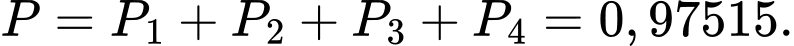Đáp án Bài tập tự luyện
Câu 1 [275897]: Vận động viên Tùng thi bắn súng. Biết xác suất để Tùng bắn trúng vòng 10 là 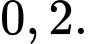 Mỗi vận động viên được bắn hai lần và hai lần bắn độc lập. Vận động viên đạt huy chương vàng nếu cả hai lần bắn trúng vòng 10. Xác suất để vận động viên Tùng đạt huy chương vàng là
Mỗi vận động viên được bắn hai lần và hai lần bắn độc lập. Vận động viên đạt huy chương vàng nếu cả hai lần bắn trúng vòng 10. Xác suất để vận động viên Tùng đạt huy chương vàng là
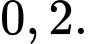 Mỗi vận động viên được bắn hai lần và hai lần bắn độc lập. Vận động viên đạt huy chương vàng nếu cả hai lần bắn trúng vòng 10. Xác suất để vận động viên Tùng đạt huy chương vàng là
Mỗi vận động viên được bắn hai lần và hai lần bắn độc lập. Vận động viên đạt huy chương vàng nếu cả hai lần bắn trúng vòng 10. Xác suất để vận động viên Tùng đạt huy chương vàng là A, 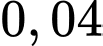
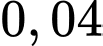
B, 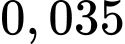
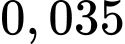
C, 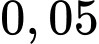
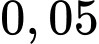
D, 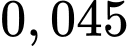
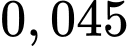
Xác suất để vận động viên Tùng đạt huy chương vàng là: 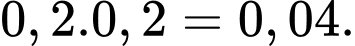
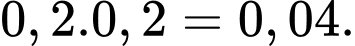
Chọn đáp án A.
Đáp án: A
Câu 2 [806045]: (THPTCHUVĂNAN-HKI-2018) Có hai hộp, mỗi hộp chứa  tấm thẻ đánh số từ
tấm thẻ đánh số từ  đến
đến  . Rút ngẫu nhiên từ mỗi hộp
. Rút ngẫu nhiên từ mỗi hộp 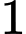 tấm thẻ. Tính xác suất để
tấm thẻ. Tính xác suất để 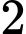 thẻ rút ra đều ghi số chẵn.
thẻ rút ra đều ghi số chẵn.
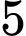 tấm thẻ đánh số từ
tấm thẻ đánh số từ 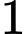 đến
đến 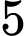 . Rút ngẫu nhiên từ mỗi hộp
. Rút ngẫu nhiên từ mỗi hộp 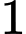 tấm thẻ. Tính xác suất để
tấm thẻ. Tính xác suất để 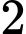 thẻ rút ra đều ghi số chẵn.
thẻ rút ra đều ghi số chẵn. A, 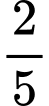 .
.
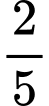 .
.B, 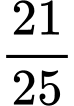 .
.
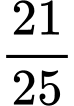 .
.C, 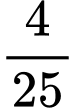 .
.
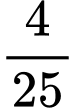 .
.D, 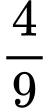 .
.
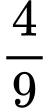 .
.
Thẻ thứ nhất có 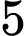 cách rút, thẻ thứ hai có
cách rút, thẻ thứ hai có 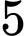 cách rút do đó số phần tử của không gian mẫu là
cách rút do đó số phần tử của không gian mẫu là 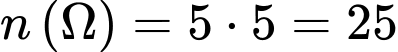 .
.
Gọi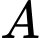 là biến cố “Hai thẻ rút ra đều mang số chẵn”.
là biến cố “Hai thẻ rút ra đều mang số chẵn”.
Rút được thẻ thứ nhất mang số chẵn có 2 cách (rút được 2 hoặc 4), tương tự với thẻ thứ hai.
Vậy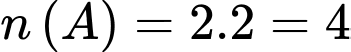 .
.
Vậy xác suất cần tìm là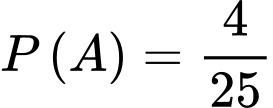 . Đáp án: C
. Đáp án: C
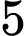 cách rút, thẻ thứ hai có
cách rút, thẻ thứ hai có 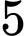 cách rút do đó số phần tử của không gian mẫu là
cách rút do đó số phần tử của không gian mẫu là 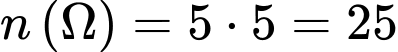 .
.Gọi
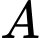 là biến cố “Hai thẻ rút ra đều mang số chẵn”.
là biến cố “Hai thẻ rút ra đều mang số chẵn”.Rút được thẻ thứ nhất mang số chẵn có 2 cách (rút được 2 hoặc 4), tương tự với thẻ thứ hai.
Vậy
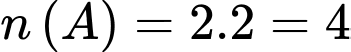 .
.Vậy xác suất cần tìm là
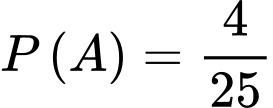 . Đáp án: C
. Đáp án: C
Câu 3 [519399]: Gieo một con súc sắc 3 lần. Xác suất để được mặt số hai xuất hiện cả 3 lần là:
A, 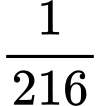
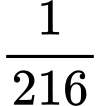
B, 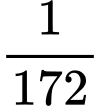
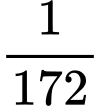
C, 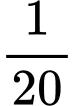
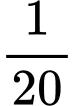
D, 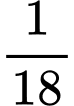
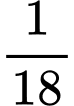
Giả sử súc sắc đã cho có 6 mặt. Không gian mẫu khi gieo 3 lần: 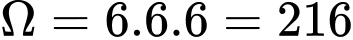
Số trường hợp mặt số 2 xuất hiện cả 3 lần:
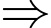 Xác suất cần tìm:
Xác suất cần tìm: 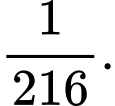 Chọn A. Đáp án: A
Chọn A. Đáp án: A
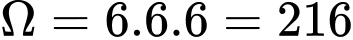
Số trường hợp mặt số 2 xuất hiện cả 3 lần:

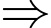 Xác suất cần tìm:
Xác suất cần tìm: 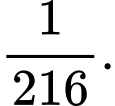 Chọn A. Đáp án: A
Chọn A. Đáp án: A
Câu 4 [227604]: Cả hai xạ thủ cùng bắn vào bia. Xác suất người thứ nhất bắn trúng bia là 0,8; người thứ hai bắn trúng bia là 0,7. Hãy tính xác suất để cả hai người cùng không bắn trúng;
A, 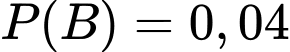
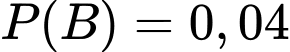
B, 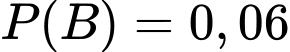
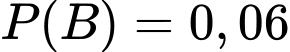
C, 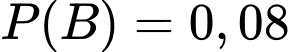
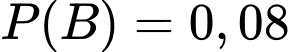
D, 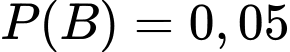
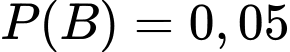
Gọi B là biến cố "Cả hai người bắn không trúng bia".
Ta thấy 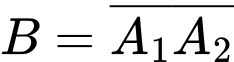 .
.
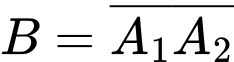 .
. Hai biến cố 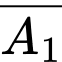 và
và 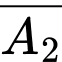 là hai biến cố độc lập nên
là hai biến cố độc lập nên
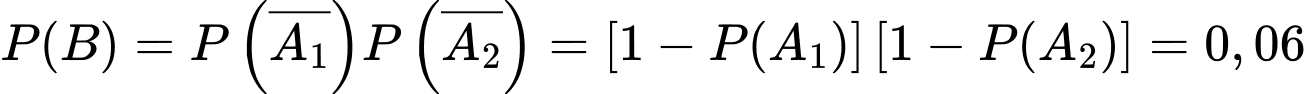 .
.
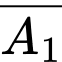 và
và 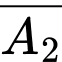 là hai biến cố độc lập nên
là hai biến cố độc lập nên
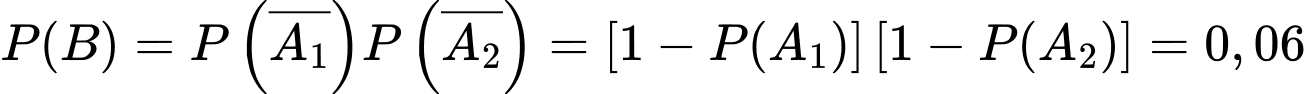 .
. Chọn B.
Đáp án: B
Câu 5 [275899]: Hai bạn An và Bình tham gia một trò chơi độc lập với nhau. Xác suất để An và Bình giành giải thưởng tương ứng là 0,8 và 0,6. Xác suất để có ít nhất một bạn giành giải thưởng là
A, 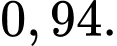
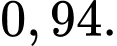
B, 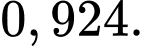
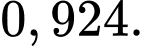
C, 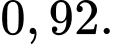
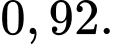
D, 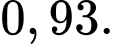
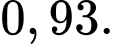
Xác suất để có ít nhất một bạn giành giải thưởng là: 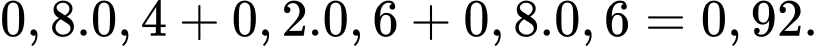
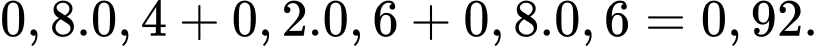
Chọn đáp án C.
Đáp án: C
Câu 6 [518964]: Xác suất bắn trúng mục tiêu của một vận động viên khi bắn một viên đạn là 0,6. Người đó bắn hai viên một cách độc lập. Xác suất để một viên trúng và một viên trượt mục tiêu là:
A, 0,24
B, 0,45
C, 0,4
D, 0,48
HD : Một viên trúng và một viên trượt thì có thể là viên đầu tiên trúng, viên thứ hai trượt hoặc ngược lại, do đó xác suất cần tìm là: 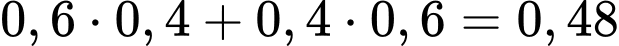
Chọn D. Đáp án: D
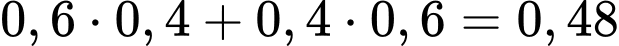
Chọn D. Đáp án: D
Câu 7 [806150]: Xác suất sút bóng thành công tại chấm  mét của hai cầu thủ Quang Hải và Văn Đức lần lượt là
mét của hai cầu thủ Quang Hải và Văn Đức lần lượt là 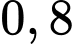 và
và 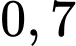 . Biết mỗi cầu thủ sút một quả tại chấm
. Biết mỗi cầu thủ sút một quả tại chấm  mét và hai người sút độc lập. Tính xác suất để ít nhất một người sút bóng thành công.
mét và hai người sút độc lập. Tính xác suất để ít nhất một người sút bóng thành công.
 mét của hai cầu thủ Quang Hải và Văn Đức lần lượt là
mét của hai cầu thủ Quang Hải và Văn Đức lần lượt là 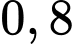 và
và 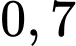 . Biết mỗi cầu thủ sút một quả tại chấm
. Biết mỗi cầu thủ sút một quả tại chấm  mét và hai người sút độc lập. Tính xác suất để ít nhất một người sút bóng thành công.
mét và hai người sút độc lập. Tính xác suất để ít nhất một người sút bóng thành công. A, 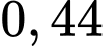 .
.
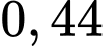 .
.B, 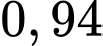 .
.
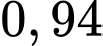 .
.C, 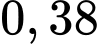 .
.
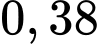 .
.D, 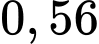 .
.
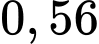 .
.
Chọn B
Xác suất sút không thành công tại chấm của cầu thủ Quang Hải là
của cầu thủ Quang Hải là 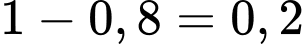
Xác suất sút không thành công tại chấm của cầu thủ Văn Đức là
của cầu thủ Văn Đức là 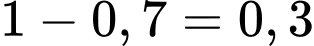
Xác suất cả hai cầu thủ sút không thành công tại chấm là
là 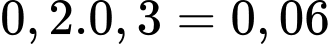
Suy ra: Xác suất để ít nhất một người sút bóng thành công là: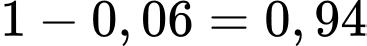 . Đáp án: B
. Đáp án: B
Xác suất sút không thành công tại chấm
 của cầu thủ Quang Hải là
của cầu thủ Quang Hải là 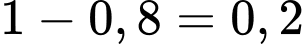
Xác suất sút không thành công tại chấm
 của cầu thủ Văn Đức là
của cầu thủ Văn Đức là 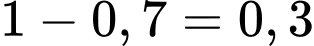
Xác suất cả hai cầu thủ sút không thành công tại chấm
 là
là 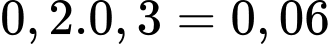
Suy ra: Xác suất để ít nhất một người sút bóng thành công là:
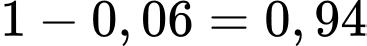 . Đáp án: B
. Đáp án: B
Câu 8 [579688]: [Đề mẫu HSA 2024]: Hai xạ thủ  độc lập với nhau bắn vào mục tiêu. Biết rằng xác suất bắn trúng mục tiêu của
độc lập với nhau bắn vào mục tiêu. Biết rằng xác suất bắn trúng mục tiêu của  tương ứng là
tương ứng là 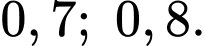 Xác suất để có duy nhất một xạ thủ bắn trúng mục tiêu là
Xác suất để có duy nhất một xạ thủ bắn trúng mục tiêu là
 độc lập với nhau bắn vào mục tiêu. Biết rằng xác suất bắn trúng mục tiêu của
độc lập với nhau bắn vào mục tiêu. Biết rằng xác suất bắn trúng mục tiêu của  tương ứng là
tương ứng là 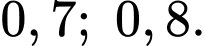 Xác suất để có duy nhất một xạ thủ bắn trúng mục tiêu là
Xác suất để có duy nhất một xạ thủ bắn trúng mục tiêu là A, 0,24.
B, 0,38.
C, 0,50.
D, 0,56.
+) Trường hợp 1:  bắn trúng,
bắn trúng, 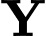 bắn trượt, xác suất là
bắn trượt, xác suất là 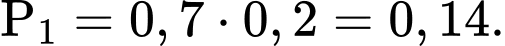
+) Trường hợp bắn trượt,
bắn trượt, 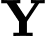 bắn trúng, xác suất là
bắn trúng, xác suất là 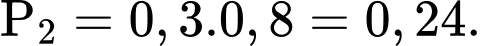
 Xác suất để chỉ có một xạ thủ bắn trúng là
Xác suất để chỉ có một xạ thủ bắn trúng là 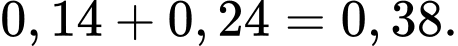
Chọn B. Đáp án: B
 bắn trúng,
bắn trúng,  bắn trượt, xác suất là
bắn trượt, xác suất là 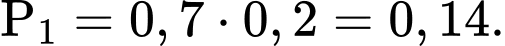
+) Trường hợp
 bắn trượt,
bắn trượt,  bắn trúng, xác suất là
bắn trúng, xác suất là 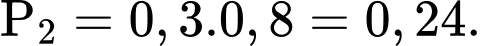
 Xác suất để chỉ có một xạ thủ bắn trúng là
Xác suất để chỉ có một xạ thủ bắn trúng là 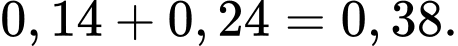
Chọn B. Đáp án: B
Câu 9 [579689]: [Đề mẫu HSA 2024]: Trong một khu dân cư, tỉ lệ gia đình nuôi chó là 0,2; tỉ lệ gia đình nuôi mèo là 0,25; tỉ lệ gia đình nuôi cả chó và mèo là 0,05. Chọn ngẫu nhiên một gia đình trong khu dân cư đó, xác suất để gia đình được chọn không nuôi con vật nào trong hai con vật chó và mèo gần nhất với giá trị nào sau đây?
A, 0,50.
B, 0,45.
C, 0,55.
D, 0,60.
Tỉ lệ gia đình nuôi chó là 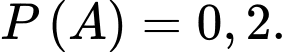
Tỉ lệ gia đình nuôi mèo là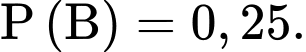
Tỉ lệ gia đình nuôi cả chó và mèo là
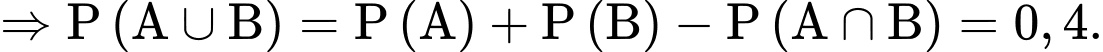
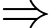 Tỉ lệ gia đình không nuôi cả chó và mèo là
Tỉ lệ gia đình không nuôi cả chó và mèo là 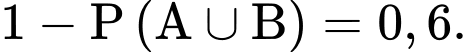
Chọn D. Đáp án: D
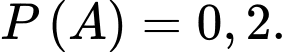
Tỉ lệ gia đình nuôi mèo là
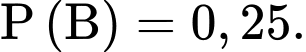
Tỉ lệ gia đình nuôi cả chó và mèo là

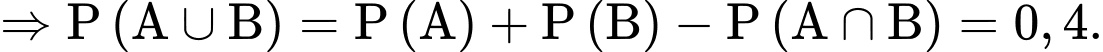
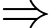 Tỉ lệ gia đình không nuôi cả chó và mèo là
Tỉ lệ gia đình không nuôi cả chó và mèo là 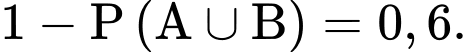
Chọn D. Đáp án: D
Câu 10 [792283]: Một công ty may mặc có hai hệ thống máy chạy song song. Xác suất để hệ thống máy thứ nhất hoạt động tốt là 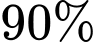 , xác suất để hệ thống máy thứ hai hoạt động tốt là
, xác suất để hệ thống máy thứ hai hoạt động tốt là 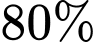 . Công ty chỉ có thể hoàn thành đơn hàng đúng hạn nếu ít nhất một trong hai hệ thống máy hoạt động tốt. Xác suất để công ty hoàn thành đúng hạn là
. Công ty chỉ có thể hoàn thành đơn hàng đúng hạn nếu ít nhất một trong hai hệ thống máy hoạt động tốt. Xác suất để công ty hoàn thành đúng hạn là
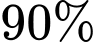 , xác suất để hệ thống máy thứ hai hoạt động tốt là
, xác suất để hệ thống máy thứ hai hoạt động tốt là 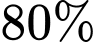 . Công ty chỉ có thể hoàn thành đơn hàng đúng hạn nếu ít nhất một trong hai hệ thống máy hoạt động tốt. Xác suất để công ty hoàn thành đúng hạn là
. Công ty chỉ có thể hoàn thành đơn hàng đúng hạn nếu ít nhất một trong hai hệ thống máy hoạt động tốt. Xác suất để công ty hoàn thành đúng hạn là A, 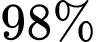 .
.
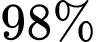 .
.B, 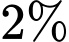 .
.
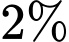 .
.C, 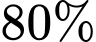 .
.
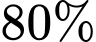 .
.D, 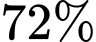 .
.
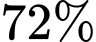 .
.
Chọn A
Goi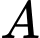 là biến cố : « Hệ thống máy thứ nhất hoạt động tốt »
là biến cố : « Hệ thống máy thứ nhất hoạt động tốt »
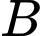 là biến cố : « Hệ thống máy thứ hai hoạt động tốt »
là biến cố : « Hệ thống máy thứ hai hoạt động tốt »
 là biến cố : « Công ty hoàn thành đúng hạn »
là biến cố : « Công ty hoàn thành đúng hạn »
Ta có là biến cố : « Hệ thống máy thứ nhất hoạt động không tốt »
là biến cố : « Hệ thống máy thứ nhất hoạt động không tốt »
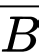 là biến cố : « Hệ thống máy thứ hai hoạt động không tốt »
là biến cố : « Hệ thống máy thứ hai hoạt động không tốt »
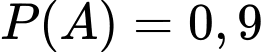 ;
; 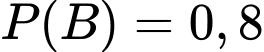 ;
;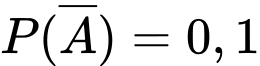 ;
; 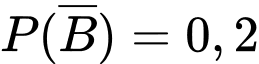 .
.
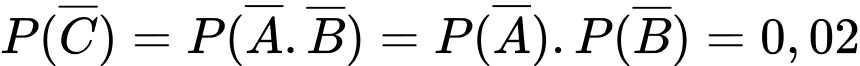
 . Đáp án: A
. Đáp án: A
Goi
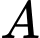 là biến cố : « Hệ thống máy thứ nhất hoạt động tốt »
là biến cố : « Hệ thống máy thứ nhất hoạt động tốt » 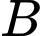 là biến cố : « Hệ thống máy thứ hai hoạt động tốt »
là biến cố : « Hệ thống máy thứ hai hoạt động tốt »  là biến cố : « Công ty hoàn thành đúng hạn »
là biến cố : « Công ty hoàn thành đúng hạn » Ta có
 là biến cố : « Hệ thống máy thứ nhất hoạt động không tốt »
là biến cố : « Hệ thống máy thứ nhất hoạt động không tốt » 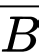 là biến cố : « Hệ thống máy thứ hai hoạt động không tốt »
là biến cố : « Hệ thống máy thứ hai hoạt động không tốt » 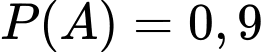 ;
; 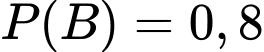 ;
;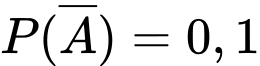 ;
; 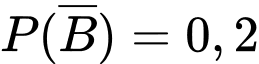 .
.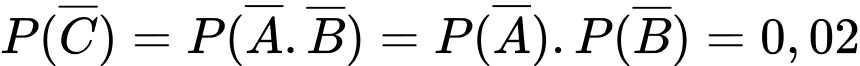
 . Đáp án: A
. Đáp án: A
Câu 11 [806130]: Một chiếc ôtô với hai động cơ độc lập đang gặp trục trặc kĩ thuật. Xác suất để động cơ 1 gặp trục trặc là 0,5. Xác suất để động cơ 2 gặp trục trặc là 0,4. Biết rằng xe chỉ không thể chạy được khi cả hai động cơ bị hỏng. Tính xác suất để xe đi được.
A, 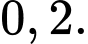
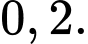
B, 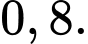
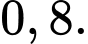
C, 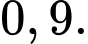
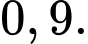
D, 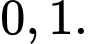
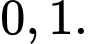
Gọi 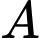 là biến cố “động cơ 1 bị hỏng”, gọi
là biến cố “động cơ 1 bị hỏng”, gọi 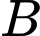 là biến cố “động cơ 2 bị hỏng”.
là biến cố “động cơ 2 bị hỏng”.
Suy ra là biến cố “cả hai động cơ bị hỏng”
là biến cố “cả hai động cơ bị hỏng”  “ xe không chạy được nữa”.
“ xe không chạy được nữa”.
Lại thấy hai động cơ hoạt động độc lập nên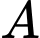 và
và 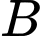 là hai biến cố độc lập.
là hai biến cố độc lập.
 Áp dụng quy tắc nhân xác suất ta được xác suất để xe phải dừng lại giữa đường là
Áp dụng quy tắc nhân xác suất ta được xác suất để xe phải dừng lại giữa đường là 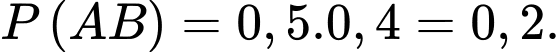
Vậy xác suất để xe đi được là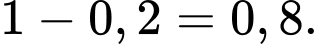 Đáp án: B
Đáp án: B
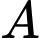 là biến cố “động cơ 1 bị hỏng”, gọi
là biến cố “động cơ 1 bị hỏng”, gọi 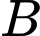 là biến cố “động cơ 2 bị hỏng”.
là biến cố “động cơ 2 bị hỏng”. Suy ra
 là biến cố “cả hai động cơ bị hỏng”
là biến cố “cả hai động cơ bị hỏng”  “ xe không chạy được nữa”.
“ xe không chạy được nữa”. Lại thấy hai động cơ hoạt động độc lập nên
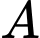 và
và 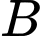 là hai biến cố độc lập.
là hai biến cố độc lập. 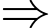 Áp dụng quy tắc nhân xác suất ta được xác suất để xe phải dừng lại giữa đường là
Áp dụng quy tắc nhân xác suất ta được xác suất để xe phải dừng lại giữa đường là 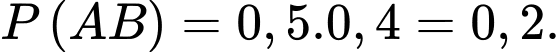
Vậy xác suất để xe đi được là
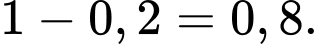 Đáp án: B
Đáp án: B
Câu 12 [582520]:
Cho hai biến cố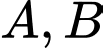 đôc lập với nhau. Biết
đôc lập với nhau. Biết 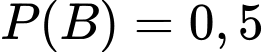 và
và 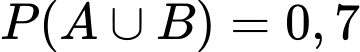 . Hãy tính xác suất của biến cố
. Hãy tính xác suất của biến cố 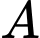 .
.
A,
0,4.
B,
0,6.
C,
0,5.
D,
0,3.
Do 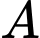 và
và 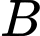 là hai biến cố độc lập nên
là hai biến cố độc lập nên 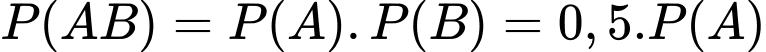 .
.
Ta có: 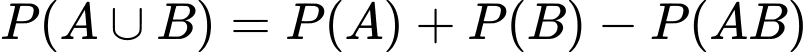
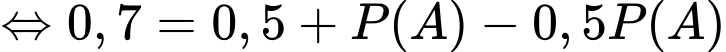

Câu 13 [582521]:
Cho 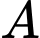 và
và 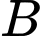 là hai biến cố độc lập. Biết
là hai biến cố độc lập. Biết 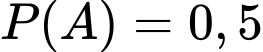 và
và 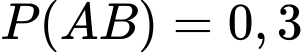 . Hãy tính xác suất của các biến cố
. Hãy tính xác suất của các biến cố 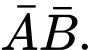
A, 0,2.
B, 0,3.
C, 0,4.
D, 0,1.
Do 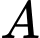 và
và 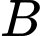 là hai biến cố độc lập nên
là hai biến cố độc lập nên 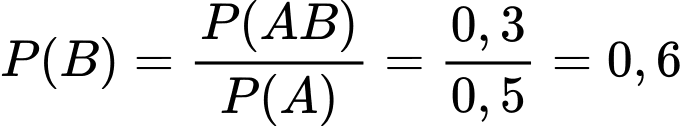 .
.
Vì  là biến cố đối của
là biến cố đối của 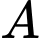 nên
nên 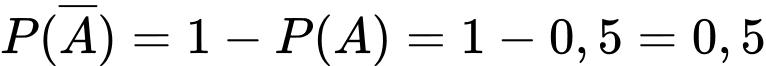 .
.
Do  và
và 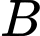 độc lập nên
độc lập nên 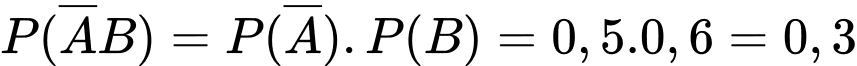 .
.
Vì 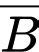 là biến cố đối của
là biến cố đối của 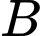 nên
nên 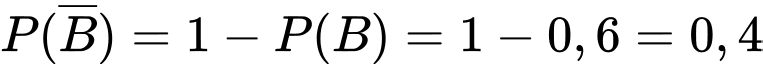 . Do
. Do  và
và 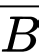 độc lập nên
độc lập nên 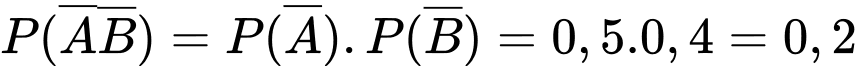 .
.
Câu 14 [227602]: Một người bắn liên tiếp vào một mục tiêu khi viên đạn trúng mục tiêu thì thôi (các phát súng độc lập nhau ). Biết rằng xác suất trúng mục tiêu của mỗi lần bắn như nhau và bằng 0,6 .Tính xác suất để bắn đến viên thứ 4 thì ngừng bắn
A, 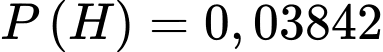
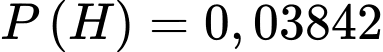
B, . 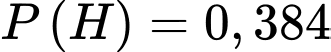
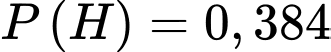
C, 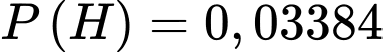
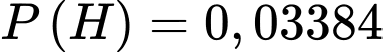
D, 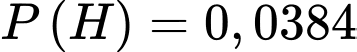
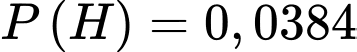
Gọi 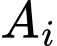 là biến cố trúng đích lần thứ 4
H là biến cố bắn lần thứ 4 thì ngừng
là biến cố trúng đích lần thứ 4
H là biến cố bắn lần thứ 4 thì ngừng 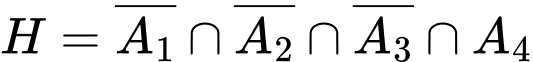
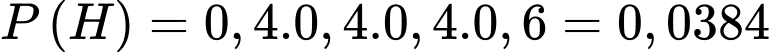 . Đáp án: D
. Đáp án: D
 là biến cố trúng đích lần thứ 4
H là biến cố bắn lần thứ 4 thì ngừng
là biến cố trúng đích lần thứ 4
H là biến cố bắn lần thứ 4 thì ngừng 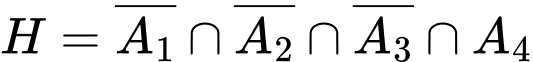
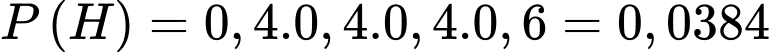 .
. Chọn D.
Câu 15 [806133]: (CHUYÊNVINH-LẦN2-2018) Đầu tiết học, cô giáo kiểm tra bài cũ bằng cách gọi lần lượt từng người từ đầu danh sách lớp lên bảng trả lời câu hỏi. Biết rằng học sinh đâu tiên trong danh sách lớp là An, Bình, Cường với xác suất thuộc bài lần lượt là 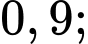
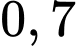 và
và 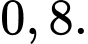 Cô giáo sẽ dừng kiểm tra sau khi đã có 2 học sinh thuộc bài. Tính xác suất cô giáo chỉ kiểm tra bài cũ đúng 3 bạn trên.
Cô giáo sẽ dừng kiểm tra sau khi đã có 2 học sinh thuộc bài. Tính xác suất cô giáo chỉ kiểm tra bài cũ đúng 3 bạn trên.
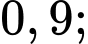
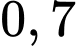 và
và 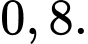 Cô giáo sẽ dừng kiểm tra sau khi đã có 2 học sinh thuộc bài. Tính xác suất cô giáo chỉ kiểm tra bài cũ đúng 3 bạn trên.
Cô giáo sẽ dừng kiểm tra sau khi đã có 2 học sinh thuộc bài. Tính xác suất cô giáo chỉ kiểm tra bài cũ đúng 3 bạn trên. A, 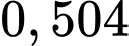 .
.
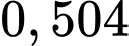 .
.B, 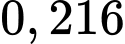 .
.
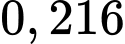 .
.C,  .
.
 .
.D, 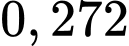 .
.
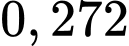 .
.
Trường hợp 1. An thuộc bài, Bình không thuộc bài, Cường thuộc bài ta có xác suất:
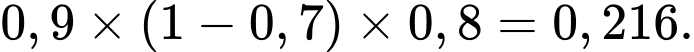
Trường hợp 2. An không thuộc bài, Bình thuộc bài, Cường thuộc bài ta có xác suất:
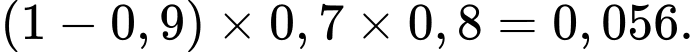
Vậy xác suất cần tìm là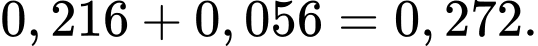 Đáp án: D
Đáp án: D
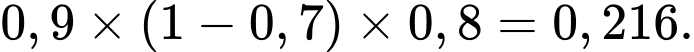
Trường hợp 2. An không thuộc bài, Bình thuộc bài, Cường thuộc bài ta có xác suất:
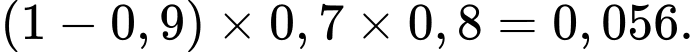
Vậy xác suất cần tìm là
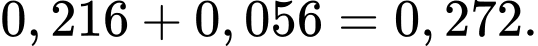 Đáp án: D
Đáp án: D
Câu 16 [519395]: Trong một trò chơi điện tử, xác suất để An thắng một trận là 0,4 (không có hòa). Hỏi An phải chơi tối thiểu bao nhiêu trận để xác suất An thắng ít nhất một trận trong loạt chơi đó lớn hơn 0,95
A, 4.
B, 5.
C, 6.
D, 7.
Giả sử An chơi  trận thì xác suất An thua hết cả
trận thì xác suất An thua hết cả 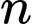 trận đó là
trận đó là 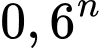
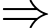 Xác suất An thắng ít nhất trong 1 trận đó là:
Xác suất An thắng ít nhất trong 1 trận đó là: 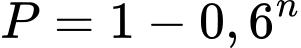
Dễ thấy với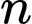 càng lớn thì
càng lớn thì 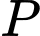 càng lớn. Ta cần:
càng lớn. Ta cần:
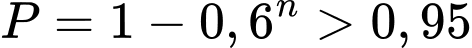
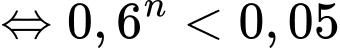
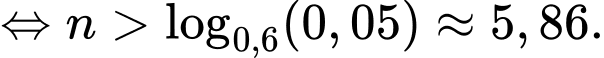
Chọn C. Đáp án: C
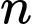 trận thì xác suất An thua hết cả
trận thì xác suất An thua hết cả 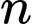 trận đó là
trận đó là 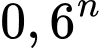
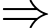 Xác suất An thắng ít nhất trong 1 trận đó là:
Xác suất An thắng ít nhất trong 1 trận đó là: 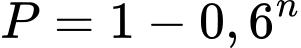
Dễ thấy với
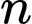 càng lớn thì
càng lớn thì 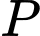 càng lớn. Ta cần:
càng lớn. Ta cần:
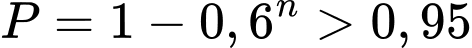
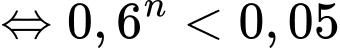
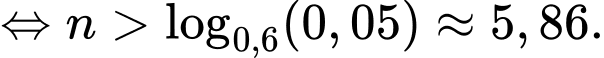
Chọn C. Đáp án: C
Câu 17 [806132]: (THPTĐoànThượng-HảiDương-HKI18-19) Hai người ngang tài ngang sức tranh chức vô địch của một cuộc thi cờ tướng. Người giành chiến thắng là người đầu tiên thắng được năm ván cờ. tại thời điểm người chơi thứ nhất đã thắng 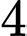 ván và ngưởi chới thứ hai mới thắng
ván và ngưởi chới thứ hai mới thắng 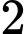 ván, tính xác suất để người chơi thứ nhất giành chiến thắng.
ván, tính xác suất để người chơi thứ nhất giành chiến thắng.
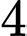 ván và ngưởi chới thứ hai mới thắng
ván và ngưởi chới thứ hai mới thắng 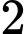 ván, tính xác suất để người chơi thứ nhất giành chiến thắng.
ván, tính xác suất để người chơi thứ nhất giành chiến thắng. A, 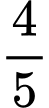 .
.
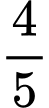 .
.B, 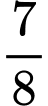 .
.
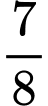 .
.C, 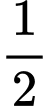 .
.
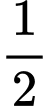 .
.D, 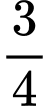 .
.
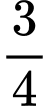 .
.
Chọn B
Cách 1:Hai người ngang sức nên xác suất người thứ nhất thắng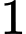 trận là
trận là 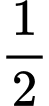 ; thua
; thua 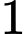 trận là
trận là 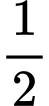 .
.
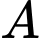 là biến cố: “Người thứ nhất giành chiến thắng chung cuộc”
là biến cố: “Người thứ nhất giành chiến thắng chung cuộc”
Vậy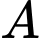 = “Người thứ nhất thắng ngay trận đầu” hoặc “người thứ nhất thắng sau 2 trận” hoặc “người thứ nhất thắng sau 3 trận”
= “Người thứ nhất thắng ngay trận đầu” hoặc “người thứ nhất thắng sau 2 trận” hoặc “người thứ nhất thắng sau 3 trận”
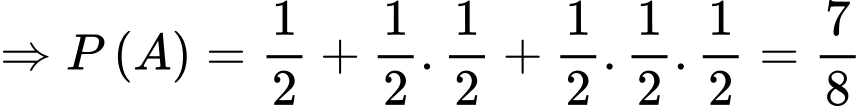 .
.
Cách 2: Hai người ngang sức nên xác suất người thứ hai thắng trận là
trận là 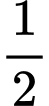 ; thua
; thua 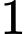 trận là
trận là 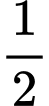 .
.
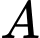 là biến cố: “Người thứ nhất giành chiến thắng chung cuộc”
là biến cố: “Người thứ nhất giành chiến thắng chung cuộc”
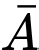 = “người thứ hai thắng chung cuộc”
= “người thứ hai thắng chung cuộc”
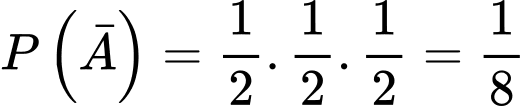
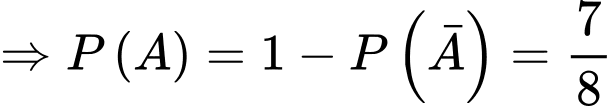 . Đáp án: B
. Đáp án: B
Cách 1:Hai người ngang sức nên xác suất người thứ nhất thắng
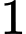 trận là
trận là 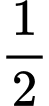 ; thua
; thua 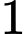 trận là
trận là 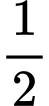 .
.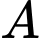 là biến cố: “Người thứ nhất giành chiến thắng chung cuộc”
là biến cố: “Người thứ nhất giành chiến thắng chung cuộc” Vậy
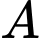 = “Người thứ nhất thắng ngay trận đầu” hoặc “người thứ nhất thắng sau 2 trận” hoặc “người thứ nhất thắng sau 3 trận”
= “Người thứ nhất thắng ngay trận đầu” hoặc “người thứ nhất thắng sau 2 trận” hoặc “người thứ nhất thắng sau 3 trận” 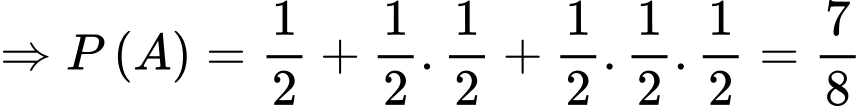 .
.Cách 2: Hai người ngang sức nên xác suất người thứ hai thắng
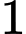 trận là
trận là 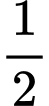 ; thua
; thua 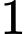 trận là
trận là 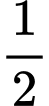 .
.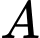 là biến cố: “Người thứ nhất giành chiến thắng chung cuộc”
là biến cố: “Người thứ nhất giành chiến thắng chung cuộc” 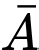 = “người thứ hai thắng chung cuộc”
= “người thứ hai thắng chung cuộc” 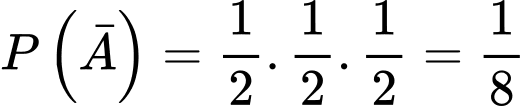
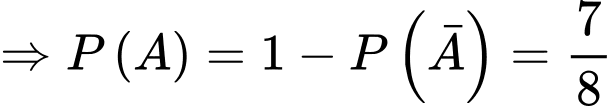 . Đáp án: B
. Đáp án: B
Câu 18 [806162]: (CHUYÊNTRẦNPHÚ-HẢIPHÒNG-LẦN1-2018) Ba xạ thủ cùng bắn vào một tấm bia một cách độc lập, xác suất bắn trúng đích lần lượt là 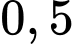 ;
; 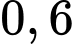 và
và 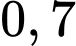 . Xác suất để có đúng hai người bắn trúng bia là
. Xác suất để có đúng hai người bắn trúng bia là
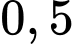 ;
; 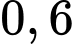 và
và 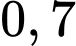 . Xác suất để có đúng hai người bắn trúng bia là
. Xác suất để có đúng hai người bắn trúng bia là A, 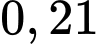 .
.
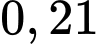 .
.B, 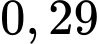 .
.
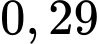 .
.C, 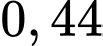 .
.
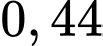 .
.D, 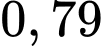 .
.
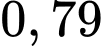 .
.
Gọi 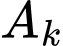 là biến cố người thứ
là biến cố người thứ 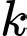 bắn trúng bia với xác suất tương ứng là
bắn trúng bia với xác suất tương ứng là 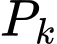
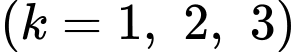 .
.
Biến cố có đúng hai người bắn trúng bia là: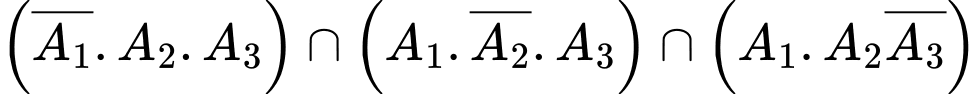 .
.
Xác suất của biến cố này là:
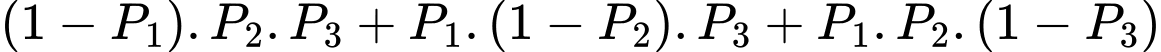
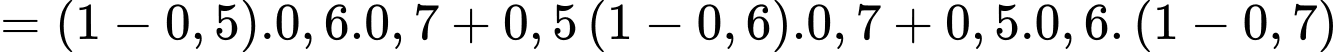
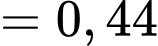 .
.
Vậy xác suất để có đúng hai người bắn trúng bia là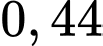 . Đáp án: C
. Đáp án: C
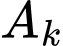 là biến cố người thứ
là biến cố người thứ 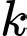 bắn trúng bia với xác suất tương ứng là
bắn trúng bia với xác suất tương ứng là 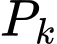
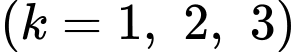 .
.Biến cố có đúng hai người bắn trúng bia là:
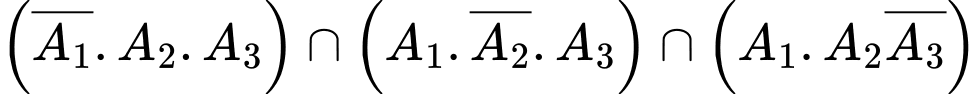 .
.Xác suất của biến cố này là:
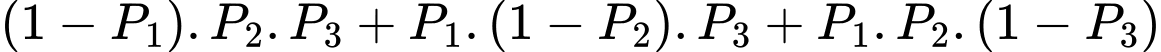
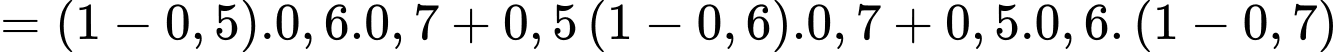
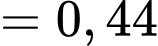 .
.Vậy xác suất để có đúng hai người bắn trúng bia là
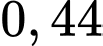 . Đáp án: C
. Đáp án: C
Câu 19 [806158]: Một xạ thủ bắn bia. Biết rằng xác suất bắn trúng vòng tròn  là
là 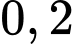 ; vòng
; vòng 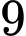 là
là 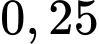 và vòng
và vòng 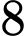 là
là 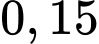 . Nếu trúng vòng
. Nếu trúng vòng 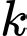 thì được
thì được 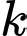 điểm. Giả sử xạ thủ đó bắn ba phát súng một cách độc lập. Xả thủ đạt loại giỏi nếu anh ta đạt ít nhấ
điểm. Giả sử xạ thủ đó bắn ba phát súng một cách độc lập. Xả thủ đạt loại giỏi nếu anh ta đạt ít nhấ 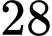 điểm. Xác suất để xả thủ này đạt loại giỏi
điểm. Xác suất để xả thủ này đạt loại giỏi
 là
là 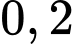 ; vòng
; vòng 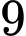 là
là 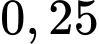 và vòng
và vòng 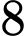 là
là 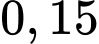 . Nếu trúng vòng
. Nếu trúng vòng 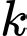 thì được
thì được 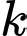 điểm. Giả sử xạ thủ đó bắn ba phát súng một cách độc lập. Xả thủ đạt loại giỏi nếu anh ta đạt ít nhấ
điểm. Giả sử xạ thủ đó bắn ba phát súng một cách độc lập. Xả thủ đạt loại giỏi nếu anh ta đạt ít nhấ 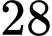 điểm. Xác suất để xả thủ này đạt loại giỏi
điểm. Xác suất để xả thủ này đạt loại giỏi A, 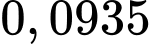 .
.
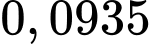 .
.B,  .
.
 .
.C,  .
.
 .
.D, 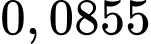 .
.
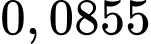 .
.
Chọn A
Gọi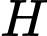 là biến cố: “Xạ thủ bắn đạt loại giỏi”.
là biến cố: “Xạ thủ bắn đạt loại giỏi”. 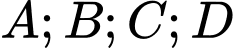 là các biến cố sau:
là các biến cố sau:
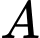 : “Ba viên trúng vòng
: “Ba viên trúng vòng  ”
”
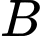 : “Hai viên trúng vòng
: “Hai viên trúng vòng  và một viên trúng vòng
và một viên trúng vòng 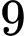 ”
”
 : “Một viên trúng vòng
: “Một viên trúng vòng  và hai viên trúng vòng
và hai viên trúng vòng 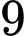 ”
”
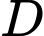 : “Hai viên trúng vòng
: “Hai viên trúng vòng  và một viên trúng vòng
và một viên trúng vòng 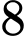 ”
”
Các biến cố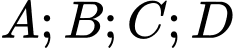 là các biến cố xung khắc từng đôi một và
là các biến cố xung khắc từng đôi một và 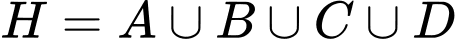
Suy ra theo quy tắc cộng mở rộng ta có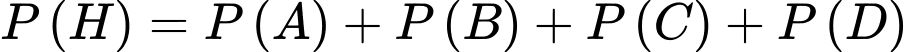
Mặt khác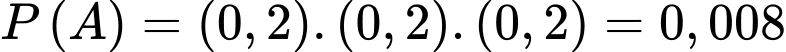
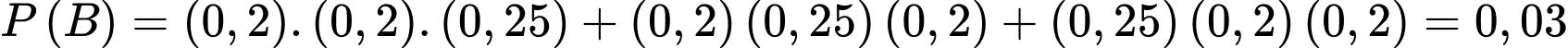
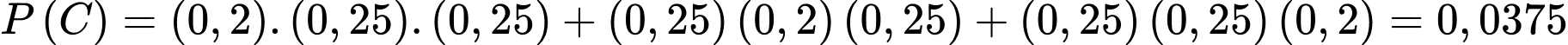
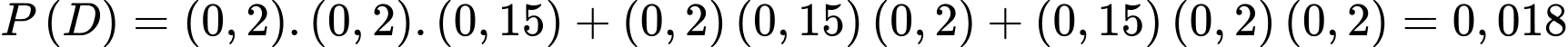
Do đó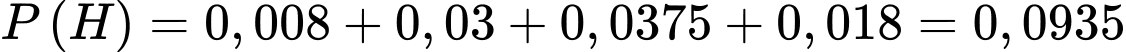 Đáp án: A
Đáp án: A
Gọi
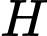 là biến cố: “Xạ thủ bắn đạt loại giỏi”.
là biến cố: “Xạ thủ bắn đạt loại giỏi”. 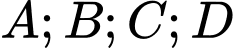 là các biến cố sau:
là các biến cố sau: 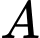 : “Ba viên trúng vòng
: “Ba viên trúng vòng  ”
”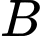 : “Hai viên trúng vòng
: “Hai viên trúng vòng  và một viên trúng vòng
và một viên trúng vòng 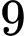 ”
” : “Một viên trúng vòng
: “Một viên trúng vòng  và hai viên trúng vòng
và hai viên trúng vòng 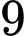 ”
”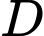 : “Hai viên trúng vòng
: “Hai viên trúng vòng  và một viên trúng vòng
và một viên trúng vòng 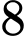 ”
”Các biến cố
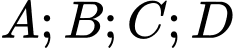 là các biến cố xung khắc từng đôi một và
là các biến cố xung khắc từng đôi một và 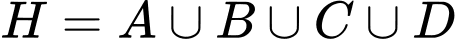
Suy ra theo quy tắc cộng mở rộng ta có
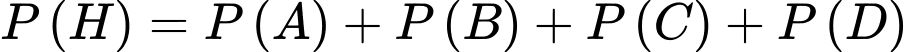
Mặt khác
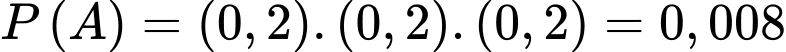
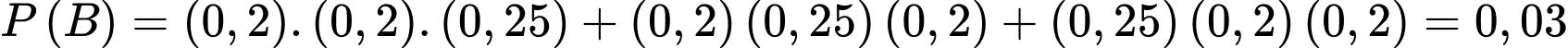
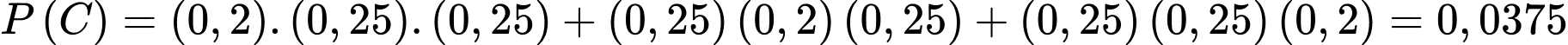
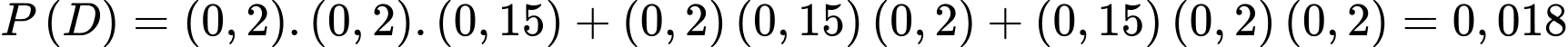
Do đó
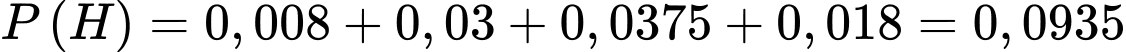 Đáp án: A
Đáp án: A
Câu 20 [581409]: Một ngân hàng đề thi có 20 hạng mục, mỗi hạng mục có 10 câu hỏi. Đề thi có 20 câu hỏi tương ứng 20 hạng mục sao cho mỗi hạng mục có đúng 1 câu hỏi. Máy tính chọn từ ngân hàng ngẫu nhiên 2 đề thi thỏa mãn tiêu chí trên. Tìm xác suất để 2 đề thi có ít nhất 3 câu hỏi trùng nhau. (Kết quả làm tròn đến hàng phần nghìn).
A, 0,167.
B, 0,593.
C, 0,190.
D, 0,323.
Giả sử đề 1 đã được máy tính chọn ra. Ta xét xác suất để đề 2 giống đề 1
Ở mỗi hạng mục, xác suất để câu hỏi của 2 đề giống nhau và khác nhau là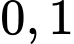 và
và 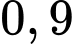
Xác suất để 2 đề không trùng nhau câu hỏi nào là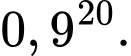
Xác suất để 2 đề trùng nhau đúng 1 câu hỏi là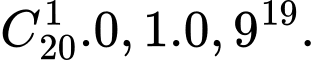
Xác suất để 2 đề trùng nhau đúng 2 câu hỏi là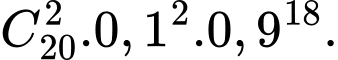
Xác suất để 2 đề trùng nhau từ 3 câu hỏi trở lên là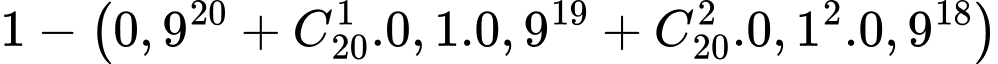
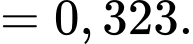
Chọn D. Đáp án: D
Ở mỗi hạng mục, xác suất để câu hỏi của 2 đề giống nhau và khác nhau là
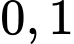 và
và 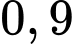
Xác suất để 2 đề không trùng nhau câu hỏi nào là
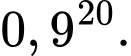
Xác suất để 2 đề trùng nhau đúng 1 câu hỏi là
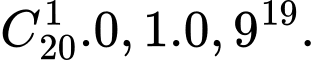
Xác suất để 2 đề trùng nhau đúng 2 câu hỏi là
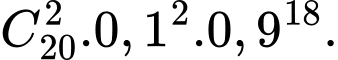
Xác suất để 2 đề trùng nhau từ 3 câu hỏi trở lên là
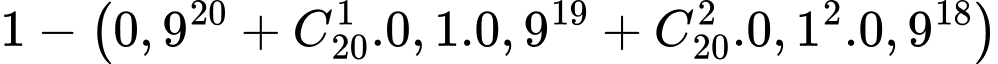
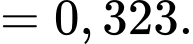
Chọn D. Đáp án: D
Câu 21 [275831]: Tại các trường trung học phổ thông của một tỉnh, thống kê cho thấy có 63% giáo viên môn Toán tham khảo bộ sách giáo khoa A, 56% giáo viên môn Toán tham khảo bộ sách giáo khoa B và 28,5% giáo viên môn Toán tham khỏa cả hai bộ sách giáo khoa A và B. Tính tỉ lệ giáo viên môn Toán các trường trung học phô thông của tỉnh đó không tham khảo cả hai bộ sách giáo khoa A và B.
Gọi C: “Giáo viên môn Toán tham khảo bộ sách giáo khoa A”; D: “Giáo viên bộ môn Toán tham khảo bộ sách giáo khoa B”.
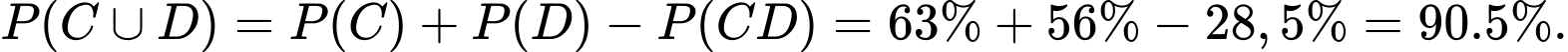

Vậy tỉ lệ giáo viên môn Toán các trường trung học phổ thông của tỉnh đó không tham khảo cả hai bộ sách giáo khoa A và B là 9,5\%.
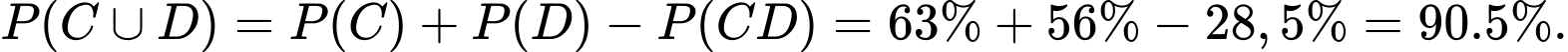

Vậy tỉ lệ giáo viên môn Toán các trường trung học phổ thông của tỉnh đó không tham khảo cả hai bộ sách giáo khoa A và B là 9,5\%.
Câu 22 [405592]: Một cậu bé và một cô bé được hỏi sinh vào ngày nào trong tuần. Tìm xác suất sao cho:
a) Bé trai sinh vào thứ Hai và bé gái sinh vào Thứ Tư.
b) Bé trai sinh vào ngày cuối tuần (Thứ Bảy và Chủ nhật) còn bé gái thì không.
Xác suất để bé trai sinh vào cuối tuần là 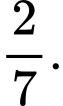
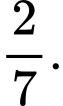
Xác suất để bé gái sinh không sinh vào cuối tuần là 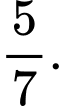
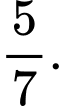
Bé trai sinh vào ngày cuối tuần (Thứ bảy và Chủ nhật) còn bé gái thì không là 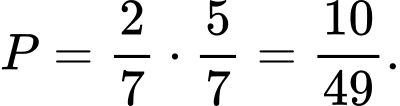
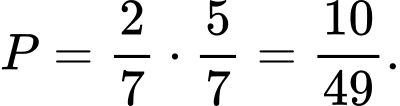
Đáp án: 0,2
Câu 23 [405591]: Một trường học có hai máy photocopy. Vào một ngày bất kỳ, máy  có
có  khả năng bị kẹt giấy và máy
khả năng bị kẹt giấy và máy 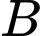 có
có 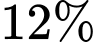 khả năng bị kẹt giấy. Xác suất để vào một ngày bất kỳ, cả hai máy sẽ làm việc liên tục là bao nhiêu phần trăm. Làm tròn kết quả đến hàng đơn vị.
khả năng bị kẹt giấy. Xác suất để vào một ngày bất kỳ, cả hai máy sẽ làm việc liên tục là bao nhiêu phần trăm. Làm tròn kết quả đến hàng đơn vị.
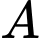 có
có  khả năng bị kẹt giấy và máy
khả năng bị kẹt giấy và máy 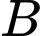 có
có 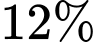 khả năng bị kẹt giấy. Xác suất để vào một ngày bất kỳ, cả hai máy sẽ làm việc liên tục là bao nhiêu phần trăm. Làm tròn kết quả đến hàng đơn vị.
khả năng bị kẹt giấy. Xác suất để vào một ngày bất kỳ, cả hai máy sẽ làm việc liên tục là bao nhiêu phần trăm. Làm tròn kết quả đến hàng đơn vị.
Gọi 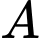 là biến cố "Máy
là biến cố "Máy 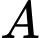 bị kẹt giấy".
bị kẹt giấy".
Gọi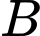 là biến cố "Biến cố máy
là biến cố "Biến cố máy 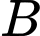 bị kẹt giấy".
bị kẹt giấy".
Ta có: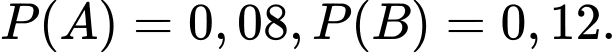
Vì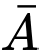 và
và 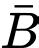 là hai biến cố độc lập, nên xác suất cả hai máy làm việc liên tục (không bị kẹt giấy) là
là hai biến cố độc lập, nên xác suất cả hai máy làm việc liên tục (không bị kẹt giấy) là 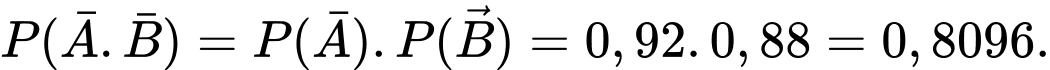
Điền đáp số: 81
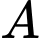 là biến cố "Máy
là biến cố "Máy 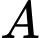 bị kẹt giấy".
bị kẹt giấy".Gọi
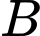 là biến cố "Biến cố máy
là biến cố "Biến cố máy 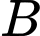 bị kẹt giấy".
bị kẹt giấy".Ta có:
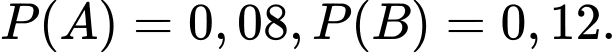
Vì
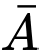 và
và 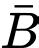 là hai biến cố độc lập, nên xác suất cả hai máy làm việc liên tục (không bị kẹt giấy) là
là hai biến cố độc lập, nên xác suất cả hai máy làm việc liên tục (không bị kẹt giấy) là 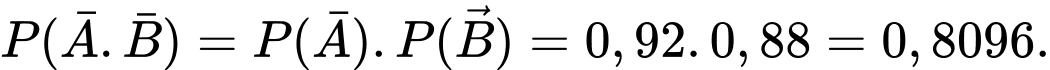
Điền đáp số: 81
Câu 24 [405589]: Một bình đựng 7 viên bi trắng và 5 viên bi đen. Lần lượt lấy ngẫu nhiên ra 2 bi, sau khi lấy lần thứ nhất ta để lại viên bi vào bình rồi mới lấy tiếp lần thứ hai. Tính xác suất để lấy được bi thứ 1 màu trắng và bi thứ 2 màu đen?
Gọi 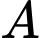 là biến cố lần thứ nhất lấy được bi màu trắng.
là biến cố lần thứ nhất lấy được bi màu trắng. 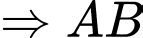 là biến cố lần thứ nhất lấy được bi màu trắng và lần thứ hai lấy được bi màu đen.
là biến cố lần thứ nhất lấy được bi màu trắng và lần thứ hai lấy được bi màu đen.
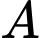 là biến cố lần thứ nhất lấy được bi màu trắng.
là biến cố lần thứ nhất lấy được bi màu trắng. Gọi 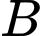 là biến cố lần thứ hai lấy được bi màu đen.
là biến cố lần thứ hai lấy được bi màu đen.
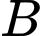 là biến cố lần thứ hai lấy được bi màu đen.
là biến cố lần thứ hai lấy được bi màu đen. 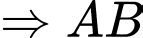 là biến cố lần thứ nhất lấy được bi màu trắng và lần thứ hai lấy được bi màu đen.
là biến cố lần thứ nhất lấy được bi màu trắng và lần thứ hai lấy được bi màu đen. Vì sau khi lấy viên bi thứ nhất xong, ta để lại viên bi vào bình, nên không làm ảnh hưởng xác suất lấy viên bi lần thứ hai. Ta thấy 2 biến cố 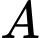 và
và 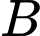 độc lập với nhau.
độc lập với nhau.
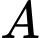 và
và 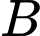 độc lập với nhau.
độc lập với nhau. Xác suất để lần thứ nhất lấy được bi màu trắng là: 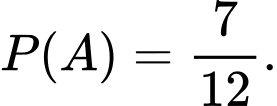
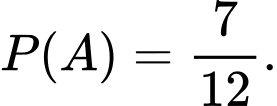
Xác suất để lần thứ hai lấy được bi màu đen là 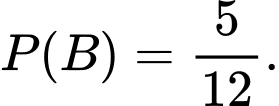
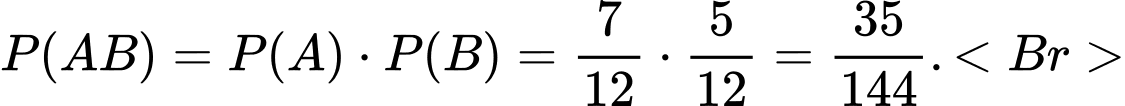
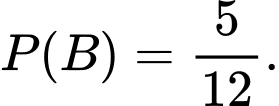
Áp dụng quy tắc nhân xác suất, xác suất để lấy được bi thứ 1 màu trắng và bi thứ 2 màu đen là:
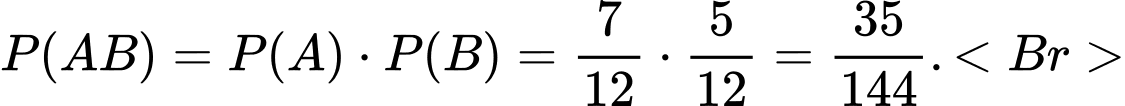
Điền: 0,24
Câu 25 [274339]: Một bệnh truyền nhiễm có xác suất truyền bệnh là 0,8 nếu tiếp xúc với người bệnh mà không đeo khẩu trang; là 0,1 nếu tiếp xúc với người bệnh mà có đeo khẩu trang. Anh Lâm tiếp xúc với 1 người bệnh hai lần, trong đó có 1 lần đeo khẩu trang và một lần không đeo khẩu trang. Tính xác suất anh Lâm bị lây bệnh từ người bệnh mà anh tiếp xúc.
Gọi 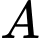 là biến cố: "A Lâm bị nhiễm bệnh khi tiếp xúc người bệnh mà không đeo khẩu trang" và
là biến cố: "A Lâm bị nhiễm bệnh khi tiếp xúc người bệnh mà không đeo khẩu trang" và 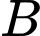 : "A Lâm bị nhiễm bệnh khi tiếp xúc với người bệnh dù có đeo khẩu trang”. Dễ thấy
: "A Lâm bị nhiễm bệnh khi tiếp xúc với người bệnh dù có đeo khẩu trang”. Dễ thấy 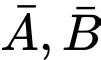 là hai biến cố độc lập.
Xác suất để A Lâm không nhiễm bệnh trong cả hai lần tiếp xúc với người bệnh là
là hai biến cố độc lập.
Xác suất để A Lâm không nhiễm bệnh trong cả hai lần tiếp xúc với người bệnh là 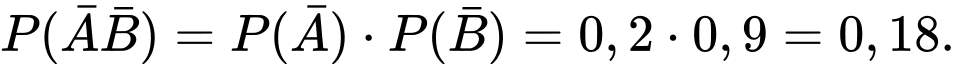
Gọi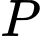 là xác suất để A Lâm bị lây bệnh khi tiếp xúc người bệnh, ta có:
là xác suất để A Lâm bị lây bệnh khi tiếp xúc người bệnh, ta có: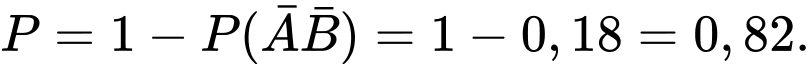
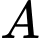 là biến cố: "A Lâm bị nhiễm bệnh khi tiếp xúc người bệnh mà không đeo khẩu trang" và
là biến cố: "A Lâm bị nhiễm bệnh khi tiếp xúc người bệnh mà không đeo khẩu trang" và 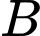 : "A Lâm bị nhiễm bệnh khi tiếp xúc với người bệnh dù có đeo khẩu trang”. Dễ thấy
: "A Lâm bị nhiễm bệnh khi tiếp xúc với người bệnh dù có đeo khẩu trang”. Dễ thấy 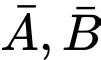 là hai biến cố độc lập.
Xác suất để A Lâm không nhiễm bệnh trong cả hai lần tiếp xúc với người bệnh là
là hai biến cố độc lập.
Xác suất để A Lâm không nhiễm bệnh trong cả hai lần tiếp xúc với người bệnh là 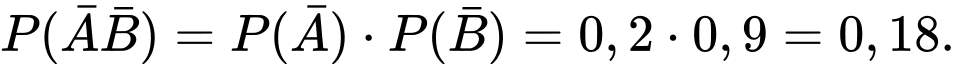
Gọi
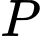 là xác suất để A Lâm bị lây bệnh khi tiếp xúc người bệnh, ta có:
là xác suất để A Lâm bị lây bệnh khi tiếp xúc người bệnh, ta có: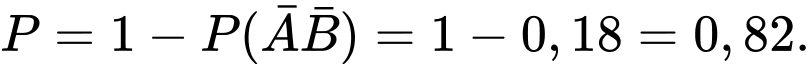
Câu 26 [405577]: Trong một trận đấu bóng đá quan trọng ở vòng đấu loại trực tiếp, khi trận đấu buộc phải giải quyết bằng loạt sút luân lưu  huấn luyện viên đội
huấn luyện viên đội  đưa danh sách lần lượt 5 cầu thủ có xác suất sút luân lưu
đưa danh sách lần lượt 5 cầu thủ có xác suất sút luân lưu  thành công là 0,
thành công là 0,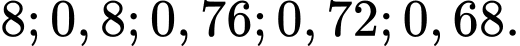 Tìm xác suất để chỉ có cầu thủ cuối cùng sút trượt luân lưu (làm tròn kết quả đến hàng phần trăm).
Tìm xác suất để chỉ có cầu thủ cuối cùng sút trượt luân lưu (làm tròn kết quả đến hàng phần trăm).
 huấn luyện viên đội
huấn luyện viên đội 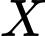 đưa danh sách lần lượt 5 cầu thủ có xác suất sút luân lưu
đưa danh sách lần lượt 5 cầu thủ có xác suất sút luân lưu  thành công là 0,
thành công là 0,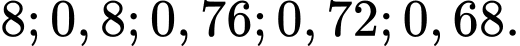 Tìm xác suất để chỉ có cầu thủ cuối cùng sút trượt luân lưu (làm tròn kết quả đến hàng phần trăm).
Tìm xác suất để chỉ có cầu thủ cuối cùng sút trượt luân lưu (làm tròn kết quả đến hàng phần trăm).
Gọi 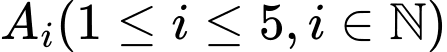 là biến cố: "Cầu thủ thứ
là biến cố: "Cầu thủ thứ 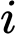 của đội
của đội 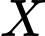 sút luân lưu thành công".
sút luân lưu thành công".
Xác suất cần tìm là:
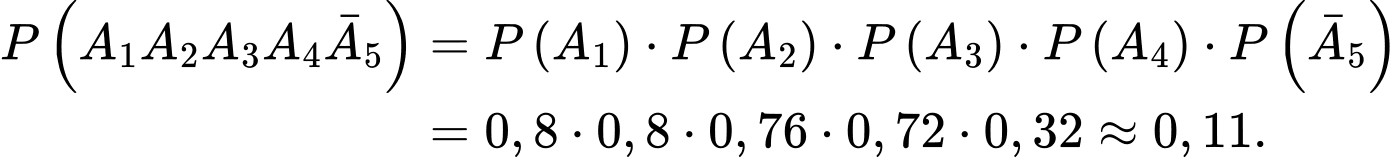
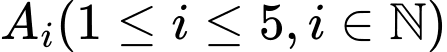 là biến cố: "Cầu thủ thứ
là biến cố: "Cầu thủ thứ 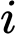 của đội
của đội 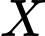 sút luân lưu thành công".
sút luân lưu thành công". Xác suất cần tìm là:
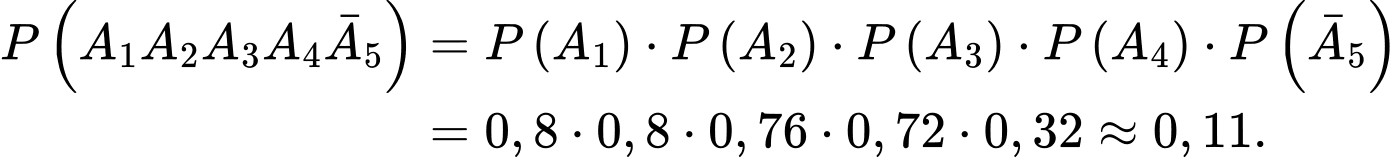
Câu 27 [276454]: Hai bạn Việt và Nam cùng tham gia một kì thi trắc nghiệm môn Toán và môn Tiếng anh một cách độc lập. Đề thi của mỗi môn gồm 6 mã đề khác nhau và các môn khác nhau thì mã đề khác nhau. Đề thi được sắp xếp và phát cho học sinh một cách ngẫu nhiên. Tính xác suất để hai bạn Việt và Nam có chung đúng một mã đề thi trong kì thi đó.
Không gian mẫu 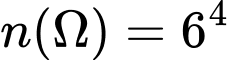 .
. 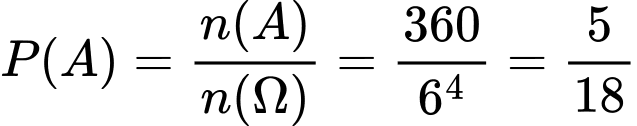 .
.
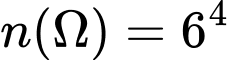 .
. Gọi biến cố A: “Hai bạn Việt và Nam có chung đúng một mã đề thi trong kì thi đó”.
Biến cố B: “Hai bạn Việt và Nam có chung một mã đề thi môn Toán trong kì thi đó”.
Biến cố C: “ Hai bạn Việt và Nam có chung một mã đề thi môn Tiếng Anh trong kì thi đó”.
Khi đó: 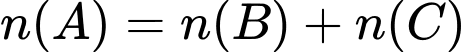 .
.
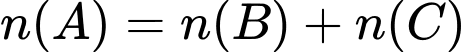 .
. Số các kết quả thuận lợi cho biến cố B là: 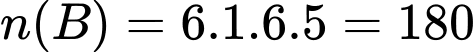 .
.
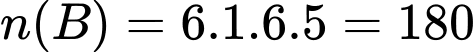 .
. Số các kết quả thuận lợi cho biến cố C là: 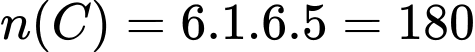 .
.
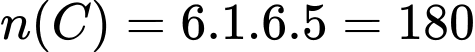 .
. Số các kết quả thuận lợi cho biến cố  là:
là: 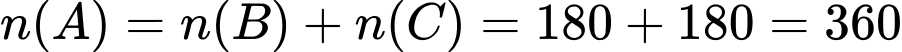 .
.
 là:
là: 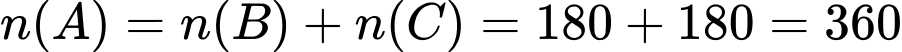 .
. Xác suất để hai bạn Việt và Nam có chung đúng một mã đề thi trong kì thi đó là:
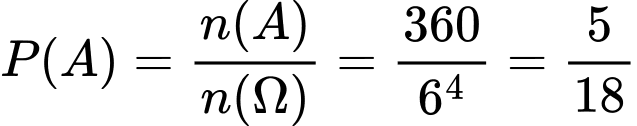 .
.
Câu 28 [275912]: Một máy bay có 4 động cơ trong đó 2 động cơ ở cánh phải và 2 động cơ ở cánh trái. Chuyến bay hạ cánh an toàn khi trên mỗi cánh của nó có ít nhất một động cơ không bị lỗi. Giả sử mỗi động cơ ở cánh phải có xác suất bị lỗi là 0,01 và mỗi động cơ ở cánh trái có xác suất bị lỗi là 0,015. Các động cơ hoạt động độc lập với nhau. Tính xác suất để chuyến bay hạ cánh an toàn.
Xác suất để 1 động cơ trái không bị lỗi, 2 động cơ phải không bị lỗi: 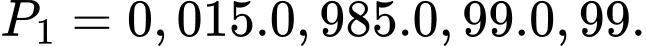
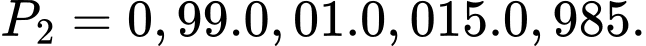
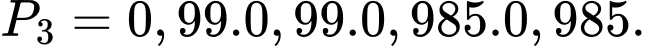
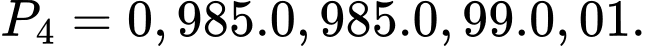
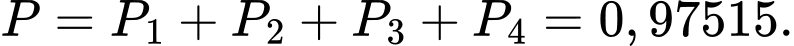
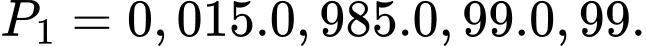
Xác suất để 1 động cơ trái không bị lỗi, 1 động cơ phải không bị lỗi:
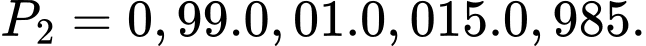
Xác suất để 2 động cơ trái không bị lỗi, 2 động cơ phải không bị lỗi:
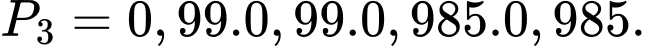
Xác suất để 2 động cơ trái không bị lỗi, 1 động cơ phải không bị lỗi:
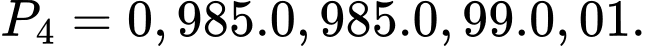
Xác suất để chuyến bay hạ cánh an toàn là: