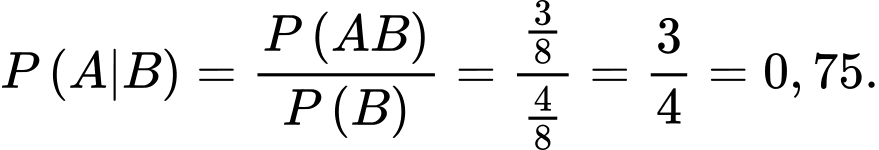Đáp án Bài tập tự luyện
Câu 1 [135712]: Một lớp có 60 em học sinh, 40 em có y phục màu xanh, 10 em có y phục có cả màu xanh và màu trắng. Chọn ngẫu nhiên một em. Tính xác suất để em đó y phục có màu trắng với điều kiện y phục của em đó có màu xanh.
A, 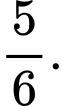
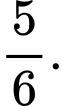
B, 

C, 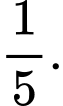
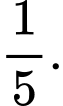
D, 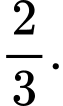
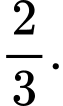
Gọi A là biến cố chọn được em y phục có màu trắng.
Gọi B là biến cố chọn được em y phục có màu xanh.
Ta phải tính 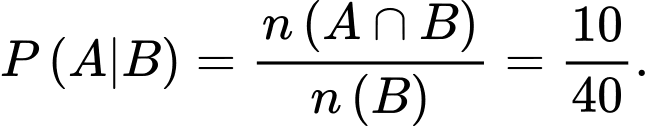
Đáp án: B 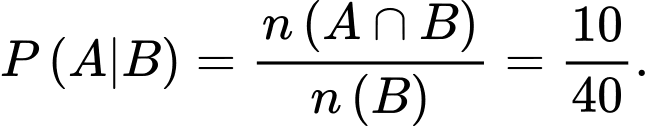
Chọn B.
Câu 2 [135717]: Thống kê 2000 sinh viên một khóa của trường đại học theo giới tính và ngành
học thu được các số liệu sau 

Lấy ngẫu nhiên một sinh viên khóa đó. Nếu đã chọn được một sinh viên nam hãy tính xác suất để người đó học tài chính ngân hàng bằng bao nhiêu?
A, 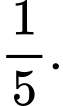
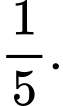
B, 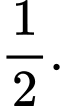
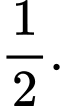
C, 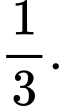
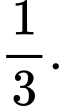
D, 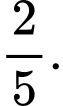
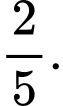
Gọi A là biến cố học sinh đó học tài chính ngân hàng
Gọi B là biến cố học sinh đó là nam
Ta phải tính 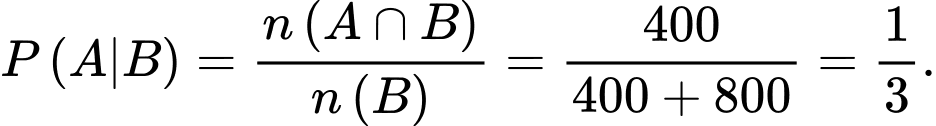
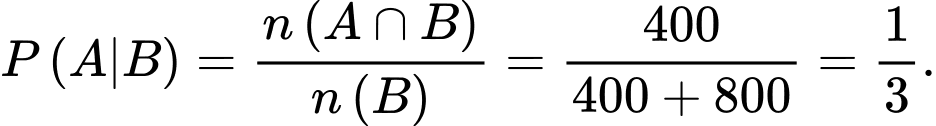
Chọn C.
Đáp án: C
Câu 3 [135722]: Khảo sát 100 người trong đó có 49 nam và 51 nữ về việc có nuôi thú cưng không thì được bảng sau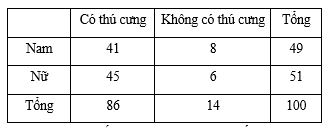

Chọn ngẫu nhiên một người trong số người được khảo sát. Biết người đó là nam, tính xác suất của biến cố người được chọn nuôi thú cưng?
A, 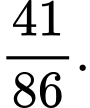
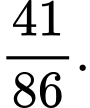
B, 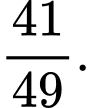
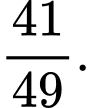
C, 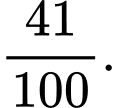
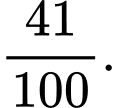
D, 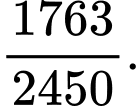
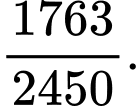
Gọi 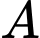 là biến cố học sinh đó nuôi thú cưng
là biến cố học sinh đó nuôi thú cưng
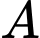 là biến cố học sinh đó nuôi thú cưng
là biến cố học sinh đó nuôi thú cưng Gọi 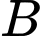 là biến cố học sinh đó là nam
là biến cố học sinh đó là nam
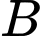 là biến cố học sinh đó là nam
là biến cố học sinh đó là nam Ta phải tính 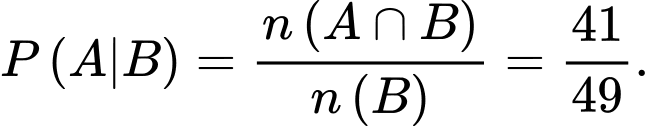
Đáp án: B 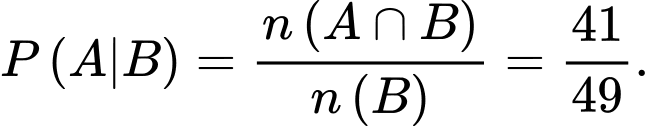
Chọn B.
Câu 4 [135781]: [Trích SGK Cùng Khám Phá]: Một công ty vừa ra mắt sản phẩm X và tổ chức ngày trải nghiệm sản phẩm. Họ thống kê được trong 200 người đến tham quan ngày trải nghiệm có 60 người là nam giới và 140 người là nữ giới. Trong số những người được thống kê này, có 120 người mua sản phẩm X, gồm 40 khách hàng nam và 80 khách hàng nữ, còn lại là không mua sản phẩm X. Chọn ngẫu nhiên một người trong số 200 người được thống kê. Tính xác suất để người này mua sản phẩm X, biết rằng người được chọn là nữ giới (làm tròn kết quả đến hàng phần trăm).
A, 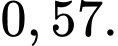
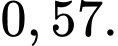
B, 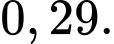
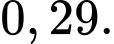
C, 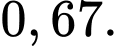
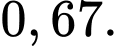
D, 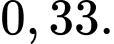
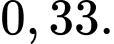
Gọi 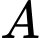 là biến cố người này mua sản phẩm
là biến cố người này mua sản phẩm
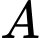 là biến cố người này mua sản phẩm
là biến cố người này mua sản phẩm Gọi 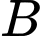 là biến cố người này là nữ giới.
là biến cố người này là nữ giới.
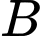 là biến cố người này là nữ giới.
là biến cố người này là nữ giới. Ta có: 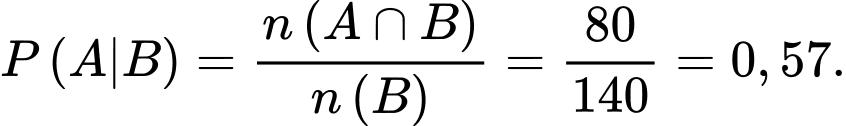
Đáp án: A 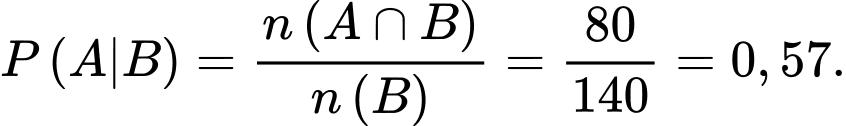
Chọn A.
Câu 5 [135791]: Ở một trường đại học, 60% sinh viên đậu môn Kế toán, 70% đậu môn Tiếng Anh và 30% đậu cả hai khóa học này. Chọn ngẫu nhiên một học sinh. Xác suất bạn ấy đậu môn Kế toán biết bạn ấy đậu môn tiếng Anh là
A, 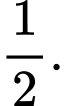
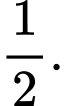
B, 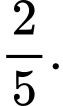
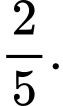
C, 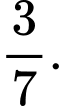
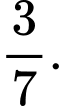
D, 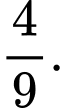
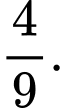
Gọi 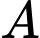 : “Đậu môn Kế toán”,
: “Đậu môn Kế toán”, 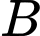 : “Đậu môn Tiếng Anh”.
: “Đậu môn Tiếng Anh”. 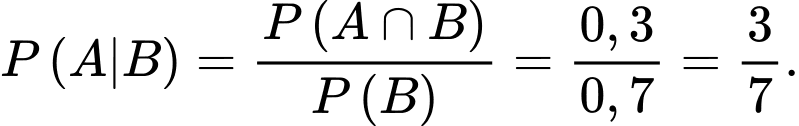 Đáp án: C
Đáp án: C
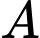 : “Đậu môn Kế toán”,
: “Đậu môn Kế toán”, 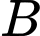 : “Đậu môn Tiếng Anh”.
: “Đậu môn Tiếng Anh”. Khi đó, 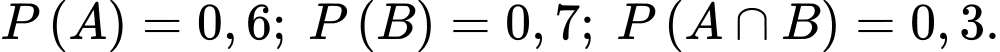 Xác suất học sinh chọn đậu môn Kế toán biết bạn ấy đậu môn tiếng Anh là
Xác suất học sinh chọn đậu môn Kế toán biết bạn ấy đậu môn tiếng Anh là
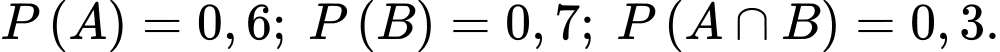 Xác suất học sinh chọn đậu môn Kế toán biết bạn ấy đậu môn tiếng Anh là
Xác suất học sinh chọn đậu môn Kế toán biết bạn ấy đậu môn tiếng Anh là 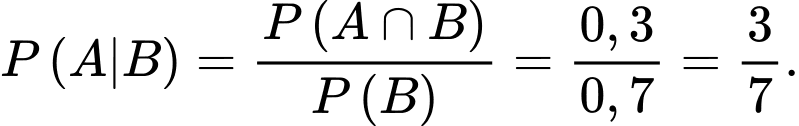
Chọn C.
Câu 6 [360669]: Một lô sản phẩm có 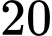 sản phẩm, trong đó có
sản phẩm, trong đó có 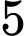 sản phẩm chất lượng thấp. Lấy liên tiếp
sản phẩm chất lượng thấp. Lấy liên tiếp 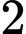 sản phẩm trong lô sản phẩm trên, trong đó sản phẩm lấy ra ở lần thứ nhất không được bỏ lại vào lô sản phẩm. Tính xác suất để cả hai sảm phẩm được lấy ra đều có chất lượng thấp.
sản phẩm trong lô sản phẩm trên, trong đó sản phẩm lấy ra ở lần thứ nhất không được bỏ lại vào lô sản phẩm. Tính xác suất để cả hai sảm phẩm được lấy ra đều có chất lượng thấp.
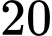 sản phẩm, trong đó có
sản phẩm, trong đó có 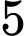 sản phẩm chất lượng thấp. Lấy liên tiếp
sản phẩm chất lượng thấp. Lấy liên tiếp 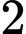 sản phẩm trong lô sản phẩm trên, trong đó sản phẩm lấy ra ở lần thứ nhất không được bỏ lại vào lô sản phẩm. Tính xác suất để cả hai sảm phẩm được lấy ra đều có chất lượng thấp.
sản phẩm trong lô sản phẩm trên, trong đó sản phẩm lấy ra ở lần thứ nhất không được bỏ lại vào lô sản phẩm. Tính xác suất để cả hai sảm phẩm được lấy ra đều có chất lượng thấp. A, 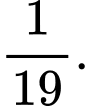
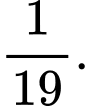
B, 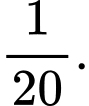
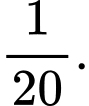
C, 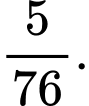
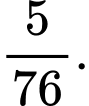
D, 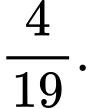
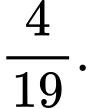
Gọi 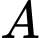 là biến cố sản phẩm được lấy lần 1 có chất lượng thấp,
là biến cố sản phẩm được lấy lần 1 có chất lượng thấp, 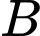 là biến cố sản phẩm được lấy lần 2 có chất lượng thấp,
là biến cố sản phẩm được lấy lần 2 có chất lượng thấp,
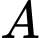 là biến cố sản phẩm được lấy lần 1 có chất lượng thấp,
là biến cố sản phẩm được lấy lần 1 có chất lượng thấp, 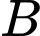 là biến cố sản phẩm được lấy lần 2 có chất lượng thấp,
là biến cố sản phẩm được lấy lần 2 có chất lượng thấp, Khi đó 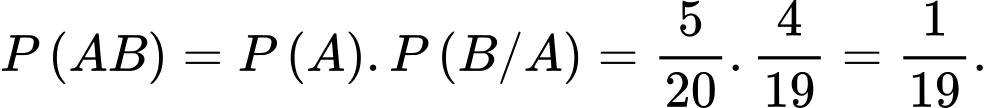
Đáp án: A 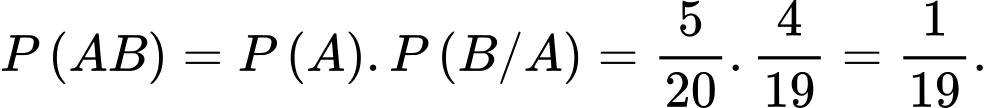
Chọn A.
Câu 7 [134769]: Cho 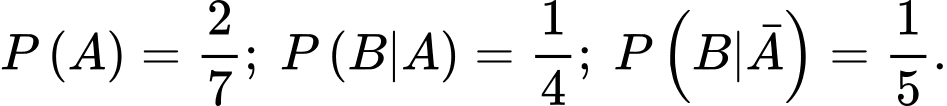 Giá trị
Giá trị 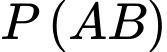 là
là
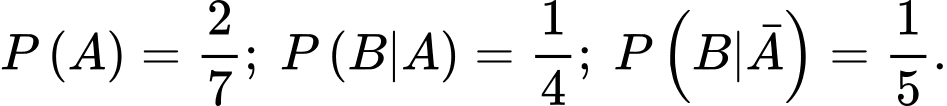 Giá trị
Giá trị 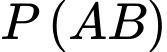 là
là A, 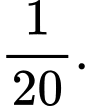
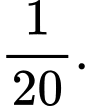
B, 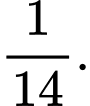
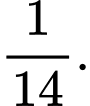
C, 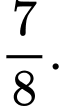
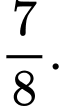
D, 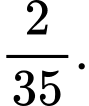
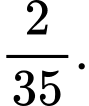
Ta có: 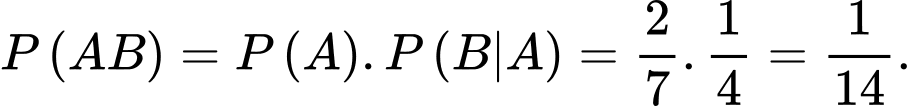 Chọn B. Đáp án: B
Chọn B. Đáp án: B
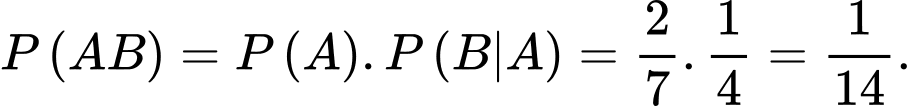 Chọn B. Đáp án: B
Chọn B. Đáp án: B
Câu 8 [134800]: Cho hai biến cố 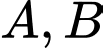 có có
có có 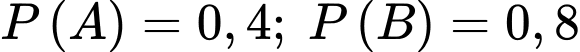 và
và 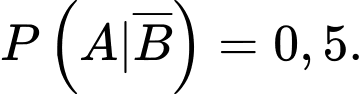 Tính
Tính 
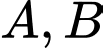 có có
có có 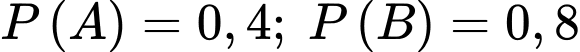 và
và 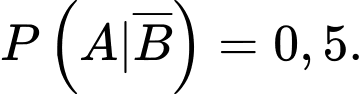 Tính
Tính 
A, 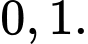
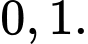
B, 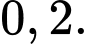
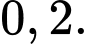
C, 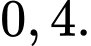
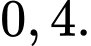
D, 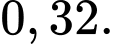
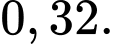
Ta có: 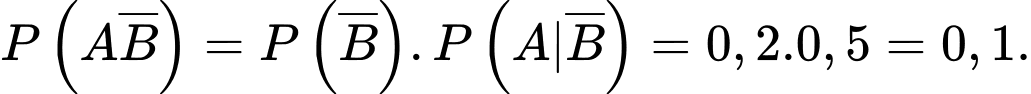 Chọn A. Đáp án: A
Chọn A. Đáp án: A
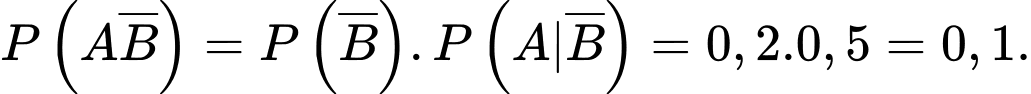 Chọn A. Đáp án: A
Chọn A. Đáp án: A
Câu 9 [134803]: Cho 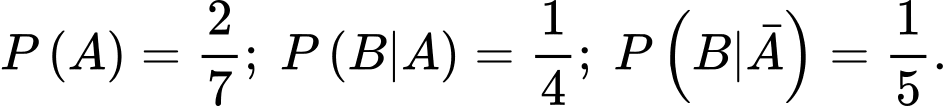 Giá trị
Giá trị  là
là
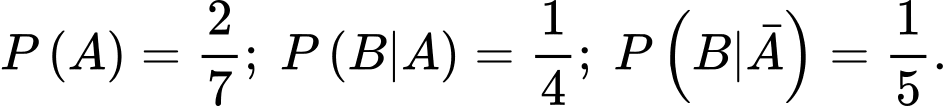 Giá trị
Giá trị  là
là A, 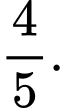
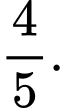
B, 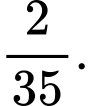
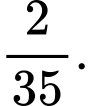
C, 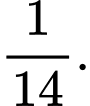
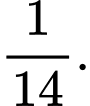
D, 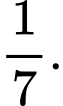
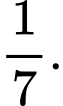
Chọn đáp án D.
Ta có: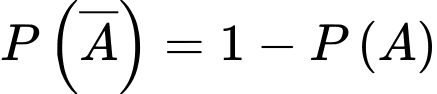
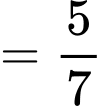
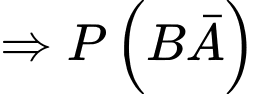
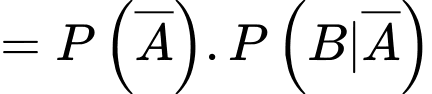
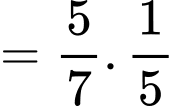
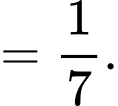 Đáp án: D
Đáp án: D
Ta có:
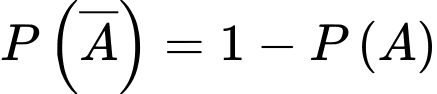
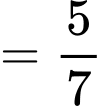
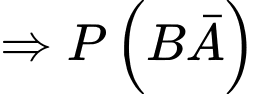
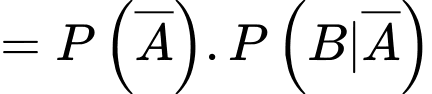
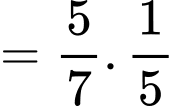
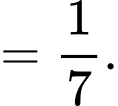 Đáp án: D
Đáp án: D
Câu 10 [134807]: Cho hai biến cố 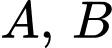 sao cho
sao cho 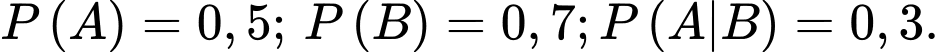 Tính
Tính 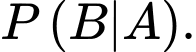
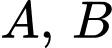 sao cho
sao cho 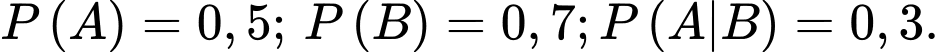 Tính
Tính 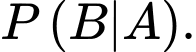
A, 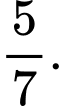
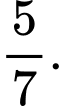
B, 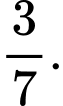
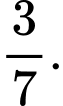
C, 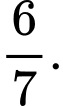
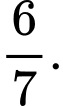
D, 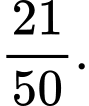
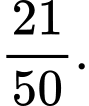
Chọn đáp án D.
Ta có: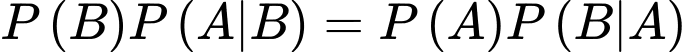
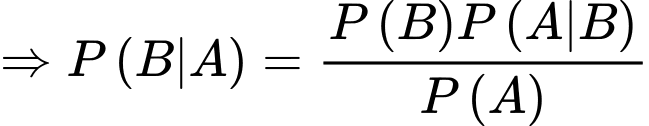
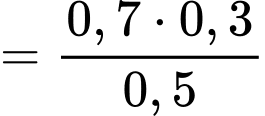
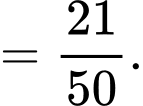 Đáp án: D
Đáp án: D
Ta có:
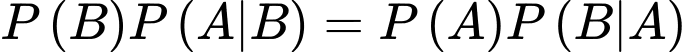
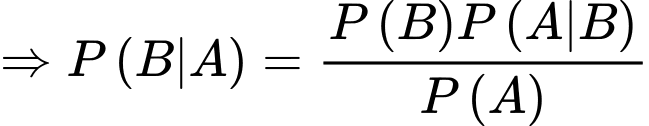
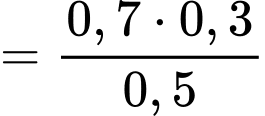
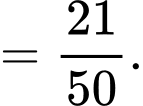 Đáp án: D
Đáp án: D
Câu 11 [145267]: Cho hai biến cố 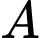 và
và 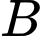 có
có 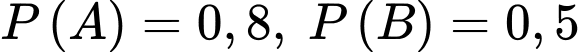 và
và 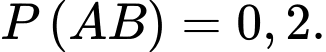 Xác suất của biến cố
Xác suất của biến cố 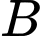 không xảy ra với điều kiện biến cố
không xảy ra với điều kiện biến cố 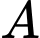 xảy ra là
xảy ra là
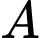 và
và 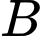 có
có 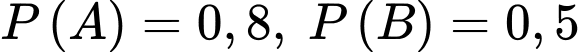 và
và 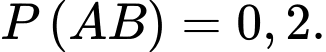 Xác suất của biến cố
Xác suất của biến cố 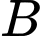 không xảy ra với điều kiện biến cố
không xảy ra với điều kiện biến cố 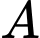 xảy ra là
xảy ra là A, 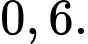
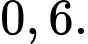
B, 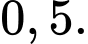
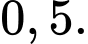
C, 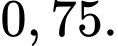
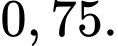
D, 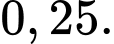
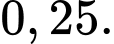
Ta có: 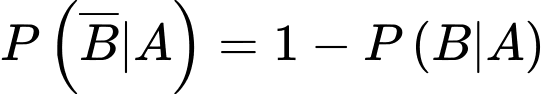
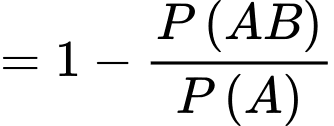
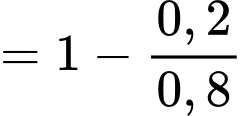
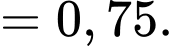
Chọn C. Đáp án: C
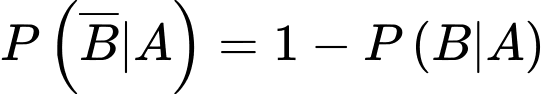
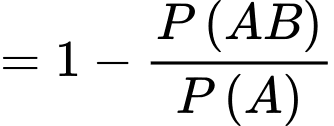
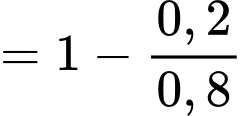
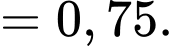
Chọn C. Đáp án: C
Câu 12 [134811]: Cho hai biến cố 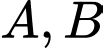 có
có 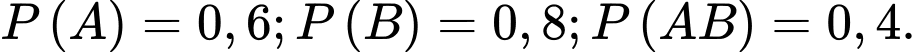 Tính xác suất của biến cố
Tính xác suất của biến cố 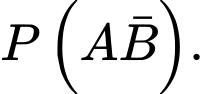
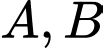 có
có 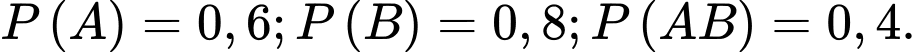 Tính xác suất của biến cố
Tính xác suất của biến cố 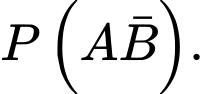
A, 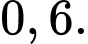
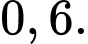
B, 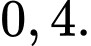
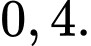
C, 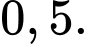
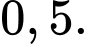
D, 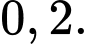
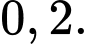
Vì  và
và  là hai biến cố xung khắc và
là hai biến cố xung khắc và  nên theo tính chất của xác suất, ta có:
nên theo tính chất của xác suất, ta có: 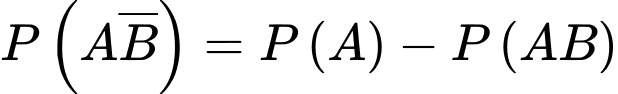
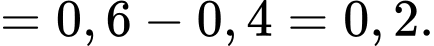
Chọn D. Đáp án: D
 và
và  là hai biến cố xung khắc và
là hai biến cố xung khắc và  nên theo tính chất của xác suất, ta có:
nên theo tính chất của xác suất, ta có: 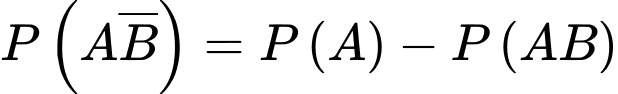
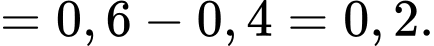
Chọn D. Đáp án: D
Câu 13 [134813]: Cho hai biến cố A và B có 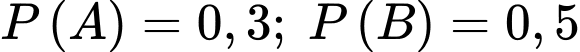 và
và  Tính
Tính 
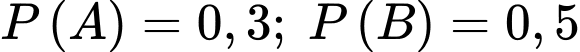 và
và  Tính
Tính 
A, 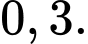
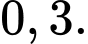
B, 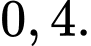
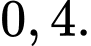
C, 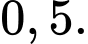
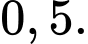
D, 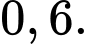
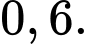
Chọn đáp án A.
Ta có: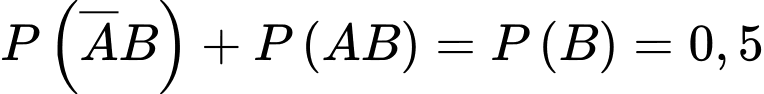
Mặt khác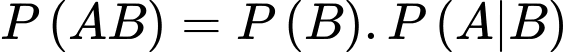
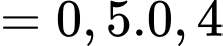
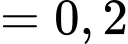
Suy ra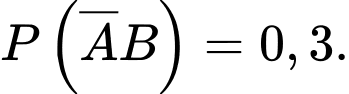 Đáp án: A
Đáp án: A
Ta có:
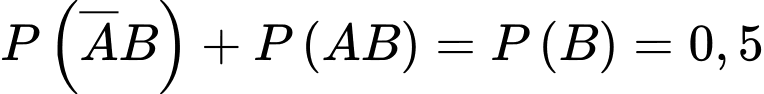
Mặt khác
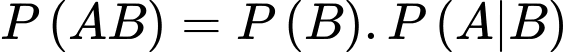
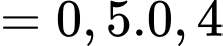
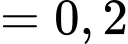
Suy ra
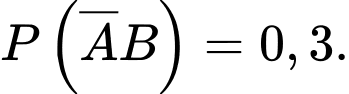 Đáp án: A
Đáp án: A
Câu 14 [134808]: Cho hai biến cố 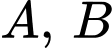 sao cho
sao cho 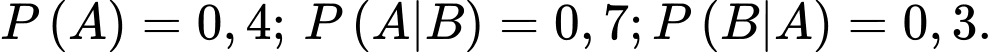 Tính
Tính 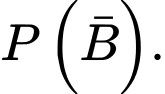
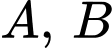 sao cho
sao cho 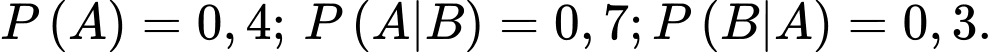 Tính
Tính 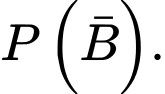
A, 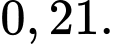
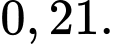
B, 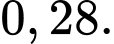
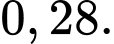
C, 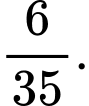
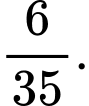
D, 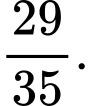
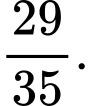
Ta có: 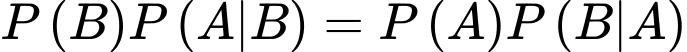
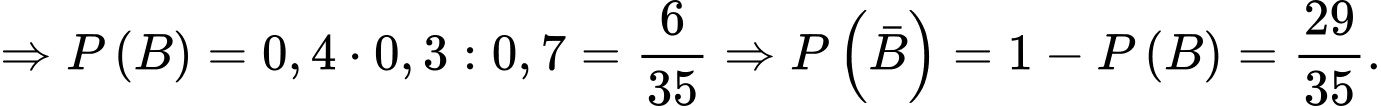
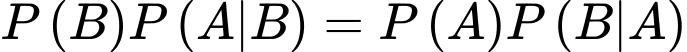
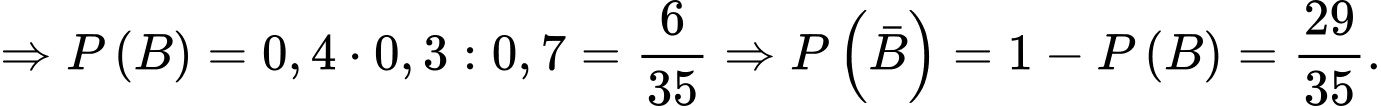
Chọn D.
Đáp án: D
Câu 15 [145261]: [Trích SGK Cùng Khám Phá]: Cho 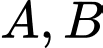 là các biến cố thoả mãn
là các biến cố thoả mãn 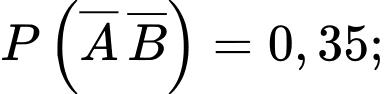
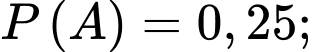
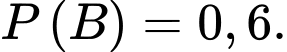 Giá trị của
Giá trị của  bằng
bằng
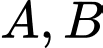 là các biến cố thoả mãn
là các biến cố thoả mãn 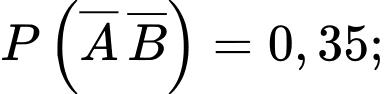
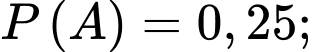
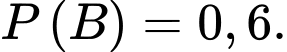 Giá trị của
Giá trị của  bằng
bằng A, 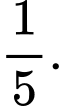
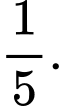
B, 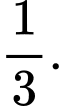
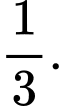
C, 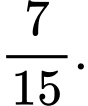
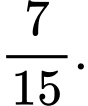
D, 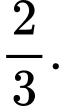
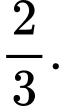
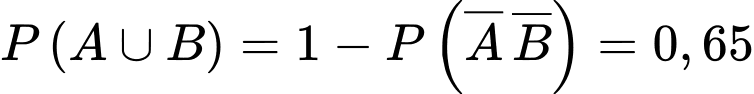
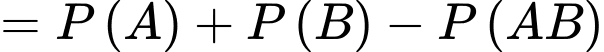
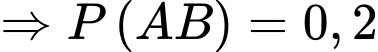
Do đó
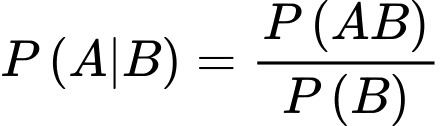
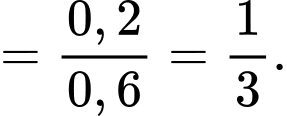
Chọn B. Đáp án: B
Câu 16 [579691]: [Đề mẫu HSA 2024]: Cho các biến cố  và
và 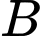 thỏa mãn
thỏa mãn 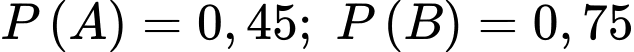 và
và 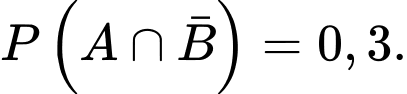 Khi đó
Khi đó  bằng
bằng
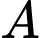 và
và 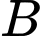 thỏa mãn
thỏa mãn 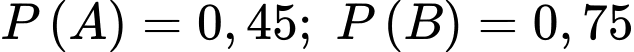 và
và 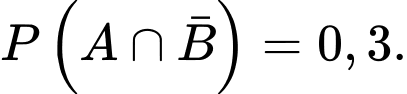 Khi đó
Khi đó  bằng
bằng A, 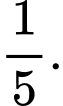
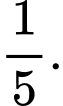
B, 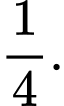
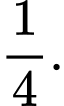
C, 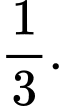
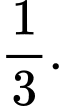
D, 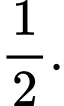
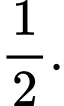
Ta có: 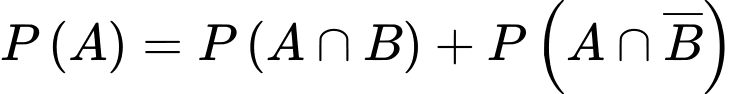
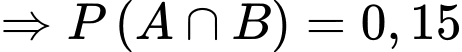
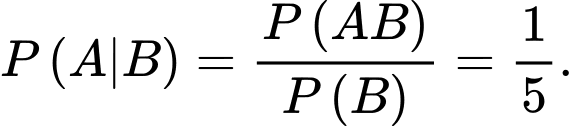
Chọn A. Đáp án: A
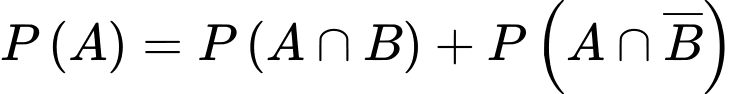
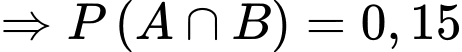
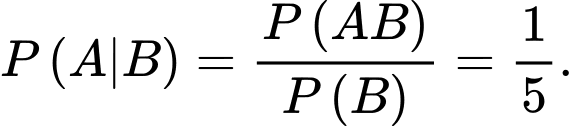
Chọn A. Đáp án: A
Câu 17 [135752]: Một hộp có 8 viên bi màu đỏ và 5 viên bi màu vàng; các viên bi có kích thước và khối lượng như nhau. Có 5 viên bi trong hộp được đánh số, trong đó có 3 viên bi màu đỏ và 2 viên bi màu vàng. Lấy ngẫu nhiên một viên bi trong hộp. Tính xác suất để viên bi được lấy ra có màu đỏ, biết rằng viên bi đó được đánh số.
A, 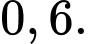
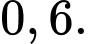
B, 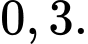
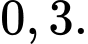
C, 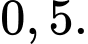
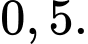
D, 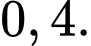
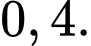
Gọi 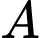 là biến cố viên bi lấy ra có màu đỏ.
là biến cố viên bi lấy ra có màu đỏ.
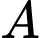 là biến cố viên bi lấy ra có màu đỏ.
là biến cố viên bi lấy ra có màu đỏ. Gọi 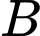 là biến cố viên bi đó được đánh số.
là biến cố viên bi đó được đánh số.
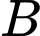 là biến cố viên bi đó được đánh số.
là biến cố viên bi đó được đánh số. Ta phải tính 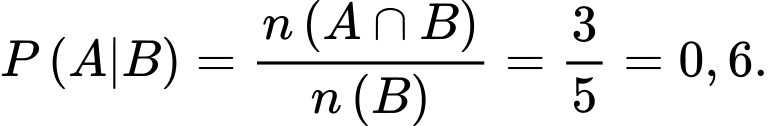
Đáp án: A 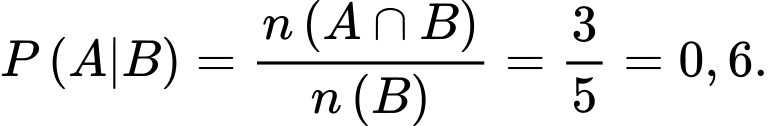
Chọn A.
Câu 18 [360660]: Một hộp có 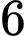 quả bóng màu xanh,
quả bóng màu xanh, 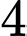 quả bóng màu đỏ; các quả bóng có kích thước và khối lượng như nhau. Lấy ngẫu nhiên lần lượt hai quả bóng trong hộp, lấy không hoàn lại. Tìm xác suất để lần thứ hai lấy được quả bóng màu đỏ, biết rằng lần thứ nhất đã lấy được quả bóng màu xanh.
quả bóng màu đỏ; các quả bóng có kích thước và khối lượng như nhau. Lấy ngẫu nhiên lần lượt hai quả bóng trong hộp, lấy không hoàn lại. Tìm xác suất để lần thứ hai lấy được quả bóng màu đỏ, biết rằng lần thứ nhất đã lấy được quả bóng màu xanh.
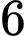 quả bóng màu xanh,
quả bóng màu xanh, 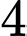 quả bóng màu đỏ; các quả bóng có kích thước và khối lượng như nhau. Lấy ngẫu nhiên lần lượt hai quả bóng trong hộp, lấy không hoàn lại. Tìm xác suất để lần thứ hai lấy được quả bóng màu đỏ, biết rằng lần thứ nhất đã lấy được quả bóng màu xanh.
quả bóng màu đỏ; các quả bóng có kích thước và khối lượng như nhau. Lấy ngẫu nhiên lần lượt hai quả bóng trong hộp, lấy không hoàn lại. Tìm xác suất để lần thứ hai lấy được quả bóng màu đỏ, biết rằng lần thứ nhất đã lấy được quả bóng màu xanh. A, 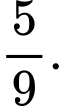
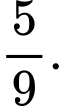
B, 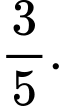
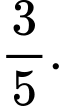
C, 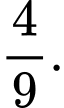
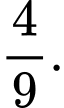
D, 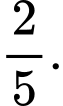
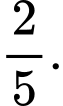
Gọi  là biến cố lần thứ hai lấy được quả bóng màu đỏ.
là biến cố lần thứ hai lấy được quả bóng màu đỏ.
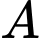 là biến cố lần thứ hai lấy được quả bóng màu đỏ.
là biến cố lần thứ hai lấy được quả bóng màu đỏ. Gọi 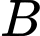 là biến cố lần thứ nhất lấy được quả bóng màu xanh.
là biến cố lần thứ nhất lấy được quả bóng màu xanh.
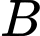 là biến cố lần thứ nhất lấy được quả bóng màu xanh.
là biến cố lần thứ nhất lấy được quả bóng màu xanh. Ta phải tính 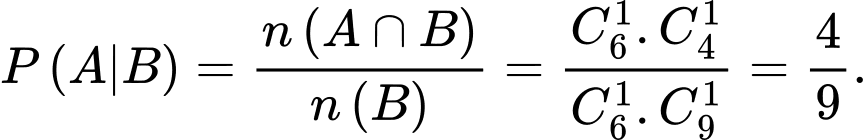
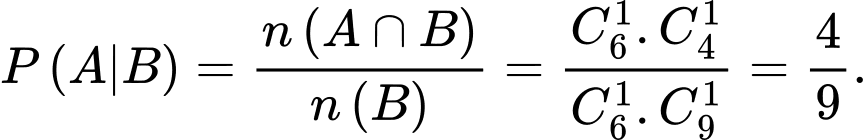
Chọn C.
Đáp án: C
Câu 19 [134814]: Cho hai biến cố 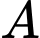 và
và 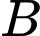 có
có 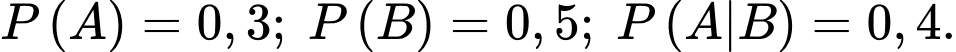 Tính
Tính 
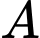 và
và 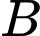 có
có 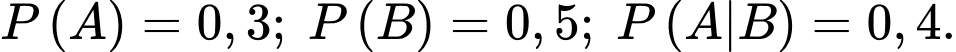 Tính
Tính 
A, 0,2.
B, 0,4.
C, 0,6.
D, 0,8.
Ta có: 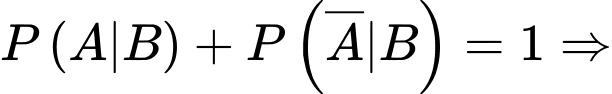
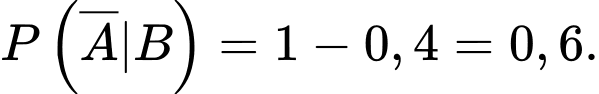 Đáp án: C
Đáp án: C
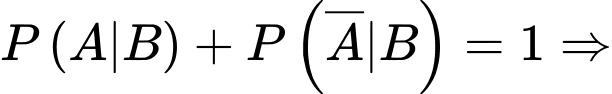
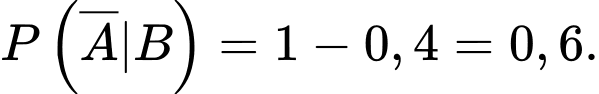 Đáp án: C
Đáp án: C
Câu 20 [134819]: Cho hai biến cố 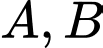 có
có 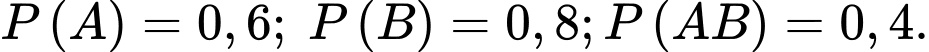 Tính xác suất của biến cố
Tính xác suất của biến cố 
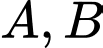 có
có 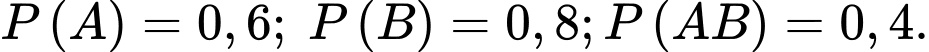 Tính xác suất của biến cố
Tính xác suất của biến cố 
A, 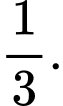
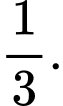
B, 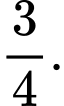
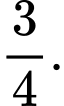
C, 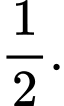
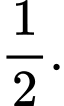
D, 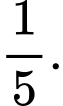
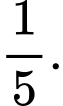
Ta có: 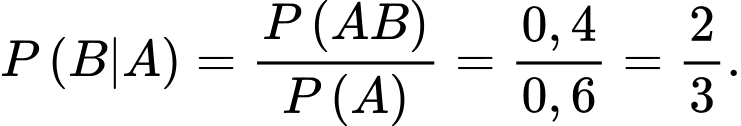
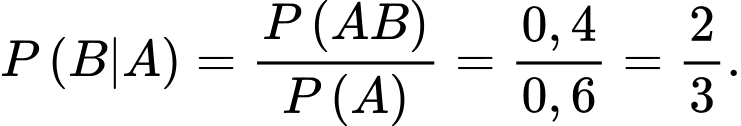
Mặt khác: 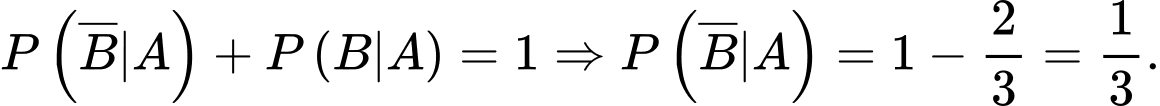
Đáp án: A 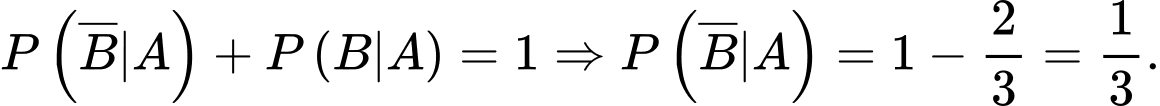
Chọn A.
Câu 21 [134823]: Cho hai biến cố  có có
có có 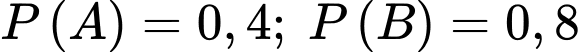 và
và 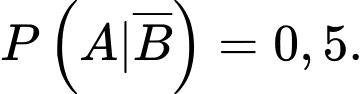 Tính
Tính 
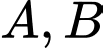 có có
có có 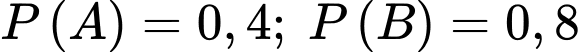 và
và 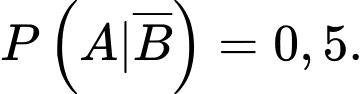 Tính
Tính 
A, 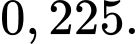
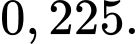
B, 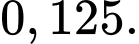
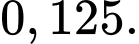
C, 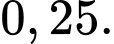
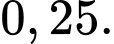
D, 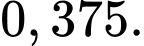
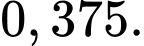
Ta có: 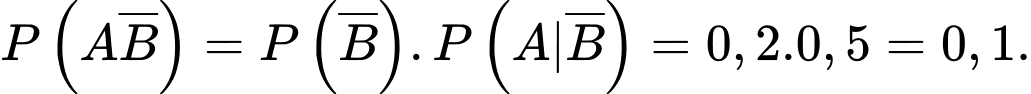
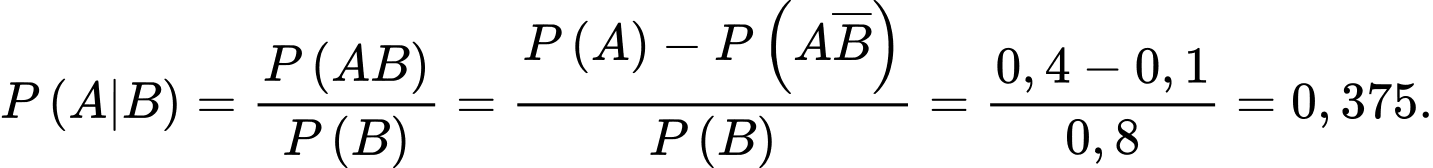
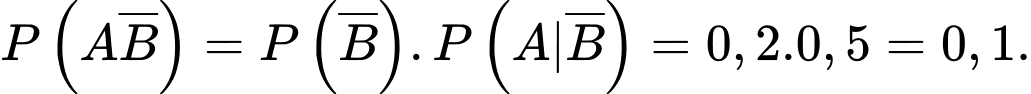
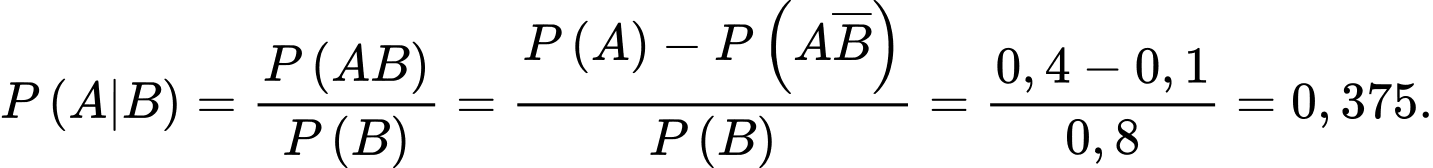
Chọn D.
Đáp án: D
Câu 22 [135780]: Một túi có  hộp sữa chua dâu và
hộp sữa chua dâu và  hộp sữa chua nha đam; các hộp sữa chua có kích thước và khối lượng như nhau. Có
hộp sữa chua nha đam; các hộp sữa chua có kích thước và khối lượng như nhau. Có  hộp sữa chua trong túi là sữa chua không đường, trong đó có
hộp sữa chua trong túi là sữa chua không đường, trong đó có 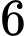 hộp sữa chua dâu và
hộp sữa chua dâu và 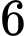 hộp sữa chua nha đam. Lấy ngẫu nhiên một hộp sữa chua trong túi. Tính xác suất để hộp sữa chua được lấy ra là hộp sữa chua dâu, biết rằng hộp sữa chua đó là sữa chua không đường.
hộp sữa chua nha đam. Lấy ngẫu nhiên một hộp sữa chua trong túi. Tính xác suất để hộp sữa chua được lấy ra là hộp sữa chua dâu, biết rằng hộp sữa chua đó là sữa chua không đường.
 hộp sữa chua dâu và
hộp sữa chua dâu và  hộp sữa chua nha đam; các hộp sữa chua có kích thước và khối lượng như nhau. Có
hộp sữa chua nha đam; các hộp sữa chua có kích thước và khối lượng như nhau. Có  hộp sữa chua trong túi là sữa chua không đường, trong đó có
hộp sữa chua trong túi là sữa chua không đường, trong đó có 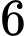 hộp sữa chua dâu và
hộp sữa chua dâu và 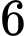 hộp sữa chua nha đam. Lấy ngẫu nhiên một hộp sữa chua trong túi. Tính xác suất để hộp sữa chua được lấy ra là hộp sữa chua dâu, biết rằng hộp sữa chua đó là sữa chua không đường.
hộp sữa chua nha đam. Lấy ngẫu nhiên một hộp sữa chua trong túi. Tính xác suất để hộp sữa chua được lấy ra là hộp sữa chua dâu, biết rằng hộp sữa chua đó là sữa chua không đường. A, 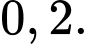
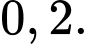
B, 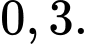
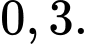
C, 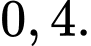
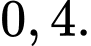
D, 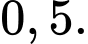
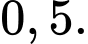
Gọi 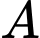 là biến cố hộp sữa chua được lấy ra là hộp sữa chua dâu.
là biến cố hộp sữa chua được lấy ra là hộp sữa chua dâu.
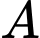 là biến cố hộp sữa chua được lấy ra là hộp sữa chua dâu.
là biến cố hộp sữa chua được lấy ra là hộp sữa chua dâu. Gọi 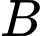 là biến cố hộp sữa chua được lấy ra là hộp sữa chua không đường.
là biến cố hộp sữa chua được lấy ra là hộp sữa chua không đường.
 là biến cố hộp sữa chua được lấy ra là hộp sữa chua không đường.
là biến cố hộp sữa chua được lấy ra là hộp sữa chua không đường. Ta phải tính 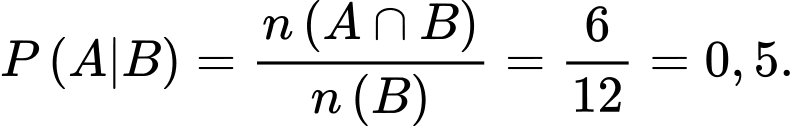
Đáp án: D 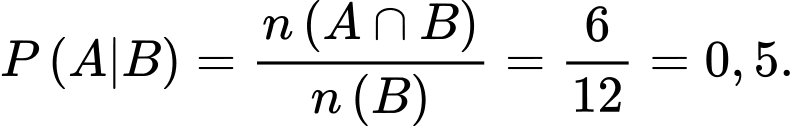
Chọn D.
Câu 23 [135801]: Một thủ quỹ có một chùm chìa khóa gồm 9 chiếc chìa giống hệt nhau trong đó chỉ có 2 chìa có thể mở được tủ sắt. Anh ta thử ngẫu nhiên từng chìa (chìa không trúng được bỏ ra trong lần thử kế tiếp). Tìm xác suất để anh ta mở được tủ vào đúng lần thứ ba.
A, 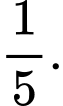
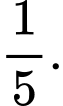
B, 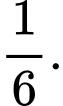
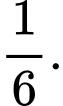
C, 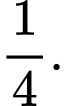
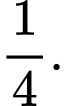
D, 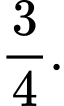
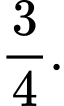
Chọn đáp án B.
Số cách sử dụng chìa khoá đến lần thứ ba là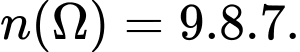
Số cách mở được cửa ở lần thứ ba là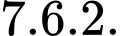
Xác suất cần tính bằng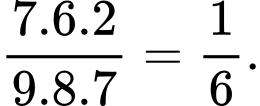 Đáp án: B
Đáp án: B
Số cách sử dụng chìa khoá đến lần thứ ba là
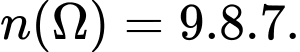
Số cách mở được cửa ở lần thứ ba là
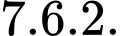
Xác suất cần tính bằng
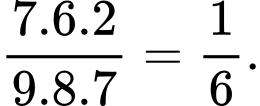 Đáp án: B
Đáp án: B
Câu 24 [135701]: Cho hai biến cố 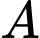 và
và 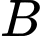 với
với 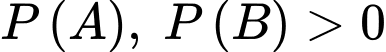 và
và 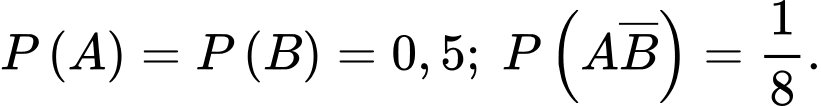 Tính
Tính 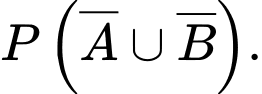
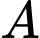 và
và 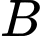 với
với 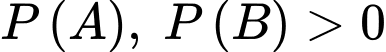 và
và 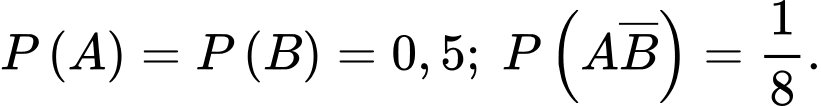 Tính
Tính 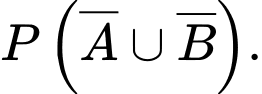
A, 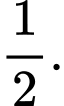
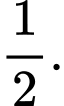
B, 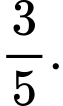
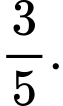
C, 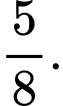
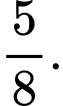
D, 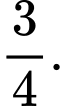
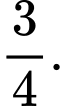
Ta có: 

Lại có: 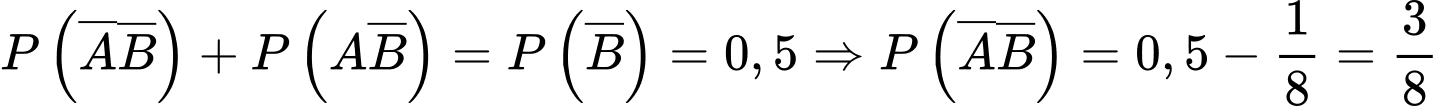 nên
nên 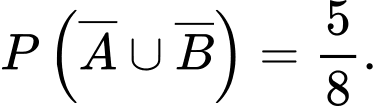
Đáp án: C 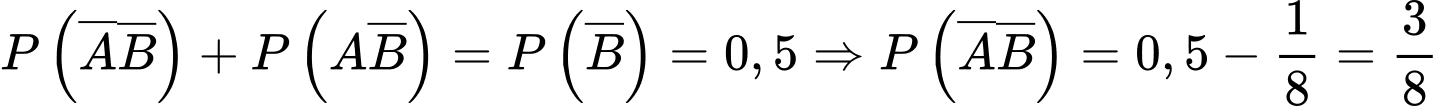 nên
nên 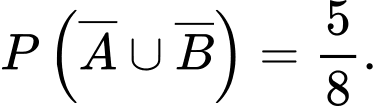
Câu 25 [135703]: Cho hai biến cố 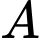 và
và 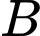 với
với 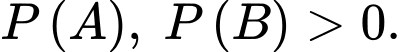 Biết
Biết 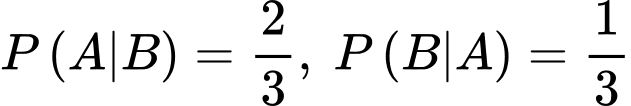 và
và 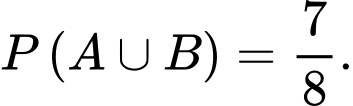 Tính
Tính 
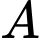 và
và 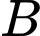 với
với 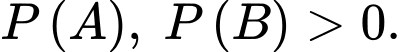 Biết
Biết 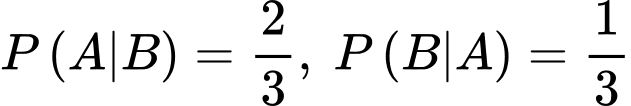 và
và 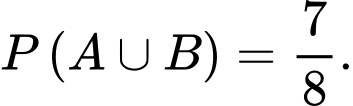 Tính
Tính 
A, 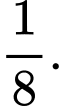
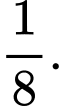
B, 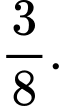
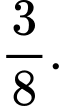
C, 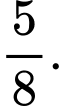
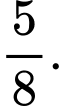
D, 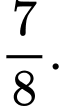
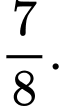
Từ 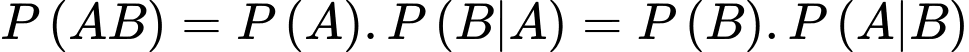
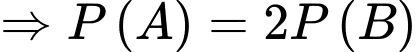
Vậy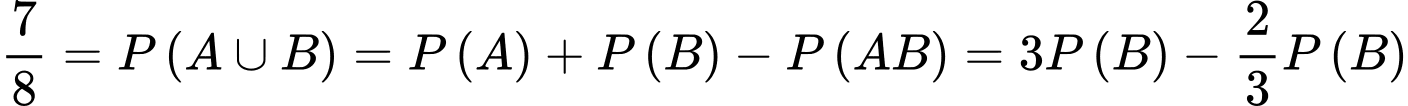 hay
hay 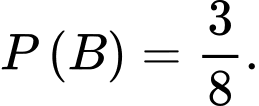
Chọn B. Đáp án: B
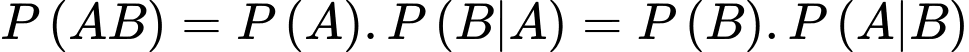
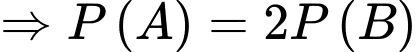
Vậy
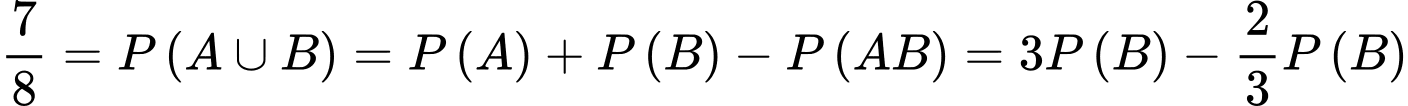 hay
hay 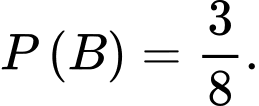
Chọn B. Đáp án: B
Câu 26 [135784]: [Trích SGK Cánh Diều]: Trên giá sách có  quyển sách Khoa học và
quyển sách Khoa học và  quyển sách Nghệ thuật. Có
quyển sách Nghệ thuật. Có 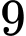 quyển sách viết bằng tiếng Anh, trong đó
quyển sách viết bằng tiếng Anh, trong đó 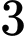 quyển sách Khoa học và
quyển sách Khoa học và 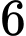 quyển sách Nghệ thuật, các quyển sách còn lại viết bằng tiếng Việt. Lấy ngẫu nhiên một quyển sách. Tính xác suất để quyển sách được lấy ra là sách viết bằng tiếng Việt, biết rằng quyển sách đó là sách Khoa học.
quyển sách Nghệ thuật, các quyển sách còn lại viết bằng tiếng Việt. Lấy ngẫu nhiên một quyển sách. Tính xác suất để quyển sách được lấy ra là sách viết bằng tiếng Việt, biết rằng quyển sách đó là sách Khoa học.
 quyển sách Khoa học và
quyển sách Khoa học và  quyển sách Nghệ thuật. Có
quyển sách Nghệ thuật. Có 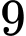 quyển sách viết bằng tiếng Anh, trong đó
quyển sách viết bằng tiếng Anh, trong đó 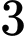 quyển sách Khoa học và
quyển sách Khoa học và 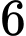 quyển sách Nghệ thuật, các quyển sách còn lại viết bằng tiếng Việt. Lấy ngẫu nhiên một quyển sách. Tính xác suất để quyển sách được lấy ra là sách viết bằng tiếng Việt, biết rằng quyển sách đó là sách Khoa học.
quyển sách Nghệ thuật, các quyển sách còn lại viết bằng tiếng Việt. Lấy ngẫu nhiên một quyển sách. Tính xác suất để quyển sách được lấy ra là sách viết bằng tiếng Việt, biết rằng quyển sách đó là sách Khoa học.
Gọi 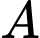 là biến cố quyển sách được lấy ra là sách viết bằng Tiếng Việt.
là biến cố quyển sách được lấy ra là sách viết bằng Tiếng Việt. 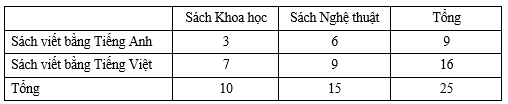
Ta phải tính 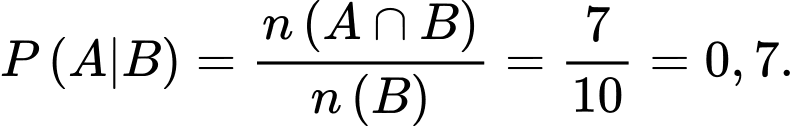
 là biến cố quyển sách được lấy ra là sách viết bằng Tiếng Việt.
là biến cố quyển sách được lấy ra là sách viết bằng Tiếng Việt. Gọi  là biến cố quyển sách được lấy ra là sách Khoa học.
là biến cố quyển sách được lấy ra là sách Khoa học.
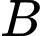 là biến cố quyển sách được lấy ra là sách Khoa học.
là biến cố quyển sách được lấy ra là sách Khoa học. Ta có bảng sau:

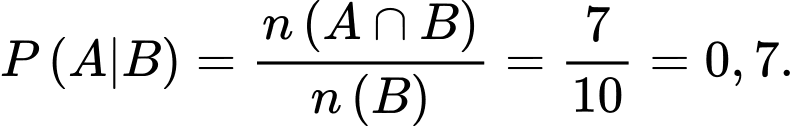
Câu 27 [135859]: [Trích SGK Kết Nối Tri Thức]:Trong một hộp kín có 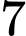 chiếc bút bi xanh và
chiếc bút bi xanh và 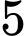 chiếc bút bi đen, các chiếc bút có cùng kích thước và khối lượng. Bạn Sơn lấy ngẫu nhiên một chiếc bút bi từ trong hộp, không trả lại. Sau đó bạn Tùng lấy ngẫu nhiên một trong
chiếc bút bi đen, các chiếc bút có cùng kích thước và khối lượng. Bạn Sơn lấy ngẫu nhiên một chiếc bút bi từ trong hộp, không trả lại. Sau đó bạn Tùng lấy ngẫu nhiên một trong  chiếc bút còn lại. Tính xác suất để hai chiếc bút lấy ra có cùng màu. Viết kết quả làm tròn đến hàng phần trăm.
chiếc bút còn lại. Tính xác suất để hai chiếc bút lấy ra có cùng màu. Viết kết quả làm tròn đến hàng phần trăm.
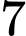 chiếc bút bi xanh và
chiếc bút bi xanh và 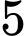 chiếc bút bi đen, các chiếc bút có cùng kích thước và khối lượng. Bạn Sơn lấy ngẫu nhiên một chiếc bút bi từ trong hộp, không trả lại. Sau đó bạn Tùng lấy ngẫu nhiên một trong
chiếc bút bi đen, các chiếc bút có cùng kích thước và khối lượng. Bạn Sơn lấy ngẫu nhiên một chiếc bút bi từ trong hộp, không trả lại. Sau đó bạn Tùng lấy ngẫu nhiên một trong  chiếc bút còn lại. Tính xác suất để hai chiếc bút lấy ra có cùng màu. Viết kết quả làm tròn đến hàng phần trăm.
chiếc bút còn lại. Tính xác suất để hai chiếc bút lấy ra có cùng màu. Viết kết quả làm tròn đến hàng phần trăm.
Xác suất để hai chiếc bút lấy ra cùng màu xanh là: 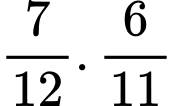
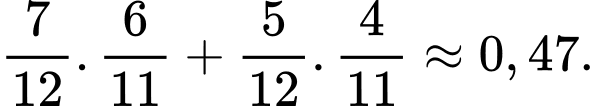
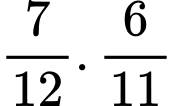
Xác suất để hai chiếc bút lấy ra cùng màu đen là: 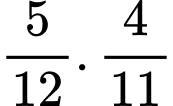
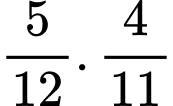
Xác suất để hai chiếc bút lấy ra có cùng màu là
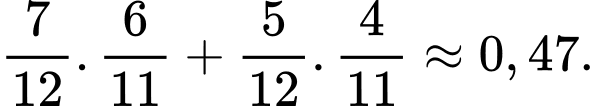
Câu 28 [143805]: Trong thời gian có dịch ở một vung cứ 100 người mắc dịch thì có 10 người phải cấp cứu. Xác suất gặp một người mắc dịch và phải đi cấp cứu ở vùng đó là 0,06. Tìm tỷ lệ mắc bệnh dịch của vùng đó.
Đặt A – gặp người mắc dịch, B – gặp người bị cấp cứu và ta
phải tìm P(A).
phải tìm P(A).
Từ đầu bài ta có: P(B|A) = 10/100 = 0,1; P(AB) =0,06.
Mặt khác P(B|A) = P(AB)/P(A), từ đo suy ra 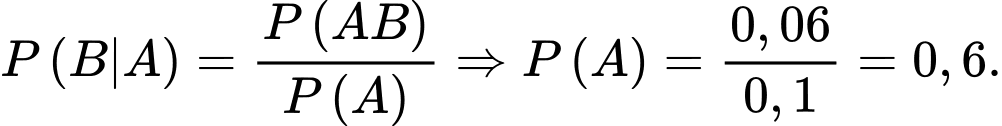
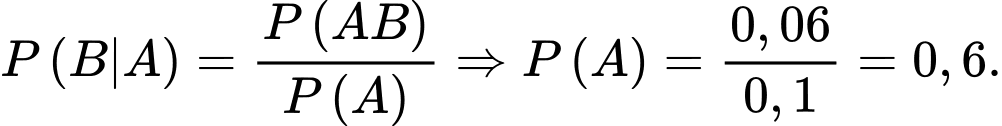
Câu 29 [145403]: Một lớp có 3 tổ sinh viên: tổ I có 12 người, tổ II có 10 người và tổ III có 15 người. Chọn ngẫu nhiên ra một nhóm sinh viên gồm 4 người. Biết trong nhóm có đúng một sinh viên tổ I, tính xác suất để trong nhóm đó có đúng một sinh viên tổ III. Viết kết quả làm tròn đến hàng phần trăm.
Gọi A là biến cố: “Trong nhóm có đúng 1 sinh viên tổ 1”
B là biến cố: Trong nhóm có đúng 1 sinh viên tổ 3”
Ta có: 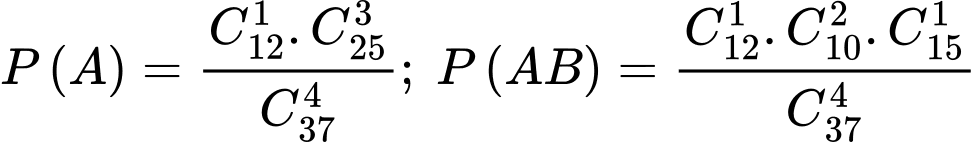
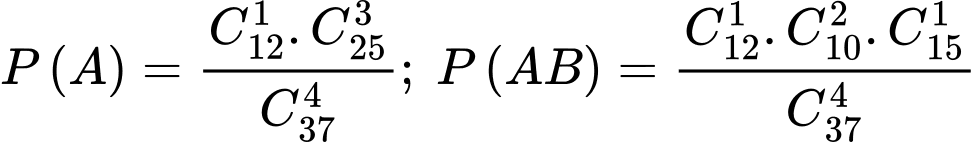
Suy ra 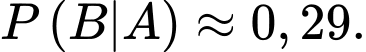
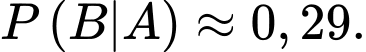
Câu 30 [135692]: Theo thống kê ở các gia đình có hai con thì xác suất để con thứ nhất và con thứ hai đều là trai là 0,27 và hai con đều là gái là 0,23, còn xác suất con thứ nhất và con thứ hai có một trai và một gái là bằng nhau. Chọn ngẫu nhiên một gia đình thì gặp gia đình có con thứ nhất là gái, tìm xác suất để con thứ hai là trai. Viết kết quả làm tròn đến hàng phần trăm.
Gọi A là biến cố "con thứ nhất là con gái” và B là biến cố "con thứ hai là con trai thì theo đề bài ta có: 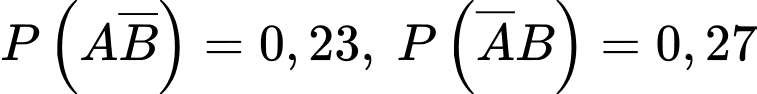
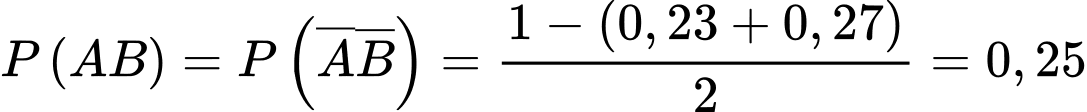
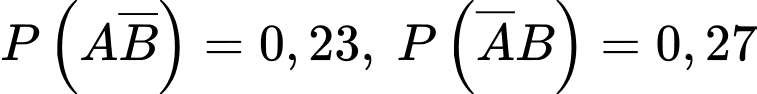
Vì xác suất con thứ nhất và con thứ hai có một trai và một gái là bằng nhau nên
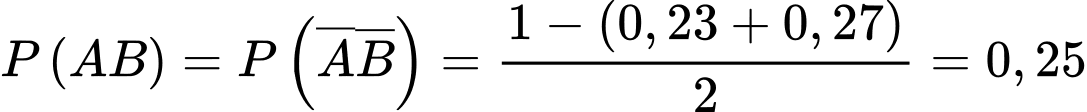
Ta cần tính: 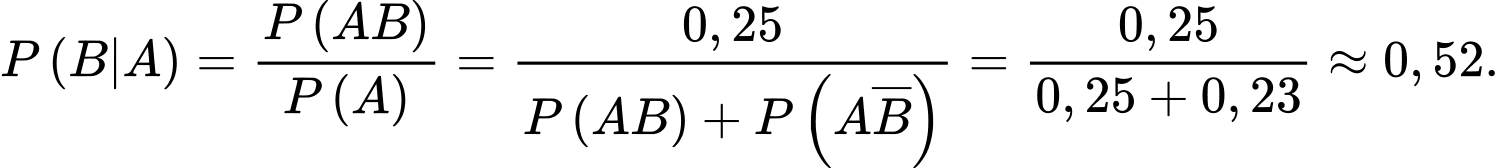
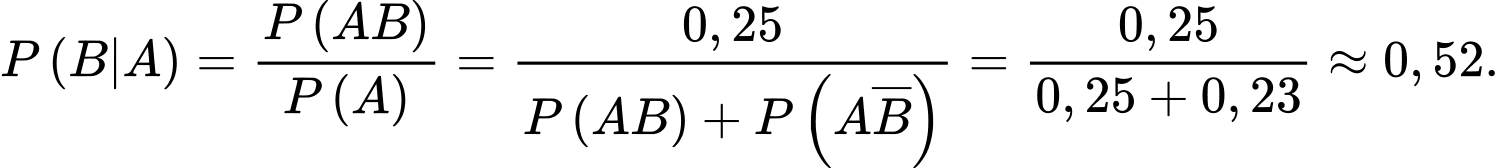
Câu 31 [146672]: Một lô hàng có 6 sản phẩm tốt, 4 sản phẩm xấu. Lấy ngẫu nhiên không hoàn lại từng sản phẩm cho đến khi lấy được 2 sản phẩm tốt thì ngừng, Biết đã ngừng lại ở lần lấy sản phẩm thứ 4. Tính xác suất để lần lấy thứ nhất lấy được sản phẩm tốt. Viết kết quả làm tròn đến hàng phần trăm.
Điền đáp án: 0,33.
Gọi A là biến cố: lần thứ nhất lấy được sản phẩm tốt
B là biến cố: Ngưng lại ở lần thứ 4
Ta có: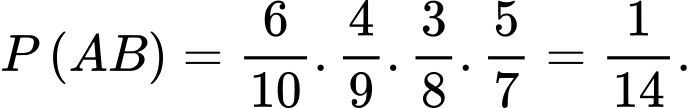
Mặt khác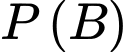
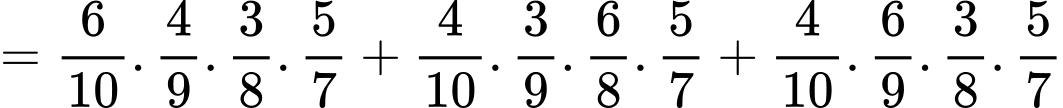
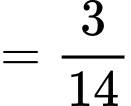
Do đó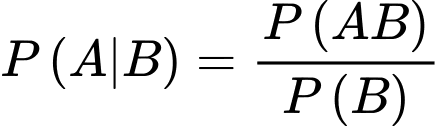
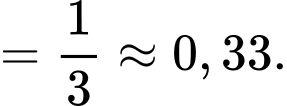
Gọi A là biến cố: lần thứ nhất lấy được sản phẩm tốt
B là biến cố: Ngưng lại ở lần thứ 4
Ta có:
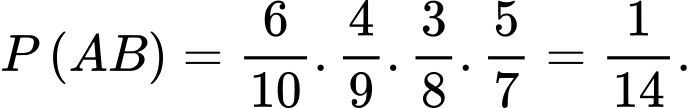
Mặt khác
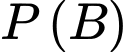
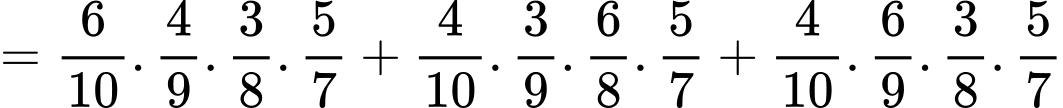
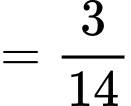
Do đó
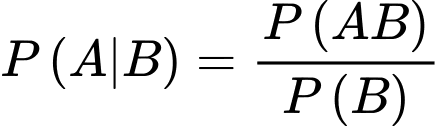
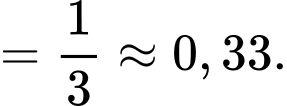
Câu 32 [135871]: Một gia đình có 3 đứa trẻ. Biết rằng có ít nhất 2 đứa trẻ là con trai và xác suất sinh con trai và con gái là như nhau ở mỗi lần sinh. Xác suất để gia đình có 2 đứa trẻ là con trai và 1 đứa trẻ là con gái bằng bao nhiêu?
Do gia đình có 3 đứa trẻ nên sẽ có thể xảy ra 8 khả năng: (trai, trai, trai), (gái, gái, gái), (gái, trai, trai), (trai, gái, trai), (trai, trai, gái), (trai, gái, gái), (gái, trai, gái), (gái, gái, trai).
Gọi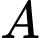 là biến cố “Có 2 đứa trẻ là con trai và 1 đứa trẻ là con gái ” và
là biến cố “Có 2 đứa trẻ là con trai và 1 đứa trẻ là con gái ” và 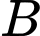 là biến cố “Có ít nhất hai đứa trẻ là con trai” thì có
là biến cố “Có ít nhất hai đứa trẻ là con trai” thì có 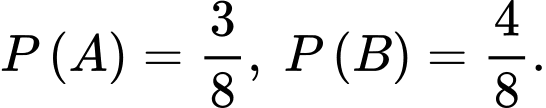
Do nếu xảy ra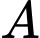 thì đương nhiên sẽ xảy ra
thì đương nhiên sẽ xảy ra 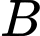 nên ta có:
nên ta có: 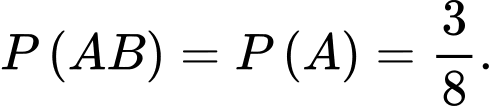
Suy ra, xác suất để cả hai đứa trẻ đều là con gái khi biết ít nhất có một đứa trẻ là gái là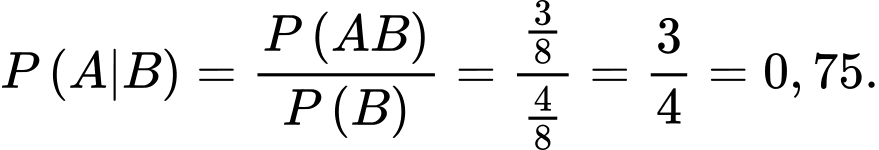
Gọi
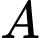 là biến cố “Có 2 đứa trẻ là con trai và 1 đứa trẻ là con gái ” và
là biến cố “Có 2 đứa trẻ là con trai và 1 đứa trẻ là con gái ” và 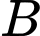 là biến cố “Có ít nhất hai đứa trẻ là con trai” thì có
là biến cố “Có ít nhất hai đứa trẻ là con trai” thì có 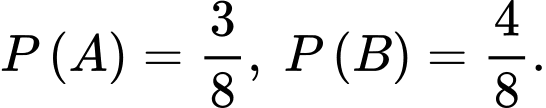
Do nếu xảy ra
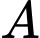 thì đương nhiên sẽ xảy ra
thì đương nhiên sẽ xảy ra 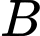 nên ta có:
nên ta có: 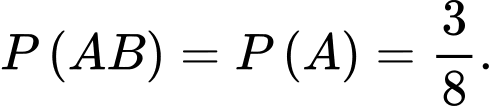
Suy ra, xác suất để cả hai đứa trẻ đều là con gái khi biết ít nhất có một đứa trẻ là gái là