Đáp án Bài tập tự luyện
Câu 1 [805159]: An muốn qua nhà Bình để cùng Bình đến chơi nhà Cường. Từ nhà An đến nhà Bình có 4 con
đường đi, từ nhà Bình đến nhà Cường có 6 con đường đi. Hỏi An có bao nhiêu cách chọn
đường đi đến nhà Cường cùng Bình (như hình vẽ dưới đây và không có con đường nào khác)?


A, 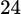 .
.
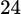 .
.B, 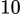 .
.
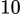 .
.C, 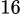 .
.
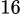 .
.D, 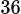 .
.
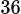 .
.
Chọn A
Chọn đường đi từ nhà An đến nhà Bình có 4 cách chọn.
Chọn đường đi từ nhà Bình đến nhà Cường có 6 cách chọn.
Vậy theo quy tắc nhân có cách cho An chọn đường đi đến nhà Cường cùng Bình. Đáp án: A
cách cho An chọn đường đi đến nhà Cường cùng Bình. Đáp án: A
Chọn đường đi từ nhà An đến nhà Bình có 4 cách chọn.
Chọn đường đi từ nhà Bình đến nhà Cường có 6 cách chọn.
Vậy theo quy tắc nhân có
 cách cho An chọn đường đi đến nhà Cường cùng Bình. Đáp án: A
cách cho An chọn đường đi đến nhà Cường cùng Bình. Đáp án: A
Câu 2 [805173]: Có 3 kiểu mặt đồng hồ đeo tay (vuông, tròn, elip) và 4 kiểu dây (kim loại, da, vải và nhựa). Hỏi có bao nhiêu cách chọn một chiếc đồng hồ gồm một mặt và một dây?
A,  .
.
 .
.B,  .
.
 .
.C,  .
.
 .
.D, 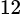 .
.
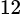 .
.
Chọn D
Chọn 1 kiểu mặt từ 3 kiểu mặt có 3 cách.
Chọn 1 kiểu dây từ 4 kiểu dây có 4 cách
Vậy theo quy tắc nhân có 12 cách chọn 1 chiếc đồng hồ gồm một mặt và một dây. Đáp án: D
Chọn 1 kiểu mặt từ 3 kiểu mặt có 3 cách.
Chọn 1 kiểu dây từ 4 kiểu dây có 4 cách
Vậy theo quy tắc nhân có 12 cách chọn 1 chiếc đồng hồ gồm một mặt và một dây. Đáp án: D
Câu 3 [601908]: Có  cặp vợ chồng đi dự tiệc. Tổng số cách chọn một người đàn ông và một người đàn bà trong bữa tiệc phát biểu ý kiến sao cho hai người đó không là vợ chồng?
cặp vợ chồng đi dự tiệc. Tổng số cách chọn một người đàn ông và một người đàn bà trong bữa tiệc phát biểu ý kiến sao cho hai người đó không là vợ chồng?
 cặp vợ chồng đi dự tiệc. Tổng số cách chọn một người đàn ông và một người đàn bà trong bữa tiệc phát biểu ý kiến sao cho hai người đó không là vợ chồng?
cặp vợ chồng đi dự tiệc. Tổng số cách chọn một người đàn ông và một người đàn bà trong bữa tiệc phát biểu ý kiến sao cho hai người đó không là vợ chồng? A, 100.
B, 91.
C, 10.
D, 90.
Để chọn một người đàn ông và một người đàn bà không là vợ chồng, ta có
 Có
Có  cách chọn người đàn ông.
cách chọn người đàn ông.
 Có
Có 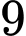 cách chọn người đàn bà.
cách chọn người đàn bà.
Vậy theo qui tắc nhân ta có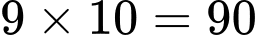 cách. Chọn D.
Đáp án: D
cách. Chọn D.
Đáp án: D
 Có
Có  cách chọn người đàn ông.
cách chọn người đàn ông. Có
Có 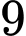 cách chọn người đàn bà.
cách chọn người đàn bà.Vậy theo qui tắc nhân ta có
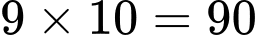 cách. Chọn D.
Đáp án: D
cách. Chọn D.
Đáp án: D
Câu 4 [601914]: Biển số xe máy của tỉnh 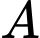 (nếu không kể mã số tỉnh) có
(nếu không kể mã số tỉnh) có 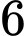 kí tự, trong đó kí tự ở vị trí đầu tiên là một chữ cái (trong bảng
kí tự, trong đó kí tự ở vị trí đầu tiên là một chữ cái (trong bảng 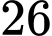 cái tiếng Anh), kí tự ở vị trí thứ hai là một chữ số thuộc tập
cái tiếng Anh), kí tự ở vị trí thứ hai là một chữ số thuộc tập  mỗi kí tự ở bốn vị trí tiếp theo là một chữ số thuộc tập
mỗi kí tự ở bốn vị trí tiếp theo là một chữ số thuộc tập 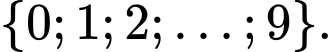 Hỏi nếu chỉ dùng một mã số tỉnh thì tỉnh
Hỏi nếu chỉ dùng một mã số tỉnh thì tỉnh 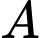 có thể làm được nhiều nhất bao nhiêu biển số xe máy khác nhau?
có thể làm được nhiều nhất bao nhiêu biển số xe máy khác nhau?
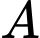 (nếu không kể mã số tỉnh) có
(nếu không kể mã số tỉnh) có 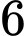 kí tự, trong đó kí tự ở vị trí đầu tiên là một chữ cái (trong bảng
kí tự, trong đó kí tự ở vị trí đầu tiên là một chữ cái (trong bảng 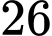 cái tiếng Anh), kí tự ở vị trí thứ hai là một chữ số thuộc tập
cái tiếng Anh), kí tự ở vị trí thứ hai là một chữ số thuộc tập  mỗi kí tự ở bốn vị trí tiếp theo là một chữ số thuộc tập
mỗi kí tự ở bốn vị trí tiếp theo là một chữ số thuộc tập 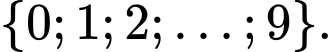 Hỏi nếu chỉ dùng một mã số tỉnh thì tỉnh
Hỏi nếu chỉ dùng một mã số tỉnh thì tỉnh 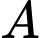 có thể làm được nhiều nhất bao nhiêu biển số xe máy khác nhau?
có thể làm được nhiều nhất bao nhiêu biển số xe máy khác nhau? A, 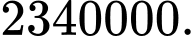
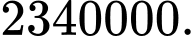
B, 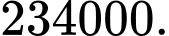
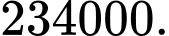
C, 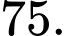
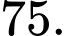
D, 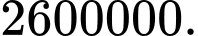
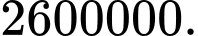
Giả sử biển số xe là 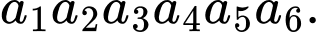
 Có
Có 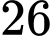 cách chọn
cách chọn 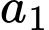
 Có
Có 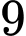 cách chọn
cách chọn 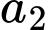
 Có
Có  cách chọn
cách chọn 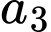
 Có
Có  cách chọn
cách chọn 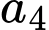
 Có
Có  cách chọn
cách chọn 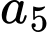
 Có
Có  cách chọn
cách chọn 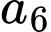
Vậy theo qui tắc nhân ta có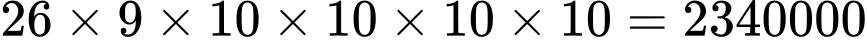 biển số xe. Chọn A.
Đáp án: A
biển số xe. Chọn A.
Đáp án: A
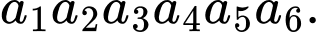
 Có
Có 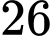 cách chọn
cách chọn 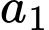
 Có
Có 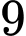 cách chọn
cách chọn 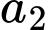
 Có
Có  cách chọn
cách chọn 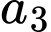
 Có
Có  cách chọn
cách chọn 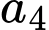
 Có
Có  cách chọn
cách chọn 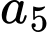
 Có
Có  cách chọn
cách chọn 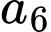
Vậy theo qui tắc nhân ta có
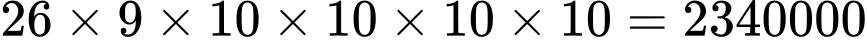 biển số xe. Chọn A.
Đáp án: A
biển số xe. Chọn A.
Đáp án: A
Câu 5 [805439]: (DHSP HÀ NỘI HKI 2017-2018) Đội thanh niên xung kích của một trường trung học phổ thông có  người, gồm
người, gồm 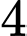 học sinh lớp
học sinh lớp  ,
, 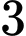 học sinh lớp
học sinh lớp 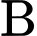 ,
, 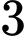 học sinh lớp
học sinh lớp  . Hỏi có bao nhiêu cách chọn ra
. Hỏi có bao nhiêu cách chọn ra 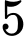 học sinh đi làm nhiệm vụ mà số học sinh lớp
học sinh đi làm nhiệm vụ mà số học sinh lớp 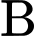 bằng số học sinh lớp
bằng số học sinh lớp  ?
?
 người, gồm
người, gồm 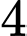 học sinh lớp
học sinh lớp  ,
, 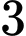 học sinh lớp
học sinh lớp 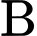 ,
, 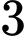 học sinh lớp
học sinh lớp  . Hỏi có bao nhiêu cách chọn ra
. Hỏi có bao nhiêu cách chọn ra 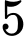 học sinh đi làm nhiệm vụ mà số học sinh lớp
học sinh đi làm nhiệm vụ mà số học sinh lớp 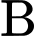 bằng số học sinh lớp
bằng số học sinh lớp  ?
? A, 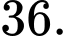
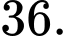
B, 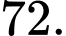
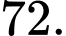
C, 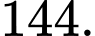
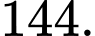
D, 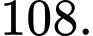
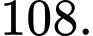
Chọn B
Trường hợp 1: Lớp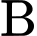 và lớp
và lớp  có
có 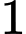 học sinh, lớp
học sinh, lớp  có
có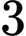 học sinh. Khi đó, số cách chọn là
học sinh. Khi đó, số cách chọn là  .
.
Trường hợp 2: Lớp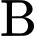 và lớp
và lớp  có
có 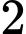 học sinh, lớp
học sinh, lớp  có
có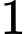 học sinh. Khi đó, số cách chọn là
học sinh. Khi đó, số cách chọn là  .
.
Áp dụng quy tắc cộng ta có số cách chọn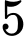 học sinh đi làm nhiệm vụ mà số học sinh lớp
học sinh đi làm nhiệm vụ mà số học sinh lớp 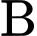 bằng số học sinh lớp
bằng số học sinh lớp  là
là 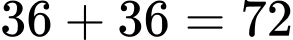 cách. Đáp án: B
cách. Đáp án: B
Trường hợp 1: Lớp
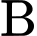 và lớp
và lớp  có
có 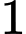 học sinh, lớp
học sinh, lớp  có
có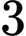 học sinh. Khi đó, số cách chọn là
học sinh. Khi đó, số cách chọn là  .
.Trường hợp 2: Lớp
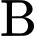 và lớp
và lớp  có
có 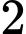 học sinh, lớp
học sinh, lớp  có
có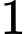 học sinh. Khi đó, số cách chọn là
học sinh. Khi đó, số cách chọn là  .
.Áp dụng quy tắc cộng ta có số cách chọn
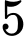 học sinh đi làm nhiệm vụ mà số học sinh lớp
học sinh đi làm nhiệm vụ mà số học sinh lớp 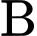 bằng số học sinh lớp
bằng số học sinh lớp  là
là 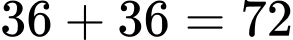 cách. Đáp án: B
cách. Đáp án: B
Câu 6 [805177]: Từ tập 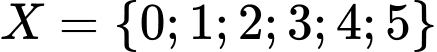 có thể lập được bao nhiêu số tự nhiên có ba chữ số khác nhau mà số đó chia hết cho 5?
có thể lập được bao nhiêu số tự nhiên có ba chữ số khác nhau mà số đó chia hết cho 5?
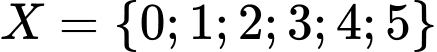 có thể lập được bao nhiêu số tự nhiên có ba chữ số khác nhau mà số đó chia hết cho 5?
có thể lập được bao nhiêu số tự nhiên có ba chữ số khác nhau mà số đó chia hết cho 5? A, 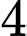 .
.
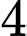 .
.B, 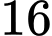 .
.
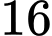 .
.C, 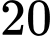 .
.
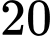 .
.D, 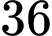 .
.
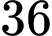 .
.
Chọn D
* Th1: Số cần tìm có dạng : có
: có 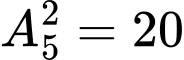 số.
số.
* Th2: Số cần tìm có dạng : có
: có 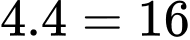 số.
số.
Vậy có: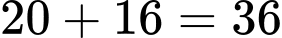 số thỏa yêu cầu đề bài. Đáp án: D
số thỏa yêu cầu đề bài. Đáp án: D
* Th1: Số cần tìm có dạng
 : có
: có 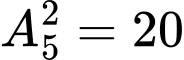 số.
số. * Th2: Số cần tìm có dạng
 : có
: có 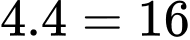 số.
số. Vậy có:
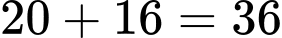 số thỏa yêu cầu đề bài. Đáp án: D
số thỏa yêu cầu đề bài. Đáp án: D
Câu 7 [601949]: Cho tập 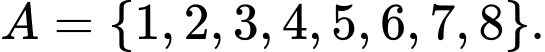 Từ tập A có thể lập được bao nhiêu số gồm 8 chữ số đôi một khác nhau sao các số này lẻ không chia hết cho 5.
Từ tập A có thể lập được bao nhiêu số gồm 8 chữ số đôi một khác nhau sao các số này lẻ không chia hết cho 5.
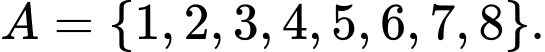 Từ tập A có thể lập được bao nhiêu số gồm 8 chữ số đôi một khác nhau sao các số này lẻ không chia hết cho 5.
Từ tập A có thể lập được bao nhiêu số gồm 8 chữ số đôi một khác nhau sao các số này lẻ không chia hết cho 5. A, 15120.
B, 23523.
C, 16862.
D, 23145.
Chọn A.
Vì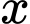 lẻ và không chia hết cho 5 nên
lẻ và không chia hết cho 5 nên 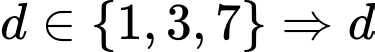 có 3 cách chọn
có 3 cách chọn
Số các chọn các chữ số còn lại là: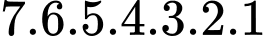
Vậy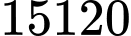 số thỏa yêu cầu bài toán. Đáp án: A
số thỏa yêu cầu bài toán. Đáp án: A
Vì
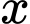 lẻ và không chia hết cho 5 nên
lẻ và không chia hết cho 5 nên 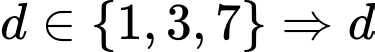 có 3 cách chọn
có 3 cách chọnSố các chọn các chữ số còn lại là:
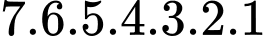
Vậy
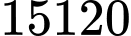 số thỏa yêu cầu bài toán. Đáp án: A
số thỏa yêu cầu bài toán. Đáp án: A
Câu 8 [519318]: Một hội đồng gồm 5 nam và 4 nữ được tuyển vào một ban quản trị gồm 4 người. Biết rằng ban quản trị có ít nhất một nam và một nữ. Hỏi có bao nhiêu cách tuyển chọn?
A, 240.
B, 260.
C, 126.
D, 120.
HD: Số cách chọn ban quản trị gồm 1 nam và 3 nữ là 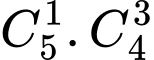 cách.
cách.
Số cách chọn ban quản trị gồm 2 nam và 2 nữ là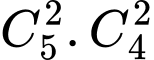 cách.
cách.
Số cách chọn ban quản trị gồm 3 nam và 1 nữ là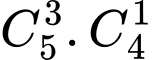 cách.
cách.
Vậy tổng số cách chọn cần tìm là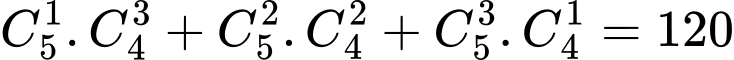 cách. Chọn D. Đáp án: D
cách. Chọn D. Đáp án: D
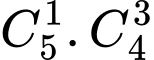 cách.
cách.
Số cách chọn ban quản trị gồm 2 nam và 2 nữ là
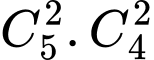 cách.
cách.
Số cách chọn ban quản trị gồm 3 nam và 1 nữ là
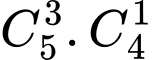 cách.
cách.
Vậy tổng số cách chọn cần tìm là
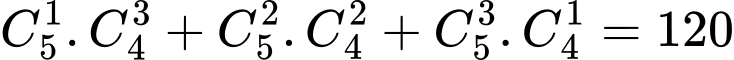 cách. Chọn D. Đáp án: D
cách. Chọn D. Đáp án: D
Câu 9 [805444]: (THPT Yên Mỹ Hưng Yên lần 1 - 2019) Trong hộp có 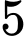 quả cầu đỏ và
quả cầu đỏ và 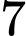 quả cầu xanh kích thước giống nhau. Lấy ngẫu nhiên
quả cầu xanh kích thước giống nhau. Lấy ngẫu nhiên 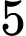 quả cầu từ hộp. Hỏi có bao nhiêu khả năng lấy được số quả cầu đỏ nhiều hơn số quả cầu xanh.
quả cầu từ hộp. Hỏi có bao nhiêu khả năng lấy được số quả cầu đỏ nhiều hơn số quả cầu xanh.
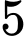 quả cầu đỏ và
quả cầu đỏ và 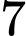 quả cầu xanh kích thước giống nhau. Lấy ngẫu nhiên
quả cầu xanh kích thước giống nhau. Lấy ngẫu nhiên 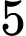 quả cầu từ hộp. Hỏi có bao nhiêu khả năng lấy được số quả cầu đỏ nhiều hơn số quả cầu xanh.
quả cầu từ hộp. Hỏi có bao nhiêu khả năng lấy được số quả cầu đỏ nhiều hơn số quả cầu xanh. A, 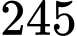 .
.
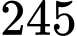 .
.B, 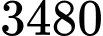 .
.
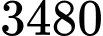 .
.C, 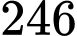 .
.
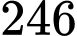 .
.D, 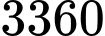 .
.
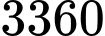 .
.
Chọn C
Lấy ngẫu nhiên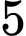 quả cầu từ hộp
quả cầu từ hộp  quả cầu, để số quả cẩu đỏ nhiều hơn số quả cầu xanh, những trường hợp có thể xảy ra là
quả cầu, để số quả cẩu đỏ nhiều hơn số quả cầu xanh, những trường hợp có thể xảy ra là
Trường hợp 1: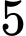 cầu đỏ
cầu đỏ
Số khả năng: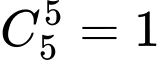 khả năng.
khả năng.
Trường hợp 1: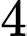 cầu đỏ,
cầu đỏ, 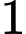 cầu xanh
cầu xanh
Số khả năng: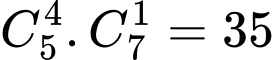 khả năng.
khả năng.
Trường hợp 2: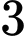 cầu đỏ,
cầu đỏ, 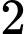 cầu xanh
cầu xanh
Số khả năng: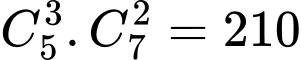 khả năng.
khả năng.
Áp dụng quy tắc cộng: có tất cả: khả năng. Đáp án: C
khả năng. Đáp án: C
Lấy ngẫu nhiên
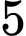 quả cầu từ hộp
quả cầu từ hộp  quả cầu, để số quả cẩu đỏ nhiều hơn số quả cầu xanh, những trường hợp có thể xảy ra là
quả cầu, để số quả cẩu đỏ nhiều hơn số quả cầu xanh, những trường hợp có thể xảy ra làTrường hợp 1:
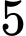 cầu đỏ
cầu đỏSố khả năng:
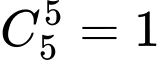 khả năng.
khả năng. Trường hợp 1:
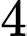 cầu đỏ,
cầu đỏ, 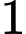 cầu xanh
cầu xanhSố khả năng:
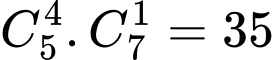 khả năng.
khả năng. Trường hợp 2:
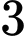 cầu đỏ,
cầu đỏ, 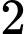 cầu xanh
cầu xanhSố khả năng:
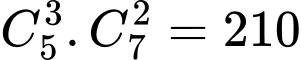 khả năng.
khả năng. Áp dụng quy tắc cộng: có tất cả:
 khả năng. Đáp án: C
khả năng. Đáp án: C
Câu 10 [519443]: Cho 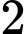 đường thẳng
đường thẳng  , trên đường thẳng
, trên đường thẳng 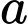 lấy
lấy 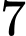 điểm phân biệt, trên đường thẳng
điểm phân biệt, trên đường thẳng 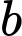 lấy
lấy 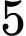 điểm phân biệt. Hỏi có thể dựng được bao nhiêu tam giác từ
điểm phân biệt. Hỏi có thể dựng được bao nhiêu tam giác từ  điểm đã cho ?
điểm đã cho ?
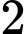 đường thẳng
đường thẳng  , trên đường thẳng
, trên đường thẳng 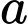 lấy
lấy 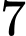 điểm phân biệt, trên đường thẳng
điểm phân biệt, trên đường thẳng 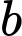 lấy
lấy 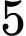 điểm phân biệt. Hỏi có thể dựng được bao nhiêu tam giác từ
điểm phân biệt. Hỏi có thể dựng được bao nhiêu tam giác từ  điểm đã cho ?
điểm đã cho ? A, 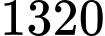
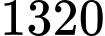
B, 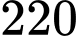
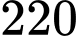
C, 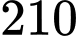
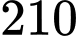
D, 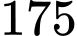
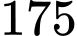
HD : Số tam giác có đỉnh nằm trên 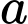 và cạnh nằm trên
và cạnh nằm trên 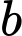 là
là 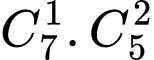
Số tam giác có đỉnh nằm trên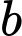 và cạnh nằm trên
và cạnh nằm trên 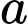 là
là 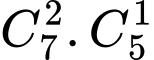
Do đó số tam giác có thể dựng được là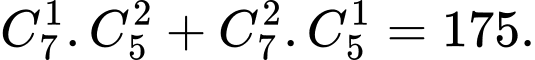 Chọn D. Đáp án: D
Chọn D. Đáp án: D
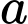 và cạnh nằm trên
và cạnh nằm trên 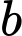 là
là 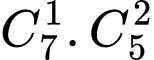
Số tam giác có đỉnh nằm trên
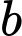 và cạnh nằm trên
và cạnh nằm trên 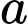 là
là 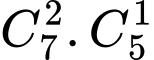
Do đó số tam giác có thể dựng được là
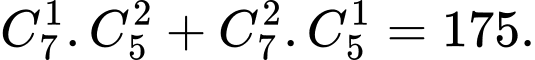 Chọn D. Đáp án: D
Chọn D. Đáp án: D
Câu 11 [805447]: Trong kho đèn trang trí đang còn 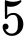 bóng đèn loại I,
bóng đèn loại I, 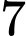 bóng đèn loại II, các bóng đèn đều khác nhau về màu sắc và hình dáng. Lấy ra
bóng đèn loại II, các bóng đèn đều khác nhau về màu sắc và hình dáng. Lấy ra 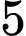 bóng đèn bất kỳ. Hỏi có bao nhiêu khả năng xảy ra số bóng đèn loại I nhiều hơn số bóng đèn loại II?
bóng đèn bất kỳ. Hỏi có bao nhiêu khả năng xảy ra số bóng đèn loại I nhiều hơn số bóng đèn loại II?
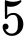 bóng đèn loại I,
bóng đèn loại I, 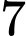 bóng đèn loại II, các bóng đèn đều khác nhau về màu sắc và hình dáng. Lấy ra
bóng đèn loại II, các bóng đèn đều khác nhau về màu sắc và hình dáng. Lấy ra 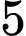 bóng đèn bất kỳ. Hỏi có bao nhiêu khả năng xảy ra số bóng đèn loại I nhiều hơn số bóng đèn loại II?
bóng đèn bất kỳ. Hỏi có bao nhiêu khả năng xảy ra số bóng đèn loại I nhiều hơn số bóng đèn loại II? A, 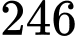 .
.
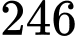 .
.B, 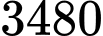 .
.
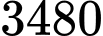 .
.C, 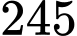 .
.
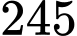 .
.D, 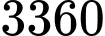 .
.
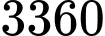 .
.
Có 3 trường hợp xảy ra:
TH1: Lấy được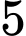 bóng đèn loại I: có
bóng đèn loại I: có 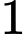 cách
cách
TH2: Lấy được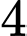 bóng đèn loại I,
bóng đèn loại I, 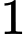 bóng đèn loại II: có
bóng đèn loại II: có 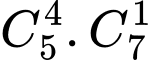 cách
cách
TH3: Lấy được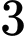 bóng đèn loại I,
bóng đèn loại I, 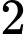 bóng đèn loại II: có
bóng đèn loại II: có 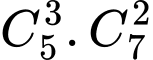 cách
cách
Theo quy tắc cộng, có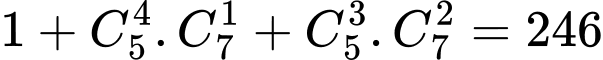 cách Đáp án: A
cách Đáp án: A
TH1: Lấy được
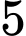 bóng đèn loại I: có
bóng đèn loại I: có 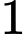 cách
cáchTH2: Lấy được
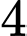 bóng đèn loại I,
bóng đèn loại I, 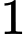 bóng đèn loại II: có
bóng đèn loại II: có 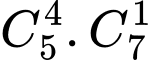 cách
cáchTH3: Lấy được
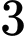 bóng đèn loại I,
bóng đèn loại I, 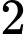 bóng đèn loại II: có
bóng đèn loại II: có 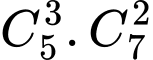 cách
cáchTheo quy tắc cộng, có
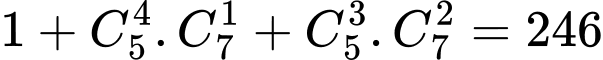 cách Đáp án: A
cách Đáp án: A
Câu 12 [805451]: Bình A chứa  quả cầu xanh,
quả cầu xanh, 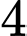 quả cầu đỏ và
quả cầu đỏ và 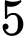 quả cầu trắng. Bình B chứa
quả cầu trắng. Bình B chứa 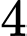 quả cầu xanh,
quả cầu xanh, 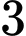 quả cầu đỏ và
quả cầu đỏ và 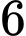 quả cầu trắng. Bình C chứa
quả cầu trắng. Bình C chứa 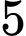 quả cầu xanh,
quả cầu xanh, 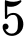 quả cầu đỏ và
quả cầu đỏ và 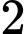 quả cầu trắng. Từ mỗi bình lấy ra một quả cầu. Có bao nhiêu cách lấy để cuối cùng được
quả cầu trắng. Từ mỗi bình lấy ra một quả cầu. Có bao nhiêu cách lấy để cuối cùng được 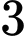 quả có màu giống nhau.
quả có màu giống nhau.
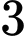 quả cầu xanh,
quả cầu xanh, 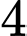 quả cầu đỏ và
quả cầu đỏ và 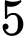 quả cầu trắng. Bình B chứa
quả cầu trắng. Bình B chứa 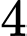 quả cầu xanh,
quả cầu xanh, 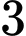 quả cầu đỏ và
quả cầu đỏ và 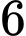 quả cầu trắng. Bình C chứa
quả cầu trắng. Bình C chứa 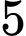 quả cầu xanh,
quả cầu xanh, 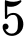 quả cầu đỏ và
quả cầu đỏ và 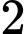 quả cầu trắng. Từ mỗi bình lấy ra một quả cầu. Có bao nhiêu cách lấy để cuối cùng được
quả cầu trắng. Từ mỗi bình lấy ra một quả cầu. Có bao nhiêu cách lấy để cuối cùng được 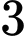 quả có màu giống nhau.
quả có màu giống nhau. A, 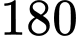 .
.
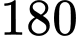 .
.B, 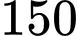 .
.
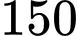 .
.C, 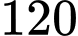 .
.
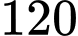 .
.D, 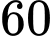 .
.
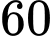 .
.
Trường hợp 1: Lấy được 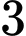 quả cầu xanh từ
quả cầu xanh từ 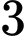 bình: Số cách lấy:
bình: Số cách lấy: 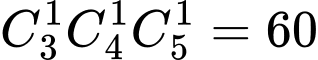 (cách)
(cách)
Trường hợp 2: Lấy được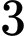 quả cầu đỏ từ
quả cầu đỏ từ 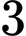 bình: Số cách lấy:
bình: Số cách lấy: 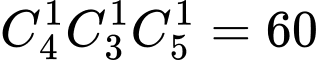 (cách)
(cách)
Trường hợp 3: Lấy được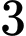 quả cầu trắng từ
quả cầu trắng từ 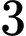 bình: Số cách lấy:
bình: Số cách lấy: 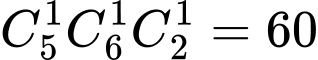 (cách)
(cách)
Vậy có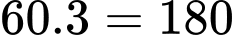 cách lấy được
cách lấy được 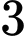 quả cùng màu từ
quả cùng màu từ 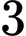 bình. Đáp án: A
bình. Đáp án: A
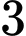 quả cầu xanh từ
quả cầu xanh từ 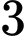 bình: Số cách lấy:
bình: Số cách lấy: 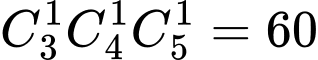 (cách)
(cách) Trường hợp 2: Lấy được
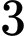 quả cầu đỏ từ
quả cầu đỏ từ 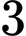 bình: Số cách lấy:
bình: Số cách lấy: 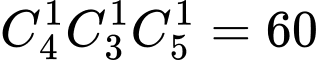 (cách)
(cách) Trường hợp 3: Lấy được
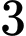 quả cầu trắng từ
quả cầu trắng từ 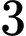 bình: Số cách lấy:
bình: Số cách lấy: 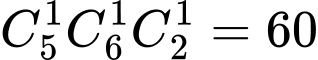 (cách)
(cách) Vậy có
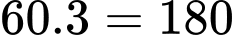 cách lấy được
cách lấy được 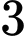 quả cùng màu từ
quả cùng màu từ 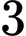 bình. Đáp án: A
bình. Đáp án: A
Câu 13 [805452]: Tổ 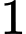 lớp 11A có
lớp 11A có 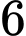 học sinh nam và
học sinh nam và 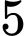 học sinh nữ. Giáo viên chủ nhiệm cần chọn ra
học sinh nữ. Giáo viên chủ nhiệm cần chọn ra 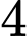 học sinh của tổ
học sinh của tổ 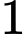 để lao động vệ sinh cùng cả trường. Hỏi có bao nhiêu cách chọn
để lao động vệ sinh cùng cả trường. Hỏi có bao nhiêu cách chọn 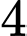 học sinh trong đó có ít nhất một học sinh nam?
học sinh trong đó có ít nhất một học sinh nam?
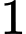 lớp 11A có
lớp 11A có 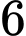 học sinh nam và
học sinh nam và 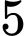 học sinh nữ. Giáo viên chủ nhiệm cần chọn ra
học sinh nữ. Giáo viên chủ nhiệm cần chọn ra 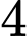 học sinh của tổ
học sinh của tổ 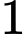 để lao động vệ sinh cùng cả trường. Hỏi có bao nhiêu cách chọn
để lao động vệ sinh cùng cả trường. Hỏi có bao nhiêu cách chọn 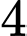 học sinh trong đó có ít nhất một học sinh nam?
học sinh trong đó có ít nhất một học sinh nam? A,  .
.
 .
.B, 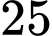 .
.
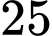 .
.C, 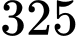 .
.
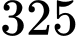 .
.D, 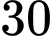 .
.
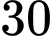 .
.
Trường hợp 1: Chọn 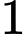 nam và
nam và 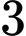 nữ.
nữ.
Trường hợp 2: Chọn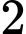 nam và
nam và 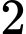 nữ.
nữ.
Trường hợp 3: Chọn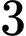 nam và
nam và 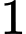 nữ.
nữ.
Trường hợp 4: Chọn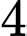 nam.
nam.
Số cách chọn cần tìm là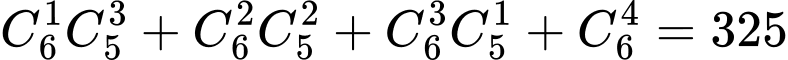 cách chọn. Đáp án: C
cách chọn. Đáp án: C
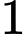 nam và
nam và 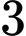 nữ.
nữ. Trường hợp 2: Chọn
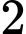 nam và
nam và 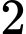 nữ.
nữ. Trường hợp 3: Chọn
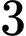 nam và
nam và 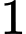 nữ.
nữ. Trường hợp 4: Chọn
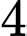 nam.
nam. Số cách chọn cần tìm là
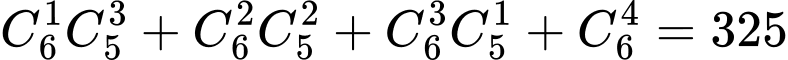 cách chọn. Đáp án: C
cách chọn. Đáp án: C
Câu 14 [629656]: Từ các chữ số 0, 1, 2, 3, 4, 5, 6, 7, 8 có thể lập được bao nhiêu số có 4 chữ số khác nhau và chia hết cho 2:
A, 1512.
B, 2568.
C, 2120.
D, 1680.
HD : Giả sử số đó là 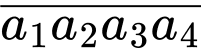
Trường hợp 1 :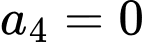 chọn
chọn 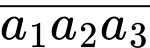 có
có 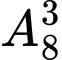 cách nên có
cách nên có 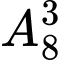 số thỏa mãn
số thỏa mãn
Trường hợp 2: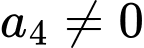 chọn
chọn 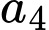 có 4 cách chọn, chọn
có 4 cách chọn, chọn 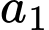 có 7 cách chọn, chọn
có 7 cách chọn, chọn 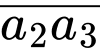 có
có 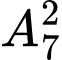 cách chọn nên có
cách chọn nên có 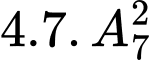 số thỏa mãn. Do đó có
số thỏa mãn. Do đó có 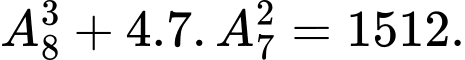 Chọn A. Đáp án: A
Chọn A. Đáp án: A
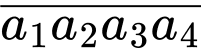
Trường hợp 1 :
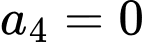 chọn
chọn 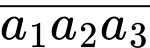 có
có 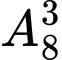 cách nên có
cách nên có 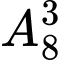 số thỏa mãn
số thỏa mãnTrường hợp 2:
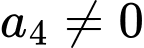 chọn
chọn 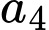 có 4 cách chọn, chọn
có 4 cách chọn, chọn 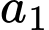 có 7 cách chọn, chọn
có 7 cách chọn, chọn 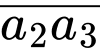 có
có 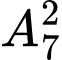 cách chọn nên có
cách chọn nên có 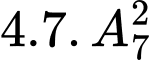 số thỏa mãn. Do đó có
số thỏa mãn. Do đó có 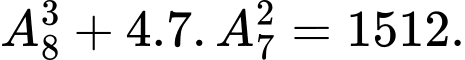 Chọn A. Đáp án: A
Chọn A. Đáp án: A
Câu 15 [922188]: Số 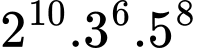 có bao nhiêu ước số nguyên dương
có bao nhiêu ước số nguyên dương
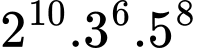 có bao nhiêu ước số nguyên dương
có bao nhiêu ước số nguyên dương A, 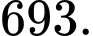
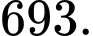
B, 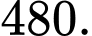
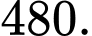
C, 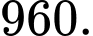
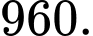
D, 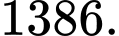
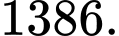
Đáp án: A
Câu 16 [220943]: Có 3 viên bi đen khác nhau, 4 viên bi đỏ khác nhau, 5 viên bi xanh khác nhau. Hỏi có bao nhiêu cách sắp xếp các viên bi trên thành một dãy sao cho các viên bi cùng màu ở cạnh nhau?
A, 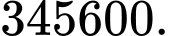
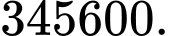
B, 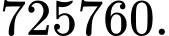
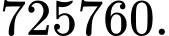
C, 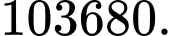
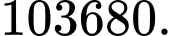
D, 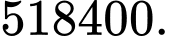
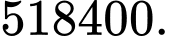
Lời giải.
Số các hoán vị về màu bi khi xếp thành dãy là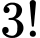
Số cách xếp 3 viên bi đen khác nhau thành dãy là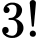
Số cách xếp 4 viên bi đỏ khác nhau thành dãy là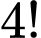
Số cách xếp 5 viên bi xanh khác nhau thành dãy là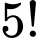
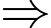 Số cách xếp các viên bi trên thành một dãy sao cho các viên bi cùng màu ở cạnh nhau là
Số cách xếp các viên bi trên thành một dãy sao cho các viên bi cùng màu ở cạnh nhau là 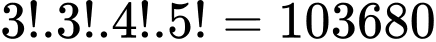 cách. Chọn C. Đáp án: C
cách. Chọn C. Đáp án: C
Số các hoán vị về màu bi khi xếp thành dãy là
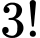
Số cách xếp 3 viên bi đen khác nhau thành dãy là
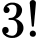
Số cách xếp 4 viên bi đỏ khác nhau thành dãy là
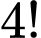
Số cách xếp 5 viên bi xanh khác nhau thành dãy là
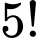
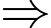 Số cách xếp các viên bi trên thành một dãy sao cho các viên bi cùng màu ở cạnh nhau là
Số cách xếp các viên bi trên thành một dãy sao cho các viên bi cùng màu ở cạnh nhau là 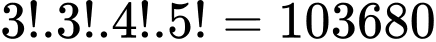 cách. Chọn C. Đáp án: C
cách. Chọn C. Đáp án: C
Câu 17 [805305]: Có 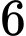 học sinh và
học sinh và 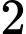 thầy giáo được xếp thành hàng ngang. Hỏi có bao nhiêu cách xếp sao cho hai thầy giáo không đứng cạnh nhau?
thầy giáo được xếp thành hàng ngang. Hỏi có bao nhiêu cách xếp sao cho hai thầy giáo không đứng cạnh nhau?
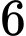 học sinh và
học sinh và 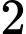 thầy giáo được xếp thành hàng ngang. Hỏi có bao nhiêu cách xếp sao cho hai thầy giáo không đứng cạnh nhau?
thầy giáo được xếp thành hàng ngang. Hỏi có bao nhiêu cách xếp sao cho hai thầy giáo không đứng cạnh nhau? A, 30240 cách.
B, 720 cách.
C, 362880 cách.
D, 1440 cách.
Chọn A
Xếp 8 người thành hàng ngang có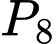 cách.
cách.
Xếp 8 người thành hàng ngang sao cho 2 thầy giáo đứng cạnh nhau có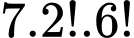 cách.
cách.
Vậy số cách xếp cần tìm là: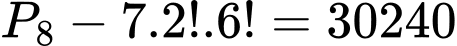 cách. Đáp án: A
cách. Đáp án: A
Xếp 8 người thành hàng ngang có
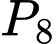 cách.
cách. Xếp 8 người thành hàng ngang sao cho 2 thầy giáo đứng cạnh nhau có
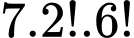 cách.
cách. Vậy số cách xếp cần tìm là:
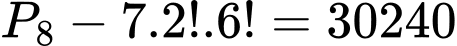 cách. Đáp án: A
cách. Đáp án: A
Câu 18 [805418]: Có tất cả bao nhiêu cách chia  người thành hai nhóm, một nhóm có
người thành hai nhóm, một nhóm có 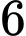 người và một nhóm có
người và một nhóm có 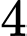 người?
người?
 người thành hai nhóm, một nhóm có
người thành hai nhóm, một nhóm có 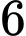 người và một nhóm có
người và một nhóm có 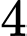 người?
người? A, 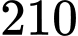 .
.
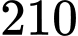 .
.B, 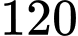 .
.
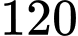 .
.C, 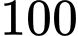 .
.
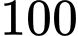 .
.D, 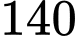 .
.
 .
.
Số cách phân nhóm 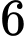 người trong
người trong  người là
người là 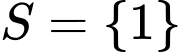 . Sau khi phân nhóm
. Sau khi phân nhóm  người còn lại
người còn lại 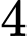 người được phân nhóm vào nhóm còn lại. Vậy có
người được phân nhóm vào nhóm còn lại. Vậy có 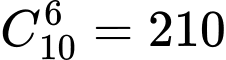 cách. Đáp án: A
cách. Đáp án: A
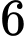 người trong
người trong  người là
người là 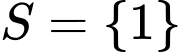 . Sau khi phân nhóm
. Sau khi phân nhóm 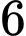 người còn lại
người còn lại 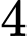 người được phân nhóm vào nhóm còn lại. Vậy có
người được phân nhóm vào nhóm còn lại. Vậy có 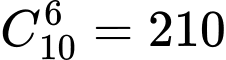 cách. Đáp án: A
cách. Đáp án: A
Câu 19 [302589]: Một đội thanh niên tình nguyện có 15 người gồm 12 nam và 3 nữ. Hỏi có bao nhiêu cách phân công đội thanh niên tình nguyện đó về 3 tỉnh miền núi sao cho mỗi tỉnh có 4 nam và 1 nữ?
A, 2037131.
B, 3912363.
C, 207900.
D, 213930.
HD: Chọn 4 nam và 1 nữ cho tỉnh 1 có 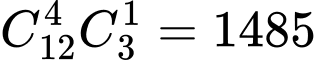 cách.
cách.
Chọn 4 nam và 1 nữ cho tỉnh 1 có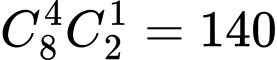 cách.
cách.
Còn lại ta đã chọn xong cho tỉnh 3.
Do đó có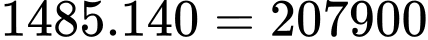 cách thỏa mãn. Chọn C Đáp án: C
cách thỏa mãn. Chọn C Đáp án: C
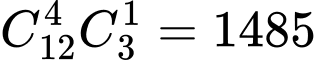 cách.
cách.
Chọn 4 nam và 1 nữ cho tỉnh 1 có
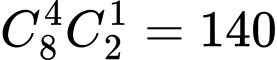 cách.
cách.
Còn lại ta đã chọn xong cho tỉnh 3.
Do đó có
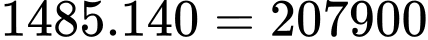 cách thỏa mãn. Chọn C Đáp án: C
cách thỏa mãn. Chọn C Đáp án: C
Câu 20 [601953]: Từ các chữ số  ,
, 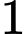 ,
, 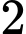 ,
, 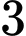 ,
, 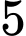 ,
, 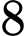 có thể lập được bao nhiêu số tự nhiên lẻ có bốn chữ số đôi một khác nhau và phải có mặt chữ số
có thể lập được bao nhiêu số tự nhiên lẻ có bốn chữ số đôi một khác nhau và phải có mặt chữ số 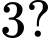
 ,
, 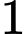 ,
, 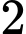 ,
, 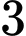 ,
, 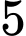 ,
, 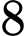 có thể lập được bao nhiêu số tự nhiên lẻ có bốn chữ số đôi một khác nhau và phải có mặt chữ số
có thể lập được bao nhiêu số tự nhiên lẻ có bốn chữ số đôi một khác nhau và phải có mặt chữ số 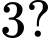
A, 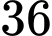 số.
số.
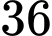 số.
số.B, 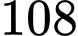 số.
số.
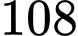 số.
số.C, 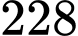 số.
số.
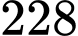 số.
số.D, 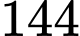 số.
số.
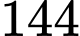 số.
số.
Chọn B
Gọi số tự nhiên có bốn chữ số khác nhau là Do số cần lập là số lẻ và phải có mặt chữ số
Do số cần lập là số lẻ và phải có mặt chữ số 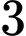 nên ta có các trường hợp.
nên ta có các trường hợp.
TH1: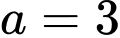 khi đó số có dạng
khi đó số có dạng 
Có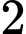 cách chọn
cách chọn 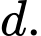
Có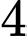 cách chọn
cách chọn 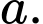
Có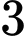 cách chọn
cách chọn 
Theo quy tắc nhân có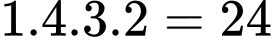 (số).
(số).
TH2: khi đó số có dạng
khi đó số có dạng 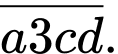
Có cách chọn
cách chọn 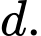
Có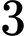 cách chọn
cách chọn 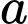 (do
(do 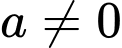 ).
).
Có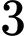 cách chọn
cách chọn 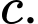
Theo quy tắc nhân có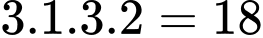 (số).
(số).
TH3: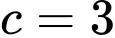 khi đó số có dạng
khi đó số có dạng 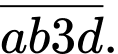
Có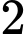 cách chọn
cách chọn 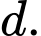
Có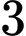 cách chọn
cách chọn 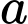 (do
(do 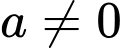 ).
).
Có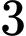 cách chọn
cách chọn 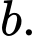
Theo quy tắc nhân có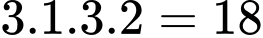 (số).
(số).
TH4: khi đó số có dạng
khi đó số có dạng 
Có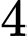 cách chọn
cách chọn 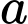 (do
(do 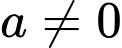 ).
).
Có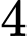 cách chọn
cách chọn 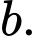
Có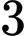 cách chọn
cách chọn 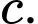
Theo quy tắc nhân có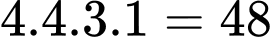 (số).
(số).
Theo quy tắc cộng có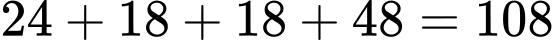 (số). Đáp án: B
(số). Đáp án: B
Gọi số tự nhiên có bốn chữ số khác nhau là
 Do số cần lập là số lẻ và phải có mặt chữ số
Do số cần lập là số lẻ và phải có mặt chữ số 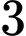 nên ta có các trường hợp.
nên ta có các trường hợp.TH1:
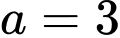 khi đó số có dạng
khi đó số có dạng 
Có
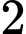 cách chọn
cách chọn 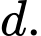
Có
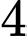 cách chọn
cách chọn 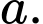
Có
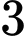 cách chọn
cách chọn 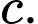
Theo quy tắc nhân có
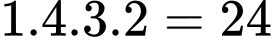 (số).
(số).TH2:
 khi đó số có dạng
khi đó số có dạng 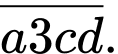
Có
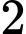 cách chọn
cách chọn 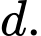
Có
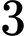 cách chọn
cách chọn 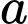 (do
(do 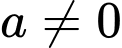 ).
).Có
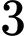 cách chọn
cách chọn 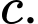
Theo quy tắc nhân có
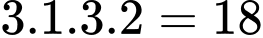 (số).
(số).TH3:
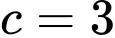 khi đó số có dạng
khi đó số có dạng 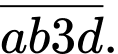
Có
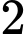 cách chọn
cách chọn 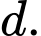
Có
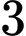 cách chọn
cách chọn 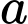 (do
(do 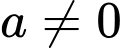 ).
).Có
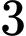 cách chọn
cách chọn 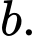
Theo quy tắc nhân có
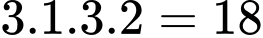 (số).
(số).TH4:
 khi đó số có dạng
khi đó số có dạng 
Có
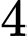 cách chọn
cách chọn 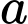 (do
(do 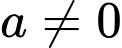 ).
).Có
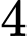 cách chọn
cách chọn 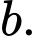
Có
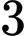 cách chọn
cách chọn 
Theo quy tắc nhân có
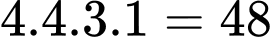 (số).
(số).Theo quy tắc cộng có
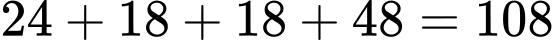 (số). Đáp án: B
(số). Đáp án: B
Câu 21 [805311]: Có bao nhiêu cách sắp xếp  nữ sinh,
nữ sinh, 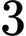 nam sinh thành một hàng dọc sao cho các bạn nam và nữ ngồi xen kẽ?
nam sinh thành một hàng dọc sao cho các bạn nam và nữ ngồi xen kẽ?
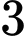 nữ sinh,
nữ sinh, 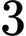 nam sinh thành một hàng dọc sao cho các bạn nam và nữ ngồi xen kẽ?
nam sinh thành một hàng dọc sao cho các bạn nam và nữ ngồi xen kẽ? A, 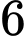 .
.
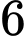 .
.B, 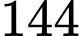 .
.
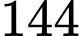 .
.C, 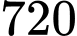 .
.
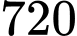 .
.D, 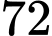 .
.
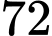 .
.
Chọn D
Đánh số thứ tự các vị trí theo hàng dọc từ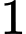 đến
đến  .
.
* Trường hợp 1: Nam đứng trước, nữ đứng sau.
* Xếp nam (vào các vị trí đánh số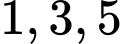 ): Có
): Có 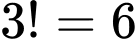 cách.
cách.
* Xếp nữ (vào các vị trí đánh số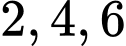 ): Có
): Có 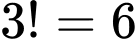 cách.
cách.
Vậy trường hợp này có: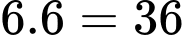 cách.
cách.
* Trường hợp 2: Nữ đứng trước, nam đứng sau.
* Xếp nữ (vào các vị trí đánh số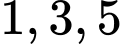 ): Có
): Có 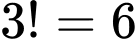 cách.
cách.
* Xếp nam (vào các vị trí đánh số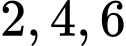 ): Có
): Có 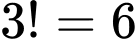 cách.
cách.
Vậy trường hợp này có: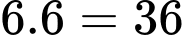 cách.
cách.
Theo quy tắc cộng ta có: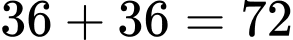 cách sắp xếp
cách sắp xếp 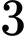 nữ sinh,
nữ sinh, 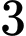 nam sinh thành một hàng dọc sao cho các bạn nam và nữ ngồi xen kẽ Đáp án: D
nam sinh thành một hàng dọc sao cho các bạn nam và nữ ngồi xen kẽ Đáp án: D
Đánh số thứ tự các vị trí theo hàng dọc từ
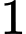 đến
đến 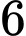 .
.* Trường hợp 1: Nam đứng trước, nữ đứng sau.
* Xếp nam (vào các vị trí đánh số
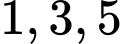 ): Có
): Có 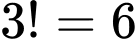 cách.
cách. * Xếp nữ (vào các vị trí đánh số
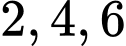 ): Có
): Có 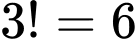 cách.
cách. Vậy trường hợp này có:
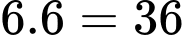 cách.
cách. * Trường hợp 2: Nữ đứng trước, nam đứng sau.
* Xếp nữ (vào các vị trí đánh số
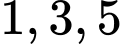 ): Có
): Có 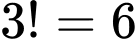 cách.
cách. * Xếp nam (vào các vị trí đánh số
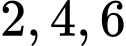 ): Có
): Có 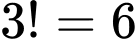 cách.
cách. Vậy trường hợp này có:
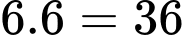 cách.
cách. Theo quy tắc cộng ta có:
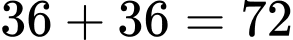 cách sắp xếp
cách sắp xếp 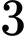 nữ sinh,
nữ sinh,  nam sinh thành một hàng dọc sao cho các bạn nam và nữ ngồi xen kẽ Đáp án: D
nam sinh thành một hàng dọc sao cho các bạn nam và nữ ngồi xen kẽ Đáp án: D
Câu 22 [629624]: Cho tập 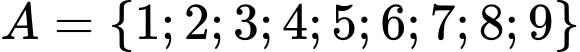 . Từ tập A có thể lập được bao nhiêu số tự nhiên chẵn có 5 chữ số đôi một khác nhau sao cho số đó không bắt đầu bởi 125?
. Từ tập A có thể lập được bao nhiêu số tự nhiên chẵn có 5 chữ số đôi một khác nhau sao cho số đó không bắt đầu bởi 125?
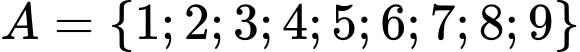 . Từ tập A có thể lập được bao nhiêu số tự nhiên chẵn có 5 chữ số đôi một khác nhau sao cho số đó không bắt đầu bởi 125?
. Từ tập A có thể lập được bao nhiêu số tự nhiên chẵn có 5 chữ số đôi một khác nhau sao cho số đó không bắt đầu bởi 125? A, 265
B, 262
C, 6702
D, 6705
HD: Gọi 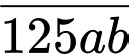 là số bắt đầu bởi 125 và có 5 chữ số đôi một khác nhau.
là số bắt đầu bởi 125 và có 5 chữ số đôi một khác nhau.
Suy ra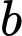 có 3 cách chọn,
có 3 cách chọn, 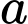 có 5 cách chọn
có 5 cách chọn  có
có 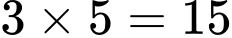 số.
số.
Số các số chã̃n có 5 chữ số đôi một khác nhau được lập từ tập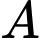 là
là 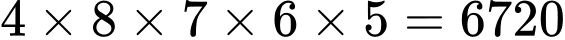 số.
số.
Suy ra có tất cả số cần tìm. Chọn D. Đáp án: D
số cần tìm. Chọn D. Đáp án: D
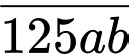 là số bắt đầu bởi 125 và có 5 chữ số đôi một khác nhau.
là số bắt đầu bởi 125 và có 5 chữ số đôi một khác nhau.
Suy ra
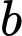 có 3 cách chọn,
có 3 cách chọn, 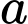 có 5 cách chọn
có 5 cách chọn  có
có 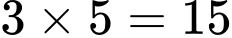 số.
số.
Số các số chã̃n có 5 chữ số đôi một khác nhau được lập từ tập
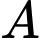 là
là 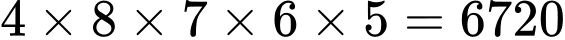 số.
số.
Suy ra có tất cả
 số cần tìm. Chọn D. Đáp án: D
số cần tìm. Chọn D. Đáp án: D
Câu 23 [251883]: Mùa giải  , giải bóng đá vô địch quốc gia (V. League) có
, giải bóng đá vô địch quốc gia (V. League) có 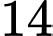 đội bóng tham giá. Các đội bóng đấu vòng tròn hai lượt đi và về. Hỏi cả giải đấu có bao nhiêu trận đấu?
đội bóng tham giá. Các đội bóng đấu vòng tròn hai lượt đi và về. Hỏi cả giải đấu có bao nhiêu trận đấu?
 , giải bóng đá vô địch quốc gia (V. League) có
, giải bóng đá vô địch quốc gia (V. League) có 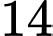 đội bóng tham giá. Các đội bóng đấu vòng tròn hai lượt đi và về. Hỏi cả giải đấu có bao nhiêu trận đấu?
đội bóng tham giá. Các đội bóng đấu vòng tròn hai lượt đi và về. Hỏi cả giải đấu có bao nhiêu trận đấu?
Chọn 2 đội trong 14 đội bóng tham gia để tthi đấu lượt đi là một tổ hợp chập 2 của 14
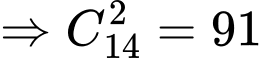 (trận)
(trận)
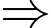 Cả giải đấu lượt đi và về có số trận đấu là:
Cả giải đấu lượt đi và về có số trận đấu là: 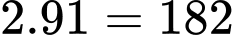 (trận)
(trận)
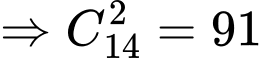 (trận)
(trận)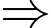 Cả giải đấu lượt đi và về có số trận đấu là:
Cả giải đấu lượt đi và về có số trận đấu là: 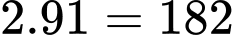 (trận)
(trận)
Câu 24 [219707]: Cho A={0, 1, 2, 3, 4, 5}. Từ tập A có thể lập được bao nhiêu số tự nhiên có 3 chữ số chia hết cho 5?
Gọi số tự nhiên chẵn có 3 chữ số cần tìm là: 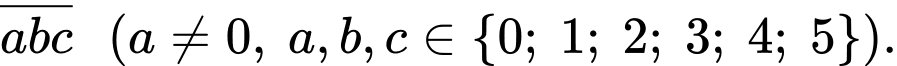
Chọn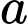 có 5 cách, chọn
có 5 cách, chọn 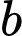 có 6 cách, chọn
có 6 cách, chọn  có 2 cách.
có 2 cách.
Do đó, có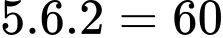 số thoả mãn.
số thoả mãn.
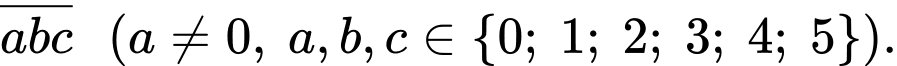
Chọn
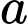 có 5 cách, chọn
có 5 cách, chọn 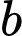 có 6 cách, chọn
có 6 cách, chọn  có 2 cách.
có 2 cách.Do đó, có
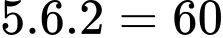 số thoả mãn.
số thoả mãn.
Câu 25 [251881]: Một nhóm gồm 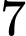 bạn đến trung tâm chăm sóc người cao tuổi làm từ thiện. Theo chỉ dẫn của trung tâm,
bạn đến trung tâm chăm sóc người cao tuổi làm từ thiện. Theo chỉ dẫn của trung tâm, 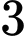 bạn hỗ trợ đi lại,
bạn hỗ trợ đi lại, 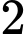 bạn hỗ trợ tắm rửa và
bạn hỗ trợ tắm rửa và 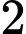 bạn hỗ trợ ăn uống. Có bao nhiêu cách phân công các bạn trong nhóm làm các công việc trên?
bạn hỗ trợ ăn uống. Có bao nhiêu cách phân công các bạn trong nhóm làm các công việc trên?
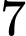 bạn đến trung tâm chăm sóc người cao tuổi làm từ thiện. Theo chỉ dẫn của trung tâm,
bạn đến trung tâm chăm sóc người cao tuổi làm từ thiện. Theo chỉ dẫn của trung tâm, 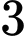 bạn hỗ trợ đi lại,
bạn hỗ trợ đi lại, 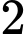 bạn hỗ trợ tắm rửa và
bạn hỗ trợ tắm rửa và 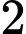 bạn hỗ trợ ăn uống. Có bao nhiêu cách phân công các bạn trong nhóm làm các công việc trên?
bạn hỗ trợ ăn uống. Có bao nhiêu cách phân công các bạn trong nhóm làm các công việc trên?
Việc phân công các bạn trong nhóm làm các công việc theo chỉ dần của trung tâm gồm 3 công đoạn:
- CĐ1: Chọn 3 bạn hỗ trợ đi lại trong 7 bạn đến trung tâm là một tổ hợp chập 3 của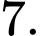
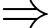 Có:
Có: 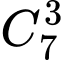 (cách chọn)
(cách chọn)
- CĐ2: Chọn 2 bạn hỗ trợ tắm rửa trong 6 bạn còn lại là một tổ hợp chập 2 của 7
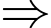 Có:
Có: 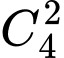 (cách chọn)
(cách chọn)
- CĐ3: Chọn 2 bạn hỗ trợ ăn uống trong 5 bạn còn lại là một tổ hợp chập 2 của 5
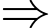 Có:
Có: 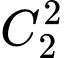 (cách chọn)
(cách chọn)
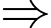 Áp dụng quy tắc nhân có:
Áp dụng quy tắc nhân có: 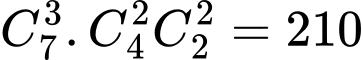 cách chọn thỏa mãn yêu cầu đề.
cách chọn thỏa mãn yêu cầu đề.
- CĐ1: Chọn 3 bạn hỗ trợ đi lại trong 7 bạn đến trung tâm là một tổ hợp chập 3 của
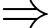 Có:
Có: 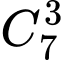 (cách chọn)
(cách chọn)- CĐ2: Chọn 2 bạn hỗ trợ tắm rửa trong 6 bạn còn lại là một tổ hợp chập 2 của 7
 Có:
Có: 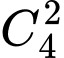 (cách chọn)
(cách chọn)- CĐ3: Chọn 2 bạn hỗ trợ ăn uống trong 5 bạn còn lại là một tổ hợp chập 2 của 5
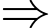 Có:
Có: 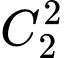 (cách chọn)
(cách chọn)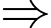 Áp dụng quy tắc nhân có:
Áp dụng quy tắc nhân có: 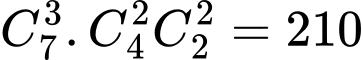 cách chọn thỏa mãn yêu cầu đề.
cách chọn thỏa mãn yêu cầu đề.
Câu 26 [251882]: Có 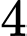 đường thẳng song song cắt
đường thẳng song song cắt 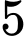 đường thẳng song song khác tạo thành những hình bình hành (như Hình
đường thẳng song song khác tạo thành những hình bình hành (như Hình  ). Có bao nhiêu hình bình hành được tạo thành?
). Có bao nhiêu hình bình hành được tạo thành?
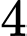 đường thẳng song song cắt
đường thẳng song song cắt  đường thẳng song song khác tạo thành những hình bình hành (như Hình
đường thẳng song song khác tạo thành những hình bình hành (như Hình  ). Có bao nhiêu hình bình hành được tạo thành?
). Có bao nhiêu hình bình hành được tạo thành?
Vì cứ hai đường thẳng song song trong nhóm này và 2 đường thẳng song song trong nhóm kia cắt nhau tạo thành một hình bình hành.
- CĐ1: Chọn 2 đường thẳng song song trong nhóm 4 đường thẳng song song có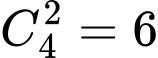 (cách)
(cách)
- CĐ2: Chọn 2 đường thẳng song song trong nhóm 5 đường thẳng song song có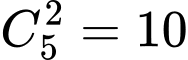 (cách)
(cách)
Vậy có tất cả 6.10=60 hình bình hành được tạo thành.
- CĐ1: Chọn 2 đường thẳng song song trong nhóm 4 đường thẳng song song có
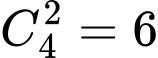 (cách)
(cách)
- CĐ2: Chọn 2 đường thẳng song song trong nhóm 5 đường thẳng song song có
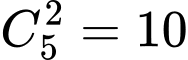 (cách)
(cách)
Vậy có tất cả 6.10=60 hình bình hành được tạo thành.
Câu 27 [219702]: Cho hai đường thẳng 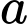 và
và 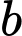 song song với nhau. Trên đường thẳng
song song với nhau. Trên đường thẳng 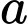 có 5 điểm phân biệt và trên đường thẳng
có 5 điểm phân biệt và trên đường thẳng 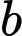 có 10 điểm phân biệt. Hỏi có thể tạo được bao nhiêu tam giác có các đỉnh là các điểm nằm trên 2 đường thẳng
có 10 điểm phân biệt. Hỏi có thể tạo được bao nhiêu tam giác có các đỉnh là các điểm nằm trên 2 đường thẳng 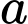 và
và 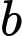 đã cho?
đã cho?
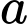 và
và 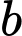 song song với nhau. Trên đường thẳng
song song với nhau. Trên đường thẳng 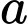 có 5 điểm phân biệt và trên đường thẳng
có 5 điểm phân biệt và trên đường thẳng 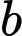 có 10 điểm phân biệt. Hỏi có thể tạo được bao nhiêu tam giác có các đỉnh là các điểm nằm trên 2 đường thẳng
có 10 điểm phân biệt. Hỏi có thể tạo được bao nhiêu tam giác có các đỉnh là các điểm nằm trên 2 đường thẳng 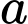 và
và 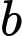 đã cho?
đã cho?
Hướng dẫn giải:
TH1: Chọn 2 đỉnh trên đường thẳng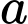 và 1 đỉnh trên đường thẳng
và 1 đỉnh trên đường thẳng 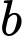 có:
có: 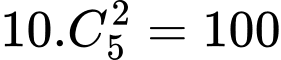 (cách).
(cách).
TH2: Chọn 2 đỉnh trên đường thẳng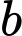 và 1 đỉnh trên đường thẳng
và 1 đỉnh trên đường thẳng 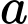 có:
có: 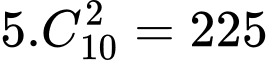 (cách).
(cách).
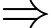 Có
Có 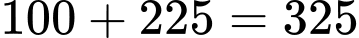 tam giác có các đỉnh là các điểm nằm trên 2 đường thẳng
tam giác có các đỉnh là các điểm nằm trên 2 đường thẳng 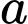 và
và 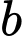 đã cho.
đã cho.
TH1: Chọn 2 đỉnh trên đường thẳng
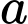 và 1 đỉnh trên đường thẳng
và 1 đỉnh trên đường thẳng 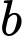 có:
có: 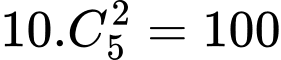 (cách).
(cách).TH2: Chọn 2 đỉnh trên đường thẳng
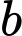 và 1 đỉnh trên đường thẳng
và 1 đỉnh trên đường thẳng 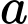 có:
có: 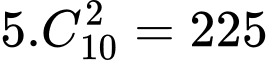 (cách).
(cách).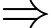 Có
Có 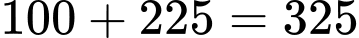 tam giác có các đỉnh là các điểm nằm trên 2 đường thẳng
tam giác có các đỉnh là các điểm nằm trên 2 đường thẳng 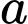 và
và 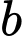 đã cho.
đã cho.
Câu 28 [581410]: Một nhóm gồm 2 học sinh lớp 10, 2 học sinh lớp 11 và 2 học sinh lớp 12 xếp thành hai hàng ngang để chụp ảnh, mỗi hàng 3 người. Hỏi có bao nhiêu cách xếp sao cho 2 học sinh lớp 10 đứng ở hàng phía trước và 2 học sinh lớp 12 đứng ở hàng phía sau?
Số cách xếp hai học sinh lớp 10 ở hàng phía trước là 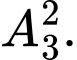
Số cách xếp hai học sinh lớp 12 ở hàng phía sau là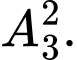
Số cách xếp hai học sinh lớp 11 ở hai vị trí còn lại là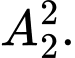
Vậy tổng số cách xếp có thể là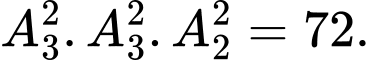
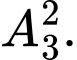
Số cách xếp hai học sinh lớp 12 ở hàng phía sau là
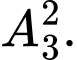
Số cách xếp hai học sinh lớp 11 ở hai vị trí còn lại là
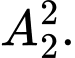
Vậy tổng số cách xếp có thể là
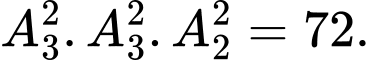
Câu 29 [219704]: Nhà trường tổ chức than quan dã ngoại cho 10 thành viên tiêu biểu của câu lạc bộ Toán học và 10 thành viên tiêu biểu của câu lạc bộ Tiếng Anh. Sau một trò chơi, ban tổ chức chọn ngẫu nhiên 5 thành viên tham gia trò chơi. Số cách chọn sao cho 5 thành viên được chọn, mỗi câu lạc bộ có ít nhất 1 thành viên:
Hướng dẫn giải
Tổng số thành viên là 20.
Có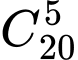 cách chọn 5 thành viên từ 20 thành viên.
cách chọn 5 thành viên từ 20 thành viên.
Có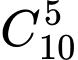 cách chọn 5 thành viên từ 10 thành viên của câu lạc bộ Toán.
cách chọn 5 thành viên từ 10 thành viên của câu lạc bộ Toán.
Có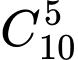 cách chọn 5 thành viên từ 10 thành viên của câu lạc bộ Tiếng Anh.
cách chọn 5 thành viên từ 10 thành viên của câu lạc bộ Tiếng Anh.
Suy ra số cách chọn 5 thành viên mà mỗi câu lạc bộ có ít nhất một thành viên là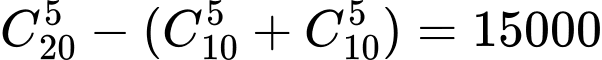
Tổng số thành viên là 20.
Có
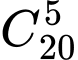 cách chọn 5 thành viên từ 20 thành viên.
cách chọn 5 thành viên từ 20 thành viên.Có
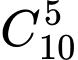 cách chọn 5 thành viên từ 10 thành viên của câu lạc bộ Toán.
cách chọn 5 thành viên từ 10 thành viên của câu lạc bộ Toán.Có
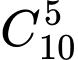 cách chọn 5 thành viên từ 10 thành viên của câu lạc bộ Tiếng Anh.
cách chọn 5 thành viên từ 10 thành viên của câu lạc bộ Tiếng Anh.Suy ra số cách chọn 5 thành viên mà mỗi câu lạc bộ có ít nhất một thành viên là
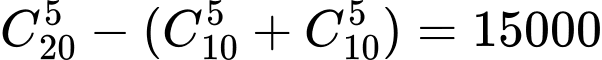
Câu 30 [219705]: Đội văn nghệ của một nhà trường gồm 4 học sinh lớp 12A, 3 học sinh lớp 12B và 2 học sinh lớp 12C. Chọn ngẫu nhiên 5 học sinh từ đội văn nghệ đó biểu diễn trong lễ bế giảng. Hỏi có bao nhiêu cách chọn sao cho lớp nào cũng có học sinh được chọn và có ít nhất 2 học sinh lớp 12A
Hướng dẫn
Từ giả thiết suy ra có 3 khả năng xảy ra như sau
12A 12B 12C
2 học sinh 2 học sinh 1 học sinh
2 học sinh 1 học sinh 2 học sinh
3 học sinh 1 học sinh 1 học sinh
Từ đó suy ra số cách chọn là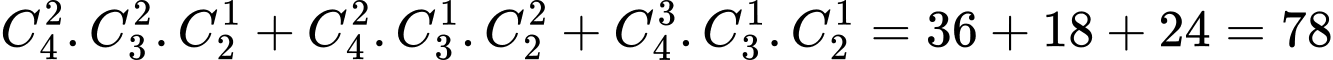
Từ giả thiết suy ra có 3 khả năng xảy ra như sau
12A 12B 12C
2 học sinh 2 học sinh 1 học sinh
2 học sinh 1 học sinh 2 học sinh
3 học sinh 1 học sinh 1 học sinh
Từ đó suy ra số cách chọn là