Đáp án Bài tập tự luyện
Câu 1 [45919]: Chọn ngẫu nhiên hai số khác nhau từ 23 số nguyên dương đầu tiên. Xác suất để chọn được hai số có tổng là một số chẵn bằng
A, 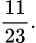
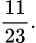
B, 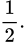
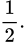
C, 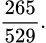
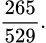
D, 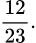
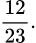
Đáp án: A
Câu 2 [322507]: Một hộp chứa 11 quả cầu gồm 5 quả cầu màu xanh và 6 quả cầu màu đỏ. Chọn ngẫu nhiên đồng thời 2 quả cầu từ hộp đó. Xác suất để 2 quả cầu chọn ra cùng màu bằng
A, 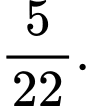
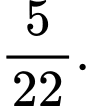
B, 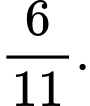
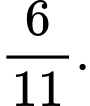
C, 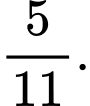
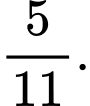
D, 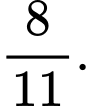
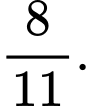
Số cách để chọn 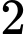 quả cầu từ hộp là
quả cầu từ hộp là 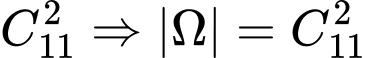
Tiếp theo ta sẽ tìm số cách để lấy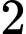 quả cầu cùng màu từ hộp
quả cầu cùng màu từ hộp
Trường hợp 1: Chọn được hai quả cầu màu xanh có
có 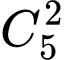 cách chọn
cách chọn
Trường hợp 2: Chọn được hai quả cầu màu đỏ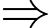 có
có 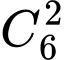 cách chọn
cách chọn
Do đó số cách chọn được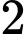 quả cầu cùng màu là
quả cầu cùng màu là
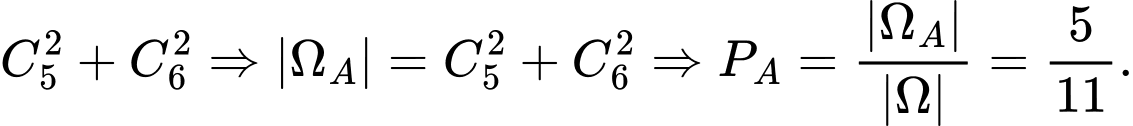 Chọn C. Đáp án: C
Chọn C. Đáp án: C
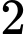 quả cầu từ hộp là
quả cầu từ hộp là 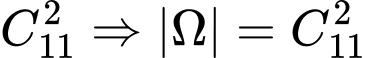
Tiếp theo ta sẽ tìm số cách để lấy
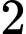 quả cầu cùng màu từ hộp
quả cầu cùng màu từ hộpTrường hợp 1: Chọn được hai quả cầu màu xanh
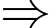 có
có 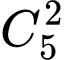 cách chọn
cách chọnTrường hợp 2: Chọn được hai quả cầu màu đỏ
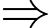 có
có 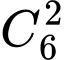 cách chọn
cách chọnDo đó số cách chọn được
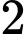 quả cầu cùng màu là
quả cầu cùng màu là 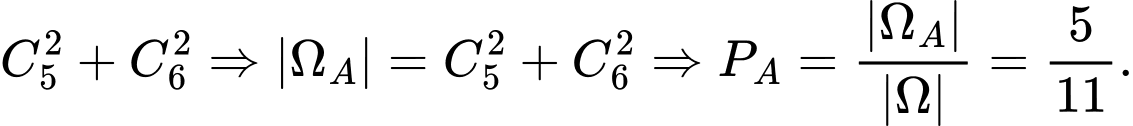 Chọn C. Đáp án: C
Chọn C. Đáp án: C
Câu 3 [805836]: (DHSPHÀNỘIHKI2017-2018) Trong một tổ có 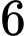 học sinh nam và
học sinh nam và 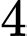 học sinh nữ. Chọn ngẫu nhiên
học sinh nữ. Chọn ngẫu nhiên 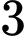 bạn trong tổ tham gia đội tình nguyện của trường. Tính xác suất để
bạn trong tổ tham gia đội tình nguyện của trường. Tính xác suất để 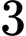 bạn được chọn toàn là nam.
bạn được chọn toàn là nam.
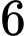 học sinh nam và
học sinh nam và 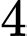 học sinh nữ. Chọn ngẫu nhiên
học sinh nữ. Chọn ngẫu nhiên 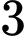 bạn trong tổ tham gia đội tình nguyện của trường. Tính xác suất để
bạn trong tổ tham gia đội tình nguyện của trường. Tính xác suất để 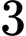 bạn được chọn toàn là nam.
bạn được chọn toàn là nam. A, 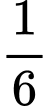 .
.
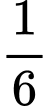 .
.B, 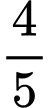 .
.
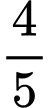 .
.C, 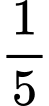 .
.
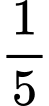 .
.D, 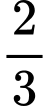 .
.
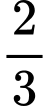 .
.
Chọn A
Xét phép thử: Chọn ngẫu nhiên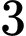 trong
trong  bạn trong tổ, ta có
bạn trong tổ, ta có 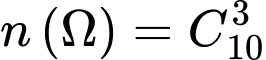 .
.
Gọi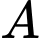 là biến cố: “
là biến cố: “ 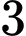 bạn được chọn toàn nam”, ta có
bạn được chọn toàn nam”, ta có 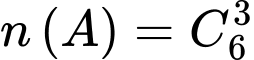 .
.
Xác suất của biến cố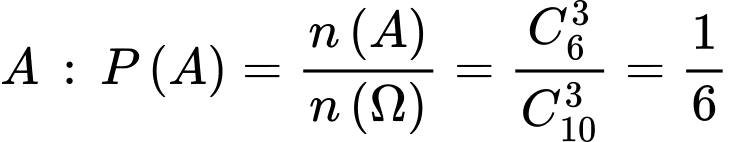 . Đáp án: A
. Đáp án: A
Xét phép thử: Chọn ngẫu nhiên
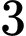 trong
trong  bạn trong tổ, ta có
bạn trong tổ, ta có 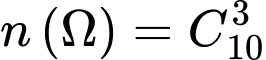 .
.Gọi
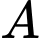 là biến cố: “
là biến cố: “ 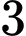 bạn được chọn toàn nam”, ta có
bạn được chọn toàn nam”, ta có 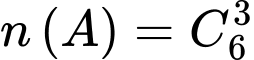 .
.Xác suất của biến cố
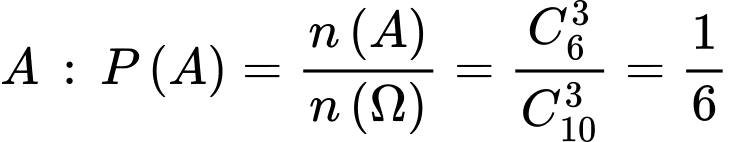 . Đáp án: A
. Đáp án: A
Câu 4 [792229]: Để kiểm tra chất lượng sản phẩm từ một công ty sữa, người ta đã gửi đến bộ phận kiểm nghiệm 5 hộp sữa cam, 4 hộp sữa dâu và 3 hộp sữa nho. Bộ phận kiểm nghiệm chọn ra 3 hộp sữa để phân tích mẫu. Tính xác suất để 3 hộp sữa được chọn có đủ cả 3 loại.
A, 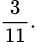
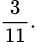
B, 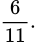
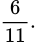
C, 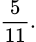
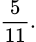
D, 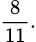
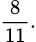
Xác suất để 3 hộp sữa được chọn có đủ cả 3 loại là: 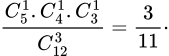
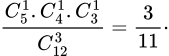
Chọn đáp án A.
Đáp án: A
Câu 5 [805835]: (HỌCKỲIĐANPHƯỢNGHÀNỘI2017-2018) Một hộp đèn có 12 bóng, trong đó có 4 bóng hỏng. Lấy ngẫu nhiên 3 bóng. Tính xác suất để trong 3 bóng có 1 bóng hỏng.
A, 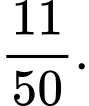
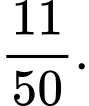
B, 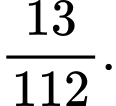
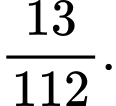
C, 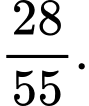
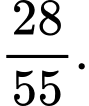
D, 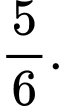
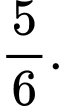
Chọn C
Trong 3 bóng có 1 bóng hỏng
Ta có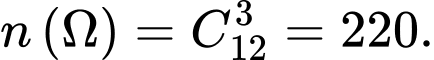
Gọi biến cố A : “Trong 3 bóng lấy ra có 1 bóng hỏng”.
Tính được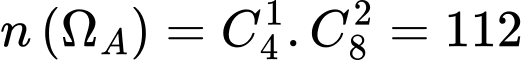
Vậy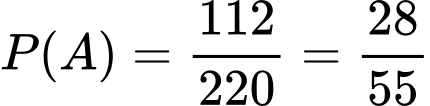 Đáp án: C
Đáp án: C
Trong 3 bóng có 1 bóng hỏng
Ta có
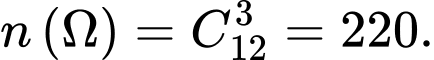
Gọi biến cố A : “Trong 3 bóng lấy ra có 1 bóng hỏng”.
Tính được
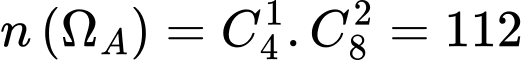
Vậy
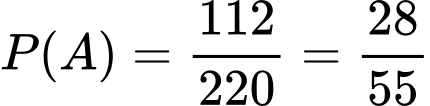 Đáp án: C
Đáp án: C
Câu 6 [792231]: (TRƯỜNG THPT CHUYÊN BẮC NINH) Lớp 11B có 25 đoàn viên trong đó 10 nam và 15 nữ. Chọn ngẫu nhiên 3 đoàn viên trong lớp để tham dự hội trại ngày 26 tháng 3. Tính xác suất để 3 đoàn viên được chọn có 2 nam và 1 nữ
A, 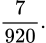
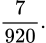
B, 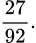
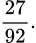
C, 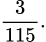
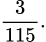
D, 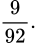
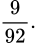
Đáp án: B
Câu 7 [792239]: Trên giá sách có 4 quyển sách toán, 3 quyển sách lý, 2 quyển sách hóa. Lấy ngẫu nhiên 3 quyển sách. Xác suất để 3 quyển được lấy ra có ít nhất một quyển là toán bằng
A, 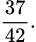
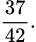
B, 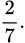
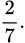
C, 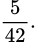
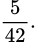
D, 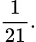
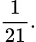
Xác suất để 3 quyển được lấy ra có ít nhất một quyển là toán bằng:
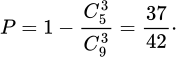
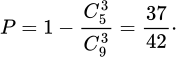
Chọn đáp án A.
Đáp án: A
Câu 8 [792234]: (THPT Chuyên Đại Học Vinh - Nghệ An - 2018) Lấy ngẫu nhiên hai viên bi từ một thùng gồm 4 bi xanh, 5 bi đỏ và 6 bi vàng. Tính xác suất để lấy được hai viên bi khác màu?
A, 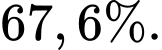
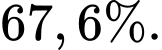
B, 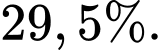
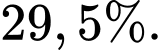
C, 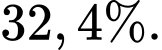
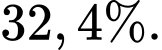
D, 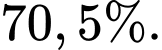
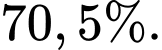
Không gian mẫu: 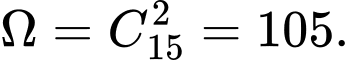
Xác suất để lấy được hai viên bi khác màu là: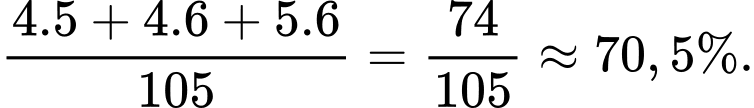 Đáp án: D
Đáp án: D
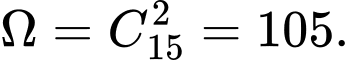
Xác suất để lấy được hai viên bi khác màu là:
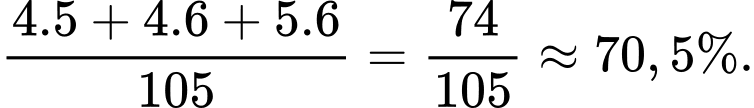 Đáp án: D
Đáp án: D
Câu 9 [792237]: (THPT CHUYÊN BẮC NINH) Một tổ có 5 học sinh nam và 6 học sinh nữ. Giáo viên chọn ngẫu nhiên 3 học sinh để làm trực nhật. Tính xác suất để 3 học sinh được chọn có cả nam và nữ
A, 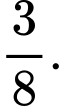
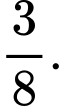
B, 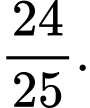
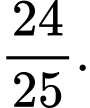
C, 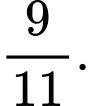
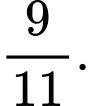
D, 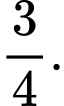
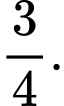
Xác suất để 3 học sinh được chọn có cả nam và nữ là: 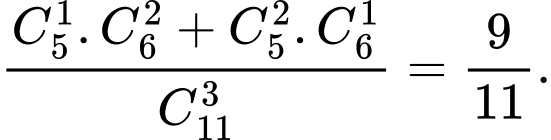 Đáp án: C
Đáp án: C
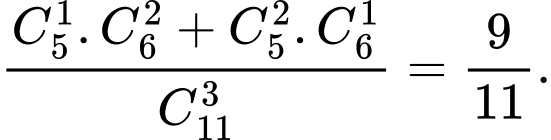 Đáp án: C
Đáp án: C
Câu 10 [792232]: Trong một đợt kiểm tra vệ sinh an toàn thực phẩm của ngành y tế tại chợ, ban quản lý chợ lấy ra mẫu thịt lợn trong đó có 4 mẫu ở quầy 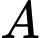 , 5 mẫu ở quầy
, 5 mẫu ở quầy 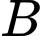 , 6 mẫu ở quầy
, 6 mẫu ở quầy  . Đoàn kiểm tra lấy ngẫu nhiên 4 mẫu để phân tích xem trong thịt lợn có chứa hóa chất tạo nạc hay không. Xác suất để mẫu thịt của cả 3 quầy
. Đoàn kiểm tra lấy ngẫu nhiên 4 mẫu để phân tích xem trong thịt lợn có chứa hóa chất tạo nạc hay không. Xác suất để mẫu thịt của cả 3 quầy 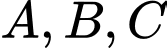 đều được chọn bằng
đều được chọn bằng
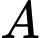 , 5 mẫu ở quầy
, 5 mẫu ở quầy 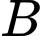 , 6 mẫu ở quầy
, 6 mẫu ở quầy  . Đoàn kiểm tra lấy ngẫu nhiên 4 mẫu để phân tích xem trong thịt lợn có chứa hóa chất tạo nạc hay không. Xác suất để mẫu thịt của cả 3 quầy
. Đoàn kiểm tra lấy ngẫu nhiên 4 mẫu để phân tích xem trong thịt lợn có chứa hóa chất tạo nạc hay không. Xác suất để mẫu thịt của cả 3 quầy 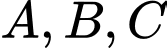 đều được chọn bằng
đều được chọn bằng A, 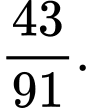
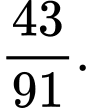
B, 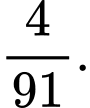
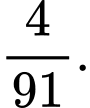
C, 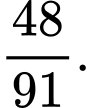
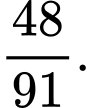
D, 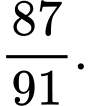
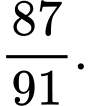
Đáp án: C
Câu 11 [792233]: Một đội ngũ giáo viên gồm 8 thầy giáo dạy toán, 5 cô giáo dạy vật lý và 3 cô giáo dạy hóa học. Sở giáo dục cần chọn ra 4 người để chấm bài thi THPT quốc gia, tính xác suất trong 4 người được chọn phải có cô giáo và có đủ ba bộ môn
A, 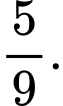
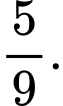
B, 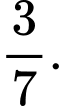
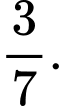
C, 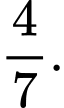
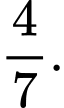
D, 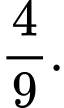
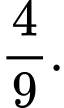
Không gian mẫu: 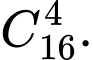
TH1: Số cách chọn 1 thầy giáo dạy toán, 1 cô giáo dạy vật lí, 2 cô giáo dạy hoá học là: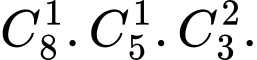
TH2: Số cách chọn 1 thầy giáo dạy toán, 2 cô giáo dạy vật lí, 1 cô giáo dạy hoá học là: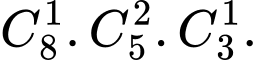
TH3: Số cách chọn 2 thầy giáo dạy toán, 1 cô giáo dạy vật lí, 1 cô giáo dạy hoá học là: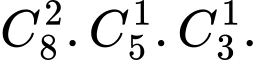
Số cách chọn 4 người có cô giáo và có đủ ba bộ môn là:
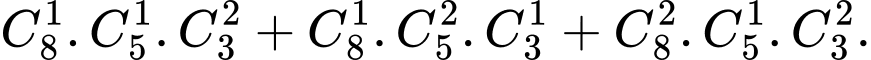
Vậy xác suất trong 4 người được chọn phải có cô giáo và có đủ ba bộ môn là: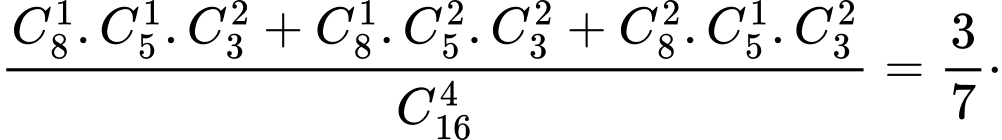
Chọn đáp án B. Đáp án: B
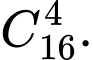
TH1: Số cách chọn 1 thầy giáo dạy toán, 1 cô giáo dạy vật lí, 2 cô giáo dạy hoá học là:
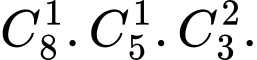
TH2: Số cách chọn 1 thầy giáo dạy toán, 2 cô giáo dạy vật lí, 1 cô giáo dạy hoá học là:
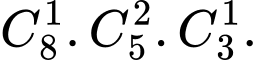
TH3: Số cách chọn 2 thầy giáo dạy toán, 1 cô giáo dạy vật lí, 1 cô giáo dạy hoá học là:
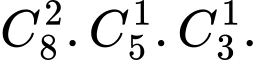
Số cách chọn 4 người có cô giáo và có đủ ba bộ môn là:
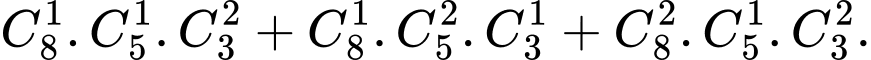
Vậy xác suất trong 4 người được chọn phải có cô giáo và có đủ ba bộ môn là:
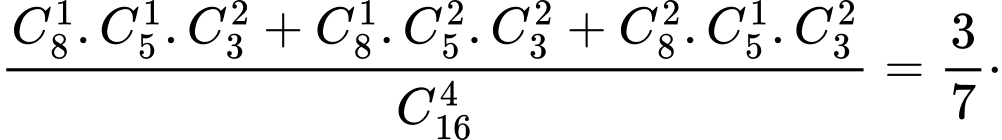
Chọn đáp án B. Đáp án: B
Câu 12 [792280]: Một chiếc hộp chứa 9 quả cầu gồm 4 quả màu xanh, 3 quả màu đỏ và 2 quả màu vàng. Lấy ngẫu nhiên 3 quả cầu từ hộp đó. Xác suất để trong 3 quả cầu lấy được có ít nhất 1 quả màu đỏ bằng
A, 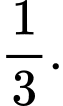
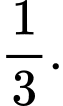
B, 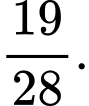
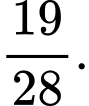
C, 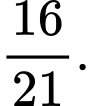
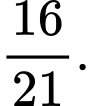
D, 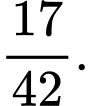
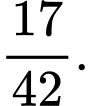
Chọn C
Ta có: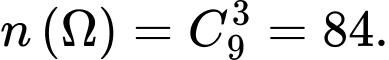
Gọi biến cố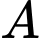 : “3 quả cầu có ít nhất 1 quả màu đỏ”.
: “3 quả cầu có ít nhất 1 quả màu đỏ”.
Suy biến cố đối là : “3 quả cầu không có quả màu đỏ”.
: “3 quả cầu không có quả màu đỏ”.
Vậy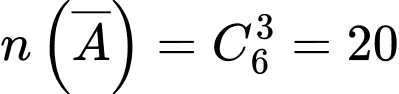
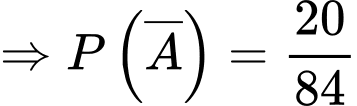
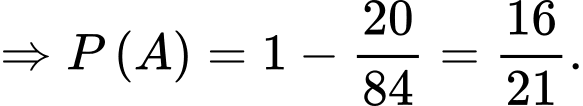 Đáp án: C
Đáp án: C
Ta có:
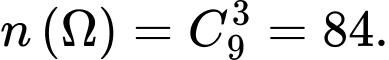
Gọi biến cố
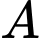 : “3 quả cầu có ít nhất 1 quả màu đỏ”.
: “3 quả cầu có ít nhất 1 quả màu đỏ”. Suy biến cố đối là
 : “3 quả cầu không có quả màu đỏ”.
: “3 quả cầu không có quả màu đỏ”. Vậy
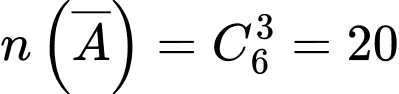
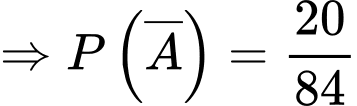
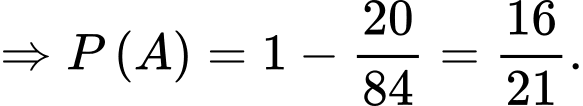 Đáp án: C
Đáp án: C
Câu 13 [806037]: Một tổ gồm 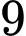 học sinh gồm
học sinh gồm 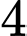 học sinh nữ và
học sinh nữ và 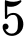 học sinh nam. Chọn ngẫu nhiên từ tổ đó ra
học sinh nam. Chọn ngẫu nhiên từ tổ đó ra 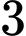 học sinh. Xác suất để trong
học sinh. Xác suất để trong 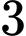 học sinh chọn ra có số học sinh nam nhiều hơn số học sinh nữ bằng
học sinh chọn ra có số học sinh nam nhiều hơn số học sinh nữ bằng
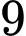 học sinh gồm
học sinh gồm 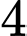 học sinh nữ và
học sinh nữ và 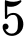 học sinh nam. Chọn ngẫu nhiên từ tổ đó ra
học sinh nam. Chọn ngẫu nhiên từ tổ đó ra 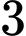 học sinh. Xác suất để trong
học sinh. Xác suất để trong 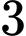 học sinh chọn ra có số học sinh nam nhiều hơn số học sinh nữ bằng
học sinh chọn ra có số học sinh nam nhiều hơn số học sinh nữ bằng A, 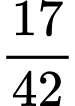 .
.
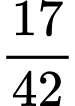 .
.B, 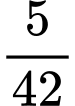 .
.
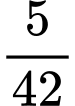 .
.C, 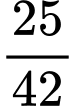 .
.
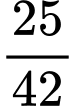 .
.D, 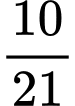 .
.
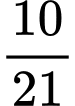 .
.
Có 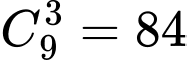 cách chọn
cách chọn 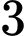 học sinh bất kì.
học sinh bất kì.
Chọn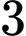 học sinh mà số học sinh nam nhiều hơn số học sinh nữ có các trường hợp
học sinh mà số học sinh nam nhiều hơn số học sinh nữ có các trường hợp
+ Có 3 học sinh nam: Có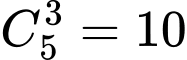 cách chọn
cách chọn
+ Có 2 học sinh nam,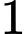 học sinh nữ: Có
học sinh nữ: Có 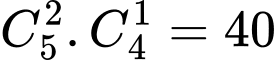 cách chọn
cách chọn
Xác suất cần tìm là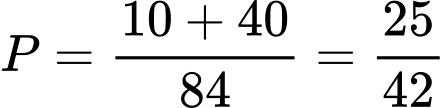 . Đáp án: C
. Đáp án: C
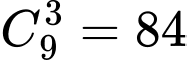 cách chọn
cách chọn 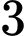 học sinh bất kì.
học sinh bất kì. Chọn
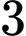 học sinh mà số học sinh nam nhiều hơn số học sinh nữ có các trường hợp
học sinh mà số học sinh nam nhiều hơn số học sinh nữ có các trường hợp+ Có 3 học sinh nam: Có
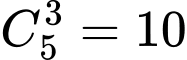 cách chọn
cách chọn+ Có 2 học sinh nam,
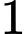 học sinh nữ: Có
học sinh nữ: Có 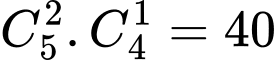 cách chọn
cách chọnXác suất cần tìm là
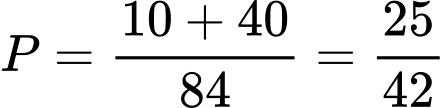 . Đáp án: C
. Đáp án: C
Câu 14 [806085]: Cho hai đường thẳng song song 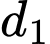 ,
, 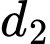 . Trên
. Trên 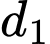 có 6 điểm phân biệt được tô màu đỏ, trên
có 6 điểm phân biệt được tô màu đỏ, trên 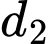 có 4 điểm phân biệt được tô màu xanh. Xét tất cả các tam giác được tạo thành khi nối các điểm đó với nhau. Chọn ngẫu nhiên một tam giác, khi đó xác suất để thu được tam giác có hai đỉnh màu đỏ là.
có 4 điểm phân biệt được tô màu xanh. Xét tất cả các tam giác được tạo thành khi nối các điểm đó với nhau. Chọn ngẫu nhiên một tam giác, khi đó xác suất để thu được tam giác có hai đỉnh màu đỏ là.
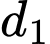 ,
, 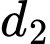 . Trên
. Trên 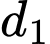 có 6 điểm phân biệt được tô màu đỏ, trên
có 6 điểm phân biệt được tô màu đỏ, trên 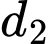 có 4 điểm phân biệt được tô màu xanh. Xét tất cả các tam giác được tạo thành khi nối các điểm đó với nhau. Chọn ngẫu nhiên một tam giác, khi đó xác suất để thu được tam giác có hai đỉnh màu đỏ là.
có 4 điểm phân biệt được tô màu xanh. Xét tất cả các tam giác được tạo thành khi nối các điểm đó với nhau. Chọn ngẫu nhiên một tam giác, khi đó xác suất để thu được tam giác có hai đỉnh màu đỏ là. A, 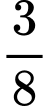 .
.
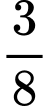 .
.B, 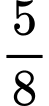 .
.
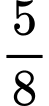 .
.C, 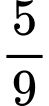 .
.
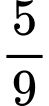 .
.D, 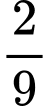 .
.
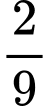 .
.
Chọn B
Mỗi tam giác được tạo thành khi lấy 2 điểm trên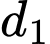 và 1 điểm trên
và 1 điểm trên 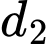 , hoặc 2 điểm trên
, hoặc 2 điểm trên 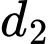 và 1 điểm trên
và 1 điểm trên 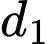 . Số tam giác được tạo thành là:
. Số tam giác được tạo thành là: 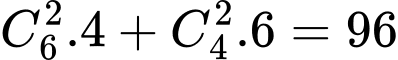 .
.
Số tam giác có hai đỉnh màu đỏ là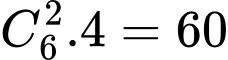 . Vậy xác suất để thu được tam giác có hai đỉnh màu đỏ là:
. Vậy xác suất để thu được tam giác có hai đỉnh màu đỏ là: 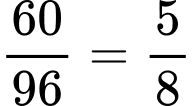 . Đáp án: B
. Đáp án: B
Mỗi tam giác được tạo thành khi lấy 2 điểm trên
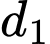 và 1 điểm trên
và 1 điểm trên 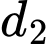 , hoặc 2 điểm trên
, hoặc 2 điểm trên 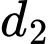 và 1 điểm trên
và 1 điểm trên 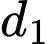 . Số tam giác được tạo thành là:
. Số tam giác được tạo thành là: 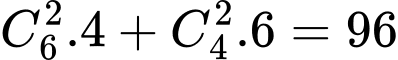 .
.Số tam giác có hai đỉnh màu đỏ là
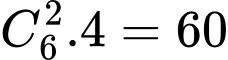 . Vậy xác suất để thu được tam giác có hai đỉnh màu đỏ là:
. Vậy xác suất để thu được tam giác có hai đỉnh màu đỏ là: 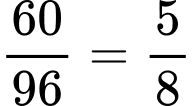 . Đáp án: B
. Đáp án: B
Câu 15 [806106]: Trên giá sách có 4 quyển sách toán, 3 quyển sách lý, 2 quyển sách hóa. Lấy ngẫu nhiên 3 quyển sách. Tính xác suất để 3 quyển được lấy ra có ít nhất một quyển là toán.
A, 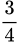 .
.
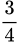 .
.B, 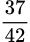 .
.
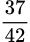 .
.C, 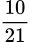 .
.
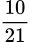 .
.D, 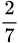 .
.
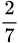 .
.
Chọn B
Trên giá có tất cả: (quyển sách) bao gồm cả 3 môn: toán, lý và hóa.
(quyển sách) bao gồm cả 3 môn: toán, lý và hóa.
Lấy 3 quyển sách từ 9 quyển sách, số cách lấy ra là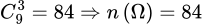
Gọi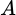 là biến cố: “3 quyển lấy ra có ít nhất 1 quyển toán”.
là biến cố: “3 quyển lấy ra có ít nhất 1 quyển toán”.
Suy ra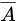 : “3 quyển lấy ra không có quyển toán nào”
: “3 quyển lấy ra không có quyển toán nào” 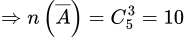 .
.
Vậy xác suất để 3 quyển được lấy ra có ít nhất một quyển sách toán là:
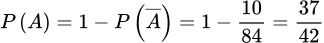 . Đáp án: B
. Đáp án: B
Trên giá có tất cả:
 (quyển sách) bao gồm cả 3 môn: toán, lý và hóa.
(quyển sách) bao gồm cả 3 môn: toán, lý và hóa. Lấy 3 quyển sách từ 9 quyển sách, số cách lấy ra là
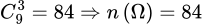
Gọi
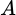 là biến cố: “3 quyển lấy ra có ít nhất 1 quyển toán”.
là biến cố: “3 quyển lấy ra có ít nhất 1 quyển toán”. Suy ra
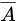 : “3 quyển lấy ra không có quyển toán nào”
: “3 quyển lấy ra không có quyển toán nào” 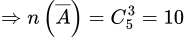 .
.Vậy xác suất để 3 quyển được lấy ra có ít nhất một quyển sách toán là:
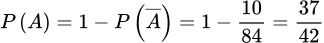 . Đáp án: B
. Đáp án: B
Câu 16 [806040]: Gọi 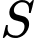 là tập các số tự nhiên có
là tập các số tự nhiên có 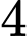 chữ số khác nhau được tạo từ tập
chữ số khác nhau được tạo từ tập 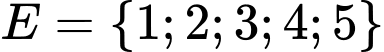 . Chọn ngẫu nhiên một số từ tập
. Chọn ngẫu nhiên một số từ tập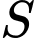 . Tính xác suất để số được chọn là một số chẵn.
. Tính xác suất để số được chọn là một số chẵn.
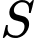 là tập các số tự nhiên có
là tập các số tự nhiên có 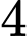 chữ số khác nhau được tạo từ tập
chữ số khác nhau được tạo từ tập 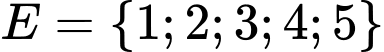 . Chọn ngẫu nhiên một số từ tập
. Chọn ngẫu nhiên một số từ tập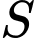 . Tính xác suất để số được chọn là một số chẵn.
. Tính xác suất để số được chọn là một số chẵn. A, 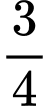 .
.
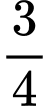 .
.B, 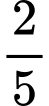 .
.
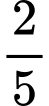 .
.C, 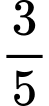 .
.
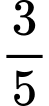 .
.D, 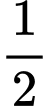 .
.
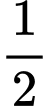 .
.
Chọn B
Gọi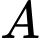 là biến cố chọn ngẫu nhiên một số từ tập
là biến cố chọn ngẫu nhiên một số từ tập 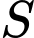 sao cho số đó là số chẵn.
sao cho số đó là số chẵn.
Số phần tử không gian mẫu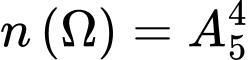
Gọi số có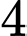 chữ số khác nhau là số chẵn có dạng
chữ số khác nhau là số chẵn có dạng 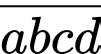
Chọn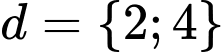 có
có 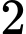 cách. Chọn ba số xếp vào ba vị trí
cách. Chọn ba số xếp vào ba vị trí 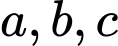 có
có 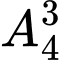
Vậy có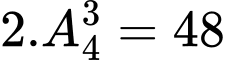 số chẵn có
số chẵn có 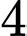 chữ số khác nhau
chữ số khác nhau 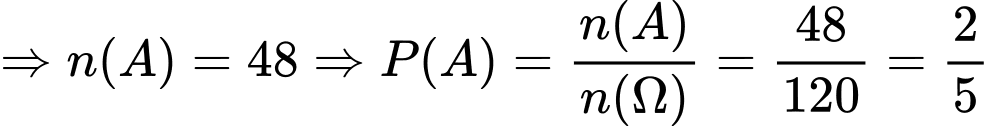 . Đáp án: B
. Đáp án: B
Gọi
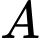 là biến cố chọn ngẫu nhiên một số từ tập
là biến cố chọn ngẫu nhiên một số từ tập 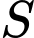 sao cho số đó là số chẵn.
sao cho số đó là số chẵn. Số phần tử không gian mẫu
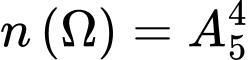
Gọi số có
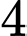 chữ số khác nhau là số chẵn có dạng
chữ số khác nhau là số chẵn có dạng 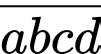
Chọn
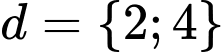 có
có 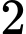 cách. Chọn ba số xếp vào ba vị trí
cách. Chọn ba số xếp vào ba vị trí 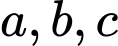 có
có 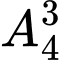
Vậy có
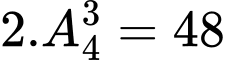 số chẵn có
số chẵn có 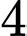 chữ số khác nhau
chữ số khác nhau 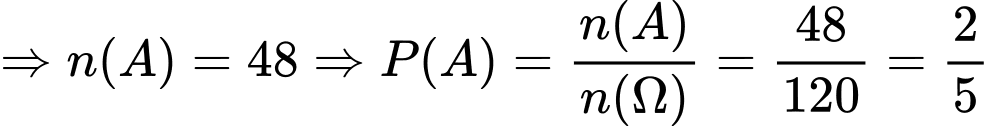 . Đáp án: B
. Đáp án: B
Câu 17 [806062]: Gọi 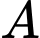 là tập hợp các số tự nhiên có
là tập hợp các số tự nhiên có 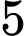 chữ số đôi một khác nhau. Chọn ngẫu nhiên một số tự nhiên thuộc tập
chữ số đôi một khác nhau. Chọn ngẫu nhiên một số tự nhiên thuộc tập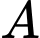 . Tính xác suất để chọn được một số thuộc
. Tính xác suất để chọn được một số thuộc 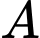 và số đó chia hết cho
và số đó chia hết cho 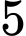 .
.
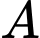 là tập hợp các số tự nhiên có
là tập hợp các số tự nhiên có 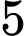 chữ số đôi một khác nhau. Chọn ngẫu nhiên một số tự nhiên thuộc tập
chữ số đôi một khác nhau. Chọn ngẫu nhiên một số tự nhiên thuộc tập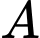 . Tính xác suất để chọn được một số thuộc
. Tính xác suất để chọn được một số thuộc 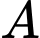 và số đó chia hết cho
và số đó chia hết cho 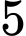 .
. A, 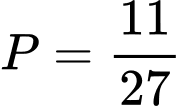 .
.
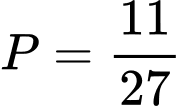 .
.B, 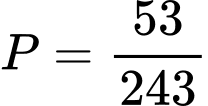 .
.
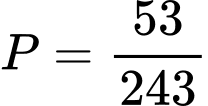 .
.C, 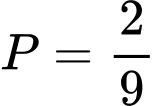 .
.
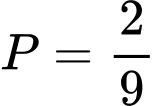 .
.D, 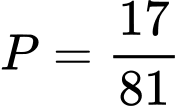 .
.
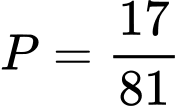 .
.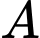 là tập hợp các số tự nhiên có
là tập hợp các số tự nhiên có 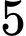 chữ số đôi một khác nhau
chữ số đôi một khác nhau 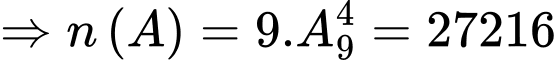
Chọn ngẫu nhiên một số thuộc tập
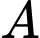 có
có 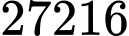 cách chọn
cách chọn 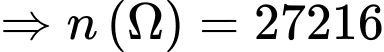
Gọi
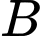 là biến cố “Chọn được một số thuộc
là biến cố “Chọn được một số thuộc 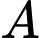 và số đó chia hết cho
và số đó chia hết cho 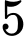 ”
”Gọi số chia hết cho
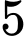 thuộc tập
thuộc tập 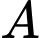 là
là 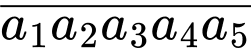
Trường hợp 1: Chữ số tận cùng là

Có
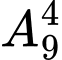 cách chọn
cách chọn 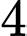 chữ số còn lại.
chữ số còn lại. Trường hợp 2: Chữ số tận cùng là
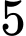
Chọn chữ số
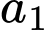 có
có 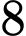 cách
cáchChọn
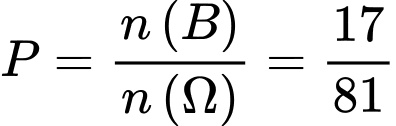 chữ số còn lại có
chữ số còn lại có 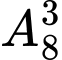
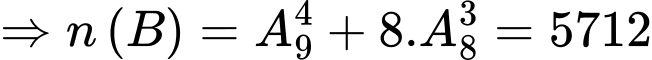 .
.Vậy
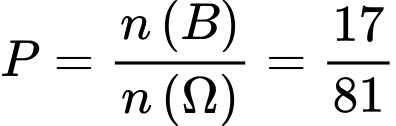 . Đáp án: D
. Đáp án: D
Câu 18 [806086]: Cho năm đoạn thẳng có độ dài: 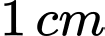 ,
, 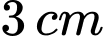 ,
, 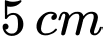 ,
,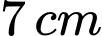 ,
, 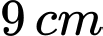 . Lấy ngẫu nhiên ba đoạn thẳng trong năm đoạn thẳng đó. Xác suất để ba đoạn thẳng lấy ra là ba cạnh của một tam giác là
. Lấy ngẫu nhiên ba đoạn thẳng trong năm đoạn thẳng đó. Xác suất để ba đoạn thẳng lấy ra là ba cạnh của một tam giác là
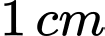 ,
, 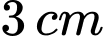 ,
, 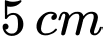 ,
,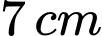 ,
, 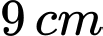 . Lấy ngẫu nhiên ba đoạn thẳng trong năm đoạn thẳng đó. Xác suất để ba đoạn thẳng lấy ra là ba cạnh của một tam giác là
. Lấy ngẫu nhiên ba đoạn thẳng trong năm đoạn thẳng đó. Xác suất để ba đoạn thẳng lấy ra là ba cạnh của một tam giác là A, 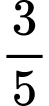 .
.
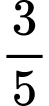 .
.B, 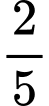 .
.
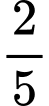 .
.C, 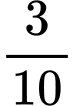 .
.
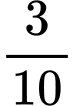 .
.D, 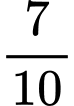 .
.
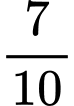 .
.
Chọn C
* Lấy ngẫu nhiên ba đoạn thẳng trong năm đoạn thẳng đã cho có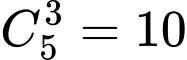 cách.
cách.
Suy ra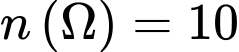 .
.
* Gọi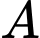 là biến cố "lấy được ba đoạn thẳng là ba cạnh của một tam giác".
là biến cố "lấy được ba đoạn thẳng là ba cạnh của một tam giác".
Các trường hợp ba đoạn thẳng là ba cạnh của một tam giác là:
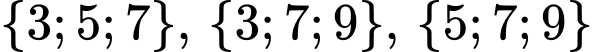 (thỏa mãn: hiệu hai cạnh bé hơn cạnh còn lại, tổng hai cạnh lớn hơn cạnh còn lại).
(thỏa mãn: hiệu hai cạnh bé hơn cạnh còn lại, tổng hai cạnh lớn hơn cạnh còn lại).
Do đó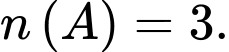 Vậy sác xuất cần tìm là
Vậy sác xuất cần tìm là 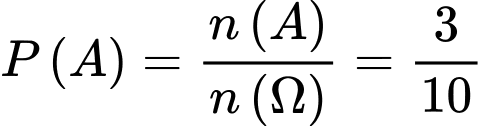 . Đáp án: C
. Đáp án: C
* Lấy ngẫu nhiên ba đoạn thẳng trong năm đoạn thẳng đã cho có
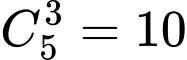 cách.
cách. Suy ra
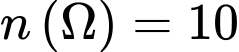 .
.* Gọi
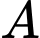 là biến cố "lấy được ba đoạn thẳng là ba cạnh của một tam giác".
là biến cố "lấy được ba đoạn thẳng là ba cạnh của một tam giác".Các trường hợp ba đoạn thẳng là ba cạnh của một tam giác là:
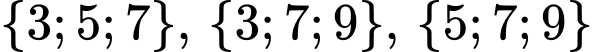 (thỏa mãn: hiệu hai cạnh bé hơn cạnh còn lại, tổng hai cạnh lớn hơn cạnh còn lại).
(thỏa mãn: hiệu hai cạnh bé hơn cạnh còn lại, tổng hai cạnh lớn hơn cạnh còn lại). Do đó
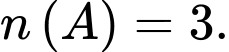 Vậy sác xuất cần tìm là
Vậy sác xuất cần tìm là 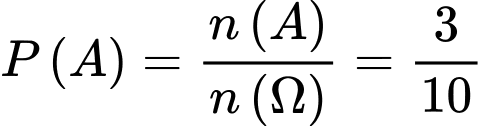 . Đáp án: C
. Đáp án: C
Câu 19 [806148]: Túi I chứa 3 bi trắng, 7 bi đỏ, 15 bi xanh. Túi II chứa 10 bi trắng, 6 bi đỏ, 9 bi xanh. Từ mỗi túi lấy ngẫu nhiên 1 viên bi. Tính xác suất để lấy được hai viên cùng màu.
A, 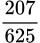 .
.
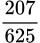 .
.B, 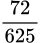 .
.
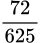 .
.C, 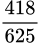 .
.
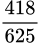 .
.D, 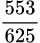 .
.
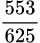 .
.
Gọi 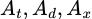 lần lượt là biến cố bi rút được từ túi I là trắng, đỏ, xanh.
lần lượt là biến cố bi rút được từ túi I là trắng, đỏ, xanh.
Gọi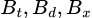 lần lượt là biến cố bi rút được từ túi II là trắng, đỏ, xanh.
lần lượt là biến cố bi rút được từ túi II là trắng, đỏ, xanh.
Các biến cố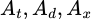 độc lập với
độc lập với 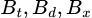 .
.
Vậy xác suất để lấy được hai bi cùng màu là
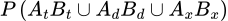
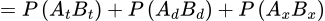
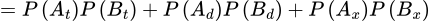
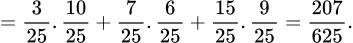 Đáp án: A
Đáp án: A
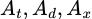 lần lượt là biến cố bi rút được từ túi I là trắng, đỏ, xanh.
lần lượt là biến cố bi rút được từ túi I là trắng, đỏ, xanh. Gọi
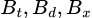 lần lượt là biến cố bi rút được từ túi II là trắng, đỏ, xanh.
lần lượt là biến cố bi rút được từ túi II là trắng, đỏ, xanh. Các biến cố
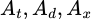 độc lập với
độc lập với 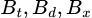 .
.Vậy xác suất để lấy được hai bi cùng màu là
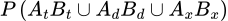
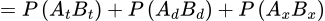
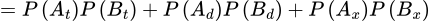
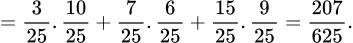 Đáp án: A
Đáp án: A
Câu 20 [805833]: Hộp 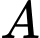 có
có 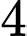 viên bi trắng,
viên bi trắng, 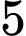 viên bi đỏ và
viên bi đỏ và 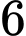 viên bi xanh. Hộp
viên bi xanh. Hộp 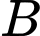 có
có 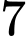 viên bi trắng,
viên bi trắng, 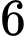 viên bi đỏ và
viên bi đỏ và 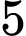 viên bi xanh. Lấy ngẫu nhiên mỗi hộp một viên bi, tính xác suất để hai viên bi được lấy ra có cùng màu.
viên bi xanh. Lấy ngẫu nhiên mỗi hộp một viên bi, tính xác suất để hai viên bi được lấy ra có cùng màu.
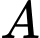 có
có 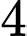 viên bi trắng,
viên bi trắng, 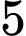 viên bi đỏ và
viên bi đỏ và 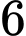 viên bi xanh. Hộp
viên bi xanh. Hộp 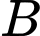 có
có 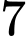 viên bi trắng,
viên bi trắng, 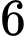 viên bi đỏ và
viên bi đỏ và 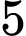 viên bi xanh. Lấy ngẫu nhiên mỗi hộp một viên bi, tính xác suất để hai viên bi được lấy ra có cùng màu.
viên bi xanh. Lấy ngẫu nhiên mỗi hộp một viên bi, tính xác suất để hai viên bi được lấy ra có cùng màu. A, 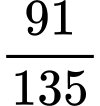 .
.
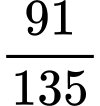 .
.B, 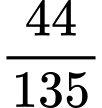 .
.
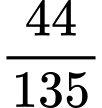 .
.C, 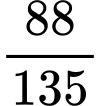 .
.
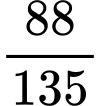 .
.D, 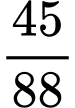 .
.
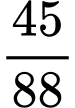 .
.
Chọn B
Số phần tử của không gian mẫu: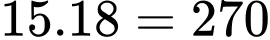 .
.
Số cách chọn từ mỗi hộp 1 viên bi sau cho 2 viên bi cùng màu là: .
.
Vậy xác suất cần tìm là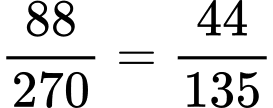 . Đáp án: B
. Đáp án: B
Số phần tử của không gian mẫu:
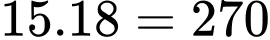 .
.Số cách chọn từ mỗi hộp 1 viên bi sau cho 2 viên bi cùng màu là:
 .
.Vậy xác suất cần tìm là
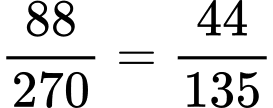 . Đáp án: B
. Đáp án: B
Câu 21 [792250]: Tổ một có 3 học sinh nam và 4 học sinh nữ. Tổ hai có 5 học sinh nam và 2 học sinh nữ. Chọn ngẫu nhiên mỗi tổ một học sinh đi làm nhiệm vụ. Tính xác suất sao cho chọn được hai học sinh có cả nam và nữ.
A, 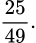
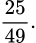
B, 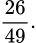
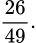
C, 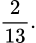
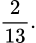
D, 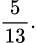
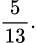
Ta có 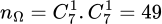
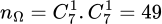
Gọi B là xác suất chọn được hai học sinh có cả nam và nữ (chọn mỗi tổ một học sinh) đi làm nhiệm vụ.
Có 2 trường hợp:
TH1: Tổ 1 chọn được 1 nam và tổ 2 chọn được 1 nữ: 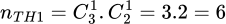
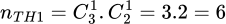
TH2: Tổ 1 chọn được 1 nữ và tổ 2 chọn được 1 nam: 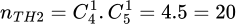
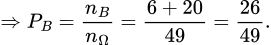 Chọn đáp án B.
Chọn đáp án B.
Đáp án: B 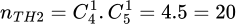
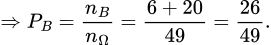 Chọn đáp án B.
Chọn đáp án B.
Câu 22 [554586]: Trên hai tia 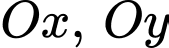 của góc nhọn
của góc nhọn 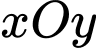 lần lượt cho 5 điểm và 8 điểm phân biệt khác
lần lượt cho 5 điểm và 8 điểm phân biệt khác  Chọn ngẫu nhiên 3 điểm từ 14 điểm (gồm điểm
Chọn ngẫu nhiên 3 điểm từ 14 điểm (gồm điểm  và 13 điểm đã cho), xác suất để 3 điểm chọn được là ba đỉnh của một tam giác bằng
và 13 điểm đã cho), xác suất để 3 điểm chọn được là ba đỉnh của một tam giác bằng
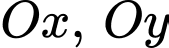 của góc nhọn
của góc nhọn 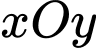 lần lượt cho 5 điểm và 8 điểm phân biệt khác
lần lượt cho 5 điểm và 8 điểm phân biệt khác  Chọn ngẫu nhiên 3 điểm từ 14 điểm (gồm điểm
Chọn ngẫu nhiên 3 điểm từ 14 điểm (gồm điểm  và 13 điểm đã cho), xác suất để 3 điểm chọn được là ba đỉnh của một tam giác bằng
và 13 điểm đã cho), xác suất để 3 điểm chọn được là ba đỉnh của một tam giác bằng A, 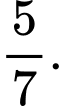
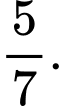
B, 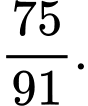
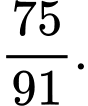
C, 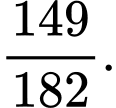
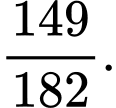
D, 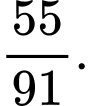
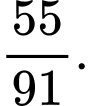
Ta có:
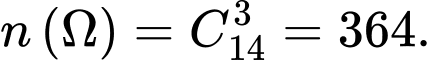
Gọi
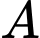 là biến cố: “
là biến cố: “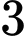 điểm chọn được là ba đỉnh của một tam giác”.
điểm chọn được là ba đỉnh của một tam giác”.
Xét
 điểm nằm trên hai tia
điểm nằm trên hai tia 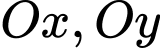 không tính điểm
không tính điểm 
TH1: Tam giác có
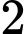 đỉnh thuộc
đỉnh thuộc 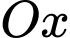 và
và 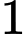 đỉnh thuộc
đỉnh thuộc 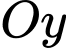 có:
có:
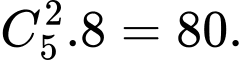
TH2: Tam giác có
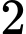 đỉnh thuộc
đỉnh thuộc 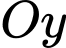 và
và 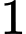 đỉnh thuộc
đỉnh thuộc 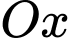 có:
có: 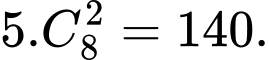
Xét tam giác có
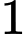 đỉnh là
đỉnh là 
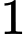 đỉnh thuộc
đỉnh thuộc 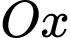 có:
có: 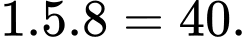
Vậy
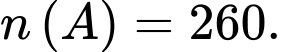
Vậy
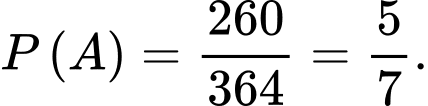
Đáp án: A. Đáp án: A
Câu 23 [579686]: [Đề mẫu HSA 2024]: Cô giáo có 12 phần quà gồm 4 phần loại  và 8 phần loại
và 8 phần loại  được đựng trong 12 hộp kín giống nhau. Cô chia đều cho 3 bạn, mỗi bạn 4 phần quà. Xác suất để mỗi bạn đều nhận được cả hai loại quà là
được đựng trong 12 hộp kín giống nhau. Cô chia đều cho 3 bạn, mỗi bạn 4 phần quà. Xác suất để mỗi bạn đều nhận được cả hai loại quà là
 và 8 phần loại
và 8 phần loại  được đựng trong 12 hộp kín giống nhau. Cô chia đều cho 3 bạn, mỗi bạn 4 phần quà. Xác suất để mỗi bạn đều nhận được cả hai loại quà là
được đựng trong 12 hộp kín giống nhau. Cô chia đều cho 3 bạn, mỗi bạn 4 phần quà. Xác suất để mỗi bạn đều nhận được cả hai loại quà là A, 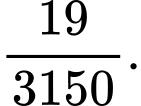
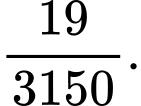
B, 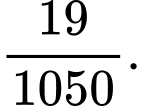
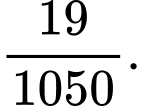
C, 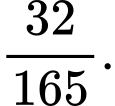
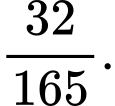
D, 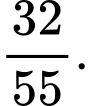
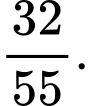
Số phần tử không gian mẫu là 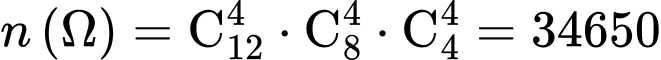
Do mỗi bạn đều có hai loại quà nên mỗi phần quà cho mỗi bạn được chia phải có cả hai loại I và II, mà ta có 4 quà loại I
Có ít nhất 1 bạn nhận được 2 mòn quà loại 1
Ta có: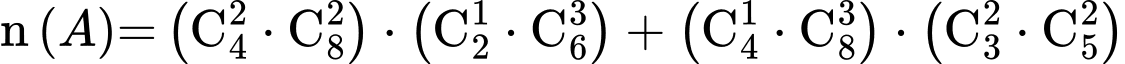
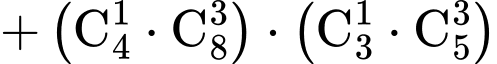 cách chia.
cách chia.
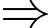 Xác suất cần tìm là
Xác suất cần tìm là 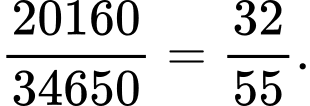
Chọn D. Đáp án: D
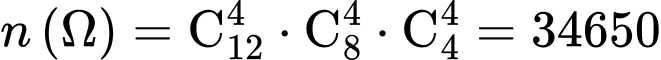
Do mỗi bạn đều có hai loại quà nên mỗi phần quà cho mỗi bạn được chia phải có cả hai loại I và II, mà ta có 4 quà loại I
Có ít nhất 1 bạn nhận được 2 mòn quà loại 1
Ta có:
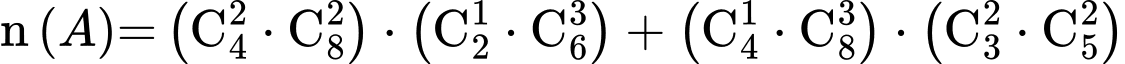
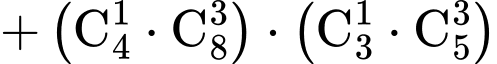 cách chia.
cách chia. 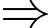 Xác suất cần tìm là
Xác suất cần tìm là 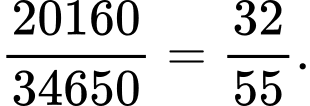
Chọn D. Đáp án: D
Câu 24 [251694]: Có hộp I và hộp II, mỗi hộp chứa 5 tấm thẻ đánh số từ 1 đến 5. Từ mỗi hộp, rút ngẫu nhiên ra một tấm thẻ. Tính xác suất để thẻ rút ra từ hộp II mang số lớn hơn số trên thẻ rút ra từ hộp I.
Rút từ hộp I có 5 cách, từ hợp II có 5 cách, số khả năng xảy ra khi rút mỗi hộp 1 thẻ là: 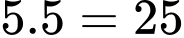 , hay
, hay 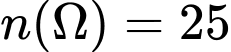 .
.

Biến cố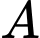 : "Thẻ rút ra từ hộp II mang số lớn hơn số trên thẻ rút ra từ hộp I".
: "Thẻ rút ra từ hộp II mang số lớn hơn số trên thẻ rút ra từ hộp I".
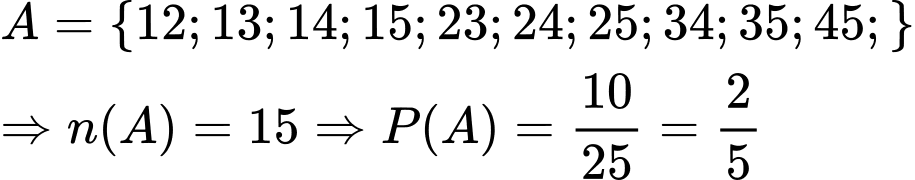
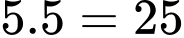 , hay
, hay 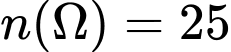 .
.
Biến cố
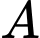 : "Thẻ rút ra từ hộp II mang số lớn hơn số trên thẻ rút ra từ hộp I".
: "Thẻ rút ra từ hộp II mang số lớn hơn số trên thẻ rút ra từ hộp I".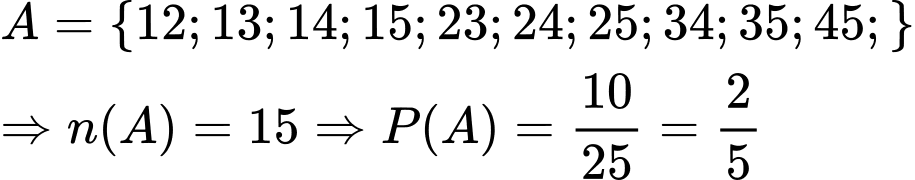
Câu 25 [792295]: Có hai dãy ghế đối diện nhau, mỗi dãy có ba ghế. Xếp ngẫu nhiên 6 học sinh gồm 3 nam 3 nữngồi vào hai dãy ghế đó sao cho mỗi ghế có đúng một học sinh ngồi. Xác suất để mỗi học
sinh nam đều ngồi đối diện với một học sinh nữ bằng
A, 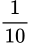 .
.
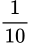 .
.B, 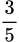 .
.
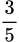 .
.C, 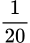
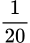
D, 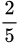 .
.
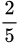 .
.
Chọn D
Sắp 6 học sinh vào 6 cái ghế có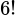 cách.
cách.
Suy ra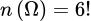 .
.
Đánh số thự tự 6 cái ghế như hình bên dưới

Gọi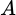 là biến cố: “Nam nữ ngồi đối diện”.
là biến cố: “Nam nữ ngồi đối diện”.
Học sinh nam thứ nhất có 6 cách chọn một vị trí ngồi.
Học sinh nam thứ hai có 4 cách chọn một vị trị ngồi (trừ vị trí đối diện với người nam thứ nhất).
Học sinh nam thứ ba có hai cách chọn một vị trí ngồi (trừ hai vị trí đối diện với hai nam thứ nhất và thứ hai).
Xếp ba học sinh nữ vào ba vị trí còn lại có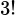 cách.
cách.
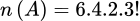
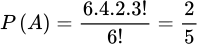 . Đáp án: D
. Đáp án: D
Sắp 6 học sinh vào 6 cái ghế có
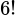 cách.
cách. Suy ra
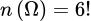 .
.Đánh số thự tự 6 cái ghế như hình bên dưới

Gọi
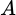 là biến cố: “Nam nữ ngồi đối diện”.
là biến cố: “Nam nữ ngồi đối diện”. Học sinh nam thứ nhất có 6 cách chọn một vị trí ngồi.
Học sinh nam thứ hai có 4 cách chọn một vị trị ngồi (trừ vị trí đối diện với người nam thứ nhất).
Học sinh nam thứ ba có hai cách chọn một vị trí ngồi (trừ hai vị trí đối diện với hai nam thứ nhất và thứ hai).
Xếp ba học sinh nữ vào ba vị trí còn lại có
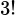 cách.
cách. 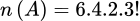
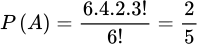 . Đáp án: D
. Đáp án: D
Câu 26 [792297]: Có  học sinh gồm
học sinh gồm 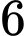 nam và
nam và 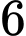 nữ ngồi vào hai hàng ghế đối diện nhau tùy ý. Xác suất để mỗi một em nam ngồi đối diện với một em nữ là?
nữ ngồi vào hai hàng ghế đối diện nhau tùy ý. Xác suất để mỗi một em nam ngồi đối diện với một em nữ là?

 học sinh gồm
học sinh gồm 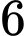 nam và
nam và 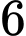 nữ ngồi vào hai hàng ghế đối diện nhau tùy ý. Xác suất để mỗi một em nam ngồi đối diện với một em nữ là?
nữ ngồi vào hai hàng ghế đối diện nhau tùy ý. Xác suất để mỗi một em nam ngồi đối diện với một em nữ là? 
A, 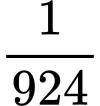 .
.
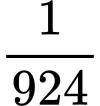 .
.B, 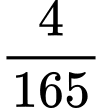 .
.
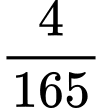 .
.C, 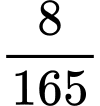 .
.
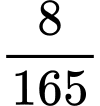 .
.D, 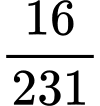 .
.
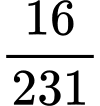 .
.
Chọn D
Số cách xếp học sinh vào
học sinh vào  chỗ là
chỗ là 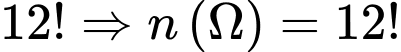
Gọi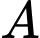 là biến cố “Xếp mỗi một em nam ngồi đối diện với một em nữ”.
là biến cố “Xếp mỗi một em nam ngồi đối diện với một em nữ”.

Ta có vị trí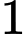 có
có  cách chọn; vị trí
cách chọn; vị trí 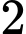 có
có 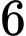 cách chọn; vị trí
cách chọn; vị trí 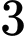 có
có  cách chọn;; vị trí
cách chọn;; vị trí 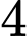 có
có 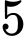 cách chọn.
cách chọn.
Nên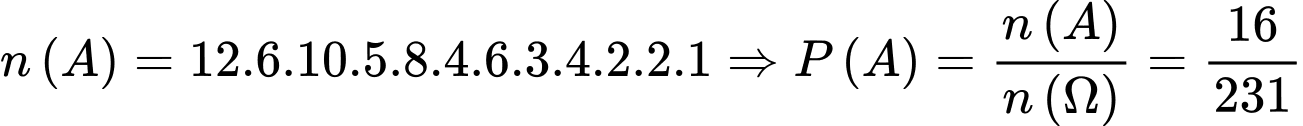 Đáp án: D
Đáp án: D
Số cách xếp
 học sinh vào
học sinh vào  chỗ là
chỗ là 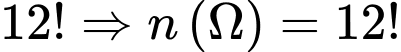
Gọi
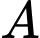 là biến cố “Xếp mỗi một em nam ngồi đối diện với một em nữ”.
là biến cố “Xếp mỗi một em nam ngồi đối diện với một em nữ”. 
Ta có vị trí
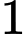 có
có  cách chọn; vị trí
cách chọn; vị trí 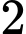 có
có 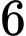 cách chọn; vị trí
cách chọn; vị trí 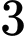 có
có  cách chọn;; vị trí
cách chọn;; vị trí 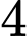 có
có 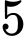 cách chọn.
cách chọn. Nên
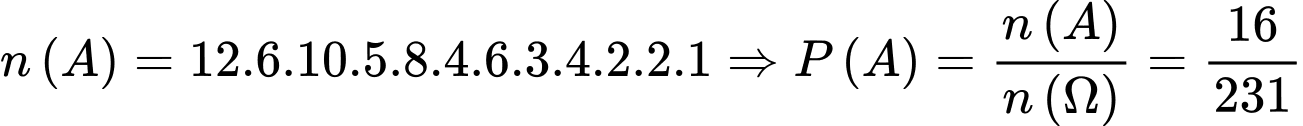 Đáp án: D
Đáp án: D
Câu 27 [803769]: Có 10 học sinh, gồm 5 bạn lớp 12A và 5 bạn lớp 12B tham gia một trò chơi. Để thực hiện trò chơi, người điều khiển ghép ngẫu nhiên 10 học sinh đó thành 5 cặp. Xác suất để không có cặp nào gồm hai học sinh cùng lớp bằng
A, 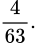
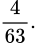
B, 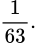
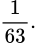
C, 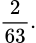
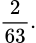
D, 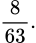
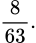
Xác suất để không có cặp nào gồm hai học sinh cùng lớp bằng: 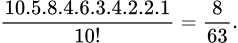
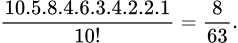
Chọn đáp án D.
Đáp án: D
Câu 28 [792276]: Có 6 chiếc ghế được kê thành một hàng ngang. Xếp ngẫu nhiên 6 học sinh, gồm 3 học sinh lớp 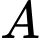 , 2 học sinh lớp
, 2 học sinh lớp 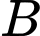 và 1 học sinh lớp
và 1 học sinh lớp  ngồi vào hàng ghế đó, sao cho mỗi ghế có đúng một học sinh. Xác suất để học sinh lớp
ngồi vào hàng ghế đó, sao cho mỗi ghế có đúng một học sinh. Xác suất để học sinh lớp  chỉ ngồi cạnh học sinh lớp
chỉ ngồi cạnh học sinh lớp 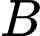 bằng
bằng
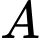 , 2 học sinh lớp
, 2 học sinh lớp 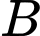 và 1 học sinh lớp
và 1 học sinh lớp  ngồi vào hàng ghế đó, sao cho mỗi ghế có đúng một học sinh. Xác suất để học sinh lớp
ngồi vào hàng ghế đó, sao cho mỗi ghế có đúng một học sinh. Xác suất để học sinh lớp  chỉ ngồi cạnh học sinh lớp
chỉ ngồi cạnh học sinh lớp 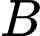 bằng
bằng A, 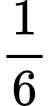 .
.
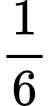 .
.B, 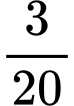 .
.
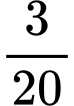 .
.C, 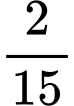 .
.
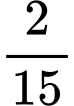 .
.D, 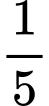 .
.
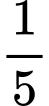 .
.
Chọn D
Xếp ngẫu nhiên 6 học sinh thành hàng ngang, không gian mẫu có số phần tử là: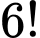 .
.
Gọi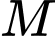 là biến cố “học sinh lớp
là biến cố “học sinh lớp  chỉ ngồi cạnh học sinh lớp
chỉ ngồi cạnh học sinh lớp 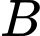 ”.
”.
Xét các trường hợp:
Trường hợp 1. Học sinh lớp ngồi đầu dãy
ngồi đầu dãy
+ Chọn vị trí cho học sinh lớp có 2 cách.
có 2 cách.
+ Chọn 1 học sinh lớp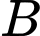 ngồi cạnh học sinh lớp
ngồi cạnh học sinh lớp  có 2 cách.
có 2 cách.
+ Hoán vị các học sinh còn lại cho nhau có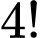 cách.
cách.
Trường hợp này thu được: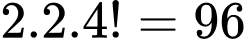 cách.
cách.
Trường hợp 2. Học sinh lớp ngồi giữa hai học sinh lớp
ngồi giữa hai học sinh lớp 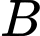 , ta gộp thành 1 nhóm, khi đó:
, ta gộp thành 1 nhóm, khi đó:
+ Hoán vị 4 phần tử gồm 3 học sinh lớp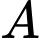 và nhóm gồm học sinh lớp
và nhóm gồm học sinh lớp 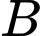 và lớp
và lớp  có:
có: 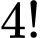 cách.
cách.
+ Hoán vị hai học sinh lớp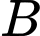 cho nhau có:
cho nhau có: 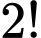 cách.
cách.
Trường hợp này thu được: cách.
cách.
Như vậy số phần tử của biến cố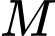 là:
là: 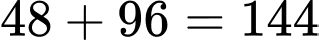 .
.
Xác suất của biến cố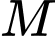 là
là 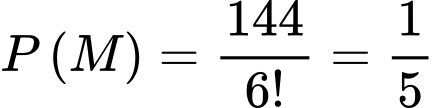 . Đáp án: D
. Đáp án: D
Xếp ngẫu nhiên 6 học sinh thành hàng ngang, không gian mẫu có số phần tử là:
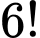 .
.Gọi
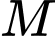 là biến cố “học sinh lớp
là biến cố “học sinh lớp  chỉ ngồi cạnh học sinh lớp
chỉ ngồi cạnh học sinh lớp 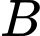 ”.
”.Xét các trường hợp:
Trường hợp 1. Học sinh lớp
 ngồi đầu dãy
ngồi đầu dãy+ Chọn vị trí cho học sinh lớp
 có 2 cách.
có 2 cách. + Chọn 1 học sinh lớp
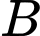 ngồi cạnh học sinh lớp
ngồi cạnh học sinh lớp  có 2 cách.
có 2 cách. + Hoán vị các học sinh còn lại cho nhau có
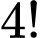 cách.
cách. Trường hợp này thu được:
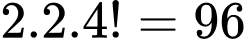 cách.
cách. Trường hợp 2. Học sinh lớp
 ngồi giữa hai học sinh lớp
ngồi giữa hai học sinh lớp 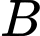 , ta gộp thành 1 nhóm, khi đó:
, ta gộp thành 1 nhóm, khi đó: + Hoán vị 4 phần tử gồm 3 học sinh lớp
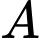 và nhóm gồm học sinh lớp
và nhóm gồm học sinh lớp 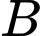 và lớp
và lớp  có:
có: 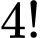 cách.
cách. + Hoán vị hai học sinh lớp
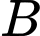 cho nhau có:
cho nhau có: 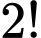 cách.
cách. Trường hợp này thu được:
 cách.
cách. Như vậy số phần tử của biến cố
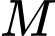 là:
là: 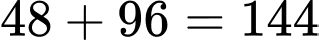 .
.Xác suất của biến cố
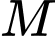 là
là 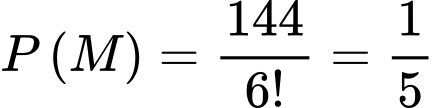 . Đáp án: D
. Đáp án: D
Câu 29 [792277]: Cho đa giác đều 12 đỉnh nội tiếp đường tròn tâm 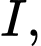 chọn ngẫu nhiên 3 đỉnh của đa giác đó. Tính xác suất để 3 đỉnh được chọn tạo thành một tam giác không có cạnh nào là cạnh của đa giác đã cho.
chọn ngẫu nhiên 3 đỉnh của đa giác đó. Tính xác suất để 3 đỉnh được chọn tạo thành một tam giác không có cạnh nào là cạnh của đa giác đã cho.
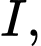 chọn ngẫu nhiên 3 đỉnh của đa giác đó. Tính xác suất để 3 đỉnh được chọn tạo thành một tam giác không có cạnh nào là cạnh của đa giác đã cho.
chọn ngẫu nhiên 3 đỉnh của đa giác đó. Tính xác suất để 3 đỉnh được chọn tạo thành một tam giác không có cạnh nào là cạnh của đa giác đã cho. A, 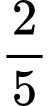 .
.
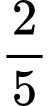 .
.B, 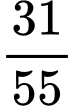 .
.
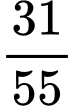 .
.C, 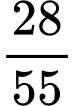 .
.
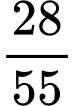 .
.D, 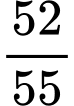 .
.
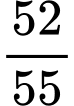 .
.
Chọn C
Số tam giác được tạo thành là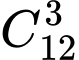 .
.
Số tam giác có chung 1 cạnh với đa giác là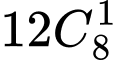 .
.
Số tam giác có chung 2 cạnh với đa giác là .
.
Vậy xác suất để được tam giác không có chung cạnh với đa giác là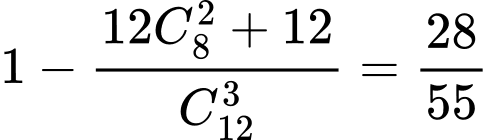 . Đáp án: C
. Đáp án: C
Số tam giác được tạo thành là
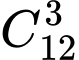 .
.Số tam giác có chung 1 cạnh với đa giác là
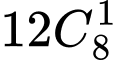 .
.Số tam giác có chung 2 cạnh với đa giác là
 .
.Vậy xác suất để được tam giác không có chung cạnh với đa giác là
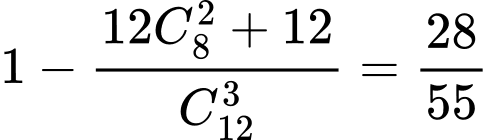 . Đáp án: C
. Đáp án: C
Câu 30 [792290]: Cho một đa giác đều 18 đỉnh nội tiếp trong một đường tròn tâm  . Gọi
. Gọi 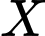 là tập hợp tất cả các tam giác có các đỉnh là các đỉnh của đa giác trên. Tính xác suất
là tập hợp tất cả các tam giác có các đỉnh là các đỉnh của đa giác trên. Tính xác suất 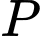 để chọn được một tam giác từ tập
để chọn được một tam giác từ tập 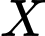 là tam giác cân nhưng không phải tam giác đều.
là tam giác cân nhưng không phải tam giác đều.
 . Gọi
. Gọi 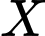 là tập hợp tất cả các tam giác có các đỉnh là các đỉnh của đa giác trên. Tính xác suất
là tập hợp tất cả các tam giác có các đỉnh là các đỉnh của đa giác trên. Tính xác suất 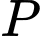 để chọn được một tam giác từ tập
để chọn được một tam giác từ tập 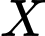 là tam giác cân nhưng không phải tam giác đều.
là tam giác cân nhưng không phải tam giác đều. A, 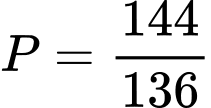 .
.
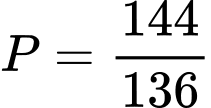 .
.B, 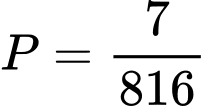 .
.
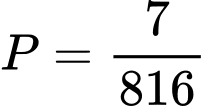 .
.C, 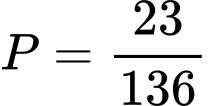 .
.
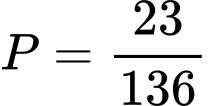 .
.D, 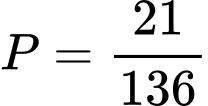 .
.
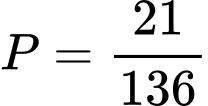 .
.
Chọn C
Số phần tử của không gian mẫu là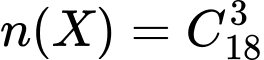 .
.
Ký hiệu đa giác là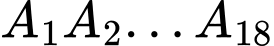 nội tiếp đường tròn
nội tiếp đường tròn  , xét đường kính
, xét đường kính 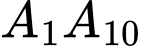 khi đó số tam giác cân có đỉnh cân là
khi đó số tam giác cân có đỉnh cân là 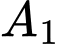 hoặc
hoặc 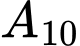 là
là 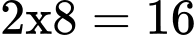 (tam giác cân); Mà có tất cả là 9 đường kính do vậy số tam giác cân có các đỉnh là đỉnh của đa giác là
(tam giác cân); Mà có tất cả là 9 đường kính do vậy số tam giác cân có các đỉnh là đỉnh của đa giác là 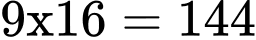 (tam giác cân).
(tam giác cân).
Ta lại có số tam giác đều có các đỉnh là đỉnh của đa giác đều 18 đỉnh là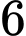 .
.
Vậy xác suất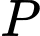 để chọn được một tam giác từ tập
để chọn được một tam giác từ tập 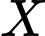 là tam giác cân nhưng không phải tam giác đều là
là tam giác cân nhưng không phải tam giác đều là 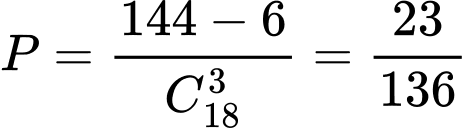 . Đáp án: C
. Đáp án: C
Số phần tử của không gian mẫu là
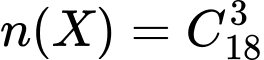 .
.Ký hiệu đa giác là
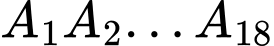 nội tiếp đường tròn
nội tiếp đường tròn  , xét đường kính
, xét đường kính 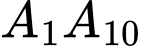 khi đó số tam giác cân có đỉnh cân là
khi đó số tam giác cân có đỉnh cân là 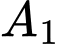 hoặc
hoặc 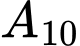 là
là 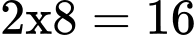 (tam giác cân); Mà có tất cả là 9 đường kính do vậy số tam giác cân có các đỉnh là đỉnh của đa giác là
(tam giác cân); Mà có tất cả là 9 đường kính do vậy số tam giác cân có các đỉnh là đỉnh của đa giác là 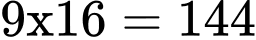 (tam giác cân).
(tam giác cân). Ta lại có số tam giác đều có các đỉnh là đỉnh của đa giác đều 18 đỉnh là
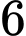 .
.Vậy xác suất
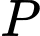 để chọn được một tam giác từ tập
để chọn được một tam giác từ tập 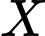 là tam giác cân nhưng không phải tam giác đều là
là tam giác cân nhưng không phải tam giác đều là 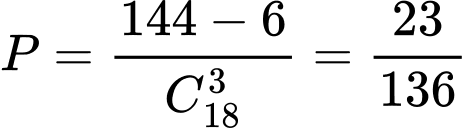 . Đáp án: C
. Đáp án: C