Đáp án Bài tập tự luyện
Câu 1 [237733]: Số phần tử của tập hợp  là
là
 là
là A, 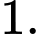
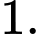
B, 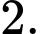
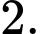
C, 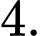
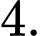
D, 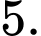
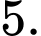
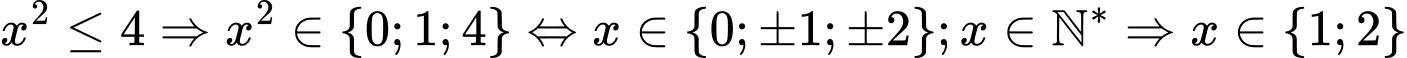 . Chọn B. Đáp án: B
. Chọn B. Đáp án: B
Câu 2 [240079]: Cho hai tập hợp 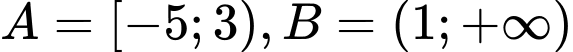 . Khi đó
. Khi đó  là tập nào sau đây?
là tập nào sau đây?
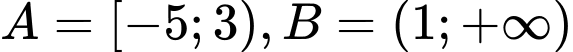 . Khi đó
. Khi đó  là tập nào sau đây?
là tập nào sau đây? A, 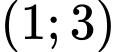 .
.
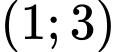 .
.B, 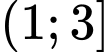 .
.
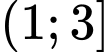 .
.C, 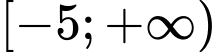 .
.
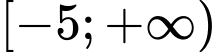 .
.D, 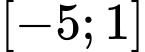 .
.
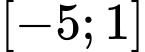 .
.
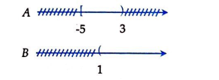
Ta có thể biểu diễn hai tập hợp A và B, tập  là phần không bị gạch ở cả A và B nên
là phần không bị gạch ở cả A và B nên 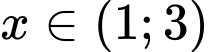 .
Đáp án A.
.
Đáp án A.
 Đáp án: A
Đáp án: A
 là phần không bị gạch ở cả A và B nên
là phần không bị gạch ở cả A và B nên 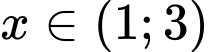 .
Đáp án A.
.
Đáp án A. Đáp án: A
Đáp án: A
Câu 3 [237734]: Hãy liệt kê các phần tử của tập 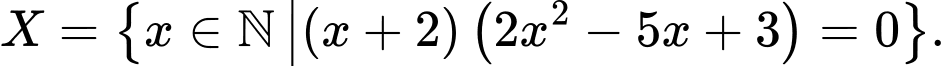
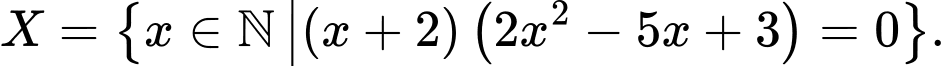
A, 

B, 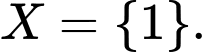
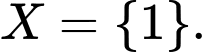
C, 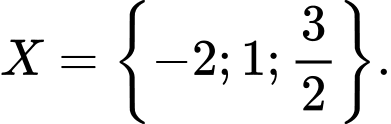
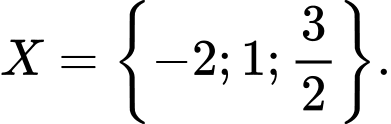
D, 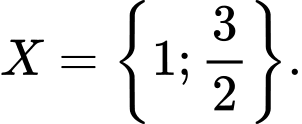
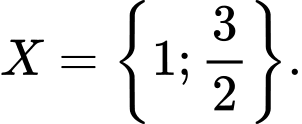
Ta có 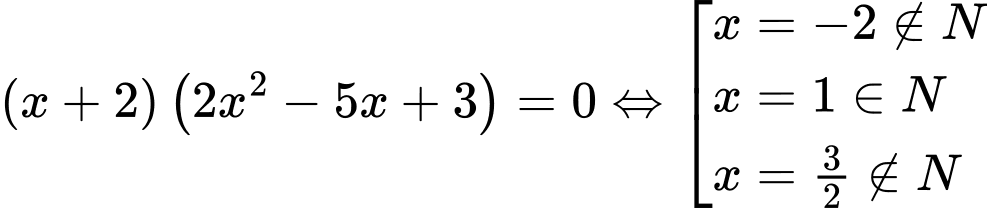 nên
nên 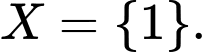 Chọn B.
Đáp án: B
Chọn B.
Đáp án: B
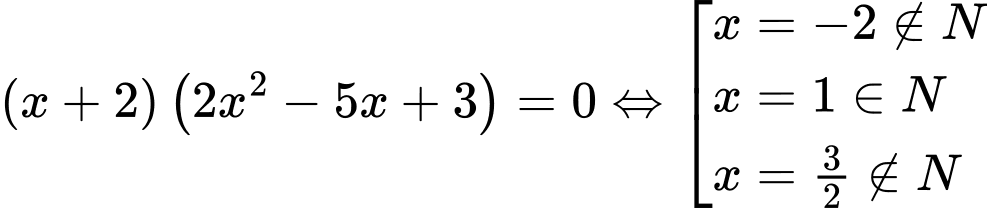 nên
nên 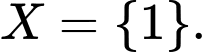 Chọn B.
Đáp án: B
Chọn B.
Đáp án: B
Câu 4 [237741]: Trong các tập hợp sau, tập hợp nào khác rỗng?
A, 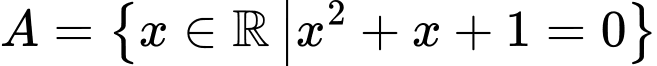 .
.
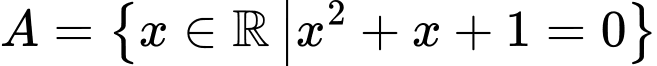 .
.B, 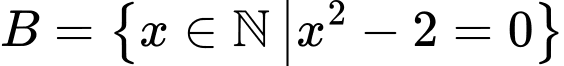 .
.
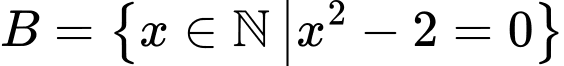 .
.C, 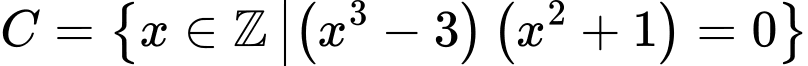 .
.
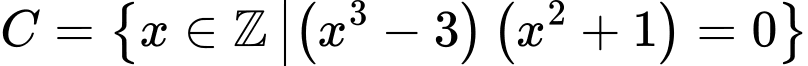 .
.D, 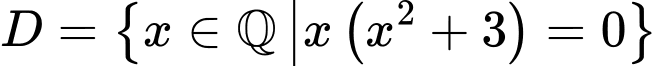 .
.
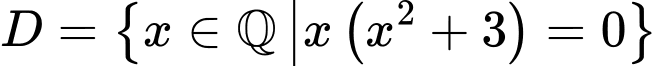 .
.
Chọn D.
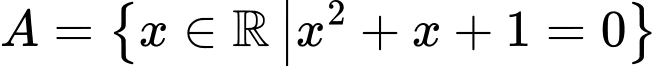 . Ta có
. Ta có 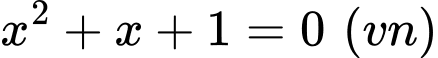
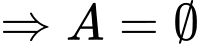 .
.
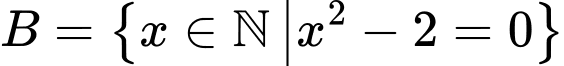 . Ta có
. Ta có 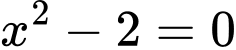
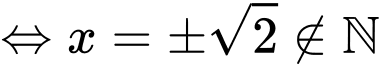
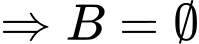
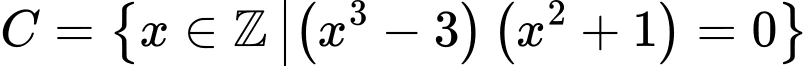 . Ta có
. Ta có 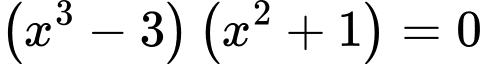
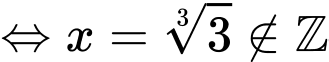
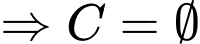
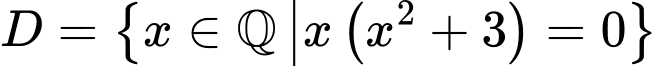 . Ta có
. Ta có 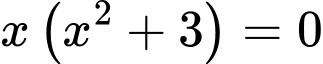
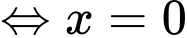
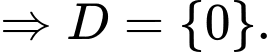 Đáp án: D
Đáp án: D
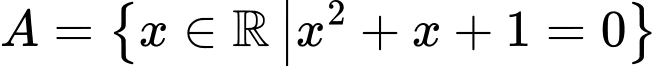 . Ta có
. Ta có 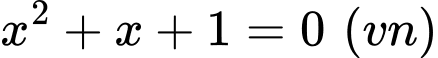
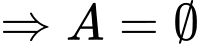 .
.
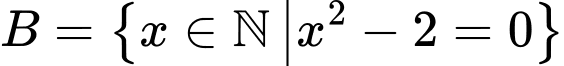 . Ta có
. Ta có 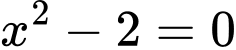
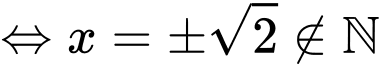
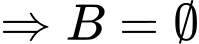
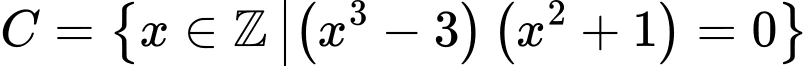 . Ta có
. Ta có 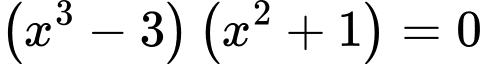
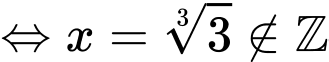
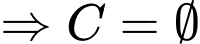
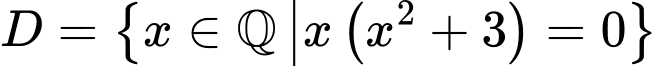 . Ta có
. Ta có 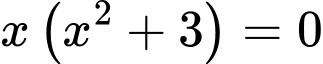
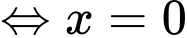
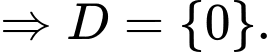 Đáp án: D
Đáp án: D
Câu 5 [237752]: Cho tập hợp 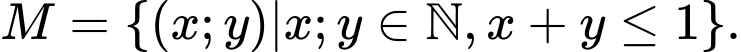 Hỏi tập
Hỏi tập 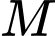 có bao nhiêu phần tử?
có bao nhiêu phần tử?
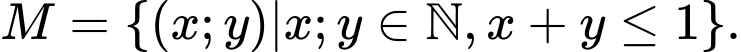 Hỏi tập
Hỏi tập 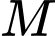 có bao nhiêu phần tử?
có bao nhiêu phần tử? A, 4.
B, 1.
C, 2.
D, 3.
Vì 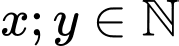 nên x, y thuộc vào tập
nên x, y thuộc vào tập 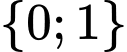
Vậy cặp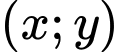 là
là 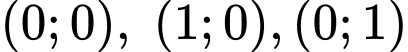 thỏa mãn
thỏa mãn 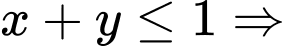 Có 3 cặp hay M có 3 phần tử.
Đáp án D. Đáp án: D
Có 3 cặp hay M có 3 phần tử.
Đáp án D. Đáp án: D
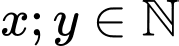 nên x, y thuộc vào tập
nên x, y thuộc vào tập 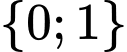
Vậy cặp
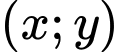 là
là 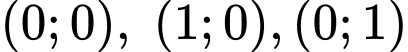 thỏa mãn
thỏa mãn 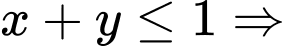 Có 3 cặp hay M có 3 phần tử.
Đáp án D. Đáp án: D
Có 3 cặp hay M có 3 phần tử.
Đáp án D. Đáp án: D
Câu 6 [237766]: Cho tập hợp A có 4 phần tử. Hỏi tập A có bao nhiêu tập con khác rỗng?
A, 16.
B, 15.
C, 12.
D, 7.
Đáp án B.
Vì số tập con của tập 4 phần tử là 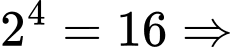 Số tập con khác rỗng là
Số tập con khác rỗng là 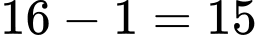 . Đáp án: B
. Đáp án: B
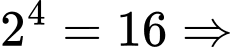 Số tập con khác rỗng là
Số tập con khác rỗng là 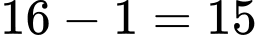 . Đáp án: B
. Đáp án: B
Câu 7 [237780]: Tập 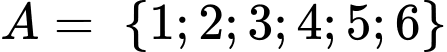 có bao nhiêu tập hợp con có đúng hai phần tử?
có bao nhiêu tập hợp con có đúng hai phần tử?
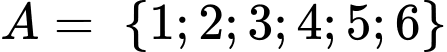 có bao nhiêu tập hợp con có đúng hai phần tử?
có bao nhiêu tập hợp con có đúng hai phần tử? A, 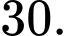
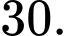
B, 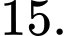
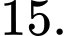
C, 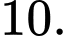
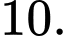
D, 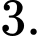
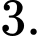
Các tập con có hai phần tử của tập 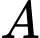 là:
là: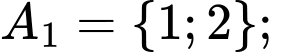
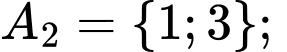
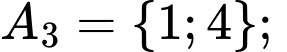
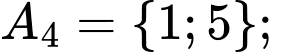
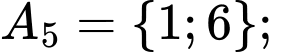
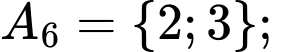
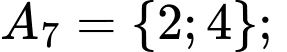
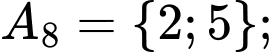
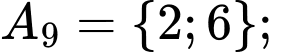
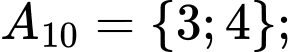
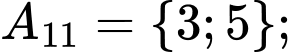
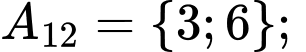
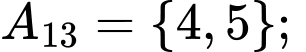
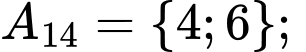
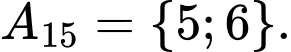 Chọn B. Đáp án: B
Chọn B. Đáp án: B
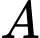 là:
là: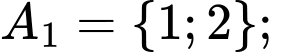
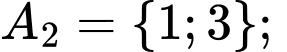
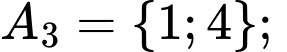
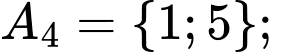
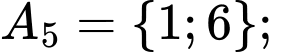
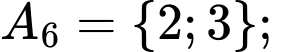
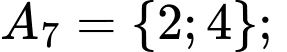
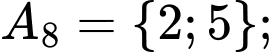
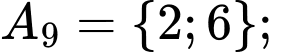
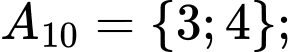
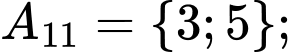
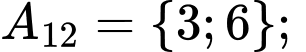
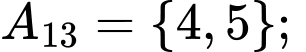
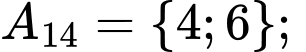
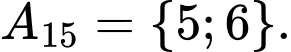 Chọn B. Đáp án: B
Chọn B. Đáp án: B
Câu 8 [240051]: Tập 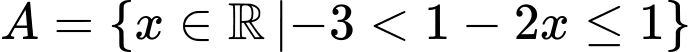 được viết lại dưới dạng đoạn, khoảng, nửa khoảng là
được viết lại dưới dạng đoạn, khoảng, nửa khoảng là
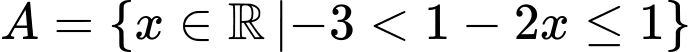 được viết lại dưới dạng đoạn, khoảng, nửa khoảng là
được viết lại dưới dạng đoạn, khoảng, nửa khoảng là A, 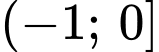 .
.
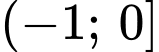 .
.B, 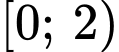 .
.
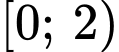 .
.C, 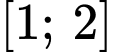 .
.
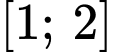 .
.D, 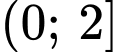 .
.
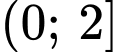 .
.
Chọn B
Ta có: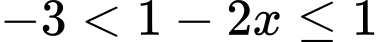
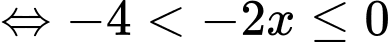
 .
.
Do đó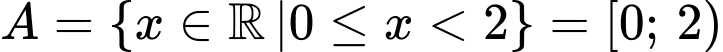 . Đáp án: B
. Đáp án: B
Ta có:
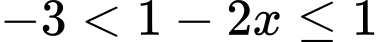
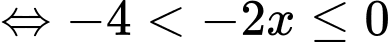
 .
.
Do đó
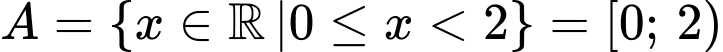 . Đáp án: B
. Đáp án: B
Câu 9 [237788]: Số tập con của tập hợp: 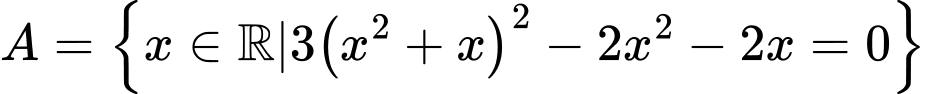 là
là
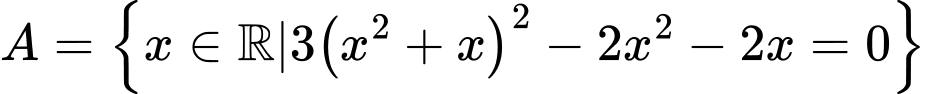 là
là A, 16.
B, 8.
C, 12.
D, 10.
Đáp án. A.
Giải phương trình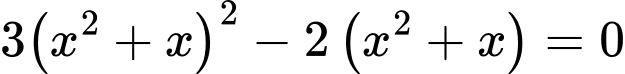
Đặt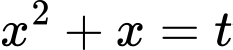 ta có phương trình
ta có phương trình 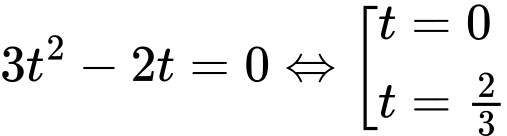
Với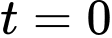 ta có
ta có 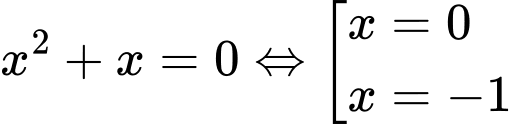
Với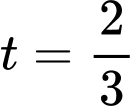 ta có:
ta có: 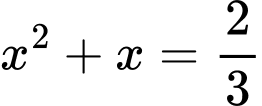
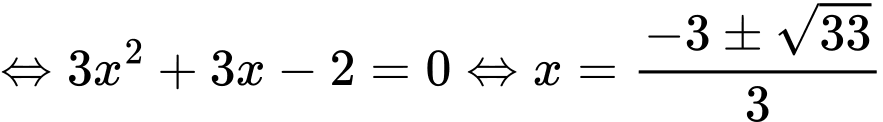 Vậy A có 4 phần tử suy ra số tập con của A là
Vậy A có 4 phần tử suy ra số tập con của A là 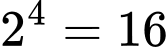 . Đáp án: A
. Đáp án: A
Giải phương trình
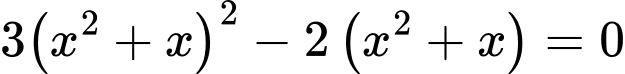
Đặt
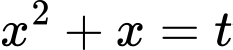 ta có phương trình
ta có phương trình 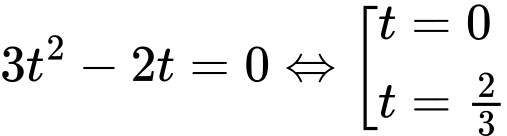
Với
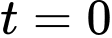 ta có
ta có 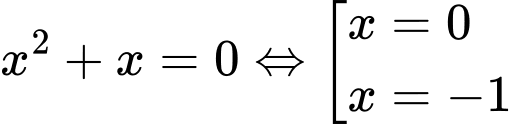
Với
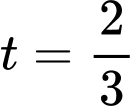 ta có:
ta có: 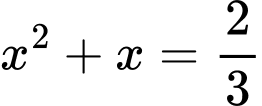
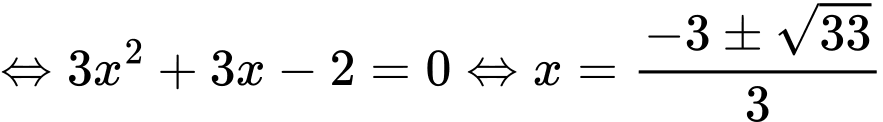 Vậy A có 4 phần tử suy ra số tập con của A là
Vậy A có 4 phần tử suy ra số tập con của A là 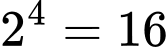 . Đáp án: A
. Đáp án: A
Câu 10 [237446]: Cho hai tập hợp 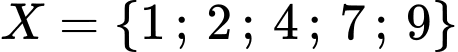 và
và 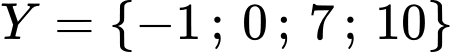 . Tập hợp
. Tập hợp  có bao nhiêu phần tử?
có bao nhiêu phần tử?
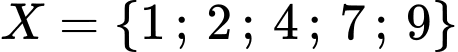 và
và 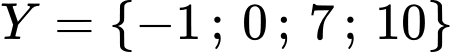 . Tập hợp
. Tập hợp  có bao nhiêu phần tử?
có bao nhiêu phần tử? A, 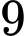 .
.
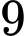 .
.B, 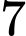 .
.
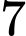 .
.C, 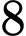 .
.
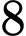 .
.D,  .
.
 .
.
Chọn C
Ta có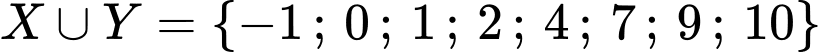 . Do đó
. Do đó  có
có 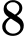 phần tử. Đáp án: C
phần tử. Đáp án: C
Ta có
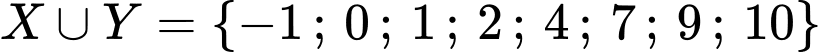 . Do đó
. Do đó  có
có 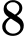 phần tử. Đáp án: C
phần tử. Đáp án: C
Câu 11 [237468]: Cho 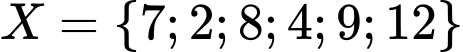 ;
;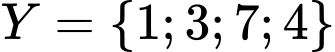 . Tập nào sau đây bằng tập
. Tập nào sau đây bằng tập  ?
?
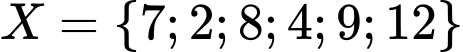 ;
;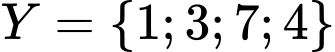 . Tập nào sau đây bằng tập
. Tập nào sau đây bằng tập  ?
? A, 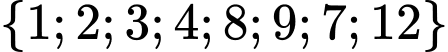 .
.
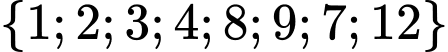 .
.B, 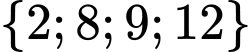 .
.
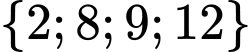 .
.C, 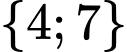 .
.
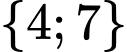 .
.D, 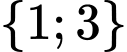 .
.
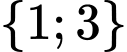 .
.
Chọn C
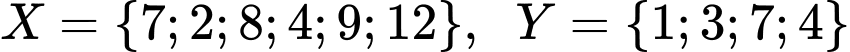
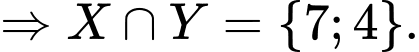 . Đáp án: C
. Đáp án: C
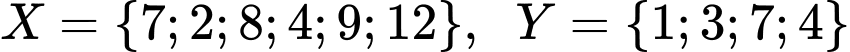
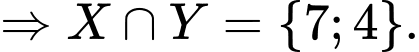 . Đáp án: C
. Đáp án: C
Câu 12 [237441]: Cho hai tập hợp 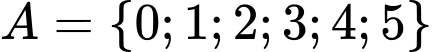 và
và 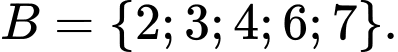 Khẳng định nào sau đây đúng?
Khẳng định nào sau đây đúng?
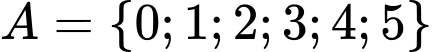 và
và 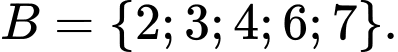 Khẳng định nào sau đây đúng?
Khẳng định nào sau đây đúng? A, 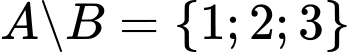 .
.
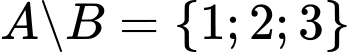 .
.B, 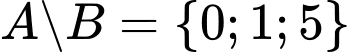 .
.
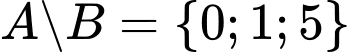 .
.C, 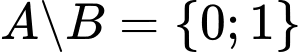 .
.
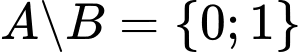 .
.D, 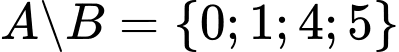 .
.
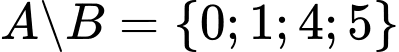 .
.
Kí hiệu 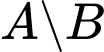 được hiểu là tập hợp các phần tử thuộc
được hiểu là tập hợp các phần tử thuộc 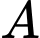 và không thuộc
và không thuộc 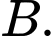
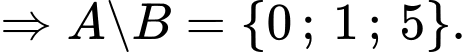 Chọn B. Đáp án: B
Chọn B. Đáp án: B
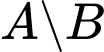 được hiểu là tập hợp các phần tử thuộc
được hiểu là tập hợp các phần tử thuộc 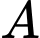 và không thuộc
và không thuộc 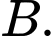
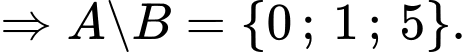 Chọn B. Đáp án: B
Chọn B. Đáp án: B
Câu 13 [240081]: Cho hai tập hợp 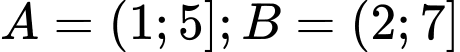 . Tập hợp
. Tập hợp 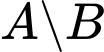 là
là
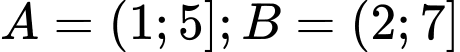 . Tập hợp
. Tập hợp 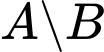 là
là A, 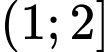 .
.
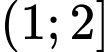 .
.B, 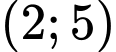 .
.
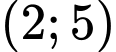 .
.C, 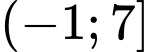 .
.
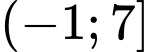 .
.D, 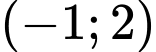 .
.
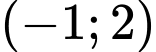 .
.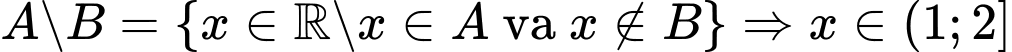 .
Đáp án A.
.
Đáp án A.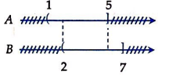 Đáp án: A
Đáp án: A
Câu 14 [237453]: Cho hai tập hợp 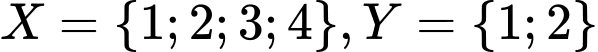 .
. 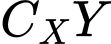 là tập hợp sau đây?
là tập hợp sau đây?
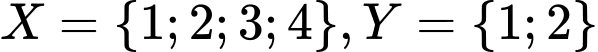 .
. 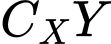 là tập hợp sau đây?
là tập hợp sau đây? A, 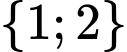 .
.
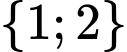 .
.B, 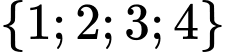 .
.
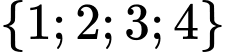 .
.C, 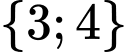 .
.
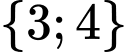 .
.D, 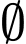 .
.
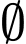 .
.
Vì  nên
nên 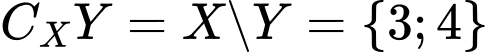
Đáp án. C. Đáp án: C
 nên
nên 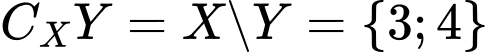
Đáp án. C. Đáp án: C
Câu 15 [240086]: Cho 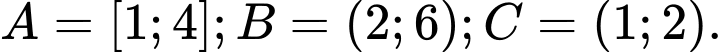 Tìm
Tìm 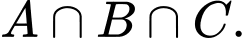
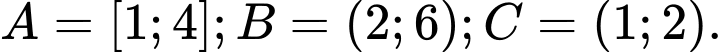 Tìm
Tìm 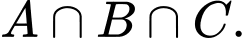
A, 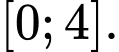
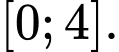
B, 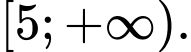
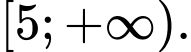
C, 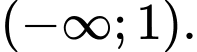
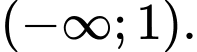
D, 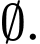
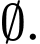
Chọn D
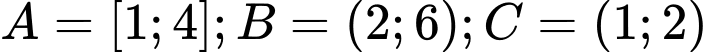
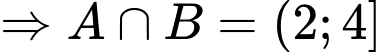
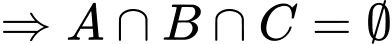 . Đáp án: D
. Đáp án: D
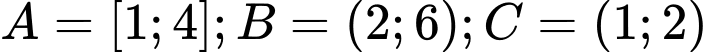
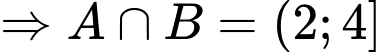
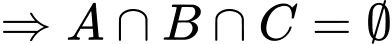 . Đáp án: D
. Đáp án: D
Câu 16 [237476]: Cho 2 tập hợp 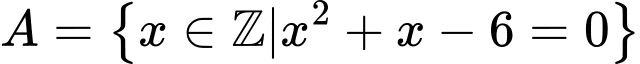 ,
, 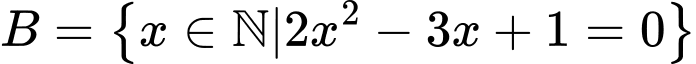 . Chọn khẳng định đúng.
. Chọn khẳng định đúng.
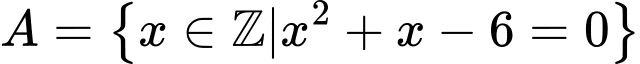 ,
, 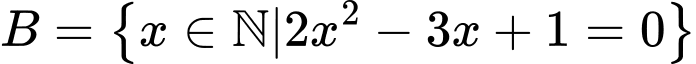 . Chọn khẳng định đúng.
. Chọn khẳng định đúng. A, 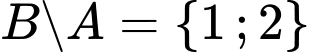 .
.
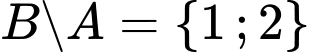 .
.B, 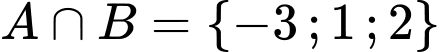 .
.
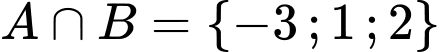 .
.C, 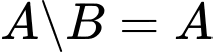 .
.
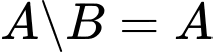 .
.D, 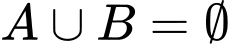 .
.
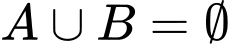 .
.
Chọn C
Ta có:
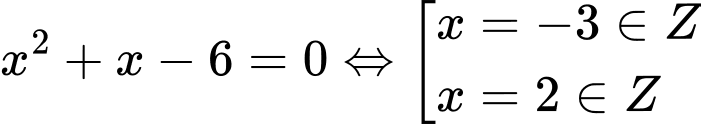

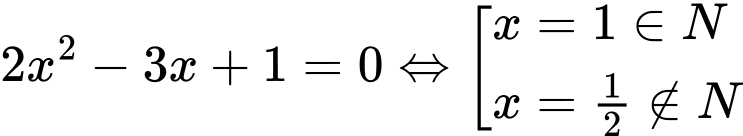
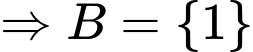
Suy ra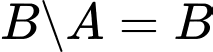 ;
; 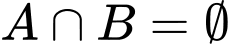 ;
; 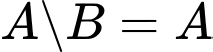 ;
; 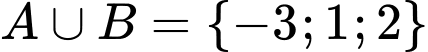 .
Đáp án: C
.
Đáp án: C
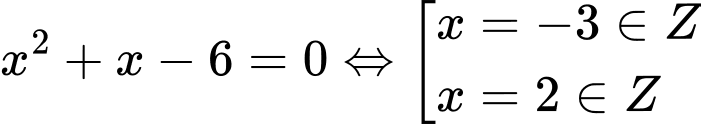

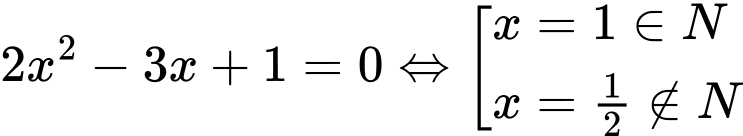
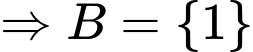
Suy ra
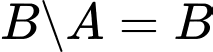 ;
; 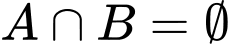 ;
; 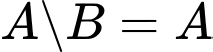 ;
; 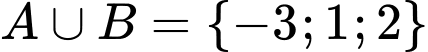 .
Đáp án: C
.
Đáp án: C
Câu 17 [237470]: Cho 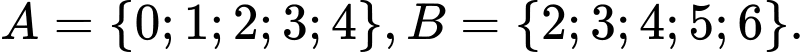 Tập hợp
Tập hợp  bằng
bằng
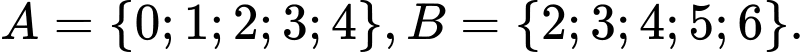 Tập hợp
Tập hợp  bằng
bằng A, 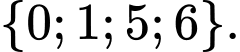
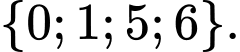
B, 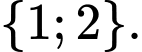
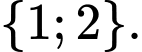
C, 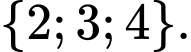
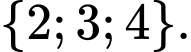
D, 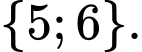
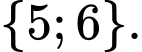
Chọn A
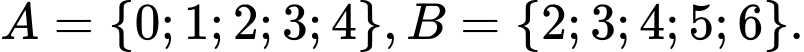
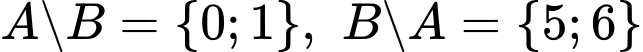
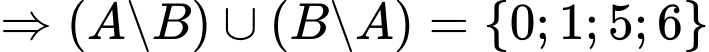 . Đáp án: A
. Đáp án: A
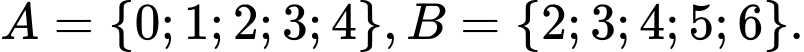
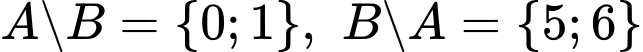
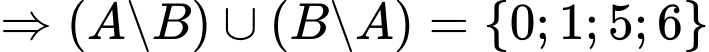 . Đáp án: A
. Đáp án: A
Câu 18 [237483]: Cho 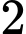 tập hợp
tập hợp 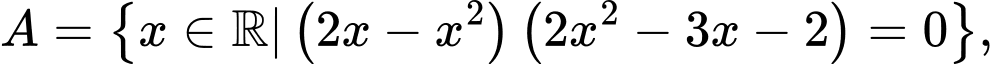
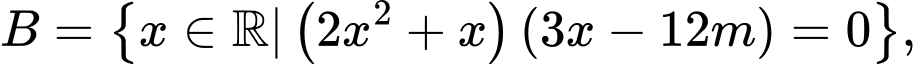 với giá trị nào của
với giá trị nào của 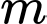 thì
thì 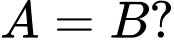
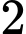 tập hợp
tập hợp 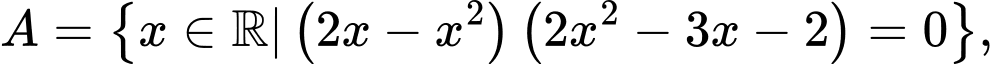
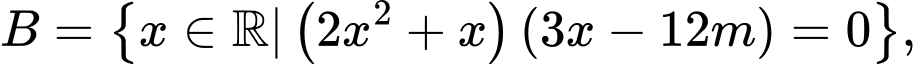 với giá trị nào của
với giá trị nào của 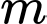 thì
thì 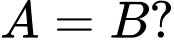
A, 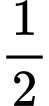 .
.
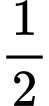 .
.B, 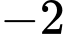 .
.
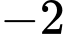 .
.C, 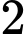 .
.
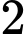 .
.D, 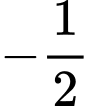 .
.
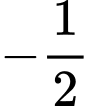 .
.
Chọn AXét tập hợp 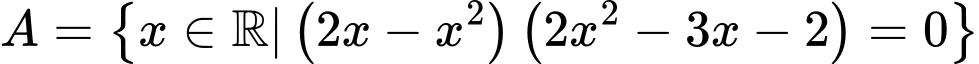 ta có:
ta có: 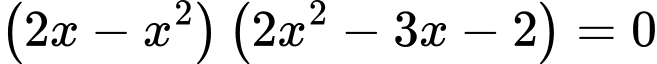
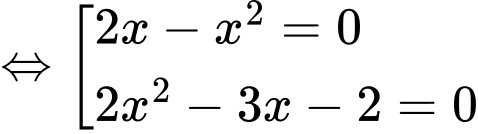
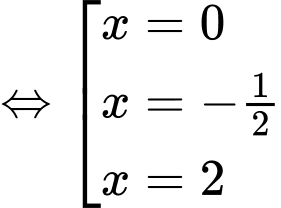
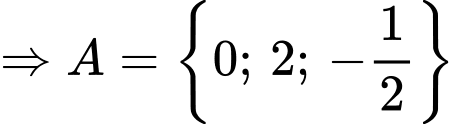 .
.
Xét tập hợp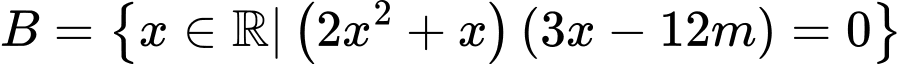
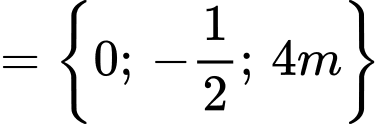 .
.
Để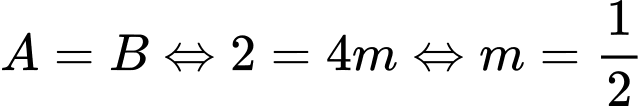 . Đáp án: A
. Đáp án: A
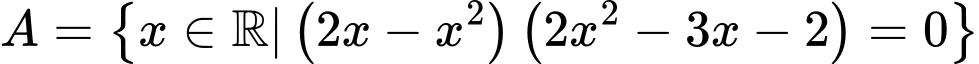 ta có:
ta có: 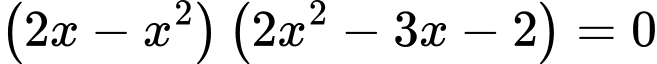
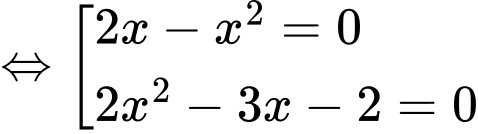
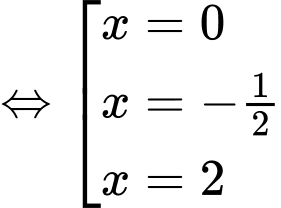
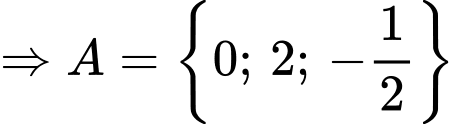 .
.Xét tập hợp
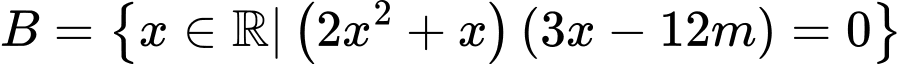
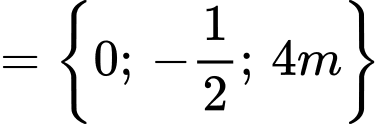 .
.Để
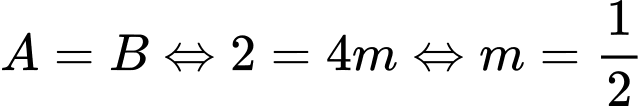 . Đáp án: A
. Đáp án: A
Câu 19 [237547]: Mỗi học sinh lớp 10B đều chơi bóng đá hoặc bóng chuyền. Biết rằng có 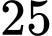 bạn chơi bóng đá,
bạn chơi bóng đá, 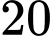 bạn chơi bóng chuyền và
bạn chơi bóng chuyền và  bạn chơi cả hai môn. Hỏi lớp 10B có bao nhiêu học sinh?
bạn chơi cả hai môn. Hỏi lớp 10B có bao nhiêu học sinh?
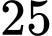 bạn chơi bóng đá,
bạn chơi bóng đá, 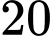 bạn chơi bóng chuyền và
bạn chơi bóng chuyền và  bạn chơi cả hai môn. Hỏi lớp 10B có bao nhiêu học sinh?
bạn chơi cả hai môn. Hỏi lớp 10B có bao nhiêu học sinh? A, 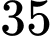 .
.
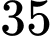 .
.B, 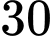 .
.
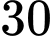 .
.C, 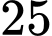 .
.
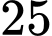 .
.D, 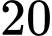 .
.
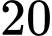 .
.
Chọn A
Giả sử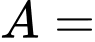 “Hs chơi bóng đá”.
“Hs chơi bóng đá”.
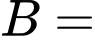 “Hs chơi bóng chuyền”
“Hs chơi bóng chuyền”
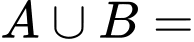 “Hs chơi bóng đá hoặc bóng chuyền”
“Hs chơi bóng đá hoặc bóng chuyền”
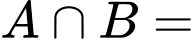 “Hs chơi cả hai môn”.
“Hs chơi cả hai môn”.
Số phần tử của là:
là: 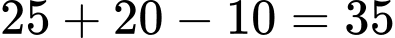 .
.
Số Hs chơi bóng đá hoặc bóng chuyền là số Hs của lớp: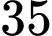 . Đáp án: A
. Đáp án: A
Giả sử
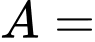 “Hs chơi bóng đá”.
“Hs chơi bóng đá”.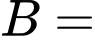 “Hs chơi bóng chuyền”
“Hs chơi bóng chuyền”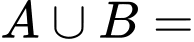 “Hs chơi bóng đá hoặc bóng chuyền”
“Hs chơi bóng đá hoặc bóng chuyền”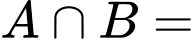 “Hs chơi cả hai môn”.
“Hs chơi cả hai môn”.Số phần tử của
 là:
là: 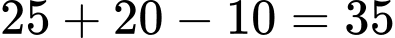 .
.Số Hs chơi bóng đá hoặc bóng chuyền là số Hs của lớp:
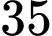 . Đáp án: A
. Đáp án: A
Câu 20 [237541]: Một lớp học có 25 học sinh chơi bóng đá, 23 học sinh chơi bóng bàn, 14 học sinh chơi cả bóng đá và bóng bàn và 6 học sinh không chơi môn nào. Số học sinh chỉ chơi 1 môn thể thao là
A, 48.
B, 20.
C, 34.
D, 28.
Đáp án B.
Gọi A là tập hợp các học sinh chơi bóng đá
B là tập hợp các học sinh chơi bóng bàn
C là tập hợp các học sinh không chơi môn nào
Khi đó số học sinh chỉ chơi bóng đá là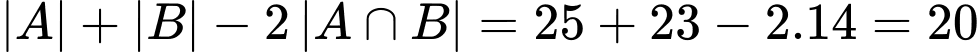 Đáp án: B
Đáp án: B
Gọi A là tập hợp các học sinh chơi bóng đá
B là tập hợp các học sinh chơi bóng bàn
C là tập hợp các học sinh không chơi môn nào
Khi đó số học sinh chỉ chơi bóng đá là
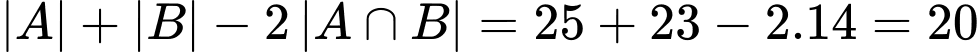 Đáp án: B
Đáp án: B
Câu 21 [237538]: Trong một lớp học có 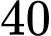 học sinh, trong đó có
học sinh, trong đó có 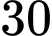 học sinh đạt học sinh giỏi môn Toán,
học sinh đạt học sinh giỏi môn Toán, 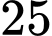 học sinh đạt học sinh giỏi môn Văn. Biết rằng chỉ có
học sinh đạt học sinh giỏi môn Văn. Biết rằng chỉ có 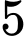 học sinh không đạt danh hiệu học sinh giỏi môn nào trong cả hai môn Toán và Văn. Hỏi có bao nhiêu học sinh chỉ học giỏi một môn trong hai môn Toán hoặc Văn?
học sinh không đạt danh hiệu học sinh giỏi môn nào trong cả hai môn Toán và Văn. Hỏi có bao nhiêu học sinh chỉ học giỏi một môn trong hai môn Toán hoặc Văn?
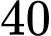 học sinh, trong đó có
học sinh, trong đó có 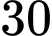 học sinh đạt học sinh giỏi môn Toán,
học sinh đạt học sinh giỏi môn Toán, 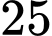 học sinh đạt học sinh giỏi môn Văn. Biết rằng chỉ có
học sinh đạt học sinh giỏi môn Văn. Biết rằng chỉ có 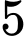 học sinh không đạt danh hiệu học sinh giỏi môn nào trong cả hai môn Toán và Văn. Hỏi có bao nhiêu học sinh chỉ học giỏi một môn trong hai môn Toán hoặc Văn?
học sinh không đạt danh hiệu học sinh giỏi môn nào trong cả hai môn Toán và Văn. Hỏi có bao nhiêu học sinh chỉ học giỏi một môn trong hai môn Toán hoặc Văn? A, 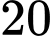 .
.
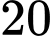 .
.B,  .
.
 .
.C,  .
.
 .
.D,  .
.
 .
.
B.
Gọi là tập hợp các học sinh đạt học sinh giỏi môn Toán.
là tập hợp các học sinh đạt học sinh giỏi môn Toán.
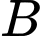 là tập hợp các học sinh đạt học sinh giỏi môn Văn.
là tập hợp các học sinh đạt học sinh giỏi môn Văn.
 là tập hợp các học sinh đạt học sinh giỏi cả hai môn Toán và Văn.
là tập hợp các học sinh đạt học sinh giỏi cả hai môn Toán và Văn.
Số học sinh đạt học sinh giỏi môn Toán, Văn của lớp là: 40-5=35 (học sinh).
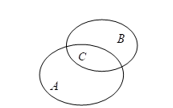
Theo sơ đồ Ven ta có: .
.
Do vậy ta có:
Số học sinh chỉ giỏi môn Toán là: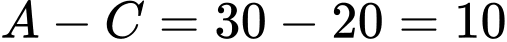 (học sinh).
(học sinh).
Số học sinh chỉ giỏi môn Văn là: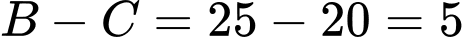 (học sinh).
Nên số học sinh chỉ giỏi một trong hai môn Toán hoặc Văn là:
(học sinh).
Nên số học sinh chỉ giỏi một trong hai môn Toán hoặc Văn là: 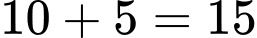 (học sinh).
Vậy ta chọn đáp án
(học sinh).
Vậy ta chọn đáp án 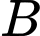 . Đáp án: B
. Đáp án: B

Gọi
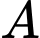 là tập hợp các học sinh đạt học sinh giỏi môn Toán.
là tập hợp các học sinh đạt học sinh giỏi môn Toán.
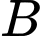 là tập hợp các học sinh đạt học sinh giỏi môn Văn.
là tập hợp các học sinh đạt học sinh giỏi môn Văn.
 là tập hợp các học sinh đạt học sinh giỏi cả hai môn Toán và Văn.
là tập hợp các học sinh đạt học sinh giỏi cả hai môn Toán và Văn.
Số học sinh đạt học sinh giỏi môn Toán, Văn của lớp là: 40-5=35 (học sinh).
Theo sơ đồ Ven ta có:
 .
.
Do vậy ta có:
Số học sinh chỉ giỏi môn Toán là:
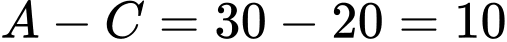 (học sinh).
(học sinh).
Số học sinh chỉ giỏi môn Văn là:
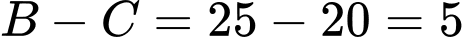 (học sinh).
Nên số học sinh chỉ giỏi một trong hai môn Toán hoặc Văn là:
(học sinh).
Nên số học sinh chỉ giỏi một trong hai môn Toán hoặc Văn là: 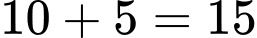 (học sinh).
Vậy ta chọn đáp án
(học sinh).
Vậy ta chọn đáp án 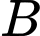 . Đáp án: B
. Đáp án: B
Câu 22 [237545]: Lớp 10A có 40 học sinh trong đó có 10 bạn học sinh giỏi Toán, 15 bạn học sinh giỏi Lý, và 22 bạn không giỏi môn học nào trong hai môn Toán, Lý. Hỏi lớp 10A có bao nhiêu bạn học sinh vừa giỏi Toán vừa giỏi Lý?
A, 7.
B, 25.
C, 10.
D, 18
Ta có tổng số học sinh giỏi Toán và Lý là:
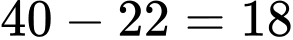 (học sinh)
(học sinh)
Suy ra số học sinh giỏi cả hai môn là:
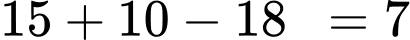 (học sinh)
(học sinh)
Chọn A. Đáp án: A
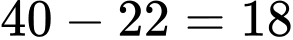 (học sinh)
(học sinh)Suy ra số học sinh giỏi cả hai môn là:
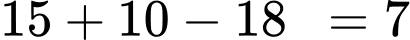 (học sinh)
(học sinh)Chọn A. Đáp án: A
Câu 23 [240128]: Cho hai tập hợp  và
và 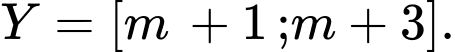 Tìm tất cả các giá trị
Tìm tất cả các giá trị 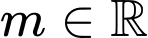 sao cho
sao cho 
 và
và 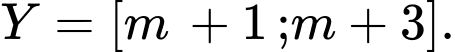 Tìm tất cả các giá trị
Tìm tất cả các giá trị 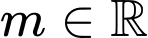 sao cho
sao cho 
A, 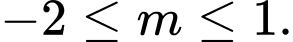
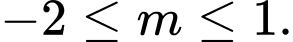
B, 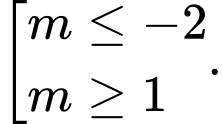
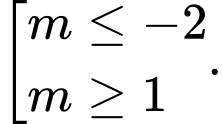
C, 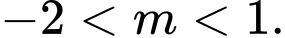
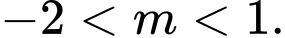
D, 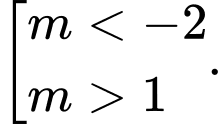
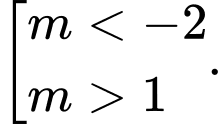
Chọn A

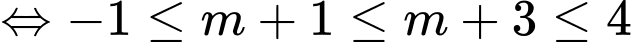

Vậy chọn đáp án A.
HS chọn đáp án B và D do đọc không kỹ đề hoặc hiểu sai khái niệm tập hợp con thành HS chọn đáp án C do hiểu khái niệm tập hợp con thành khái niệm tập hợp con thực sự. Đáp án: A
HS chọn đáp án C do hiểu khái niệm tập hợp con thành khái niệm tập hợp con thực sự. Đáp án: A

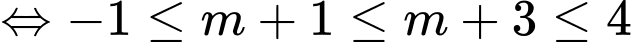

Vậy chọn đáp án A.
HS chọn đáp án B và D do đọc không kỹ đề hoặc hiểu sai khái niệm tập hợp con thành
 HS chọn đáp án C do hiểu khái niệm tập hợp con thành khái niệm tập hợp con thực sự. Đáp án: A
HS chọn đáp án C do hiểu khái niệm tập hợp con thành khái niệm tập hợp con thực sự. Đáp án: A
Câu 24 [240133]: Cho 2 tập khác rỗng 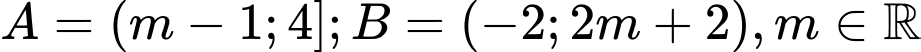 . Tìm m để
. Tìm m để 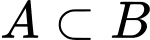 .
.
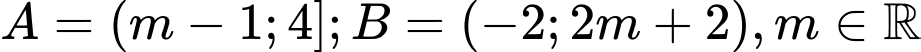 . Tìm m để
. Tìm m để 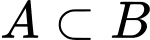 .
. A, 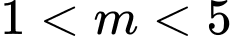 .
.
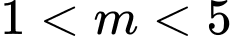 .
.B,  .
.
 .
.C, 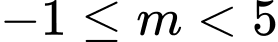 .
.
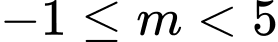 .
.D, 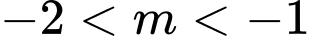 .
.
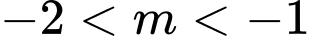 .
.
Chọn A
Với 2 tập khác rỗng ,
, 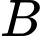 ta có điều kiện
ta có điều kiện 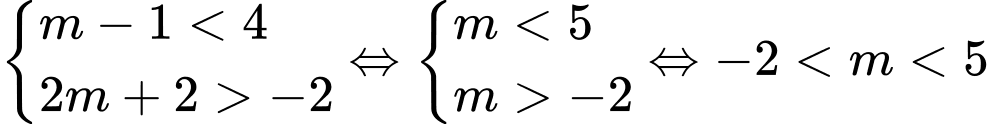 .
.
Để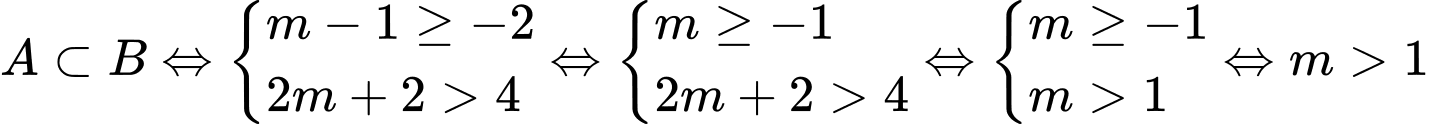 . So với điều kiện
. So với điều kiện 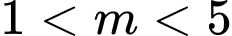 . Đáp án: A
. Đáp án: A
Với 2 tập khác rỗng
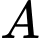 ,
, 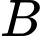 ta có điều kiện
ta có điều kiện 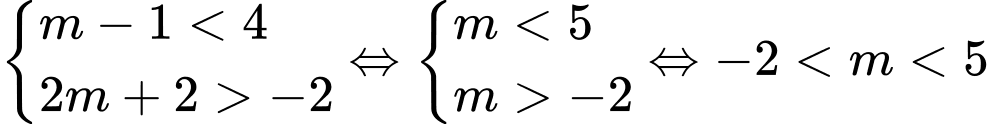 .
.
Để
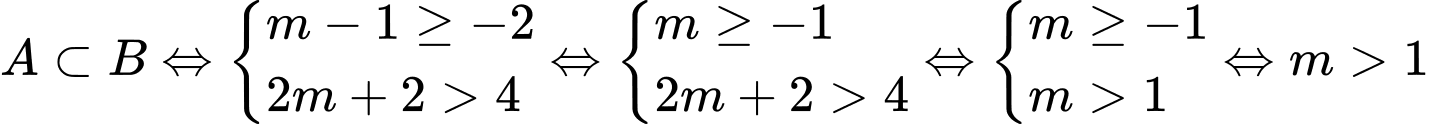 . So với điều kiện
. So với điều kiện 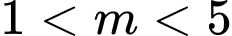 . Đáp án: A
. Đáp án: A
Câu 25 [240117]: Cho tập hợp 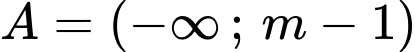 , tập
, tập 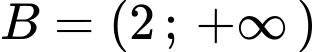 , tìm
, tìm 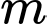 để
để 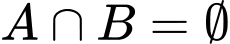 .
.
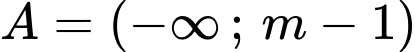 , tập
, tập 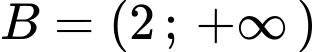 , tìm
, tìm 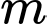 để
để 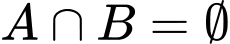 .
. A,  .
.
 .
.B,  .
.
 .
.C,  .
.
 .
.D,  .
.
 .
.
Chọn B
Biểu diễn 2 tập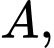
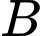 trên 2 trục số ta được:
trên 2 trục số ta được:

Suy ra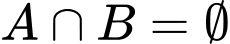
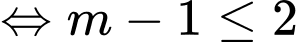
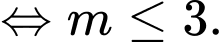 Đáp án: B
Đáp án: B
Biểu diễn 2 tập
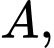
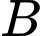 trên 2 trục số ta được:
trên 2 trục số ta được:
Suy ra
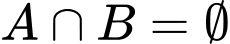
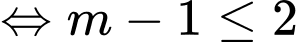
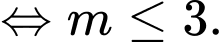 Đáp án: B
Đáp án: B
Câu 26 [240121]: Cho hai tập hợp 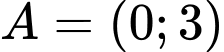 và
và 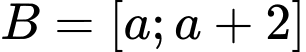 , với giá trị nào của
, với giá trị nào của 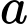 thì
thì 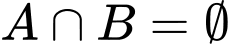 ?
?
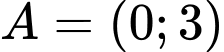 và
và 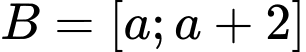 , với giá trị nào của
, với giá trị nào của 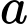 thì
thì 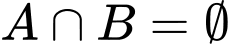 ?
? A, 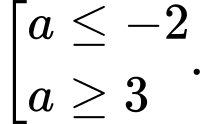
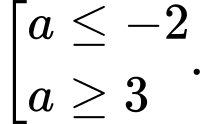
B, 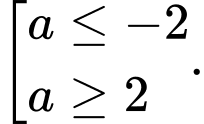
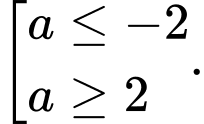
C, 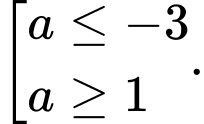
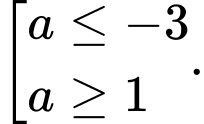
D, 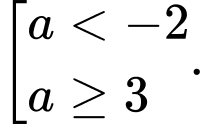
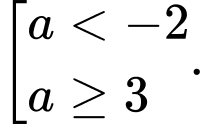
Chọn A
Để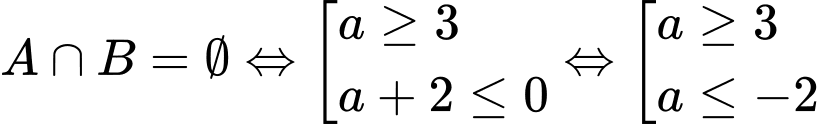 . Đáp án: A
. Đáp án: A
Để
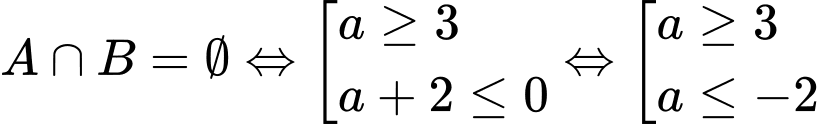 . Đáp án: A
. Đáp án: A
Câu 27 [237485]: Cho tập hợp 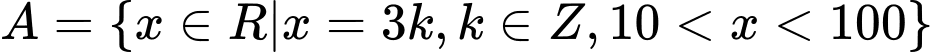 . Tổng các phần tử của tập hợp
. Tổng các phần tử của tập hợp 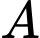 bằng
bằng
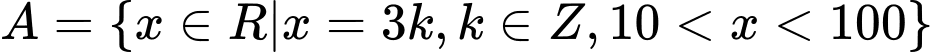 . Tổng các phần tử của tập hợp
. Tổng các phần tử của tập hợp 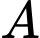 bằng
bằng A, 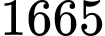 .
.
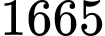 .
.B, 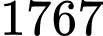 .
.
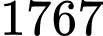 .
.C, 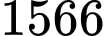 .
.
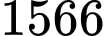 .
.D, 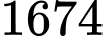 .
.
 .
.
Chọn A
Ta có: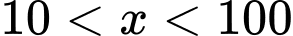
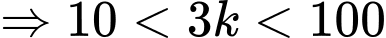
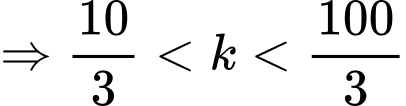
Vì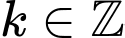 nên
nên 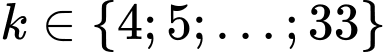 .
.
Suy ra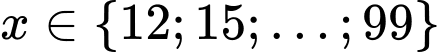 .
.
Tổng các phần tử của tập hợp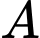 bằng:
bằng: 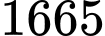 . Đáp án: A
. Đáp án: A
Ta có:
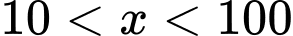
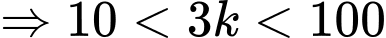
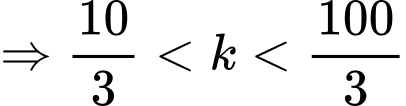
Vì
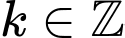 nên
nên 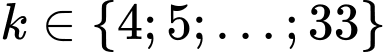 .
.
Suy ra
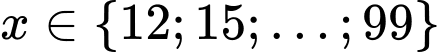 .
.
Tổng các phần tử của tập hợp
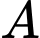 bằng:
bằng: 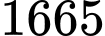 . Đáp án: A
. Đáp án: A
Câu 28 [240108]: Cho số thực  .Điều kiện cần và đủ để
.Điều kiện cần và đủ để 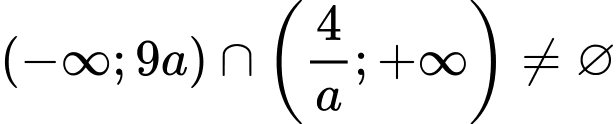 là
là
 .Điều kiện cần và đủ để
.Điều kiện cần và đủ để 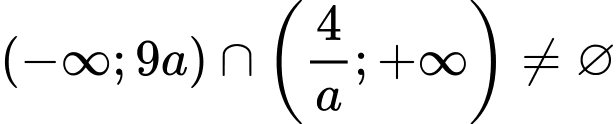 là
là A, 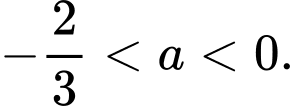
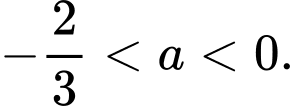
B, 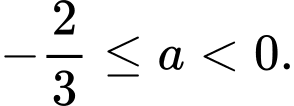
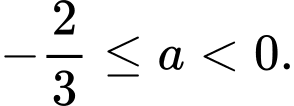
C, 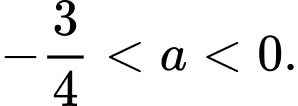
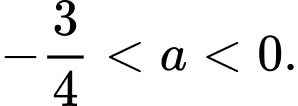
D, 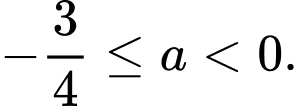
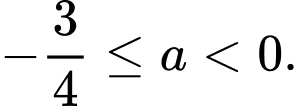
Chọn A
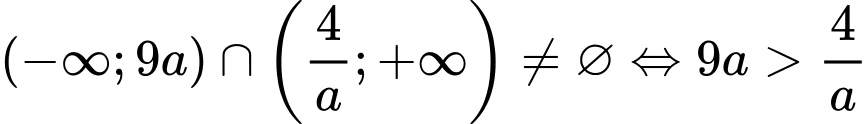
Khi đó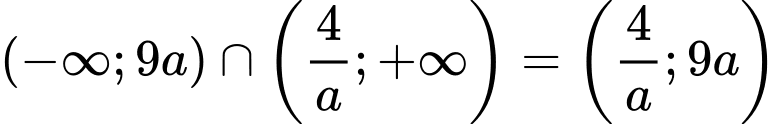
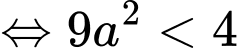 (vì
(vì  nên ta nhân 2 vế với a phải đổi chiều BPT)
nên ta nhân 2 vế với a phải đổi chiều BPT)
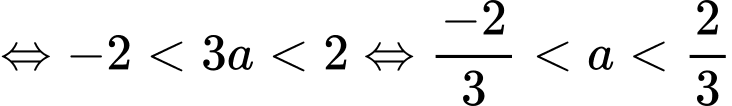
Kết hợp suy ra
suy ra 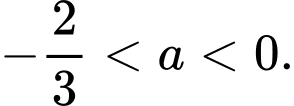 Đáp án: A
Đáp án: A
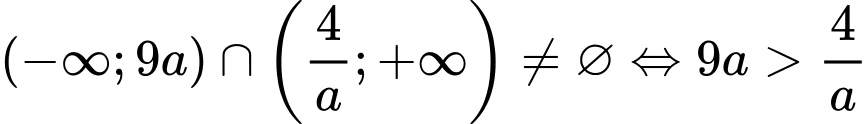
Khi đó
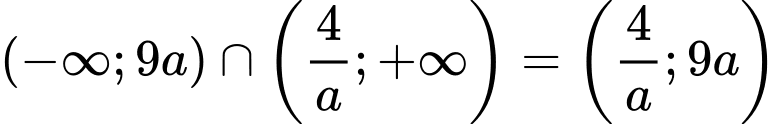
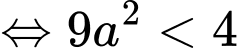 (vì
(vì  nên ta nhân 2 vế với a phải đổi chiều BPT)
nên ta nhân 2 vế với a phải đổi chiều BPT)
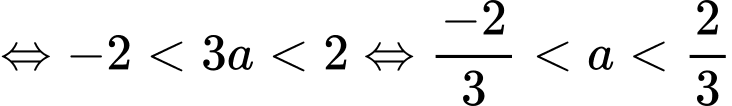
Kết hợp
 suy ra
suy ra 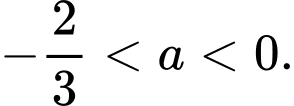 Đáp án: A
Đáp án: A
Câu 29 [237540]: Lớp 10A có 45 học sinh trong đó có 25 em học giỏi môn Toán, 23 em học giỏi môn Lý, 20 em học giỏi môn Hóa, 11 em học giỏi cả môn Toán và môn Lý, 8 em học giỏi cả môn Lý và môn Hóa, 9 em học giỏi cả môn Toán và môn Hóa) Hỏi lớp 10A có bao nhiêu bạn học giỏi cả ba môn Toán, Lý, Hóa, biết rằng mỗi học sinh trong lớp học giỏi ít nhất một trong 3 môn Toán, Lý, Hóa?
A, 3.
B, 4.
C, 5.
D, 6.
Gọi T, L, H lần lượt là tập hợp các học sinh giỏi môn Toán, Lý, Hóa)
Khi đó tương tự Ví dụ 13 ta có công thức: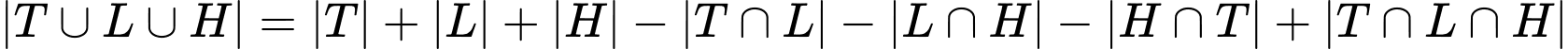
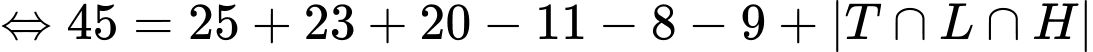
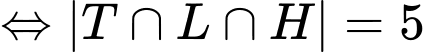
Vậy có 5 học sinh giỏi cả 3 môn. Đáp án. C.
 Đáp án: C
Đáp án: C
Khi đó tương tự Ví dụ 13 ta có công thức:
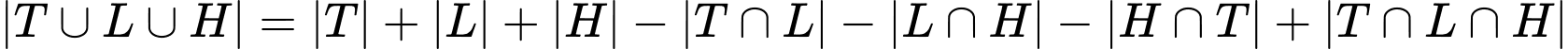
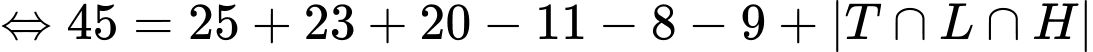
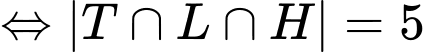
Vậy có 5 học sinh giỏi cả 3 môn. Đáp án. C.
 Đáp án: C
Đáp án: C
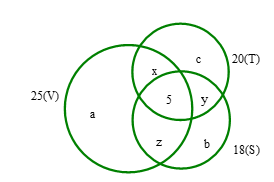
Câu 30 [237529]: Trong lớp 10C có 45 học sinh trong đó có 25 em thích môn Văn, 20 em thích môn Toán,18 em thích môn Sử, 6 em không thích môn nào, 5 em thích cả ba môn. Tính số em thích chỉ một môn trong ba môn trên.
A, 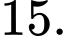
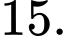
B, 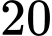 .
.
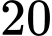 .
.C, 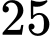 .
.
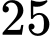 .
.D, 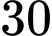 .
.
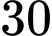 .
.
Chọn B
Gọi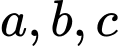 theo thứ tự là số học sinh chỉ thích môn Văn, Sử, Toán;
theo thứ tự là số học sinh chỉ thích môn Văn, Sử, Toán;
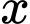 là số học sịnh chỉ thích hai môn là văn và toán
là số học sịnh chỉ thích hai môn là văn và toán
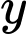 là số học sịnh chỉ thích hai môn là Sử và toán
là số học sịnh chỉ thích hai môn là Sử và toán
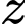 là số học sịnh chỉ thích hai môn là văn và Sử
là số học sịnh chỉ thích hai môn là văn và Sử
Ta có số em thích ít nhất một môn là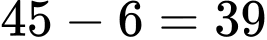
Dựa vào biểu đồ ven ta có hệ phương trình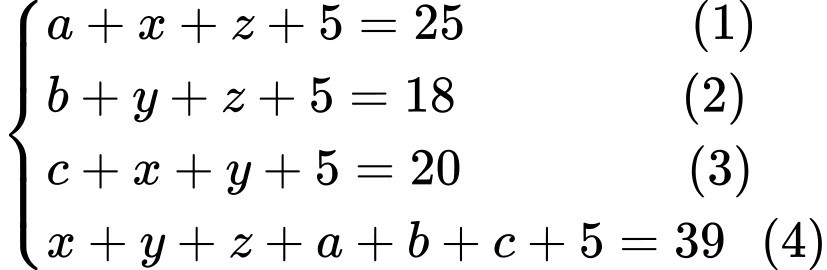
Cộng vế với vế (1), (2), (3) ta có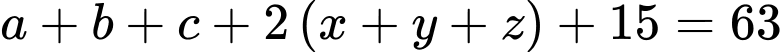 (5)
(5)
Từ (4) và (5) ta có
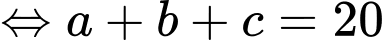 Vậy chỉ có 20 em thích chỉ một môn trong ba môn trên.
Vậy chỉ có 20 em thích chỉ một môn trong ba môn trên.
 Đáp án: B
Đáp án: B
Gọi
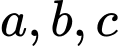 theo thứ tự là số học sinh chỉ thích môn Văn, Sử, Toán;
theo thứ tự là số học sinh chỉ thích môn Văn, Sử, Toán;
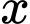 là số học sịnh chỉ thích hai môn là văn và toán
là số học sịnh chỉ thích hai môn là văn và toán
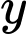 là số học sịnh chỉ thích hai môn là Sử và toán
là số học sịnh chỉ thích hai môn là Sử và toán
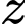 là số học sịnh chỉ thích hai môn là văn và Sử
là số học sịnh chỉ thích hai môn là văn và Sử
Ta có số em thích ít nhất một môn là
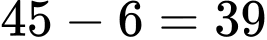
Dựa vào biểu đồ ven ta có hệ phương trình
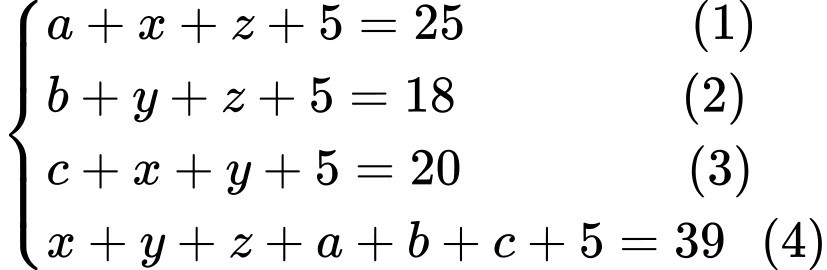
Cộng vế với vế (1), (2), (3) ta có
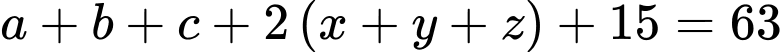 (5)
(5)
Từ (4) và (5) ta có

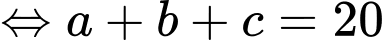 Vậy chỉ có 20 em thích chỉ một môn trong ba môn trên.
Vậy chỉ có 20 em thích chỉ một môn trong ba môn trên. Đáp án: B
Đáp án: B
Câu 31 [237531]: Lớp 10A có  học sinh giỏi Toán,
học sinh giỏi Toán,  học sinh giỏi Lý,
học sinh giỏi Lý,  học sinh giỏi hóa,
học sinh giỏi hóa, 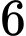 học sinh giỏi cả Toán và Lý,
học sinh giỏi cả Toán và Lý, 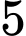 học sinh giỏi cả Hóa và Lý,
học sinh giỏi cả Hóa và Lý, 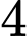 học sinh giỏi cả Toán và Hóa,
học sinh giỏi cả Toán và Hóa, 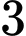 học sinh giỏi cả ba môn Toán, Lý, Hóa) Số học sinh giỏi ít nhất một trong ba môn (Toán, Lý, Hóa) của lớp 10A là
học sinh giỏi cả ba môn Toán, Lý, Hóa) Số học sinh giỏi ít nhất một trong ba môn (Toán, Lý, Hóa) của lớp 10A là
 học sinh giỏi Toán,
học sinh giỏi Toán,  học sinh giỏi Lý,
học sinh giỏi Lý,  học sinh giỏi hóa,
học sinh giỏi hóa, 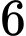 học sinh giỏi cả Toán và Lý,
học sinh giỏi cả Toán và Lý, 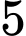 học sinh giỏi cả Hóa và Lý,
học sinh giỏi cả Hóa và Lý, 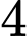 học sinh giỏi cả Toán và Hóa,
học sinh giỏi cả Toán và Hóa, 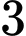 học sinh giỏi cả ba môn Toán, Lý, Hóa) Số học sinh giỏi ít nhất một trong ba môn (Toán, Lý, Hóa) của lớp 10A là
học sinh giỏi cả ba môn Toán, Lý, Hóa) Số học sinh giỏi ít nhất một trong ba môn (Toán, Lý, Hóa) của lớp 10A là A, 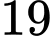 .
.
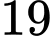 .
.B,  .
.
 .
.C, 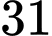 .
.
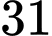 .
.D, 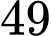 .
.
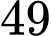 .
.
Chọn A
Theo giả thiết đề bài cho, ta có biểu đồ Ven:
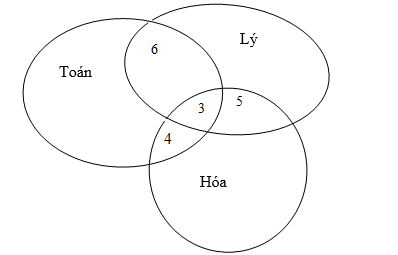
Dựa vào biểu đồ Ven ta thấy:
Số học sinh chỉ giỏi Toán và Lý (không giỏi Hóa) là: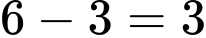 (em)
(em)
Số học sinh chỉ giỏi Toán và Hóa (không giỏi Lý) là: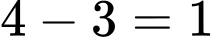 (em)
(em)
Số học sinh chỉ giỏi Lý và Hóa (không giỏi Toán) là: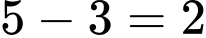 (em)
(em)
Số học sinh chỉ giỏi một môn Toán là: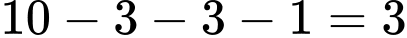 (em)
(em)
Số học sinh chỉ giỏi một môn Lý là: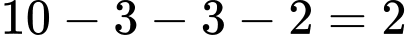 (em)
(em)
Số học sinh chỉ giỏi một môn Hóa là: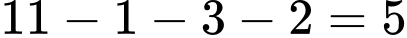 (em)
(em)
Số học sinh giỏi ít nhất một trong ba môn là:
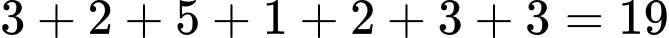 (em) Đáp án: A
(em) Đáp án: A
Theo giả thiết đề bài cho, ta có biểu đồ Ven:

Dựa vào biểu đồ Ven ta thấy:
Số học sinh chỉ giỏi Toán và Lý (không giỏi Hóa) là:
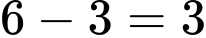 (em)
(em)
Số học sinh chỉ giỏi Toán và Hóa (không giỏi Lý) là:
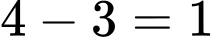 (em)
(em)
Số học sinh chỉ giỏi Lý và Hóa (không giỏi Toán) là:
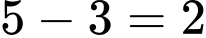 (em)
(em)
Số học sinh chỉ giỏi một môn Toán là:
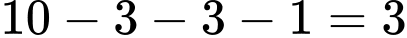 (em)
(em)
Số học sinh chỉ giỏi một môn Lý là:
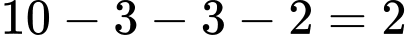 (em)
(em)
Số học sinh chỉ giỏi một môn Hóa là:
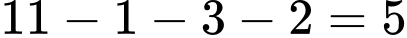 (em)
(em)
Số học sinh giỏi ít nhất một trong ba môn là:
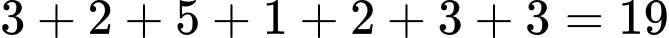 (em) Đáp án: A
(em) Đáp án: A
Câu 32 [240377]: Một cuộc khảo sát về khách du lịch thăm vịnh Hạ Long cho thấy trong 1410 khách du lịch được phỏng vấn có 789 khách du lịch đến thăm động Thiên Cung, 690 khách du lịch đến đảo Titop. Toàn bộ khách được phỏng vấn đã đến ît nhất một trong hai địa điểm trên. Hỏi có bao nhiêu khách du lịch vừa đến thăm động Thiên Cung vừa đến thăm đảo Titop ở vịnh Hạ Long?
Gọi A là tập hợp các khách du lịch đến thăm động Thiên Cung
B là tập hợp các khách du lịch đến đảo Titop.
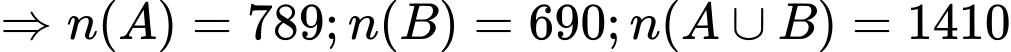
Biểu đồ Ven
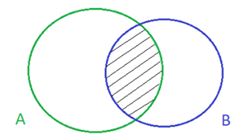
Tổng số khách du lịch = Số khách đến động Thiên Cung + Số khách đến đảo Titop - Số khách du lịch đến cả hai địa điểm.
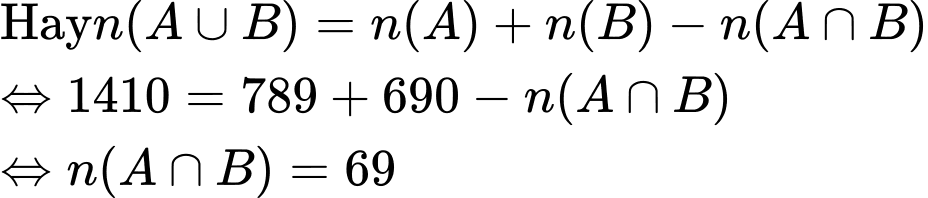
Vậy có 69 khách du lịch vừa đến thăm động Thiên cung vừa đến thăm đảo Titop ở vịnh Hạ Long.
B là tập hợp các khách du lịch đến đảo Titop.
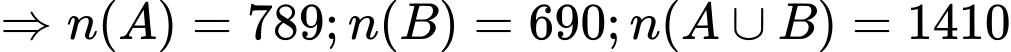
Biểu đồ Ven

Tổng số khách du lịch = Số khách đến động Thiên Cung + Số khách đến đảo Titop - Số khách du lịch đến cả hai địa điểm.
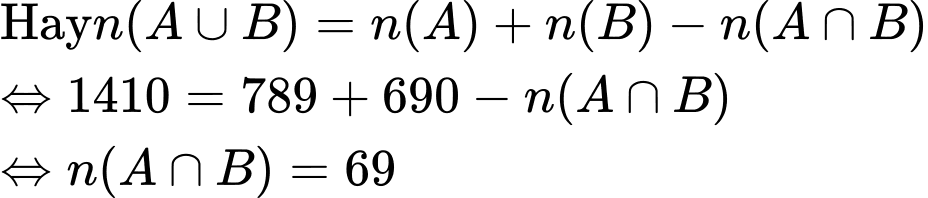
Vậy có 69 khách du lịch vừa đến thăm động Thiên cung vừa đến thăm đảo Titop ở vịnh Hạ Long.
Câu 33 [237776]: Tìm các tập 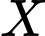 thỏa mãn
thỏa mãn 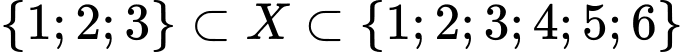 .
.
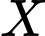 thỏa mãn
thỏa mãn 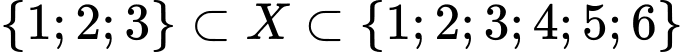 .
. 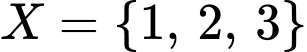 hoặc
hoặc 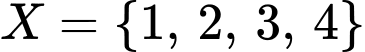 hoặc
hoặc 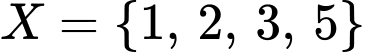 hoặc
hoặc 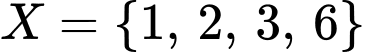 hoặc
hoặc 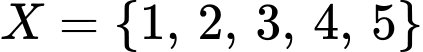 hoặc
hoặc 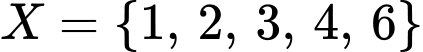 hoặc
hoặc 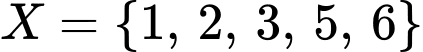 hoặc
hoặc 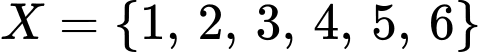 .
.
Vậy có 8 tập hợp thoả mãn đề bài
Câu 34 [237777]: Tìm tất cả các tập hợp 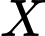 sao cho:
sao cho: 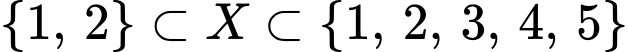 .
.
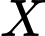 sao cho:
sao cho: 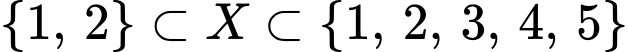 .
. 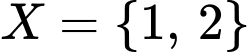 hoặc
hoặc 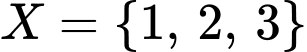 hoặc
hoặc 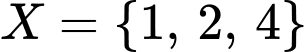 hoặc
hoặc 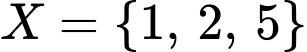 hoặc
hoặc 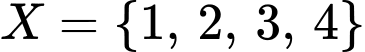 hoặc
hoặc 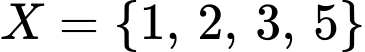 hoặc
hoặc 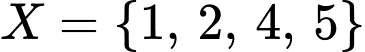 hoặc
hoặc 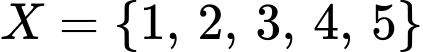 .
.
Câu 35 [240126]: Cho hai tập hợp 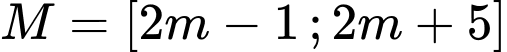 và
và 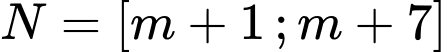 (với
(với 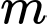 là tham số thực). Tổng tất cả các giá trị của
là tham số thực). Tổng tất cả các giá trị của 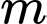 để hợp của hai tập hợp
để hợp của hai tập hợp 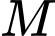 và
và 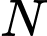 là một đoạn có độ dài bằng 10 là
là một đoạn có độ dài bằng 10 là
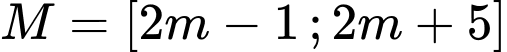 và
và 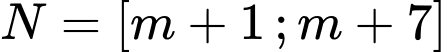 (với
(với 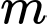 là tham số thực). Tổng tất cả các giá trị của
là tham số thực). Tổng tất cả các giá trị của 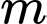 để hợp của hai tập hợp
để hợp của hai tập hợp 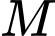 và
và 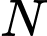 là một đoạn có độ dài bằng 10 là
là một đoạn có độ dài bằng 10 là A, 4.
B, -2.
C, 6.
D, 10.
Chọn A
Nhận thấy là hai đoạn cùng có độ dài bằng 6, nên để
là hai đoạn cùng có độ dài bằng 6, nên để  là một đoạn có độ dài bằng 10 thì ta có các trường hợp sau:
là một đoạn có độ dài bằng 10 thì ta có các trường hợp sau:
*
Khi đó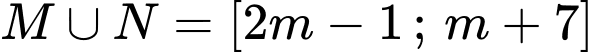 , nên
, nên  là một đoạn có độ dài bằng 10 khi:
là một đoạn có độ dài bằng 10 khi:
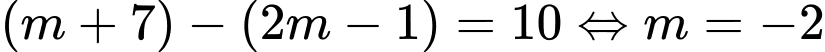 (thỏa mãn
(thỏa mãn  ).
).
*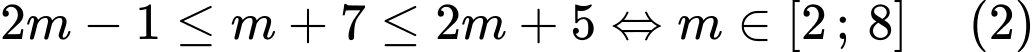
Khi đó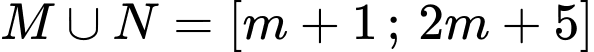 , nên
, nên  là một đoạn có độ dài bằng 10 khi:
là một đoạn có độ dài bằng 10 khi:
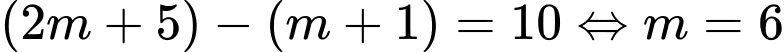 (thỏa mãn
(thỏa mãn  ).
).
Vậy Tổng tất cả các giá trị của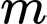 để hợp của hai tập hợp
để hợp của hai tập hợp 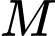 và
và 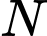 là một đoạn có độ dài bằng 10 là
là một đoạn có độ dài bằng 10 là 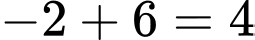 . Đáp án: A
. Đáp án: A
Nhận thấy
 là hai đoạn cùng có độ dài bằng 6, nên để
là hai đoạn cùng có độ dài bằng 6, nên để  là một đoạn có độ dài bằng 10 thì ta có các trường hợp sau:
là một đoạn có độ dài bằng 10 thì ta có các trường hợp sau:
*

Khi đó
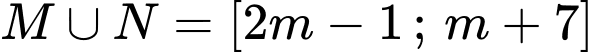 , nên
, nên  là một đoạn có độ dài bằng 10 khi:
là một đoạn có độ dài bằng 10 khi:
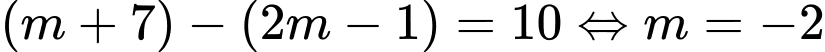 (thỏa mãn
(thỏa mãn  ).
).
*
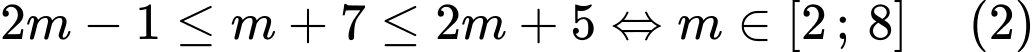
Khi đó
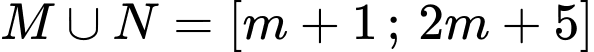 , nên
, nên  là một đoạn có độ dài bằng 10 khi:
là một đoạn có độ dài bằng 10 khi:
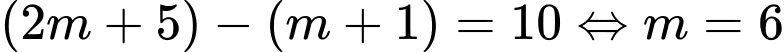 (thỏa mãn
(thỏa mãn  ).
).
Vậy Tổng tất cả các giá trị của
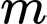 để hợp của hai tập hợp
để hợp của hai tập hợp 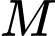 và
và 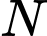 là một đoạn có độ dài bằng 10 là
là một đoạn có độ dài bằng 10 là 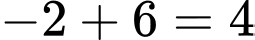 . Đáp án: A
. Đáp án: A
Câu 36 [237532]: Một nhóm học sinh giỏi các môn: Anh, Toán, Văn. Có  em giỏi Văn,
em giỏi Văn,  em giỏi Anh,
em giỏi Anh,  em giỏi Toán,
em giỏi Toán, 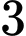 em giỏi Văn và Toán,
em giỏi Văn và Toán, 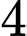 em giỏi Toán và Anh,
em giỏi Toán và Anh, 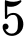 em giỏi Văn và Anh,
em giỏi Văn và Anh, 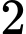 em giỏi cả ba môn. Hỏi nhóm đó có bao nhiêu em học sinh?
em giỏi cả ba môn. Hỏi nhóm đó có bao nhiêu em học sinh?
 em giỏi Văn,
em giỏi Văn,  em giỏi Anh,
em giỏi Anh,  em giỏi Toán,
em giỏi Toán, 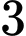 em giỏi Văn và Toán,
em giỏi Văn và Toán, 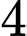 em giỏi Toán và Anh,
em giỏi Toán và Anh, 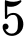 em giỏi Văn và Anh,
em giỏi Văn và Anh, 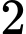 em giỏi cả ba môn. Hỏi nhóm đó có bao nhiêu em học sinh?
em giỏi cả ba môn. Hỏi nhóm đó có bao nhiêu em học sinh? A, 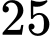 .
.
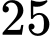 .
.B, 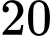 .
.
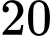 .
.C, 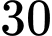 .
.
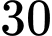 .
.D, Đáp án khác.
C.
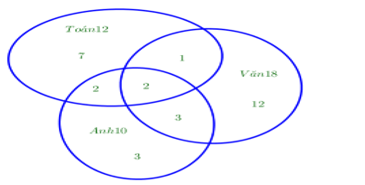
Vì có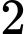 em giỏi cùng lúc ba môn, nên ta có :
em giỏi cùng lúc ba môn, nên ta có :
- Số học sinh giỏi hai môn Toán và Văn, không giỏi Anh là :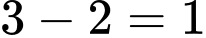 .
.
- Số học sinh giỏi hai môn Toán và Anh, không giỏi Văn là :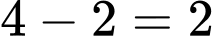 .
.
- Số học sinh giỏi hai môn Văn và Anh, không giỏi Toán là :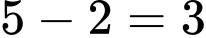 .
.
Lúc đó :
- Số em giỏi mình môn Văn là :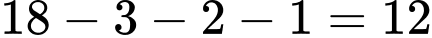 .
.
- Số em giỏi mình môn Toán là :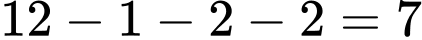 .
.
- Số em giỏi mình môn Anh là :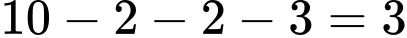 .
Vậy cả nhóm có tổng số học sinh là :
.
Vậy cả nhóm có tổng số học sinh là : 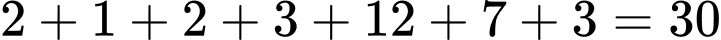 . Đáp án: C
. Đáp án: C

Vì có
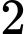 em giỏi cùng lúc ba môn, nên ta có :
em giỏi cùng lúc ba môn, nên ta có :
- Số học sinh giỏi hai môn Toán và Văn, không giỏi Anh là :
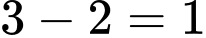 .
.
- Số học sinh giỏi hai môn Toán và Anh, không giỏi Văn là :
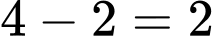 .
.
- Số học sinh giỏi hai môn Văn và Anh, không giỏi Toán là :
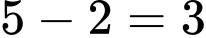 .
.
Lúc đó :
- Số em giỏi mình môn Văn là :
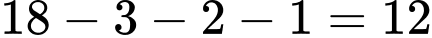 .
.
- Số em giỏi mình môn Toán là :
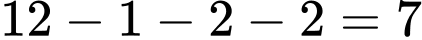 .
.
- Số em giỏi mình môn Anh là :
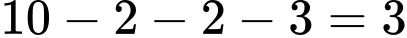 .
Vậy cả nhóm có tổng số học sinh là :
.
Vậy cả nhóm có tổng số học sinh là : 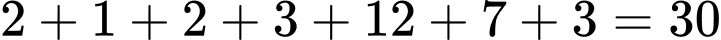 . Đáp án: C
. Đáp án: C
Câu 37 [237535]: Hội khỏe Phù Đổng của trường Trần Phú, lớp 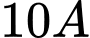 có 45 học sinh, trong đó có 25 học sinh thi điền kinh, 20 học sinh thi nhảy xa, 15 học sinh thi nhảy cao, 7 em không tham gia môn nào, 5 em tham gia cả 3 môn. Hỏi số em tham gia chỉ một môn trong ba môn trên là bao nhiêu?
có 45 học sinh, trong đó có 25 học sinh thi điền kinh, 20 học sinh thi nhảy xa, 15 học sinh thi nhảy cao, 7 em không tham gia môn nào, 5 em tham gia cả 3 môn. Hỏi số em tham gia chỉ một môn trong ba môn trên là bao nhiêu?
 có 45 học sinh, trong đó có 25 học sinh thi điền kinh, 20 học sinh thi nhảy xa, 15 học sinh thi nhảy cao, 7 em không tham gia môn nào, 5 em tham gia cả 3 môn. Hỏi số em tham gia chỉ một môn trong ba môn trên là bao nhiêu?
có 45 học sinh, trong đó có 25 học sinh thi điền kinh, 20 học sinh thi nhảy xa, 15 học sinh thi nhảy cao, 7 em không tham gia môn nào, 5 em tham gia cả 3 môn. Hỏi số em tham gia chỉ một môn trong ba môn trên là bao nhiêu? A, 20.
B, 45.
C, 38.
D, 21.
D.
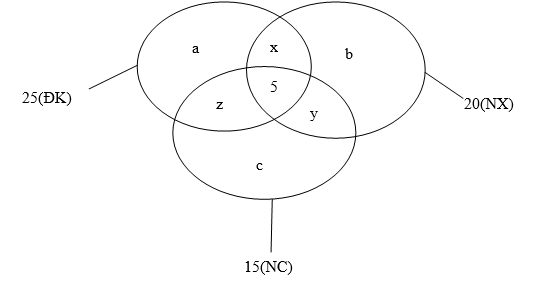
Gọi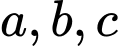 theo thứ tự là số học sinh chỉ thi môn điền kinh, nhảy xa, nhảy cao.
theo thứ tự là số học sinh chỉ thi môn điền kinh, nhảy xa, nhảy cao.
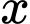 là số học sinh chỉ thi hai môn điền kinh và nhảy xa
là số học sinh chỉ thi hai môn điền kinh và nhảy xa
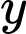 là số học sinh chỉ thi hai môn nhảy xa và nhảy cao
là số học sinh chỉ thi hai môn nhảy xa và nhảy cao
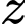 là số học sinh chỉ thi hai môn điền kinh và nhảy cao
là số học sinh chỉ thi hai môn điền kinh và nhảy cao
Số em thi ít nhất một môn là: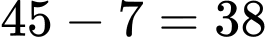
Dựa vào biểu đồ ven ta có hệ phương trình sau: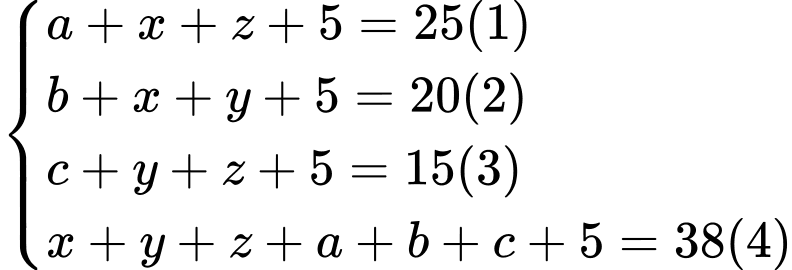
Cộng vế với vế của ta có:
ta có: 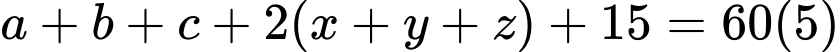
Từ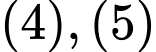 ta có:
ta có: 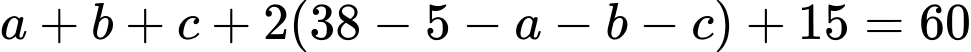
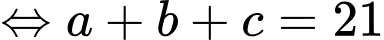 Vậy có 21 học sinh chỉ thi một trong ba nội dung trên. Đáp án: D
Vậy có 21 học sinh chỉ thi một trong ba nội dung trên. Đáp án: D

Gọi
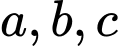 theo thứ tự là số học sinh chỉ thi môn điền kinh, nhảy xa, nhảy cao.
theo thứ tự là số học sinh chỉ thi môn điền kinh, nhảy xa, nhảy cao.
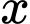 là số học sinh chỉ thi hai môn điền kinh và nhảy xa
là số học sinh chỉ thi hai môn điền kinh và nhảy xa
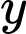 là số học sinh chỉ thi hai môn nhảy xa và nhảy cao
là số học sinh chỉ thi hai môn nhảy xa và nhảy cao
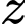 là số học sinh chỉ thi hai môn điền kinh và nhảy cao
là số học sinh chỉ thi hai môn điền kinh và nhảy cao
Số em thi ít nhất một môn là:
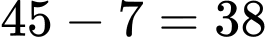
Dựa vào biểu đồ ven ta có hệ phương trình sau:
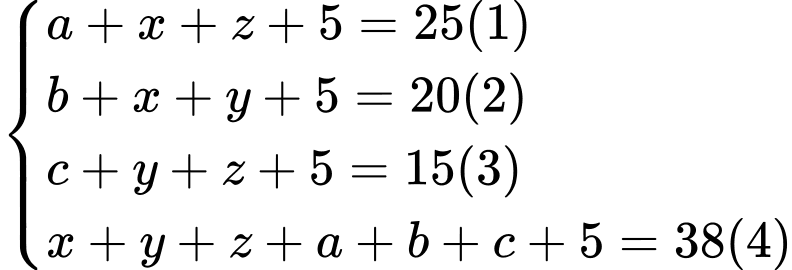
Cộng vế với vế của
 ta có:
ta có: 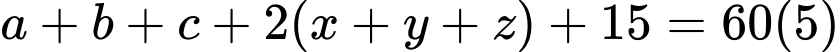
Từ
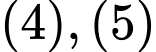 ta có:
ta có: 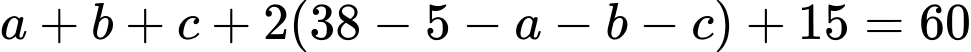
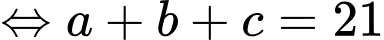 Vậy có 21 học sinh chỉ thi một trong ba nội dung trên. Đáp án: D
Vậy có 21 học sinh chỉ thi một trong ba nội dung trên. Đáp án: D
Câu 38 [237527]: Trong một khoảng thời gian nhất định, tại một địa phương, Đài khí tượng thủy văn đã thống kê được: Số ngày mưa: 10 ngày; Số ngày có gió: 8 ngày; Số ngày lạnh: 6 ngày; Số ngày mưa và gió: 5 ngày; Số ngày mưa và lạnh: 4 ngày; Số ngày lạnh và có gió: 3 ngày; Số ngày mưa, lạnh và có gió: 1 ngày.Vậy có bao nhiêu ngày thời tiết xấu (Có gió, mưa hay lạnh)?
A, 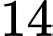 .
.
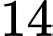 .
.B,  .
.
 .
.C,  .
.
 .
.D, 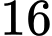 .
.
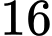 .
.
Ký hiệu A là tập hợp những ngày mưa, B là tập hợp những ngày có gió, C là tập hợp những ngày lạnh.
Theo giả thiết ta có: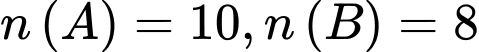 ,
, 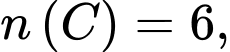
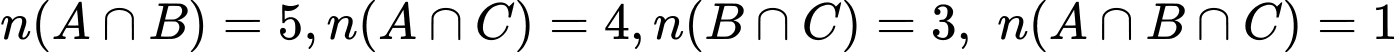
Để tìm số ngày thời tiết xấu ta sử dụng biểu đồ Ven(hình vẽ). Ta cần tính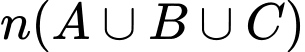 .
.
Xét tổng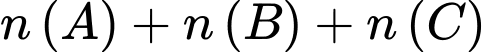 : trong tổng này, mỗi phần tử của A giao B, B giao C, C giao A được tính làm hai lần nên trong tổng
: trong tổng này, mỗi phần tử của A giao B, B giao C, C giao A được tính làm hai lần nên trong tổng 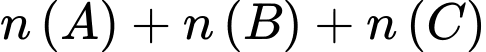 ta phải trừ đi tổng
ta phải trừ đi tổng 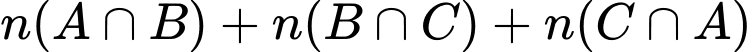 .
.
Trong tổng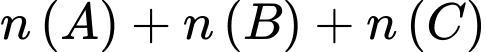 được tính
được tính 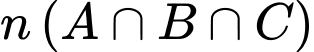 3 lần, trong
3 lần, trong 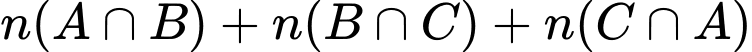 cũng được tính
cũng được tính 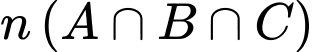 3 lần. Vì vậy
3 lần. Vì vậy
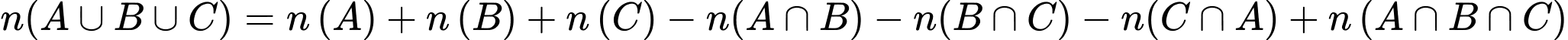
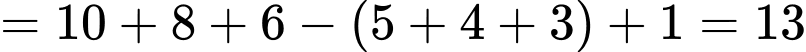
Vậy số ngày thời tiết xấu là 13 ngày.
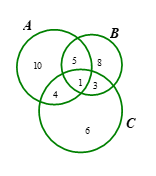 Đáp án: B
Đáp án: B
Theo giả thiết ta có:
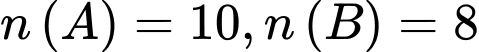 ,
, 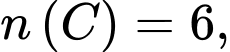
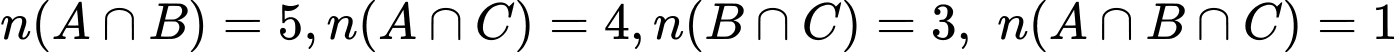
Để tìm số ngày thời tiết xấu ta sử dụng biểu đồ Ven(hình vẽ). Ta cần tính
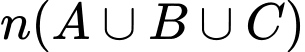 .
.
Xét tổng
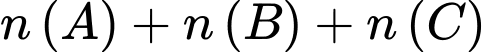 : trong tổng này, mỗi phần tử của A giao B, B giao C, C giao A được tính làm hai lần nên trong tổng
: trong tổng này, mỗi phần tử của A giao B, B giao C, C giao A được tính làm hai lần nên trong tổng 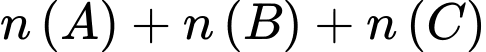 ta phải trừ đi tổng
ta phải trừ đi tổng 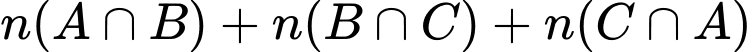 .
.
Trong tổng
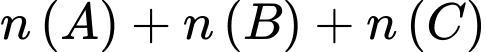 được tính
được tính 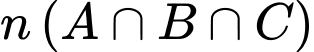 3 lần, trong
3 lần, trong 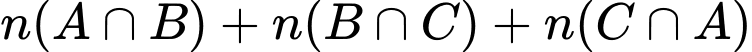 cũng được tính
cũng được tính 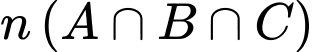 3 lần. Vì vậy
3 lần. Vì vậy
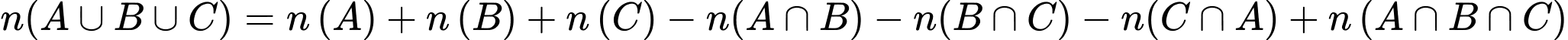
Vậy số ngày thời tiết xấu là 13 ngày.
 Đáp án: B
Đáp án: B