Đáp án Bài tập tự luyện
Câu 1 [245743]: Số nghiệm của phương trình 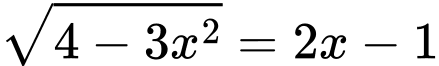 là
là
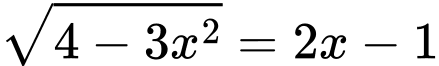 là
là A, 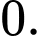
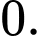
B, 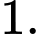
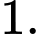
C, 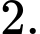
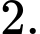
D, 
Chọn B
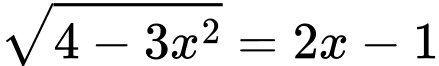
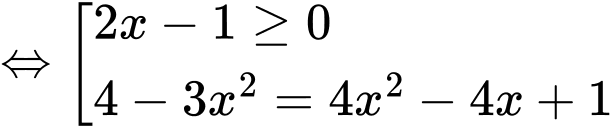
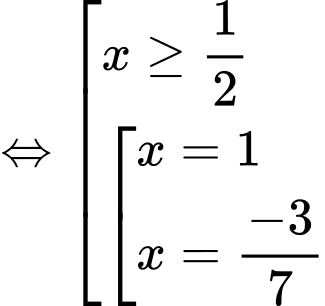
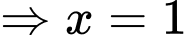
Vậy phương trình có 1 nghiệm Đáp án: B
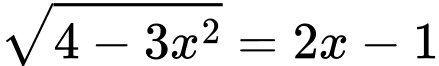
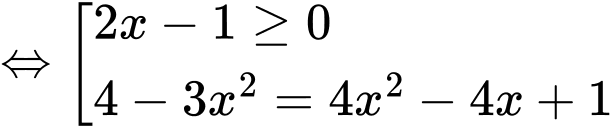
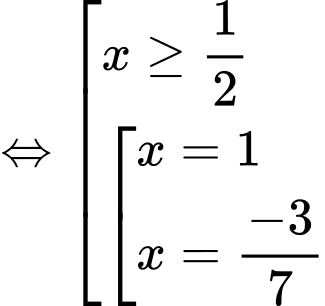
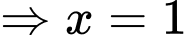
Vậy phương trình có 1 nghiệm Đáp án: B
Câu 2 [245751]: Phương trình 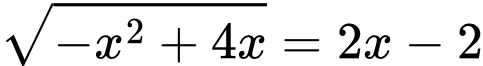 có bao nhiêu nghiệm?
có bao nhiêu nghiệm?
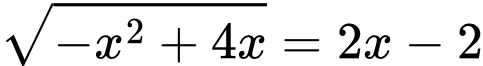 có bao nhiêu nghiệm?
có bao nhiêu nghiệm? A, 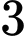 .
.
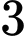 .
.B,  .
.
 .
.C, 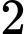 .
.
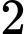 .
.D,  .
.
 .
.
Chọn D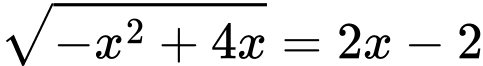
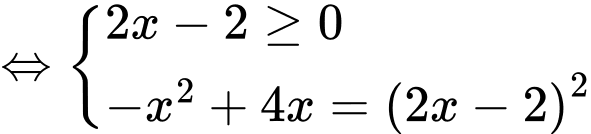
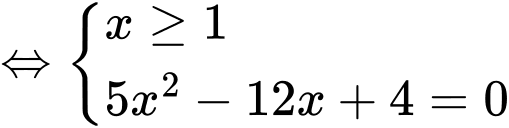
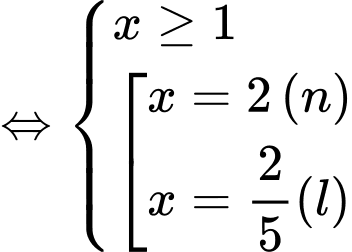 .Vậy
.Vậy 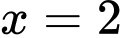 là nghiệm của phương trình. Đáp án: D
là nghiệm của phương trình. Đáp án: D
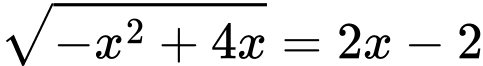
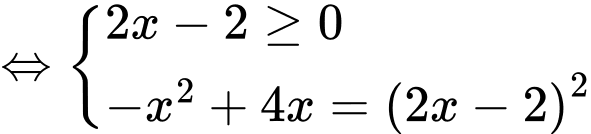
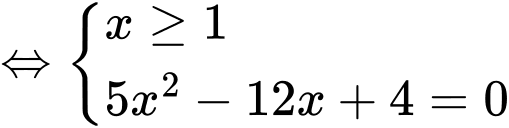
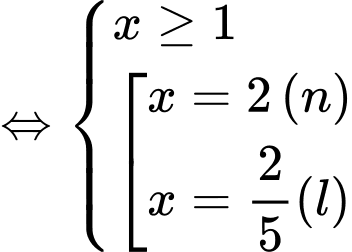 .Vậy
.Vậy 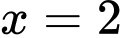 là nghiệm của phương trình. Đáp án: D
là nghiệm của phương trình. Đáp án: D
Câu 3 [581793]: Phương trình 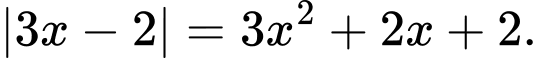 có bao nhiêu nghiệm thực?
có bao nhiêu nghiệm thực?
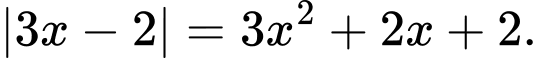 có bao nhiêu nghiệm thực?
có bao nhiêu nghiệm thực? A, 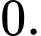
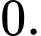
B, 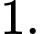
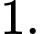
C, 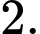
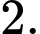
D, 
Áp dụng: 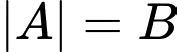 với
với  thì
thì  hoặc
hoặc 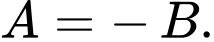
Ta có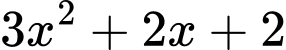
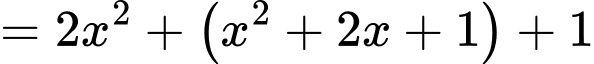
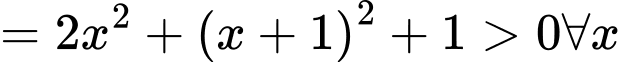
Khi đó, phương trình đã cho trở thành:
TH1: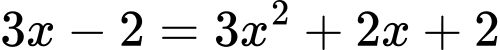
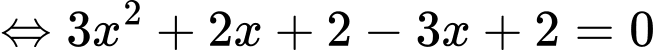
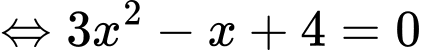
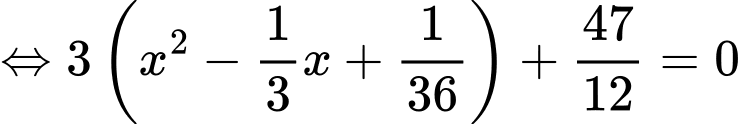
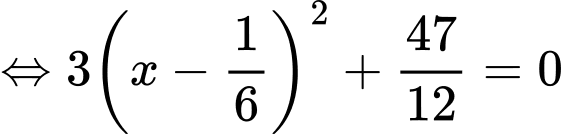 (vô lí vì vế trái luôn dương)
(vô lí vì vế trái luôn dương)
TH2: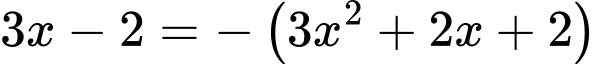
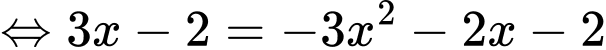
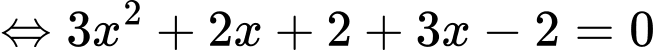

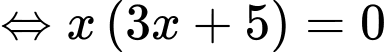
+)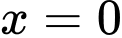
+)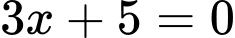 suy ra
suy ra 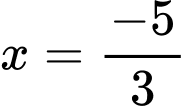
Vậy phương trình đã cho có hai nghiệm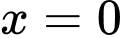 và
và 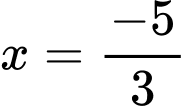
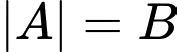 với
với  thì
thì  hoặc
hoặc 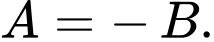
Ta có
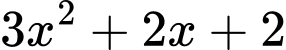
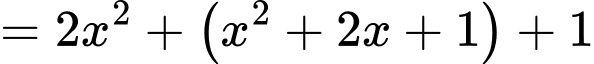
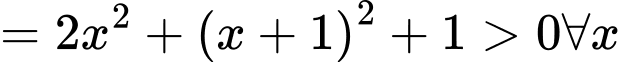
Khi đó, phương trình đã cho trở thành:
TH1:
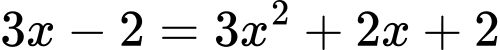
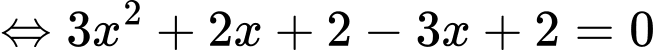
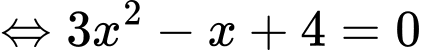
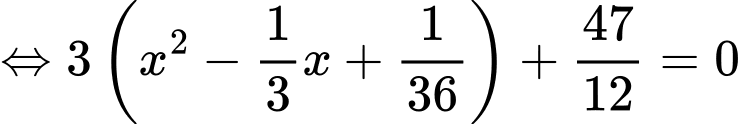
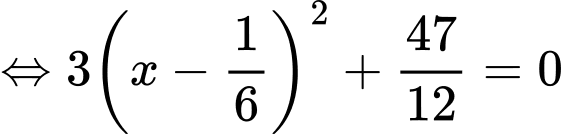 (vô lí vì vế trái luôn dương)
(vô lí vì vế trái luôn dương)
TH2:
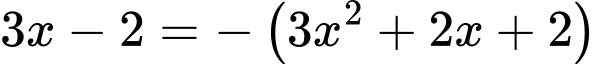
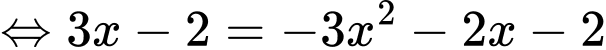
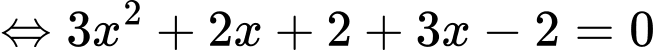

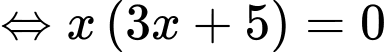
+)
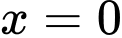
+)
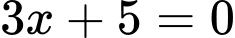 suy ra
suy ra 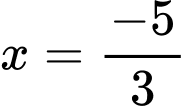
Vậy phương trình đã cho có hai nghiệm
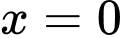 và
và 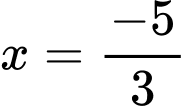
Câu 4 [581794]: Phương trình 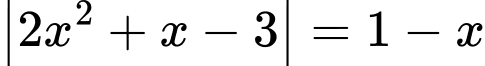 có bao nhiêu nghiệm thực?
có bao nhiêu nghiệm thực?
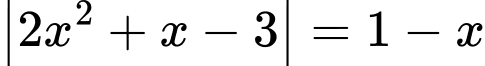 có bao nhiêu nghiệm thực?
có bao nhiêu nghiệm thực? A, 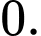
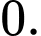
B, 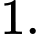
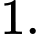
C, 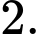
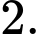
D, 
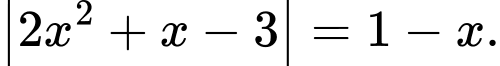
Ta có
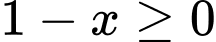 suy ra
suy ra 
TH1:
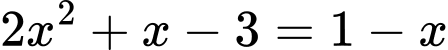
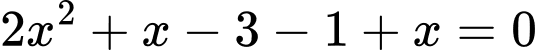
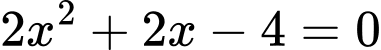
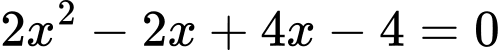
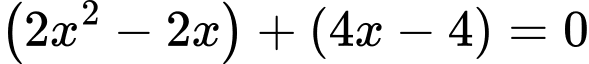
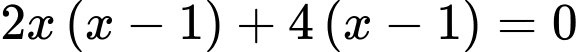
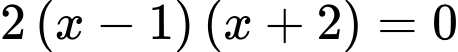
Suy ra
 hoặc
hoặc 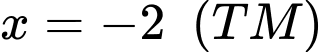
TH2:
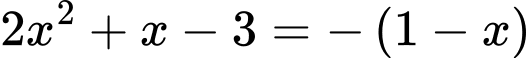
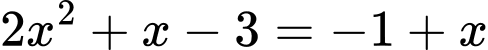
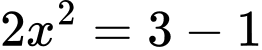
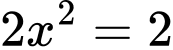
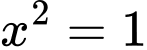
Suy ra
 hoặc
hoặc 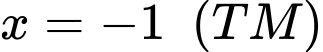
Vậy phương trình đã cho có ba nghiệm
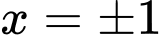 và
và 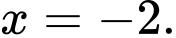
Đáp án: D. Đáp án: D
Câu 5 [245752]: Số nghiệm của phương trình 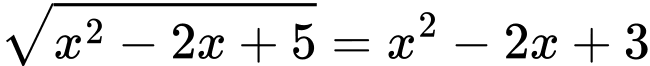 là
là
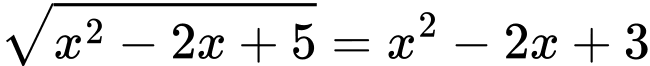 là
là A, 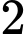 .
.
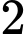 .
.B, 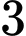 .
.
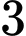 .
.C, 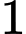 .
.
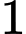 .
.D,  .
.
 .
.
Chọn C
Ta có: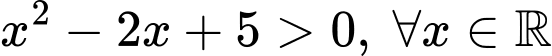
Đặt , ta có phương trình trở thành
, ta có phương trình trở thành 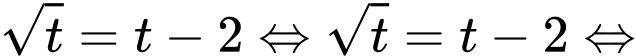
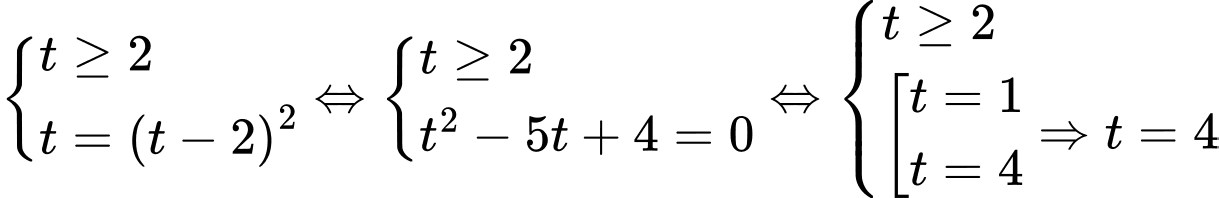
Khi đó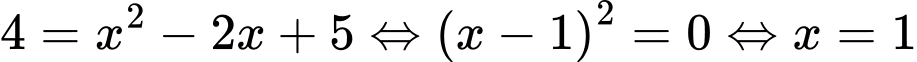 . Thử lại ta thấy
. Thử lại ta thấy 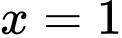 thỏa mãn.
thỏa mãn.
Suy ra phương trình đã cho có một nghiệm. Đáp án: C
Ta có:
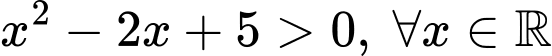
Đặt
 , ta có phương trình trở thành
, ta có phương trình trở thành 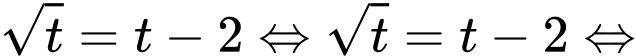
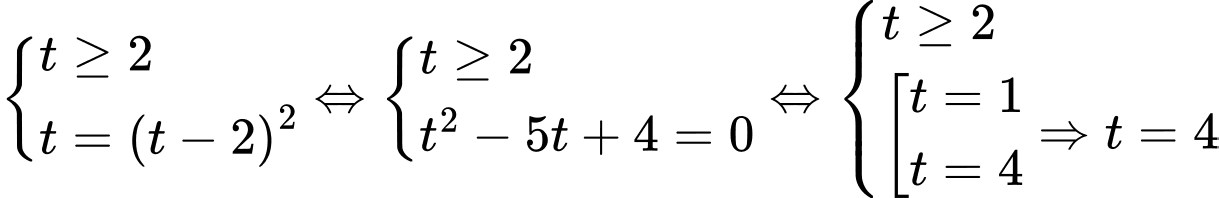
Khi đó
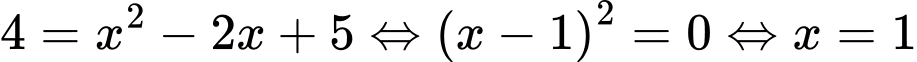 . Thử lại ta thấy
. Thử lại ta thấy 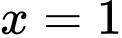 thỏa mãn.
thỏa mãn.
Suy ra phương trình đã cho có một nghiệm. Đáp án: C
Câu 6 [245753]: Tích các nghiệm của phương trình 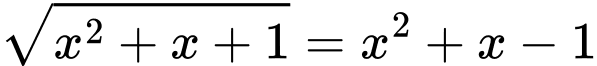 là
là
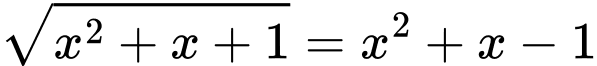 là
là A, 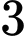 .
.
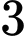 .
.B, 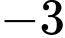 .
.
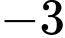 .
.C, 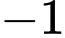 .
.
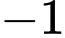 .
.D,  .
.
 .
.
Chọn B
Ta có: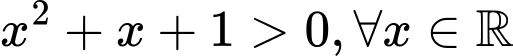
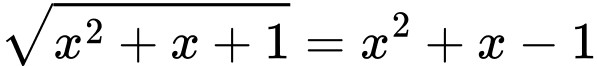
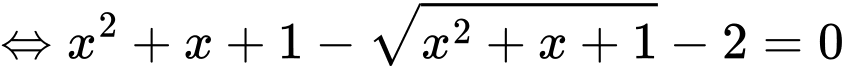
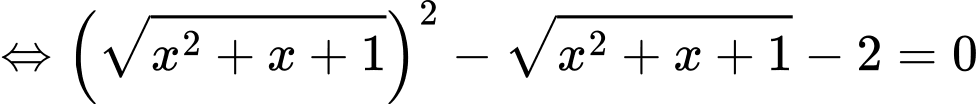
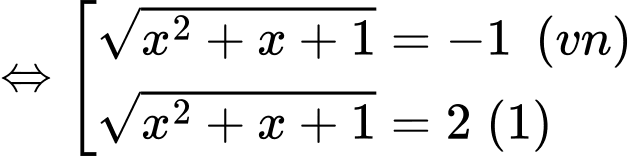
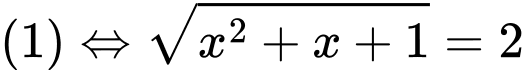
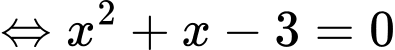 Do đó:
Do đó: 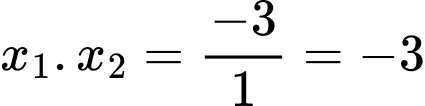 . Đáp án: B
. Đáp án: B
Ta có:
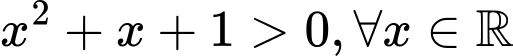
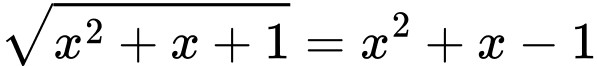
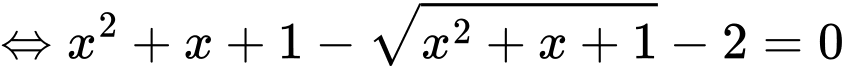
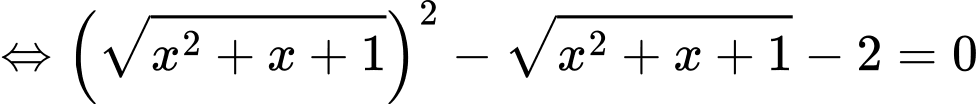
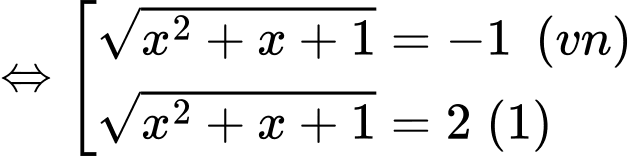
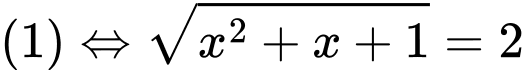
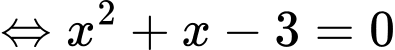 Do đó:
Do đó: 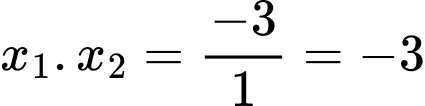 . Đáp án: B
. Đáp án: B
Câu 7 [245744]: Số nghiệm của phương trình 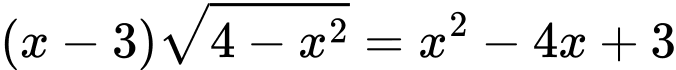 là
là
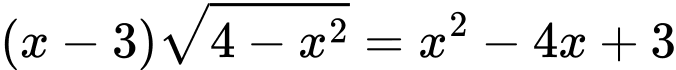 là
là A, 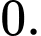
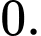
B, 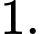
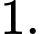
C, 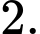
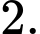
D, 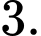
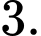
Chọn B
Điều kiện xác định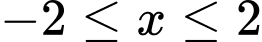
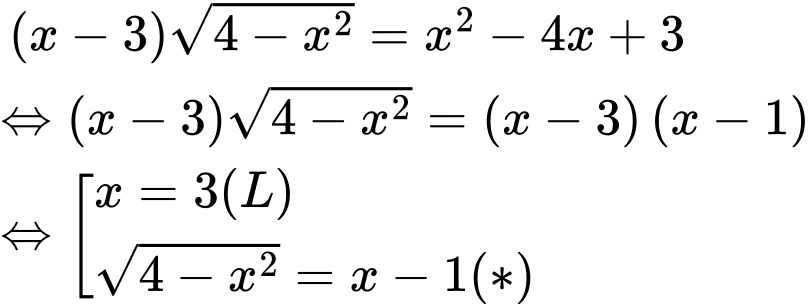
Giải (*)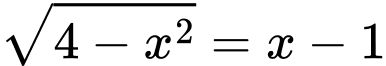
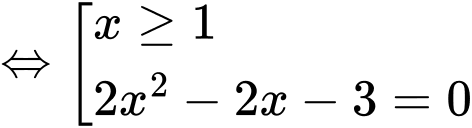
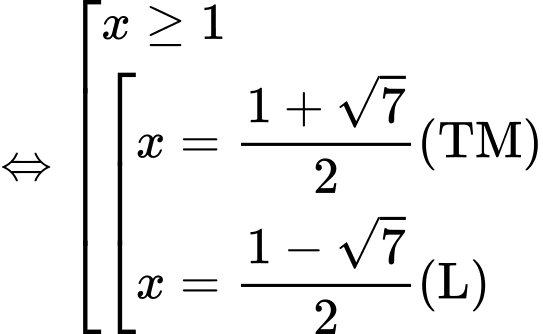
Vậy phương trình có 1 nghiệm Đáp án: B
Điều kiện xác định
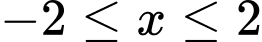
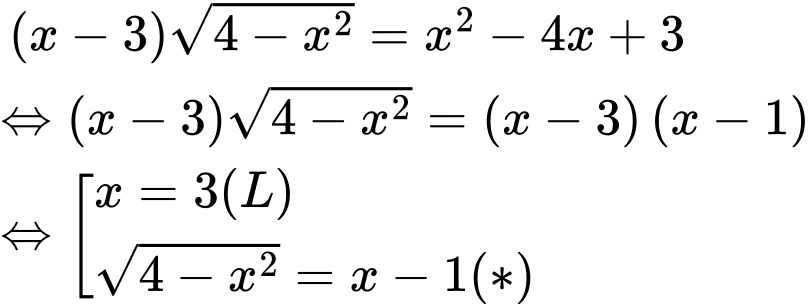
Giải (*)
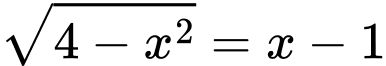
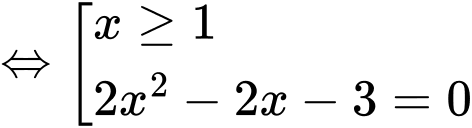
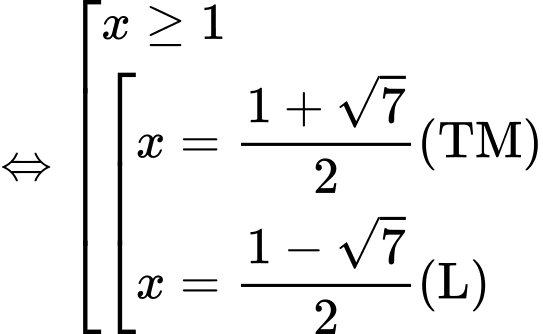
Vậy phương trình có 1 nghiệm Đáp án: B
Câu 8 [245745]: Tổng các nghiệm của phương trình 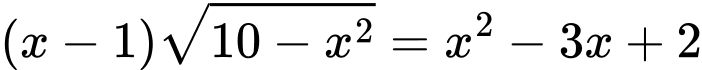 là
là
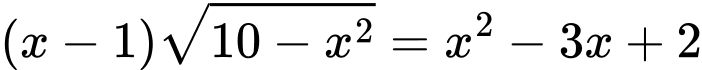 là
là A, 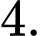
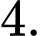
B, 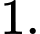
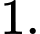
C, 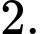
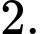
D, 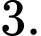
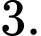
Chọn A
Điều kiện xác định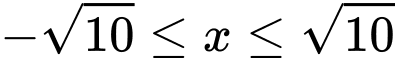
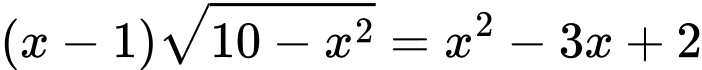
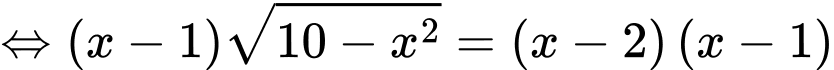
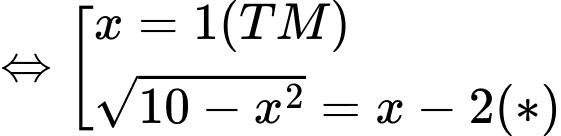
Giải (*)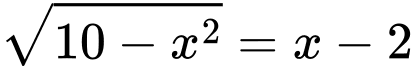
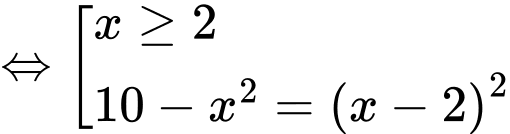
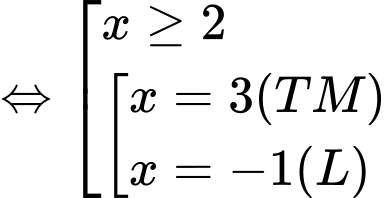
Vậy tổng các nghiệm của phương trình bằng 4 Đáp án: A
Điều kiện xác định
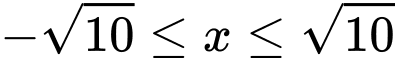
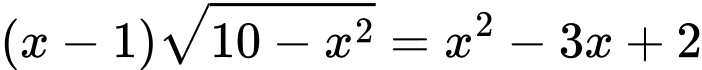
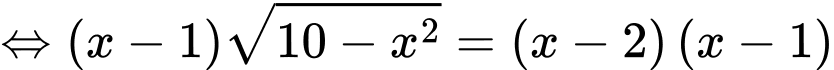
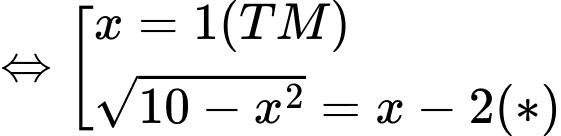
Giải (*)
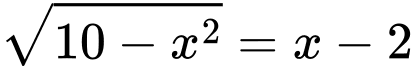
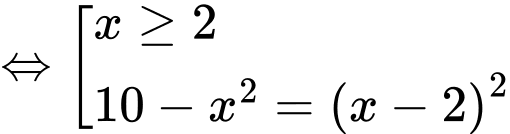
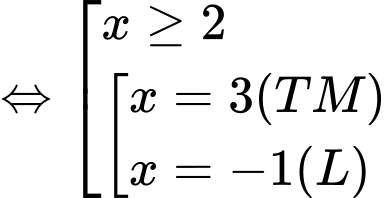
Vậy tổng các nghiệm của phương trình bằng 4 Đáp án: A
Câu 9 [581790]: có bao nhiêu giá trị thực của tham số 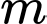 để phương trình
để phương trình 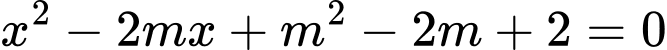 có hai nghiệm phân biệt
có hai nghiệm phân biệt 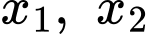 thỏa mãn
thỏa mãn 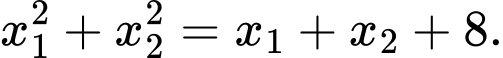
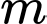 để phương trình
để phương trình 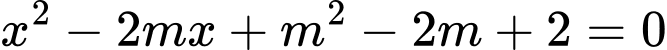 có hai nghiệm phân biệt
có hai nghiệm phân biệt 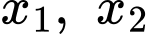 thỏa mãn
thỏa mãn 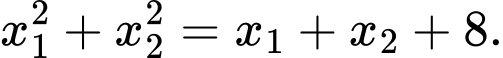
A, 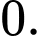
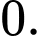
B,
C,
D,
Xét phương trình 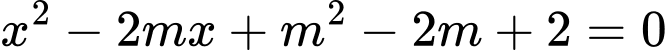 có
có 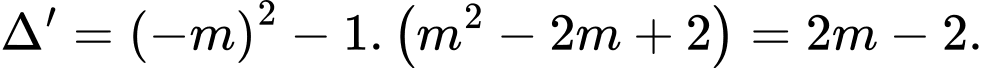
Để phương trình đã cho có hai nghiệm phân biệt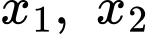 thì
thì  suy ra
suy ra 
Áp dụng hệ thức Viet, ta có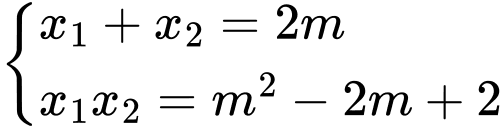
Ta có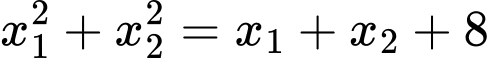
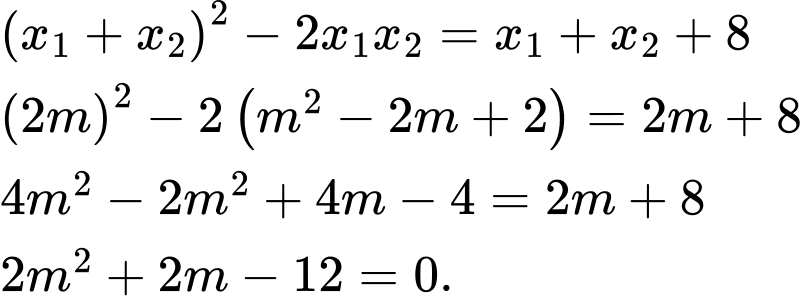
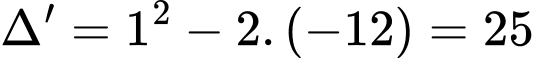 nên phương trình trên có hai nghiệm phân biệt
nên phương trình trên có hai nghiệm phân biệt 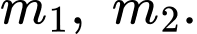
Khi đó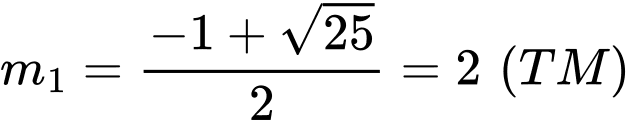 và
và 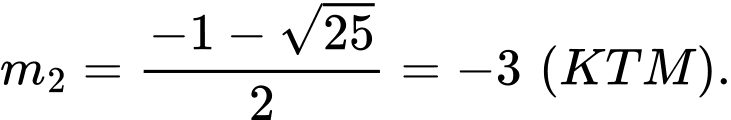 Đáp án: B
Đáp án: B
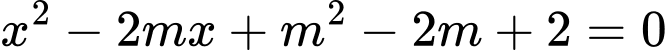 có
có 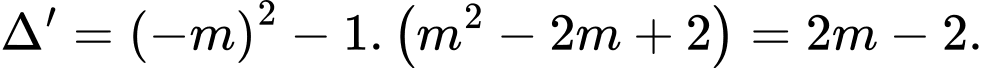
Để phương trình đã cho có hai nghiệm phân biệt
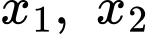 thì
thì  suy ra
suy ra 
Áp dụng hệ thức Viet, ta có
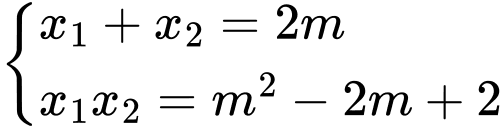
Ta có
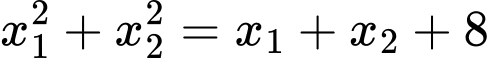
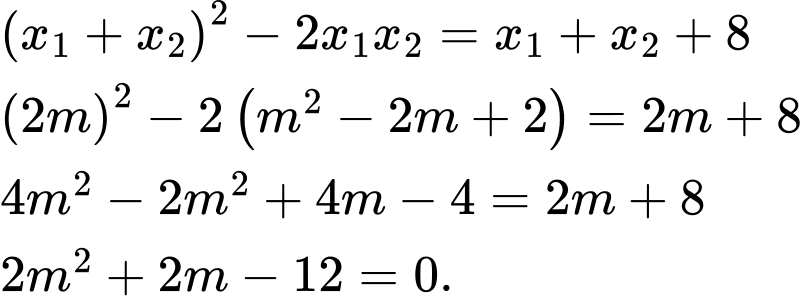
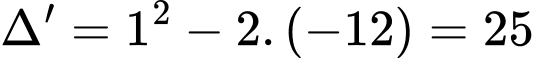 nên phương trình trên có hai nghiệm phân biệt
nên phương trình trên có hai nghiệm phân biệt 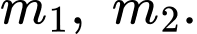
Khi đó
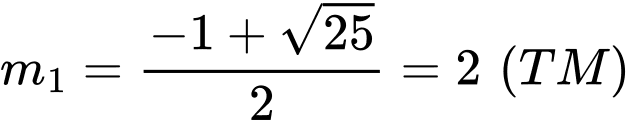 và
và 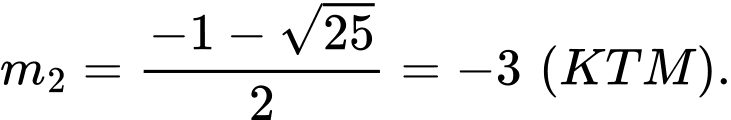 Đáp án: B
Đáp án: B
Câu 10 [245909]: Tìm 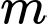 để phương trình
để phương trình 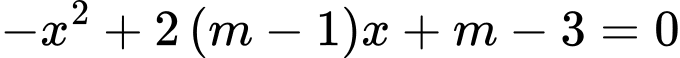 có hai nghiệm phân biệt.
có hai nghiệm phân biệt.
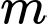 để phương trình
để phương trình 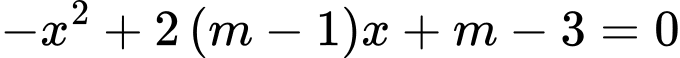 có hai nghiệm phân biệt.
có hai nghiệm phân biệt. A, 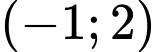 .
.
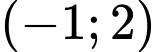 .
.B, 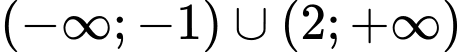 .
.
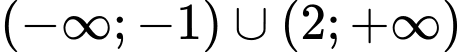 .
.C, 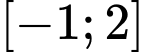 .
.
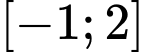 .
.D,  .
.
 .
.
Chọn B
Phương trình có hai nghiệm phân biệt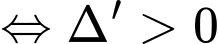

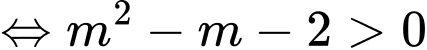
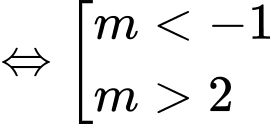
Vậy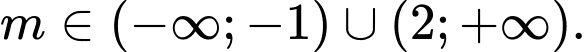 Đáp án: B
Đáp án: B
Phương trình có hai nghiệm phân biệt
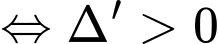

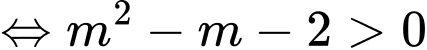
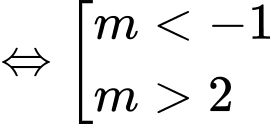
Vậy
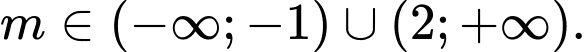 Đáp án: B
Đáp án: B
Câu 11 [581795]:
Cho phương trình 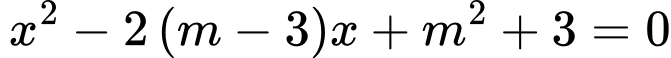 (
(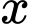 là ẩn số,
là ẩn số, 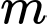 là tham số).
là tham số).
Có bao nhiêu giá trị của 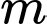 để phương trình có hai nghiệm
để phương trình có hai nghiệm 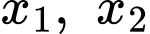 thỏa mãn hệ thức
thỏa mãn hệ thức 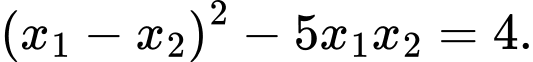
A, 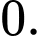
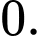
B, 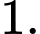
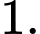
C, 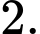
D, 
Chọn C.
Xét phương trình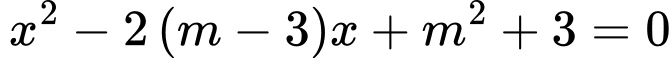 có
có
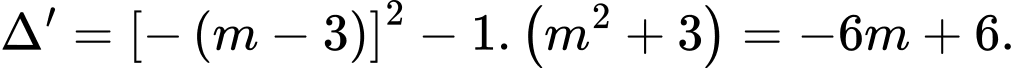
Để phương trình đã cho có hai nghiệm thì nên
nên 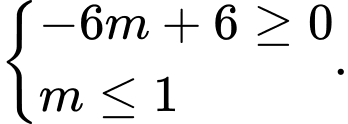
Áp dụng hệ thức Viet, ta có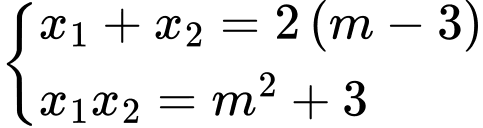
Ta có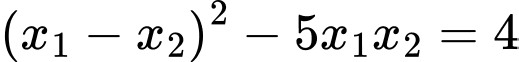
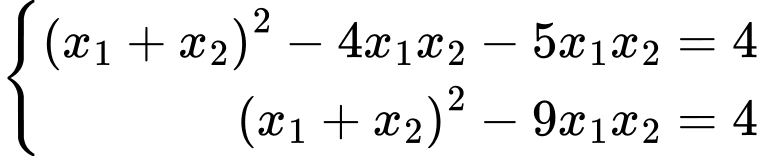
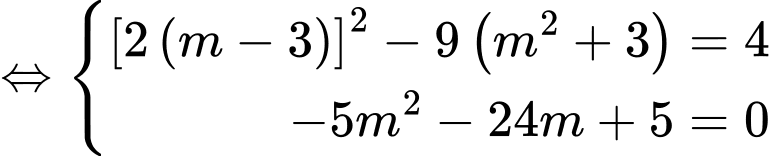
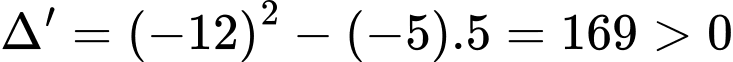 nên phương trình trên có hai nghiệm phân biệt
nên phương trình trên có hai nghiệm phân biệt 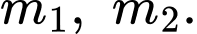
Khi đó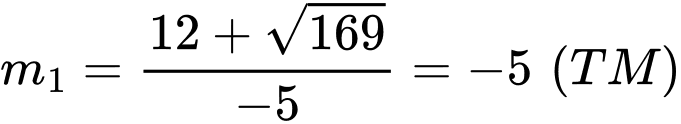 và
và 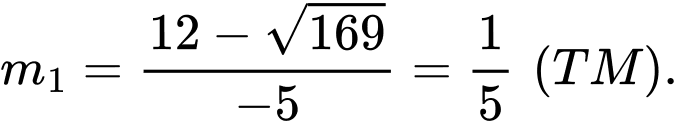 Đáp án: C
Đáp án: C
Xét phương trình
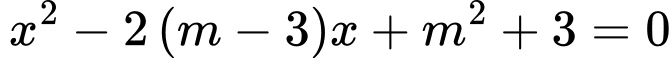 có
có
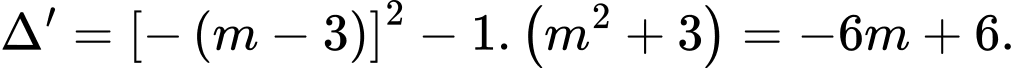
Để phương trình đã cho có hai nghiệm thì
 nên
nên 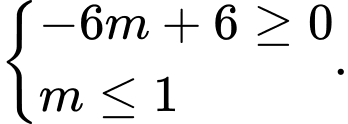
Áp dụng hệ thức Viet, ta có
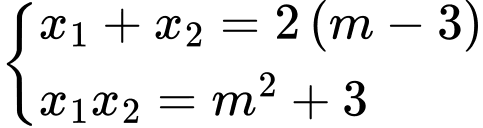
Ta có
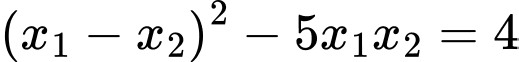
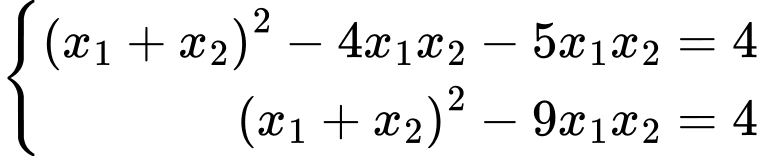
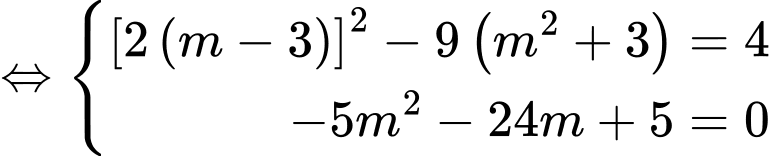
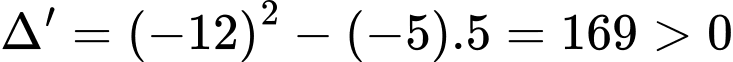 nên phương trình trên có hai nghiệm phân biệt
nên phương trình trên có hai nghiệm phân biệt 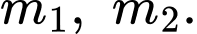
Khi đó
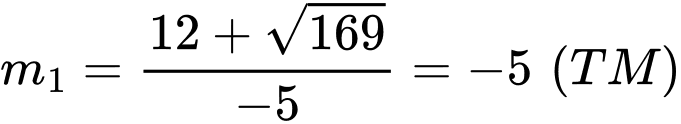 và
và 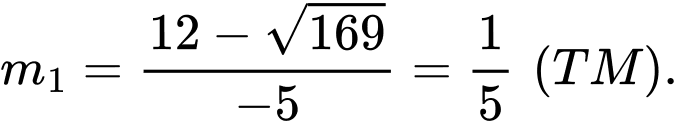 Đáp án: C
Đáp án: C
Câu 12 [245934]: Phương trình 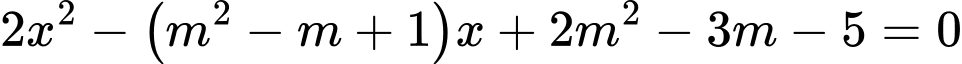 có hai nghiệm phân biệt trái dấu khi và chỉ khi
có hai nghiệm phân biệt trái dấu khi và chỉ khi
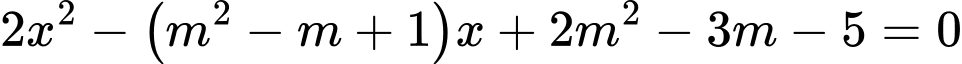 có hai nghiệm phân biệt trái dấu khi và chỉ khi
có hai nghiệm phân biệt trái dấu khi và chỉ khi A,  hoặc
hoặc 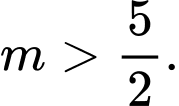
 hoặc
hoặc 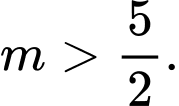
B, 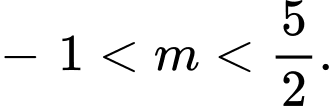
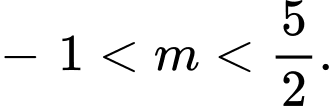
C,  hoặc
hoặc 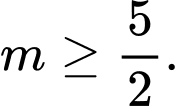
 hoặc
hoặc 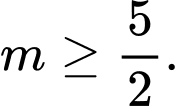
D, 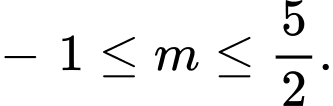
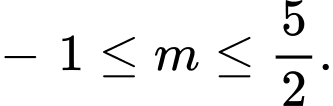
Phương trình đã cho có hai nghiệm trái dấu khi và chỉ khi
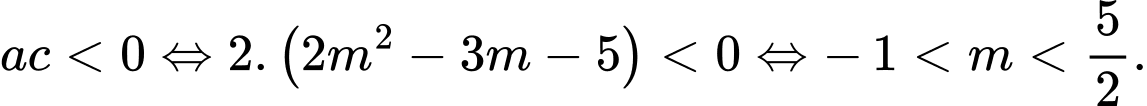 Chọn B. Đáp án: B
Chọn B. Đáp án: B
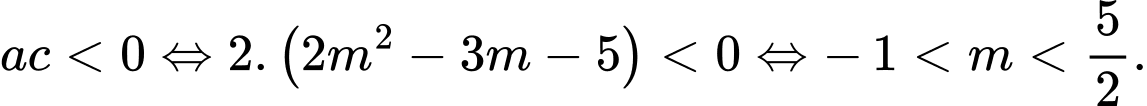 Chọn B. Đáp án: B
Chọn B. Đáp án: B
Câu 13 [245926]: Tìm tất cả các giá trị của tham số 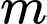 để phương trình
để phương trình 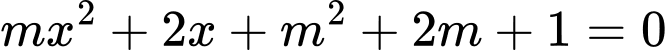 có hai nghiệm trái dấu.
có hai nghiệm trái dấu.
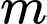 để phương trình
để phương trình 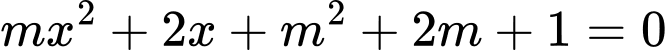 có hai nghiệm trái dấu.
có hai nghiệm trái dấu. A, 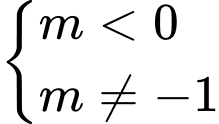 .
.
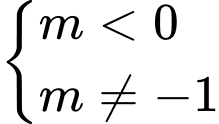 .
.B,  .
.
 .
.C, 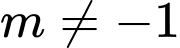 .
.
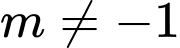 .
.D, 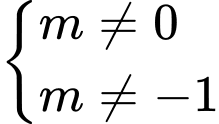 .
.
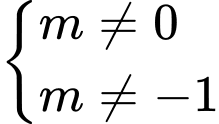 .
.
Chọn A.
Dễ thấy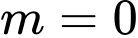 không thỏa mãn yêu cầu bài toán.
không thỏa mãn yêu cầu bài toán.
Với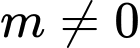 , phương trình đã cho là phương trình bậc hai.
, phương trình đã cho là phương trình bậc hai.
Phương trình có hai nghiệm trái dấu khi và chỉ khi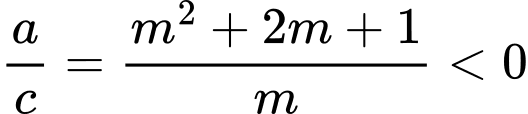
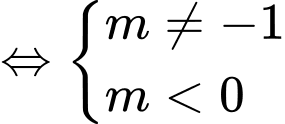 . Đáp án: A
. Đáp án: A
Dễ thấy
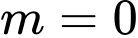 không thỏa mãn yêu cầu bài toán.
không thỏa mãn yêu cầu bài toán.
Với
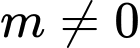 , phương trình đã cho là phương trình bậc hai.
, phương trình đã cho là phương trình bậc hai.
Phương trình có hai nghiệm trái dấu khi và chỉ khi
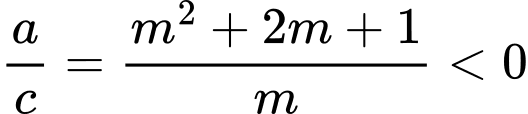
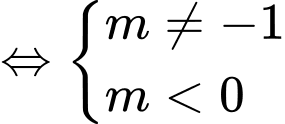 . Đáp án: A
. Đáp án: A
Câu 14 [245932]: Tìm tất cả các giá trị thực của tham số 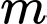 sao cho phương trình
sao cho phương trình 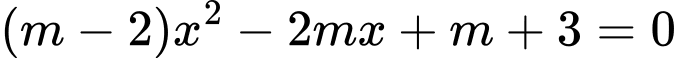 có hai nghiệm dương phân biệt.
có hai nghiệm dương phân biệt.
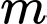 sao cho phương trình
sao cho phương trình 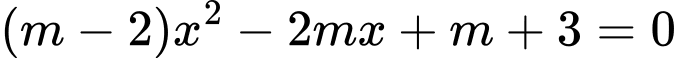 có hai nghiệm dương phân biệt.
có hai nghiệm dương phân biệt. A, 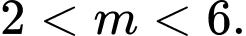
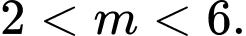
B,  hoặc
hoặc 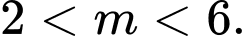
 hoặc
hoặc 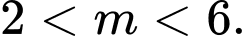
C,  hoặc
hoặc 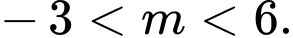
 hoặc
hoặc 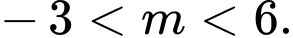
D, 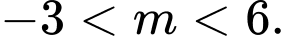
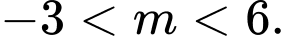
Yêu cầu bài toán 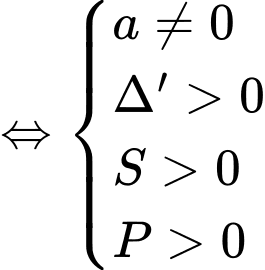
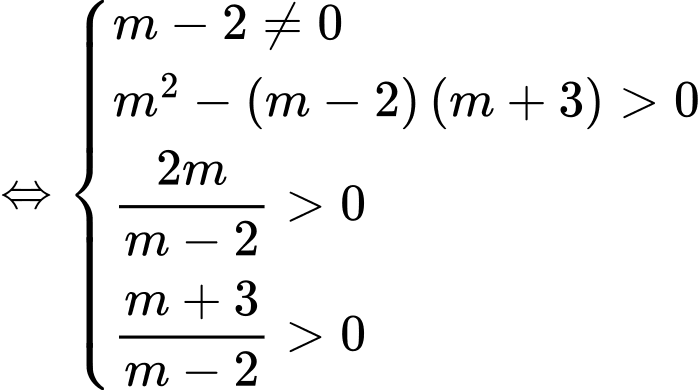
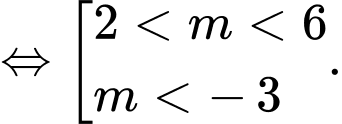 Chọn B. Đáp án: B
Chọn B. Đáp án: B
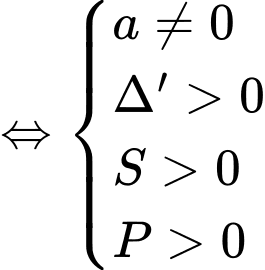
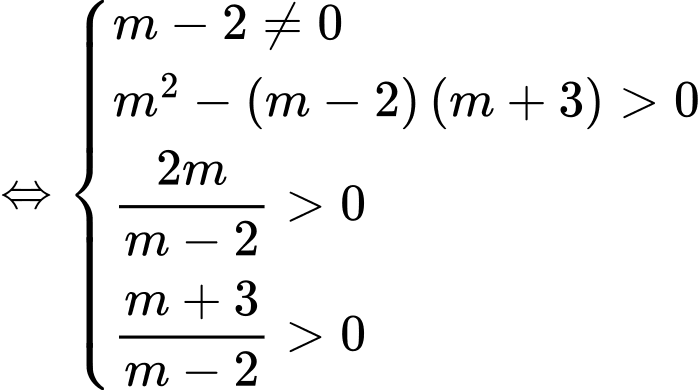
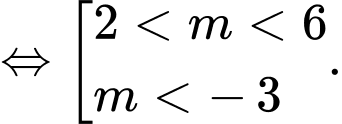 Chọn B. Đáp án: B
Chọn B. Đáp án: B
Câu 15 [189051]: Một cuộc thi có 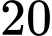 câu hỏi với quy định cho điểm như sau: Với mỗi câu hỏi, nếu trả lời đúng thì được cộng
câu hỏi với quy định cho điểm như sau: Với mỗi câu hỏi, nếu trả lời đúng thì được cộng 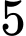 điểm, trả lời sai thì bị trừ
điểm, trả lời sai thì bị trừ 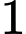 điểm, không trả lời thì không được điểm. Bạn Minh được
điểm, không trả lời thì không được điểm. Bạn Minh được 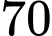 điểm trong cuộc thi đó. Hỏi bạn Minh đã trả lời đúng được bao nhiêu câu? Biết rằng bạn Minh đã trả lời tất cả các câu hỏi trong cuộc thi.
điểm trong cuộc thi đó. Hỏi bạn Minh đã trả lời đúng được bao nhiêu câu? Biết rằng bạn Minh đã trả lời tất cả các câu hỏi trong cuộc thi.
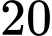 câu hỏi với quy định cho điểm như sau: Với mỗi câu hỏi, nếu trả lời đúng thì được cộng
câu hỏi với quy định cho điểm như sau: Với mỗi câu hỏi, nếu trả lời đúng thì được cộng 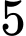 điểm, trả lời sai thì bị trừ
điểm, trả lời sai thì bị trừ 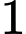 điểm, không trả lời thì không được điểm. Bạn Minh được
điểm, không trả lời thì không được điểm. Bạn Minh được 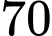 điểm trong cuộc thi đó. Hỏi bạn Minh đã trả lời đúng được bao nhiêu câu? Biết rằng bạn Minh đã trả lời tất cả các câu hỏi trong cuộc thi.
điểm trong cuộc thi đó. Hỏi bạn Minh đã trả lời đúng được bao nhiêu câu? Biết rằng bạn Minh đã trả lời tất cả các câu hỏi trong cuộc thi.
Gọi số câu bạn Minh đã trả lời đúng là 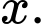 Suy ra số câu bạn Minh trả lời sai là
Suy ra số câu bạn Minh trả lời sai là 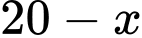 Bạn Minh được
Bạn Minh được 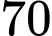 điểm nên ta có:
điểm nên ta có:
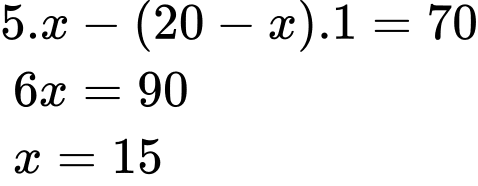 Vậy bạn Minh trả lời đúng
Vậy bạn Minh trả lời đúng  câu.
câu.
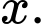 Suy ra số câu bạn Minh trả lời sai là
Suy ra số câu bạn Minh trả lời sai là 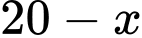 Bạn Minh được
Bạn Minh được 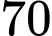 điểm nên ta có:
điểm nên ta có:
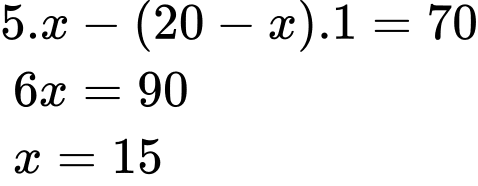 Vậy bạn Minh trả lời đúng
Vậy bạn Minh trả lời đúng  câu.
câu.
Câu 16 [189895]: Một công xưởng sản xuất một lượng hàng, theo kế hoạch mỗi ngày phải sản xuất được 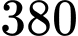 sản phẩm. Nhưng khi thực hiện, do cải tiến kĩ thuật mỗi ngày công xưởng sản xuất được
sản phẩm. Nhưng khi thực hiện, do cải tiến kĩ thuật mỗi ngày công xưởng sản xuất được 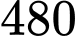 sản phẩm. Do đó, công xưởng đã hoàn thành kế hoạch trước
sản phẩm. Do đó, công xưởng đã hoàn thành kế hoạch trước 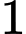 ngày và còn vươt mức
ngày và còn vươt mức 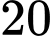 sản phẩm. Hỏi theo kế hoạch, công xưởng phải sản xuất bao nhiêu sản phẩm?
sản phẩm. Hỏi theo kế hoạch, công xưởng phải sản xuất bao nhiêu sản phẩm?
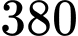 sản phẩm. Nhưng khi thực hiện, do cải tiến kĩ thuật mỗi ngày công xưởng sản xuất được
sản phẩm. Nhưng khi thực hiện, do cải tiến kĩ thuật mỗi ngày công xưởng sản xuất được 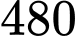 sản phẩm. Do đó, công xưởng đã hoàn thành kế hoạch trước
sản phẩm. Do đó, công xưởng đã hoàn thành kế hoạch trước 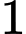 ngày và còn vươt mức
ngày và còn vươt mức 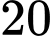 sản phẩm. Hỏi theo kế hoạch, công xưởng phải sản xuất bao nhiêu sản phẩm?
sản phẩm. Hỏi theo kế hoạch, công xưởng phải sản xuất bao nhiêu sản phẩm?
Gọi số sản phẩm theo kế hoạch công xưởng phải sản xuất là x sản phẩm( )
) 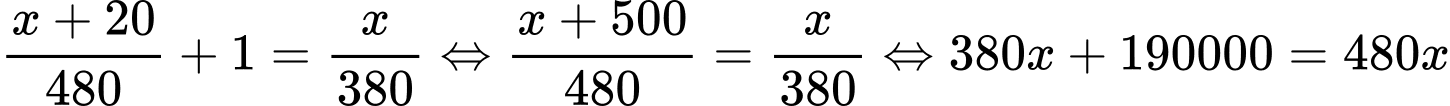
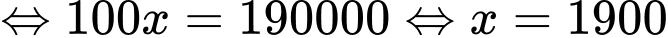 (thỏa mãn điều kiện)
(thỏa mãn điều kiện)
 )
) Theo kế hoạch mỗi ngày sản xuất 380 sản phẩm nên số ngày theo kế hoạch hoàn thành công việc là 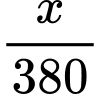 (ngày)
(ngày)
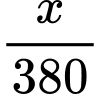 (ngày)
(ngày) Số sản phẩm thực tế xưởng sản xuất là:  (sản phẩm )
(sản phẩm )
 (sản phẩm )
(sản phẩm ) Thực tế số ngày để công xưởng hoàn thành công việc là: 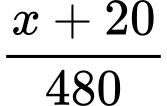 (ngày)
(ngày)
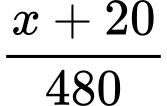 (ngày)
(ngày) Vì công xưởng hoàn thành kế hoạch sớm hơn 1 ngày nên ta có phương trình:
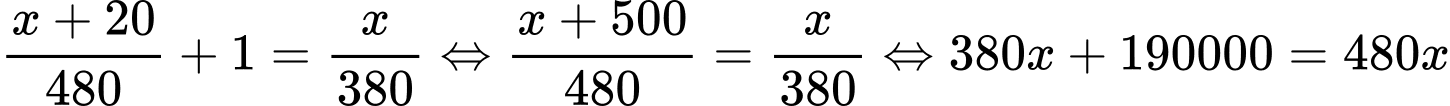
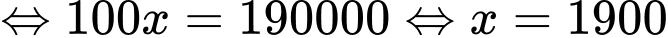 (thỏa mãn điều kiện)
(thỏa mãn điều kiện) Vậy theo kế hoạch, công xưởng phải sản xuất 1900 sản phẩm
Câu 17 [581786]: Phương trình 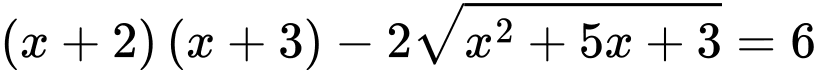 có bao nhiêu nghiệm.
có bao nhiêu nghiệm.
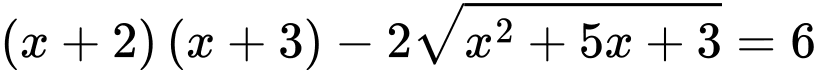 có bao nhiêu nghiệm.
có bao nhiêu nghiệm. 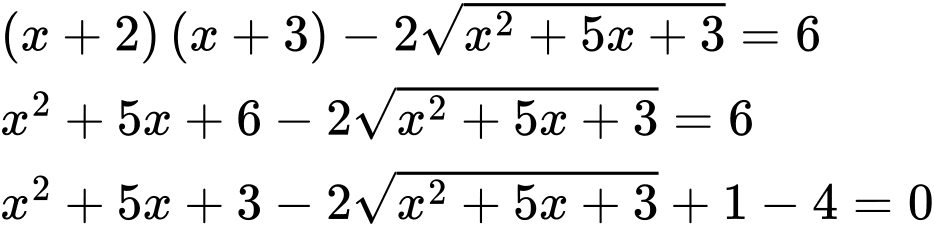
Điều kiện:
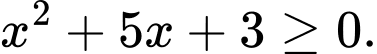
Đặt
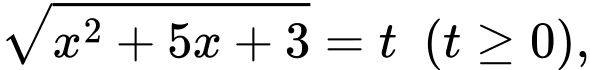 phương trình đã cho trở thành:
phương trình đã cho trở thành: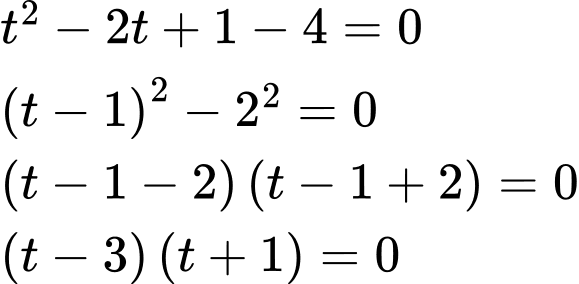
TH1:
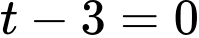 suy ra
suy ra 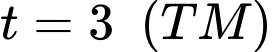 nên
nên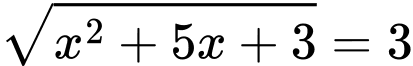
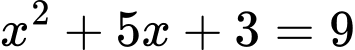
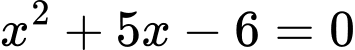
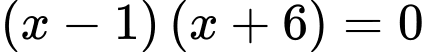
Suy ra
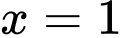 hoặc
hoặc 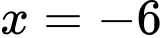
TH2:
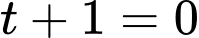 suy ra
suy ra 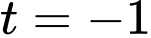 (KTM)
(KTM)Thử lại ta thấy
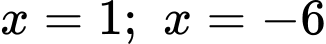 thoả mãn
thoả mãn 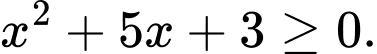
Vậy phương trình đã cho có hai nghiệm
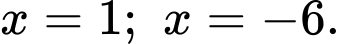
Câu 18 [581792]: Số nghiệm của phương trình 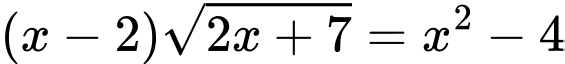 bằng
bằng
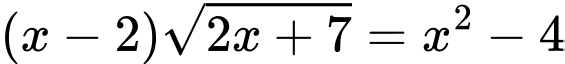 bằng
bằng 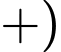 Điều kiện:
Điều kiện: 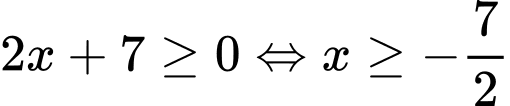 .
.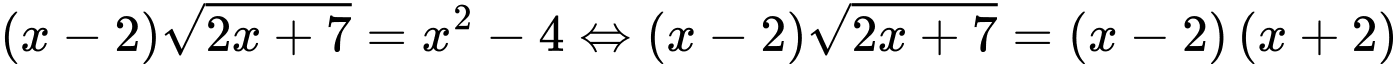
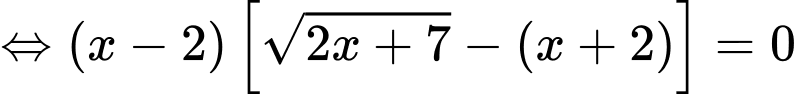
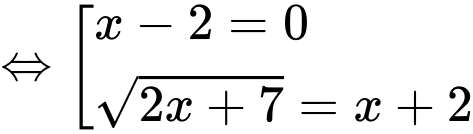 .
.
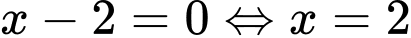 ( thỏa mãn ).
( thỏa mãn ).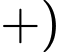
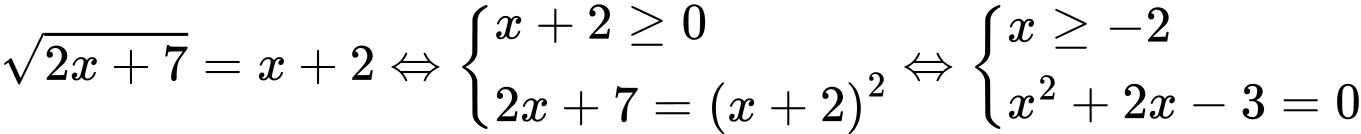 .
.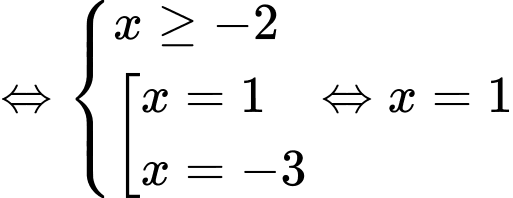 ( thỏa mãn ).
( thỏa mãn ).
Vậy phương trình có hai nghiệm 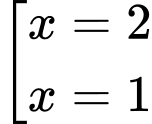 .
.
Câu 19 [189066]: (Bài toán nói về cuộc đời của nhà toán học Diofantos, được lấy trong Hợp tuyển Hy Lạp – Cuốn sách gồm 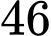 bài toán về số, viết dưới dạng thơ trào phúng).
bài toán về số, viết dưới dạng thơ trào phúng).
Thời thơ ấu của Diofantos chiếm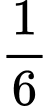 cuộc đời
cuộc đời
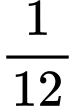 cuộc đời tiếp theo là thời thanh niên sôi nổi
cuộc đời tiếp theo là thời thanh niên sôi nổi
Thêm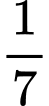 cuộc đời nữa ông sống độc thân
cuộc đời nữa ông sống độc thân
Sau khi lập gia đình được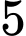 năm thì sinh một con trai
năm thì sinh một con trai
Nhưng số mệnh chỉ cho con sống bằng nửa đời cha
Ông đã từ trần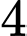 năm sau khi con mất
năm sau khi con mất
Diofantos sống bao nhiêu tuổi, hãy tính cho ra?
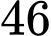 bài toán về số, viết dưới dạng thơ trào phúng).
bài toán về số, viết dưới dạng thơ trào phúng).Thời thơ ấu của Diofantos chiếm
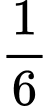 cuộc đời
cuộc đời 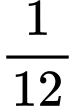 cuộc đời tiếp theo là thời thanh niên sôi nổi
cuộc đời tiếp theo là thời thanh niên sôi nổiThêm
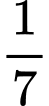 cuộc đời nữa ông sống độc thân
cuộc đời nữa ông sống độc thânSau khi lập gia đình được
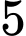 năm thì sinh một con trai
năm thì sinh một con traiNhưng số mệnh chỉ cho con sống bằng nửa đời cha
Ông đã từ trần
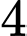 năm sau khi con mất
năm sau khi con mất Diofantos sống bao nhiêu tuổi, hãy tính cho ra?
Gọi số tuổi của Diofantos là 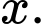 Số tuổi thời thơ ấu là
Số tuổi thời thơ ấu là 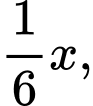 số tuổi thời thanh niên là
số tuổi thời thanh niên là 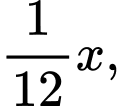 thêm
thêm 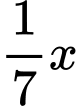 tuổi sống độc thân.
tuổi sống độc thân.
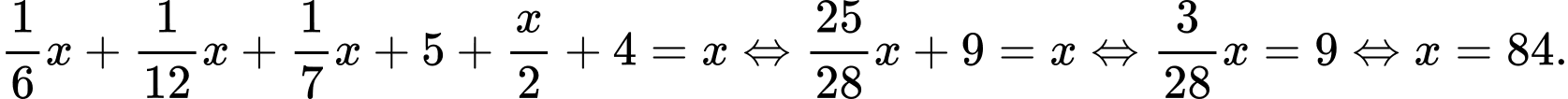
Vậy số tuổi của Diofantos là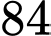 tuổi.
tuổi.
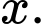 Số tuổi thời thơ ấu là
Số tuổi thời thơ ấu là 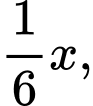 số tuổi thời thanh niên là
số tuổi thời thanh niên là 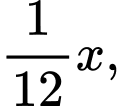 thêm
thêm 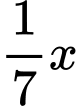 tuổi sống độc thân.
tuổi sống độc thân.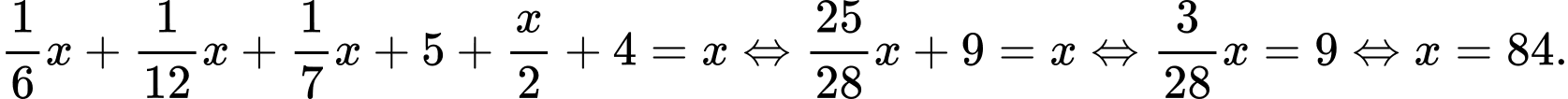
Vậy số tuổi của Diofantos là
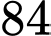 tuổi.
tuổi.
Câu 20 [300259]: Bác An có một mảnh đất hình chữ nhật với chiều dài 14 m và chiều rộng 12 m. Bác dự định xây nhà trên mảnh đất đó và dành một phân diện tích đất để làm sân vườn như hình vẽ. Biết diện tích đất làm nhà là 100 m2. Hỏi 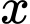 bằng bao nhiêu mét?
bằng bao nhiêu mét?
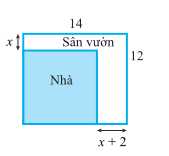
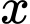 bằng bao nhiêu mét?
bằng bao nhiêu mét?
Diện tích của mảnh đất đó là 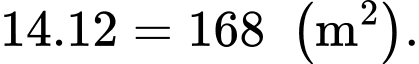
Kích thước của phần đất làm nhà lần lượt là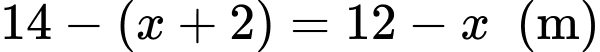 và
và 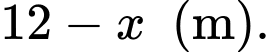
Vì diện tích đất làm nhà là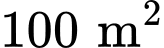 nên ta có phương trình:
nên ta có phương trình:
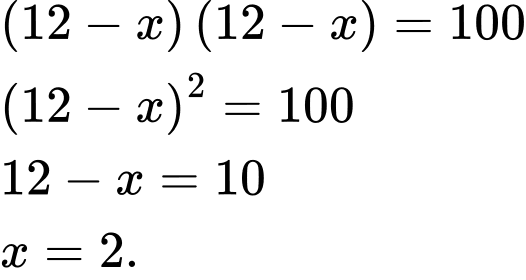
Vậy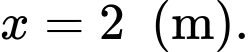
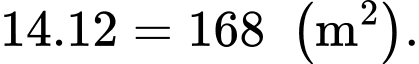
Kích thước của phần đất làm nhà lần lượt là
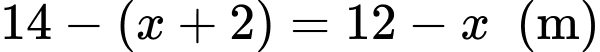 và
và 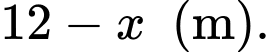
Vì diện tích đất làm nhà là
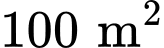 nên ta có phương trình:
nên ta có phương trình: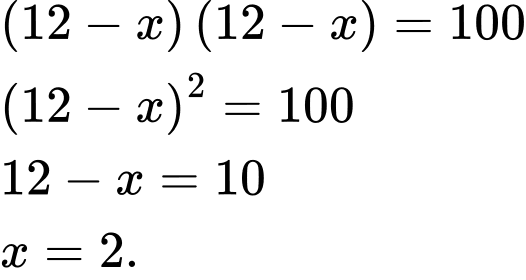
Vậy
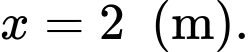
Câu 21 [300265]: Một khu vườn hình chữ nhật có chiều dài hơn chiều rộng 4 m. Nếu tăng chiều dài thêm 7 m và giảm chiều rộng 5 m thì diện tích giảm 29 m2. Tính chu vi của khu vườn ban đầu.
Gọi chiều rộng của khu vườn đó là 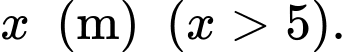
Chiều dài của khu vườn đó là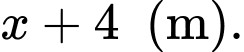
Diện tích của khu vườn đó là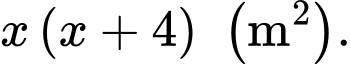
Vì nếu tăng chiều dài thêm 7 m và giảm chiều rộng 5 m thì diện tích giảm 29 m2 nên ta có phương trình:
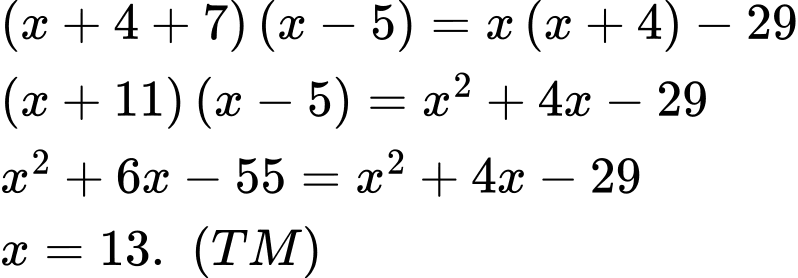
Suy ra chiều rộng của khu vườn đó là 13 m, chiều dài của khu vườn đó là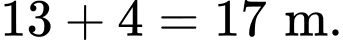
Vậy chu vi của khu vườn đó là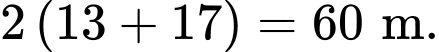
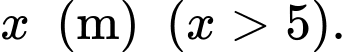
Chiều dài của khu vườn đó là
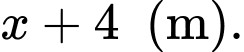
Diện tích của khu vườn đó là
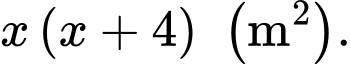
Vì nếu tăng chiều dài thêm 7 m và giảm chiều rộng 5 m thì diện tích giảm 29 m2 nên ta có phương trình:
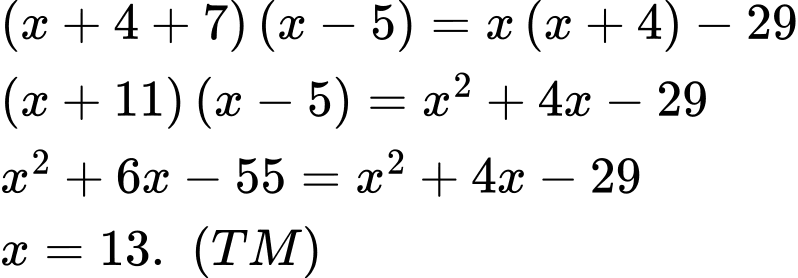
Suy ra chiều rộng của khu vườn đó là 13 m, chiều dài của khu vườn đó là
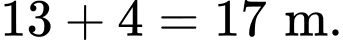
Vậy chu vi của khu vườn đó là
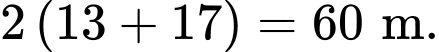
Câu 22 [581787]: Gọi 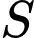 là tập hợp các giá trị của tham số
là tập hợp các giá trị của tham số 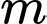 để phương trình
để phương trình 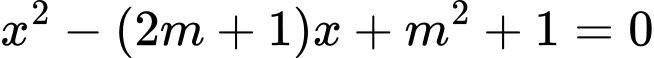 có hai nghiệm phân biệt
có hai nghiệm phân biệt 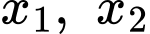 thỏa mãn
thỏa mãn 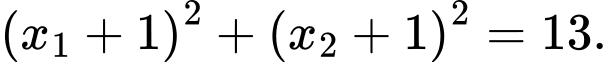 Số phần tử của tập
Số phần tử của tập 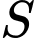 bằng bao nhiêu?
bằng bao nhiêu?
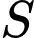 là tập hợp các giá trị của tham số
là tập hợp các giá trị của tham số 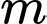 để phương trình
để phương trình 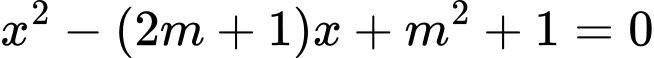 có hai nghiệm phân biệt
có hai nghiệm phân biệt 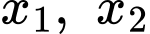 thỏa mãn
thỏa mãn 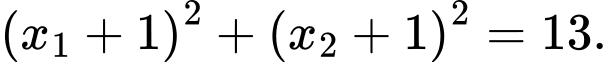 Số phần tử của tập
Số phần tử của tập 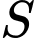 bằng bao nhiêu?
bằng bao nhiêu?
Xét phương trình 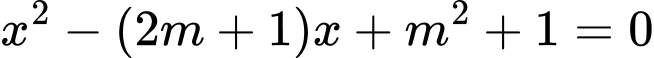 có
có 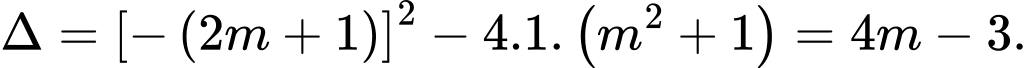
Để phương trình đã cho có hai nghiệm phân biệt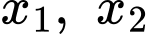 thì
thì  nên
nên 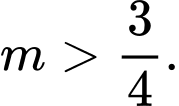
Áp dụng hệ thức Viet, ta có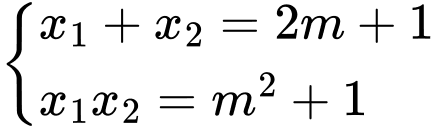
Ta có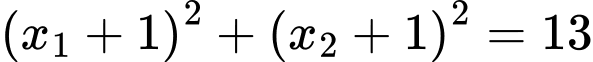
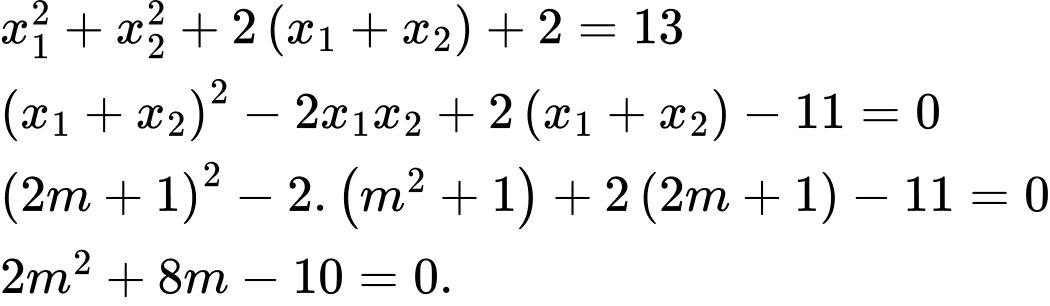
Đáp án: 1 phần tử là 1
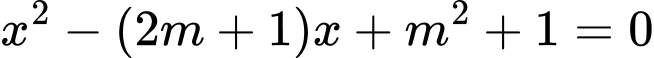 có
có 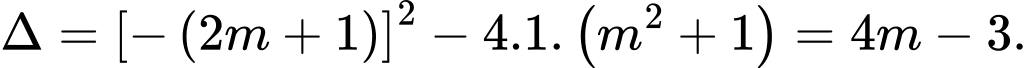
Để phương trình đã cho có hai nghiệm phân biệt
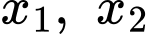 thì
thì  nên
nên 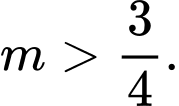
Áp dụng hệ thức Viet, ta có
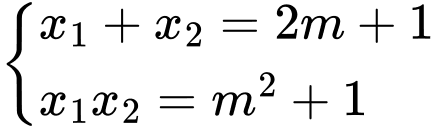
Ta có
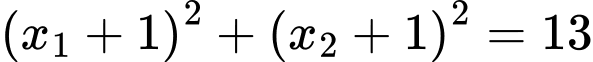
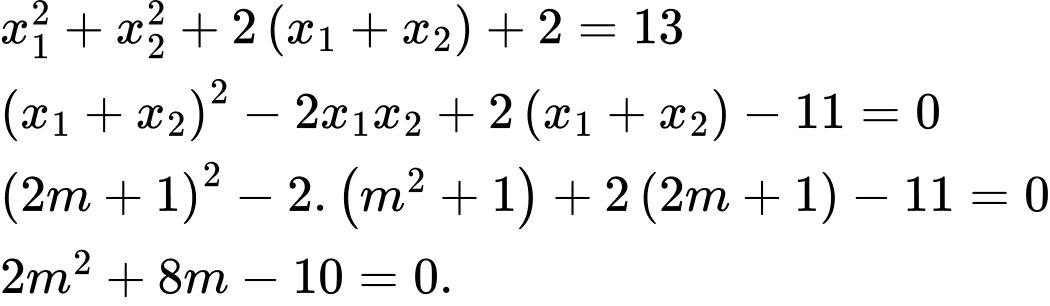
Đáp án: 1 phần tử là 1
Câu 23 [581788]: Cho phương trình 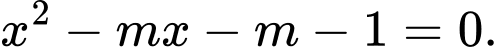 Gọi
Gọi 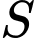 là tập hợp các giá trị của
là tập hợp các giá trị của 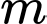 để phương trình có hai nghiệm phân biệt
để phương trình có hai nghiệm phân biệt 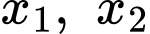 thỏa mãn
thỏa mãn 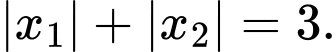 Tổng các phần tử của tập hợp
Tổng các phần tử của tập hợp 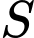 bằng bao nhiêu?
bằng bao nhiêu?
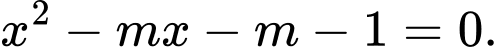 Gọi
Gọi 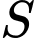 là tập hợp các giá trị của
là tập hợp các giá trị của 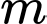 để phương trình có hai nghiệm phân biệt
để phương trình có hai nghiệm phân biệt 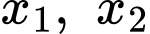 thỏa mãn
thỏa mãn 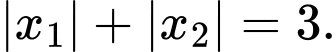 Tổng các phần tử của tập hợp
Tổng các phần tử của tập hợp 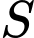 bằng bao nhiêu?
bằng bao nhiêu?
Xét phương trình 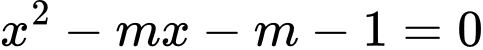 có
có
Do nên phương trình có hai nghiệm
nên phương trình có hai nghiệm 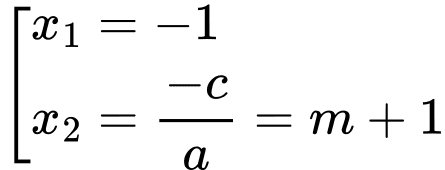
Để phương trình đã cho luôn có hai nghiệm phân biệt thì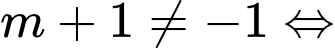
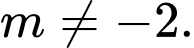
Ta có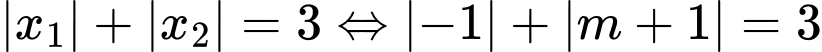
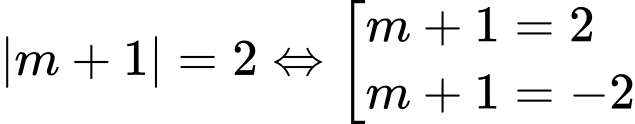
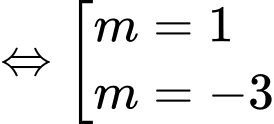
Vậy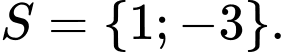 Tổng các phần tử bằng
Tổng các phần tử bằng 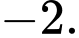
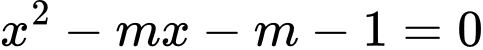 có
cóDo
 nên phương trình có hai nghiệm
nên phương trình có hai nghiệm 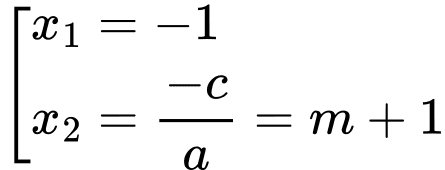
Để phương trình đã cho luôn có hai nghiệm phân biệt thì
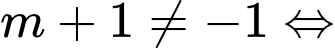
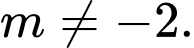
Ta có
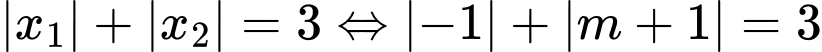
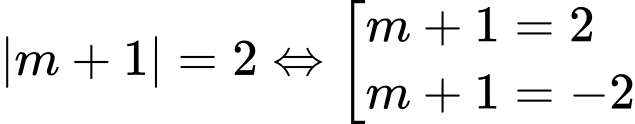
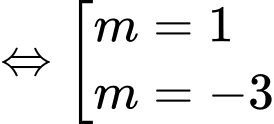
Vậy
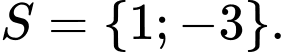 Tổng các phần tử bằng
Tổng các phần tử bằng 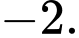
Câu 24 [581789]: Cho phương trình 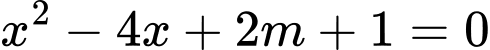 với
với 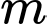 là tham số. Gọi
là tham số. Gọi 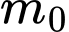 là giá trị của tham số
là giá trị của tham số 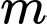 để phương trình đã cho có hai nghiệm phân biệt
để phương trình đã cho có hai nghiệm phân biệt 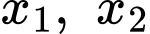 thỏa mãn
thỏa mãn 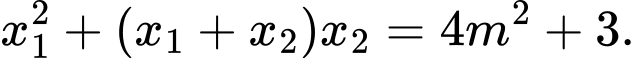 Tính
Tính 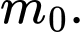
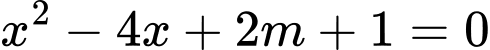 với
với 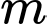 là tham số. Gọi
là tham số. Gọi 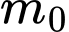 là giá trị của tham số
là giá trị của tham số 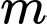 để phương trình đã cho có hai nghiệm phân biệt
để phương trình đã cho có hai nghiệm phân biệt 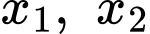 thỏa mãn
thỏa mãn 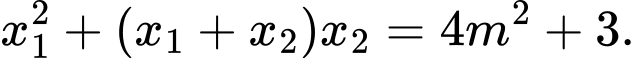 Tính
Tính 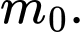
Xét phương trình 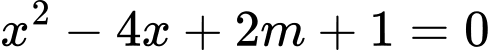 có
có 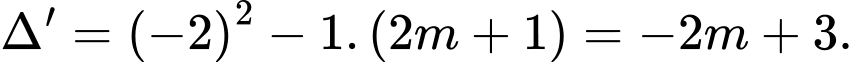
Để phương trình đã cho luôn có hai nghiệm phân biệt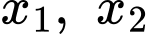 thì
thì  suy ra
suy ra 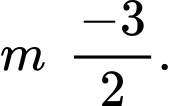
Áp dụng hệ thức Viet, ta có: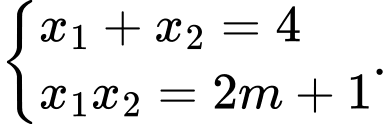
Ta có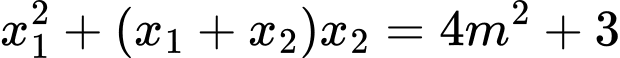
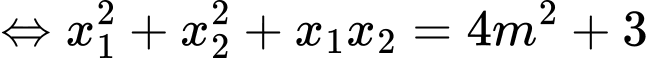
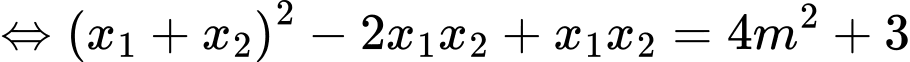
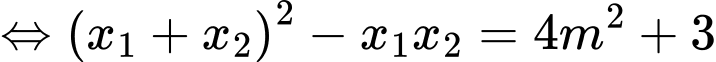
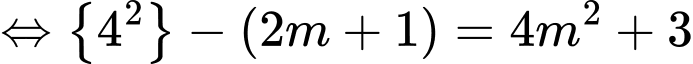
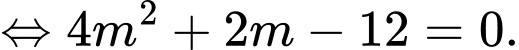
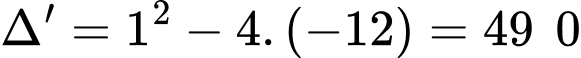 nên phương trình trên có hai nghiệm phân biệt
nên phương trình trên có hai nghiệm phân biệt 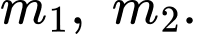
Khi đó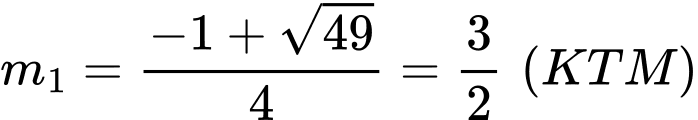 và
và 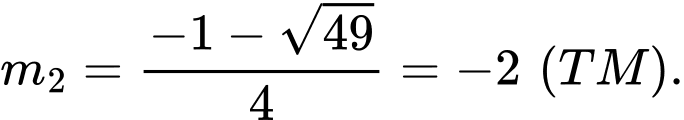
Vậy giá trị của m là -2.
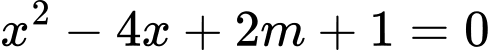 có
có 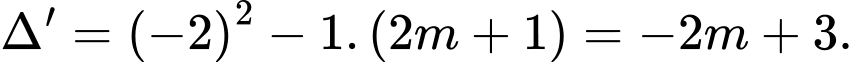
Để phương trình đã cho luôn có hai nghiệm phân biệt
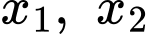 thì
thì  suy ra
suy ra 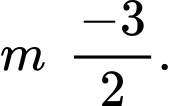
Áp dụng hệ thức Viet, ta có:
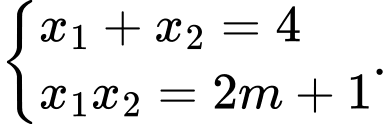
Ta có
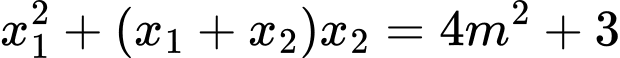
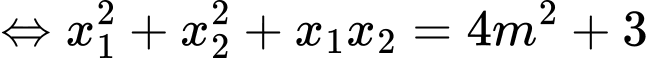
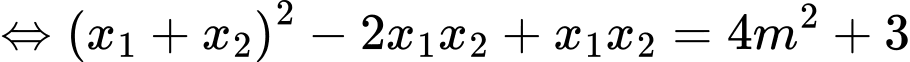
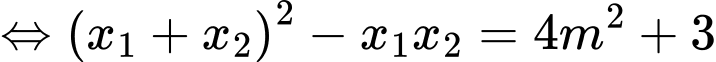
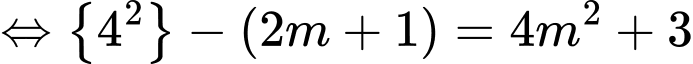
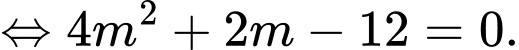
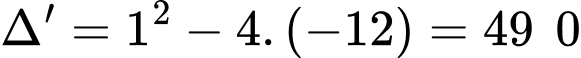 nên phương trình trên có hai nghiệm phân biệt
nên phương trình trên có hai nghiệm phân biệt 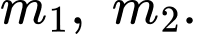
Khi đó
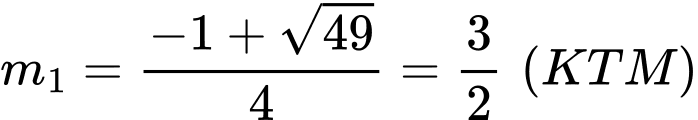 và
và 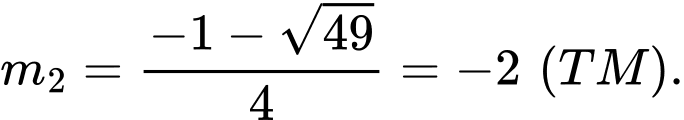
Vậy giá trị của m là -2.
Câu 25 [581791]: Cho phương trình 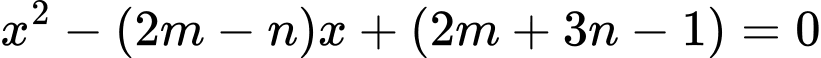 với
với 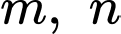 là tham số. Gọi
là tham số. Gọi 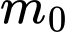 và
và 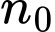 là các giá trị của
là các giá trị của 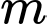 và
và 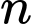 để phương trình đã cho có hai nghiệm
để phương trình đã cho có hai nghiệm 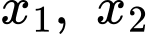 thỏa mãn
thỏa mãn 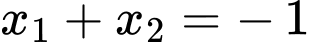 và
và 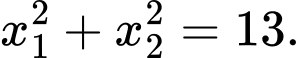 Tính
Tính 
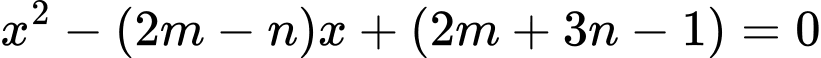 với
với 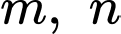 là tham số. Gọi
là tham số. Gọi 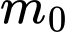 và
và 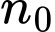 là các giá trị của
là các giá trị của 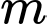 và
và 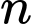 để phương trình đã cho có hai nghiệm
để phương trình đã cho có hai nghiệm 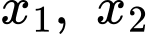 thỏa mãn
thỏa mãn 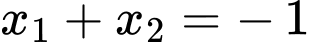 và
và 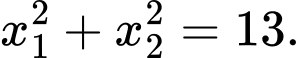 Tính
Tính 
Xét phương trình 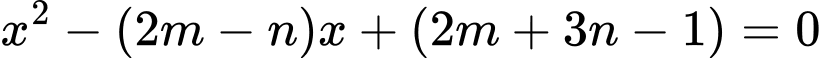 có
có
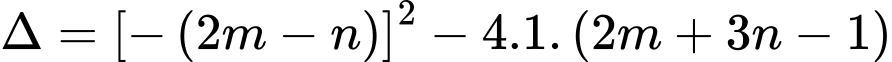
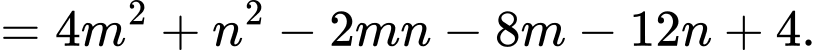
Áp dụng hệ thức Viet, ta có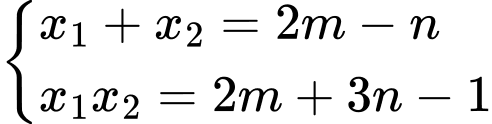
Ta có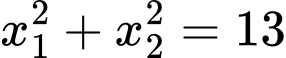
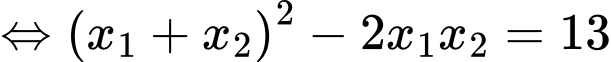
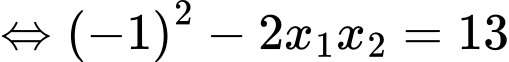
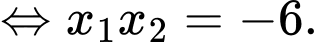
Xét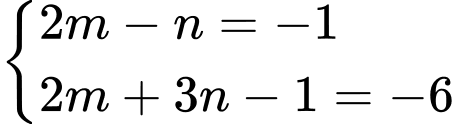
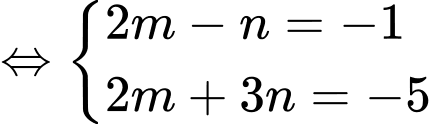
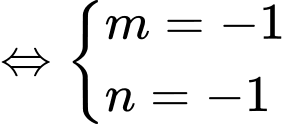
Thử lại ta thấy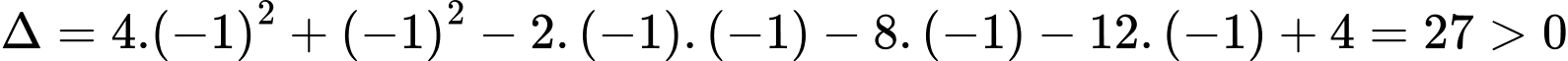 nên thỏa mãn phương trình đã cho có hai nghiệm phân biệt
nên thỏa mãn phương trình đã cho có hai nghiệm phân biệt 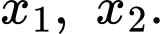
Đáp án: 2.
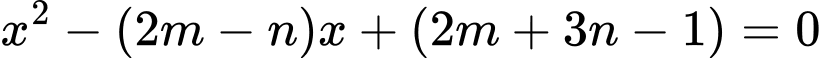 có
có
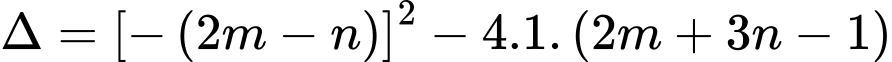
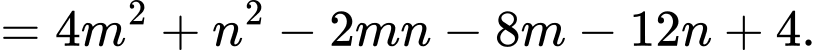
Áp dụng hệ thức Viet, ta có
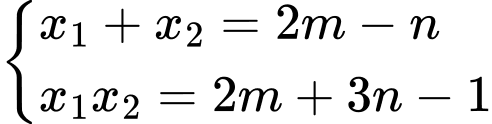
Ta có
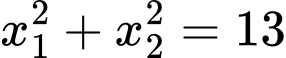
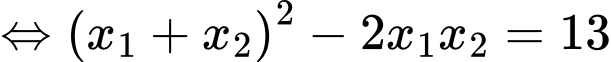
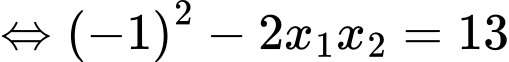
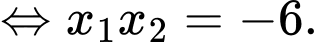
Xét
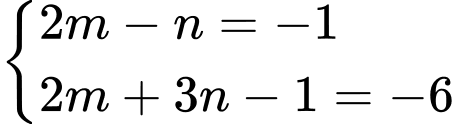
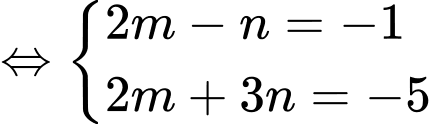
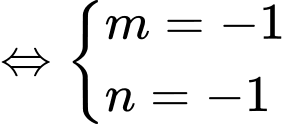
Thử lại ta thấy
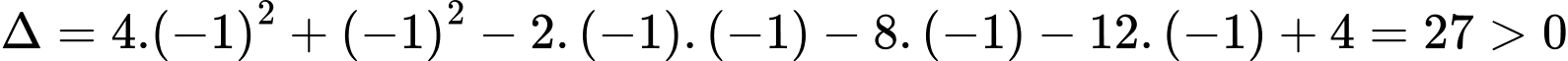 nên thỏa mãn phương trình đã cho có hai nghiệm phân biệt
nên thỏa mãn phương trình đã cho có hai nghiệm phân biệt 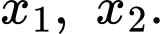
Đáp án: 2.
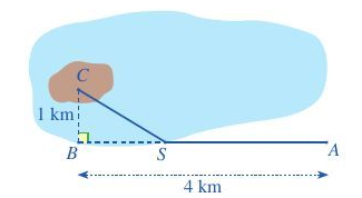
Câu 26 [239876]: Một kĩ sư thiết kế đường dây điện từ vị trí  đến vị trí S và từ vị trí S đến vị trí C trên cù lao như hình. Tiền công thiết kế mỗi ki-lômét đường dây từ
đến vị trí S và từ vị trí S đến vị trí C trên cù lao như hình. Tiền công thiết kế mỗi ki-lômét đường dây từ  đến
đến  và từ
và từ  đến
đến  lần lượt là 3 triệu đồng và 5 triệu đồng. Biết tổng số tiền công là 16 triệu đồng. Tính tổng số ki-lô-mét đường dây điện đã thiết kế.
lần lượt là 3 triệu đồng và 5 triệu đồng. Biết tổng số tiền công là 16 triệu đồng. Tính tổng số ki-lô-mét đường dây điện đã thiết kế.
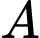 đến vị trí S và từ vị trí S đến vị trí C trên cù lao như hình. Tiền công thiết kế mỗi ki-lômét đường dây từ
đến vị trí S và từ vị trí S đến vị trí C trên cù lao như hình. Tiền công thiết kế mỗi ki-lômét đường dây từ 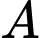 đến
đến  và từ
và từ 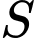 đến
đến  lần lượt là 3 triệu đồng và 5 triệu đồng. Biết tổng số tiền công là 16 triệu đồng. Tính tổng số ki-lô-mét đường dây điện đã thiết kế.
lần lượt là 3 triệu đồng và 5 triệu đồng. Biết tổng số tiền công là 16 triệu đồng. Tính tổng số ki-lô-mét đường dây điện đã thiết kế. 
Gọi khoảng cách từ 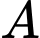 đến
đến 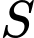 là
là 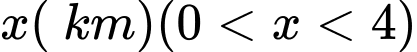
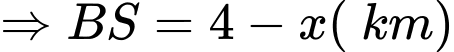
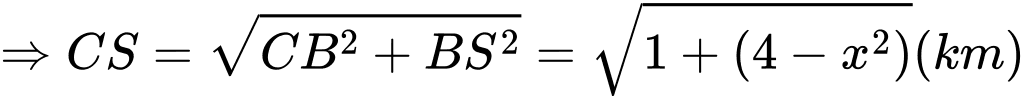
Tổng số tiền từ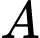 đến
đến  là:
là:
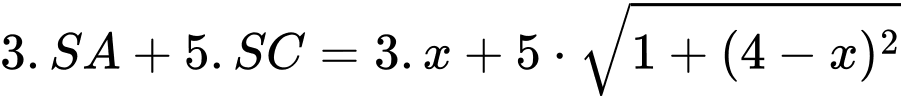 (triệu đồng)
(triệu đồng)
Khi đó ta có phương trình:
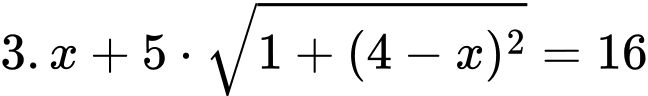
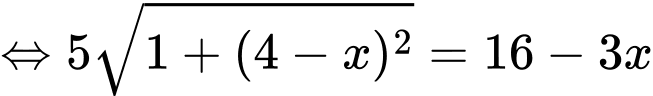
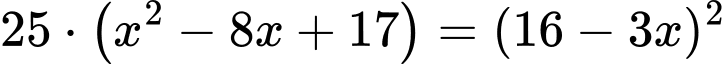
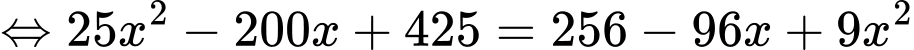
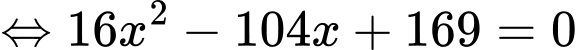
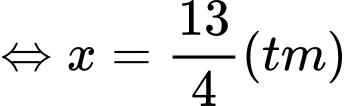
Do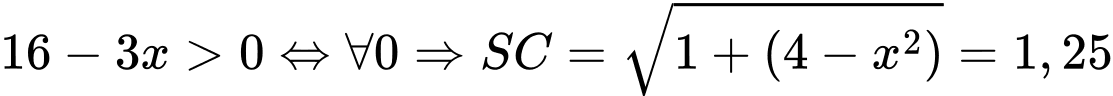
Vậy tổng ki-lô-mét đường dây điện đã thiết kế là

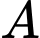 đến
đến 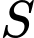 là
là 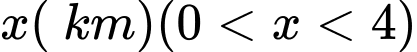
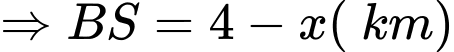
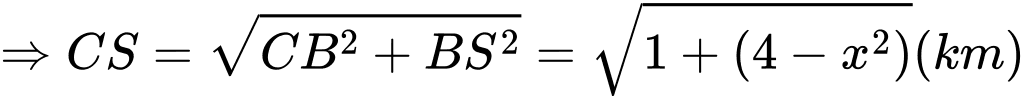
Tổng số tiền từ
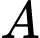 đến
đến  là:
là: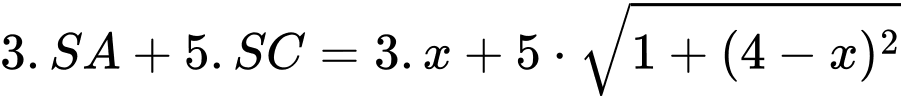 (triệu đồng)
(triệu đồng)Khi đó ta có phương trình:
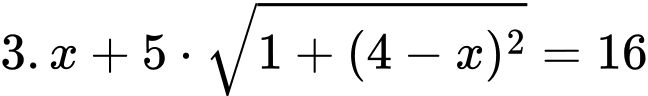
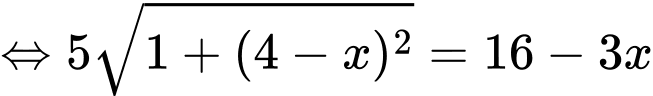
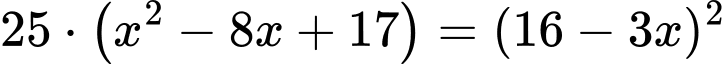
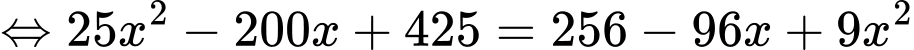
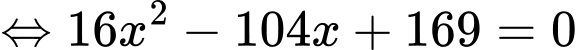
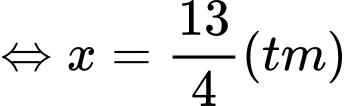
Do
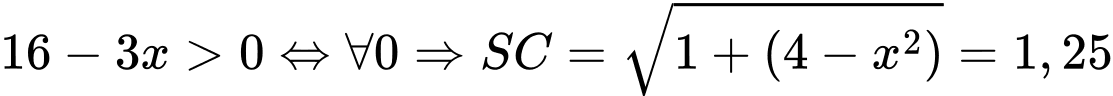
Vậy tổng ki-lô-mét đường dây điện đã thiết kế là

Câu 27 [239865]: Để leo lên một bức tường, bác Nam dùng một chiếc thang có chiều dài cao hơn bức tường đó 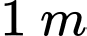 . Ban đầu, bác Nam đặt chiếc thang mà đầu trên của chiếc thang đó vừa chạm đúng vào mép trên bức tường (Hình a). Sau đó, bác Nam dịch chuyển chân thang vào gần chân tường thêm 0,5
. Ban đầu, bác Nam đặt chiếc thang mà đầu trên của chiếc thang đó vừa chạm đúng vào mép trên bức tường (Hình a). Sau đó, bác Nam dịch chuyển chân thang vào gần chân tường thêm 0,5 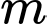 thì bác Nam nhận thấy thang tạo với mặt đất một góc
thì bác Nam nhận thấy thang tạo với mặt đất một góc 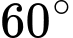 (Hình
(Hình 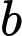 ). Bức tường cao bao nhiêu mét (làm tròn kết quả đến hàng phần mười)?
). Bức tường cao bao nhiêu mét (làm tròn kết quả đến hàng phần mười)?
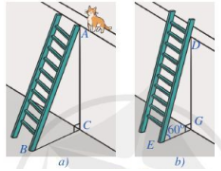
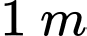 . Ban đầu, bác Nam đặt chiếc thang mà đầu trên của chiếc thang đó vừa chạm đúng vào mép trên bức tường (Hình a). Sau đó, bác Nam dịch chuyển chân thang vào gần chân tường thêm 0,5
. Ban đầu, bác Nam đặt chiếc thang mà đầu trên của chiếc thang đó vừa chạm đúng vào mép trên bức tường (Hình a). Sau đó, bác Nam dịch chuyển chân thang vào gần chân tường thêm 0,5 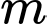 thì bác Nam nhận thấy thang tạo với mặt đất một góc
thì bác Nam nhận thấy thang tạo với mặt đất một góc 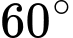 (Hình
(Hình 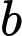 ). Bức tường cao bao nhiêu mét (làm tròn kết quả đến hàng phần mười)?
). Bức tường cao bao nhiêu mét (làm tròn kết quả đến hàng phần mười)? 
Gọi chiều cao bức tường
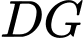 là
là 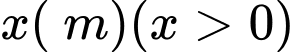
Chiều dài chiếc thang là
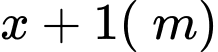
Khoảng cách từ chân thang sau khi bác Nam điều chỉnh là:
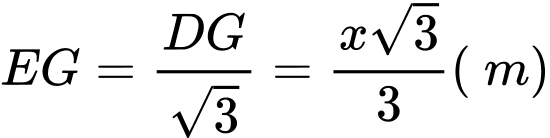
Áp dụng định lý Py-ta-go cho tam giác vuông ABC ta có:
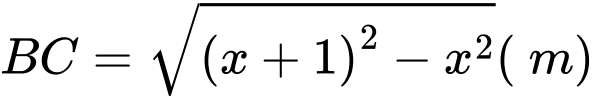
Bác Nam dịch chuyển chân thang vào gần chân tường thêm
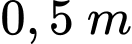 nên ta có:
nên ta có: 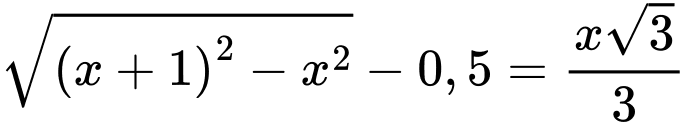
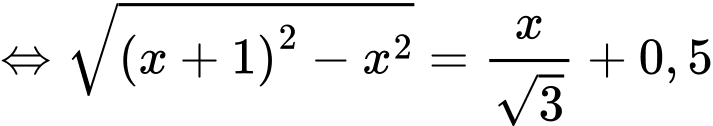
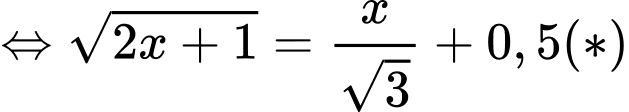
Ta có
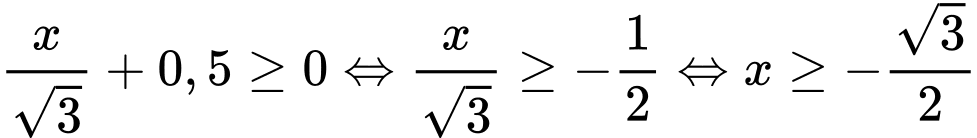 (Luôn đúng do
(Luôn đúng do 
Ta bình phương hai vế (*) ta được:
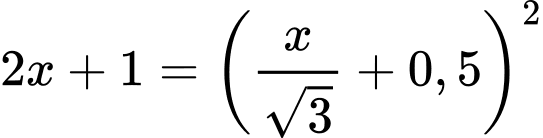
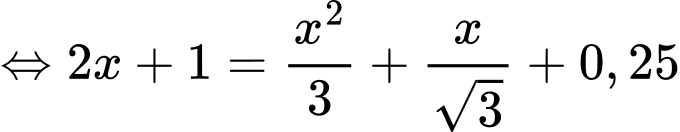
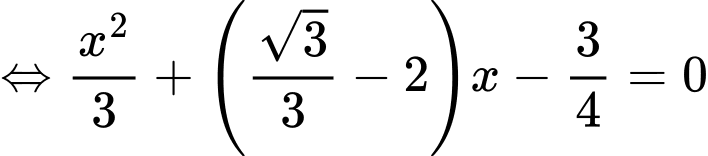
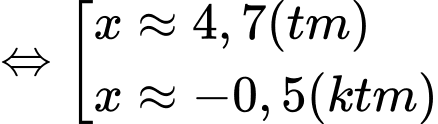
Vậy chiều cao của bức tường là 4,7 m.
Câu 28 [239866]: Một người đứng ở điểm A trên một bờ sông rộng 300 m, chèo thuyền đến vị trí 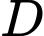 , sau đó chạy bộ đến vị trí B cách C một khoảng
, sau đó chạy bộ đến vị trí B cách C một khoảng 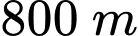 như Hình. Vận tốc chèo thuyền là
như Hình. Vận tốc chèo thuyền là 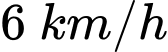 , vận tốc chạy bộ là
, vận tốc chạy bộ là 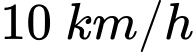 và giả sử vận tốc dòng nước không đáng kể. Tính khoảng cách từ vị trí
và giả sử vận tốc dòng nước không đáng kể. Tính khoảng cách từ vị trí  đến
đến 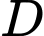 , biết tổng thời gian người đó chèo thuyền và chạy bộ từ
, biết tổng thời gian người đó chèo thuyền và chạy bộ từ 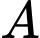 đến
đến 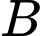 là 7,2 phút.
là 7,2 phút.
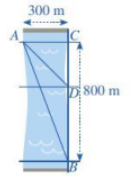
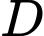 , sau đó chạy bộ đến vị trí B cách C một khoảng
, sau đó chạy bộ đến vị trí B cách C một khoảng 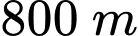 như Hình. Vận tốc chèo thuyền là
như Hình. Vận tốc chèo thuyền là 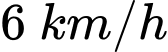 , vận tốc chạy bộ là
, vận tốc chạy bộ là 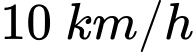 và giả sử vận tốc dòng nước không đáng kể. Tính khoảng cách từ vị trí
và giả sử vận tốc dòng nước không đáng kể. Tính khoảng cách từ vị trí  đến
đến 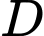 , biết tổng thời gian người đó chèo thuyền và chạy bộ từ
, biết tổng thời gian người đó chèo thuyền và chạy bộ từ 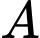 đến
đến 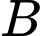 là 7,2 phút.
là 7,2 phút. 
Câu 29 [239867]: Một ngọn hải đăng đặt tại vị trí 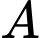 cách bờ biển một khoảng cách
cách bờ biển một khoảng cách 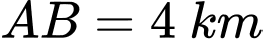 . Trên bờ biển có một cái kho ở vị trí C cách
. Trên bờ biển có một cái kho ở vị trí C cách 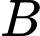 một khoảng là 7 km. Người canh hải đăng có thể chèo thuyền từ
một khoảng là 7 km. Người canh hải đăng có thể chèo thuyền từ 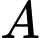 đến vị trí
đến vị trí 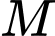 trên bờ biển với vận tốc
trên bờ biển với vận tốc 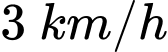 rồi đi bộ đến
rồi đi bộ đến  với vận tốc
với vận tốc 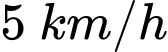 như Hình 35 . Tính khoảng cách từ vị trí
như Hình 35 . Tính khoảng cách từ vị trí 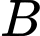 đến
đến 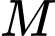 , biết thời gian người đó đi từ
, biết thời gian người đó đi từ 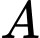 đến
đến  là 148 phút.
là 148 phút.

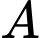 cách bờ biển một khoảng cách
cách bờ biển một khoảng cách 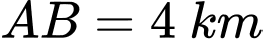 . Trên bờ biển có một cái kho ở vị trí C cách
. Trên bờ biển có một cái kho ở vị trí C cách 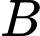 một khoảng là 7 km. Người canh hải đăng có thể chèo thuyền từ
một khoảng là 7 km. Người canh hải đăng có thể chèo thuyền từ 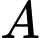 đến vị trí
đến vị trí 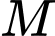 trên bờ biển với vận tốc
trên bờ biển với vận tốc 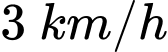 rồi đi bộ đến
rồi đi bộ đến  với vận tốc
với vận tốc 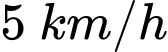 như Hình 35 . Tính khoảng cách từ vị trí
như Hình 35 . Tính khoảng cách từ vị trí 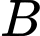 đến
đến 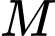 , biết thời gian người đó đi từ
, biết thời gian người đó đi từ 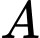 đến
đến  là 148 phút.
là 148 phút. 
Gọi BM 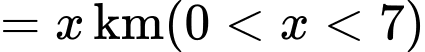
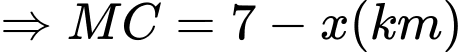
Ta có: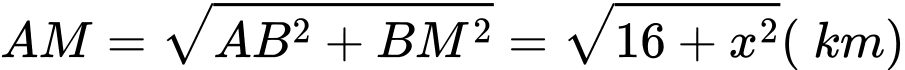
Thời gian từ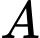 đến
đến 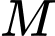 là:
là: 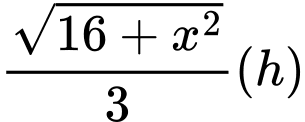
Thời gian từ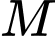 đến C là:
đến C là: 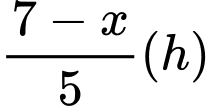
Tổng thời gian từ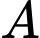 đến C là 148 phút nên ta có:
đến C là 148 phút nên ta có:
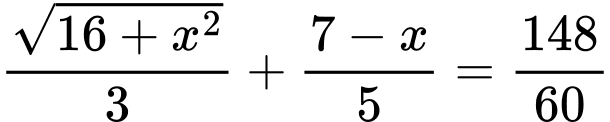
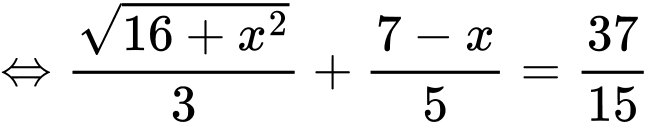
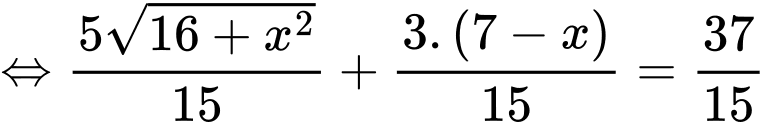
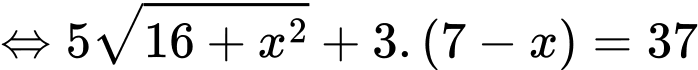
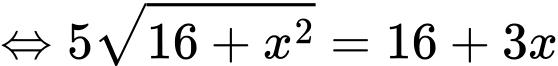
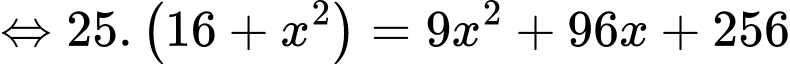

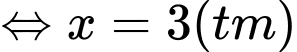
Vậy khoảng cách từ vị trí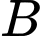 đến
đến 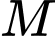 là 3 km.
là 3 km.
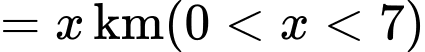
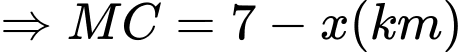
Ta có:
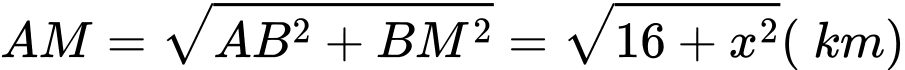
Thời gian từ
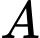 đến
đến 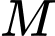 là:
là: 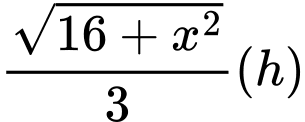
Thời gian từ
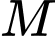 đến C là:
đến C là: 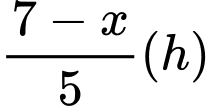
Tổng thời gian từ
 đến C là 148 phút nên ta có:
đến C là 148 phút nên ta có: 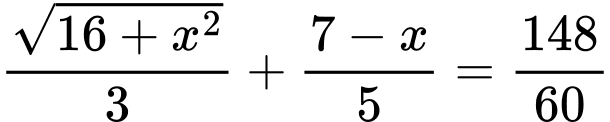
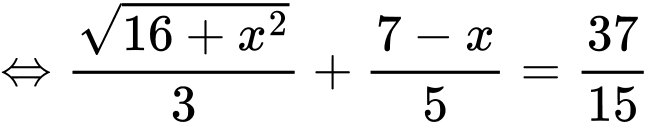
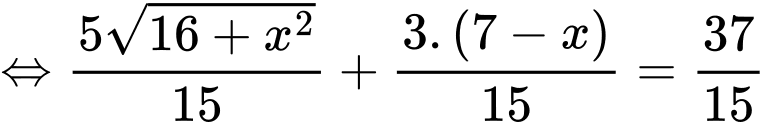
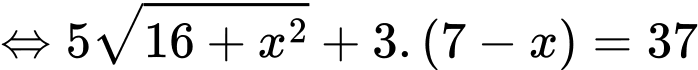
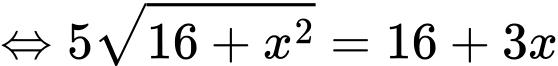
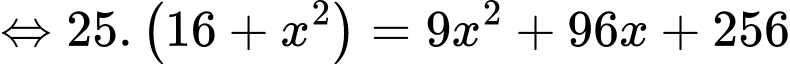

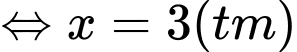
Vậy khoảng cách từ vị trí
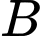 đến
đến 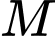 là 3 km.
là 3 km.
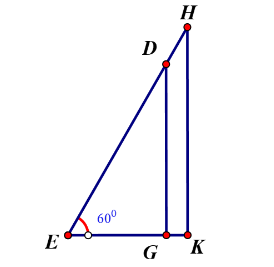
Câu 30 [251601]: Cho tứ giác 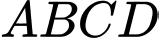 có
có 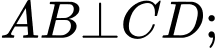
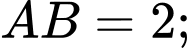
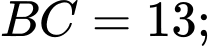
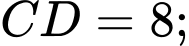
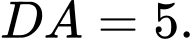 Gọi
Gọi 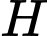 là giao điểm của
là giao điểm của  và
và 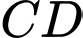 và đặt
và đặt 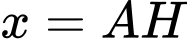 . Hãy thiết lập một phương trình để tính độ dài
. Hãy thiết lập một phương trình để tính độ dài 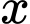 , từ đó tính diện tích tứ giác
, từ đó tính diện tích tứ giác 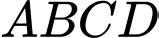 .
.

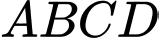 có
có 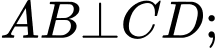
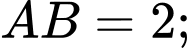
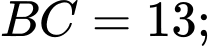
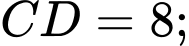
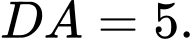 Gọi
Gọi 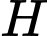 là giao điểm của
là giao điểm của  và
và 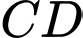 và đặt
và đặt 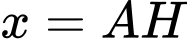 . Hãy thiết lập một phương trình để tính độ dài
. Hãy thiết lập một phương trình để tính độ dài 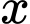 , từ đó tính diện tích tứ giác
, từ đó tính diện tích tứ giác 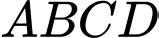 .
.
- Xét tam giác 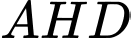 vuông tại
vuông tại 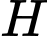 có:
có: 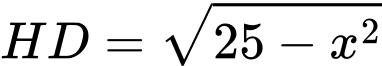 (áp dụng định lí Pytago).
(áp dụng định lí Pytago).
- Xét tam giác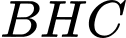 vuông tại
vuông tại 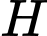 có:
có: 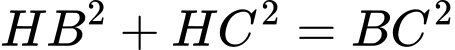
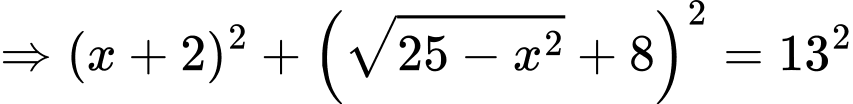
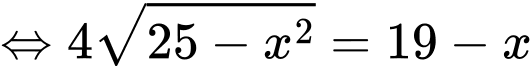
Bình phương hai vế ta được:
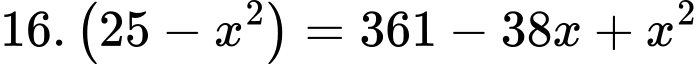
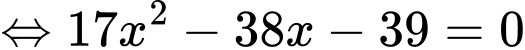
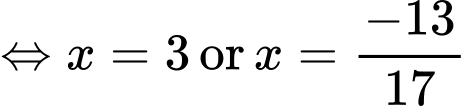
Thử lại phương trình và điều kiện , giá trị
, giá trị 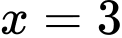 thỏa mãn.
thỏa mãn.
Vậy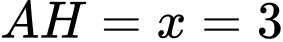 .
.
- Diện tích tam giác HAD là: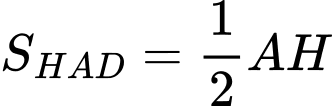 .
. 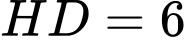
- Diện tích tam giác HBC là: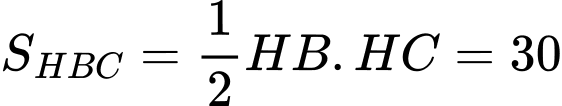
Vậy diện tích tứ giác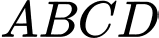 là: 30 - 6 = 24 (đơn vị diện tích).
là: 30 - 6 = 24 (đơn vị diện tích).
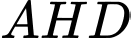 vuông tại
vuông tại 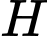 có:
có: 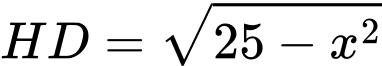 (áp dụng định lí Pytago).
(áp dụng định lí Pytago).- Xét tam giác
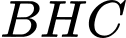 vuông tại
vuông tại 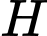 có:
có: 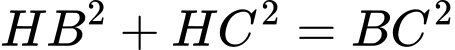
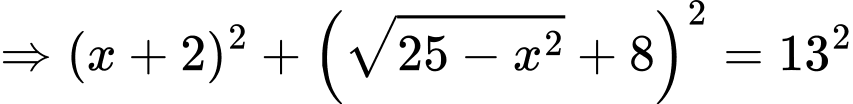
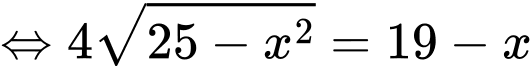
Bình phương hai vế ta được:
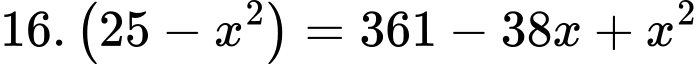
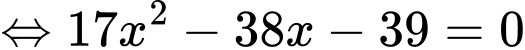
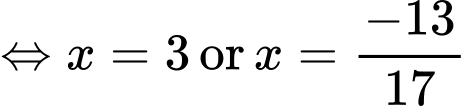
Thử lại phương trình và điều kiện
 , giá trị
, giá trị 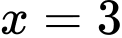 thỏa mãn.
thỏa mãn. Vậy
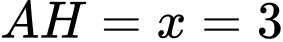 .
.- Diện tích tam giác HAD là:
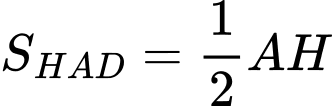 .
. 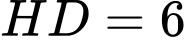
- Diện tích tam giác HBC là:
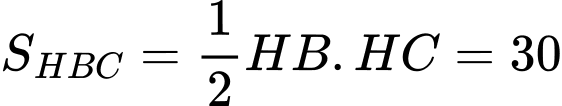
Vậy diện tích tứ giác
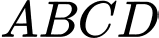 là: 30 - 6 = 24 (đơn vị diện tích).
là: 30 - 6 = 24 (đơn vị diện tích).