Đáp án Bài tập tự luyện
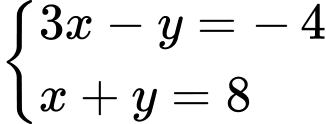 có nghiệm là
có nghiệm là 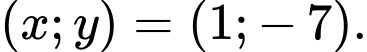
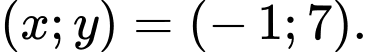
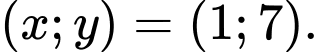
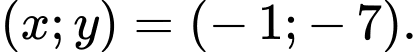
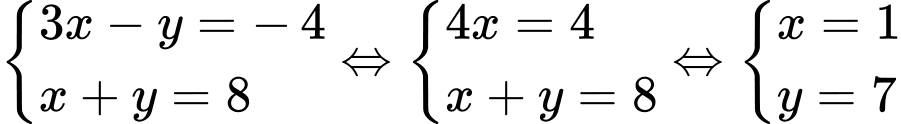 Đáp án: C
Đáp án: C 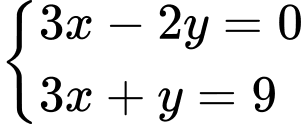 có nghiệm là
có nghiệm là  thì
thì 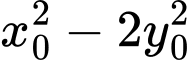 bằng
bằng 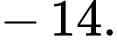
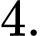
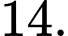
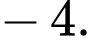
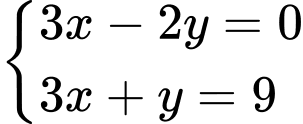
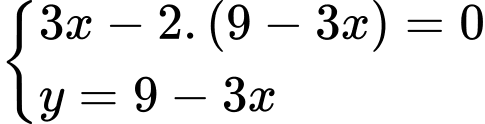
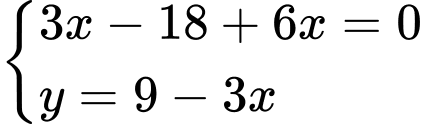
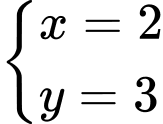
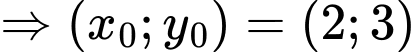
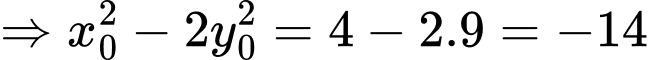 Đáp án: A
Đáp án: A 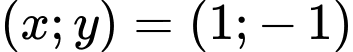 đều là nghiệm của hai phương trình
đều là nghiệm của hai phương trình 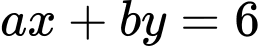 và
và 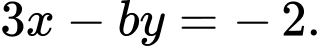 Tính giá trị của biểu thức
Tính giá trị của biểu thức 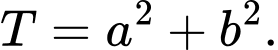
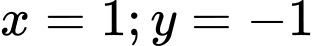 thay vào phương trình
thay vào phương trình 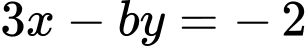 ta được:
ta được: 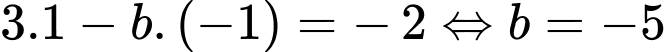
Với
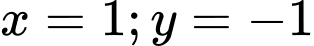 thay vào phương trình
thay vào phương trình 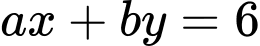 ta được
ta được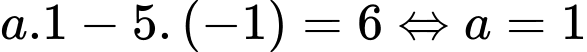
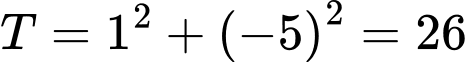 Đáp án: D
Đáp án: D 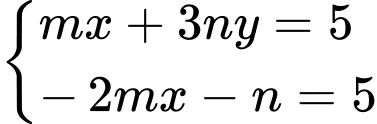 (
(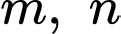 là tham số) có nghiệm duy nhất là
là tham số) có nghiệm duy nhất là 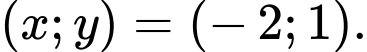 Giá trị của biểu thức
Giá trị của biểu thức  bằng
bằng 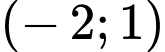 vào hệ phương trình ta được:
vào hệ phương trình ta được: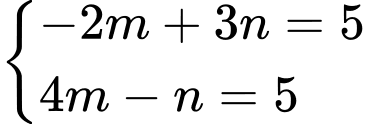
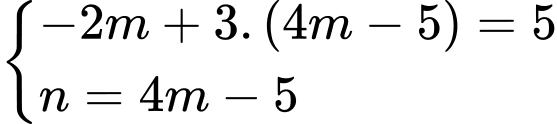
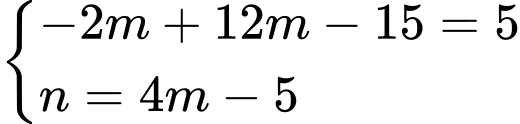
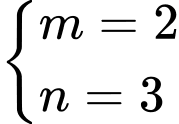
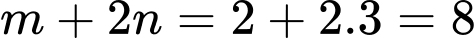 Đáp án: C
Đáp án: C  để hệ phương trình
để hệ phương trình 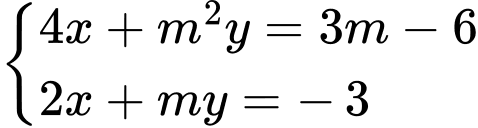 có vô số nghiệm?
có vô số nghiệm? 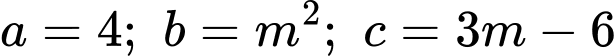 và
và 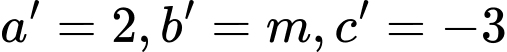
TH1:
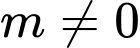
Để hệ phương trình có vô số nghiệm thì:
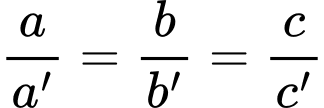
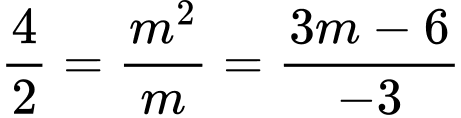
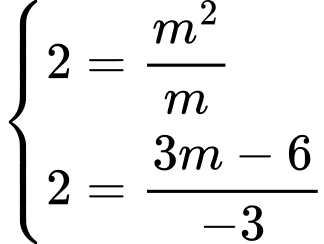
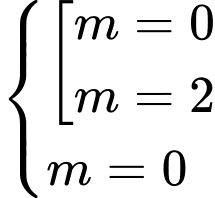
Kết hợp ĐKXĐ không có giá trị
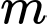 thỏa mãn.
thỏa mãn.TH2:
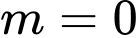
Thay
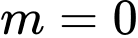 vào hệ phương trình, ta được:
vào hệ phương trình, ta được: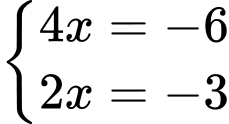
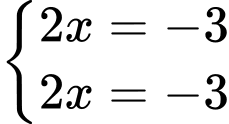
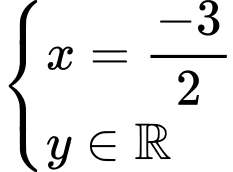
Vậy
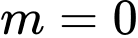 là giá trị cần tìm.
là giá trị cần tìm.Chọn đáp án B. Đáp án: D
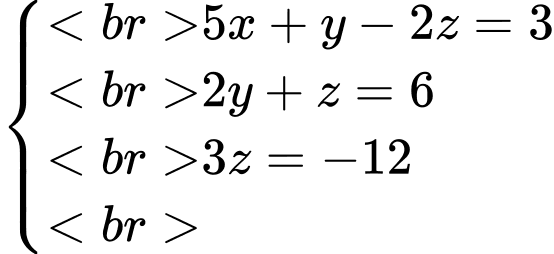 có nghiệm là
có nghiệm là 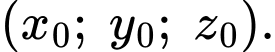 Giá trị của biểu thức
Giá trị của biểu thức 

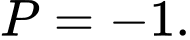


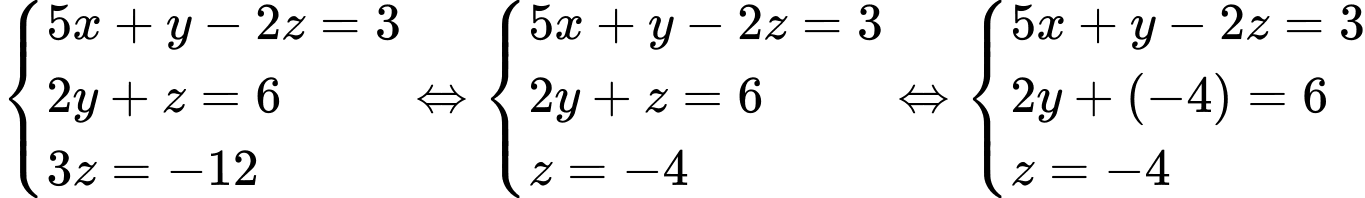 <
<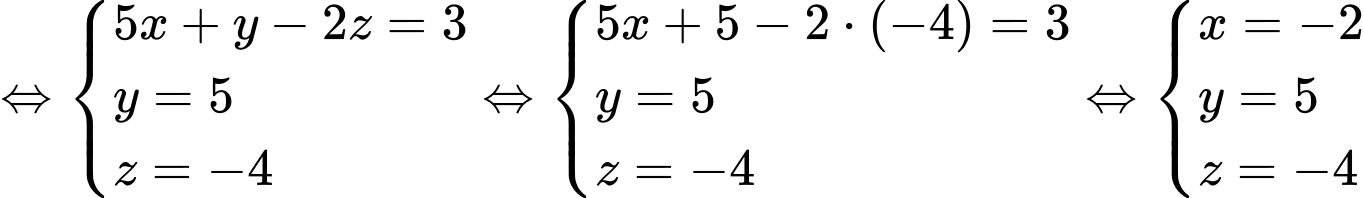
Nhận xét: Phương pháp giải hệ phương trình bậc nhất ba ẩn bằng cách biến đổi hệ đó về hệ có dạng tam giác gọi là phương pháp khử dần ẩn số hay phuơng pháp Gauss
Vậy 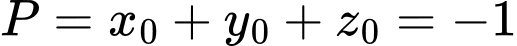
Hệ phương trình:  có nghiệm là
có nghiệm là 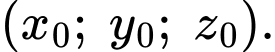 Giá trị của biểu thức
Giá trị của biểu thức 

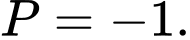


Ta có: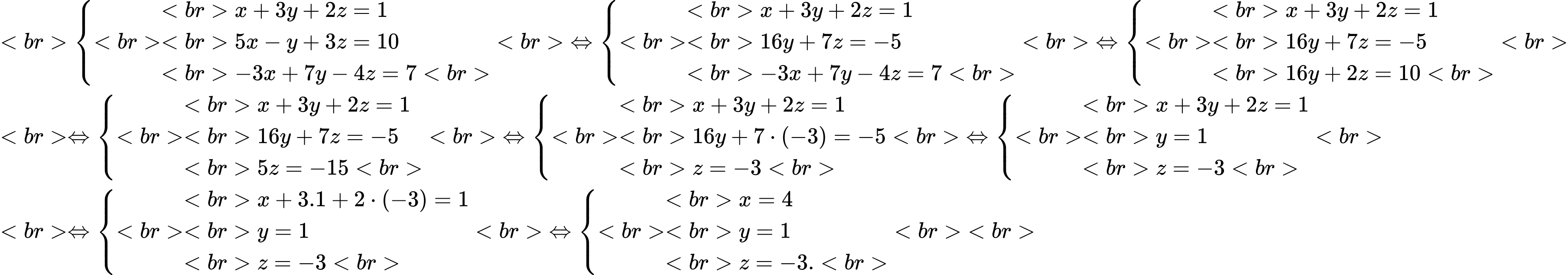
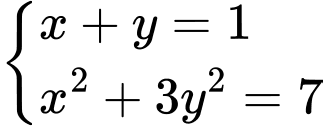 có nghiệm là
có nghiệm là 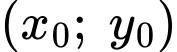 với
với 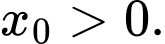 Tính giá trị của biểu thức
Tính giá trị của biểu thức 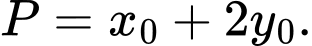

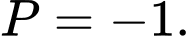


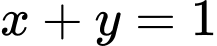 ta rút
ta rút 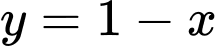 thế vào phương trình
thế vào phương trình 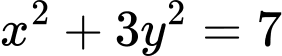 ta được:
ta được: 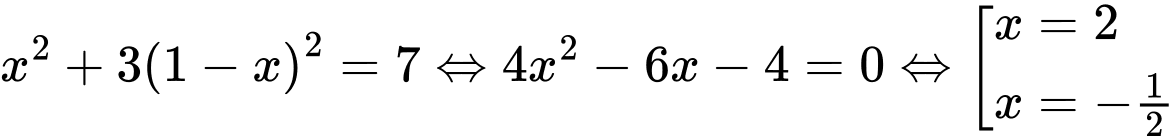
Vì
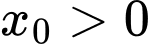 nên chọn
nên chọn 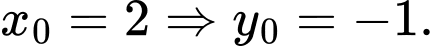 Vậy
Vậy 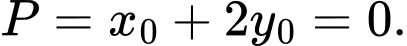
Chọn đáp án C. Đáp án: C
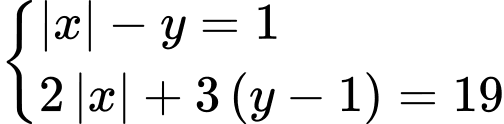 là
là 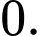
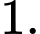
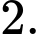
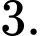
 khi đó hệ phương trình đã cho trở thành:
khi đó hệ phương trình đã cho trở thành: 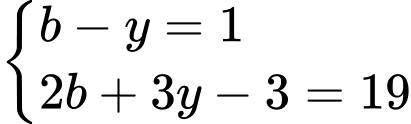
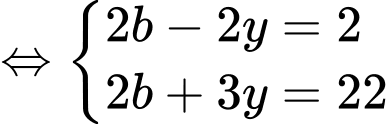
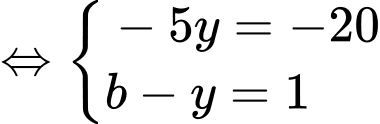
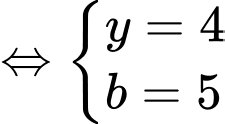 (TMĐK).
(TMĐK). ▪ Với
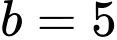
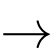
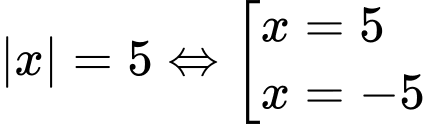
Vậy hệ phương trình đã cho có nghiệm là
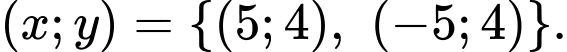
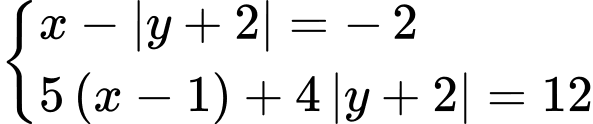 có bao nhiêu nghiệm?
có bao nhiêu nghiệm? 
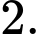
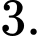
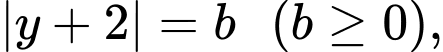 khi đó hệ phương trình đã cho trở thành:
khi đó hệ phương trình đã cho trở thành: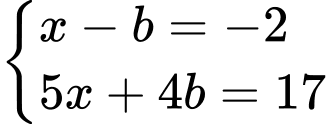
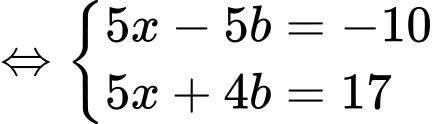
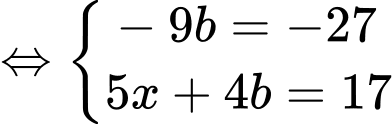
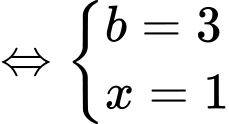 (TMĐK).
(TMĐK).▪ Với

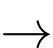

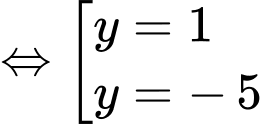
Vậy hệ phương trình đã cho có nghiệm là
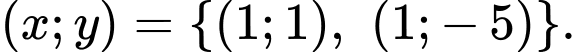
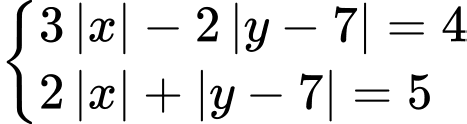 có bao nhiêu nghiệm
có bao nhiêu nghiệm 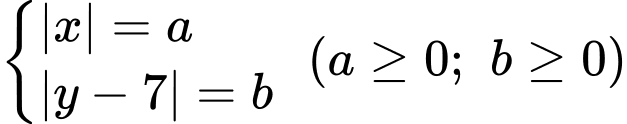
Khi đó hệ phương trình đã cho trở thành:

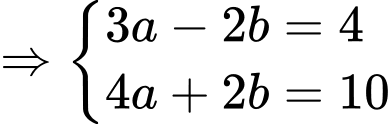
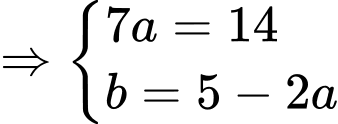
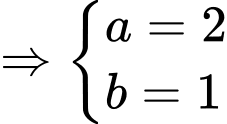 (TMĐK).
(TMĐK).▪ Với
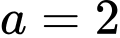
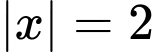

▪ Với
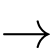
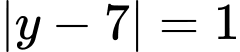
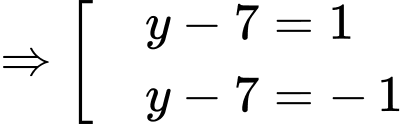
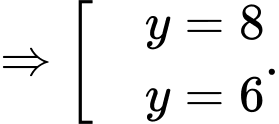
Vậy hệ phương trình đã cho có 4 nghiệm là
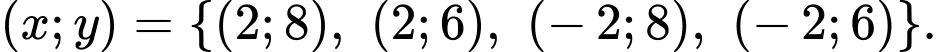 Đáp án: D
Đáp án: D 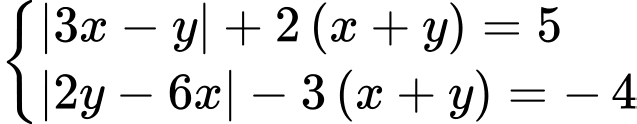 có bao nhiêu nghiệm
có bao nhiêu nghiệm 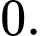
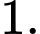
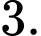
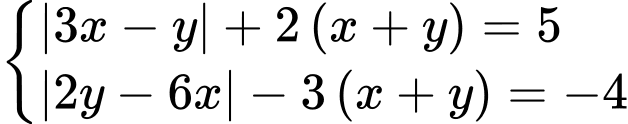
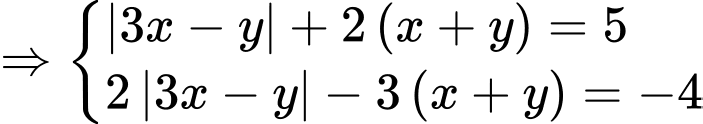
Đặt
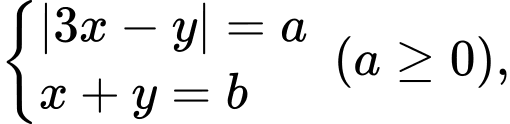 khi đó hệ phương trình đã cho trở thành:
khi đó hệ phương trình đã cho trở thành: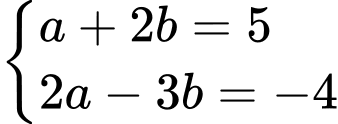
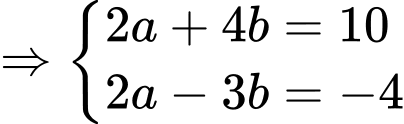
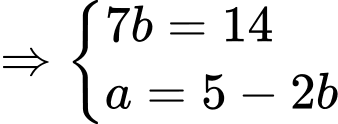
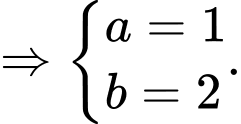 (TMĐK).
(TMĐK).▪ Với
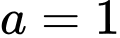
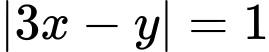
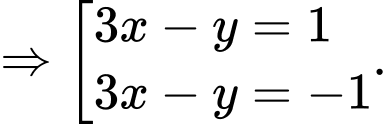
Kết hợp với phương trình
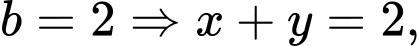 ta được:
ta được:TH1:
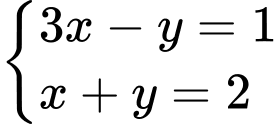
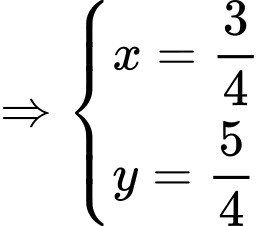
TH2:
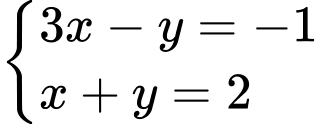
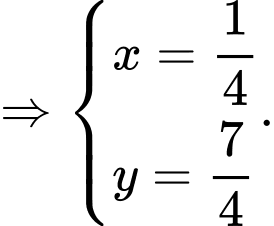
Vậy hệ phương trình đã cho có 2 nghiệm là
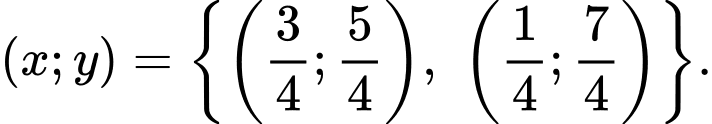 Đáp án: C
Đáp án: C 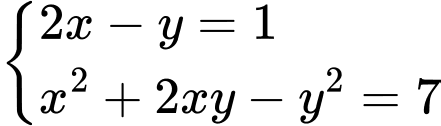 có bao nhiêu nghiệm
có bao nhiêu nghiệm
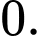
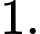
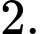
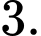
Giải chi tiết:
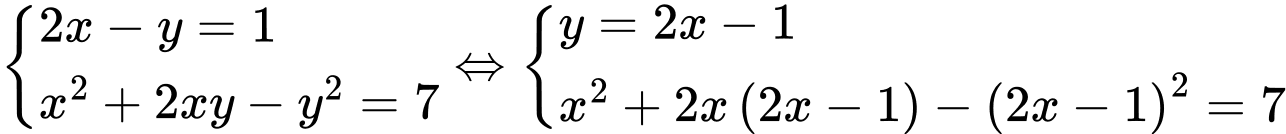
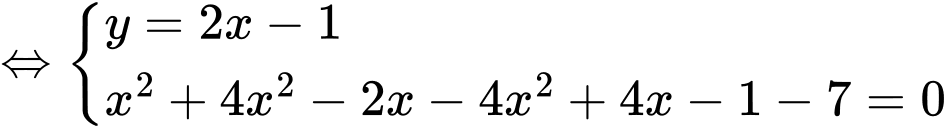
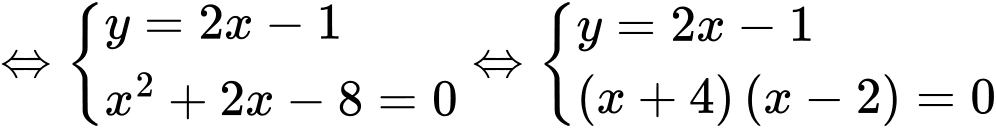
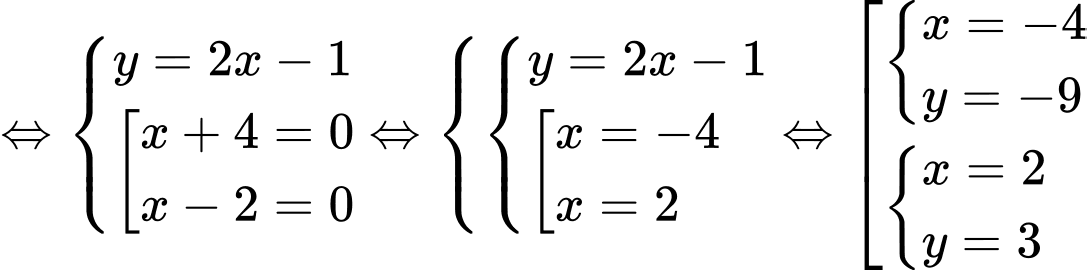 . Chọn C.
. Chọn C.
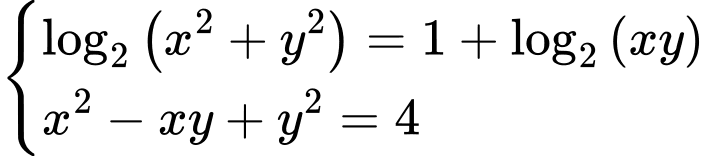 có bao nhiêu nghiệm
có bao nhiêu nghiệm
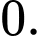
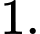
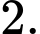
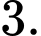
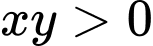
Khi đó hệ
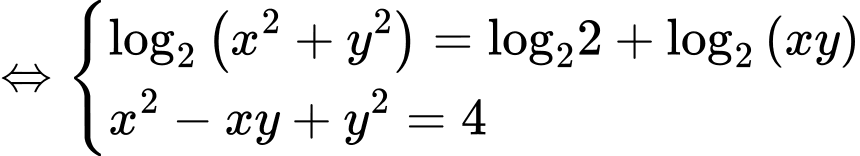
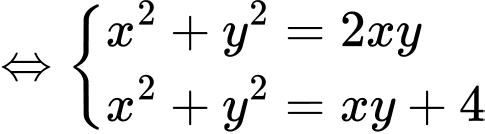
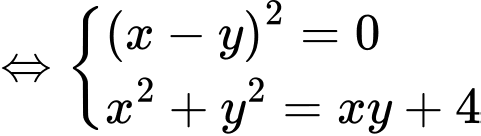
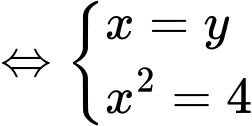
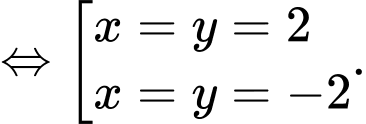 Chọn C.
Chọn C.
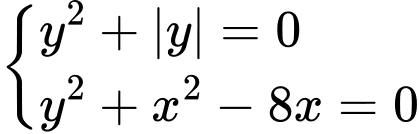
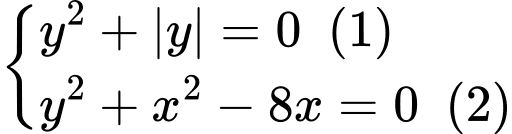
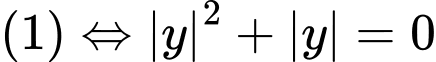
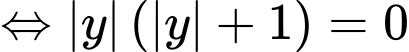
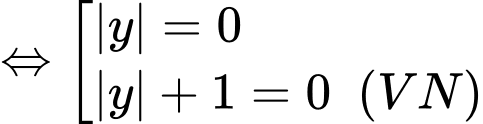
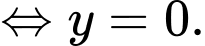
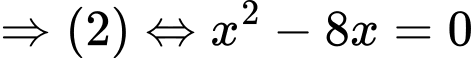

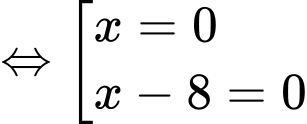
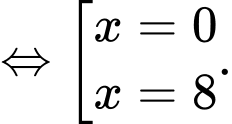
Vậy hệ phương trình đã cho có 2 nghiệm
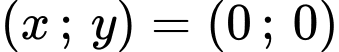 hoặc
hoặc 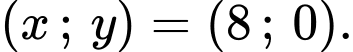
Chọn C. Đáp án: C
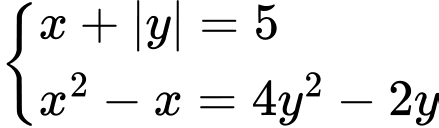 có bao nhiêu nghiệm?
có bao nhiêu nghiệm? 
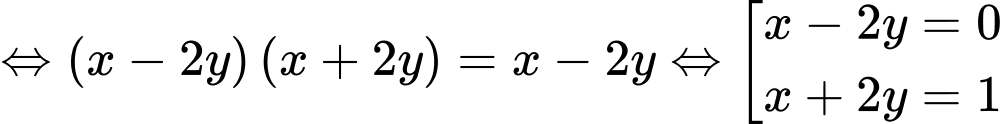
Khi đó, ta xét hai trường hợp sau:
TH1:
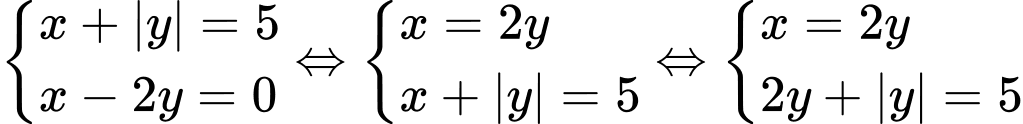
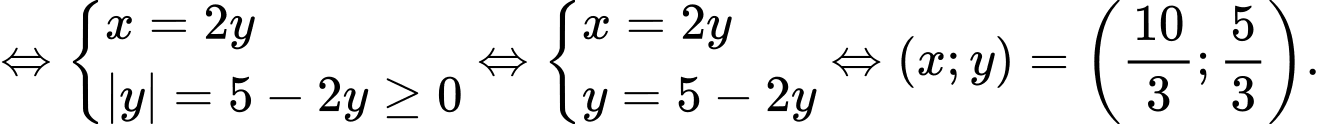
TH2:
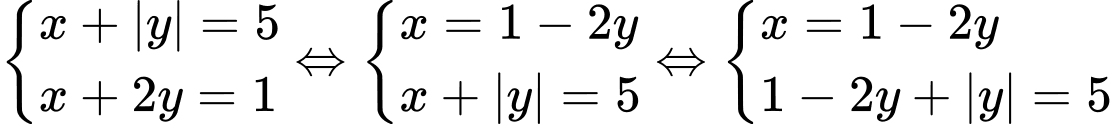
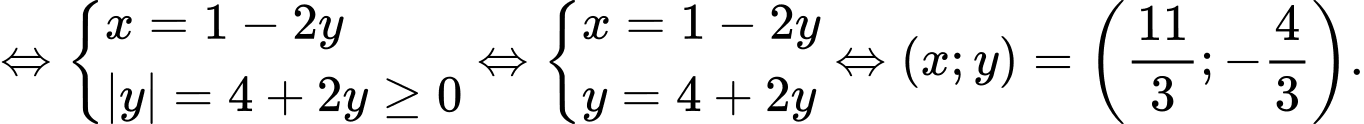
Chọn đáp án D Đáp án: D
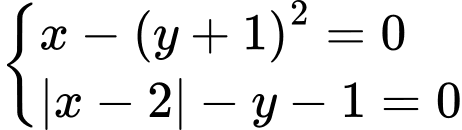 là
là 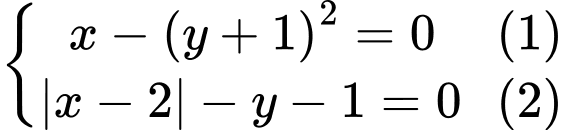
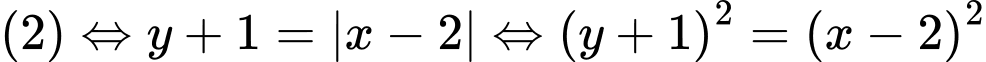
 ta được
ta được 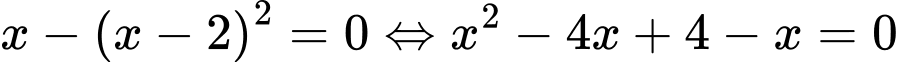
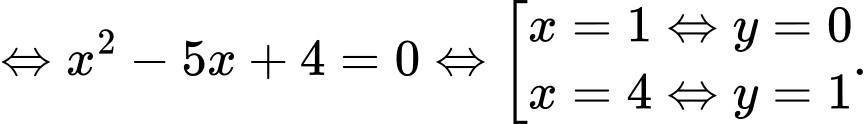
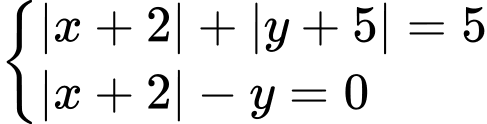 có tất cả bao nhiêu nghiệm?
có tất cả bao nhiêu nghiệm?  ta được:
ta được: 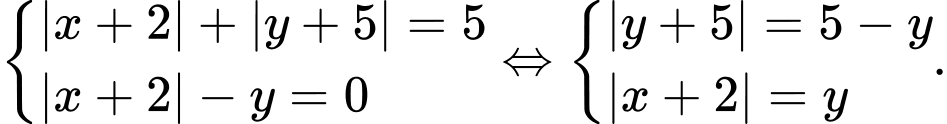
Nếu
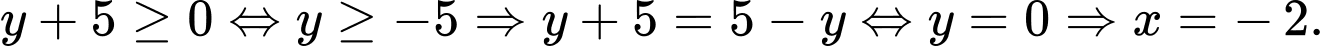
Nếu
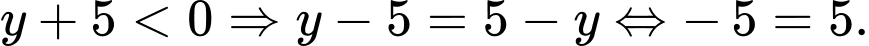 (Vô lý)
(Vô lý)
Vậy nghiệm của hệ phương trình là
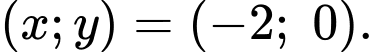
Chọn đáp án A. Đáp án: A
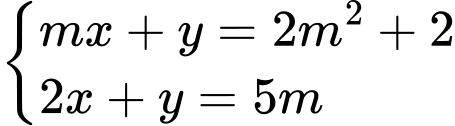 (
(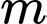 là tham số) có nghiệm duy nhất
là tham số) có nghiệm duy nhất 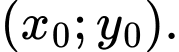 Giá trị lớn nhất của biểu thức
Giá trị lớn nhất của biểu thức 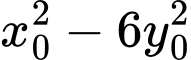 bằng
bằng 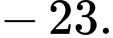
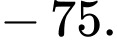
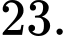
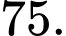
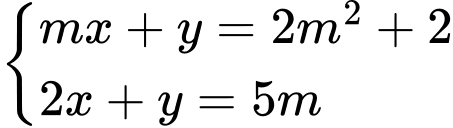 có nghiệm duy nhất khi
có nghiệm duy nhất khi 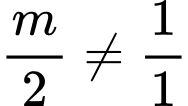 suy ra
suy ra 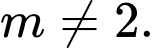
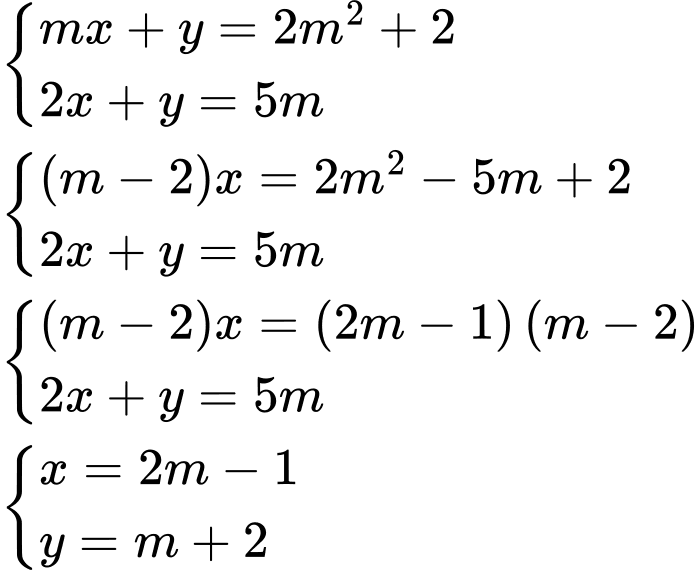
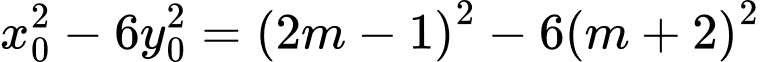
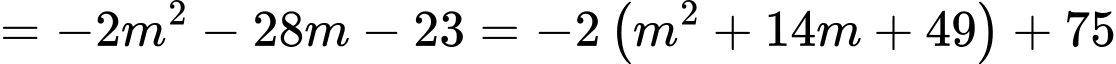
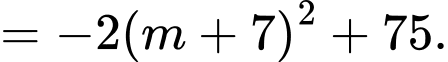
Ta có
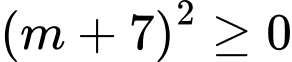 nên
nên 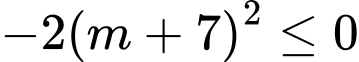 suy ra
suy ra 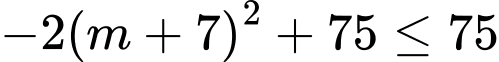 hay
hay 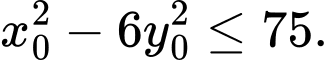
Vậy giá trị lớn nhất của
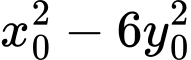 là 75.
là 75.Chọn đáp án D Đáp án: D
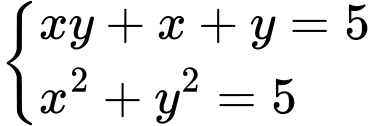 là
là 
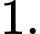
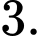
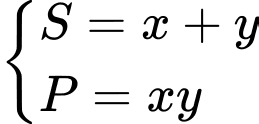 (Điều kiện :
(Điều kiện : 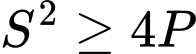 )
)Ta được hệ phương trình:
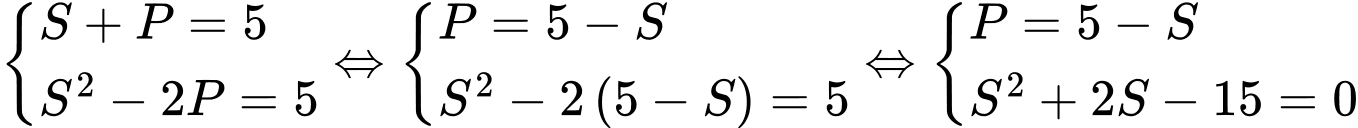
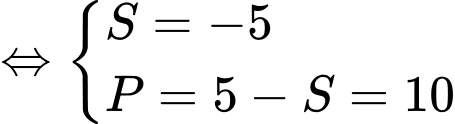 hoặc
hoặc 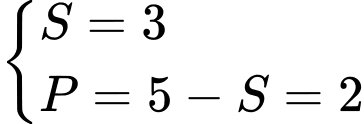
Với
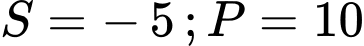 thì
thì  nên ta loại trường hợp này.
nên ta loại trường hợp này.Với
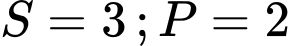 thì
thì 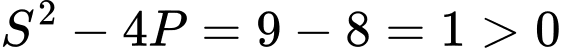 nên khi đó
nên khi đó  là nghiệm của phương trình
là nghiệm của phương trình 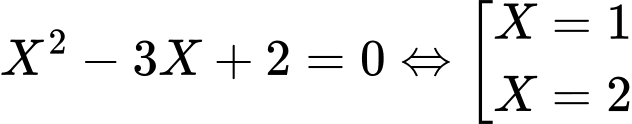
Ta có nghiệm hệ phương trình là
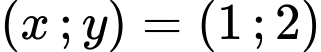 hoặc
hoặc 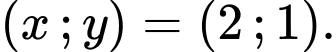
Chọn đáp án A. Đáp án: A
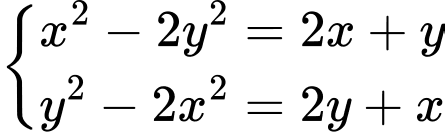 có bao nhiêu nghiệm?
có bao nhiêu nghiệm? 
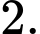
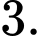
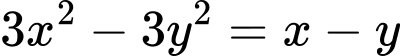
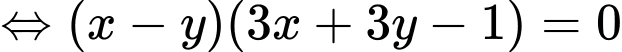
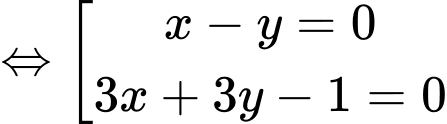
Kết hợp với hệ phương trình ta có:
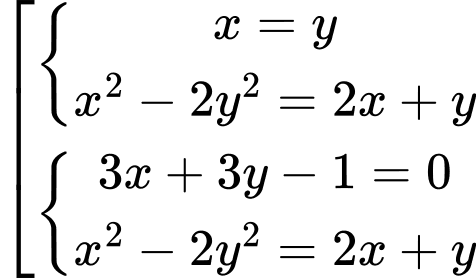
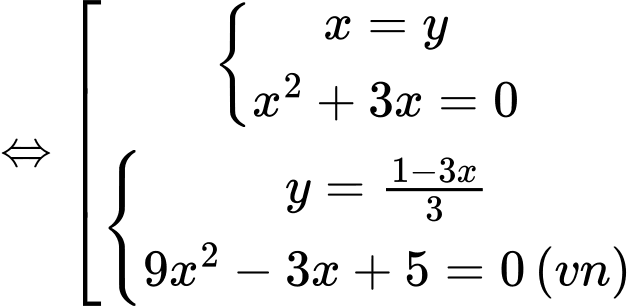
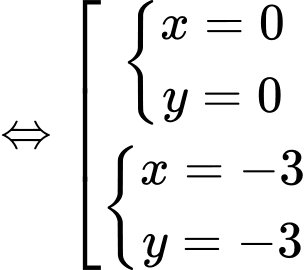
Vậy hệ phương trình đã cho có 2 nghiệm (0;0), (-3;-3).
Chọn đáp án B. Đáp án: B
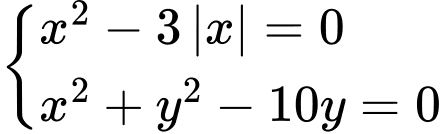 có bao nhiêu nghiệm?
có bao nhiêu nghiệm? Ta có: 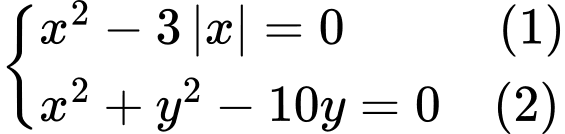
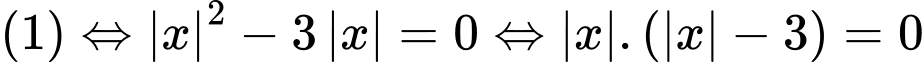
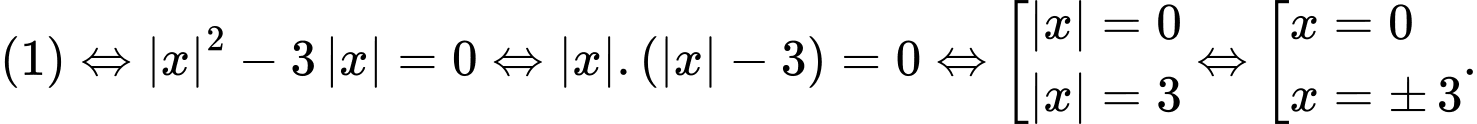
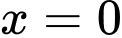 thay vào
thay vào  ta có
ta có 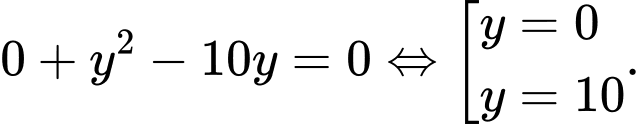
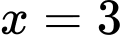 thay vào
thay vào  ta có
ta có 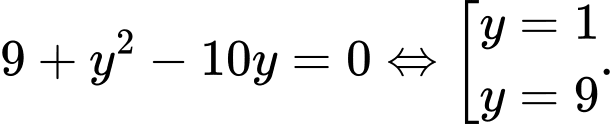
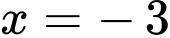 thay vào
thay vào  ta có
ta có 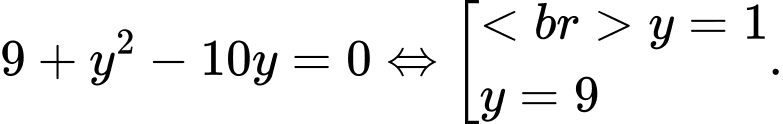
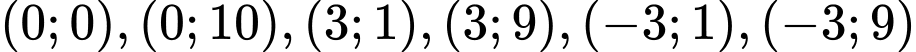 .
.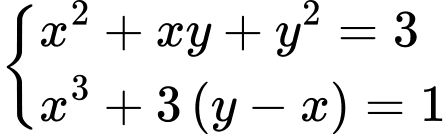 là
là 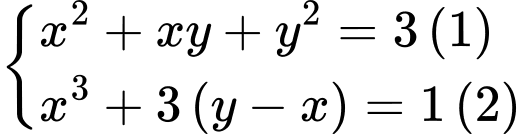
Thay
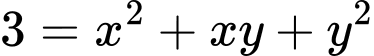 vào
vào  ta được:
ta được:
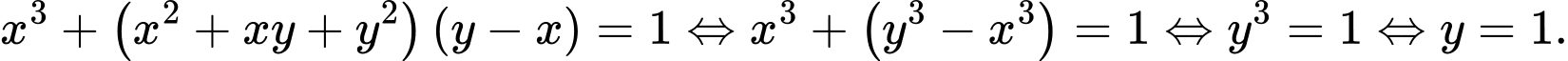
Thay
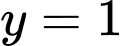 vào
vào  ta được:
ta được: 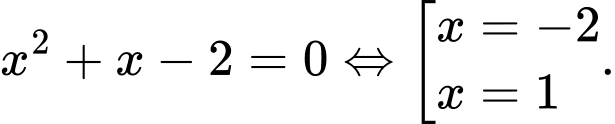
Vậy hệ phương trình có 2 nghiệm.
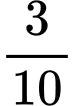 bể. Nếu chỉ mở vòi I thì sau bao lâu sẽ đầy bể?
bể. Nếu chỉ mở vòi I thì sau bao lâu sẽ đầy bể?  Gọi thời gian vòi thứ nhất người thứ nhất, vòi thứ hai chảy một mình xong công việc lần lượt là
Gọi thời gian vòi thứ nhất người thứ nhất, vòi thứ hai chảy một mình xong công việc lần lượt là 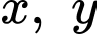 (giờ). Điều kiện:
(giờ). Điều kiện: 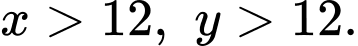
 Trong
Trong 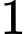 giờ vòi thứ nhất chảy được
giờ vòi thứ nhất chảy được 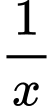 , thứ hai chảy được
, thứ hai chảy được 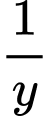 (bể).
(bể).
Sau 12 giờ vòi thứ nhất chảy được 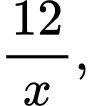 vòi thứ hai làm được
vòi thứ hai làm được 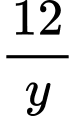 (bể).
(bể).
Do hai vòi chảy chung thì sau 12 giờ đầy bể nên ta có phương trình: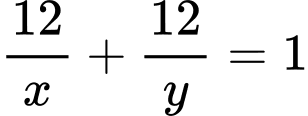
 Trong 4 giờ vòi thứ nhất chảy được
Trong 4 giờ vòi thứ nhất chảy được  (bể)
(bể)
Trong 3 giờ vòi thứ hai làm được 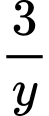 (bể)
(bể)
Do vòi thứ nhất chảy trong 4 giờ rồi khóa lại và vòi thứ hai chảy tiếp 3 giờ nữa thì được 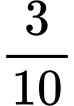 bể nên ta có phương trình:
bể nên ta có phương trình: 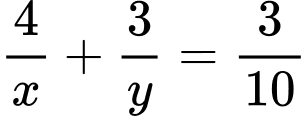
Đặt 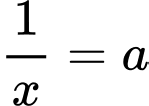 và
và 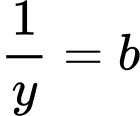 nên ta có hệ phương trình
nên ta có hệ phương trình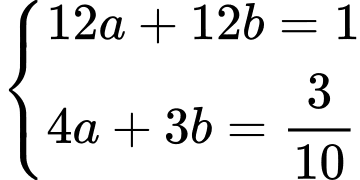
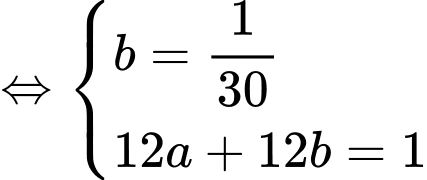
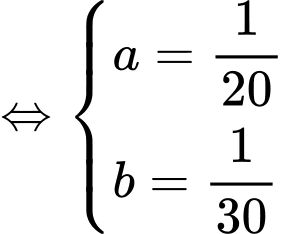
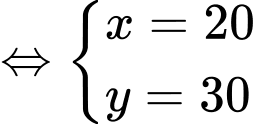 (TM)
(TM)
Vậy vòi thứ nhất làm một mình trong 20 giờ thì đầy bể, vòi thứ hai làm một mình trong 30 giờ thì đầy bể.
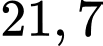 triệu đồng, kể cả thuế giá trị gia tăng
triệu đồng, kể cả thuế giá trị gia tăng 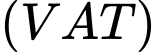 với mức
với mức 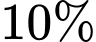 đối với loại hàng thứ nhất và
đối với loại hàng thứ nhất và 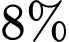 đối với loại hàng thứ hai. Nếu thuế
đối với loại hàng thứ hai. Nếu thuế 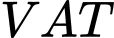 là
là 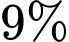 đối với cả hai loại hàng thì người đó phải trả tổng cộng
đối với cả hai loại hàng thì người đó phải trả tổng cộng 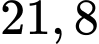 triệu đồng. Hỏi nếu không kể thuế
triệu đồng. Hỏi nếu không kể thuế 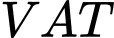 thì người đó phải trả bao nhiêu tiền cho loại hàng thứ hai. Viết kết quả theo đơn vị triệu đồng.
thì người đó phải trả bao nhiêu tiền cho loại hàng thứ hai. Viết kết quả theo đơn vị triệu đồng. 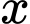 (triệu đồng)
(triệu đồng) 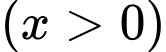
Giá của loại hàng thứ hai nếu không kể thuế VAT là
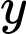 (triệu đồng)
(triệu đồng) 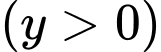
Vì loại hàng thứ nhất chịu thuế VAT 10% và loại hàng thứ hai chịu thuê VAT 8% thì người mua phải trả 21,7 triệu đồng cho hai loại hàng nên ta có phương trình
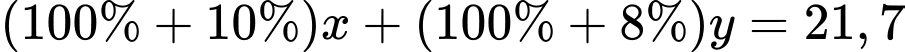 hay
hay  (1)
(1)Vì nếu thuế VAT là 9% cho cả hai loại hàng thì người mua phải trả 21,8 triệu đồng cho hai loại hàng nên ta có phương trình
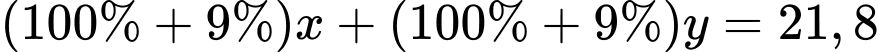 hay
hay 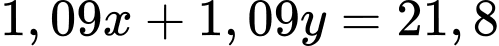 (2)
(2)Từ (1) và (2) ta có hệ phương trình
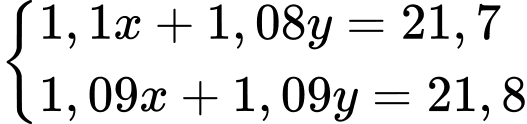 suy ra
suy ra 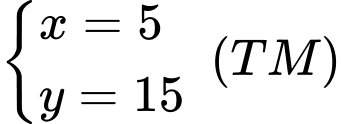
Vậy giá của loại hàng thứ nhất nếu không kể thuế VAT là 5 triệu đồng, giá của loại hàng thứ hai nếu không kể thuê VAT là 15 triệu đồng.
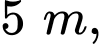 diện tích khu vườn là
diện tích khu vườn là 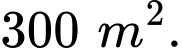 Người ta dùng lưới
Người ta dùng lưới  rào xung quanh khu vườn. Số tiền dùng để mua lưới
rào xung quanh khu vườn. Số tiền dùng để mua lưới  để rào khu vườn là bao nhiêu nghìn đồng, biết giá tiền mua
để rào khu vườn là bao nhiêu nghìn đồng, biết giá tiền mua 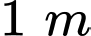 lưới là 48 000 đồng.
lưới là 48 000 đồng. 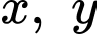
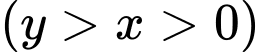 lần lượt là chiều rộng, chiều dài của mảnh vườn hình chữ nhật.
lần lượt là chiều rộng, chiều dài của mảnh vườn hình chữ nhật.Mảnh vườn hình chữ nhật có chiều dài hơn chiều rộng
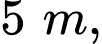 nên ta có
nên ta có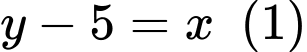
Diện tích khu vườn là
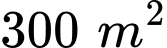 nên ta có
nên ta có 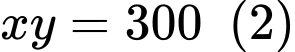
Từ
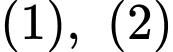 ta có hệ phương trình
ta có hệ phương trình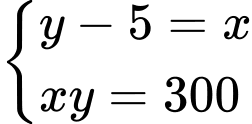
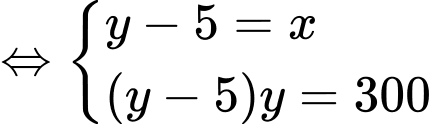
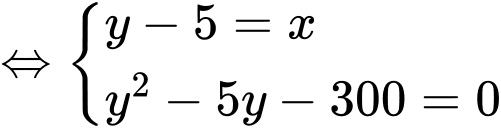
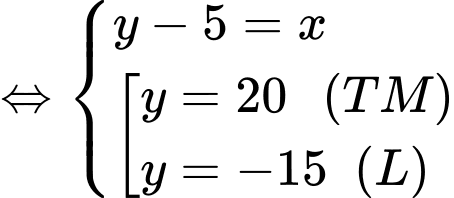
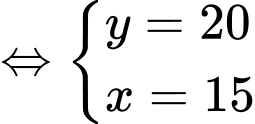 (TMĐK)
(TMĐK)Chu vi mảnh vườn là
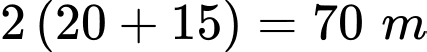
Số tiền dùng để mua lưới
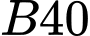 để rào khu vườn là
để rào khu vườn là 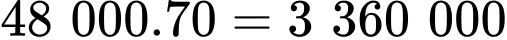 đồng
đồngVậy số tiền cần dùng là
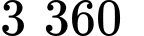 nghìn đồng.
nghìn đồng. 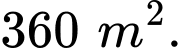 Nếu tăng chiều rộng
Nếu tăng chiều rộng 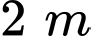 và giảm chiều dài
và giảm chiều dài 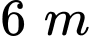 thì diện tích mảnh đất không đổi. Tính chu vi của mảnh đất.
thì diện tích mảnh đất không đổi. Tính chu vi của mảnh đất. 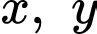
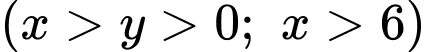 lần lượt là chiều dài, chiều rộng của mảnh đất.
lần lượt là chiều dài, chiều rộng của mảnh đất.Mảnh đất hình chữ nhật có diện tích
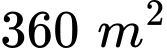 nên ta có
nên ta có 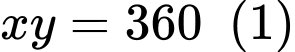
Nếu tăng chiều rộng
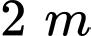 và giảm chiều dài
và giảm chiều dài 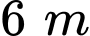 thì diện tích mảnh đất không đổi nên ta có
thì diện tích mảnh đất không đổi nên ta có 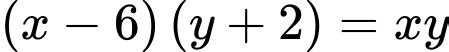
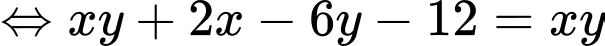
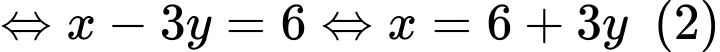
Từ
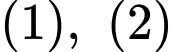 ta có hệ phương trình
ta có hệ phương trình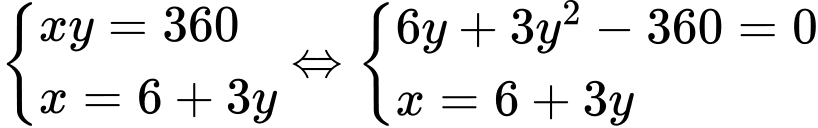
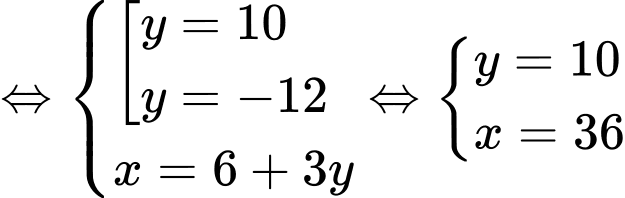 (TMĐK)
(TMĐK)Chu vi của mảnh đất là
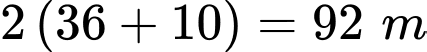
Vậy chu vi của mảnh đất là
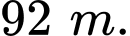
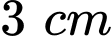 và cạnh huyền bằng
và cạnh huyền bằng 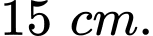 Tính chu vi tam giác đó.
Tính chu vi tam giác đó. 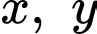
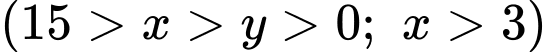 lần lượt là hai cạnh góc vuông của tam giác.
lần lượt là hai cạnh góc vuông của tam giác.Hai cạnh góc vuông có độ dài hơn kém nhau
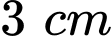 nên ta có
nên ta có 
Cạnh huyền của một tam giác vuông bằng
 nên ta có
nên ta có 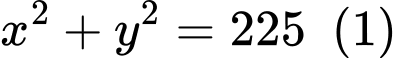
Từ
 ta có hệ phươmg trình
ta có hệ phươmg trình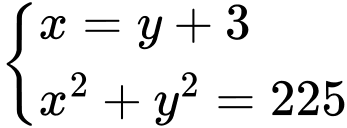
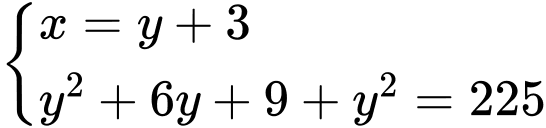
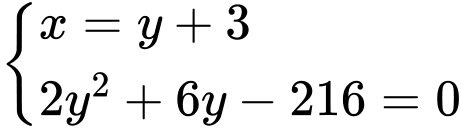
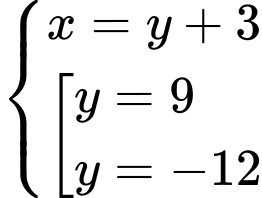
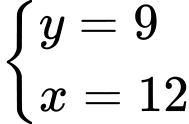 (TMĐK)
(TMĐK)Chu vi của tam giác vuông là

Vậy chu vi của tam giác vuông là
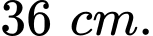
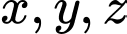 lần lượt là số vé trẻ em, vé học sinh và vé người lớn đã được bán ra.
lần lượt là số vé trẻ em, vé học sinh và vé người lớn đã được bán ra.Có 900 vé đã được bán ra, ta có
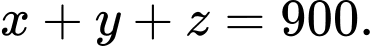
Tổng số tiền thu được trong buổi biểu diễn này là 50600000 đồng, ta có
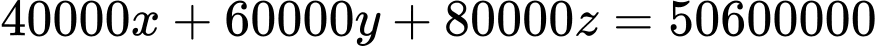
hay
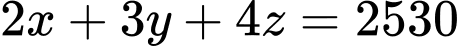 .
.Số vé người lớn bằng một nửa số vé trẻ em và học sinh cộng lại, ta có
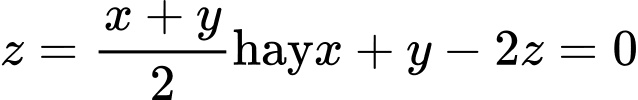
Từ đó, ta có hệ phương trình
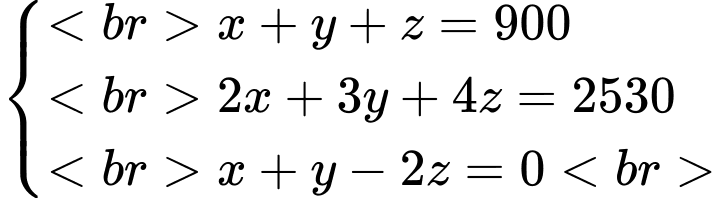
Sử dụng máy tính cầm tay giải hệ phương trình, ta được:
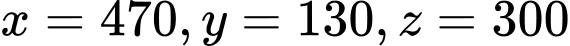 . Vậy có 470 vé trẻ em
. Vậy có 470 vé trẻ em 
Biết tổng thời gian thi đấu ba môn phối hợp của Hùng là 1 giờ 1 phút 30 giây, của Dũng là 1 giờ 3 phút 40 giây và của Mạnh là 1 giờ 1 phút 55 giây. Cự li của chặng đua chạy là bao nhiêu km.
Đổi: 1 giờ 1 phút 30 giây 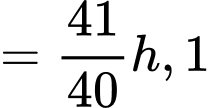 giờ 3 phút 40 giây
giờ 3 phút 40 giây 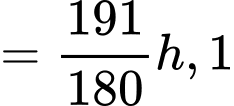 giờ 1 phút 55 giây
giờ 1 phút 55 giây 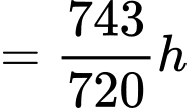 .
.
Gọi cự li của mỗi chặng đua chạy, bơi và đạp xe lần lượt là x, y, z (km).
Dựa vào bảng trên ta có hệ phương trình: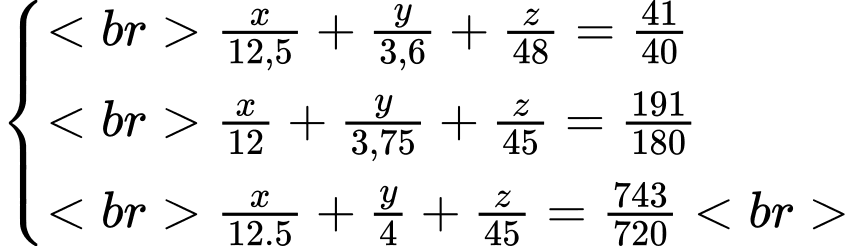
Giải hệ này ta được 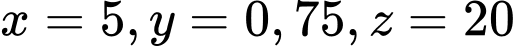 .
.
Vậy cự li của chặng đua chạy là 5 km
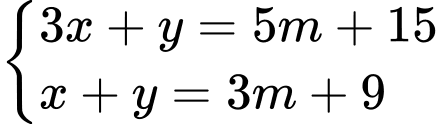 có nghiệm
có nghiệm 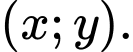 Tìm giá tr nhỏ nhất của biểu thức
Tìm giá tr nhỏ nhất của biểu thức 
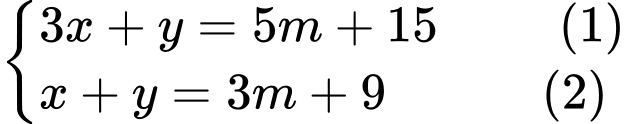
 Lấy
Lấy  ta được
ta được 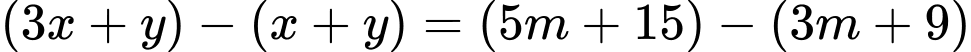

Thay
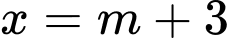 vào phương trình
vào phương trình 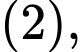 ta được
ta được 
 Khi đó
Khi đó 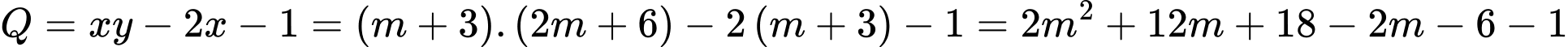
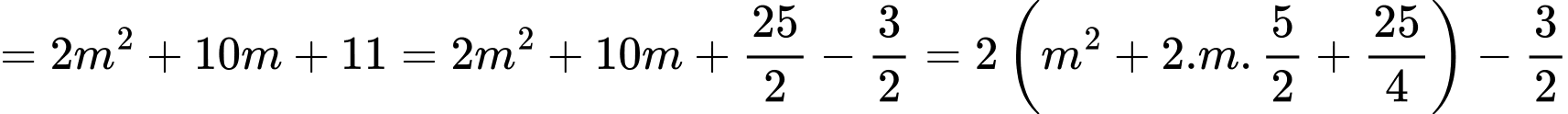
 mà
mà 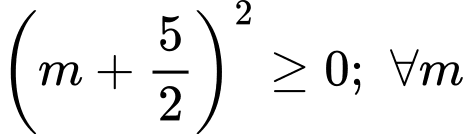 nên
nên 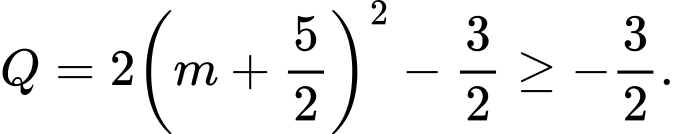
Dấu bằng xảy ra khi và chỉ khi:
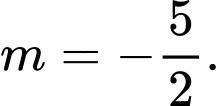
Vậy giá trị nhỏ nhất của
 là
là 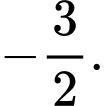
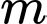 để nghiệm
để nghiệm 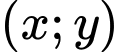 của hệ phương trình
của hệ phương trình 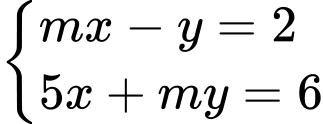 thỏa mãn biểu thức
thỏa mãn biểu thức 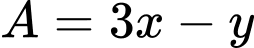 nhận giá trị nguyên bằng
nhận giá trị nguyên bằng 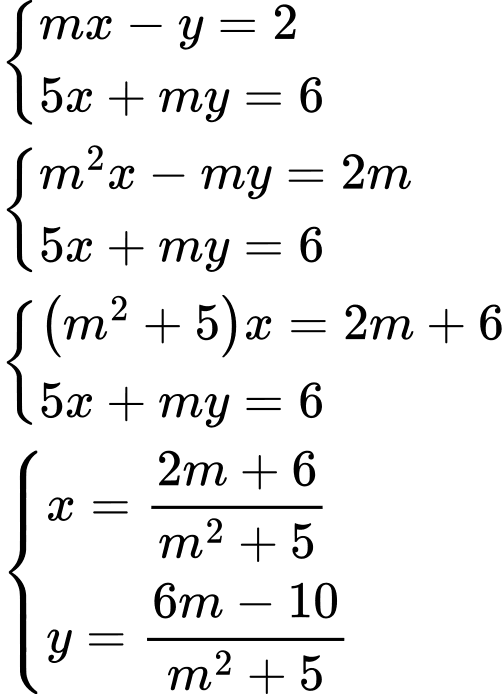
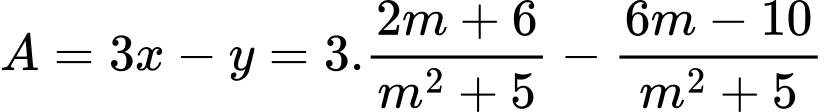
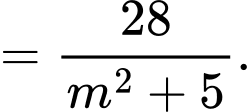
Để 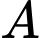 nhận giá trị nguyên thì
nhận giá trị nguyên thì  Ư(28)
Ư(28)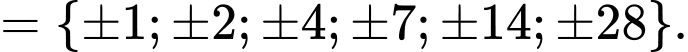
Vì 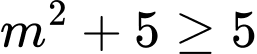 nên
nên 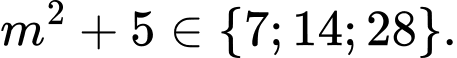
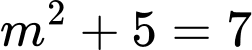 suy ra
suy ra 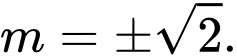
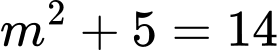 suy ra
suy ra 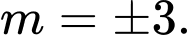
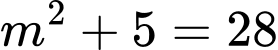 suy ra
suy ra 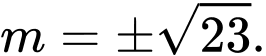
Vậy có 6 giá trị của  .
.