Đáp án Bài tập tự luyện
Câu 1 [245725]: Tập nghiệm của bất phương trình 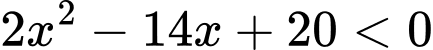 là
là
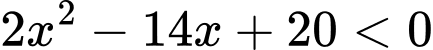 là
là A, 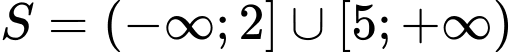 .
.
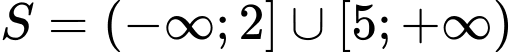 .
.B, 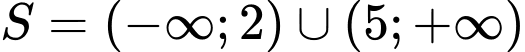 .
.
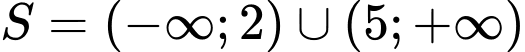 .
.C, 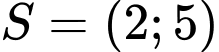 .
.
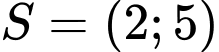 .
.D, 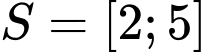 .
.
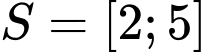 .
.
Chọn C
Bất phương trình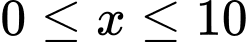
 .
Vậy
.
Vậy 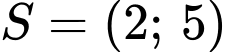 . Đáp án: C
. Đáp án: C
Bất phương trình
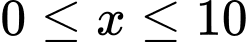
 .
Vậy
.
Vậy 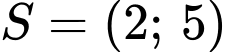 . Đáp án: C
. Đáp án: C
Câu 2 [245730]: Tập xác định của hàm số 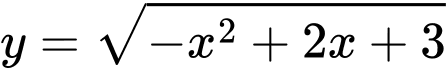 là
là
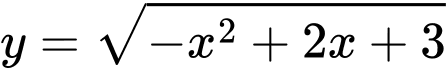 là
là A, 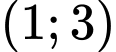 .
.
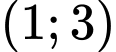 .
.B, 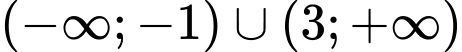 .
.
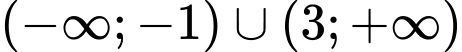 .
.C, 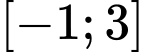 .
.
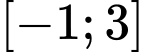 .
.D,  .
.
 .
.
Chọn C
Hàm số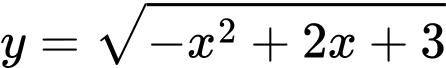 xác định khi
xác định khi 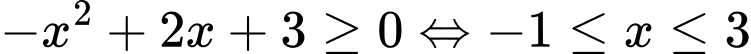 .
Vậy tập xác định của hàm số là
.
Vậy tập xác định của hàm số là  . Đáp án: C
. Đáp án: C
Hàm số
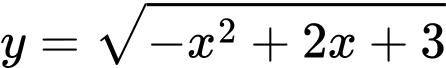 xác định khi
xác định khi 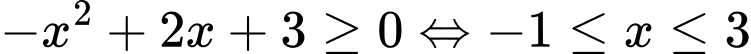 .
Vậy tập xác định của hàm số là
.
Vậy tập xác định của hàm số là  . Đáp án: C
. Đáp án: C
Câu 3 [245735]: Số nghiệm nguyên của bất phương trình 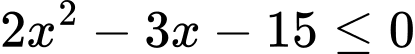 là
là
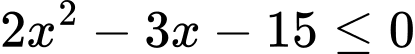 là
là A, 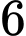 .
.
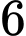 .
.B, 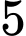 .
.
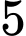 .
.C, 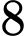 .
.
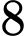 .
.D, 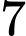 .
.
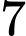 .
.
Chọn A.
Xét 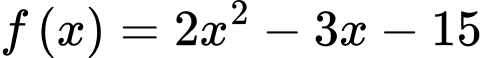 .
.
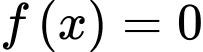
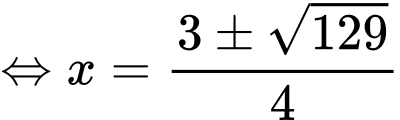 .
.
Ta có bảng xét dấu:
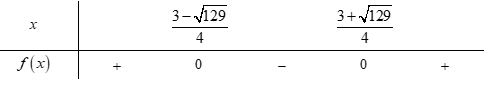
Tập nghiệm của bất phương trình là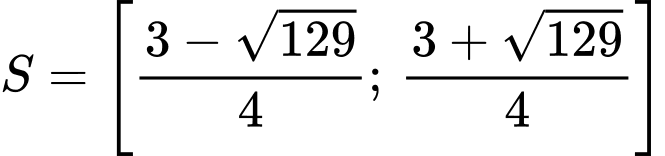 .
.
Do đó bất phương trình có 6 nghiệm nguyên là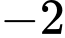 ,
, 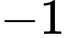 ,
,  ,
, 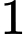 ,
, 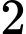 ,
, 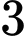 .
Đáp án: A
.
Đáp án: A
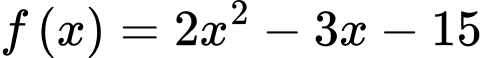 .
.
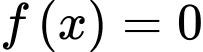
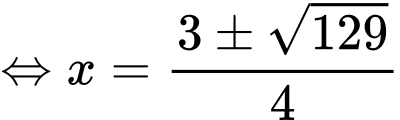 .
.
Ta có bảng xét dấu:
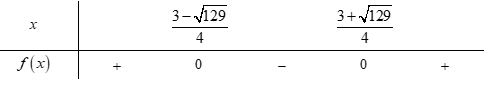
Tập nghiệm của bất phương trình là
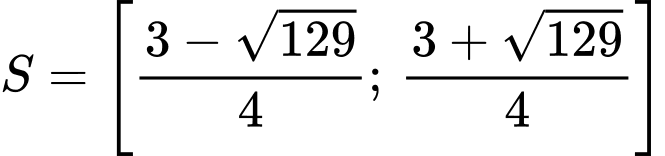 .
.
Do đó bất phương trình có 6 nghiệm nguyên là
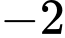 ,
,  ,
,  ,
,  ,
,  ,
,  .
Đáp án: A
.
Đáp án: A
Câu 4 [581397]: Bất phương trình 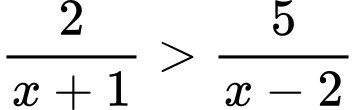 có số nghiệm nguyên thuộc đoạn
có số nghiệm nguyên thuộc đoạn 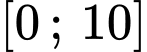 là
là
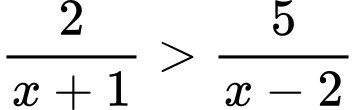 có số nghiệm nguyên thuộc đoạn
có số nghiệm nguyên thuộc đoạn 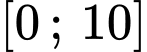 là
là A, 2.
B, 3.
C, 8.
D, 9.
Điều kiện xác định: 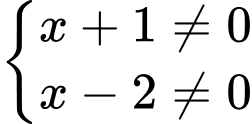
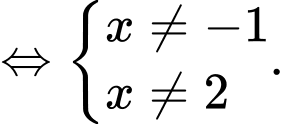 Ta có
Ta có 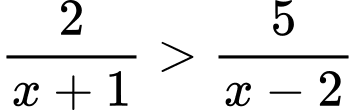
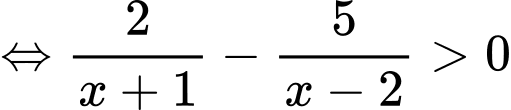
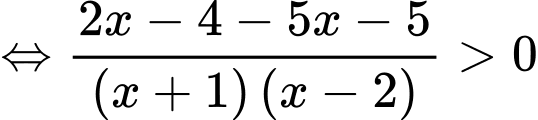
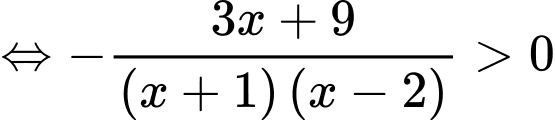
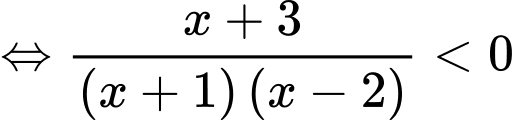
Ta có bảng xét dấu: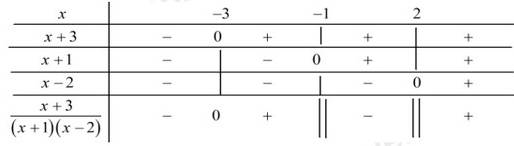
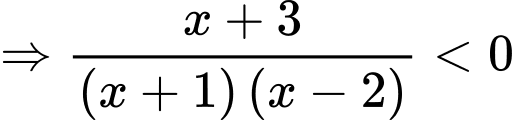
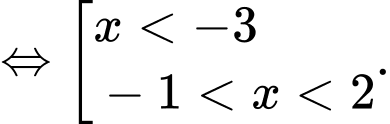
Lại có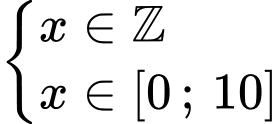
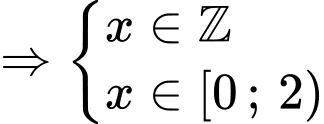
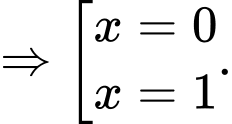
Vậy bất phương trình có 2 nghiệm nguyên thuộc đoạn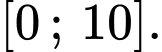
Chọn A.
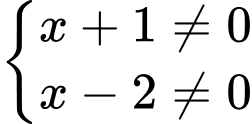
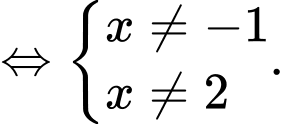 Ta có
Ta có 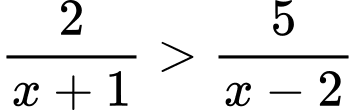
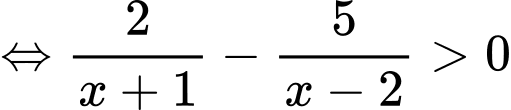
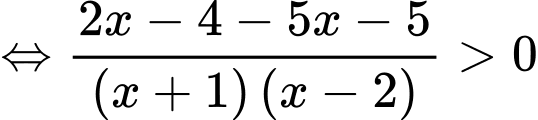
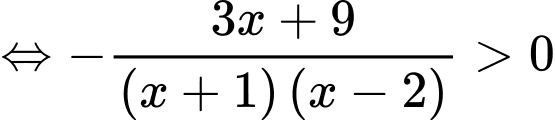
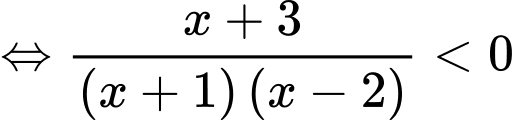
Ta có bảng xét dấu:

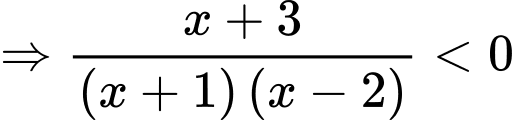
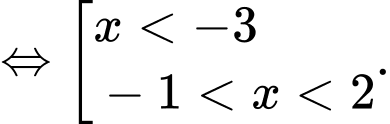
Lại có
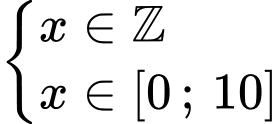
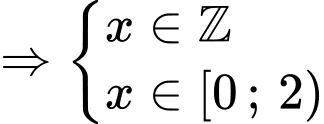
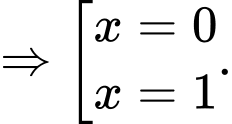
Vậy bất phương trình có 2 nghiệm nguyên thuộc đoạn
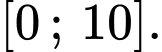
Chọn A.
Câu 5 [361854]: Có bao nhiêu số nguyên 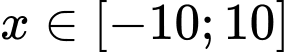 thoả mãn
thoả mãn 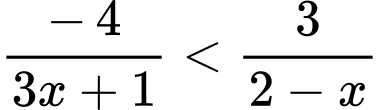 ?
?
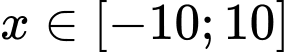 thoả mãn
thoả mãn 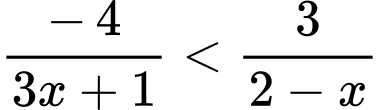 ?
? A, 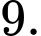
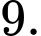
B, 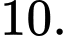
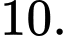
C, 

D, 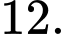
Điều kiện: 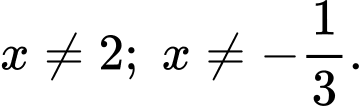
Ta có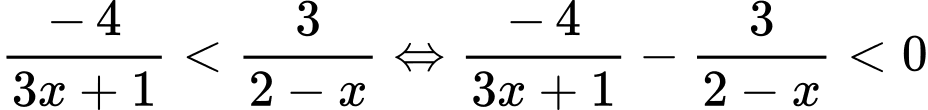
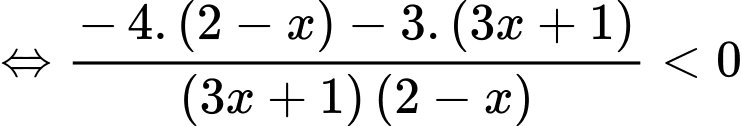
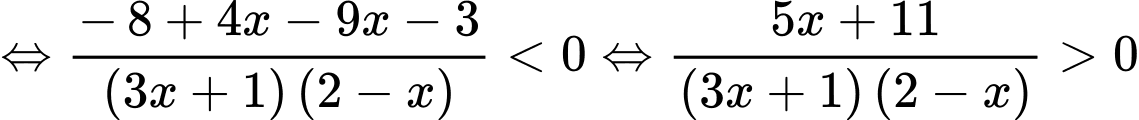
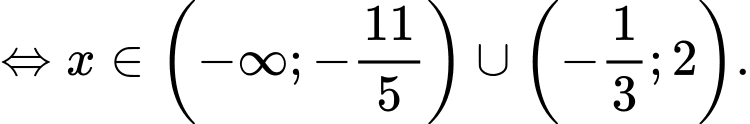
Mà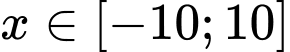 suy ra
suy ra 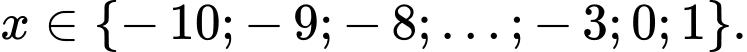
Vậy có 10 giá trị nguyên của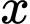 thỏa mãn yêu cầu bài toán.
thỏa mãn yêu cầu bài toán.
Chọn đáp án B. Đáp án: B
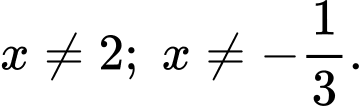
Ta có
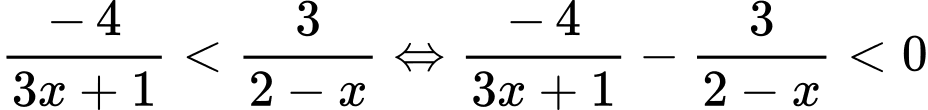
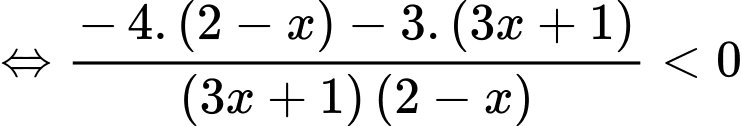
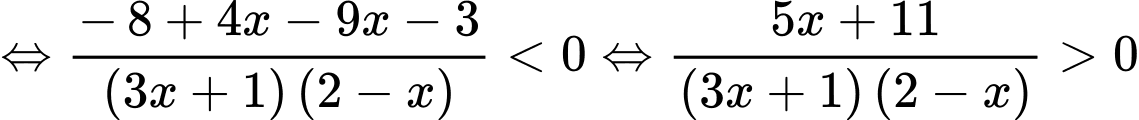
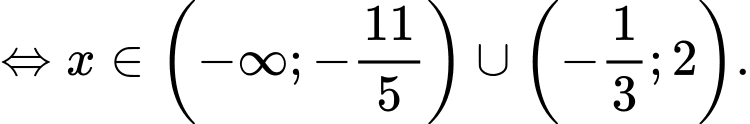
Mà
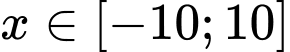 suy ra
suy ra 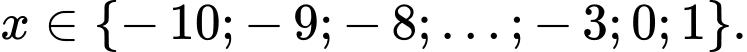
Vậy có 10 giá trị nguyên của
 thỏa mãn yêu cầu bài toán.
thỏa mãn yêu cầu bài toán.Chọn đáp án B. Đáp án: B
Câu 6 [361954]: Số nghiệm nguyên dương của bất phương trình 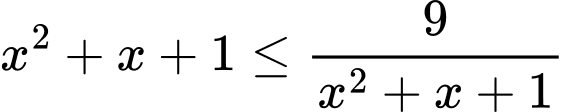 là
là
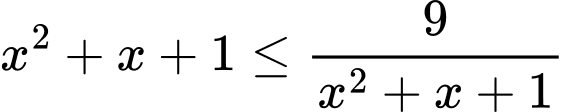 là
là A, 
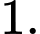
B, 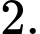
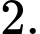
C, 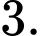
D, 
Điều kiện: 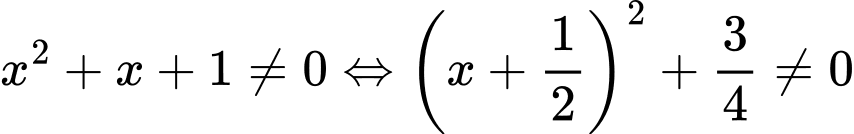 (luôn đúng)
(luôn đúng)
Ta có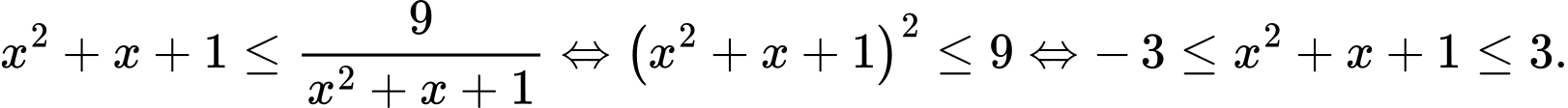
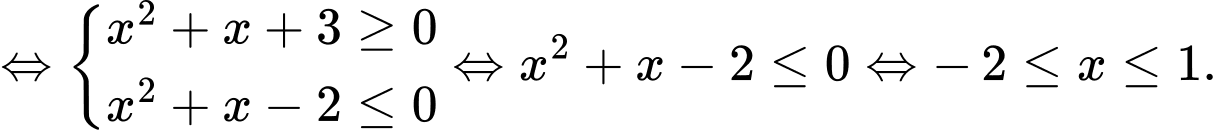
Số nghiệm nguyên dương của bất phương trình là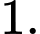
Chọn đáp án A Đáp án: A
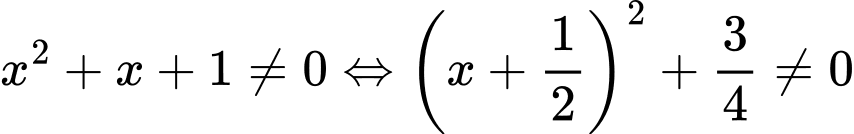 (luôn đúng)
(luôn đúng)
Ta có
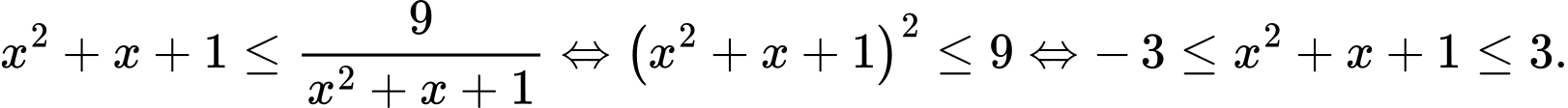
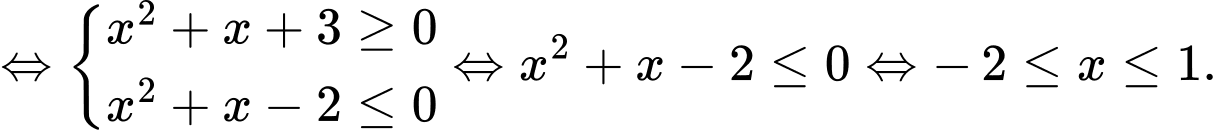
Số nghiệm nguyên dương của bất phương trình là
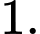
Chọn đáp án A Đáp án: A
Câu 7 [362112]: Số nghiệm nguyên của bất phương trình 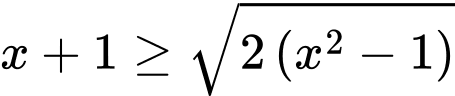 là
là
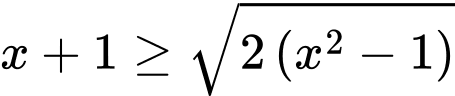 là
là A, 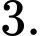
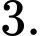
B, 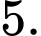
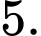
C, 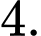
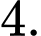
D, 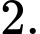
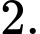
Ta có: 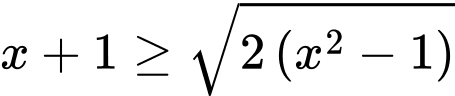
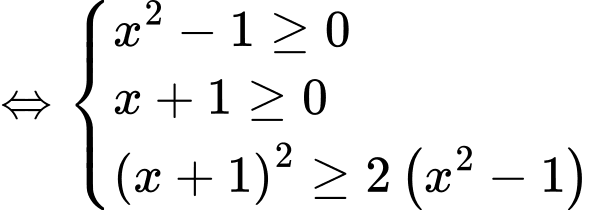
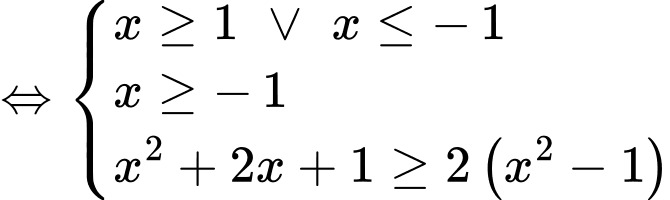
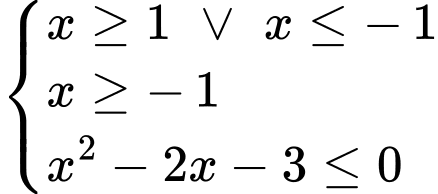
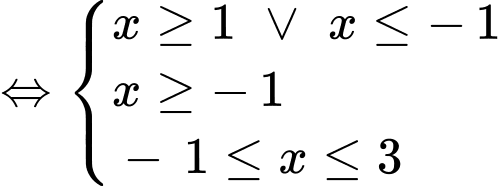
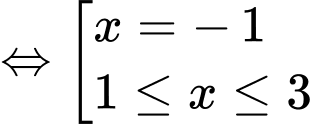
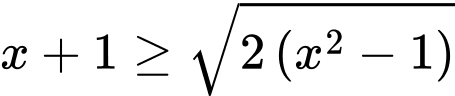
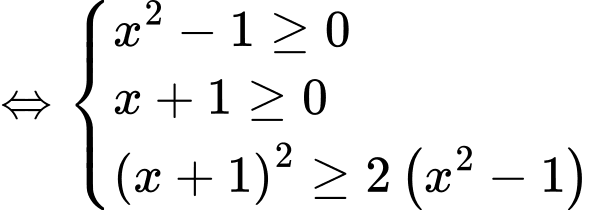
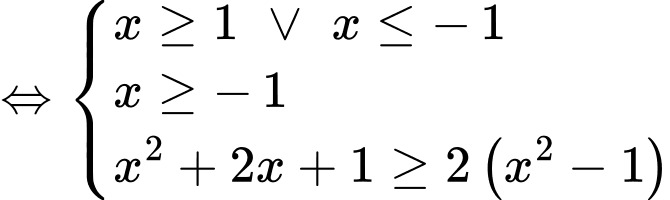
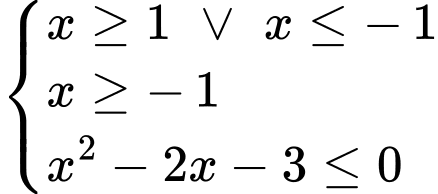
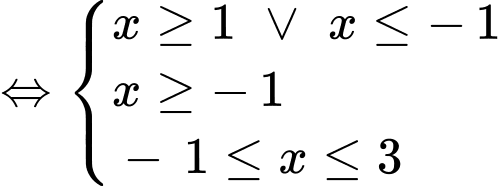
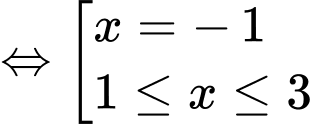
Vậy có 4 giá trị nguyên của 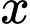 thỏa mãn bất phương trình.
thỏa mãn bất phương trình.
Đáp án: C 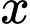 thỏa mãn bất phương trình.
thỏa mãn bất phương trình. Chọn đáp án C.
Câu 8 [362162]: Số nghiệm nguyên 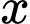 thuộc đoạn
thuộc đoạn 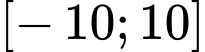 thoả mãn
thoả mãn 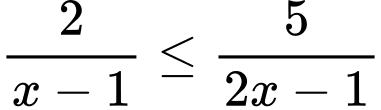 là
là
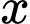 thuộc đoạn
thuộc đoạn 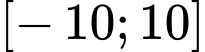 thoả mãn
thoả mãn 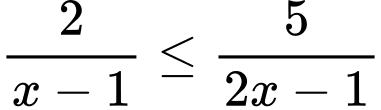 là
là A, 

B, 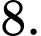
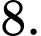
C, 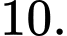
D, 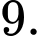
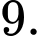
Điều kiện: 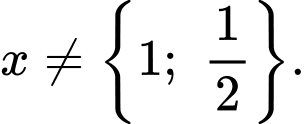
Ta có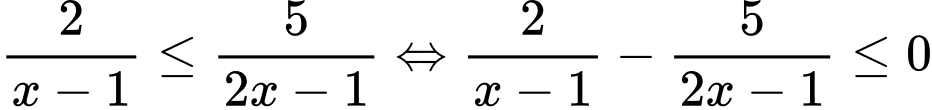
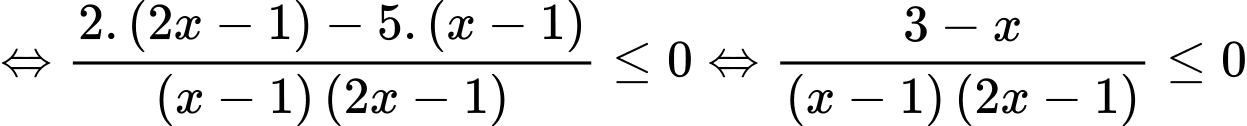
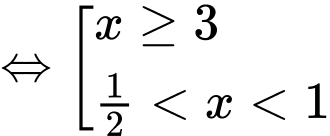 mà
mà 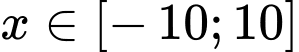 và
và 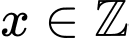 nên
nên 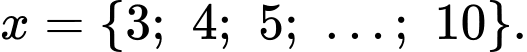
Chọn đáp án B. Đáp án: B
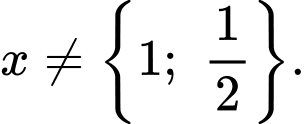
Ta có
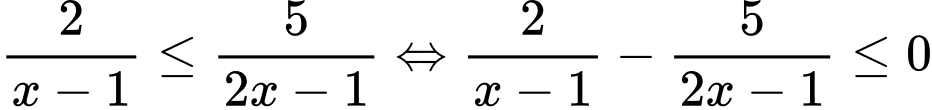
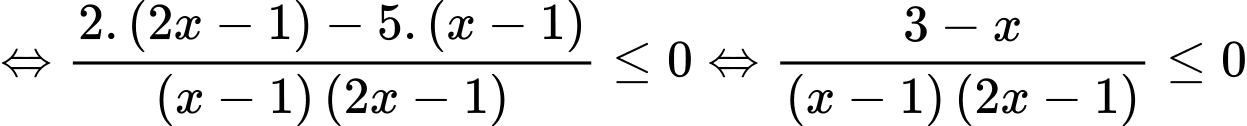
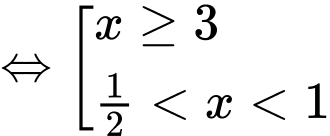 mà
mà 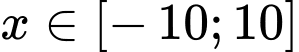 và
và 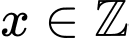 nên
nên 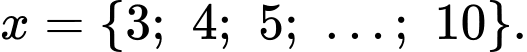
Chọn đáp án B. Đáp án: B
Câu 9 [362294]: Tập nghiệm của bất phương trình 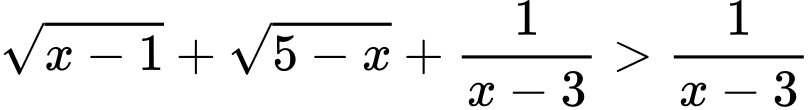 là
là
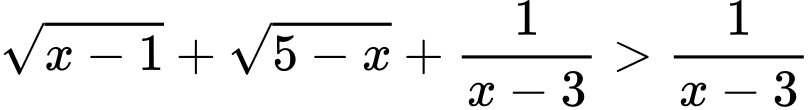 là
là A, 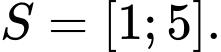
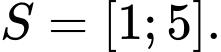
B, 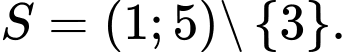
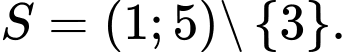
C, 

D, 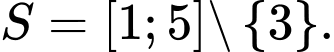
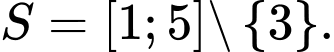
Điều kiện: 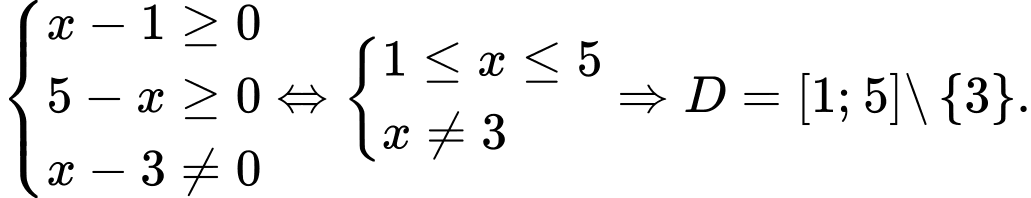
Bất phương trình trở thành: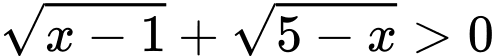
Mà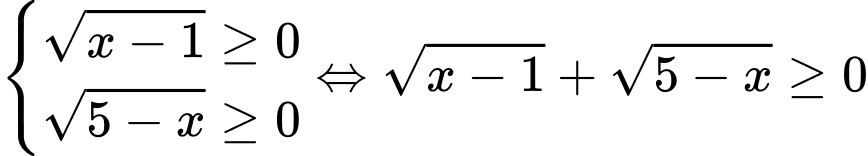 với mọi
với mọi 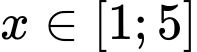
Dấu “=” xảy ra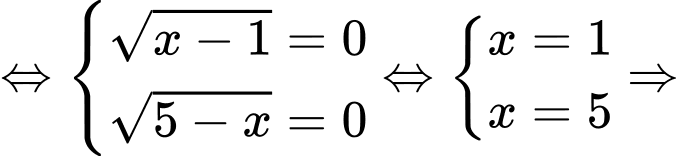 Vô lý.
Vô lý.
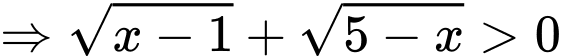 với mọi
với mọi 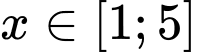
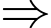 Bất phương trình ban đầu luôn đúng
Bất phương trình ban đầu luôn đúng 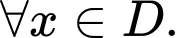 Vậy tập nghiệm của bất phương trình là
Vậy tập nghiệm của bất phương trình là 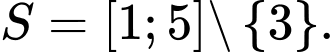
Chọn đáp án D. Đáp án: D
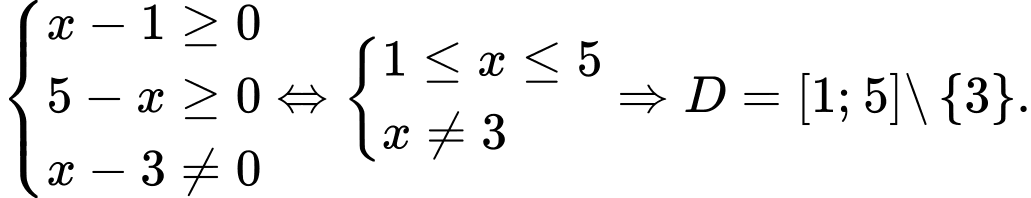
Bất phương trình trở thành:
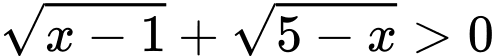
Mà
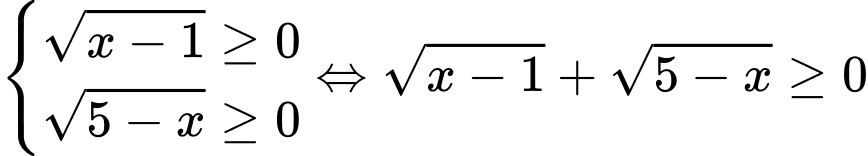 với mọi
với mọi 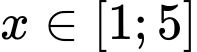
Dấu “=” xảy ra
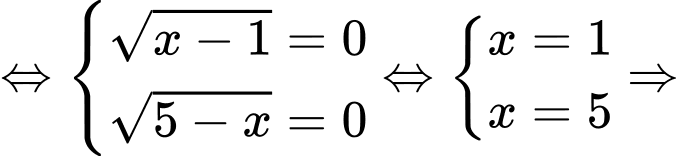 Vô lý.
Vô lý. 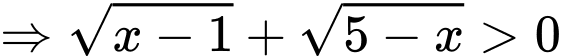 với mọi
với mọi 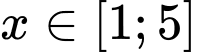
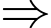 Bất phương trình ban đầu luôn đúng
Bất phương trình ban đầu luôn đúng 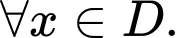 Vậy tập nghiệm của bất phương trình là
Vậy tập nghiệm của bất phương trình là 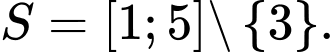
Chọn đáp án D. Đáp án: D
Câu 10 [579649]: [Đề mẫu HSA 2024]: Số giá trị nguyên của tham số 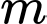 trên đoạn
trên đoạn 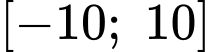 để bất phương trình
để bất phương trình  thỏa mãn với mọi số thực
thỏa mãn với mọi số thực 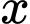 là
là
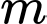 trên đoạn
trên đoạn 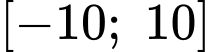 để bất phương trình
để bất phương trình  thỏa mãn với mọi số thực
thỏa mãn với mọi số thực 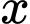 là
là A, 10.
B, 11.
C, 18.
D, 20.
TH1: 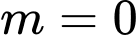 suy ra
suy ra 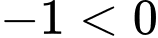 (thoả mãn)
(thoả mãn)
TH2: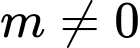
Ta có điều kiện
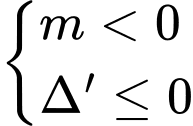
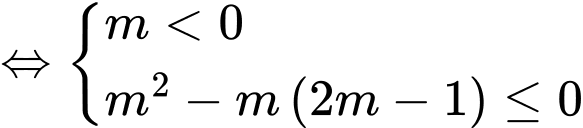
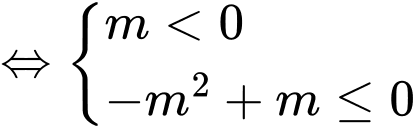
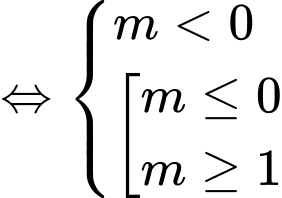
Kết hợp hai trường hợp suy ra
Và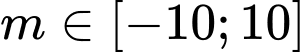 suy ra
suy ra 
Vậy có 11 giá trị của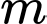 thoả mãn.
thoả mãn.
Chọn B. Đáp án: B
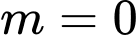 suy ra
suy ra 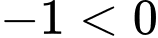 (thoả mãn)
(thoả mãn) TH2:
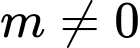
Ta có điều kiện
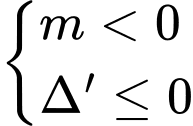
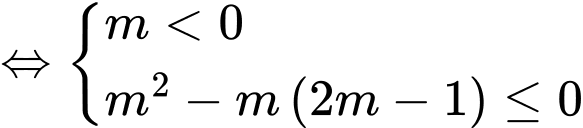
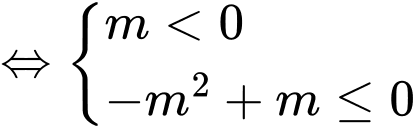
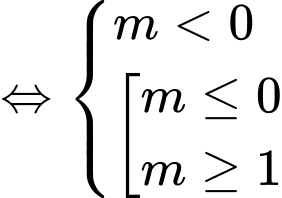
Kết hợp hai trường hợp suy ra

Và
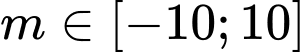 suy ra
suy ra 
Vậy có 11 giá trị của
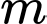 thoả mãn.
thoả mãn. Chọn B. Đáp án: B
Câu 11 [251606]: Bất phương trình 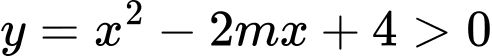 nghiệm đúng với mọi
nghiệm đúng với mọi 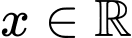 khi
khi
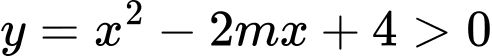 nghiệm đúng với mọi
nghiệm đúng với mọi 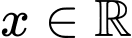 khi
khi A, 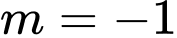 .
.
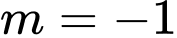 .
.B, 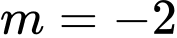 .
.
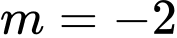 .
.C, 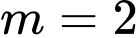 .
.
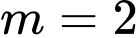 .
.D,  .
.
 .
.
Đáp án A
 Đáp án: A
Đáp án: A
 Đáp án: A
Đáp án: A
Câu 12 [245940]: Tìm tất cả các giá trị của tham số 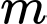 để bất phương trình
để bất phương trình 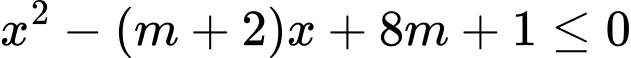 vô nghiệm.
vô nghiệm.
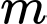 để bất phương trình
để bất phương trình 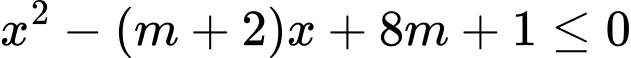 vô nghiệm.
vô nghiệm. A,  .
.
 .
.B,  .
.
 .
.C, 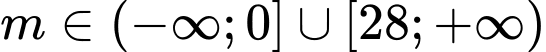 .
.
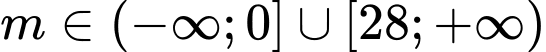 .
.D,  .
.
 .
.
Chọn D
Bất phương trình vô nghiệm khi và chỉ khi 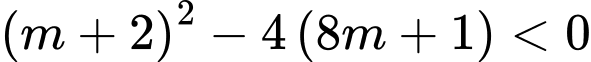
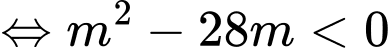
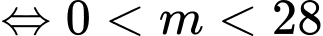 . Đáp án: D
. Đáp án: D
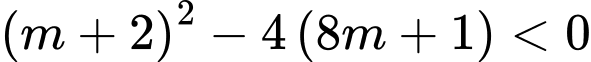
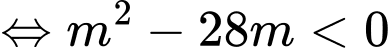
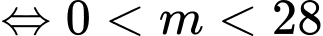 . Đáp án: D
. Đáp án: D
Câu 13 [245941]: Tam thức 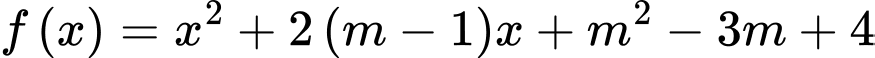 không âm với mọi giá trị của
không âm với mọi giá trị của 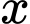 khi
khi
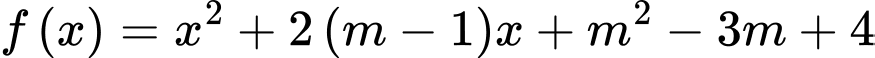 không âm với mọi giá trị của
không âm với mọi giá trị của 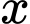 khi
khi A,  .
.
 .
.B,  .
.
 .
.C,  .
.
 .
.D,  .
.
 .
.
Chọn D
Yêu cầu bài toán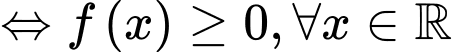
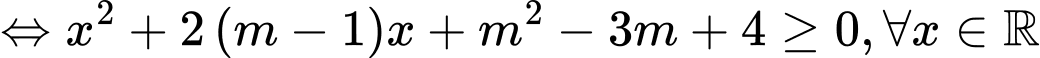
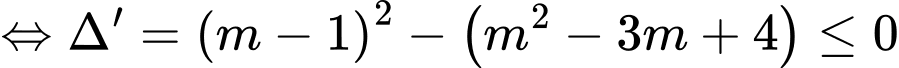
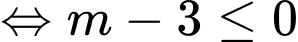
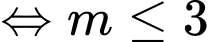 .
Vậy
.
Vậy  thỏa mãn yêu cầu bài toán Đáp án: D
thỏa mãn yêu cầu bài toán Đáp án: D
Yêu cầu bài toán
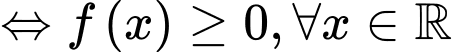
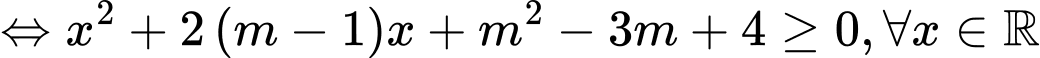
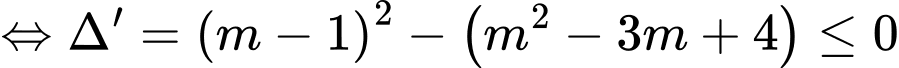
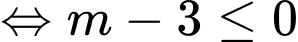
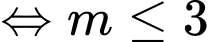 .
Vậy
.
Vậy  thỏa mãn yêu cầu bài toán Đáp án: D
thỏa mãn yêu cầu bài toán Đáp án: D
Câu 14 [245943]: Tìm các giá trị của m để biểu thức 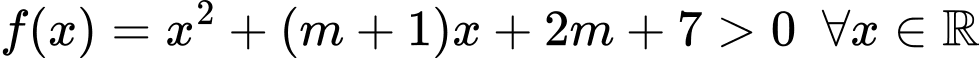 .
.
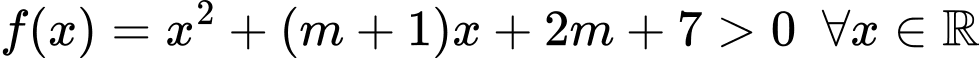 .
. A,  .
.
 .
.B, 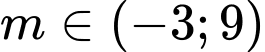 .
.
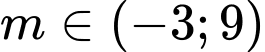 .
.C, 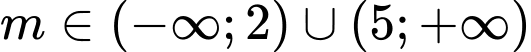 .
.
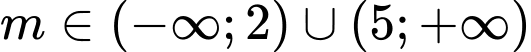 .
.D, 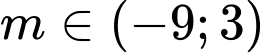 .
.
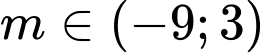 .
.
Chọn B
Ta có :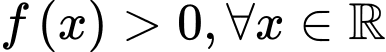
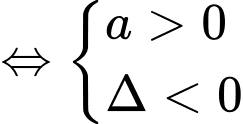
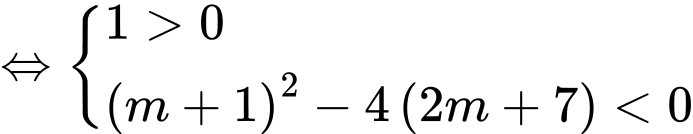
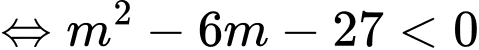
 Đáp án: B
Đáp án: B
Ta có :
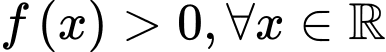
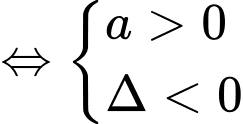
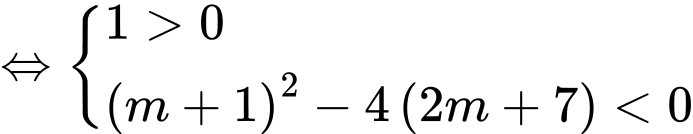
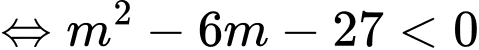
 Đáp án: B
Đáp án: B
Câu 15 [245949]: Tìm tất cả các giá trị của m để bất phương trình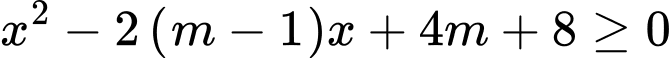 nghiệm đúng với mọi
nghiệm đúng với mọi 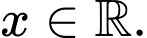
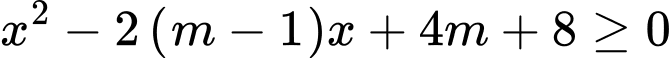 nghiệm đúng với mọi
nghiệm đúng với mọi 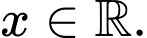
A, 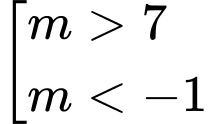 .
.
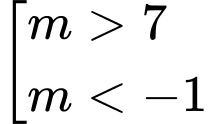 .
.B, 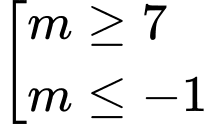 .
.
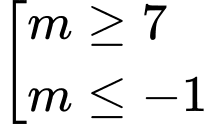 .
.C, 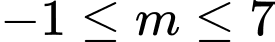 .
.
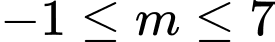 .
.D, 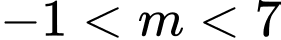 .
.
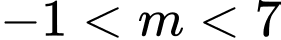 .
.
Chọn C
BPT nghiệm đúng
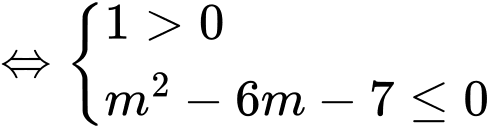
 . Đáp án: C
. Đáp án: C
BPT nghiệm đúng

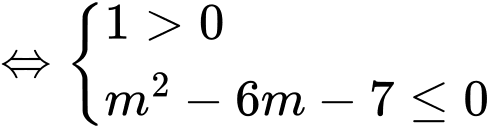
 . Đáp án: C
. Đáp án: C
Câu 16 [245956]: Có bao nhiêu giá trị nguyên của tham số 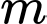 để hàm số
để hàm số 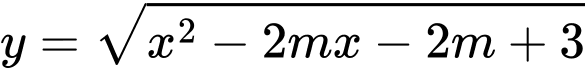 có tập xác định là
có tập xác định là 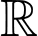 ?
?
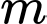 để hàm số
để hàm số 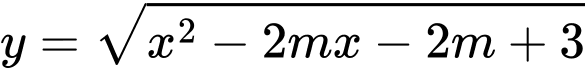 có tập xác định là
có tập xác định là 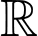 ?
? A, 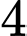 .
.
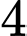 .
.B, 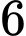 .
.
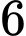 .
.C, 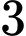 .
.
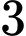 .
.D, 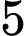 .
.
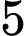 .
.
Chọn D.
Hàm số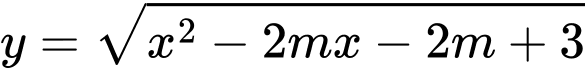 có tập xác định là
có tập xác định là 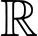 khi
khi 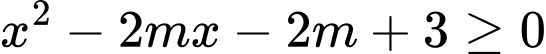 với mọi
với mọi 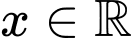
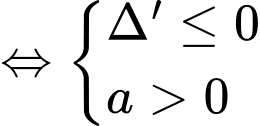
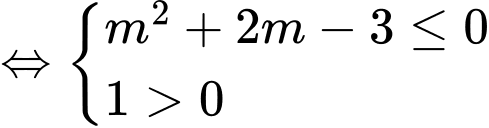
 . Do
. Do 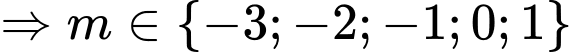 . Vậy có
. Vậy có 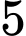 giá trị nguyên của
giá trị nguyên của 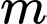 thỏa yêu cầu bài toán. Đáp án: D
thỏa yêu cầu bài toán. Đáp án: D
Hàm số
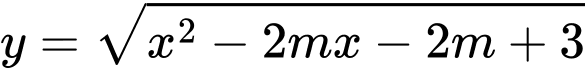 có tập xác định là
có tập xác định là 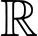 khi
khi 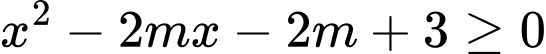 với mọi
với mọi 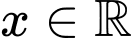
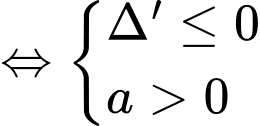
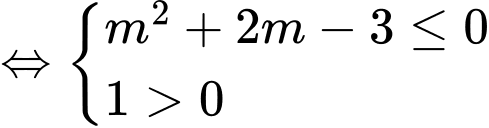
 . Do
. Do 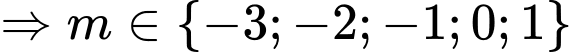 . Vậy có
. Vậy có 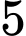 giá trị nguyên của
giá trị nguyên của 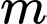 thỏa yêu cầu bài toán. Đáp án: D
thỏa yêu cầu bài toán. Đáp án: D
Câu 17 [245953]: Tìm tập hợp các giá trị của 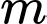 để hàm số
để hàm số 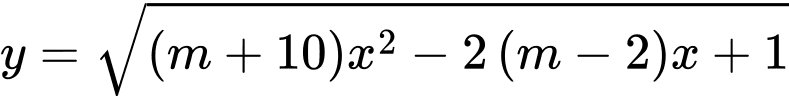 có tập xác định
có tập xác định 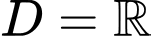 .
.
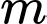 để hàm số
để hàm số 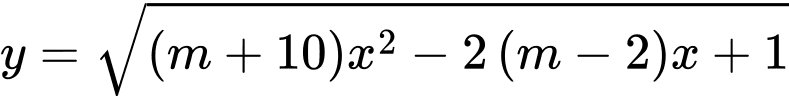 có tập xác định
có tập xác định 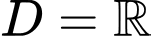 .
. A, 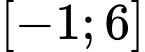 .
.
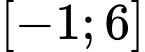 .
.B, 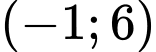 .
.
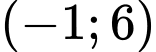 .
.C, 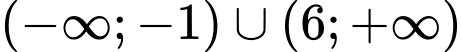 .
.
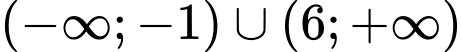 .
.D, 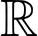 .
.
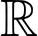 .
.
Chọn A
Hàm số xác định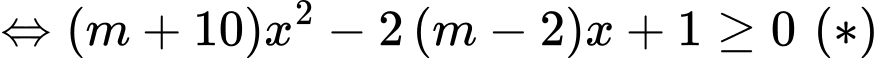 .
.
Hàm số có tập xác định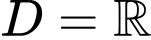 khi và chỉ khi
khi và chỉ khi  đúng với
đúng với 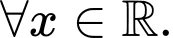
+)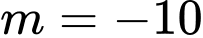 :
:  trở thành:
trở thành: 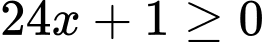 không đúng với
không đúng với  . Suy ra
. Suy ra 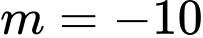 loại.
loại.
+)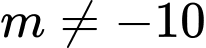 :
:  đúng với
đúng với 
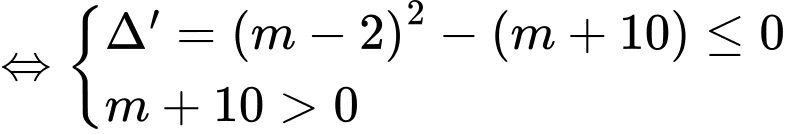
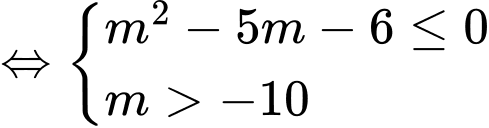
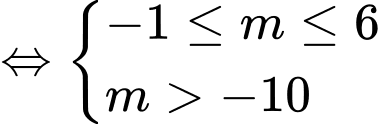

Vậy với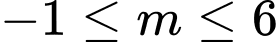 thì hàm số đã cho có tập xác định
thì hàm số đã cho có tập xác định 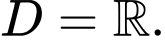 Đáp án: A
Đáp án: A
Hàm số xác định
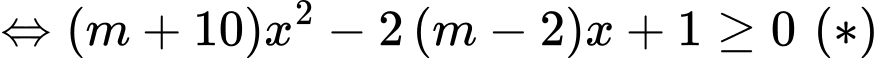 .
.Hàm số có tập xác định
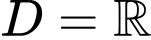 khi và chỉ khi
khi và chỉ khi  đúng với
đúng với 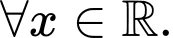
+)
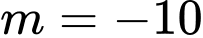 :
:  trở thành:
trở thành: 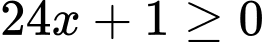 không đúng với
không đúng với  . Suy ra
. Suy ra 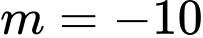 loại.
loại.+)
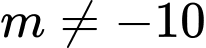 :
:  đúng với
đúng với 
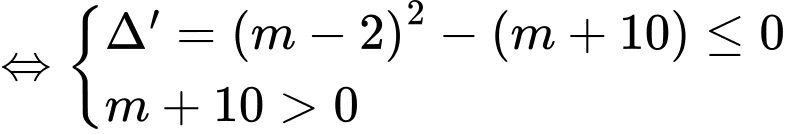
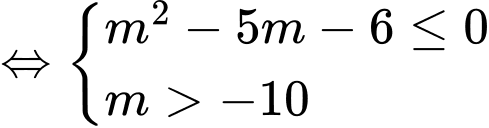
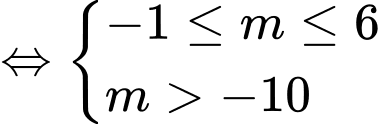

Vậy với
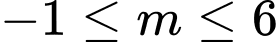 thì hàm số đã cho có tập xác định
thì hàm số đã cho có tập xác định 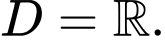 Đáp án: A
Đáp án: A
Câu 18 [245961]: Tìm 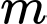 để
để 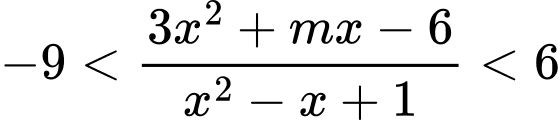 nghiệm đúng với
nghiệm đúng với  .
.
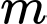 để
để 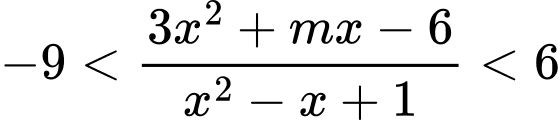 nghiệm đúng với
nghiệm đúng với  .
. A, 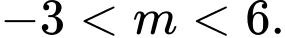
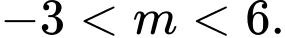
B, 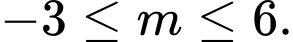
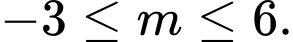
C, 

D, 

Bất phương trình đã cho tương tương với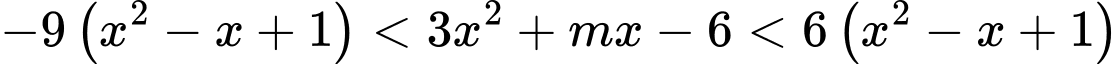 (do
(do 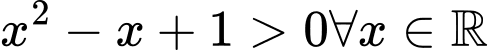 )
)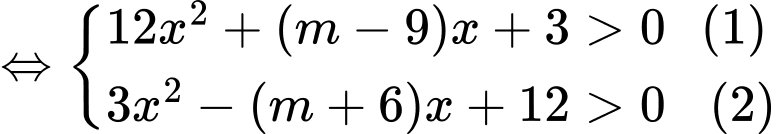
Yêu cầu (1) và (2) nghiệm đúng
(1) và (2) nghiệm đúng 
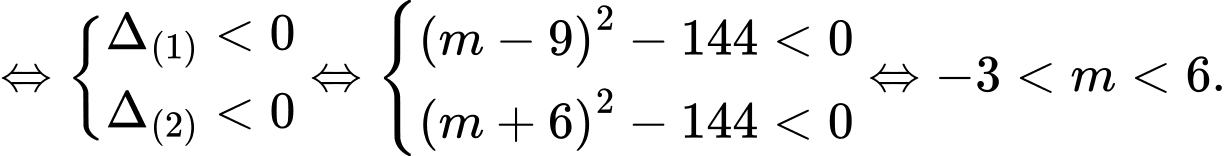 Đáp án: A
Đáp án: A
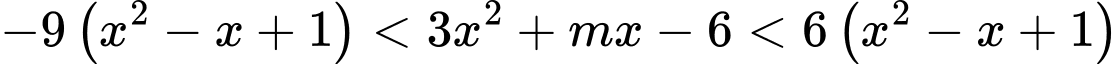 (do
(do 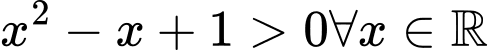 )
)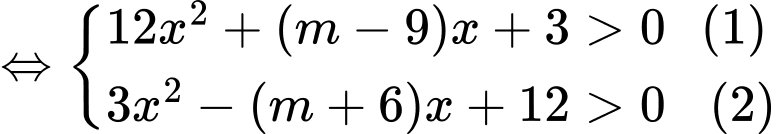
Yêu cầu
 (1) và (2) nghiệm đúng
(1) và (2) nghiệm đúng 
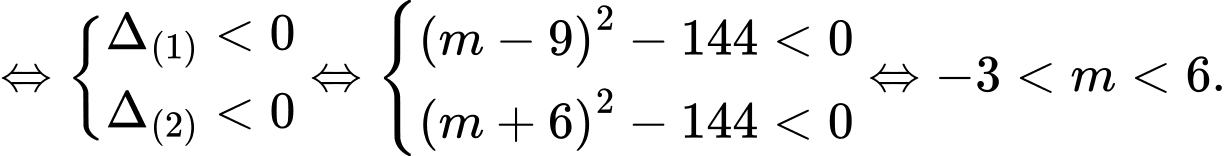 Đáp án: A
Đáp án: A
Câu 19 [245962]: Xác định 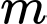 để với mọi
để với mọi 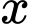 ta có
ta có 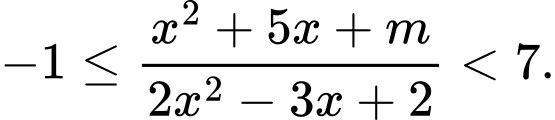
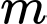 để với mọi
để với mọi 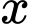 ta có
ta có 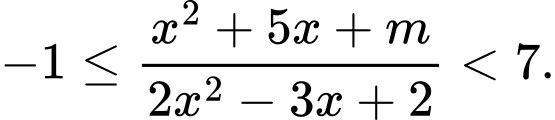
A, 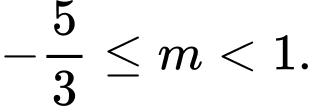
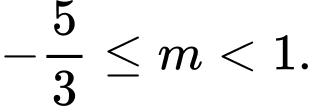
B, 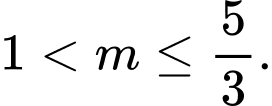
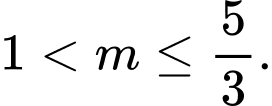
C, 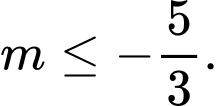
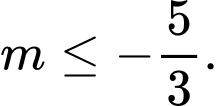
D, 

Bất phương trình tương đương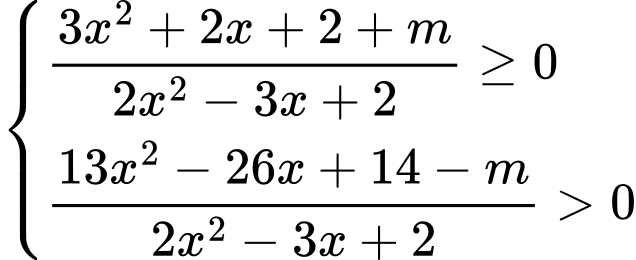
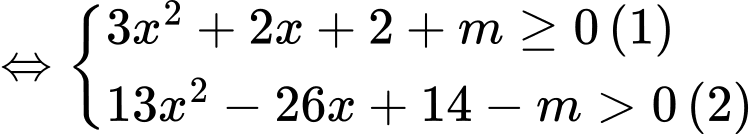 .
.
Yêu cầu (1) và (2) nghiệm đúng
(1) và (2) nghiệm đúng 
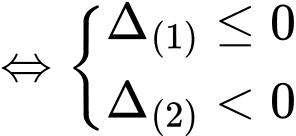
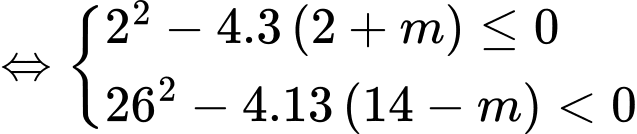
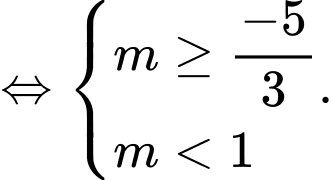 Chọn A. Đáp án: A
Chọn A. Đáp án: A
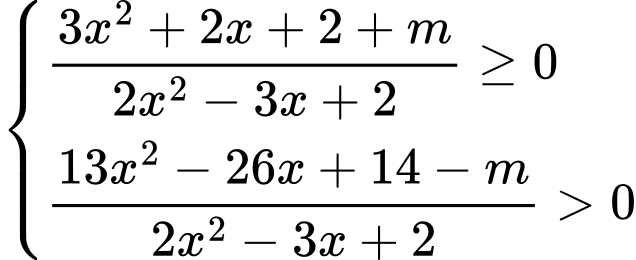
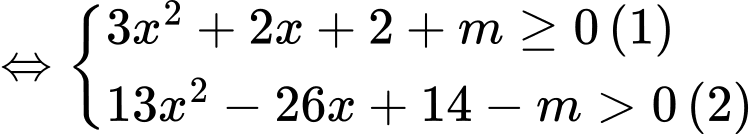 .
.Yêu cầu
 (1) và (2) nghiệm đúng
(1) và (2) nghiệm đúng 
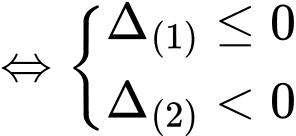
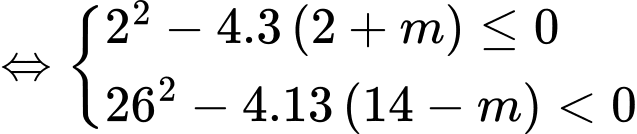
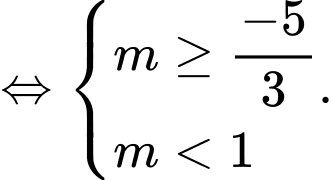 Chọn A. Đáp án: A
Chọn A. Đáp án: A
Câu 20 [300185]: Tìm giá trị 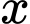 nguyên lớn nhất để giá trị của biểu thức
nguyên lớn nhất để giá trị của biểu thức  không lớn hơn giá trị của biểu thức
không lớn hơn giá trị của biểu thức 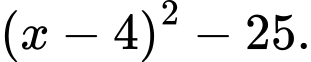
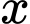 nguyên lớn nhất để giá trị của biểu thức
nguyên lớn nhất để giá trị của biểu thức  không lớn hơn giá trị của biểu thức
không lớn hơn giá trị của biểu thức 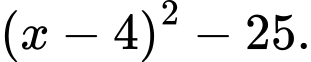
Để giá trị của biểu thức  không lớn hơn giá trị của biểu thức
không lớn hơn giá trị của biểu thức 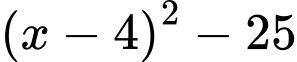 thì:
thì:
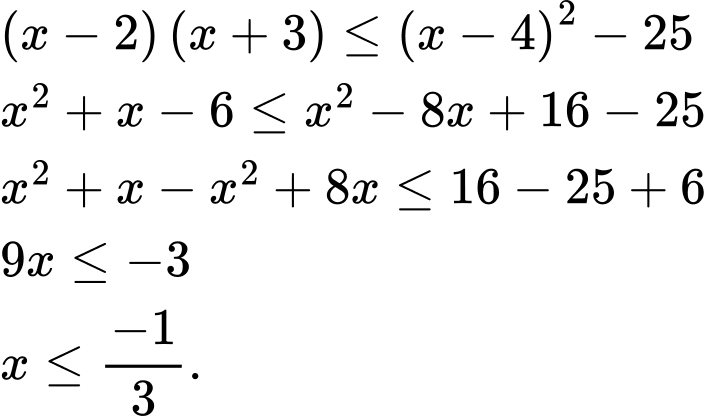
Với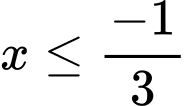 thì giá trị nguyên lớn nhất của
thì giá trị nguyên lớn nhất của 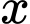 là
là 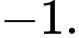
Vậy để giá trị của biểu thức không lớn hơn giá trị của biểu thức
không lớn hơn giá trị của biểu thức 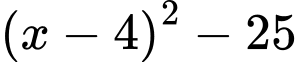 thì giá trị nguyên lớn nhất của
thì giá trị nguyên lớn nhất của 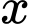 là
là 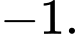
 không lớn hơn giá trị của biểu thức
không lớn hơn giá trị của biểu thức 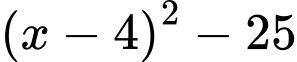 thì:
thì: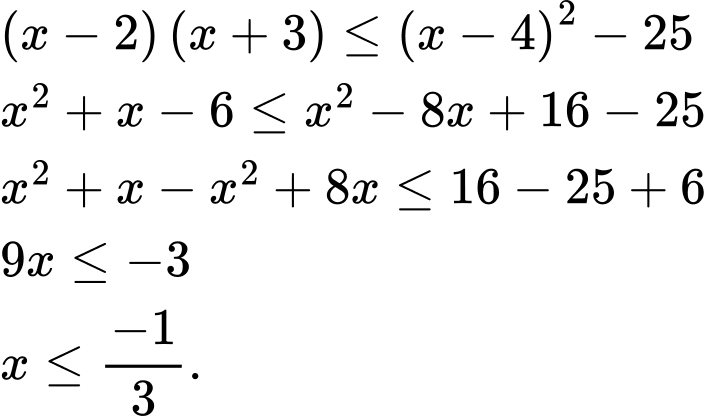
Với
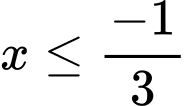 thì giá trị nguyên lớn nhất của
thì giá trị nguyên lớn nhất của 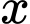 là
là 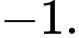
Vậy để giá trị của biểu thức
 không lớn hơn giá trị của biểu thức
không lớn hơn giá trị của biểu thức 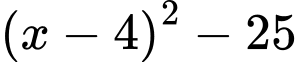 thì giá trị nguyên lớn nhất của
thì giá trị nguyên lớn nhất của 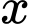 là
là 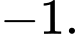
Câu 21 [582023]: Có bao nhiêu giá trị nguyên của tham số 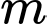 để với mọi
để với mọi 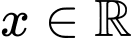 biểu thức
biểu thức 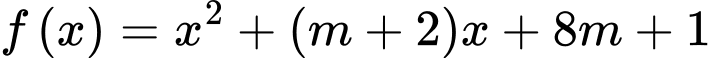 luôn nhận giá trị dương?
luôn nhận giá trị dương?
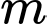 để với mọi
để với mọi 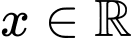 biểu thức
biểu thức 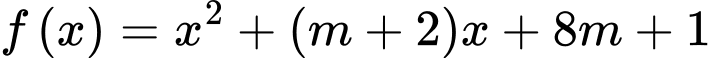 luôn nhận giá trị dương?
luôn nhận giá trị dương? 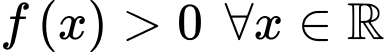
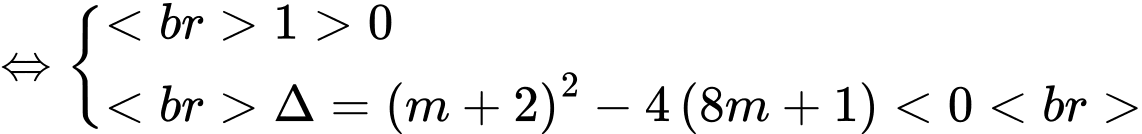

Vậy có 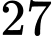 giá trị nguyên của tham số
giá trị nguyên của tham số 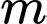 thỏa mãn yêu cầu bài toán.
thỏa mãn yêu cầu bài toán.
Câu 22 [581990]: Có bao nhiêu số tự nhiên 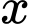 thoả mãn đồng thời hai bất phương trình sau:
thoả mãn đồng thời hai bất phương trình sau:
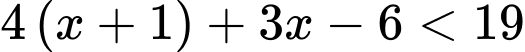 và
và 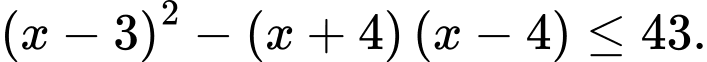
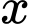 thoả mãn đồng thời hai bất phương trình sau:
thoả mãn đồng thời hai bất phương trình sau: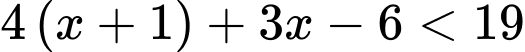 và
và 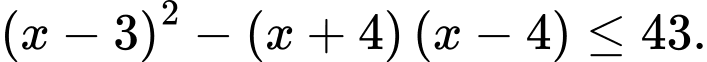
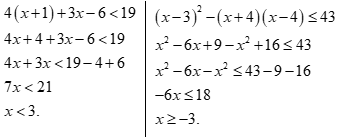
Để 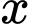 thỏa mãn cả hai bất phương trình thì
thỏa mãn cả hai bất phương trình thì 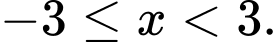
Vậy có 3 số tự nhiên 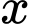 thỏa mãn đồng thời hai bất phương trình
thỏa mãn đồng thời hai bất phương trình 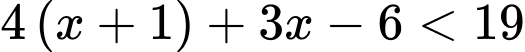 và
và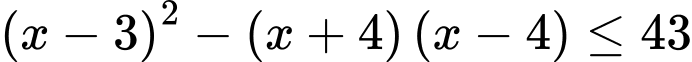 là
là 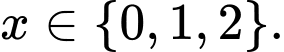
Câu 23 [582046]: Có bao nhiêu giá trị nguyên của 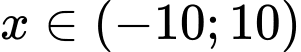 để biểu thức
để biểu thức 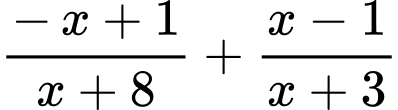 nhận giá trị dương.
nhận giá trị dương.
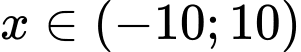 để biểu thức
để biểu thức 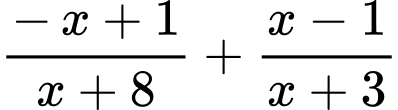 nhận giá trị dương.
nhận giá trị dương.
Để biểu thức 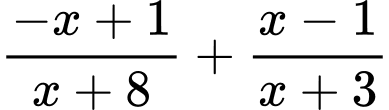 nhận giá trị dương thì:
nhận giá trị dương thì:
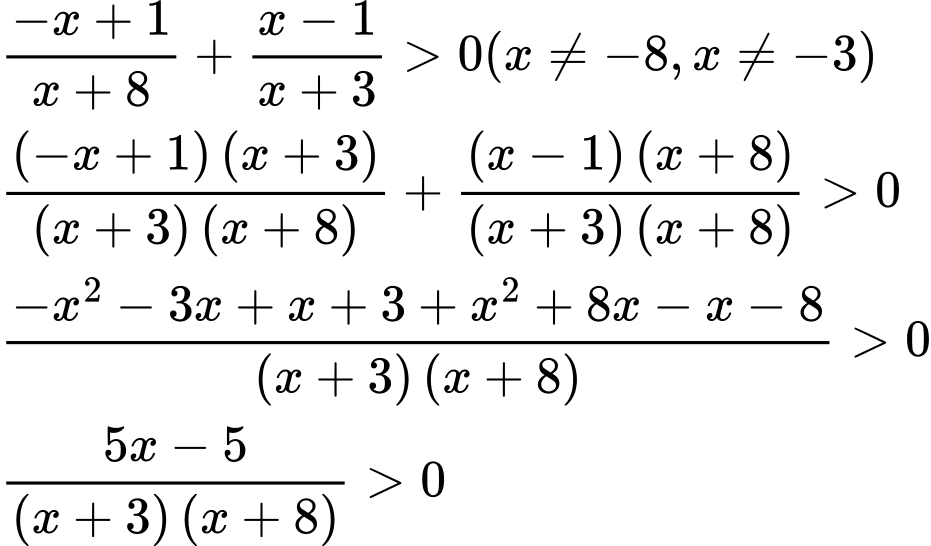
Lập bảng xét dấu ta có kết luận
Vậy bất phương trình đã cho có nghiệm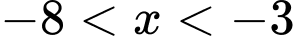 hoặc
hoặc  suy ra có 12 giá trị của
suy ra có 12 giá trị của 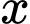 thoả mãn.
thoả mãn.
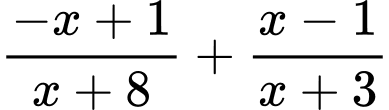 nhận giá trị dương thì:
nhận giá trị dương thì: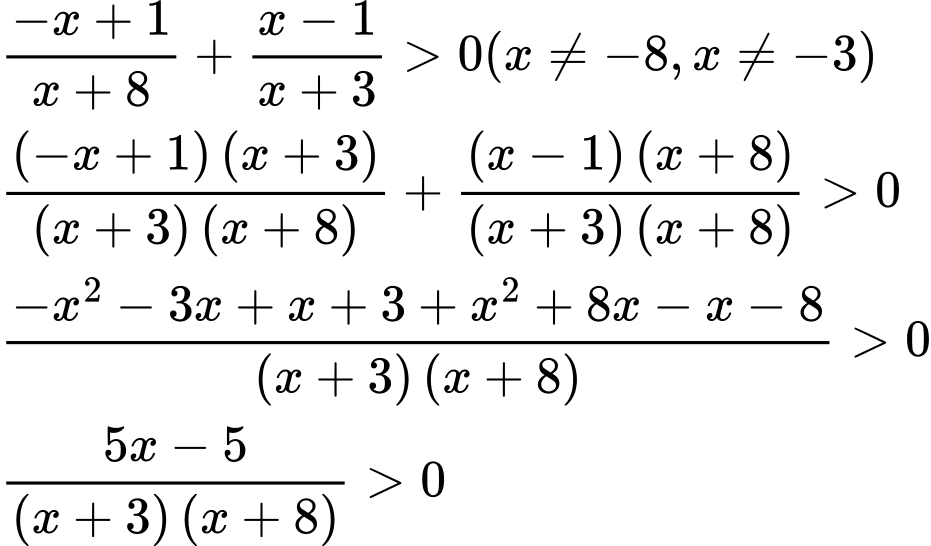
Lập bảng xét dấu ta có kết luận
Vậy bất phương trình đã cho có nghiệm
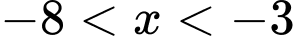 hoặc
hoặc  suy ra có 12 giá trị của
suy ra có 12 giá trị của 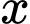 thoả mãn.
thoả mãn.
Câu 24 [582000]: Tìm số nghiệm nguyên của bất phương trình 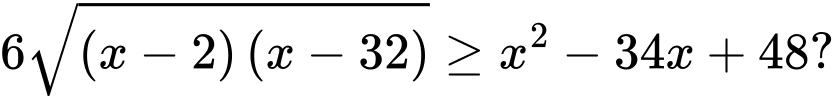
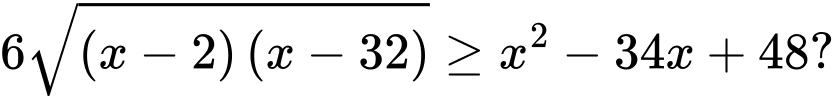
Ta có 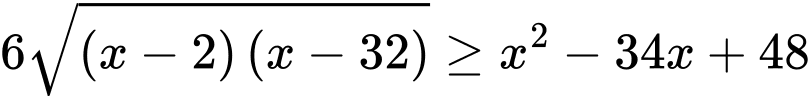
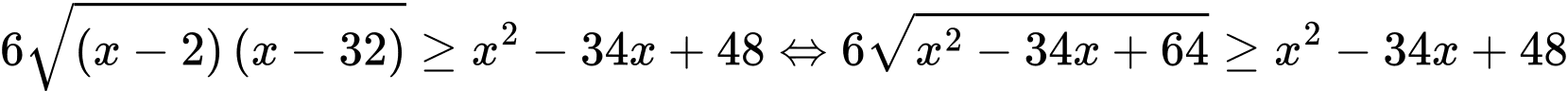
Đặt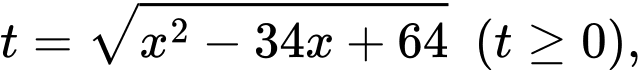 suy ra
suy ra 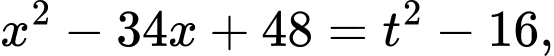
Bất phương trình trở thành: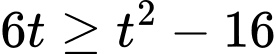
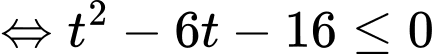
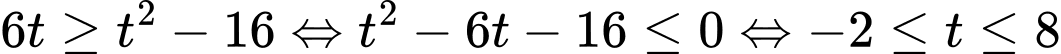
Kết hợp điều kiện, suy ra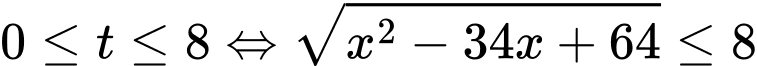
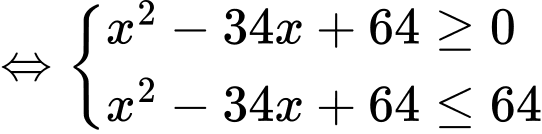
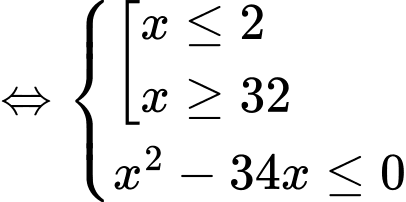
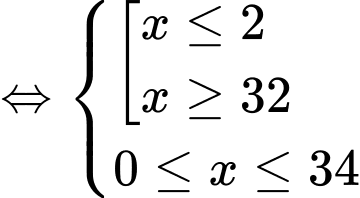
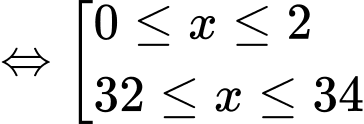
Vậy bất phương trình có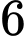 nghiệm nguyên
nghiệm nguyên 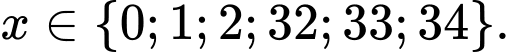
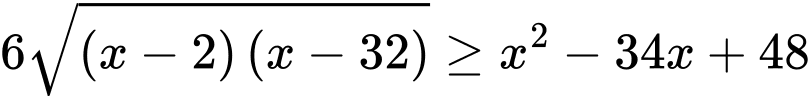
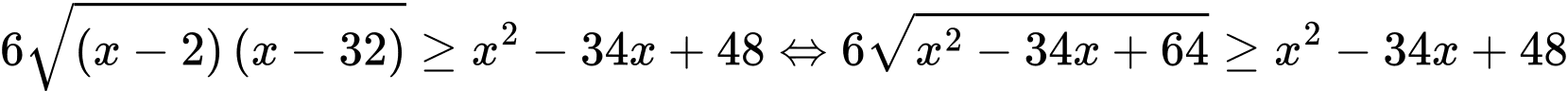
Đặt
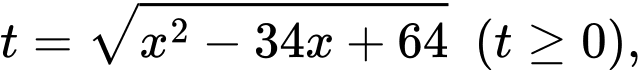 suy ra
suy ra 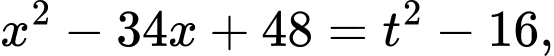
Bất phương trình trở thành:
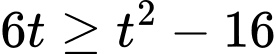
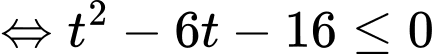
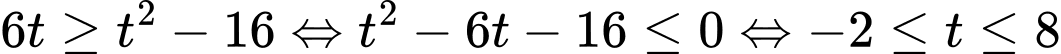
Kết hợp điều kiện, suy ra
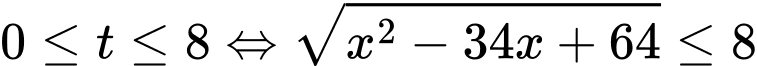
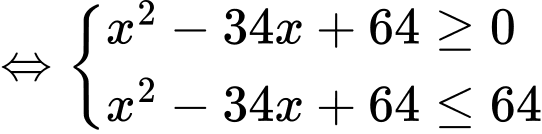
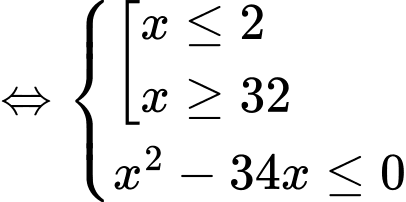
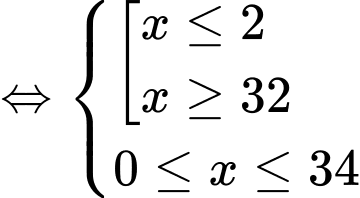
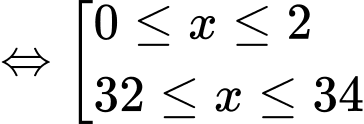
Vậy bất phương trình có
 nghiệm nguyên
nghiệm nguyên 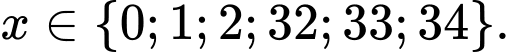
Câu 25 [582001]: Biết tập nghiệm của bất phương trình 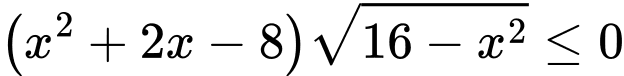 có dạng
có dạng 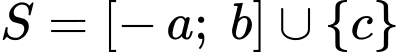 với
với 
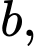
 là các số nguyên dương. Tính
là các số nguyên dương. Tính 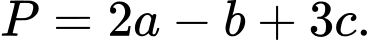
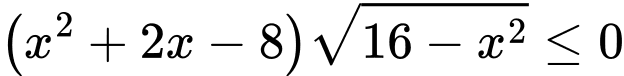 có dạng
có dạng 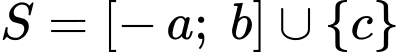 với
với 
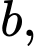
 là các số nguyên dương. Tính
là các số nguyên dương. Tính 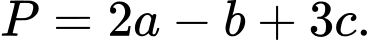
Ta có: 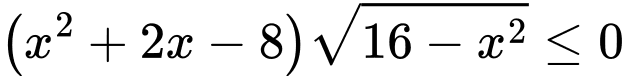
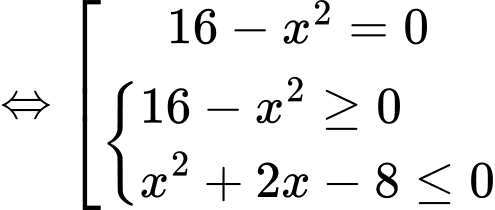
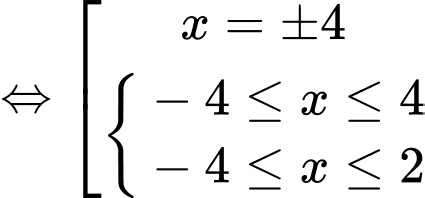
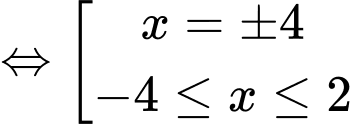
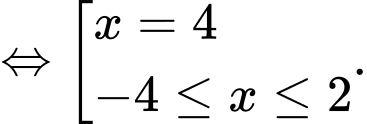
Vậy tập nghiệm của bất phương trình là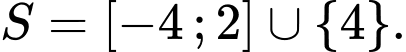
Suy ra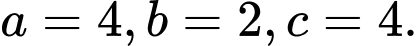
Vậy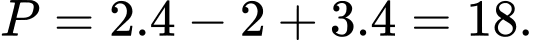
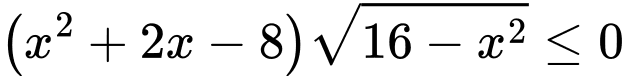
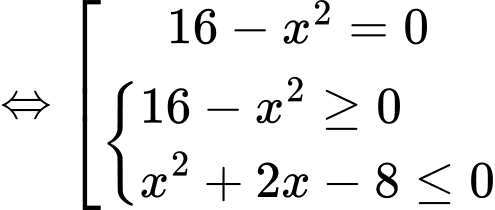
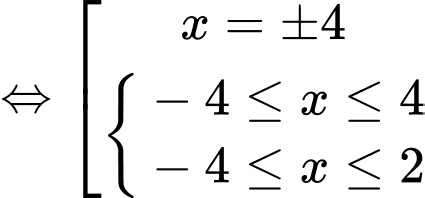
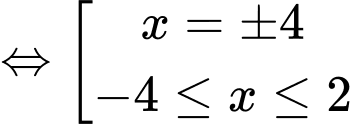
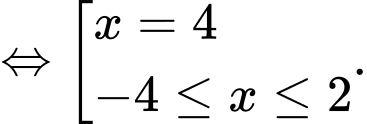
Vậy tập nghiệm của bất phương trình là
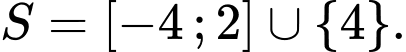
Suy ra
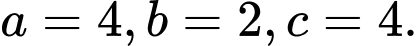
Vậy
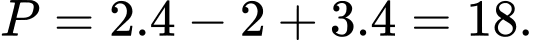
Câu 26 [251597]: Một vật được ném theo phương thẳng đứng xuống dưới từ độ cao 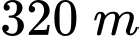 với vận tốc ban đầu
với vận tốc ban đầu 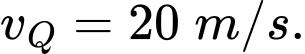 Hỏi sau ít nhất bao nhiêu giấy, vật đó cách mặt đất không quá
Hỏi sau ít nhất bao nhiêu giấy, vật đó cách mặt đất không quá 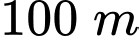 ? Giả thiết rằng sức cản của không khí là không đáng kể. Lấy gia tốc trọng trường
? Giả thiết rằng sức cản của không khí là không đáng kể. Lấy gia tốc trọng trường 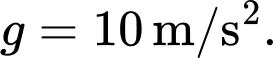
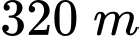 với vận tốc ban đầu
với vận tốc ban đầu 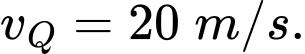 Hỏi sau ít nhất bao nhiêu giấy, vật đó cách mặt đất không quá
Hỏi sau ít nhất bao nhiêu giấy, vật đó cách mặt đất không quá 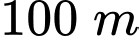 ? Giả thiết rằng sức cản của không khí là không đáng kể. Lấy gia tốc trọng trường
? Giả thiết rằng sức cản của không khí là không đáng kể. Lấy gia tốc trọng trường 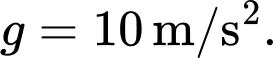
Chọn trục Oy thẳng đứng, chiều dương hướng xuống, gốc tọa độ  tại mặt đất và gốc thời gian là lúc ném.
tại mặt đất và gốc thời gian là lúc ném.
Ta có độ cao của vật là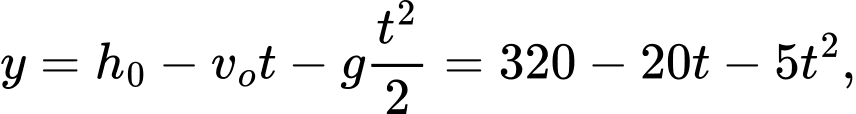 với g là gia tốc tự do lấy
với g là gia tốc tự do lấy 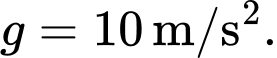
Để vật đó cách mặt đất không quá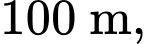 thì
thì 
Ta có bất phương trình: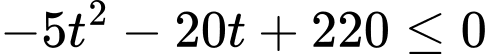
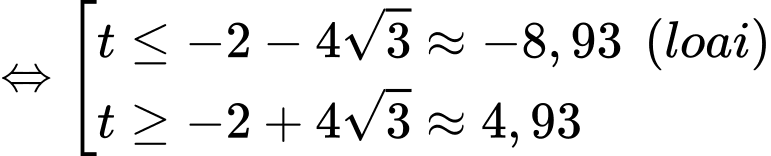
Vậy sau ít nhất 4,93 giây thì vật đó cách mặt đất không quá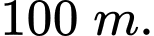
 tại mặt đất và gốc thời gian là lúc ném.
tại mặt đất và gốc thời gian là lúc ném.Ta có độ cao của vật là
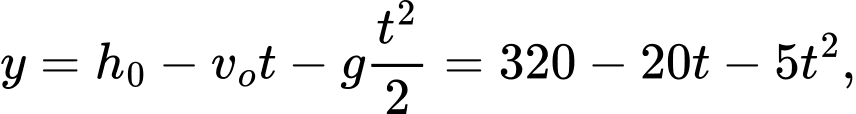 với g là gia tốc tự do lấy
với g là gia tốc tự do lấy 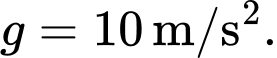
Để vật đó cách mặt đất không quá
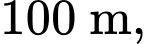 thì
thì 
Ta có bất phương trình:
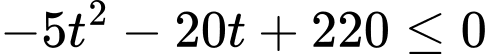
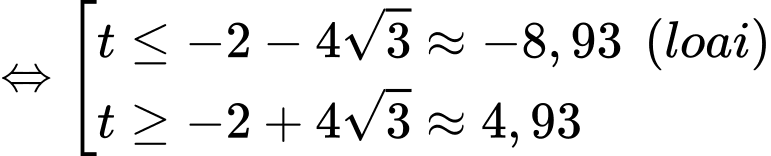
Vậy sau ít nhất 4,93 giây thì vật đó cách mặt đất không quá
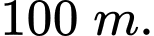
Câu 27 [251869]: Một quả bóng được bắn thẳng lên từ độ cao 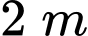 với vận tốc ban đầu là
với vận tốc ban đầu là 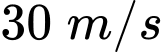 . Khoảng cách của bóng so với mặt đất sau t giây được cho bởi hàm số:
. Khoảng cách của bóng so với mặt đất sau t giây được cho bởi hàm số: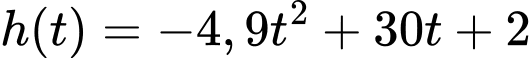 với h(t) tính bằng đơn vị mét. Hỏi quả bóng nằm ở độ cao trên
với h(t) tính bằng đơn vị mét. Hỏi quả bóng nằm ở độ cao trên 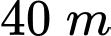 trong thời gian bao lâu? Làm tròn kết quả đến hàng phần mười.
trong thời gian bao lâu? Làm tròn kết quả đến hàng phần mười.
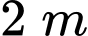 với vận tốc ban đầu là
với vận tốc ban đầu là 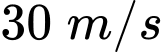 . Khoảng cách của bóng so với mặt đất sau t giây được cho bởi hàm số:
. Khoảng cách của bóng so với mặt đất sau t giây được cho bởi hàm số: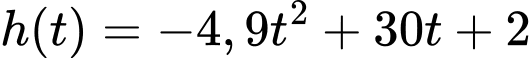 với h(t) tính bằng đơn vị mét. Hỏi quả bóng nằm ở độ cao trên
với h(t) tính bằng đơn vị mét. Hỏi quả bóng nằm ở độ cao trên 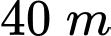 trong thời gian bao lâu? Làm tròn kết quả đến hàng phần mười.
trong thời gian bao lâu? Làm tròn kết quả đến hàng phần mười.
Khi quả bóng nằm ở độ cao trên 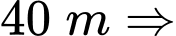 Khi đó
Khi đó 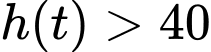
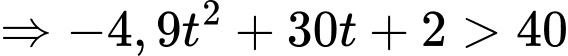
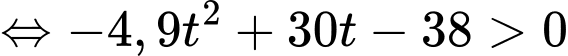
Tam thức bậc hai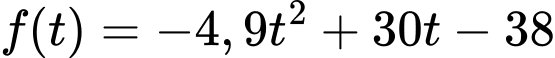 có hai nghiệm phân biệt
có hai nghiệm phân biệt 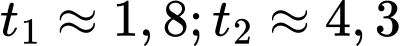
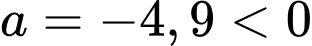 nên
nên 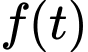 dương với mọi x thuộc khoảng
dương với mọi x thuộc khoảng 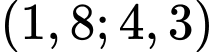 .
.
Vậy quả bóng nằm ở độ cao trên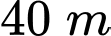 trong thời gian là: 4,3 - 1,8=2,5
trong thời gian là: 4,3 - 1,8=2,5 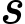 .
.
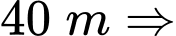 Khi đó
Khi đó 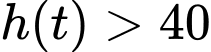
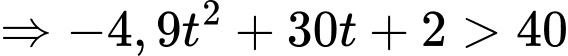
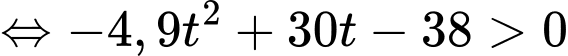
Tam thức bậc hai
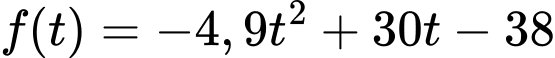 có hai nghiệm phân biệt
có hai nghiệm phân biệt 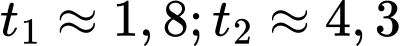
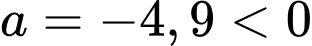 nên
nên 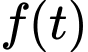 dương với mọi x thuộc khoảng
dương với mọi x thuộc khoảng 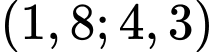 .
.Vậy quả bóng nằm ở độ cao trên
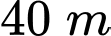 trong thời gian là: 4,3 - 1,8=2,5
trong thời gian là: 4,3 - 1,8=2,5 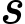 .
.
Câu 28 [582024]: Một công ty bắt đầu sản xuất và bán một loại máy tính xách tay từ năm 2018. Số lượng loại máy tính đó bán được trong hai năm liên tiếp 2018 và 2019 lần lượt là 3,2 nghìn và 4 nghìn chiếc. Theo nghiên cứu dự báo thị trường của công ty, trong khoảng 10 năm kể từ năm 2018, số lượng máy tính loại đó bán được mỗi năm có thể được xấp xỉ bởi một hàm bậc hai.
Giả sử t là thời gian (theo đơn vị năm) tính từ năm 2018. Số lượng loại máy tính đó bán được trong năm 2018 và năm 2019 lần lượt được biểu diên bởi các điểm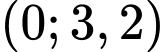 và
và 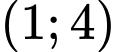 . Giả sử điểm
. Giả sử điểm 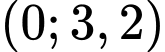 là đỉnh đồ thị của hàm số bậc hai này. Đến năm bao nhiêu thì số lượng máy tính xách tay đó được bán trong năm sẽ vượt mức 52 nghìn chiếc?
là đỉnh đồ thị của hàm số bậc hai này. Đến năm bao nhiêu thì số lượng máy tính xách tay đó được bán trong năm sẽ vượt mức 52 nghìn chiếc?
Giả sử t là thời gian (theo đơn vị năm) tính từ năm 2018. Số lượng loại máy tính đó bán được trong năm 2018 và năm 2019 lần lượt được biểu diên bởi các điểm
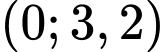 và
và 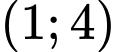 . Giả sử điểm
. Giả sử điểm 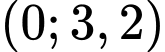 là đỉnh đồ thị của hàm số bậc hai này. Đến năm bao nhiêu thì số lượng máy tính xách tay đó được bán trong năm sẽ vượt mức 52 nghìn chiếc?
là đỉnh đồ thị của hàm số bậc hai này. Đến năm bao nhiêu thì số lượng máy tính xách tay đó được bán trong năm sẽ vượt mức 52 nghìn chiếc? Gọi hàm số bậc hai mô tả số lượng máy tính xách tay bán qua từng năm có dạng: 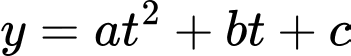
Với y là số lượng máy tính bán ra (đơn vị: nghìn chiếc), t là thời gian (đơn vị năm). Điều kiện  .
.
- Do đồ thị hàm số có đỉnh là 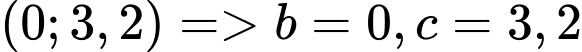 .
.
- Đồ thị đi qua điểm 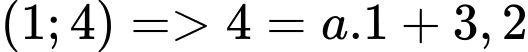 , hay
, hay 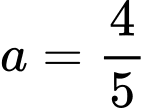
Vậy hàm số có dạng 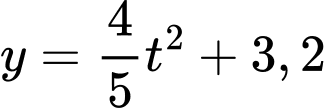
Xét phương trình: 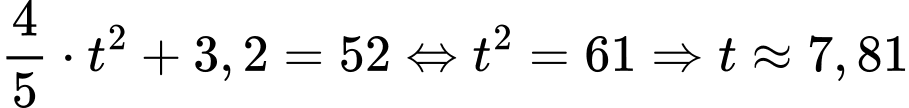
Ứng với t = 8 là năm 2026.
Vậy đến năm 2026 thì số lượng máy tính bán ra trong năm vượt mức 52 nghìn chiếc.