Đáp án Bài tập tự luyện
Câu 1 [237941]: Miền nghiệm của bất phương trình 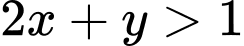 không chứa điểm nào sau đây?
không chứa điểm nào sau đây?
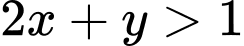 không chứa điểm nào sau đây?
không chứa điểm nào sau đây? A, 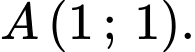
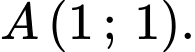
B, 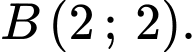
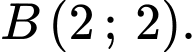
C, 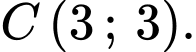
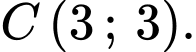
D, 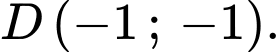
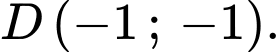
Thay từng cặp điểm ở 4 phương án vào bất phương trình đã cho ta có:
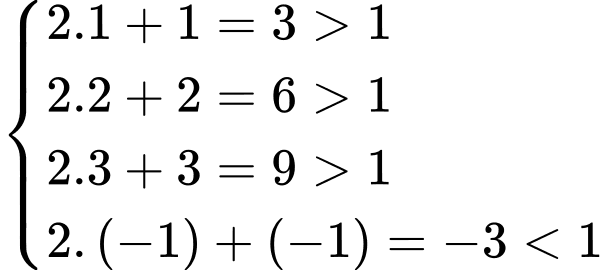 nên chỉ điểm
nên chỉ điểm 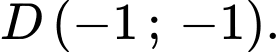 không thuộc miền nghiệm của bất phương trình đã cho. Chọn D. Đáp án: D
không thuộc miền nghiệm của bất phương trình đã cho. Chọn D. Đáp án: D
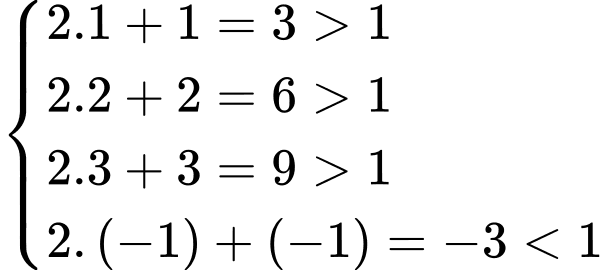 nên chỉ điểm
nên chỉ điểm 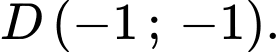 không thuộc miền nghiệm của bất phương trình đã cho. Chọn D. Đáp án: D
không thuộc miền nghiệm của bất phương trình đã cho. Chọn D. Đáp án: D
Câu 2 [237942]: Cặp số 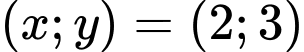 là nghiệm của bất phương trình nào sau đây?
là nghiệm của bất phương trình nào sau đây?
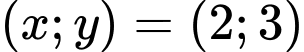 là nghiệm của bất phương trình nào sau đây?
là nghiệm của bất phương trình nào sau đây? A, 

B, 

C, 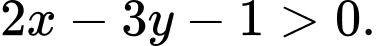
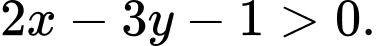
D, 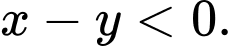
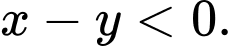
Ta có 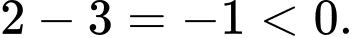 Chọn D. Đáp án: D
Chọn D. Đáp án: D
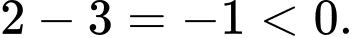 Chọn D. Đáp án: D
Chọn D. Đáp án: D
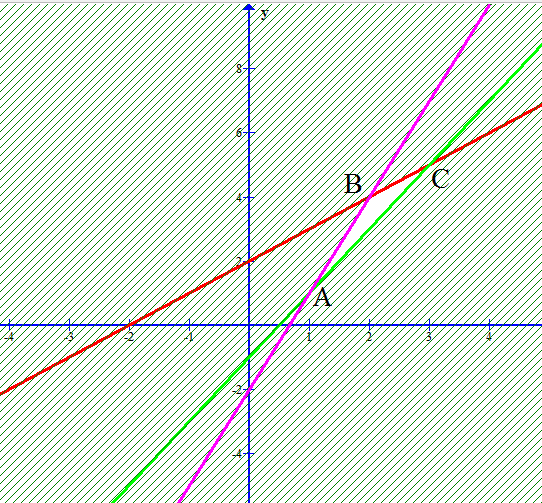
Câu 3 [237944]: Miền nghiệm của bất phương trình 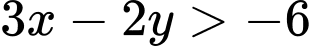 là
là
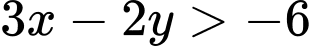 là
là A, 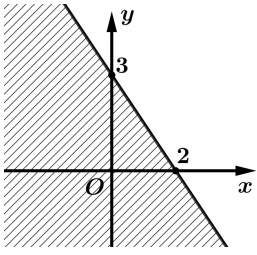

B, 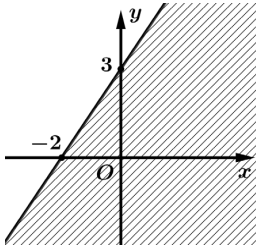

C, 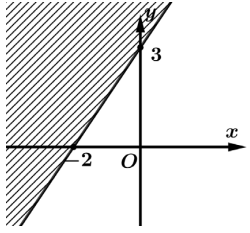

D, 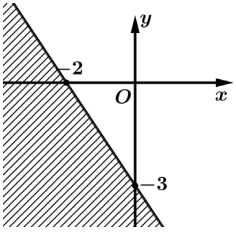

Chọn C.
Trước hết, ta vẽ đường thẳng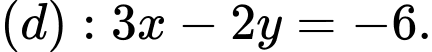 Ta thấy
Ta thấy 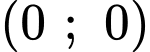 là nghiệm của bất phương trình đã cho. Vậy miền nghiệm cần tìm là nửa mặt phẳng bờ
là nghiệm của bất phương trình đã cho. Vậy miền nghiệm cần tìm là nửa mặt phẳng bờ  chứa điểm
chứa điểm 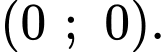
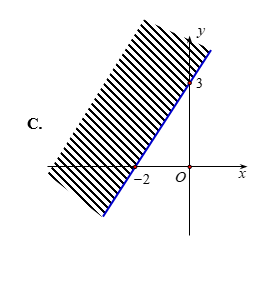 Đáp án: C
Đáp án: C
Trước hết, ta vẽ đường thẳng
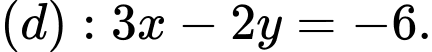 Ta thấy
Ta thấy 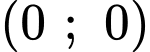 là nghiệm của bất phương trình đã cho. Vậy miền nghiệm cần tìm là nửa mặt phẳng bờ
là nghiệm của bất phương trình đã cho. Vậy miền nghiệm cần tìm là nửa mặt phẳng bờ  chứa điểm
chứa điểm 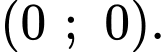
 Đáp án: C
Đáp án: C
Câu 4 [237953]: Miền nghiệm của bất phương trình 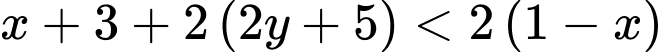 là nửa mặt phẳng không chứa điểm nào dưới đây?
là nửa mặt phẳng không chứa điểm nào dưới đây?
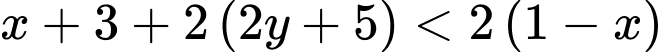 là nửa mặt phẳng không chứa điểm nào dưới đây?
là nửa mặt phẳng không chứa điểm nào dưới đây? A, 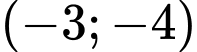 .
.
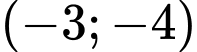 .
.B, 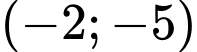 .
.
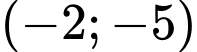 .
.C, 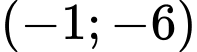 .
.
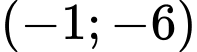 .
.D, 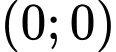 .
.
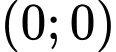 .
.
Chọn D.
Biến đổi bất phương trình: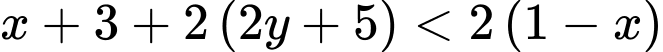
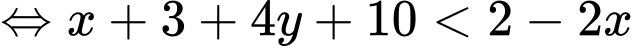
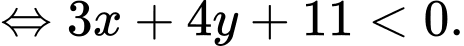
Dễ thấy tại điểm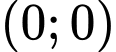 ta có:
ta có: 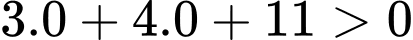 nên miên nghiệm của BPT không chứa
nên miên nghiệm của BPT không chứa 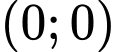 Đáp án: D
Đáp án: D
Biến đổi bất phương trình:
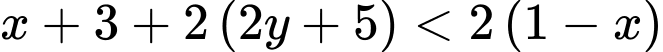
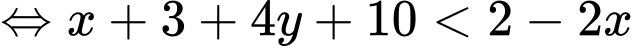
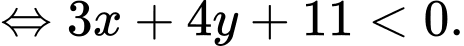
Dễ thấy tại điểm
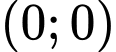 ta có:
ta có: 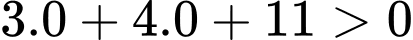 nên miên nghiệm của BPT không chứa
nên miên nghiệm của BPT không chứa 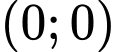 Đáp án: D
Đáp án: D
Câu 5 [365702]: Tìm số các giá trị nguyên của tham số 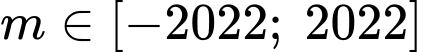 sao cho
sao cho 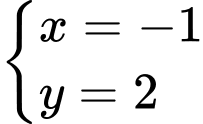 là nghiệm của bất phương trình
là nghiệm của bất phương trình 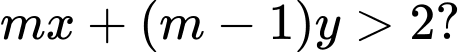
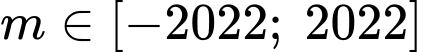 sao cho
sao cho 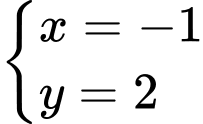 là nghiệm của bất phương trình
là nghiệm của bất phương trình 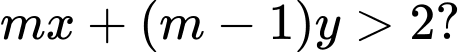
A, 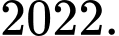
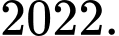
B, 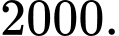
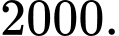
C, 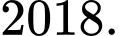
D, 
Ta có 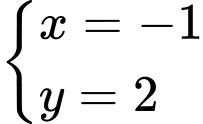 là nghiệm của bất phương trình
là nghiệm của bất phương trình 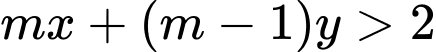 nên
nên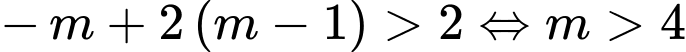
Mà nên
nên 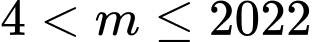
Do nên
nên 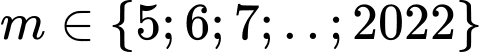
Số các giá trị nguyên của tham số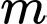 thỏa mãn đề là
thỏa mãn đề là  (số)
(số)
Chọn đáp án C. Đáp án: C
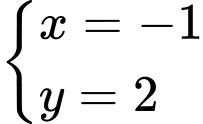 là nghiệm của bất phương trình
là nghiệm của bất phương trình 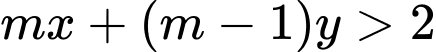 nên
nên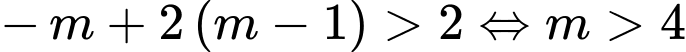
Mà
 nên
nên 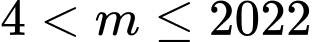
Do
 nên
nên 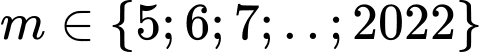
Số các giá trị nguyên của tham số
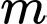 thỏa mãn đề là
thỏa mãn đề là  (số)
(số)
Chọn đáp án C. Đáp án: C
Câu 6 [238024]: Trong các cặp số sau, cặp nào không là nghiệm của hệ bất phương trình 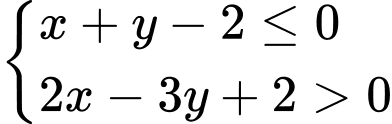 ?
?
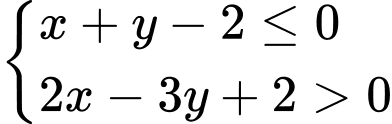 ?
? A, 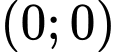 .
.
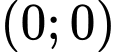 .
.B, 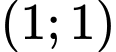 .
.
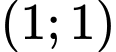 .
.C, 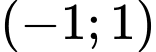 .
.
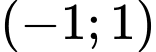 .
.D, 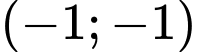 .
.
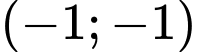 .
.
Lời giải: ChọnC.
Ta thay cặp số 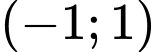 vào hệ ta thấy không thỏa mãn. Đáp án: C
vào hệ ta thấy không thỏa mãn. Đáp án: C
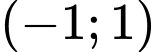 vào hệ ta thấy không thỏa mãn. Đáp án: C
vào hệ ta thấy không thỏa mãn. Đáp án: C
Câu 7 [240837]: Miền nghiệm của hệ bất phương trình 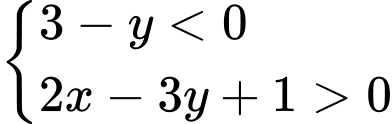 chứa điểm nào sau đây?
chứa điểm nào sau đây?
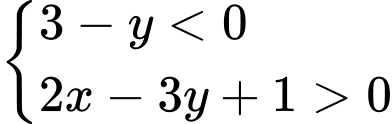 chứa điểm nào sau đây?
chứa điểm nào sau đây? A, 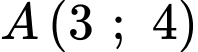 .
.
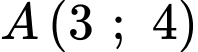 .
.B, 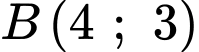 .
.
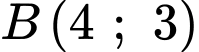 .
.C, 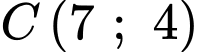 .
.
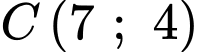 .
.D, 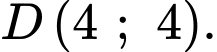
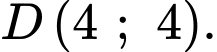
Chọn C.
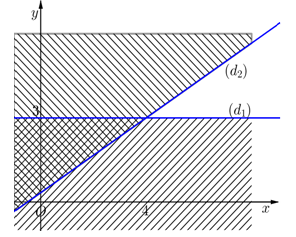
Trước hết, ta vẽ hai đường thẳng:
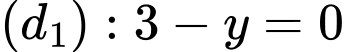
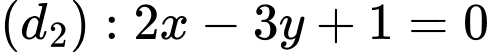
Ta thấy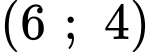 là nghiệm của hai bất phương trình. Điều đó có nghĩa điểm
là nghiệm của hai bất phương trình. Điều đó có nghĩa điểm 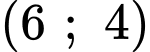 thuộc cả hai miền nghiệm của hai bất phương trình. Sau khi gạch bỏ các miền không thích hợp, miền không bị gạch là miền nghiệm của hệ. Đáp án: C
thuộc cả hai miền nghiệm của hai bất phương trình. Sau khi gạch bỏ các miền không thích hợp, miền không bị gạch là miền nghiệm của hệ. Đáp án: C

Trước hết, ta vẽ hai đường thẳng:
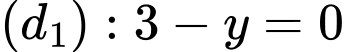
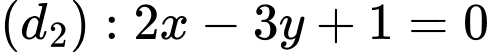
Ta thấy
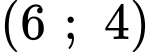 là nghiệm của hai bất phương trình. Điều đó có nghĩa điểm
là nghiệm của hai bất phương trình. Điều đó có nghĩa điểm 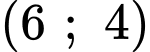 thuộc cả hai miền nghiệm của hai bất phương trình. Sau khi gạch bỏ các miền không thích hợp, miền không bị gạch là miền nghiệm của hệ. Đáp án: C
thuộc cả hai miền nghiệm của hai bất phương trình. Sau khi gạch bỏ các miền không thích hợp, miền không bị gạch là miền nghiệm của hệ. Đáp án: C
Câu 8 [238025]: Điểm nào sau đây không thuộc miền nghiệm của hệ bất phương trình 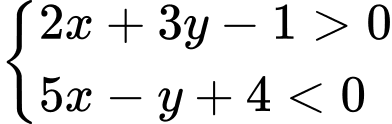 ?
?
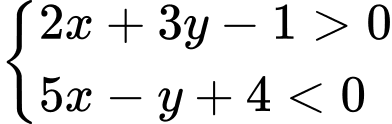 ?
? A, 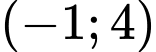 .
.
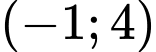 .
.B, 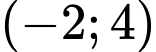 .
.
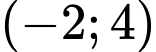 .
.C, 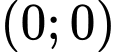 .
.
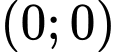 .
.D, 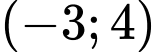 .
.
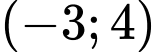 .
.
Nhận xét: chỉ có điểm 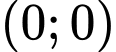 không thỏa mãn hệ. Đáp án: C
không thỏa mãn hệ. Đáp án: C
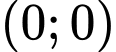 không thỏa mãn hệ. Đáp án: C
không thỏa mãn hệ. Đáp án: C
Câu 9 [240834]: Miền nghiệm của hệ bất phương trình 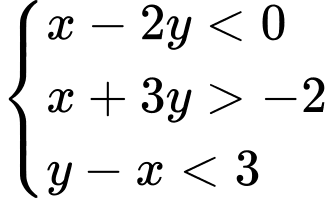 chứa điểm nào sau đây?
chứa điểm nào sau đây?
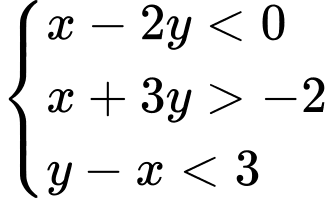 chứa điểm nào sau đây?
chứa điểm nào sau đây? A, 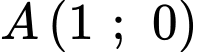 .
.
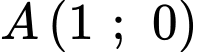 .
.B, 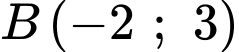 .
.
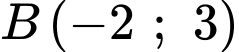 .
.C, 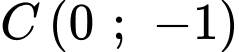 .
.
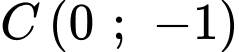 .
.D, 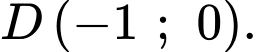
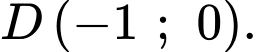
Chọn D.
Trước hết, ta vẽ ba đường thẳng:

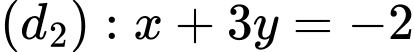
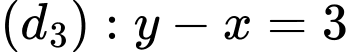
Ta thấy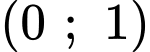 là nghiệm của cả ba bất phương trình. Điều đó có nghĩa điểm
là nghiệm của cả ba bất phương trình. Điều đó có nghĩa điểm 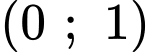 thuộc cả ba miền nghiệm của ba bất phương trình. Sau khi gạch bỏ các miền không thích hợp, miền không bị gạch là miền nghiệm của hệ. Đáp án: D
thuộc cả ba miền nghiệm của ba bất phương trình. Sau khi gạch bỏ các miền không thích hợp, miền không bị gạch là miền nghiệm của hệ. Đáp án: D
Trước hết, ta vẽ ba đường thẳng:

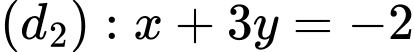
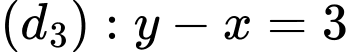
Ta thấy
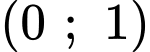 là nghiệm của cả ba bất phương trình. Điều đó có nghĩa điểm
là nghiệm của cả ba bất phương trình. Điều đó có nghĩa điểm 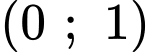 thuộc cả ba miền nghiệm của ba bất phương trình. Sau khi gạch bỏ các miền không thích hợp, miền không bị gạch là miền nghiệm của hệ. Đáp án: D
thuộc cả ba miền nghiệm của ba bất phương trình. Sau khi gạch bỏ các miền không thích hợp, miền không bị gạch là miền nghiệm của hệ. Đáp án: D
Câu 10 [582047]: Bác Ngọc thực hiện chế độ ăn kiêng với yêu cầu tối thiểu hằng ngày qua thức uống là  đơn vị vitamin
đơn vị vitamin 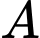 và 90 đơn vị vitamin C. Một cốc đồ uống ăn kiêng thứ nhất cung cấp 60 ca-lo, 12 đơn vị vitamin
và 90 đơn vị vitamin C. Một cốc đồ uống ăn kiêng thứ nhất cung cấp 60 ca-lo, 12 đơn vị vitamin 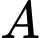 và 10 đơn vị vitamin C. Một cốc đổ uống ăn kiêng thứ hai cung cấp
và 10 đơn vị vitamin C. Một cốc đổ uống ăn kiêng thứ hai cung cấp  đơn vị vitamin
đơn vị vitamin 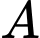 và 30 đơn vị vitamin C. Viết hệ bất phương trình mô tả số lượng cốc cho đồ uống thứ nhất và thứ hai mà bác Ngọc nên uống mỗi ngày để đáp ứng nhu cầu cần thiết đối với số ca-lo và số đơn vị vitamin hấp thụ.
và 30 đơn vị vitamin C. Viết hệ bất phương trình mô tả số lượng cốc cho đồ uống thứ nhất và thứ hai mà bác Ngọc nên uống mỗi ngày để đáp ứng nhu cầu cần thiết đối với số ca-lo và số đơn vị vitamin hấp thụ.
 đơn vị vitamin
đơn vị vitamin 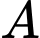 và 90 đơn vị vitamin C. Một cốc đồ uống ăn kiêng thứ nhất cung cấp 60 ca-lo, 12 đơn vị vitamin
và 90 đơn vị vitamin C. Một cốc đồ uống ăn kiêng thứ nhất cung cấp 60 ca-lo, 12 đơn vị vitamin 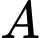 và 10 đơn vị vitamin C. Một cốc đổ uống ăn kiêng thứ hai cung cấp
và 10 đơn vị vitamin C. Một cốc đổ uống ăn kiêng thứ hai cung cấp  đơn vị vitamin
đơn vị vitamin 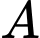 và 30 đơn vị vitamin C. Viết hệ bất phương trình mô tả số lượng cốc cho đồ uống thứ nhất và thứ hai mà bác Ngọc nên uống mỗi ngày để đáp ứng nhu cầu cần thiết đối với số ca-lo và số đơn vị vitamin hấp thụ.
và 30 đơn vị vitamin C. Viết hệ bất phương trình mô tả số lượng cốc cho đồ uống thứ nhất và thứ hai mà bác Ngọc nên uống mỗi ngày để đáp ứng nhu cầu cần thiết đối với số ca-lo và số đơn vị vitamin hấp thụ. A, 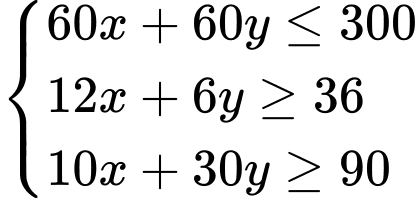
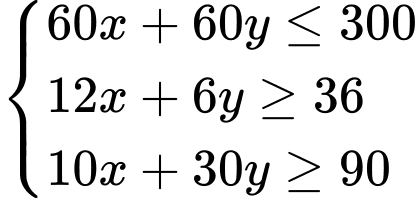
B, 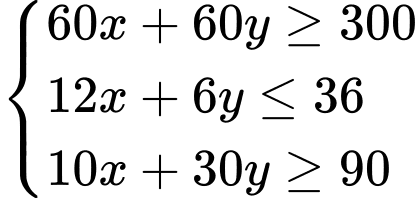
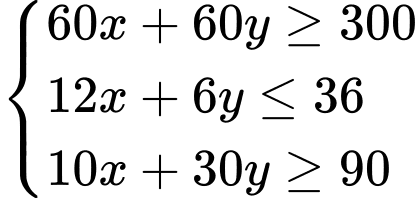
C, 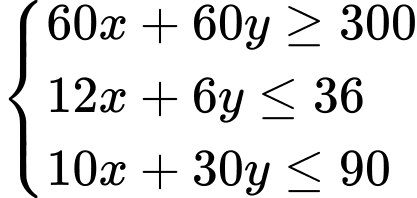
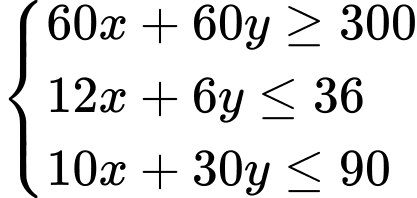
D, 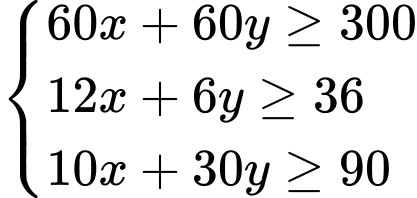
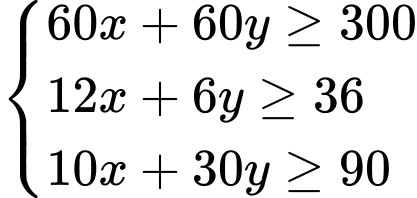
Gọi x, y lần lượt là số lượng cốc cho đồ uống thứ nhất và thứ hai cần tìm.
Lượng calo trong cả 2 đồ uống là:
Lượng vitamin A trong 2 đồ uống là: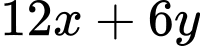
Lượng vitamin C trong 2 đồ uống là:
Ta có hệ bất phương trình:
Lượng calo trong cả 2 đồ uống là:

Lượng vitamin A trong 2 đồ uống là:
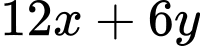
Lượng vitamin C trong 2 đồ uống là:

Ta có hệ bất phương trình:
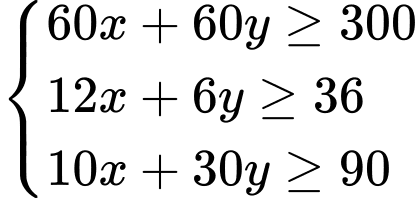
Câu 11 [292516]: Miền nghiệm của hệ bất phương trình 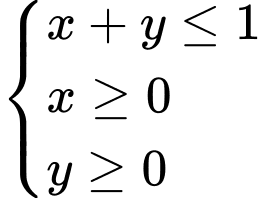 là?
là?
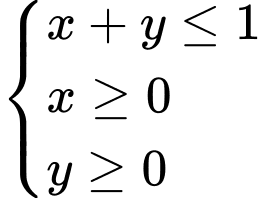 là?
là? A, Miền ngũ giác.
B, Miền tam giác.
C, Miền lục giác.
D, Miền tứ giác.

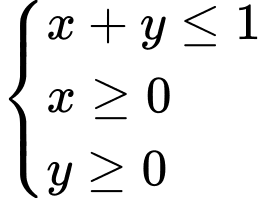 là miền được tô trên hình vẽ
là miền được tô trên hình vẽ Ta nhận thấy miền được tô này là miền tam giác vuông cân tại O với cạnh góc vuông 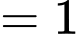
 Chọn Ⓑ
Chọn Ⓑ
Đáp án: B 
 Chọn Ⓑ
Chọn Ⓑ
Câu 12 [238034]: Miền tam giác 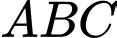 kể cả ba cạnh sau đây là miền nghiệm của hệ bất phương trình nào trong bốn hệ bất phương trình dưới đây?
kể cả ba cạnh sau đây là miền nghiệm của hệ bất phương trình nào trong bốn hệ bất phương trình dưới đây?
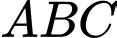 kể cả ba cạnh sau đây là miền nghiệm của hệ bất phương trình nào trong bốn hệ bất phương trình dưới đây?
kể cả ba cạnh sau đây là miền nghiệm của hệ bất phương trình nào trong bốn hệ bất phương trình dưới đây?
A, 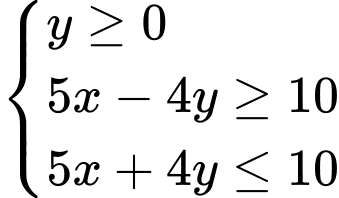 .
.
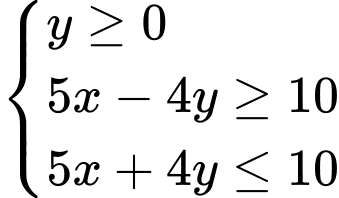 .
.B, 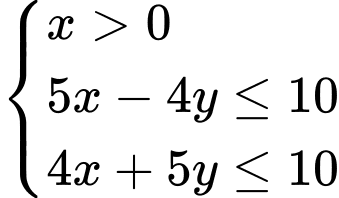 .
.
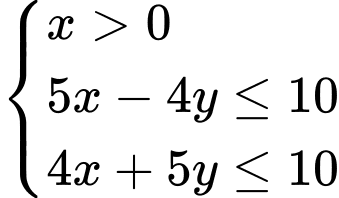 .
.C, 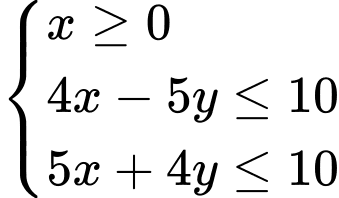 .
.
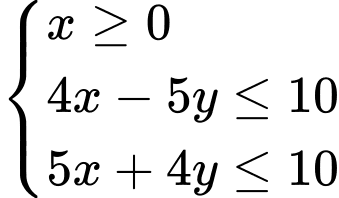 .
.D, 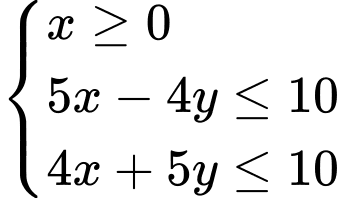 .
.
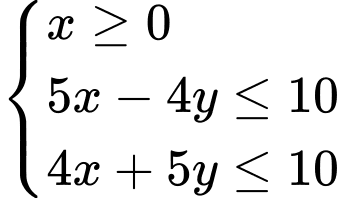 .
.
Chọn D.
Cạnh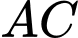 có phương trình
có phương trình 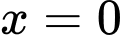 và cạnh
và cạnh 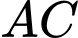 nằm trong miền nghiệm nên
nằm trong miền nghiệm nên  là một bất phương trình của hệ.
là một bất phương trình của hệ.
Cạnh qua hai điểm
qua hai điểm 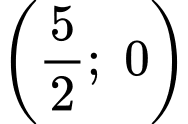 và
và 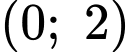 nên có phương trình dạng:
nên có phương trình dạng: 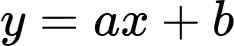
Ta có: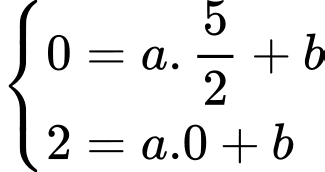
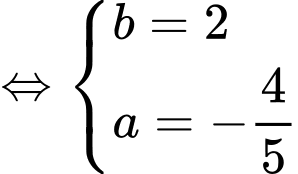
suy ra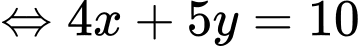 .
.
Vậy hệ bất phương trình cần tìm là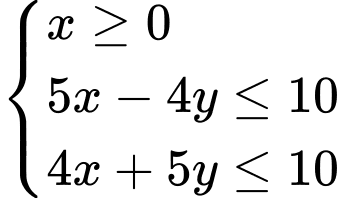 .
Đáp án: D
.
Đáp án: D
Cạnh
 có phương trình
có phương trình  và cạnh
và cạnh 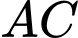 nằm trong miền nghiệm nên
nằm trong miền nghiệm nên  là một bất phương trình của hệ.
là một bất phương trình của hệ.
Cạnh
 qua hai điểm
qua hai điểm 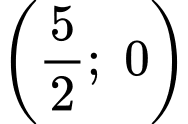 và
và 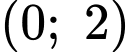 nên có phương trình dạng:
nên có phương trình dạng: 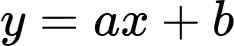
Ta có:
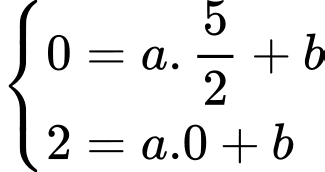
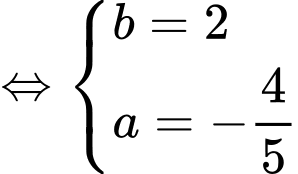
suy ra
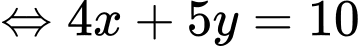 .
.
Vậy hệ bất phương trình cần tìm là
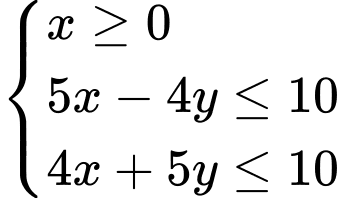 .
Đáp án: D
.
Đáp án: D
Câu 13 [238041]: Giá trị nhỏ nhất của biểu thức 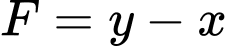 trên miền xác định bởi hệ
trên miền xác định bởi hệ 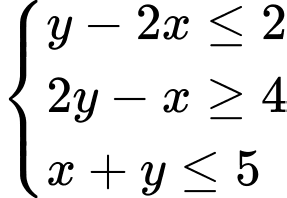 là
là
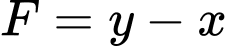 trên miền xác định bởi hệ
trên miền xác định bởi hệ 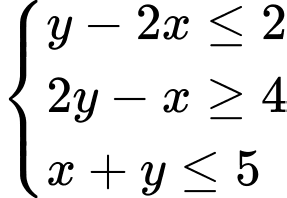 là
là A, 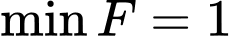 khi
khi 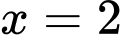 ,
, 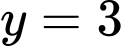 .
.
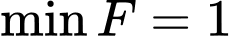 khi
khi 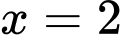 ,
, 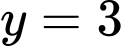 .
.B, 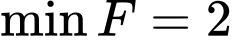 khi
khi 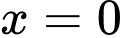 ,
, 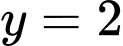 .
.
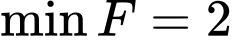 khi
khi 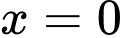 ,
, 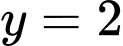 .
.C, 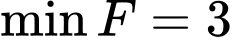 khi
khi 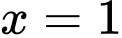 ,
, 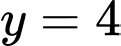 .
.
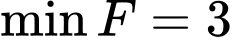 khi
khi 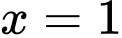 ,
, 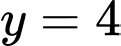 .
.D, 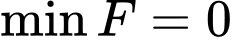 khi
khi 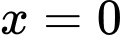 ,
, 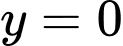 .
.
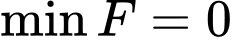 khi
khi 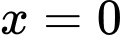 ,
, 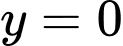 .
.
Chọn A.
Miền nghiệm của hệ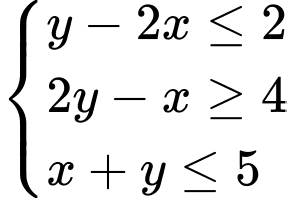 là miền trong của tam giác
là miền trong của tam giác 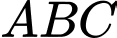 kể cả biên (như hình)
kể cả biên (như hình)
Ta thấy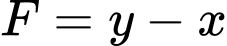 đạt giá trị nhỏ nhất chỉ có thể tại các điểm
đạt giá trị nhỏ nhất chỉ có thể tại các điểm 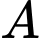 ,
, 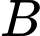 ,
,  .
.
Tại thì
thì 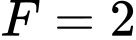 .
.
Tại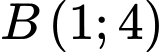 thì
thì 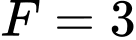
Tại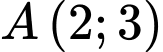 thì
thì 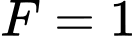 .
.
Vậy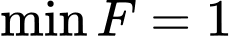 khi
khi 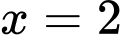 ,
, 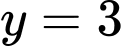 . Đáp án: A
. Đáp án: A
Miền nghiệm của hệ
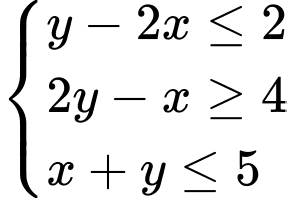 là miền trong của tam giác
là miền trong của tam giác 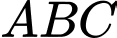 kể cả biên (như hình)
kể cả biên (như hình)
Ta thấy
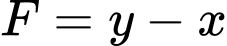 đạt giá trị nhỏ nhất chỉ có thể tại các điểm
đạt giá trị nhỏ nhất chỉ có thể tại các điểm 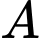 ,
, 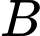 ,
,  .
.
Tại
 thì
thì 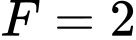 .
.
Tại
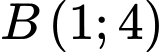 thì
thì 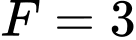
Tại
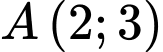 thì
thì 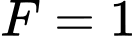 .
.
Vậy
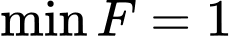 khi
khi 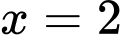 ,
, 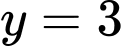 . Đáp án: A
. Đáp án: A
Câu 14 [238046]: Biểu thức 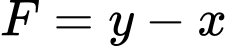 đạt giá trị nhỏ nhất với điều kiện
đạt giá trị nhỏ nhất với điều kiện 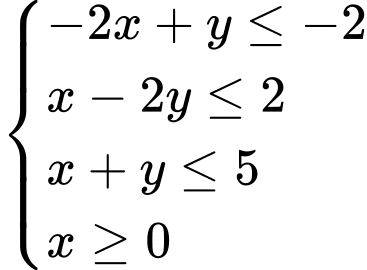 tại điểm
tại điểm 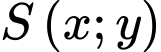 có toạ độ là
có toạ độ là
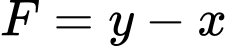 đạt giá trị nhỏ nhất với điều kiện
đạt giá trị nhỏ nhất với điều kiện 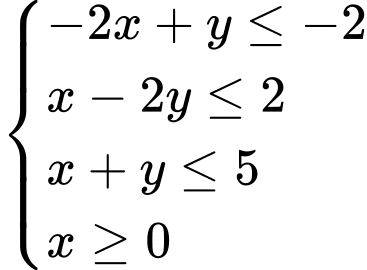 tại điểm
tại điểm 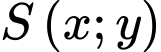 có toạ độ là
có toạ độ là A, 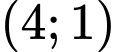 .
.
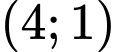 .
.B, 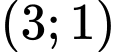 .
.
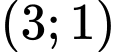 .
.C, 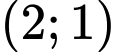 .
.
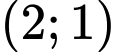 .
.D, 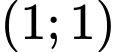 .
.
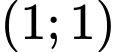 .
.
Lời giải: Chọn A.
Biểu diễn miền ngiệm của hệ bất phương trình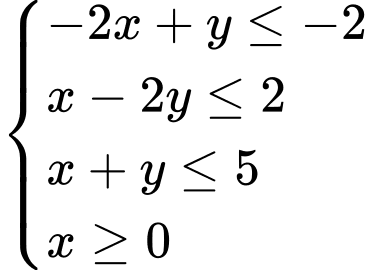 trên hệ trục tọa độ như dưới đây:
trên hệ trục tọa độ như dưới đây:
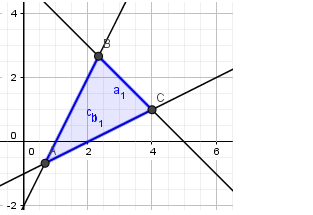
Nhận thấy biểu thức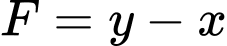 chỉ đạt giá trị nhỏ nhất tại các điểm
chỉ đạt giá trị nhỏ nhất tại các điểm 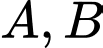 hoặc
hoặc  . Đáp án: A
. Đáp án: A
Biểu diễn miền ngiệm của hệ bất phương trình
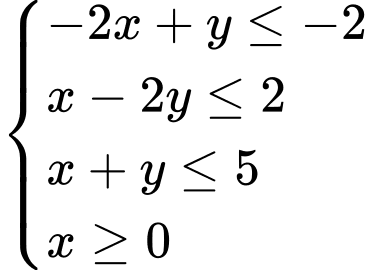 trên hệ trục tọa độ như dưới đây:
trên hệ trục tọa độ như dưới đây:
Nhận thấy biểu thức
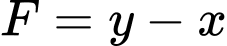 chỉ đạt giá trị nhỏ nhất tại các điểm
chỉ đạt giá trị nhỏ nhất tại các điểm 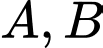 hoặc
hoặc  . Đáp án: A
. Đáp án: A
Câu 15 [238045]: Giá trị nhỏ nhất của biết thức 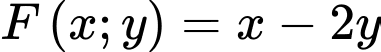 với điều kiện
với điều kiện 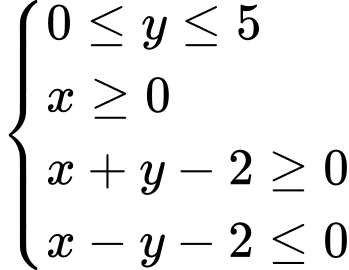 là
là
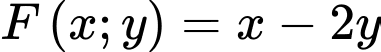 với điều kiện
với điều kiện 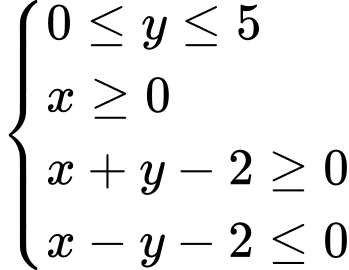 là
là A, 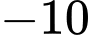 .
.
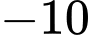 .
.B,  .
.
 .
.C, 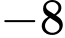 .
.
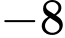 .
.D, 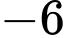 .
.
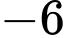 .
.
Lời giải: Chọn A.
Biểu diễn miền ngiệm của hệ bất phương trình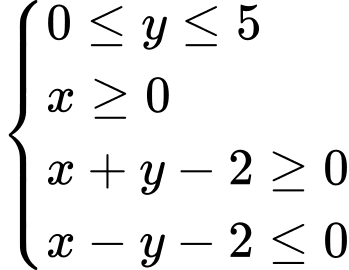 trên hệ trục tọa độ như dưới đây:
trên hệ trục tọa độ như dưới đây:
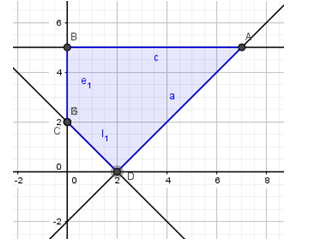
Nhận thấy biết thức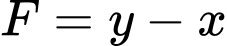 chỉ đạt giá trị nhỏ nhất tại các điểm
chỉ đạt giá trị nhỏ nhất tại các điểm 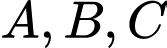 hoặc
hoặc 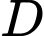 .
.
Ta có: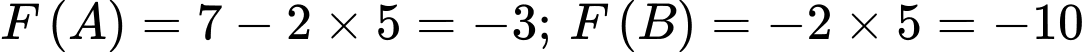 .
.
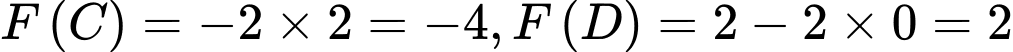 .
Vậy
.
Vậy 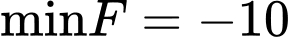 khi
khi 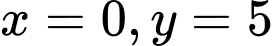 . Đáp án: A
. Đáp án: A
Biểu diễn miền ngiệm của hệ bất phương trình
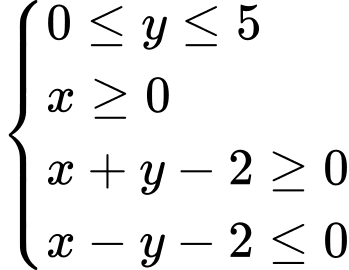 trên hệ trục tọa độ như dưới đây:
trên hệ trục tọa độ như dưới đây:
Nhận thấy biết thức
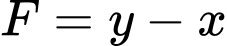 chỉ đạt giá trị nhỏ nhất tại các điểm
chỉ đạt giá trị nhỏ nhất tại các điểm 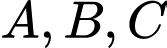 hoặc
hoặc 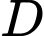 .
.
Ta có:
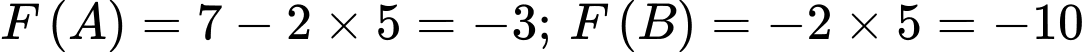 .
.
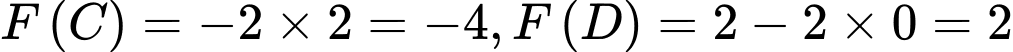 .
Vậy
.
Vậy 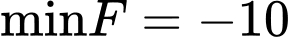 khi
khi 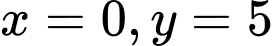 . Đáp án: A
. Đáp án: A
Câu 16 [238048]: Trong một cuộc thi pha chế, hai đội A, B được sử dụng tối đa 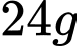 hương liệu,
hương liệu, 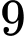 lít nước và
lít nước và 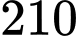 g đường để pha chế nước cam và nước táo. Để pha chế
g đường để pha chế nước cam và nước táo. Để pha chế 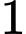 lít nước cam cần
lít nước cam cần 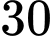 g đường,
g đường, 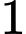 lít nước và
lít nước và 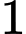 g hương liệu; pha chế
g hương liệu; pha chế 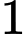 lít nước táo cần
lít nước táo cần  g đường,
g đường, 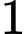 lít nước và
lít nước và 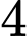 g hương liệu. Mỗi lít nước cam nhận được
g hương liệu. Mỗi lít nước cam nhận được 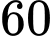 điểm thưởng, mỗi lít nước táo nhận được
điểm thưởng, mỗi lít nước táo nhận được 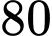 điểm thưởng. Đội A pha chế được
điểm thưởng. Đội A pha chế được 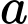 lít nước cam và
lít nước cam và 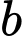 lít nước táo và dành được điểm thưởng cao nhất. Hiệu số
lít nước táo và dành được điểm thưởng cao nhất. Hiệu số 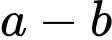 là
là
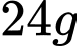 hương liệu,
hương liệu, 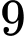 lít nước và
lít nước và 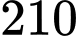 g đường để pha chế nước cam và nước táo. Để pha chế
g đường để pha chế nước cam và nước táo. Để pha chế 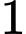 lít nước cam cần
lít nước cam cần 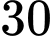 g đường,
g đường, 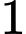 lít nước và
lít nước và 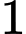 g hương liệu; pha chế
g hương liệu; pha chế 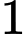 lít nước táo cần
lít nước táo cần  g đường,
g đường, 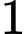 lít nước và
lít nước và 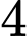 g hương liệu. Mỗi lít nước cam nhận được
g hương liệu. Mỗi lít nước cam nhận được 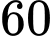 điểm thưởng, mỗi lít nước táo nhận được
điểm thưởng, mỗi lít nước táo nhận được 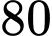 điểm thưởng. Đội A pha chế được
điểm thưởng. Đội A pha chế được 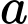 lít nước cam và
lít nước cam và 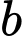 lít nước táo và dành được điểm thưởng cao nhất. Hiệu số
lít nước táo và dành được điểm thưởng cao nhất. Hiệu số 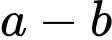 là
là A, 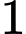 .
.
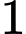 .
.B, 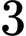 .
.
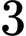 .
.C, 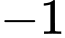 .
.
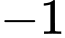 .
.D, 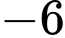 .
.
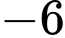 .
.
Lời giải: Chọn C
Gọi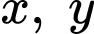 lần lượt là số lít nước cam và nước táo mà mỗi đội cần pha chế
lần lượt là số lít nước cam và nước táo mà mỗi đội cần pha chế 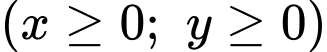 .
.
Để pha chế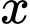 lít nước cam cần
lít nước cam cần 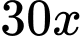 g đường,
g đường, 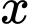 lít nước và
lít nước và 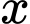 g hương liệu.
g hương liệu.
Để pha chế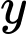 lít nước táo cần
lít nước táo cần 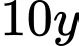 g đường,
g đường, 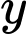 lít nước và
lít nước và 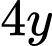 g hương liệu.
g hương liệu.
Theo bài ra ta có hệ bất phương trình: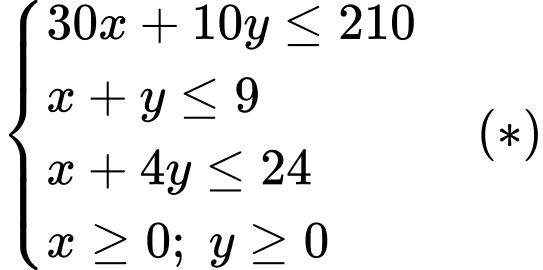 .
.
Số điểm đạt được khi pha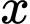 lít nước cam và
lít nước cam và 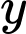 lít nước táo là
lít nước táo là 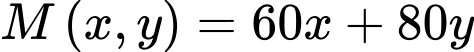 . Bài toán trở thành tìm
. Bài toán trở thành tìm 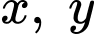 để
để 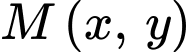 đạt giá trị lớn nhất.
đạt giá trị lớn nhất.
Ta biểu diễn miền nghiệm của hệ trên mặt phẳng tọa độ như sau:
trên mặt phẳng tọa độ như sau:

Miền nghiệm là ngũ giác .
.
Tọa độ các điểm: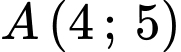 ,
, 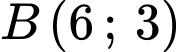 ,
, 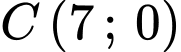 ,
, 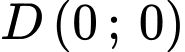 ,
, 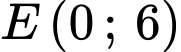 .
.
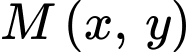 sẽ đạt giá trị lớn nhất, giá trị nhỏ nhất tại các đỉnh của miền nghiệm nên thay tọa độ các điểm vào biểu thức
sẽ đạt giá trị lớn nhất, giá trị nhỏ nhất tại các đỉnh của miền nghiệm nên thay tọa độ các điểm vào biểu thức 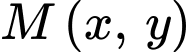 ta được:
ta được:
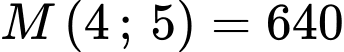 ;
; 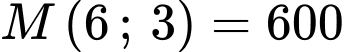 ,
, 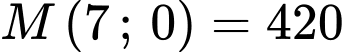 ,
, 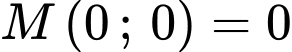 ,
, 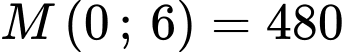 .
.
Vậy giá trị lớn nhất của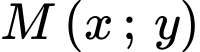 bằng
bằng 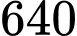 khi
khi 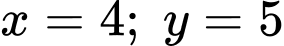
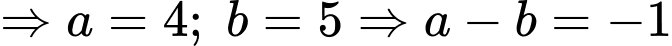 . Đáp án: C
. Đáp án: C
Gọi
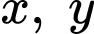 lần lượt là số lít nước cam và nước táo mà mỗi đội cần pha chế
lần lượt là số lít nước cam và nước táo mà mỗi đội cần pha chế 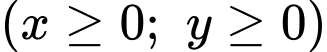 .
.
Để pha chế
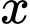 lít nước cam cần
lít nước cam cần 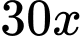 g đường,
g đường, 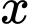 lít nước và
lít nước và 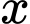 g hương liệu.
g hương liệu.
Để pha chế
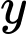 lít nước táo cần
lít nước táo cần 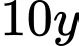 g đường,
g đường, 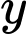 lít nước và
lít nước và 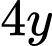 g hương liệu.
g hương liệu.
Theo bài ra ta có hệ bất phương trình:
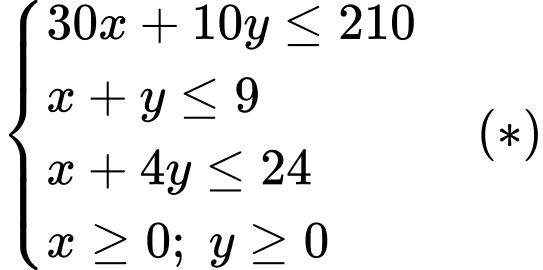 .
.
Số điểm đạt được khi pha
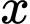 lít nước cam và
lít nước cam và 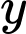 lít nước táo là
lít nước táo là 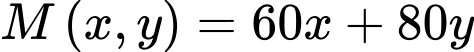 . Bài toán trở thành tìm
. Bài toán trở thành tìm 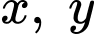 để
để 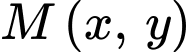 đạt giá trị lớn nhất.
đạt giá trị lớn nhất.
Ta biểu diễn miền nghiệm của hệ
 trên mặt phẳng tọa độ như sau:
trên mặt phẳng tọa độ như sau:
Miền nghiệm là ngũ giác
 .
.
Tọa độ các điểm:
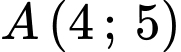 ,
, 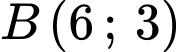 ,
, 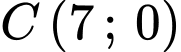 ,
, 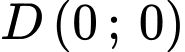 ,
, 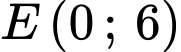 .
.
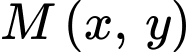 sẽ đạt giá trị lớn nhất, giá trị nhỏ nhất tại các đỉnh của miền nghiệm nên thay tọa độ các điểm vào biểu thức
sẽ đạt giá trị lớn nhất, giá trị nhỏ nhất tại các đỉnh của miền nghiệm nên thay tọa độ các điểm vào biểu thức 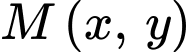 ta được:
ta được:
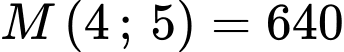 ;
; 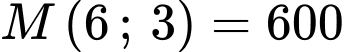 ,
, 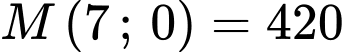 ,
, 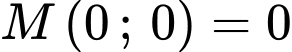 ,
, 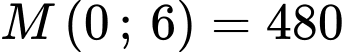 .
.
Vậy giá trị lớn nhất của
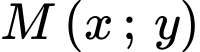 bằng
bằng 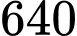 khi
khi 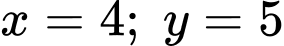
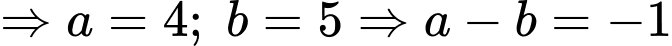 . Đáp án: C
. Đáp án: C
Câu 17 [238050]: Một công ty TNHH trong một đợt quảng cáo và bán khuyến mãi hàng hóa ( sản phẩm mới của công ty) cần thuê xe để chở trên
sản phẩm mới của công ty) cần thuê xe để chở trên 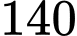 người và trên
người và trên 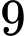 tấn hàng. Nơi thuê chỉ có hai loại xe
tấn hàng. Nơi thuê chỉ có hai loại xe 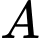 và
và 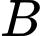 . Trong đó xe loại
. Trong đó xe loại 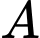 có
có  chiếc, xe loại
chiếc, xe loại 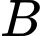 có
có 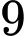 chiếc. Một chiếc xe loại
chiếc. Một chiếc xe loại 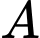 cho thuê với giá
cho thuê với giá 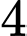 triệu, loại
triệu, loại 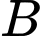 giá
giá 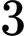 triệu. Hỏi phải thuê bao nhiêu xe mỗi loại để chi phí vận chuyển là thấp nhấ? Biết rằng xe
triệu. Hỏi phải thuê bao nhiêu xe mỗi loại để chi phí vận chuyển là thấp nhấ? Biết rằng xe 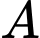 chỉ chở tối đa
chỉ chở tối đa 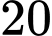 người và
người và 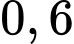 tấn hàng. Xe
tấn hàng. Xe 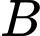 chở tối đa
chở tối đa  người và
người và 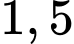 tấn hàng.
tấn hàng.
 sản phẩm mới của công ty) cần thuê xe để chở trên
sản phẩm mới của công ty) cần thuê xe để chở trên 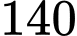 người và trên
người và trên 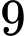 tấn hàng. Nơi thuê chỉ có hai loại xe
tấn hàng. Nơi thuê chỉ có hai loại xe 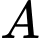 và
và 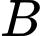 . Trong đó xe loại
. Trong đó xe loại 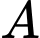 có
có  chiếc, xe loại
chiếc, xe loại 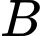 có
có 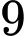 chiếc. Một chiếc xe loại
chiếc. Một chiếc xe loại 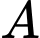 cho thuê với giá
cho thuê với giá 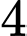 triệu, loại
triệu, loại 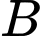 giá
giá 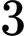 triệu. Hỏi phải thuê bao nhiêu xe mỗi loại để chi phí vận chuyển là thấp nhấ? Biết rằng xe
triệu. Hỏi phải thuê bao nhiêu xe mỗi loại để chi phí vận chuyển là thấp nhấ? Biết rằng xe 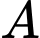 chỉ chở tối đa
chỉ chở tối đa 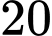 người và
người và 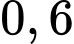 tấn hàng. Xe
tấn hàng. Xe 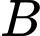 chở tối đa
chở tối đa  người và
người và 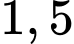 tấn hàng.
tấn hàng. A, 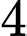 xe
xe 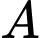 và
và 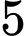 xe
xe 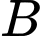 .
.
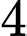 xe
xe 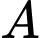 và
và 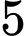 xe
xe 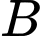 .
.B, 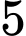 xe
xe 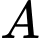 và
và 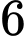 xe
xe 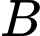 .
.
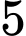 xe
xe 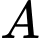 và
và 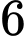 xe
xe 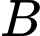 .
.C, 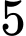 xe
xe 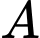 và
và 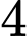 xe
xe 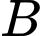 .
.
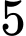 xe
xe 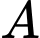 và
và 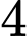 xe
xe 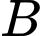 .
.D, 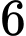 xe
xe 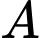 và
và 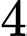 xe
xe 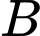 .
.
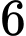 xe
xe 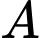 và
và 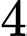 xe
xe 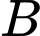 .
.
Chọn C
Gọi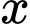 là số xe loại
là số xe loại 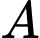
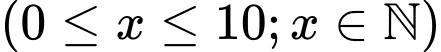 ,
, 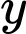 là số xe loại
là số xe loại 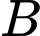
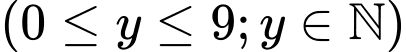 . Khi đó tổng chi phí thuê xe là
. Khi đó tổng chi phí thuê xe là 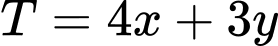 (triệu đồng).
(triệu đồng).
Xe chở tối đa
chở tối đa  người, xe
người, xe 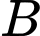 chở tối đa
chở tối đa  người nên tổng số người
người nên tổng số người 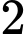 xe chở tối đa được là
xe chở tối đa được là  (người).
(người).
Xe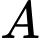 chở được
chở được 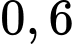 tấn hàng, xe
tấn hàng, xe 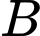 chở được
chở được 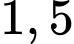 tấn hàng nên tổng lượng hàng
tấn hàng nên tổng lượng hàng 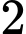 xe chở được là
xe chở được là  (tấn).
(tấn).
Theo giả thiết, ta có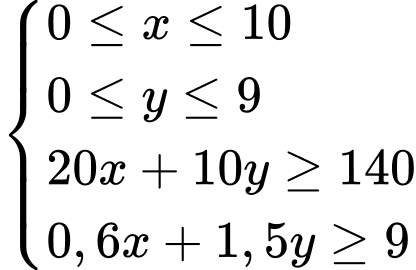

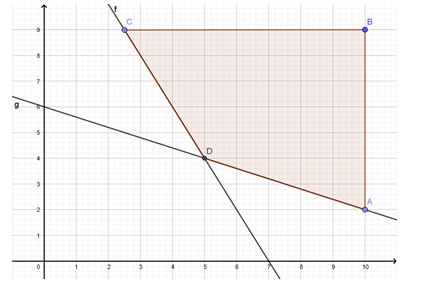
Biểu diễn miền nghiệm của hệ bất phương trình là tứ giác
là tứ giác  kể cả miền trong của tứ giác (như hình vẽ trên).
kể cả miền trong của tứ giác (như hình vẽ trên).
Biểu thức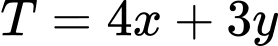 đạt giá trị nhỏ nhất tại một trong các đỉnh của tứ giác
đạt giá trị nhỏ nhất tại một trong các đỉnh của tứ giác  .
.
Tại các đỉnh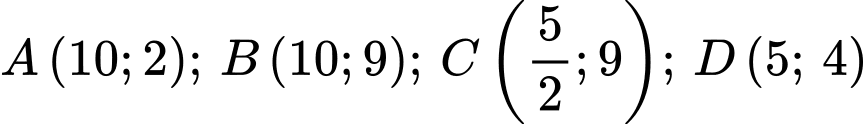 , ta thấy
, ta thấy 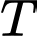 đạt giá trị nhỏ nhất tại
đạt giá trị nhỏ nhất tại 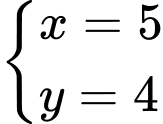 .
.
Khi đó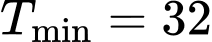 (triệu đồng). Đáp án: C
(triệu đồng). Đáp án: C
Gọi
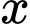 là số xe loại
là số xe loại 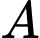
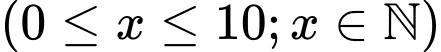 ,
,  là số xe loại
là số xe loại 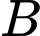
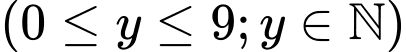 . Khi đó tổng chi phí thuê xe là
. Khi đó tổng chi phí thuê xe là 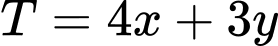 (triệu đồng).
(triệu đồng).Xe
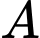 chở tối đa
chở tối đa 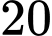 người, xe
người, xe 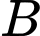 chở tối đa
chở tối đa  người nên tổng số người
người nên tổng số người 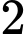 xe chở tối đa được là
xe chở tối đa được là  (người).
(người).Xe
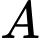 chở được
chở được 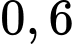 tấn hàng, xe
tấn hàng, xe 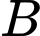 chở được
chở được 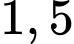 tấn hàng nên tổng lượng hàng
tấn hàng nên tổng lượng hàng 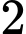 xe chở được là
xe chở được là  (tấn).
(tấn).Theo giả thiết, ta có
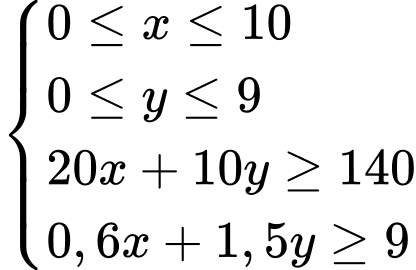


Biểu diễn miền nghiệm của hệ bất phương trình
 là tứ giác
là tứ giác  kể cả miền trong của tứ giác (như hình vẽ trên).
kể cả miền trong của tứ giác (như hình vẽ trên).Biểu thức
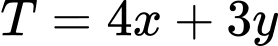 đạt giá trị nhỏ nhất tại một trong các đỉnh của tứ giác
đạt giá trị nhỏ nhất tại một trong các đỉnh của tứ giác  .
.Tại các đỉnh
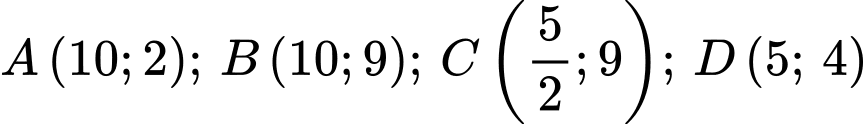 , ta thấy
, ta thấy 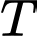 đạt giá trị nhỏ nhất tại
đạt giá trị nhỏ nhất tại 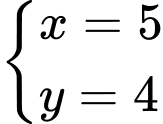 .
.Khi đó
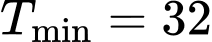 (triệu đồng). Đáp án: C
(triệu đồng). Đáp án: C
Câu 18 [582048]: Tổng các nghiệm nguyên của hệ bất phương trình 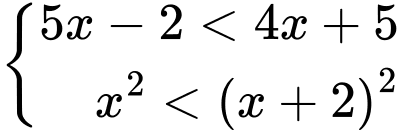 bằng
bằng
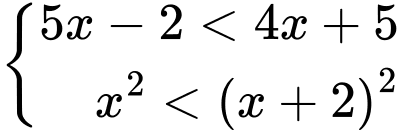 bằng
bằng
Ta có 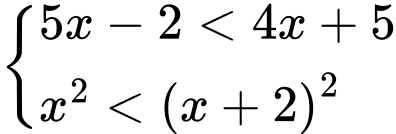
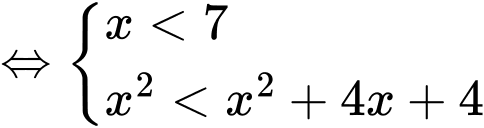
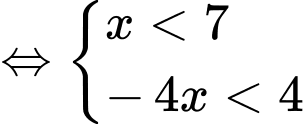
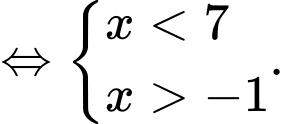
Vậy tập nghiệm của hệ bất phương trình là
Suy ra các nghiệm nguyên của hệ bất phương trình là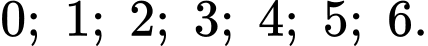
Vậy tổng tất cả các nghiệm của hệ bất phương trình là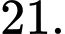
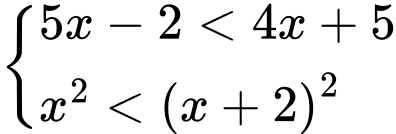
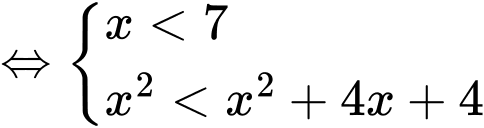
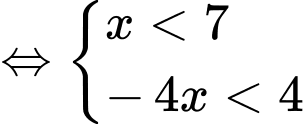
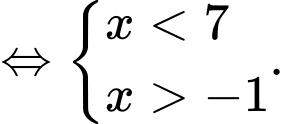
Vậy tập nghiệm của hệ bất phương trình là

Suy ra các nghiệm nguyên của hệ bất phương trình là
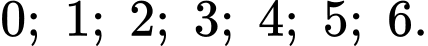
Vậy tổng tất cả các nghiệm của hệ bất phương trình là
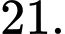
Câu 19 [557999]: Cho các giá trị 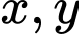 thỏa mãn điều kiện
thỏa mãn điều kiện 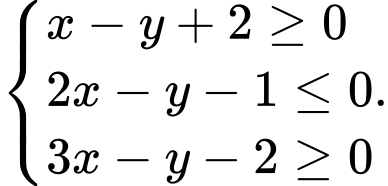 Tìm giá trị lớn nhất của biểu thức
Tìm giá trị lớn nhất của biểu thức 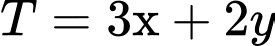
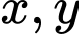 thỏa mãn điều kiện
thỏa mãn điều kiện 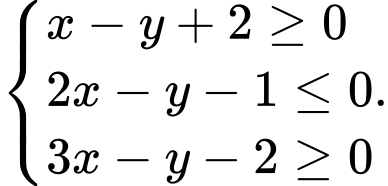 Tìm giá trị lớn nhất của biểu thức
Tìm giá trị lớn nhất của biểu thức 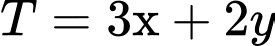
 (Kể cả đường biên) trong đó
(Kể cả đường biên) trong đó 
Giá trị lớn nhất của 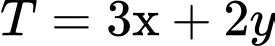 đạt được tại các đỉnh của tam giác
đạt được tại các đỉnh của tam giác 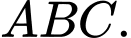
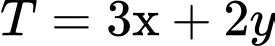 đạt được tại các đỉnh của tam giác
đạt được tại các đỉnh của tam giác 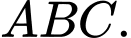
Do 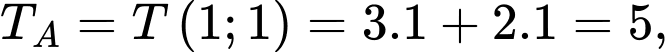
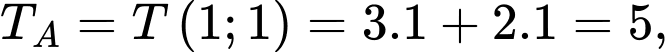
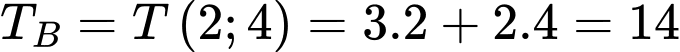 và
và 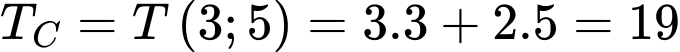 nên giá
trị lớn nhất của
nên giá
trị lớn nhất của 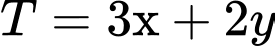 là
là 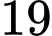 đạt được khi
đạt được khi 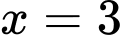 và
và 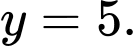
Đáp số: 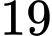
Câu 20 [582049]: Một xưởng cơ khí có hai công nhân là Chiến và Bình. Xưởng sản xuất loại sản phẩm 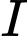 và
và 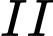 . Mỗi sản phẩm
. Mỗi sản phẩm 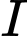 bán lãi
bán lãi  nghìn đồng, mỗi sản phẩm
nghìn đồng, mỗi sản phẩm 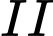 bán lãi
bán lãi 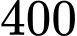 nghìn đồng. Để sản xuất được một sản phẩm
nghìn đồng. Để sản xuất được một sản phẩm 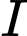 thì Chiến phải làm việc trong
thì Chiến phải làm việc trong 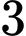 giờ, Bình phải làm việc trong
giờ, Bình phải làm việc trong 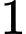 giờ. Để sản xuất được một sản phẩm
giờ. Để sản xuất được một sản phẩm 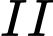 thì Chiến phải làm việc trong
thì Chiến phải làm việc trong 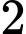 giờ, Bình phải làm việc trong
giờ, Bình phải làm việc trong 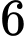 giờ. Một người không thể làm được đồng thời hai sản phẩm. Biết rằng trong một tháng Chiến không thể làm việc quá
giờ. Một người không thể làm được đồng thời hai sản phẩm. Biết rằng trong một tháng Chiến không thể làm việc quá 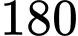 giờ và Bình không thể làm việc quá
giờ và Bình không thể làm việc quá 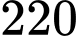 giờ. Số tiền lãi lớn nhất trong một tháng của xưởng là
giờ. Số tiền lãi lớn nhất trong một tháng của xưởng là
 và
và 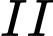 . Mỗi sản phẩm
. Mỗi sản phẩm 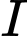 bán lãi
bán lãi  nghìn đồng, mỗi sản phẩm
nghìn đồng, mỗi sản phẩm 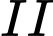 bán lãi
bán lãi 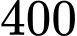 nghìn đồng. Để sản xuất được một sản phẩm
nghìn đồng. Để sản xuất được một sản phẩm 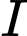 thì Chiến phải làm việc trong
thì Chiến phải làm việc trong 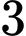 giờ, Bình phải làm việc trong
giờ, Bình phải làm việc trong 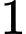 giờ. Để sản xuất được một sản phẩm
giờ. Để sản xuất được một sản phẩm 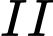 thì Chiến phải làm việc trong
thì Chiến phải làm việc trong 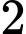 giờ, Bình phải làm việc trong
giờ, Bình phải làm việc trong 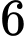 giờ. Một người không thể làm được đồng thời hai sản phẩm. Biết rằng trong một tháng Chiến không thể làm việc quá
giờ. Một người không thể làm được đồng thời hai sản phẩm. Biết rằng trong một tháng Chiến không thể làm việc quá 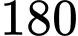 giờ và Bình không thể làm việc quá
giờ và Bình không thể làm việc quá 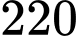 giờ. Số tiền lãi lớn nhất trong một tháng của xưởng là
giờ. Số tiền lãi lớn nhất trong một tháng của xưởng là
Gọi 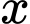 ,
, 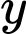 lần lượt là số sản phẩm loại
lần lượt là số sản phẩm loại 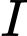 và loại
và loại 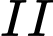 được sản xuất ra. Điều kiện
được sản xuất ra. Điều kiện 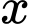 ,
, 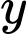 nguyên dương.
nguyên dương.
Ta có hệ bất phương trình sau: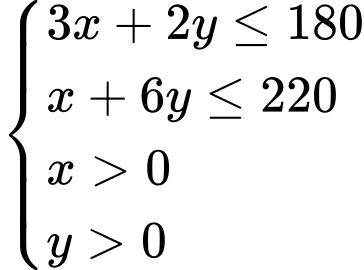
Miền nghiệm của hệ trên là
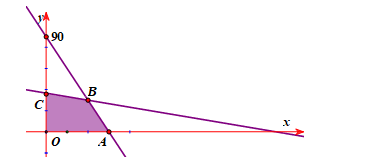
Tiền lãi trong một tháng của xưởng là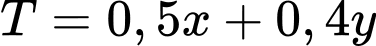 (triệu đồng).
(triệu đồng).
Ta thấy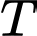 đạt giá trị lớn nhất chỉ có thể tại các điểm
đạt giá trị lớn nhất chỉ có thể tại các điểm 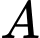 ,
, 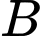 ,
,  . Vì
. Vì  có tọa độ không nguyên nên loại.
có tọa độ không nguyên nên loại.
Tại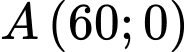 thì
thì 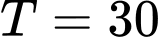 triệu đồng.
triệu đồng.
Tại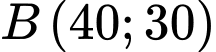 thì
thì 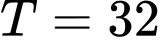 triệu đồng.
triệu đồng.
Vậy tiền lãi lớn nhất trong một tháng của xưởng là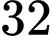 triệu đồng.
triệu đồng.
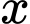 ,
, 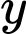 lần lượt là số sản phẩm loại
lần lượt là số sản phẩm loại 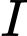 và loại
và loại 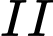 được sản xuất ra. Điều kiện
được sản xuất ra. Điều kiện 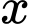 ,
, 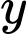 nguyên dương.
nguyên dương. Ta có hệ bất phương trình sau:
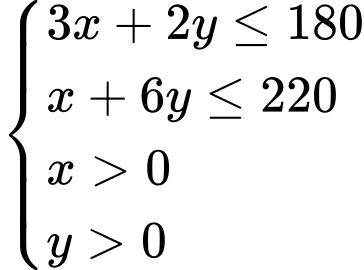
Miền nghiệm của hệ trên là

Tiền lãi trong một tháng của xưởng là
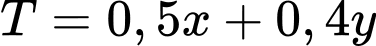 (triệu đồng).
(triệu đồng). Ta thấy
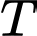 đạt giá trị lớn nhất chỉ có thể tại các điểm
đạt giá trị lớn nhất chỉ có thể tại các điểm 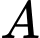 ,
, 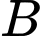 ,
,  . Vì
. Vì  có tọa độ không nguyên nên loại.
có tọa độ không nguyên nên loại. Tại
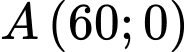 thì
thì 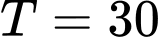 triệu đồng.
triệu đồng. Tại
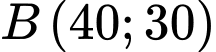 thì
thì 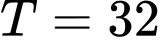 triệu đồng.
triệu đồng.Vậy tiền lãi lớn nhất trong một tháng của xưởng là
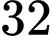 triệu đồng.
triệu đồng.
Câu 21 [582050]: Một học sinh dự định vẽ các tấm thiệp xuân làm bằng tay để bán trong một hội chợ Tết. Cần 2 giờ để vẽ một tấm thiệp loại nhỏ có giá 10 nghìn đồng và 3 giờ để vẽ một tấm thiệp loại lớn có giá 20 nghìn đồng. Học sinh này chỉ có 30 giờ để vẽ và ban tổ chức hội chợ yêu cầu phải vẽ ít nhất 12 tấm. Hãy cho biết số tiền lớn nhất mà bạn ấy thu được là bao nhiêu?
Ta có các điều kiện ràng buộc đối với x, y như sau:
- Hiển nhiên 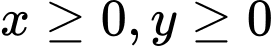
- Tổng số giờ vẽ không quá 30 giờ nên 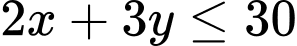
- Số tấm thiệp tối thiểu là 12 tấm nên 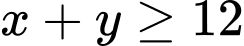
Từ đó ta có hệ bất phương trình: 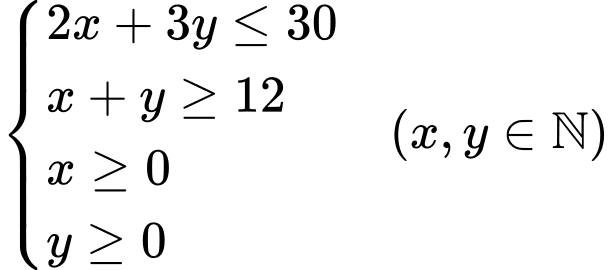
Biểu diễn từng miền nghiệm của hệ bất phương trình trên hệ trục tọa độ  , ta được như hình dưới.
, ta được như hình dưới.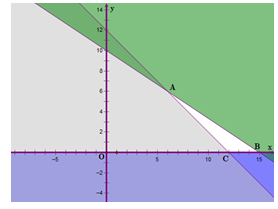
Miền không tô màu (miền tam giác 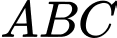 , bao gồm cả các cạnh) trong hình trên là phần giao của các miền nghiệm và cũng là phần biểu diễn nghiệm của hệ bất phươnng trình.
, bao gồm cả các cạnh) trong hình trên là phần giao của các miền nghiệm và cũng là phần biểu diễn nghiệm của hệ bất phươnng trình.
Với các đỉnh 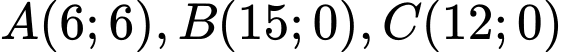 .
.
Gọi F là số tiền (đơn vị: nghìn đồng) thu được, ta có: 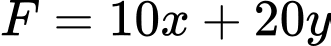
Tính giá trị của F tại các đỉnh của tam giác:
Tại 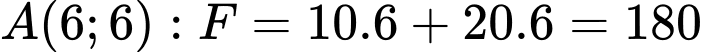
Tại 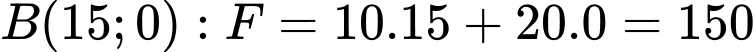
Tại 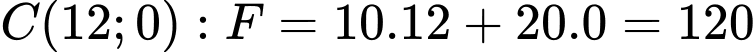
F đạt giá trị lớn nhất bằng 180 tại 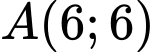 .
.
Vậy bạn học sinh đó cần vẽ 6 tấm thiệp loại nhỏ và 6 tấm thiệp loại to để có được nhiều tiền nhất.
Câu 22 [238051]: Một gia đình cần ít nhất 900 đơn vị protein và 400 đơn vị lipit trong thức ăn mỗi ngày. Mỗi kilogam thịt bò chứa 800 đơn vị protein và 200 đơn vị lipit. Mỗi kilogam thịt lợn chứa 600 đơn vị protein và 400 đơn vị lipit. Biết rằng gia đình này chỉ mua nhiều nhất 1,6 kg thịt bò và 1,1 kg thịt lợn. Giá tiền một kg thịt bò là 160 nghìn đồng, 1 kg thịt lợn là 110 nghìn đồng. Gọi 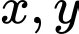 lần lượt là số kg thịt bò và thịt lợn mà gia đình đó cần mua để tổng số tiền họ phải trả là ít nhất mà vẫn đảm bảo lượng protein và lipit trong thức ăn. Tính
lần lượt là số kg thịt bò và thịt lợn mà gia đình đó cần mua để tổng số tiền họ phải trả là ít nhất mà vẫn đảm bảo lượng protein và lipit trong thức ăn. Tính 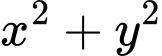 .
.
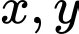 lần lượt là số kg thịt bò và thịt lợn mà gia đình đó cần mua để tổng số tiền họ phải trả là ít nhất mà vẫn đảm bảo lượng protein và lipit trong thức ăn. Tính
lần lượt là số kg thịt bò và thịt lợn mà gia đình đó cần mua để tổng số tiền họ phải trả là ít nhất mà vẫn đảm bảo lượng protein và lipit trong thức ăn. Tính 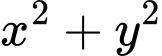 .
. A, 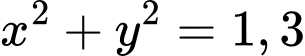 .
.
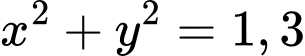 .
.B, 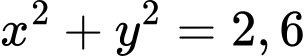 .
.
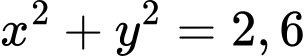 .
.C, 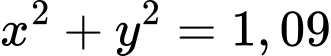 .
.
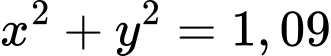 .
.D, 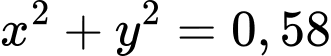 .
.
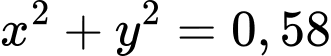 .
.
Chọn A
Điều kiện: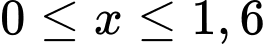 ;
; 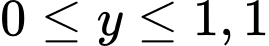
Khi đó số protein có được là và số lipit có được là
và số lipit có được là 
Vì gia đình đó cần ít nhất 900 đơn vị protein và 400 đơn vị lipit trong thức ăn mỗi ngày nên điều kiện tương ứng là: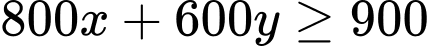 và
và 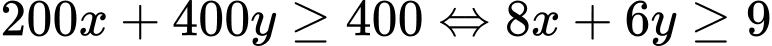 và
và 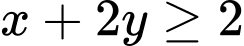
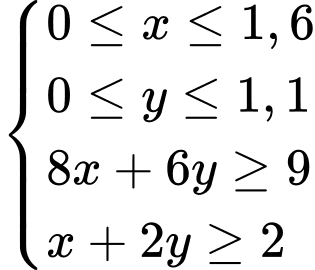
Miền nghiệm của hệ trên là miền nghiệm của tứ giác ABCD (kể cả biên)
Chi phí để mua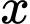 kg thịt bò và
kg thịt bò và 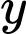 kg thịt
lợn là
kg thịt
lợn là 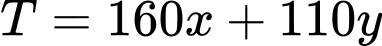
Biết T đạt giá trị nhỏ nhất tại một trong các đỉnh của tứ giác ABCD
Tại A: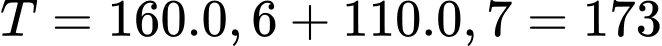 (nghìn)
(nghìn)
Tại B: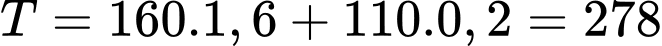 (nghìn)
(nghìn)
Tại C: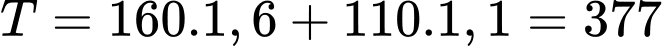 (nghìn)
(nghìn)
Tại D: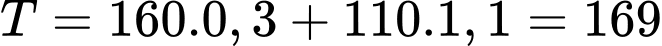 (nghìn)
(nghìn)
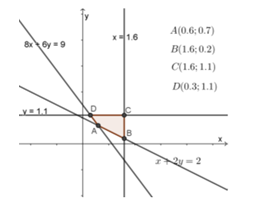
Vậy T đạt GTNN khi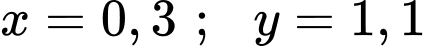
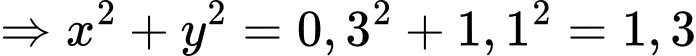 . Đáp án: A
. Đáp án: A
Điều kiện:
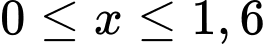 ;
; 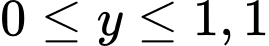
Khi đó số protein có được là
 và số lipit có được là
và số lipit có được là 
Vì gia đình đó cần ít nhất 900 đơn vị protein và 400 đơn vị lipit trong thức ăn mỗi ngày nên điều kiện tương ứng là:
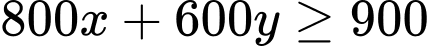 và
và 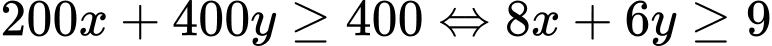 và
và 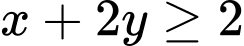
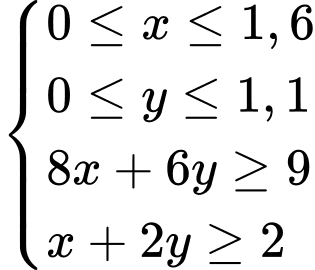
Miền nghiệm của hệ trên là miền nghiệm của tứ giác ABCD (kể cả biên)
Chi phí để mua
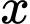 kg thịt bò và
kg thịt bò và 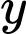 kg thịt
lợn là
kg thịt
lợn là 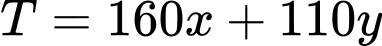
Biết T đạt giá trị nhỏ nhất tại một trong các đỉnh của tứ giác ABCD
Tại A:
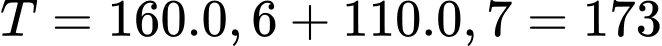 (nghìn)
(nghìn)
Tại B:
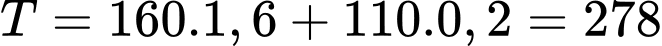 (nghìn)
(nghìn)
Tại C:
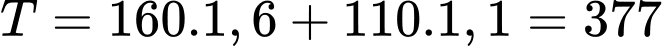 (nghìn)
(nghìn)
Tại D:
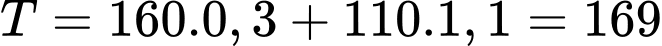 (nghìn)
(nghìn)
Vậy T đạt GTNN khi
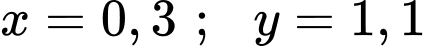
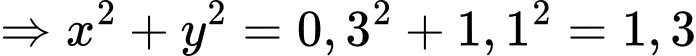 . Đáp án: A
. Đáp án: A
Câu 23 [558001]: Một công ty điện tử sản xuất hai kiểu radio trên hai dây chuyền độc lập. Radio kiểu một sản xuất trên dây chuyền một với công suất 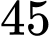 radio/ngày, radio kiểu hai sản xuất trên dây chuyền hai với công suất
radio/ngày, radio kiểu hai sản xuất trên dây chuyền hai với công suất 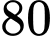 radio/ngày. Để sản xuất một chiếc radio kiểu một cần
radio/ngày. Để sản xuất một chiếc radio kiểu một cần  linh kiện, để sản xuất một chiếc radio kiểu hai cần 9 linh kiện. Tiền lãi khi bán một chiếc radio kiểu một là
linh kiện, để sản xuất một chiếc radio kiểu hai cần 9 linh kiện. Tiền lãi khi bán một chiếc radio kiểu một là 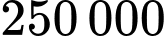 đồng, lãi thu được khi bán một chiếc radio kiểu hai là
đồng, lãi thu được khi bán một chiếc radio kiểu hai là 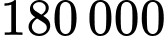 đồng. Biết rằng số linh kiện có thể sử dụng tối đa trong một ngày là
đồng. Biết rằng số linh kiện có thể sử dụng tối đa trong một ngày là 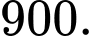 Gọi
Gọi 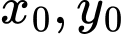 lần lượt là số radio kiểu một và radio kiểu hai sản suất được trong một ngày để tiền lãi thu được là nhiều nhất. Khi đó tổng
lần lượt là số radio kiểu một và radio kiểu hai sản suất được trong một ngày để tiền lãi thu được là nhiều nhất. Khi đó tổng 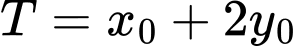 bằng
bằng
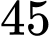 radio/ngày, radio kiểu hai sản xuất trên dây chuyền hai với công suất
radio/ngày, radio kiểu hai sản xuất trên dây chuyền hai với công suất 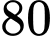 radio/ngày. Để sản xuất một chiếc radio kiểu một cần
radio/ngày. Để sản xuất một chiếc radio kiểu một cần  linh kiện, để sản xuất một chiếc radio kiểu hai cần 9 linh kiện. Tiền lãi khi bán một chiếc radio kiểu một là
linh kiện, để sản xuất một chiếc radio kiểu hai cần 9 linh kiện. Tiền lãi khi bán một chiếc radio kiểu một là 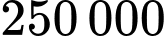 đồng, lãi thu được khi bán một chiếc radio kiểu hai là
đồng, lãi thu được khi bán một chiếc radio kiểu hai là 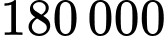 đồng. Biết rằng số linh kiện có thể sử dụng tối đa trong một ngày là
đồng. Biết rằng số linh kiện có thể sử dụng tối đa trong một ngày là 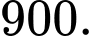 Gọi
Gọi 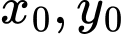 lần lượt là số radio kiểu một và radio kiểu hai sản suất được trong một ngày để tiền lãi thu được là nhiều nhất. Khi đó tổng
lần lượt là số radio kiểu một và radio kiểu hai sản suất được trong một ngày để tiền lãi thu được là nhiều nhất. Khi đó tổng 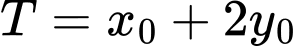 bằng
bằng
Gọi 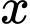 và
và  lần lượt là số radio kiểu một và số radio kiểu hai mà công ty này sản xuất trong một ngày (
lần lượt là số radio kiểu một và số radio kiểu hai mà công ty này sản xuất trong một ngày (
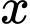 và
và 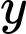 lần lượt là số radio kiểu một và số radio kiểu hai mà công ty này sản xuất trong một ngày (
lần lượt là số radio kiểu một và số radio kiểu hai mà công ty này sản xuất trong một ngày (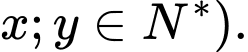
Số tiền lãi mà công ty này thu về hàng ngày là 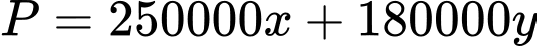 (đồng).
(đồng).
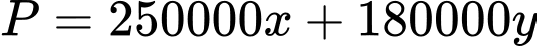 (đồng).
(đồng). Ta có hệ bất phương trình 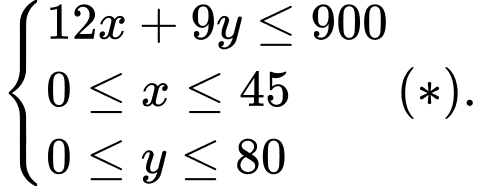
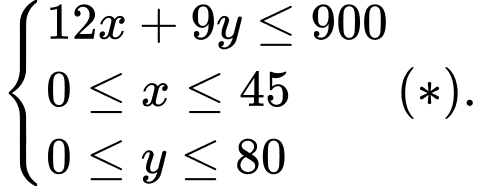
Bài toán trở thành tìm giá trị lớn nhất của biểu thức 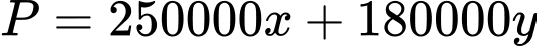 trên miền nghiệm của hệ bất phương trình (*).
trên miền nghiệm của hệ bất phương trình (*).
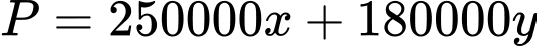 trên miền nghiệm của hệ bất phương trình (*).
trên miền nghiệm của hệ bất phương trình (*). 
Miền nghiệm của hệ bất phương trình (*) là miền ngũ giác  trong đó
trong đó 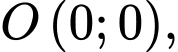
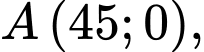
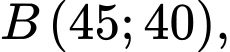

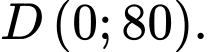
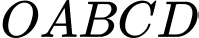 trong đó
trong đó 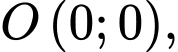
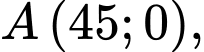
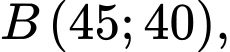

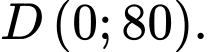
Tại  ta có
ta có 
 ta có
ta có 
Tại 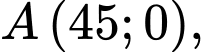 ta có
ta có 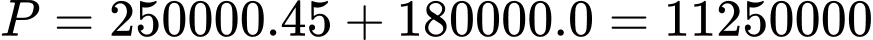
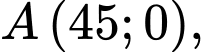 ta có
ta có 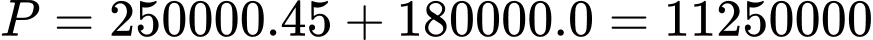
Tại 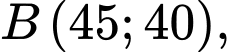 ta có
ta có 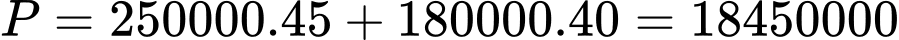
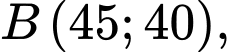 ta có
ta có 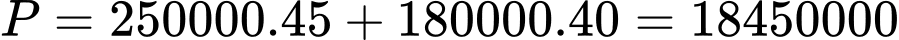
Tại 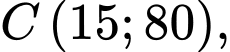 ta có
ta có 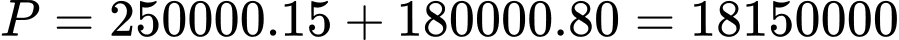
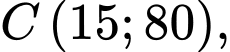 ta có
ta có 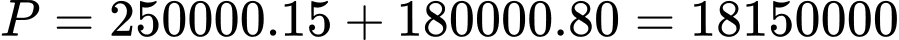
Tại 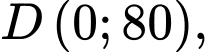 ta có
ta có 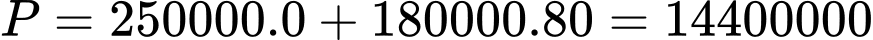
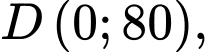 ta có
ta có 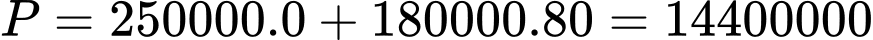
Vậy biểu thức 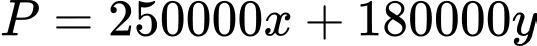 đạt giác trị lớn nhất khi x
đạt giác trị lớn nhất khi x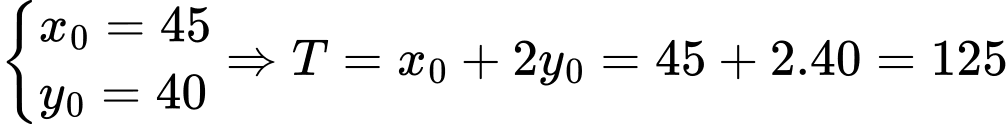
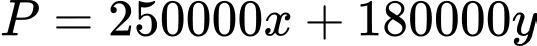 đạt giác trị lớn nhất khi x
đạt giác trị lớn nhất khi x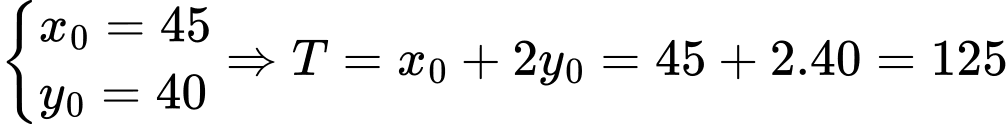
Đáp án: 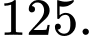
Câu 24 [558002]: Gia đình chị Minh dự định trồng rau và hoa trên một mảnh đất có diện tích 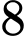 ha. Nếu trồng
ha. Nếu trồng 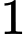 ha rau thì cần
ha rau thì cần 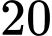 ngày công và thu lợi
ngày công và thu lợi 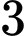 triệu đồng. Nếu trồng
triệu đồng. Nếu trồng 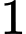 ha hoa thì cần
ha hoa thì cần 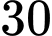 ngày công và thu lợi
ngày công và thu lợi 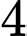 triệu đồng. Biết rằng, gia đình chị Minh chỉ có thể sử dụng không quá
triệu đồng. Biết rằng, gia đình chị Minh chỉ có thể sử dụng không quá 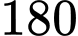 ngày công cho công việc trồng rau và hoa. Hỏi từ việc trồng rau và hoa nói trên, chị Minh có thể thu về lợi nhuận cao nhất là bao nhiêu triệu đồng
ngày công cho công việc trồng rau và hoa. Hỏi từ việc trồng rau và hoa nói trên, chị Minh có thể thu về lợi nhuận cao nhất là bao nhiêu triệu đồng
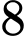 ha. Nếu trồng
ha. Nếu trồng 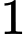 ha rau thì cần
ha rau thì cần 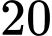 ngày công và thu lợi
ngày công và thu lợi 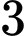 triệu đồng. Nếu trồng
triệu đồng. Nếu trồng 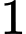 ha hoa thì cần
ha hoa thì cần 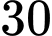 ngày công và thu lợi
ngày công và thu lợi 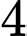 triệu đồng. Biết rằng, gia đình chị Minh chỉ có thể sử dụng không quá
triệu đồng. Biết rằng, gia đình chị Minh chỉ có thể sử dụng không quá 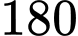 ngày công cho công việc trồng rau và hoa. Hỏi từ việc trồng rau và hoa nói trên, chị Minh có thể thu về lợi nhuận cao nhất là bao nhiêu triệu đồng
ngày công cho công việc trồng rau và hoa. Hỏi từ việc trồng rau và hoa nói trên, chị Minh có thể thu về lợi nhuận cao nhất là bao nhiêu triệu đồng
Gọi 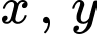
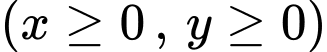 lần lượt là số ha đất trồng rau và hoa.
lần lượt là số ha đất trồng rau và hoa.
Diện tích đất trồng canh tác không vượt quá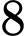 ha nên ta có:
ha nên ta có: 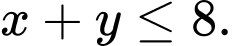
Số ngày công sử dụng không vượt quá 180 ngày nên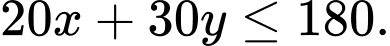
Từ đó, ta có hệ bất phương trình: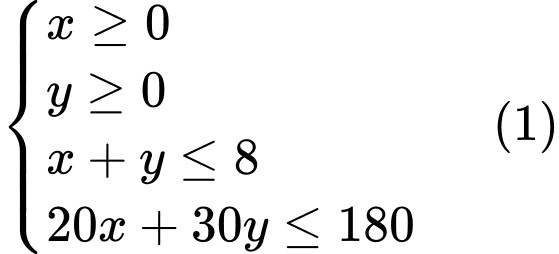
Ta cần tìm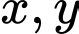 sao cho
sao cho 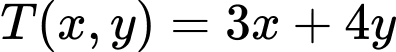 lớn nhất
lớn nhất
Miền nghiệm của hệ được biểu diễn như sau:
được biểu diễn như sau:
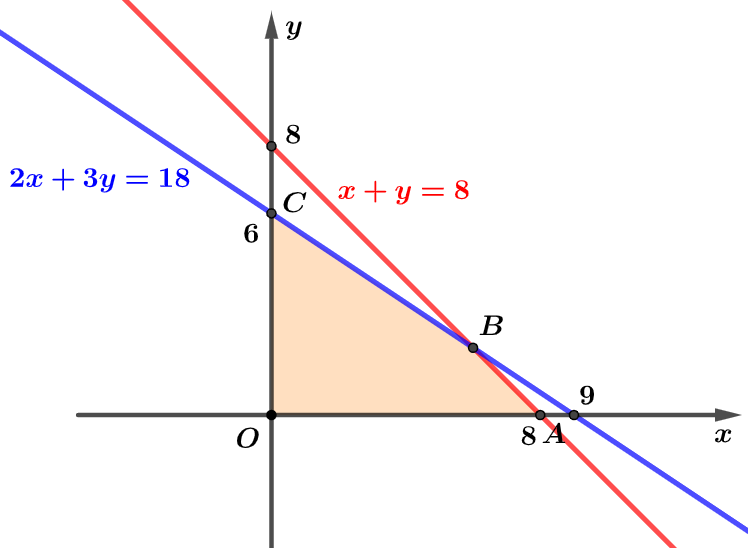
Miền nghiệm của hệ bất phương trình trên là miền trong của tứ giác kể cả
kể cả 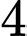 cạnh của tứ giác đó, với
cạnh của tứ giác đó, với 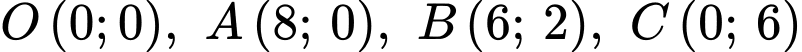
Tại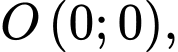 ta có:
ta có: 
Tại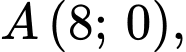 ta có:
ta có: 
Tại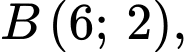 ta có:
ta có: 
Tại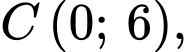 ta có:
ta có: 
Vậy số lợi nhuận cao nhất mà gia đình chị Minh thu được từ trồng rau và hoa là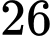 triệu đồng.
triệu đồng.
Đáp án: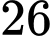 triệu đồng.
triệu đồng.
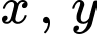
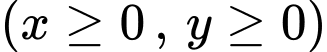 lần lượt là số ha đất trồng rau và hoa.
lần lượt là số ha đất trồng rau và hoa.Diện tích đất trồng canh tác không vượt quá
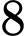 ha nên ta có:
ha nên ta có: 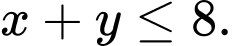
Số ngày công sử dụng không vượt quá 180 ngày nên
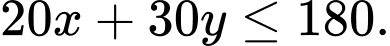
Từ đó, ta có hệ bất phương trình:
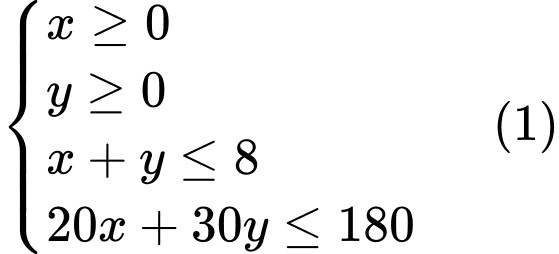
Ta cần tìm
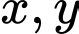 sao cho
sao cho 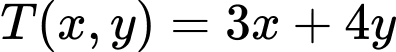 lớn nhất
lớn nhấtMiền nghiệm của hệ
 được biểu diễn như sau:
được biểu diễn như sau:
Miền nghiệm của hệ bất phương trình trên là miền trong của tứ giác
 kể cả
kể cả 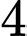 cạnh của tứ giác đó, với
cạnh của tứ giác đó, với 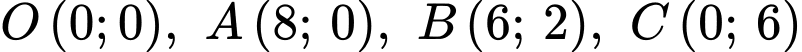
Tại
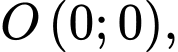 ta có:
ta có: 
Tại
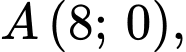 ta có:
ta có: 
Tại
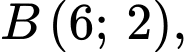 ta có:
ta có: 
Tại
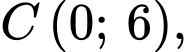 ta có:
ta có: 
Vậy số lợi nhuận cao nhất mà gia đình chị Minh thu được từ trồng rau và hoa là
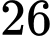 triệu đồng.
triệu đồng.Đáp án:
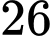 triệu đồng.
triệu đồng.