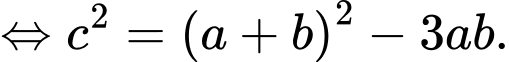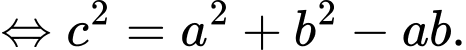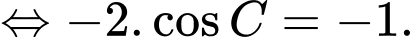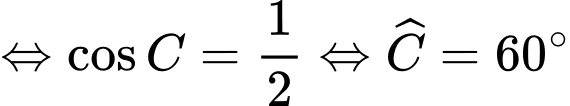Đáp án Bài tập tự luyện
Câu 1 [238415]: Cho tam giác 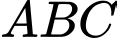 có
có 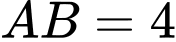 cm,
cm, 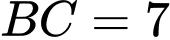 cm,
cm, 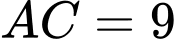 cm. Tính
cm. Tính 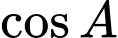 .
.
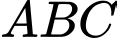 có
có 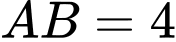 cm,
cm, 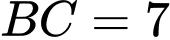 cm,
cm, 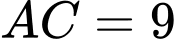 cm. Tính
cm. Tính 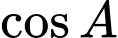 .
. A, 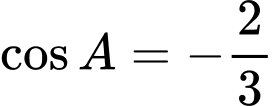 .
.
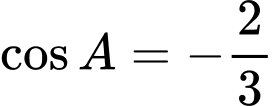 .
.B, 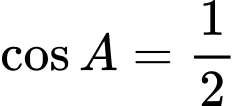 .
.
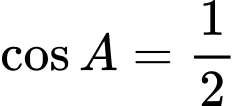 .
.C, 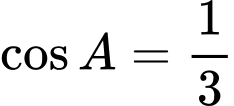 .
.
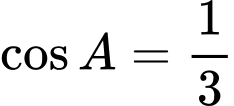 .
.D, 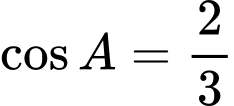 .
.
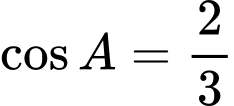 .
.
Chọn D
Ta có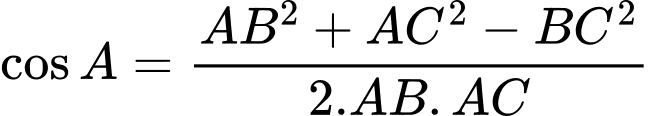
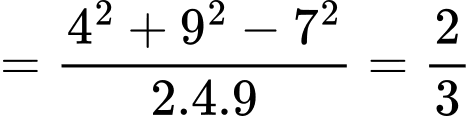 . Đáp án: D
. Đáp án: D
Ta có
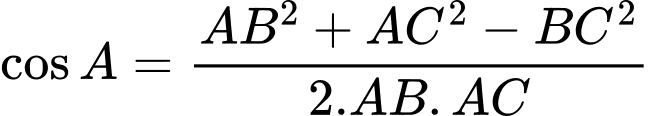
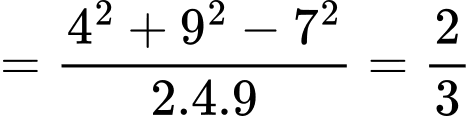 . Đáp án: D
. Đáp án: D
Câu 2 [238451]: Cho tam giác  có
có 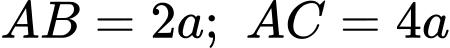 và
và 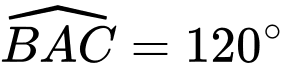 . Tính diện tích tam giác
. Tính diện tích tam giác 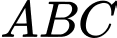 .
.
 có
có 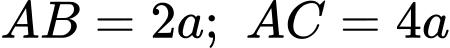 và
và 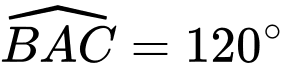 . Tính diện tích tam giác
. Tính diện tích tam giác 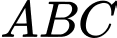 .
. A, 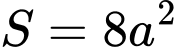 .
.
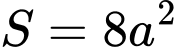 .
.B, 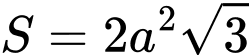 .
.
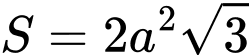 .
.C, 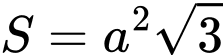 .
.
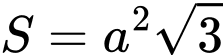 .
.D, 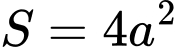 .
.
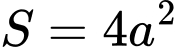 .
.
Chọn B
Diện tích của tam giác  là
là 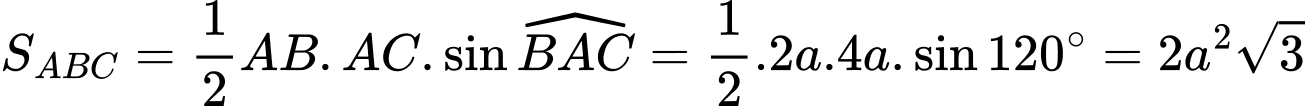 (đvdt). Đáp án: B
(đvdt). Đáp án: B
 là
là 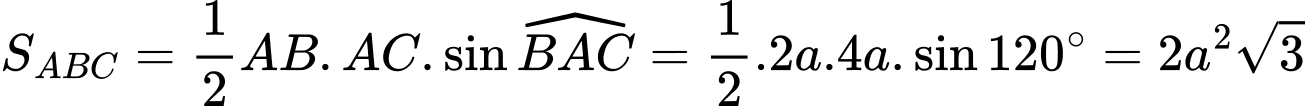 (đvdt). Đáp án: B
(đvdt). Đáp án: B
Câu 3 [238436]: Cho tam giác  thoả mãn hệ thức
thoả mãn hệ thức  . Trong các mệnh đề sau, mệnh đề nào đúng?
. Trong các mệnh đề sau, mệnh đề nào đúng?
 thoả mãn hệ thức
thoả mãn hệ thức 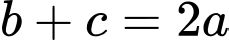 . Trong các mệnh đề sau, mệnh đề nào đúng?
. Trong các mệnh đề sau, mệnh đề nào đúng? A, 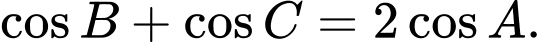
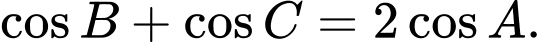
B, 

C, 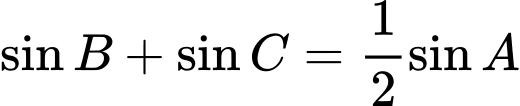 .
.
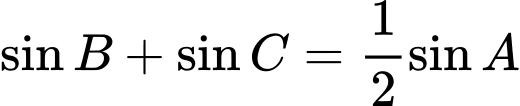 .
.D, 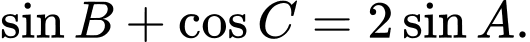
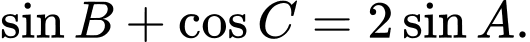
Chọn B.
Ta có: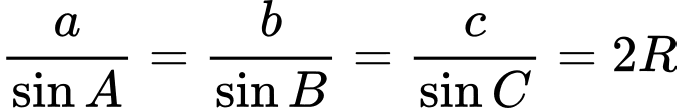
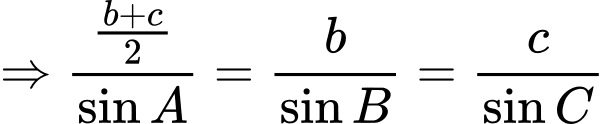
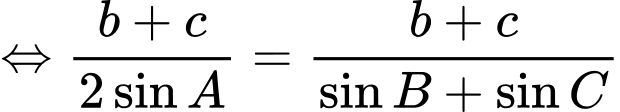
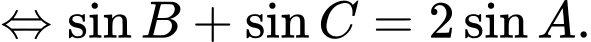 Đáp án: B
Đáp án: B
Ta có:
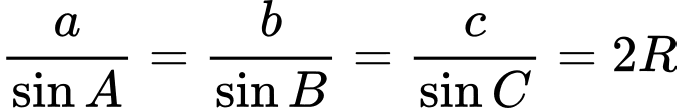
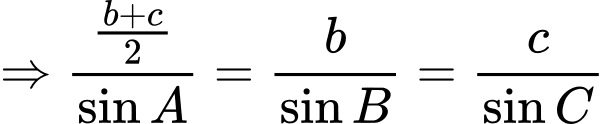
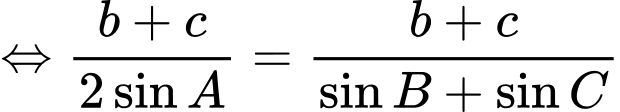
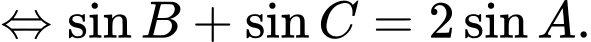 Đáp án: B
Đáp án: B
Câu 4 [238435]: Cho 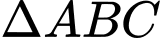 có
có 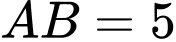 ;
;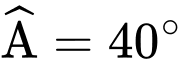 ;
;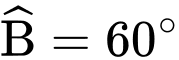 . Độ dài
. Độ dài 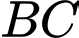 gần nhất với kết quả nào?
gần nhất với kết quả nào?
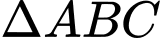 có
có 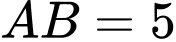 ;
;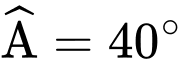 ;
;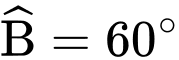 . Độ dài
. Độ dài 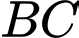 gần nhất với kết quả nào?
gần nhất với kết quả nào? A, 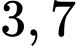 .
.
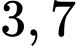 .
.B, 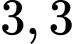 .
.
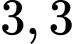 .
.C, 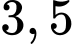 .
.
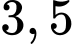 .
.D, 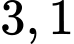 .
.
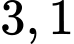 .
.
Chọn B
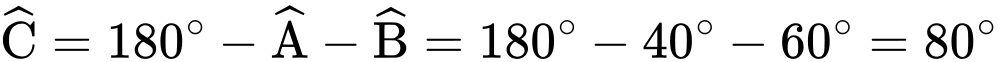 Áp dụng định lý sin:
Áp dụng định lý sin: 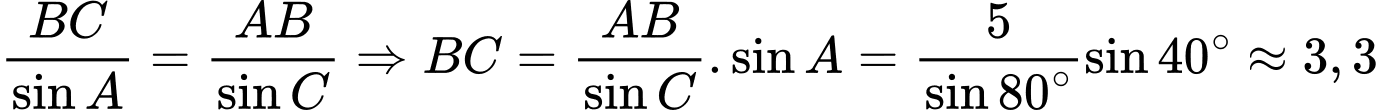 . Đáp án: B
. Đáp án: B
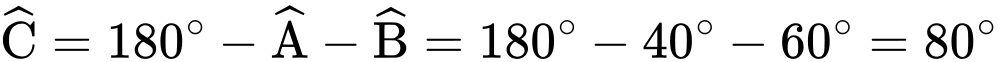 Áp dụng định lý sin:
Áp dụng định lý sin: 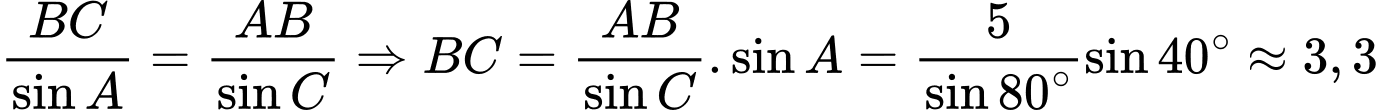 . Đáp án: B
. Đáp án: B
Câu 5 [238448]: Cho tam giác  . Biết
. Biết  ;
; 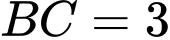 và
và  . Tính chu vi và diện tích tam giác
. Tính chu vi và diện tích tam giác 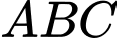 .
.
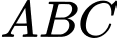 . Biết
. Biết 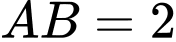 ;
; 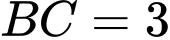 và
và  . Tính chu vi và diện tích tam giác
. Tính chu vi và diện tích tam giác 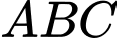 .
. A, 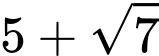 và
và 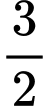 .
.
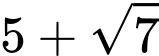 và
và 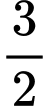 .
.B, 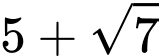 và
và 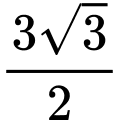 .
.
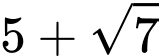 và
và 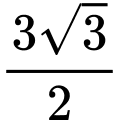 .
.C, 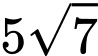 và
và 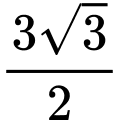 .
.
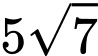 và
và 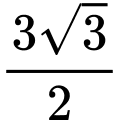 .
.D, 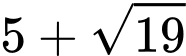 và
và 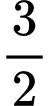 .
.
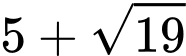 và
và 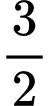 .
.
Chọn B
Ta có:
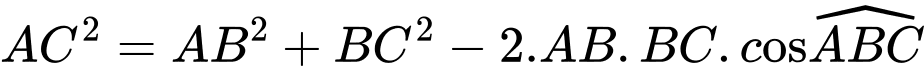
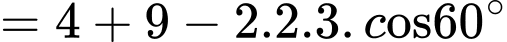
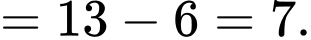
Suy ra
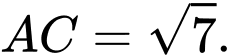
Chu vi tam giác
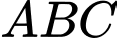 là
là 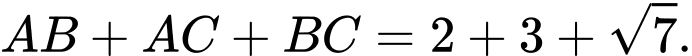
Diện tích tam giác
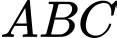 là
là 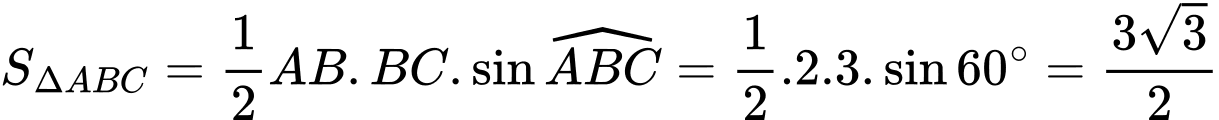 (đvdt). Đáp án: B
(đvdt). Đáp án: B
Câu 6 [238441]: Tính diện tích tam giác 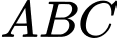 biết
biết 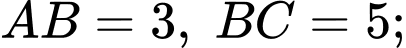
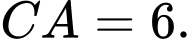
 biết
biết 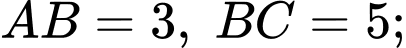
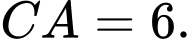
A, 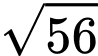 .
.
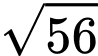 .
.B, 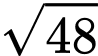 .
.
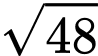 .
.C, 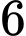 .
.
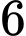 .
.D, 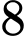 .
.
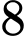 .
.
Chọn A
Ta có: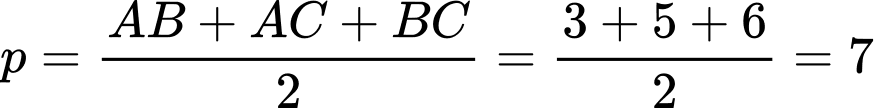 .
.
Vậy diện tích tam giác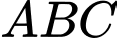 là:
là: 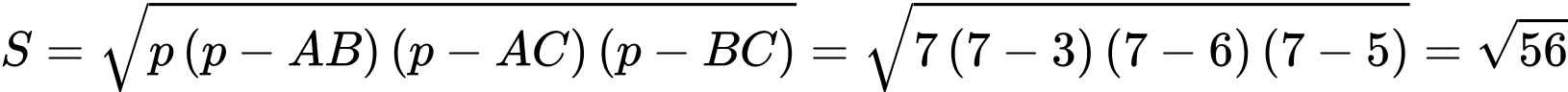 . Đáp án: A
. Đáp án: A
Ta có:
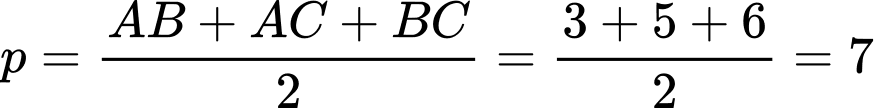 .
.Vậy diện tích tam giác
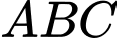 là:
là: 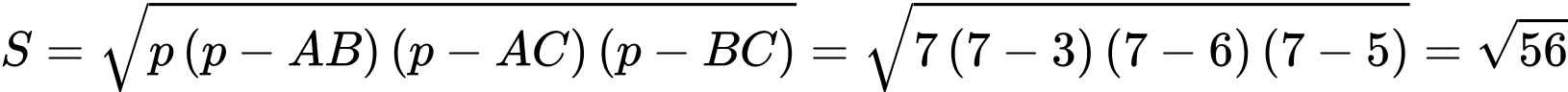 . Đáp án: A
. Đáp án: A
Câu 7 [284587]: Mảnh vườn hình tam giác của gia đình nhà bạn An có chiều dài các cạnh là 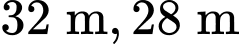 và
và 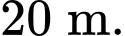 Hỏi diện tích mảnh vườn của gia đình bạn An là bao nhiêu mét vuông(làm tròn đến hàng phần mười)?
Hỏi diện tích mảnh vườn của gia đình bạn An là bao nhiêu mét vuông(làm tròn đến hàng phần mười)?
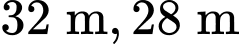 và
và 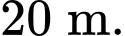 Hỏi diện tích mảnh vườn của gia đình bạn An là bao nhiêu mét vuông(làm tròn đến hàng phần mười)?
Hỏi diện tích mảnh vườn của gia đình bạn An là bao nhiêu mét vuông(làm tròn đến hàng phần mười)? A, 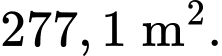
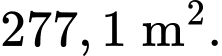
B, 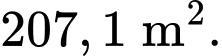
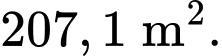
C, 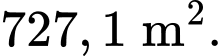
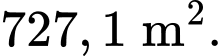
D, 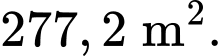
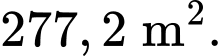
Cách 1:
Nửa chu vi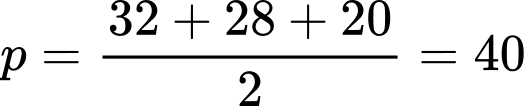
Diên tích tam giác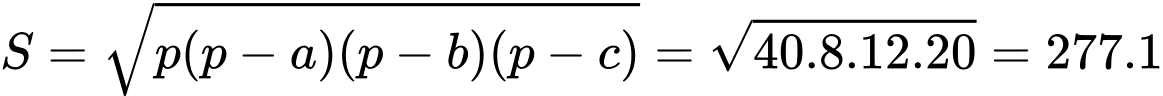
Cách 2: Xét tam giác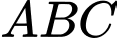 có ba cạnh
có ba cạnh 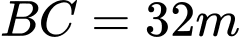 và
và 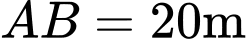 và
và 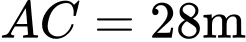
Theo định lý hàm cos trong tam giác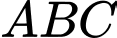 ta có:
ta có:
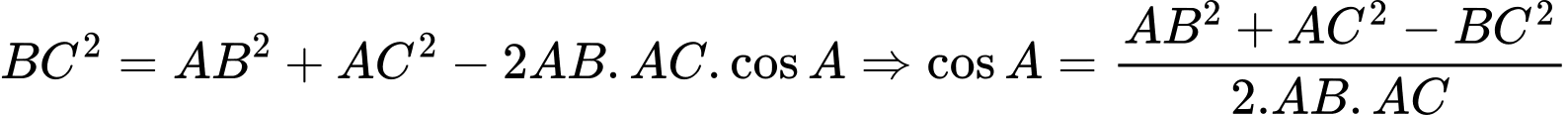
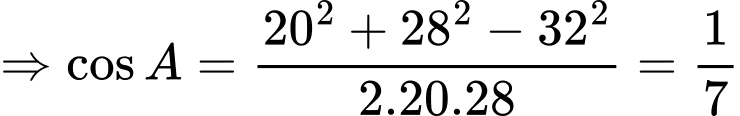
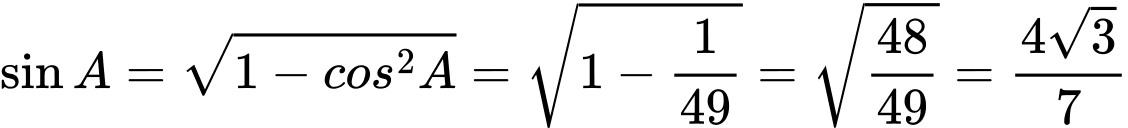
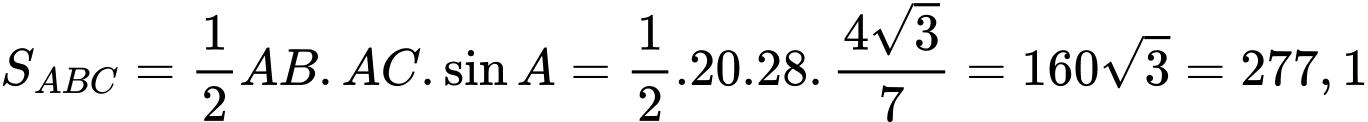 Đáp án: A
Đáp án: A
Nửa chu vi
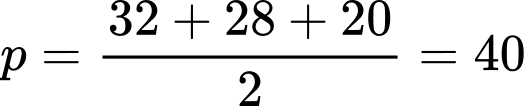
Diên tích tam giác
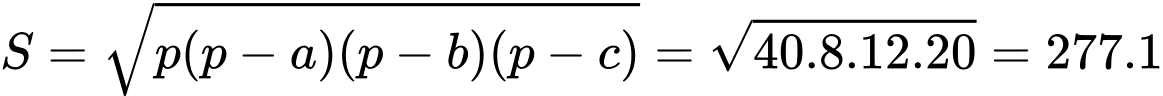
Cách 2: Xét tam giác
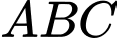 có ba cạnh
có ba cạnh 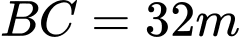 và
và 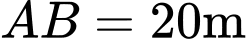 và
và 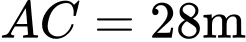
Theo định lý hàm cos trong tam giác
 ta có:
ta có: 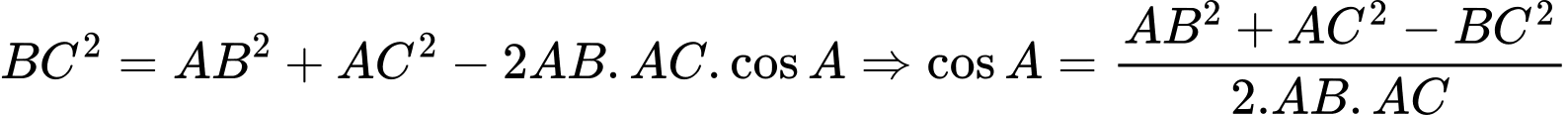
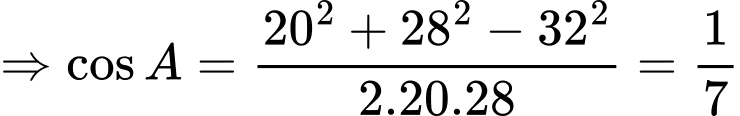
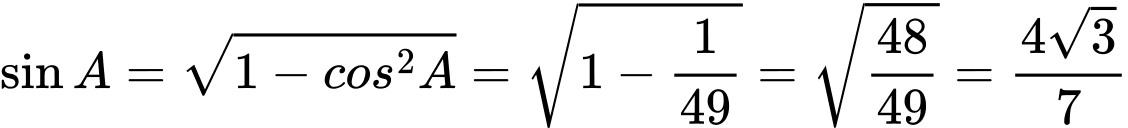
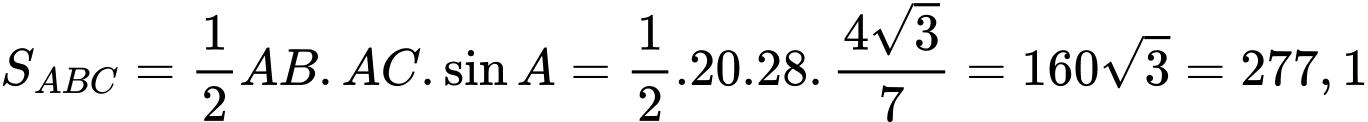 Đáp án: A
Đáp án: A
Câu 8 [238417]: Cho tam giác  thoả mãn:
thoả mãn: 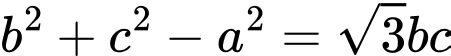 . Khi đó
. Khi đó
 thoả mãn:
thoả mãn: 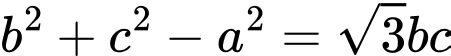 . Khi đó
. Khi đó A, 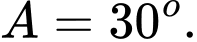
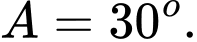
B, 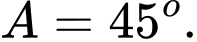
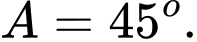
C, 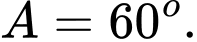
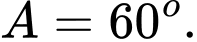
D, 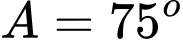 .
.
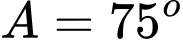 .
.
Chọn A.Ta có: 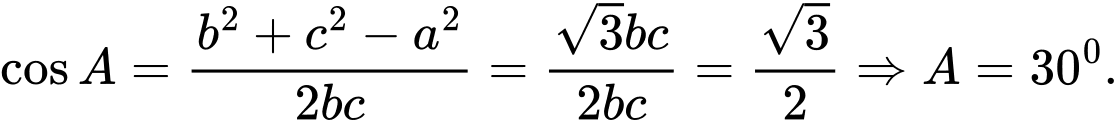 Đáp án: A
Đáp án: A
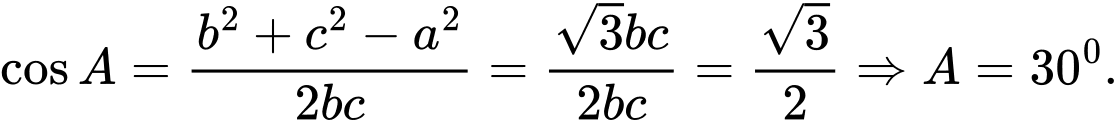 Đáp án: A
Đáp án: A
Câu 9 [238467]: Hai chiếc tàu thuỷ cùng xuất phát từ vị trí  , đi thẳng theo hai hướng tạo với nhau một góc
, đi thẳng theo hai hướng tạo với nhau một góc 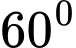 . Tàu thứ nhất chạy với tốc độ
. Tàu thứ nhất chạy với tốc độ 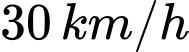 , tàu thứ hai chạy với tốc độ
, tàu thứ hai chạy với tốc độ 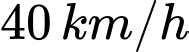 . Hỏi sau
. Hỏi sau  giờ hai tàu cách nhau bao nhiêu
giờ hai tàu cách nhau bao nhiêu 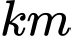 ?
?
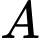 , đi thẳng theo hai hướng tạo với nhau một góc
, đi thẳng theo hai hướng tạo với nhau một góc 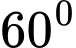 . Tàu thứ nhất chạy với tốc độ
. Tàu thứ nhất chạy với tốc độ 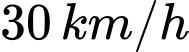 , tàu thứ hai chạy với tốc độ
, tàu thứ hai chạy với tốc độ 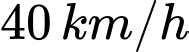 . Hỏi sau
. Hỏi sau 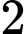 giờ hai tàu cách nhau bao nhiêu
giờ hai tàu cách nhau bao nhiêu 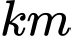 ?
? A, 
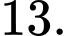
B, 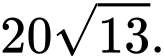
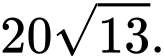
C, 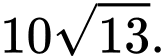
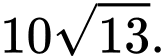
D, 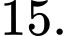
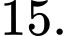
Chọn B.
Ta có: Sau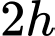 quãng đường tàu thứ nhất chạy được là:
quãng đường tàu thứ nhất chạy được là: 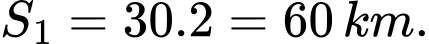
Sau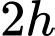 quãng đường tàu thứ hai chạy được là:
quãng đường tàu thứ hai chạy được là: 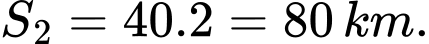 Vậy: sau
Vậy: sau 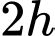 hai tàu cách nhau là:
hai tàu cách nhau là: 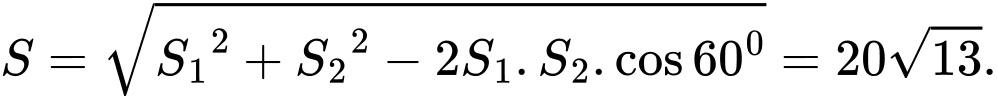 Đáp án: B
Đáp án: B
Ta có: Sau
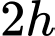 quãng đường tàu thứ nhất chạy được là:
quãng đường tàu thứ nhất chạy được là: 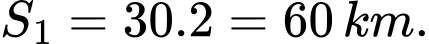
Sau
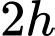 quãng đường tàu thứ hai chạy được là:
quãng đường tàu thứ hai chạy được là: 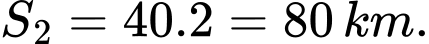 Vậy: sau
Vậy: sau 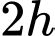 hai tàu cách nhau là:
hai tàu cách nhau là: 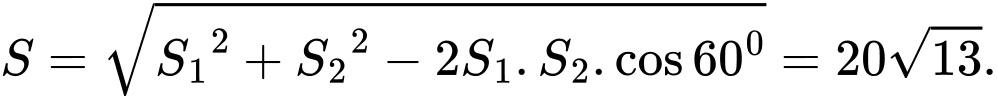 Đáp án: B
Đáp án: B
Câu 10 [238457]: Cho 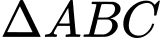 có
có 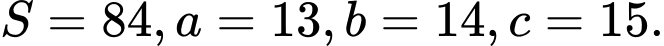 Độ dài bán kính đường tròn ngoại tiếp
Độ dài bán kính đường tròn ngoại tiếp 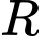 của tam giác trên là
của tam giác trên là
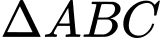 có
có 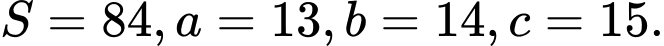 Độ dài bán kính đường tròn ngoại tiếp
Độ dài bán kính đường tròn ngoại tiếp 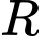 của tam giác trên là
của tam giác trên là A, 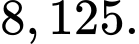
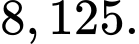
B, 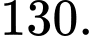
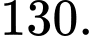
C, 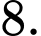
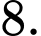
D, 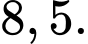
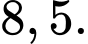
Chọn A.
Ta có: 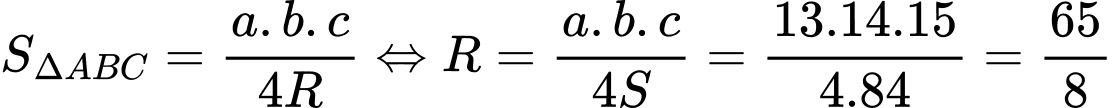 . Đáp án: A
. Đáp án: A
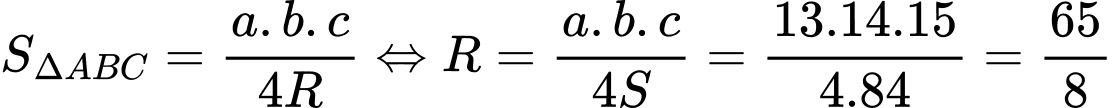 . Đáp án: A
. Đáp án: A
Câu 11 [238453]: Cho tam giác  có chu vi bằng 12 và bán kính đường tròn nội tiếp bằng 1. Diện tích của tam giác
có chu vi bằng 12 và bán kính đường tròn nội tiếp bằng 1. Diện tích của tam giác  bằng
bằng
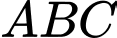 có chu vi bằng 12 và bán kính đường tròn nội tiếp bằng 1. Diện tích của tam giác
có chu vi bằng 12 và bán kính đường tròn nội tiếp bằng 1. Diện tích của tam giác  bằng
bằng A,  .
.
 .
.B, 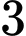 .
.
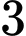 .
.C, 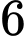 .
.
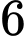 .
.D, 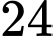 .
.
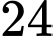 .
.
Chọn C
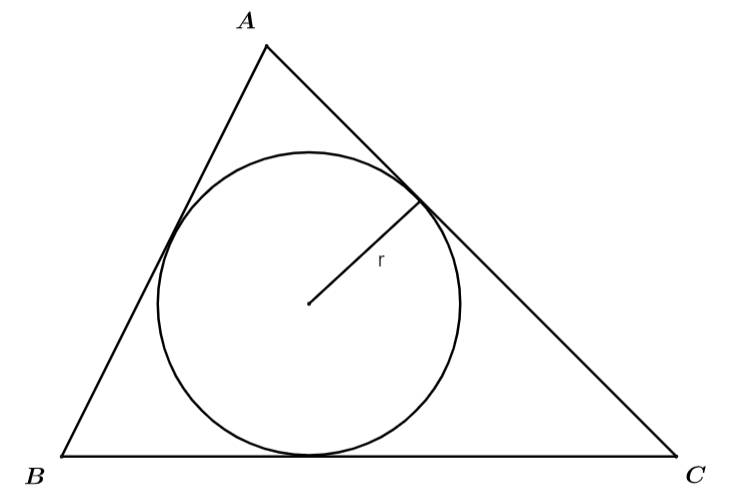
Theo đề bài tam giác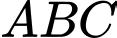 có chu vi bằng 12 nên nửa chu vi là
có chu vi bằng 12 nên nửa chu vi là 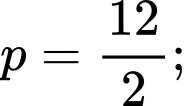 bán kính đường tròn nội tiếp bằng 1, tức là ta có:
bán kính đường tròn nội tiếp bằng 1, tức là ta có: 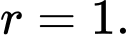
Diện tích tam giác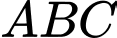 là:
là: 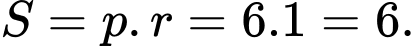 Đáp án: C
Đáp án: C

Theo đề bài tam giác
 có chu vi bằng 12 nên nửa chu vi là
có chu vi bằng 12 nên nửa chu vi là 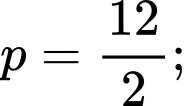 bán kính đường tròn nội tiếp bằng 1, tức là ta có:
bán kính đường tròn nội tiếp bằng 1, tức là ta có: 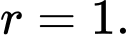
Diện tích tam giác
 là:
là: 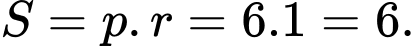 Đáp án: C
Đáp án: C
Câu 12 [238458]: Cho  có
có 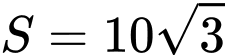 , nửa chu vi
, nửa chu vi 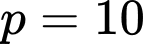 . Độ dài bán kính đường tròn nội tiếp
. Độ dài bán kính đường tròn nội tiếp 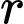 của tam giác trên là
của tam giác trên là
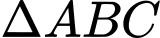 có
có 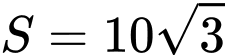 , nửa chu vi
, nửa chu vi 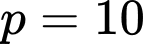 . Độ dài bán kính đường tròn nội tiếp
. Độ dài bán kính đường tròn nội tiếp 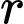 của tam giác trên là
của tam giác trên là A, 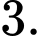
B, 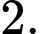
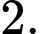
C, 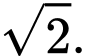
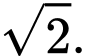
D, 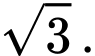
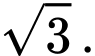
Chọn D.
Ta có: 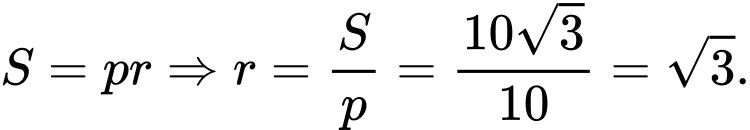 Đáp án: D
Đáp án: D
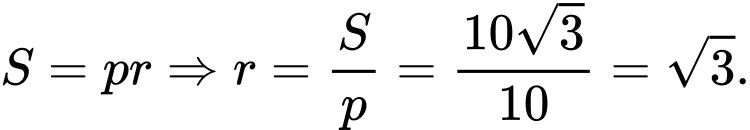 Đáp án: D
Đáp án: D
Câu 13 [238456]: Cho tam giác  có
có 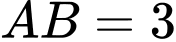 ,
, 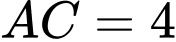 ,
, 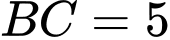 . Bán kính đường tròn nội tiếp tam giác bằng
. Bán kính đường tròn nội tiếp tam giác bằng
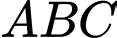 có
có 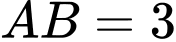 ,
, 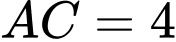 ,
, 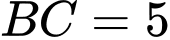 . Bán kính đường tròn nội tiếp tam giác bằng
. Bán kính đường tròn nội tiếp tam giác bằng A, 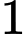 .
.
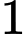 .
.B, 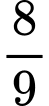 .
.
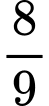 .
.C, 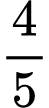 .
.
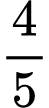 .
.D, 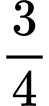 .
.
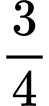 .
.
Chọn A
Vì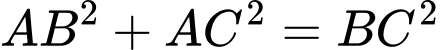 nên tam giác
nên tam giác 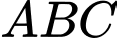 vuông tại
vuông tại 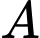 .
Do đó bán kính đường tròn nội tiếp
.
Do đó bán kính đường tròn nội tiếp 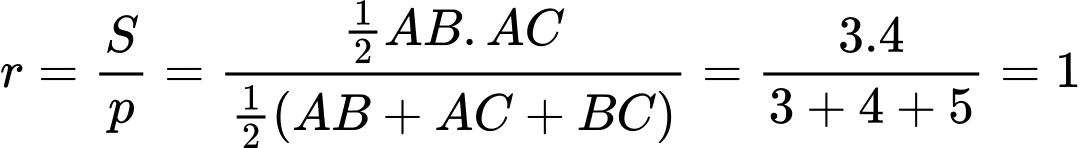 . Đáp án: A
. Đáp án: A
Vì
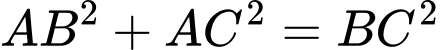 nên tam giác
nên tam giác 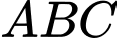 vuông tại
vuông tại 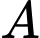 .
Do đó bán kính đường tròn nội tiếp
.
Do đó bán kính đường tròn nội tiếp 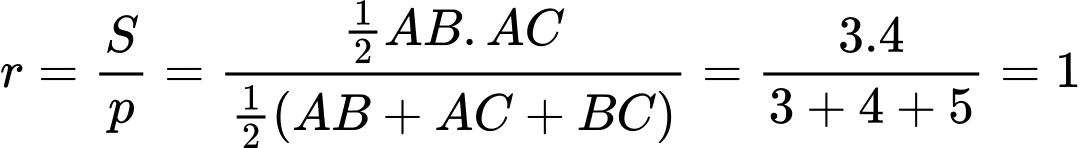 . Đáp án: A
. Đáp án: A
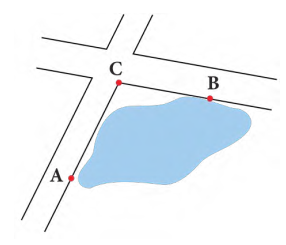
Câu 14 [239890]: Để tính khoảng cách giữa hai địa điểm 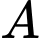 và
và 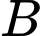 mà ta không thể đi trực tiếp từ
mà ta không thể đi trực tiếp từ 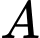 đến
đến 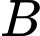 (hai địa điểm nằm ở hai bên bờ một hồ nước, một đầm lầy, ...), người ta tiến hành như sau: Chọn một địa điểm
(hai địa điểm nằm ở hai bên bờ một hồ nước, một đầm lầy, ...), người ta tiến hành như sau: Chọn một địa điểm  sao cho ta đo được các khoảng cách
sao cho ta đo được các khoảng cách 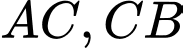 và góc
và góc  . Sau khi đo, ta nhận được:
. Sau khi đo, ta nhận được:  và
và 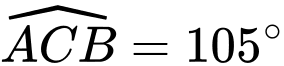 (Hình 31). Tính khoảng cách
(Hình 31). Tính khoảng cách  (làm tròn kết quả đến hàng phần mười đơn vị mét).
(làm tròn kết quả đến hàng phần mười đơn vị mét).
 và
và 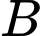 mà ta không thể đi trực tiếp từ
mà ta không thể đi trực tiếp từ 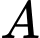 đến
đến 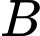 (hai địa điểm nằm ở hai bên bờ một hồ nước, một đầm lầy, ...), người ta tiến hành như sau: Chọn một địa điểm
(hai địa điểm nằm ở hai bên bờ một hồ nước, một đầm lầy, ...), người ta tiến hành như sau: Chọn một địa điểm  sao cho ta đo được các khoảng cách
sao cho ta đo được các khoảng cách 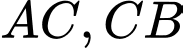 và góc
và góc  . Sau khi đo, ta nhận được:
. Sau khi đo, ta nhận được:  và
và 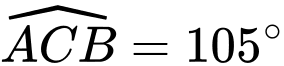 (Hình 31). Tính khoảng cách
(Hình 31). Tính khoảng cách  (làm tròn kết quả đến hàng phần mười đơn vị mét).
(làm tròn kết quả đến hàng phần mười đơn vị mét).
Đổi: 1 km = 1000 m. Do đó 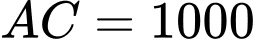 m.
m.
Áp dụng định lí cosin trong tam giác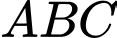 ta có:
ta có:
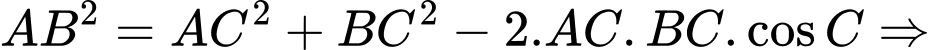
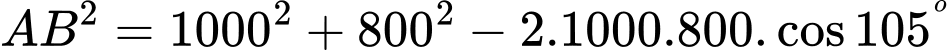
 ≈
≈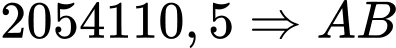 ≈
≈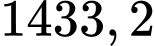
Vậy khoảng cách là 1433,2 m.
là 1433,2 m.
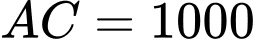 m.
m. Áp dụng định lí cosin trong tam giác
 ta có:
ta có: 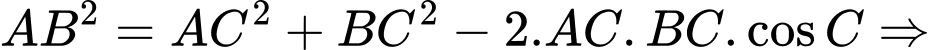
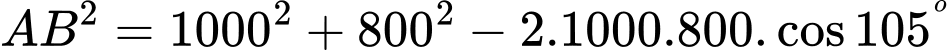
 ≈
≈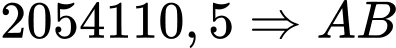 ≈
≈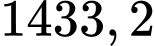
Vậy khoảng cách
 là 1433,2 m.
là 1433,2 m.
Câu 15 [239354]: Để lắp đường dây diện cao thế từ vị trí 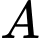 đến vị trí B, do phải tránh một ngọn núi nên người ta phải nối đường dây từ vị trí
đến vị trí B, do phải tránh một ngọn núi nên người ta phải nối đường dây từ vị trí 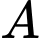 đến vị trí
đến vị trí  dài
dài 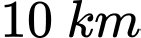 , sau đó nối đường dây từ vị trí
, sau đó nối đường dây từ vị trí  đến vị trí
đến vị trí  dài
dài 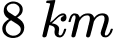 . Góc tạo bởi hai đoạn dây
. Góc tạo bởi hai đoạn dây  và
và  là
là 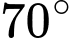 . Tính chiều dài tăng thêm vì không thể nối trực tiếp từ
. Tính chiều dài tăng thêm vì không thể nối trực tiếp từ  đến
đến  .
.
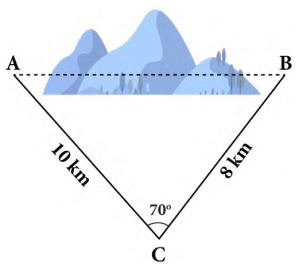
 đến vị trí B, do phải tránh một ngọn núi nên người ta phải nối đường dây từ vị trí
đến vị trí B, do phải tránh một ngọn núi nên người ta phải nối đường dây từ vị trí 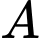 đến vị trí
đến vị trí  dài
dài 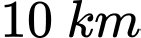 , sau đó nối đường dây từ vị trí
, sau đó nối đường dây từ vị trí  đến vị trí
đến vị trí 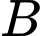 dài
dài 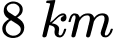 . Góc tạo bởi hai đoạn dây
. Góc tạo bởi hai đoạn dây 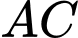 và
và 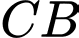 là
là 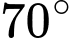 . Tính chiều dài tăng thêm vì không thể nối trực tiếp từ
. Tính chiều dài tăng thêm vì không thể nối trực tiếp từ 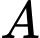 đến
đến 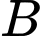 .
.
Áp dụng định lí cosin, ta có:
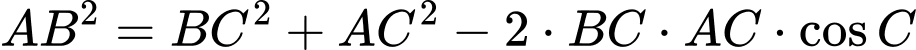
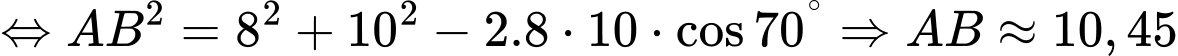
Vậy chiều dài tăng thêm vì không thể nối trực tiếp là:
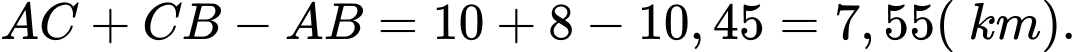
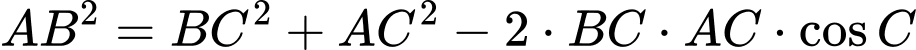
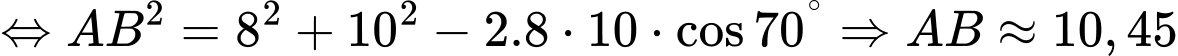
Vậy chiều dài tăng thêm vì không thể nối trực tiếp là:
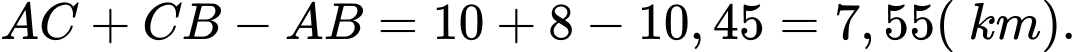
Câu 16 [238397]: Hai chiếc tàu thủy cùng xuất phát từ một vị trí 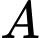 , đi thẳng theo hai hướng tạo với nhau góc
, đi thẳng theo hai hướng tạo với nhau góc 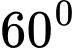 . Tàu
. Tàu 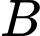 chạy với tốc độ
chạy với tốc độ 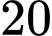 hải lí một giờ. Tàu
hải lí một giờ. Tàu  chạy với tốc độ
chạy với tốc độ  hải lí một giờ. Sau hai giờ, hai tàu cách nhau bao nhiêu hải lí?
hải lí một giờ. Sau hai giờ, hai tàu cách nhau bao nhiêu hải lí?
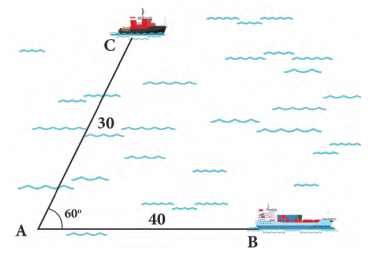
 , đi thẳng theo hai hướng tạo với nhau góc
, đi thẳng theo hai hướng tạo với nhau góc  . Tàu
. Tàu  chạy với tốc độ
chạy với tốc độ 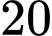 hải lí một giờ. Tàu
hải lí một giờ. Tàu  chạy với tốc độ
chạy với tốc độ  hải lí một giờ. Sau hai giờ, hai tàu cách nhau bao nhiêu hải lí?
hải lí một giờ. Sau hai giờ, hai tàu cách nhau bao nhiêu hải lí?
Sau 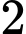 giờ tàu
giờ tàu 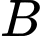 đi được
đi được 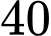 hải lí, tàu
hải lí, tàu  đi được
đi được 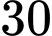 hải lí. Vậy tam giác
hải lí. Vậy tam giác 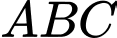 có
có 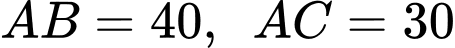 và
và 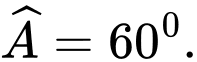
Áp dụng định lí côsin vào tam giác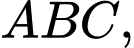 ta có:
ta có:
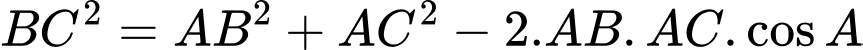
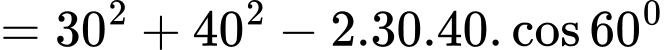
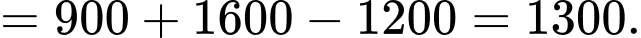
Vậy (hải lí).
(hải lí).
Sau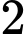 giờ, hai tàu cách nhau khoảng
giờ, hai tàu cách nhau khoảng 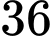 hải lí.
hải lí.
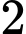 giờ tàu
giờ tàu 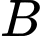 đi được
đi được 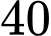 hải lí, tàu
hải lí, tàu  đi được
đi được 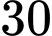 hải lí. Vậy tam giác
hải lí. Vậy tam giác 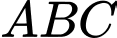 có
có 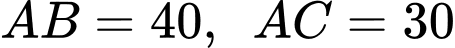 và
và 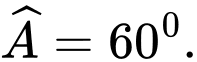
Áp dụng định lí côsin vào tam giác
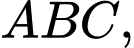 ta có:
ta có:
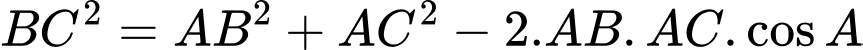
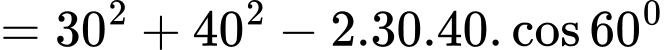
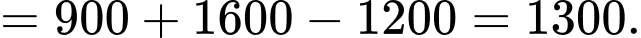
Vậy
 (hải lí).
(hải lí).
Sau
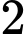 giờ, hai tàu cách nhau khoảng
giờ, hai tàu cách nhau khoảng 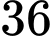 hải lí.
hải lí.
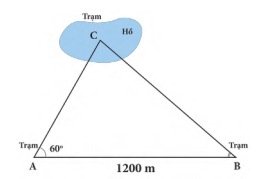
Câu 17 [584174]: Có hai trạm quan sát 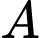 và
và 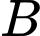 ven hồ và một trạn quan sát
ven hồ và một trạn quan sát  ở giữa hồ. Để tính khoảng cách từ
ở giữa hồ. Để tính khoảng cách từ 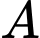 và từ
và từ 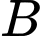 đến
đến  , người ta làm như sau (Hình ):
, người ta làm như sau (Hình ):
- Đo góc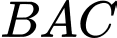 được
được 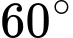 , đo góc
, đo góc  được
được 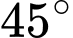 ;
;
- Đo khoảng cách được
được 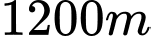 .
.
Khoảng cách từ trạm đến các trạm
đến các trạm  và
và  bằng bao nhiêu mét (làm tròn kết quả đến hàng đơn vị)?
bằng bao nhiêu mét (làm tròn kết quả đến hàng đơn vị)?
 và
và  ven hồ và một trạn quan sát
ven hồ và một trạn quan sát  ở giữa hồ. Để tính khoảng cách từ
ở giữa hồ. Để tính khoảng cách từ  và từ
và từ  đến
đến  , người ta làm như sau (Hình ):
, người ta làm như sau (Hình ):- Đo góc
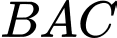 được
được 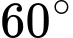 , đo góc
, đo góc  được
được 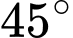 ;
;- Đo khoảng cách
 được
được 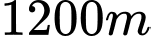 .
.Khoảng cách từ trạm
 đến các trạm
đến các trạm 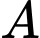 và
và 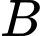 bằng bao nhiêu mét (làm tròn kết quả đến hàng đơn vị)?
bằng bao nhiêu mét (làm tròn kết quả đến hàng đơn vị)?
Ba vị trí A, B, C tạo thành 3 đỉnh của tam giác 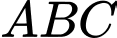 .
.
Ta có: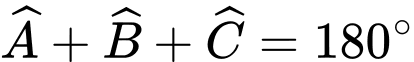 (định lí tổng ba góc trong tam giác
(định lí tổng ba góc trong tam giác 
Suy ra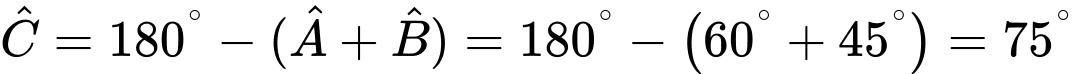
Áp dụng định lí sin trong tam giác ta có:
ta có: 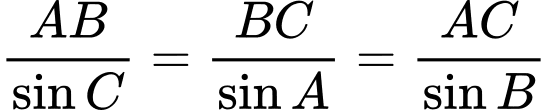
Do đó: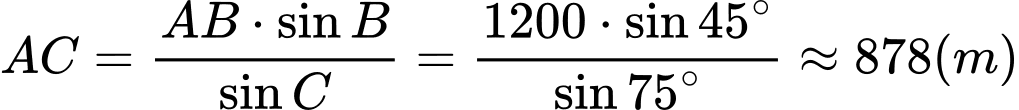 ;
;
Vậy khoảng cách từ' trạm C đến trạm A khoảng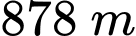
 .
.Ta có:
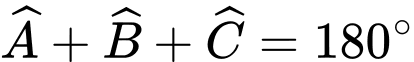 (định lí tổng ba góc trong tam giác
(định lí tổng ba góc trong tam giác 
Suy ra
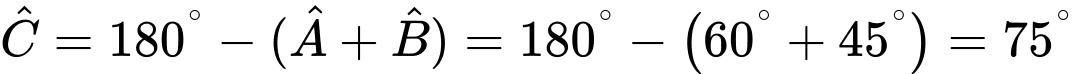
Áp dụng định lí sin trong tam giác
 ta có:
ta có: 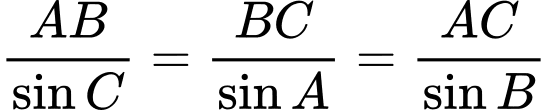
Do đó:
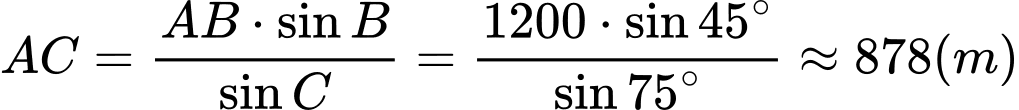 ;
;Vậy khoảng cách từ' trạm C đến trạm A khoảng
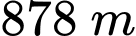
Câu 18 [240346]: Một người đứng ở bờ sông, muốn đo độ rộng của khúc sông chảy qua vị trí đang đứng (khúc sông tương đối thẳng, có thể xem hai bờ song song với nhau).
Từ vị trí đang đứng , người đó đo được góc nghiêng
, người đó đo được góc nghiêng 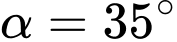 so với bờ sông tới một vị trí
so với bờ sông tới một vị trí  quan sát được ở phía bờ bên kia. Sau đó di chuyển dọc bờ sông đến vị trí
quan sát được ở phía bờ bên kia. Sau đó di chuyển dọc bờ sông đến vị trí  cách
cách  một khoảng
một khoảng 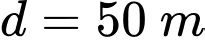 và tiếp tục đo được góc nghiêng
và tiếp tục đo được góc nghiêng 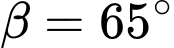 so với bờ bên kia tới vị trí
so với bờ bên kia tới vị trí  đã chọn (Hình).
đã chọn (Hình).
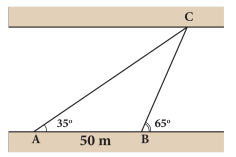
Hỏi độ rộng của khúc sông chảy qua vị trí người đó đang đứng là bao nhiêu mét (làm tròn kết quả đến hàng phẩn mười)?
Từ vị trí đang đứng
 , người đó đo được góc nghiêng
, người đó đo được góc nghiêng 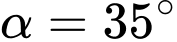 so với bờ sông tới một vị trí
so với bờ sông tới một vị trí  quan sát được ở phía bờ bên kia. Sau đó di chuyển dọc bờ sông đến vị trí
quan sát được ở phía bờ bên kia. Sau đó di chuyển dọc bờ sông đến vị trí  cách
cách 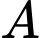 một khoảng
một khoảng 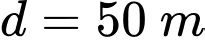 và tiếp tục đo được góc nghiêng
và tiếp tục đo được góc nghiêng 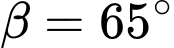 so với bờ bên kia tới vị trí
so với bờ bên kia tới vị trí  đã chọn (Hình).
đã chọn (Hình).
Hỏi độ rộng của khúc sông chảy qua vị trí người đó đang đứng là bao nhiêu mét (làm tròn kết quả đến hàng phẩn mười)?
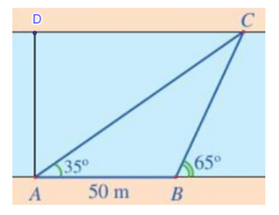
Dựng
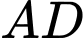 vuông góc với hai bên bờ sông, khi đó AD là độ rộng của khúc sông chạy qua vị trí của người đó đang đứng. Ta cần tính khoảng cách AD.
vuông góc với hai bên bờ sông, khi đó AD là độ rộng của khúc sông chạy qua vị trí của người đó đang đứng. Ta cần tính khoảng cách AD. Xét tam giác
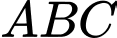 ta có:
ta có: 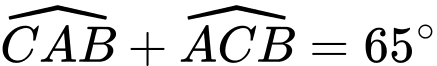 (tính chất góc ngoài tại đỉnh
(tính chất góc ngoài tại đỉnh 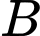 của tam giác)
của tam giác) 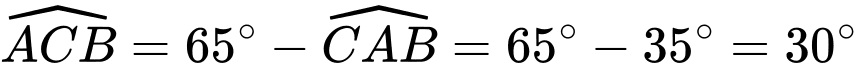 . Lại có
. Lại có  .
.Áp dụng định lí sin trong tam giác
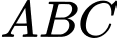 ta có:
ta có: 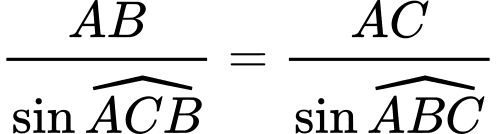 .
.Suy ra
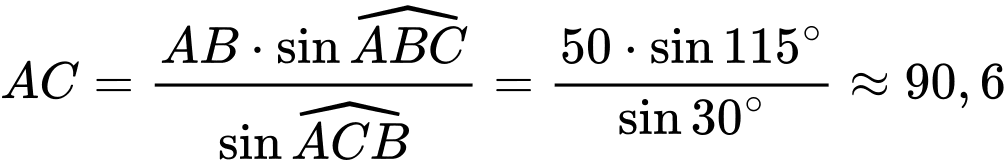 . Ta có:
. Ta có: 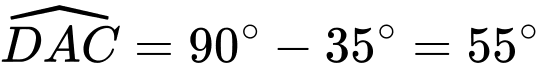 .
.Tam giác ADC vuông tại
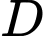 nên
nên 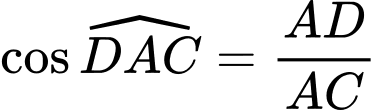
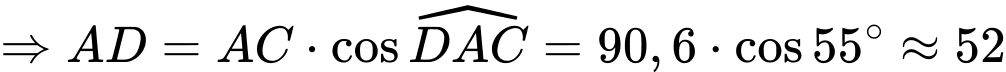
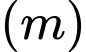 .
.Vậy độ rộng của khúc sông chảy qua vị trí người đó đang đứng là
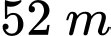 .
.
Câu 19 [558025]: Cho tam giác 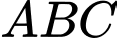 có
có 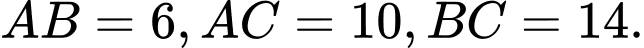 Độ dài đường cao
Độ dài đường cao 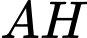 của tam giác
của tam giác 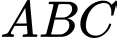 bằng bao nhiêu(làm tròn đến 1 chữ số sau dấu thập phân) ?
bằng bao nhiêu(làm tròn đến 1 chữ số sau dấu thập phân) ?
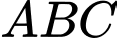 có
có 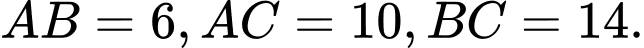 Độ dài đường cao
Độ dài đường cao 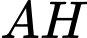 của tam giác
của tam giác  bằng bao nhiêu(làm tròn đến 1 chữ số sau dấu thập phân) ?
bằng bao nhiêu(làm tròn đến 1 chữ số sau dấu thập phân) ?
Áp dụng định lí côsin cho tam giác  ta có:
ta có:
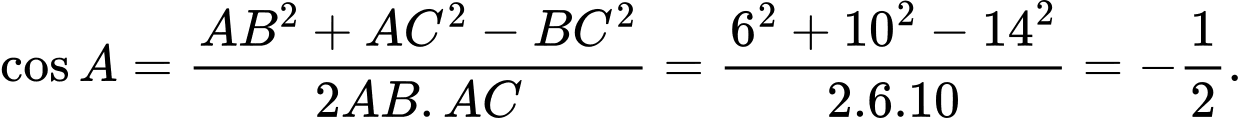
Do đó,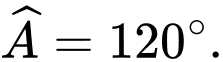
Diện tích tam giác là:
là: 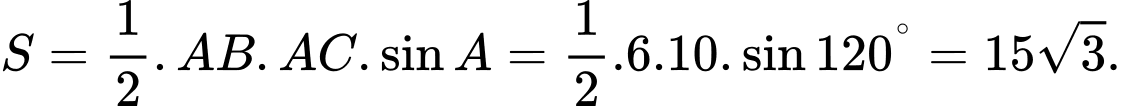
Độ dài đường cao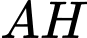 là:
là: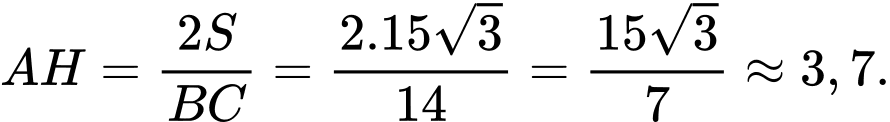
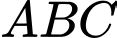 ta có:
ta có: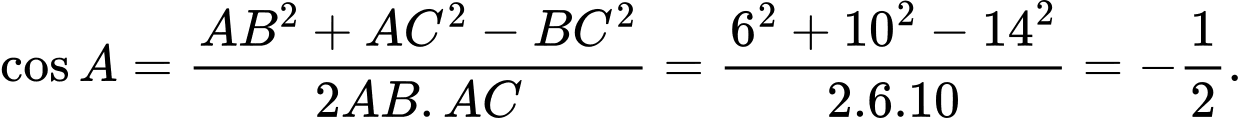
Do đó,
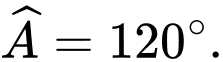
Diện tích tam giác
 là:
là: 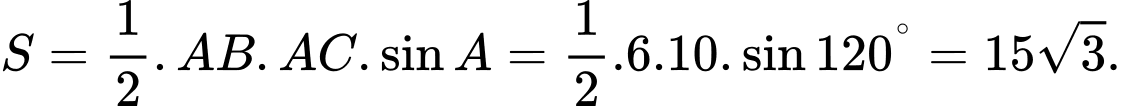
Độ dài đường cao
 là:
là: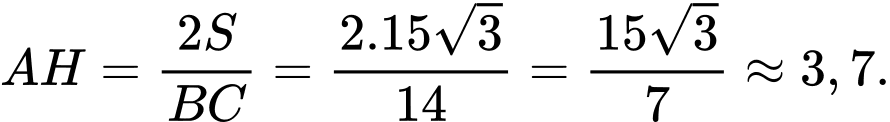
Câu 20 [238422]: Tam giác  có
có 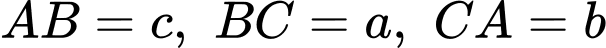 . Các cạnh
. Các cạnh 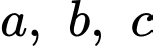 liên hệ với nhau bởi đẳng thức
liên hệ với nhau bởi đẳng thức 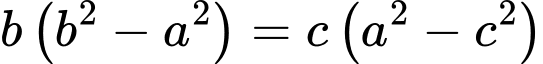 . Khi đó góc
. Khi đó góc  bằng bao nhiêu độ?
bằng bao nhiêu độ?
 có
có 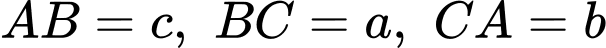 . Các cạnh
. Các cạnh 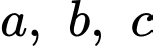 liên hệ với nhau bởi đẳng thức
liên hệ với nhau bởi đẳng thức 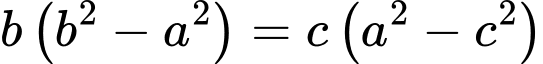 . Khi đó góc
. Khi đó góc 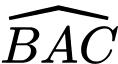 bằng bao nhiêu độ?
bằng bao nhiêu độ? A, 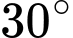 .
.
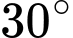 .
.B, 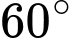 .
.
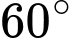 .
.C, 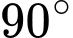 .
.
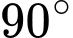 .
.D, 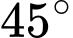 .
.
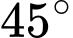 .
.
Chọn B
Theo bài ra, ta có: 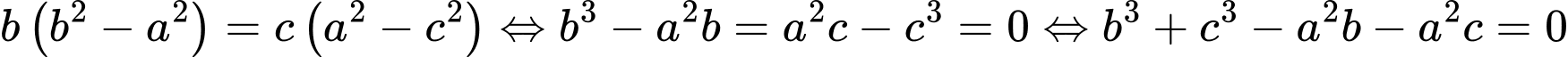
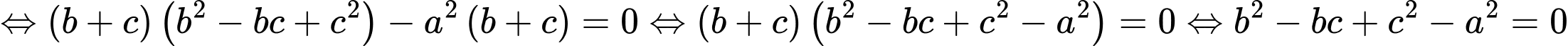 (do
(do 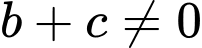 )
)
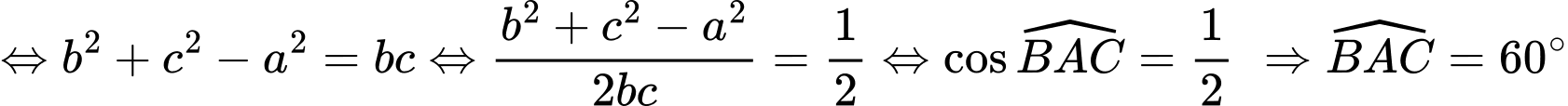 . Đáp án: B
. Đáp án: B
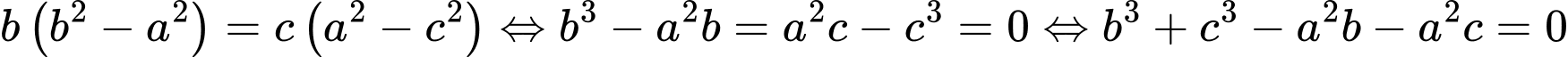
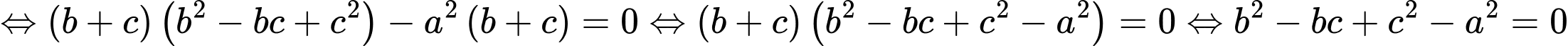 (do
(do 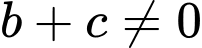 )
)
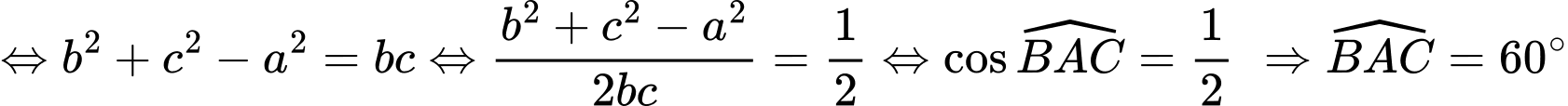 . Đáp án: B
. Đáp án: B
Câu 21 [238460]: Một tam giác có ba cạnh là  Bán kính đường tròn ngoại tiếp là
Bán kính đường tròn ngoại tiếp là
 Bán kính đường tròn ngoại tiếp là
Bán kính đường tròn ngoại tiếp là A, 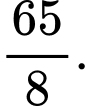
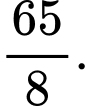
B, 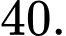
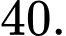
C, 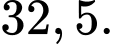
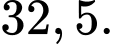
D, 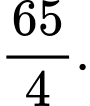
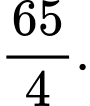
Chọn C.
Ta có: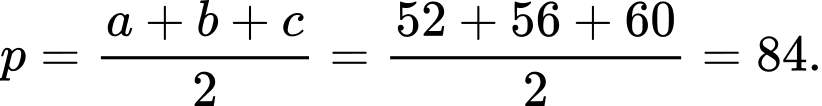
Suy ra: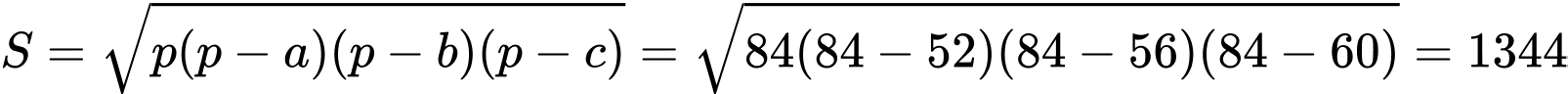 .
.
Mà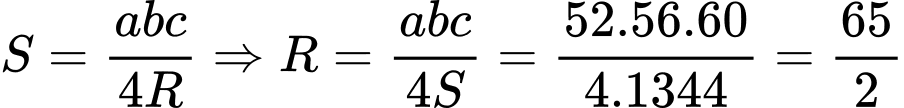 . Đáp án: C
. Đáp án: C
Ta có:
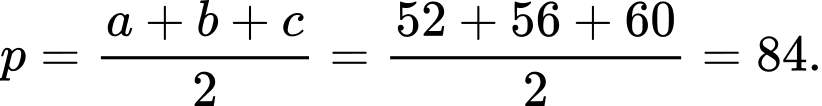
Suy ra:
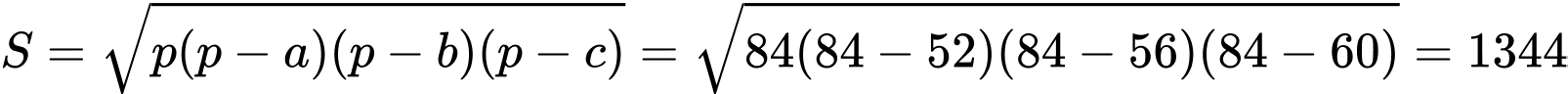 .
.
Mà
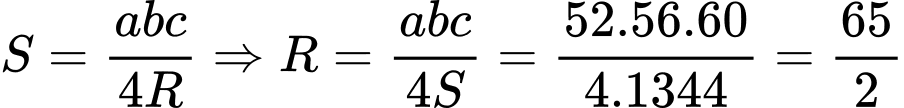 . Đáp án: C
. Đáp án: C
Câu 22 [238459]: Một tam giác có ba cạnh là 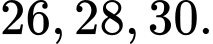 Bán kính đường tròn nội tiếp là
Bán kính đường tròn nội tiếp là
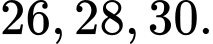 Bán kính đường tròn nội tiếp là
Bán kính đường tròn nội tiếp là A, 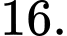
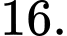
B, 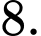
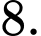
C, 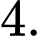
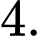
D, 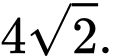
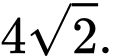
Chọn B.
Ta có: 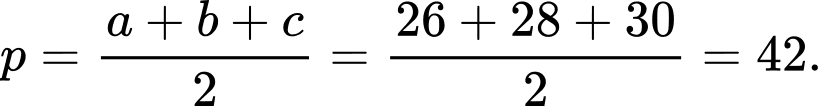
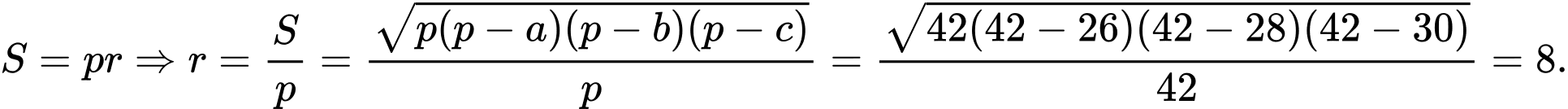 Đáp án: B
Đáp án: B
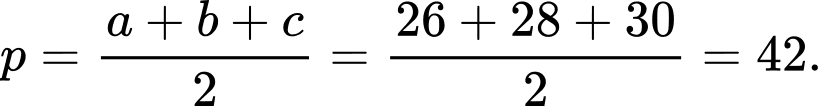
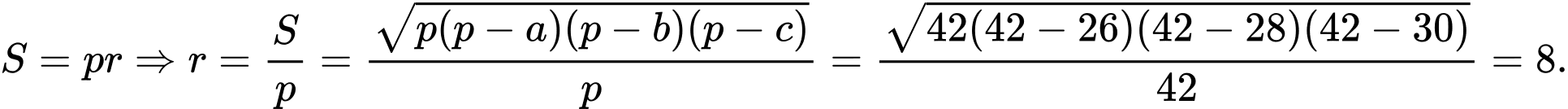 Đáp án: B
Đáp án: B
Câu 23 [583167]: Cho tam giác  có
có 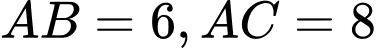 và
và 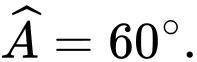 Gọi
Gọi  là tâm đường tròn ngoại tiếp tam giác
là tâm đường tròn ngoại tiếp tam giác 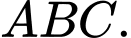 Tính diện tích tam giác
Tính diện tích tam giác 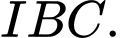 Viết kết quả làm tròn đến hàng phần mười.
Viết kết quả làm tròn đến hàng phần mười.
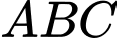 có
có 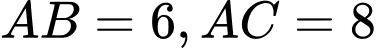 và
và 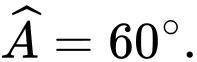 Gọi
Gọi 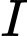 là tâm đường tròn ngoại tiếp tam giác
là tâm đường tròn ngoại tiếp tam giác 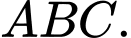 Tính diện tích tam giác
Tính diện tích tam giác 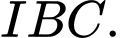 Viết kết quả làm tròn đến hàng phần mười.
Viết kết quả làm tròn đến hàng phần mười. 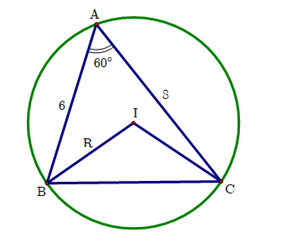
Đặt 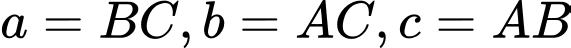 .
.
Áp dụng định lí cosin cho tam giác 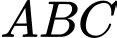 ta được:
ta được: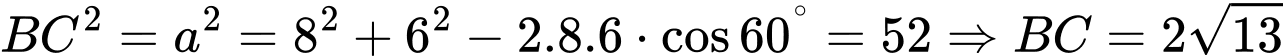
Xét tam giác IBC ta có:
Góc  (góc ở tâm và góc nội tiếp cùng chắn một cung)
(góc ở tâm và góc nội tiếp cùng chắn một cung)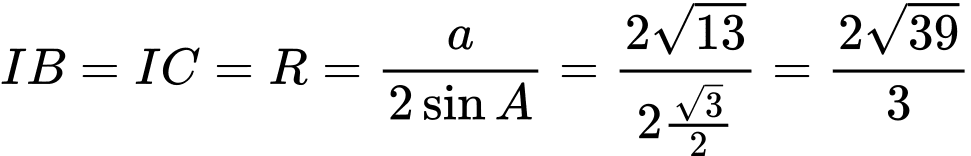
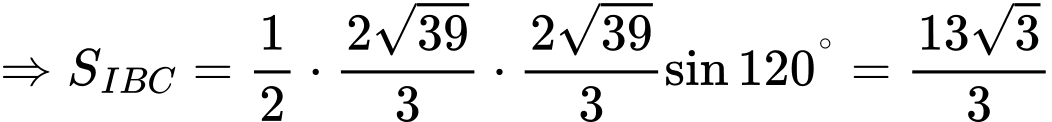
Câu 24 [558023]: Cho tam giác 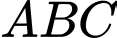 có các cạnh
có các cạnh 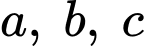 thỏa mãn điều kiện
thỏa mãn điều kiện  Tính số đo của góc
Tính số đo của góc 
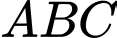 có các cạnh
có các cạnh 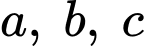 thỏa mãn điều kiện
thỏa mãn điều kiện  Tính số đo của góc
Tính số đo của góc 
Trong tam giác 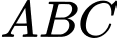 ta luôn có
ta luôn có 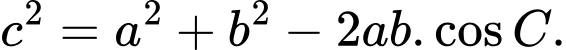
Ta có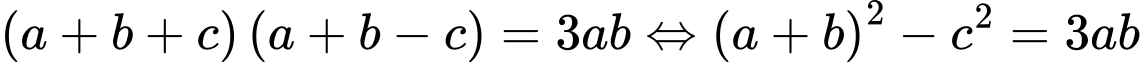 .
.
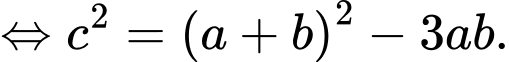
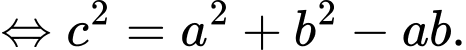

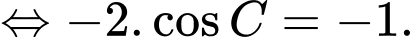
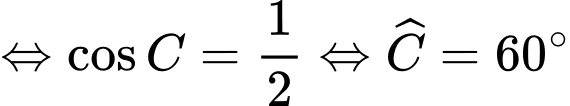
 ta luôn có
ta luôn có 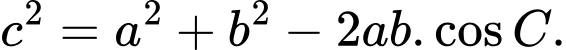
Ta có
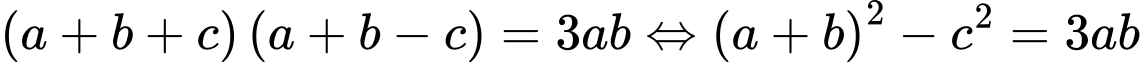 .
.