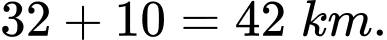Đáp án Bài tập tự luyện
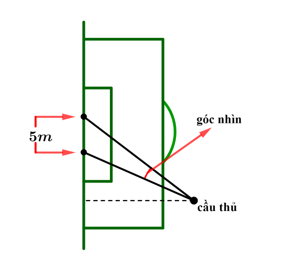
Câu 1 [243347]: Một khung thành bóng đá rộng 5 mét. Một cầu thủ đứng ở vị trí cách cột dọc khung thành 26 mét và cách cột dọc còn lại 23 mét, sút vào khung thành. Tính góc nhìn của cầu thủ đến hai cột khung thành trên.

Ta có: 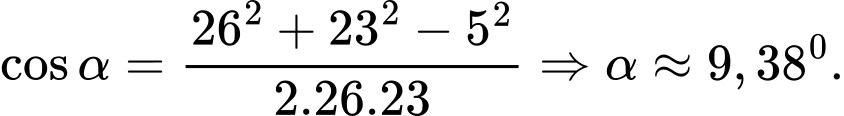
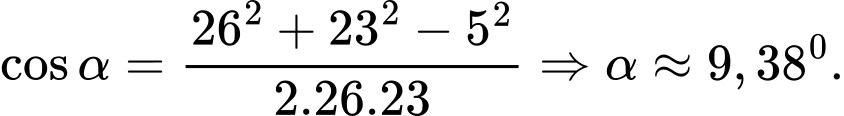
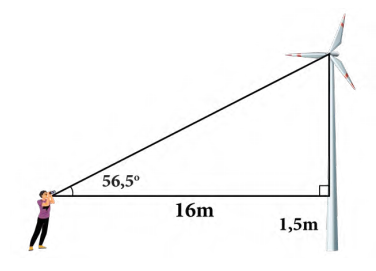
Câu 2 [239355]: Một người đứng cách thân một cái quạt gió 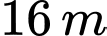 và nhìn thấy tâm của cánh quạt với góc nâng
và nhìn thấy tâm của cánh quạt với góc nâng 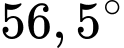 (hình vẽ). Tính khoảng cách từ tâm của cánh quạt đến mặt đất. Cho biết khoảng cách từ mắt của người đó đến mặt đất là
(hình vẽ). Tính khoảng cách từ tâm của cánh quạt đến mặt đất. Cho biết khoảng cách từ mắt của người đó đến mặt đất là 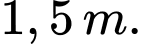
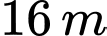 và nhìn thấy tâm của cánh quạt với góc nâng
và nhìn thấy tâm của cánh quạt với góc nâng 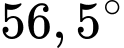 (hình vẽ). Tính khoảng cách từ tâm của cánh quạt đến mặt đất. Cho biết khoảng cách từ mắt của người đó đến mặt đất là
(hình vẽ). Tính khoảng cách từ tâm của cánh quạt đến mặt đất. Cho biết khoảng cách từ mắt của người đó đến mặt đất là 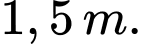

Kí hiệu các điểm A, B, C như hình
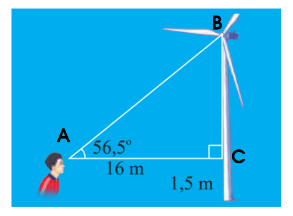
Cách 1:
Ta có: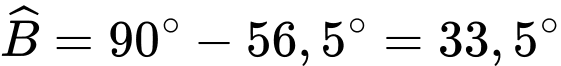
Áp dụng định lísin, ta có:

Vậy khoảng cách từ tâm của cánh quạt đến mặt đất là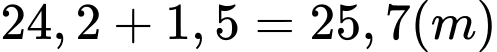
Cách 2:
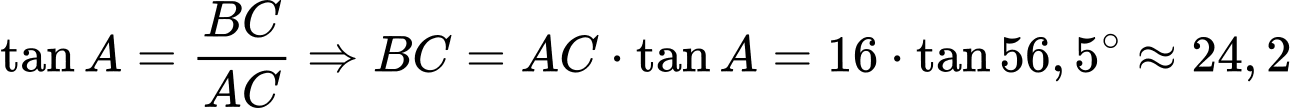
Vậy khoảng cách từ tâm của cánh quạt đến mặt đất là
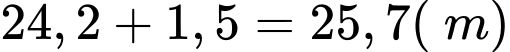

Cách 1:
Ta có:
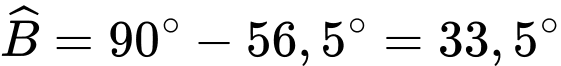
Áp dụng định lísin, ta có:


Vậy khoảng cách từ tâm của cánh quạt đến mặt đất là
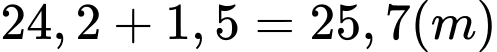
Cách 2:
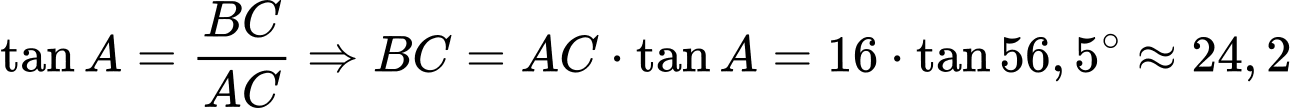
Vậy khoảng cách từ tâm của cánh quạt đến mặt đất là
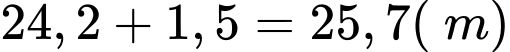
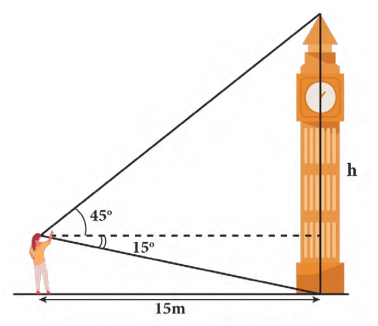
Câu 3 [238396]: Một người quan sát đứng cách một cái tháp 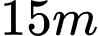 , nhìn thấy đỉnh tháp một góc
, nhìn thấy đỉnh tháp một góc 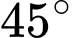 và nhìn dưới chân tháp một góc
và nhìn dưới chân tháp một góc 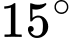 so với phương nằm ngang như trong hình vẽ. Tính chiều cao
so với phương nằm ngang như trong hình vẽ. Tính chiều cao 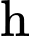 của tháp.
của tháp.
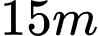 , nhìn thấy đỉnh tháp một góc
, nhìn thấy đỉnh tháp một góc 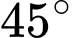 và nhìn dưới chân tháp một góc
và nhìn dưới chân tháp một góc 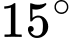 so với phương nằm ngang như trong hình vẽ. Tính chiều cao
so với phương nằm ngang như trong hình vẽ. Tính chiều cao  của tháp.
của tháp.
Ta có
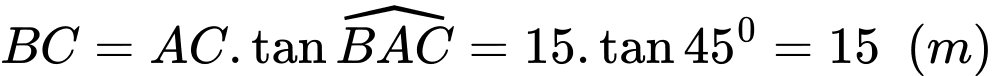
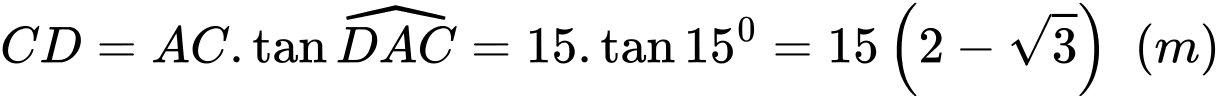
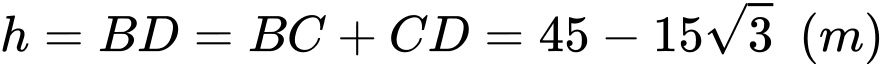 .Vậy chiều cao của tháp là
.Vậy chiều cao của tháp là 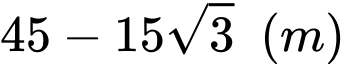 .
.
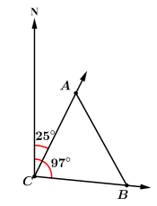
Câu 4 [243356]: Vào lúc 1 giờ chiều, hai vận động viên A và B xuất phát từ cùng một vị trí. Vận động viên A chạy với vận tốc 14 km/h theo một góc định hướng là 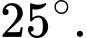 Vận động viên B chạy với vận tốc 12 km/h theo một góc định hướng là
Vận động viên B chạy với vận tốc 12 km/h theo một góc định hướng là 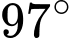 (tham khảo hình vẽ). Tại thời điểm nào A sẽ cách B một khoảng 20 km?
(tham khảo hình vẽ). Tại thời điểm nào A sẽ cách B một khoảng 20 km?
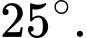 Vận động viên B chạy với vận tốc 12 km/h theo một góc định hướng là
Vận động viên B chạy với vận tốc 12 km/h theo một góc định hướng là 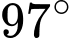 (tham khảo hình vẽ). Tại thời điểm nào A sẽ cách B một khoảng 20 km?
(tham khảo hình vẽ). Tại thời điểm nào A sẽ cách B một khoảng 20 km?
Sau 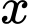 giờ thì vận động viên A chạy được
giờ thì vận động viên A chạy được  vận động viên B chạy được
vận động viên B chạy được 
Ta có: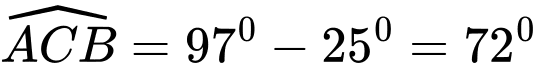
Áp dụng định lý cosin ta được: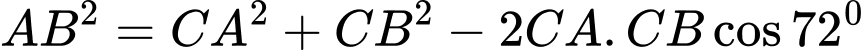
Suy ra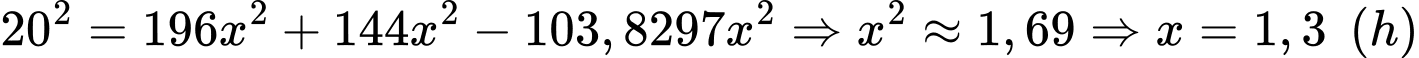
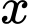 giờ thì vận động viên A chạy được
giờ thì vận động viên A chạy được  vận động viên B chạy được
vận động viên B chạy được 
Ta có:
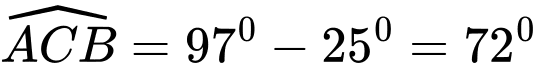
Áp dụng định lý cosin ta được:
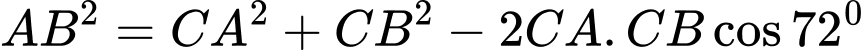
Suy ra
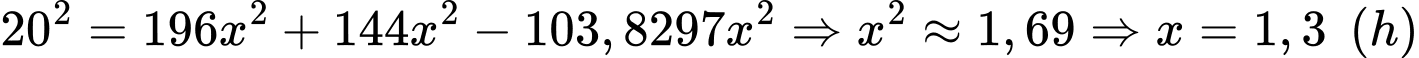
Câu 5 [243351]: An và Bắc đang xem xét mua một mảnh đất. Nhân viên nhà đất cung cấp cho họ một bản vẽ chi tiết như hình vẽ. Hãy tính diện tích mảnh đất.


Ta có: 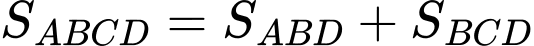
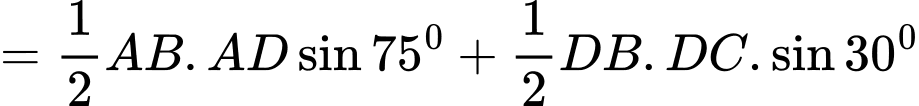
Trong đó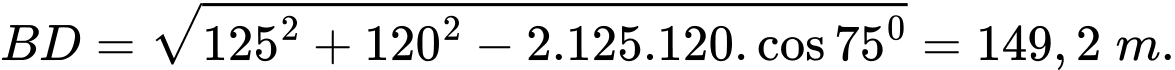
Suy ra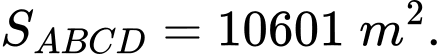
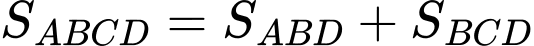
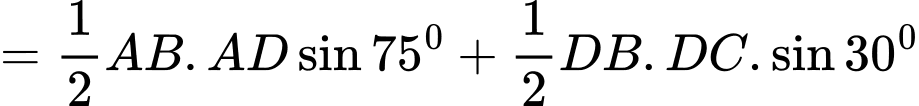
Trong đó
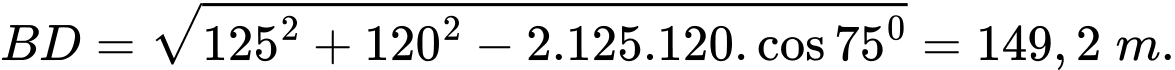
Suy ra
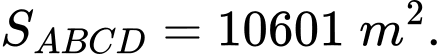
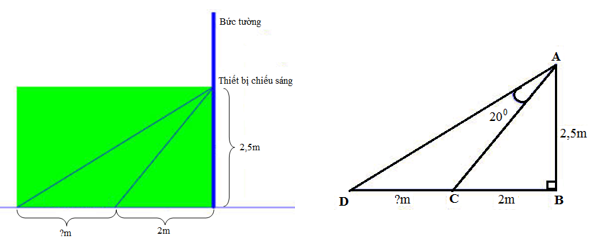
Câu 6 [242533]: Người ta cần lắp đặt một thiết bị chiếu sáng gắn trên tường cho một phòng triển lãm như hình vẽ. Thiết bị này có góc chiếu sáng là 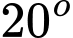 và cần đặt cao hơn mặt đất là 2,5m. Người ta đặt thiết bị chiếu sáng này sát tường và được canh chỉnh sao cho trên mặt đất dải ánh sáng bắt đầu từ vị trí cách tường 2m. Hãy tính độ dài vùng được chiếu sáng trên mặt đất.
và cần đặt cao hơn mặt đất là 2,5m. Người ta đặt thiết bị chiếu sáng này sát tường và được canh chỉnh sao cho trên mặt đất dải ánh sáng bắt đầu từ vị trí cách tường 2m. Hãy tính độ dài vùng được chiếu sáng trên mặt đất.
 và cần đặt cao hơn mặt đất là 2,5m. Người ta đặt thiết bị chiếu sáng này sát tường và được canh chỉnh sao cho trên mặt đất dải ánh sáng bắt đầu từ vị trí cách tường 2m. Hãy tính độ dài vùng được chiếu sáng trên mặt đất.
và cần đặt cao hơn mặt đất là 2,5m. Người ta đặt thiết bị chiếu sáng này sát tường và được canh chỉnh sao cho trên mặt đất dải ánh sáng bắt đầu từ vị trí cách tường 2m. Hãy tính độ dài vùng được chiếu sáng trên mặt đất.
Xét 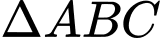 vuông tại B, ta có:
vuông tại B, ta có: 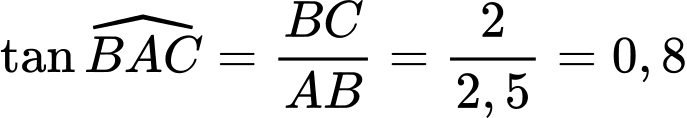
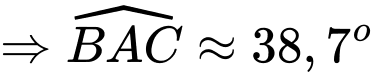
Ta có: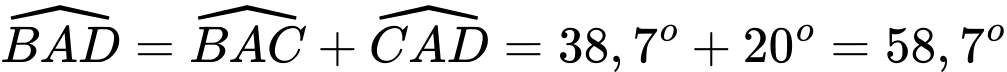
Xét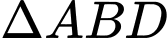 vuông tại B, Ta có:
vuông tại B, Ta có: 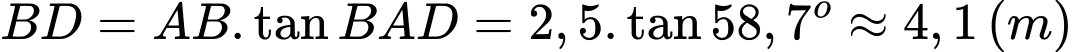
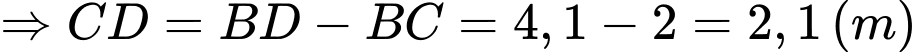
Vậy độ dài vùng được chiếu sáng trên mặt đất là 2,1 (m).
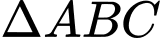 vuông tại B, ta có:
vuông tại B, ta có: 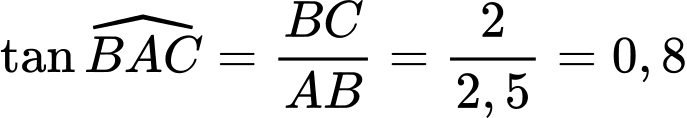
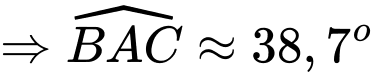
Ta có:
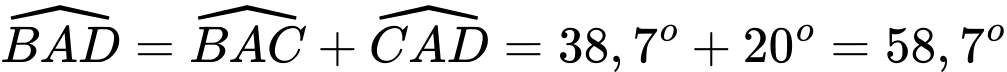
Xét
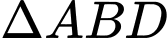 vuông tại B, Ta có:
vuông tại B, Ta có: 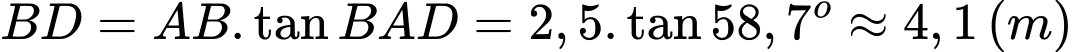
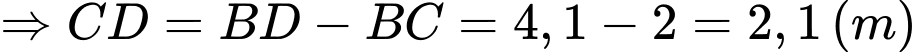
Vậy độ dài vùng được chiếu sáng trên mặt đất là 2,1 (m).
Câu 7 [239891]: Một người đi dọc bờ biển từ vị trí 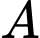 đến vị trí
đến vị trí 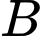 và quan sát một ngọn hải đăng. Góc nghiêng của phương quan sát từ các vị trí A, B tới ngọn hải đăng với đường đi của người quan sát là
và quan sát một ngọn hải đăng. Góc nghiêng của phương quan sát từ các vị trí A, B tới ngọn hải đăng với đường đi của người quan sát là 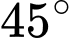 và
và 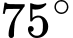 . Biết khoảng cách giữa hai vị trí A, B là
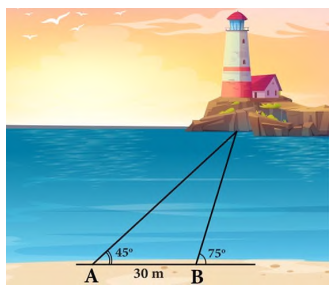
. Biết khoảng cách giữa hai vị trí A, B là 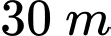 (Hình). Ngọn hải đăng cách bờ biển bao nhiêu mét (làm tròn kết quả đến hàng đơn vị)?
(Hình). Ngọn hải đăng cách bờ biển bao nhiêu mét (làm tròn kết quả đến hàng đơn vị)?
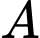 đến vị trí
đến vị trí 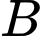 và quan sát một ngọn hải đăng. Góc nghiêng của phương quan sát từ các vị trí A, B tới ngọn hải đăng với đường đi của người quan sát là
và quan sát một ngọn hải đăng. Góc nghiêng của phương quan sát từ các vị trí A, B tới ngọn hải đăng với đường đi của người quan sát là 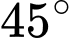 và
và 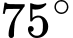 . Biết khoảng cách giữa hai vị trí A, B là
. Biết khoảng cách giữa hai vị trí A, B là 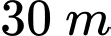 (Hình). Ngọn hải đăng cách bờ biển bao nhiêu mét (làm tròn kết quả đến hàng đơn vị)?
(Hình). Ngọn hải đăng cách bờ biển bao nhiêu mét (làm tròn kết quả đến hàng đơn vị)?
Gọi C là vị trí ngọn hải đăng và H là hình chiếu của C trên  .
.
Khi đó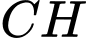 là khoảng cách từ ngọn hải đăng tới bờ biển.
là khoảng cách từ ngọn hải đăng tới bờ biển.
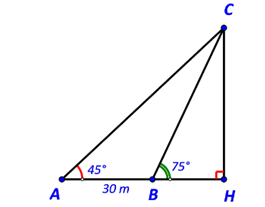
Ta có: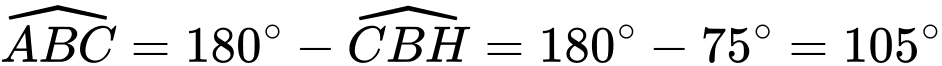
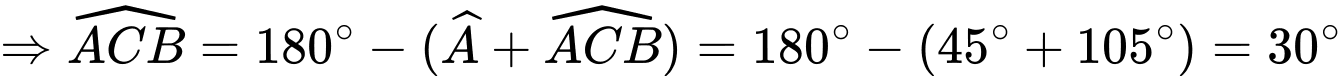 Áp dụng định lí sin trong tam giác
Áp dụng định lí sin trong tam giác 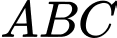 ta có:
ta có: 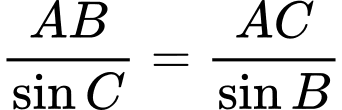
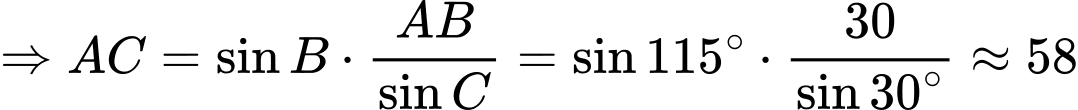
Tam giác ACH vuông tại H nên ta có:
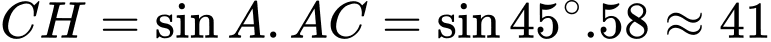
Vậy ngọn hải đăng cách bờ biển .
.
 .
.Khi đó
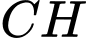 là khoảng cách từ ngọn hải đăng tới bờ biển.
là khoảng cách từ ngọn hải đăng tới bờ biển. 
Ta có:
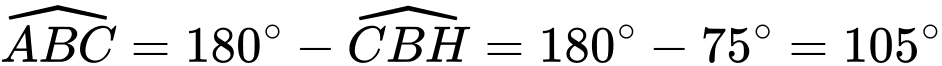
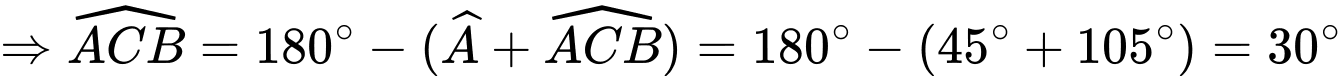 Áp dụng định lí sin trong tam giác
Áp dụng định lí sin trong tam giác 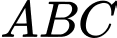 ta có:
ta có: 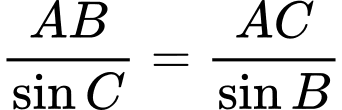
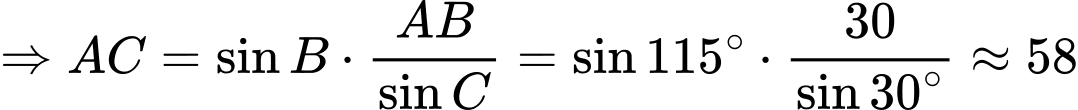
Tam giác ACH vuông tại H nên ta có:
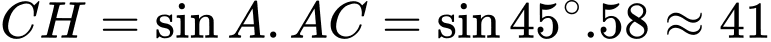
Vậy ngọn hải đăng cách bờ biển
 .
.
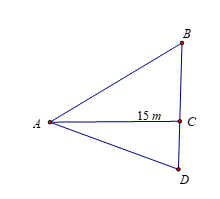
Câu 8 [239356]: Tính chiều cao  của một ngọn núi. Biết tại hai điểm C, D cách nhau 1 km trên mặt đất (B, C, D thẳng hàng), người ta nhìn thấy đỉnh A của núi với góc nâng lần lượt là
của một ngọn núi. Biết tại hai điểm C, D cách nhau 1 km trên mặt đất (B, C, D thẳng hàng), người ta nhìn thấy đỉnh A của núi với góc nâng lần lượt là 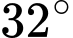 và
và 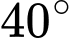 (Hình).
(Hình).
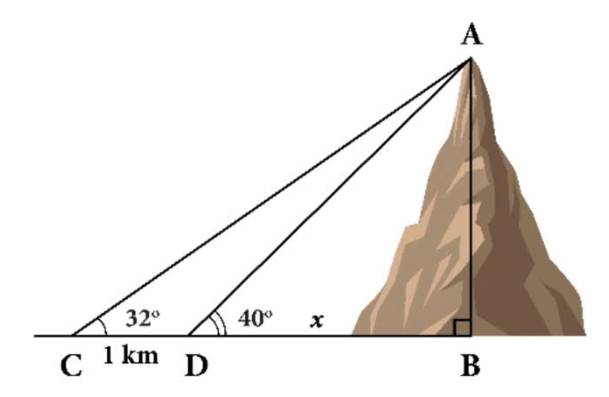
 của một ngọn núi. Biết tại hai điểm C, D cách nhau 1 km trên mặt đất (B, C, D thẳng hàng), người ta nhìn thấy đỉnh A của núi với góc nâng lần lượt là
của một ngọn núi. Biết tại hai điểm C, D cách nhau 1 km trên mặt đất (B, C, D thẳng hàng), người ta nhìn thấy đỉnh A của núi với góc nâng lần lượt là 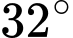 và
và 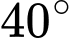 (Hình).
(Hình).
Tam giác 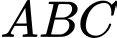 vuông tại
vuông tại 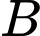 nên ta có:
nên ta có:
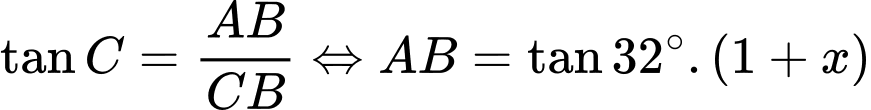
Tam giác ADB vuông tại B nên ta có:
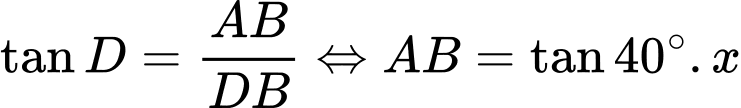
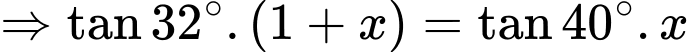

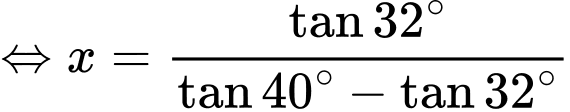
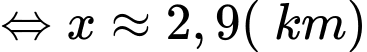
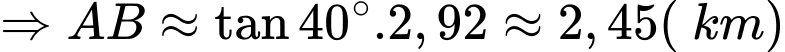
Vậy chiều cao của ngọn núi là 2,45 km.
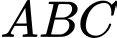 vuông tại
vuông tại 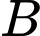 nên ta có:
nên ta có: 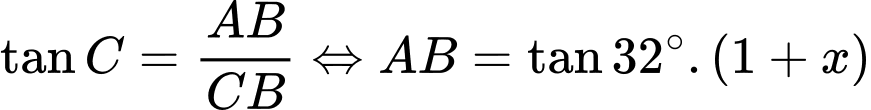
Tam giác ADB vuông tại B nên ta có:
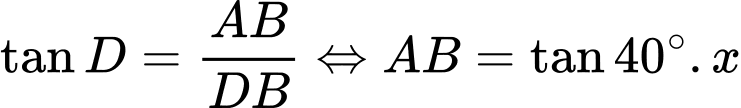
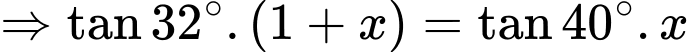

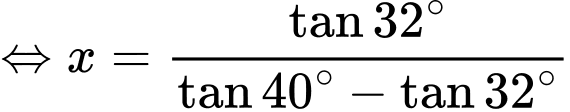
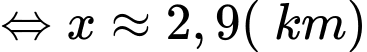
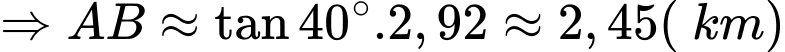
Vậy chiều cao của ngọn núi là 2,45 km.
Câu 9 [238395]: Các góc nhìn đến đỉnh núi so với mực nước biển được đo từ hai đèn tín hiệu A và B trên biển được thể hiện trên hình vẽ. Nếu các đèn tín hiệu cách nhau 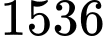 m thì ngọn núi cao bao nhiêu (tính gần đúng sau dấu phẩy hai chữ số)?
m thì ngọn núi cao bao nhiêu (tính gần đúng sau dấu phẩy hai chữ số)?
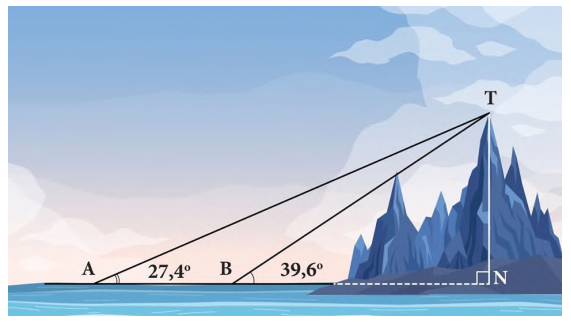
 m thì ngọn núi cao bao nhiêu (tính gần đúng sau dấu phẩy hai chữ số)?
m thì ngọn núi cao bao nhiêu (tính gần đúng sau dấu phẩy hai chữ số)?
Ta có 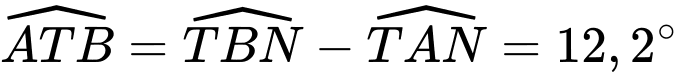 .
.
Áp dụng định lí sin cho tam giác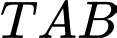 :
: 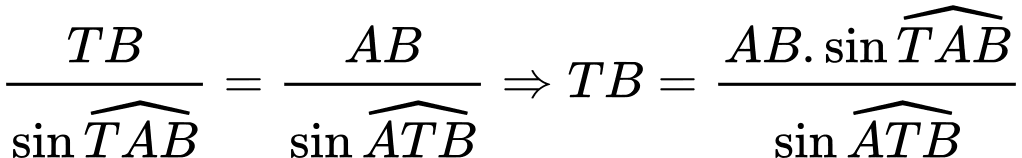 .
.
Xét tam giác vuông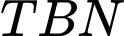 ta có:
ta có:
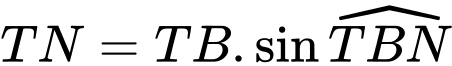
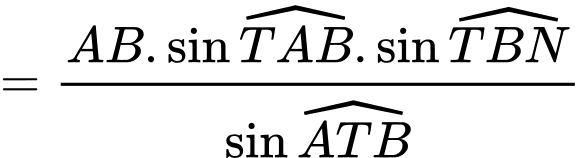
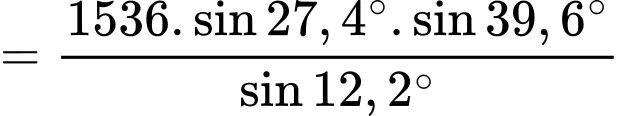
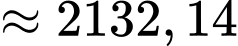 .
.
Vậy chiều cao ngọn núi xấp xỉ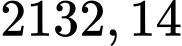 m.
m.
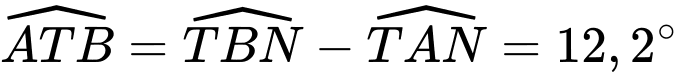 .
.Áp dụng định lí sin cho tam giác
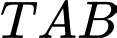 :
: 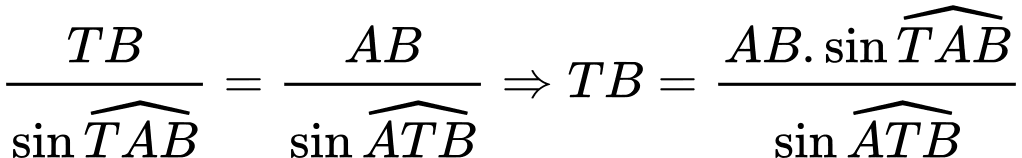 .
.Xét tam giác vuông
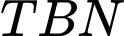 ta có:
ta có: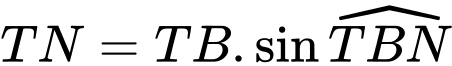
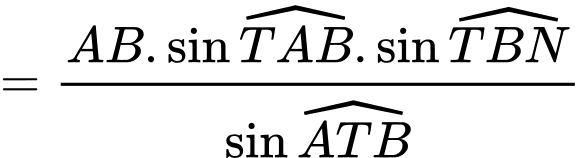
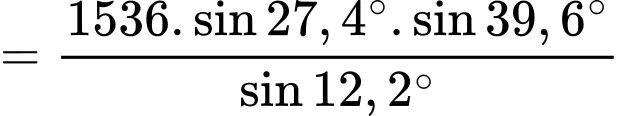
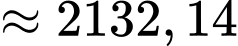 .
.Vậy chiều cao ngọn núi xấp xỉ
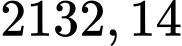 m.
m.
Câu 10 [238401]: Từ hai vị trí 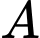 ,
,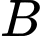 người ta quan sát một cái cây (hình vẽ). Lấy
người ta quan sát một cái cây (hình vẽ). Lấy  là điểm gốc cây,
là điểm gốc cây, 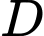 là điểm ngọn cây.
là điểm ngọn cây. 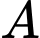 ,
,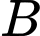 cùng thẳng hàng với điểm
cùng thẳng hàng với điểm 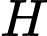 thuộc chiều cao
thuộc chiều cao 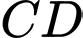 của cây. Người ta đo được
của cây. Người ta đo được 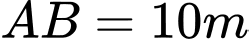 ,
, 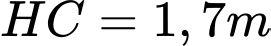 ,
, 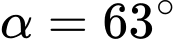 ,
, 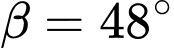 . Tính chiều cao của cây đó.
. Tính chiều cao của cây đó.
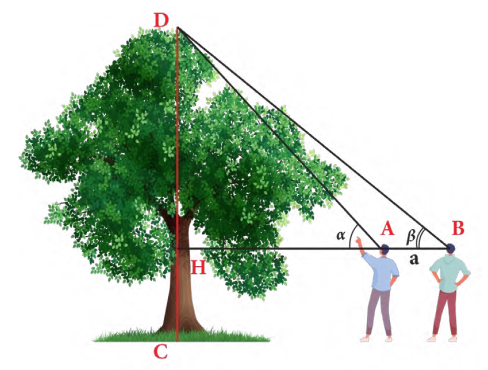
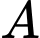 ,
,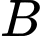 người ta quan sát một cái cây (hình vẽ). Lấy
người ta quan sát một cái cây (hình vẽ). Lấy  là điểm gốc cây,
là điểm gốc cây, 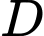 là điểm ngọn cây.
là điểm ngọn cây. 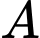 ,
,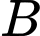 cùng thẳng hàng với điểm
cùng thẳng hàng với điểm 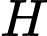 thuộc chiều cao
thuộc chiều cao 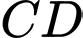 của cây. Người ta đo được
của cây. Người ta đo được 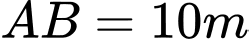 ,
, 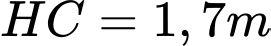 ,
, 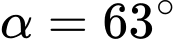 ,
, 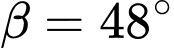 . Tính chiều cao của cây đó.
. Tính chiều cao của cây đó.
Ta có 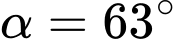
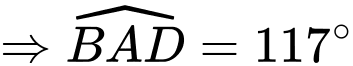
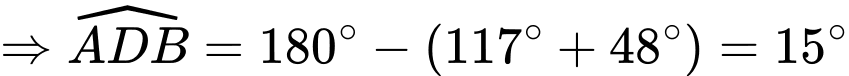
Áp dụng định lý sin trong tam giác ABD ta có: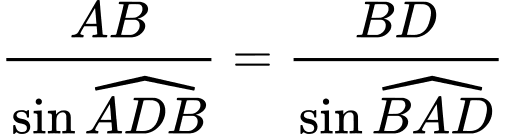
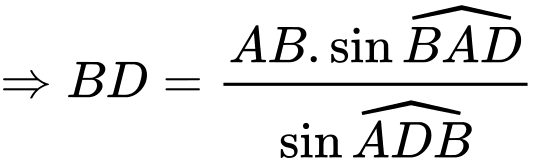
Tam giác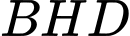 vuông tại
vuông tại 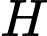 nên có:
nên có: 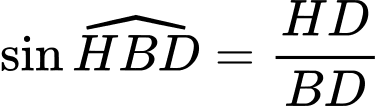
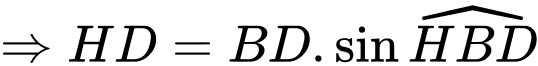
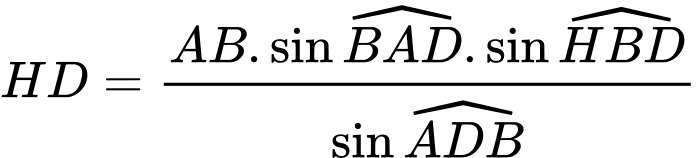
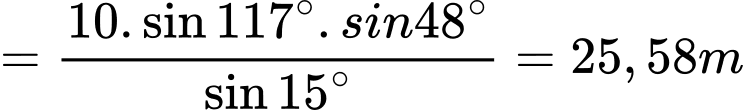 .
.
Vây chiều cao của cây là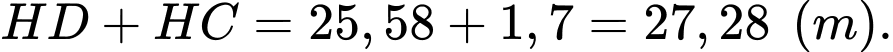
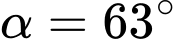
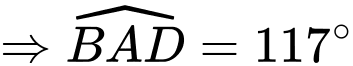
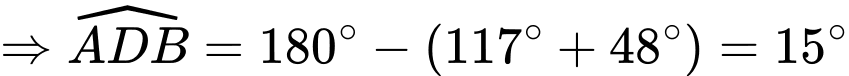
Áp dụng định lý sin trong tam giác ABD ta có:
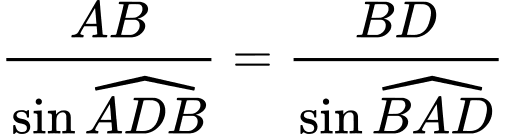
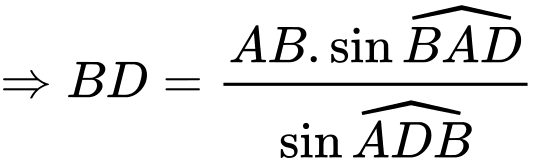
Tam giác
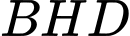 vuông tại
vuông tại 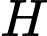 nên có:
nên có: 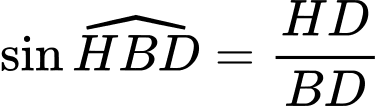
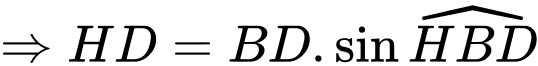
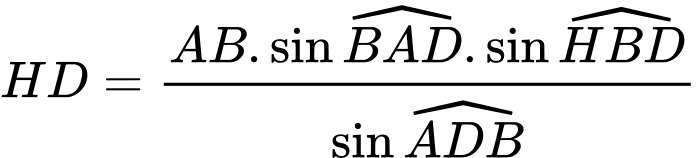
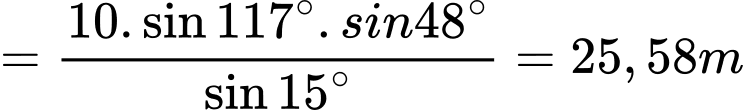 .
. Vây chiều cao của cây là
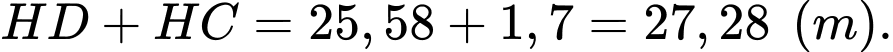
Câu 11 [243348]: Một tòa tháp cao 42 mét đứng trên đỉnh một ngọn đồi. Từ một điểm trên mặt đất cách xa chân đồi, có thể nhìn thấy đỉnh tháp và chân tháp dưới góc 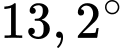 và
và  so với mặt đất. Tính chiều cao của ngọn đồi.
so với mặt đất. Tính chiều cao của ngọn đồi.

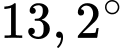 và
và  so với mặt đất. Tính chiều cao của ngọn đồi.
so với mặt đất. Tính chiều cao của ngọn đồi.
Ta có: 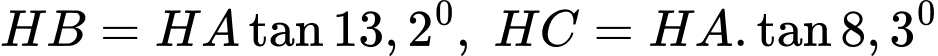
Lại có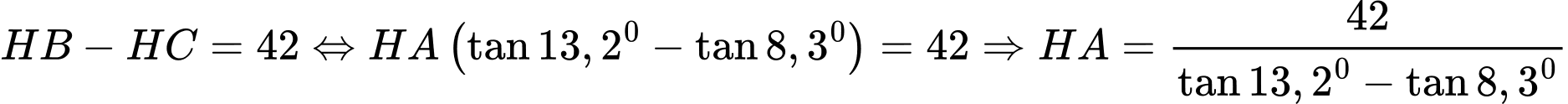
Suy ra chiều cao ngọn đồi là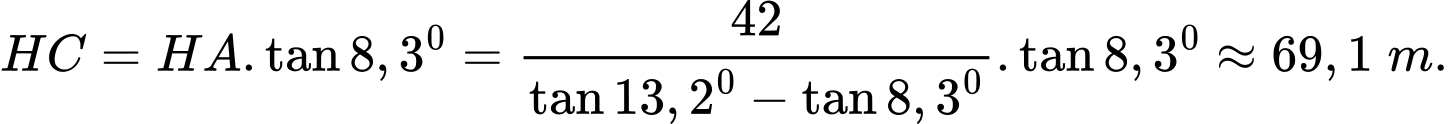
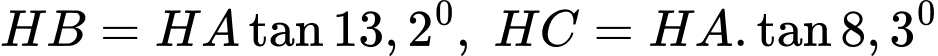
Lại có
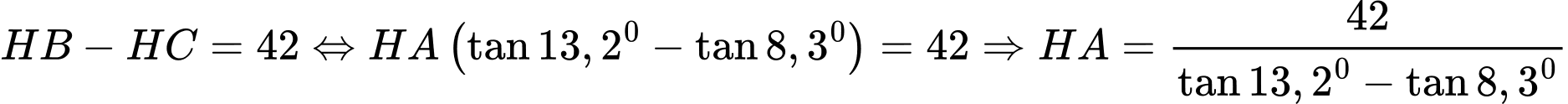
Suy ra chiều cao ngọn đồi là
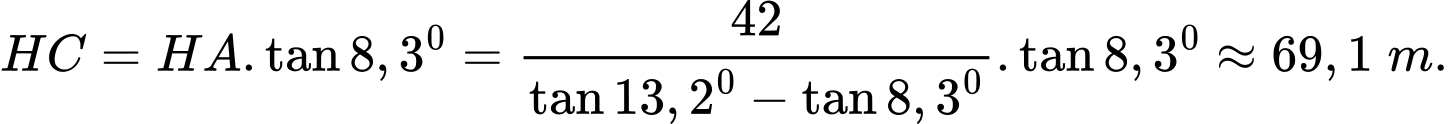
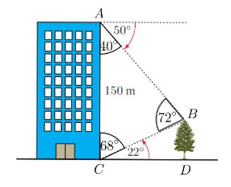
Câu 12 [580931]: Đứng ở chân của một tòa nhà Nam phải nhìn hướng lên 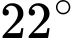 để thấy ngọn của một cái cây. Nếu đứng ở đỉnh của tòa nhà đó cao 150 mét so với mặt đất, Nam phải nhìn hướng xuống một góc
để thấy ngọn của một cái cây. Nếu đứng ở đỉnh của tòa nhà đó cao 150 mét so với mặt đất, Nam phải nhìn hướng xuống một góc 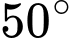 so với phương nằm ngang để thấy ngọn của cái đây đó. Tính khoảng cách từ tòa nhà đến cây.
so với phương nằm ngang để thấy ngọn của cái đây đó. Tính khoảng cách từ tòa nhà đến cây.
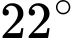 để thấy ngọn của một cái cây. Nếu đứng ở đỉnh của tòa nhà đó cao 150 mét so với mặt đất, Nam phải nhìn hướng xuống một góc
để thấy ngọn của một cái cây. Nếu đứng ở đỉnh của tòa nhà đó cao 150 mét so với mặt đất, Nam phải nhìn hướng xuống một góc 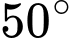 so với phương nằm ngang để thấy ngọn của cái đây đó. Tính khoảng cách từ tòa nhà đến cây.
so với phương nằm ngang để thấy ngọn của cái đây đó. Tính khoảng cách từ tòa nhà đến cây.
HD: Ta có: 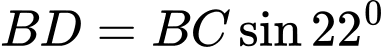 (1)là chiều cao cái cây
(1)là chiều cao cái cây
Lại có: 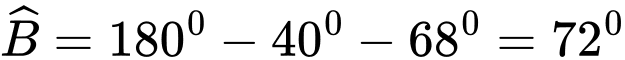
Áp dụng định lý sin ta có: 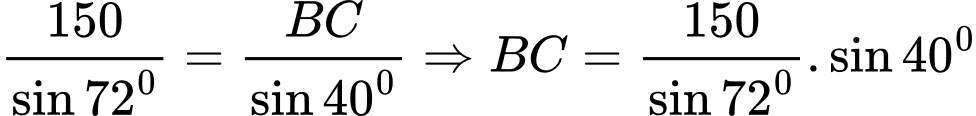 thay vào (1) ta tính được chiều cao xấp sỹ 38 mét.
thay vào (1) ta tính được chiều cao xấp sỹ 38 mét.
Khoảng cách từ tòa nhà đến cái cây là 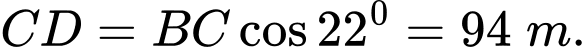
Câu 13 [238402]: Một người quan sát đỉnh của một ngọn núi nhân tạo từ hai vị trí khác nhau của tòa nhà. Lần đầu tiên người đó quan sát đỉnh núi từ tầng trệt với phương nhìn tạo với phương nằm ngang 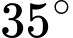 và lần thứ hai người này quan sát tại sân thượng của cùng tòa nhà đó với phương nằm ngang
và lần thứ hai người này quan sát tại sân thượng của cùng tòa nhà đó với phương nằm ngang 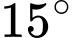 (như hình vẽ). Tính chiều cao ngọn núi biết rằng tòa nhà cao
(như hình vẽ). Tính chiều cao ngọn núi biết rằng tòa nhà cao 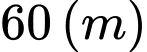 .
.
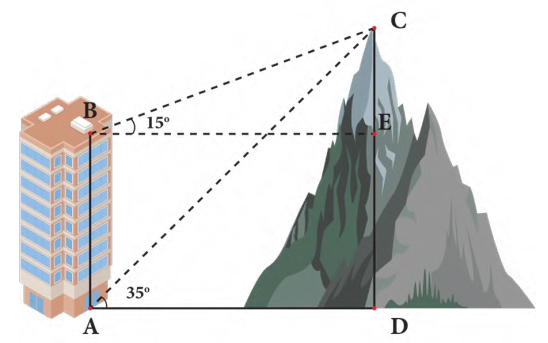
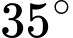 và lần thứ hai người này quan sát tại sân thượng của cùng tòa nhà đó với phương nằm ngang
và lần thứ hai người này quan sát tại sân thượng của cùng tòa nhà đó với phương nằm ngang 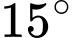 (như hình vẽ). Tính chiều cao ngọn núi biết rằng tòa nhà cao
(như hình vẽ). Tính chiều cao ngọn núi biết rằng tòa nhà cao 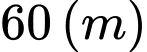 .
.
Ta có: 


Áp dụng định lý hàm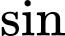 cho
cho 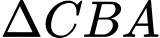 ta có
ta có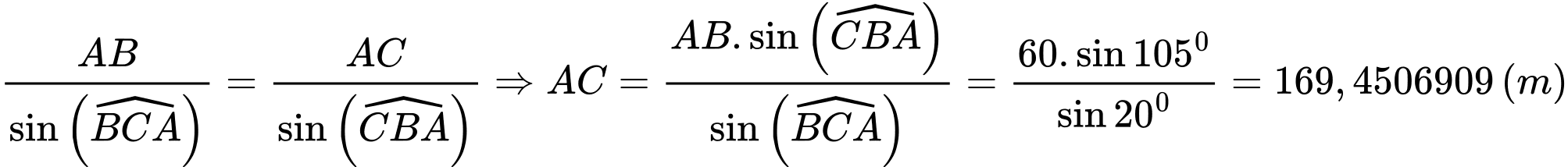
Xét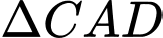 vuông tại
vuông tại 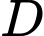 , ta có
, ta có  .
.



Áp dụng định lý hàm
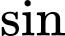 cho
cho 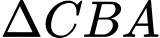 ta có
ta có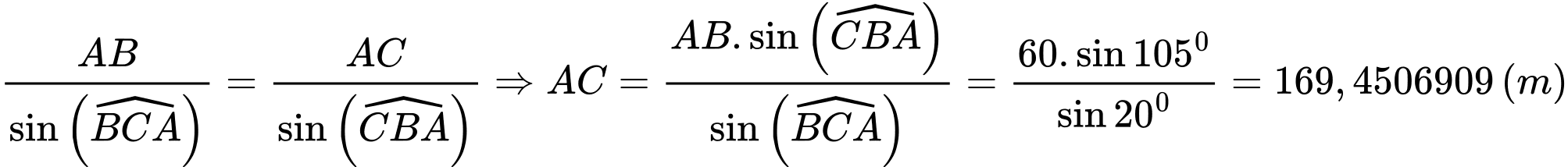
Xét
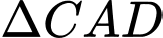 vuông tại
vuông tại 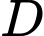 , ta có
, ta có  .
.
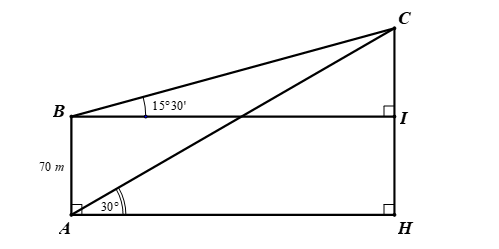
Câu 14 [238394]: Từ hai vị trí 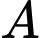 và
và 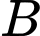 của một tòa nhà, người ta quan sát đỉnh
của một tòa nhà, người ta quan sát đỉnh  của ngọn núi. Biết rằng độ cao
của ngọn núi. Biết rằng độ cao 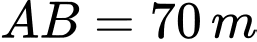 , phương nhìn
, phương nhìn 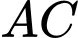 tạo với phương nằm ngang một góc
tạo với phương nằm ngang một góc 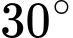 , phương nhìn
, phương nhìn 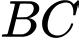 tạo với phương nằm ngang một góc
tạo với phương nằm ngang một góc 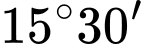 (như hình vẽ). Tính độ cao
(như hình vẽ). Tính độ cao 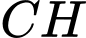 của ngọn núi so với mặt đất.
của ngọn núi so với mặt đất.
 và
và  của một tòa nhà, người ta quan sát đỉnh
của một tòa nhà, người ta quan sát đỉnh  của ngọn núi. Biết rằng độ cao
của ngọn núi. Biết rằng độ cao 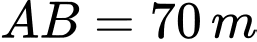 , phương nhìn
, phương nhìn 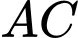 tạo với phương nằm ngang một góc
tạo với phương nằm ngang một góc 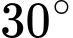 , phương nhìn
, phương nhìn 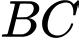 tạo với phương nằm ngang một góc
tạo với phương nằm ngang một góc 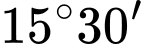 (như hình vẽ). Tính độ cao
(như hình vẽ). Tính độ cao 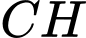 của ngọn núi so với mặt đất.
của ngọn núi so với mặt đất.
Cách 1:
+ Ta có:
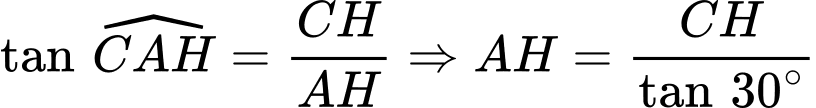 .
.
+ Lại có:
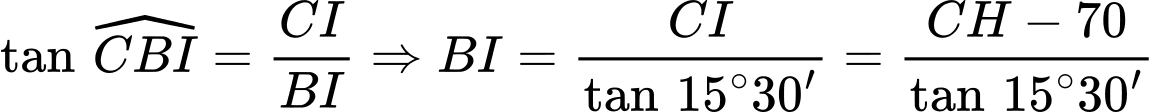 .
.
+ Do
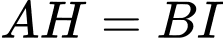 nên
nên 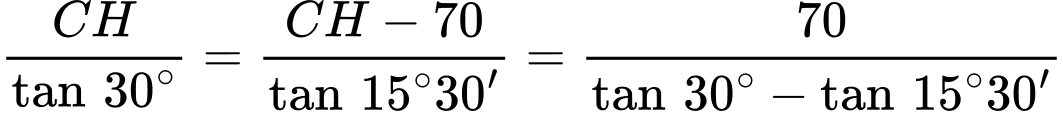 .
.
+ Vậy
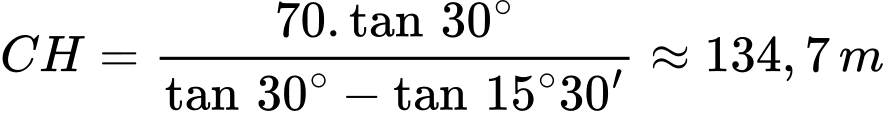 .
.
Cách 2:
+ Ta có:
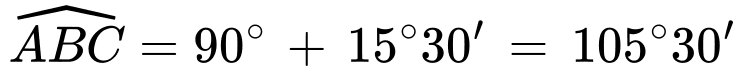 .
.
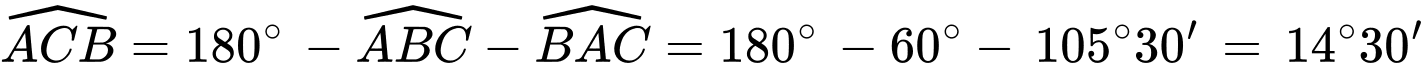 .
.
+ Áp dụng định lí sin trong tam giác
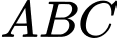 , ta có:
, ta có:
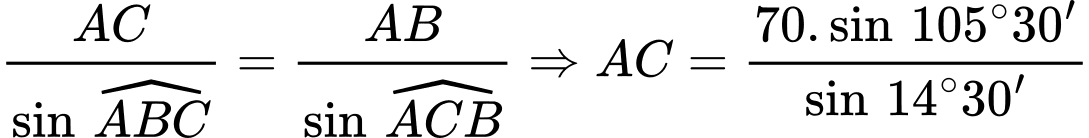 .
.
+ Lại có:
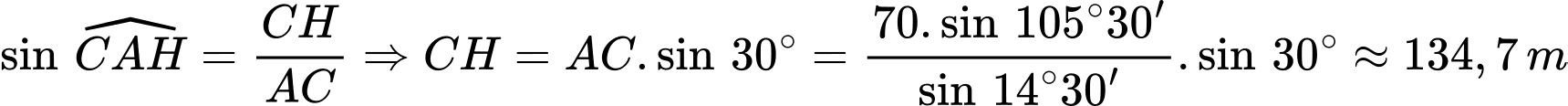 .
.
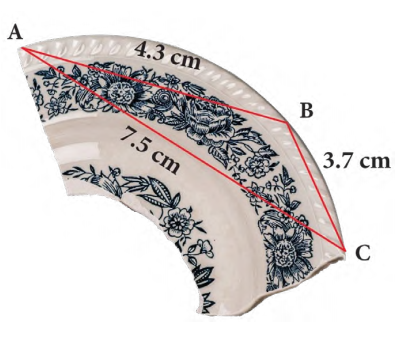
Câu 15 [238470]: Trong khi khai quật một ngôi mộ cổ, các nhà khảo cổ học đã tìm được một chiếc đĩa cổ hình tròn bị vỡ, các nhà khảo cổ muốn khôi phục lại hình dạng chiếc đĩa này. Để xác định bán kính của chiếc đĩa, các nhà khảo cổ lấy 3 điểm trên chiếc đĩa và tiến hành đo đạc thu được kết quả như hình vẽ (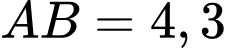 cm;
cm;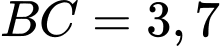 cm;
cm; 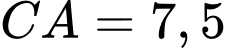 cm). Bán kính của chiếc đĩa này bằng (kết quả làm tròn tới hai chữ số sau dấu phẩy).
cm). Bán kính của chiếc đĩa này bằng (kết quả làm tròn tới hai chữ số sau dấu phẩy).
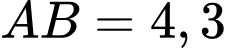 cm;
cm;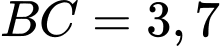 cm;
cm; 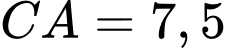 cm). Bán kính của chiếc đĩa này bằng (kết quả làm tròn tới hai chữ số sau dấu phẩy).
cm). Bán kính của chiếc đĩa này bằng (kết quả làm tròn tới hai chữ số sau dấu phẩy).
A, 5,73 cm.
B, 6,01cm.
C, 5,85cm.
D, 4,57cm.
Chọn A
Bán kính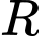 của chiếc đĩa bằng bán kính đường tròn ngoại tiếp tam giác
của chiếc đĩa bằng bán kính đường tròn ngoại tiếp tam giác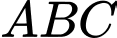 .
.
Nửa chu vi của tam giác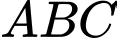 là:
là: 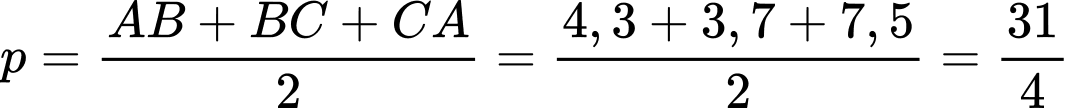 cm.
cm.
Diện tích tam giác là:
là: 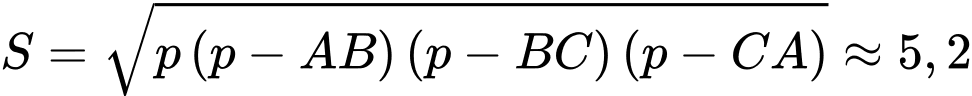 cm2.
cm2.
Mà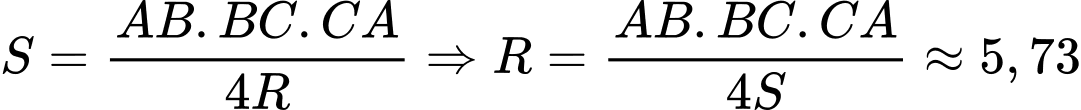 cm. Đáp án: A
cm. Đáp án: A
Bán kính
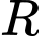 của chiếc đĩa bằng bán kính đường tròn ngoại tiếp tam giác
của chiếc đĩa bằng bán kính đường tròn ngoại tiếp tam giác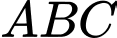 .
.
Nửa chu vi của tam giác
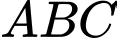 là:
là: 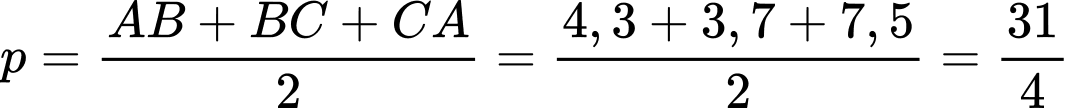 cm.
cm.
Diện tích tam giác
 là:
là: 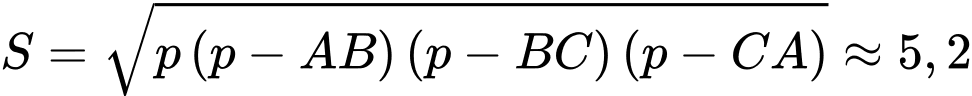 cm2.
cm2.
Mà
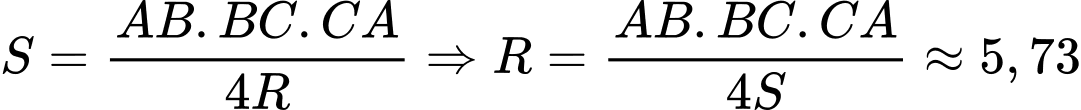 cm. Đáp án: A
cm. Đáp án: A
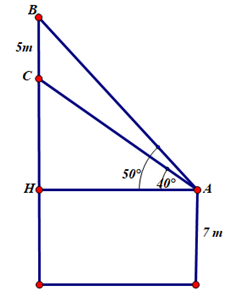
Câu 16 [580932]: Trên nóc một tòa nhà có một cột ăng-ten cao 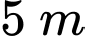 . Từ một vị trí quan sát A cao 7 m so với mặt đất có thể nhìn thấy đỉnh
. Từ một vị trí quan sát A cao 7 m so với mặt đất có thể nhìn thấy đỉnh 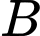 và chân
và chân  của cột ăng-ten, với các góc tương ứng là
của cột ăng-ten, với các góc tương ứng là 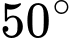 và
và 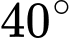 so với phương nằm ngang
so với phương nằm ngang 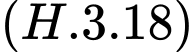
Tính chiều cao của tòa nhà.
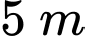 . Từ một vị trí quan sát A cao 7 m so với mặt đất có thể nhìn thấy đỉnh
. Từ một vị trí quan sát A cao 7 m so với mặt đất có thể nhìn thấy đỉnh 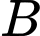 và chân
và chân  của cột ăng-ten, với các góc tương ứng là
của cột ăng-ten, với các góc tương ứng là 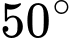 và
và 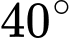 so với phương nằm ngang
so với phương nằm ngang 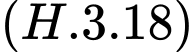

Tính chiều cao của tòa nhà.
Tính các góc của tam giác 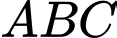 .
.
Gọi H là hình chiếu của 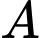 lên đường thẳng
lên đường thẳng 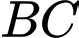 .
.
Xét tam giác 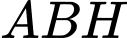 , vuông tại H ta có:
, vuông tại H ta có: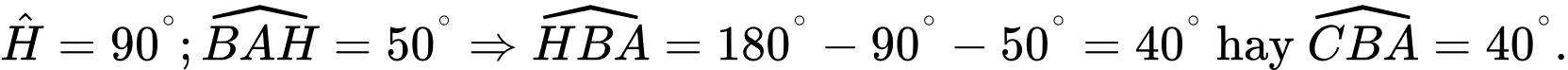
Từ  và
và  , suy ra:
, suy ra: 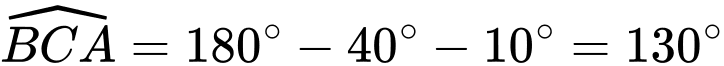 .
.
Vậy ba góc của tam giác 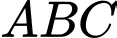 lần lượt là:
lần lượt là: 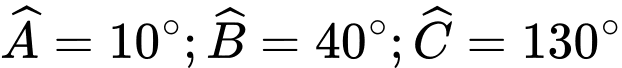 .
.
Tính chiều cao của tòa nhà.
Áp dụng định lý sin cho tam giác 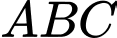 , ta được:
, ta được: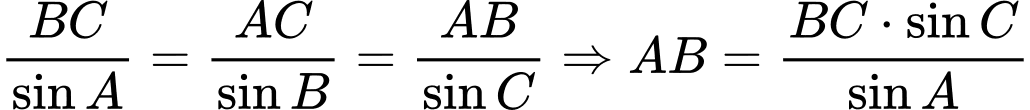
Mà 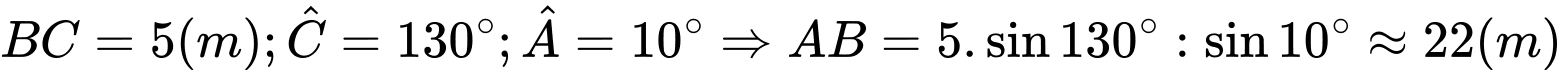
Xét tam giác 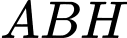 , vuông tại H ta có:
, vuông tại H ta có: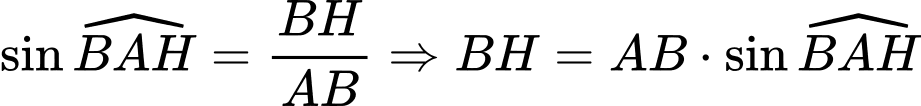
Mà: 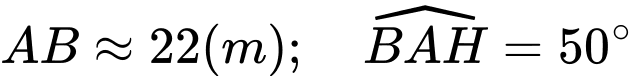
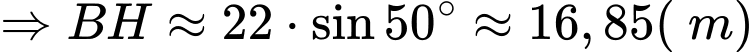
Vậy chiều cao của tòa nhà là: 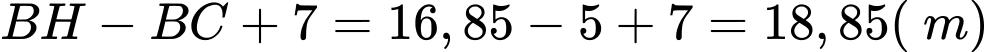
Câu 17 [579669]: [Đề mẫu HSA 2024]: Để đo chiều cao tòa tháp người ta dùng dụng cụ đo góc có chiều cao 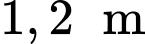 đặt tại hai vị trí trên mặt đất cách nhau một khoảng
đặt tại hai vị trí trên mặt đất cách nhau một khoảng 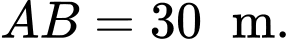 Tại vị trí
Tại vị trí 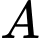 và
và 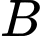 góc đo thu được so với phương ngang lần lượt là
góc đo thu được so với phương ngang lần lượt là 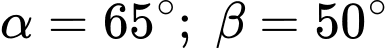 (hình minh họa). Chiều cao
(hình minh họa). Chiều cao  của tòa tháp (từ điểm
của tòa tháp (từ điểm 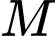 tới mặt đất) là bao nhiêu?
tới mặt đất) là bao nhiêu?
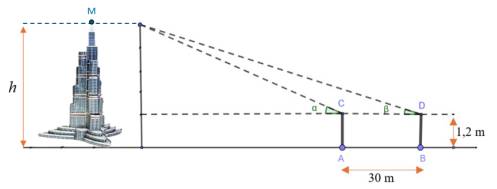
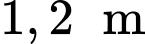 đặt tại hai vị trí trên mặt đất cách nhau một khoảng
đặt tại hai vị trí trên mặt đất cách nhau một khoảng 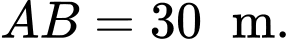 Tại vị trí
Tại vị trí 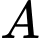 và
và 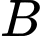 góc đo thu được so với phương ngang lần lượt là
góc đo thu được so với phương ngang lần lượt là 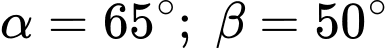 (hình minh họa). Chiều cao
(hình minh họa). Chiều cao  của tòa tháp (từ điểm
của tòa tháp (từ điểm 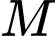 tới mặt đất) là bao nhiêu?
tới mặt đất) là bao nhiêu? 
A, 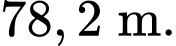
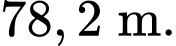
B, 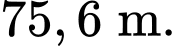
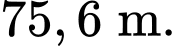
C, 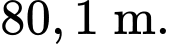
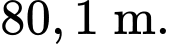
D, 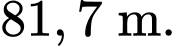
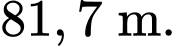
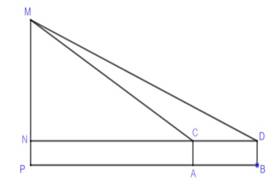
Xét
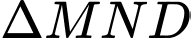 vuông:
vuông: 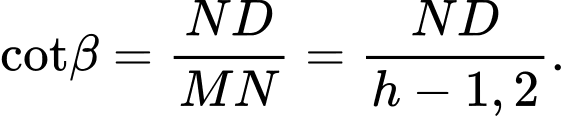
Xét
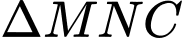 vuông:
vuông: 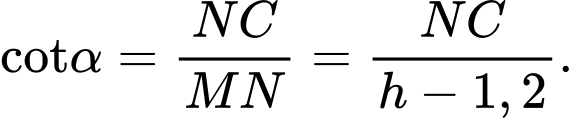
Suy ra
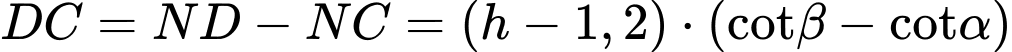
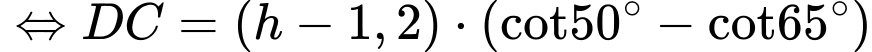
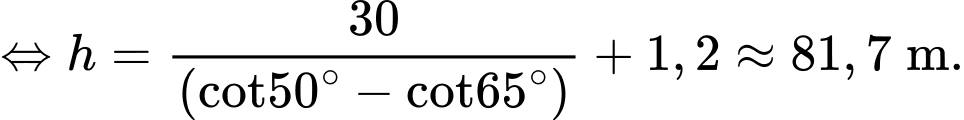
Chọn D. Đáp án: D
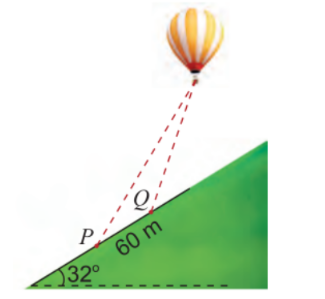
Câu 18 [239357]: Hai người quan sát khinh khí cầu tại hai địa điểm 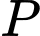 và
và  nằm ở sườn đồi nghiêng
nằm ở sườn đồi nghiêng 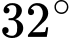 so với phương ngang, cách nhau
so với phương ngang, cách nhau 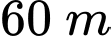 (Hình 10). Người quan sát tại
(Hình 10). Người quan sát tại 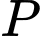 xác định góc nâng của khinh khí cầu là
xác định góc nâng của khinh khí cầu là 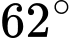 . Cùng lúc đó, người quan sát tại
. Cùng lúc đó, người quan sát tại  xác định góc nâng của khinh khí cầu đó là
xác định góc nâng của khinh khí cầu đó là 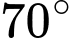 . Tính khoảng cách từ
. Tính khoảng cách từ  đến khinh khí cầu.
đến khinh khí cầu.
 và
và  nằm ở sườn đồi nghiêng
nằm ở sườn đồi nghiêng 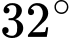 so với phương ngang, cách nhau
so với phương ngang, cách nhau 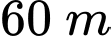 (Hình 10). Người quan sát tại
(Hình 10). Người quan sát tại 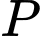 xác định góc nâng của khinh khí cầu là
xác định góc nâng của khinh khí cầu là 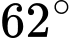 . Cùng lúc đó, người quan sát tại
. Cùng lúc đó, người quan sát tại  xác định góc nâng của khinh khí cầu đó là
xác định góc nâng của khinh khí cầu đó là 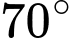 . Tính khoảng cách từ
. Tính khoảng cách từ  đến khinh khí cầu.
đến khinh khí cầu. 
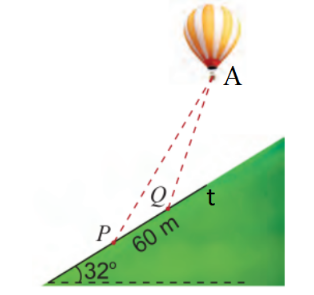
Gọi A là vị trí của khinh khí cầu, Pt là đường sườn đồi như hình.
Ta có:
Tại
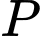 , góc nâng của khinh khí cầu là
, góc nâng của khinh khí cầu là 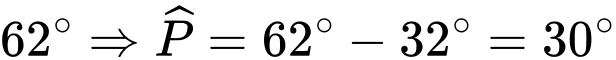
Tại Q, góc nâng của khinh khí cầu là
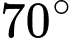
 và
và 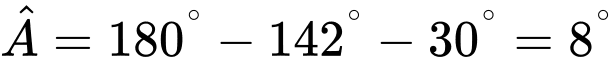
Áp dụng định lí sin trong tam giác APQ, ta có:

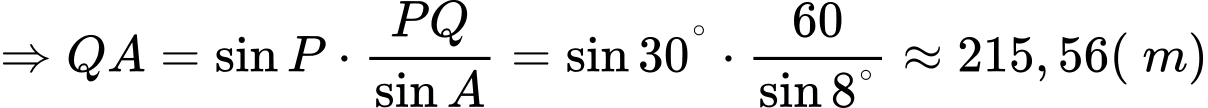
Vậy khoảng cách từ'
 đến khinh khí cầu là 215,56 m.
đến khinh khí cầu là 215,56 m.
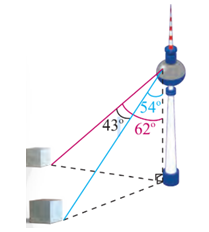
Câu 19 [239358]: Một người đứng ở trên một tháp truyền hình cao 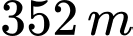 so với mặt đất, muốn xác định khoảng cách giữa hai cột mốc trên mặt đất bên dưới. Người đó quan sát thấy góc được tạo bởi hai đường ngắm tới hai mốc này là
so với mặt đất, muốn xác định khoảng cách giữa hai cột mốc trên mặt đất bên dưới. Người đó quan sát thấy góc được tạo bởi hai đường ngắm tới hai mốc này là 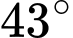 , góc giữa phương thẳng đứng và đường ngắm tới một điểm mốc trên mặt đất là
, góc giữa phương thẳng đứng và đường ngắm tới một điểm mốc trên mặt đất là 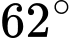 và đến điểm mốc khác là
và đến điểm mốc khác là 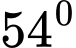 (hình vẽ). Tính khoảng cách giữa hai cột mốc này.
(hình vẽ). Tính khoảng cách giữa hai cột mốc này.
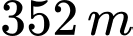 so với mặt đất, muốn xác định khoảng cách giữa hai cột mốc trên mặt đất bên dưới. Người đó quan sát thấy góc được tạo bởi hai đường ngắm tới hai mốc này là
so với mặt đất, muốn xác định khoảng cách giữa hai cột mốc trên mặt đất bên dưới. Người đó quan sát thấy góc được tạo bởi hai đường ngắm tới hai mốc này là 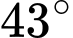 , góc giữa phương thẳng đứng và đường ngắm tới một điểm mốc trên mặt đất là
, góc giữa phương thẳng đứng và đường ngắm tới một điểm mốc trên mặt đất là 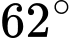 và đến điểm mốc khác là
và đến điểm mốc khác là 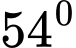 (hình vẽ). Tính khoảng cách giữa hai cột mốc này.
(hình vẽ). Tính khoảng cách giữa hai cột mốc này. 
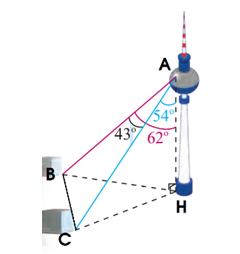
Gọi các điểm A, B, C, H như hình trên.
Xét tam giác
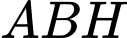 ta có:
ta có: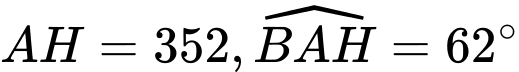
Mà
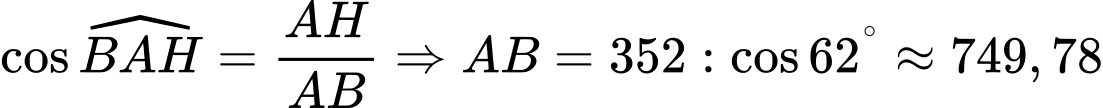
Tương tự, ta có:
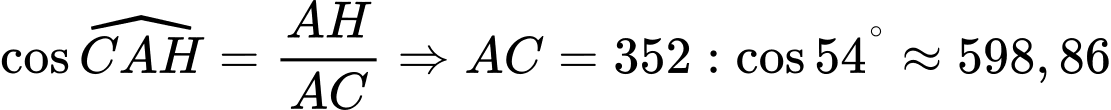
Áp dụng định lí cosin cho tam giác
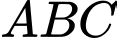 , ta có:
, ta có: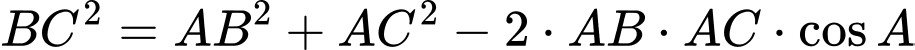
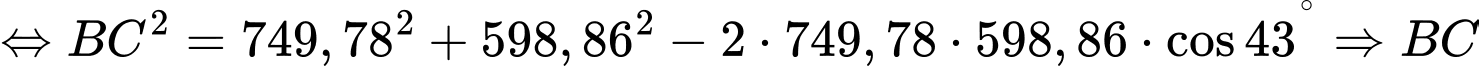
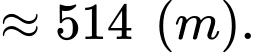
Vậy khoảng cách giữa hai cột mốc này là 514 m.
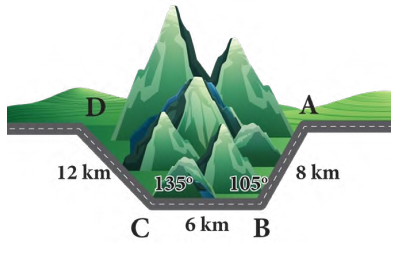
Câu 20 [240465]: Để tránh núi, giao thông hiện tại phải đi vòng như mô hình trong Hình. Để rút ngắn khoảng cách và tránh sạt lở núi, người ta dự định làm đường hầm xuyên núi, nối thẳng từ 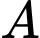 tới
tới 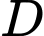 . Hỏi độ dài đường mới sẽ giảm bao nhiêu kilômét so với đường cũ?
. Hỏi độ dài đường mới sẽ giảm bao nhiêu kilômét so với đường cũ?
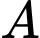 tới
tới 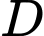 . Hỏi độ dài đường mới sẽ giảm bao nhiêu kilômét so với đường cũ?
. Hỏi độ dài đường mới sẽ giảm bao nhiêu kilômét so với đường cũ?
Bước 1:
Áp dụng định lí cos trong tam giác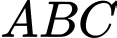 ta có:
ta có:

Bước 2:
Lại có: Theo định lí sin thì
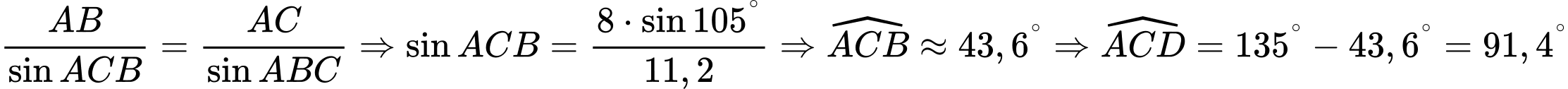
Bước 3:
Áp dụng định lí cos trong tam giác ACD ta có:
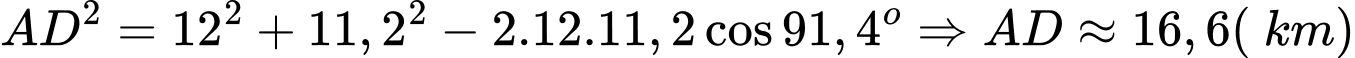
Bước 4:
Độ dài đường mới giảm số kilomet so với đường cũ là: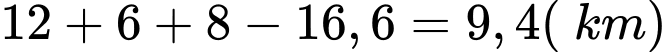
Áp dụng định lí cos trong tam giác
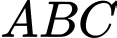 ta có:
ta có: 
Bước 2:
Lại có: Theo định lí sin thì
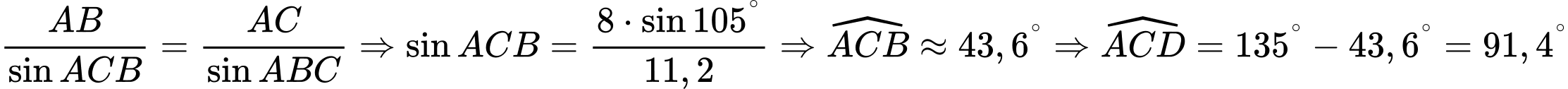
Bước 3:
Áp dụng định lí cos trong tam giác ACD ta có:
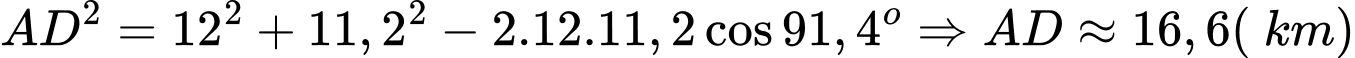
Bước 4:
Độ dài đường mới giảm số kilomet so với đường cũ là:
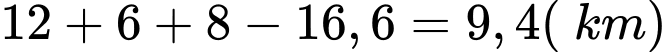
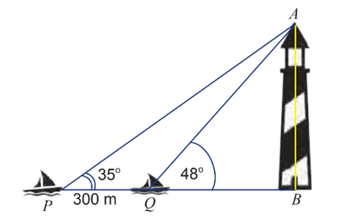
Câu 21 [239421]: Hai chiếc tàu thủy 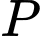 và
và  cách nhau
cách nhau 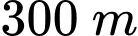 và thẳng hàng với chân
và thẳng hàng với chân 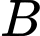 của tháp hải đăng
của tháp hải đăng  ở trên bờ biển (Hình). Từ
ở trên bờ biển (Hình). Từ 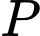 và
và  , người ta nhìn thấy tháp hải đăng
, người ta nhìn thấy tháp hải đăng  dưới các góc
dưới các góc 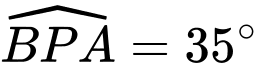 và
và 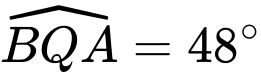 . Tính chiều cao của tháp hải đăng đó.
. Tính chiều cao của tháp hải đăng đó.
 và
và  cách nhau
cách nhau 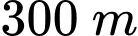 và thẳng hàng với chân
và thẳng hàng với chân 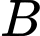 của tháp hải đăng
của tháp hải đăng  ở trên bờ biển (Hình). Từ
ở trên bờ biển (Hình). Từ 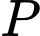 và
và  , người ta nhìn thấy tháp hải đăng
, người ta nhìn thấy tháp hải đăng  dưới các góc
dưới các góc 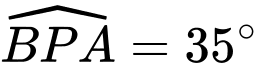 và
và 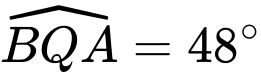 . Tính chiều cao của tháp hải đăng đó.
. Tính chiều cao của tháp hải đăng đó. 
Xét tam giác 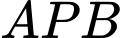 và
và  , ta có:
, ta có:
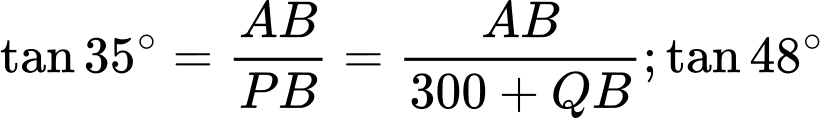
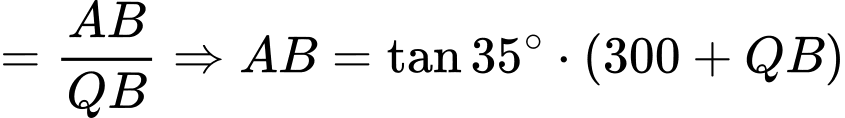
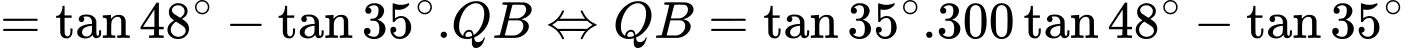
 =
= 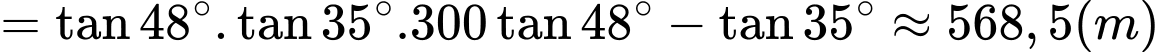
Vậy tháp hải đăng cao khoảng 568,5 m.
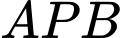 và
và  , ta có:
, ta có: 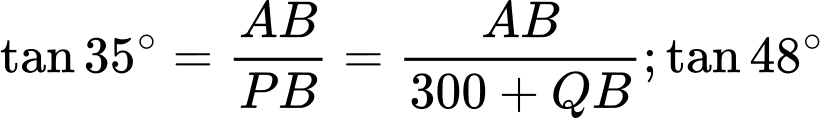
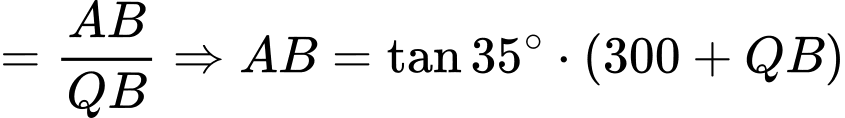
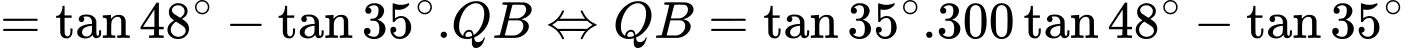
 =
= 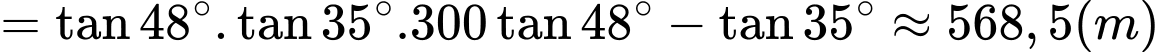
Vậy tháp hải đăng cao khoảng 568,5 m.
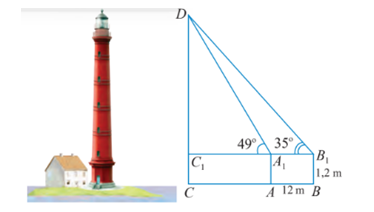
Câu 22 [239422]: Muốn đo chiều cao của một ngọn tháp, người ta lấy hai điểm A, B trên mặt đất có khoảng cách 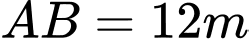 cùng thẳng hàng với chân
cùng thẳng hàng với chân  của tháp để đặt hai giác kế. Chân của hai giác kế có chiều cao là
của tháp để đặt hai giác kế. Chân của hai giác kế có chiều cao là 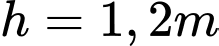 . Gọi
. Gọi 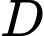 là đỉnh tháp và hai điểm
là đỉnh tháp và hai điểm 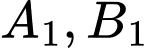 cùng thẳng hàng với
cùng thẳng hàng với  thuộc chiều cao
thuộc chiều cao 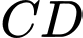 của tháp. Người ta do được
của tháp. Người ta do được 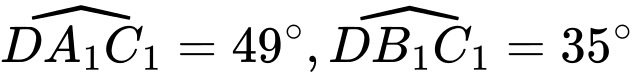 . Tính chiều cao
. Tính chiều cao 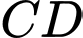 của tháp.
của tháp.
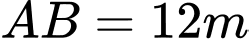 cùng thẳng hàng với chân
cùng thẳng hàng với chân  của tháp để đặt hai giác kế. Chân của hai giác kế có chiều cao là
của tháp để đặt hai giác kế. Chân của hai giác kế có chiều cao là 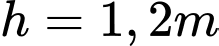 . Gọi
. Gọi 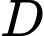 là đỉnh tháp và hai điểm
là đỉnh tháp và hai điểm 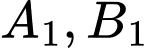 cùng thẳng hàng với
cùng thẳng hàng với  thuộc chiều cao
thuộc chiều cao 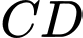 của tháp. Người ta do được
của tháp. Người ta do được 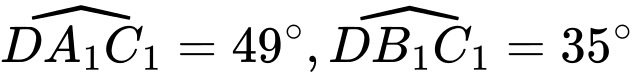 . Tính chiều cao
. Tính chiều cao 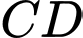 của tháp.
của tháp. 
Ta có:
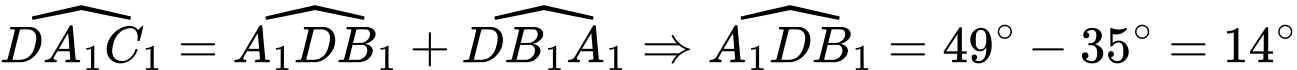
Áp dụng định lí sin trong tam giác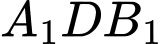 , ta có:
, ta có:

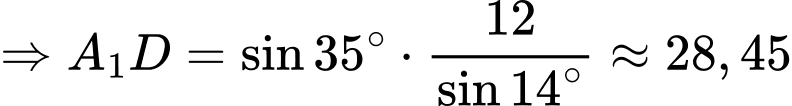
Áp dụng định lí sin trong tam giác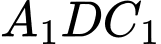 , ta có:
, ta có:
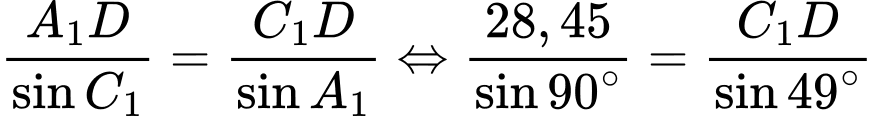
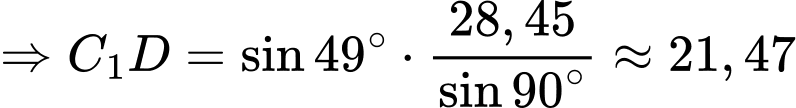
Do đó, chiều cao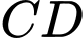 của tháp là:
của tháp là: 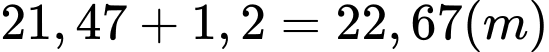
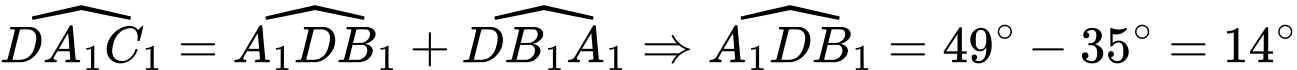
Áp dụng định lí sin trong tam giác
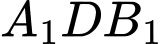 , ta có:
, ta có: 
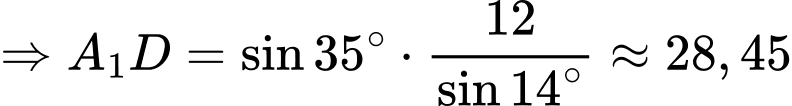
Áp dụng định lí sin trong tam giác
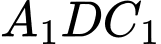 , ta có:
, ta có: 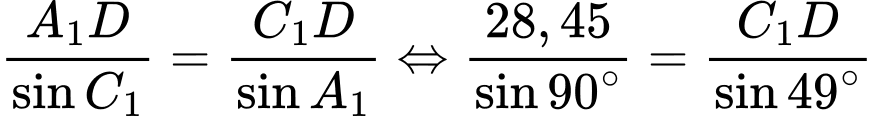
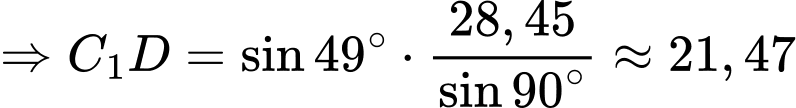
Do đó, chiều cao
 của tháp là:
của tháp là: 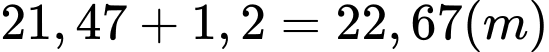
Câu 23 [238400]: Giả sử chúng ta cần đo chiều cao  của một tòa tháp với
của một tòa tháp với  là chân tháp và
là chân tháp và  là đỉnh tháp. Vì không thể đến chân tháp được nên từ hai điểm
là đỉnh tháp. Vì không thể đến chân tháp được nên từ hai điểm  và
và 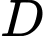 có khoảng cách
có khoảng cách 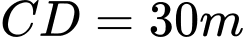 sao cho ba điểm
sao cho ba điểm 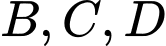 thẳng hàng người ta đo các góc
thẳng hàng người ta đo các góc 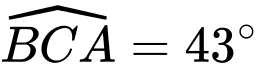 và góc
và góc 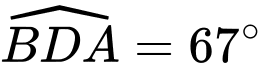 . Hãy tính chiều cao
. Hãy tính chiều cao  của tòa tháp.
của tòa tháp.
 của một tòa tháp với
của một tòa tháp với 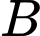 là chân tháp và
là chân tháp và 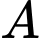 là đỉnh tháp. Vì không thể đến chân tháp được nên từ hai điểm
là đỉnh tháp. Vì không thể đến chân tháp được nên từ hai điểm  và
và 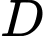 có khoảng cách
có khoảng cách 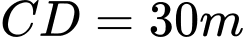 sao cho ba điểm
sao cho ba điểm 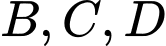 thẳng hàng người ta đo các góc
thẳng hàng người ta đo các góc 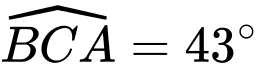 và góc
và góc 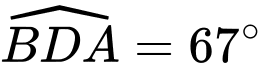 . Hãy tính chiều cao
. Hãy tính chiều cao  của tòa tháp.
của tòa tháp. 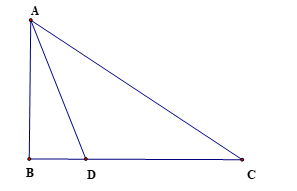
Trong tam giác
 : có góc
: có góc 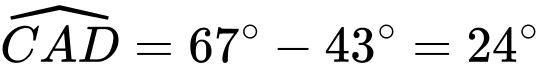
Áp dụng định lý sin trong tam giác
 ta có:
ta có:
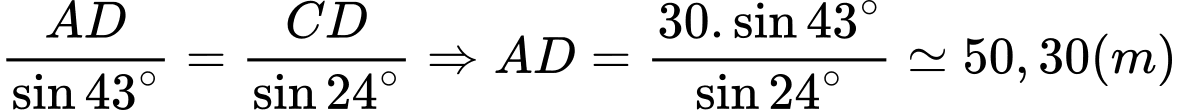
Trong tam giác vuông
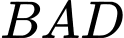 ta có
ta có 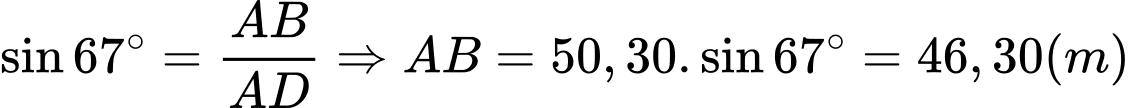
Vậy chiều cao của tòa tháp là
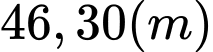
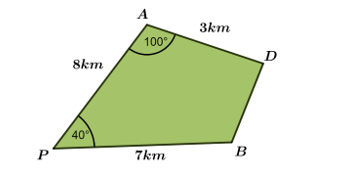
Câu 24 [243355]: An và Bắc cùng xuất phát từ điểm 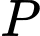 đi theo hai hướng khác nhau và tạo với nhau một góc
đi theo hai hướng khác nhau và tạo với nhau một góc 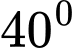 để đến đích là điểm
để đến đích là điểm  Biết rằng họ dừng lại để ăn trưa lần lượt tại
Biết rằng họ dừng lại để ăn trưa lần lượt tại 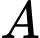 và
và 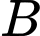 (như hình vẽ). Hỏi Bắc phải đi bao xa nữa để đến đích?
(như hình vẽ). Hỏi Bắc phải đi bao xa nữa để đến đích?
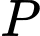 đi theo hai hướng khác nhau và tạo với nhau một góc
đi theo hai hướng khác nhau và tạo với nhau một góc 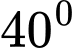 để đến đích là điểm
để đến đích là điểm  Biết rằng họ dừng lại để ăn trưa lần lượt tại
Biết rằng họ dừng lại để ăn trưa lần lượt tại 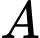 và
và 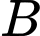 (như hình vẽ). Hỏi Bắc phải đi bao xa nữa để đến đích?
(như hình vẽ). Hỏi Bắc phải đi bao xa nữa để đến đích?
Ta cần tính 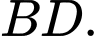 Ta có:
Ta có: 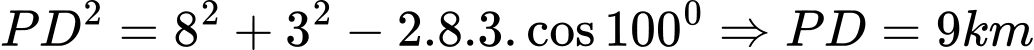
Mặt khác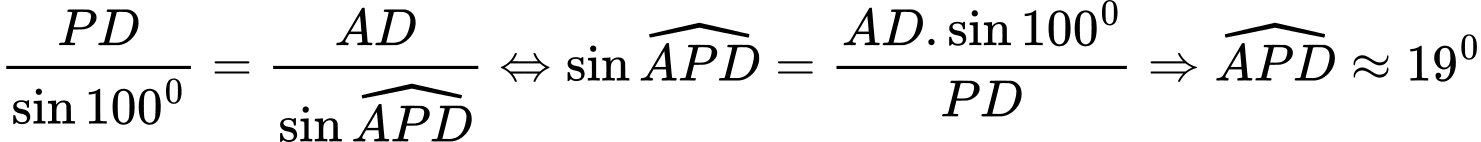
Do đó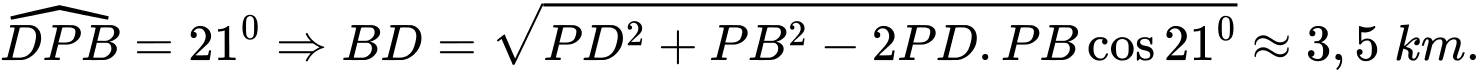
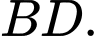 Ta có:
Ta có: 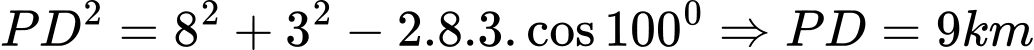
Mặt khác
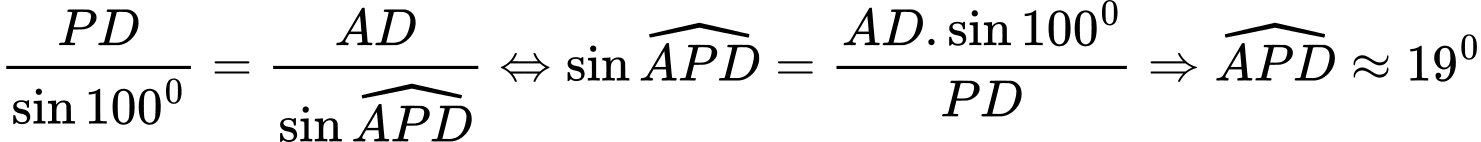
Do đó
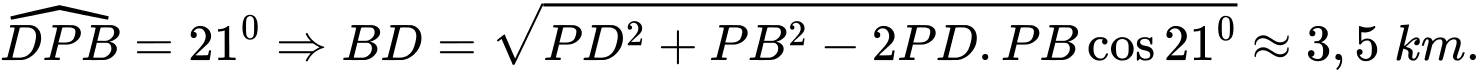
Câu 25 [243353]: Một chiếc thuyền dự định đi trực tiếp từ A đến B. Tuy nhiên, nó đã đi thẳng đến trước khi thuyền trưởng nhận ra rằng ông ta đa đi lệch khỏi hải trình. Chiếc thuyền đã đổi hướng một góc 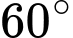 rồi đi thêm 10 km để đến B. Hành trình lẽ ra đã ngắn hơn 4 km nếu thuyền đi thẳng từ A đến B. Hỏi thuyền đã đi bao xa?
rồi đi thêm 10 km để đến B. Hành trình lẽ ra đã ngắn hơn 4 km nếu thuyền đi thẳng từ A đến B. Hỏi thuyền đã đi bao xa?
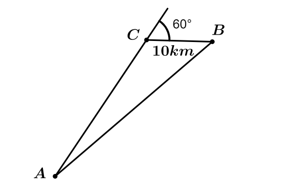
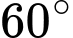 rồi đi thêm 10 km để đến B. Hành trình lẽ ra đã ngắn hơn 4 km nếu thuyền đi thẳng từ A đến B. Hỏi thuyền đã đi bao xa?
rồi đi thêm 10 km để đến B. Hành trình lẽ ra đã ngắn hơn 4 km nếu thuyền đi thẳng từ A đến B. Hỏi thuyền đã đi bao xa?
Theo giả thiết bài toán ta có: 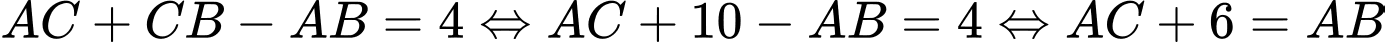
Đặt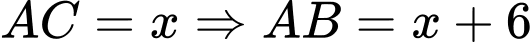
Ta có: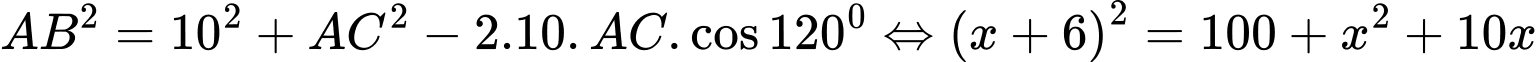
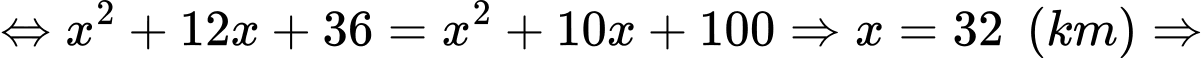 thuyền đã đi
thuyền đã đi 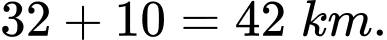
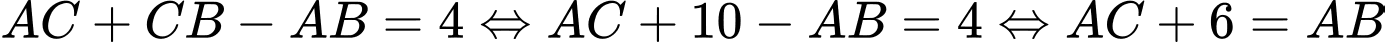
Đặt
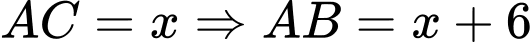
Ta có:
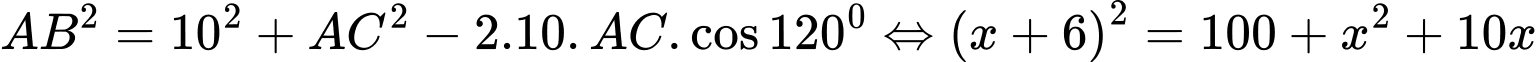
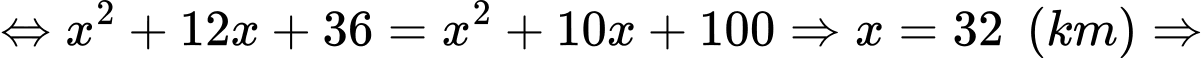 thuyền đã đi
thuyền đã đi