Đáp án Bài tập tự luyện
Câu 1 [239177]: Cho hình bình hành 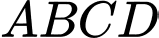 . Trong các khẳng định sau, khẳng định nào sai?
. Trong các khẳng định sau, khẳng định nào sai?
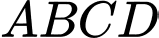 . Trong các khẳng định sau, khẳng định nào sai?
. Trong các khẳng định sau, khẳng định nào sai? A, 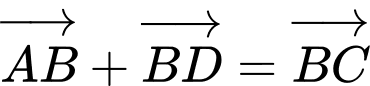 .
.
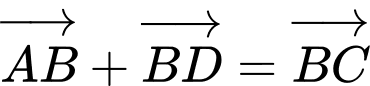 .
.B, 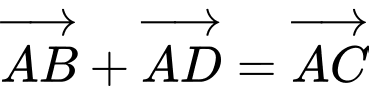 .
.
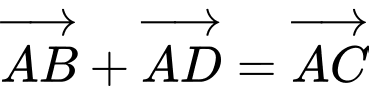 .
.C, 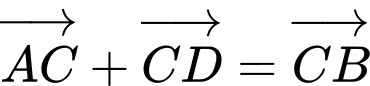 .
.
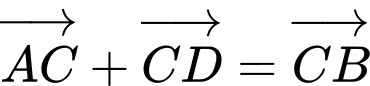 .
.D, 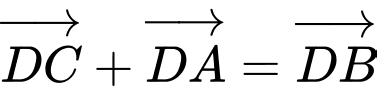 .
.
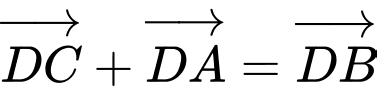 .
.
Chọn C
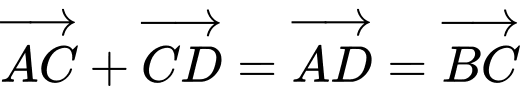 . Đáp án: C
. Đáp án: C
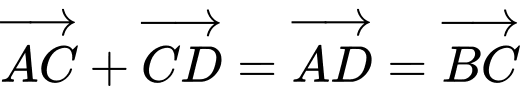 . Đáp án: C
. Đáp án: C
Câu 2 [239182]: Gọi  là tâm hình bình hành
là tâm hình bình hành 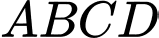 . Đẳng thức nào sau đây sai?
. Đẳng thức nào sau đây sai?
 là tâm hình bình hành
là tâm hình bình hành 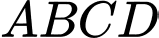 . Đẳng thức nào sau đây sai?
. Đẳng thức nào sau đây sai? A, 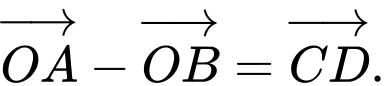 .
.
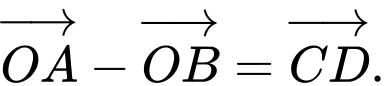 .
.B, 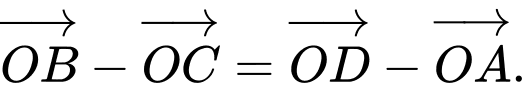 .
.
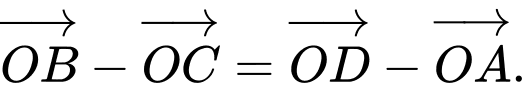 .
.C, 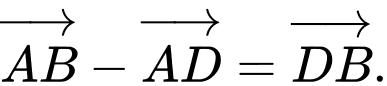 .
.
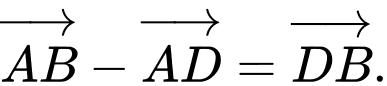 .
.D, 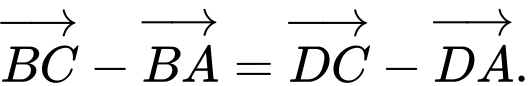 .
.
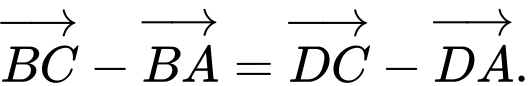 .
.
B.
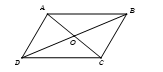
Xét các đáp án:
Đáp án A. Ta có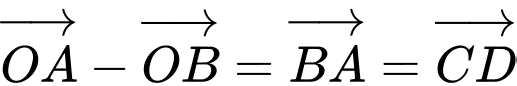 . Vậy A đúng.
. Vậy A đúng.
Đáp án B. Ta có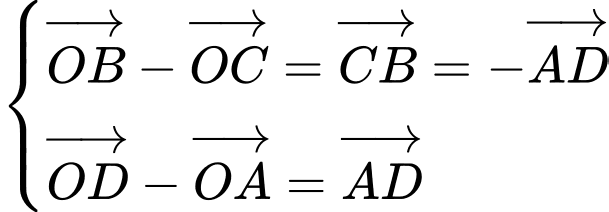 . Vậy B sai.
. Vậy B sai.
Đáp án C. Ta có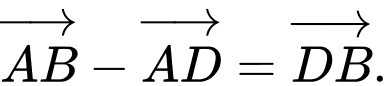 Vậy C đúng.
Vậy C đúng.
Đáp án D. Ta có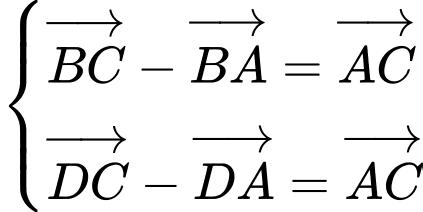 . Vậy D đúng Đáp án: B
. Vậy D đúng Đáp án: B

Xét các đáp án:
Đáp án A. Ta có
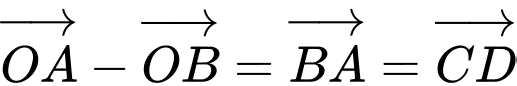 . Vậy A đúng.
. Vậy A đúng.
Đáp án B. Ta có
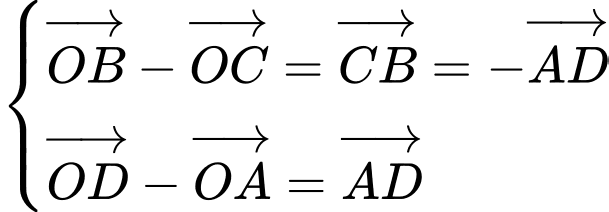 . Vậy B sai.
. Vậy B sai.
Đáp án C. Ta có
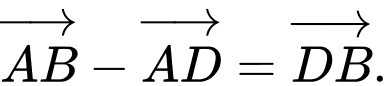 Vậy C đúng.
Vậy C đúng.
Đáp án D. Ta có
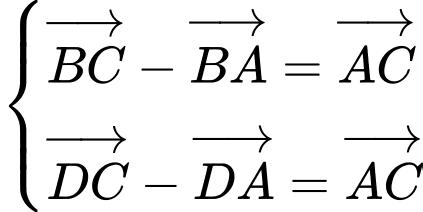 . Vậy D đúng Đáp án: B
. Vậy D đúng Đáp án: B
Câu 3 [240689]: Cho hình vuông 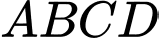 cạnh
cạnh 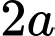 . Tính
. Tính 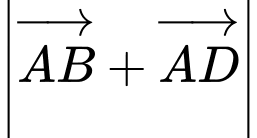 .
.
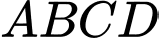 cạnh
cạnh 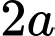 . Tính
. Tính 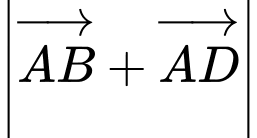 .
. A, 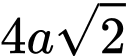 .
.
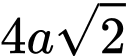 .
.B, 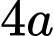 .
.
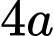 .
.C, 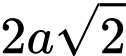 .
.
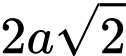 .
.D, 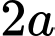 .
.
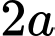 .
.
C.
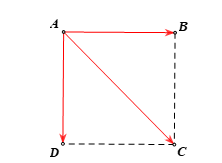
Ta có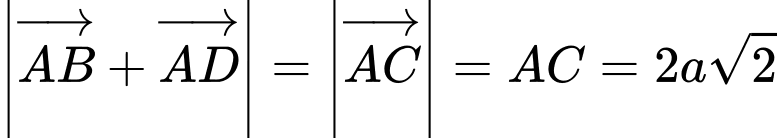 . Đáp án: C
. Đáp án: C

Ta có
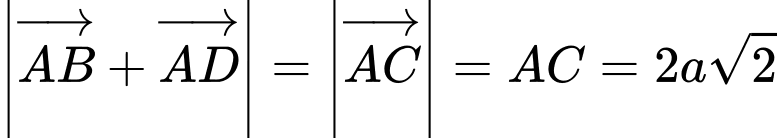 . Đáp án: C
. Đáp án: C
Câu 4 [240661]: Cho tam giác 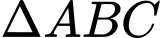 vuông tại A có
vuông tại A có 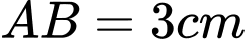 ,
, 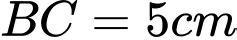 . Khi đó độ dài
. Khi đó độ dài 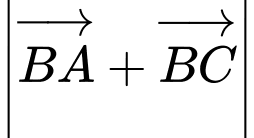 là
là
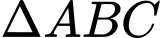 vuông tại A có
vuông tại A có 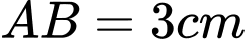 ,
, 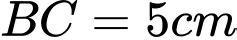 . Khi đó độ dài
. Khi đó độ dài 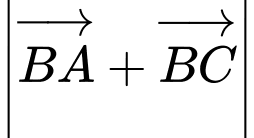 là
là A, 4.
B, 8.
C, 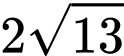 .
.
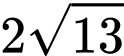 .
.D, 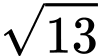 .
.
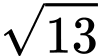 .
.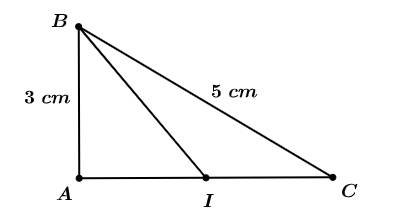
Gọi
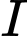 là trung điểm của
là trung điểm của 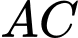
Ta có

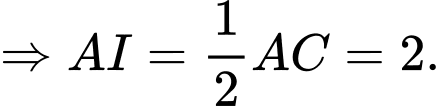
Ta có
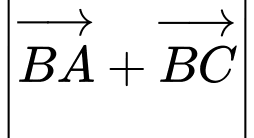
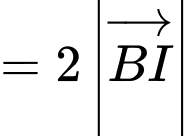 (theo quy tắc đường trung tuyến)
(theo quy tắc đường trung tuyến)
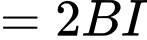

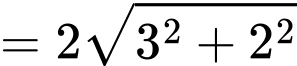
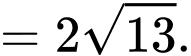
Chọn C. Đáp án: C
Câu 5 [240667]: Cho hình vuông ABCD có cạnh là a. O là giao điểm của hai đường chéo. Tính 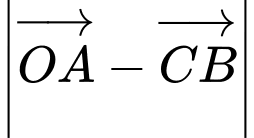 .
.
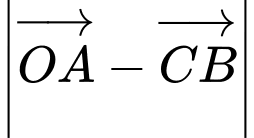 .
. A, 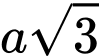
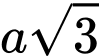
B, 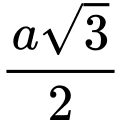
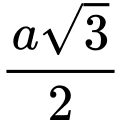
C, 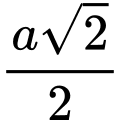 .
.
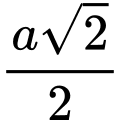 .
.D, 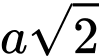 .
.
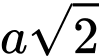 .
.
C.
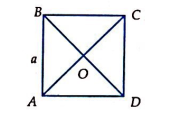
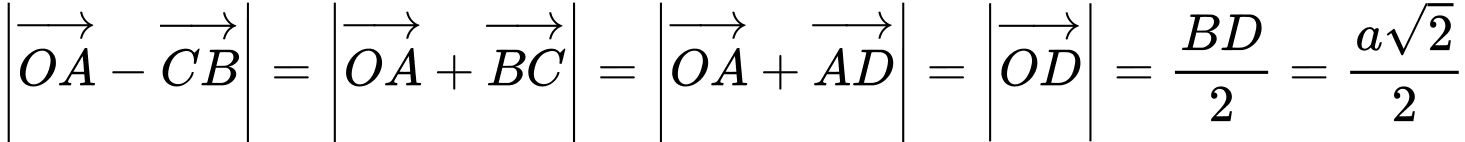 Đáp án: C
Đáp án: C

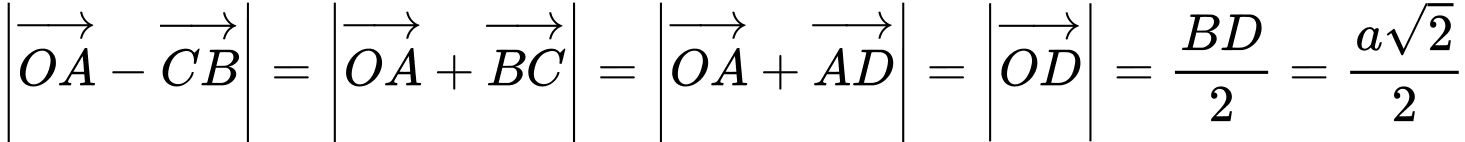 Đáp án: C
Đáp án: C
Câu 6 [239178]: Cho tam giác 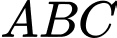 và
và 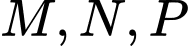 lần lượt là trung điểm của
lần lượt là trung điểm của 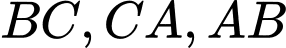 . Trong các khẳng định sau, khẳng định nào sai?
. Trong các khẳng định sau, khẳng định nào sai?
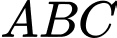 và
và 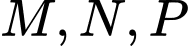 lần lượt là trung điểm của
lần lượt là trung điểm của 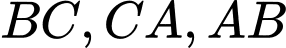 . Trong các khẳng định sau, khẳng định nào sai?
. Trong các khẳng định sau, khẳng định nào sai? A, 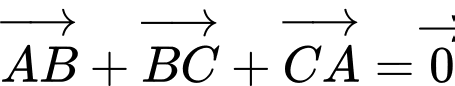 .
.
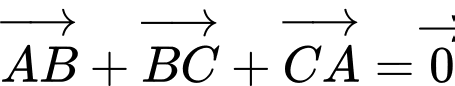 .
.B, 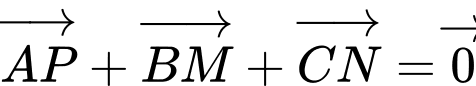 .
.
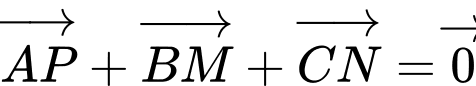 .
.C, 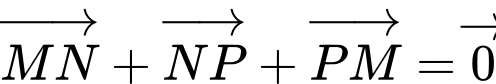 .
.
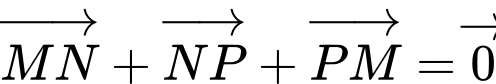 .
.D, 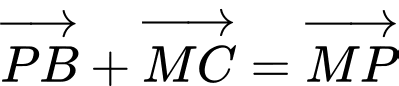 .
.
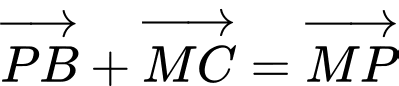 .
.
Chọn D
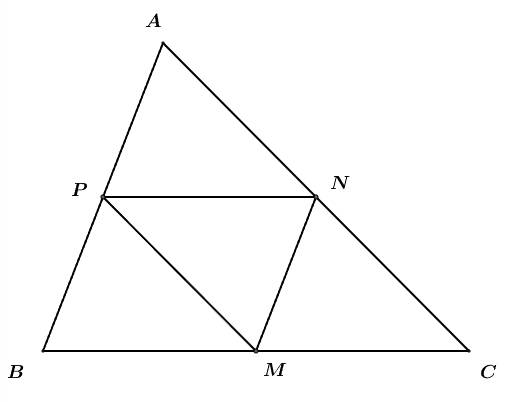
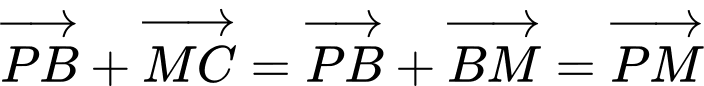 . Đáp án: D
. Đáp án: D

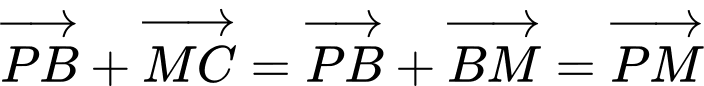 . Đáp án: D
. Đáp án: D
Câu 7 [239691]: Cho tam giác đều 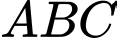 có cạnh bằng
có cạnh bằng 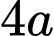 .Tích vô hướng của hai vectơ
.Tích vô hướng của hai vectơ 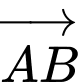 và
và 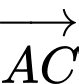 là
là
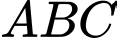 có cạnh bằng
có cạnh bằng 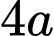 .Tích vô hướng của hai vectơ
.Tích vô hướng của hai vectơ 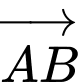 và
và 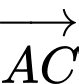 là
là A, 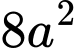 .
.
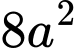 .
.B, 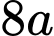 .
.
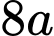 .
.C, 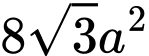 .
.
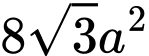 .
.D, 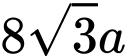 .
.
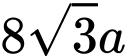 .
.
Chọn A
Ta có
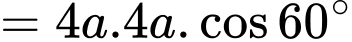
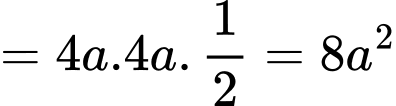 . Đáp án: A
. Đáp án: A
Ta có

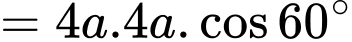
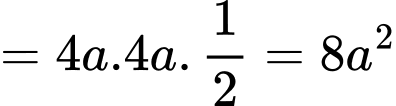 . Đáp án: A
. Đáp án: A
Câu 8 [239267]: Biết rằng hai vectơ 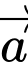 và
và 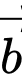 không cùng phương nhưng hai vectơ
không cùng phương nhưng hai vectơ 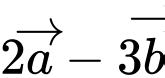 và
và 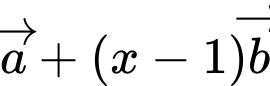 cùng phương. Khi đó giá trị của
cùng phương. Khi đó giá trị của 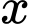 là
là
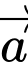 và
và 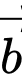 không cùng phương nhưng hai vectơ
không cùng phương nhưng hai vectơ 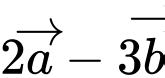 và
và 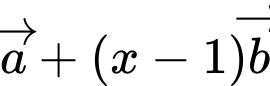 cùng phương. Khi đó giá trị của
cùng phương. Khi đó giá trị của 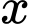 là
là A, 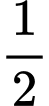 .
.
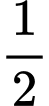 .
.B, 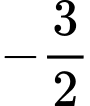 .
.
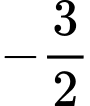 .
.C, 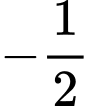 .
.
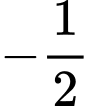 .
.D, 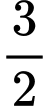 .
.
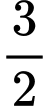 .
.
Vì 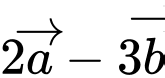 và
và 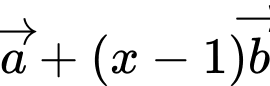 cùng phương nên ta có tỉ lệ
cùng phương nên ta có tỉ lệ 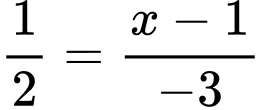
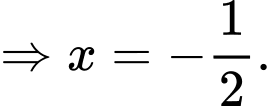
Chọn C. Đáp án: C
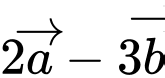 và
và 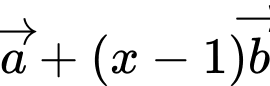 cùng phương nên ta có tỉ lệ
cùng phương nên ta có tỉ lệ 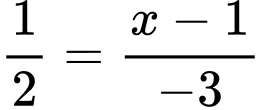
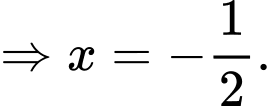
Chọn C. Đáp án: C
Câu 9 [239635]: Cho tam giác đều 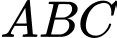 cạnh bằng
cạnh bằng 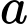 và
và 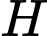 là trung điểm
là trung điểm 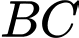 . Tính
. Tính 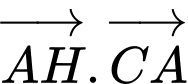 .
.
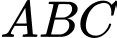 cạnh bằng
cạnh bằng 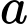 và
và 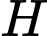 là trung điểm
là trung điểm 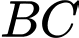 . Tính
. Tính 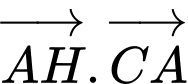 .
. A, 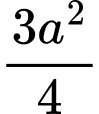 .
.
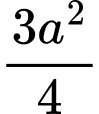 .
.B, 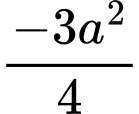 .
.
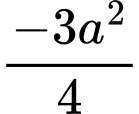 .
.C, 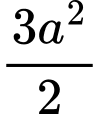 .
.
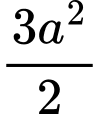 .
.D, 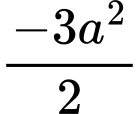 .
.
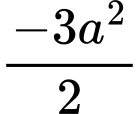 .
.
Chọn B
Ta có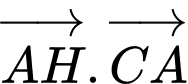

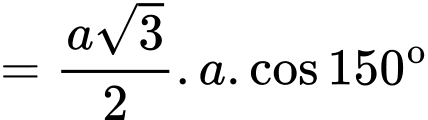
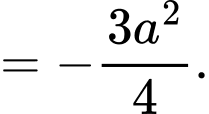 Đáp án: B
Đáp án: B
Ta có
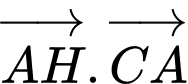

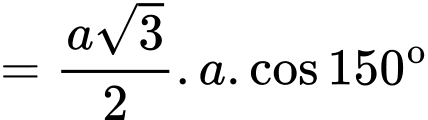
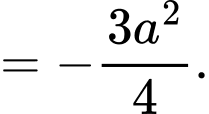 Đáp án: B
Đáp án: B
Câu 10 [240691]: Tam giác 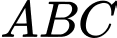 thỏa mãn:
thỏa mãn: 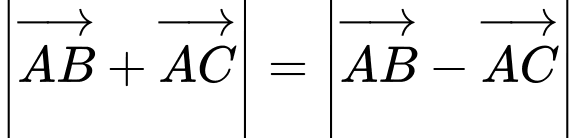 thì tam giác
thì tam giác 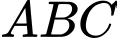 là
là
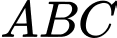 thỏa mãn:
thỏa mãn: 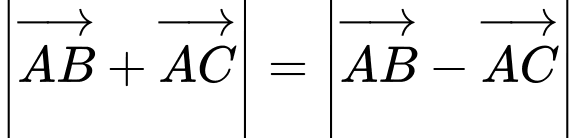 thì tam giác
thì tam giác 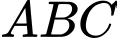 là
là A, Tam giác vuông 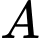 .
.
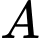 .
.B, Tam giác vuông  .
.
 .
.C, Tam giác vuông 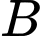 .
.
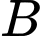 .
.D, Tam giác cân tại  .
.
 .
.
Chọn A.
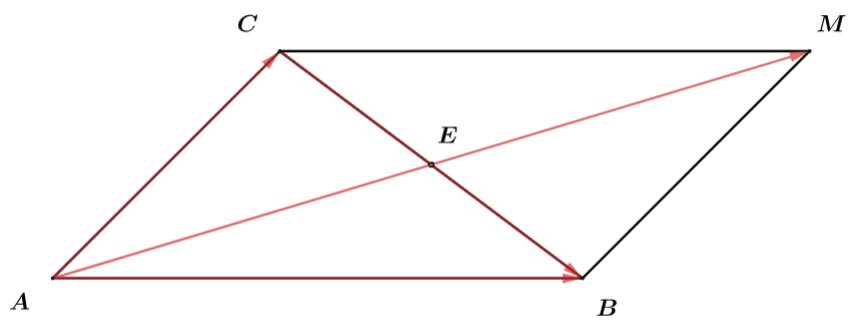
Gọi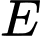 là trung điểm
là trung điểm 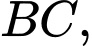
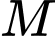 là điểm thỏa
là điểm thỏa 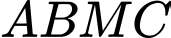 là hình bình hành.
là hình bình hành.
Ta có: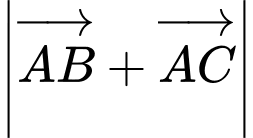
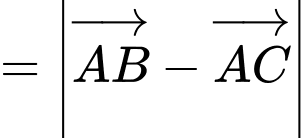
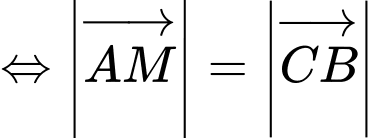
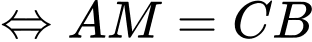
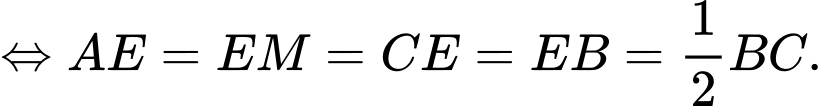
Trung tuyến kẻ từ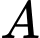 bằng một nửa cạnh
bằng một nửa cạnh 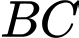 nên tam giác
nên tam giác 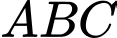 vuông tại
vuông tại 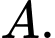 Đáp án: A
Đáp án: A

Gọi
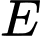 là trung điểm
là trung điểm 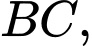
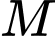 là điểm thỏa
là điểm thỏa 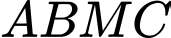 là hình bình hành.
là hình bình hành.
Ta có:
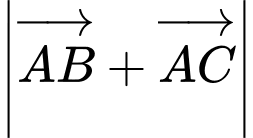
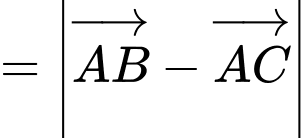
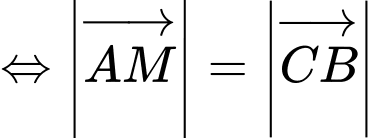
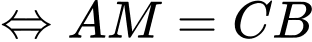
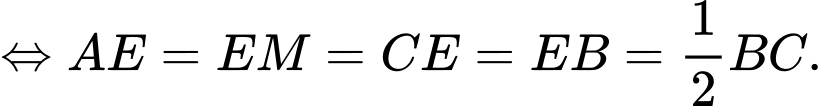
Trung tuyến kẻ từ
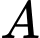 bằng một nửa cạnh
bằng một nửa cạnh 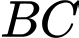 nên tam giác
nên tam giác 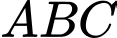 vuông tại
vuông tại 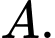 Đáp án: A
Đáp án: A
Câu 11 [239637]: Cho 2 vectơ 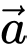 và
và 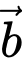 có
có 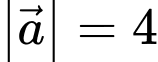 ,
, 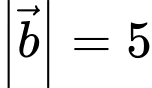 và
và 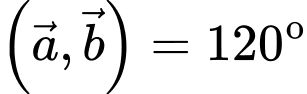 .Tính
.Tính 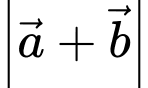 .
.
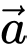 và
và 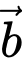 có
có 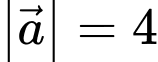 ,
, 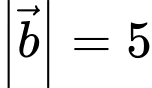 và
và 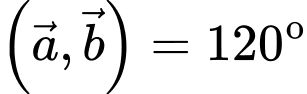 .Tính
.Tính 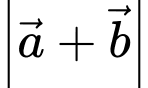 .
. A, 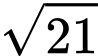 .
.
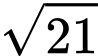 .
.B, 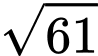 .
.
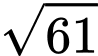 .
.C, 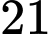 .
.
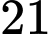 .
.D, 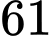 .
.
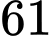 .
.
Chọn A
Ta có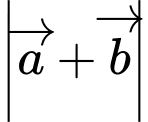
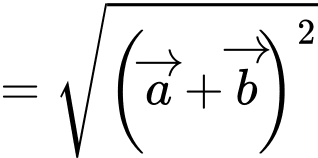
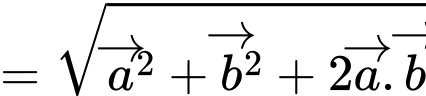
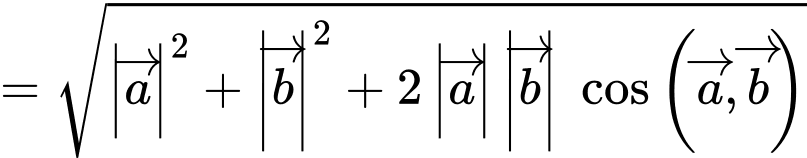
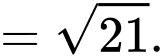 Đáp án: A
Đáp án: A
Ta có
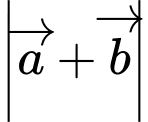
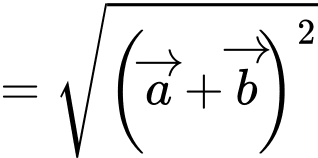
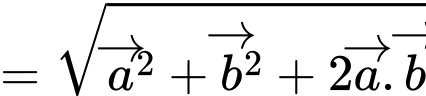
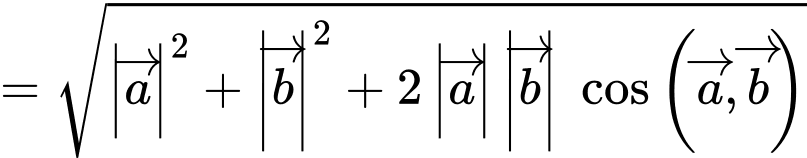
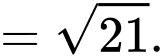 Đáp án: A
Đáp án: A
Câu 12 [239696]: Cho tam giác 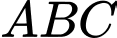 có
có 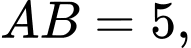
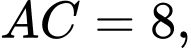
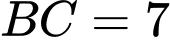 thì
thì 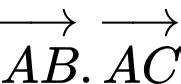 bằng
bằng
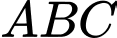 có
có 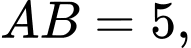
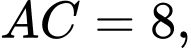
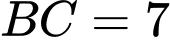 thì
thì 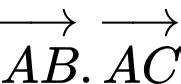 bằng
bằng A, -20.
B, 40.
C, 10.
D, 20.
Chọn D
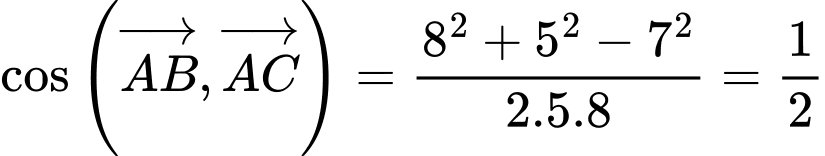
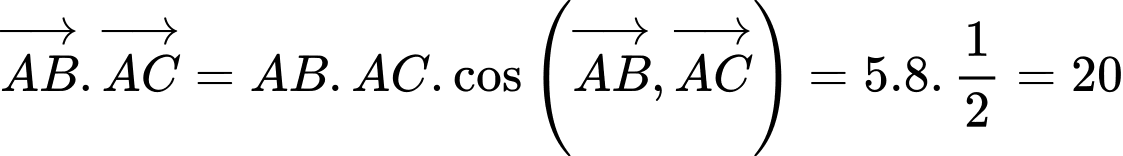 Đáp án: D
Đáp án: D
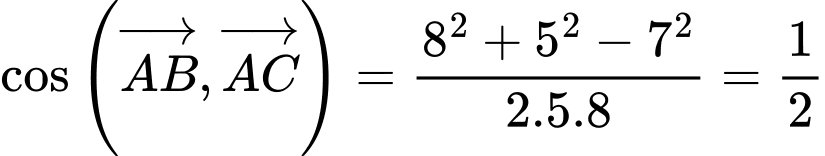
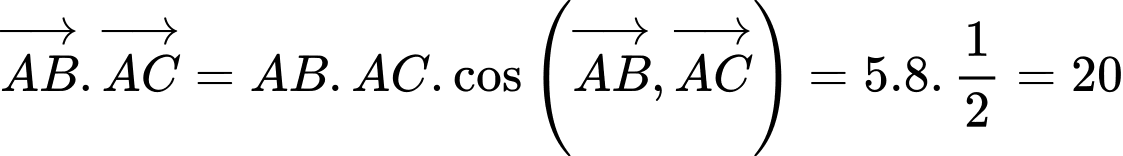 Đáp án: D
Đáp án: D
Câu 13 [239689]: Cho hai vectơ 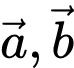 thỏa mãn:
thỏa mãn: 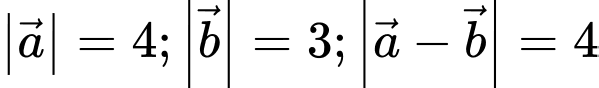 . Gọi
. Gọi 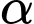 là góc giữa hai vectơ
là góc giữa hai vectơ 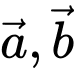 . Chọn phát biểu đúng.
. Chọn phát biểu đúng.
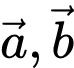 thỏa mãn:
thỏa mãn: 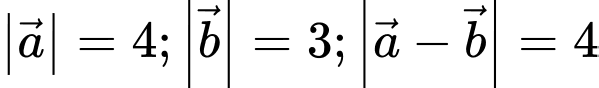 . Gọi
. Gọi 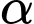 là góc giữa hai vectơ
là góc giữa hai vectơ 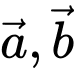 . Chọn phát biểu đúng.
. Chọn phát biểu đúng. A, 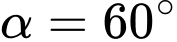 .
.
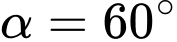 .
.B, 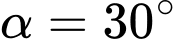 .
.
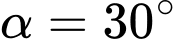 .
.C, 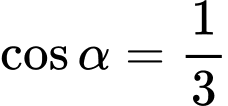 .
.
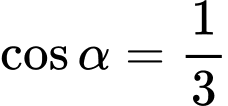 .
.D, 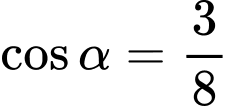 .
.
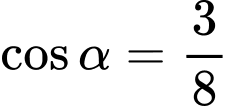 .
.
Chọn D
Ta có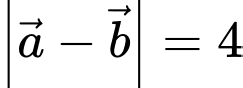
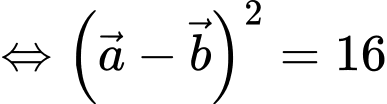
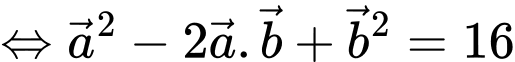
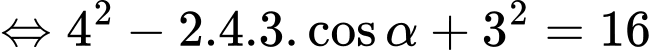
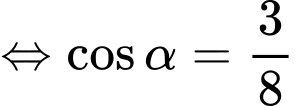 Đáp án: D
Đáp án: D
Ta có
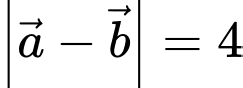
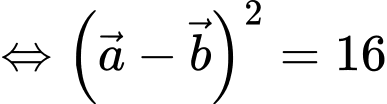
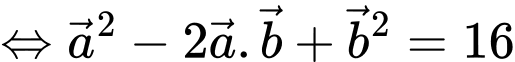
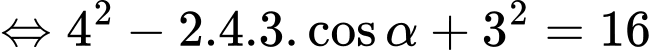
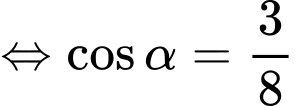 Đáp án: D
Đáp án: D
Câu 14 [239679]: Cho tam giác vuông cân 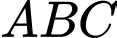 với
với 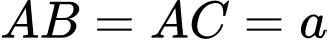 . Khi đó
. Khi đó 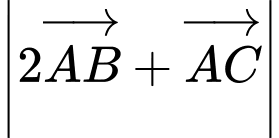 bằng
bằng
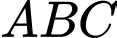 với
với 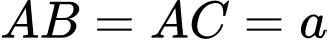 . Khi đó
. Khi đó 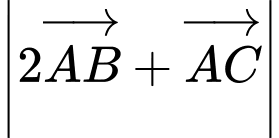 bằng
bằng A, 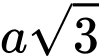 .
.
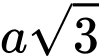 .
.B, 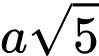 .
.
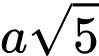 .
.C, 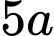 .
.
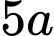 .
.D, 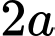 .
.
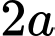 .
.
Chọn B
Ta có: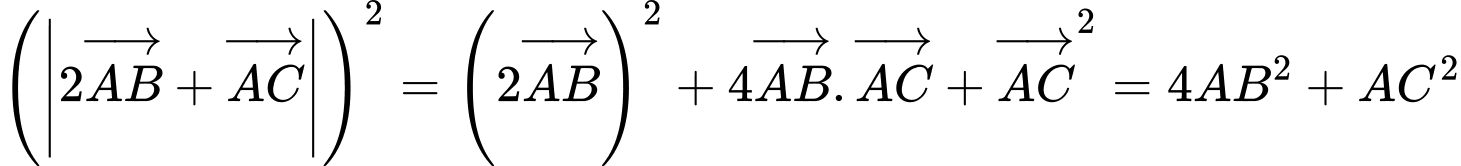 ( vì
( vì 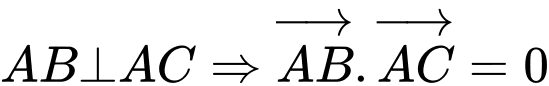 )
)
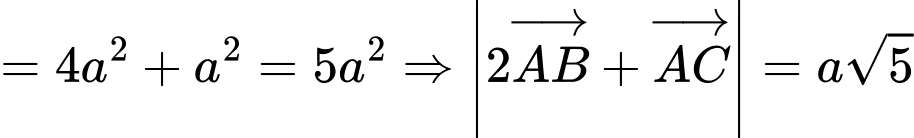 . Đáp án: B
. Đáp án: B
Ta có:
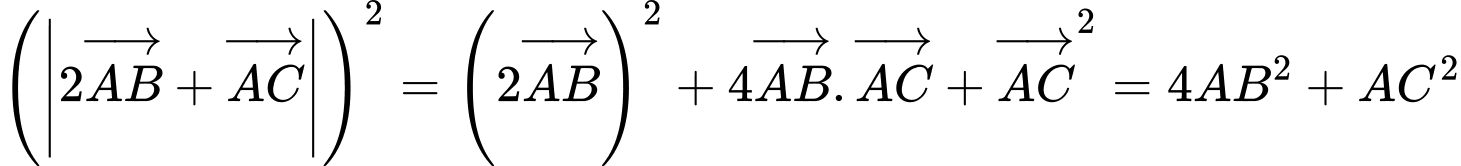 ( vì
( vì 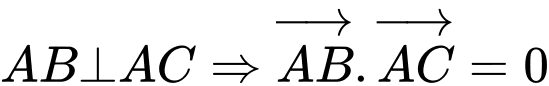 )
)
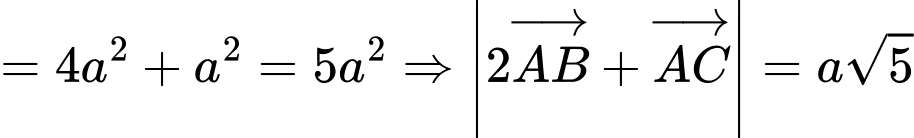 . Đáp án: B
. Đáp án: B
Câu 15 [237251]: Cho hình chữ nhật 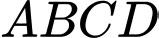 có hai cạnh
có hai cạnh 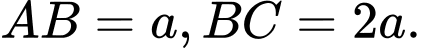 Khi đó
Khi đó 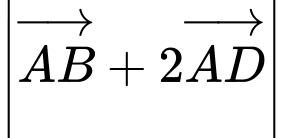 bằng
bằng
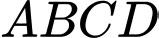 có hai cạnh
có hai cạnh 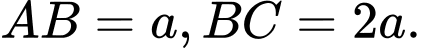 Khi đó
Khi đó 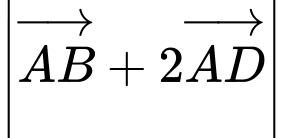 bằng
bằng A, 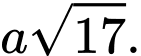
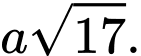
B, 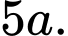
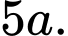
C, 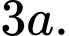
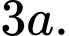
D, 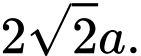
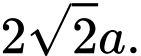
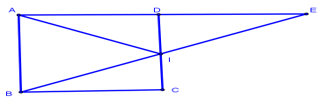
Dựng điểm
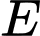 sao cho
sao cho 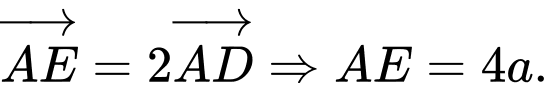 Gọi
Gọi 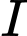 là trung điểm của
là trung điểm của 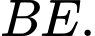
Xét tam giác vuông
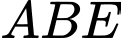 có
có 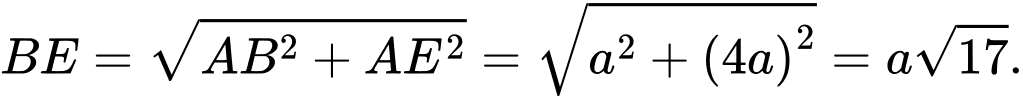
Ta có
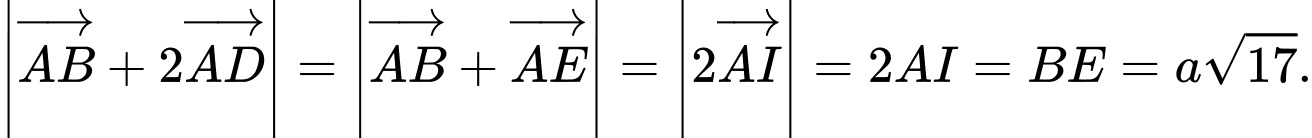 Đáp án: A
Đáp án: A
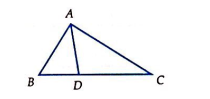
Câu 16 [239392]: Cho 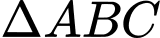 . Trên BC lấy điểm D sao cho
. Trên BC lấy điểm D sao cho 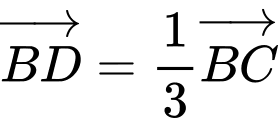 . Khi đó phân tích
. Khi đó phân tích  theo các vectơ
theo các vectơ 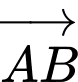 và
và 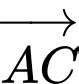 .
.
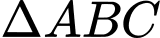 . Trên BC lấy điểm D sao cho
. Trên BC lấy điểm D sao cho 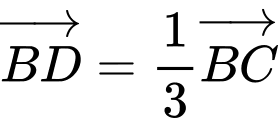 . Khi đó phân tích
. Khi đó phân tích  theo các vectơ
theo các vectơ 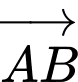 và
và 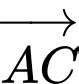 .
. A, 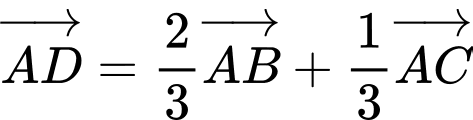 .
.
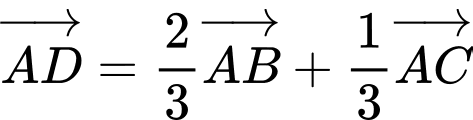 .
.B, 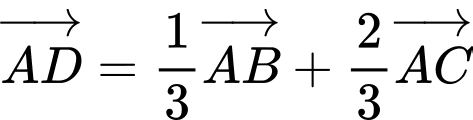 .
.
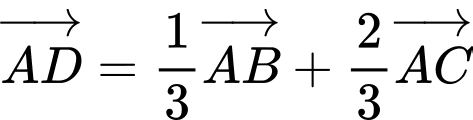 .
.C, 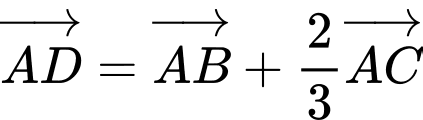 .
.
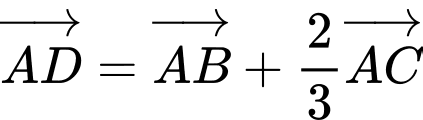 .
.D, 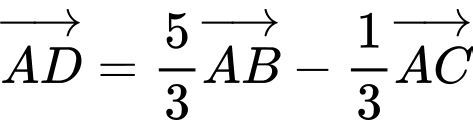 .
.
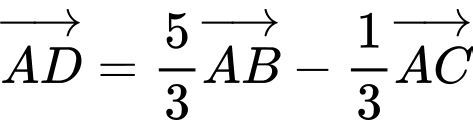 .
.
A
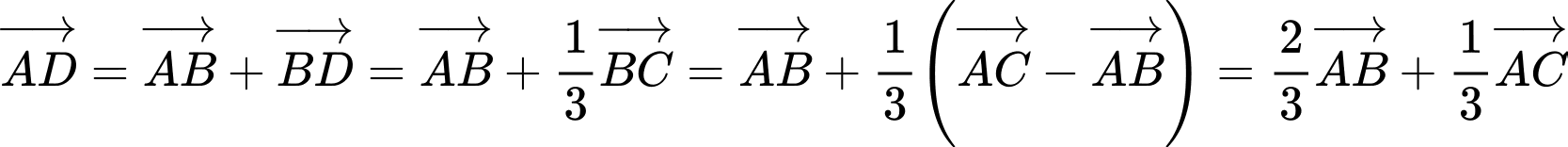 Đáp án: A
Đáp án: A

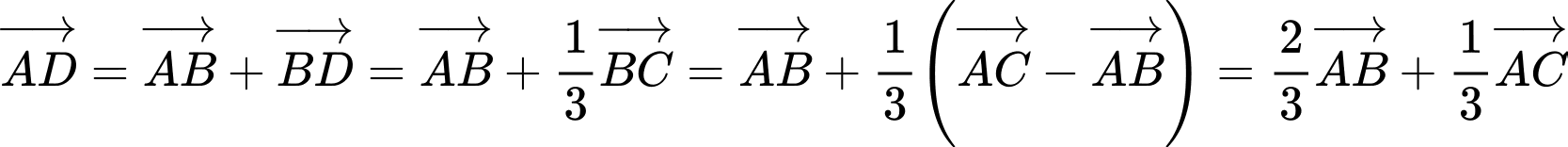 Đáp án: A
Đáp án: A
Câu 17 [239379]: Trên đường thẳng chứa cạnh 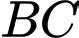 của tam giác
của tam giác 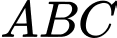 lấy một điểm
lấy một điểm 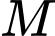 sao cho
sao cho 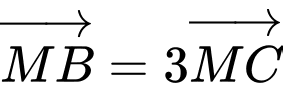 . Khi đó đẳng thức nào sau đây đúng?
. Khi đó đẳng thức nào sau đây đúng?
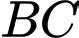 của tam giác
của tam giác 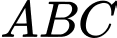 lấy một điểm
lấy một điểm 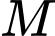 sao cho
sao cho 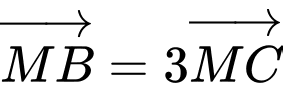 . Khi đó đẳng thức nào sau đây đúng?
. Khi đó đẳng thức nào sau đây đúng? A, 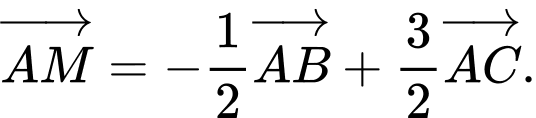
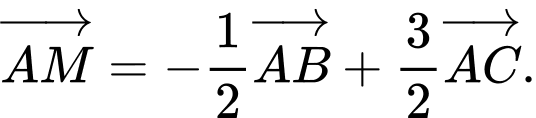
B, 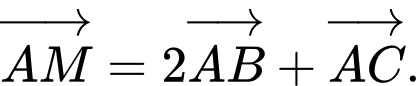
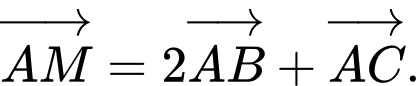
C, 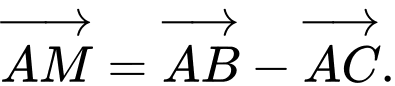
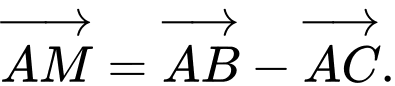
D, 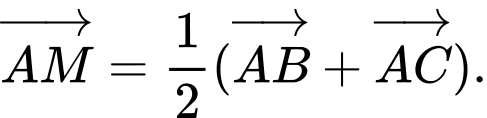
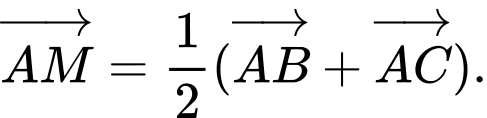
Chọn đáp án A.
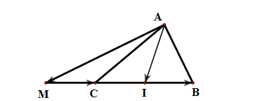
Gọi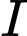 là trung điểm của
là trung điểm của 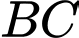 . Khi đó
. Khi đó  là trung điểm của
là trung điểm của 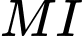 . Ta có:
. Ta có:
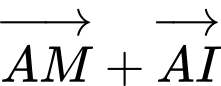
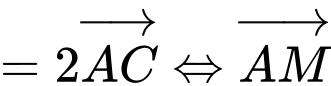
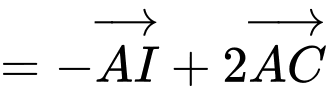
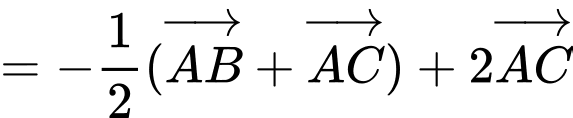
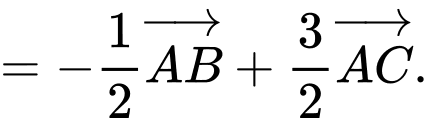 Đáp án: A
Đáp án: A

Gọi
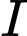 là trung điểm của
là trung điểm của 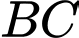 . Khi đó
. Khi đó  là trung điểm của
là trung điểm của 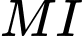 . Ta có:
. Ta có: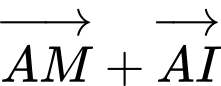
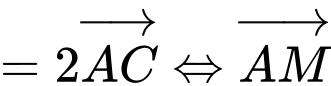
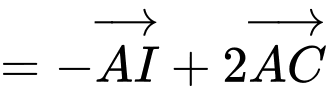
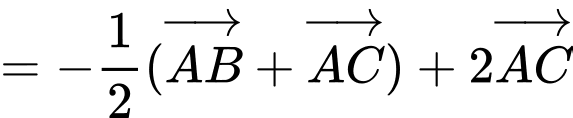
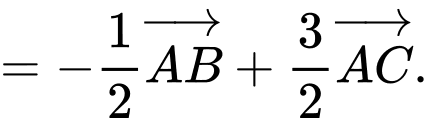 Đáp án: A
Đáp án: A
Câu 18 [239403]: Cho hình bình hành ABCD. Gọi M, N là các điểm nằm trên các cạnh AB và CD sao cho 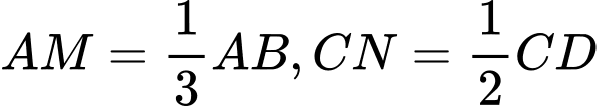 . Gọi G là trọng tâm của
. Gọi G là trọng tâm của 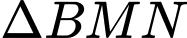 . Hãy phân tích
. Hãy phân tích 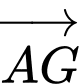 theo hai vectơ
theo hai vectơ 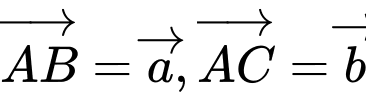 .
.
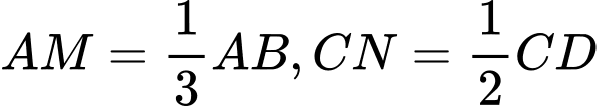 . Gọi G là trọng tâm của
. Gọi G là trọng tâm của 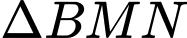 . Hãy phân tích
. Hãy phân tích 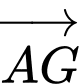 theo hai vectơ
theo hai vectơ 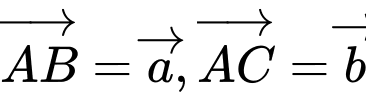 .
. A, 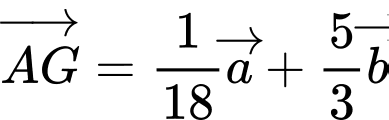 .
.
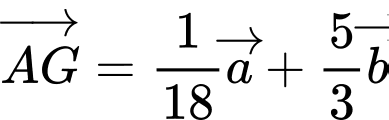 .
.B, 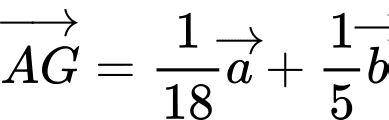 .
.
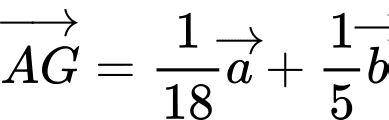 .
.C, 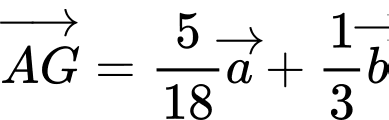 .
.
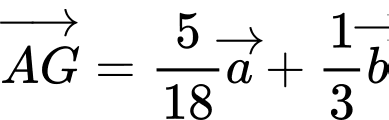 .
.D, 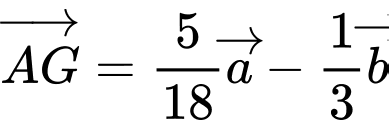 .
.
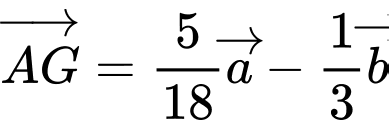 .
.
Ta có 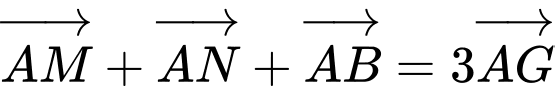 mà
mà 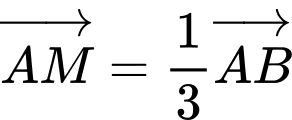
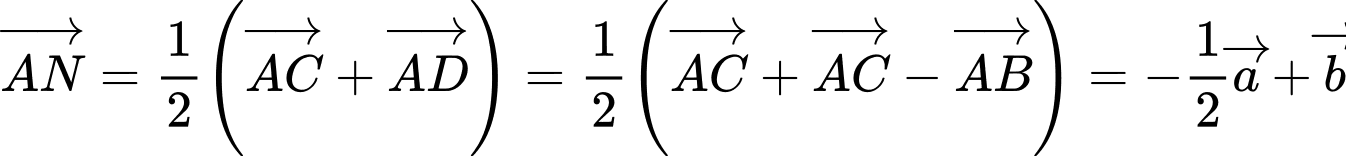
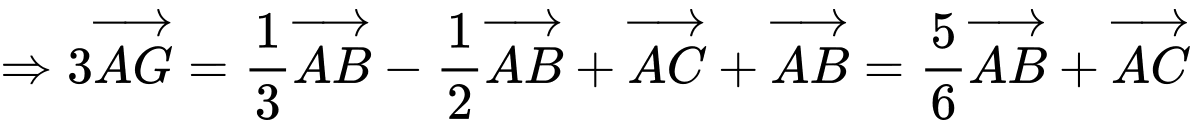
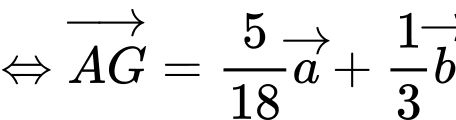 .
.
Đáp án C. Đáp án: C
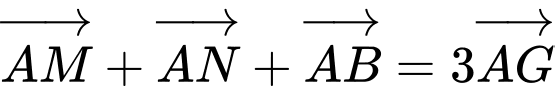 mà
mà 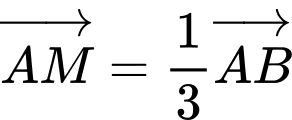
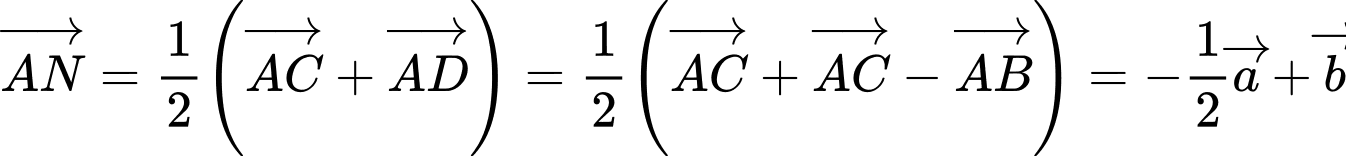
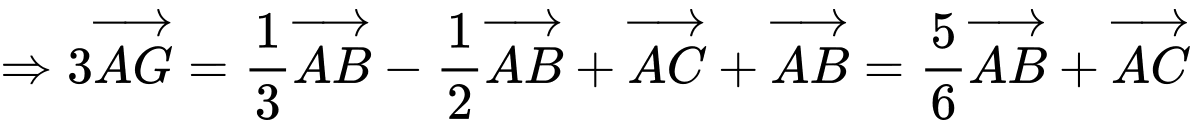
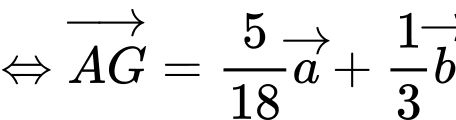 .
.Đáp án C. Đáp án: C
Câu 19 [240692]: Cho hai lực 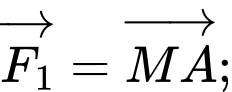
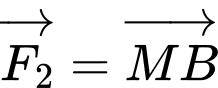 cùng tác động vào một vật tại điểm
cùng tác động vào một vật tại điểm 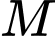 cường độ hai lực
cường độ hai lực 
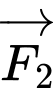 lần lượt là
lần lượt là 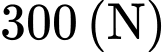 và
và 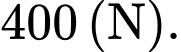
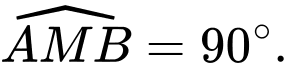 Tìm cường độ của lực tổng hợp tác động vào vật.
Tìm cường độ của lực tổng hợp tác động vào vật.
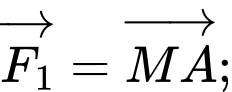
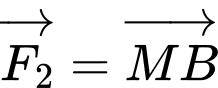 cùng tác động vào một vật tại điểm
cùng tác động vào một vật tại điểm 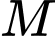 cường độ hai lực
cường độ hai lực 
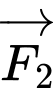 lần lượt là
lần lượt là 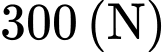 và
và 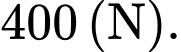
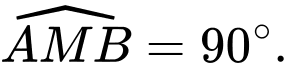 Tìm cường độ của lực tổng hợp tác động vào vật.
Tìm cường độ của lực tổng hợp tác động vào vật. A, 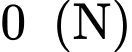 .
.
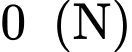 .
.B, 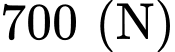 .
.
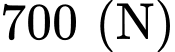 .
.C, 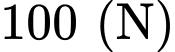 .
.
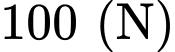 .
.D, 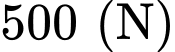 .
.
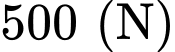 .
.
D.
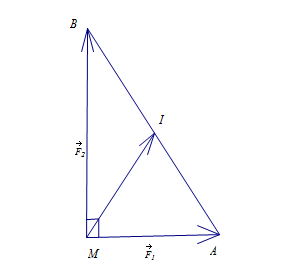
Cường độ lực tổng hợp của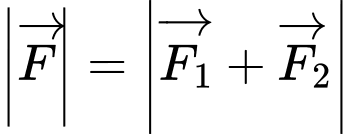
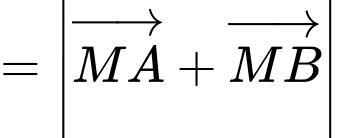
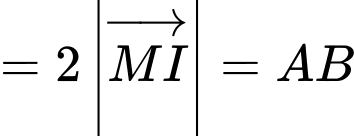 (
(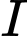 là trung điểm của
là trung điểm của  ). Ta có
). Ta có 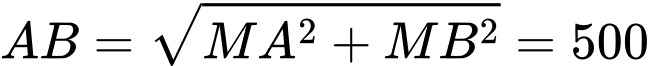 suy ra
suy ra 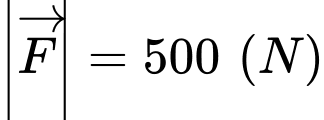 . Đáp án: D
. Đáp án: D

Cường độ lực tổng hợp của
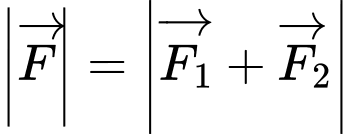
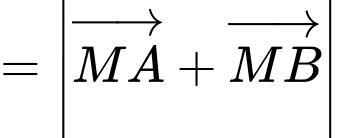
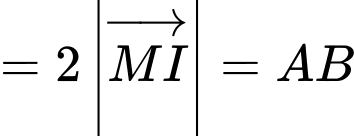 (
(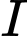 là trung điểm của
là trung điểm của  ). Ta có
). Ta có 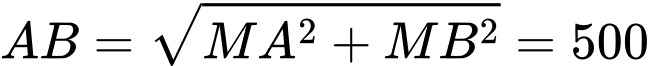 suy ra
suy ra 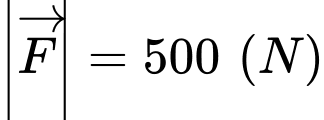 . Đáp án: D
. Đáp án: D
Câu 20 [240682]: Có hai lực 
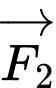 cùng tác động vào một vật đứng tại điểm
cùng tác động vào một vật đứng tại điểm  , biết hai lực
, biết hai lực 
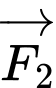 đều có cường độ là
đều có cường độ là  và chúng hợp với nhau một góc
và chúng hợp với nhau một góc 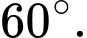 Hỏi vật đó phải chịu một lực tổng hợp có cường độ bằng bao nhiêu?
Hỏi vật đó phải chịu một lực tổng hợp có cường độ bằng bao nhiêu?

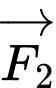 cùng tác động vào một vật đứng tại điểm
cùng tác động vào một vật đứng tại điểm  , biết hai lực
, biết hai lực 
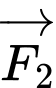 đều có cường độ là
đều có cường độ là  và chúng hợp với nhau một góc
và chúng hợp với nhau một góc 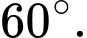 Hỏi vật đó phải chịu một lực tổng hợp có cường độ bằng bao nhiêu?
Hỏi vật đó phải chịu một lực tổng hợp có cường độ bằng bao nhiêu? A, 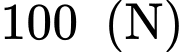 .
.
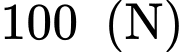 .
.B, 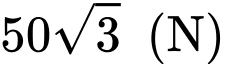 .
.
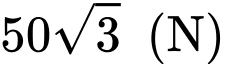 .
.C, 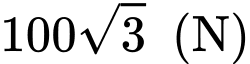 .
.
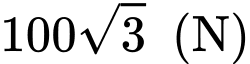 .
.D, Đáp án khác.
B.
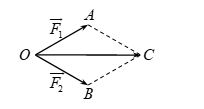
Giả sử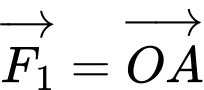 ,
, 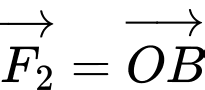 .
.
Theo quy tắc hình bình hành, suy ra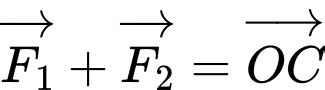 , như hình vẽ.
, như hình vẽ.
Ta có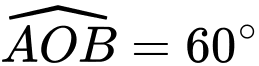 ,
, 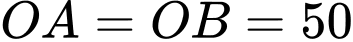 , nên tam giác
, nên tam giác 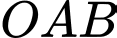 đều, suy ra
đều, suy ra 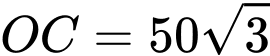 .Vậy
.Vậy  . Đáp án: B
. Đáp án: B

Giả sử
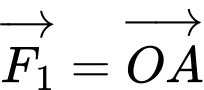 ,
, 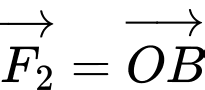 .
.Theo quy tắc hình bình hành, suy ra
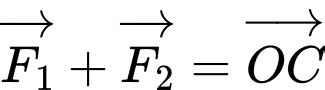 , như hình vẽ.
, như hình vẽ.Ta có
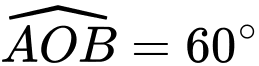 ,
, 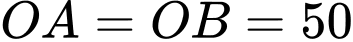 , nên tam giác
, nên tam giác 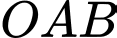 đều, suy ra
đều, suy ra 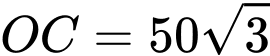 .Vậy
.Vậy  . Đáp án: B
. Đáp án: B
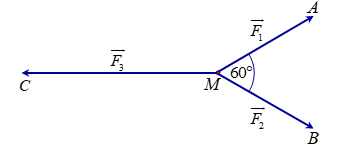
Câu 21 [240686]: Cho ba lực 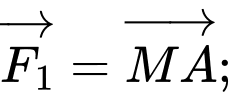
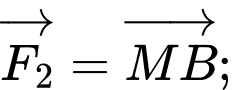
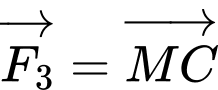 cùng tác động vào một vật tại điểm
cùng tác động vào một vật tại điểm 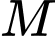 và vật đứng yên. Cho biết cường độ của
và vật đứng yên. Cho biết cường độ của 
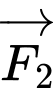 đều bằng
đều bằng 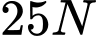 và góc
và góc 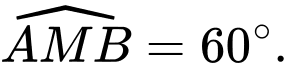 Khi đó cường độ lực của
Khi đó cường độ lực của 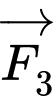 là
là
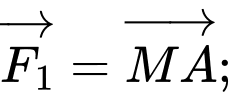
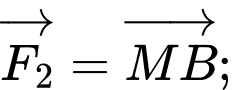
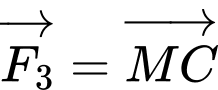 cùng tác động vào một vật tại điểm
cùng tác động vào một vật tại điểm 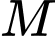 và vật đứng yên. Cho biết cường độ của
và vật đứng yên. Cho biết cường độ của 
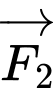 đều bằng
đều bằng 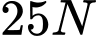 và góc
và góc 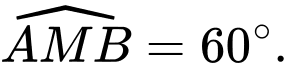 Khi đó cường độ lực của
Khi đó cường độ lực của 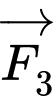 là
là
A, 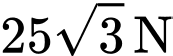 .
.
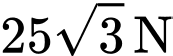 .
.B, 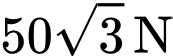 .
.
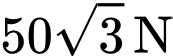 .
.C, 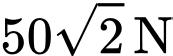 .
.
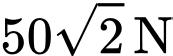 .
.D, 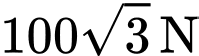 .
.
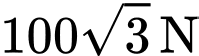 .
.
Chọn A.
Vật đứng yên nên ba lực đã cho cân bằng. Ta được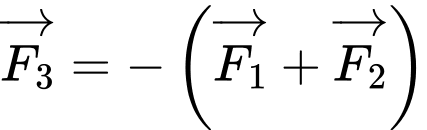 .
.

Dựng hình bình hành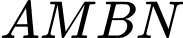 . Ta có
. Ta có 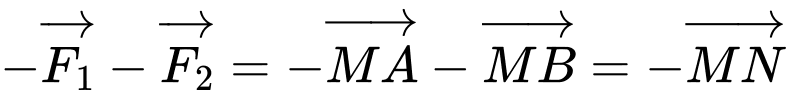 .Suy ra
.Suy ra 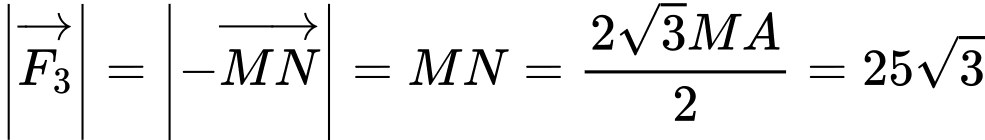 . Đáp án: A
. Đáp án: A
Vật đứng yên nên ba lực đã cho cân bằng. Ta được
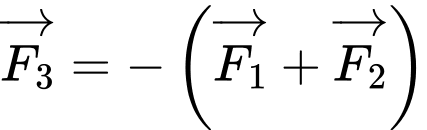 .
.
Dựng hình bình hành
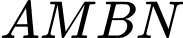 . Ta có
. Ta có 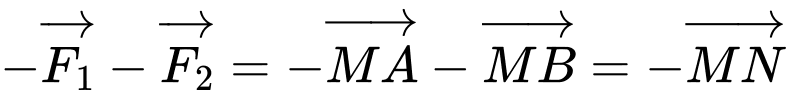 .Suy ra
.Suy ra 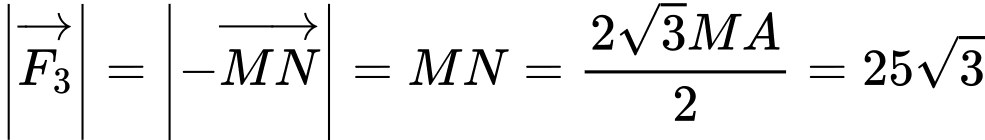 . Đáp án: A
. Đáp án: A
Câu 22 [239716]: Cho tam giác 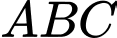 đều cạnh bằng
đều cạnh bằng 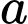 . Tập hợp các điểm
. Tập hợp các điểm 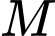 thỏa mãn đẳng thức
thỏa mãn đẳng thức 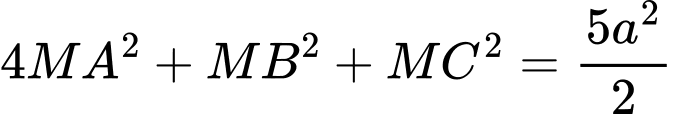 nằm trên một đường tròn
nằm trên một đường tròn  có bán kính
có bán kính 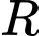 . Tính
. Tính 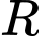 .
.
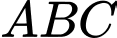 đều cạnh bằng
đều cạnh bằng 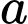 . Tập hợp các điểm
. Tập hợp các điểm 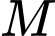 thỏa mãn đẳng thức
thỏa mãn đẳng thức 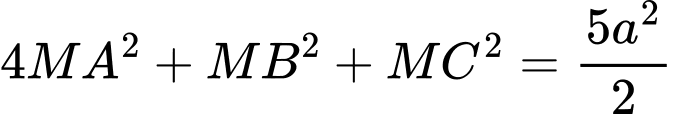 nằm trên một đường tròn
nằm trên một đường tròn  có bán kính
có bán kính 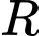 . Tính
. Tính 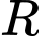 .
. A, 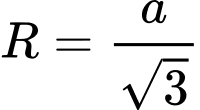 .
.
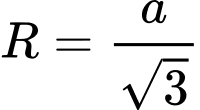 .
.B, 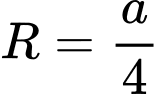 .
.
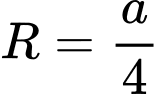 .
.C, 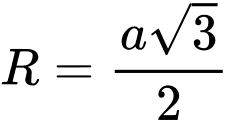 .
.
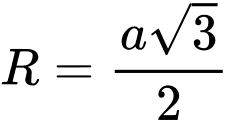 .
.D, 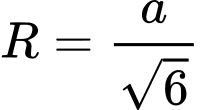 .
.
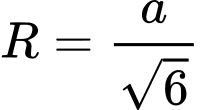 .
.
D
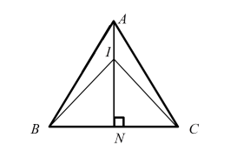
Gọi là trung điểm đoạn
là trung điểm đoạn 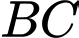 .
.
Gọi là điểm thỏa:
là điểm thỏa: 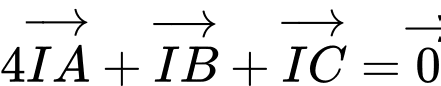
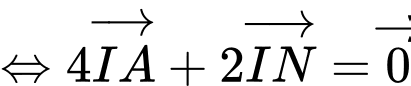
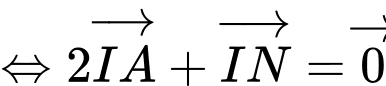 , nên điểm
, nên điểm 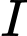 thuộc đoạn thẳng
thuộc đoạn thẳng 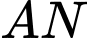 sao cho
sao cho 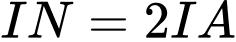 .
.
Khi đó: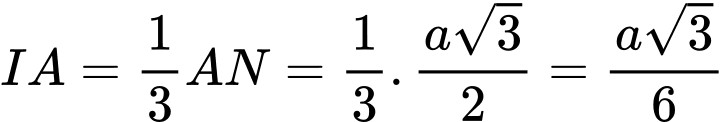 , và
, và 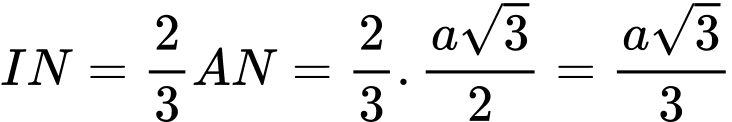 .
.
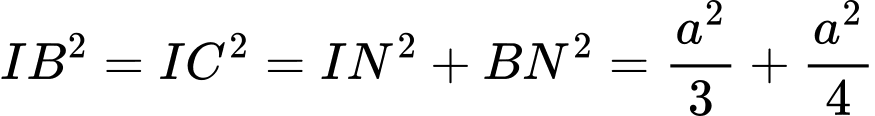
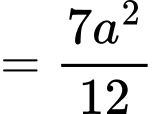 .
.
Ta có: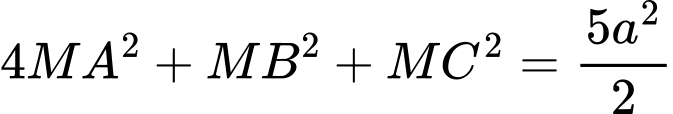
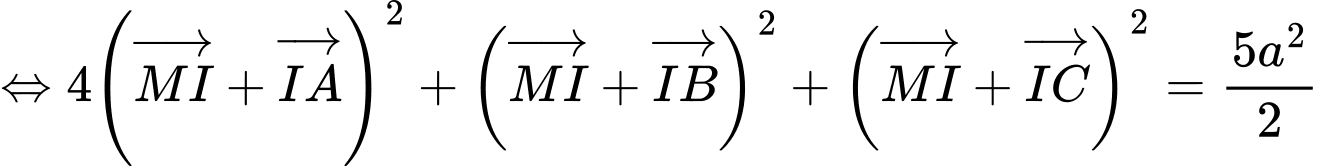 .
.
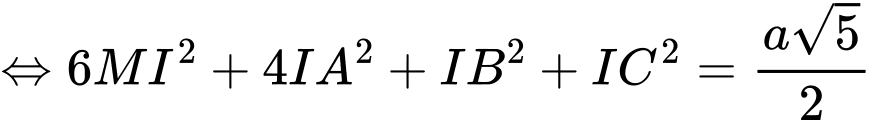
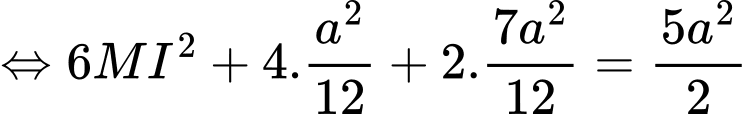
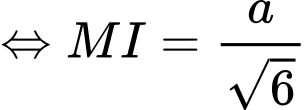 . Đáp án: D
. Đáp án: D

Gọi
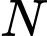 là trung điểm đoạn
là trung điểm đoạn 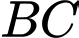 .
.
Gọi
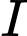 là điểm thỏa:
là điểm thỏa: 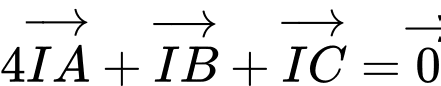
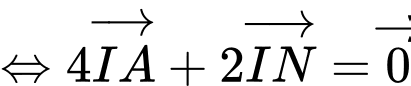
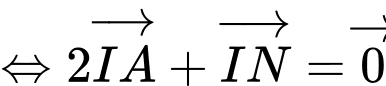 , nên điểm
, nên điểm 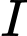 thuộc đoạn thẳng
thuộc đoạn thẳng 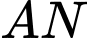 sao cho
sao cho 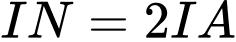 .
.
Khi đó:
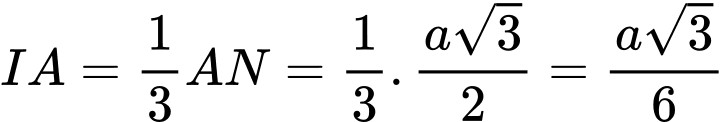 , và
, và 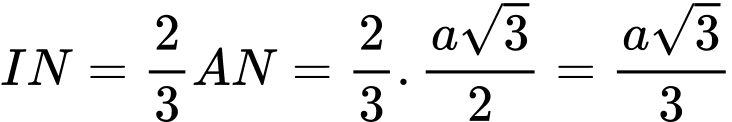 .
.
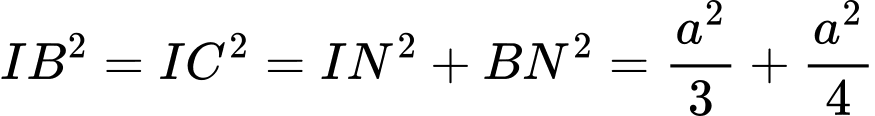
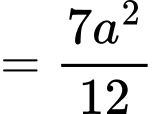 .
.
Ta có:
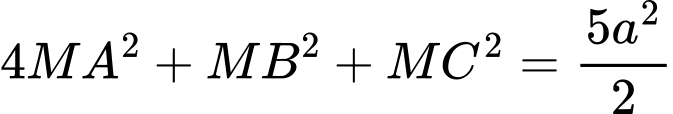
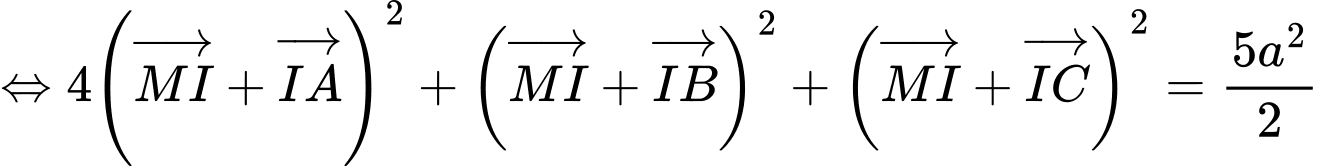 .
.
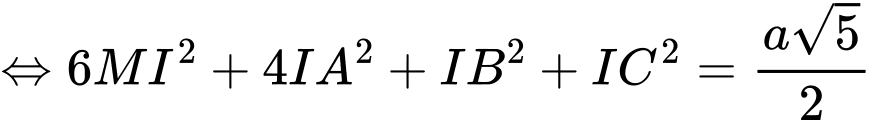
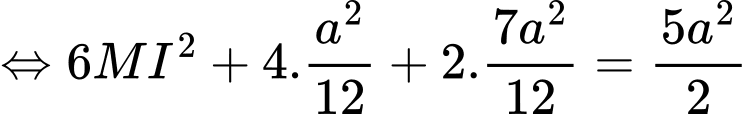
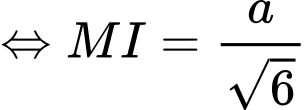 . Đáp án: D
. Đáp án: D
Câu 23 [285149]: Cho tam giác 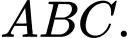 Tập hơp các diểm
Tập hơp các diểm 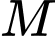 thỏa mãn
thỏa mãn 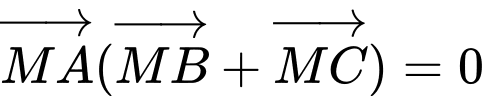 là
là
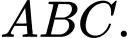 Tập hơp các diểm
Tập hơp các diểm 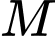 thỏa mãn
thỏa mãn 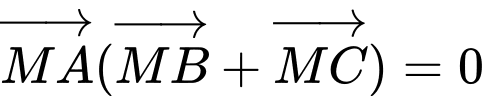 là
là A, đường thẳng.
B, một điểm.
C, đoạn thẳng.
D, đường tròn.
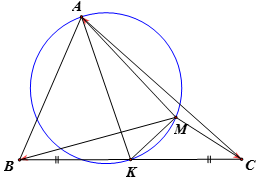
Gọi
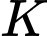 là trung điểm
là trung điểm 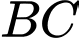
Ta có
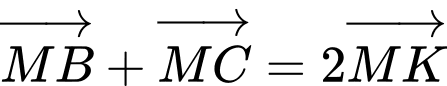
Thay vào giả thiết
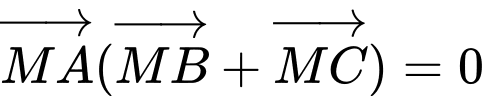
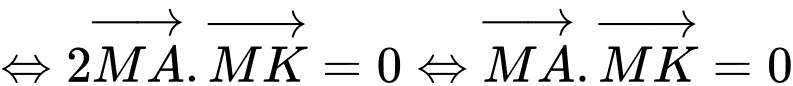
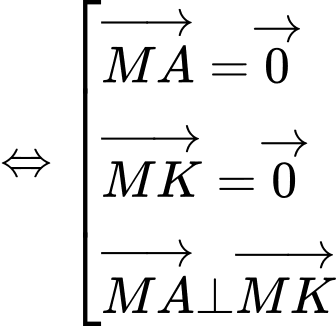
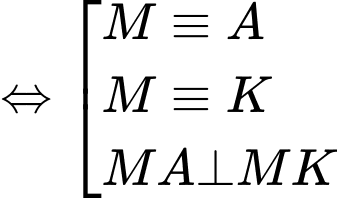 hay là tập hợp điểm
hay là tập hợp điểm 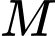 là đường tròn đường kính
là đường tròn đường kính 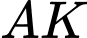 ( lấy cả hai điểm
( lấy cả hai điểm 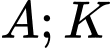 ). Đáp án: D
). Đáp án: D
Câu 24 [558075]: Cho hình chữ nhật 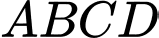 có
có 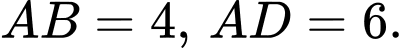 Độ dài của vectơ
Độ dài của vectơ 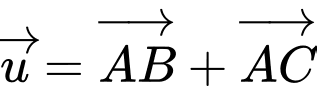 bằng bao nhiêu?
bằng bao nhiêu?
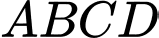 có
có 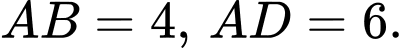 Độ dài của vectơ
Độ dài của vectơ 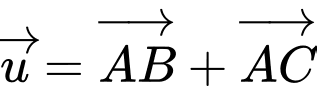 bằng bao nhiêu?
bằng bao nhiêu? 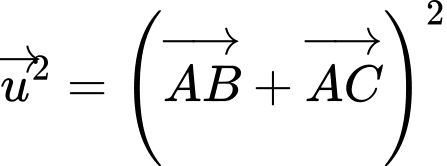
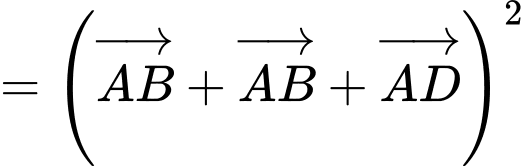
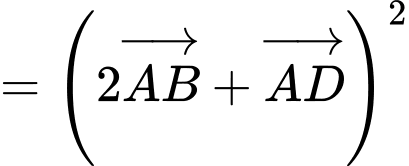
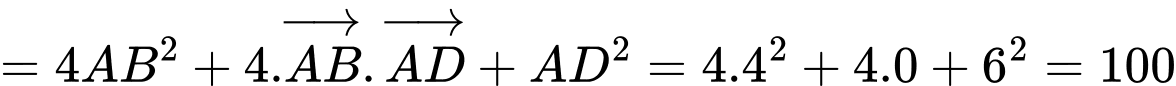
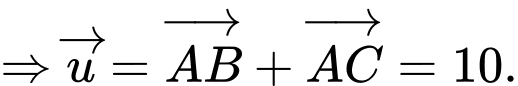
Câu 25 [239641]: Cho 2 vectơ 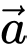 và
và 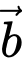 có độ dài đều bằng 1 thỏa
có độ dài đều bằng 1 thỏa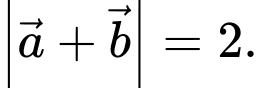 Hãy xác định
Hãy xác định 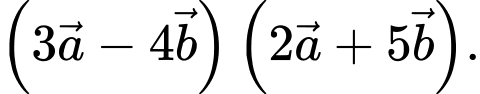
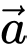 và
và 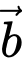 có độ dài đều bằng 1 thỏa
có độ dài đều bằng 1 thỏa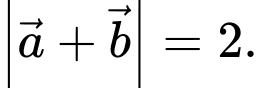 Hãy xác định
Hãy xác định 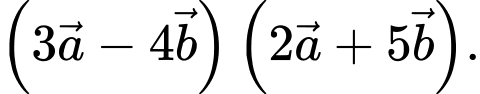
A, 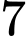 .
.
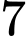 .
.B, 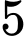 .
.
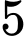 .
.C, 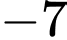 .
.
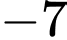 .
.D, 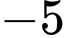 .
.
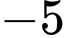 .
.
Chọn C
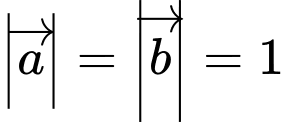 ,
, 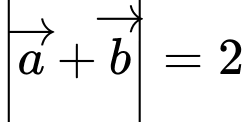
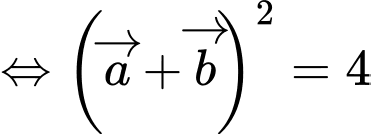
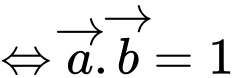 ,
, 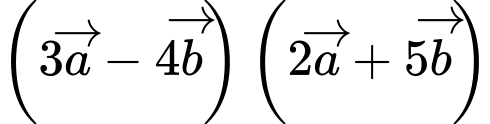
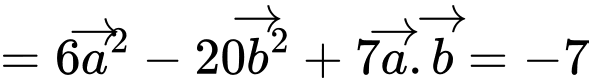 . Đáp án: C
. Đáp án: C
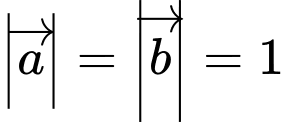 ,
, 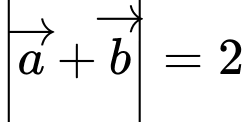
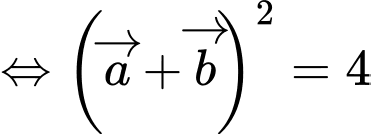
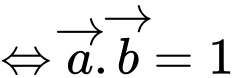 ,
, 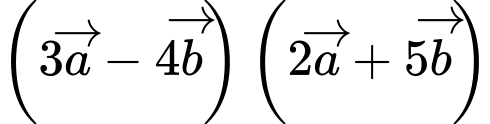
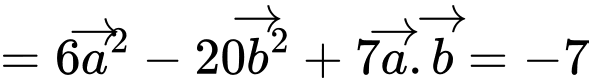 . Đáp án: C
. Đáp án: C
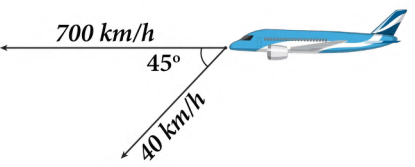
Câu 26 [240044]: Một máy bay đang bay từ hướng đông sang hướng tây với tốc độ 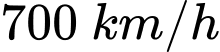 thì gặp luồng gió thổi từ hướng đông bắc sang hướng tây nam với tốc độ
thì gặp luồng gió thổi từ hướng đông bắc sang hướng tây nam với tốc độ 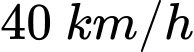 (Hình). Máy bay bị thay đổi vận tốc sau khi gặp gió thổi. Tìm tốc độ mới của máy bay (làm tròn kết quả đến hàng phần trăm theo đơn vị km/h).
(Hình). Máy bay bị thay đổi vận tốc sau khi gặp gió thổi. Tìm tốc độ mới của máy bay (làm tròn kết quả đến hàng phần trăm theo đơn vị km/h).
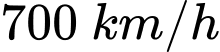 thì gặp luồng gió thổi từ hướng đông bắc sang hướng tây nam với tốc độ
thì gặp luồng gió thổi từ hướng đông bắc sang hướng tây nam với tốc độ 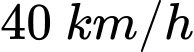 (Hình). Máy bay bị thay đổi vận tốc sau khi gặp gió thổi. Tìm tốc độ mới của máy bay (làm tròn kết quả đến hàng phần trăm theo đơn vị km/h).
(Hình). Máy bay bị thay đổi vận tốc sau khi gặp gió thổi. Tìm tốc độ mới của máy bay (làm tròn kết quả đến hàng phần trăm theo đơn vị km/h).
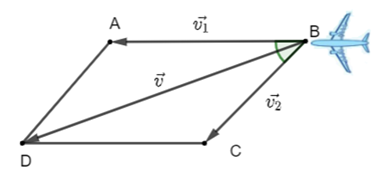
Khi đó ta có:
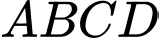 là hình bình hành có
là hình bình hành có  .
.Suy ra:
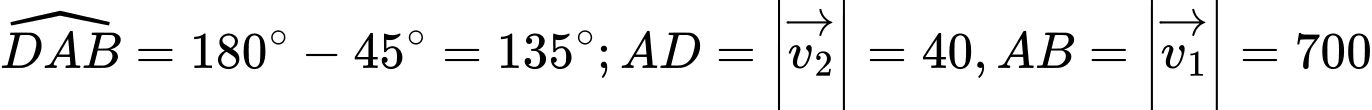 .
.Ta cần tính độ dài đoạn thẳng
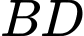 , đây chính là độ dài vectơ
, đây chính là độ dài vectơ 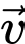 .
.Áp dụng định lí sin trong tam giác
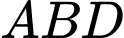 , ta có:
, ta có: 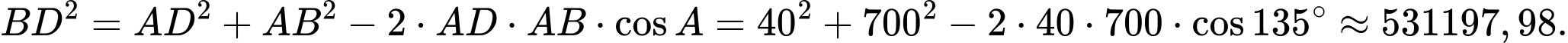
Suy ra
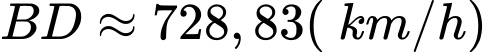 .
.Vậy tốc độ mới của máy bay sau khi gặp gió thổi là 728,83km/h.
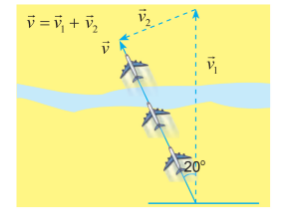
Câu 27 [239459]: Một chiếc máy bay được biết là đang bay về phía Bắc với tốc độ 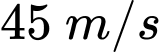 , mặc dù vận tốc của nó so với mặt đất là
, mặc dù vận tốc của nó so với mặt đất là 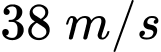 theo hướng nghiêng một góc
theo hướng nghiêng một góc 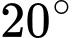 về phía tây bắc (hình). Tính tốc độ của gió
về phía tây bắc (hình). Tính tốc độ của gió
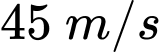 , mặc dù vận tốc của nó so với mặt đất là
, mặc dù vận tốc của nó so với mặt đất là 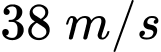 theo hướng nghiêng một góc
theo hướng nghiêng một góc 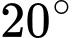 về phía tây bắc (hình). Tính tốc độ của gió
về phía tây bắc (hình). Tính tốc độ của gió
Từ giả thiết ta có:
+) Vectơ tương ứng với vận tốc máy bay là vectơ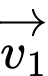
+) Vectơ tương ứng với vận tốc máy bay so với mặt đất là vectơ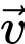
+) Vectơ tương ứng với vận tốc gió là vectơ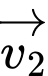
Ta có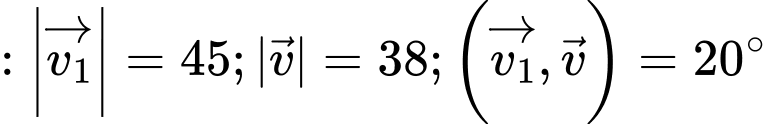
Áp dụng định lý cosin ta có:
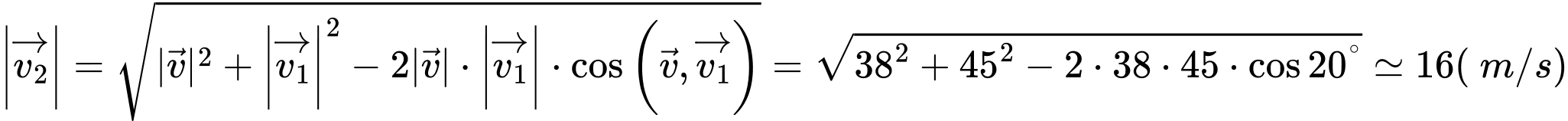
Vậy tốc độ của gió gần bằng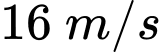
+) Vectơ tương ứng với vận tốc máy bay là vectơ
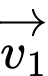
+) Vectơ tương ứng với vận tốc máy bay so với mặt đất là vectơ
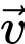
+) Vectơ tương ứng với vận tốc gió là vectơ
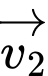
Ta có
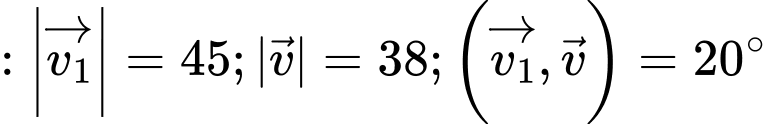
Áp dụng định lý cosin ta có:
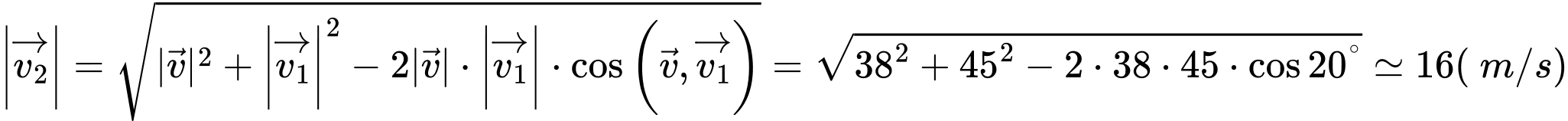
Vậy tốc độ của gió gần bằng
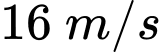
Câu 28 [239434]: Cho ba lực 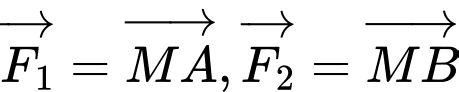 và
và 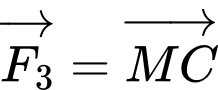 cùng tác động vào một vật tại điểm
cùng tác động vào một vật tại điểm 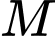 và vật đứng yên. Cho biết cường độ của
và vật đứng yên. Cho biết cường độ của 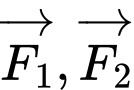 đều là
đều là 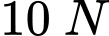 và
và 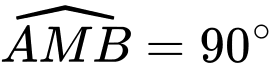 Tìm độ lớn của lực
Tìm độ lớn của lực 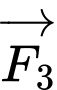 .
.
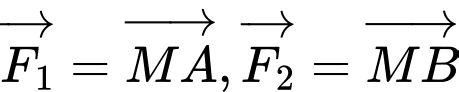 và
và 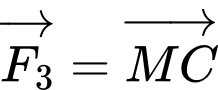 cùng tác động vào một vật tại điểm
cùng tác động vào một vật tại điểm 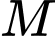 và vật đứng yên. Cho biết cường độ của
và vật đứng yên. Cho biết cường độ của 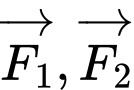 đều là
đều là 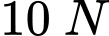 và
và 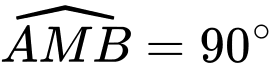 Tìm độ lớn của lực
Tìm độ lớn của lực 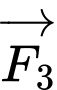 .
.
Ba lực 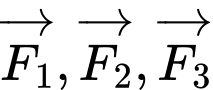 cùng tác dụng vào
cùng tác dụng vào 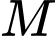 và vật đứng yên nên hợp lực của chúng có giá trị bằng không, hay:
và vật đứng yên nên hợp lực của chúng có giá trị bằng không, hay:
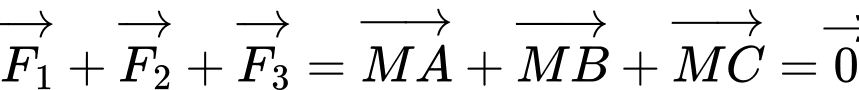
Dựng hình bình hành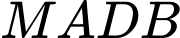 , khi đó:
, khi đó: 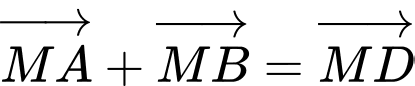

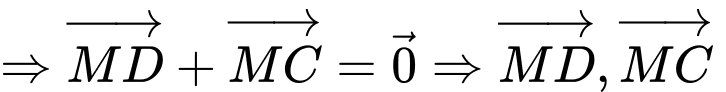 (hai vectơ đối nhau)
(hai vectơ đối nhau)
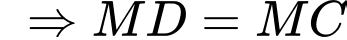
Xét hình bình hành MADB, ta có:
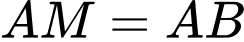 và
và 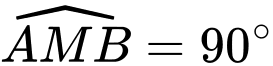
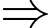 MADB là hình vuông, cạnh
MADB là hình vuông, cạnh 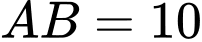
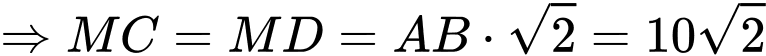
Vậy độ lớn của lực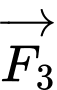 |à
|à 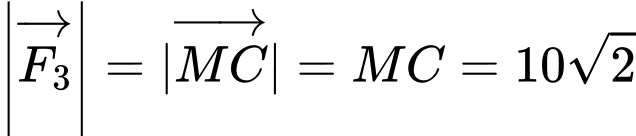 (N)
(N)
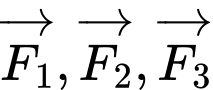 cùng tác dụng vào
cùng tác dụng vào 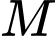 và vật đứng yên nên hợp lực của chúng có giá trị bằng không, hay:
và vật đứng yên nên hợp lực của chúng có giá trị bằng không, hay: 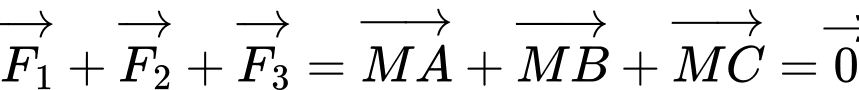
Dựng hình bình hành
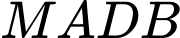 , khi đó:
, khi đó: 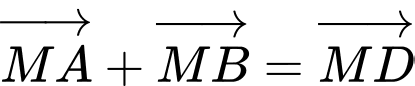

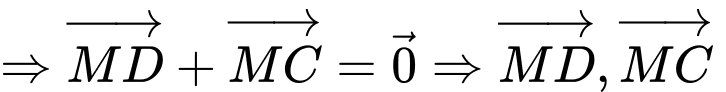 (hai vectơ đối nhau)
(hai vectơ đối nhau) 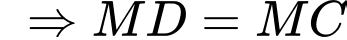
Xét hình bình hành MADB, ta có:
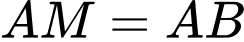 và
và 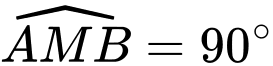
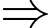 MADB là hình vuông, cạnh
MADB là hình vuông, cạnh 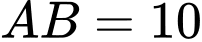
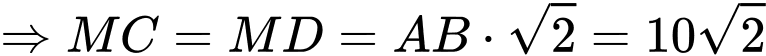
Vậy độ lớn của lực
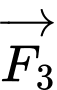 |à
|à 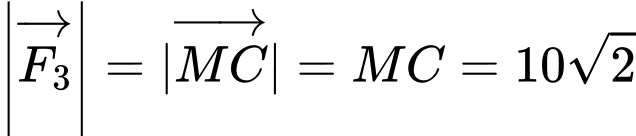 (N)
(N)