Đáp án Bài tập tự luyện
Câu 1 [246094]: Trong mặt phẳng với hệ tọa độ 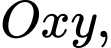 cho đường thẳng
cho đường thẳng 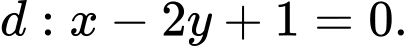 Một vectơ chỉ phương của đường thẳng
Một vectơ chỉ phương của đường thẳng 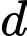 là
là
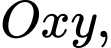 cho đường thẳng
cho đường thẳng 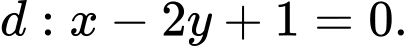 Một vectơ chỉ phương của đường thẳng
Một vectơ chỉ phương của đường thẳng 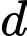 là
là A, 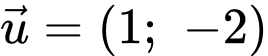 .
.
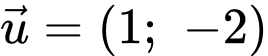 .
.B, 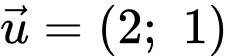 .
.
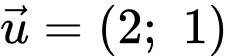 .
.C, 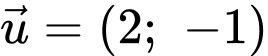 .
.
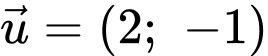 .
.D, 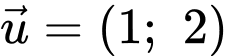 .
.
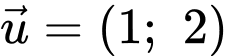 .
.
Chọn B
Đường thẳng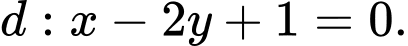 có vectơ pháp tuyến là
có vectơ pháp tuyến là 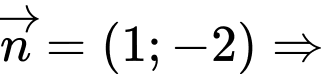 Vectơ chỉ phương của
Vectơ chỉ phương của 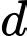 là
là 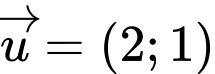 . Đáp án: B
. Đáp án: B
Đường thẳng
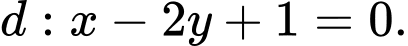 có vectơ pháp tuyến là
có vectơ pháp tuyến là 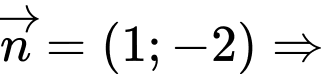 Vectơ chỉ phương của
Vectơ chỉ phương của 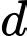 là
là 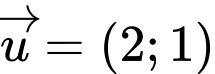 . Đáp án: B
. Đáp án: B
Câu 2 [246098]: Đường thẳng 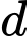 có một vectơ pháp tuyến là
có một vectơ pháp tuyến là 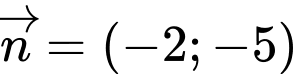 . Đường thẳng
. Đường thẳng  vuông góc với
vuông góc với 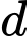 có một vectơ chỉ phương là
có một vectơ chỉ phương là
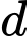 có một vectơ pháp tuyến là
có một vectơ pháp tuyến là 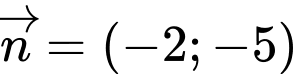 . Đường thẳng
. Đường thẳng  vuông góc với
vuông góc với 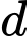 có một vectơ chỉ phương là
có một vectơ chỉ phương là A, 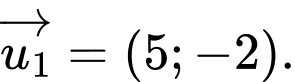
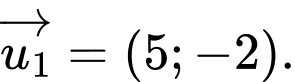
B, 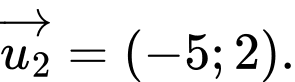
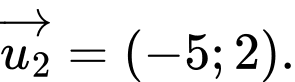
C, 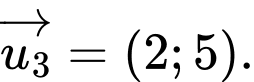
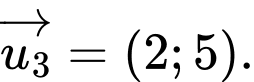
D, 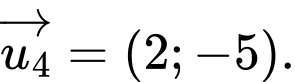
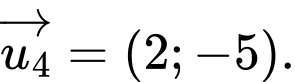
hay chọn 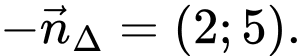 Chọn C. Đáp án: C
Chọn C. Đáp án: C
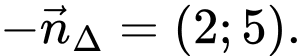 Chọn C. Đáp án: C
Chọn C. Đáp án: C
Câu 3 [246106]: Phương trình tham số của đường thẳng qua 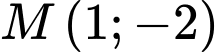 ,
, 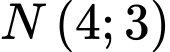 là
là
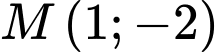 ,
, 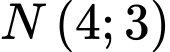 là
là A, 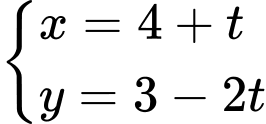 .
.
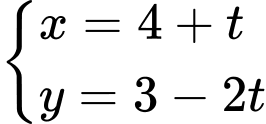 .
.B, 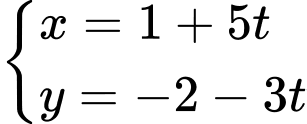 .
.
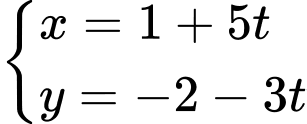 .
.C, 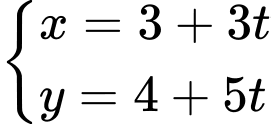 .
.
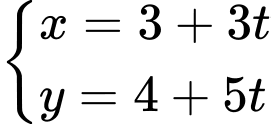 .
.D, 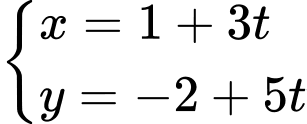 .
.
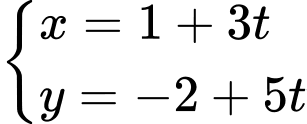 .
.
Chọn D
Đường thẳng có vectơ chỉ phương là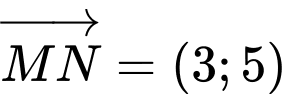 và đi qua
và đi qua 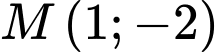 nên có phương trình tham số là
nên có phương trình tham số là 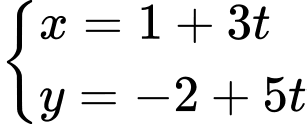 . Đáp án: D
. Đáp án: D
Đường thẳng có vectơ chỉ phương là
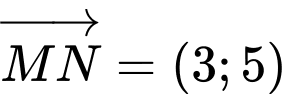 và đi qua
và đi qua 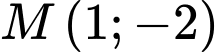 nên có phương trình tham số là
nên có phương trình tham số là 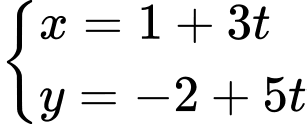 . Đáp án: D
. Đáp án: D
Câu 4 [246110]: Trong mặt phẳng 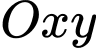 cho điểm
cho điểm 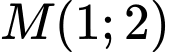 . Gọi
. Gọi 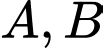 là hình chiếu của
là hình chiếu của 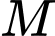 lên
lên 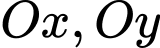 . Viết phương trình đường thẳng
. Viết phương trình đường thẳng  .
.
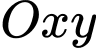 cho điểm
cho điểm 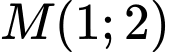 . Gọi
. Gọi 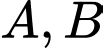 là hình chiếu của
là hình chiếu của 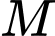 lên
lên 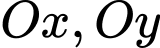 . Viết phương trình đường thẳng
. Viết phương trình đường thẳng  .
. A, 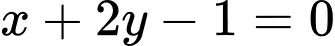 .
.
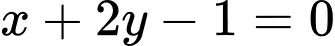 .
.B, 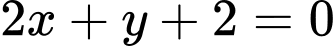 .
.
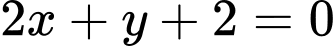 .
.C, 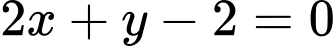 .
.
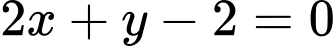 .
.D,  .
.
 .
.
Chọn C.
Ta có hình chiếu của điểm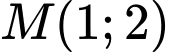 lên
lên 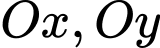 lần lượt là A(1;0) và B(0;2). Do đó phương
trình đường thẳng AB là
lần lượt là A(1;0) và B(0;2). Do đó phương
trình đường thẳng AB là 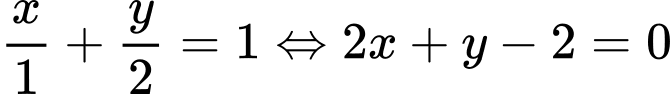 . Đáp án: C
. Đáp án: C
Ta có hình chiếu của điểm
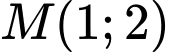 lên
lên 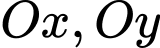 lần lượt là A(1;0) và B(0;2). Do đó phương
trình đường thẳng AB là
lần lượt là A(1;0) và B(0;2). Do đó phương
trình đường thẳng AB là 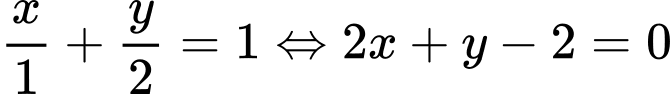 . Đáp án: C
. Đáp án: C
Câu 5 [246140]: Đường trung trực của đoạn  với
với 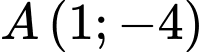 và
và 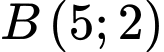 có phương trình là
có phương trình là
 với
với 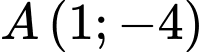 và
và 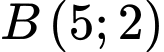 có phương trình là
có phương trình là A, 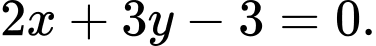
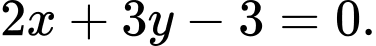
B, 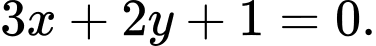
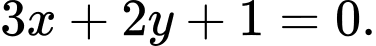
C, 

D, 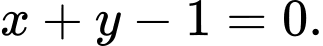
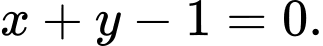
Ta có: 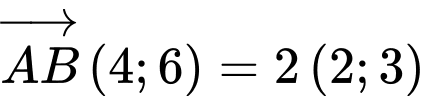
Trung điểm của là
là 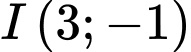
Phương trình trung trực của là:
là: 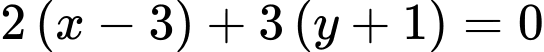
Hay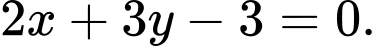 Chọn A.
Đáp án: A
Chọn A.
Đáp án: A
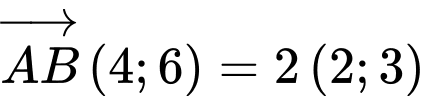
Trung điểm của
 là
là 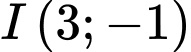
Phương trình trung trực của
 là:
là: 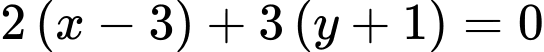
Hay
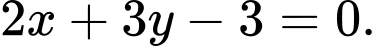 Chọn A.
Đáp án: A
Chọn A.
Đáp án: A
Câu 6 [246109]: Cho đường thẳng 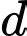 có phương trình tham số
có phương trình tham số 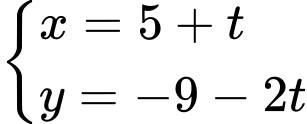 . Phương trình tổng quát của đường thẳng
. Phương trình tổng quát của đường thẳng 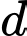 là
là
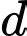 có phương trình tham số
có phương trình tham số 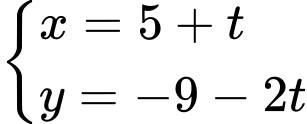 . Phương trình tổng quát của đường thẳng
. Phương trình tổng quát của đường thẳng 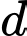 là
là A, 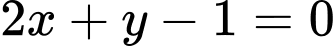 .
.
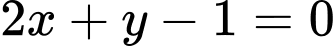 .
.B, 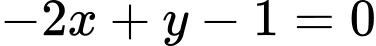 .
.
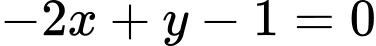 .
.C, 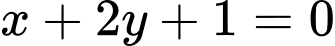 .
.
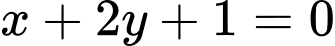 .
.D, 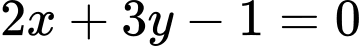 .
.
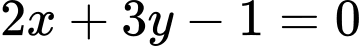 .
.
Chọn A
Đường thẳng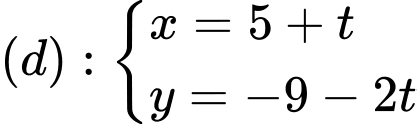
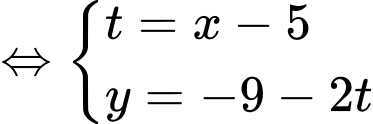
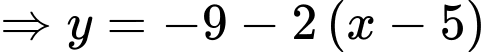
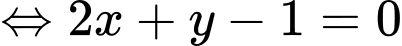 . Đáp án: A
. Đáp án: A
Đường thẳng
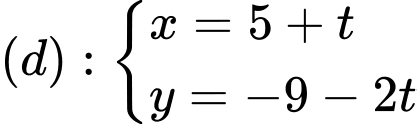
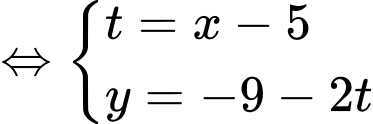
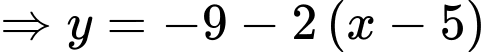
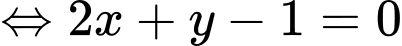 . Đáp án: A
. Đáp án: A
Câu 7 [240398]: Cho 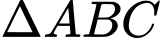 có
có 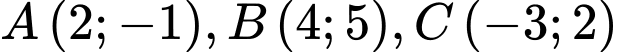 . Đường cao
. Đường cao 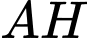 của
của 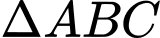 có phương trình là
có phương trình là
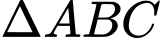 có
có 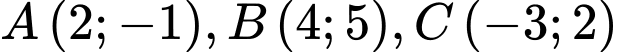 . Đường cao
. Đường cao 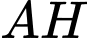 của
của 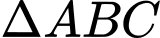 có phương trình là
có phương trình là A, 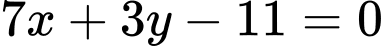 .
.
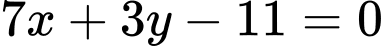 .
.B, 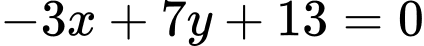 .
.
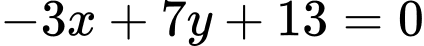 .
.C, 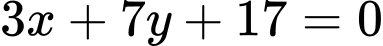 .
.
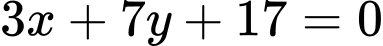 .
.D, 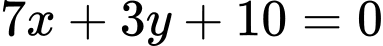 .
.
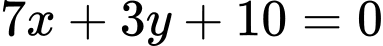 .
.
Đường cao 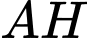 đi qua điểm
đi qua điểm 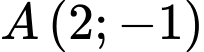 và có VTPT là
và có VTPT là 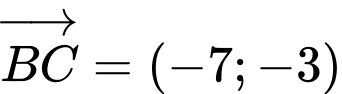 .
.
Vậy phương trình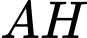 là
là 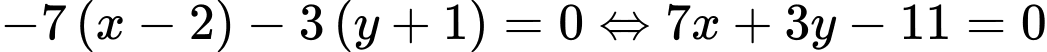 . Đáp án: A
. Đáp án: A
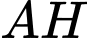 đi qua điểm
đi qua điểm 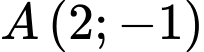 và có VTPT là
và có VTPT là 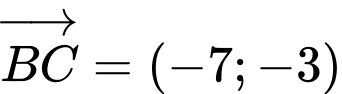 .
.
Vậy phương trình
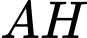 là
là 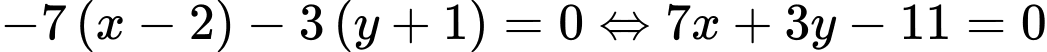 . Đáp án: A
. Đáp án: A
Câu 8 [246123]: Trong mặt phẳng với hệ tọa độ 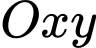 , cho hình bình hành
, cho hình bình hành 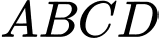 có đỉnh
có đỉnh 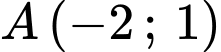 và phương trình đường thẳng chứa cạnh
và phương trình đường thẳng chứa cạnh 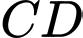 là
là 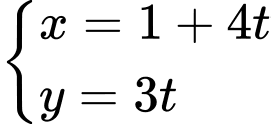 . Viết phương trình tham số của đường thẳng chứa cạnh
. Viết phương trình tham số của đường thẳng chứa cạnh  .
.
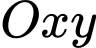 , cho hình bình hành
, cho hình bình hành 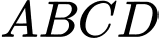 có đỉnh
có đỉnh 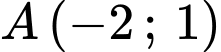 và phương trình đường thẳng chứa cạnh
và phương trình đường thẳng chứa cạnh 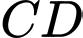 là
là 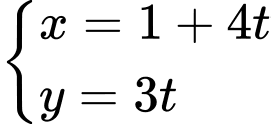 . Viết phương trình tham số của đường thẳng chứa cạnh
. Viết phương trình tham số của đường thẳng chứa cạnh  .
. A, 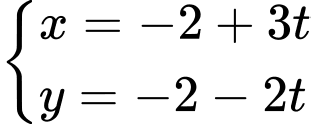 .
.
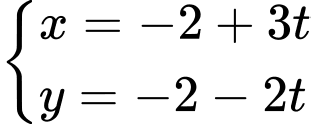 .
.B, 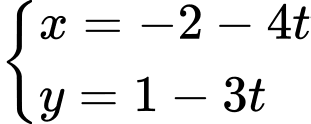 .
.
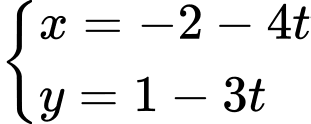 .
.C, 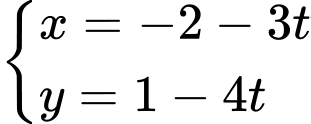
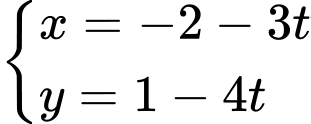
D, 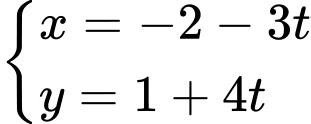
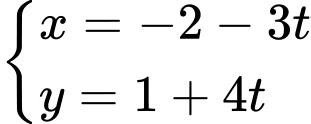
Đường thẳng chứa cạnh CD có VTCP là 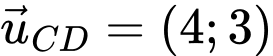
Vì . Suy ra
. Suy ra 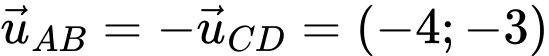
Vậy đường thẳng chứa cạnh AB là đường thẳng qua A và có VTCP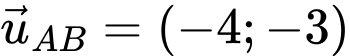 là:
là: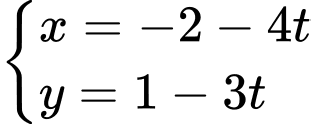 Đáp án: B
Đáp án: B
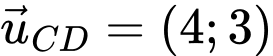
Vì
 . Suy ra
. Suy ra 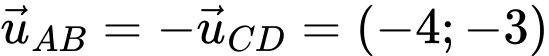
Vậy đường thẳng chứa cạnh AB là đường thẳng qua A và có VTCP
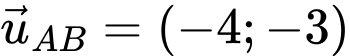 là:
là: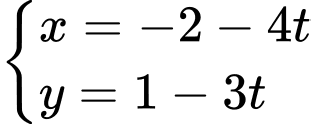 Đáp án: B
Đáp án: B
Câu 9 [246203]: Khoảng cách từ điểm 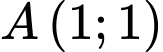 đến đường thẳng
đến đường thẳng 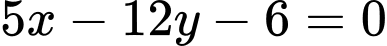 là
là
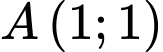 đến đường thẳng
đến đường thẳng 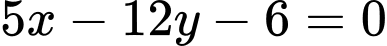 là
là A,  .
.
 .
.B, 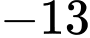 .
.
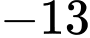 .
.C, 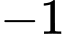 .
.
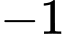 .
.D, 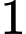 .
.
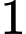 .
.
Chọn D
Khoảng cách từ điểm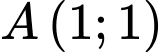 đến đường thẳng
đến đường thẳng 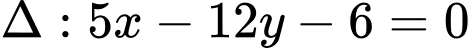 là
là
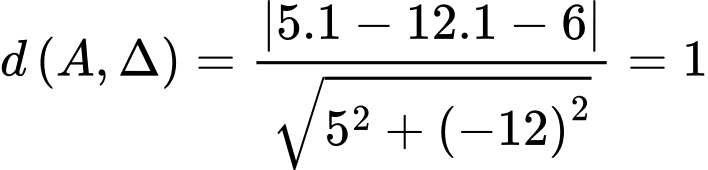 . Đáp án: D
. Đáp án: D
Khoảng cách từ điểm
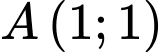 đến đường thẳng
đến đường thẳng 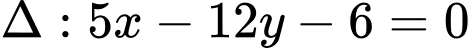 là
là
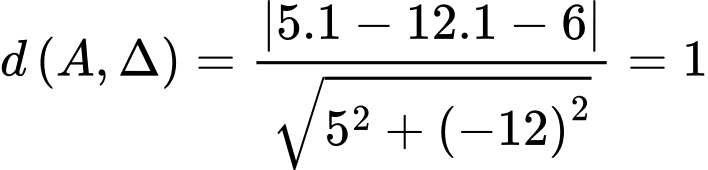 . Đáp án: D
. Đáp án: D
Câu 10 [246183]: Cho hai đường thẳng 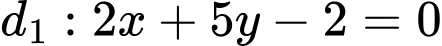 và
và 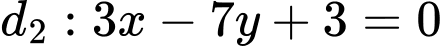 . Góc tạo bởi đường thẳng
. Góc tạo bởi đường thẳng 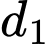 và
và 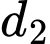 bằng
bằng
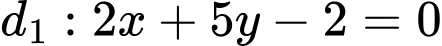 và
và 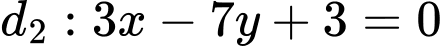 . Góc tạo bởi đường thẳng
. Góc tạo bởi đường thẳng 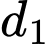 và
và 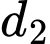 bằng
bằng A, 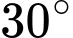 .
.
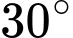 .
.B, 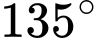 .
.
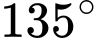 .
.C, 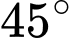 .
.
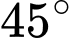 .
.D, 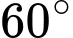 .
.
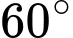 .
.
Chọn C
Đường thẳng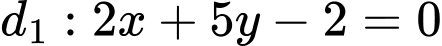 có vectơ pháp tuyến
có vectơ pháp tuyến 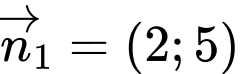 .
.
Đường thẳng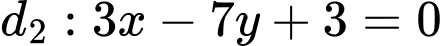 có vectơ pháp tuyến
có vectơ pháp tuyến 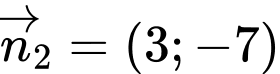 .
.
Góc giữa hai đường thẳng được tính bằng công thức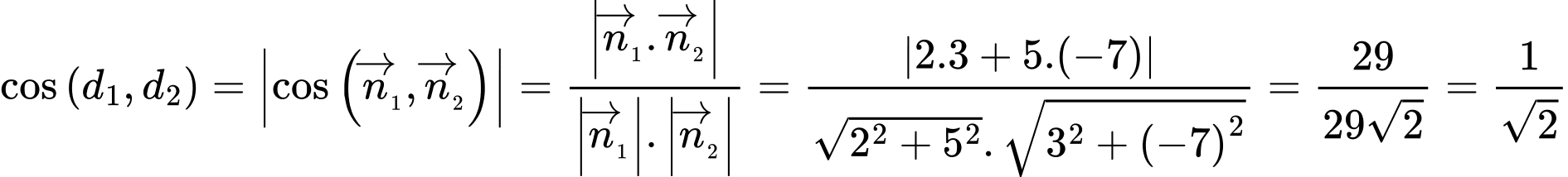
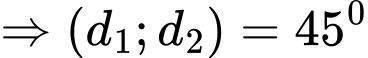
Vậy góc tạo bởi đường thẳng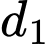 và
và 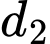 bằng
bằng 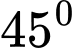 . Đáp án: C
. Đáp án: C
Đường thẳng
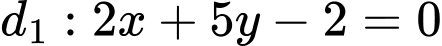 có vectơ pháp tuyến
có vectơ pháp tuyến 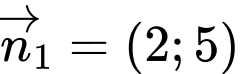 .
.Đường thẳng
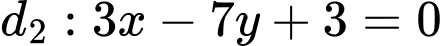 có vectơ pháp tuyến
có vectơ pháp tuyến 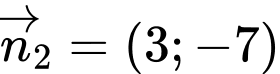 .
.Góc giữa hai đường thẳng được tính bằng công thức
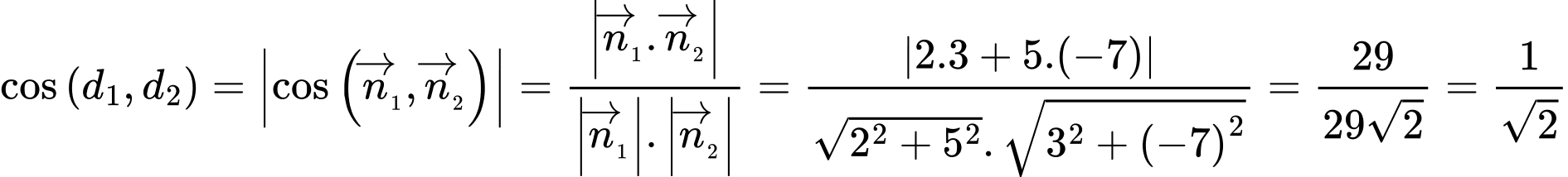
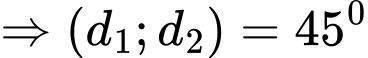
Vậy góc tạo bởi đường thẳng
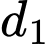 và
và 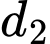 bằng
bằng 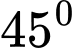 . Đáp án: C
. Đáp án: C
Câu 11 [246192]: Tính góc tạo bởi giữa hai đường thẳng
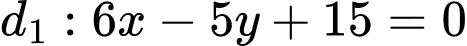 và
và 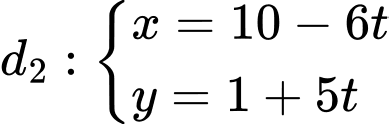
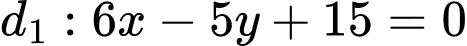 và
và 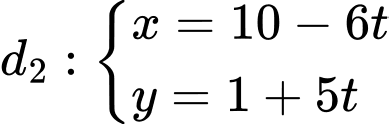
A, 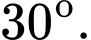
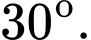
B, 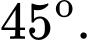
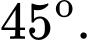
C, 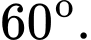
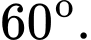
D, 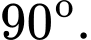
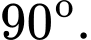
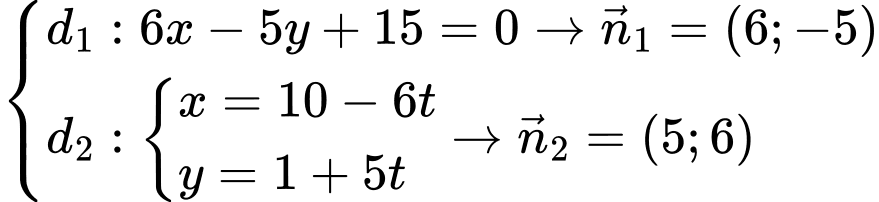
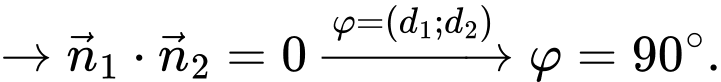 Đáp án: D
Đáp án: D
Câu 12 [246221]: Đường tròn  có tâm
có tâm 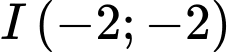 và tiếp xúc với đường thẳng
và tiếp xúc với đường thẳng 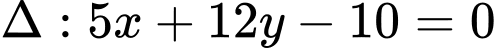 . Bán kính
. Bán kính 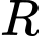 của đường tròn
của đường tròn  bằng
bằng
 có tâm
có tâm 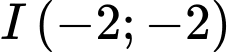 và tiếp xúc với đường thẳng
và tiếp xúc với đường thẳng 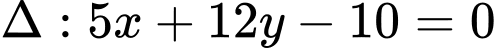 . Bán kính
. Bán kính 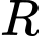 của đường tròn
của đường tròn  bằng
bằng A, 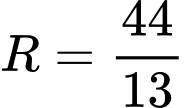 .
.
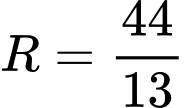 .
.B, 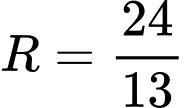 .
.
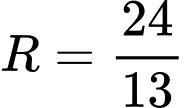 .
.C, 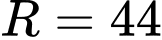 .
.
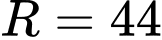 .
.D, 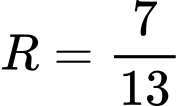 .
.
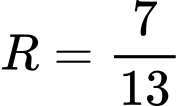 .
.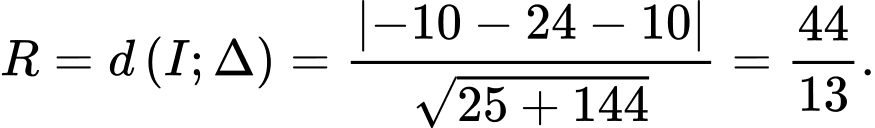 Chọn A. Đáp án: A
Chọn A. Đáp án: A
Câu 13 [246212]: Khoảng cách từ giao điểm của hai đường thẳng 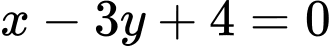 và
và 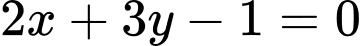 đến đường thẳng
đến đường thẳng 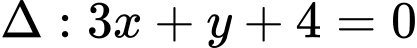 bằng
bằng
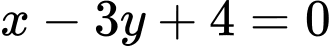 và
và 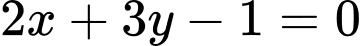 đến đường thẳng
đến đường thẳng 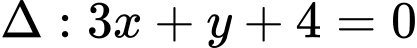 bằng
bằng A, 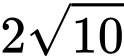 .
.
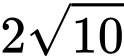 .
.B, 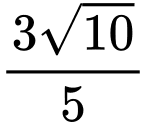 .
.
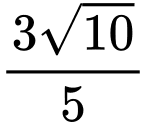 .
.C, 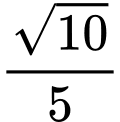 .
.
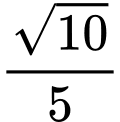 .
.D, 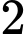 .
.
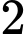 .
.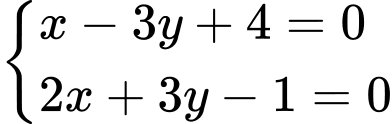
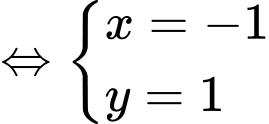
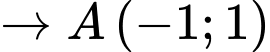
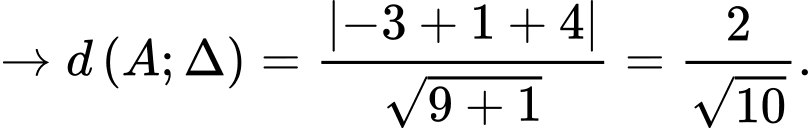 Chọn C. Đáp án: C
Chọn C. Đáp án: C
Câu 14 [246213]: Trong mặt phẳng với hệ tọa độ 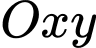 , cho tam giác
, cho tam giác 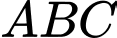 có
có 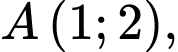
 và
và 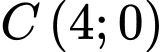 . Chiều cao của tam giác kẻ từ đỉnh
. Chiều cao của tam giác kẻ từ đỉnh 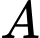 bằng
bằng
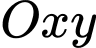 , cho tam giác
, cho tam giác 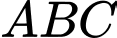 có
có 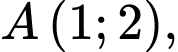
 và
và 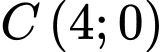 . Chiều cao của tam giác kẻ từ đỉnh
. Chiều cao của tam giác kẻ từ đỉnh 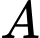 bằng
bằng A, 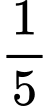 .
.
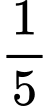 .
.B, 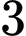 .
.
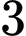 .
.C, 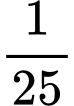 .
.
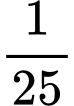 .
.D, 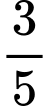 .
.
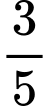 .
.
Ta có: 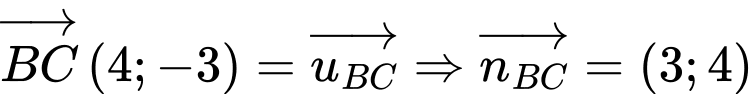
Phương trình đường thẳng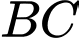 là:
là: 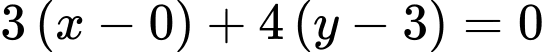
Hay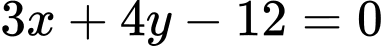
Suy ra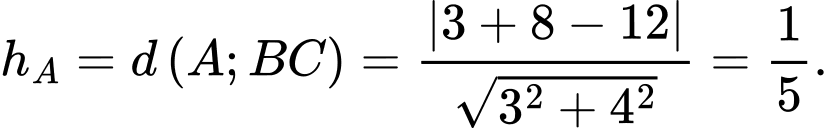 Chọn A.
Đáp án: A
Chọn A.
Đáp án: A
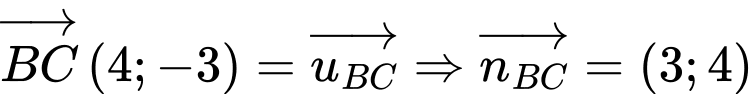
Phương trình đường thẳng
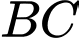 là:
là: 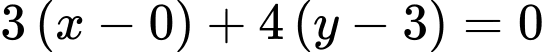
Hay
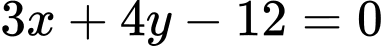
Suy ra
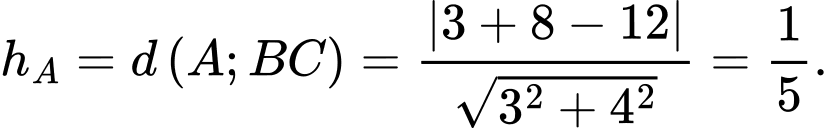 Chọn A.
Đáp án: A
Chọn A.
Đáp án: A
Câu 15 [246251]: Trong mặt phẳng với hệ trục tọa độ 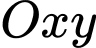 , cho tam giác
, cho tam giác 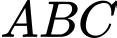 có
có 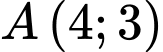 ,
, 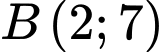 ,
, 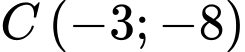 . Tọa độ chân đường cao kẻ từ đỉnh
. Tọa độ chân đường cao kẻ từ đỉnh 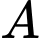 xuống cạnh
xuống cạnh 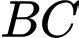 là
là
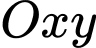 , cho tam giác
, cho tam giác 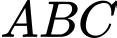 có
có 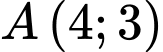 ,
, 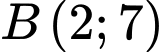 ,
, 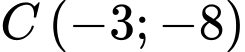 . Tọa độ chân đường cao kẻ từ đỉnh
. Tọa độ chân đường cao kẻ từ đỉnh 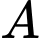 xuống cạnh
xuống cạnh 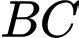 là
là A, 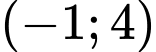 .
.
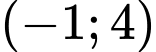 .
.B, 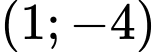 .
.
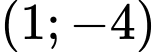 .
.C, 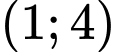 .
.
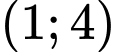 .
.D, 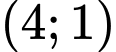 .
.
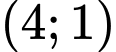 .
.
Chọn C
Phương trình đường thẳng đi qua hai điểm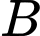 và
và  có dạng:
có dạng: 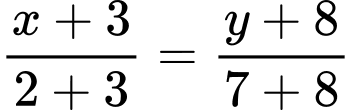
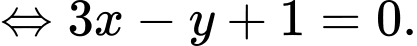
Đường thẳng đi qua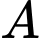 và vuông góc với
và vuông góc với 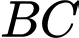 có phương trình:
có phương trình: 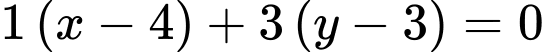
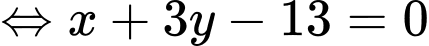
Tọa độ chân đường cao kẻ từ đỉnh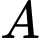 xuống cạnh
xuống cạnh 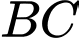 là nghiệm của hệ phương trình:
là nghiệm của hệ phương trình: 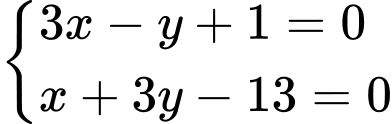
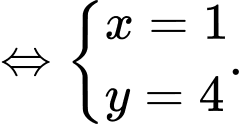 Đáp án: C
Đáp án: C
Phương trình đường thẳng đi qua hai điểm
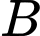 và
và  có dạng:
có dạng: 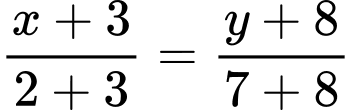
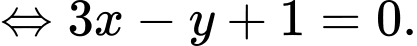
Đường thẳng đi qua
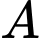 và vuông góc với
và vuông góc với 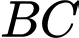 có phương trình:
có phương trình: 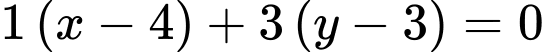
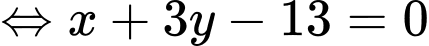
Tọa độ chân đường cao kẻ từ đỉnh
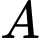 xuống cạnh
xuống cạnh 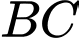 là nghiệm của hệ phương trình:
là nghiệm của hệ phương trình: 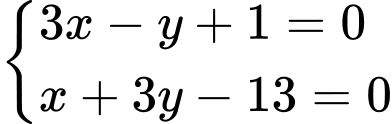
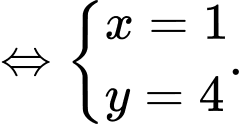 Đáp án: C
Đáp án: C
Câu 16 [246260]: Trong mặt phẳng với hệ tọa độ 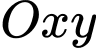 , cho hai đường thẳng
, cho hai đường thẳng 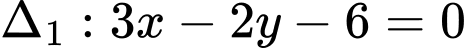 và
và 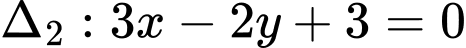 . Tìm điểm
. Tìm điểm 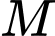 thuộc trục hoành sao cho
thuộc trục hoành sao cho 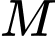 cách đều hai đường thẳng đã cho.
cách đều hai đường thẳng đã cho.
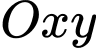 , cho hai đường thẳng
, cho hai đường thẳng 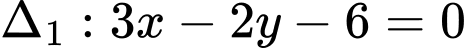 và
và 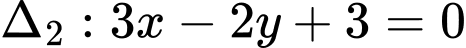 . Tìm điểm
. Tìm điểm 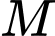 thuộc trục hoành sao cho
thuộc trục hoành sao cho 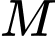 cách đều hai đường thẳng đã cho.
cách đều hai đường thẳng đã cho. A, 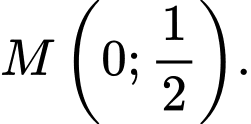
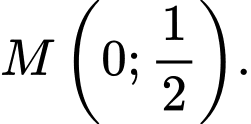
B, 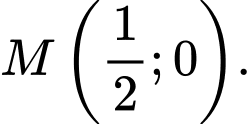
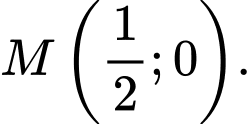
C, 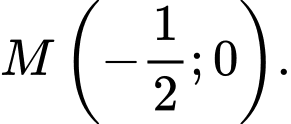
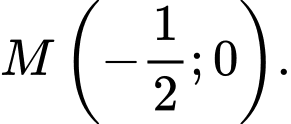
D, 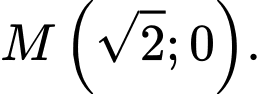
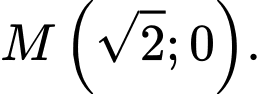
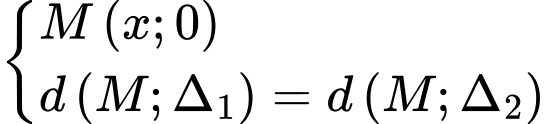
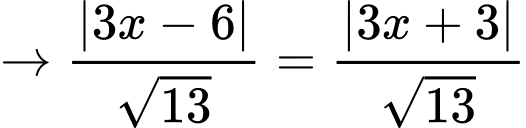
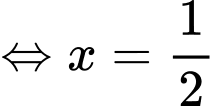
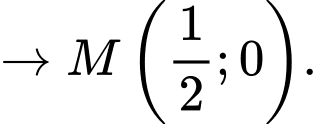 Chọn B. Đáp án: B
Chọn B. Đáp án: B
Câu 17 [246143]: Trong mặt phẳng với hệ tọa độ 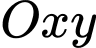 , cho điểm
, cho điểm 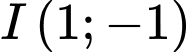 và hai đường thẳng
và hai đường thẳng 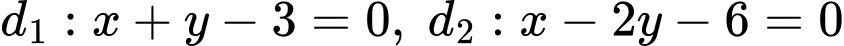 . Hai điểm
. Hai điểm 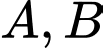 lần lượt thuộc hai đường thẳng
lần lượt thuộc hai đường thẳng 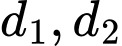 sao cho
sao cho 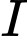 là trung điểm của đoạn thẳng
là trung điểm của đoạn thẳng  . Đường thẳng
. Đường thẳng  có một vectơ chỉ phương là
có một vectơ chỉ phương là
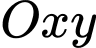 , cho điểm
, cho điểm 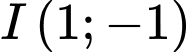 và hai đường thẳng
và hai đường thẳng 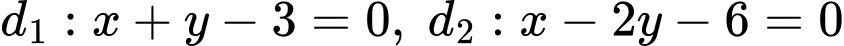 . Hai điểm
. Hai điểm 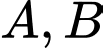 lần lượt thuộc hai đường thẳng
lần lượt thuộc hai đường thẳng 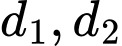 sao cho
sao cho 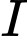 là trung điểm của đoạn thẳng
là trung điểm của đoạn thẳng  . Đường thẳng
. Đường thẳng  có một vectơ chỉ phương là
có một vectơ chỉ phương là A, 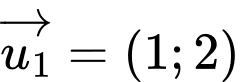 .
.
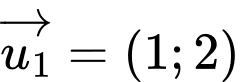 .
.B, 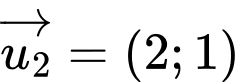 .
.
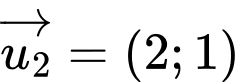 .
.C, 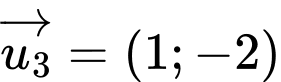 .
.
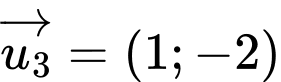 .
.D, 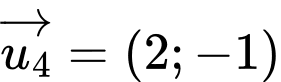 .
.
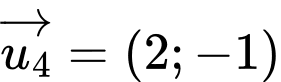 .
.
Chọn A
Vì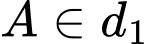 , giả sử
, giả sử 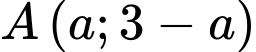 ; Vì
; Vì 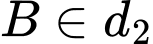 , giả sử
, giả sử 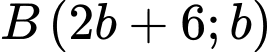
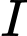 là trung điểm của đoạn thẳng
là trung điểm của đoạn thẳng  khi và chỉ khi
khi và chỉ khi 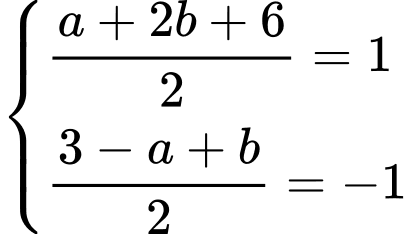
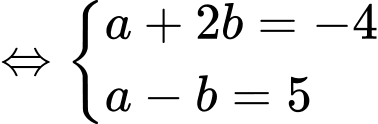
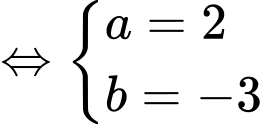
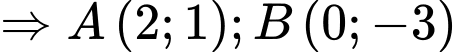
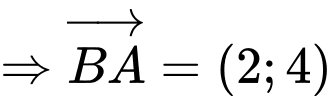
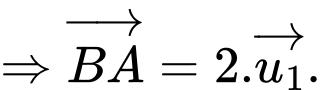
Vậy đường thẳng có một vectơ chỉ phương là
có một vectơ chỉ phương là 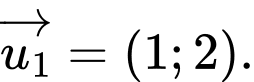 Đáp án: A
Đáp án: A
Vì
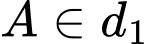 , giả sử
, giả sử 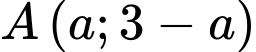 ; Vì
; Vì 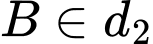 , giả sử
, giả sử 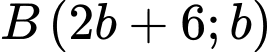
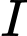 là trung điểm của đoạn thẳng
là trung điểm của đoạn thẳng  khi và chỉ khi
khi và chỉ khi 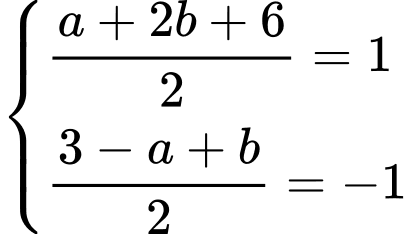
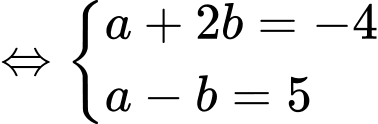
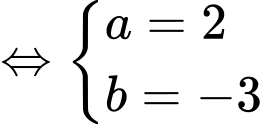
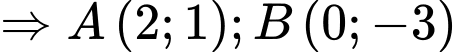
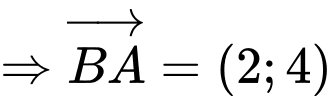
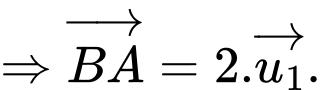
Vậy đường thẳng
 có một vectơ chỉ phương là
có một vectơ chỉ phương là 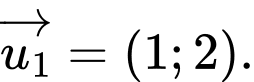 Đáp án: A
Đáp án: A
Câu 18 [246264]: Trong mặt phẳng với hệ tọa độ 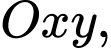 giả sử điểm
giả sử điểm 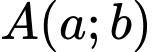 thuộc đường thẳng
thuộc đường thẳng 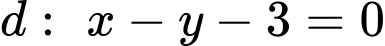 và cách
và cách 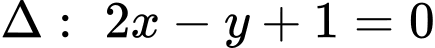 một khoảng bằng
một khoảng bằng 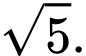 Tính
Tính 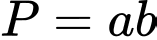 biết
biết 
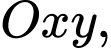 giả sử điểm
giả sử điểm 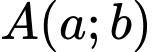 thuộc đường thẳng
thuộc đường thẳng 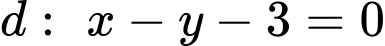 và cách
và cách 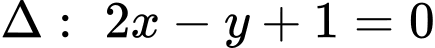 một khoảng bằng
một khoảng bằng 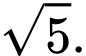 Tính
Tính 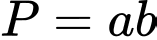 biết
biết 
A, 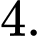
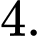
B, 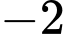
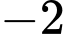
C, 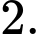
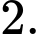
D, 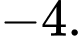
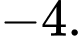
Chọn B
Do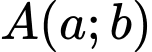 thuộc đường thẳng
thuộc đường thẳng 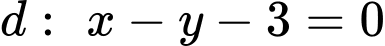 nên
nên 
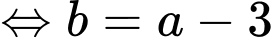
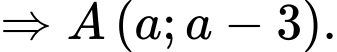
Khoảng cách từ điểm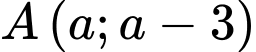 đến đường thẳng
đến đường thẳng 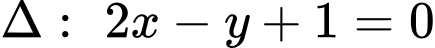 là
là 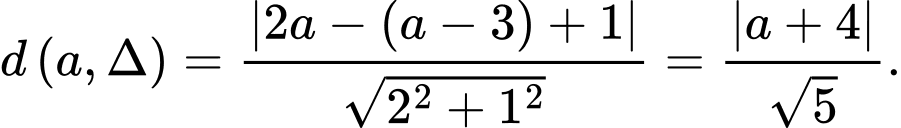
Theo đề bài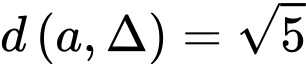
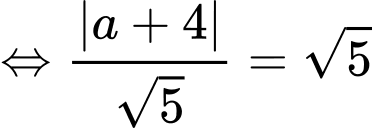
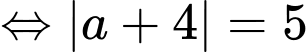
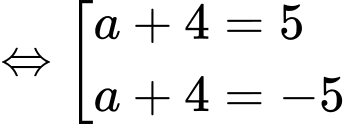
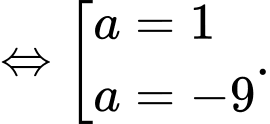
Theo đề bài điểm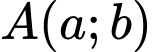 có hoành độ dương nên
có hoành độ dương nên 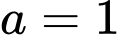
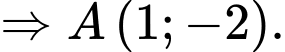 Vậy
Vậy 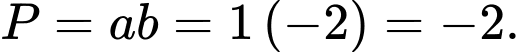 Đáp án: B
Đáp án: B
Do
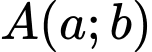 thuộc đường thẳng
thuộc đường thẳng 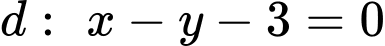 nên
nên 
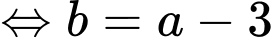
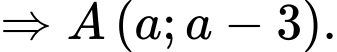
Khoảng cách từ điểm
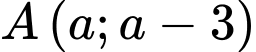 đến đường thẳng
đến đường thẳng 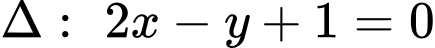 là
là 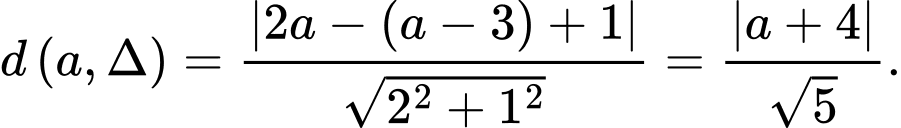
Theo đề bài
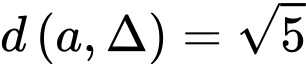
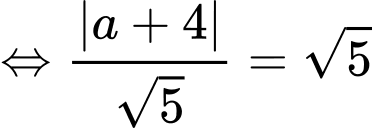
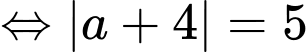
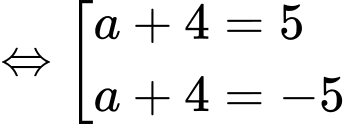
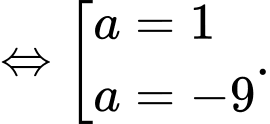
Theo đề bài điểm
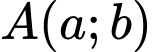 có hoành độ dương nên
có hoành độ dương nên 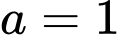
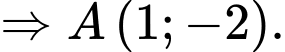 Vậy
Vậy 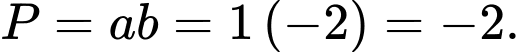 Đáp án: B
Đáp án: B
Câu 19 [246267]: Trong mặt phẳng tọa độ 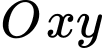 , cho điểm
, cho điểm 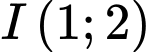 và đường thẳng
và đường thẳng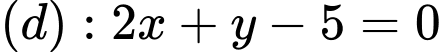 . Biết rằng có hai điểm
. Biết rằng có hai điểm 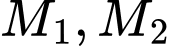 thuộc (d) sao cho
thuộc (d) sao cho  . Tổng các hoành độ của
. Tổng các hoành độ của 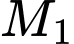 và
và 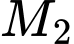 là
là
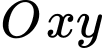 , cho điểm
, cho điểm 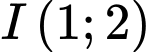 và đường thẳng
và đường thẳng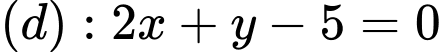 . Biết rằng có hai điểm
. Biết rằng có hai điểm 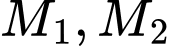 thuộc (d) sao cho
thuộc (d) sao cho  . Tổng các hoành độ của
. Tổng các hoành độ của 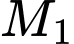 và
và 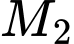 là
là A, 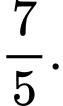
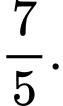
B, 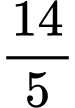 .
.
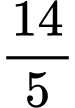 .
.C, 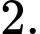
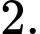
D, 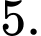
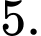
Chọn B
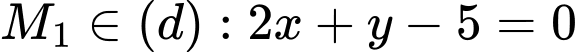
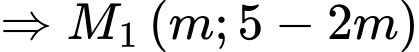
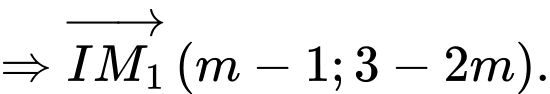
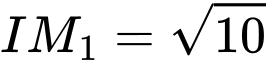
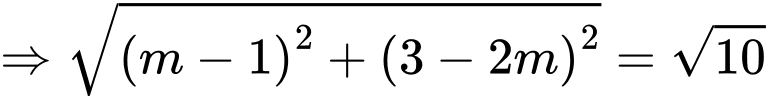
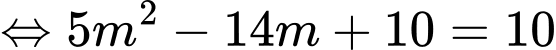
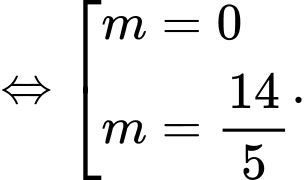
 có 2 điểm thỏa mãn yêu cầu bài toán là
có 2 điểm thỏa mãn yêu cầu bài toán là 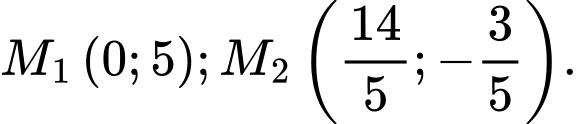 Tổng các hoành độ của
Tổng các hoành độ của  và
và  là:
là: 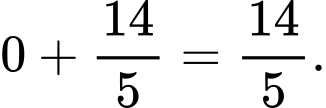 Đáp án: B
Đáp án: B
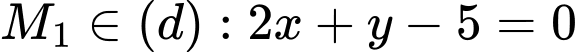
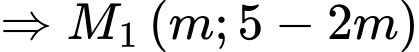
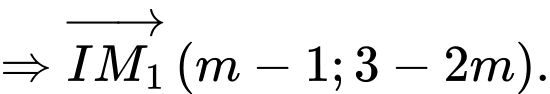
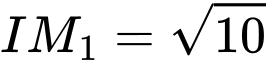
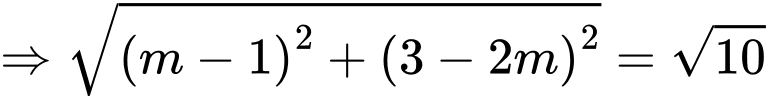
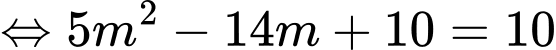
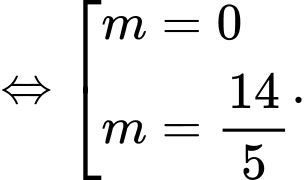
 có 2 điểm thỏa mãn yêu cầu bài toán là
có 2 điểm thỏa mãn yêu cầu bài toán là 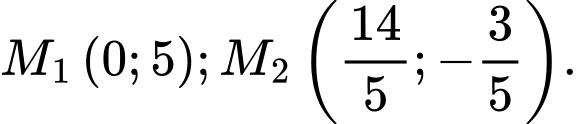 Tổng các hoành độ của
Tổng các hoành độ của 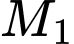 và
và 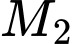 là:
là: 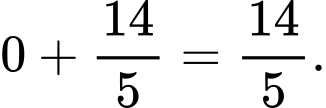 Đáp án: B
Đáp án: B
Câu 20 [581038]: Trong mặt phẳng với hệ tọa độ 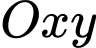 , cho hai điểm
, cho hai điểm 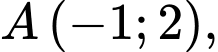
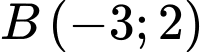 và đường thẳng
và đường thẳng 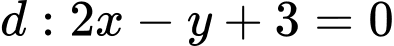 . Điểm
. Điểm  thuộc
thuộc 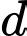 sao cho tam giác
sao cho tam giác 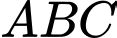 cân tại
cân tại  Tìm tung độ của điểm
Tìm tung độ của điểm 
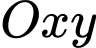 , cho hai điểm
, cho hai điểm 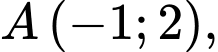
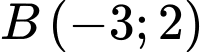 và đường thẳng
và đường thẳng 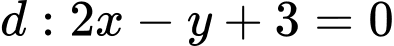 . Điểm
. Điểm  thuộc
thuộc 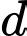 sao cho tam giác
sao cho tam giác 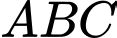 cân tại
cân tại  Tìm tung độ của điểm
Tìm tung độ của điểm 
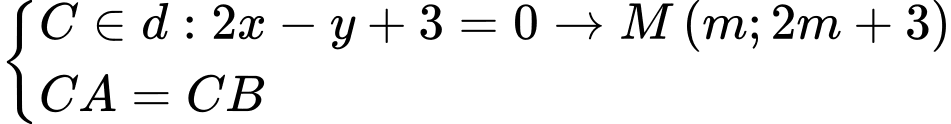
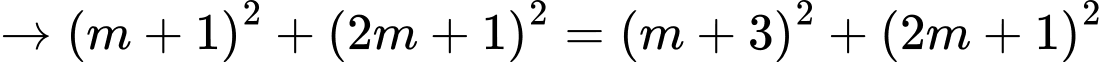
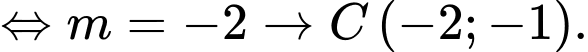
Do đó tung độ điểm
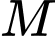 bằng
bằng 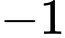 .
.
Câu 21 [246270]: Trong mặt phẳng với hệ tọa độ 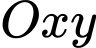 , cho
, cho 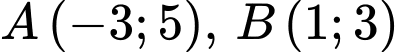 và đường thẳng
và đường thẳng 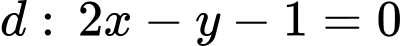 , đường thẳng
, đường thẳng  cắt
cắt 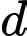 tại
tại 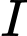 . Tính tỉ số
. Tính tỉ số 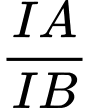 .
.
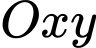 , cho
, cho 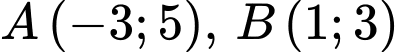 và đường thẳng
và đường thẳng 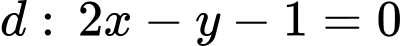 , đường thẳng
, đường thẳng  cắt
cắt 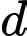 tại
tại 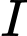 . Tính tỉ số
. Tính tỉ số 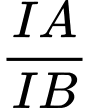 .
. A, 6.
B, 2.
C, 4.
D, 1.
Chọn A
Vetơ chỉ phương của AB là: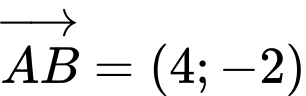
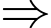 vectơ pháp tuyến của AB là:
vectơ pháp tuyến của AB là: 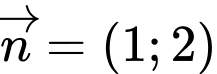
Phương trình đường thẳng là:
là: 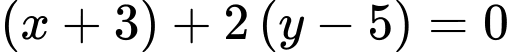
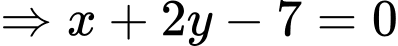
Tọa độ điểm I là nghiệm của hệ phương trình: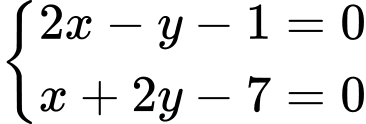
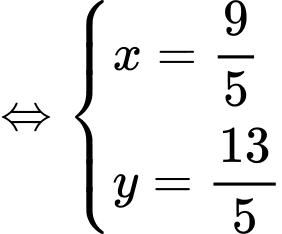
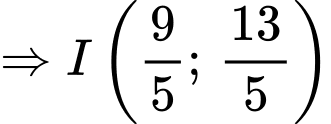 .
.
Vậy tỉ số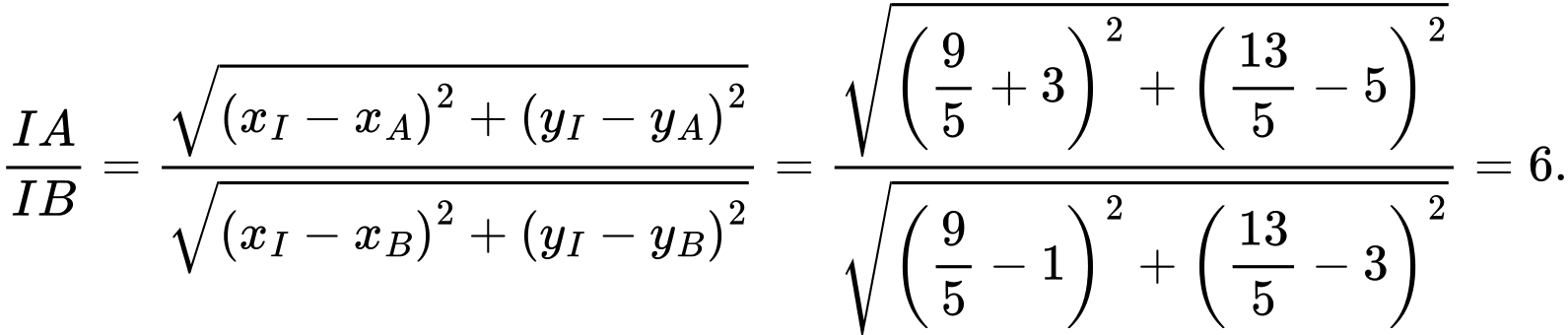 Đáp án: A
Đáp án: A
Vetơ chỉ phương của AB là:
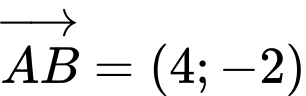
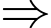 vectơ pháp tuyến của AB là:
vectơ pháp tuyến của AB là: 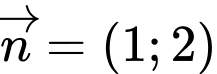
Phương trình đường thẳng
 là:
là: 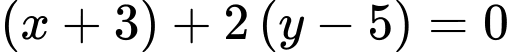
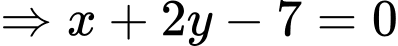
Tọa độ điểm I là nghiệm của hệ phương trình:
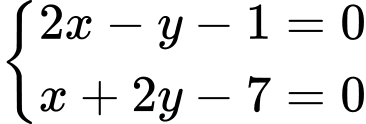
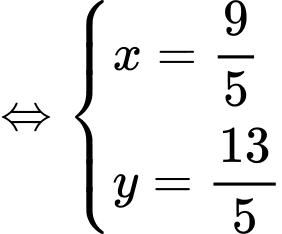
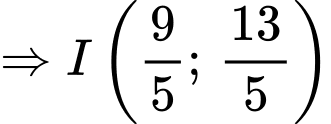 .
.Vậy tỉ số
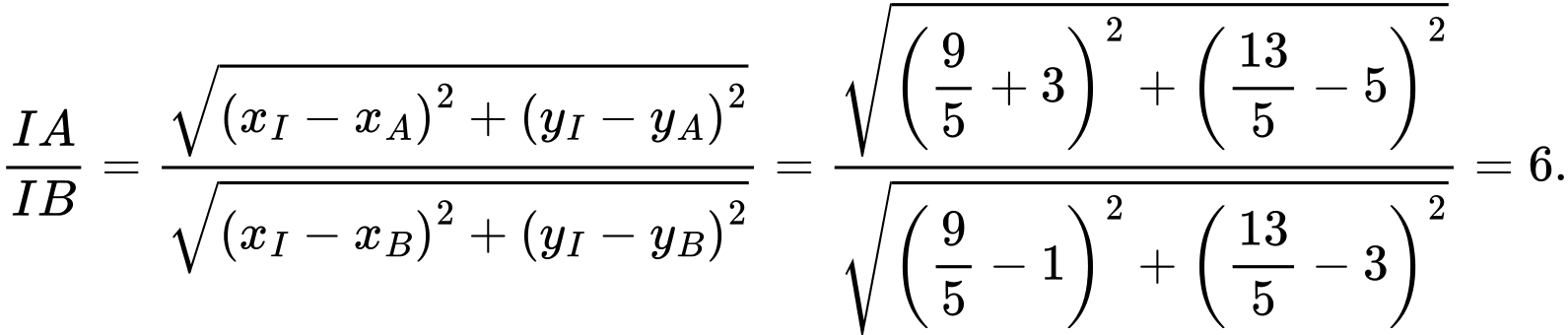 Đáp án: A
Đáp án: A
Câu 22 [581040]: Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có 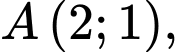 đường cao
đường cao 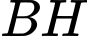 có phương trình
có phương trình 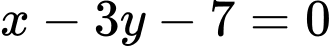 và trung tuyến
và trung tuyến 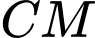 có phương trình
có phương trình  Tìm hoành độ của đỉnh
Tìm hoành độ của đỉnh 
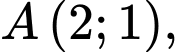 đường cao
đường cao 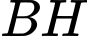 có phương trình
có phương trình 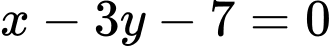 và trung tuyến
và trung tuyến 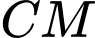 có phương trình
có phương trình  Tìm hoành độ của đỉnh
Tìm hoành độ của đỉnh 
Điểm  thuộc đường trung tuyến
thuộc đường trung tuyến 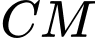 nên gọi tọa độ điểm
nên gọi tọa độ điểm 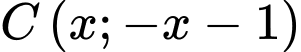 .
.
Tọa độ 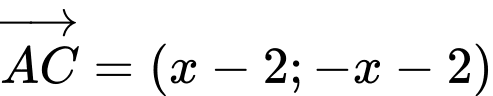 , tọa độ vectơ chỉ phương của đường thẳng
, tọa độ vectơ chỉ phương của đường thẳng 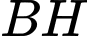 là
là 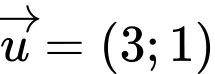 .
.
Vì  nên
nên 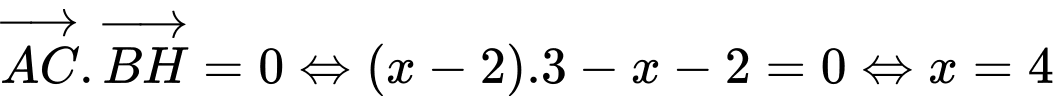 .
.
Vậy 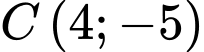 .
.
Câu 23 [246268]: Trong hệ tọa độ 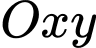 cho
cho 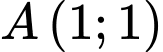 ,
, 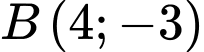 . Gọi
. Gọi 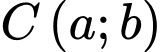 thuộc đường thẳng
thuộc đường thẳng 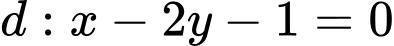 sao cho khoảng cách từ
sao cho khoảng cách từ  đến đường thẳng
đến đường thẳng  bằng 6. Biết rằng
bằng 6. Biết rằng  có hoành độ nguyên, tính
có hoành độ nguyên, tính  .
.
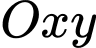 cho
cho 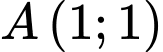 ,
, 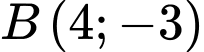 . Gọi
. Gọi 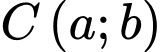 thuộc đường thẳng
thuộc đường thẳng 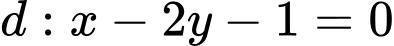 sao cho khoảng cách từ
sao cho khoảng cách từ  đến đường thẳng
đến đường thẳng  bằng 6. Biết rằng
bằng 6. Biết rằng  có hoành độ nguyên, tính
có hoành độ nguyên, tính  .
. A, 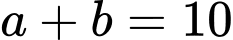 .
.
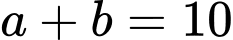 .
.B, 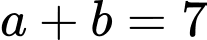 .
.
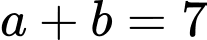 .
.C, 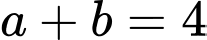 .
.
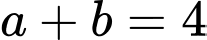 .
.D, 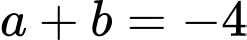 .
.
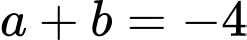 .
.
Chọn A
Ta có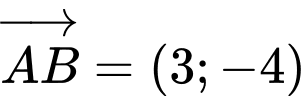 .
.
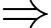 phương trình tổng quát của đường thẳng
phương trình tổng quát của đường thẳng  có dạng
có dạng 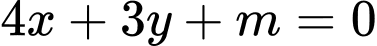 .
.
Vì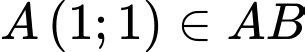 nên
nên 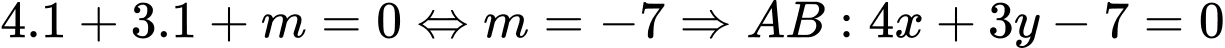 .
.
Vì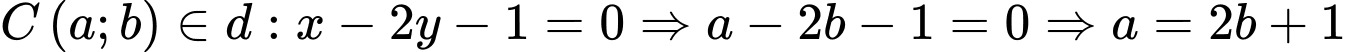 .
.
Theo đề ra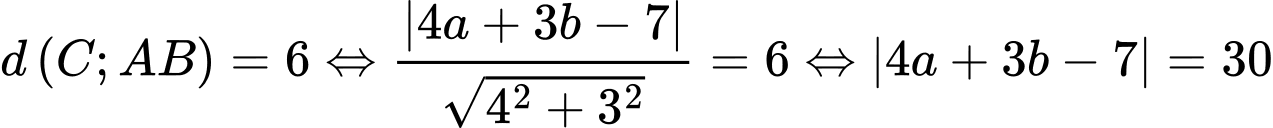 .
.
Thay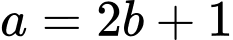 vào ta được:
vào ta được: 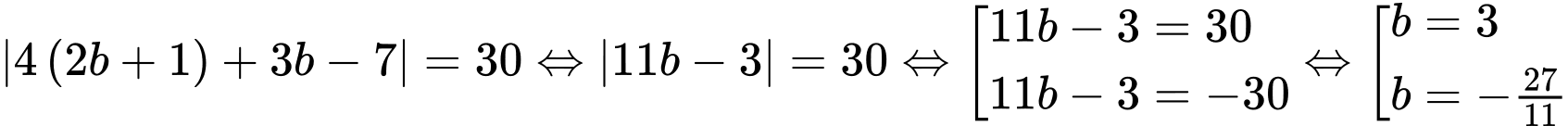 .
.
Do có tọa độ nguyên nên
có tọa độ nguyên nên 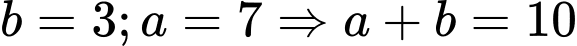 . Đáp án: A
. Đáp án: A
Ta có
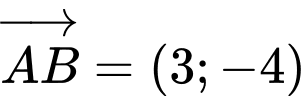 .
.
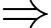 phương trình tổng quát của đường thẳng
phương trình tổng quát của đường thẳng  có dạng
có dạng 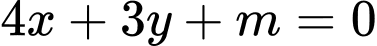 .
.
Vì
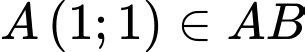 nên
nên 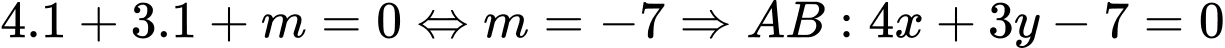 .
.
Vì
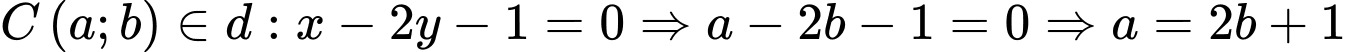 .
.
Theo đề ra
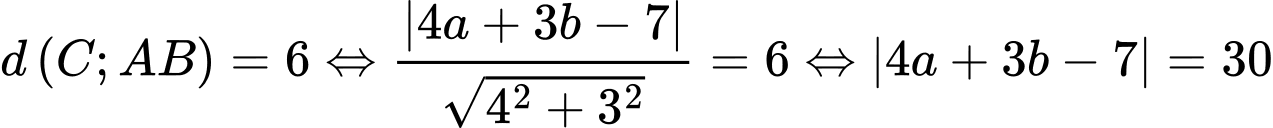 .
.
Thay
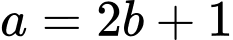 vào ta được:
vào ta được: 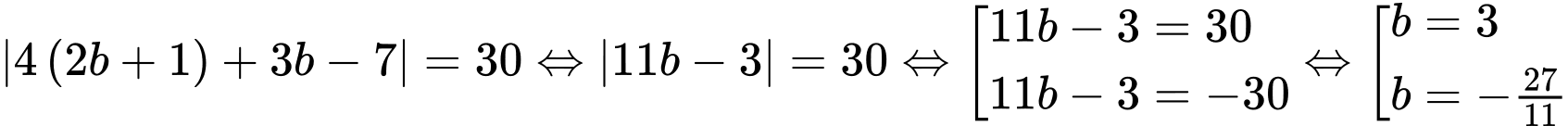 .
.
Do
 có tọa độ nguyên nên
có tọa độ nguyên nên 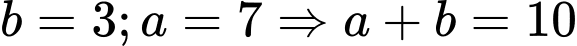 . Đáp án: A
. Đáp án: A
Câu 24 [581039]: Có hai con tài 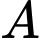 và
và 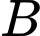 cùng xuất phát từ hai bến, chuyển động đều theo đường thẳng ngoài biển. Trên màn hình ra đa của trạm điều khiển (được coi như mặt phẳng tọa độ Oxy với đơn vị trên các trục tính theo ki - lô - mét), sau khi xuất phát
cùng xuất phát từ hai bến, chuyển động đều theo đường thẳng ngoài biển. Trên màn hình ra đa của trạm điều khiển (được coi như mặt phẳng tọa độ Oxy với đơn vị trên các trục tính theo ki - lô - mét), sau khi xuất phát 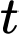 (giờ)
(giờ) 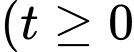 ), vị trí của tàu
), vị trí của tàu 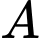 có tọa độ được xác định bởi công thức:
có tọa độ được xác định bởi công thức: 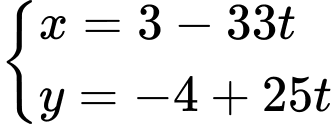 , vị trí của tàu
, vị trí của tàu 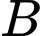 có tọa độ là (4-30t;3-40t). Nếu tàu
có tọa độ là (4-30t;3-40t). Nếu tàu  đứng yên ở vị trí ban đầu, tàu
đứng yên ở vị trí ban đầu, tàu  chạy thì khoảng cách ngắn nhất giứa hai tàu bằng bao nhiêu km? Viết kết quả làm tròn đến hàng phần mười.
chạy thì khoảng cách ngắn nhất giứa hai tàu bằng bao nhiêu km? Viết kết quả làm tròn đến hàng phần mười.
 và
và  cùng xuất phát từ hai bến, chuyển động đều theo đường thẳng ngoài biển. Trên màn hình ra đa của trạm điều khiển (được coi như mặt phẳng tọa độ Oxy với đơn vị trên các trục tính theo ki - lô - mét), sau khi xuất phát
cùng xuất phát từ hai bến, chuyển động đều theo đường thẳng ngoài biển. Trên màn hình ra đa của trạm điều khiển (được coi như mặt phẳng tọa độ Oxy với đơn vị trên các trục tính theo ki - lô - mét), sau khi xuất phát 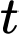 (giờ)
(giờ) 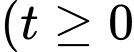 ), vị trí của tàu
), vị trí của tàu 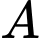 có tọa độ được xác định bởi công thức:
có tọa độ được xác định bởi công thức: 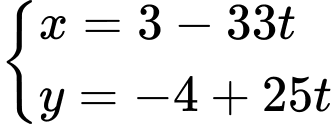 , vị trí của tàu
, vị trí của tàu  có tọa độ là (4-30t;3-40t). Nếu tàu
có tọa độ là (4-30t;3-40t). Nếu tàu  đứng yên ở vị trí ban đầu, tàu
đứng yên ở vị trí ban đầu, tàu  chạy thì khoảng cách ngắn nhất giứa hai tàu bằng bao nhiêu km? Viết kết quả làm tròn đến hàng phần mười.
chạy thì khoảng cách ngắn nhất giứa hai tàu bằng bao nhiêu km? Viết kết quả làm tròn đến hàng phần mười.
>Khi tàu  đứng yên ở vị trí ban đầu
đứng yên ở vị trí ban đầu 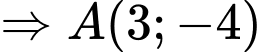 . Khi đó khoảng cách ngắn nhất giữa tàu
. Khi đó khoảng cách ngắn nhất giữa tàu 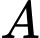 và tàu
và tàu 
Vì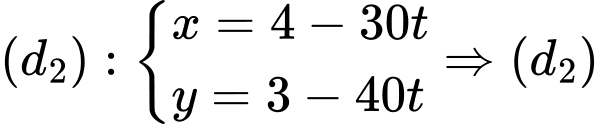 qua
qua 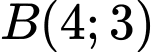 , nhận vecto pháp tuyến
, nhận vecto pháp tuyến 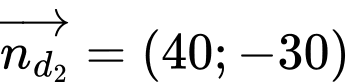
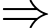 Phương trình tổng quát của (d):
Phương trình tổng quát của (d): 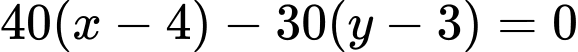 hay (d):
hay (d): 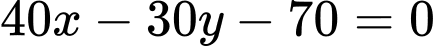
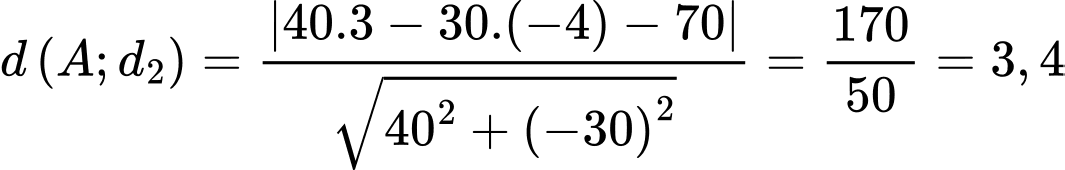
Vậy khoảng cách ngắn nhất giữa hai tàu bằng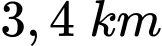 .
.
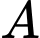 đứng yên ở vị trí ban đầu
đứng yên ở vị trí ban đầu 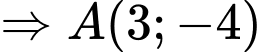 . Khi đó khoảng cách ngắn nhất giữa tàu
. Khi đó khoảng cách ngắn nhất giữa tàu 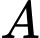 và tàu
và tàu 
Vì
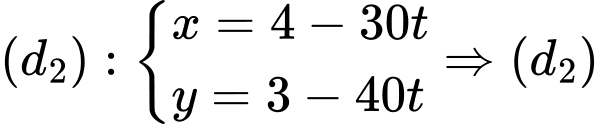 qua
qua 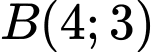 , nhận vecto pháp tuyến
, nhận vecto pháp tuyến 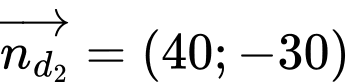
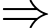 Phương trình tổng quát của (d):
Phương trình tổng quát của (d): 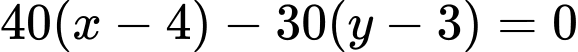 hay (d):
hay (d): 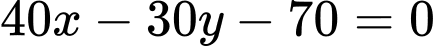
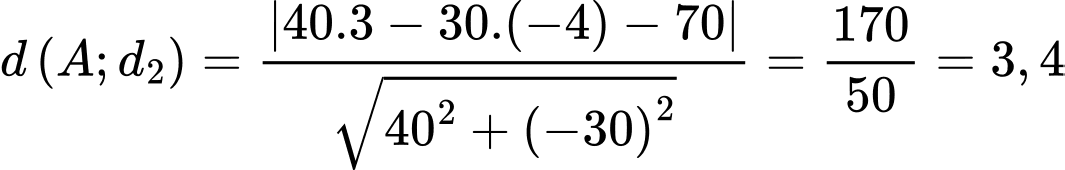
Vậy khoảng cách ngắn nhất giữa hai tàu bằng
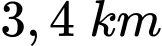 .
.
Câu 25 [558682]: Một ao cá có dạng hình chữ nhật 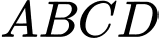 với chiều dài
với chiều dài 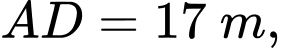 chiều rộng
chiều rộng 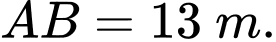 Phần tam giác
Phần tam giác 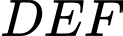 người ta để nuôi vịt, biết
người ta để nuôi vịt, biết 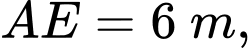
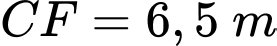 (minh họa như hình vẽ). Tính khoảng cách từ vị trí người đứng ở vị trí
(minh họa như hình vẽ). Tính khoảng cách từ vị trí người đứng ở vị trí 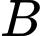 câu cá đến vách ngăn nuôi vịt là đường thẳng
câu cá đến vách ngăn nuôi vịt là đường thẳng 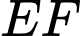 (Kết quả làm tròn đến hàng phần trăm).
(Kết quả làm tròn đến hàng phần trăm).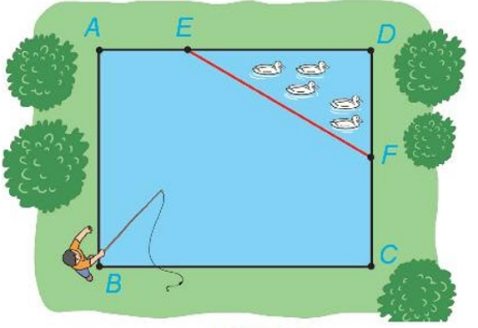
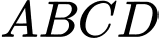 với chiều dài
với chiều dài 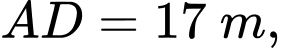 chiều rộng
chiều rộng 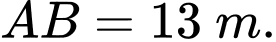 Phần tam giác
Phần tam giác 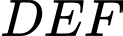 người ta để nuôi vịt, biết
người ta để nuôi vịt, biết 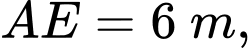
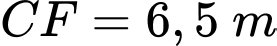 (minh họa như hình vẽ). Tính khoảng cách từ vị trí người đứng ở vị trí
(minh họa như hình vẽ). Tính khoảng cách từ vị trí người đứng ở vị trí 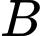 câu cá đến vách ngăn nuôi vịt là đường thẳng
câu cá đến vách ngăn nuôi vịt là đường thẳng 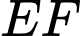 (Kết quả làm tròn đến hàng phần trăm).
(Kết quả làm tròn đến hàng phần trăm).
Chọn hệ trục toạ độ 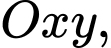 có điểm
có điểm  trùng với điểm
trùng với điểm 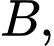 các tia
các tia 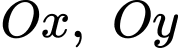 tương ứng trùng với các tia
tương ứng trùng với các tia 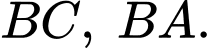 Chọn 1 đơn vị độ dài trên mặt phẳng toạ độ tương ứng với
Chọn 1 đơn vị độ dài trên mặt phẳng toạ độ tương ứng với  trong thực tế.
trong thực tế.
Khi đó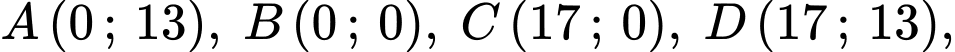
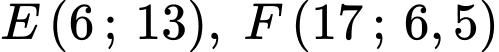
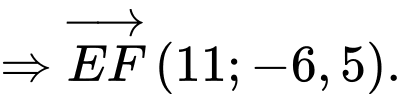
Đường thẳng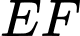 có vectơ chỉ phương là
có vectơ chỉ phương là 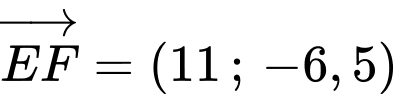 nên có vectơ pháp tuyến
nên có vectơ pháp tuyến 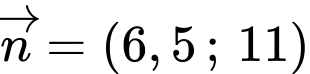 và đi qua điểm
và đi qua điểm 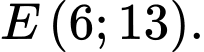
Suy ra phương trình tổng quát của đường thẳng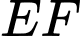 là:
là: 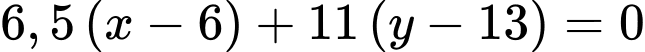 hay
hay 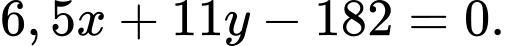
Khoảng cách từ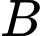 đến đường thẳng
đến đường thẳng 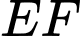 là
là 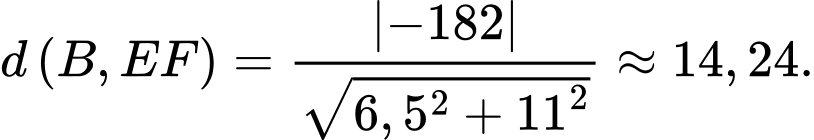
Vậy khoảng cách từ vị trí người đứng ở vị trí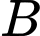 câu cá đến vách ngăn nuôi vịt là đường thẳng
câu cá đến vách ngăn nuôi vịt là đường thẳng 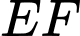 bằng
bằng 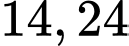 mét.
mét.
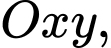 có điểm
có điểm  trùng với điểm
trùng với điểm 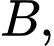 các tia
các tia 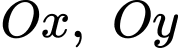 tương ứng trùng với các tia
tương ứng trùng với các tia 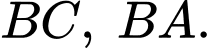 Chọn 1 đơn vị độ dài trên mặt phẳng toạ độ tương ứng với
Chọn 1 đơn vị độ dài trên mặt phẳng toạ độ tương ứng với  trong thực tế.
trong thực tế.Khi đó
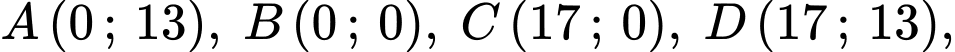
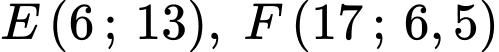
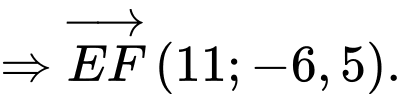
Đường thẳng
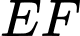 có vectơ chỉ phương là
có vectơ chỉ phương là 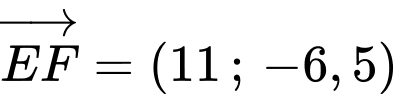 nên có vectơ pháp tuyến
nên có vectơ pháp tuyến 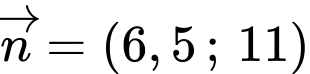 và đi qua điểm
và đi qua điểm 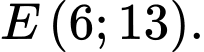
Suy ra phương trình tổng quát của đường thẳng
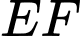 là:
là: 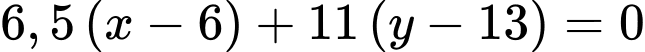 hay
hay 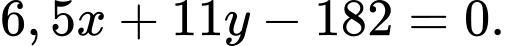
Khoảng cách từ
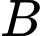 đến đường thẳng
đến đường thẳng 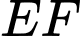 là
là 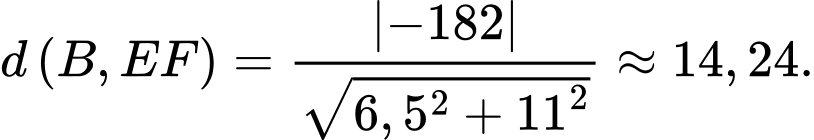
Vậy khoảng cách từ vị trí người đứng ở vị trí
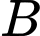 câu cá đến vách ngăn nuôi vịt là đường thẳng
câu cá đến vách ngăn nuôi vịt là đường thẳng 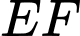 bằng
bằng 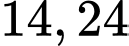 mét.
mét.
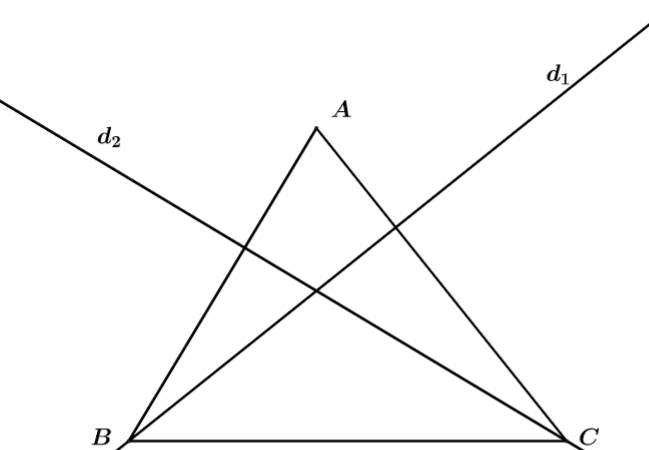
Câu 26 [581041]: Trong mặt phẳng với hệ tọa độ 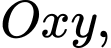 cho tam giác
cho tam giác 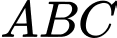 có phương trình cạnh
có phương trình cạnh 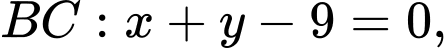 đường cao qua đỉnh
đường cao qua đỉnh 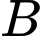 và
và  lần lượt có phương trình
lần lượt có phương trình 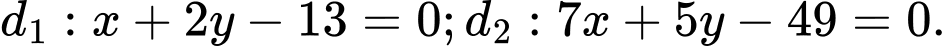 Tìm tung độ của đỉnh
Tìm tung độ của đỉnh 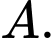
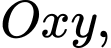 cho tam giác
cho tam giác 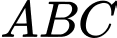 có phương trình cạnh
có phương trình cạnh 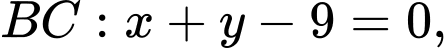 đường cao qua đỉnh
đường cao qua đỉnh 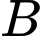 và
và  lần lượt có phương trình
lần lượt có phương trình 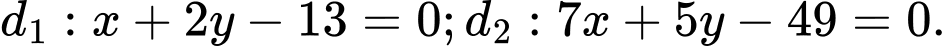 Tìm tung độ của đỉnh
Tìm tung độ của đỉnh 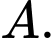
Do
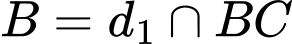 nên tọa độ của
nên tọa độ của 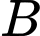 là nghiệm của hệ:
là nghiệm của hệ: 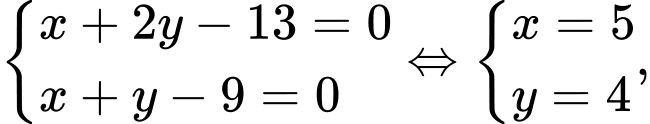 ta được
ta được 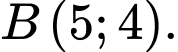
Do
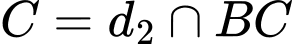 nên
nên 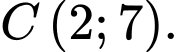
Cạnh
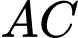 đi qua
đi qua  và vuông góc với
và vuông góc với 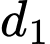 nên
nên 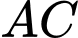 có phương trình
có phương trình 
Cạnh
 đi qua
đi qua 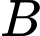 và vuông góc với
và vuông góc với 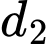 nên
nên  có phương trình
có phương trình 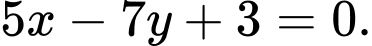
Do
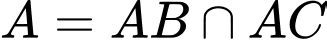 nên
nên 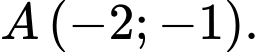
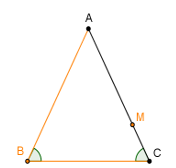
Câu 27 [240418]: Trong mặt phẳng với hệ tọa độ 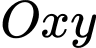 , cho tam giác cân
, cho tam giác cân 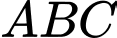 có cạnh đáy
có cạnh đáy 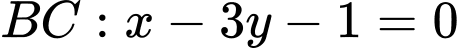 , cạnh bên
, cạnh bên 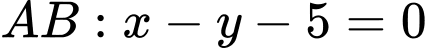 . Đường thẳng
. Đường thẳng 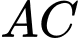 đi qua
đi qua 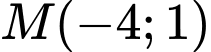 . Giả sử toạ độ đỉnh
. Giả sử toạ độ đỉnh 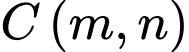 .Tính
.Tính 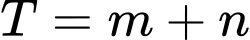 .
.
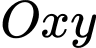 , cho tam giác cân
, cho tam giác cân 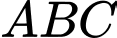 có cạnh đáy
có cạnh đáy 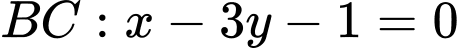 , cạnh bên
, cạnh bên 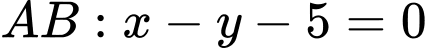 . Đường thẳng
. Đường thẳng 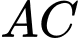 đi qua
đi qua 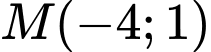 . Giả sử toạ độ đỉnh
. Giả sử toạ độ đỉnh 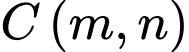 .Tính
.Tính 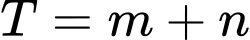 .
. A, 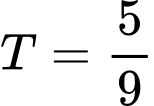 .
.
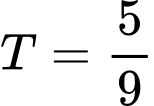 .
.B, 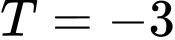 .
.
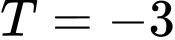 .
.C, 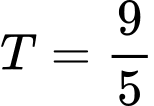 .
.
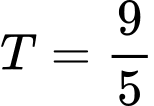 .
.D, 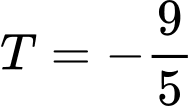 .
.
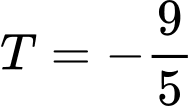 .
.
Chọn C
Gọi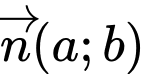 với
với 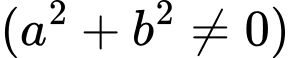 là vectơ pháp tuyến của
là vectơ pháp tuyến của 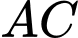 , vectơ
, vectơ 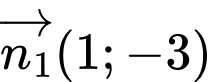 là vectơ pháp tuyến của đường thẳng
là vectơ pháp tuyến của đường thẳng 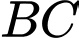 ,
, 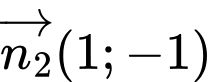 là
vectơ pháp tuyến của đường thẳng
là
vectơ pháp tuyến của đường thẳng  .
.
Ta có: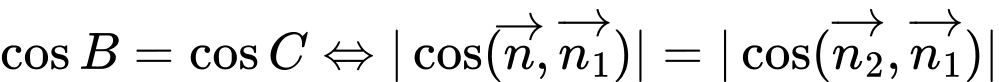
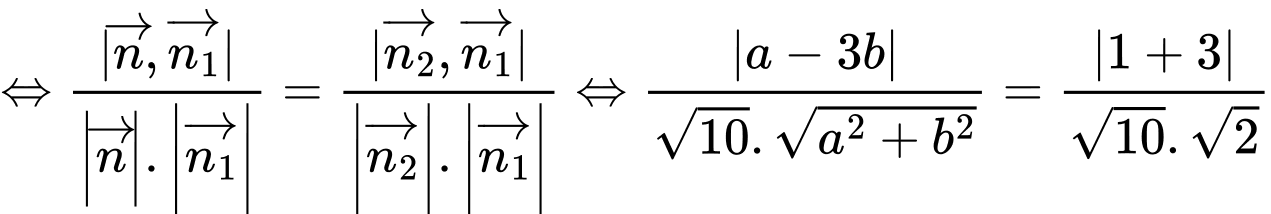
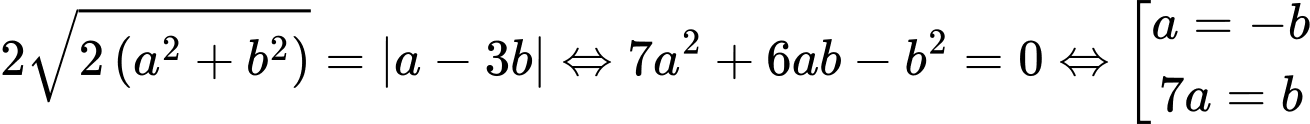
+ Với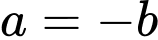 chọn
chọn 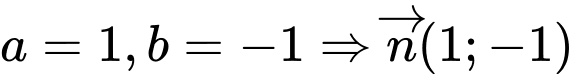 loại vì
loại vì 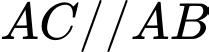
+ Với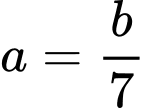 chọn
chọn 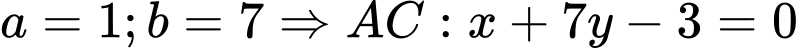 . Điểm
. Điểm 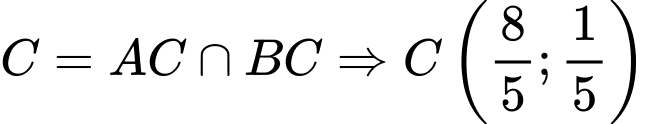
 Đáp án: C
Đáp án: C
Gọi
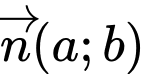 với
với 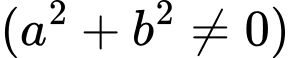 là vectơ pháp tuyến của
là vectơ pháp tuyến của 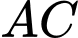 , vectơ
, vectơ 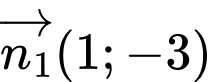 là vectơ pháp tuyến của đường thẳng
là vectơ pháp tuyến của đường thẳng 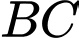 ,
, 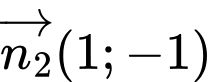 là
vectơ pháp tuyến của đường thẳng
là
vectơ pháp tuyến của đường thẳng  .
.
Ta có:
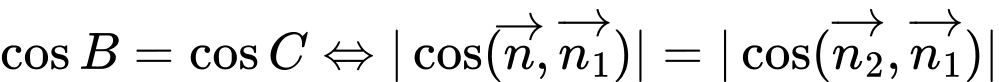
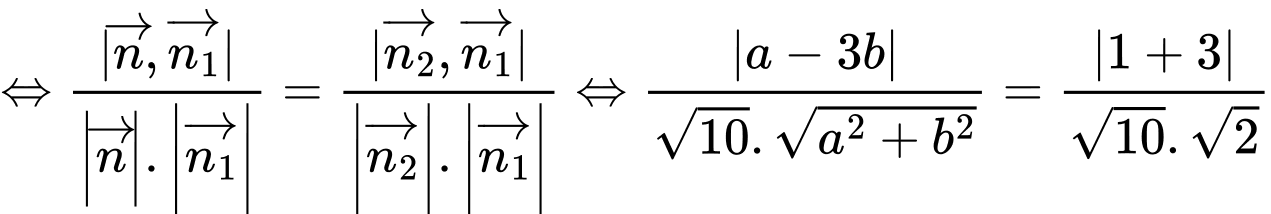
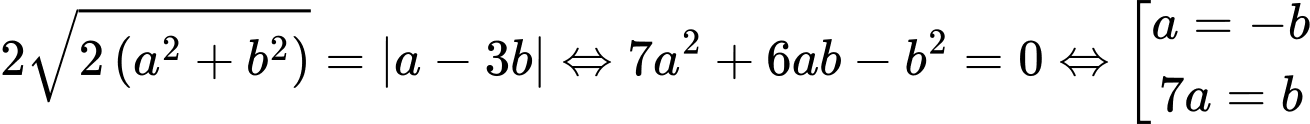
+ Với
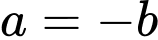 chọn
chọn 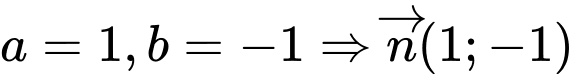 loại vì
loại vì 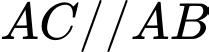
+ Với
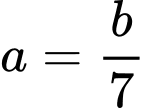 chọn
chọn 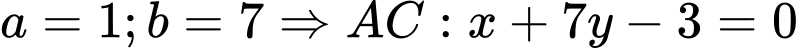 . Điểm
. Điểm 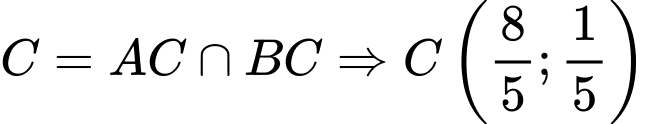
 Đáp án: C
Đáp án: C