Đáp án Bài tập tự luyện
Câu 1 [246313]: Đường tròn 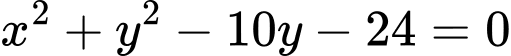 có bán kính bằng bao nhiêu?
có bán kính bằng bao nhiêu?
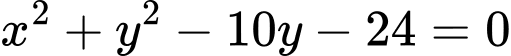 có bán kính bằng bao nhiêu?
có bán kính bằng bao nhiêu? A, 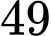 .
.
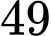 .
.B, 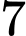 .
.
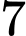 .
.C, 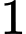 .
.
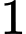 .
.D,  .
.
 .
.
Chọn B
Đường tròn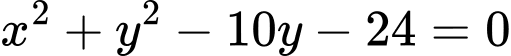 có tâm
có tâm 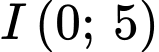 , bán kính
, bán kính 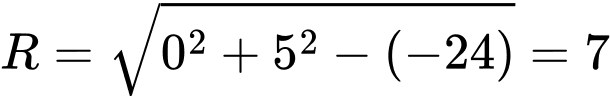 . Đáp án: B
. Đáp án: B
Đường tròn
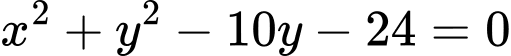 có tâm
có tâm 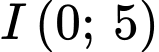 , bán kính
, bán kính 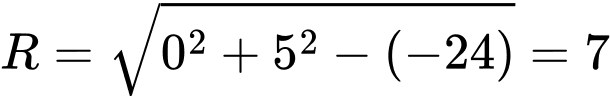 . Đáp án: B
. Đáp án: B
Câu 2 [246318]: Đường tròn 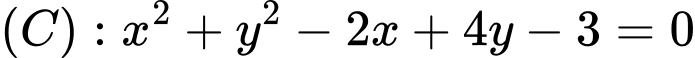 có tâm
có tâm 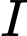 , bán kính
, bán kính  là
là
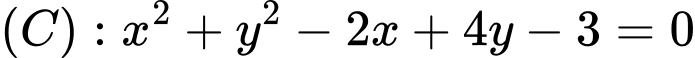 có tâm
có tâm  , bán kính
, bán kính  là
là A, 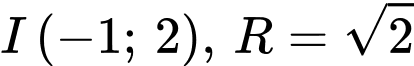 .
.
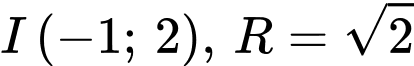 .
.B, 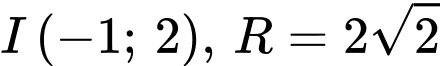 .
.
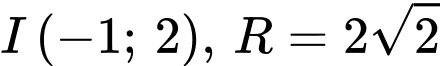 .
.C, 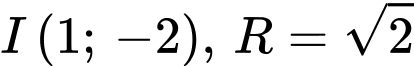 .
.
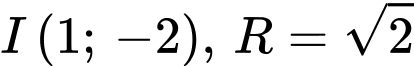 .
.D, 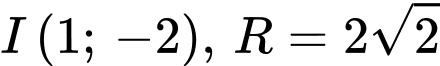 .
.
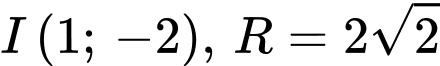 .
.
Chọn D
Tâm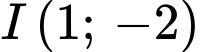 , bán kính
, bán kính  . Đáp án: D
. Đáp án: D
Tâm
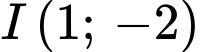 , bán kính
, bán kính  . Đáp án: D
. Đáp án: D
Câu 3 [246309]: Phương trình nào sau đây là phương trình của đường tròn?
A, 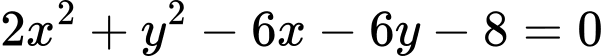 .
.
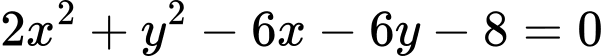 .
.B, 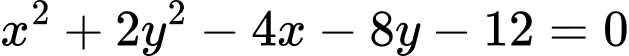 .
.
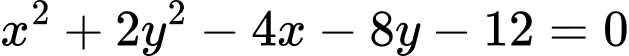 .
.C, 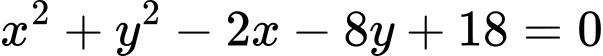 .
.
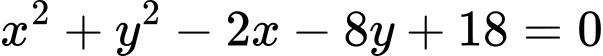 .
.D, 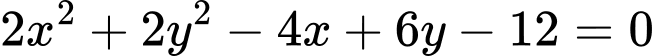 .
.
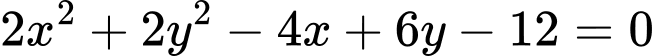 .
.
Chọn D
Biết rằng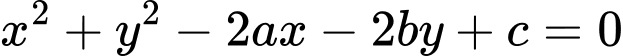 là phương trình của một đường tròn khi và chỉ khi
là phương trình của một đường tròn khi và chỉ khi  .
.
Ta thấy phương trình trong phương án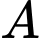 và
và 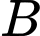 có hệ số của
có hệ số của 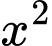 ,
, 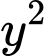 không bằng nhau nên đây không phải là phương trình đường tròn.
không bằng nhau nên đây không phải là phương trình đường tròn.
Với phương án có
có 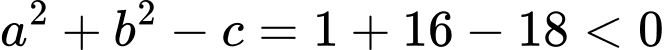 nên đây không phải là phương trình đường tròn. Vậy ta chọn đáp án
nên đây không phải là phương trình đường tròn. Vậy ta chọn đáp án 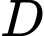 . Đáp án: D
. Đáp án: D
Biết rằng
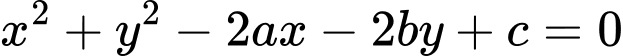 là phương trình của một đường tròn khi và chỉ khi
là phương trình của một đường tròn khi và chỉ khi  .
.
Ta thấy phương trình trong phương án
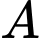 và
và 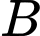 có hệ số của
có hệ số của 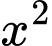 ,
, 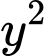 không bằng nhau nên đây không phải là phương trình đường tròn.
không bằng nhau nên đây không phải là phương trình đường tròn.
Với phương án
 có
có 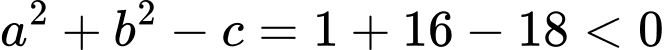 nên đây không phải là phương trình đường tròn. Vậy ta chọn đáp án
nên đây không phải là phương trình đường tròn. Vậy ta chọn đáp án 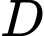 . Đáp án: D
. Đáp án: D
Câu 4 [246307]: Tìm tất cả các giá trị của tham số 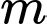 để phương trình
để phương trình 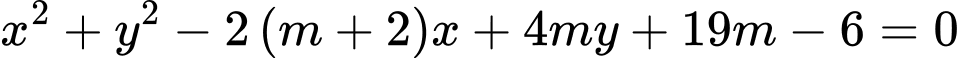 là phương trình đường tròn.
là phương trình đường tròn.
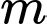 để phương trình
để phương trình 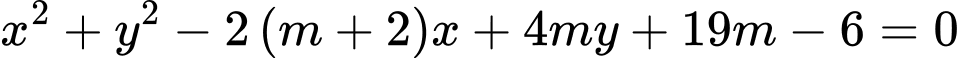 là phương trình đường tròn.
là phương trình đường tròn. A, 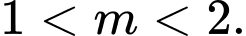
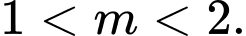
B,  hoặc
hoặc  .
.
 hoặc
hoặc  .
.C,  hoặc
hoặc  .
.
 hoặc
hoặc  .
.D,  hoặc
hoặc  .
.
 hoặc
hoặc  .
.
Chọn D
Ta có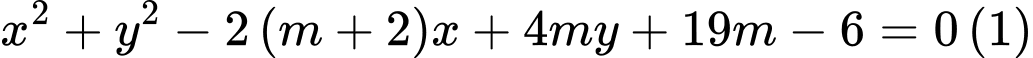
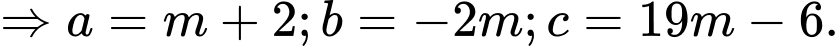
Phương trình là phương trình đường tròn
là phương trình đường tròn 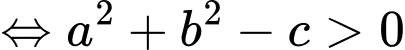
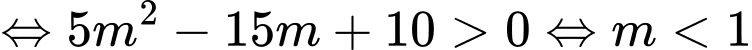 hoặc
hoặc  . Đáp án: D
. Đáp án: D
Ta có
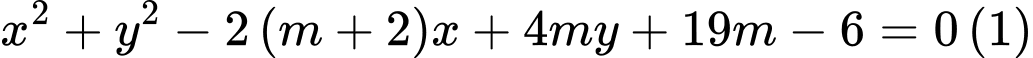
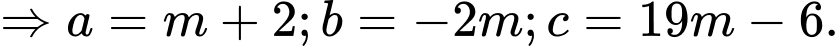
Phương trình
 là phương trình đường tròn
là phương trình đường tròn 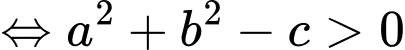
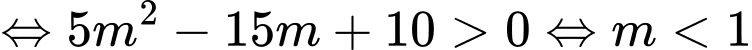 hoặc
hoặc  . Đáp án: D
. Đáp án: D
Câu 5 [246385]: Trên hệ trục tọa độ 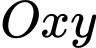 , cho đường tròn
, cho đường tròn  có tâm
có tâm 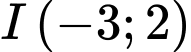 và một tiếp tuyến của nó có phương trình là
và một tiếp tuyến của nó có phương trình là 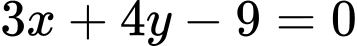 . Viết phương trình của đường tròn
. Viết phương trình của đường tròn  .
.
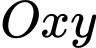 , cho đường tròn
, cho đường tròn  có tâm
có tâm 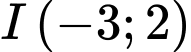 và một tiếp tuyến của nó có phương trình là
và một tiếp tuyến của nó có phương trình là 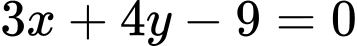 . Viết phương trình của đường tròn
. Viết phương trình của đường tròn  .
. A, 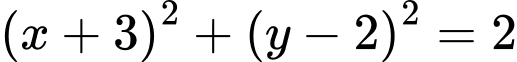 .
.
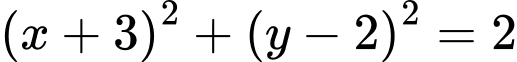 .
.B, 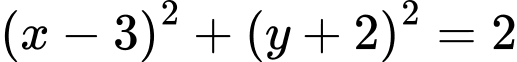 .
.
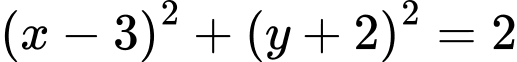 .
.C, 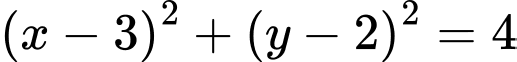 .
.
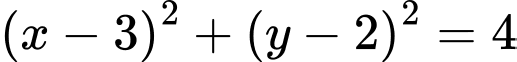 .
.D, 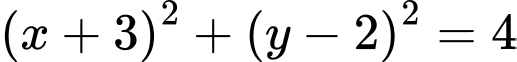 .
.
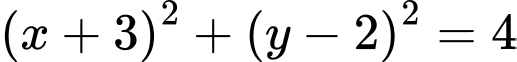 .
.
Chọn D
Vì đường tròn có tâm
có tâm 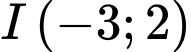 và một tiếp tuyến của nó là đường thẳng
và một tiếp tuyến của nó là đường thẳng  có phương trình là
có phương trình là 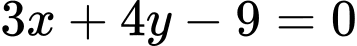 nên bán kính của đường tròn là
nên bán kính của đường tròn là 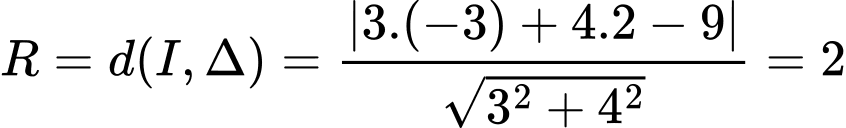
Vậy phương trình đường tròn là: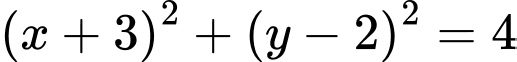 Đáp án: D
Đáp án: D
Vì đường tròn
 có tâm
có tâm 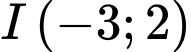 và một tiếp tuyến của nó là đường thẳng
và một tiếp tuyến của nó là đường thẳng  có phương trình là
có phương trình là 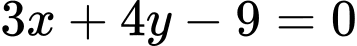 nên bán kính của đường tròn là
nên bán kính của đường tròn là 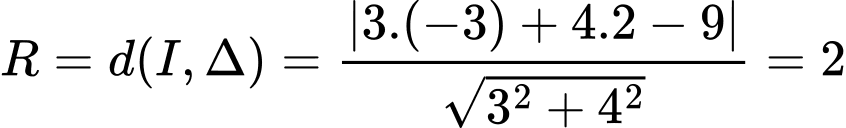
Vậy phương trình đường tròn là:
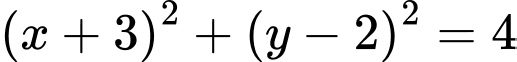 Đáp án: D
Đáp án: D
Câu 6 [246383]: Một đường tròn có tâm 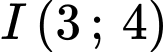 tiếp xúc với đường thẳng
tiếp xúc với đường thẳng 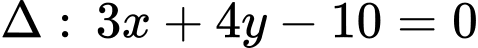 . Hỏi bán kính đường tròn bằng bao nhiêu?
. Hỏi bán kính đường tròn bằng bao nhiêu?
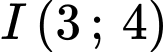 tiếp xúc với đường thẳng
tiếp xúc với đường thẳng 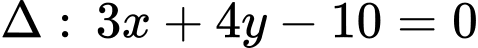 . Hỏi bán kính đường tròn bằng bao nhiêu?
. Hỏi bán kính đường tròn bằng bao nhiêu? A, 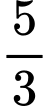 .
.
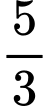 .
.B, 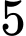 .
.
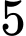 .
.C, 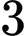 .
.
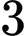 .
.D, 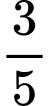 .
.
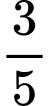 .
.
Chọn C
Đường tròn tâm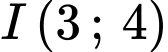 tiếp xúc với đường thẳng
tiếp xúc với đường thẳng 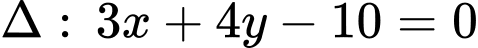 nên bán kính đường tròn chính là khoảng cách từ tâm
nên bán kính đường tròn chính là khoảng cách từ tâm 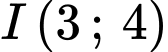 tới đường thẳng
tới đường thẳng 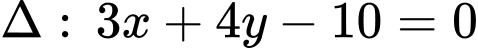 .
.
Ta có: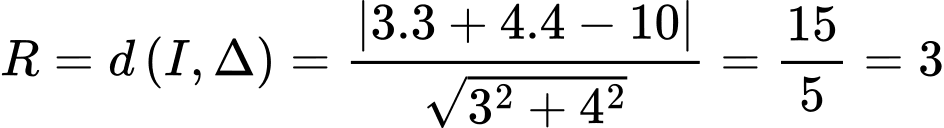 . Đáp án: C
. Đáp án: C
Đường tròn tâm
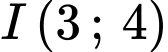 tiếp xúc với đường thẳng
tiếp xúc với đường thẳng 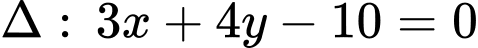 nên bán kính đường tròn chính là khoảng cách từ tâm
nên bán kính đường tròn chính là khoảng cách từ tâm 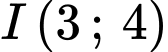 tới đường thẳng
tới đường thẳng 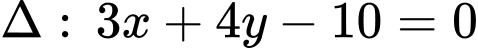 .
.Ta có:
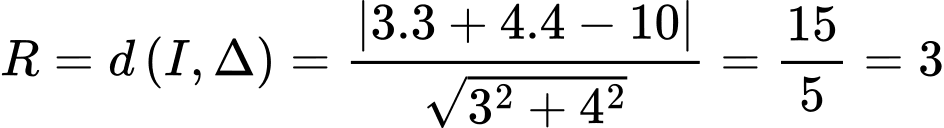 . Đáp án: C
. Đáp án: C
Câu 7 [246373]: Đường tròn  đi qua hai điểm
đi qua hai điểm 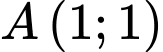 ,
, 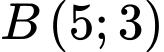 và có tâm
và có tâm 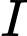 thuộc trục hoành có phương trình là
thuộc trục hoành có phương trình là
 đi qua hai điểm
đi qua hai điểm 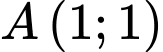 ,
, 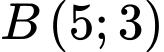 và có tâm
và có tâm 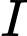 thuộc trục hoành có phương trình là
thuộc trục hoành có phương trình là A, 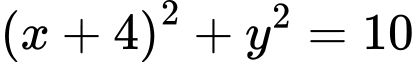 .
.
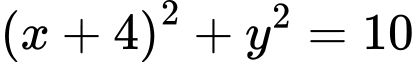 .
.B, 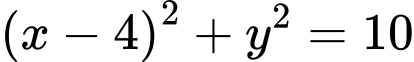 .
.
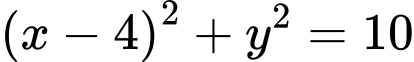 .
.C, 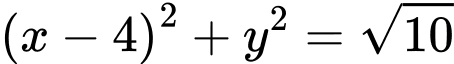 .
.
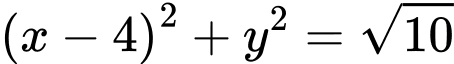 .
.D, 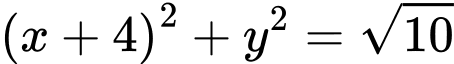 .
.
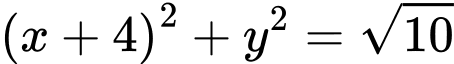 .
.
Chọn B
Gọi ;
; 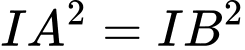
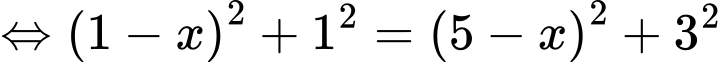
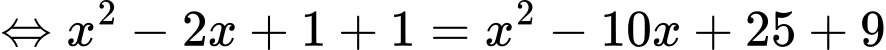
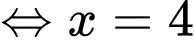 . Vậy tâm đường tròn là
. Vậy tâm đường tròn là 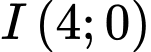 và bán kính
và bán kính 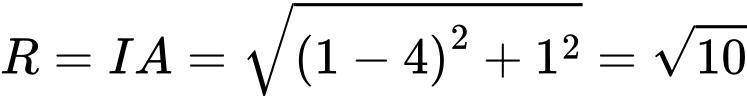 .
.
Phương trình đường tròn có dạng
có dạng 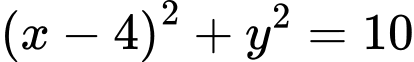 . Đáp án: B
. Đáp án: B
Gọi
 ;
; 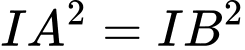
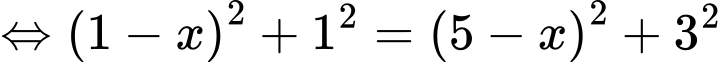
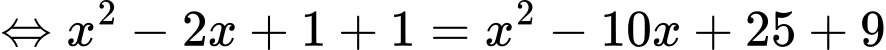
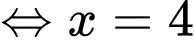 . Vậy tâm đường tròn là
. Vậy tâm đường tròn là 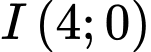 và bán kính
và bán kính 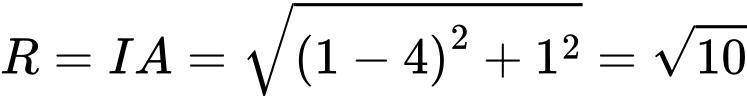 .
.
Phương trình đường tròn
 có dạng
có dạng 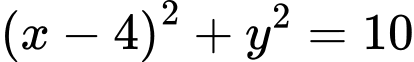 . Đáp án: B
. Đáp án: B
Câu 8 [246377]: Lập phương trình đường tròn đi qua hai điểm 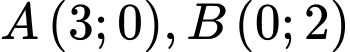 và có tâm thuộc đường thẳng
và có tâm thuộc đường thẳng 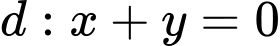 .
.
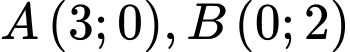 và có tâm thuộc đường thẳng
và có tâm thuộc đường thẳng 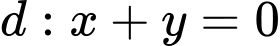 .
. A, 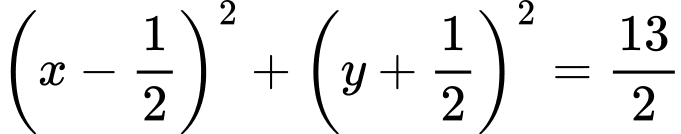 .
.
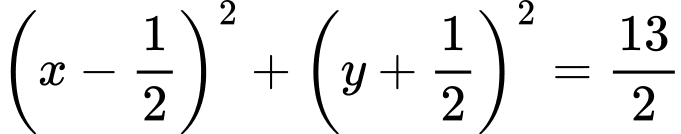 .
.B, 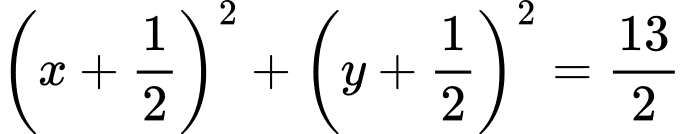 .
.
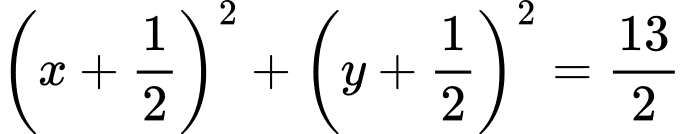 .
.C, 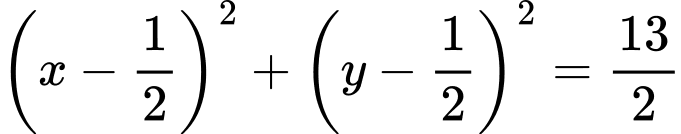 .
.
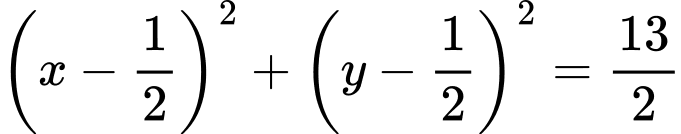 .
.D, 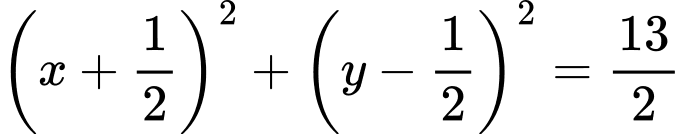 .
.
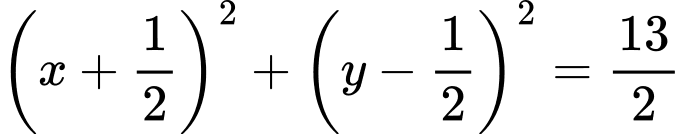 .
.
Chọn A
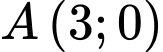 ,
,  ,
, 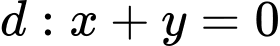 .
.
Gọi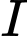 là tâm đường tròn vậy
là tâm đường tròn vậy 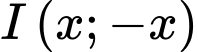 vì
vì 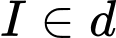 .
.
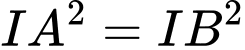
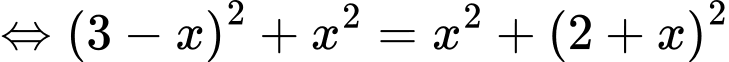
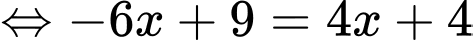
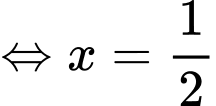 . Vậy
. Vậy 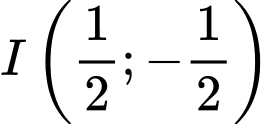 .
.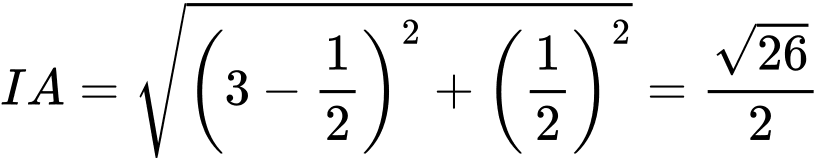 là bán kính đường tròn.
là bán kính đường tròn.
Phương trình đường tròn cần lập là: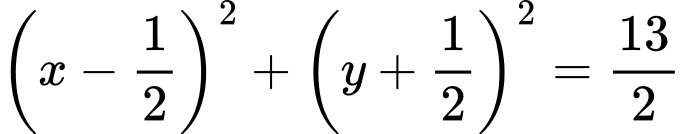 . Đáp án: A
. Đáp án: A
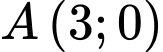 ,
,  ,
, 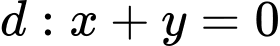 .
.Gọi
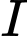 là tâm đường tròn vậy
là tâm đường tròn vậy 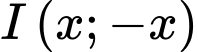 vì
vì 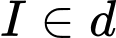 .
.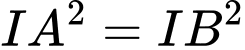
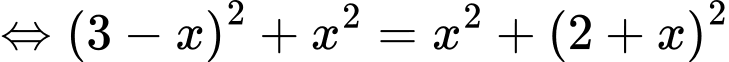
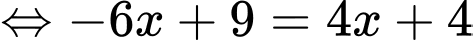
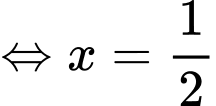 . Vậy
. Vậy 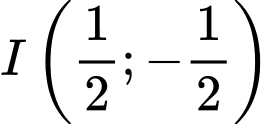 .
.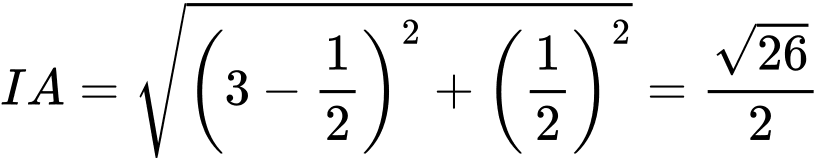 là bán kính đường tròn.
là bán kính đường tròn.Phương trình đường tròn cần lập là:
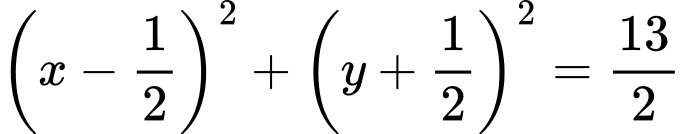 . Đáp án: A
. Đáp án: A
Câu 9 [246322]: Cho đường tròn 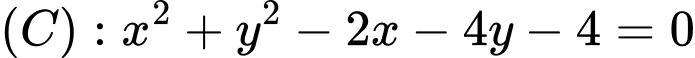 và điểm
và điểm 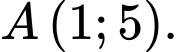 Đường thẳng nào trong các đường thẳng dưới đây là tiếp tuyến của đường tròn
Đường thẳng nào trong các đường thẳng dưới đây là tiếp tuyến của đường tròn  tại điểm
tại điểm 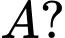
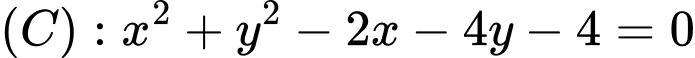 và điểm
và điểm 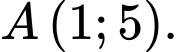 Đường thẳng nào trong các đường thẳng dưới đây là tiếp tuyến của đường tròn
Đường thẳng nào trong các đường thẳng dưới đây là tiếp tuyến của đường tròn  tại điểm
tại điểm 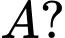
A, 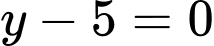 .
.
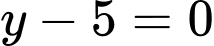 .
.B, 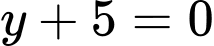 .
.
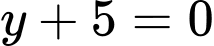 .
.C,  .
.
 .
.D,  .
.
 .
.
Chọn A
Đường tròn có tâm
có tâm 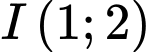
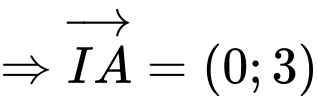 .
.
Gọi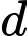 là tiếp tuyến của
là tiếp tuyến của  tại điểm
tại điểm 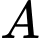 , khi đó
, khi đó 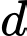 đi qua
đi qua 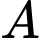 và nhận vectơ
và nhận vectơ  là một VTPT.
là một VTPT.
Chọn một VTPT của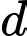 là
là 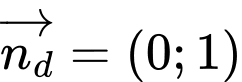 . Vậy phương trình đường thẳng
. Vậy phương trình đường thẳng 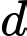 là
là 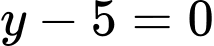 . Đáp án: A
. Đáp án: A
Đường tròn
 có tâm
có tâm 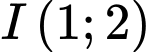
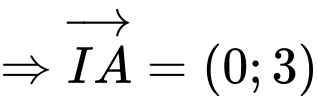 .
.Gọi
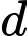 là tiếp tuyến của
là tiếp tuyến của  tại điểm
tại điểm 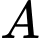 , khi đó
, khi đó 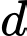 đi qua
đi qua 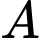 và nhận vectơ
và nhận vectơ  là một VTPT.
là một VTPT.Chọn một VTPT của
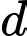 là
là 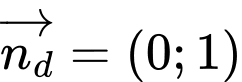 . Vậy phương trình đường thẳng
. Vậy phương trình đường thẳng 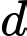 là
là 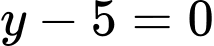 . Đáp án: A
. Đáp án: A
Câu 10 [581404]: Trên mặt phẳng toạ độ 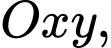 cho đường tròn
cho đường tròn 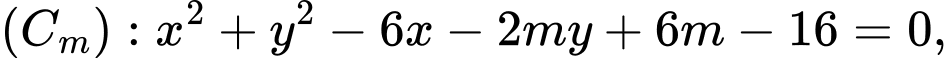 với
với 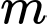 là tham số thực. Khi
là tham số thực. Khi 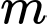 thay đổi, bán kính đường tròn
thay đổi, bán kính đường tròn 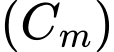 đạt giá trị nhỏ nhất bằng bao nhiêu?
đạt giá trị nhỏ nhất bằng bao nhiêu?
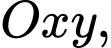 cho đường tròn
cho đường tròn 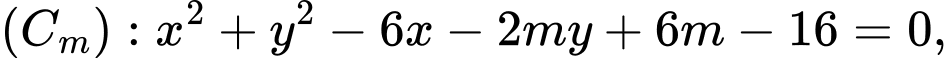 với
với 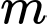 là tham số thực. Khi
là tham số thực. Khi 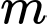 thay đổi, bán kính đường tròn
thay đổi, bán kính đường tròn 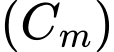 đạt giá trị nhỏ nhất bằng bao nhiêu?
đạt giá trị nhỏ nhất bằng bao nhiêu? A, 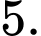
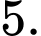
B, 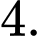
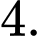
C, 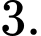
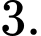
D, 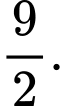
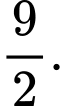
Bán kính đường tròn 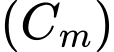 là
là 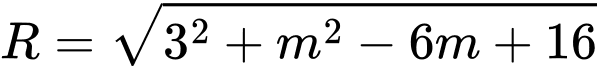
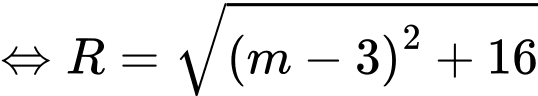
Có: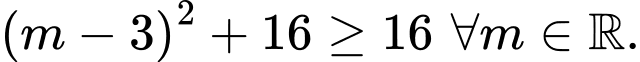
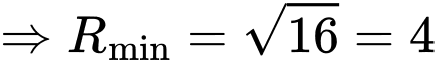 dấu bằng xảy ra
dấu bằng xảy ra 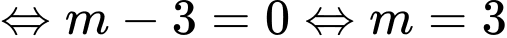
Vậy giá trị nhỏ nhất của bán kính đường tròn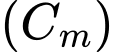 bằng
bằng 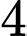 , đạt được khi
, đạt được khi 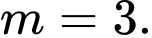
Chọn B. Đáp án: B
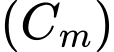 là
là 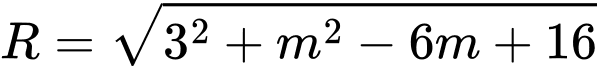
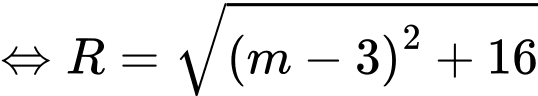
Có:
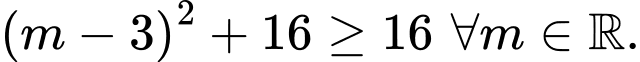
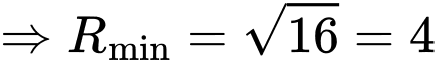 dấu bằng xảy ra
dấu bằng xảy ra 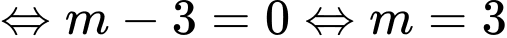
Vậy giá trị nhỏ nhất của bán kính đường tròn
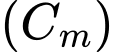 bằng
bằng 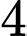 , đạt được khi
, đạt được khi 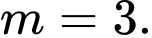
Chọn B. Đáp án: B
Câu 11 [246328]: Trong mặt phẳng 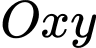 , cho đường tròn
, cho đường tròn 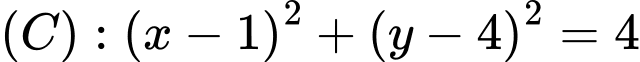 . Phương trình tiếp tuyến với đường tròn
. Phương trình tiếp tuyến với đường tròn  , biết tiếp tuyến đó song song với đường thẳng
, biết tiếp tuyến đó song song với đường thẳng 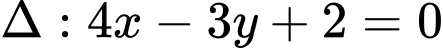 là
là
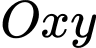 , cho đường tròn
, cho đường tròn 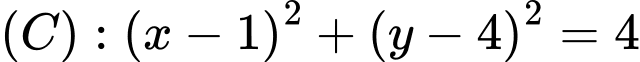 . Phương trình tiếp tuyến với đường tròn
. Phương trình tiếp tuyến với đường tròn  , biết tiếp tuyến đó song song với đường thẳng
, biết tiếp tuyến đó song song với đường thẳng 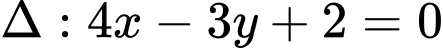 là
là A, 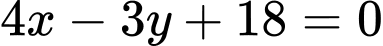 và
và 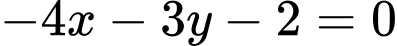 .
.
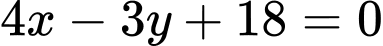 và
và 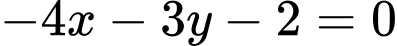 .
.B, 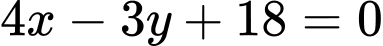 và
và 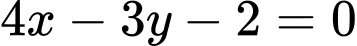 .
.
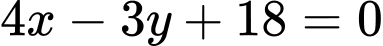 và
và 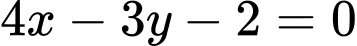 .
.C, 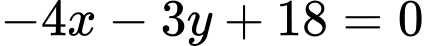 và
và 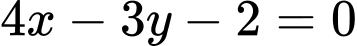 .
.
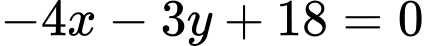 và
và 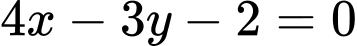 .
.D, 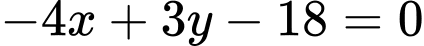 và
và 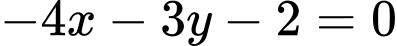 .
.
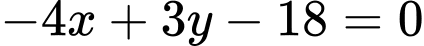 và
và 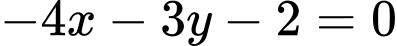 .
.
Chọn B
Đường tròn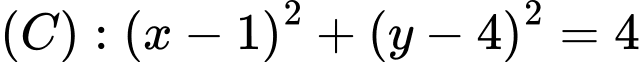 có tâm
có tâm 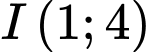 và bán kính
và bán kính 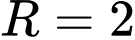 .
.
Gọi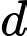 là tiếp tuyến của
là tiếp tuyến của  .
.
Vì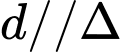 nên đường thẳng
nên đường thẳng 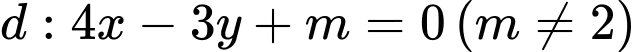 .
.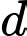 là tiếp tuyến của
là tiếp tuyến của 
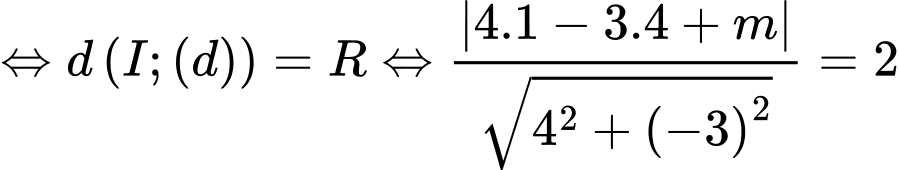
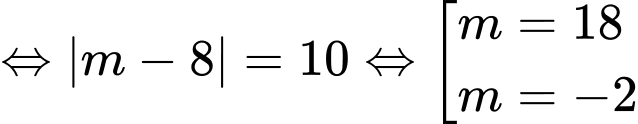 (thỏa mãn điều kiện)
(thỏa mãn điều kiện)
Vậy có 2 tiếp tuyến cần tìm :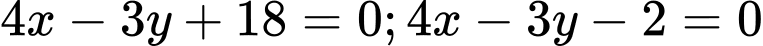 . Đáp án: B
. Đáp án: B
Đường tròn
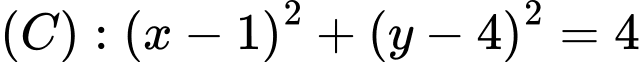 có tâm
có tâm 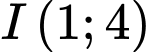 và bán kính
và bán kính 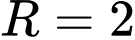 .
.Gọi
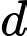 là tiếp tuyến của
là tiếp tuyến của  .
.Vì
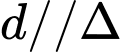 nên đường thẳng
nên đường thẳng 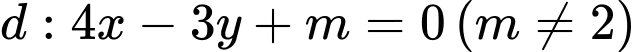 .
.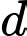 là tiếp tuyến của
là tiếp tuyến của 
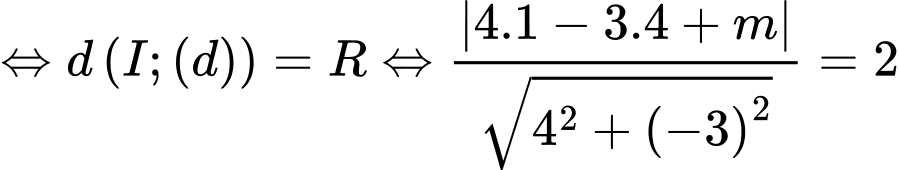
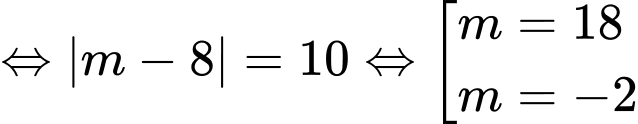 (thỏa mãn điều kiện)
(thỏa mãn điều kiện)Vậy có 2 tiếp tuyến cần tìm :
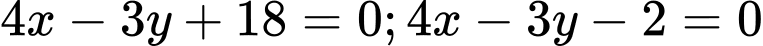 . Đáp án: B
. Đáp án: B
Câu 12 [246374]: Trong mặt phẳng với hệ tọa độ 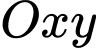 , tìm tọa độ tâm
, tìm tọa độ tâm 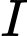 của đường tròn đi qua ba điểm
của đường tròn đi qua ba điểm  ,
, 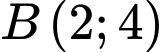 ,
, 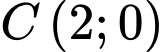 .
.
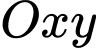 , tìm tọa độ tâm
, tìm tọa độ tâm 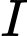 của đường tròn đi qua ba điểm
của đường tròn đi qua ba điểm  ,
, 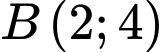 ,
, 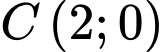 .
. A, 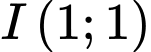 .
.
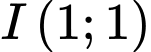 .
.B, 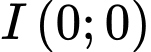 .
.
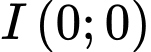 .
.C, 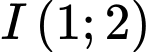 .
.
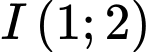 .
.D, 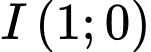 .
.
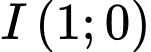 .
.
Chọn C
Giả sử phương trình đường tròn đi qua 3 điểm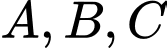 có dạng
có dạng 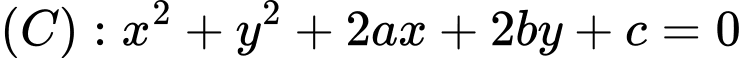
Thay tọa độ 3 điểm ,
, 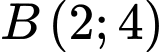 ,
, 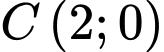 ta được:
ta được: 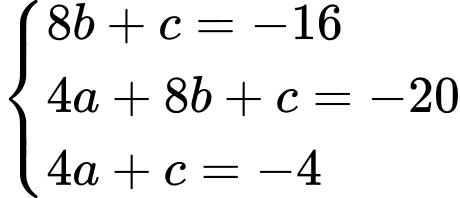
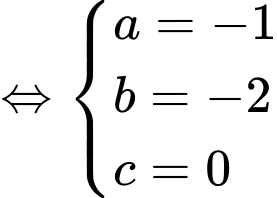
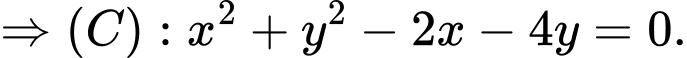
Vậy có tâm
có tâm 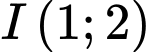 và bán kính
và bán kính 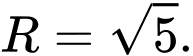 Đáp án: C
Đáp án: C
Giả sử phương trình đường tròn đi qua 3 điểm
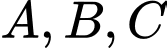 có dạng
có dạng 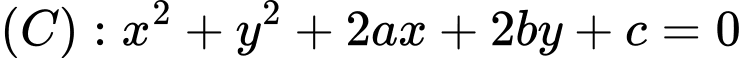
Thay tọa độ 3 điểm
 ,
, 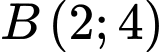 ,
, 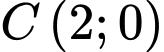 ta được:
ta được: 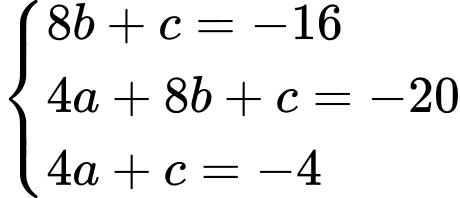
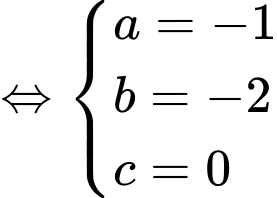
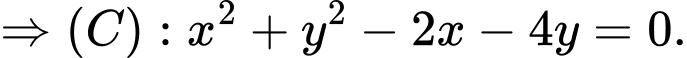
Vậy
 có tâm
có tâm 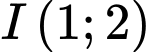 và bán kính
và bán kính 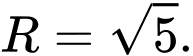 Đáp án: C
Đáp án: C
Câu 13 [246327]: Trong mặt phẳng tọa độ Oxy, cho đường tròn  có phương trình
có phương trình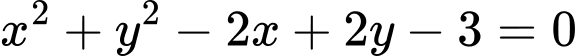 . Từ điểm
. Từ điểm 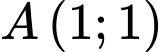 kẻ được bao nhiêu tiếp tuyến đến đường tròn
kẻ được bao nhiêu tiếp tuyến đến đường tròn  ?
?
 có phương trình
có phương trình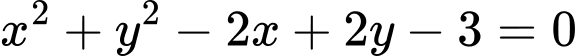 . Từ điểm
. Từ điểm 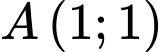 kẻ được bao nhiêu tiếp tuyến đến đường tròn
kẻ được bao nhiêu tiếp tuyến đến đường tròn  ?
? A, 1.
B, 2.
C, Vô số.
D, 0.
Chọn D
 có tâm
có tâm 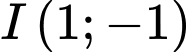 bán kính
bán kính 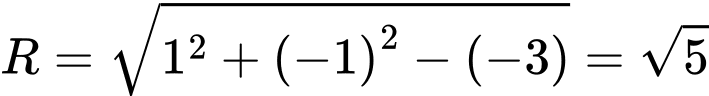
Vì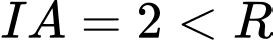 nên A nằm bên trong
nên A nằm bên trong  .Vì vậy không kẻ được tiếp tuyến nào tới đường tròn
.Vì vậy không kẻ được tiếp tuyến nào tới đường tròn  . Đáp án: D
. Đáp án: D
 có tâm
có tâm 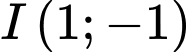 bán kính
bán kính 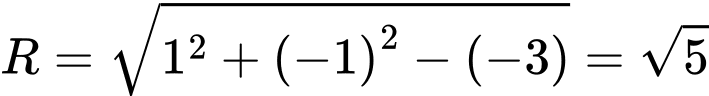
Vì
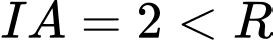 nên A nằm bên trong
nên A nằm bên trong  .Vì vậy không kẻ được tiếp tuyến nào tới đường tròn
.Vì vậy không kẻ được tiếp tuyến nào tới đường tròn  . Đáp án: D
. Đáp án: D
Câu 14 [246376]: Trong mặt phẳng 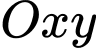 , đường tròn đi qua ba điểm
, đường tròn đi qua ba điểm 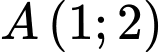 ,
, 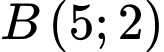 ,
, 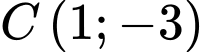 có phương trình là
có phương trình là
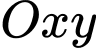 , đường tròn đi qua ba điểm
, đường tròn đi qua ba điểm 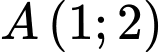 ,
, 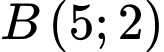 ,
, 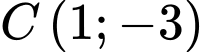 có phương trình là
có phương trình là A, 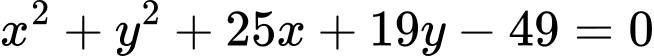 .
.
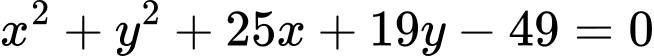 .
.B, 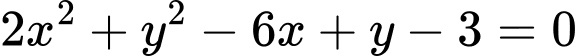 .
.
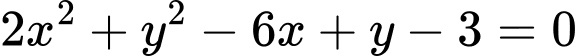 .
.C, 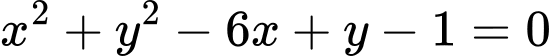 .
.
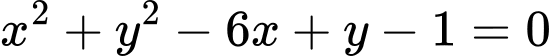 .
.D, 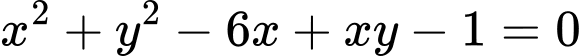 .
.
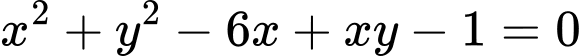 .
.
Chọn C
Phương trình đường tròn có dạng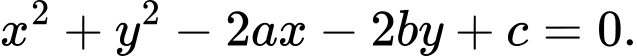 Đường tròn này qua
Đường tròn này qua 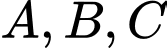 nên
nên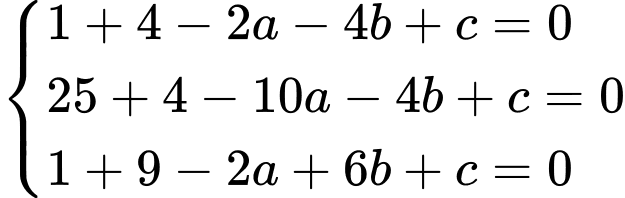
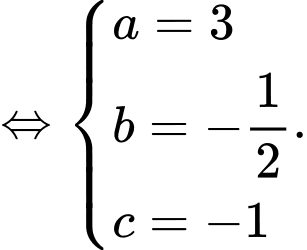
Vậy phương trình đường tròn cần tìm là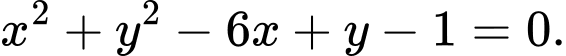 Đáp án: C
Đáp án: C
Phương trình đường tròn có dạng
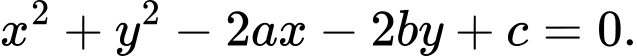 Đường tròn này qua
Đường tròn này qua 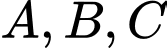 nên
nên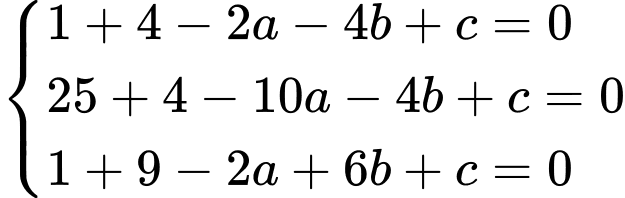
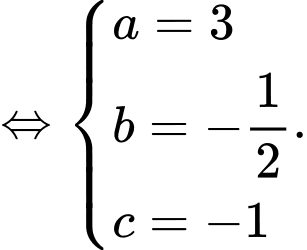
Vậy phương trình đường tròn cần tìm là
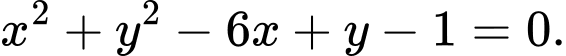 Đáp án: C
Đáp án: C
Câu 15 [246335]: Trong mặt phẳng tọa độ 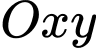 cho đường tròn
cho đường tròn  có tâm
có tâm 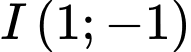 bán kính
bán kính 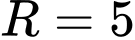 . Biết rằng đường thẳng
. Biết rằng đường thẳng 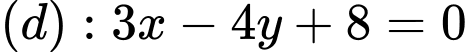 cắt đường tròn
cắt đường tròn  tại hai điểm phân biệt
tại hai điểm phân biệt 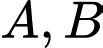 . Tính độ dài đoạn thẳng
. Tính độ dài đoạn thẳng  .
.
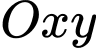 cho đường tròn
cho đường tròn  có tâm
có tâm 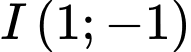 bán kính
bán kính 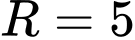 . Biết rằng đường thẳng
. Biết rằng đường thẳng 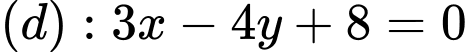 cắt đường tròn
cắt đường tròn  tại hai điểm phân biệt
tại hai điểm phân biệt 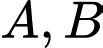 . Tính độ dài đoạn thẳng
. Tính độ dài đoạn thẳng  .
. A, 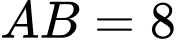 .
.
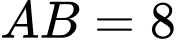 .
.B, 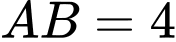 .
.
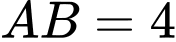 .
.C, 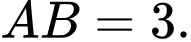 .
.
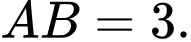 .
.D, 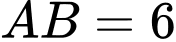 .
.
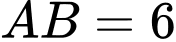 .
.
A
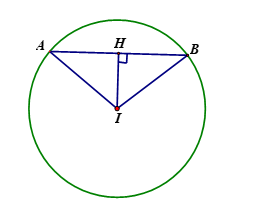
Gọi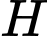 là trung điểm của đoạn thẳng
là trung điểm của đoạn thẳng  . Ta có
. Ta có  và
và 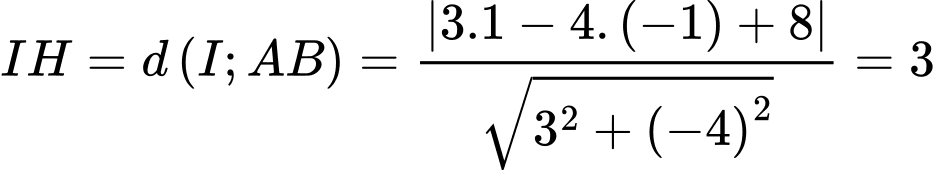 .
.
Xét tam giác vuông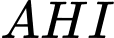 ta có:
ta có: 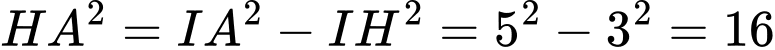
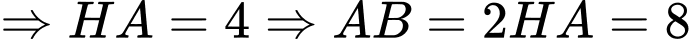 Đáp án: A
Đáp án: A

Gọi
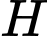 là trung điểm của đoạn thẳng
là trung điểm của đoạn thẳng  . Ta có
. Ta có  và
và 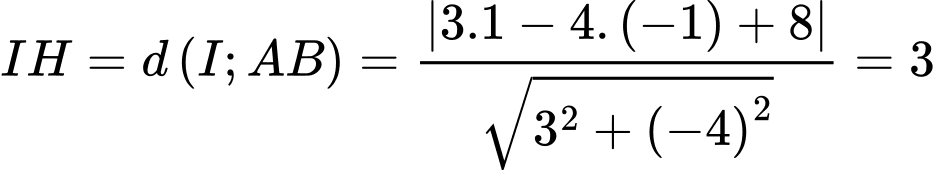 .
.
Xét tam giác vuông
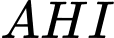 ta có:
ta có: 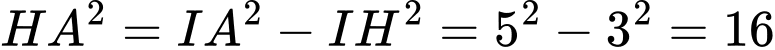
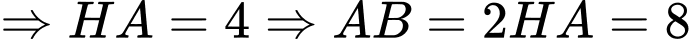 Đáp án: A
Đáp án: A
Câu 16 [246386]: Trên mặt phẳng toạ độ 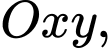 cho các điểm
cho các điểm 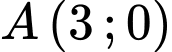 và
và 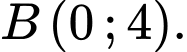 Đường tròn nội tiếp tam giác
Đường tròn nội tiếp tam giác 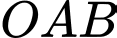 có phương trình
có phương trình
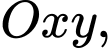 cho các điểm
cho các điểm 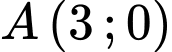 và
và 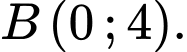 Đường tròn nội tiếp tam giác
Đường tròn nội tiếp tam giác 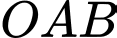 có phương trình
có phương trình A, 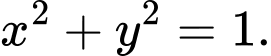
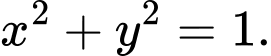
B, 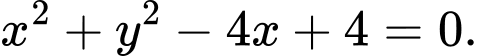
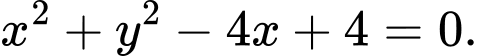
C, 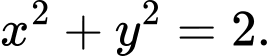
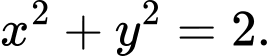
D, 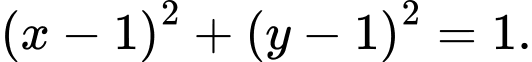
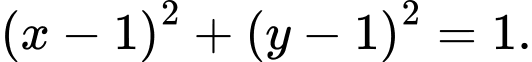
Chọn đáp án D.
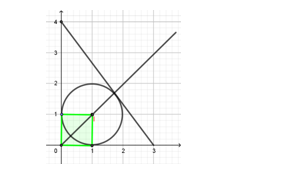
Vì các điểm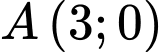 và
và  nằm trong góc phần tư thứ nhất nên tam giác
nằm trong góc phần tư thứ nhất nên tam giác 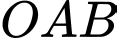 cũng nằm trong góc phần tư thứ nhất. Do vậy gọi tâm đường tròn nội tiếp là
cũng nằm trong góc phần tư thứ nhất. Do vậy gọi tâm đường tròn nội tiếp là 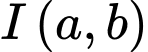 thì
thì 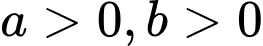 .
.
Theo đề ra ta có: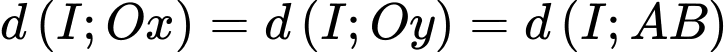 .
.
Phương trình theo đoạn chắn của AB là: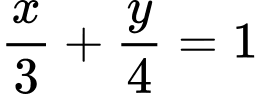 hay
hay 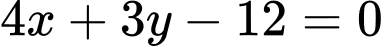 .
.
Do vậy ta có: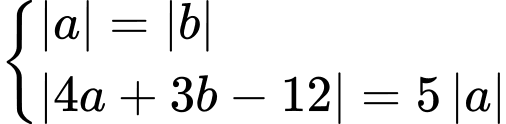
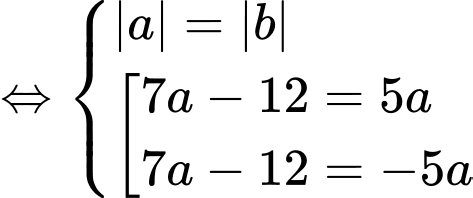
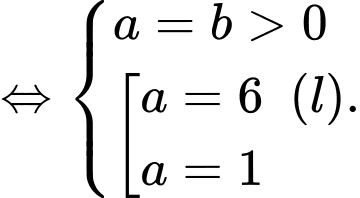
Vậy phương trình đường tròn cần tìm là: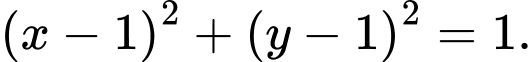 Đáp án: D
Đáp án: D

Vì các điểm
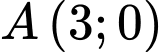 và
và  nằm trong góc phần tư thứ nhất nên tam giác
nằm trong góc phần tư thứ nhất nên tam giác 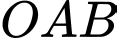 cũng nằm trong góc phần tư thứ nhất. Do vậy gọi tâm đường tròn nội tiếp là
cũng nằm trong góc phần tư thứ nhất. Do vậy gọi tâm đường tròn nội tiếp là 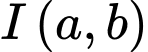 thì
thì 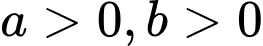 .
.Theo đề ra ta có:
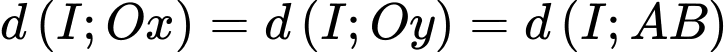 .
.Phương trình theo đoạn chắn của AB là:
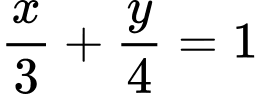 hay
hay 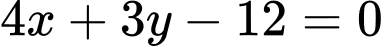 .
.Do vậy ta có:
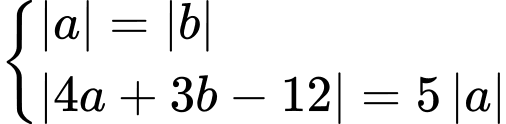
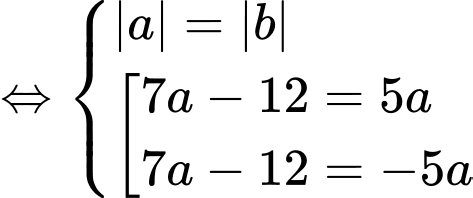
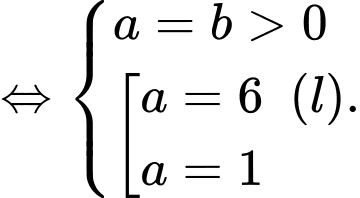
Vậy phương trình đường tròn cần tìm là:
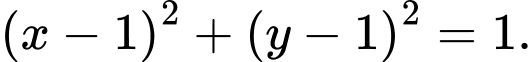 Đáp án: D
Đáp án: D
Câu 17 [246344]: Trong mặt phẳng với hệ tọa độ 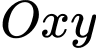 , cho đường thẳng
, cho đường thẳng 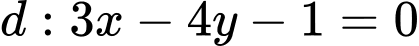 và điểm
và điểm 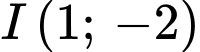 . Gọi
. Gọi  là đường tròn có tâm I và cắt đường thẳng d tại hai điểm A và B sao cho tam giác IAB có diện tích bằng 4. Phương trình đường tròn
là đường tròn có tâm I và cắt đường thẳng d tại hai điểm A và B sao cho tam giác IAB có diện tích bằng 4. Phương trình đường tròn  là
là
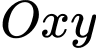 , cho đường thẳng
, cho đường thẳng 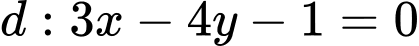 và điểm
và điểm 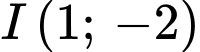 . Gọi
. Gọi  là đường tròn có tâm I và cắt đường thẳng d tại hai điểm A và B sao cho tam giác IAB có diện tích bằng 4. Phương trình đường tròn
là đường tròn có tâm I và cắt đường thẳng d tại hai điểm A và B sao cho tam giác IAB có diện tích bằng 4. Phương trình đường tròn  là
là A, 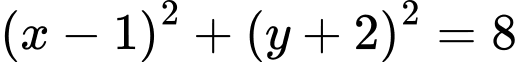 .
.
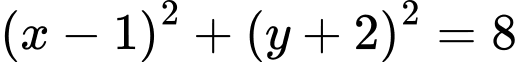 .
.B, 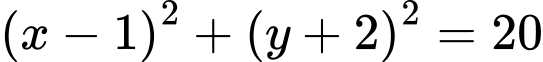 .
.
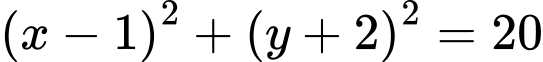 .
.C, 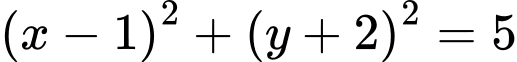 .
.
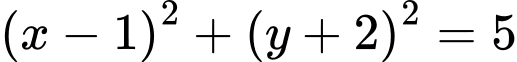 .
.D, 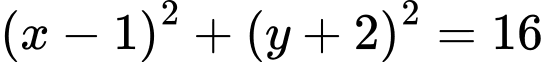 .
.
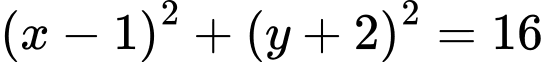 .
.
A
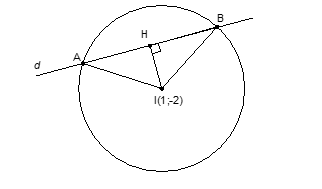
Ta có: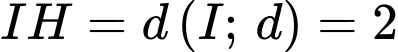 .
.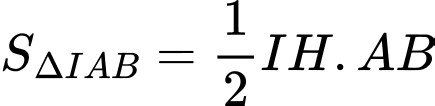
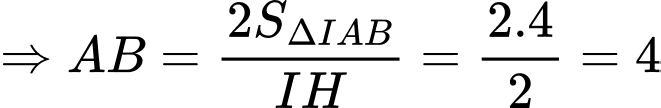
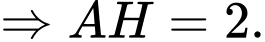
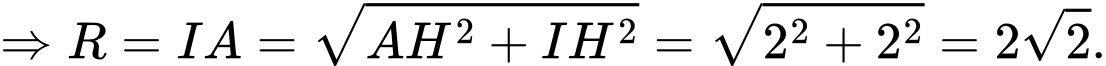
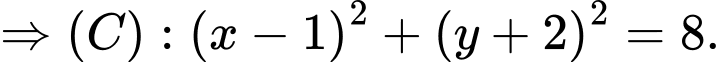 Đáp án: A
Đáp án: A

Ta có:
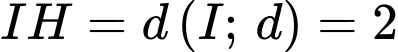 .
.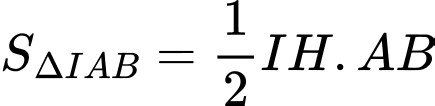
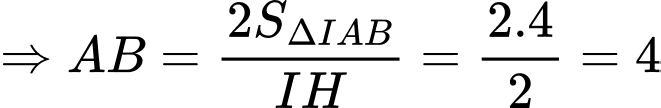
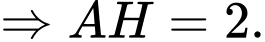
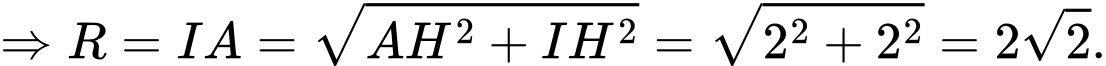
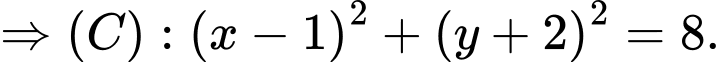 Đáp án: A
Đáp án: A
Câu 18 [246378]: Cho tam giác 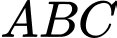 biết
biết 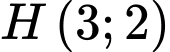 ,
, 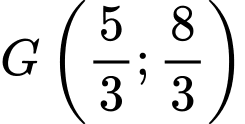 lần lượt là trực tâm và trọng tâm của tam giác, đường thẳng
lần lượt là trực tâm và trọng tâm của tam giác, đường thẳng 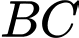 có phương trình
có phương trình 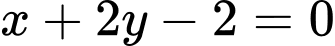 . Tìm phương trình đường tròn ngoại tiếp tam giác
. Tìm phương trình đường tròn ngoại tiếp tam giác 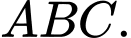
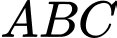 biết
biết 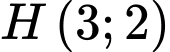 ,
, 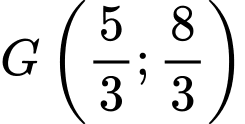 lần lượt là trực tâm và trọng tâm của tam giác, đường thẳng
lần lượt là trực tâm và trọng tâm của tam giác, đường thẳng 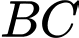 có phương trình
có phương trình 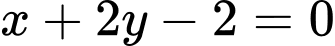 . Tìm phương trình đường tròn ngoại tiếp tam giác
. Tìm phương trình đường tròn ngoại tiếp tam giác 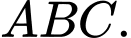
A, 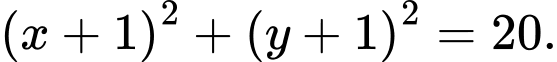
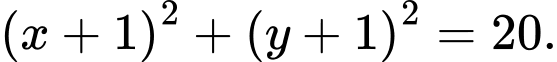
B, 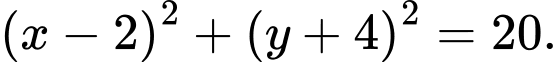
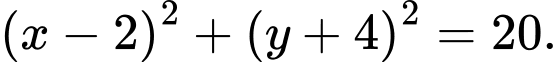
C, 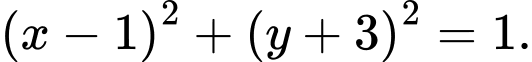
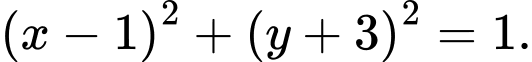
D, 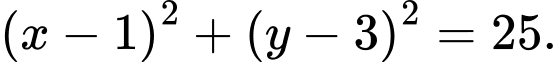
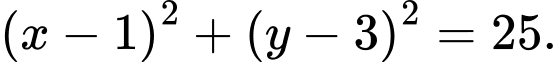
D
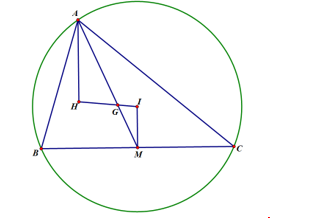
*) Gọi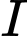 là tâm đường tròn ngoại tiếp tam giác
là tâm đường tròn ngoại tiếp tam giác 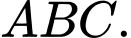
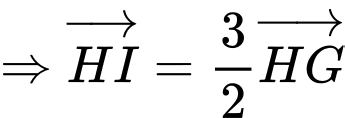
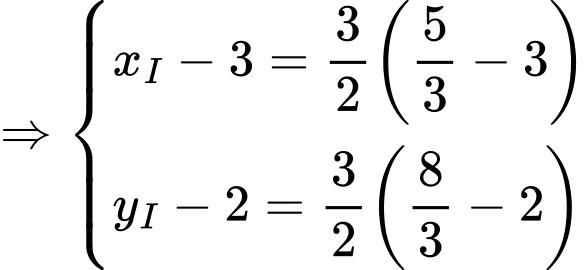
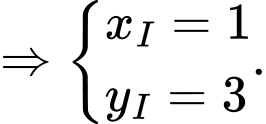
(Do đó ta có thể chọn đáp án D luôn mà không cần tính bán kính).
*) Gọi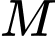 là trung điểm của
là trung điểm của 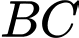
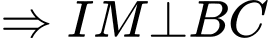
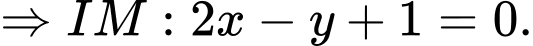
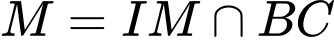
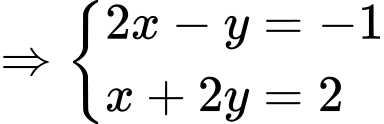
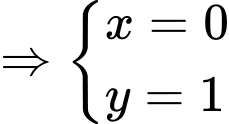
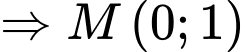 .
.
Lại có: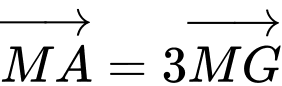
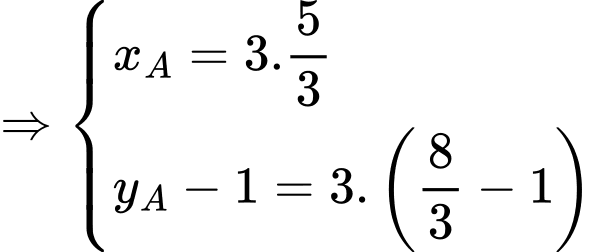
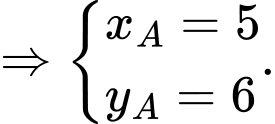
Suy ra: bán kính đường tròn ngoại tiếp tam giác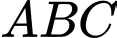 là
là 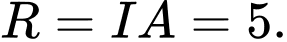
Vậy phương trình đường tròn ngoại tiếp tam giác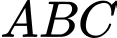 là
là 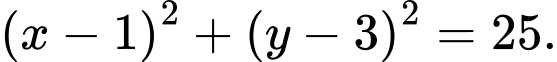 Đáp án: D
Đáp án: D

*) Gọi
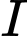 là tâm đường tròn ngoại tiếp tam giác
là tâm đường tròn ngoại tiếp tam giác 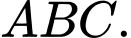
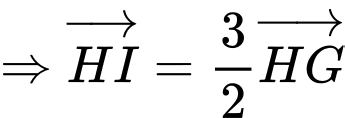
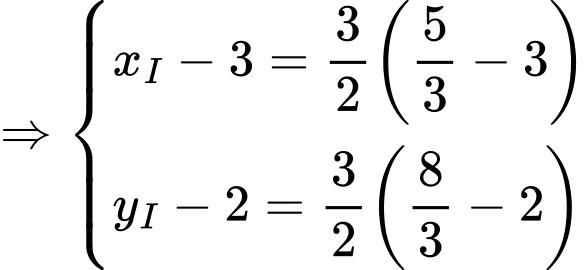
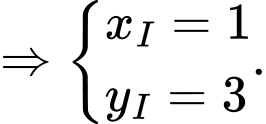
(Do đó ta có thể chọn đáp án D luôn mà không cần tính bán kính).
*) Gọi
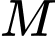 là trung điểm của
là trung điểm của 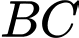
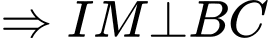
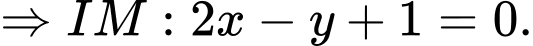
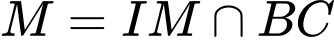
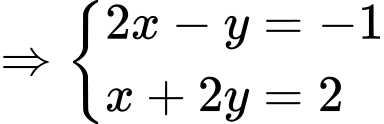
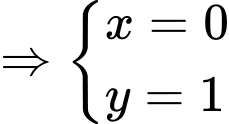
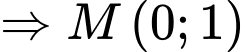 .
.Lại có:
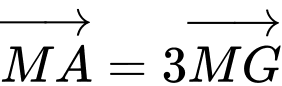
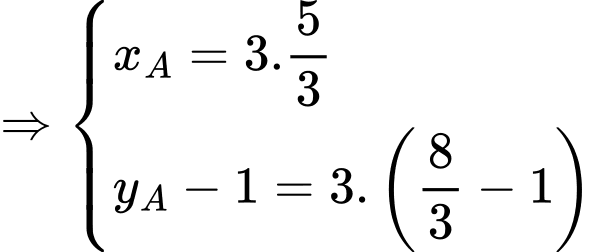
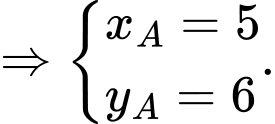
Suy ra: bán kính đường tròn ngoại tiếp tam giác
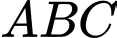 là
là 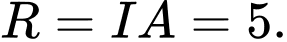
Vậy phương trình đường tròn ngoại tiếp tam giác
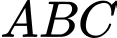 là
là 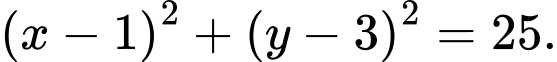 Đáp án: D
Đáp án: D
Câu 19 [581058]: Chuyển động của một vật thể trong khoảng thời gian 180 phút được thể hiện trong mặt phẳng tọa độ. Theo đó, tại thời điểm 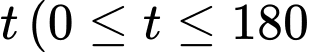 ) vật thể ở vị trí có tọa độ
) vật thể ở vị trí có tọa độ 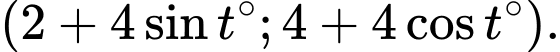 Quỹ đạo chuyển động của vật thể là đường tròn có bán kính bằng bao nhiêu?
Quỹ đạo chuyển động của vật thể là đường tròn có bán kính bằng bao nhiêu?
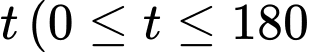 ) vật thể ở vị trí có tọa độ
) vật thể ở vị trí có tọa độ 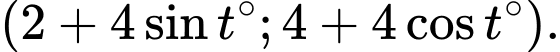 Quỹ đạo chuyển động của vật thể là đường tròn có bán kính bằng bao nhiêu?
Quỹ đạo chuyển động của vật thể là đường tròn có bán kính bằng bao nhiêu?
Gọi điểm 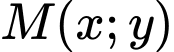 thuộc vào quỹ đạo chuyển động của vật thể.
thuộc vào quỹ đạo chuyển động của vật thể.
Ta có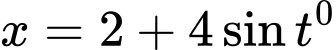 và
và 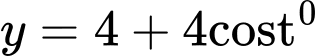
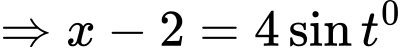 và
và 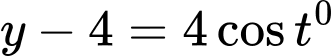
Mà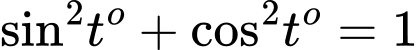
Nên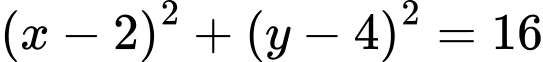
Vậy quỹ đạo chuyển động của vật thể là đường tròn có tâm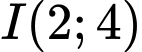 và bán kính bằng
và bán kính bằng 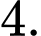
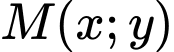 thuộc vào quỹ đạo chuyển động của vật thể.
thuộc vào quỹ đạo chuyển động của vật thể.
Ta có
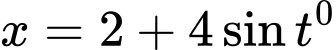 và
và 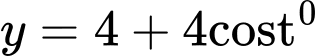
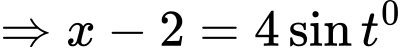 và
và 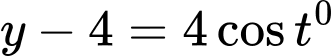
Mà
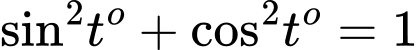
Nên
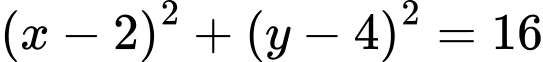
Vậy quỹ đạo chuyển động của vật thể là đường tròn có tâm
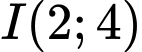 và bán kính bằng
và bán kính bằng 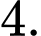
Câu 20 [581059]: Hình mô phỏng một trạm thu phát sóng điện thoại di động đặt ở vị trí 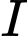 có toạ độ
có toạ độ 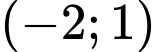 trong mặt phẳng toạ độ (đơn vị trên hai trục là ki-lô-mét).
trong mặt phẳng toạ độ (đơn vị trên hai trục là ki-lô-mét).
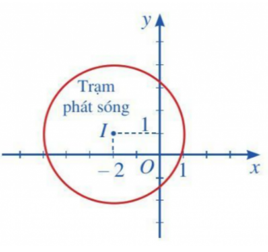
Tính theo đường chim bay, xác định khoảng cách ngắn nhất để một người ở vị trí có tọạ độ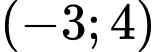 di chuyển được tới vùng phủ sóng theo đơn vị ki-lô-mét (làm tròn kết quả đến hàng phần trăm).
di chuyển được tới vùng phủ sóng theo đơn vị ki-lô-mét (làm tròn kết quả đến hàng phần trăm).
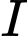 có toạ độ
có toạ độ 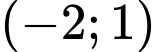 trong mặt phẳng toạ độ (đơn vị trên hai trục là ki-lô-mét).
trong mặt phẳng toạ độ (đơn vị trên hai trục là ki-lô-mét).
Tính theo đường chim bay, xác định khoảng cách ngắn nhất để một người ở vị trí có tọạ độ
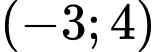 di chuyển được tới vùng phủ sóng theo đơn vị ki-lô-mét (làm tròn kết quả đến hàng phần trăm).
di chuyển được tới vùng phủ sóng theo đơn vị ki-lô-mét (làm tròn kết quả đến hàng phần trăm).
c.
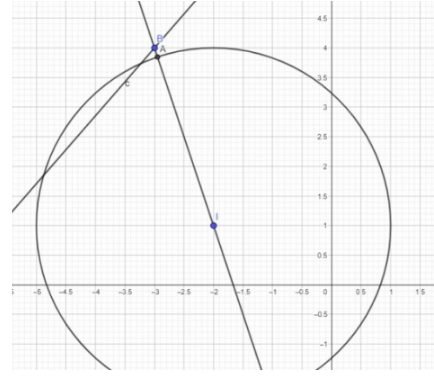
Giả sử vị trí đứng của người đó là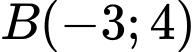 .
.
Ta có: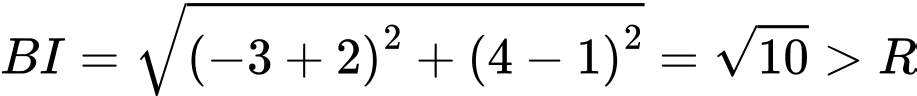
 Khoảng cách ngắn nhất để người đó di chuyển được từ vị trí
Khoảng cách ngắn nhất để người đó di chuyển được từ vị trí 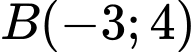 tới vùng phủ sóng là
tới vùng phủ sóng là 

Giả sử vị trí đứng của người đó là
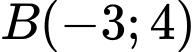 .
.Ta có:
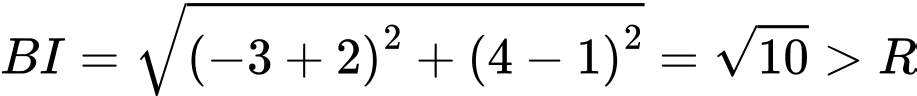
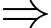 Khoảng cách ngắn nhất để người đó di chuyển được từ vị trí
Khoảng cách ngắn nhất để người đó di chuyển được từ vị trí 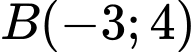 tới vùng phủ sóng là
tới vùng phủ sóng là 
Câu 21 [579676]: [Đề mẫu HSA 2024]: Trong mặt phẳng tọa độ 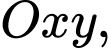 đường tròn
đường tròn  đi qua hai điểm
đi qua hai điểm 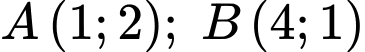 và có tâm thuộc đường thẳng
và có tâm thuộc đường thẳng 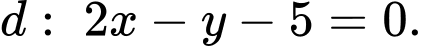 Tính bán kính đường tròn
Tính bán kính đường tròn 
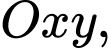 đường tròn
đường tròn  đi qua hai điểm
đi qua hai điểm 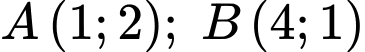 và có tâm thuộc đường thẳng
và có tâm thuộc đường thẳng 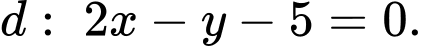 Tính bán kính đường tròn
Tính bán kính đường tròn 
Gọi tâm của đường tròn  là
là 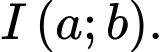
Vì tâm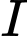 thuộc đường thẳng
thuộc đường thẳng 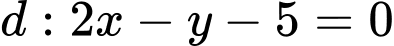 nên
nên 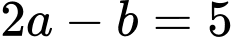
Ta có: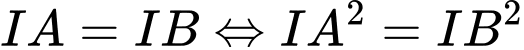
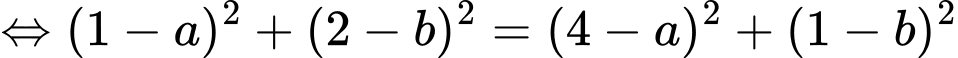
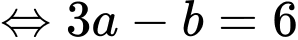
Suy ra hệ phương trình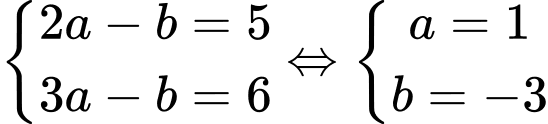
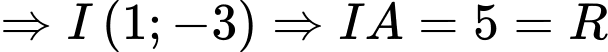
Bán kính đường tròn là 5.
là 5.
Đáp án: 5
 là
là 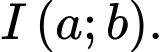
Vì tâm
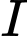 thuộc đường thẳng
thuộc đường thẳng 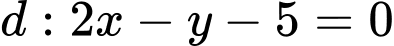 nên
nên 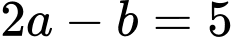
Ta có:
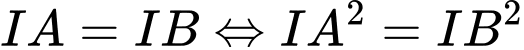
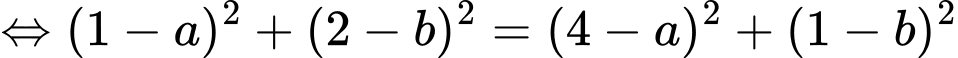
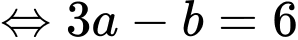
Suy ra hệ phương trình
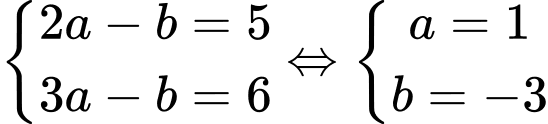
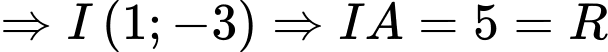
Bán kính đường tròn
 là 5.
là 5.Đáp án: 5
Câu 22 [581053]: Trong mặt phẳng với hệ tọa độ 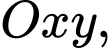 cho đường thẳng
cho đường thẳng 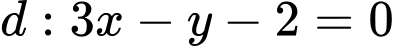 và hai điểm
và hai điểm 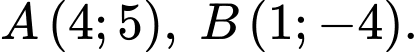 Đường tròn
Đường tròn  có tâm thuộc
có tâm thuộc 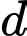 và đi qua hai điểm
và đi qua hai điểm 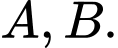 có đường kính bằng bao nhiêu?
có đường kính bằng bao nhiêu?
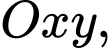 cho đường thẳng
cho đường thẳng 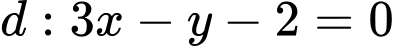 và hai điểm
và hai điểm 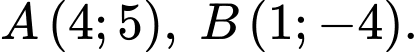 Đường tròn
Đường tròn  có tâm thuộc
có tâm thuộc 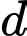 và đi qua hai điểm
và đi qua hai điểm 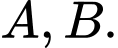 có đường kính bằng bao nhiêu?
có đường kính bằng bao nhiêu?
HD: Trung điểm của  là
là 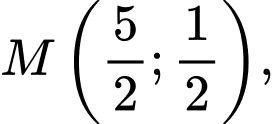
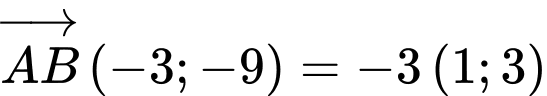
Phương trình đường thẳng trung trực của là đường thẳng qua
là đường thẳng qua 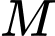 và có vectơ pháp tuyến là
và có vectơ pháp tuyến là 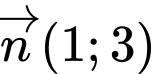 là:
là: 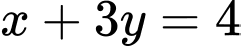
Toạ độ tâm của đường tròn là nghiệm của hệ phương trình
là nghiệm của hệ phương trình
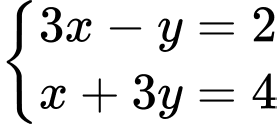
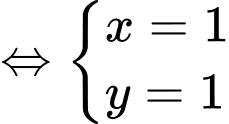
Vậy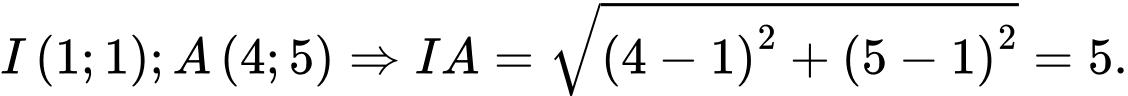
Bán kính đường tròn bằng 5 nên đường kính đường tròn bằng 10.
 là
là 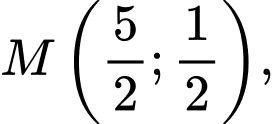
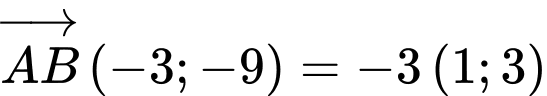
Phương trình đường thẳng trung trực của
 là đường thẳng qua
là đường thẳng qua 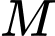 và có vectơ pháp tuyến là
và có vectơ pháp tuyến là 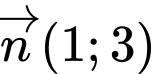 là:
là: 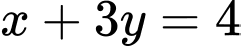
Toạ độ tâm của đường tròn
 là nghiệm của hệ phương trình
là nghiệm của hệ phương trình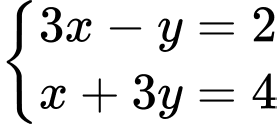
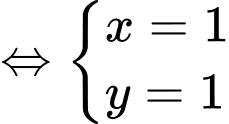
Vậy
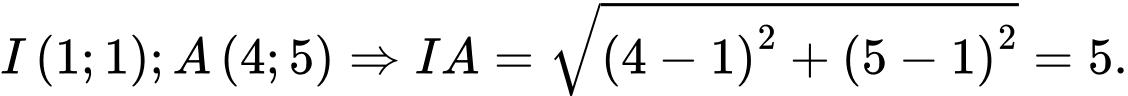
Bán kính đường tròn bằng 5 nên đường kính đường tròn bằng 10.
Câu 23 [558645]: Đường tròn  có tâm
có tâm 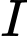 (có hoành độ dương) thuộc đường thẳng
(có hoành độ dương) thuộc đường thẳng 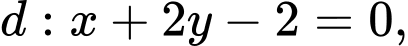 bán kính
bán kính 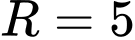 và tiếp xúc với đường thẳng
và tiếp xúc với đường thẳng 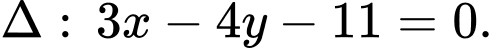 Phương trình của đường tròn
Phương trình của đường tròn  có dạng
có dạng 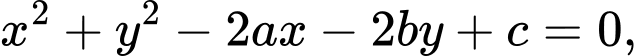 khi đó
khi đó 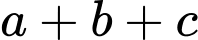 bằng bao nhiêu?
bằng bao nhiêu?
 có tâm
có tâm 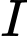 (có hoành độ dương) thuộc đường thẳng
(có hoành độ dương) thuộc đường thẳng 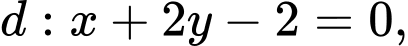 bán kính
bán kính 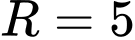 và tiếp xúc với đường thẳng
và tiếp xúc với đường thẳng 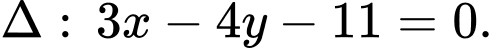 Phương trình của đường tròn
Phương trình của đường tròn  có dạng
có dạng 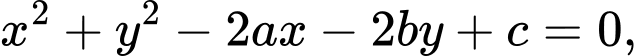 khi đó
khi đó 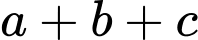 bằng bao nhiêu?
bằng bao nhiêu?
Ta có: 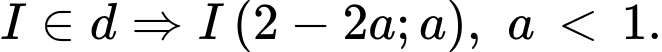
Do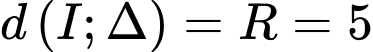
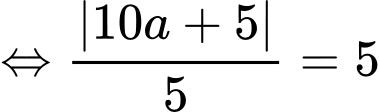

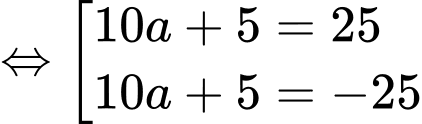
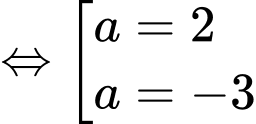
Do vậy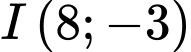

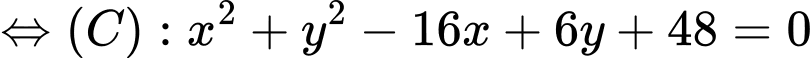
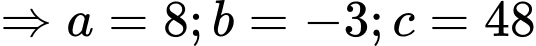
Vậy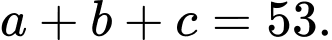
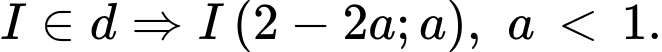
Do
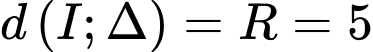
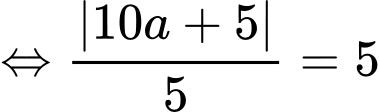

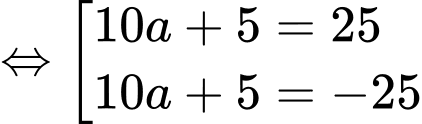
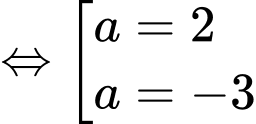
Do vậy
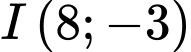

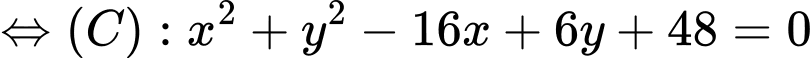
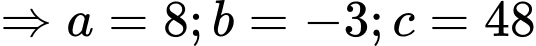
Vậy
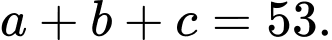
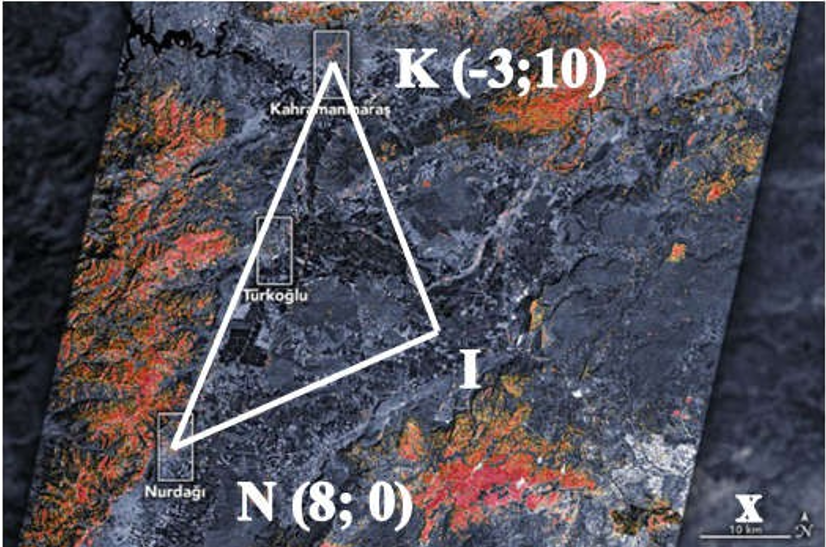
Câu 24 [558660]: Ngày 6/2/2023, một trận động đất 7,8 độ richter có tâm chấn tại Thổ Nhĩ Kì (hình minh họa). Biết rằng đường tròn tác động đi qua 2 thành phố Kahramanmaras và Nurdagi có tọa độ lần lượt là 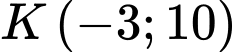 và
và  . Mặt khác, tâm chấn xác định được nằm trên một đường thẳng có phương trình
. Mặt khác, tâm chấn xác định được nằm trên một đường thẳng có phương trình 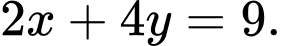
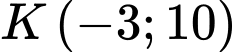 và
và  . Mặt khác, tâm chấn xác định được nằm trên một đường thẳng có phương trình
. Mặt khác, tâm chấn xác định được nằm trên một đường thẳng có phương trình 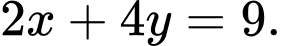

Hãy xác định bán kính tác động (km) tính từ tâm chấn (Tâm I), kết quả làm tròn 2 số sau dấy phẩy là
Phương trình đường tròn tác động có dạng: 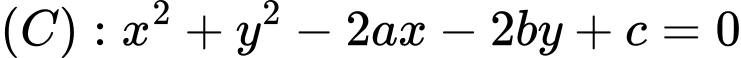 có tâm
có tâm 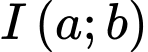 đi qua
đi qua 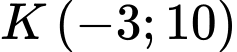 và
và  nên ta có hệ phương trình:
nên ta có hệ phương trình:
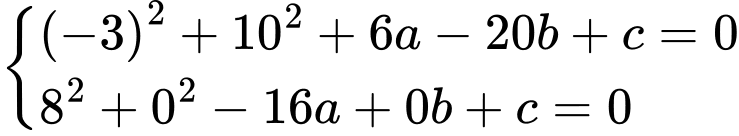
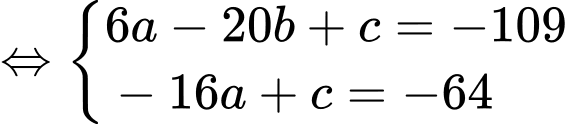

Tâm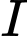 thuộc đường thẳng
thuộc đường thẳng 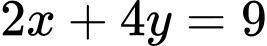 nên
nên 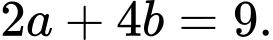
Từ và
và  suy ra
suy ra 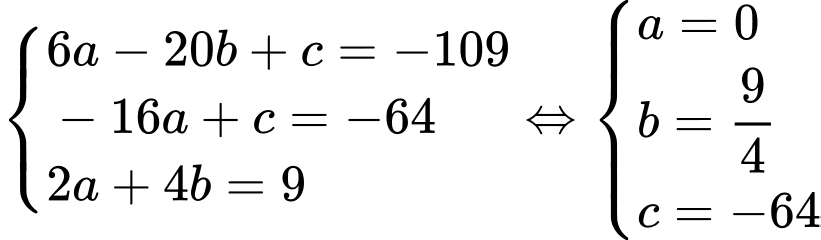
Vậy bán kính tác động tính từ tâm chấn là: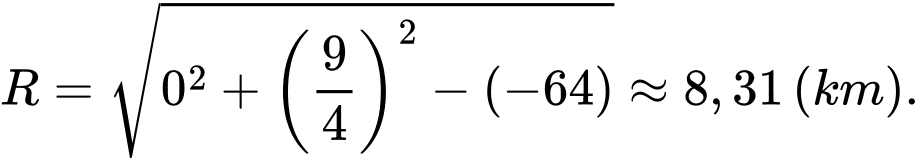
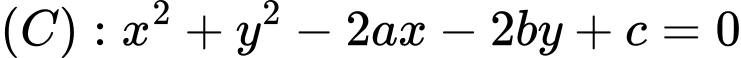 có tâm
có tâm 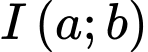 đi qua
đi qua 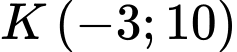 và
và  nên ta có hệ phương trình:
nên ta có hệ phương trình: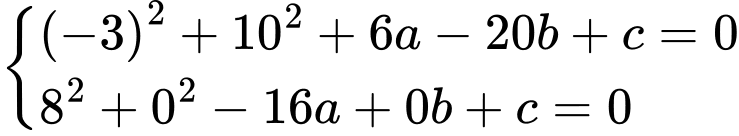
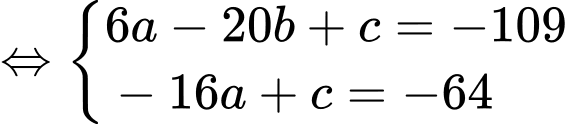

Tâm
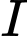 thuộc đường thẳng
thuộc đường thẳng 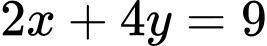 nên
nên 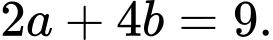
Từ
 và
và  suy ra
suy ra 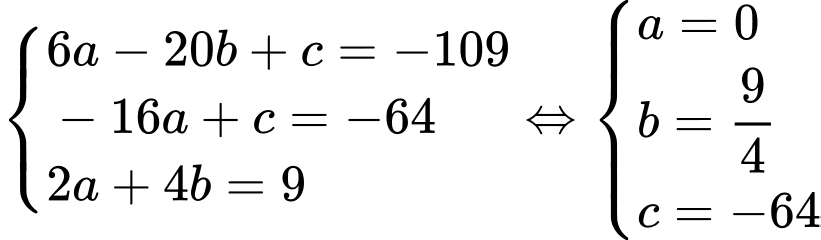
Vậy bán kính tác động tính từ tâm chấn là:
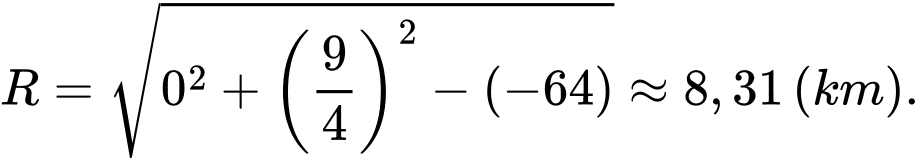
Câu 25 [246334]: Cho đường thẳng 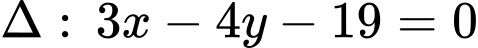 và đường tròn
và đường tròn 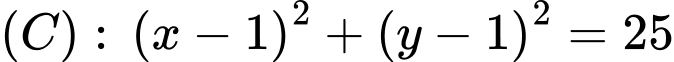 . Biết đường thẳng
. Biết đường thẳng  cắt
cắt  tại hai điểm phân biệt
tại hai điểm phân biệt 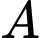 và
và 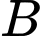 , khi đó độ dài đọan thẳng
, khi đó độ dài đọan thẳng  là
là
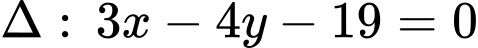 và đường tròn
và đường tròn 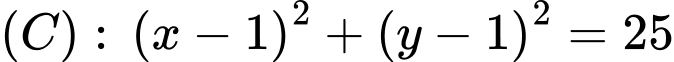 . Biết đường thẳng
. Biết đường thẳng  cắt
cắt  tại hai điểm phân biệt
tại hai điểm phân biệt 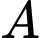 và
và 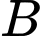 , khi đó độ dài đọan thẳng
, khi đó độ dài đọan thẳng  là
là A, 6.
B, 3.
C, 4.
D, 8.
Chọn A
Từ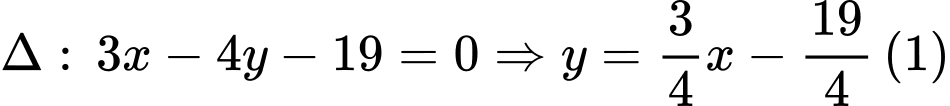 .
.
Thế vào
vào  ta được
ta được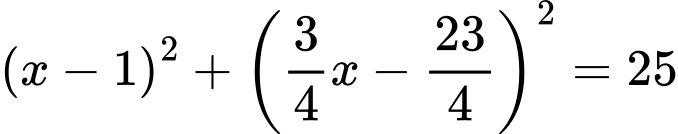
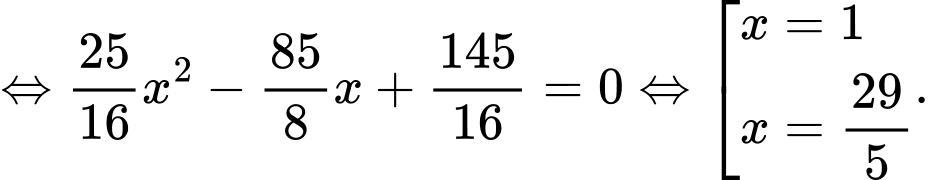
+)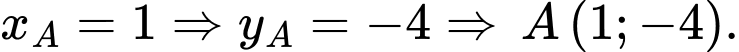
+)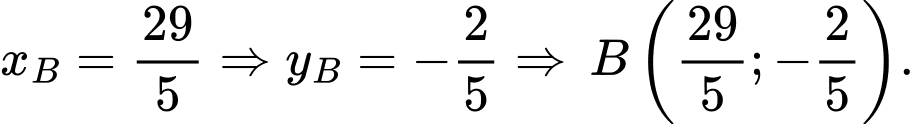
Độ dài đoạn thẳng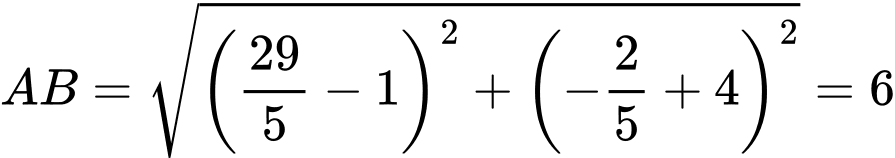 . Đáp án: A
. Đáp án: A
Từ
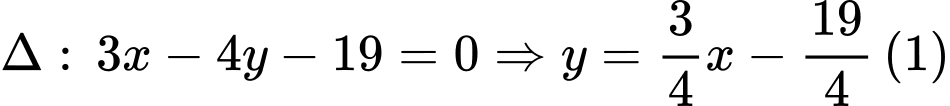 .
.Thế
 vào
vào  ta được
ta được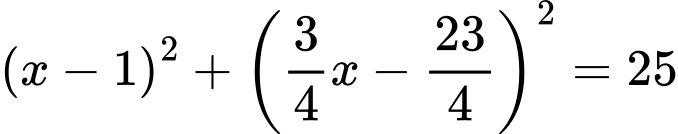
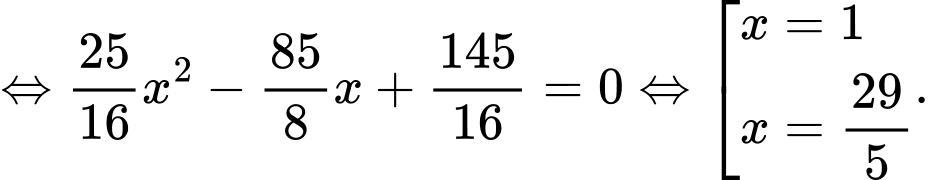
+)
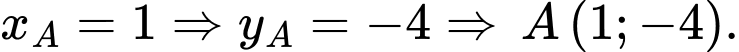
+)
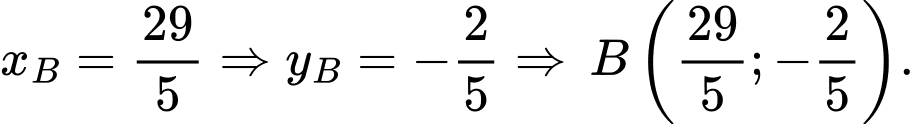
Độ dài đoạn thẳng
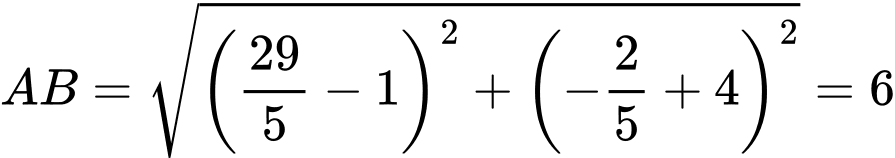 . Đáp án: A
. Đáp án: A
Câu 26 [558655]: Trong mặt phẳng với hệ toạ độ 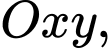 cho đường tròn
cho đường tròn  đi qua hai điểm
đi qua hai điểm 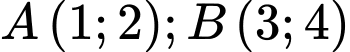 và tiếp xúc với đường thẳng
và tiếp xúc với đường thẳng 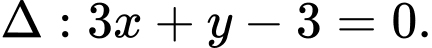 Gọi
Gọi 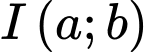 là tâm của đường tròn
là tâm của đường tròn  Tính giá trị biểu thức
Tính giá trị biểu thức 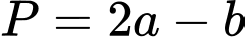 (với
(với 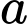 là số không nguyên).
là số không nguyên).
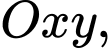 cho đường tròn
cho đường tròn  đi qua hai điểm
đi qua hai điểm 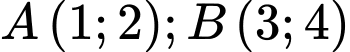 và tiếp xúc với đường thẳng
và tiếp xúc với đường thẳng 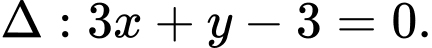 Gọi
Gọi 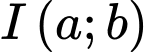 là tâm của đường tròn
là tâm của đường tròn  Tính giá trị biểu thức
Tính giá trị biểu thức 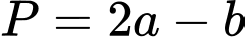 (với
(với 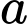 là số không nguyên).
là số không nguyên).
Ta có: Phương trình đường thẳng  là:
là: 
Gọi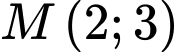 là trung điểm của đoạn
là trung điểm của đoạn 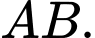
Khi đó đường trung trực của đoạn thẳng có phương trình là:
có phương trình là: 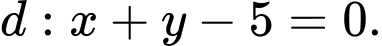
Vì đi qua hai điểm
đi qua hai điểm 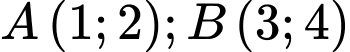 và tiếp xúc với đường thẳng
và tiếp xúc với đường thẳng 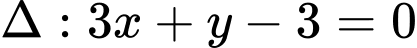 nên
nên 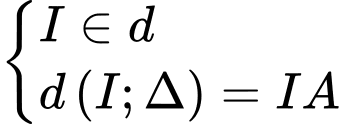
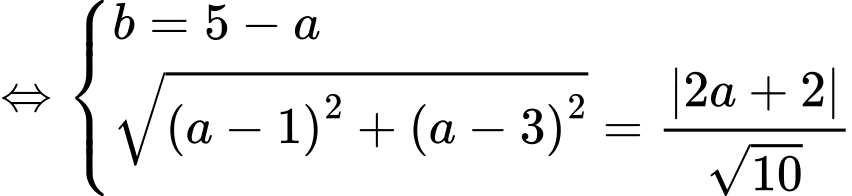
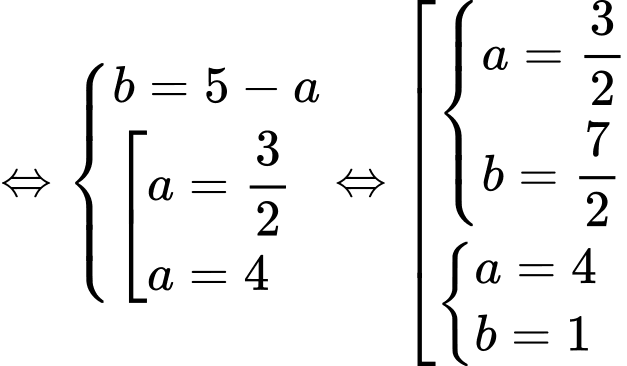
Vậy với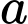 là số không nguyên thì biểu thức
là số không nguyên thì biểu thức 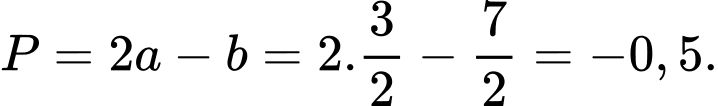
 là:
là: 
Gọi
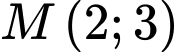 là trung điểm của đoạn
là trung điểm của đoạn 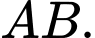
Khi đó đường trung trực của đoạn thẳng
 có phương trình là:
có phương trình là: 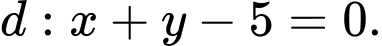
Vì
 đi qua hai điểm
đi qua hai điểm 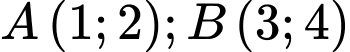 và tiếp xúc với đường thẳng
và tiếp xúc với đường thẳng 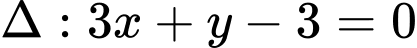 nên
nên 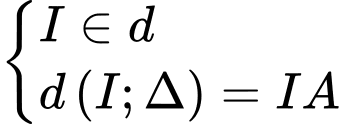
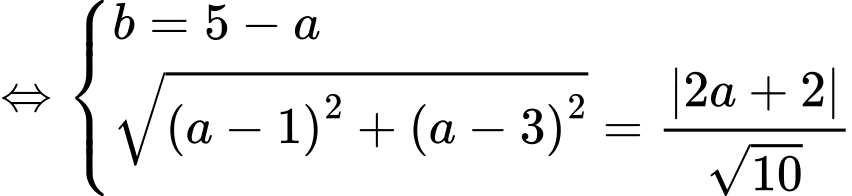
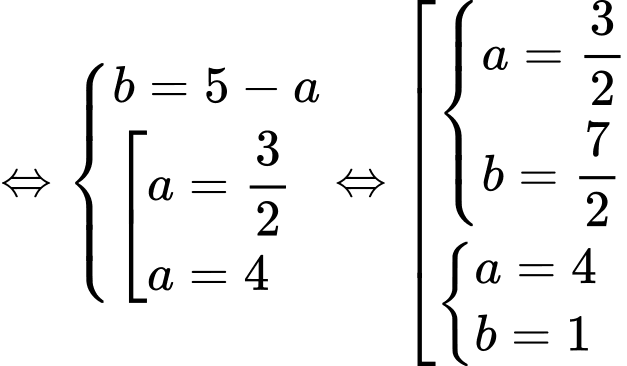
Vậy với
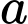 là số không nguyên thì biểu thức
là số không nguyên thì biểu thức 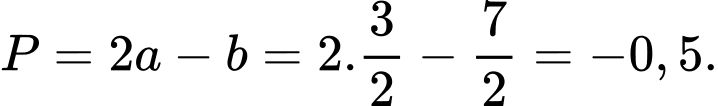
Câu 27 [246343]: Trong mặt phẳng tọa độ 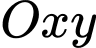 , cho hai đường thẳng
, cho hai đường thẳng 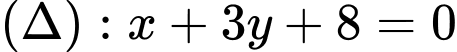 ;
; 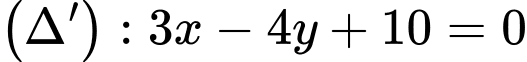 và điểm
và điểm 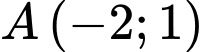 . Đường tròn có tâm
. Đường tròn có tâm 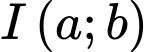 thuộc đường thẳng
thuộc đường thẳng  ,đi qua
,đi qua 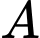 và tiếp xúc với đường thẳng
và tiếp xúc với đường thẳng 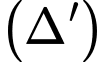 . Tính
. Tính  .
.
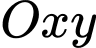 , cho hai đường thẳng
, cho hai đường thẳng 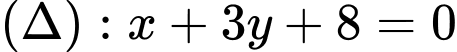 ;
; 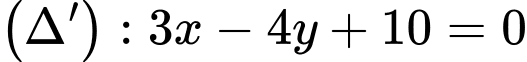 và điểm
và điểm 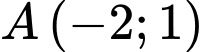 . Đường tròn có tâm
. Đường tròn có tâm 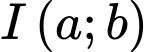 thuộc đường thẳng
thuộc đường thẳng  ,đi qua
,đi qua 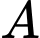 và tiếp xúc với đường thẳng
và tiếp xúc với đường thẳng 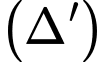 . Tính
. Tính  .
. A, 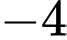 .
.
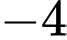 .
.B, 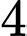 .
.
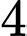 .
.C, 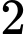 .
.
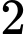 .
.D, 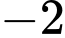 .
.
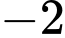 .
.
Chọn D
.
Vì nên
nên 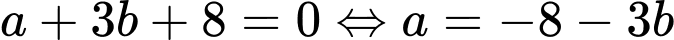 .
.
Vì đường tròn đi qua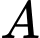 và tiếp xúc với đường thẳng
và tiếp xúc với đường thẳng 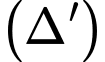 nên:
nên:
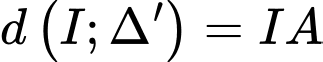
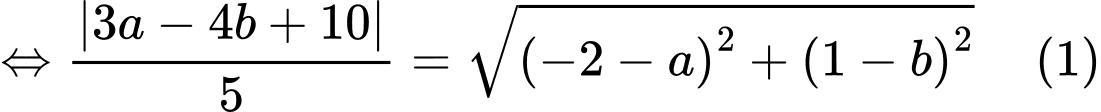 .
.
Thay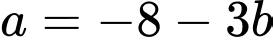 vào
vào  ta có:
ta có:
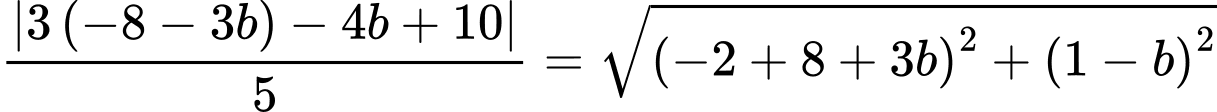
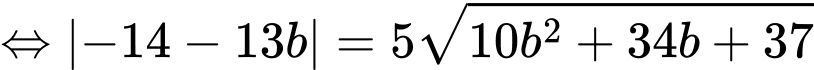
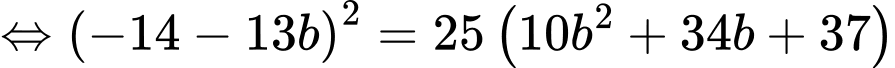
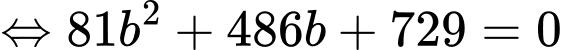
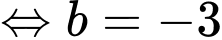 .
.
Với .
.
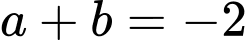 .
.
 Đáp án: D
Đáp án: D
Vì
 nên
nên 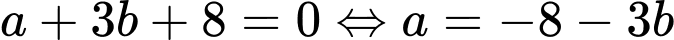 .
.
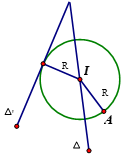
Vì đường tròn đi qua
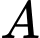 và tiếp xúc với đường thẳng
và tiếp xúc với đường thẳng 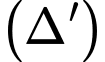 nên:
nên:
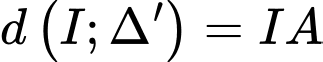
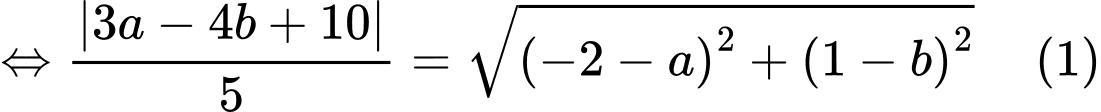 .
.
Thay
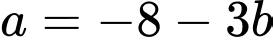 vào
vào  ta có:
ta có:
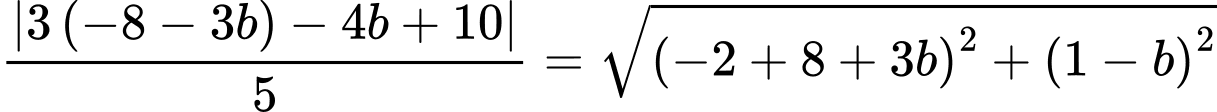
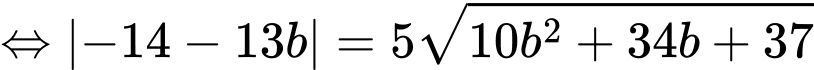
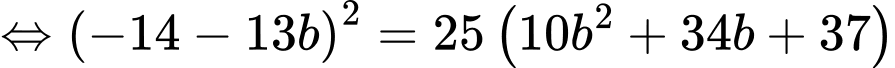
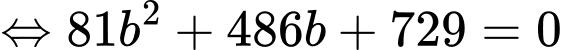
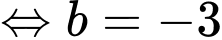 .
.
Với
 .
.
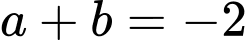 .
. Đáp án: D
Đáp án: D
Câu 28 [581055]: Trong mặt phẳng với hệ tọa độ 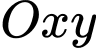 . Cho đường tròn
. Cho đường tròn 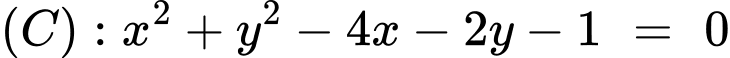 và đường thẳng
và đường thẳng 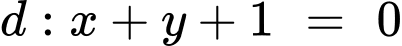 . Biết rằng có hai điểm
. Biết rằng có hai điểm 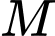 thuộc đường thẳng
thuộc đường thẳng 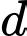 sao cho từ điểm
sao cho từ điểm 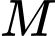 kẻ được đến
kẻ được đến  hai tiếp tuyến hợp với nhau góc
hai tiếp tuyến hợp với nhau góc 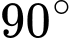 . Tổng tung độ của hai điểm đó bằng bao nhiêu.
. Tổng tung độ của hai điểm đó bằng bao nhiêu.
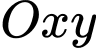 . Cho đường tròn
. Cho đường tròn 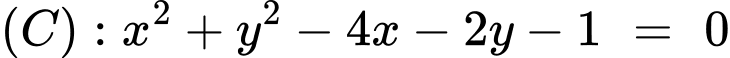 và đường thẳng
và đường thẳng 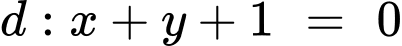 . Biết rằng có hai điểm
. Biết rằng có hai điểm 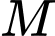 thuộc đường thẳng
thuộc đường thẳng 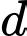 sao cho từ điểm
sao cho từ điểm 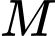 kẻ được đến
kẻ được đến  hai tiếp tuyến hợp với nhau góc
hai tiếp tuyến hợp với nhau góc 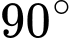 . Tổng tung độ của hai điểm đó bằng bao nhiêu.
. Tổng tung độ của hai điểm đó bằng bao nhiêu. 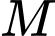 thuộc
thuộc 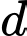 suy ra
suy ra 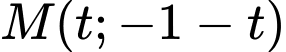 . Nếu 2 tiếp tuyến vuông góc với nhau thì
. Nếu 2 tiếp tuyến vuông góc với nhau thì 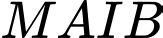 là hình vuông (
là hình vuông (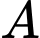 ,
,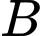 là 2 tiếp điểm). Do đó
là 2 tiếp điểm). Do đó 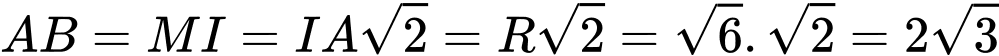
Ta có :
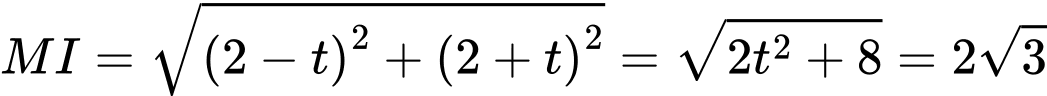
- Do đó :
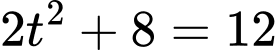
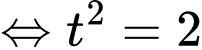
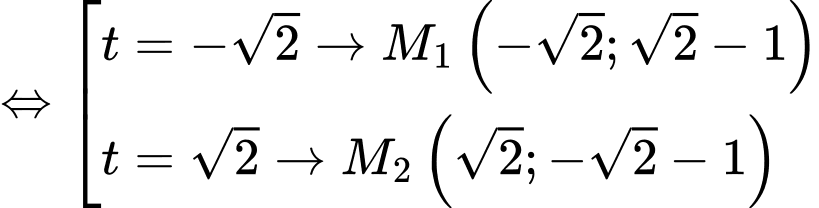 .
.
Suy ra tổng tung độ của hai điểm bằng -2.
Câu 29 [581056]: Trong mặt phẳng 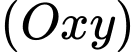 , cho
, cho 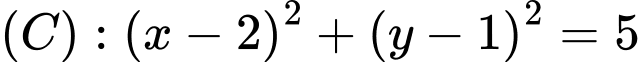 . Điểm
. Điểm 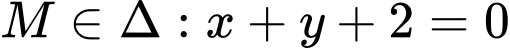 có hoành độ dương sao cho qua
có hoành độ dương sao cho qua 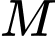 kẻ được tới
kẻ được tới  hai tiếp tuyến
hai tiếp tuyến 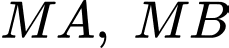 thỏa mãn diện tích tứ giác
thỏa mãn diện tích tứ giác 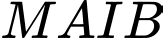 bằng
bằng  , với
, với 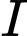 là tâm đường tròn. Tìm hoành độ của điểm
là tâm đường tròn. Tìm hoành độ của điểm 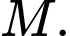
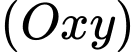 , cho
, cho 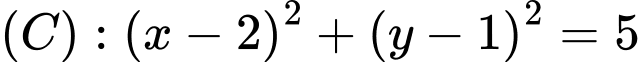 . Điểm
. Điểm 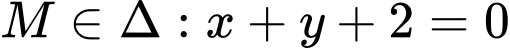 có hoành độ dương sao cho qua
có hoành độ dương sao cho qua 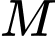 kẻ được tới
kẻ được tới  hai tiếp tuyến
hai tiếp tuyến 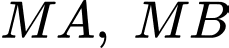 thỏa mãn diện tích tứ giác
thỏa mãn diện tích tứ giác 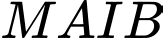 bằng
bằng  , với
, với 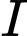 là tâm đường tròn. Tìm hoành độ của điểm
là tâm đường tròn. Tìm hoành độ của điểm 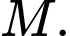
 có tâm
có tâm 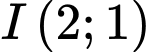 , bán kính
, bán kính 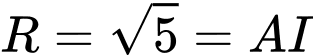
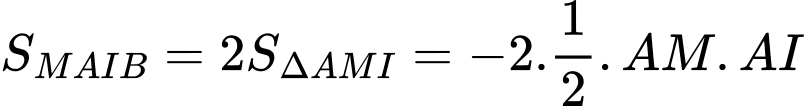
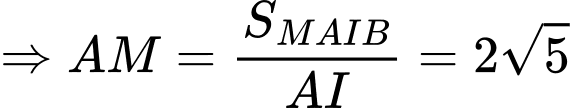


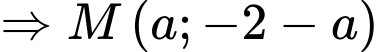
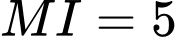
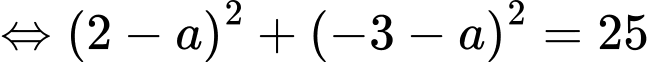
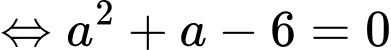
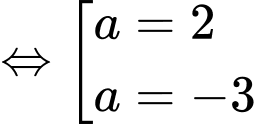
Điểm thỏa mãn điều kiện có hoành độ bằng 2.
Câu 30 [581057]: Trong mặt phẳng 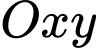 cho
cho 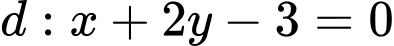 và
và 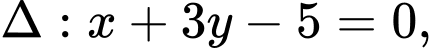 đường tròn
đường tròn  có bán kính bằng
có bán kính bằng 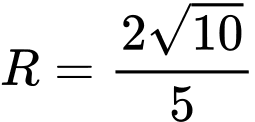 , có tâm
, có tâm 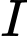 thuộc
thuộc 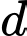 và tiếp xúc với
và tiếp xúc với  . Biết điểm
. Biết điểm 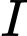 có hoành độ âm. Tính tung độ của điểm
có hoành độ âm. Tính tung độ của điểm 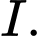
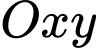 cho
cho 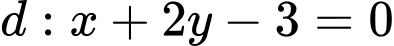 và
và 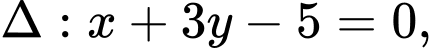 đường tròn
đường tròn  có bán kính bằng
có bán kính bằng 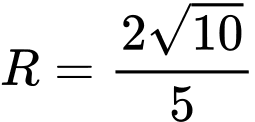 , có tâm
, có tâm 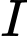 thuộc
thuộc 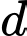 và tiếp xúc với
và tiếp xúc với  . Biết điểm
. Biết điểm 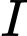 có hoành độ âm. Tính tung độ của điểm
có hoành độ âm. Tính tung độ của điểm 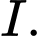
Gọi 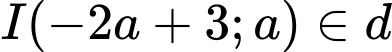 là tâm của (C). Ta có
là tâm của (C). Ta có
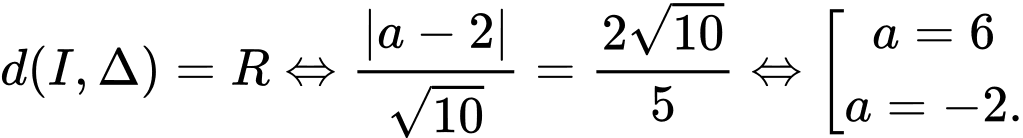
Với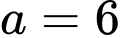 suy ra I( -9; 6) (thoả mãn). Vậy tung độ điểm I là 6.
suy ra I( -9; 6) (thoả mãn). Vậy tung độ điểm I là 6.
Với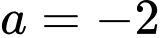 suy ra I( 7; -2) (không thoả mãn).
suy ra I( 7; -2) (không thoả mãn).
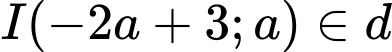 là tâm của (C). Ta có
là tâm của (C). Ta có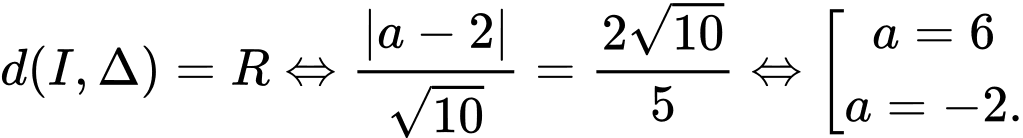
Với
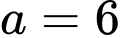 suy ra I( -9; 6) (thoả mãn). Vậy tung độ điểm I là 6.
suy ra I( -9; 6) (thoả mãn). Vậy tung độ điểm I là 6.Với
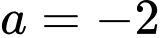 suy ra I( 7; -2) (không thoả mãn).
suy ra I( 7; -2) (không thoả mãn).