Đáp án Bài tập tự luyện số 1
Câu 1 [265692]: Số đo theo đơn vị rađian của góc 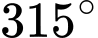 là
là
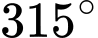 là
là A, 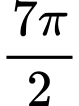 .
.
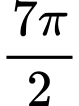 .
.B, 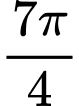 .
.
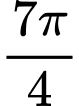 .
.C, 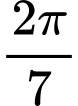 .
.
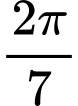 .
.D, 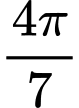 .
.
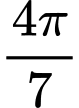 .
.
Ta có 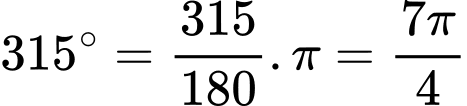 (rađian). Đáp án: B
(rađian). Đáp án: B
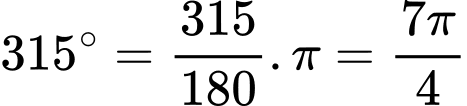 (rađian). Đáp án: B
(rađian). Đáp án: B
Câu 2 [265700]: Một bánh xe có 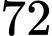 răng. Số đo góc mà bánh xe đã quay được khi di chuyển
răng. Số đo góc mà bánh xe đã quay được khi di chuyển  răng là
răng là
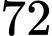 răng. Số đo góc mà bánh xe đã quay được khi di chuyển
răng. Số đo góc mà bánh xe đã quay được khi di chuyển  răng là
răng là A, 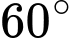 .
.
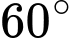 .
.B, 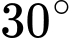 .
.
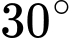 .
.C, 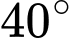 .
.
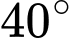 .
.D, 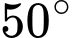 .
.
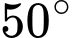 .
.
Chọn D
+ 1 bánh răng tương ứng với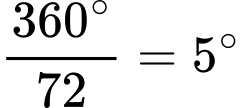
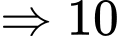 bánh răng là
bánh răng là 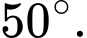 Đáp án: D
Đáp án: D
+ 1 bánh răng tương ứng với
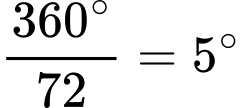
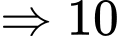 bánh răng là
bánh răng là 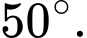 Đáp án: D
Đáp án: D
Câu 3 [269912]: Cho 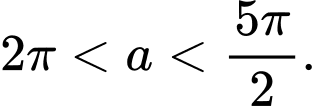 Chọn khẳng định đúng.
Chọn khẳng định đúng.
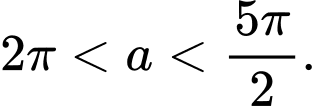 Chọn khẳng định đúng.
Chọn khẳng định đúng. A, 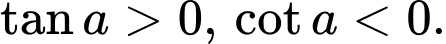
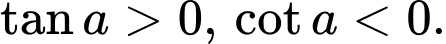
B, 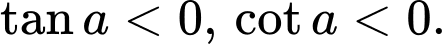
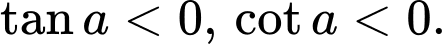
C, 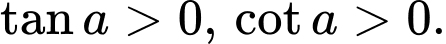
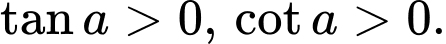
D, 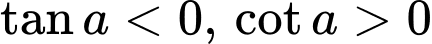 .
.
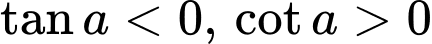 .
.
Chọn C
Đặt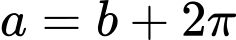 .
. 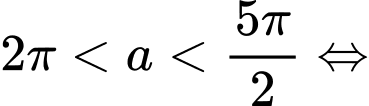
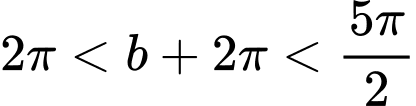
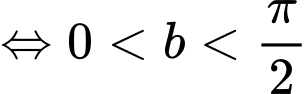
Có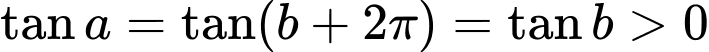 ,
, 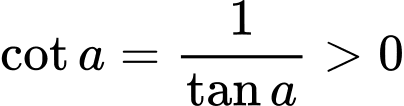 .
.
Vậy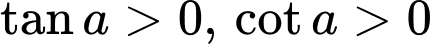 . Đáp án: C
. Đáp án: C
Đặt
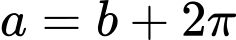 .
. 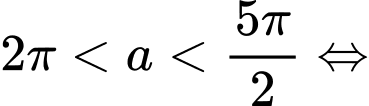
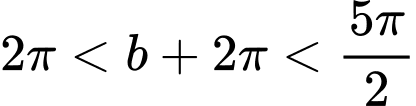
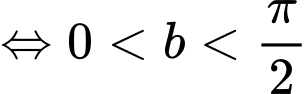
Có
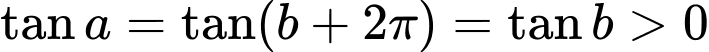 ,
, 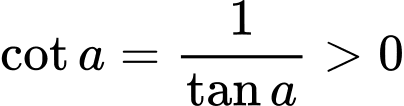 .
.Vậy
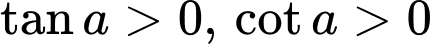 . Đáp án: C
. Đáp án: C
Câu 4 [269938]: Cho 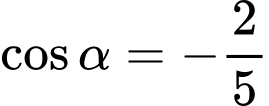
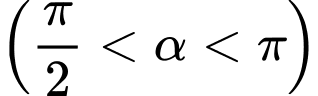 . Khi đó
. Khi đó 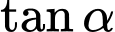 bằng
bằng
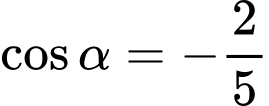
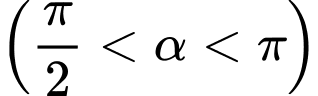 . Khi đó
. Khi đó 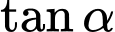 bằng
bằng A, 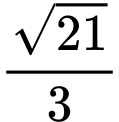 .
.
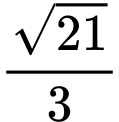 .
.B, 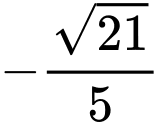 .
.
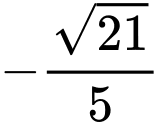 .
.C, 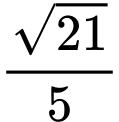 .
.
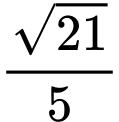 .
.D, 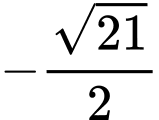 .
.
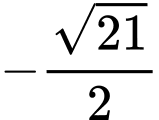 .
.
Chọn D
Với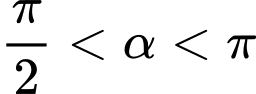
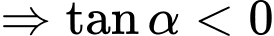 .
.
Ta có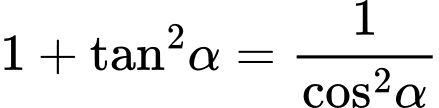
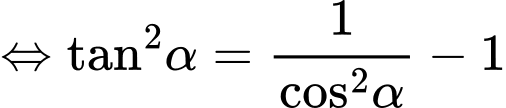
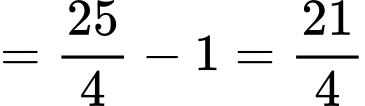
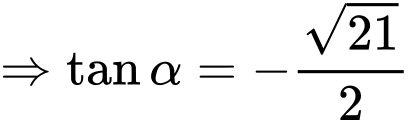 . Đáp án: D
. Đáp án: D
Với
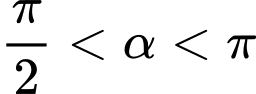
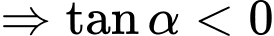 .
.Ta có
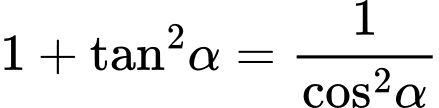
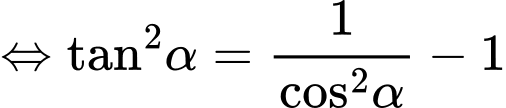
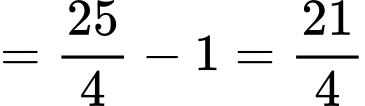
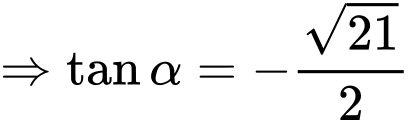 . Đáp án: D
. Đáp án: D
Câu 5 [269940]: Cho  . Tính
. Tính 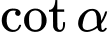 .
.
 . Tính
. Tính 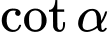 .
. A, 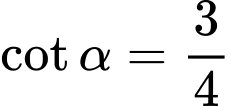 .
.
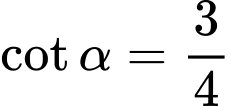 .
.B, 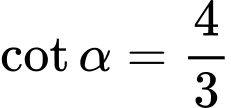 .
.
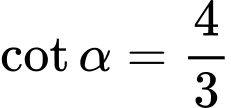 .
.C, 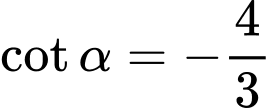 .
.
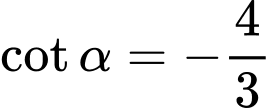 .
.D, 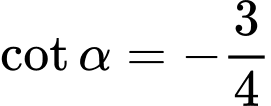 .
.
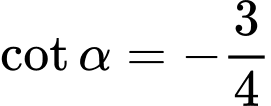 .
.
Chọn C
Ta có: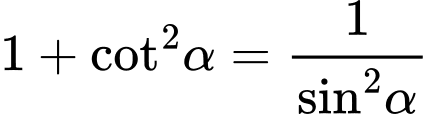
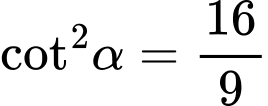
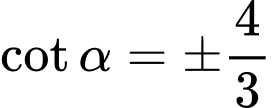 .
.
Vì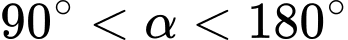 nên
nên 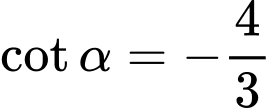 . Đáp án: C
. Đáp án: C
Ta có:
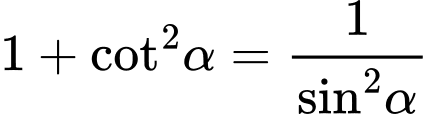
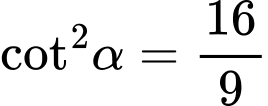
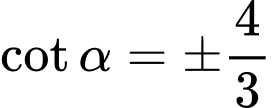 .
.Vì
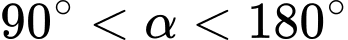 nên
nên 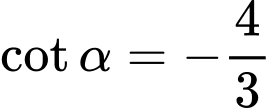 . Đáp án: C
. Đáp án: C
Câu 6 [518837]: Cho 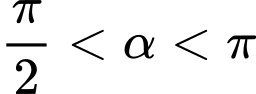 và
và 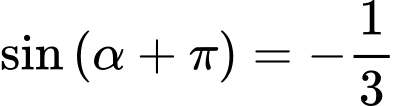 . Tính
. Tính 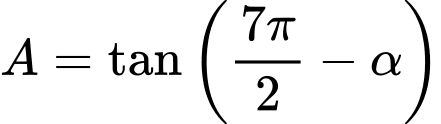 .
.
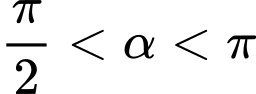 và
và 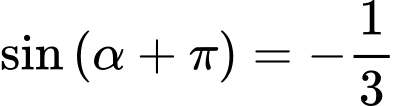 . Tính
. Tính 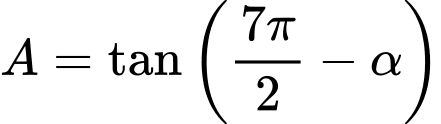 .
. A, 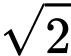 .
.
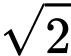 .
.B, 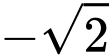 .
.
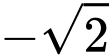 .
.C, 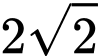 .
.
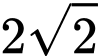 .
. D, 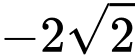 .
.
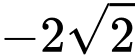 .
.
HD: 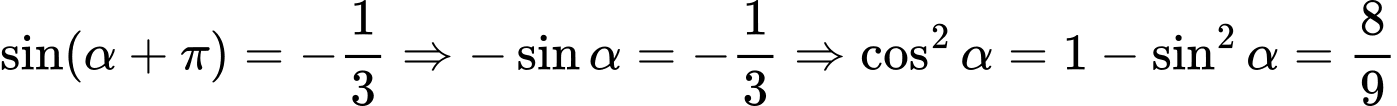
Do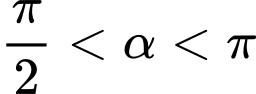 nên
nên  do đó
do đó 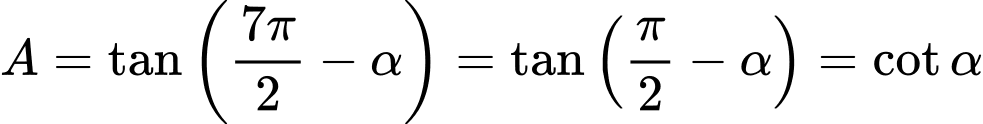
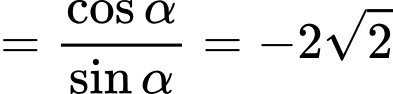
Chọn D. Đáp án: D
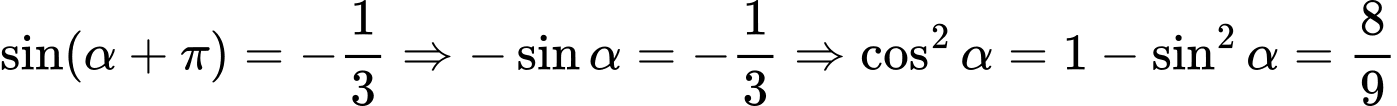
Do
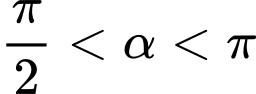 nên
nên  do đó
do đó 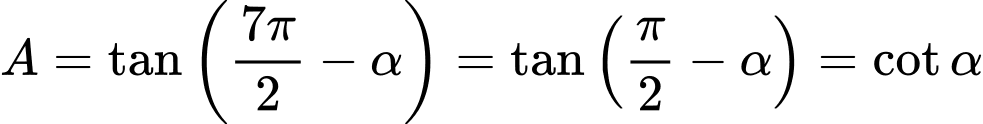
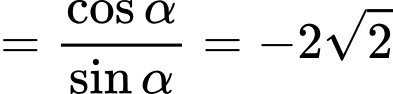
Chọn D. Đáp án: D
Câu 7 [269971]: Đơn giản biểu thức 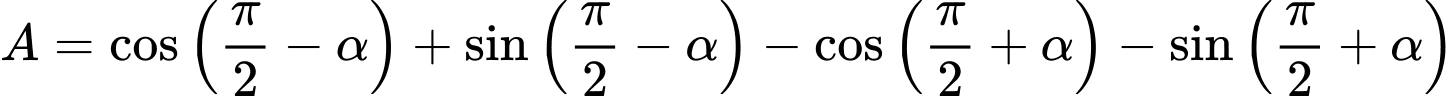 , ta có
, ta có
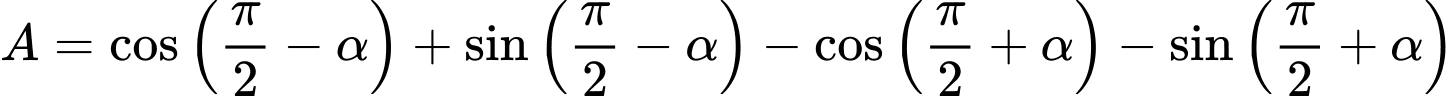 , ta có
, ta có A, 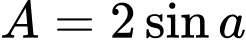 .
.
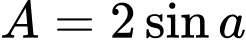 .
.B, 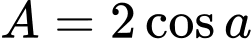 .
.
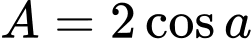 .
.C, 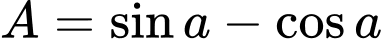 .
.
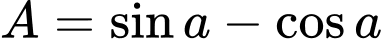 .
.D, 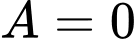 .
.
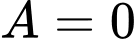 .
.
Chọn A.
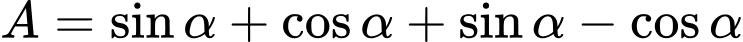
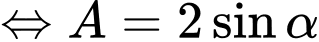 . Đáp án: A
. Đáp án: A
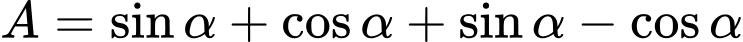
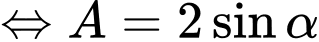 . Đáp án: A
. Đáp án: A
Câu 8 [269948]: Cho 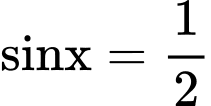 và cosx nhận giá trị âm, giá trị của biểu thức
và cosx nhận giá trị âm, giá trị của biểu thức 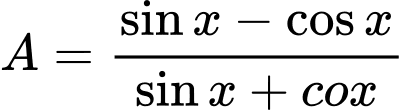 bằng
bằng
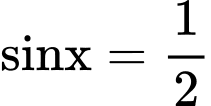 và cosx nhận giá trị âm, giá trị của biểu thức
và cosx nhận giá trị âm, giá trị của biểu thức 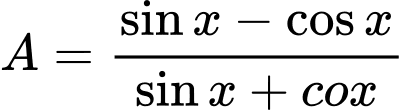 bằng
bằng A,  .
.
 .
.B, 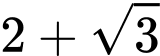 .
.
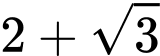 .
.C,  .
.
 .
.D,  .
.
 .
.
Chọn A
Vì cosx nhận giá trị âm.
Ta có: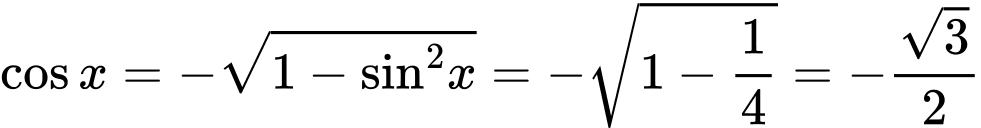
Suy ra: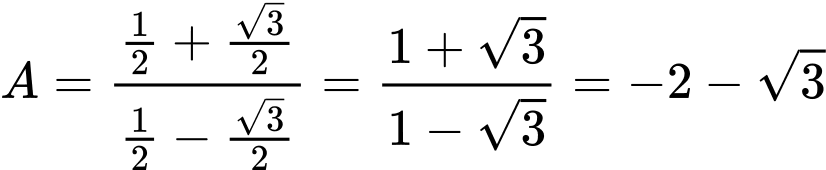 Đáp án: A
Đáp án: A
Vì cosx nhận giá trị âm.
Ta có:
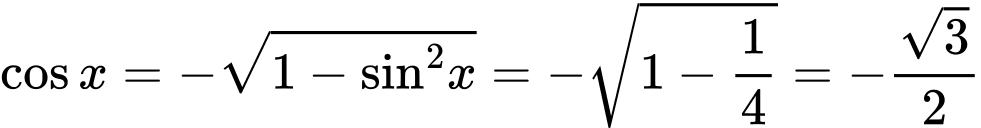
Suy ra:
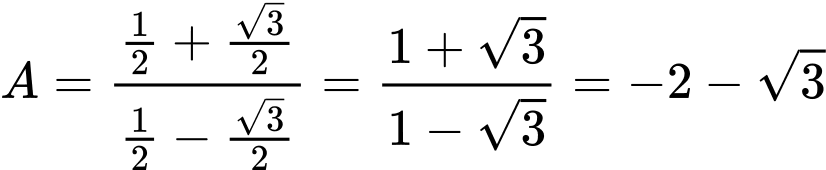 Đáp án: A
Đáp án: A
Câu 9 [269947]: Cho 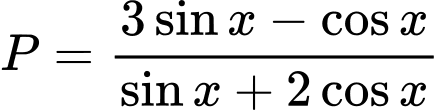 với
với 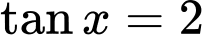 . Giá trị của
. Giá trị của 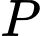 bằng
bằng
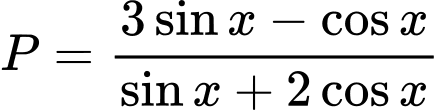 với
với 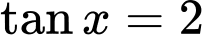 . Giá trị của
. Giá trị của 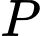 bằng
bằng A, 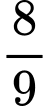 .
.
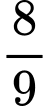 .
.B, 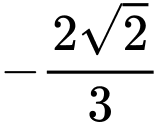 .
.
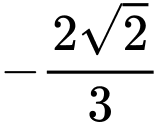 .
.C, 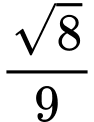 .
.
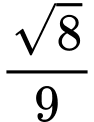 .
.D, 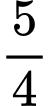 .
.
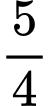 .
.
Chọn D
Ta có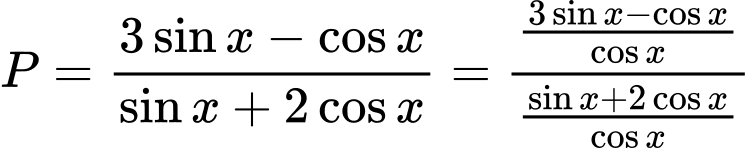
Suy ra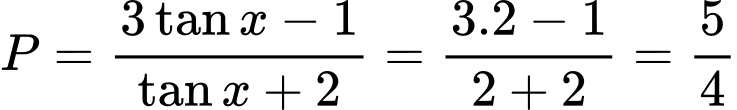 Đáp án: D
Đáp án: D
Ta có
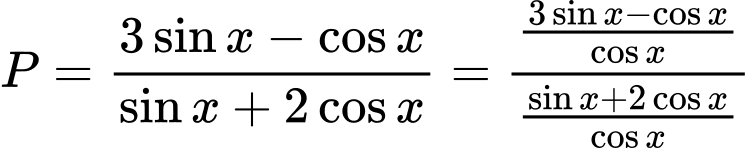
Suy ra
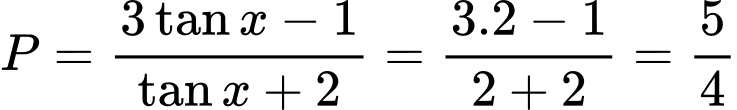 Đáp án: D
Đáp án: D
Câu 10 [269972]: Biểu thức 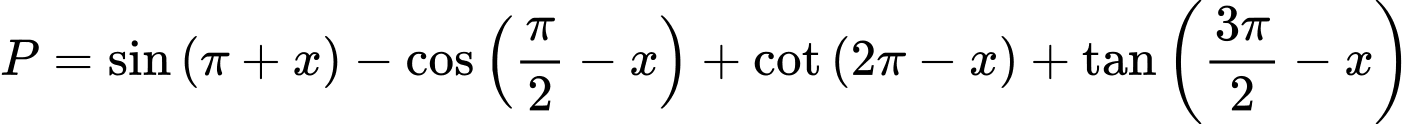 có biểu thức rút gọn là
có biểu thức rút gọn là
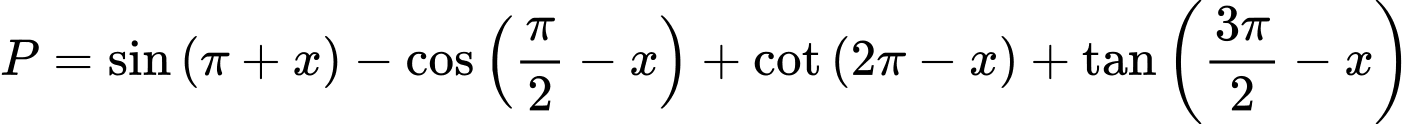 có biểu thức rút gọn là
có biểu thức rút gọn là A, 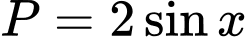 .
.
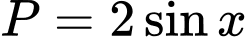 .
.B, 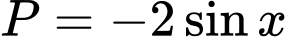 .
.
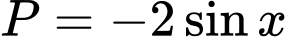 .
.C, 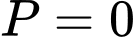 .
.
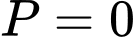 .
.D, 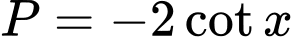 .
.
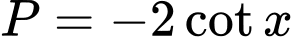 .
.
Chọn B

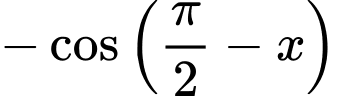
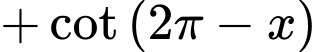
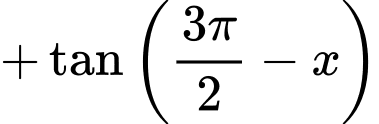
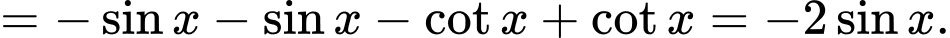 Đáp án: B
Đáp án: B

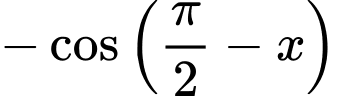
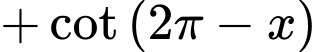
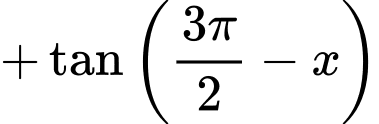
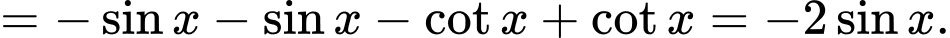 Đáp án: B
Đáp án: B
Câu 11 [269963]: Biểu thức rút gọn của A = 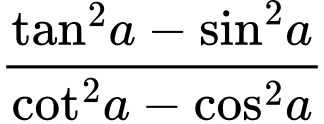 bằng
bằng
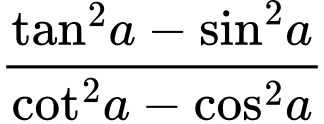 bằng
bằng A, 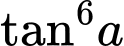 .
.
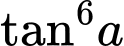 .
.B,  .
.
 .
.C, 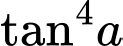 .
.
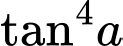 .
.D, 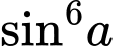 .
.
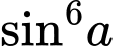 .
.
Chọn A
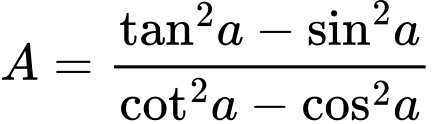
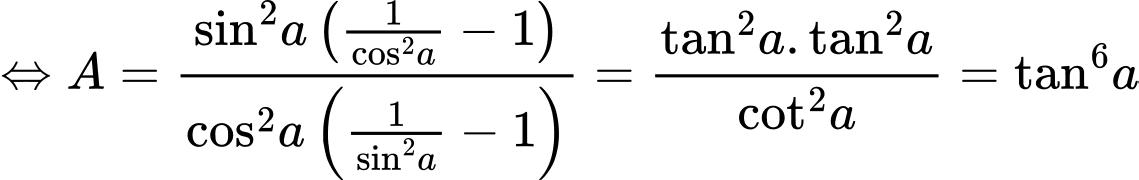 . Đáp án: A
. Đáp án: A
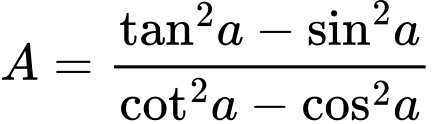
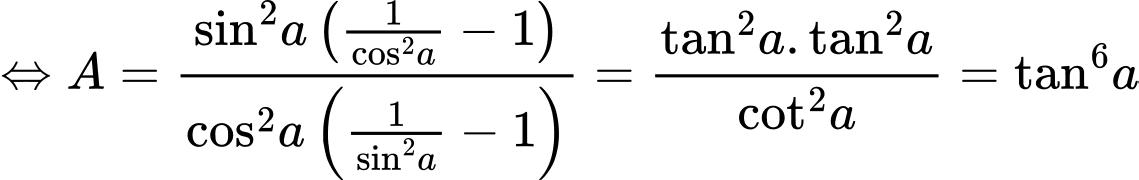 . Đáp án: A
. Đáp án: A
Câu 12 [269970]: Đơn giản biểu thức  ta có
ta có
 ta có
ta có A, 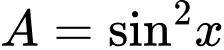 .
.
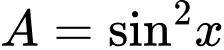 .
.B, 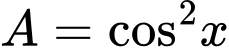 .
.
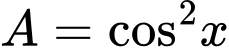 .
.C, 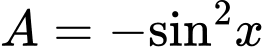 .
.
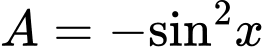 .
.D, 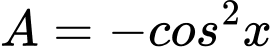 .
.
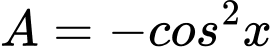 .
.
Chọn A

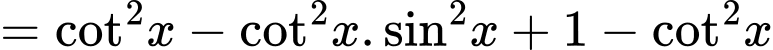
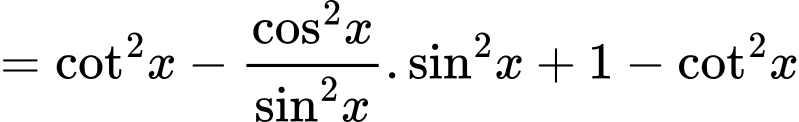
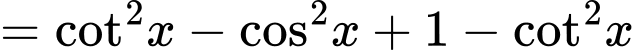
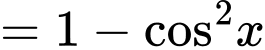
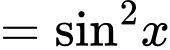 . Đáp án: A
. Đáp án: A

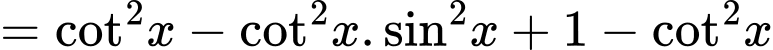
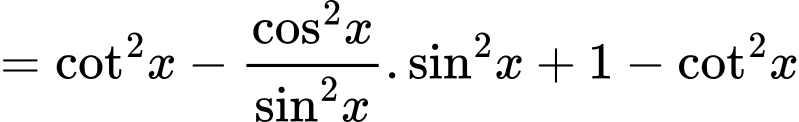
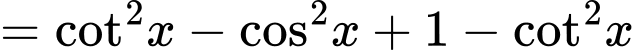
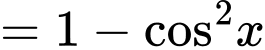
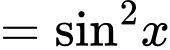 . Đáp án: A
. Đáp án: A
Câu 13 [397399]: Một cái đồng hồ treo tường có đường kính bằng 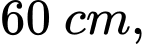 ta xem vành ngoài chiếc đồng hồ là một đường tròn với các điểm
ta xem vành ngoài chiếc đồng hồ là một đường tròn với các điểm 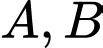 lần lượt tương ứng với vị trí các số
lần lượt tương ứng với vị trí các số 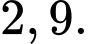
Tính độ dài cung nhỏ (kết quả tính theo đơn vị centimét và làm tròn đến hàng phần chục).
(kết quả tính theo đơn vị centimét và làm tròn đến hàng phần chục).

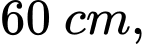 ta xem vành ngoài chiếc đồng hồ là một đường tròn với các điểm
ta xem vành ngoài chiếc đồng hồ là một đường tròn với các điểm 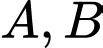 lần lượt tương ứng với vị trí các số
lần lượt tương ứng với vị trí các số 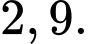
Tính độ dài cung nhỏ
 (kết quả tính theo đơn vị centimét và làm tròn đến hàng phần chục).
(kết quả tính theo đơn vị centimét và làm tròn đến hàng phần chục). 
Bán kính đường tròn là 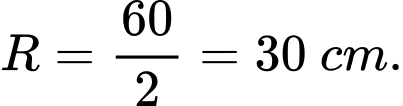
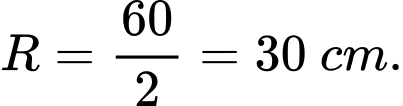
Ta có: 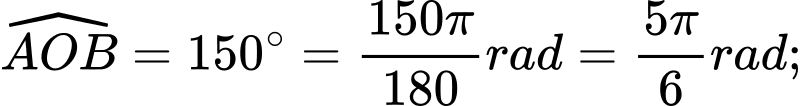 suy ra độ dài cung nhỏ
suy ra độ dài cung nhỏ  là
là 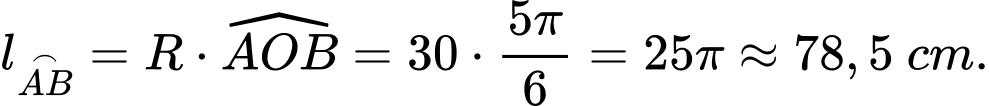
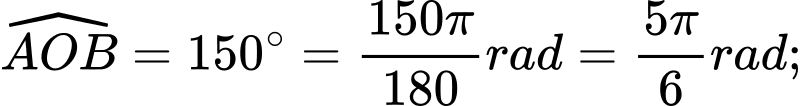 suy ra độ dài cung nhỏ
suy ra độ dài cung nhỏ  là
là 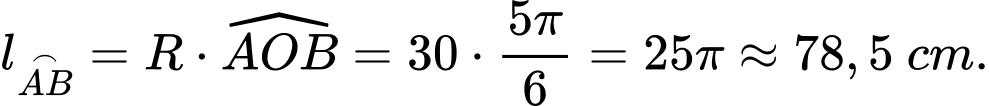
Câu 14 [397404]: Một bánh xe có đường kính kể cả lốp xe là  Nếu xe chạy với tốc độ
Nếu xe chạy với tốc độ 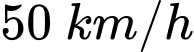 thì trong một giây bánh xe quay được bao nhiêu vòng? (Kết quả được làm tròn đến hàng phần trăm).
thì trong một giây bánh xe quay được bao nhiêu vòng? (Kết quả được làm tròn đến hàng phần trăm).
 Nếu xe chạy với tốc độ
Nếu xe chạy với tốc độ 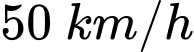 thì trong một giây bánh xe quay được bao nhiêu vòng? (Kết quả được làm tròn đến hàng phần trăm).
thì trong một giây bánh xe quay được bao nhiêu vòng? (Kết quả được làm tròn đến hàng phần trăm).
Tốc độ xe là: 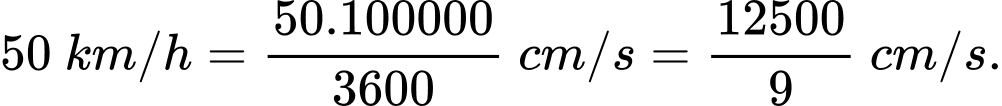
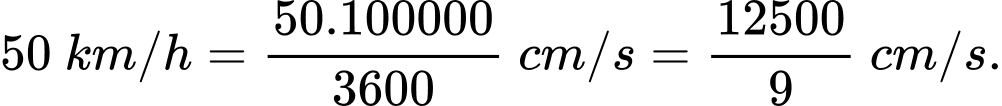
Mỗi vòng bánh  e có chiều dài:
e có chiều dài: 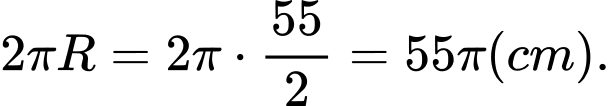
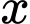 e có chiều dài:
e có chiều dài: 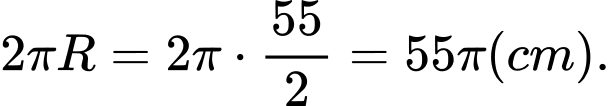
Vậy mỗi giây thì bánh xe lăn được số vòng là 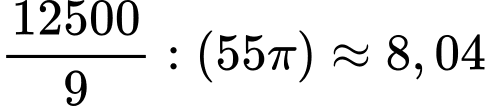 (vòng).
(vòng).
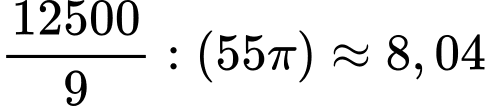 (vòng).
(vòng).
Câu 15 [270928]: Hải lí là một đơn vị chiều dài hàng hải, được tính bằng độ dài một cung chắn một góc 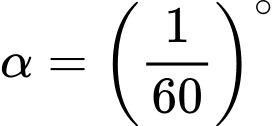 của đường kinh tuyến (Hình 17). Đổi số đo
của đường kinh tuyến (Hình 17). Đổi số đo 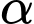 sang radian và cho biết 1 hải lí bằng khoảng bao nhiêu kilômét, biết bán kính trung bình của Trái Đất là
sang radian và cho biết 1 hải lí bằng khoảng bao nhiêu kilômét, biết bán kính trung bình của Trái Đất là 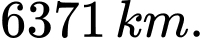 Làm tròn kết quả đến hàng phần trăm.
Làm tròn kết quả đến hàng phần trăm. 
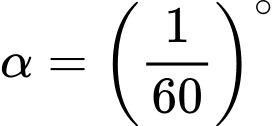 của đường kinh tuyến (Hình 17). Đổi số đo
của đường kinh tuyến (Hình 17). Đổi số đo 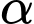 sang radian và cho biết 1 hải lí bằng khoảng bao nhiêu kilômét, biết bán kính trung bình của Trái Đất là
sang radian và cho biết 1 hải lí bằng khoảng bao nhiêu kilômét, biết bán kính trung bình của Trái Đất là 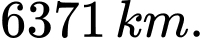 Làm tròn kết quả đến hàng phần trăm.
Làm tròn kết quả đến hàng phần trăm. 
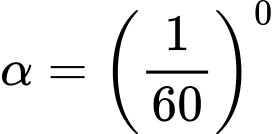
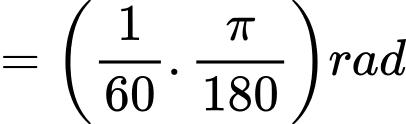
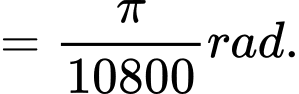
Độ dài một cung chắn một góc
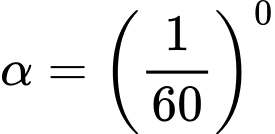 của đường kinh tuyến là:
của đường kinh tuyến là: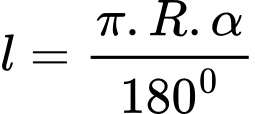
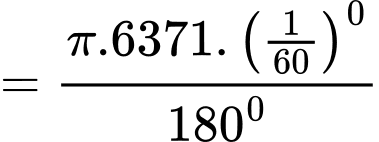
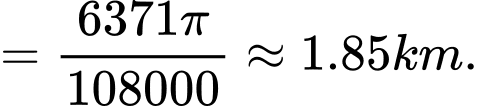
Vậy 1 hải lí bằng 1,85 km.
Câu 16 [159539]: Kim phút của đồng hồ dài gấp 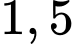 lần kim giờ. Từ lúc
lần kim giờ. Từ lúc 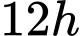 hai kim gặp nhau thì sau khoảng thời gian ngắn nhất là
hai kim gặp nhau thì sau khoảng thời gian ngắn nhất là 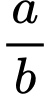 (giờ) (với
(giờ) (với 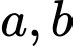 là số nguyên dương và phân số
là số nguyên dương và phân số 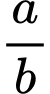 tối giản) hai kim lại gặp nhau lần tiếp theo. Tính
tối giản) hai kim lại gặp nhau lần tiếp theo. Tính 
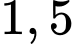 lần kim giờ. Từ lúc
lần kim giờ. Từ lúc 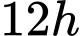 hai kim gặp nhau thì sau khoảng thời gian ngắn nhất là
hai kim gặp nhau thì sau khoảng thời gian ngắn nhất là 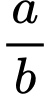 (giờ) (với
(giờ) (với 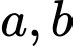 là số nguyên dương và phân số
là số nguyên dương và phân số 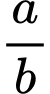 tối giản) hai kim lại gặp nhau lần tiếp theo. Tính
tối giản) hai kim lại gặp nhau lần tiếp theo. Tính 
Tốc độ góc của kim phút là 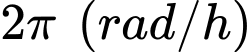
Tốc độ góc của kim giờ là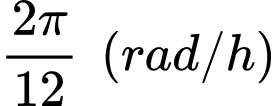
Sau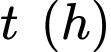 kim phút quét một góc
kim phút quét một góc 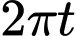 và kim giờ quét một góc
và kim giờ quét một góc 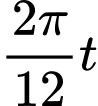
Để hai kim gặp lại nhau thì kim phút quét một góc hơn kim giờ đúng một vòng
Suy ra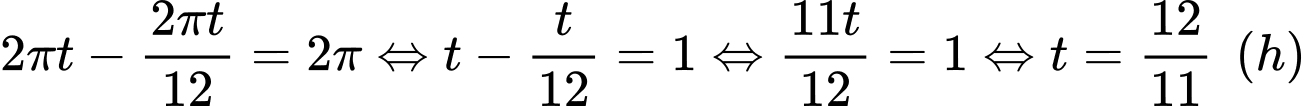
Do đó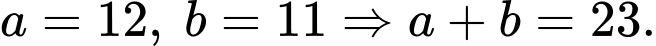
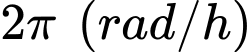
Tốc độ góc của kim giờ là
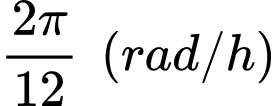
Sau
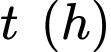 kim phút quét một góc
kim phút quét một góc 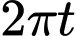 và kim giờ quét một góc
và kim giờ quét một góc 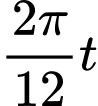
Để hai kim gặp lại nhau thì kim phút quét một góc hơn kim giờ đúng một vòng

Suy ra
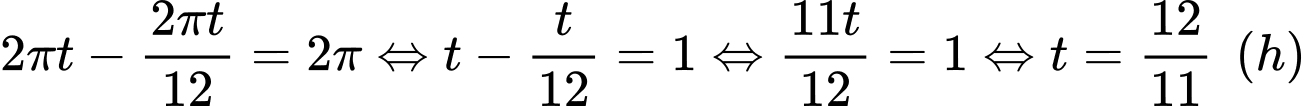
Do đó
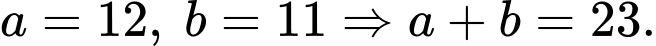
Câu 17 [518834]: Cho 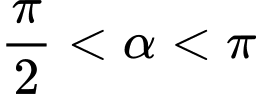 và
và 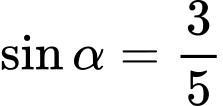 . Tính
. Tính 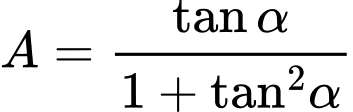 .
.
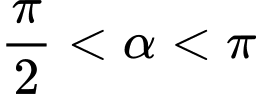 và
và 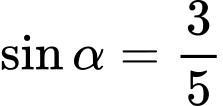 . Tính
. Tính 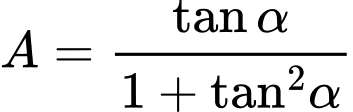 .
.
Ta có: 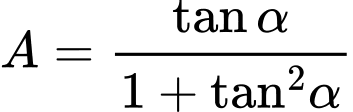
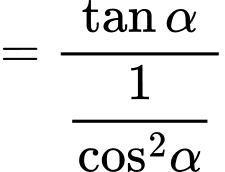
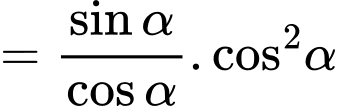
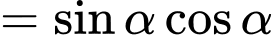
Do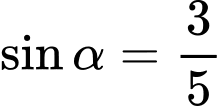
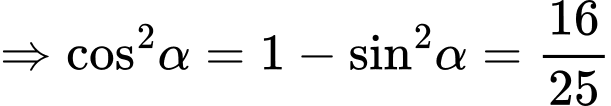
Với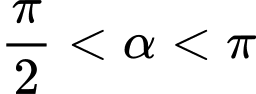 ta suy ra
ta suy ra 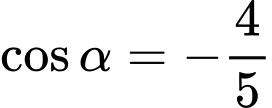
Do đó: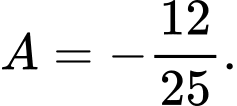
Đáp án: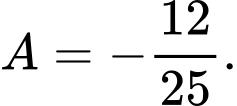 Đáp án: A
Đáp án: A
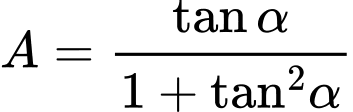
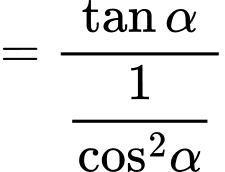
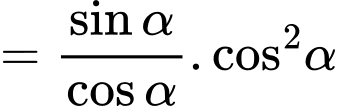
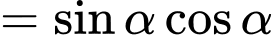
Do
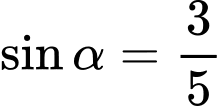
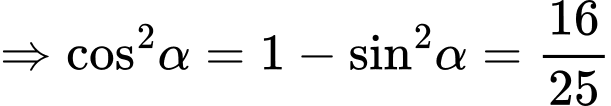
Với
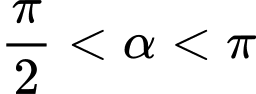 ta suy ra
ta suy ra 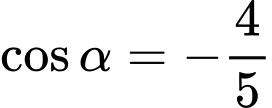
Do đó:
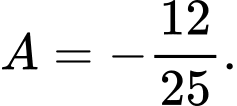
Đáp án:
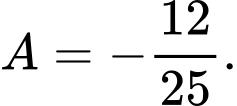 Đáp án: A
Đáp án: A
Câu 18 [269951]: Cho 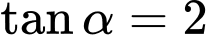 . Tính giá trị biểu thức
. Tính giá trị biểu thức 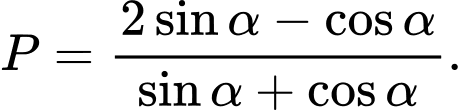
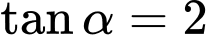 . Tính giá trị biểu thức
. Tính giá trị biểu thức 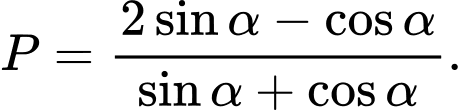
Ta có: 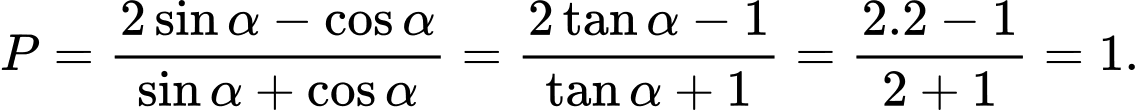 Đáp án: B
Đáp án: B
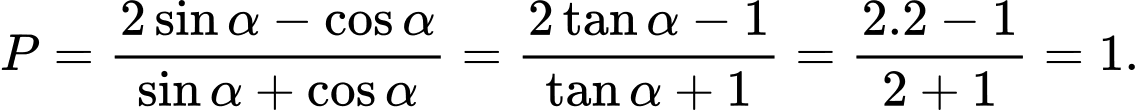 Đáp án: B
Đáp án: B
Câu 19 [272554]: Thanh  quay ngược chiều kim đồng hồ quanh trục
quay ngược chiều kim đồng hồ quanh trục  của nó trên một mặt phẳng thẳng đứng và in bóng vuông góc xuống mặt đất như Hình 12. Vị trí ban đầu của thanh là
của nó trên một mặt phẳng thẳng đứng và in bóng vuông góc xuống mặt đất như Hình 12. Vị trí ban đầu của thanh là  . Hỏi độ dài bóng
. Hỏi độ dài bóng  của
của 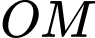 khi thanh quay được
khi thanh quay được 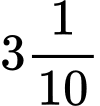 vòng là bao nhiêu, biết độ dài thanh
vòng là bao nhiêu, biết độ dài thanh 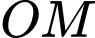 là
là 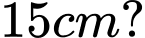 Kết quả làm tròn đến hàng phần mười.
Kết quả làm tròn đến hàng phần mười.
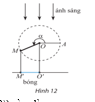
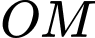 quay ngược chiều kim đồng hồ quanh trục
quay ngược chiều kim đồng hồ quanh trục  của nó trên một mặt phẳng thẳng đứng và in bóng vuông góc xuống mặt đất như Hình 12. Vị trí ban đầu của thanh là
của nó trên một mặt phẳng thẳng đứng và in bóng vuông góc xuống mặt đất như Hình 12. Vị trí ban đầu của thanh là 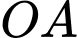 . Hỏi độ dài bóng
. Hỏi độ dài bóng 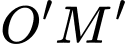 của
của 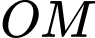 khi thanh quay được
khi thanh quay được 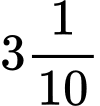 vòng là bao nhiêu, biết độ dài thanh
vòng là bao nhiêu, biết độ dài thanh 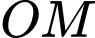 là
là 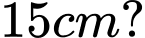 Kết quả làm tròn đến hàng phần mười.
Kết quả làm tròn đến hàng phần mười.
Độ dài bóng 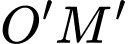 của
của 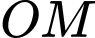 khi thanh quay được
khi thanh quay được 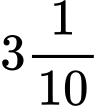 vòng là:
vòng là:
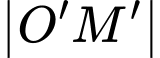
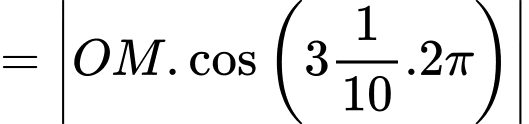
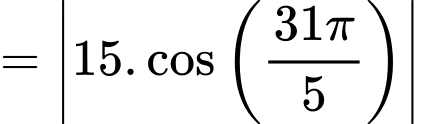
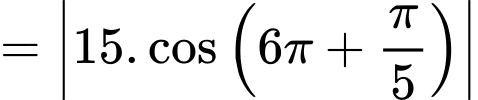
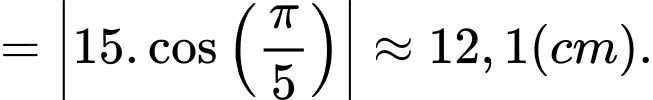
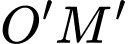 của
của 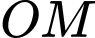 khi thanh quay được
khi thanh quay được 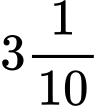 vòng là:
vòng là: 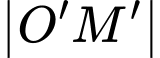
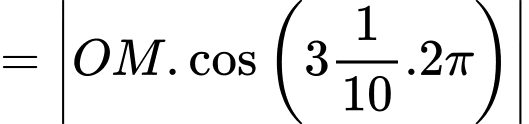
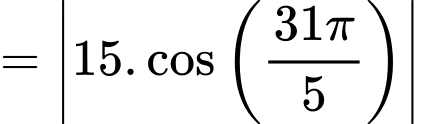
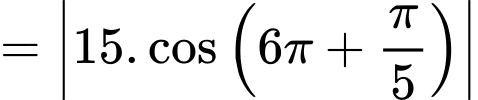
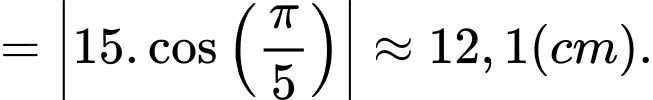
Câu 20 [397647]: Một chiếc đu quay có bán kính 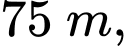 tâm của vòng quay ở độ cao
tâm của vòng quay ở độ cao 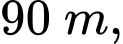 thời gian thực hiện mỗi vòng quay của đu quay là 30 phút. Nếu một người vào cabin tại vị trí thấp nhất của vòng quay, thì sau 20 phút quay, người đó ở độ cao bao nhiêu mét?
thời gian thực hiện mỗi vòng quay của đu quay là 30 phút. Nếu một người vào cabin tại vị trí thấp nhất của vòng quay, thì sau 20 phút quay, người đó ở độ cao bao nhiêu mét?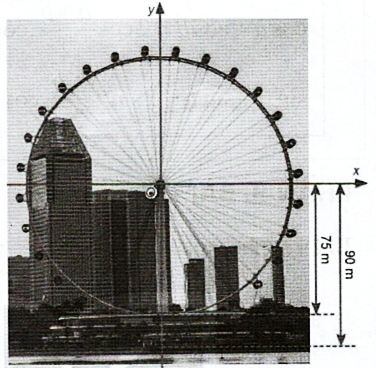
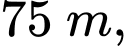 tâm của vòng quay ở độ cao
tâm của vòng quay ở độ cao 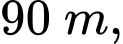 thời gian thực hiện mỗi vòng quay của đu quay là 30 phút. Nếu một người vào cabin tại vị trí thấp nhất của vòng quay, thì sau 20 phút quay, người đó ở độ cao bao nhiêu mét?
thời gian thực hiện mỗi vòng quay của đu quay là 30 phút. Nếu một người vào cabin tại vị trí thấp nhất của vòng quay, thì sau 20 phút quay, người đó ở độ cao bao nhiêu mét?
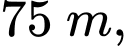 tâm của vòng quay ở độ cao
tâm của vòng quay ở độ cao 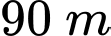 vào hệ trục tọa độ
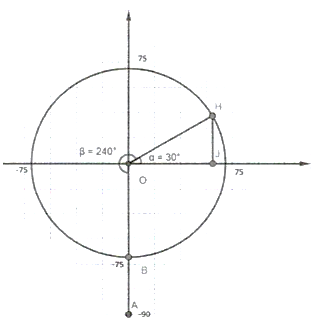
vào hệ trục tọa độ 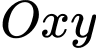 ta được hình bên:
ta được hình bên: Sau 20 phút quay cabin đi được một góc là 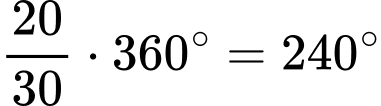 tức là đến vị trí điểm
tức là đến vị trí điểm 
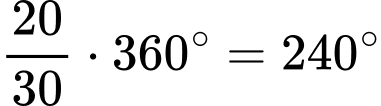 tức là đến vị trí điểm
tức là đến vị trí điểm 
Khi đó góc 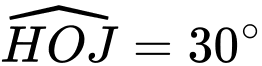 và
và 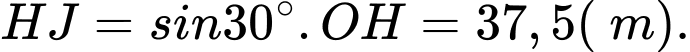
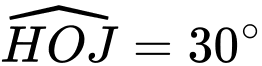 và
và 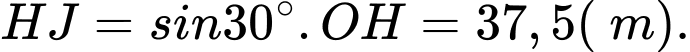
Vậy sau 20 phút quay, người đó ở độ cao 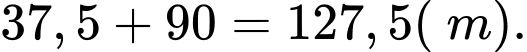
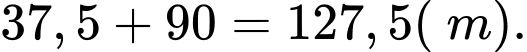
Câu 21 [397889]: Từ một vị trí  người ta buộc hai sợi cáp
người ta buộc hai sợi cáp  và
và 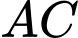 đến một cái trụ cao
đến một cái trụ cao 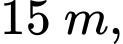 được dựng vuông góc với mặt đất, chân trụ ở vị trí
được dựng vuông góc với mặt đất, chân trụ ở vị trí  Biết
Biết  và
và 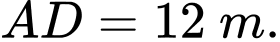 Tìm góc nhọn
Tìm góc nhọn 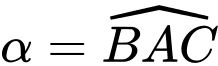 tạo bởi hai sợi dây cáp đó, đồng thời tính gần đúng
tạo bởi hai sợi dây cáp đó, đồng thời tính gần đúng 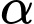 (làm tròn đến hàng phần chục, đơn vị độ).
(làm tròn đến hàng phần chục, đơn vị độ).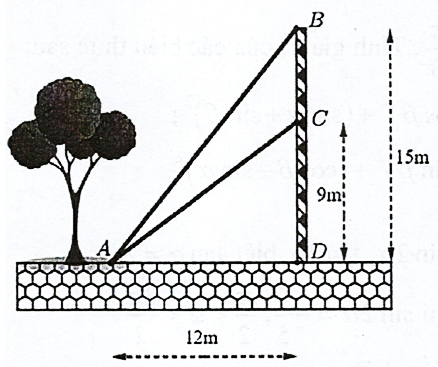
 người ta buộc hai sợi cáp
người ta buộc hai sợi cáp  và
và  đến một cái trụ cao
đến một cái trụ cao 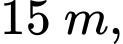 được dựng vuông góc với mặt đất, chân trụ ở vị trí
được dựng vuông góc với mặt đất, chân trụ ở vị trí  Biết
Biết  và
và 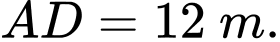 Tìm góc nhọn
Tìm góc nhọn 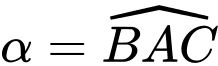 tạo bởi hai sợi dây cáp đó, đồng thời tính gần đúng
tạo bởi hai sợi dây cáp đó, đồng thời tính gần đúng 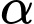 (làm tròn đến hàng phần chục, đơn vị độ).
(làm tròn đến hàng phần chục, đơn vị độ).
Ta có:
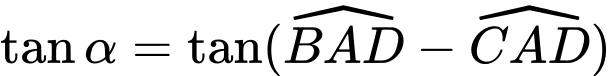
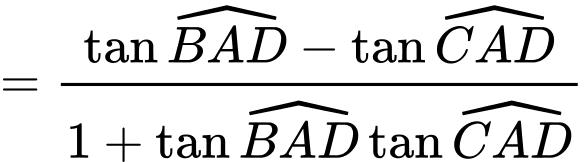
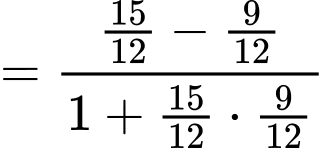
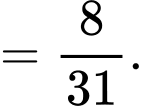
Vì vậy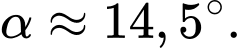
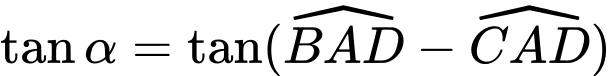
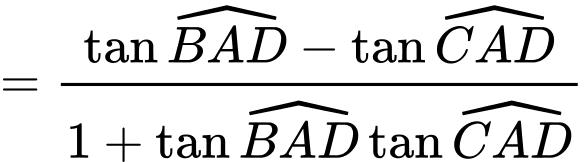
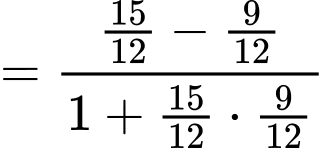
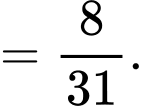
Vì vậy
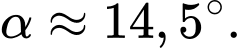
Câu 22 [581239]: Trên nóc một toà nhà có một cột ăng-ten cao 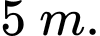 Từ vị trí quan sát
Từ vị trí quan sát 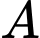 cao
cao 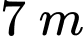 so với mặt đất, có thể nhìn thấy đỉnh
so với mặt đất, có thể nhìn thấy đỉnh 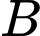 và chân
và chân  của cột ăng-ten dưới góc
của cột ăng-ten dưới góc 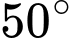 và
và 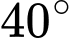 so với phương nằm ngang. Tính chiều cao của toà nhà. Làm tròn kết quả đến hàng phần chục.
so với phương nằm ngang. Tính chiều cao của toà nhà. Làm tròn kết quả đến hàng phần chục.
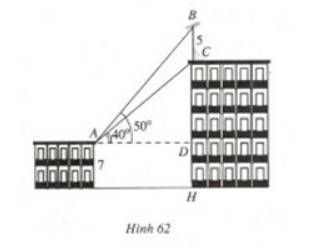
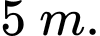 Từ vị trí quan sát
Từ vị trí quan sát 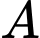 cao
cao 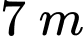 so với mặt đất, có thể nhìn thấy đỉnh
so với mặt đất, có thể nhìn thấy đỉnh 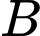 và chân
và chân  của cột ăng-ten dưới góc
của cột ăng-ten dưới góc 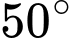 và
và 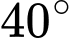 so với phương nằm ngang. Tính chiều cao của toà nhà. Làm tròn kết quả đến hàng phần chục.
so với phương nằm ngang. Tính chiều cao của toà nhà. Làm tròn kết quả đến hàng phần chục.
Đặt 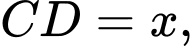 ta có:
ta có:
Xét tam giác vuông tại
vuông tại 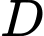 có:
có:
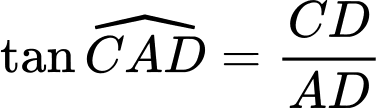
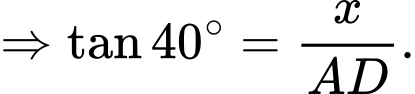
Xét tam giác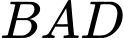 vuông tại
vuông tại 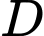 có:
có:
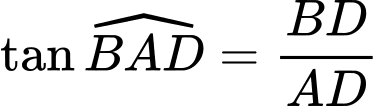
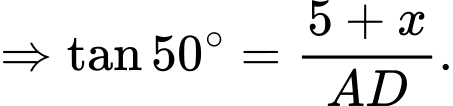
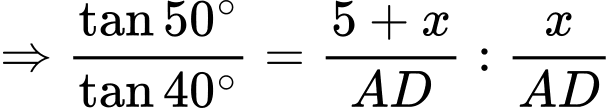
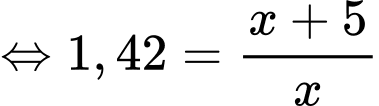
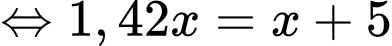
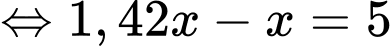
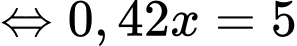
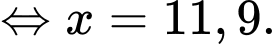 Vậy chiều cao toà nhà là CH và bằng 7+11,9=18,9.
Vậy chiều cao toà nhà là CH và bằng 7+11,9=18,9.
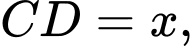 ta có:
ta có:Xét tam giác
 vuông tại
vuông tại  có:
có: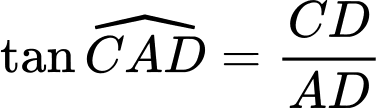
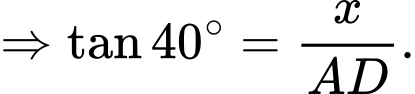
Xét tam giác
 vuông tại
vuông tại  có:
có: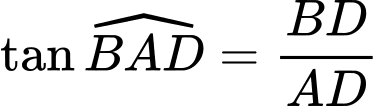
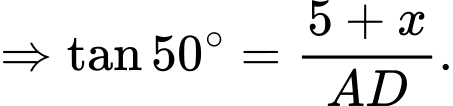
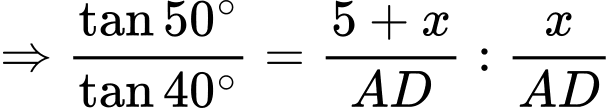
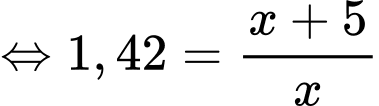
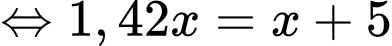
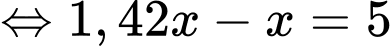
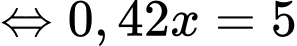
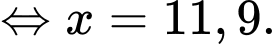 Vậy chiều cao toà nhà là CH và bằng 7+11,9=18,9.
Vậy chiều cao toà nhà là CH và bằng 7+11,9=18,9.