Đáp án Bài tập tự luyện số 2
Câu 1 [541067]: Cho hai góc 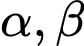 thoả mãn
thoả mãn 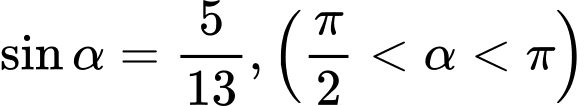 và
và 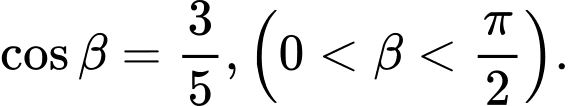 Tính giá trị đúng của
Tính giá trị đúng của 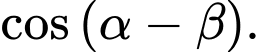
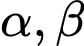 thoả mãn
thoả mãn 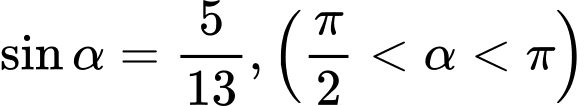 và
và 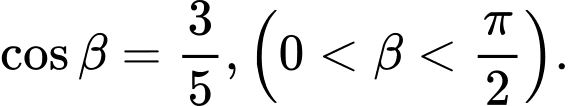 Tính giá trị đúng của
Tính giá trị đúng của 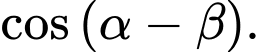
A, 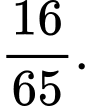
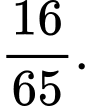
B, 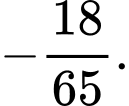
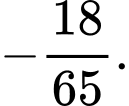
C, 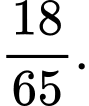
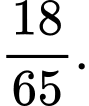
D, 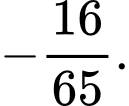
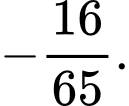
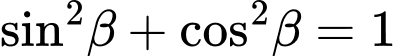

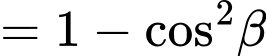
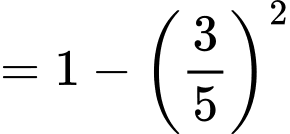
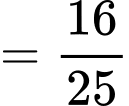
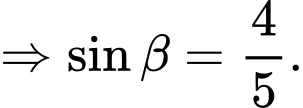
+)
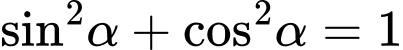
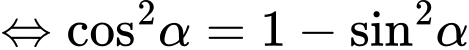
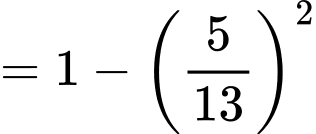
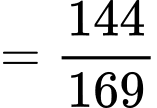
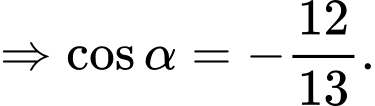
+)
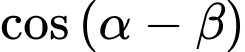
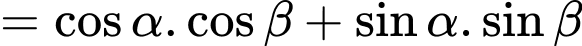
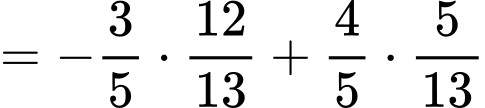
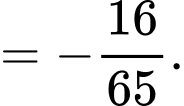
Chọn đáp án D. Đáp án: D
Câu 2 [541069]: Biểu thức 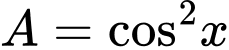
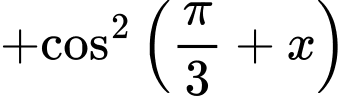
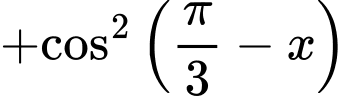 bằng
bằng
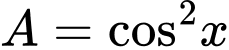
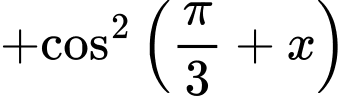
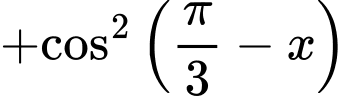 bằng
bằng A, 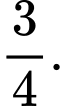
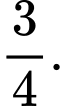
B, 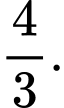
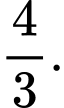
C, 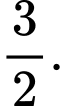
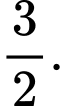
D, 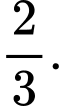
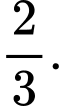
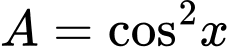
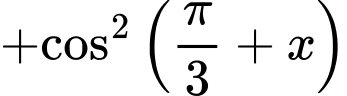
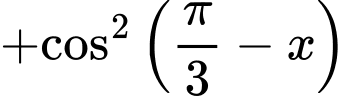

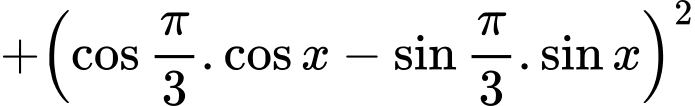
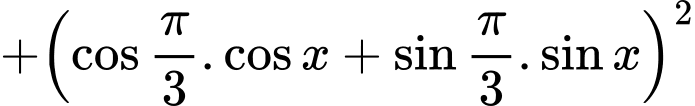
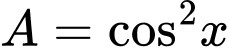
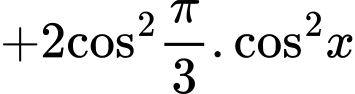
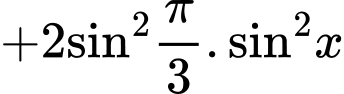

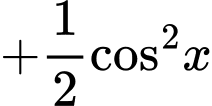
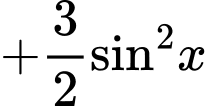
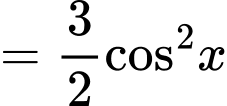
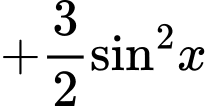
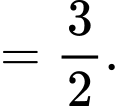
Chọn đáp án C. Đáp án: C
Câu 3 [541070]: Cho 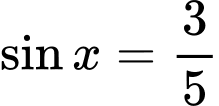 với
với 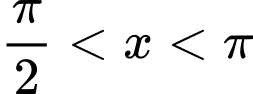 khi đó
khi đó 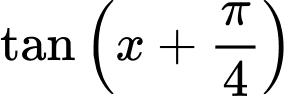 bằng
bằng
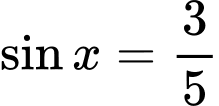 với
với 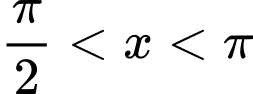 khi đó
khi đó 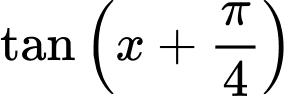 bằng
bằng A, 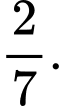
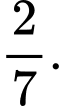
B, 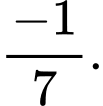
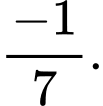
C, 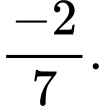
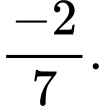
D, 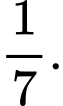
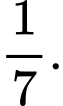
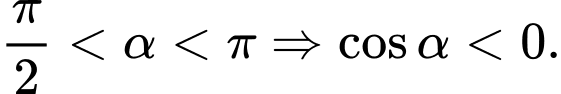
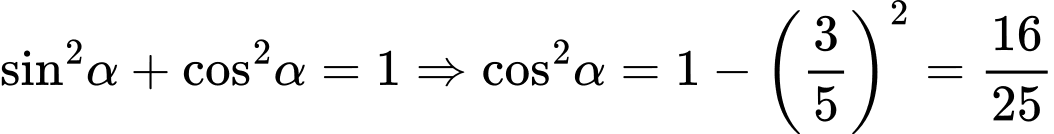
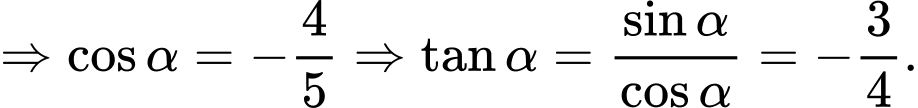
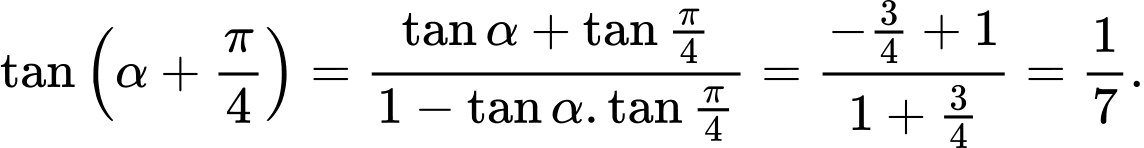
Chọn đáp án D.
Câu 4 [541071]: Cho hai góc nhọn 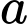 và
và 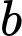 với
với 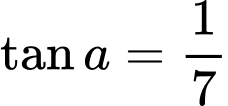 và
và 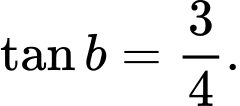 Tính
Tính 
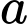 và
và 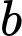 với
với 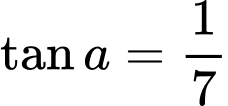 và
và 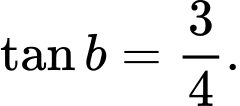 Tính
Tính 
A, 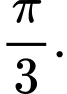
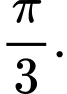
B, 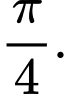
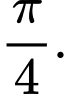
C, 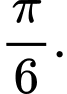
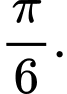
D, 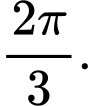
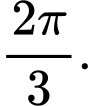
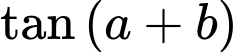
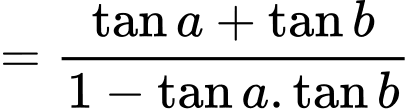
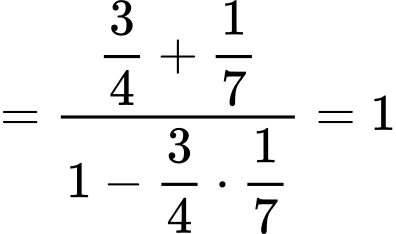
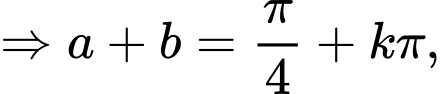 với
với 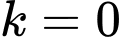
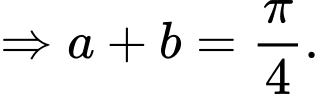
Chọn đáp án B. Đáp án: B
Câu 5 [541072]: Cho 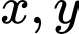 là các góc nhọn,
là các góc nhọn, 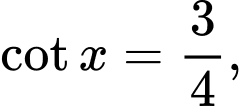
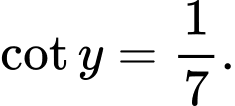 Tổng
Tổng  bằng
bằng
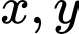 là các góc nhọn,
là các góc nhọn, 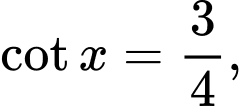
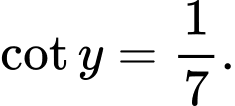 Tổng
Tổng  bằng
bằng A, 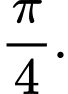
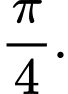
B, 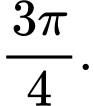
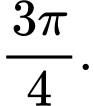
C, 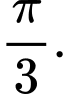
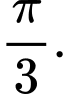
D, 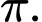
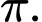
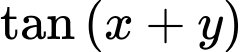
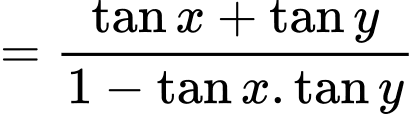
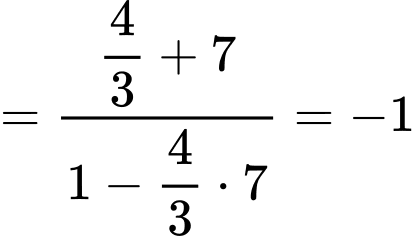
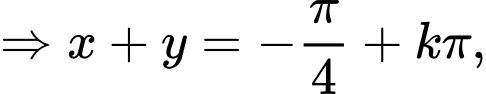 với
với 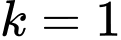
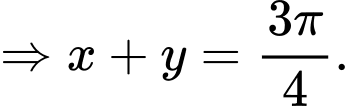
Chọn đáp án B. Đáp án: B
Câu 6 [519413]: Cho 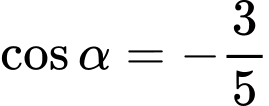 với
với 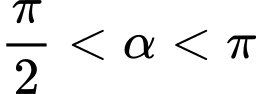 . Tính giá trị
. Tính giá trị 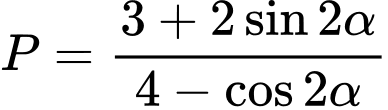 .
.
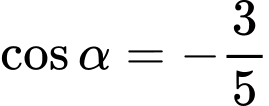 với
với 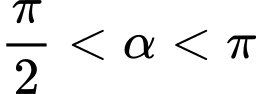 . Tính giá trị
. Tính giá trị 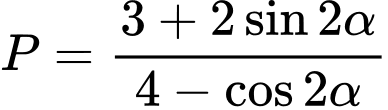 .
. A, 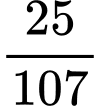 .
.
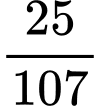 .
. B, 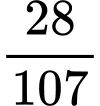 .
.
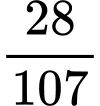 .
.C, 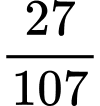 .
.
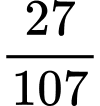 .
.D, 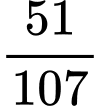 .
.
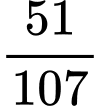 .
.
Ta có:
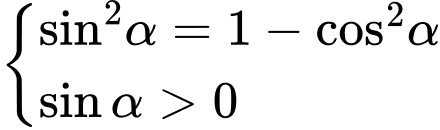
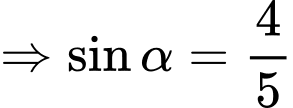
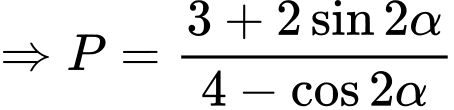
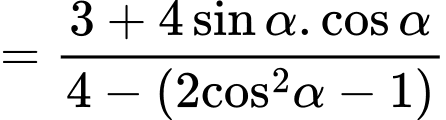
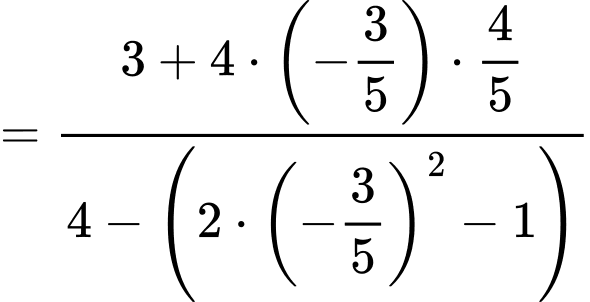
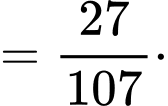
Chọn đáp án C.
Đáp án: C
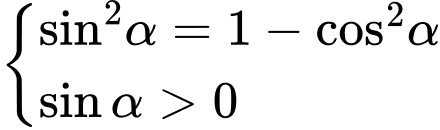
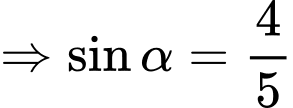
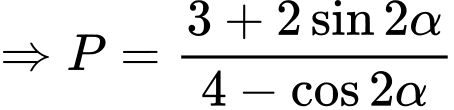
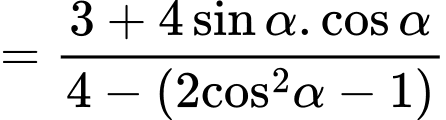
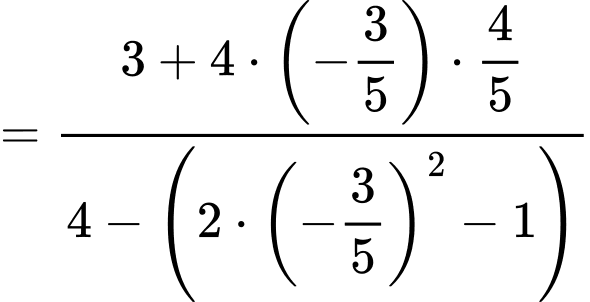
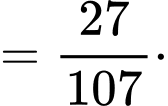
Chọn đáp án C.
Đáp án: C
Câu 7 [519417]: Tính giá trị của biểu thức 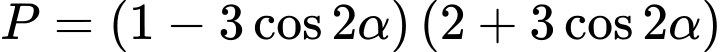 biết
biết 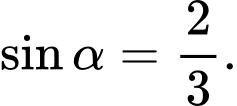
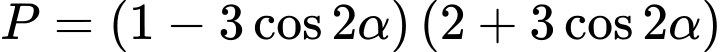 biết
biết 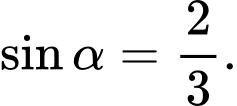
A, 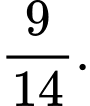
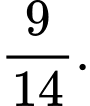
B, 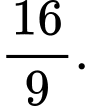
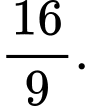
C, 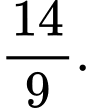
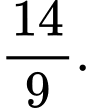
D, 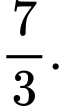
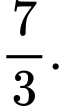
Ta có 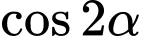
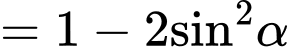
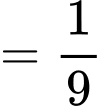
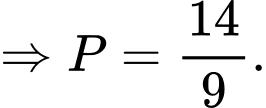
Chọn C. Đáp án: C
Câu 8 [519414]: Cho 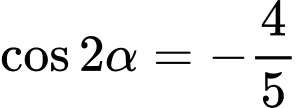 với
với 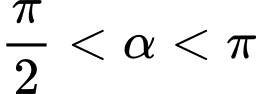 . Tính giá trị
. Tính giá trị 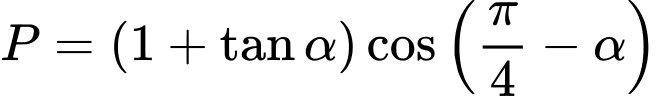 .
.
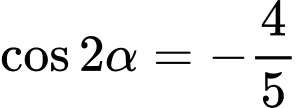 với
với 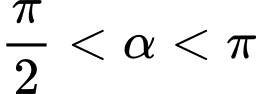 . Tính giá trị
. Tính giá trị 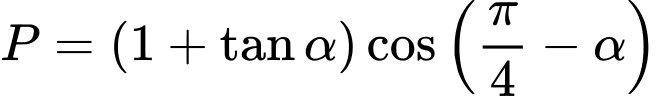 .
. A, 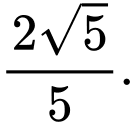
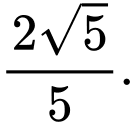
B, 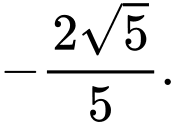
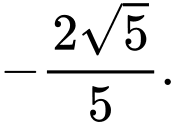
C, 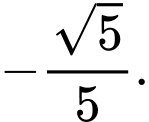
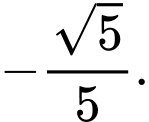
D, 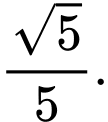
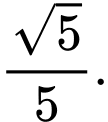
Ta có 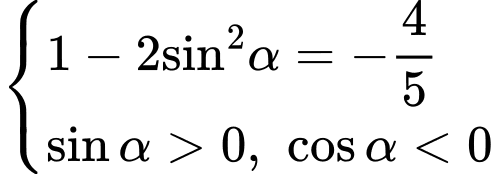
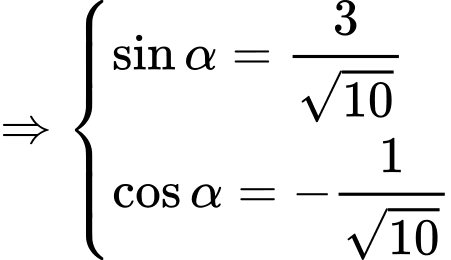
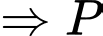
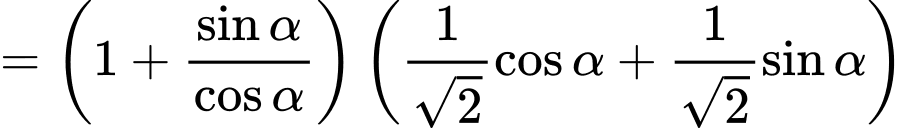
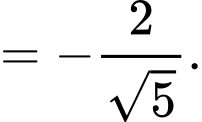
Chọn B. Đáp án: B
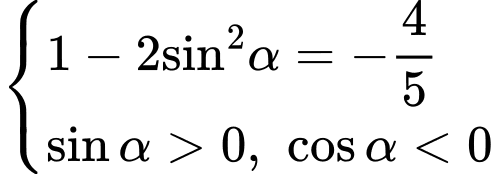
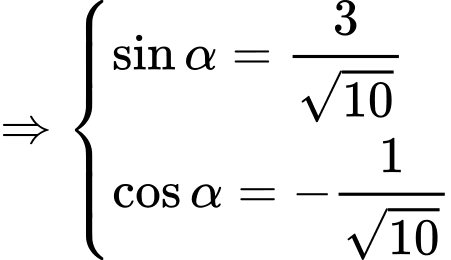
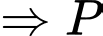
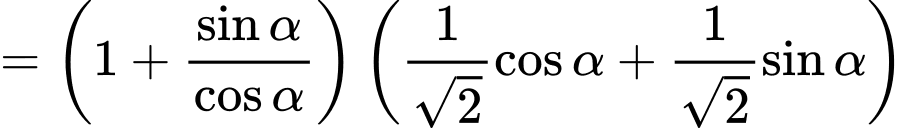
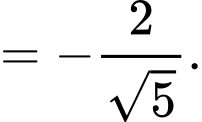
Chọn B. Đáp án: B
Câu 9 [519420]: Cho 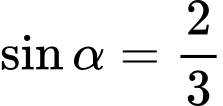 với
với 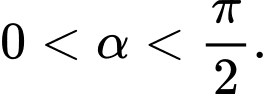 Tính giá trị
Tính giá trị 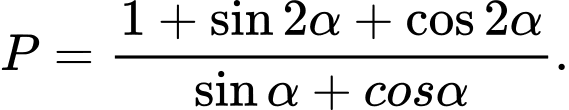
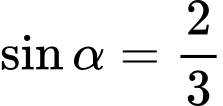 với
với 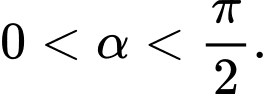 Tính giá trị
Tính giá trị 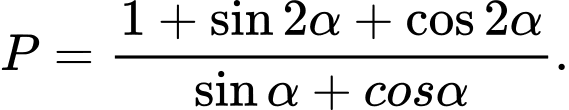
A, 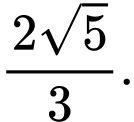
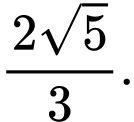
B, 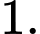
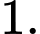
C, 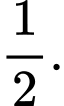
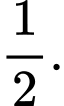
D, 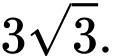
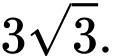
Ta có 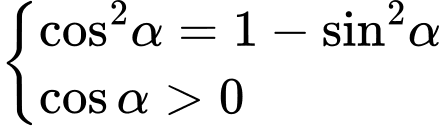
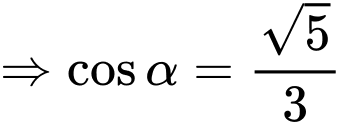
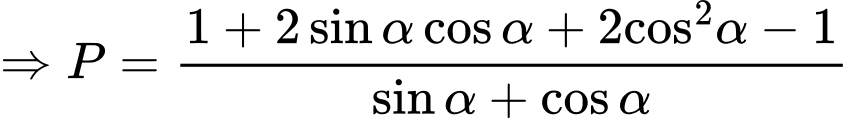
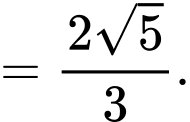
Chọn A. Đáp án: A
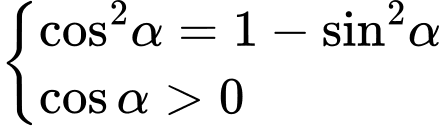
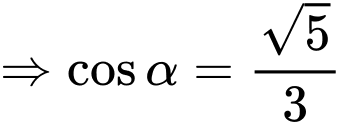
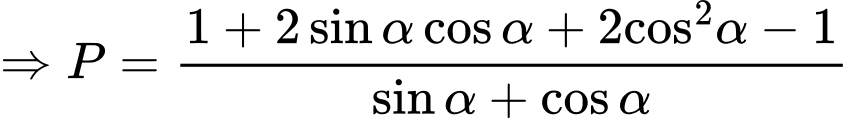
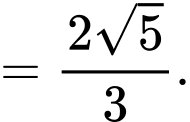
Chọn A. Đáp án: A
Câu 10 [270423]: Rút gọn biểu thức 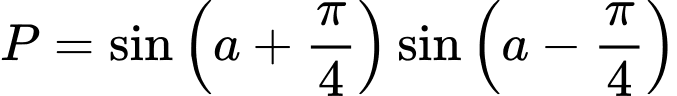 .
.
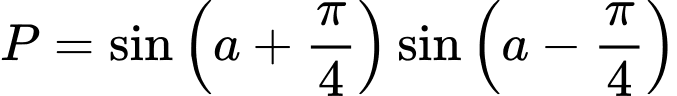 .
. A, 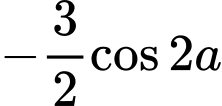 .
.
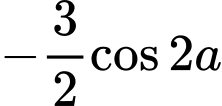 .
.B,  .
.
 .
.C, 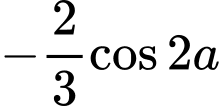 .
.
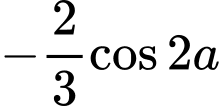 .
.D, 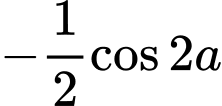 .
.
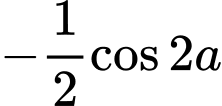 .
.
Chọn D
Ta có:
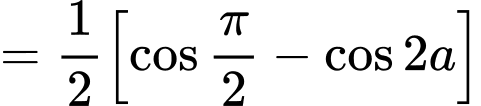
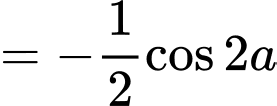 . Đáp án: D
. Đáp án: D
Ta có:

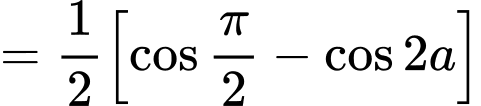
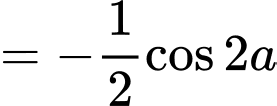 . Đáp án: D
. Đáp án: D
Câu 11 [270417]: Cho số thực 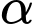 thỏa mãn
thỏa mãn 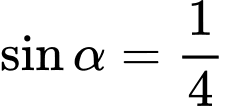 . Tính
. Tính 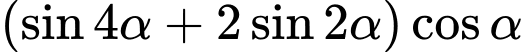 .
.
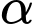 thỏa mãn
thỏa mãn 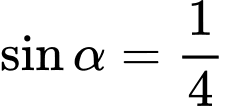 . Tính
. Tính 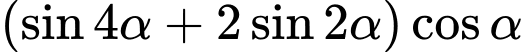 .
. A, 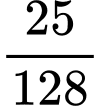 .
.
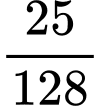 .
.B, 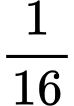 .
.
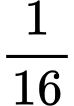 .
.C, 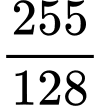 .
.
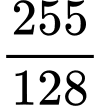 .
.D, 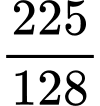 .
.
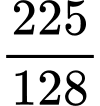 .
.
Ta có 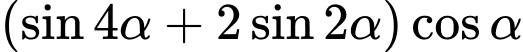
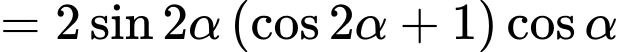
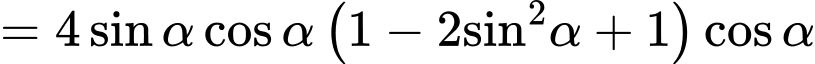
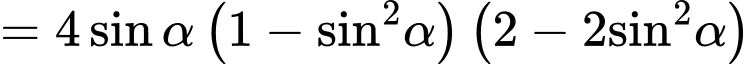
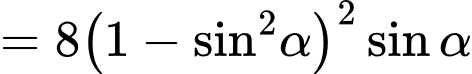
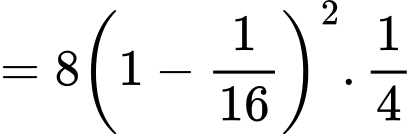
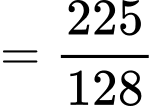 . Đáp án: C
. Đáp án: C
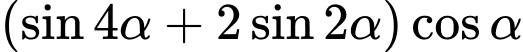
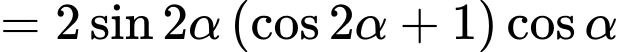
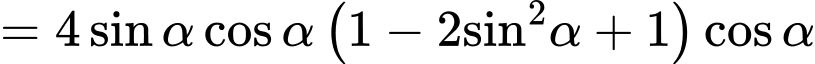
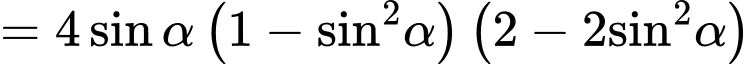
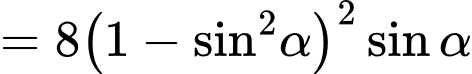
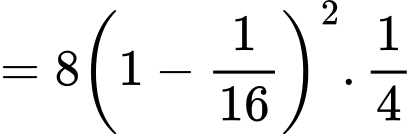
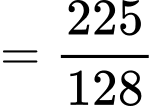 . Đáp án: C
. Đáp án: C
Câu 12 [270442]: Cho 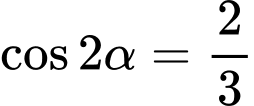 . Tính giá trị của biểu thức
. Tính giá trị của biểu thức 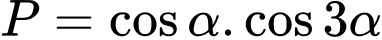 .
.
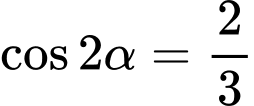 . Tính giá trị của biểu thức
. Tính giá trị của biểu thức 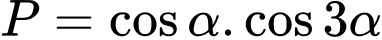 .
. A, 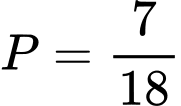 .
.
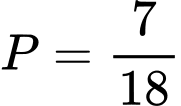 .
.B, 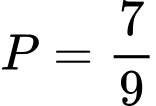 .
.
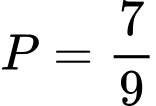 .
.C, 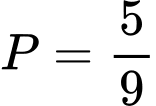 .
.
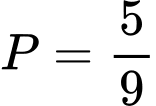 .
.D, 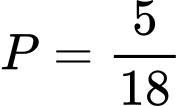 .
.
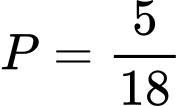 .
.
Chọn D
Ta có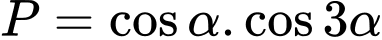
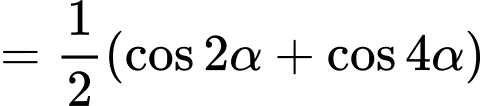
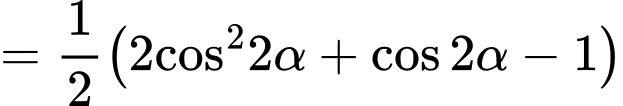
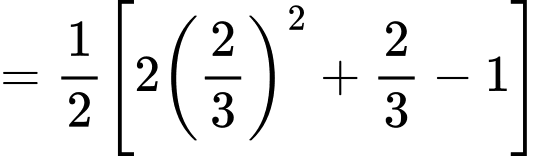
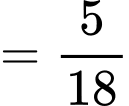 . Đáp án: D
. Đáp án: D
Ta có
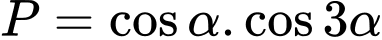
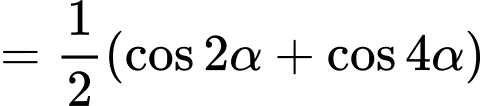
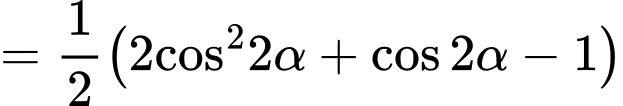
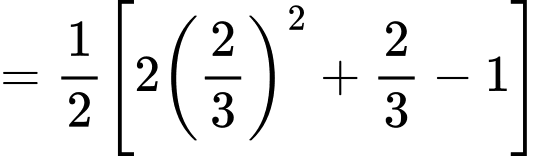
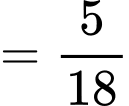 . Đáp án: D
. Đáp án: D
Câu 13 [270416]: Cho 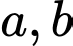 là hai góc nhọn. Biết
là hai góc nhọn. Biết 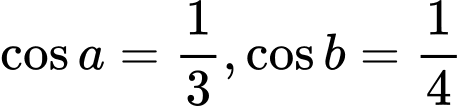 . Giá trị của biểu thức
. Giá trị của biểu thức 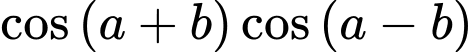 bằng
bằng
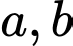 là hai góc nhọn. Biết
là hai góc nhọn. Biết 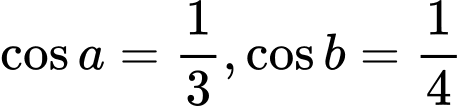 . Giá trị của biểu thức
. Giá trị của biểu thức 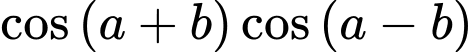 bằng
bằng A, 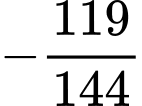 .
.
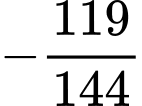 .
.B, 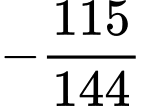 .
.
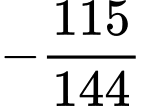 .
.C, 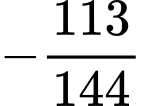 .
.
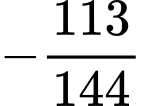 .
.D, 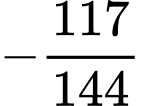 .
.
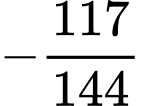 .
.
Chọn A
Từ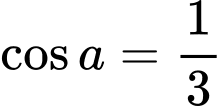
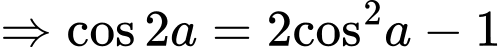
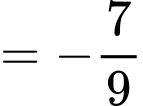
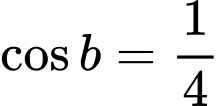
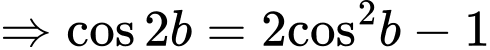
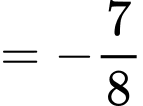
Ta có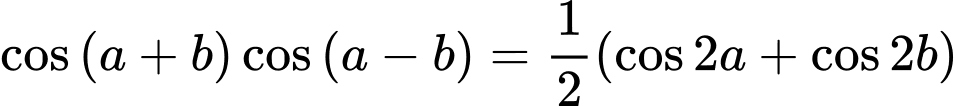
 Đáp án: A
Đáp án: A
Từ
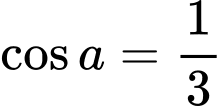
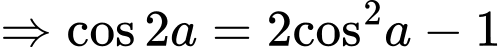
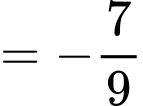
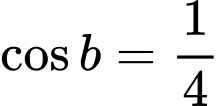
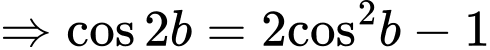
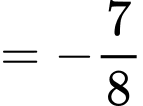
Ta có
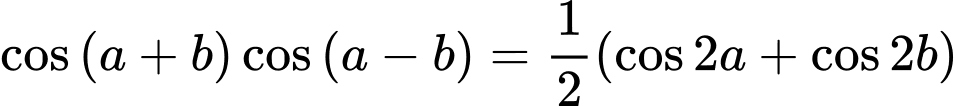
 Đáp án: A
Đáp án: A
Câu 14 [579694]: [Đề mẫu HSA 2024]: Lúc 6 giờ 00 sáng kim phút và kim giờ của đồng hồ tạo thành hai tia đối nhau. Biết rằng sau ít nhất 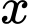 phút thì kim phút và kim giờ lại tạo thành hai tia đối nhau. Hỏi
phút thì kim phút và kim giờ lại tạo thành hai tia đối nhau. Hỏi 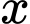 gần nhất với giá trị nào sau đây?
gần nhất với giá trị nào sau đây?

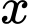 phút thì kim phút và kim giờ lại tạo thành hai tia đối nhau. Hỏi
phút thì kim phút và kim giờ lại tạo thành hai tia đối nhau. Hỏi 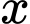 gần nhất với giá trị nào sau đây?
gần nhất với giá trị nào sau đây? 
A, 65,3.
B, 65,5.
C, 65,7.
D, 65,9.
Gọi 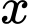 là số phút cần tìm.
là số phút cần tìm.
Giả sử chiều quay cùng chiều kim đồng hồ là chiều dương.
Sau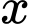 phút, kim phút quét được góc:
phút, kim phút quét được góc: 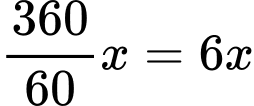
Sau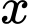 phút, kim giờ quét được góc có số đo so với số 12 trên đồng hồ là
phút, kim giờ quét được góc có số đo so với số 12 trên đồng hồ là
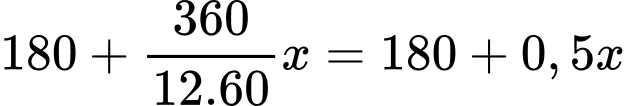
Để tạo thành 2 tia đối nhau thì góc của 2 kim phải chênh lệch nhau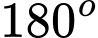 , ta có
, ta có
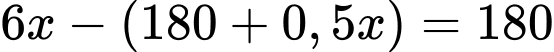
Giải phương trình, ta được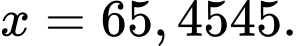
Chọn B. Đáp án: B
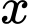 là số phút cần tìm.
là số phút cần tìm. Giả sử chiều quay cùng chiều kim đồng hồ là chiều dương.
Sau
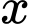 phút, kim phút quét được góc:
phút, kim phút quét được góc: 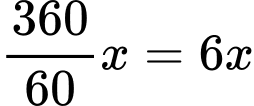
Sau
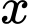 phút, kim giờ quét được góc có số đo so với số 12 trên đồng hồ là
phút, kim giờ quét được góc có số đo so với số 12 trên đồng hồ là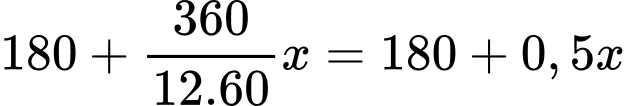
Để tạo thành 2 tia đối nhau thì góc của 2 kim phải chênh lệch nhau
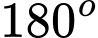 , ta có
, ta có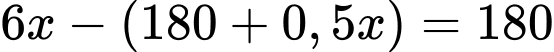
Giải phương trình, ta được
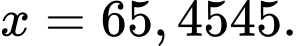
Chọn B. Đáp án: B
Câu 15 [159537]: Bánh xe của một xe máy có đường kính 100 cm quay được 6390 vòng trong 3 phút. Hỏi vận tốc 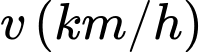 của người đi xe máy đó là bao nhiêu? (làm tròn đến hàng đơn vị).
của người đi xe máy đó là bao nhiêu? (làm tròn đến hàng đơn vị).
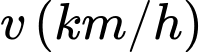 của người đi xe máy đó là bao nhiêu? (làm tròn đến hàng đơn vị).
của người đi xe máy đó là bao nhiêu? (làm tròn đến hàng đơn vị).
Bán kính của bánh xe là: 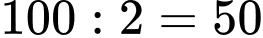 (cm)
(cm)
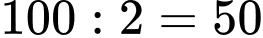 (cm)
(cm) Trong 1 phút bánh xe quay được: 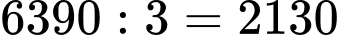 (vòng).
(vòng).
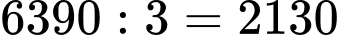 (vòng).
(vòng). Trong 1 giờ bánh xe quay được: 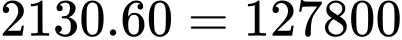 (vòng).
(vòng).
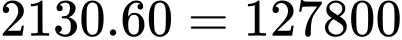 (vòng).
(vòng). Trong 1 giờ bánh xe đi được quãng đường là: 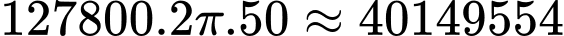 (cm).
(cm).
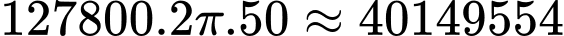 (cm).
(cm). Vậy vận tốc của người đi xe máy là: 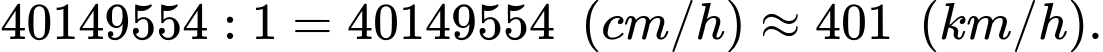
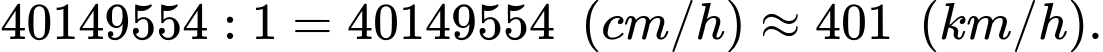
Bài toán này ra đáp số hơi phi thực tế (nếu cho quay được 639 vòng/3 phút) thì sẽ chuẩn với thực tế hơn các em nhé, chứ xe máy đâu mà chạy được 401 km/h
Câu 16 [159534]: Một người đi xe đạp đã đi được quãng đường 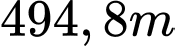 trong thời gian 2 phút. Biết rằng đường kính bánh xe là
trong thời gian 2 phút. Biết rằng đường kính bánh xe là 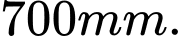 Hỏi trong 3 giây bánh xe quay được một góc lượng giác có số đo (đơn vị Radian) là bao nhiêu (giả sử bánh xe quay theo chiều dương, kết quả làm tròn đến một chữ số sau dấu phẩy)?
Hỏi trong 3 giây bánh xe quay được một góc lượng giác có số đo (đơn vị Radian) là bao nhiêu (giả sử bánh xe quay theo chiều dương, kết quả làm tròn đến một chữ số sau dấu phẩy)?
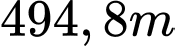 trong thời gian 2 phút. Biết rằng đường kính bánh xe là
trong thời gian 2 phút. Biết rằng đường kính bánh xe là 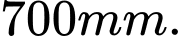 Hỏi trong 3 giây bánh xe quay được một góc lượng giác có số đo (đơn vị Radian) là bao nhiêu (giả sử bánh xe quay theo chiều dương, kết quả làm tròn đến một chữ số sau dấu phẩy)?
Hỏi trong 3 giây bánh xe quay được một góc lượng giác có số đo (đơn vị Radian) là bao nhiêu (giả sử bánh xe quay theo chiều dương, kết quả làm tròn đến một chữ số sau dấu phẩy)?
Đổi đơn vị: 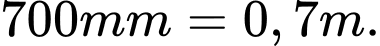
Ta có chu vi bánh xe là: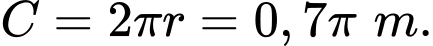
Trong 2 phút (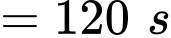 ) bánh xe quay được số vòng là:
) bánh xe quay được số vòng là: 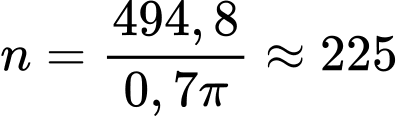 (vòng).
(vòng).
Suy ra trong 3 giây bánh xe quay được số vòng là: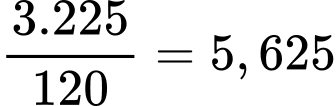 (vòng)
(vòng)
Mỗi vòng bánh xe quay được một góc là (radian).
(radian).
Suy ra trong 3 giây bánh xe đã quay được góc lượng giác có số đo là: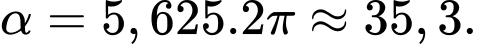
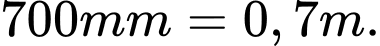
Ta có chu vi bánh xe là:
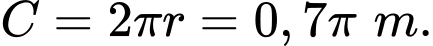
Trong 2 phút (
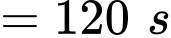 ) bánh xe quay được số vòng là:
) bánh xe quay được số vòng là: 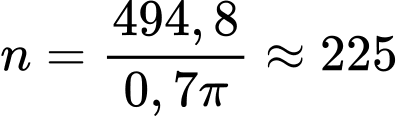 (vòng).
(vòng).
Suy ra trong 3 giây bánh xe quay được số vòng là:
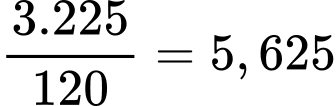 (vòng)
(vòng)
Mỗi vòng bánh xe quay được một góc là
 (radian).
(radian).
Suy ra trong 3 giây bánh xe đã quay được góc lượng giác có số đo là:
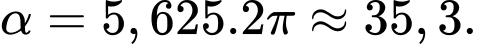
Câu 17 [518839]: Cho 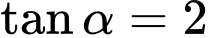 . Tính
. Tính 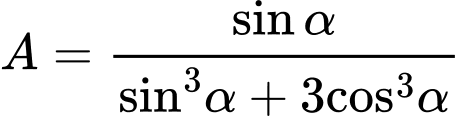 .
.
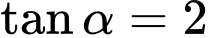 . Tính
. Tính 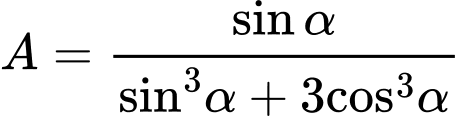 .
. A,
B,
C,
D,
Ta có: 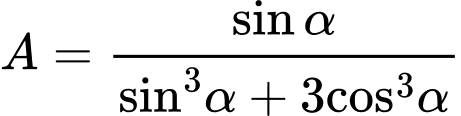
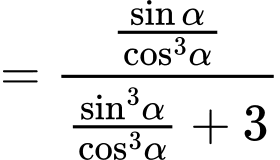
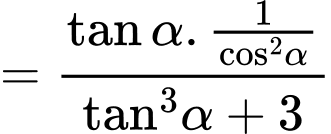
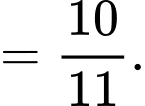
Đáp án: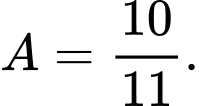 Đáp án: B
Đáp án: B
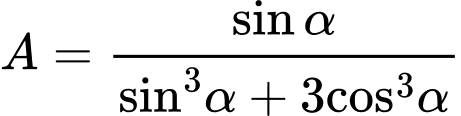
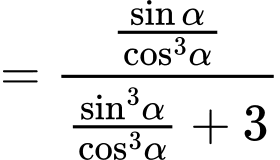
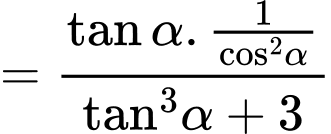
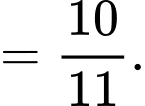
Đáp án:
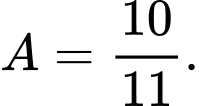 Đáp án: B
Đáp án: B
Câu 18 [269955]: Cho 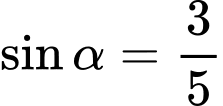 và
và 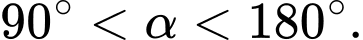 Giá trị của biểu thức
Giá trị của biểu thức 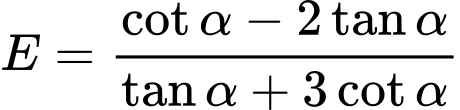 là
là
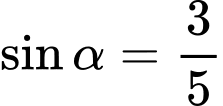 và
và 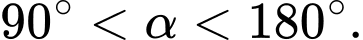 Giá trị của biểu thức
Giá trị của biểu thức 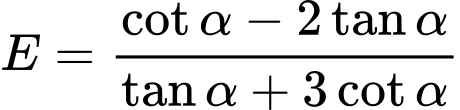 là
là
Ta có: 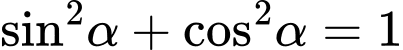
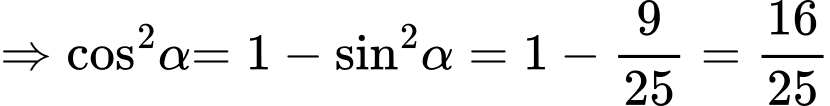
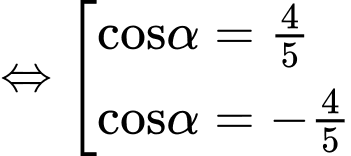
Vì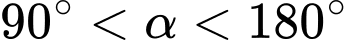
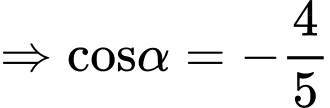 .
.
Vậy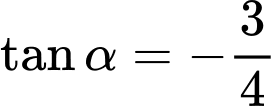 và
và 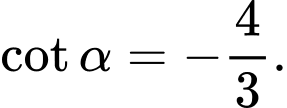
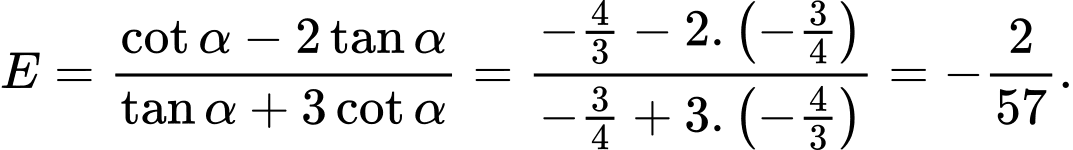
Đáp án: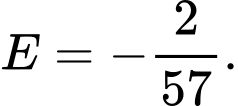 Đáp án: B
Đáp án: B
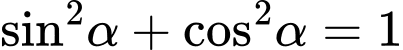
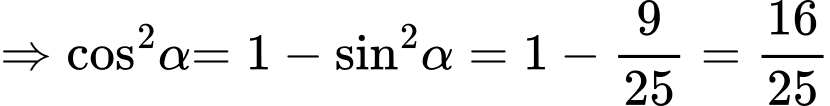
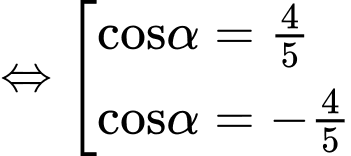
Vì
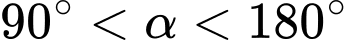
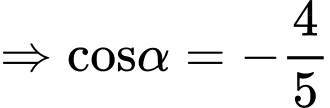 .
.
Vậy
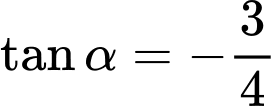 và
và 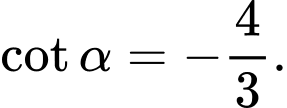
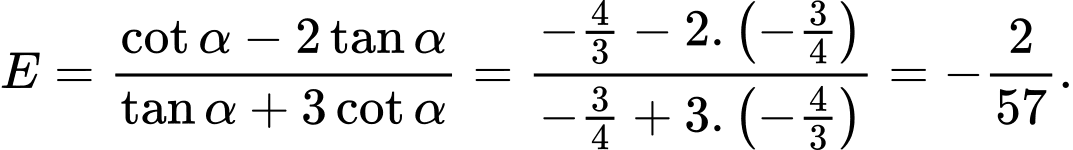
Đáp án:
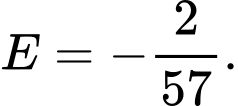 Đáp án: B
Đáp án: B
Câu 19 [270439]: Cho biết 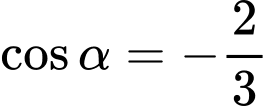 . Giá trị của biểu thức
. Giá trị của biểu thức 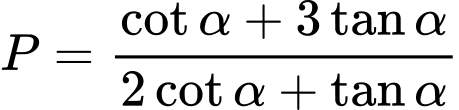 bằng bao nhiêu?
bằng bao nhiêu?
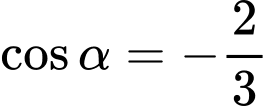 . Giá trị của biểu thức
. Giá trị của biểu thức 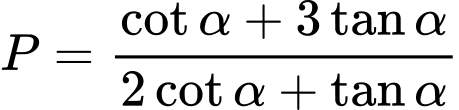 bằng bao nhiêu?
bằng bao nhiêu?
Ta có: 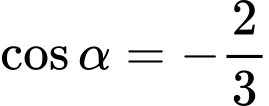
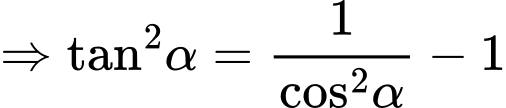
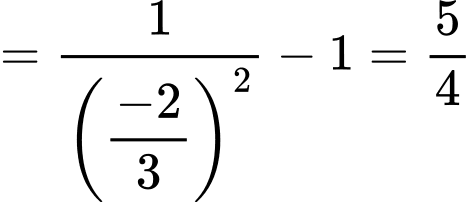
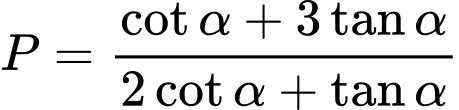
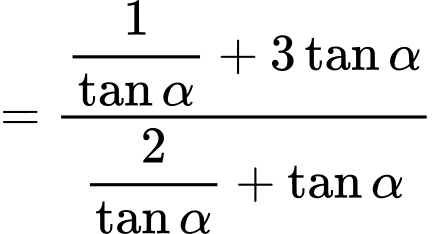
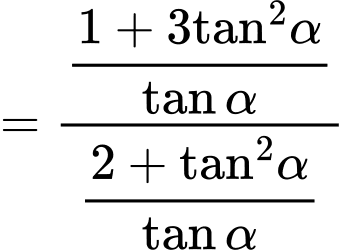
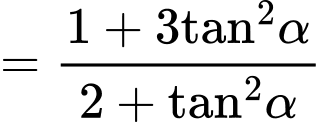
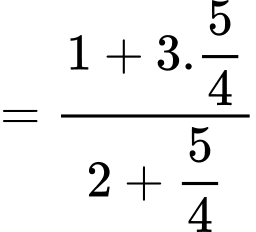
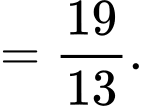
Đáp án: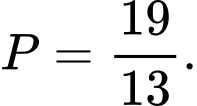 Đáp án: A
Đáp án: A
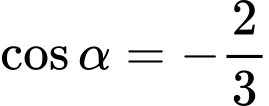
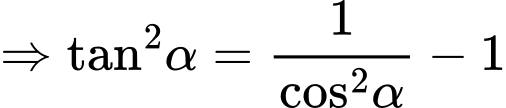
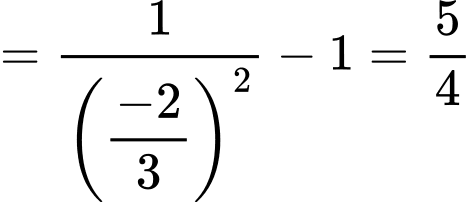
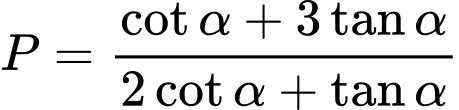
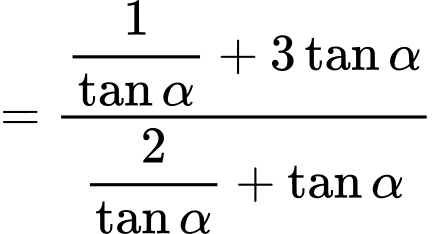
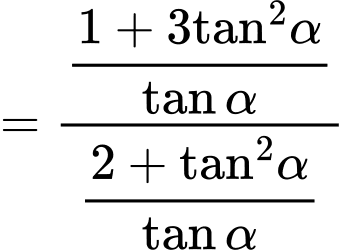
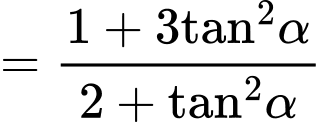
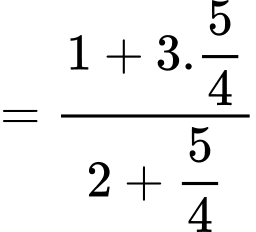
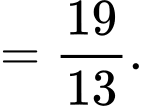
Đáp án:
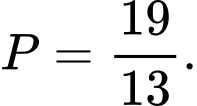 Đáp án: A
Đáp án: A
Câu 20 [269961]: Cho biết 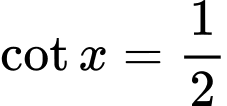 . Giá trị biểu thức
. Giá trị biểu thức 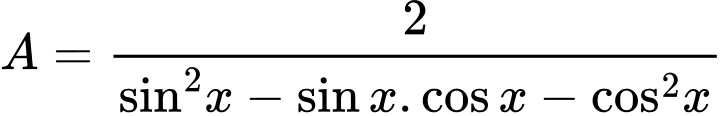 bằng
bằng
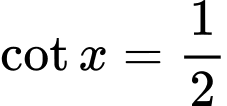 . Giá trị biểu thức
. Giá trị biểu thức 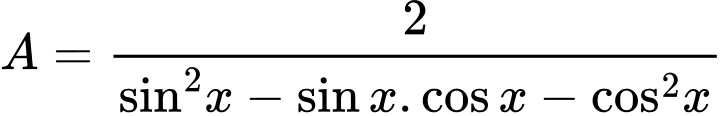 bằng
bằng A, 6.
B, 8.
C, 10.
D, 12.
Chọn C
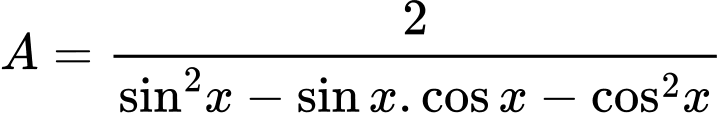
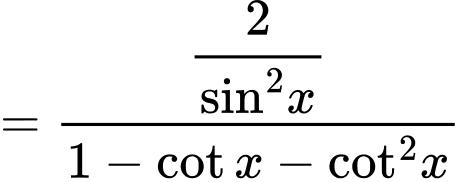
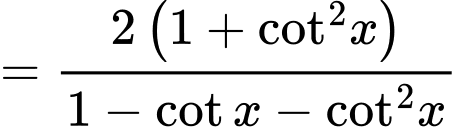
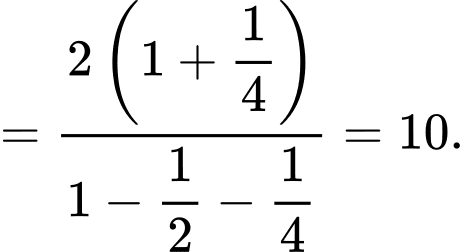 Đáp án: C
Đáp án: C
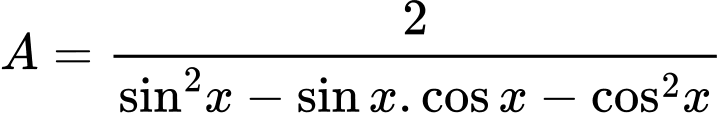
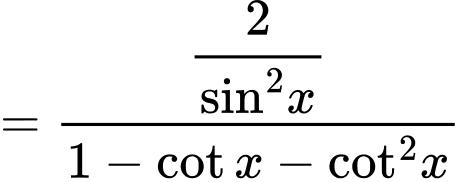
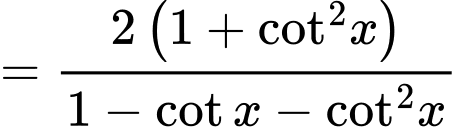
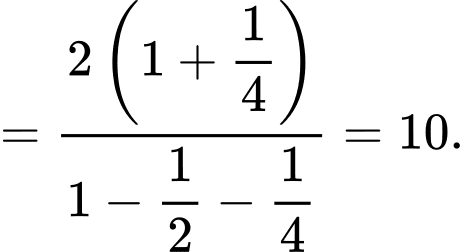 Đáp án: C
Đáp án: C
Câu 21 [272555]: Khi xe đạp di chuyển, van  của bánh xe quay quanh trục
của bánh xe quay quanh trục  theo chiều kim đồng hồ với tốc độ góc không đổi là
theo chiều kim đồng hồ với tốc độ góc không đổi là 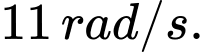 (Hình 13). Ban đầu van nằm ở vị trí
(Hình 13). Ban đầu van nằm ở vị trí 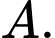 Hỏi sau một phút di chuyển, khoảng cách từ van đến mặt đất là bao nhiêu, biết bán kính
Hỏi sau một phút di chuyển, khoảng cách từ van đến mặt đất là bao nhiêu, biết bán kính 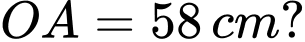 Giả sử độ dày của lốp xe không đáng kể. Kết quả làm tròn đến hàng phần mười.
Giả sử độ dày của lốp xe không đáng kể. Kết quả làm tròn đến hàng phần mười. 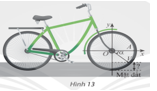
 của bánh xe quay quanh trục
của bánh xe quay quanh trục  theo chiều kim đồng hồ với tốc độ góc không đổi là
theo chiều kim đồng hồ với tốc độ góc không đổi là 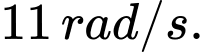 (Hình 13). Ban đầu van nằm ở vị trí
(Hình 13). Ban đầu van nằm ở vị trí 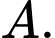 Hỏi sau một phút di chuyển, khoảng cách từ van đến mặt đất là bao nhiêu, biết bán kính
Hỏi sau một phút di chuyển, khoảng cách từ van đến mặt đất là bao nhiêu, biết bán kính 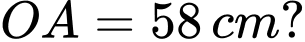 Giả sử độ dày của lốp xe không đáng kể. Kết quả làm tròn đến hàng phần mười.
Giả sử độ dày của lốp xe không đáng kể. Kết quả làm tròn đến hàng phần mười. 
Sau một phút di chuyển, khoảng cách từ van đến mặt đất là :
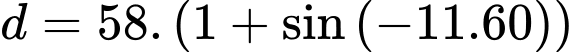
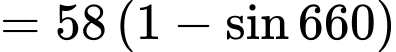
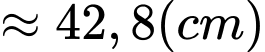
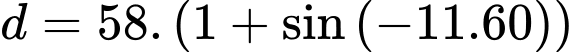
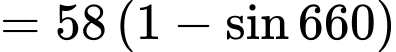
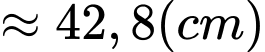
Câu 22 [581237]: Trong hình 3, tam giác 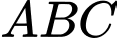 vuông tại
vuông tại 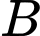 và có hai cạnh góc vuông là
và có hai cạnh góc vuông là 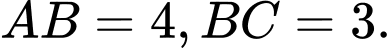 Vẽ điểm
Vẽ điểm 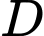 nằm trên tia đối của tia
nằm trên tia đối của tia 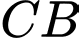 thoả mãn
thoả mãn 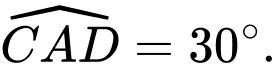 Tính độ dài cạnh
Tính độ dài cạnh 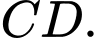 Viết kết quả làm tròn đến hàng phần chục.
Viết kết quả làm tròn đến hàng phần chục.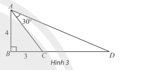
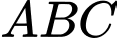 vuông tại
vuông tại 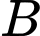 và có hai cạnh góc vuông là
và có hai cạnh góc vuông là 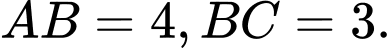 Vẽ điểm
Vẽ điểm 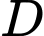 nằm trên tia đối của tia
nằm trên tia đối của tia 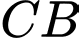 thoả mãn
thoả mãn 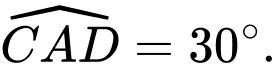 Tính độ dài cạnh
Tính độ dài cạnh 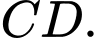 Viết kết quả làm tròn đến hàng phần chục.
Viết kết quả làm tròn đến hàng phần chục.
Xét tam giác 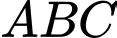 vuông tại
vuông tại 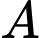 có
có 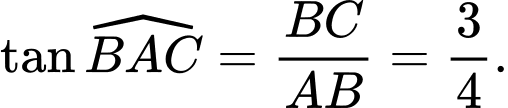
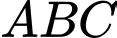 vuông tại
vuông tại 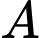 có
có 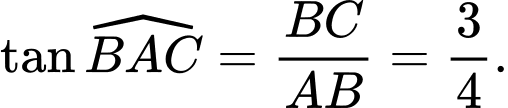
Ta có:

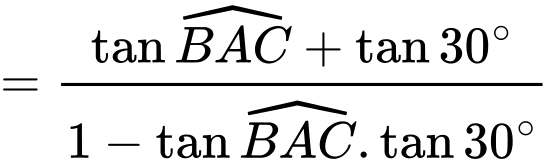
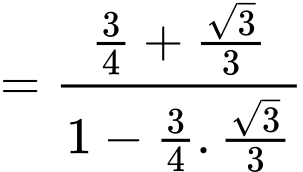
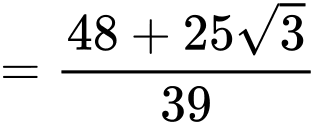

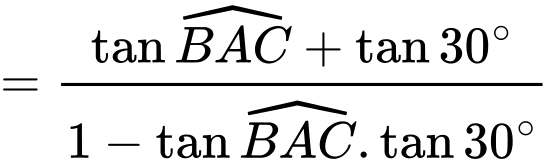
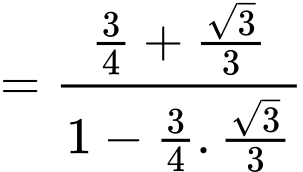
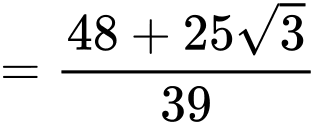
Xét tam giác 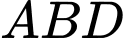 vuông tại
vuông tại 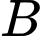 có:
có: 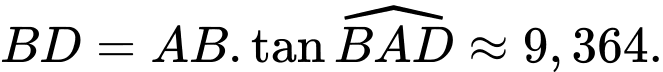
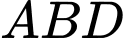 vuông tại
vuông tại 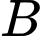 có:
có: 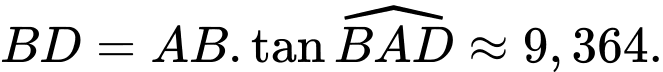
Vậy 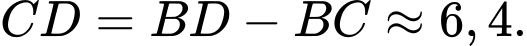
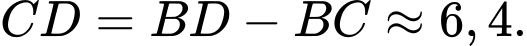
Câu 23 [270820]: Có hai chung cư cao cấp xây canh nhau với khoảng cách giữa chúng 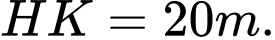 Để đảm bảo an ninh, trên nóc chung cư thứ hai người ta lắp camera ở vị trí
Để đảm bảo an ninh, trên nóc chung cư thứ hai người ta lắp camera ở vị trí  Gọi
Gọi 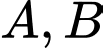 lần lượt là vị trí thấp nhất, cao nhất trên chung cư thứ nhất mà camera có thể quan sát được ( Hình
lần lượt là vị trí thấp nhất, cao nhất trên chung cư thứ nhất mà camera có thể quan sát được ( Hình 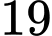 ). Hãy tính số đo góc
). Hãy tính số đo góc  (phạm vi camera có thể quan sát được ở chung cư thứ nhất). Biết rằng chiều cao của chung cư thứ hai là
(phạm vi camera có thể quan sát được ở chung cư thứ nhất). Biết rằng chiều cao của chung cư thứ hai là 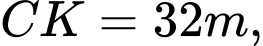
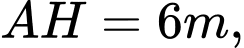
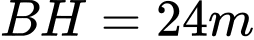 (làm tròn kết quả đến hàng phần mười theo đơn vị độ).
(làm tròn kết quả đến hàng phần mười theo đơn vị độ).

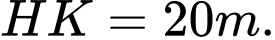 Để đảm bảo an ninh, trên nóc chung cư thứ hai người ta lắp camera ở vị trí
Để đảm bảo an ninh, trên nóc chung cư thứ hai người ta lắp camera ở vị trí  Gọi
Gọi 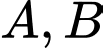 lần lượt là vị trí thấp nhất, cao nhất trên chung cư thứ nhất mà camera có thể quan sát được ( Hình
lần lượt là vị trí thấp nhất, cao nhất trên chung cư thứ nhất mà camera có thể quan sát được ( Hình 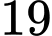 ). Hãy tính số đo góc
). Hãy tính số đo góc  (phạm vi camera có thể quan sát được ở chung cư thứ nhất). Biết rằng chiều cao của chung cư thứ hai là
(phạm vi camera có thể quan sát được ở chung cư thứ nhất). Biết rằng chiều cao của chung cư thứ hai là 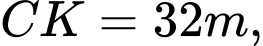
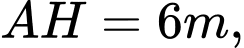
 (làm tròn kết quả đến hàng phần mười theo đơn vị độ).
(làm tròn kết quả đến hàng phần mười theo đơn vị độ).
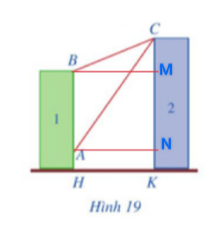
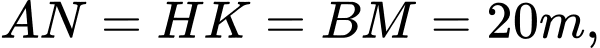
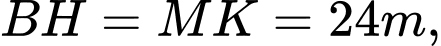
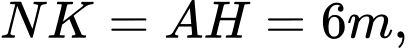
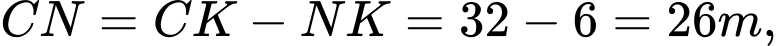
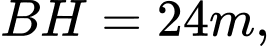
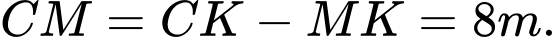
a)
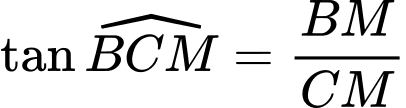
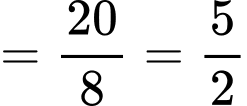
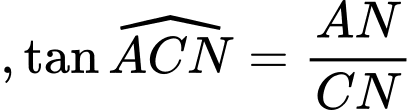
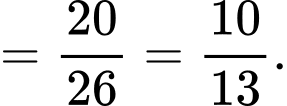
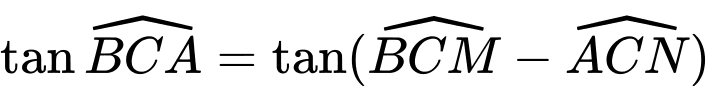
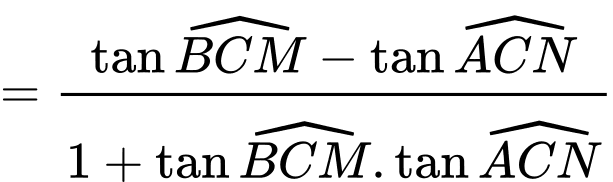
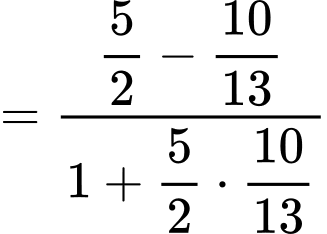
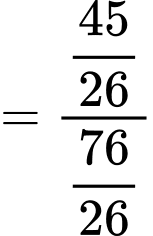
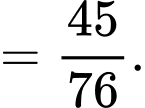
b)
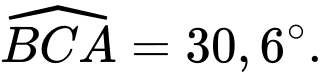
Câu 24 [581238]: Kim giờ dài 6 cm và kim phút dài 11 cm của đồng hồ chỉ 4 giờ. Hỏi thời gian ít nhất đề 2 kim vuông góc với nhau là bao nhiêu giờ?
Một giờ, kim phút quét được một góc lượng giác 2π; kim giờ quét được một góc 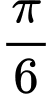 .
.
Hiệu vận tốc giữa kim phút và kim giờ là 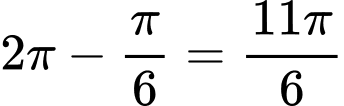 .
.
Vào lúc 4 giờ hai kim tạo với nhau một góc là 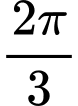 .
.
Khoảng thời gian ít nhất để hai kim vuông góc với nhau là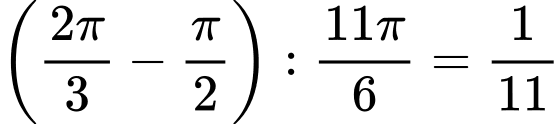 (giờ).
(giờ).
Vậy sau 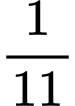 (giờ) hai kim sẽ vuông góc với nhau.
(giờ) hai kim sẽ vuông góc với nhau.