Đáp án Bài tập tự luyện
Câu 1 [802194]: (THPT CHU VĂN AN - HKI - 2018) Hàm số nào sau đây là hàm số chẵn?
A, 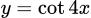 .
.
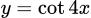 .
.B, 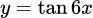 .
.
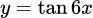 .
.C, 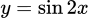 .
.
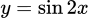 .
.D, 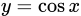 .
.
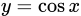 .
.
Xét hàm 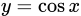 .
.
TXĐ: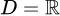 .
.
Khi đó .
.
Ta có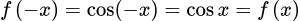 .
.
Vậy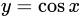 là hàm số chẵn. Đáp án: D
là hàm số chẵn. Đáp án: D
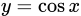 .
.TXĐ:
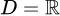 .
.Khi đó
 .
.Ta có
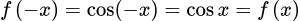 .
.Vậy
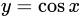 là hàm số chẵn. Đáp án: D
là hàm số chẵn. Đáp án: D
Câu 2 [522487]: Tập xác định của hàm số 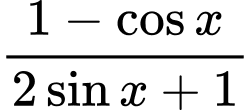 là
là
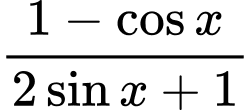 là
là A, 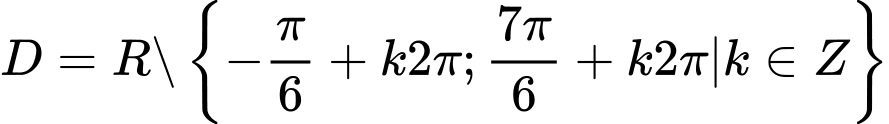 .
.
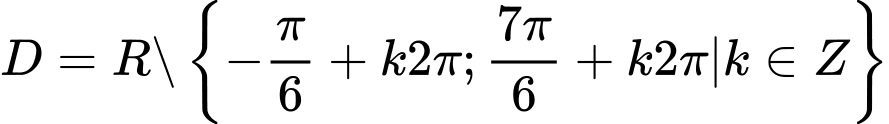 .
.B, 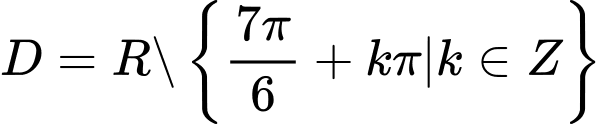 .
.
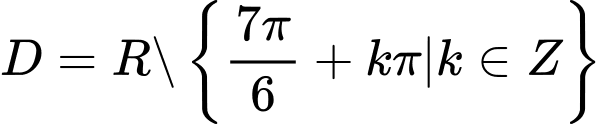 .
.C, 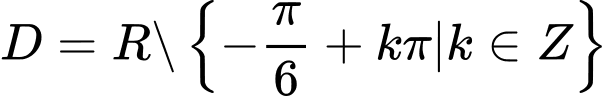 .
.
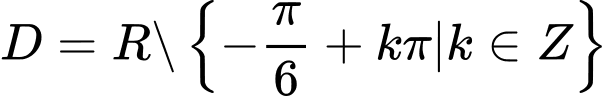 .
.D, 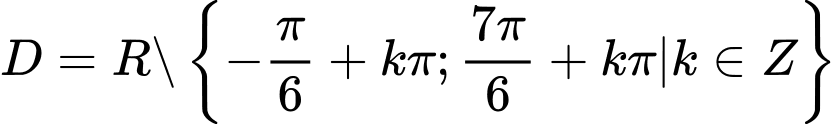 .
.
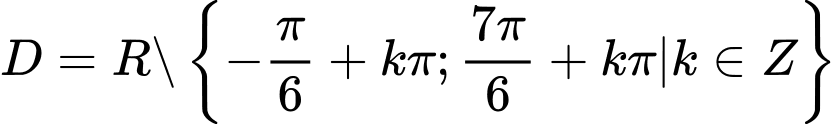 .
.
ĐK: 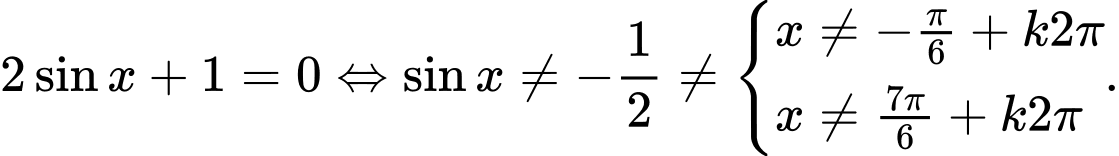
Tập xác định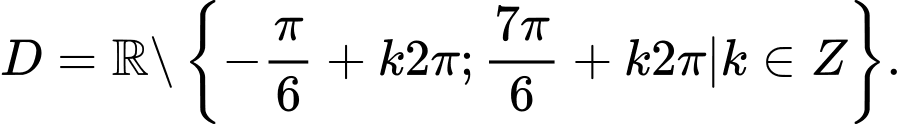
Chọn A. Đáp án: A
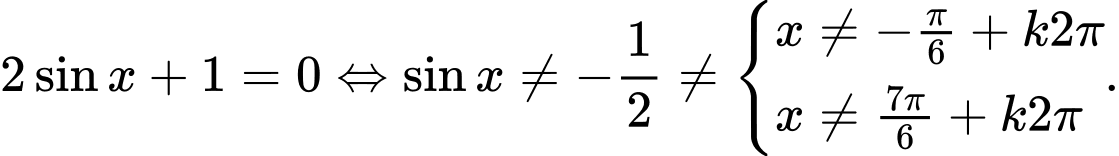
Tập xác định
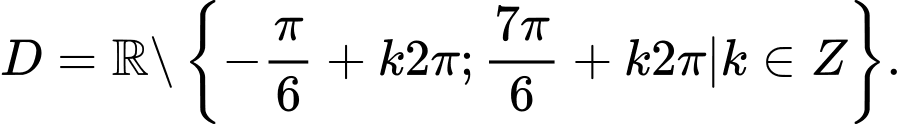
Chọn A. Đáp án: A
Câu 3 [802148]: (THPT THIỆU HÓA – THANH HÓA NĂM 2018 - 2019 LẦN 01) Tìm tập xác định 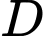 của hàm số
của hàm số 
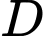 của hàm số
của hàm số 
A, 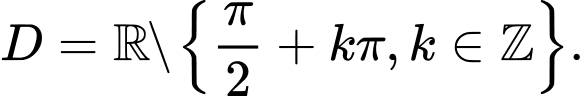
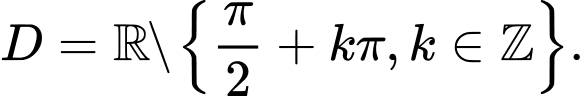
B, 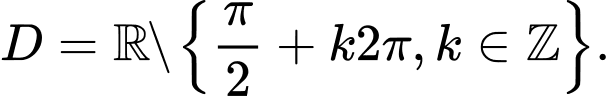
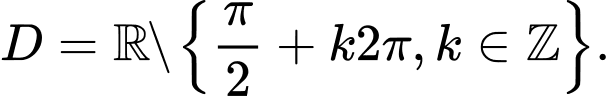
C, 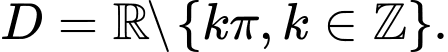
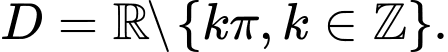
D, 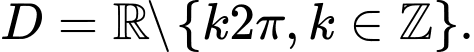
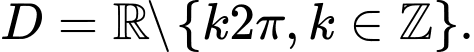
Chọn C
Hàm số xác định khi: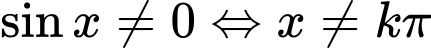 .
.
Vậy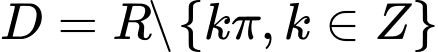 Đáp án: C
Đáp án: C
Hàm số xác định khi:
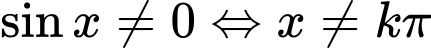 .
.Vậy
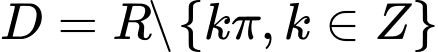 Đáp án: C
Đáp án: C
Câu 4 [802152]: (GKI THPT NGHĨA HƯNG NAM ĐỊNH NĂM 2018 - 2019) Tập xác định của hàm số 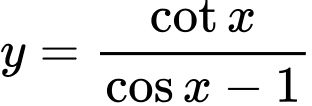 là
là
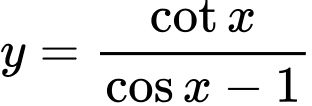 là
là A, 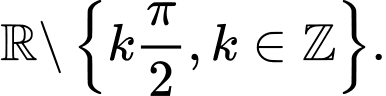
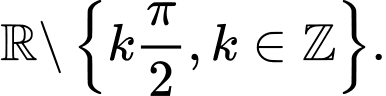
B, 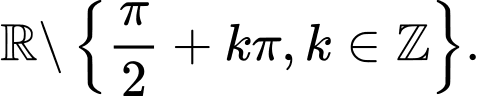
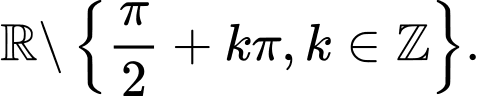
C, 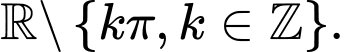
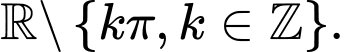
D, 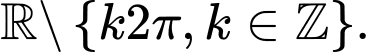
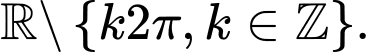
Chọn C
Điều kiện xác định của hàm số là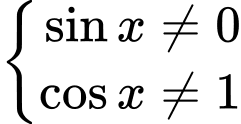
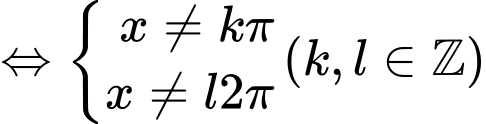
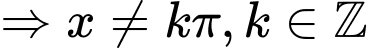 .
.
Vậy tập xác định của hàm số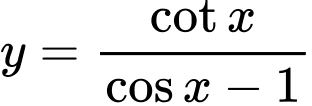 là
là 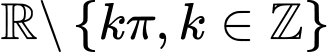 . Đáp án: C
. Đáp án: C
Điều kiện xác định của hàm số là
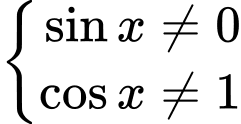
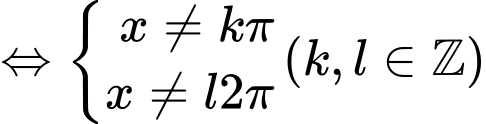
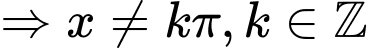 .
.Vậy tập xác định của hàm số
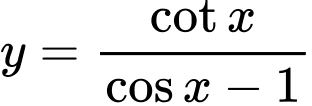 là
là 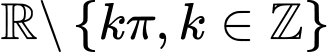 . Đáp án: C
. Đáp án: C
Câu 5 [802155]: (CHUYÊN TRẦN PHÚ HẢI PHÒNG NĂM 2018-2019 LẦN 02) Điều kiện xác định của hàm số 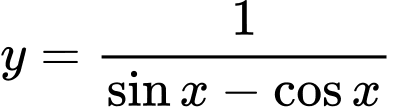 là
là
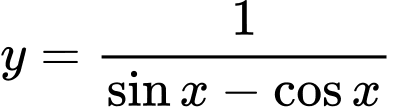 là
là A, 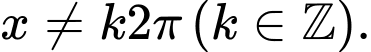
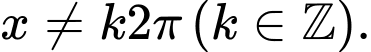
B, 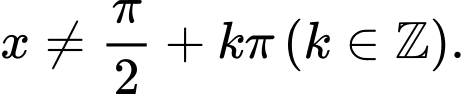
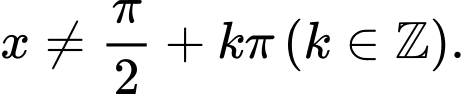
C, 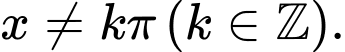
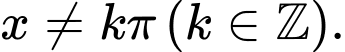
D, 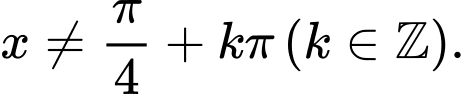
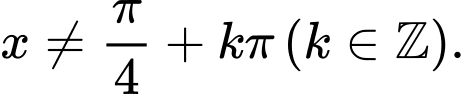
Điều kiện 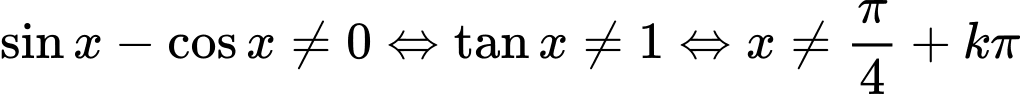 Đáp án: D
Đáp án: D
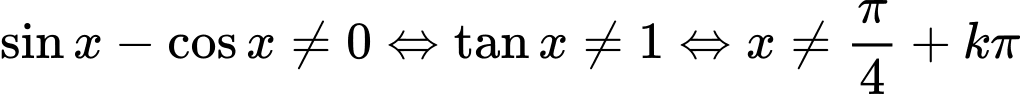 Đáp án: D
Đáp án: D
Câu 6 [522512]: Hãy chỉ ra hàm số nào là hàm số lẻ?
A, 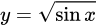 .
.
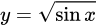 .
.B, 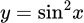 .
.
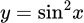 .
.C, 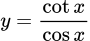 .
.
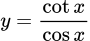 .
.D, 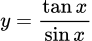 .
.
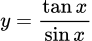 .
.
Với A: do khi 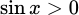 thì
thì 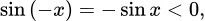 do đó
do đó 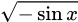 không tồn tại, ta loại A
không tồn tại, ta loại A
Với B: Tập xác định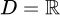 là tập đối xứng.
là tập đối xứng.
Ta có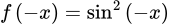
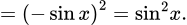 Vậy hàm số ở phương án C là hàm số lẻ. Chọn C.
Vậy hàm số ở phương án C là hàm số lẻ. Chọn C.
Đáp án: C
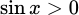 thì
thì 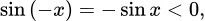 do đó
do đó 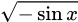 không tồn tại, ta loại A
không tồn tại, ta loại A Với B: Tập xác định
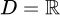 là tập đối xứng.
là tập đối xứng. Ta có
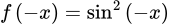
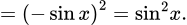 Vậy hàm số ở phương án C là hàm số lẻ. Chọn C.
Vậy hàm số ở phương án C là hàm số lẻ. Chọn C.Đáp án: C
Câu 7 [522516]: Hàm số nào sau đây là hàm số chẵn?
A, 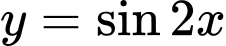 .
.
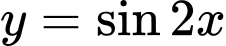 .
.B, 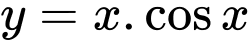 .
.
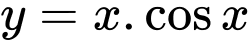 .
.C, 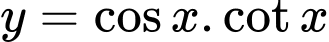 .
.
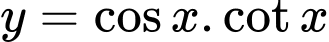 .
.D, 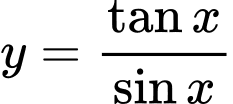 .
.
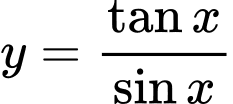 .
.
Dễ thấy hàm số 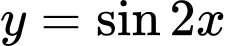 là hàm số lẻ.
là hàm số lẻ.
Với B ta có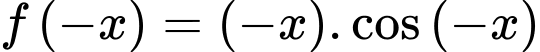
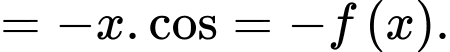
Vậy hàm số ở B là hàm số lẻ.
Với C ta có TXĐ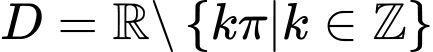 là tập đối xứng.
là tập đối xứng.
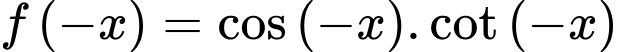
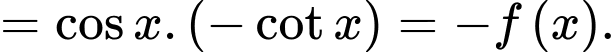
Vậy hàm số ở C là hàm số lẻ. Chọn D.
Đáp án: D
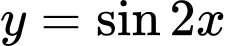 là hàm số lẻ.
là hàm số lẻ. Với B ta có
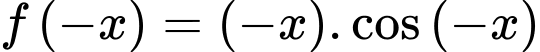
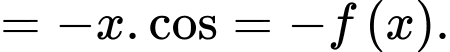
Vậy hàm số ở B là hàm số lẻ.
Với C ta có TXĐ
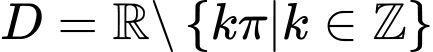 là tập đối xứng.
là tập đối xứng. 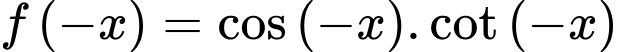
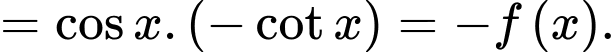
Vậy hàm số ở C là hàm số lẻ. Chọn D.
Đáp án: D
Câu 8 [522517]: Hàm số nào sau đây là hàm số chẵn?
A, 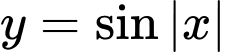 .
.
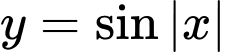 .
.B, 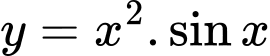 .
.
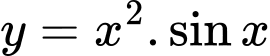 .
.C, 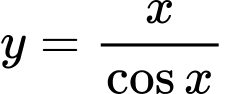 .
.
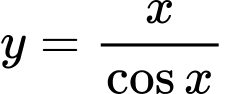 .
.D, 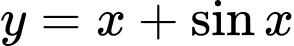 .
.
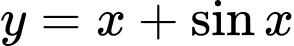 .
.
Ta chọn luôn A vì ở phần ví dụ ta có đưa ra hàm số 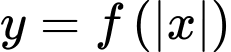 là hàm số chẵn trên D. Chọn A. Đáp án: A
là hàm số chẵn trên D. Chọn A. Đáp án: A
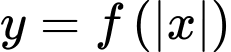 là hàm số chẵn trên D. Chọn A. Đáp án: A
là hàm số chẵn trên D. Chọn A. Đáp án: A
Câu 9 [523475]: Trong các hàm số sau đây, hàm số nào là hàm số tuần hoàn?
A, 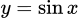 .
.
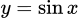 .
.B, 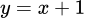 .
.
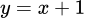 .
.C, 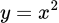 .
.
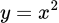 .
.D, 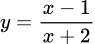 .
.
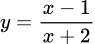 .
.
Tập xác định của hàm số: 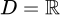 .
.
Với mọi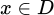 ,
, 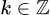 ta có
ta có 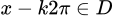 và
và 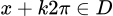 ,
, 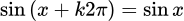 .
.
Vậy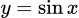 là hàm số tuần hoàn. Chọn A.
là hàm số tuần hoàn. Chọn A.
Đáp án: A
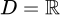 .
.Với mọi
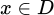 ,
, 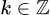 ta có
ta có 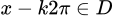 và
và 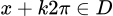 ,
, 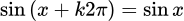 .
.Vậy
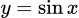 là hàm số tuần hoàn. Chọn A.
là hàm số tuần hoàn. Chọn A.Đáp án: A
Câu 10 [523478]: Trong các hàm số sau đây, hàm số nào là hàm số tuần hoàn?
A, 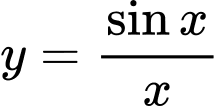 .
.
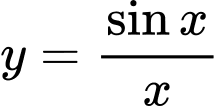 .
.B, 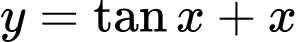 .
.
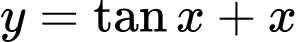 .
.C, 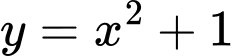 .
.
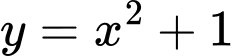 .
.D,  .
.
 .
.
Xét hàm số  ,
,
Tập xác định :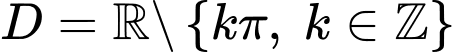
Với mọi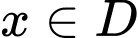 ,
, 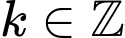 ta có
ta có 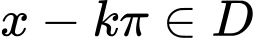 và
và 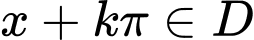 ,
, 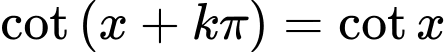 .
.
Vậy là hàm tuần hoàn. Chọn D.
là hàm tuần hoàn. Chọn D.
Đáp án: D
 ,
,Tập xác định :
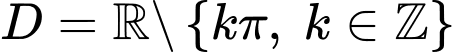
Với mọi
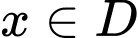 ,
, 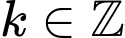 ta có
ta có 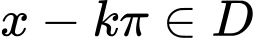 và
và 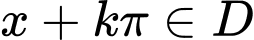 ,
, 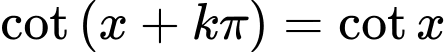 .
.Vậy
 là hàm tuần hoàn. Chọn D.
là hàm tuần hoàn. Chọn D.Đáp án: D
Câu 11 [523472]: Hàm số 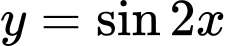 có chu kỳ là
có chu kỳ là
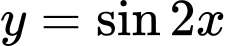 có chu kỳ là
có chu kỳ là A, 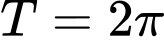 .
.
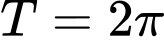 .
.B, 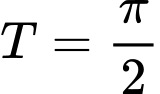 .
.
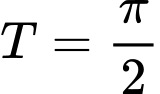 .
.C, 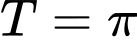 .
.
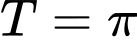 .
.D, 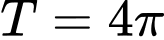 .
.
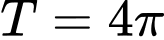 .
.
Hàm số 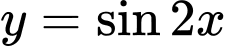 tuần hoàn với chu kỳ
tuần hoàn với chu kỳ 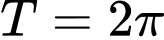 nên hàm số
nên hàm số 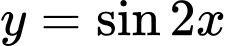 tuần hoàn với chu kỳ
tuần hoàn với chu kỳ 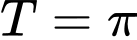 . Chọn C. Đáp án: C
. Chọn C. Đáp án: C
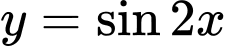 tuần hoàn với chu kỳ
tuần hoàn với chu kỳ 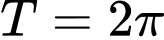 nên hàm số
nên hàm số 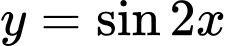 tuần hoàn với chu kỳ
tuần hoàn với chu kỳ 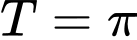 . Chọn C. Đáp án: C
. Chọn C. Đáp án: C
Câu 12 [523473]: Chu kỳ của hàm số 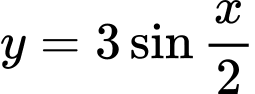 là số nào sau đây?
là số nào sau đây?
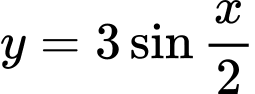 là số nào sau đây?
là số nào sau đây? A,  .
.
 .
.B, 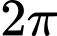 .
.
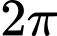 .
.C, 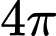 .
.
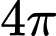 .
.D, 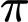 .
.
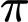 .
.
Chu kì của hàm số 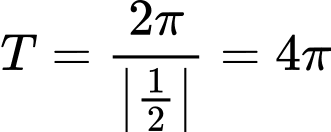 . Chọn C Đáp án: C
. Chọn C Đáp án: C
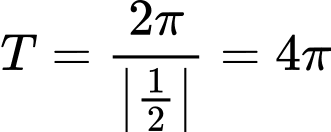 . Chọn C Đáp án: C
. Chọn C Đáp án: C
Câu 13 [523488]: Tìm chu kì  của hàm số
của hàm số 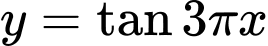 .
.
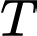 của hàm số
của hàm số 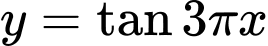 .
. A, 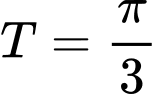 .
.
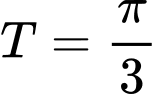 .
.B, 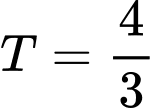 .
.
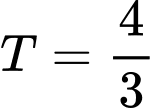 .
.C, 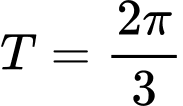 .
.
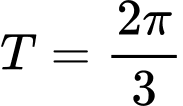 .
.D, 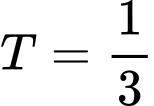 .
.
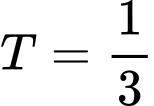 .
.
Chọn D
Hàm số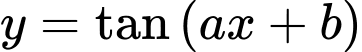 tuần hoàn với chu kì
tuần hoàn với chu kì 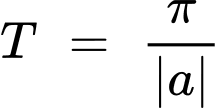 .
.
Áp dụng: Hàm số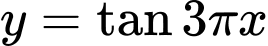 tuần hoàn với chu kì
tuần hoàn với chu kì 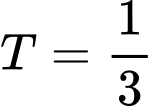 . Đáp án: D
. Đáp án: D
Hàm số
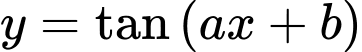 tuần hoàn với chu kì
tuần hoàn với chu kì 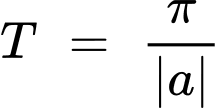 .
.Áp dụng: Hàm số
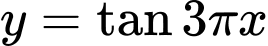 tuần hoàn với chu kì
tuần hoàn với chu kì 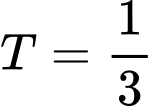 . Đáp án: D
. Đáp án: D
Câu 14 [518043]: Tìm giá trị nhỏ nhất, giá trị lớn nhất của hàm số 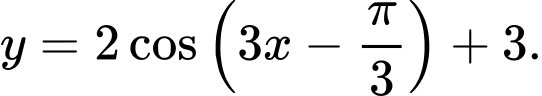
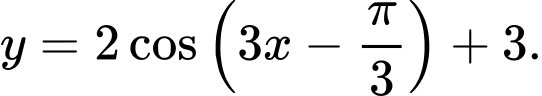
A, 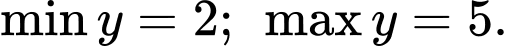
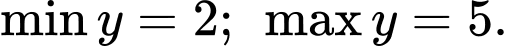
B, 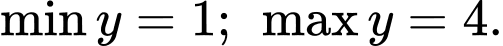
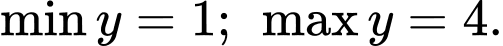
C, 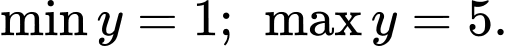
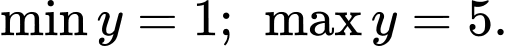
D, 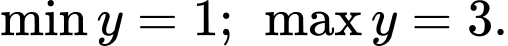
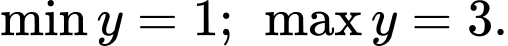
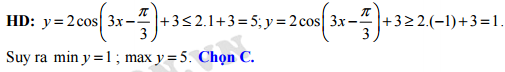 Đáp án: C
Đáp án: C
Câu 15 [518039]: Tìm giá trị nhỏ nhất, giá trị lớn nhất của hàm số 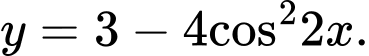
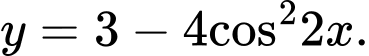
A, 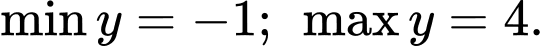
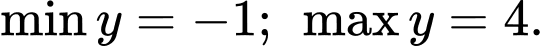
B, 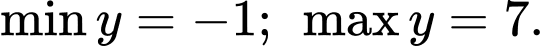
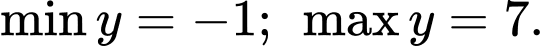
C, 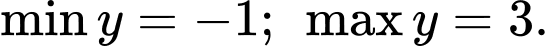
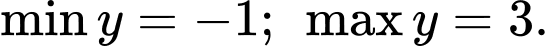
D, 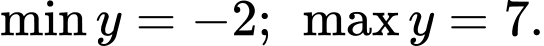
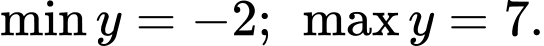
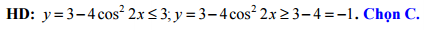 Đáp án: C
Đáp án: C
Câu 16 [518032]: Tìm giá trị nhỏ nhất, giá trị lớn nhất của hàm số 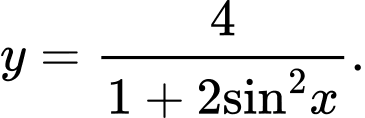
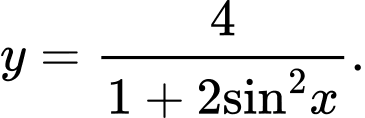
A, 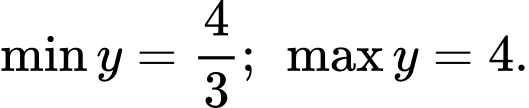
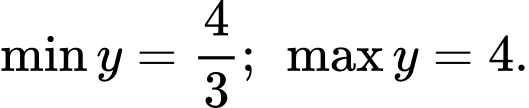
B, 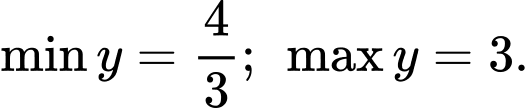
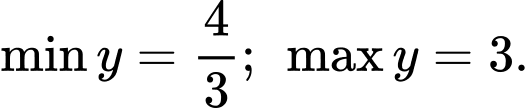
C, 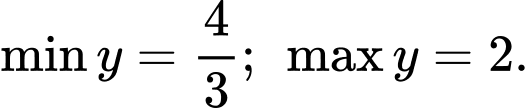
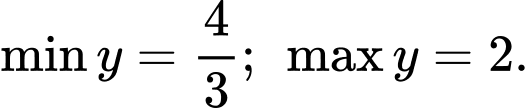
D, 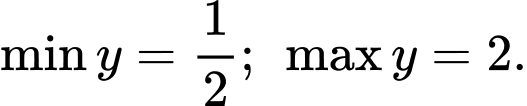
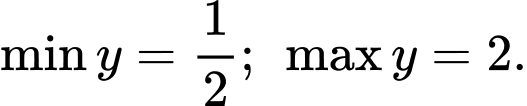
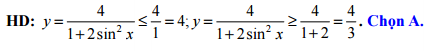 Đáp án: A
Đáp án: A
Câu 17 [802238]: (THPTHOALƯA-LẦN1-2018) Tìm tập giá trị của hàm số 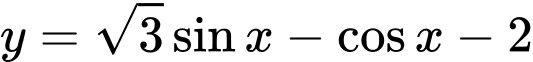 .
.
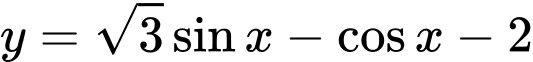 .
. A, 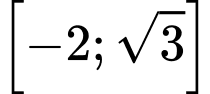 .
.
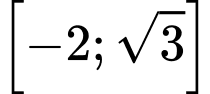 .
.B, 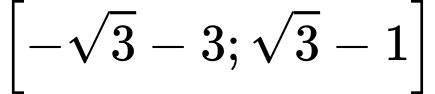 .
.
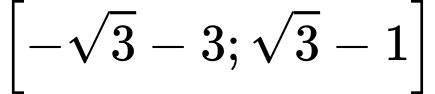 .
.C, 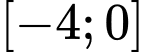 .
.
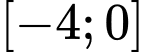 .
.D, 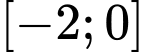
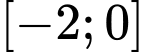
Xét 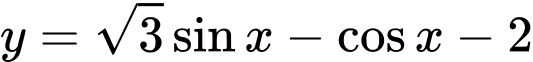
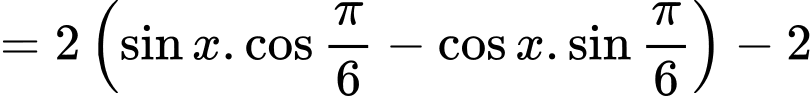
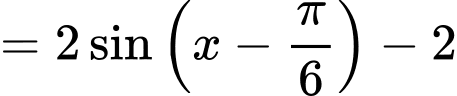
Ta có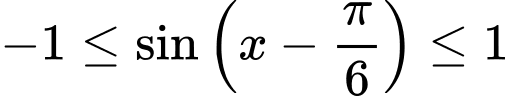
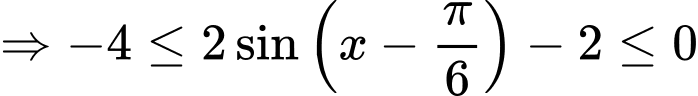
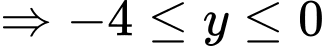 với mọi
với mọi
Vậy tập giá trị của hàm số là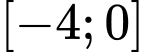 .
.
Đáp án: C
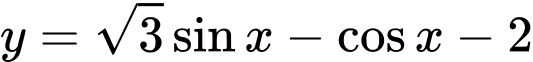
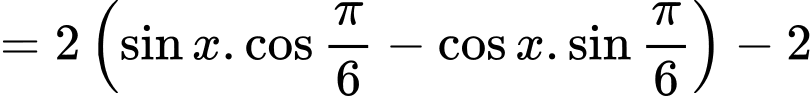
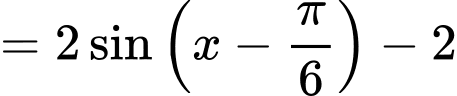
Ta có
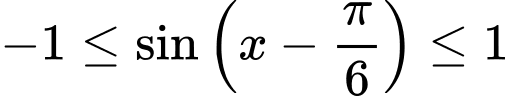
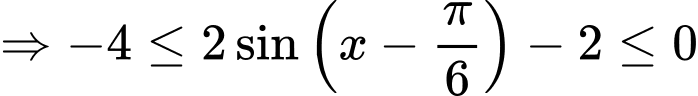
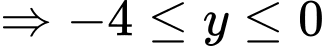 với mọi
với mọi Vậy tập giá trị của hàm số là
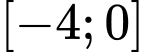 .
.Đáp án: C
Câu 18 [737087]: Tập giá trị của hàm số 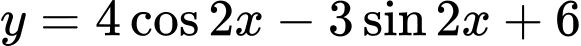 là:
là:
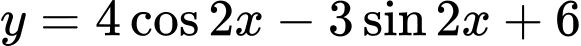 là:
là: A, 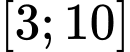
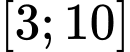
B, 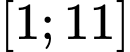
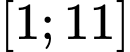
C, 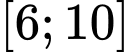
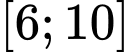
D, 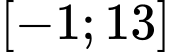
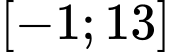
Áp dụng bất đẳng thức 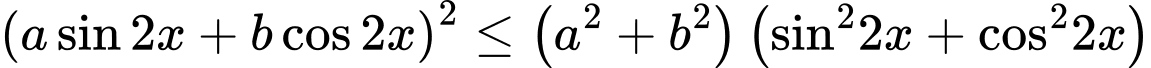
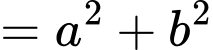
Ta được: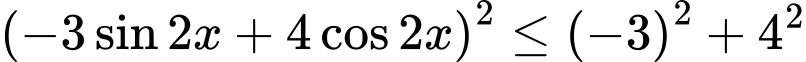
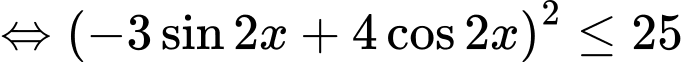
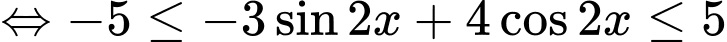
Cộng mỗi vế với 6 ta được: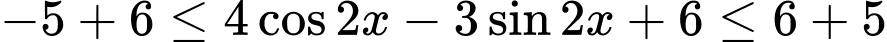
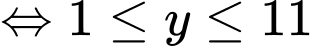
 Chọn B. Đáp án: B
Chọn B. Đáp án: B
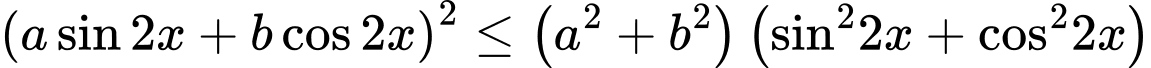
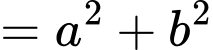
Ta được:
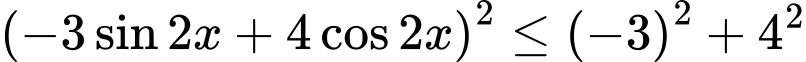
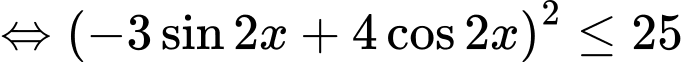
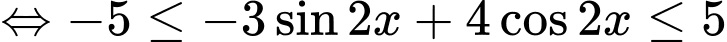
Cộng mỗi vế với 6 ta được:
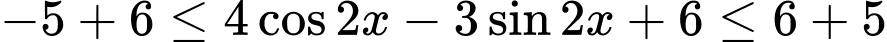
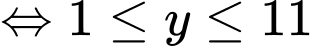
 Chọn B. Đáp án: B
Chọn B. Đáp án: B
Câu 19 [802244]: Giá trị nhỏ nhất của hàm số 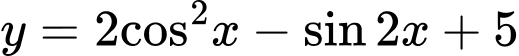
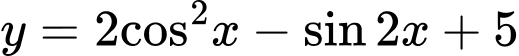
A, 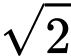 .
.
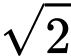 .
.B, 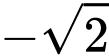 .
.
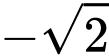 .
.C,  .
.
 .
.D, 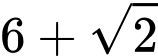 .
.
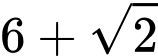 .
.
Ta có 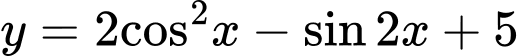
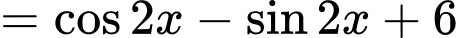
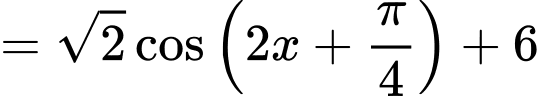 .
.
Do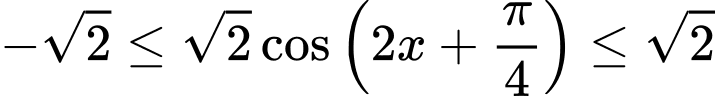 nên
nên 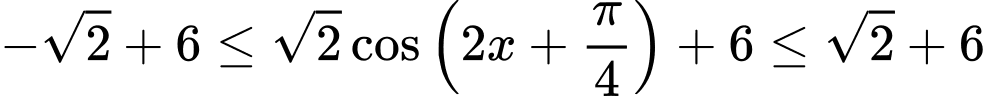 .
.
Vậy giá trị nhỏ nhất của hàm số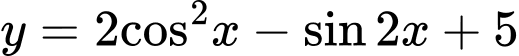 là
là  .
.
Đáp án: C
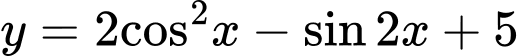
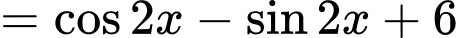
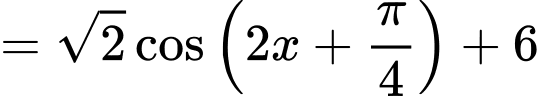 .
.Do
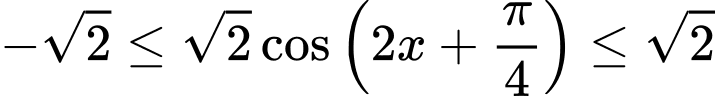 nên
nên 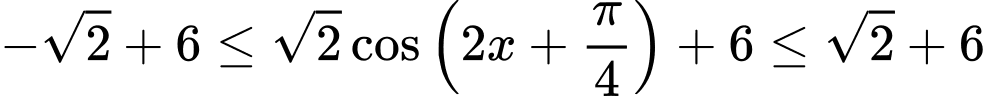 .
.Vậy giá trị nhỏ nhất của hàm số
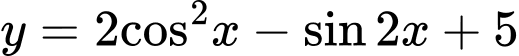 là
là  .
.Đáp án: C
Câu 20 [518046]: Tìm giá trị nhỏ nhất, giá trị lớn nhất của hàm số 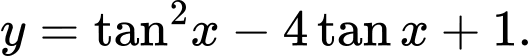
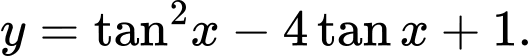
A, 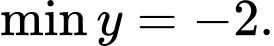
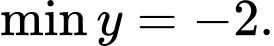
B, 
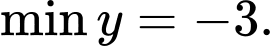
C, 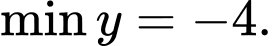
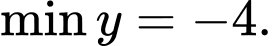
D, 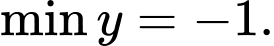
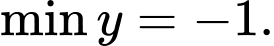
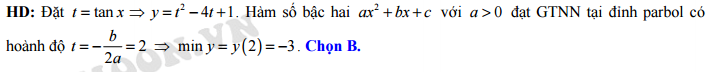 Đáp án: B
Đáp án: B
Câu 21 [518851]: Giá trị nhỏ nhất của hàm số 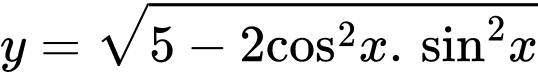 bằng:
bằng:
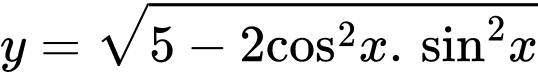 bằng:
bằng: A, 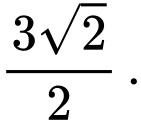
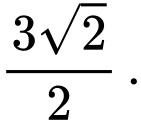
B, 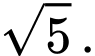
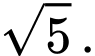
C, 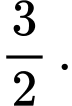
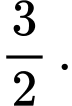
D, 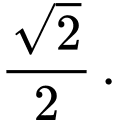
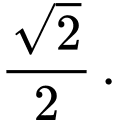
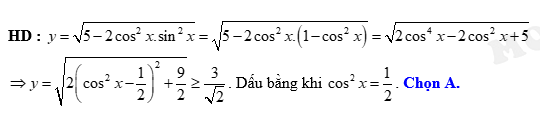 Đáp án: A
Đáp án: A
Câu 22 [523495]: Tìm chu kì 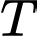 của hàm số
của hàm số 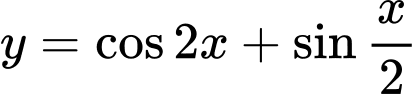 .
.
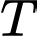 của hàm số
của hàm số 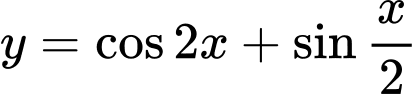 .
. A, 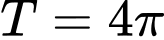 .
.
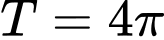 .
.B, 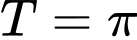 .
.
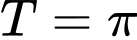 .
.C, 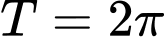 .
.
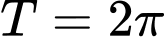 .
.D, 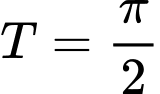 .
.
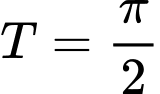 .
.
Chọn A
Hàm số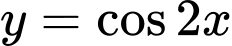 tuần hoàn với chu kì
tuần hoàn với chu kì 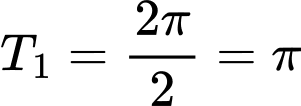 .
.
Hàm số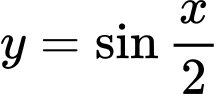 tuần hoàn với chu kì
tuần hoàn với chu kì 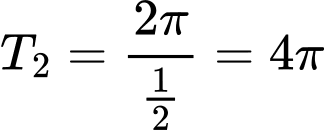 .
.
Suy ra hàm số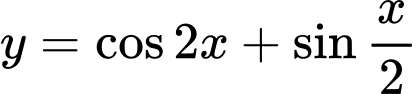 tuần hoàn với chu kì
tuần hoàn với chu kì 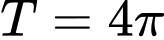 .
.
Nhận xét: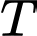 là bội chung nhỏ nhất của
là bội chung nhỏ nhất của 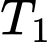 và
và 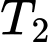 . Đáp án: A
. Đáp án: A
Hàm số
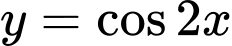 tuần hoàn với chu kì
tuần hoàn với chu kì 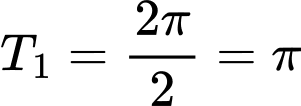 .
.Hàm số
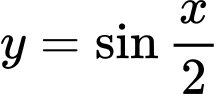 tuần hoàn với chu kì
tuần hoàn với chu kì 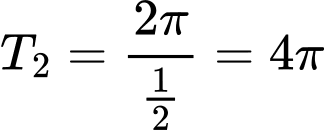 .
.Suy ra hàm số
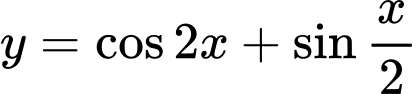 tuần hoàn với chu kì
tuần hoàn với chu kì 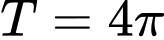 .
.Nhận xét:
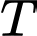 là bội chung nhỏ nhất của
là bội chung nhỏ nhất của 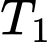 và
và 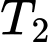 . Đáp án: A
. Đáp án: A
Câu 23 [523496]: Tìm chu kì 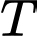 của hàm số
của hàm số 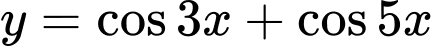 .
.
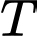 của hàm số
của hàm số 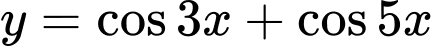 .
. A, 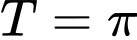 .
.
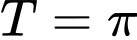 .
.B, 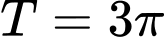 .
.
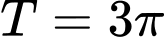 .
.C, 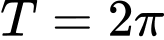 .
.
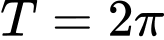 .
.D, 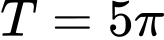 .
.
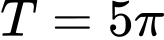 .
.
Chọn C
Hàm số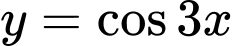 tuần hoàn với chu kì
tuần hoàn với chu kì 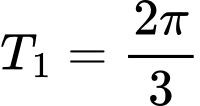 .
.
Hàm số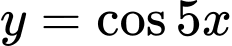 tuần hoàn với chu kì
tuần hoàn với chu kì 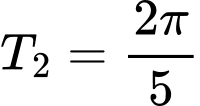 .
.
Suy ra hàm số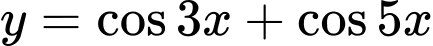 tuần hoàn với chu kì
tuần hoàn với chu kì 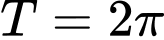 . Đáp án: C
. Đáp án: C
Hàm số
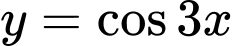 tuần hoàn với chu kì
tuần hoàn với chu kì 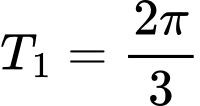 .
.Hàm số
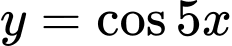 tuần hoàn với chu kì
tuần hoàn với chu kì 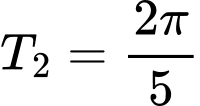 .
.Suy ra hàm số
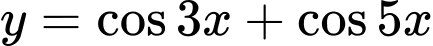 tuần hoàn với chu kì
tuần hoàn với chu kì 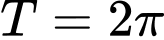 . Đáp án: C
. Đáp án: C
Câu 24 [802256]: Hình nào dưới đây biểu diễn đồ thị hàm số 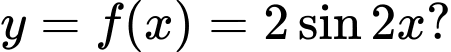
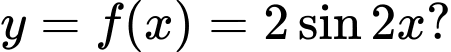
A, 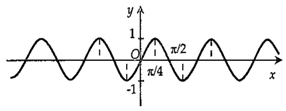

B, 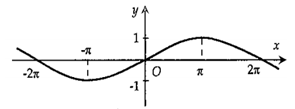

C, 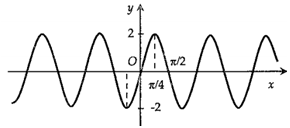

D, 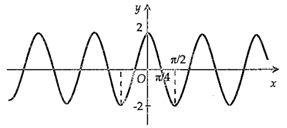

Chọn C.
Ta thấy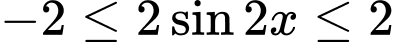 nên ta có loại A và B.
nên ta có loại A và B.
Tiếp theo với C và D ta có:
Từ phần lý thuyết ở trên ta có hàm số tuần hoàn với chu kì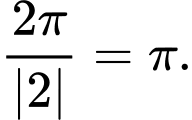
Ta thấy với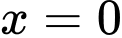 thì
thì 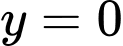 nên đồ thị hàm số đi qua gốc tọa độ. Từ đây ta chọn đáp án C.
Đáp án: C
nên đồ thị hàm số đi qua gốc tọa độ. Từ đây ta chọn đáp án C.
Đáp án: C
Ta thấy
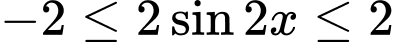 nên ta có loại A và B.
nên ta có loại A và B. Tiếp theo với C và D ta có:
Từ phần lý thuyết ở trên ta có hàm số tuần hoàn với chu kì
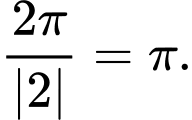
Ta thấy với
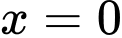 thì
thì 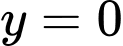 nên đồ thị hàm số đi qua gốc tọa độ. Từ đây ta chọn đáp án C.
Đáp án: C
nên đồ thị hàm số đi qua gốc tọa độ. Từ đây ta chọn đáp án C.
Đáp án: C
Câu 25 [802257]: Hình vẽ nào sau đây biểu diễn đồ thị hàm số 

A, 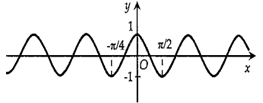

B, 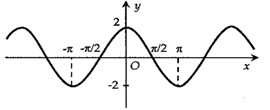

C, 

D, 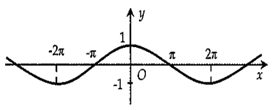

Chọn D
Ta thấy nên ta loại B.
nên ta loại B.
Tiếp theo ta có hàm số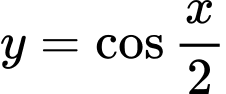 có chu kì tuần hoàn là
có chu kì tuần hoàn là 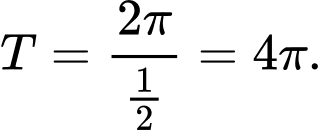
Ta thấy với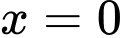 thì
thì 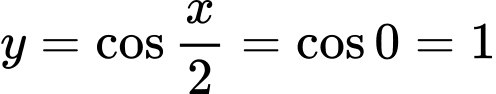 nên ta chọn D.
Đáp án: D
nên ta chọn D.
Đáp án: D
Ta thấy
 nên ta loại B.
nên ta loại B. Tiếp theo ta có hàm số
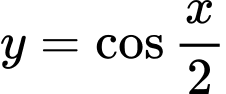 có chu kì tuần hoàn là
có chu kì tuần hoàn là 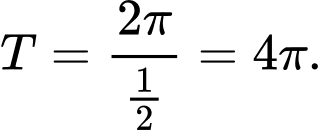
Ta thấy với
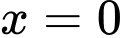 thì
thì 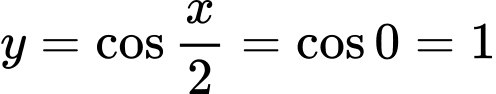 nên ta chọn D.
Đáp án: D
nên ta chọn D.
Đáp án: D
Câu 26 [581240]: Giả sử khi một cơn sóng biển đi qua một cái cọc ở ngoài khơi, chiều cao của nước được mô hình hóa bởi hàm số 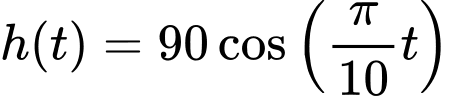 , trong đó
, trong đó  là độ cao tính bằng centimét trên mực nước biển trung bình tại thời điểm
là độ cao tính bằng centimét trên mực nước biển trung bình tại thời điểm  giây. Chiều cao của sóng la bao nhiêu cm, tức là khoảng cách theo phương thẳng đứng giữa đáy và đỉnh của sóng.
giây. Chiều cao của sóng la bao nhiêu cm, tức là khoảng cách theo phương thẳng đứng giữa đáy và đỉnh của sóng.
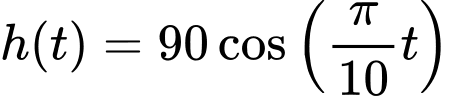 , trong đó
, trong đó 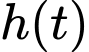 là độ cao tính bằng centimét trên mực nước biển trung bình tại thời điểm
là độ cao tính bằng centimét trên mực nước biển trung bình tại thời điểm 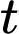 giây. Chiều cao của sóng la bao nhiêu cm, tức là khoảng cách theo phương thẳng đứng giữa đáy và đỉnh của sóng.
giây. Chiều cao của sóng la bao nhiêu cm, tức là khoảng cách theo phương thẳng đứng giữa đáy và đỉnh của sóng.
Chiều cao của sóng là: 2.90 = 180(cm).
Câu 27 [581241]: Huyết áp được tạo ra do lực co bóp của cơ tim và sức cản của thành động mạch. Mỗi lần tim đập, huyết áp của chúng ta tăng rồi giảm giữa các nhịp. Huyết áp tối đa và huyết áp tối thiểu được gọi tương ứng là huyết áp tâm thu và tâm trương. Chỉ số huyết áp của chúng được viết là huyết áp tâm thu, huyết áp tâm trương. Chỉ số huyết áp 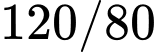 là huyết áp bình thường. Giả sử huyết áp của một người nào đó được mô hình hóa bởi hàm số:
là huyết áp bình thường. Giả sử huyết áp của một người nào đó được mô hình hóa bởi hàm số: 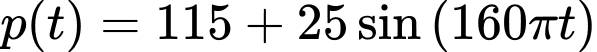 ,
,
Trong đó,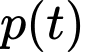 là huyết áp tính theo đơn vị mmHg (milimét thủy ngân) và thời gian
là huyết áp tính theo đơn vị mmHg (milimét thủy ngân) và thời gian 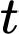 tính theo phút. Tìm số nhịp tim một phút.
tính theo phút. Tìm số nhịp tim một phút.
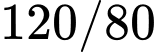 là huyết áp bình thường. Giả sử huyết áp của một người nào đó được mô hình hóa bởi hàm số:
là huyết áp bình thường. Giả sử huyết áp của một người nào đó được mô hình hóa bởi hàm số: 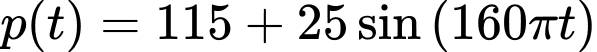 ,
,
Trong đó,
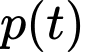 là huyết áp tính theo đơn vị mmHg (milimét thủy ngân) và thời gian
là huyết áp tính theo đơn vị mmHg (milimét thủy ngân) và thời gian 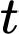 tính theo phút. Tìm số nhịp tim một phút.
tính theo phút. Tìm số nhịp tim một phút.
Chu kì của hàm số 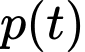 là:
là: 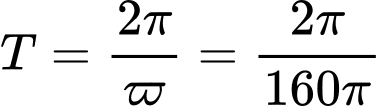
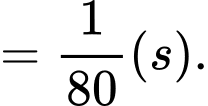
Số nhịp tim mỗi phút là: 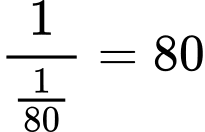 (nhịp).
(nhịp).
Câu 28 [802243]: (THPT CHUYÊN QUANG TRUNG - BP - LẦN1 - 2018) Tập giá trị của hàm số 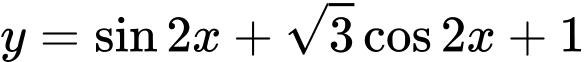 là đoạn
là đoạn 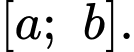 Tính tổng
Tính tổng 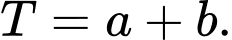
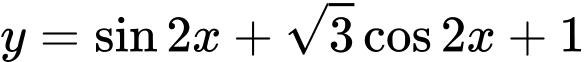 là đoạn
là đoạn 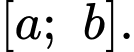 Tính tổng
Tính tổng 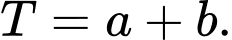
A, 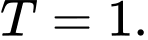
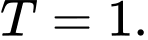
B, 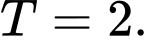
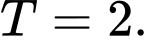
C, 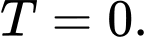
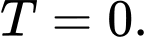
D, 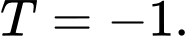
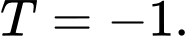
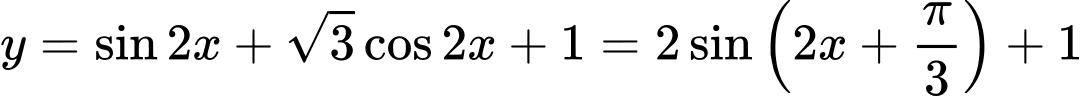
Do
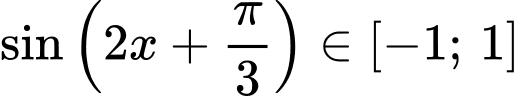 nên
nên 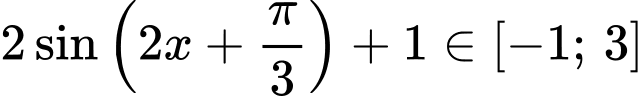 .
.Vậy
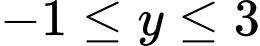 .( Ta thấy
.( Ta thấy 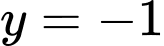 khi
khi 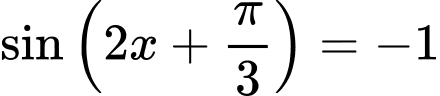 ,
,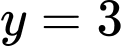 khi
khi 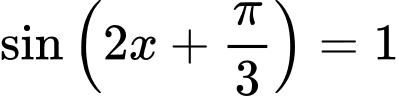 ). Đáp án: B
). Đáp án: B
Câu 29 [802246]: Gọi 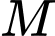 và
và 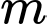 lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số
lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số 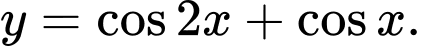 Khi đó
Khi đó  bằng bao nhiêu?
bằng bao nhiêu?
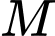 và
và 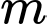 lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số
lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số 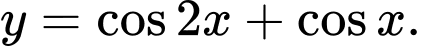 Khi đó
Khi đó  bằng bao nhiêu?
bằng bao nhiêu? A, 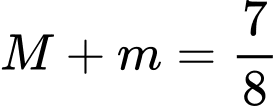 .
.
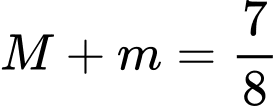 .
.B, 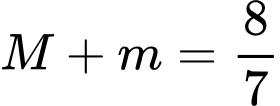 .
.
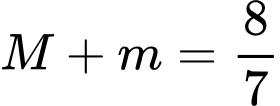 .
.C, 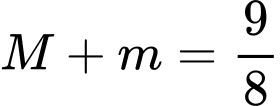 .
.
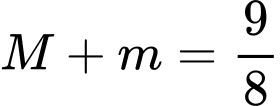 .
.D, 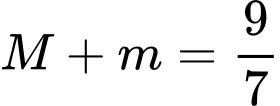 .
.
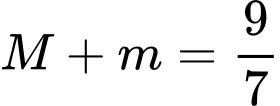 .
.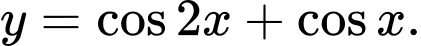 TXĐ: .
TXĐ: .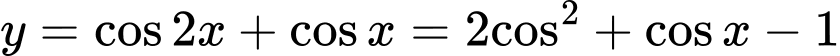 .
.Đặt:
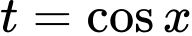 ,
,  .
.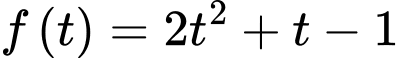 .
.Đồ thị của hàm số
 là parabol có đỉnh
là parabol có đỉnh 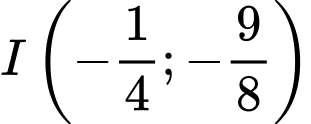 .
.BBT:
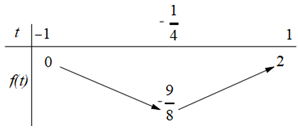
Dựa vào BBT ta có:
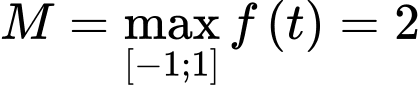 ,
, 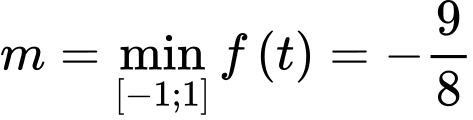 .
.Vậy
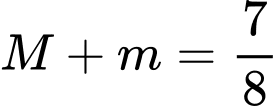 .
.Đáp án: A
Câu 30 [581242]: Tìm giá trị nhỏ nhất của biểu thức: 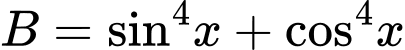
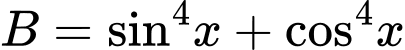
Ta có 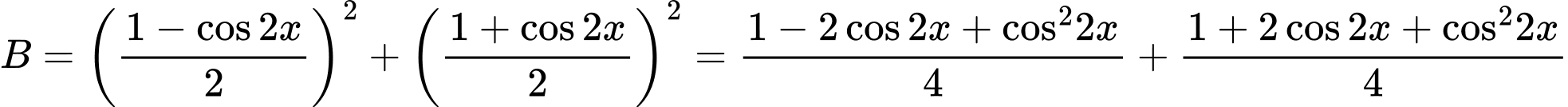
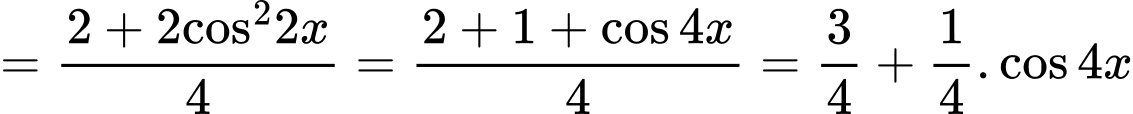
Vì 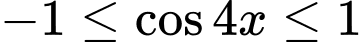 nên
nên 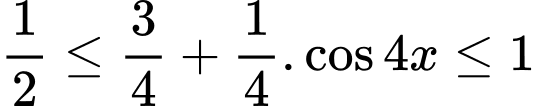 suy ra
suy ra 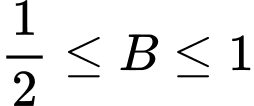 .
.