Đáp án Bài tập tự luyện
Câu 1 [185130]: Cho hàm số 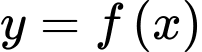 có bảng biến thiên như sau:
có bảng biến thiên như sau:
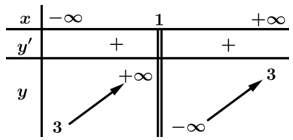
Tiệm cận đứng của đồ thị hàm số đã cho có phương trình là
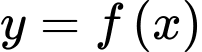 có bảng biến thiên như sau:
có bảng biến thiên như sau:
Tiệm cận đứng của đồ thị hàm số đã cho có phương trình là
A, 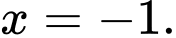
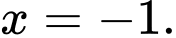
B, 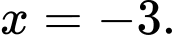
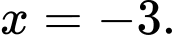
C, 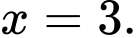
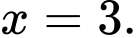
D, 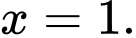
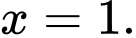
Từ đồ thị ta thấy 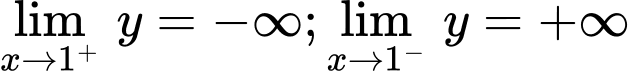
Vậy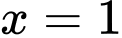 là tiệm cận đứng của đồ thị hàm số. Đáp án: D
là tiệm cận đứng của đồ thị hàm số. Đáp án: D
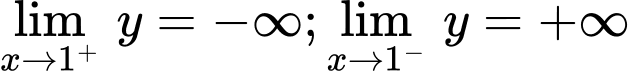
Vậy
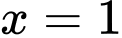 là tiệm cận đứng của đồ thị hàm số. Đáp án: D
là tiệm cận đứng của đồ thị hàm số. Đáp án: D
Câu 2 [522403]: Cho hàm số 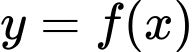 liên tục trên
liên tục trên 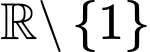 có bảng biến thiên như hình vẽ. Tổng số đường tiệm cận đứng và đường tiệm cận ngang của đồ thị hàm số
có bảng biến thiên như hình vẽ. Tổng số đường tiệm cận đứng và đường tiệm cận ngang của đồ thị hàm số 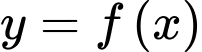 là
là
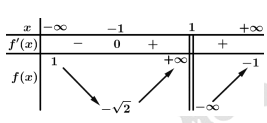
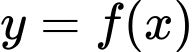 liên tục trên
liên tục trên 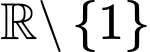 có bảng biến thiên như hình vẽ. Tổng số đường tiệm cận đứng và đường tiệm cận ngang của đồ thị hàm số
có bảng biến thiên như hình vẽ. Tổng số đường tiệm cận đứng và đường tiệm cận ngang của đồ thị hàm số 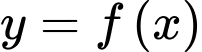 là
là
A, 1.
B, 4.
C, 2.
D, 3.
Lời giải: Ta có: 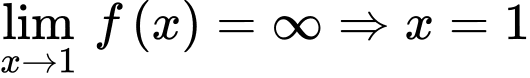 là tiệm cận đứng của đồ thị hàm số.
là tiệm cận đứng của đồ thị hàm số.
Lại có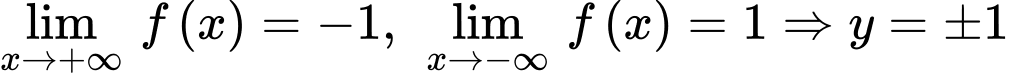 là tiệm cận ngang của đồ thị hàm số.
là tiệm cận ngang của đồ thị hàm số.
Do đó đồ thị hàm số có 3 đường tiệm cận. Chọn D. Đáp án: D
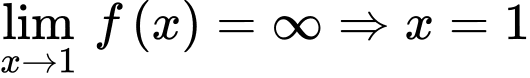 là tiệm cận đứng của đồ thị hàm số.
là tiệm cận đứng của đồ thị hàm số.Lại có
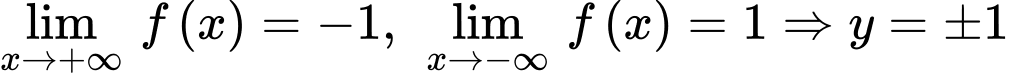 là tiệm cận ngang của đồ thị hàm số.
là tiệm cận ngang của đồ thị hàm số.Do đó đồ thị hàm số có 3 đường tiệm cận. Chọn D. Đáp án: D
Câu 3 [46009]: Cho hàm số 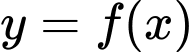 có bảng biến thiên như sau:
có bảng biến thiên như sau:
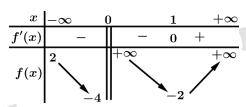
Tổng số tiệm cận đứng và tiệm cận ngang của đồ thị hàm số đã cho là
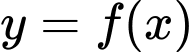 có bảng biến thiên như sau:
có bảng biến thiên như sau:
Tổng số tiệm cận đứng và tiệm cận ngang của đồ thị hàm số đã cho là
A, 4.
B, 1.
C, 3.
D, 2.
Ta có 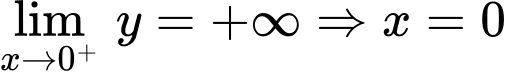 là tiệm cận đứng của đồ thị hàm số.
là tiệm cận đứng của đồ thị hàm số.
Từ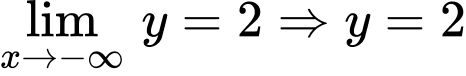 là tiệm cận ngang của đồ thị hàm số.
là tiệm cận ngang của đồ thị hàm số.
Tổng số tiệm cận đứng và tiệm cận ngang của đồ thị hàm số đã cho là 2. Chọn D. Đáp án: D
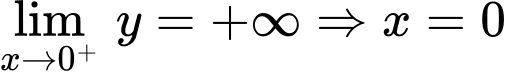 là tiệm cận đứng của đồ thị hàm số.
là tiệm cận đứng của đồ thị hàm số.Từ
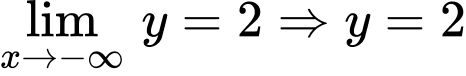 là tiệm cận ngang của đồ thị hàm số.
là tiệm cận ngang của đồ thị hàm số. Tổng số tiệm cận đứng và tiệm cận ngang của đồ thị hàm số đã cho là 2. Chọn D. Đáp án: D
Câu 4 [522398]: Cho hàm số 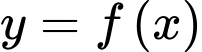 có bảng biến thiên như sau:
có bảng biến thiên như sau:
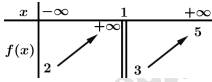
Tổng số tiệm cận ngang và số tiệm cận đứng của đồ thị hàm số đã cho là
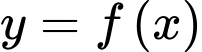 có bảng biến thiên như sau:
có bảng biến thiên như sau:
Tổng số tiệm cận ngang và số tiệm cận đứng của đồ thị hàm số đã cho là
A, 4.
B, 1.
C, 3.
D, 2.
Ta có 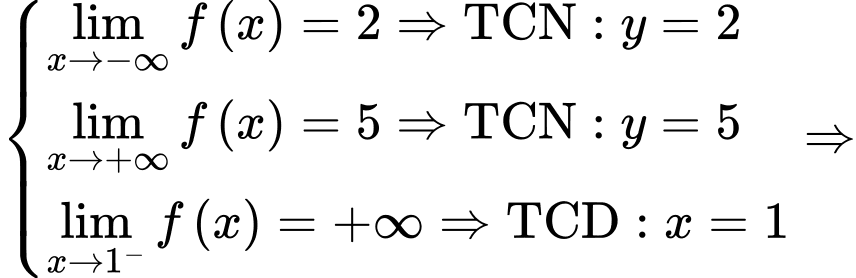 Chọn C.
Đáp án: C
Chọn C.
Đáp án: C
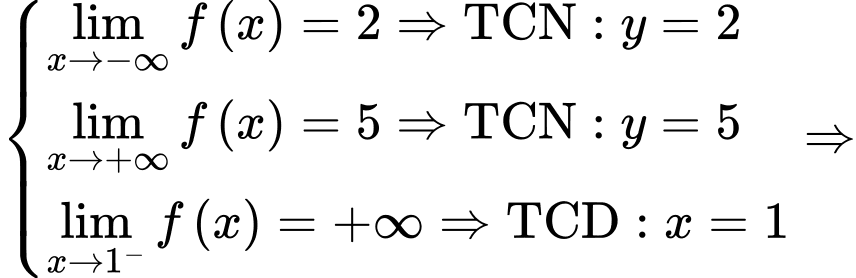 Chọn C.
Đáp án: C
Chọn C.
Đáp án: C
Câu 5 [522400]: Cho hàm số 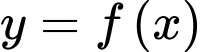 có bảng biến thiên như hình vẽ dưới đây. Hỏi đồ thị của hàm số đã cho có bao nhiêu đường tiệm cận?
có bảng biến thiên như hình vẽ dưới đây. Hỏi đồ thị của hàm số đã cho có bao nhiêu đường tiệm cận?
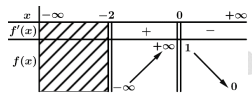
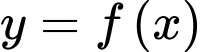 có bảng biến thiên như hình vẽ dưới đây. Hỏi đồ thị của hàm số đã cho có bao nhiêu đường tiệm cận?
có bảng biến thiên như hình vẽ dưới đây. Hỏi đồ thị của hàm số đã cho có bao nhiêu đường tiệm cận?
A, 1.
B, 3.
C, 2.
D, 4.
Lời giải: Dựa vào bảng biến thiên ta có: 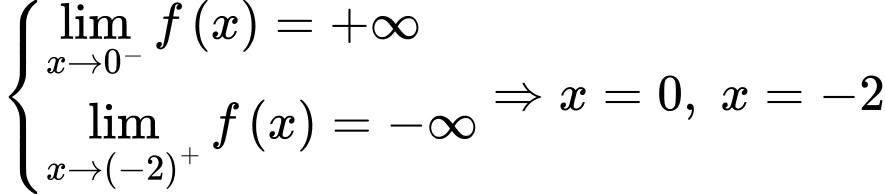 là tiệm cận đứng của đồ thị hàm số. Mặt khác:
là tiệm cận đứng của đồ thị hàm số. Mặt khác: 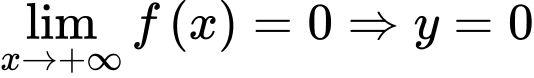 là tiệm cận ngang của đồ thị hàm số.
là tiệm cận ngang của đồ thị hàm số.
Vậy đồ thị đã cho có 3 tiệm cận. Chọn B. Đáp án: B
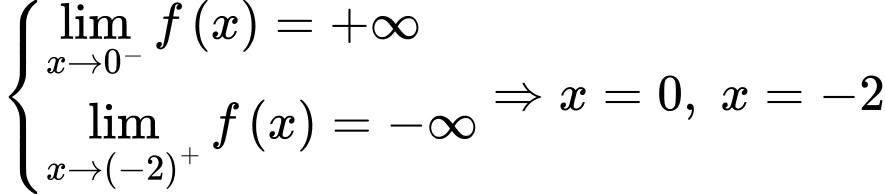 là tiệm cận đứng của đồ thị hàm số. Mặt khác:
là tiệm cận đứng của đồ thị hàm số. Mặt khác: 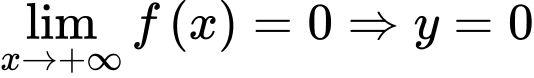 là tiệm cận ngang của đồ thị hàm số.
là tiệm cận ngang của đồ thị hàm số.Vậy đồ thị đã cho có 3 tiệm cận. Chọn B. Đáp án: B
Câu 6 [339512]: Cho hàm số 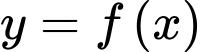 có bảng biến thiên như sau:
có bảng biến thiên như sau:
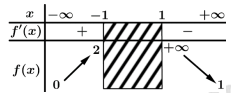
Tổng số đường tiệm cận đứng và đường tiệm cận ngang của đồ thị hàm số đã cho là
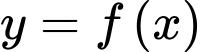 có bảng biến thiên như sau:
có bảng biến thiên như sau:
Tổng số đường tiệm cận đứng và đường tiệm cận ngang của đồ thị hàm số đã cho là
A, 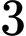 .
.
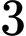 .
.B, 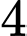 .
.
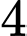 .
.C, 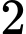 .
.
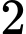 .
.D, 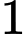 .
.
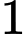 .
.
Chọn A
Dựa vào hình vẽ bảng biến thiên hàm số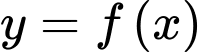 ta thấy
ta thấy
+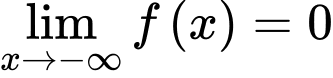 suy ra đường thẳng
suy ra đường thẳng 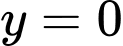 là một tiệm cận ngang của đồ thị hàm số
là một tiệm cận ngang của đồ thị hàm số 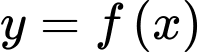 .
.
+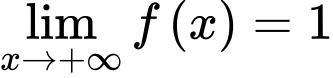 suy ra đường thẳng
suy ra đường thẳng 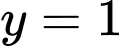 là một tiệm cận ngang của đồ thị hàm số
là một tiệm cận ngang của đồ thị hàm số 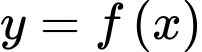 .
.
+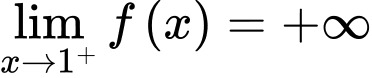 suy ra đường thẳng
suy ra đường thẳng 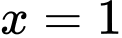 là một tiệm cận đứng của đồ thị hàm số
là một tiệm cận đứng của đồ thị hàm số 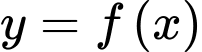 .
.
+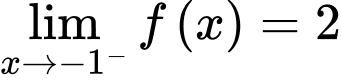 suy ra đường thẳng
suy ra đường thẳng 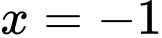 không là tiệm cận đứng của đồ thị hàm số
không là tiệm cận đứng của đồ thị hàm số 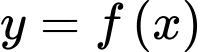 .
.
Vậy tổng số đường tiệm cận đứng và đường tiệm cận ngang của đồ thị hàm số đã cho là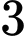 . Đáp án: A
. Đáp án: A
Dựa vào hình vẽ bảng biến thiên hàm số
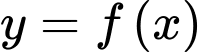 ta thấy
ta thấy+
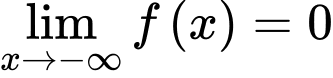 suy ra đường thẳng
suy ra đường thẳng 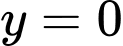 là một tiệm cận ngang của đồ thị hàm số
là một tiệm cận ngang của đồ thị hàm số 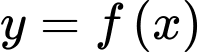 .
.+
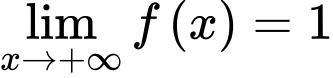 suy ra đường thẳng
suy ra đường thẳng 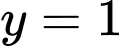 là một tiệm cận ngang của đồ thị hàm số
là một tiệm cận ngang của đồ thị hàm số 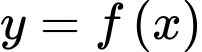 .
.+
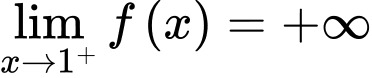 suy ra đường thẳng
suy ra đường thẳng 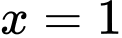 là một tiệm cận đứng của đồ thị hàm số
là một tiệm cận đứng của đồ thị hàm số 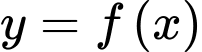 .
.+
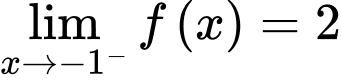 suy ra đường thẳng
suy ra đường thẳng 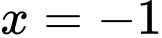 không là tiệm cận đứng của đồ thị hàm số
không là tiệm cận đứng của đồ thị hàm số 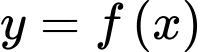 .
.Vậy tổng số đường tiệm cận đứng và đường tiệm cận ngang của đồ thị hàm số đã cho là
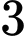 . Đáp án: A
. Đáp án: A
Câu 7 [378481]: Cho hàm số 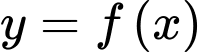 thoả mãn:
thoả mãn: 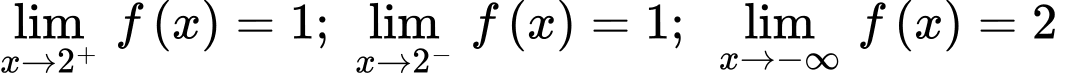 và
và 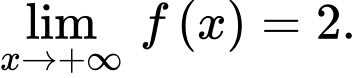 Khẳng định nào sau đây là đúng?
Khẳng định nào sau đây là đúng?
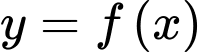 thoả mãn:
thoả mãn: 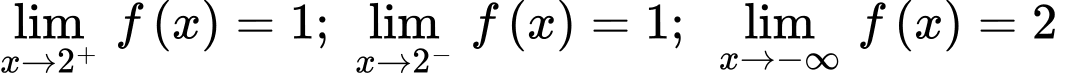 và
và 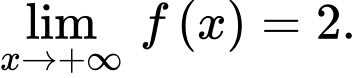 Khẳng định nào sau đây là đúng?
Khẳng định nào sau đây là đúng? A, Đường thẳng 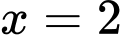 là tiệm cận đứng của đồ thị hàm số.
là tiệm cận đứng của đồ thị hàm số.
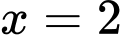 là tiệm cận đứng của đồ thị hàm số.
là tiệm cận đứng của đồ thị hàm số.B, Đường thẳng 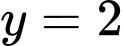 là tiệm cận ngang của đồ thị hàm số.
là tiệm cận ngang của đồ thị hàm số.
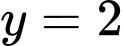 là tiệm cận ngang của đồ thị hàm số.
là tiệm cận ngang của đồ thị hàm số.C, Đường thẳng 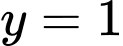 là tiệm cận ngang của đồ thị hàm số.
là tiệm cận ngang của đồ thị hàm số.
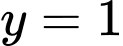 là tiệm cận ngang của đồ thị hàm số.
là tiệm cận ngang của đồ thị hàm số.D, Đường thẳng 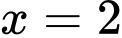 là tiệm cận ngang của đồ thị hàm số.
là tiệm cận ngang của đồ thị hàm số.
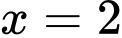 là tiệm cận ngang của đồ thị hàm số.
là tiệm cận ngang của đồ thị hàm số.
Từ đồ thị ta thấy 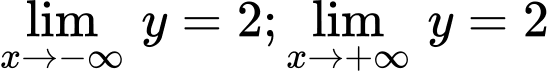
Vậy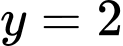 là tiệm cận ngang của đồ thị hàm số. Đáp án: B
là tiệm cận ngang của đồ thị hàm số. Đáp án: B
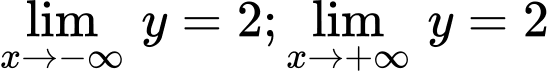
Vậy
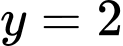 là tiệm cận ngang của đồ thị hàm số. Đáp án: B
là tiệm cận ngang của đồ thị hàm số. Đáp án: B
Câu 8 [378483]: Cho hàm số 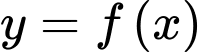 xác định trên
xác định trên 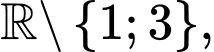 liên tục trên mỗi khoảng xác định và có bảng biến thiên như sau:
liên tục trên mỗi khoảng xác định và có bảng biến thiên như sau: 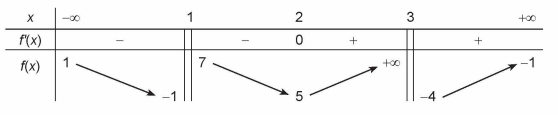
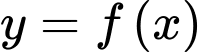 xác định trên
xác định trên 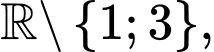 liên tục trên mỗi khoảng xác định và có bảng biến thiên như sau:
liên tục trên mỗi khoảng xác định và có bảng biến thiên như sau: 
Khẳng định nào sau đây là sai?
A, Đường thẳng 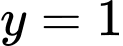 là tiệm cận ngang của đồ thị hàm số đã cho.
là tiệm cận ngang của đồ thị hàm số đã cho.
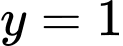 là tiệm cận ngang của đồ thị hàm số đã cho.
là tiệm cận ngang của đồ thị hàm số đã cho.B, Đường thẳng 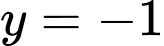 là tiệm cận ngang của đồ thị hàm số đã cho.
là tiệm cận ngang của đồ thị hàm số đã cho.
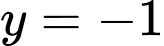 là tiệm cận ngang của đồ thị hàm số đã cho.
là tiệm cận ngang của đồ thị hàm số đã cho.C, Đường thẳng 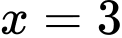 là tiệm cận đứng của đồ thị hàm số đã cho.
là tiệm cận đứng của đồ thị hàm số đã cho.
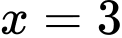 là tiệm cận đứng của đồ thị hàm số đã cho.
là tiệm cận đứng của đồ thị hàm số đã cho.D, Đường thẳng 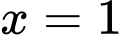 là tiệm cận đứng của đồ thị hàm số đã cho.
là tiệm cận đứng của đồ thị hàm số đã cho.
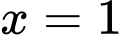 là tiệm cận đứng của đồ thị hàm số đã cho.
là tiệm cận đứng của đồ thị hàm số đã cho.
Từ đồ thị ta thấy 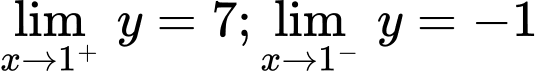
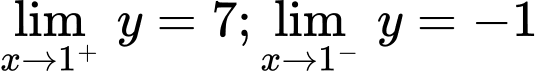
Vậy 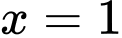 không là tiệm cận đứng của đồ thị hàm số.
không là tiệm cận đứng của đồ thị hàm số.
Đáp án: D 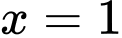 không là tiệm cận đứng của đồ thị hàm số.
không là tiệm cận đứng của đồ thị hàm số.
Câu 9 [501907]: Cho hàm số 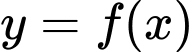 có bảng biến thiên như hình vẽ dưới đây.
có bảng biến thiên như hình vẽ dưới đây.
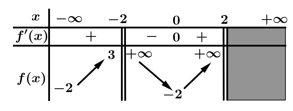
Tổng số đường tiệm cận đứng và tiệm cận ngang là
 có bảng biến thiên như hình vẽ dưới đây.
có bảng biến thiên như hình vẽ dưới đây. 
Tổng số đường tiệm cận đứng và tiệm cận ngang là
A,
B,
C,
D,
Tập xác định của hàm số : 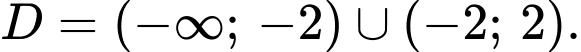
Ta có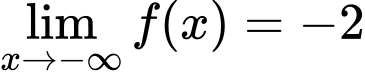
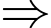 Đường thẳng có phương trình:
Đường thẳng có phương trình: 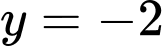 là tiệm cận ngang.
là tiệm cận ngang.
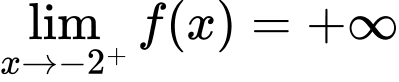
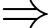 Đường thẳng có phương trình:
Đường thẳng có phương trình: 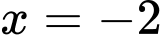 là tiệm cận đứng.
là tiệm cận đứng.
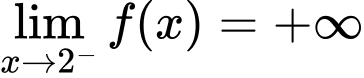
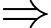 Đường thẳng có phương trình:
Đường thẳng có phương trình: 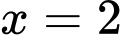 là tiệm cận đứng.
là tiệm cận đứng.
Vậy đồ thị hàm số có 3 đường tiệm cận. Đáp án: D
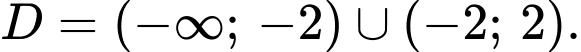
Ta có
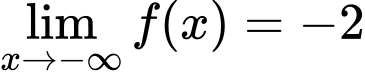
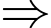 Đường thẳng có phương trình:
Đường thẳng có phương trình: 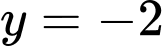 là tiệm cận ngang.
là tiệm cận ngang.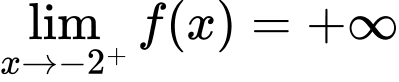
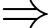 Đường thẳng có phương trình:
Đường thẳng có phương trình: 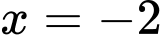 là tiệm cận đứng.
là tiệm cận đứng.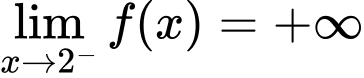
 Đường thẳng có phương trình:
Đường thẳng có phương trình: 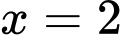 là tiệm cận đứng.
là tiệm cận đứng.Vậy đồ thị hàm số có 3 đường tiệm cận. Đáp án: D
Câu 10 [185161]: Tiệm cận đứng của đồ thị hàm số 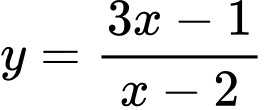 có phương trình là
có phương trình là
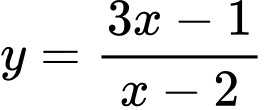 có phương trình là
có phương trình là A, 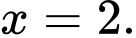
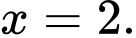
B, 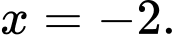
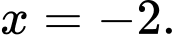
C, 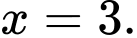
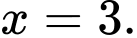
D, 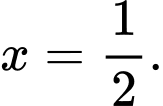
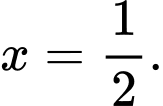
Ta có 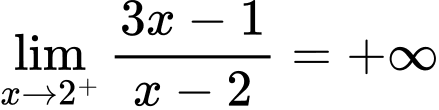 và
và 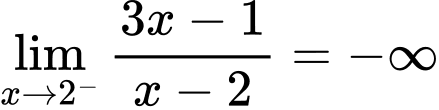 nên tiệm cận đứng của đồ thị hàm số
nên tiệm cận đứng của đồ thị hàm số 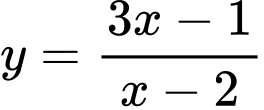 có phương trình là
có phương trình là 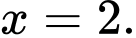 Đáp án: A
Đáp án: A
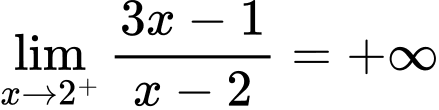 và
và 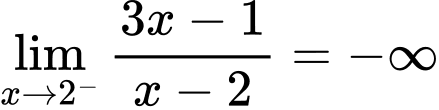 nên tiệm cận đứng của đồ thị hàm số
nên tiệm cận đứng của đồ thị hàm số 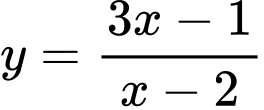 có phương trình là
có phương trình là 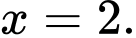 Đáp án: A
Đáp án: A
Câu 11 [975578]: Phương trình đường tiệm cận ngang của đồ thị hàm số 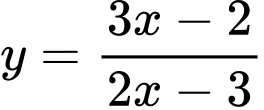 là
là
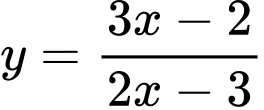 là
là A, 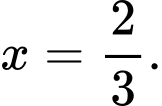
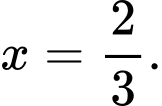
B, 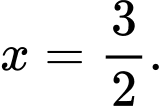
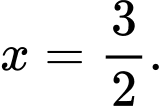
C, 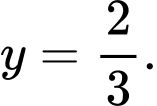
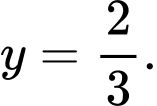
D, 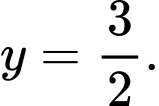
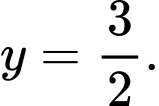
HD: Đồ thị hàm số 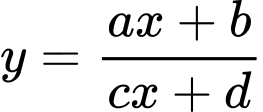 có tiệm cận ngang là
có tiệm cận ngang là 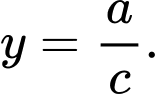 Chọn D. Đáp án: D
Chọn D. Đáp án: D
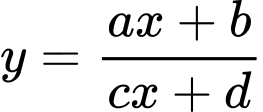 có tiệm cận ngang là
có tiệm cận ngang là 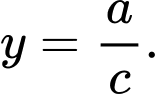 Chọn D. Đáp án: D
Chọn D. Đáp án: D
Câu 12 [801837]: Tiệm cận ngang của đồ thị hàm số 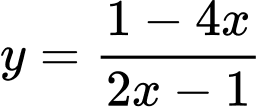 .
.
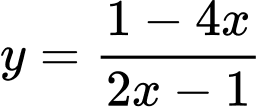 .
. A, 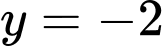 .
.
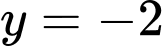 .
.B, 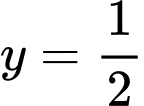 .
.
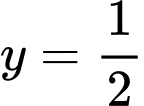 .
.C, 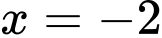 .
.
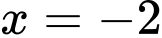 .
.D, 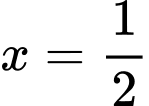 .
.
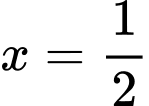 .
.
Chọn A
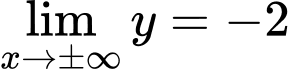
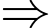 ĐTHS có TCN:
ĐTHS có TCN: 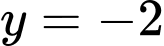 Đáp án: A
Đáp án: A
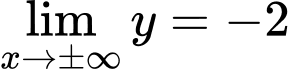
 ĐTHS có TCN:
ĐTHS có TCN: 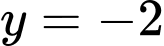 Đáp án: A
Đáp án: A
Câu 13 [382470]: Nếu trong một ngày, một xưởng sản xuất được 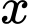 kilôgam sản phẩm thì chi phí trung bình (tính bằng nghìn đồng) cho một sản phẩm được cho bởi công thức:
kilôgam sản phẩm thì chi phí trung bình (tính bằng nghìn đồng) cho một sản phẩm được cho bởi công thức: 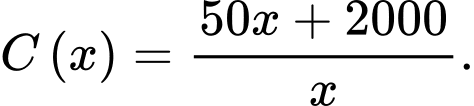 Tiệm cận ngang của đồ thị hàm số
Tiệm cận ngang của đồ thị hàm số  là:
là:
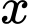 kilôgam sản phẩm thì chi phí trung bình (tính bằng nghìn đồng) cho một sản phẩm được cho bởi công thức:
kilôgam sản phẩm thì chi phí trung bình (tính bằng nghìn đồng) cho một sản phẩm được cho bởi công thức: 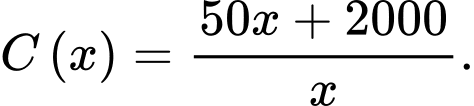 Tiệm cận ngang của đồ thị hàm số
Tiệm cận ngang của đồ thị hàm số  là:
là: A, 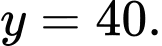
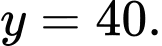
B, 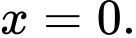
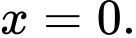
C, 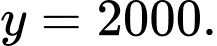
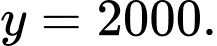
D, 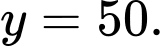
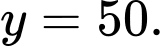
Ta có: 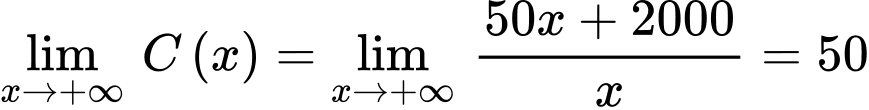
Vậy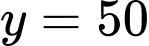 là tiệm cận ngang của đồ thị hàm số. Đáp án: D
là tiệm cận ngang của đồ thị hàm số. Đáp án: D
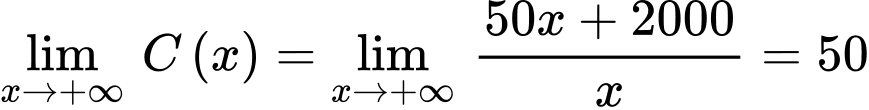
Vậy
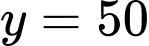 là tiệm cận ngang của đồ thị hàm số. Đáp án: D
là tiệm cận ngang của đồ thị hàm số. Đáp án: D
Câu 14 [382471]: Số lượng sản phẩm bán được của một công ty trong 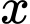 (tháng) được tính theo công thức
(tháng) được tính theo công thức 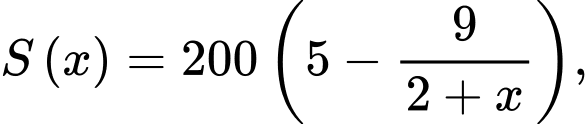 trong đó
trong đó 
(Nguồn: R. Larson and B. Edwards, Calculus 10e, Cengage 2014)
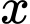 (tháng) được tính theo công thức
(tháng) được tính theo công thức 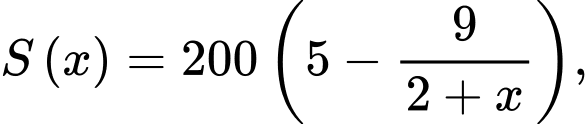 trong đó
trong đó 
(Nguồn: R. Larson and B. Edwards, Calculus 10e, Cengage 2014)
Xem 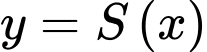 là một số hàm số xác định trên nửa khoảng
là một số hàm số xác định trên nửa khoảng 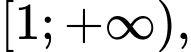 tiệm cận ngang của đồ thị của hàm số đó là
tiệm cận ngang của đồ thị của hàm số đó là
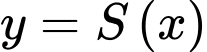 là một số hàm số xác định trên nửa khoảng
là một số hàm số xác định trên nửa khoảng 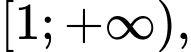 tiệm cận ngang của đồ thị của hàm số đó là
tiệm cận ngang của đồ thị của hàm số đó làA, 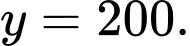
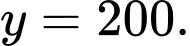
B, 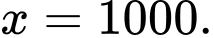
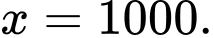
C, 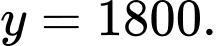
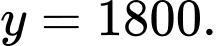
D, 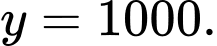
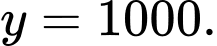
Ta có: 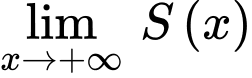
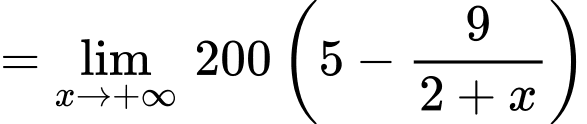
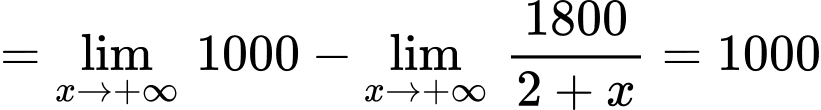
Vậy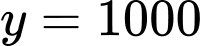 là tiệm cận ngang của đồ thị hàm số . Đáp án: D
là tiệm cận ngang của đồ thị hàm số . Đáp án: D
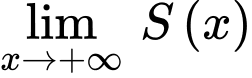
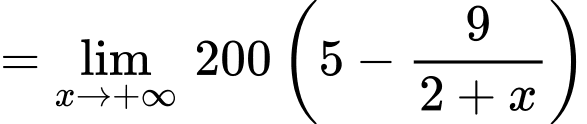
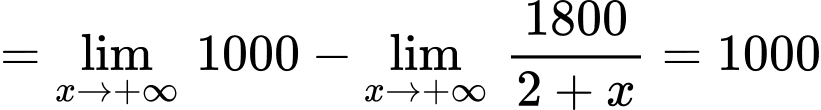
Vậy
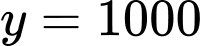 là tiệm cận ngang của đồ thị hàm số . Đáp án: D
là tiệm cận ngang của đồ thị hàm số . Đáp án: D
Câu 15 [31230]: Tìm giao điểm hai đường tiệm cận của đồ thị hàm số 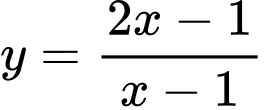 .
.
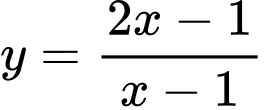 .
. A, 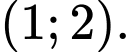
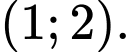
B, 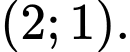
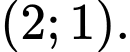
C, 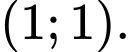
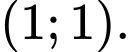
D, 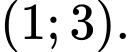
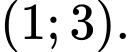
HD: ĐTHS có tiệm cận đứng 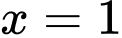 và tiệm cận ngang
và tiệm cận ngang 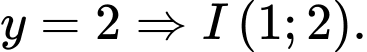 Chọn A Đáp án: A
Chọn A Đáp án: A
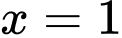 và tiệm cận ngang
và tiệm cận ngang 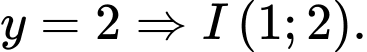 Chọn A Đáp án: A
Chọn A Đáp án: A
Câu 16 [306980]: Đường thẳng 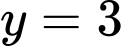 là tiệm cận ngang của đồ thị hàm số nào sau đây?
là tiệm cận ngang của đồ thị hàm số nào sau đây?
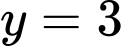 là tiệm cận ngang của đồ thị hàm số nào sau đây?
là tiệm cận ngang của đồ thị hàm số nào sau đây? A, 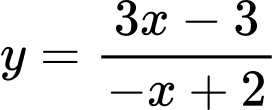 .
.
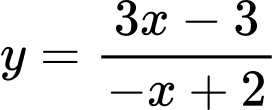 .
.B, 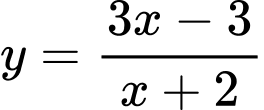 .
.
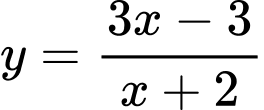 .
.C, 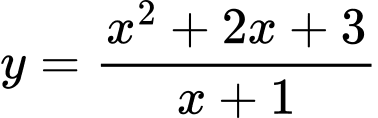 .
.
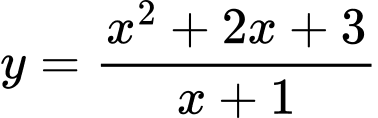 .
.D, 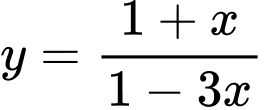 .
.
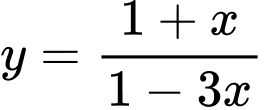 .
.
Chọn B
Ta có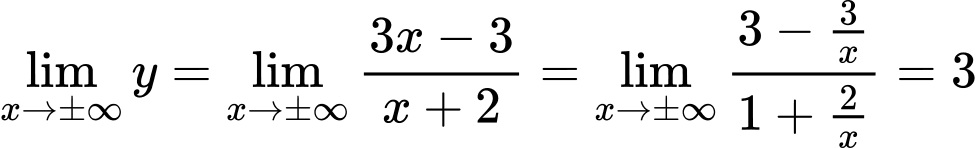 suy ra đường thẳng
suy ra đường thẳng 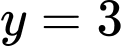 là tiệm cận ngang của đồ thị hàm số
là tiệm cận ngang của đồ thị hàm số 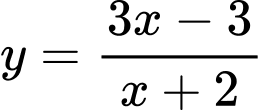 . Đáp án: B
. Đáp án: B
Ta có
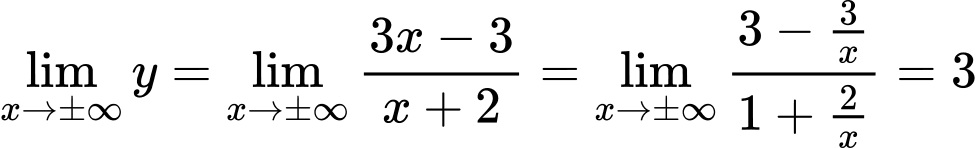 suy ra đường thẳng
suy ra đường thẳng 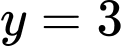 là tiệm cận ngang của đồ thị hàm số
là tiệm cận ngang của đồ thị hàm số 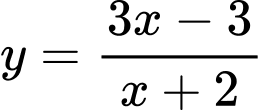 . Đáp án: B
. Đáp án: B
Câu 17 [382472]: Một đơn vị sản xuất hàng tiêu dùng ước tính chi phí để sản xuất 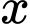 đơn vị sản phẩm là
đơn vị sản phẩm là 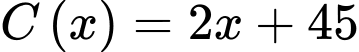 (triệu đồng). Khi đó, chi phí trung bình cho mỗi đơn vị sản phẩm là
(triệu đồng). Khi đó, chi phí trung bình cho mỗi đơn vị sản phẩm là 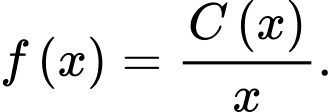 Nhận xét nào sau đây là đúng?
Nhận xét nào sau đây là đúng?
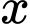 đơn vị sản phẩm là
đơn vị sản phẩm là 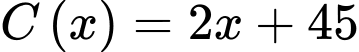 (triệu đồng). Khi đó, chi phí trung bình cho mỗi đơn vị sản phẩm là
(triệu đồng). Khi đó, chi phí trung bình cho mỗi đơn vị sản phẩm là 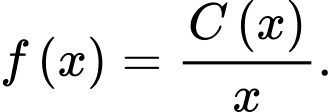 Nhận xét nào sau đây là đúng?
Nhận xét nào sau đây là đúng? A, Chi phí trung bình luôn tăng khi 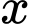 tăng dần.
tăng dần.
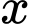 tăng dần.
tăng dần.B, Chi phí trung bình luôn giảm khi 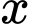 tăng dần và luôn lớn hơn 2 triệu đồng/sản phẩm.
tăng dần và luôn lớn hơn 2 triệu đồng/sản phẩm.
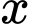 tăng dần và luôn lớn hơn 2 triệu đồng/sản phẩm.
tăng dần và luôn lớn hơn 2 triệu đồng/sản phẩm.C, Chi phí trung bình luôn giảm khi 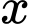 tăng dần và luôn nhỏ hơn 2 triệu đồng/sản phẩm.
tăng dần và luôn nhỏ hơn 2 triệu đồng/sản phẩm.
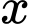 tăng dần và luôn nhỏ hơn 2 triệu đồng/sản phẩm.
tăng dần và luôn nhỏ hơn 2 triệu đồng/sản phẩm.D, Chi phí trung bình luôn giảm khi 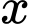 tăng dần và luôn nhỏ hơn 45 triệu đồng/sản phẩm.
tăng dần và luôn nhỏ hơn 45 triệu đồng/sản phẩm.
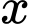 tăng dần và luôn nhỏ hơn 45 triệu đồng/sản phẩm.
tăng dần và luôn nhỏ hơn 45 triệu đồng/sản phẩm.
Ta có: 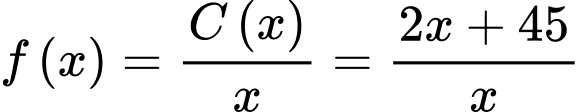
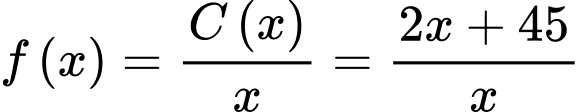
Có 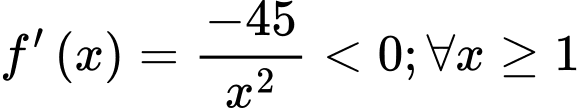 nên hàm số
nên hàm số 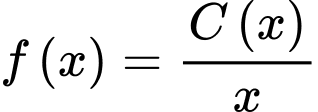 là hàm số giảm.
là hàm số giảm.
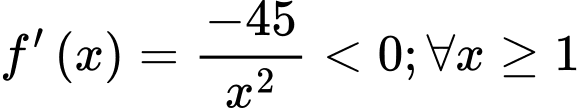 nên hàm số
nên hàm số 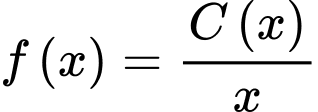 là hàm số giảm.
là hàm số giảm. Có 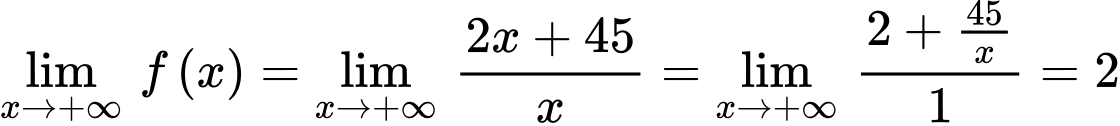
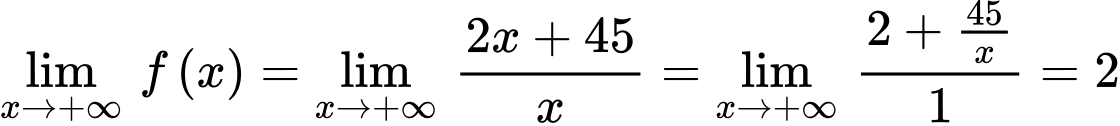
Do đó chi phí trung bình giảm theo x nhưng luôn lớn hơn 2 triệu đồng/sản phẩm.
Đáp án: B
Câu 18 [522404]: Tìm số tiệm cận đứng của đồ thị hàm số 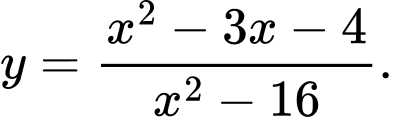
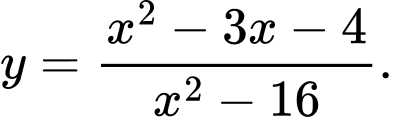
A, 2.
B, 3.
C, 0.
D, 1.
Lời giải: TXĐ: 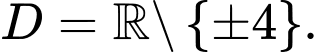 Khi đó:
Khi đó: 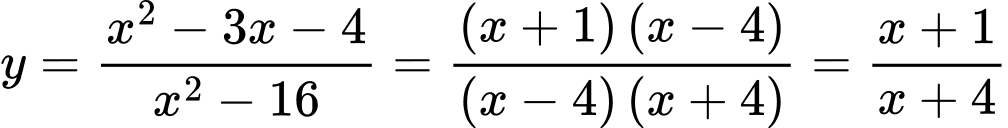
Suy ra đồ thị hàm số có một đường tiệm cận đứng là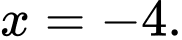 Chọn D.
Đáp án: D
Chọn D.
Đáp án: D
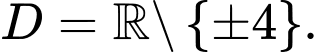 Khi đó:
Khi đó: 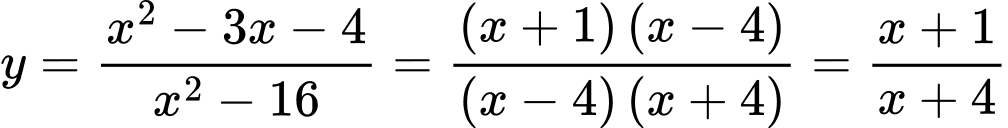
Suy ra đồ thị hàm số có một đường tiệm cận đứng là
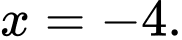 Chọn D.
Đáp án: D
Chọn D.
Đáp án: D
Câu 19 [358933]: Số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số 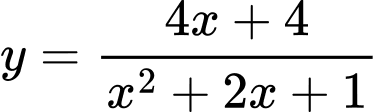 là:
là:
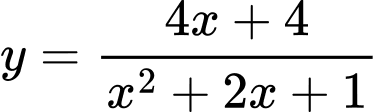 là:
là: A, 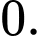
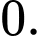
B, 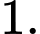
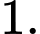
C, 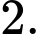
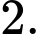
D, 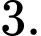
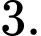
Ta có: 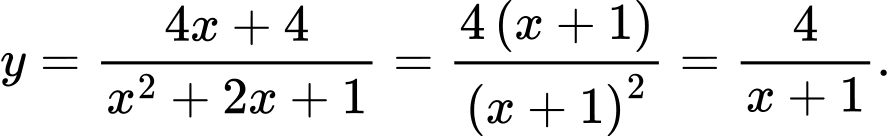
ĐKXĐ: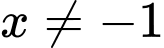
Do đó đồ thị hàm số có đường tiệm cận đứng là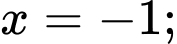 đường tiệm cận ngang là
đường tiệm cận ngang là 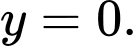
Vậy đồ thị hàm số đã cho có hai đường tiệm cận. Đáp án: C
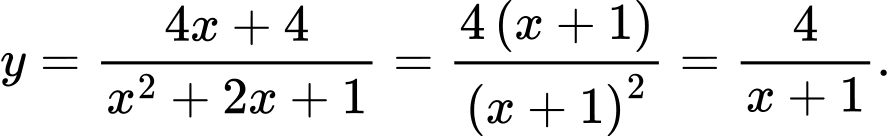
ĐKXĐ:
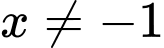
Do đó đồ thị hàm số có đường tiệm cận đứng là
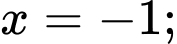 đường tiệm cận ngang là
đường tiệm cận ngang là 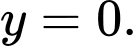
Vậy đồ thị hàm số đã cho có hai đường tiệm cận. Đáp án: C
Câu 20 [382474]: [Nguồn SGK Cùng Khám Phá] Tại một công ty sản xuất đồ chơi A, công ty phải chi 50 000 USD để thiết lập dây chuyền sản xuất ban đầu. Sau đó, cứ sản xuất được một sản phẩm đồ chơi A, công ty phải trả 5 USD cho nguyên liệu thô và nhân công. Gọi 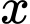 là số đồ chơi A mà công ty đã sản xuất và
là số đồ chơi A mà công ty đã sản xuất và 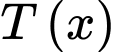 (đơn vị USD) là tổng số tiền bao gồm cả chi phí ban đầu mà công ty phải chi trả khi sản xuất x đồ chơi A. Người ta xác định chi phí trung bình cho mỗi sản phẩm đồ chơi A là
(đơn vị USD) là tổng số tiền bao gồm cả chi phí ban đầu mà công ty phải chi trả khi sản xuất x đồ chơi A. Người ta xác định chi phí trung bình cho mỗi sản phẩm đồ chơi A là 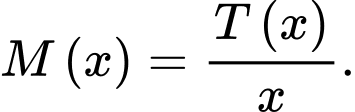 Xem
Xem 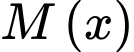 là hàm số theo
là hàm số theo 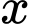 xác định trên nửa khoảng
xác định trên nửa khoảng 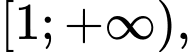 tiệm cận ngang của đồ thị hàm số này là:
tiệm cận ngang của đồ thị hàm số này là:
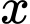 là số đồ chơi A mà công ty đã sản xuất và
là số đồ chơi A mà công ty đã sản xuất và 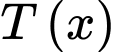 (đơn vị USD) là tổng số tiền bao gồm cả chi phí ban đầu mà công ty phải chi trả khi sản xuất x đồ chơi A. Người ta xác định chi phí trung bình cho mỗi sản phẩm đồ chơi A là
(đơn vị USD) là tổng số tiền bao gồm cả chi phí ban đầu mà công ty phải chi trả khi sản xuất x đồ chơi A. Người ta xác định chi phí trung bình cho mỗi sản phẩm đồ chơi A là 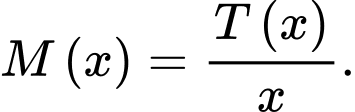 Xem
Xem 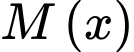 là hàm số theo
là hàm số theo 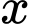 xác định trên nửa khoảng
xác định trên nửa khoảng 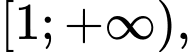 tiệm cận ngang của đồ thị hàm số này là:
tiệm cận ngang của đồ thị hàm số này là: A, 

B, 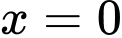
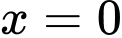
C, 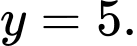
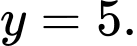
D, 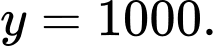
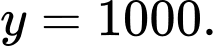
Ta có: 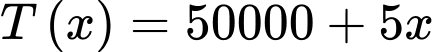 .
.
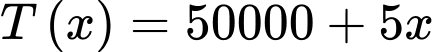 .
. Suy ra 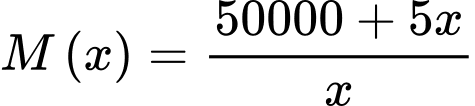 .
.
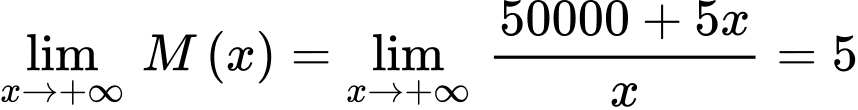
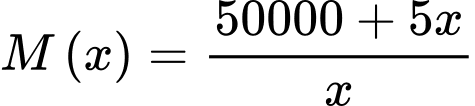 .
.
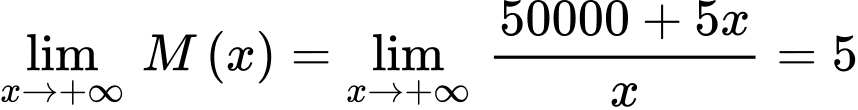
Vậy 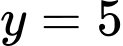 là tiệm cận ngang của đồ thị hàm số.
là tiệm cận ngang của đồ thị hàm số.
Đáp án: C 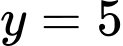 là tiệm cận ngang của đồ thị hàm số.
là tiệm cận ngang của đồ thị hàm số.
Câu 21 [31268]: Biết đồ thị hàm số $y = \frac{{\left( {4a - b} \right){x^2} + ax + 1}}{{{x^2} + ax + b - 12}}$ nhận trục hoành và trục tung làm hai tiệm cận thì giá trị $a + b$ bằng
A,
B,
C,
D,
Do đồ thị nhận trục hoành làm tiệm cận ngang mà $\underset{x\to +\infty }{\mathop{\lim }}\,y=4a-b=0\Rightarrow b=4a.$
Đáp án: D
Do đồ thị nhận trục tung làm tiệm cận đứng $\Rightarrow $ Biểu thức ${{x}^{2}}+ax+b-12$ nhận $x=0$ làm nghiệm $\Rightarrow b=12$ $\Rightarrow a=3$ $\Rightarrow a+b=15.$