Đáp án Bài tập tự luyện
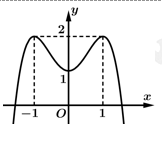
Câu 1 [677863]: Cho hàm số bậc bốn 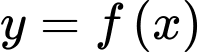 có đồ thị là đường cong trong hình bên. Số nghiệm thực của phương trình
có đồ thị là đường cong trong hình bên. Số nghiệm thực của phương trình 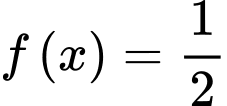 là
là
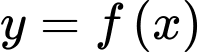 có đồ thị là đường cong trong hình bên. Số nghiệm thực của phương trình
có đồ thị là đường cong trong hình bên. Số nghiệm thực của phương trình 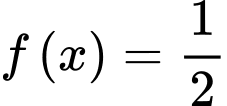 là
là 
A, 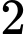 .
.
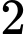 .
.B, 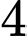 .
.
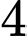 .
.C, 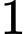 .
.
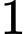 .
.D, 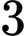 .
.
 .
.
Chọn A
Số nghiệm thực của phương trình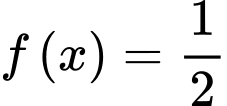 chính là số giao điểm của đồ thị hàm số
chính là số giao điểm của đồ thị hàm số 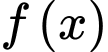 với đường thẳng
với đường thẳng 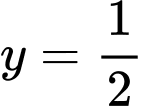
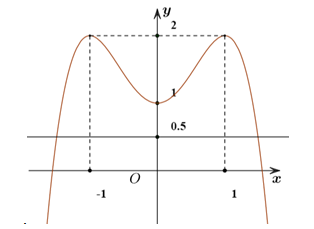
Dựa vào hình trên ta thấy đồ thị hàm số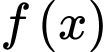 với đường thẳng
với đường thẳng 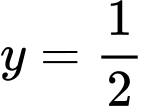 có 2 giao điểm.
có 2 giao điểm.
Vậy phương trình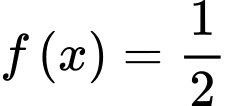 có hai nghiệm.
Đáp án: A
có hai nghiệm.
Đáp án: A
Số nghiệm thực của phương trình
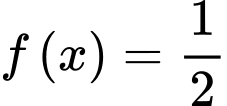 chính là số giao điểm của đồ thị hàm số
chính là số giao điểm của đồ thị hàm số 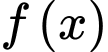 với đường thẳng
với đường thẳng 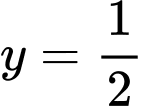

Dựa vào hình trên ta thấy đồ thị hàm số
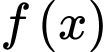 với đường thẳng
với đường thẳng 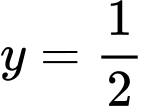 có 2 giao điểm.
có 2 giao điểm. Vậy phương trình
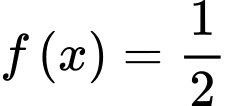 có hai nghiệm.
Đáp án: A
có hai nghiệm.
Đáp án: A
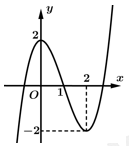
Câu 2 [185160]: Cho hàm số bậc ba 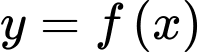 có đồ thị là đường cong trong hình bên. Số nghiệm thực của phương trình
có đồ thị là đường cong trong hình bên. Số nghiệm thực của phương trình 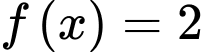 là
là
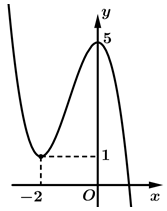
 có đồ thị là đường cong trong hình bên. Số nghiệm thực của phương trình
có đồ thị là đường cong trong hình bên. Số nghiệm thực của phương trình 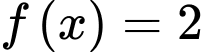 là
là
A, 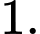
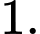
B, 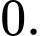
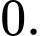
C, 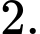
D, 
Số nghiệm của phương trình bằng số giao điểm của hai đồ thị.
Do số giao điểm của đồ thị hàm số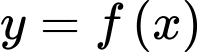 và đường thẳng
và đường thẳng 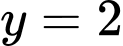 là 3 nên số nghiệm thực của phương trình
là 3 nên số nghiệm thực của phương trình 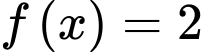 là 3.
Đáp án: D
là 3.
Đáp án: D
Do số giao điểm của đồ thị hàm số
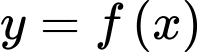 và đường thẳng
và đường thẳng 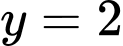 là 3 nên số nghiệm thực của phương trình
là 3 nên số nghiệm thực của phương trình 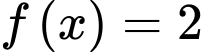 là 3.
Đáp án: D
là 3.
Đáp án: D
Câu 3 [132930]: Cho hàm số 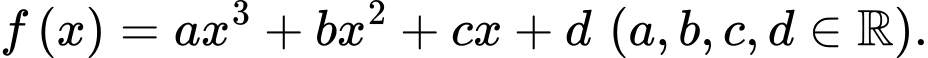 Đồ thị của hàm số
Đồ thị của hàm số  như hình vẽ bên. Số nghiệm thực của phương trình
như hình vẽ bên. Số nghiệm thực của phương trình  là
là
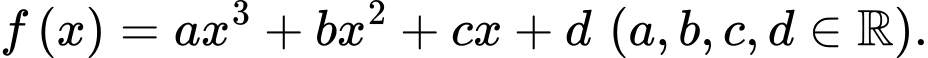 Đồ thị của hàm số
Đồ thị của hàm số 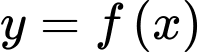 như hình vẽ bên. Số nghiệm thực của phương trình
như hình vẽ bên. Số nghiệm thực của phương trình  là
là

A, 3.
B, 0.
C, 1.
D, 2.
Ta có 
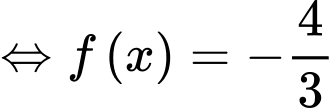 .
.
Dựa vào đồ thị thì đường thẳng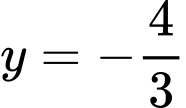 cắt đồ thị hàm số
cắt đồ thị hàm số 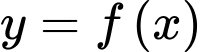 tại đúng 3 điểm phân biệt.
tại đúng 3 điểm phân biệt.

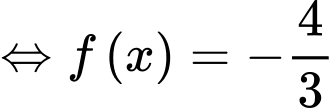 .
.Dựa vào đồ thị thì đường thẳng
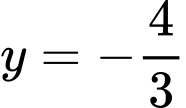 cắt đồ thị hàm số
cắt đồ thị hàm số 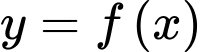 tại đúng 3 điểm phân biệt.
tại đúng 3 điểm phân biệt. Vậy phương trình  có đúng 3 nghiệm phân biệt. Chọn A.
có đúng 3 nghiệm phân biệt. Chọn A.
Đáp án: A  có đúng 3 nghiệm phân biệt. Chọn A.
có đúng 3 nghiệm phân biệt. Chọn A.
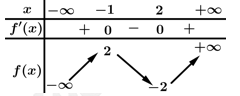
Câu 4 [45910]: Cho hàm số 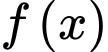 có bảng biến thiên như sau:
có bảng biến thiên như sau:
Số nghiệm thực của phương trình là
là
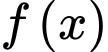 có bảng biến thiên như sau:
có bảng biến thiên như sau:
Số nghiệm thực của phương trình
 là
là A, 3.
B, 1.
C, 2.
D, 0.
Ta có: 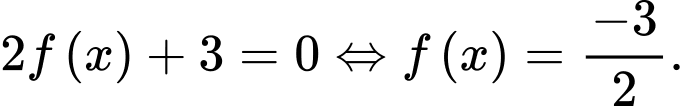
Dựa vào bảng biến thiên dễ thấy đường thẳng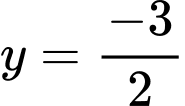 cắt đồ thị hàm số
cắt đồ thị hàm số 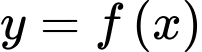 tại đúng 3 điểm phân biệt.
tại đúng 3 điểm phân biệt.
Vậy phương trình có đúng 3 nghiệm phân biệt.
có đúng 3 nghiệm phân biệt.
Chọn A. Đáp án: A
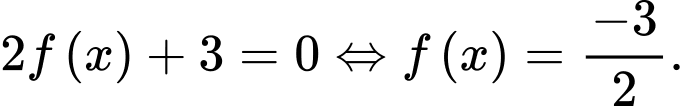
Dựa vào bảng biến thiên dễ thấy đường thẳng
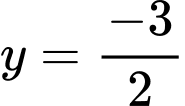 cắt đồ thị hàm số
cắt đồ thị hàm số 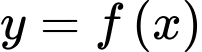 tại đúng 3 điểm phân biệt.
tại đúng 3 điểm phân biệt.
Vậy phương trình
 có đúng 3 nghiệm phân biệt.
có đúng 3 nghiệm phân biệt.
Chọn A. Đáp án: A
Câu 5 [975575]: Cho hàm số 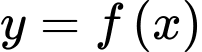 có bảng biến thiên như hình vẽ.
có bảng biến thiên như hình vẽ.
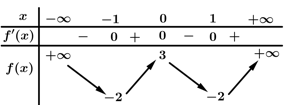
Số nghiệm thực dương phân biệt của phương trình là
là
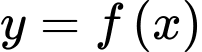 có bảng biến thiên như hình vẽ.
có bảng biến thiên như hình vẽ.
Số nghiệm thực dương phân biệt của phương trình
 là
là A, 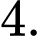
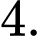
B, 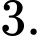
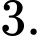
C, 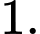
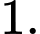
D, 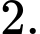
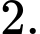
HD: Ta có: 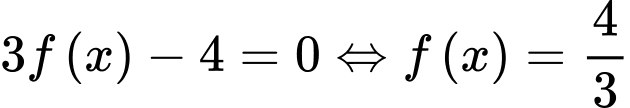
Kẻ đường thẳng nằm ngang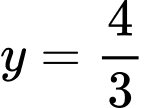 ta thấy đồ thị hàm số
ta thấy đồ thị hàm số 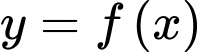 và đường thẳng
và đường thẳng 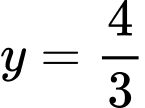 cắt nhau tại 4 điểm phân biệt trong đó có 2 điểm có hoành độ dương (Đọc kỹ đề ko bị lừa :v). Chọn D. Đáp án: D
cắt nhau tại 4 điểm phân biệt trong đó có 2 điểm có hoành độ dương (Đọc kỹ đề ko bị lừa :v). Chọn D. Đáp án: D
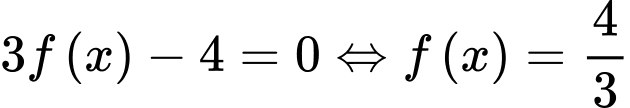
Kẻ đường thẳng nằm ngang
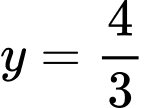 ta thấy đồ thị hàm số
ta thấy đồ thị hàm số 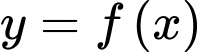 và đường thẳng
và đường thẳng 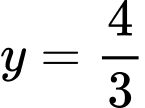 cắt nhau tại 4 điểm phân biệt trong đó có 2 điểm có hoành độ dương (Đọc kỹ đề ko bị lừa :v). Chọn D. Đáp án: D
cắt nhau tại 4 điểm phân biệt trong đó có 2 điểm có hoành độ dương (Đọc kỹ đề ko bị lừa :v). Chọn D. Đáp án: D
Câu 6 [506184]: Cho hàm số 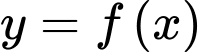 có bảng biến thiên như sau
có bảng biến thiên như sau
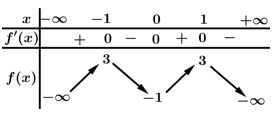
Số nghiệm của phương trình là
là
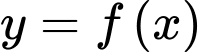 có bảng biến thiên như sau
có bảng biến thiên như sau
Số nghiệm của phương trình
 là
là A, 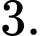
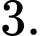
B, 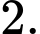
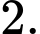
C, 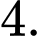
D, 
Chọn A.
Ta có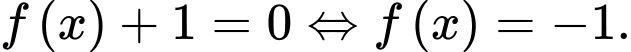
Số nghiệm của phương trình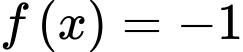 bằng số giao điểm của đồ thị hàm số
bằng số giao điểm của đồ thị hàm số 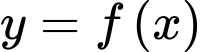 và đường thẳng
và đường thẳng 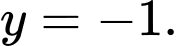
Ta có
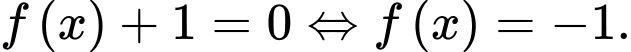
Số nghiệm của phương trình
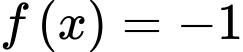 bằng số giao điểm của đồ thị hàm số
bằng số giao điểm của đồ thị hàm số 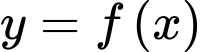 và đường thẳng
và đường thẳng 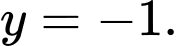
Quan sát bảng biến thiên suy ra phương trình có 3 nghiệm.
Đáp án: A
Câu 7 [310237]: Cho hàm số 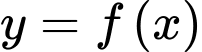 có bảng biến thiên như hình vẽ sau
có bảng biến thiên như hình vẽ sau
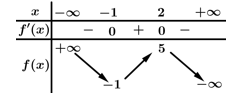
Số nghiệm của phương trình là
là
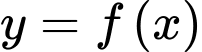 có bảng biến thiên như hình vẽ sau
có bảng biến thiên như hình vẽ sau
Số nghiệm của phương trình
 là
là A, 3.
B, 4.
C, 5.
D, 6.
HD: Phương trình 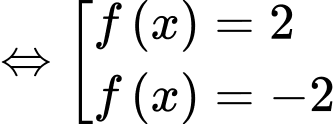
Phương trình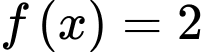 có đúng 3 nghiệm phân biệt và phương trình
có đúng 3 nghiệm phân biệt và phương trình 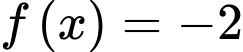 có 1 nghiệm duy nhất.
có 1 nghiệm duy nhất.
Các nghiệm này không trùng nhau.
Vậy phương trình đã cho có đúng 4 nghiệm phân biệt. Chọn B. Đáp án: B
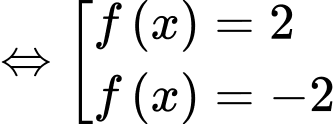
Phương trình
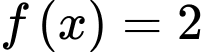 có đúng 3 nghiệm phân biệt và phương trình
có đúng 3 nghiệm phân biệt và phương trình 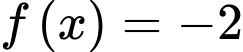 có 1 nghiệm duy nhất.
có 1 nghiệm duy nhất.
Các nghiệm này không trùng nhau.
Vậy phương trình đã cho có đúng 4 nghiệm phân biệt. Chọn B. Đáp án: B
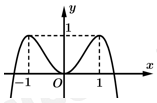
Câu 8 [29583]: Cho hàm số 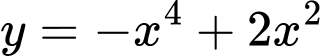 có đồ thị như hình bên dưới. Tìm tất cả các giá trị thực của tham số
có đồ thị như hình bên dưới. Tìm tất cả các giá trị thực của tham số 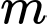 để phương trình
để phương trình 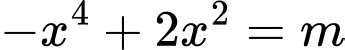 có bốn nghiệm thực phân biệt.
có bốn nghiệm thực phân biệt.
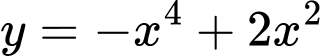 có đồ thị như hình bên dưới. Tìm tất cả các giá trị thực của tham số
có đồ thị như hình bên dưới. Tìm tất cả các giá trị thực của tham số 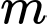 để phương trình
để phương trình 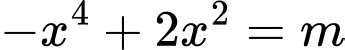 có bốn nghiệm thực phân biệt.
có bốn nghiệm thực phân biệt.
A, 

B, 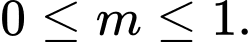
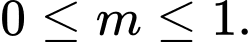
C, 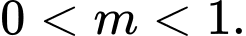
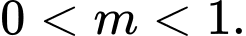
D, 

Số nghiệm của phương trình phụ thuộc vào số giao điểm của đồ thị hàm số và đường thẳng. Dựa vào hình vẽ suy ra PT đã cho có 4 nghiệm khi 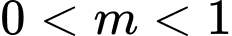 . Chọn C. Đáp án: C
. Chọn C. Đáp án: C
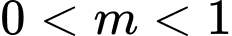 . Chọn C. Đáp án: C
. Chọn C. Đáp án: C
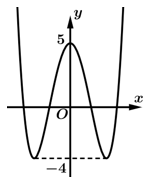
Câu 9 [185148]: Cho hàm số bậc bốn 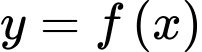 có đồ thị là đường cong trong hình bên. Có bao nhiêu giá trị nguyên của
có đồ thị là đường cong trong hình bên. Có bao nhiêu giá trị nguyên của 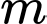 sao cho ứng với mỗi
sao cho ứng với mỗi 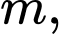 phương trình
phương trình 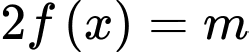 có 4 nghiệm thực phân biệt?
có 4 nghiệm thực phân biệt?
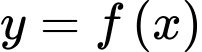 có đồ thị là đường cong trong hình bên. Có bao nhiêu giá trị nguyên của
có đồ thị là đường cong trong hình bên. Có bao nhiêu giá trị nguyên của 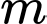 sao cho ứng với mỗi
sao cho ứng với mỗi 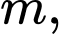 phương trình
phương trình 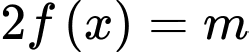 có 4 nghiệm thực phân biệt?
có 4 nghiệm thực phân biệt?
A, 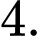
B, 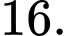
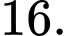
C, 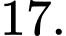
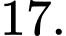
D, 
Ta có: 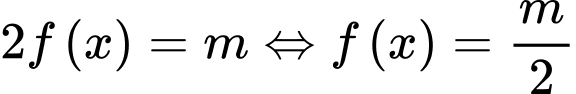 .
.
Để phương trình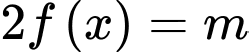 có 4 nghiệm phân biệt thì đồ thị hàm số
có 4 nghiệm phân biệt thì đồ thị hàm số 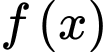 và đường thẳng
và đường thẳng 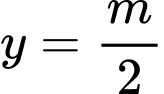 cắt nhau tại 4 điểm phân biệt.
cắt nhau tại 4 điểm phân biệt.
Khi đó: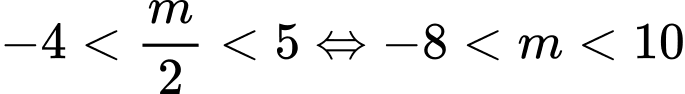 .Mà
.Mà  . Suy ra có 17 giá trị
. Suy ra có 17 giá trị 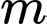 thoả mãn.
thoả mãn.
Vậy có 17 giá trị nguyên của m sao cho ứng với mỗi m, phương trình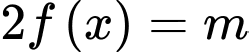 có 4 nghiệm phân biệt.
Đáp án: C
có 4 nghiệm phân biệt.
Đáp án: C
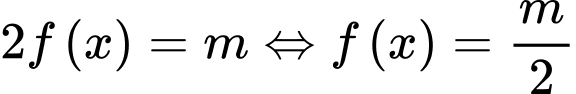 .
.
Để phương trình
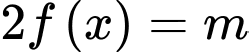 có 4 nghiệm phân biệt thì đồ thị hàm số
có 4 nghiệm phân biệt thì đồ thị hàm số 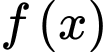 và đường thẳng
và đường thẳng 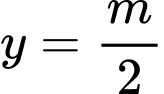 cắt nhau tại 4 điểm phân biệt.
cắt nhau tại 4 điểm phân biệt.
Khi đó:
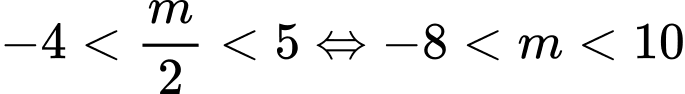 .Mà
.Mà  . Suy ra có 17 giá trị
. Suy ra có 17 giá trị 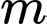 thoả mãn.
thoả mãn.
Vậy có 17 giá trị nguyên của m sao cho ứng với mỗi m, phương trình
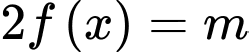 có 4 nghiệm phân biệt.
Đáp án: C
có 4 nghiệm phân biệt.
Đáp án: C
Câu 10 [975576]: Đồ thị hàm số 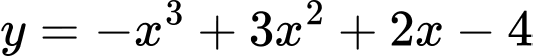 cắt trục tung tại điểm
cắt trục tung tại điểm
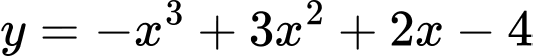 cắt trục tung tại điểm
cắt trục tung tại điểm A, 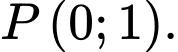
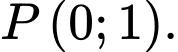
B, 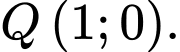
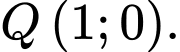
C, 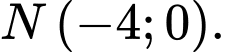
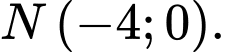
D, 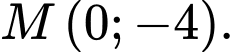
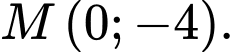
Giao điểm của đồ thị hàm số với trục tung có hoành độ 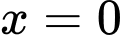
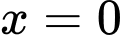
Cho 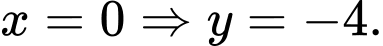
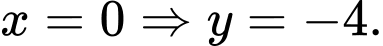
Vậy tọa độ giao điểm là 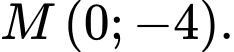
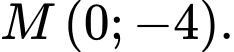
Chọn D.
Đáp án: D
Câu 11 [801781]: Tọa độ giao điểm 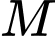 của đồ thị hàm số
của đồ thị hàm số 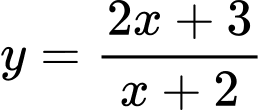 với trục hoành là
với trục hoành là
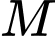 của đồ thị hàm số
của đồ thị hàm số 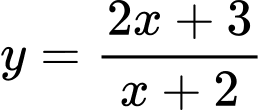 với trục hoành là
với trục hoành là A, 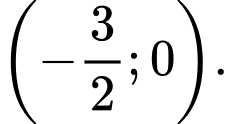
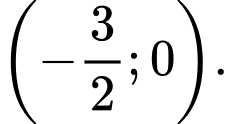
B, 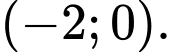
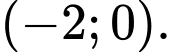
C, 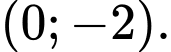
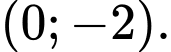
D, 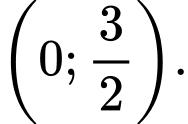
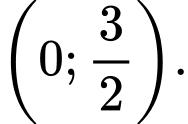
Chọn A.
Cho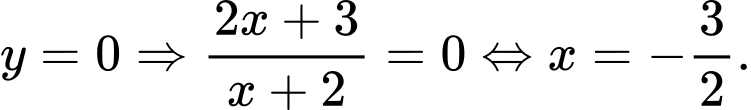
Vậy đồ thị hàm số cắt trục hoành tại điểm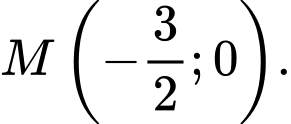 Đáp án: A
Đáp án: A
Cho
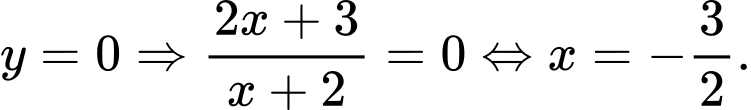
Vậy đồ thị hàm số cắt trục hoành tại điểm
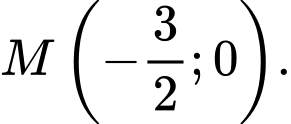 Đáp án: A
Đáp án: A
Câu 12 [677917]: Số giao điểm của đồ thị hàm số 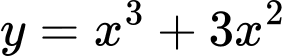 và đồ thị hàm số
và đồ thị hàm số 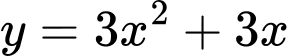 là
là
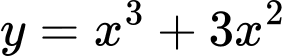 và đồ thị hàm số
và đồ thị hàm số 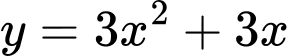 là
là A, 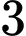 .
.
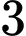 .
.B, 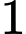 .
.
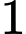 .
.C, 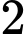 .
.
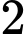 .
.D,  .
.
 .
.
Chọn A
Phương trình hoành độ giao điểm của hai đồ thị đã cho là:
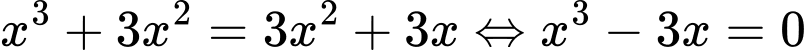
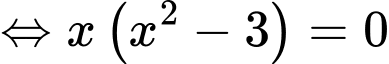
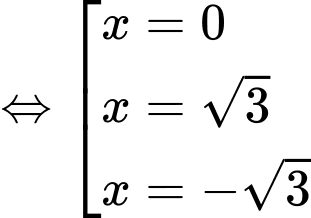 .
.
Hai đồ thị đã cho cắt nhau tại 3 điểm. Đáp án: A
Phương trình hoành độ giao điểm của hai đồ thị đã cho là:
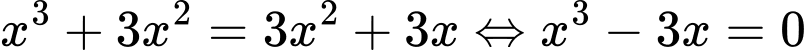
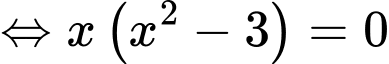
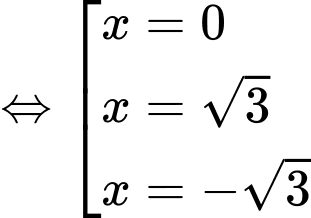 .
.Hai đồ thị đã cho cắt nhau tại 3 điểm. Đáp án: A
Câu 13 [185185]: Biết đường thẳng 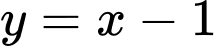 cắt đồ thị hàm số
cắt đồ thị hàm số 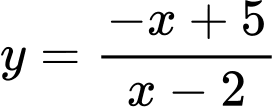 tại hai điểm phân biệt có hoành độ là
tại hai điểm phân biệt có hoành độ là 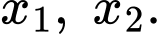 Giá trị của
Giá trị của  bằng
bằng
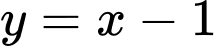 cắt đồ thị hàm số
cắt đồ thị hàm số 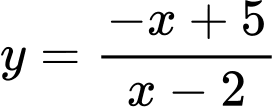 tại hai điểm phân biệt có hoành độ là
tại hai điểm phân biệt có hoành độ là 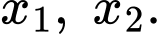 Giá trị của
Giá trị của  bằng
bằng A, 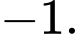
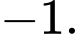
B, 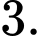
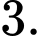
C, 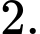
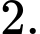
D, 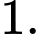
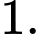
Phương trình hoành độ giao điểm là:
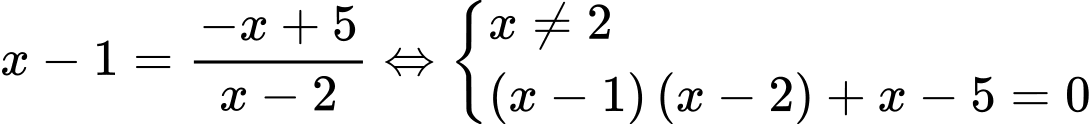
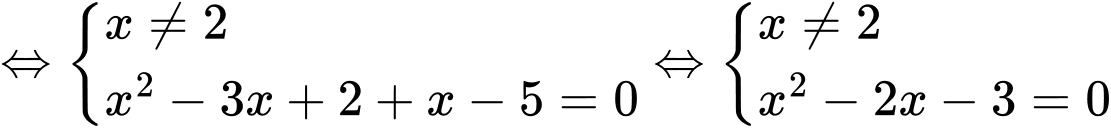
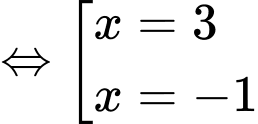
Suy ra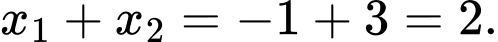 Đáp án: C
Đáp án: C
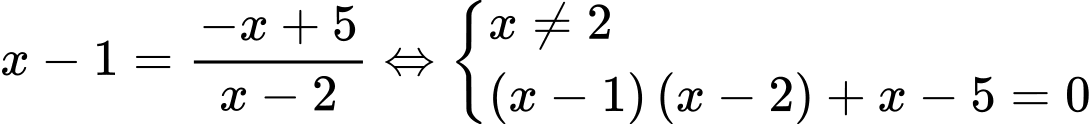
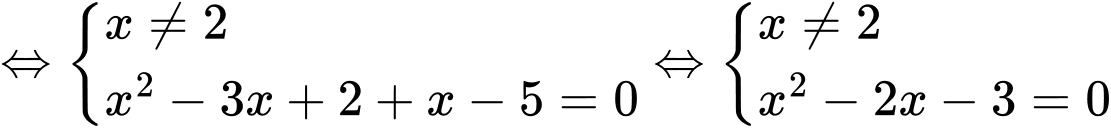
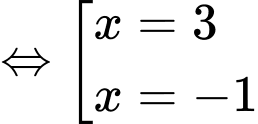
Suy ra
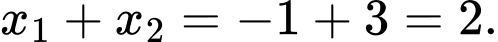 Đáp án: C
Đáp án: C
Câu 14 [318846]: Biết đồ thị hai hàm số 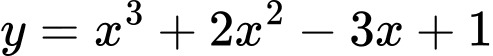 và
và 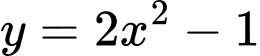 cắt nhau tại hai điểm
cắt nhau tại hai điểm 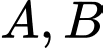 . Tính độ dài đoạn
. Tính độ dài đoạn  .
.
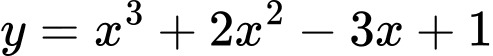 và
và 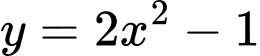 cắt nhau tại hai điểm
cắt nhau tại hai điểm 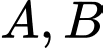 . Tính độ dài đoạn
. Tính độ dài đoạn  .
. A, 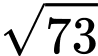 .
.
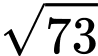 .
.B, 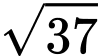 .
.
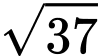 .
.C, 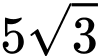 .
.
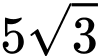 .
.D, 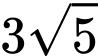 .
.
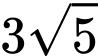 .
.
Chọn D
Ta có phương trình hoành độ giao điểm của đồ thị hai hàm số đã cho:
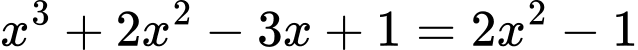
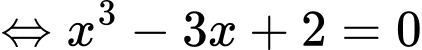
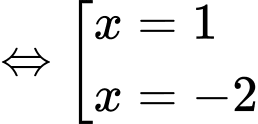
+ Với .
.
+ Với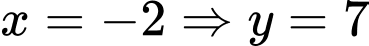 .
.
Do đó đồ thị hàm số cắt nhau tại hai điểm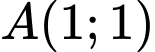 và
và 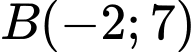 .
.
Khi đó ta có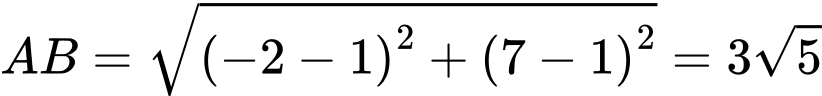 . Đáp án: D
. Đáp án: D
Ta có phương trình hoành độ giao điểm của đồ thị hai hàm số đã cho:
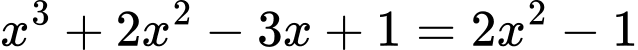
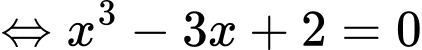
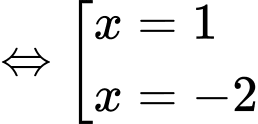
+ Với
 .
.+ Với
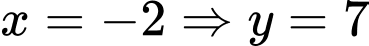 .
.Do đó đồ thị hàm số cắt nhau tại hai điểm
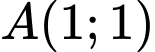 và
và 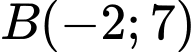 .
.Khi đó ta có
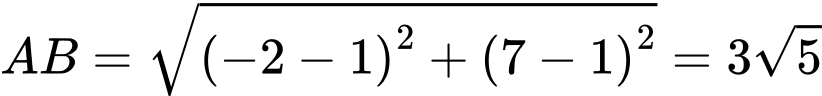 . Đáp án: D
. Đáp án: D
Câu 15 [512250]: Tìm tất cả các giá trị của tham số 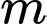 sao cho đồ thị hàm số
sao cho đồ thị hàm số 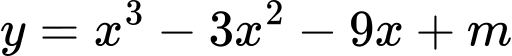 cắt trục hoành tại ba điểm phân biệt
cắt trục hoành tại ba điểm phân biệt
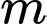 sao cho đồ thị hàm số
sao cho đồ thị hàm số 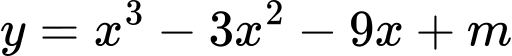 cắt trục hoành tại ba điểm phân biệt
cắt trục hoành tại ba điểm phân biệt A,  .
.
 .
.B, 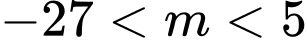 .
.
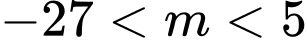 .
.C, 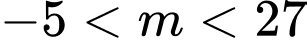 .
.
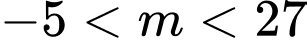 .
.D, 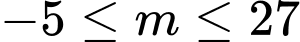 .
.
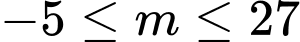 .
.
Chọn C
Đồ thị hàm số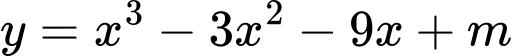 cắt trục hoành tại ba điểm phân biệt khi phương trình
cắt trục hoành tại ba điểm phân biệt khi phương trình
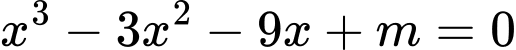
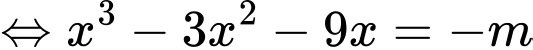 có ba nghiệm phân biệt.
có ba nghiệm phân biệt.
Xét hàm số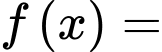
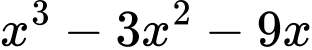
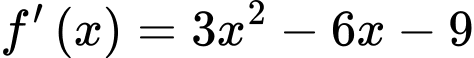
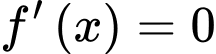
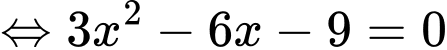
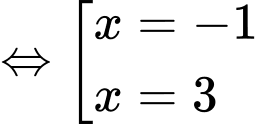 .
.
Bảng biến thiên của hàm số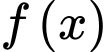 như sau
như sau
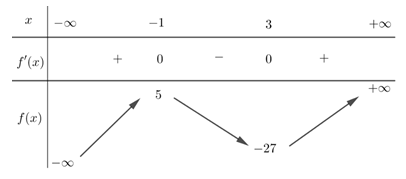
Từ bảng biến thiên suy ra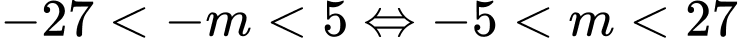 . Đáp án: C
. Đáp án: C
Đồ thị hàm số
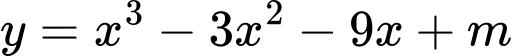 cắt trục hoành tại ba điểm phân biệt khi phương trình
cắt trục hoành tại ba điểm phân biệt khi phương trình
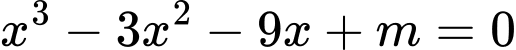
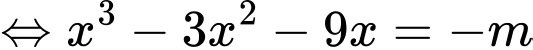 có ba nghiệm phân biệt.
có ba nghiệm phân biệt. Xét hàm số
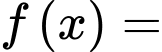
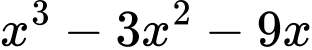
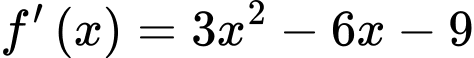
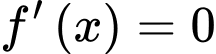
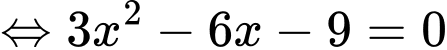
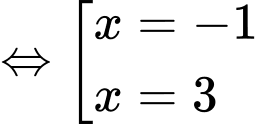 .
.Bảng biến thiên của hàm số
 như sau
như sau
Từ bảng biến thiên suy ra
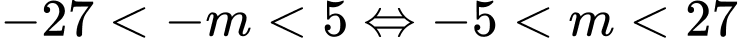 . Đáp án: C
. Đáp án: C
Câu 16 [280806]: Có bao nhiêu giá trị nguyên của tham số 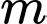 để hàm số
để hàm số 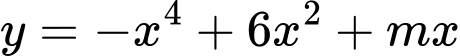 có ba điểm cực trị?
có ba điểm cực trị?
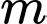 để hàm số
để hàm số 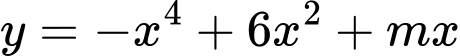 có ba điểm cực trị?
có ba điểm cực trị? A, 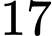 .
.
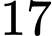 .
.B,  .
.
 .
.C, 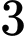 .
.
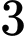 .
.D, 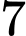 .
.
 .
.
Chọn B
Ta có: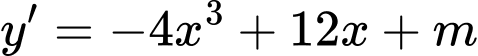 . Xét phương trình
. Xét phương trình 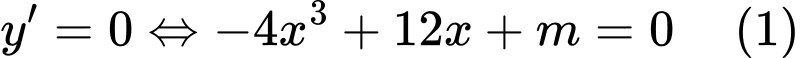 .
.
Để hàm số có ba điểm cực trị thì phương trình phải có 3 nghiệm phân biệt.
phải có 3 nghiệm phân biệt.
Ta có: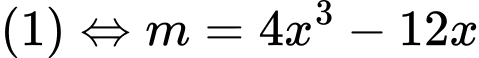 .
.
Xét hàm số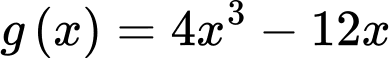 có
có 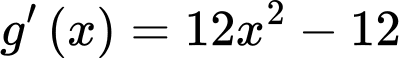 . Cho
. Cho 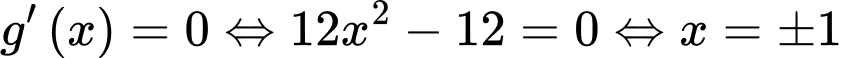 .
.
Bảng biến thiên của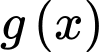
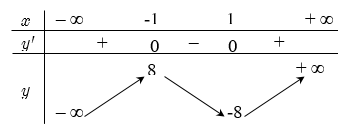
Dựa vào bảng biến thiên ta thấy, phương trình có 3 nghiệm phân biệt khi
có 3 nghiệm phân biệt khi 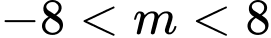 .
.
Do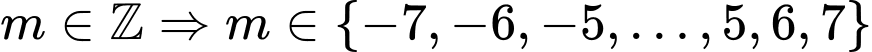 .
.
Vậy có 15 giá trị nguyên của tham số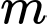 thỏa yêu cầu đề bài. Đáp án: B
thỏa yêu cầu đề bài. Đáp án: B
Ta có:
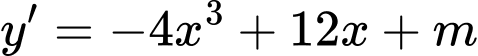 . Xét phương trình
. Xét phương trình 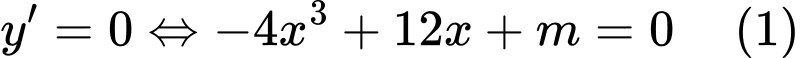 .
.Để hàm số có ba điểm cực trị thì phương trình
 phải có 3 nghiệm phân biệt.
phải có 3 nghiệm phân biệt.Ta có:
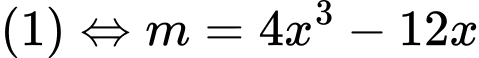 .
.Xét hàm số
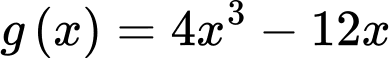 có
có 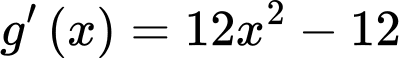 . Cho
. Cho 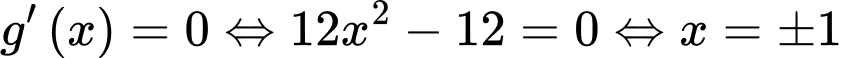 .
.Bảng biến thiên của
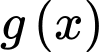

Dựa vào bảng biến thiên ta thấy, phương trình
 có 3 nghiệm phân biệt khi
có 3 nghiệm phân biệt khi 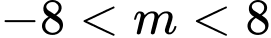 .
.
Do
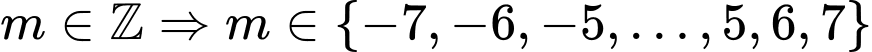 .
.
Vậy có 15 giá trị nguyên của tham số
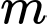 thỏa yêu cầu đề bài. Đáp án: B
thỏa yêu cầu đề bài. Đáp án: B
Câu 17 [184822]: [Câu 41 – Mã 104]: Có bao nhiêu giá trị nguyên của tham số 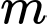 sao cho ứng với mỗi
sao cho ứng với mỗi 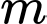 hàm số
hàm số 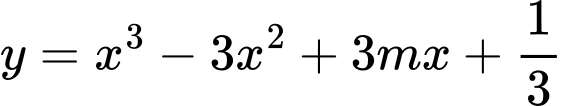 có đúng một điểm cực trị thuộc khoảng
có đúng một điểm cực trị thuộc khoảng 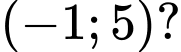
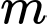 sao cho ứng với mỗi
sao cho ứng với mỗi 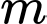 hàm số
hàm số 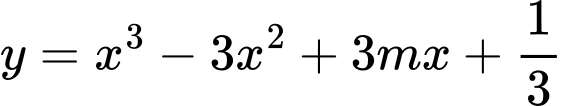 có đúng một điểm cực trị thuộc khoảng
có đúng một điểm cực trị thuộc khoảng 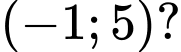
A, 
B, 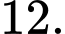
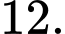
C, 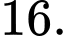
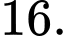
D, 

Ta có: 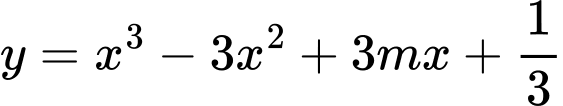
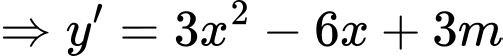 .
.
Hàm số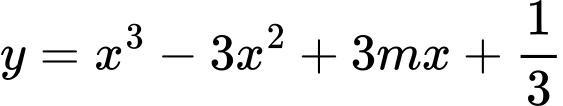 có đúng 1 cực trị thuộc khoảng
có đúng 1 cực trị thuộc khoảng  khi và chỉ khi
khi và chỉ khi 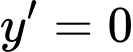 có 1 nghiệm thuộc khoảng
có 1 nghiệm thuộc khoảng 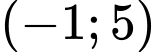
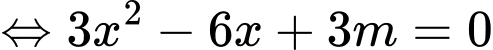 có 1 nghiệm thuộc khoảng
có 1 nghiệm thuộc khoảng 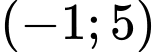 .
.
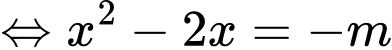 có 1 nghiệm thuộc khoảng
có 1 nghiệm thuộc khoảng 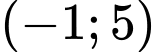 .
.
Đặt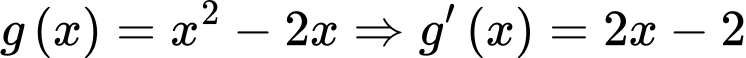
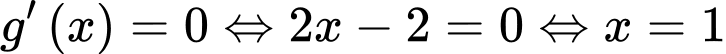
Bảng biến thiên
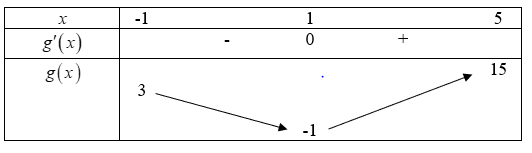
Để có 1 nghiệm thuộc khoảng
có 1 nghiệm thuộc khoảng  thì
thì  .
.
Vậy có 12 giá trị nguyên của m sao cho ứng với mỗi m hàm số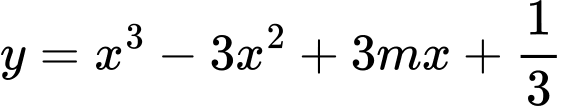 có đúng 1 cực trị thuộc khoảng
có đúng 1 cực trị thuộc khoảng 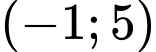 .
Đáp án: B
.
Đáp án: B
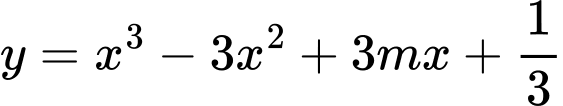
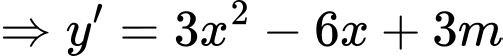 .
.
Hàm số
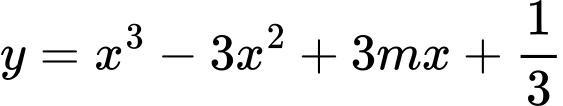 có đúng 1 cực trị thuộc khoảng
có đúng 1 cực trị thuộc khoảng 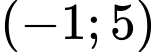 khi và chỉ khi
khi và chỉ khi 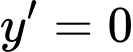 có 1 nghiệm thuộc khoảng
có 1 nghiệm thuộc khoảng 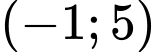
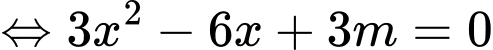 có 1 nghiệm thuộc khoảng
có 1 nghiệm thuộc khoảng 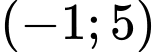 .
.
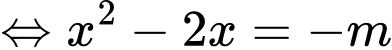 có 1 nghiệm thuộc khoảng
có 1 nghiệm thuộc khoảng 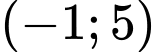 .
.
Đặt
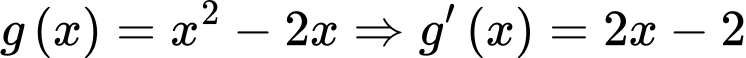
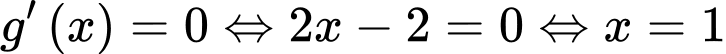
Bảng biến thiên

Để
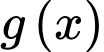 có 1 nghiệm thuộc khoảng
có 1 nghiệm thuộc khoảng 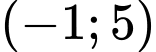 thì
thì 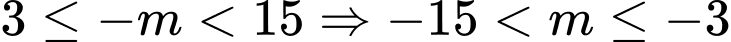 .
.
Vậy có 12 giá trị nguyên của m sao cho ứng với mỗi m hàm số
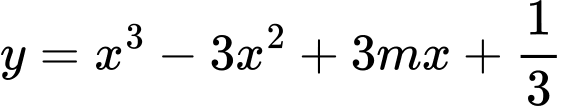 có đúng 1 cực trị thuộc khoảng
có đúng 1 cực trị thuộc khoảng 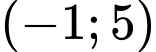 .
Đáp án: B
.
Đáp án: B
Câu 18 [382763]: [Trích Đề Mẫu ĐGNL HN]: Số giá trị nguyên của tham số 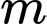 để phương trình
để phương trình 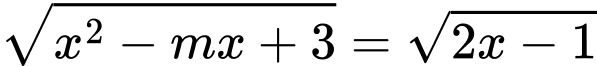 có hai nghiệm phân biệt là
có hai nghiệm phân biệt là
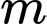 để phương trình
để phương trình 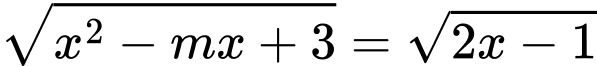 có hai nghiệm phân biệt là
có hai nghiệm phân biệt là
Ta có: 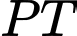

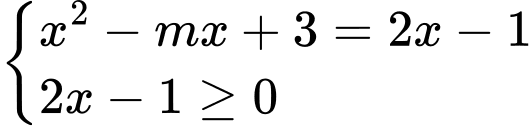

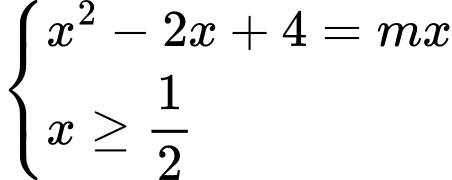

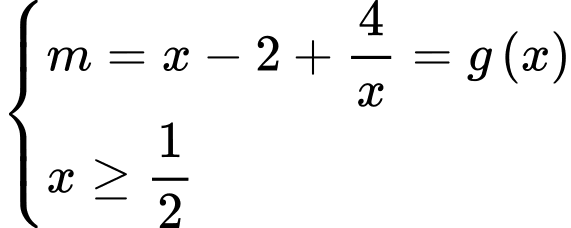
Lập bảng biến thiên của hàm số trên
trên 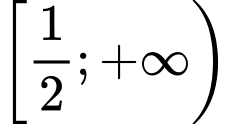

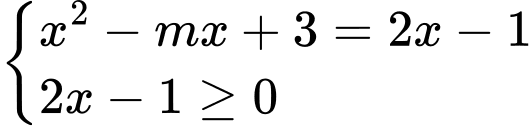

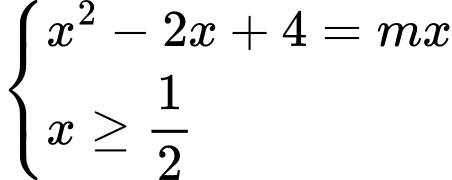

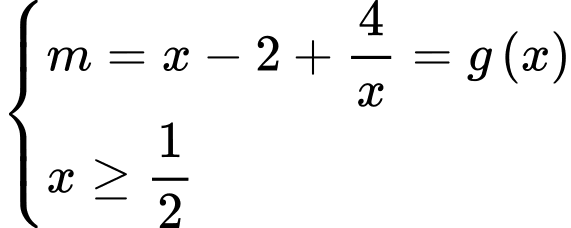
Lập bảng biến thiên của hàm số
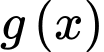 trên
trên 
Ta có 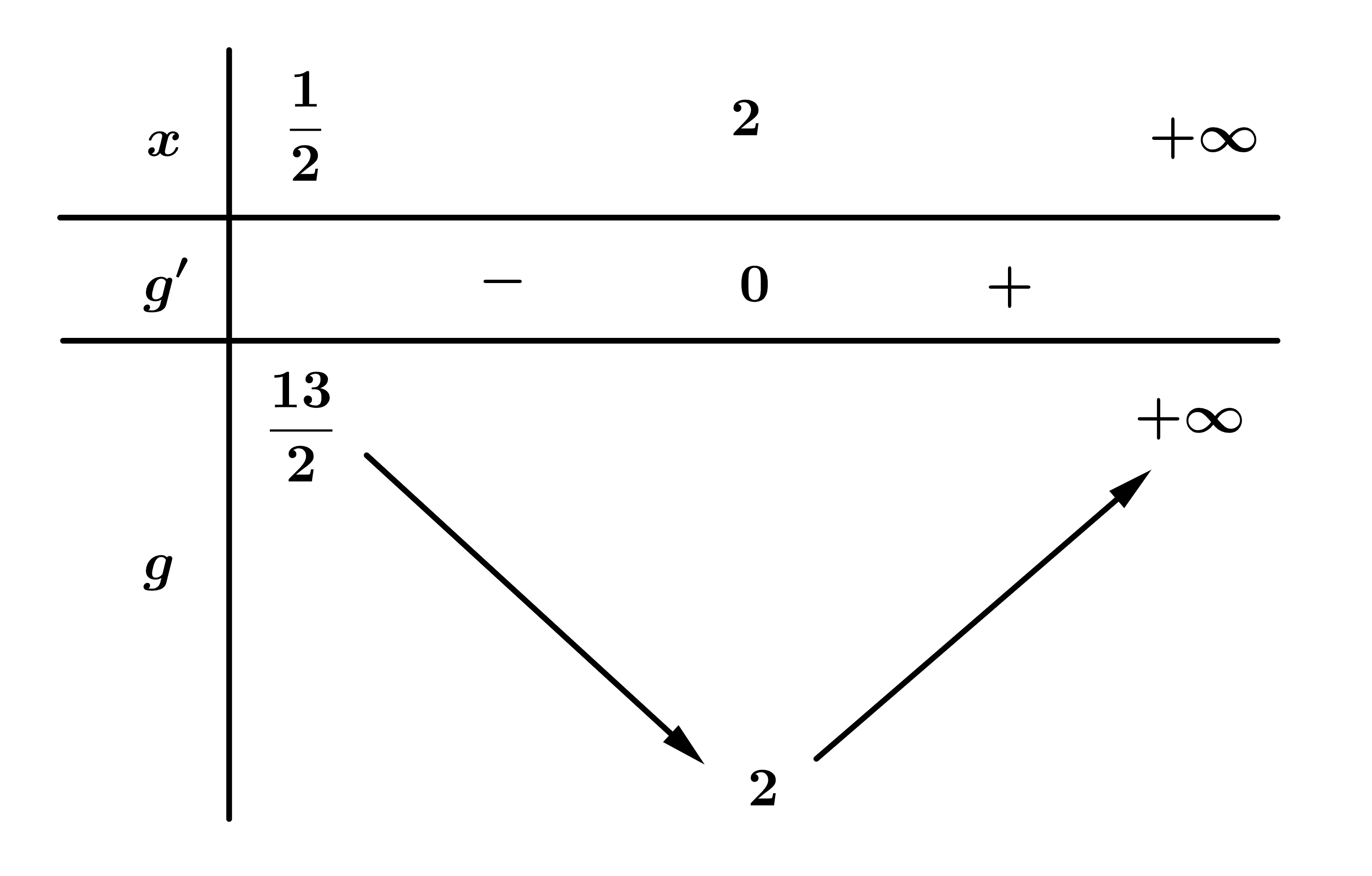

Vậy phương trình có 2 nghiệm phân biệt khi và chỉ khi 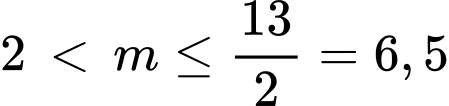
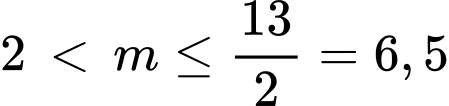
Mà 

Vậy có 4 giá trị của 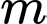 thoả mãn ycbt.
thoả mãn ycbt.
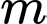 thoả mãn ycbt.
thoả mãn ycbt.
Câu 19 [791427]: Điều kiện để phương trình 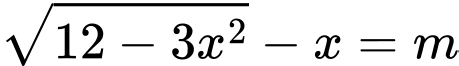 có nghiệm là
có nghiệm là  . Khi đó
. Khi đó 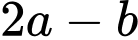 bằng
bằng
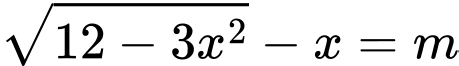 có nghiệm là
có nghiệm là  . Khi đó
. Khi đó 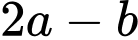 bằng
bằng A, 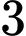 .
.
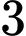 .
.B, 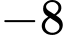 .
.
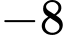 .
.C, 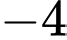 .
.
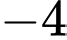 .
.D,  .
.
 .
.
Chọn B
ĐK: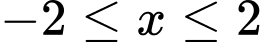 .
.
Xét hàm số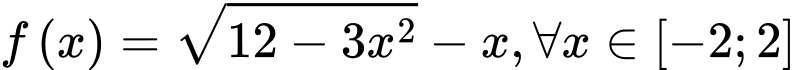 .
.
Ta có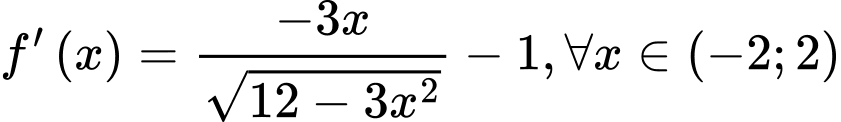 .
.
Cho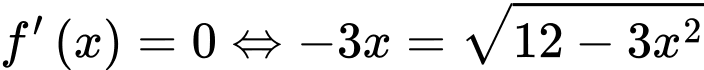
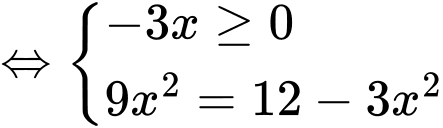
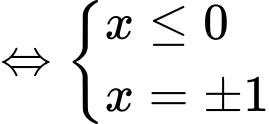
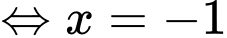 .
.
Bảng biến thiên:
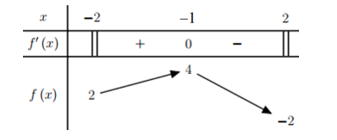
Vậy YCBT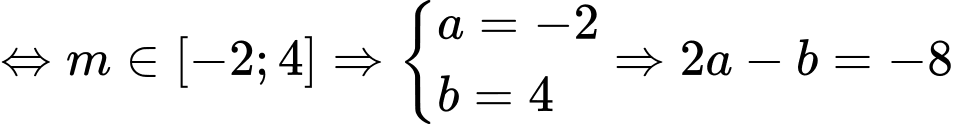 . Đáp án: B
. Đáp án: B
ĐK:
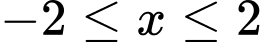 .
.Xét hàm số
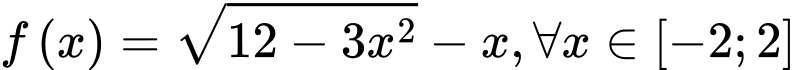 .
.Ta có
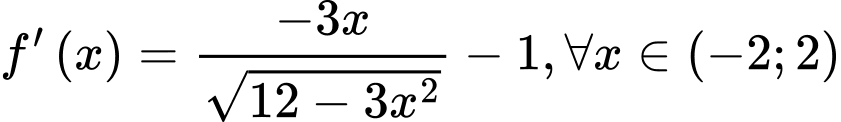 .
.Cho
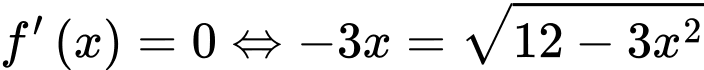
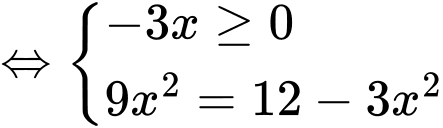
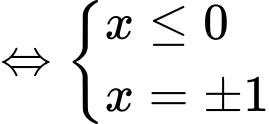
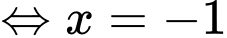 .
.Bảng biến thiên:

Vậy YCBT
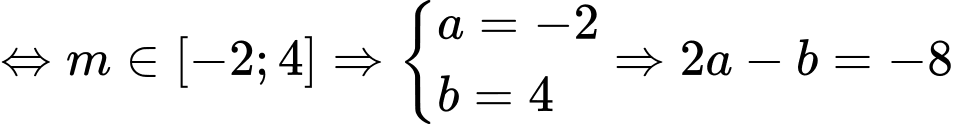 . Đáp án: B
. Đáp án: B
Câu 20 [508164]: Cho đồ thị hàm số 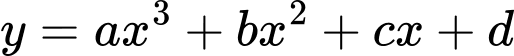 như hình vẽ dưới đây:
như hình vẽ dưới đây:
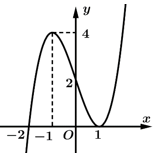
Đồ thị của hàm số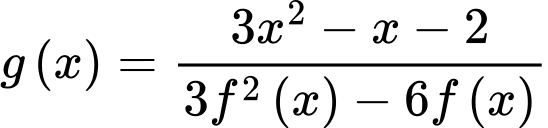 có bao nhiêu đường tiệm cận đứng?
có bao nhiêu đường tiệm cận đứng?
 như hình vẽ dưới đây:
như hình vẽ dưới đây:
Đồ thị của hàm số
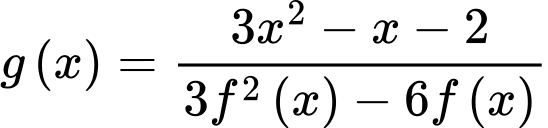 có bao nhiêu đường tiệm cận đứng?
có bao nhiêu đường tiệm cận đứng? A, 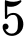 .
.
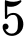 .
.B, 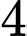 .
.
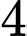 .
.C, 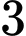 .
.
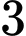 .
.D, 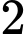 .
.
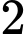 .
.
Chọn A
Xét phương trình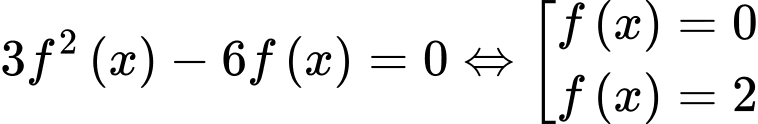
Dựa vào đồ thị, ta có
+) Phương trình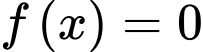
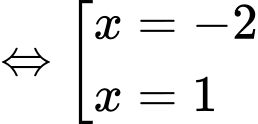 (trong đó
(trong đó 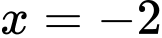 là nghiệm đơn và
là nghiệm đơn và 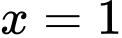 là nghiệm bội 2)
là nghiệm bội 2)
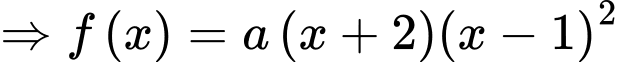 ,
, 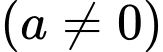 .
.
+) Phương trình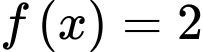
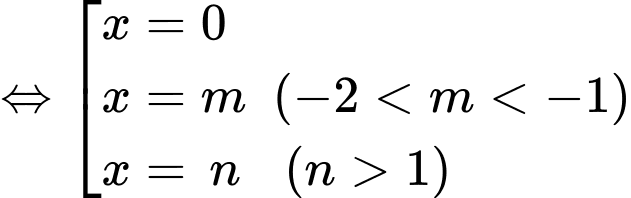 (
(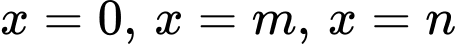 đều là các nghiệm đơn)
đều là các nghiệm đơn) 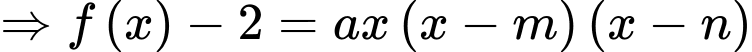 ,
, 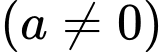 .
.
Suy ra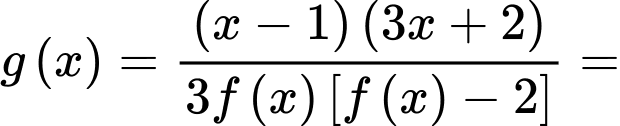
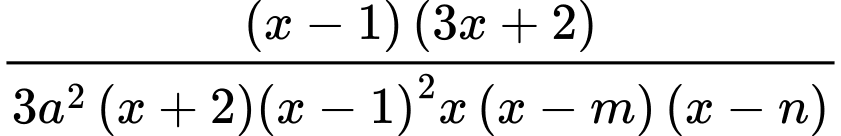 ,
, 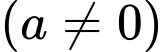 .
.
Vậy đồ thị hàm số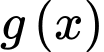 có
có 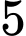 đường tiệm cận đứng. Đáp án: A
đường tiệm cận đứng. Đáp án: A
Xét phương trình
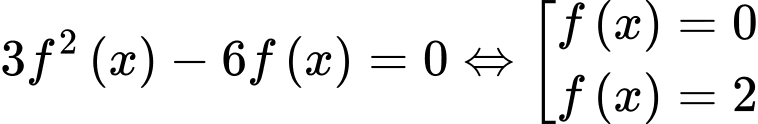
Dựa vào đồ thị, ta có
+) Phương trình
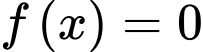
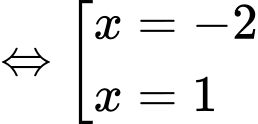 (trong đó
(trong đó 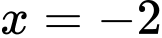 là nghiệm đơn và
là nghiệm đơn và 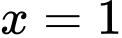 là nghiệm bội 2)
là nghiệm bội 2)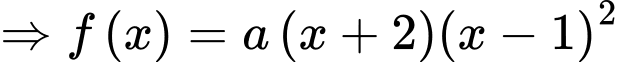 ,
, 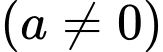 .
.+) Phương trình
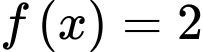
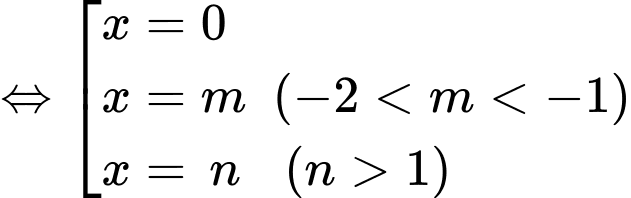 (
(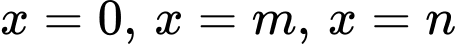 đều là các nghiệm đơn)
đều là các nghiệm đơn) 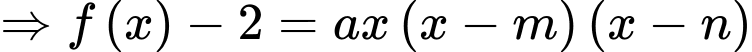 ,
, 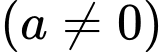 .
.Suy ra
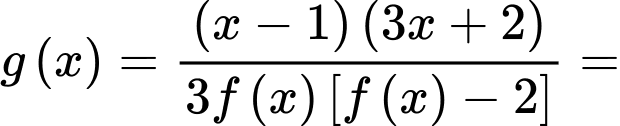
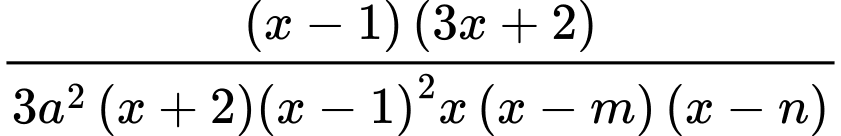 ,
, 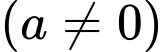 .
.Vậy đồ thị hàm số
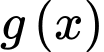 có
có 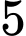 đường tiệm cận đứng. Đáp án: A
đường tiệm cận đứng. Đáp án: A