Đáp án Bài tập tự luyện
Câu 1 [509244]: [Đề thi tham khảo BGD-ĐT năm 2020]: Có bao nhiêu giá trị nguyên của tham số 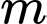 để hàm số
để hàm số 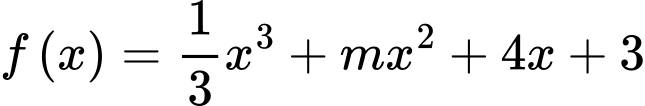 đồng biến trên
đồng biến trên 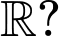
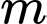 để hàm số
để hàm số 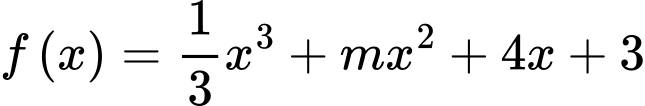 đồng biến trên
đồng biến trên 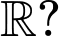
A, 5
B, 4
C, 3
D, 2
Chọn đáp án A. 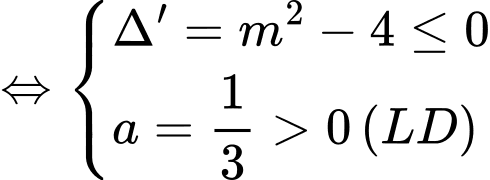

Ta có: 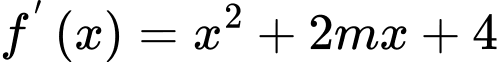 .
.
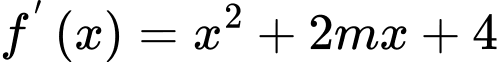 .
. Để hàm số đã cho đồng biến trên 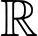 khi và chỉ khi
khi và chỉ khi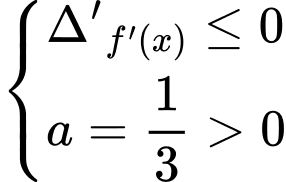
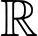 khi và chỉ khi
khi và chỉ khi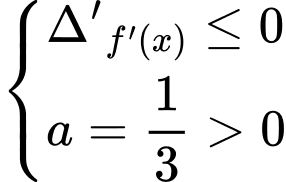
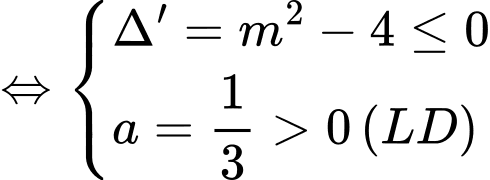

Vậy có 5 giá trị nguyên của m thỏa mãn yêu cầu bài toán.
Đáp án: A
Câu 2 [6314]: Tìm tập hợp tất cả các tham số thực của 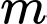 để hàm số
để hàm số 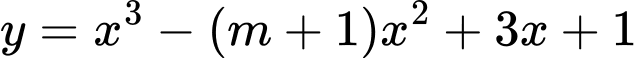 đồng biến trên khoảng
đồng biến trên khoảng 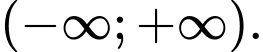
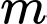 để hàm số
để hàm số 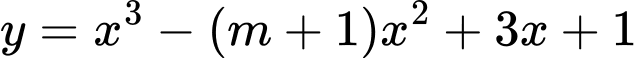 đồng biến trên khoảng
đồng biến trên khoảng 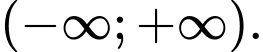
A, 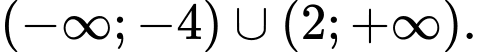
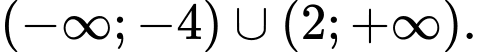
B, 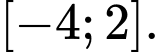
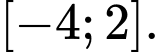
C, 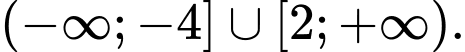
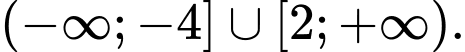
D, 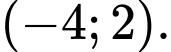
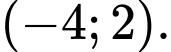
Ta có 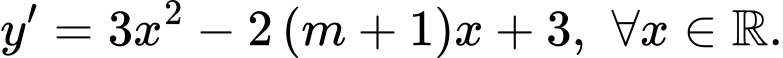
Để hàm số đồng biến trên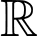
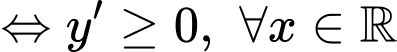
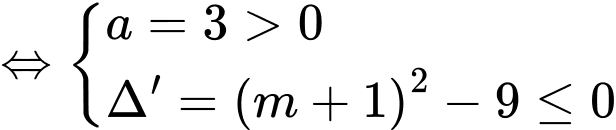
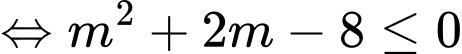

Chọn đáp án B. Đáp án: B
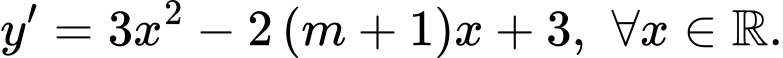
Để hàm số đồng biến trên
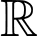
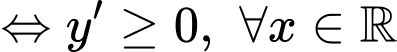
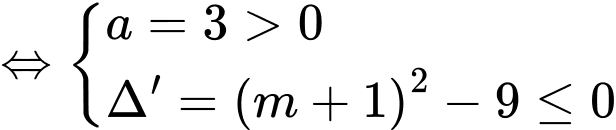
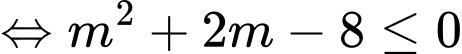

Chọn đáp án B. Đáp án: B
Câu 3 [791249]: Tìm giá trị thực của tham số 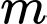 để hàm số
để hàm số 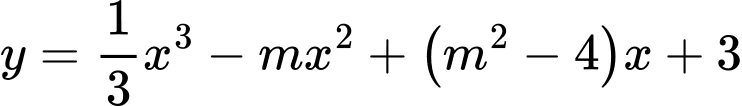 đạt cực đại tại
đạt cực đại tại 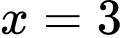
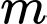 để hàm số
để hàm số 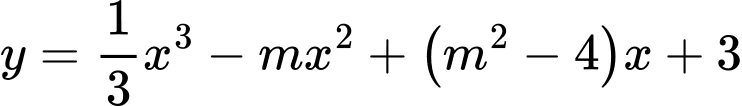 đạt cực đại tại
đạt cực đại tại 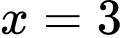
A, 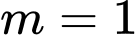 .
.
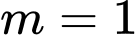 .
.B, 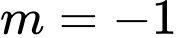 .
.
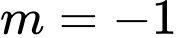 .
.C, 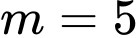 .
.
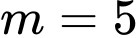 .
.D, 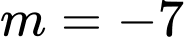 .
.
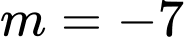 .
.
Đáp án C
Ta có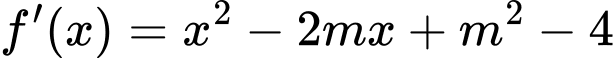
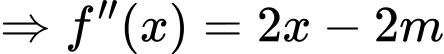 .
.
Điều kiện hàm đạt cực đại là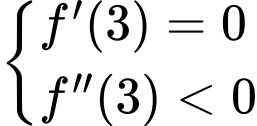
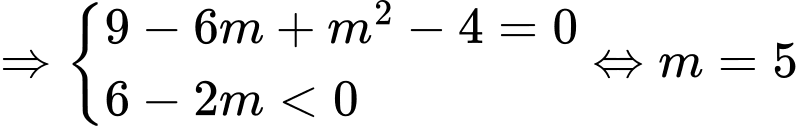 . Đáp án: C
. Đáp án: C
Ta có
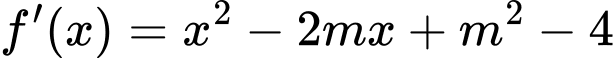
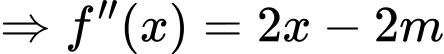 .
.
Điều kiện hàm đạt cực đại là
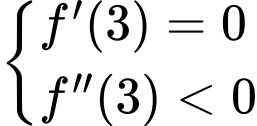
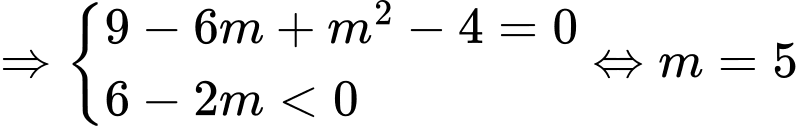 . Đáp án: C
. Đáp án: C
Câu 4 [308221]: Cho hàm số 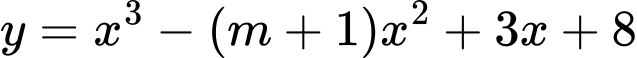 với
với 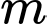 là tham số. Gọi
là tham số. Gọi 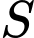 là tập hợp tất cả các giá trị nguyên của
là tập hợp tất cả các giá trị nguyên của 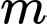 để hàm số đồng biến trên
để hàm số đồng biến trên 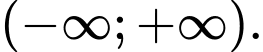 Tìm số phần tử của
Tìm số phần tử của 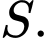
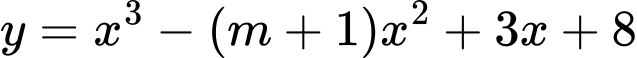 với
với 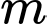 là tham số. Gọi
là tham số. Gọi 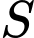 là tập hợp tất cả các giá trị nguyên của
là tập hợp tất cả các giá trị nguyên của 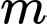 để hàm số đồng biến trên
để hàm số đồng biến trên 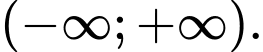 Tìm số phần tử của
Tìm số phần tử của 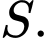
A, 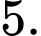
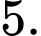
B, 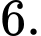
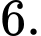
C, Vô số.
D, 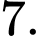
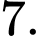
Chọn D
Có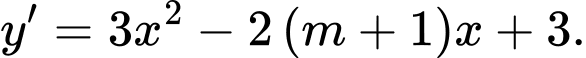
Hàm số đã cho đồng biến trên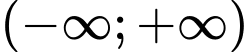 khi và chỉ khi phương trình
khi và chỉ khi phương trình 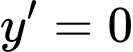 vô nghiệm hoặc có nghiệm kép.
vô nghiệm hoặc có nghiệm kép.
Hay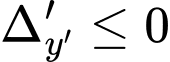
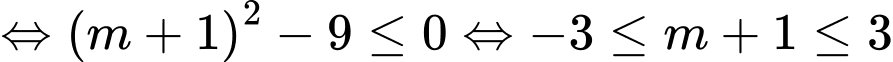

Vậy có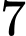 giá trị nguyên của tham số
giá trị nguyên của tham số 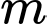 thỏa
thỏa 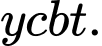 Đáp án: D
Đáp án: D
Có
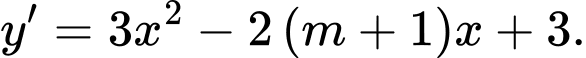
Hàm số đã cho đồng biến trên
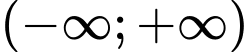 khi và chỉ khi phương trình
khi và chỉ khi phương trình 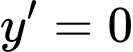 vô nghiệm hoặc có nghiệm kép.
vô nghiệm hoặc có nghiệm kép.
Hay
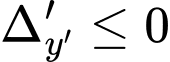
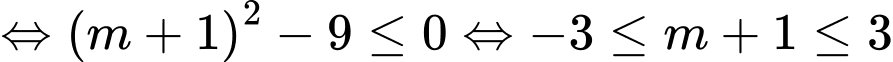

Vậy có
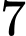 giá trị nguyên của tham số
giá trị nguyên của tham số 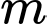 thỏa
thỏa 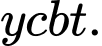 Đáp án: D
Đáp án: D
Câu 5 [2837]: Cho hàm số 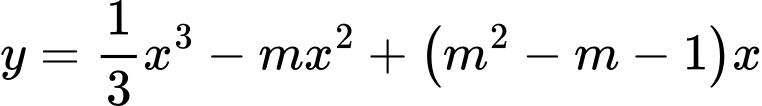 . Với giá trị nào của
. Với giá trị nào của 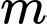 thì hàm số đã cho đạt cực đại tại
thì hàm số đã cho đạt cực đại tại 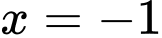 ?
?
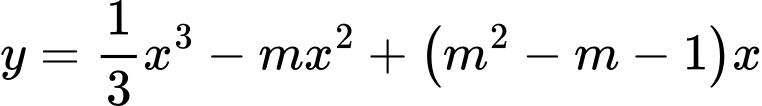 . Với giá trị nào của
. Với giá trị nào của 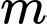 thì hàm số đã cho đạt cực đại tại
thì hàm số đã cho đạt cực đại tại 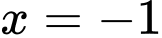 ?
? A, 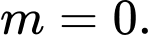
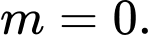
B, 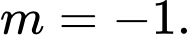
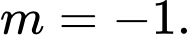
C, 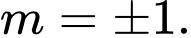
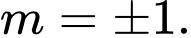
D, 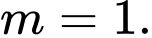
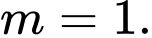
Ta có 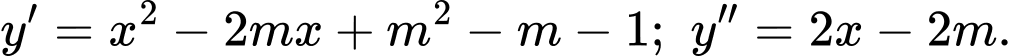
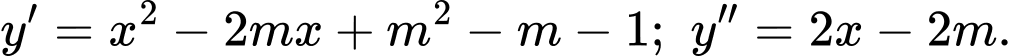
YCBT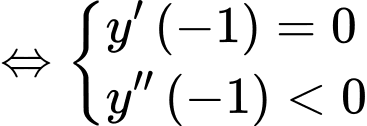
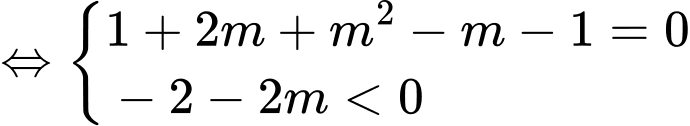
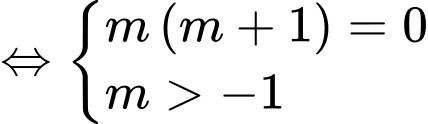
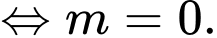
Chọn đáp án A. Đáp án: A
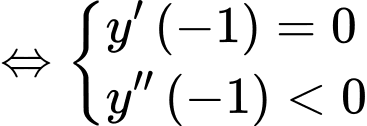
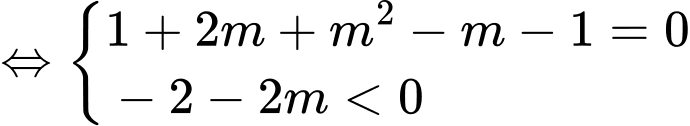
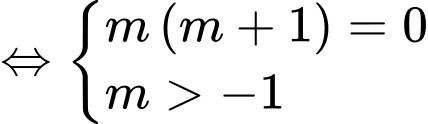
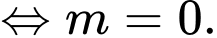
Chọn đáp án A. Đáp án: A
Câu 6 [15704]: Tìm tham số 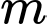 để hàm số
để hàm số 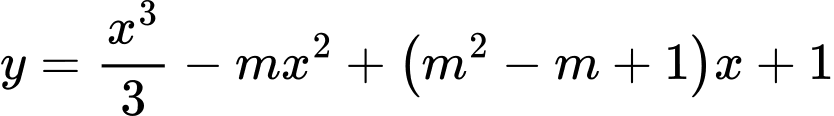 đạt cực tiểu tại
đạt cực tiểu tại 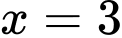 .
.
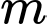 để hàm số
để hàm số 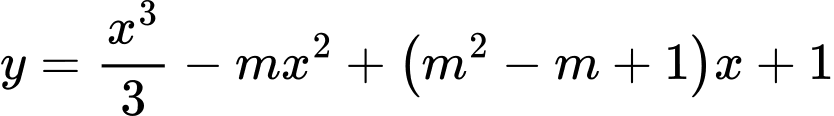 đạt cực tiểu tại
đạt cực tiểu tại 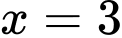 .
. A, 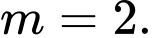
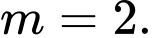
B, 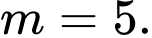
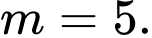
C, 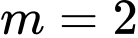 và
và 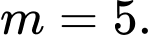
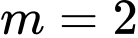 và
và 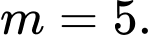
D, Không tồn tại 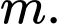
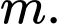
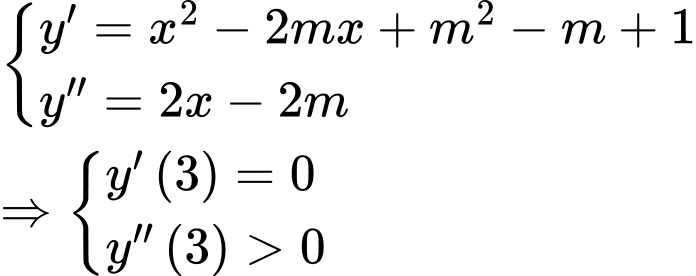
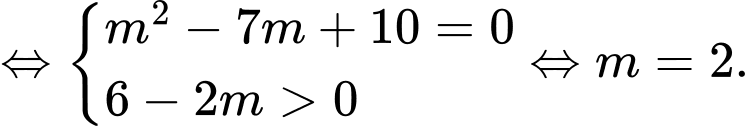
Câu 7 [2824]: Tìm 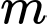 để hàm số
để hàm số 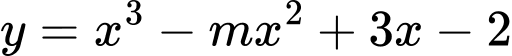 đạt cực tiểu tại
đạt cực tiểu tại 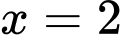 .
.
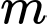 để hàm số
để hàm số 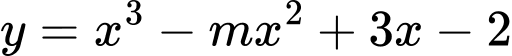 đạt cực tiểu tại
đạt cực tiểu tại 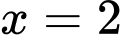 .
. A, 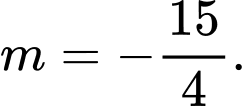
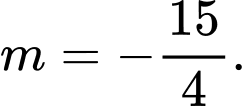
B, 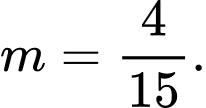
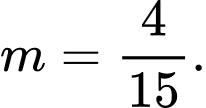
C, 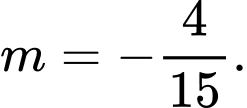
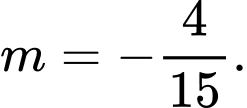
D, 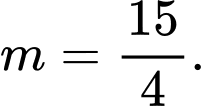
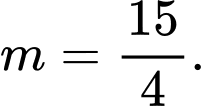
Ta có 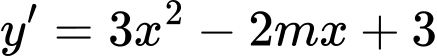
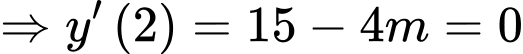
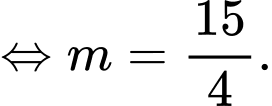
Khi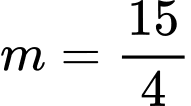
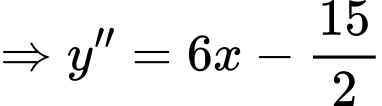
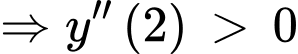 do đó hàm số đạt cực tiểu tại
do đó hàm số đạt cực tiểu tại 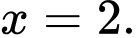
Chọn đáp án D. Đáp án: D
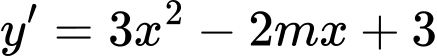
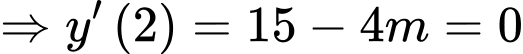
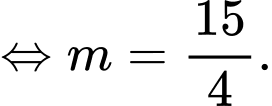
Khi
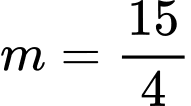
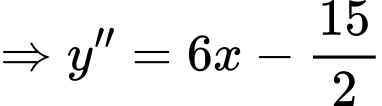
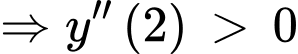 do đó hàm số đạt cực tiểu tại
do đó hàm số đạt cực tiểu tại 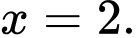
Chọn đáp án D. Đáp án: D
Câu 8 [2576]: Cho hàm số 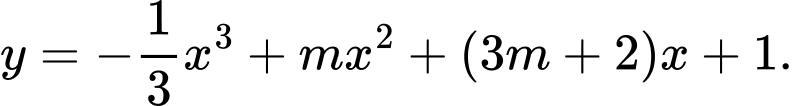 Số giá trị nguyên của
Số giá trị nguyên của 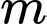 để hàm số nghịch biến trên
để hàm số nghịch biến trên 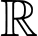 là
là
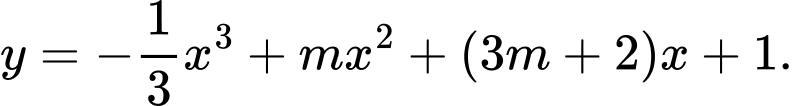 Số giá trị nguyên của
Số giá trị nguyên của 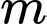 để hàm số nghịch biến trên
để hàm số nghịch biến trên 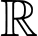 là
là A, 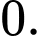
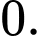
B, 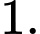
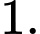
C, 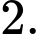
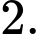
D, 
Hệ số  Hàm số nghịch biến trên
Hàm số nghịch biến trên 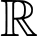 khi
khi 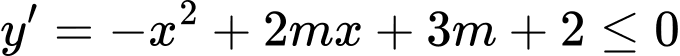
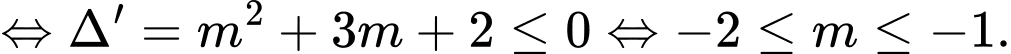
 Hàm số nghịch biến trên
Hàm số nghịch biến trên 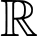 khi
khi 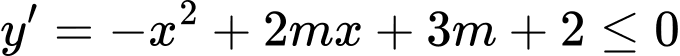
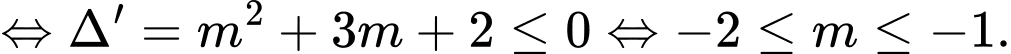
Mà 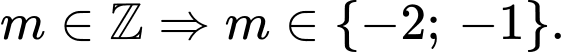
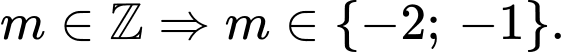
Vậy có 2 giá trị của 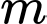 thoả mãn ycbt.
thoả mãn ycbt.
Đáp án: C 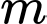 thoả mãn ycbt.
thoả mãn ycbt. Chọn đáp án C.
Câu 9 [509245]: [Trích đề thi THPT QG năm 2017]: Cho hàm số 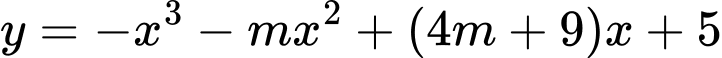 với
với 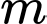 là tham số. Có bao nhiêu giá trị nguyên của để hàm số nghịch biến trên khoảng
là tham số. Có bao nhiêu giá trị nguyên của để hàm số nghịch biến trên khoảng 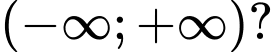
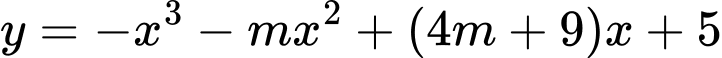 với
với 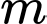 là tham số. Có bao nhiêu giá trị nguyên của để hàm số nghịch biến trên khoảng
là tham số. Có bao nhiêu giá trị nguyên của để hàm số nghịch biến trên khoảng 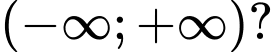
A, 4.
B, 6.
C, 7.
D, 5.
Ta có 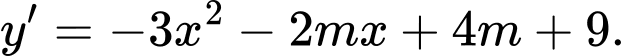
Hàm số nghịch biến trên khoảng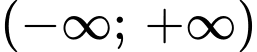
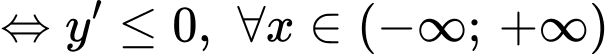
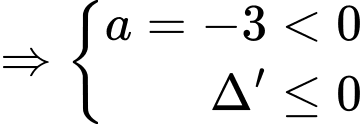
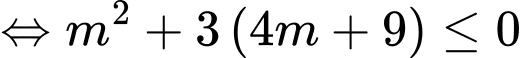
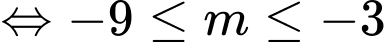
Mà
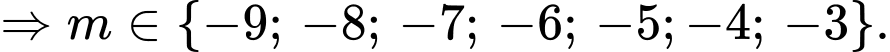
Vậy có 7 giá trị của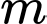 thỏa mãn ycbt.
thỏa mãn ycbt.
Chọn đáp án C. Đáp án: C
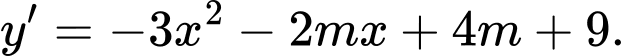
Hàm số nghịch biến trên khoảng
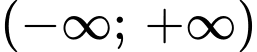
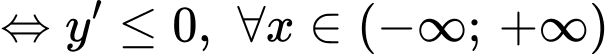
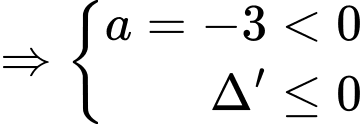
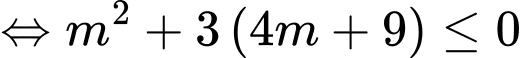
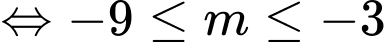
Mà

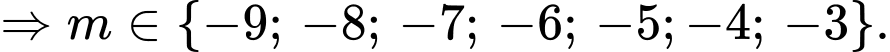
Vậy có 7 giá trị của
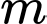 thỏa mãn ycbt.
thỏa mãn ycbt. Chọn đáp án C. Đáp án: C
Câu 10 [802006]: Hàm số 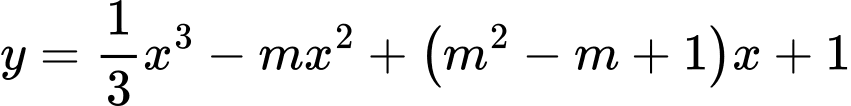 đạt cực đại tại điểm
đạt cực đại tại điểm 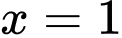 khi
khi
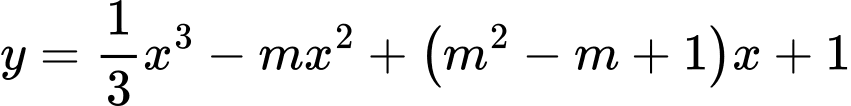 đạt cực đại tại điểm
đạt cực đại tại điểm 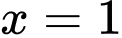 khi
khi A, 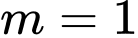 hoặc
hoặc 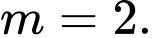
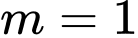 hoặc
hoặc 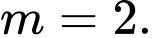
B, 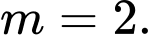
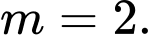
C, 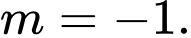
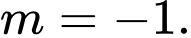
D, 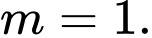
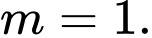
Chọn B
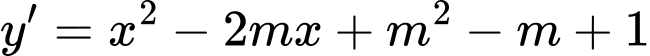
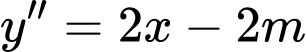
Hàm số đạt cực đại tại
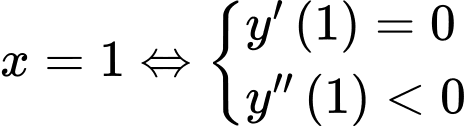
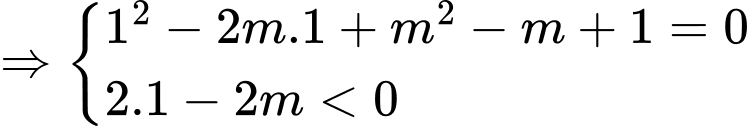
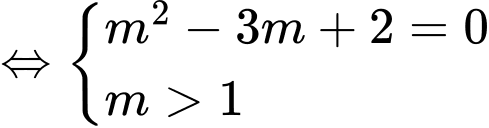
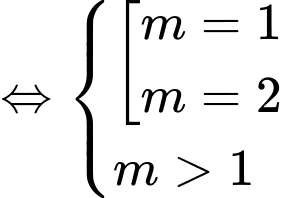
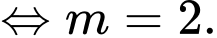 Đáp án: B
Đáp án: B
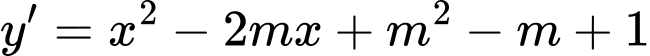
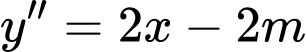
Hàm số đạt cực đại tại
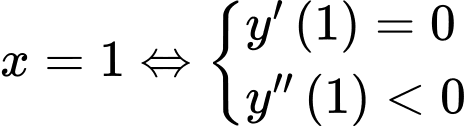
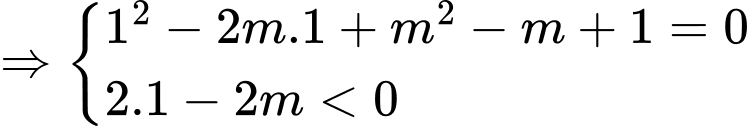
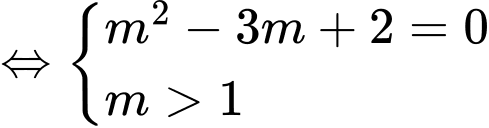
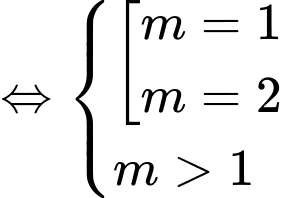
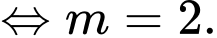 Đáp án: B
Đáp án: B