Đáp án Bài tập tự luyện
Câu 1 [6309]: Tìm tập hợp tất cả các giá trị của tham số 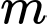 để hàm số
để hàm số 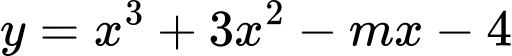 đồng biến trên khoảng
đồng biến trên khoảng 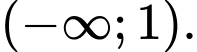
 để hàm số
để hàm số 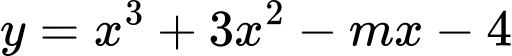 đồng biến trên khoảng
đồng biến trên khoảng 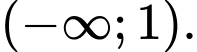
A, 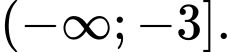
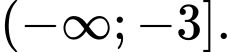
B, 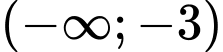 .
.
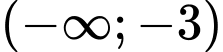 .
.C, 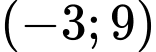 .
.
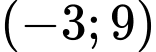 .
.D, 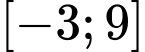 .
.
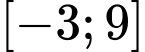 .
.
Ta có 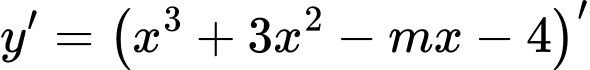
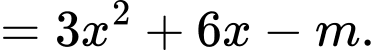
Hàm số đồng biến trên khoảng
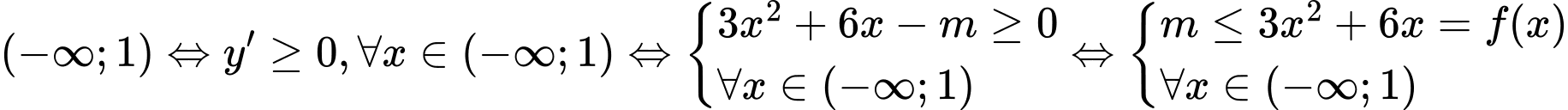
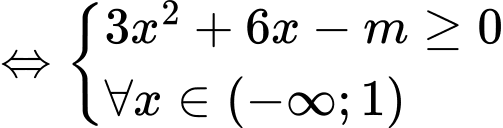
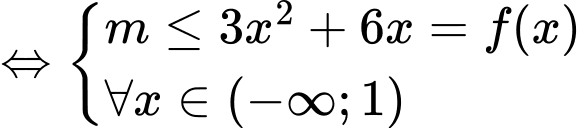
Ta có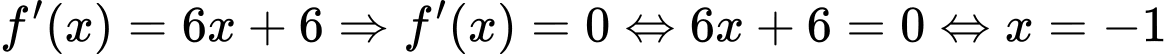 .
.
Xét bảng biến thiên của hàm số trên đoạn ta thấy
ta thấy 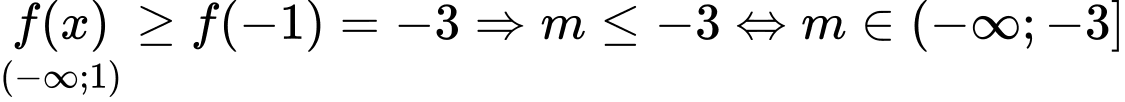 .
.
Chọn A. Đáp án: A
Hàm số đồng biến trên khoảng

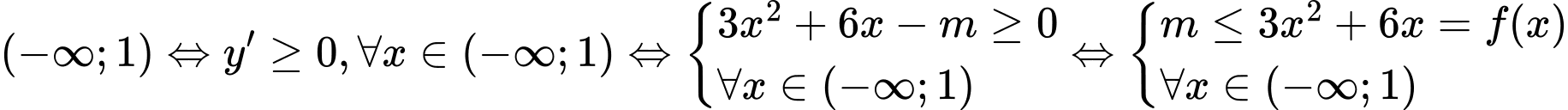
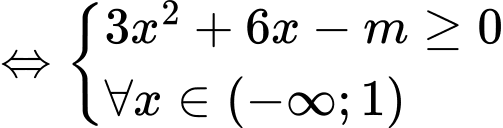
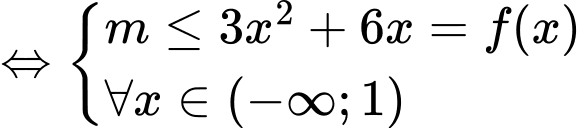
Ta có
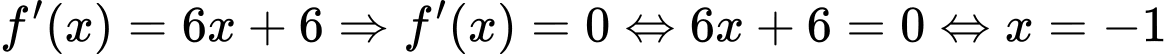 .
.
Xét bảng biến thiên của hàm số trên đoạn
 ta thấy
ta thấy 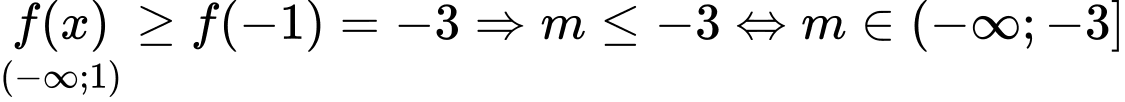 .
.
Chọn A. Đáp án: A
Câu 2 [677877]: Tập hợp tất cả các giá trị thực của tham số 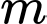 để hàm số
để hàm số 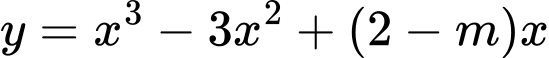 đồng biến trên khoảng
đồng biến trên khoảng 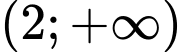 là
là
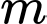 để hàm số
để hàm số 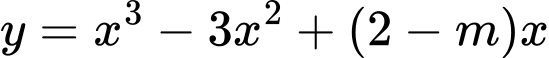 đồng biến trên khoảng
đồng biến trên khoảng 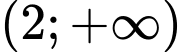 là
là A, 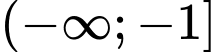 .
.
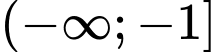 .
.B,  .
.
 .
.C, 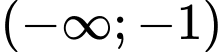 .
.
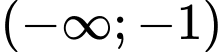 .
.D, 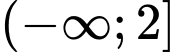 .
.
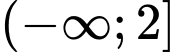 .
.
Chọn D
Ta có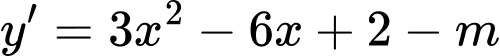 .
.
Để hàm số đồng biến trênkhoảng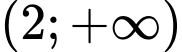 khi và chỉ khi
khi và chỉ khi 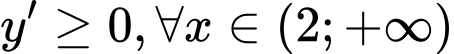
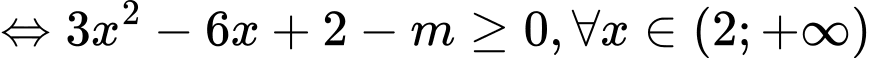
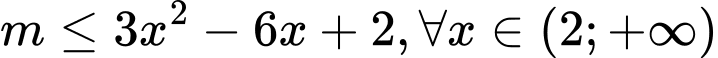 .
.
Xét hàm số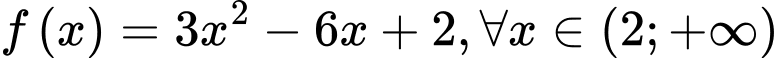 .
.
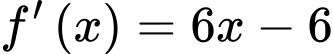 ;
; 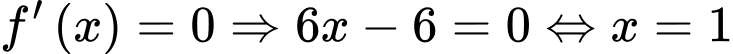 .
.
Bảng biến thiên:
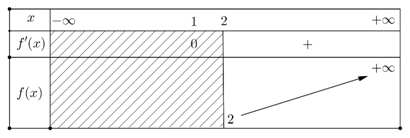
Từ bảng biến thiên ta thấy . Vậy
. Vậy  . Đáp án: D
. Đáp án: D
Ta có
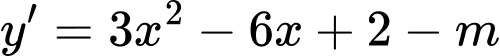 .
. Để hàm số đồng biến trênkhoảng
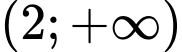 khi và chỉ khi
khi và chỉ khi 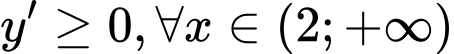
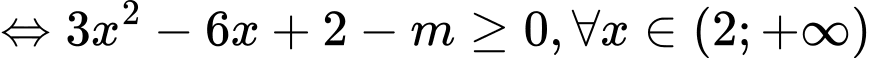
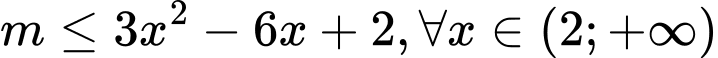 .
.Xét hàm số
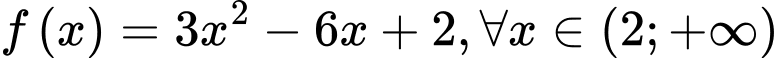 .
.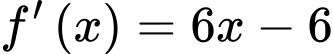 ;
; 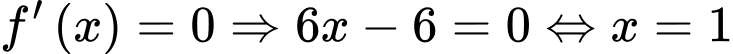 .
.Bảng biến thiên:

Từ bảng biến thiên ta thấy
 . Vậy
. Vậy  . Đáp án: D
. Đáp án: D
Câu 3 [2527]: Tìm 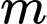 để hàm số
để hàm số 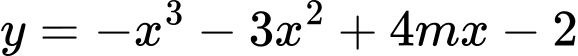 nghịch biến trên
nghịch biến trên 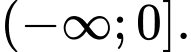
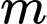 để hàm số
để hàm số 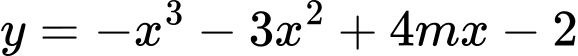 nghịch biến trên
nghịch biến trên 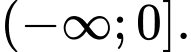
A, 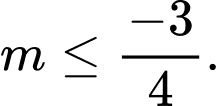
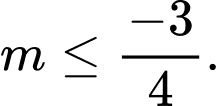
B, 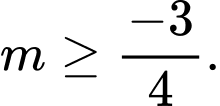
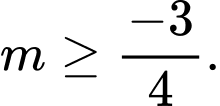
C, 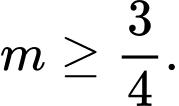
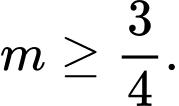
D, 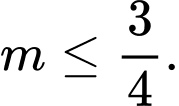
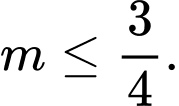
Theo bài ra, hàm số nghịch biến trên miền đang xét khi 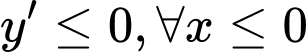
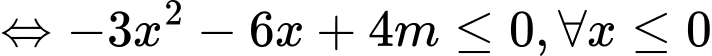
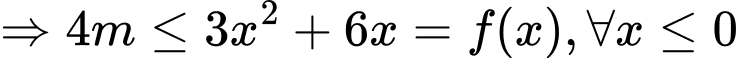

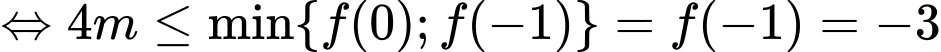
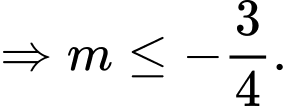 Đáp án: A
Đáp án: A
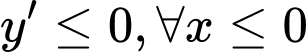
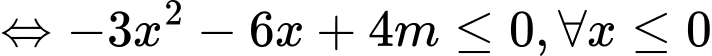
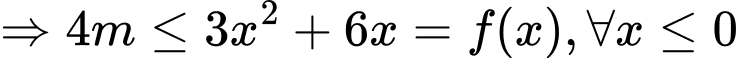

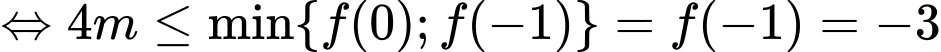
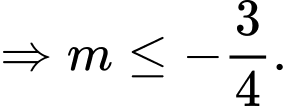 Đáp án: A
Đáp án: A
Câu 4 [517772]: [Đề thi tham khảo của Bộ GD&ĐT năm 2019]: Tập hợp các giá trị thực của tham số 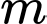 để hàm số
để hàm số 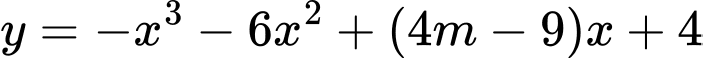 nghịch biến trên khoảng
nghịch biến trên khoảng 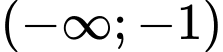 là
là
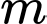 để hàm số
để hàm số 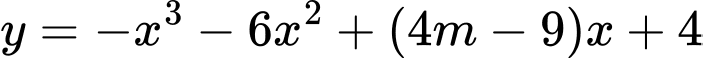 nghịch biến trên khoảng
nghịch biến trên khoảng 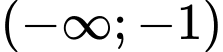 là
là A, 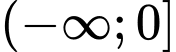
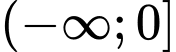
B, 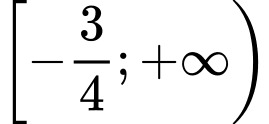
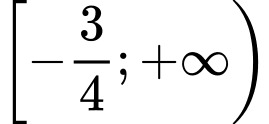
C, 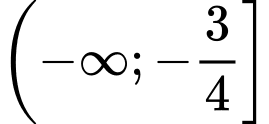
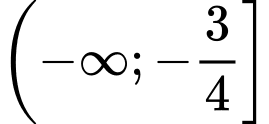
D, 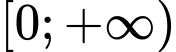
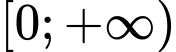
Lời giải: Ta có 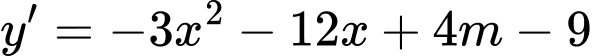
Hàm số nghịch biến trên khoảng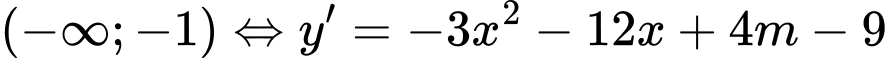


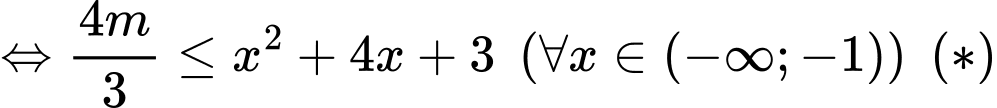
Xét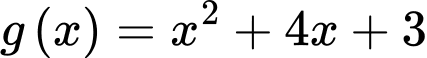 trên khoảng
trên khoảng 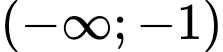 ta có:
ta có: 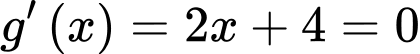
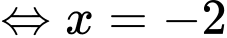
Ta tìm được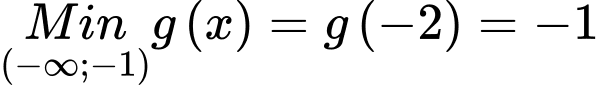
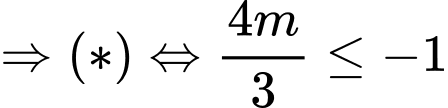
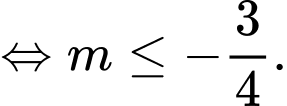 Chọn C. Đáp án: C
Chọn C. Đáp án: C
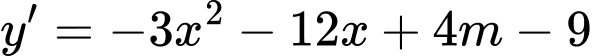
Hàm số nghịch biến trên khoảng
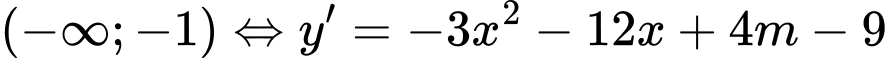


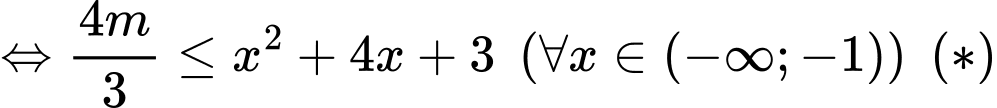
Xét
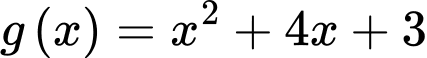 trên khoảng
trên khoảng 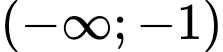 ta có:
ta có: 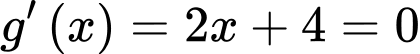
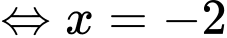
Ta tìm được
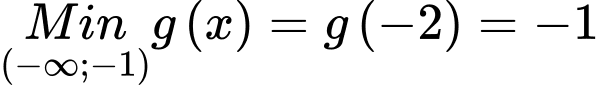
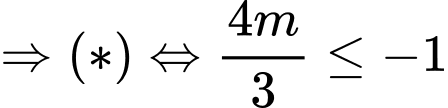
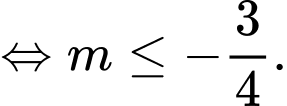 Chọn C. Đáp án: C
Chọn C. Đáp án: C
Câu 5 [2570]: Cho hàm số 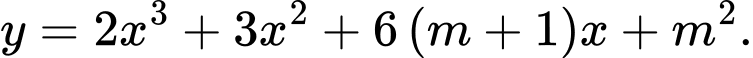 Số giá trị nguyên của
Số giá trị nguyên của  để hàm số nghịch biến trên khoảng
để hàm số nghịch biến trên khoảng 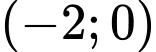 là
là
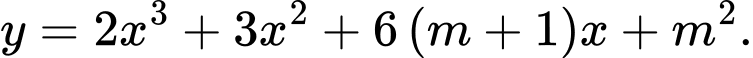 Số giá trị nguyên của
Số giá trị nguyên của  để hàm số nghịch biến trên khoảng
để hàm số nghịch biến trên khoảng 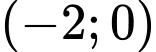 là
là A, 
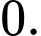
B, 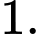
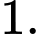
C, 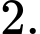
D, 
Ta có 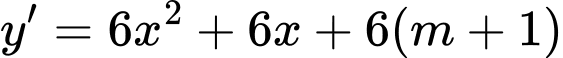
Để hàm số nghịch biến trên khoảng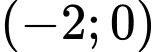 thì
thì 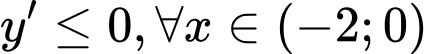
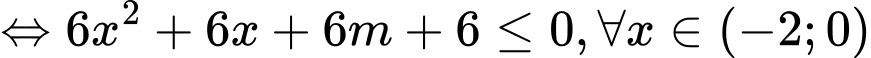
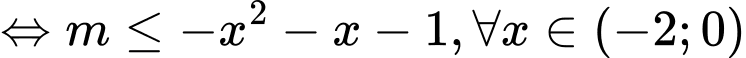
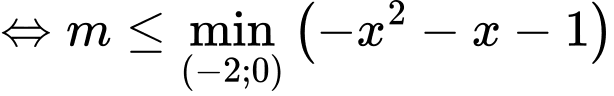
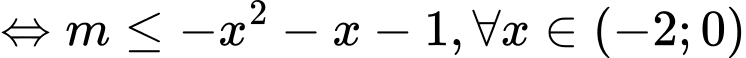
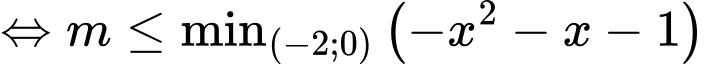
Xét hàm số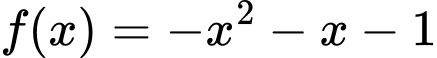 với
với  (do hàm số
(do hàm số 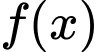 liên tục trên
liên tục trên 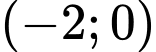 )
)
Ta có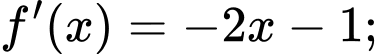
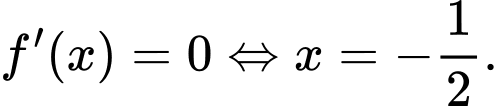
Ta có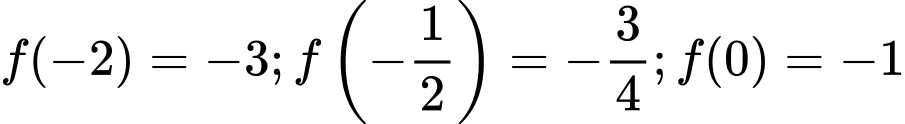
Do đó giá trị nhỏ nhất của hàm số là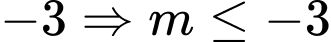 mà
mà  Chọn D. Đáp án: D
Chọn D. Đáp án: D
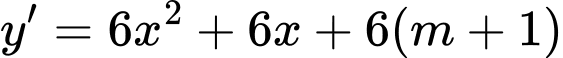
Để hàm số nghịch biến trên khoảng
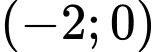 thì
thì 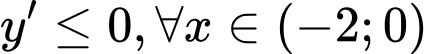
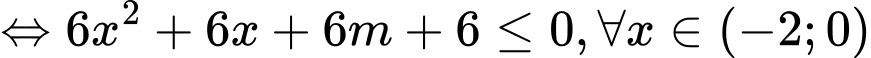
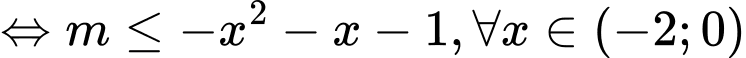
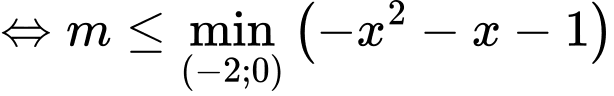
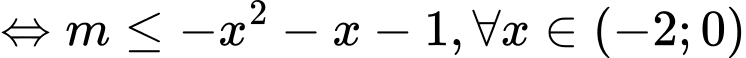
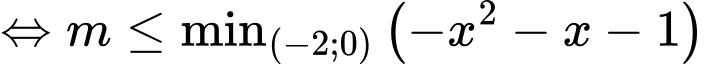
Xét hàm số
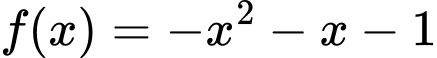 với
với  (do hàm số
(do hàm số 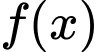 liên tục trên
liên tục trên 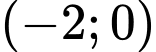 )
)Ta có
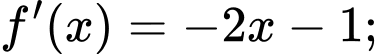
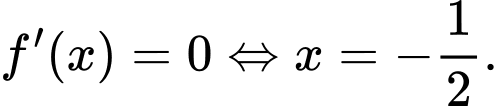
Ta có
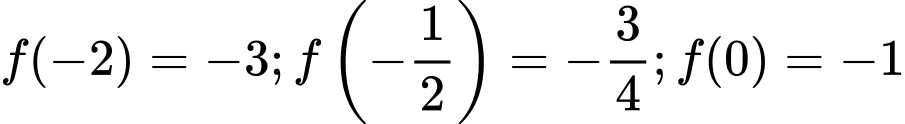
Do đó giá trị nhỏ nhất của hàm số là
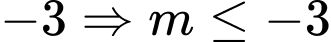 mà
mà  Chọn D. Đáp án: D
Chọn D. Đáp án: D
Câu 6 [384324]: [Đề mẫu ĐGNL ĐHQG Hà Nội]: Tập hợp các giá trị của tham số 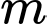 để hàm số
để hàm số 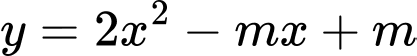 đồng biến trên khoảng
đồng biến trên khoảng 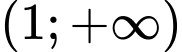 là
là
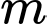 để hàm số
để hàm số 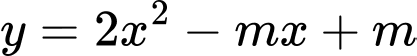 đồng biến trên khoảng
đồng biến trên khoảng 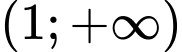 là
là A, 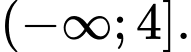
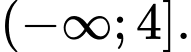
B, 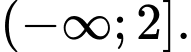
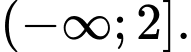
C, 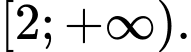
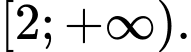
D, 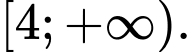
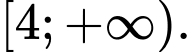
Chọn đáp án A.
Có: 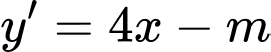 Để hàm số đã cho đồng biến trên khoảng
Để hàm số đã cho đồng biến trên khoảng 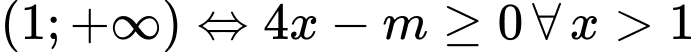
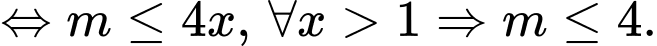
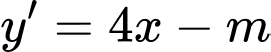 Để hàm số đã cho đồng biến trên khoảng
Để hàm số đã cho đồng biến trên khoảng 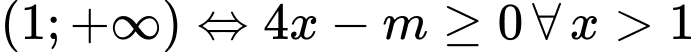
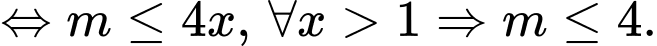
Câu 7 [6317]: Tìm tất cả các giá trị thực của tham số 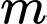 để hàm số
để hàm số 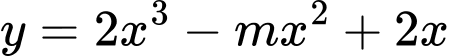 đồng biến trên khoảng
đồng biến trên khoảng 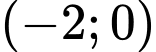 .
.
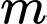 để hàm số
để hàm số 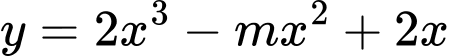 đồng biến trên khoảng
đồng biến trên khoảng 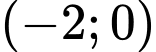 .
. A, 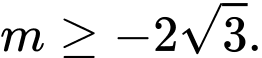
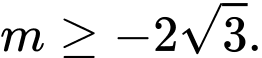
B, 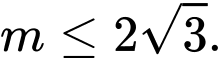
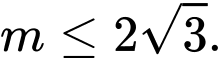
C, 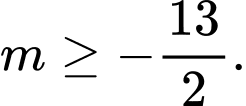
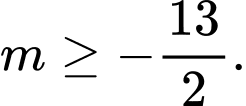
D, 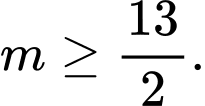
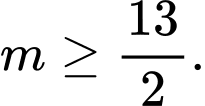
Ta có: 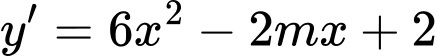 . Hàm số đồng biến trên khoảng
. Hàm số đồng biến trên khoảng 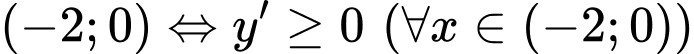
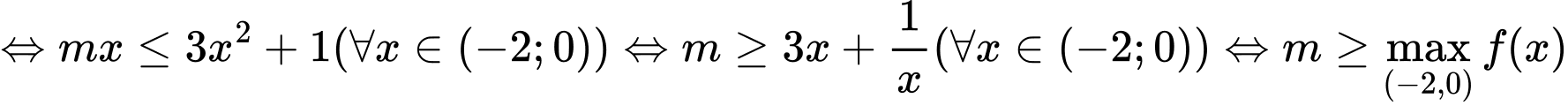
Xét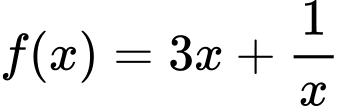 với
với  ta có:
ta có: 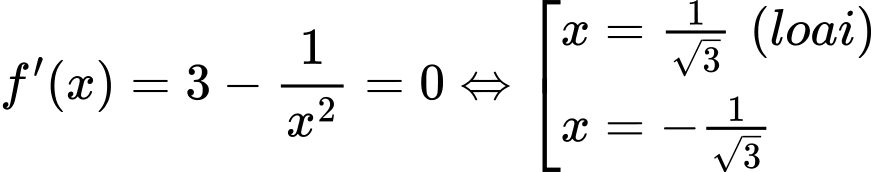
Lại có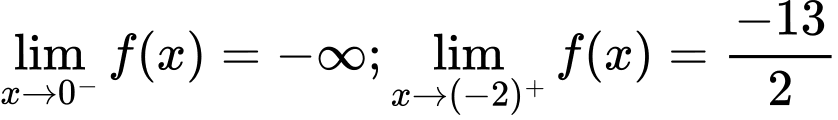 và
và 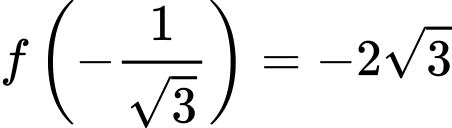
Vậy . Chọn
. Chọn 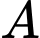 .
.
Cách 2: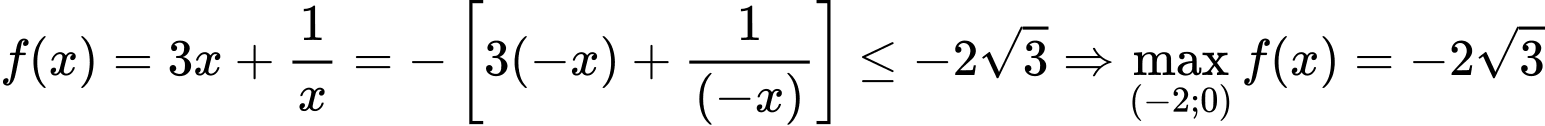 khi
khi 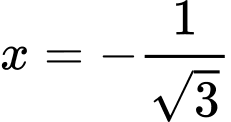 Đáp án: A
Đáp án: A
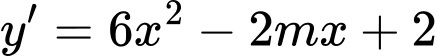 . Hàm số đồng biến trên khoảng
. Hàm số đồng biến trên khoảng 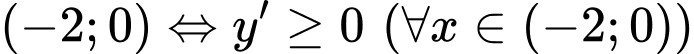
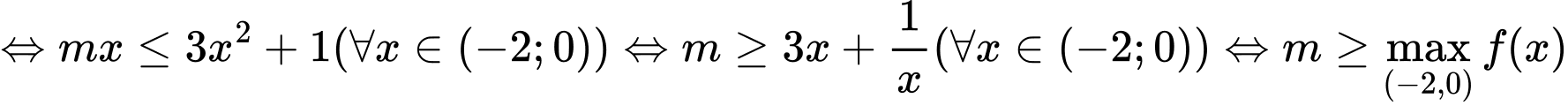
Xét
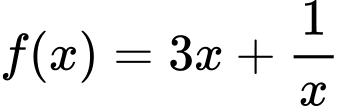 với
với  ta có:
ta có: 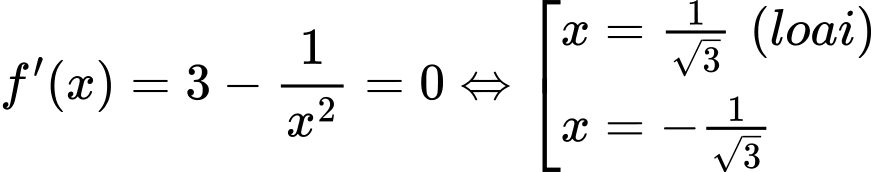
Lại có
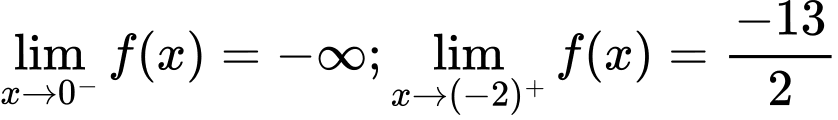 và
và 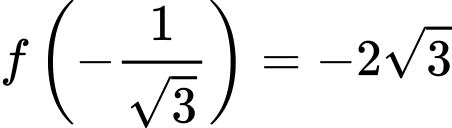
Vậy
 . Chọn
. Chọn 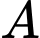 .
.
Cách 2:
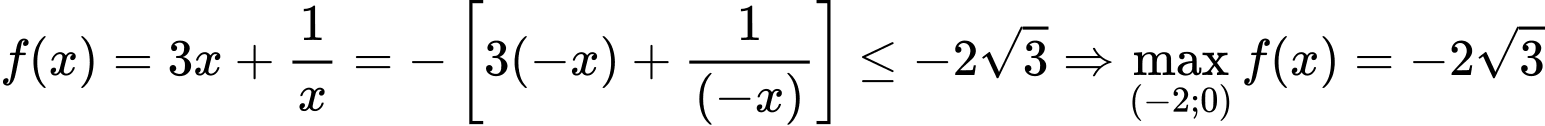 khi
khi 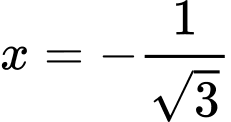 Đáp án: A
Đáp án: A
Câu 8 [308074]: Tập hợp tất cả các giá trị thực của tham số  để hàm số
để hàm số 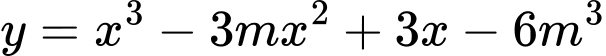 đồng biến trên khoảng
đồng biến trên khoảng 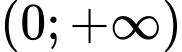 là
là
 để hàm số
để hàm số 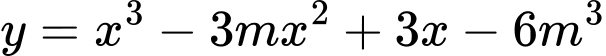 đồng biến trên khoảng
đồng biến trên khoảng 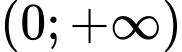 là
là A, 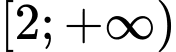 .
.
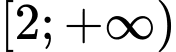 .
.B, 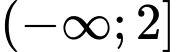 .
.
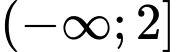 .
.C, 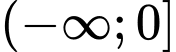 .
.
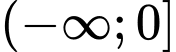 .
.D, 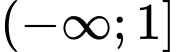 .
.
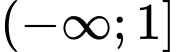 .
.
Chọn D
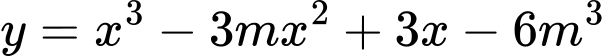
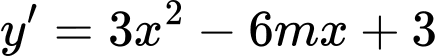 .
.
Để hàm số đồng biến trên khoảng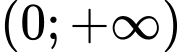

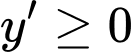 ,
, 
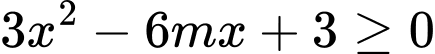 ,
, 

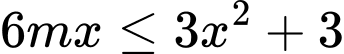 ,
, 

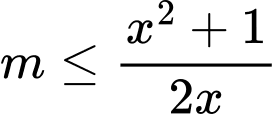 ,
, 

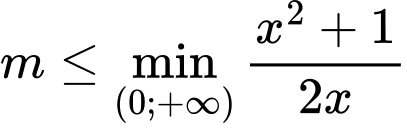 .
.
Gọi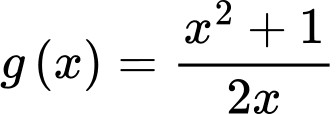
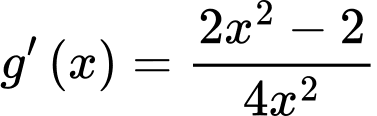 ;
; 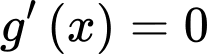

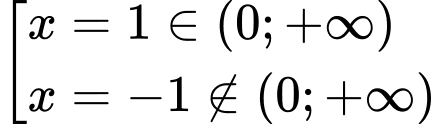 .
.
Bảng biến thiên của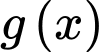 :
:
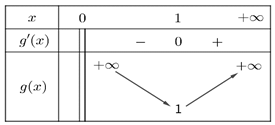
Vậy . Đáp án: D
. Đáp án: D
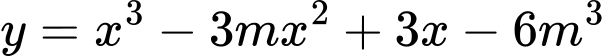
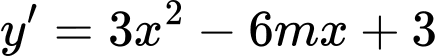 .
.
Để hàm số đồng biến trên khoảng
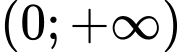

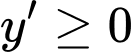 ,
, 
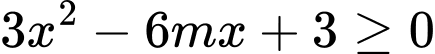 ,
, 

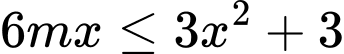 ,
, 

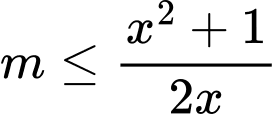 ,
, 

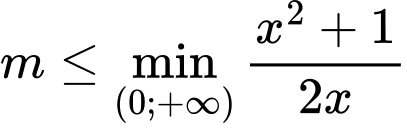 .
.
Gọi
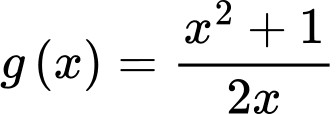
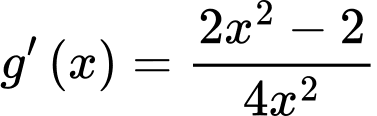 ;
; 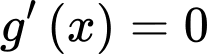

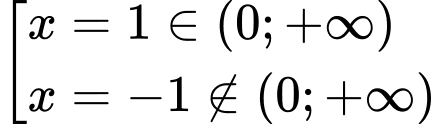 .
.
Bảng biến thiên của
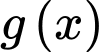 :
:
Vậy
 . Đáp án: D
. Đáp án: D
Câu 9 [6330]: Tìm 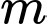 để hàm số
để hàm số 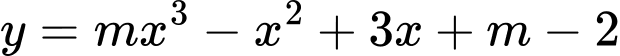 đồng biến trên khoảng
đồng biến trên khoảng 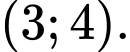
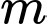 để hàm số
để hàm số 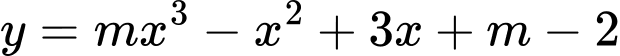 đồng biến trên khoảng
đồng biến trên khoảng 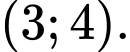
A, 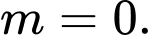
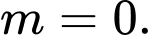
B, 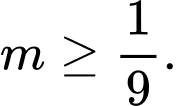
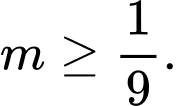
C, 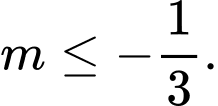
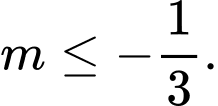
D, 

Ta có 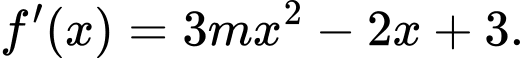
Hàm số đã cho đồng biến trên (3;4) khi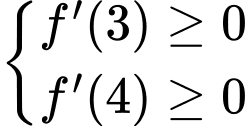
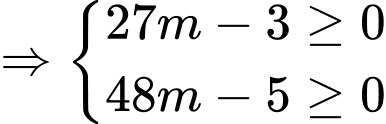
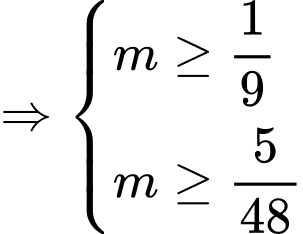
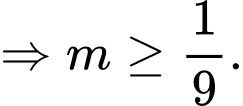 Đáp án: B
Đáp án: B
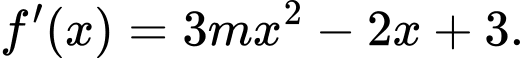
Hàm số đã cho đồng biến trên (3;4) khi
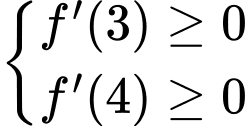
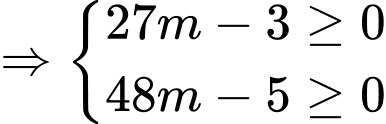
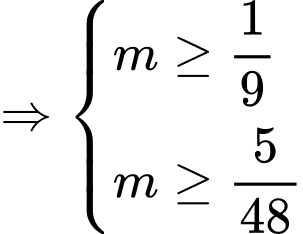
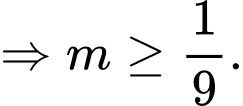 Đáp án: B
Đáp án: B