Đáp án Bài tập tự luyện
Câu 1 [45895]: Cho hàm số 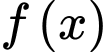 có bảng biến thiên như sau
có bảng biến thiên như sau
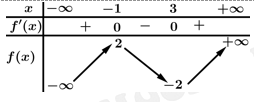
Hàm số đã cho đạt cực tiểu tại
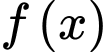 có bảng biến thiên như sau
có bảng biến thiên như sau
Hàm số đã cho đạt cực tiểu tại
A, 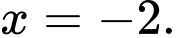
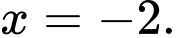
B, 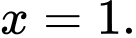
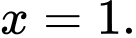
C, 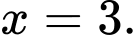
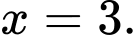
D, 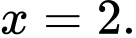
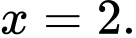
Chọn đáp án C Đáp án: C
Câu 2 [508514]: Cho hàm số 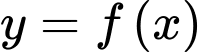 có bảng biến thiên như sau:
có bảng biến thiên như sau:
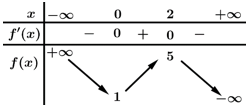
Giá trị cực đại của hàm số đã cho bằng
 có bảng biến thiên như sau:
có bảng biến thiên như sau:
Giá trị cực đại của hàm số đã cho bằng
A, 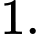
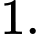
B, 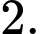
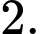
C, 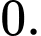
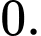
D, 
Đáp án D. Giá trị cực đại của hàm số bằng 5. Đáp án: D
Câu 3 [378875]: Cho hàm số 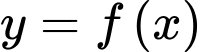 xác định trên
xác định trên 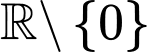 và có bảng biến thiên như sau:
và có bảng biến thiên như sau:
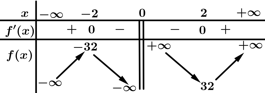
Cực đại của hàm số đã cho bằng
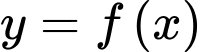 xác định trên
xác định trên 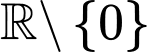 và có bảng biến thiên như sau:
và có bảng biến thiên như sau:
Cực đại của hàm số đã cho bằng
A, 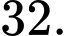
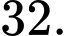
B, 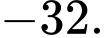
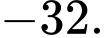
C, 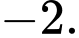
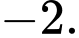
D, 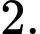
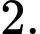
Cực đại ý nói giá trị cực đại Đáp án: B
Câu 4 [185179]: Cho hàm số 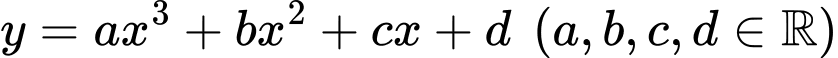 có đồ thị là đường cong trong hình bên. Giá trị cực đại của hàm số đã cho bằng
có đồ thị là đường cong trong hình bên. Giá trị cực đại của hàm số đã cho bằng
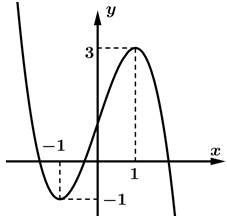
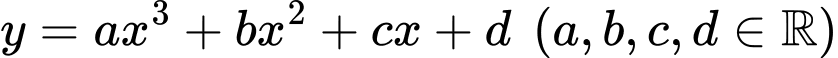 có đồ thị là đường cong trong hình bên. Giá trị cực đại của hàm số đã cho bằng
có đồ thị là đường cong trong hình bên. Giá trị cực đại của hàm số đã cho bằng
A, 
B, 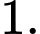
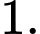
C, 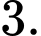
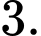
D, 
Giá trị cực đại của hàm số là 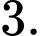 Đáp án: C
Đáp án: C
 Đáp án: C
Đáp án: C
Câu 5 [377570]: Cho hàm số 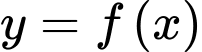 có bảng biến thiên như hình vẽ.
có bảng biến thiên như hình vẽ. 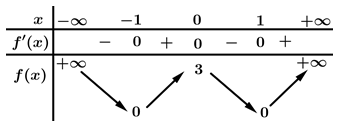
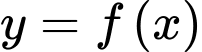 có bảng biến thiên như hình vẽ.
có bảng biến thiên như hình vẽ. 
Các mệnh đề sau đúng hay sai
A, a) Hàm số có ba điểm cực trị.
B, b) Hàm số có giá trị cực đại bằng 3.
C, c) Hàm số có giá trị cực đại bằng 0.
D, d) Hàm số có hai điểm cực tiểu.
a) Đúng. Hàm số có ba điểm cực trị là: 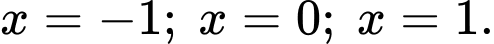
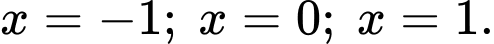
b) Đúng. Hàm số có giá trị cực đại bằng 3.
c) Sai. Hàm số có giá trị cực đại bằng 3.
d) Đúng. Hàm số có hai điểm cực tiểu là: 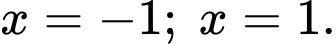
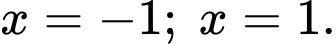
Câu 6 [377571]: Cho hàm số 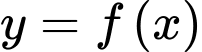 có bảng biến thiên như hình vẽ.
có bảng biến thiên như hình vẽ. 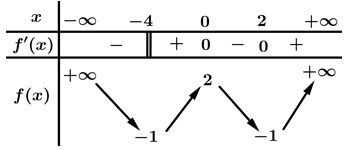
Các mệnh đề sau đúng hay sai
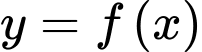 có bảng biến thiên như hình vẽ.
có bảng biến thiên như hình vẽ. 
A, a) Hàm số có ba điểm cực trị
B, b) Hàm số có có hai điểm cực tiểu.
C, c) Hàm số có giá trị cực đại bằng 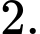
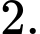
D, d) Hàm số có hai cực tiểu.
a) Đúng. Hàm số có ba điểm cực trị là: 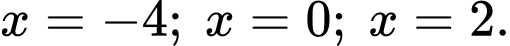
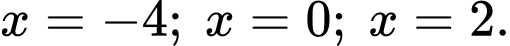
b) Đúng. Hàm số có hai điểm cực tiểu.
c) Đúng.
d) Sai. Cực tiểu ý nói giá trị cực tiểu. Hàm số có một cực tiểu bằng 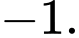
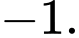
Câu 7 [377572]: Cho hàm số 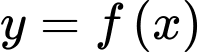 xác định trên
xác định trên 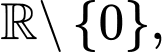 liên tục trên từng khoảng xác định và có bảng biến thiên như hình vẽ.
liên tục trên từng khoảng xác định và có bảng biến thiên như hình vẽ. 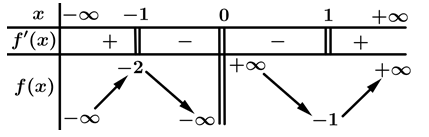
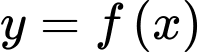 xác định trên
xác định trên 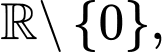 liên tục trên từng khoảng xác định và có bảng biến thiên như hình vẽ.
liên tục trên từng khoảng xác định và có bảng biến thiên như hình vẽ. 
Các mệnh đề sau đúng hay sai
A, a) Hàm số không có điểm cực trị.
B, b) Giá trị cực đại của hàm số bằng 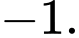
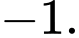
C, c) Hàm số nghịch biến trên khoảng 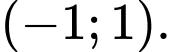
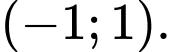
D, d) Hàm số có giá trị cực đại lớn hơn giá trị cực tiểu.
a) Sai. Hàm số có 2 điểm cực trị 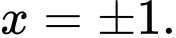
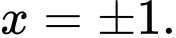
b) Sai. Giá trị cực đại của hàm số bằng 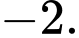
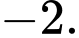
c) Sai. Hàm số nghịch biến trên mỗi khoảng 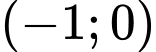 và
và 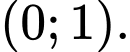
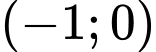 và
và 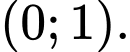
d) Sai. Hàm số có giá trị cực đại (bằng 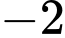 ) nhỏ hơn giá trị cực tiểu (bằng
) nhỏ hơn giá trị cực tiểu (bằng 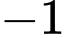 ).
).
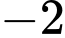 ) nhỏ hơn giá trị cực tiểu (bằng
) nhỏ hơn giá trị cực tiểu (bằng 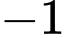 ).
).
Câu 8 [378878]: Cho hàm số 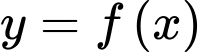 có bảng biến thiên như hình vẽ. Các mệnh đề sau đúng hay sai
có bảng biến thiên như hình vẽ. Các mệnh đề sau đúng hay sai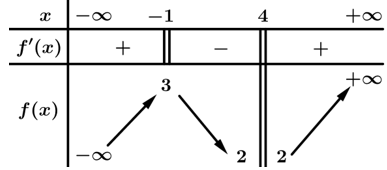
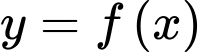 có bảng biến thiên như hình vẽ. Các mệnh đề sau đúng hay sai
có bảng biến thiên như hình vẽ. Các mệnh đề sau đúng hay sai
A, a) Hàm số đạt cực đại tại điểm 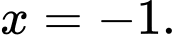
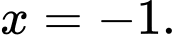
B, b) Giá trị cực tiểu của hàm số đã cho bằng 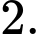
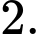
C, c) Hàm số đã cho không có điểm cực trị.
D, d) Hàm số đã cho đồng biến trên khoảng 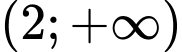
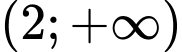
a, Đúng
b, Sai
c, Sai. Hàm số đã cho có điểm cực trị.
d, Sai. Hàm số đã cho đồng biến trên khoảng 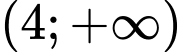 và
và 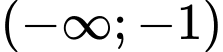
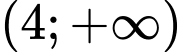 và
và 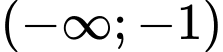
Câu 9 [378877]: Cho hàm số 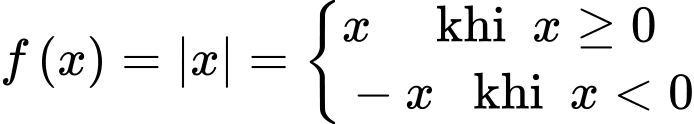 và có đồ thị như hình vẽ. Xét tính đúng sai của các mệnh đề sau:
và có đồ thị như hình vẽ. Xét tính đúng sai của các mệnh đề sau:
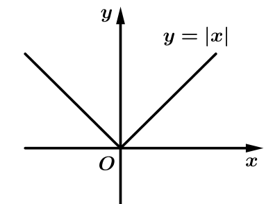
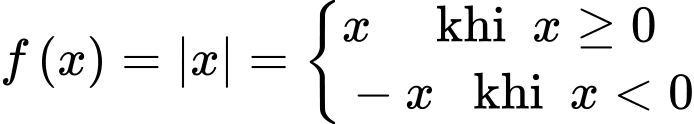 và có đồ thị như hình vẽ. Xét tính đúng sai của các mệnh đề sau:
và có đồ thị như hình vẽ. Xét tính đúng sai của các mệnh đề sau:

A, a) Hàm số 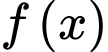 có
có 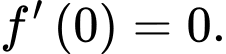
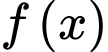 có
có 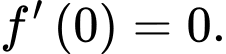
B, b) Hàm số 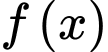 không có đạo hàm tại điểm
không có đạo hàm tại điểm 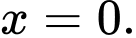
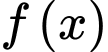 không có đạo hàm tại điểm
không có đạo hàm tại điểm 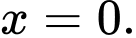
C, c) Hàm số 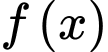 đạt cực tiểu tại điểm
đạt cực tiểu tại điểm 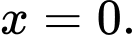
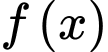 đạt cực tiểu tại điểm
đạt cực tiểu tại điểm 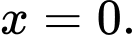
D, d) Giá trị cực tiểu của hàm số 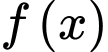 bằng
bằng 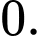
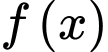 bằng
bằng 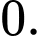
a, Sai b, Đúng c, Đúng d, Đúng
Hàm số đã cho xác định và liên tục trên R
Ta có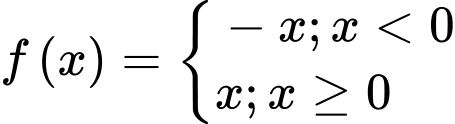
Do đó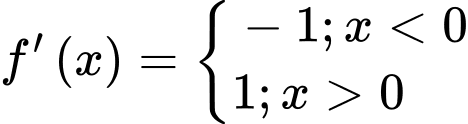 .
.
Hàm số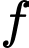 không có đạo hàm tại điểm
không có đạo hàm tại điểm 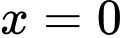
Bảng biến thiên
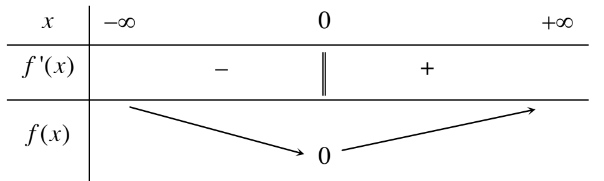
Vậy hàm số đạt cực tiểu tại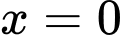 và giá trị cực tiểu của hàm số là
và giá trị cực tiểu của hàm số là 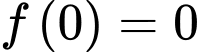
Hàm số đã cho xác định và liên tục trên R
Ta có
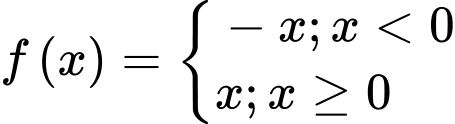
Do đó
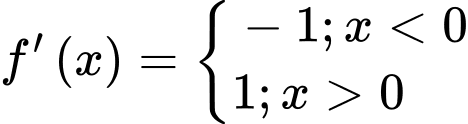 .
.
Hàm số
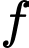 không có đạo hàm tại điểm
không có đạo hàm tại điểm 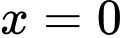
Bảng biến thiên

Vậy hàm số đạt cực tiểu tại
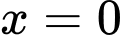 và giá trị cực tiểu của hàm số là
và giá trị cực tiểu của hàm số là 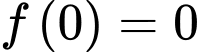
Câu 10 [386946]: Giá trị cực đại của hàm số 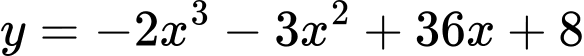 bằng
bằng
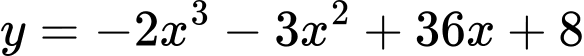 bằng
bằng Đáp số:………………………
Ta có 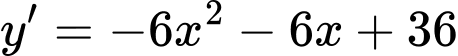

Bảng biến thiên

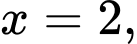
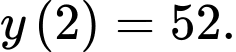
Câu 11 [386947]: Giá trị cực tiểu của hàm số 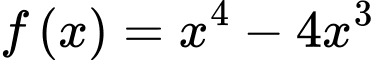 bằng
bằng
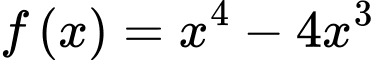 bằng
bằng Đáp số:………………………
Ta có 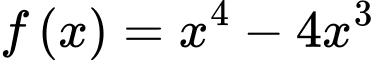
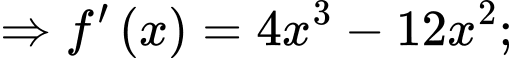
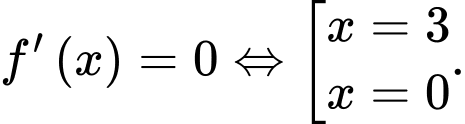
Trong 2 nghiệm thì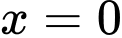 là nghiệm bội chẵn nên ta không cần phải điền trên trục.
là nghiệm bội chẵn nên ta không cần phải điền trên trục.
BBT như sau

Vậy hàm số đạt cực tiểu tại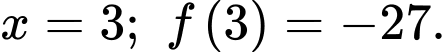
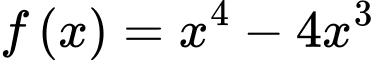
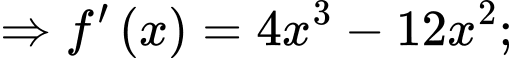
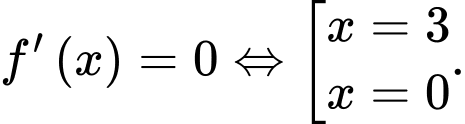
Trong 2 nghiệm thì
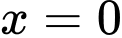 là nghiệm bội chẵn nên ta không cần phải điền trên trục.
là nghiệm bội chẵn nên ta không cần phải điền trên trục.BBT như sau

Vậy hàm số đạt cực tiểu tại
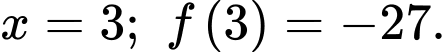
Câu 12 [386949]: Tìm cực đại của hàm số 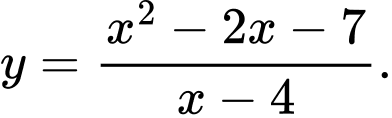
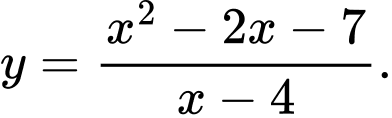
Ta có 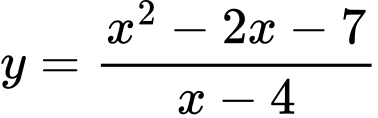
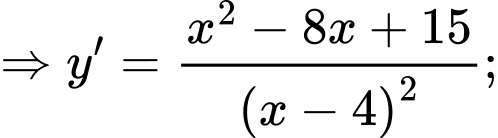
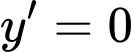
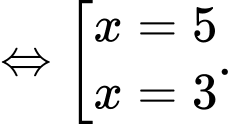
Bảng biến thiên

Vậy hàm số đạt cực đại tại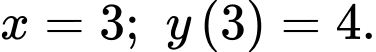
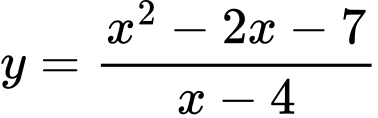
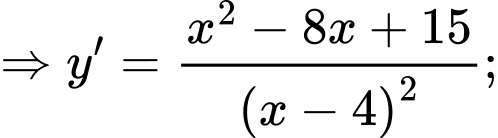
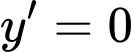
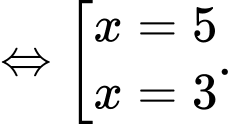
Bảng biến thiên

Vậy hàm số đạt cực đại tại
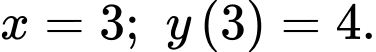
Câu 13 [383395]: [SGK Chân Trời Sáng Tạo]: Một phần lát cắt của dãy núi (xem hình vẽ) có độ cao so với mặt đất tính bằng mét được mô tả bởi hàm số: 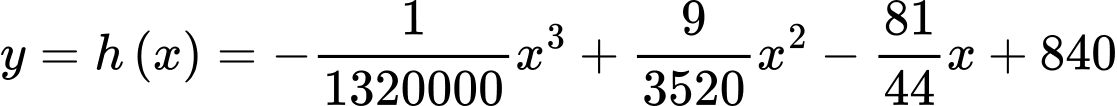 với
với 
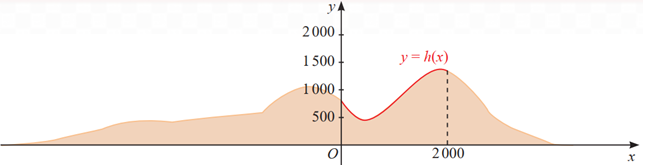
Hỏi đỉnh núi cách mặt đất một khoảng bằng bao nhiêu mét (làm tròn kết quả đến hàng đơn vị)
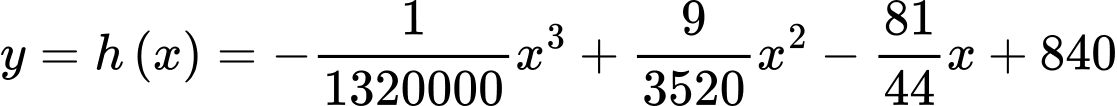 với
với 

Tập xác định: D = 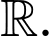
Có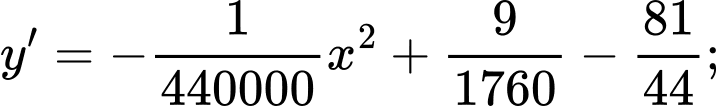
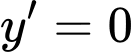
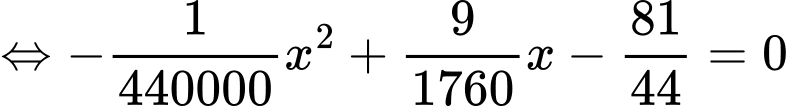
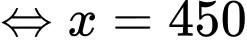 hoặc
hoặc 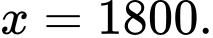
Bảng biến thiên:
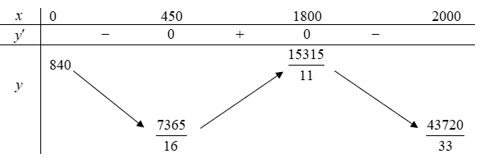
Dựa vào bảng biến thiên, khoảng cách giữa đỉnh núi và mặt đất là: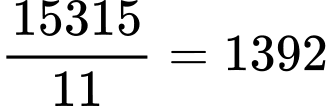 (m).
(m).
Có
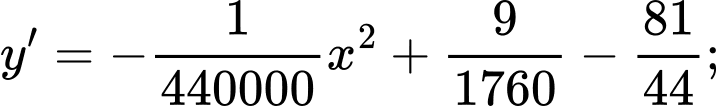
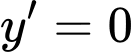
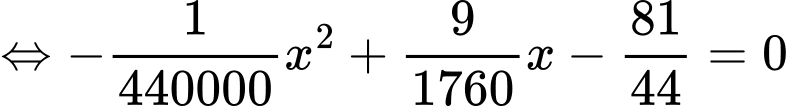
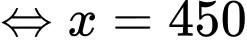 hoặc
hoặc 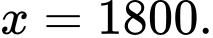
Bảng biến thiên:

Dựa vào bảng biến thiên, khoảng cách giữa đỉnh núi và mặt đất là:
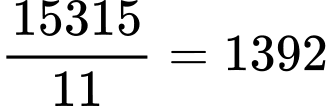 (m).
(m).
Câu 14 [628852]: Hàm số 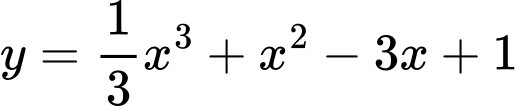 đạt cực tiểu tại điểm
đạt cực tiểu tại điểm
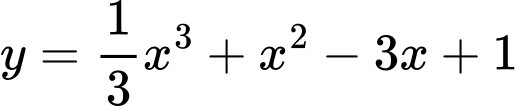 đạt cực tiểu tại điểm
đạt cực tiểu tại điểm A, 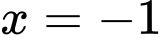 .
.
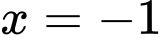 .
.B, 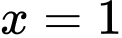 .
.
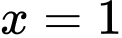 .
.C, 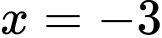 .
.
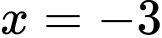 .
.D, 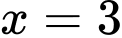 .
.
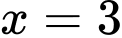 .
.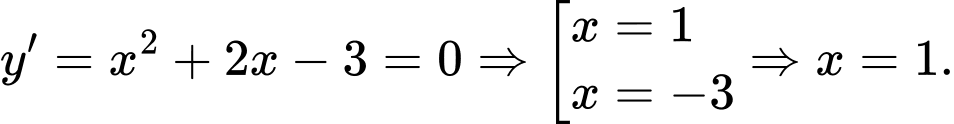 Đáp án: B
Đáp án: B
Câu 15 [2834]: Hàm số 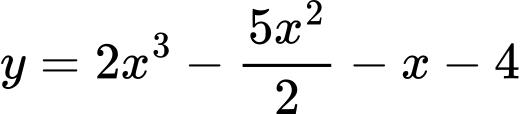 đạt cực đại tại điểm
đạt cực đại tại điểm
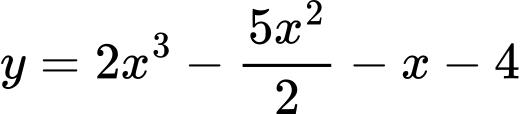 đạt cực đại tại điểm
đạt cực đại tại điểm A, 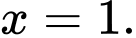
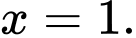
B, 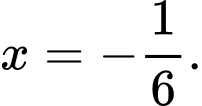
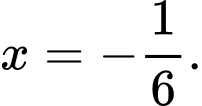
C, 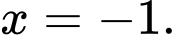
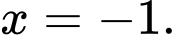
D, 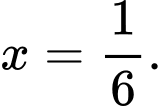
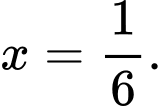
Ta có 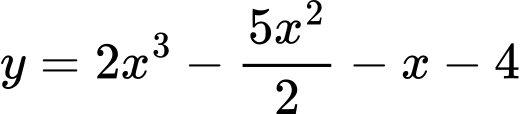
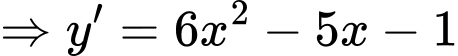
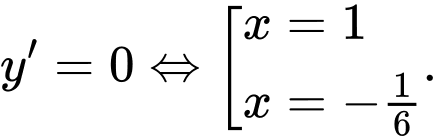
Ta có trục xét dấu
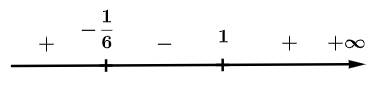
Suy ra hàm số đạt cực đại tại điểm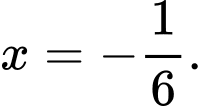 Chọn B. Đáp án: B
Chọn B. Đáp án: B
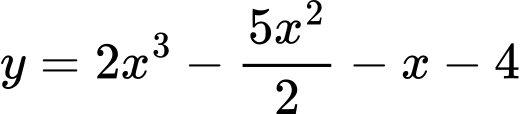
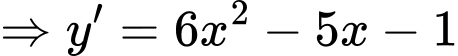
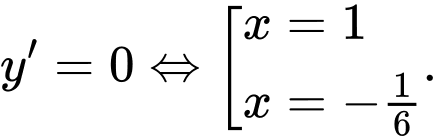
Ta có trục xét dấu
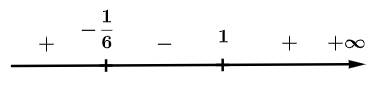
Suy ra hàm số đạt cực đại tại điểm
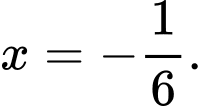 Chọn B. Đáp án: B
Chọn B. Đáp án: B
Câu 16 [629180]: Điểm cực tiểu của đồ thị hàm số 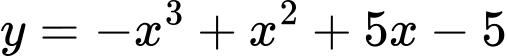 là
là
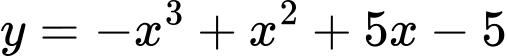 là
là A, 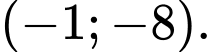
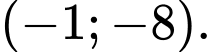
B, 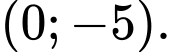
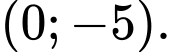
C, 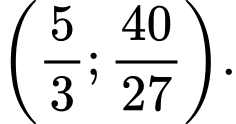
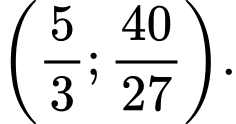
D, 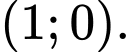
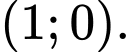
Đồ thị hình chữ N ngươc, hoành độ cực tiểu nhỏ hơn. 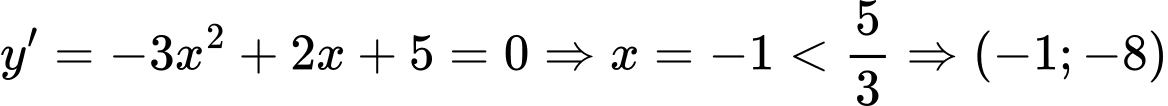 là điểm cực tiểu của đồ thị hàm số.
Đáp án: A
là điểm cực tiểu của đồ thị hàm số.
Đáp án: A
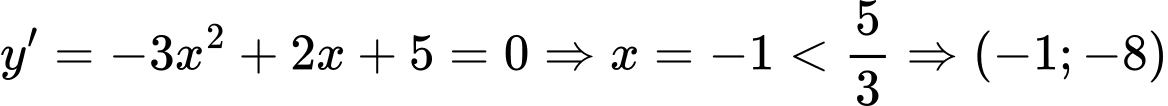 là điểm cực tiểu của đồ thị hàm số.
là điểm cực tiểu của đồ thị hàm số.
Câu 17 [319619]: Hàm số nào sau đây có đúng một điểm cực trị?
A, 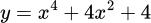 .
.
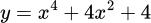 .
.B, 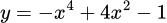 .
.
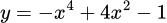 .
.C, 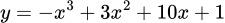 .
.
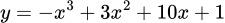 .
.D, 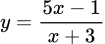 .
.
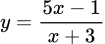 .
.
Chọn A.
Xét hàm số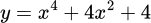 .
.
Ta có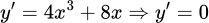
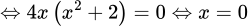 .
.
Bảng biến thiên
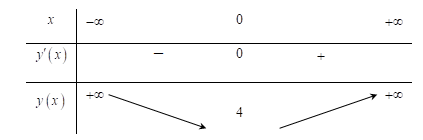
Vậy hàm số có đúng một điểm cực trị.
Hàm số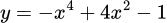 có ba điểm cực trị.
có ba điểm cực trị.
Hàm số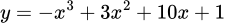 có hai điểm cực trị.
có hai điểm cực trị.
Hàm số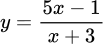 không có điểm cực trị. Đáp án: A
không có điểm cực trị. Đáp án: A
Xét hàm số
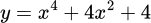 .
.Ta có
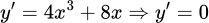
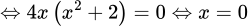 .
.Bảng biến thiên

Vậy hàm số có đúng một điểm cực trị.
Hàm số
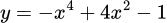 có ba điểm cực trị.
có ba điểm cực trị.Hàm số
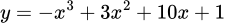 có hai điểm cực trị.
có hai điểm cực trị.Hàm số
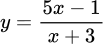 không có điểm cực trị. Đáp án: A
không có điểm cực trị. Đáp án: A
Câu 18 [378478]: Hàm số nào dưới đây không có cực trị?
A, 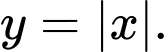
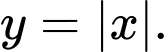
B, 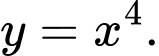
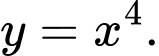
C, 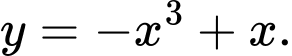
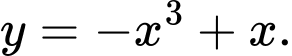
D, 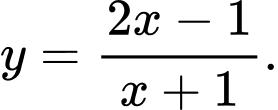
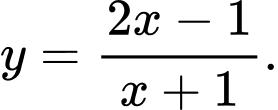
Chọn đáp án D. Vì ta có 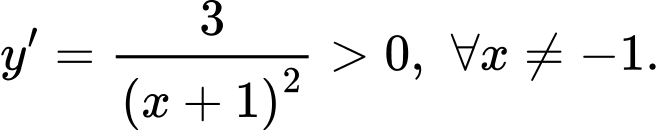
Suy ra hàm số đồng biến trên toàn tập xác định. Nên hàm số không có cực trị. Đáp án: D
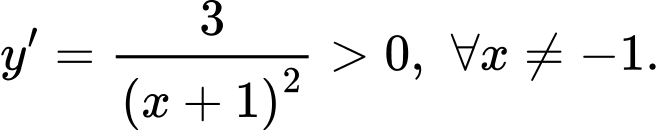
Suy ra hàm số đồng biến trên toàn tập xác định. Nên hàm số không có cực trị. Đáp án: D
Câu 19 [319955]: Điểm cực đại của đồ thị hàm số 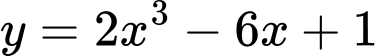 là
là
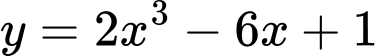 là
là A, 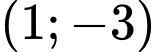 .
.
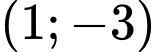 .
.B, 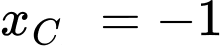 .
.
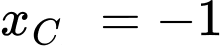 .
.C, 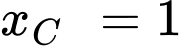 .
.
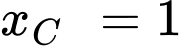 .
.D, 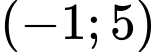 .
.
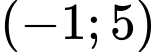 .
.
Chọn D
Tập xác định của hàm số là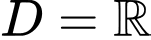 .
.
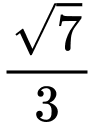
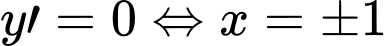 .
.
Bảng biến thiên
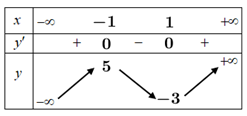
Suy ra điểm cực đại của đồ thị hàm số đã cho là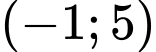 . Đáp án: D
. Đáp án: D
Tập xác định của hàm số là
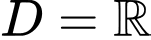 .
.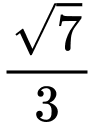
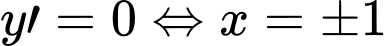 .
.Bảng biến thiên

Suy ra điểm cực đại của đồ thị hàm số đã cho là
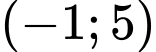 . Đáp án: D
. Đáp án: D
Câu 20 [378479]: Giá trị cực tiểu của hàm số 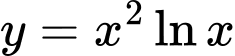 là
là
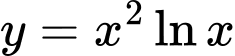 là
là A, 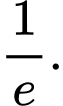
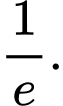
B, 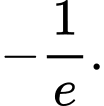
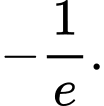
C, 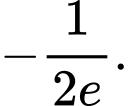
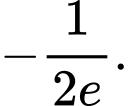
D, 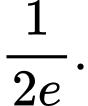
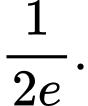
Ta có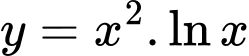 . ĐKXĐ
. ĐKXĐ  .
. 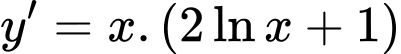
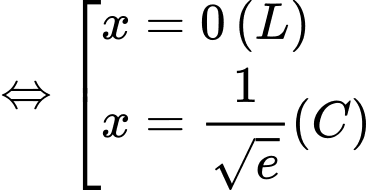
Vậy giá trị cực tiểu của hàm số là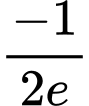 . Đáp án: C
. Đáp án: C
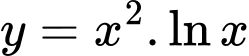 . ĐKXĐ
. ĐKXĐ  .
. 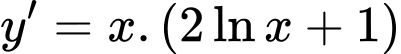
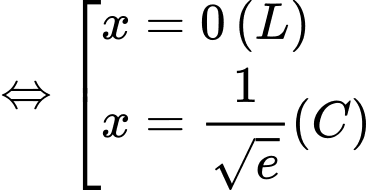
Vậy giá trị cực tiểu của hàm số là
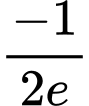 . Đáp án: C
. Đáp án: C
Câu 21 [377575]: Cho hàm số 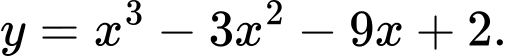 Các mệnh đề sau đúng hay sai
Các mệnh đề sau đúng hay sai
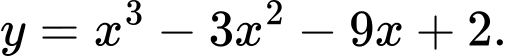 Các mệnh đề sau đúng hay sai
Các mệnh đề sau đúng hay sai A, a) Điểm cực tiểu của hàm số là 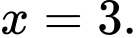
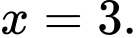
B, b) Cực đại của hàm số đã cho bằng 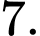
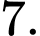
C, c) Hàm số đã cho đồng biến trên khoảng 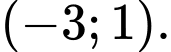
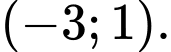
D, d) Điểm cực tiểu của hàm số đã cho là 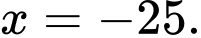
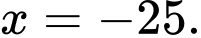
Ta có:
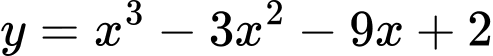
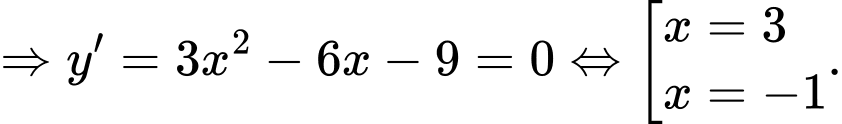
Ta có bảng biến thiên:
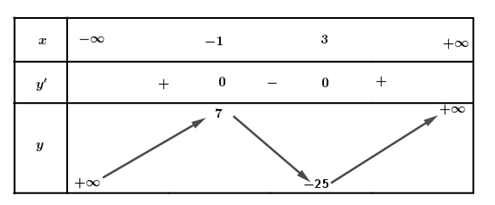
a) Đúng. Điểm cực tiểu của hàm số là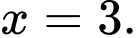
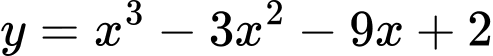
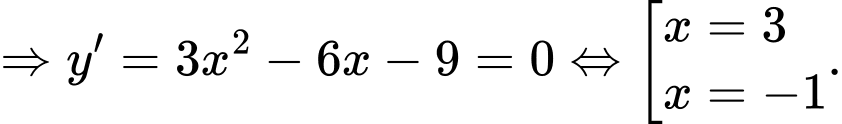
Ta có bảng biến thiên:

a) Đúng. Điểm cực tiểu của hàm số là
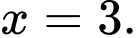
b) Đúng. Cực đại của hàm số đã cho bằng 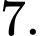
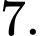
c) Sai. Hàm số đã cho đồng biến trên khoảng 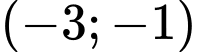 và nghịch biến trên
và nghịch biến trên 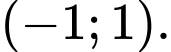
d) Sai. Điểm cực tiểu của hàm số đã cho là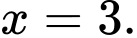
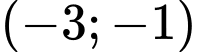 và nghịch biến trên
và nghịch biến trên 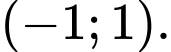
d) Sai. Điểm cực tiểu của hàm số đã cho là
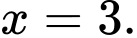
Câu 22 [377576]: Cho hàm số 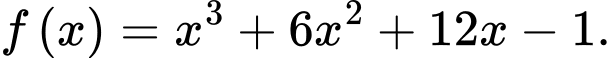 Các mệnh đề sau đúng hay sai
Các mệnh đề sau đúng hay sai
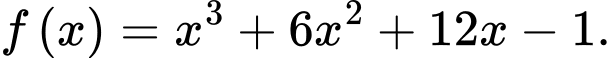 Các mệnh đề sau đúng hay sai
Các mệnh đề sau đúng hay sai A, a) Hàm số đã cho có một điểm cực trị
B, b) Hàm số đã cho đồng biến trên 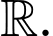
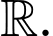
C, c) Giá trị cực tiểu của hàm số đã cho bằng 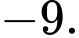
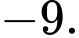
D, d) Hàm số 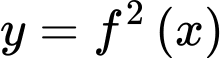 có hai điểm cực trị.
có hai điểm cực trị.
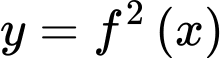 có hai điểm cực trị.
có hai điểm cực trị.
Ta có:

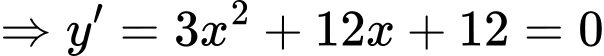
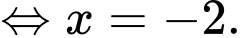
Ta có bảng biến thiên:
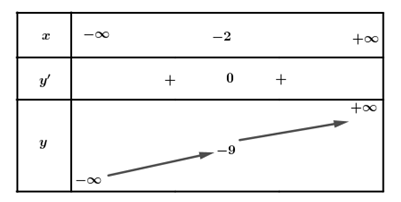
a) Sai. Hàm số đã cho không có cực trị.
b) Đúng. Hàm số đã cho đồng biến trên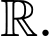
c) Sai. Hàm số không có giá trị cực tiểu.
d) Sai.
Ta có: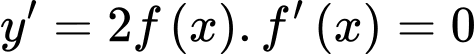
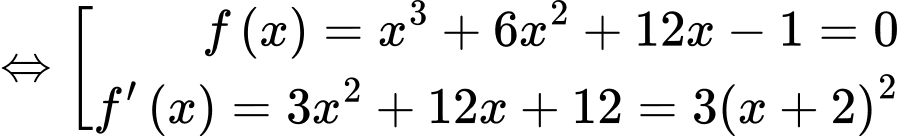
Hệ phương trình trên có 1 nghiệm bội lẻ duy nhất nên hàm số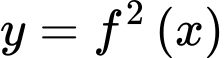 có 1 điểm cực trị.
có 1 điểm cực trị.

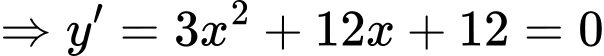
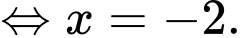
Ta có bảng biến thiên:

a) Sai. Hàm số đã cho không có cực trị.
b) Đúng. Hàm số đã cho đồng biến trên
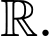
c) Sai. Hàm số không có giá trị cực tiểu.
d) Sai.
Ta có:
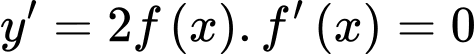
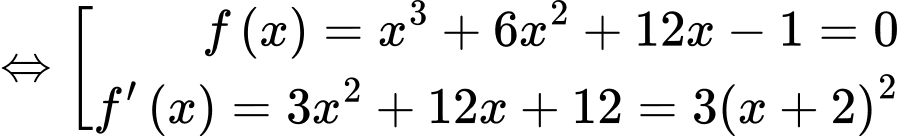
Hệ phương trình trên có 1 nghiệm bội lẻ duy nhất nên hàm số
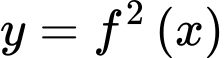 có 1 điểm cực trị.
có 1 điểm cực trị.
Câu 23 [378881]: Gọi 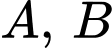 là 2 điểm cực trị của đồ thị hàm số
là 2 điểm cực trị của đồ thị hàm số 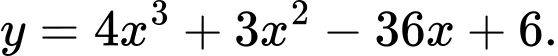 Hỏi diện tích tam giác
Hỏi diện tích tam giác 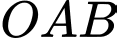 là bao nhiêu?
là bao nhiêu?
Đáp số:………………
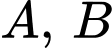 là 2 điểm cực trị của đồ thị hàm số
là 2 điểm cực trị của đồ thị hàm số 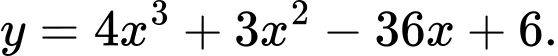 Hỏi diện tích tam giác
Hỏi diện tích tam giác 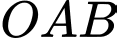 là bao nhiêu?
là bao nhiêu?Đáp số:………………
Ta có: 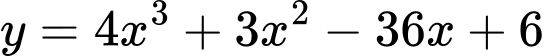
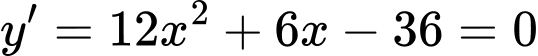
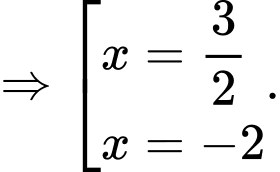
Suy ra 2 điểm cực trị của đồ thị hàm số là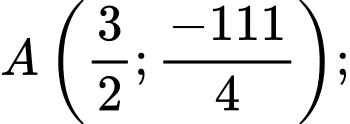
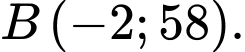
Tính diện tích tam giác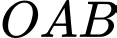
+) Cách 1:
Ta có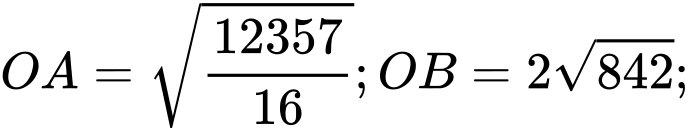
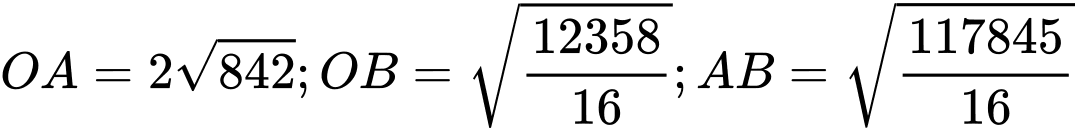
Áp dụng công thức Heron có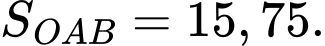
+) Cách 2:
Ta có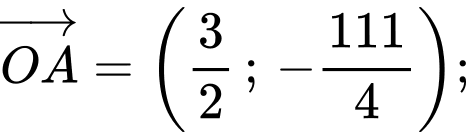
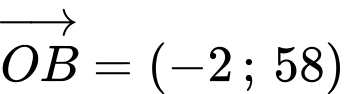
Suy ra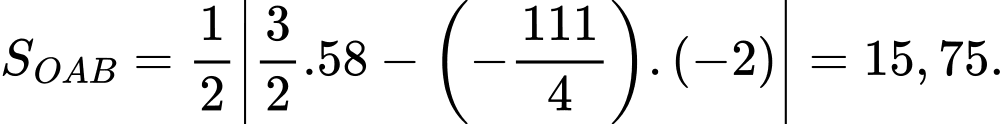
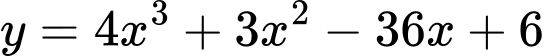
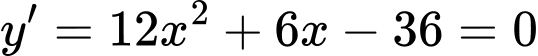
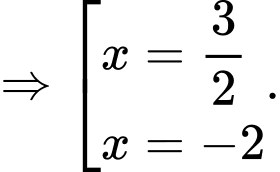
Suy ra 2 điểm cực trị của đồ thị hàm số là
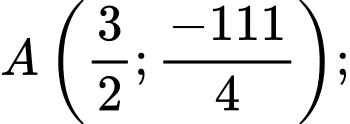
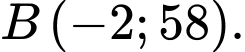
Tính diện tích tam giác
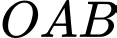
+) Cách 1:
Ta có
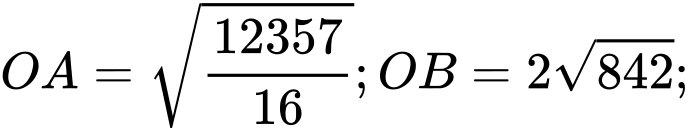
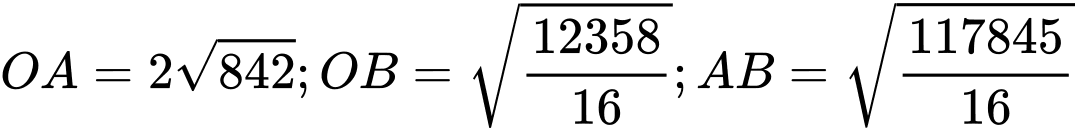
Áp dụng công thức Heron có
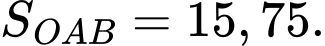
+) Cách 2:
Ta có
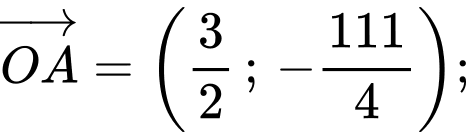
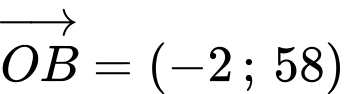
Suy ra
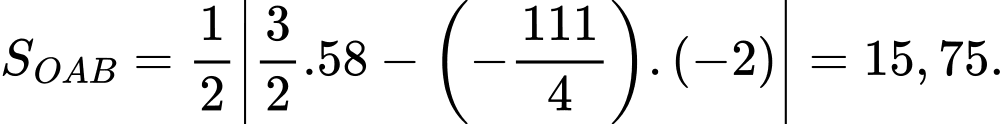
Câu 24 [501296]: Gọi 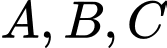 là 3 điểm cực trị của đồ thị hàm số
là 3 điểm cực trị của đồ thị hàm số 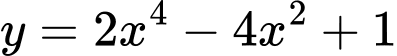 . Hỏi diện tích tam giác
. Hỏi diện tích tam giác 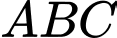 là bao nhiêu?
là bao nhiêu?
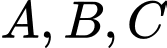 là 3 điểm cực trị của đồ thị hàm số
là 3 điểm cực trị của đồ thị hàm số 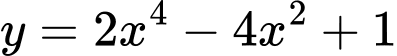 . Hỏi diện tích tam giác
. Hỏi diện tích tam giác 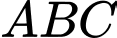 là bao nhiêu?
là bao nhiêu? A, 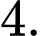
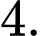
B, 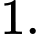
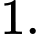
C, 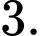
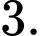
D, 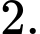
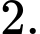
Đáp án D
Cách 1: Sử dụng công thức nhanh đối với diện tích tam giác đồ thị hàm trùng phương
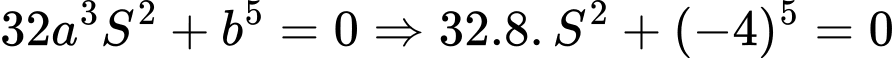
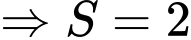 .
.
Cách 2: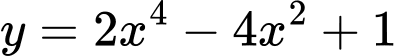
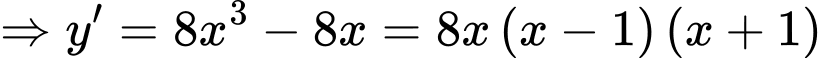
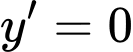
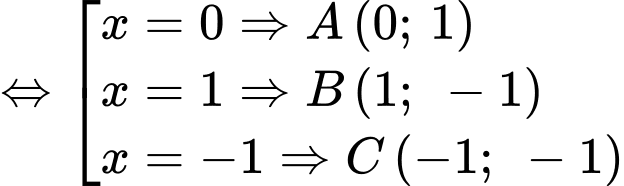
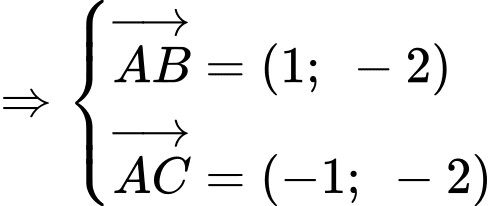
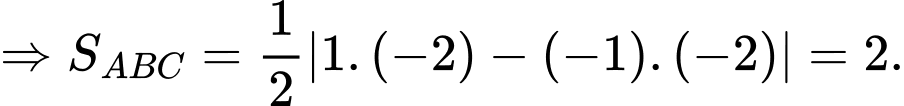
Cách 3: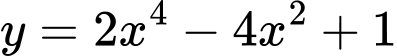
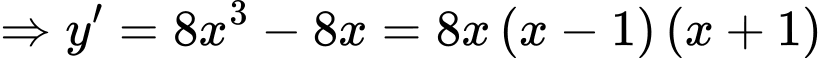
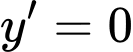
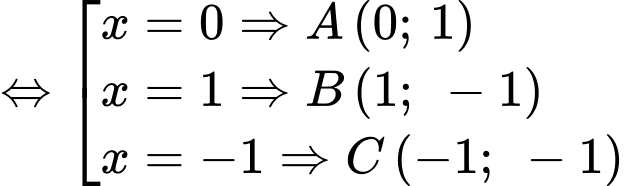
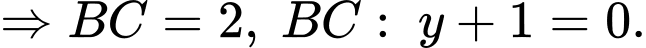
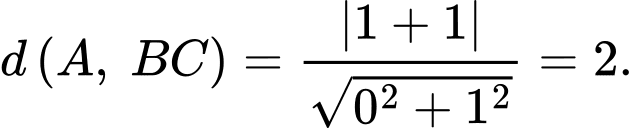
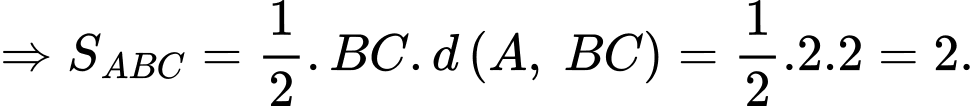 Đáp án: D
Đáp án: D
Cách 1: Sử dụng công thức nhanh đối với diện tích tam giác đồ thị hàm trùng phương
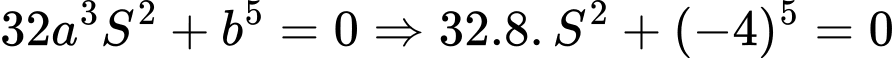
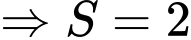 .
. Cách 2:
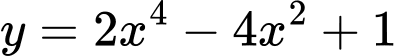
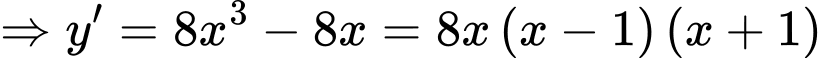
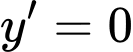
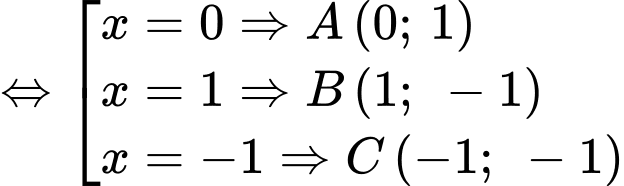
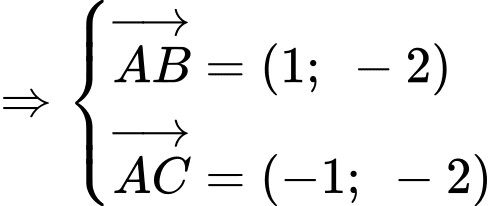
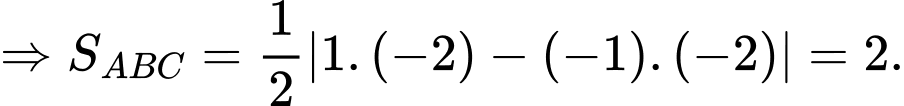
Cách 3:
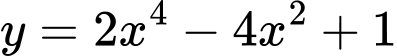
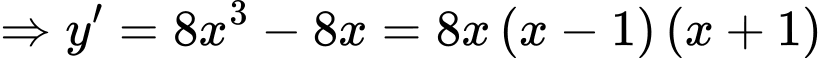
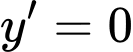
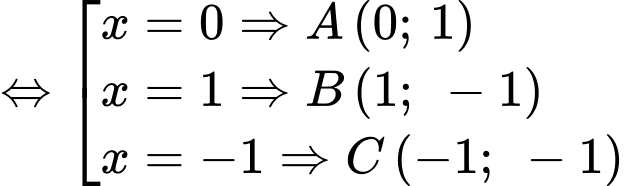
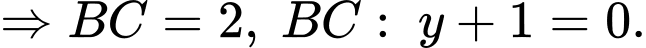
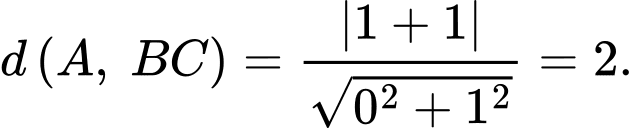
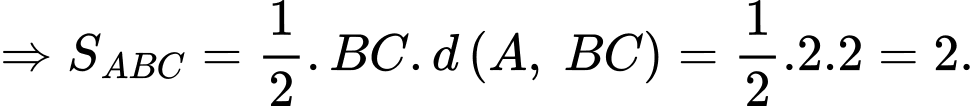 Đáp án: D
Đáp án: D
Câu 25 [45911]: Cho hàm số 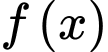 có đạo hàm
có đạo hàm 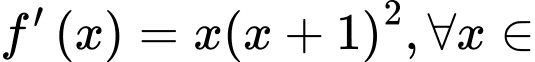
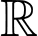 . Số điểm cực trị của hàm số đã cho là
. Số điểm cực trị của hàm số đã cho là
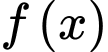 có đạo hàm
có đạo hàm 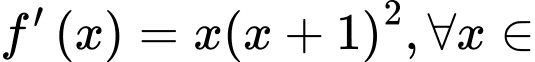
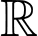 . Số điểm cực trị của hàm số đã cho là
. Số điểm cực trị của hàm số đã cho là A, 0.
B, 1.
C, 2.
D, 3.
Hàm số 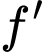 có 1 nghiệm bội lẻ là
có 1 nghiệm bội lẻ là 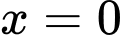 . Nên hàm số đã cho có 1 cực trị. Đáp án: B
. Nên hàm số đã cho có 1 cực trị. Đáp án: B
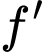 có 1 nghiệm bội lẻ là
có 1 nghiệm bội lẻ là 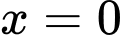 . Nên hàm số đã cho có 1 cực trị. Đáp án: B
. Nên hàm số đã cho có 1 cực trị. Đáp án: B
Câu 26 [909045]: Cho hàm số 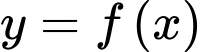 có bảng xét dấu đạo hàm như hình vẽ.
có bảng xét dấu đạo hàm như hình vẽ.
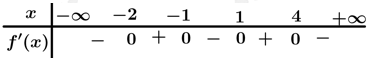
Số điểm cực trị của hàm số đã cho là
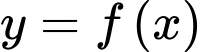 có bảng xét dấu đạo hàm như hình vẽ.
có bảng xét dấu đạo hàm như hình vẽ.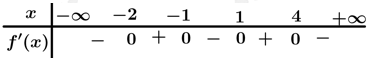
Số điểm cực trị của hàm số đã cho là
A, 
B, 
C, 
D, 
Chọn D
Dựa vào bảng xét dấu,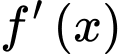 đổi dấu khi qua các điểm
đổi dấu khi qua các điểm 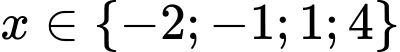 .
.
Vậy số điểm cực trị của hàm số đã cho là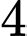 .
Đáp án: D
.
Đáp án: D
Dựa vào bảng xét dấu,
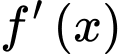 đổi dấu khi qua các điểm
đổi dấu khi qua các điểm 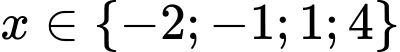 .
.Vậy số điểm cực trị của hàm số đã cho là
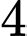 .
Đáp án: D
.
Đáp án: D
Câu 27 [677871]: Cho hàm số 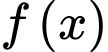 có đạo hàm
có đạo hàm 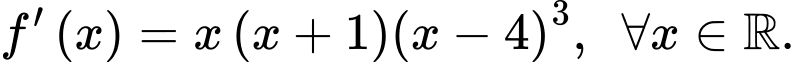 Số điểm cực đại của hàm số đã cho là
Số điểm cực đại của hàm số đã cho là
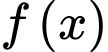 có đạo hàm
có đạo hàm 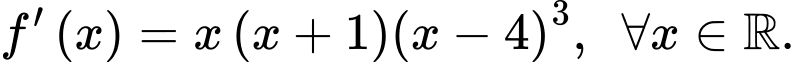 Số điểm cực đại của hàm số đã cho là
Số điểm cực đại của hàm số đã cho là A, 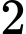 .
.
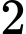 .
.B, 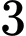 .
.
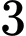 .
.C, 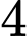 .
.
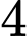 .
.D, 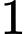 .
.
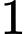 .
.
Chọn D
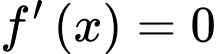
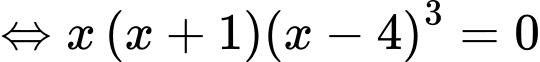
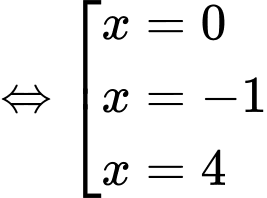 .
.
Lập bảng biến thiên của hàm số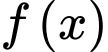
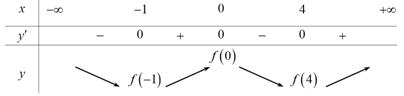
Vậy hàm số đã cho có một điểm cực đại.
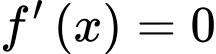
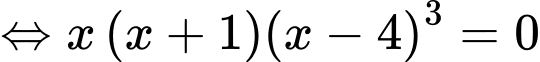
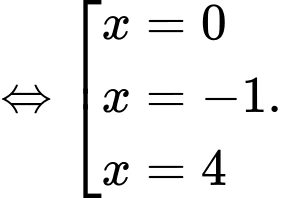 Đáp án: D
Đáp án: D
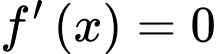
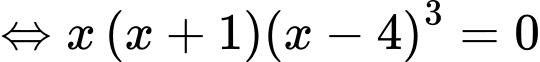
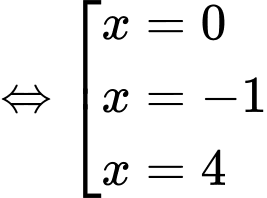 .
.Lập bảng biến thiên của hàm số
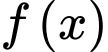

Vậy hàm số đã cho có một điểm cực đại.
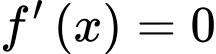
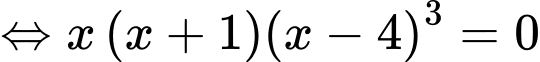
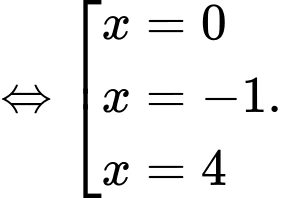 Đáp án: D
Đáp án: D
Câu 28 [677924]: Cho hàm số 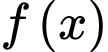 liên tục trên R và có bảng xét dấu của
liên tục trên R và có bảng xét dấu của 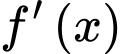 như sau:
như sau:
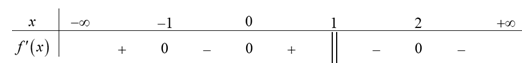
Số điểm cực đại của hàm số đã cho là
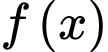 liên tục trên R và có bảng xét dấu của
liên tục trên R và có bảng xét dấu của 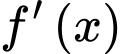 như sau:
như sau: 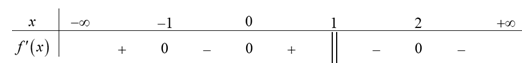
Số điểm cực đại của hàm số đã cho là
A, 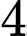 .
.
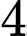 .
.B, 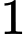 .
.
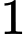 .
.C, 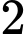 .
.
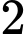 .
.D, 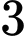 .
.
 .
.
Chọn C
Do hàm số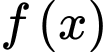 liên tục trên
liên tục trên 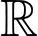 ,
, 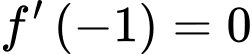 ,
,
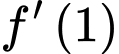 không xác định nhưng do hàm số liên tục trên
không xác định nhưng do hàm số liên tục trên 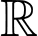 nên tồn tại
nên tồn tại 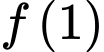
và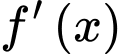 đổi dấu từ
đổi dấu từ  sang
sang 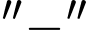 khi đi qua các điểm
khi đi qua các điểm 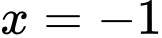 ,
, 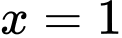 nên hàm số đã cho đạt cực đại tại 2 điểm này.
nên hàm số đã cho đạt cực đại tại 2 điểm này.
Vậy số điểm cực đại của hàm số đã cho là 2. Đáp án: C
Do hàm số
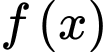 liên tục trên
liên tục trên 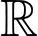 ,
, 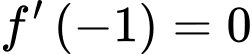 ,
, 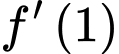 không xác định nhưng do hàm số liên tục trên
không xác định nhưng do hàm số liên tục trên 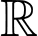 nên tồn tại
nên tồn tại 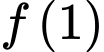
và
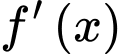 đổi dấu từ
đổi dấu từ  sang
sang 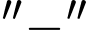 khi đi qua các điểm
khi đi qua các điểm 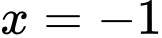 ,
, 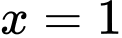 nên hàm số đã cho đạt cực đại tại 2 điểm này.
nên hàm số đã cho đạt cực đại tại 2 điểm này. Vậy số điểm cực đại của hàm số đã cho là 2. Đáp án: C
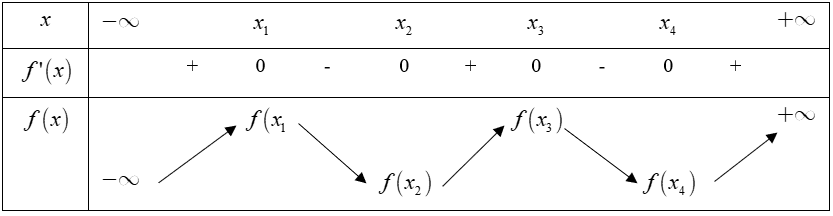
Câu 29 [378884]: Cho hàm số 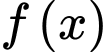 có đạo hàm cấp hai
có đạo hàm cấp hai 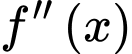 và bảng biến thiên của
và bảng biến thiên của 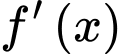 như sau:
như sau: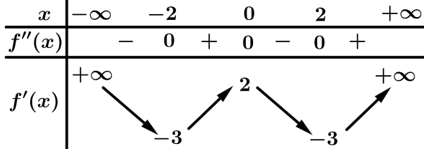



Số điểm cực trị của hàm số 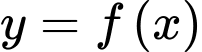 là
là
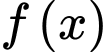 có đạo hàm cấp hai
có đạo hàm cấp hai 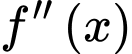 và bảng biến thiên của
và bảng biến thiên của 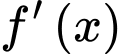 như sau:
như sau:
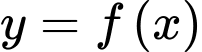 là
là A, 4.
B, 3.
C, 5.
D, 2.
Từ đồ thị ta thấy 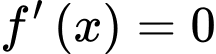 có 4 nghiệm phân biệt là
có 4 nghiệm phân biệt là 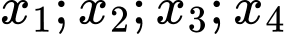
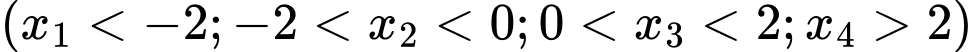
Đáp án: A
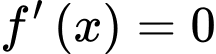 có 4 nghiệm phân biệt là
có 4 nghiệm phân biệt là 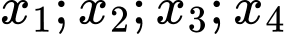
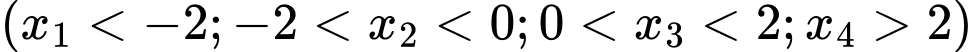
Bảng biến thiên

Vậy hàm số đã cho có 4 cực trị
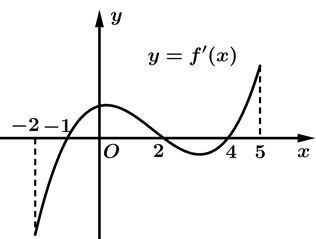
Câu 30 [378882]: Cho hàm số 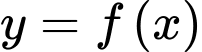 có đồ thị hàm số
có đồ thị hàm số 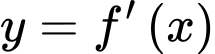 như hình vẽ. Các mệnh đề sau đúng hay
như hình vẽ. Các mệnh đề sau đúng hay
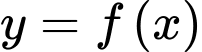 có đồ thị hàm số
có đồ thị hàm số 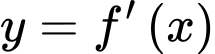 như hình vẽ. Các mệnh đề sau đúng hay
như hình vẽ. Các mệnh đề sau đúng hay 
A, a) Hàm số 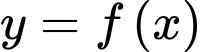 đạt cực tiểu tại điểm
đạt cực tiểu tại điểm 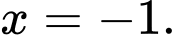
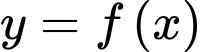 đạt cực tiểu tại điểm
đạt cực tiểu tại điểm 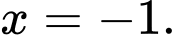
B, b) Hàm số 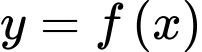 có hai điểm cực trị trên khoảng
có hai điểm cực trị trên khoảng 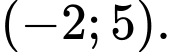
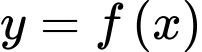 có hai điểm cực trị trên khoảng
có hai điểm cực trị trên khoảng 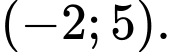
C, c) Hàm số 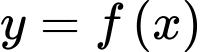 đạt cực đại tại điểm
đạt cực đại tại điểm 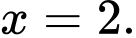
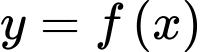 đạt cực đại tại điểm
đạt cực đại tại điểm 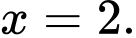
D, d) 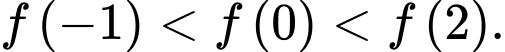
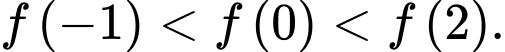
Từ đồ thị của 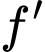 ta có bảng biến thiên
ta có bảng biến thiên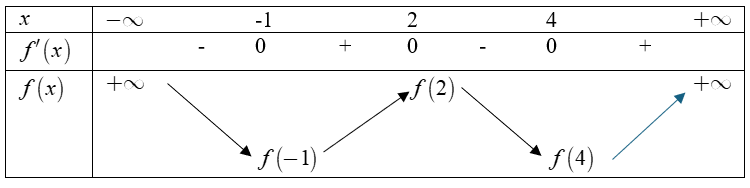
Dựa vào bảng biến thiên có
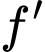 ta có bảng biến thiên
ta có bảng biến thiên
Dựa vào bảng biến thiên có
a, Đúng b, Sai c, Đúng d, Đúng