Đáp án Bài tập tự luyện
Câu 1 [380650]: Cho tứ diện 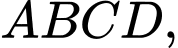 khi đó
khi đó 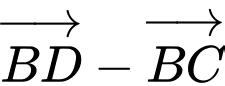 bằng
bằng
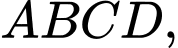 khi đó
khi đó 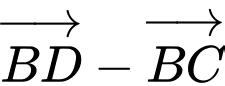 bằng
bằng A, 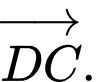
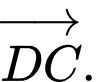
B, 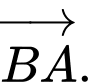
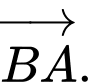
C, 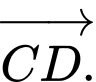
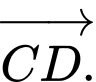
D, 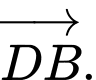
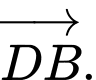
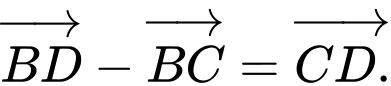
Chọn C. Đáp án: C
Câu 2 [976980]: Cho hình hộp  (hình vẽ minh hoạ).
(hình vẽ minh hoạ).

Mệnh đề nào sau đây đúng?
 (hình vẽ minh hoạ).
(hình vẽ minh hoạ). 
Mệnh đề nào sau đây đúng?
A, 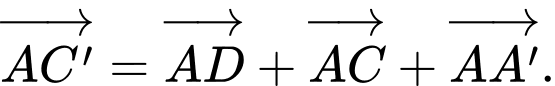
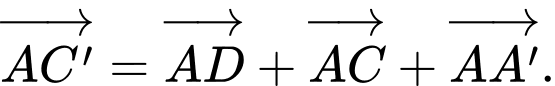
B, 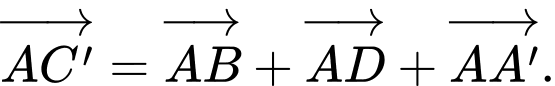
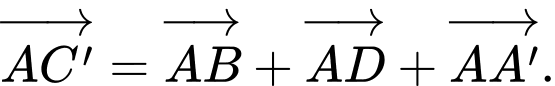
C, 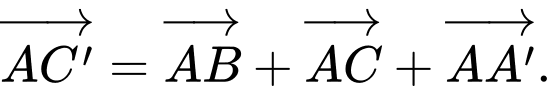
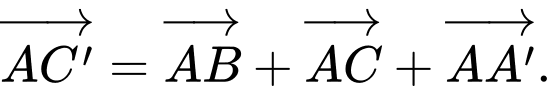
D, 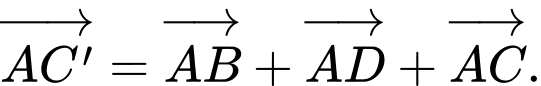
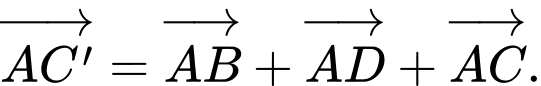
Áp dụng quy tắc hình hộp. Ta có: 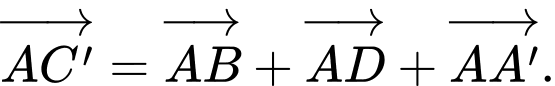
Chọn B. Đáp án: B
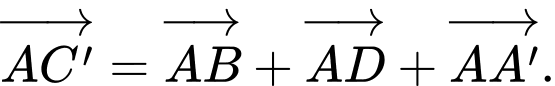
Chọn B. Đáp án: B
Câu 3 [976993]: Cho hình chóp 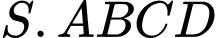 có đáy là hình bình hành (hình vẽ minh hoạ). Hãy chọn khẳng định đúng.
có đáy là hình bình hành (hình vẽ minh hoạ). Hãy chọn khẳng định đúng.
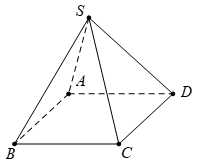
 có đáy là hình bình hành (hình vẽ minh hoạ). Hãy chọn khẳng định đúng.
có đáy là hình bình hành (hình vẽ minh hoạ). Hãy chọn khẳng định đúng.
A, 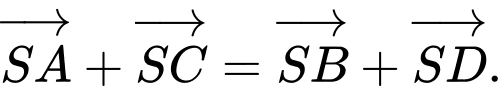
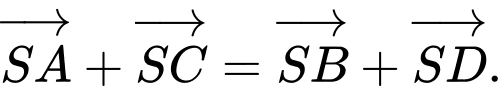
B, 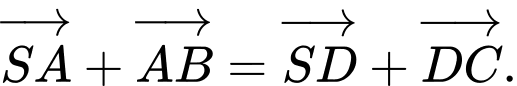
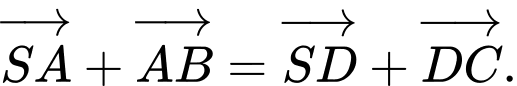
C, 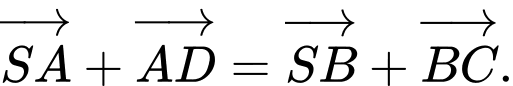
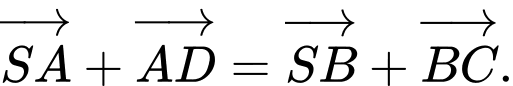
D, 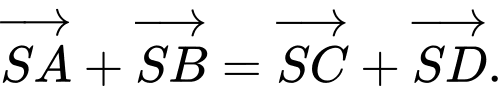
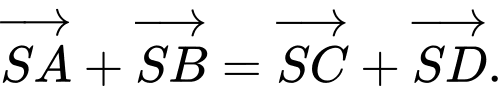
Chọn đáp án A.
A. Ta có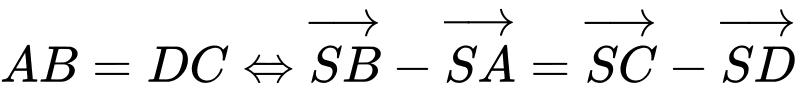
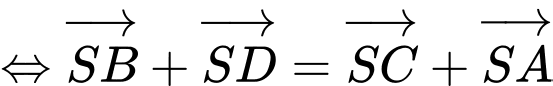
Suy ra A đúng.
B.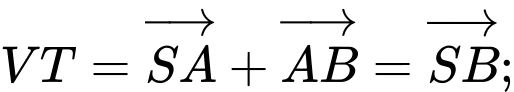
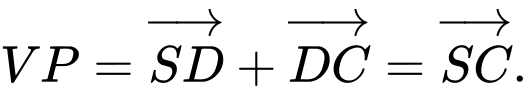
Mà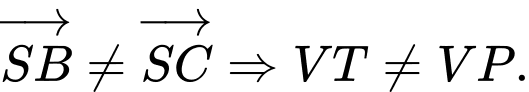
Suy ra B sai.
C.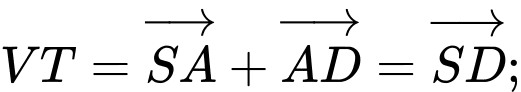
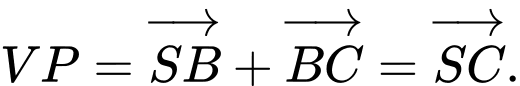
Mà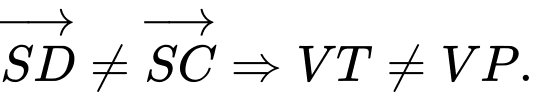
Suy ra C sai.
D.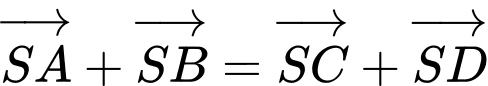
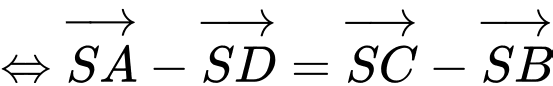
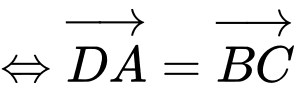 (điều này là sai) Vì
(điều này là sai) Vì 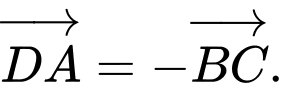
Suy ra D sai. Đáp án: A
A. Ta có
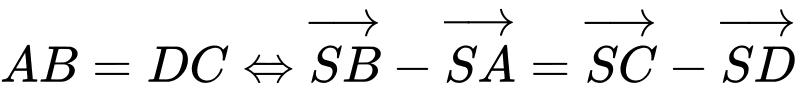
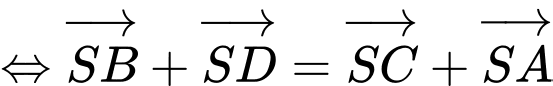
Suy ra A đúng.
B.
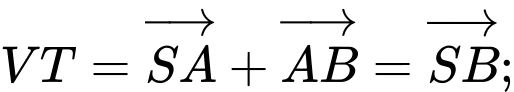
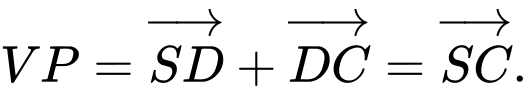
Mà
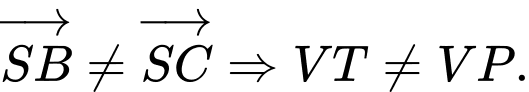
Suy ra B sai.
C.
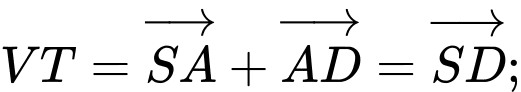
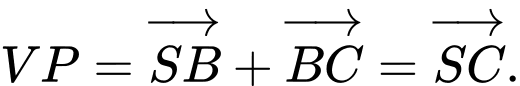
Mà
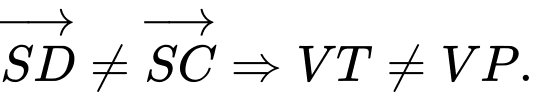
Suy ra C sai.
D.
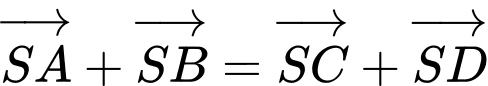
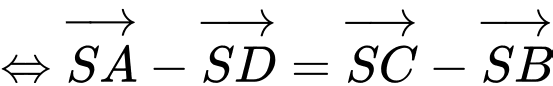
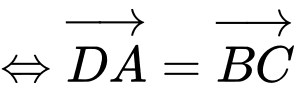 (điều này là sai) Vì
(điều này là sai) Vì 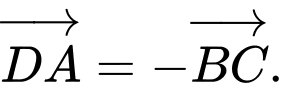
Suy ra D sai. Đáp án: A
Câu 4 [358949]: Cho hình hộp 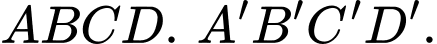 Vectơ
Vectơ 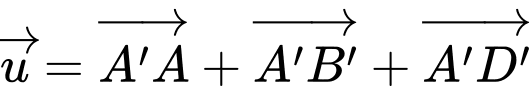 bằng vectơ nào dưới đây?
bằng vectơ nào dưới đây?
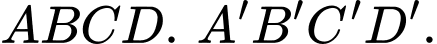 Vectơ
Vectơ 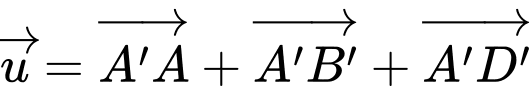 bằng vectơ nào dưới đây?
bằng vectơ nào dưới đây? A, 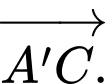
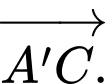
B, 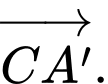
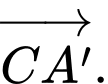
C, 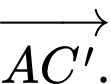
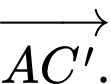
D, 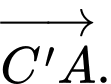
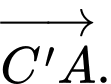

Theo quy tắc hình hộp, với A' là gốc và A'C là đường chéo. Đáp án A.
Đáp án: A
Câu 5 [379191]: Cho tứ diện 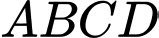 có
có 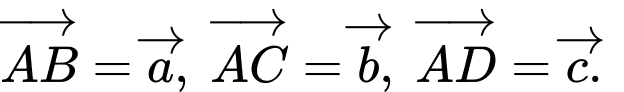 Gọi
Gọi 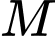 là trung điểm của
là trung điểm của 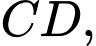 , I là trung điểm của BM. Khẳng định nào sau đây là đúng?
, I là trung điểm của BM. Khẳng định nào sau đây là đúng?
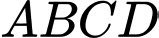 có
có 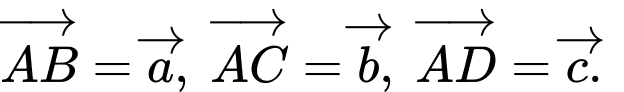 Gọi
Gọi 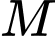 là trung điểm của
là trung điểm của 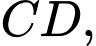 , I là trung điểm của BM. Khẳng định nào sau đây là đúng?
, I là trung điểm của BM. Khẳng định nào sau đây là đúng? A, 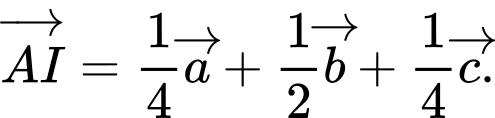
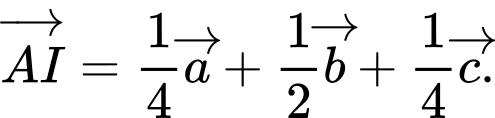
B, 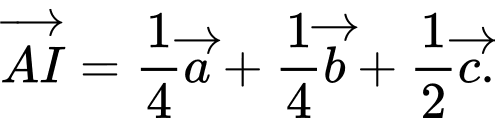
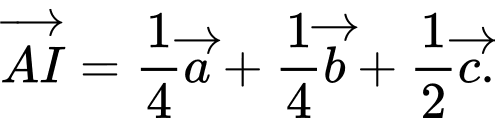
C, 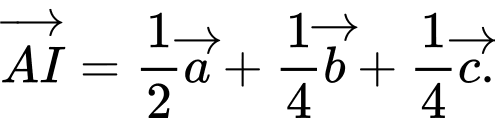
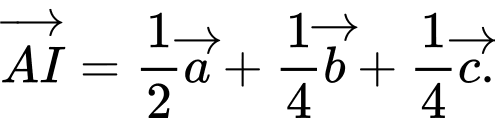
D, 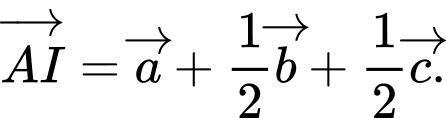
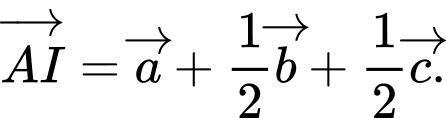
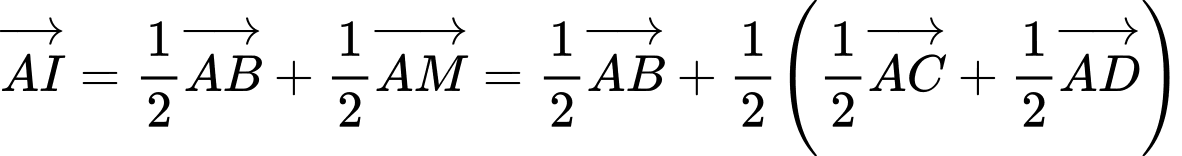
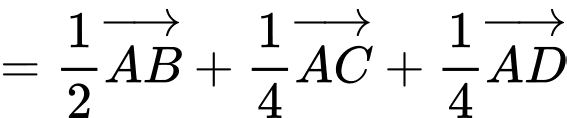
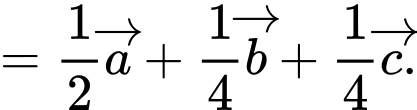 Đáp án: C
Đáp án: C
Câu 6 [975608]: Cho tứ diện 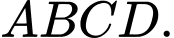 Đặt
Đặt 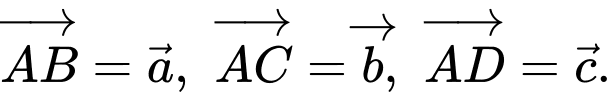 Gọi
Gọi  là trọng tâm của tam giác
là trọng tâm của tam giác  Trong các đẳng thức sau, đẳng thức nào đúng?
Trong các đẳng thức sau, đẳng thức nào đúng?
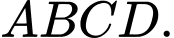 Đặt
Đặt 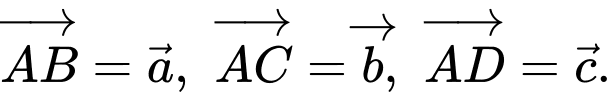 Gọi
Gọi  là trọng tâm của tam giác
là trọng tâm của tam giác  Trong các đẳng thức sau, đẳng thức nào đúng?
Trong các đẳng thức sau, đẳng thức nào đúng? A, 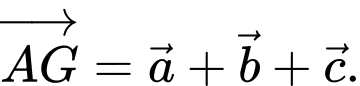
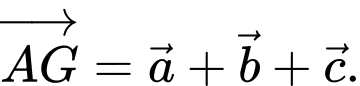
B, 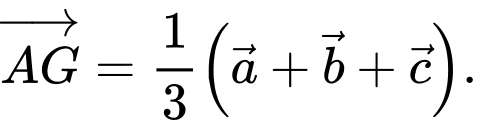
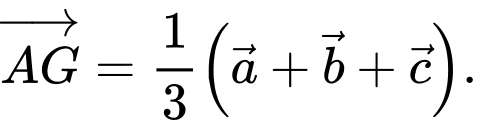
C, 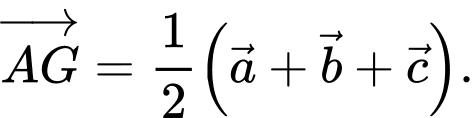
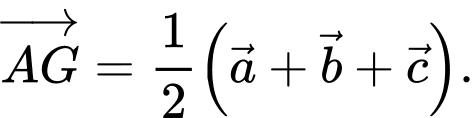
D, 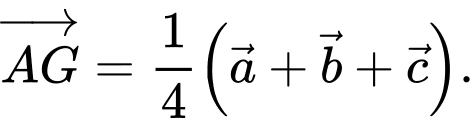
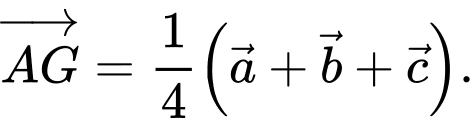
HD: Do  là trọng tâm tam giác
là trọng tâm tam giác  nên
nên 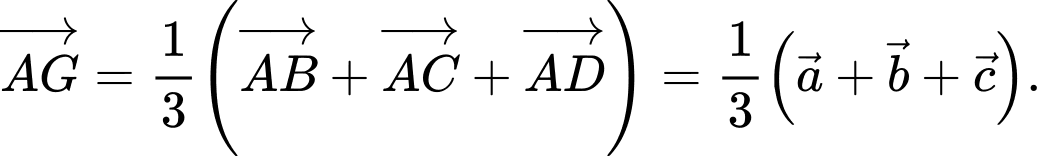 Chọn B. Đáp án: B
Chọn B. Đáp án: B
 là trọng tâm tam giác
là trọng tâm tam giác  nên
nên 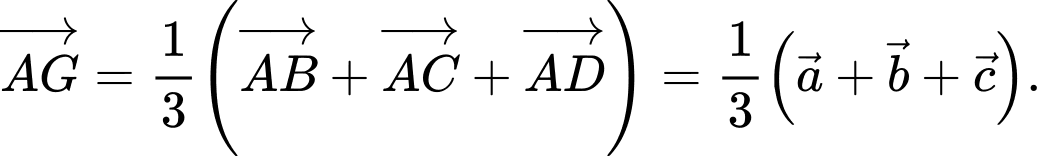 Chọn B. Đáp án: B
Chọn B. Đáp án: B
Câu 7 [49592]: Cho lăng trụ tam giác  có
có 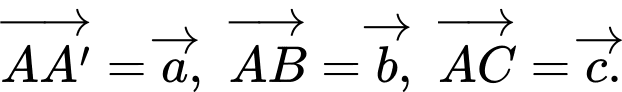 Hãy phân tích (biểu thị) vectơ
Hãy phân tích (biểu thị) vectơ 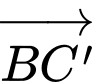 qua các vectơ
qua các vectơ 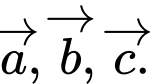
 có
có 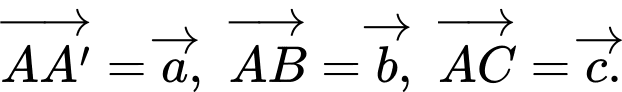 Hãy phân tích (biểu thị) vectơ
Hãy phân tích (biểu thị) vectơ 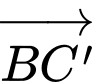 qua các vectơ
qua các vectơ 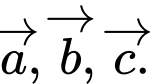
A, 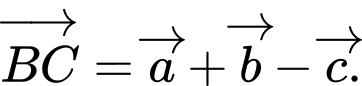
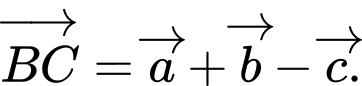
B, 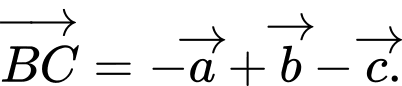
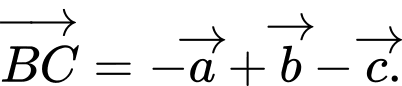
C, 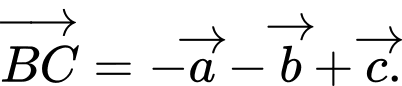
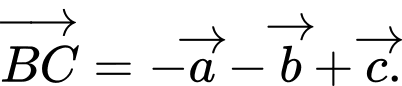
D, 


Ta có
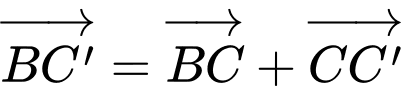
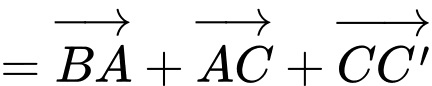
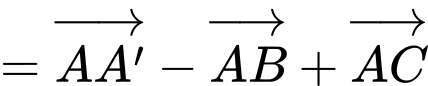
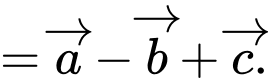
Chọn D. Đáp án: D
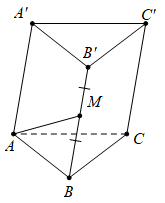
Câu 8 [975604]: Cho hình lăng trụ  Gọi
Gọi 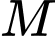 là trung điểm của cạnh
là trung điểm của cạnh 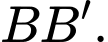 Đặt
Đặt 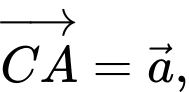
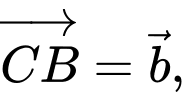
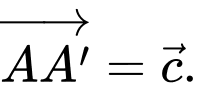 Khẳng định nào dưới đây là đúng?
Khẳng định nào dưới đây là đúng?
 Gọi
Gọi 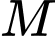 là trung điểm của cạnh
là trung điểm của cạnh 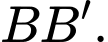 Đặt
Đặt 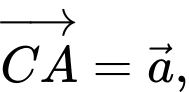
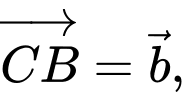
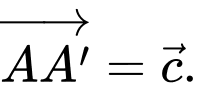 Khẳng định nào dưới đây là đúng?
Khẳng định nào dưới đây là đúng? A, 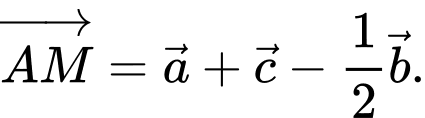
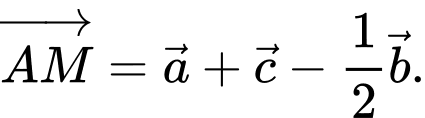
B, 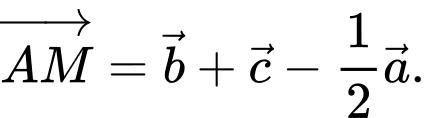
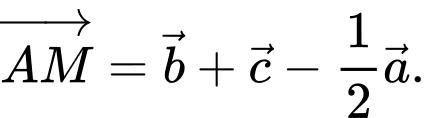
C, 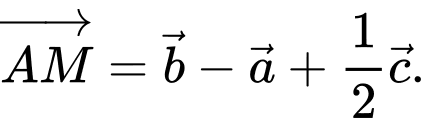
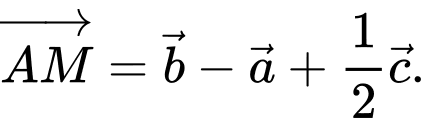
D, 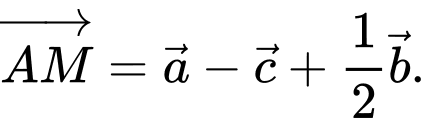
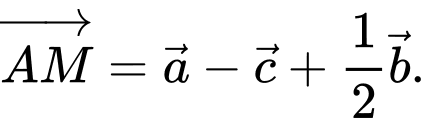
Chọn đáp án C.
Ta có:
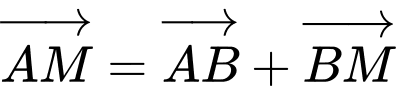
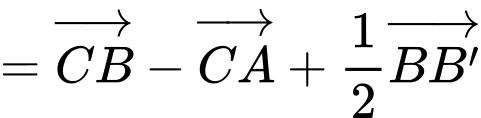
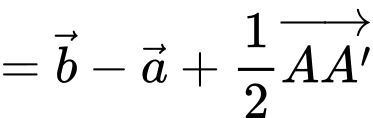
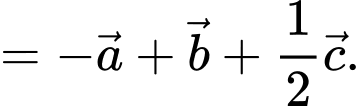 Đáp án: C
Đáp án: C

Ta có:
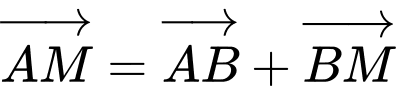
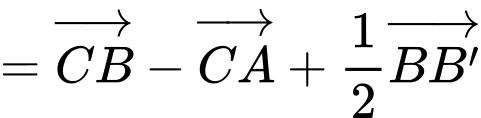
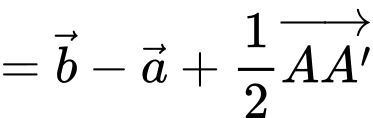
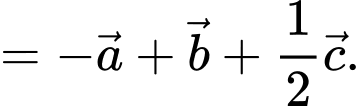 Đáp án: C
Đáp án: C
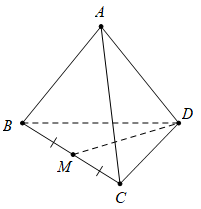
Câu 9 [975609]: Cho tứ diện 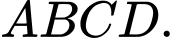 Đặt
Đặt 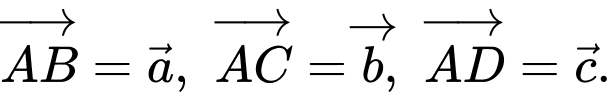 Gọi
Gọi 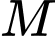 là trung điểm của đoạn thẳng
là trung điểm của đoạn thẳng 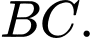 Đẳng thức nào dưới đây là đúng?
Đẳng thức nào dưới đây là đúng?
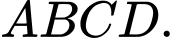 Đặt
Đặt 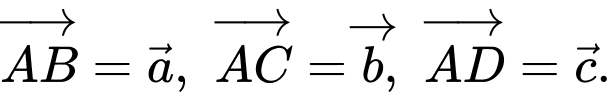 Gọi
Gọi 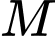 là trung điểm của đoạn thẳng
là trung điểm của đoạn thẳng 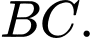 Đẳng thức nào dưới đây là đúng?
Đẳng thức nào dưới đây là đúng? A, 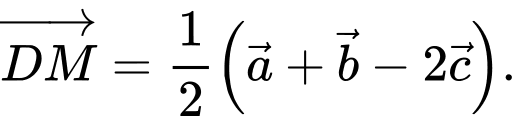
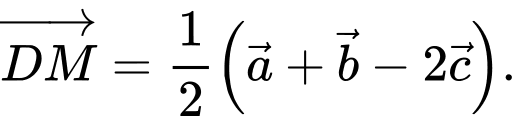
B, 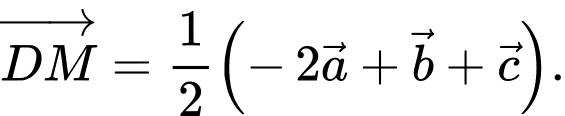
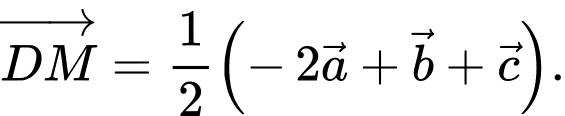
C, 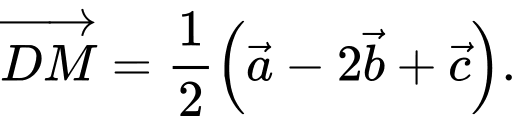
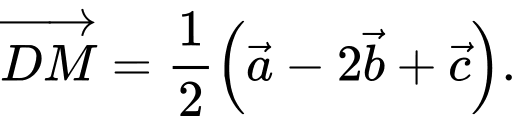
D, 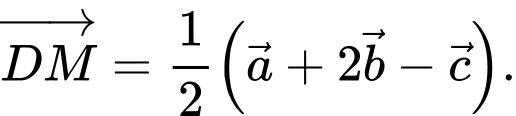
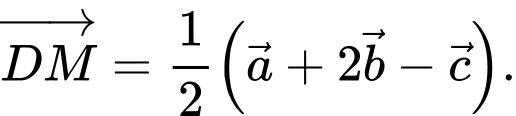
HD: Ta có:
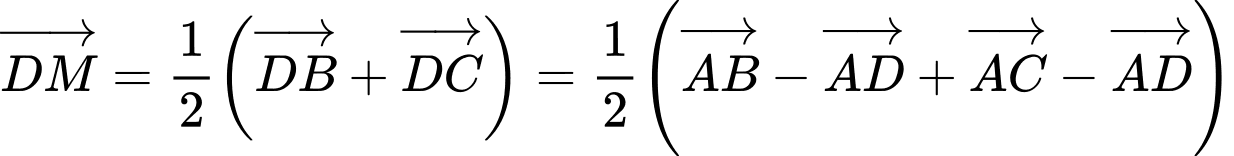
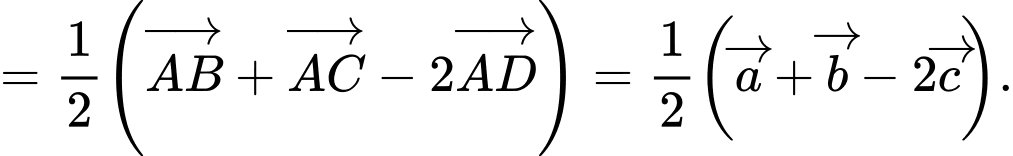 Chọn A.
Đáp án: A
Chọn A.
Đáp án: A
Câu 10 [49597]: Cho tứ diện 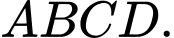 Gọi
Gọi 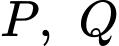 là trung điểm của
là trung điểm của  và
và 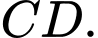 Chọn khẳng định đúng.
Chọn khẳng định đúng.
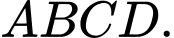 Gọi
Gọi 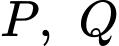 là trung điểm của
là trung điểm của  và
và 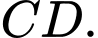 Chọn khẳng định đúng.
Chọn khẳng định đúng. A, 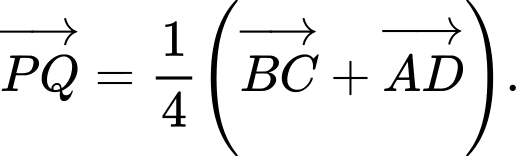
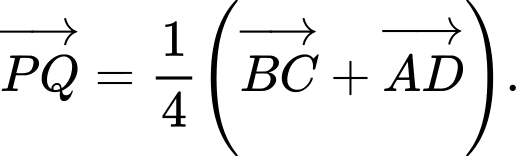
B, 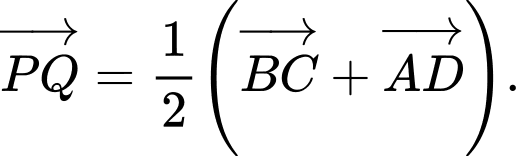
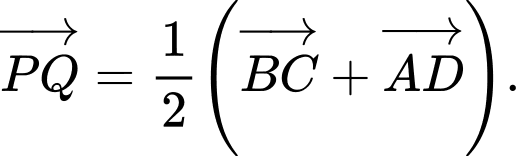
C, 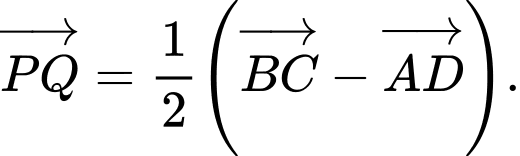
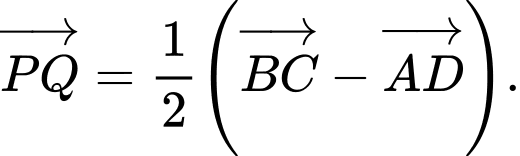
D, 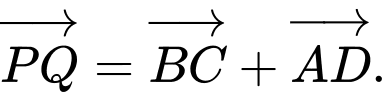
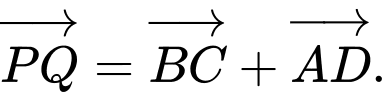
Ta có 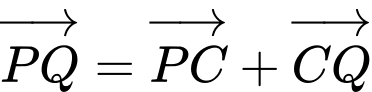
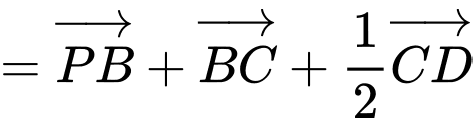
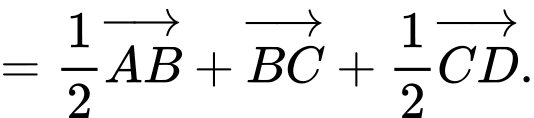
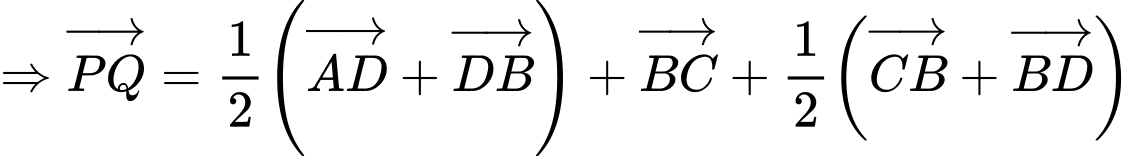
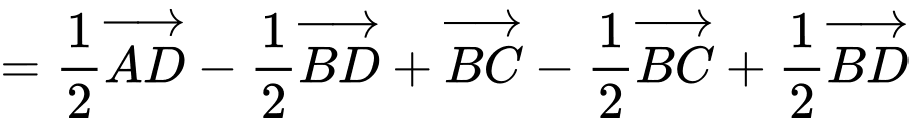
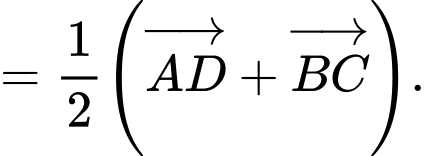
Chọn B. Đáp án: B
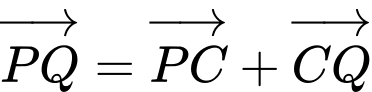
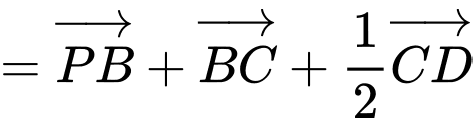
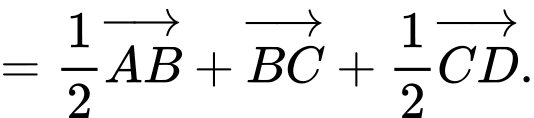
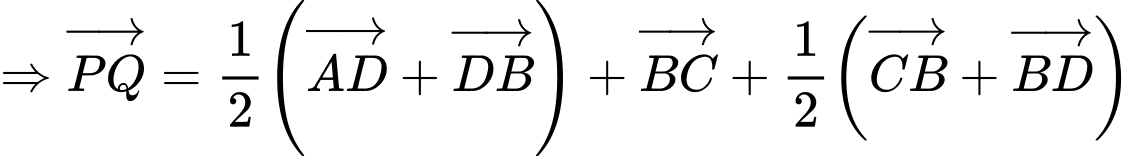
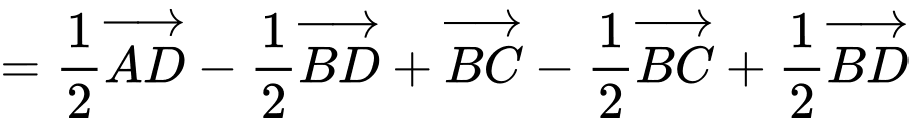
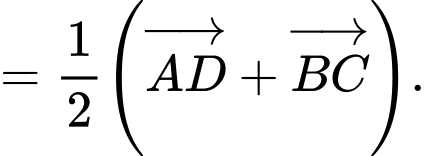
Chọn B. Đáp án: B
Câu 11 [378993]: Trong không gian cho hình chóp 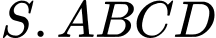 có đáy
có đáy 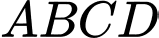 là hình bình hành tâm
là hình bình hành tâm  Xét tính đúng sai của các mệnh đề sau
Xét tính đúng sai của các mệnh đề sau
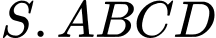 có đáy
có đáy 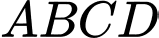 là hình bình hành tâm
là hình bình hành tâm  Xét tính đúng sai của các mệnh đề sau
Xét tính đúng sai của các mệnh đề sau 
a) Đúng.
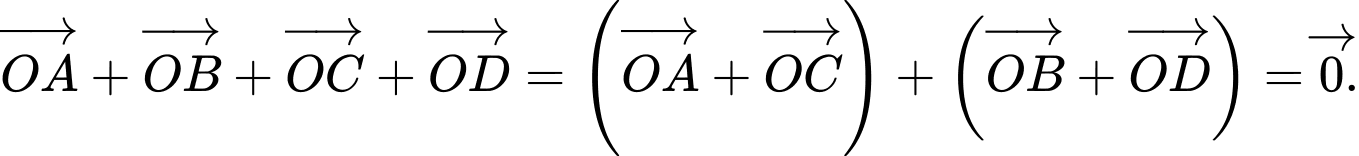
b) Đúng.
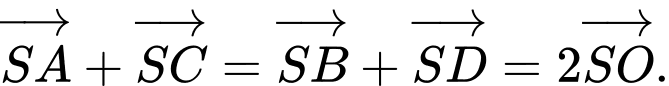
c) Sai.
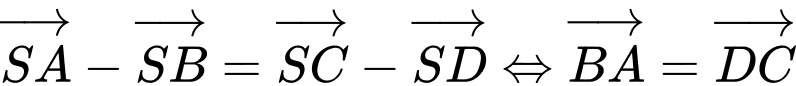 (sai)
(sai)d) Sai.
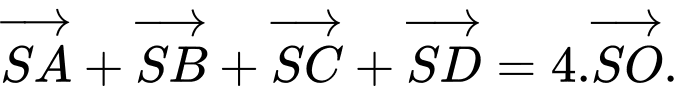
Câu 12 [378994]: Cho tứ diện 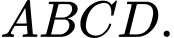 Các mệnh đề sau đúng hay sai
Các mệnh đề sau đúng hay sai
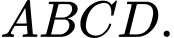 Các mệnh đề sau đúng hay sai
Các mệnh đề sau đúng hay sai A, a) 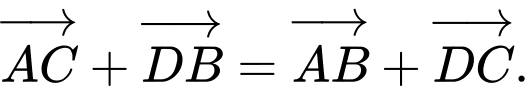
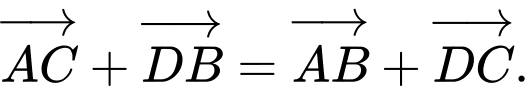
B, b) 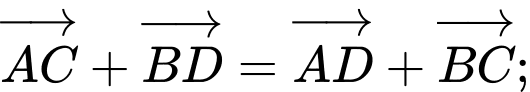
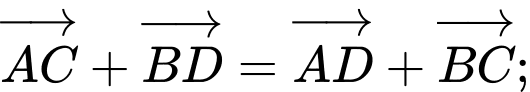
C, c) 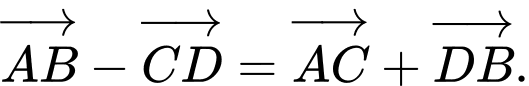
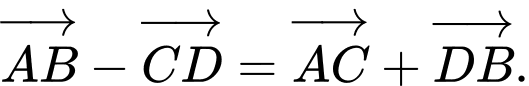
D, d) 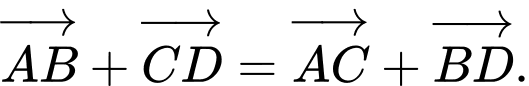
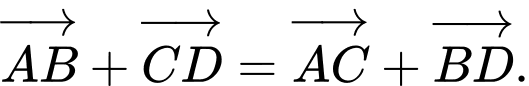
a) Đúng. Ta có: 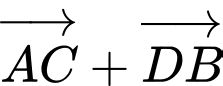
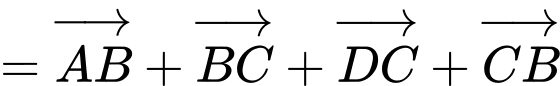
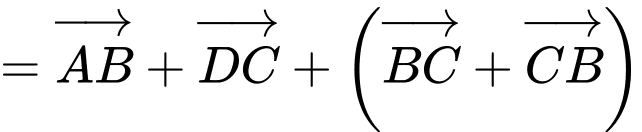
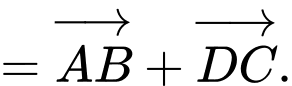
b) Đúng. Ta có: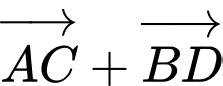
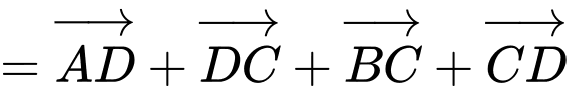
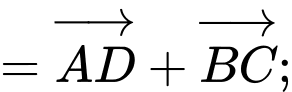
c) Đúng.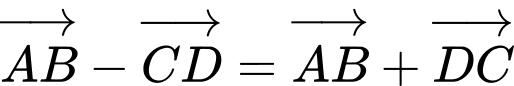
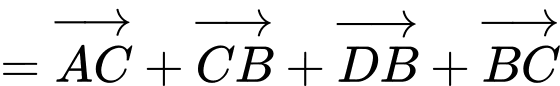
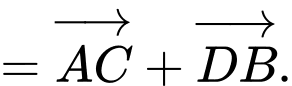
d) Sai.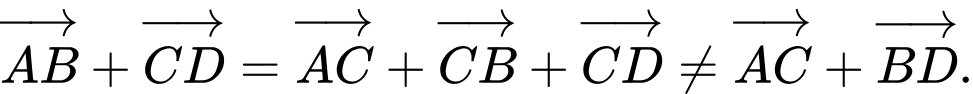
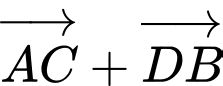
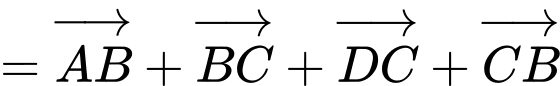
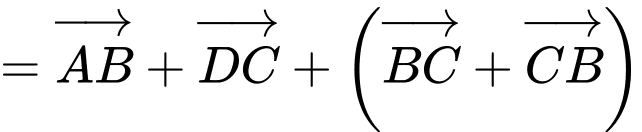
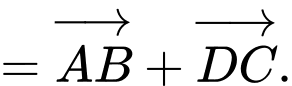
b) Đúng. Ta có:
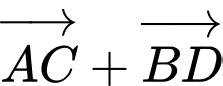
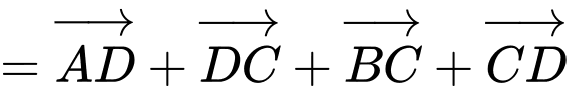
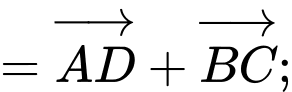
c) Đúng.
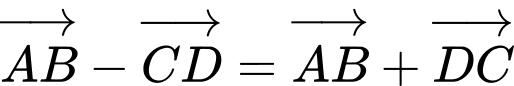
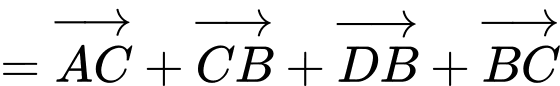
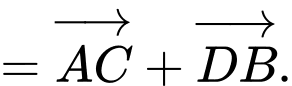
d) Sai.
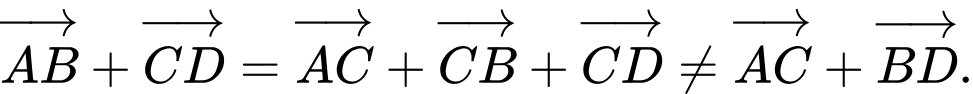
Câu 13 [379982]: Cho tứ diện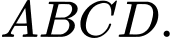 Gọi
Gọi 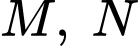 lần lượt là trung điểm của
lần lượt là trung điểm của 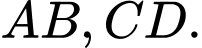 Các mệnh đề sau đúng hay sai
Các mệnh đề sau đúng hay sai
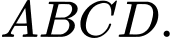 Gọi
Gọi 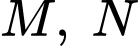 lần lượt là trung điểm của
lần lượt là trung điểm của 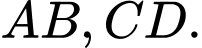 Các mệnh đề sau đúng hay sai
Các mệnh đề sau đúng hay sai A, a) 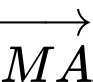 và
và 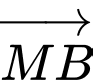 là hai vectơ đối nhau.
là hai vectơ đối nhau.
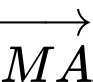 và
và 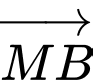 là hai vectơ đối nhau.
là hai vectơ đối nhau.B, b) 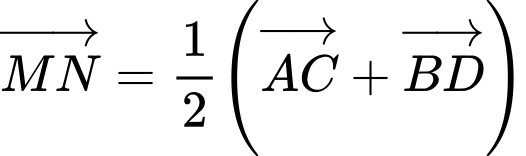
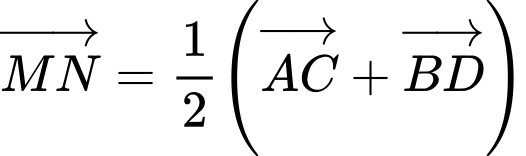
C, c) 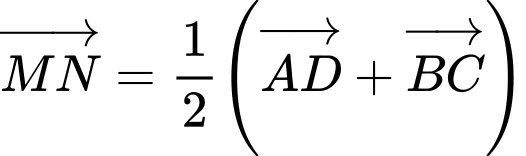
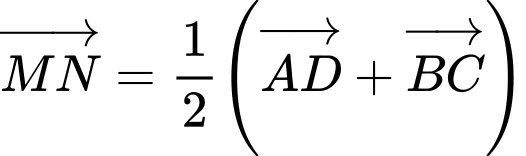
D, d) 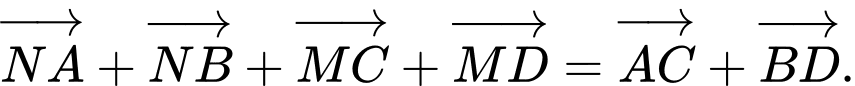
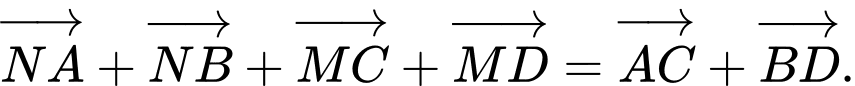
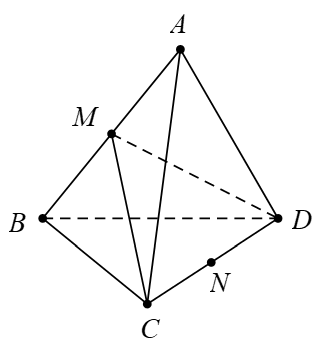
a) Đúng
b) Đúng.
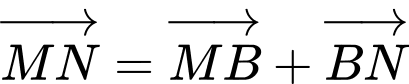
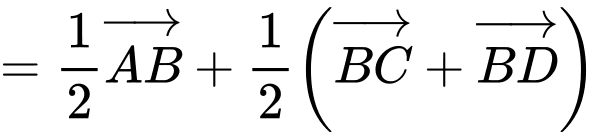
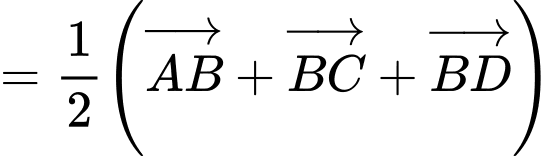
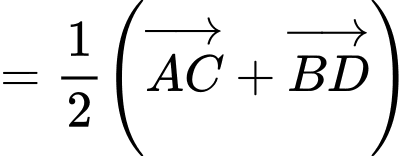
c) Đúng.
d) Sai.
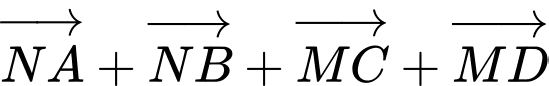
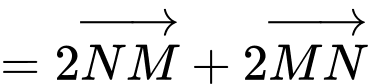
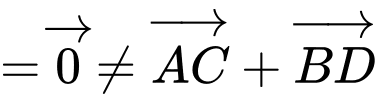
Câu 14 [379373]: Cho hình chóp 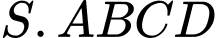 có đáy là hình bình hành. Gọi
có đáy là hình bình hành. Gọi 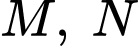 lần lượt là trung điểm của
lần lượt là trung điểm của  và
và 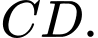 Xét tính đúng sai của các mệnh đề sau
Xét tính đúng sai của các mệnh đề sau
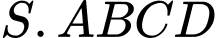 có đáy là hình bình hành. Gọi
có đáy là hình bình hành. Gọi 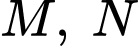 lần lượt là trung điểm của
lần lượt là trung điểm của  và
và 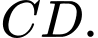 Xét tính đúng sai của các mệnh đề sau
Xét tính đúng sai của các mệnh đề sau A, a) 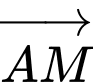 và
và 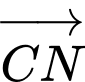 là hai vectơ đối nhau.
là hai vectơ đối nhau.
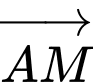 và
và 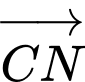 là hai vectơ đối nhau.
là hai vectơ đối nhau.B, b) 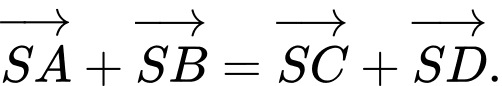
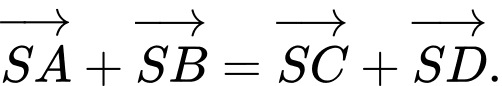
C, c) 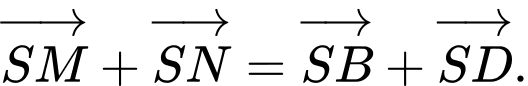
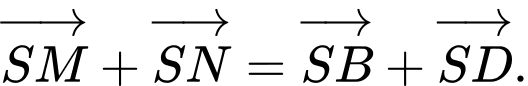
D, d) 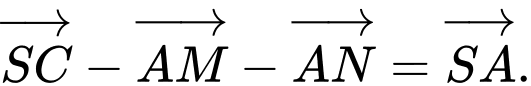
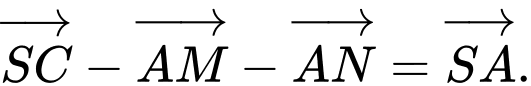
Đính chính câu hỏi: " Các em thêm dữ kiện đáy là hình bình hành nhé"
Thầy Tuấn-Xin lỗi các em về lỗi đề (sách 3000 bài tập nên không thể tránh khỏi trong lần đầu xuất bản) - Các em sửa lại đề theo đề Web nhé!. Cảm ơn các em nhiều!
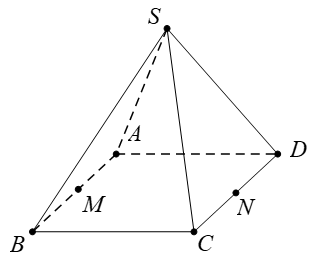
a) Đúng.
b) Sai.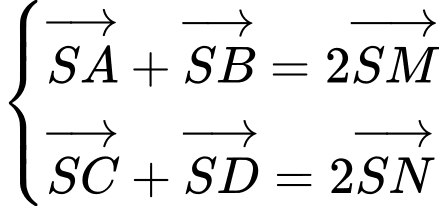
c) Đúng.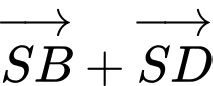
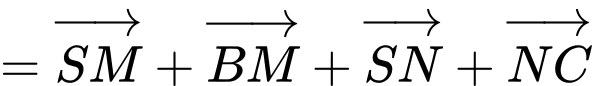
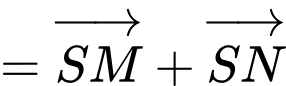
d) Đúng.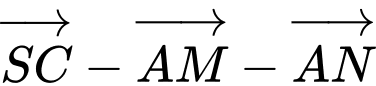
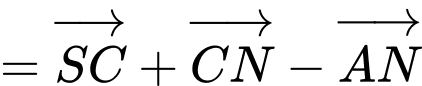
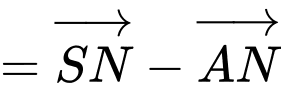
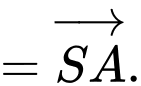
Thầy Tuấn-Xin lỗi các em về lỗi đề (sách 3000 bài tập nên không thể tránh khỏi trong lần đầu xuất bản) - Các em sửa lại đề theo đề Web nhé!. Cảm ơn các em nhiều!

a) Đúng.
b) Sai.
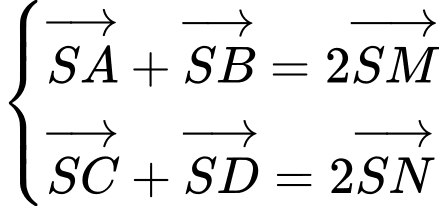
c) Đúng.
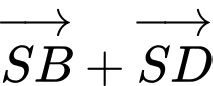
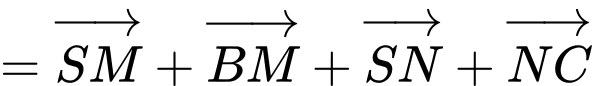
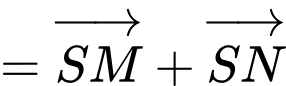
d) Đúng.
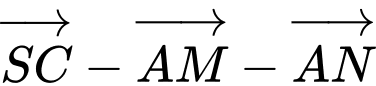
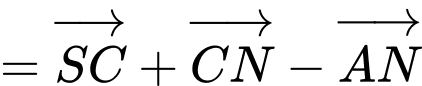
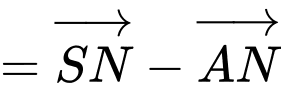
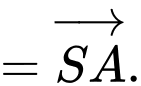
Câu 15 [379374]: Cho tứ diện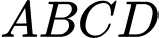 có
có 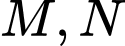 lần lượt là trung điểm của các cạnh
lần lượt là trung điểm của các cạnh 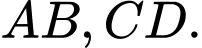 Gọi
Gọi  là trung điểm của đoạn thẳng
là trung điểm của đoạn thẳng 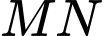 và
và  là trọng tâm tam giác
là trọng tâm tam giác 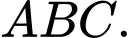 Xét tính đúng sai của các mệnh đề sau
Xét tính đúng sai của các mệnh đề sau
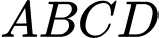 có
có 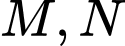 lần lượt là trung điểm của các cạnh
lần lượt là trung điểm của các cạnh 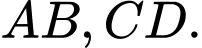 Gọi
Gọi  là trung điểm của đoạn thẳng
là trung điểm của đoạn thẳng 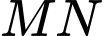 và
và  là trọng tâm tam giác
là trọng tâm tam giác 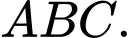 Xét tính đúng sai của các mệnh đề sau
Xét tính đúng sai của các mệnh đề sau 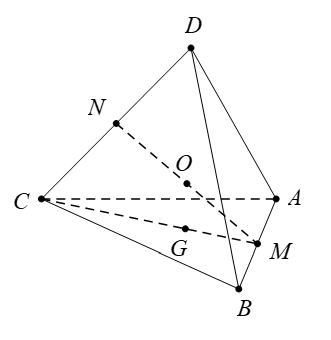
a) Đúng. (Theo quy tắc trung tuyến)
b) Sai. Ta có
 (áp dụng quy tắc trung tuyến)
(áp dụng quy tắc trung tuyến) 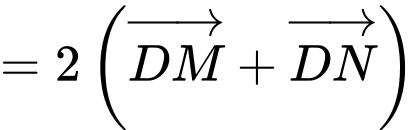
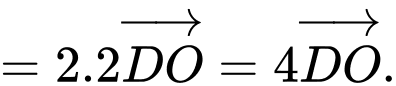
c) Sai. Áp dụng quy tắc trọng tâm ta được:
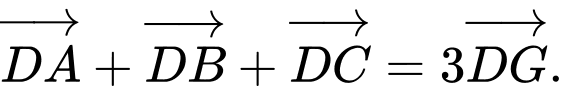
d) Sai. Dựa vào kết quả của phần b và c ta được
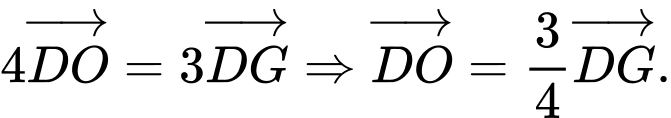
Câu 16 [379941]: Cho tứ diện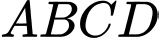 có
có 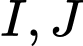 lần lượt là trung điểm của các cạnh
lần lượt là trung điểm của các cạnh 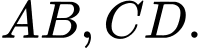 Gọi
Gọi  là trung điểm của đoạn thẳng
là trung điểm của đoạn thẳng  Xét tính đúng sai của các mệnh đề sau
Xét tính đúng sai của các mệnh đề sau
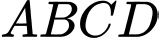 có
có 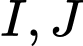 lần lượt là trung điểm của các cạnh
lần lượt là trung điểm của các cạnh 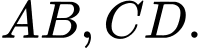 Gọi
Gọi  là trung điểm của đoạn thẳng
là trung điểm của đoạn thẳng  Xét tính đúng sai của các mệnh đề sau
Xét tính đúng sai của các mệnh đề sau A, a) 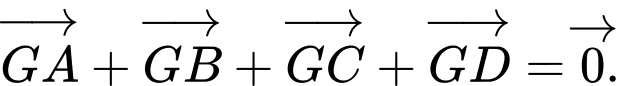
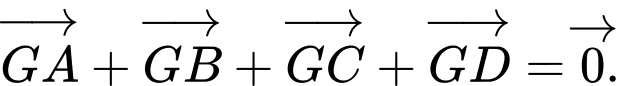
B, b) 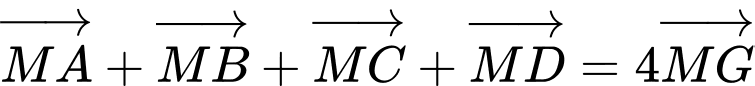 với
với 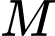 là một điểm tuỳ ý.
là một điểm tuỳ ý.
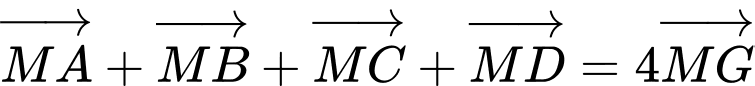 với
với 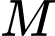 là một điểm tuỳ ý.
là một điểm tuỳ ý.C, c) 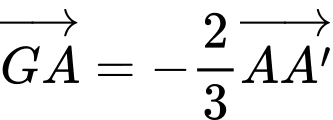 với
với 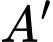 là trọng tâm tam giác
là trọng tâm tam giác 
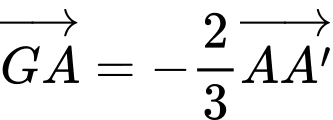 với
với 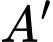 là trọng tâm tam giác
là trọng tâm tam giác 
D,
d) 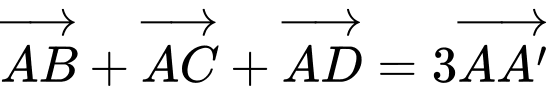 với
với 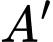 là trọng tâm tam giác
là trọng tâm tam giác 

a) Đúng. Ta có:
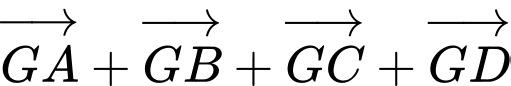
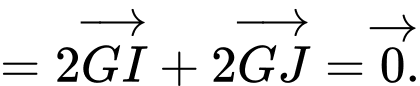
b) Đúng.
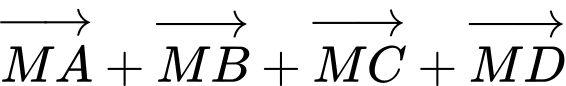
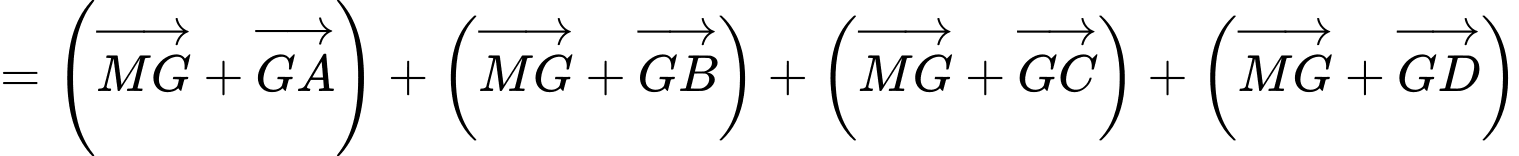
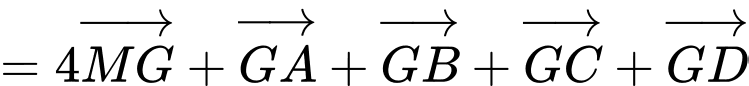
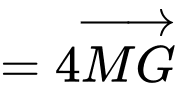

c) Sai. Ta có:
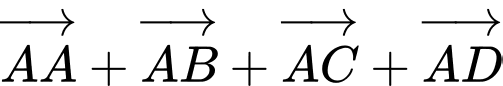
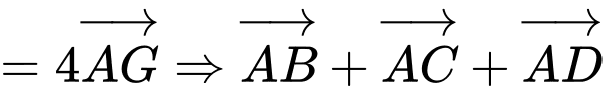
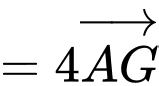
Mặt khác
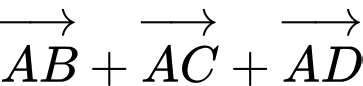
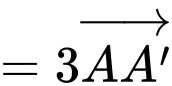 suy ra
suy ra 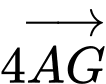
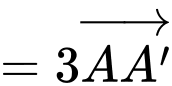
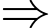
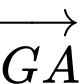
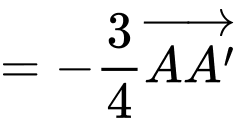
d) Đúng.
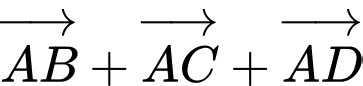
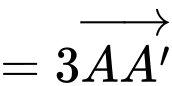 (tính chất trọng tâm)
(tính chất trọng tâm)
Câu 17 [378997]: Cho hình tứ diện 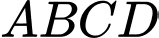 có
có 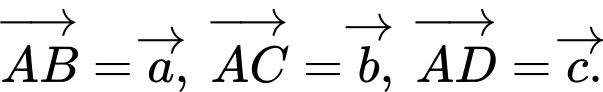 Gọi
Gọi 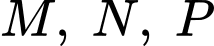 và
và  lần lượt là trung điểm của
lần lượt là trung điểm của 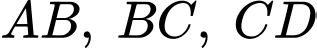 và
và 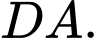 Xác định tính đúng sai của các mệnh đề sau:
Xác định tính đúng sai của các mệnh đề sau:
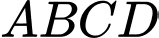 có
có 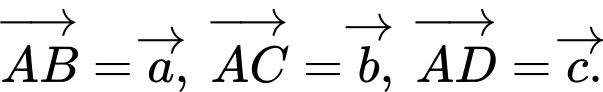 Gọi
Gọi 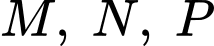 và
và  lần lượt là trung điểm của
lần lượt là trung điểm của 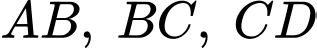 và
và 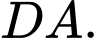 Xác định tính đúng sai của các mệnh đề sau:
Xác định tính đúng sai của các mệnh đề sau: 
a) Sai. 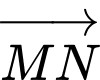
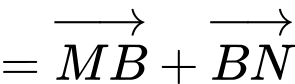
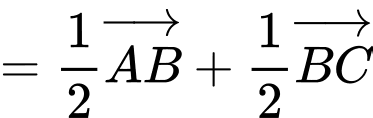
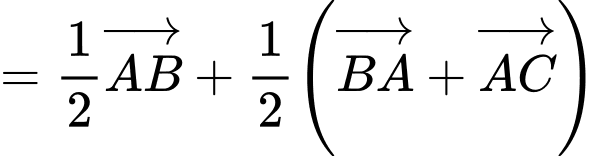
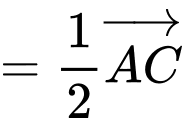
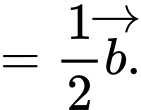
b) Đúng. 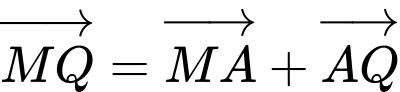
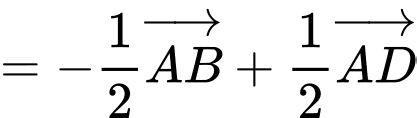
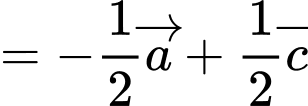
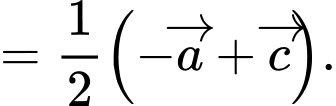
c) Đúng. 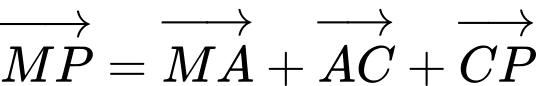
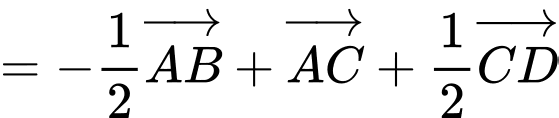
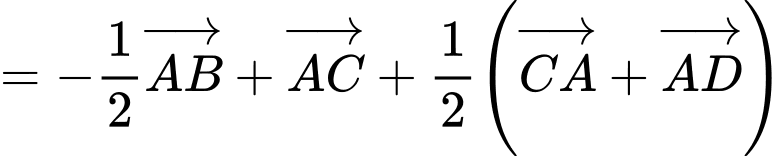
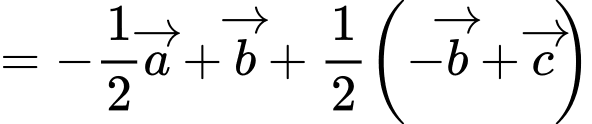
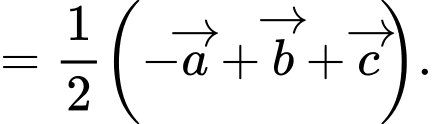
d) Đúng. Từ câu a), b), c) ta có: 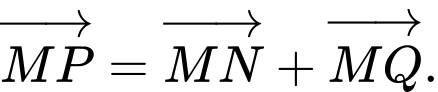
Câu 18 [380656]: Cho hai hình bình hành 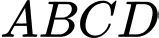 và
và 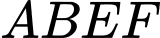 không cùng nằm trong một mặt phẳng. Trên các đường chéo
không cùng nằm trong một mặt phẳng. Trên các đường chéo 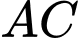 và
và 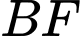 lấy các điểm
lấy các điểm 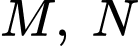 sao cho
sao cho 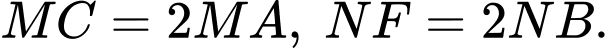 Khi đó biểu diễn vectơ
Khi đó biểu diễn vectơ 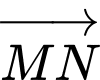 theo ba vectơ
theo ba vectơ 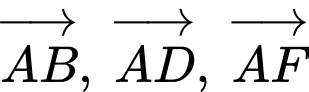 ta được:
ta được: 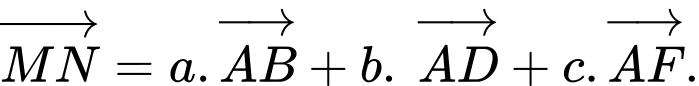 Tính giá trị của
Tính giá trị của 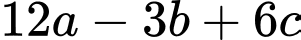
Đáp số:………………………….
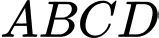 và
và 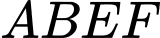 không cùng nằm trong một mặt phẳng. Trên các đường chéo
không cùng nằm trong một mặt phẳng. Trên các đường chéo 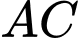 và
và 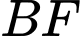 lấy các điểm
lấy các điểm 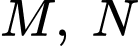 sao cho
sao cho 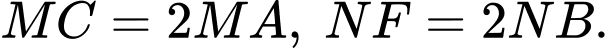 Khi đó biểu diễn vectơ
Khi đó biểu diễn vectơ 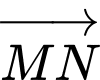 theo ba vectơ
theo ba vectơ 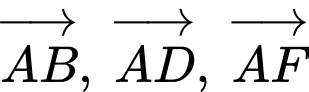 ta được:
ta được: 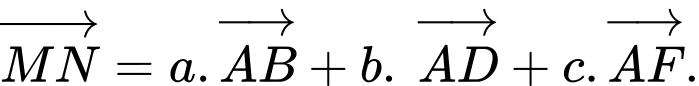 Tính giá trị của
Tính giá trị của 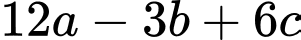
Đáp số:………………………….

Ta có: 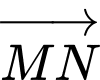
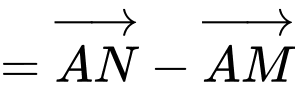
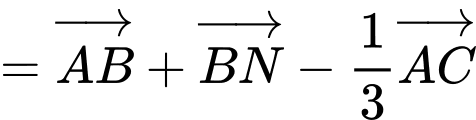
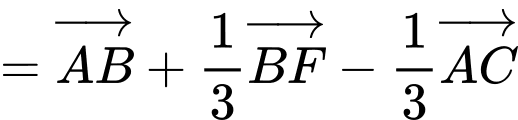
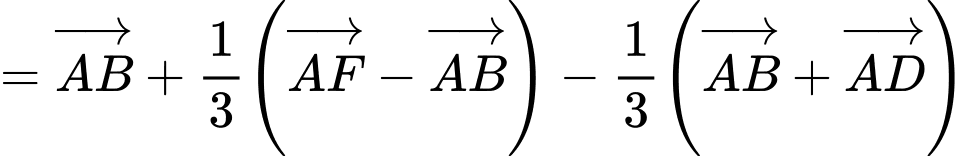
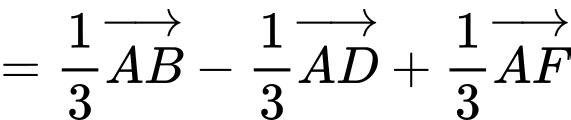
Suy ra 
Câu 19 [379002]: Cho tứ diện 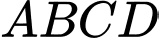 có
có 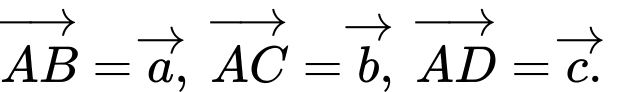 Gọi
Gọi 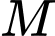 là trung điểm của
là trung điểm của 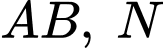 là điểm trên cạnh
là điểm trên cạnh 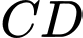 sao cho
sao cho 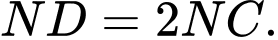 Gọi
Gọi  là trung điểm của đoạn thẳng
là trung điểm của đoạn thẳng 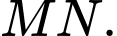 Biết rằng
Biết rằng 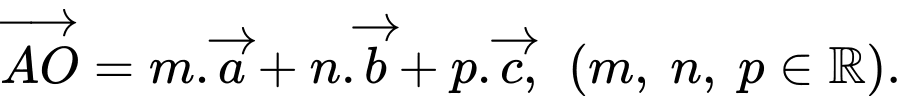 Tính giá trị của
Tính giá trị của 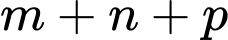
Đáp số:………………………….
 có
có 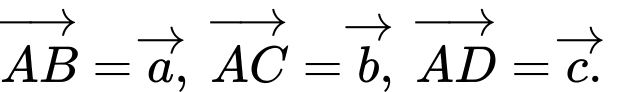 Gọi
Gọi 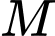 là trung điểm của
là trung điểm của 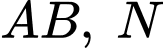 là điểm trên cạnh
là điểm trên cạnh 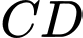 sao cho
sao cho 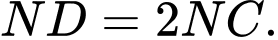 Gọi
Gọi  là trung điểm của đoạn thẳng
là trung điểm của đoạn thẳng 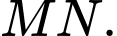 Biết rằng
Biết rằng 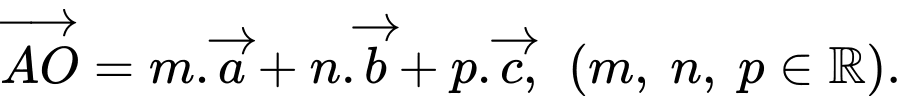 Tính giá trị của
Tính giá trị của 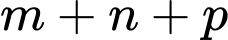
Đáp số:………………………….
HD: Ta có: 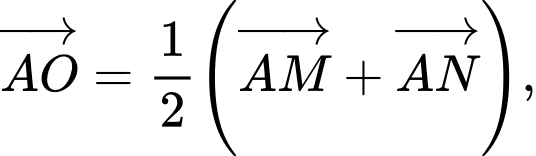 trong đó
trong đó 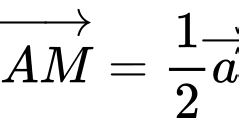 và
và
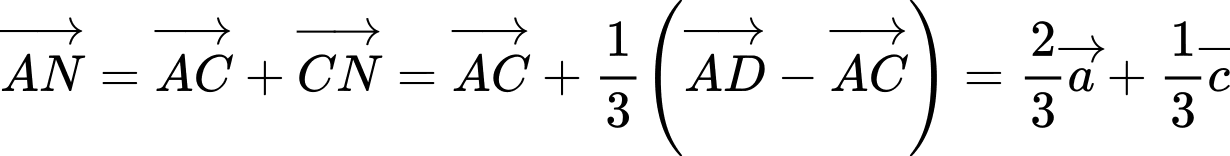
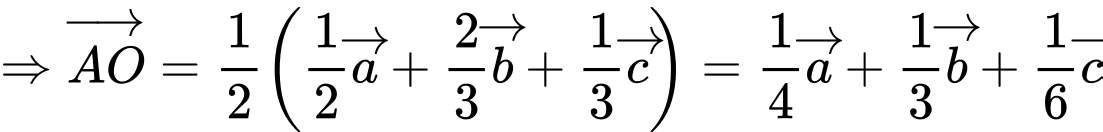
Do đó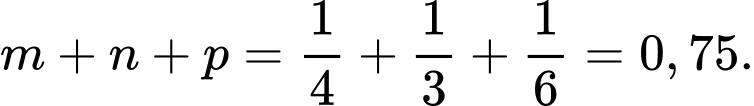
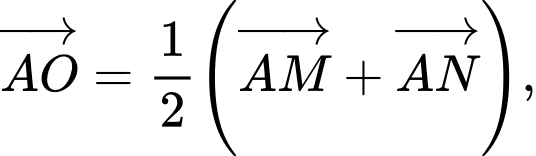 trong đó
trong đó 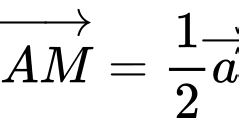 và
và
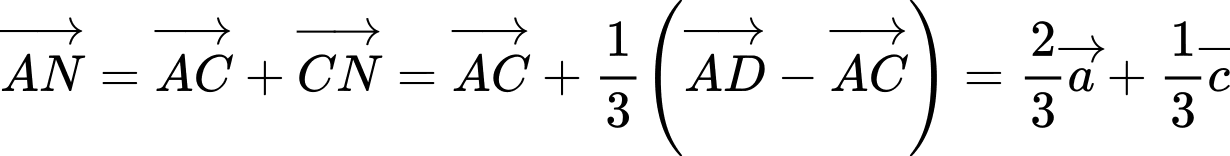
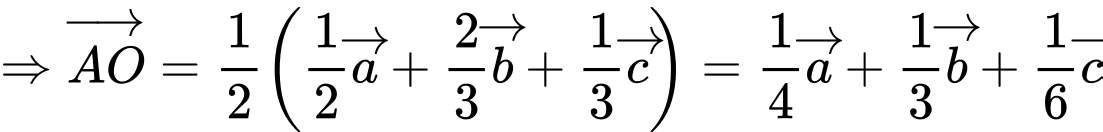
Do đó
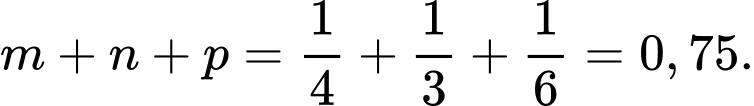
Đáp số: 0,75
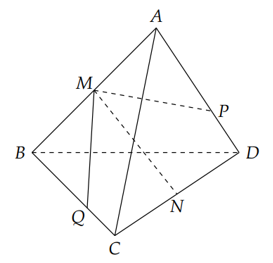
Câu 20 [379356]: Cho tứ diện 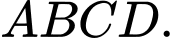 Gọi
Gọi 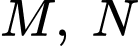 lần lượt là trung điểm của
lần lượt là trung điểm của  và
và 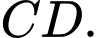 Trên cạnh
Trên cạnh 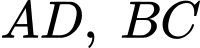 lần lượt lấy các điểm
lần lượt lấy các điểm 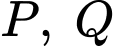 sao cho
sao cho 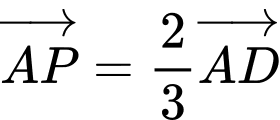 và
và 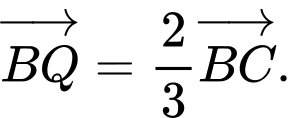 Biết rằng
Biết rằng 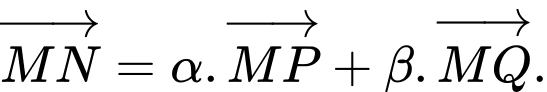 Hãy tính tổng
Hãy tính tổng 
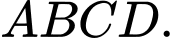 Gọi
Gọi 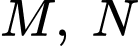 lần lượt là trung điểm của
lần lượt là trung điểm của  và
và 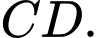 Trên cạnh
Trên cạnh 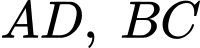 lần lượt lấy các điểm
lần lượt lấy các điểm 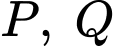 sao cho
sao cho 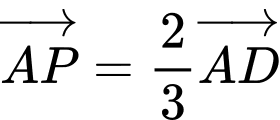 và
và 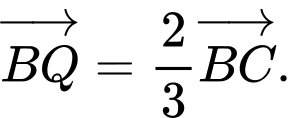 Biết rằng
Biết rằng 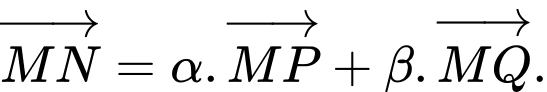 Hãy tính tổng
Hãy tính tổng 
Ta có: 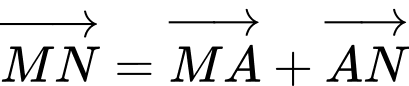
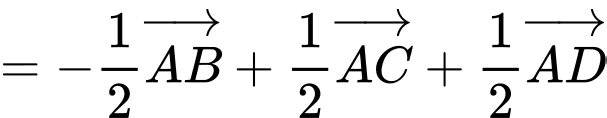
Mặt khác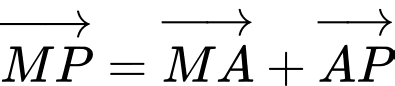
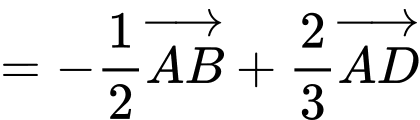 ;
;
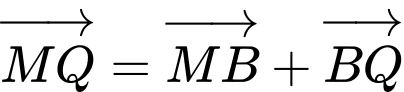
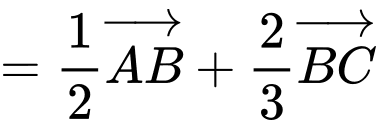
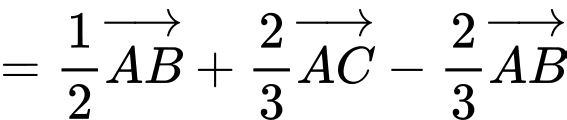
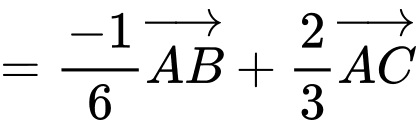
Đồng nhất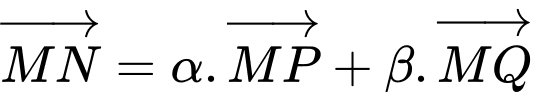 ta được
ta được 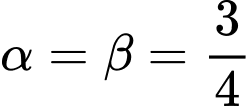
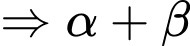
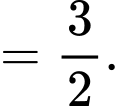
Đáp số 1,5.
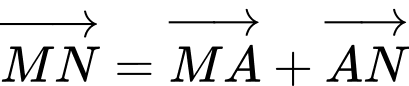
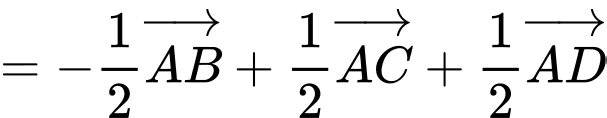

Mặt khác
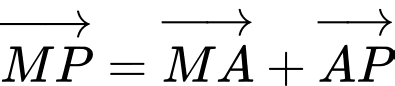
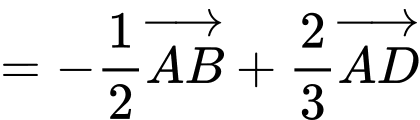 ;
; 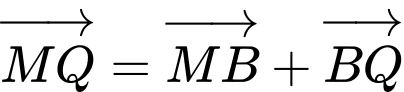
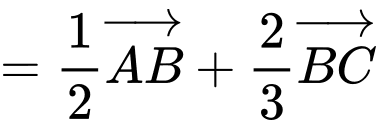
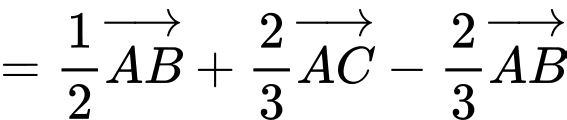
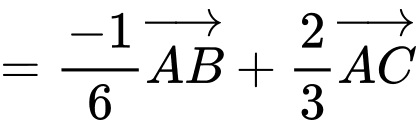
Đồng nhất
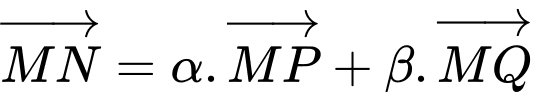 ta được
ta được 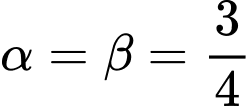
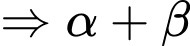
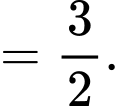
Đáp số 1,5.