Đáp án Bài tập tự luyện
Câu 1 [151426]: Trong không gian với hệ tọa độ 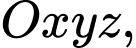 cho vật thể
cho vật thể  được giới hạn bởi hai mặt phẳng có phương trình
được giới hạn bởi hai mặt phẳng có phương trình 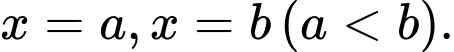 Gọi
Gọi 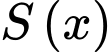 là diện tích thiết diện của
là diện tích thiết diện của  bị cắt bởi mặt phẳng vuông góc với trục
bị cắt bởi mặt phẳng vuông góc với trục 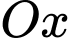 tại điểm có hoành độ là
tại điểm có hoành độ là 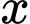
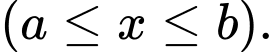 Giả sử hàm số
Giả sử hàm số 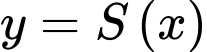 liên tục trên đoạn
liên tục trên đoạn 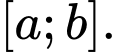 Khi đó thể tích
Khi đó thể tích  của vật thể được cho bởi công thức
của vật thể được cho bởi công thức
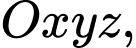 cho vật thể
cho vật thể  được giới hạn bởi hai mặt phẳng có phương trình
được giới hạn bởi hai mặt phẳng có phương trình 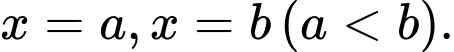 Gọi
Gọi 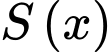 là diện tích thiết diện của
là diện tích thiết diện của  bị cắt bởi mặt phẳng vuông góc với trục
bị cắt bởi mặt phẳng vuông góc với trục 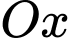 tại điểm có hoành độ là
tại điểm có hoành độ là 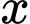
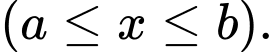 Giả sử hàm số
Giả sử hàm số 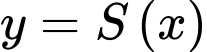 liên tục trên đoạn
liên tục trên đoạn 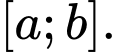 Khi đó thể tích
Khi đó thể tích  của vật thể được cho bởi công thức
của vật thể được cho bởi công thức A, 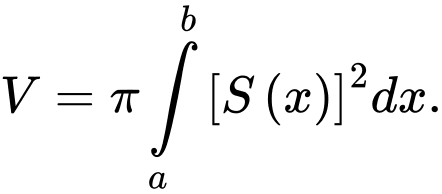
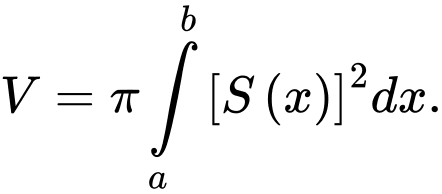
B, 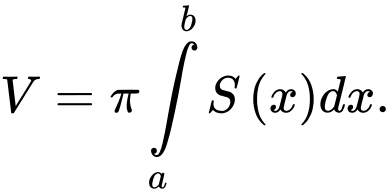
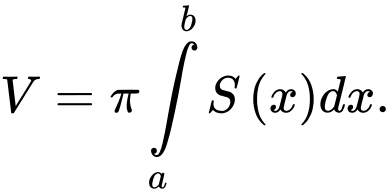
C, 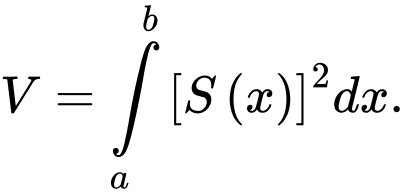
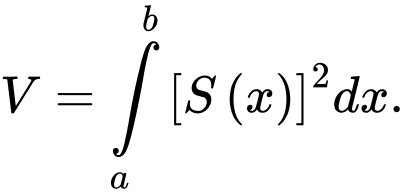
D, 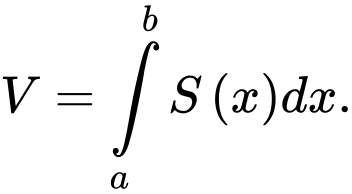
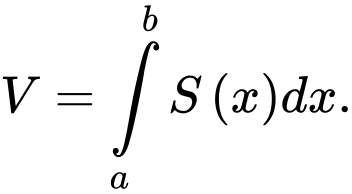
Chọn đáp án D. Đáp án: D
Câu 2 [151428]: Tính thể tích  của vật thể giới hạn bởi hai mặt phẳng
của vật thể giới hạn bởi hai mặt phẳng 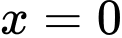 và
và 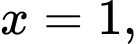 biết rằng khi cắt vật thể bởi mặt phẳng tùy ý vuông góc với trục
biết rằng khi cắt vật thể bởi mặt phẳng tùy ý vuông góc với trục 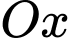 tại điểm có hoành độ
tại điểm có hoành độ 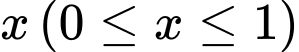 thì được thiết diện là hình vuông có cạnh bằng
thì được thiết diện là hình vuông có cạnh bằng  .
.
 của vật thể giới hạn bởi hai mặt phẳng
của vật thể giới hạn bởi hai mặt phẳng 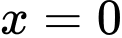 và
và 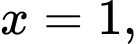 biết rằng khi cắt vật thể bởi mặt phẳng tùy ý vuông góc với trục
biết rằng khi cắt vật thể bởi mặt phẳng tùy ý vuông góc với trục 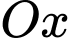 tại điểm có hoành độ
tại điểm có hoành độ 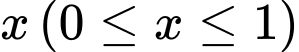 thì được thiết diện là hình vuông có cạnh bằng
thì được thiết diện là hình vuông có cạnh bằng  .
. A, 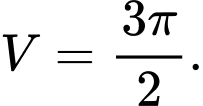
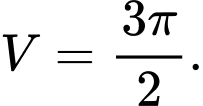
B, 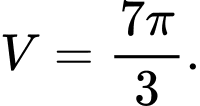
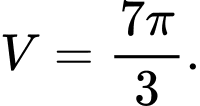
C, 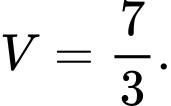
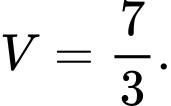
D, 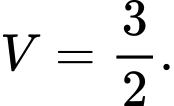
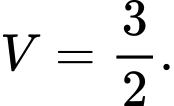
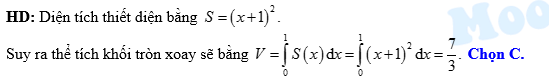 Đáp án: C
Đáp án: C
Câu 3 [151431]: Cho phần vật thể 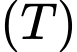 giới hạn bởi hai mặt phẳng có phương trình
giới hạn bởi hai mặt phẳng có phương trình 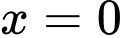 và
và 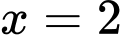 . Cắt phần vật thể
. Cắt phần vật thể 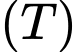 bởi mặt phẳng vuông góc với trục
bởi mặt phẳng vuông góc với trục 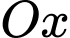 tại điểm có hoành độ
tại điểm có hoành độ 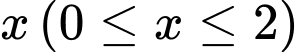 , ta được thiết diện là một tam giác đều có độ dài cạnh bằng
, ta được thiết diện là một tam giác đều có độ dài cạnh bằng 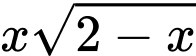 . Tính thể tích
. Tính thể tích  của phần vật thể
của phần vật thể 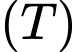 .
.
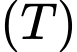 giới hạn bởi hai mặt phẳng có phương trình
giới hạn bởi hai mặt phẳng có phương trình 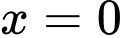 và
và 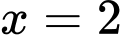 . Cắt phần vật thể
. Cắt phần vật thể 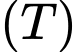 bởi mặt phẳng vuông góc với trục
bởi mặt phẳng vuông góc với trục 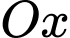 tại điểm có hoành độ
tại điểm có hoành độ 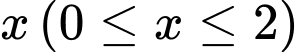 , ta được thiết diện là một tam giác đều có độ dài cạnh bằng
, ta được thiết diện là một tam giác đều có độ dài cạnh bằng 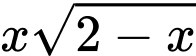 . Tính thể tích
. Tính thể tích  của phần vật thể
của phần vật thể 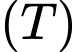 .
. A, 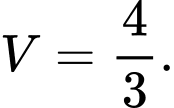
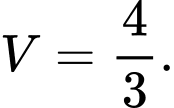
B, 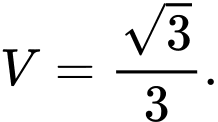
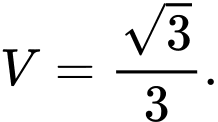
C, 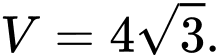
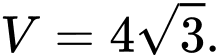
D, 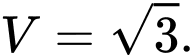
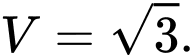
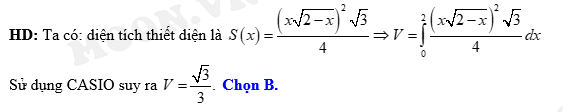 Đáp án: B
Đáp án: B
Câu 4 [360293]: Thể tích khối tròn xoay tạo thành khi cho hình phẳng giới hạn bởi đồ thị hàm số 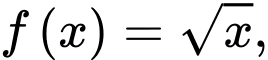 trục hoành và hai đường thẳng
trục hoành và hai đường thẳng 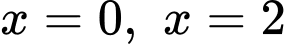 quay quanh trục
quay quanh trục 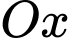 là:
là:
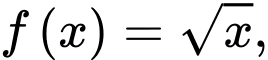 trục hoành và hai đường thẳng
trục hoành và hai đường thẳng 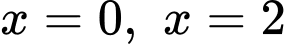 quay quanh trục
quay quanh trục 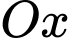 là:
là: A, 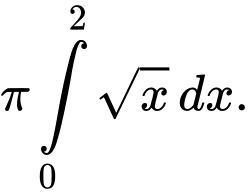
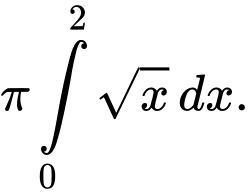
B, 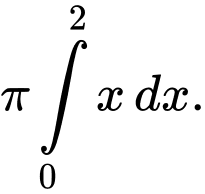
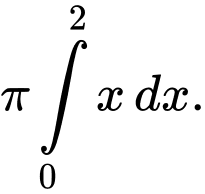
C, 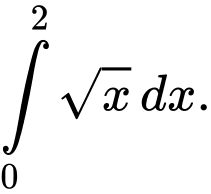
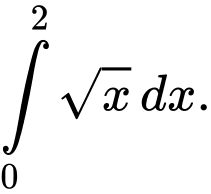
D, 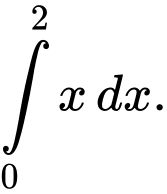
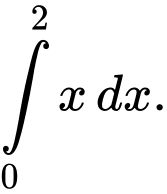
Thể tích của khối tròn xoay đó là 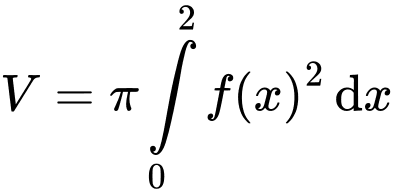
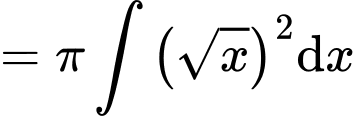
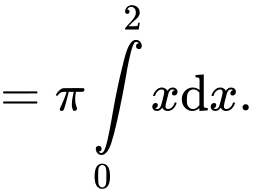
Chọn B. Đáp án: B
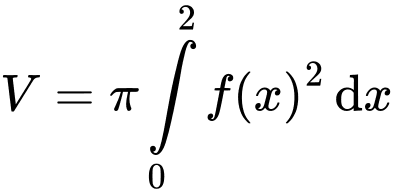
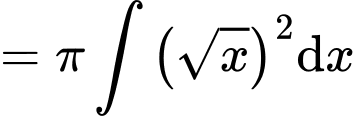
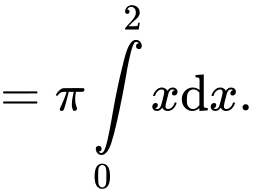
Chọn B. Đáp án: B
Câu 5 [151627]: Cho hình phẳng 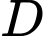 giới hạn bởi đồ thị hàm số
giới hạn bởi đồ thị hàm số 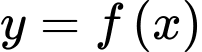 , trục
, trục 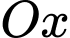 và hai đường thẳng
và hai đường thẳng 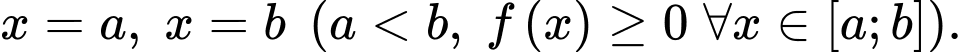 Công thức tính thể tích vật thể tròn xoay nhận được khi hình phẳng
Công thức tính thể tích vật thể tròn xoay nhận được khi hình phẳng 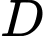 quay quanh trục
quay quanh trục 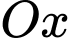 là
là
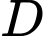 giới hạn bởi đồ thị hàm số
giới hạn bởi đồ thị hàm số 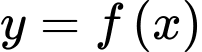 , trục
, trục 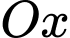 và hai đường thẳng
và hai đường thẳng 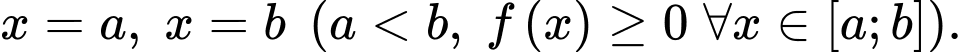 Công thức tính thể tích vật thể tròn xoay nhận được khi hình phẳng
Công thức tính thể tích vật thể tròn xoay nhận được khi hình phẳng 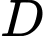 quay quanh trục
quay quanh trục 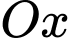 là
là A, 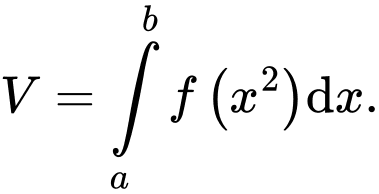
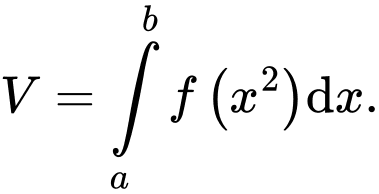
B, 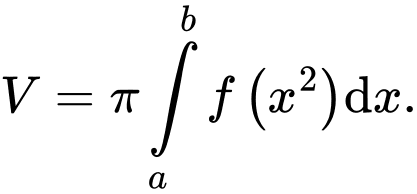
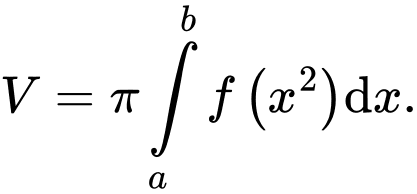
C, 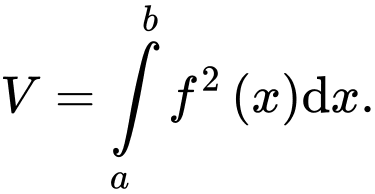
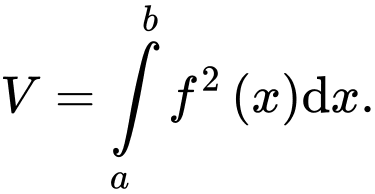
D, 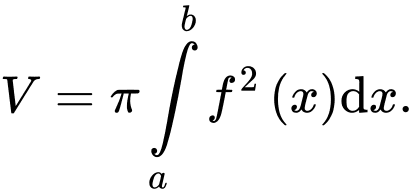
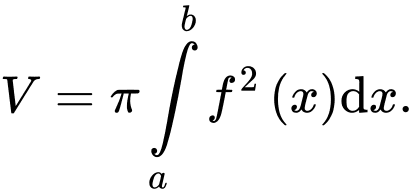
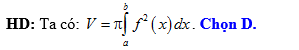 Đáp án: D
Đáp án: D
Câu 6 [151629]: Cho hình phẳng  giới hạn bởi các đường
giới hạn bởi các đường 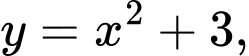
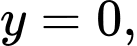
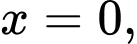
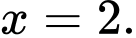 Gọi
Gọi  là thể tích khối tròn xoay được tạo thành khi quay
là thể tích khối tròn xoay được tạo thành khi quay  xung quanh trục
xung quanh trục 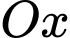 . Mệnh đề nào sau đây đúng?
. Mệnh đề nào sau đây đúng?
 giới hạn bởi các đường
giới hạn bởi các đường 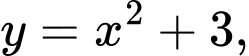
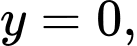
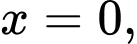
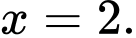 Gọi
Gọi  là thể tích khối tròn xoay được tạo thành khi quay
là thể tích khối tròn xoay được tạo thành khi quay  xung quanh trục
xung quanh trục 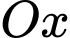 . Mệnh đề nào sau đây đúng?
. Mệnh đề nào sau đây đúng? A, 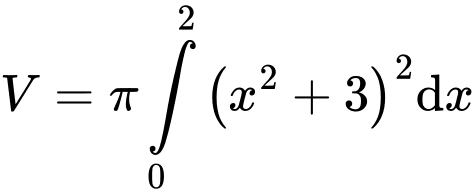 .
.
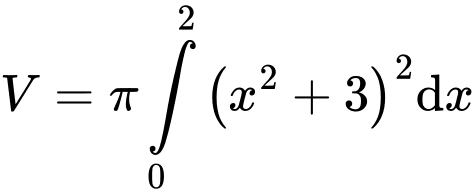 .
.B, 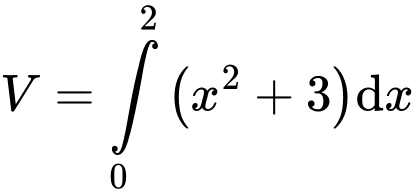 .
.
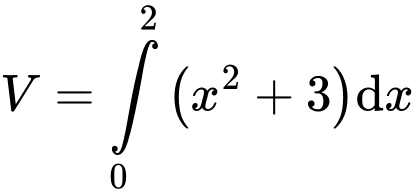 .
.C, 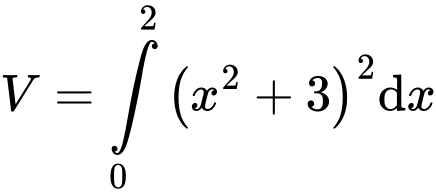 .
.
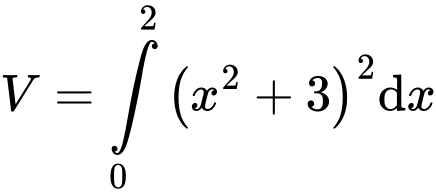 .
.D, 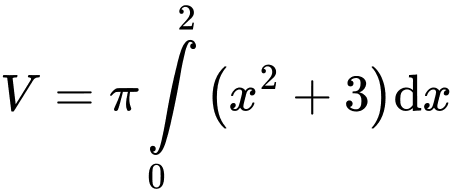 .
.
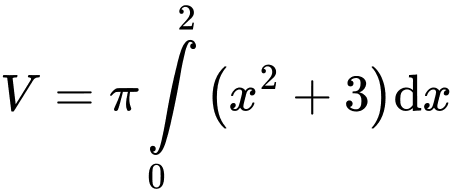 .
.
Đáp án A
Thể tích của vật thể được tạo nên là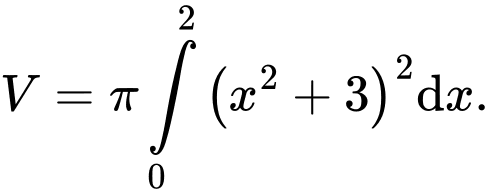 Đáp án: A
Đáp án: A
Thể tích của vật thể được tạo nên là
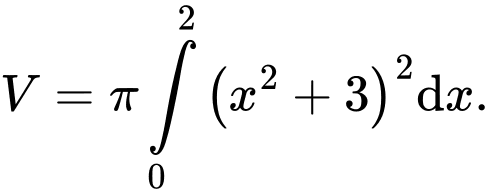 Đáp án: A
Đáp án: A
Câu 7 [151631]: Thể tích khối tròn xoay tạo thành khi quay hình phẳng giới hạn bởi các đường 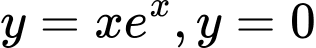 và
và 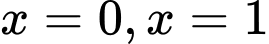 xung quanh trục
xung quanh trục 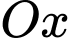 là
là
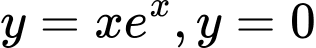 và
và 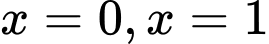 xung quanh trục
xung quanh trục 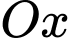 là
là A, 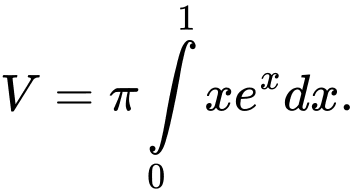
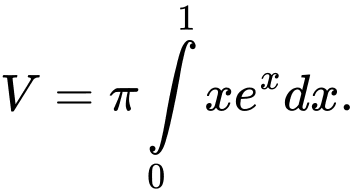
B, 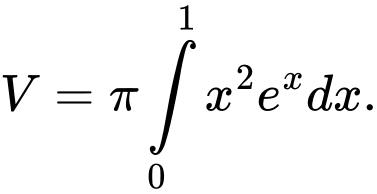
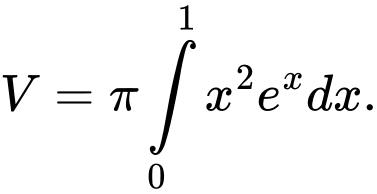
C, 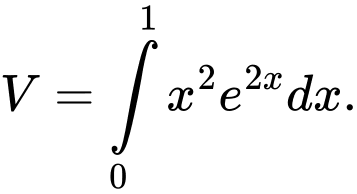
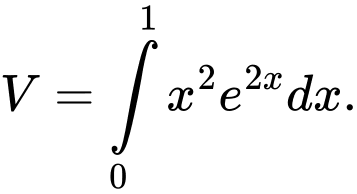
D, 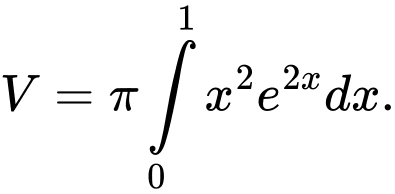
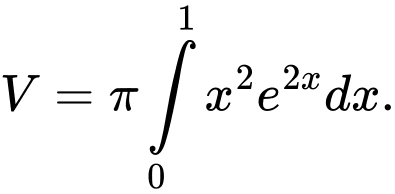
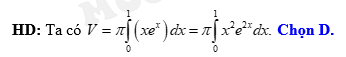 Đáp án: D
Đáp án: D
Câu 8 [16452]: Cho hình phẳng 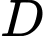 giới hạn bởi đường cong
giới hạn bởi đường cong 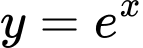 , trục hoành và các đường thẳng
, trục hoành và các đường thẳng 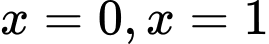 . Khối tròn xoay tạo thành khi quay
. Khối tròn xoay tạo thành khi quay 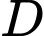 quanh trục hoành có thể tích là
quanh trục hoành có thể tích là
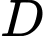 giới hạn bởi đường cong
giới hạn bởi đường cong 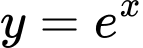 , trục hoành và các đường thẳng
, trục hoành và các đường thẳng 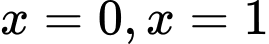 . Khối tròn xoay tạo thành khi quay
. Khối tròn xoay tạo thành khi quay 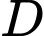 quanh trục hoành có thể tích là
quanh trục hoành có thể tích là A, 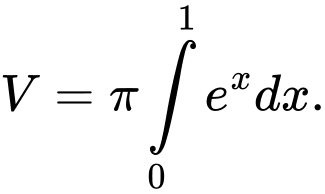
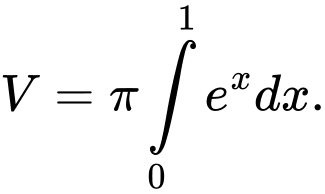
B, 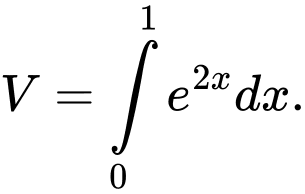
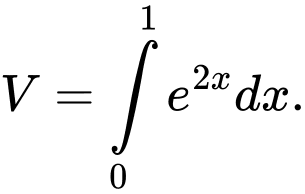
C, 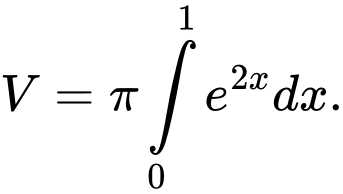
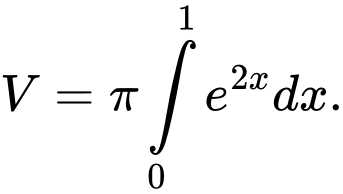
D, 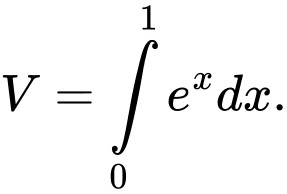
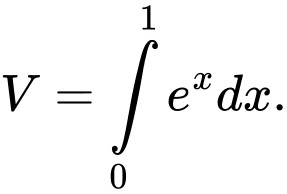
Đáp án C
Ta có thể tích của khối tròn xoay khi quay hình phẳng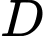 là:
là: 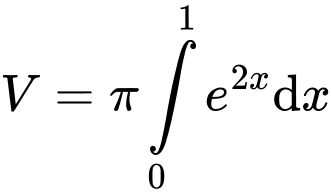 Đáp án: C
Đáp án: C
Ta có thể tích của khối tròn xoay khi quay hình phẳng
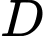 là:
là: 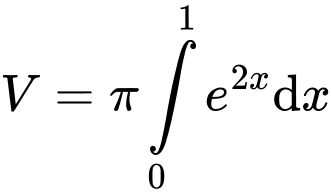 Đáp án: C
Đáp án: C
Câu 9 [151632]: Gọi 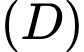 là hình phẳng giới hạn bởi các đường
là hình phẳng giới hạn bởi các đường 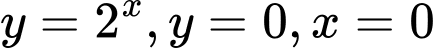 và
và 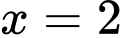 . Thể tích
. Thể tích  của khối tròn xoay tạo thành khi quay
của khối tròn xoay tạo thành khi quay 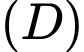 quanh trục
quanh trục 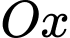 được định bởi công thức
được định bởi công thức
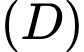 là hình phẳng giới hạn bởi các đường
là hình phẳng giới hạn bởi các đường 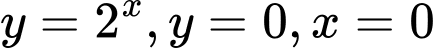 và
và 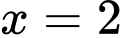 . Thể tích
. Thể tích  của khối tròn xoay tạo thành khi quay
của khối tròn xoay tạo thành khi quay 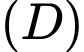 quanh trục
quanh trục 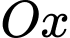 được định bởi công thức
được định bởi công thức A, 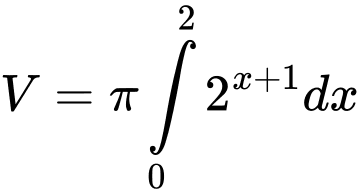 .
.
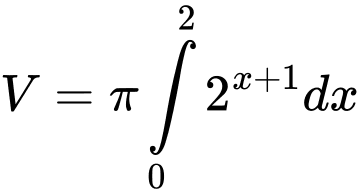 .
.B, 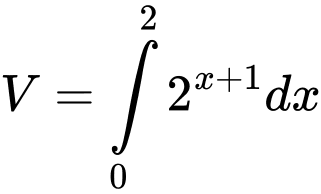 .
.
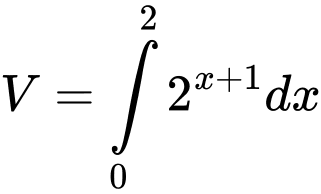 .
.C, 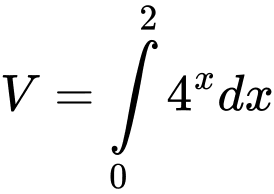 .
.
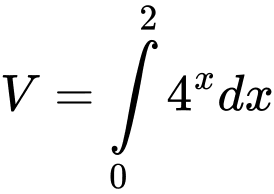 .
.D, 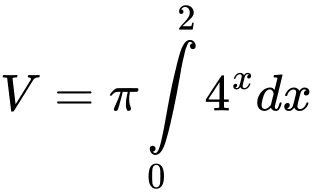 .
.
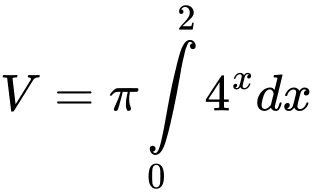 .
. Đáp án: D
Đáp án: D
Câu 10 [378616]: Cho hình phẳng 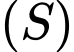 giới hạn bởi đồ thị hàm số
giới hạn bởi đồ thị hàm số 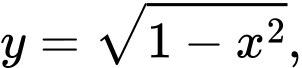 trục hoành và hai đường thẳng
trục hoành và hai đường thẳng 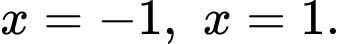 Thể tích của khối tròn xoay khi quay
Thể tích của khối tròn xoay khi quay 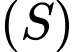 quanh
quanh 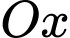 là
là
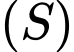 giới hạn bởi đồ thị hàm số
giới hạn bởi đồ thị hàm số 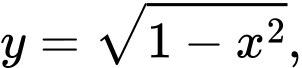 trục hoành và hai đường thẳng
trục hoành và hai đường thẳng 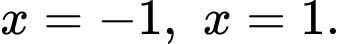 Thể tích của khối tròn xoay khi quay
Thể tích của khối tròn xoay khi quay 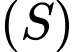 quanh
quanh 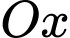 là
là A, 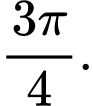
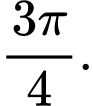
B, 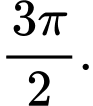
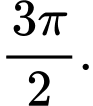
C, 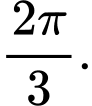
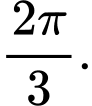
D, 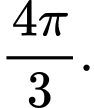
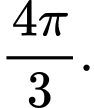
Thể tích của khối tròn xoay đó là 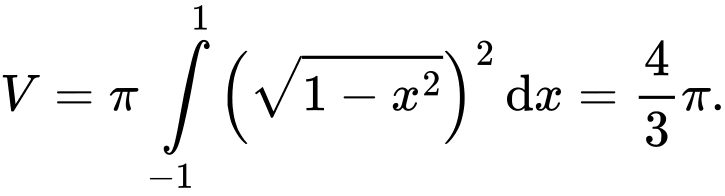
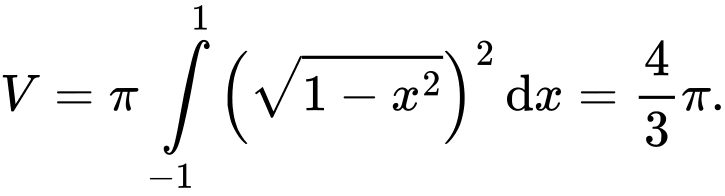
Chọn đáp án D.
Đáp án: D
Câu 11 [151641]: Gọi  là hình phẳng giới hạn bởi đồ thị hàm số
là hình phẳng giới hạn bởi đồ thị hàm số 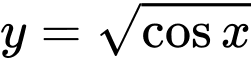 , trục hoành và các đường thẳng
, trục hoành và các đường thẳng 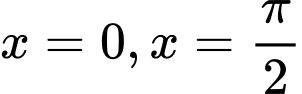 . Tính thể tích
. Tính thể tích  của khối tròn xoay tạo thành khi quay hình
của khối tròn xoay tạo thành khi quay hình  quanh trục
quanh trục 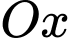 .
.
 là hình phẳng giới hạn bởi đồ thị hàm số
là hình phẳng giới hạn bởi đồ thị hàm số 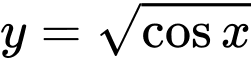 , trục hoành và các đường thẳng
, trục hoành và các đường thẳng 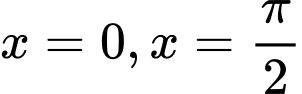 . Tính thể tích
. Tính thể tích  của khối tròn xoay tạo thành khi quay hình
của khối tròn xoay tạo thành khi quay hình  quanh trục
quanh trục 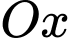 .
. A, 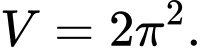
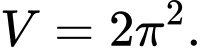
B, 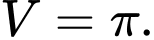
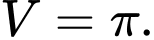
C, 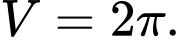
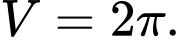
D, 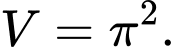
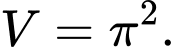
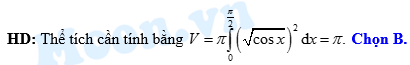 Đáp án: B
Đáp án: B
Câu 12 [161581]: Cho hình phẳng giới hạn bởi các đường 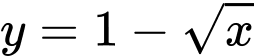 , trục hoành và
, trục hoành và 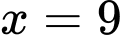 quay xung quanh trục
quay xung quanh trục 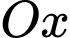 . Tính thể tích khối tròn xoay tạo thành.
. Tính thể tích khối tròn xoay tạo thành.
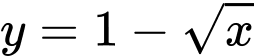 , trục hoành và
, trục hoành và 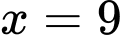 quay xung quanh trục
quay xung quanh trục 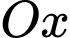 . Tính thể tích khối tròn xoay tạo thành.
. Tính thể tích khối tròn xoay tạo thành. A, 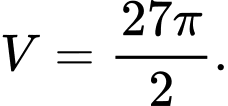
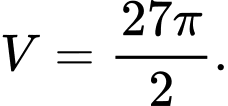
B, 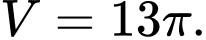
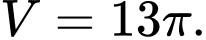
C, 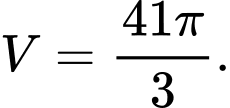
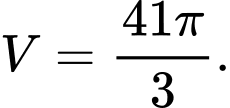
D, 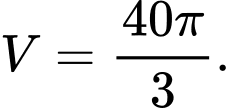
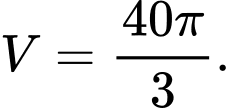
Chọn D
Phương trình hoành độ giao điểm của đồ thị hàm số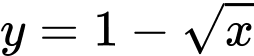 và trục hoành:
và trục hoành: 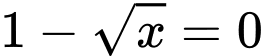
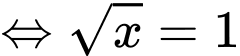
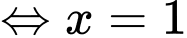 .
Thể tích của khối tròn xoay tạo thành là:
.
Thể tích của khối tròn xoay tạo thành là:
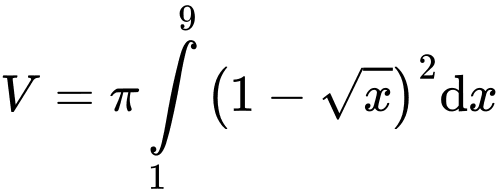
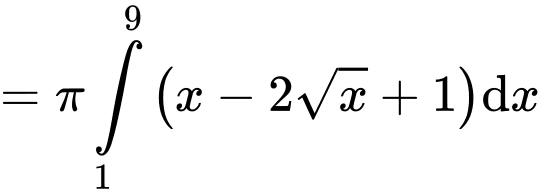
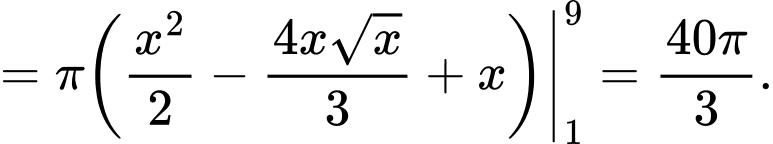 Đáp án: D
Đáp án: D
Phương trình hoành độ giao điểm của đồ thị hàm số
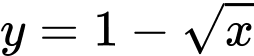 và trục hoành:
và trục hoành: 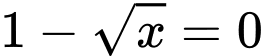
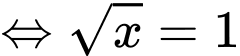
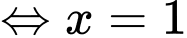 .
Thể tích của khối tròn xoay tạo thành là:
.
Thể tích của khối tròn xoay tạo thành là:
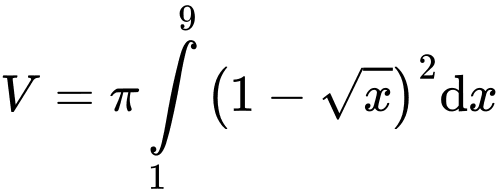
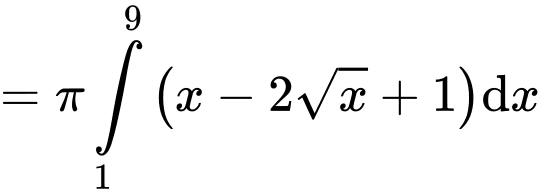
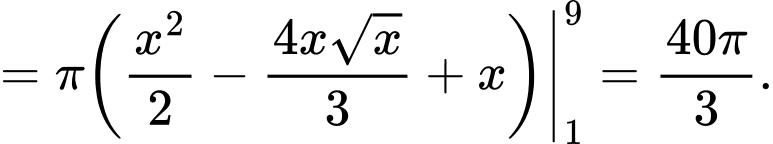 Đáp án: D
Đáp án: D
Câu 13 [151636]: Thể tích vật thể tròn xoay sinh bởi khi quay hình phẳng giới hạn bởi đồ thị hàm số 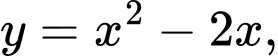 trục hoành, đường thẳng
trục hoành, đường thẳng 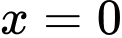 và đường thẳng
và đường thẳng 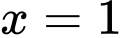 quay quanh trục hoành là
quay quanh trục hoành là
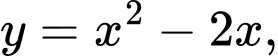 trục hoành, đường thẳng
trục hoành, đường thẳng 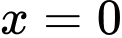 và đường thẳng
và đường thẳng 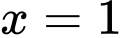 quay quanh trục hoành là
quay quanh trục hoành là A, 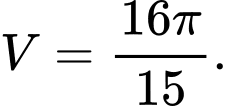
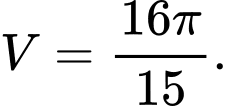
B, 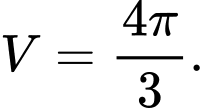
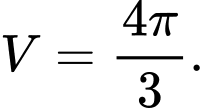
C, 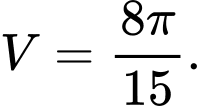
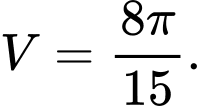
D, 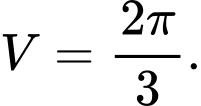
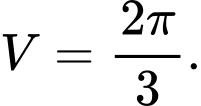
HD: Thể tích cần tính bằng 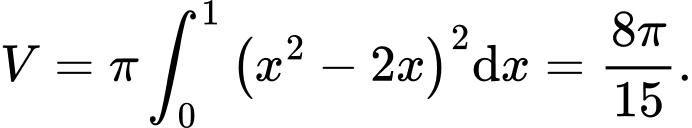 Chọn C. Đáp án: C
Chọn C. Đáp án: C
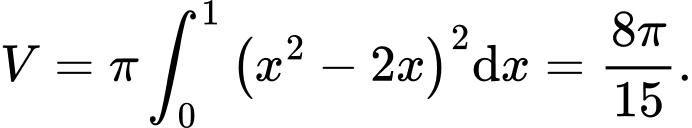 Chọn C. Đáp án: C
Chọn C. Đáp án: C
Câu 14 [151643]: Cho hình phẳng 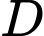 giới hạn bởi đường cong
giới hạn bởi đường cong 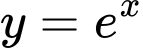 , trục hoành và các đường thẳng
, trục hoành và các đường thẳng 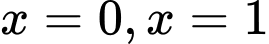 . Khối tròn xoay tạo thành khi quay
. Khối tròn xoay tạo thành khi quay 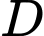 quanh trục hoành có thể tích
quanh trục hoành có thể tích  bằng bao
nhiêu?
bằng bao
nhiêu?
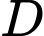 giới hạn bởi đường cong
giới hạn bởi đường cong 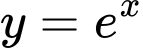 , trục hoành và các đường thẳng
, trục hoành và các đường thẳng 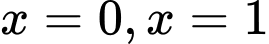 . Khối tròn xoay tạo thành khi quay
. Khối tròn xoay tạo thành khi quay 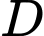 quanh trục hoành có thể tích
quanh trục hoành có thể tích  bằng bao
nhiêu?
bằng bao
nhiêu? A, 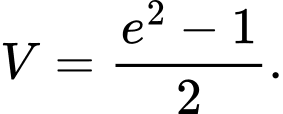
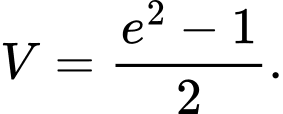
B, 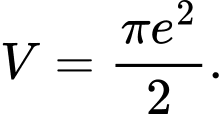
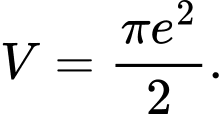
C, 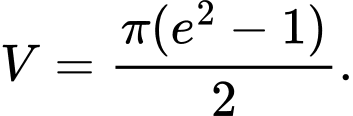
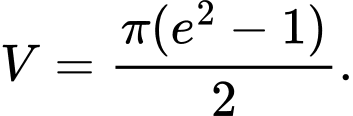
D, 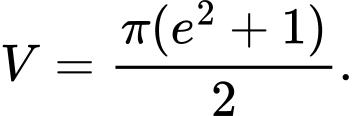
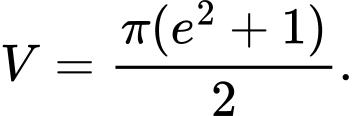
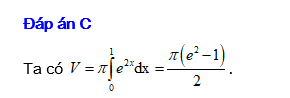 Đáp án: C
Đáp án: C
Câu 15 [151648]: Cho hàm số  với
với 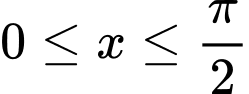 , có đồ thị là
, có đồ thị là  như hình vẽ bên, quay hình
như hình vẽ bên, quay hình  quanh trục
quanh trục 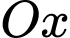 tạo thành khối tròn xoay có thể tích bằng bao nhiêu?
tạo thành khối tròn xoay có thể tích bằng bao nhiêu?
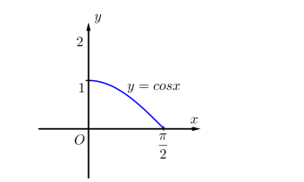
 với
với 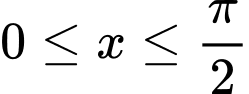 , có đồ thị là
, có đồ thị là  như hình vẽ bên, quay hình
như hình vẽ bên, quay hình  quanh trục
quanh trục 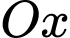 tạo thành khối tròn xoay có thể tích bằng bao nhiêu?
tạo thành khối tròn xoay có thể tích bằng bao nhiêu?
A, 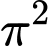 .
.
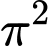 .
.B, 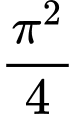 .
.
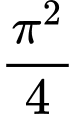 .
.C, 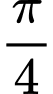 .
.
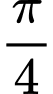 .
.D, 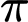 .
.
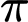 .
.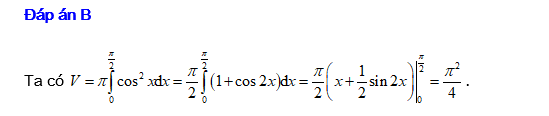 Đáp án: B
Đáp án: B
Câu 16 [161521]: Cho hình phẳng  giới hạn bởi đường cong
giới hạn bởi đường cong 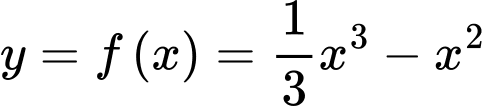 và trục hoành. Các mệnh đề sau đúng hay sai?
và trục hoành. Các mệnh đề sau đúng hay sai?
 giới hạn bởi đường cong
giới hạn bởi đường cong 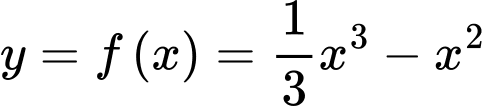 và trục hoành. Các mệnh đề sau đúng hay sai?
và trục hoành. Các mệnh đề sau đúng hay sai? A, a) Hàm số 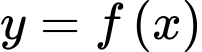 cắt trục hoành tại hai điểm phân biệt.
cắt trục hoành tại hai điểm phân biệt.
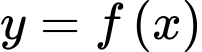 cắt trục hoành tại hai điểm phân biệt.
cắt trục hoành tại hai điểm phân biệt.B, b) 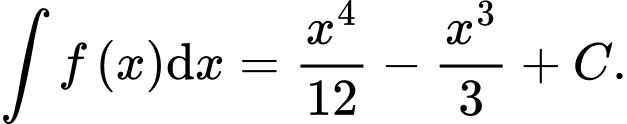
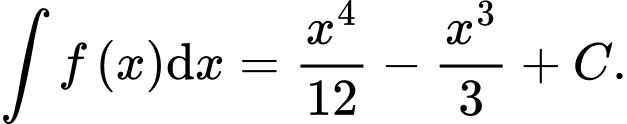
C, c) Diện tích hình phẳng  bằng
bằng 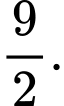
 bằng
bằng 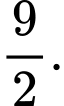
D, d) Thể tích khối tròn xoay khi quay hình phẳng  quanh trục
quanh trục 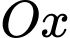 (làm tròn đến hàng phần chục) bằng
(làm tròn đến hàng phần chục) bằng 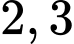 (đơn vị thể tích).
(đơn vị thể tích).
 quanh trục
quanh trục 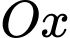 (làm tròn đến hàng phần chục) bằng
(làm tròn đến hàng phần chục) bằng 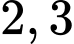 (đơn vị thể tích).
(đơn vị thể tích).
a) Đúng.
Số giao điểm của đồ thị hàm số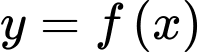 và
và 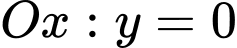 là số nghiệm của phương trình
là số nghiệm của phương trình 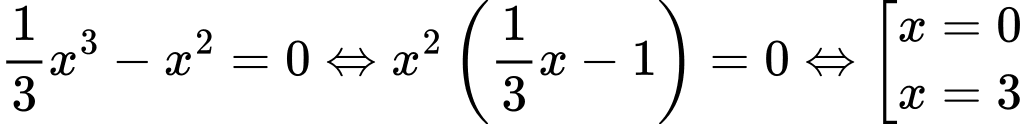
Vậy hàm số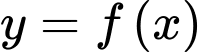 cắt trục hoành tại hai điểm phân biệt.
cắt trục hoành tại hai điểm phân biệt.
b) Đúng.
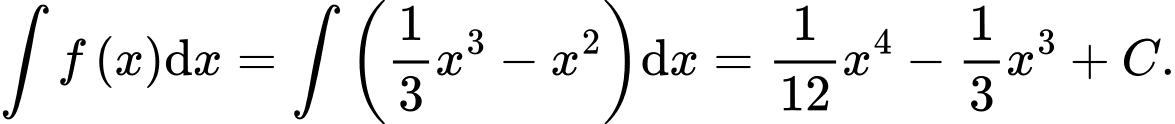
c) Sai.
Hoành độ giao điểm của đồ thị hàm số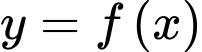 và trục hoành
và trục hoành 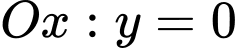 là
là 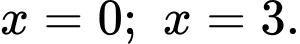
Vậy hình phẳng giới hạn bởi đồ thị hàm số
giới hạn bởi đồ thị hàm số 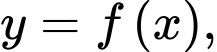 trục hoành và hai đường thẳng
trục hoành và hai đường thẳng 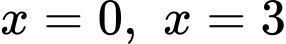 sẽ có diện tích là:
sẽ có diện tích là: 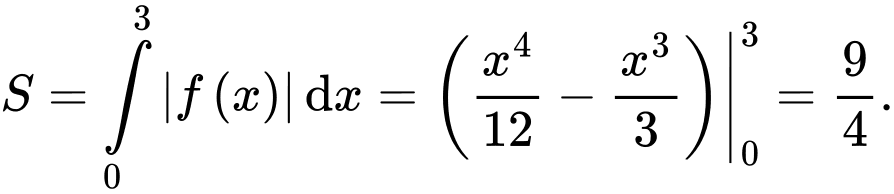
d) Sai.
Khối tròn xoay khi quay hình phẳng quanh trục
quanh trục 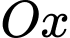 có nghĩa là khối tròn xoay sinh được khi quay
có nghĩa là khối tròn xoay sinh được khi quay 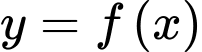 quanh trục hoành và bị giới hạn bởi hai đường thẳng
quanh trục hoành và bị giới hạn bởi hai đường thẳng 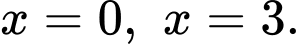
Vậy thể tích khối tròn xoay đó là: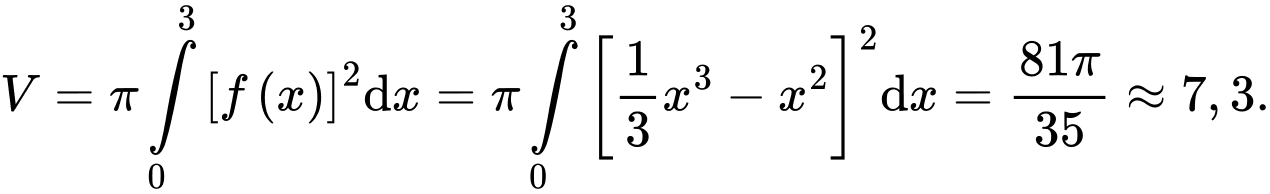
Số giao điểm của đồ thị hàm số
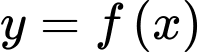 và
và 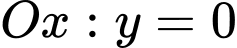 là số nghiệm của phương trình
là số nghiệm của phương trình 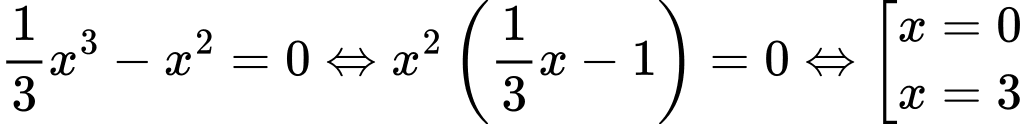
Vậy hàm số
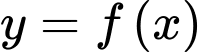 cắt trục hoành tại hai điểm phân biệt.
cắt trục hoành tại hai điểm phân biệt.
b) Đúng.
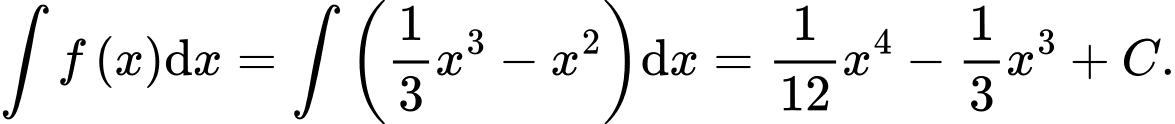
c) Sai.
Hoành độ giao điểm của đồ thị hàm số
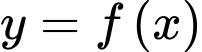 và trục hoành
và trục hoành 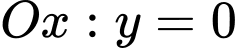 là
là 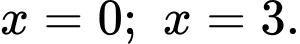
Vậy hình phẳng
 giới hạn bởi đồ thị hàm số
giới hạn bởi đồ thị hàm số 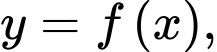 trục hoành và hai đường thẳng
trục hoành và hai đường thẳng 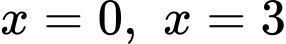 sẽ có diện tích là:
sẽ có diện tích là: 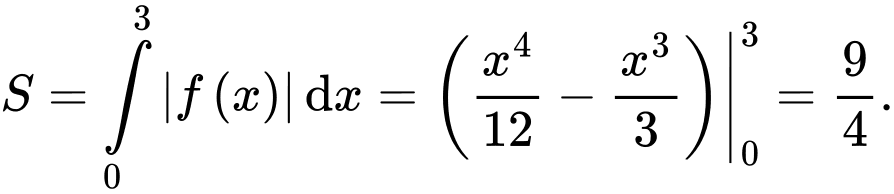
d) Sai.
Khối tròn xoay khi quay hình phẳng
 quanh trục
quanh trục 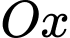 có nghĩa là khối tròn xoay sinh được khi quay
có nghĩa là khối tròn xoay sinh được khi quay 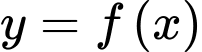 quanh trục hoành và bị giới hạn bởi hai đường thẳng
quanh trục hoành và bị giới hạn bởi hai đường thẳng 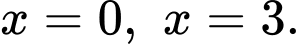
Vậy thể tích khối tròn xoay đó là:
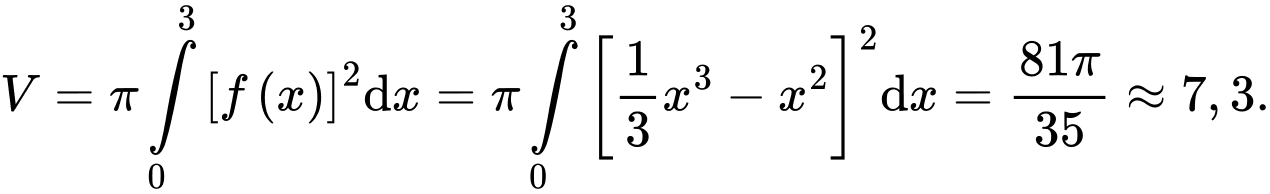
Câu 17 [161623]: Cho hàm số 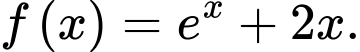
Xét tính đúng sai của các phát biểu sau:
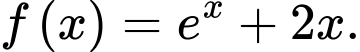
Xét tính đúng sai của các phát biểu sau:
A, a) 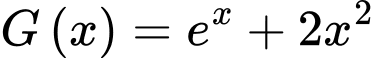 là một nguyên hàm của
là một nguyên hàm của 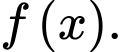
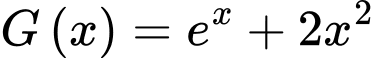 là một nguyên hàm của
là một nguyên hàm của 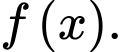
B, b) Thể tích khối tròn xoay sinh ra khi quay quanh trục 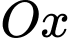 hình phẳng giới hạn bởi đồ thị hàm số
hình phẳng giới hạn bởi đồ thị hàm số 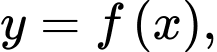 trục hoành và hai đường thẳng
trục hoành và hai đường thẳng 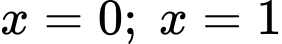 là
là 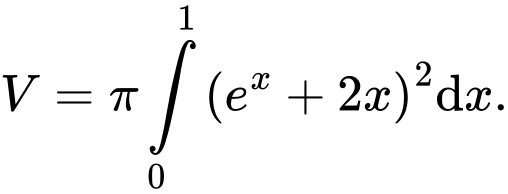
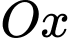 hình phẳng giới hạn bởi đồ thị hàm số
hình phẳng giới hạn bởi đồ thị hàm số 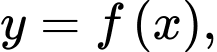 trục hoành và hai đường thẳng
trục hoành và hai đường thẳng 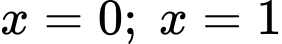 là
là 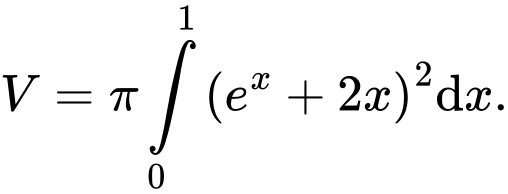
C, c) Tích phân 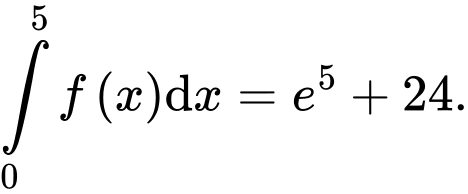
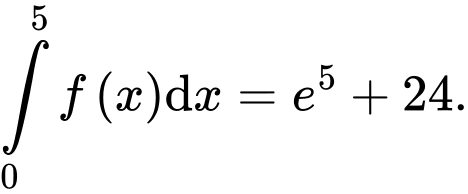
D, d) Cho 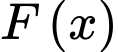 là một nguyên hàm của hàm số
là một nguyên hàm của hàm số 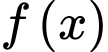 thỏa mãn
thỏa mãn 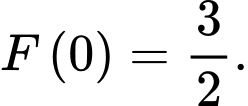 Khi đó
Khi đó 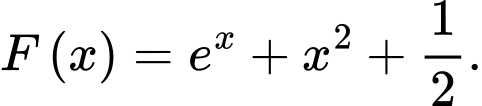
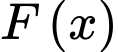 là một nguyên hàm của hàm số
là một nguyên hàm của hàm số 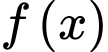 thỏa mãn
thỏa mãn 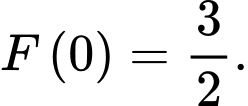 Khi đó
Khi đó 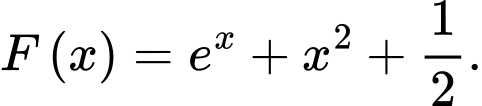
a) Sai.
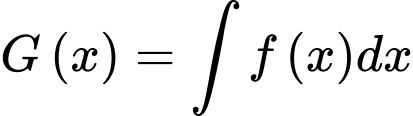
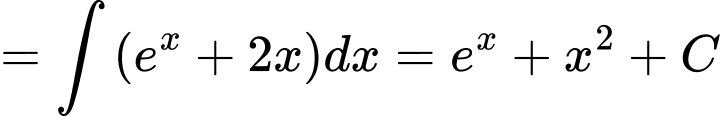
b) Đúng.
Thể tích khối tròn xoay sinh ra khi quay quanh trục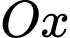 hình phẳng giới hạn bởi đồ thị hàm số
hình phẳng giới hạn bởi đồ thị hàm số 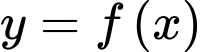 , trục hoành và hai đường thẳng
, trục hoành và hai đường thẳng 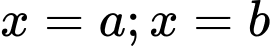 là
là 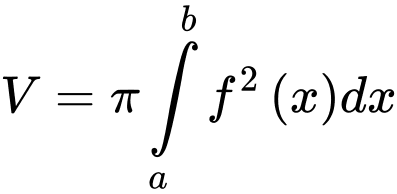
c) Đúng.
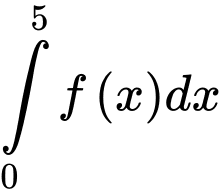
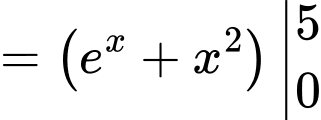
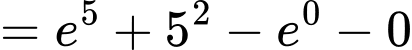
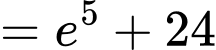 .
.
d) Đúng.
Vì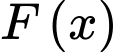 là một nguyên hàm của hàm số
là một nguyên hàm của hàm số 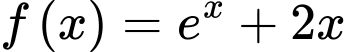 nên
nên
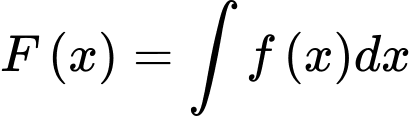
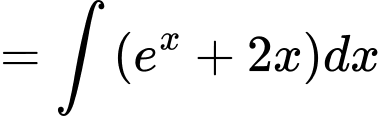
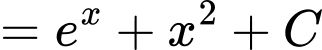 .
.
Khi đó: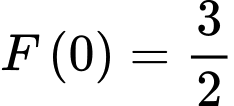
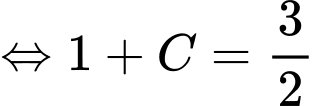
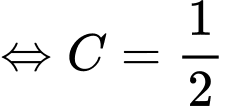 .
.
Vậy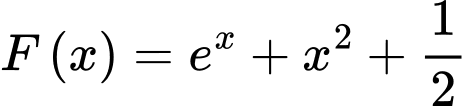 .
.
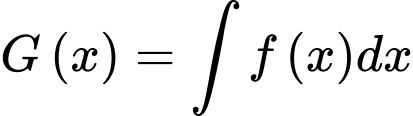
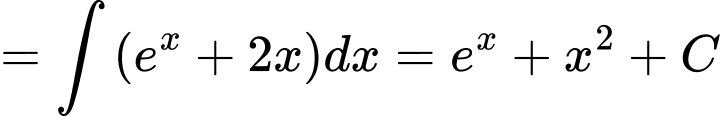
b) Đúng.
Thể tích khối tròn xoay sinh ra khi quay quanh trục
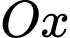 hình phẳng giới hạn bởi đồ thị hàm số
hình phẳng giới hạn bởi đồ thị hàm số 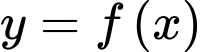 , trục hoành và hai đường thẳng
, trục hoành và hai đường thẳng 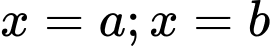 là
là 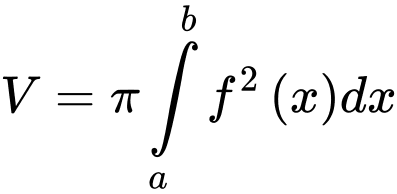
c) Đúng.
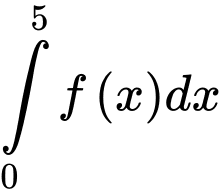
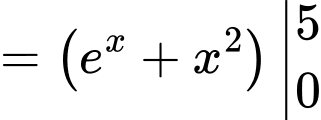
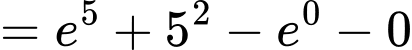
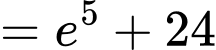 .
.
d) Đúng.
Vì
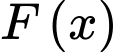 là một nguyên hàm của hàm số
là một nguyên hàm của hàm số 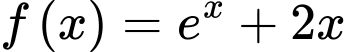 nên
nên
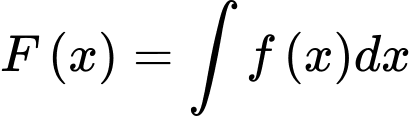
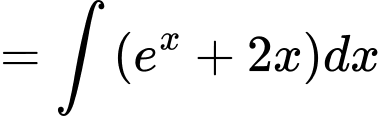
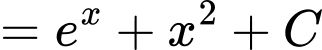 .
.
Khi đó:
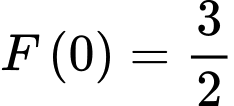
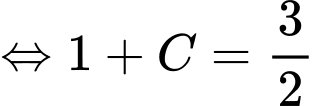
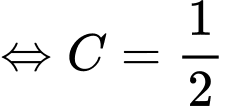 .
.
Vậy
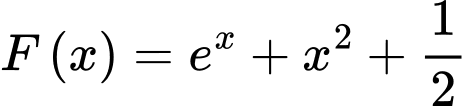 .
.
Câu 18 [163175]: Cho hàm số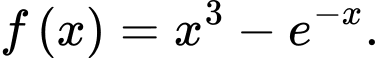 Gọi
Gọi  là hình phẳng giới hạn bởi đồ thị hàm số
là hình phẳng giới hạn bởi đồ thị hàm số 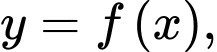 trục hoành và hai đường thẳng
trục hoành và hai đường thẳng 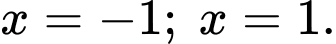 Xét tính đúng sai của các phát biểu sau:
Xét tính đúng sai của các phát biểu sau:
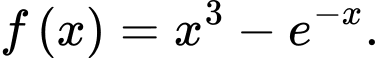 Gọi
Gọi  là hình phẳng giới hạn bởi đồ thị hàm số
là hình phẳng giới hạn bởi đồ thị hàm số 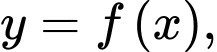 trục hoành và hai đường thẳng
trục hoành và hai đường thẳng 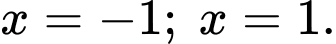 Xét tính đúng sai của các phát biểu sau:
Xét tính đúng sai của các phát biểu sau: A,
a) Hàm số 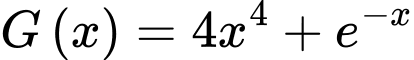 là một nguyên hàm của hàm số
là một nguyên hàm của hàm số 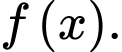
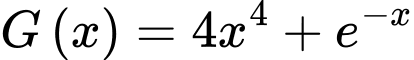 là một nguyên hàm của hàm số
là một nguyên hàm của hàm số 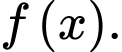
B,
b) Diện tích hình phẳng  bằng
bằng 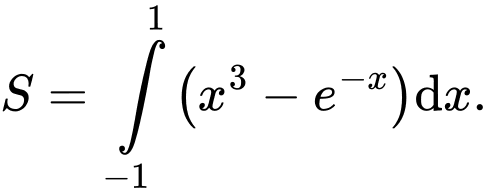
 bằng
bằng 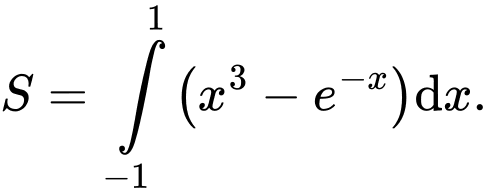
C,
c) Thể tích khối tròn xoay sinh ra khi quay  quanh trục
quanh trục 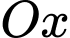 (làm tròn đến hàng đơn vị) là
(làm tròn đến hàng đơn vị) là 
 quanh trục
quanh trục 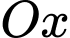 (làm tròn đến hàng đơn vị) là
(làm tròn đến hàng đơn vị) là 
D,
d) Cho 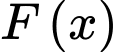 là một nguyên hàm của hàm số
là một nguyên hàm của hàm số 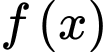 thỏa mãn
thỏa mãn  . Khi đó
. Khi đó 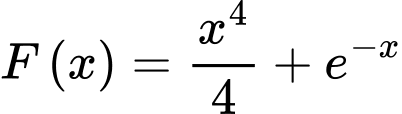 .
.
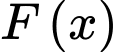 là một nguyên hàm của hàm số
là một nguyên hàm của hàm số 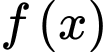 thỏa mãn
thỏa mãn  . Khi đó
. Khi đó 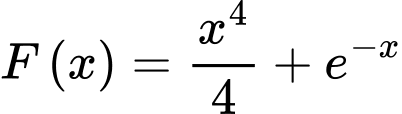 .
.
a) Sai 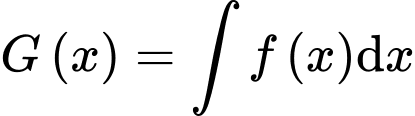
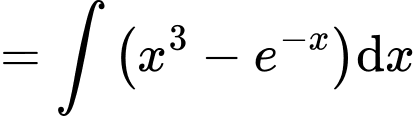
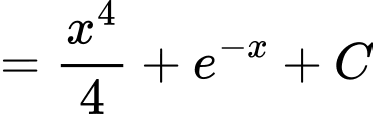 .
. 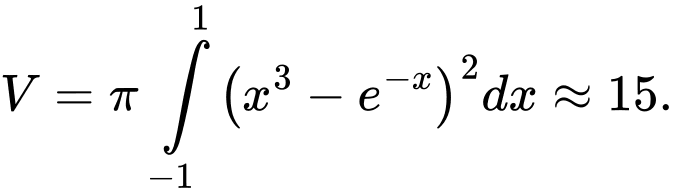 .
. 
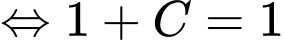
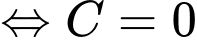 .
.
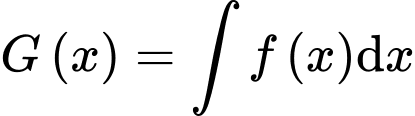
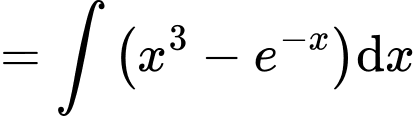
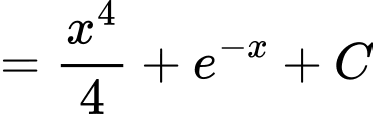 .
. b) Sai.
Diện tích hình phẳng  bằng
bằng 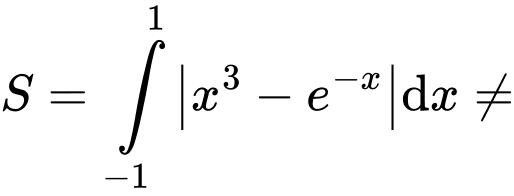
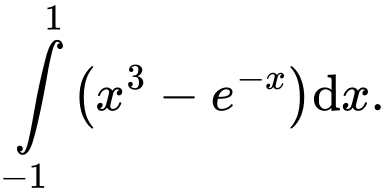
 bằng
bằng 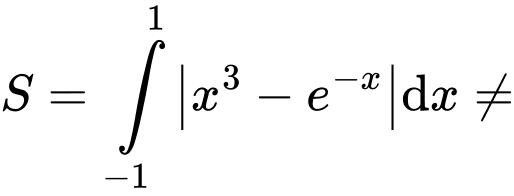
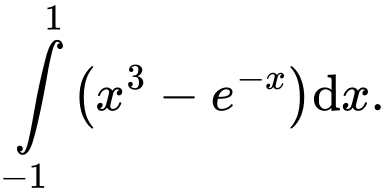
c) Đúng
Thể tích khối tròn xoay là
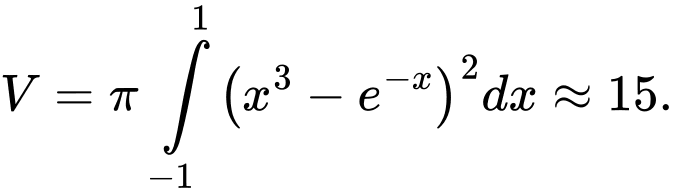 .
. d) Đúng
Vì 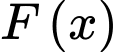 là một nguyên hàm của hàm số
là một nguyên hàm của hàm số 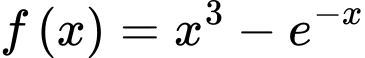 nên
nên
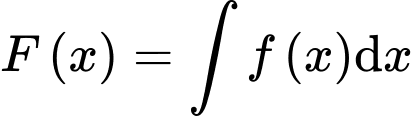
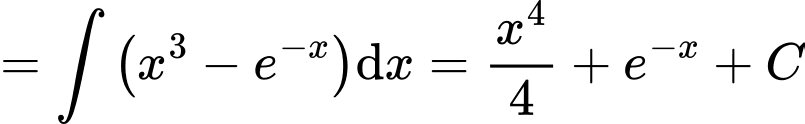 .
.
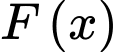 là một nguyên hàm của hàm số
là một nguyên hàm của hàm số 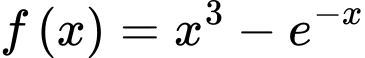 nên
nên
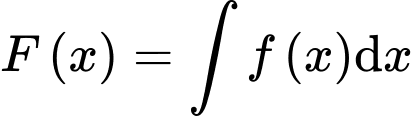
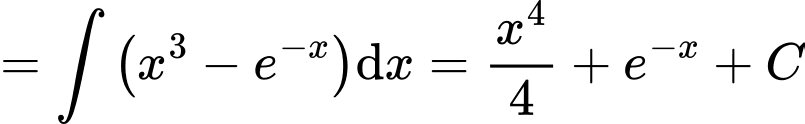 .
. Khi đó:

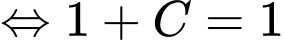
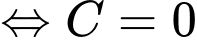 .
. Vậy 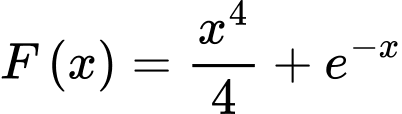 .
.
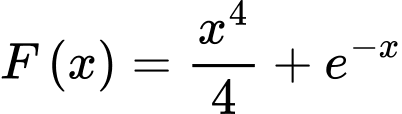 .
.
Câu 19 [161625]: Cho 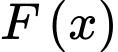 là nguyên hàm của hàm số
là nguyên hàm của hàm số 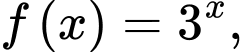 thỏa mãn
thỏa mãn 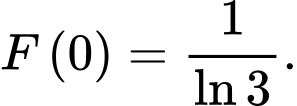 Xét tính đúng sai của các phát biểu sau:
Xét tính đúng sai của các phát biểu sau:
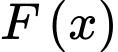 là nguyên hàm của hàm số
là nguyên hàm của hàm số 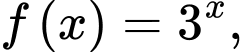 thỏa mãn
thỏa mãn 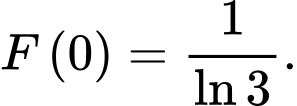 Xét tính đúng sai của các phát biểu sau:
Xét tính đúng sai của các phát biểu sau: A, a) 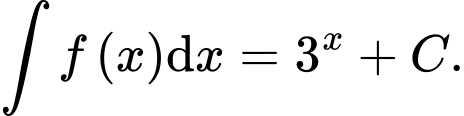
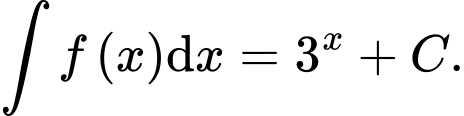
B, b) 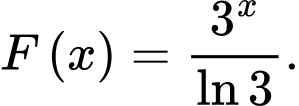
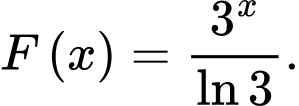
C, c) Giá trị biểu thức 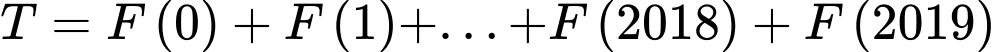 bằng
bằng 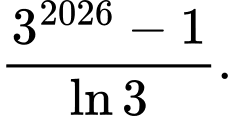
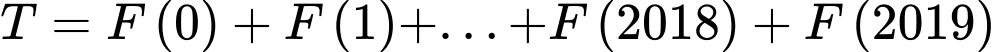 bằng
bằng 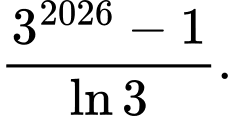
D, d) Cho hình phẳng  giới hạn bởi đồ thị các hàm số
giới hạn bởi đồ thị các hàm số 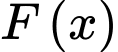 , trục tung, trục hoành và đường thẳng
, trục tung, trục hoành và đường thẳng 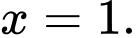 Thể tích của khối tròn xoay tạo thành khi quay
Thể tích của khối tròn xoay tạo thành khi quay  quanh trục
quanh trục 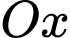 bằng
bằng 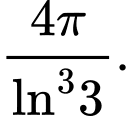
 giới hạn bởi đồ thị các hàm số
giới hạn bởi đồ thị các hàm số 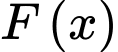 , trục tung, trục hoành và đường thẳng
, trục tung, trục hoành và đường thẳng 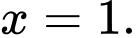 Thể tích của khối tròn xoay tạo thành khi quay
Thể tích của khối tròn xoay tạo thành khi quay  quanh trục
quanh trục 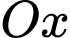 bằng
bằng 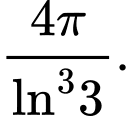
a) Sai 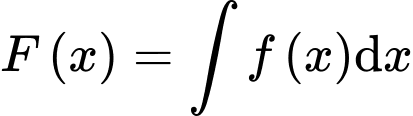
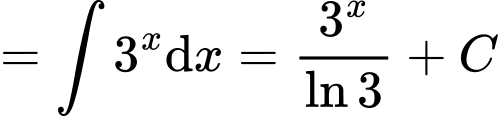 .
. 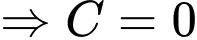
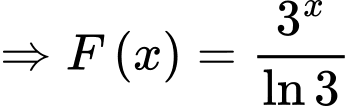 .
. 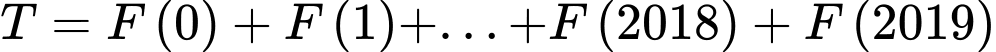
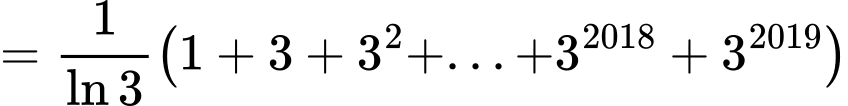
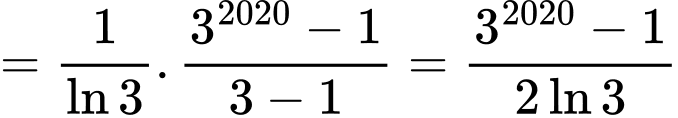
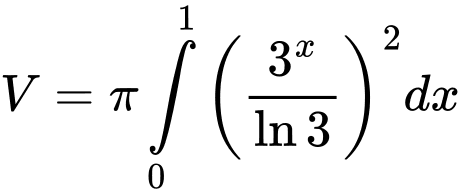
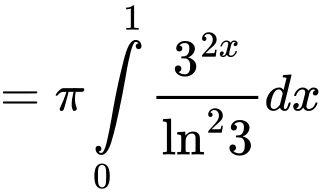
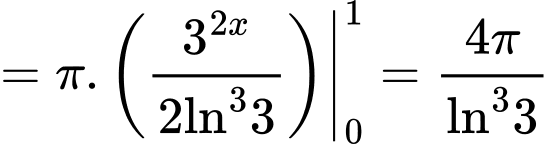 .
.
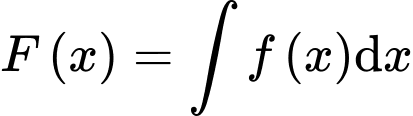
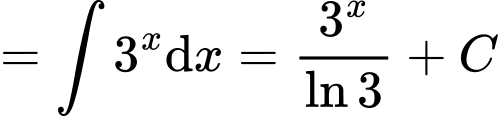 .
. b) Đúng
Ta có: 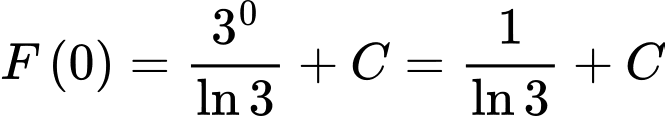 mà
mà 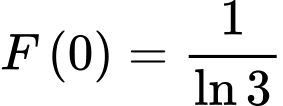
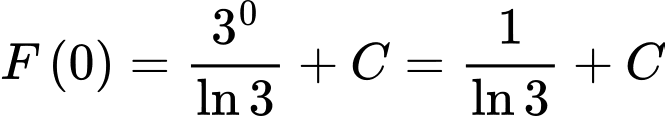 mà
mà 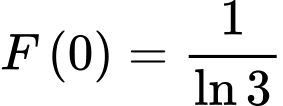
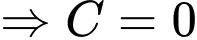
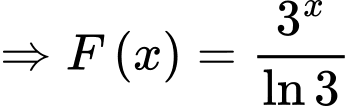 .
. c) Sai
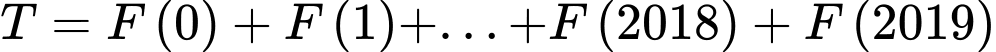
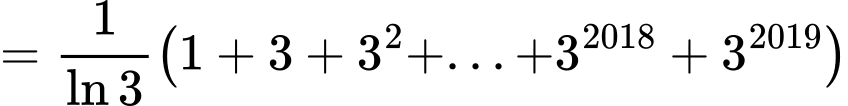
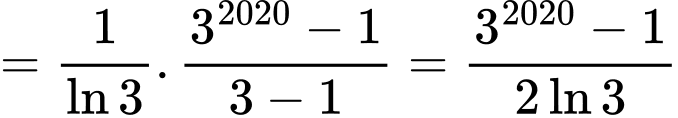
d) Đúng
Ta có thể tích của khối tròn xoay tạo thành khi quay  quanh trục
quanh trục 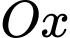 bằng :
bằng :
 quanh trục
quanh trục 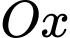 bằng :
bằng : 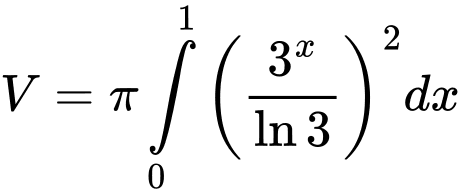
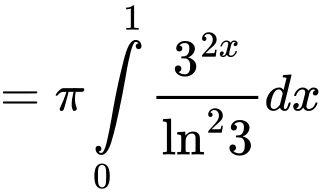
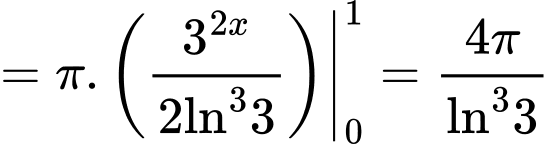 .
.
Câu 20 [161569]: Cho hình phẳng 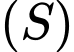 giới hạn bởi đồ thị hàm số
giới hạn bởi đồ thị hàm số 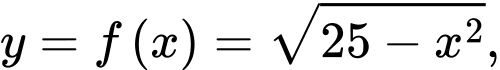 trục hoành và hai đường thẳng
trục hoành và hai đường thẳng 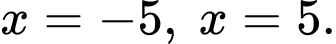 Các mệnh đề sau đúng hay sai?
Các mệnh đề sau đúng hay sai?
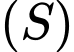 giới hạn bởi đồ thị hàm số
giới hạn bởi đồ thị hàm số 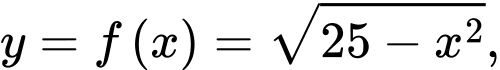 trục hoành và hai đường thẳng
trục hoành và hai đường thẳng 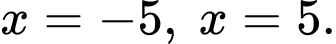 Các mệnh đề sau đúng hay sai?
Các mệnh đề sau đúng hay sai? A, a) Đạo hàm của hàm số 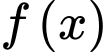 bằng
bằng 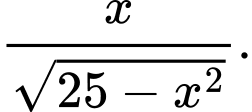
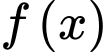 bằng
bằng 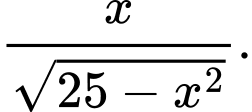
B, b) Diện tích hình phẳng 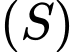 bằng
bằng 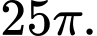
 bằng
bằng 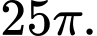
C, c) Thể tích của khối tròn xoay khi quay 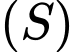 quanh
quanh 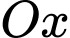 là
là 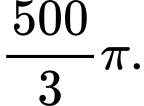
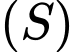 quanh
quanh 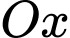 là
là 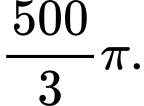
D, d) Diện tích hình phẳng giới hạn bởi đồ thị hàm số 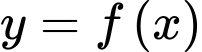 và đường thẳng
và đường thẳng 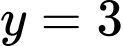 bằng
bằng 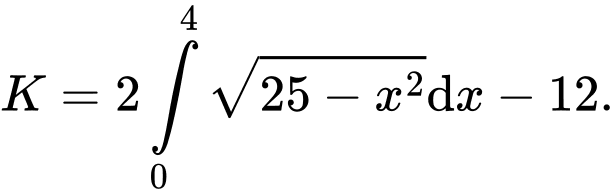
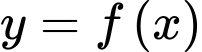 và đường thẳng
và đường thẳng 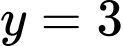 bằng
bằng 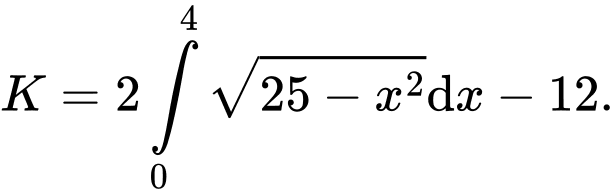
a) Sai.
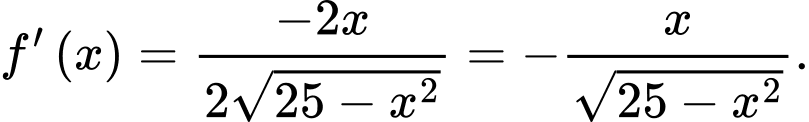
b) Sai.
Diện tích hình phẳng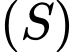 là
là 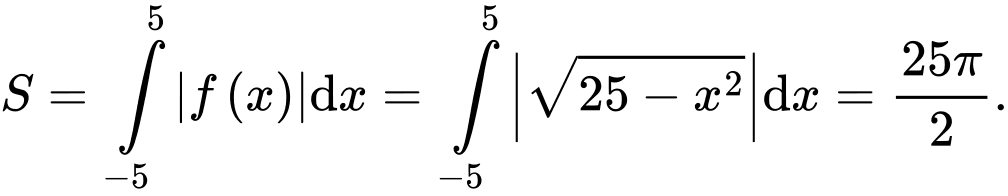
c) Đúng.
Tập xác định của hàm số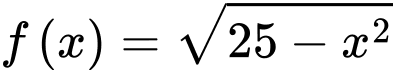 là
là 
Nên ta sẽ được khối tròn xoay tạo bởi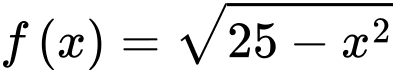 quay quanh trục hoành và giới hạn bởi hai đường thẳng
quay quanh trục hoành và giới hạn bởi hai đường thẳng 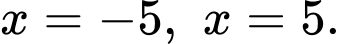
Suy ra thể tích khối tròn xoay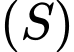 là
là 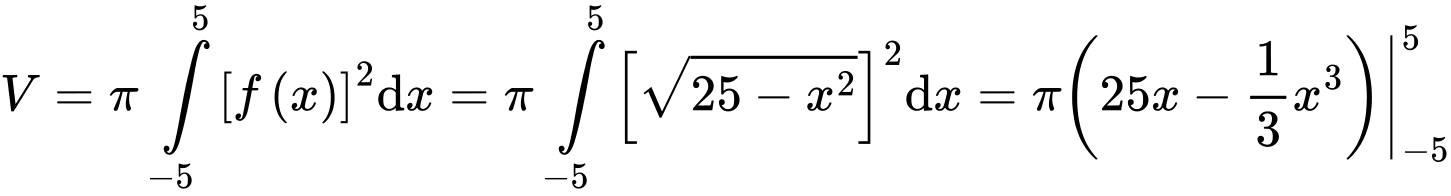
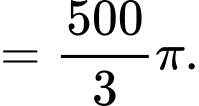
d) Sai.
Hoành độ giao điểm của đồ thị hàm số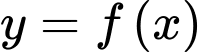 và đường thẳng
và đường thẳng 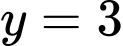 là nghiệm của phương trình:
là nghiệm của phương trình: 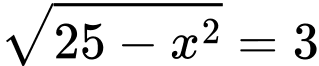

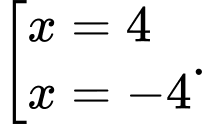
Suy ra diện tích hình phẳng giới hạn bởi đồ thị hàm số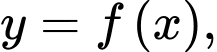 đường thẳng
đường thẳng 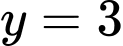 và hai đường thẳng
và hai đường thẳng 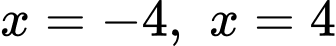 được tính theo công thức là
được tính theo công thức là
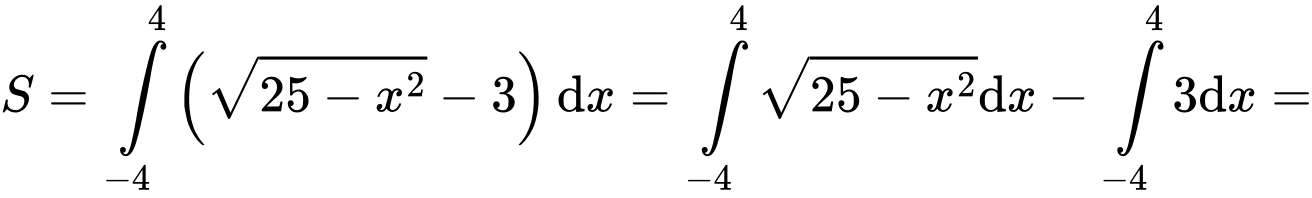
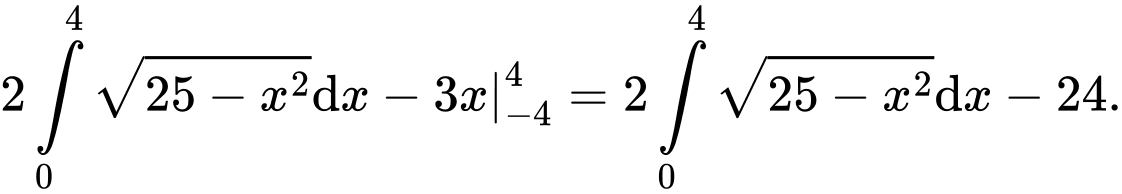
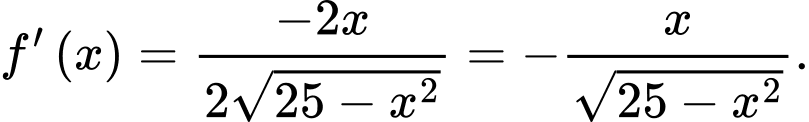
b) Sai.
Diện tích hình phẳng
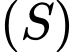 là
là 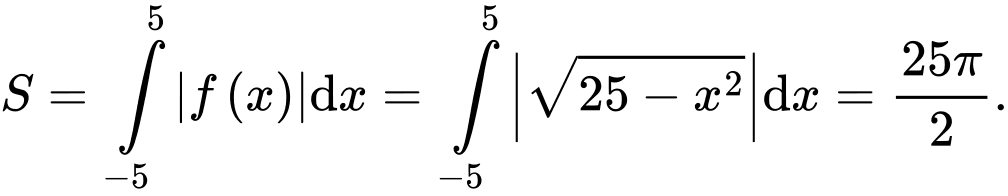
c) Đúng.
Tập xác định của hàm số
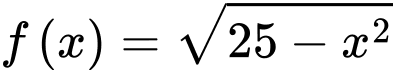 là
là 
Nên ta sẽ được khối tròn xoay tạo bởi
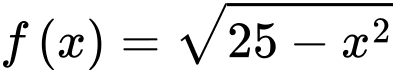 quay quanh trục hoành và giới hạn bởi hai đường thẳng
quay quanh trục hoành và giới hạn bởi hai đường thẳng 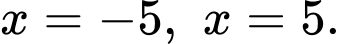
Suy ra thể tích khối tròn xoay
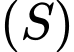 là
là 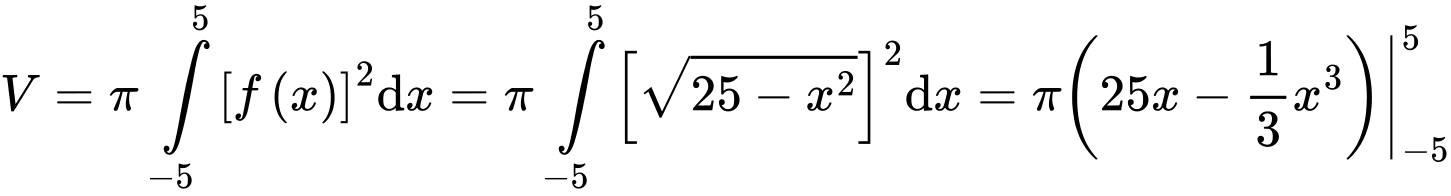
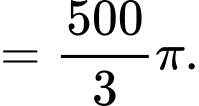
d) Sai.
Hoành độ giao điểm của đồ thị hàm số
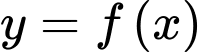 và đường thẳng
và đường thẳng 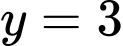 là nghiệm của phương trình:
là nghiệm của phương trình: 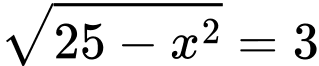

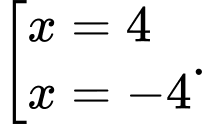
Suy ra diện tích hình phẳng giới hạn bởi đồ thị hàm số
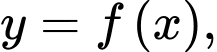 đường thẳng
đường thẳng 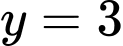 và hai đường thẳng
và hai đường thẳng 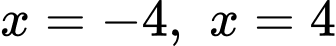 được tính theo công thức là
được tính theo công thức là
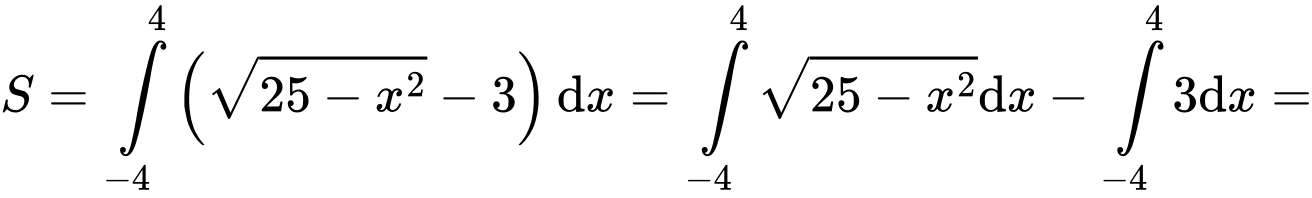
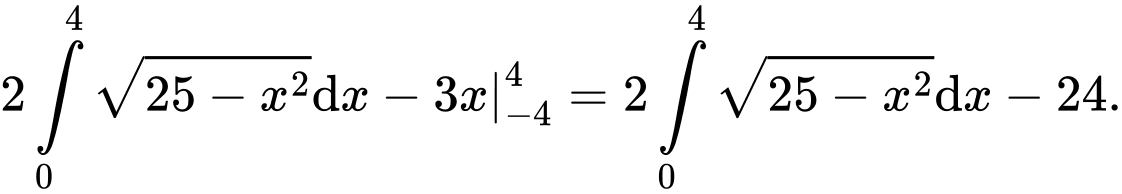
Câu 21 [161570]: Cho hàm số 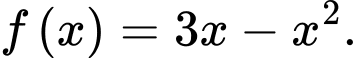 Gọi
Gọi  là hình phẳng giới hạn bởi đồ thị hàm số
là hình phẳng giới hạn bởi đồ thị hàm số 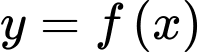 và trục hoành. Các mệnh đề sau đúng hay sai?
và trục hoành. Các mệnh đề sau đúng hay sai?
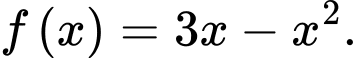 Gọi
Gọi  là hình phẳng giới hạn bởi đồ thị hàm số
là hình phẳng giới hạn bởi đồ thị hàm số 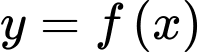 và trục hoành. Các mệnh đề sau đúng hay sai?
và trục hoành. Các mệnh đề sau đúng hay sai? A, a) Hàm số 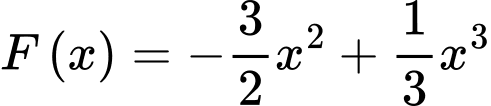 là một nguyên hàm của hàm số
là một nguyên hàm của hàm số 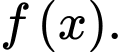
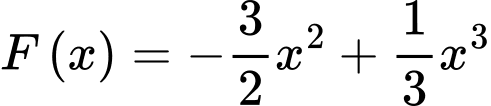 là một nguyên hàm của hàm số
là một nguyên hàm của hàm số 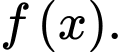
B, b) Diện tích hình phẳng  bằng
bằng 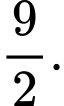
 bằng
bằng 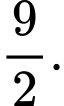
C, c) Diện tích hình phẳng giới hạn bởi đồ thị hàm số 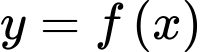 và đường thẳng
và đường thẳng 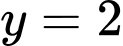 bằng
bằng 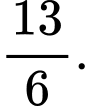
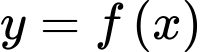 và đường thẳng
và đường thẳng 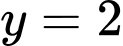 bằng
bằng 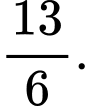
D, d) Thể tích khối tròn xoay được tạo thành khi quay hình phẳng  quanh trục hoành bằng
quanh trục hoành bằng 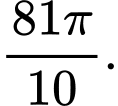
 quanh trục hoành bằng
quanh trục hoành bằng 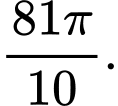
a) Sai. 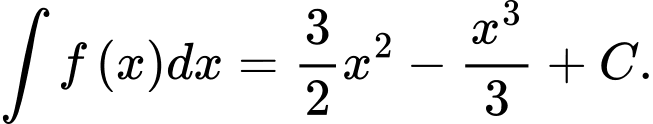
b) Đúng. Diện tích hình phẳng bằng
bằng 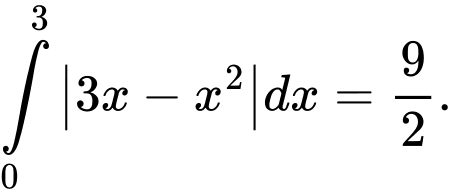
c) Sai. Ta có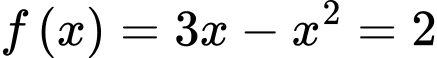

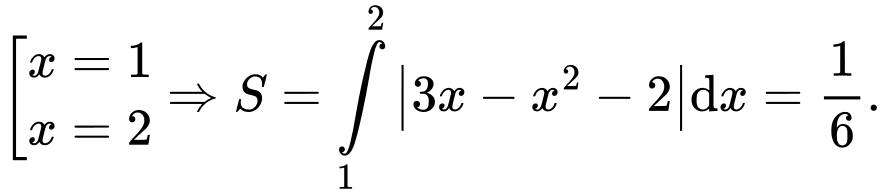
d) Đúng. Ta có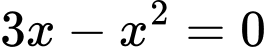

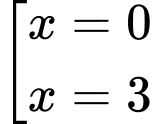
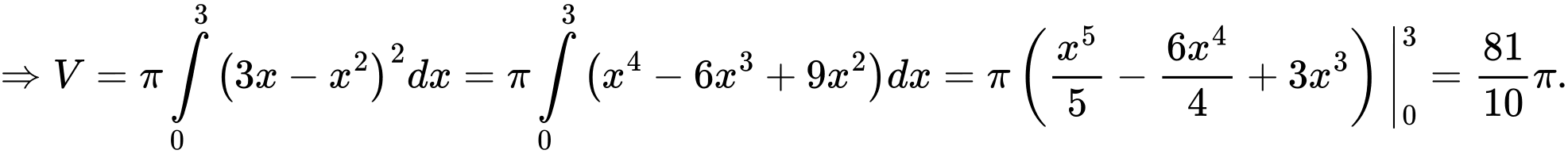
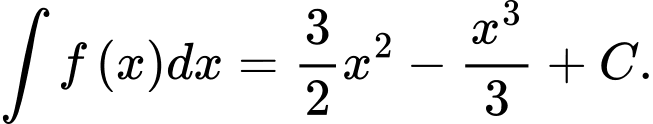
b) Đúng. Diện tích hình phẳng
 bằng
bằng 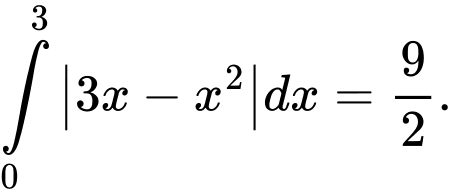
c) Sai. Ta có
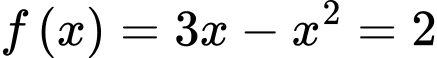

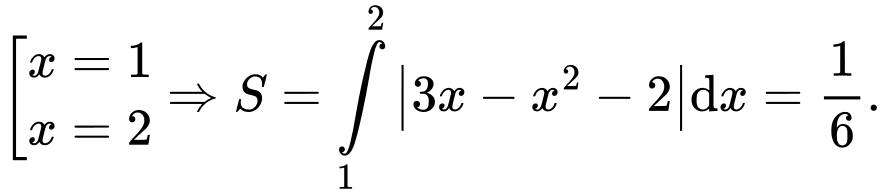
d) Đúng. Ta có
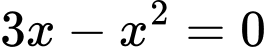

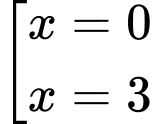
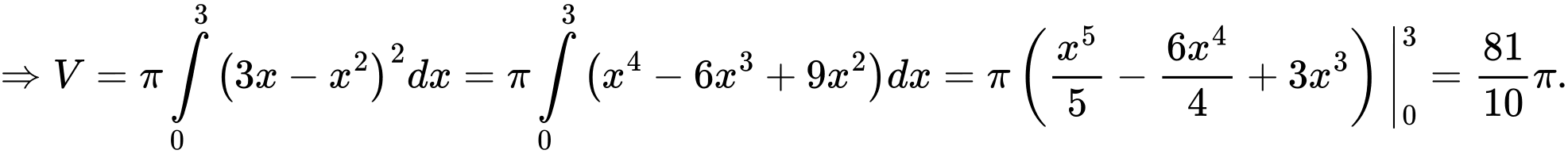
Câu 22 [161573]: Gọi  là hình phẳng giới hạn bởi các đường
là hình phẳng giới hạn bởi các đường 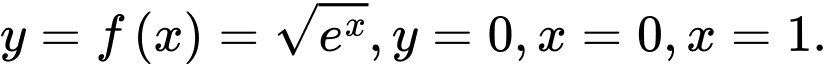 Các mệnh đề sau đúng hay sai?
Các mệnh đề sau đúng hay sai?
 là hình phẳng giới hạn bởi các đường
là hình phẳng giới hạn bởi các đường 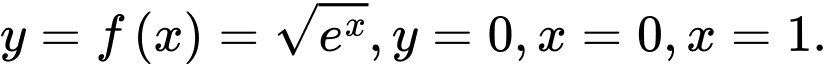 Các mệnh đề sau đúng hay sai?
Các mệnh đề sau đúng hay sai? A, a) 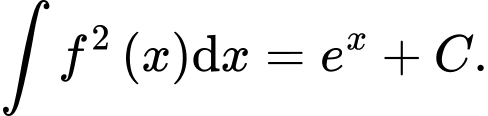
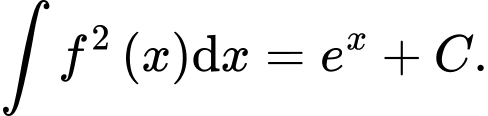
B, b) 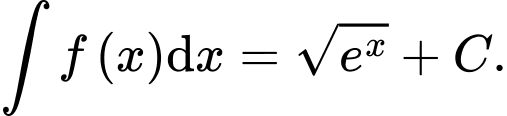
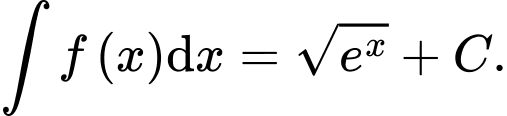
C, c) Diện tích hình phẳng  bằng
bằng 
 bằng
bằng 
D, d) Thể tích  của khối tròn xoay được sinh ra khi quay hình phẳng
của khối tròn xoay được sinh ra khi quay hình phẳng quanh trục
quanh trục 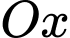 (làm tròn đến hàng phần trăm) bằng
(làm tròn đến hàng phần trăm) bằng 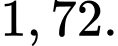
 của khối tròn xoay được sinh ra khi quay hình phẳng
của khối tròn xoay được sinh ra khi quay hình phẳng quanh trục
quanh trục 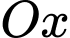 (làm tròn đến hàng phần trăm) bằng
(làm tròn đến hàng phần trăm) bằng 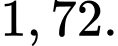
a) Đúng. 
b) Sai.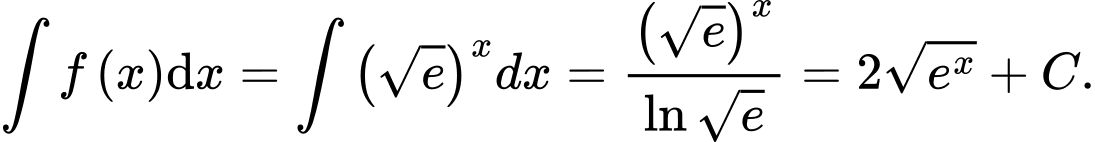
c) Sai.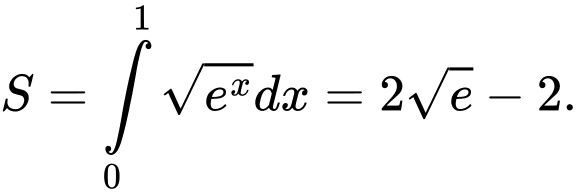
d) Sai.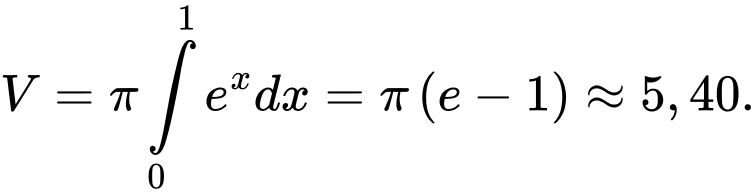

b) Sai.
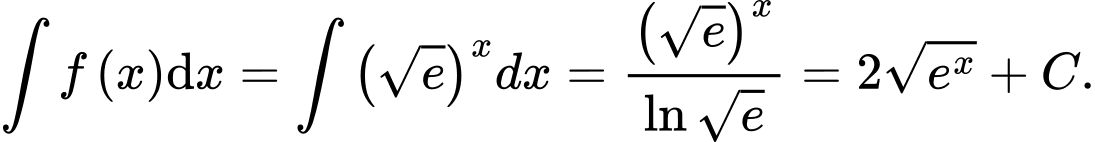
c) Sai.
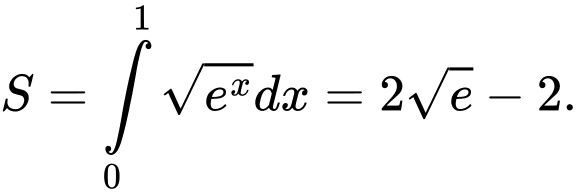
d) Sai.
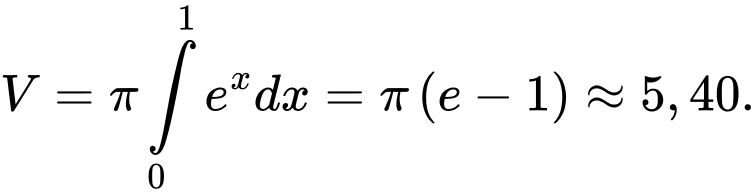
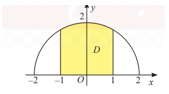
Câu 23 [372589]: Trên mặt phẳng toạ độ 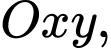 vẽ nửa đường tròn tâm
vẽ nửa đường tròn tâm  bán kính
bán kính 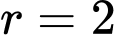 nằm phía trên trục
nằm phía trên trục 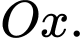 Gọi
Gọi 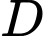 là hình phẳng giới hạn bởi nửa đường tròn, trục
là hình phẳng giới hạn bởi nửa đường tròn, trục 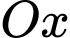 và hai đường thẳng
và hai đường thẳng 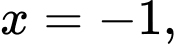
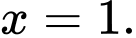 Tính thể tích khối tròn xoay tạo thành khi quay
Tính thể tích khối tròn xoay tạo thành khi quay 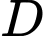 quanh trục
quanh trục 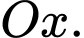
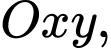 vẽ nửa đường tròn tâm
vẽ nửa đường tròn tâm  bán kính
bán kính 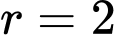 nằm phía trên trục
nằm phía trên trục 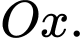 Gọi
Gọi 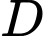 là hình phẳng giới hạn bởi nửa đường tròn, trục
là hình phẳng giới hạn bởi nửa đường tròn, trục 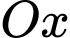 và hai đường thẳng
và hai đường thẳng 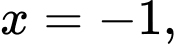
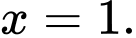 Tính thể tích khối tròn xoay tạo thành khi quay
Tính thể tích khối tròn xoay tạo thành khi quay 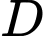 quanh trục
quanh trục 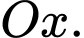

Phương trình nửa đường tròn trong hình vẽ là: 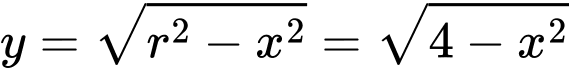
Thể tích khối tròn xoay cần tìm là: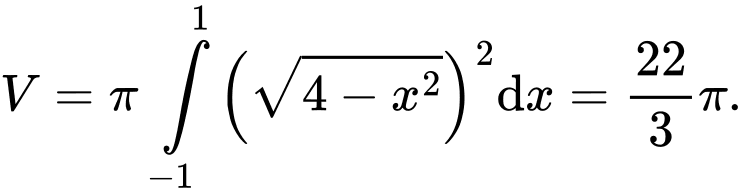
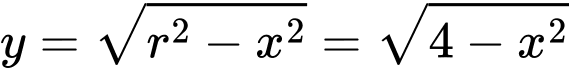
Thể tích khối tròn xoay cần tìm là:
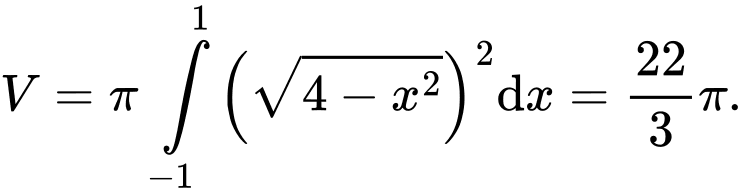
Câu 24 [42008]: Tính thể tích  của phần vật thể giới hạn bởi hai mặt phẳng
của phần vật thể giới hạn bởi hai mặt phẳng 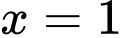 và
và  , biết rằng khi cắt vật thể bởi mặt phẳng tùy ý vuông góc với trục
, biết rằng khi cắt vật thể bởi mặt phẳng tùy ý vuông góc với trục 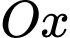 tại điểm có hoành độ
tại điểm có hoành độ 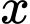 (
(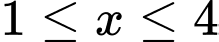 ) thì được thiết diện là một hình lục giác đều có độ dài cạnh là
) thì được thiết diện là một hình lục giác đều có độ dài cạnh là 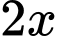 .
.
 của phần vật thể giới hạn bởi hai mặt phẳng
của phần vật thể giới hạn bởi hai mặt phẳng 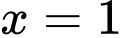 và
và  , biết rằng khi cắt vật thể bởi mặt phẳng tùy ý vuông góc với trục
, biết rằng khi cắt vật thể bởi mặt phẳng tùy ý vuông góc với trục 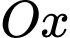 tại điểm có hoành độ
tại điểm có hoành độ 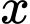 (
(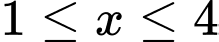 ) thì được thiết diện là một hình lục giác đều có độ dài cạnh là
) thì được thiết diện là một hình lục giác đều có độ dài cạnh là 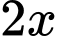 .
. A, 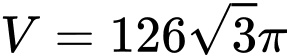 .
.
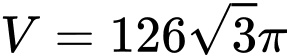 .
.B, 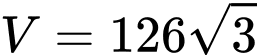 .
.
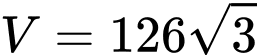 .
.C, 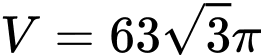 .
.
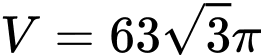 .
.D, 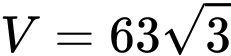 .
.
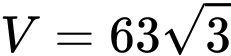 .
. Đáp án: B
Đáp án: B
Câu 25 [371990]: Khi cắt một vật thể hình chiếc nêm bởi mặt phẳng vuông góc với trục 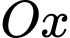 tại điểm có hoành độ
tại điểm có hoành độ 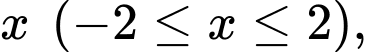 mặt cắt là tam giác vuông có một góc
mặt cắt là tam giác vuông có một góc 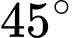 và độ dài một cạnh góc vuông là
và độ dài một cạnh góc vuông là 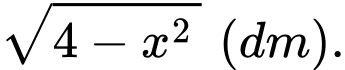 Tính thể tích của vật thể theo đơn vị
Tính thể tích của vật thể theo đơn vị 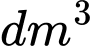 . Làm tròn kết quả đến hàng phần chục.
. Làm tròn kết quả đến hàng phần chục. 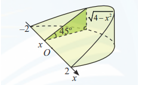
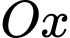 tại điểm có hoành độ
tại điểm có hoành độ 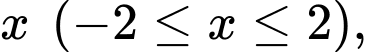 mặt cắt là tam giác vuông có một góc
mặt cắt là tam giác vuông có một góc 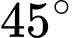 và độ dài một cạnh góc vuông là
và độ dài một cạnh góc vuông là 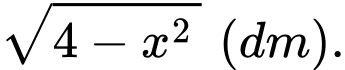 Tính thể tích của vật thể theo đơn vị
Tính thể tích của vật thể theo đơn vị 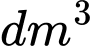 . Làm tròn kết quả đến hàng phần chục.
. Làm tròn kết quả đến hàng phần chục. 
Vì mặt cắt là tam giác vuông có một góc 45° nên mặt cắt là tam giác vuông cân.
Do đó diện tích của mặt cắt là: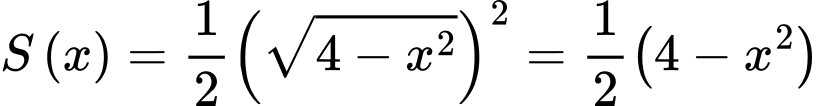
Thể tích vật thể là: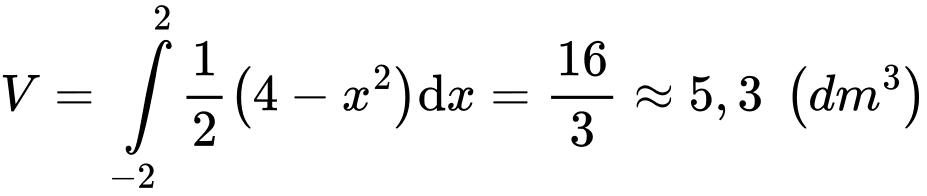
Do đó diện tích của mặt cắt là:
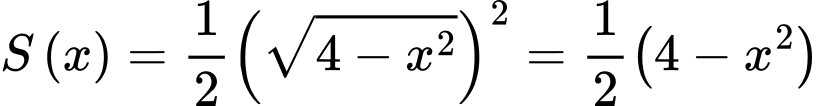
Thể tích vật thể là:
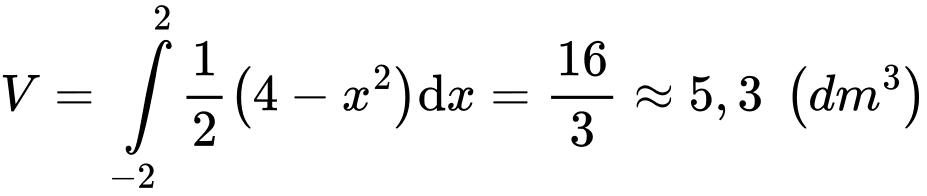
Câu 26 [372588]: Một chiếc lều mái vòm có hình dạng như hình. Nếu cắt lều bằng mặt phẳng song song với mặt đáy và cách mặt đáy một khoảng 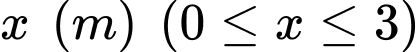 thì được hình vuông có cạnh
thì được hình vuông có cạnh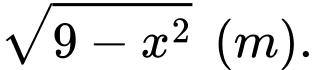 Tính thể tích của lều.
Tính thể tích của lều. 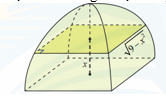
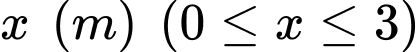 thì được hình vuông có cạnh
thì được hình vuông có cạnh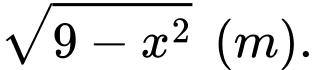 Tính thể tích của lều.
Tính thể tích của lều. 
Vì mặt cắt là hình vuông nên diện tích của mặt cắt là:
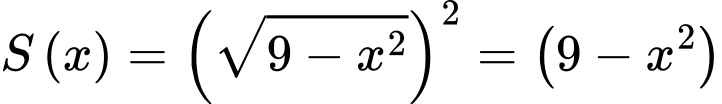
Thể tích vật thể là: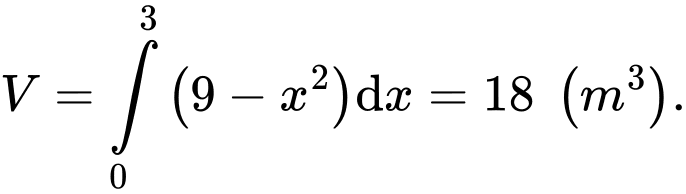
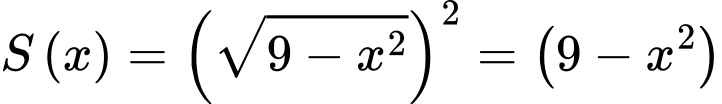
Thể tích vật thể là:
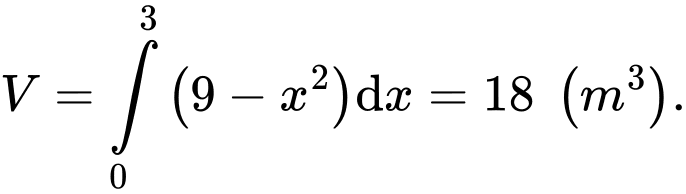
Câu 27 [372587]: Nếu cắt chậu nước có hình dạng như hình bằng mặt phẳng song song và cách mặt đáy 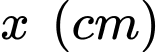
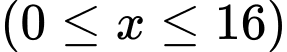 thì mặt cắt là hình tròn có bán kính
thì mặt cắt là hình tròn có bán kính 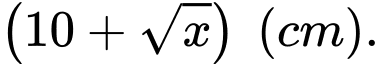 Tính dung tích của chậu.
Tính dung tích của chậu. 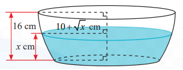
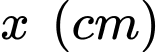
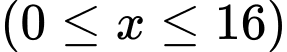 thì mặt cắt là hình tròn có bán kính
thì mặt cắt là hình tròn có bán kính 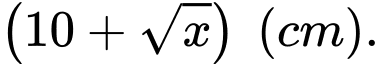 Tính dung tích của chậu.
Tính dung tích của chậu. 
Diện tích mặt cắt là 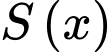
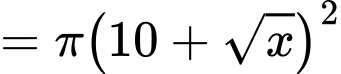
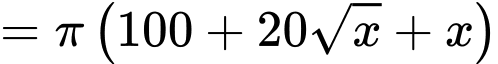
Suy ra dung tích của chậu là
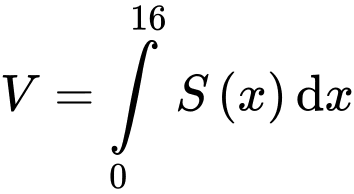
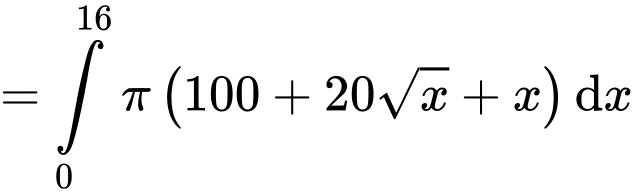
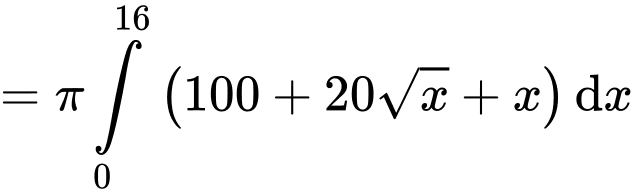
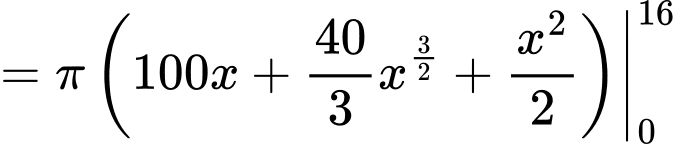
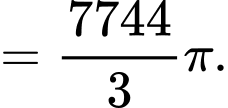
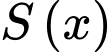
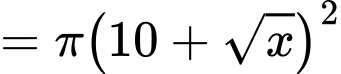
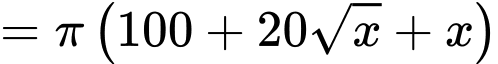
Suy ra dung tích của chậu là
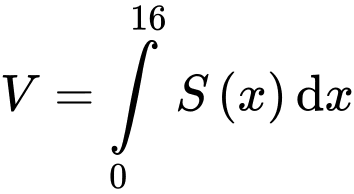
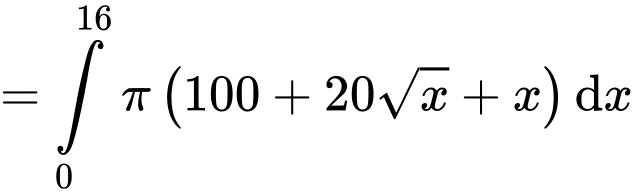
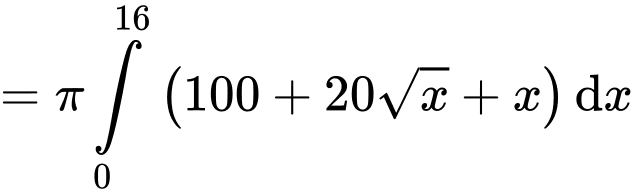
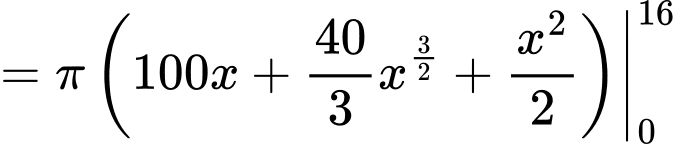
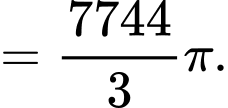
Câu 28 [376851]: Xét chiếc chén trong bộ ấm chén uống trà, bạn Dương ước lượng được rằng chiếc chén được tạo thành khi cho hình phẳng giới hạn bởi đồ thị hàm số 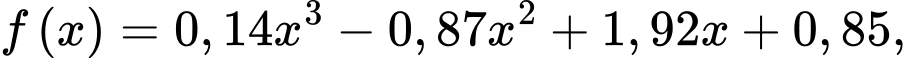 trục hoành và hai đường thẳng
trục hoành và hai đường thẳng 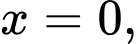
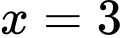 quay quanh trục
quay quanh trục 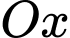 (đơn vị trên mỗi trục toạ độ là centimét). Tính thể tích của chiếc chén (làm tròn kết quả đến hàng đơn vị của centimét khối).
(đơn vị trên mỗi trục toạ độ là centimét). Tính thể tích của chiếc chén (làm tròn kết quả đến hàng đơn vị của centimét khối).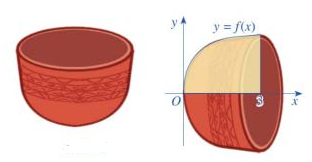
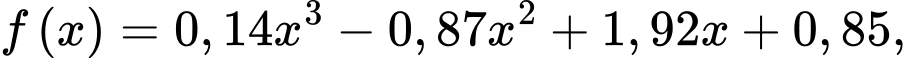 trục hoành và hai đường thẳng
trục hoành và hai đường thẳng 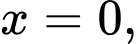
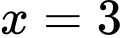 quay quanh trục
quay quanh trục 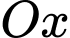 (đơn vị trên mỗi trục toạ độ là centimét). Tính thể tích của chiếc chén (làm tròn kết quả đến hàng đơn vị của centimét khối).
(đơn vị trên mỗi trục toạ độ là centimét). Tính thể tích của chiếc chén (làm tròn kết quả đến hàng đơn vị của centimét khối).
Ta có thể tích của chiếc chén là: 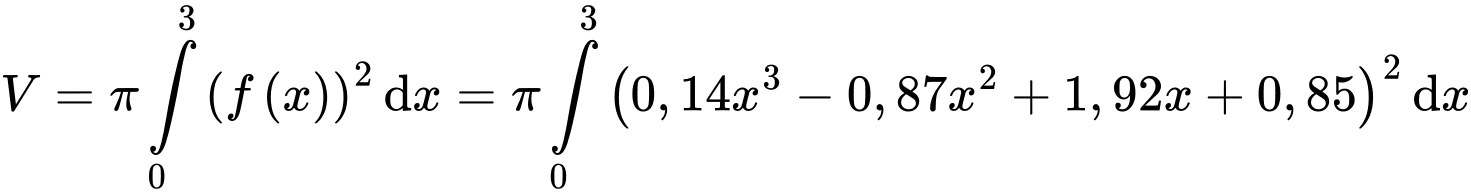
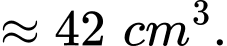
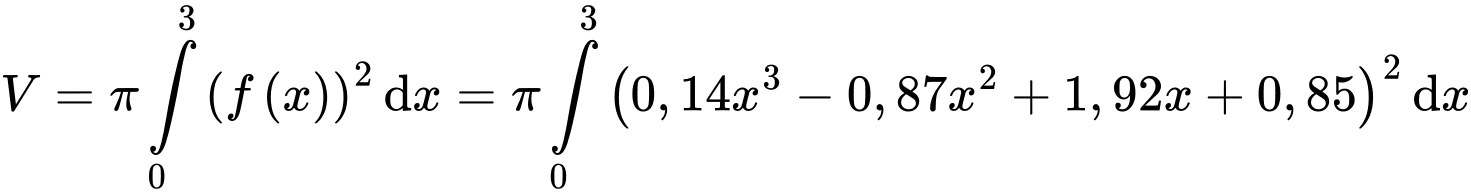
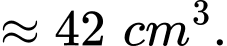
Vậy thể tích của chiếc chén là 
