Đáp án Bài tập tự luyện
Câu 1 [360298]: Người ta dự định lắp kính cho cửa của một mái vòm có dạng hình parabol. Hãy tính diện tích mặt kính cần lắp vào, biết rằng vòm cửa cao  và rộng
và rộng 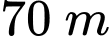 (Hình 33).
(Hình 33).
 và rộng
và rộng 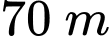 (Hình 33).
(Hình 33).
Giả sử parabol có dạng: 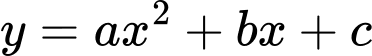
Theo giả thiết,
+) Vòm cửa cao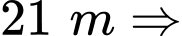 Parabol đi qua điểm
Parabol đi qua điểm 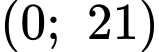
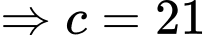
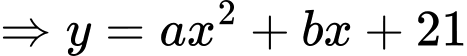
+) Vòm cửa rộng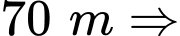 Parabol đi qua hai điểm
Parabol đi qua hai điểm 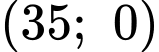 và
và 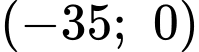
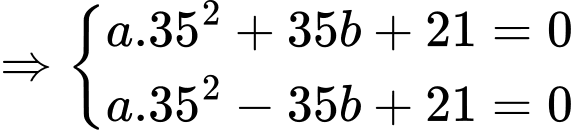
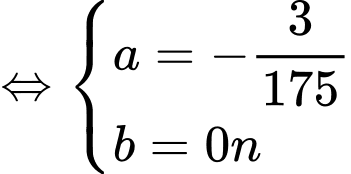
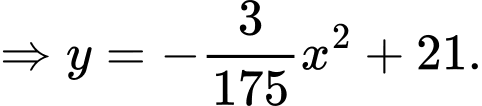
Diện tích cần lắp kính là diện tích giới hạn bởi parabol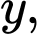 trục
trục 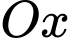 (mặt đất) và hai đường thẳng
(mặt đất) và hai đường thẳng 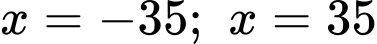
Vậy diện tích cần lắp kính bằng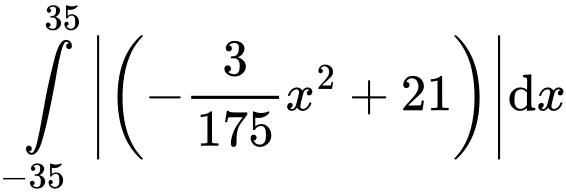
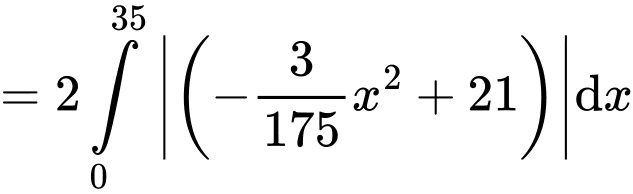
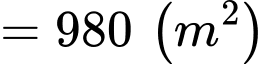
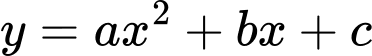
Theo giả thiết,
+) Vòm cửa cao
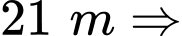 Parabol đi qua điểm
Parabol đi qua điểm 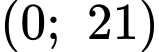
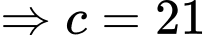
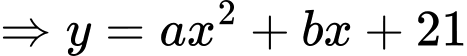
+) Vòm cửa rộng
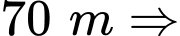 Parabol đi qua hai điểm
Parabol đi qua hai điểm 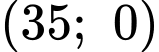 và
và 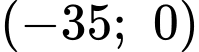
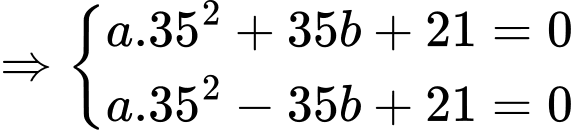
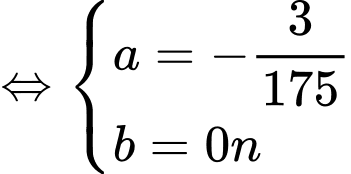
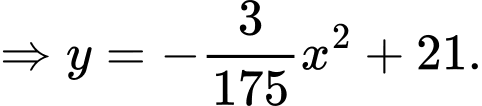
Diện tích cần lắp kính là diện tích giới hạn bởi parabol
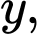 trục
trục 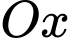 (mặt đất) và hai đường thẳng
(mặt đất) và hai đường thẳng 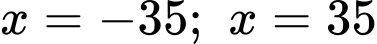
Vậy diện tích cần lắp kính bằng
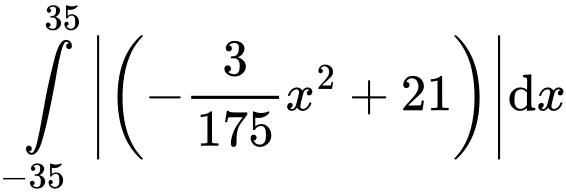
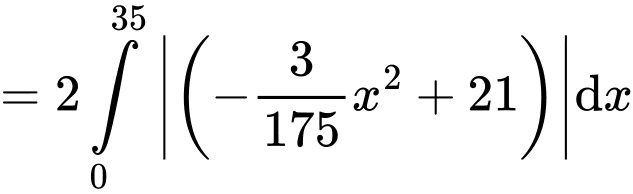
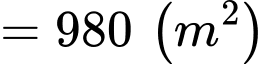
Câu 2 [151396]: Bạn An cần mua một chiếc gương có đường viền là đường Parabol bậc 2 (xem hình vẽ).
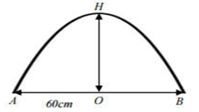
Biết rằng khoảng cách đoạn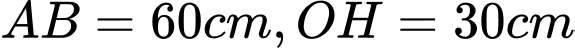 . Diện tích của chiếc gương bạn An mua là bao nhiêu
. Diện tích của chiếc gương bạn An mua là bao nhiêu 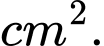

Biết rằng khoảng cách đoạn
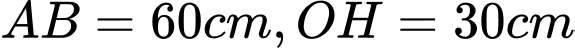 . Diện tích của chiếc gương bạn An mua là bao nhiêu
. Diện tích của chiếc gương bạn An mua là bao nhiêu 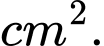
A, 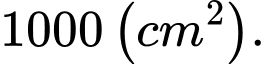
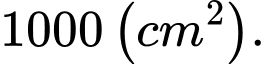
B, 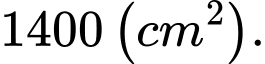
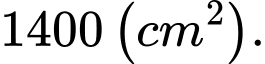
C, 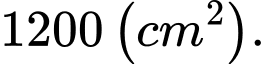
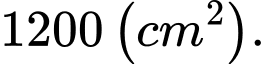
D, 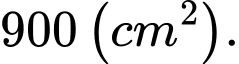
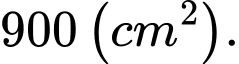
Cách 1:
Chọn hệ trục tọa độ như hình vẽ
Đường Parabol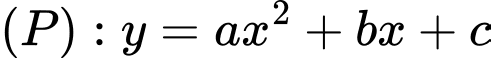 đi qua các điểm
đi qua các điểm 
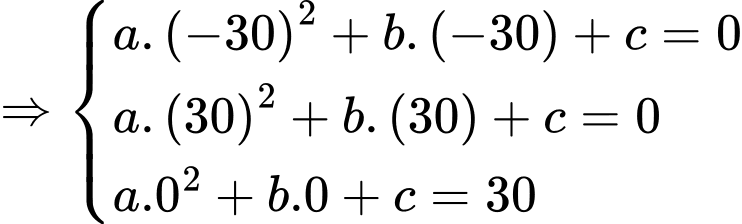
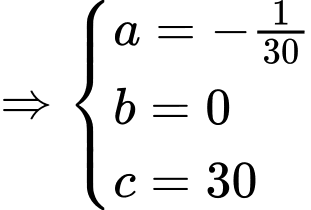
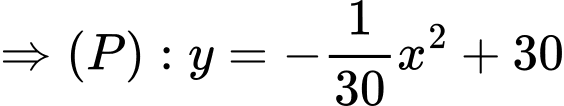
Diện tích chiếc gương là: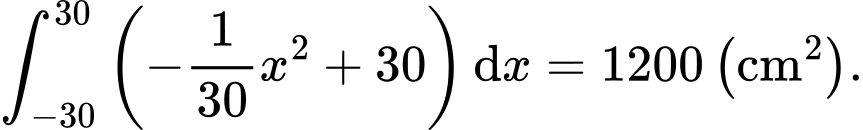
Cách 2:
Dùng công thức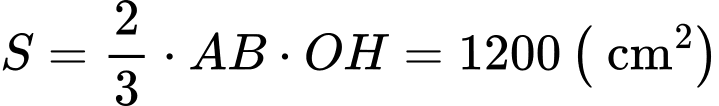 Đáp án: C
Đáp án: C
Chọn hệ trục tọa độ như hình vẽ

Đường Parabol
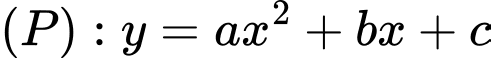 đi qua các điểm
đi qua các điểm 
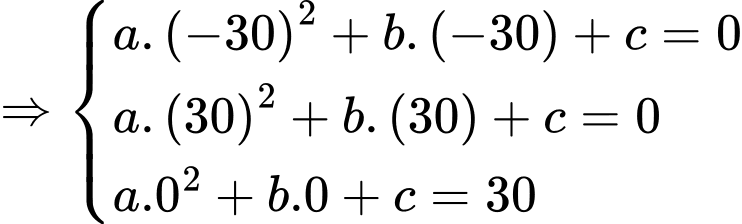
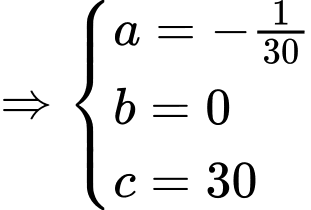
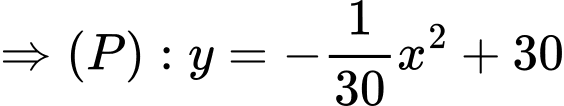
Diện tích chiếc gương là:
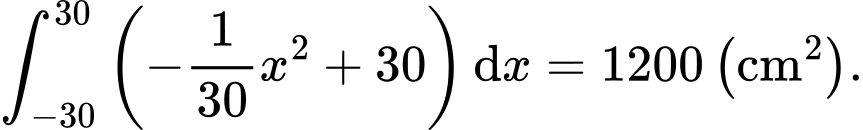
Cách 2:
Dùng công thức
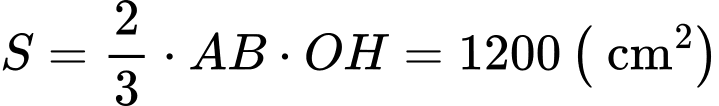 Đáp án: C
Đáp án: C
Câu 3 [153542]: [Đề ĐGNL ĐHSP HN 2024]: Bạn Bình vẽ một hình phẳng giới hạn bởi hai đường parabol sao cho các đỉnh và các giao điểm của hai parabol đó lần lượt là trung điểm các cạnh của hình chữ nhật với hai kích thước là 6 cm và 4,5 cm (như hình vẽ bên). Diện tích của hình phẳng được tô màu đậm bằng bao nhiêu 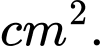
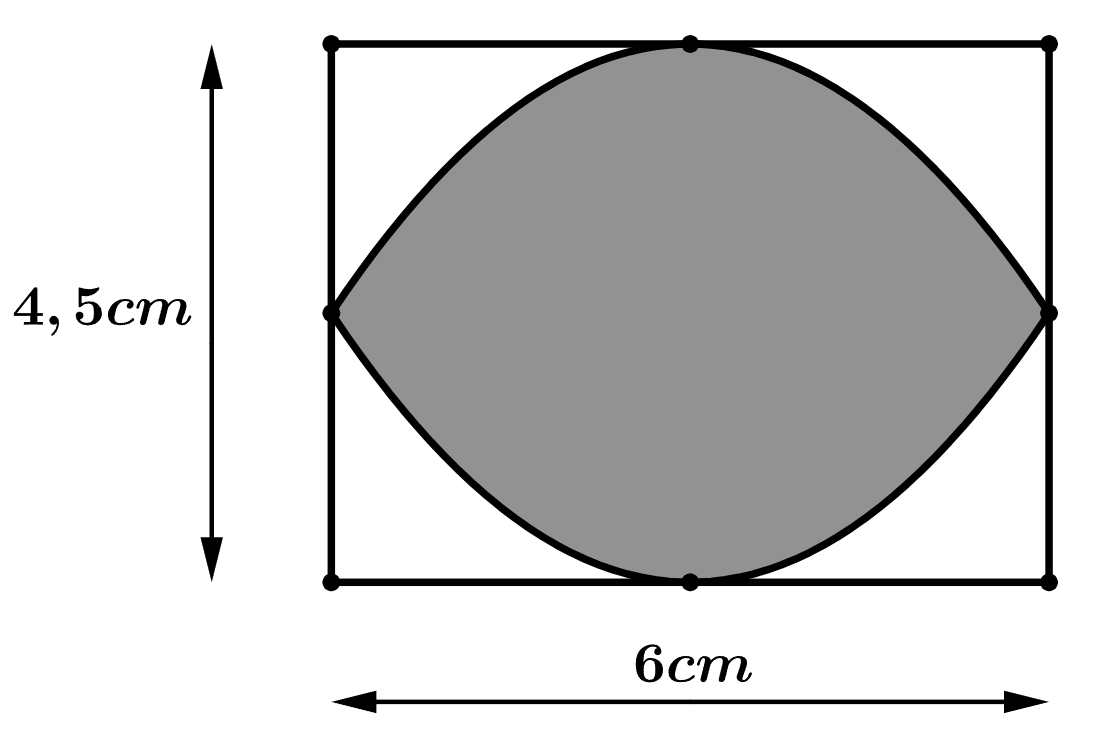
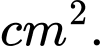

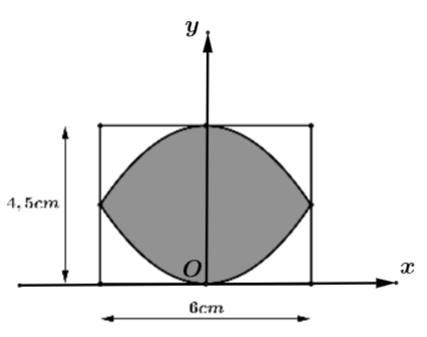
Ta đặt hình vào hệ trục như hình vẽ và chia đôi hình theo phương ngang ta được hình chữ nhật cạnh 2,5 cm và 6 cm.
Ta có đường cong bài cho có dạng parabol. Suy ra đường cong có phương trình là:
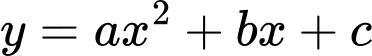
Đường cong đi qua gốc tọa độ O và đi qua 2 điểm
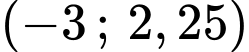 và
và 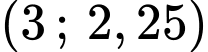
Ta có hệ:
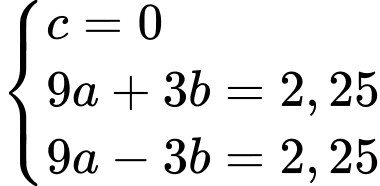
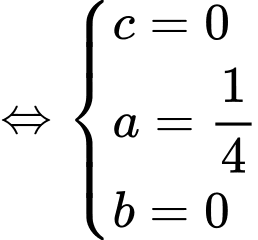
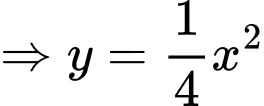
Ta có diện tích nửa hình cần tìm có diện tích là tích phân của
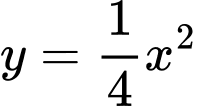 và
và 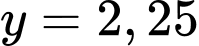 với cận -3 và 3.
với cận -3 và 3.
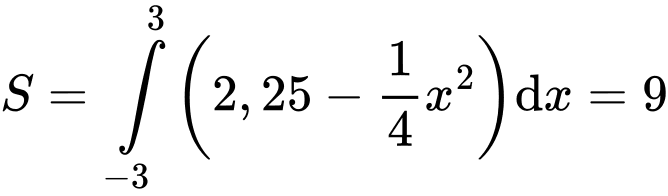
Vậy diện tích cần tìm là:
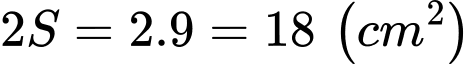
Đáp án:

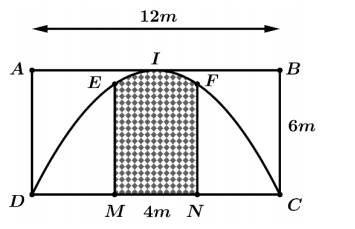
Câu 4 [151413]: Trong đợt hội trại “Khi tôi 18” được tổ chức tại THPT X, Đoàn trường có thực hiện một dự án trưng bày trên một pano có dạng parabol như hình vẽ. Biết rằng Đoàn trường sẽ yêu cầu các lớp gửi dự thi và dán lên khu vực hình chữ nhật 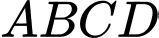 , phần còn lại sẽ được trang trí hoa văn cho phù hợp. Chi phí dán hoa văn là
, phần còn lại sẽ được trang trí hoa văn cho phù hợp. Chi phí dán hoa văn là  đồng cho một
đồng cho một 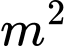 bảng. Hỏi chi phí thấp nhất cho việc hoàn tất hoa văn trên pano sẽ là bao nhiêu nghìn đồng. Kết quả làm tròn đến hàng đơn vị của nghìn đồng.
bảng. Hỏi chi phí thấp nhất cho việc hoàn tất hoa văn trên pano sẽ là bao nhiêu nghìn đồng. Kết quả làm tròn đến hàng đơn vị của nghìn đồng.
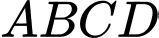 , phần còn lại sẽ được trang trí hoa văn cho phù hợp. Chi phí dán hoa văn là
, phần còn lại sẽ được trang trí hoa văn cho phù hợp. Chi phí dán hoa văn là  đồng cho một
đồng cho một 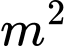 bảng. Hỏi chi phí thấp nhất cho việc hoàn tất hoa văn trên pano sẽ là bao nhiêu nghìn đồng. Kết quả làm tròn đến hàng đơn vị của nghìn đồng.
bảng. Hỏi chi phí thấp nhất cho việc hoàn tất hoa văn trên pano sẽ là bao nhiêu nghìn đồng. Kết quả làm tròn đến hàng đơn vị của nghìn đồng.
A,  đồng.
đồng.
 đồng.
đồng.B,  đồng.
đồng.
 đồng.
đồng.C,  đồng.
đồng.
 đồng.
đồng.D,  đồng.
đồng.
 đồng.
đồng.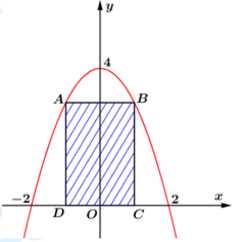
Gọi là diện tích hình phằng giới hạn bởi Parabol có phương trình
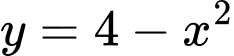 và trục hoành.
và trục hoành.
Suy ra
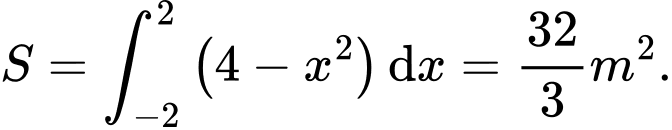
Gọi điềm
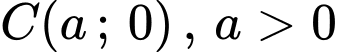 suy ra
suy ra 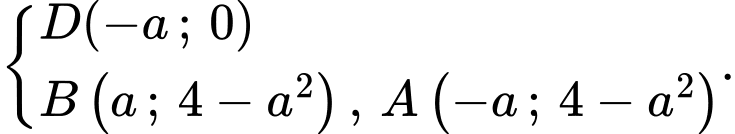
Gọi
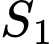 là diện tích
là diện tích 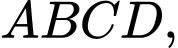 suy ra
suy ra 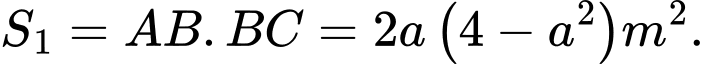
Gọi
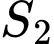 là diện tích có hoa văn, suy ra
là diện tích có hoa văn, suy ra 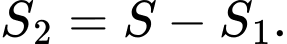
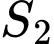 nhỏ nhất khi và chỉ khi
nhỏ nhất khi và chỉ khi 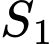 lớn nhất.
lớn nhất.
Xét hàm số
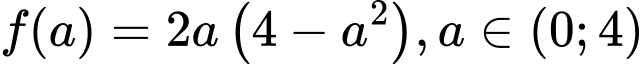
Ta có
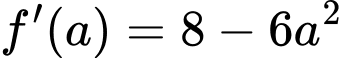
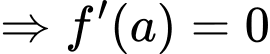
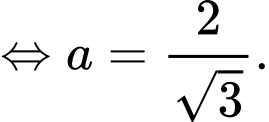
Xét bảng biến thiên hàm số
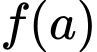 với
với 
Suy ra
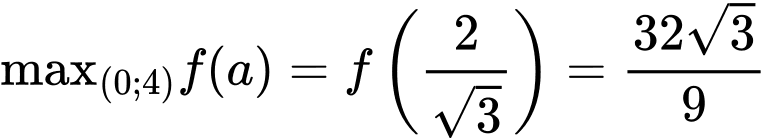
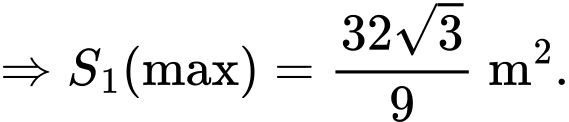
Suy ra
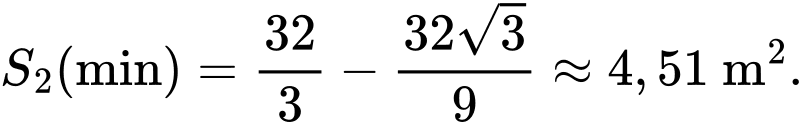
Suy ra số tiền cần bằng 451.000 đồng.
Chọn C. Đáp án: C
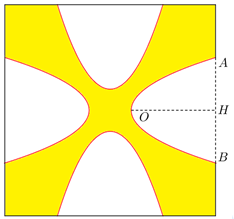
Câu 5 [151399]: Một hoa văn trang trí được tạo ra từ một miếng bìa mỏng hình vuông cạnh 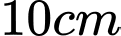 bằng cách khoét bỏ đi bốn phần bằng nhau có hình dạng parabol như hình bên. Biết rằng
bằng cách khoét bỏ đi bốn phần bằng nhau có hình dạng parabol như hình bên. Biết rằng 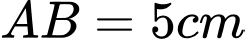 đồng thời
đồng thời 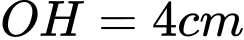 . Diện tích bề mặt hoa văn đó là bao nhiêu
. Diện tích bề mặt hoa văn đó là bao nhiêu 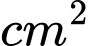 .
.
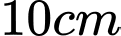 bằng cách khoét bỏ đi bốn phần bằng nhau có hình dạng parabol như hình bên. Biết rằng
bằng cách khoét bỏ đi bốn phần bằng nhau có hình dạng parabol như hình bên. Biết rằng 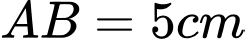 đồng thời
đồng thời 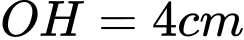 . Diện tích bề mặt hoa văn đó là bao nhiêu
. Diện tích bề mặt hoa văn đó là bao nhiêu 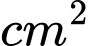 .
.
Chọn đáp án A.
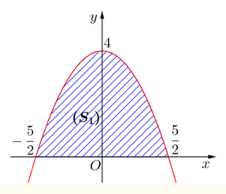
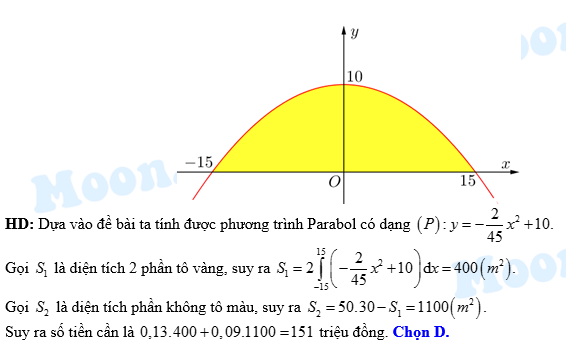
Dựa vào đề bài ta tính được Parabol có PT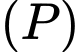 :
: 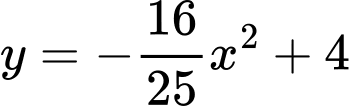 .
.
Gọi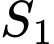 là diện tích hình phẳng trong hình bên Suy ra:
là diện tích hình phẳng trong hình bên Suy ra: 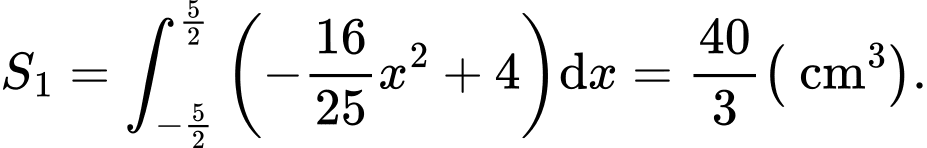
Gọi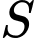 là diện tich hoa vān cần tính Suy ra
là diện tich hoa vān cần tính Suy ra 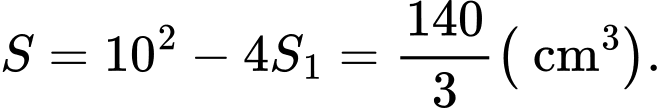

Dựa vào đề bài ta tính được Parabol có PT
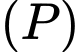 :
: 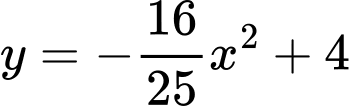 .
.Gọi
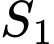 là diện tích hình phẳng trong hình bên Suy ra:
là diện tích hình phẳng trong hình bên Suy ra: 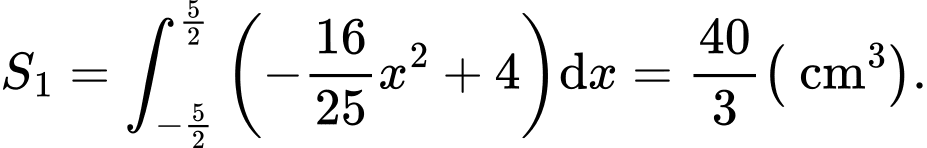
Gọi
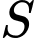 là diện tich hoa vān cần tính Suy ra
là diện tich hoa vān cần tính Suy ra 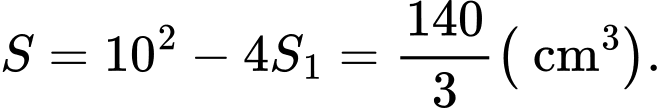
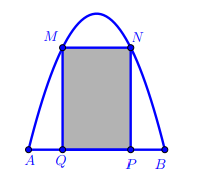
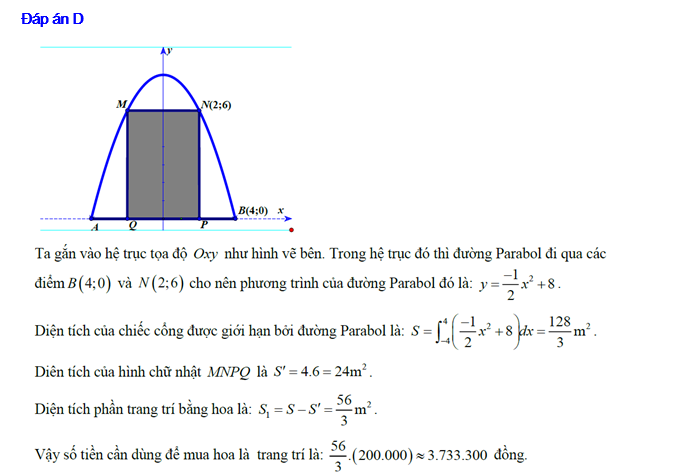
Câu 6 [151407]: Một chiếc cổng có hình dạng là một Parabol có khoảng cách giữa hai chân cổng là 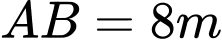 . Người ta treo một tấm phông hình chữ nhật có hai đỉnh
. Người ta treo một tấm phông hình chữ nhật có hai đỉnh 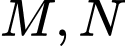 nằm trên Parabol và hai đỉnh
nằm trên Parabol và hai đỉnh 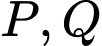 nằm trên mặt đất (như hình vẽ). Ở phần phía ngoài phông (phần không tô đen) người ta mua hoa để trang trí với chi phí cho
nằm trên mặt đất (như hình vẽ). Ở phần phía ngoài phông (phần không tô đen) người ta mua hoa để trang trí với chi phí cho 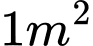 cần số tiền mua hoa là
cần số tiền mua hoa là  đồng cho
đồng cho 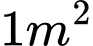 . Biết
. Biết 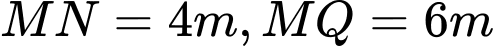 . Hỏi số tiền dùng để mua hoa trang trí chiếc cổng là bao nhiêu nghìn đồng? Kết quả làm tròn đến hàng đơn vị của nghìn đồng
. Hỏi số tiền dùng để mua hoa trang trí chiếc cổng là bao nhiêu nghìn đồng? Kết quả làm tròn đến hàng đơn vị của nghìn đồng
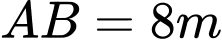 . Người ta treo một tấm phông hình chữ nhật có hai đỉnh
. Người ta treo một tấm phông hình chữ nhật có hai đỉnh 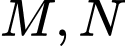 nằm trên Parabol và hai đỉnh
nằm trên Parabol và hai đỉnh 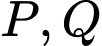 nằm trên mặt đất (như hình vẽ). Ở phần phía ngoài phông (phần không tô đen) người ta mua hoa để trang trí với chi phí cho
nằm trên mặt đất (như hình vẽ). Ở phần phía ngoài phông (phần không tô đen) người ta mua hoa để trang trí với chi phí cho 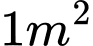 cần số tiền mua hoa là
cần số tiền mua hoa là  đồng cho
đồng cho 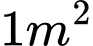 . Biết
. Biết 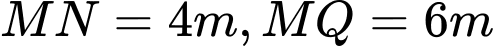 . Hỏi số tiền dùng để mua hoa trang trí chiếc cổng là bao nhiêu nghìn đồng? Kết quả làm tròn đến hàng đơn vị của nghìn đồng
. Hỏi số tiền dùng để mua hoa trang trí chiếc cổng là bao nhiêu nghìn đồng? Kết quả làm tròn đến hàng đơn vị của nghìn đồng
Điền đáp số: 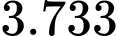 nghìn đồng
nghìn đồng
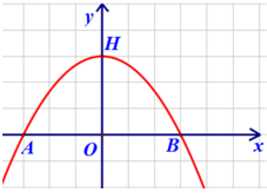
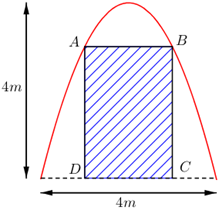
Câu 7 [408113]: Hình bên là cánh cửa gỗ, phía dưới có dạng hình chữ nhật 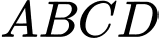 và mép trên được thiết kế là một phần của đường parabol với các kích thước như sau:
và mép trên được thiết kế là một phần của đường parabol với các kích thước như sau: 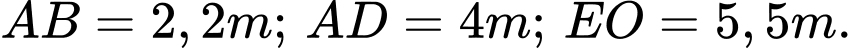 Biết giá thành sản xuất cửa gỗ là 30 triệu đồng/1
Biết giá thành sản xuất cửa gỗ là 30 triệu đồng/1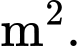 Chi phí để sản xuất của gỗ đã cho là…………..triệu đồng?
Chi phí để sản xuất của gỗ đã cho là…………..triệu đồng?
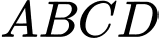 và mép trên được thiết kế là một phần của đường parabol với các kích thước như sau:
và mép trên được thiết kế là một phần của đường parabol với các kích thước như sau: 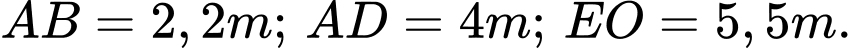 Biết giá thành sản xuất cửa gỗ là 30 triệu đồng/1
Biết giá thành sản xuất cửa gỗ là 30 triệu đồng/1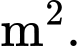 Chi phí để sản xuất của gỗ đã cho là…………..triệu đồng?
Chi phí để sản xuất của gỗ đã cho là…………..triệu đồng?
Chọn hệ trục 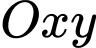 như hình vẽ, khi đó ta có
như hình vẽ, khi đó ta có 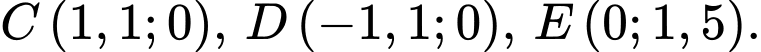
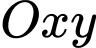 như hình vẽ, khi đó ta có
như hình vẽ, khi đó ta có 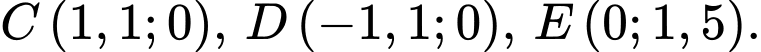
Phương trình của parabol có dạng 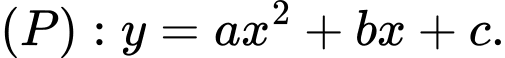
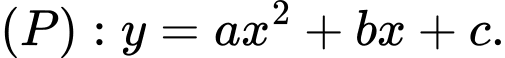
Do 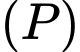 đi qua
đi qua 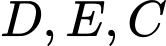 nên có phương trình
nên có phương trình
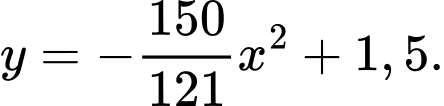
 đi qua
đi qua 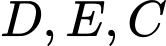 nên có phương trình
nên có phương trình
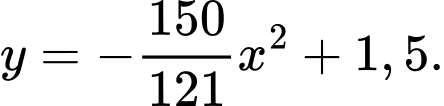
Vậy diện tích của cánh cửa gỗ là 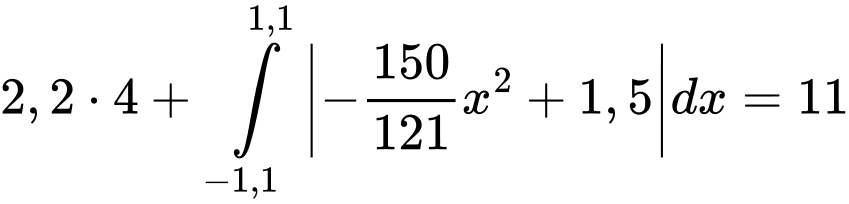
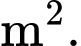
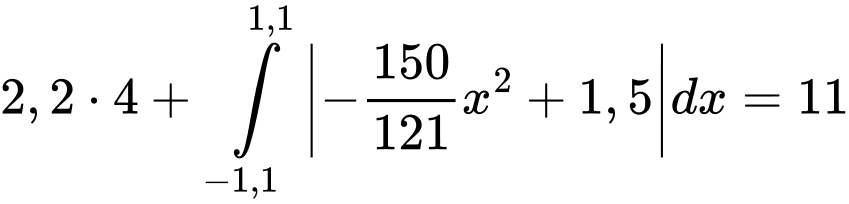
Suy ra cho phí sản xuất cánh cửa là 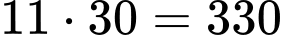 (triệu đồng).
(triệu đồng).
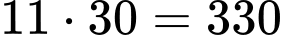 (triệu đồng).
(triệu đồng).
Câu 8 [153546]: Hình bên minh hoạ mặt cắt đứng của một con kênh đặt trong hệ trục toạ độ 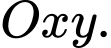 Đáy của con kênh là một đường cong
Đáy của con kênh là một đường cong  cho bởi hàm số bậc ba có dạng
cho bởi hàm số bậc ba có dạng 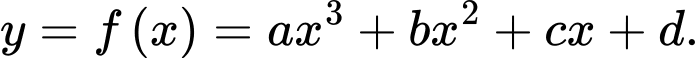 Hãy tính diện tích
Hãy tính diện tích
hình phẳng tô đậm trong hình vẽ, biết đơn vị trên mỗi trục toạ độ là mét và đồ thị hàm số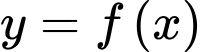 nhận gốc toạ độ
nhận gốc toạ độ  và điểm
và điểm 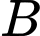 là các điểm cực trị. Viết kết quả làm tròn đến hàng đơn vị của
là các điểm cực trị. Viết kết quả làm tròn đến hàng đơn vị của 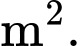
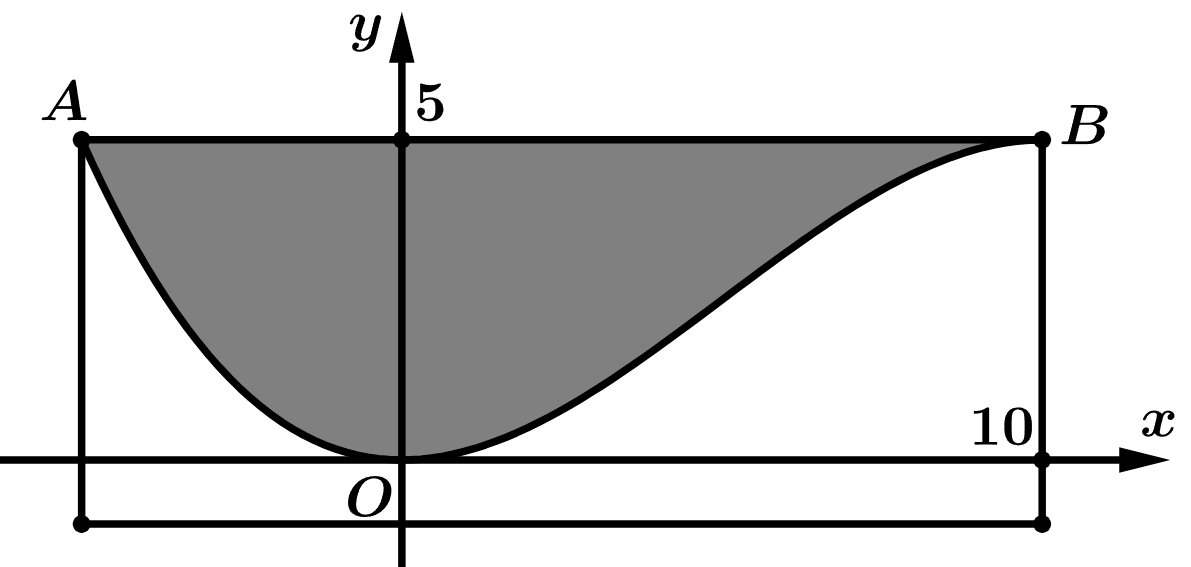
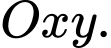 Đáy của con kênh là một đường cong
Đáy của con kênh là một đường cong  cho bởi hàm số bậc ba có dạng
cho bởi hàm số bậc ba có dạng 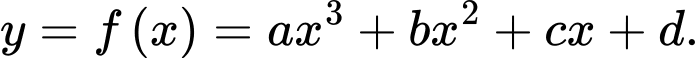 Hãy tính diện tích
Hãy tính diện tích hình phẳng tô đậm trong hình vẽ, biết đơn vị trên mỗi trục toạ độ là mét và đồ thị hàm số
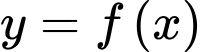 nhận gốc toạ độ
nhận gốc toạ độ  và điểm
và điểm 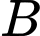 là các điểm cực trị. Viết kết quả làm tròn đến hàng đơn vị của
là các điểm cực trị. Viết kết quả làm tròn đến hàng đơn vị của 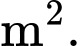

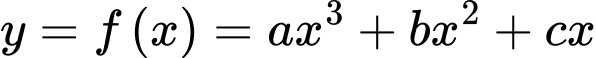 mà
mà 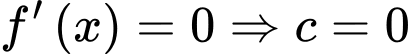
Mặt khác 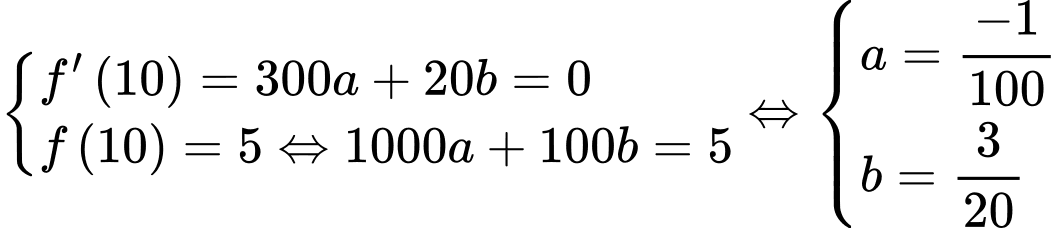
Do đó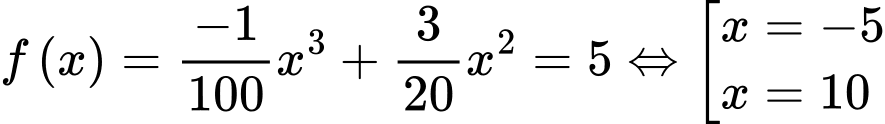
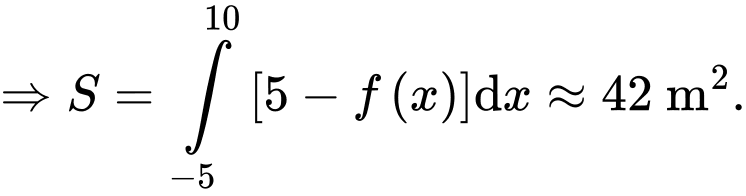
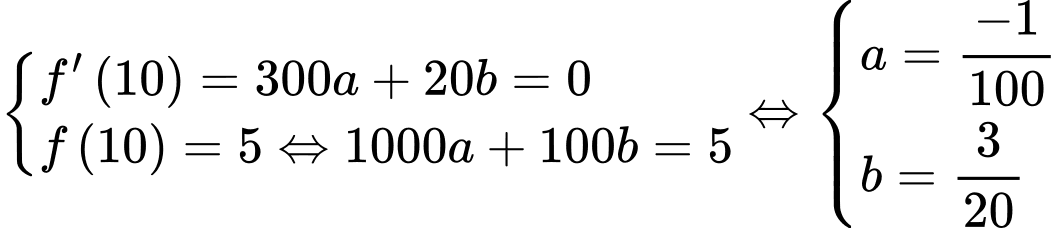
Do đó
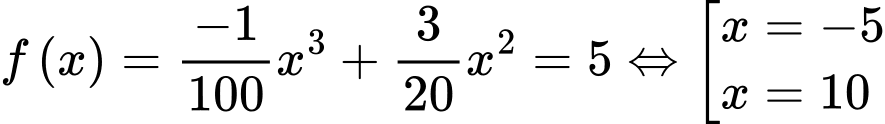
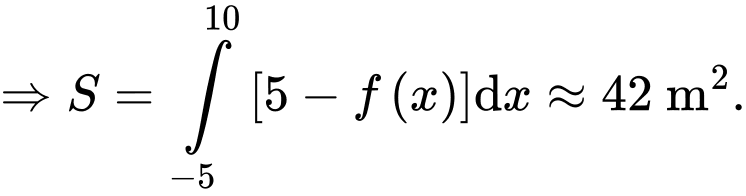
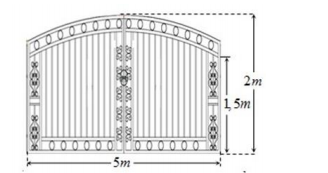
Câu 9 [80749]: Ông A muốn làm cửa rào sắt có hình dạng và kích thước như hình vẽ bên, biết đường cong phía trên là một Parabol. Giá  của rào sắt là
của rào sắt là  đồng. Hỏi ông An phải trả bao nhiêu nghìn đồng để làm cái cửa sắt như vậy. Viết kết quả làm tròn đến hàng đơn vị của nghìn đồng.
đồng. Hỏi ông An phải trả bao nhiêu nghìn đồng để làm cái cửa sắt như vậy. Viết kết quả làm tròn đến hàng đơn vị của nghìn đồng.
 của rào sắt là
của rào sắt là  đồng. Hỏi ông An phải trả bao nhiêu nghìn đồng để làm cái cửa sắt như vậy. Viết kết quả làm tròn đến hàng đơn vị của nghìn đồng.
đồng. Hỏi ông An phải trả bao nhiêu nghìn đồng để làm cái cửa sắt như vậy. Viết kết quả làm tròn đến hàng đơn vị của nghìn đồng.
A, 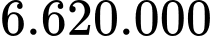 đồng.
đồng.
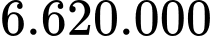 đồng.
đồng.B, 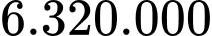 đồng
đồng
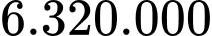 đồng
đồngC, 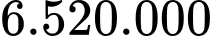 đồng.
đồng.
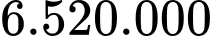 đồng.
đồng.D, 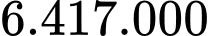 đồng.
đồng.
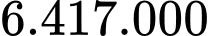 đồng.
đồng.
Chọn đáp án D.
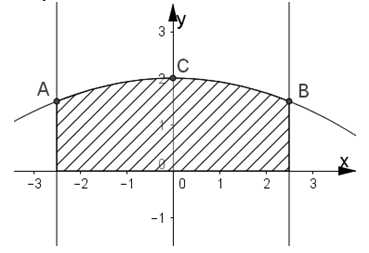
Chọn hệ trục tọa độ như hình vẽ.
Trong đó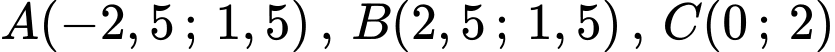 .
.
Giả sử đường cong trên là một Parabol có dạng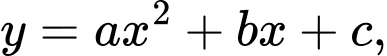 với
với 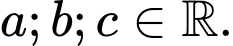
Do Parabol đi qua các điểm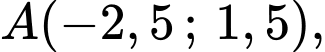
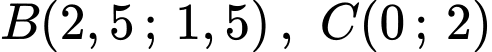 nên ta có hệ phương trình
nên ta có hệ phương trình
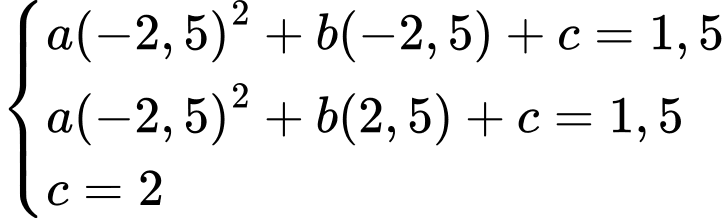
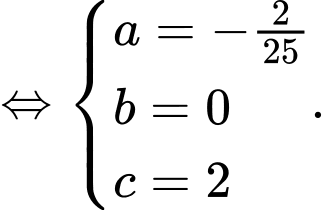
Khi đó phương trình Parabol là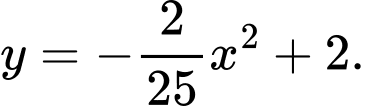
Diện tích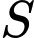 của cửa rào sắt là diện tích phần hình phẳng giới bởi đồ thị hàm số
của cửa rào sắt là diện tích phần hình phẳng giới bởi đồ thị hàm số 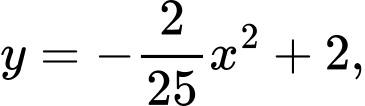 trục hoành và hai đường thẳng
trục hoành và hai đường thẳng 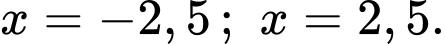
Ta có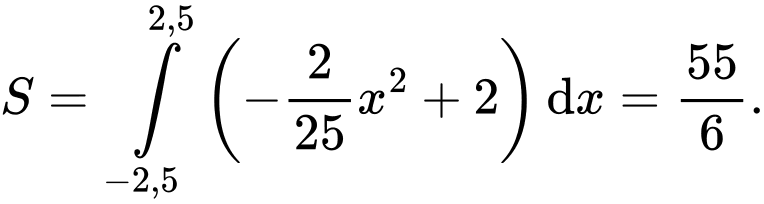
Vậy ông An phải trả số tiền để làm cái cửa sắt là :
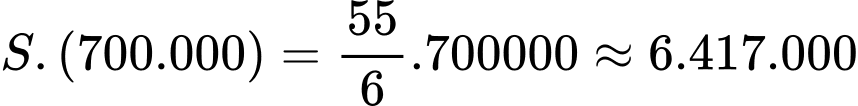 (đồng). Đáp án: D
(đồng). Đáp án: D

Chọn hệ trục tọa độ như hình vẽ.
Trong đó
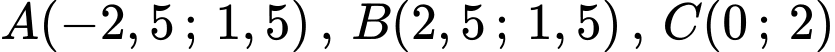 .
.
Giả sử đường cong trên là một Parabol có dạng
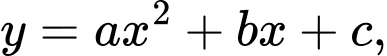 với
với 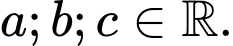
Do Parabol đi qua các điểm
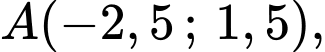
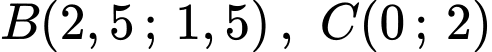 nên ta có hệ phương trình
nên ta có hệ phương trình
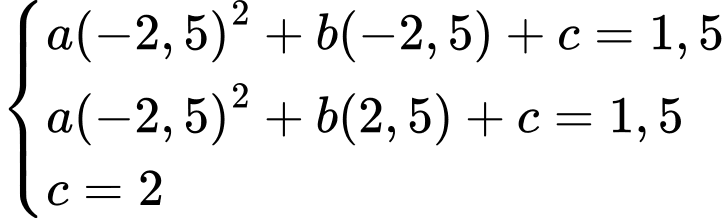
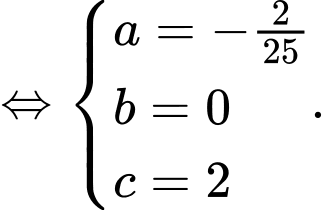
Khi đó phương trình Parabol là
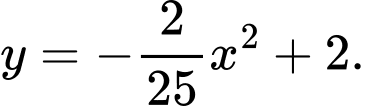
Diện tích
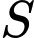 của cửa rào sắt là diện tích phần hình phẳng giới bởi đồ thị hàm số
của cửa rào sắt là diện tích phần hình phẳng giới bởi đồ thị hàm số 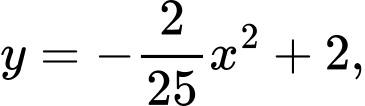 trục hoành và hai đường thẳng
trục hoành và hai đường thẳng 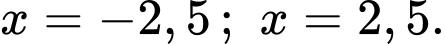
Ta có
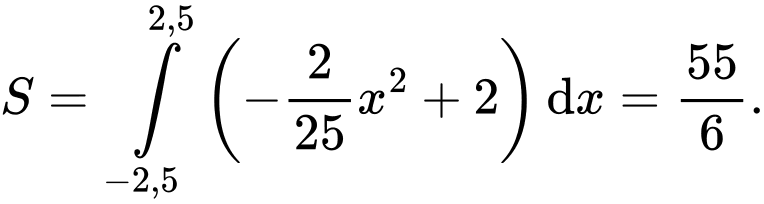
Vậy ông An phải trả số tiền để làm cái cửa sắt là :
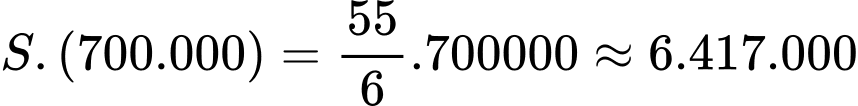 (đồng). Đáp án: D
(đồng). Đáp án: D
Câu 10 [151397]: Một công ty quảng cáo 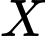 muốn làm một bức tranh trang trí hình
muốn làm một bức tranh trang trí hình 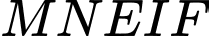 ở chính giữa một bức tường hình chữ nhật
ở chính giữa một bức tường hình chữ nhật 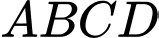 có chiều cao
có chiều cao 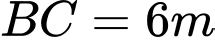 , chiều dài
, chiều dài 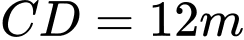 (hình vẽ bên). Cho biết
(hình vẽ bên). Cho biết 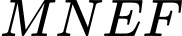 là hình chữ nhật có
là hình chữ nhật có 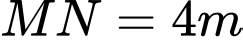 , cung
, cung 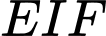 có hình dạng là một phần của cung parabol có đỉnh
có hình dạng là một phần của cung parabol có đỉnh 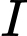 là trung điểm của cạnh
là trung điểm của cạnh  và đi qua hai điểm
và đi qua hai điểm 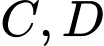 . Kinh phí làm bức tranh là
. Kinh phí làm bức tranh là  đồng/
đồng/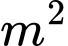 . Công ty
. Công ty 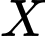 cần
cần 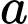 triệu đồng để làm bức tranh đó. Tìm
triệu đồng để làm bức tranh đó. Tìm  viết kết quả làm tròn đến hàng phần chục.
viết kết quả làm tròn đến hàng phần chục.
 muốn làm một bức tranh trang trí hình
muốn làm một bức tranh trang trí hình  ở chính giữa một bức tường hình chữ nhật
ở chính giữa một bức tường hình chữ nhật 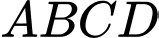 có chiều cao
có chiều cao 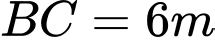 , chiều dài
, chiều dài 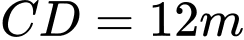 (hình vẽ bên). Cho biết
(hình vẽ bên). Cho biết 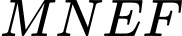 là hình chữ nhật có
là hình chữ nhật có 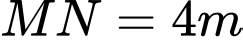 , cung
, cung 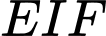 có hình dạng là một phần của cung parabol có đỉnh
có hình dạng là một phần của cung parabol có đỉnh 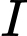 là trung điểm của cạnh
là trung điểm của cạnh  và đi qua hai điểm
và đi qua hai điểm 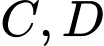 . Kinh phí làm bức tranh là
. Kinh phí làm bức tranh là  đồng/
đồng/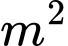 . Công ty
. Công ty  cần
cần 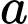 triệu đồng để làm bức tranh đó. Tìm
triệu đồng để làm bức tranh đó. Tìm 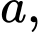 viết kết quả làm tròn đến hàng phần chục.
viết kết quả làm tròn đến hàng phần chục.
Gọi  là trung điểm của
là trung điểm của 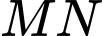 và trùng với gốc toạ độ
và trùng với gốc toạ độ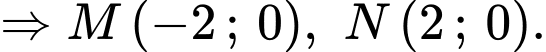
Phương trình parabol có đỉnh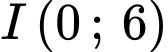 và đi qua hai điểm
và đi qua hai điểm 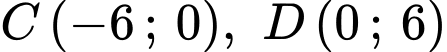 là
là 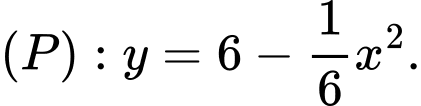
Bức tranh là mặt phẳng bị giới hạn bởi hàm số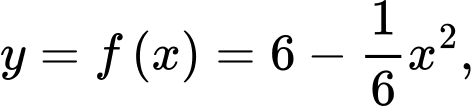
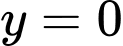 và các đường thẳng
và các đường thẳng 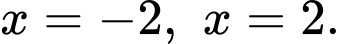
Khi đó diện tích bức tranh là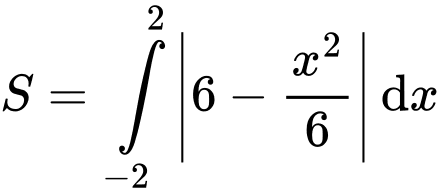
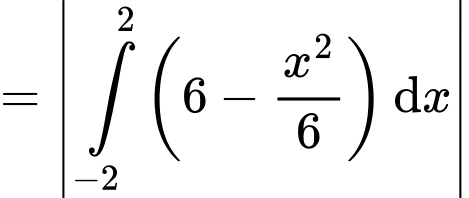
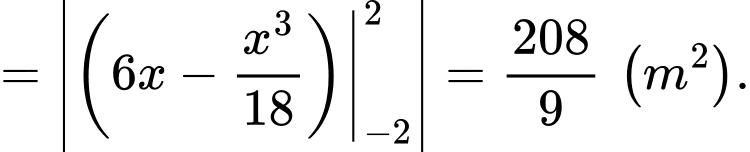
Vậy số tiền công ty X cần dùng để làm bức tranh là
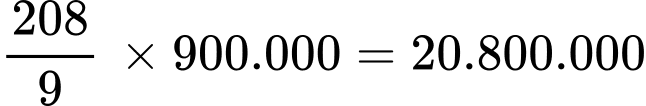
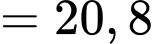 triệu đồng.
triệu đồng.
Vậy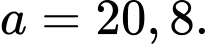 Đáp án: C
Đáp án: C
 là trung điểm của
là trung điểm của 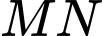 và trùng với gốc toạ độ
và trùng với gốc toạ độ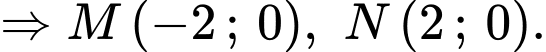
Phương trình parabol có đỉnh
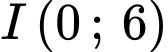 và đi qua hai điểm
và đi qua hai điểm 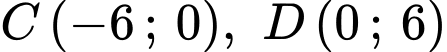 là
là 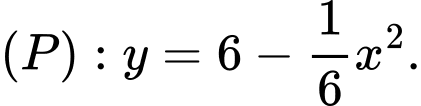
Bức tranh là mặt phẳng bị giới hạn bởi hàm số
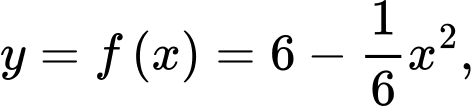
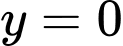 và các đường thẳng
và các đường thẳng 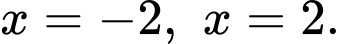
Khi đó diện tích bức tranh là
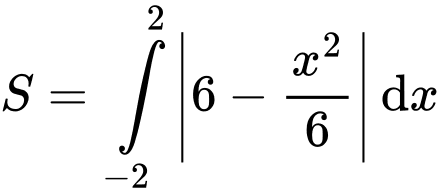
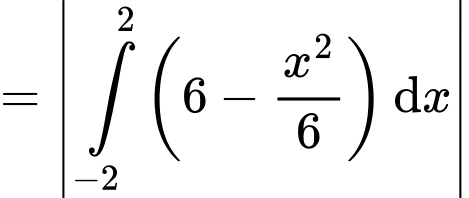
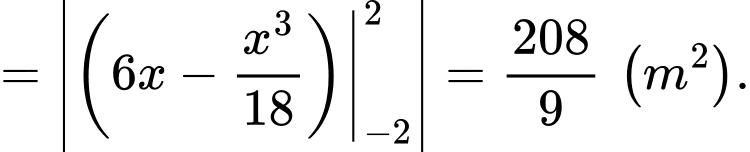
Vậy số tiền công ty X cần dùng để làm bức tranh là
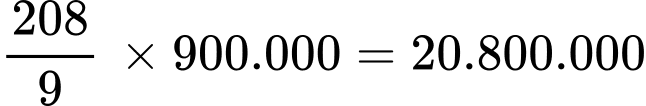
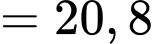 triệu đồng.
triệu đồng.Vậy
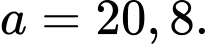 Đáp án: C
Đáp án: C
Câu 11 [301711]: Ông Tuấn làm một logo bằng tấm nhựa phẳng, có hình dạng là một hình có trục đối xứng. Biết đường viền 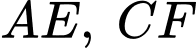 ở hai bên là hai nhánh của một parabol và phần lõm
ở hai bên là hai nhánh của một parabol và phần lõm 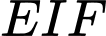 phía dưới đáy cũng là một parabol, hai nhánh phía trên là hai đoạn thẳng như hình bên dưới. Cho biết
phía dưới đáy cũng là một parabol, hai nhánh phía trên là hai đoạn thẳng như hình bên dưới. Cho biết 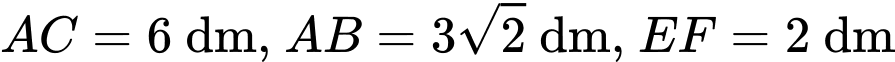 và khoảng cách giữa
và khoảng cách giữa 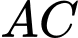 và
và 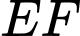 bằng
bằng 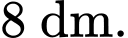 Hỏi diện tích của logo đó bằng bao nhiêu
Hỏi diện tích của logo đó bằng bao nhiêu  Viết kết quả dưới dạng số thập phân. Viết kết quả làm tròn đến hàng phần trăm.
Viết kết quả dưới dạng số thập phân. Viết kết quả làm tròn đến hàng phần trăm.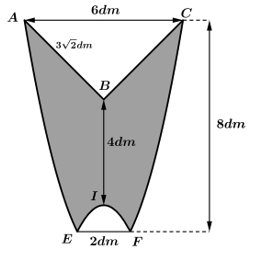
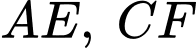 ở hai bên là hai nhánh của một parabol và phần lõm
ở hai bên là hai nhánh của một parabol và phần lõm 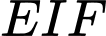 phía dưới đáy cũng là một parabol, hai nhánh phía trên là hai đoạn thẳng như hình bên dưới. Cho biết
phía dưới đáy cũng là một parabol, hai nhánh phía trên là hai đoạn thẳng như hình bên dưới. Cho biết 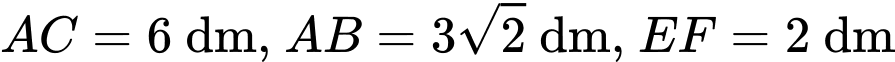 và khoảng cách giữa
và khoảng cách giữa 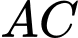 và
và 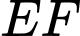 bằng
bằng 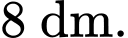 Hỏi diện tích của logo đó bằng bao nhiêu
Hỏi diện tích của logo đó bằng bao nhiêu  Viết kết quả dưới dạng số thập phân. Viết kết quả làm tròn đến hàng phần trăm.
Viết kết quả dưới dạng số thập phân. Viết kết quả làm tròn đến hàng phần trăm.
Xét hệ toạ độ 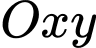 như hình vẽ.
như hình vẽ.
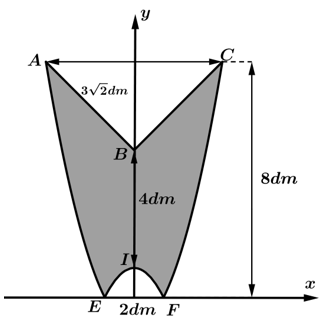
Khi đó nửa bên phải trục tung là hình phẳng giới hạn bởi các đường:
giới hạn bởi các đường: 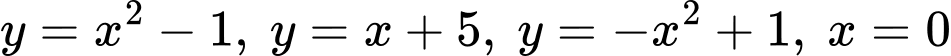
Ta có: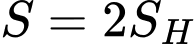
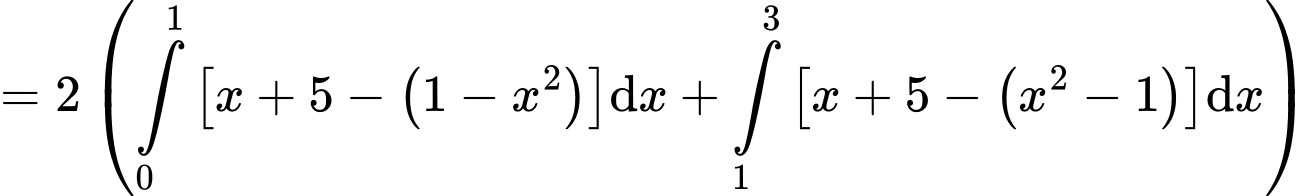
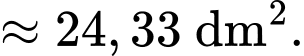
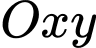 như hình vẽ.
như hình vẽ.
Khi đó nửa bên phải trục tung là hình phẳng
 giới hạn bởi các đường:
giới hạn bởi các đường: 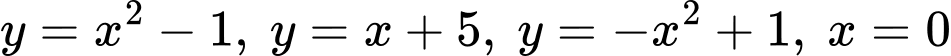
Ta có:
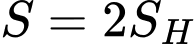
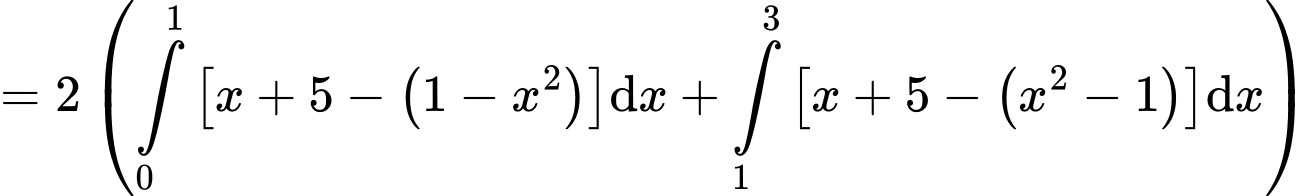
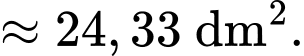
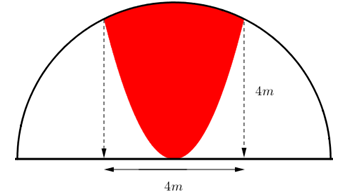
Câu 12 [151402]: Một khuôn viên dạng nửa hình tròn có đường kính bằng 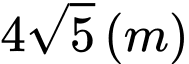 . Trên đó người thiết kế hai phần để trồng hoa và trồng cỏ Nhật Bản. Phần trồng hoa có dạng của một cánh hoa hình parabol có đỉnh trùng với tâm nửa hình tròn và hai đầu mút của cánh hoa nằm trên nửa đường tròn (phần tô màu) cách nhau một khoảng bằng
. Trên đó người thiết kế hai phần để trồng hoa và trồng cỏ Nhật Bản. Phần trồng hoa có dạng của một cánh hoa hình parabol có đỉnh trùng với tâm nửa hình tròn và hai đầu mút của cánh hoa nằm trên nửa đường tròn (phần tô màu) cách nhau một khoảng bằng 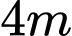 , phần còn lại của khuôn viên (phần không tô màu) để dành trồng cỏ Nhật Bản. Biết các kích thước cho như hình vẽ và kinh phí để trồng cỏ Nhật Bản là
, phần còn lại của khuôn viên (phần không tô màu) để dành trồng cỏ Nhật Bản. Biết các kích thước cho như hình vẽ và kinh phí để trồng cỏ Nhật Bản là  đồng/
đồng/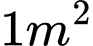 . Hỏi cần bao nhiêu nghìn đồng để trồng cỏ Nhật Bản trên phần đất đó? Kết quả làm tròn đến hàng đơn vị của nghìn đồng.
. Hỏi cần bao nhiêu nghìn đồng để trồng cỏ Nhật Bản trên phần đất đó? Kết quả làm tròn đến hàng đơn vị của nghìn đồng.
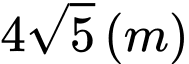 . Trên đó người thiết kế hai phần để trồng hoa và trồng cỏ Nhật Bản. Phần trồng hoa có dạng của một cánh hoa hình parabol có đỉnh trùng với tâm nửa hình tròn và hai đầu mút của cánh hoa nằm trên nửa đường tròn (phần tô màu) cách nhau một khoảng bằng
. Trên đó người thiết kế hai phần để trồng hoa và trồng cỏ Nhật Bản. Phần trồng hoa có dạng của một cánh hoa hình parabol có đỉnh trùng với tâm nửa hình tròn và hai đầu mút của cánh hoa nằm trên nửa đường tròn (phần tô màu) cách nhau một khoảng bằng 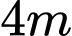 , phần còn lại của khuôn viên (phần không tô màu) để dành trồng cỏ Nhật Bản. Biết các kích thước cho như hình vẽ và kinh phí để trồng cỏ Nhật Bản là
, phần còn lại của khuôn viên (phần không tô màu) để dành trồng cỏ Nhật Bản. Biết các kích thước cho như hình vẽ và kinh phí để trồng cỏ Nhật Bản là  đồng/
đồng/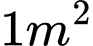 . Hỏi cần bao nhiêu nghìn đồng để trồng cỏ Nhật Bản trên phần đất đó? Kết quả làm tròn đến hàng đơn vị của nghìn đồng.
. Hỏi cần bao nhiêu nghìn đồng để trồng cỏ Nhật Bản trên phần đất đó? Kết quả làm tròn đến hàng đơn vị của nghìn đồng.
A, 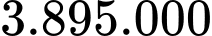 đồng.
đồng.
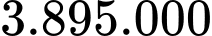 đồng.
đồng.B, 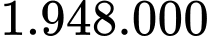 đồng.
đồng.
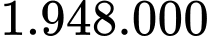 đồng.
đồng.C, 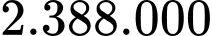 đồng.
đồng.
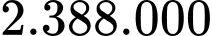 đồng.
đồng.D, 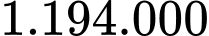 đồng.
đồng.
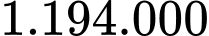 đồng.
đồng.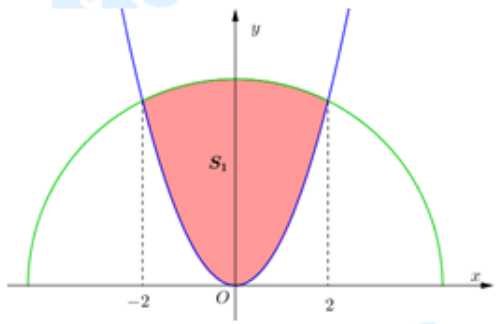
HD:Ta có
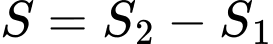
Trong đó
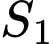 là diện tích hình phẳng giới hạn bởi các đường
là diện tích hình phẳng giới hạn bởi các đường 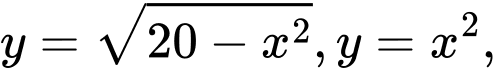
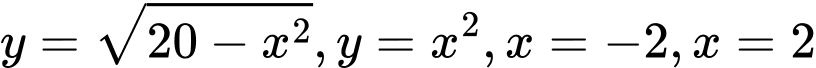 được tô màu trong hình bên,
được tô màu trong hình bên, 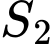 là diện tích nửa hình tròn có bán kính bằng
là diện tích nửa hình tròn có bán kính bằng 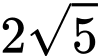 .
.
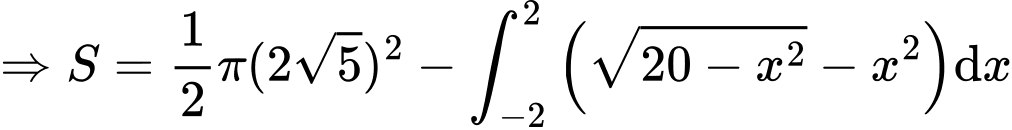
Suy ra
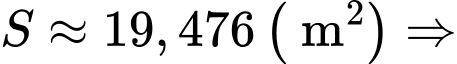 Chi phí sẽ bằng
Chi phí sẽ bằng 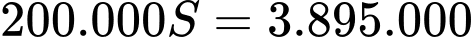 đồng.
đồng.
Chọn A. Đáp án: A
Câu 13 [151398]: Ông An xây dựng sân bóng đá mini hình chữ nhật có chiều rộng 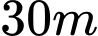 và chiều dài
và chiều dài 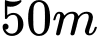 . Để giảm bớt chi phí cho việc trồng cỏ nhân tạo, ông An chia sân bóng ra làm hai phần (tô màu và không tô màu) như hình vẽ:
. Để giảm bớt chi phí cho việc trồng cỏ nhân tạo, ông An chia sân bóng ra làm hai phần (tô màu và không tô màu) như hình vẽ:
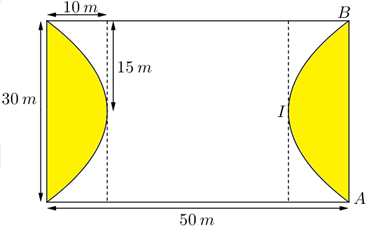
- Phần tô màu gồm hai miền diện tích bằng nhau và đường cong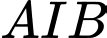 là một parabol có đỉnh
là một parabol có đỉnh 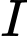 .
.
- Phần tô màu được trồng cỏ nhân tạo với giá 130 nghìn đồng/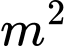 và phần còn lại được trồng cỏ nhân tạo với giá 90 nghìn đồng/
và phần còn lại được trồng cỏ nhân tạo với giá 90 nghìn đồng/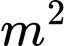 .
.
- Hỏi ông An phải trả bao nhiêu tiền để trồng cỏ nhân tạo cho sân bóng?
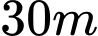 và chiều dài
và chiều dài 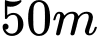 . Để giảm bớt chi phí cho việc trồng cỏ nhân tạo, ông An chia sân bóng ra làm hai phần (tô màu và không tô màu) như hình vẽ:
. Để giảm bớt chi phí cho việc trồng cỏ nhân tạo, ông An chia sân bóng ra làm hai phần (tô màu và không tô màu) như hình vẽ:
- Phần tô màu gồm hai miền diện tích bằng nhau và đường cong
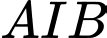 là một parabol có đỉnh
là một parabol có đỉnh 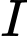 .
.- Phần tô màu được trồng cỏ nhân tạo với giá 130 nghìn đồng/
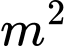 và phần còn lại được trồng cỏ nhân tạo với giá 90 nghìn đồng/
và phần còn lại được trồng cỏ nhân tạo với giá 90 nghìn đồng/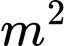 .
.- Hỏi ông An phải trả bao nhiêu tiền để trồng cỏ nhân tạo cho sân bóng?
A, 165 triệu đồng.
B, 195 triệu đồng.
C, 135 triệu đồng.
D, 151 triệu đồng.
 Đáp án: D
Đáp án: D
Câu 14 [151400]: Một mảnh vườn toán học có dạng hình chữ nhật, chiều dài là 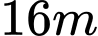 và chiều rộng là
và chiều rộng là 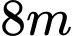 . Các nhà Toán học dùng hai đường parabol, mỗi parabol có đỉnh là trung điểm của một cạnh dài và đi qua 2 mút của cạnh dài đối diện; phần mảnh vườn nằm ở miền trong của cả hai parabol (phần gạch sọc như hình vẽ minh họa) được trồng hoa Hồng. Biết chi phí để trồng hoa Hồng là
. Các nhà Toán học dùng hai đường parabol, mỗi parabol có đỉnh là trung điểm của một cạnh dài và đi qua 2 mút của cạnh dài đối diện; phần mảnh vườn nằm ở miền trong của cả hai parabol (phần gạch sọc như hình vẽ minh họa) được trồng hoa Hồng. Biết chi phí để trồng hoa Hồng là 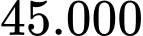 đồng/
đồng/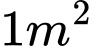 . Hỏi các nhà Toán học phải chi bao nhiêu tiền (đơn vị nghìn đồng) để trồng hoa trên phần mảnh vườn đó.
. Hỏi các nhà Toán học phải chi bao nhiêu tiền (đơn vị nghìn đồng) để trồng hoa trên phần mảnh vườn đó.
Viết kết quả làm tròn đến hàng đơn vị của nghìn đồng.
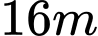 và chiều rộng là
và chiều rộng là 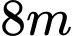 . Các nhà Toán học dùng hai đường parabol, mỗi parabol có đỉnh là trung điểm của một cạnh dài và đi qua 2 mút của cạnh dài đối diện; phần mảnh vườn nằm ở miền trong của cả hai parabol (phần gạch sọc như hình vẽ minh họa) được trồng hoa Hồng. Biết chi phí để trồng hoa Hồng là
. Các nhà Toán học dùng hai đường parabol, mỗi parabol có đỉnh là trung điểm của một cạnh dài và đi qua 2 mút của cạnh dài đối diện; phần mảnh vườn nằm ở miền trong của cả hai parabol (phần gạch sọc như hình vẽ minh họa) được trồng hoa Hồng. Biết chi phí để trồng hoa Hồng là 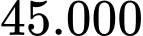 đồng/
đồng/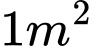 . Hỏi các nhà Toán học phải chi bao nhiêu tiền (đơn vị nghìn đồng) để trồng hoa trên phần mảnh vườn đó.
. Hỏi các nhà Toán học phải chi bao nhiêu tiền (đơn vị nghìn đồng) để trồng hoa trên phần mảnh vườn đó.Viết kết quả làm tròn đến hàng đơn vị của nghìn đồng.
A, 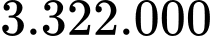 đồng.
đồng.
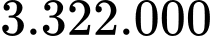 đồng.
đồng.B, 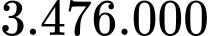 đồng.
đồng.
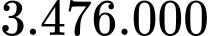 đồng.
đồng.C, 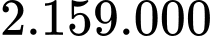 đồng.
đồng.
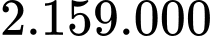 đồng.
đồng.D, 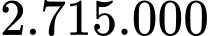 đồng.
đồng.
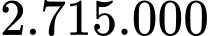 đồng.
đồng.
Dựa vào đề bài ta tính được 2 parabol có phương trình là 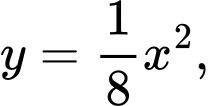
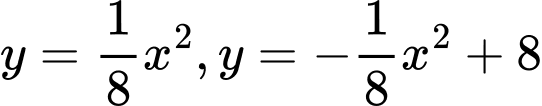
PT hoành độ giao điểm là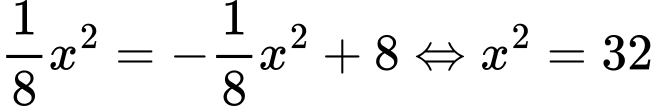
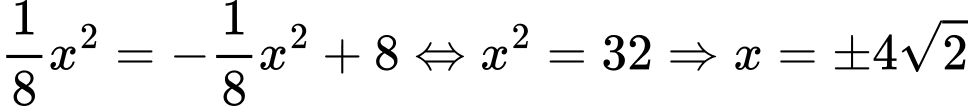
Suy ra diện tích trồng hoa bằng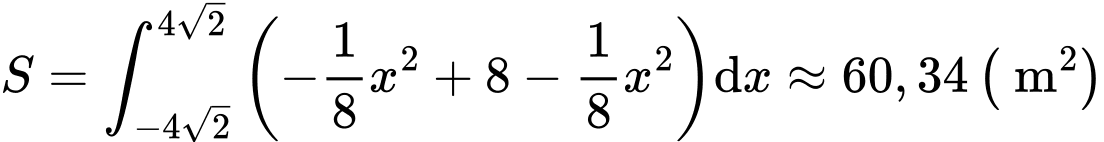
Suy ra số tiền cần dùng bằng 2.715.000 đồng.
Chọn D. Đáp án: D
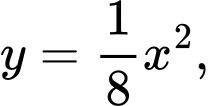
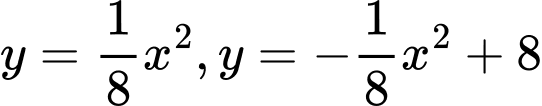
PT hoành độ giao điểm là
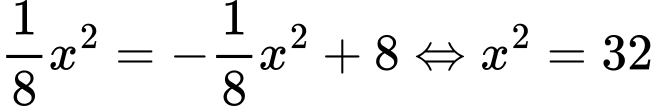
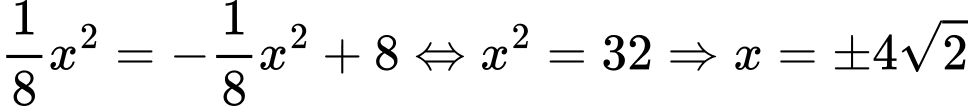
Suy ra diện tích trồng hoa bằng
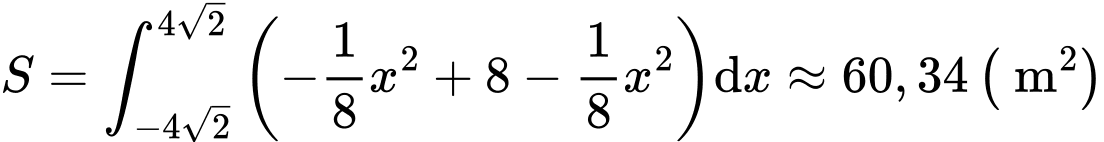
Suy ra số tiền cần dùng bằng 2.715.000 đồng.
Chọn D. Đáp án: D
Câu 15 [151409]: Để trang trí tòa nhà người ta vẽ lên tường một hình như sau: trên mỗi cạnh hình lục giác đều có cạnh là 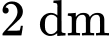 là một cánh hoa hình parabol mà đỉnh parabol
là một cánh hoa hình parabol mà đỉnh parabol 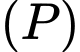 cách cạnh lục giác là
cách cạnh lục giác là 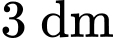 và nằm phía ngoài lục giác, 2 đầu mút của cạnh cũng là 2 điểm giới hạn của đường
và nằm phía ngoài lục giác, 2 đầu mút của cạnh cũng là 2 điểm giới hạn của đường 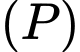 đó. Hãy tính diện tích hình trên (kể cả lục giác) (đơn vị
đó. Hãy tính diện tích hình trên (kể cả lục giác) (đơn vị 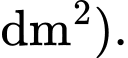 Viết kết quả làm tròn đến hàng đơn vị.
Viết kết quả làm tròn đến hàng đơn vị.

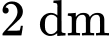 là một cánh hoa hình parabol mà đỉnh parabol
là một cánh hoa hình parabol mà đỉnh parabol 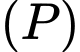 cách cạnh lục giác là
cách cạnh lục giác là 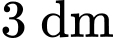 và nằm phía ngoài lục giác, 2 đầu mút của cạnh cũng là 2 điểm giới hạn của đường
và nằm phía ngoài lục giác, 2 đầu mút của cạnh cũng là 2 điểm giới hạn của đường 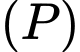 đó. Hãy tính diện tích hình trên (kể cả lục giác) (đơn vị
đó. Hãy tính diện tích hình trên (kể cả lục giác) (đơn vị 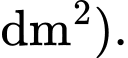 Viết kết quả làm tròn đến hàng đơn vị.
Viết kết quả làm tròn đến hàng đơn vị. 
Điền đáp án: 34.
Xét cánh hoa hình parabol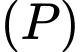 đi qua các điểm
đi qua các điểm 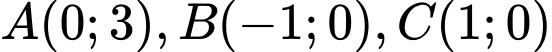 với
với 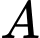 là đỉnh của
là đỉnh của 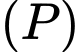 và
và 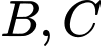 là hai đầu mút thỏa mãn
là hai đầu mút thỏa mãn 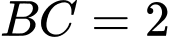 là độ dài cạnh của hình lục giác đều.
là độ dài cạnh của hình lục giác đều.
Gọi phương trình parabol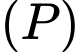 là
là 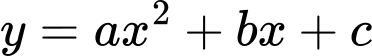 , điểm
, điểm 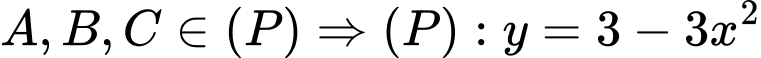 .
.
Diện tích hình cánh hoa được giới hạn bởi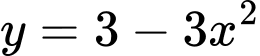 , trục hoành và hai đường thẳng
, trục hoành và hai đường thẳng 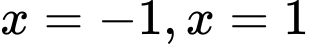 là
là
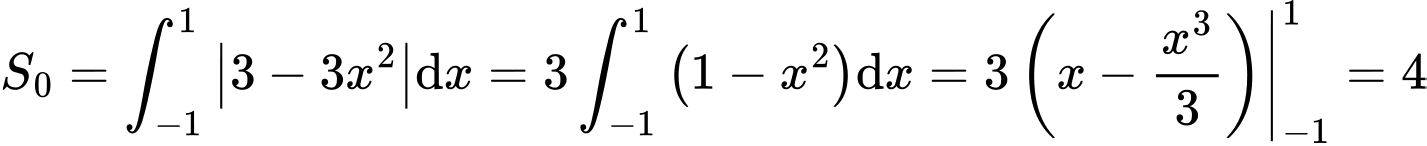
Vậy diện tích cần tính là tổng diện tích của sáu cánh hoa ứng với sáu cạnh của lục giác cộng với diện tích của lục giác đều và bằng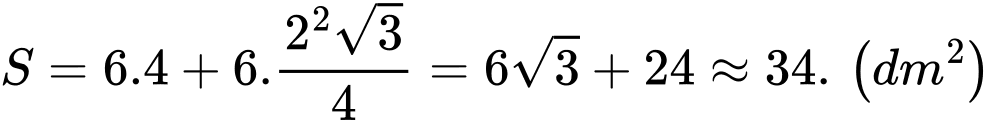
Xét cánh hoa hình parabol
 đi qua các điểm
đi qua các điểm 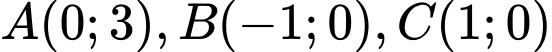 với
với  là đỉnh của
là đỉnh của 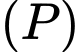 và
và 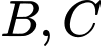 là hai đầu mút thỏa mãn
là hai đầu mút thỏa mãn 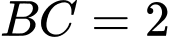 là độ dài cạnh của hình lục giác đều.
là độ dài cạnh của hình lục giác đều.Gọi phương trình parabol
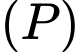 là
là 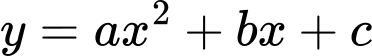 , điểm
, điểm 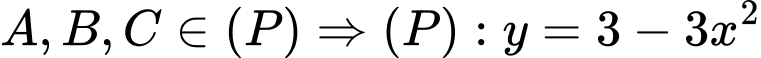 .
.Diện tích hình cánh hoa được giới hạn bởi
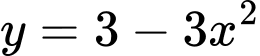 , trục hoành và hai đường thẳng
, trục hoành và hai đường thẳng 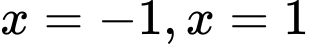 là
là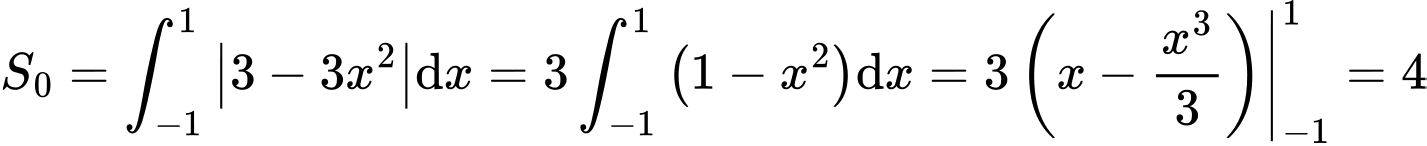
Vậy diện tích cần tính là tổng diện tích của sáu cánh hoa ứng với sáu cạnh của lục giác cộng với diện tích của lục giác đều và bằng
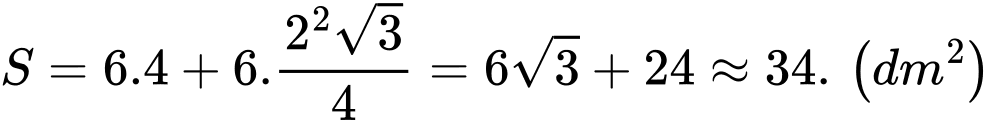
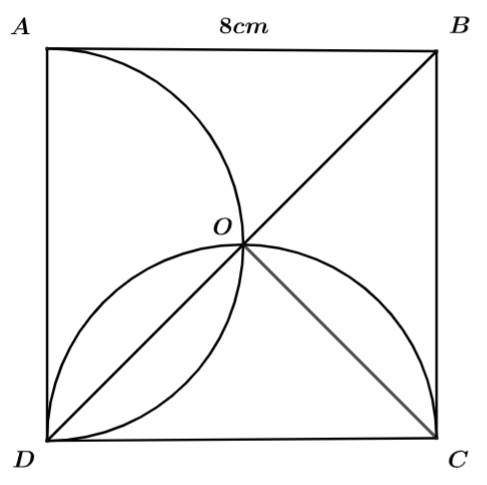
Câu 16 [301738]: Cho hình vuông 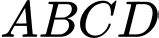 có cạnh bằng
có cạnh bằng  Vẽ nửa đường tròn đường kính
Vẽ nửa đường tròn đường kính 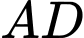 và
và 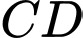 (như hình vẽ). Diện tích phần tô đậm là bao nhiêu
(như hình vẽ). Diện tích phần tô đậm là bao nhiêu  Viết kết quả làm tròn đến hàng đơn vị.
Viết kết quả làm tròn đến hàng đơn vị.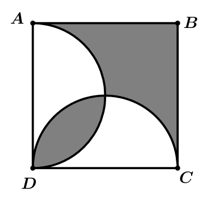
 có cạnh bằng
có cạnh bằng  Vẽ nửa đường tròn đường kính
Vẽ nửa đường tròn đường kính 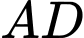 và
và 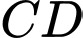 (như hình vẽ). Diện tích phần tô đậm là bao nhiêu
(như hình vẽ). Diện tích phần tô đậm là bao nhiêu 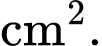 Viết kết quả làm tròn đến hàng đơn vị.
Viết kết quả làm tròn đến hàng đơn vị.
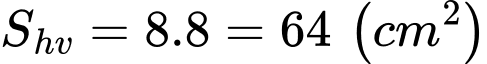
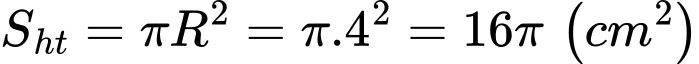
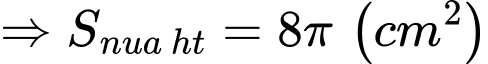
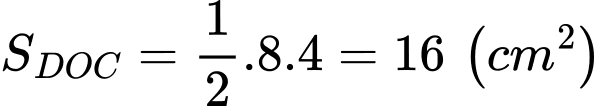

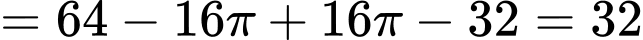
Đáp án: 32
Câu 17 [398646]: Trên một tuyến đường thẳng có một đoạn phải đi xuyên qua một quả núi nhỏ, do đó người ta đã tạo một hầm chui để thuận tiện cho các phương tiện giao thông di chuyển, vòm của hầm chui được đổ bê tông có dạng như hình vẽ dưới đây
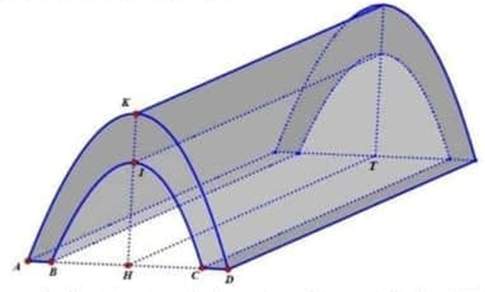
với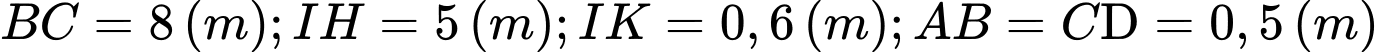
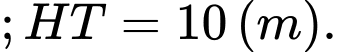 Biết khi cắt vòm của hầm chui bằng mặt phẳng vuông góc với trục của tuyến đường ta luôn có thiết diện là một hình phẳng được giới hạn bởi hai parabol và giao tuyến của mặt cắt với mặt đường. Tính thể tích vòm của hầm chui được đổ bê tông.
Biết khi cắt vòm của hầm chui bằng mặt phẳng vuông góc với trục của tuyến đường ta luôn có thiết diện là một hình phẳng được giới hạn bởi hai parabol và giao tuyến của mặt cắt với mặt đường. Tính thể tích vòm của hầm chui được đổ bê tông.

với
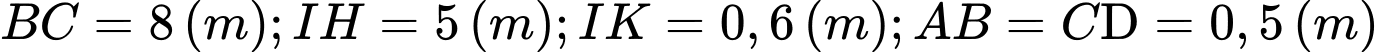
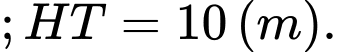 Biết khi cắt vòm của hầm chui bằng mặt phẳng vuông góc với trục của tuyến đường ta luôn có thiết diện là một hình phẳng được giới hạn bởi hai parabol và giao tuyến của mặt cắt với mặt đường. Tính thể tích vòm của hầm chui được đổ bê tông.
Biết khi cắt vòm của hầm chui bằng mặt phẳng vuông góc với trục của tuyến đường ta luôn có thiết diện là một hình phẳng được giới hạn bởi hai parabol và giao tuyến của mặt cắt với mặt đường. Tính thể tích vòm của hầm chui được đổ bê tông. A, 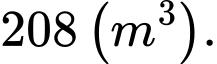
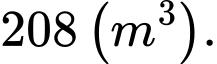
B, 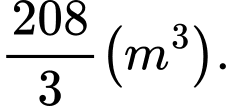
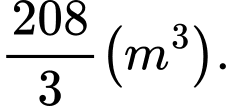
C, 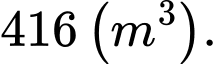
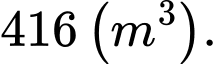
D, 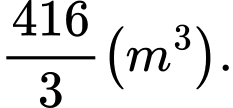
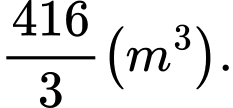
Chọn B
Gọi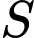 là diện tích hình phẳng giới hạn bởi hai parabol và giao tuyến của mặt cắt với mặt đường.
là diện tích hình phẳng giới hạn bởi hai parabol và giao tuyến của mặt cắt với mặt đường.
Thể tích vòm của hầm chui được đổ bê tông là: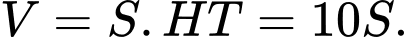
Gắn phần diện tích vào hệ trục tọa độ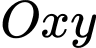 , ta có đồ thị như hình vẽ.
, ta có đồ thị như hình vẽ.
Từ đồ thị, ta xác định được hai hàm số parabol:
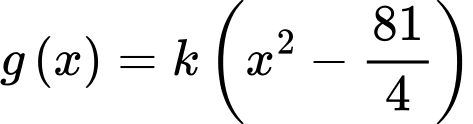
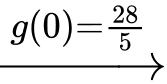
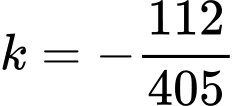
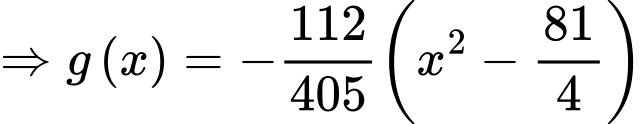
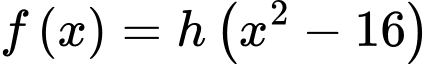
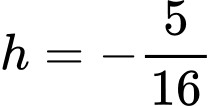
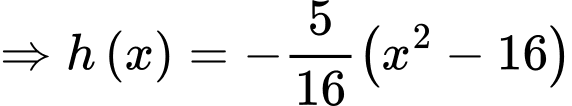
Khi đó,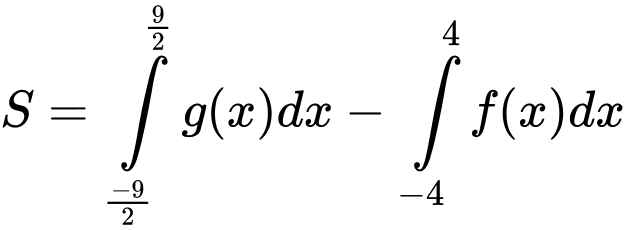
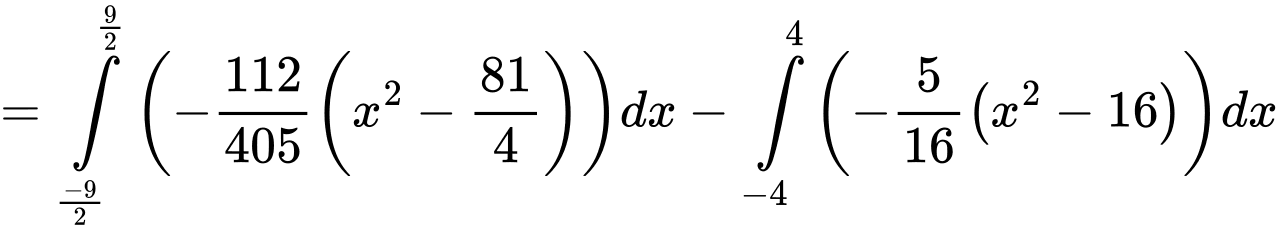
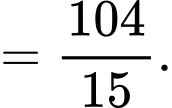
Vậy thể tích của vòm là: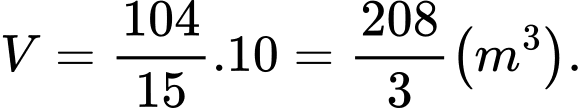 Đáp án: B
Đáp án: B
Gọi
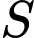 là diện tích hình phẳng giới hạn bởi hai parabol và giao tuyến của mặt cắt với mặt đường.
là diện tích hình phẳng giới hạn bởi hai parabol và giao tuyến của mặt cắt với mặt đường. Thể tích vòm của hầm chui được đổ bê tông là:
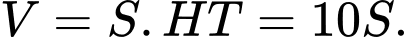
Gắn phần diện tích vào hệ trục tọa độ
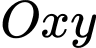 , ta có đồ thị như hình vẽ.
, ta có đồ thị như hình vẽ. 
Từ đồ thị, ta xác định được hai hàm số parabol:
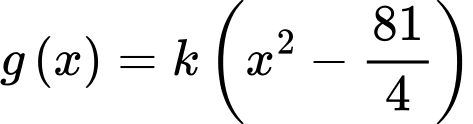
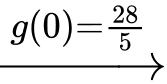
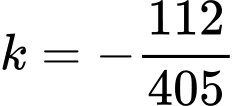
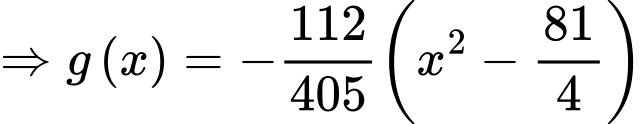
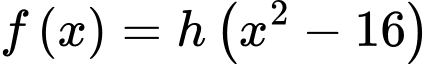
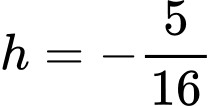
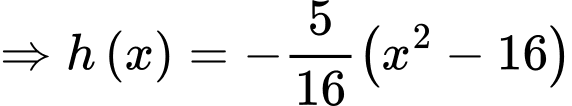
Khi đó,
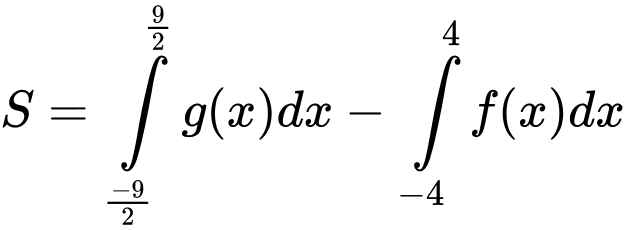
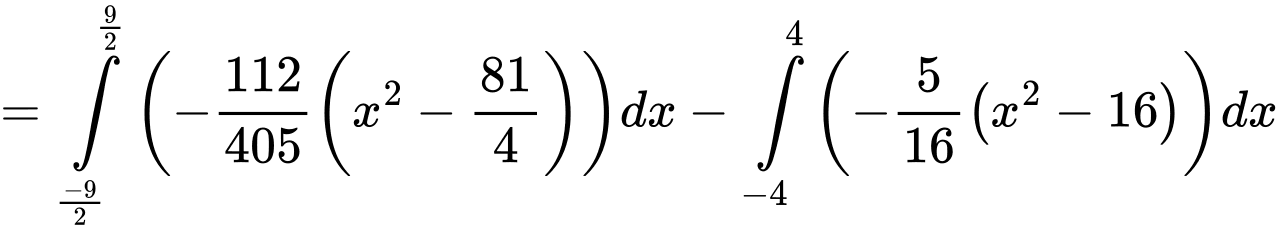
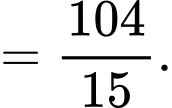
Vậy thể tích của vòm là:
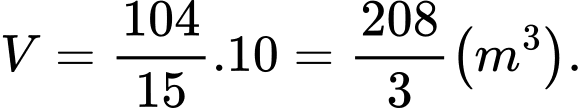 Đáp án: B
Đáp án: B
Câu 18 [151411]: Một viên gạch hoa hình vuông cạnh 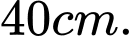 Người thiết kế đã sử dụng bốn đường parabol có chung đỉnh tại tâm của viên gạch để tạo ra bốn cánh hoa (được tô màu sẫm như hình vẽ bên). Diện tích mỗi cánh hoa của viên gạch bằng
Người thiết kế đã sử dụng bốn đường parabol có chung đỉnh tại tâm của viên gạch để tạo ra bốn cánh hoa (được tô màu sẫm như hình vẽ bên). Diện tích mỗi cánh hoa của viên gạch bằng
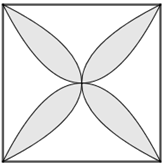
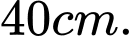 Người thiết kế đã sử dụng bốn đường parabol có chung đỉnh tại tâm của viên gạch để tạo ra bốn cánh hoa (được tô màu sẫm như hình vẽ bên). Diện tích mỗi cánh hoa của viên gạch bằng
Người thiết kế đã sử dụng bốn đường parabol có chung đỉnh tại tâm của viên gạch để tạo ra bốn cánh hoa (được tô màu sẫm như hình vẽ bên). Diện tích mỗi cánh hoa của viên gạch bằng
A, 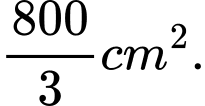
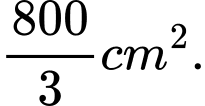
B, 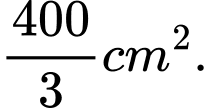
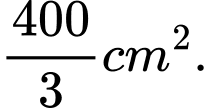
C, 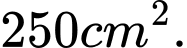
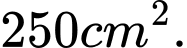
D, 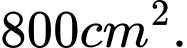
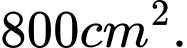
 Đáp án: B
Đáp án: B
Câu 19 [151416]: Từ một miếng tôn hình vuông, người thợ làm chậu cảnh đã tạo mẫu và cắt đi phần hình phẳng không tô đậm trên hình, phần tô đậm được giữ lại làm khuôn quay thành các đôn để đặt các chậu hoa. Tính diện tích hình phẳng đã bị cắt bỏ (đơn vị 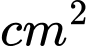 ) biết đường cong trong hình là một parabol có đỉnh nằm trên đường chéo của hình vuông.
) biết đường cong trong hình là một parabol có đỉnh nằm trên đường chéo của hình vuông.
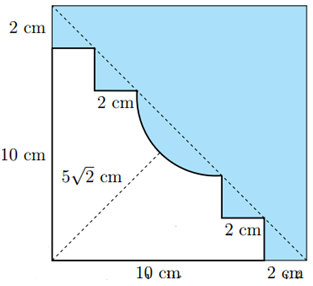
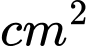 ) biết đường cong trong hình là một parabol có đỉnh nằm trên đường chéo của hình vuông.
) biết đường cong trong hình là một parabol có đỉnh nằm trên đường chéo của hình vuông.
A, 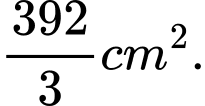
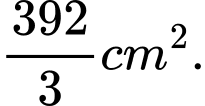
B, 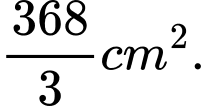
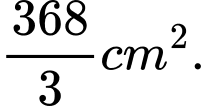
C, 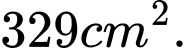
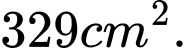
D, 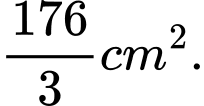
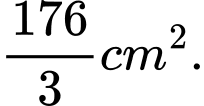
 Đáp án: D
Đáp án: D
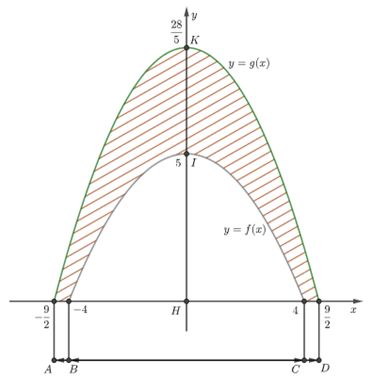
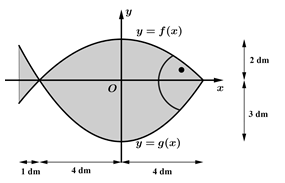
Câu 20 [392145]: Hoạ sĩ thiết kế logo hình con cá cho một doanh nghiệp kinh doanh hải sản. Logo là hình phẳng giới hạn bởi hai parabol với các kích thước được cho trong Hình vẽ bên (đơn vị trên mỗi trục toạ độ là decimét). Diện tích logo là bao nhiêu  Kết quả làm tròn đến hàng đơn vị.
Kết quả làm tròn đến hàng đơn vị.
 Kết quả làm tròn đến hàng đơn vị.
Kết quả làm tròn đến hàng đơn vị.
Dựa vào đồ thị, ta có diện tích logo là diện tích được giới hạn bởi hai đường parabol 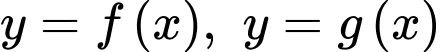 và hai đường thẳng
và hai đường thẳng 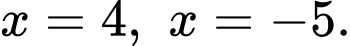 Quan sát đồ thị, ta thấy +) Parabol
Quan sát đồ thị, ta thấy +) Parabol 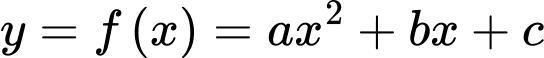 đi qua 3 điểm
đi qua 3 điểm 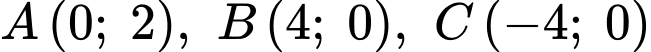
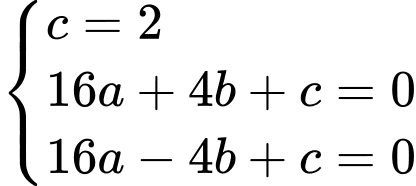
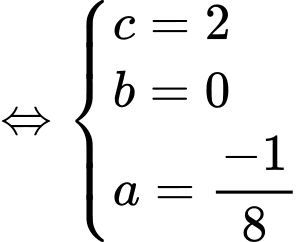
+) Parabol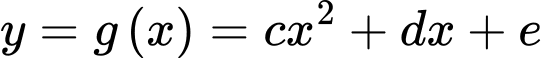 đi qua 3 điểm
đi qua 3 điểm 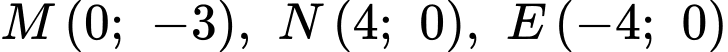
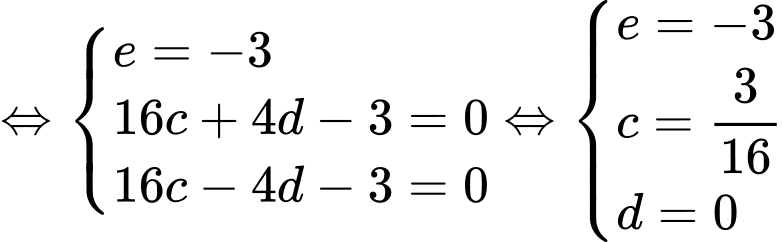
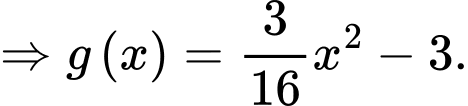
Vậy diện tích logo bằng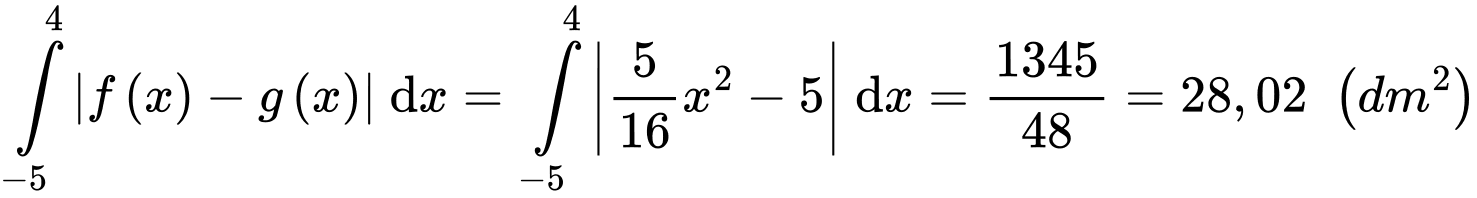
Điền đáp án: 28
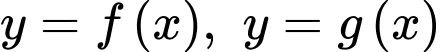 và hai đường thẳng
và hai đường thẳng 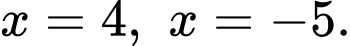 Quan sát đồ thị, ta thấy +) Parabol
Quan sát đồ thị, ta thấy +) Parabol 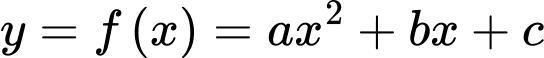 đi qua 3 điểm
đi qua 3 điểm 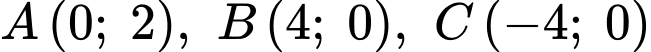
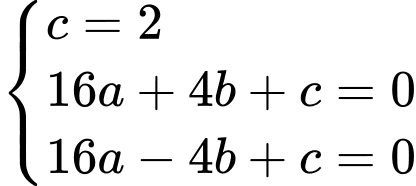
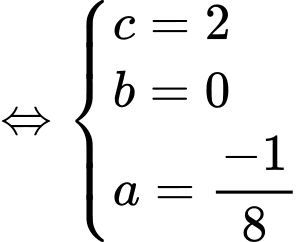
+) Parabol
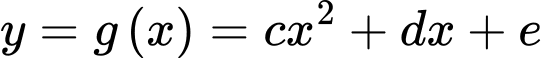 đi qua 3 điểm
đi qua 3 điểm 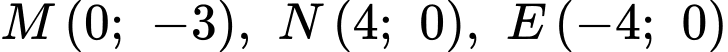
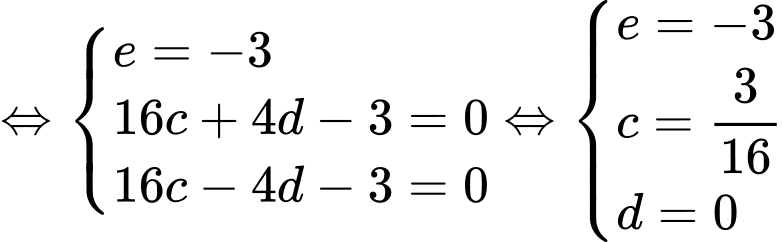
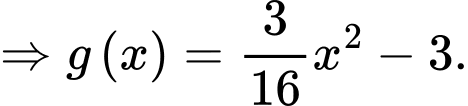
Vậy diện tích logo bằng
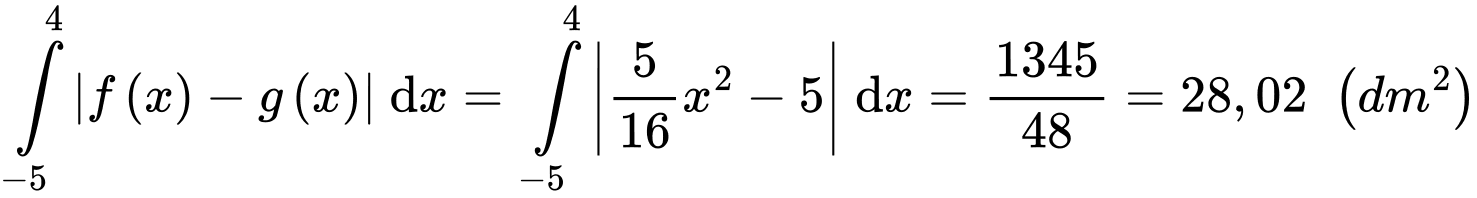
Điền đáp án: 28
Câu 21 [151405]: Trên bức tường cần trang trí một hình phẳng dạng parabol đỉnh 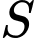 như hình vẽ, biết
như hình vẽ, biết
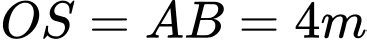 ,
,  là trung điểm
là trung điểm  , parabol được chia thành ba phần để sơn ba màu khác nhau với mức chi phí: phần trên là phần kẻ sọc
, parabol được chia thành ba phần để sơn ba màu khác nhau với mức chi phí: phần trên là phần kẻ sọc  đồng/
đồng/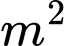 , phần giữa là hình quạt tâm
, phần giữa là hình quạt tâm  , bán kính
, bán kính 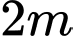 được tô đậm
được tô đậm  đồng/
đồng/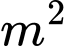 , phần còn lại
, phần còn lại  đồng/
đồng/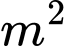 . Tổng chi phí để sơn cả 3 phần là bao nhiêu nghìn đồng. Kết quả làm tròn đến hàng đơn vị của nghìn đồng.
. Tổng chi phí để sơn cả 3 phần là bao nhiêu nghìn đồng. Kết quả làm tròn đến hàng đơn vị của nghìn đồng.
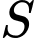 như hình vẽ, biết
như hình vẽ, biết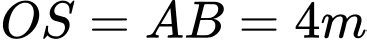 ,
,  là trung điểm
là trung điểm  , parabol được chia thành ba phần để sơn ba màu khác nhau với mức chi phí: phần trên là phần kẻ sọc
, parabol được chia thành ba phần để sơn ba màu khác nhau với mức chi phí: phần trên là phần kẻ sọc  đồng/
đồng/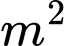 , phần giữa là hình quạt tâm
, phần giữa là hình quạt tâm  , bán kính
, bán kính 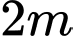 được tô đậm
được tô đậm  đồng/
đồng/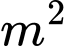 , phần còn lại
, phần còn lại  đồng/
đồng/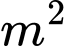 . Tổng chi phí để sơn cả 3 phần là bao nhiêu nghìn đồng. Kết quả làm tròn đến hàng đơn vị của nghìn đồng.
. Tổng chi phí để sơn cả 3 phần là bao nhiêu nghìn đồng. Kết quả làm tròn đến hàng đơn vị của nghìn đồng. A, 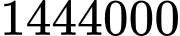 đồng.
đồng.
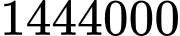 đồng.
đồng.B, 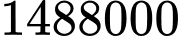 đồng.
đồng.
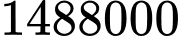 đồng.
đồng.C, 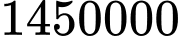 đồng.
đồng.
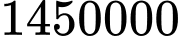 đồng.
đồng.D, 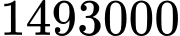 đồng.
đồng.
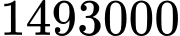 đồng.
đồng.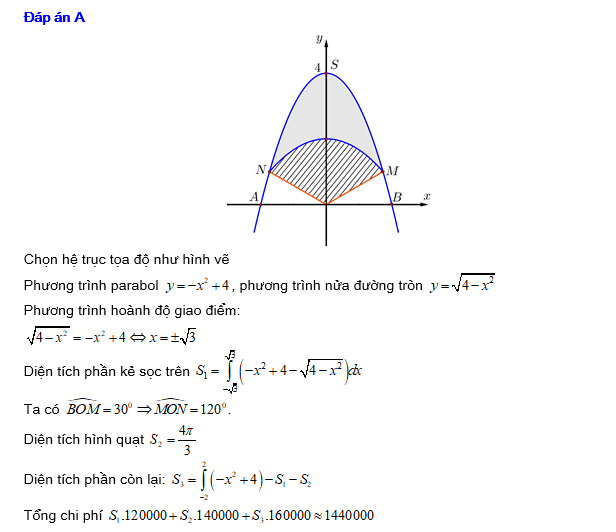 Đáp án: A
Đáp án: A