Đáp án Bài tập tự luyện
Câu 1 [57138]: Trong không gian 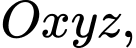 cho hai mặt phẳng
cho hai mặt phẳng  và
và 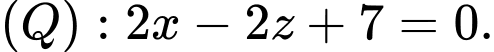 Góc giữa hai mặt phẳng
Góc giữa hai mặt phẳng 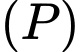 và
và  là
là
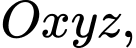 cho hai mặt phẳng
cho hai mặt phẳng  và
và 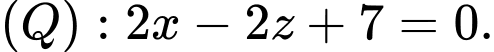 Góc giữa hai mặt phẳng
Góc giữa hai mặt phẳng 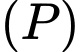 và
và  là
là A, 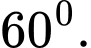
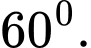
B, 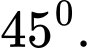
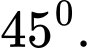
C, 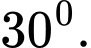
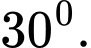
D, 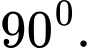
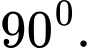
Chọn đáp án A.
Các vtpt của hai mặt phẳng là: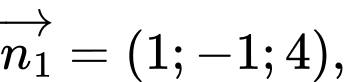
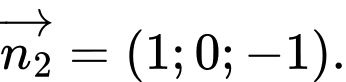 Gọi
Gọi 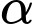 là góc giữa hai mặt phẳng.
là góc giữa hai mặt phẳng.
Ta có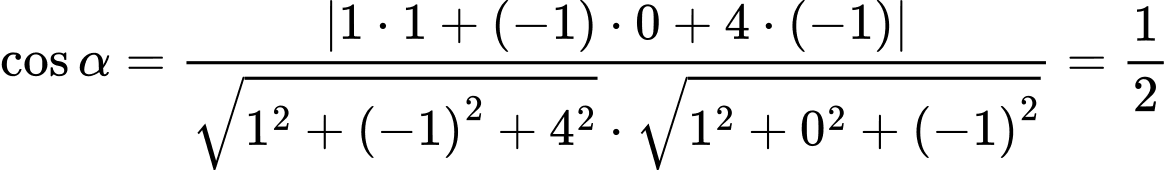
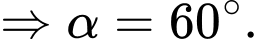 Đáp án: A
Đáp án: A
Các vtpt của hai mặt phẳng là:
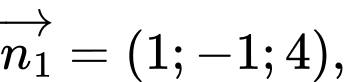
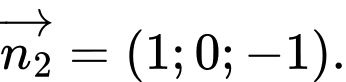 Gọi
Gọi 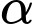 là góc giữa hai mặt phẳng.
là góc giữa hai mặt phẳng.
Ta có
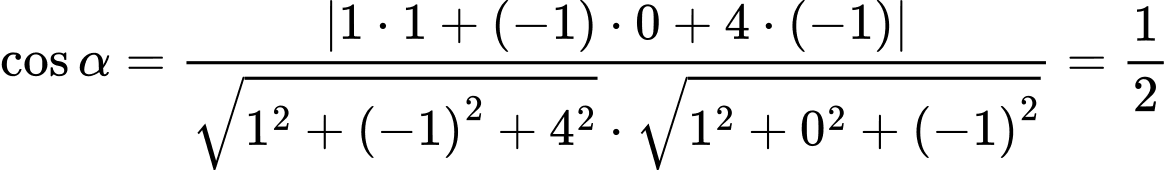
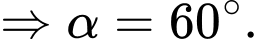 Đáp án: A
Đáp án: A
Câu 2 [57135]: Trong không gian với hệ toạ độ 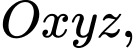 cho mặt phẳng
cho mặt phẳng 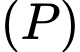 có phương trình là
có phương trình là  . Tính góc giữa
. Tính góc giữa 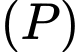 và mặt phẳng
và mặt phẳng 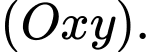
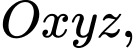 cho mặt phẳng
cho mặt phẳng 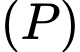 có phương trình là
có phương trình là  . Tính góc giữa
. Tính góc giữa 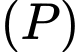 và mặt phẳng
và mặt phẳng 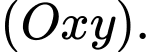
A, 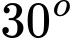 .
.
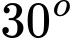 .
.B, 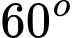 .
.
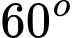 .
.C, 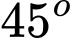 .
.
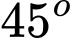 .
.D, 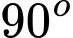 .
.
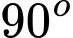 .
.
Chọn đáp án C.
Vectơ pháp tuyến của mặt phẳng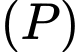 là
là 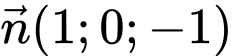
Vectơ pháp tuyến của mặt phẳng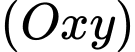 là
là 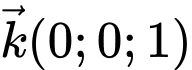
Gọi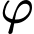 là góc hợp bởi mặt phẳng
là góc hợp bởi mặt phẳng 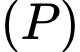 và mặt phảng
và mặt phảng 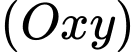
Ta có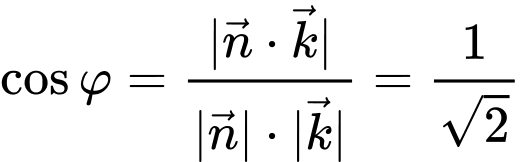
Vậy góc hợp bời mặt phẳng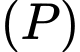 mặt phả̉ng
mặt phả̉ng 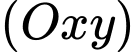 là
là 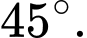 Đáp án: C
Đáp án: C
Vectơ pháp tuyến của mặt phẳng
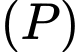 là
là 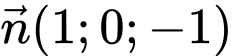
Vectơ pháp tuyến của mặt phẳng
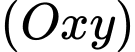 là
là 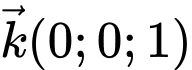
Gọi
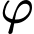 là góc hợp bởi mặt phẳng
là góc hợp bởi mặt phẳng 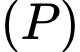 và mặt phảng
và mặt phảng 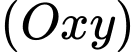
Ta có
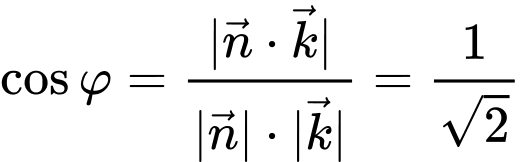
Vậy góc hợp bời mặt phẳng
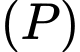 mặt phả̉ng
mặt phả̉ng 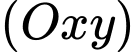 là
là 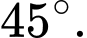 Đáp án: C
Đáp án: C
Câu 3 [57254]: Trong không gian với hệ tọa độ 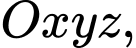 số đo của góc tạo bởi hai đường thẳng
số đo của góc tạo bởi hai đường thẳng 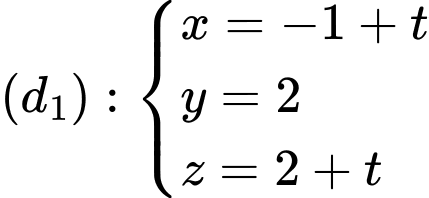 và
và 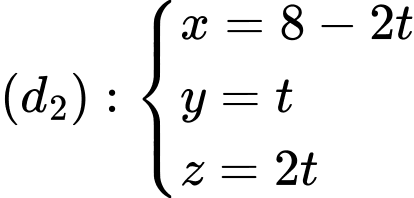 là
là
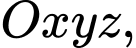 số đo của góc tạo bởi hai đường thẳng
số đo của góc tạo bởi hai đường thẳng 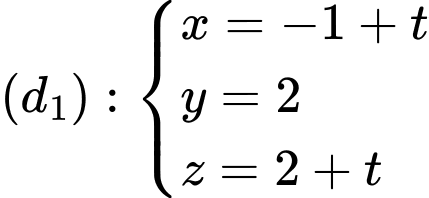 và
và 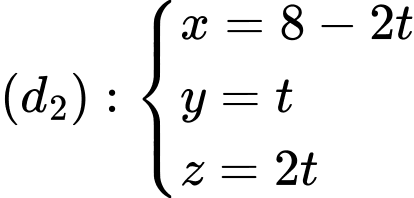 là
là A, 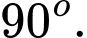
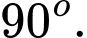
B, 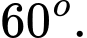
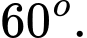
C, 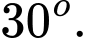
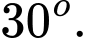
D, 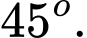
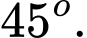
Chọn đáp án A.
Ta có vectơ chỉ phương của đường thẳng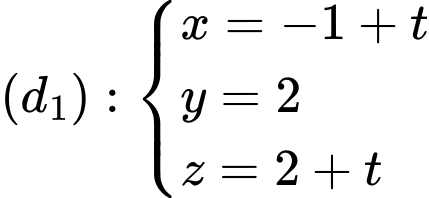 và
và 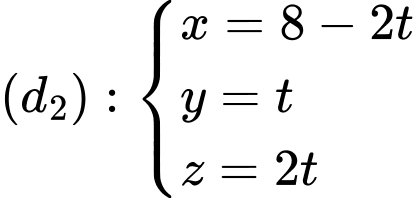 lần lượt là
lần lượt là 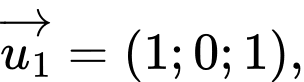
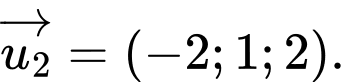
Suy ra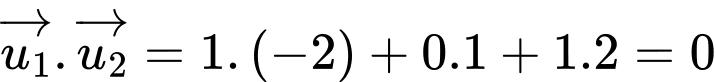
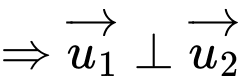 nên góc giữa hai đường thẳng
nên góc giữa hai đường thẳng 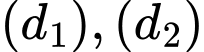 bằng
bằng 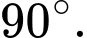 Đáp án: A
Đáp án: A
Ta có vectơ chỉ phương của đường thẳng
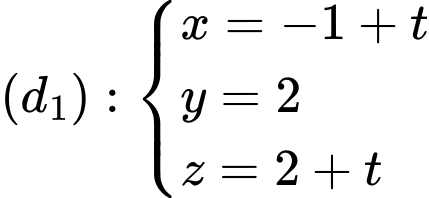 và
và 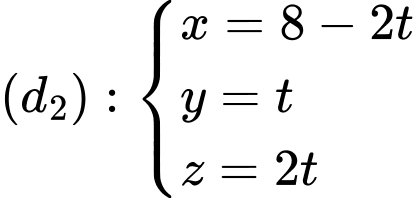 lần lượt là
lần lượt là 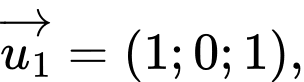
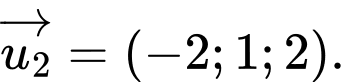
Suy ra
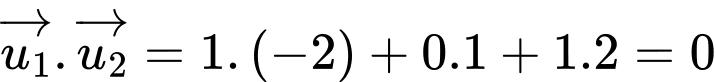
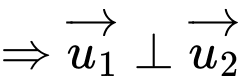 nên góc giữa hai đường thẳng
nên góc giữa hai đường thẳng 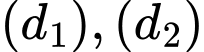 bằng
bằng 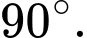 Đáp án: A
Đáp án: A
Câu 4 [57256]: Trong không gian với hệ tọa độ 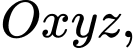 cho hai đường thẳng
cho hai đường thẳng 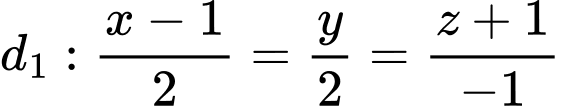 và
và 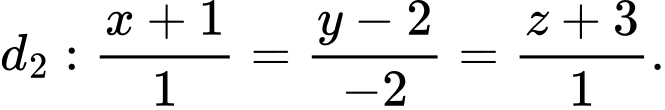 Tính côsin của góc giữa hai đường thẳng
Tính côsin của góc giữa hai đường thẳng 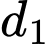 và
và 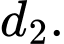
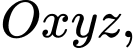 cho hai đường thẳng
cho hai đường thẳng 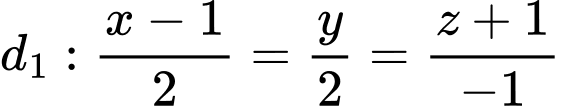 và
và 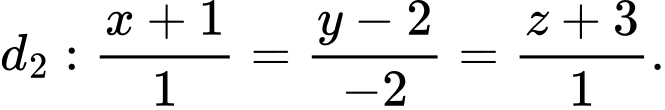 Tính côsin của góc giữa hai đường thẳng
Tính côsin của góc giữa hai đường thẳng 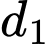 và
và 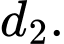
A, 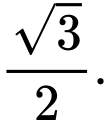
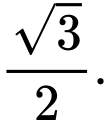
B, 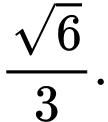
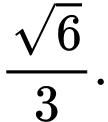
C, 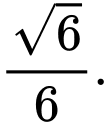
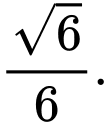
D, 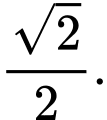
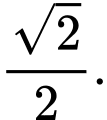
HD: Gọi 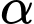 là góc giữa hai đường thẳng
là góc giữa hai đường thẳng 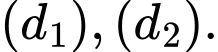
Ta có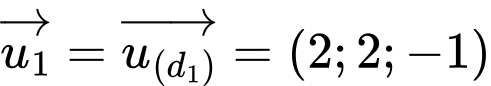 và
và 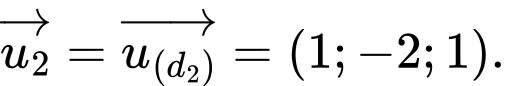
Khi đó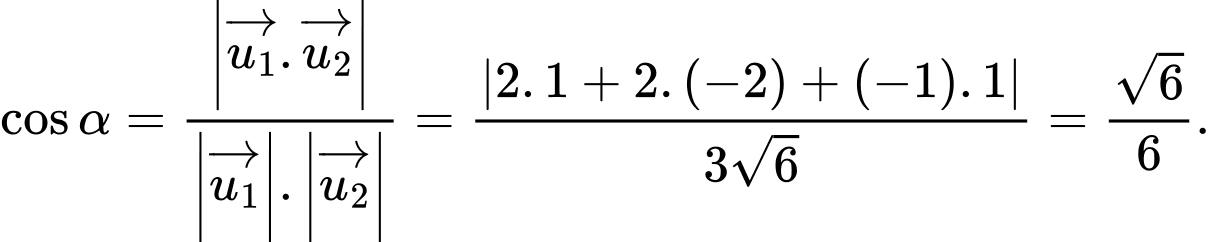 Chọn C. Đáp án: C
Chọn C. Đáp án: C
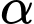 là góc giữa hai đường thẳng
là góc giữa hai đường thẳng 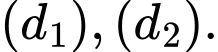
Ta có
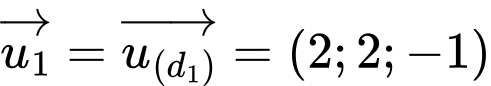 và
và 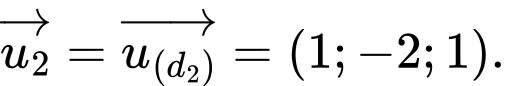
Khi đó
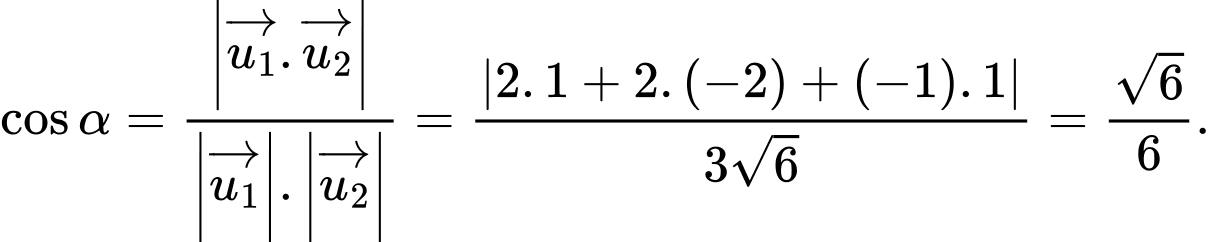 Chọn C. Đáp án: C
Chọn C. Đáp án: C
Câu 5 [57289]: Trong không gian tọa độ 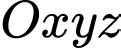 cho đường thẳng
cho đường thẳng 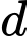 và mặt phẳng
và mặt phẳng 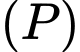
 Gọi
Gọi 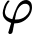 là góc giữa
là góc giữa 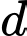 và
và 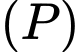
 Khẳng định nào sau đây là đúng?
Khẳng định nào sau đây là đúng?
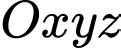 cho đường thẳng
cho đường thẳng 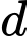 và mặt phẳng
và mặt phẳng 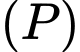
 Gọi
Gọi 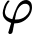 là góc giữa
là góc giữa 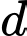 và
và 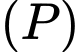
 Khẳng định nào sau đây là đúng?
Khẳng định nào sau đây là đúng? A, 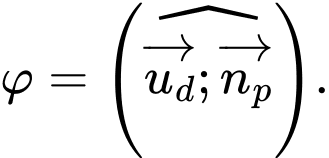
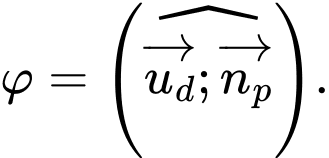
B, 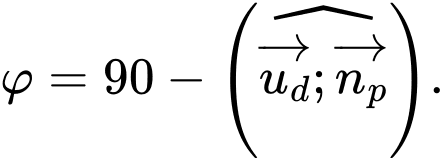
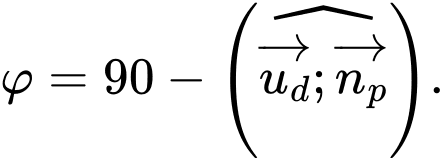
C, 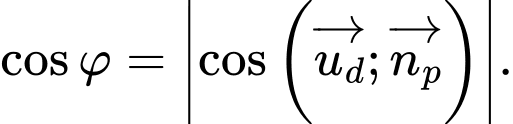
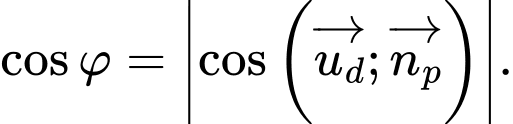
D, 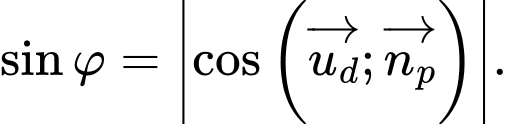
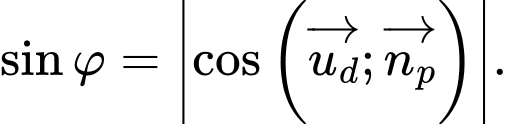
Theo công thức tính góc giữa đường thẳng và mặt phẳng ta có: 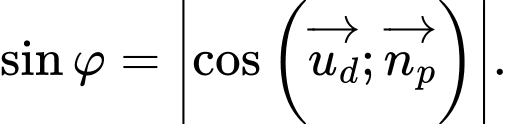 Chọn D. Đáp án: D
Chọn D. Đáp án: D
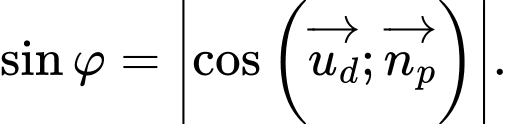 Chọn D. Đáp án: D
Chọn D. Đáp án: D
Câu 6 [57261]: Trong không gian với hệ trục tọa độ 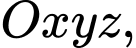 cho hình lăng trụ đứng
cho hình lăng trụ đứng  có
có 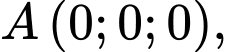
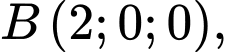
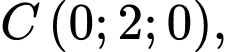
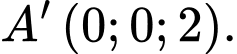 Góc giữa
Góc giữa 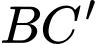 và
và 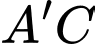 bằng
bằng
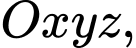 cho hình lăng trụ đứng
cho hình lăng trụ đứng  có
có 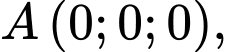
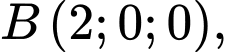
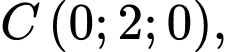
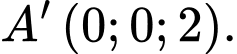 Góc giữa
Góc giữa 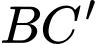 và
và 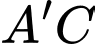 bằng
bằng A, 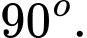
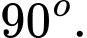
B, 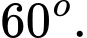
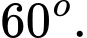
C, 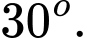
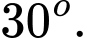
D, 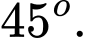
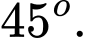
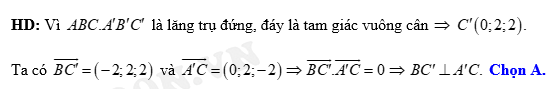 Đáp án: A
Đáp án: A
Câu 7 [57274]: Trong không gian với hệ tọa độ 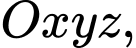 cho đường thẳng
cho đường thẳng 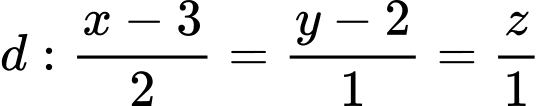 và mặt phẳng
và mặt phẳng 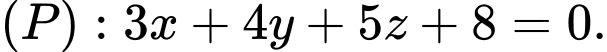 Góc giữa đường thẳng
Góc giữa đường thẳng 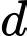 và mặt phẳng
và mặt phẳng 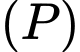 có số đo là
có số đo là
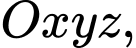 cho đường thẳng
cho đường thẳng 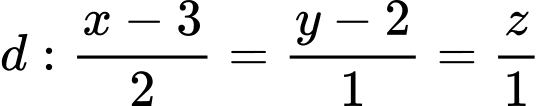 và mặt phẳng
và mặt phẳng 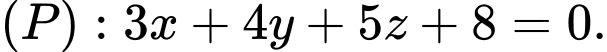 Góc giữa đường thẳng
Góc giữa đường thẳng 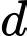 và mặt phẳng
và mặt phẳng 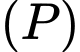 có số đo là
có số đo là A, 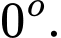
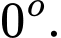
B, 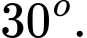
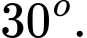
C, 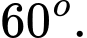
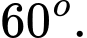
D, 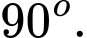
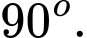
Chọn đáp án C.
Gọi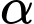 là góc giữa đường thẳng
là góc giữa đường thẳng 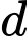 và mặt phẳng
và mặt phẳng 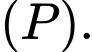 Ta có
Ta có 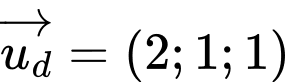 và
và 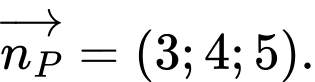
Khi đó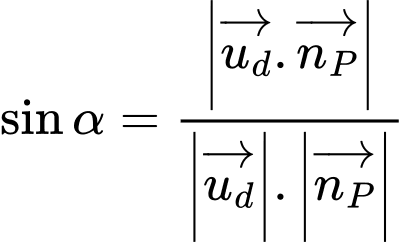
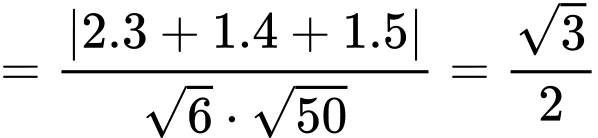
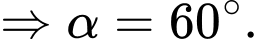 Đáp án: C
Đáp án: C
Gọi
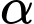 là góc giữa đường thẳng
là góc giữa đường thẳng 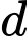 và mặt phẳng
và mặt phẳng 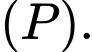 Ta có
Ta có 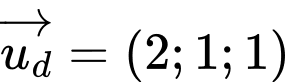 và
và 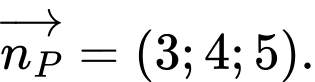
Khi đó
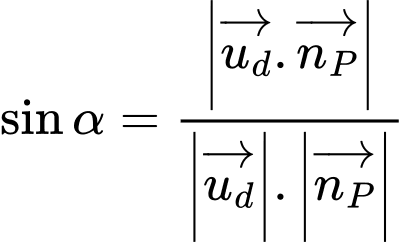
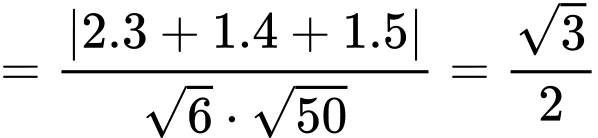
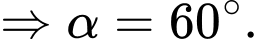 Đáp án: C
Đáp án: C
Câu 8 [57282]: Trong không gian với hệ trục tọa độ 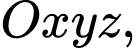 cho mặt phẳng
cho mặt phẳng 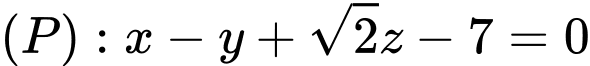 và đường thẳng
và đường thẳng 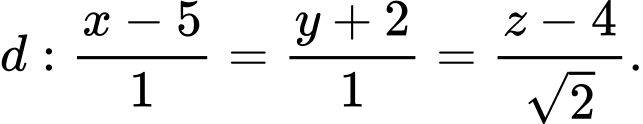 Góc giữa đường thẳng
Góc giữa đường thẳng 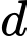 và mặt phẳng
và mặt phẳng 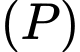 là
là
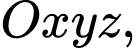 cho mặt phẳng
cho mặt phẳng 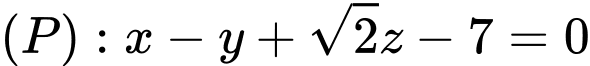 và đường thẳng
và đường thẳng 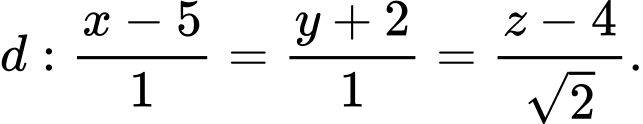 Góc giữa đường thẳng
Góc giữa đường thẳng 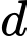 và mặt phẳng
và mặt phẳng 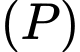 là
là A, 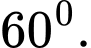
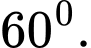
B, 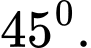
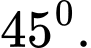
C, 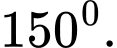
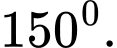
D, 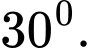
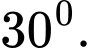
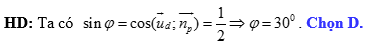 Đáp án: D
Đáp án: D
Câu 9 [899530]: Trong không gian 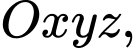 cho mặt phẳng
cho mặt phẳng 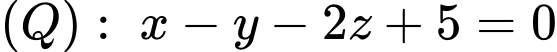 và điểm
và điểm 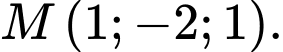 Khoảng cách từ điểm
Khoảng cách từ điểm 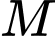 đến mặt phẳng
đến mặt phẳng  bằng
bằng
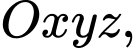 cho mặt phẳng
cho mặt phẳng 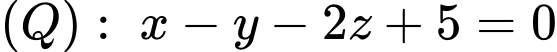 và điểm
và điểm 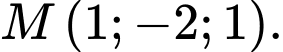 Khoảng cách từ điểm
Khoảng cách từ điểm 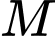 đến mặt phẳng
đến mặt phẳng  bằng
bằng A, 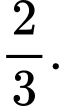
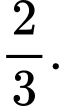
B, 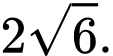
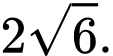
C, 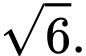
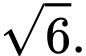
D, 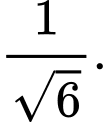
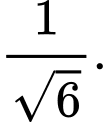
Áp dụng công thức ta có: 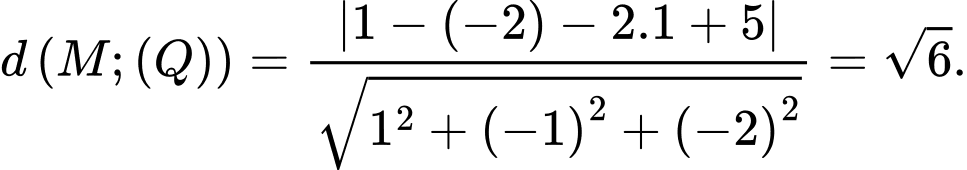 Chọn C. Đáp án: C
Chọn C. Đáp án: C
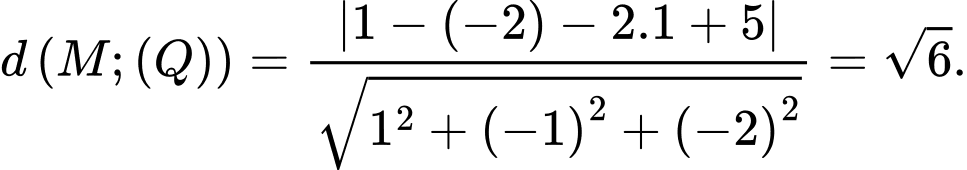 Chọn C. Đáp án: C
Chọn C. Đáp án: C
Câu 10 [57293]: Trong không gian 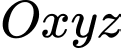 , khoảng cách từ điểm
, khoảng cách từ điểm 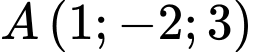 đến
đến 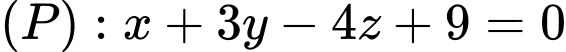 là
là
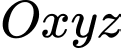 , khoảng cách từ điểm
, khoảng cách từ điểm 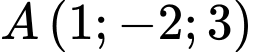 đến
đến 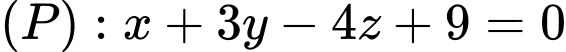 là
là A, 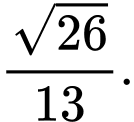
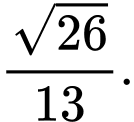
B, 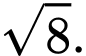
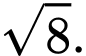
C, 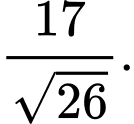
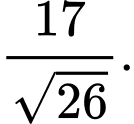
D, 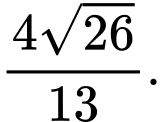
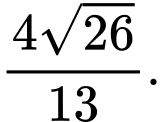
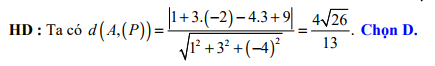 Đáp án: D
Đáp án: D
Câu 11 [57309]: Trong không gian 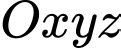 cho mặt phẳng
cho mặt phẳng 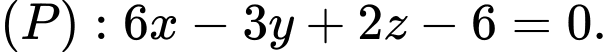 Tính khoảng cách
Tính khoảng cách 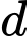 từ điểm
từ điểm 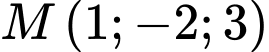 đến mặt phẳng
đến mặt phẳng 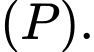
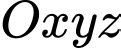 cho mặt phẳng
cho mặt phẳng 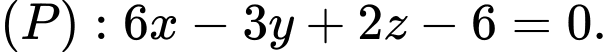 Tính khoảng cách
Tính khoảng cách 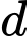 từ điểm
từ điểm 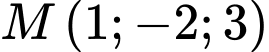 đến mặt phẳng
đến mặt phẳng 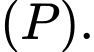
A, 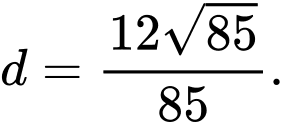
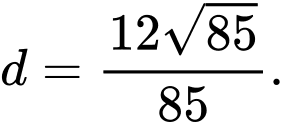
B, 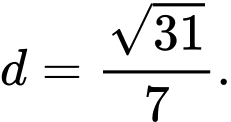
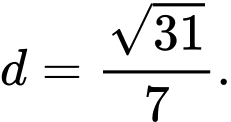
C, 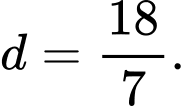
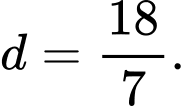
D, 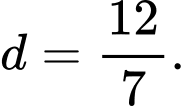
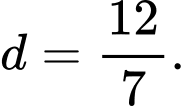
HD: Khoảng cách từ điểm 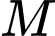 đến mặt phẳng
đến mặt phẳng 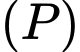 là
là 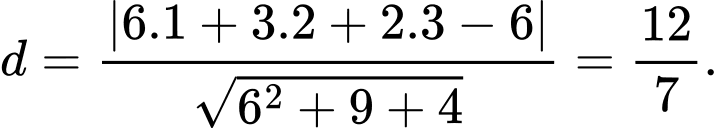 Chọn D. Đáp án: D
Chọn D. Đáp án: D
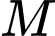 đến mặt phẳng
đến mặt phẳng 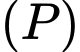 là
là 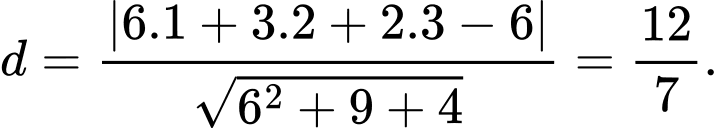 Chọn D. Đáp án: D
Chọn D. Đáp án: D
Câu 12 [360649]: Khoảng cách từ điểm 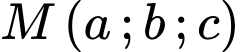 đến mặt phẳng
đến mặt phẳng 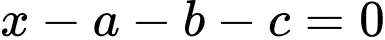 là:
là:
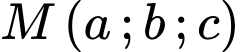 đến mặt phẳng
đến mặt phẳng 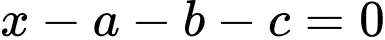 là:
là: A, 

B, 

C, 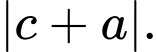
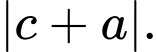
D, 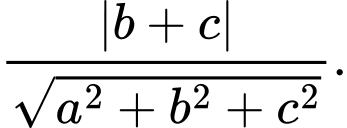
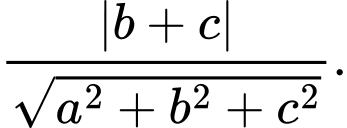
Khoảng cách từ 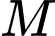 đến mặt phẳng
đến mặt phẳng 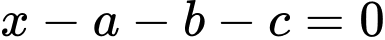 bằng
bằng
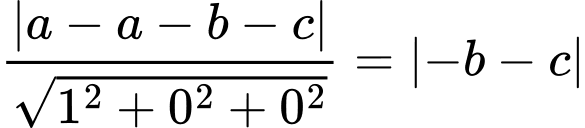
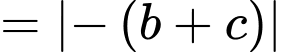
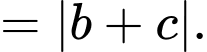 Chọn B. Đáp án: B
Chọn B. Đáp án: B
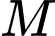 đến mặt phẳng
đến mặt phẳng 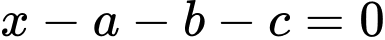 bằng
bằng 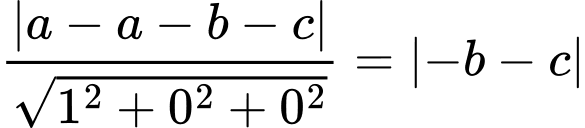
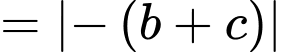
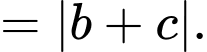 Chọn B. Đáp án: B
Chọn B. Đáp án: B
Câu 13 [322584]: Trong không gian 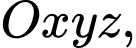 khoảng cách giữa hai mặt phẳng
khoảng cách giữa hai mặt phẳng  và
và 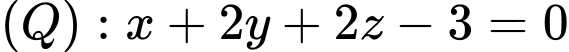 bằng
bằng
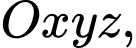 khoảng cách giữa hai mặt phẳng
khoảng cách giữa hai mặt phẳng  và
và 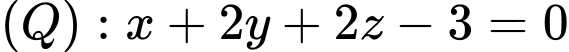 bằng
bằng A, 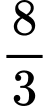
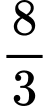
B, 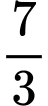
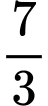
C, 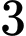
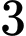
D, 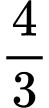
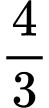
Chọn đáp án B.
Ta có: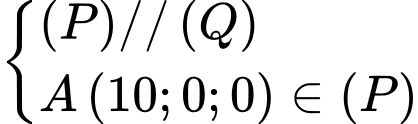
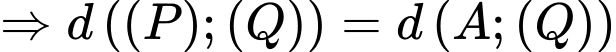
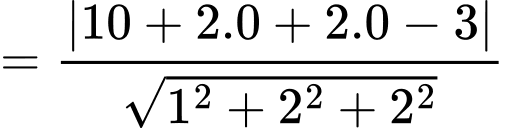
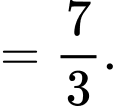 Đáp án: B
Đáp án: B
Ta có:
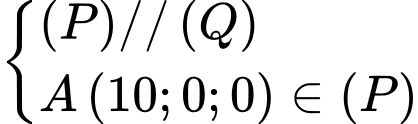
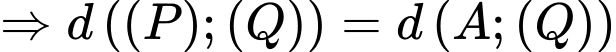
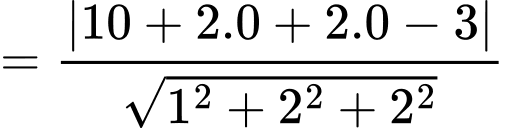
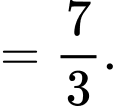 Đáp án: B
Đáp án: B
Câu 14 [899536]: Trong không gian 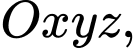 cho hai mặt phẳng song song
cho hai mặt phẳng song song 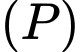 và
và  lần lượt có phương trình
lần lượt có phương trình 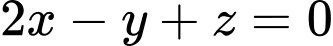 và
và 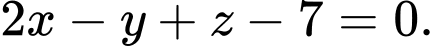 Khoảng cách giữa hai mặt phẳng
Khoảng cách giữa hai mặt phẳng 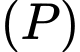 và
và  bằng
bằng
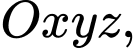 cho hai mặt phẳng song song
cho hai mặt phẳng song song 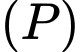 và
và  lần lượt có phương trình
lần lượt có phương trình 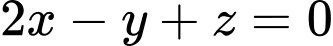 và
và 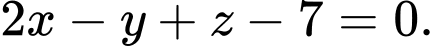 Khoảng cách giữa hai mặt phẳng
Khoảng cách giữa hai mặt phẳng 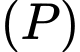 và
và  bằng
bằng A, 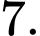
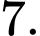
B, 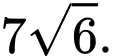
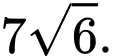
C, 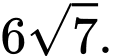
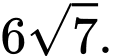
D, 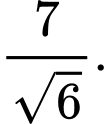
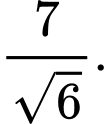
Xét 2 mặt phẳng 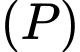 và
và  ta có:
ta có: 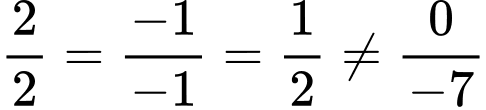 nên
nên 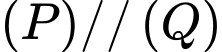 .
.
Do đó: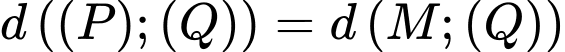 với
với 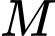 là điểm bất kì thuộc
là điểm bất kì thuộc 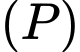 .
.
Chọn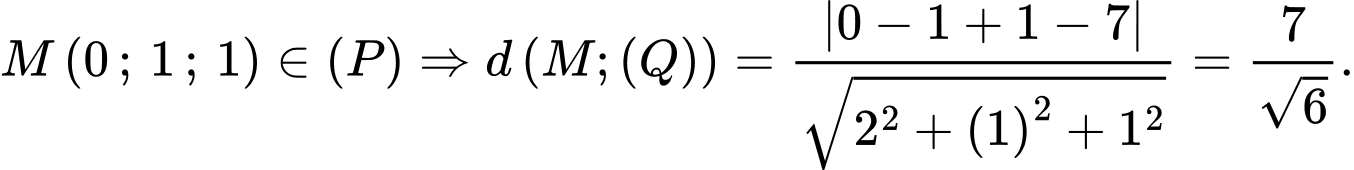 Chọn D.
Đáp án: D
Chọn D.
Đáp án: D
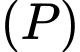 và
và  ta có:
ta có: 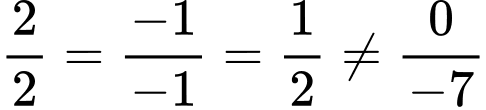 nên
nên 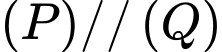 .
. Do đó:
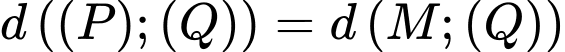 với
với 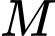 là điểm bất kì thuộc
là điểm bất kì thuộc 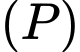 .
. Chọn
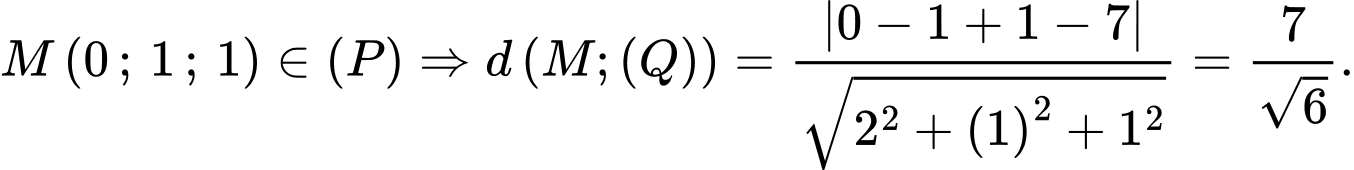 Chọn D.
Đáp án: D
Chọn D.
Đáp án: D
Câu 15 [57310]: Trong không gian tọa độ 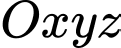 , cho
, cho 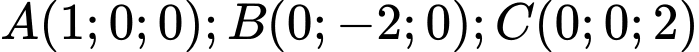 . Tính khoảng cách từ điểm
. Tính khoảng cách từ điểm  đến mặt phẳng
đến mặt phẳng 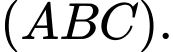
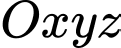 , cho
, cho 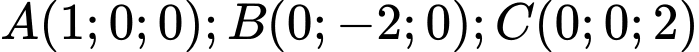 . Tính khoảng cách từ điểm
. Tính khoảng cách từ điểm  đến mặt phẳng
đến mặt phẳng 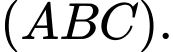
A, 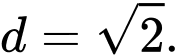
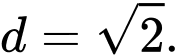
B, 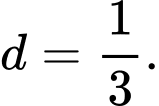
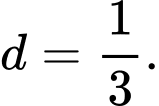
C, 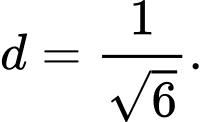
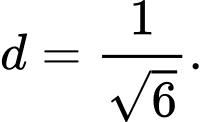
D, 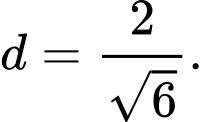
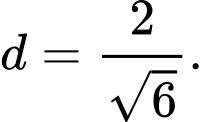
 Đáp án: D
Đáp án: D
Câu 16 [899531]: Trong không gian tọa độ 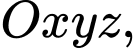 cho các điểm
cho các điểm  Khoảng cách từ gốc tọa độ
Khoảng cách từ gốc tọa độ  đến mặt phẳng
đến mặt phẳng 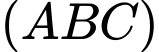 bằng
bằng
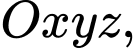 cho các điểm
cho các điểm  Khoảng cách từ gốc tọa độ
Khoảng cách từ gốc tọa độ  đến mặt phẳng
đến mặt phẳng 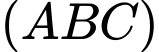 bằng
bằng A, 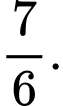
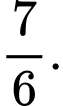
B, 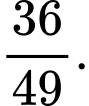
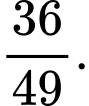
C, 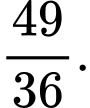
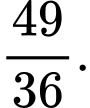
D, 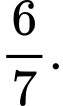
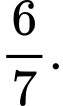
Phương trình mặt phẳng 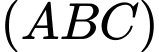 theo đoạn chắn là
theo đoạn chắn là
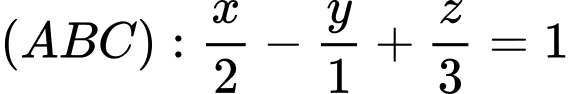 hay
hay 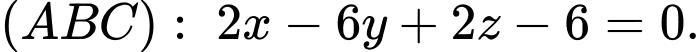
Khoảng cách từ gốc tọa độ đến mặt phẳng
đến mặt phẳng 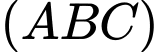 là
là 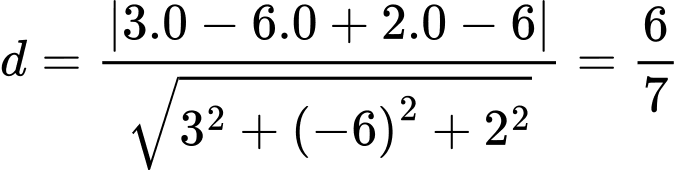 . Chọn D. Đáp án: D
. Chọn D. Đáp án: D
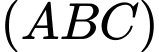 theo đoạn chắn là
theo đoạn chắn là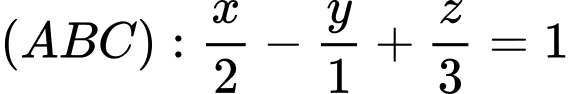 hay
hay 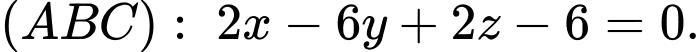
Khoảng cách từ gốc tọa độ
 đến mặt phẳng
đến mặt phẳng 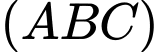 là
là 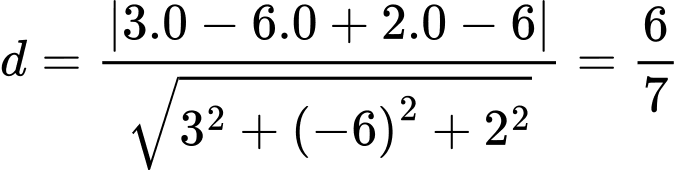 . Chọn D. Đáp án: D
. Chọn D. Đáp án: D
Câu 17 [398642]: Trong không gian 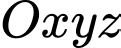 , cho các điểm
, cho các điểm 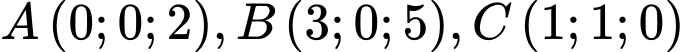 và
và 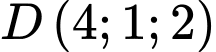 . Khoảng cách từ
. Khoảng cách từ 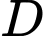 đến mặt phẳng
đến mặt phẳng 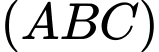 bằng
bằng
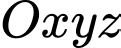 , cho các điểm
, cho các điểm 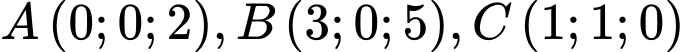 và
và 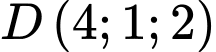 . Khoảng cách từ
. Khoảng cách từ 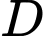 đến mặt phẳng
đến mặt phẳng 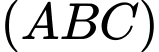 bằng
bằng A,  .
.
 .
. B, 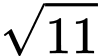 .
.
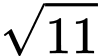 .
.C, 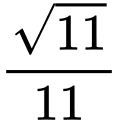 .
.
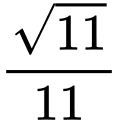 .
.D, 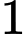 .
.
 .
.
Ta có 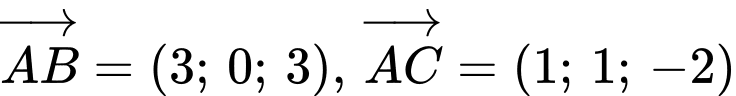 Mặt phẳng
Mặt phẳng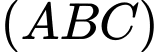 có vectơ pháp tuyến
có vectơ pháp tuyến 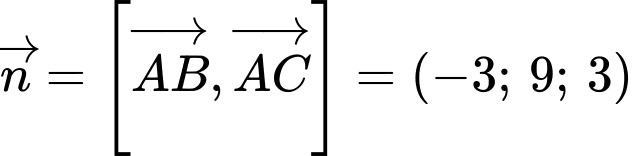 Phương trình mặt phẳng
Phương trình mặt phẳng 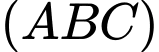 là :
là : 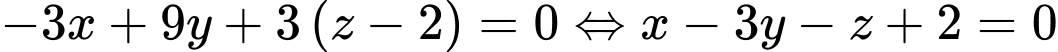 Khoảng cách từ
Khoảng cách từ 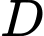 đến mặt phẳng
đến mặt phẳng 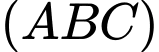 là
là
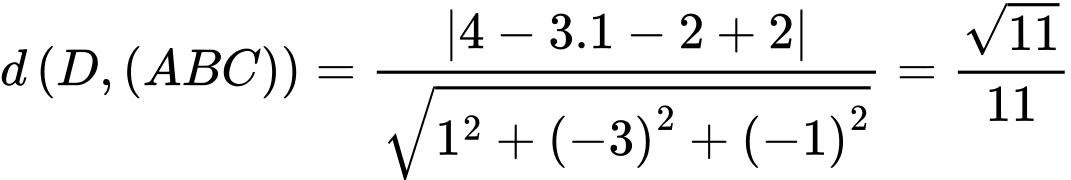 . Đáp án: C
. Đáp án: C
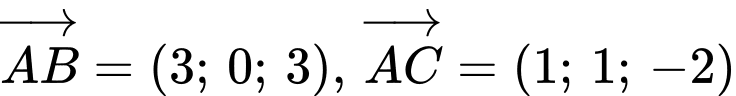 Mặt phẳng
Mặt phẳng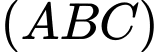 có vectơ pháp tuyến
có vectơ pháp tuyến 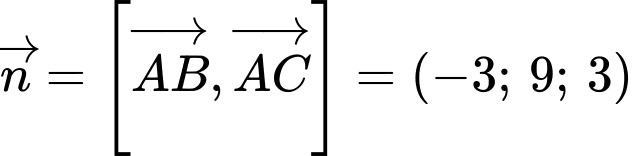 Phương trình mặt phẳng
Phương trình mặt phẳng 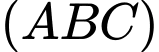 là :
là : 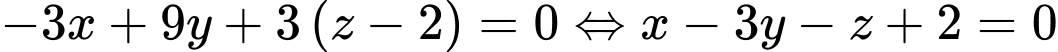 Khoảng cách từ
Khoảng cách từ 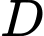 đến mặt phẳng
đến mặt phẳng 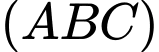 là
là
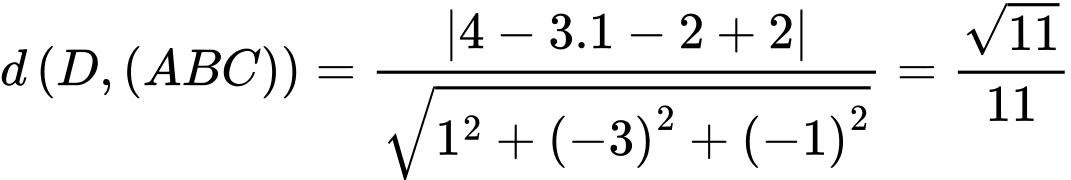 . Đáp án: C
. Đáp án: C
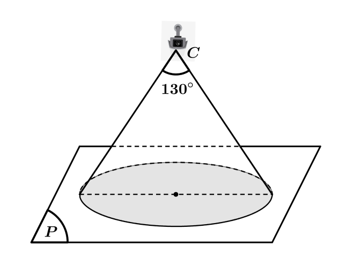
Câu 18 [408111]: Góc quan sát ngang của một camera là 130°. Trong không gian Oxyz, camera được đặt tại điểm 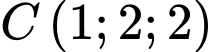 và chiếu thẳng về phía mặt phẳng
và chiếu thẳng về phía mặt phẳng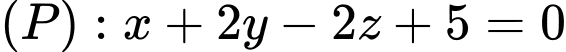 . Hỏi vùng quan sát được trên mặt phẳng (P) của camera là hình tròn có diện tích bằng bao nhiêu? (Làm tròn kết quả đến chữ số thập phân thứ nhất).
. Hỏi vùng quan sát được trên mặt phẳng (P) của camera là hình tròn có diện tích bằng bao nhiêu? (Làm tròn kết quả đến chữ số thập phân thứ nhất).
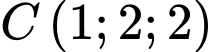 và chiếu thẳng về phía mặt phẳng
và chiếu thẳng về phía mặt phẳng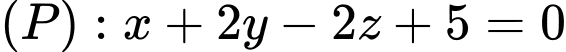 . Hỏi vùng quan sát được trên mặt phẳng (P) của camera là hình tròn có diện tích bằng bao nhiêu? (Làm tròn kết quả đến chữ số thập phân thứ nhất).
. Hỏi vùng quan sát được trên mặt phẳng (P) của camera là hình tròn có diện tích bằng bao nhiêu? (Làm tròn kết quả đến chữ số thập phân thứ nhất).
A, 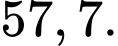
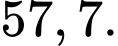
B, 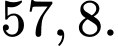
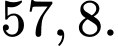
C, 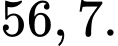
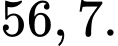
D, 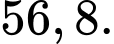
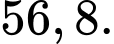
Chọn B.
Khoảng cách từ điểm C tới mặt phẳng (P) là
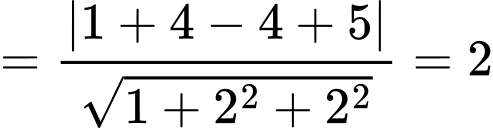
Khoảng cách từ điểm C tới mặt phẳng (P) là

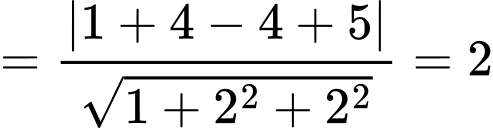
Vùng quan sát là diện tích hình tròn tâm H bán kính HA và vùng quan sát có diện tích
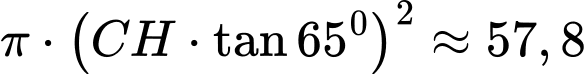 .
.
Đáp án: B 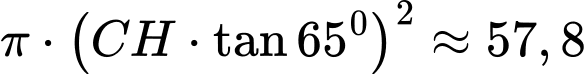 .
.