Đáp án Bài tập tự luyện
Câu 1 [80335]: Tính bán kính mặt cầu đi qua 4 điểm 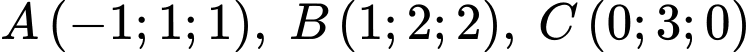 và
và 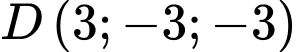
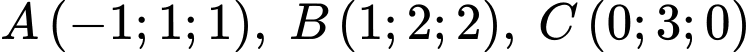 và
và 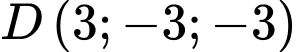
A, 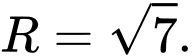
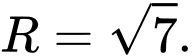
B, 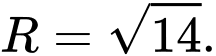
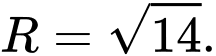
C, 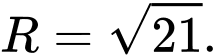
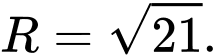
D, 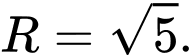
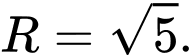
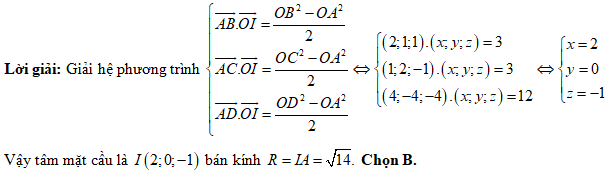 Đáp án: B
Đáp án: B
Câu 2 [57462]: Trong không gian với hệ tọa độ 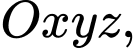 cho các điểm
cho các điểm 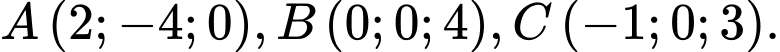 Phương trình mặt cầu ngoại tiếp tứ diện
Phương trình mặt cầu ngoại tiếp tứ diện 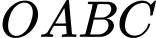 là
là
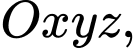 cho các điểm
cho các điểm 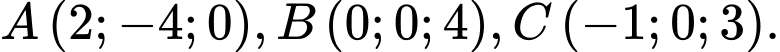 Phương trình mặt cầu ngoại tiếp tứ diện
Phương trình mặt cầu ngoại tiếp tứ diện 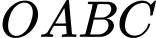 là
là A, 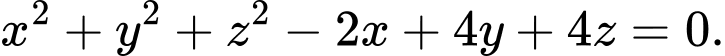
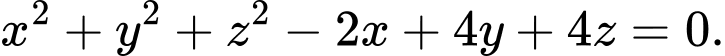
B, 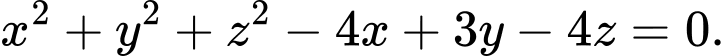
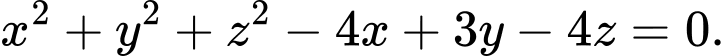
C, 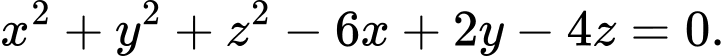
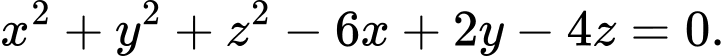
D, 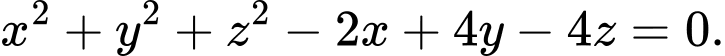
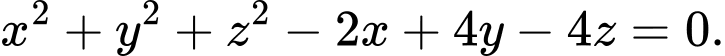
 Đáp án: D
Đáp án: D
Câu 3 [80354]: Trong không gian tọa độ 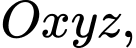 tính bán kính mặt cầu
tính bán kính mặt cầu 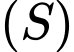 đi qua 3 điểm
đi qua 3 điểm
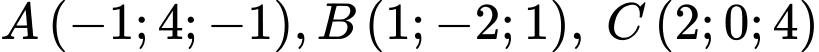 và có tâm thuộc mặt phẳng
và có tâm thuộc mặt phẳng 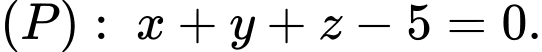
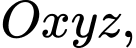 tính bán kính mặt cầu
tính bán kính mặt cầu 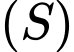 đi qua 3 điểm
đi qua 3 điểm
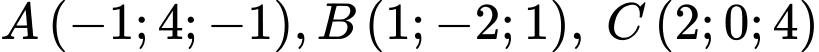 và có tâm thuộc mặt phẳng
và có tâm thuộc mặt phẳng 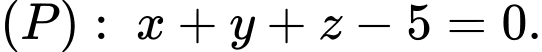
A, 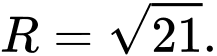
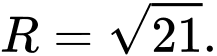
B, 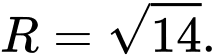
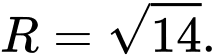
C, 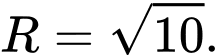
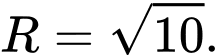
D, 

 Đáp án: A
Đáp án: A
Câu 4 [58176]: Trong không gian với hệ tọa độ 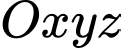 , phương trình nào dưới đây là phương trình mặt cầu đi qua ba điểm
, phương trình nào dưới đây là phương trình mặt cầu đi qua ba điểm 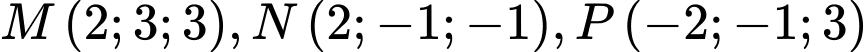 và có tâm thuộc mặt phẳng
và có tâm thuộc mặt phẳng 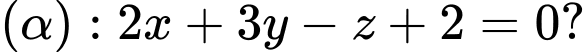
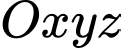 , phương trình nào dưới đây là phương trình mặt cầu đi qua ba điểm
, phương trình nào dưới đây là phương trình mặt cầu đi qua ba điểm 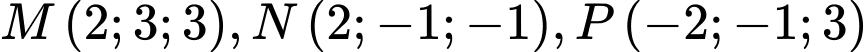 và có tâm thuộc mặt phẳng
và có tâm thuộc mặt phẳng 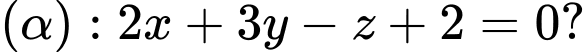
A, 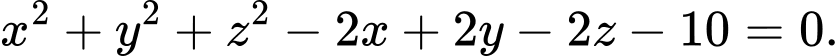
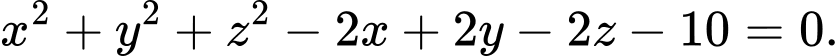
B, 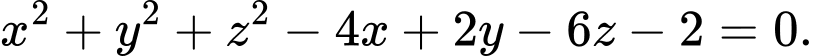
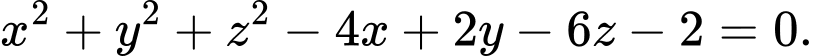
C, 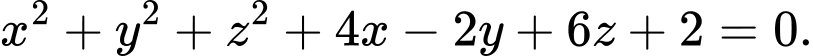
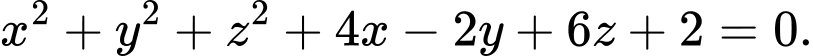
D, 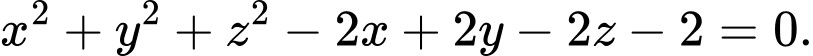
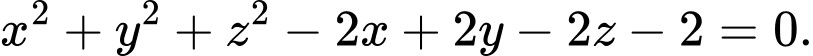
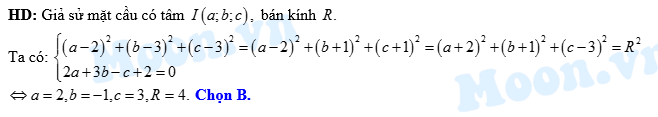 Đáp án: B
Đáp án: B
Câu 5 [57474]: Trong không gian với hệ tọa độ 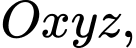 mặt cầu
mặt cầu 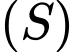 đi qua
đi qua 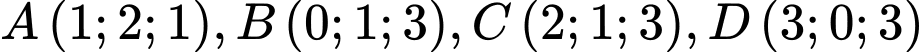 có phương trình là
có phương trình là
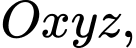 mặt cầu
mặt cầu 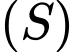 đi qua
đi qua 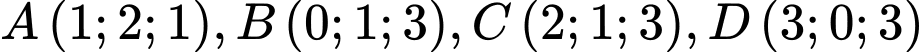 có phương trình là
có phương trình là A, 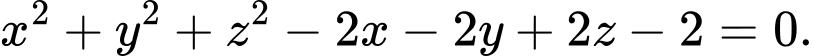
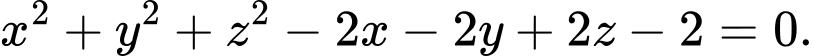
B, 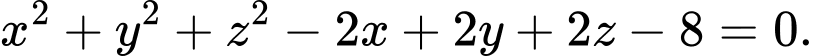
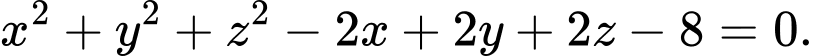
C, 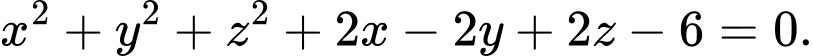
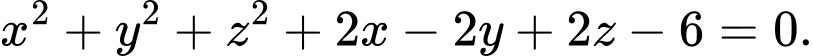
D, 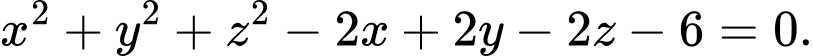
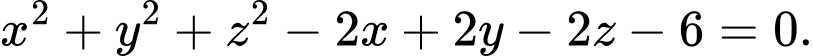
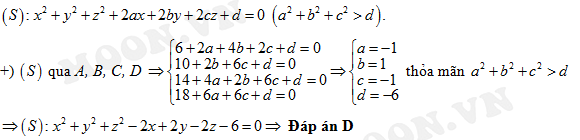 Đáp án: D
Đáp án: D
Câu 6 [57475]: Trong không gian với hệ toạ độ 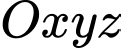 cho 4 điểm
cho 4 điểm 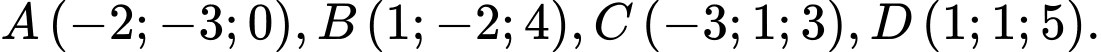 Viết phương trình mặt cầu đi qua 4 điểm
Viết phương trình mặt cầu đi qua 4 điểm 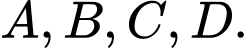
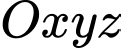 cho 4 điểm
cho 4 điểm 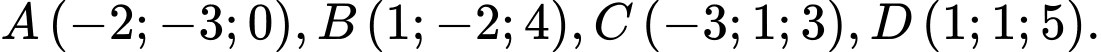 Viết phương trình mặt cầu đi qua 4 điểm
Viết phương trình mặt cầu đi qua 4 điểm 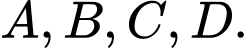
A, 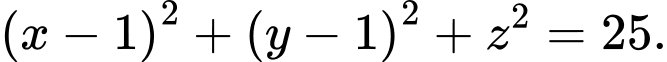
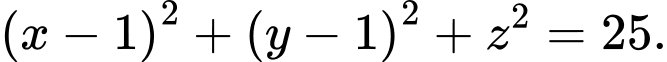
B, 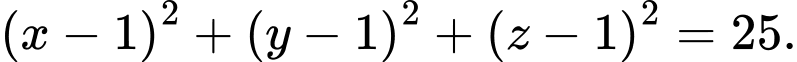
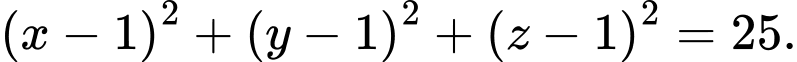
C, 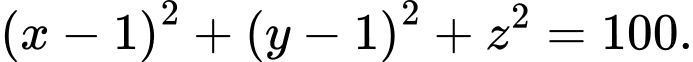
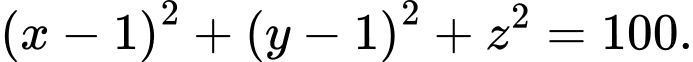
D, 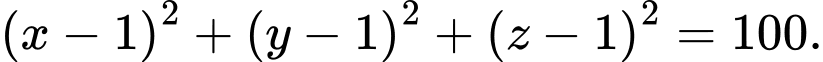
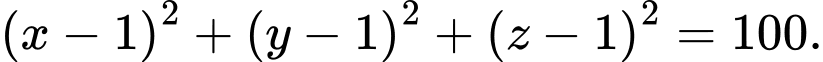
Chọn đáp án A.
Gọi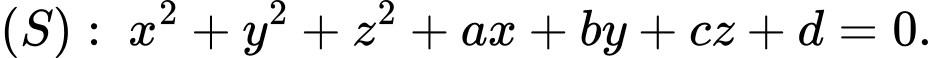
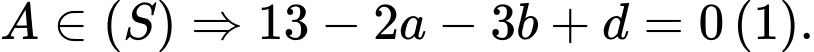
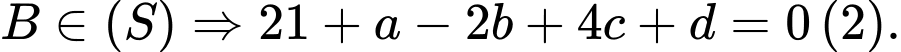
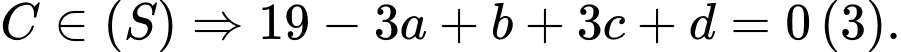

Từ (1), (2), (3) và (4) ta có: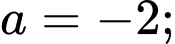
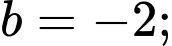
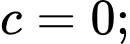
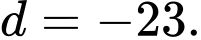
Vậy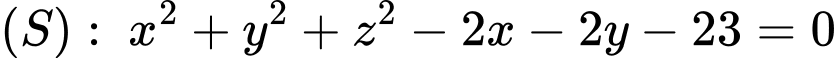 hay
hay 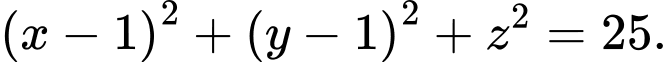 Đáp án: A
Đáp án: A
Gọi
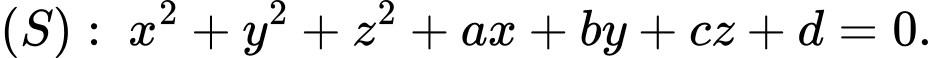
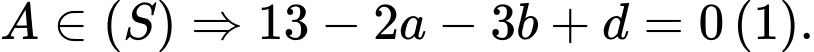
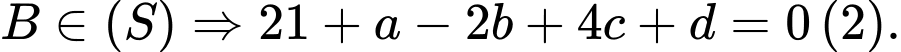
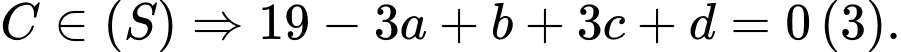

Từ (1), (2), (3) và (4) ta có:
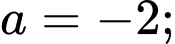
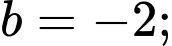
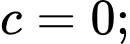
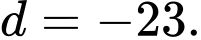
Vậy
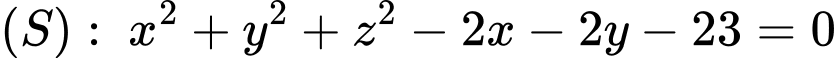 hay
hay 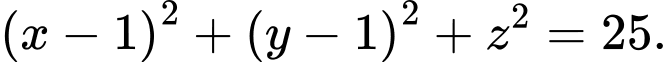 Đáp án: A
Đáp án: A
Câu 7 [57461]: Trong không gian với hệ tọa độ 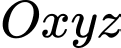 , cho tứ diện
, cho tứ diện 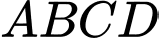 có tọa độ các đỉnh là
có tọa độ các đỉnh là 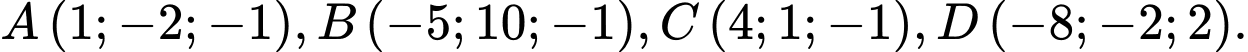 Tâm
Tâm 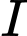 của mặt cầu ngoại tiếp tứ diện
của mặt cầu ngoại tiếp tứ diện 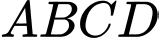 là
là
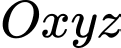 , cho tứ diện
, cho tứ diện 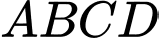 có tọa độ các đỉnh là
có tọa độ các đỉnh là 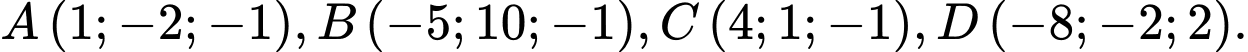 Tâm
Tâm 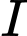 của mặt cầu ngoại tiếp tứ diện
của mặt cầu ngoại tiếp tứ diện 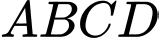 là
là A, 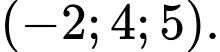
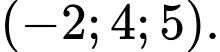
B, 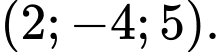
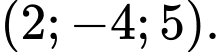
C, 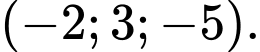
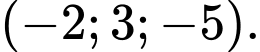
D, 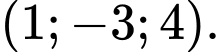
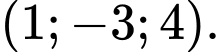
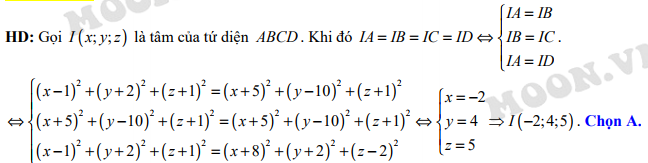 Đáp án: A
Đáp án: A
Câu 8 [57464]: Trong không gian với hệ trục tọa độ 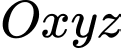 , gọi
, gọi 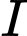 là tâm mặt cầu đi qua bốn điểm
là tâm mặt cầu đi qua bốn điểm 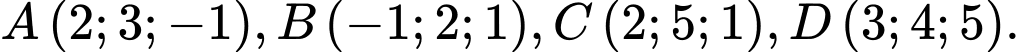 Tính độ dài đoạn thẳng
Tính độ dài đoạn thẳng 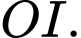
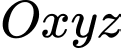 , gọi
, gọi 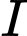 là tâm mặt cầu đi qua bốn điểm
là tâm mặt cầu đi qua bốn điểm 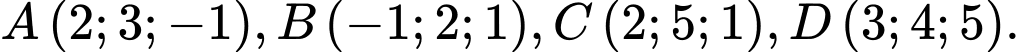 Tính độ dài đoạn thẳng
Tính độ dài đoạn thẳng 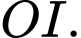
A, 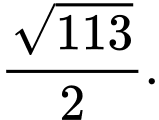
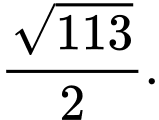
B, 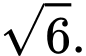
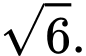
C, 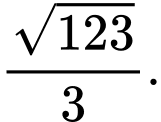
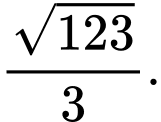
D, 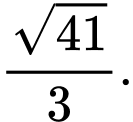
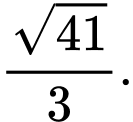
 Đáp án: C
Đáp án: C
Câu 9 [57468]: Trong không gian với hệ tọa độ 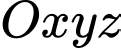 cho bốn điểm
cho bốn điểm 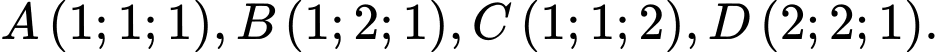 Tâm
Tâm 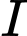 của mặt cầu ngoại tiếp tứ diện
của mặt cầu ngoại tiếp tứ diện 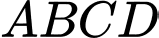 có tọa độ
có tọa độ
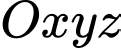 cho bốn điểm
cho bốn điểm 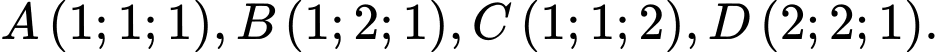 Tâm
Tâm 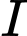 của mặt cầu ngoại tiếp tứ diện
của mặt cầu ngoại tiếp tứ diện 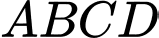 có tọa độ
có tọa độ A, 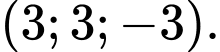
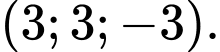
B, 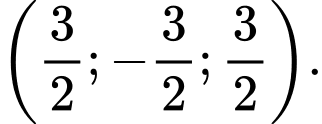
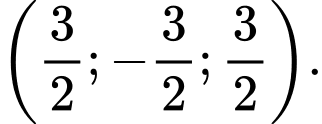
C, 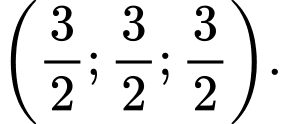
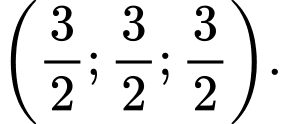
D, 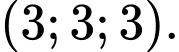
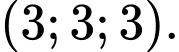
Chọn đáp án C.
Gọi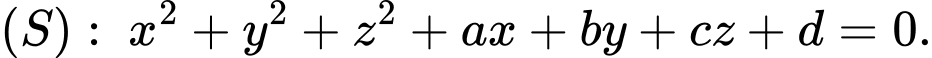

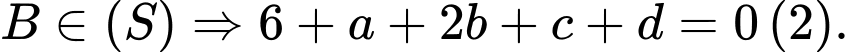
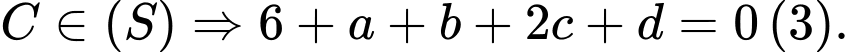

Từ (1), (2), (3) và (4) ta có: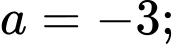
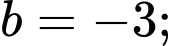
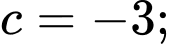

Vậy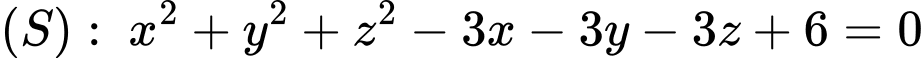 hay
hay 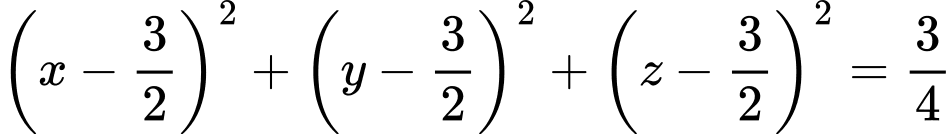 có tâm
có tâm 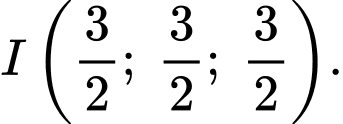 Đáp án: C
Đáp án: C
Gọi
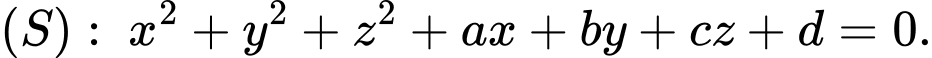

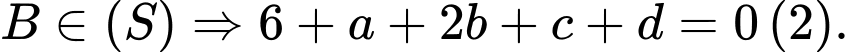
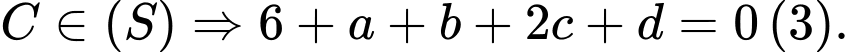

Từ (1), (2), (3) và (4) ta có:
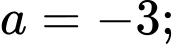
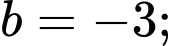
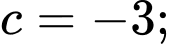

Vậy
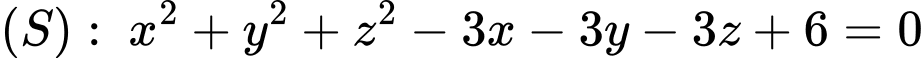 hay
hay 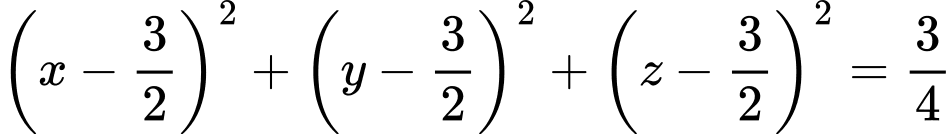 có tâm
có tâm 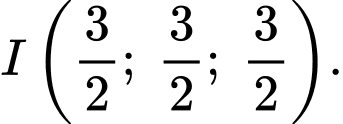 Đáp án: C
Đáp án: C
Câu 10 [57470]: Trong không gian 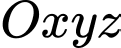 , cho bốn điểm
, cho bốn điểm 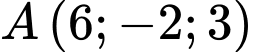 ;
; 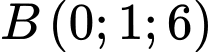 ;
; 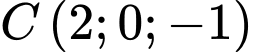 ;
; 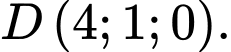 Gọi
Gọi 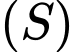 là mặt cầu đi qua 4 điểm
là mặt cầu đi qua 4 điểm 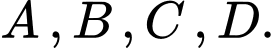 Hãy viết phương trình mặt phẳng tiếp xúc với mặt cầu
Hãy viết phương trình mặt phẳng tiếp xúc với mặt cầu 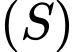 tại điểm
tại điểm 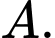
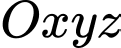 , cho bốn điểm
, cho bốn điểm 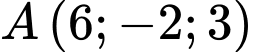 ;
; 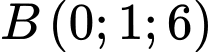 ;
; 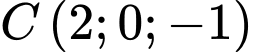 ;
; 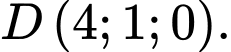 Gọi
Gọi 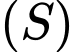 là mặt cầu đi qua 4 điểm
là mặt cầu đi qua 4 điểm 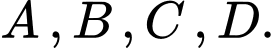 Hãy viết phương trình mặt phẳng tiếp xúc với mặt cầu
Hãy viết phương trình mặt phẳng tiếp xúc với mặt cầu 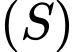 tại điểm
tại điểm 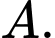
A, 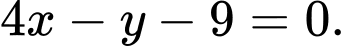
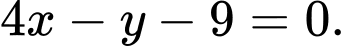
B, 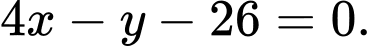
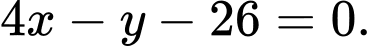
C, 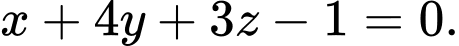
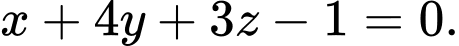
D, 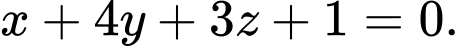
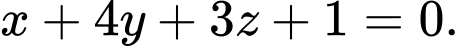
 Đáp án: B
Đáp án: B
Câu 11 [57472]: Cho điểm 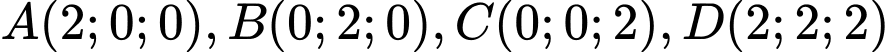 . Mặt cầu ngoại tiếp tứ diện
. Mặt cầu ngoại tiếp tứ diện 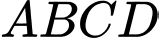 có bán kính là
có bán kính là
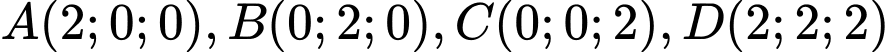 . Mặt cầu ngoại tiếp tứ diện
. Mặt cầu ngoại tiếp tứ diện 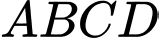 có bán kính là
có bán kính là A, 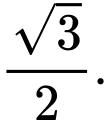
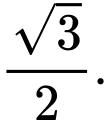
B, 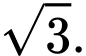
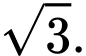
C, 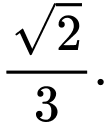
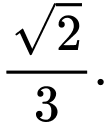
D, 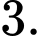
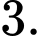
 Đáp án: B
Đáp án: B
Câu 12 [57463]: Trong không gian với hệ tọa độ 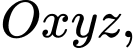 cho điểm
cho điểm 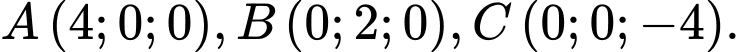 Viết phương trình mặt cầu
Viết phương trình mặt cầu 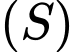 ngoại tiếp tứ diện
ngoại tiếp tứ diện 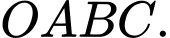
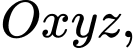 cho điểm
cho điểm 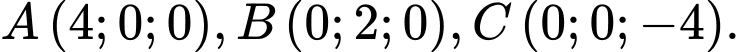 Viết phương trình mặt cầu
Viết phương trình mặt cầu 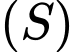 ngoại tiếp tứ diện
ngoại tiếp tứ diện 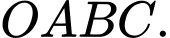
A, 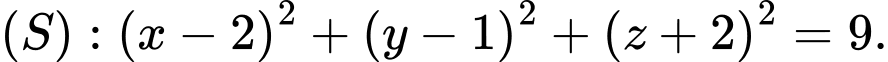
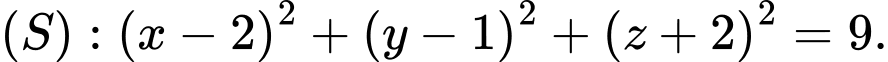
B, 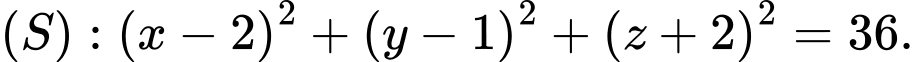
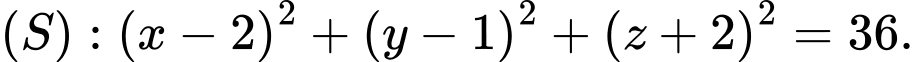
C, 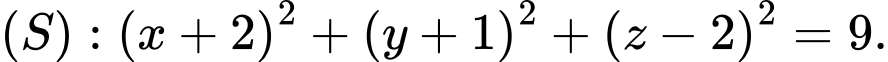
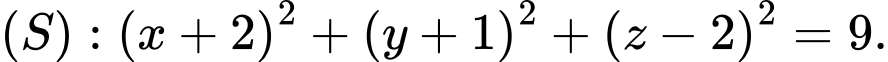
D, 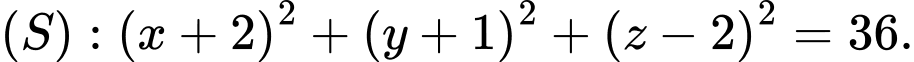
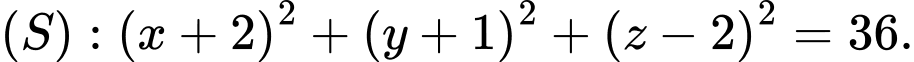
Trung điểm của  là
là 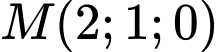 , trục đường tròn ngoại tiếp tam giác
, trục đường tròn ngoại tiếp tam giác 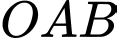 là
là 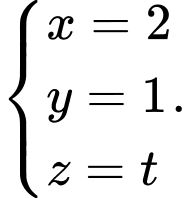
Suy ra tâm mặt cầu của tứ diện là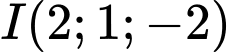 bán kính
bán kính 
Do đó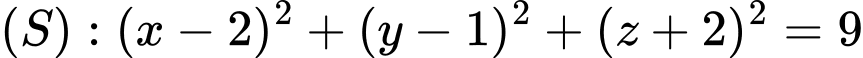 .
.
Chọn A. Đáp án: A
 là
là 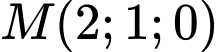 , trục đường tròn ngoại tiếp tam giác
, trục đường tròn ngoại tiếp tam giác 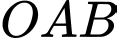 là
là 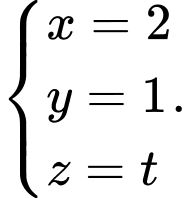
Suy ra tâm mặt cầu của tứ diện là
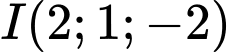 bán kính
bán kính 
Do đó
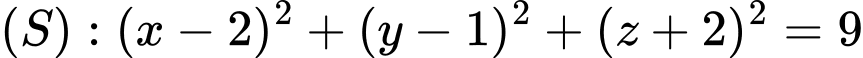 .
.
Chọn A. Đáp án: A
Câu 13 [57465]: Trong không gian với hệ trục tọa độ 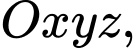 cho ba điểm
cho ba điểm 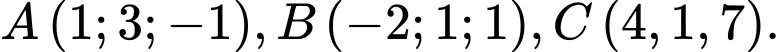 Tìm bán kính
Tìm bán kính 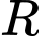 của mặt cầu đi qua 4 điểm
của mặt cầu đi qua 4 điểm 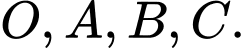
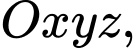 cho ba điểm
cho ba điểm 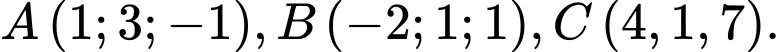 Tìm bán kính
Tìm bán kính 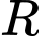 của mặt cầu đi qua 4 điểm
của mặt cầu đi qua 4 điểm 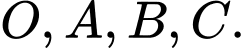
A, 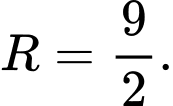
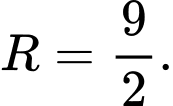
B, 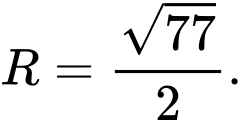
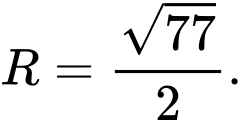
C, 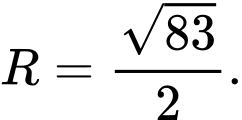
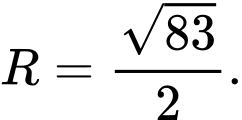
D, 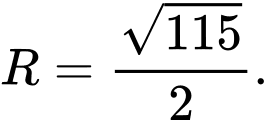
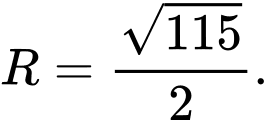
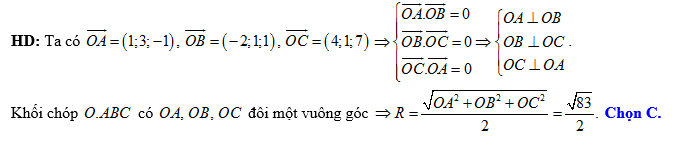 Đáp án: C
Đáp án: C
Câu 14 [57466]: Trong không gian 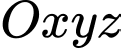 , viết phương trình mặt cầu
, viết phương trình mặt cầu 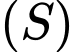 đi qua bốn điểm
đi qua bốn điểm 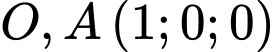 và
và 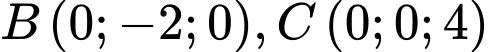
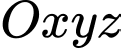 , viết phương trình mặt cầu
, viết phương trình mặt cầu 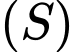 đi qua bốn điểm
đi qua bốn điểm 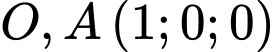 và
và 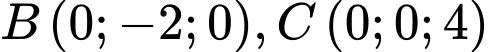
A, 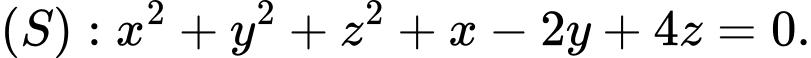
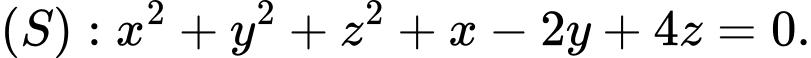
B, 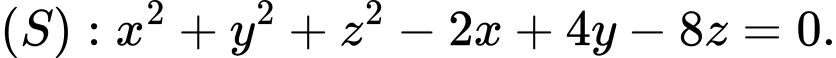
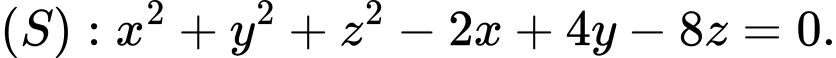
C, 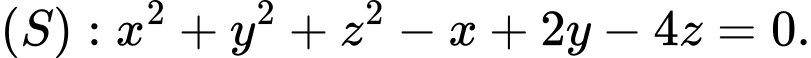
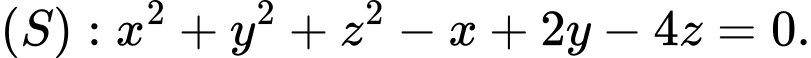
D, 

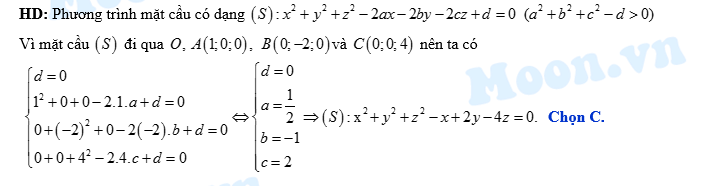 Đáp án: C
Đáp án: C
Câu 15 [57471]: Trong không gian với hệ trục tọa độ 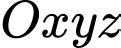 cho
cho 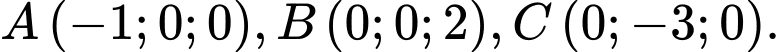 Bán kính mặt cầu ngoại tiếp tứ diện
Bán kính mặt cầu ngoại tiếp tứ diện 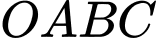 là
là
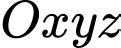 cho
cho 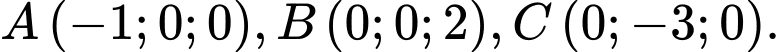 Bán kính mặt cầu ngoại tiếp tứ diện
Bán kính mặt cầu ngoại tiếp tứ diện 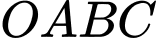 là
là A, 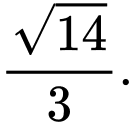
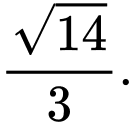
B, 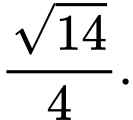
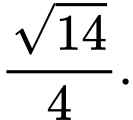
C, 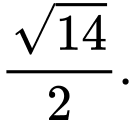
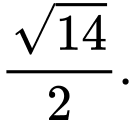
D, 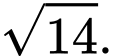
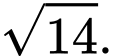
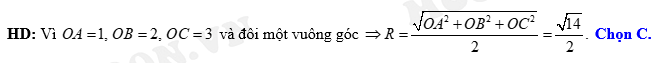 Đáp án: C
Đáp án: C
Câu 16 [58180]: Trong không gian với hệ tọa độ 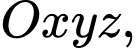 cho các điểm
cho các điểm 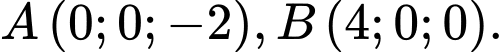 Mặt cầu
Mặt cầu 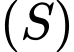 có bán kính nhỏ nhất đi qua
có bán kính nhỏ nhất đi qua 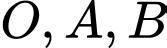 có tâm là
có tâm là
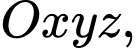 cho các điểm
cho các điểm 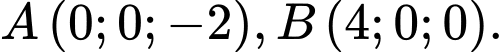 Mặt cầu
Mặt cầu 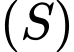 có bán kính nhỏ nhất đi qua
có bán kính nhỏ nhất đi qua 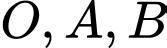 có tâm là
có tâm là A, 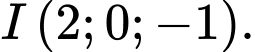
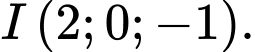
B, 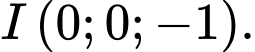
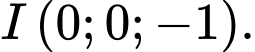
C, 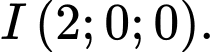
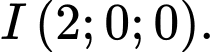
D, 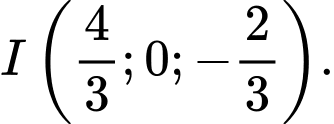
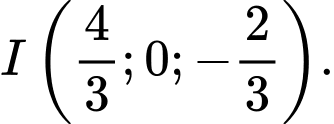
Chọn đáp án A.
Ta có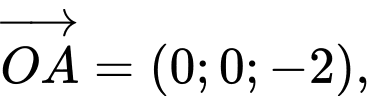
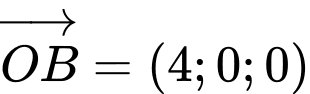 suy ra
suy ra 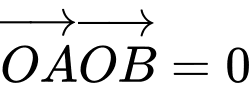
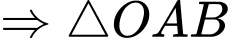 vuông tại
vuông tại 
Do đó, mặt cầu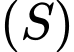 có bán kính
có bán kính  và đi qua
và đi qua 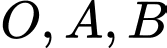 có tâm là trung điểm của
có tâm là trung điểm của 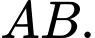
Vậy tọa độ tâm mặt cầu là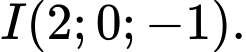 Đáp án: A
Đáp án: A
Ta có
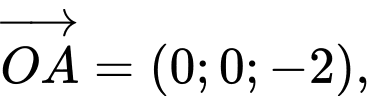
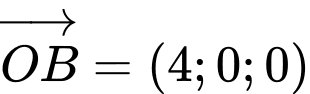 suy ra
suy ra 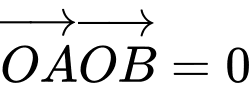
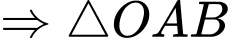 vuông tại
vuông tại 
Do đó, mặt cầu
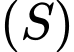 có bán kính
có bán kính  và đi qua
và đi qua 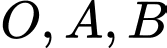 có tâm là trung điểm của
có tâm là trung điểm của 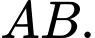
Vậy tọa độ tâm mặt cầu là
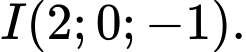 Đáp án: A
Đáp án: A
Câu 17 [58182]: Trong không gian với hệ tọa độ 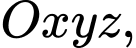 cho 3 điểm
cho 3 điểm 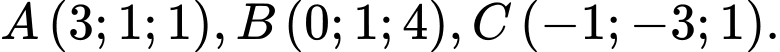 Phương trình mặt cầu
Phương trình mặt cầu 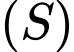 qua
qua 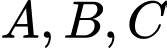 có tâm nằm trên mặt phẳng
có tâm nằm trên mặt phẳng 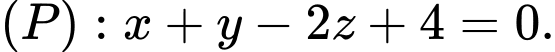
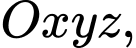 cho 3 điểm
cho 3 điểm 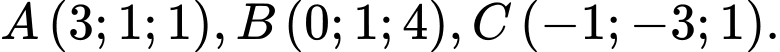 Phương trình mặt cầu
Phương trình mặt cầu 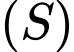 qua
qua 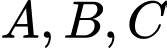 có tâm nằm trên mặt phẳng
có tâm nằm trên mặt phẳng 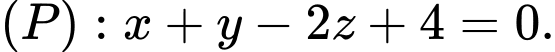
A, 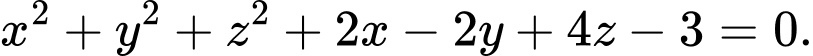
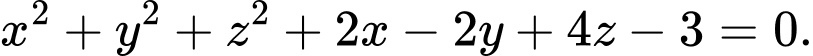
B, 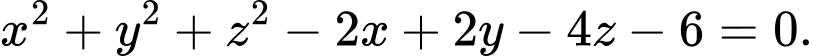
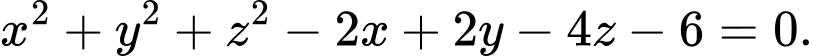
C, 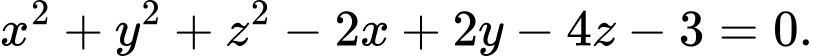
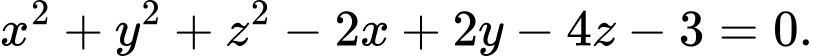
D, 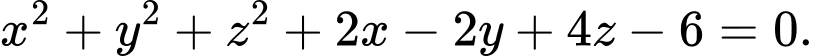
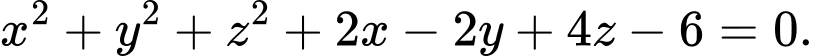
Chọn đáp án C.
Gọi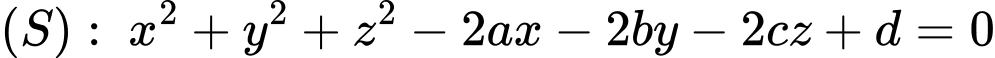 có tâm
có tâm 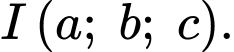
Tâm nằm trên mặt phẳng nên
nên 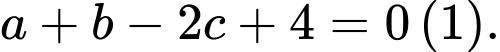
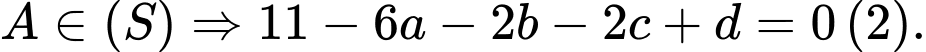
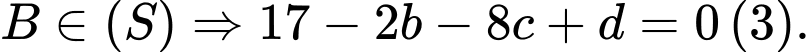

Từ (1), (2), (3) và (4) ta có: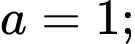
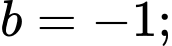
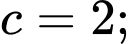

Vậy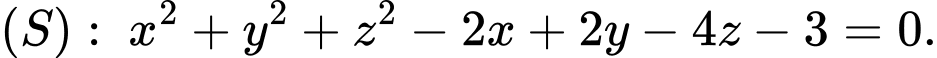 Đáp án: C
Đáp án: C
Gọi
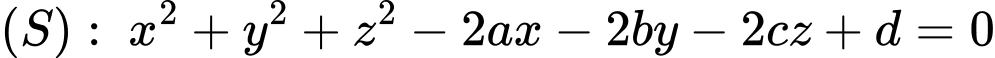 có tâm
có tâm 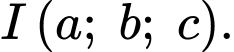
Tâm nằm trên mặt phẳng
 nên
nên 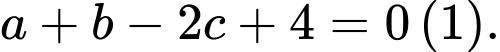
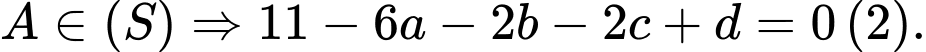
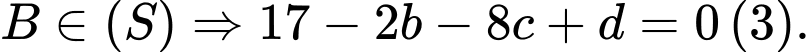

Từ (1), (2), (3) và (4) ta có:
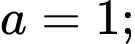
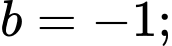
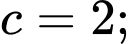

Vậy
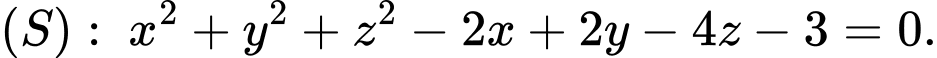 Đáp án: C
Đáp án: C
Câu 18 [80356]: Trong không gian tọa độ 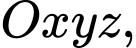 cho 2 điểm
cho 2 điểm 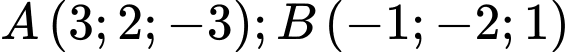 và mặt phẳng
và mặt phẳng 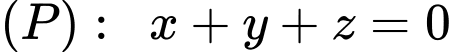 . Viết phương trình mặt cầu
. Viết phương trình mặt cầu 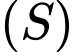 có tâm
có tâm 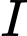 thuộc
thuộc 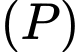 đi qua A,B sao cho tam giác OIA vuông tại gốc tọa độ
đi qua A,B sao cho tam giác OIA vuông tại gốc tọa độ 
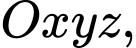 cho 2 điểm
cho 2 điểm 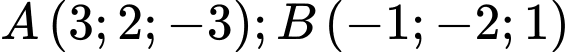 và mặt phẳng
và mặt phẳng 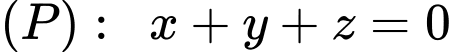 . Viết phương trình mặt cầu
. Viết phương trình mặt cầu 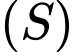 có tâm
có tâm 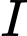 thuộc
thuộc 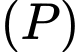 đi qua A,B sao cho tam giác OIA vuông tại gốc tọa độ
đi qua A,B sao cho tam giác OIA vuông tại gốc tọa độ 
A, 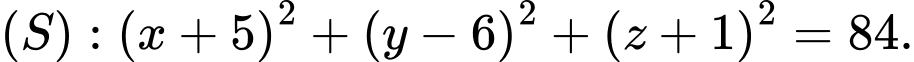
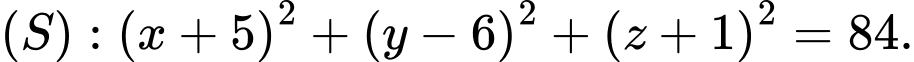
B, 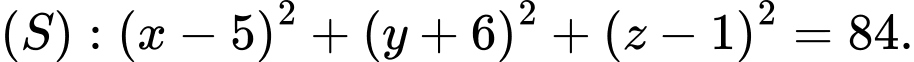
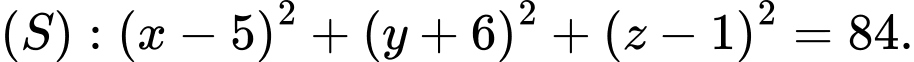
C, 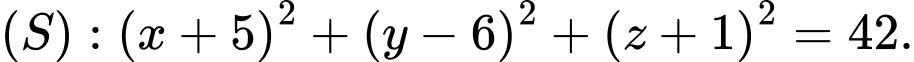
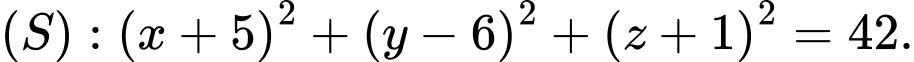
D, 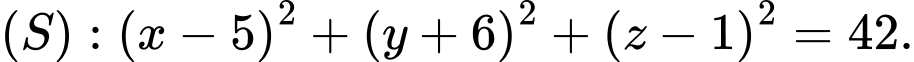
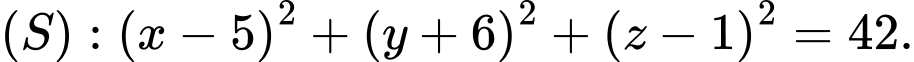
 Đáp án: A
Đáp án: A
Câu 19 [392167]: Trong không gian toạ độ 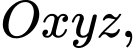 cho bốn điểm
cho bốn điểm 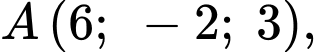
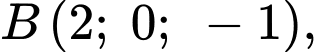
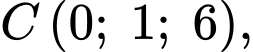
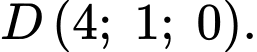 Các mệnh đề sau đây đúng hay sai?
Các mệnh đề sau đây đúng hay sai?
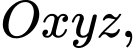 cho bốn điểm
cho bốn điểm 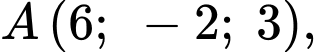
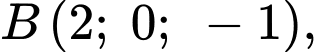
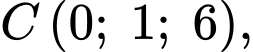
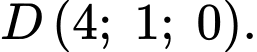 Các mệnh đề sau đây đúng hay sai?
Các mệnh đề sau đây đúng hay sai? A, a) Đường thẳng 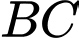 có phương trình là:
có phương trình là: 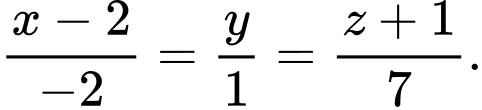
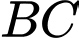 có phương trình là:
có phương trình là: 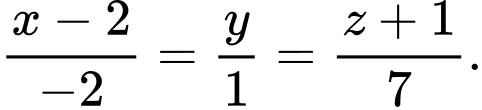
B, b) Mặt cầu đường kính  có phương trình là
có phương trình là 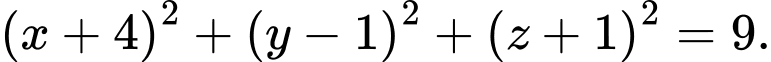
 có phương trình là
có phương trình là 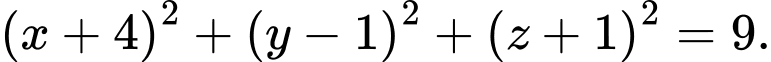
C, c) Phương trình mặt phẳng 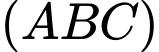 là:
là: 
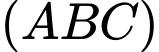 là:
là: 
D, d) Mặt cầu ngoại tiếp tứ diện 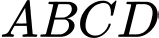 có bán kính bằng
có bán kính bằng 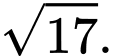
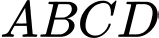 có bán kính bằng
có bán kính bằng 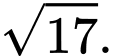
a) Đúng b) Sai c) Đúng d) Đúng 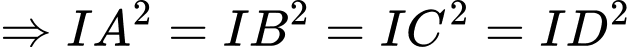
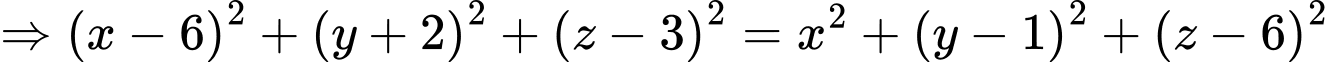
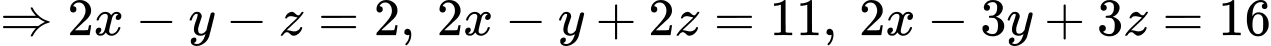
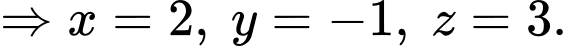
a) 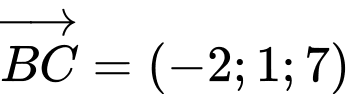
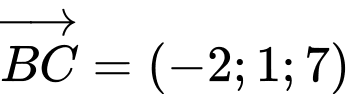
Đường thẳng 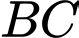 có phương trình là:
có phương trình là: 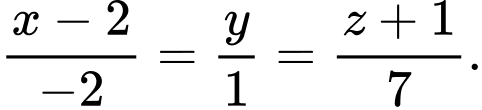
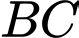 có phương trình là:
có phương trình là: 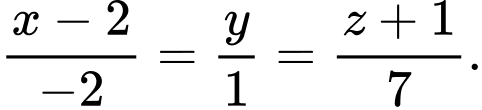
b) Tâm 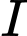 của mặt cầu là trung điểm
của mặt cầu là trung điểm 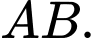
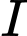 của mặt cầu là trung điểm
của mặt cầu là trung điểm 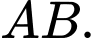
Nên ta có 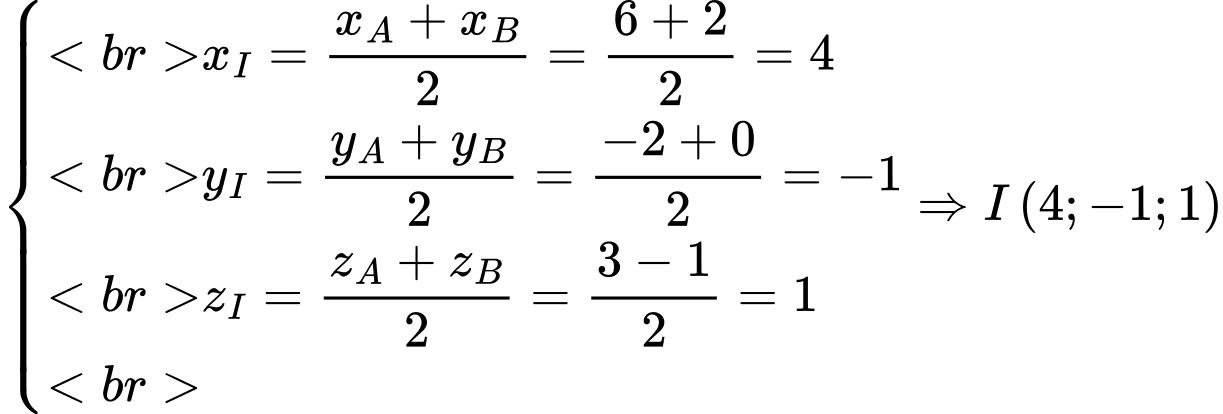
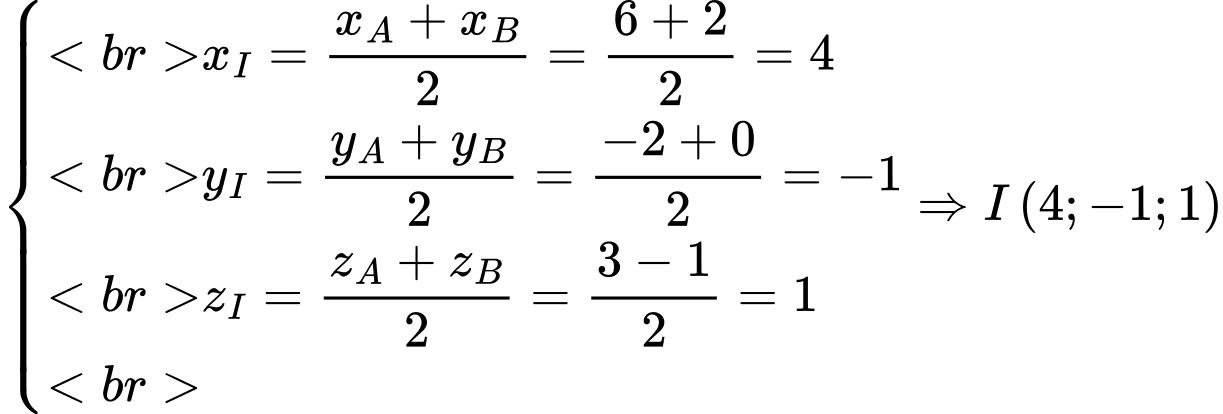
Bán kính mặt cầu 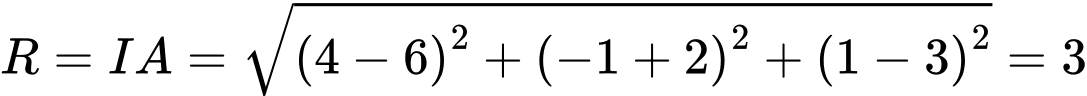
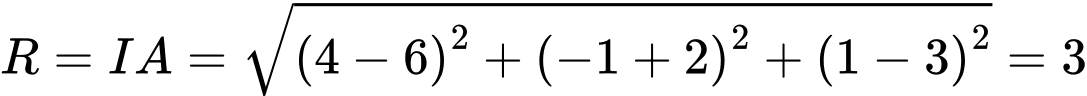
Vậy phương trình mặt cầu đường kính  là
là 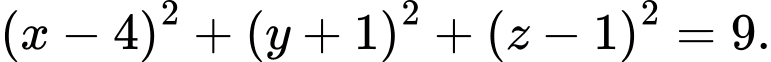
 là
là 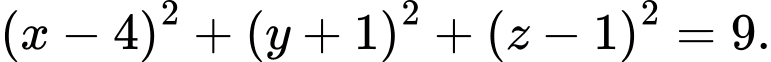
c) Mặt phẳng 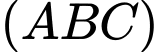 có vecto chỉ phương là
có vecto chỉ phương là 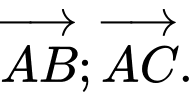
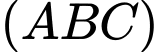 có vecto chỉ phương là
có vecto chỉ phương là 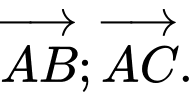
Nên 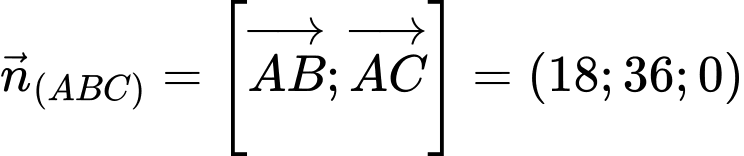 hay
hay 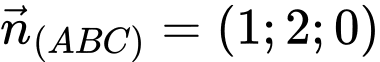
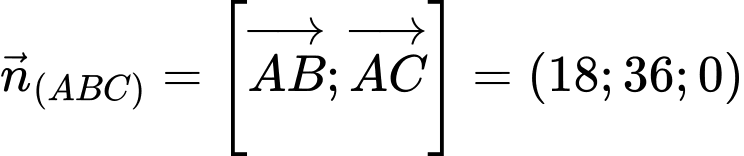 hay
hay 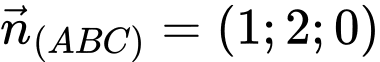
Phương trình mặt phẳng 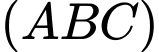 là:
là: 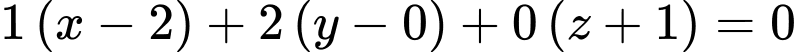
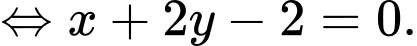
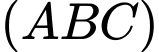 là:
là: 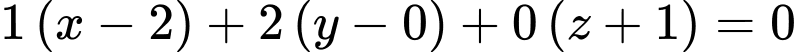
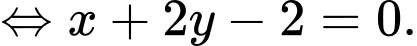
d) Gọi 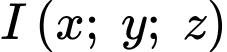 là tâm của mặt cầu ngoại tiếp tứ diện
là tâm của mặt cầu ngoại tiếp tứ diện 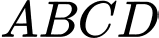
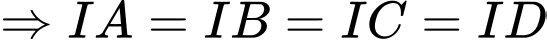
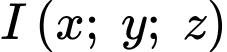 là tâm của mặt cầu ngoại tiếp tứ diện
là tâm của mặt cầu ngoại tiếp tứ diện 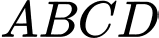
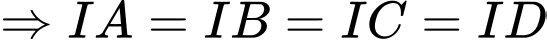
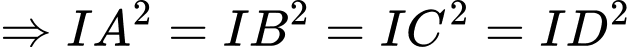
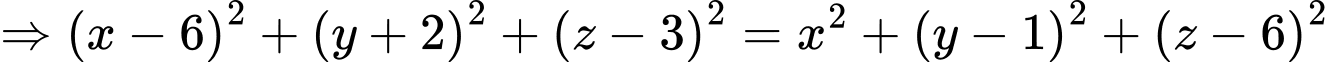
Và 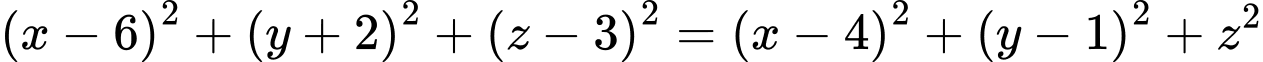
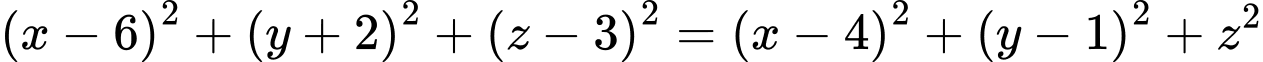
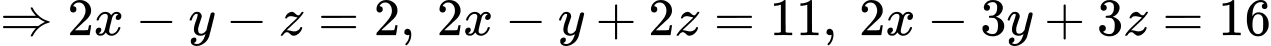
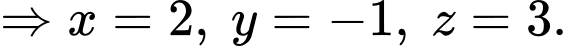
Vậy tâm mặt cầu ngoại tiếp tứ diện 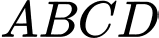 là
là 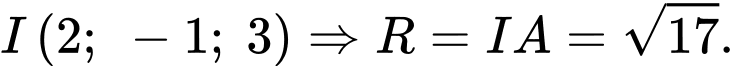
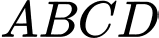 là
là 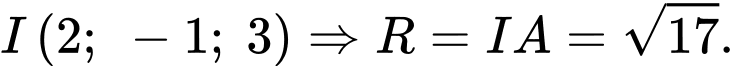
Câu 20 [408105]: Trong không gian toạ độ 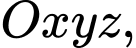 cho bốn điểm
cho bốn điểm 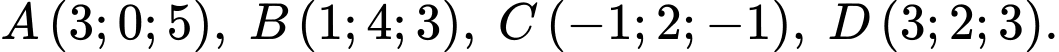 Các mệnh đề sau đây đúng hay sai?
Các mệnh đề sau đây đúng hay sai?
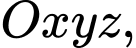 cho bốn điểm
cho bốn điểm 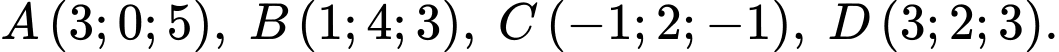 Các mệnh đề sau đây đúng hay sai?
Các mệnh đề sau đây đúng hay sai? A, Đường thẳng  có phương trình là:
có phương trình là: 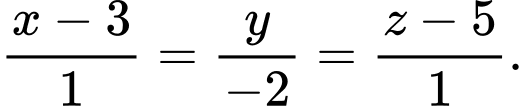
 có phương trình là:
có phương trình là: 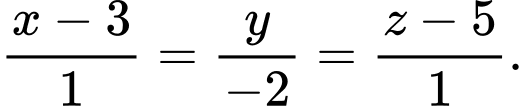
B, Một vectơ pháp tuyến của mặt phẳng 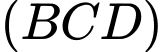 là
là 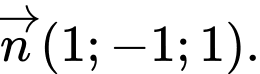
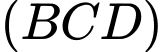 là
là 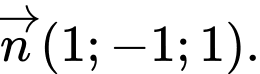
C, Mặt cầu tâm 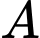 tiếp xúc với mặt phẳng
tiếp xúc với mặt phẳng 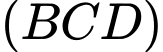 có bán kính là
có bán kính là 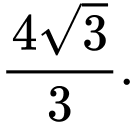
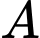 tiếp xúc với mặt phẳng
tiếp xúc với mặt phẳng 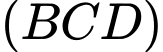 có bán kính là
có bán kính là 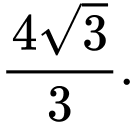
D, Mặt cầu ngoại tiếp tứ diện 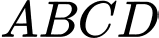 có bán kính bằng
có bán kính bằng 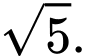
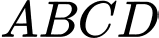 có bán kính bằng
có bán kính bằng 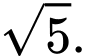
a) Đúng. 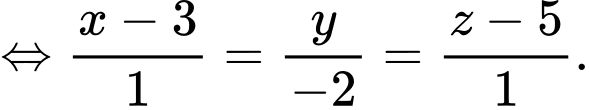
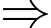 Một vectơ pháp tuyến của mặt phẳng
Một vectơ pháp tuyến của mặt phẳng 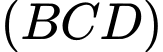 là
là 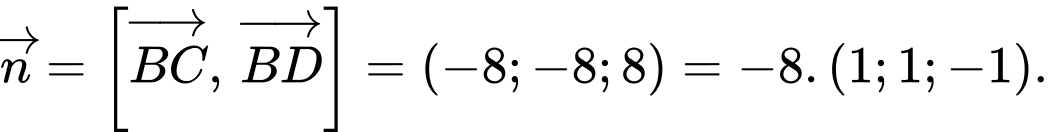
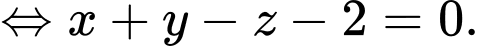
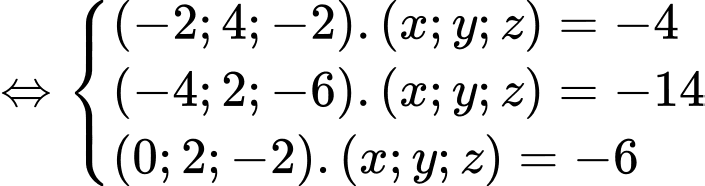
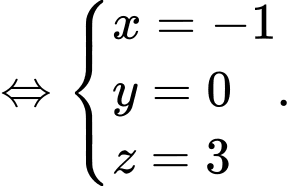
Đường thẳng  đi qua điểm
đi qua điểm 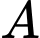 và có vectơ chỉ phương
và có vectơ chỉ phương 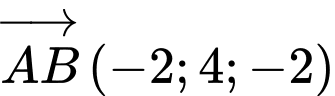 có phương trình là
có phương trình là
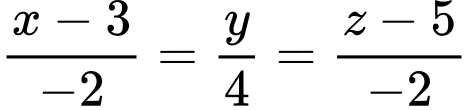
 đi qua điểm
đi qua điểm 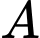 và có vectơ chỉ phương
và có vectơ chỉ phương 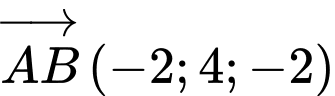 có phương trình là
có phương trình là
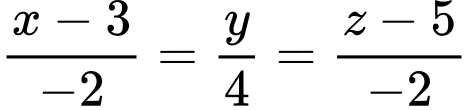
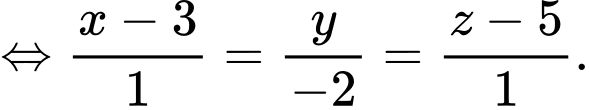
b) Sai.
Mặt phẳng 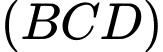 có 2 vectơ chỉ phương là
có 2 vectơ chỉ phương là 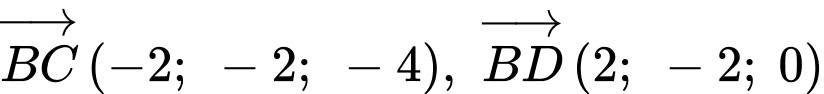
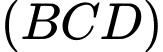 có 2 vectơ chỉ phương là
có 2 vectơ chỉ phương là 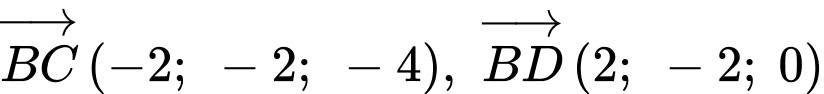
 Một vectơ pháp tuyến của mặt phẳng
Một vectơ pháp tuyến của mặt phẳng 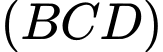 là
là 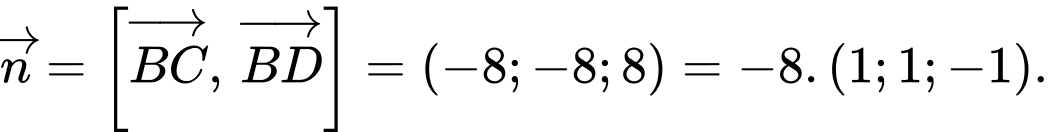
c) Đúng.
Mặt phẳng 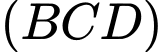 đi qua điểm
đi qua điểm 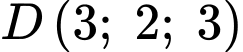 và có vectơ pháp tuyến
và có vectơ pháp tuyến 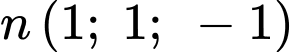 có phương trình là
có phương trình là 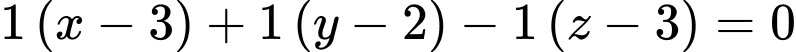
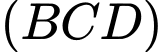 đi qua điểm
đi qua điểm 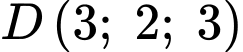 và có vectơ pháp tuyến
và có vectơ pháp tuyến 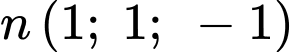 có phương trình là
có phương trình là 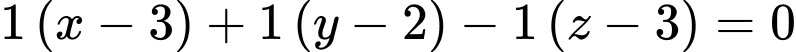
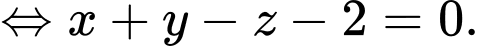
Vì mặt cầu tâm 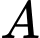 tiếp xúc với mặt phẳng
tiếp xúc với mặt phẳng 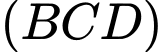 nên ta có
nên ta có 
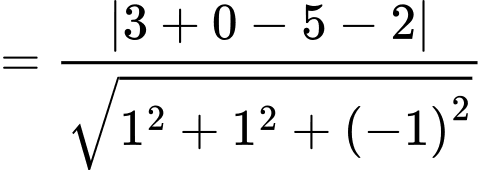
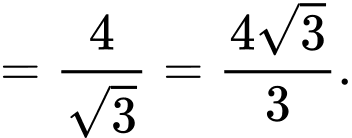
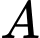 tiếp xúc với mặt phẳng
tiếp xúc với mặt phẳng 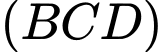 nên ta có
nên ta có 
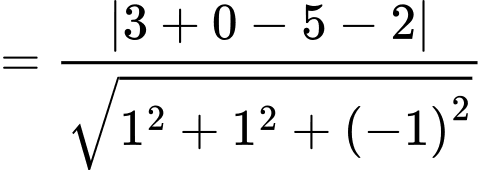
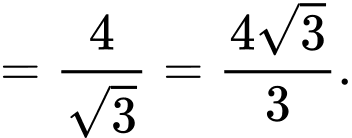
d) Sai.
Giải hệ phương trình 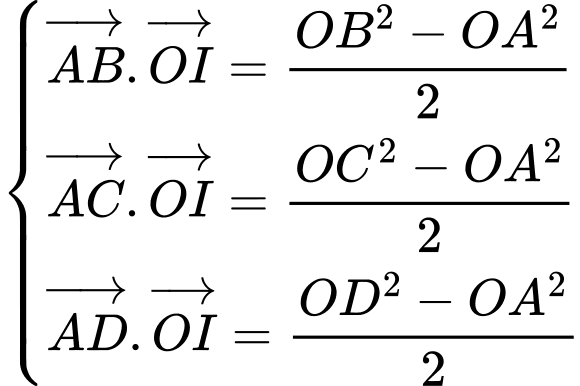
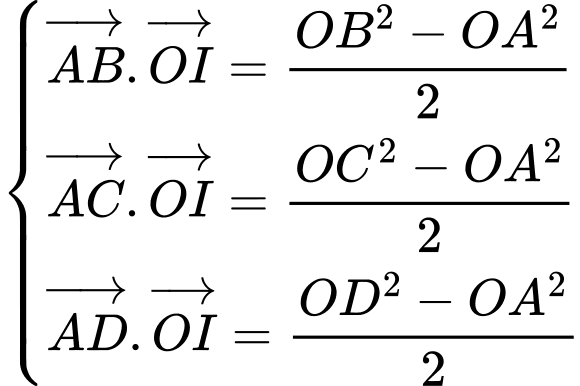
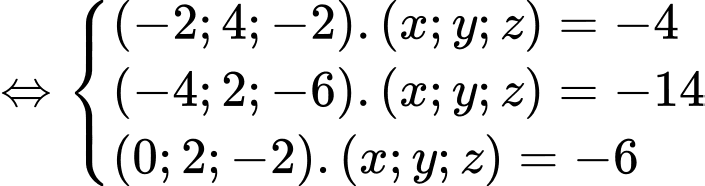
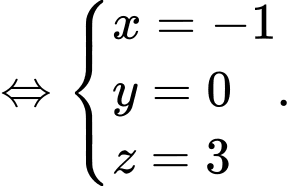
Suy ra 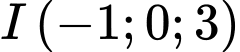 và bán kính mặt cầu là
và bán kính mặt cầu là 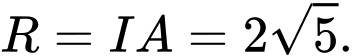
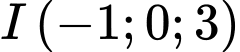 và bán kính mặt cầu là
và bán kính mặt cầu là 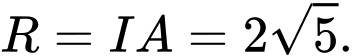
Câu 21 [408106]: Trong không gian toạ độ 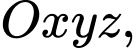 cho ba điểm
cho ba điểm 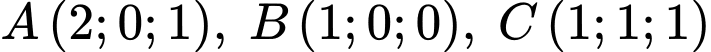 và mặt phẳng
và mặt phẳng 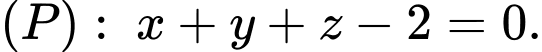 Các mệnh đề sau đây đúng hay sai?
Các mệnh đề sau đây đúng hay sai?
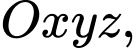 cho ba điểm
cho ba điểm 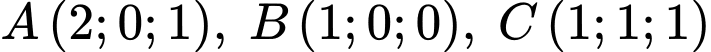 và mặt phẳng
và mặt phẳng 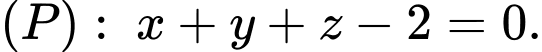 Các mệnh đề sau đây đúng hay sai?
Các mệnh đề sau đây đúng hay sai? A, Độ dài đoạn thẳng  bằng
bằng 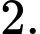
 bằng
bằng 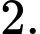
B, Phương trình mặt phẳng 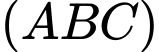 là:
là: 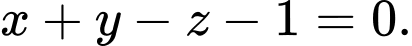
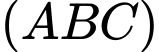 là:
là: 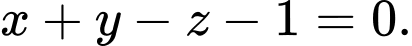
C, Mặt cầu tâm 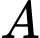 và tiếp xúc với mặt phẳng
và tiếp xúc với mặt phẳng 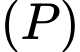 có bán kính bằng
có bán kính bằng 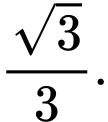
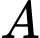 và tiếp xúc với mặt phẳng
và tiếp xúc với mặt phẳng 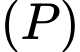 có bán kính bằng
có bán kính bằng 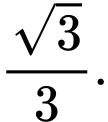
D, Gọi 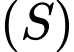 mặt cầu đi qua
mặt cầu đi qua 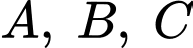 và có tâm
và có tâm  thì bán kính mặt cầu
thì bán kính mặt cầu 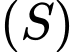 bằng
bằng 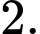
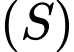 mặt cầu đi qua
mặt cầu đi qua 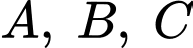 và có tâm
và có tâm  thì bán kính mặt cầu
thì bán kính mặt cầu 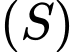 bằng
bằng 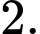
a) Sai. 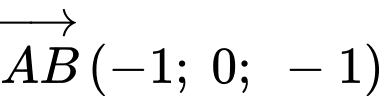
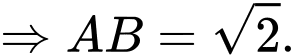
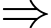 Một vectơ pháp tuyến của mặt phẳng
Một vectơ pháp tuyến của mặt phẳng 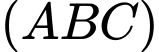 là
là 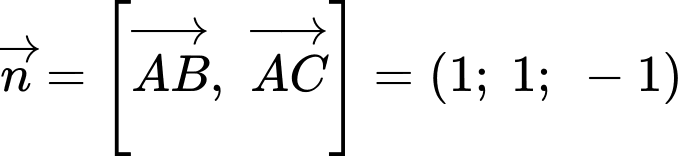
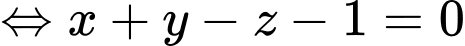
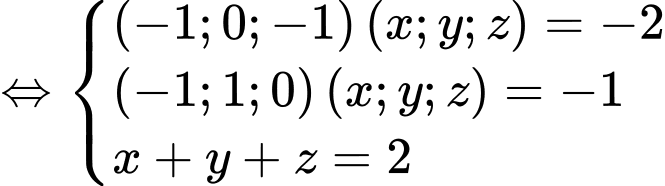
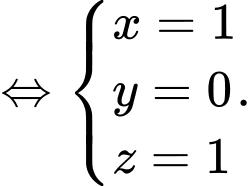
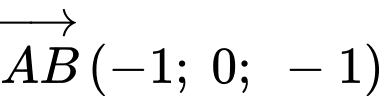
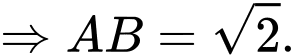
b) Đúng.
Mặt phẳng 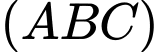 có 2 vectơ chỉ phương là
có 2 vectơ chỉ phương là 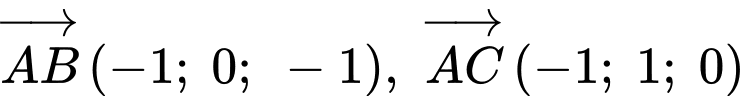
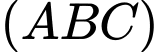 có 2 vectơ chỉ phương là
có 2 vectơ chỉ phương là 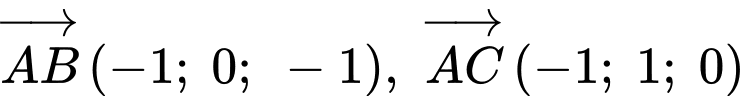
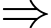 Một vectơ pháp tuyến của mặt phẳng
Một vectơ pháp tuyến của mặt phẳng 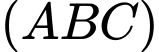 là
là 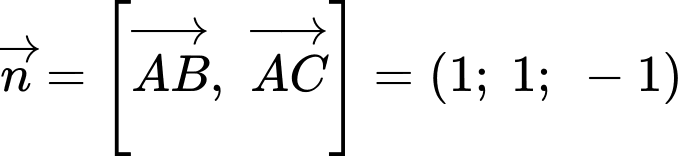
Mặt phẳng 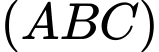 đi qua điểm
đi qua điểm 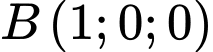 và có vectơ pháp tuyến
và có vectơ pháp tuyến 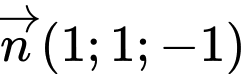 có phương trình là
có phương trình là
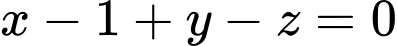
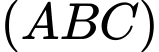 đi qua điểm
đi qua điểm 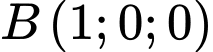 và có vectơ pháp tuyến
và có vectơ pháp tuyến 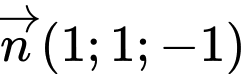 có phương trình là
có phương trình là
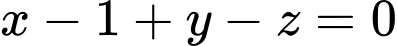
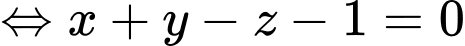
c) Đúng.
Vì mặt cầu tâm tâm 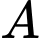 và tiếp xúc với mặt phẳng
và tiếp xúc với mặt phẳng 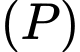 nên ta có
nên ta có 
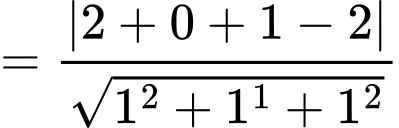
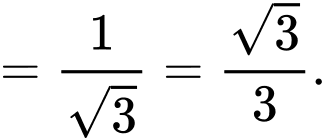
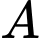 và tiếp xúc với mặt phẳng
và tiếp xúc với mặt phẳng 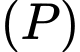 nên ta có
nên ta có 
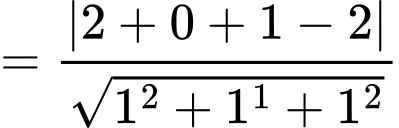
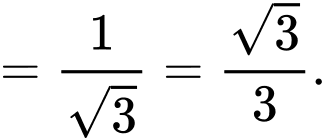
d) Sai.
Giải hệ phương trình 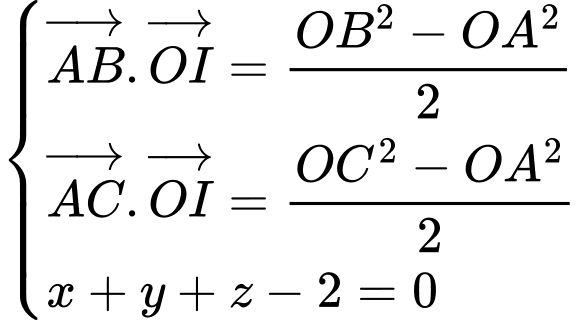
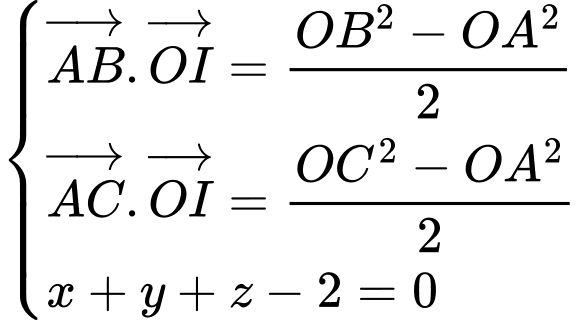
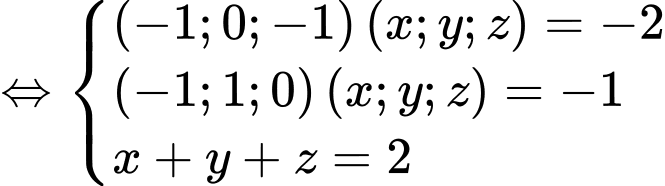
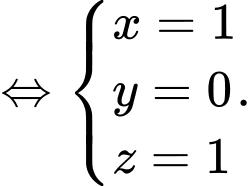
Suy ra 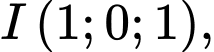 bán kính mặt cầu
bán kính mặt cầu 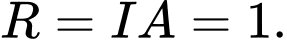
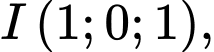 bán kính mặt cầu
bán kính mặt cầu 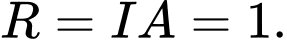
Khi đó phương trình mặt cầu là 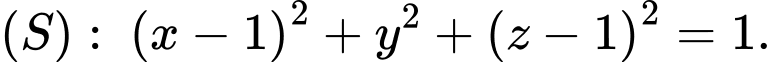
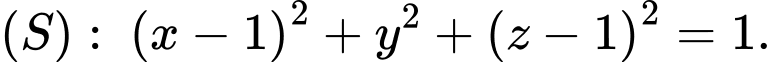
Câu 22 [408107]: Trong không gian 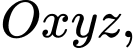 cho ba điểm
cho ba điểm 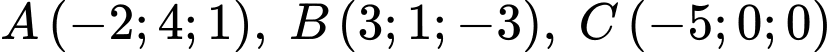 và mặt phẳng
và mặt phẳng 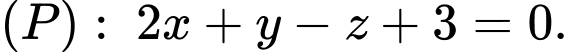 Các mệnh đề sau đây đúng hay sai?
Các mệnh đề sau đây đúng hay sai?
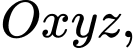 cho ba điểm
cho ba điểm 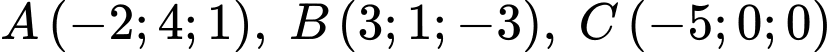 và mặt phẳng
và mặt phẳng 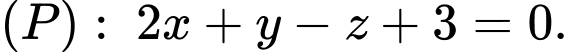 Các mệnh đề sau đây đúng hay sai?
Các mệnh đề sau đây đúng hay sai? A, Một vectơ pháp tuyến của mặt phẳng 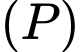 là
là 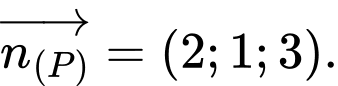
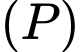 là
là 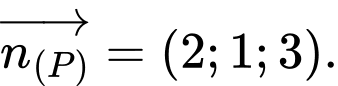
B, Phương trình đường thẳng 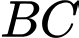 là:
là: 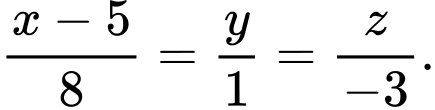
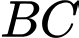 là:
là: 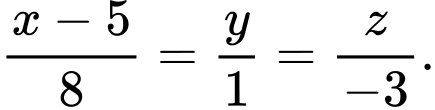
C, Phương trình mặt cầu đường kính  là:
là: 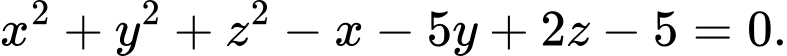
 là:
là: 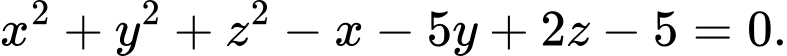
D, Gọi 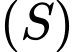 mặt cầu đi qua
mặt cầu đi qua 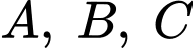 và có tâm
và có tâm  thì bán kính mặt cầu
thì bán kính mặt cầu 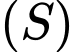 bằng
bằng 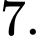
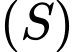 mặt cầu đi qua
mặt cầu đi qua 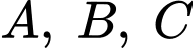 và có tâm
và có tâm  thì bán kính mặt cầu
thì bán kính mặt cầu 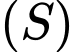 bằng
bằng 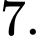
a) Sai. 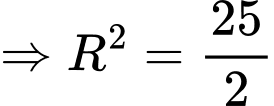
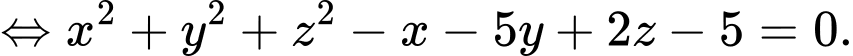
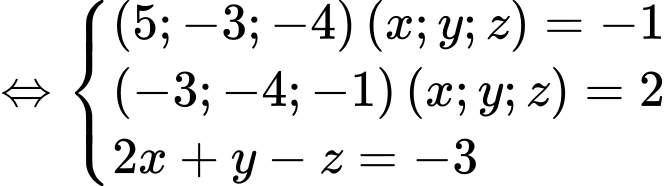
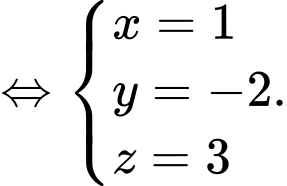
Một vectơ pháp tuyến của mặt phẳng 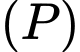 là
là 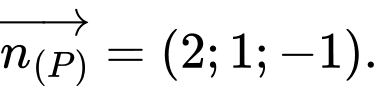
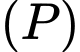 là
là 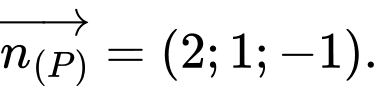
b) Sai.
Ta có 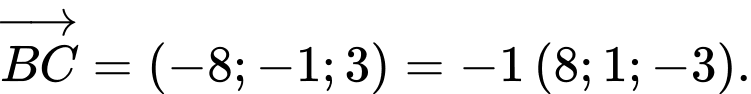
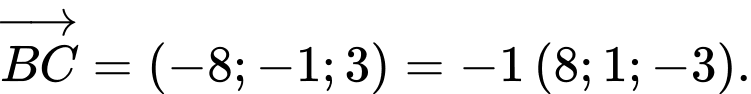
Phương trình đường thẳng 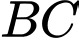 đi qua điểm
đi qua điểm  và có vectơ chỉ phương
và có vectơ chỉ phương 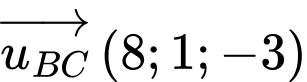 là
là
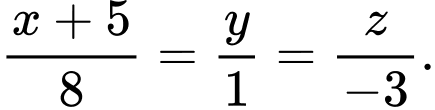
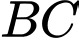 đi qua điểm
đi qua điểm  và có vectơ chỉ phương
và có vectơ chỉ phương 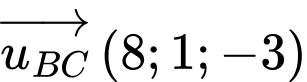 là
là
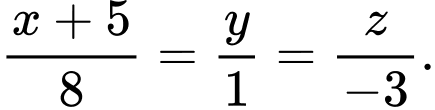
c) Đúng.
Mặt cầu đường kính  có
có
 có
có +) Tâm 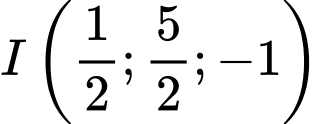
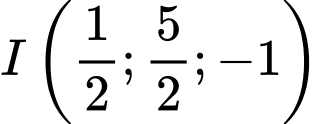
+) Bán kính 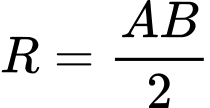
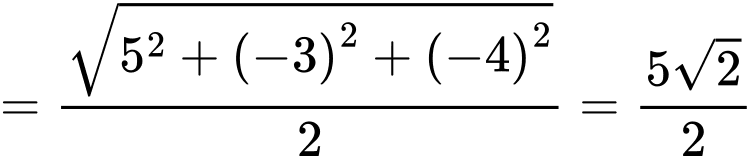
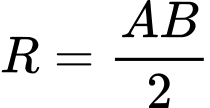
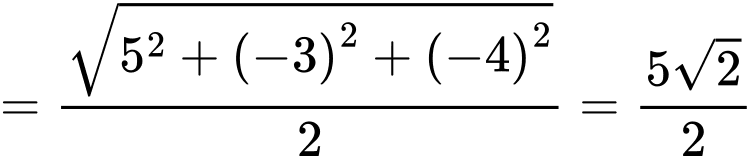
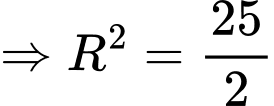
Suy ra phương trình mặt cầu đường kính  là:
là: 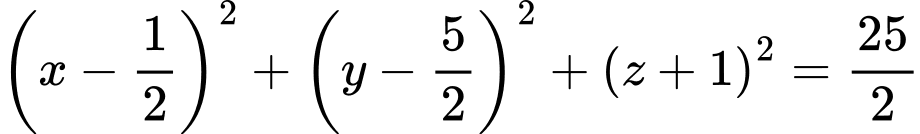
 là:
là: 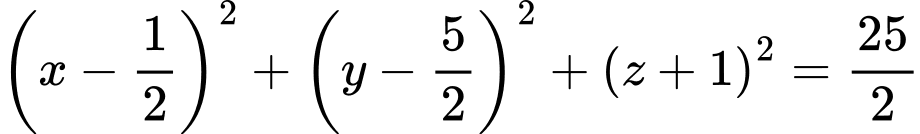
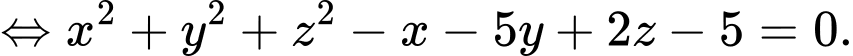
d) Đúng.
Giải hệ phương trình 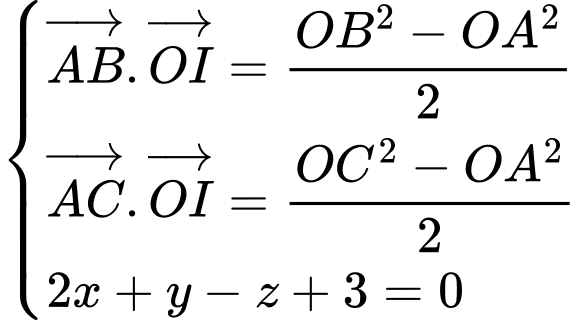
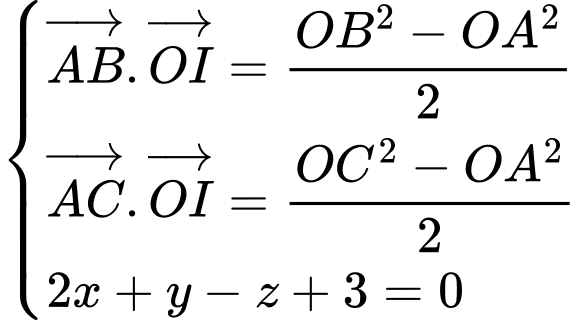
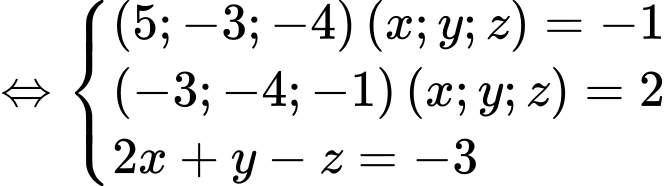
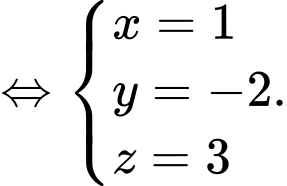
Suy ra 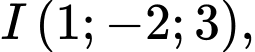 bán kính mặt cầu
bán kính mặt cầu 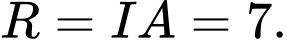
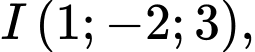 bán kính mặt cầu
bán kính mặt cầu 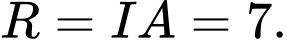
Câu 23 [392169]: Trong không gian 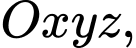 cho hình chóp đều
cho hình chóp đều 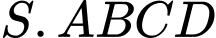 có
có 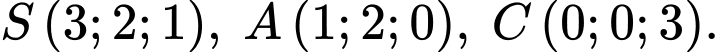 Gọi
Gọi 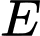 là trung điểm của
là trung điểm của 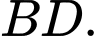 Gọi
Gọi 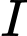 là tâm mặt cầu
là tâm mặt cầu 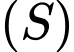 ngoại tiếp của hình chóp
ngoại tiếp của hình chóp 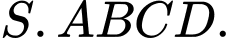 Mỗi mệnh đề sau đúng hay sai?
Mỗi mệnh đề sau đúng hay sai?
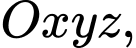 cho hình chóp đều
cho hình chóp đều 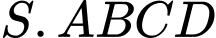 có
có 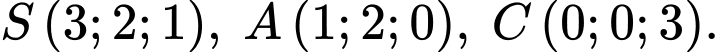 Gọi
Gọi 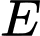 là trung điểm của
là trung điểm của 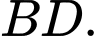 Gọi
Gọi 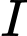 là tâm mặt cầu
là tâm mặt cầu 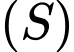 ngoại tiếp của hình chóp
ngoại tiếp của hình chóp 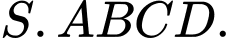 Mỗi mệnh đề sau đúng hay sai?
Mỗi mệnh đề sau đúng hay sai? A, a) 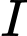 cách đều ba điểm
cách đều ba điểm 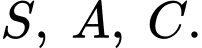
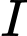 cách đều ba điểm
cách đều ba điểm 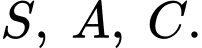
B, b) 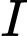 thuộc đường thẳng
thuộc đường thẳng 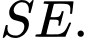
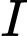 thuộc đường thẳng
thuộc đường thẳng 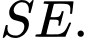
C, c) 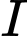 cách đều mặt đáy và mặt bên của hình chóp.
cách đều mặt đáy và mặt bên của hình chóp.
 cách đều mặt đáy và mặt bên của hình chóp.
cách đều mặt đáy và mặt bên của hình chóp.D, d) Phương trình mặt cầu 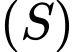 là
là 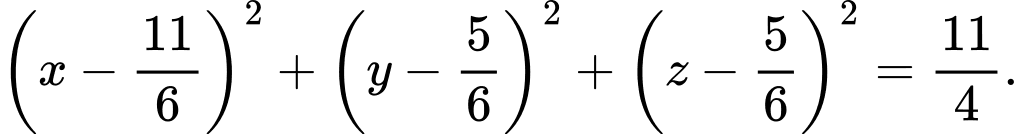
 là
là 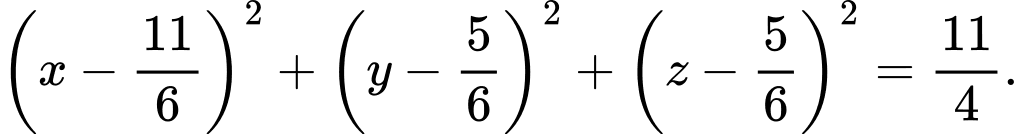
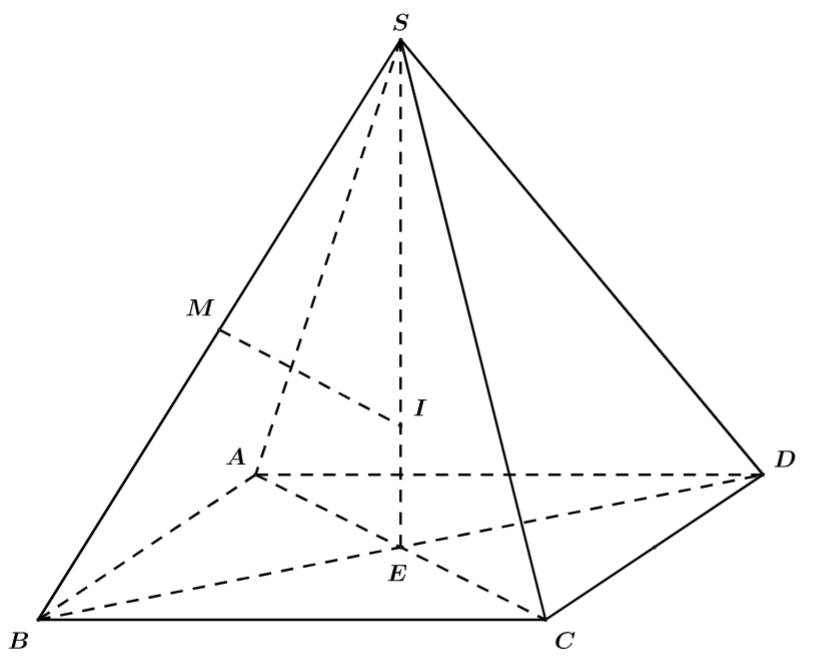
Theo bài cho ta có:
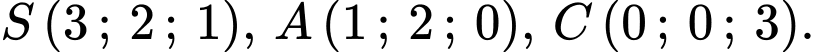
Ta có:
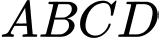 là hình vuông có tâm
là hình vuông có tâm 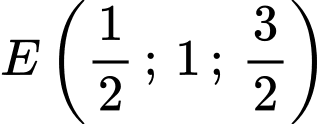 là trung điểm của
là trung điểm của 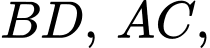 Phương trình đường thẳng
Phương trình đường thẳng 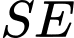 có vecto
có vecto 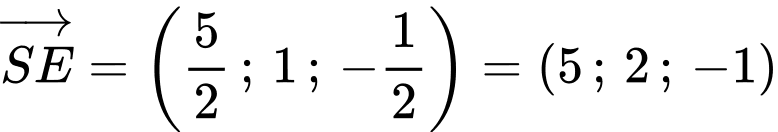 Là:
Là:
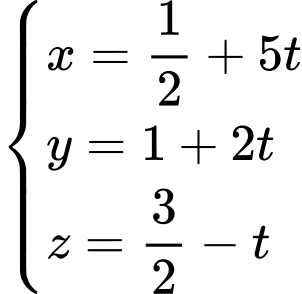
Trung điểm của
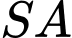 là
là 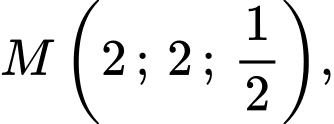
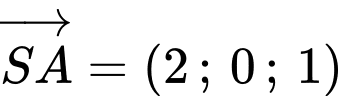
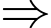 Phương trình mặt phẳng trung trực của
Phương trình mặt phẳng trung trực của 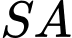 là
là 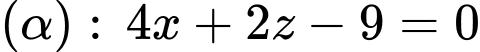
Tâm
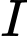 của mặt cầu cần tìm là giao của
của mặt cầu cần tìm là giao của  và
và 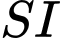
Giải phương trình:
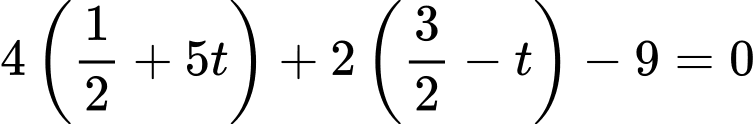
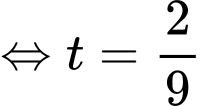
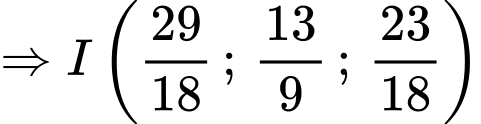
Bán kính mặt cầu bình phương:
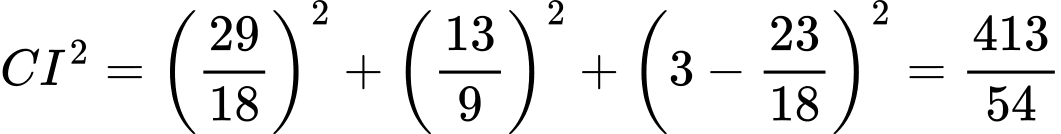
Phương trình mặt cầu:
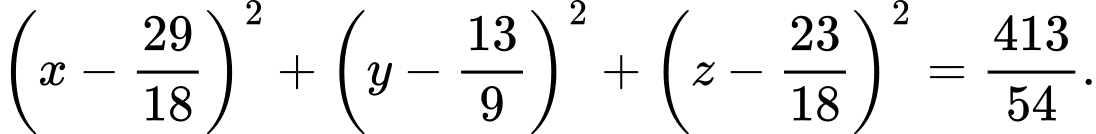
A.Đúng, vì:
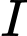 là tâm mặt cầu
là tâm mặt cầu 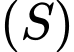 ngoại tiếp của hình chóp
ngoại tiếp của hình chóp 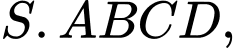 nên
nên 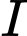 sẽ cách đều 3 điểm
sẽ cách đều 3 điểm 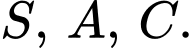
B. Đúng, vì: Tâm
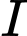 của mặt cầu cần tìm là giao của
của mặt cầu cần tìm là giao của  và
và 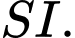
C. Đúng, vì:
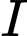 là tâm mặt cầu ngoại tiếp khối chóp đều trùng với tâm mặt cầu nội tiếp khối chóp đều.
là tâm mặt cầu ngoại tiếp khối chóp đều trùng với tâm mặt cầu nội tiếp khối chóp đều.
D. Sai, vì: Phương trình mặt cầu:
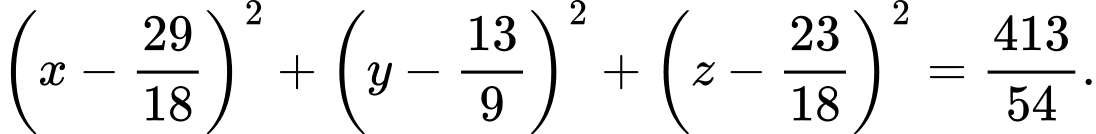
Câu 24 [57469]: Trong không gian với hệ tọa độ 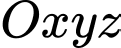 , cho 4 điểm
, cho 4 điểm  Mặt cầu đi qua bốn điểm
Mặt cầu đi qua bốn điểm 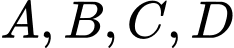 có bán kính bằng
có bán kính bằng
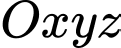 , cho 4 điểm
, cho 4 điểm  Mặt cầu đi qua bốn điểm
Mặt cầu đi qua bốn điểm 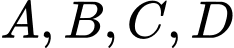 có bán kính bằng
có bán kính bằng A, 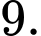
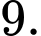
B, 

C, 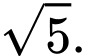
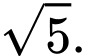
D, 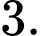
Chọn đáp án D.
Gọi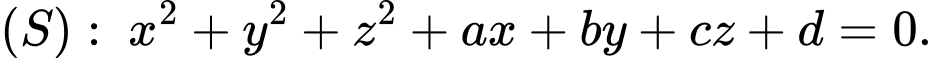
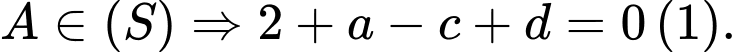
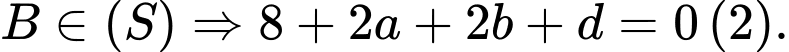
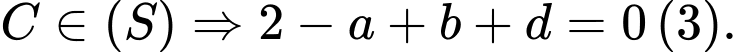
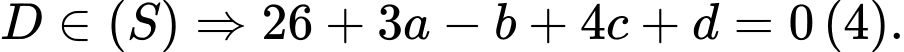
Từ (1), (2), (3) và (4) ta có: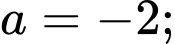
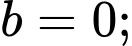
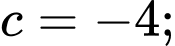
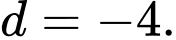
Vậy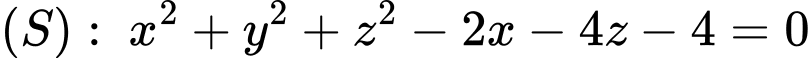 hay
hay 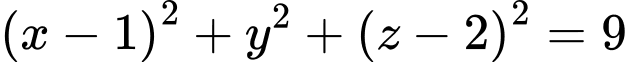 với bán kính
với bán kính 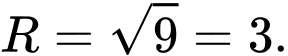 Đáp án: D
Đáp án: D
Gọi
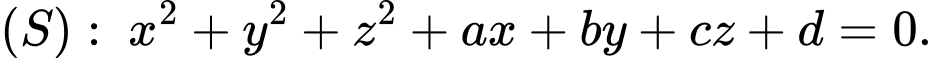
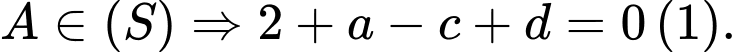
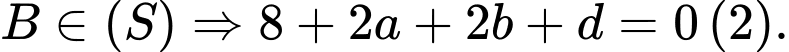
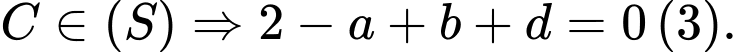
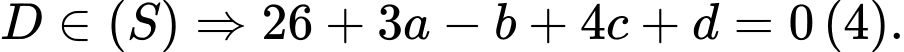
Từ (1), (2), (3) và (4) ta có:
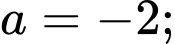
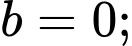
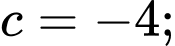
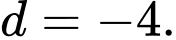
Vậy
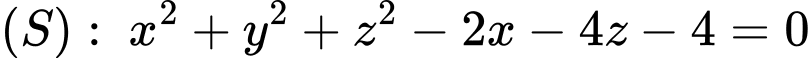 hay
hay 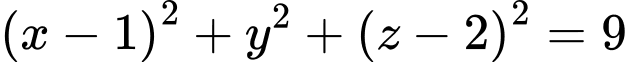 với bán kính
với bán kính 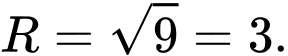 Đáp án: D
Đáp án: D
Câu 25 [80352]: Trong không gian tọa độ 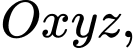 tính bán kính
tính bán kính 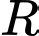 của mặt cầu
của mặt cầu 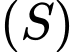 đi qua 3 điểm
đi qua 3 điểm
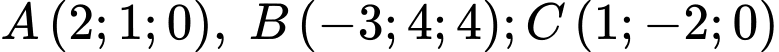 và có tâm thuộc mặt phẳng
và có tâm thuộc mặt phẳng 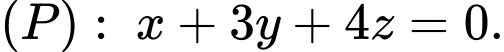
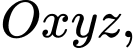 tính bán kính
tính bán kính 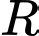 của mặt cầu
của mặt cầu 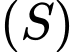 đi qua 3 điểm
đi qua 3 điểm
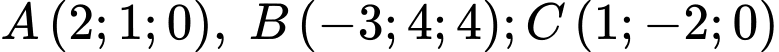 và có tâm thuộc mặt phẳng
và có tâm thuộc mặt phẳng 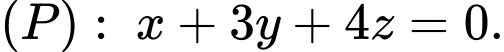
A, 

B, 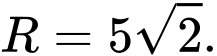
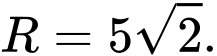
C, 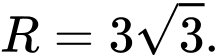
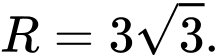
D, 

 Đáp án: D
Đáp án: D
Câu 26 [396454]: Trong không gian tọa độ 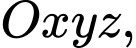 mặt cầu
mặt cầu 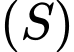 có tâm
có tâm 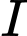 đi qua 3 điểm
đi qua 3 điểm
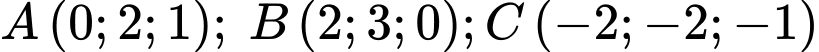 và
và 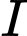 thuộc mặt phẳng
thuộc mặt phẳng 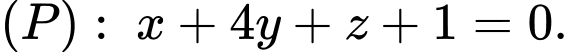 Tính
Tính 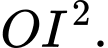
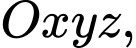 mặt cầu
mặt cầu 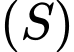 có tâm
có tâm 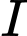 đi qua 3 điểm
đi qua 3 điểm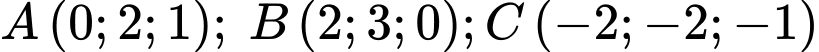 và
và 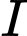 thuộc mặt phẳng
thuộc mặt phẳng 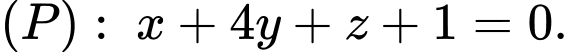 Tính
Tính 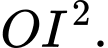
Gọi 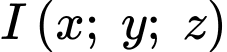 là tâm mặt cầu.
là tâm mặt cầu.
Giải hệ phương trình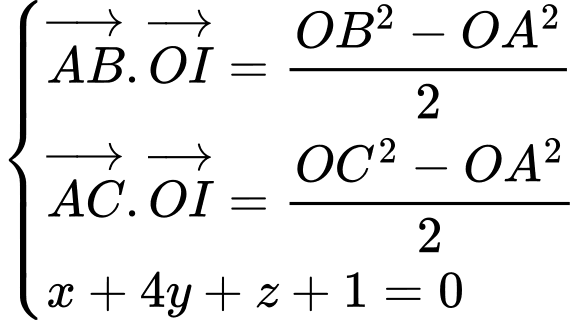
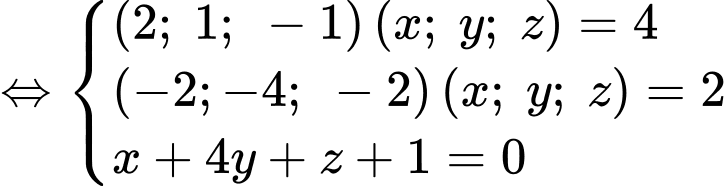
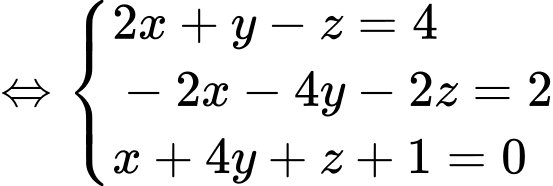
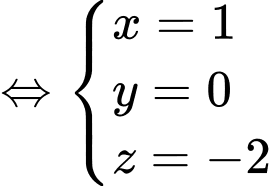
Suy ra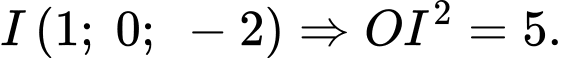
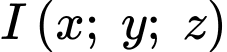 là tâm mặt cầu.
là tâm mặt cầu.
Giải hệ phương trình
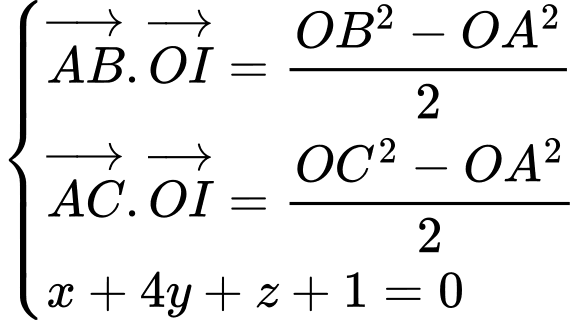
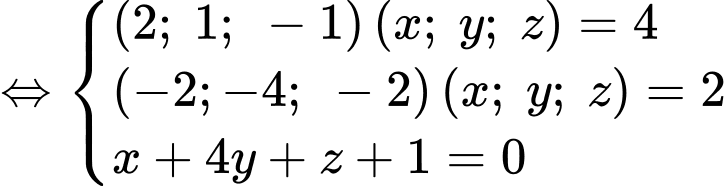
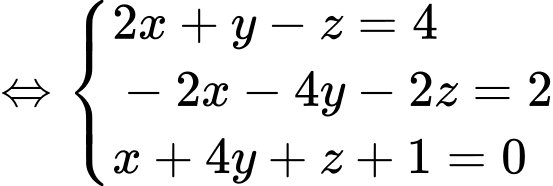
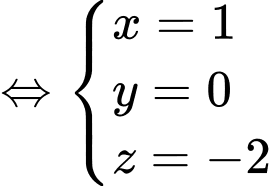
Suy ra
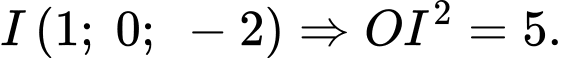
Câu 27 [396456]: Trong không gian với hệ tọa độ 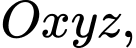 mặt cầu đi qua 4 điểm
mặt cầu đi qua 4 điểm 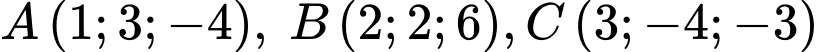 và
và 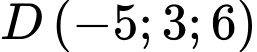 có tâm là
có tâm là 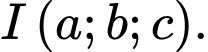 Tính
Tính 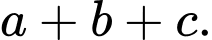
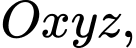 mặt cầu đi qua 4 điểm
mặt cầu đi qua 4 điểm 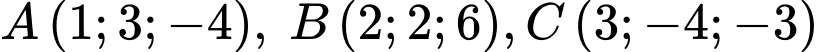 và
và 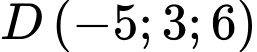 có tâm là
có tâm là 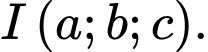 Tính
Tính 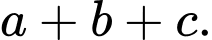
Giải hệ phương trình 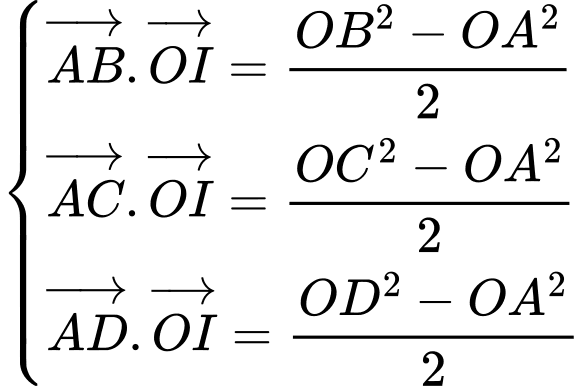
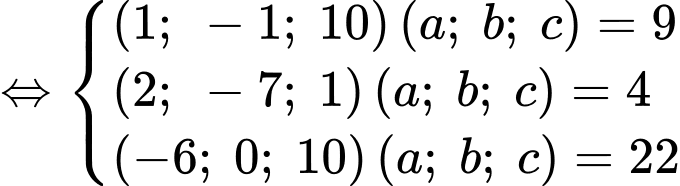
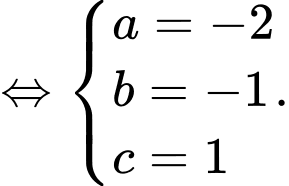
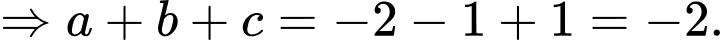
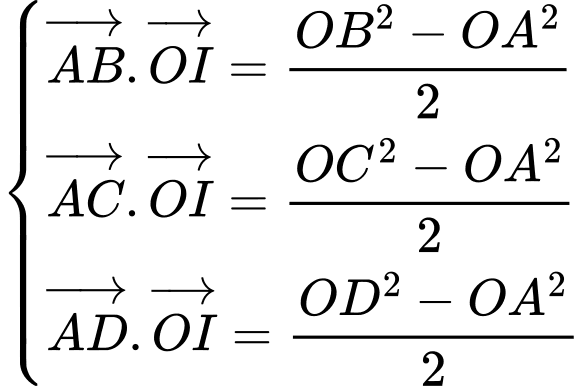
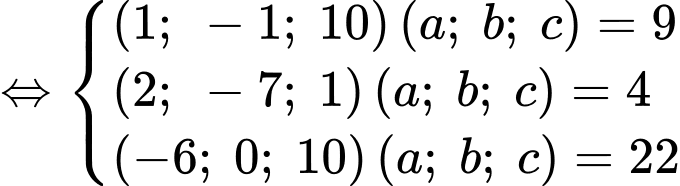
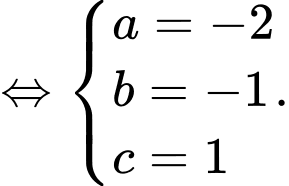
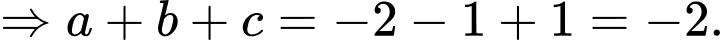
Câu 28 [59136]: Trong không gian với hệ tọa độ 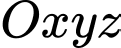 , cho ba điểm
, cho ba điểm 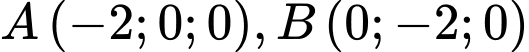 và
và 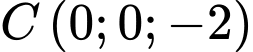 . Gọi
. Gọi 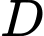 là điểm khác
là điểm khác  sao cho
sao cho  đôi một vuông góc với nhau và
đôi một vuông góc với nhau và 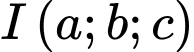 là tâm mặt cầu ngoại tiếp tứ diện
là tâm mặt cầu ngoại tiếp tứ diện 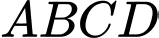 . Tính
. Tính  .
.
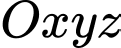 , cho ba điểm
, cho ba điểm 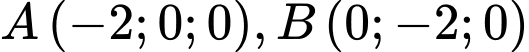 và
và 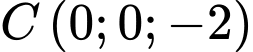 . Gọi
. Gọi 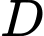 là điểm khác
là điểm khác  sao cho
sao cho  đôi một vuông góc với nhau và
đôi một vuông góc với nhau và 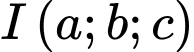 là tâm mặt cầu ngoại tiếp tứ diện
là tâm mặt cầu ngoại tiếp tứ diện 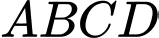 . Tính
. Tính  .
. A, 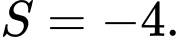
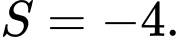
B, 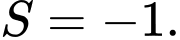
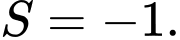
C, 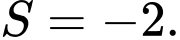
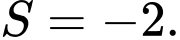
D, 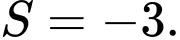
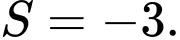
Chọn đáp án B.
Phương trình trục đường tròn ngoại tiếp tam giác đều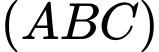 là đường thẳng qua điểm
là đường thẳng qua điểm 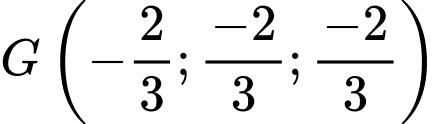 và vuông góc với mặt phẳng
và vuông góc với mặt phẳng 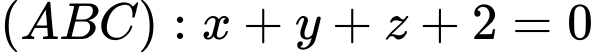 là
là 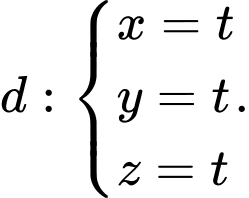
Khi đó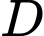 và
và 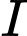 đều thuộc đường thắng
đều thuộc đường thắng 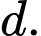
Gọi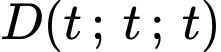 ta có:
ta có: 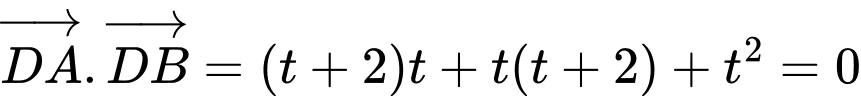
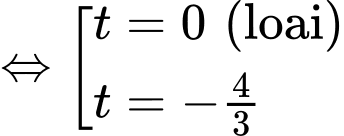
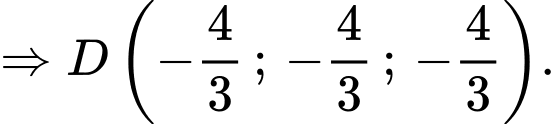
Gọi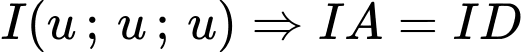
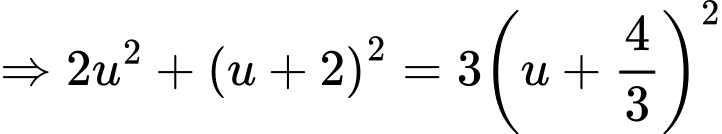
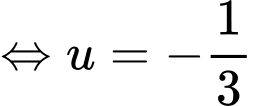
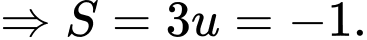 Đáp án: B
Đáp án: B
Phương trình trục đường tròn ngoại tiếp tam giác đều
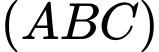 là đường thẳng qua điểm
là đường thẳng qua điểm 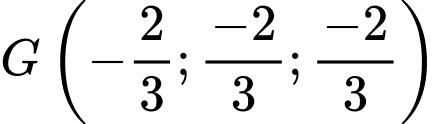 và vuông góc với mặt phẳng
và vuông góc với mặt phẳng 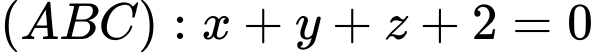 là
là 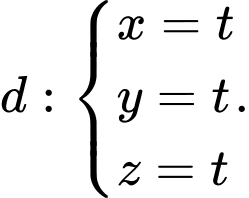
Khi đó
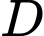 và
và 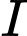 đều thuộc đường thắng
đều thuộc đường thắng 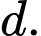
Gọi
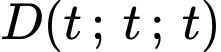 ta có:
ta có: 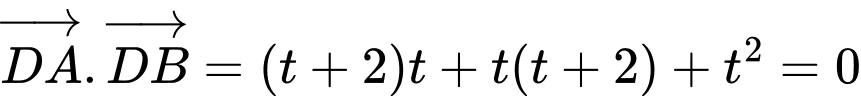
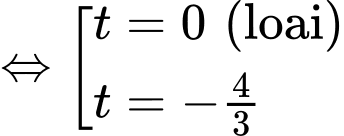
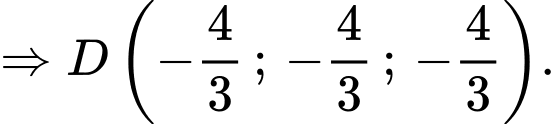
Gọi
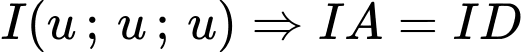
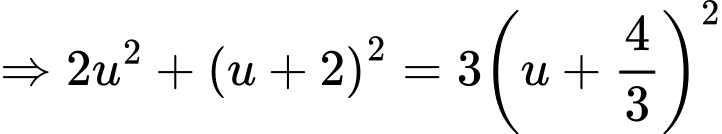
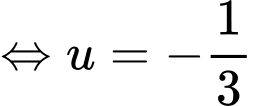
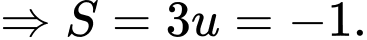 Đáp án: B
Đáp án: B
Câu 29 [202969]: Giả sử Trái Đất có dạng hình cầu và bạn An đang đứng trên mặt đất. Có 3 vệ tinh báo về máy chủ tiếp nhận thông tin rằng vệ tinh thứ nhất đang cách An 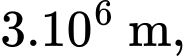 vệ tinh thứ hai đang cách An
vệ tinh thứ hai đang cách An 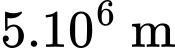 và vệ tinh thứ ba đang cách An
và vệ tinh thứ ba đang cách An 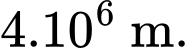 Biết rằng trong hệ trục toạ độ
Biết rằng trong hệ trục toạ độ 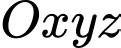 cho trước với
cho trước với  là tâm Trái Đất (1 đơn vị =
là tâm Trái Đất (1 đơn vị = 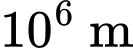 ), tại thời điểm vệ tinh thông báo về máy chủ thì toạ độ của các vệ tinh lần lượt là
), tại thời điểm vệ tinh thông báo về máy chủ thì toạ độ của các vệ tinh lần lượt là 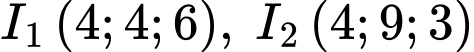 và
và 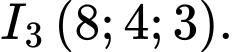 Giả sử bạn An đang đứng ở vị trí có toạ độ là
Giả sử bạn An đang đứng ở vị trí có toạ độ là 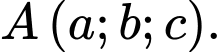 Hãy tính
Hãy tính 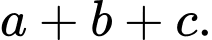
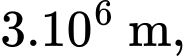 vệ tinh thứ hai đang cách An
vệ tinh thứ hai đang cách An 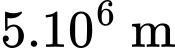 và vệ tinh thứ ba đang cách An
và vệ tinh thứ ba đang cách An 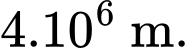 Biết rằng trong hệ trục toạ độ
Biết rằng trong hệ trục toạ độ 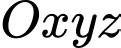 cho trước với
cho trước với  là tâm Trái Đất (1 đơn vị =
là tâm Trái Đất (1 đơn vị = 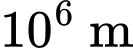 ), tại thời điểm vệ tinh thông báo về máy chủ thì toạ độ của các vệ tinh lần lượt là
), tại thời điểm vệ tinh thông báo về máy chủ thì toạ độ của các vệ tinh lần lượt là 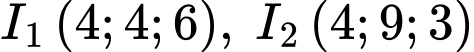 và
và 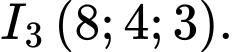 Giả sử bạn An đang đứng ở vị trí có toạ độ là
Giả sử bạn An đang đứng ở vị trí có toạ độ là 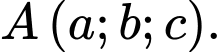 Hãy tính
Hãy tính 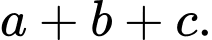
Gọi 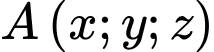 thì
thì 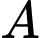 chính là giao điểm của bốn mặt cầu: Trái Đất và ba mặt cầu tâm lần lượt
chính là giao điểm của bốn mặt cầu: Trái Đất và ba mặt cầu tâm lần lượt 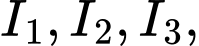 có bán kính lần lượt là khoảng cách từ các vệ tinh đến An.
có bán kính lần lượt là khoảng cách từ các vệ tinh đến An.
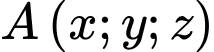 thì
thì 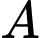 chính là giao điểm của bốn mặt cầu: Trái Đất và ba mặt cầu tâm lần lượt
chính là giao điểm của bốn mặt cầu: Trái Đất và ba mặt cầu tâm lần lượt 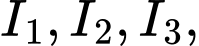 có bán kính lần lượt là khoảng cách từ các vệ tinh đến An.
có bán kính lần lượt là khoảng cách từ các vệ tinh đến An. Ta có hệ phương trình
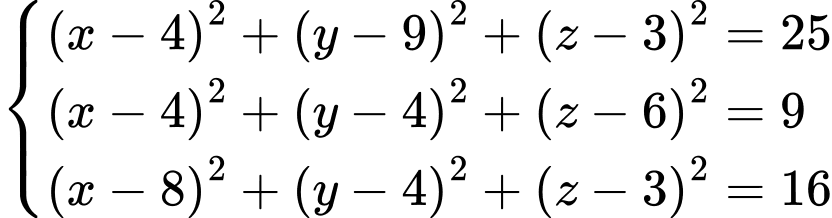
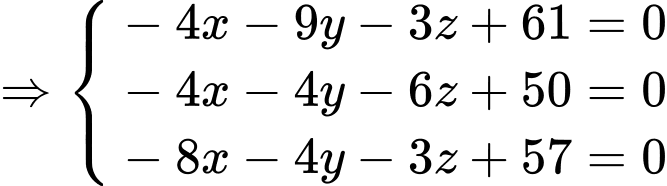
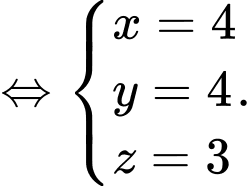
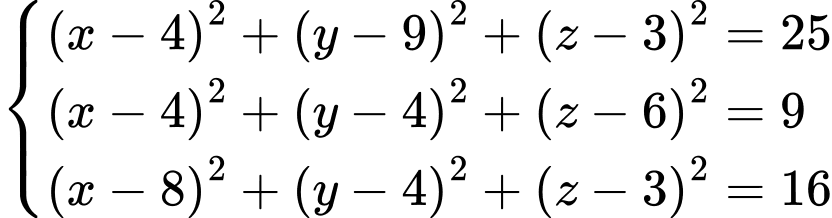
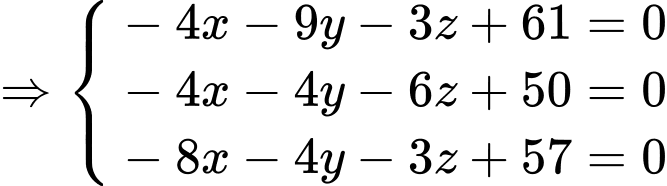
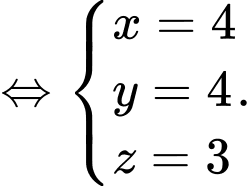
Vậy toạ độ bạn An là 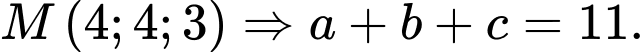
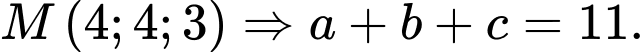
Câu 30 [360644]: Hệ thống định vị toàn cầu (tên tiếng Anh là: Global Positioning System, viết tắt là GPS) là một hệ thống cho phép xác định chính xác vị trí của một vật thể trong không gian (Hình 42).
Ta có thể mô phỏng cơ chế hoạt động của hệ thống GPS trong không gian như sau: Trong cùng một thời điểm, toạ độ của một điểm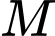 trong không gian sẽ được xác định bởi bốn vệ tinh cho trước, trên mỗi vệ tinh có một máy thu tín hiệu. Bằng cách so sánh sự sai lệch về thời gian từ lúc tín hiệu được phát đi với thời gian nhận phản hồi tín hiệu đó, mỗi máy thu tín hiệu xác định được khoảng cách từ vệ tinh đến vị trí
trong không gian sẽ được xác định bởi bốn vệ tinh cho trước, trên mỗi vệ tinh có một máy thu tín hiệu. Bằng cách so sánh sự sai lệch về thời gian từ lúc tín hiệu được phát đi với thời gian nhận phản hồi tín hiệu đó, mỗi máy thu tín hiệu xác định được khoảng cách từ vệ tinh đến vị trí 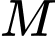 cần tìm toạ độ. Như vậy, điểm
cần tìm toạ độ. Như vậy, điểm 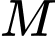 là giao điểm của bốn mặt cầu với tâm lần lượt là bốn vệ tinh đã cho.
là giao điểm của bốn mặt cầu với tâm lần lượt là bốn vệ tinh đã cho.
Ta xét một ví dụ cụ thể như sau:
Trong không gian với hệ toạ độ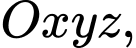 cho bốn vệ tinh
cho bốn vệ tinh 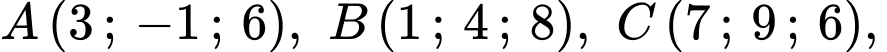
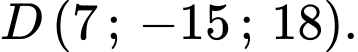 Toạ độ của điểm
Toạ độ của điểm 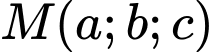 trong không gian biết khoảng cách từ vệ tinh đến điểm
trong không gian biết khoảng cách từ vệ tinh đến điểm 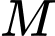 lần lượt là
lần lượt là 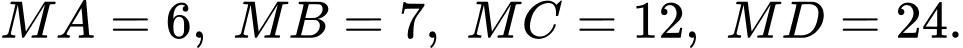

. Tính 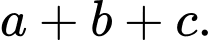
Ta có thể mô phỏng cơ chế hoạt động của hệ thống GPS trong không gian như sau: Trong cùng một thời điểm, toạ độ của một điểm
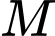 trong không gian sẽ được xác định bởi bốn vệ tinh cho trước, trên mỗi vệ tinh có một máy thu tín hiệu. Bằng cách so sánh sự sai lệch về thời gian từ lúc tín hiệu được phát đi với thời gian nhận phản hồi tín hiệu đó, mỗi máy thu tín hiệu xác định được khoảng cách từ vệ tinh đến vị trí
trong không gian sẽ được xác định bởi bốn vệ tinh cho trước, trên mỗi vệ tinh có một máy thu tín hiệu. Bằng cách so sánh sự sai lệch về thời gian từ lúc tín hiệu được phát đi với thời gian nhận phản hồi tín hiệu đó, mỗi máy thu tín hiệu xác định được khoảng cách từ vệ tinh đến vị trí 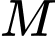 cần tìm toạ độ. Như vậy, điểm
cần tìm toạ độ. Như vậy, điểm 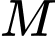 là giao điểm của bốn mặt cầu với tâm lần lượt là bốn vệ tinh đã cho.
là giao điểm của bốn mặt cầu với tâm lần lượt là bốn vệ tinh đã cho. Ta xét một ví dụ cụ thể như sau:
Trong không gian với hệ toạ độ
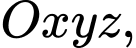 cho bốn vệ tinh
cho bốn vệ tinh 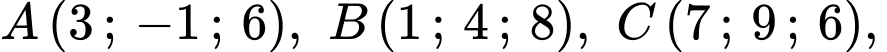
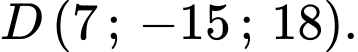 Toạ độ của điểm
Toạ độ của điểm 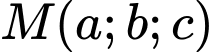 trong không gian biết khoảng cách từ vệ tinh đến điểm
trong không gian biết khoảng cách từ vệ tinh đến điểm 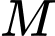 lần lượt là
lần lượt là 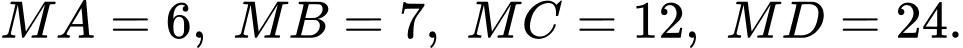

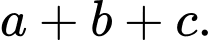
Theo bài ra ta có: 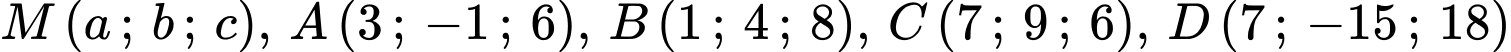 và
và 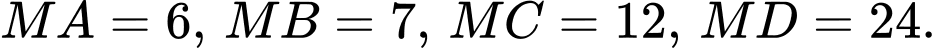
Ta có:
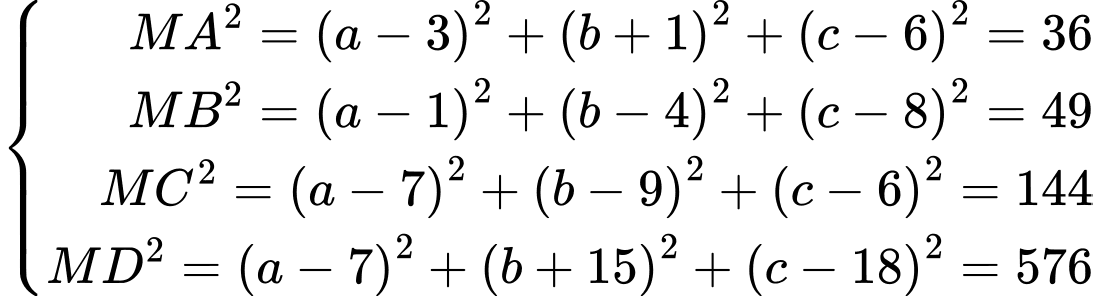
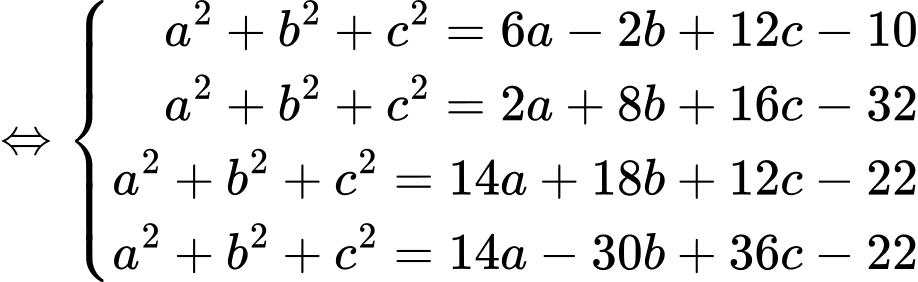
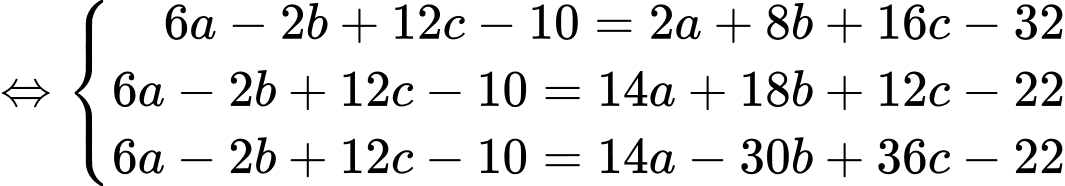
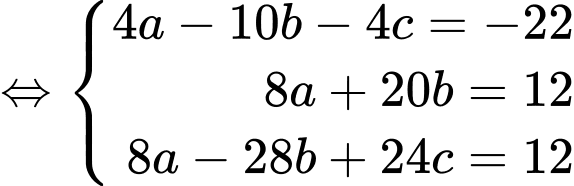
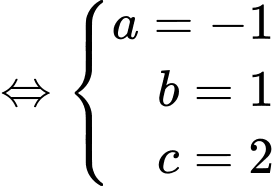
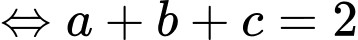
Đáp án: 2.
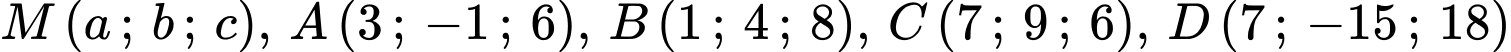 và
và 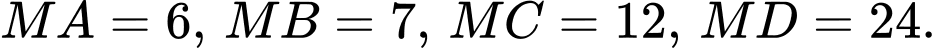
Ta có:
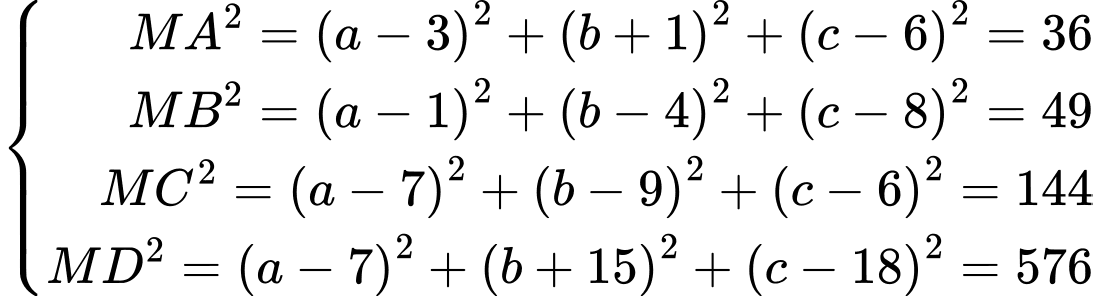
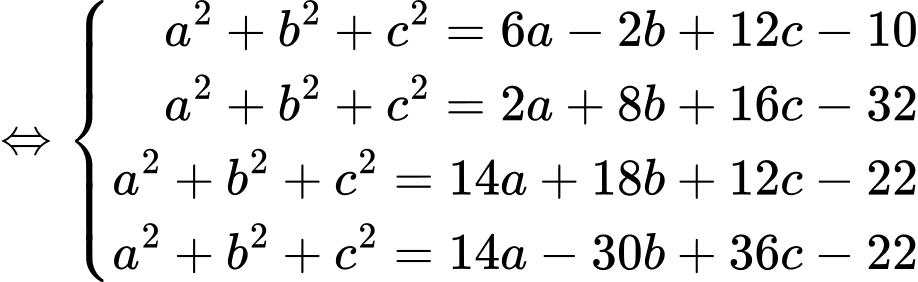
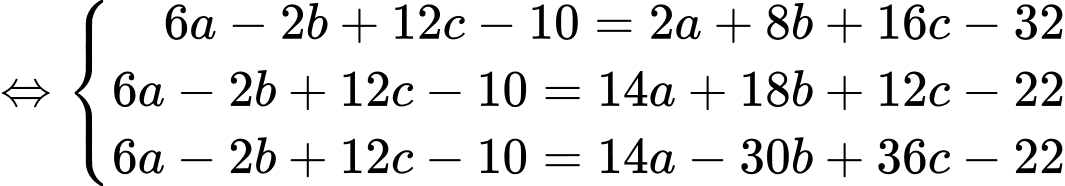
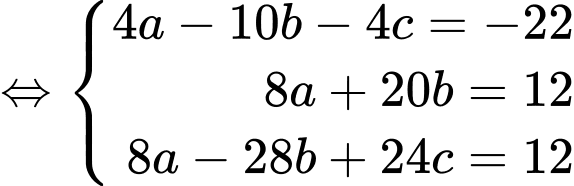
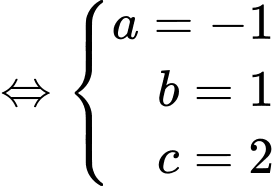
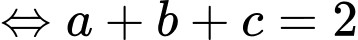
Đáp án: 2.