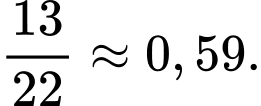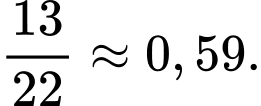Đáp án Bài tập tự luyện
Câu 1 [143806]: Cho 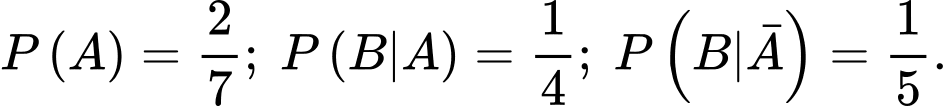 Giá trị
Giá trị 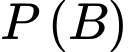 là
là
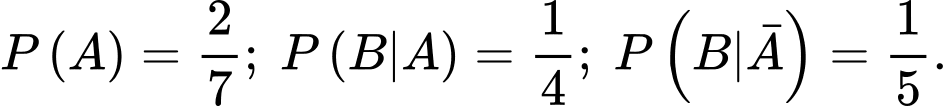 Giá trị
Giá trị 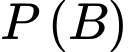 là
là A, 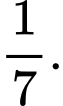
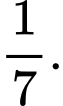
B, 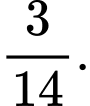
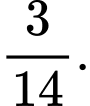
C, 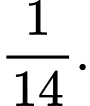
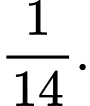
D, 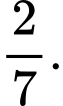
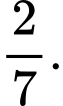
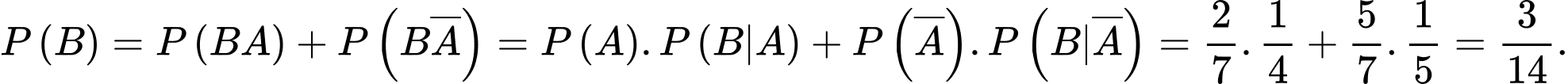 Chọn B. Đáp án: B
Chọn B. Đáp án: B
Câu 2 [143807]: Một học sinh đi học muộn với xác suất là 0,3. Nếu người đó đi học muộn thì xác suất để người đó ăn sáng là 0,2. Nếu người đó không đi học muộn thì xác suất để người đó ăn sáng là 0,6. Ta có sơ đồ hình cây như sau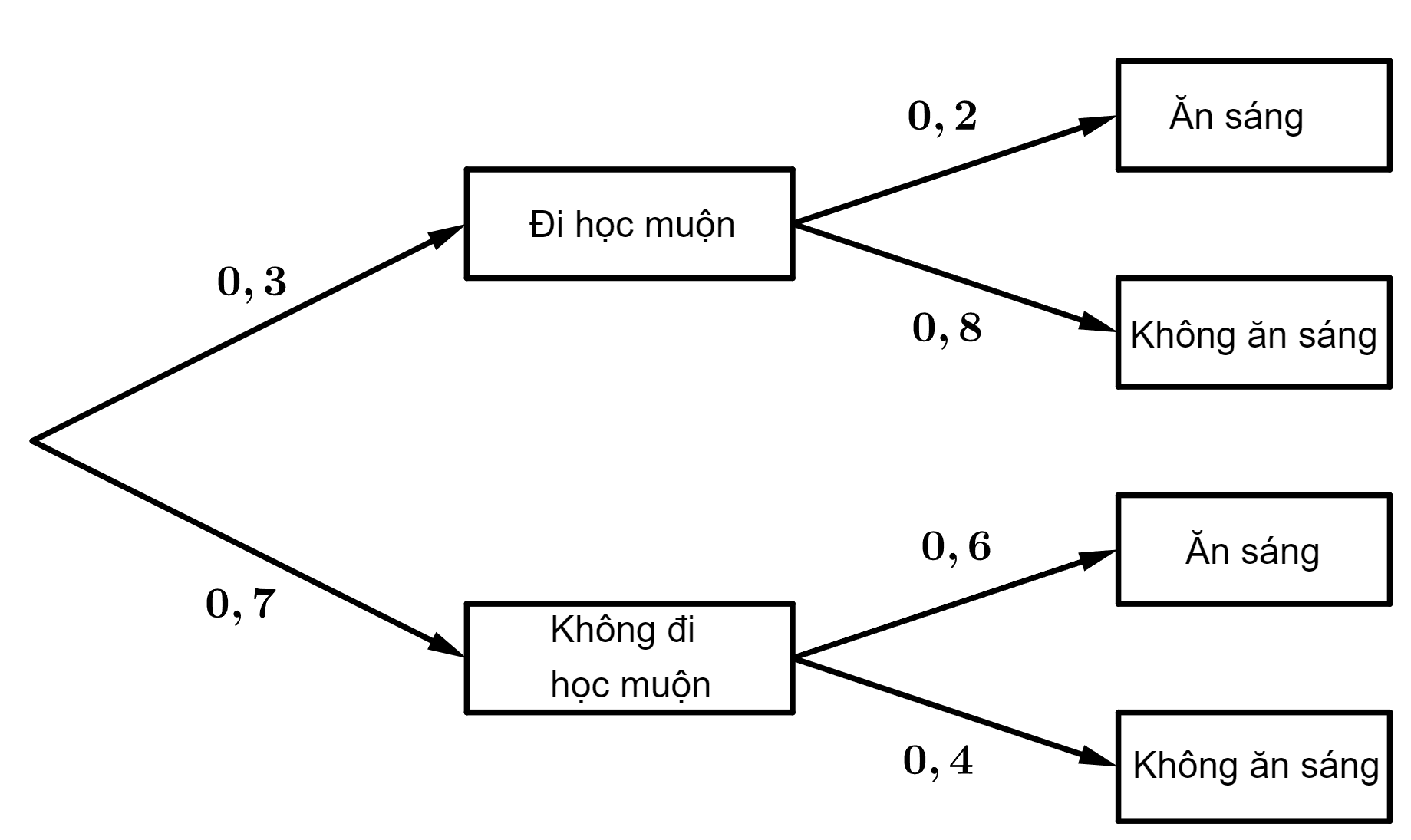

Xác suất của biến cố người đó ăn sáng là
A, 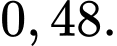
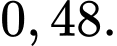
B, 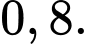
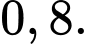
C, 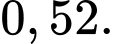
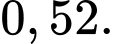
D, 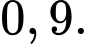
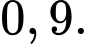
Xác suất của biến cố người đó ăn sáng là: 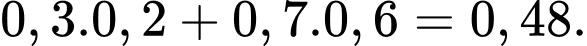
Chọn A. Đáp án: A
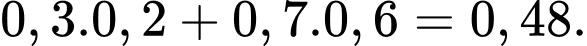
Chọn A. Đáp án: A
Câu 3 [360676]: Cho hai biến cố 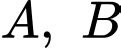 với
với 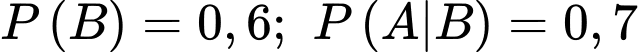 và
và 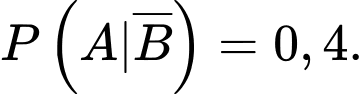 Khi đó,
Khi đó, 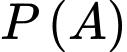 bằng:
bằng:
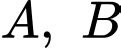 với
với 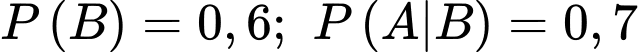 và
và 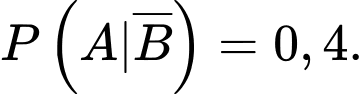 Khi đó,
Khi đó, 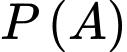 bằng:
bằng: A, 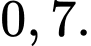
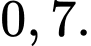
B, 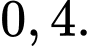
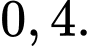
C, 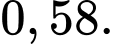
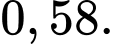
D, 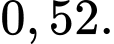
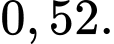
Ta có: 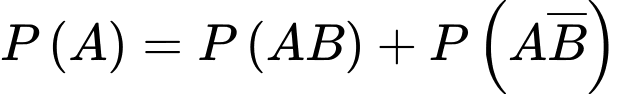
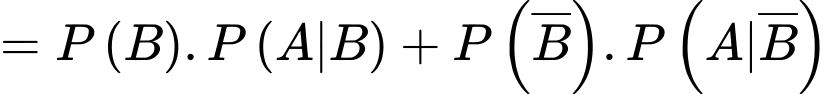
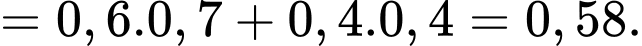
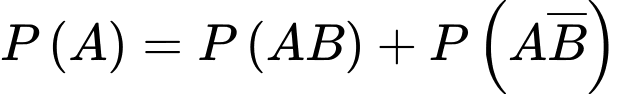
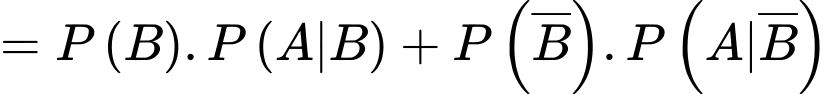
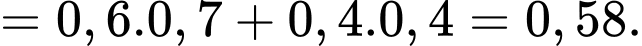
Chọn C.
Đáp án: C
Câu 4 [378729]: Cho 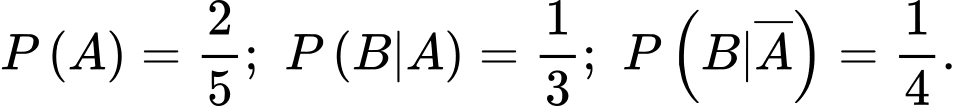
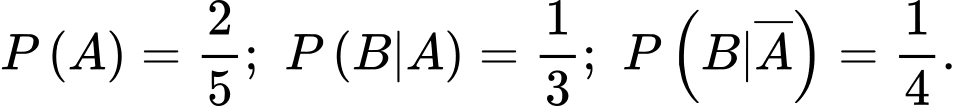
Giá trị của 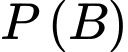 là
là
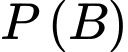 là
là
A, 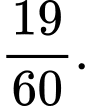
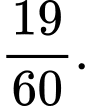
B, 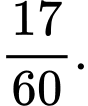
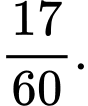
C, 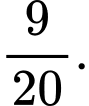
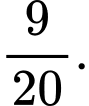
D, 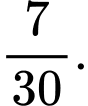
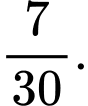
Ta có: 
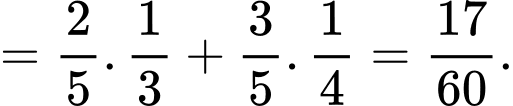 Đáp án: B
Đáp án: B

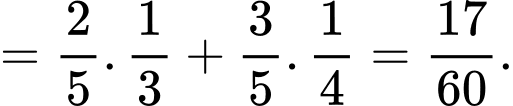
Chọn B.
Câu 5 [378717]: Số khán giả đến xem buổi biểu diễn ca nhạc ngoài trời phụ thuộc vào thời tiết. Giả sử, nếu trời không mưa thì xác suất để bán hết vé là 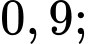 còn nếu trời mưa thì xác suất để bán hết vé chỉ là
còn nếu trời mưa thì xác suất để bán hết vé chỉ là 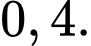 Dự báo thời tiết cho thấy xác suất để trời mưa vào buổi biểu diễn là
Dự báo thời tiết cho thấy xác suất để trời mưa vào buổi biểu diễn là 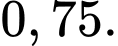 Tính xác suất để nhà tổ chức sự kiện bán hết vé.
Tính xác suất để nhà tổ chức sự kiện bán hết vé.
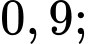 còn nếu trời mưa thì xác suất để bán hết vé chỉ là
còn nếu trời mưa thì xác suất để bán hết vé chỉ là 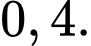 Dự báo thời tiết cho thấy xác suất để trời mưa vào buổi biểu diễn là
Dự báo thời tiết cho thấy xác suất để trời mưa vào buổi biểu diễn là 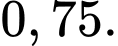 Tính xác suất để nhà tổ chức sự kiện bán hết vé.
Tính xác suất để nhà tổ chức sự kiện bán hết vé. A, 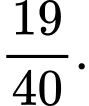
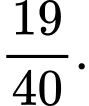
B, 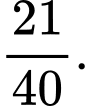
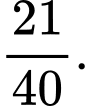
C, 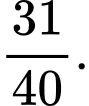
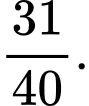
D, 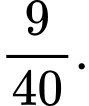
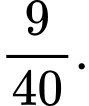
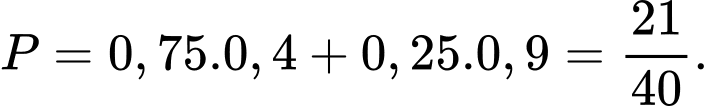 Đáp án: B
Đáp án: B
Câu 6 [145258]: [Trích SGK Cùng Khám Phá]: Người ta khảo sát khả năng chơi nhạc cụ của một nhóm học sinh tại trường X. Nhóm này có 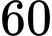 học sinh là nam. Kết quả khảo sát cho thấy có
học sinh là nam. Kết quả khảo sát cho thấy có 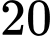 học sinh nam và
học sinh nam và  học sinh nữ biết chơi ít nhất một nhạc cụ. Chọn ngẫu nhiên một học sinh trong nhóm này. Tính xác suất để chọn được học sinh biết chơi ít nhất một nhạc cụ.
học sinh nữ biết chơi ít nhất một nhạc cụ. Chọn ngẫu nhiên một học sinh trong nhóm này. Tính xác suất để chọn được học sinh biết chơi ít nhất một nhạc cụ.
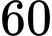 học sinh là nam. Kết quả khảo sát cho thấy có
học sinh là nam. Kết quả khảo sát cho thấy có 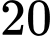 học sinh nam và
học sinh nam và  học sinh nữ biết chơi ít nhất một nhạc cụ. Chọn ngẫu nhiên một học sinh trong nhóm này. Tính xác suất để chọn được học sinh biết chơi ít nhất một nhạc cụ.
học sinh nữ biết chơi ít nhất một nhạc cụ. Chọn ngẫu nhiên một học sinh trong nhóm này. Tính xác suất để chọn được học sinh biết chơi ít nhất một nhạc cụ. A, 18%.
B, 66%.
C, 34%.
D, 82%.
Xét phép thử chọn ngẫu nhiên một học sinh trong nhóm.
Gọi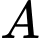 là biến cố "Chọn được một học sinh biết chơi ít nhất một nhạc cụ" và
là biến cố "Chọn được một học sinh biết chơi ít nhất một nhạc cụ" và 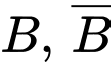 lần lượt là các biến cố
lần lượt là các biến cố
"Chọn được một học sinh nam" và "Chọn được một học sinh nữ".
Theo đề bài: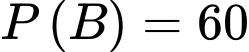
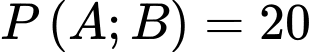
Áp dụng công thức xác suất toàn phần, ta có: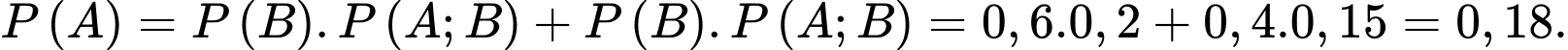
Vậy xác suất để chọn được một học sinh biết chơi nhạc cụ là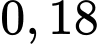 hay
hay 
Chọn A. Đáp án: A
Gọi
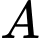 là biến cố "Chọn được một học sinh biết chơi ít nhất một nhạc cụ" và
là biến cố "Chọn được một học sinh biết chơi ít nhất một nhạc cụ" và 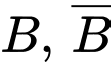 lần lượt là các biến cố
lần lượt là các biến cố"Chọn được một học sinh nam" và "Chọn được một học sinh nữ".
Theo đề bài:
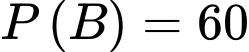
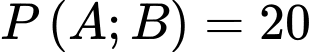
Áp dụng công thức xác suất toàn phần, ta có:
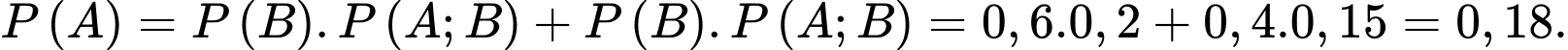
Vậy xác suất để chọn được một học sinh biết chơi nhạc cụ là
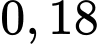 hay
hay 
Chọn A. Đáp án: A
Câu 7 [143809]: Một cậu bé có một hộp bi gồm 6 viên bi đỏ và 4 viên bi trắng. Một hôm cậu thấy mất 1 viên bi mà không biết viên bi đó màu gì. Tính xác suất để khi lấy ngẫu nhiên ra một viên bi từ hộp thì ta được bi đỏ.
A, 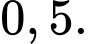
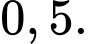
B, 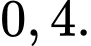
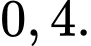
C, 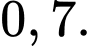
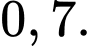
D, 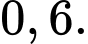
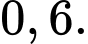
Chọn đáp án D.
Vì ta chưa biết viên bi bị mất là màu nào. Nên ta gọi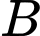 là biến cố “Viên bi bị mất màu đỏ”,
là biến cố “Viên bi bị mất màu đỏ”, 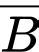 là biến cố “Viên bị mất màu trắng”.
là biến cố “Viên bị mất màu trắng”.
Xét trường hợp biến cố viên bi đỏ bị mất thì trong hộp còn lại tổng cộng 9 viên bi, trong đó có 5 viên bi đỏ. Và với trường hợp biến cố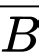 xảy ra thì trong hộp còn lại tổng cộng 9 viên bi, trong đó có 6 viên bi đỏ.
xảy ra thì trong hộp còn lại tổng cộng 9 viên bi, trong đó có 6 viên bi đỏ.
Ta có sơ đồ cây như sau:
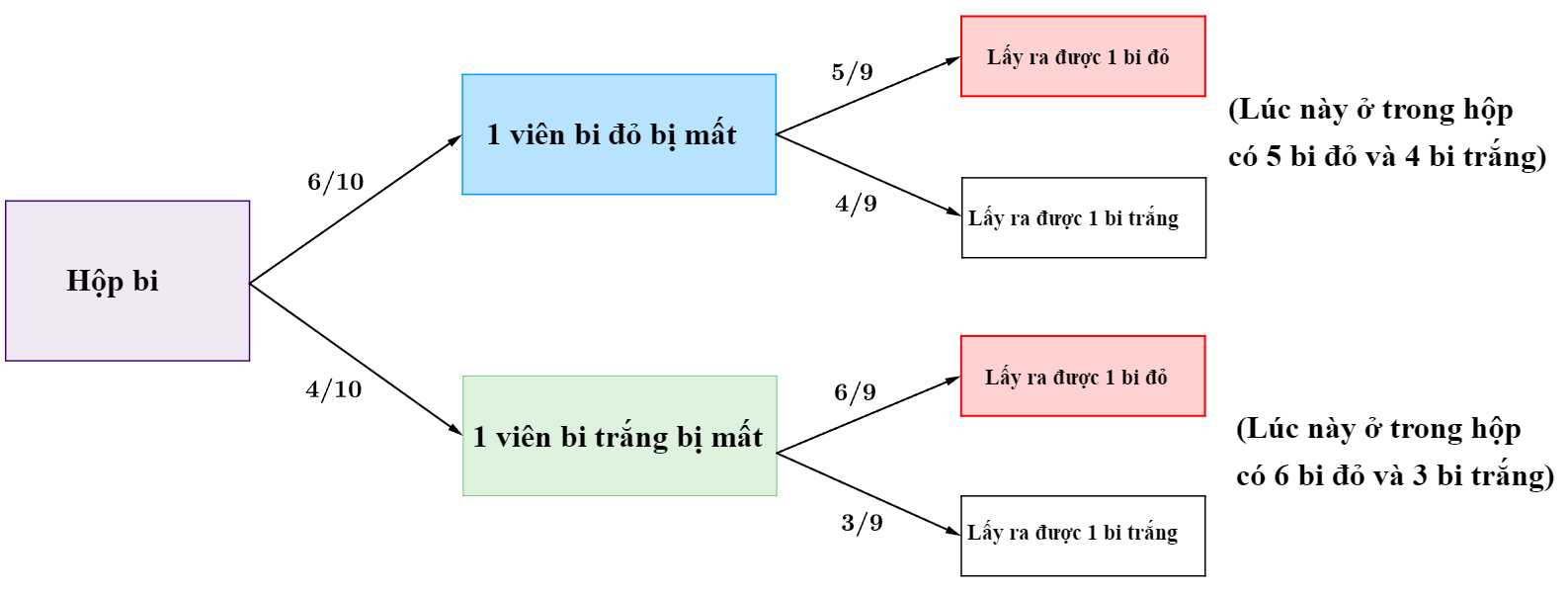
Áp dụng công thức xác suất toàn phần, ta có xác suất lấy được một viên bi đỏ từ hộp bằng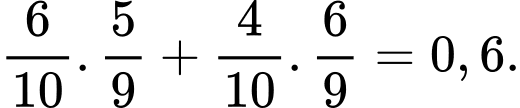 Đáp án: D
Đáp án: D
Vì ta chưa biết viên bi bị mất là màu nào. Nên ta gọi
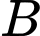 là biến cố “Viên bi bị mất màu đỏ”,
là biến cố “Viên bi bị mất màu đỏ”, 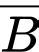 là biến cố “Viên bị mất màu trắng”.
là biến cố “Viên bị mất màu trắng”.
Xét trường hợp biến cố viên bi đỏ bị mất thì trong hộp còn lại tổng cộng 9 viên bi, trong đó có 5 viên bi đỏ. Và với trường hợp biến cố
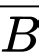 xảy ra thì trong hộp còn lại tổng cộng 9 viên bi, trong đó có 6 viên bi đỏ.
xảy ra thì trong hộp còn lại tổng cộng 9 viên bi, trong đó có 6 viên bi đỏ.
Ta có sơ đồ cây như sau:

Áp dụng công thức xác suất toàn phần, ta có xác suất lấy được một viên bi đỏ từ hộp bằng
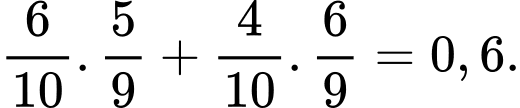 Đáp án: D
Đáp án: D
Câu 8 [143810]: Hai nhà máy cùng sản xuất 1 loại linh kiện điện tử. Năng suất nhà máy hai
gấp 3 lần năng suất nhà máy một. Tỷ lệ hỏng của nhà máy một và hai lần lượt là 0,1% và
0,2%. Giả sử linh kiện bán ở Trung tâm chỉ do hai nhà máy này sản xuất. Mua 1 linh
kiện ở Trung tâm. Tính xác suất để linh kiện ấy hỏng
gấp 3 lần năng suất nhà máy một. Tỷ lệ hỏng của nhà máy một và hai lần lượt là 0,1% và
0,2%. Giả sử linh kiện bán ở Trung tâm chỉ do hai nhà máy này sản xuất. Mua 1 linh
kiện ở Trung tâm. Tính xác suất để linh kiện ấy hỏng
A, 0,175%.
B, 0,125%.
C, 0,225%.
D, 0,233%.
Gọi  lần lượt là biến cố linh kiện điện tử do nhà máy I và nhà máy II sản xuất.
lần lượt là biến cố linh kiện điện tử do nhà máy I và nhà máy II sản xuất.
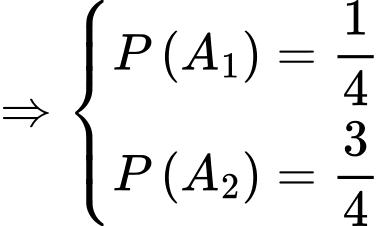
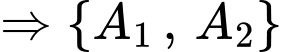 là một hệ đầy đủ.
là một hệ đầy đủ.
Gọi B là biến cố linh kiện điện tử bị hỏng
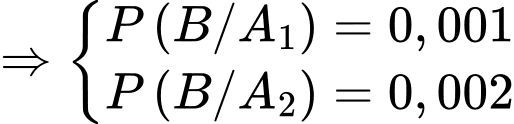
Xác suất linh kiện bán ra là một linh kiện bị hỏng là:
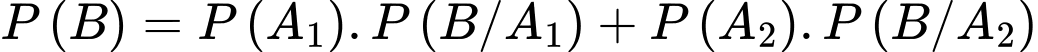
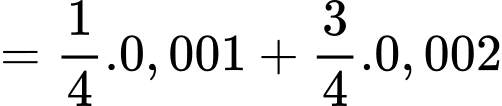
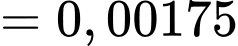
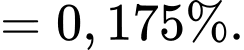
Đáp án: A. Đáp án: A
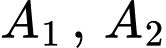 lần lượt là biến cố linh kiện điện tử do nhà máy I và nhà máy II sản xuất.
lần lượt là biến cố linh kiện điện tử do nhà máy I và nhà máy II sản xuất.
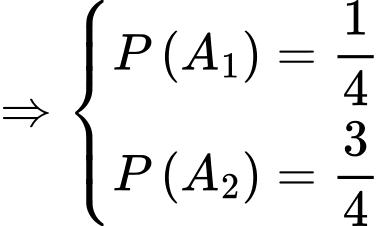
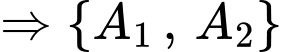 là một hệ đầy đủ.
là một hệ đầy đủ.
Gọi B là biến cố linh kiện điện tử bị hỏng
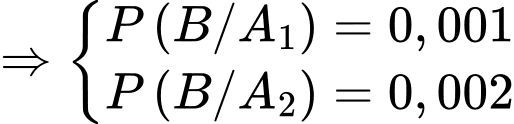
Xác suất linh kiện bán ra là một linh kiện bị hỏng là:
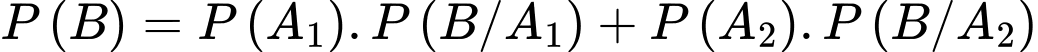
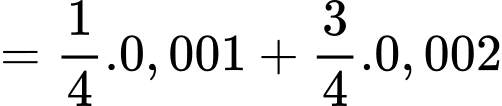
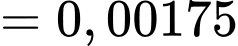
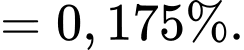
Đáp án: A. Đáp án: A
Câu 9 [143808]: Có hai chuồng thỏ. Chuồng I có 6 con thỏ đen và 10 con thỏ trắng. Chuồng II có 8 con thỏ đen và 4 con thỏ trắng. Trước tiên, từ chuồng I lấy ra ngẫu nhiên 1 con thỏ rồi cho vào chuồng II. Sau đó, từ chuồng II lấy ra ngẫu nhiên 1 con thỏ. Tính xác suất để con thỏ được lấy ra là con thỏ trắng.
A, 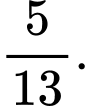
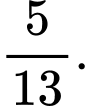
B, 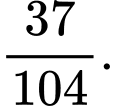
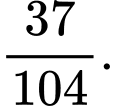
C, 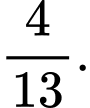
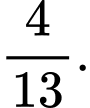
D, 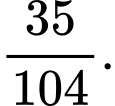
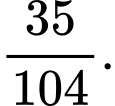
Chọn đáp án B.
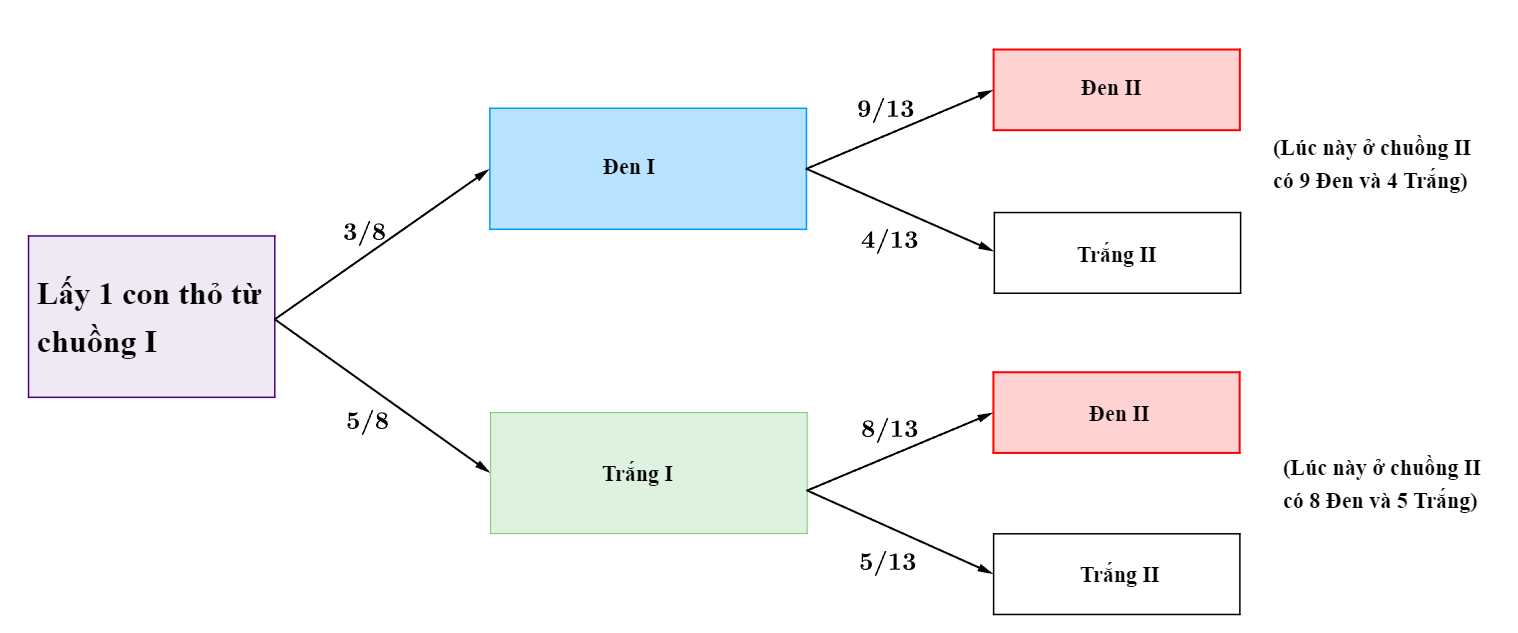
Từ dữ kiện đề bài, ta có sơ đồ cây như sau:
Áp dụng công thức xác suất toàn phần, ta có xác suất lấy được con thỏ được lấy ra từ chuồng II là con thỏ trắng bằng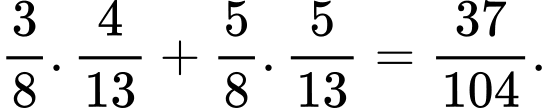 Đáp án: B
Đáp án: B
Từ dữ kiện đề bài, ta có sơ đồ cây như sau:

Áp dụng công thức xác suất toàn phần, ta có xác suất lấy được con thỏ được lấy ra từ chuồng II là con thỏ trắng bằng
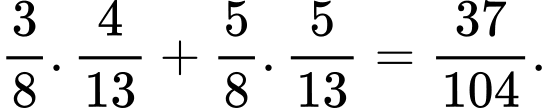 Đáp án: B
Đáp án: B
Câu 10 [378723]: Có hai chuồng thỏ. Chuồng I có 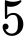 con thỏ đen và
con thỏ đen và  con thỏ trắng. Chuồng II có
con thỏ trắng. Chuồng II có 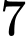 con thỏ đen và
con thỏ đen và 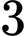 con thỏ trắng. Trước tiên, từ chuồng II lấy ra ngẫu nhiên
con thỏ trắng. Trước tiên, từ chuồng II lấy ra ngẫu nhiên 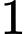 con thỏ rồi cho vào chuồng I. Sau đó, từ chuồng I lấy ra ngẫu nhiên
con thỏ rồi cho vào chuồng I. Sau đó, từ chuồng I lấy ra ngẫu nhiên 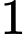 con thỏ. Tính xác suất để con thỏ được lấy ra là con thỏ trắng.
con thỏ. Tính xác suất để con thỏ được lấy ra là con thỏ trắng.
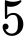 con thỏ đen và
con thỏ đen và  con thỏ trắng. Chuồng II có
con thỏ trắng. Chuồng II có 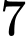 con thỏ đen và
con thỏ đen và 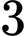 con thỏ trắng. Trước tiên, từ chuồng II lấy ra ngẫu nhiên
con thỏ trắng. Trước tiên, từ chuồng II lấy ra ngẫu nhiên 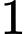 con thỏ rồi cho vào chuồng I. Sau đó, từ chuồng I lấy ra ngẫu nhiên
con thỏ rồi cho vào chuồng I. Sau đó, từ chuồng I lấy ra ngẫu nhiên 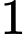 con thỏ. Tính xác suất để con thỏ được lấy ra là con thỏ trắng.
con thỏ. Tính xác suất để con thỏ được lấy ra là con thỏ trắng. A, 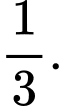
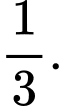
B, 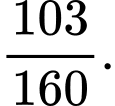
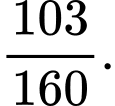
C, 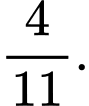
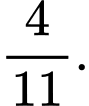
D, 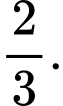
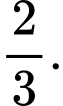
Gọi biến cố A: “Lấy chuồng II ra được thỏ trắng”;
B: “Lấy chuồng I ra được thỏ trắng”;
Ta có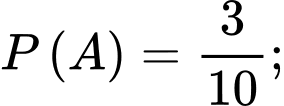
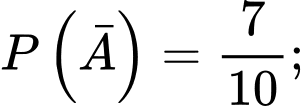
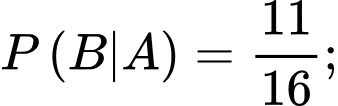
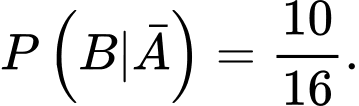
Ta cần tính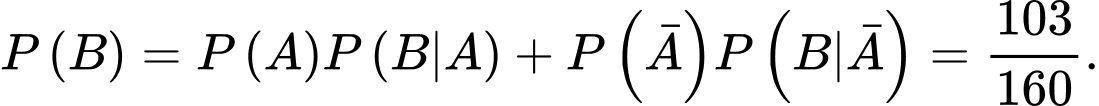 Chọn B. Đáp án: B
Chọn B. Đáp án: B
B: “Lấy chuồng I ra được thỏ trắng”;
Ta có
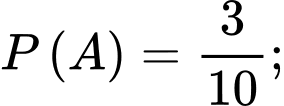
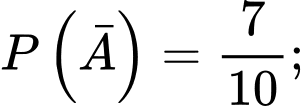
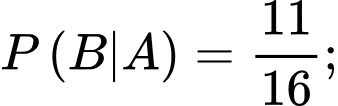
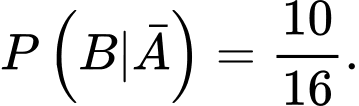
Ta cần tính
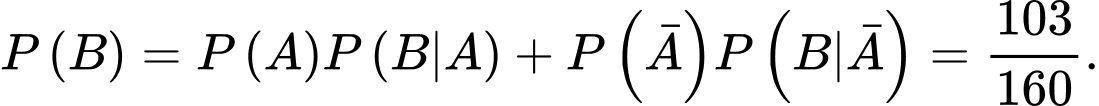 Chọn B. Đáp án: B
Chọn B. Đáp án: B
Câu 11 [146776]: Một người có 5 con gà mái, 2 con gà trống nhốt chung trong một cái lồng.Một người đến mua, người bán gà bắt ngẫu nhiên 1 con. Người mua chấp nhận mua con gà đó. Xét tính đúng sai của mệnh đề sau:
a) Đúng. Xác suất để người đó mua được con gà mái là 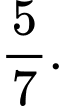
b) Sai. Xác suất để người đó mua được con gà trống là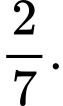
c) Đúng. Một người thứ hai lại đến mua gà, người bán gà lại bắt ngẫu nhiên ra 1 con, xác suất để người thứ hai mua được con gà trống là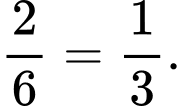
d) Sai. Gọi A là biến cố: “ người thứ hai mua được gà trống”
B là biến cố: Người thứ nhất mua được gà mái”
Ta có: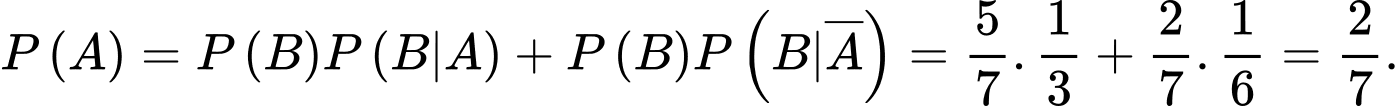
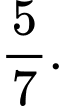
b) Sai. Xác suất để người đó mua được con gà trống là
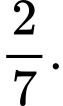
c) Đúng. Một người thứ hai lại đến mua gà, người bán gà lại bắt ngẫu nhiên ra 1 con, xác suất để người thứ hai mua được con gà trống là
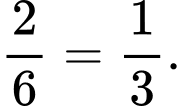
d) Sai. Gọi A là biến cố: “ người thứ hai mua được gà trống”
B là biến cố: Người thứ nhất mua được gà mái”
Ta có:
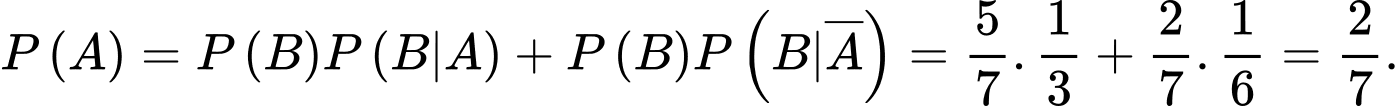
Câu 12 [143811]: Có 2 xạ thủ loại I và 8 xạ thủ loại II, xác suất bắn trúng đích của các loại xạ
thủ loại I là 0,9 và loại II là 0,7. Chọn ngẫu nhiên ra một xạ thủ và xạ thủ đó bắn một viên đạn. Tìm xác suất để viên đạn đó trúng đích.
Gọi A là biến cố “Viên đạn bắn trúng đích”
 lần lượt là biến cố “Chọn được xạ thủ loại 1, 2”
lần lượt là biến cố “Chọn được xạ thủ loại 1, 2” 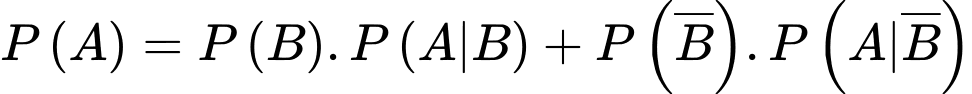
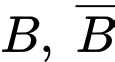 lần lượt là biến cố “Chọn được xạ thủ loại 1, 2”
lần lượt là biến cố “Chọn được xạ thủ loại 1, 2” Ta có: 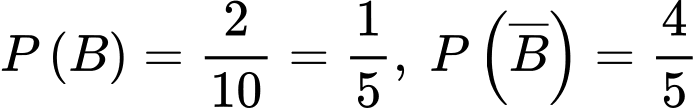
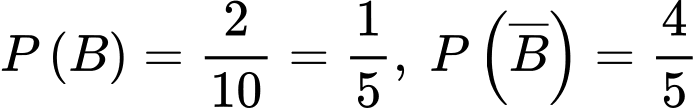
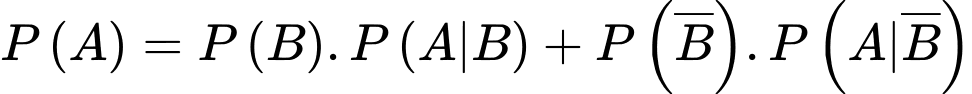
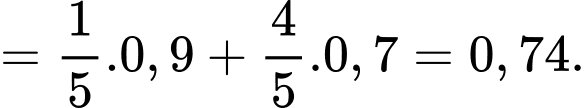
Câu 13 [143812]: Theo thống kê xác suất để hai ngày liên tiếp có mưa ở một thành phố vào mùa hè là0,5; còn không mưa là 0,3. Biết các sự kiện có một ngày mưa, một ngày không mưa là đồng khả năng. Tính xác suất để ngày thứ hai có mưa, biết ngày đầu không mưa.
Điền đáp án: 0,25.
Gọi A là “ngày đầu mưa" và B là “ngày thứ hai mưa" thì ta có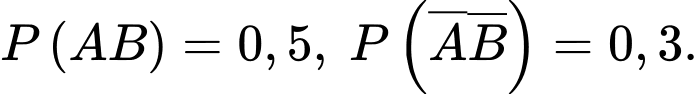
Vì các sự kiện có một ngày mưa, một ngày không mưa là đồng khả năng nên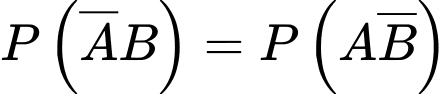
Lại có: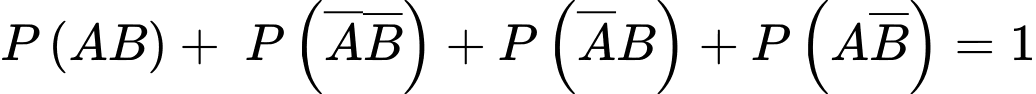 nên
nên 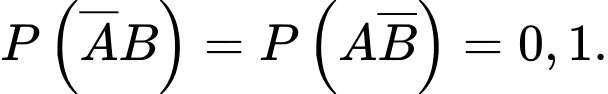
Xác suất cần tính là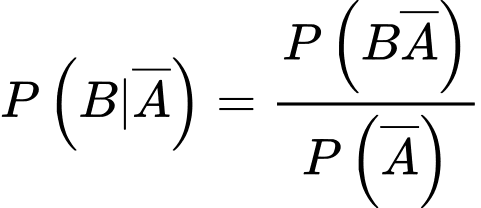
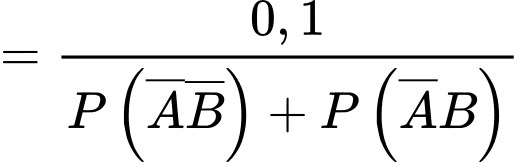
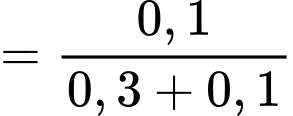
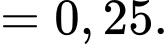
Gọi A là “ngày đầu mưa" và B là “ngày thứ hai mưa" thì ta có
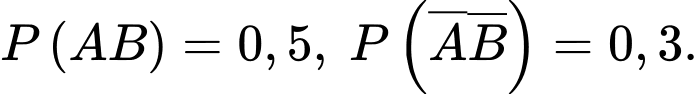
Vì các sự kiện có một ngày mưa, một ngày không mưa là đồng khả năng nên
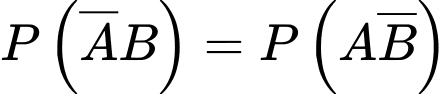
Lại có:
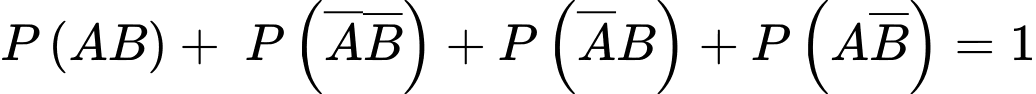 nên
nên 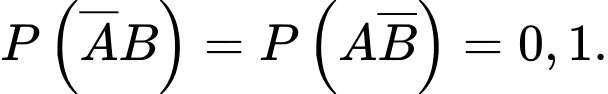
Xác suất cần tính là
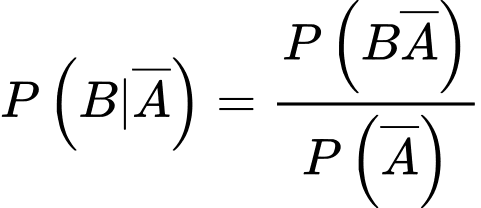
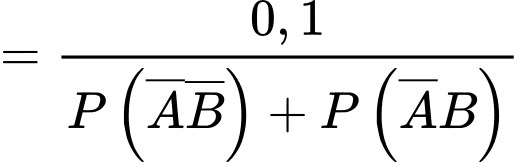
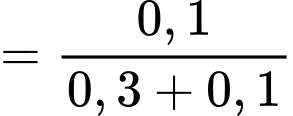
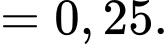
Câu 14 [378735]: Chuồng I có 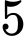 con gà mái,
con gà mái, 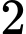 con gà trống. Chuồng II có
con gà trống. Chuồng II có 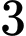 con gà mái,
con gà mái, 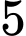 con gà trống. Bác Mai bắt một con gà trong số đó theo cách sau: “Bác tung một con xúc xắc cân đối, đồng chất. Nếu số chấm chia hết cho
con gà trống. Bác Mai bắt một con gà trong số đó theo cách sau: “Bác tung một con xúc xắc cân đối, đồng chất. Nếu số chấm chia hết cho 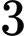 thì bác chọn chuồng I. Nếu số chấm không chia hết cho
thì bác chọn chuồng I. Nếu số chấm không chia hết cho 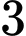 thì bác chọn chuồng II. Sau đó, từ chuồng đã chọn bác bắt ngẫu nhiên một con gà”. Tính xác suất để bác Mai bắt được con gà mái. Viết kết quả làm tròn đến hàng phần trăm.
thì bác chọn chuồng II. Sau đó, từ chuồng đã chọn bác bắt ngẫu nhiên một con gà”. Tính xác suất để bác Mai bắt được con gà mái. Viết kết quả làm tròn đến hàng phần trăm.
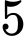 con gà mái,
con gà mái, 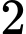 con gà trống. Chuồng II có
con gà trống. Chuồng II có 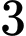 con gà mái,
con gà mái, 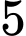 con gà trống. Bác Mai bắt một con gà trong số đó theo cách sau: “Bác tung một con xúc xắc cân đối, đồng chất. Nếu số chấm chia hết cho
con gà trống. Bác Mai bắt một con gà trong số đó theo cách sau: “Bác tung một con xúc xắc cân đối, đồng chất. Nếu số chấm chia hết cho 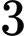 thì bác chọn chuồng I. Nếu số chấm không chia hết cho
thì bác chọn chuồng I. Nếu số chấm không chia hết cho 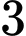 thì bác chọn chuồng II. Sau đó, từ chuồng đã chọn bác bắt ngẫu nhiên một con gà”. Tính xác suất để bác Mai bắt được con gà mái. Viết kết quả làm tròn đến hàng phần trăm.
thì bác chọn chuồng II. Sau đó, từ chuồng đã chọn bác bắt ngẫu nhiên một con gà”. Tính xác suất để bác Mai bắt được con gà mái. Viết kết quả làm tròn đến hàng phần trăm.
Gọi A là biến cố: "Chọn chuồng I ";
B là biến cố: "Bắt được gà mái".
Vì nếu tung xúc xắc mà số chấm xuất hiện chia hết cho 3 thì bác chọn chuồng I nên ta có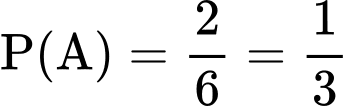 . Suy ra
. Suy ra 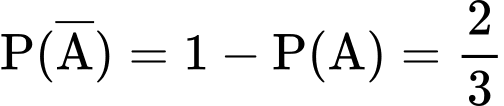 .
.
Từ dữ kiện bài ra, ta suy ra được: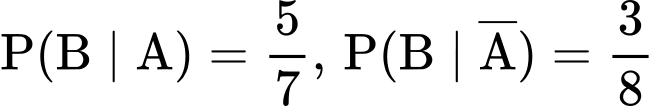 .
.
Áp dụng công thức xác suất toàn phần, ta có:

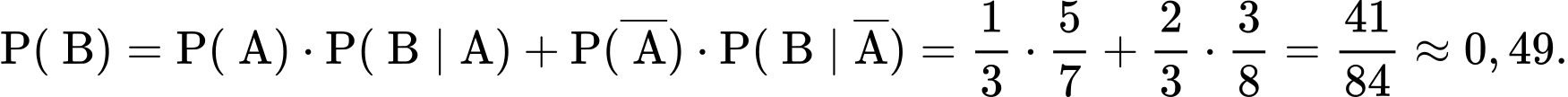
Vậy xác suất để bác Mai bắt được con gà mái là 0,49
B là biến cố: "Bắt được gà mái".
Vì nếu tung xúc xắc mà số chấm xuất hiện chia hết cho 3 thì bác chọn chuồng I nên ta có
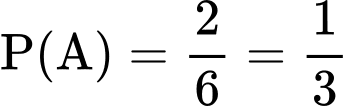 . Suy ra
. Suy ra 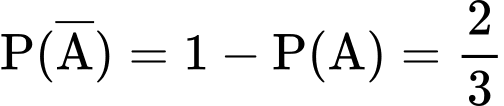 .
.Từ dữ kiện bài ra, ta suy ra được:
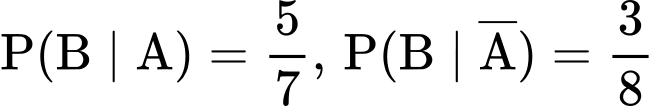 .
.Áp dụng công thức xác suất toàn phần, ta có:

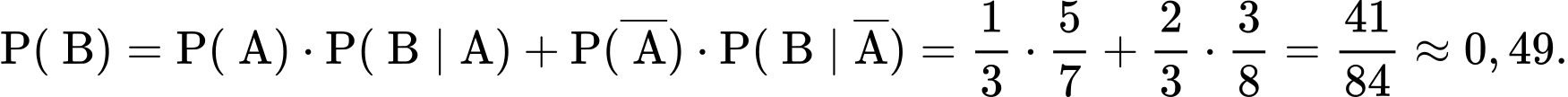
Vậy xác suất để bác Mai bắt được con gà mái là 0,49
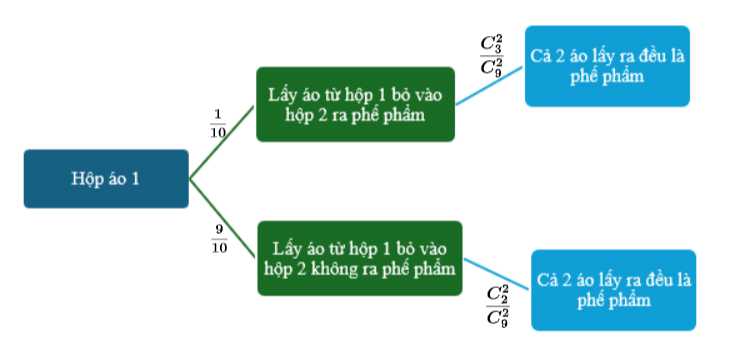
Câu 15 [143814]: Có 2 hộp áo; hộp một có 10 áo trong đó có 1 phế phẩm; hộp hai có 8 áo trong đó có 2 phế phẩm. Lấy ngẫu nhiên 1 áo từ hộp một bỏ sang hộp hai; sau đó từ hộp này chọn ngẫu nhiên ra 2 áo. Gọi 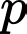 là xác suất để cả 2 áo này đều là phế phẩm. Tính
là xác suất để cả 2 áo này đều là phế phẩm. Tính 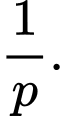
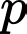 là xác suất để cả 2 áo này đều là phế phẩm. Tính
là xác suất để cả 2 áo này đều là phế phẩm. Tính 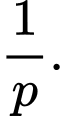
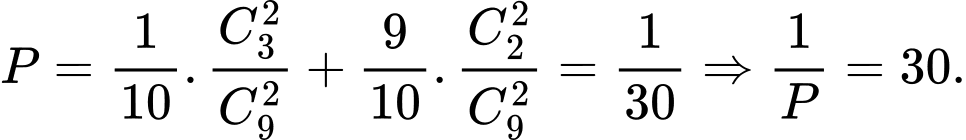
Câu 16 [378722]: Trong quân sự, một máy bay chiến đấu của đối phương có thể xuất hiện ở vị trí X với xác suất 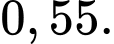 Nếu máy bay đó không xuất hiện ở vị trí X thì nó xuất hiện ở vị trí Y. Để phòng thủ, các bệ phóng tên lửa được bố trí tại các vị trí X và Y. Khi máy bay đối phương xuất hiện ở vị trí X hoặc Y thì tên lửa sẽ được phóng để hạ máy bay đó.
Nếu máy bay đó không xuất hiện ở vị trí X thì nó xuất hiện ở vị trí Y. Để phòng thủ, các bệ phóng tên lửa được bố trí tại các vị trí X và Y. Khi máy bay đối phương xuất hiện ở vị trí X hoặc Y thì tên lửa sẽ được phóng để hạ máy bay đó.
Xét phương án tác chiến sau: Nếu máy bay xuất hiện tại X thì bắn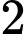 quả tên lửa và nếu máy bay xuất hiện tại Y thì bắn một quả tên lửa.
quả tên lửa và nếu máy bay xuất hiện tại Y thì bắn một quả tên lửa.
Biết rằng, xác suất bắn trúng máy bay của mỗi quả tên lửa là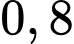 và các bệ phóng tên lửa hoạt động độc lập. Máy bay bị bắn hạ nếu nó trúng ít nhất
và các bệ phóng tên lửa hoạt động độc lập. Máy bay bị bắn hạ nếu nó trúng ít nhất 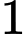 quả tên lửa. Tính xác suất bắn hạ máy bay đối phương trong phương án tác chiến nêu trên. Viết kết quả làm tròn đến hàng phần trăm.
quả tên lửa. Tính xác suất bắn hạ máy bay đối phương trong phương án tác chiến nêu trên. Viết kết quả làm tròn đến hàng phần trăm.
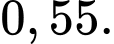 Nếu máy bay đó không xuất hiện ở vị trí X thì nó xuất hiện ở vị trí Y. Để phòng thủ, các bệ phóng tên lửa được bố trí tại các vị trí X và Y. Khi máy bay đối phương xuất hiện ở vị trí X hoặc Y thì tên lửa sẽ được phóng để hạ máy bay đó.
Nếu máy bay đó không xuất hiện ở vị trí X thì nó xuất hiện ở vị trí Y. Để phòng thủ, các bệ phóng tên lửa được bố trí tại các vị trí X và Y. Khi máy bay đối phương xuất hiện ở vị trí X hoặc Y thì tên lửa sẽ được phóng để hạ máy bay đó.Xét phương án tác chiến sau: Nếu máy bay xuất hiện tại X thì bắn
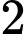 quả tên lửa và nếu máy bay xuất hiện tại Y thì bắn một quả tên lửa.
quả tên lửa và nếu máy bay xuất hiện tại Y thì bắn một quả tên lửa.Biết rằng, xác suất bắn trúng máy bay của mỗi quả tên lửa là
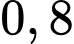 và các bệ phóng tên lửa hoạt động độc lập. Máy bay bị bắn hạ nếu nó trúng ít nhất
và các bệ phóng tên lửa hoạt động độc lập. Máy bay bị bắn hạ nếu nó trúng ít nhất 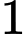 quả tên lửa. Tính xác suất bắn hạ máy bay đối phương trong phương án tác chiến nêu trên. Viết kết quả làm tròn đến hàng phần trăm.
quả tên lửa. Tính xác suất bắn hạ máy bay đối phương trong phương án tác chiến nêu trên. Viết kết quả làm tròn đến hàng phần trăm.
Gọi 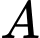 là biến cố: “Máy bay xuất hiện ở vị trí
là biến cố: “Máy bay xuất hiện ở vị trí 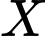 ”;
”;
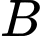 là biến cố: “Máy bay bị bắn rơi”.
là biến cố: “Máy bay bị bắn rơi”.
Theo bài ra ta có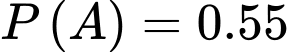 .
.
Suy ra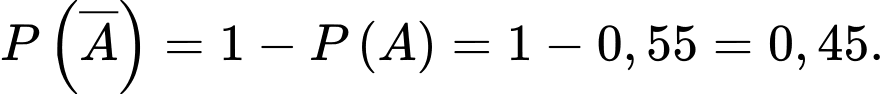
Nếu máy bay xuất hiện tại X thì có hai quả tên lửa bắn lên.
Khi đó, là xác suất để máy bay bị bắn rơi khi có hai quả tên lửa bắn lên.
là xác suất để máy bay bị bắn rơi khi có hai quả tên lửa bắn lên.
Ta tính xác suất của biến cố đối : “Máy bay không rơi khi có hai quả tên lửa bắn lên”. Ta có
: “Máy bay không rơi khi có hai quả tên lửa bắn lên”. Ta có 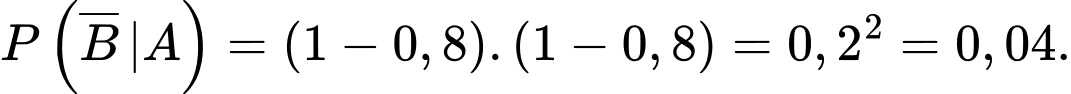
Vậy
 : Nếu máy bay xuất hiện tại Y thì có một quả tên lửa bắn lên. Máy bay rơi khi bị quả tên lửa này bắn trúng. Do đó
: Nếu máy bay xuất hiện tại Y thì có một quả tên lửa bắn lên. Máy bay rơi khi bị quả tên lửa này bắn trúng. Do đó  .
.
Theo công thức xác suất toàn phần ta có:
Vậy xác suất bắn hạ máy bay đối phương trong phương án tác chiến nêu trên là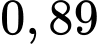 .
.
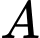 là biến cố: “Máy bay xuất hiện ở vị trí
là biến cố: “Máy bay xuất hiện ở vị trí 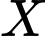 ”;
”; 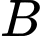 là biến cố: “Máy bay bị bắn rơi”.
là biến cố: “Máy bay bị bắn rơi”.Theo bài ra ta có
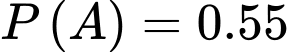 .
. Suy ra
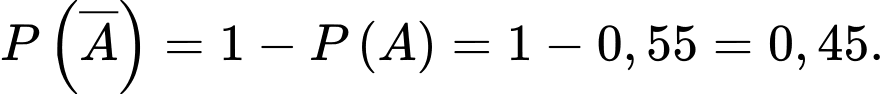
Nếu máy bay xuất hiện tại X thì có hai quả tên lửa bắn lên.
Khi đó,
 là xác suất để máy bay bị bắn rơi khi có hai quả tên lửa bắn lên.
là xác suất để máy bay bị bắn rơi khi có hai quả tên lửa bắn lên.Ta tính xác suất của biến cố đối
 : “Máy bay không rơi khi có hai quả tên lửa bắn lên”. Ta có
: “Máy bay không rơi khi có hai quả tên lửa bắn lên”. Ta có 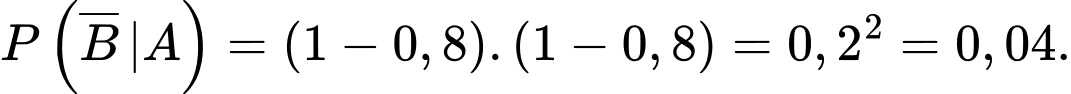
Vậy

 : Nếu máy bay xuất hiện tại Y thì có một quả tên lửa bắn lên. Máy bay rơi khi bị quả tên lửa này bắn trúng. Do đó
: Nếu máy bay xuất hiện tại Y thì có một quả tên lửa bắn lên. Máy bay rơi khi bị quả tên lửa này bắn trúng. Do đó  .
.Theo công thức xác suất toàn phần ta có:

Vậy xác suất bắn hạ máy bay đối phương trong phương án tác chiến nêu trên là
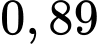 .
.
Câu 17 [143815]: Một chiếc máy bay có thể xuất hiện ở vị trí A với xác suất 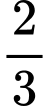 và ở vị trí B với xác suất
và ở vị trí B với xác suất 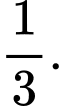 Người ta đặt 3 khẩu súng ở vị trí A và 1 khẩu súng ở vị trí B. Biết rằng xác suất bắn trúng máy bay của mỗi khẩu pháo là 0,7 và các khẩu pháo hoạt động độc lập với nhau, tính xác suất máy bay rơi, biết rằng máy bay sẽ rơi nếu bị bắn trúng. Viết kết quả làm tròn đến hàng phần trăm.
Người ta đặt 3 khẩu súng ở vị trí A và 1 khẩu súng ở vị trí B. Biết rằng xác suất bắn trúng máy bay của mỗi khẩu pháo là 0,7 và các khẩu pháo hoạt động độc lập với nhau, tính xác suất máy bay rơi, biết rằng máy bay sẽ rơi nếu bị bắn trúng. Viết kết quả làm tròn đến hàng phần trăm.
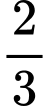 và ở vị trí B với xác suất
và ở vị trí B với xác suất 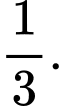 Người ta đặt 3 khẩu súng ở vị trí A và 1 khẩu súng ở vị trí B. Biết rằng xác suất bắn trúng máy bay của mỗi khẩu pháo là 0,7 và các khẩu pháo hoạt động độc lập với nhau, tính xác suất máy bay rơi, biết rằng máy bay sẽ rơi nếu bị bắn trúng. Viết kết quả làm tròn đến hàng phần trăm.
Người ta đặt 3 khẩu súng ở vị trí A và 1 khẩu súng ở vị trí B. Biết rằng xác suất bắn trúng máy bay của mỗi khẩu pháo là 0,7 và các khẩu pháo hoạt động độc lập với nhau, tính xác suất máy bay rơi, biết rằng máy bay sẽ rơi nếu bị bắn trúng. Viết kết quả làm tròn đến hàng phần trăm.
3 khẩu đặt tại A thì để máy bay rơi cần ít nhất một khẩu bắn trúng. Xác suất để ít nhất một khẩu tại A bắn trúng máy bay là: 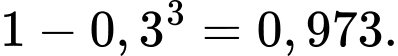
Xác suất để ở vị trí A không có khẩu pháo nào bắn trúng là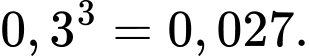
Theo công thức xác suất toàn phần. Xác suất để máy bay rơi là:
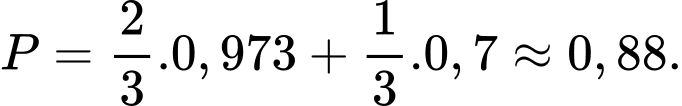
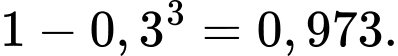
Xác suất để ở vị trí A không có khẩu pháo nào bắn trúng là
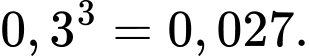
Theo công thức xác suất toàn phần. Xác suất để máy bay rơi là:
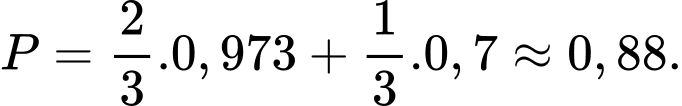
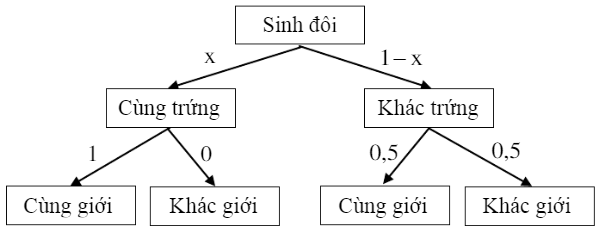
Câu 18 [143816]: Một cặp trẻ sinh đôi có thể do cùng một trứng hay do hai trứng khác nhau sinh ra. Các cặp sinh đôi cùng trứng luôn có cùng giới tính. Cặp sinh đôi khác trứng thì giới tính của mỗi đứa độc lập với nhau và có xác suất 0,5 là con trai. Thống kê cho thấy 34% cặp sinh đôi đều là trai, 30% cặp sinh đôi đều là gái và 36% cặp sinh đôi có giới tính khác nhau. Tìm tỷ lệ cặp sinh đôi cùng trứng.
Gọi A là biến cố: Cặp sinh đôi cùng trứng
B là biến cố: Cặp sinh đôi khác trứng
Gọi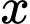 là tỷ lệ sinh đôi cùng trứng thì
là tỷ lệ sinh đôi cùng trứng thì 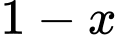 là tỷ lệ sinh đôi khác trứng.
là tỷ lệ sinh đôi khác trứng.
Ta có sơ đồ hình cây sau:
Áp dụng công thức xác suất toàn phần ta có: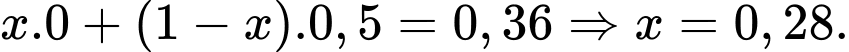
B là biến cố: Cặp sinh đôi khác trứng
Gọi
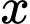 là tỷ lệ sinh đôi cùng trứng thì
là tỷ lệ sinh đôi cùng trứng thì 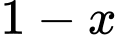 là tỷ lệ sinh đôi khác trứng.
là tỷ lệ sinh đôi khác trứng.Ta có sơ đồ hình cây sau:

Áp dụng công thức xác suất toàn phần ta có:
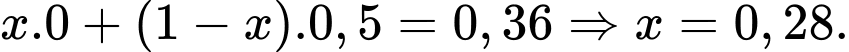
Câu 19 [143813]: Có 2 hộp đựng sản phẩm. Hộp thứ nhất có 10 sản phẩm trong đó có 9 sản phẩm tốt và 1 sản phẩm xấu. Hộp thứ hai có 20 sản phẩm trong đó có 18 sản phẩm tốt và 2 sản phẩm xấu. Từ hộp thứ nhất lấy ngẫu nhiên một sản phẩm bỏ sang hộp thứ hai. Tìm xác suất để lấy ngẫu nhiên một sản phẩm từ hộp thứ hai được sản phẩm tốt.
Gọi A là biến cố "Lấy được sản phẩm tốt từ hộp hai".
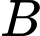 - Sản phẩm bỏ từ hộp thứ nhất sang hộp thứ hai là sản phẩm tốt.
- Sản phẩm bỏ từ hộp thứ nhất sang hộp thứ hai là sản phẩm tốt.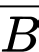 - Sản phẩm bỏ từ hộp thứ nhất sang hộp thứ hai là 2 sản phẩm xấu.
- Sản phẩm bỏ từ hộp thứ nhất sang hộp thứ hai là 2 sản phẩm xấu.
Xác suất để từ hộp một bỏ sang hộp hai sản phẩm tốt bằng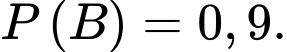
Xác suất để từ hộp một bở sang hộp hai phế phẩm bằng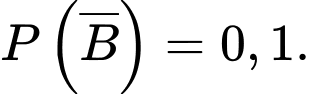
Xác suất có điều kiện để từ hộp hai lấy được sản phẩm tốt khi các giả thuyết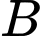 và
và 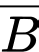 đã xảy ra là
đã xảy ra là 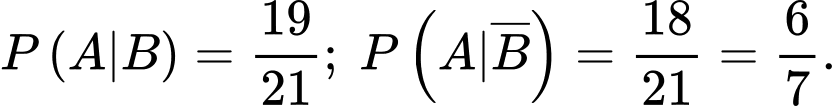
Do đó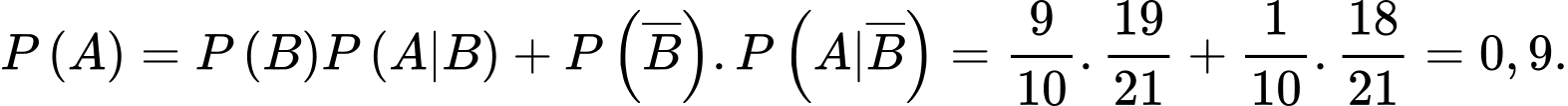
 - Sản phẩm bỏ từ hộp thứ nhất sang hộp thứ hai là sản phẩm tốt.
- Sản phẩm bỏ từ hộp thứ nhất sang hộp thứ hai là sản phẩm tốt. - Sản phẩm bỏ từ hộp thứ nhất sang hộp thứ hai là 2 sản phẩm xấu.
- Sản phẩm bỏ từ hộp thứ nhất sang hộp thứ hai là 2 sản phẩm xấu.
Xác suất để từ hộp một bỏ sang hộp hai sản phẩm tốt bằng
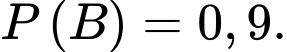
Xác suất để từ hộp một bở sang hộp hai phế phẩm bằng
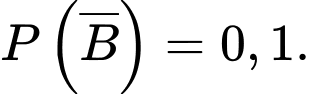
Xác suất có điều kiện để từ hộp hai lấy được sản phẩm tốt khi các giả thuyết
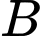 và
và 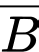 đã xảy ra là
đã xảy ra là 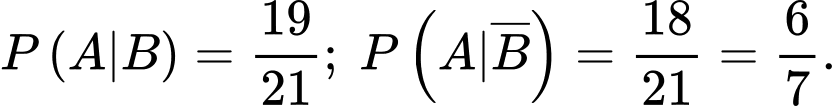
Do đó
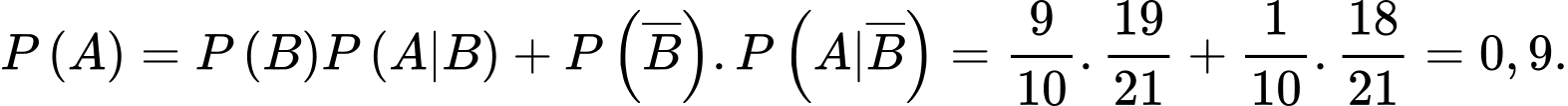
Câu 20 [145259]: [Trích SGK Cùng Khám Phá]: Có hai hộp đựng các viên bi cùng kích thước và khối lượng. Hộp thứ nhất chứa 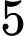 viên bi đỏ và
viên bi đỏ và 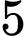 viên bi xanh, hộp thứ hai chứa
viên bi xanh, hộp thứ hai chứa 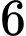 viên bi đỏ và
viên bi đỏ và 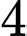 viên bi xanh. Lấy ngẫu nhiên một viên bi từ hộp thứ nhất chuyển sang hộp thứ hai, sau đó lấy ra ngẫu nhiên một viên bi từ hộp thứ hai. Tính xác suất để viên bi được lấy ra từ hộp thứ hai là viên bi đỏ. Viết kết quả làm tròn đến hàng phần trăm.
viên bi xanh. Lấy ngẫu nhiên một viên bi từ hộp thứ nhất chuyển sang hộp thứ hai, sau đó lấy ra ngẫu nhiên một viên bi từ hộp thứ hai. Tính xác suất để viên bi được lấy ra từ hộp thứ hai là viên bi đỏ. Viết kết quả làm tròn đến hàng phần trăm.
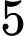 viên bi đỏ và
viên bi đỏ và 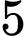 viên bi xanh, hộp thứ hai chứa
viên bi xanh, hộp thứ hai chứa 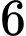 viên bi đỏ và
viên bi đỏ và 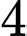 viên bi xanh. Lấy ngẫu nhiên một viên bi từ hộp thứ nhất chuyển sang hộp thứ hai, sau đó lấy ra ngẫu nhiên một viên bi từ hộp thứ hai. Tính xác suất để viên bi được lấy ra từ hộp thứ hai là viên bi đỏ. Viết kết quả làm tròn đến hàng phần trăm.
viên bi xanh. Lấy ngẫu nhiên một viên bi từ hộp thứ nhất chuyển sang hộp thứ hai, sau đó lấy ra ngẫu nhiên một viên bi từ hộp thứ hai. Tính xác suất để viên bi được lấy ra từ hộp thứ hai là viên bi đỏ. Viết kết quả làm tròn đến hàng phần trăm.
Xét phép thử lấy ngẫu nhiên một viên bi từ hộp thứ nhất chuyển sang hộp thứ hai, sau đó lấy ra ngẫu nhiên một viên bi từ hộp thứ hai.
Gọi:
•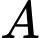 là biến cố "Viên bi được lấy ra từ hộp thứ hai là bi đỏ";
là biến cố "Viên bi được lấy ra từ hộp thứ hai là bi đỏ";
•
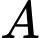 là biến cố "Viên bi được lấy ra từ hộp thứ hai là bi đỏ";
là biến cố "Viên bi được lấy ra từ hộp thứ hai là bi đỏ"; • 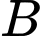 là biến cố "Viên bi được lấy ra từ hộp thứ nhất chuyển sang hộp thứ hai là bi đỏ";
là biến cố "Viên bi được lấy ra từ hộp thứ nhất chuyển sang hộp thứ hai là bi đỏ";
•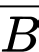 là biến cố "Viên bi được lấy ra từ hộp thứ nhất chuyển sang hộp thứ hai là bi xanh".
là biến cố "Viên bi được lấy ra từ hộp thứ nhất chuyển sang hộp thứ hai là bi xanh".
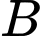 là biến cố "Viên bi được lấy ra từ hộp thứ nhất chuyển sang hộp thứ hai là bi đỏ";
là biến cố "Viên bi được lấy ra từ hộp thứ nhất chuyển sang hộp thứ hai là bi đỏ"; •
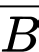 là biến cố "Viên bi được lấy ra từ hộp thứ nhất chuyển sang hộp thứ hai là bi xanh".
là biến cố "Viên bi được lấy ra từ hộp thứ nhất chuyển sang hộp thứ hai là bi xanh". Ta có: 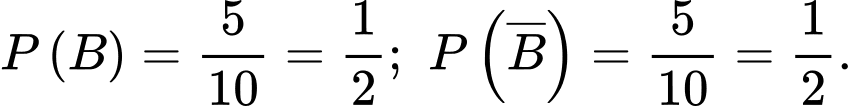
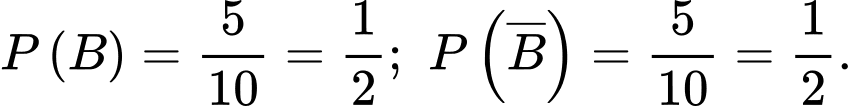
Nếu viên bi được lấy ra từ hộp thứ nhất chuyển sang hộp thứ hai là bi đỏ thì sau khi chuyển, hộp thứ hai có 7 bi đỏ và 4 bi xanh.
Do đó 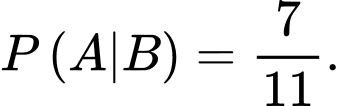
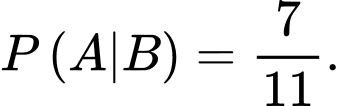
Nếu viên bi được lấy ra từ hộp thứ nhất chuyển sang hộp thứ hai là bi xanh thì sau khi chuyển, hộp thứ hai có 6 bi đỏ và 5 bi xanh.
Do đó 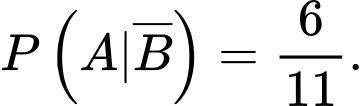
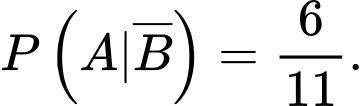
Áp dụng công thức xác suất toàn phần, ta có:
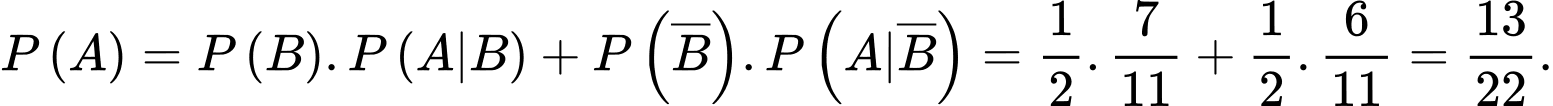
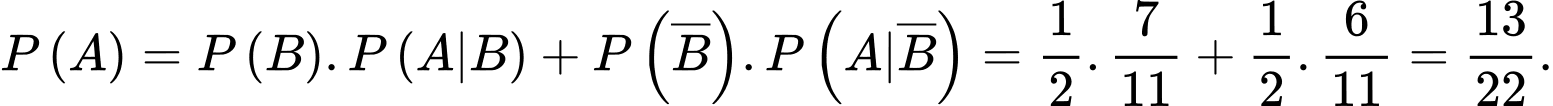
Vậy xác suất để viên bi được lấy ra từ hộp thứ hai là bi đỏ bằng