PHẦN I. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Câu 1 [805500]: Cho dãy số 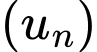 có số hạng tổng quát
có số hạng tổng quát 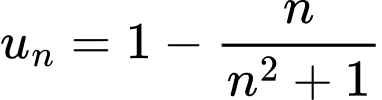 (với
(với  ). Số hạng đầu tiên của dãy là
). Số hạng đầu tiên của dãy là
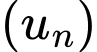 có số hạng tổng quát
có số hạng tổng quát 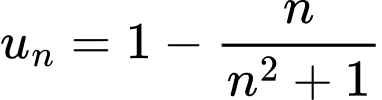 (với
(với  ). Số hạng đầu tiên của dãy là
). Số hạng đầu tiên của dãy là A, 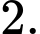
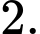
B, 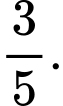
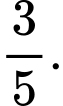
C, 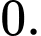
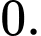
D, 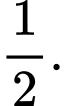
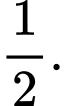
Chọn đáp án D.
Ta có: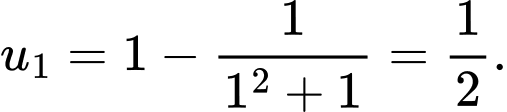 Đáp án: D
Đáp án: D
Ta có:
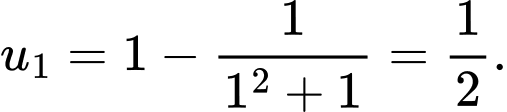 Đáp án: D
Đáp án: D
Câu 2 [311296]: Tìm họ nguyên hàm của hàm số 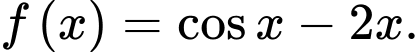
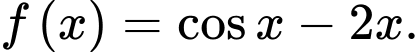
A, 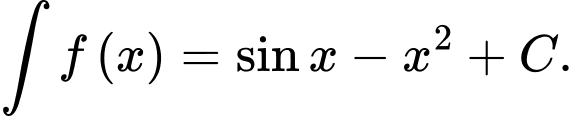
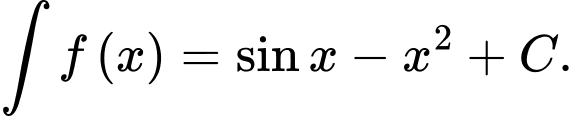
B, 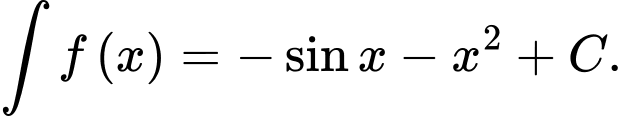
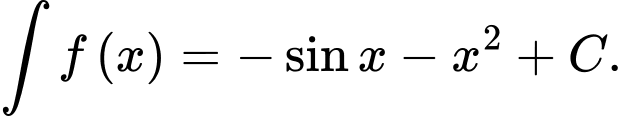
C, 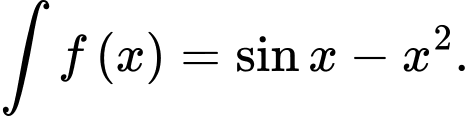
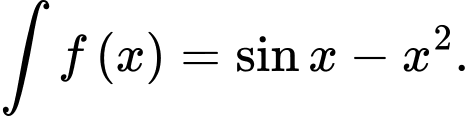
D, 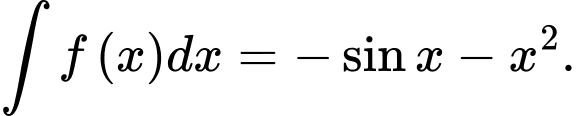
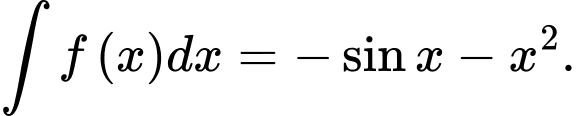
Chọn đáp án A.
Ta có: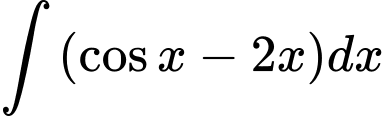
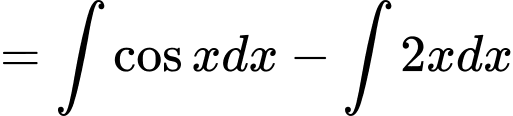
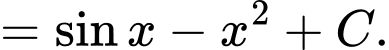 Đáp án: A
Đáp án: A
Ta có:
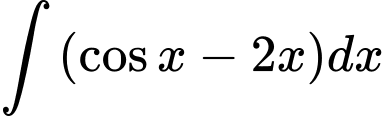
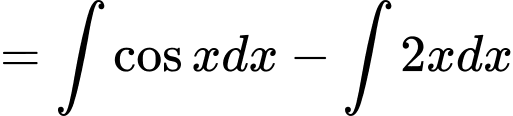
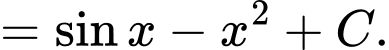 Đáp án: A
Đáp án: A
Câu 3 [53319]: Cho đường thẳng  đi qua điểm
đi qua điểm 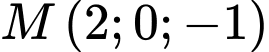 và vecto chỉ phương
và vecto chỉ phương 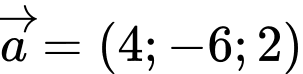 . Phương trình tham số của đường thẳng
. Phương trình tham số của đường thẳng  là
là
 đi qua điểm
đi qua điểm 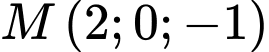 và vecto chỉ phương
và vecto chỉ phương 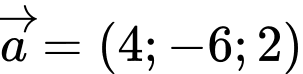 . Phương trình tham số của đường thẳng
. Phương trình tham số của đường thẳng  là
là A, 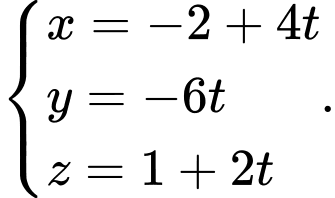
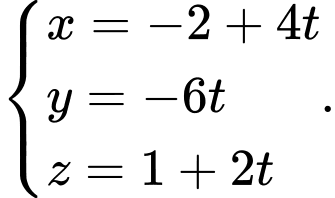
B, 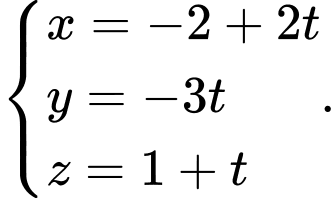
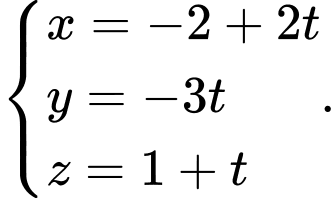
C, 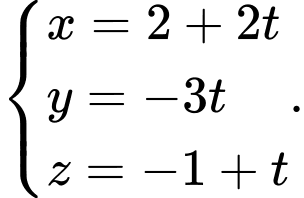
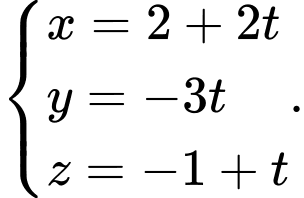
D, 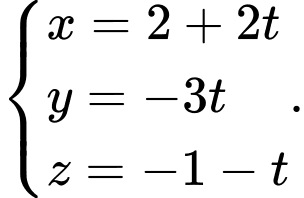
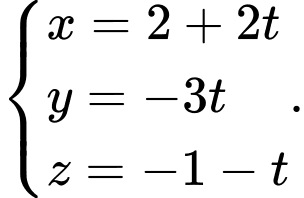
Chọn đáp án C.
Phương trình đường thẳng cần tìm là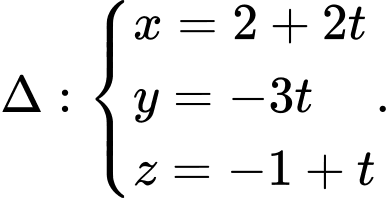 Đáp án: C
Đáp án: C
Phương trình đường thẳng cần tìm là
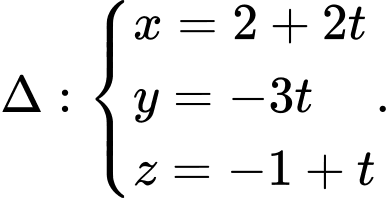 Đáp án: C
Đáp án: C
Câu 4 [516427]: Nghiệm của phương trình 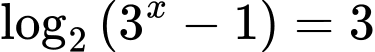 là
là
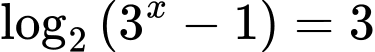 là
là A, 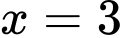 .
.
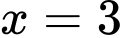 .
.B, 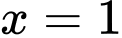 .
.
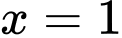 .
.C, 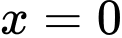 .
.
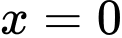 .
.D, 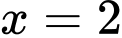 .
.
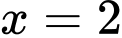 .
.
Chọn đáp án D.
Điều kiện: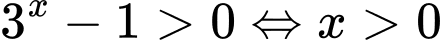 .
.
Khi đó: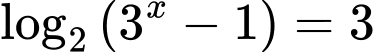
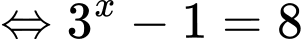
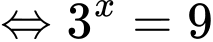
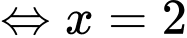 ( thỏa mãn).
( thỏa mãn).
Vậy phương trình có nghiệm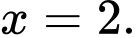 Đáp án: D
Đáp án: D
Điều kiện:
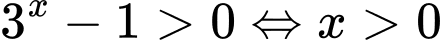 .
. Khi đó:
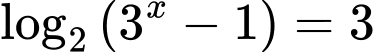
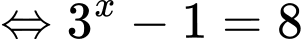
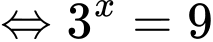
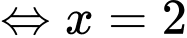 ( thỏa mãn).
( thỏa mãn). Vậy phương trình có nghiệm
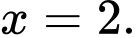 Đáp án: D
Đáp án: D
Câu 5 [42030]: Cho 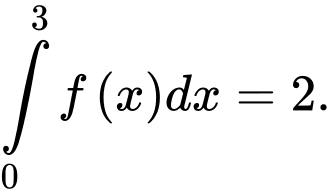 Tính giá trị của tích phân
Tính giá trị của tích phân 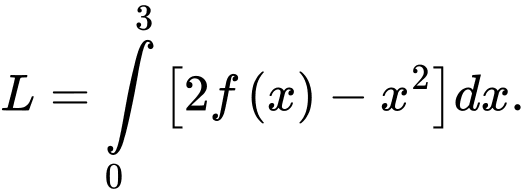
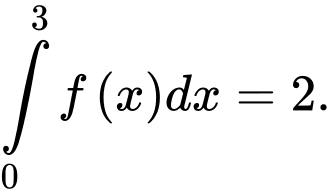 Tính giá trị của tích phân
Tính giá trị của tích phân 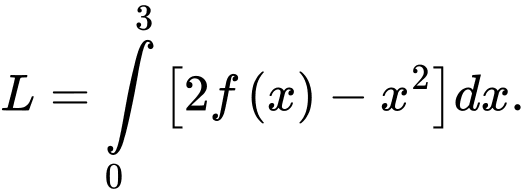
A, 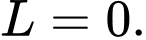
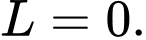
B, 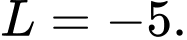
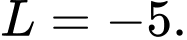
C, 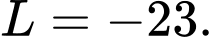
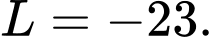
D, 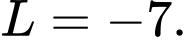
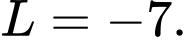
Chọn đáp án B.
Phương pháp
Sử dụng các tính chất tích phân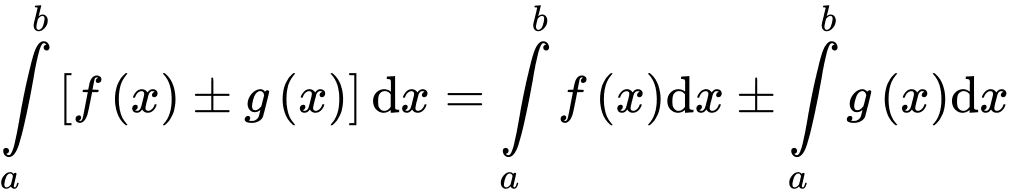 và
và 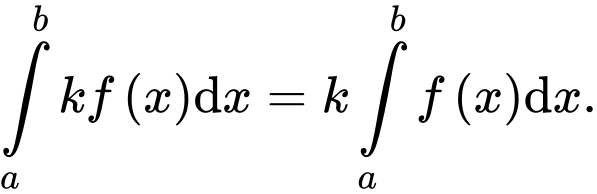
Cách giải
Ta có:
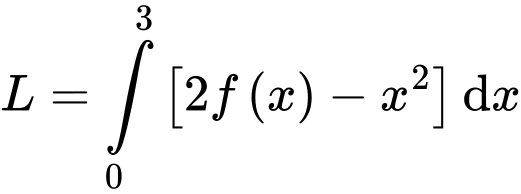
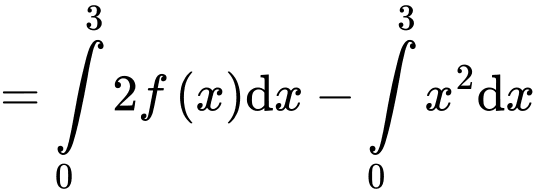
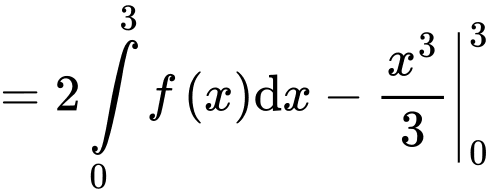
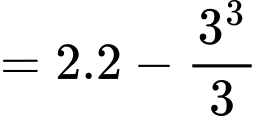
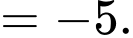 Đáp án: B
Đáp án: B
Phương pháp
Sử dụng các tính chất tích phân
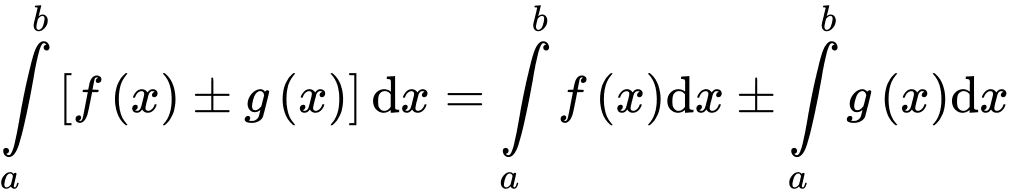 và
và 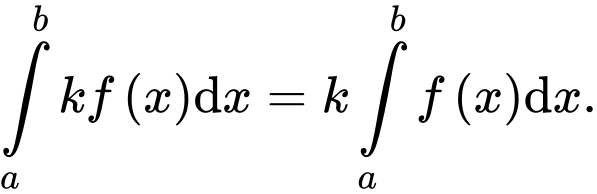
Cách giải
Ta có:
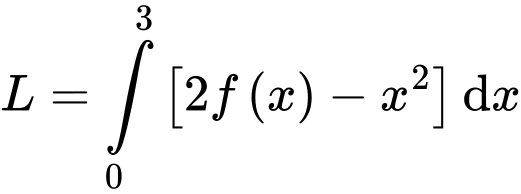
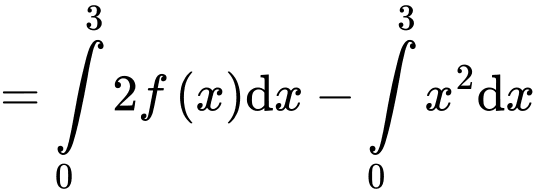
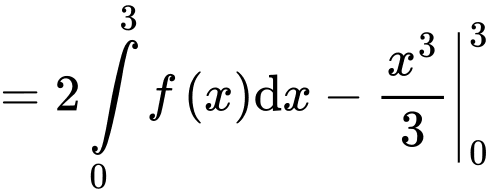
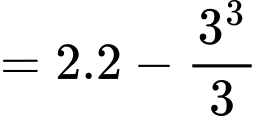
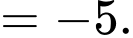 Đáp án: B
Đáp án: B
Câu 6 [600333]: Cho 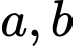 là hai số thực dương thoả mãn
là hai số thực dương thoả mãn 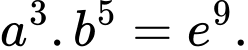 Giá trị của
Giá trị của  bằng
bằng
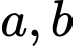 là hai số thực dương thoả mãn
là hai số thực dương thoả mãn 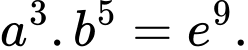 Giá trị của
Giá trị của  bằng
bằng A, 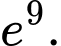
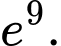
B, 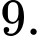
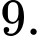
C, 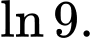
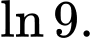
D, 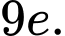
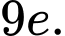
Chọn đáp án B.
Ta có:
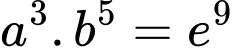
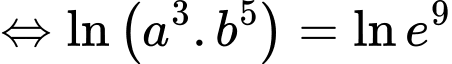
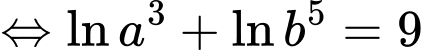
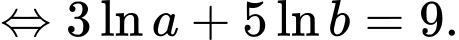
Vậy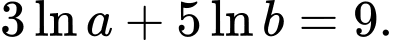 Đáp án: B
Đáp án: B
Ta có:
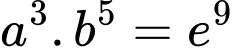
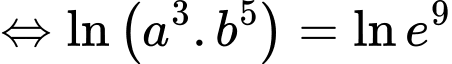
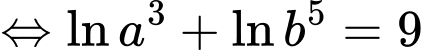
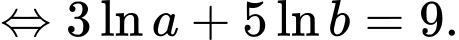
Vậy
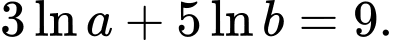 Đáp án: B
Đáp án: B
Câu 7 [333922]: Trong không gian 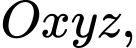 cho mặt cầu
cho mặt cầu 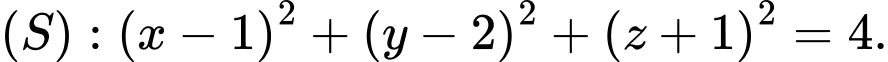 Tọa độ tâm
Tọa độ tâm 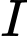 và bán kính
và bán kính 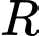 của mặt cầu
của mặt cầu 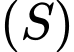 là
là
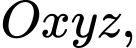 cho mặt cầu
cho mặt cầu 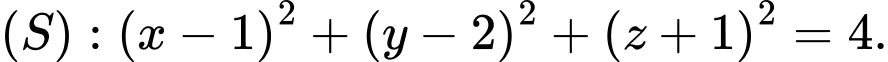 Tọa độ tâm
Tọa độ tâm 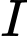 và bán kính
và bán kính 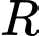 của mặt cầu
của mặt cầu 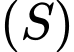 là
là A, 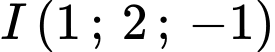 và
và 
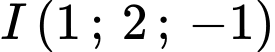 và
và 
B, 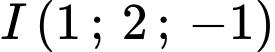 và
và 
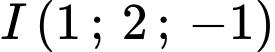 và
và 
C, 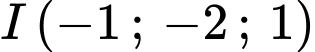 và
và 
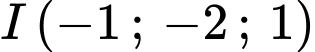 và
và 
D, 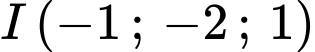 và
và 
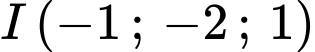 và
và 
Chọn đáp án A.
Mặt cầu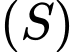 có tâm
có tâm 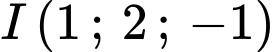 và bán kính
và bán kính  Đáp án: A
Đáp án: A
Mặt cầu
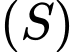 có tâm
có tâm 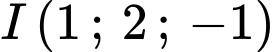 và bán kính
và bán kính  Đáp án: A
Đáp án: A
Câu 8 [333949]: Cho khối lăng trụ tam giác đều có tất cả các cạnh bằng 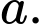 Thể tích của khối lăng trụ là
Thể tích của khối lăng trụ là
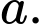 Thể tích của khối lăng trụ là
Thể tích của khối lăng trụ là A, 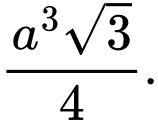
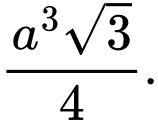
B, 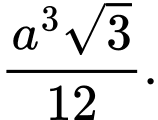
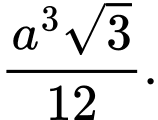
C, 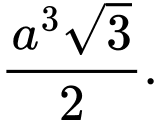
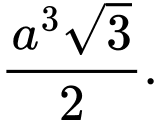
D, 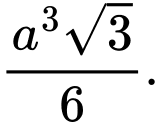
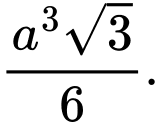
Chọn đáp án A.
Diện tích đáy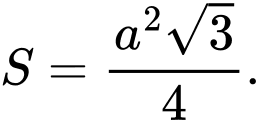
Thể tích khối lăng trụ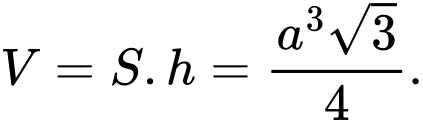 Đáp án: A
Đáp án: A
Diện tích đáy
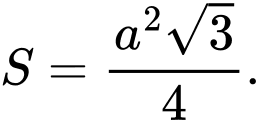
Thể tích khối lăng trụ
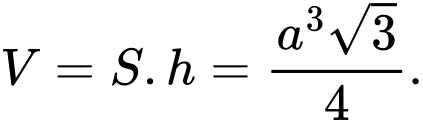 Đáp án: A
Đáp án: A Sử dụng thông tin dưới đây để trả lời câu 9 và câu 10
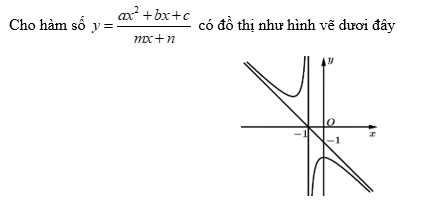
Câu 9 [698986]: Tiệm cận đứng của đồ thị hàm số là đường thẳng có phương trình
A, 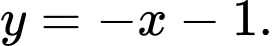
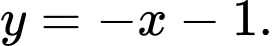
B, 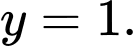
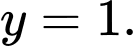
C, 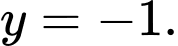
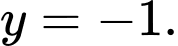
D, 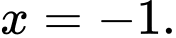
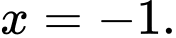
Chọn đáp án D.
Nhìn vào đồ thị hàm số ta có tiệm cận đứng của đồ thị hàm số là đường thẳng có phương trình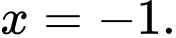 Đáp án: D
Đáp án: D
Nhìn vào đồ thị hàm số ta có tiệm cận đứng của đồ thị hàm số là đường thẳng có phương trình
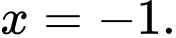 Đáp án: D
Đáp án: D
Câu 10 [698987]: Hình vẽ trên là đồ thị của hàm số nào trong các hàm số dưới đây.
A, 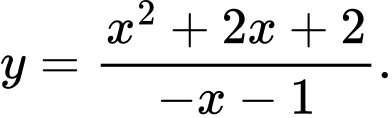
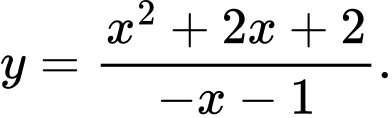
B, 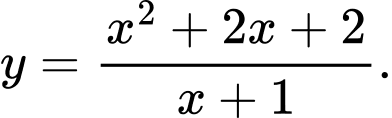
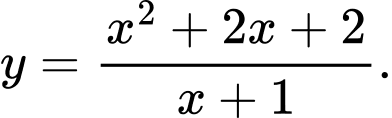
C, 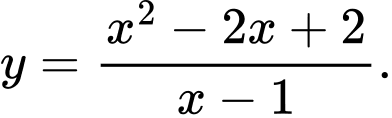
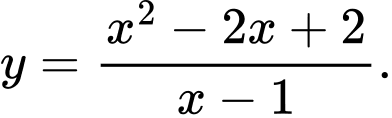
D, 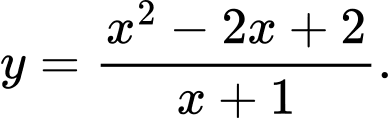
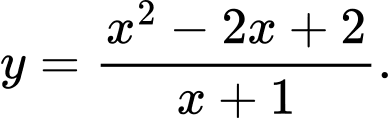
Chọn đáp án A.
Ta có: tiệm cận đứng của đồ thị hàm số là đường thẳng có phương trình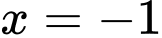 do đó loại C.
do đó loại C.
Đồ thị đi qua điểm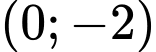 do đó ta loại B, D. Đáp án: A
do đó ta loại B, D. Đáp án: A
Ta có: tiệm cận đứng của đồ thị hàm số là đường thẳng có phương trình
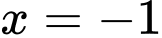 do đó loại C.
do đó loại C.
Đồ thị đi qua điểm
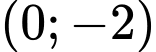 do đó ta loại B, D. Đáp án: A
do đó ta loại B, D. Đáp án: A
Câu 11 [803785]: Trong không gian 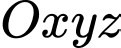 , cho
, cho 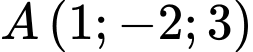 ,
, 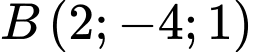 ,
, 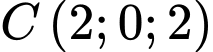 , khi đó tích vô hướng
, khi đó tích vô hướng 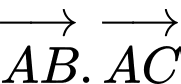 bằng.
bằng.
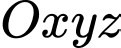 , cho
, cho 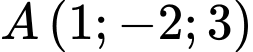 ,
, 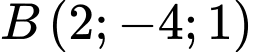 ,
, 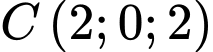 , khi đó tích vô hướng
, khi đó tích vô hướng 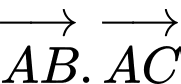 bằng.
bằng. A, 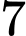 .
.
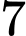 .
.B, 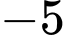 .
.
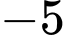 .
.C, 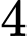 .
.
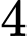 .
.D, 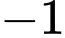 .
.
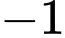 .
.
Chọn đáp án D.
* Ta có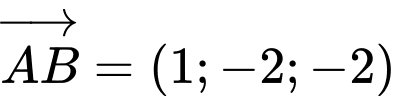 ;
; 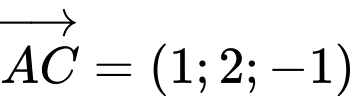 .
.
* Khi đó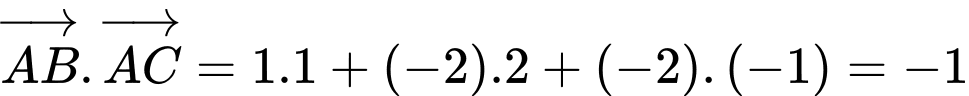 . Đáp án: D
. Đáp án: D
* Ta có
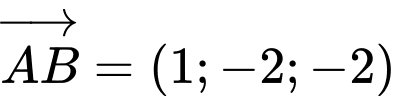 ;
; 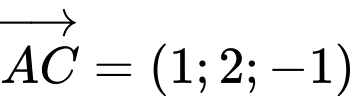 .
.* Khi đó
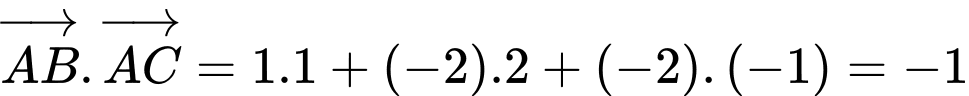 . Đáp án: D
. Đáp án: D
Câu 12 [694832]: Kết quả điều tra về số giờ làm thêm trong 1 tuần của một nhóm sinh viên được cho ở bảng sau:
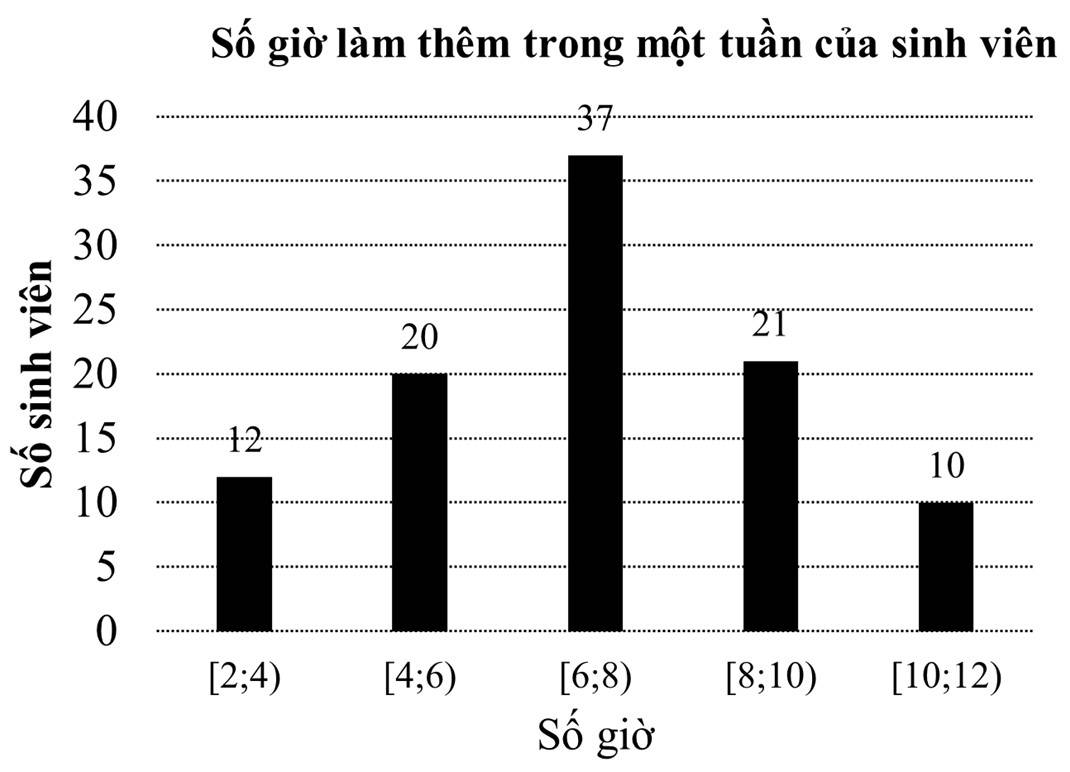
Khoảng tứ phân vị của mẫu số liệu ghép nhóm cho bởi biểu đồ trên gần nhất với giá trị nào dưới đây

Khoảng tứ phân vị của mẫu số liệu ghép nhóm cho bởi biểu đồ trên gần nhất với giá trị nào dưới đây
A, 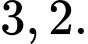
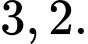
B, 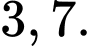
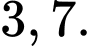
C, 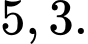
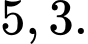
D, 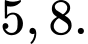
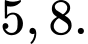
Chọn đáp án A.
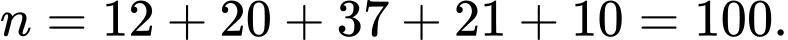
Gọi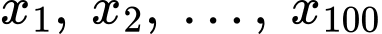 là mẫu số liệu được xếp theo thứ tự không giảm.
là mẫu số liệu được xếp theo thứ tự không giảm.
Khi đó: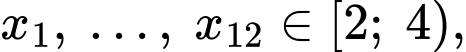
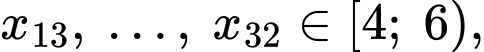
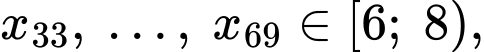
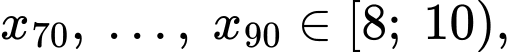
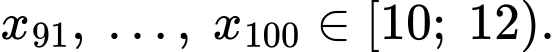
Tứ phân vị thứ nhất của dãy số liệu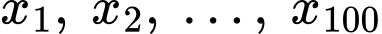 là
là 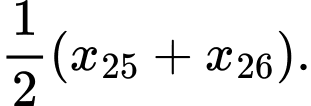
Do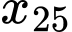 và
và 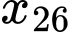 cùng thuộc nhóm
cùng thuộc nhóm 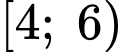 nên tứ phân vị thứ nhất của mẫu số liệu ghép nhóm là
nên tứ phân vị thứ nhất của mẫu số liệu ghép nhóm là
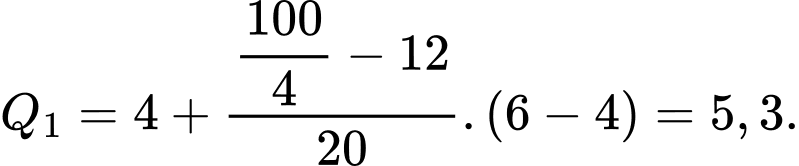
Tứ phân vị thứ ba của dãy số liệu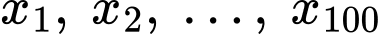 là
là 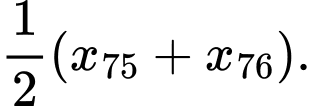
Do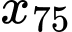 và
và 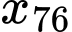 cùng thuộc nhóm
cùng thuộc nhóm 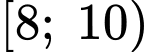 nên tứ phân vị thứ nhất của mẫu số liệu ghép nhóm là
nên tứ phân vị thứ nhất của mẫu số liệu ghép nhóm là
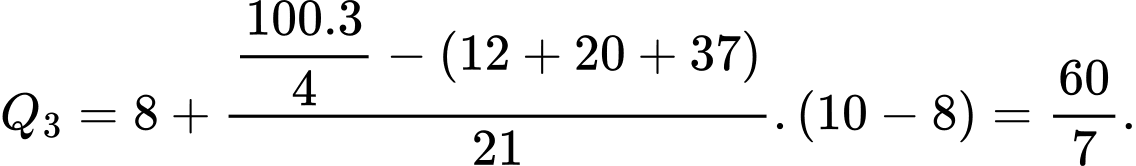
Khoảng tứ phân vị của mẫu số liệu ghép nhóm trên là
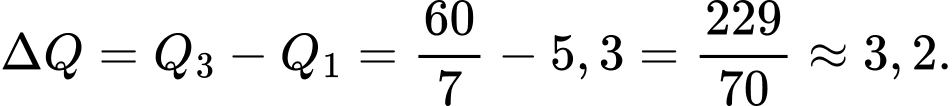 Đáp án: A
Đáp án: A
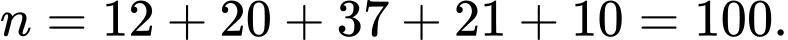
Gọi
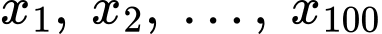 là mẫu số liệu được xếp theo thứ tự không giảm.
là mẫu số liệu được xếp theo thứ tự không giảm. Khi đó:
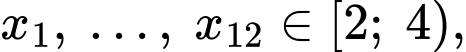
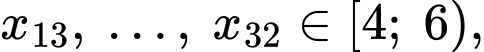
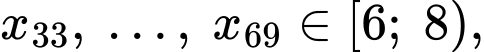
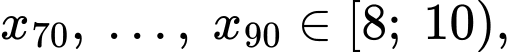
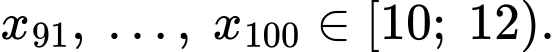
Tứ phân vị thứ nhất của dãy số liệu
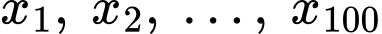 là
là 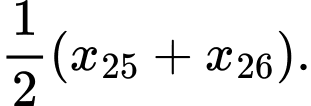
Do
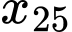 và
và 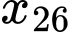 cùng thuộc nhóm
cùng thuộc nhóm 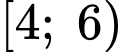 nên tứ phân vị thứ nhất của mẫu số liệu ghép nhóm là
nên tứ phân vị thứ nhất của mẫu số liệu ghép nhóm là 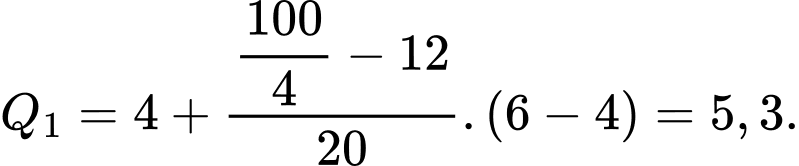
Tứ phân vị thứ ba của dãy số liệu
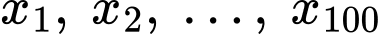 là
là 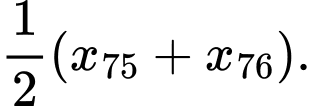
Do
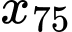 và
và 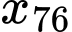 cùng thuộc nhóm
cùng thuộc nhóm 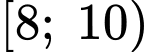 nên tứ phân vị thứ nhất của mẫu số liệu ghép nhóm là
nên tứ phân vị thứ nhất của mẫu số liệu ghép nhóm là 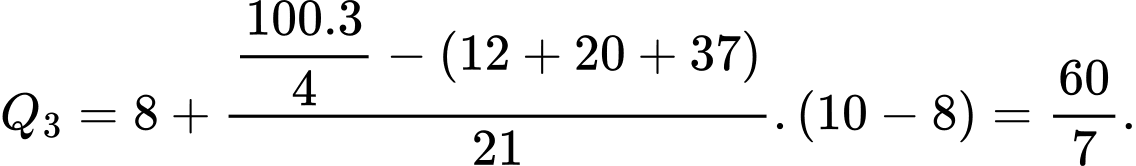
Khoảng tứ phân vị của mẫu số liệu ghép nhóm trên là
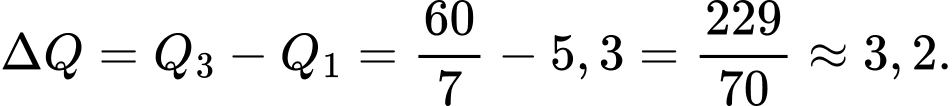 Đáp án: A
Đáp án: A PHẦN II. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Câu 13 [694833]: Cho hàm số 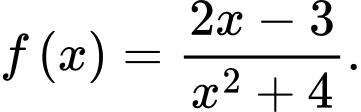
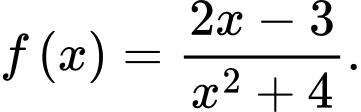
a) Đúng.
ĐKXĐ: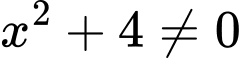
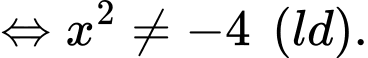
Vậy hàm số đã cho xác định với mọi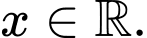
b) Đúng.
Ta có: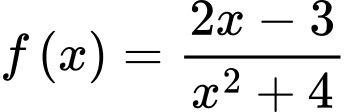
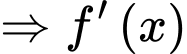
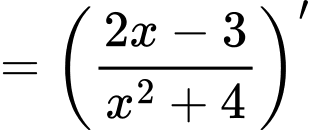
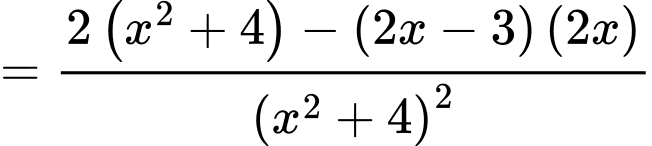
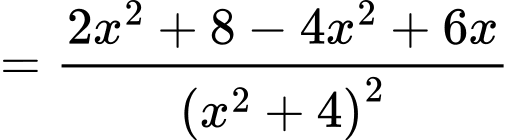
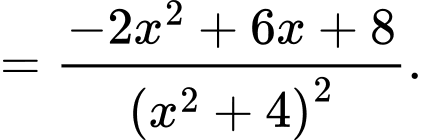
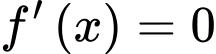
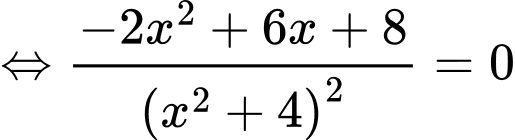
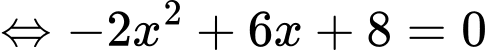
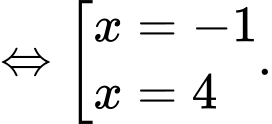
c) Đúng.
Bảng biến thiên hàm số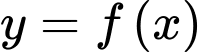 :
:
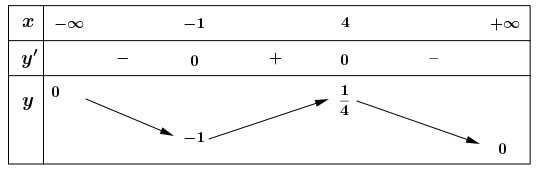
Vậy giá trị cực đại của hàm số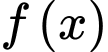 là
là 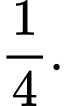
d) Sai.
Dựa vào BBT ta có: Tập giá trị của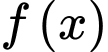 là
là 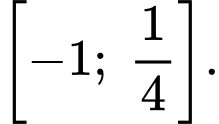
Vậy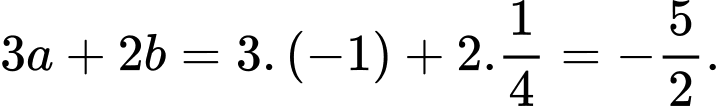
ĐKXĐ:
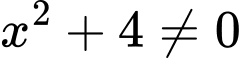
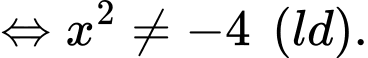
Vậy hàm số đã cho xác định với mọi
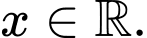
b) Đúng.
Ta có:
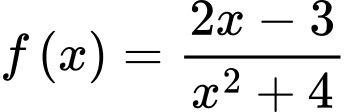
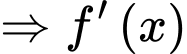
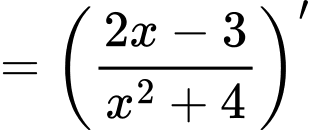
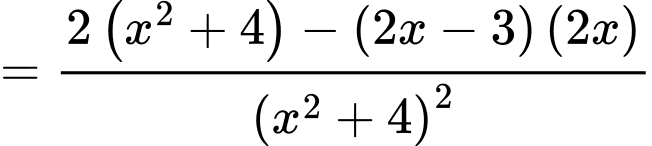
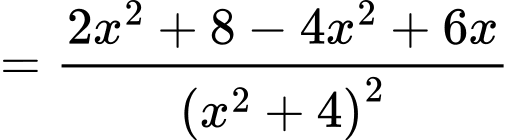
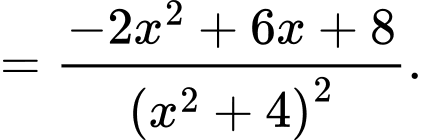
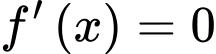
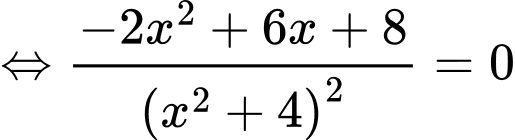
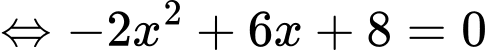
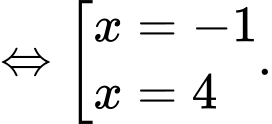
c) Đúng.
Bảng biến thiên hàm số
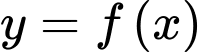 :
: 
Vậy giá trị cực đại của hàm số
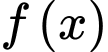 là
là 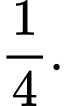
d) Sai.
Dựa vào BBT ta có: Tập giá trị của
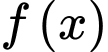 là
là 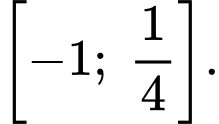
Vậy
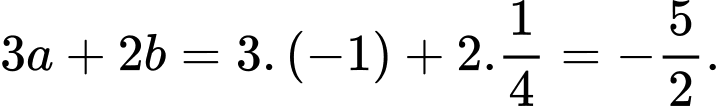
Câu 14 [694835]: Nam đang tham gia một bài học từ mới môn Tiếng Anh trong vòng 60 phút. Biết rằng 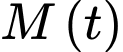 là số từ mới mà Nam có thể ghi nhớ trong
là số từ mới mà Nam có thể ghi nhớ trong 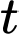 phút. Tốc độ ghi nhớ từ mới của Nam được xác định bởi hàm số
phút. Tốc độ ghi nhớ từ mới của Nam được xác định bởi hàm số 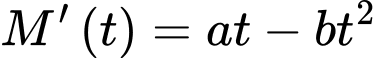 (với
(với 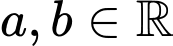 ) (từ/phút) và đạt cao nhất tại thời điểm 40 phút. Biết rằng Nam có thể ghi nhớ được 18 từ mới trong 10 phút đầu tiên của bài học.
) (từ/phút) và đạt cao nhất tại thời điểm 40 phút. Biết rằng Nam có thể ghi nhớ được 18 từ mới trong 10 phút đầu tiên của bài học.
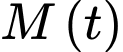 là số từ mới mà Nam có thể ghi nhớ trong
là số từ mới mà Nam có thể ghi nhớ trong 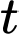 phút. Tốc độ ghi nhớ từ mới của Nam được xác định bởi hàm số
phút. Tốc độ ghi nhớ từ mới của Nam được xác định bởi hàm số 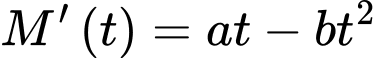 (với
(với 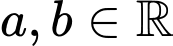 ) (từ/phút) và đạt cao nhất tại thời điểm 40 phút. Biết rằng Nam có thể ghi nhớ được 18 từ mới trong 10 phút đầu tiên của bài học.
) (từ/phút) và đạt cao nhất tại thời điểm 40 phút. Biết rằng Nam có thể ghi nhớ được 18 từ mới trong 10 phút đầu tiên của bài học.
a) Sai.
Tốc độ ghi nhớ từ mới của Nam đạt cao nhất tại thời điểm 40 phút nên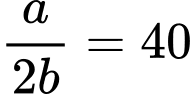 hay
hay 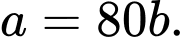
Số từ mới mà Nam có thể ghi nhớ trong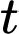 phút là
phút là
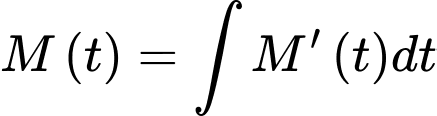
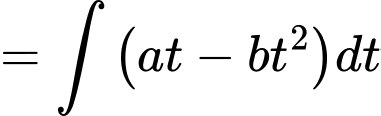
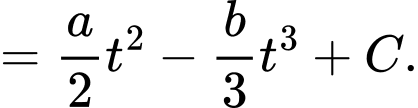
Mặt khác,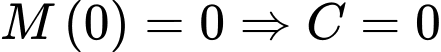
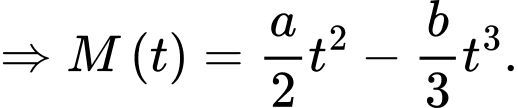
Nam có thể ghi nhớ được 18 từ mới trong 10 phút đầu tiên của bài học nên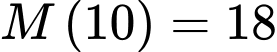 hay
hay 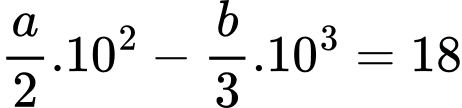
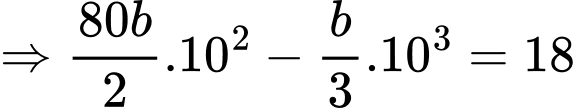
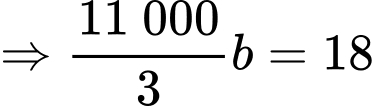
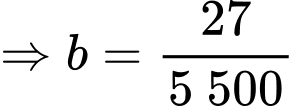
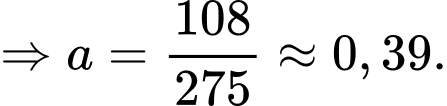
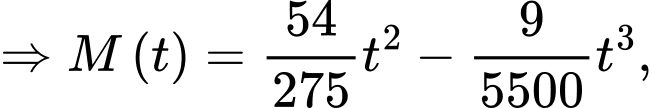
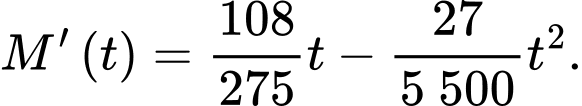
b) Sai.
Khả năng ghi nhớ của Nam tại thời điểm 20 phút là
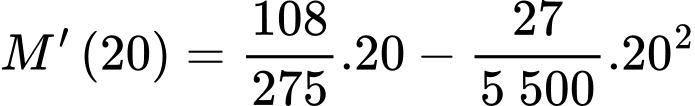
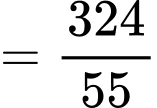
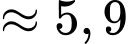 (từ/ phút).
(từ/ phút).
c) Sai.
Trong cả tiết học Nam ghi nhớ được tổng cộng số từ mới là:
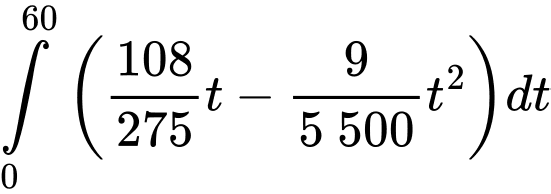
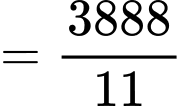
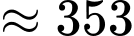 (từ).
(từ).
d) Sai.
Tốc độ học trung bình của Nam trong cả tiết học là
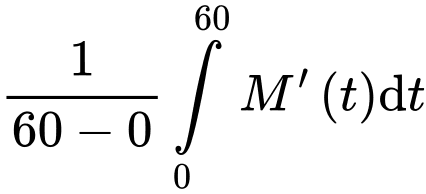
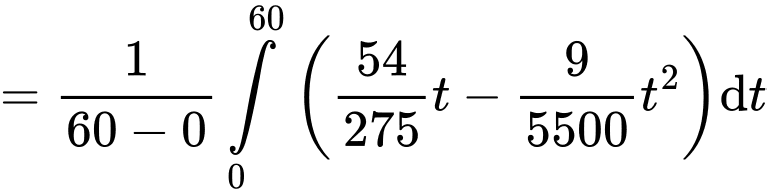
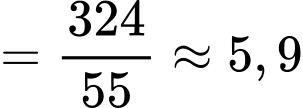 (từ/ phút).
(từ/ phút).
Tốc độ ghi nhớ từ mới của Nam đạt cao nhất tại thời điểm 40 phút nên
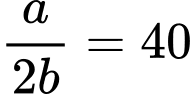 hay
hay 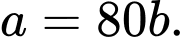
Số từ mới mà Nam có thể ghi nhớ trong
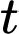 phút là
phút là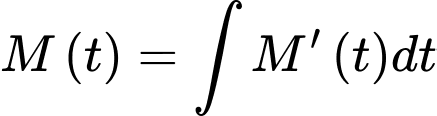
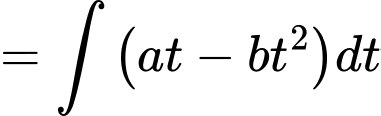
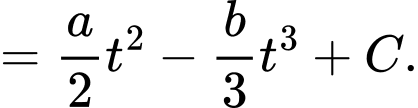
Mặt khác,
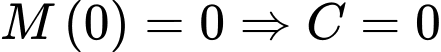
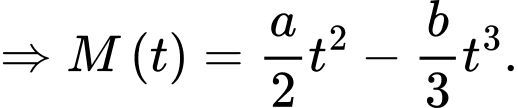
Nam có thể ghi nhớ được 18 từ mới trong 10 phút đầu tiên của bài học nên
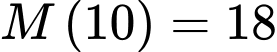 hay
hay 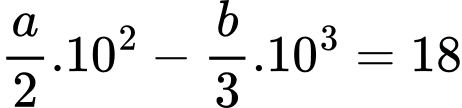
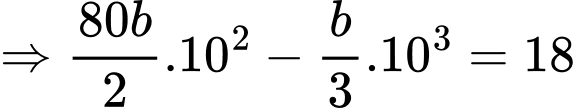
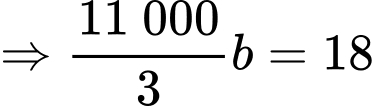
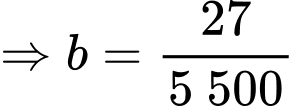
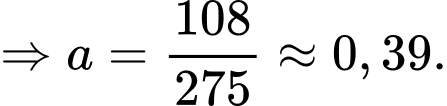
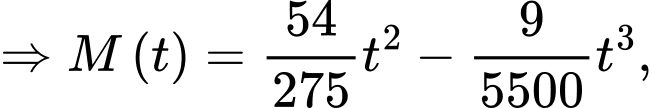
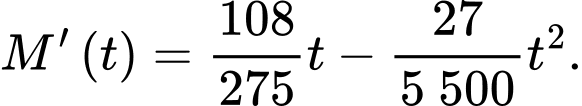
b) Sai.
Khả năng ghi nhớ của Nam tại thời điểm 20 phút là
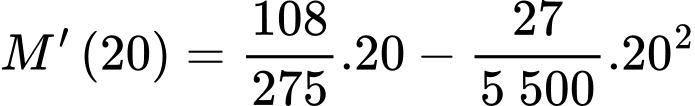
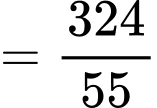
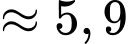 (từ/ phút).
(từ/ phút).c) Sai.
Trong cả tiết học Nam ghi nhớ được tổng cộng số từ mới là:
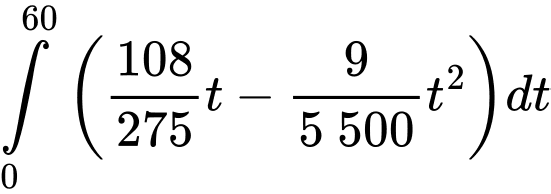
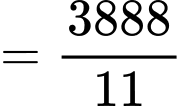
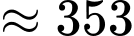 (từ).
(từ).d) Sai.
Tốc độ học trung bình của Nam trong cả tiết học là
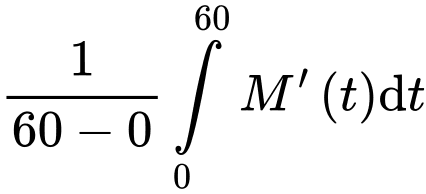
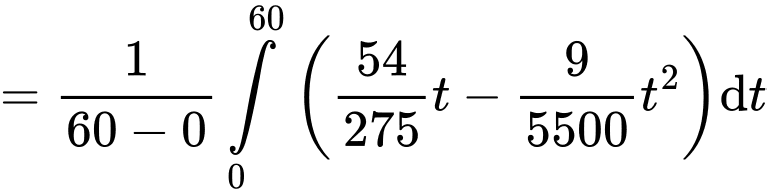
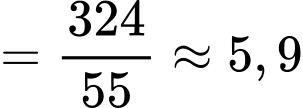 (từ/ phút).
(từ/ phút).
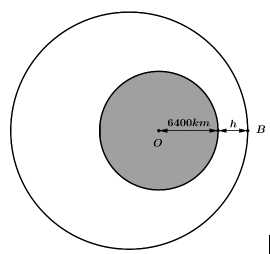
Câu 15 [694834]: Vệ tinh hoạt động dựa trên nguyên lý của vật lý Newton - một vật thể bị kéo bởi một lực hấp dẫn từ một vật thể khác sẽ chuyển động theo một quỹ đạo elip xung quanh vật thể đó. Để đưa vệ tinh lên quỹ đạo, người ta sử dụng các loại tên lửa đẩy khác nhau để cung cấp cho vệ tinh động lượng cần thiết để thoát khỏi trọng lực của Trái Đất và duy trì quỹ đạo ổn định. Để thuận tiện ta quy ước một quỹ đạo gần tròn thành một đường tròn. Trong hệ tọa độ 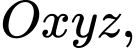 gốc tọa độ là tâm trái đất, một vệ tinh nhân tạo có quỹ đạo được coi như một đường tròn có bán kính
gốc tọa độ là tâm trái đất, một vệ tinh nhân tạo có quỹ đạo được coi như một đường tròn có bán kính 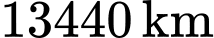 có điểm xuất phát là điểm
có điểm xuất phát là điểm 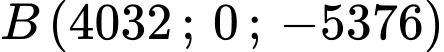 và đây cũng là điểm gần Trái Đất nhất của vệ tinh. Quỹ đạo của vệ tinh này nằm trên mặt phẳng vuông góc với trục tung và có tâm nằm trên đường thẳng
và đây cũng là điểm gần Trái Đất nhất của vệ tinh. Quỹ đạo của vệ tinh này nằm trên mặt phẳng vuông góc với trục tung và có tâm nằm trên đường thẳng 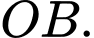 Coi trái đất là hình cầu hoàn hảo có bán kính bằng
Coi trái đất là hình cầu hoàn hảo có bán kính bằng 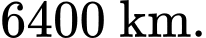
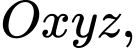 gốc tọa độ là tâm trái đất, một vệ tinh nhân tạo có quỹ đạo được coi như một đường tròn có bán kính
gốc tọa độ là tâm trái đất, một vệ tinh nhân tạo có quỹ đạo được coi như một đường tròn có bán kính 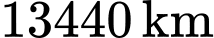 có điểm xuất phát là điểm
có điểm xuất phát là điểm 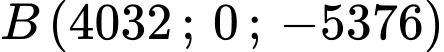 và đây cũng là điểm gần Trái Đất nhất của vệ tinh. Quỹ đạo của vệ tinh này nằm trên mặt phẳng vuông góc với trục tung và có tâm nằm trên đường thẳng
và đây cũng là điểm gần Trái Đất nhất của vệ tinh. Quỹ đạo của vệ tinh này nằm trên mặt phẳng vuông góc với trục tung và có tâm nằm trên đường thẳng 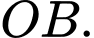 Coi trái đất là hình cầu hoàn hảo có bán kính bằng
Coi trái đất là hình cầu hoàn hảo có bán kính bằng 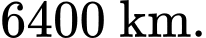

a) Sai.
Quỹ đạo của vệ tinh này nằm trên mặt phẳng vuông góc với trục tung nên một vectơ chỉ phương của mặt phẳng chứa quỹ đoạ của vệ tinh là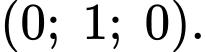
Khi đó, phương trình mặt phẳng chứa quỹ đạo của vệ tinh có dạng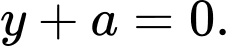
Quỹ đạo đi qua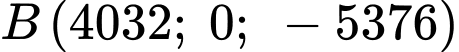 nên
nên 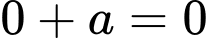 hay
hay 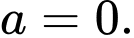
Vậy phương trình mặt phẳng chứa quỹ đạo của vệ tinh là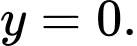
b) Đúng.
Khoảng cách ngắn nhất từ Trái Đất đến vệ tinh bằng:
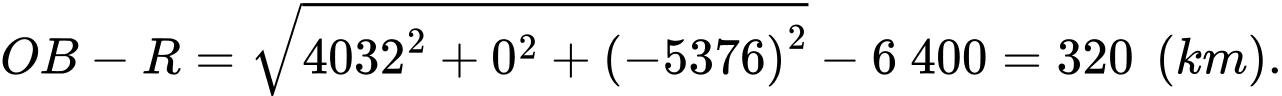
Vậy khi xuất phát tại điểm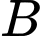 vệ tinh đang ở độ cao
vệ tinh đang ở độ cao 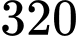 km so với mặt đất.
km so với mặt đất.
c) Sai.
Quỹ đạo của vệ tinh có tâm nằm trên đường thẳng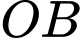 nên tâm
nên tâm 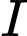 nằm trên đường thẳng
nằm trên đường thẳng 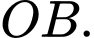
Mặt khác: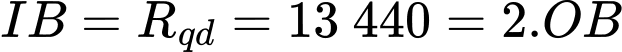 nên
nên  là trung điểm của
là trung điểm của 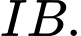
Khi đó: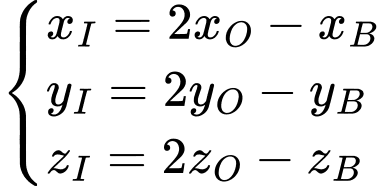
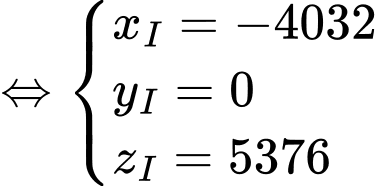
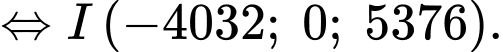
d) Sai.
Gọi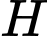 là hình chiếu của
là hình chiếu của 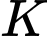 trên mặt phẳng chứa quỹ đạo
trên mặt phẳng chứa quỹ đạo 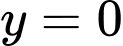
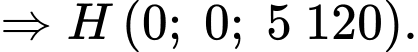
Ta có:
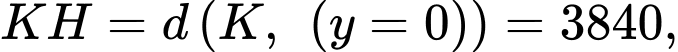
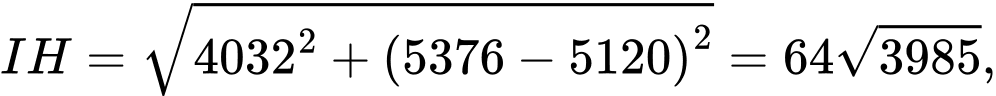
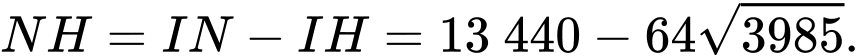
Nối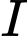 và
và 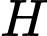 cắt vệ tinh tại
cắt vệ tinh tại 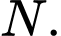 Khi đó:
Khi đó:
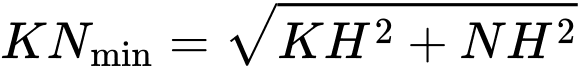

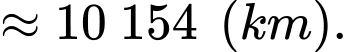
Quỹ đạo của vệ tinh này nằm trên mặt phẳng vuông góc với trục tung nên một vectơ chỉ phương của mặt phẳng chứa quỹ đoạ của vệ tinh là
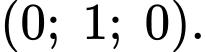
Khi đó, phương trình mặt phẳng chứa quỹ đạo của vệ tinh có dạng
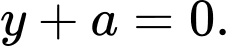
Quỹ đạo đi qua
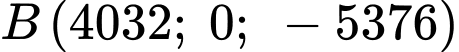 nên
nên 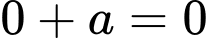 hay
hay 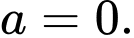
Vậy phương trình mặt phẳng chứa quỹ đạo của vệ tinh là
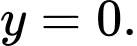
b) Đúng.
Khoảng cách ngắn nhất từ Trái Đất đến vệ tinh bằng:
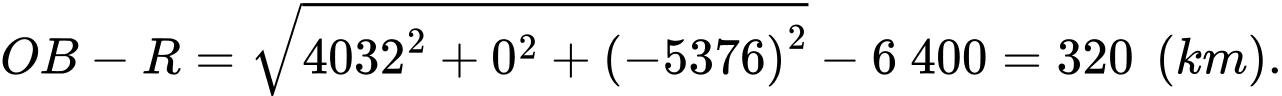
Vậy khi xuất phát tại điểm
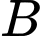 vệ tinh đang ở độ cao
vệ tinh đang ở độ cao 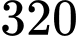 km so với mặt đất.
km so với mặt đất.
c) Sai.
Quỹ đạo của vệ tinh có tâm nằm trên đường thẳng
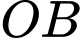 nên tâm
nên tâm 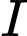 nằm trên đường thẳng
nằm trên đường thẳng 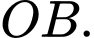
Mặt khác:
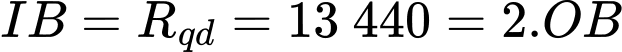 nên
nên  là trung điểm của
là trung điểm của 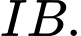
Khi đó:
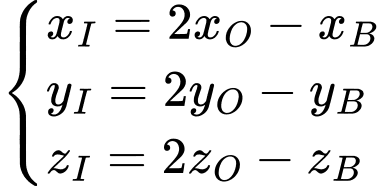
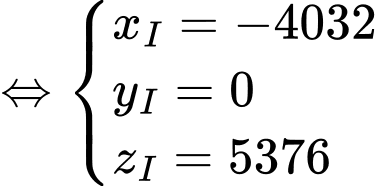
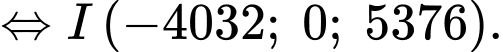
d) Sai.
Gọi
 là hình chiếu của
là hình chiếu của 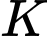 trên mặt phẳng chứa quỹ đạo
trên mặt phẳng chứa quỹ đạo 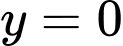
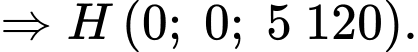
Ta có:
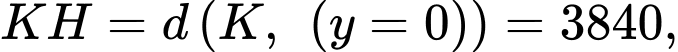
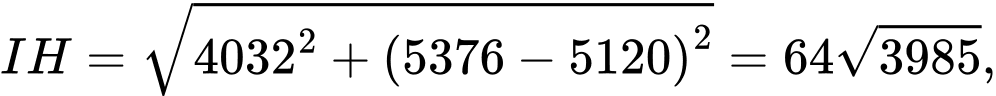
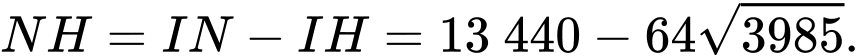
Nối
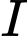 và
và 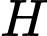 cắt vệ tinh tại
cắt vệ tinh tại 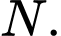 Khi đó:
Khi đó: 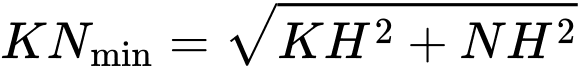

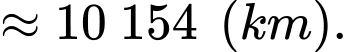
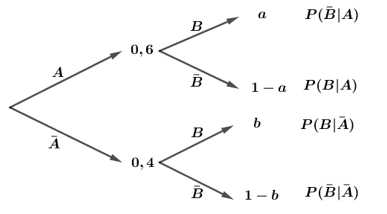
Câu 16 [694836]: Khi trả lời câu hỏi trong một bài thi trắc nghiệm, học sinh có thể biết đáp án hoặc dự đoán đáp án. Các câu hỏi trắc nghiệm có 4 đáp án nhưng chỉ có 1 đáp án đúng. Giả sử bạn Tuấn có xác suất biết đáp án đúng là 0,6 và xác suất Tuấn không biết đáp án đúng là 0,4. Trong trường hợp không biết đáp án Tuấn sẽ dự đoán đáp án đúng bằng cách chọn ngẫu nhiên một trong 4 đáp án của đề thi. Giả sử Tuấn gặp một câu hỏi trắc nghiệm
Gọi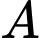 là biến cố “Câu trả lời của Tuấn là đúng”
là biến cố “Câu trả lời của Tuấn là đúng”
Gọi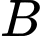 là biến cố “Câu hỏi đó Tuấn đã biết đáp án”
là biến cố “Câu hỏi đó Tuấn đã biết đáp án”
Gọi
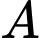 là biến cố “Câu trả lời của Tuấn là đúng”
là biến cố “Câu trả lời của Tuấn là đúng”Gọi
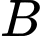 là biến cố “Câu hỏi đó Tuấn đã biết đáp án”
là biến cố “Câu hỏi đó Tuấn đã biết đáp án”
a) Đúng.
Với mỗi câu hỏi bạn Tuấn có xác suất biết đáp án đúng là 0,6 và xác suất Tuấn không biết đáp án đúng là 0,4 nên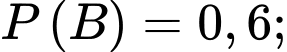
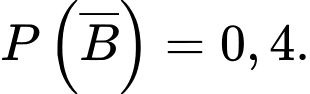
b) Sai.
Xác suất câu trả lời của Tuấn là đúng khi Tuấn đã biết đáp án bằng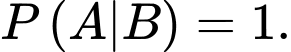
Xác suất câu trả lời của Tuấn là đúng khi Tuấn chưa biết đáp án bằng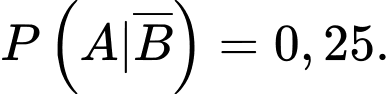
c) Sai.
Áp dụng công thức xác suất toàn phần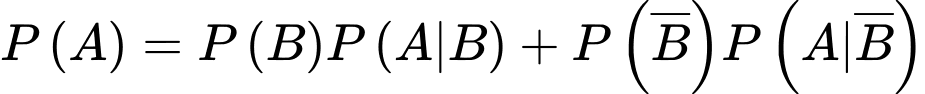 ta có:
ta có:
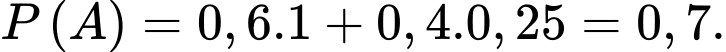
Vậy xác suất để câu trả lời của Tuấn đúng là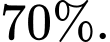
d) Đúng.
Áp dụng công thức Bayes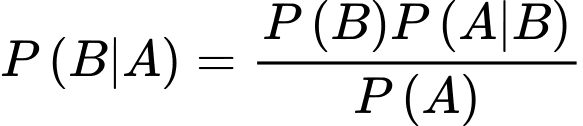 ta có:
ta có:
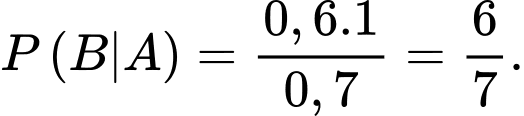
Vậy với câu trắc nghiệm mà câu trả lời của Tuấn là đúng thì xác suất để câu đó là câu mà Tuấn biết đáp án đúng là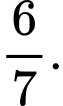
Với mỗi câu hỏi bạn Tuấn có xác suất biết đáp án đúng là 0,6 và xác suất Tuấn không biết đáp án đúng là 0,4 nên
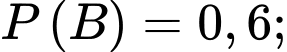
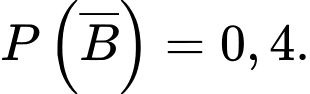
b) Sai.
Xác suất câu trả lời của Tuấn là đúng khi Tuấn đã biết đáp án bằng
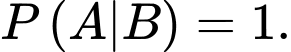
Xác suất câu trả lời của Tuấn là đúng khi Tuấn chưa biết đáp án bằng
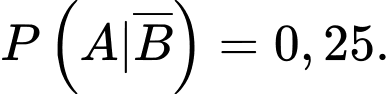
c) Sai.
Áp dụng công thức xác suất toàn phần
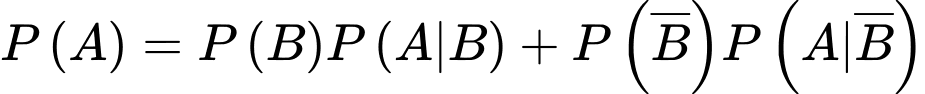 ta có:
ta có: 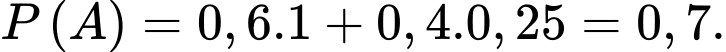
Vậy xác suất để câu trả lời của Tuấn đúng là
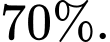
d) Đúng.
Áp dụng công thức Bayes
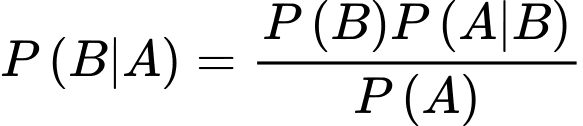 ta có:
ta có: 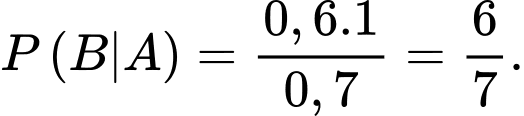
Vậy với câu trắc nghiệm mà câu trả lời của Tuấn là đúng thì xác suất để câu đó là câu mà Tuấn biết đáp án đúng là
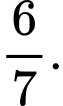
PHẦN III. Thí sinh trả lời từ câu 1 đến câu 6.
Câu 17 [694837]: Cho hình lập phương 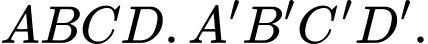 Số đo của góc nhị diện
Số đo của góc nhị diện 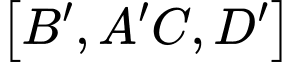 bằng bao nhiêu độ?
bằng bao nhiêu độ?
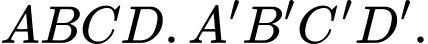 Số đo của góc nhị diện
Số đo của góc nhị diện 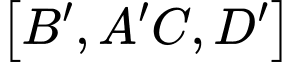 bằng bao nhiêu độ?
bằng bao nhiêu độ?
Điền đáp án: 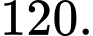
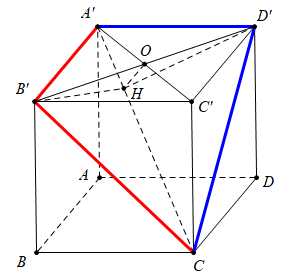
Ta có:
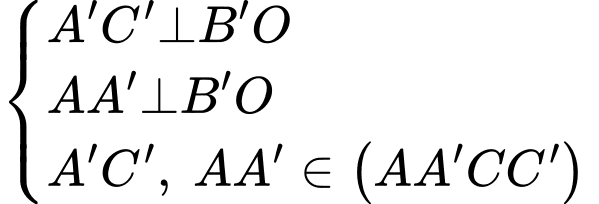


Lại có:
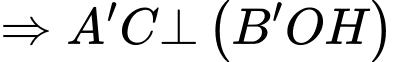
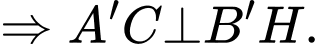
Tương tự ta chứng minh được
=> góc nhị diện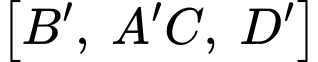 là góc
là góc 
Cho các cạnh hình lập phương là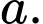
Ta có:
Xét tam giác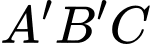 vuông tại
vuông tại 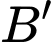 ta có:
ta có:
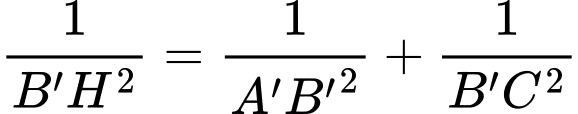
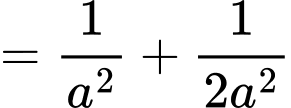
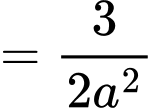
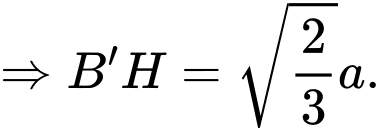
Tương tự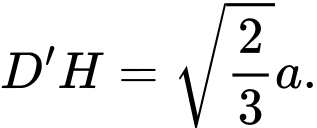
Ta có: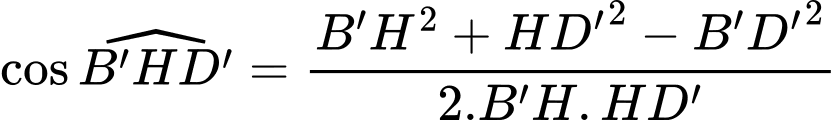
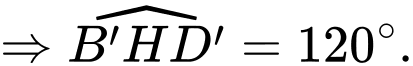
Vậy số đo của góc nhị diện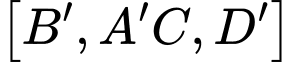 bằng
bằng 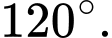
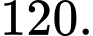

Ta có:


Lại có:

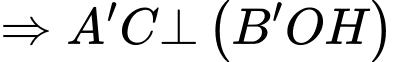
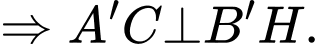
Tương tự ta chứng minh được

=> góc nhị diện
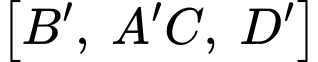 là góc
là góc 
Cho các cạnh hình lập phương là
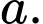
Ta có:

Xét tam giác
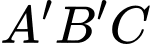 vuông tại
vuông tại 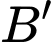 ta có:
ta có: 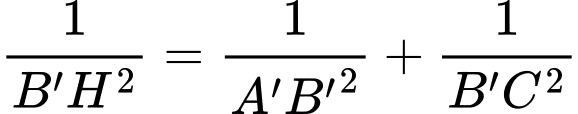
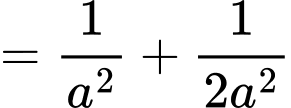
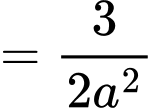
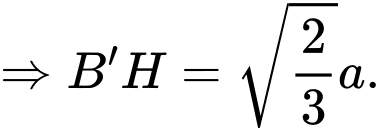
Tương tự
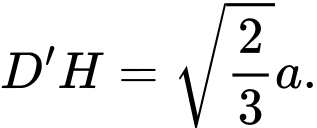
Ta có:
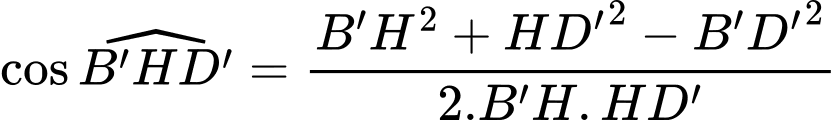
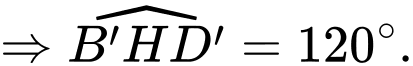
Vậy số đo của góc nhị diện
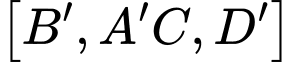 bằng
bằng 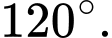
Câu 18 [694838]: Một chai soda có giá 1 đô. Sau khi uống, hai chai rỗng sẽ được đổi lấy một chai soda. Bạn có thể uống nhiều nhất bao nhiêu chai soda nếu bạn có 100 đô?


Điền đáp án: 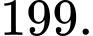
Mua số lượng chai soda ban đầu:
Với 100 đô ta sẽ mua được 100 chai soda.
Đổi chai rỗng lấy soda: Sau khi uống 100 chai, ta sẽ có 100 chai rỗng. 100 chai rỗng ta sẽ đổi được 50 chai soda mới.
Tiếp tục quy trình:
Sau khi uống 50 chai soda mới, ta được 50 chai rỗng.
Đổi 50 chai rỗng lấy 25 chai soda mới.
Lặp lại quy trình:
Uống 25 chai so da mới, ta được 25 chai rỗng.
Đổi 25 chai rỗng ta được 12 chai soda mới và dư 1 chai rỗng.
Tiếp tục đổi:
Uống 12 chai soda mới ta sẽ có 12 chai rỗng.
Đổi 12 chai rỗng ta được 6 chai so đa mới.
Lặp lại quy trình:
Uống 6 chai so da mới, ta được 6 chai rỗng.
Đổi 6 chai rỗng ta được 3 chai soda mới.
Tiếp tục đổi:
Uống chai 3 soda mới vừa đổi ta được 3 chai rỗng.
Cộng với 1 chai rỗng còn dư ở phía trên ta được 4 chai rỗng và đổi thêm được 2 chai soda mới.
Kết thúc:
Uống 2 chai so da mới, ta được 2 chai rỗng.
Đổi 2 chai rỗng ta được 1 chai soda mới.
Uống chai 1 soda mới vừa đổi ta được 1 chai rỗng.
Vậy ta có thể uống được nhiều nhất là chai.
chai.
Mua số lượng chai soda ban đầu:
Với 100 đô ta sẽ mua được 100 chai soda.
Đổi chai rỗng lấy soda: Sau khi uống 100 chai, ta sẽ có 100 chai rỗng. 100 chai rỗng ta sẽ đổi được 50 chai soda mới.
Tiếp tục quy trình:
Sau khi uống 50 chai soda mới, ta được 50 chai rỗng.
Đổi 50 chai rỗng lấy 25 chai soda mới.
Lặp lại quy trình:
Uống 25 chai so da mới, ta được 25 chai rỗng.
Đổi 25 chai rỗng ta được 12 chai soda mới và dư 1 chai rỗng.
Tiếp tục đổi:
Uống 12 chai soda mới ta sẽ có 12 chai rỗng.
Đổi 12 chai rỗng ta được 6 chai so đa mới.
Lặp lại quy trình:
Uống 6 chai so da mới, ta được 6 chai rỗng.
Đổi 6 chai rỗng ta được 3 chai soda mới.
Tiếp tục đổi:
Uống chai 3 soda mới vừa đổi ta được 3 chai rỗng.
Cộng với 1 chai rỗng còn dư ở phía trên ta được 4 chai rỗng và đổi thêm được 2 chai soda mới.
Kết thúc:
Uống 2 chai so da mới, ta được 2 chai rỗng.
Đổi 2 chai rỗng ta được 1 chai soda mới.
Uống chai 1 soda mới vừa đổi ta được 1 chai rỗng.
Vậy ta có thể uống được nhiều nhất là
 chai.
chai.
Câu 19 [696355]: Từ một tấm tôn phẳng hình chữ nhật có chiều dài 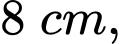 chiều rộng
chiều rộng  có gắn hệ toạ độ
có gắn hệ toạ độ 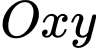 như hình vẽ.
như hình vẽ.
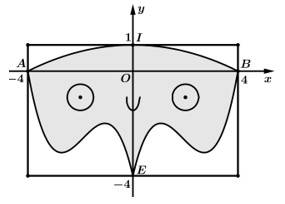
Thầy Tuấn cắt miếng tôn theo ba đường: Đường cong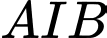 là một phần của Parabol, các đường cong
là một phần của Parabol, các đường cong 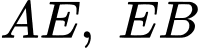 là một phần đồ thị hàm số bậc ba. Trang trí phần còn lại để tạo thành một chiếc mặt nạ đồ chơi có trục đối xứng là trục
là một phần đồ thị hàm số bậc ba. Trang trí phần còn lại để tạo thành một chiếc mặt nạ đồ chơi có trục đối xứng là trục 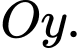 Biết đường cong
Biết đường cong 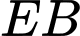 đi qua các điểm
đi qua các điểm 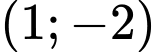 và
và 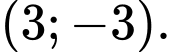 Tính diện tích chiếc mặt nạ đồ chơi của thầy Tuấn. Làm tròn đến hàng phần mười theo đơn vị
Tính diện tích chiếc mặt nạ đồ chơi của thầy Tuấn. Làm tròn đến hàng phần mười theo đơn vị 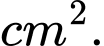
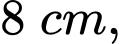 chiều rộng
chiều rộng  có gắn hệ toạ độ
có gắn hệ toạ độ 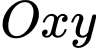 như hình vẽ.
như hình vẽ. 
Thầy Tuấn cắt miếng tôn theo ba đường: Đường cong
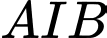 là một phần của Parabol, các đường cong
là một phần của Parabol, các đường cong 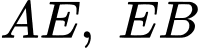 là một phần đồ thị hàm số bậc ba. Trang trí phần còn lại để tạo thành một chiếc mặt nạ đồ chơi có trục đối xứng là trục
là một phần đồ thị hàm số bậc ba. Trang trí phần còn lại để tạo thành một chiếc mặt nạ đồ chơi có trục đối xứng là trục 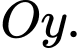 Biết đường cong
Biết đường cong 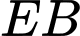 đi qua các điểm
đi qua các điểm 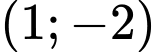 và
và 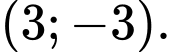 Tính diện tích chiếc mặt nạ đồ chơi của thầy Tuấn. Làm tròn đến hàng phần mười theo đơn vị
Tính diện tích chiếc mặt nạ đồ chơi của thầy Tuấn. Làm tròn đến hàng phần mười theo đơn vị 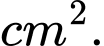
Điền đáp án: 24,9.
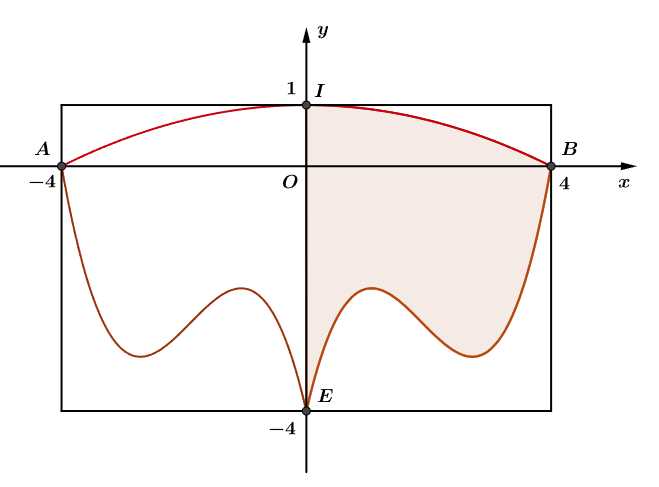
Giả sử đường cong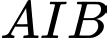 có phương trình là
có phương trình là 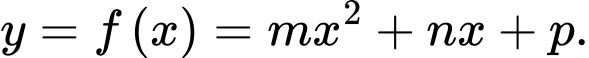
Đường cong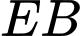 có phương trình là
có phương trình là 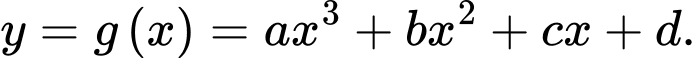
Vì mặt nạ đối xứng qua trục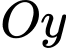 nên diện tích của mặt nạ bằng
nên diện tích của mặt nạ bằng 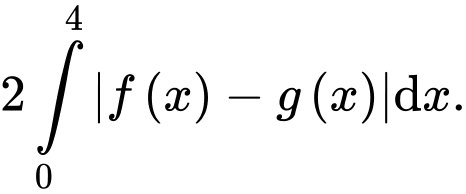
+) Viết phương trình của
Ta có đường cong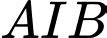 đi qua các điểm
đi qua các điểm 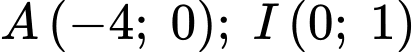 và
và 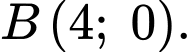 Từ đó ta có hệ phương trình:
Từ đó ta có hệ phương trình: 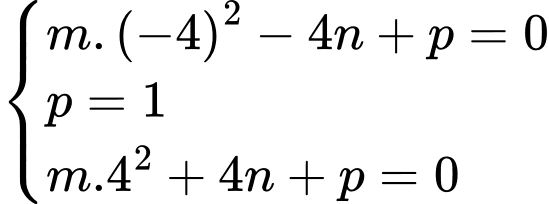
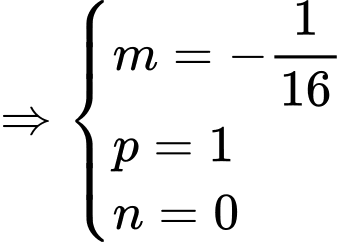
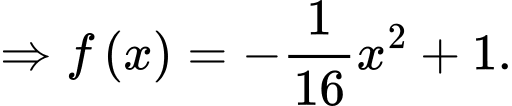
+) Viết phương trình của
Vì đồ thị hàm số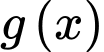 đi qua điểm
đi qua điểm 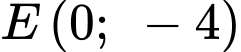 nên suy ra
nên suy ra 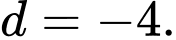
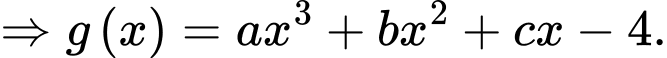
Lại có đường cong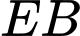 đi qua các điểm
đi qua các điểm 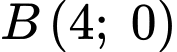 và các điểm
và các điểm 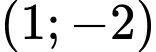 và
và 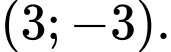 Từ đó, ta có hệ phương trình:
Từ đó, ta có hệ phương trình: 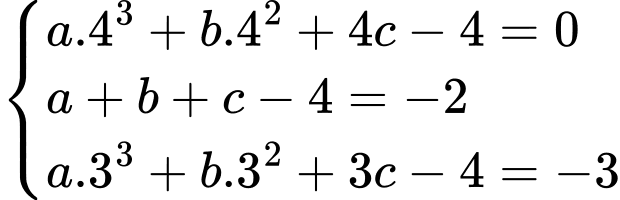
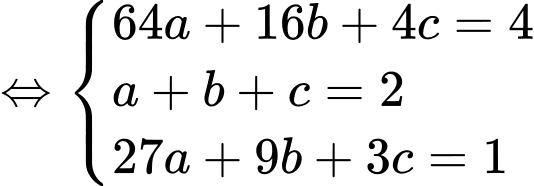
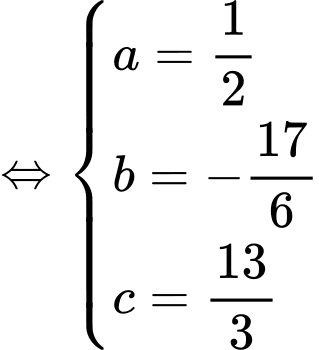
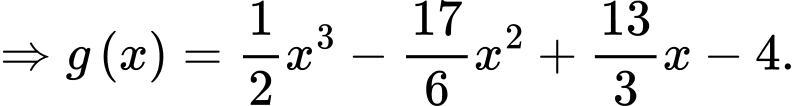
Suy ra diện tích của mặt nạ bằng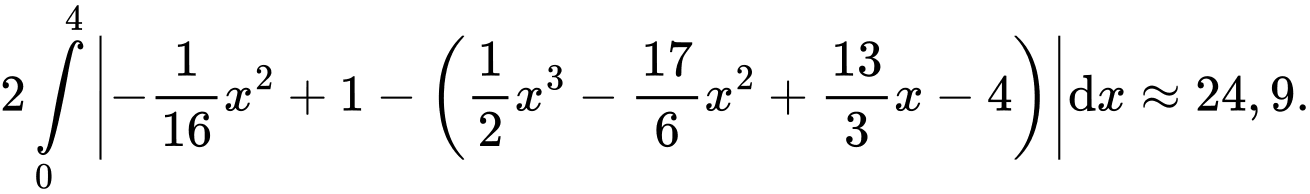

Giả sử đường cong
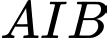 có phương trình là
có phương trình là 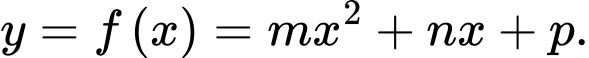
Đường cong
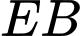 có phương trình là
có phương trình là 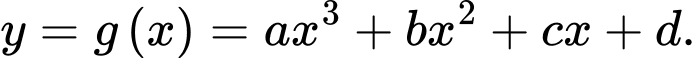
Vì mặt nạ đối xứng qua trục
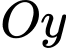 nên diện tích của mặt nạ bằng
nên diện tích của mặt nạ bằng 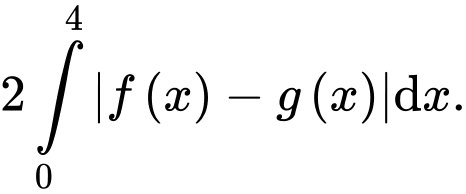
+) Viết phương trình của

Ta có đường cong
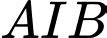 đi qua các điểm
đi qua các điểm 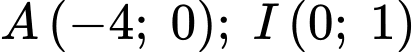 và
và 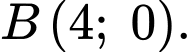 Từ đó ta có hệ phương trình:
Từ đó ta có hệ phương trình: 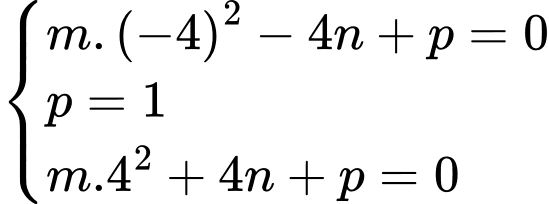
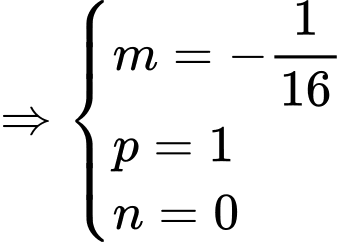
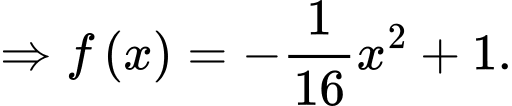
+) Viết phương trình của

Vì đồ thị hàm số
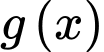 đi qua điểm
đi qua điểm 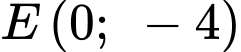 nên suy ra
nên suy ra 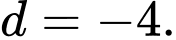
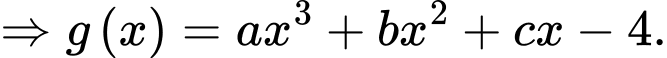
Lại có đường cong
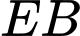 đi qua các điểm
đi qua các điểm 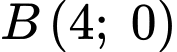 và các điểm
và các điểm 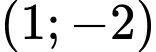 và
và 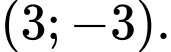 Từ đó, ta có hệ phương trình:
Từ đó, ta có hệ phương trình: 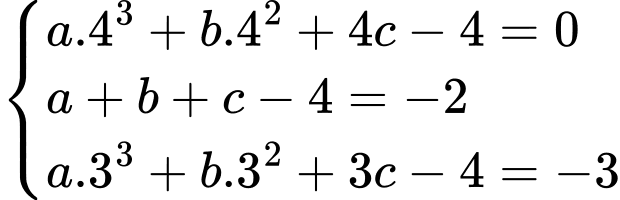
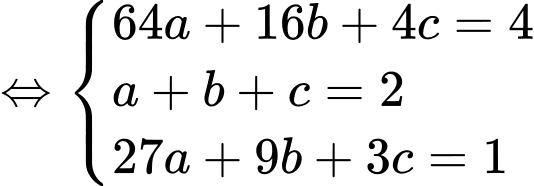
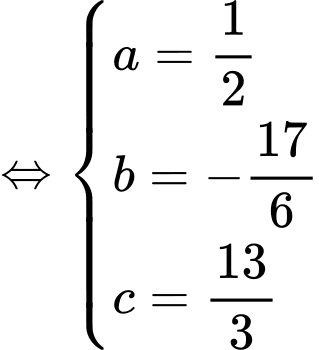
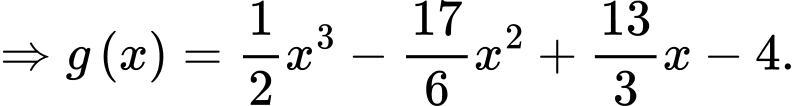
Suy ra diện tích của mặt nạ bằng
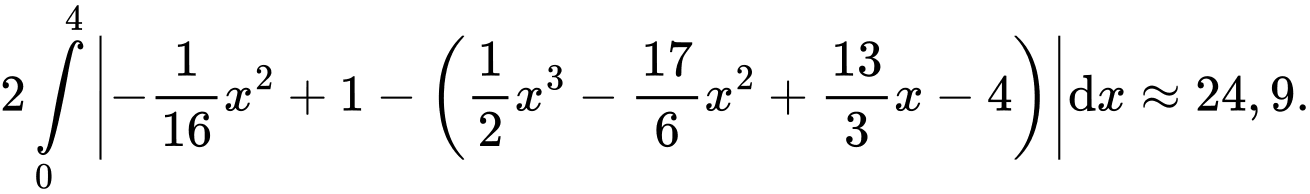
Câu 20 [693323]: Một hồi cứu về một bệnh nhân ung thư vú đã phẫu thuật cho kết quả với tỉ lệ sống trên 5 năm là 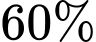 và tỉ lệ di căn là
và tỉ lệ di căn là 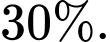 Biết rằng số bệnh nhân vừa sống trên 5 năm vừa di căn chỉ bằng một nửa số bệnh nhân vừa không di căn vừa sống không quá 5 năm. Một bệnh nhân bị ung thư vú và không di căn, tính xác suất để người này sống trên 5 năm. Làm tròn kết quả đến chữ số thập phân thứ 2.
Biết rằng số bệnh nhân vừa sống trên 5 năm vừa di căn chỉ bằng một nửa số bệnh nhân vừa không di căn vừa sống không quá 5 năm. Một bệnh nhân bị ung thư vú và không di căn, tính xác suất để người này sống trên 5 năm. Làm tròn kết quả đến chữ số thập phân thứ 2.
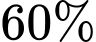 và tỉ lệ di căn là
và tỉ lệ di căn là 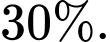 Biết rằng số bệnh nhân vừa sống trên 5 năm vừa di căn chỉ bằng một nửa số bệnh nhân vừa không di căn vừa sống không quá 5 năm. Một bệnh nhân bị ung thư vú và không di căn, tính xác suất để người này sống trên 5 năm. Làm tròn kết quả đến chữ số thập phân thứ 2.
Biết rằng số bệnh nhân vừa sống trên 5 năm vừa di căn chỉ bằng một nửa số bệnh nhân vừa không di căn vừa sống không quá 5 năm. Một bệnh nhân bị ung thư vú và không di căn, tính xác suất để người này sống trên 5 năm. Làm tròn kết quả đến chữ số thập phân thứ 2.
Điền đáp án: 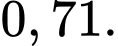
Gọi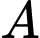 là biến cố: “Người này sống trên 5 năm”,
là biến cố: “Người này sống trên 5 năm”, 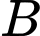 là biến cố: “Người này có di căn”.
là biến cố: “Người này có di căn”.
Khi đó: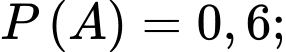
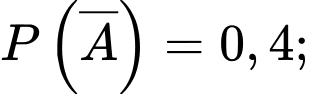
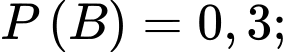
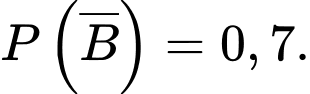
Gọi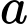 là số người di căn trong số những người sống trên 5 năm,
là số người di căn trong số những người sống trên 5 năm, 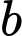 là số người di căn trong số những người sống không quá 5 năm.
là số người di căn trong số những người sống không quá 5 năm.
Ta có: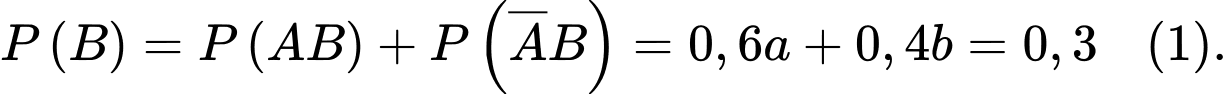
Số bệnh nhân vừa sống trên 5 năm vừa di căn chỉ bằng một nửa số bệnh nhân vừa không di căn vừa sống không quá 5 năm nên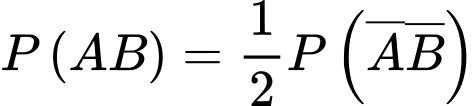
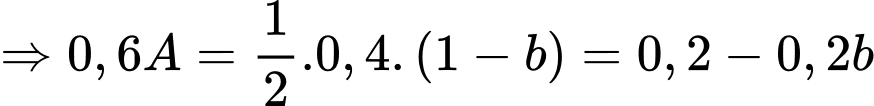
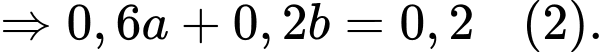
Từ và
và  ta có:
ta có: 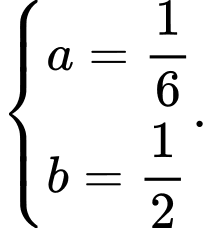
Xác suất một bệnh nhân bị ung thư vú và không di căn sống trên 5 năm bằng:
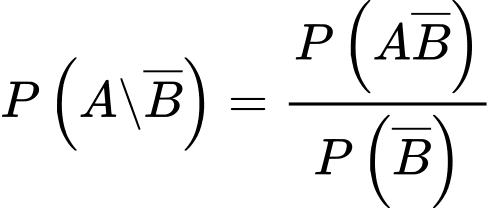
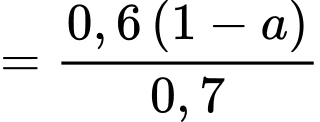
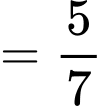
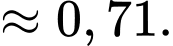
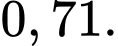

Gọi
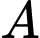 là biến cố: “Người này sống trên 5 năm”,
là biến cố: “Người này sống trên 5 năm”, 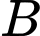 là biến cố: “Người này có di căn”.
là biến cố: “Người này có di căn”. Khi đó:
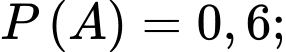
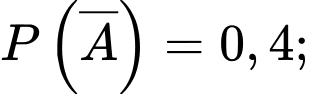
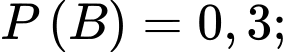
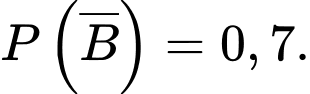
Gọi
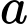 là số người di căn trong số những người sống trên 5 năm,
là số người di căn trong số những người sống trên 5 năm, 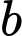 là số người di căn trong số những người sống không quá 5 năm.
là số người di căn trong số những người sống không quá 5 năm.Ta có:
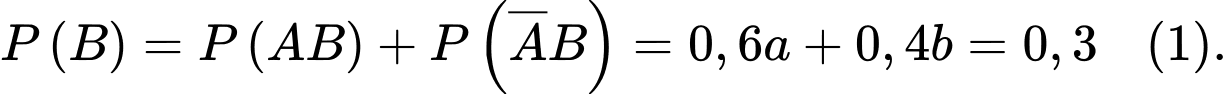
Số bệnh nhân vừa sống trên 5 năm vừa di căn chỉ bằng một nửa số bệnh nhân vừa không di căn vừa sống không quá 5 năm nên
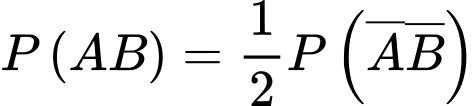
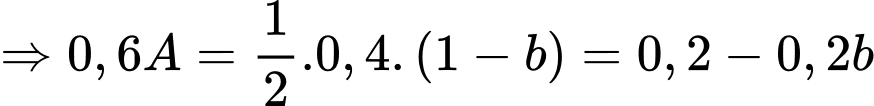
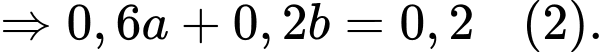
Từ
 và
và  ta có:
ta có: 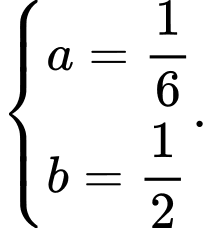
Xác suất một bệnh nhân bị ung thư vú và không di căn sống trên 5 năm bằng:
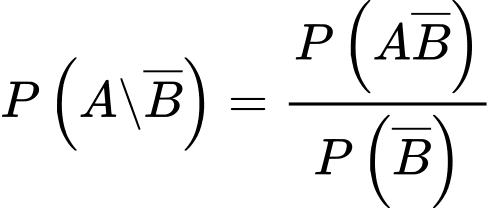
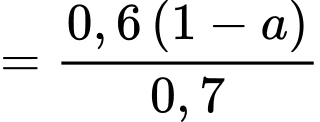
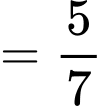
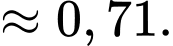
Câu 21 [702940]: Một chiếc phà chạy giữa đất liền và đảo Dedlos. Phà có công suất tối đa là 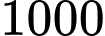 xe hơi mỗi chuyến, nhưng việc tải gần hết công suất rất tốn thời gian. Biết rằng số lượng xe hơi đưa lên phà mỗi chuyến là
xe hơi mỗi chuyến, nhưng việc tải gần hết công suất rất tốn thời gian. Biết rằng số lượng xe hơi đưa lên phà mỗi chuyến là 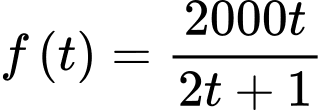 và mất một khoảng thời gian là
và mất một khoảng thời gian là 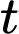 (giờ). Mỗi xe cần trung bình
(giờ). Mỗi xe cần trung bình 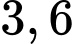 giây để dỡ xuống khi đến điểm đích. Thời gian di chuyển đến đảo và thời gian vòng về đều mất
giây để dỡ xuống khi đến điểm đích. Thời gian di chuyển đến đảo và thời gian vòng về đều mất 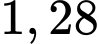 giờ. Nên tải bao nhiêu xe lên phà cho mỗi chuyến đi để lượng xe trung bình di chuyển qua lại đảo mỗi giờ đạt lớn nhất? (làm tròn kết quả đến hàng đơn vị).
giờ. Nên tải bao nhiêu xe lên phà cho mỗi chuyến đi để lượng xe trung bình di chuyển qua lại đảo mỗi giờ đạt lớn nhất? (làm tròn kết quả đến hàng đơn vị).
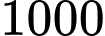 xe hơi mỗi chuyến, nhưng việc tải gần hết công suất rất tốn thời gian. Biết rằng số lượng xe hơi đưa lên phà mỗi chuyến là
xe hơi mỗi chuyến, nhưng việc tải gần hết công suất rất tốn thời gian. Biết rằng số lượng xe hơi đưa lên phà mỗi chuyến là 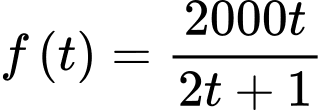 và mất một khoảng thời gian là
và mất một khoảng thời gian là 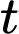 (giờ). Mỗi xe cần trung bình
(giờ). Mỗi xe cần trung bình 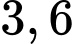 giây để dỡ xuống khi đến điểm đích. Thời gian di chuyển đến đảo và thời gian vòng về đều mất
giây để dỡ xuống khi đến điểm đích. Thời gian di chuyển đến đảo và thời gian vòng về đều mất 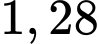 giờ. Nên tải bao nhiêu xe lên phà cho mỗi chuyến đi để lượng xe trung bình di chuyển qua lại đảo mỗi giờ đạt lớn nhất? (làm tròn kết quả đến hàng đơn vị).
giờ. Nên tải bao nhiêu xe lên phà cho mỗi chuyến đi để lượng xe trung bình di chuyển qua lại đảo mỗi giờ đạt lớn nhất? (làm tròn kết quả đến hàng đơn vị).
Điền đáp án: 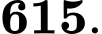
Để đưa được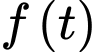 xe lên phà cần
xe lên phà cần 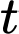 giờ.
giờ.
Tổng thời gian để đưa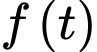 xe qua đảo hoặc từ đảo về bằng
xe qua đảo hoặc từ đảo về bằng 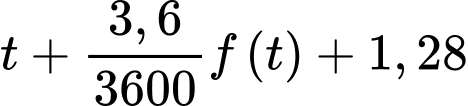 (giờ).
(giờ).
Số xe di chuyển trung bình mỗi giờ bằng:
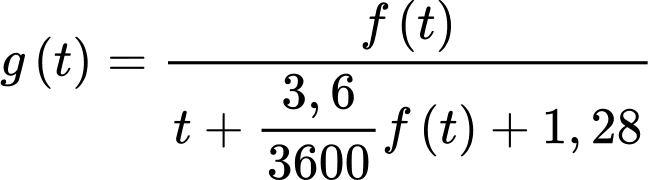
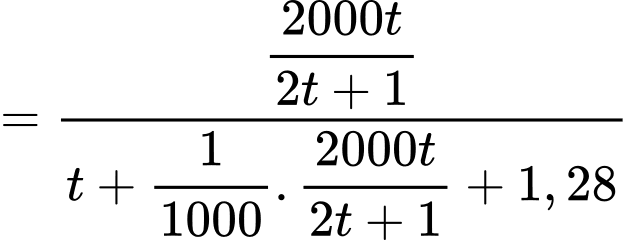
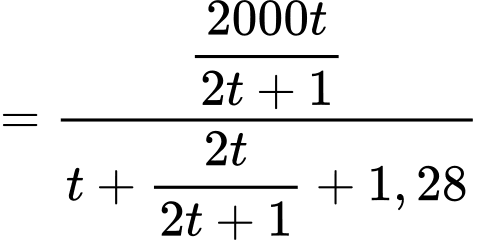
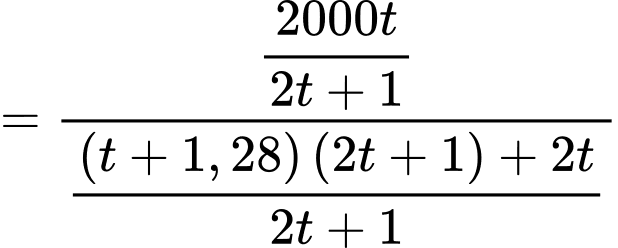
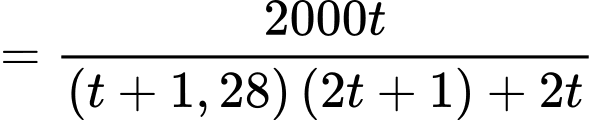
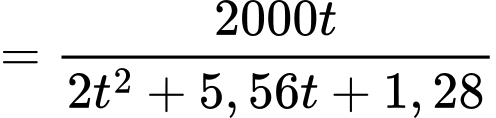
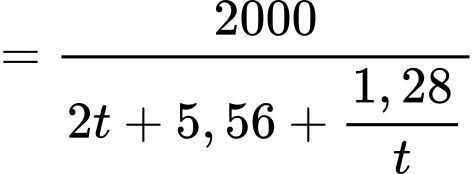
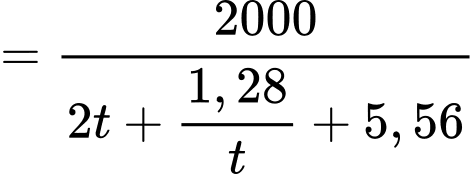
Áp dụng bất đẳng thức Côsi cho 2 số dương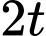 và
và 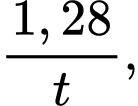 ta có
ta có 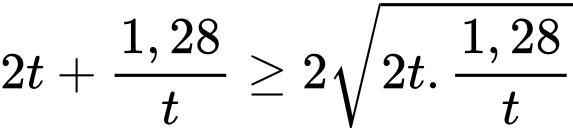
Suy ra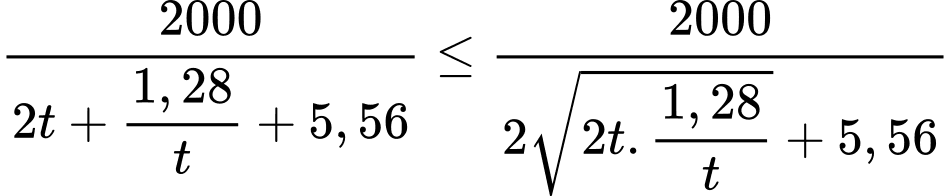
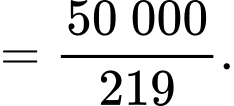
Dấu bằng xảy ra khi: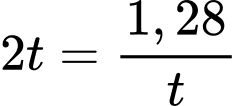
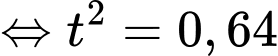
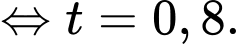
Vậy để lượng xe trung bình di chuyển qua lại đảo mỗi giờ đạt lớn nhất cần tải lên phà mỗi chuyến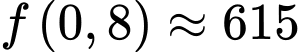 xe.
xe.
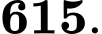
Để đưa được
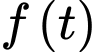 xe lên phà cần
xe lên phà cần 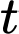 giờ.
giờ.Tổng thời gian để đưa
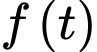 xe qua đảo hoặc từ đảo về bằng
xe qua đảo hoặc từ đảo về bằng 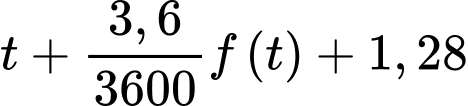 (giờ).
(giờ). Số xe di chuyển trung bình mỗi giờ bằng:
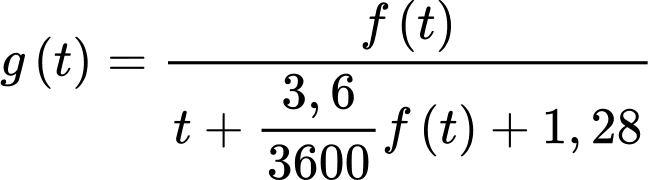
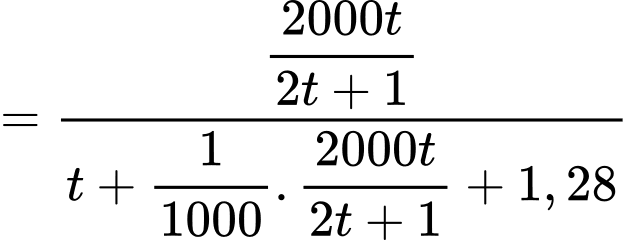
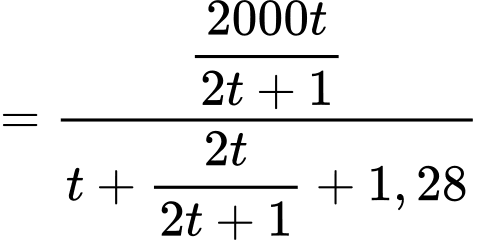
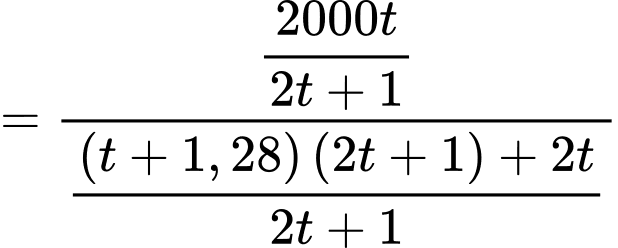
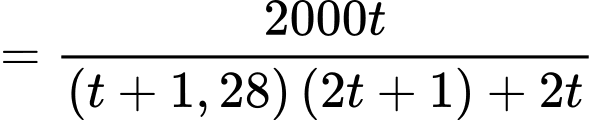
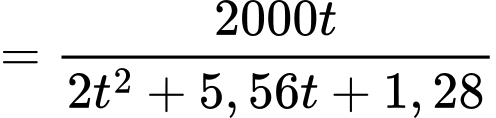
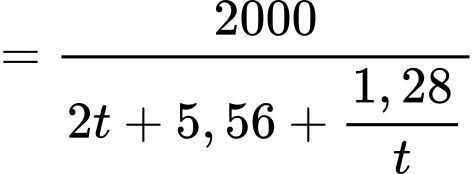
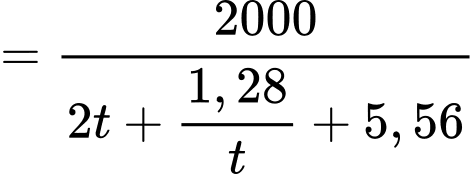
Áp dụng bất đẳng thức Côsi cho 2 số dương
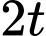 và
và 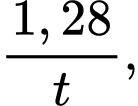 ta có
ta có 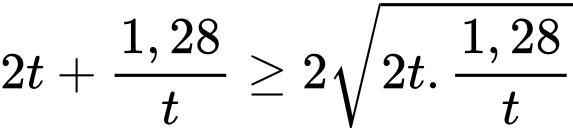
Suy ra
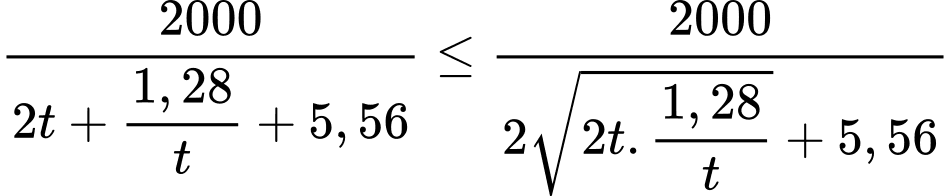
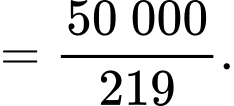
Dấu bằng xảy ra khi:
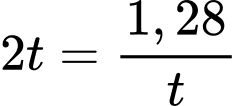
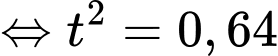
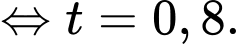
Vậy để lượng xe trung bình di chuyển qua lại đảo mỗi giờ đạt lớn nhất cần tải lên phà mỗi chuyến
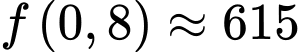 xe.
xe.
Câu 22 [694842]: Trong không gian 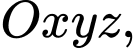 cho hình lăng trụ tam giác đều
cho hình lăng trụ tam giác đều 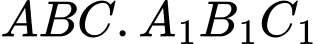 có
có 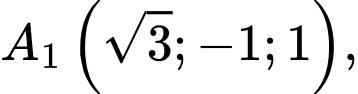 hai đỉnh
hai đỉnh 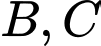 thuộc trục
thuộc trục  và
và 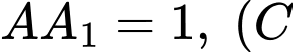 không trùng với
không trùng với  ). Biết
). Biết 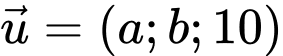 là một véc tơ chỉ phương của đường thẳng
là một véc tơ chỉ phương của đường thẳng 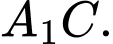 Giá trị của
Giá trị của  bằng bao nhiêu?
bằng bao nhiêu?
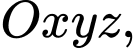 cho hình lăng trụ tam giác đều
cho hình lăng trụ tam giác đều 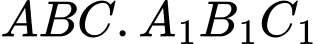 có
có 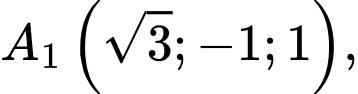 hai đỉnh
hai đỉnh 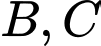 thuộc trục
thuộc trục  và
và 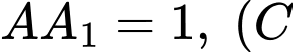 không trùng với
không trùng với  ). Biết
). Biết 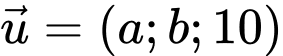 là một véc tơ chỉ phương của đường thẳng
là một véc tơ chỉ phương của đường thẳng 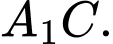 Giá trị của
Giá trị của  bằng bao nhiêu?
bằng bao nhiêu?
Điền đáp án: 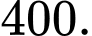
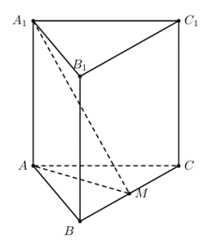
Gọi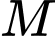 là trung điểm
là trung điểm 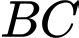 khi đó
khi đó  .
.
Ta có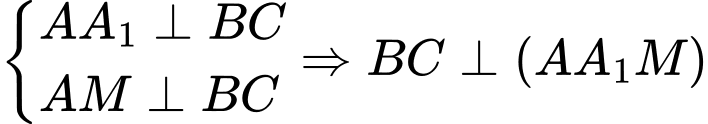 .
.
Mặt phẳng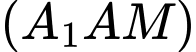 đi qua
đi qua 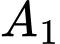 và nhận
và nhận 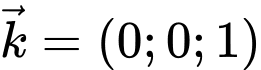 làm VTPT nên
làm VTPT nên 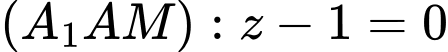 .
.
Mà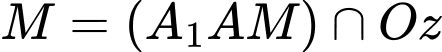 nên
nên 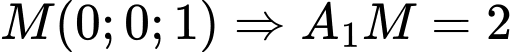 .
.
Trong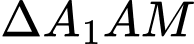 có
có 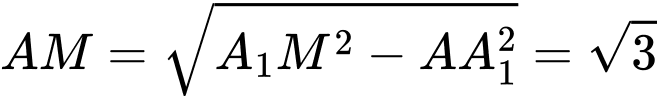 .
.
Ta có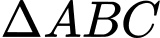 đều nên
đều nên 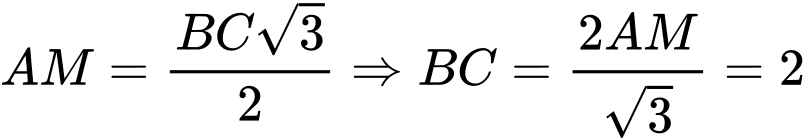 .
.
Gọi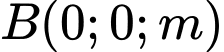 mà
mà 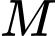 là trung điểm
là trung điểm 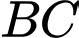 nên
nên 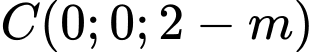 .
.
Có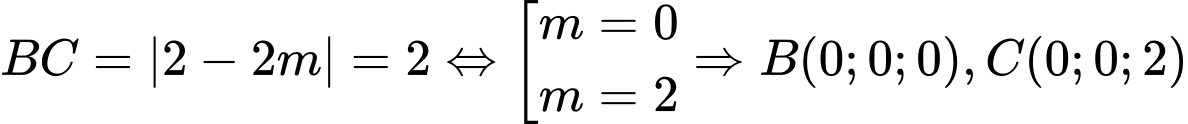 ,( vì
,( vì  không trùng với
không trùng với  ).
).
Do đó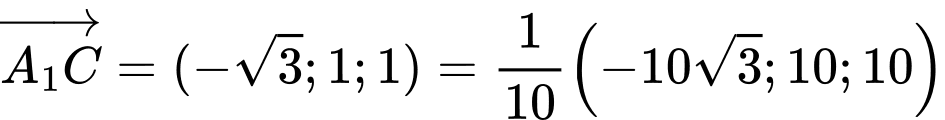
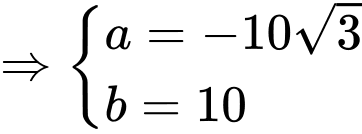 .
.
Vậy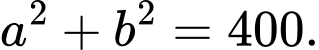
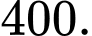

Gọi
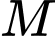 là trung điểm
là trung điểm 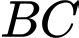 khi đó
khi đó  .
.Ta có
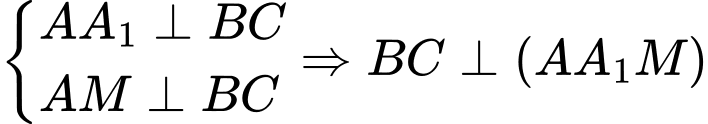 .
.Mặt phẳng
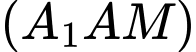 đi qua
đi qua 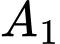 và nhận
và nhận 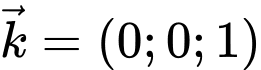 làm VTPT nên
làm VTPT nên 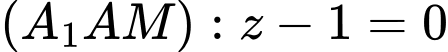 .
.Mà
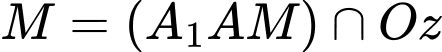 nên
nên 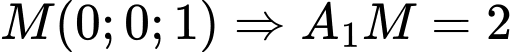 .
.Trong
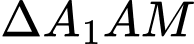 có
có 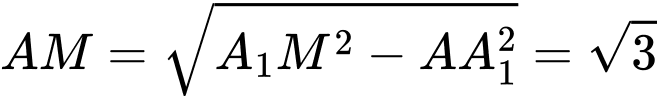 .
.Ta có
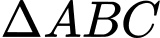 đều nên
đều nên 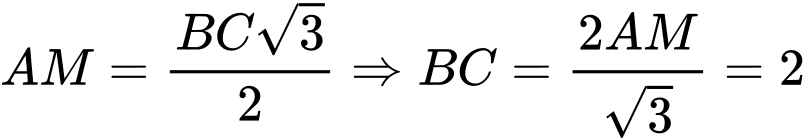 .
.Gọi
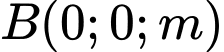 mà
mà 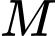 là trung điểm
là trung điểm 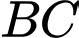 nên
nên 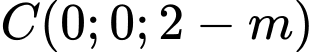 .
.Có
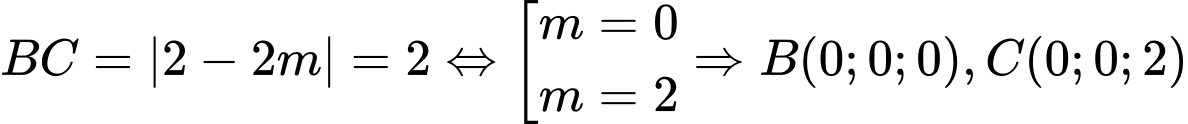 ,( vì
,( vì  không trùng với
không trùng với  ).
).Do đó
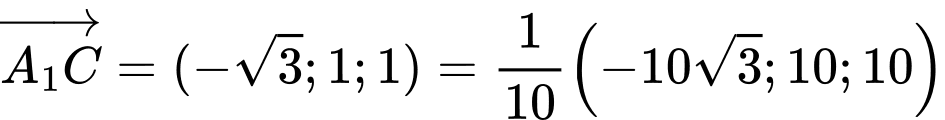
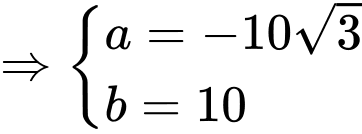 .
.Vậy