PHẦN I. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Câu 1 [503005]: Cho hàm số 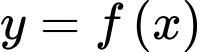 có đồ thị như hình bên.
có đồ thị như hình bên.
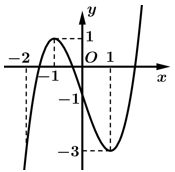
Hàm số đã cho nghịch biến trên khoảng nào dưới đây?
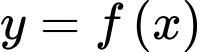 có đồ thị như hình bên.
có đồ thị như hình bên.
Hàm số đã cho nghịch biến trên khoảng nào dưới đây?
A, 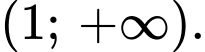
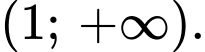
B, 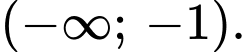
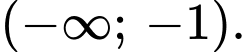
C, 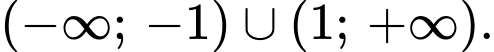
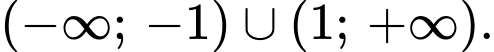
D, 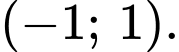
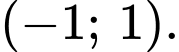
Chọn đáp án D.
Dựa vào đồ thị ta thấy hàm số đã cho nghịch biến trên khoảng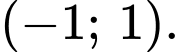 Đáp án: D
Đáp án: D
Dựa vào đồ thị ta thấy hàm số đã cho nghịch biến trên khoảng
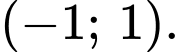 Đáp án: D
Đáp án: D
Câu 2 [809911]: Cho cấp số nhân 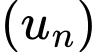 biết
biết 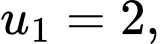
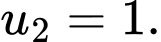 Công bội của cấp số nhân đó là
Công bội của cấp số nhân đó là
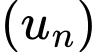 biết
biết 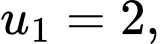
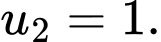 Công bội của cấp số nhân đó là
Công bội của cấp số nhân đó là A, 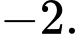
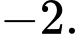
B, 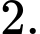
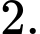
C, 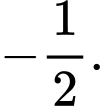
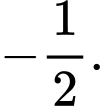
D, 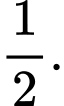
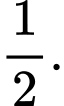
Chọn đáp án D.
Ta có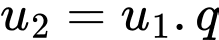
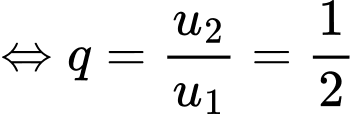 Đáp án: D
Đáp án: D
Ta có
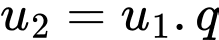
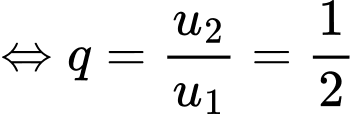 Đáp án: D
Đáp án: D
Câu 3 [809921]: Tích phân 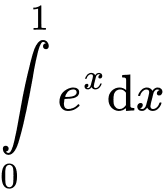 bằng
bằng
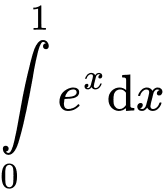 bằng
bằng A, 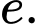
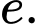
B, 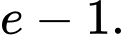
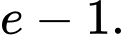
C, 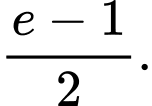
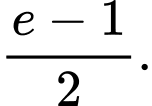
D, 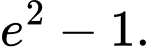
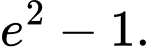
Chọn đáp án B.
Ta có: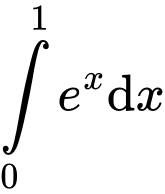
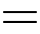
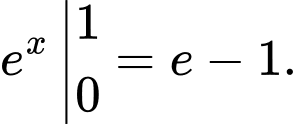 Đáp án: B
Đáp án: B
Ta có:
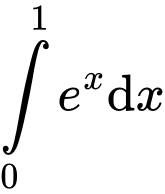
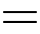
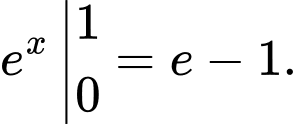 Đáp án: B
Đáp án: B
Câu 4 [809808]: Cho khối chóp có thể tích bằng 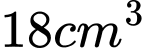 và diện tích đáy bằng
và diện tích đáy bằng  Chiều cao của khối chóp đó là
Chiều cao của khối chóp đó là
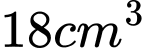 và diện tích đáy bằng
và diện tích đáy bằng  Chiều cao của khối chóp đó là
Chiều cao của khối chóp đó là A, 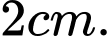
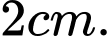
B, 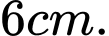
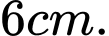
C, 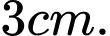
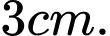
D, 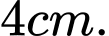
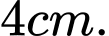
Chọn đáp án B.
Chiều cao của khối chóp :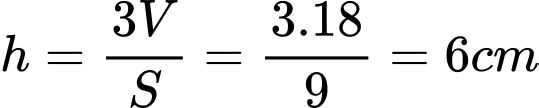 Đáp án: B
Đáp án: B
Chiều cao của khối chóp :
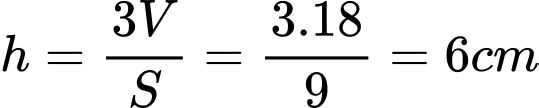 Đáp án: B
Đáp án: B
Câu 5 [605010]: Tập nghiệm của bất phương trình 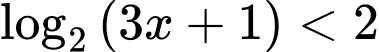 là
là
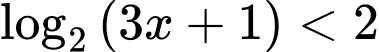 là
là A, 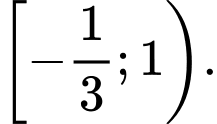
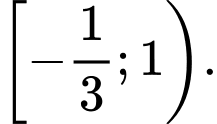
B, 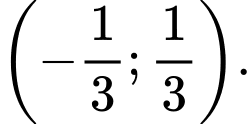
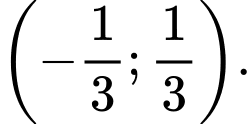
C, 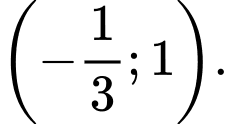
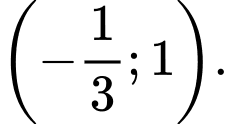
D, 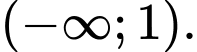
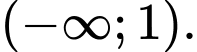
Chọn đáp án C.
Ta có: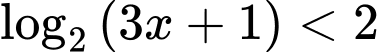
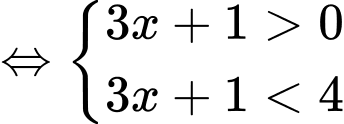
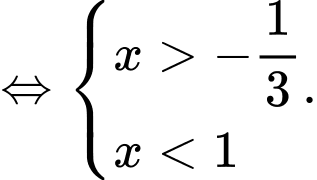
Vậy bất phương trình có tập nghiệm: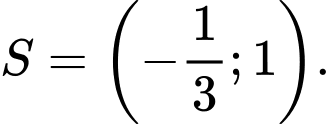 Đáp án: C
Đáp án: C
Ta có:
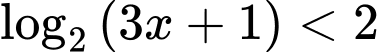
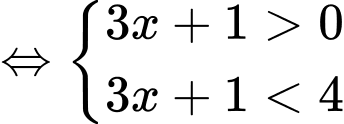
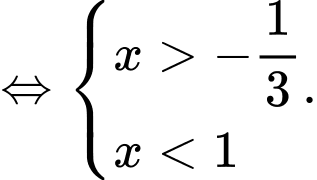
Vậy bất phương trình có tập nghiệm:
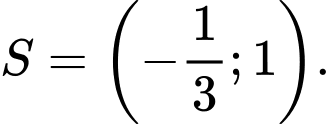 Đáp án: C
Đáp án: C
Câu 6 [809899]: Họ các nguyên hàm của hàm số 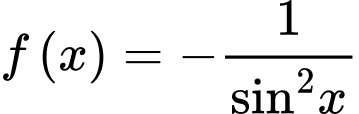 là
là
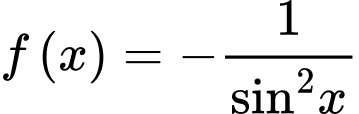 là
là A, 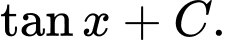
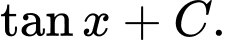
B, 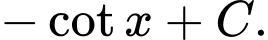
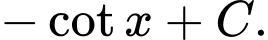
C, 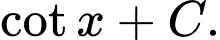
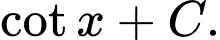
D, 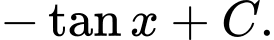
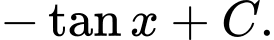
Chọn đáp án C.
Ta có: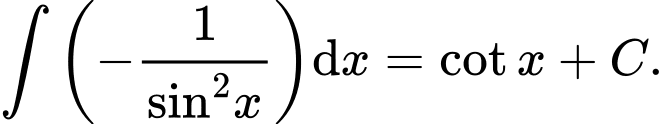 Đáp án: C
Đáp án: C
Ta có:
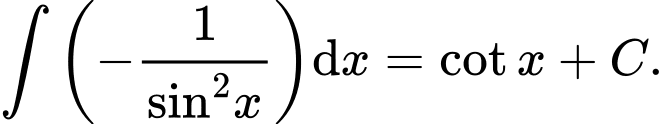 Đáp án: C
Đáp án: C
Câu 7 [809920]: Đường tiệm cận ngang của đồ thị hàm số 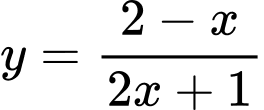 là
là
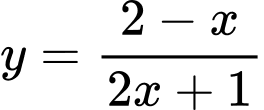 là
là A, 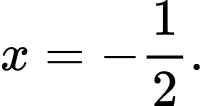
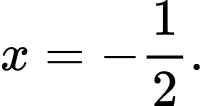
B, 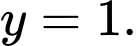
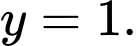
C, 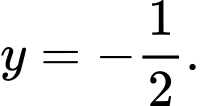
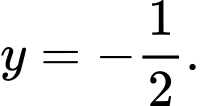
D, 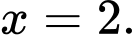
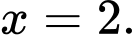
Chọn đáp án C.
Ta có: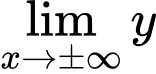
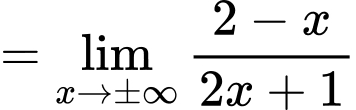
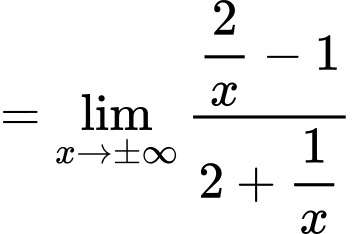
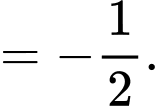
Do đó đồ thị đã cho có đường tiệm cần ngang là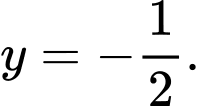 Đáp án: C
Đáp án: C
Ta có:
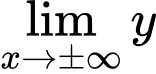
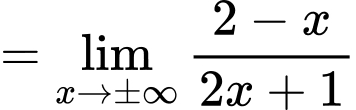
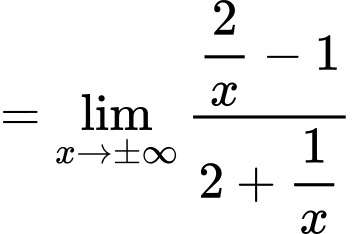
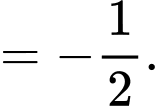
Do đó đồ thị đã cho có đường tiệm cần ngang là
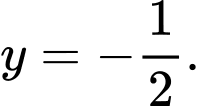 Đáp án: C
Đáp án: C
Câu 8 [809841]: Với 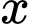 là số thực dương tùy ý,
là số thực dương tùy ý, 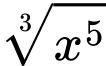 bằng
bằng
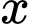 là số thực dương tùy ý,
là số thực dương tùy ý, 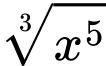 bằng
bằng A, 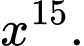
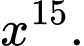
B, 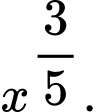
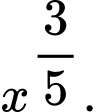
C, 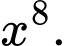
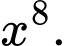
D, 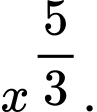
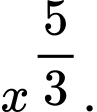
Chọn đáp án D.
Ta có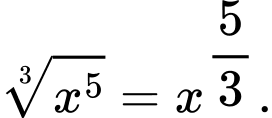 Đáp án: D
Đáp án: D
Ta có
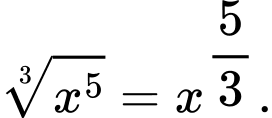 Đáp án: D
Đáp án: D Sử dụng thông tin dưới đây để trả lời câu 9 và câu 10
Trong không gian Oxyz, cho điểm A(- 4;0;1) và mặt phẳng (P):x - 2y - z + 4 = 0. Mặt phẳng (Q) đi qua điểm A và song song với mặt phẳng (P).
Câu 9 [699661]: Mặt phẳng  đi qua điểm
đi qua điểm  và song song với mặt phẳng
và song song với mặt phẳng 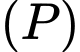 có phương trình là
có phương trình là
 đi qua điểm
đi qua điểm 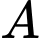 và song song với mặt phẳng
và song song với mặt phẳng 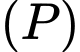 có phương trình là
có phương trình là A, 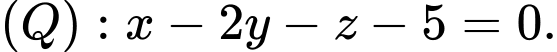
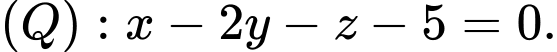
B, 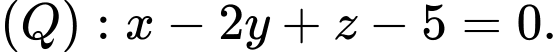
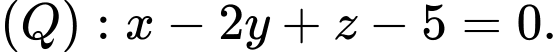
C, 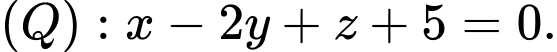
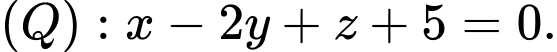
D, 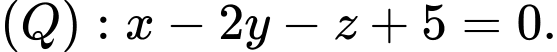
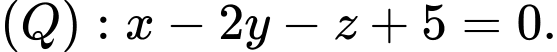
Chọn đáp án D.
Mặt phẳng song song với mặt phẳng
song song với mặt phẳng 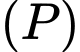 nên phương trình có dạng
nên phương trình có dạng 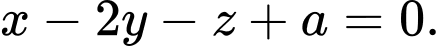
Mặt phẳng đi qua
đi qua 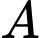 nên
nên 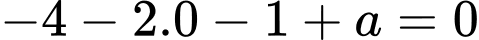
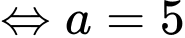
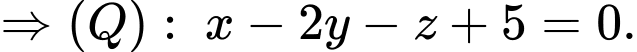 Đáp án: D
Đáp án: D
Mặt phẳng
 song song với mặt phẳng
song song với mặt phẳng 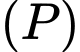 nên phương trình có dạng
nên phương trình có dạng 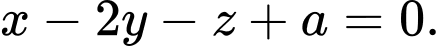
Mặt phẳng
 đi qua
đi qua 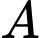 nên
nên 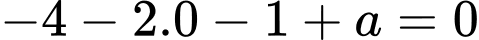
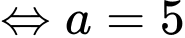
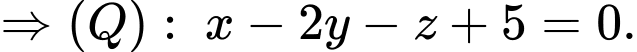 Đáp án: D
Đáp án: D
Câu 10 [699662]: Khoảng cách giữa hai mặt phẳng 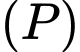 và
và  bằng
bằng
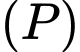 và
và  bằng
bằng A, 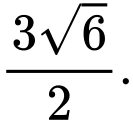
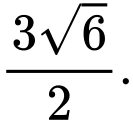
B, 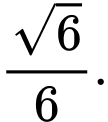
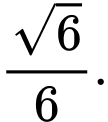
C, 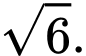
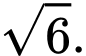
D, 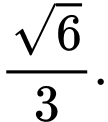
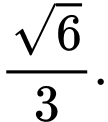
Chọn đáp án B.
Khoảng cách giữa hai mặt phẳng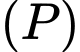 và
và  là
là
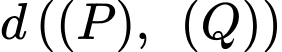
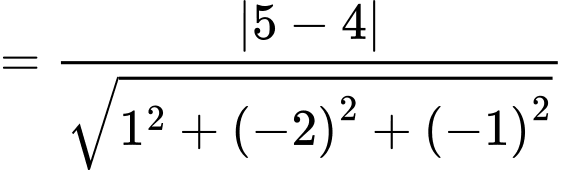
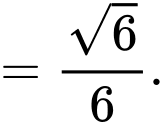 Đáp án: B
Đáp án: B
Khoảng cách giữa hai mặt phẳng
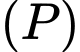 và
và  là
là 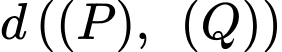
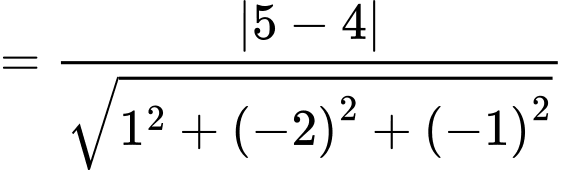
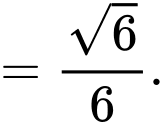 Đáp án: B
Đáp án: B
Câu 11 [547614]: Thời gian chạy cự li 100m (đơn vị: giây) của 40 học sinh được cho bởi mẫu số liệu ghép nhóm sau:

Nhóm chứa trung vị của mẫu số liệu trên là

Nhóm chứa trung vị của mẫu số liệu trên là
A, [24;28).
B, [20;24).
C, [12;16).
D, [16;20).
Chọn đáp án D.
Nhóm chứa trung vị của mẫu số liệu trên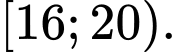 Đáp án: D
Đáp án: D
Nhóm chứa trung vị của mẫu số liệu trên
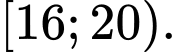 Đáp án: D
Đáp án: D
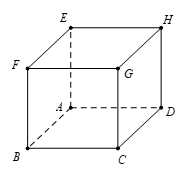
Câu 12 [597378]: Cho hình hộp 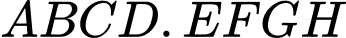 . Gọi
. Gọi  là trung điểm
là trung điểm  . Khẳng định nào sau đây là khẳng định đúng?
. Khẳng định nào sau đây là khẳng định đúng?
 . Gọi
. Gọi  là trung điểm
là trung điểm  . Khẳng định nào sau đây là khẳng định đúng?
. Khẳng định nào sau đây là khẳng định đúng?
A, 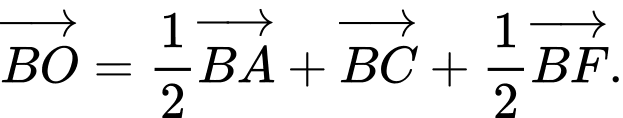
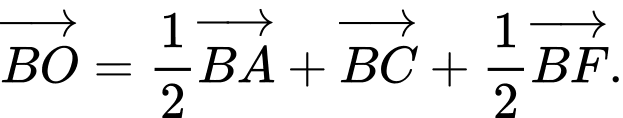
B, 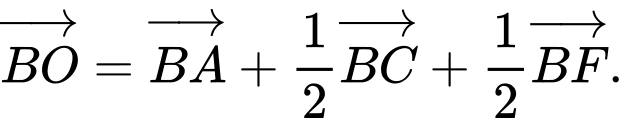
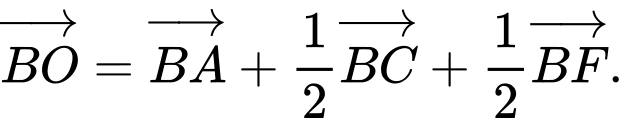
C, 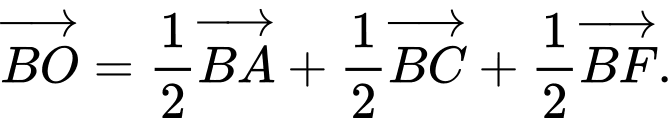
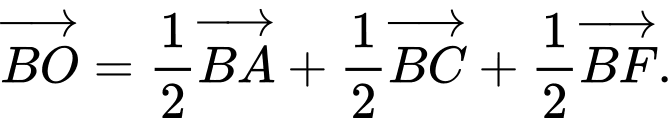
D, 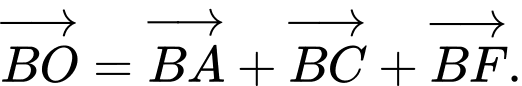
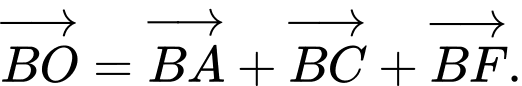
Chọn đáp án A.
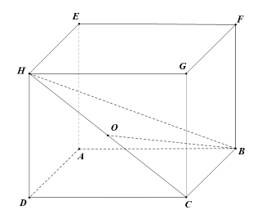
Ta có
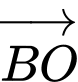
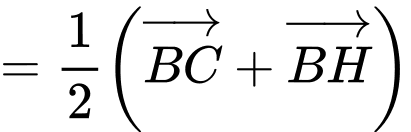
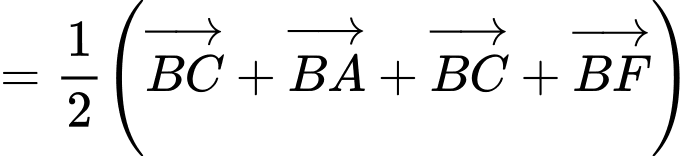
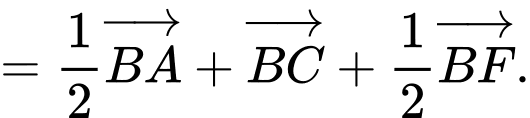 Đáp án: A
Đáp án: A

Ta có
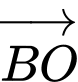
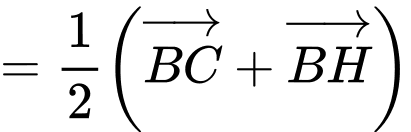
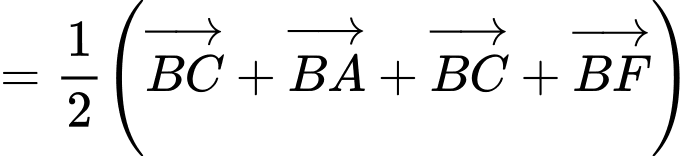
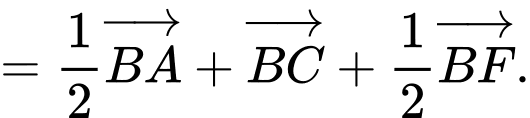 Đáp án: A
Đáp án: A PHẦN II. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Câu 13 [693317]: Trong không gian với hệ tọa độ 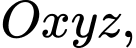 cho hai điểm
cho hai điểm 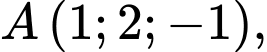
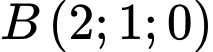 và mặt phẳng
và mặt phẳng 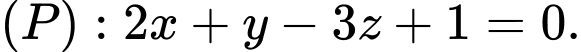 Gọi
Gọi  là mặt phẳng chứa
là mặt phẳng chứa 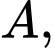
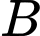 và vuông góc với
và vuông góc với 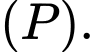
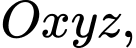 cho hai điểm
cho hai điểm 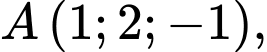
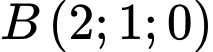 và mặt phẳng
và mặt phẳng 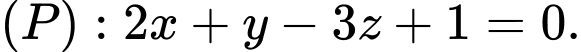 Gọi
Gọi  là mặt phẳng chứa
là mặt phẳng chứa 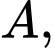
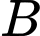 và vuông góc với
và vuông góc với 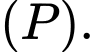
a) Đúng.
Mặt phẳng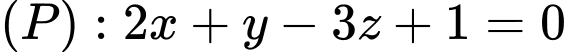 có một vectơ pháp tuyến là
có một vectơ pháp tuyến là 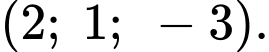
b) Sai.
Ta có: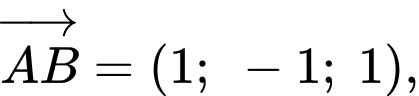
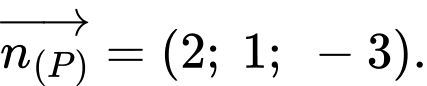
Mặt phẳng chứa
chứa 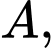
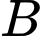 Q vuông góc với
Q vuông góc với 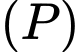 nên
nên 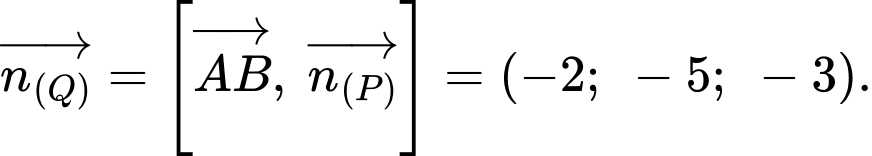
c) Đúng.
Phương trình mặt phẳng đi qua
đi qua 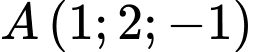 và có vectơ pháp tuyến
và có vectơ pháp tuyến 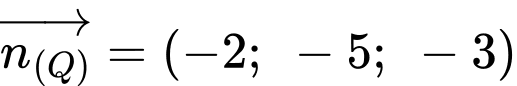 là:
là:  hay
hay 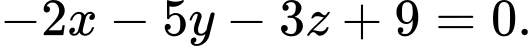
Vậy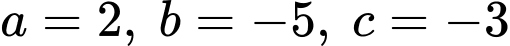

d) Sai.
Khoảng cách từ đến
đến  bằng:
bằng:
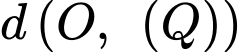
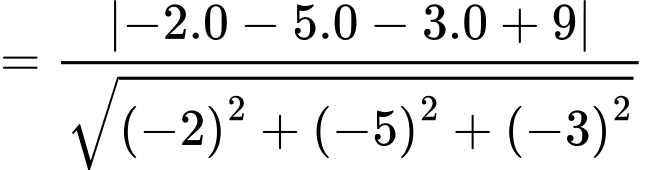
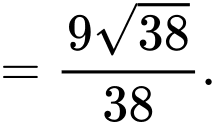
Mặt phẳng
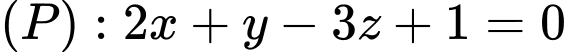 có một vectơ pháp tuyến là
có một vectơ pháp tuyến là 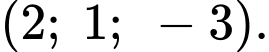
b) Sai.
Ta có:
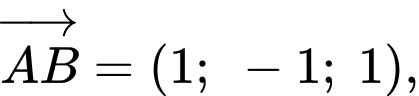
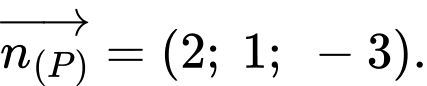
Mặt phẳng
 chứa
chứa 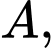
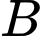 Q vuông góc với
Q vuông góc với 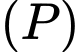 nên
nên 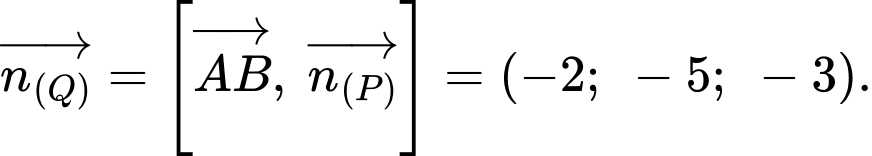
c) Đúng.
Phương trình mặt phẳng
 đi qua
đi qua 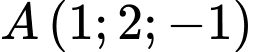 và có vectơ pháp tuyến
và có vectơ pháp tuyến 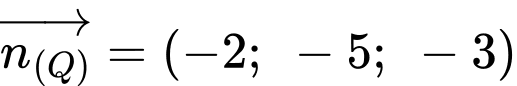 là:
là:  hay
hay 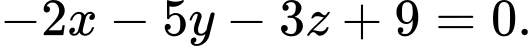
Vậy
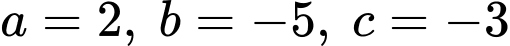

d) Sai.
Khoảng cách từ
 đến
đến  bằng:
bằng: 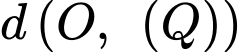
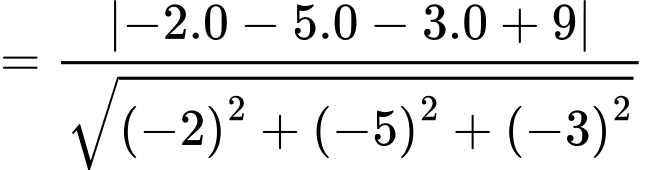
Câu 14 [702939]: Trong một số trường hợp, tin đồn lan truyền và được mô hình hoá bằng hàm số: 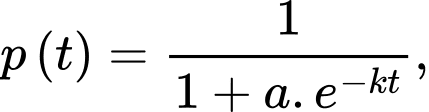 trong đó
trong đó 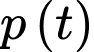 là tỉ lệ dân số biết tin đồn tại thời điểm t (giờ) và a và k là hằng số dương.
là tỉ lệ dân số biết tin đồn tại thời điểm t (giờ) và a và k là hằng số dương.
Giả sử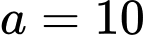 và
và 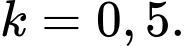 Khi đó:
Khi đó:
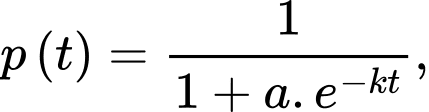 trong đó
trong đó 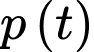 là tỉ lệ dân số biết tin đồn tại thời điểm t (giờ) và a và k là hằng số dương.
là tỉ lệ dân số biết tin đồn tại thời điểm t (giờ) và a và k là hằng số dương.Giả sử
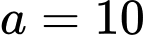 và
và 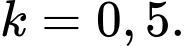 Khi đó:
Khi đó:
a) Đúng.
Ta có: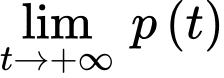
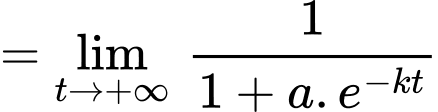
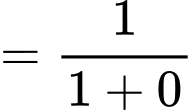
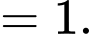
b) Sai.
Tốc độ lan truyền tin đồn là:
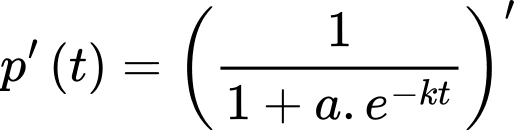
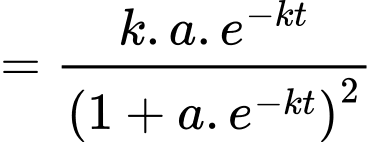
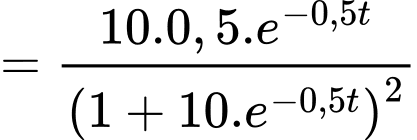
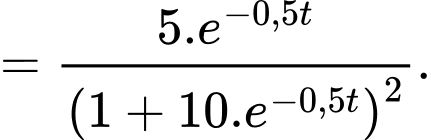
c) Sai.
Đặt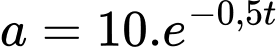 khi đó:
khi đó:
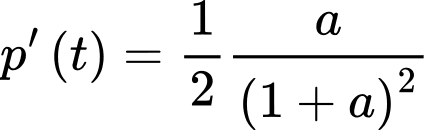
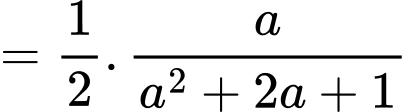
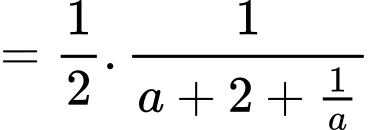
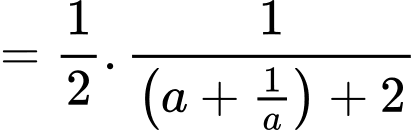
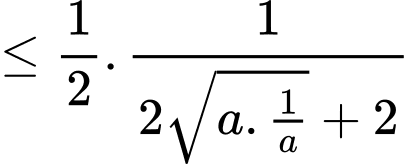 (BĐT Cô-si)
(BĐT Cô-si) 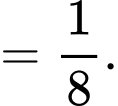
Dấu bằng xảy ra khi: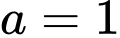
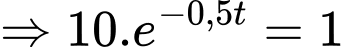
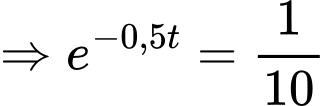
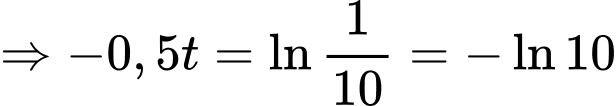
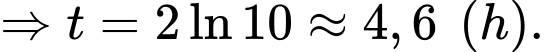
d) Đúng.
Tại thời điểm tin đồn lan truyền với tốc độ lớn nhất thì tỉ lệ dân số biết tin đồn là
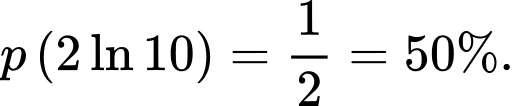
Ta có:
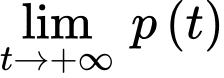
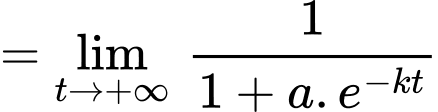
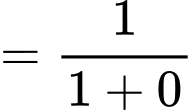
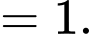
b) Sai.
Tốc độ lan truyền tin đồn là:
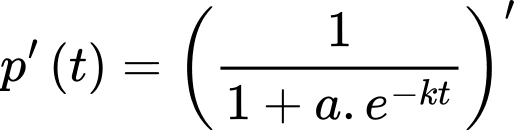
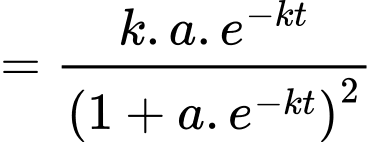
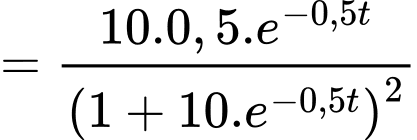
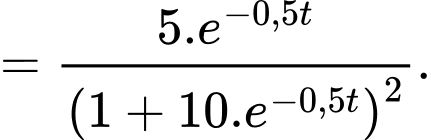
c) Sai.
Đặt
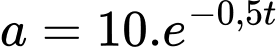 khi đó:
khi đó: 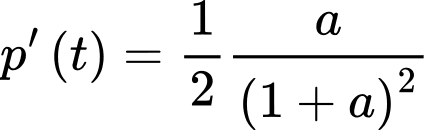
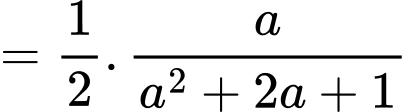
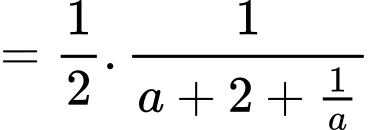
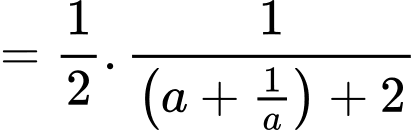
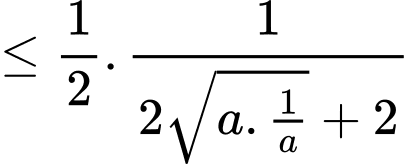 (BĐT Cô-si)
(BĐT Cô-si) 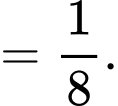
Dấu bằng xảy ra khi:
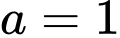
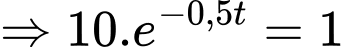
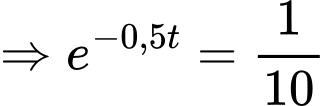
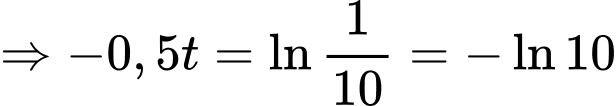
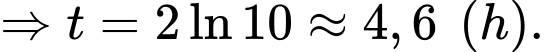
d) Đúng.
Tại thời điểm tin đồn lan truyền với tốc độ lớn nhất thì tỉ lệ dân số biết tin đồn là
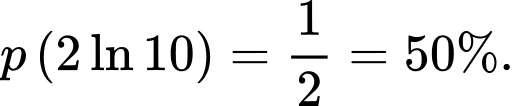
Câu 15 [693319]: Trong một kì thi tốt nghiệp trung học phổ thông, một tỉnh X có 70% học sinh lựa chọn tổ hợp A00 (gồm các môn Toán, Vật lí, Hóa học). Biết rằng, nếu một học sinh chọn tổ hợp A00 thì xác suất để học sinh đó đỗ đại học là 0,55; còn nếu học sinh không chọn tổ hợp A00 thì xác suất để học sinh đó đỗ đại học là 0,6. Chọn ngẫu nhiên một học sinh của tỉnh X đã tốt nghiệp trung học phổ thông trong kì thi trên.
Gọi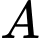 là biến cố: “Chọn được học sinh lựa chọn khối A00”
là biến cố: “Chọn được học sinh lựa chọn khối A00”
Gọi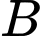 là biến cố: : “Chọn được học sinh đỗ đại học”
là biến cố: : “Chọn được học sinh đỗ đại học”
Gọi
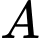 là biến cố: “Chọn được học sinh lựa chọn khối A00”
là biến cố: “Chọn được học sinh lựa chọn khối A00”Gọi
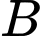 là biến cố: : “Chọn được học sinh đỗ đại học”
là biến cố: : “Chọn được học sinh đỗ đại học”
a) Đúng.
Xét các biến cố:
 : “Chọn được học sinh không lựa chọn khối A00”.
: “Chọn được học sinh không lựa chọn khối A00”.
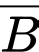 : “Chọn được học sinh không đỗ đại học”.
: “Chọn được học sinh không đỗ đại học”.
Có 70% học sinh lựa chọn tổ hợp A00

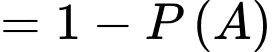
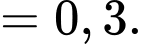
b) Sai.
Nếu một học sinh chọn tổ hợp A00 thì xác suất để học sinh đó đỗ đại học là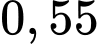
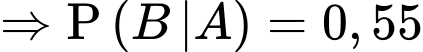 .
.
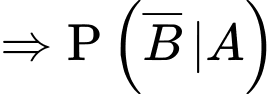
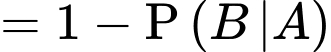
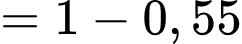
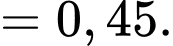
Nếu học sinh không chọn tổ hợp A00 thì xác suất để học sinh đó đỗ đại học là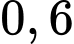
 .
.

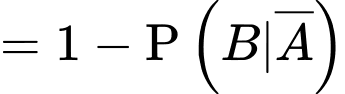

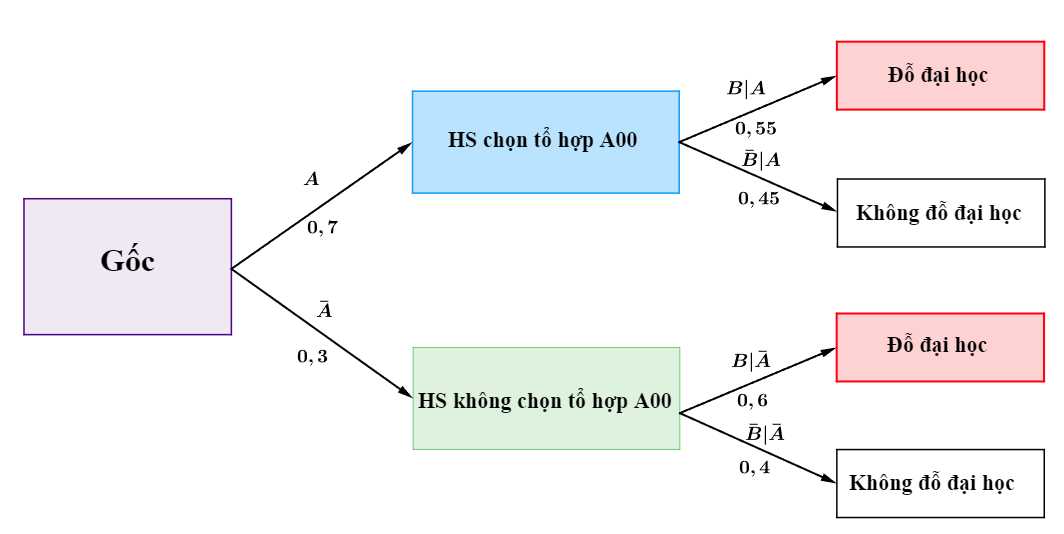
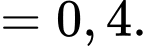 Từ đó, ta có sơ đồ cây sau:
Từ đó, ta có sơ đồ cây sau:
c) Sai.
Xác suất để học sinh đó chọn tổ hợp A00, biết học sinh không đỗ đại học là

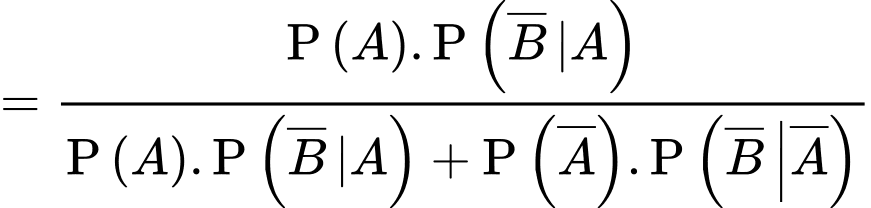
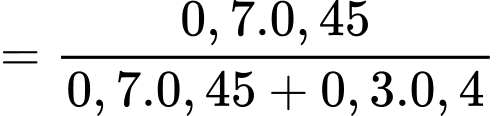
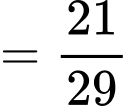 .
.
d) Sai.
Xác suất để học sinh đó không chọn tổ hợp A00, biết học sinh không đỗ đại học là
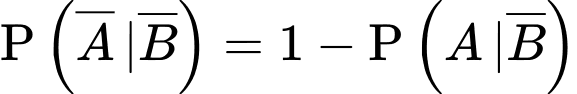
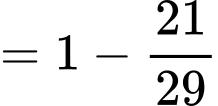
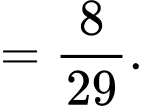
Xét các biến cố:
 : “Chọn được học sinh không lựa chọn khối A00”.
: “Chọn được học sinh không lựa chọn khối A00”.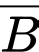 : “Chọn được học sinh không đỗ đại học”.
: “Chọn được học sinh không đỗ đại học”.Có 70% học sinh lựa chọn tổ hợp A00


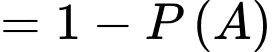
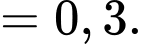
b) Sai.
Nếu một học sinh chọn tổ hợp A00 thì xác suất để học sinh đó đỗ đại học là
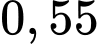
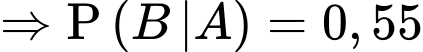 .
.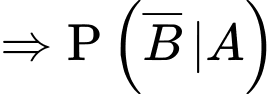
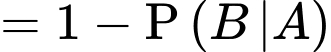
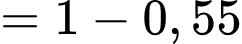
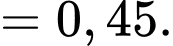
Nếu học sinh không chọn tổ hợp A00 thì xác suất để học sinh đó đỗ đại học là
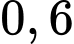
 .
.
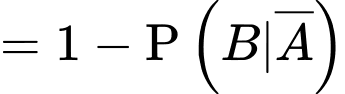

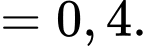 Từ đó, ta có sơ đồ cây sau:
Từ đó, ta có sơ đồ cây sau:
c) Sai.
Xác suất để học sinh đó chọn tổ hợp A00, biết học sinh không đỗ đại học là

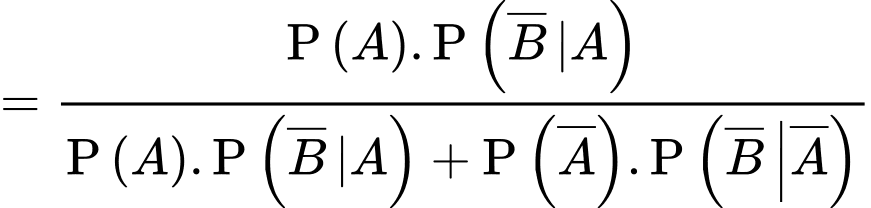
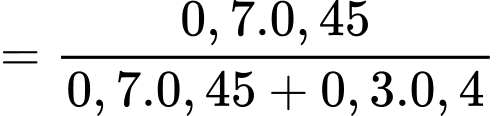
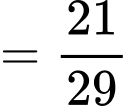 .
.d) Sai.
Xác suất để học sinh đó không chọn tổ hợp A00, biết học sinh không đỗ đại học là
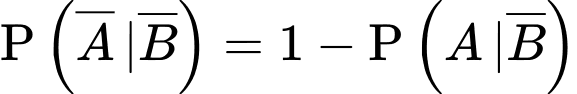
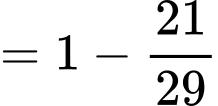
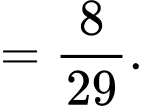
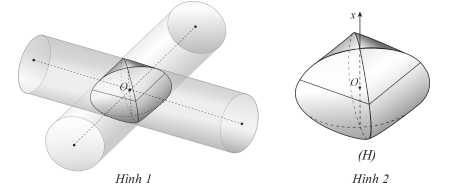
Câu 16 [693320]: Cho hai hình trụ có cùng bán kính bằng 3 được đặt lồng vào nhau sao cho trục của hai hình trụ vuông góc với nhau và cắt nhau tại  (hình 1). Gọi
(hình 1). Gọi  là phần giao nhau của hai hình trụ (hình 2). Chọn trục
là phần giao nhau của hai hình trụ (hình 2). Chọn trục 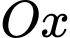 vuông góc với hai trục của hình trụ như hình vẽ. Cắt khối
vuông góc với hai trục của hình trụ như hình vẽ. Cắt khối  bởi mặt phẳng vuông góc với trục
bởi mặt phẳng vuông góc với trục 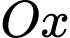 tại điểm có hoành độ
tại điểm có hoành độ 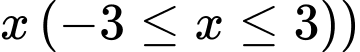 ta được thiết diện có diện tích là
ta được thiết diện có diện tích là 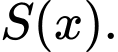
 (hình 1). Gọi
(hình 1). Gọi  là phần giao nhau của hai hình trụ (hình 2). Chọn trục
là phần giao nhau của hai hình trụ (hình 2). Chọn trục 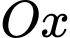 vuông góc với hai trục của hình trụ như hình vẽ. Cắt khối
vuông góc với hai trục của hình trụ như hình vẽ. Cắt khối  bởi mặt phẳng vuông góc với trục
bởi mặt phẳng vuông góc với trục 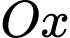 tại điểm có hoành độ
tại điểm có hoành độ 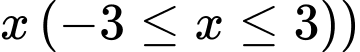 ta được thiết diện có diện tích là
ta được thiết diện có diện tích là 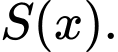

a) Sai.
Hình khối không là một khối tròn xoay.
không là một khối tròn xoay.
b) Sai.
Công thức tính thể tích khối là
là 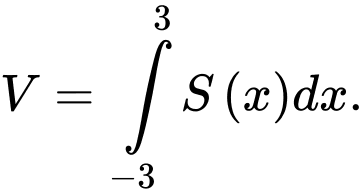
c) Sai.
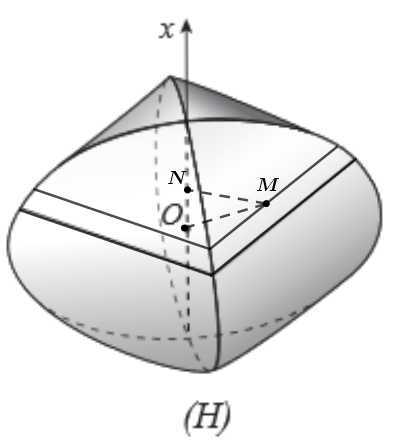
Ta có: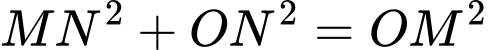
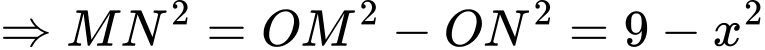
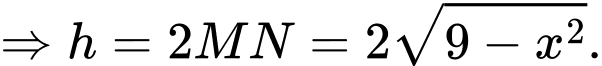
Khi đó: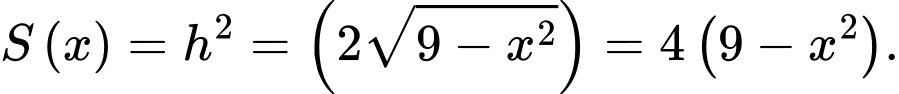
d) Đúng.
Thể tích khối là:
là:
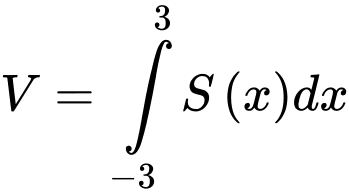
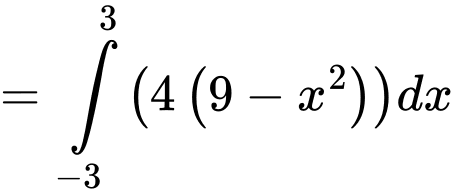
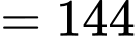 (đvtt).
(đvtt).
Hình khối
 không là một khối tròn xoay.
không là một khối tròn xoay.b) Sai.
Công thức tính thể tích khối
 là
là 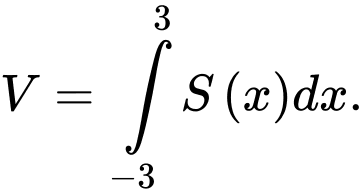
c) Sai.

Ta có:
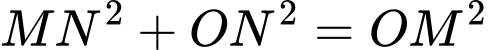
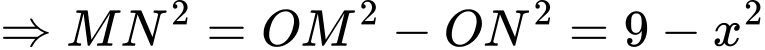
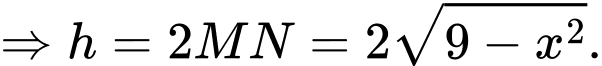
Khi đó:
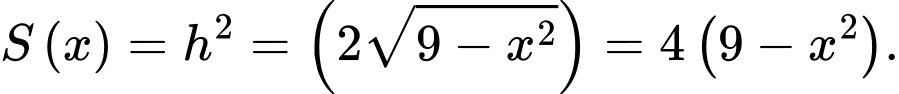
d) Đúng.
Thể tích khối
 là:
là: 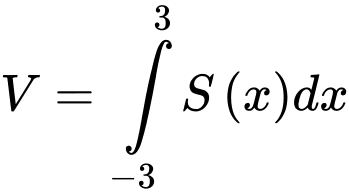
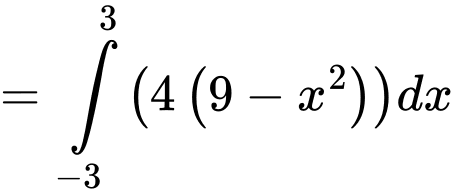
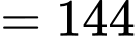 (đvtt).
(đvtt). PHẦN III. Thí sinh trả lời từ câu 1 đến câu 6.
Câu 17 [699671]: Cho chóp 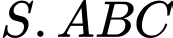 có đáy
có đáy 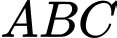 là tam giác vuông cân tại
là tam giác vuông cân tại 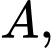 tam giác
tam giác 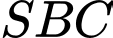 là tam giác đều cạnh
là tam giác đều cạnh 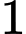 và thuộc mặt phẳng vuông góc với đáy. Tính khoảng cách giữa 2 đường thẳng
và thuộc mặt phẳng vuông góc với đáy. Tính khoảng cách giữa 2 đường thẳng 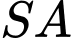 và
và 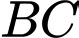 (làm tròn kết quả đến hàng phần trăm).
(làm tròn kết quả đến hàng phần trăm).
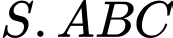 có đáy
có đáy 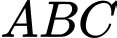 là tam giác vuông cân tại
là tam giác vuông cân tại 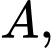 tam giác
tam giác 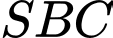 là tam giác đều cạnh
là tam giác đều cạnh 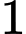 và thuộc mặt phẳng vuông góc với đáy. Tính khoảng cách giữa 2 đường thẳng
và thuộc mặt phẳng vuông góc với đáy. Tính khoảng cách giữa 2 đường thẳng 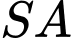 và
và 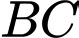 (làm tròn kết quả đến hàng phần trăm).
(làm tròn kết quả đến hàng phần trăm).
Điền đáp án: 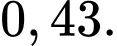
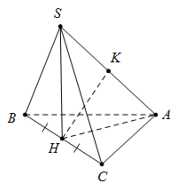
Gọi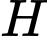 là trung điểm của
là trung điểm của 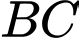 khi đó
khi đó 
Mặt khác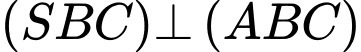 do đó
do đó 
Ta có: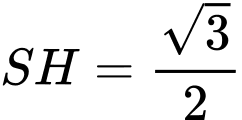 và
và 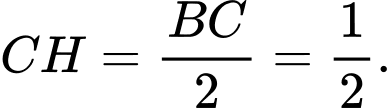 Do
Do 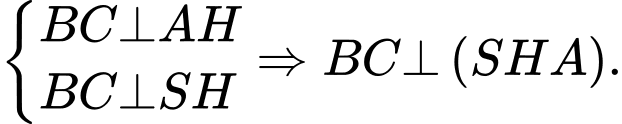
Dựng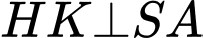 khi đó
khi đó 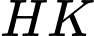 là đoạn vuông góc chung của
là đoạn vuông góc chung của 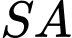 và
và 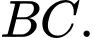
Lại có: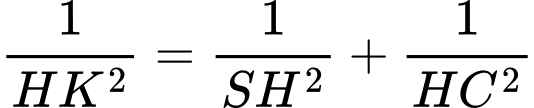
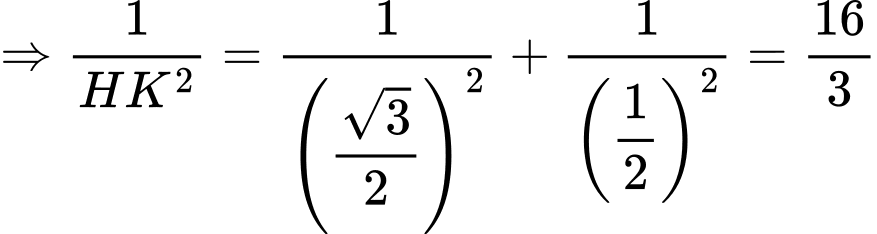
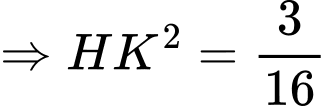
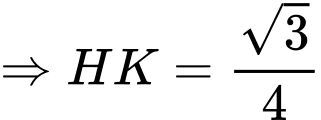
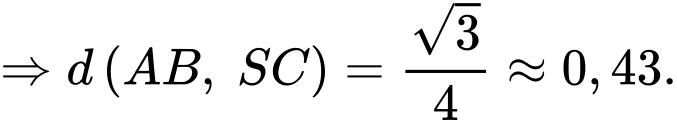
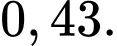

Gọi
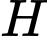 là trung điểm của
là trung điểm của 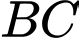 khi đó
khi đó 
Mặt khác
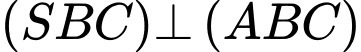 do đó
do đó 
Ta có:
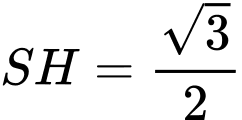 và
và 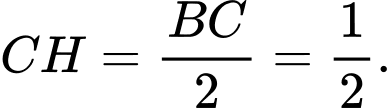 Do
Do 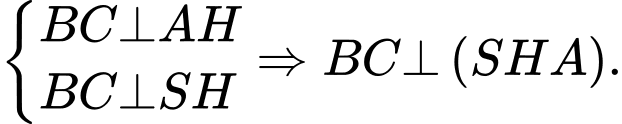
Dựng
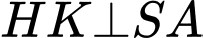 khi đó
khi đó 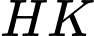 là đoạn vuông góc chung của
là đoạn vuông góc chung của 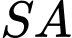 và
và 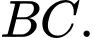
Lại có:
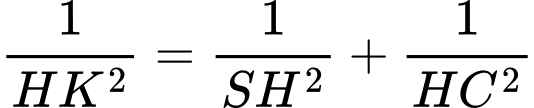
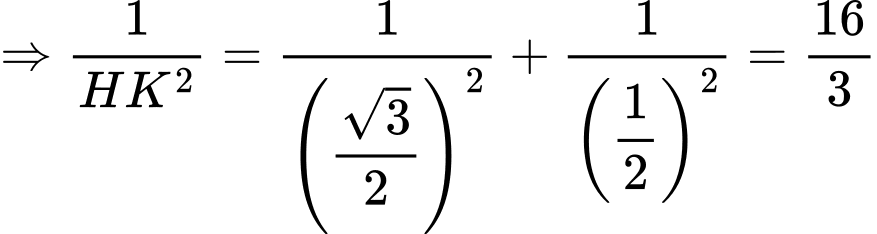
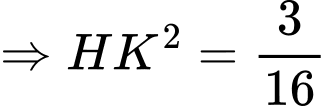
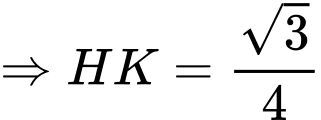
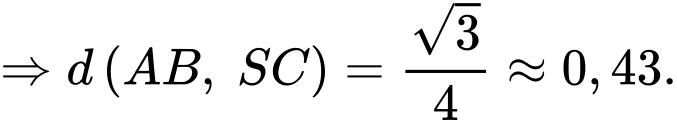
Câu 18 [695181]: Hai tên cướp bịt mặt tấn công 1 ngân hàng. Tuy nhiên, người thu ngân đã kịp thời nhấn chuông báo động và khóa cửa ra vào. Các tên cướp nhận ra rằng chúng đã mắc kẹt, vì vậy quyết định cởi mặt nạ và trà trộn vào đám đông. Đối mặt với 40 người trong ngân hàng đều tự nhận mình vô tội, cảnh sát quyết định sử dụng máy phát hiện nói dối. Giả sử xác suất 1 người phạm tội bị máy phát hiện nói dối báo động là 0,85, xác suất 1 người vô tội bị máy báo động 0,08. Tính xác suất ông Tuấn là 1 trong 2 tên cướp, biết rằng ông Tuấn bị máy phát hiện nói dối báo động. Kết quả làm tròn đến hàng phần trăm.
Điền đáp án: 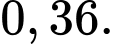
Gọi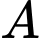 là biến cố: “Ông Tuấn là 1 trong hai tên cướp”.
là biến cố: “Ông Tuấn là 1 trong hai tên cướp”.
Gọi là biến cố: “Máy phát hiện nói dối báo động”.
Từ dữ kiện đề bài, ta có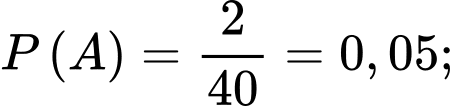
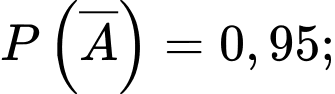
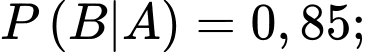
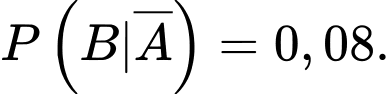
Ta có sơ đồ cây sau:
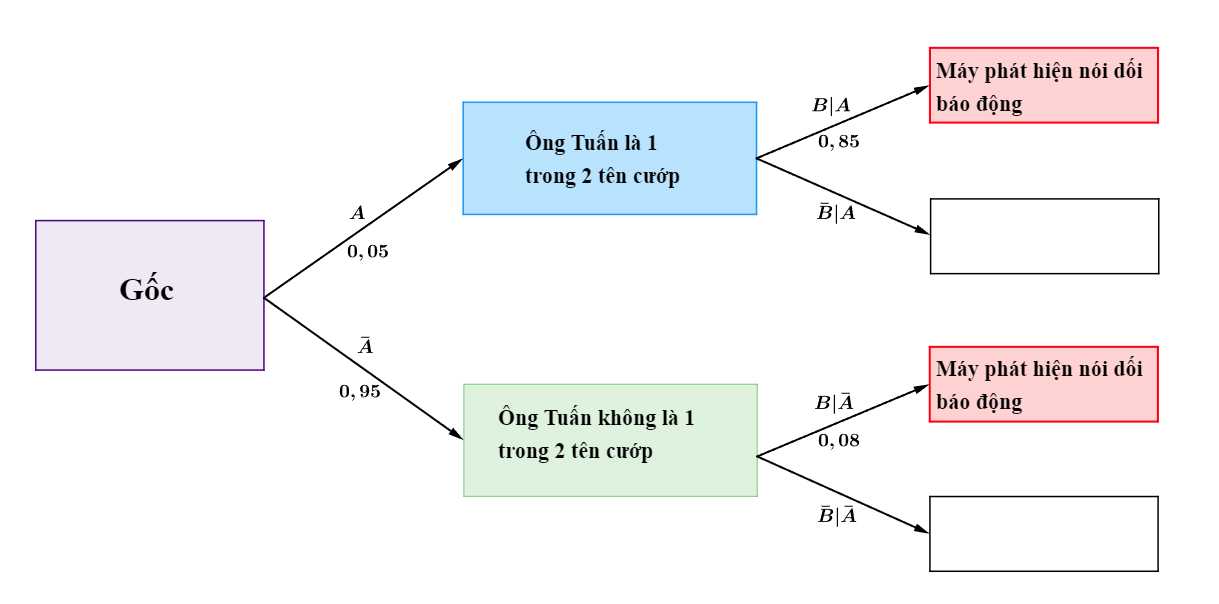
Suy ra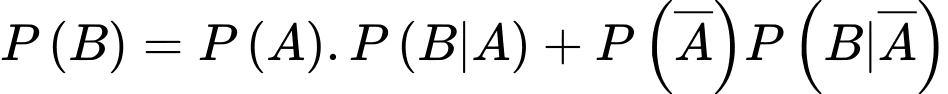
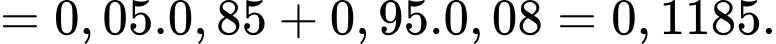
Áp dụng công thức Bayes, ta có xcas xuất ông Tuấn là 1 trong 2 tên cướp, biết rằng ông Tuấn bị máy phát hiện nói dối báo động là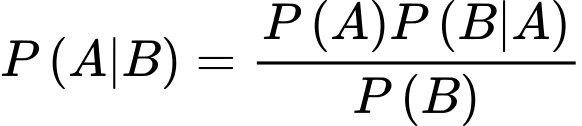
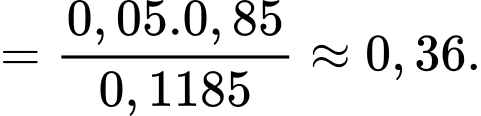
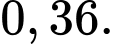
Gọi
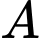 là biến cố: “Ông Tuấn là 1 trong hai tên cướp”.
là biến cố: “Ông Tuấn là 1 trong hai tên cướp”.
Gọi là biến cố: “Máy phát hiện nói dối báo động”.
Từ dữ kiện đề bài, ta có
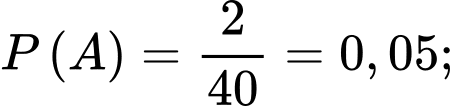
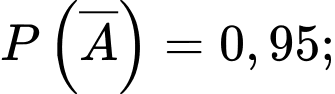
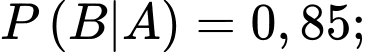
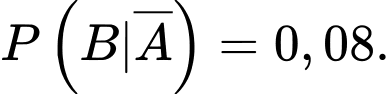
Ta có sơ đồ cây sau:

Suy ra
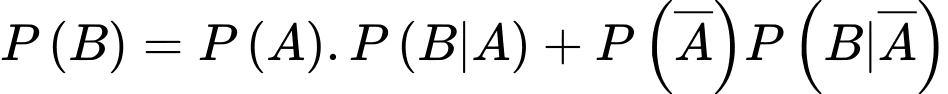
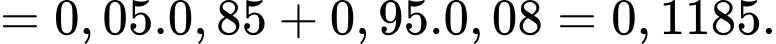
Áp dụng công thức Bayes, ta có xcas xuất ông Tuấn là 1 trong 2 tên cướp, biết rằng ông Tuấn bị máy phát hiện nói dối báo động là
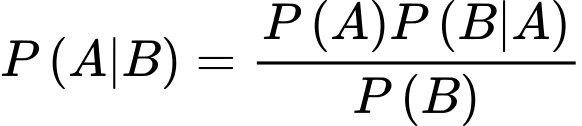
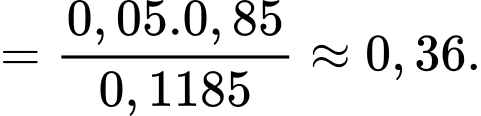
Câu 19 [546932]: Một vật trang trí có dạng một khối tròn xoay được tạo thành khi quay miền  (phần được tô màu trong hình vẽ bên) quanh trục
(phần được tô màu trong hình vẽ bên) quanh trục 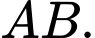 Miền
Miền  được giới hạn bởi các cạnh
được giới hạn bởi các cạnh 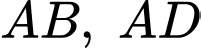 của hình vuông
của hình vuông 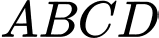 và các cung phần tư của các đường tròn bán kính bằng
và các cung phần tư của các đường tròn bán kính bằng 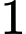 cm với tâm lần lượt là trung điểm của các cạnh
cm với tâm lần lượt là trung điểm của các cạnh 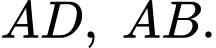 Tính thể tích của vật trang trí đó, làm tròn kết quả đến hàng phần mười của centimét khối.
Tính thể tích của vật trang trí đó, làm tròn kết quả đến hàng phần mười của centimét khối.

 (phần được tô màu trong hình vẽ bên) quanh trục
(phần được tô màu trong hình vẽ bên) quanh trục 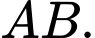 Miền
Miền  được giới hạn bởi các cạnh
được giới hạn bởi các cạnh 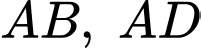 của hình vuông
của hình vuông 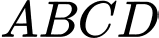 và các cung phần tư của các đường tròn bán kính bằng
và các cung phần tư của các đường tròn bán kính bằng 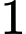 cm với tâm lần lượt là trung điểm của các cạnh
cm với tâm lần lượt là trung điểm của các cạnh 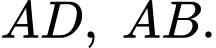 Tính thể tích của vật trang trí đó, làm tròn kết quả đến hàng phần mười của centimét khối.
Tính thể tích của vật trang trí đó, làm tròn kết quả đến hàng phần mười của centimét khối.
Điền đáp án: 
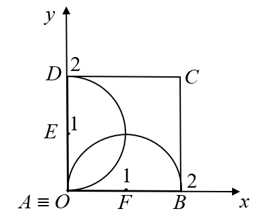
Chọn trục chứa điểm
chứa điểm  trục
trục 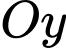 chứa điểm
chứa điểm 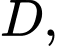 và gốc tọa độ
và gốc tọa độ  trùng điểm
trùng điểm 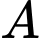 (như hình vẽ).
(như hình vẽ).
Gọi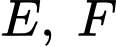 lần lượt là trung điểm của
lần lượt là trung điểm của 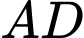 ,
,  . Khi đó
. Khi đó 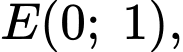
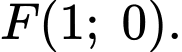
*Phương trình đường tròn có tâm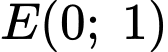 và đường kính
và đường kính 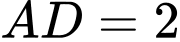 là:
là: 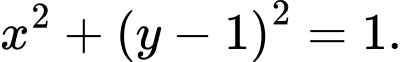
Suy ra phương trình cung trên của đường tròn tâm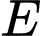 là:
là: 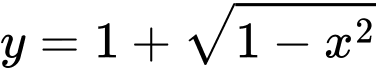
*Phương trình đường tròn có tâm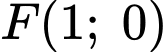 và đường kính
và đường kính 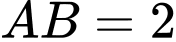 là:
là: 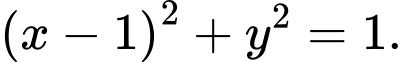
Suy ra phương trình cung trên của đường tròn tâm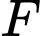 là:
là: 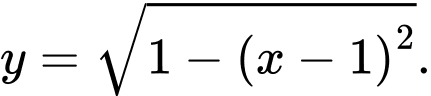
Vậy, thể tích vật trang trí là:
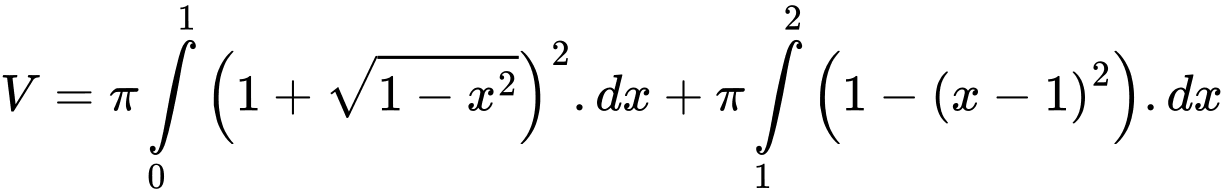
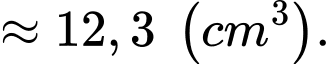
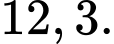

Chọn trục
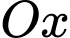 chứa điểm
chứa điểm 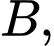 trục
trục 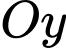 chứa điểm
chứa điểm 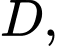 và gốc tọa độ
và gốc tọa độ  trùng điểm
trùng điểm 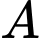 (như hình vẽ).
(như hình vẽ).
Gọi
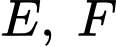 lần lượt là trung điểm của
lần lượt là trung điểm của 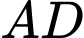 ,
,  . Khi đó
. Khi đó 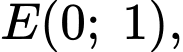
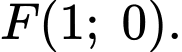
*Phương trình đường tròn có tâm
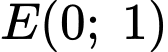 và đường kính
và đường kính 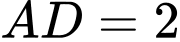 là:
là: 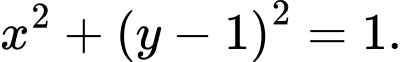
Suy ra phương trình cung trên của đường tròn tâm
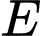 là:
là: 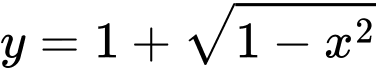
*Phương trình đường tròn có tâm
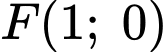 và đường kính
và đường kính 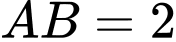 là:
là: 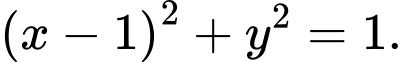
Suy ra phương trình cung trên của đường tròn tâm
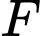 là:
là: 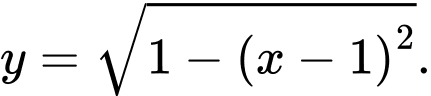
Vậy, thể tích vật trang trí là:
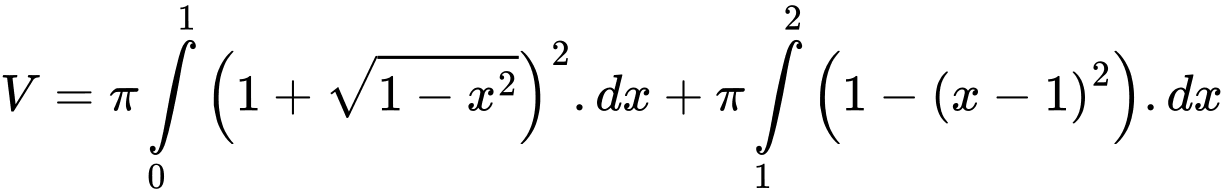
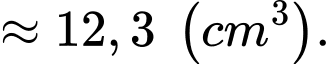
Câu 20 [693324]: Trong một phần mềm 3D mô phỏng một trò chơi điện tử, có hai chất điểm 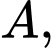
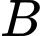 luôn chuyển động trên một mặt cầu
luôn chuyển động trên một mặt cầu 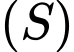 và cách nhau một khoảng không đổi bằng
và cách nhau một khoảng không đổi bằng 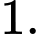 Nếu đặt trong không gian toạ độ
Nếu đặt trong không gian toạ độ 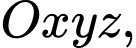 mặt cầu
mặt cầu 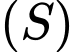 có phương trình là
có phương trình là 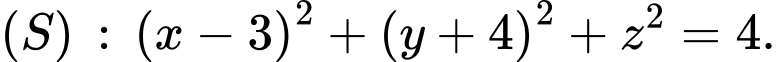 Tìm giá trị nhỏ nhất của biểu thức
Tìm giá trị nhỏ nhất của biểu thức  ?
?
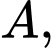
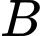 luôn chuyển động trên một mặt cầu
luôn chuyển động trên một mặt cầu 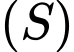 và cách nhau một khoảng không đổi bằng
và cách nhau một khoảng không đổi bằng 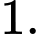 Nếu đặt trong không gian toạ độ
Nếu đặt trong không gian toạ độ 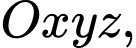 mặt cầu
mặt cầu 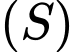 có phương trình là
có phương trình là 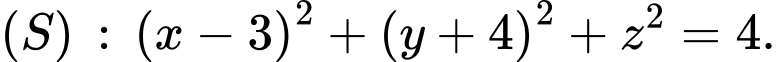 Tìm giá trị nhỏ nhất của biểu thức
Tìm giá trị nhỏ nhất của biểu thức  ?
?
Điền đáp án: 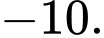
Mặt cầu có tâm
có tâm 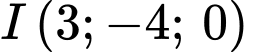 và bán kính
và bán kính 
Ta có: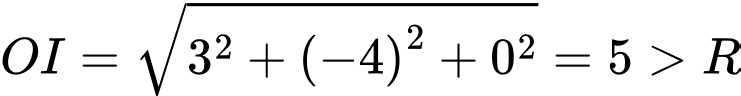 , Suy ra
, Suy ra  nằm ngoài mặt cầu
nằm ngoài mặt cầu 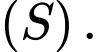
Ta có:
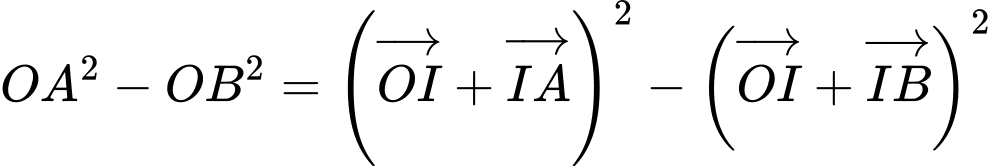
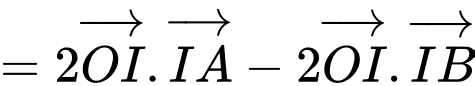
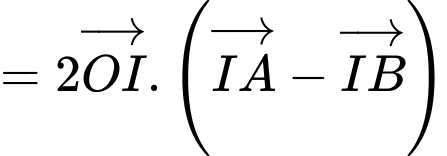
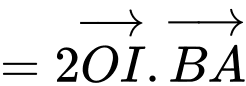
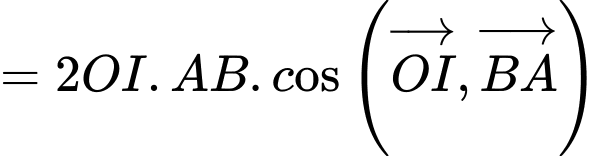
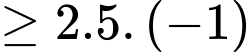
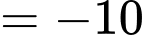
Vậy đạt giá trị nhỏ nhất là
đạt giá trị nhỏ nhất là 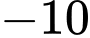 khi và chỉ khi
khi và chỉ khi 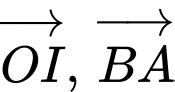 ngược hướng.
ngược hướng.
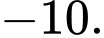
Mặt cầu
 có tâm
có tâm 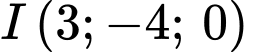 và bán kính
và bán kính 
Ta có:
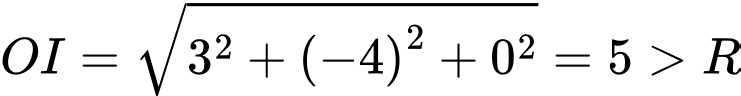 , Suy ra
, Suy ra  nằm ngoài mặt cầu
nằm ngoài mặt cầu 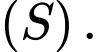
Ta có:
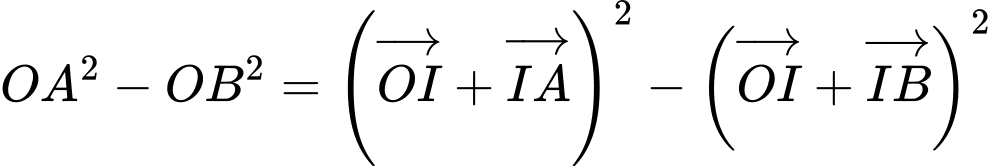
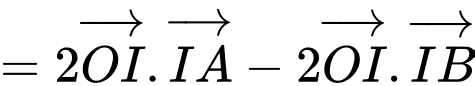
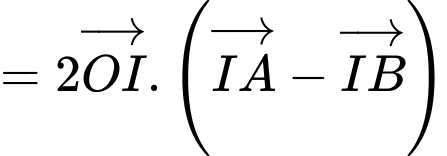
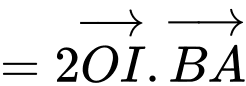
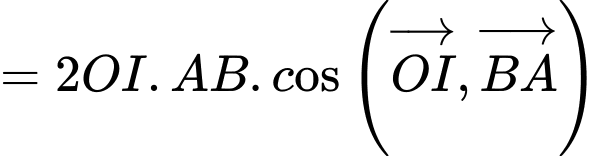
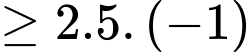
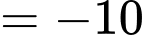
Vậy
 đạt giá trị nhỏ nhất là
đạt giá trị nhỏ nhất là 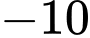 khi và chỉ khi
khi và chỉ khi 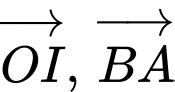 ngược hướng.
ngược hướng.
Câu 21 [703160]: Đường đi của một khinh khí cầu được gắn trong hệ trục tọa độ là một phần của đường cong bậc hai trên bậc nhất có đồ thị cắt trục hoành tại hai điểm có tọa độ là 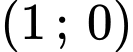 và
và 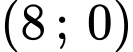 với đơn vị trên hệ trục tọa độ là
với đơn vị trên hệ trục tọa độ là 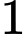 km.
km.
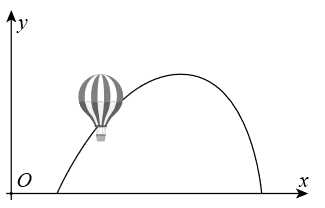
Biết rằng điểm cực đại của đồ thị hàm số là điểm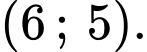 Hỏi khi khí cầu đi qua điểm cực đại và cách mặt đất
Hỏi khi khí cầu đi qua điểm cực đại và cách mặt đất 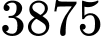 m thì khí cầu cách gốc tọa độ theo phương ngang bao nhiêu? (đơn vị: km).
m thì khí cầu cách gốc tọa độ theo phương ngang bao nhiêu? (đơn vị: km).
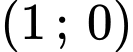 và
và 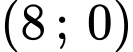 với đơn vị trên hệ trục tọa độ là
với đơn vị trên hệ trục tọa độ là 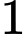 km.
km.
Biết rằng điểm cực đại của đồ thị hàm số là điểm
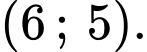 Hỏi khi khí cầu đi qua điểm cực đại và cách mặt đất
Hỏi khi khí cầu đi qua điểm cực đại và cách mặt đất 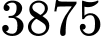 m thì khí cầu cách gốc tọa độ theo phương ngang bao nhiêu? (đơn vị: km).
m thì khí cầu cách gốc tọa độ theo phương ngang bao nhiêu? (đơn vị: km).
Điền đáp án: 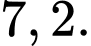
Cách 1:
Gọi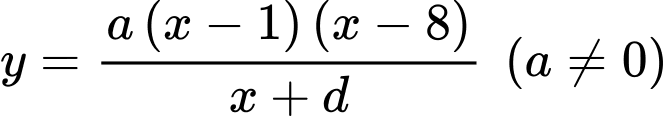 là đường đi của khinh khí cầu.
là đường đi của khinh khí cầu.
Khi đó, phương trình đường thẳng đi qua 2 điểm cực trị là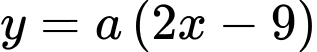 , phương trình đường thẳng này đi qua điểm
, phương trình đường thẳng này đi qua điểm 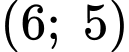 suy ra
suy ra 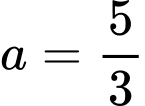
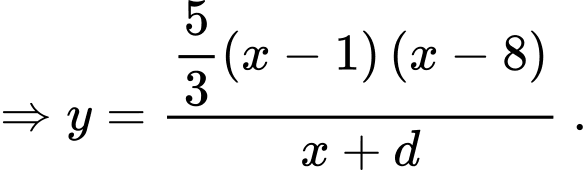
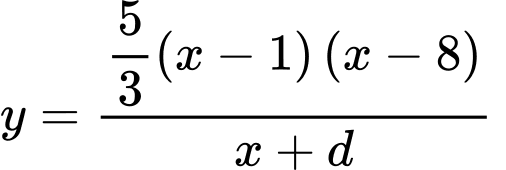 đi qua điểm
đi qua điểm 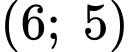 nên
nên 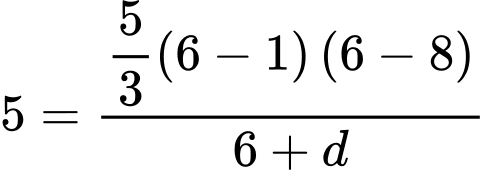
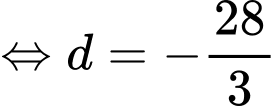
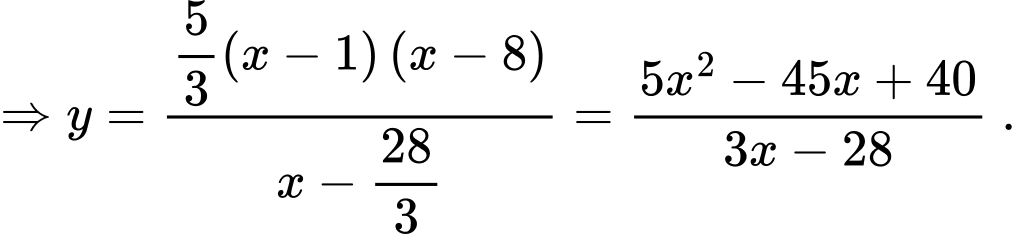
Cách 2:
Gọi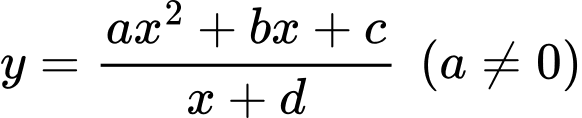 là đường đi của khinh khí cầu.
là đường đi của khinh khí cầu.
Khi đó: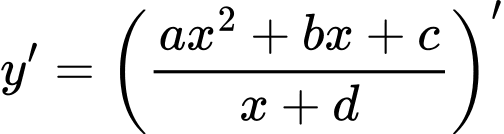
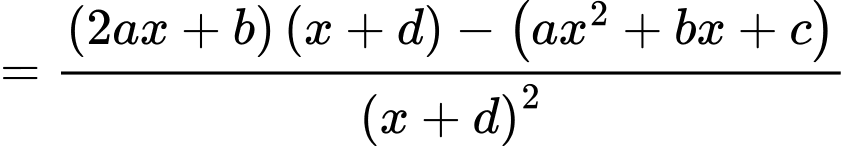
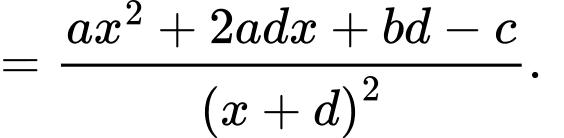
Ta có: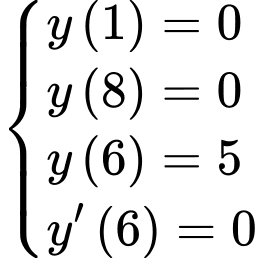
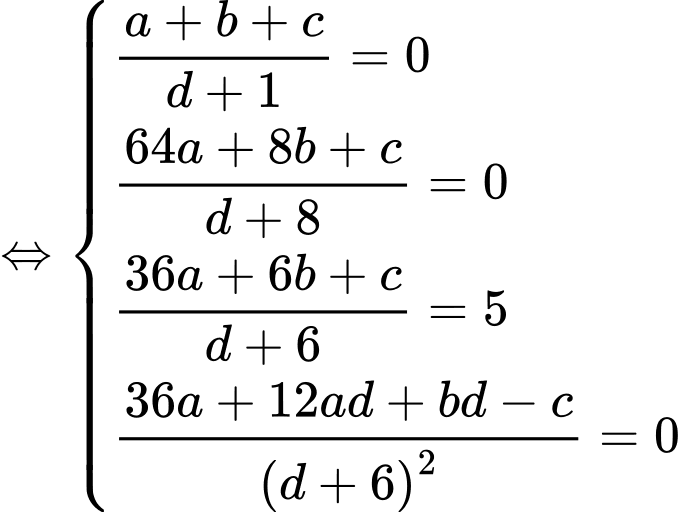
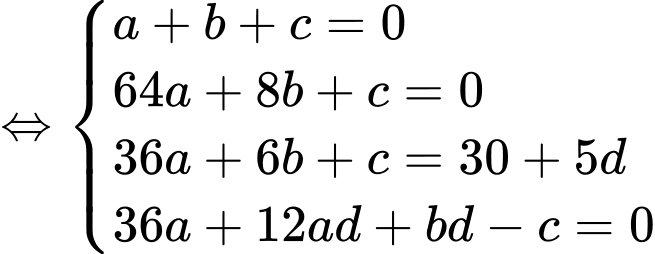
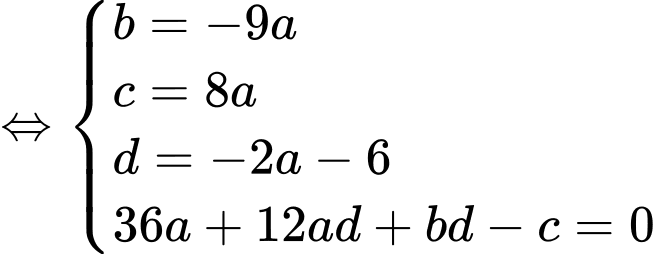
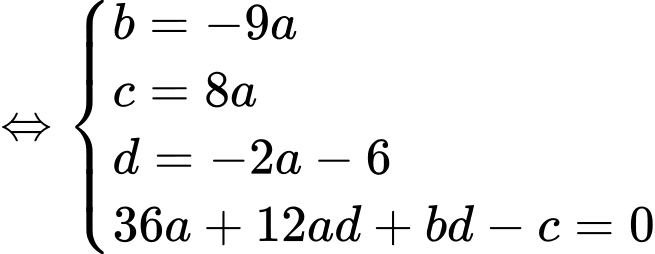
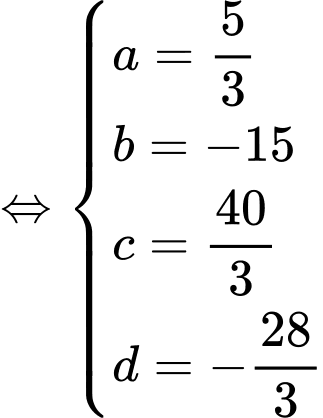
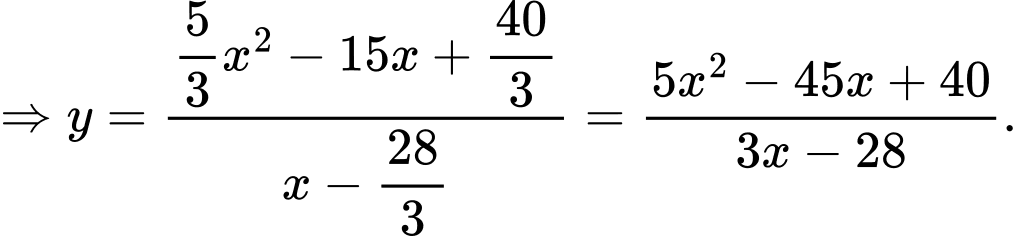
Ta có:
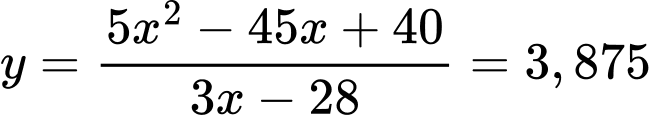
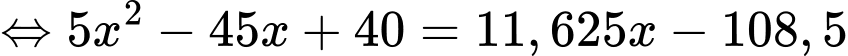
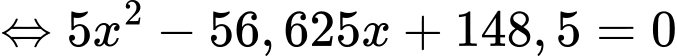
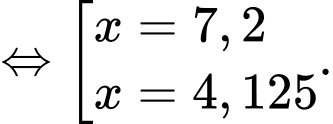
Vậy khi khí cầu đi qua điểm cực đại và cách mặt đất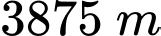 thì khí cầu cách gốc tọa độ theo phương ngang
thì khí cầu cách gốc tọa độ theo phương ngang 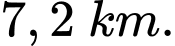
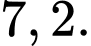
Cách 1:
Gọi
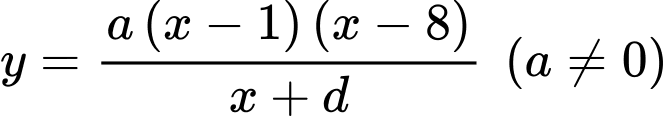 là đường đi của khinh khí cầu.
là đường đi của khinh khí cầu. Khi đó, phương trình đường thẳng đi qua 2 điểm cực trị là
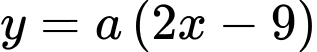 , phương trình đường thẳng này đi qua điểm
, phương trình đường thẳng này đi qua điểm 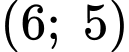 suy ra
suy ra 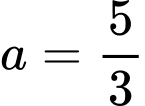
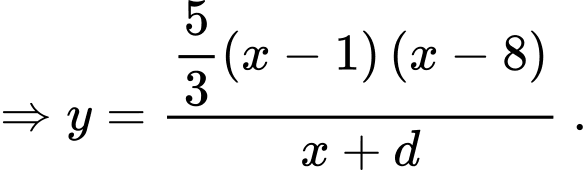
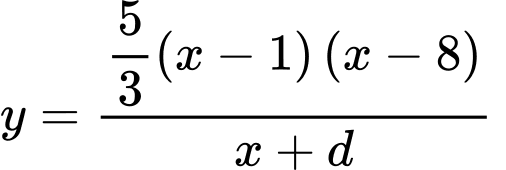 đi qua điểm
đi qua điểm 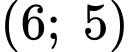 nên
nên 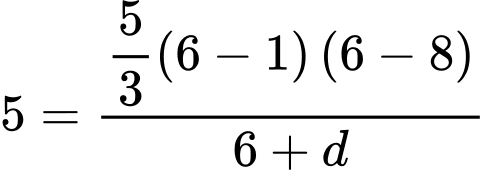
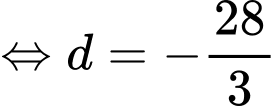
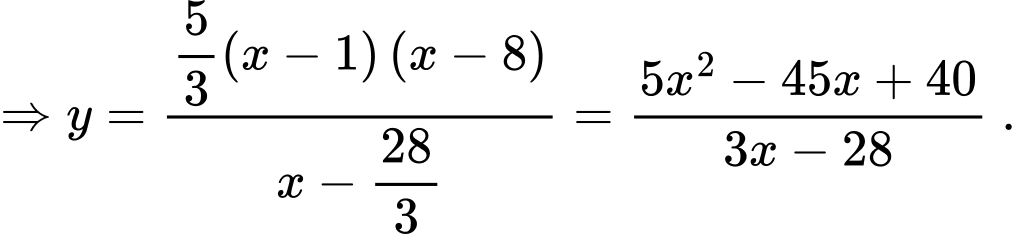
Cách 2:
Gọi
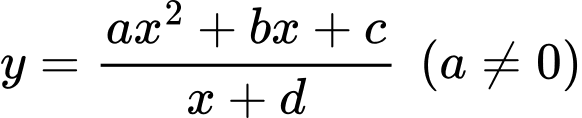 là đường đi của khinh khí cầu.
là đường đi của khinh khí cầu. Khi đó:
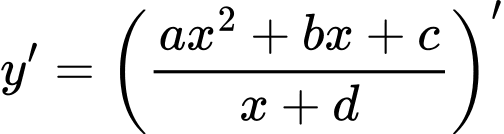
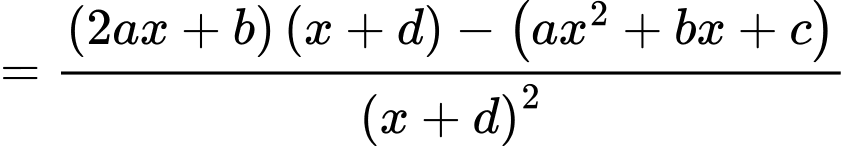
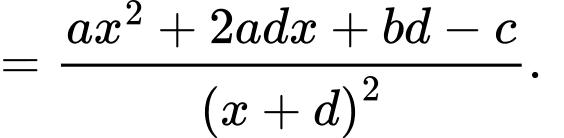
Ta có:
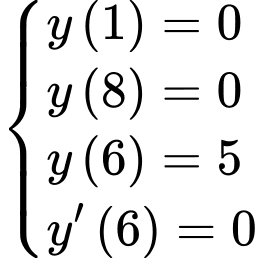
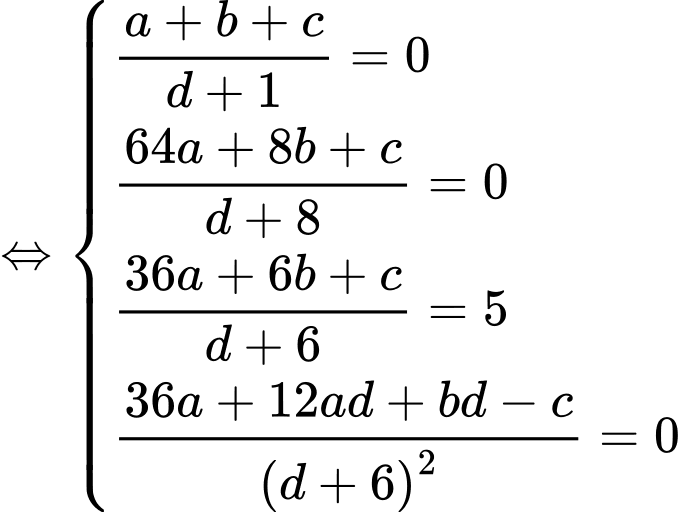
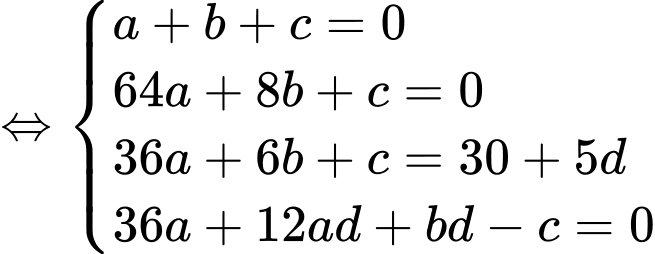
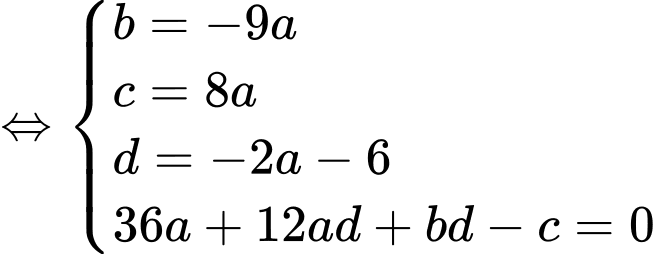
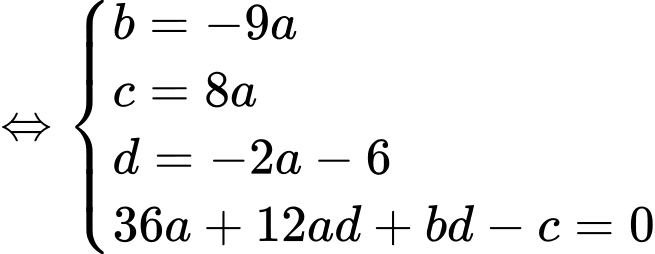
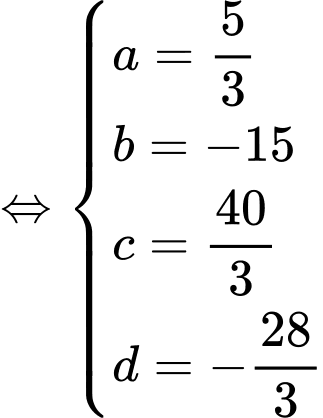
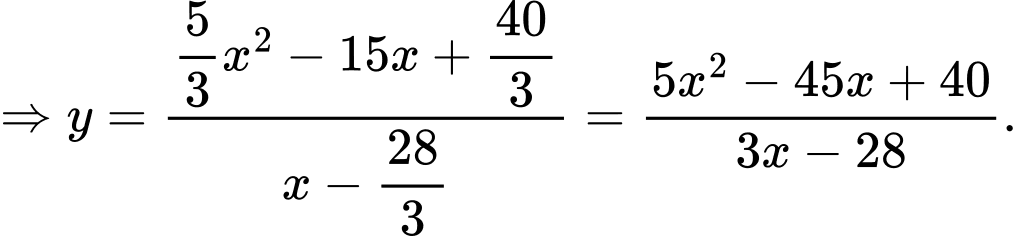
Ta có:
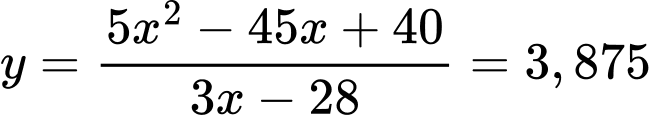
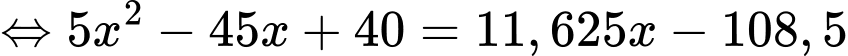
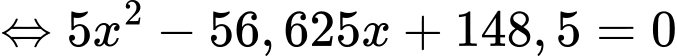
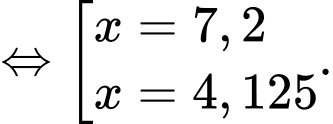
Vậy khi khí cầu đi qua điểm cực đại và cách mặt đất
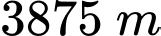 thì khí cầu cách gốc tọa độ theo phương ngang
thì khí cầu cách gốc tọa độ theo phương ngang 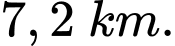
Câu 22 [693322]: Trên hồ có 10 lá cây hoa súng xếp thành một hàng ngang. Trên lá ngoài cùng có một con ếch.

Mỗi bước, con ếch sẽ nhảy qua lá kế bên lá nó đang đứng hoặc nhảy bỏ qua lá đó để sang lá tiếp theo. Con ếch không bao giờ nhảy lùi. Hỏi con ếch có bao nhiêu cách để nhảy sang lá ngoài cùng bên phải?

Mỗi bước, con ếch sẽ nhảy qua lá kế bên lá nó đang đứng hoặc nhảy bỏ qua lá đó để sang lá tiếp theo. Con ếch không bao giờ nhảy lùi. Hỏi con ếch có bao nhiêu cách để nhảy sang lá ngoài cùng bên phải?
Điền đáp án: 
Cách 1:
Tổ hợpGọi số lần nhảy 1 bước, 2 bước của con ếch lần lượt là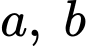 với
với 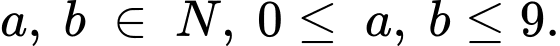
Với mỗi cặp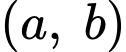 ta có số cách di chuyển của con ếch là
ta có số cách di chuyển của con ếch là 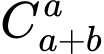 ( cách ).
( cách ).
Theo giả thiết ta có :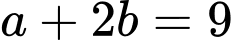 suy ra
suy ra 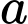 lẻ nên
lẻ nên 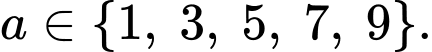
Với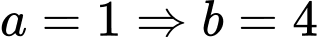 : Số cách di chuyển của con ếch là
: Số cách di chuyển của con ếch là 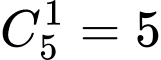 ( cách ).
( cách ).
Với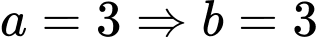 : Số cách di chuyển của con ếch là
: Số cách di chuyển của con ếch là 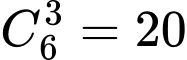 ( cách ).
( cách ).
Với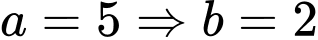 : Số cách di chuyển của con ếch là
: Số cách di chuyển của con ếch là 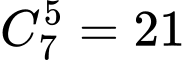 ( cách ).
( cách ).
Với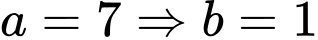 : Số cách di chuyển của con ếch là
: Số cách di chuyển của con ếch là 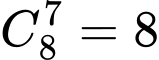 ( cách ).
( cách ).
Với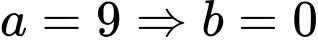 : Số cách di chuyển của con ếch là
: Số cách di chuyển của con ếch là 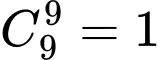 ( cách ).
( cách ).
Số sách di chuyển của con ếch là cách.
cách.
Cách 2: Dãy số fibonacci
Gọi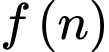 là số cách nhảy để nhảy đến lá thứ
là số cách nhảy để nhảy đến lá thứ 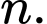
Con ếch bắt đầu xuất phát từ lá 1.
Ta có :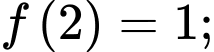
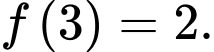
Vì để nhảy đến lá thứ 4 thì sẽ phải nhảy qua lá thứ 2 hoặc lá thứ 3 nên ta có số cách nhảy đến lá thứ 4 là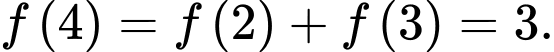
Tương tự ta có :
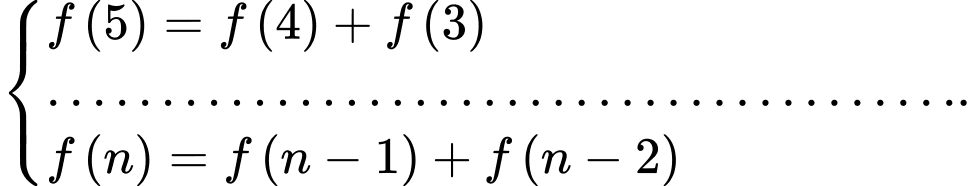
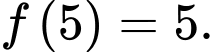
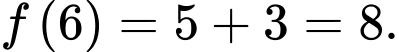
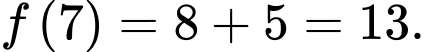
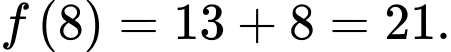
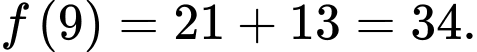
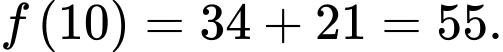
Vậy con ếch có tất cả 55 cách nhảy.
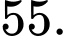
Cách 1:
Tổ hợpGọi số lần nhảy 1 bước, 2 bước của con ếch lần lượt là
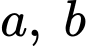 với
với 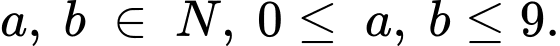
Với mỗi cặp
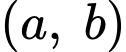 ta có số cách di chuyển của con ếch là
ta có số cách di chuyển của con ếch là 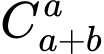 ( cách ).
( cách ).Theo giả thiết ta có :
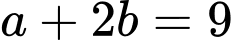 suy ra
suy ra 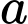 lẻ nên
lẻ nên 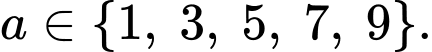
Với
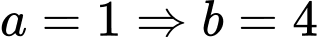 : Số cách di chuyển của con ếch là
: Số cách di chuyển của con ếch là 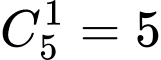 ( cách ).
( cách ).Với
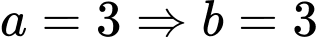 : Số cách di chuyển của con ếch là
: Số cách di chuyển của con ếch là 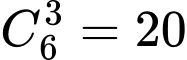 ( cách ).
( cách ).Với
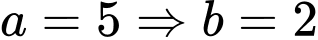 : Số cách di chuyển của con ếch là
: Số cách di chuyển của con ếch là 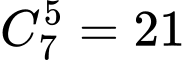 ( cách ).
( cách ).Với
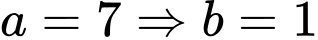 : Số cách di chuyển của con ếch là
: Số cách di chuyển của con ếch là 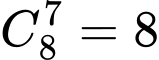 ( cách ).
( cách ).Với
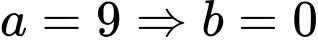 : Số cách di chuyển của con ếch là
: Số cách di chuyển của con ếch là 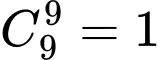 ( cách ).
( cách ).Số sách di chuyển của con ếch là
 cách.
cách.Cách 2: Dãy số fibonacci
Gọi
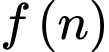 là số cách nhảy để nhảy đến lá thứ
là số cách nhảy để nhảy đến lá thứ 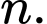
Con ếch bắt đầu xuất phát từ lá 1.
Ta có :
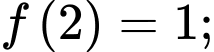
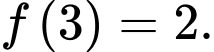
Vì để nhảy đến lá thứ 4 thì sẽ phải nhảy qua lá thứ 2 hoặc lá thứ 3 nên ta có số cách nhảy đến lá thứ 4 là
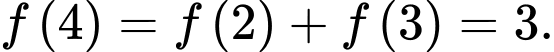
Tương tự ta có :
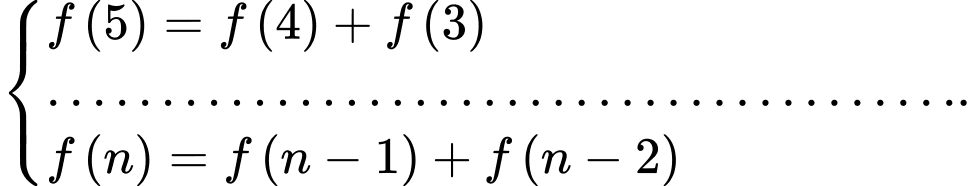
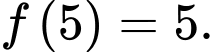
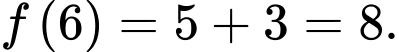
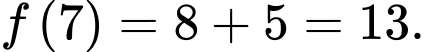
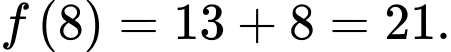
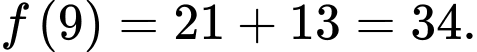
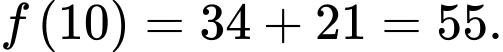
Vậy con ếch có tất cả 55 cách nhảy.