PHẦN I. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Câu 1 [693325]: 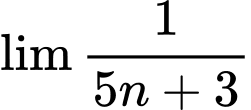 bằng
bằng
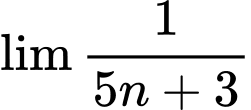 bằng
bằng A, 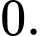
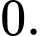
B, 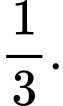
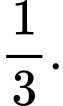
C, 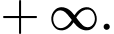
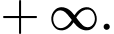
D, 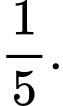
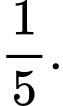
Chọn đáp án A.
Ta có: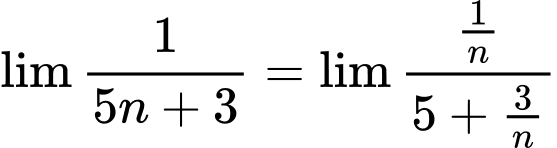
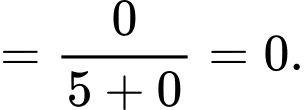 Đáp án: A
Đáp án: A
Ta có:
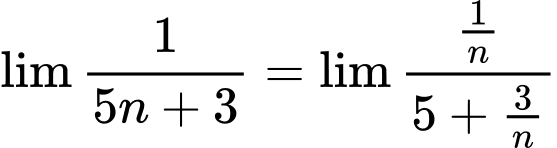
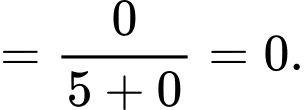 Đáp án: A
Đáp án: A
Câu 2 [547585]: Điểm kiểm tra giữa học kì I của lớp 11T được thống kê theo bảng sau:

Độ dài các nhóm của mẫu số liệu là

Độ dài các nhóm của mẫu số liệu là
A,  .
.
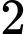 .
.B, 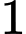 .
.
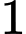 .
.C, 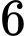 .
.
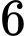 .
.D, 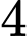 .
.
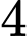 .
.
Chọn đáp án A.
Gọi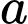 là số ở đầu mút trái,
là số ở đầu mút trái, 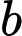 là số ở đầu mút phải của các nhóm của mẫu số liệu.
là số ở đầu mút phải của các nhóm của mẫu số liệu.
Ta có: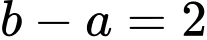 là độ dài của nhóm. Đáp án: A
là độ dài của nhóm. Đáp án: A
Gọi
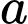 là số ở đầu mút trái,
là số ở đầu mút trái, 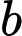 là số ở đầu mút phải của các nhóm của mẫu số liệu.
là số ở đầu mút phải của các nhóm của mẫu số liệu.Ta có:
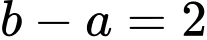 là độ dài của nhóm. Đáp án: A
là độ dài của nhóm. Đáp án: A
Câu 3 [685467]: Cho hàm số 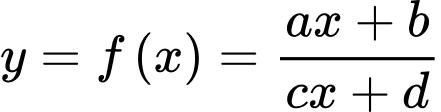 có đồ thị như hình vẽ sau:
có đồ thị như hình vẽ sau:
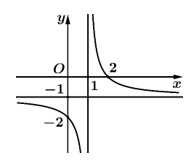
Tâm đối xứng của đồ thị hàm số có tọa độ là
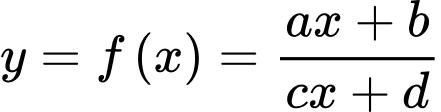 có đồ thị như hình vẽ sau:
có đồ thị như hình vẽ sau: 
Tâm đối xứng của đồ thị hàm số có tọa độ là
A, 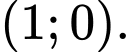
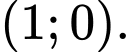
B, 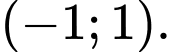
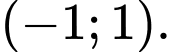
C, 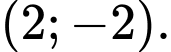
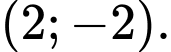
D, 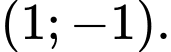
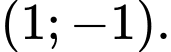
Chọn đáp án D.
Ta có tâm đối xứng của đồ thị là giao của các đường tiệm cận của hàm số. Suy ra từ đồ thị hàm số suy ra tâm đối xứng là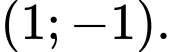 Đáp án: D
Đáp án: D
Ta có tâm đối xứng của đồ thị là giao của các đường tiệm cận của hàm số. Suy ra từ đồ thị hàm số suy ra tâm đối xứng là
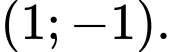 Đáp án: D
Đáp án: D
Câu 4 [699673]: Trong không gian 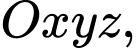 cho hai vectơ
cho hai vectơ 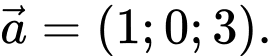 Độ dài của vectơ
Độ dài của vectơ 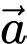 là
là
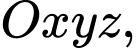 cho hai vectơ
cho hai vectơ 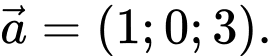 Độ dài của vectơ
Độ dài của vectơ 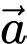 là
là A, 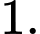
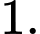
B, 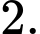
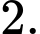
C, 
D, 

Chọn đáp án D.
Ta có: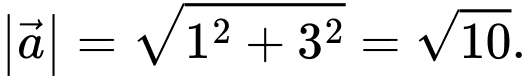 Đáp án: D
Đáp án: D
Ta có:
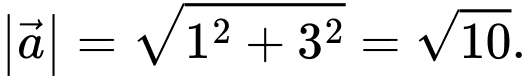 Đáp án: D
Đáp án: D
Câu 5 [520556]: Tập nghiệm của bất phương trình 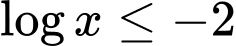 là
là
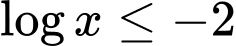 là
là A, 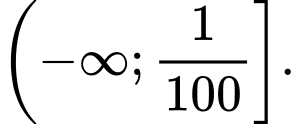
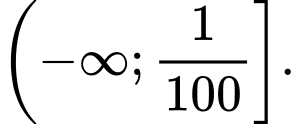
B, 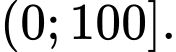
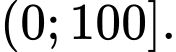
C, 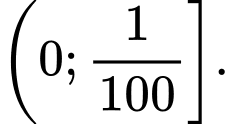
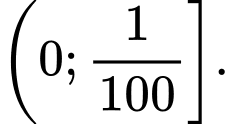
D, 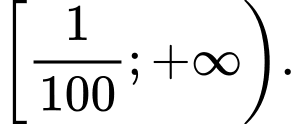
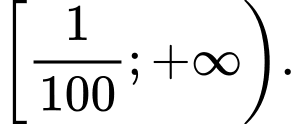
Chọn đáp án C .
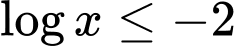
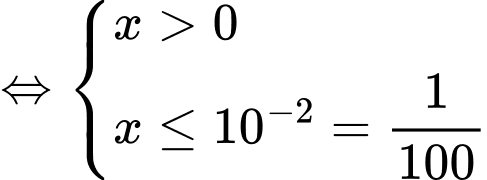
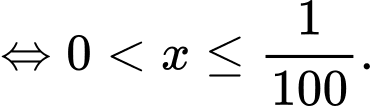 Đáp án: C
Đáp án: C
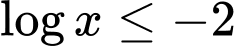
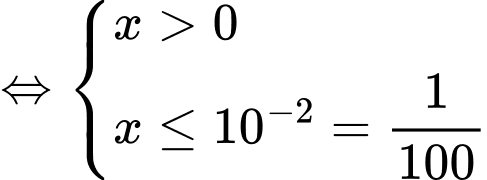
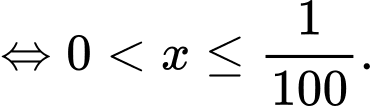 Đáp án: C
Đáp án: C
Câu 6 [693327]: Cho hàm số 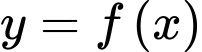 có đạo hàm
có đạo hàm 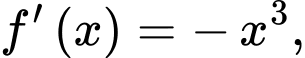
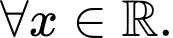 Hàm số đã cho đồng biến trên khoảng nào sau đây?
Hàm số đã cho đồng biến trên khoảng nào sau đây?
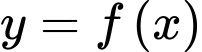 có đạo hàm
có đạo hàm 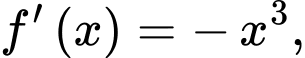
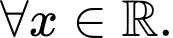 Hàm số đã cho đồng biến trên khoảng nào sau đây?
Hàm số đã cho đồng biến trên khoảng nào sau đây? A, 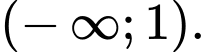
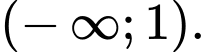
B, 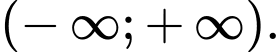
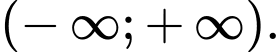
C, 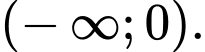
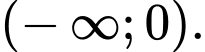
D, 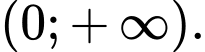
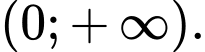
Chọn đáp án C.
Ta có: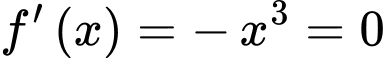
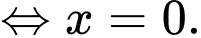
Ta có trục xét dấu của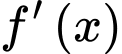 như sau:
như sau:
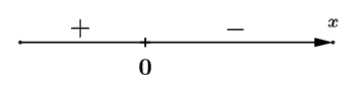
Suy ra hàm số đồng biến trên khoảng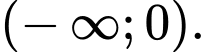 Đáp án: C
Đáp án: C
Ta có:
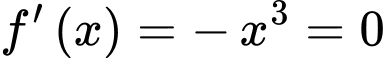
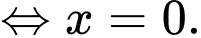
Ta có trục xét dấu của
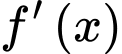 như sau:
như sau: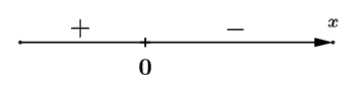
Suy ra hàm số đồng biến trên khoảng
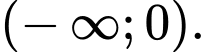 Đáp án: C
Đáp án: C
Câu 7 [699674]: 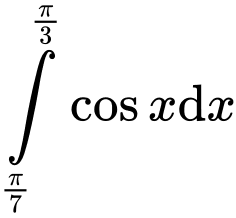 bằng
bằng
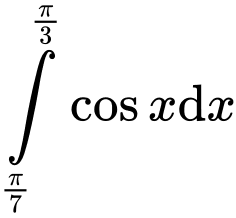 bằng
bằng A, 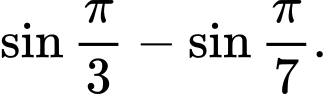
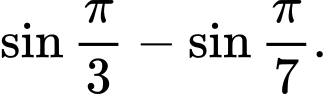
B, 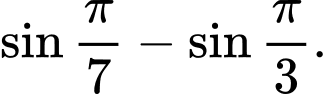
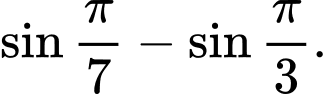
C, 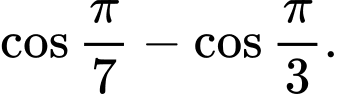
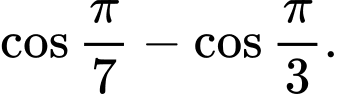
D, 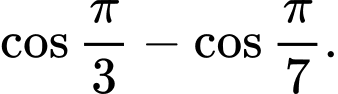
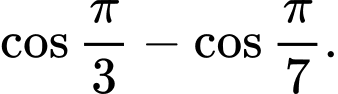
Chọn đáp án A.
Ta có: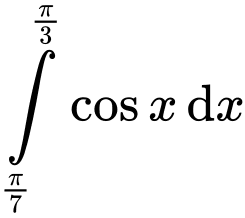
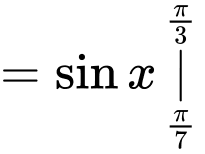
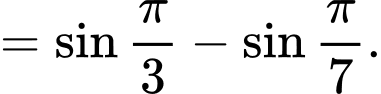 Đáp án: A
Đáp án: A
Ta có:
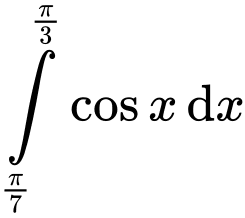
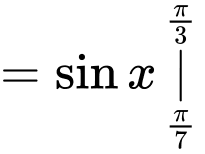
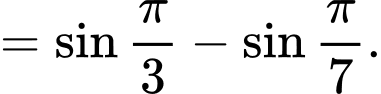 Đáp án: A
Đáp án: A
Câu 8 [693329]: Tập xác định của hàm số 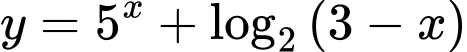 là
là
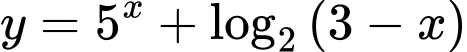 là
là A, 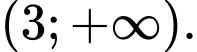
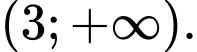
B, 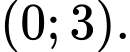
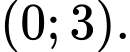
C, 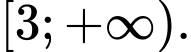
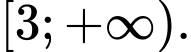
D, 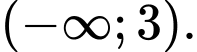
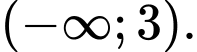
Chọn đáp án D.
ĐKXĐ: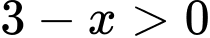
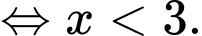 Đáp án: D
Đáp án: D
ĐKXĐ:
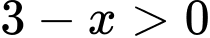
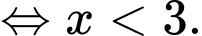 Đáp án: D
Đáp án: D
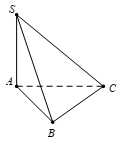
Câu 9 [693330]: Cho hình chóp 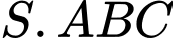 có đáy
có đáy 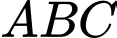 là tam giác vuông tại
là tam giác vuông tại 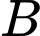 và cạnh bên
và cạnh bên 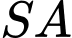 vuông góc với mặt phẳng đáy. Phát biểu sau đây là sai?
vuông góc với mặt phẳng đáy. Phát biểu sau đây là sai?
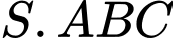 có đáy
có đáy 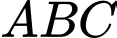 là tam giác vuông tại
là tam giác vuông tại 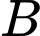 và cạnh bên
và cạnh bên 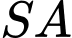 vuông góc với mặt phẳng đáy. Phát biểu sau đây là sai?
vuông góc với mặt phẳng đáy. Phát biểu sau đây là sai?
A, 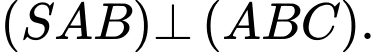
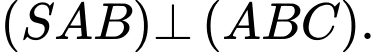
B, 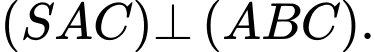
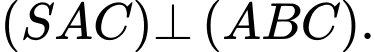
C, 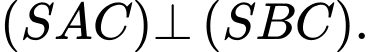
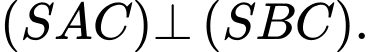
D, 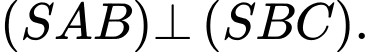
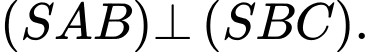
Chọn đáp án C.
Ta có:
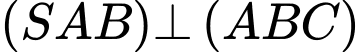 do có
do có 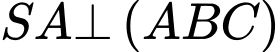 mà
mà 
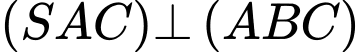 do có
do có 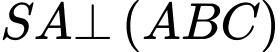 mà
mà 
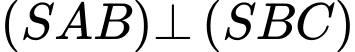 do có
do có 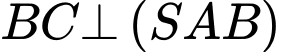 (do có
(do có  và
và  ).
).
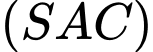 và
và 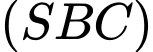 không vuông góc với nhau. Đáp án: C
không vuông góc với nhau. Đáp án: C
Ta có:
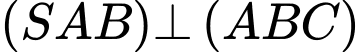 do có
do có 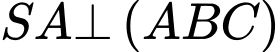 mà
mà 
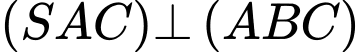 do có
do có 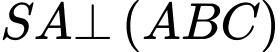 mà
mà 
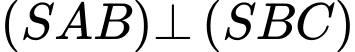 do có
do có 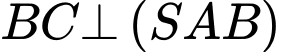 (do có
(do có  và
và  ).
).
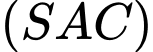 và
và 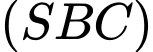 không vuông góc với nhau. Đáp án: C
không vuông góc với nhau. Đáp án: C
Câu 10 [693332]: Cho tứ diện 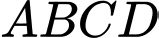 có
có  là trọng tâm của tam giác
là trọng tâm của tam giác  Đặt
Đặt 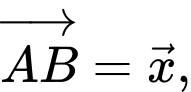
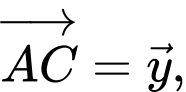
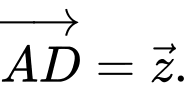 Phát biểu sau đây là đúng?
Phát biểu sau đây là đúng?
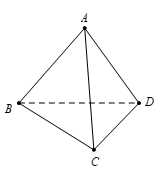
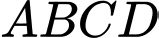 có
có  là trọng tâm của tam giác
là trọng tâm của tam giác  Đặt
Đặt 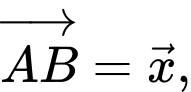
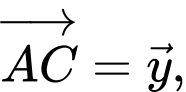
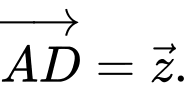 Phát biểu sau đây là đúng?
Phát biểu sau đây là đúng?
A, 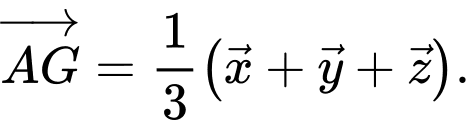
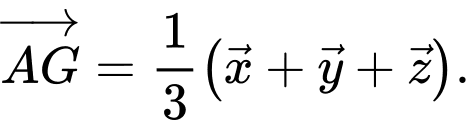
B, 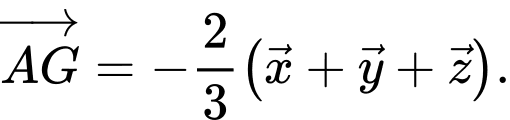
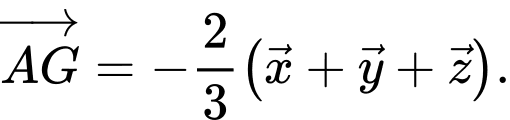
C, 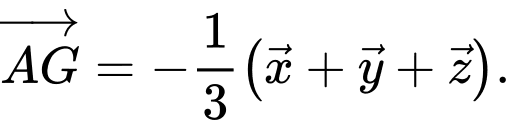
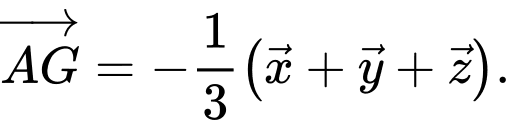
D, 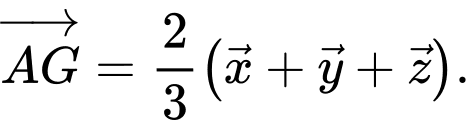
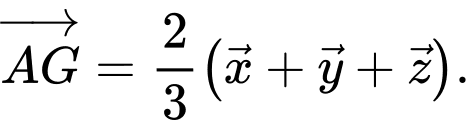
Chọn đáp án A.
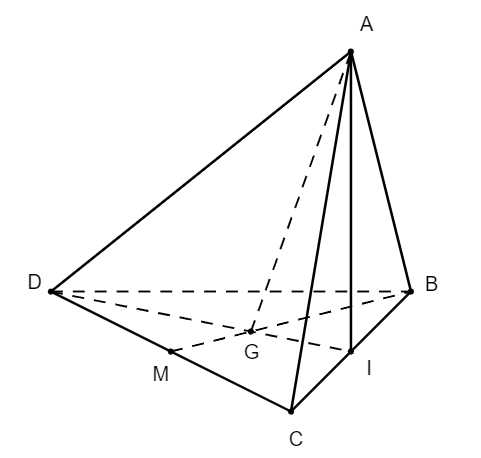
Ta có: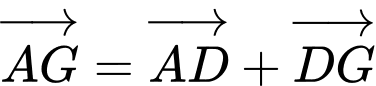
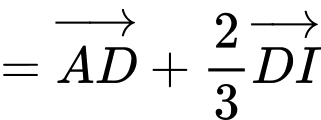
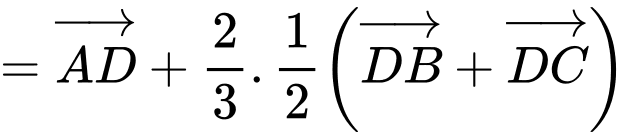
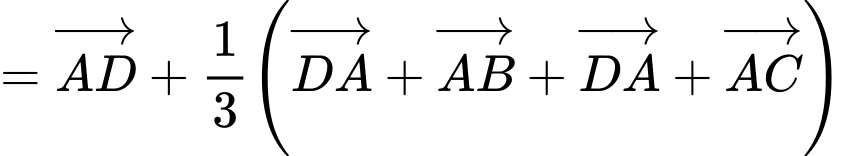
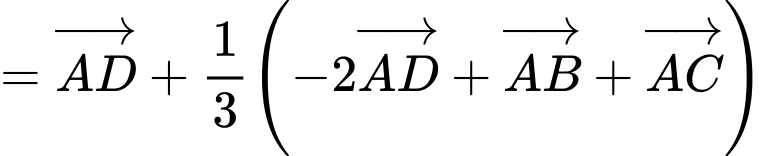
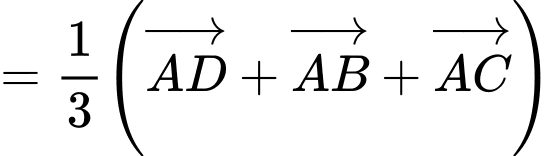
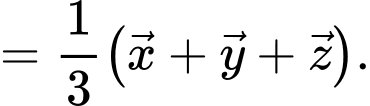 Đáp án: A
Đáp án: A

Ta có:
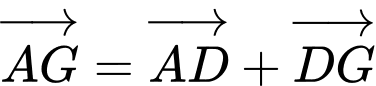
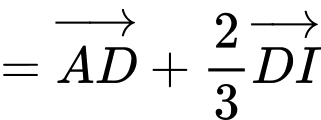
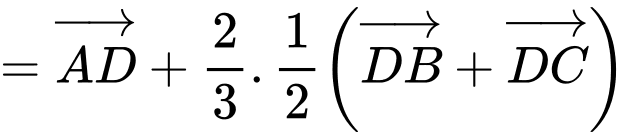
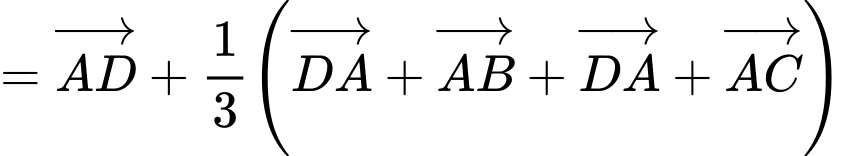
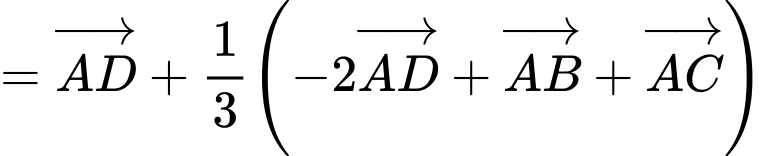
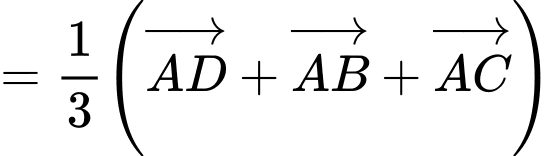
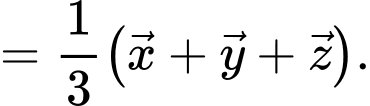 Đáp án: A
Đáp án: A
Câu 11 [256696]: Trong không gian 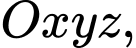 đường thẳng
đường thẳng 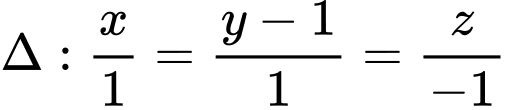 song song với mặt phẳng nào sau đây?
song song với mặt phẳng nào sau đây?
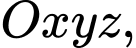 đường thẳng
đường thẳng 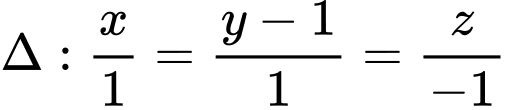 song song với mặt phẳng nào sau đây?
song song với mặt phẳng nào sau đây? A, 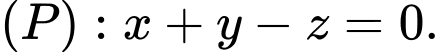
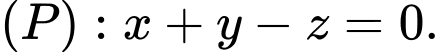
B, 

C, 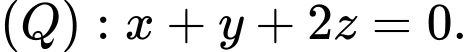
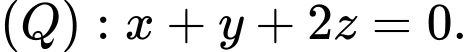
D, 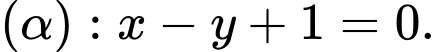
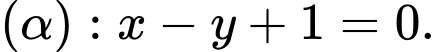
Chọn đáp án C.
Ta có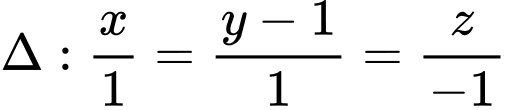
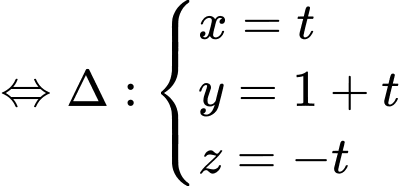
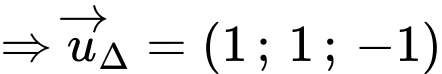
Xét lần lượt các mặt phẳng với đường thẳng ta được:
ta được:
+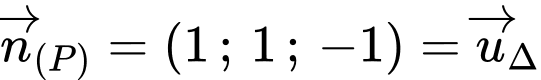
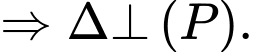
+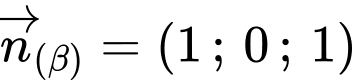
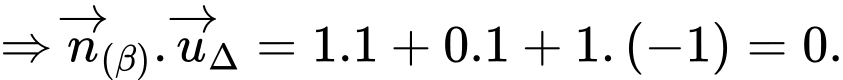
Mặt khác: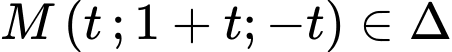 ta thay điểm
ta thay điểm 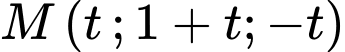 vào mặt phẳng
vào mặt phẳng  ta có:
ta có:
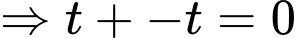
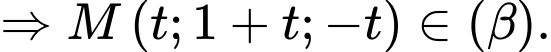
Suy ra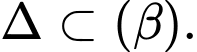
+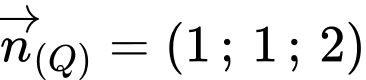
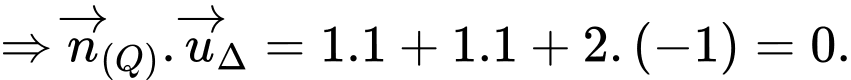
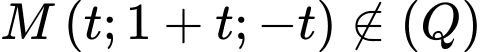
Suy ra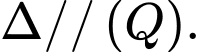
+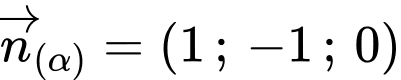
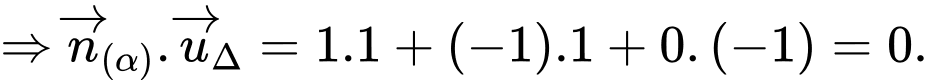
Mặt khác: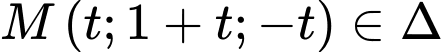 ta thay điểm
ta thay điểm 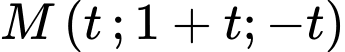 vào mặt phẳng
vào mặt phẳng  ta có:
ta có:
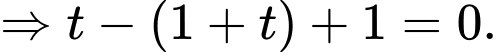
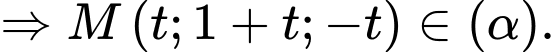
Suy ra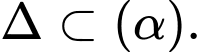 Đáp án: C
Đáp án: C
Ta có
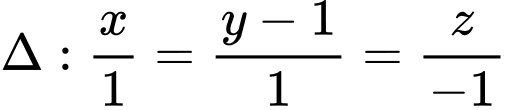
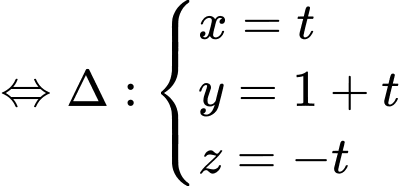
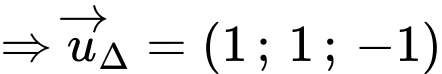
Xét lần lượt các mặt phẳng với đường thẳng
 ta được:
ta được:+
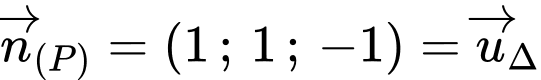
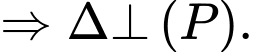
+
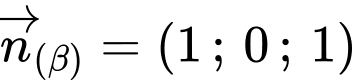
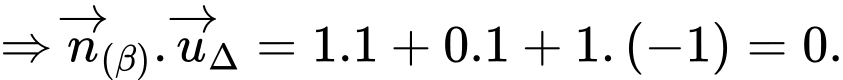
Mặt khác:
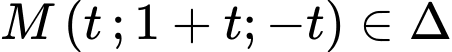 ta thay điểm
ta thay điểm 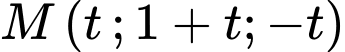 vào mặt phẳng
vào mặt phẳng  ta có:
ta có: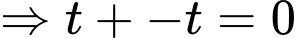
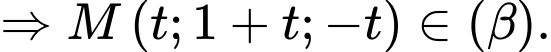
Suy ra
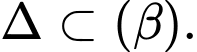
+
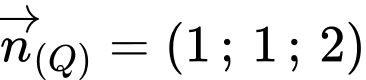
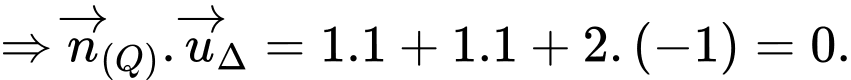
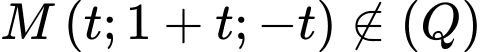
Suy ra
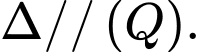
+
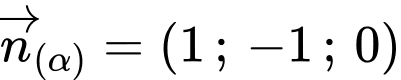
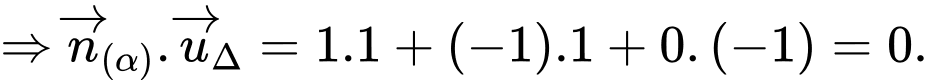
Mặt khác:
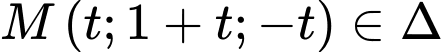 ta thay điểm
ta thay điểm 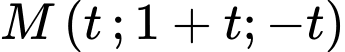 vào mặt phẳng
vào mặt phẳng  ta có:
ta có: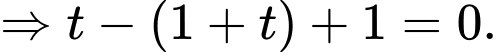
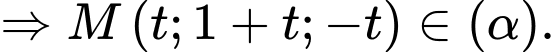
Suy ra
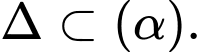 Đáp án: C
Đáp án: C
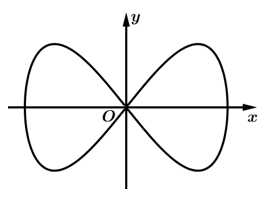
Câu 12 [693333]: Đường cong trong hình bên có tên gọi là đường Lemmiscate. Trong mặt phẳng 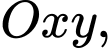 phương trình của đường Lemmiscate đã cho là
phương trình của đường Lemmiscate đã cho là 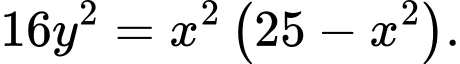 Thể tích vật thể tròn xoay tạo thành khi cho hình phẳng giới hạn bởi đường cong đó quay quanh trục
Thể tích vật thể tròn xoay tạo thành khi cho hình phẳng giới hạn bởi đường cong đó quay quanh trục 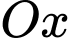 bằng
bằng
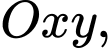 phương trình của đường Lemmiscate đã cho là
phương trình của đường Lemmiscate đã cho là 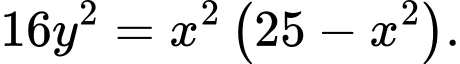 Thể tích vật thể tròn xoay tạo thành khi cho hình phẳng giới hạn bởi đường cong đó quay quanh trục
Thể tích vật thể tròn xoay tạo thành khi cho hình phẳng giới hạn bởi đường cong đó quay quanh trục 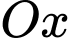 bằng
bằng
A, 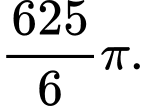
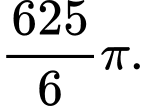
B, 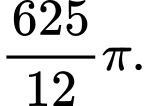
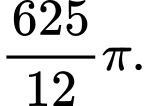
C, 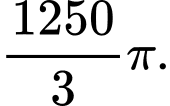
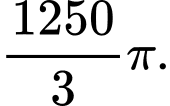
D, 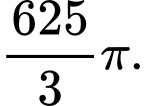
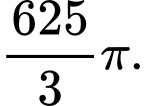
Chọn đáp án B.
Hoành độ giao điểm của đồ thị với trục hoành là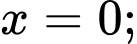
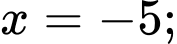
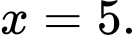
Dễ thấy thể tích vật thể xoay tạo thành khi cho hình phẳng giới hạn bởi đường cong đó quay quanh trục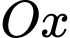 bao gồm 4 phần bằng nhau
bao gồm 4 phần bằng nhau
Có: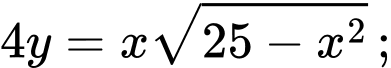
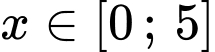
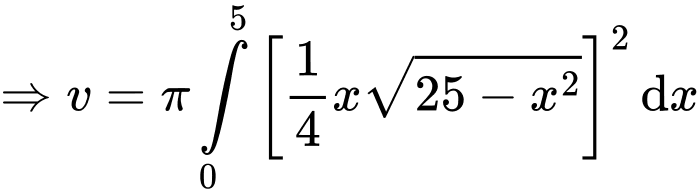
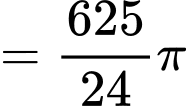
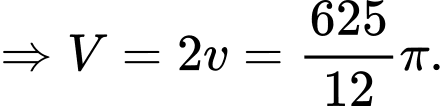 Đáp án: B
Đáp án: B
Hoành độ giao điểm của đồ thị với trục hoành là
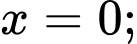
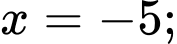
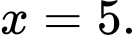
Dễ thấy thể tích vật thể xoay tạo thành khi cho hình phẳng giới hạn bởi đường cong đó quay quanh trục
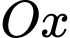 bao gồm 4 phần bằng nhau
bao gồm 4 phần bằng nhauCó:
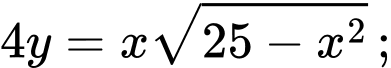
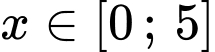
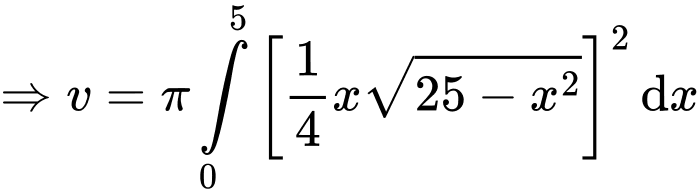
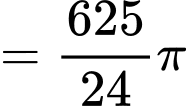
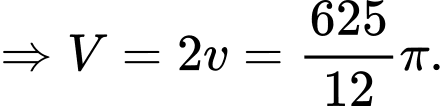 Đáp án: B
Đáp án: B PHẦN II. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Câu 13 [693335]: Biết 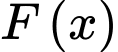 là một nguyên hàm của hàm số
là một nguyên hàm của hàm số 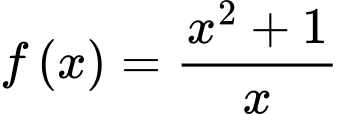 trên khoảng
trên khoảng 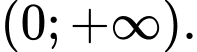
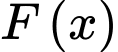 là một nguyên hàm của hàm số
là một nguyên hàm của hàm số 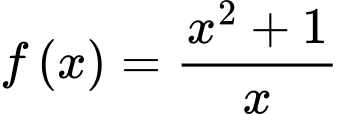 trên khoảng
trên khoảng 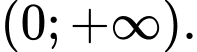
a) Đúng.
Ta có: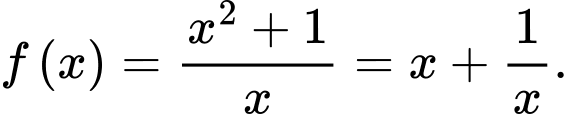
b) Sai.
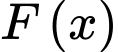 là một nguyên hàm của hàm số
là một nguyên hàm của hàm số 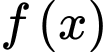 nên
nên 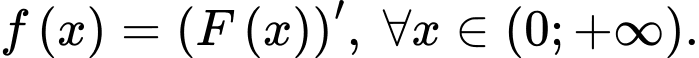
c) Sai.
Ta có: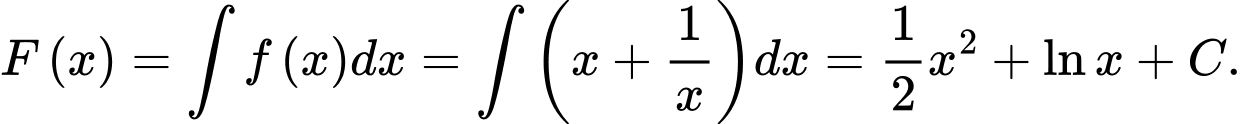
d) Sai.
Đồ thị của hàm số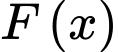 đi qua
đi qua 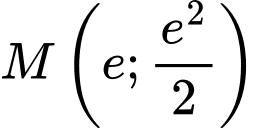 nên
nên 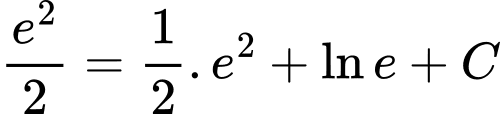
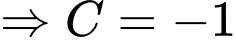
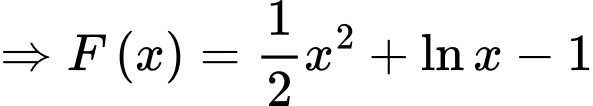
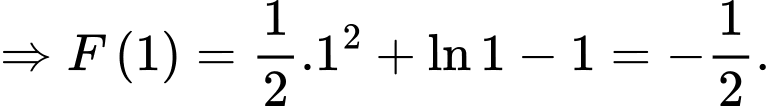
Ta có:
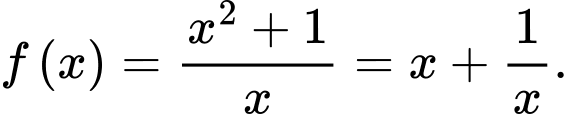
b) Sai.
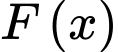 là một nguyên hàm của hàm số
là một nguyên hàm của hàm số 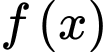 nên
nên 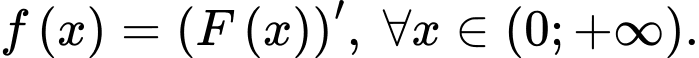
c) Sai.
Ta có:
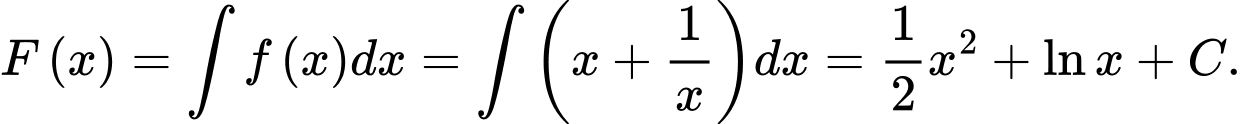
d) Sai.
Đồ thị của hàm số
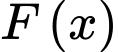 đi qua
đi qua 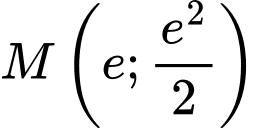 nên
nên 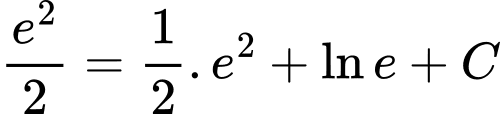
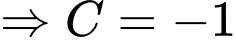
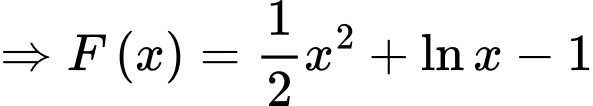
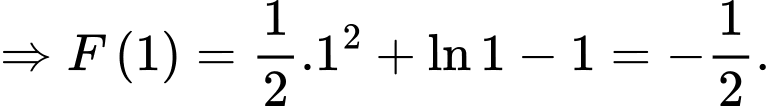
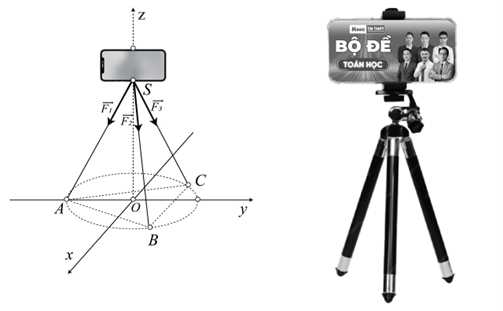
Câu 14 [693336]: Một chiếc điện thoại iphone được đặt trên một giá đỡ có ba chân với điểm đặt 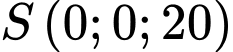 và các điểm chạm mặt đất của ba chân lần lượt là
và các điểm chạm mặt đất của ba chân lần lượt là 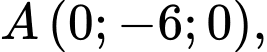
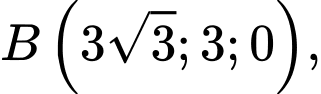
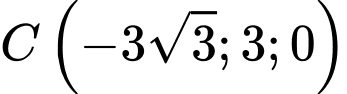 (đơn vị cm). Cho biết điện thoại có trọng lượng là
(đơn vị cm). Cho biết điện thoại có trọng lượng là  và ba lực tác dụng lên giá đỡ được phân bố như hình vẽ là ba lực
và ba lực tác dụng lên giá đỡ được phân bố như hình vẽ là ba lực 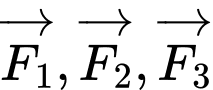 có độ lớn bằng nhau và đo bằng đơn vị Niuton.
có độ lớn bằng nhau và đo bằng đơn vị Niuton.
 và các điểm chạm mặt đất của ba chân lần lượt là
và các điểm chạm mặt đất của ba chân lần lượt là 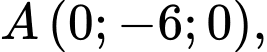
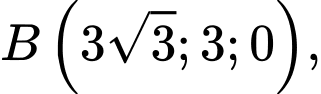
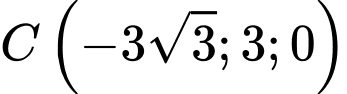 (đơn vị cm). Cho biết điện thoại có trọng lượng là
(đơn vị cm). Cho biết điện thoại có trọng lượng là  và ba lực tác dụng lên giá đỡ được phân bố như hình vẽ là ba lực
và ba lực tác dụng lên giá đỡ được phân bố như hình vẽ là ba lực 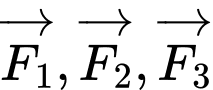 có độ lớn bằng nhau và đo bằng đơn vị Niuton.
có độ lớn bằng nhau và đo bằng đơn vị Niuton.
a) Đúng.
Ta có: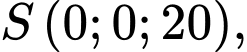
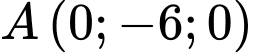
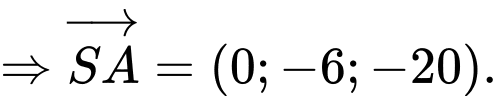
b) Sai.
Gọi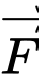 là trọng lực tác dụng lên điện thoại
là trọng lực tác dụng lên điện thoại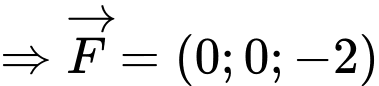
Điện thoại có trọng lượng là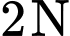 và ba lực tác dụng lên giá đỡ được phân bố như hình vẽ là ba lực
và ba lực tác dụng lên giá đỡ được phân bố như hình vẽ là ba lực 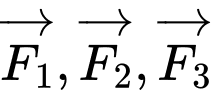 nên
nên 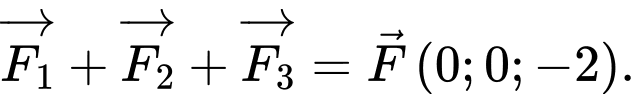
c) Sai.
Ta có:
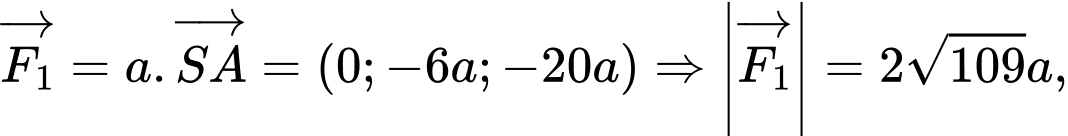
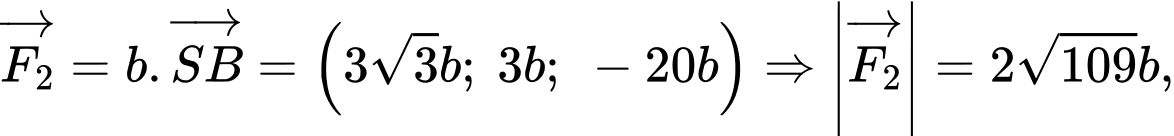
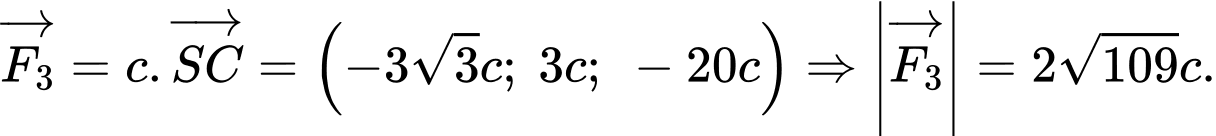
Ba lực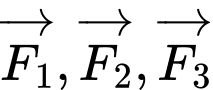 có độ lớn bằng nhau nên
có độ lớn bằng nhau nên 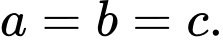
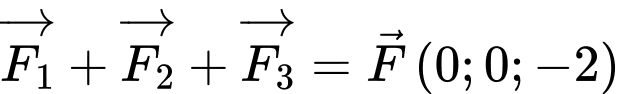
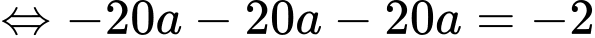
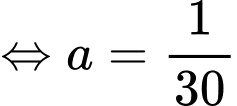
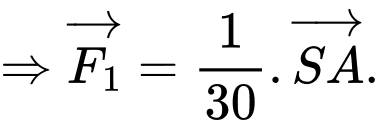
d) Đúng.
Ta có: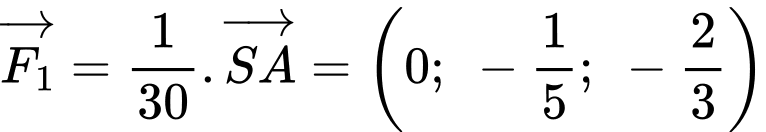
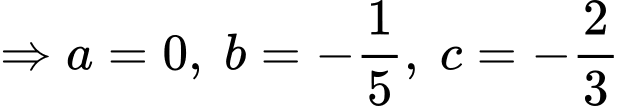
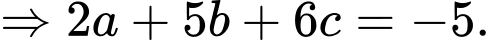
Ta có:
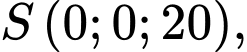
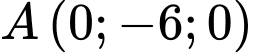
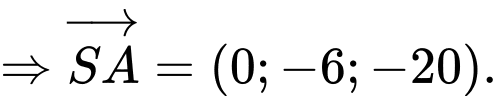
b) Sai.
Gọi
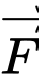 là trọng lực tác dụng lên điện thoại
là trọng lực tác dụng lên điện thoại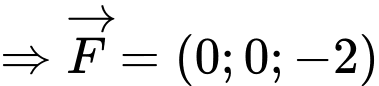
Điện thoại có trọng lượng là
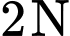 và ba lực tác dụng lên giá đỡ được phân bố như hình vẽ là ba lực
và ba lực tác dụng lên giá đỡ được phân bố như hình vẽ là ba lực 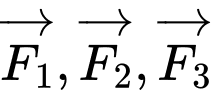 nên
nên 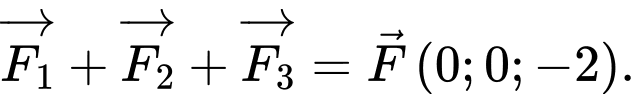
c) Sai.
Ta có:
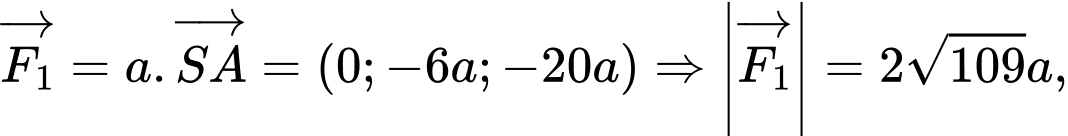
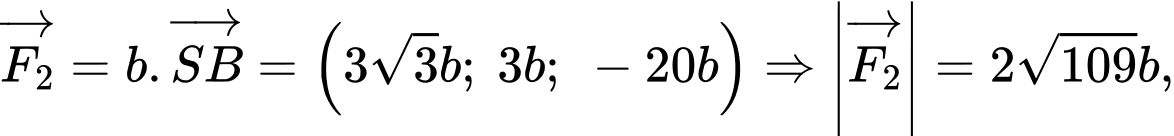
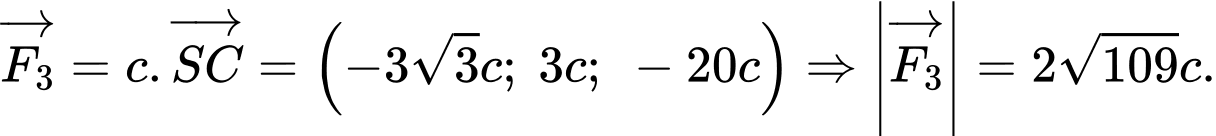
Ba lực
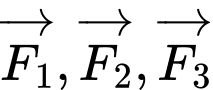 có độ lớn bằng nhau nên
có độ lớn bằng nhau nên 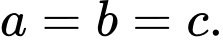
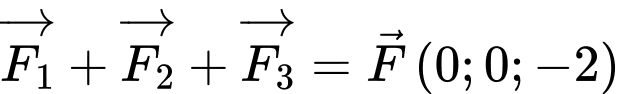
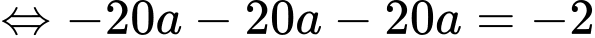
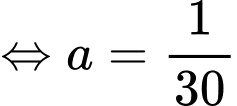
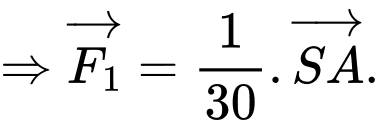
d) Đúng.
Ta có:
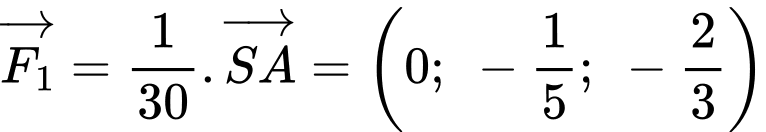
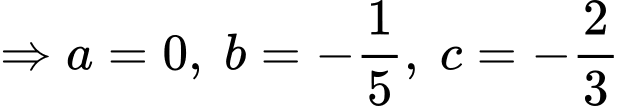
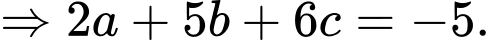
Câu 15 [693337]: Một thùng chứa 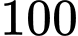 quả táo trong đó có
quả táo trong đó có 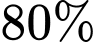 số quả táo được dán nhãn, số còn lại không được dán nhãn. Bạn Hoàng lấy ra một quả trong thùng, sau đó bạn Hà lấy ra một quả thứ hai.
số quả táo được dán nhãn, số còn lại không được dán nhãn. Bạn Hoàng lấy ra một quả trong thùng, sau đó bạn Hà lấy ra một quả thứ hai.
Gọi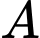 là biến cố “Quả táo bạn Hoàng lấy ra có dán nhãn”;
là biến cố “Quả táo bạn Hoàng lấy ra có dán nhãn”;
Gọi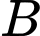 là biến cố “Quả táo bạn Hà lấy ra có dán nhãn”.
là biến cố “Quả táo bạn Hà lấy ra có dán nhãn”.
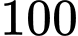 quả táo trong đó có
quả táo trong đó có 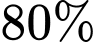 số quả táo được dán nhãn, số còn lại không được dán nhãn. Bạn Hoàng lấy ra một quả trong thùng, sau đó bạn Hà lấy ra một quả thứ hai.
số quả táo được dán nhãn, số còn lại không được dán nhãn. Bạn Hoàng lấy ra một quả trong thùng, sau đó bạn Hà lấy ra một quả thứ hai. Gọi
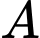 là biến cố “Quả táo bạn Hoàng lấy ra có dán nhãn”;
là biến cố “Quả táo bạn Hoàng lấy ra có dán nhãn”; Gọi
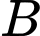 là biến cố “Quả táo bạn Hà lấy ra có dán nhãn”.
là biến cố “Quả táo bạn Hà lấy ra có dán nhãn”.
a) Đúng.
Số quả táo trong thùng được dán nhãn là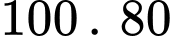 (quả).
(quả).
Ta có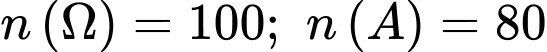
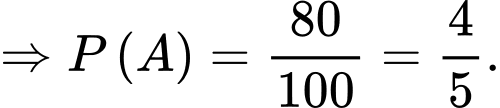
b) Sai.
Vì Hoàng đã lấy ra một quả có nhãn nên số quả táo trong thùng còn lại 99 quả, trong đó có 79 quả có dán nhãn. Suy ra xác suất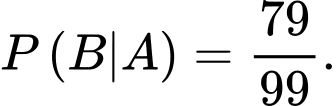
c) Đúng.
Ta có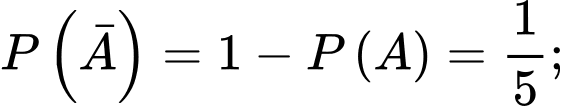
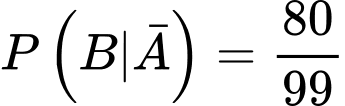 .
.
Ta có sơ đồ cây sau:
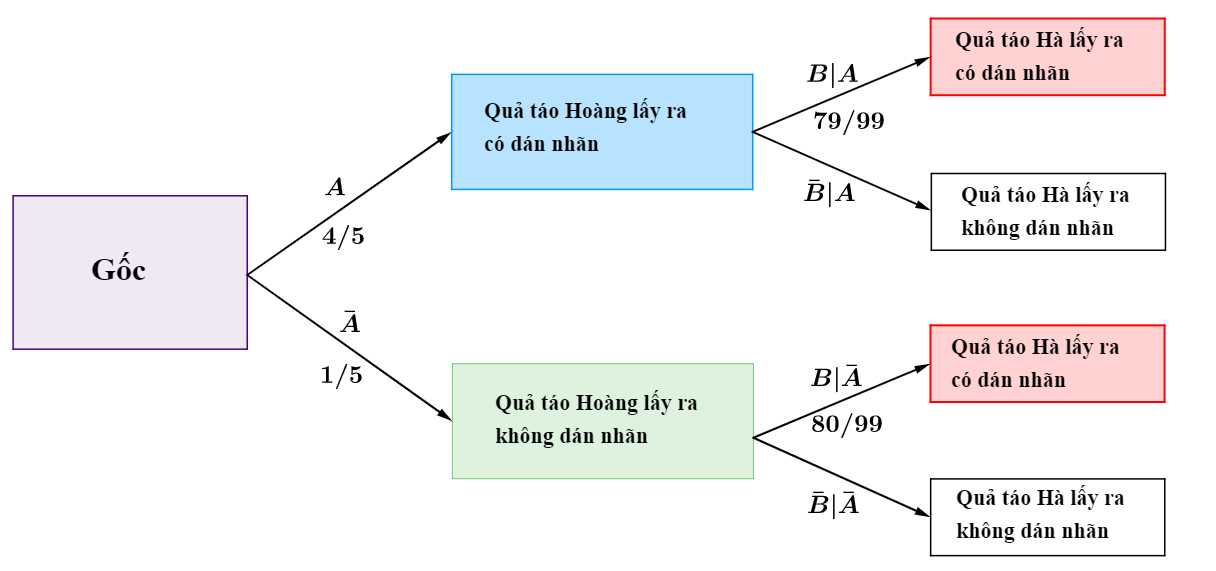
Vậy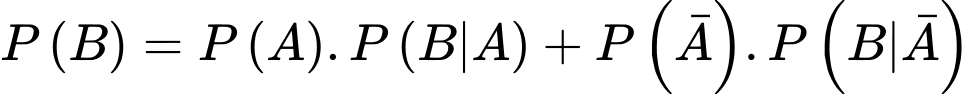
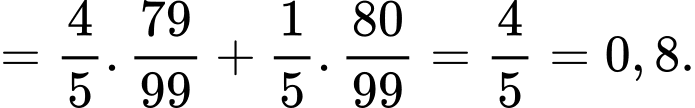
d) Sai.
Xác suất để Hoàng cũng lấy ra quả táo có dán nhãn khi biết Hà lấy được quả táo có dán nhãn là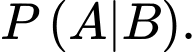
Áp dụng công thức Bayes, ta có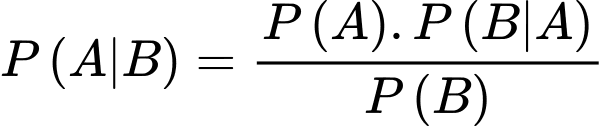
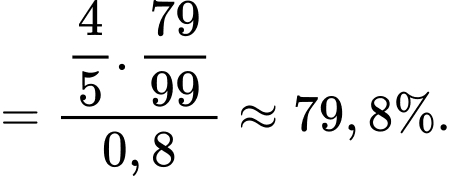
Số quả táo trong thùng được dán nhãn là
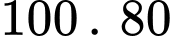 (quả).
(quả).Ta có
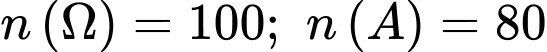
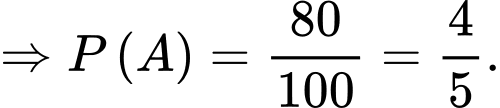
b) Sai.
Vì Hoàng đã lấy ra một quả có nhãn nên số quả táo trong thùng còn lại 99 quả, trong đó có 79 quả có dán nhãn. Suy ra xác suất
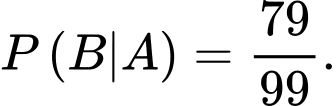
c) Đúng.
Ta có
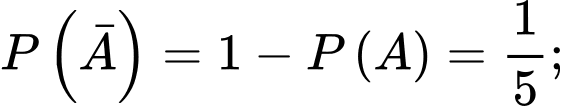
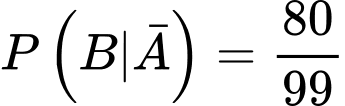 .
.Ta có sơ đồ cây sau:

Vậy
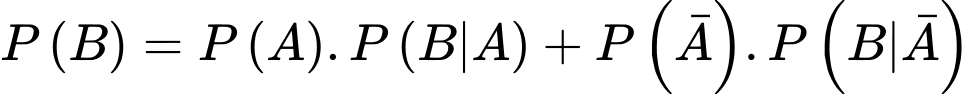
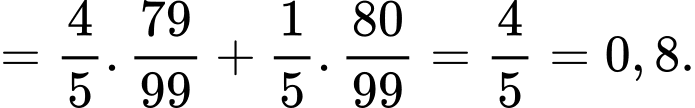
d) Sai.
Xác suất để Hoàng cũng lấy ra quả táo có dán nhãn khi biết Hà lấy được quả táo có dán nhãn là
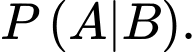
Áp dụng công thức Bayes, ta có
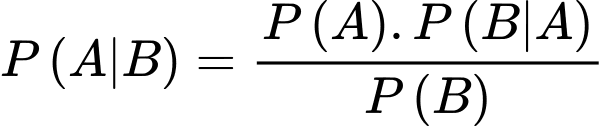
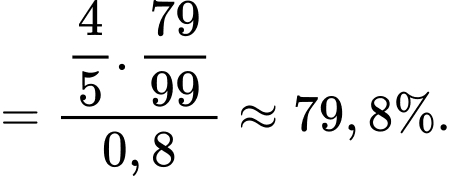
Câu 16 [693338]: Trên trục 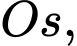 cho hai chất điểm chuyển động có toạ độ theo thời gian
cho hai chất điểm chuyển động có toạ độ theo thời gian 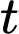 (giây) lần lượt là
(giây) lần lượt là 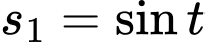 và
và 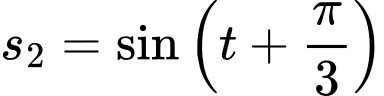 (đơn vị: mét).
(đơn vị: mét).
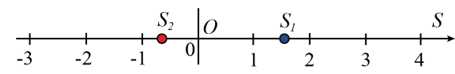
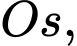 cho hai chất điểm chuyển động có toạ độ theo thời gian
cho hai chất điểm chuyển động có toạ độ theo thời gian 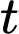 (giây) lần lượt là
(giây) lần lượt là 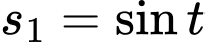 và
và 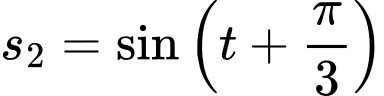 (đơn vị: mét).
(đơn vị: mét).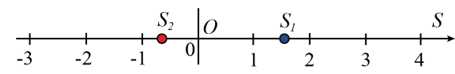
a) Sai.
Tại thời điểm ban đầu hai chất điểm cách nhau một khoảng bằng

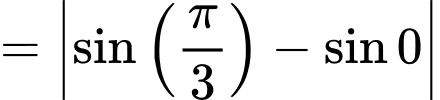
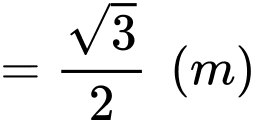
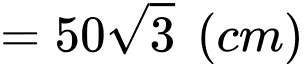
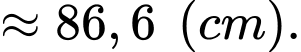
b) Sai.
Khoảng cách giữa hai chất điểm được xác định bởi hàm số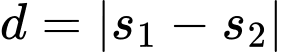 (mét).
(mét).
c) Đúng.
Ta có: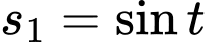
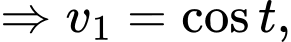
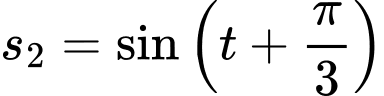

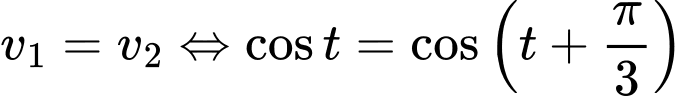
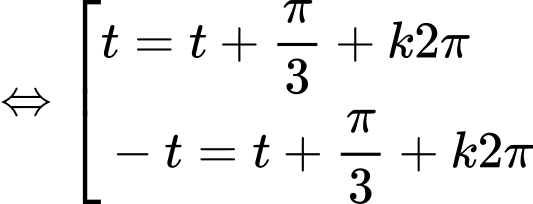
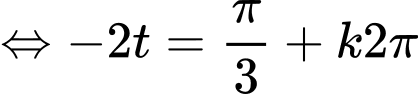
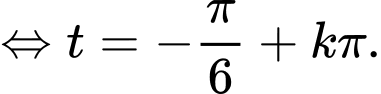
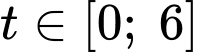
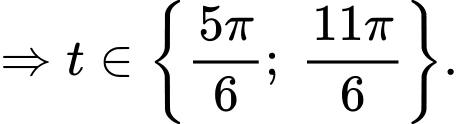
d) Đúng.
Khoảng cách giữa hai chất điểm được xác định bởi hàm số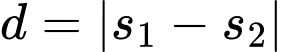 (mét).
(mét).
Ta có: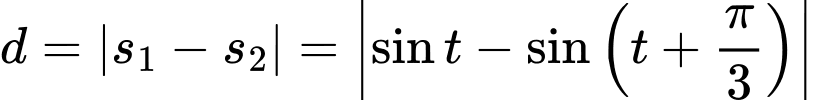
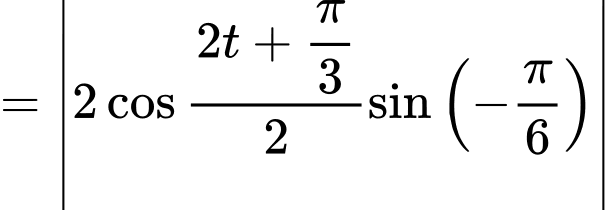
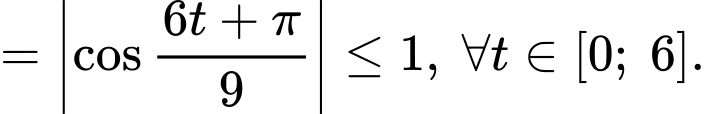
Vậy trong 6 giây đầu tiên, khoảng cách xa nhất của hai chất điểm là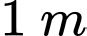 hay
hay 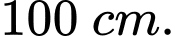
Tại thời điểm ban đầu hai chất điểm cách nhau một khoảng bằng

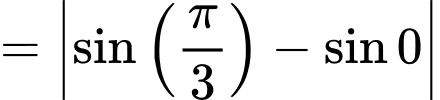
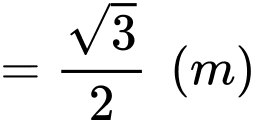
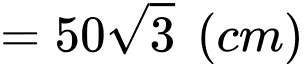
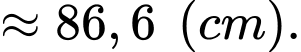
b) Sai.
Khoảng cách giữa hai chất điểm được xác định bởi hàm số
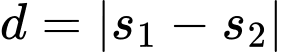 (mét).
(mét).c) Đúng.
Ta có:
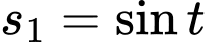
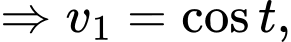
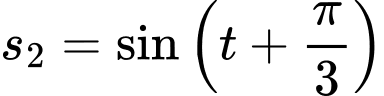

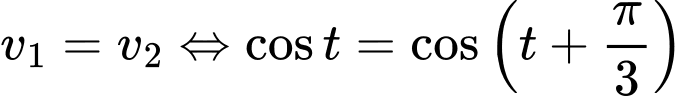
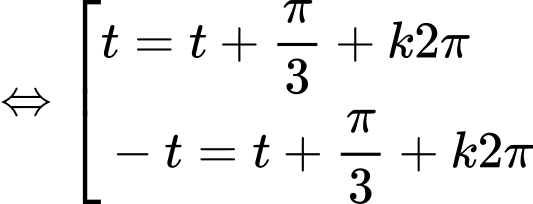
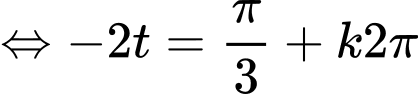
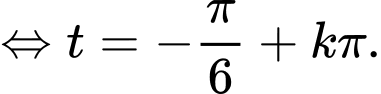
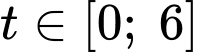
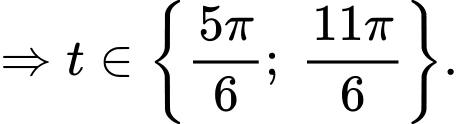
d) Đúng.
Khoảng cách giữa hai chất điểm được xác định bởi hàm số
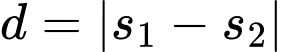 (mét).
(mét).Ta có:
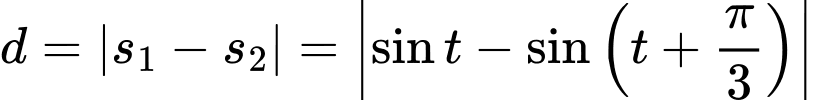
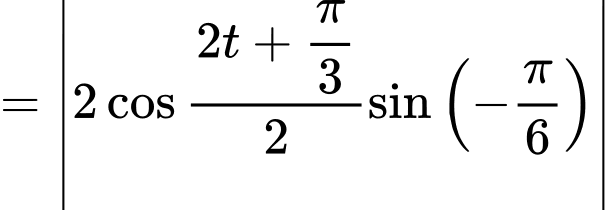
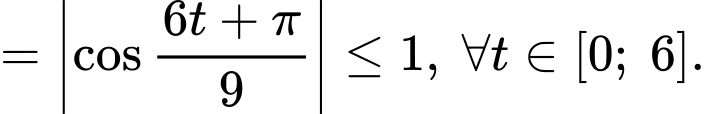
Vậy trong 6 giây đầu tiên, khoảng cách xa nhất của hai chất điểm là
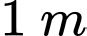 hay
hay 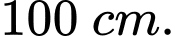
PHẦN III. Thí sinh trả lời từ câu 1 đến câu 6.
Câu 17 [693339]: Cho hình lăng trụ đứng  có đáy
có đáy 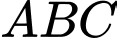 là tam giác vuông tại
là tam giác vuông tại 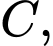
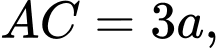
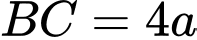 và góc giữa đường thẳng
và góc giữa đường thẳng 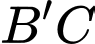 và mặt phẳng
và mặt phẳng 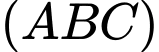 bằng
bằng 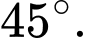 Tính sin của góc giữa đường thẳng
Tính sin của góc giữa đường thẳng 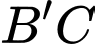 và mặt phẳng
và mặt phẳng 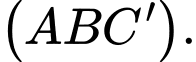
 có đáy
có đáy 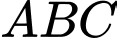 là tam giác vuông tại
là tam giác vuông tại 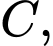
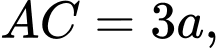
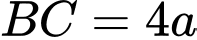 và góc giữa đường thẳng
và góc giữa đường thẳng 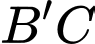 và mặt phẳng
và mặt phẳng 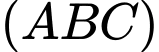 bằng
bằng 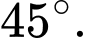 Tính sin của góc giữa đường thẳng
Tính sin của góc giữa đường thẳng 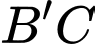 và mặt phẳng
và mặt phẳng 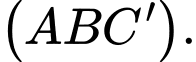
Điền đáp án: 0,73.
Gọi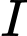 là giao điểm của
là giao điểm của 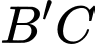 và mặt phẳng
và mặt phẳng 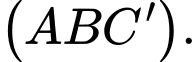
Suy ra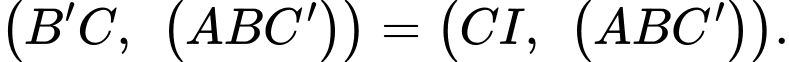
Quan sát hình minh hoạ.
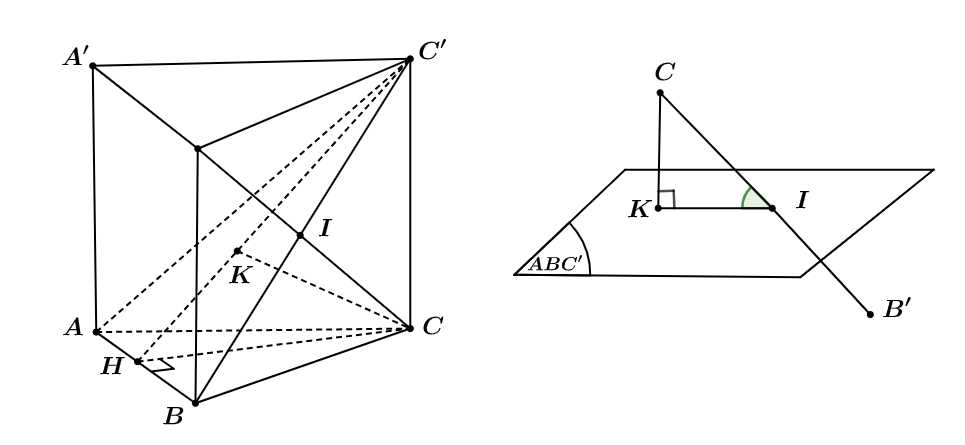
Kẻ
Ta có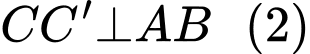 (vì
(vì  là lăng trụ đứng nên
là lăng trụ đứng nên 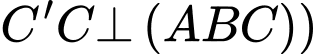
Từ (1) và (2) suy ra
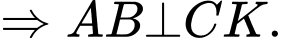
Lại có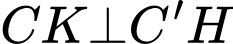 nên suy ra
nên suy ra 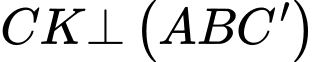 hay
hay 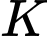 là hình chiếu của điểm
là hình chiếu của điểm  xuống mặt phẳng
xuống mặt phẳng 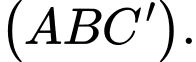
Suy ra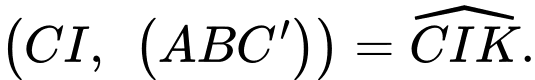
+) Trong tam giác vuông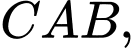 ta có
ta có 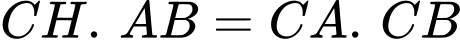
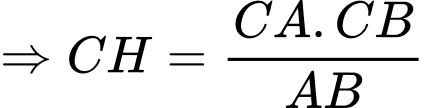
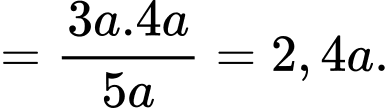
Ta có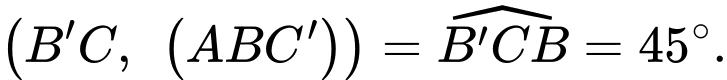
Suy ra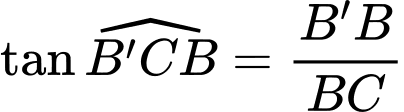
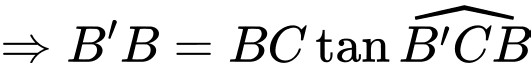
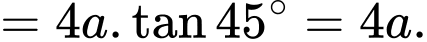
Trong tam giác vuông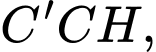 ta có
ta có
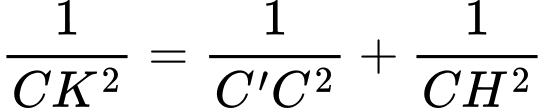
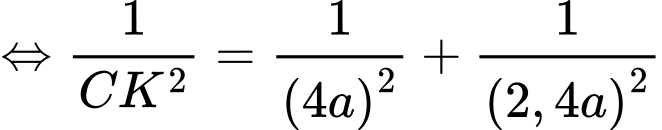
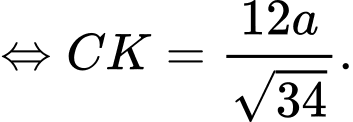
+) Ta có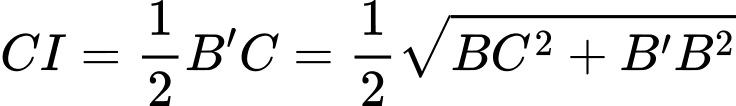
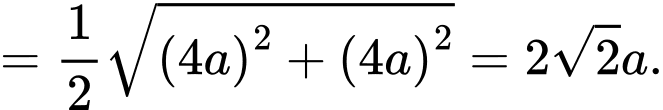
Suy ra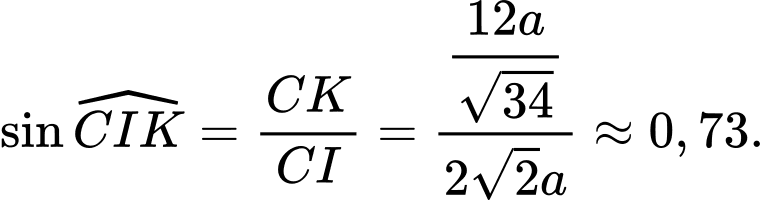
Gọi
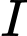 là giao điểm của
là giao điểm của 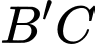 và mặt phẳng
và mặt phẳng 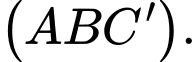
Suy ra
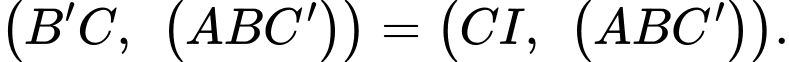
Quan sát hình minh hoạ.

Kẻ

Ta có
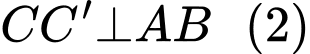 (vì
(vì  là lăng trụ đứng nên
là lăng trụ đứng nên 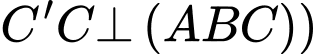
Từ (1) và (2) suy ra

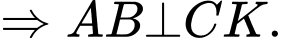
Lại có
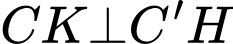 nên suy ra
nên suy ra 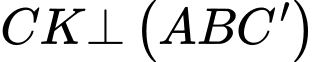 hay
hay 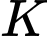 là hình chiếu của điểm
là hình chiếu của điểm  xuống mặt phẳng
xuống mặt phẳng 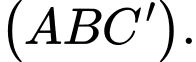
Suy ra
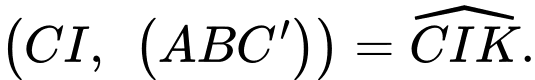
+) Trong tam giác vuông
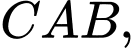 ta có
ta có 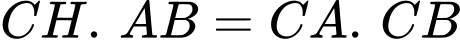
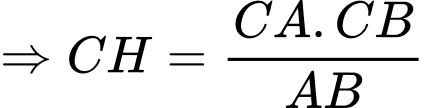
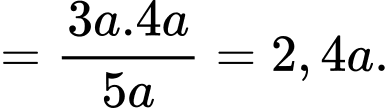
Ta có
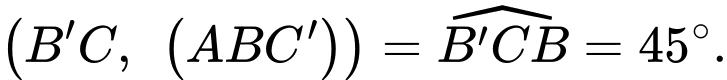
Suy ra
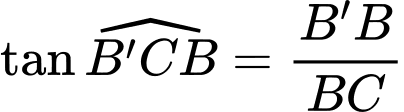
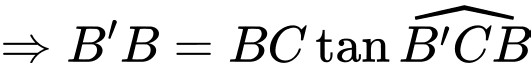
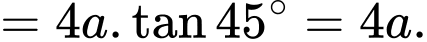
Trong tam giác vuông
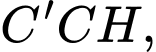 ta có
ta có 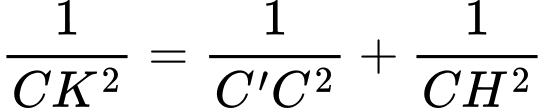
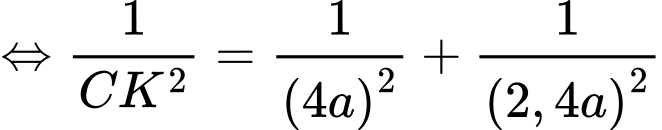
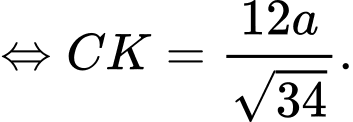
+) Ta có
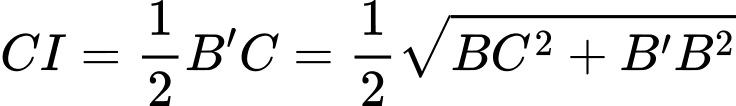
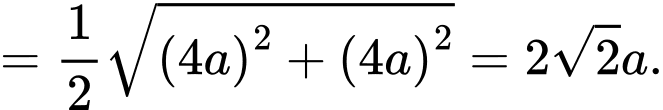
Suy ra
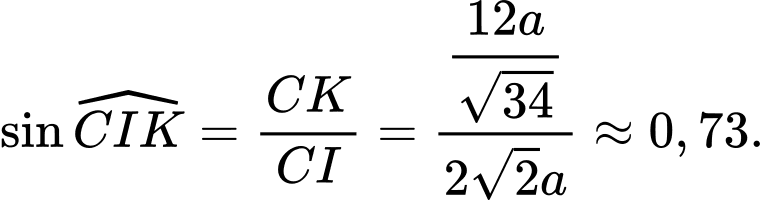
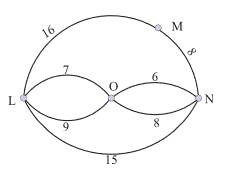
Câu 18 [693340]: Biểu đồ thể hiện các con đường nối giữa các thị trấn (đơn vị: km). Cán bộ thanh tra xuất phát từ thị trấn L đi kiểm tra tất cả các tuyến đường nối giữa các thị trấn M, N, O và quay lại L. Chiều dài quãng đường tối thiểu thanh tra cần phải đi là bao nhiêu km?

Điền đáp án: 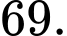
Nhận thấy đồ thị trên đều là bậc chẵn ( không có đỉnh bậc lẻ).
 Đồ thị tồn tại chu trình Euler: chu trình đi qua tất cả các cạnh của đồ thị đúng một lần (quãng đường tối thiểu).
Đồ thị tồn tại chu trình Euler: chu trình đi qua tất cả các cạnh của đồ thị đúng một lần (quãng đường tối thiểu).
 Chiều dài quãng đường tối thiểu thanh tra cần phải đi là tổng độ dài tất cả các quãng đường có trong đồ thị trên:
Chiều dài quãng đường tối thiểu thanh tra cần phải đi là tổng độ dài tất cả các quãng đường có trong đồ thị trên: 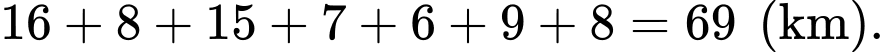
Nhận thấy đồ thị trên đều là bậc chẵn ( không có đỉnh bậc lẻ).
 Đồ thị tồn tại chu trình Euler: chu trình đi qua tất cả các cạnh của đồ thị đúng một lần (quãng đường tối thiểu).
Đồ thị tồn tại chu trình Euler: chu trình đi qua tất cả các cạnh của đồ thị đúng một lần (quãng đường tối thiểu).
 Chiều dài quãng đường tối thiểu thanh tra cần phải đi là tổng độ dài tất cả các quãng đường có trong đồ thị trên:
Chiều dài quãng đường tối thiểu thanh tra cần phải đi là tổng độ dài tất cả các quãng đường có trong đồ thị trên: 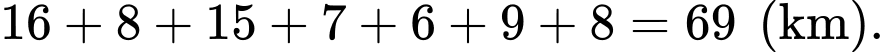
Câu 19 [693342]: Vắc xin AstraZeneca (AZD1222) được Tổ chức Y tế Thế giới (WHO) cấp phép sử dụng khẩn cấp giúp ngăn ngừa các triệu chứng nghiêm trọng và giảm tử vong do COVID-19. Vắc xin này được tiêm ở tỉnh X, thống kê cho thấy rằng: Với người có bệnh nền thì xác suất xảy ra phản ứng phụ sau tiêm là 28%, với người không có bệnh nền thì xác suất xảy ra phản ứng phụ sau tiêm là 17%. Chọn ngẫu nhiên một người được tiêm và thấy người này có phản ứng phụ. Tính xác suất để người này bị bệnh nền. Biết tỷ lệ người có bệnh nền ở tỉnh X là 12%. Làm tròn đến hàng phần trăm.
Điền đáp án: 0,18.
Gọi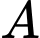 là biến cố “Người tiêm vắc xin có bệnh nền”.
là biến cố “Người tiêm vắc xin có bệnh nền”.
Và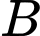 là biến cố “Xảy ra phản ứng phụ sau tiêm”.
là biến cố “Xảy ra phản ứng phụ sau tiêm”.
Ta có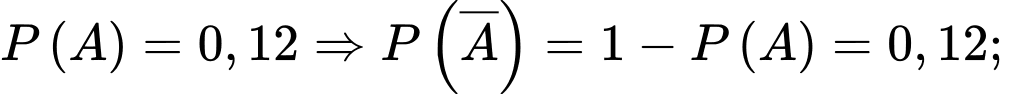
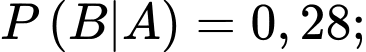
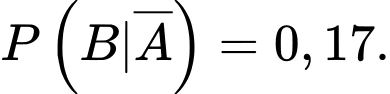
Từ dữ kiện đề bài, ta có sơ đồ cây sau:
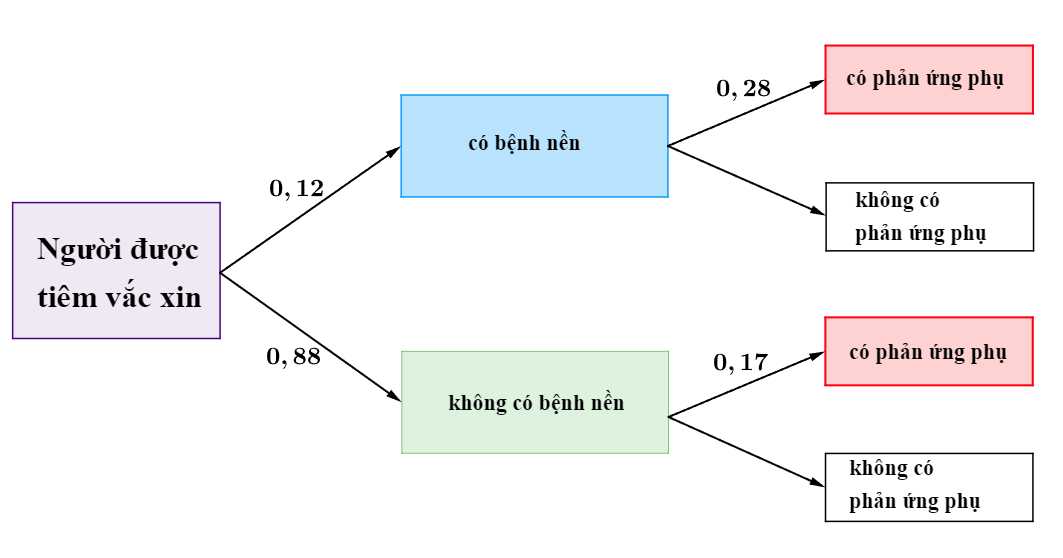
Suy ra xác suất người này có phản ứng phụ là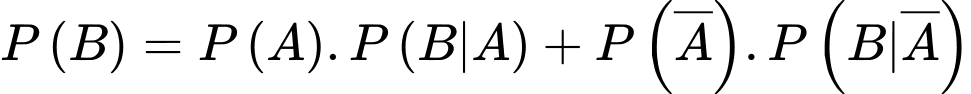
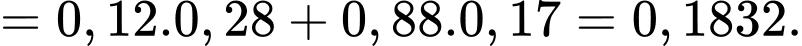
Áp dụng công thức Bayes, ta có xác suất người này có bệnh nền khi biết người này có phản ứng phụ là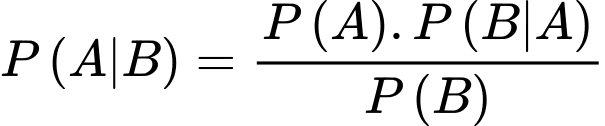
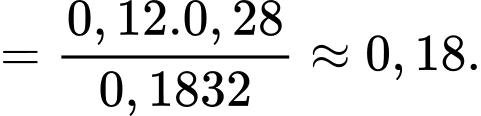
Gọi
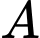 là biến cố “Người tiêm vắc xin có bệnh nền”.
là biến cố “Người tiêm vắc xin có bệnh nền”.
Và
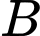 là biến cố “Xảy ra phản ứng phụ sau tiêm”.
là biến cố “Xảy ra phản ứng phụ sau tiêm”.
Ta có
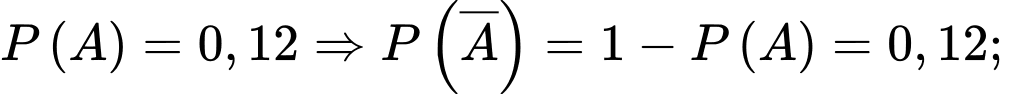
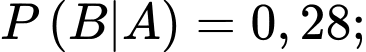
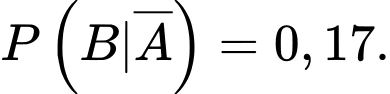
Từ dữ kiện đề bài, ta có sơ đồ cây sau:

Suy ra xác suất người này có phản ứng phụ là
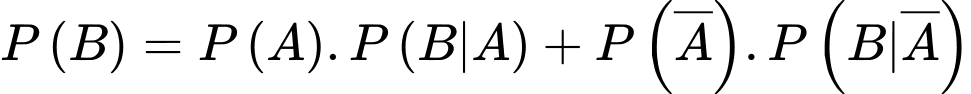
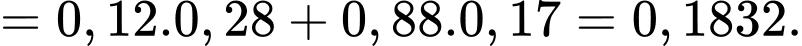
Áp dụng công thức Bayes, ta có xác suất người này có bệnh nền khi biết người này có phản ứng phụ là
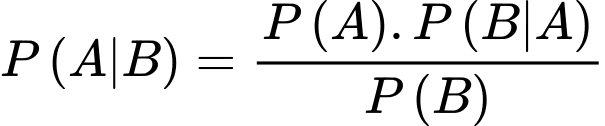
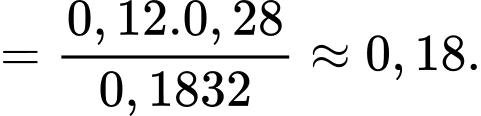
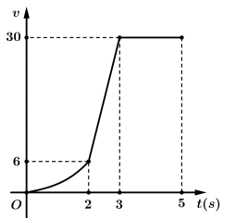
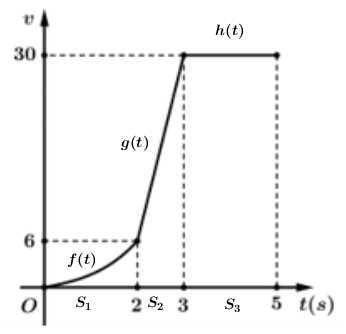
Câu 20 [505247]: Một chiếc xe đua Bugatti đang chuyển động trên đường đua. Đồ thị trên hình vẽ bên biểu thị vận tốc 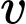 (m/s) của chiếc xe đó trong 5 giây đầu tiên. Đồ thị trong 2s đầu tiên là 1 nhánh của hàm bậc 3 nhận
(m/s) của chiếc xe đó trong 5 giây đầu tiên. Đồ thị trong 2s đầu tiên là 1 nhánh của hàm bậc 3 nhận  làm tâm đối xứng, trong giây tiếp theo xe tăng tốc với gia tốc
làm tâm đối xứng, trong giây tiếp theo xe tăng tốc với gia tốc 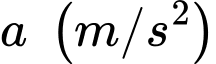 và đạt vận tốc
và đạt vận tốc 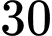 m/s tại giây thứ 3, sau đó duy trì vận tốc này đến giây thứ 5. Biết quãng đường xe đi được trong
m/s tại giây thứ 3, sau đó duy trì vận tốc này đến giây thứ 5. Biết quãng đường xe đi được trong 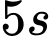 đầu bằng
đầu bằng 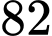 m. Vận tốc của xe tại giây đầu tiên bằng bao nhiêu? (tính theo đơn vị
m. Vận tốc của xe tại giây đầu tiên bằng bao nhiêu? (tính theo đơn vị 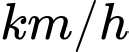 ).
).
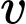 (m/s) của chiếc xe đó trong 5 giây đầu tiên. Đồ thị trong 2s đầu tiên là 1 nhánh của hàm bậc 3 nhận
(m/s) của chiếc xe đó trong 5 giây đầu tiên. Đồ thị trong 2s đầu tiên là 1 nhánh của hàm bậc 3 nhận  làm tâm đối xứng, trong giây tiếp theo xe tăng tốc với gia tốc
làm tâm đối xứng, trong giây tiếp theo xe tăng tốc với gia tốc 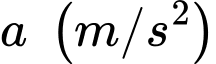 và đạt vận tốc
và đạt vận tốc 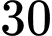 m/s tại giây thứ 3, sau đó duy trì vận tốc này đến giây thứ 5. Biết quãng đường xe đi được trong
m/s tại giây thứ 3, sau đó duy trì vận tốc này đến giây thứ 5. Biết quãng đường xe đi được trong 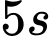 đầu bằng
đầu bằng 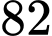 m. Vận tốc của xe tại giây đầu tiên bằng bao nhiêu? (tính theo đơn vị
m. Vận tốc của xe tại giây đầu tiên bằng bao nhiêu? (tính theo đơn vị 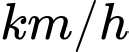 ).
).
Điền đáp án: 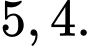
Ta có: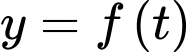 nhận
nhận  làm tâm đối xứng nên
làm tâm đối xứng nên 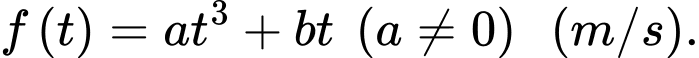
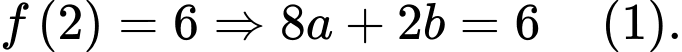
Quãng đường xe đi được trong 5 giây đầu bằng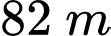 nên
nên 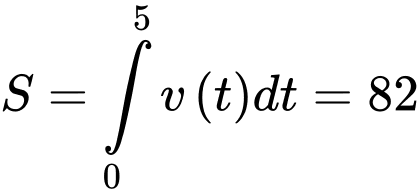
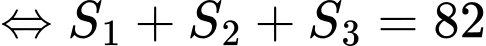
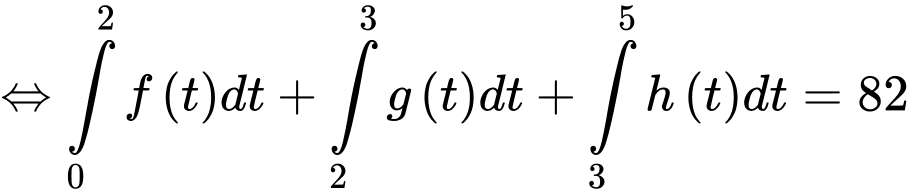
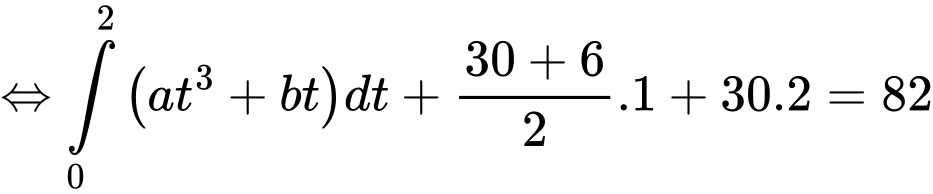
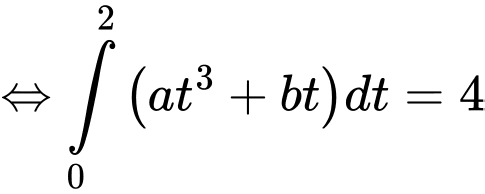
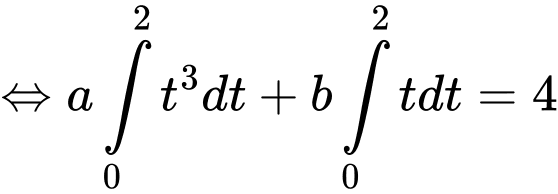
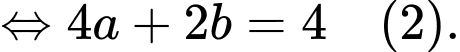
Từ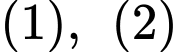 ta có:
ta có: 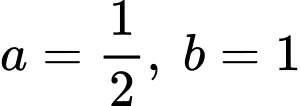
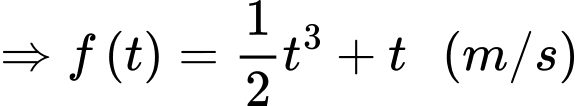
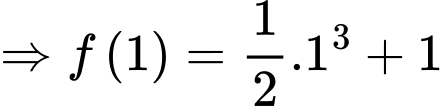
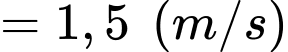

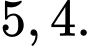

Ta có:
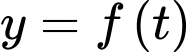 nhận
nhận  làm tâm đối xứng nên
làm tâm đối xứng nên 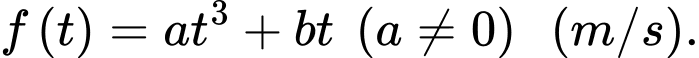
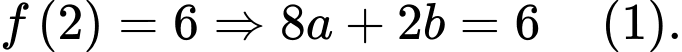
Quãng đường xe đi được trong 5 giây đầu bằng
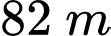 nên
nên 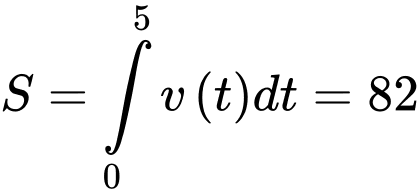
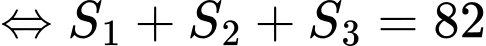
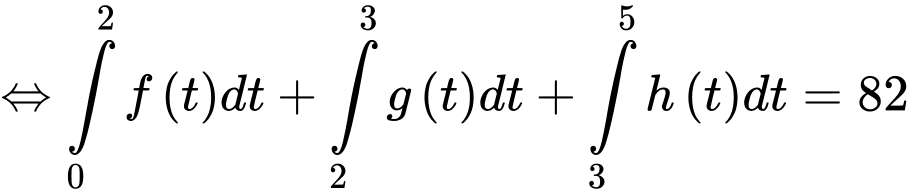
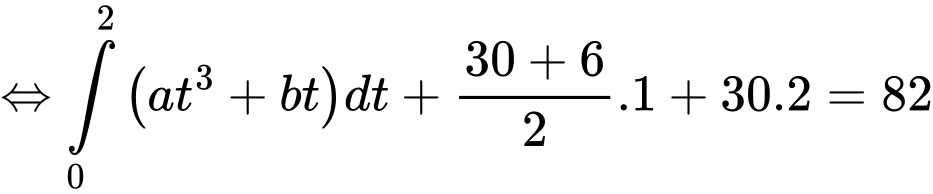
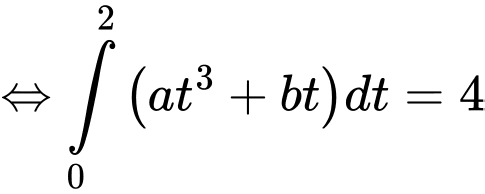
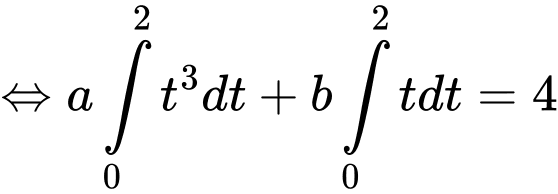
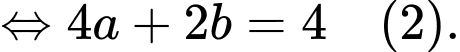
Từ
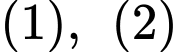 ta có:
ta có: 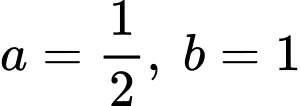
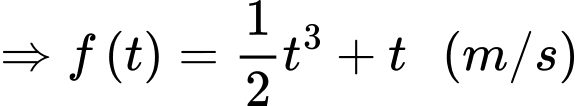
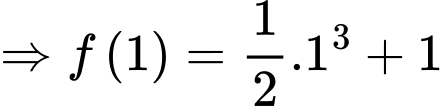
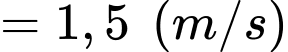

Câu 21 [693341]: Hệ thống mạch máu chứa các mạch máu gồm động mạch chính, động mạch con, mao mạch và tĩnh mạch để giúp đưa máu từ tim đến các cơ quan và ngược lại. Hệ thống hoạt động để tối ưu hoá (tối thiểu) năng lượng mà tim sử dụng trong quá trình bơm máu. Đặc biệt năng lượng này giảm khi sức cản của máu giảm. Hình vẽ dưới đây minh hoạ một mạch máu chính có bán kính 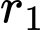 phân nhánh với một góc
phân nhánh với một góc 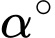 tạo thành một mạch máu nhỏ hơn với bán kính
tạo thành một mạch máu nhỏ hơn với bán kính 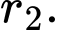
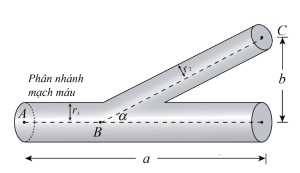
Sử dụng mô tả Định luật Poiseuille, người ta đã chứng minh được sức cản của máu theo con đường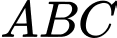 là
là 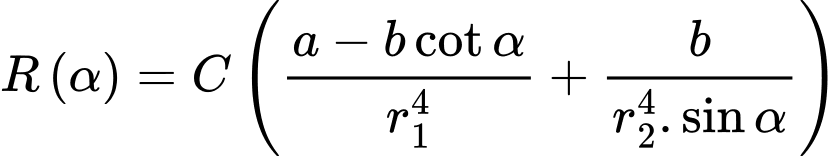 với
với 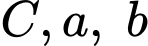 là các hằng số. Khi bán kính mạch máu nhỏ bằng
là các hằng số. Khi bán kính mạch máu nhỏ bằng 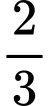 bán kính mạch máu chính. Xác định
bán kính mạch máu chính. Xác định 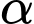 để sức cản này là nhỏ nhất. Làm tròn đến hàng đơn vị.
để sức cản này là nhỏ nhất. Làm tròn đến hàng đơn vị.
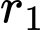 phân nhánh với một góc
phân nhánh với một góc 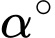 tạo thành một mạch máu nhỏ hơn với bán kính
tạo thành một mạch máu nhỏ hơn với bán kính 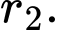

Sử dụng mô tả Định luật Poiseuille, người ta đã chứng minh được sức cản của máu theo con đường
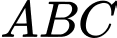 là
là 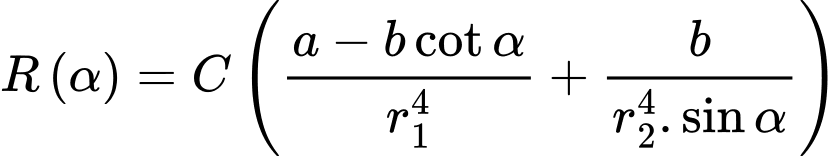 với
với 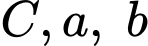 là các hằng số. Khi bán kính mạch máu nhỏ bằng
là các hằng số. Khi bán kính mạch máu nhỏ bằng 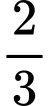 bán kính mạch máu chính. Xác định
bán kính mạch máu chính. Xác định 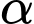 để sức cản này là nhỏ nhất. Làm tròn đến hàng đơn vị.
để sức cản này là nhỏ nhất. Làm tròn đến hàng đơn vị.
Điền đáp án: 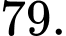
Ta có:
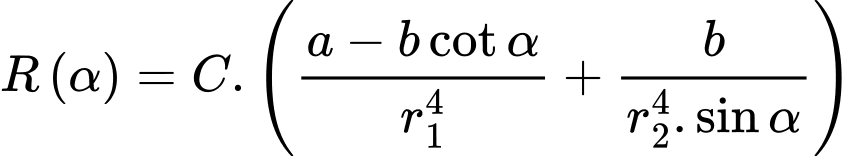
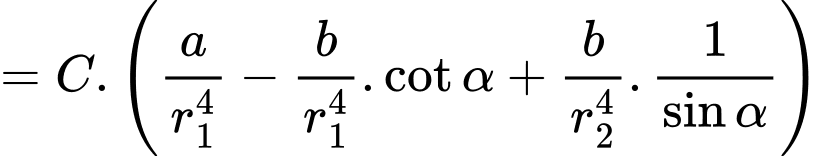
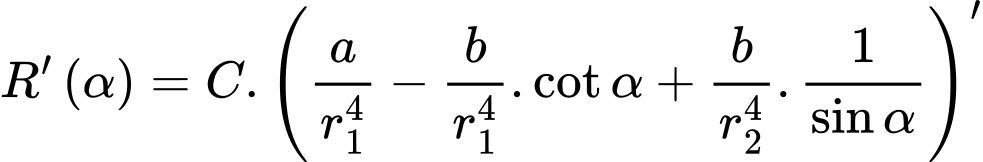
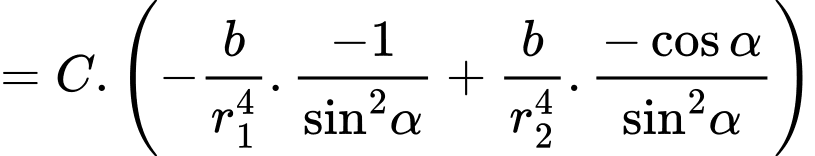
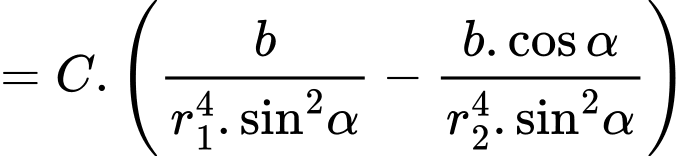
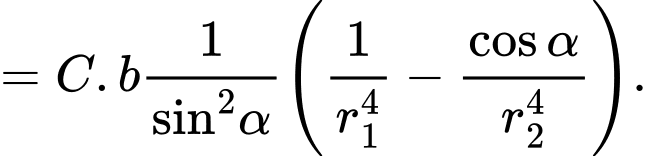
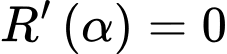
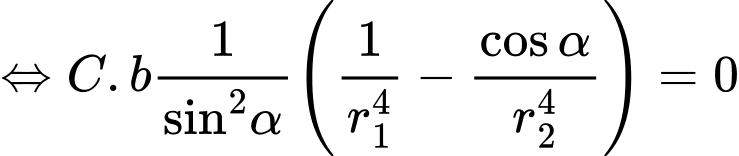
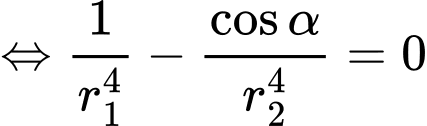
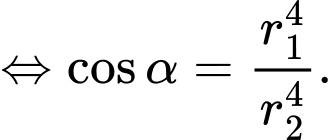
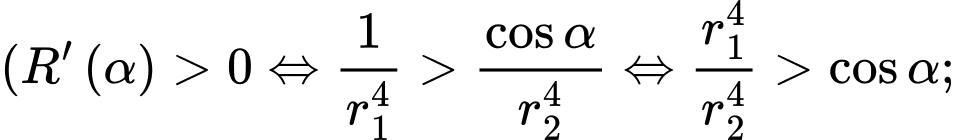
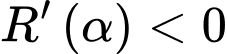
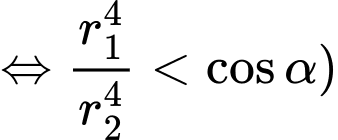
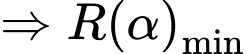 khi
khi 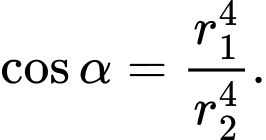
Do đó: Khi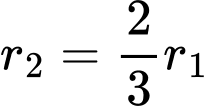
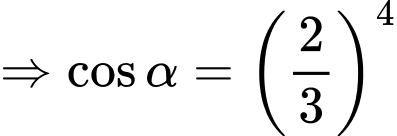
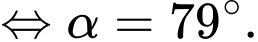
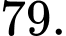
Ta có:
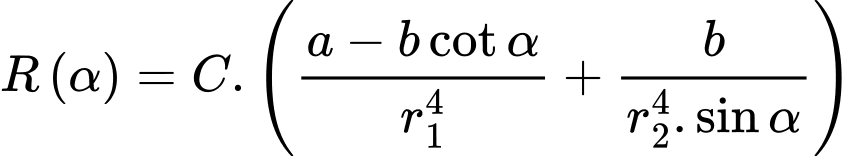
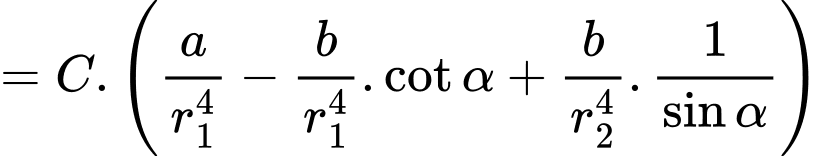
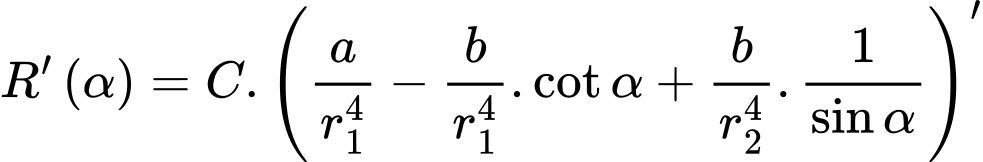
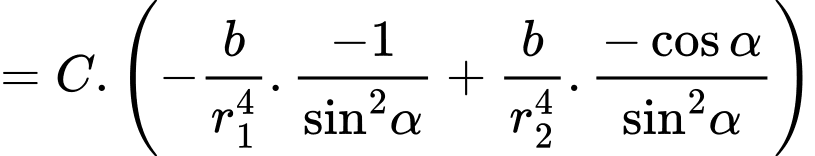
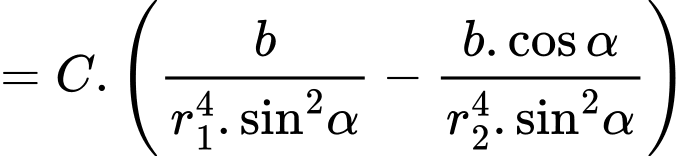
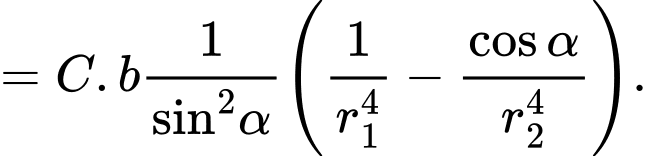
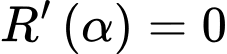
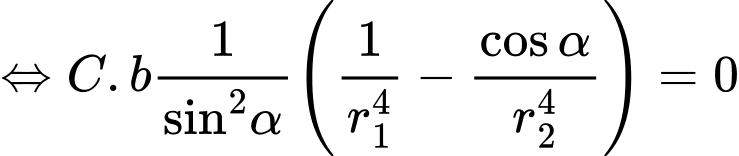
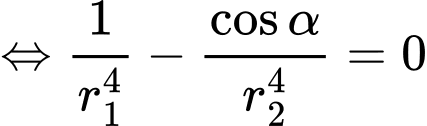
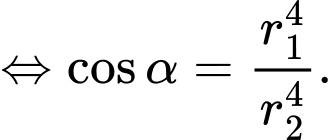
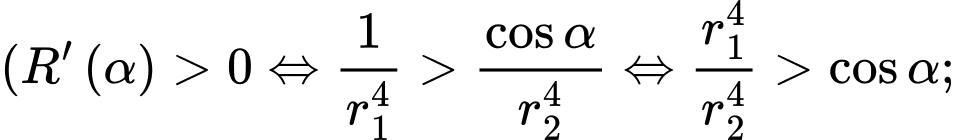
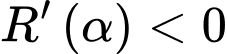
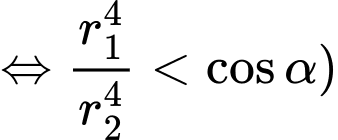
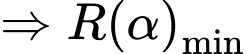 khi
khi 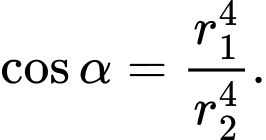
Do đó: Khi
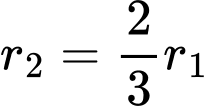
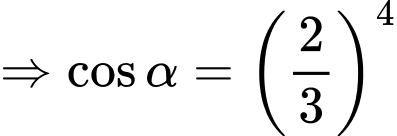
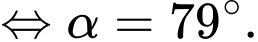
Câu 22 [693343]: Trong hệ toạ độ 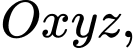 có một mặt mặt cầu
có một mặt mặt cầu 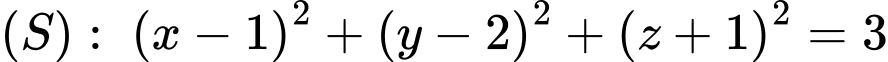 và đường thẳng
và đường thẳng 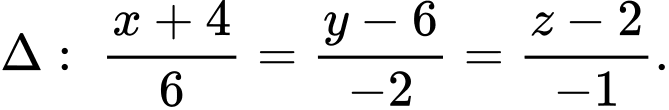 Từ điểm
Từ điểm 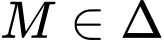 kẻ các tiếp tuyến đến mặt cầu
kẻ các tiếp tuyến đến mặt cầu 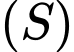 và gọi
và gọi  là tập hợp các tiếp điểm. Biết diện tích hình phẳng giới hạn bởi
là tập hợp các tiếp điểm. Biết diện tích hình phẳng giới hạn bởi  đạt giá trị nhỏ nhất thì
đạt giá trị nhỏ nhất thì  thuộc mặt phẳng
thuộc mặt phẳng 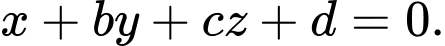 Tìm
Tìm 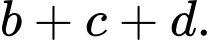
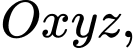 có một mặt mặt cầu
có một mặt mặt cầu 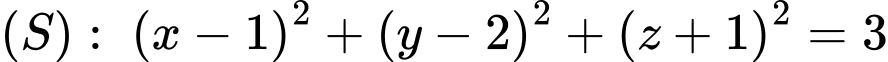 và đường thẳng
và đường thẳng 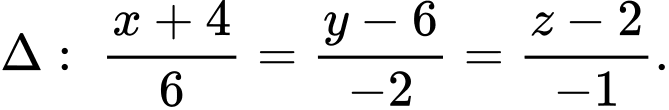 Từ điểm
Từ điểm 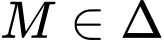 kẻ các tiếp tuyến đến mặt cầu
kẻ các tiếp tuyến đến mặt cầu 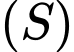 và gọi
và gọi  là tập hợp các tiếp điểm. Biết diện tích hình phẳng giới hạn bởi
là tập hợp các tiếp điểm. Biết diện tích hình phẳng giới hạn bởi  đạt giá trị nhỏ nhất thì
đạt giá trị nhỏ nhất thì  thuộc mặt phẳng
thuộc mặt phẳng 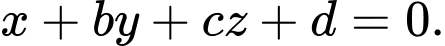 Tìm
Tìm 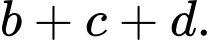
Điền đáp án: 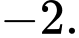
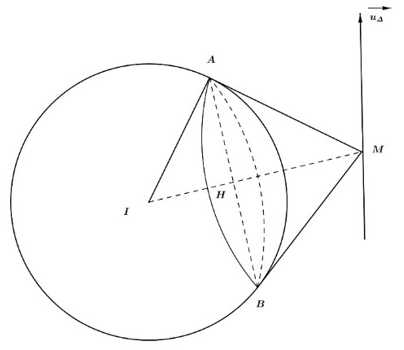
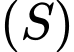 có tâm
có tâm 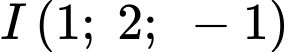 và bán kính
và bán kính 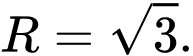
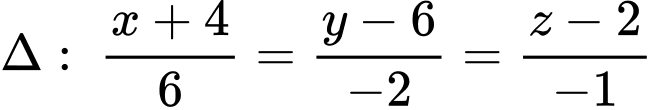 hay
hay 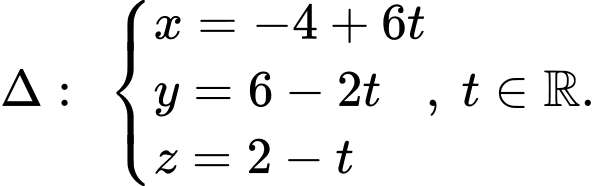 Lấy
Lấy 
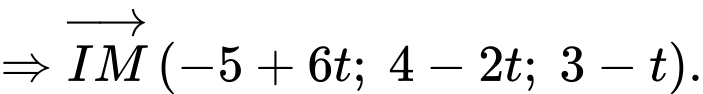
Diện tích hình phẳng giới hạn bởi bằng
bằng 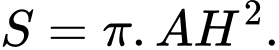
Do đó: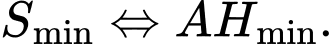
Mà
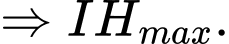
Lại có: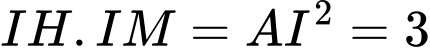
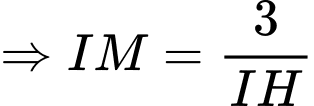
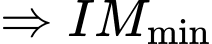
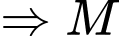 là hình chiếu của
là hình chiếu của 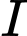 xuống
xuống 
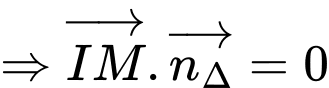
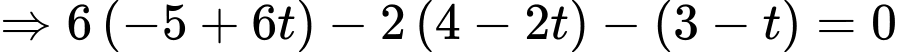
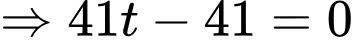
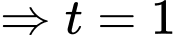
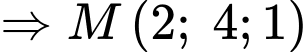
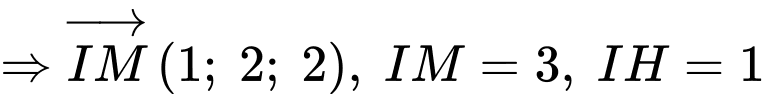
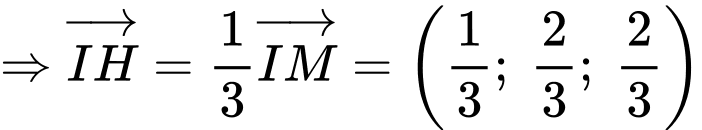
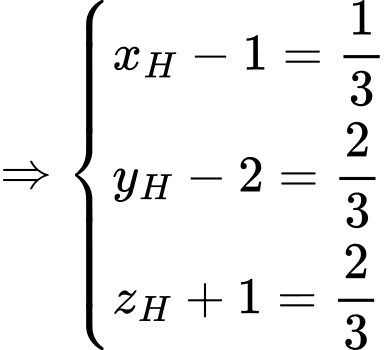
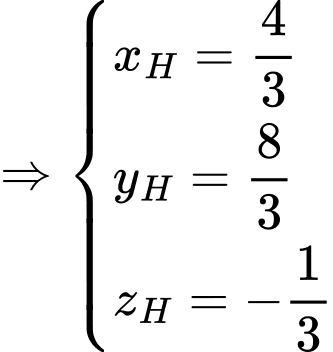
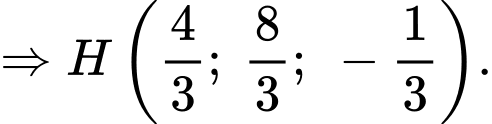
 đi qua
đi qua 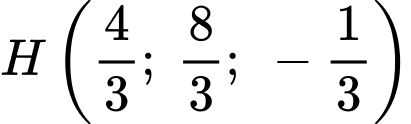 và có vectơ pháp tuyến
và có vectơ pháp tuyến 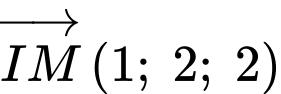 có phương trình là
có phương trình là 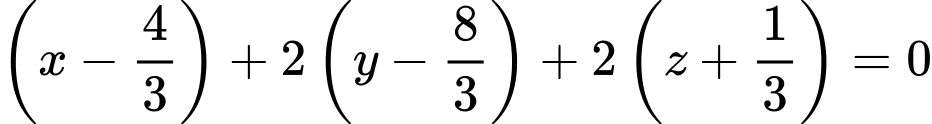 hay
hay 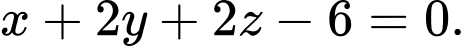
Vậy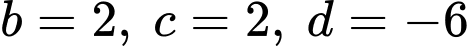 hay
hay 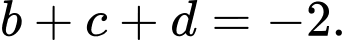
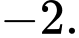

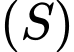 có tâm
có tâm 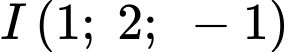 và bán kính
và bán kính 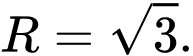
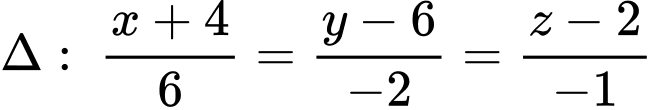 hay
hay 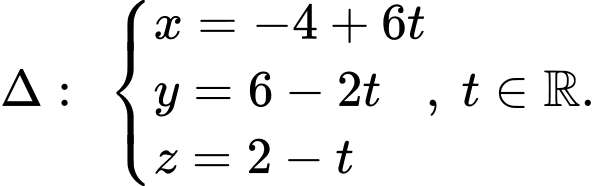 Lấy
Lấy 
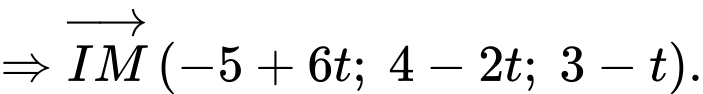
Diện tích hình phẳng giới hạn bởi
 bằng
bằng 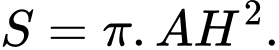
Do đó:
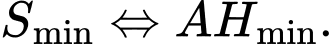
Mà

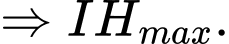
Lại có:
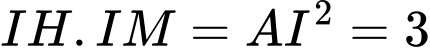
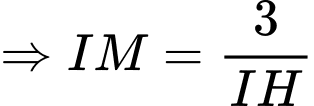
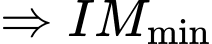
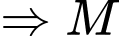 là hình chiếu của
là hình chiếu của 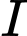 xuống
xuống 
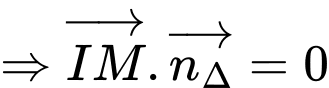
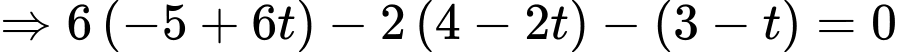
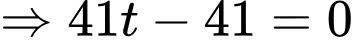
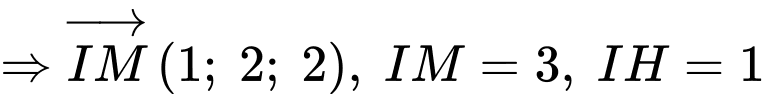
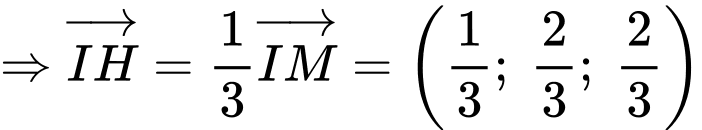
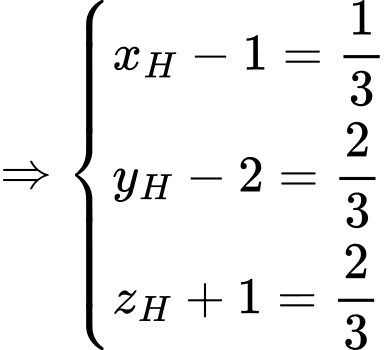
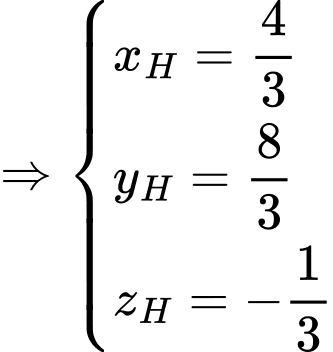
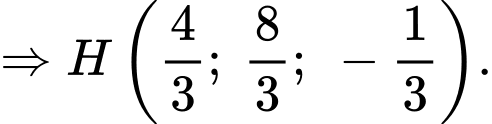
 đi qua
đi qua 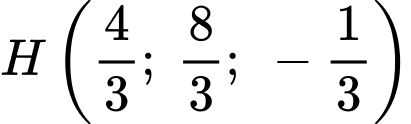 và có vectơ pháp tuyến
và có vectơ pháp tuyến 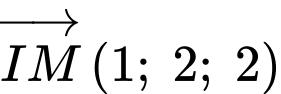 có phương trình là
có phương trình là 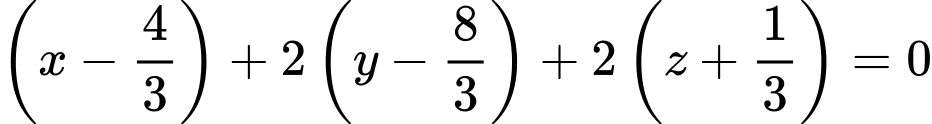 hay
hay 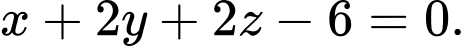
Vậy
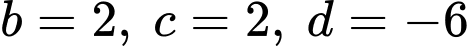 hay
hay