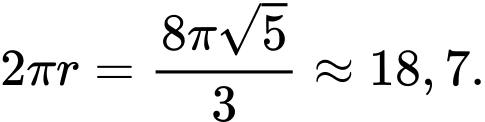PHẦN I. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Câu 1 [695045]: Hàm số 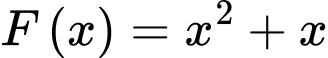 là một nguyên hàm của hàm số nào dưới đây?
là một nguyên hàm của hàm số nào dưới đây?
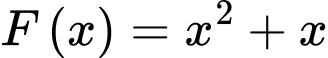 là một nguyên hàm của hàm số nào dưới đây?
là một nguyên hàm của hàm số nào dưới đây? A, 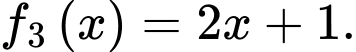
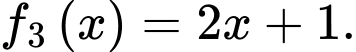
B, 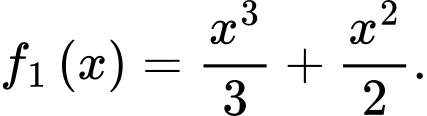
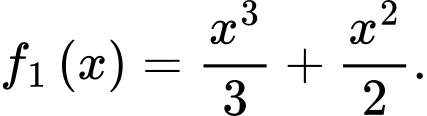
C, 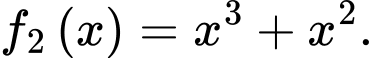
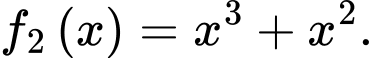
D, 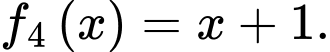
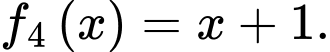
Chọn đáp án A.
Ta có: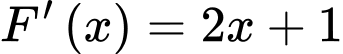 Đáp án: A
Đáp án: A
Ta có:
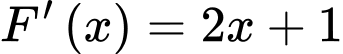 Đáp án: A
Đáp án: A
Câu 2 [547586]: Khảo sát thời gian xem ti vi trong một ngày của một số học sinh khối 11 thu được mẫu số liệu ghép nhóm sau:

Số học sinh xem ti vi từ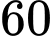 phút đến dưới
phút đến dưới 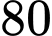 phút là
phút là

Số học sinh xem ti vi từ
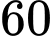 phút đến dưới
phút đến dưới 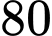 phút là
phút là A, 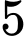 .
.
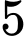 .
.B,  .
.
 .
.C, 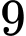 .
.
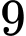 .
.D,  .
.
 .
.
Chọn đáp án D.
Dựa vào bảng trên ta thấy số học sinh thuộc nửa khoảng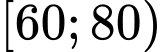 là 10. Đáp án: D
là 10. Đáp án: D
Dựa vào bảng trên ta thấy số học sinh thuộc nửa khoảng
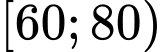 là 10. Đáp án: D
là 10. Đáp án: D Sử dụng thông tin dưới đây để trả lời câu 3 và câu 4
Trong không gian với hệ tọa độ Oxyz, cho 3 điểm A( - 1;0;0), B( 0;3;0), C(0;0;4).
Câu 3 [699817]: Phương trình nào dưới đây là phương trình của mặt phẳng 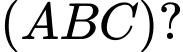
A, 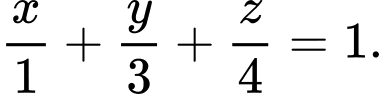
B, 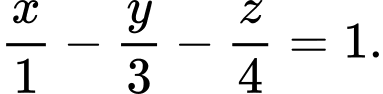
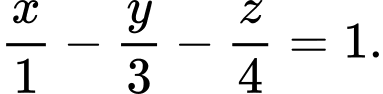
C, 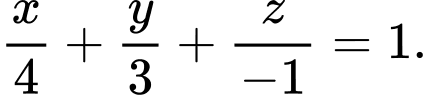
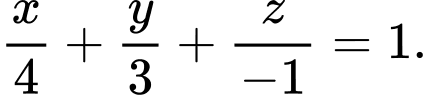
D, 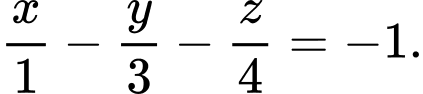
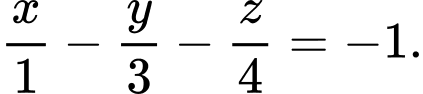
Chọn đáp án D.
Mặt phẳng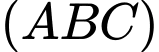 đi qua ba điểm
đi qua ba điểm 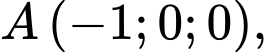
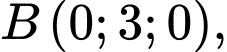
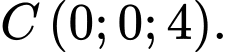
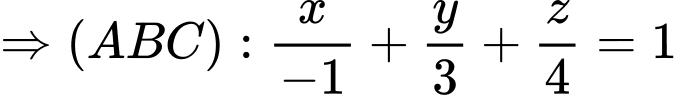
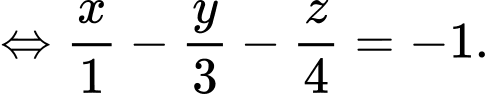 Đáp án: D
Đáp án: D
Mặt phẳng
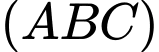 đi qua ba điểm
đi qua ba điểm 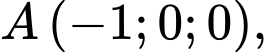
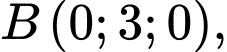
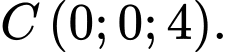
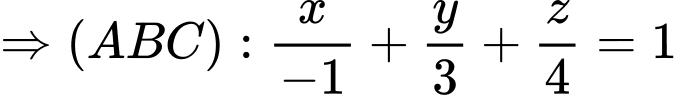
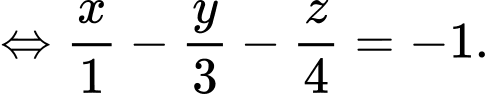 Đáp án: D
Đáp án: D
Câu 4 [699818]: Phương trình tham số của đường thẳng  là
là
 là
là A, 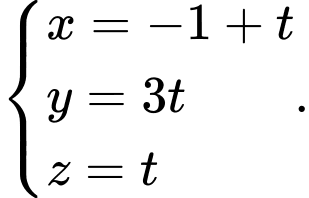
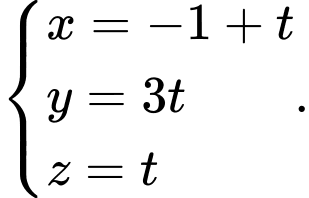
B, 
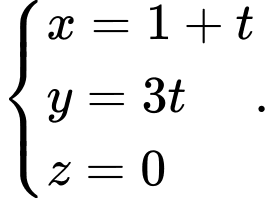
C, 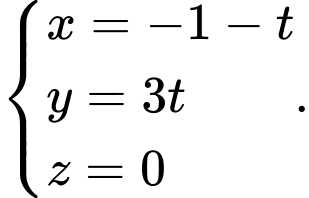
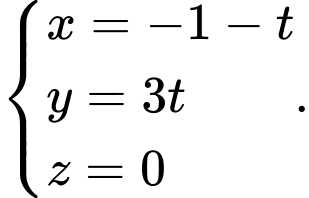
D, 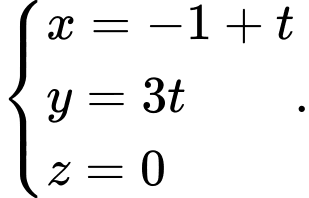
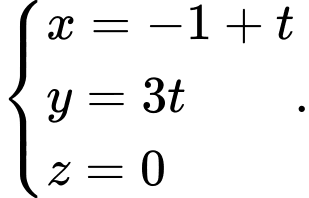
Chọn đáp án D.
Ta có vecto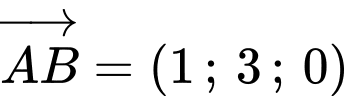
Phương trình đường thẳng nhận
nhận 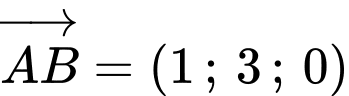 làm vecto chỉ phương và đi qua điểm
làm vecto chỉ phương và đi qua điểm 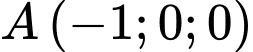 là:
là:
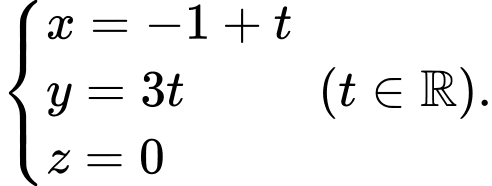 Đáp án: D
Đáp án: D
Ta có vecto
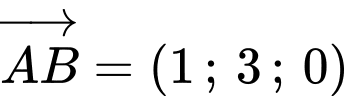
Phương trình đường thẳng
 nhận
nhận 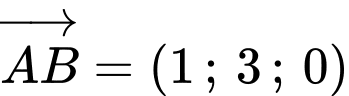 làm vecto chỉ phương và đi qua điểm
làm vecto chỉ phương và đi qua điểm 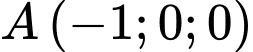 là:
là: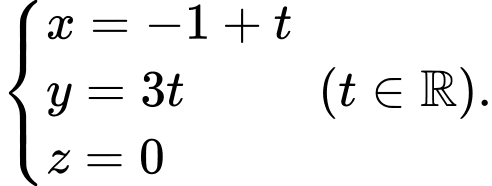 Đáp án: D
Đáp án: D
Câu 5 [256724]: Cho hàm số 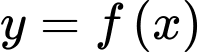 có bảng biến thiên như hình sau:
có bảng biến thiên như hình sau:

Số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số đã cho là
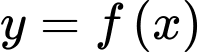 có bảng biến thiên như hình sau:
có bảng biến thiên như hình sau:
Số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số đã cho là
A, 
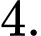
B, 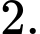
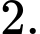
C, 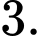
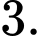
D, 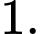
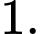
Chọn đáp án B.
Dựa vào bảng biến thiên, ta có:
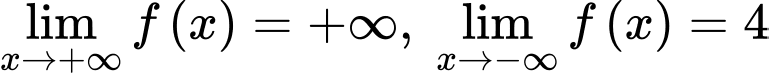 nên đồ thị hàm số có 1 TCN là
nên đồ thị hàm số có 1 TCN là 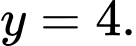
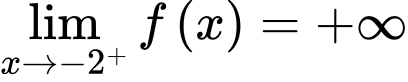 nên đồ thị hàm số có 1 TCĐ là
nên đồ thị hàm số có 1 TCĐ là 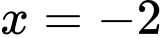 .
.
Vậy đồ thị hàm số có tổng cộng 2 đường tiệm cận. Đáp án: B
Dựa vào bảng biến thiên, ta có:
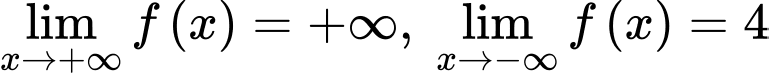 nên đồ thị hàm số có 1 TCN là
nên đồ thị hàm số có 1 TCN là 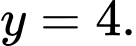
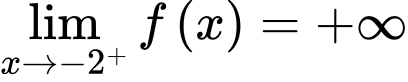 nên đồ thị hàm số có 1 TCĐ là
nên đồ thị hàm số có 1 TCĐ là 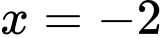 .
.Vậy đồ thị hàm số có tổng cộng 2 đường tiệm cận. Đáp án: B
Câu 6 [695046]: Bốn số 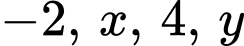 theo thứ tự lập thành cấp số cộng, khi đó
theo thứ tự lập thành cấp số cộng, khi đó  bằng
bằng
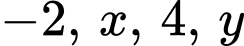 theo thứ tự lập thành cấp số cộng, khi đó
theo thứ tự lập thành cấp số cộng, khi đó  bằng
bằng A, 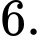
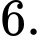
B, 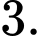
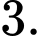
C, 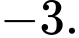
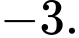
D, 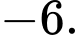
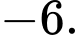
Chọn đáp án D.
Theo bài cho ta có: bốn số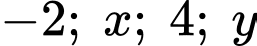 theo thứ tự lập thành cấp số cộng nên ta có hệ:
theo thứ tự lập thành cấp số cộng nên ta có hệ:
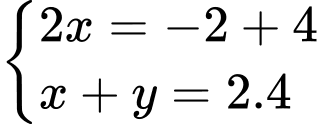
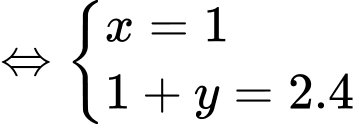
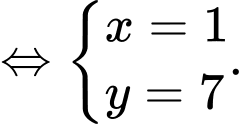
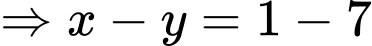
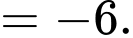 Đáp án: D
Đáp án: D
Theo bài cho ta có: bốn số
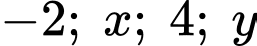 theo thứ tự lập thành cấp số cộng nên ta có hệ:
theo thứ tự lập thành cấp số cộng nên ta có hệ:
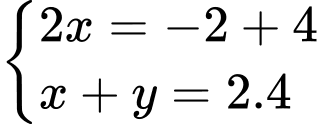
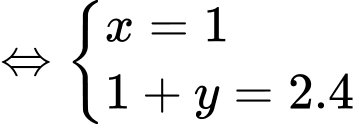
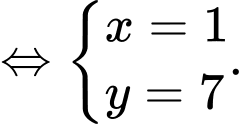
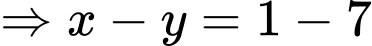
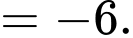 Đáp án: D
Đáp án: D
Câu 7 [695047]: Cho hình lăng trụ có thể tích bằng 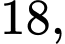 đáy là hình vuông cạnh bằng
đáy là hình vuông cạnh bằng 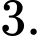 Chiều cao của khối lăng trụ đã cho bằng
Chiều cao của khối lăng trụ đã cho bằng
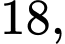 đáy là hình vuông cạnh bằng
đáy là hình vuông cạnh bằng 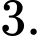 Chiều cao của khối lăng trụ đã cho bằng
Chiều cao của khối lăng trụ đã cho bằng A, 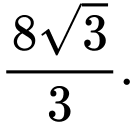
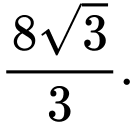
B, 
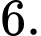
C, 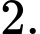
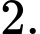
D, 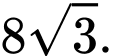
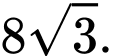
Chọn đáp án C.
Ta có: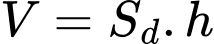
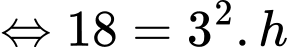
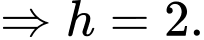 Đáp án: C
Đáp án: C
Ta có:
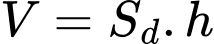
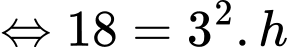
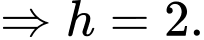 Đáp án: C
Đáp án: C
Câu 8 [695049]: Cho tứ diện đều 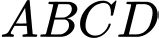 cạnh
cạnh 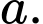 Độ dài của vectơ
Độ dài của vectơ 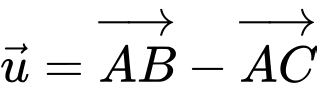 là
là
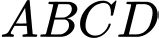 cạnh
cạnh 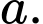 Độ dài của vectơ
Độ dài của vectơ 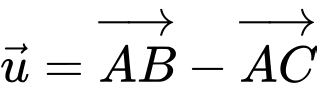 là
là A, 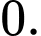
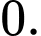
B, 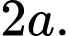
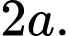
C, 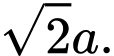
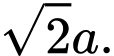
D, 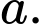
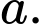
Chọn đáp án D.
Ta có: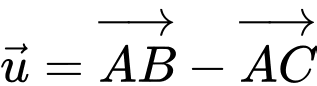
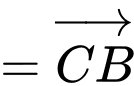
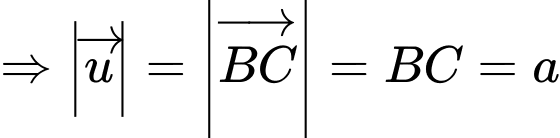 Đáp án: D
Đáp án: D
Ta có:
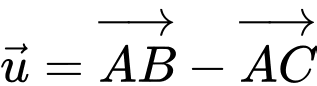
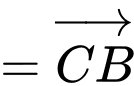
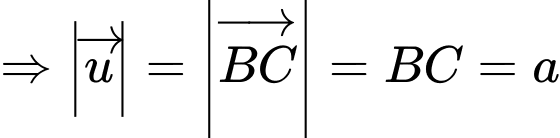 Đáp án: D
Đáp án: D
Câu 9 [50429]: Đạo hàm của hàm số 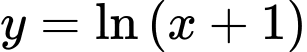 trên khoảng
trên khoảng 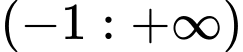 là
là
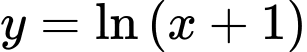 trên khoảng
trên khoảng 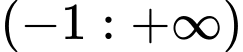 là
là A, 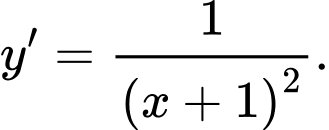
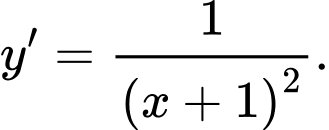
B, 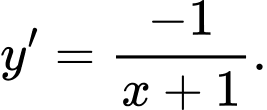
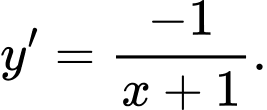
C, 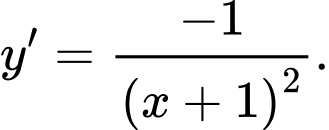
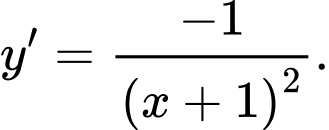
D, 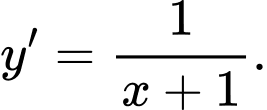
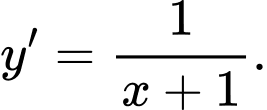
Chọn đáp án D
.
Chú ý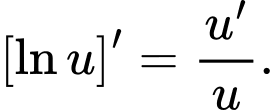
Nên ta có: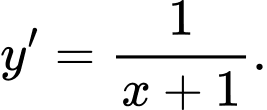 Đáp án: D
Đáp án: D
Chú ý
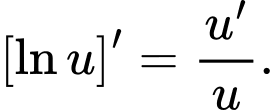
Nên ta có:
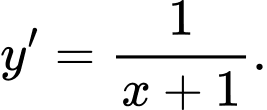 Đáp án: D
Đáp án: D
Câu 10 [699819]: Hàm số 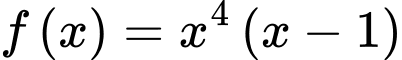 có bao nhiêu điểm cực trị?
có bao nhiêu điểm cực trị?
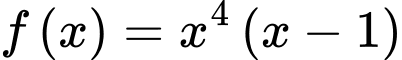 có bao nhiêu điểm cực trị?
có bao nhiêu điểm cực trị? A, 
B, 
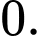
C, 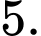
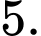
D, 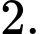
Chọn đáp án D.
Xét: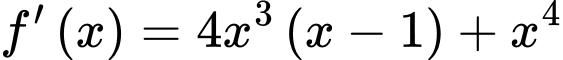
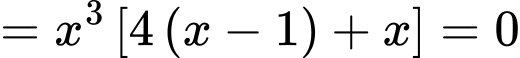
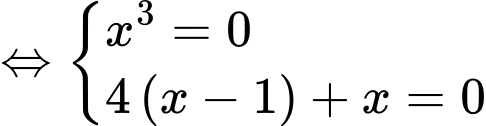
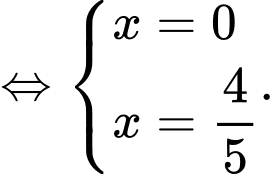
Phương trình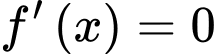 có hai nghiệm bội lẻ phân biệt
có hai nghiệm bội lẻ phân biệt
Vậy hàm số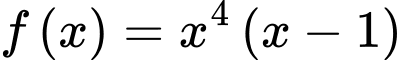 có hai điểm cực trị.
Đáp án: D
có hai điểm cực trị.
Đáp án: D
Xét:
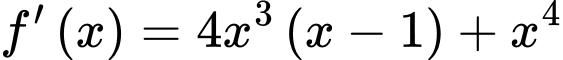
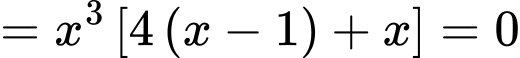
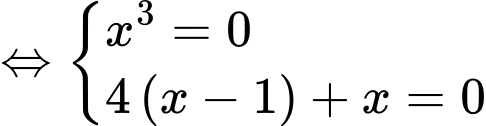
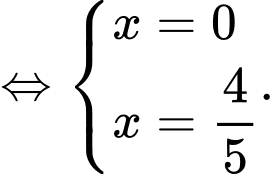
Phương trình
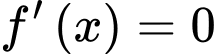 có hai nghiệm bội lẻ phân biệt
có hai nghiệm bội lẻ phân biệt
Vậy hàm số
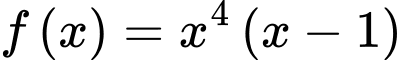 có hai điểm cực trị.
Đáp án: D
có hai điểm cực trị.
Đáp án: D
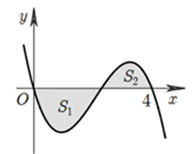
Câu 11 [256755]: Cho hàm số 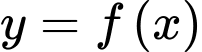 liên tục trên
liên tục trên 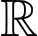 và có đồ thị như hình vẽ bên. Biết rằng các diện tích
và có đồ thị như hình vẽ bên. Biết rằng các diện tích 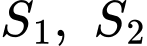 thỏa mãn
thỏa mãn 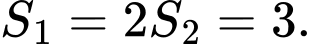 Tích phân
Tích phân 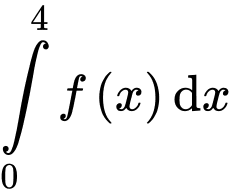 bằng
bằng
 liên tục trên
liên tục trên 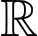 và có đồ thị như hình vẽ bên. Biết rằng các diện tích
và có đồ thị như hình vẽ bên. Biết rằng các diện tích 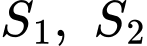 thỏa mãn
thỏa mãn 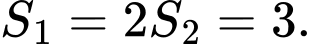 Tích phân
Tích phân 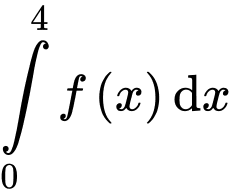 bằng
bằng
A, 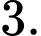
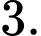
B, 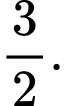
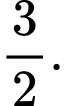
C, 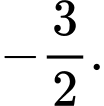
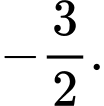
D, 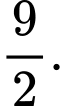
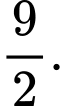
Chọn đáp án C.
Ta có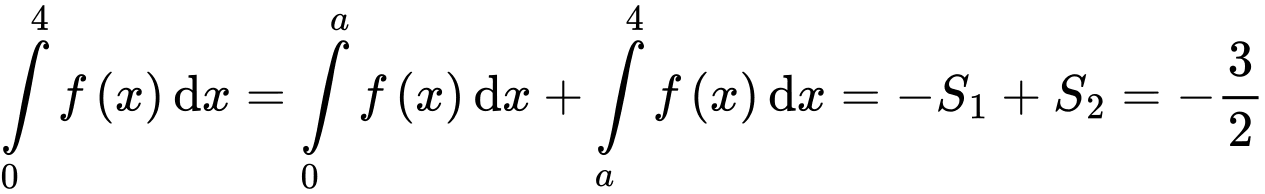 . Đáp án: C
. Đáp án: C
Ta có
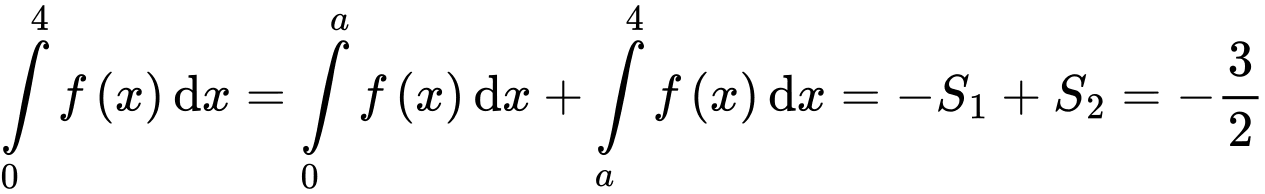 . Đáp án: C
. Đáp án: C
Câu 12 [695050]: Bất phương trình 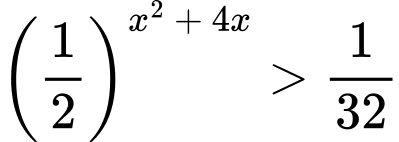 có tập nghiệm là
có tập nghiệm là  Khi đó giá trị của
Khi đó giá trị của 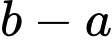 là
là
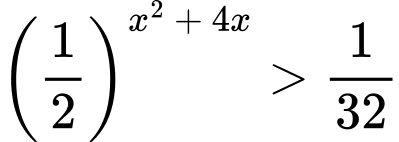 có tập nghiệm là
có tập nghiệm là  Khi đó giá trị của
Khi đó giá trị của 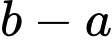 là
là A, 
B, 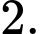
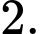
C, 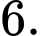
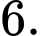
D, 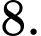
Chọn đáp án C.
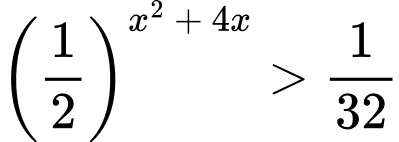
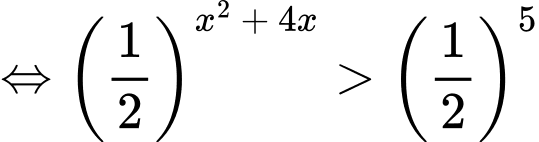
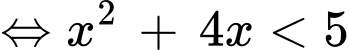
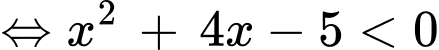

Vậy bất phương trình có tập nghiệm là 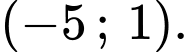 Khi đó
Khi đó 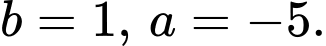
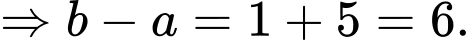 Đáp án: C
Đáp án: C
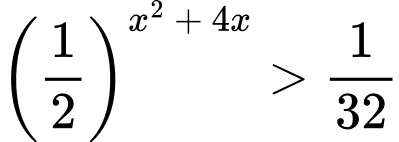
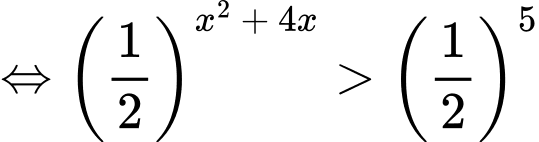
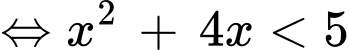
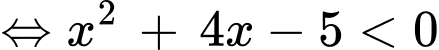

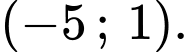 Khi đó
Khi đó 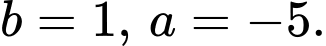
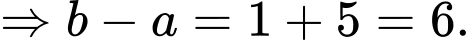 Đáp án: C
Đáp án: C PHẦN II. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Câu 13 [695053]: Trong không gian với hệ tọa độ 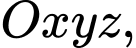 cho các điểm
cho các điểm 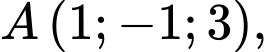
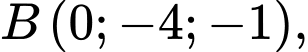
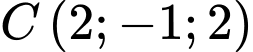 và
và 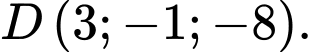 Xét tính đúng sai của các mệnh đề sau:
Xét tính đúng sai của các mệnh đề sau:
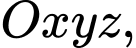 cho các điểm
cho các điểm 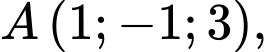
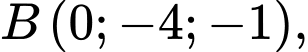
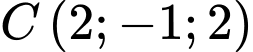 và
và 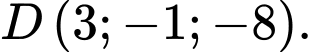 Xét tính đúng sai của các mệnh đề sau:
Xét tính đúng sai của các mệnh đề sau:
a) Đúng.
Ta có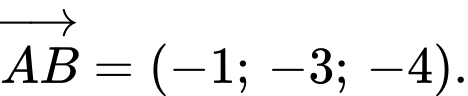
b) Đúng.
Mặt phẳng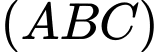 có 2 vectơ chỉ phương là
có 2 vectơ chỉ phương là 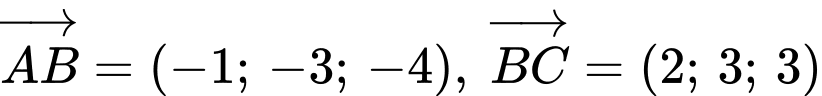
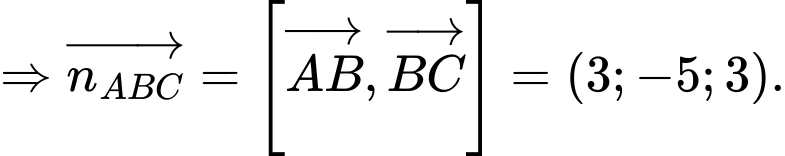
Do đó vectơ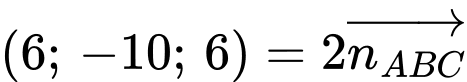 cũng là một vectơ pháp tuyến của mp
cũng là một vectơ pháp tuyến của mp 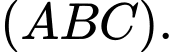
c) Đúng.
Mặt phẳng (ABC) đi qua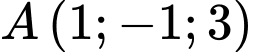 và nhận
và nhận 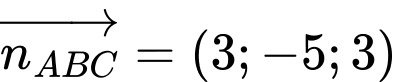 làm vectơ pháp tuyến nên có phương trình là
làm vectơ pháp tuyến nên có phương trình là 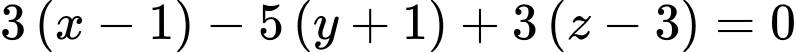
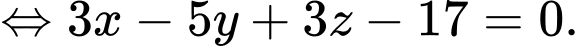
d) Sai.
Thay tọa độ điểm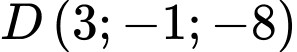 vào phương trình mp (ABC) ta thấy
vào phương trình mp (ABC) ta thấy  nên 4 điểm
nên 4 điểm 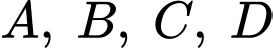 không đồng phẳng.
không đồng phẳng.
Ta có
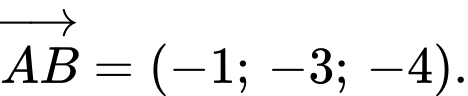
b) Đúng.
Mặt phẳng
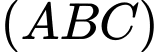 có 2 vectơ chỉ phương là
có 2 vectơ chỉ phương là 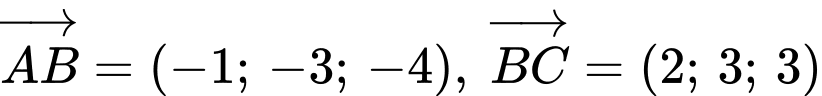
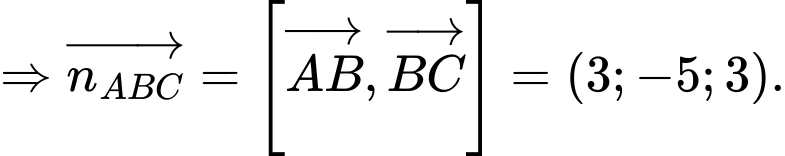
Do đó vectơ
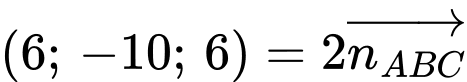 cũng là một vectơ pháp tuyến của mp
cũng là một vectơ pháp tuyến của mp 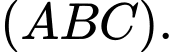
c) Đúng.
Mặt phẳng (ABC) đi qua
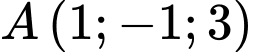 và nhận
và nhận 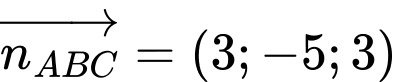 làm vectơ pháp tuyến nên có phương trình là
làm vectơ pháp tuyến nên có phương trình là 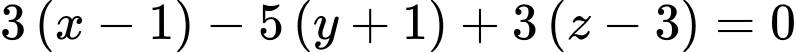
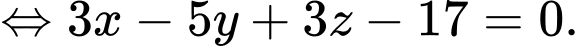
d) Sai.
Thay tọa độ điểm
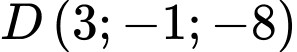 vào phương trình mp (ABC) ta thấy
vào phương trình mp (ABC) ta thấy  nên 4 điểm
nên 4 điểm 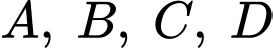 không đồng phẳng.
không đồng phẳng.
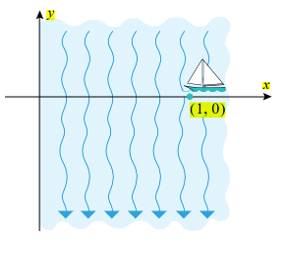
Câu 14 [693503]: Giả sử một chiếc thuyền vào sông tại điểm 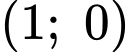 và giữ hướng về phía gốc tọa độ. Do dòng chảy mạnh, thuyền đi theo đường cong có phương trình
và giữ hướng về phía gốc tọa độ. Do dòng chảy mạnh, thuyền đi theo đường cong có phương trình 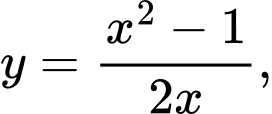 trong đó
trong đó 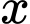 và
và 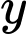 tính bằng kilomet (Như hình vẽ bên dưới).
tính bằng kilomet (Như hình vẽ bên dưới).
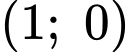 và giữ hướng về phía gốc tọa độ. Do dòng chảy mạnh, thuyền đi theo đường cong có phương trình
và giữ hướng về phía gốc tọa độ. Do dòng chảy mạnh, thuyền đi theo đường cong có phương trình 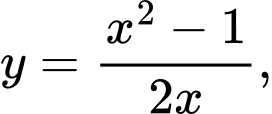 trong đó
trong đó 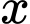 và
và 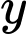 tính bằng kilomet (Như hình vẽ bên dưới).
tính bằng kilomet (Như hình vẽ bên dưới).
a) Sai.
Nếu duy trì hướng đi, thuyền sẽ đến được gốc tọa độ tức điểm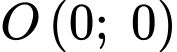 phải nằm trên phương trình đường đi của con thuyền.
phải nằm trên phương trình đường đi của con thuyền.
Vì hàm số không xác định tại điểm có toạ độ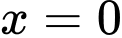 do đó hàm số sẽ không đi qua gốc toạ độ.
do đó hàm số sẽ không đi qua gốc toạ độ.
b) Sai.
Thay toạ độ của điểm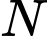 vào phương trình
vào phương trình 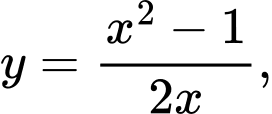 ta thấy không thoả mãn.
ta thấy không thoả mãn.
Do đó con tàu không đi qua điểm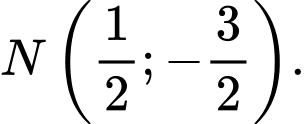
c) Sai.
Khoảng cách giữa con thuyền tại vị trí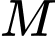 bất kì so với gốc toạ độ là
bất kì so với gốc toạ độ là 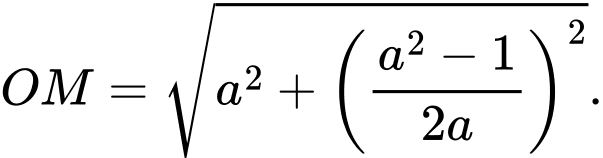
d) Sai.
Khoảng cách gần nhất giữa chiếc thuyền và gốc toạ độ bằng min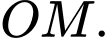
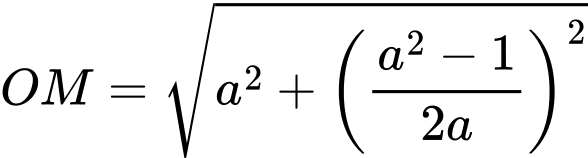
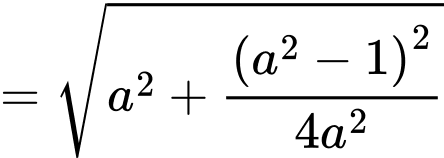
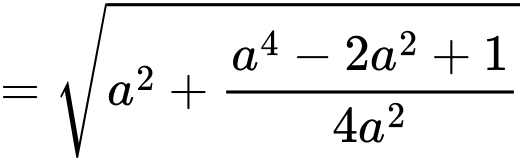
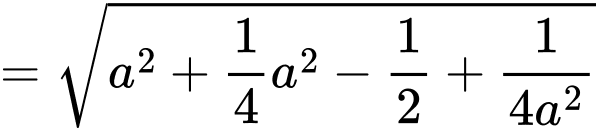
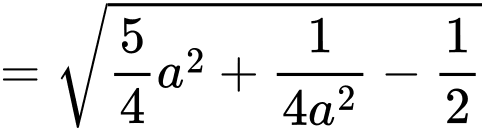
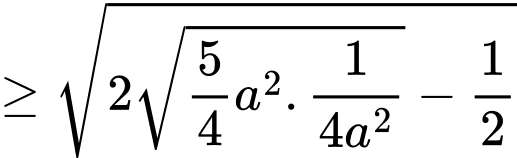
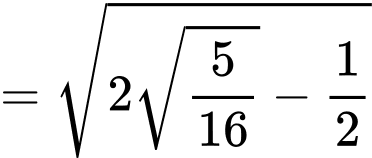
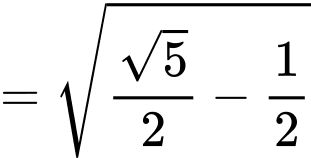
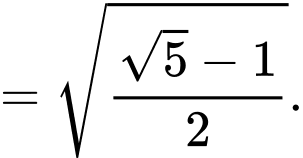
Dấu “=” xảy ra khi và chỉ khi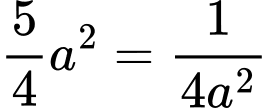
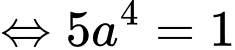
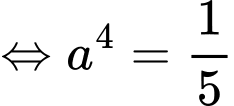
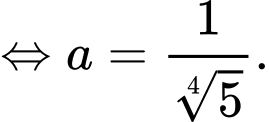
(Áp dụng bất đẳng thức Côsi cho 2 số dương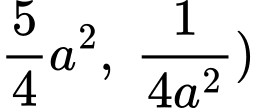
Vậy chiếc thuyền gần gốc toạ độ nhất một khoảng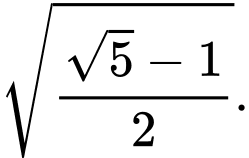
Nếu duy trì hướng đi, thuyền sẽ đến được gốc tọa độ tức điểm
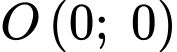 phải nằm trên phương trình đường đi của con thuyền.
phải nằm trên phương trình đường đi của con thuyền.
Vì hàm số không xác định tại điểm có toạ độ
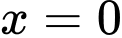 do đó hàm số sẽ không đi qua gốc toạ độ.
do đó hàm số sẽ không đi qua gốc toạ độ.
b) Sai.
Thay toạ độ của điểm
 vào phương trình
vào phương trình 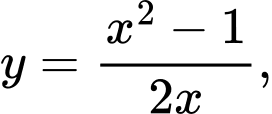 ta thấy không thoả mãn.
ta thấy không thoả mãn.
Do đó con tàu không đi qua điểm
c) Sai.
Khoảng cách giữa con thuyền tại vị trí
 bất kì so với gốc toạ độ là
bất kì so với gốc toạ độ là 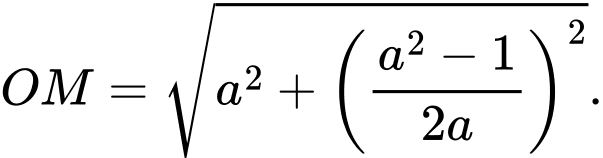
d) Sai.
Khoảng cách gần nhất giữa chiếc thuyền và gốc toạ độ bằng min
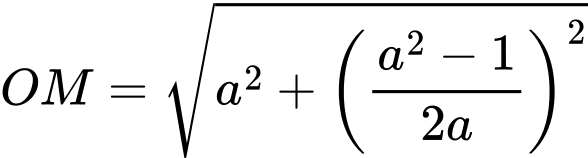
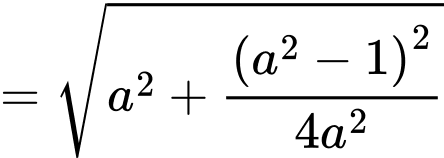
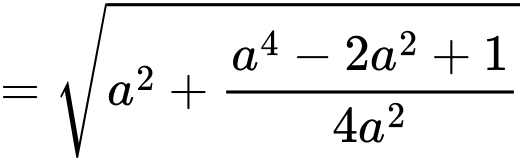
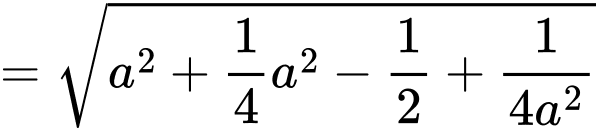
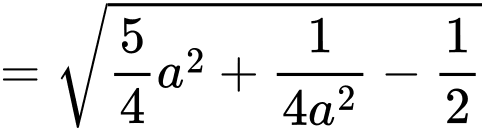
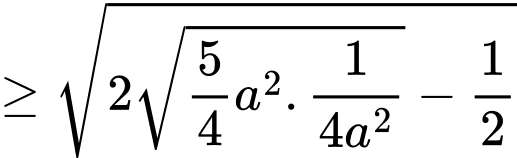
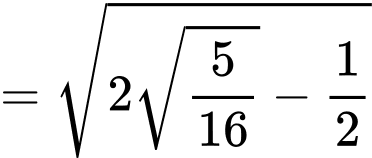
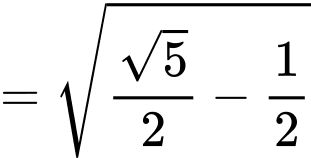
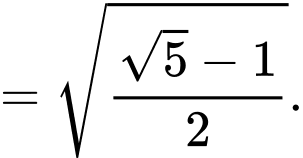
Dấu “=” xảy ra khi và chỉ khi
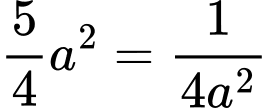
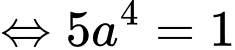
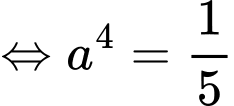
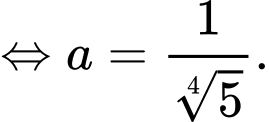
(Áp dụng bất đẳng thức Côsi cho 2 số dương
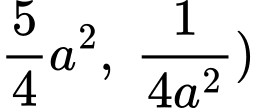
Vậy chiếc thuyền gần gốc toạ độ nhất một khoảng
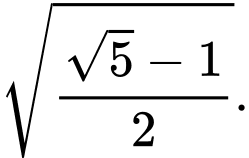
Câu 15 [695054]: Một doanh nghiệp có 45% nhân viên là nữ. Tỉ lệ nhân viên nữ và tỉ lệ nhân viên nam mua bảo hiểm nhân thọ lần lượt là 7% và 5%. Chọn ngẫu nhiên một nhân viên của doanh nghiệp
Gọi 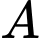 là biến cố “Nhân viên được chọn là nữ” và
là biến cố “Nhân viên được chọn là nữ” và 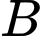 là biến cố “Nhân viên được chọn có mua bảo hiểm nhân thọ”.
là biến cố “Nhân viên được chọn có mua bảo hiểm nhân thọ”.
a) Sai.
Theo đề ta có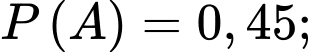
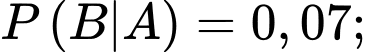
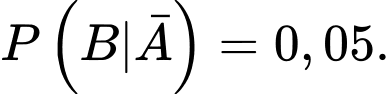 Suy ra
Suy ra 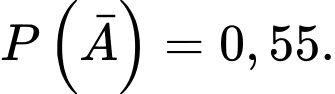
Vậy xác suất nhân viên được chọn là nam là 0,55.
b) Sai.
Ta có sơ đồ cây sau:
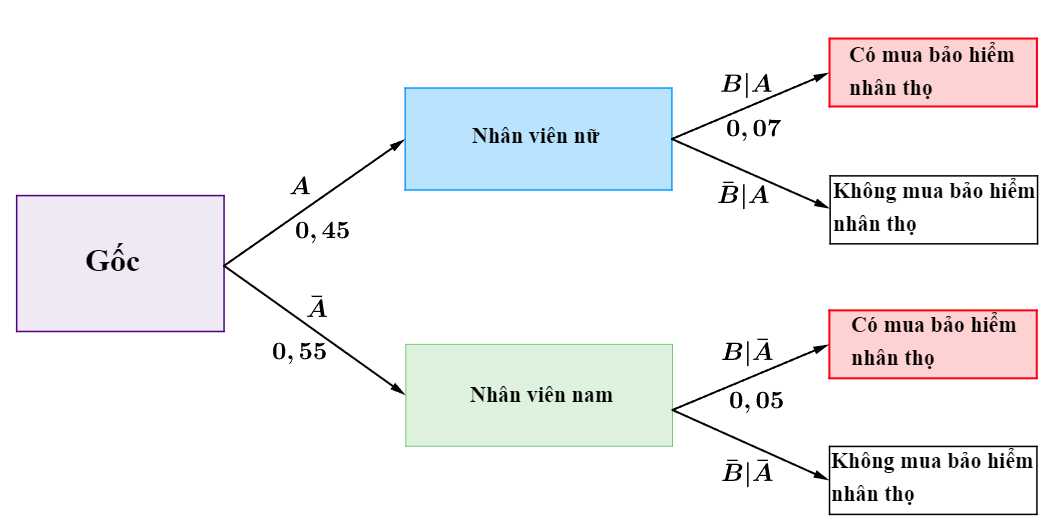
Ta có: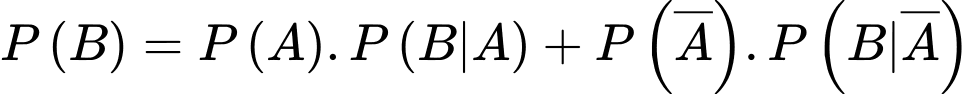 = 0,45.0,07 + 0,55.0,05 = 0,059.
= 0,45.0,07 + 0,55.0,05 = 0,059.
Vậy xác suất nhân viên được chọn có mua bảo hiểm nhân thọ là 0,059.
c) Đúng.
Ta có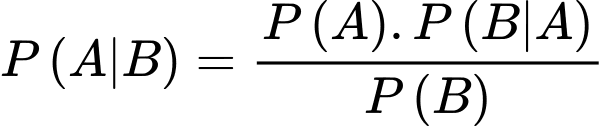
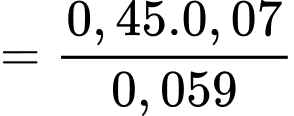
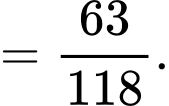
Vậy xác suất nhân viên được chọn có mua bảo hiểm nhân thọ là nữ là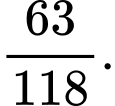
d) Sai.
Ta có: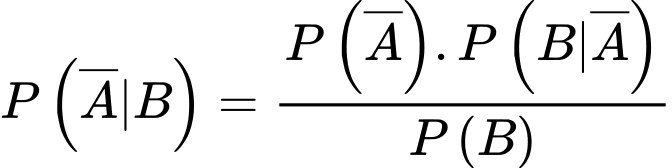
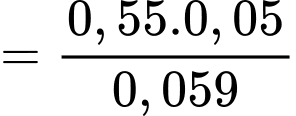
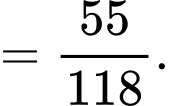
Vậy xác suất nhân viên được chọn có mua bảo hiểm nhân thọ là nam thấp hơn là nữ.
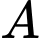 là biến cố “Nhân viên được chọn là nữ” và
là biến cố “Nhân viên được chọn là nữ” và 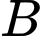 là biến cố “Nhân viên được chọn có mua bảo hiểm nhân thọ”.
là biến cố “Nhân viên được chọn có mua bảo hiểm nhân thọ”.a) Sai.
Theo đề ta có
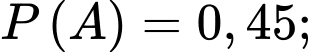
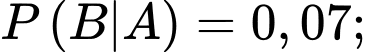
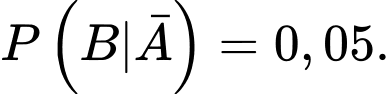 Suy ra
Suy ra 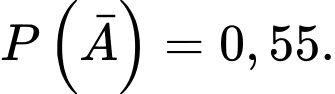
Vậy xác suất nhân viên được chọn là nam là 0,55.
b) Sai.
Ta có sơ đồ cây sau:

Ta có:
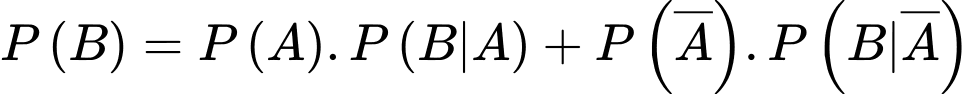 = 0,45.0,07 + 0,55.0,05 = 0,059.
= 0,45.0,07 + 0,55.0,05 = 0,059.Vậy xác suất nhân viên được chọn có mua bảo hiểm nhân thọ là 0,059.
c) Đúng.
Ta có
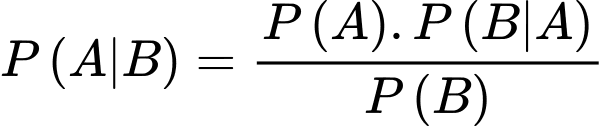
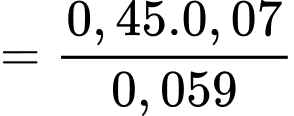
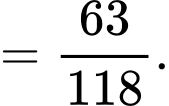
Vậy xác suất nhân viên được chọn có mua bảo hiểm nhân thọ là nữ là
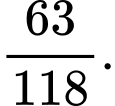
d) Sai.
Ta có:
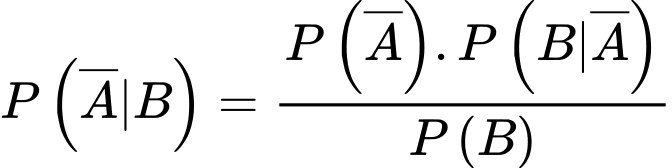
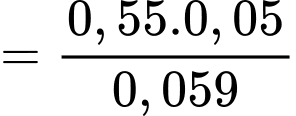
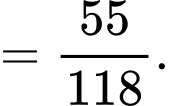
Vậy xác suất nhân viên được chọn có mua bảo hiểm nhân thọ là nam thấp hơn là nữ.
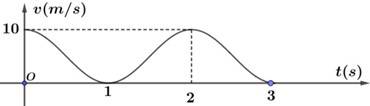
Câu 16 [695055]: Một chất điểm chuyển động trong 3 giây với vận tốc 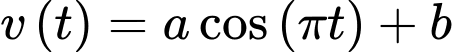 (mét/giây) (trong đó,
(mét/giây) (trong đó,  là biến thời gian;
là biến thời gian; 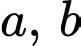 là các hằng số) có đồ thị là một đường hình sin như hình sau:
là các hằng số) có đồ thị là một đường hình sin như hình sau:
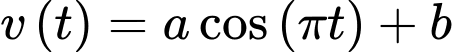 (mét/giây) (trong đó,
(mét/giây) (trong đó,  là biến thời gian;
là biến thời gian; 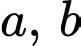 là các hằng số) có đồ thị là một đường hình sin như hình sau:
là các hằng số) có đồ thị là một đường hình sin như hình sau:
a) Đúng.
Dựa vào hình vẽ, ta thấy vận tốc của vật tại thời điểm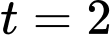 giây là
giây là  m/s.
m/s.
b) Đúng.
Quan sát hình vẽ, ta có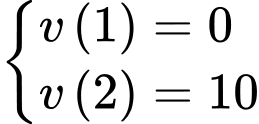
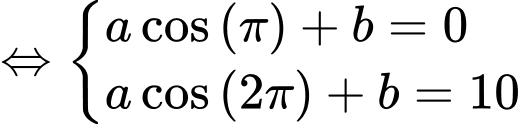
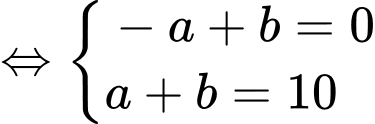
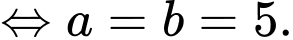
Suy ra
c) Sai.
d) Sai.
Ta có quãng đường vật đi được sau 3 giây là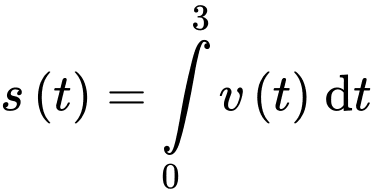
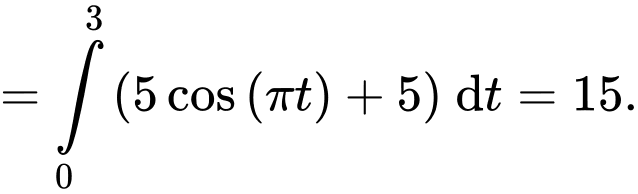
Dựa vào hình vẽ, ta thấy vận tốc của vật tại thời điểm
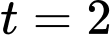 giây là
giây là  m/s.
m/s.b) Đúng.
Quan sát hình vẽ, ta có
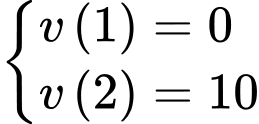
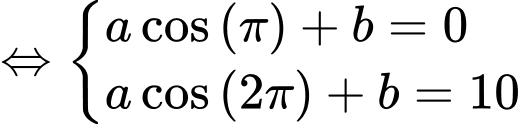
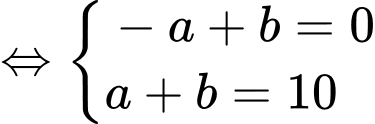
Suy ra

c) Sai.
d) Sai.
Ta có quãng đường vật đi được sau 3 giây là
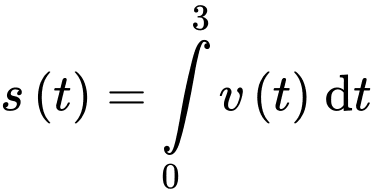
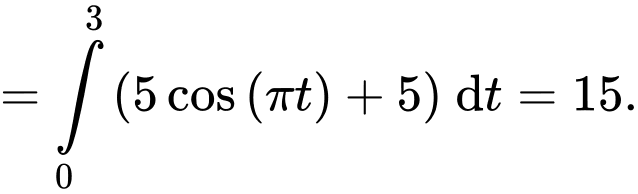
PHẦN III. Thí sinh trả lời từ câu 1 đến câu 6.
Câu 17 [695057]: Cho khối chóp đều 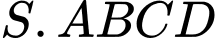 có
có 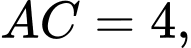 hai mặt phẳng
hai mặt phẳng 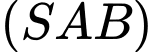 và
và  vuông góc với nhau. Thể tích của khối chóp đã cho bằng bao nhiêu? (làm tròn kết quả đến hàng phần mười).
vuông góc với nhau. Thể tích của khối chóp đã cho bằng bao nhiêu? (làm tròn kết quả đến hàng phần mười).
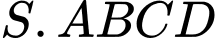 có
có 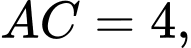 hai mặt phẳng
hai mặt phẳng 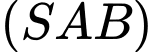 và
và  vuông góc với nhau. Thể tích của khối chóp đã cho bằng bao nhiêu? (làm tròn kết quả đến hàng phần mười).
vuông góc với nhau. Thể tích của khối chóp đã cho bằng bao nhiêu? (làm tròn kết quả đến hàng phần mười).
Điền đáp án: 
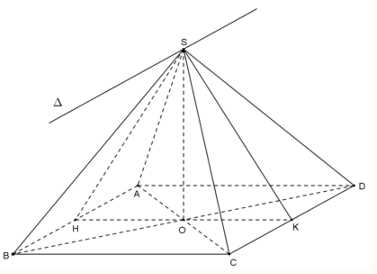
Gọi là tâm của hình vuông
là tâm của hình vuông 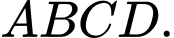
Do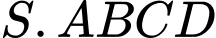 là hình chóp đều nên
là hình chóp đều nên 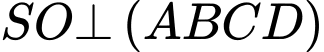

Ta có: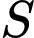 là một điểm chung của hai mặt phẳng
là một điểm chung của hai mặt phẳng 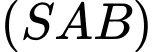 và
và 
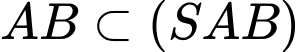 ;
; 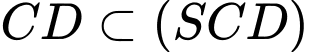 ;
; 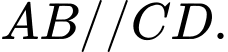
Suy ra hai mặt phẳng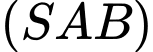 và
và  cắt nhau theo giao tuyến là đường thẳng
cắt nhau theo giao tuyến là đường thẳng  đi qua
đi qua 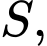 song song với
song song với  và
và 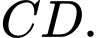
Gọi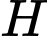 ;
; 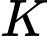 lần lượt là trung điểm của
lần lượt là trung điểm của  và
và 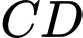
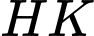 đi qua
đi qua  và
và 
Ta có: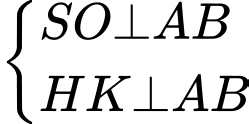

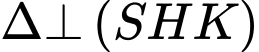 (Do
(Do 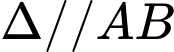 ).
).
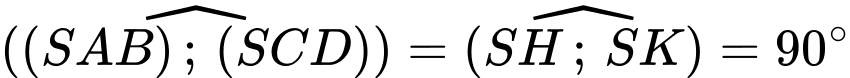
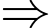

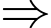 Tam giác
Tam giác 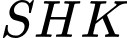 vuông tại
vuông tại 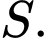
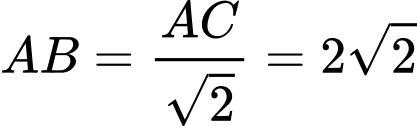 ;
; 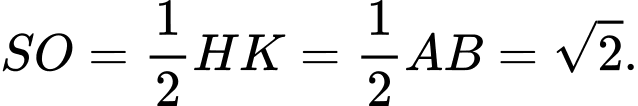
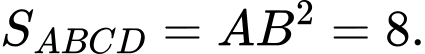
Vậy thể tích khối chóp là:
là:
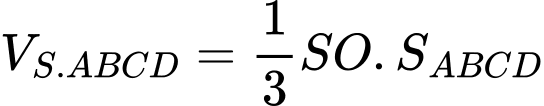
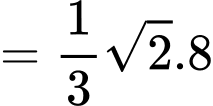
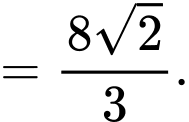

Gọi
 là tâm của hình vuông
là tâm của hình vuông 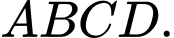
Do
 là hình chóp đều nên
là hình chóp đều nên 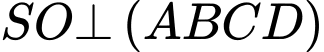

Ta có:
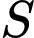 là một điểm chung của hai mặt phẳng
là một điểm chung của hai mặt phẳng 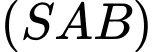 và
và 
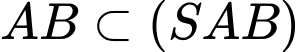 ;
; 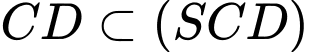 ;
; 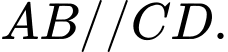
Suy ra hai mặt phẳng
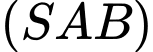 và
và  cắt nhau theo giao tuyến là đường thẳng
cắt nhau theo giao tuyến là đường thẳng  đi qua
đi qua 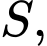 song song với
song song với  và
và 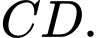
Gọi
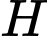 ;
; 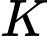 lần lượt là trung điểm của
lần lượt là trung điểm của  và
và 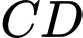
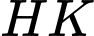 đi qua
đi qua  và
và 
Ta có:
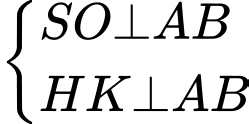

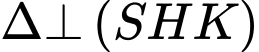 (Do
(Do 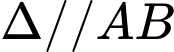 ).
).
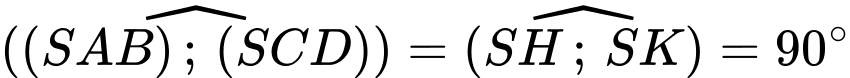

 Tam giác
Tam giác 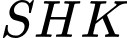 vuông tại
vuông tại 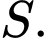
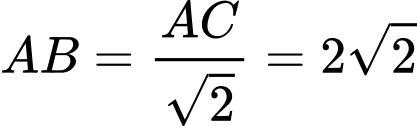 ;
; 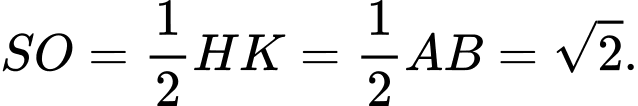
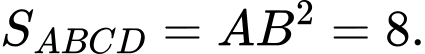
Vậy thể tích khối chóp
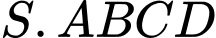 là:
là: 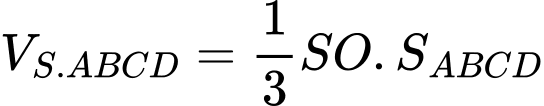
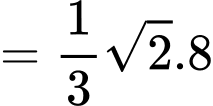
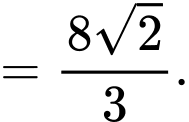
Câu 18 [695058]: Trong quán giải khát có bán các chai nước hoa quả với giá 15 000 đồng một chai, các chai rỗng sẽ đổi lấy 5 000 đồng. Bạn có thể uống được nhiều nhất bao nhiêu chai nếu trong túi bạn có 100 000 đồng?


Điền đáp án: 
Đầu tiên dùng 100 000 đồng ta sẽ mua được 6 chai nước và dư 10 000 đồng.
Uống 6 chai ta sẽ được 6 chai rỗng , sau đó đem đi đổi ta sẽ được 30 000 đồng.
Dùng 30 000 đồng trên mua được 2 chai nước mới.
Uống 2 chai nước mới ta được 2 chai rỗng, đem đi đổi ta được 10 000 đồng.
Cộng với 10 000 đồng còn dư ở phía trên ta được 20 000 đồng và mua được 1 chai nước mới.
Vậy ta có thể uống được nhiều nhất là 9 chai nước.
Đầu tiên dùng 100 000 đồng ta sẽ mua được 6 chai nước và dư 10 000 đồng.
Uống 6 chai ta sẽ được 6 chai rỗng , sau đó đem đi đổi ta sẽ được 30 000 đồng.
Dùng 30 000 đồng trên mua được 2 chai nước mới.
Uống 2 chai nước mới ta được 2 chai rỗng, đem đi đổi ta được 10 000 đồng.
Cộng với 10 000 đồng còn dư ở phía trên ta được 20 000 đồng và mua được 1 chai nước mới.
Vậy ta có thể uống được nhiều nhất là 9 chai nước.
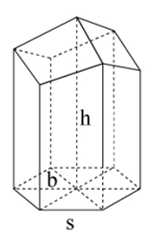
Câu 19 [695059]: Cấu trúc tổ ong là một cấu trúc đặc biệt, mỗi lỗ ong là một lăng kính hình lục giác, một đầu hở còn một đầu tạo thành một góc tam diện. Ong đã xây các lỗ này với một cách làm tối ưu về diện tích bề mặt (đã sử dụng lượng sáp ong (vật liệu) ít nhất để xây tổ). Người ta đã quan sát, nghiên cứu thì thấy rằng góc 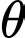 (rad) ở đỉnh nhất quán một cách đáng kinh ngạc, dựa trên cấu trúc hình học của lỗ ong đã chứng minh được diện tích bề mặt
(rad) ở đỉnh nhất quán một cách đáng kinh ngạc, dựa trên cấu trúc hình học của lỗ ong đã chứng minh được diện tích bề mặt 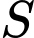 của lỗ ong là
của lỗ ong là 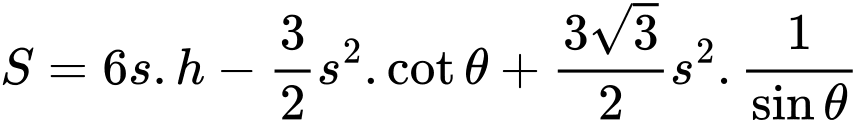
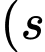 là chiều dài các cạnh của lỗ ong,
là chiều dài các cạnh của lỗ ong, 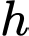 là chiều cao,
là chiều cao, 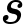 và
và 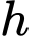 đều là hằng số). Vậy để tối thiểu hoá diện tích bề mặt (tối ưu) con ong đã xây một góc
đều là hằng số). Vậy để tối thiểu hoá diện tích bề mặt (tối ưu) con ong đã xây một góc 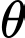 bằng bao nhiêu? Làm tròn đến hàng phần trăm.
bằng bao nhiêu? Làm tròn đến hàng phần trăm.
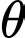 (rad) ở đỉnh nhất quán một cách đáng kinh ngạc, dựa trên cấu trúc hình học của lỗ ong đã chứng minh được diện tích bề mặt
(rad) ở đỉnh nhất quán một cách đáng kinh ngạc, dựa trên cấu trúc hình học của lỗ ong đã chứng minh được diện tích bề mặt 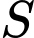 của lỗ ong là
của lỗ ong là 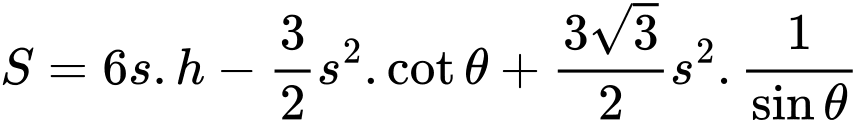
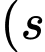 là chiều dài các cạnh của lỗ ong,
là chiều dài các cạnh của lỗ ong, 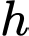 là chiều cao,
là chiều cao, 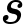 và
và 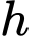 đều là hằng số). Vậy để tối thiểu hoá diện tích bề mặt (tối ưu) con ong đã xây một góc
đều là hằng số). Vậy để tối thiểu hoá diện tích bề mặt (tối ưu) con ong đã xây một góc 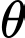 bằng bao nhiêu? Làm tròn đến hàng phần trăm.
bằng bao nhiêu? Làm tròn đến hàng phần trăm.
Điền đáp án: 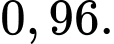
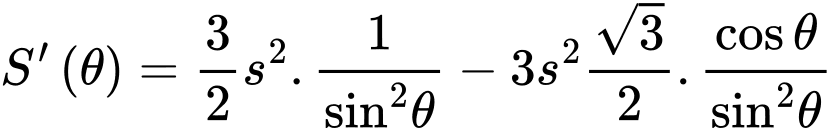
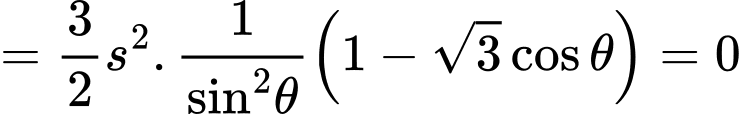
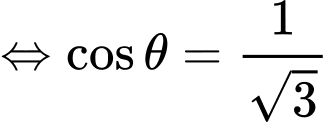
Bảng biến thiên
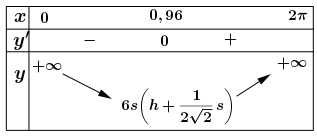
Vậy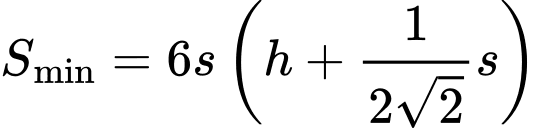 khi
khi 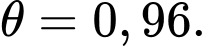
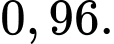
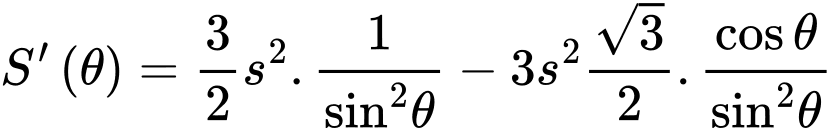
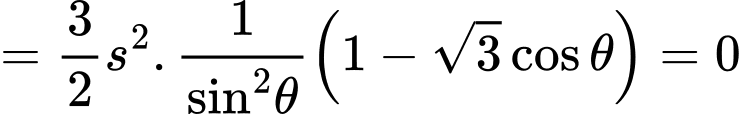
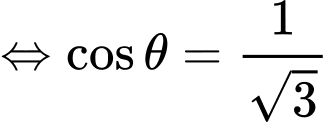
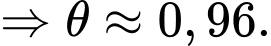
Bảng biến thiên


Vậy
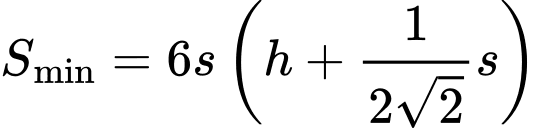 khi
khi 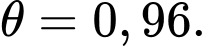
Câu 20 [695060]: Một mô hình của hệ tim mạch liên hệ thể tích 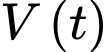 của máu trong động mạch chủ tại thời điểm
của máu trong động mạch chủ tại thời điểm 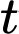 trong thời kỳ co tâm thất (giai đoạn co) với áp suất
trong thời kỳ co tâm thất (giai đoạn co) với áp suất 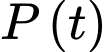 trong động mạch chủ tại cùng thời điểm được cho bởi phương trình
trong động mạch chủ tại cùng thời điểm được cho bởi phương trình 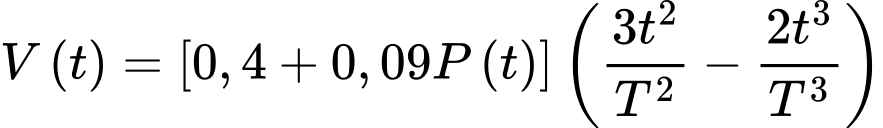 (lít) với
(lít) với 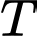 là chu kỳ của pha tâm thu (
là chu kỳ của pha tâm thu (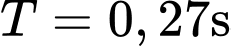 ). Giả sử áp suất động mạch chủ
). Giả sử áp suất động mạch chủ 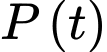 tăng đều từ
tăng đều từ  mmHg tại thời điểm
mmHg tại thời điểm 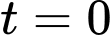 đến 30 mmHg tại thời điểm
đến 30 mmHg tại thời điểm 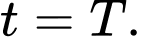 Tìm thể tích trung bình của máu trong động mạch chủ trong suốt pha tâm thu
Tìm thể tích trung bình của máu trong động mạch chủ trong suốt pha tâm thu 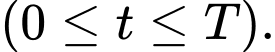 Làm tròn đến hàng phần mười.
Làm tròn đến hàng phần mười.
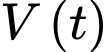 của máu trong động mạch chủ tại thời điểm
của máu trong động mạch chủ tại thời điểm 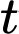 trong thời kỳ co tâm thất (giai đoạn co) với áp suất
trong thời kỳ co tâm thất (giai đoạn co) với áp suất 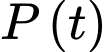 trong động mạch chủ tại cùng thời điểm được cho bởi phương trình
trong động mạch chủ tại cùng thời điểm được cho bởi phương trình 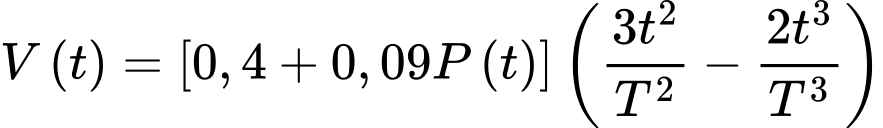 (lít) với
(lít) với 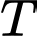 là chu kỳ của pha tâm thu (
là chu kỳ của pha tâm thu (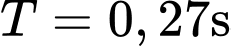 ). Giả sử áp suất động mạch chủ
). Giả sử áp suất động mạch chủ 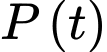 tăng đều từ
tăng đều từ  mmHg tại thời điểm
mmHg tại thời điểm 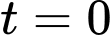 đến 30 mmHg tại thời điểm
đến 30 mmHg tại thời điểm 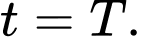 Tìm thể tích trung bình của máu trong động mạch chủ trong suốt pha tâm thu
Tìm thể tích trung bình của máu trong động mạch chủ trong suốt pha tâm thu 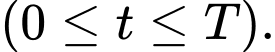 Làm tròn đến hàng phần mười.
Làm tròn đến hàng phần mười.
Điền đáp án: 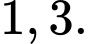
Gọi áp suất trong động mạch chủ tại thời điểm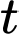 là:
là: 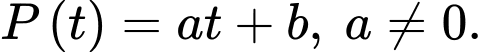
Theo bài ra ta có: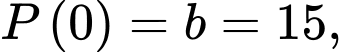
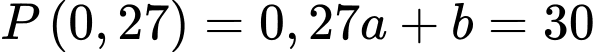
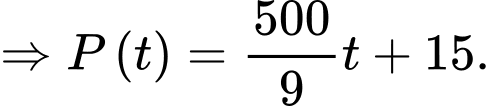
Khi đó: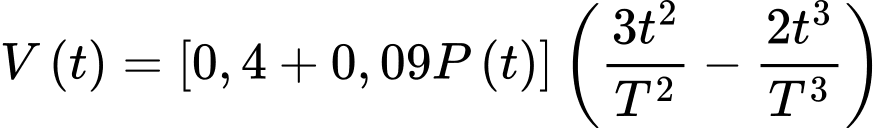
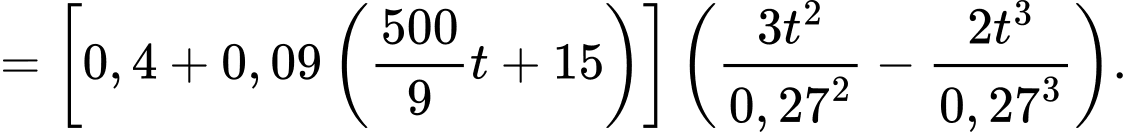
Thể tích trung bình của máu trong động mạch chủ trong suốt pha tâm thu là:
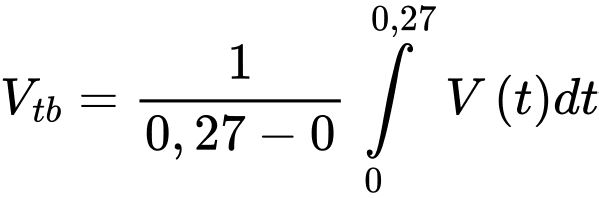
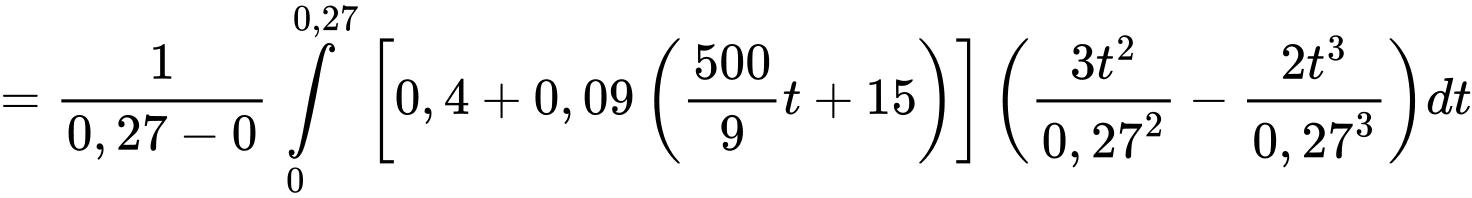
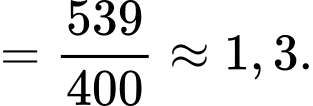
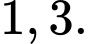
Gọi áp suất trong động mạch chủ tại thời điểm
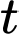 là:
là: 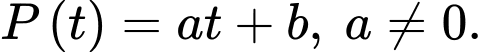
Theo bài ra ta có:
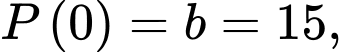
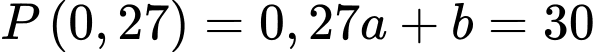
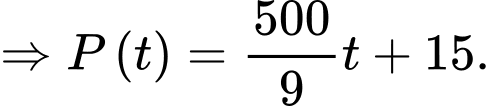
Khi đó:
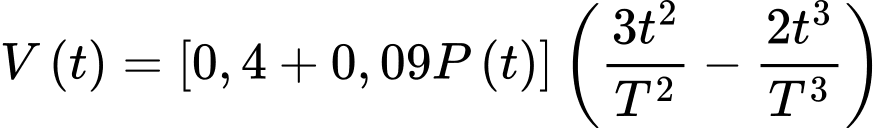
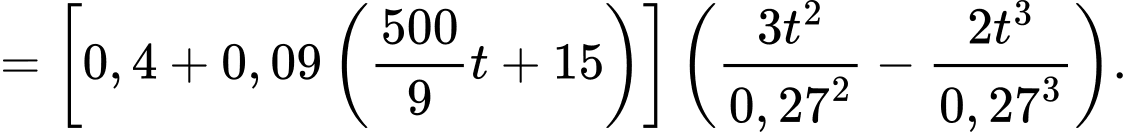
Thể tích trung bình của máu trong động mạch chủ trong suốt pha tâm thu là:
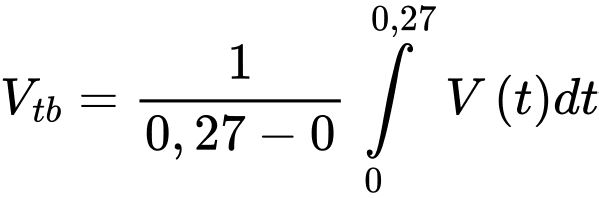
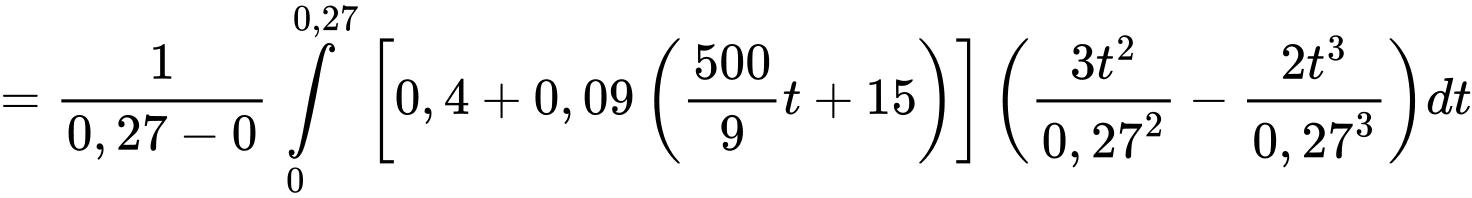
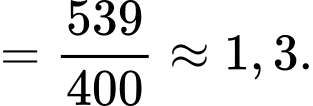
Câu 21 [695062]: Trong một báo cáo, xét nghiệm Mammography người mắc bệnh ung thư vú cho kết quả dương tính với xác suất là 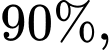 người không mắc bệnh ung thư vú cho kết quả âm tính với xác suất
người không mắc bệnh ung thư vú cho kết quả âm tính với xác suất 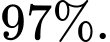 Nghiên cứu dịch tễ học chỉ ra tỉ lệ mắc ung thư vú của phụ nữ trong độ tuổi 55 là
Nghiên cứu dịch tễ học chỉ ra tỉ lệ mắc ung thư vú của phụ nữ trong độ tuổi 55 là 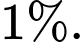 Một phụ nữ 55 tuổi, không có tiền sử ung thư vú thực hiện xét nghiệm Mammography hai lần độc lập nhau đều nhận được kết quả là dương tính. Xác suất người phụ nữ đó mắc bệnh ung thư vú là bao nhiêu %. Viết kết quả làm tròn đến hàng đơn vị.
Một phụ nữ 55 tuổi, không có tiền sử ung thư vú thực hiện xét nghiệm Mammography hai lần độc lập nhau đều nhận được kết quả là dương tính. Xác suất người phụ nữ đó mắc bệnh ung thư vú là bao nhiêu %. Viết kết quả làm tròn đến hàng đơn vị.
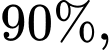 người không mắc bệnh ung thư vú cho kết quả âm tính với xác suất
người không mắc bệnh ung thư vú cho kết quả âm tính với xác suất 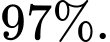 Nghiên cứu dịch tễ học chỉ ra tỉ lệ mắc ung thư vú của phụ nữ trong độ tuổi 55 là
Nghiên cứu dịch tễ học chỉ ra tỉ lệ mắc ung thư vú của phụ nữ trong độ tuổi 55 là 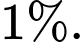 Một phụ nữ 55 tuổi, không có tiền sử ung thư vú thực hiện xét nghiệm Mammography hai lần độc lập nhau đều nhận được kết quả là dương tính. Xác suất người phụ nữ đó mắc bệnh ung thư vú là bao nhiêu %. Viết kết quả làm tròn đến hàng đơn vị.
Một phụ nữ 55 tuổi, không có tiền sử ung thư vú thực hiện xét nghiệm Mammography hai lần độc lập nhau đều nhận được kết quả là dương tính. Xác suất người phụ nữ đó mắc bệnh ung thư vú là bao nhiêu %. Viết kết quả làm tròn đến hàng đơn vị.
Điền đáp án: 90.
Xét hai biến cố:
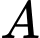 : “Người phụ nữ mắc bệnh ung thư vú”.
: “Người phụ nữ mắc bệnh ung thư vú”.
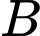 : “Kết quả xét nghiệm của người phụ nữ là dương tính”.
: “Kết quả xét nghiệm của người phụ nữ là dương tính”.
Do người phụ nữ đó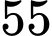 tuổi nên
tuổi nên 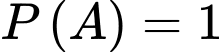
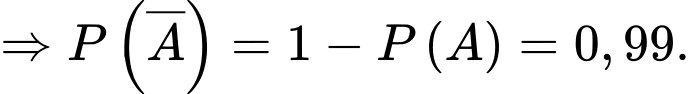
Khi đó: là xác suất người phụ nữ bị mắc bệnh ung thư vú khi có kết quả xét nghiệm dương tính.
là xác suất người phụ nữ bị mắc bệnh ung thư vú khi có kết quả xét nghiệm dương tính.
 là xác suất người phụ nữ có kết quả xét nghiệm là dương tính với điều kiện có mắc bệnh
là xác suất người phụ nữ có kết quả xét nghiệm là dương tính với điều kiện có mắc bệnh 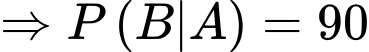
 là xác suất người phụ nữ có kết quả xét nghiệm là dương tính với điều kiện không mắc bệnh
là xác suất người phụ nữ có kết quả xét nghiệm là dương tính với điều kiện không mắc bệnh 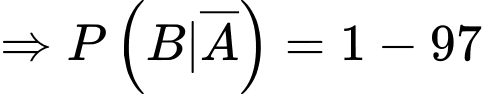
Ta có sơ đồ cây sau:
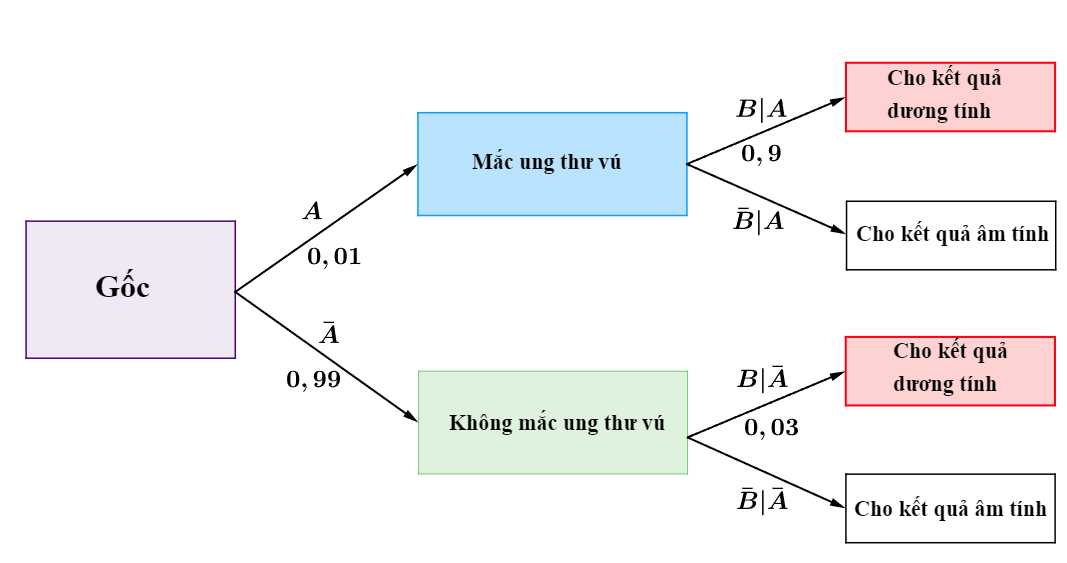
Áp dụng công thức Bayes, ta có xác suất người phụ nữ bị mắc bệnh ung thư vú khi có kết quả xét nghiệm dương tính lần thứ nhất là:
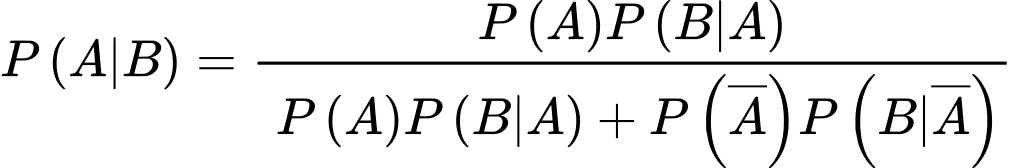
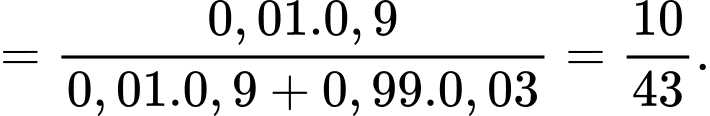
Vì người phụ nữ xét nghiệm cả lần đều ra kết quả dương tính nên ở lần thứ hai, ta xét
lần đều ra kết quả dương tính nên ở lần thứ hai, ta xét 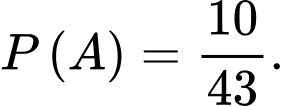
Do đó, xác suất người phụ nữ bị mắc bệnh ung thư vú khi có kết quả xét nghiệm dương tính lần thứ hai là:
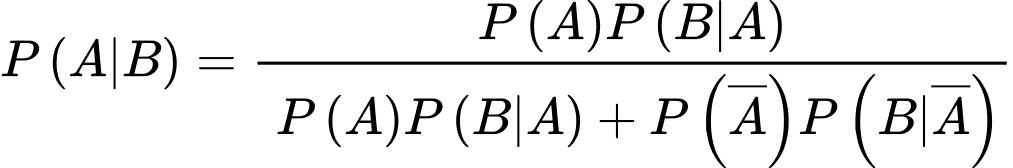
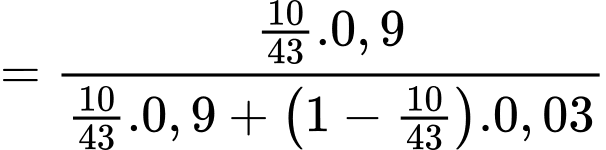
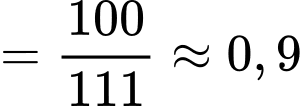 .
.
Vậy xác suất người phụ nữ bị mắc bệnh ung thư vú gần với 90%.
Xét hai biến cố:
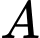 : “Người phụ nữ mắc bệnh ung thư vú”.
: “Người phụ nữ mắc bệnh ung thư vú”.
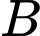 : “Kết quả xét nghiệm của người phụ nữ là dương tính”.
: “Kết quả xét nghiệm của người phụ nữ là dương tính”.
Do người phụ nữ đó
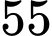 tuổi nên
tuổi nên 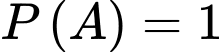
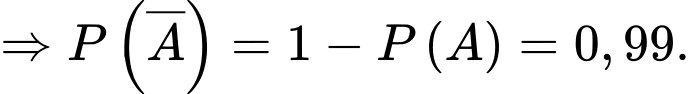
Khi đó:
 là xác suất người phụ nữ bị mắc bệnh ung thư vú khi có kết quả xét nghiệm dương tính.
là xác suất người phụ nữ bị mắc bệnh ung thư vú khi có kết quả xét nghiệm dương tính.
 là xác suất người phụ nữ có kết quả xét nghiệm là dương tính với điều kiện có mắc bệnh
là xác suất người phụ nữ có kết quả xét nghiệm là dương tính với điều kiện có mắc bệnh 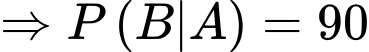
 là xác suất người phụ nữ có kết quả xét nghiệm là dương tính với điều kiện không mắc bệnh
là xác suất người phụ nữ có kết quả xét nghiệm là dương tính với điều kiện không mắc bệnh 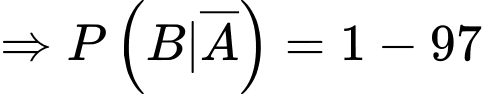
Ta có sơ đồ cây sau:

Áp dụng công thức Bayes, ta có xác suất người phụ nữ bị mắc bệnh ung thư vú khi có kết quả xét nghiệm dương tính lần thứ nhất là:
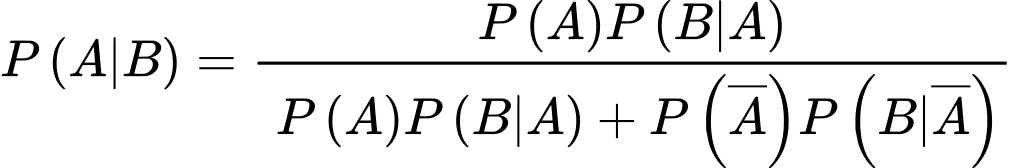
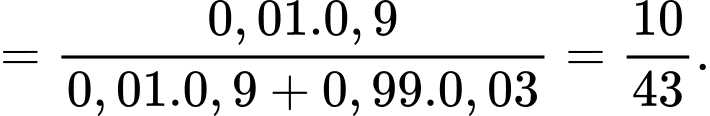
Vì người phụ nữ xét nghiệm cả
 lần đều ra kết quả dương tính nên ở lần thứ hai, ta xét
lần đều ra kết quả dương tính nên ở lần thứ hai, ta xét 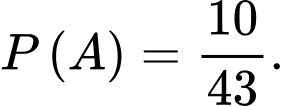
Do đó, xác suất người phụ nữ bị mắc bệnh ung thư vú khi có kết quả xét nghiệm dương tính lần thứ hai là:
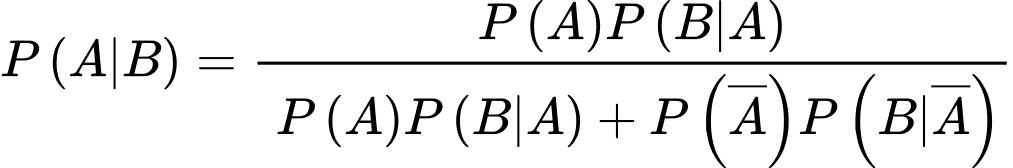
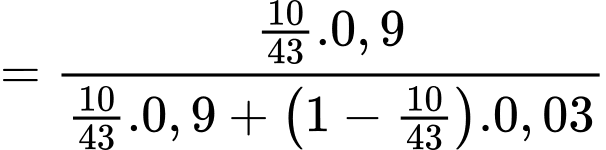
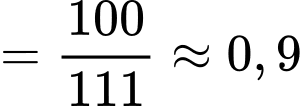 .
.
Vậy xác suất người phụ nữ bị mắc bệnh ung thư vú gần với 90%.
Câu 22 [695061]: Trong không gian với hệ tọa độ 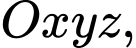 cho hai điểm
cho hai điểm 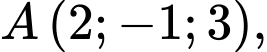
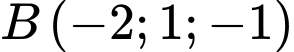 và đường thẳng
và đường thẳng 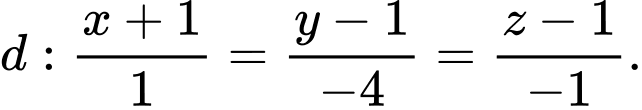 Gọi
Gọi 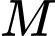 là điểm chạy trên đường thẳng
là điểm chạy trên đường thẳng 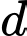 và
và 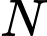 là chân đường cao hạ từ B lên đường thẳng
là chân đường cao hạ từ B lên đường thẳng 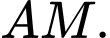 Biết điểm
Biết điểm 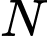 luôn chạy trên một đường cong cố định. Độ dài đường cong đó bằng bao nhiêu? (làm tròn kết quả đến hàng phần chục).
luôn chạy trên một đường cong cố định. Độ dài đường cong đó bằng bao nhiêu? (làm tròn kết quả đến hàng phần chục).
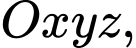 cho hai điểm
cho hai điểm 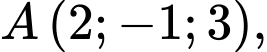
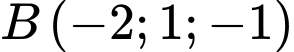 và đường thẳng
và đường thẳng 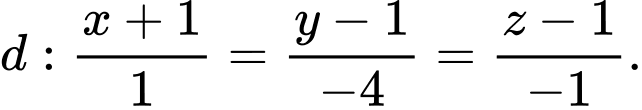 Gọi
Gọi  là điểm chạy trên đường thẳng
là điểm chạy trên đường thẳng  và
và 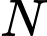 là chân đường cao hạ từ B lên đường thẳng
là chân đường cao hạ từ B lên đường thẳng 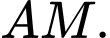 Biết điểm
Biết điểm 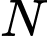 luôn chạy trên một đường cong cố định. Độ dài đường cong đó bằng bao nhiêu? (làm tròn kết quả đến hàng phần chục).
luôn chạy trên một đường cong cố định. Độ dài đường cong đó bằng bao nhiêu? (làm tròn kết quả đến hàng phần chục).
Điền đáp án: 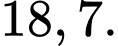
Ta có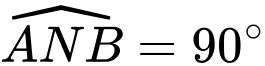 nên
nên 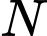 thuộc mặt cầu
thuộc mặt cầu 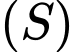 có đường kính
có đường kính 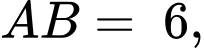 bán kính
bán kính 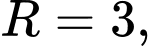 tâm
tâm 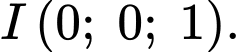
Lại có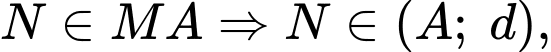 tức N chạy trên mặt phẳng
tức N chạy trên mặt phẳng 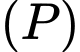 chứa
chứa 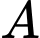 và
và 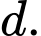
Chọn điểm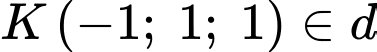
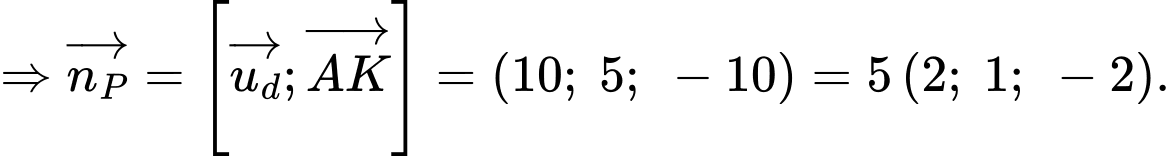
Phương trình mặt phẳng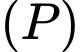 chứa
chứa 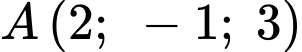 có
có 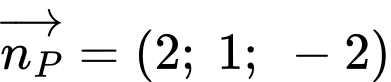 là:
là: 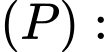
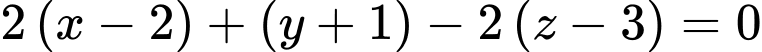 hay
hay 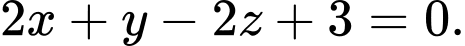
Ta có: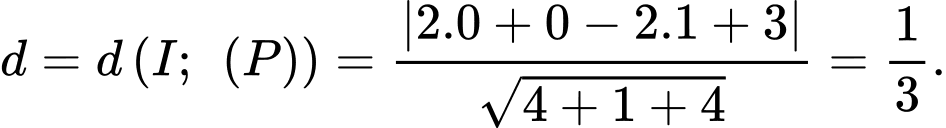
 vừa thuộc
vừa thuộc 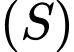 vừa thuộc
vừa thuộc 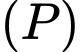 nên
nên 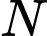 thuộc đường tròn giao tuyến của
thuộc đường tròn giao tuyến của 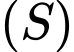 và
và 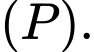
Bán kính đường tròn giao tuyến là
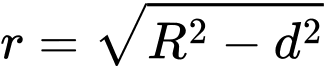
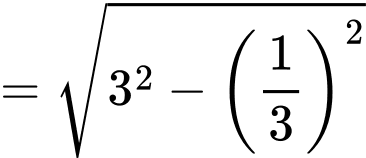
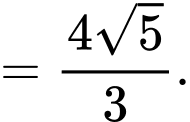
Vậy độ dài đường cong là: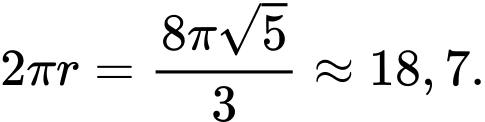
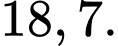
Ta có
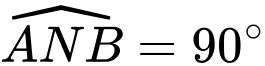 nên
nên 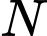 thuộc mặt cầu
thuộc mặt cầu 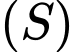 có đường kính
có đường kính 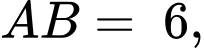 bán kính
bán kính 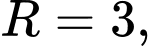 tâm
tâm 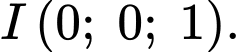
Lại có
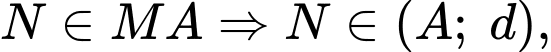 tức N chạy trên mặt phẳng
tức N chạy trên mặt phẳng 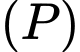 chứa
chứa 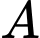 và
và 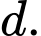
Chọn điểm
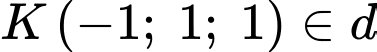
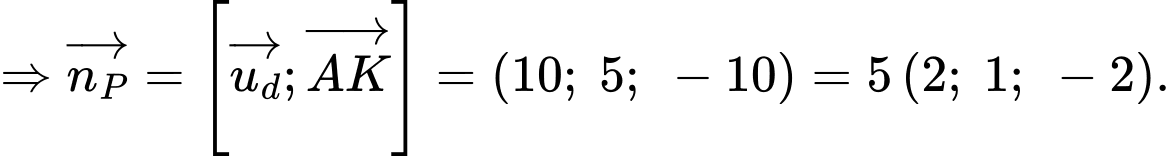
Phương trình mặt phẳng
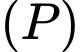 chứa
chứa 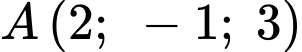 có
có 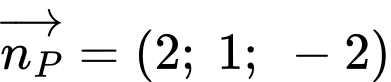 là:
là: 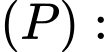
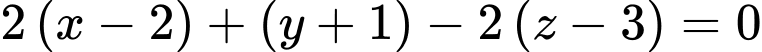 hay
hay 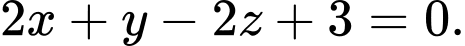
Ta có:
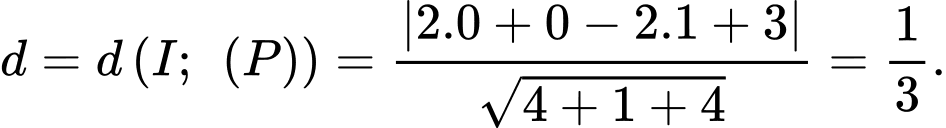
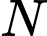 vừa thuộc
vừa thuộc 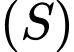 vừa thuộc
vừa thuộc 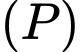 nên
nên 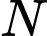 thuộc đường tròn giao tuyến của
thuộc đường tròn giao tuyến của 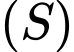 và
và 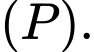
Bán kính đường tròn giao tuyến là
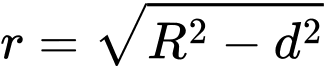
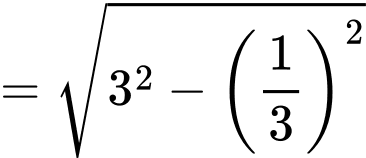
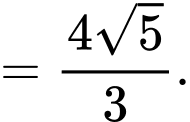
Vậy độ dài đường cong là: