PHẦN I. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Câu 1 [523988]: Cho hàm số 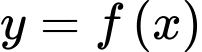 có bảng biến thiên như sau:
có bảng biến thiên như sau:
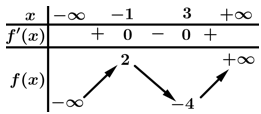
Hàm số đã cho đồng biến trên khoảng nào dưới đây?
 có bảng biến thiên như sau:
có bảng biến thiên như sau: 
Hàm số đã cho đồng biến trên khoảng nào dưới đây?
A, 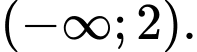
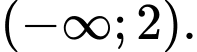
B, 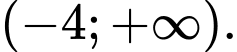
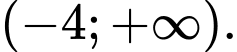
C, 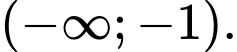
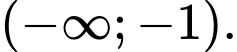
D, 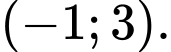
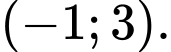
Chọn đáp án C.
Dựa vào bảng biến thiên, ta có hàm số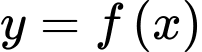 đồng biến trên các khoảng
đồng biến trên các khoảng 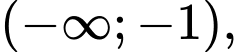
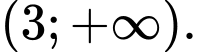 Đáp án: C
Đáp án: C
Dựa vào bảng biến thiên, ta có hàm số
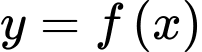 đồng biến trên các khoảng
đồng biến trên các khoảng 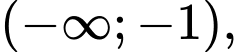
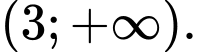 Đáp án: C
Đáp án: C
Câu 2 [810769]: Cho hàm số 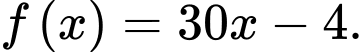 Trong các khẳng định sau khẳng định nào đúng?
Trong các khẳng định sau khẳng định nào đúng?
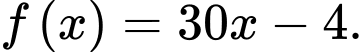 Trong các khẳng định sau khẳng định nào đúng?
Trong các khẳng định sau khẳng định nào đúng? A, 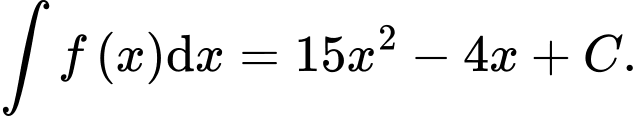
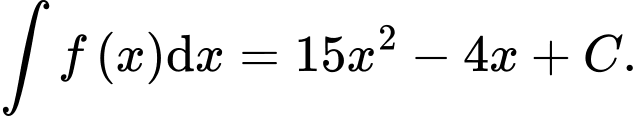
B, 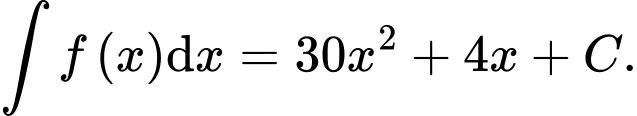
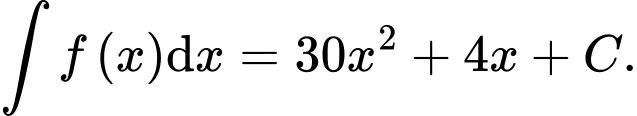
C, 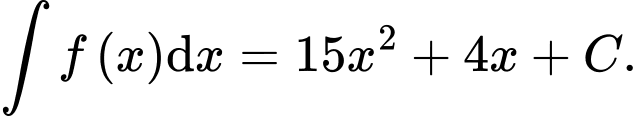
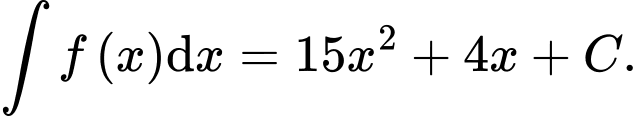
D, 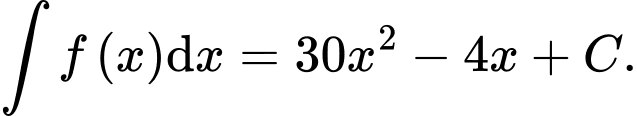
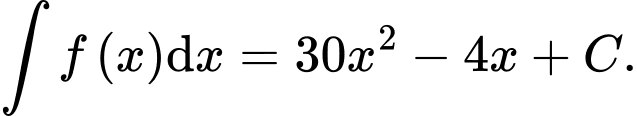
Chọn đáp án A.
Ta có: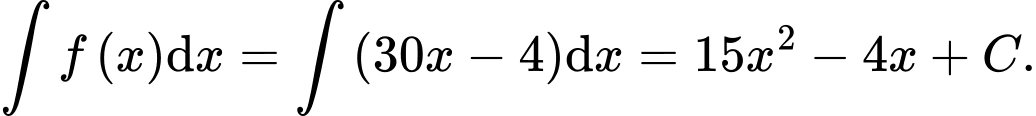 Đáp án: A
Đáp án: A
Ta có:
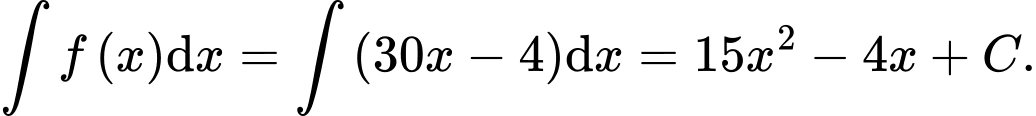 Đáp án: A
Đáp án: A
Câu 3 [900242]: Nghiệm của phương trình 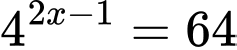 là
là
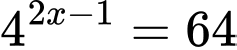 là
là A, 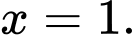
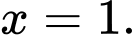
B, 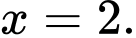
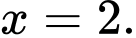
C, 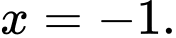
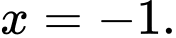
D, 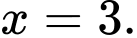
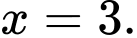
Chọn đáp án B.
Ta có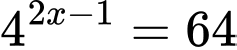
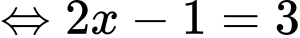
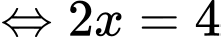
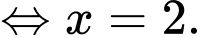 Đáp án: B
Đáp án: B
Ta có
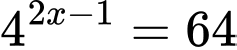
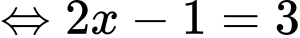
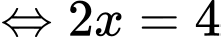
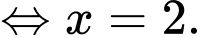 Đáp án: B
Đáp án: B
Câu 4 [810774]: Với  , đạo hàm của hàm số
, đạo hàm của hàm số 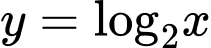 là
là
 , đạo hàm của hàm số
, đạo hàm của hàm số 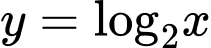 là
là A, 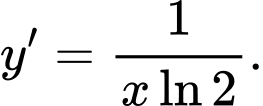
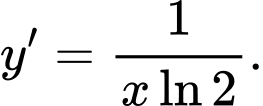
B, 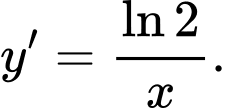
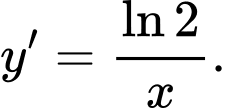
C, 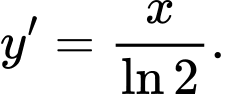
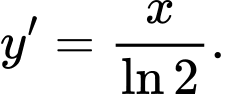
D, 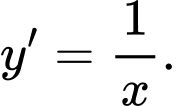
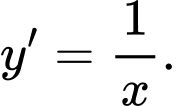
Chọn đáp án A.
Ta có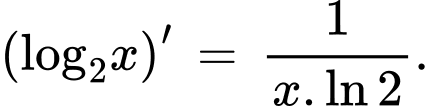 Đáp án: A
Đáp án: A
Ta có
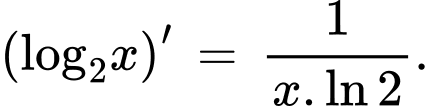 Đáp án: A
Đáp án: A
Câu 5 [810771]: Trong không gian 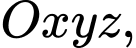 cho hai điểm
cho hai điểm 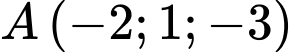 và
và 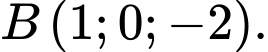 Độ dài đoạn thẳng
Độ dài đoạn thẳng  bằng
bằng
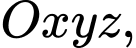 cho hai điểm
cho hai điểm 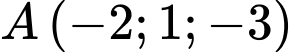 và
và 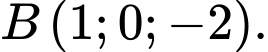 Độ dài đoạn thẳng
Độ dài đoạn thẳng  bằng
bằng A, 

B, 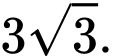
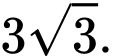
C, 

D, 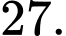
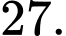
Chọn đáp án A.
Ta có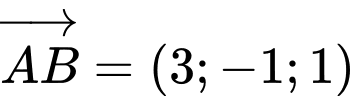
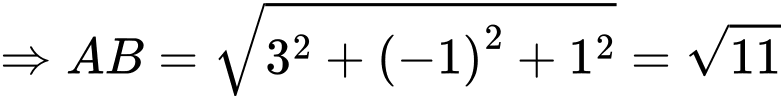 Đáp án: A
Đáp án: A
Ta có
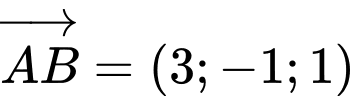
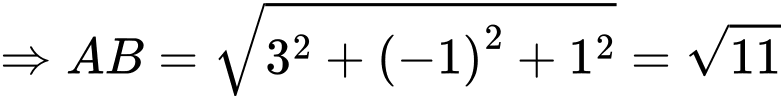 Đáp án: A
Đáp án: A
Câu 6 [693497]: Cho dãy số 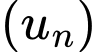 được cho bởi hệ thức truy hồi
được cho bởi hệ thức truy hồi 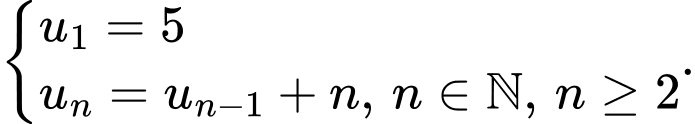 Giá trị của
Giá trị của 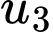 là
là
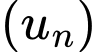 được cho bởi hệ thức truy hồi
được cho bởi hệ thức truy hồi 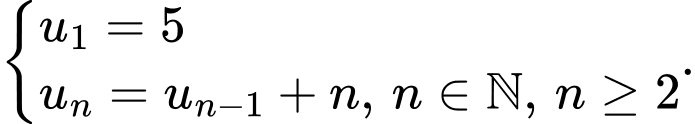 Giá trị của
Giá trị của 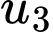 là
là A, 10.
B, 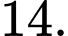
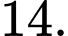
C, 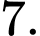
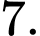
D, 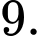
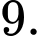
Chọn đáp án A.
Ta có: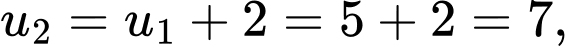
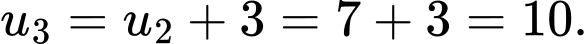 Đáp án: A
Đáp án: A
Ta có:
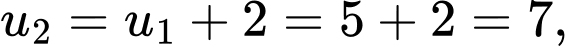
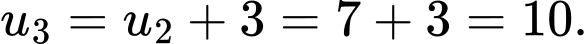 Đáp án: A
Đáp án: A
Câu 7 [809925]: Trong không gian 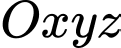 cho mặt cầu
cho mặt cầu 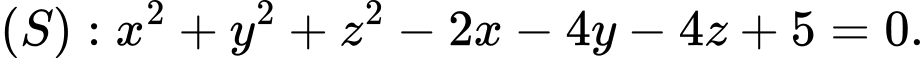 Bán kính của mặt cầu
Bán kính của mặt cầu 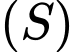 là
là
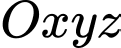 cho mặt cầu
cho mặt cầu 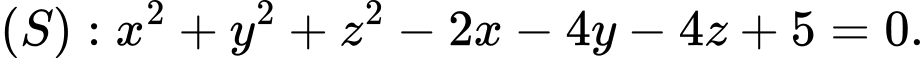 Bán kính của mặt cầu
Bán kính của mặt cầu 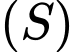 là
là A, 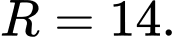
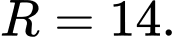
B, 

C, 

D, 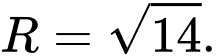
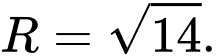
Chọn đáp án B.
Mặt cầu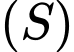 có bán kính
có bán kính 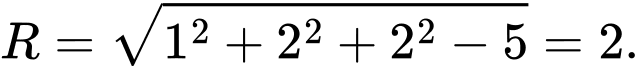 Đáp án: B
Đáp án: B
Mặt cầu
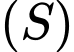 có bán kính
có bán kính 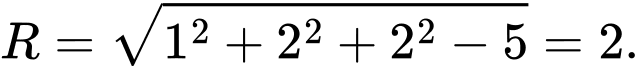 Đáp án: B
Đáp án: B Sử dụng thông tin dưới đây để trả lời câu 8 và câu 9
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, cạnh SA = a và vuông góc với mặt phẳng (ABCD).
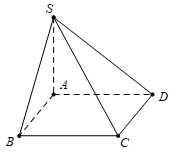

Câu 8 [699940]: Khẳng định nào dưới đây sai?
A, 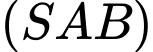 vuông góc với
vuông góc với 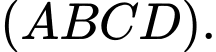
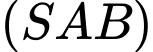 vuông góc với
vuông góc với 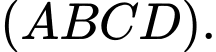
B, 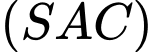 vuông góc với
vuông góc với 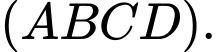
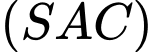 vuông góc với
vuông góc với 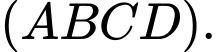
C, 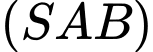 vuông góc với
vuông góc với 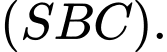
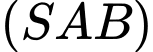 vuông góc với
vuông góc với 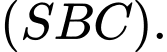
D, 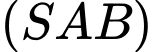 vuông góc với
vuông góc với 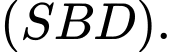
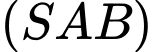 vuông góc với
vuông góc với 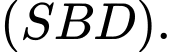
Chọn đáp án D.
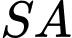 vuông góc với mặt phẳng (ABCD) nên
vuông góc với mặt phẳng (ABCD) nên 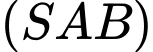 vuông góc với
vuông góc với 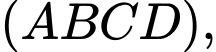
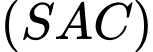 vuông góc với
vuông góc với 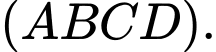 Do đó, loại A, B.
Do đó, loại A, B.
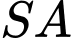 vuông góc với mặt phẳng (ABCD) nên
vuông góc với mặt phẳng (ABCD) nên 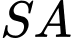 vuông góc với
vuông góc với 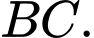
Mặt khác, ABCd là hình vuông nên vuông góc với mặt phẳng
vuông góc với mặt phẳng 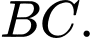
Do đó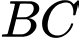 vuông góc với mặt phẳng (SAB) nên
vuông góc với mặt phẳng (SAB) nên 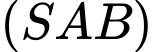 vuông góc với
vuông góc với 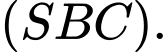 Do đó, loại C. Đáp án: D
Do đó, loại C. Đáp án: D
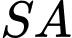 vuông góc với mặt phẳng (ABCD) nên
vuông góc với mặt phẳng (ABCD) nên 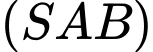 vuông góc với
vuông góc với 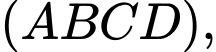
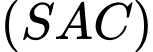 vuông góc với
vuông góc với 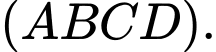 Do đó, loại A, B.
Do đó, loại A, B. 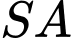 vuông góc với mặt phẳng (ABCD) nên
vuông góc với mặt phẳng (ABCD) nên 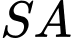 vuông góc với
vuông góc với 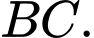
Mặt khác, ABCd là hình vuông nên
 vuông góc với mặt phẳng
vuông góc với mặt phẳng 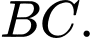
Do đó
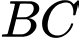 vuông góc với mặt phẳng (SAB) nên
vuông góc với mặt phẳng (SAB) nên 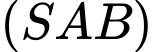 vuông góc với
vuông góc với 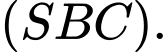 Do đó, loại C. Đáp án: D
Do đó, loại C. Đáp án: D
Câu 9 [699941]: Góc giữa hai vectơ 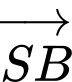 và
và 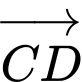 bằng
bằng
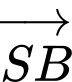 và
và 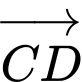 bằng
bằng A, 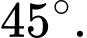
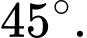
B, 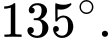
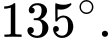
C, 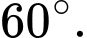
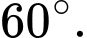
D, 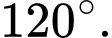
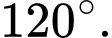
Chọn đáp án B.
Ta có: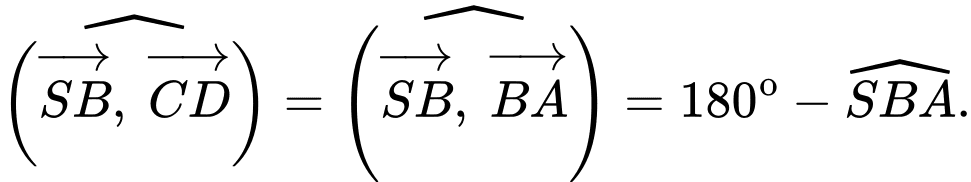
Mặt khác: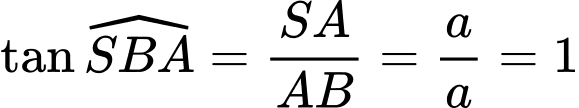

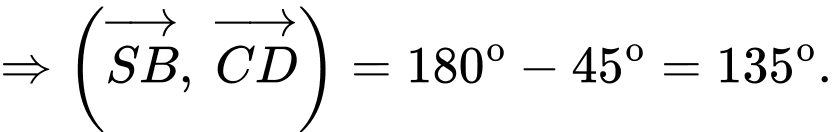 Đáp án: B
Đáp án: B
Ta có:
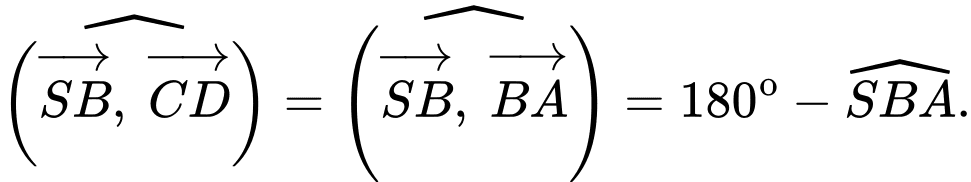
Mặt khác:
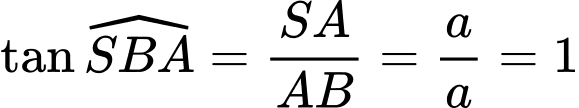

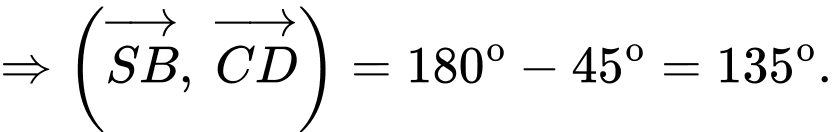 Đáp án: B
Đáp án: B
Câu 10 [693498]: Cho các hàm số 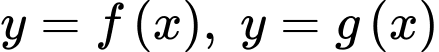 có đồ thị lần lượt là
có đồ thị lần lượt là 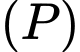 và
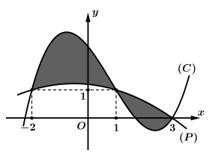
và  và hình phẳng được tô màu như hình vẽ. Công thức tính diện tích hình phẳng được tô màu là
và hình phẳng được tô màu như hình vẽ. Công thức tính diện tích hình phẳng được tô màu là
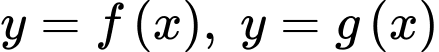 có đồ thị lần lượt là
có đồ thị lần lượt là 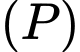 và
và  và hình phẳng được tô màu như hình vẽ. Công thức tính diện tích hình phẳng được tô màu là
và hình phẳng được tô màu như hình vẽ. Công thức tính diện tích hình phẳng được tô màu là
A, 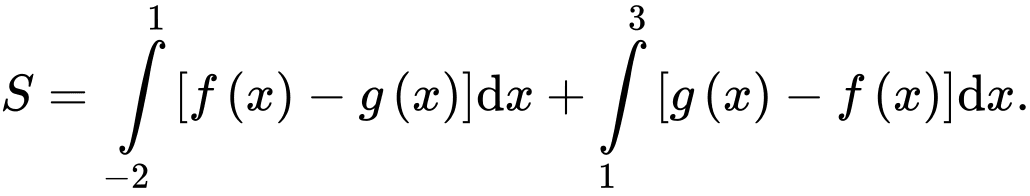
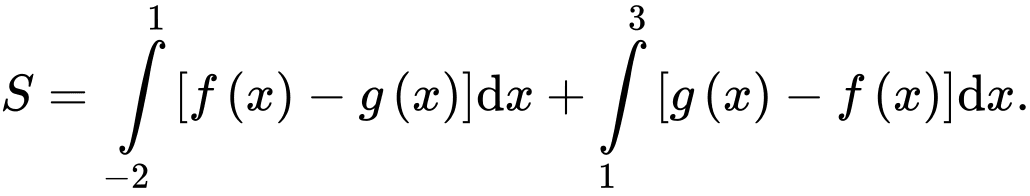
B, 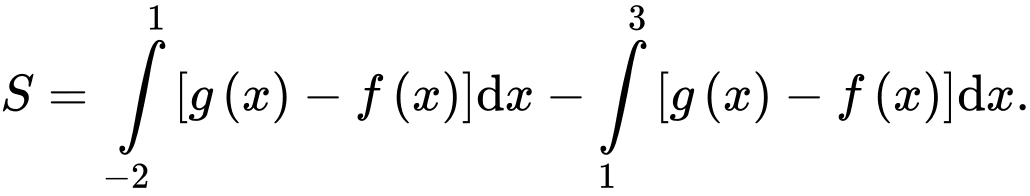
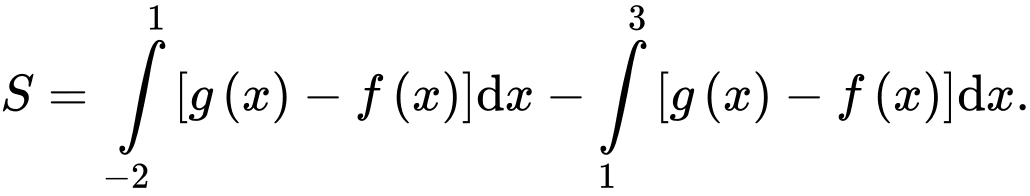
C, 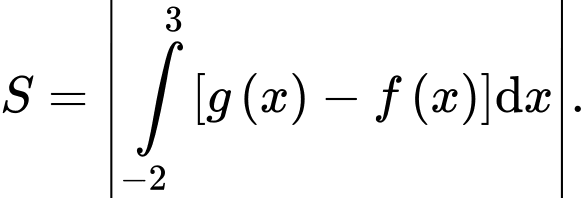
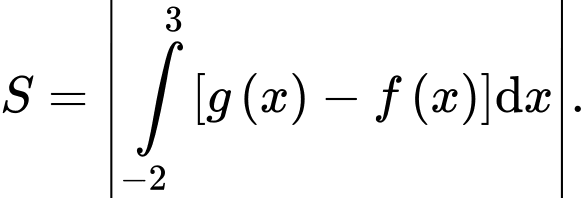
D, 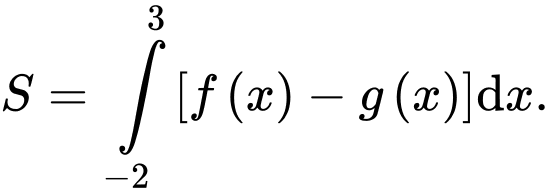
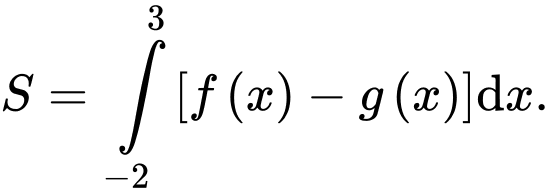
Chọn đáp án B.
Diện tích hình phẳng được tô màu là
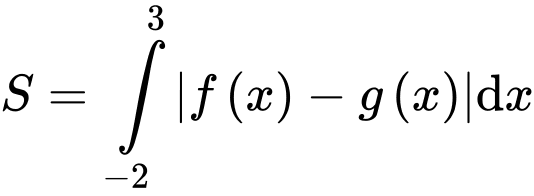
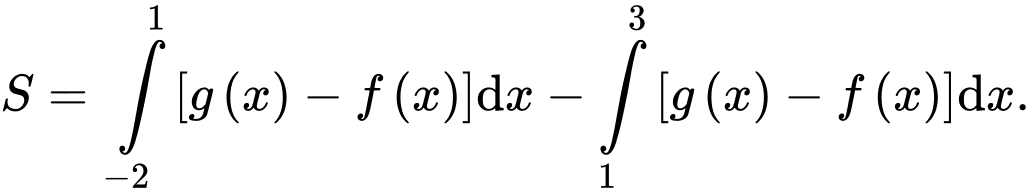 Đáp án: B
Đáp án: B
Diện tích hình phẳng được tô màu là
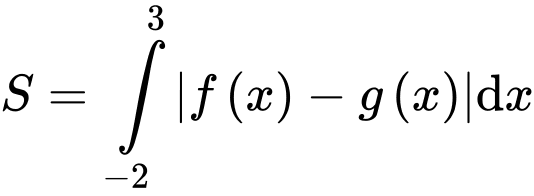
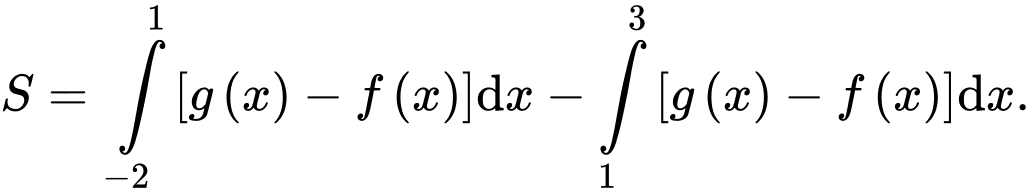 Đáp án: B
Đáp án: B
Câu 11 [810762]: Điểm cực đại của đồ thị hàm số 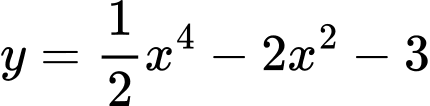 là
là
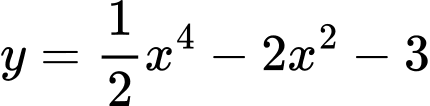 là
là A, 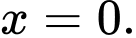
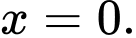
B, 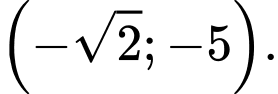
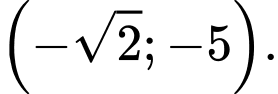
C, 

D, 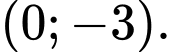
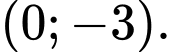
Chọn đáp án D.
Ta có: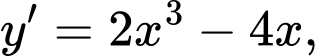
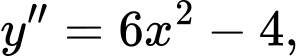
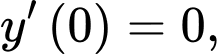
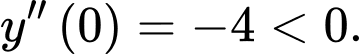
Vậy điểm cực đại của đồ thị hàm số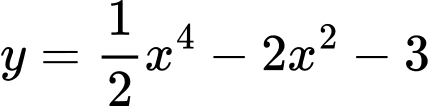 là
là 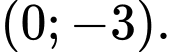 Đáp án: D
Đáp án: D
Ta có:
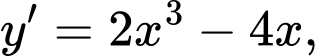
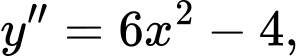
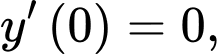
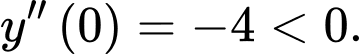
Vậy điểm cực đại của đồ thị hàm số
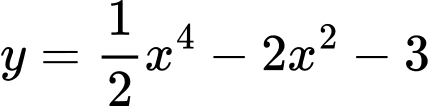 là
là 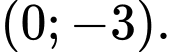 Đáp án: D
Đáp án: D
Câu 12 [693499]: Thời gian chạy bộ của bạn mỗi ngày trong thời gian gần đây của bạn An được thống kê lại ở bảng sau:

Độ lệch chuẩn của mẫu số liệu ghép nhóm đã cho bằng (làm tròn đến hàng phần trăm).

Độ lệch chuẩn của mẫu số liệu ghép nhóm đã cho bằng (làm tròn đến hàng phần trăm).
A, 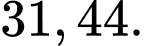
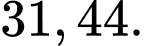
B, 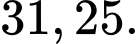
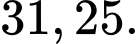
C, 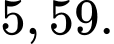
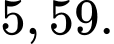
D, 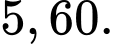
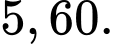
Chọn đáp án C.
Số trung bình của mấu số liệu ghép nhóm là
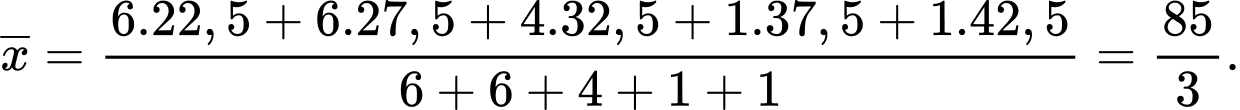
Phương sai của mẫu số liệu ghép nhóm là
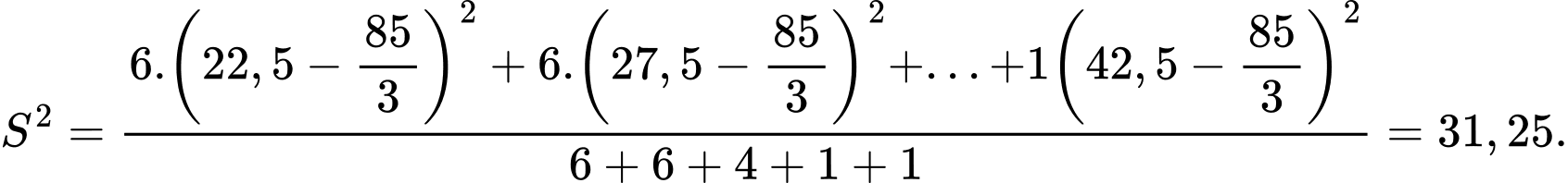
Độ lệch chuẩn của mẫu số liệu ghép nhóm là
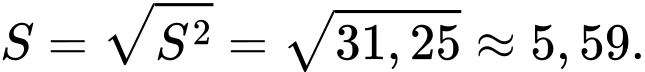 Đáp án: C
Đáp án: C
Số trung bình của mấu số liệu ghép nhóm là
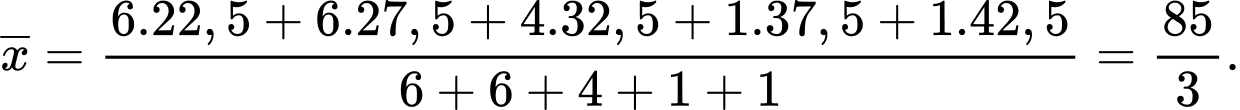
Phương sai của mẫu số liệu ghép nhóm là
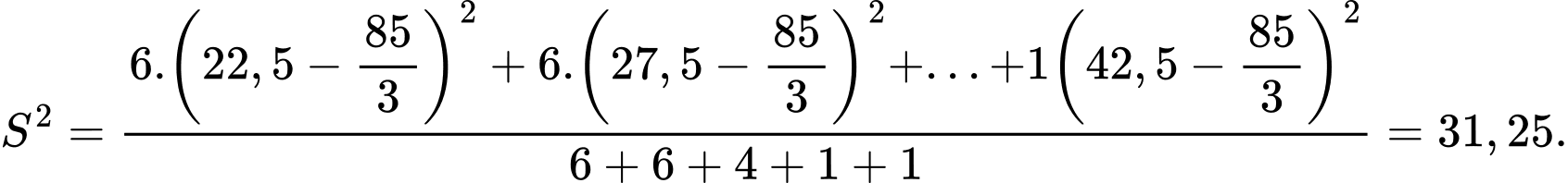
Độ lệch chuẩn của mẫu số liệu ghép nhóm là
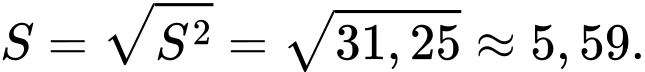 Đáp án: C
Đáp án: C PHẦN II. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Câu 13 [693500]: Trong không gian 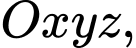 cho điểm
cho điểm 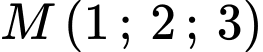 và ba điểm
và ba điểm 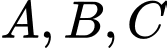 lần lượt là hình chiếu vuông góc của điểm
lần lượt là hình chiếu vuông góc của điểm 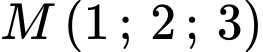 lên các trục tọa độ
lên các trục tọa độ 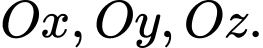 Gọi
Gọi 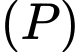 là mặt phẳng đi qua ba điểm
là mặt phẳng đi qua ba điểm 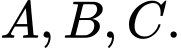
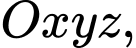 cho điểm
cho điểm 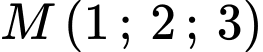 và ba điểm
và ba điểm 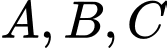 lần lượt là hình chiếu vuông góc của điểm
lần lượt là hình chiếu vuông góc của điểm 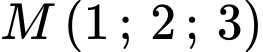 lên các trục tọa độ
lên các trục tọa độ 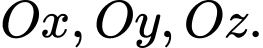 Gọi
Gọi 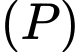 là mặt phẳng đi qua ba điểm
là mặt phẳng đi qua ba điểm 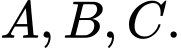
a) Đúng.
Vì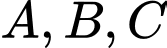 lần lượt là hình chiếu vuông góc của điểm
lần lượt là hình chiếu vuông góc của điểm 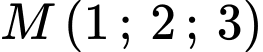 lên các trục toạ độ
lên các trục toạ độ 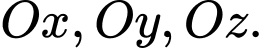
Suy ra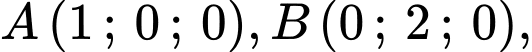
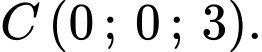
b) Sai.
Vậy phương trình mặt phẳng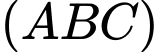 theo đoạn chắn là
theo đoạn chắn là 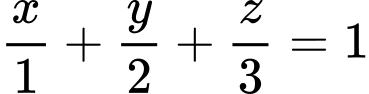

c) Sai.
Một vectơ pháp tuyến của mặt phẳng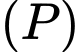 là
là 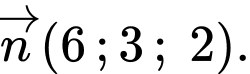
d) Sai.
Ta có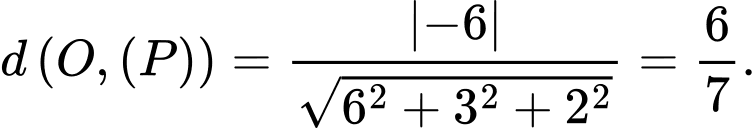
Vì
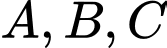 lần lượt là hình chiếu vuông góc của điểm
lần lượt là hình chiếu vuông góc của điểm 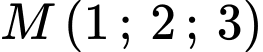 lên các trục toạ độ
lên các trục toạ độ 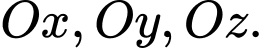
Suy ra
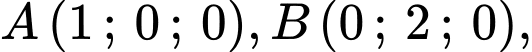
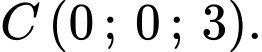
b) Sai.
Vậy phương trình mặt phẳng
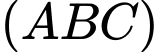 theo đoạn chắn là
theo đoạn chắn là 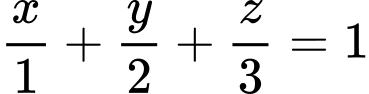

c) Sai.
Một vectơ pháp tuyến của mặt phẳng
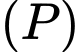 là
là 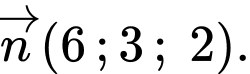
d) Sai.
Ta có
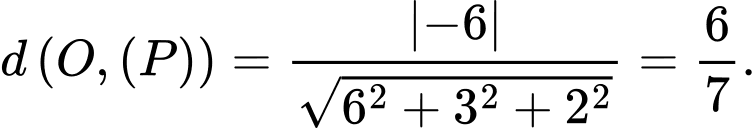
Câu 14 [699942]: Khi phát hiện một vật thể bay, xác suất một hệ thống radar phát cảnh báo là 0,9 nếu vật thể bay đó là mục tiêu thật và là 0,05 nếu đó là mục tiêu giả. Thống kê cho thấy có 99% các vật thể bay là mục tiêu giả
Gọi A là biến cố: Hệ thống radar đang phát cảnh báo khi phát hiện một vật thể bay
Gọi B là biến cố: Vật thể đó là mục tiêu thật
Gọi A là biến cố: Hệ thống radar đang phát cảnh báo khi phát hiện một vật thể bay
Gọi B là biến cố: Vật thể đó là mục tiêu thật
a) Sai.
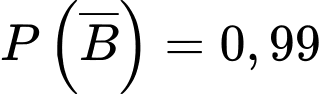
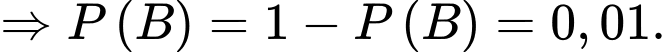
b) Đúng.
 là xác suất hệ thống radar phát cảnh báo khi biết vật thể bay đó là mục tiêu thật và bằng 0,9.
là xác suất hệ thống radar phát cảnh báo khi biết vật thể bay đó là mục tiêu thật và bằng 0,9.
c) Sai.
Ta có sơ đồ cây sau:
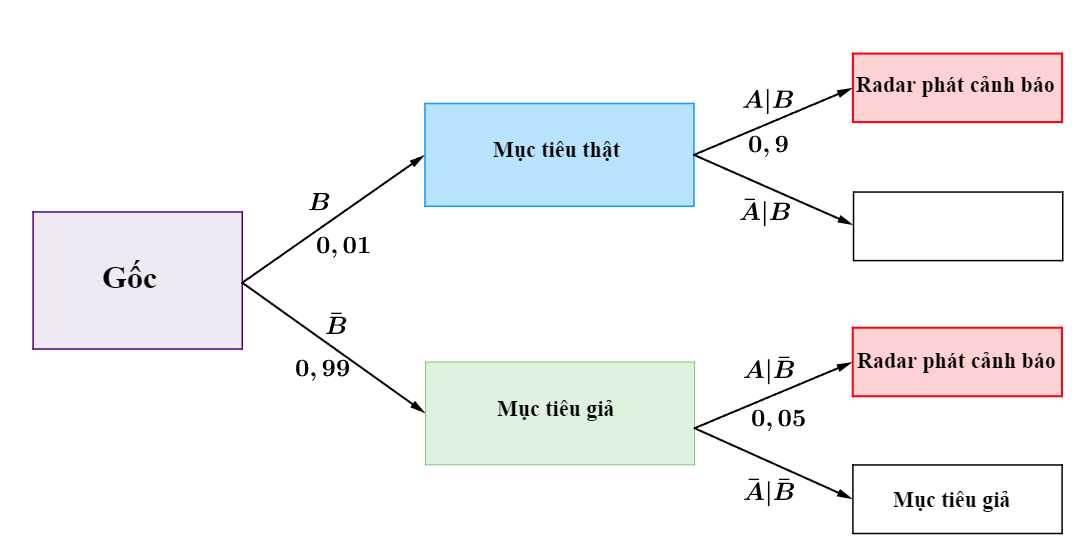
Áp dụng công thức xác suất toàn phần, ta có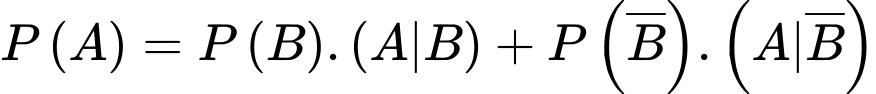
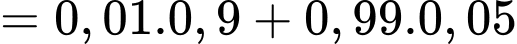
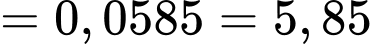
d) Đúng.
Xác vật thể đó là mục tiêu thật khi biết hệ thống radar đang phát cảnh báo là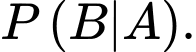
Áp dụng công thức Bayes, ta có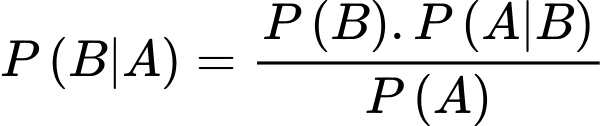
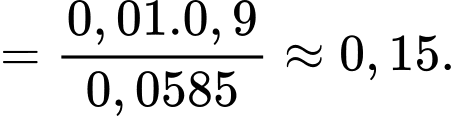
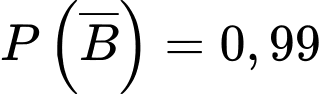
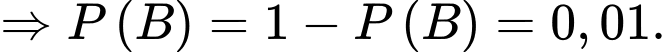
b) Đúng.
 là xác suất hệ thống radar phát cảnh báo khi biết vật thể bay đó là mục tiêu thật và bằng 0,9.
là xác suất hệ thống radar phát cảnh báo khi biết vật thể bay đó là mục tiêu thật và bằng 0,9.
c) Sai.
Ta có sơ đồ cây sau:

Áp dụng công thức xác suất toàn phần, ta có
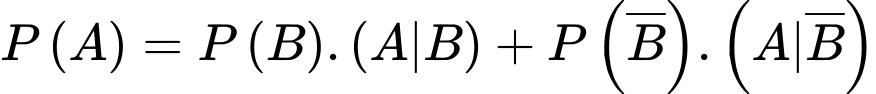
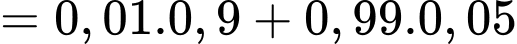
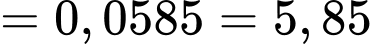
d) Đúng.
Xác vật thể đó là mục tiêu thật khi biết hệ thống radar đang phát cảnh báo là
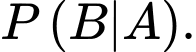
Áp dụng công thức Bayes, ta có
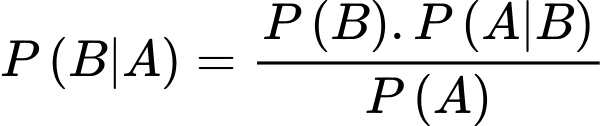
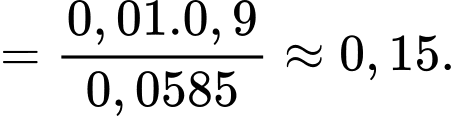
Câu 15 [696315]: Một mô hình quan trọng cho nghề cá thương mại là mô hình của Beverton và Holt. Nó bắt đầu bằng việc nghiên cứu một nhóm cá duy nhất, nghĩa là tất cả các con cá trong nghiên cứu đều được sinh ra cùng một lúc. Giả sử với một nhóm cá bơn, số lượng 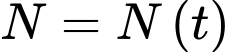 cá trong quần thể được đưa ra bởi công thức:
cá trong quần thể được đưa ra bởi công thức: 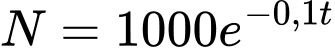 và trọng lượng
và trọng lượng 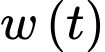 của mỗi con cá được đưa ra bởi công thức
của mỗi con cá được đưa ra bởi công thức 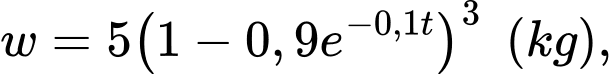
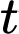 là thời gian, tính theo năm là tuổi của cá. Gọi
là thời gian, tính theo năm là tuổi của cá. Gọi 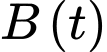 là tổng trọng lượng của nhóm cá này sau
là tổng trọng lượng của nhóm cá này sau 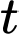 năm.
năm.
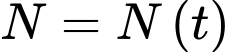 cá trong quần thể được đưa ra bởi công thức:
cá trong quần thể được đưa ra bởi công thức: 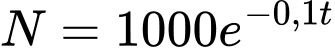 và trọng lượng
và trọng lượng 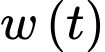 của mỗi con cá được đưa ra bởi công thức
của mỗi con cá được đưa ra bởi công thức 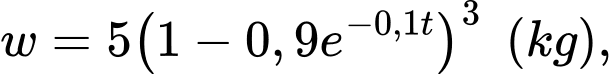
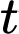 là thời gian, tính theo năm là tuổi của cá. Gọi
là thời gian, tính theo năm là tuổi của cá. Gọi 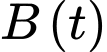 là tổng trọng lượng của nhóm cá này sau
là tổng trọng lượng của nhóm cá này sau 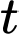 năm.
năm.
a) Sai.
Trọng lượng của con cá bơn khi mới sinh ra là
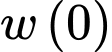
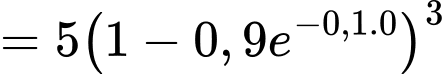
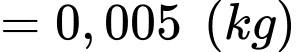
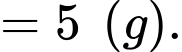
b) Đúng.
Tổng trọng lượng của nhóm cá này sau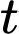 năm là:
năm là:
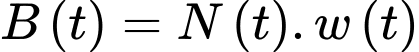
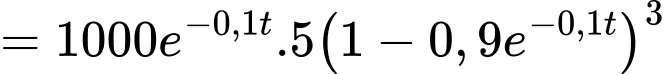
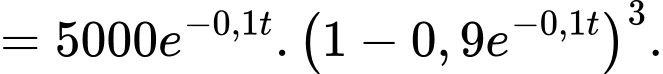
c) Sai.
Đặt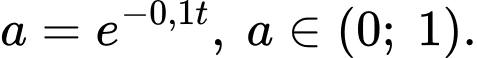
Ta có: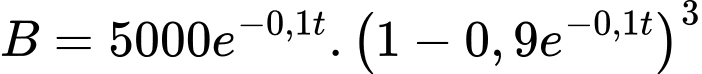
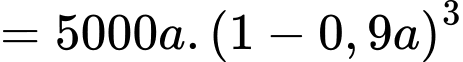
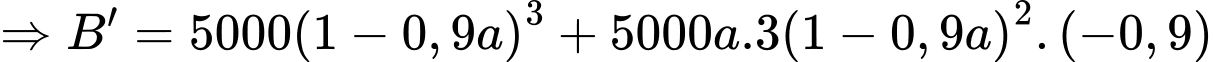
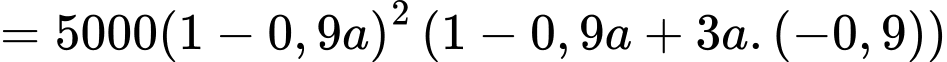
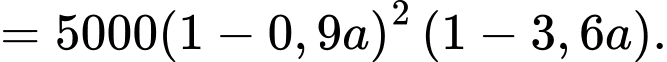
Ta có: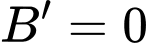
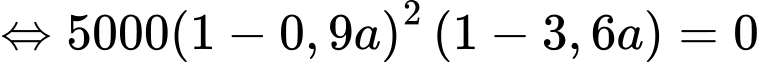
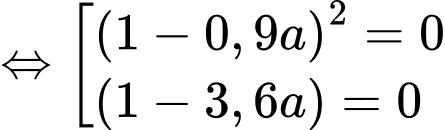
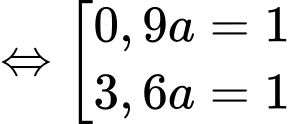
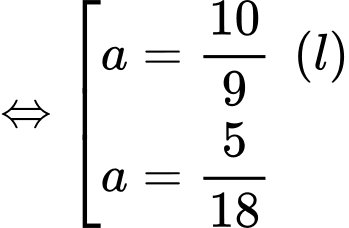
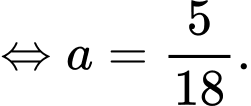
Bảng biến thiên:
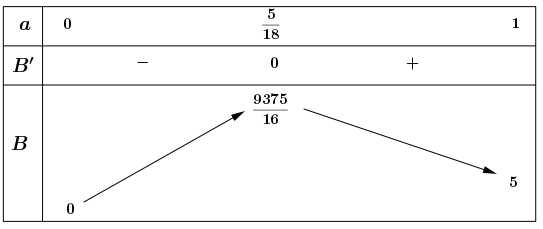
Vậy tổng trọng lượng lớn nhất của nhóm cá này là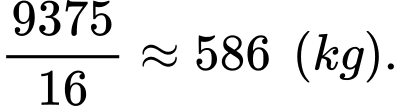
d) Đúng.
Ta có: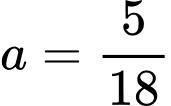
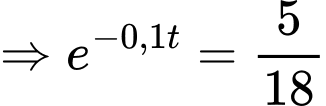
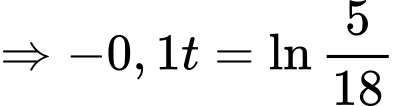
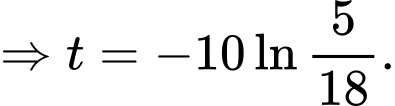
Dựa vào bảng biến thiên ta có: Tổng trọng lượng nhóm cá này lớn nhất tại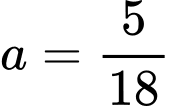 tức là sau
tức là sau 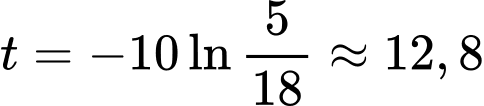 năm.
năm.
Trọng lượng của con cá bơn khi mới sinh ra là
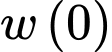
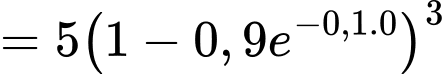
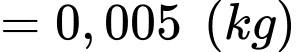
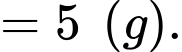
b) Đúng.
Tổng trọng lượng của nhóm cá này sau
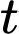 năm là:
năm là: 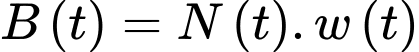
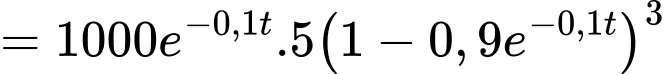
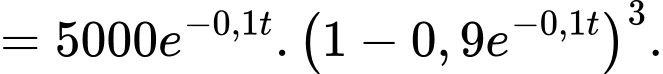
c) Sai.
Đặt
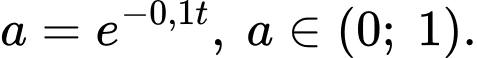
Ta có:
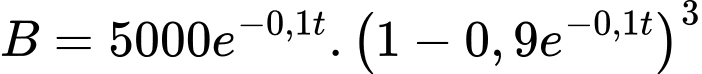
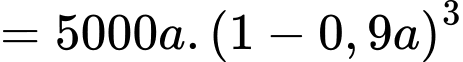
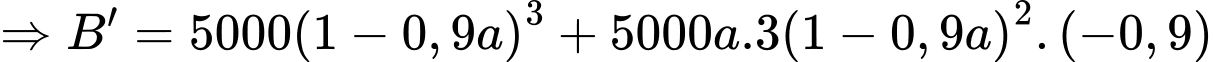
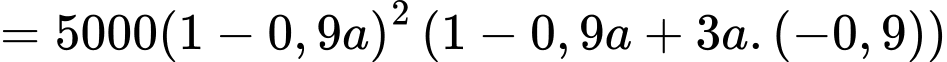
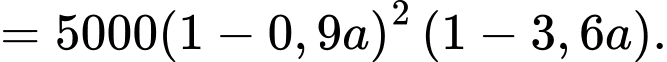
Ta có:
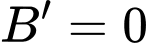
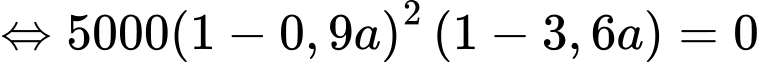
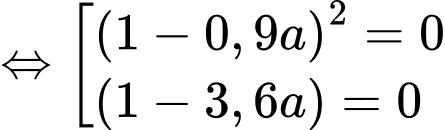
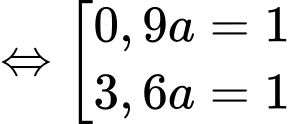
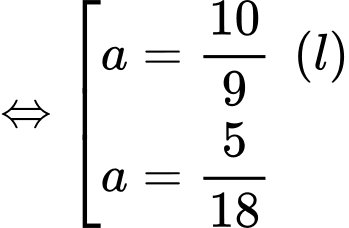
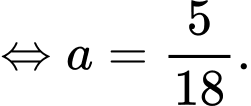
Bảng biến thiên:

Vậy tổng trọng lượng lớn nhất của nhóm cá này là
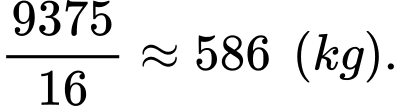
d) Đúng.
Ta có:
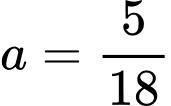
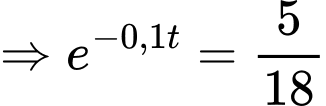
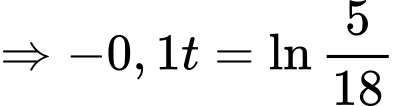
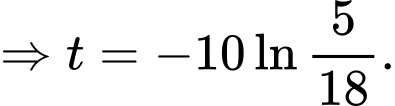
Dựa vào bảng biến thiên ta có: Tổng trọng lượng nhóm cá này lớn nhất tại
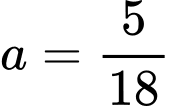 tức là sau
tức là sau 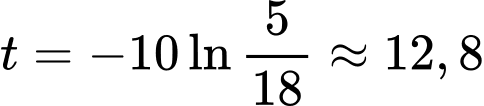 năm.
năm.
Câu 16 [699943]: Một cô gái đi máy khởi hành từ trạng thái nghỉ, tăng tốc đều đặn trong 3 phút cho đến khi đạt tốc độ  Sau đó, cô ấy duy trì tốc độ này không đổi trong vòng 4 phút cho đến khi đến một ngọn đồi. Cô ấy giảm tốc độ đều đặn trong một phút xuống còn
Sau đó, cô ấy duy trì tốc độ này không đổi trong vòng 4 phút cho đến khi đến một ngọn đồi. Cô ấy giảm tốc độ đều đặn trong một phút xuống còn  sau đó tiếp tục duy trì ở tốc độ này trong 6 phút. Khi lên đến đỉnh đồi, cô ấy giảm tốc độ đều và dừng lại sau 3 phút. Gọi
sau đó tiếp tục duy trì ở tốc độ này trong 6 phút. Khi lên đến đỉnh đồi, cô ấy giảm tốc độ đều và dừng lại sau 3 phút. Gọi 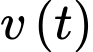 là vận tốc của cô gái tính từ trạng thái nghỉ đến khi dừng hẳn.
là vận tốc của cô gái tính từ trạng thái nghỉ đến khi dừng hẳn.
 Sau đó, cô ấy duy trì tốc độ này không đổi trong vòng 4 phút cho đến khi đến một ngọn đồi. Cô ấy giảm tốc độ đều đặn trong một phút xuống còn
Sau đó, cô ấy duy trì tốc độ này không đổi trong vòng 4 phút cho đến khi đến một ngọn đồi. Cô ấy giảm tốc độ đều đặn trong một phút xuống còn  sau đó tiếp tục duy trì ở tốc độ này trong 6 phút. Khi lên đến đỉnh đồi, cô ấy giảm tốc độ đều và dừng lại sau 3 phút. Gọi
sau đó tiếp tục duy trì ở tốc độ này trong 6 phút. Khi lên đến đỉnh đồi, cô ấy giảm tốc độ đều và dừng lại sau 3 phút. Gọi 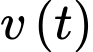 là vận tốc của cô gái tính từ trạng thái nghỉ đến khi dừng hẳn.
là vận tốc của cô gái tính từ trạng thái nghỉ đến khi dừng hẳn.
Đổi 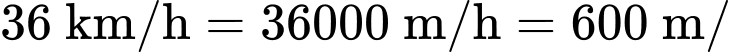 phút,
phút, 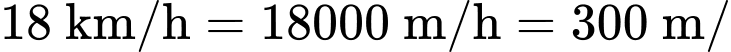 phút.
phút.
a) Sai.
Vì tốc độ từ phút thứ 4 đến phút thứ 7 là không đổi, trong khi hình vẽ đang đi xuống tại thời điểm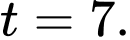
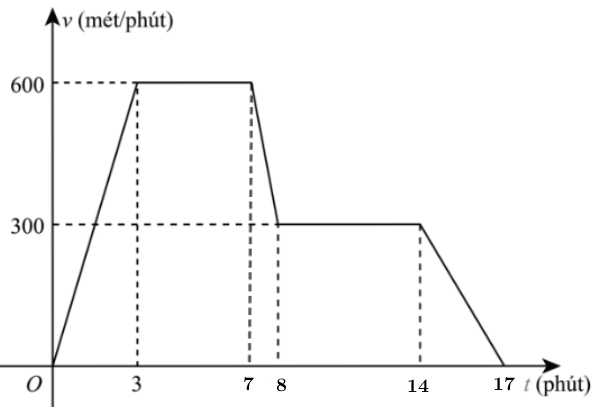
b) Sai.
Dựa vào đồ thị câu a) ta có: Tại thời điểm phút thứ 14, vận tốc của cô gái là 300 mét/phút.
c) Đúng.
Gọi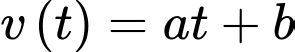 là vận tốc của cô gái đi trong 3 giây trước khi dừng lại.
là vận tốc của cô gái đi trong 3 giây trước khi dừng lại.
Ta có: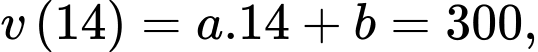
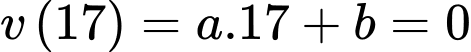
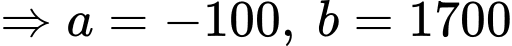
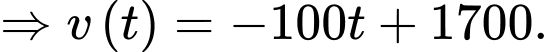
Quãng đường cô gái đi được trong 2 phút cuối là
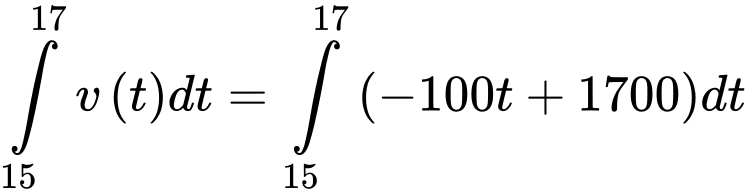
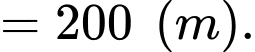
d) Sai.
Quãng đường cô gái đi trong 14 phút đầu tiên là:
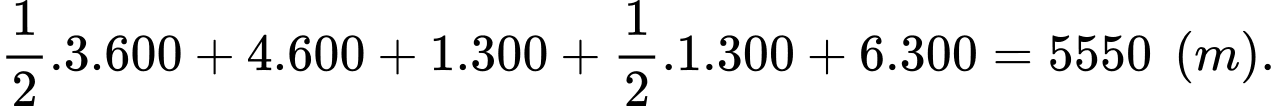
Vận tốc trung bình của cô gái trong 14 phút đầu tiên là
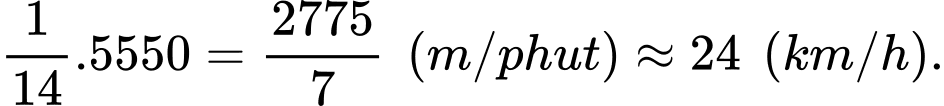
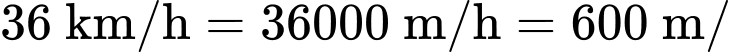 phút,
phút, 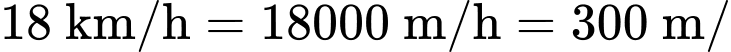 phút.
phút.a) Sai.
Vì tốc độ từ phút thứ 4 đến phút thứ 7 là không đổi, trong khi hình vẽ đang đi xuống tại thời điểm
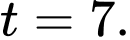

b) Sai.
Dựa vào đồ thị câu a) ta có: Tại thời điểm phút thứ 14, vận tốc của cô gái là 300 mét/phút.
c) Đúng.
Gọi
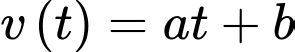 là vận tốc của cô gái đi trong 3 giây trước khi dừng lại.
là vận tốc của cô gái đi trong 3 giây trước khi dừng lại. Ta có:
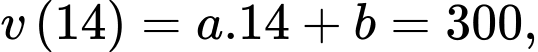
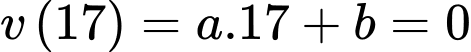
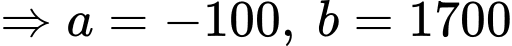
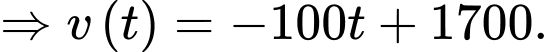
Quãng đường cô gái đi được trong 2 phút cuối là
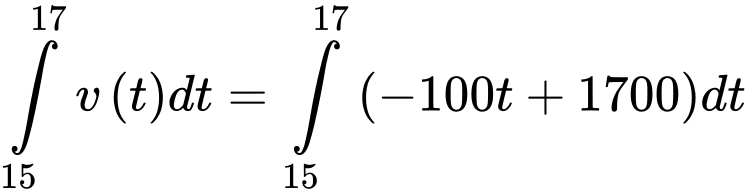
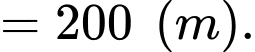
d) Sai.
Quãng đường cô gái đi trong 14 phút đầu tiên là:
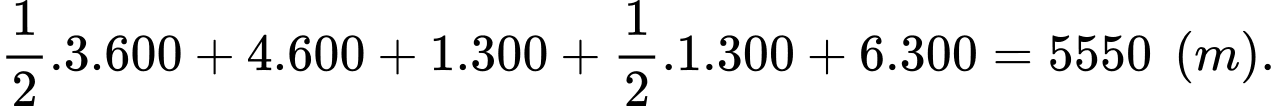
Vận tốc trung bình của cô gái trong 14 phút đầu tiên là
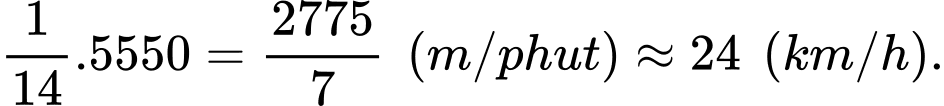
PHẦN III. Thí sinh trả lời từ câu 1 đến câu 6.
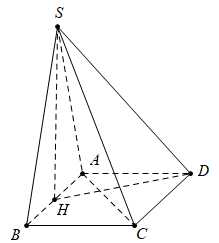
Câu 17 [693504]: Cho hình chóp 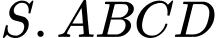 có đáy
có đáy 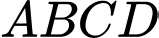 là hình thoi cạnh bằng
là hình thoi cạnh bằng 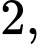
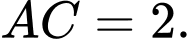 Hình chiếu của
Hình chiếu của 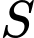 trên mặt phẳng đáy trùng với trung điểm
trên mặt phẳng đáy trùng với trung điểm 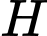 của cạnh
của cạnh 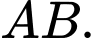 Khi
Khi 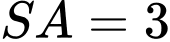 thì sin của góc giữa đường thẳng
thì sin của góc giữa đường thẳng 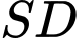 và mặt phẳng
và mặt phẳng 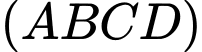 bằng bao nhiêu? (làm tròn kết quả đến hàng phần mười).
bằng bao nhiêu? (làm tròn kết quả đến hàng phần mười).
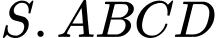 có đáy
có đáy 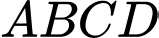 là hình thoi cạnh bằng
là hình thoi cạnh bằng 
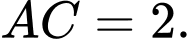 Hình chiếu của
Hình chiếu của 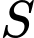 trên mặt phẳng đáy trùng với trung điểm
trên mặt phẳng đáy trùng với trung điểm 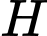 của cạnh
của cạnh 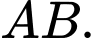 Khi
Khi 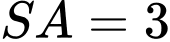 thì sin của góc giữa đường thẳng
thì sin của góc giữa đường thẳng 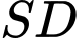 và mặt phẳng
và mặt phẳng 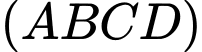 bằng bao nhiêu? (làm tròn kết quả đến hàng phần mười).
bằng bao nhiêu? (làm tròn kết quả đến hàng phần mười).
Điền đáp án: 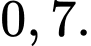
Ta có: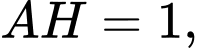

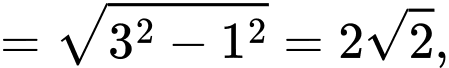
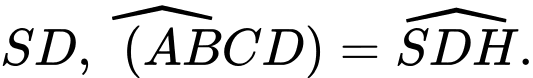
Tam giác có
có 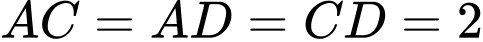
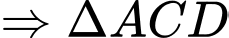 là tam giác đều.
Do đó hình thoi
là tam giác đều.
Do đó hình thoi 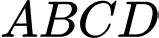 có
có 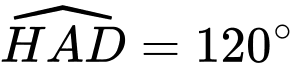
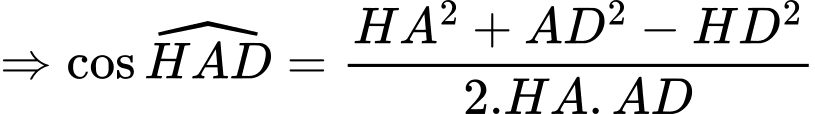
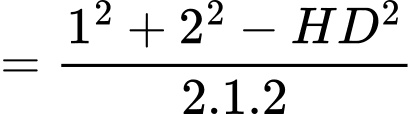
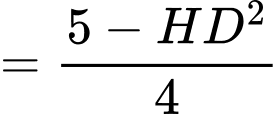
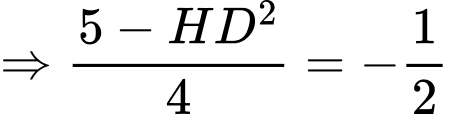
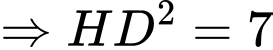
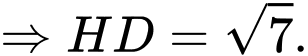
Ta có: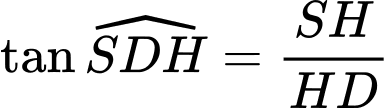
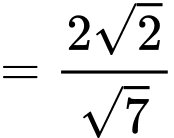
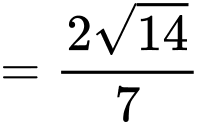
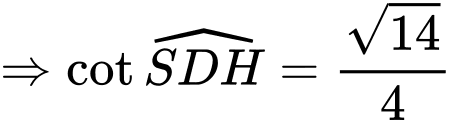
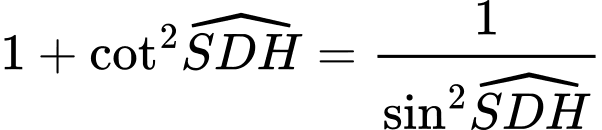
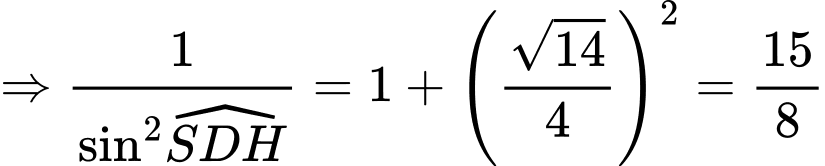

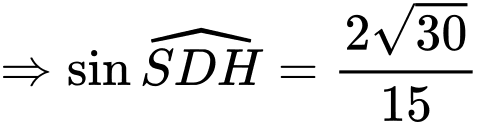
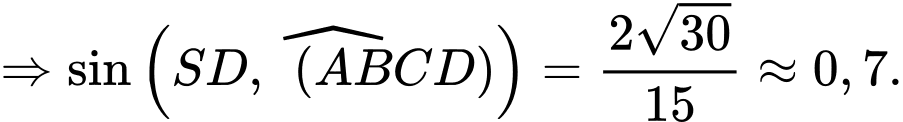
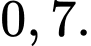

Ta có:
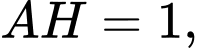

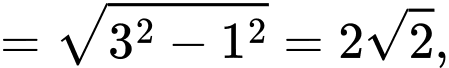
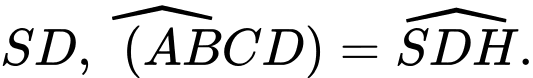
Tam giác
 có
có 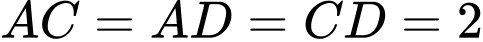
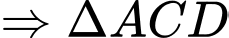 là tam giác đều.
Do đó hình thoi
là tam giác đều.
Do đó hình thoi 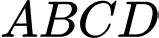 có
có 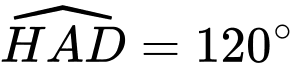
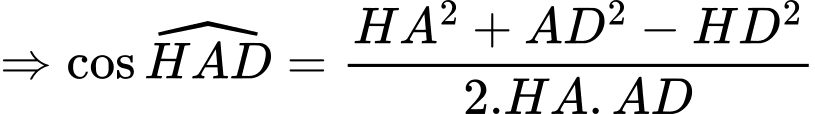
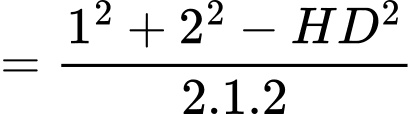
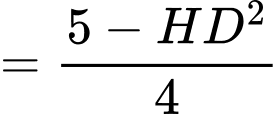
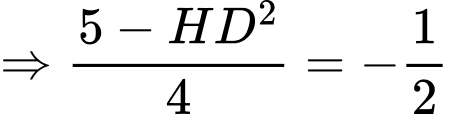
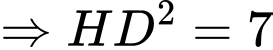
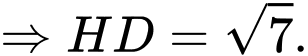
Ta có:
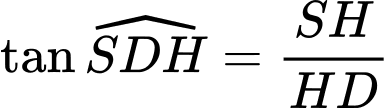
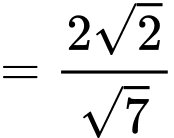
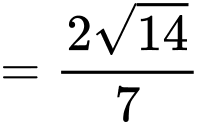
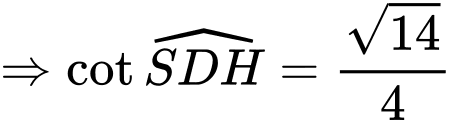
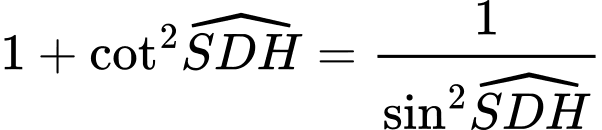
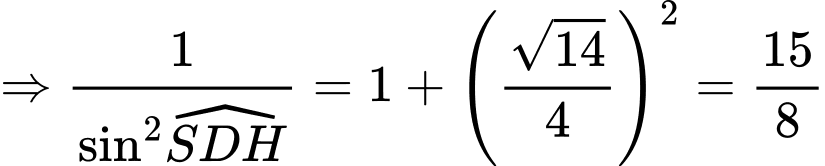

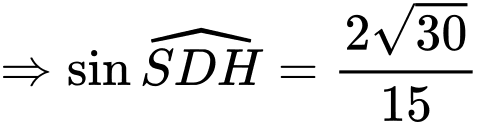
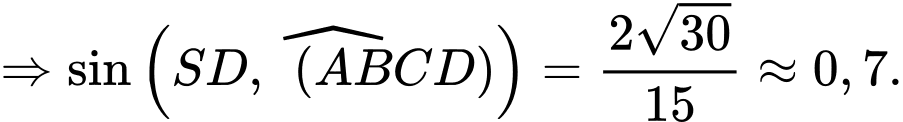
Câu 18 [693505]: Trong một đề thi trắc nghiệm môn Toán có loại câu hỏi trả lời dạng đúng sai. Một câu hỏi có 4 ý, mỗi ý học sinh chỉ cần trả lời đúng hoặc sai. Nếu 1 ý trả lời đúng đáp án thì được 0,1 điểm, đúng 2 ý được 0,25 điểm, đúng 3 ý được 0,5 điểm và đúng cả 4 ý được 1 điểm. Giả sử một thí sinh làm bài bằng cách chọn phương án ngẫu nhiên để trả lời cho 2 câu hỏi loại đúng sai này. Vậy có bao nhiêu cách chọn phương án để học sinh đó được đúng 1 điểm ở phần trả lời 2 câu hỏi này?
Điền đáp án: 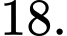
Để đạt 1 điểm sẽ có các trường hợp sau xảy ra:
TH1: Đúng cả 4 ý của 1 câu hỏi và sai cả 4 ý câu hỏi còn lại hoặc ngược lại.
TH2: Mỗi câu hỏi đúng 3 ý và sai 1 ý.
Gọi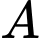 là biến cố học sinh đó được 1 điểm khi đó ta có:
là biến cố học sinh đó được 1 điểm khi đó ta có:
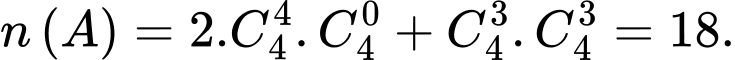
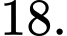
Để đạt 1 điểm sẽ có các trường hợp sau xảy ra:
TH1: Đúng cả 4 ý của 1 câu hỏi và sai cả 4 ý câu hỏi còn lại hoặc ngược lại.
TH2: Mỗi câu hỏi đúng 3 ý và sai 1 ý.
Gọi
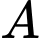 là biến cố học sinh đó được 1 điểm khi đó ta có:
là biến cố học sinh đó được 1 điểm khi đó ta có: 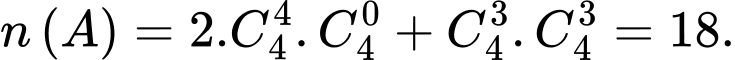
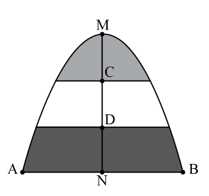
Câu 19 [693507]: Một khung cửa kính hình parabol với đỉnh 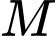 và cạnh đáy
và cạnh đáy  (minh hoạ ở hình bên). Biết chi phí để lắp phần kính màu (phần tô đậm trong hình) là 200 000 đồng/
(minh hoạ ở hình bên). Biết chi phí để lắp phần kính màu (phần tô đậm trong hình) là 200 000 đồng/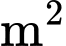 và phần kính trắng còn lại là 150 000 đồng/
và phần kính trắng còn lại là 150 000 đồng/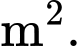 Cho
Cho 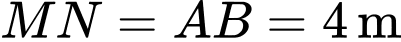 và
và 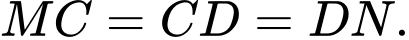 Hỏi số tiền để lắp kính cho khung cửa như trên bằng bao nhiêu triệu đồng? (làm tròn kết quả đến hàng phần mười).
Hỏi số tiền để lắp kính cho khung cửa như trên bằng bao nhiêu triệu đồng? (làm tròn kết quả đến hàng phần mười).
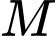 và cạnh đáy
và cạnh đáy  (minh hoạ ở hình bên). Biết chi phí để lắp phần kính màu (phần tô đậm trong hình) là 200 000 đồng/
(minh hoạ ở hình bên). Biết chi phí để lắp phần kính màu (phần tô đậm trong hình) là 200 000 đồng/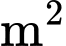 và phần kính trắng còn lại là 150 000 đồng/
và phần kính trắng còn lại là 150 000 đồng/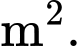 Cho
Cho 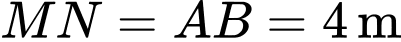 và
và 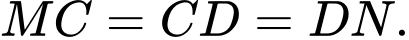 Hỏi số tiền để lắp kính cho khung cửa như trên bằng bao nhiêu triệu đồng? (làm tròn kết quả đến hàng phần mười).
Hỏi số tiền để lắp kính cho khung cửa như trên bằng bao nhiêu triệu đồng? (làm tròn kết quả đến hàng phần mười).
Điền đáp án: 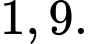

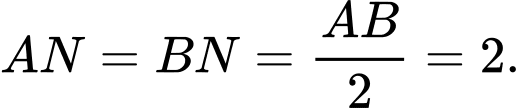
Coi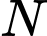 là gốc toạ độ thì ta có:
là gốc toạ độ thì ta có: 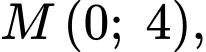
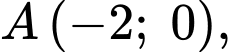
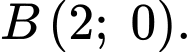
Gọi phương trình parabol là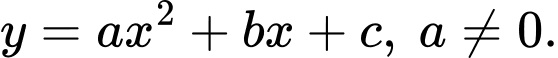
Ta có: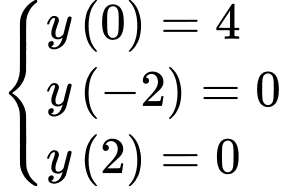
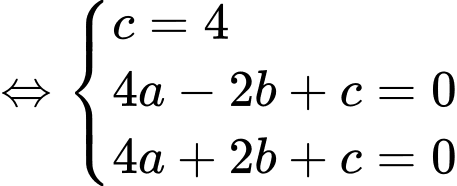
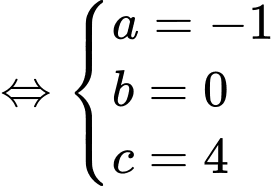
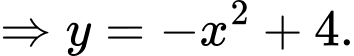
Diện tích hình phẳng giới hạn bởi parabol và trục hoành là: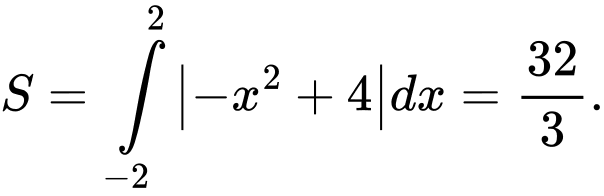
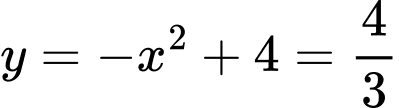
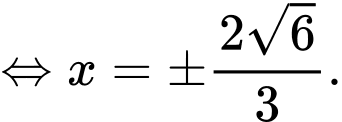
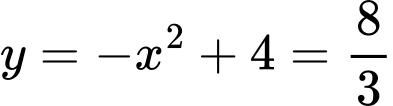
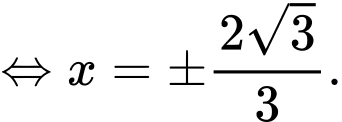
Diện tích hình phẳng giới hạn bởi parabol và đường thẳng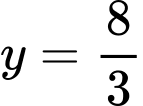 là:
là: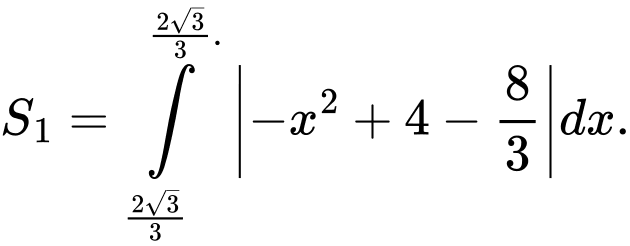
Diện tích hình phẳng giới hạn bởi parabol và đường thẳng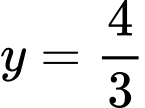 là:
là: 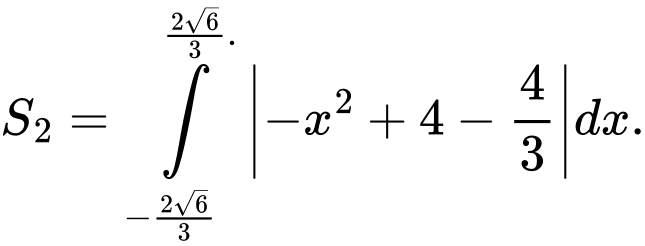
Khi đó số tiền để lắp kính là:
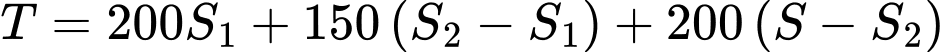
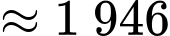 (nghìn đồng)
(nghìn đồng) 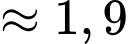 (triệu đồng).
(triệu đồng).
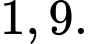

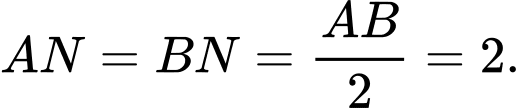
Coi
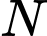 là gốc toạ độ thì ta có:
là gốc toạ độ thì ta có: 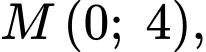
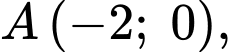
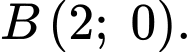
Gọi phương trình parabol là
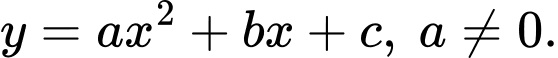
Ta có:
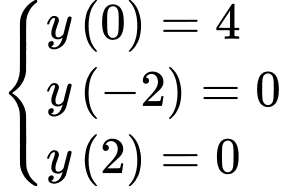
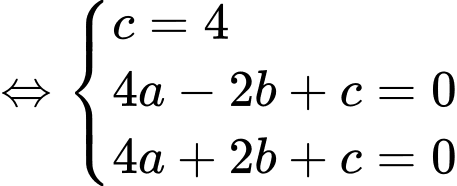
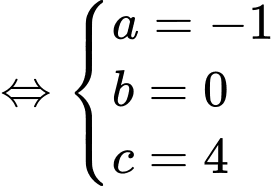
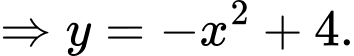
Diện tích hình phẳng giới hạn bởi parabol và trục hoành là:
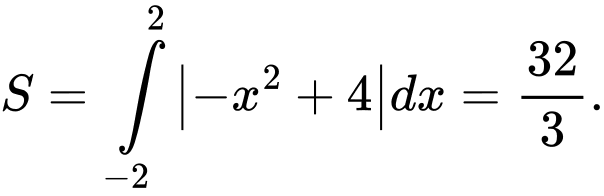
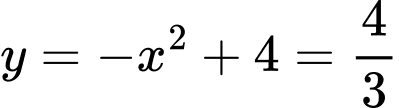
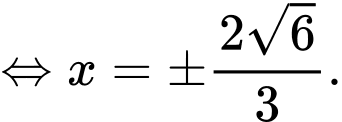
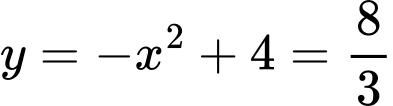
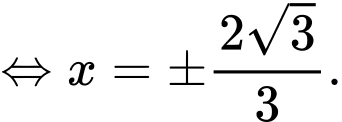
Diện tích hình phẳng giới hạn bởi parabol và đường thẳng
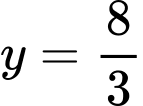 là:
là: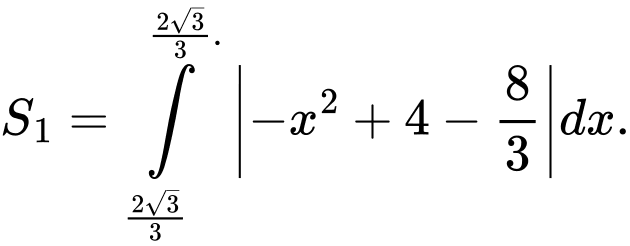
Diện tích hình phẳng giới hạn bởi parabol và đường thẳng
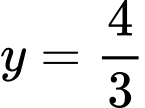 là:
là: 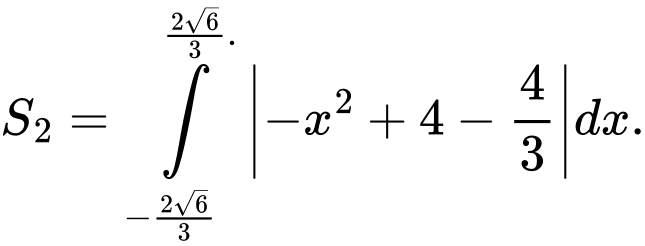
Khi đó số tiền để lắp kính là:
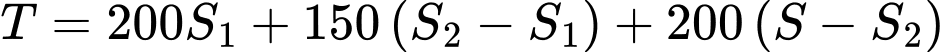
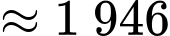 (nghìn đồng)
(nghìn đồng) 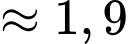 (triệu đồng).
(triệu đồng).
Câu 20 [693508]: Một người nghi ngờ bị bệnh B, với xác suất 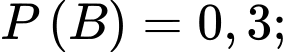 cho người này làm xét nghiệm A. Xét nghiệm A sẽ trả về hoặc dương tính, hoặc âm tính. Thống kê cho thấy, trong số những người có xét nghiệm dương tính chỉ có 80% là bị bệnh B, còn trong số những người âm tính thì có 90% không bị bệnh này. Trong y học, độ nhạy của một xét nghiệm là tỷ lệ những trường hợp thực sự có bệnh và có kết quả xét nghiệm dương tính trong toàn bộ các trường hợp có bệnh. Tính độ nhạy của xét nghiệm A. Kết quả làm tròn đến hàng phần trăm?
cho người này làm xét nghiệm A. Xét nghiệm A sẽ trả về hoặc dương tính, hoặc âm tính. Thống kê cho thấy, trong số những người có xét nghiệm dương tính chỉ có 80% là bị bệnh B, còn trong số những người âm tính thì có 90% không bị bệnh này. Trong y học, độ nhạy của một xét nghiệm là tỷ lệ những trường hợp thực sự có bệnh và có kết quả xét nghiệm dương tính trong toàn bộ các trường hợp có bệnh. Tính độ nhạy của xét nghiệm A. Kết quả làm tròn đến hàng phần trăm?
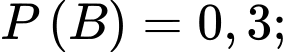 cho người này làm xét nghiệm A. Xét nghiệm A sẽ trả về hoặc dương tính, hoặc âm tính. Thống kê cho thấy, trong số những người có xét nghiệm dương tính chỉ có 80% là bị bệnh B, còn trong số những người âm tính thì có 90% không bị bệnh này. Trong y học, độ nhạy của một xét nghiệm là tỷ lệ những trường hợp thực sự có bệnh và có kết quả xét nghiệm dương tính trong toàn bộ các trường hợp có bệnh. Tính độ nhạy của xét nghiệm A. Kết quả làm tròn đến hàng phần trăm?
cho người này làm xét nghiệm A. Xét nghiệm A sẽ trả về hoặc dương tính, hoặc âm tính. Thống kê cho thấy, trong số những người có xét nghiệm dương tính chỉ có 80% là bị bệnh B, còn trong số những người âm tính thì có 90% không bị bệnh này. Trong y học, độ nhạy của một xét nghiệm là tỷ lệ những trường hợp thực sự có bệnh và có kết quả xét nghiệm dương tính trong toàn bộ các trường hợp có bệnh. Tính độ nhạy của xét nghiệm A. Kết quả làm tròn đến hàng phần trăm?
Điền đáp án: 0,76.
Gọi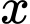 là tỷ lệ cho kết quả dương tính, khi đó
là tỷ lệ cho kết quả dương tính, khi đó 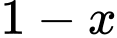 là tỷ lệ cho kết quả âm tính.
là tỷ lệ cho kết quả âm tính.
Gọi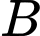 là biến cố “Người đó bị bệnh B”.
là biến cố “Người đó bị bệnh B”.
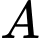 là biến cố “Xét nghiệm A trả về kết quả dương tính”
là biến cố “Xét nghiệm A trả về kết quả dương tính”
Yêu cầu bài toán tương đương với tìm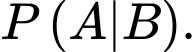
Dựa vào giả thiết, ta có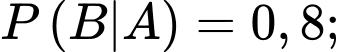
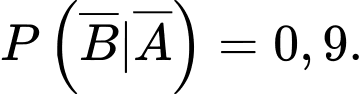
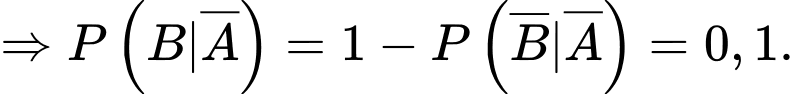
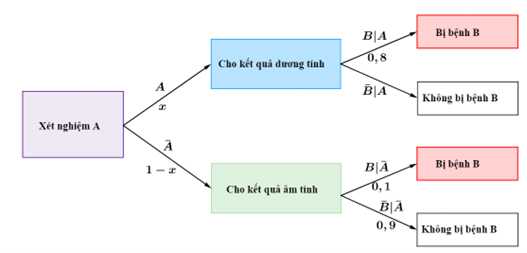
Từ đó, ta có sơ đồ cây như sau:
Ta có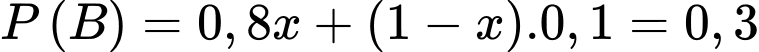
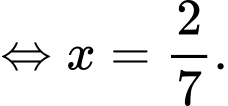
Suy ra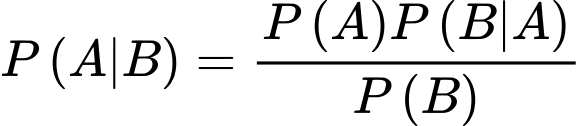
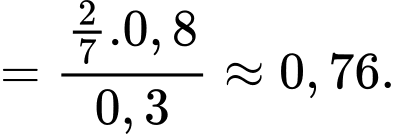
Gọi
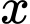 là tỷ lệ cho kết quả dương tính, khi đó
là tỷ lệ cho kết quả dương tính, khi đó 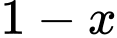 là tỷ lệ cho kết quả âm tính.
là tỷ lệ cho kết quả âm tính.Gọi
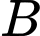 là biến cố “Người đó bị bệnh B”.
là biến cố “Người đó bị bệnh B”.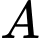 là biến cố “Xét nghiệm A trả về kết quả dương tính”
là biến cố “Xét nghiệm A trả về kết quả dương tính”Yêu cầu bài toán tương đương với tìm
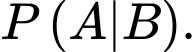
Dựa vào giả thiết, ta có
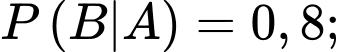
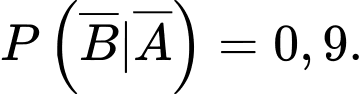
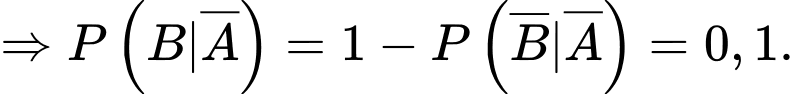
Từ đó, ta có sơ đồ cây như sau:

Ta có
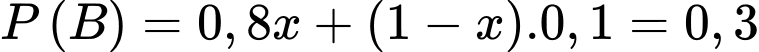
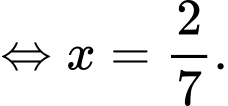
Suy ra
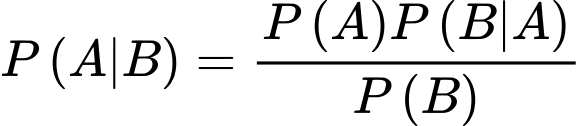
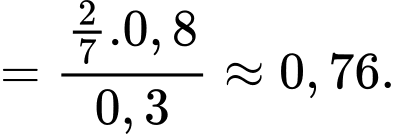
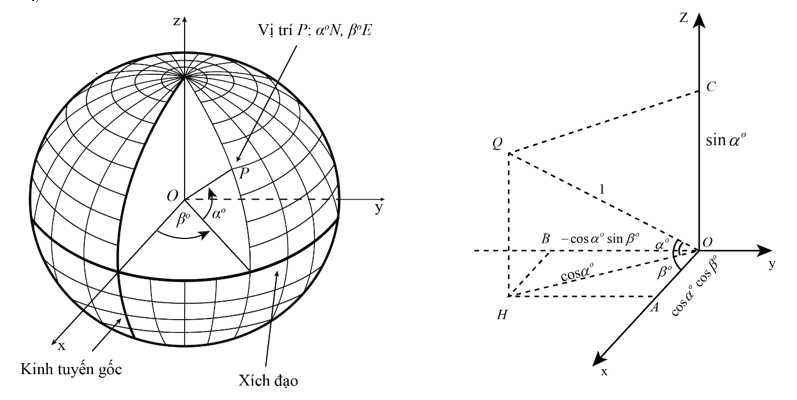
Câu 21 [693506]: Giả định rằng Trái Đất là một hình cầu hoàn hảo với bán kính R là 6371 km, trong không gian 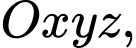 với
với  là tâm trái đất, tia
là tâm trái đất, tia 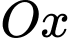 chứa giao điểm của kinh tuyến gốc và xích đạo, tia
chứa giao điểm của kinh tuyến gốc và xích đạo, tia  chứa điểm cực bắc
chứa điểm cực bắc 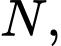 tia
tia 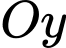 giao xích đạo tại điểm thuộc bán cầu Đông, một đơn vị dài trong không gian
giao xích đạo tại điểm thuộc bán cầu Đông, một đơn vị dài trong không gian 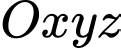 tương ứng với 6371 km trong thực tế. Biết rằng điểm
tương ứng với 6371 km trong thực tế. Biết rằng điểm 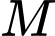 có vĩ độ và kinh độ tương ứng là
có vĩ độ và kinh độ tương ứng là 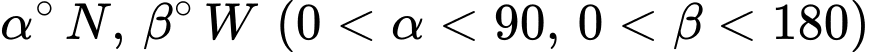 thì có tọa độ là
thì có tọa độ là 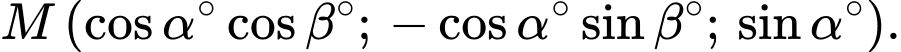 Giả sử một trạm phát sóng trên mặt đất được đặt ở vị trí
Giả sử một trạm phát sóng trên mặt đất được đặt ở vị trí 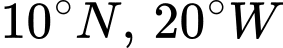 và một máy thu được đặt tại vị trí
và một máy thu được đặt tại vị trí 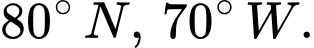 Khoảng cách giữa trạm phát sóng và trạm thu trên mặt đất bằng bao nhiêu km. Viết kết quả làm tròn đến hàng đơn vị.
Khoảng cách giữa trạm phát sóng và trạm thu trên mặt đất bằng bao nhiêu km. Viết kết quả làm tròn đến hàng đơn vị.
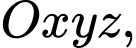 với
với  là tâm trái đất, tia
là tâm trái đất, tia 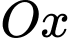 chứa giao điểm của kinh tuyến gốc và xích đạo, tia
chứa giao điểm của kinh tuyến gốc và xích đạo, tia  chứa điểm cực bắc
chứa điểm cực bắc 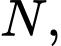 tia
tia 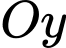 giao xích đạo tại điểm thuộc bán cầu Đông, một đơn vị dài trong không gian
giao xích đạo tại điểm thuộc bán cầu Đông, một đơn vị dài trong không gian 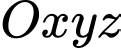 tương ứng với 6371 km trong thực tế. Biết rằng điểm
tương ứng với 6371 km trong thực tế. Biết rằng điểm 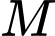 có vĩ độ và kinh độ tương ứng là
có vĩ độ và kinh độ tương ứng là 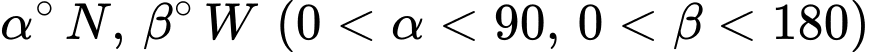 thì có tọa độ là
thì có tọa độ là 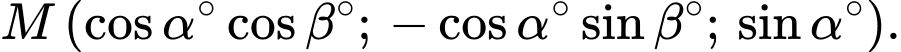 Giả sử một trạm phát sóng trên mặt đất được đặt ở vị trí
Giả sử một trạm phát sóng trên mặt đất được đặt ở vị trí 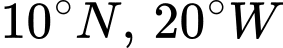 và một máy thu được đặt tại vị trí
và một máy thu được đặt tại vị trí 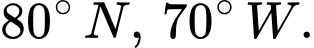 Khoảng cách giữa trạm phát sóng và trạm thu trên mặt đất bằng bao nhiêu km. Viết kết quả làm tròn đến hàng đơn vị.
Khoảng cách giữa trạm phát sóng và trạm thu trên mặt đất bằng bao nhiêu km. Viết kết quả làm tròn đến hàng đơn vị.
Điền đáp án: 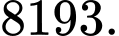
Giả sử trạm phát sóng được đặt tại điểm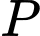 và máy thu được đặt tại điểm
và máy thu được đặt tại điểm  .
.
Khi đó: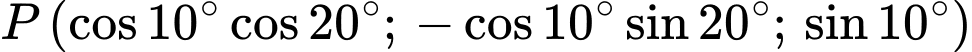 và
và 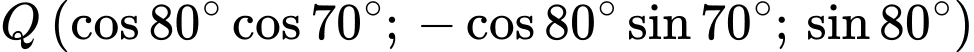 .
.
Suy ra: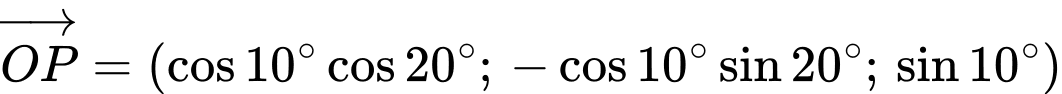 ;
; 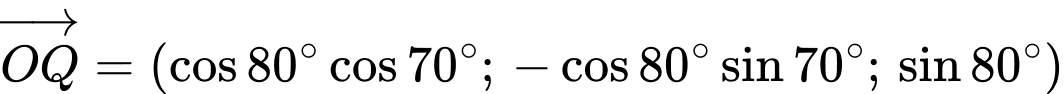 .
.
Do đó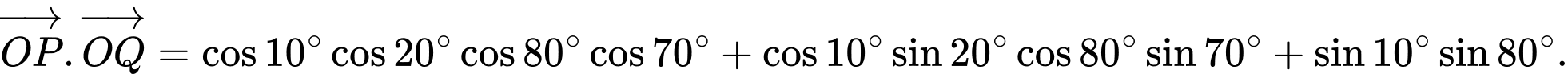
Vì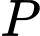 và
và  thuộc mặt đất nên
thuộc mặt đất nên 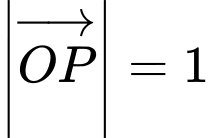 và
và 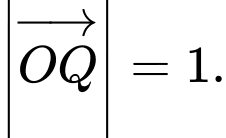
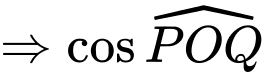
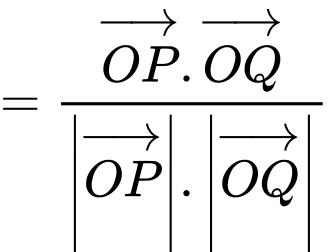
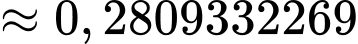
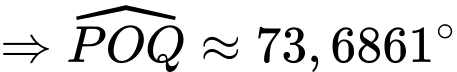 .
.
Đường tròn tâm , đi qua
, đi qua 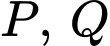 có bán kính bằng 1 và có chu vi là
có bán kính bằng 1 và có chu vi là 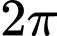 nên cung nhỏ
nên cung nhỏ 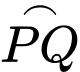 của đường tròn có độ dài xấp xỉ bằng
của đường tròn có độ dài xấp xỉ bằng 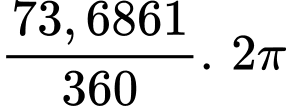 .
.
Khoảng cách trên mặt đất giữa hai vị trí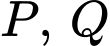 xấp xỉ bằng:
xấp xỉ bằng:
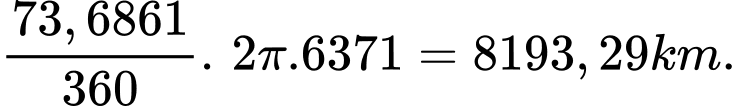
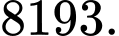
Giả sử trạm phát sóng được đặt tại điểm
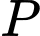 và máy thu được đặt tại điểm
và máy thu được đặt tại điểm  .
.
Khi đó:
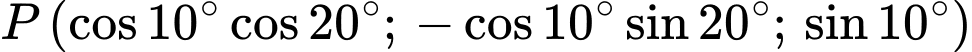 và
và 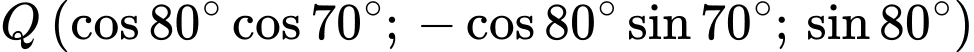 .
.
Suy ra:
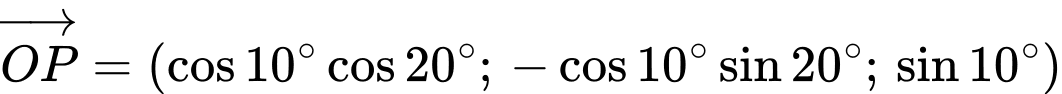 ;
; 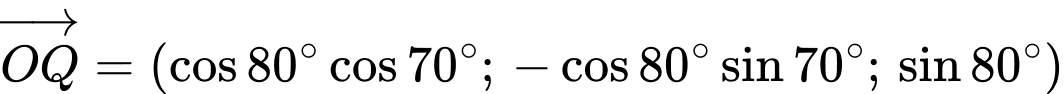 .
.
Do đó
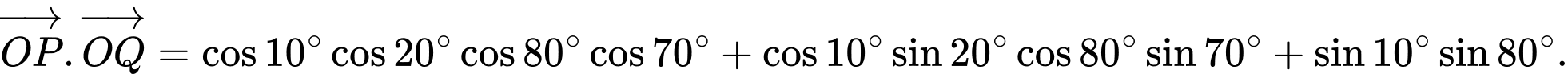
Vì
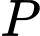 và
và  thuộc mặt đất nên
thuộc mặt đất nên 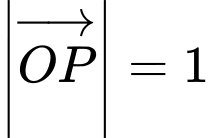 và
và 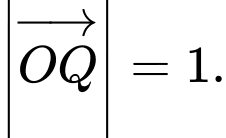
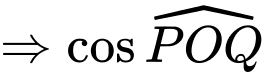
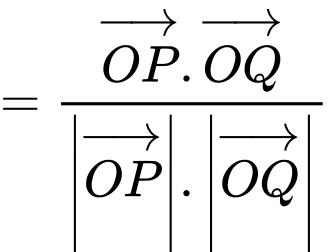
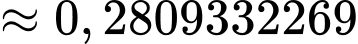
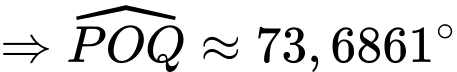 .
.
Đường tròn tâm
 , đi qua
, đi qua 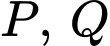 có bán kính bằng 1 và có chu vi là
có bán kính bằng 1 và có chu vi là 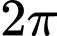 nên cung nhỏ
nên cung nhỏ 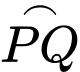 của đường tròn có độ dài xấp xỉ bằng
của đường tròn có độ dài xấp xỉ bằng 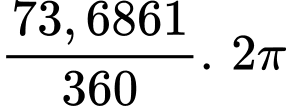 .
.
Khoảng cách trên mặt đất giữa hai vị trí
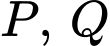 xấp xỉ bằng:
xấp xỉ bằng: 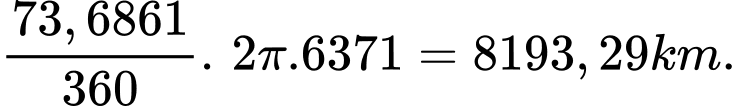
Câu 22 [702942]: Chi phí nhiên liệu của một chiếc tàu chạy trên sông được chia làm hai phần.Phần thứ nhất không phụ thuộc vào vận tốc và có chi phí mỗi giờ 480 nghìn đồng. Chi phí mỗi giờ của phần thứ hai tỉ lệ thuận với lập phương vận tốc. Khi tàu di chuyển với vận tốc 10(km/h) thì tổng chi phí cho mỗi kilomet của tàu bằng 51 nghìn đồng. Hỏi tàu phải di chuyển với vận tốc bằng bao nhiêu km/h để tổng chi phí nhiên liệu trên mỗi kilomet là nhỏ nhất?
Điền đáp án: 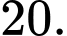
Gọi là vận tốc của tàu.
là vận tốc của tàu.
Tàu chạy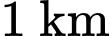 tức
tức 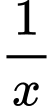 (giờ) thì chi phí phần thứ nhất tính cho mỗi
(giờ) thì chi phí phần thứ nhất tính cho mỗi 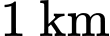 đường là
đường là 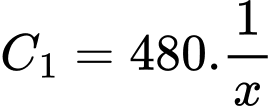 (nghìn đồng).
(nghìn đồng).
Chi phí phần thứ hai tính cho một giờ xác định bởi: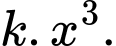
Chi phí tính cho mỗi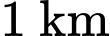 đường là
đường là 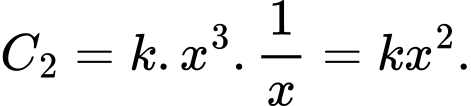
Tổng chi phí cho mỗi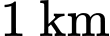 đường là
đường là 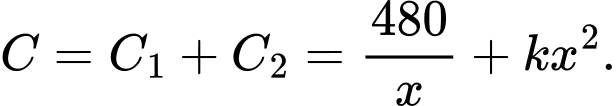
Theo bài ra ta có: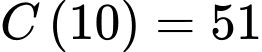
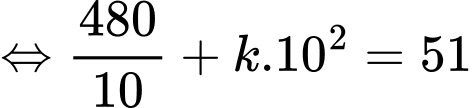
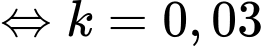
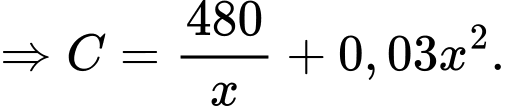
Ta có: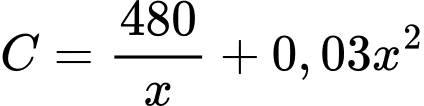
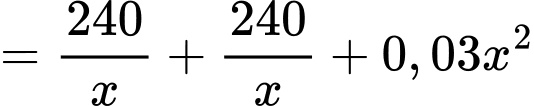
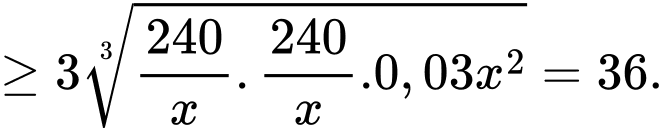
Dấu bằng xảy ra khi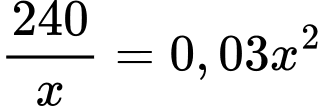
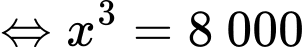
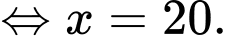
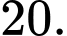
Gọi
 là vận tốc của tàu.
là vận tốc của tàu.
Tàu chạy
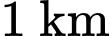 tức
tức 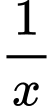 (giờ) thì chi phí phần thứ nhất tính cho mỗi
(giờ) thì chi phí phần thứ nhất tính cho mỗi 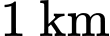 đường là
đường là 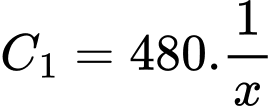 (nghìn đồng).
(nghìn đồng).
Chi phí phần thứ hai tính cho một giờ xác định bởi:
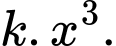
Chi phí tính cho mỗi
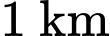 đường là
đường là 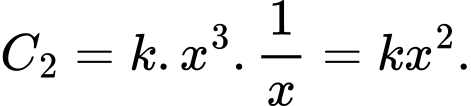
Tổng chi phí cho mỗi
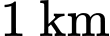 đường là
đường là 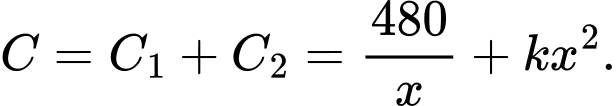
Theo bài ra ta có:
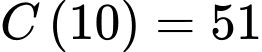
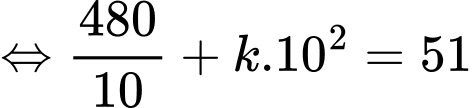
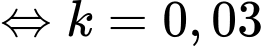
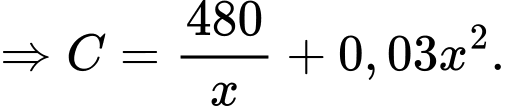
Ta có:
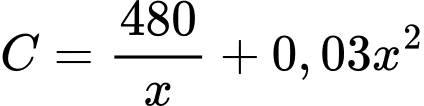
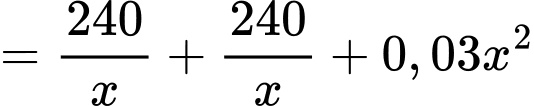
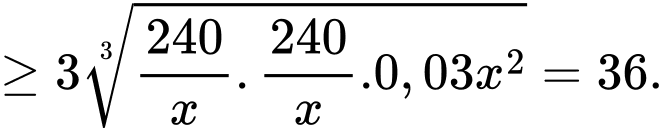
Dấu bằng xảy ra khi