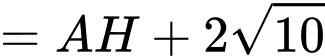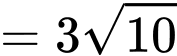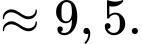PHẦN I. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Câu 1 [693524]: Nếu 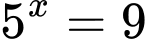 thì
thì 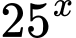 bằng
bằng
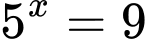 thì
thì 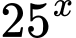 bằng
bằng A, 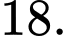
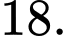
B, 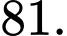
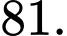
C, 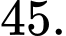
D, 
Chọn đáp án B.
Ta có: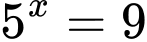
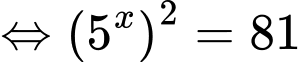
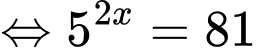
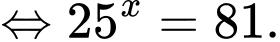 Đáp án: B
Đáp án: B
Ta có:
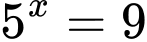
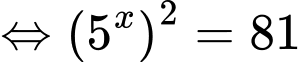
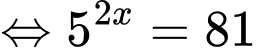
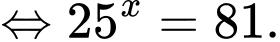 Đáp án: B
Đáp án: B
Câu 2 [693525]: Cho dãy số 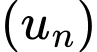 với
với 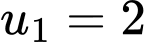 và
và 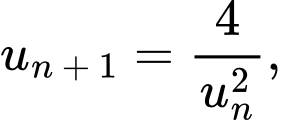
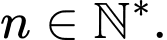 Giá trị của
Giá trị của 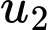 bằng
bằng
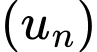 với
với 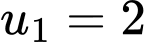 và
và 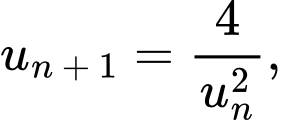
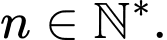 Giá trị của
Giá trị của 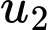 bằng
bằng A, 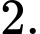
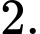
B, 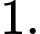
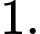
C, 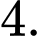
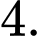
D, 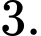
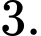
Chọn đáp án B.
Với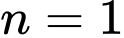 ta có:
ta có: 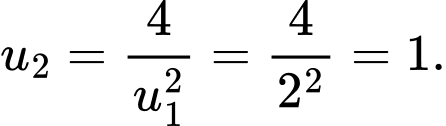 Đáp án: B
Đáp án: B
Với
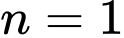 ta có:
ta có: 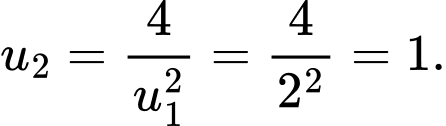 Đáp án: B
Đáp án: B
Câu 3 [693526]: Trong không gian 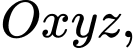 đường thẳng
đường thẳng 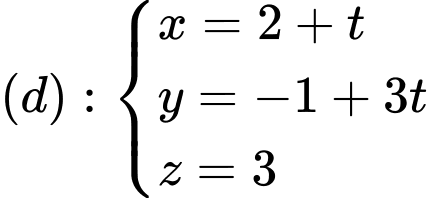 có một vectơ chỉ phương là
có một vectơ chỉ phương là
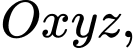 đường thẳng
đường thẳng 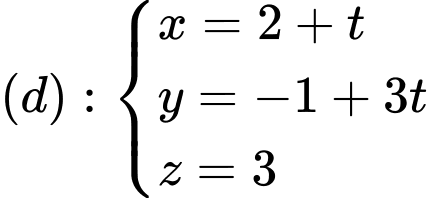 có một vectơ chỉ phương là
có một vectơ chỉ phương là A, 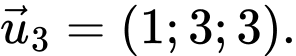
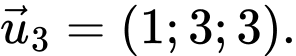
B, 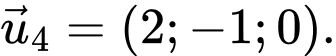
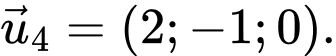
C, 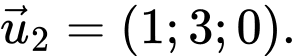
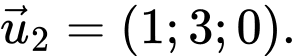
D, 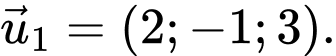
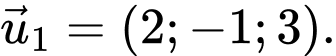
Chọn đáp án C.
Từ phương trình đường thẳng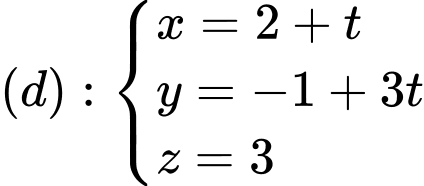 ta có vecto chỉ phương của đường thẳng
ta có vecto chỉ phương của đường thẳng  là:
là: 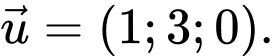 Đáp án: C
Đáp án: C
Từ phương trình đường thẳng
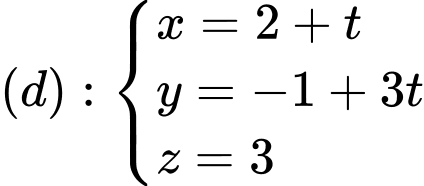 ta có vecto chỉ phương của đường thẳng
ta có vecto chỉ phương của đường thẳng  là:
là: 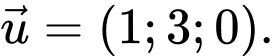 Đáp án: C
Đáp án: C
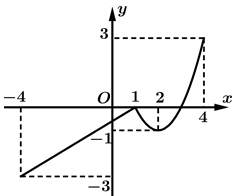
Câu 4 [256897]: Cho hàm số 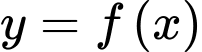 có đồ thị như hình vẽ bên. Gọi
có đồ thị như hình vẽ bên. Gọi 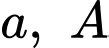 lần lượt là giá trị nhỏ nhất và giá trị lớn nhất của
lần lượt là giá trị nhỏ nhất và giá trị lớn nhất của 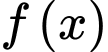 trên đoạn
trên đoạn 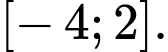 Giá trị
Giá trị 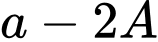 bằng
bằng
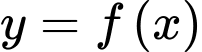 có đồ thị như hình vẽ bên. Gọi
có đồ thị như hình vẽ bên. Gọi 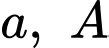 lần lượt là giá trị nhỏ nhất và giá trị lớn nhất của
lần lượt là giá trị nhỏ nhất và giá trị lớn nhất của 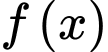 trên đoạn
trên đoạn 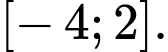 Giá trị
Giá trị 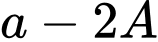 bằng
bằng
A, 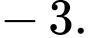
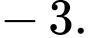
B, 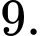
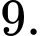
C, 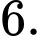
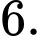
D, 

Chọn đáp án A.
Dựa vào đồ thị hàm số, ta có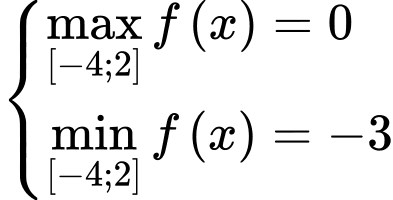
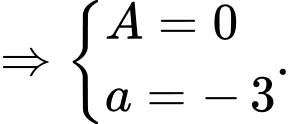
Khi đó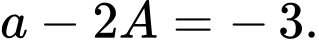 Đáp án: A
Đáp án: A
Dựa vào đồ thị hàm số, ta có
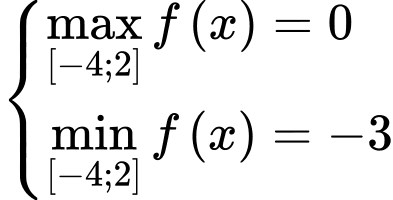
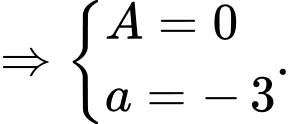
Khi đó
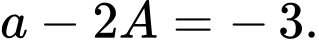 Đáp án: A
Đáp án: A
Câu 5 [693527]: Họ tất cả các nguyên hàm của hàm số 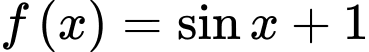 là
là
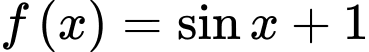 là
là A, 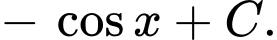
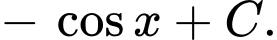
B, 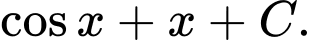
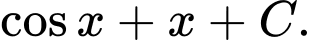
C, 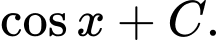
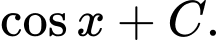
D, 

Chọn đáp án D.
Ta có: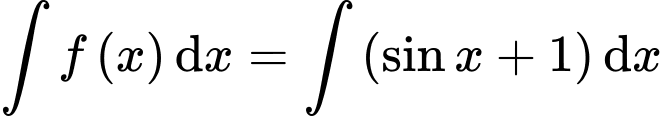
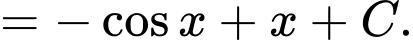
Ta có:
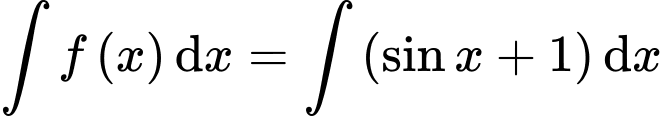
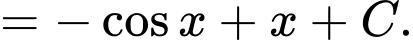
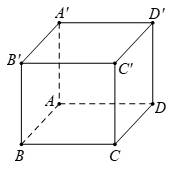
Câu 6 [693528]: Cho hình lập phương  (xem hình minh hoạ). Khẳng định nào sau đây đúng?
(xem hình minh hoạ). Khẳng định nào sau đây đúng?
 (xem hình minh hoạ). Khẳng định nào sau đây đúng?
(xem hình minh hoạ). Khẳng định nào sau đây đúng?
A, 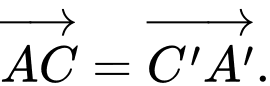
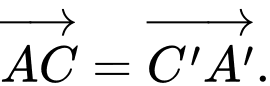
B, 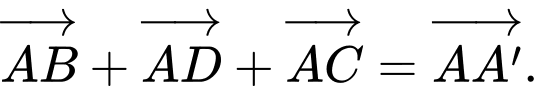
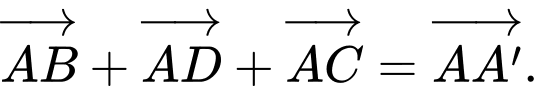
C, 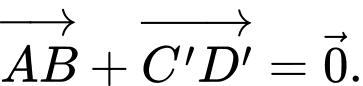
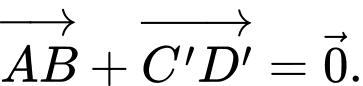
D, 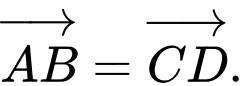
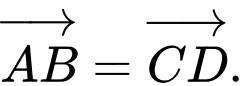
Chọn đáp án C.
Từ hình vẽ ta có:
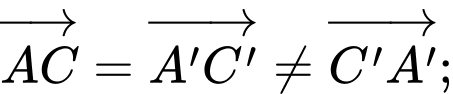
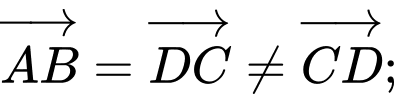
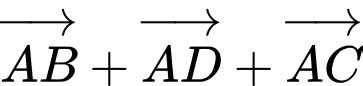
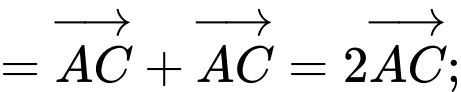
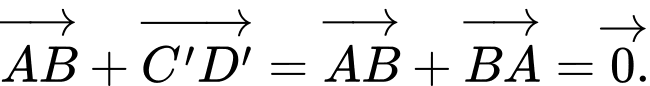
Vậy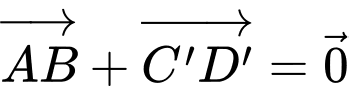 đúng. Đáp án: C
đúng. Đáp án: C
Từ hình vẽ ta có:
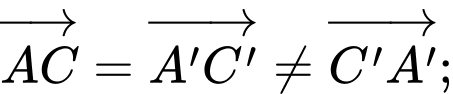
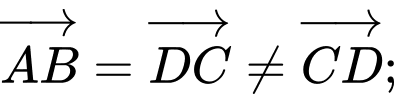
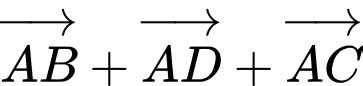
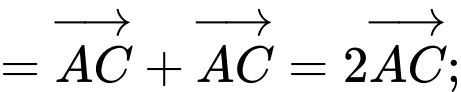
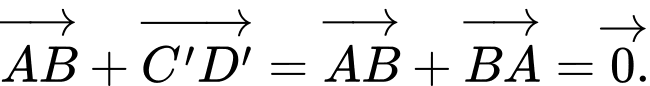
Vậy
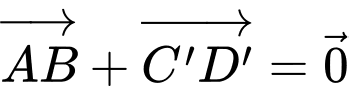 đúng. Đáp án: C
đúng. Đáp án: C
Câu 7 [693529]: Với 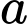 là số thực dương tuỳ ý,
là số thực dương tuỳ ý,  bằng
bằng
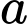 là số thực dương tuỳ ý,
là số thực dương tuỳ ý,  bằng
bằng A, 

B, 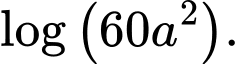
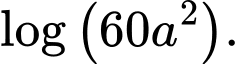
C, 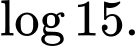
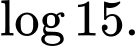
D, 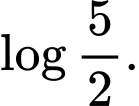
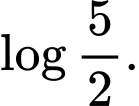
Chọn đáp án C.
Ta có:
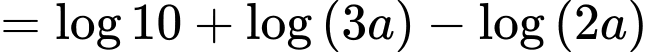
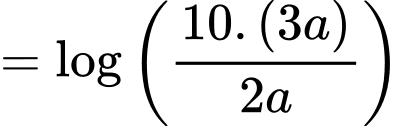
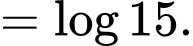 Đáp án: C
Đáp án: C
Ta có:

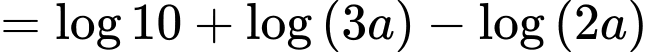
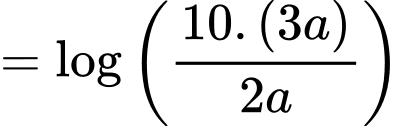
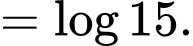 Đáp án: C
Đáp án: C
Câu 8 [699984]: Tính thể tích của khối tròn xoay thu được khi quay hình phẳng được giới hạn bởi đường cong 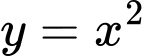 và hai đường thẳng
và hai đường thẳng 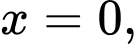
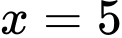 khi quay quanh trục
khi quay quanh trục 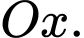
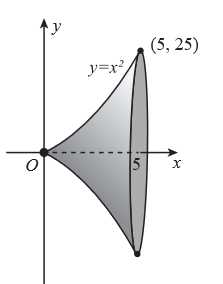
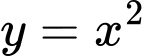 và hai đường thẳng
và hai đường thẳng 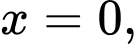
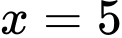 khi quay quanh trục
khi quay quanh trục 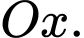

A, 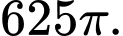
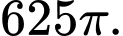
B, 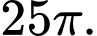
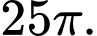
C, 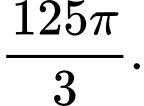
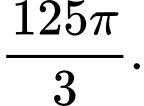
D, 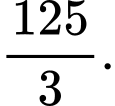
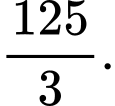
Chọn đáp án A.
Áp dụng CT tính thể tích trong tích phân ta có:
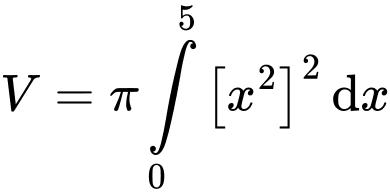
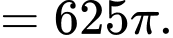 Đáp án: A
Đáp án: A
Áp dụng CT tính thể tích trong tích phân ta có:
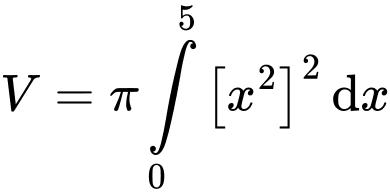
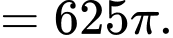 Đáp án: A
Đáp án: A
Câu 9 [693530]: Tìm hiểu thời gian hoàn thành một bài tập (đơn vị: phút) của một nhóm học sinh thu được kết quả ở bảng sau:

Thời gian trung bình (phút) để hoàn thành bài tập của các em học sinh là

Thời gian trung bình (phút) để hoàn thành bài tập của các em học sinh là
A, 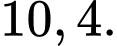
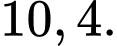
B, 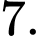
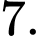
C, 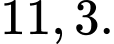
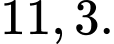
D, 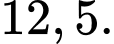
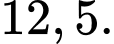
Chọn đáp án A.
Ta có: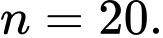
Thời gian trung bình (phút) để hoàn thành bài tập của các em học sinh là
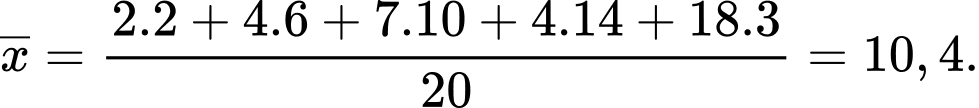 Đáp án: A
Đáp án: A
Ta có:
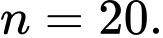
Thời gian trung bình (phút) để hoàn thành bài tập của các em học sinh là
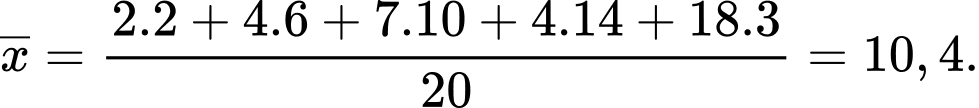 Đáp án: A
Đáp án: A
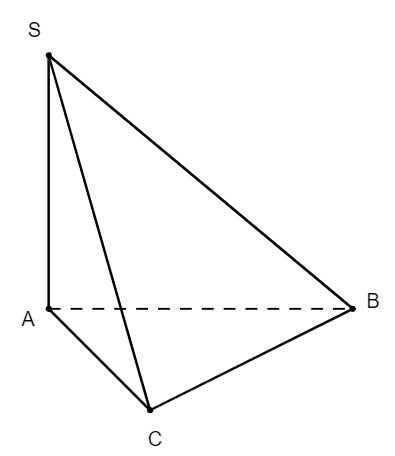
Câu 10 [693531]: Cho hình chóp 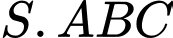 có đáy là tam giác
có đáy là tam giác 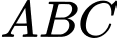 vuông tại
vuông tại 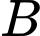 và
và 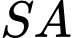 vuông góc với mặt phẳng đáy. Góc giữa đường thẳng
vuông góc với mặt phẳng đáy. Góc giữa đường thẳng 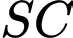 và mặt phẳng
và mặt phẳng 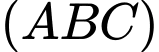 là
là
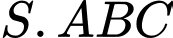 có đáy là tam giác
có đáy là tam giác 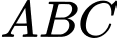 vuông tại
vuông tại 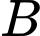 và
và 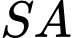 vuông góc với mặt phẳng đáy. Góc giữa đường thẳng
vuông góc với mặt phẳng đáy. Góc giữa đường thẳng 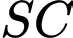 và mặt phẳng
và mặt phẳng 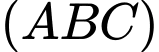 là
là A, 

B, 

C, 

D, 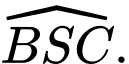
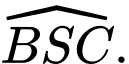
Chọn đáp án B.
Góc giữa đường thẳng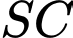 và mặt phẳng
và mặt phẳng 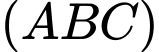 là
là  Đáp án: B
Đáp án: B

Góc giữa đường thẳng
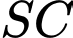 và mặt phẳng
và mặt phẳng 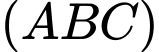 là
là  Đáp án: B
Đáp án: B
Câu 11 [256802]: Cho hàm số 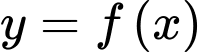 có đạo hàm trên
có đạo hàm trên 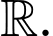 Biết
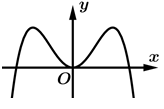
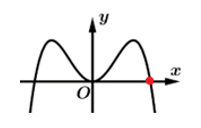
Biết 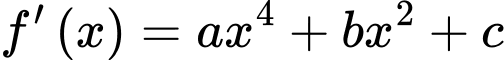 và có đồ thị như trong hình bên. Hàm số
và có đồ thị như trong hình bên. Hàm số 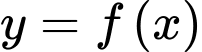 có bao nhiêu điểm cực đại?
có bao nhiêu điểm cực đại?
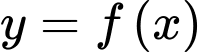 có đạo hàm trên
có đạo hàm trên 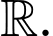 Biết
Biết 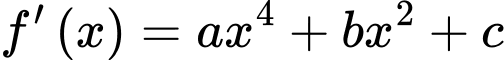 và có đồ thị như trong hình bên. Hàm số
và có đồ thị như trong hình bên. Hàm số 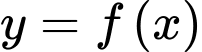 có bao nhiêu điểm cực đại?
có bao nhiêu điểm cực đại?
A, 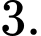
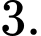
B, 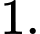
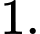
C, 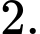
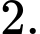
D, 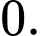
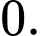
Chọn đáp án B.
Xét hàm số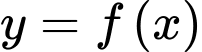 có
có 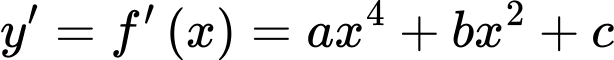
Dựa vào đồ thị hàm số, ta thấy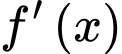 đổi dấu từ dương sang âm khi đi qua
đổi dấu từ dương sang âm khi đi qua 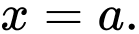
Vậy hàm số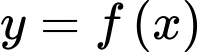 có 1 điểm cực đại.
có 1 điểm cực đại.
 Đáp án: B
Đáp án: B
Xét hàm số
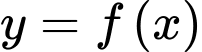 có
có 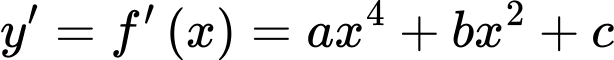
Dựa vào đồ thị hàm số, ta thấy
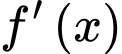 đổi dấu từ dương sang âm khi đi qua
đổi dấu từ dương sang âm khi đi qua 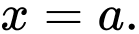
Vậy hàm số
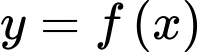 có 1 điểm cực đại.
có 1 điểm cực đại.  Đáp án: B
Đáp án: B
Câu 12 [693532]: Trong không gian 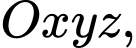 mặt phẳng
mặt phẳng 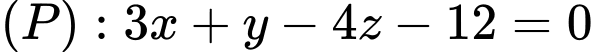 cắt trục
cắt trục 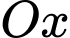 tại điểm
tại điểm 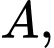 cắt trục
cắt trục  tại điểm
tại điểm 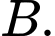 Chu vi tam giác
Chu vi tam giác 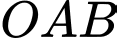 bằng
bằng
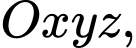 mặt phẳng
mặt phẳng 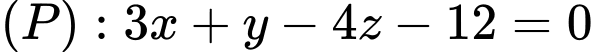 cắt trục
cắt trục 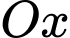 tại điểm
tại điểm 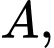 cắt trục
cắt trục  tại điểm
tại điểm 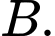 Chu vi tam giác
Chu vi tam giác 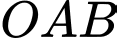 bằng
bằng A, 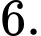
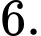
B, 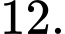
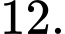
C, 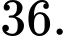
D, 
Chọn đáp án B.
Ta có: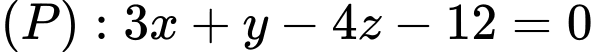 cắt
cắt 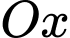 tại
tại 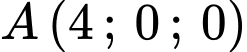 , cắt
, cắt  tại điểm
tại điểm 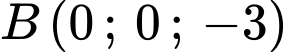 .
.
Suy ra ;
; 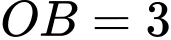 ;
; 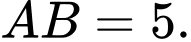
Vậy chu vi tam giác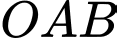 bằng
bằng  Đáp án: B
Đáp án: B
Ta có:
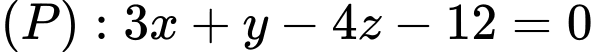 cắt
cắt 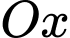 tại
tại 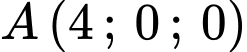 , cắt
, cắt  tại điểm
tại điểm 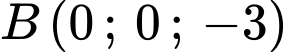 .
.Suy ra
 ;
; 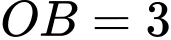 ;
; 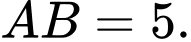
Vậy chu vi tam giác
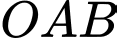 bằng
bằng  Đáp án: B
Đáp án: B PHẦN II. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Câu 13 [693534]: Trong không gian với hệ tọa độ 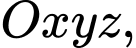 cho điểm
cho điểm 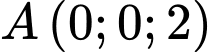 và mặt phẳng
và mặt phẳng 
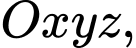 cho điểm
cho điểm 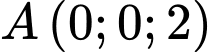 và mặt phẳng
và mặt phẳng 
a) Đúng.
Mặt phẳng có một vectơ pháp tuyến là
có một vectơ pháp tuyến là 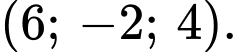
b) Đúng.
Đường thẳng đi qua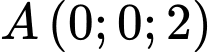 và vuông góc với
và vuông góc với 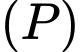 nên nhận
nên nhận 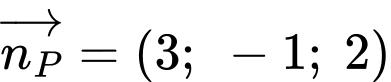 là một véc tơ chỉ phương nên có phương trình là
là một véc tơ chỉ phương nên có phương trình là 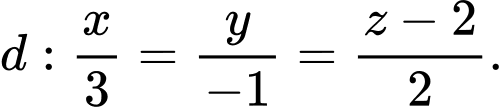
c) Đúng.
Do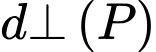 nên để
nên để 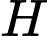 là hình chiếu vuông góc của
là hình chiếu vuông góc của 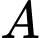 lên
lên 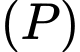 thì
thì 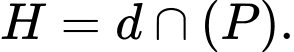
Phương trình tham số của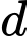 là
là 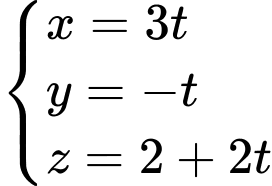
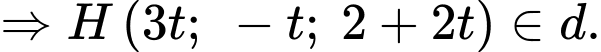
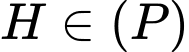
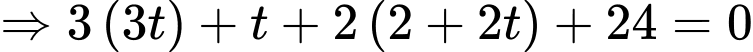
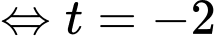
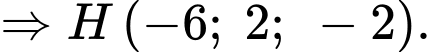
Suy ra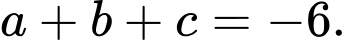
d) Đúng.
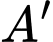 là điểm đối xứng của
là điểm đối xứng của 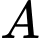 qua mặt phẳng
qua mặt phẳng 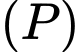
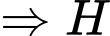 là trung điểm của
là trung điểm của 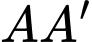
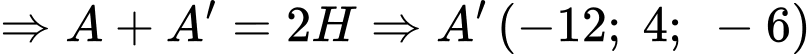
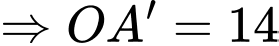
Mặt phẳng
 có một vectơ pháp tuyến là
có một vectơ pháp tuyến là 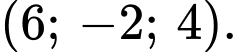
b) Đúng.
Đường thẳng đi qua
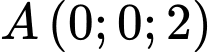 và vuông góc với
và vuông góc với 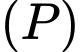 nên nhận
nên nhận 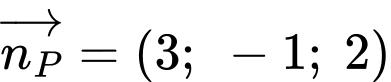 là một véc tơ chỉ phương nên có phương trình là
là một véc tơ chỉ phương nên có phương trình là 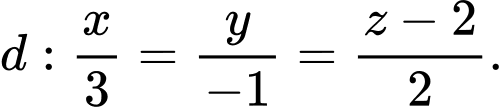
c) Đúng.
Do
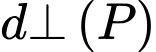 nên để
nên để 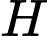 là hình chiếu vuông góc của
là hình chiếu vuông góc của 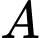 lên
lên 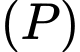 thì
thì 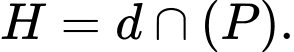
Phương trình tham số của
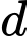 là
là 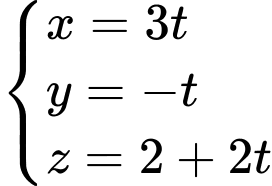
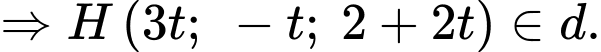
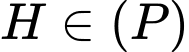
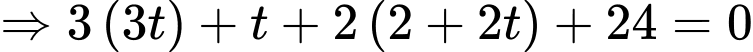
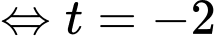
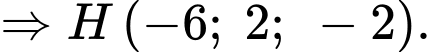
Suy ra
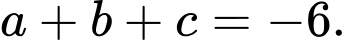
d) Đúng.
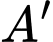 là điểm đối xứng của
là điểm đối xứng của 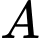 qua mặt phẳng
qua mặt phẳng 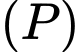
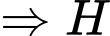 là trung điểm của
là trung điểm của 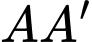
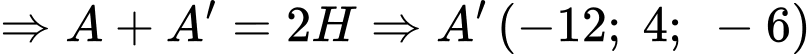
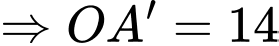
Câu 14 [693535]: Nhà máy 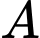 chuyên sản xuất một loại sản phẩm cho nhà máy
chuyên sản xuất một loại sản phẩm cho nhà máy 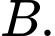 Hai nhà máy thỏa thuận rằng, hằng tháng
Hai nhà máy thỏa thuận rằng, hằng tháng 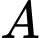 cung cấp cho
cung cấp cho 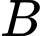 số lượng sản phẩm theo đơn đặt hàng của
số lượng sản phẩm theo đơn đặt hàng của 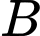 (tối đa
(tối đa 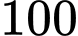 tấn sản phẩm). Nếu số lượng đặt hàng là
tấn sản phẩm). Nếu số lượng đặt hàng là 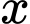 tấn sản phẩm thì giá bán cho mỗi tấn sản phẩm là
tấn sản phẩm thì giá bán cho mỗi tấn sản phẩm là 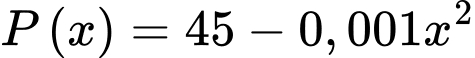 (triệu đồng). Cho phí để
(triệu đồng). Cho phí để 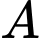 sản xuất
sản xuất 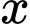 tấn sản phẩm trong một tháng là
tấn sản phẩm trong một tháng là 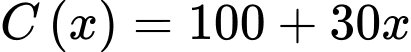 triệu đồng (gồm
triệu đồng (gồm 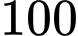 triệu đồng chi phí cố định và
triệu đồng chi phí cố định và 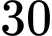 triệu đồng cho mỗi tấn sản phẩm).
triệu đồng cho mỗi tấn sản phẩm).
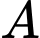 chuyên sản xuất một loại sản phẩm cho nhà máy
chuyên sản xuất một loại sản phẩm cho nhà máy 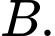 Hai nhà máy thỏa thuận rằng, hằng tháng
Hai nhà máy thỏa thuận rằng, hằng tháng 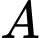 cung cấp cho
cung cấp cho 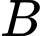 số lượng sản phẩm theo đơn đặt hàng của
số lượng sản phẩm theo đơn đặt hàng của 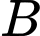 (tối đa
(tối đa 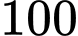 tấn sản phẩm). Nếu số lượng đặt hàng là
tấn sản phẩm). Nếu số lượng đặt hàng là 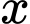 tấn sản phẩm thì giá bán cho mỗi tấn sản phẩm là
tấn sản phẩm thì giá bán cho mỗi tấn sản phẩm là 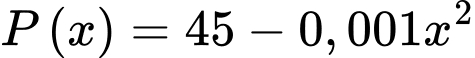 (triệu đồng). Cho phí để
(triệu đồng). Cho phí để 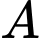 sản xuất
sản xuất 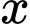 tấn sản phẩm trong một tháng là
tấn sản phẩm trong một tháng là 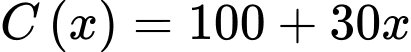 triệu đồng (gồm
triệu đồng (gồm 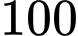 triệu đồng chi phí cố định và
triệu đồng chi phí cố định và 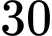 triệu đồng cho mỗi tấn sản phẩm).
triệu đồng cho mỗi tấn sản phẩm).
a) Sai.
Chi phí để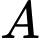 sản xuất
sản xuất  tấn sản phẩm trong một tháng là:
tấn sản phẩm trong một tháng là:
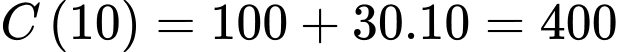 triệu đồng.
triệu đồng.
b) Đúng.
Số tiền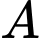 thu được khi bán
thu được khi bán  tấn sản phẩm cho
tấn sản phẩm cho 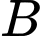 là:
là:
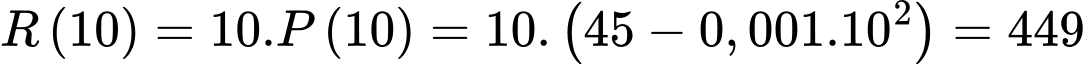 triệu đồng.
triệu đồng.
c) Sai.
Lợi nhuận mà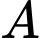 thu được là:
thu được là:
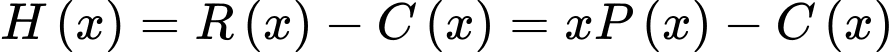
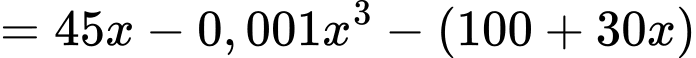
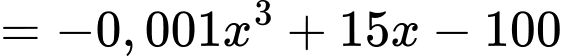 .
.
d) Sai.
Xét hàm số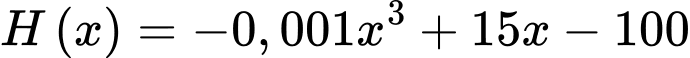 ,
, 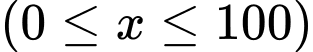 ta có:
ta có: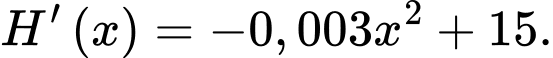 ,
,
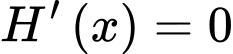
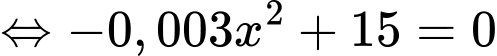
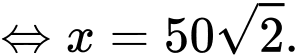
Ta có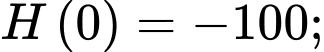
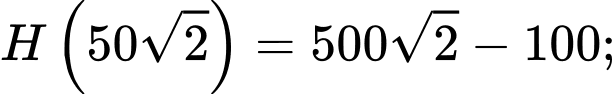
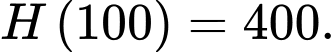
Vậy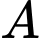 bán cho
bán cho 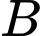 khoảng
khoảng 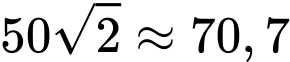 tấn sản phẩm mỗi tháng thì thu được lợi nhuận lớn nhất bằng
tấn sản phẩm mỗi tháng thì thu được lợi nhuận lớn nhất bằng 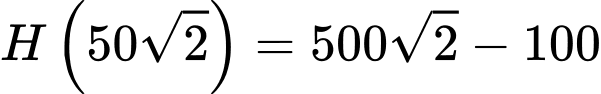 .
.
Chi phí để
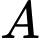 sản xuất
sản xuất  tấn sản phẩm trong một tháng là:
tấn sản phẩm trong một tháng là: 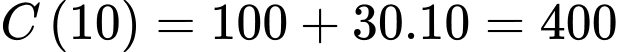 triệu đồng.
triệu đồng.b) Đúng.
Số tiền
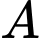 thu được khi bán
thu được khi bán  tấn sản phẩm cho
tấn sản phẩm cho 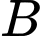 là:
là: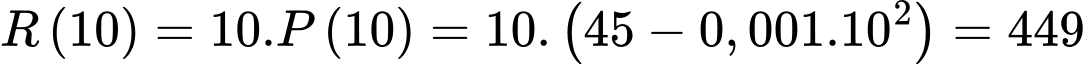 triệu đồng.
triệu đồng.c) Sai.
Lợi nhuận mà
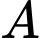 thu được là:
thu được là: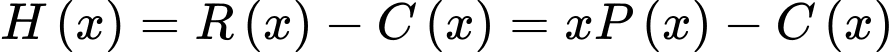
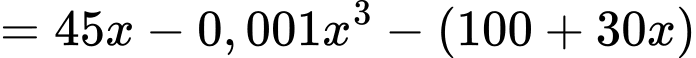
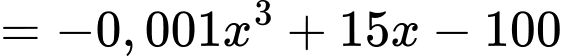 .
.d) Sai.
Xét hàm số
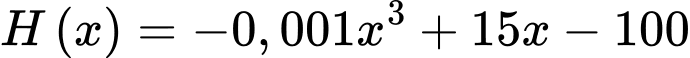 ,
, 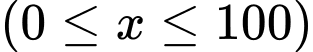 ta có:
ta có: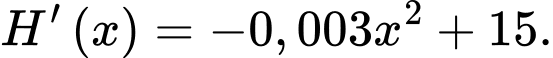 ,
, 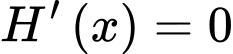
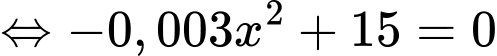
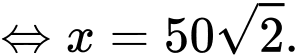
Ta có
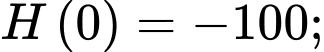
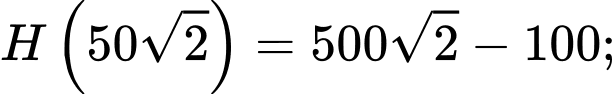
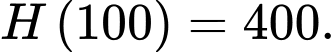
Vậy
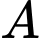 bán cho
bán cho 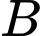 khoảng
khoảng 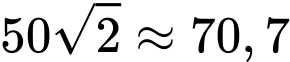 tấn sản phẩm mỗi tháng thì thu được lợi nhuận lớn nhất bằng
tấn sản phẩm mỗi tháng thì thu được lợi nhuận lớn nhất bằng 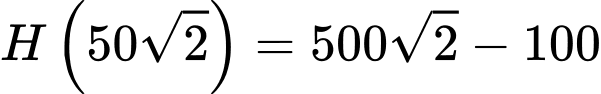 .
.
Câu 15 [693537]: Có hai hộp đựng câu hỏi thi (phiếu), mỗi phiếu ghi một câu hỏi. Hộp thứ nhất có 15 phiếu và hộp thứ hai có 9 phiếu. Biết rằng sinh viên A đi thi chỉ thuộc 10 câu ở hộp thứ nhất và 8 câu ở hộp thứ hai. Thầy giáo rút ngẫu nhiên từ mỗi hộp ra một phiếu thi, sau đó cho sinh viên A rút ngẫu nhiên ra 1 phiếu từ 2 phiếu mà thầy giáo đã rút.
Gọi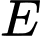 là biến cố: “sinh viên A rút ra phiếu từ hộp thứ nhất”.
là biến cố: “sinh viên A rút ra phiếu từ hộp thứ nhất”.
Gọi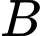 là biến cố: “Sinh viên A rút được phiếu đã thuộc bài”
là biến cố: “Sinh viên A rút được phiếu đã thuộc bài”
Gọi
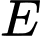 là biến cố: “sinh viên A rút ra phiếu từ hộp thứ nhất”.
là biến cố: “sinh viên A rút ra phiếu từ hộp thứ nhất”.Gọi
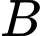 là biến cố: “Sinh viên A rút được phiếu đã thuộc bài”
là biến cố: “Sinh viên A rút được phiếu đã thuộc bài”
a) Đúng.
b) Sai.
Xác suất có điều kiện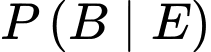 là xác suất của biến cố sinh viên đó rút được phiếu đã học thuộc khi biết đó là phiếu từ hộp thứ nhất.
là xác suất của biến cố sinh viên đó rút được phiếu đã học thuộc khi biết đó là phiếu từ hộp thứ nhất.
Điều kiện phiếu rút được là từ hộp thứ nhất, ta có trong hộp thứ nhất có 15 phiếu, số cách để thầy giáo rút 1 phiếu từ 15 phiếu là 15 cách.
Để thầy rút được phiếu mà sinh viên đó học thuộc là 10 cách.
Suy ra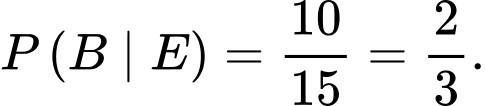
c) Sai.
Ta có xác suất sinh viên A rút ra được phiếu đã thuộc bài biết phiếu đó được rút từ hộp thứ 2 là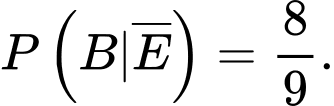
Ta có sơ đồ cây sau:
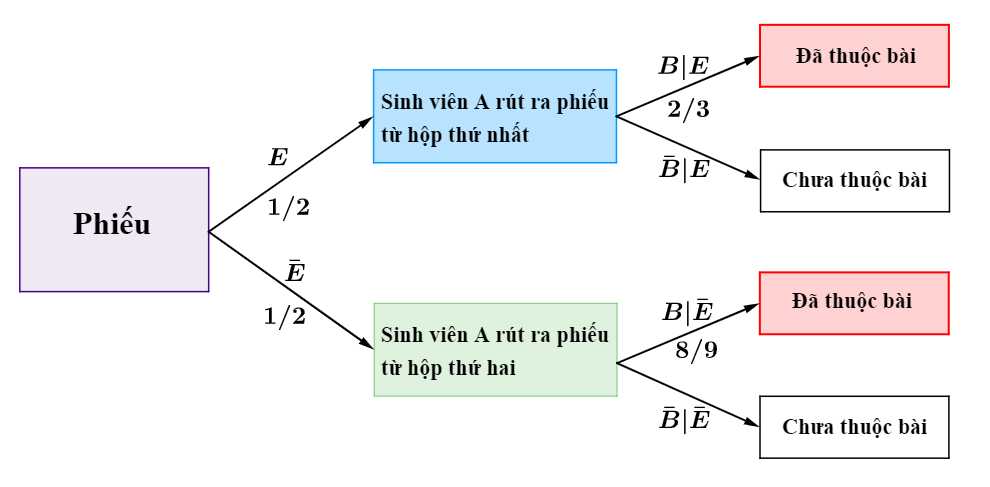
Theo công thức xác suất toàn phần, ta có
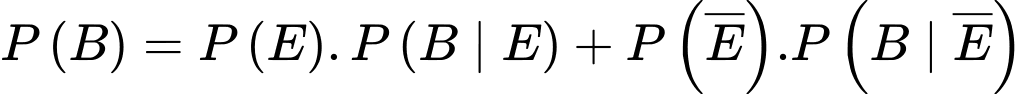
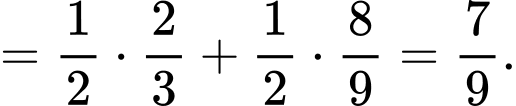
d) Đúng.
Theo công thức Bayes, ta có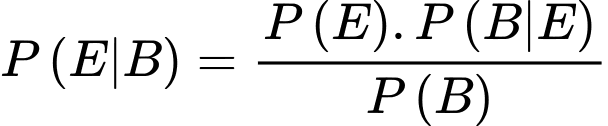
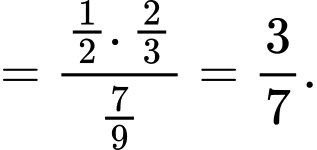
b) Sai.
Xác suất có điều kiện
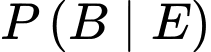 là xác suất của biến cố sinh viên đó rút được phiếu đã học thuộc khi biết đó là phiếu từ hộp thứ nhất.
là xác suất của biến cố sinh viên đó rút được phiếu đã học thuộc khi biết đó là phiếu từ hộp thứ nhất. Điều kiện phiếu rút được là từ hộp thứ nhất, ta có trong hộp thứ nhất có 15 phiếu, số cách để thầy giáo rút 1 phiếu từ 15 phiếu là 15 cách.
Để thầy rút được phiếu mà sinh viên đó học thuộc là 10 cách.
Suy ra
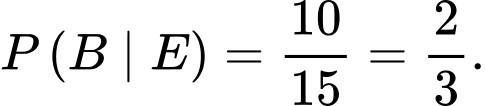
c) Sai.
Ta có xác suất sinh viên A rút ra được phiếu đã thuộc bài biết phiếu đó được rút từ hộp thứ 2 là
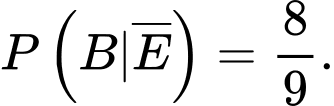
Ta có sơ đồ cây sau:

Theo công thức xác suất toàn phần, ta có
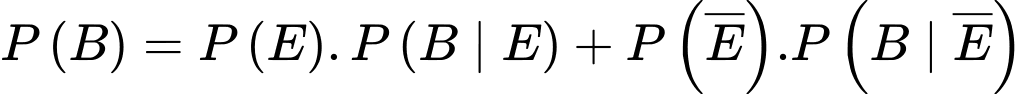
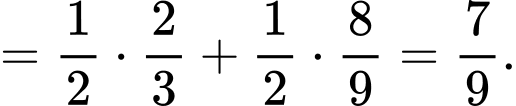
d) Đúng.
Theo công thức Bayes, ta có
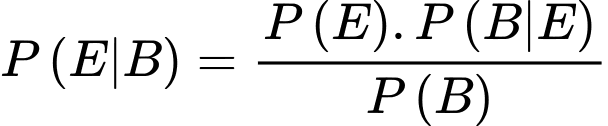
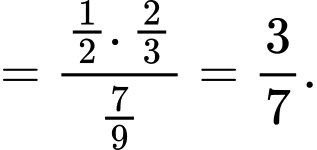
Câu 16 [693536]: Áp suất 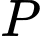 và thể tích
và thể tích  của khí trong một xilanh có chiều dài
của khí trong một xilanh có chiều dài 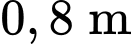 và bán kính
và bán kính 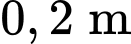 với một piston di động, liên hệ với nhau bởi công thức
với một piston di động, liên hệ với nhau bởi công thức 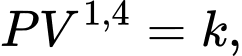 trong đó
trong đó 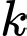 là một hằng số (Hình 1). Khi pit-tông được kéo ra hết cỡ, áp suất khí là
là một hằng số (Hình 1). Khi pit-tông được kéo ra hết cỡ, áp suất khí là 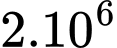 Newton/
Newton/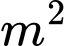 . Biết công thức thể tích khối trụ bằng
. Biết công thức thể tích khối trụ bằng 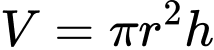 với
với 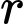 là bán kính đáy và
là bán kính đáy và 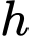 là chiều cao khối trụ
là chiều cao khối trụ
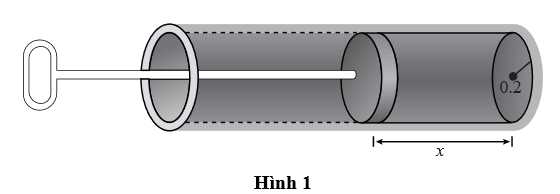
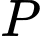 và thể tích
và thể tích  của khí trong một xilanh có chiều dài
của khí trong một xilanh có chiều dài 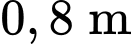 và bán kính
và bán kính 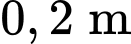 với một piston di động, liên hệ với nhau bởi công thức
với một piston di động, liên hệ với nhau bởi công thức 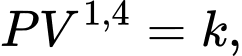 trong đó
trong đó 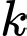 là một hằng số (Hình 1). Khi pit-tông được kéo ra hết cỡ, áp suất khí là
là một hằng số (Hình 1). Khi pit-tông được kéo ra hết cỡ, áp suất khí là 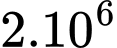 Newton/
Newton/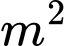 . Biết công thức thể tích khối trụ bằng
. Biết công thức thể tích khối trụ bằng 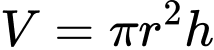 với
với 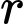 là bán kính đáy và
là bán kính đáy và 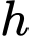 là chiều cao khối trụ
là chiều cao khối trụ 
a) Sai.
Thể tích của hình trụ như một hàm số của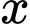 là
là
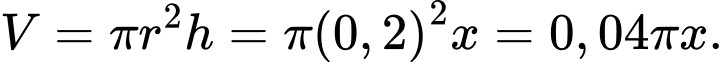
b) Đúng.
Ta có: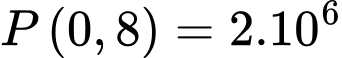 và
và 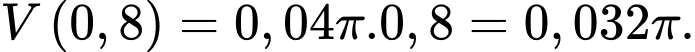
Ta có: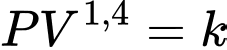
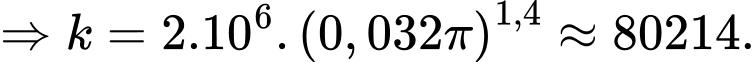
c) Sai.
Diện tích của pít-tông là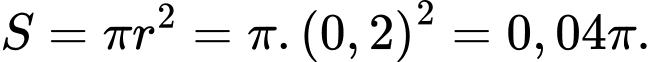
Thể tích của xi lanh là: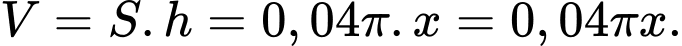
Ta có: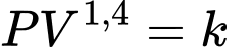
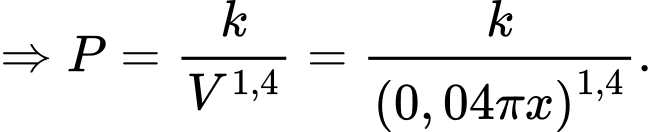
Do đó,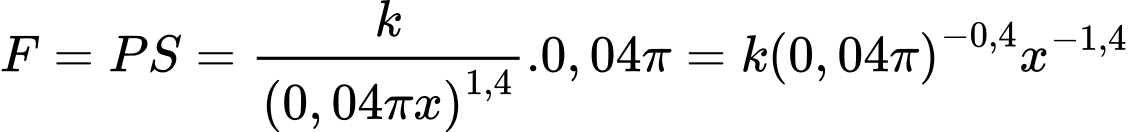
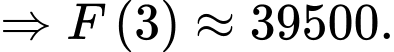
d) Đúng.
Vì lực đang đẩy ngược lại piston, để tính công, ta phải tính tích phân của lực đối, tức là
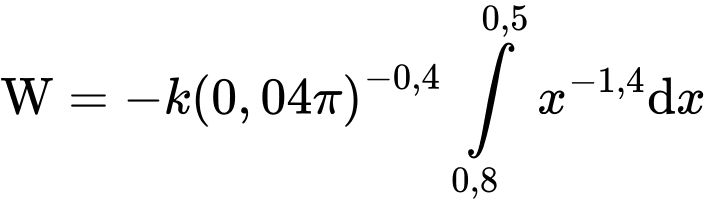
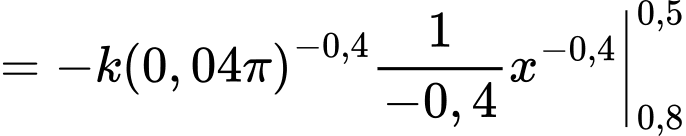
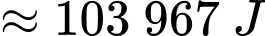
Thể tích của hình trụ như một hàm số của
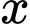 là
là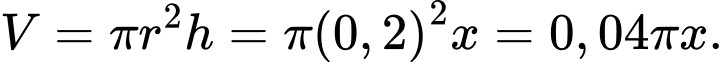
b) Đúng.
Ta có:
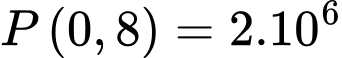 và
và 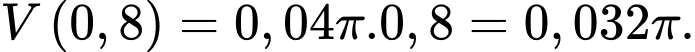
Ta có:
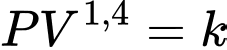
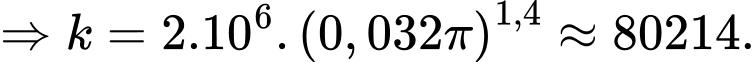
c) Sai.
Diện tích của pít-tông là
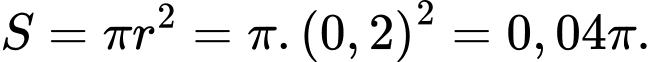
Thể tích của xi lanh là:
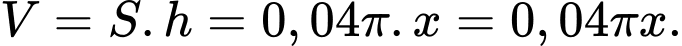
Ta có:
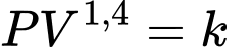
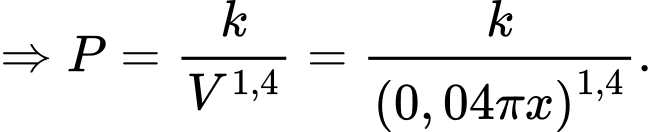
Do đó,
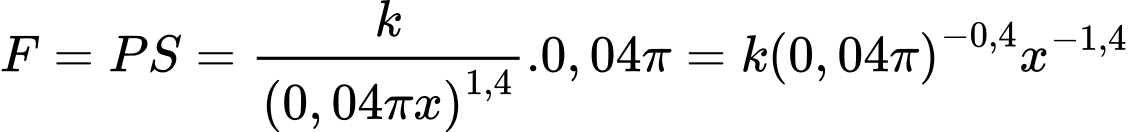
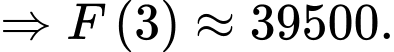
d) Đúng.
Vì lực đang đẩy ngược lại piston, để tính công, ta phải tính tích phân của lực đối, tức là
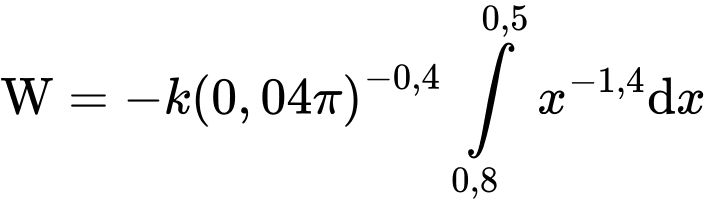
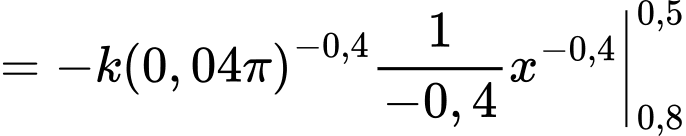
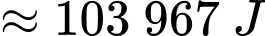
PHẦN III. Thí sinh trả lời từ câu 1 đến câu 6.
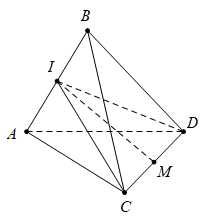
Câu 17 [693538]: Cho tứ diện 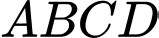 có
có 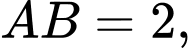 độ dài tất cả các cạnh còn lại cùng bằng
độ dài tất cả các cạnh còn lại cùng bằng 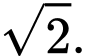 Gọi
Gọi 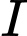 là điểm cách đều bốn đỉnh
là điểm cách đều bốn đỉnh 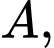
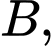
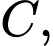
 Khoảng cách từ điểm
Khoảng cách từ điểm 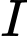 đến đường thẳng
đến đường thẳng 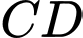 bằng bao nhiêu? (làm tròn kết quả đến hàng phần mười).
bằng bao nhiêu? (làm tròn kết quả đến hàng phần mười).
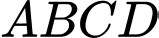 có
có 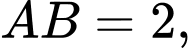 độ dài tất cả các cạnh còn lại cùng bằng
độ dài tất cả các cạnh còn lại cùng bằng 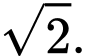 Gọi
Gọi 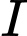 là điểm cách đều bốn đỉnh
là điểm cách đều bốn đỉnh 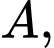
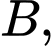
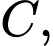
 Khoảng cách từ điểm
Khoảng cách từ điểm 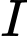 đến đường thẳng
đến đường thẳng 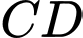 bằng bao nhiêu? (làm tròn kết quả đến hàng phần mười).
bằng bao nhiêu? (làm tròn kết quả đến hàng phần mười).
Điền đáp án: 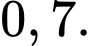
Ta có:
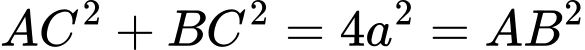
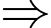 Tam giác
Tam giác 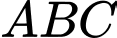 vuông tại
vuông tại 
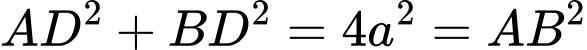
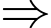 Tam giác
Tam giác 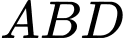 vuông tại
vuông tại 
Khi đó, gọi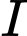 là trung điểm của
là trung điểm của  ta có
ta có  hay
hay 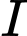 là điểm cách đều bốn đỉnh
là điểm cách đều bốn đỉnh 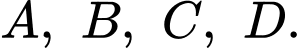 Do đó,
Do đó, 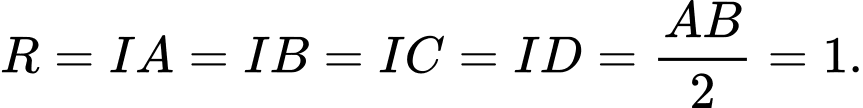
Gọi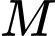 là trung điểm của
là trung điểm của 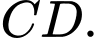
Khoảng cách từ điểm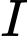 đến đường thẳng
đến đường thẳng 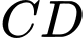 bằng
bằng

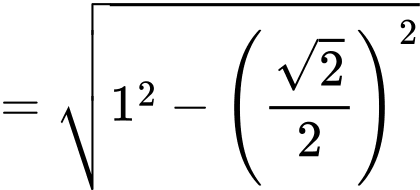
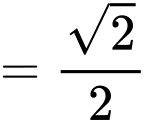
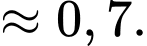
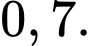

Ta có:
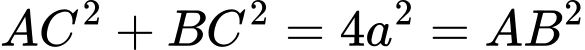
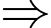 Tam giác
Tam giác 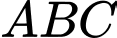 vuông tại
vuông tại 
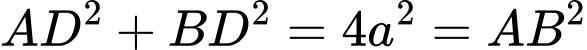
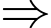 Tam giác
Tam giác 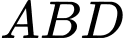 vuông tại
vuông tại 
Khi đó, gọi
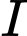 là trung điểm của
là trung điểm của  ta có
ta có  hay
hay 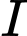 là điểm cách đều bốn đỉnh
là điểm cách đều bốn đỉnh 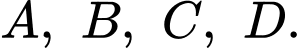 Do đó,
Do đó, 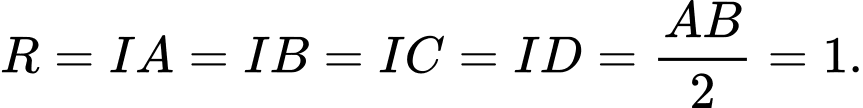
Gọi
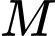 là trung điểm của
là trung điểm của 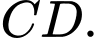
Khoảng cách từ điểm
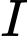 đến đường thẳng
đến đường thẳng 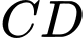 bằng
bằng 
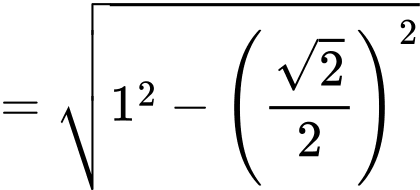
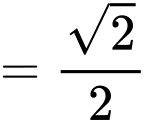
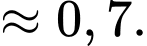
Câu 18 [693539]: Một mạng cáp quang dùng để kết nối giữa năm thị trấn. Bảng số liệu bên dưới cho biết về chi phí để lắp đặt (đơn vị: triệu đồng).
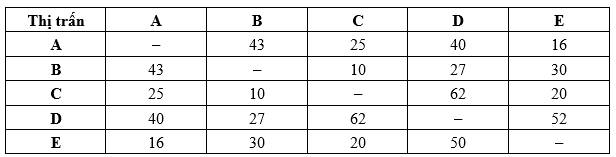
Chi phí lắp đặt tối thiểu để kết nối tất cả các thị trấn là bao nhiêu triệu đồng (hai thị trấn bất kỳ có thể kết nối qua một thị trấn trung gian)?

Chi phí lắp đặt tối thiểu để kết nối tất cả các thị trấn là bao nhiêu triệu đồng (hai thị trấn bất kỳ có thể kết nối qua một thị trấn trung gian)?
Điền đáp án: 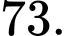
Ta mô phỏng bài toán trên dưới dạng đồ thị với năm thị trấn là năm đỉnh, chi phí để lắp đặt giữa các thị trấn là trọng số của các cạnh. Yêu cầu của bài toán là tìm cây khung nhỏ nhất.
Yêu cầu của bài toán là tìm cây khung nhỏ nhất.
Ta tìm cây khung nhỏ nhất bằng cách lần lượt thêm vào các cạnh có trọng số từ nhỏ đến lớn (hai đỉnh của cạnh được thêm vào sau không tạo thành chu trình):
Cạnh BC: 10 triệu đồng.
Cạnh AE: 16 triệu đồng.
Cạnh EC: 20 triệu đồng.
Cạnh AC: 25 triệu đồng (loại vì tạo thành chu trình).
Cạnh BD: 27 triệu đồng.
 Chi phí lắp đặt tối thiểu để kết nối tất cả các thị trấn là:
Chi phí lắp đặt tối thiểu để kết nối tất cả các thị trấn là: 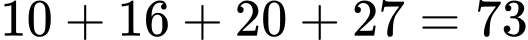 (triệu đồng).
(triệu đồng).
Ta mô phỏng bài toán trên dưới dạng đồ thị với năm thị trấn là năm đỉnh, chi phí để lắp đặt giữa các thị trấn là trọng số của các cạnh.
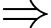 Yêu cầu của bài toán là tìm cây khung nhỏ nhất.
Yêu cầu của bài toán là tìm cây khung nhỏ nhất.
Ta tìm cây khung nhỏ nhất bằng cách lần lượt thêm vào các cạnh có trọng số từ nhỏ đến lớn (hai đỉnh của cạnh được thêm vào sau không tạo thành chu trình):
Cạnh BC: 10 triệu đồng.
Cạnh AE: 16 triệu đồng.
Cạnh EC: 20 triệu đồng.
Cạnh AC: 25 triệu đồng (loại vì tạo thành chu trình).
Cạnh BD: 27 triệu đồng.
 Chi phí lắp đặt tối thiểu để kết nối tất cả các thị trấn là:
Chi phí lắp đặt tối thiểu để kết nối tất cả các thị trấn là: 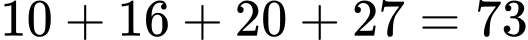 (triệu đồng).
(triệu đồng).
Câu 19 [693109]: Một người cưỡi ngựa xuất phát từ 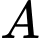 đi đến
đi đến  Điểm
Điểm 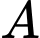 nằm trong vùng đất ướt nên vận tốc của ngựa khi đi trong vùng này là
nằm trong vùng đất ướt nên vận tốc của ngựa khi đi trong vùng này là  Điểm
Điểm  nằm trong vùng đất khô hơn nên vận tốc của ngưa khi đi trong vùng này là là
nằm trong vùng đất khô hơn nên vận tốc của ngưa khi đi trong vùng này là là  Hai phần đất này giáp nhau bởi một đường thẳng
Hai phần đất này giáp nhau bởi một đường thẳng 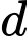 đi qua trung điểm của
đi qua trung điểm của 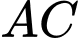 và khoảng cách từ
và khoảng cách từ 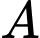 và
và  đến đường này đều bằng
đến đường này đều bằng 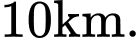 Biết
Biết 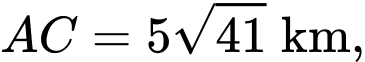 thời gian ít nhất để đi từ
thời gian ít nhất để đi từ 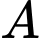 đến
đến  là mấy giờ (làm tròn kết quả đến hàng phần trăm)?
là mấy giờ (làm tròn kết quả đến hàng phần trăm)?

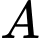 đi đến
đi đến  Điểm
Điểm 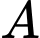 nằm trong vùng đất ướt nên vận tốc của ngựa khi đi trong vùng này là
nằm trong vùng đất ướt nên vận tốc của ngựa khi đi trong vùng này là  Điểm
Điểm  nằm trong vùng đất khô hơn nên vận tốc của ngưa khi đi trong vùng này là là
nằm trong vùng đất khô hơn nên vận tốc của ngưa khi đi trong vùng này là là  Hai phần đất này giáp nhau bởi một đường thẳng
Hai phần đất này giáp nhau bởi một đường thẳng 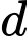 đi qua trung điểm của
đi qua trung điểm của 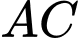 và khoảng cách từ
và khoảng cách từ 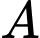 và
và  đến đường này đều bằng
đến đường này đều bằng 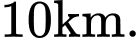 Biết
Biết 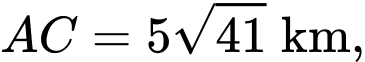 thời gian ít nhất để đi từ
thời gian ít nhất để đi từ 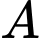 đến
đến  là mấy giờ (làm tròn kết quả đến hàng phần trăm)?
là mấy giờ (làm tròn kết quả đến hàng phần trăm)? 
Điền đáp án: 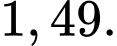
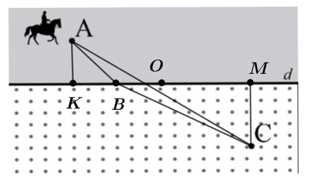
Kéo dài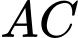 cắt
cắt 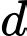 tại
tại 
Khi đó: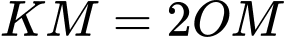
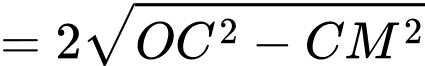
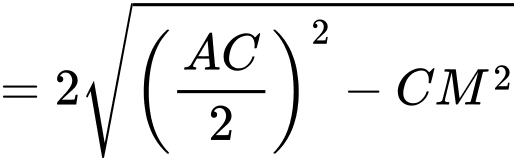
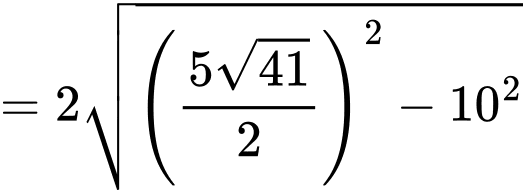
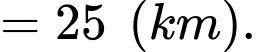
Gọi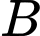 là điểm trên đường thẳng
là điểm trên đường thẳng 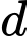 sao cho người cưỡi ngựa đi từ
sao cho người cưỡi ngựa đi từ 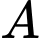 đến
đến 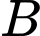 rồi đến
rồi đến 
Đặt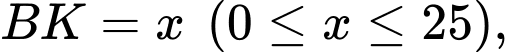 khi đó:
khi đó:
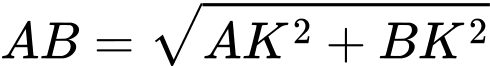
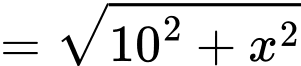
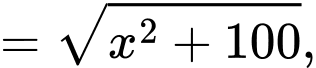
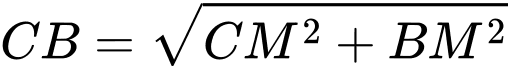
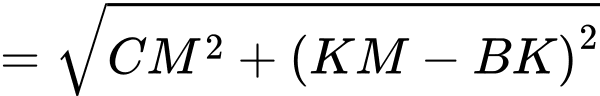
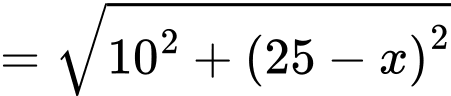
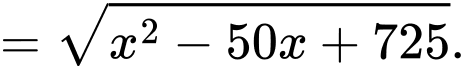
Thời gian đi từ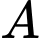 đến
đến 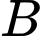 là:
là:
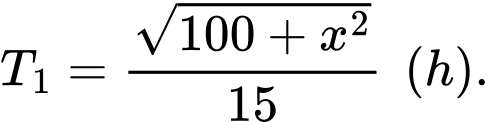
Thời gian đi từ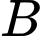 đến
đến  là:
là:
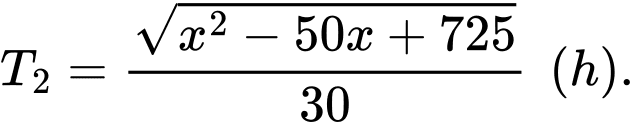
Thời gian đi từ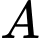 đến
đến  là:
là:
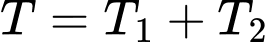
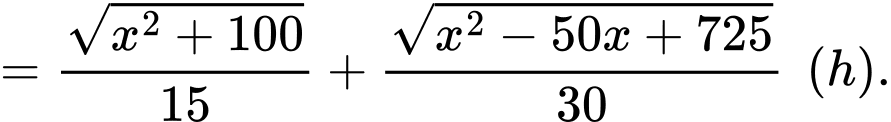
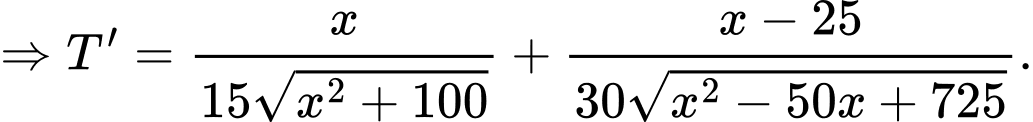
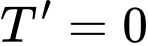
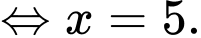
Ta có: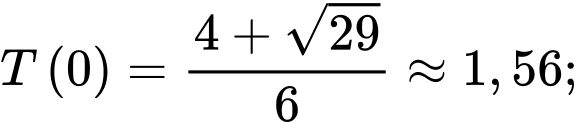
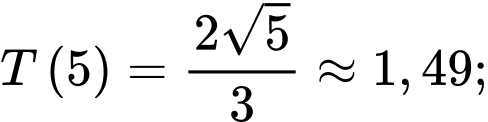
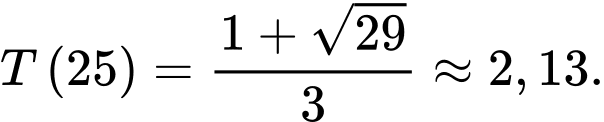
Vậy thời gian ít nhất để đi từ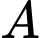 đến
đến  là 1,49 giờ.
là 1,49 giờ.
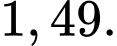

Kéo dài
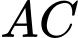 cắt
cắt 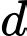 tại
tại 
Khi đó:
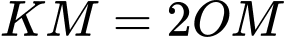
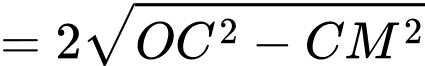
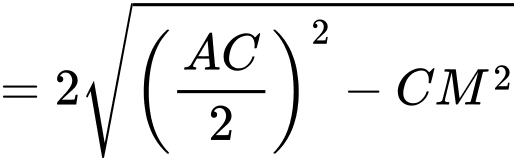
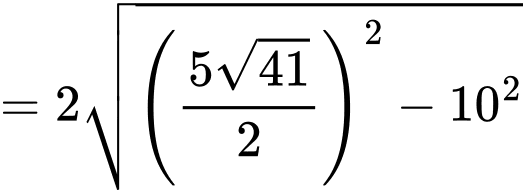
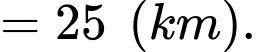
Gọi
 là điểm trên đường thẳng
là điểm trên đường thẳng 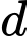 sao cho người cưỡi ngựa đi từ
sao cho người cưỡi ngựa đi từ 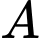 đến
đến 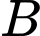 rồi đến
rồi đến 
Đặt
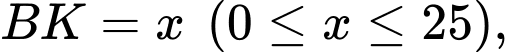 khi đó:
khi đó: 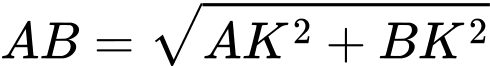
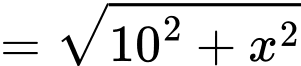
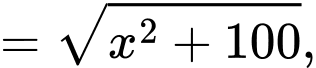
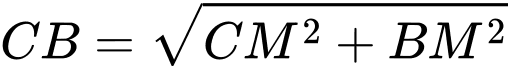
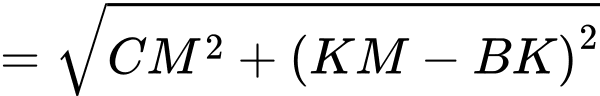
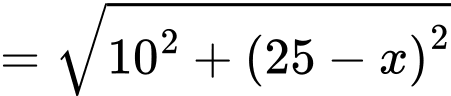
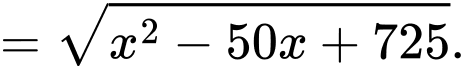
Thời gian đi từ
 đến
đến 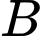 là:
là: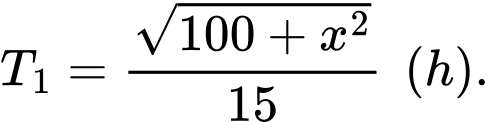
Thời gian đi từ
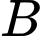 đến
đến  là:
là: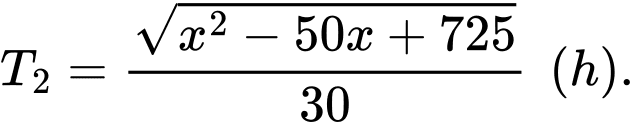
Thời gian đi từ
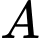 đến
đến  là:
là: 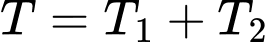
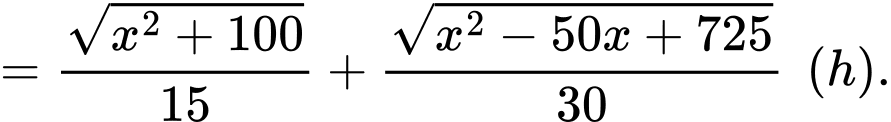
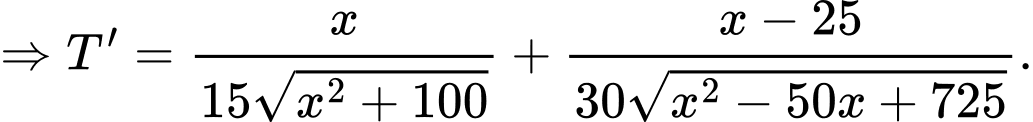
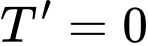
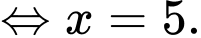
Ta có:
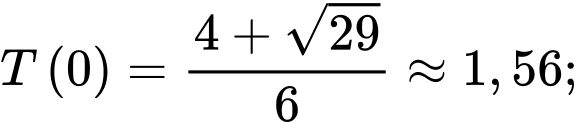
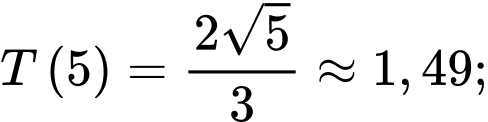
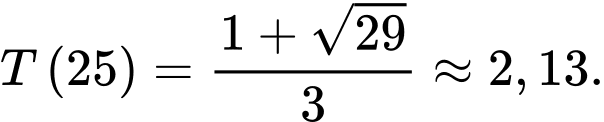
Vậy thời gian ít nhất để đi từ
 đến
đến  là 1,49 giờ.
là 1,49 giờ.
Câu 20 [693541]: ĐỀ CHƯA SỬA
Kết quả khảo sát những bệnh nhân là học sinh bị tai nạn xe máy điện về mối liên hệ giữa việc đội mũ bảo hiểm và khả năng bị chấn thương vùng đầu cho thấy:
• Tỉ lệ bệnh nhân bị chấn thương vùng đầu khi gặp tai nạn là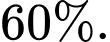
• Tỉ lệ bệnh nhân đội mũ bảo hiểm đúng cách khi gặp tai nạn là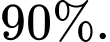
• Tỉ lệ bệnh nhân đội mũ bảo hiểm đúng cách và bị chấn thương vùng đầu là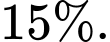
Hỏi theo kết quả điều tra trên, việc đội mũ bảo hiểm đúng cách đối với học sinh khi di chuyển bằng xe máy điện sẽ làm giảm khả năng bị chấn thương vùng đầu khi gặp tai nạn bao nhiêu lần? Kết quả viết dưới dạng số thập phân.
Nhóm tác giả xin sửa lại số liệu như sau cho hợp lí:
Kết quả khảo sát những bệnh nhân là học sinh bị tai nạn xe máy điện về mối liên hệ giữa việc đội mũ bảo hiểm và khả năng bị chấn thương vùng đầu cho thấy:
• Tỉ lệ bệnh nhân bị chấn thương vùng đầu khi gặp tai nạn là 26%.
• Tỉ lệ bệnh nhân đội mũ bảo hiểm đúng cách khi gặp tai nạn là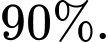
• Tỉ lệ bệnh nhân đội mũ bảo hiểm đúng cách và bị chấn thương vùng đầu là 18%.
Hỏi theo kết quả điều tra trên, việc đội mũ bảo hiểm đúng cách đối với học sinh khi di chuyển bằng xe máy điện sẽ làm giảm khả năng bị chấn thương vùng đầu khi gặp tai nạn bao nhiêu lần? Kết quả viết dưới dạng số thập phân.

Kết quả khảo sát những bệnh nhân là học sinh bị tai nạn xe máy điện về mối liên hệ giữa việc đội mũ bảo hiểm và khả năng bị chấn thương vùng đầu cho thấy:
• Tỉ lệ bệnh nhân bị chấn thương vùng đầu khi gặp tai nạn là
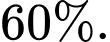
• Tỉ lệ bệnh nhân đội mũ bảo hiểm đúng cách khi gặp tai nạn là
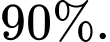
• Tỉ lệ bệnh nhân đội mũ bảo hiểm đúng cách và bị chấn thương vùng đầu là
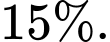
Hỏi theo kết quả điều tra trên, việc đội mũ bảo hiểm đúng cách đối với học sinh khi di chuyển bằng xe máy điện sẽ làm giảm khả năng bị chấn thương vùng đầu khi gặp tai nạn bao nhiêu lần? Kết quả viết dưới dạng số thập phân.
Nhóm tác giả xin sửa lại số liệu như sau cho hợp lí:
Kết quả khảo sát những bệnh nhân là học sinh bị tai nạn xe máy điện về mối liên hệ giữa việc đội mũ bảo hiểm và khả năng bị chấn thương vùng đầu cho thấy:
• Tỉ lệ bệnh nhân bị chấn thương vùng đầu khi gặp tai nạn là 26%.
• Tỉ lệ bệnh nhân đội mũ bảo hiểm đúng cách khi gặp tai nạn là
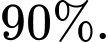
• Tỉ lệ bệnh nhân đội mũ bảo hiểm đúng cách và bị chấn thương vùng đầu là 18%.
Hỏi theo kết quả điều tra trên, việc đội mũ bảo hiểm đúng cách đối với học sinh khi di chuyển bằng xe máy điện sẽ làm giảm khả năng bị chấn thương vùng đầu khi gặp tai nạn bao nhiêu lần? Kết quả viết dưới dạng số thập phân.

Đối với đề chưa sửa:
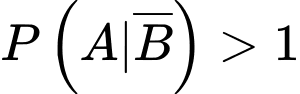 nên sẽ vô lý.
nên sẽ vô lý.
Đề sửa rồi: Ta sẽ giải như sau:
Điền đáp án: 4.
Gọi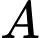 là biến cố “ Bệnh nhân bị chấn thương vùng đầu khi gặp tai nạn”.
là biến cố “ Bệnh nhân bị chấn thương vùng đầu khi gặp tai nạn”.
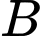 : “ Bệnh nhân đội mũ bảo hiểm đúng cách”.
: “ Bệnh nhân đội mũ bảo hiểm đúng cách”.
 : “ Bệnh nhân bị chấn thương vùng đầu khi gặp tai nạn và đội mũ bảo hiểm đúng cách ”.
: “ Bệnh nhân bị chấn thương vùng đầu khi gặp tai nạn và đội mũ bảo hiểm đúng cách ”.
Theo đề ra ta có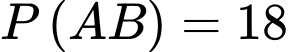
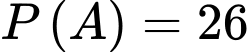
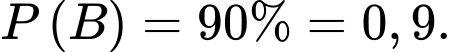
Áp dụng công thức xác suất có điều kiện, ta có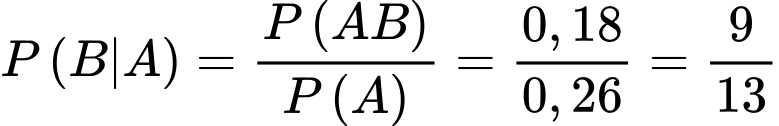
Vì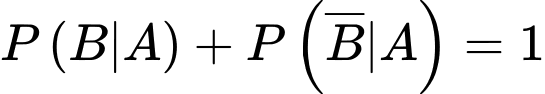
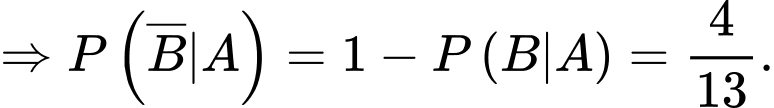
Xác suất học sinh bị chấn thương vùng đầu khi gặp tai nạn, biết học sinh đó đã đội mũ bảo hiểm đúng cách là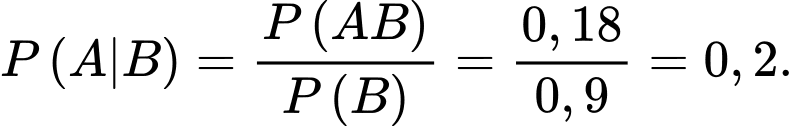
Xác suất học sinh bị chấn thương vùng đầu khi gặp tai nạn, biết học sinh đó đã không đội mũ bảo hiểm đúng cách là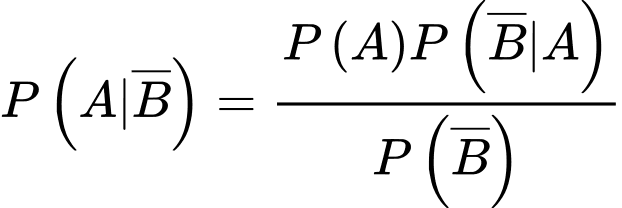
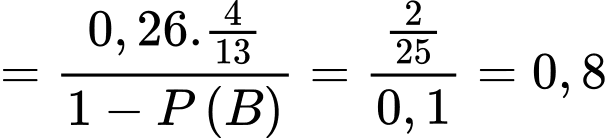
Suy ra tỉ lệ học sinh bị chấn thương vùng đầu khi gặp tai nạn khi biết học sinh đó đã đội mũ bảo hiểm đúng cách với không đội mũ bảo hiểm đúng cách là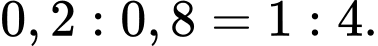
Vậy việc đội mũ bảo hiểm đúng cách đối với học sinh di chuyển bằng xe máy điện sẽ làm giảm khả năng bị chấn thương vùng đầu khi gặp tai nạn đi 4 lần.
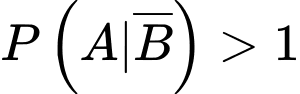 nên sẽ vô lý.
nên sẽ vô lý.Đề sửa rồi: Ta sẽ giải như sau:
Điền đáp án: 4.
Gọi
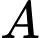 là biến cố “ Bệnh nhân bị chấn thương vùng đầu khi gặp tai nạn”.
là biến cố “ Bệnh nhân bị chấn thương vùng đầu khi gặp tai nạn”.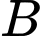 : “ Bệnh nhân đội mũ bảo hiểm đúng cách”.
: “ Bệnh nhân đội mũ bảo hiểm đúng cách”. : “ Bệnh nhân bị chấn thương vùng đầu khi gặp tai nạn và đội mũ bảo hiểm đúng cách ”.
: “ Bệnh nhân bị chấn thương vùng đầu khi gặp tai nạn và đội mũ bảo hiểm đúng cách ”.Theo đề ra ta có
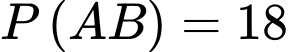
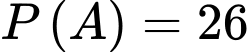
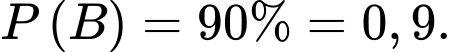
Áp dụng công thức xác suất có điều kiện, ta có
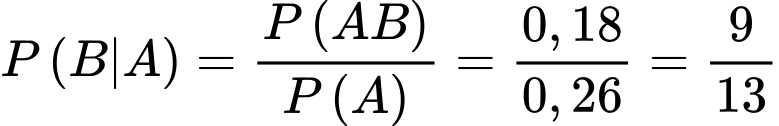
Vì
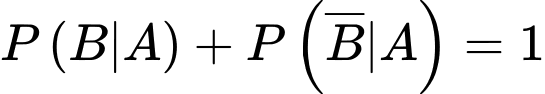
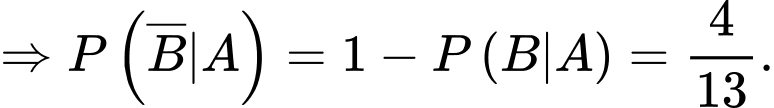
Xác suất học sinh bị chấn thương vùng đầu khi gặp tai nạn, biết học sinh đó đã đội mũ bảo hiểm đúng cách là
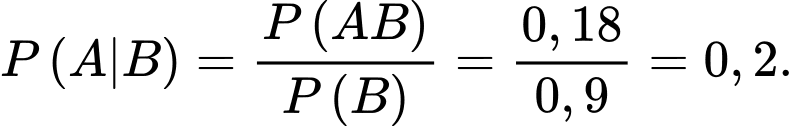
Xác suất học sinh bị chấn thương vùng đầu khi gặp tai nạn, biết học sinh đó đã không đội mũ bảo hiểm đúng cách là
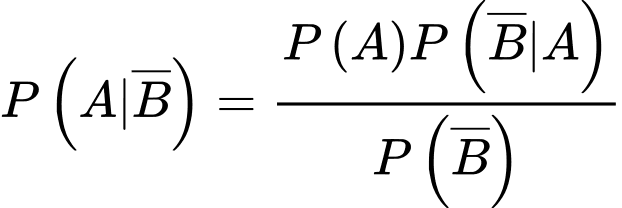
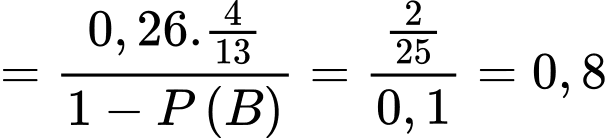
Suy ra tỉ lệ học sinh bị chấn thương vùng đầu khi gặp tai nạn khi biết học sinh đó đã đội mũ bảo hiểm đúng cách với không đội mũ bảo hiểm đúng cách là
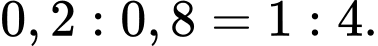
Vậy việc đội mũ bảo hiểm đúng cách đối với học sinh di chuyển bằng xe máy điện sẽ làm giảm khả năng bị chấn thương vùng đầu khi gặp tai nạn đi 4 lần.
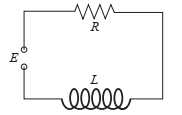
Câu 21 [702664]: Trong mạch 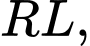 cường độ dòng điện
cường độ dòng điện 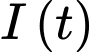 ampe luôn tăng và thay đổi thoả mãn:
ampe luôn tăng và thay đổi thoả mãn: 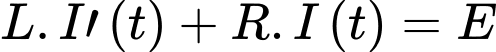 trong đó
trong đó 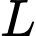 là độ tự cảm tính bằng henry,
là độ tự cảm tính bằng henry, 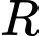 là điện trở tính bằng ôm,
là điện trở tính bằng ôm, 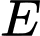 là độ giảm điện áp tính bằng vôn và
là độ giảm điện áp tính bằng vôn và 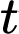 là thời gian tính bằng giây.
là thời gian tính bằng giây.
Giả sử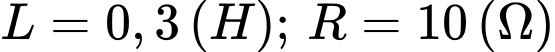 và
và 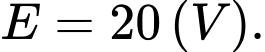 Tại thời điểm
Tại thời điểm 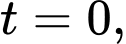 cường độ dòng điện
cường độ dòng điện 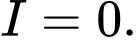 Ta coi rằng khi
Ta coi rằng khi 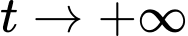 thì cường độ dòng điện tiến tới giá trị giới hạn của nó. Hỏi sau bao nhiêu giây cường độ dòng điện đạt tới
thì cường độ dòng điện tiến tới giá trị giới hạn của nó. Hỏi sau bao nhiêu giây cường độ dòng điện đạt tới 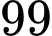 % giá trị giới hạn của nó. Làm tròn đến hàng phần trăm?
% giá trị giới hạn của nó. Làm tròn đến hàng phần trăm?
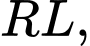 cường độ dòng điện
cường độ dòng điện 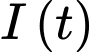 ampe luôn tăng và thay đổi thoả mãn:
ampe luôn tăng và thay đổi thoả mãn: 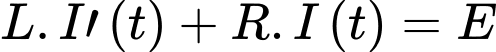 trong đó
trong đó 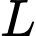 là độ tự cảm tính bằng henry,
là độ tự cảm tính bằng henry, 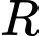 là điện trở tính bằng ôm,
là điện trở tính bằng ôm, 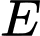 là độ giảm điện áp tính bằng vôn và
là độ giảm điện áp tính bằng vôn và 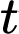 là thời gian tính bằng giây.
là thời gian tính bằng giây.
Giả sử
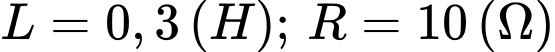 và
và 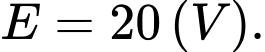 Tại thời điểm
Tại thời điểm 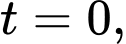 cường độ dòng điện
cường độ dòng điện 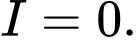 Ta coi rằng khi
Ta coi rằng khi 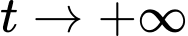 thì cường độ dòng điện tiến tới giá trị giới hạn của nó. Hỏi sau bao nhiêu giây cường độ dòng điện đạt tới
thì cường độ dòng điện tiến tới giá trị giới hạn của nó. Hỏi sau bao nhiêu giây cường độ dòng điện đạt tới 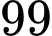 % giá trị giới hạn của nó. Làm tròn đến hàng phần trăm?
% giá trị giới hạn của nó. Làm tròn đến hàng phần trăm?
Điền đáp án: 0,14.
Theo giả thiết ta có: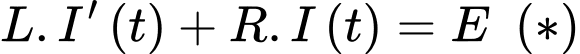
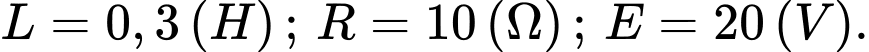
Thay số vào (*) ta có: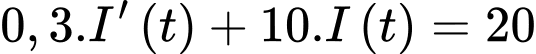
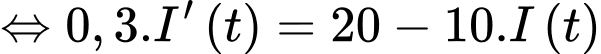
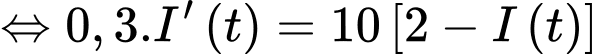
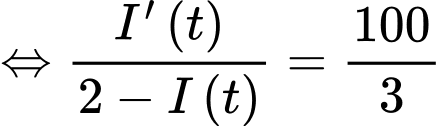
Lại có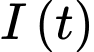 ampe luôn tăng nên ta suy ra
ampe luôn tăng nên ta suy ra 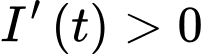
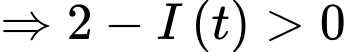
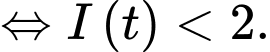
Ta có: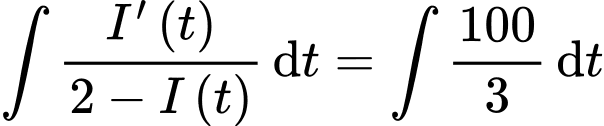
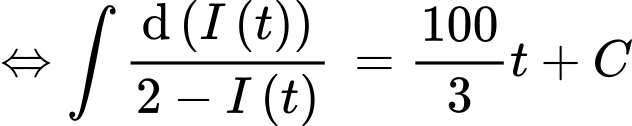
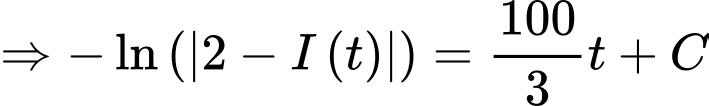 mà
mà 
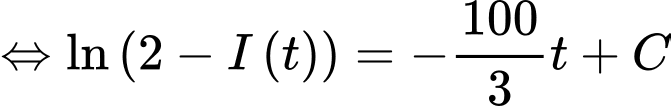
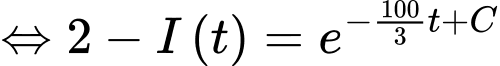
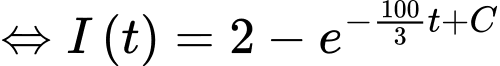
Ta có: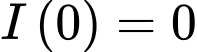
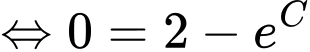
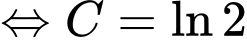
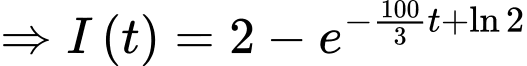
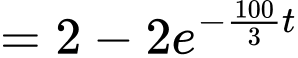
Với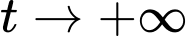 thì
thì 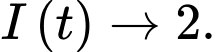
Vậy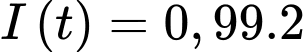
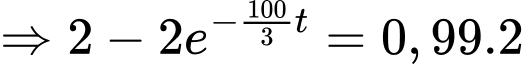
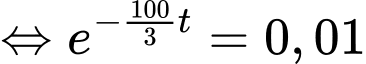
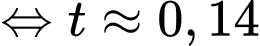 (s).
(s).
Theo giả thiết ta có:
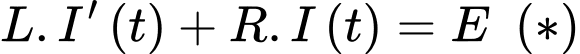
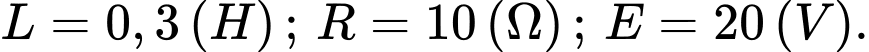
Thay số vào (*) ta có:
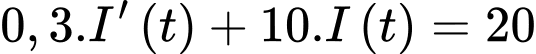
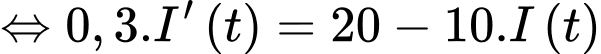
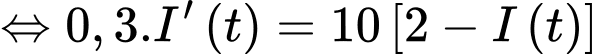
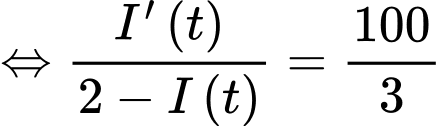
Lại có
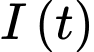 ampe luôn tăng nên ta suy ra
ampe luôn tăng nên ta suy ra 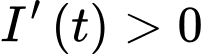
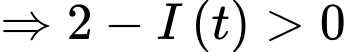
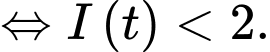
Ta có:
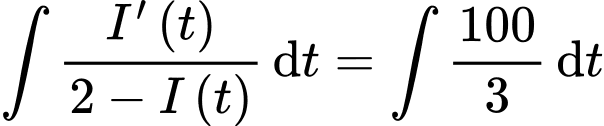
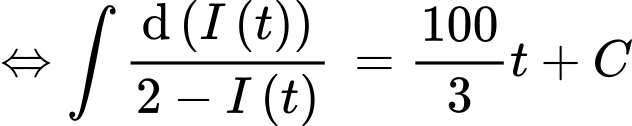
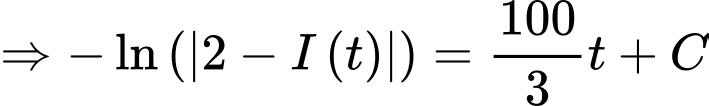 mà
mà 
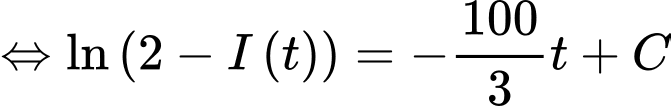
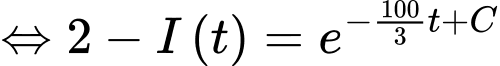
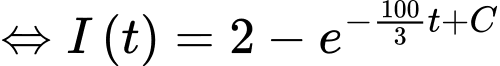
Ta có:
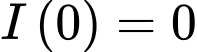
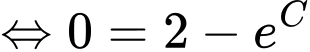
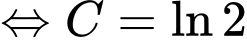
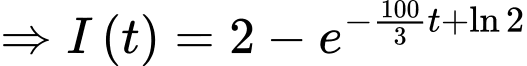
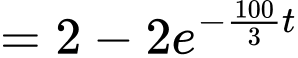
Với
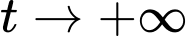 thì
thì 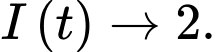
Vậy
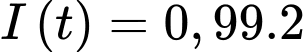
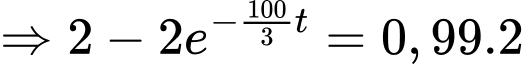
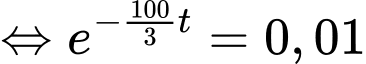
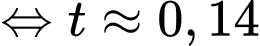 (s).
(s).
Câu 22 [693543]: Trong không gian 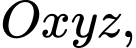 cho mặt cầu
cho mặt cầu 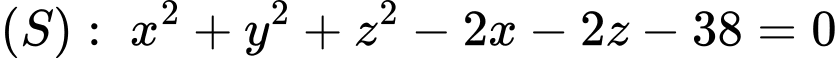 và hai mặt phẳng
và hai mặt phẳng 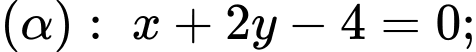
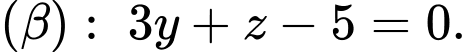 Xét
Xét 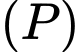 là mặt phẳng thay đổi, song song với giao tuyến của hai mặt phẳng
là mặt phẳng thay đổi, song song với giao tuyến của hai mặt phẳng 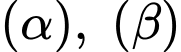 và tiếp xúc với mặt cầu
và tiếp xúc với mặt cầu 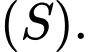 Khoảng cách lớn nhất từ điểm
Khoảng cách lớn nhất từ điểm 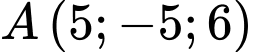 đến mặt phẳng
đến mặt phẳng 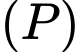 bằng bao nhiêu? Kết quả làm tròn đến hàng phần mười.
bằng bao nhiêu? Kết quả làm tròn đến hàng phần mười.
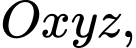 cho mặt cầu
cho mặt cầu 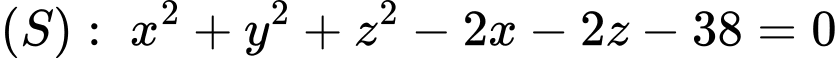 và hai mặt phẳng
và hai mặt phẳng 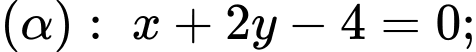
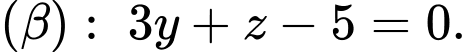 Xét
Xét 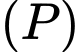 là mặt phẳng thay đổi, song song với giao tuyến của hai mặt phẳng
là mặt phẳng thay đổi, song song với giao tuyến của hai mặt phẳng 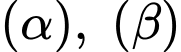 và tiếp xúc với mặt cầu
và tiếp xúc với mặt cầu 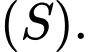 Khoảng cách lớn nhất từ điểm
Khoảng cách lớn nhất từ điểm 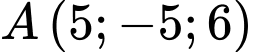 đến mặt phẳng
đến mặt phẳng 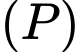 bằng bao nhiêu? Kết quả làm tròn đến hàng phần mười.
bằng bao nhiêu? Kết quả làm tròn đến hàng phần mười.
Điền đáp án: 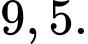
Ta có các vectơ pháp tuyến của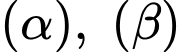 là :
là : 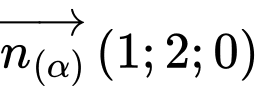 và
và 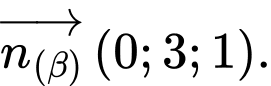
Gọi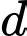 là giao tuyến của
là giao tuyến của 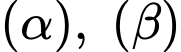 thì
thì 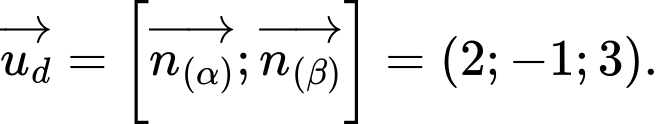
Mặt cầu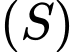 có tâm
có tâm 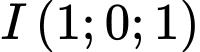 và bán kính
và bán kính 
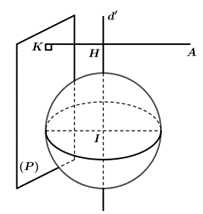
Gọi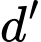 là đường thẳng qua tâm
là đường thẳng qua tâm 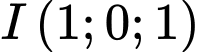 và song song với
và song song với 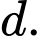
Khi đó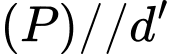 và cách
và cách 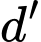 một khoảng không đổi bằng
một khoảng không đổi bằng 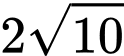 .
.
Gọi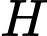 là hình chiếu vuông góc của
là hình chiếu vuông góc của 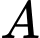 trên
trên 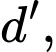 khi đó
khi đó 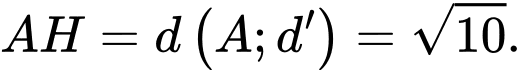
Ta có: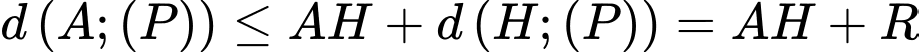 (bất đẳng thức tam giác).
(bất đẳng thức tam giác).
Khi đó:
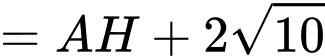
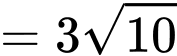
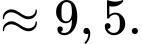
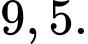
Ta có các vectơ pháp tuyến của
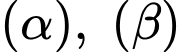 là :
là : 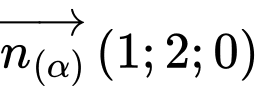 và
và 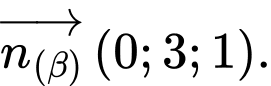
Gọi
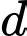 là giao tuyến của
là giao tuyến của 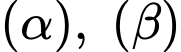 thì
thì 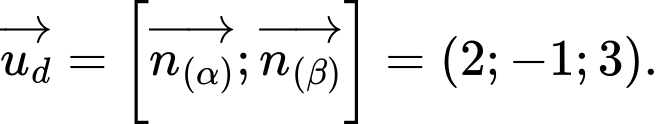
Mặt cầu
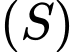 có tâm
có tâm 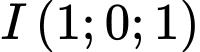 và bán kính
và bán kính 

Gọi
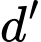 là đường thẳng qua tâm
là đường thẳng qua tâm 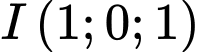 và song song với
và song song với 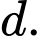
Khi đó
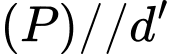 và cách
và cách 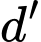 một khoảng không đổi bằng
một khoảng không đổi bằng 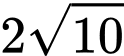 .
.Gọi
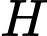 là hình chiếu vuông góc của
là hình chiếu vuông góc của 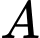 trên
trên 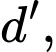 khi đó
khi đó 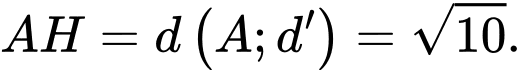
Ta có:
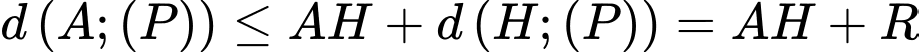 (bất đẳng thức tam giác).
(bất đẳng thức tam giác).Khi đó: