PHẦN I. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Câu 1 [256952]: Cho hàm số 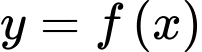 có bảng biến thiên như sau:
có bảng biến thiên như sau:
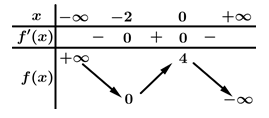
Hàm số đã cho nghịch biến trên khoảng nào sau đây?
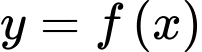 có bảng biến thiên như sau:
có bảng biến thiên như sau: 
Hàm số đã cho nghịch biến trên khoảng nào sau đây?
A, 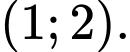
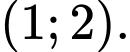
B, 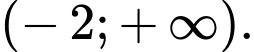
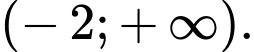
C, 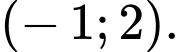
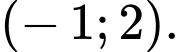
D, 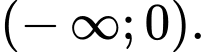
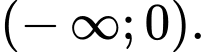
Chọn đáp án A.
Dựa vào bảng biến thiên, ta thấy hàm số nghịch biến trên các khoảng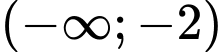 và
và 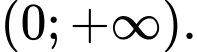
Vậy hàm số nghịch biến trên khoảng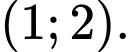 Đáp án: A
Đáp án: A
Dựa vào bảng biến thiên, ta thấy hàm số nghịch biến trên các khoảng
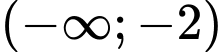 và
và 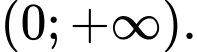
Vậy hàm số nghịch biến trên khoảng
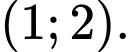 Đáp án: A
Đáp án: A
Câu 2 [693635]: Một cấp số nhân có hai số hạng liên tiếp là 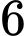 và
và 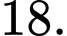 Số hạng tiếp theo là
Số hạng tiếp theo là
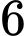 và
và 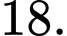 Số hạng tiếp theo là
Số hạng tiếp theo là A, 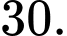
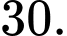
B, 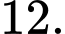
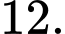
C, 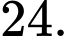
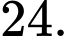
D, 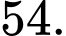
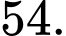
Chọn đáp án D.
Theo bài ra ta có: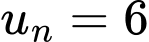 và
và 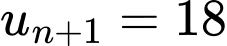
Suy ra: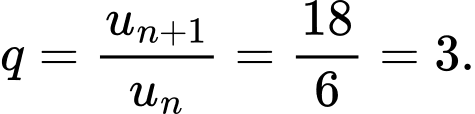
Suy ra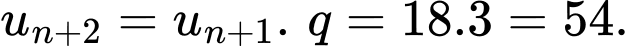 Đáp án: D
Đáp án: D
Theo bài ra ta có:
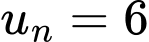 và
và 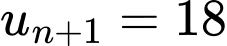
Suy ra:
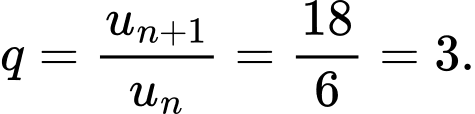
Suy ra
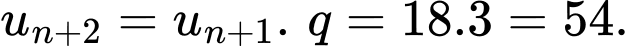 Đáp án: D
Đáp án: D
Câu 3 [520566]: Tập xác định của hàm số 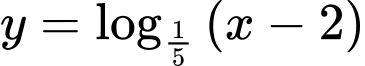 là
là
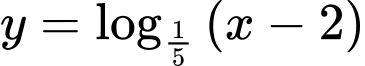 là
là A, 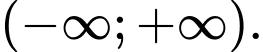
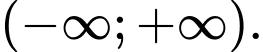
B, 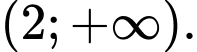
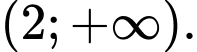
C, 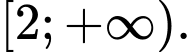
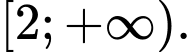
D, 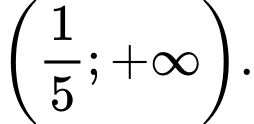
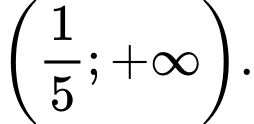
Chọn B
Hàm số đã cho xác định khi và chỉ khi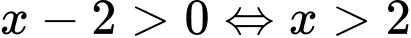 .
.
Vậy tập xác định là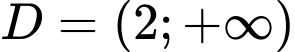 . Đáp án: B
. Đáp án: B
Hàm số đã cho xác định khi và chỉ khi
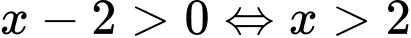 .
. Vậy tập xác định là
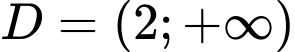 . Đáp án: B
. Đáp án: B
Câu 4 [693636]: Trong không gian 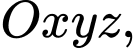 phương trình của mặt cầu có tâm
phương trình của mặt cầu có tâm  và đi qua điểm
và đi qua điểm 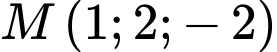 là
là
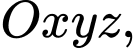 phương trình của mặt cầu có tâm
phương trình của mặt cầu có tâm  và đi qua điểm
và đi qua điểm 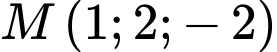 là
là A, 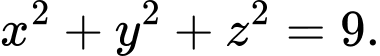
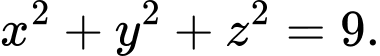
B, 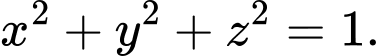
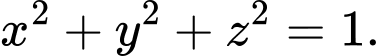
C, 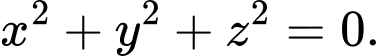
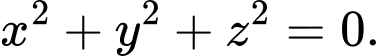
D, 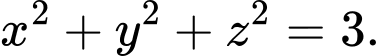
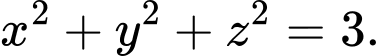
Chọn đáp án A.
Ta có phương trình của mặt cầu có tâm và đi qua điểm
và đi qua điểm 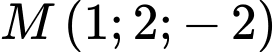

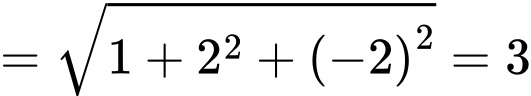 là:
là: 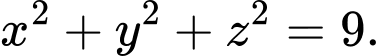 Đáp án: A
Đáp án: A
Ta có phương trình của mặt cầu có tâm
 và đi qua điểm
và đi qua điểm 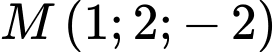

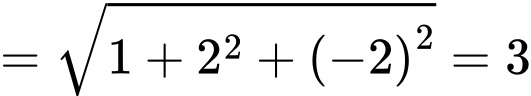 là:
là: 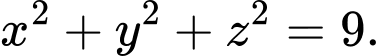 Đáp án: A
Đáp án: A
Câu 5 [693637]: Một mẫu số liệu ghép nhóm về chiều cao của một lớp (đơn vị là centimét) có phương sai là 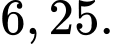 Độ lệch chuẩn của mẫu số liệu đó bằng
Độ lệch chuẩn của mẫu số liệu đó bằng
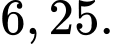 Độ lệch chuẩn của mẫu số liệu đó bằng
Độ lệch chuẩn của mẫu số liệu đó bằng A, 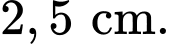
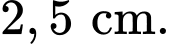
B, 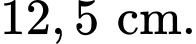
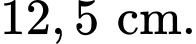
C, 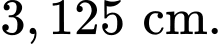
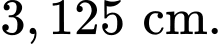
D, 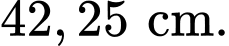
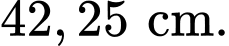
Chọn đáp án A.
Độ lệch chuẩn của mẫu số liệu đó bằng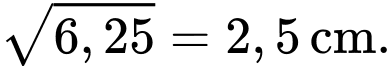 Đáp án: A
Đáp án: A
Độ lệch chuẩn của mẫu số liệu đó bằng
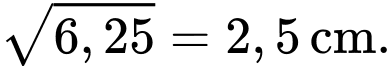 Đáp án: A
Đáp án: A
Câu 6 [693638]: Cho hình chóp tứ giác đều 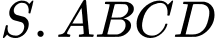 (xem hình minh hoạ bên). Đường thẳng
(xem hình minh hoạ bên). Đường thẳng 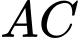 vuông góc với mặt phẳng nào sau đây?
vuông góc với mặt phẳng nào sau đây?
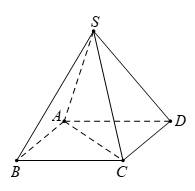
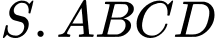 (xem hình minh hoạ bên). Đường thẳng
(xem hình minh hoạ bên). Đường thẳng 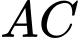 vuông góc với mặt phẳng nào sau đây?
vuông góc với mặt phẳng nào sau đây?
A, 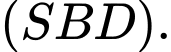
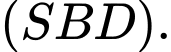
B, 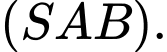
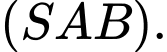
C, 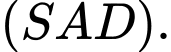
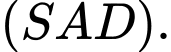
D, 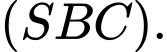
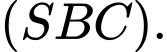
Chọn đáp án A.
Ta có: (tính chất hai đường chéo của hình vuông)
(tính chất hai đường chéo của hình vuông)
Mà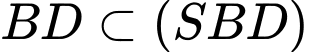
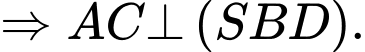 Đáp án: A
Đáp án: A
Ta có:
 (tính chất hai đường chéo của hình vuông)
(tính chất hai đường chéo của hình vuông)Mà
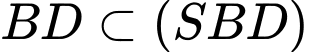
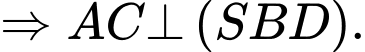 Đáp án: A
Đáp án: A
Câu 7 [700303]: Họ tất cả các nguyên hàm của hàm số 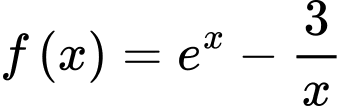 trên khoảng
trên khoảng 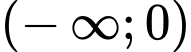 là
là
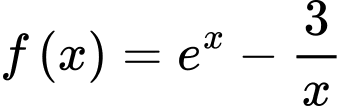 trên khoảng
trên khoảng 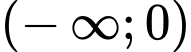 là
là A, 

B, 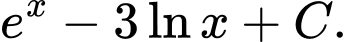
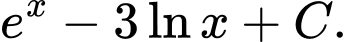
C, 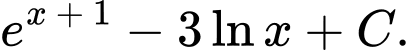
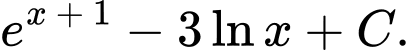
D, 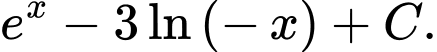
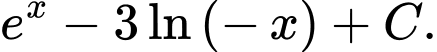
Chọn đáp án D.
Ta có: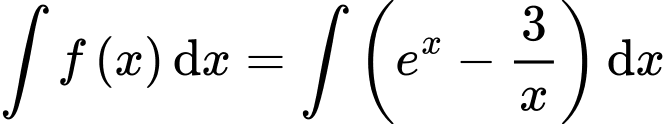
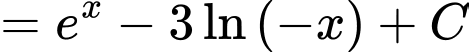 (do điều kiện của hàm trong
(do điều kiện của hàm trong 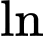 phải lớn hơn 0 mà bài cho trên khoảng
phải lớn hơn 0 mà bài cho trên khoảng 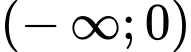 nên giá trị của
nên giá trị của 
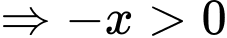 ) Đáp án: D
) Đáp án: D
Ta có:
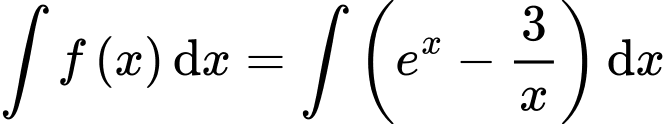
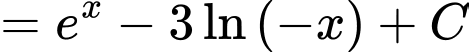 (do điều kiện của hàm trong
(do điều kiện của hàm trong 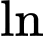 phải lớn hơn 0 mà bài cho trên khoảng
phải lớn hơn 0 mà bài cho trên khoảng 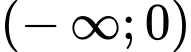 nên giá trị của
nên giá trị của 
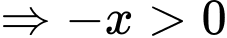 ) Đáp án: D
) Đáp án: D
Câu 8 [256778]: Với mọi số thực 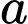 dương,
dương, 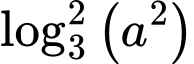 bằng
bằng
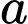 dương,
dương, 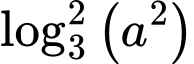 bằng
bằng A, 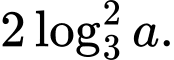
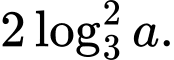
B, 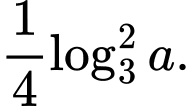
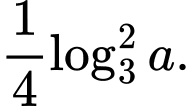
C, 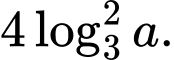
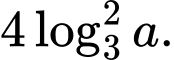
D, 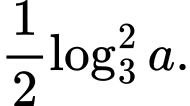
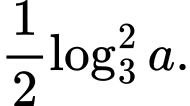
Chọn đáp án C.
Ta có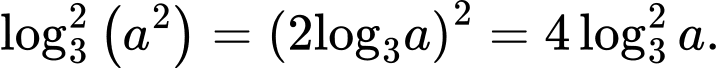 Đáp án: C
Đáp án: C
Ta có
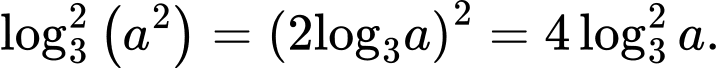 Đáp án: C
Đáp án: C
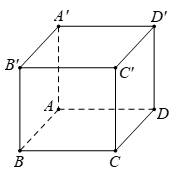
Câu 9 [693639]: Cho hình lập phương 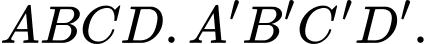 Tổng
Tổng 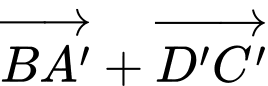 là vectơ nào sau đây?
là vectơ nào sau đây?
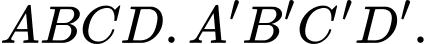 Tổng
Tổng 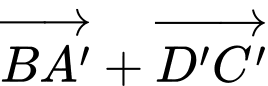 là vectơ nào sau đây?
là vectơ nào sau đây?
A, 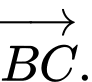
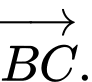
B, 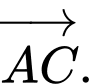
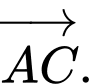
C, 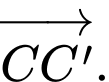
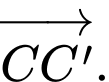
D, 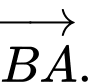
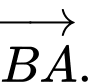
Chọn đáp án C.
Ta có: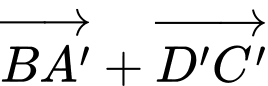
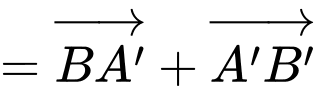

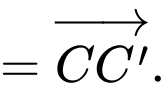 Đáp án: C
Đáp án: C
Ta có:
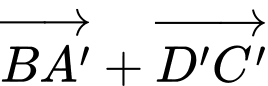
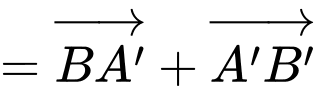

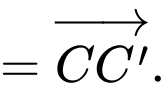 Đáp án: C
Đáp án: C
Câu 10 [693641]: Trong không gian 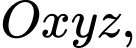 cho hai điểm
cho hai điểm 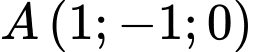 và
và 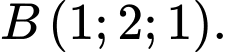 Phương trình của mặt phẳng đi qua điểm
Phương trình của mặt phẳng đi qua điểm 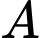 và vuông góc với
và vuông góc với  là
là
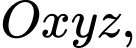 cho hai điểm
cho hai điểm 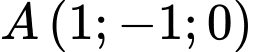 và
và 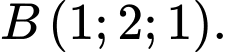 Phương trình của mặt phẳng đi qua điểm
Phương trình của mặt phẳng đi qua điểm 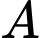 và vuông góc với
và vuông góc với  là
là A, 

B, 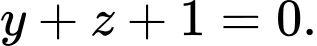
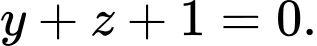
C, 

D, 

Chọn đáp án A.
Ta có: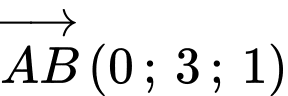
Phương trình của mặt phẳng đi qua điểm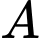 và vuông góc với
và vuông góc với  là:
là:
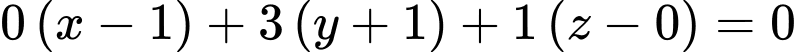
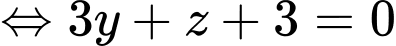 Đáp án: A
Đáp án: A
Ta có:
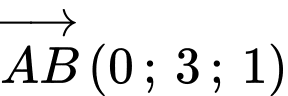
Phương trình của mặt phẳng đi qua điểm
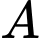 và vuông góc với
và vuông góc với  là:
là:
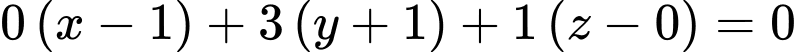
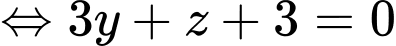 Đáp án: A
Đáp án: A
Câu 11 [693642]: Cho 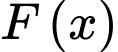 là một nguyên hàm của hàm số
là một nguyên hàm của hàm số 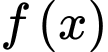 trên
trên 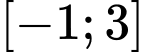 và thoả mãn
và thoả mãn 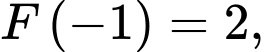
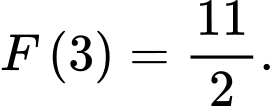 Giá trị của
Giá trị của 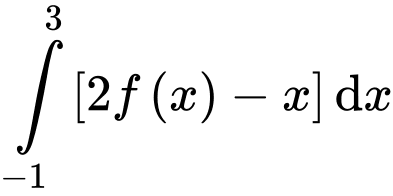 bằng
bằng
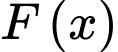 là một nguyên hàm của hàm số
là một nguyên hàm của hàm số 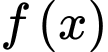 trên
trên 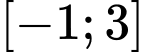 và thoả mãn
và thoả mãn 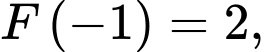
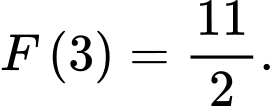 Giá trị của
Giá trị của 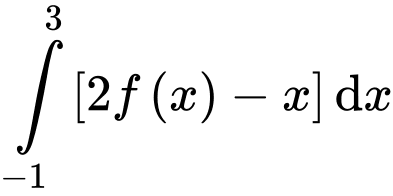 bằng
bằng A, 

B, 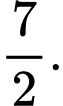
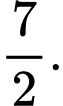
C, 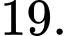
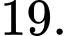
D, 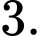
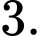
Chọn đáp án D.
Ta có: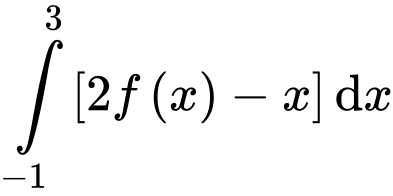
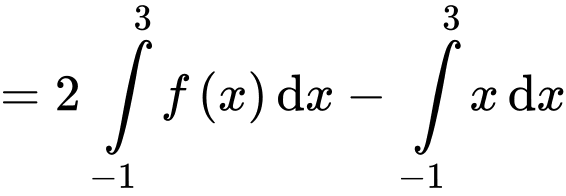
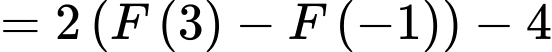
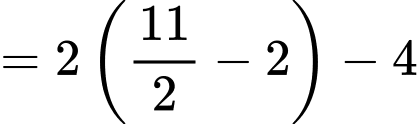
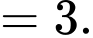 Đáp án: D
Đáp án: D
Ta có:
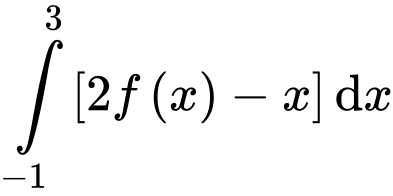
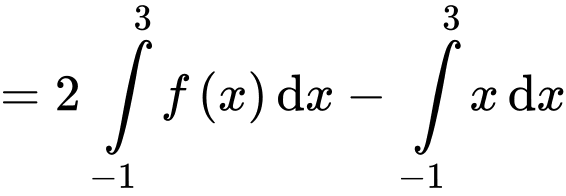
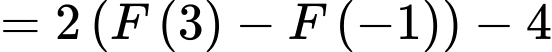
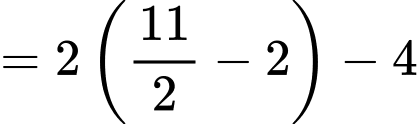
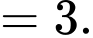 Đáp án: D
Đáp án: D
Câu 12 [693640]: Cho đồ thị hàm số 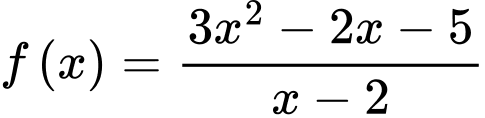 có tâm đối xứng là
có tâm đối xứng là 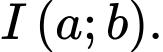 Giá trị của biểu thức
Giá trị của biểu thức  là
là
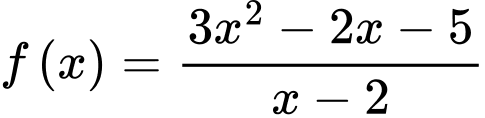 có tâm đối xứng là
có tâm đối xứng là 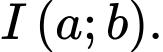 Giá trị của biểu thức
Giá trị của biểu thức  là
là A, 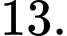
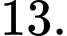
B, 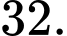
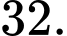
C, 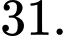
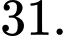
D, 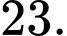
Chọn đáp án B.
Ta có:
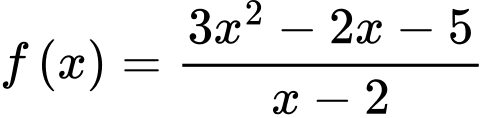
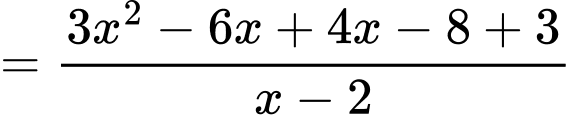
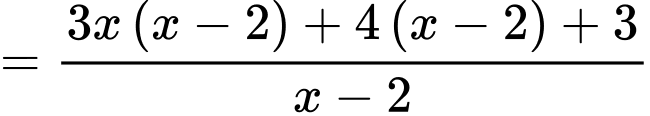
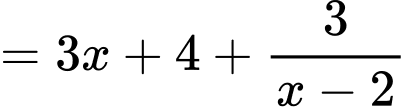
Suy ra hàm số có tiệm cận xiên là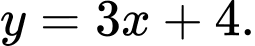
Tiệm cận đứng là: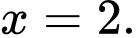
Tâm đối xứng của hàm số là giao của đường tiệm cận đứng với tiệm cận xiên nên ta có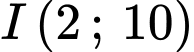
Vậy giá trị của biểu thức là
là 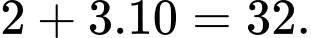 Đáp án: B
Đáp án: B
Ta có:
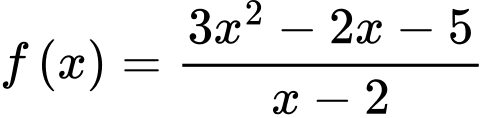
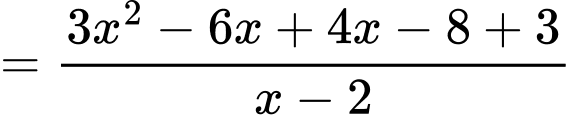
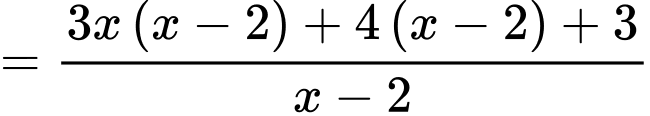
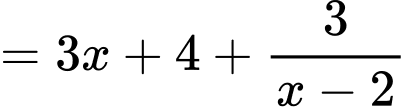
Suy ra hàm số có tiệm cận xiên là
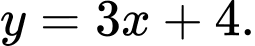
Tiệm cận đứng là:
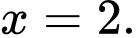
Tâm đối xứng của hàm số là giao của đường tiệm cận đứng với tiệm cận xiên nên ta có
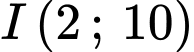
Vậy giá trị của biểu thức
 là
là 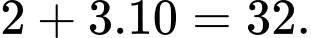 Đáp án: B
Đáp án: B PHẦN II. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Câu 13 [693643]: Cho hàm số 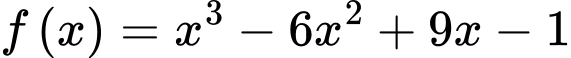 có đồ thị
có đồ thị  Gọi
Gọi 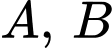 là hai điểm cực trị của
là hai điểm cực trị của 
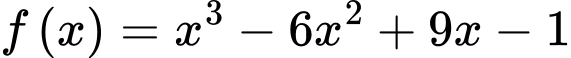 có đồ thị
có đồ thị  Gọi
Gọi 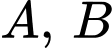 là hai điểm cực trị của
là hai điểm cực trị của 
a) Đúng.
b) Sai.
Ta có:
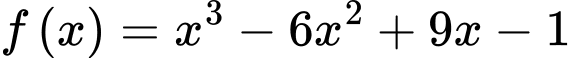
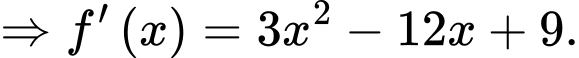
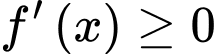
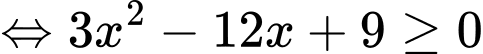
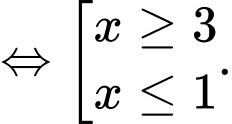
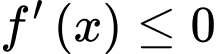
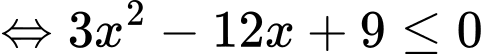
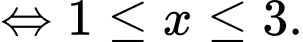
Vậy hàm số đã cho nghịch biến trên khoảng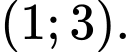
c) Đúng
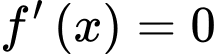
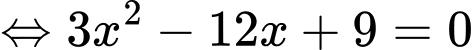
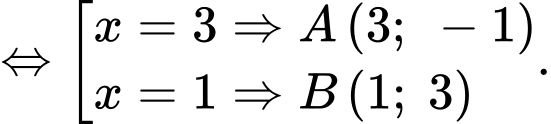
Phương trình đường thẳng đi qua hai điểm cực trị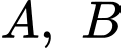 là:
là: 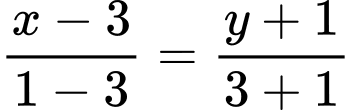 hay
hay 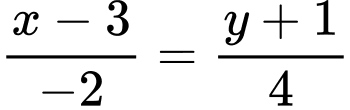
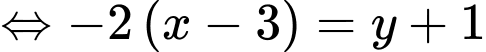
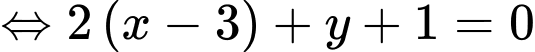
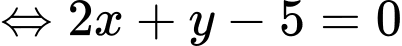
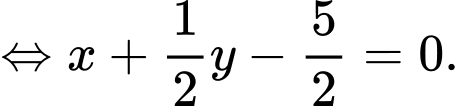
Vậy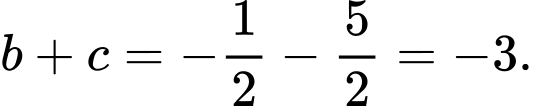
d) Sai.
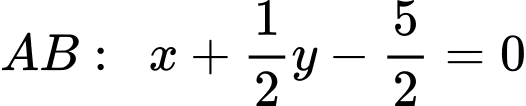
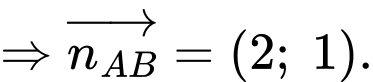
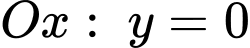
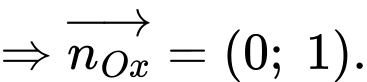
Ta có: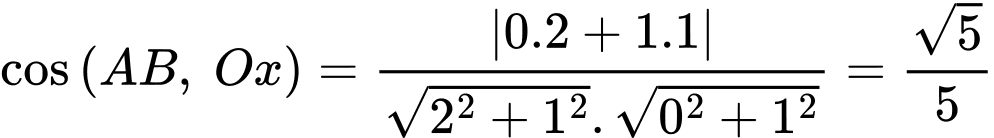
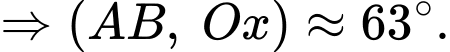
b) Sai.
Ta có:
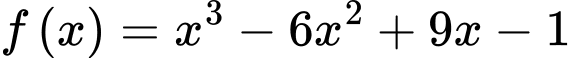
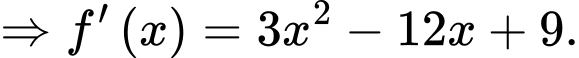
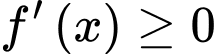
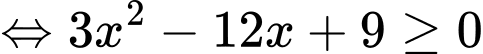
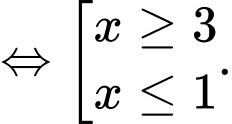
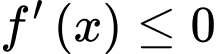
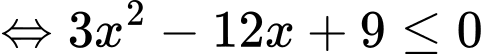
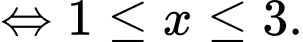
Vậy hàm số đã cho nghịch biến trên khoảng
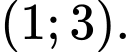
c) Đúng
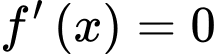
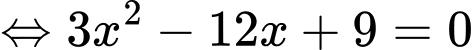
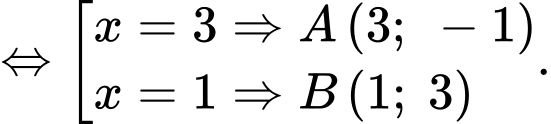
Phương trình đường thẳng đi qua hai điểm cực trị
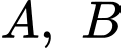 là:
là: 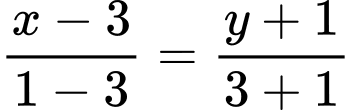 hay
hay 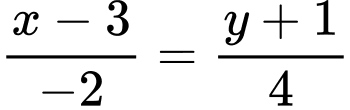
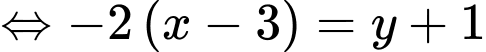
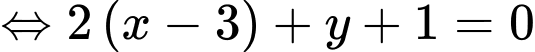
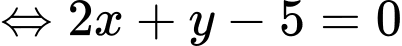
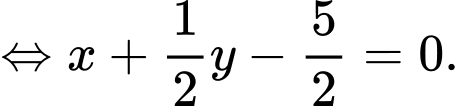
Vậy
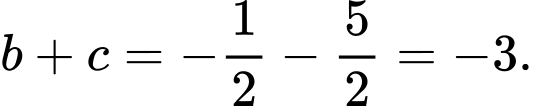
d) Sai.
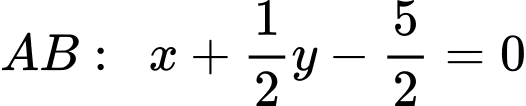
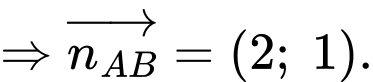
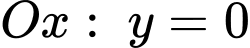
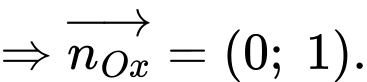
Ta có:
Câu 14 [693644]: Một vật trang trí dạng hình chóp tam giác đều có chiều cao 110 mm và đáy là tam giác đều cạnh 120 mm như hình vẽ. Chọn hệ trục tọa độ 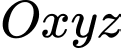 sao cho gốc tọa độ
sao cho gốc tọa độ  trùng với trung điểm của cạnh đáy
trùng với trung điểm của cạnh đáy 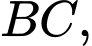 đỉnh
đỉnh 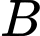 thuộc tia
thuộc tia 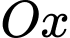 và đỉnh
và đỉnh 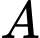 thuộc tia
thuộc tia 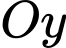 (đơn vị mỗi trục là mm, xem hình vẽ).
(đơn vị mỗi trục là mm, xem hình vẽ).
 sao cho gốc tọa độ
sao cho gốc tọa độ  trùng với trung điểm của cạnh đáy
trùng với trung điểm của cạnh đáy  đỉnh
đỉnh 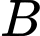 thuộc tia
thuộc tia 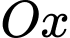 và đỉnh
và đỉnh 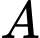 thuộc tia
thuộc tia 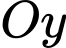 (đơn vị mỗi trục là mm, xem hình vẽ).
(đơn vị mỗi trục là mm, xem hình vẽ).
a) Đúng.
Ta có:
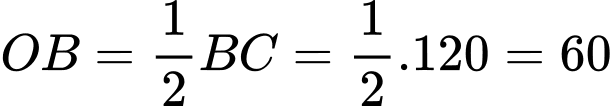
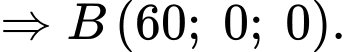
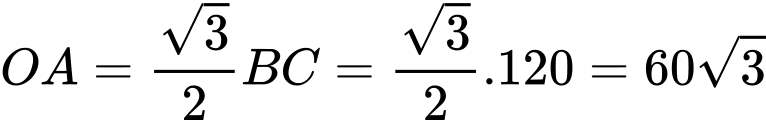
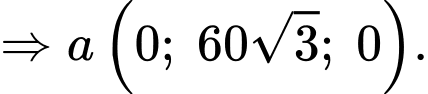
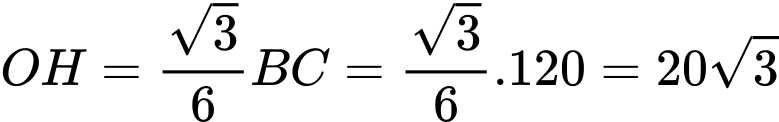
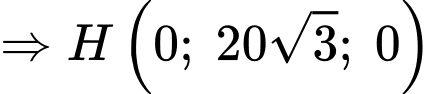
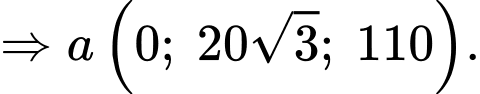
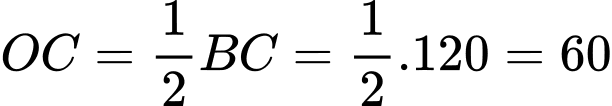
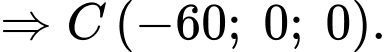
b) Sai.
Ta có: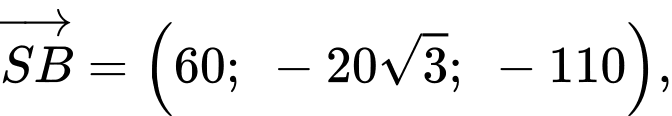
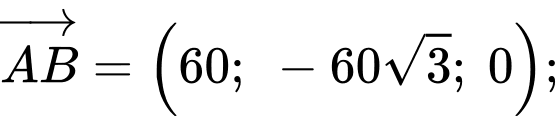
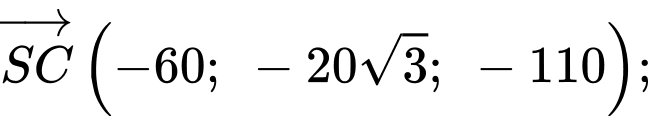
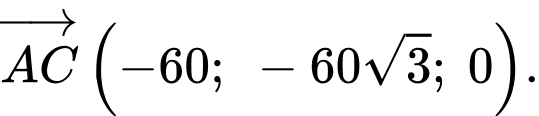
c) Sai.
Ta có: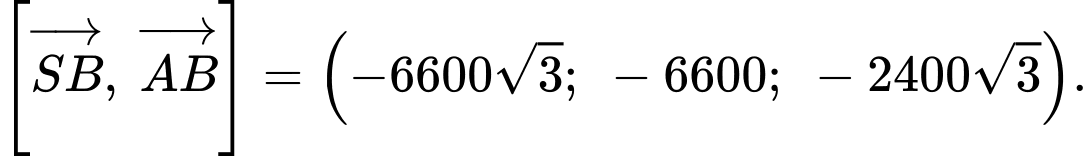
Mặt phẳng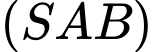 có vectơ pháp tuyến
có vectơ pháp tuyến 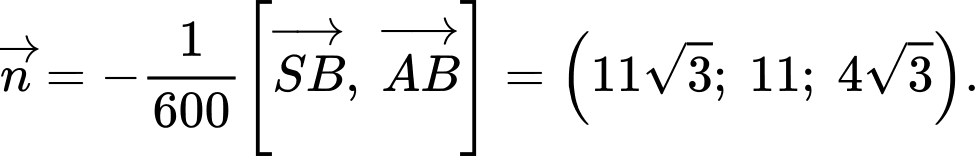 .
.
d) Sai.
Tương tự, mặt phẳng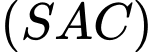 có vectơ pháp tuyến
có vectơ pháp tuyến 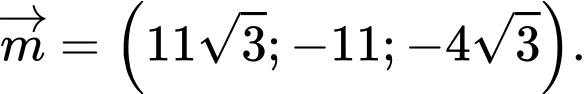
Suy ra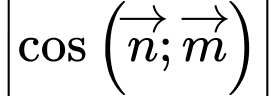
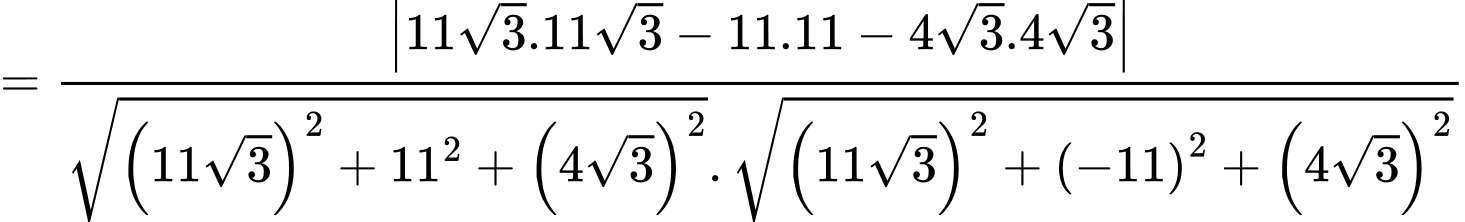
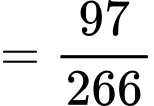
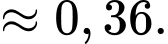
Ta có:
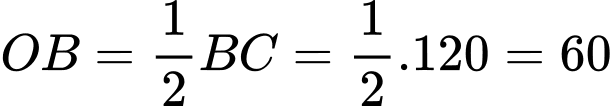
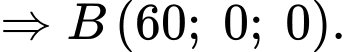
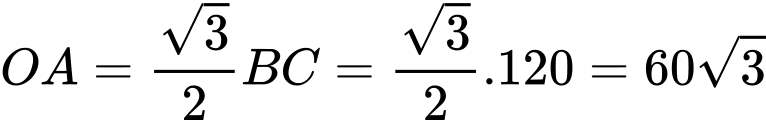
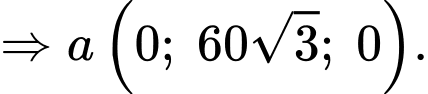
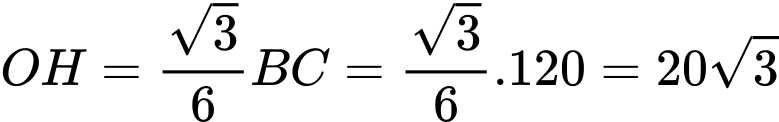
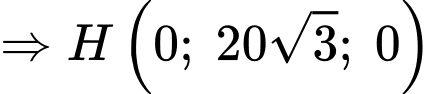
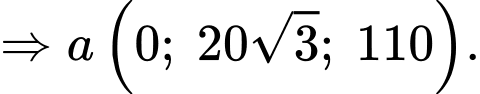
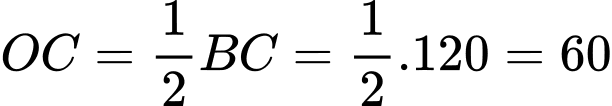
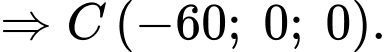
b) Sai.
Ta có:
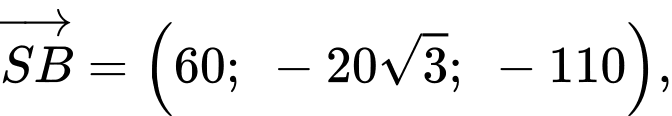
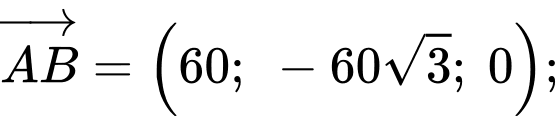
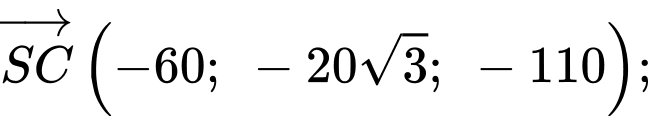
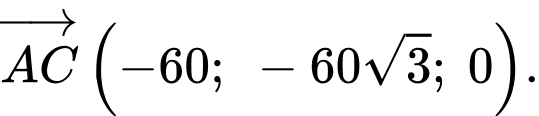
c) Sai.
Ta có:
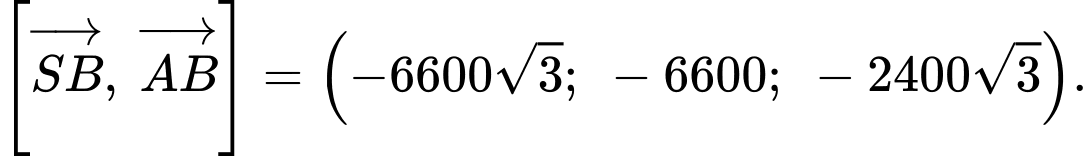
Mặt phẳng
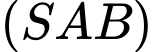 có vectơ pháp tuyến
có vectơ pháp tuyến 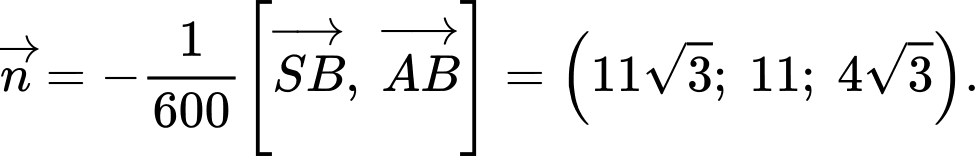 .
.
d) Sai.
Tương tự, mặt phẳng
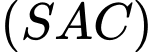 có vectơ pháp tuyến
có vectơ pháp tuyến 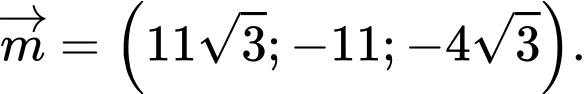
Suy ra
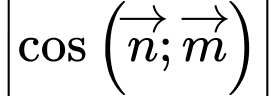
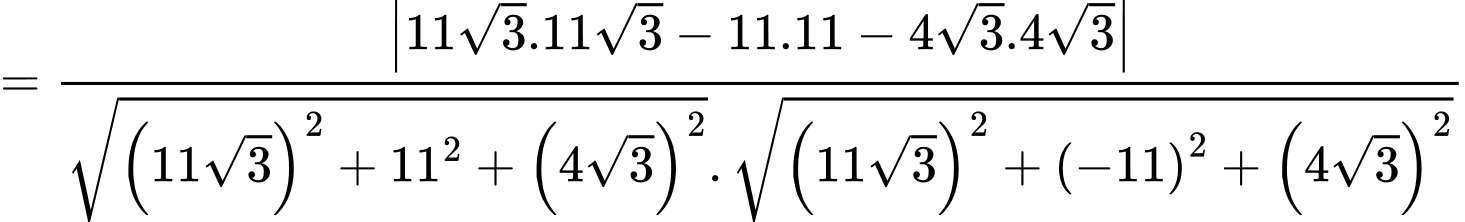
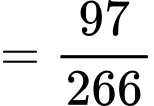
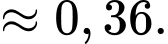
Câu 15 [693645]: Một bể bơi hình trụ trên mặt đất có đường kính  được bơm nước vào với tốc độ
được bơm nước vào với tốc độ 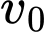 không đổi cho đến khi mực nước cao
không đổi cho đến khi mực nước cao 
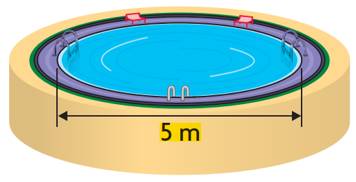
Sau khi được đổ đầy, bể bơi bị thủng ở đáy và nước rò rỉ ra ngoài. Bể bơi rò hết toàn bộ nước trong 8 giờ. Biết rằng lượng nước còn lại trong hồ được mô phỏng bởi hàm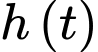 và tốc độ nước chảy ra ngoài vào thời điểm
và tốc độ nước chảy ra ngoài vào thời điểm 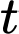 giờ (tính từ lúc bắt đầu dò) được xác định bởi hàm số
giờ (tính từ lúc bắt đầu dò) được xác định bởi hàm số 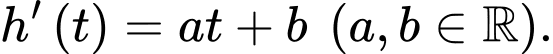 Lúc nước chảy hết ra ngoài thì vận tốc nước chảy bằng 0.
Lúc nước chảy hết ra ngoài thì vận tốc nước chảy bằng 0.
 được bơm nước vào với tốc độ
được bơm nước vào với tốc độ 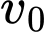 không đổi cho đến khi mực nước cao
không đổi cho đến khi mực nước cao 

Sau khi được đổ đầy, bể bơi bị thủng ở đáy và nước rò rỉ ra ngoài. Bể bơi rò hết toàn bộ nước trong 8 giờ. Biết rằng lượng nước còn lại trong hồ được mô phỏng bởi hàm
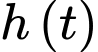 và tốc độ nước chảy ra ngoài vào thời điểm
và tốc độ nước chảy ra ngoài vào thời điểm 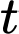 giờ (tính từ lúc bắt đầu dò) được xác định bởi hàm số
giờ (tính từ lúc bắt đầu dò) được xác định bởi hàm số 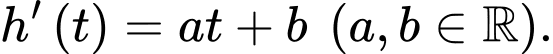 Lúc nước chảy hết ra ngoài thì vận tốc nước chảy bằng 0.
Lúc nước chảy hết ra ngoài thì vận tốc nước chảy bằng 0.
a) Sai.
Thể tích của bể sau khi dược làm đầy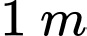 là:
là:
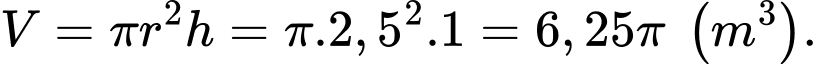
b) Đúng.
Dựa vào giả thiết: Lúc nước chảy hết ra ngoài thì vận tốc nước chảy bằng 0 nên tốc độ nước chảy ra ngoài tại thời điểm 8 giờ kể từ lúc bể bị rò bằng 0.
c) Sai.
Ta có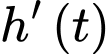 là hàm số biểu diễn tốc độ nước chảy tại thời điểm
là hàm số biểu diễn tốc độ nước chảy tại thời điểm 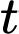 giờ.
giờ.
Dựa vào kết quả phần b), ta có tốc độ nước chảy tại thời điểm 8 giờ (tức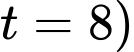 là bằng 0
là bằng 0 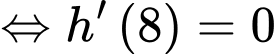
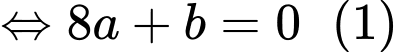
Theo công thức nguyên hàm, ta có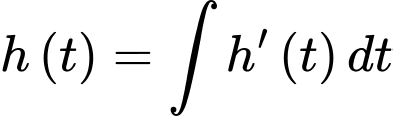
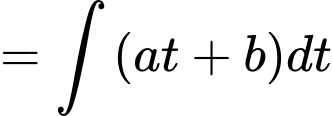
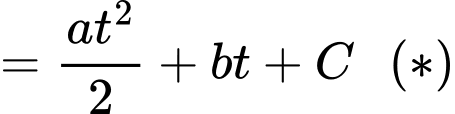
Vì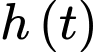 là hàm số biểu diễn thể tích nước còn lại trong hồ. Dựa vào kết quả của phần a), ta có thể tích nước trong hồ tại thời điểm ban đầu (tức
là hàm số biểu diễn thể tích nước còn lại trong hồ. Dựa vào kết quả của phần a), ta có thể tích nước trong hồ tại thời điểm ban đầu (tức 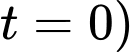 bằng
bằng 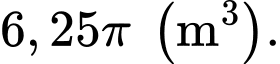
 (thay
(thay 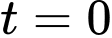 vào phương trình (*))
vào phương trình (*))
Suy ra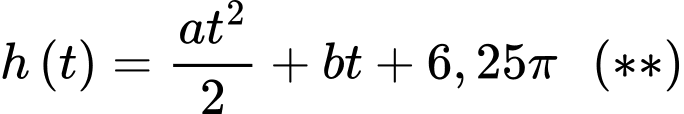
Lại có, lượng nước còn lại trong hồ sau 8 giờ là bằng 0
 (thay
(thay 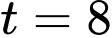 vào (**))
vào (**))
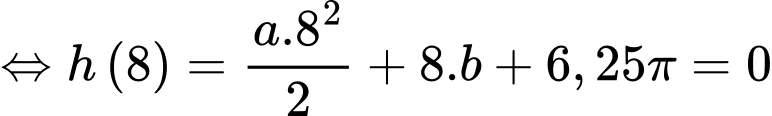
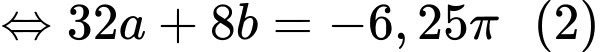
Từ (1) và (2), ta có hệ phương trình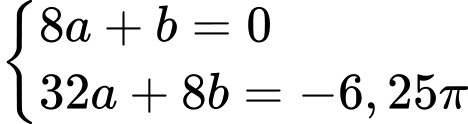
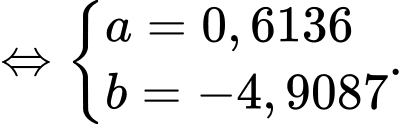
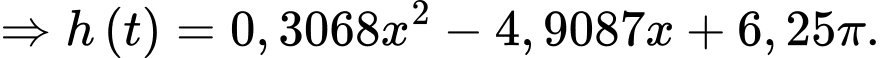
d) Sai.
Lượng nước mất đi = Lượng nước ban đầu – Lượng nước còn lại.
Ta có lượng nước còn lại sau 4 giờ là (thay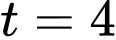 vào phương trình
vào phương trình 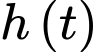 tìm được ở phần c)
tìm được ở phần c)
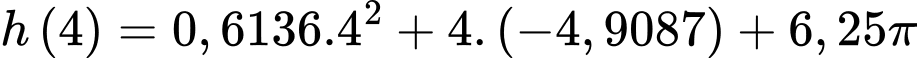
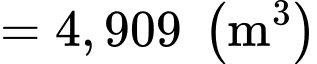
Vậy lượng nước mất đi sau 4 giờ bằng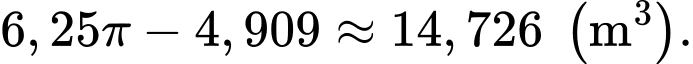
Thể tích của bể sau khi dược làm đầy
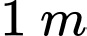 là:
là: 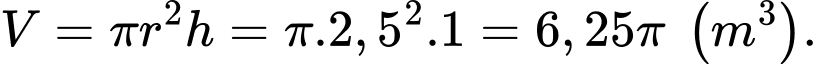
b) Đúng.
Dựa vào giả thiết: Lúc nước chảy hết ra ngoài thì vận tốc nước chảy bằng 0 nên tốc độ nước chảy ra ngoài tại thời điểm 8 giờ kể từ lúc bể bị rò bằng 0.
c) Sai.
Ta có
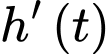 là hàm số biểu diễn tốc độ nước chảy tại thời điểm
là hàm số biểu diễn tốc độ nước chảy tại thời điểm 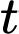 giờ.
giờ.Dựa vào kết quả phần b), ta có tốc độ nước chảy tại thời điểm 8 giờ (tức
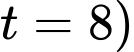 là bằng 0
là bằng 0 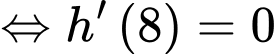
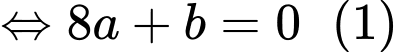
Theo công thức nguyên hàm, ta có
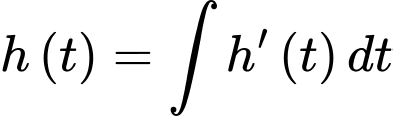
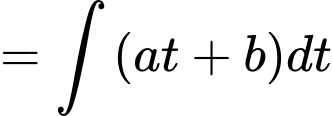
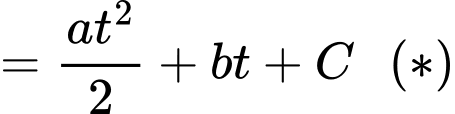
Vì
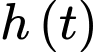 là hàm số biểu diễn thể tích nước còn lại trong hồ. Dựa vào kết quả của phần a), ta có thể tích nước trong hồ tại thời điểm ban đầu (tức
là hàm số biểu diễn thể tích nước còn lại trong hồ. Dựa vào kết quả của phần a), ta có thể tích nước trong hồ tại thời điểm ban đầu (tức 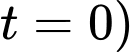 bằng
bằng 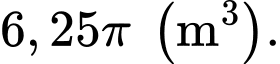
 (thay
(thay 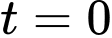 vào phương trình (*))
vào phương trình (*))Suy ra
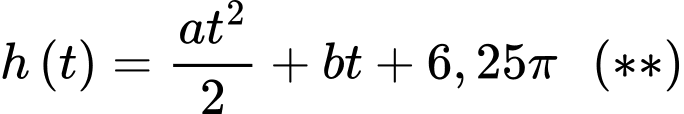
Lại có, lượng nước còn lại trong hồ sau 8 giờ là bằng 0
 (thay
(thay 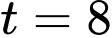 vào (**))
vào (**))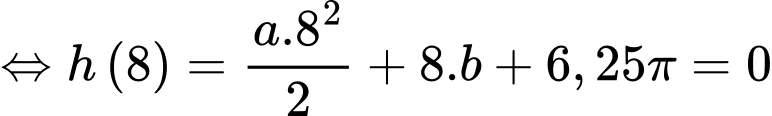
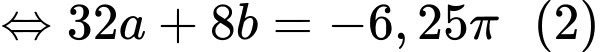
Từ (1) và (2), ta có hệ phương trình
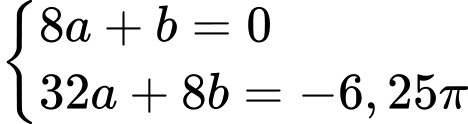
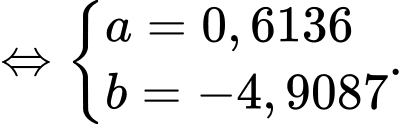
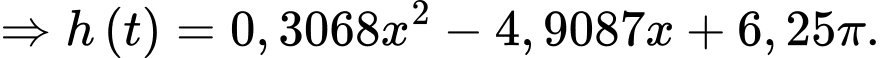
d) Sai.
Lượng nước mất đi = Lượng nước ban đầu – Lượng nước còn lại.
Ta có lượng nước còn lại sau 4 giờ là (thay
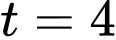 vào phương trình
vào phương trình 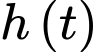 tìm được ở phần c)
tìm được ở phần c)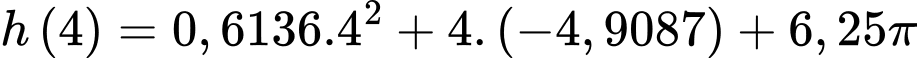
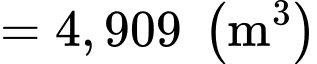
Vậy lượng nước mất đi sau 4 giờ bằng
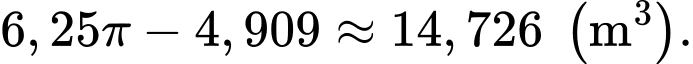
Câu 16 [693646]: Một công ty có hai chi nhánh. Sản phẩm của chi nhánh I chiếm 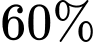 còn chi nhánh II chiếm
còn chi nhánh II chiếm 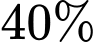 tổng sản phẩm của công ty. Tỉ lệ sản phẩm bị lỗi của chi nhánh I chiếm
tổng sản phẩm của công ty. Tỉ lệ sản phẩm bị lỗi của chi nhánh I chiếm 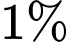 còn của chi nhánh II chiếm
còn của chi nhánh II chiếm 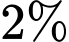 tổng sản phẩm công ty. Chọn ngẫu nhiên một sản phẩm của công ty.
tổng sản phẩm công ty. Chọn ngẫu nhiên một sản phẩm của công ty.
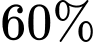 còn chi nhánh II chiếm
còn chi nhánh II chiếm 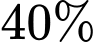 tổng sản phẩm của công ty. Tỉ lệ sản phẩm bị lỗi của chi nhánh I chiếm
tổng sản phẩm của công ty. Tỉ lệ sản phẩm bị lỗi của chi nhánh I chiếm 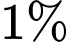 còn của chi nhánh II chiếm
còn của chi nhánh II chiếm 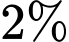 tổng sản phẩm công ty. Chọn ngẫu nhiên một sản phẩm của công ty.
tổng sản phẩm công ty. Chọn ngẫu nhiên một sản phẩm của công ty.
Gọi 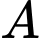 là biến cố: “Sản phẩm bị lỗi”;
là biến cố: “Sản phẩm bị lỗi”;
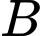 là biến cố: “Sản phẩm lấy ra do chi nhánh I sản xuất”.
là biến cố: “Sản phẩm lấy ra do chi nhánh I sản xuất”.
Suy ra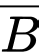 là biến cố: “Sản phẩm lấy ra do chi nhánh II sản xuất”.
là biến cố: “Sản phẩm lấy ra do chi nhánh II sản xuất”.
a) Sai.
Do sản phẩm của chi nhánh I chiếm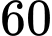 tổng sản phẩm của công ty nên
tổng sản phẩm của công ty nên 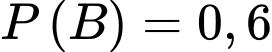 .
.
b) Đúng.
Do tỉ lệ sản phẩm bị lỗi của chi nhánh II chiếm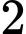 tổng sản phẩm nên
tổng sản phẩm nên 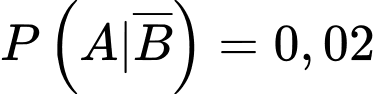 .
.
c) Sai.
Ta có: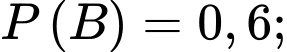
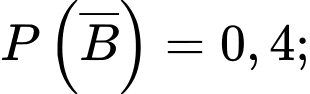
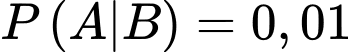 và
và 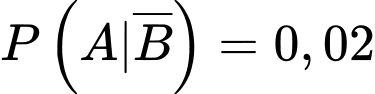 .
.
Từ đó, ta có sơ đồ cây sau:
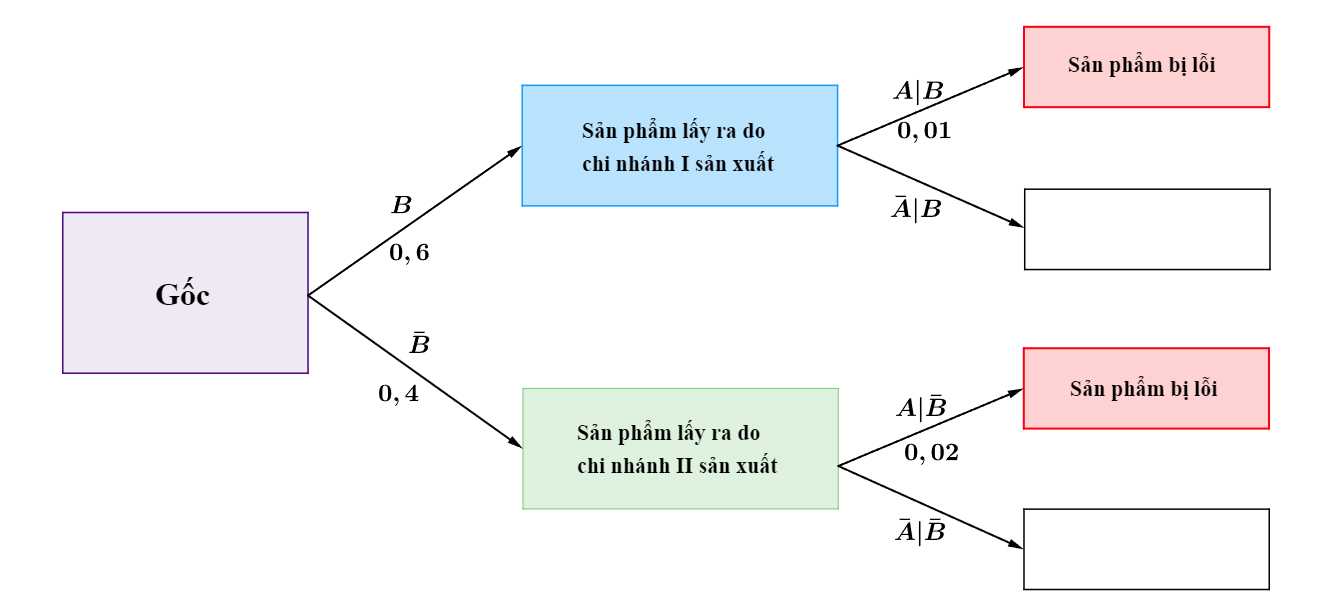
Do đó xác suất để sản phẩm lấy ra bị lỗi là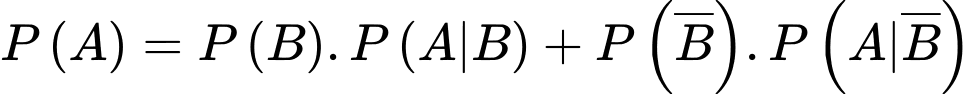
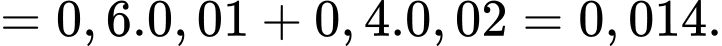
d) Sai.
Do sản phẩm lấy ra bị lỗi nên xác suất sản phẩm đó do chi nhánh I sản xuất là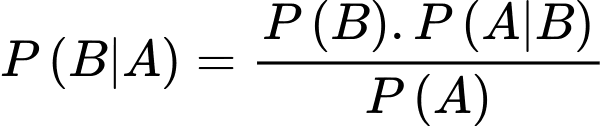
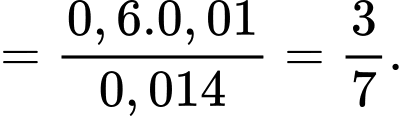
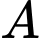 là biến cố: “Sản phẩm bị lỗi”;
là biến cố: “Sản phẩm bị lỗi”;
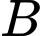 là biến cố: “Sản phẩm lấy ra do chi nhánh I sản xuất”.
là biến cố: “Sản phẩm lấy ra do chi nhánh I sản xuất”.
Suy ra
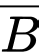 là biến cố: “Sản phẩm lấy ra do chi nhánh II sản xuất”.
là biến cố: “Sản phẩm lấy ra do chi nhánh II sản xuất”.
a) Sai.
Do sản phẩm của chi nhánh I chiếm
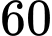 tổng sản phẩm của công ty nên
tổng sản phẩm của công ty nên 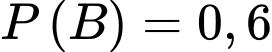 .
.
b) Đúng.
Do tỉ lệ sản phẩm bị lỗi của chi nhánh II chiếm
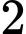 tổng sản phẩm nên
tổng sản phẩm nên 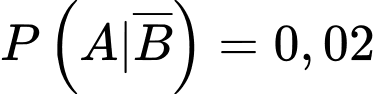 .
.
c) Sai.
Ta có:
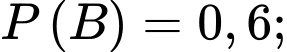
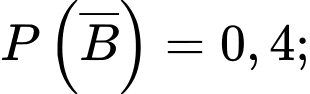
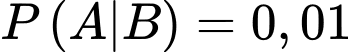 và
và 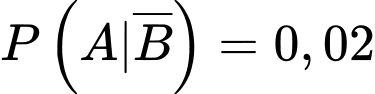 .
.
Từ đó, ta có sơ đồ cây sau:

Do đó xác suất để sản phẩm lấy ra bị lỗi là
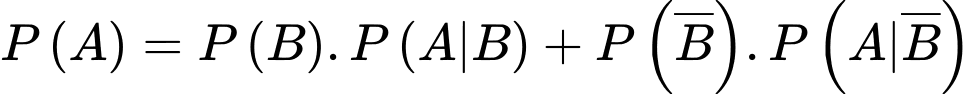
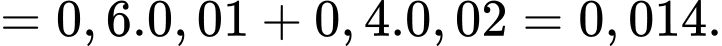
d) Sai.
Do sản phẩm lấy ra bị lỗi nên xác suất sản phẩm đó do chi nhánh I sản xuất là
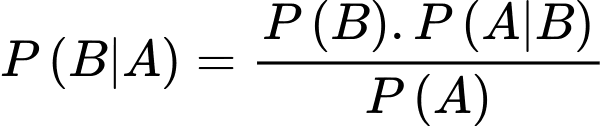
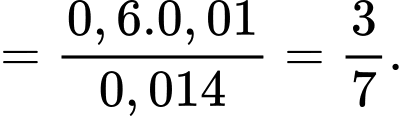
PHẦN III. Thí sinh trả lời từ câu 1 đến câu 6.
Câu 17 [693647]: Cho hình lăng trụ  có
có 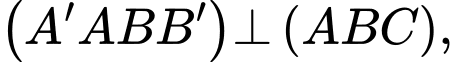
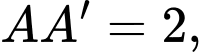
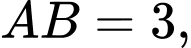
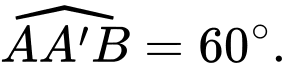 Khoảng cách giữa hai đường thẳng
Khoảng cách giữa hai đường thẳng  và
và 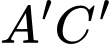 bằng bao nhiêu? (làm tròn kết quả đến hàng phần mười).
bằng bao nhiêu? (làm tròn kết quả đến hàng phần mười).
 có
có 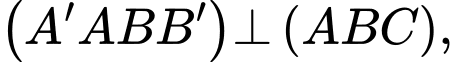
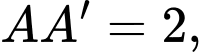
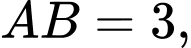
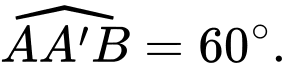 Khoảng cách giữa hai đường thẳng
Khoảng cách giữa hai đường thẳng  và
và 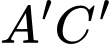 bằng bao nhiêu? (làm tròn kết quả đến hàng phần mười).
bằng bao nhiêu? (làm tròn kết quả đến hàng phần mười).
Điền đáp án: 2.
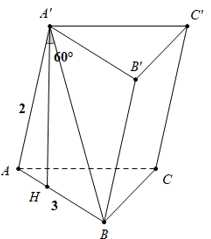
Kẻ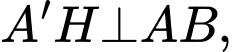 khi đó:
khi đó: 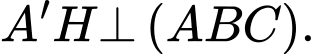
Ta có: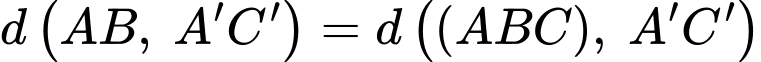
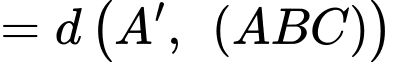
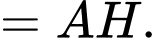
Xét tam giác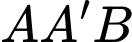 ta có
ta có 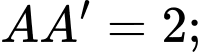
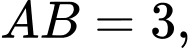
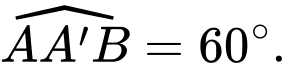
Áp dụng định lý sin, ta có: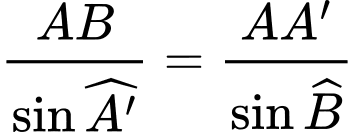
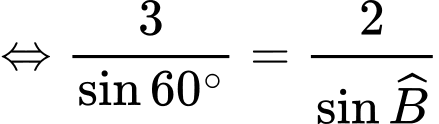
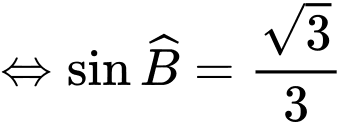
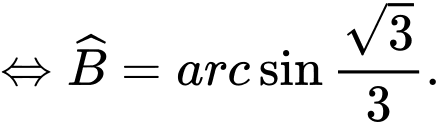
Áp dụng định lý sin, ta có: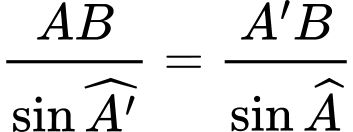
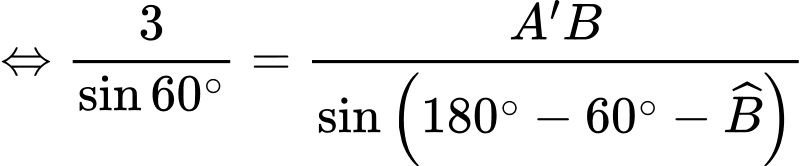
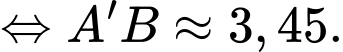
Ta có: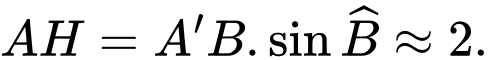
Vậy khoảng cách giữa hai đường thẳng và
và 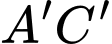 là
là 

Kẻ
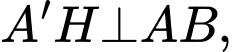 khi đó:
khi đó: 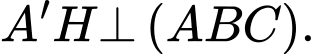
Ta có:
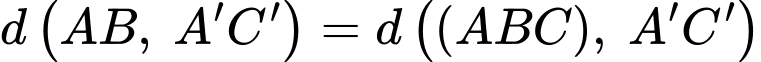
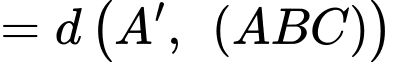
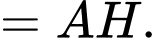
Xét tam giác
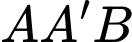 ta có
ta có 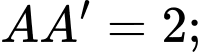
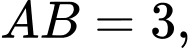
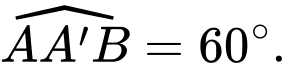
Áp dụng định lý sin, ta có:
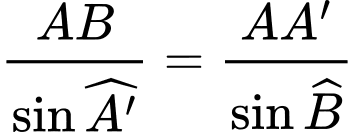
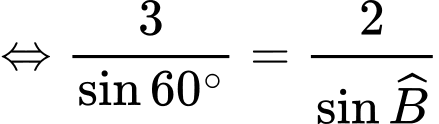
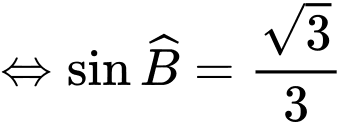
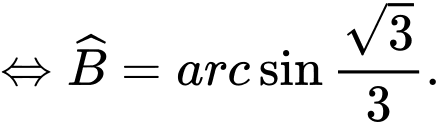
Áp dụng định lý sin, ta có:
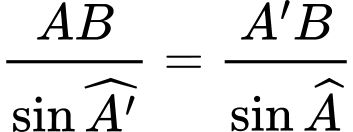
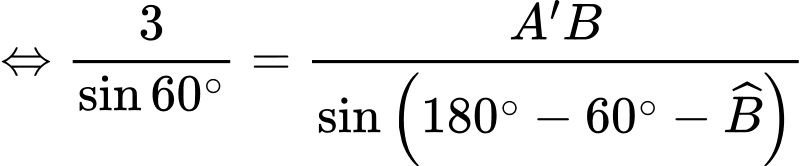
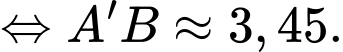
Ta có:
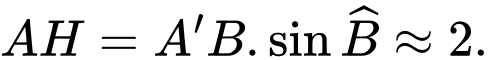
Vậy khoảng cách giữa hai đường thẳng
 và
và 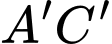 là
là 
Câu 18 [693648]: Nhân dịp khai trương, cửa hàng có một chương trình tri ân dành cho 50 người đầu tiên đứng xếp hàng (theo thứ tự từ 1 đến 50). Chủ cửa hàng sẽ tặng cho người cuối cùng một món quà đặc biệt với thể thức cuộc chơi như sau. Chủ cửa hàng nói “ Các khách hàng số lẻ sẽ bị loại”. Các khách hàng còn lại sẽ sắp xếp lại (theo thứ tự từ 1 đến hết), cuộc chơi sẽ dừng khi tìm được người cuối cùng. Vậy người may mắn nhận được quà thì ban đầu họ đứng số mấy?
Điền đáp án: 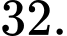
Ban đầu có 50 người, đánh số từ 1 đến 50.
Đầu tiên, những người có vị trí là số lẻ sẽ bị loại bỏ.
Những người còn lại có số thứ tự: 2, 4, 6, 8, ..., 50 (tức là còn lại 25 người).
Tiếp tục loại bỏ những người có vị trí là các số lẻ trong nhóm còn lại:
Những người còn lại có số thứ tự: 4, 8, 12, ..., 48 (tức là còn lại 12 người).
Tiếp tục loại bỏ những người có vị trí là các số lẻ trong nhóm còn lại:
Những người còn lại có số thứ tự: 8, 16, 24, 32, 40, 48 (tức là còn lại 6 người).
Tiếp tục loại bỏ những người có vị trí là các số lẻ trong nhóm còn lại:
Những người còn lại có số thứ tự: 16, 32, 48 (còn lại 3 người).
Tiếp tục loại bỏ những người có vị trí là các số lẻ trong nhóm còn lại:
Những người còn lại có số thứ tự: 32 (chỉ còn lại 1 người).
Vậy người may mắn nhận được quà ban đầu đứng vị trí số 32.
Ban đầu có 50 người, đánh số từ 1 đến 50.
Đầu tiên, những người có vị trí là số lẻ sẽ bị loại bỏ.
Những người còn lại có số thứ tự: 2, 4, 6, 8, ..., 50 (tức là còn lại 25 người).
Tiếp tục loại bỏ những người có vị trí là các số lẻ trong nhóm còn lại:
Những người còn lại có số thứ tự: 4, 8, 12, ..., 48 (tức là còn lại 12 người).
Tiếp tục loại bỏ những người có vị trí là các số lẻ trong nhóm còn lại:
Những người còn lại có số thứ tự: 8, 16, 24, 32, 40, 48 (tức là còn lại 6 người).
Tiếp tục loại bỏ những người có vị trí là các số lẻ trong nhóm còn lại:
Những người còn lại có số thứ tự: 16, 32, 48 (còn lại 3 người).
Tiếp tục loại bỏ những người có vị trí là các số lẻ trong nhóm còn lại:
Những người còn lại có số thứ tự: 32 (chỉ còn lại 1 người).
Vậy người may mắn nhận được quà ban đầu đứng vị trí số 32.
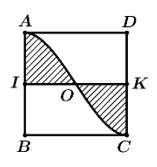
Câu 19 [693649]: Cho hình vuông 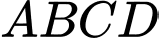 tâm
tâm  có cạnh bằng
có cạnh bằng 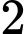 dm. Gọi
dm. Gọi 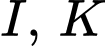 lần lượt là trung điểm cạnh
lần lượt là trung điểm cạnh 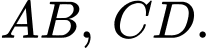 Đồ thị
Đồ thị  của hàm số bậc ba nhận
của hàm số bậc ba nhận  làm tâm đối xứng và
làm tâm đối xứng và 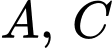 là hai điểm cực trị tạo với các đoạn thẳng
là hai điểm cực trị tạo với các đoạn thẳng 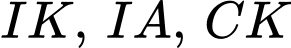 một miền phẳng
một miền phẳng  (phần gạch chéo trong hình bên). Một chiếc đồng hồ cát có dạng một khối tròn xoay được tạo thành khi quay
(phần gạch chéo trong hình bên). Một chiếc đồng hồ cát có dạng một khối tròn xoay được tạo thành khi quay  quanh trục
quanh trục 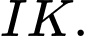 Thể tích của chiếc đồng hồ đó bằng bao nhiêu
Thể tích của chiếc đồng hồ đó bằng bao nhiêu  ? (làm tròn kết quả đến hàng phần trăm).
? (làm tròn kết quả đến hàng phần trăm).
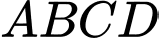 tâm
tâm  có cạnh bằng
có cạnh bằng 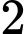 dm. Gọi
dm. Gọi 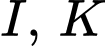 lần lượt là trung điểm cạnh
lần lượt là trung điểm cạnh 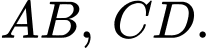 Đồ thị
Đồ thị  của hàm số bậc ba nhận
của hàm số bậc ba nhận  làm tâm đối xứng và
làm tâm đối xứng và 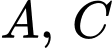 là hai điểm cực trị tạo với các đoạn thẳng
là hai điểm cực trị tạo với các đoạn thẳng 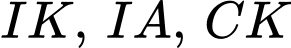 một miền phẳng
một miền phẳng  (phần gạch chéo trong hình bên). Một chiếc đồng hồ cát có dạng một khối tròn xoay được tạo thành khi quay
(phần gạch chéo trong hình bên). Một chiếc đồng hồ cát có dạng một khối tròn xoay được tạo thành khi quay  quanh trục
quanh trục 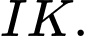 Thể tích của chiếc đồng hồ đó bằng bao nhiêu
Thể tích của chiếc đồng hồ đó bằng bao nhiêu  ? (làm tròn kết quả đến hàng phần trăm).
? (làm tròn kết quả đến hàng phần trăm).
Điền đáp án: 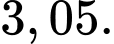
Gọi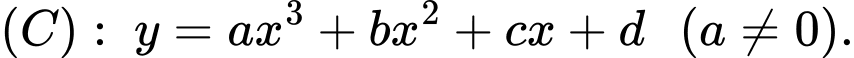
Đồ thị có
có 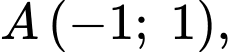
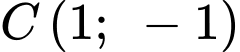 là hai điểm cực trị nên
là hai điểm cực trị nên 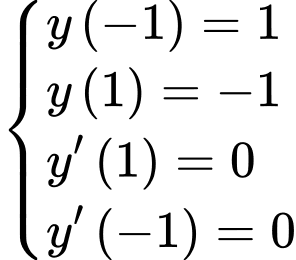
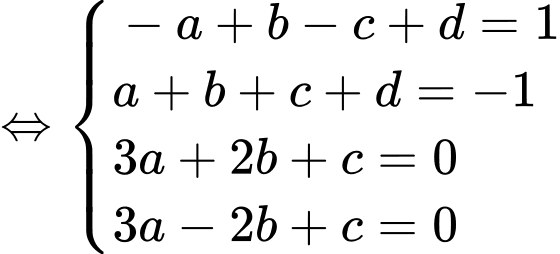
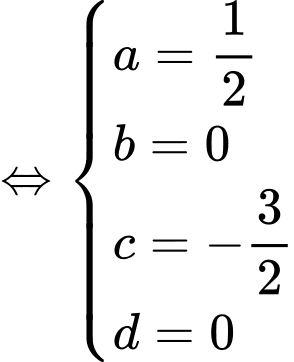
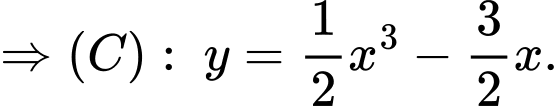
Thể tích của chiếc đồng hồ đó bằng
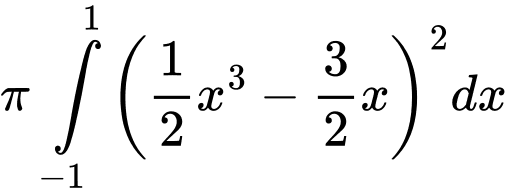
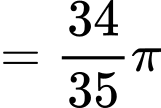
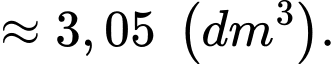
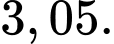
Gọi
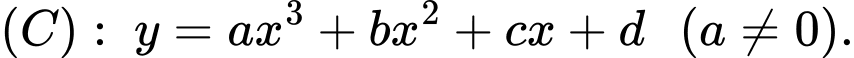
Đồ thị
 có
có 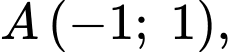
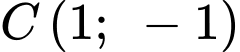 là hai điểm cực trị nên
là hai điểm cực trị nên 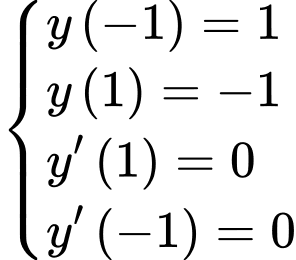
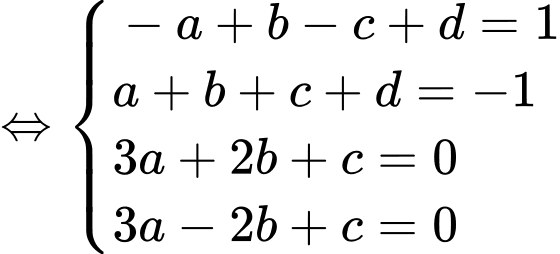
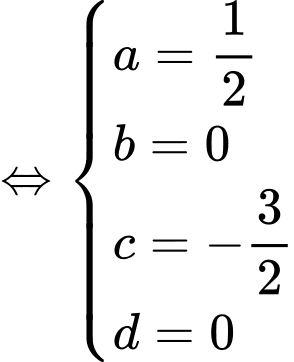
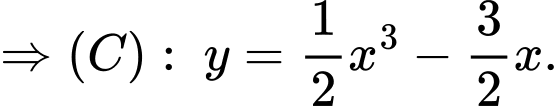
Thể tích của chiếc đồng hồ đó bằng
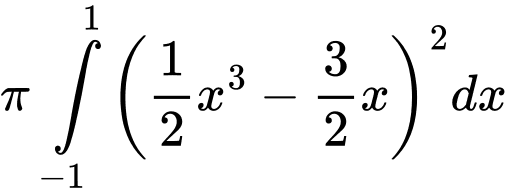
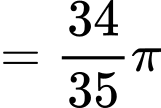
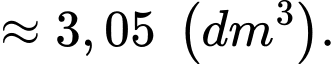
Câu 20 [693650]: Email rác hay spam email là những email hàng loạt được gửi đi mà không có sự đồng ý của người nhận, dẫn đến những trải nghiệm không tốt cho người dùng. Nội dung của spam email thường chứa các thông tin lừa đảo, quảng bá hoặc rao bán các sản phẩm, dịch vụ có vấn đề. Người ta đã sử dụng một thuật toán để phân loại thư rác, biết rằng thuật toán này có thể phân loại đến 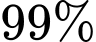 thư rác và tỉ lệ sai sót khi phân loại thư bình thường thành thư rác là
thư rác và tỉ lệ sai sót khi phân loại thư bình thường thành thư rác là 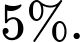 Thống kê cho thấy rằng, bình quân cứ 1000 thư được phân loại đúng thì có 410 thư rác. Tỉ lệ thư điện tử (email) gửi đến một địa chỉ là thư rác là bao nhiêu %. Kết quả làm tròn đến hàng đơn vị.
Thống kê cho thấy rằng, bình quân cứ 1000 thư được phân loại đúng thì có 410 thư rác. Tỉ lệ thư điện tử (email) gửi đến một địa chỉ là thư rác là bao nhiêu %. Kết quả làm tròn đến hàng đơn vị.
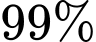 thư rác và tỉ lệ sai sót khi phân loại thư bình thường thành thư rác là
thư rác và tỉ lệ sai sót khi phân loại thư bình thường thành thư rác là 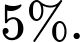 Thống kê cho thấy rằng, bình quân cứ 1000 thư được phân loại đúng thì có 410 thư rác. Tỉ lệ thư điện tử (email) gửi đến một địa chỉ là thư rác là bao nhiêu %. Kết quả làm tròn đến hàng đơn vị.
Thống kê cho thấy rằng, bình quân cứ 1000 thư được phân loại đúng thì có 410 thư rác. Tỉ lệ thư điện tử (email) gửi đến một địa chỉ là thư rác là bao nhiêu %. Kết quả làm tròn đến hàng đơn vị.
Điền đáp án: 40.
Gọi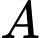 là biến cố “Thư điện tử là thư bình thường”
là biến cố “Thư điện tử là thư bình thường”
 là biến cố “Thư điện tử là thư rác”.
là biến cố “Thư điện tử là thư rác”.
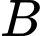 là biến cố “Thư đã được phân loại đúng”
là biến cố “Thư đã được phân loại đúng”
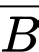 là biến cố “Thư bị phân loại sai”.
là biến cố “Thư bị phân loại sai”.
Từ giả thiết, ta có

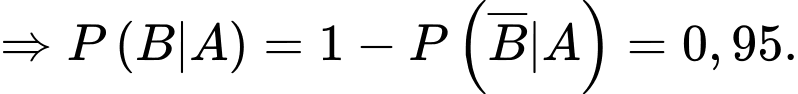
Giả sử
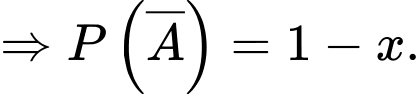
Từ đó, ta có sơ đồ cây như sau:
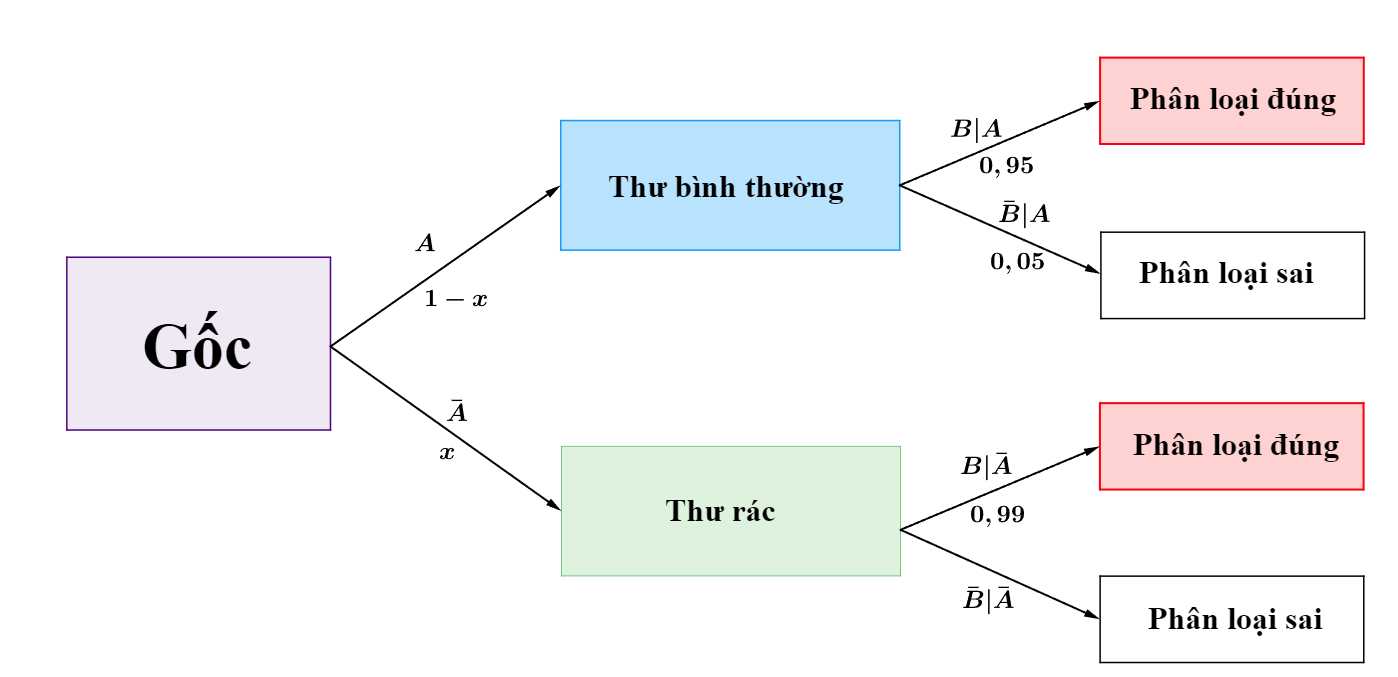
Áp dụng công thức xác suất toàn phần, ta có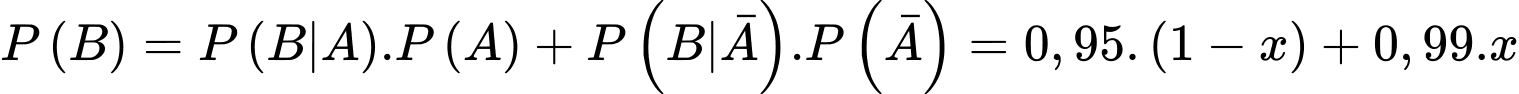
Vì bình quân cứ 1000 thư được phân loại đúng thì có 410 thư rác nên ta có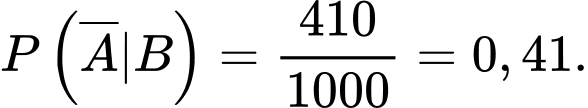
Áp dụng định lý Bayes, ta có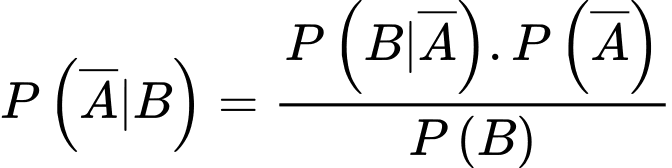
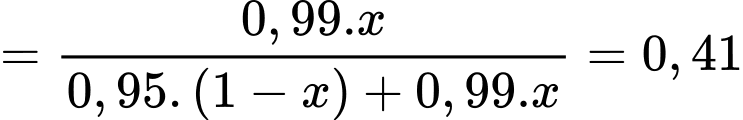
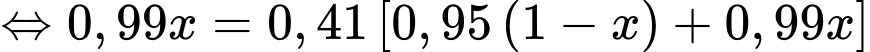
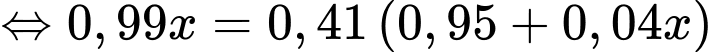
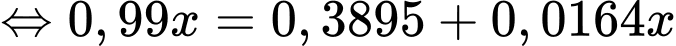
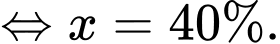
Vậy tỷ lệ thư rác là 40%.
Gọi
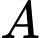 là biến cố “Thư điện tử là thư bình thường”
là biến cố “Thư điện tử là thư bình thường”
 là biến cố “Thư điện tử là thư rác”.
là biến cố “Thư điện tử là thư rác”.
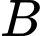 là biến cố “Thư đã được phân loại đúng”
là biến cố “Thư đã được phân loại đúng”
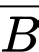 là biến cố “Thư bị phân loại sai”.
là biến cố “Thư bị phân loại sai”.
Từ giả thiết, ta có


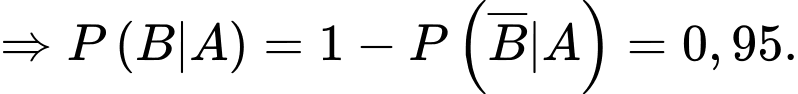
Giả sử

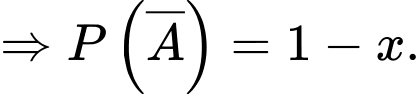
Từ đó, ta có sơ đồ cây như sau:

Áp dụng công thức xác suất toàn phần, ta có
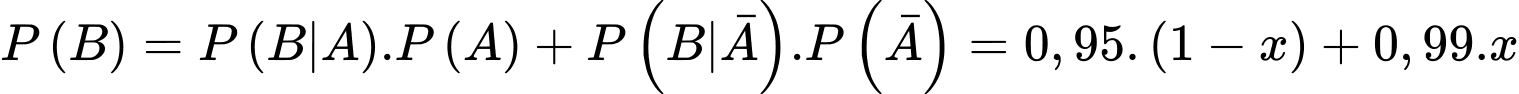
Vì bình quân cứ 1000 thư được phân loại đúng thì có 410 thư rác nên ta có
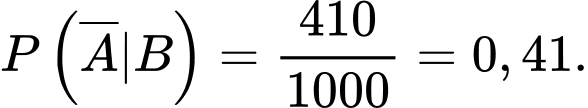
Áp dụng định lý Bayes, ta có
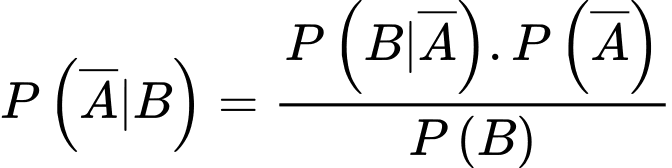
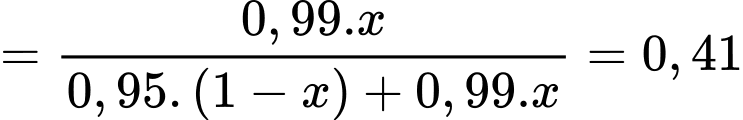
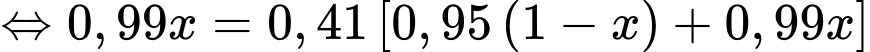
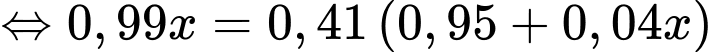
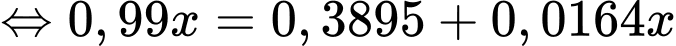
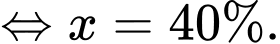
Vậy tỷ lệ thư rác là 40%.
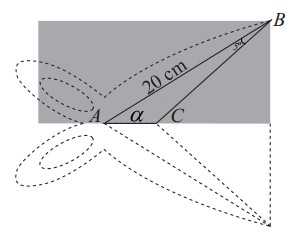
Câu 21 [696437]: Hai lưỡi của một chiếc kéo được gắn vào điểm 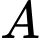 như trong hình 6.2.9. Gọi
như trong hình 6.2.9. Gọi 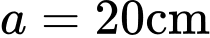 là khoảng cách từ
là khoảng cách từ 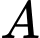 đến đầu lưỡi kéo (điểm
đến đầu lưỡi kéo (điểm 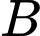 ). Gọi
). Gọi 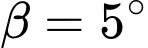 là góc ở đầu lưỡi kéo được tạo bởi đường thẳng
là góc ở đầu lưỡi kéo được tạo bởi đường thẳng  và cạnh dưới của lưỡi kéo (đường thẳng
và cạnh dưới của lưỡi kéo (đường thẳng 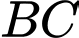 ) và gọi
) và gọi 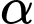 là góc giữa
là góc giữa  với phương ngang. Giả sử một mảnh giấy được cắt theo cách mà tâm của kéo tại
với phương ngang. Giả sử một mảnh giấy được cắt theo cách mà tâm của kéo tại 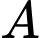 và giấy đều được cố định. Khi các lưỡi kéo đóng lại (tức là góc
và giấy đều được cố định. Khi các lưỡi kéo đóng lại (tức là góc  trong hình giảm), khoảng cách
trong hình giảm), khoảng cách 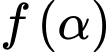 giữa
giữa 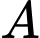 và
và  tăng lên khi cắt giấy . Giả sử
tăng lên khi cắt giấy . Giả sử 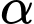 đang giảm với tốc độ không đổi là 50 độ/giây. Tại thời điểm
đang giảm với tốc độ không đổi là 50 độ/giây. Tại thời điểm 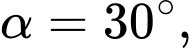 hãy tìm tốc độ (cm/s) mà giấy đang bị cắt (làm tròn đến hàng đơn vị). Biết rằng tốc độ mà giấy bị cắt bằng với tốc độ thay đổi của
hãy tìm tốc độ (cm/s) mà giấy đang bị cắt (làm tròn đến hàng đơn vị). Biết rằng tốc độ mà giấy bị cắt bằng với tốc độ thay đổi của 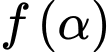 .
.
 như trong hình 6.2.9. Gọi
như trong hình 6.2.9. Gọi 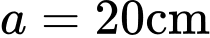 là khoảng cách từ
là khoảng cách từ 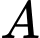 đến đầu lưỡi kéo (điểm
đến đầu lưỡi kéo (điểm 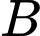 ). Gọi
). Gọi 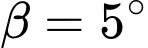 là góc ở đầu lưỡi kéo được tạo bởi đường thẳng
là góc ở đầu lưỡi kéo được tạo bởi đường thẳng  và cạnh dưới của lưỡi kéo (đường thẳng
và cạnh dưới của lưỡi kéo (đường thẳng 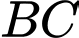 ) và gọi
) và gọi 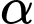 là góc giữa
là góc giữa  với phương ngang. Giả sử một mảnh giấy được cắt theo cách mà tâm của kéo tại
với phương ngang. Giả sử một mảnh giấy được cắt theo cách mà tâm của kéo tại 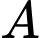 và giấy đều được cố định. Khi các lưỡi kéo đóng lại (tức là góc
và giấy đều được cố định. Khi các lưỡi kéo đóng lại (tức là góc  trong hình giảm), khoảng cách
trong hình giảm), khoảng cách 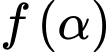 giữa
giữa 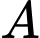 và
và  tăng lên khi cắt giấy . Giả sử
tăng lên khi cắt giấy . Giả sử 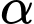 đang giảm với tốc độ không đổi là 50 độ/giây. Tại thời điểm
đang giảm với tốc độ không đổi là 50 độ/giây. Tại thời điểm 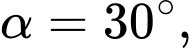 hãy tìm tốc độ (cm/s) mà giấy đang bị cắt (làm tròn đến hàng đơn vị). Biết rằng tốc độ mà giấy bị cắt bằng với tốc độ thay đổi của
hãy tìm tốc độ (cm/s) mà giấy đang bị cắt (làm tròn đến hàng đơn vị). Biết rằng tốc độ mà giấy bị cắt bằng với tốc độ thay đổi của 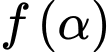 .
.
Điền đáp án: 
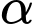 đang giảm với tốc độ không đổi là 50 độ/giây nên
đang giảm với tốc độ không đổi là 50 độ/giây nên 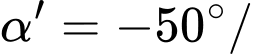 giây.
giây.
Tốc độ thay đổi của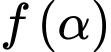 bằng
bằng 
Áp dụng định lý sin trong tam giác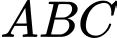 ta có:
ta có: 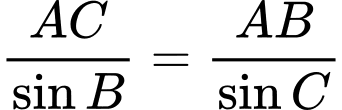 hay
hay 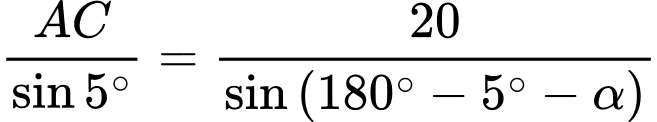
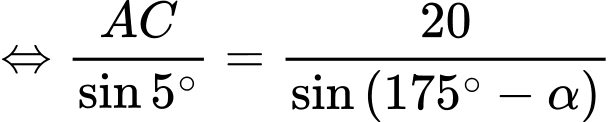
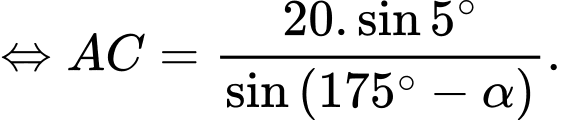
Do đó: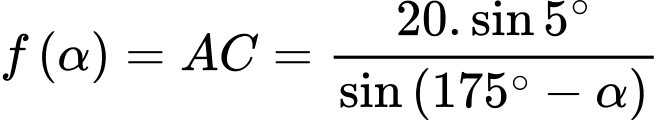
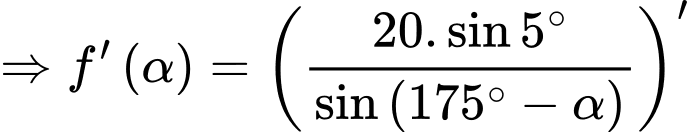
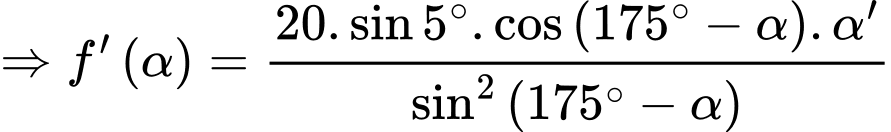
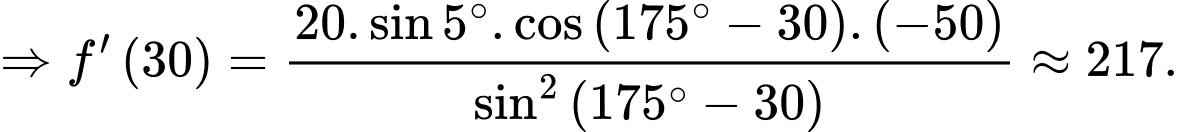
Tại thời điểm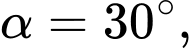 tốc độ mà giấy đang bị cắt bằng
tốc độ mà giấy đang bị cắt bằng 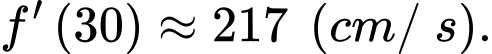

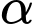 đang giảm với tốc độ không đổi là 50 độ/giây nên
đang giảm với tốc độ không đổi là 50 độ/giây nên 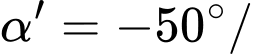 giây.
giây. Tốc độ thay đổi của
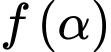 bằng
bằng 
Áp dụng định lý sin trong tam giác
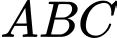 ta có:
ta có: 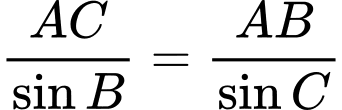 hay
hay 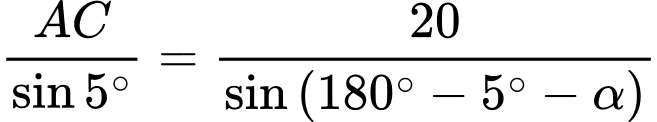
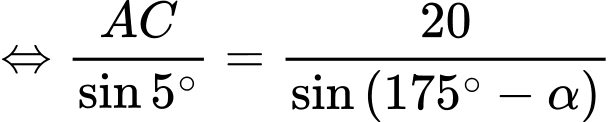
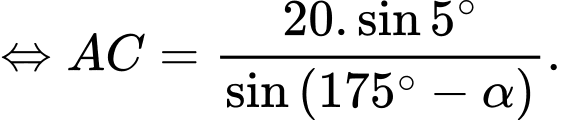
Do đó:
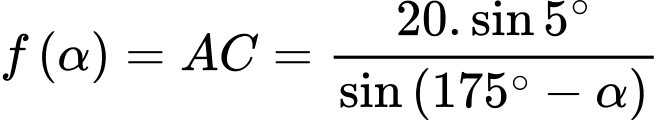
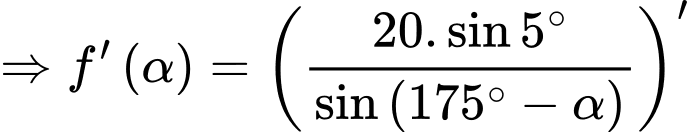
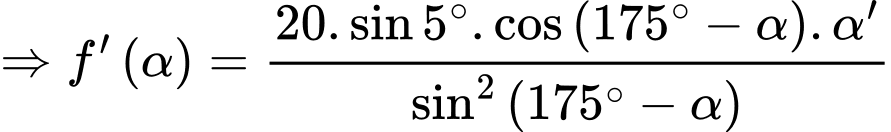
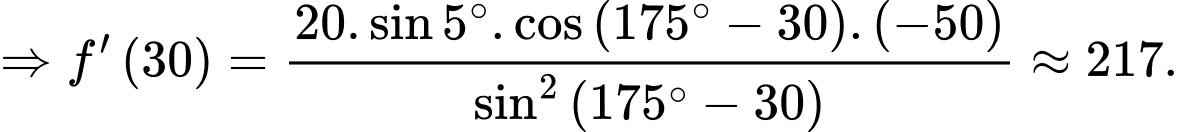
Tại thời điểm
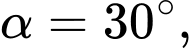 tốc độ mà giấy đang bị cắt bằng
tốc độ mà giấy đang bị cắt bằng 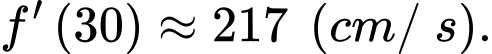
Câu 22 [693652]: Trong không gian với hệ tọa độ 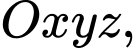 cho mặt cầu
cho mặt cầu 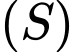 nhận mặt phẳng
nhận mặt phẳng 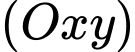 và mặt phẳng
và mặt phẳng 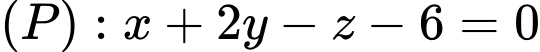 là các mặt phẳng đối xứng. Biết khoảng cách từ gốc tọa độ
là các mặt phẳng đối xứng. Biết khoảng cách từ gốc tọa độ  đến một điểm
đến một điểm 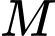 trên mặt cầu
trên mặt cầu 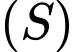 có giá trị lớn nhất và nhỏ nhất lần lượt là
có giá trị lớn nhất và nhỏ nhất lần lượt là  và
và 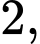 điểm
điểm  nằm ngoài khối cầu
nằm ngoài khối cầu 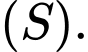 Biết tung độ tâm mặt cầu
Biết tung độ tâm mặt cầu 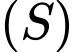 có giá trị dương, vậy tung độ tâm mặt cầu bằng bao nhiêu? (làm tròn đến hàng phần chục).
có giá trị dương, vậy tung độ tâm mặt cầu bằng bao nhiêu? (làm tròn đến hàng phần chục).
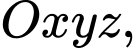 cho mặt cầu
cho mặt cầu 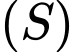 nhận mặt phẳng
nhận mặt phẳng 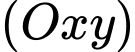 và mặt phẳng
và mặt phẳng 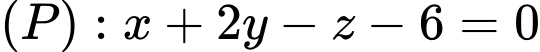 là các mặt phẳng đối xứng. Biết khoảng cách từ gốc tọa độ
là các mặt phẳng đối xứng. Biết khoảng cách từ gốc tọa độ  đến một điểm
đến một điểm 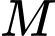 trên mặt cầu
trên mặt cầu 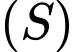 có giá trị lớn nhất và nhỏ nhất lần lượt là
có giá trị lớn nhất và nhỏ nhất lần lượt là  và
và 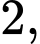 điểm
điểm  nằm ngoài khối cầu
nằm ngoài khối cầu 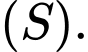 Biết tung độ tâm mặt cầu
Biết tung độ tâm mặt cầu 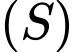 có giá trị dương, vậy tung độ tâm mặt cầu bằng bao nhiêu? (làm tròn đến hàng phần chục).
có giá trị dương, vậy tung độ tâm mặt cầu bằng bao nhiêu? (làm tròn đến hàng phần chục).
Điền đáp án: 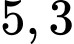 .
.
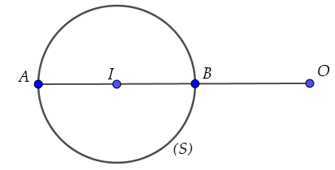
• Ta có: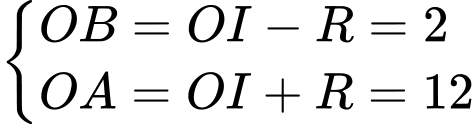
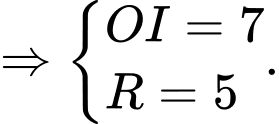
• Một mặt phẳng bất kỳ là mặt phẳng đối xứng của mặt cầu thì nó phải chứa tâm của mặt cầu.
bất kỳ là mặt phẳng đối xứng của mặt cầu thì nó phải chứa tâm của mặt cầu.
Suy ra tâm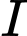 của mặt cầu phải cùng thuộc
của mặt cầu phải cùng thuộc 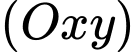 và
và 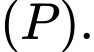
• Gọi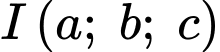
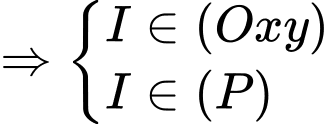
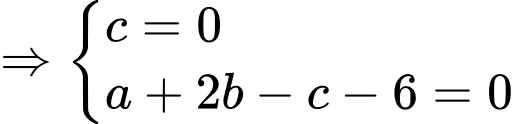
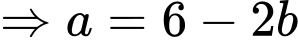
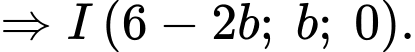
Ta có: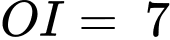
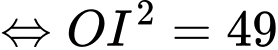
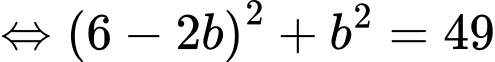

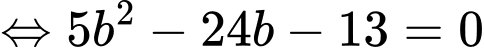
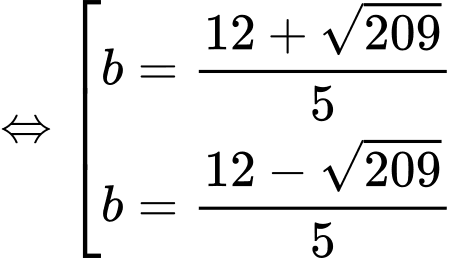
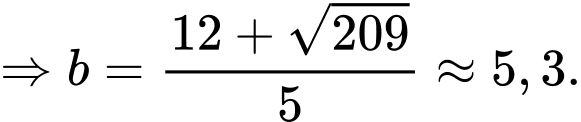
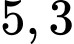 .
. 
• Ta có:
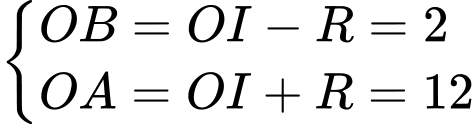
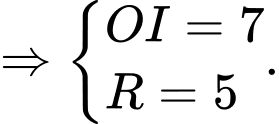
• Một mặt phẳng
 bất kỳ là mặt phẳng đối xứng của mặt cầu thì nó phải chứa tâm của mặt cầu.
bất kỳ là mặt phẳng đối xứng của mặt cầu thì nó phải chứa tâm của mặt cầu.Suy ra tâm
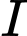 của mặt cầu phải cùng thuộc
của mặt cầu phải cùng thuộc 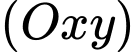 và
và 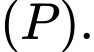
• Gọi
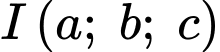
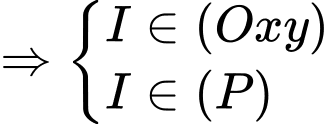
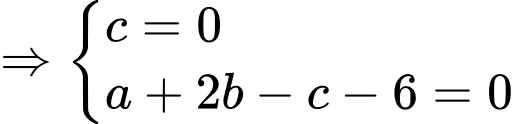
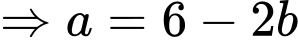
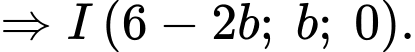
Ta có: