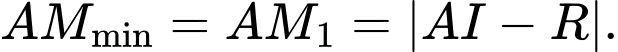PHẦN I. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Câu 1 [518263]: Cho cấp số nhân 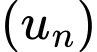 với
với 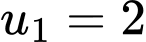 và
và 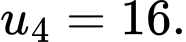 Công bội của cấp số nhân đã cho bằng
Công bội của cấp số nhân đã cho bằng
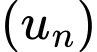 với
với 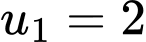 và
và 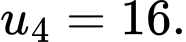 Công bội của cấp số nhân đã cho bằng
Công bội của cấp số nhân đã cho bằng A, 
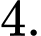
B, 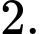
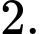
C, 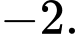
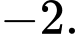
D, 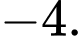
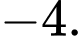
Chọn đáp án B
Ta có: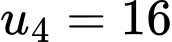
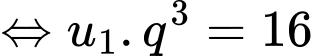
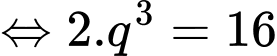
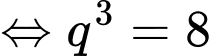
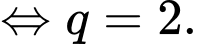
Vậy công bội của cấp số nhân đã cho bằng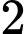 Đáp án: B
Đáp án: B
Ta có:
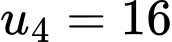
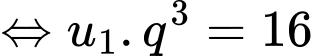
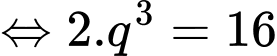
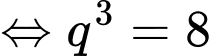
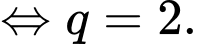
Vậy công bội của cấp số nhân đã cho bằng
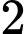 Đáp án: B
Đáp án: B
Câu 2 [315753]: Cho khối lăng trụ đứng có cạnh bên bằng 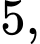 đáy là hình vuông có cạnh bằng
đáy là hình vuông có cạnh bằng 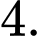 Hỏi thể tích khối lăng trụ bằng bao nhiêu?
Hỏi thể tích khối lăng trụ bằng bao nhiêu?
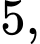 đáy là hình vuông có cạnh bằng
đáy là hình vuông có cạnh bằng 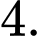 Hỏi thể tích khối lăng trụ bằng bao nhiêu?
Hỏi thể tích khối lăng trụ bằng bao nhiêu? A, 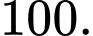
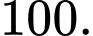
B, 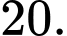
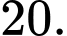
C, 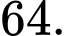
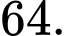
D, 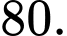
Chọn đáp án D.
Diện tích đáy là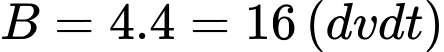
Thể tích khối lăng trụ đó là: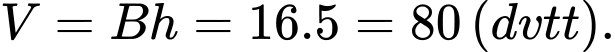 Đáp án: D
Đáp án: D
Diện tích đáy là
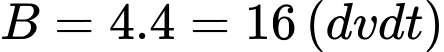
Thể tích khối lăng trụ đó là:
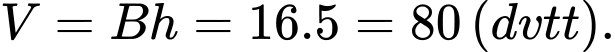 Đáp án: D
Đáp án: D Sử dụng thông tin dưới đây để trả lời câu 3 và câu 4
Cho hàm số đa thức bậc ba y=f(x) có bảng biến thiên như hình vẽ dưới đây:
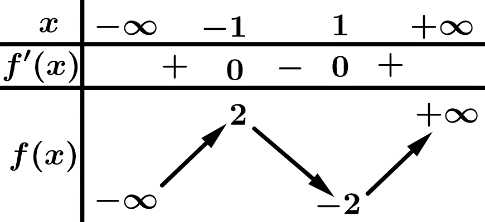

Câu 3 [697134]: Giá trị cực đại của hàm số 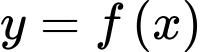 bằng
bằng
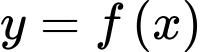 bằng
bằng A, 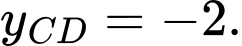
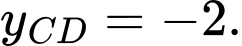
B, 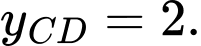
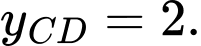
C, 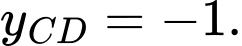
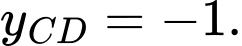
D, 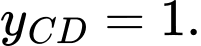
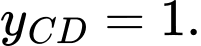
Chọn đáp án B. Đáp án: B
Câu 4 [697135]: Hàm số nào dưới đây có bảng biến thiên như hình vẽ trên?
A, 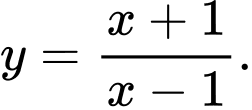
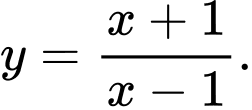
B, 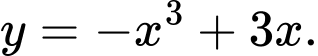
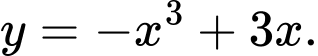
C, 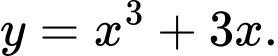
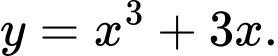
D, 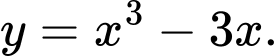
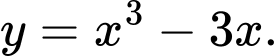
Chọn đáp án D. Đáp án: D
Câu 5 [693305]: Tập nghiệm của bất phương trình 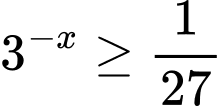 là
là
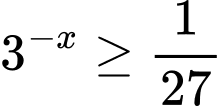 là
là A, 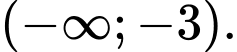
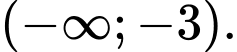
B, 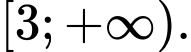
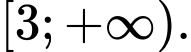
C, 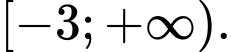
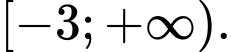
D, 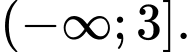
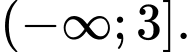
Chọn đáp án D.
Ta có: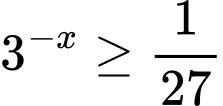
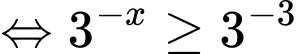
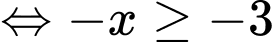
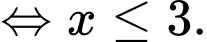 Đáp án: D
Đáp án: D
Ta có:
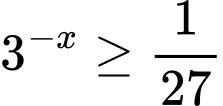
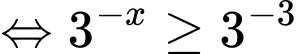
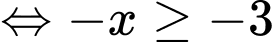
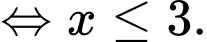 Đáp án: D
Đáp án: D
Câu 6 [312060]: Trong không gian 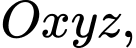 cho mặt cầu
cho mặt cầu 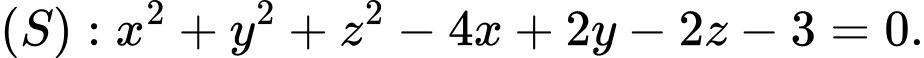 Tìm tọa độ tâm
Tìm tọa độ tâm 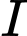 và bán kính
và bán kính 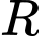 của
của 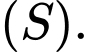
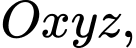 cho mặt cầu
cho mặt cầu 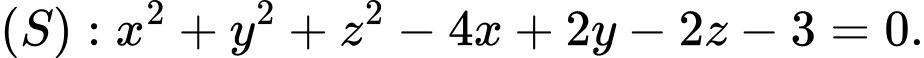 Tìm tọa độ tâm
Tìm tọa độ tâm 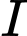 và bán kính
và bán kính 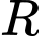 của
của 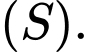
A,  và
và 
 và
và 
B, 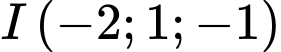 và
và 
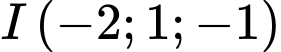 và
và 
C,  và
và 
 và
và 
D, 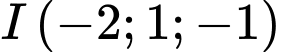 và
và 
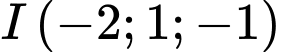 và
và 
Chọn đáp án A.
Cách 1: Một phương trình có dạng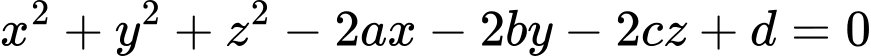 là một phương trình mặt cầu khi và chỉ khi
là một phương trình mặt cầu khi và chỉ khi 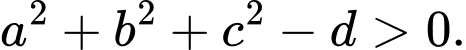 Khi đó, mặt cầu có tâm
Khi đó, mặt cầu có tâm 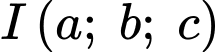 và bán kính
và bán kính 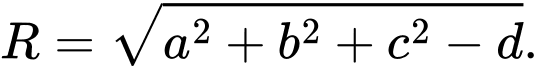
Ta phân tích phương trình đã cho như sau: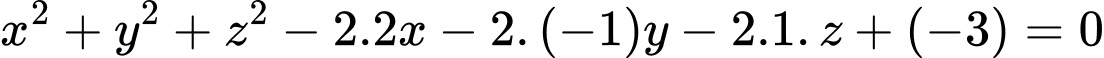
Từ đó, ta suy ra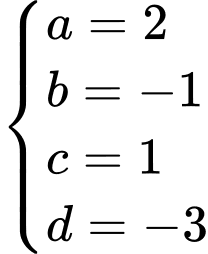
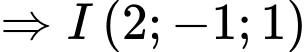 và bán kính theo công thức là
và bán kính theo công thức là 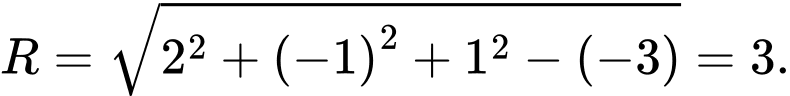
Vậy mặt cầu có tâm
có tâm  và bán kính
và bán kính 
Cách 2: Một phương trình mặt cầu có dạng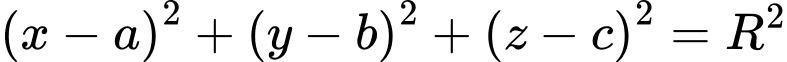 thì khi đó mặt cầu đó có tâm
thì khi đó mặt cầu đó có tâm 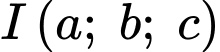 và bán kính là
và bán kính là 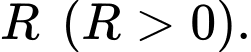
Ta sẽ biến đổi phương trình đã cho về dạng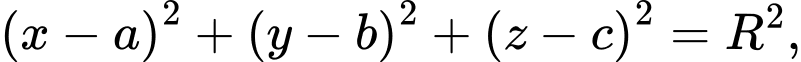 ta được
ta được 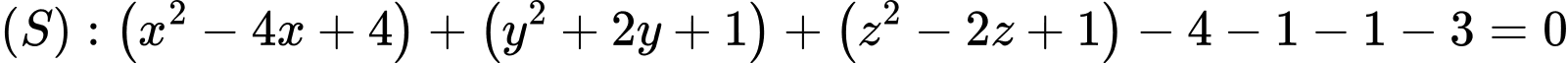
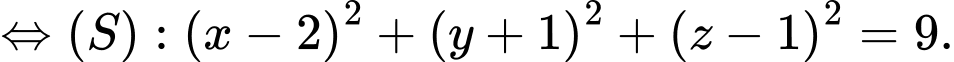
Vậy mặt cầu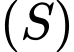 có tâm
có tâm  và bán kính
và bán kính 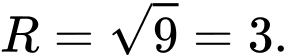 Đáp án: A
Đáp án: A
Cách 1: Một phương trình có dạng
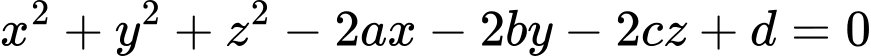 là một phương trình mặt cầu khi và chỉ khi
là một phương trình mặt cầu khi và chỉ khi 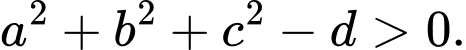 Khi đó, mặt cầu có tâm
Khi đó, mặt cầu có tâm 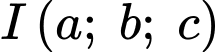 và bán kính
và bán kính 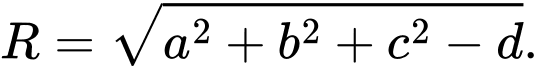
Ta phân tích phương trình đã cho như sau:
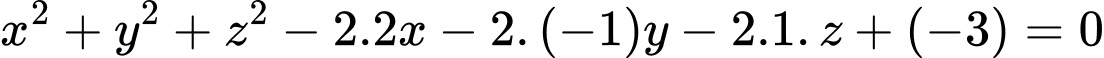
Từ đó, ta suy ra
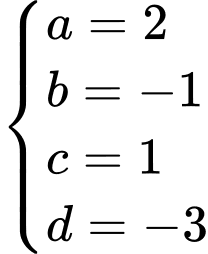
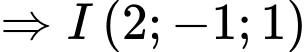 và bán kính theo công thức là
và bán kính theo công thức là 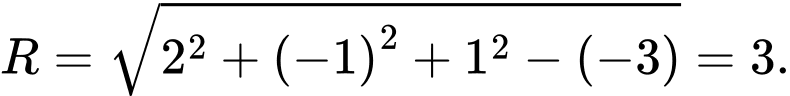
Vậy mặt cầu
 có tâm
có tâm  và bán kính
và bán kính 
Cách 2: Một phương trình mặt cầu có dạng
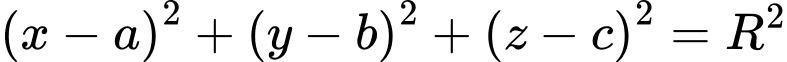 thì khi đó mặt cầu đó có tâm
thì khi đó mặt cầu đó có tâm 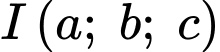 và bán kính là
và bán kính là 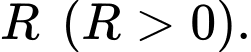
Ta sẽ biến đổi phương trình đã cho về dạng
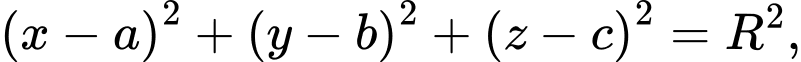 ta được
ta được 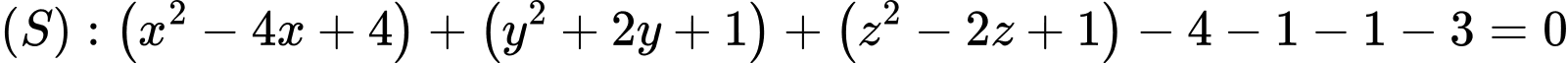
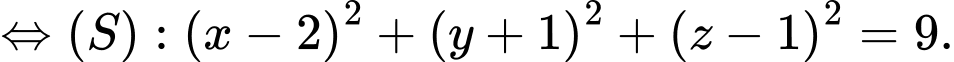
Vậy mặt cầu
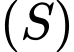 có tâm
có tâm  và bán kính
và bán kính 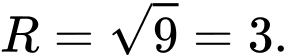 Đáp án: A
Đáp án: A
Câu 7 [520563]: Mệnh đề nào sai trong các mệnh đề sau?
A, 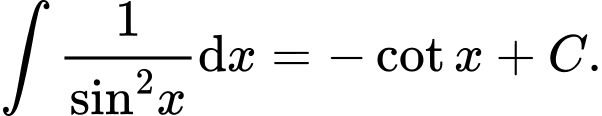
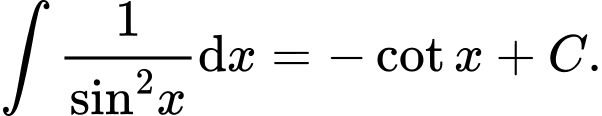
B, 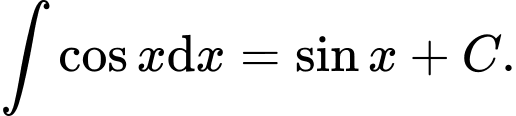
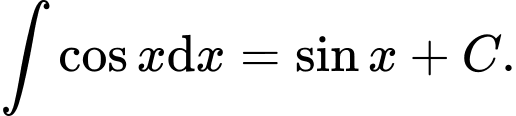
C, 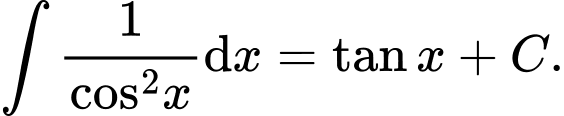
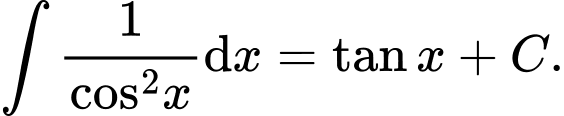
D, 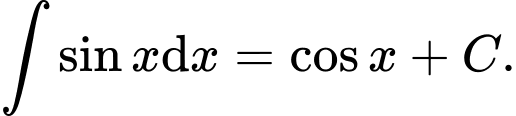
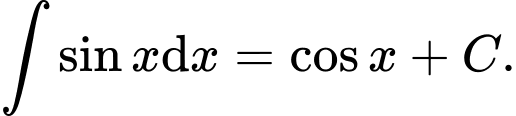
Chọn đáp án D
Ta có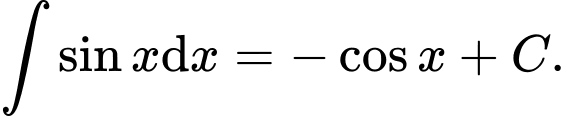 Đáp án: D
Đáp án: D
Ta có
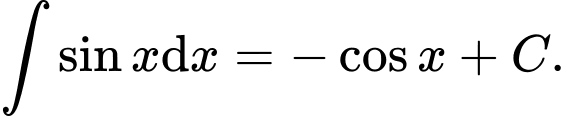 Đáp án: D
Đáp án: D
Câu 8 [513193]: Với 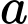 là số thực dương tùy ý,
là số thực dương tùy ý, 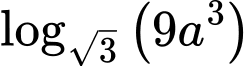 bằng
bằng
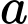 là số thực dương tùy ý,
là số thực dương tùy ý, 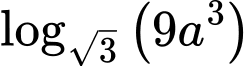 bằng
bằng A, 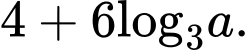
B, 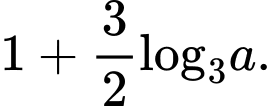
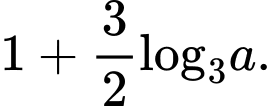
C, 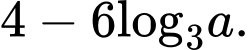
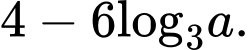
D, 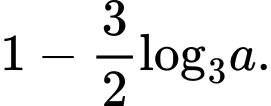
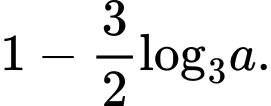
Chọn đáp án A.
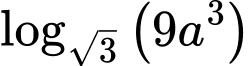
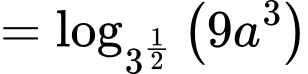
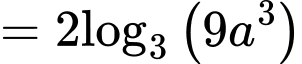
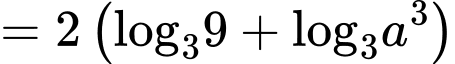
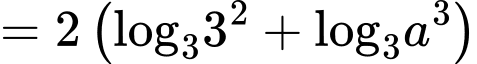
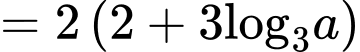
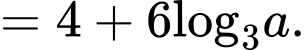 Đáp án: A
Đáp án: A
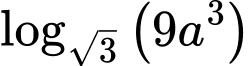
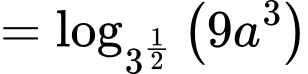
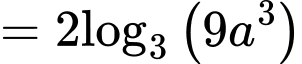
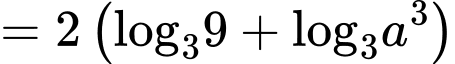
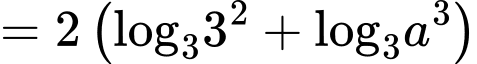
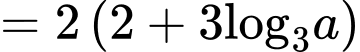
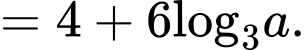 Đáp án: A
Đáp án: A
Câu 9 [976993]: Cho hình chóp  có đáy là hình bình hành (hình vẽ minh hoạ). Hãy chọn khẳng định đúng.
có đáy là hình bình hành (hình vẽ minh hoạ). Hãy chọn khẳng định đúng.
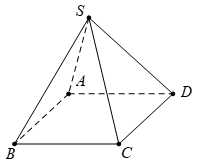
 có đáy là hình bình hành (hình vẽ minh hoạ). Hãy chọn khẳng định đúng.
có đáy là hình bình hành (hình vẽ minh hoạ). Hãy chọn khẳng định đúng.
A, 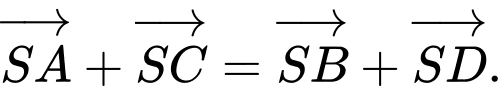
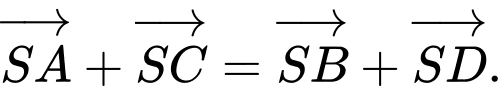
B, 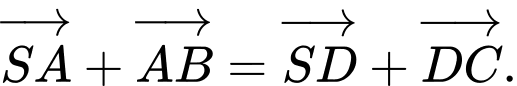
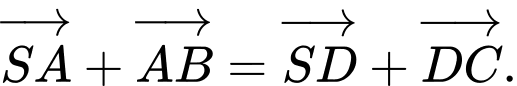
C, 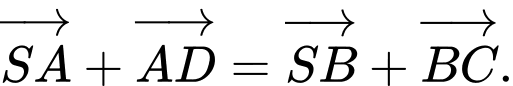
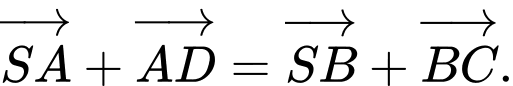
D, 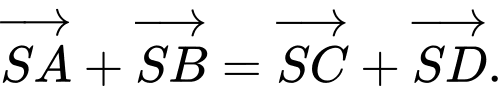
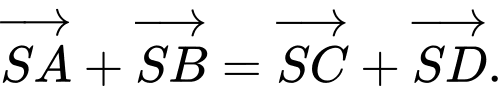
Chọn đáp án A.
A. Ta có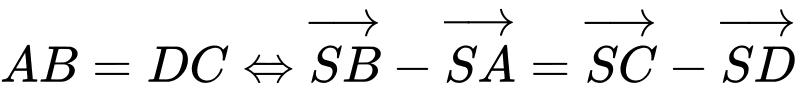
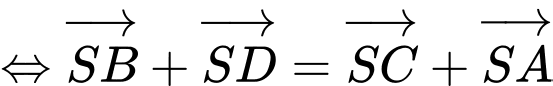
Suy ra A đúng.
B.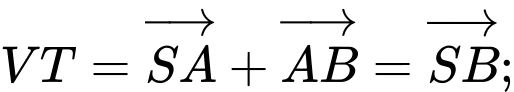
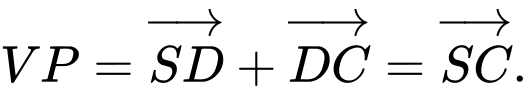
Mà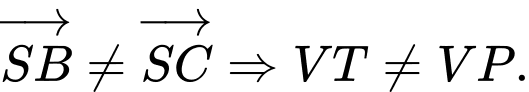
Suy ra B sai.
C.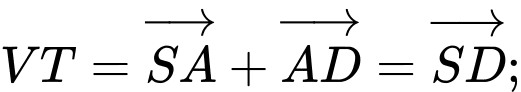
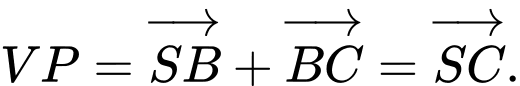
Mà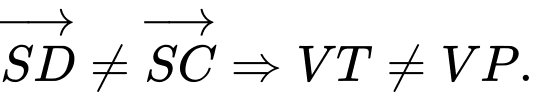
Suy ra C sai.
D.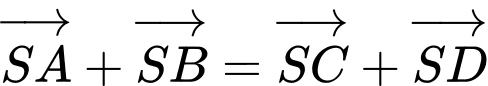
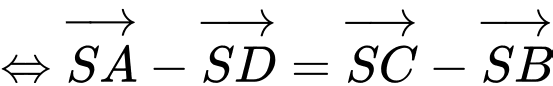
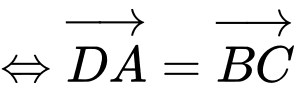 (điều này là sai) Vì
(điều này là sai) Vì 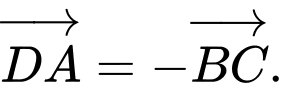
Suy ra D sai. Đáp án: A
A. Ta có
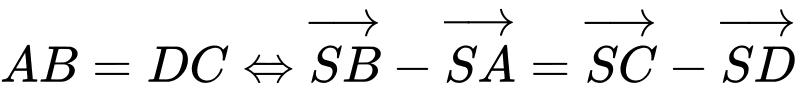
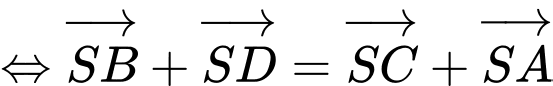
Suy ra A đúng.
B.
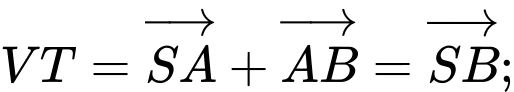
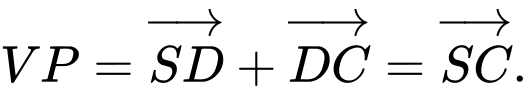
Mà
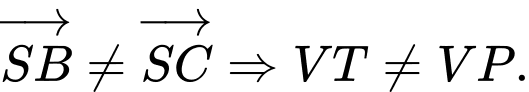
Suy ra B sai.
C.
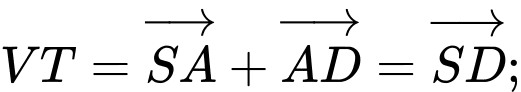
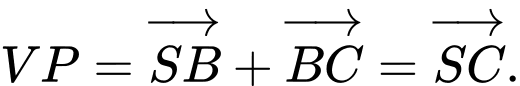
Mà
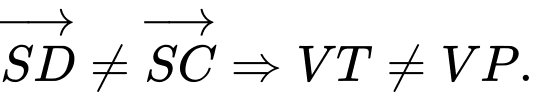
Suy ra C sai.
D.
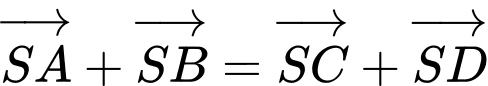
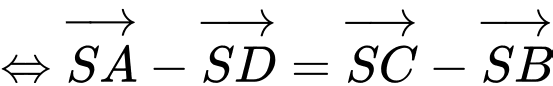
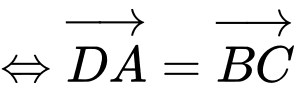 (điều này là sai) Vì
(điều này là sai) Vì 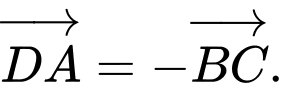
Suy ra D sai. Đáp án: A
Câu 10 [693306]: Hình thang cong 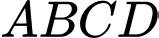 ở hình vẽ có diện tích bằng:
ở hình vẽ có diện tích bằng:
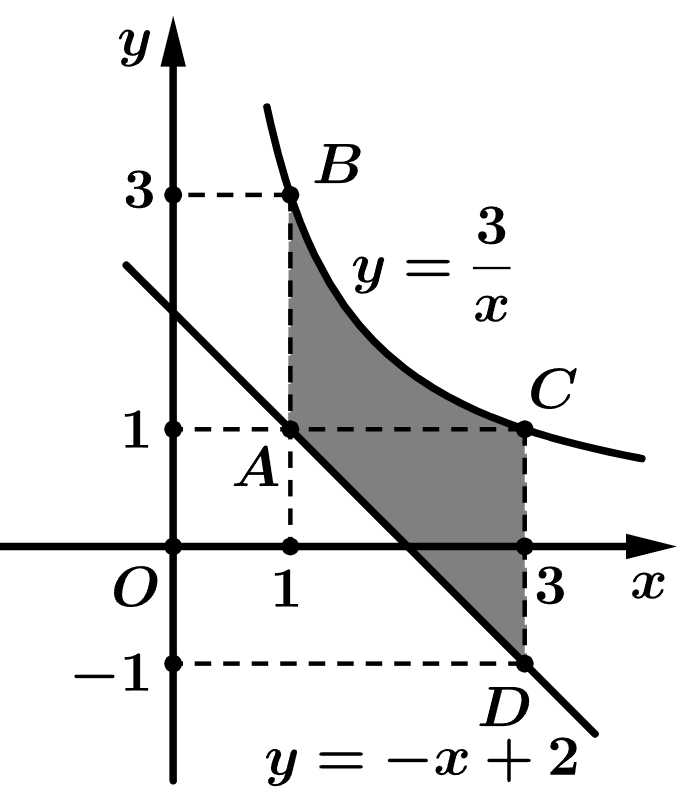
 ở hình vẽ có diện tích bằng:
ở hình vẽ có diện tích bằng:
A, 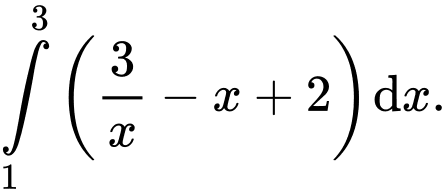
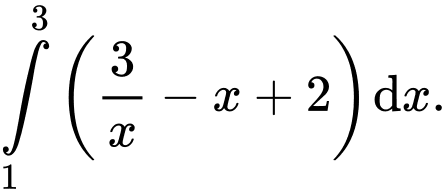
B, 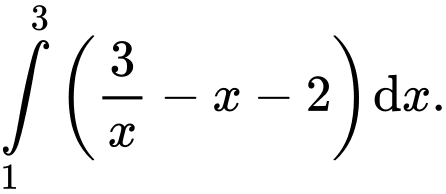
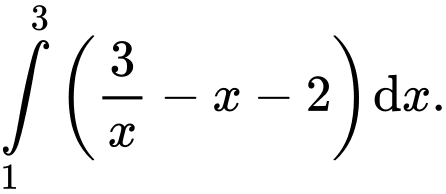
C, 

D, 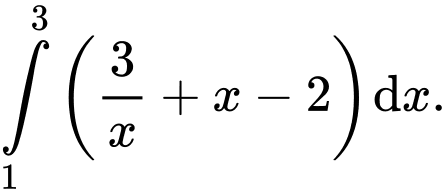
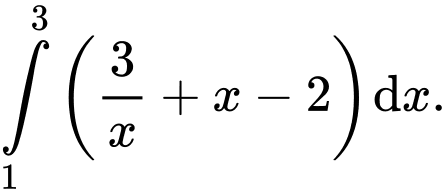
Chọn đáp án D.
Diện tích hình thang cong bằng:
bằng: 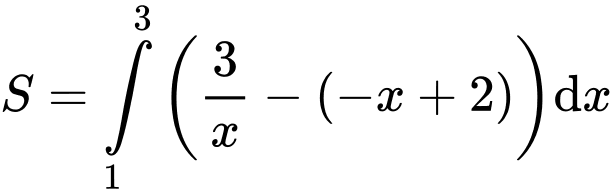
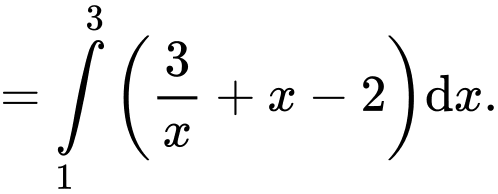 Đáp án: D
Đáp án: D
Diện tích hình thang cong
 bằng:
bằng: 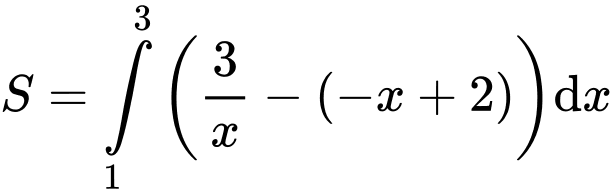
 Đáp án: D
Đáp án: D
Câu 11 [520577]: Trong không gian 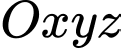 , cho mặt phẳng
, cho mặt phẳng 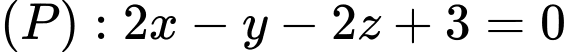 . Đường thẳng
. Đường thẳng  đi qua điểm
đi qua điểm 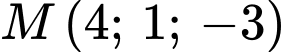 và vuông góc
và vuông góc 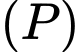 với có phương trình chính tắc là
với có phương trình chính tắc là
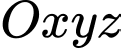 , cho mặt phẳng
, cho mặt phẳng 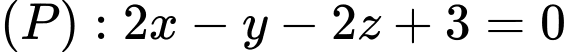 . Đường thẳng
. Đường thẳng  đi qua điểm
đi qua điểm 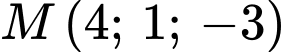 và vuông góc
và vuông góc 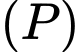 với có phương trình chính tắc là
với có phương trình chính tắc là A, 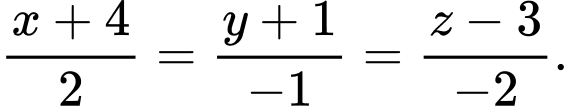
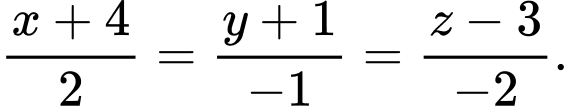
B, 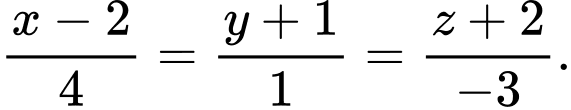
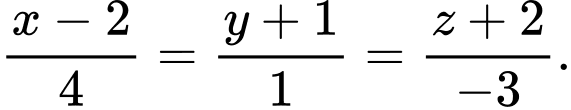
C, 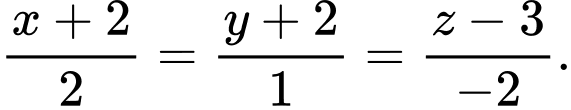
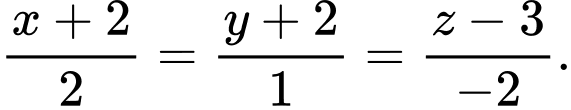
D, 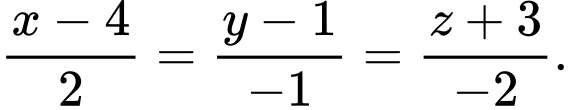
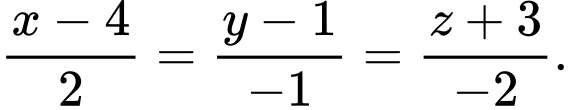
Chọn đáp án D
Ta có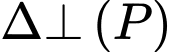
 VTCP
VTCP 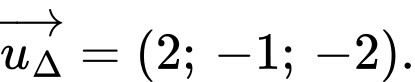
Khi đó đường thẳng đi qua điểm
đi qua điểm 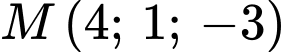 và vuông góc
và vuông góc  với có phương trình chính tắc là:
với có phương trình chính tắc là: 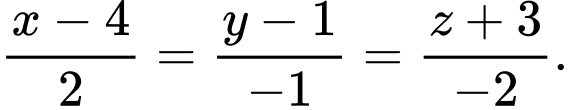 Đáp án: D
Đáp án: D
Ta có
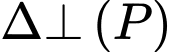
 VTCP
VTCP 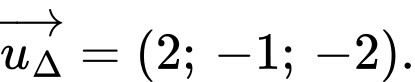
Khi đó đường thẳng
 đi qua điểm
đi qua điểm 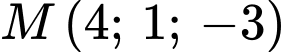 và vuông góc
và vuông góc 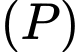 với có phương trình chính tắc là:
với có phương trình chính tắc là: 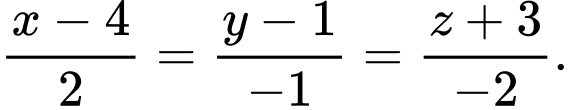 Đáp án: D
Đáp án: D
Câu 12 [693307]: Kết quả khảo sát năng suất (đơn vị tấn/ha) của một số thửa ruộng được minh họa ở biểu đồ sau:
Lập bảng tần số ghép nhóm ta tính được khoảng tứ phân vị của mẫu số liệu trên gần bằng giá trị nào dưới đây nhất.

Lập bảng tần số ghép nhóm ta tính được khoảng tứ phân vị của mẫu số liệu trên gần bằng giá trị nào dưới đây nhất.
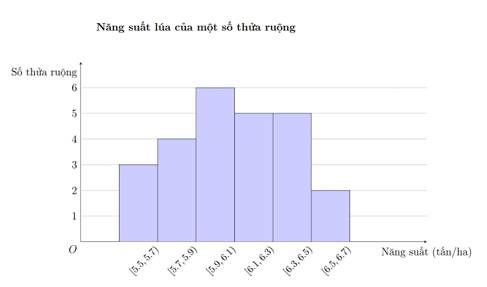
A, 
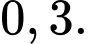
B, 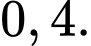
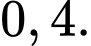
C, 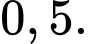
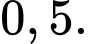
D, 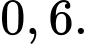
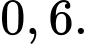
Chọn đáp án C.
+ Cỡ mẫu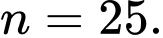
Gọi là mẫu số liệu gốc gồm năng suất của 25 thửa ruộng được sắp xếp theo thứ tự không giảm.
là mẫu số liệu gốc gồm năng suất của 25 thửa ruộng được sắp xếp theo thứ tự không giảm.
Ta có: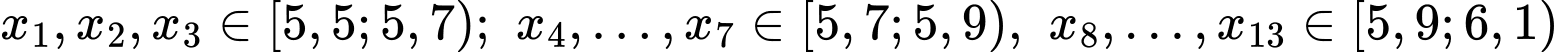 ;
; 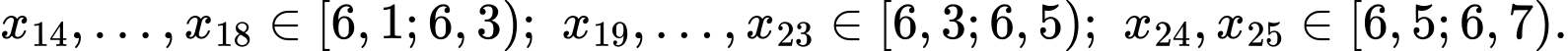
Tứ phân vị thứ nhất của mẫu số liệu gốc là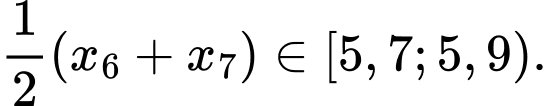 Do đó, tứ phân vị thứ nhất của mẫu số liệu ghép nhóm là:
Do đó, tứ phân vị thứ nhất của mẫu số liệu ghép nhóm là: 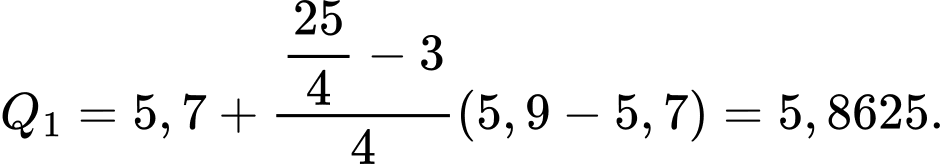
Tứ phân vị thứ ba của mẫu số liệu gốc là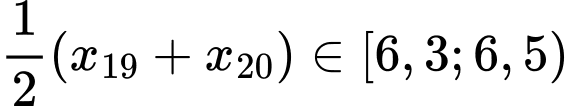 . Do đó, tứ phân vị thứ ba của mẫu số liệu ghép nhóm là:
. Do đó, tứ phân vị thứ ba của mẫu số liệu ghép nhóm là: 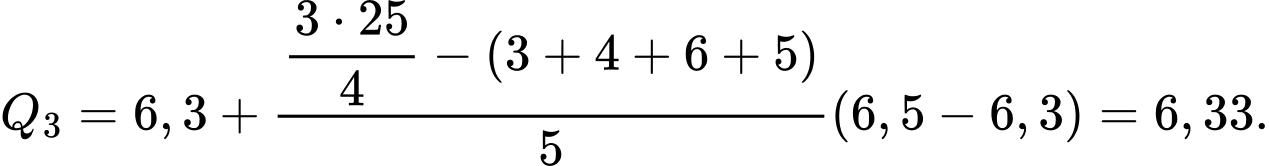
Vậy khoảng tứ phân vị của mẫu số liệu ghép nhóm là: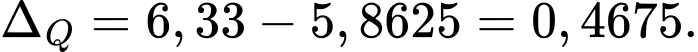 Đáp án: C
Đáp án: C
+ Cỡ mẫu
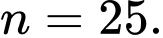
Gọi
 là mẫu số liệu gốc gồm năng suất của 25 thửa ruộng được sắp xếp theo thứ tự không giảm.
là mẫu số liệu gốc gồm năng suất của 25 thửa ruộng được sắp xếp theo thứ tự không giảm.Ta có:
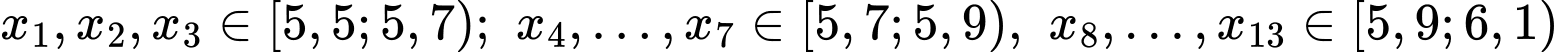 ;
; 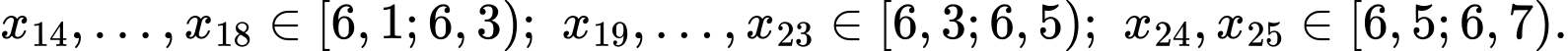
Tứ phân vị thứ nhất của mẫu số liệu gốc là
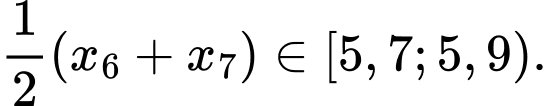 Do đó, tứ phân vị thứ nhất của mẫu số liệu ghép nhóm là:
Do đó, tứ phân vị thứ nhất của mẫu số liệu ghép nhóm là: 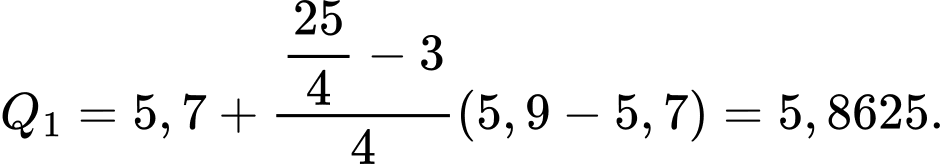
Tứ phân vị thứ ba của mẫu số liệu gốc là
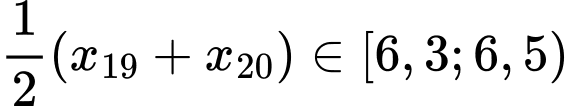 . Do đó, tứ phân vị thứ ba của mẫu số liệu ghép nhóm là:
. Do đó, tứ phân vị thứ ba của mẫu số liệu ghép nhóm là: 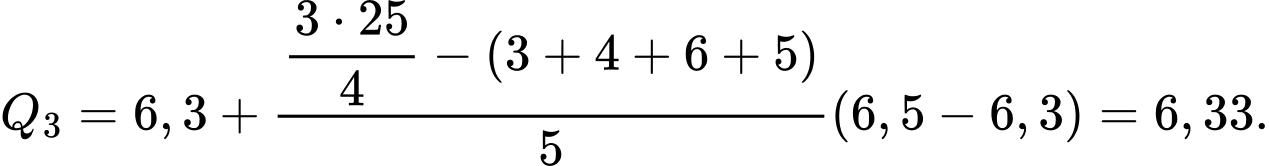
Vậy khoảng tứ phân vị của mẫu số liệu ghép nhóm là:
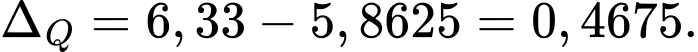 Đáp án: C
Đáp án: C PHẦN II. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Câu 13 [696328]: Cho hàm số 

a) Đúng.
b) Sai.
Ta có: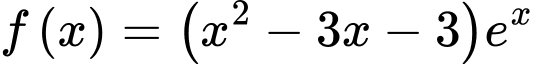
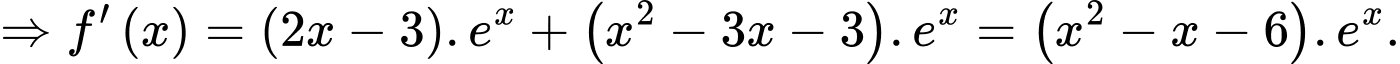
c) Đúng.
Ta có: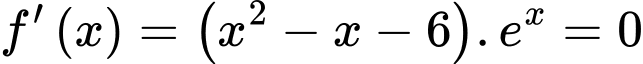
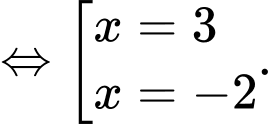
Vậy phương trình có hai nghiệm thực phân biệt.
d) Đúng.
Ta có: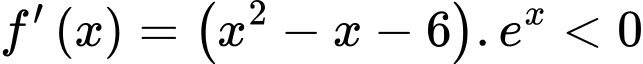

Vậy hàm số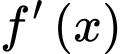 nghịch biến trên
nghịch biến trên 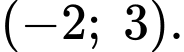
b) Sai.
Ta có:
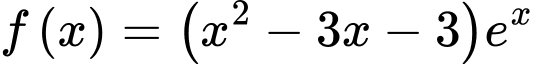
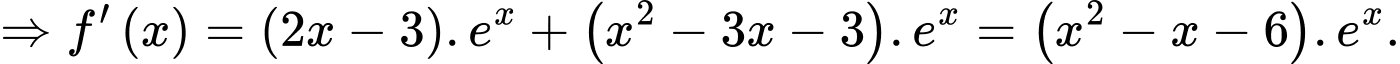
c) Đúng.
Ta có:
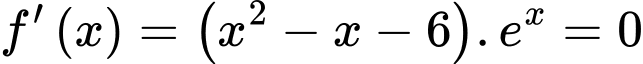
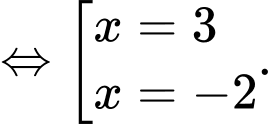
Vậy phương trình có hai nghiệm thực phân biệt.
d) Đúng.
Ta có:
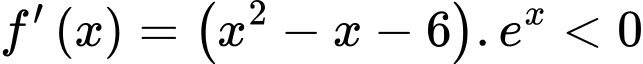

Vậy hàm số
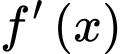 nghịch biến trên
nghịch biến trên 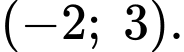
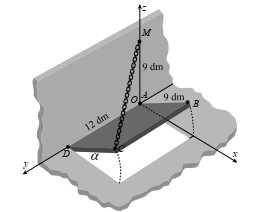
Câu 14 [693309]: Một nắp bể nước hình chữ nhật  nằm cạnh bờ tường có kích thước
nằm cạnh bờ tường có kích thước 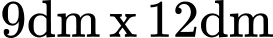 được kéo dài ra từ mặt sàn, do tác dụng của trọng lực nên nắp bể không thể mở ra được nếu không có người giữ. Người ta dùng một sợi dây xích dài
được kéo dài ra từ mặt sàn, do tác dụng của trọng lực nên nắp bể không thể mở ra được nếu không có người giữ. Người ta dùng một sợi dây xích dài 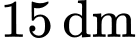 và kéo căng nối đỉnh
và kéo căng nối đỉnh  của hình chữ nhật với điểm
của hình chữ nhật với điểm 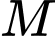 nằm phía trên bờ tường sao cho
nằm phía trên bờ tường sao cho  và
và  vuông góc với mặt sàn. Chọn hệ trục
vuông góc với mặt sàn. Chọn hệ trục 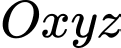 như hình vẽ, khi đó nắp bể mở ra và tạo với mặt sàn một góc
như hình vẽ, khi đó nắp bể mở ra và tạo với mặt sàn một góc 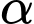 (đơn vị trên mỗi trục tọa độ tính bằng dm). Bỏ qua độ dày của nắp bể.
(đơn vị trên mỗi trục tọa độ tính bằng dm). Bỏ qua độ dày của nắp bể.
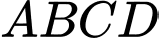 nằm cạnh bờ tường có kích thước
nằm cạnh bờ tường có kích thước 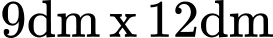 được kéo dài ra từ mặt sàn, do tác dụng của trọng lực nên nắp bể không thể mở ra được nếu không có người giữ. Người ta dùng một sợi dây xích dài
được kéo dài ra từ mặt sàn, do tác dụng của trọng lực nên nắp bể không thể mở ra được nếu không có người giữ. Người ta dùng một sợi dây xích dài 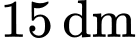 và kéo căng nối đỉnh
và kéo căng nối đỉnh  của hình chữ nhật với điểm
của hình chữ nhật với điểm 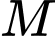 nằm phía trên bờ tường sao cho
nằm phía trên bờ tường sao cho  và
và  vuông góc với mặt sàn. Chọn hệ trục
vuông góc với mặt sàn. Chọn hệ trục 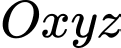 như hình vẽ, khi đó nắp bể mở ra và tạo với mặt sàn một góc
như hình vẽ, khi đó nắp bể mở ra và tạo với mặt sàn một góc 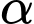 (đơn vị trên mỗi trục tọa độ tính bằng dm). Bỏ qua độ dày của nắp bể.
(đơn vị trên mỗi trục tọa độ tính bằng dm). Bỏ qua độ dày của nắp bể.
a) Sai.
Điểm M nằm trên mặt phẳng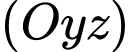 với
với 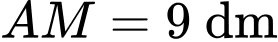
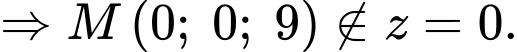
b) Sai.
Chiếu lần lượt lên các mặt phẳng ta được
lần lượt lên các mặt phẳng ta được 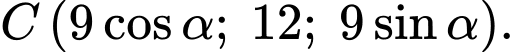
c) Sai.
Ta có: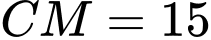
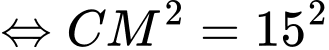
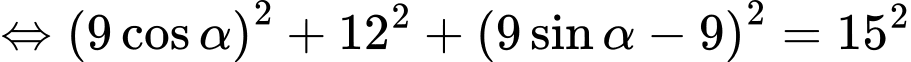
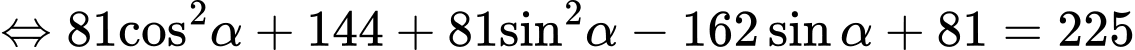
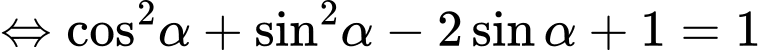
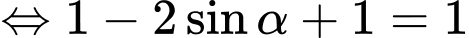
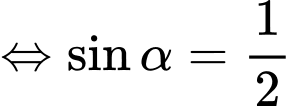
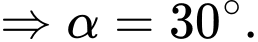
Vậy góc giữa nắp bể và mặt sàn khi kéo lên là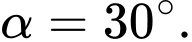
d) Đúng.d) Đúng.Cách 1: Mặt phẳng kéo lên qua điểm
qua điểm 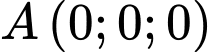 chứa
chứa  và
và 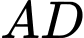
Ta có: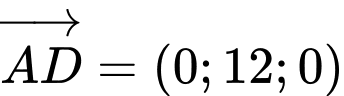 và
và 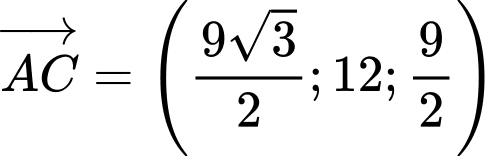
Vecto pháp tuyến của mặt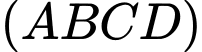 là
là 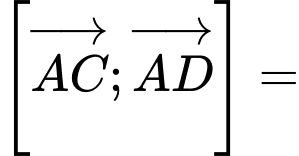
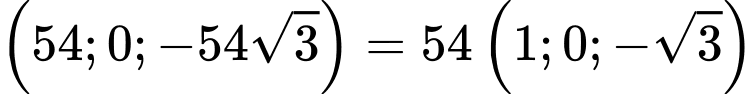
Vậy phương trình mặt phẳng chứa nắp bể sau khi kéo lên là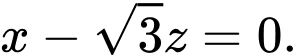 Cách2: Mặt phẳng kéo lên
Cách2: Mặt phẳng kéo lên 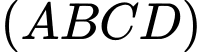 đi qua trục
đi qua trục 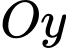 nên có phương trình tổng quát là
nên có phương trình tổng quát là 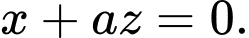
Mặt phẳng kéo lên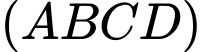 đi qua
đi qua 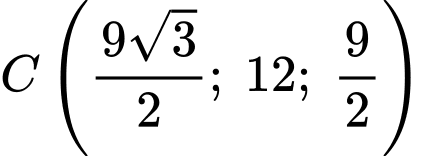 nên
nên 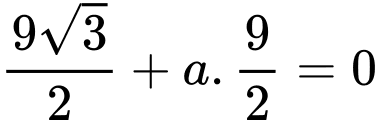
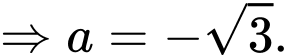
Vậy phương trình mặt phẳng chứa nắp bể sau khi kéo lên là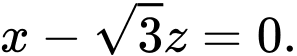
Điểm M nằm trên mặt phẳng
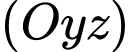 với
với 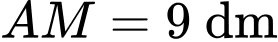
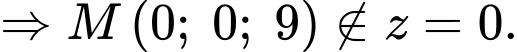
b) Sai.
Chiếu
 lần lượt lên các mặt phẳng ta được
lần lượt lên các mặt phẳng ta được 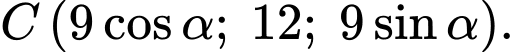
c) Sai.
Ta có:
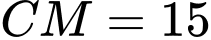
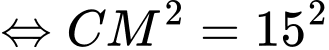
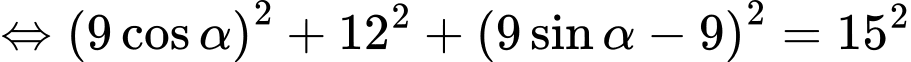
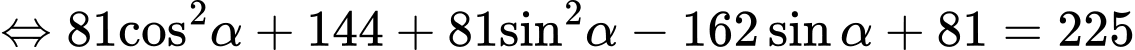
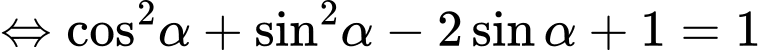
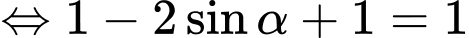
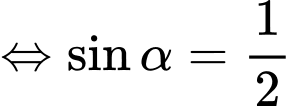
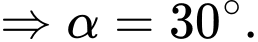
Vậy góc giữa nắp bể và mặt sàn khi kéo lên là
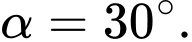
d) Đúng.d) Đúng.Cách 1: Mặt phẳng kéo lên
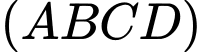 qua điểm
qua điểm 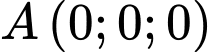 chứa
chứa  và
và 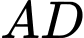
Ta có:
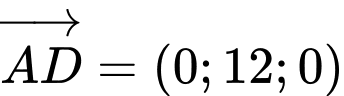 và
và 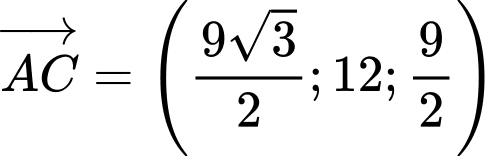
Vecto pháp tuyến của mặt
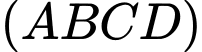 là
là 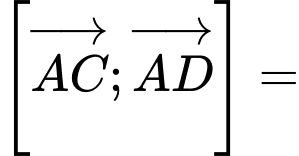
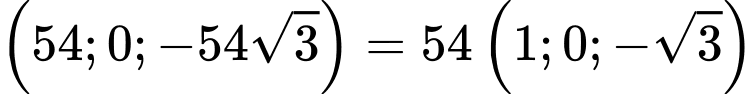
Vậy phương trình mặt phẳng chứa nắp bể sau khi kéo lên là
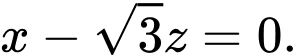 Cách2: Mặt phẳng kéo lên
Cách2: Mặt phẳng kéo lên  đi qua trục
đi qua trục  nên có phương trình tổng quát là
nên có phương trình tổng quát là 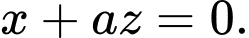
Mặt phẳng kéo lên
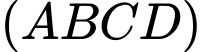 đi qua
đi qua 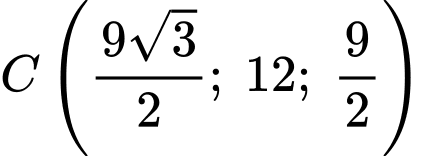 nên
nên 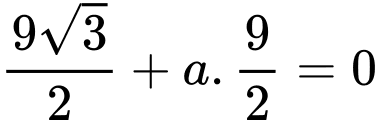
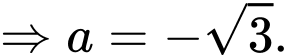
Vậy phương trình mặt phẳng chứa nắp bể sau khi kéo lên là
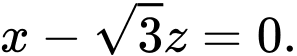
Câu 15 [693310]: Một quần thể vi khuẩn  có số lượng cá thể là
có số lượng cá thể là 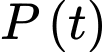 sau
sau 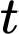 phút quan sát được phát hiện thay đổi với tốc độ là:
phút quan sát được phát hiện thay đổi với tốc độ là: 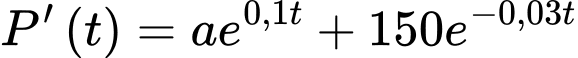
 Biết rằng lúc bắt đầu quan sát, quần thể có 200.000 vi khuẩn và đạt tốc độ tăng trưởng là 350 vi khuẩn/phút.
Biết rằng lúc bắt đầu quan sát, quần thể có 200.000 vi khuẩn và đạt tốc độ tăng trưởng là 350 vi khuẩn/phút.
 có số lượng cá thể là
có số lượng cá thể là 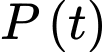 sau
sau  phút quan sát được phát hiện thay đổi với tốc độ là:
phút quan sát được phát hiện thay đổi với tốc độ là: 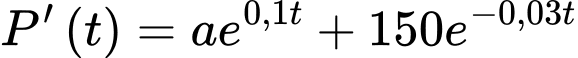
 Biết rằng lúc bắt đầu quan sát, quần thể có 200.000 vi khuẩn và đạt tốc độ tăng trưởng là 350 vi khuẩn/phút.
Biết rằng lúc bắt đầu quan sát, quần thể có 200.000 vi khuẩn và đạt tốc độ tăng trưởng là 350 vi khuẩn/phút.
a) Đúng.

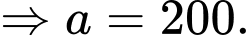
b) Sai.
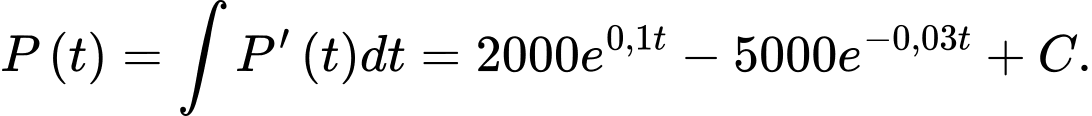
Lại có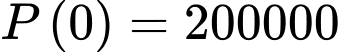 suy ra
suy ra 
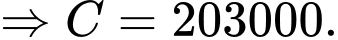
Vậy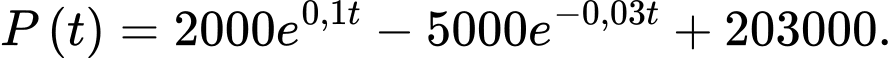
c) Đúng.

d) Sai.
Ý d tái bản đọi ngũ tác giả đã sửa lại nội dung để tránh gây hiểu nhầm
Sau 5phút vi khuẩn xuất hiện thì số lượng vi khuẩn hai quần thể bằngnhau. Nên số lượng quần thể
xuất hiện thì số lượng vi khuẩn hai quần thể bằngnhau. Nên số lượng quần thể  ở phút thứ 17 bằng số lượng quần thể
ở phút thứ 17 bằng số lượng quần thể  ở phút thứ 5
ở phút thứ 5
Tức là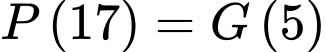 (1)
(1)

Ta có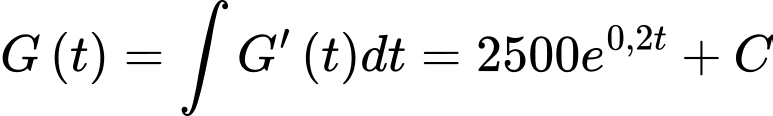
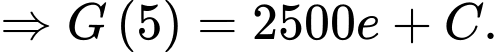
Từ (1) ta có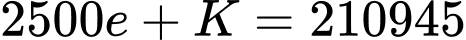
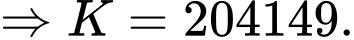
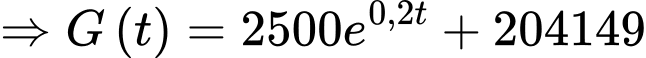
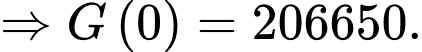

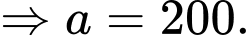
b) Sai.
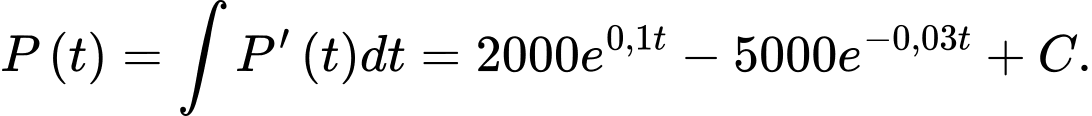
Lại có
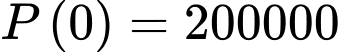 suy ra
suy ra 
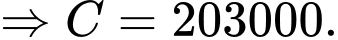
Vậy
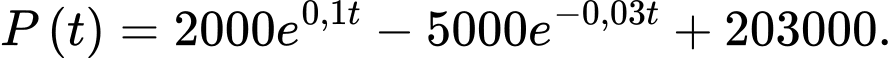
c) Đúng.

d) Sai.
Ý d tái bản đọi ngũ tác giả đã sửa lại nội dung để tránh gây hiểu nhầm
Sau 5phút vi khuẩn
 xuất hiện thì số lượng vi khuẩn hai quần thể bằngnhau. Nên số lượng quần thể
xuất hiện thì số lượng vi khuẩn hai quần thể bằngnhau. Nên số lượng quần thể  ở phút thứ 17 bằng số lượng quần thể
ở phút thứ 17 bằng số lượng quần thể  ở phút thứ 5
ở phút thứ 5Tức là
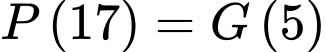 (1)
(1)
Ta có
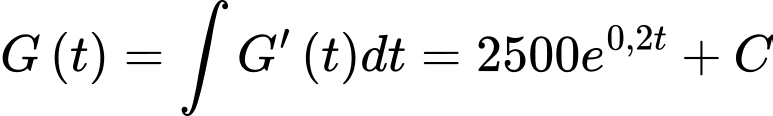
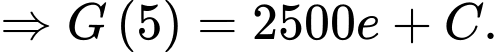
Từ (1) ta có
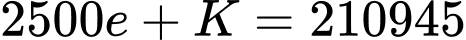
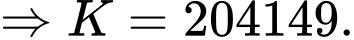
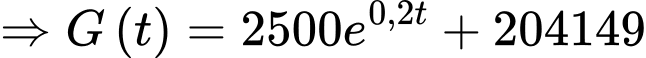
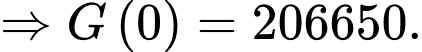
Câu 16 [693311]: Trong một ngôi làng có 500 người thì 240 người là nam. Thống kê cho thấy rằng, khả năng mắc bệnh hô hấp ở người nam trong làng là 0,6% và ở người nữ trong làng là 0,35%. Giả sử gặp một người trong làng.
Gọi là biến cố “gặp người mắc bệnh trong làng”
là biến cố “gặp người mắc bệnh trong làng”
Gọi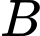 là biến cố “gặp được nam trong làng”
là biến cố “gặp được nam trong làng”
Gọi
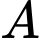 là biến cố “gặp người mắc bệnh trong làng”
là biến cố “gặp người mắc bệnh trong làng”Gọi
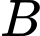 là biến cố “gặp được nam trong làng”
là biến cố “gặp được nam trong làng”
Tỉ lệ mắc bệnh chung trong làng chính là xác suất của 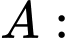 “gặp người mắc bệnh trong làng”
“gặp người mắc bệnh trong làng”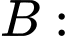 “gặp được nam trong làng”
“gặp được nam trong làng”
a) Đúng.
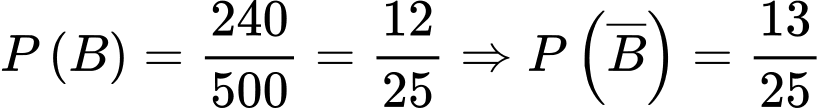
b) Sai.
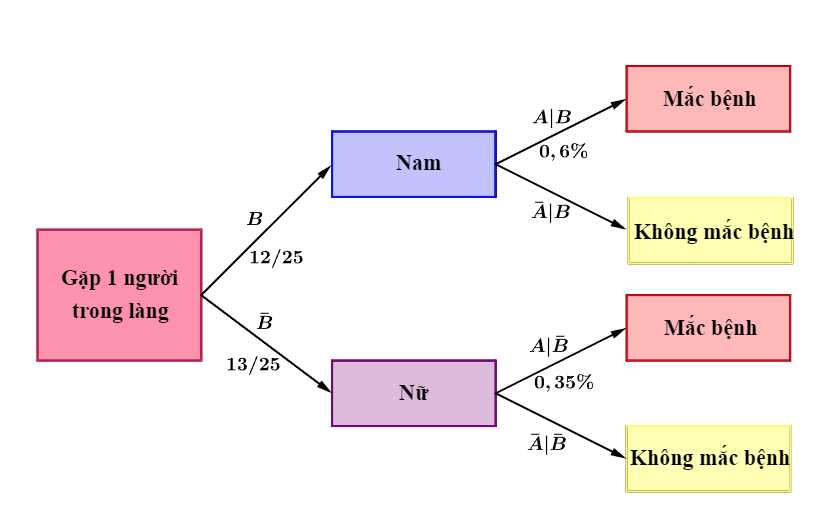
Ta có sơ đồ cây sau:
c) Sai.
Ta có: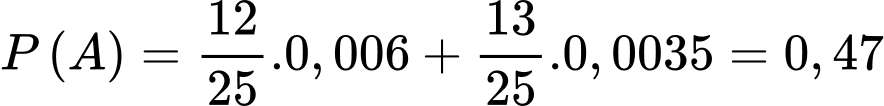
d) Sai.
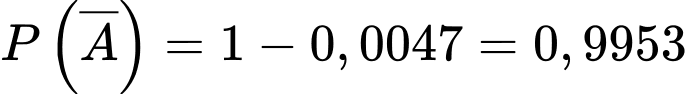
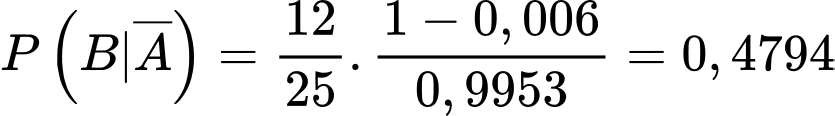
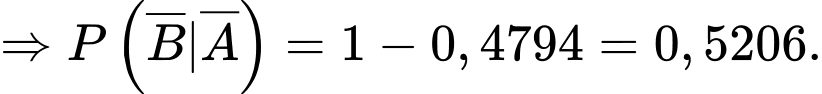
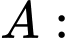 “gặp người mắc bệnh trong làng”
“gặp người mắc bệnh trong làng”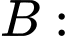 “gặp được nam trong làng”
“gặp được nam trong làng”a) Đúng.
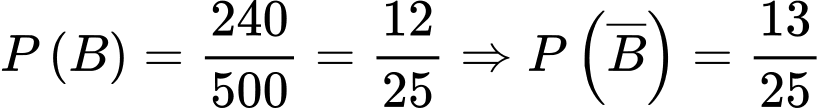
b) Sai.
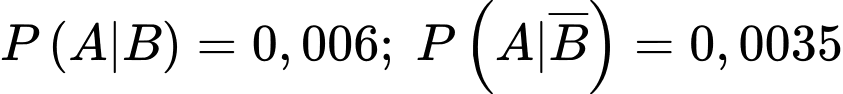
Ta có sơ đồ cây sau:

c) Sai.
Ta có:
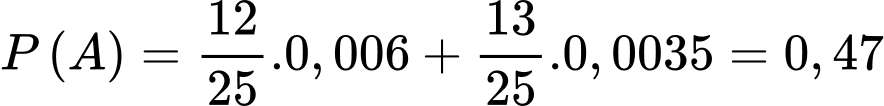
d) Sai.
PHẦN III. Thí sinh trả lời từ câu 1 đến câu 6.
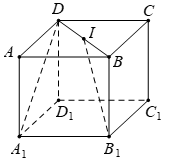
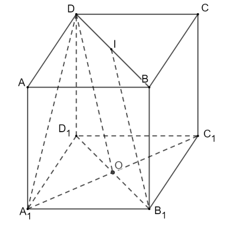
Câu 17 [257647]: Cho hình lập phương 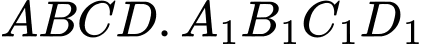 có cạnh
có cạnh 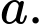 Gọi
Gọi 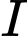 là trung điểm
là trung điểm 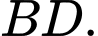 Góc giữa hai đường thẳng
Góc giữa hai đường thẳng 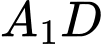 và
và 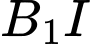 bằng
bằng
 có cạnh
có cạnh 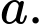 Gọi
Gọi 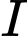 là trung điểm
là trung điểm 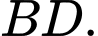 Góc giữa hai đường thẳng
Góc giữa hai đường thẳng 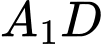 và
và 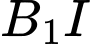 bằng
bằng
Điền đáp án: 30.
Gọi là tâm của hình vuông
là tâm của hình vuông 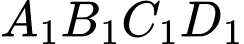 , khi đó ta có
, khi đó ta có  song song với
song song với 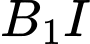 .
.
Suy ra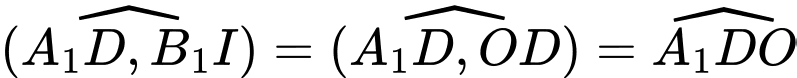 .
.
Ta có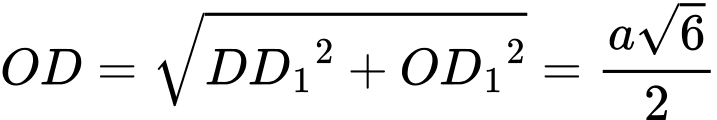 ;
; 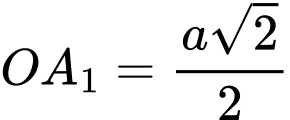 ;
; 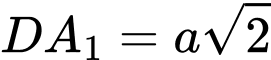 .
.
Suy ra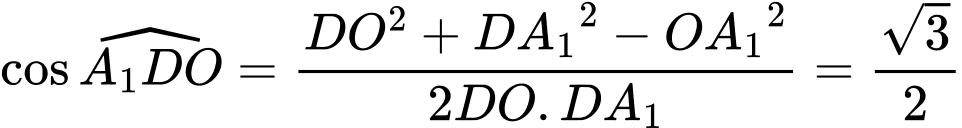 hay
hay 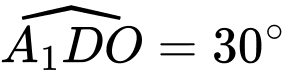 .
.
Vậy góc giữa đường thẳng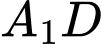 và
và 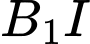 bằng
bằng 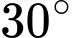 .
.
Gọi
 là tâm của hình vuông
là tâm của hình vuông  , khi đó ta có
, khi đó ta có 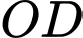 song song với
song song với 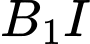 .
. Suy ra
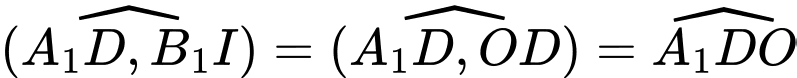 .
.Ta có
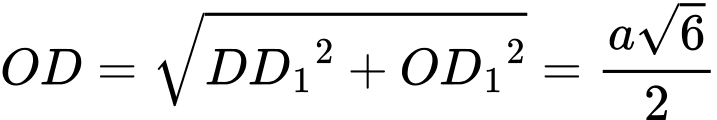 ;
; 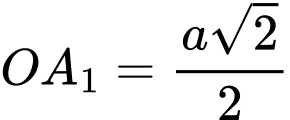 ;
; 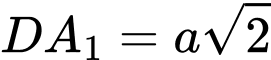 .
.Suy ra
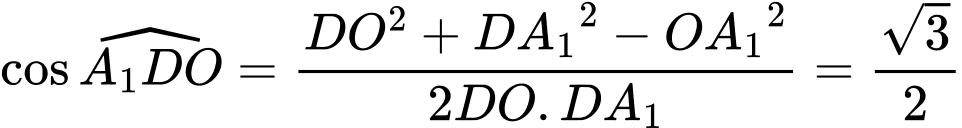 hay
hay 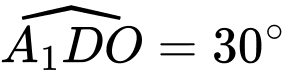 .
.Vậy góc giữa đường thẳng
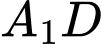 và
và 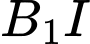 bằng
bằng 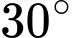 .
. 
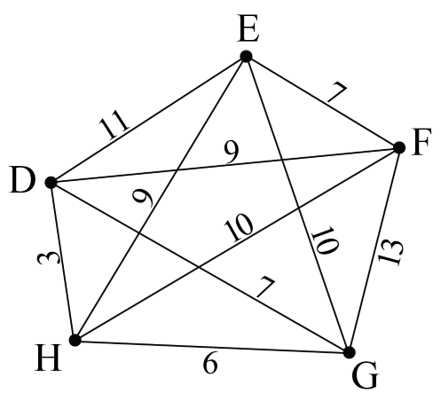
Câu 18 [693312]: Từ kho D xe bưu chính đến lấy thư từ các hộp thư tại E, F, G và H rồi quay lại kho. Sơ đồ bên hiển thị thời gian xe bưu chính di chuyển giữa các hộp thư (đơn vị: phút). Thời gian ngắn nhất để xe bưu chính thực hiện điều đó là bao nhiêu phút?

Điền đáp án: 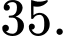
Cách 1: Tư duy
Cách 2: Kiến thức đồ thị
Áp dụng thuật toán láng giềng gần nhất, ta sẽ ưu tiên cho xe bưu chính di chuyển đến những hộp thư gần nhất và chưa được đi đến trước đó.
 Quãng đường đi của xe là:
Quãng đường đi của xe là: 
 Thời gian ngắn nhất để xe bưu chính thực hiện điều đó là: 35 phút.
Thời gian ngắn nhất để xe bưu chính thực hiện điều đó là: 35 phút.
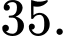
Cách 1: Tư duy
Cách 2: Kiến thức đồ thị
Áp dụng thuật toán láng giềng gần nhất, ta sẽ ưu tiên cho xe bưu chính di chuyển đến những hộp thư gần nhất và chưa được đi đến trước đó.
 Quãng đường đi của xe là:
Quãng đường đi của xe là: 
 Thời gian ngắn nhất để xe bưu chính thực hiện điều đó là: 35 phút.
Thời gian ngắn nhất để xe bưu chính thực hiện điều đó là: 35 phút.
Câu 19 [693316]: Sách ID của Moon.vn được in tại hai phân xưởng A và B và được vận chuyển về kho sau khi in xong. Xưởng A có nhiệm vụ in 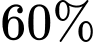 tổng số lượng sách, xưởng B sẽ in số lượng sách còn lại. Biết rằng số lượng Sách ID xưởng A và B in đạt yêu cầu về chất lượng và chuyển về kho lần lượt là
tổng số lượng sách, xưởng B sẽ in số lượng sách còn lại. Biết rằng số lượng Sách ID xưởng A và B in đạt yêu cầu về chất lượng và chuyển về kho lần lượt là 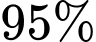 và
và 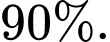 Nhân viên kiểm kho chọn ra ngẫu nhiên một cuốn Sách ID để kiểm tra thì thấy cuốn sách này không đạt yêu cầu về chất lượng. Xác suất để cuốn Sách ID đó được in ở xưởng A là bao nhiêu % (làm tròn kết quả đến hàng phần chục).
Nhân viên kiểm kho chọn ra ngẫu nhiên một cuốn Sách ID để kiểm tra thì thấy cuốn sách này không đạt yêu cầu về chất lượng. Xác suất để cuốn Sách ID đó được in ở xưởng A là bao nhiêu % (làm tròn kết quả đến hàng phần chục).

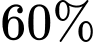 tổng số lượng sách, xưởng B sẽ in số lượng sách còn lại. Biết rằng số lượng Sách ID xưởng A và B in đạt yêu cầu về chất lượng và chuyển về kho lần lượt là
tổng số lượng sách, xưởng B sẽ in số lượng sách còn lại. Biết rằng số lượng Sách ID xưởng A và B in đạt yêu cầu về chất lượng và chuyển về kho lần lượt là 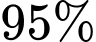 và
và 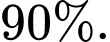 Nhân viên kiểm kho chọn ra ngẫu nhiên một cuốn Sách ID để kiểm tra thì thấy cuốn sách này không đạt yêu cầu về chất lượng. Xác suất để cuốn Sách ID đó được in ở xưởng A là bao nhiêu % (làm tròn kết quả đến hàng phần chục).
Nhân viên kiểm kho chọn ra ngẫu nhiên một cuốn Sách ID để kiểm tra thì thấy cuốn sách này không đạt yêu cầu về chất lượng. Xác suất để cuốn Sách ID đó được in ở xưởng A là bao nhiêu % (làm tròn kết quả đến hàng phần chục).
Điền đáp án: 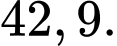
Gọi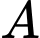 là biến cố: “Sách được in ở xưởng A”;
là biến cố: “Sách được in ở xưởng A”;
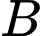 là biến cố: “Sách được in không đạt yêu cầu chất lượng”.
là biến cố: “Sách được in không đạt yêu cầu chất lượng”.
Ta tính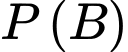 . Theo công thức xác suất toàn phần ta có:
. Theo công thức xác suất toàn phần ta có:
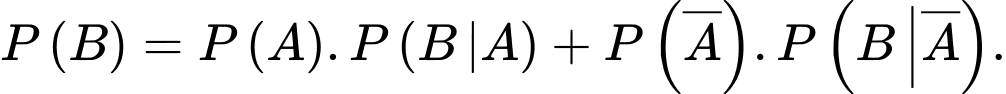
Theo giả thiết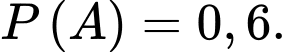
Suy ra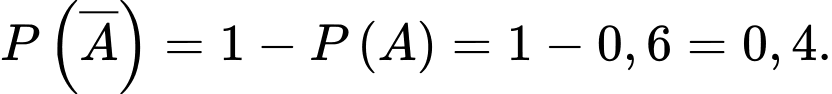
Theo giả thiết ta có
Do đó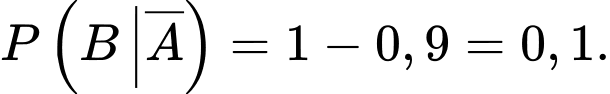
Từ đó, ta có sơ đồ cây như sau:
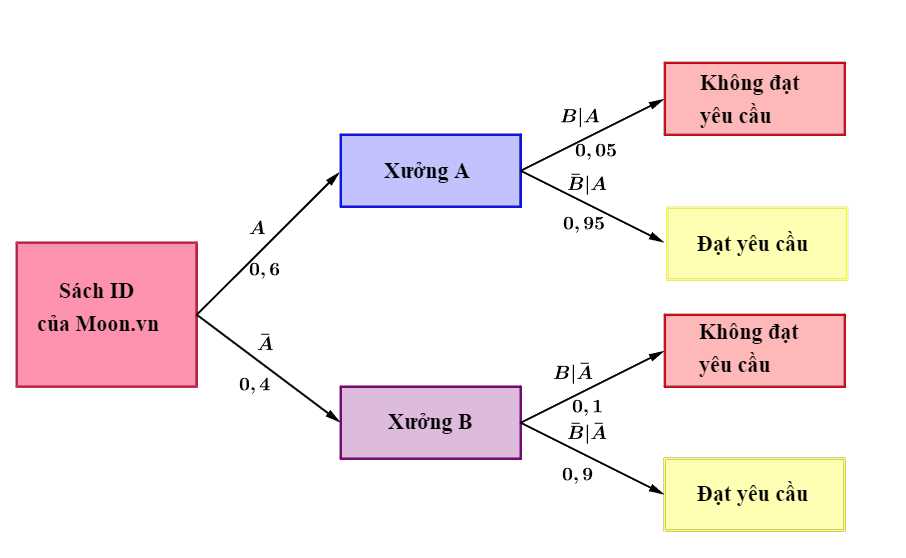
Khi đó,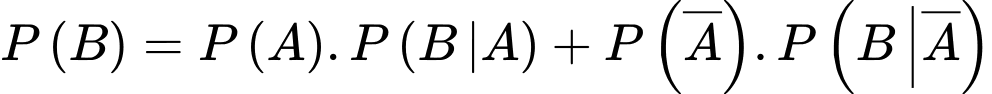
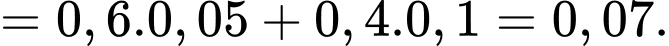
Theo Bayes ta có: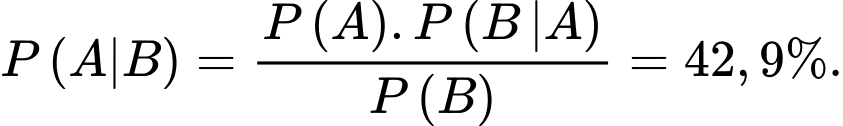
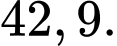
Gọi
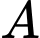 là biến cố: “Sách được in ở xưởng A”;
là biến cố: “Sách được in ở xưởng A”;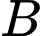 là biến cố: “Sách được in không đạt yêu cầu chất lượng”.
là biến cố: “Sách được in không đạt yêu cầu chất lượng”.Ta tính
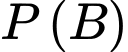 . Theo công thức xác suất toàn phần ta có:
. Theo công thức xác suất toàn phần ta có: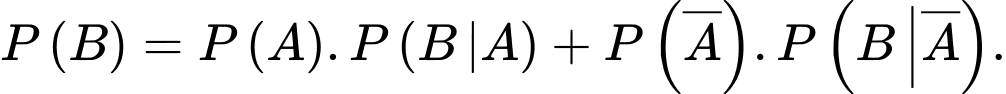
Theo giả thiết
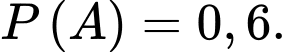
Suy ra
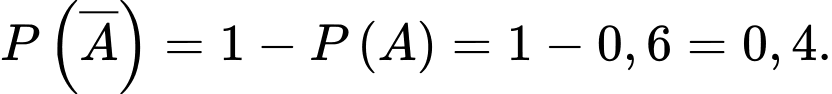
Theo giả thiết ta có

Do đó
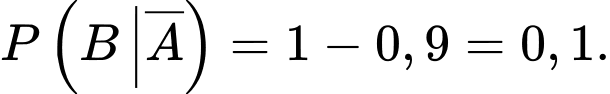
Từ đó, ta có sơ đồ cây như sau:

Khi đó,
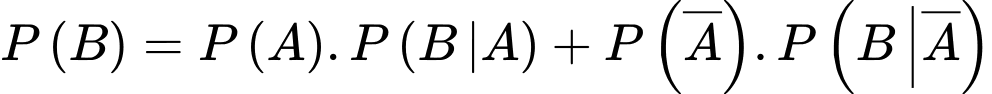
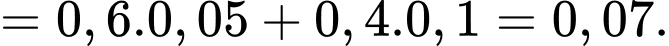
Theo Bayes ta có:
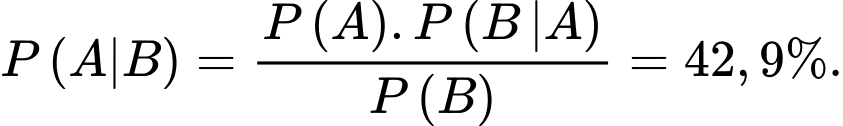
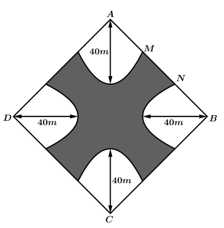
Câu 20 [693313]: Kiến trúc sư thiết kế một khu sinh hoạt cộng đồng có dạng hình vuông  có độ dài đường chéo
có độ dài đường chéo 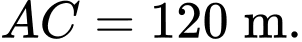 Trong đó, phần được tô màu đậm là sân chơi, phần còn lại để trồng hoa. Mỗi phần trồng hoa có đường biên cong là một phần của parabol với đỉnh thuộc một trục đối xứng của hình vuông, khoảng cách từ đỉnh đó đến đỉnh tương ứng của hình vuông bằng
Trong đó, phần được tô màu đậm là sân chơi, phần còn lại để trồng hoa. Mỗi phần trồng hoa có đường biên cong là một phần của parabol với đỉnh thuộc một trục đối xứng của hình vuông, khoảng cách từ đỉnh đó đến đỉnh tương ứng của hình vuông bằng  và
và 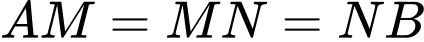 (xem hình minh họa). Diện tích của phần sân chơi là bao nhiêu mét vuông (làm tròn kết quả đến hàng đơn vị).
(xem hình minh họa). Diện tích của phần sân chơi là bao nhiêu mét vuông (làm tròn kết quả đến hàng đơn vị).
 có độ dài đường chéo
có độ dài đường chéo 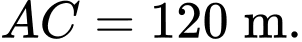 Trong đó, phần được tô màu đậm là sân chơi, phần còn lại để trồng hoa. Mỗi phần trồng hoa có đường biên cong là một phần của parabol với đỉnh thuộc một trục đối xứng của hình vuông, khoảng cách từ đỉnh đó đến đỉnh tương ứng của hình vuông bằng
Trong đó, phần được tô màu đậm là sân chơi, phần còn lại để trồng hoa. Mỗi phần trồng hoa có đường biên cong là một phần của parabol với đỉnh thuộc một trục đối xứng của hình vuông, khoảng cách từ đỉnh đó đến đỉnh tương ứng của hình vuông bằng  và
và 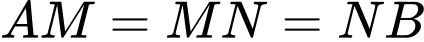 (xem hình minh họa). Diện tích của phần sân chơi là bao nhiêu mét vuông (làm tròn kết quả đến hàng đơn vị).
(xem hình minh họa). Diện tích của phần sân chơi là bao nhiêu mét vuông (làm tròn kết quả đến hàng đơn vị).
Điền đáp án: 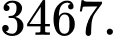
Xét hệ trục tọa độ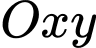 như hình vẽ ta có:
như hình vẽ ta có:
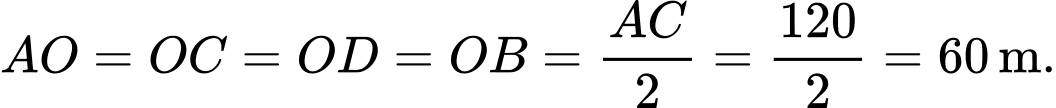
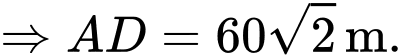
Ta có: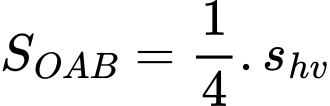
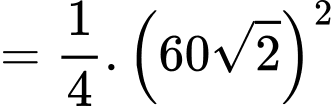
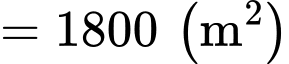
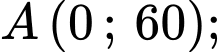
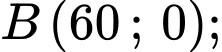
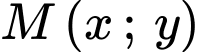
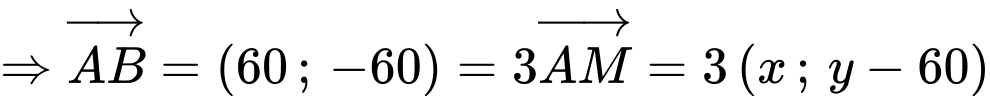
(Do bài cho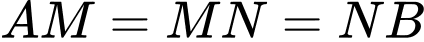 )
)

Ta xét phần hình trắng có dạng parabol như hình vẽ có: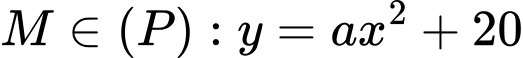
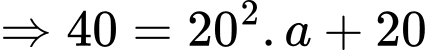
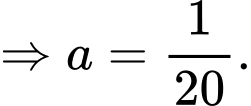
Diện tích một phần trắng là diện tích được chắn bởi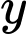 và đường thẳng
và đường thẳng 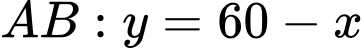 là:
là:
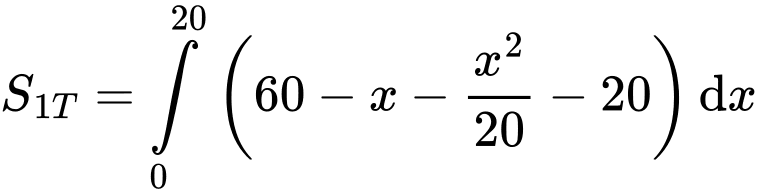
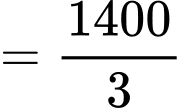
Diện tích một phần tư của sân chơi là:
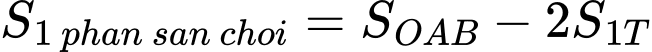
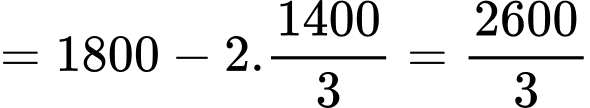
Vậy diện tích sân chơi cần tính là: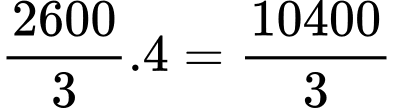
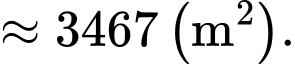
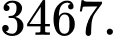

Xét hệ trục tọa độ
 như hình vẽ ta có:
như hình vẽ ta có: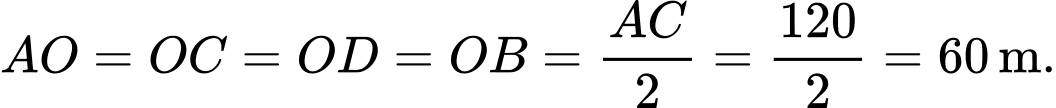
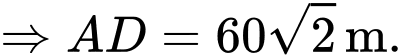
Ta có:
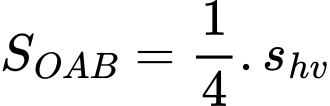
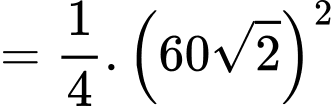
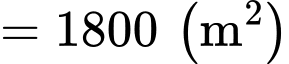
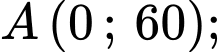
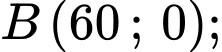
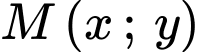
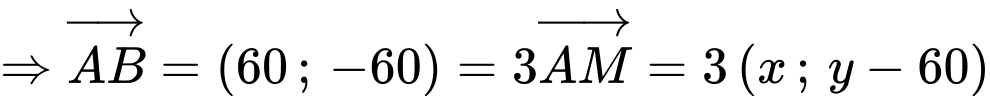
(Do bài cho
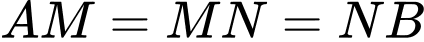 )
)
Ta xét phần hình trắng có dạng parabol như hình vẽ có:
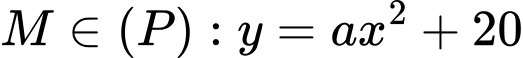
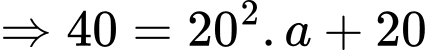
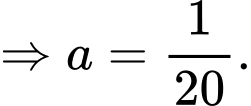
Diện tích một phần trắng là diện tích được chắn bởi
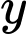 và đường thẳng
và đường thẳng 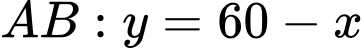 là:
là: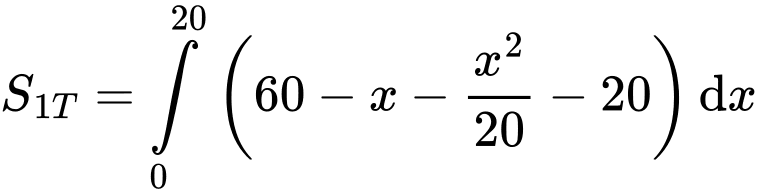
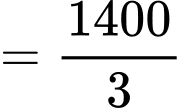
Diện tích một phần tư của sân chơi là:
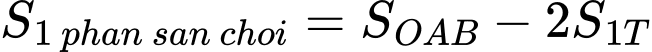
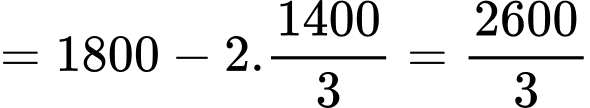
Vậy diện tích sân chơi cần tính là:
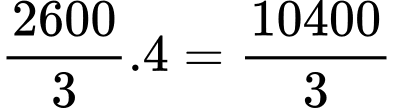
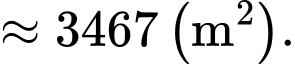
Câu 21 [696310]: Một phần của đường chạy của tàu lượn siêu tốc khi gắn hệ trục tọa độ 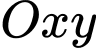 được mô phỏng ở hình 2. Biết đường chạy của nó có dạng đồ thị hàm số bậc ba
được mô phỏng ở hình 2. Biết đường chạy của nó có dạng đồ thị hàm số bậc ba 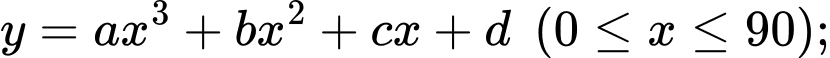 tàu lượn xuất phát từ điểm
tàu lượn xuất phát từ điểm 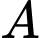 đồng thời đi qua các điểm
đồng thời đi qua các điểm 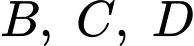 (như hình vẽ). Đơn vị mỗi trục là mét, dựa vào đồ thị hình 2, em hay tính độ cao lớn nhất (theo đơn vị mét) mà tàu lượn siêu tốc đạt được so với mặt đất (xem
(như hình vẽ). Đơn vị mỗi trục là mét, dựa vào đồ thị hình 2, em hay tính độ cao lớn nhất (theo đơn vị mét) mà tàu lượn siêu tốc đạt được so với mặt đất (xem  là mặt đất). Kết quả làm tròn đến hàng phần mười.
là mặt đất). Kết quả làm tròn đến hàng phần mười.
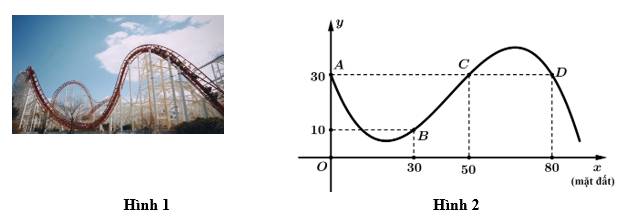
 được mô phỏng ở hình 2. Biết đường chạy của nó có dạng đồ thị hàm số bậc ba
được mô phỏng ở hình 2. Biết đường chạy của nó có dạng đồ thị hàm số bậc ba 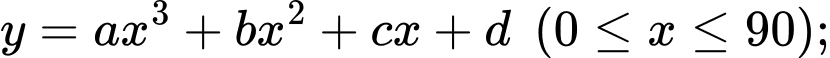 tàu lượn xuất phát từ điểm
tàu lượn xuất phát từ điểm 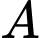 đồng thời đi qua các điểm
đồng thời đi qua các điểm 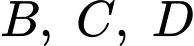 (như hình vẽ). Đơn vị mỗi trục là mét, dựa vào đồ thị hình 2, em hay tính độ cao lớn nhất (theo đơn vị mét) mà tàu lượn siêu tốc đạt được so với mặt đất (xem
(như hình vẽ). Đơn vị mỗi trục là mét, dựa vào đồ thị hình 2, em hay tính độ cao lớn nhất (theo đơn vị mét) mà tàu lượn siêu tốc đạt được so với mặt đất (xem 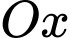 là mặt đất). Kết quả làm tròn đến hàng phần mười.
là mặt đất). Kết quả làm tròn đến hàng phần mười.
Điền đáp án: 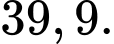
Ta có:
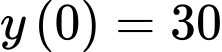
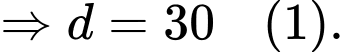
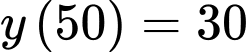
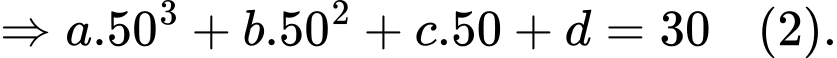
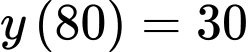
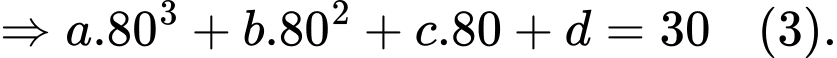
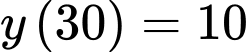
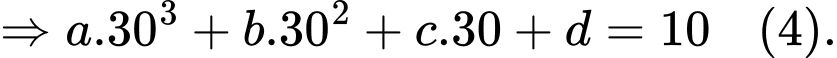
Từ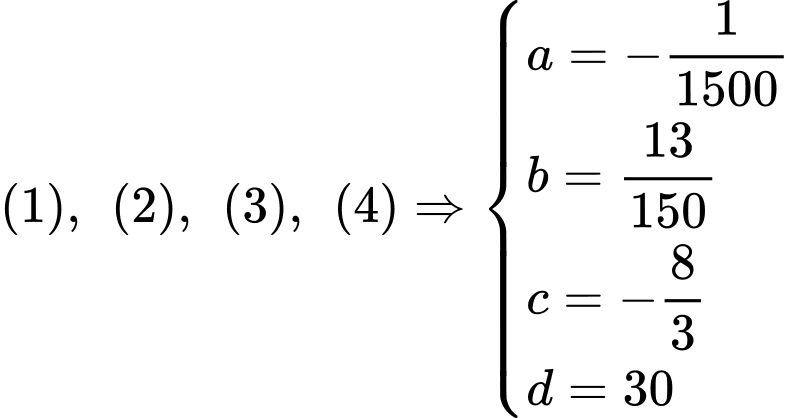
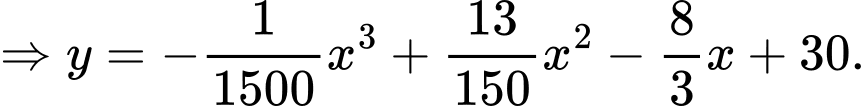
Khi đó: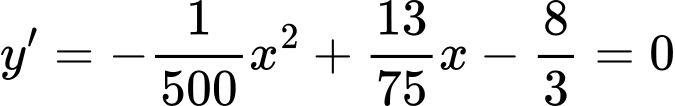
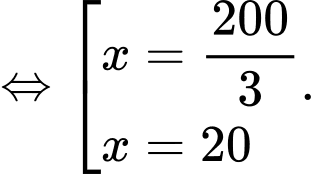
Nhìn vào đồ thị hàm số ta có: Độ cao lớn nhất mà tàu lượn siêu tốc đạt được so với mặt đất là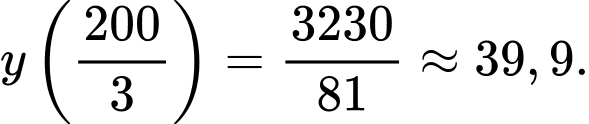
Ta có:
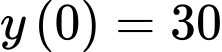
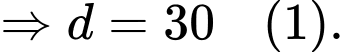
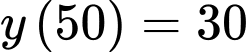
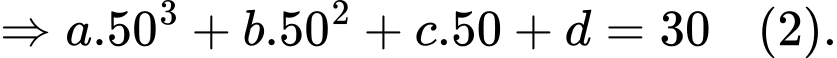
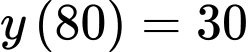
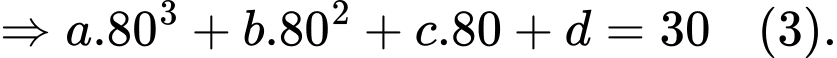
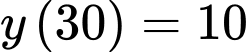
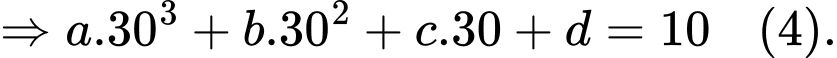
Từ
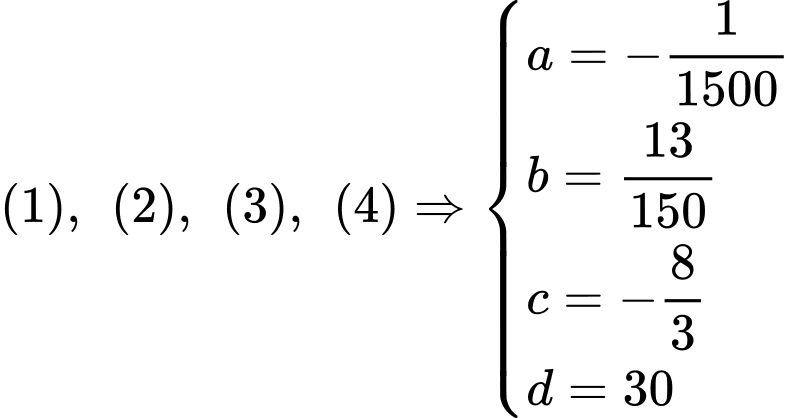
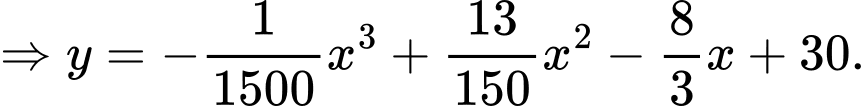
Khi đó:
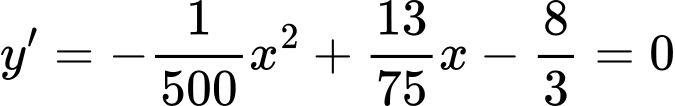
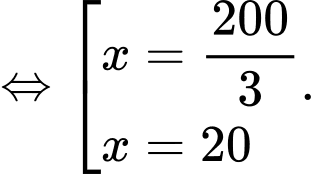
Nhìn vào đồ thị hàm số ta có: Độ cao lớn nhất mà tàu lượn siêu tốc đạt được so với mặt đất là
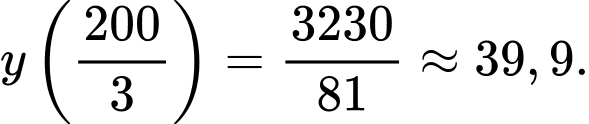
Câu 22 [693130]: Một quả bóng hình cầu có bán kính 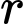 đang được treo trong một góc của tường nhà (hai bờ tường vuông góc), một điểm
đang được treo trong một góc của tường nhà (hai bờ tường vuông góc), một điểm 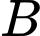 cố định nằm trên mép của hai bờ tường và cách mặt đất
cố định nằm trên mép của hai bờ tường và cách mặt đất 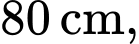 sợi dây treo bóng có độ dài
sợi dây treo bóng có độ dài 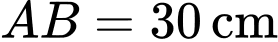 và đây cũng là độ dài ngắn nhất nối điểm
và đây cũng là độ dài ngắn nhất nối điểm 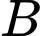 với mặt xung quanh của quả bóng. Biết rằng quả bóng tiếp xúc với hai bên bờ tường và điểm thấp nhất của quả bóng cách mặt đất
với mặt xung quanh của quả bóng. Biết rằng quả bóng tiếp xúc với hai bên bờ tường và điểm thấp nhất của quả bóng cách mặt đất  Hỏi đường kính của quả bóng là bao nhiêu centimet (làm tròn kết quả đến hàng đơn vị).
Hỏi đường kính của quả bóng là bao nhiêu centimet (làm tròn kết quả đến hàng đơn vị).
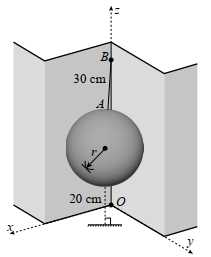
 đang được treo trong một góc của tường nhà (hai bờ tường vuông góc), một điểm
đang được treo trong một góc của tường nhà (hai bờ tường vuông góc), một điểm  cố định nằm trên mép của hai bờ tường và cách mặt đất
cố định nằm trên mép của hai bờ tường và cách mặt đất 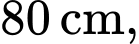 sợi dây treo bóng có độ dài
sợi dây treo bóng có độ dài 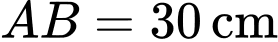 và đây cũng là độ dài ngắn nhất nối điểm
và đây cũng là độ dài ngắn nhất nối điểm  với mặt xung quanh của quả bóng. Biết rằng quả bóng tiếp xúc với hai bên bờ tường và điểm thấp nhất của quả bóng cách mặt đất
với mặt xung quanh của quả bóng. Biết rằng quả bóng tiếp xúc với hai bên bờ tường và điểm thấp nhất của quả bóng cách mặt đất  Hỏi đường kính của quả bóng là bao nhiêu centimet (làm tròn kết quả đến hàng đơn vị).
Hỏi đường kính của quả bóng là bao nhiêu centimet (làm tròn kết quả đến hàng đơn vị).
Điền đáp án: 38.
Giả sử mặt cầu có toạ độ tâm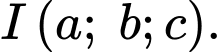 Từ giả thiết, ta thấy rằng
Từ giả thiết, ta thấy rằng 
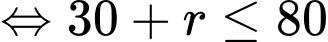

Ta khai thác dữ kiện đề bài:
Vì điểm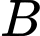 nằm trên trục
nằm trên trục  và cách mặt đất 80 cm nên
và cách mặt đất 80 cm nên 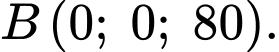
Lại có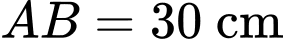 và là độ dài ngắn nhất nối điểm
và là độ dài ngắn nhất nối điểm 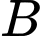 với mặt xung quanh của quả bóng, nên ta có
với mặt xung quanh của quả bóng, nên ta có 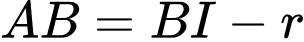
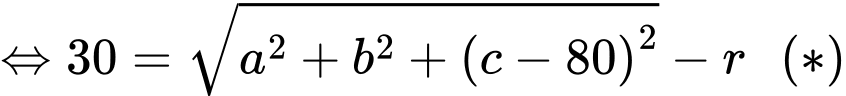
Vì quả bóng tiếp xúc với hai bên bờ tường (tức hai mặt phẳng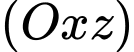 và
và 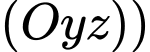 nên ta có
nên ta có 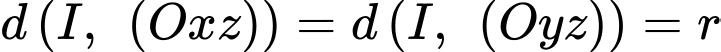 mà
mà 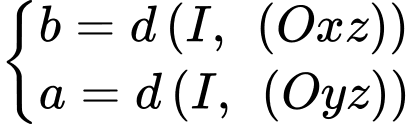
Suy ra toạ độ điểm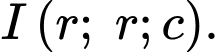
Từ giả thiết: vị trí thấp nhất của quả bóng cách mặt đất 20 cm nên ta có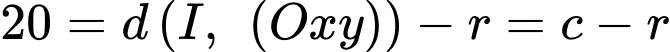
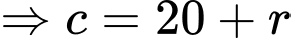
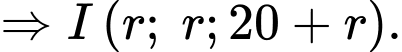
Khi đó, phương trình (*) tương đương với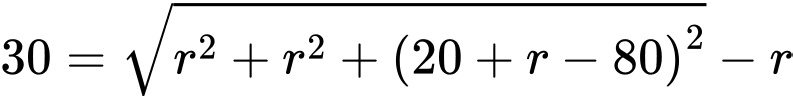
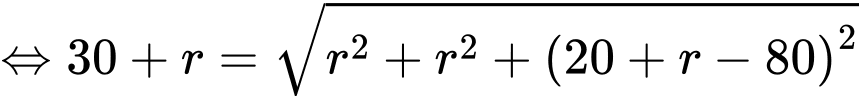
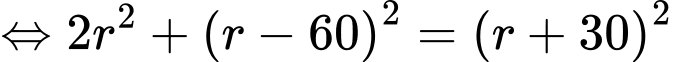
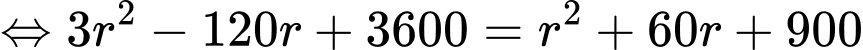
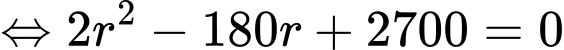
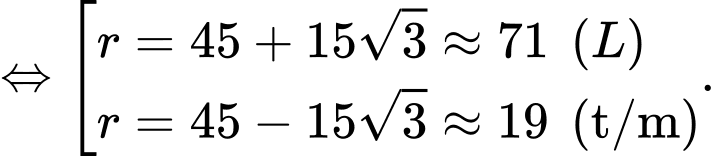
Vậy đường kính của quả bóng là 38 cm.
Note: Để chứng minh bài trên, ta sử dụng bổ đề sau:
Cho một điểm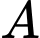 bất kì; mặt cầu
bất kì; mặt cầu 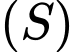 có tâm
có tâm 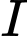 và bán kính
và bán kính 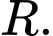 Gọi
Gọi 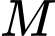 là một điểm di động trên mặt cầu
là một điểm di động trên mặt cầu  Minh hoạ như hình vẽ.
Minh hoạ như hình vẽ.
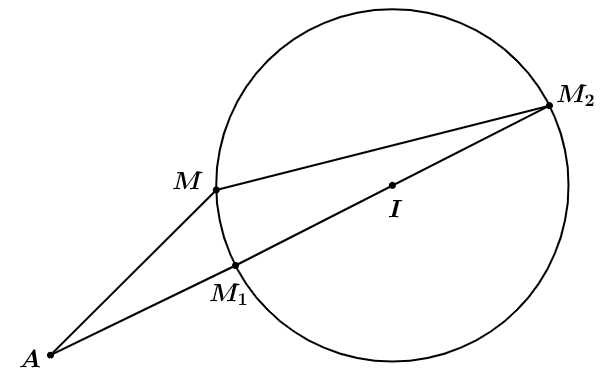
Khi đó:
+)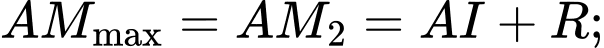
+)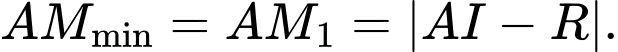
Giả sử mặt cầu có toạ độ tâm
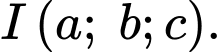 Từ giả thiết, ta thấy rằng
Từ giả thiết, ta thấy rằng 
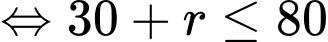

Ta khai thác dữ kiện đề bài:
Vì điểm
 nằm trên trục
nằm trên trục  và cách mặt đất 80 cm nên
và cách mặt đất 80 cm nên 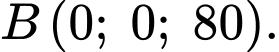
Lại có
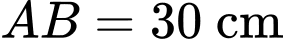 và là độ dài ngắn nhất nối điểm
và là độ dài ngắn nhất nối điểm 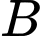 với mặt xung quanh của quả bóng, nên ta có
với mặt xung quanh của quả bóng, nên ta có 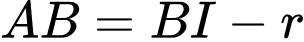
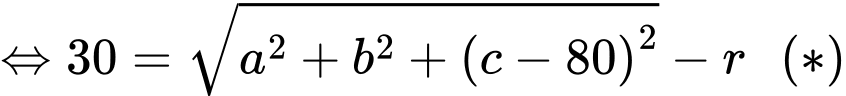
Vì quả bóng tiếp xúc với hai bên bờ tường (tức hai mặt phẳng
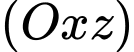 và
và 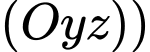 nên ta có
nên ta có 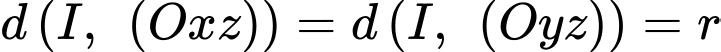 mà
mà 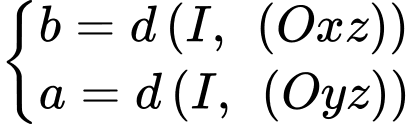
Suy ra toạ độ điểm
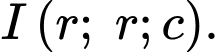
Từ giả thiết: vị trí thấp nhất của quả bóng cách mặt đất 20 cm nên ta có
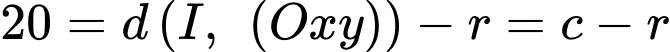
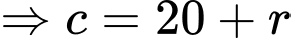
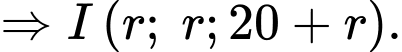
Khi đó, phương trình (*) tương đương với
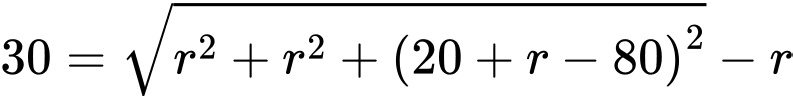
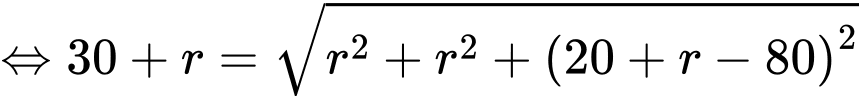
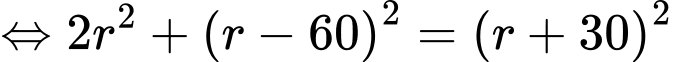
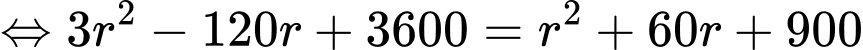
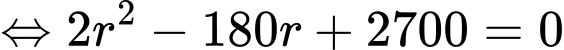
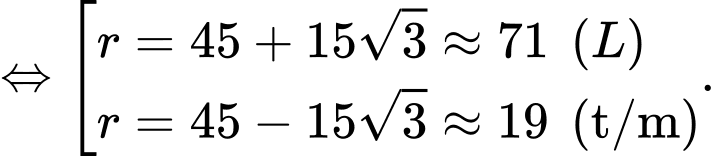
Vậy đường kính của quả bóng là 38 cm.
Note: Để chứng minh bài trên, ta sử dụng bổ đề sau:
Cho một điểm
 bất kì; mặt cầu
bất kì; mặt cầu 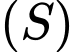 có tâm
có tâm 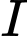 và bán kính
và bán kính 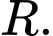 Gọi
Gọi 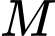 là một điểm di động trên mặt cầu
là một điểm di động trên mặt cầu 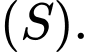 Minh hoạ như hình vẽ.
Minh hoạ như hình vẽ.
Khi đó:
+)
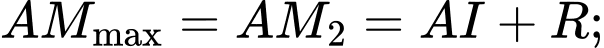
+)