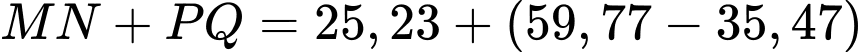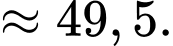PHẦN I. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Câu 1 [890256]: Trong không gian với hệ trục tọa độ 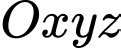 , cho điểm
, cho điểm 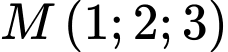 . Hình chiếu của
. Hình chiếu của 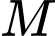 lên trục
lên trục 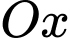 là điểm
là điểm
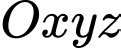 , cho điểm
, cho điểm 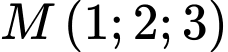 . Hình chiếu của
. Hình chiếu của 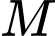 lên trục
lên trục 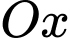 là điểm
là điểm A, 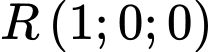 .
.
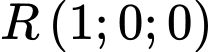 .
.B, 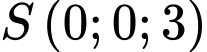 .
.
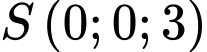 .
.C, 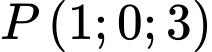 .
.
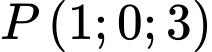 .
.D, 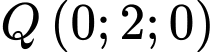 .
.
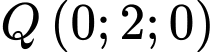 .
.
Chọn đáp án A.
Gọi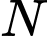 là hình chiếu của
là hình chiếu của 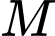 lên trục
lên trục 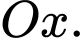
Do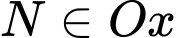

Do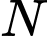 là hình chiếu của
là hình chiếu của 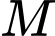 lên trục
lên trục 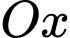
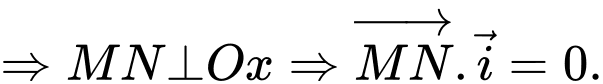
Trong đó: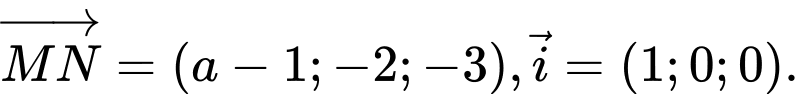
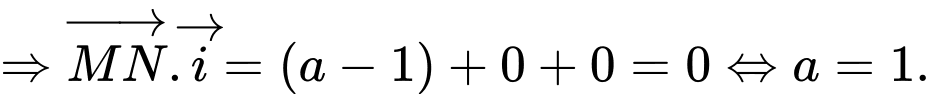
Vậy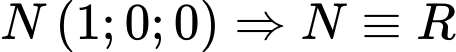 Đáp án: A
Đáp án: A
Gọi
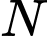 là hình chiếu của
là hình chiếu của 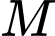 lên trục
lên trục 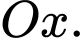
Do
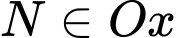

Do
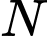 là hình chiếu của
là hình chiếu của 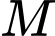 lên trục
lên trục 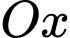
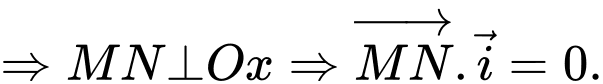
Trong đó:
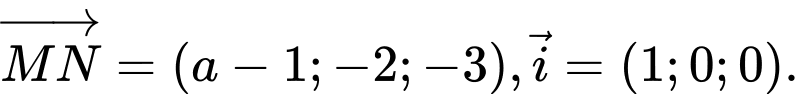
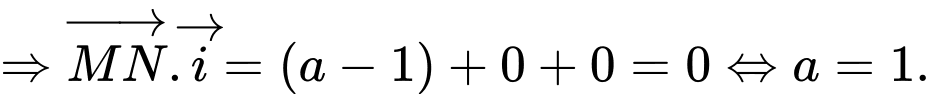
Vậy
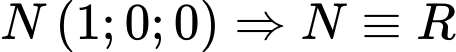 Đáp án: A
Đáp án: A
Câu 2 [256785]: Trên khoảng 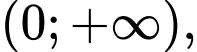 họ nguyên hàm của hàm số
họ nguyên hàm của hàm số 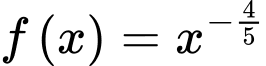 là
là
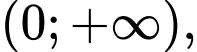 họ nguyên hàm của hàm số
họ nguyên hàm của hàm số 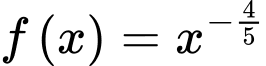 là
là A, 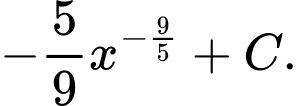
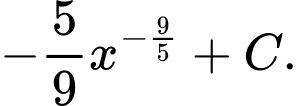
B, 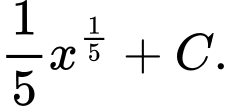
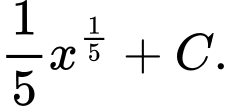
C, 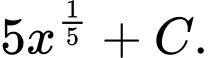
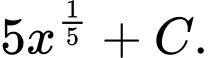
D, 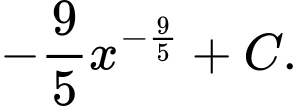
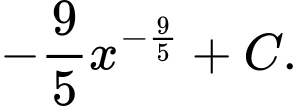
Chọn đáp án C.
Ta có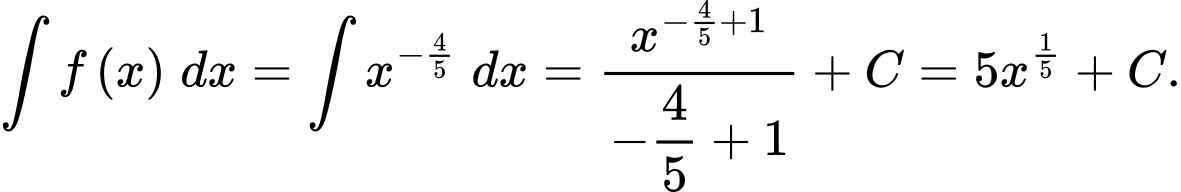 Đáp án: C
Đáp án: C
Ta có
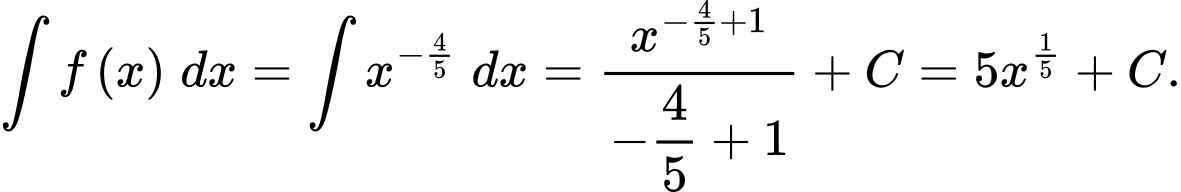 Đáp án: C
Đáp án: C
Câu 3 [256938]: Cho hàm số 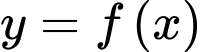 liên tục trên
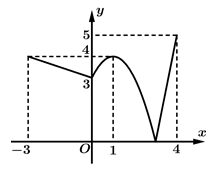
liên tục trên 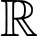 và có đồ thị như hình vẽ bên. Trên đoạn
và có đồ thị như hình vẽ bên. Trên đoạn 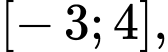 hàm số đã cho có bao nhiêu điểm cực trị?
hàm số đã cho có bao nhiêu điểm cực trị?
 liên tục trên
liên tục trên  và có đồ thị như hình vẽ bên. Trên đoạn
và có đồ thị như hình vẽ bên. Trên đoạn 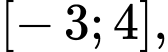 hàm số đã cho có bao nhiêu điểm cực trị?
hàm số đã cho có bao nhiêu điểm cực trị? 
A, 4.
B, 3.
C, 2.
D, 1.
Chọn đáp án B.
Dựa vào đồ thị hàm số, trên đoạn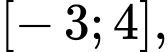 hàm số có 3 điểm cực trị. Đáp án: B
hàm số có 3 điểm cực trị. Đáp án: B
Dựa vào đồ thị hàm số, trên đoạn
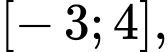 hàm số có 3 điểm cực trị. Đáp án: B
hàm số có 3 điểm cực trị. Đáp án: B
Câu 4 [256905]: Cho cấp số cộng 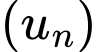 thỏa mãn
thỏa mãn 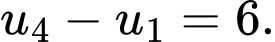 Công sai của
Công sai của 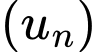 bằng
bằng
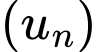 thỏa mãn
thỏa mãn 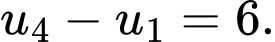 Công sai của
Công sai của 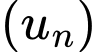 bằng
bằng A, 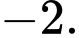
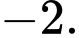
B, 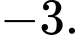
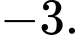
C, 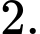
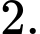
D, 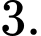
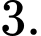
Chọn đáp án C.
Ta có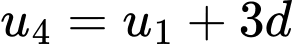
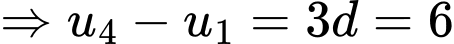
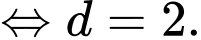
Vậy công sai của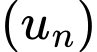 bằng
bằng 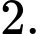 Đáp án: C
Đáp án: C
Ta có
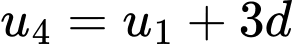
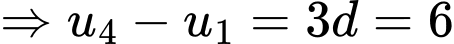
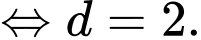
Vậy công sai của
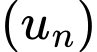 bằng
bằng 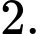 Đáp án: C
Đáp án: C
Câu 5 [693676]: Cho hình chóp 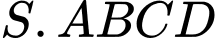 có đáy
có đáy 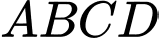 là hình bình hành tâm
là hình bình hành tâm  Hai mặt phẳng
Hai mặt phẳng 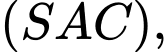
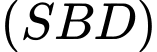 cùng vuông góc với mặt phẳng đáy. Khẳng định nào sau đây đúng?
cùng vuông góc với mặt phẳng đáy. Khẳng định nào sau đây đúng?
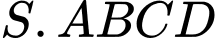 có đáy
có đáy 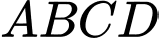 là hình bình hành tâm
là hình bình hành tâm  Hai mặt phẳng
Hai mặt phẳng 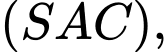
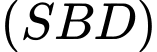 cùng vuông góc với mặt phẳng đáy. Khẳng định nào sau đây đúng?
cùng vuông góc với mặt phẳng đáy. Khẳng định nào sau đây đúng? A, 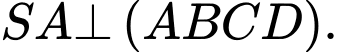
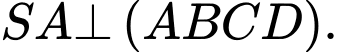
B, 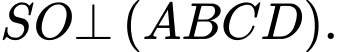
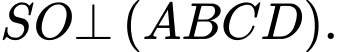
C, 

D, 

Chọn đáp án B.
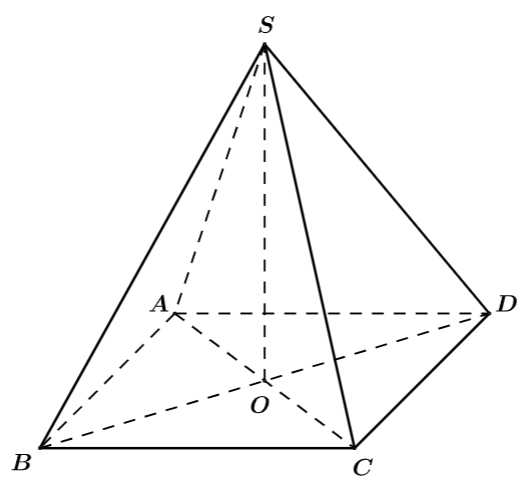
Xét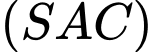 và
và 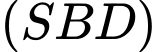 có:
có:
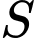 chung
chung
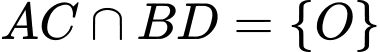
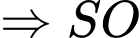 là giao tuyến của hai mặt phẳng
là giao tuyến của hai mặt phẳng 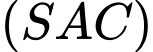 và
và 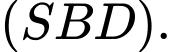
Mà hai mặt phẳng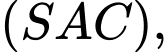
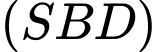 cùng vuông góc với mặt phẳng đáy.
cùng vuông góc với mặt phẳng đáy.
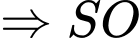 vuông góc với mặt phẳng đáy.
vuông góc với mặt phẳng đáy.
Hay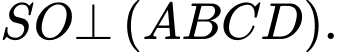 Đáp án: B
Đáp án: B

Xét
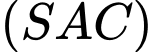 và
và 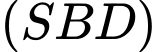 có:
có: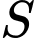 chung
chung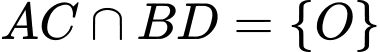
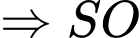 là giao tuyến của hai mặt phẳng
là giao tuyến của hai mặt phẳng 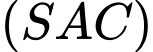 và
và 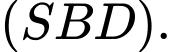
Mà hai mặt phẳng
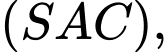
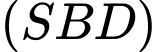 cùng vuông góc với mặt phẳng đáy.
cùng vuông góc với mặt phẳng đáy.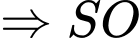 vuông góc với mặt phẳng đáy.
vuông góc với mặt phẳng đáy.Hay
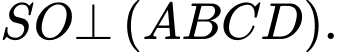 Đáp án: B
Đáp án: B
Câu 6 [693677]: Giá trị nhỏ nhất của hàm số 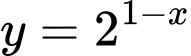 trên đoạn
trên đoạn 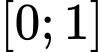 bằng
bằng
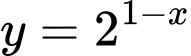 trên đoạn
trên đoạn 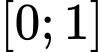 bằng
bằng A, 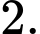
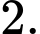
B, 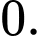
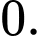
C, 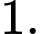
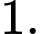
D, 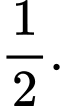
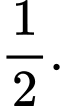
Chọn đáp án C.
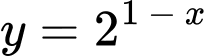
Ta có: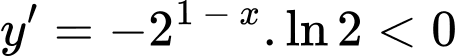 với
với 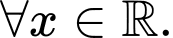
Suy ra hàm số nghịch biến trên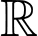 hay hàm số nghịch biến trên đoạn
hay hàm số nghịch biến trên đoạn 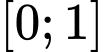
Vậy giá trị nhỏ nhất của hàm số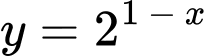 trên đoạn
trên đoạn 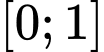 là
là 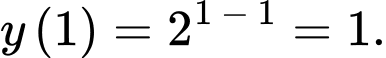 Đáp án: C
Đáp án: C
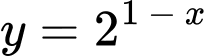
Ta có:
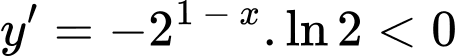 với
với 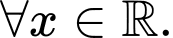
Suy ra hàm số nghịch biến trên
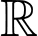 hay hàm số nghịch biến trên đoạn
hay hàm số nghịch biến trên đoạn 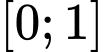
Vậy giá trị nhỏ nhất của hàm số
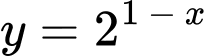 trên đoạn
trên đoạn 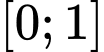 là
là 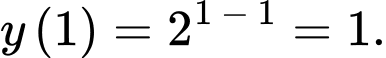 Đáp án: C
Đáp án: C
Câu 7 [693679]: Tập nghiệm của bất phương trình 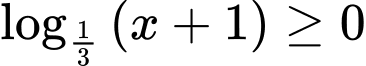 là
là
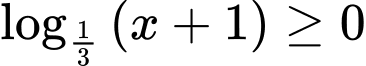 là
là A, 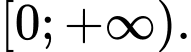
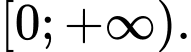
B, 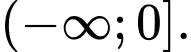
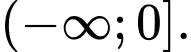
C, 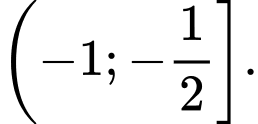
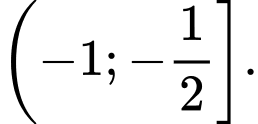
D, 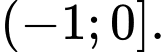
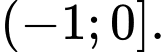
Chọn đáp án D.
ĐKXĐ: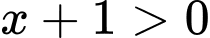


Ta có: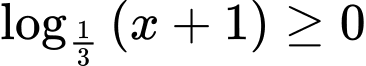
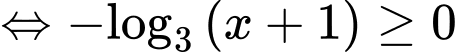
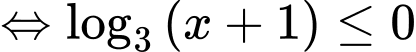

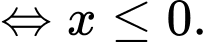
Vậy tập nghiệm của bất phương trình là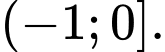 Đáp án: D
Đáp án: D
ĐKXĐ:
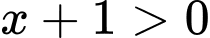


Ta có:
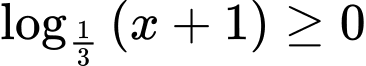
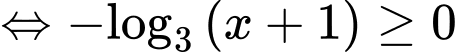
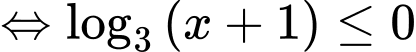

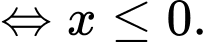
Vậy tập nghiệm của bất phương trình là
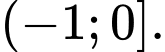 Đáp án: D
Đáp án: D
Câu 8 [616565]: Cho hình phẳng  giới hạn bởi các đường
giới hạn bởi các đường 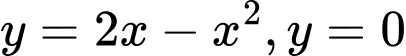 . Quay
. Quay  quanh trục hoành tạo thành khối tròn xoay có thể tích là
quanh trục hoành tạo thành khối tròn xoay có thể tích là
 giới hạn bởi các đường
giới hạn bởi các đường 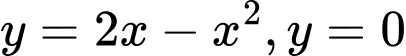 . Quay
. Quay  quanh trục hoành tạo thành khối tròn xoay có thể tích là
quanh trục hoành tạo thành khối tròn xoay có thể tích là A, 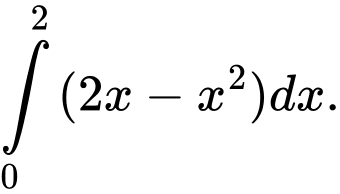
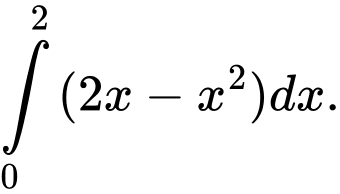
B, 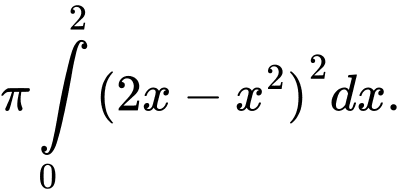
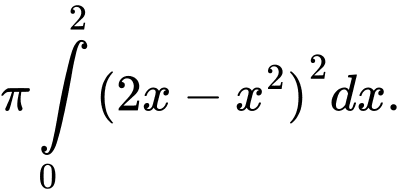
C, 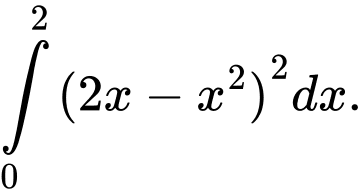
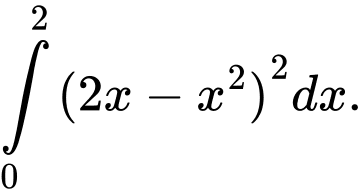
D, 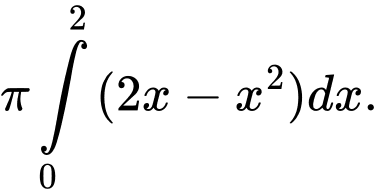
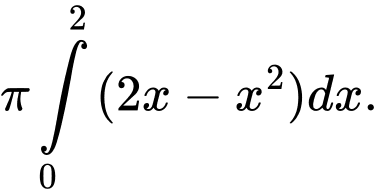
Chọn đáp án B.
Ta có: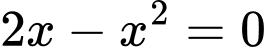

Theo công thức thể tích giới hạn bởi các đường ta có: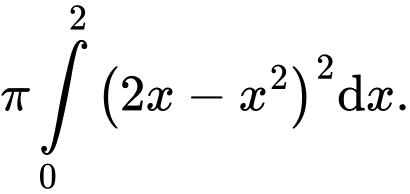 Đáp án: B
Đáp án: B
Ta có:
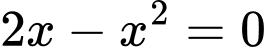

Theo công thức thể tích giới hạn bởi các đường ta có:
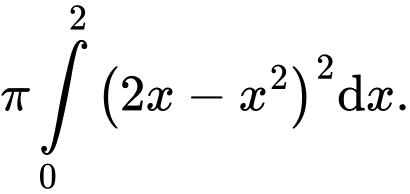 Đáp án: B
Đáp án: B
Câu 9 [810778]: Trong không gian 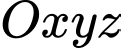 , cho mặt cầu
, cho mặt cầu 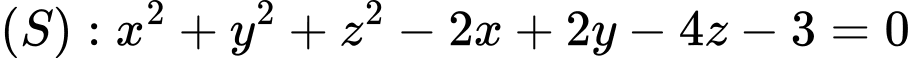 . Tâm của mặt cầu
. Tâm của mặt cầu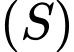 có tọa độ là
có tọa độ là
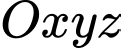 , cho mặt cầu
, cho mặt cầu 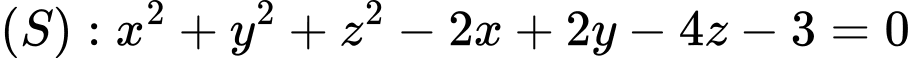 . Tâm của mặt cầu
. Tâm của mặt cầu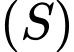 có tọa độ là
có tọa độ là A, 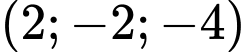 .
.
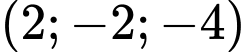 .
.B, 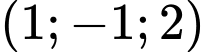 .
.
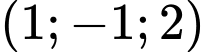 .
.C, 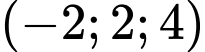 .
.
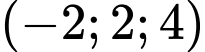 .
.D, 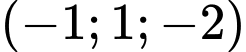 .
.
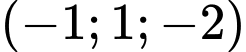 .
.
Chọn đáp án B.
Tâm của mặt cầu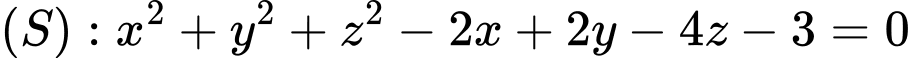 là
là 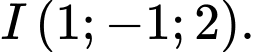 Đáp án: B
Đáp án: B
Tâm của mặt cầu
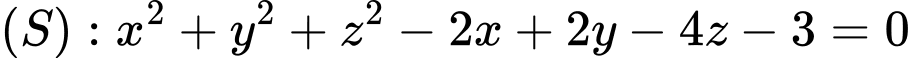 là
là 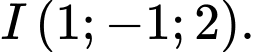 Đáp án: B
Đáp án: B
Câu 10 [693680]: Cho hàm số bậc ba 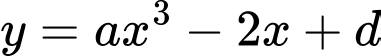
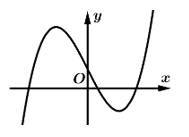
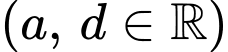 có đồ thị như hình vẽ bên. Khẳng định nào sau đây đúng?
có đồ thị như hình vẽ bên. Khẳng định nào sau đây đúng?
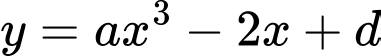
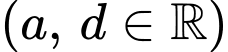 có đồ thị như hình vẽ bên. Khẳng định nào sau đây đúng?
có đồ thị như hình vẽ bên. Khẳng định nào sau đây đúng?
A, 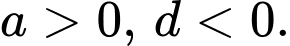
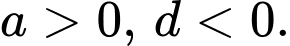
B, 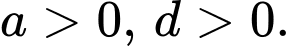
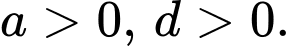
C, 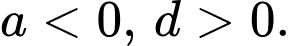
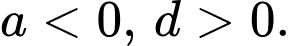
D, 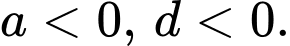
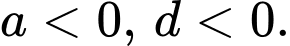
Chọn đáp án B.
Từ đồ thị hình vẽ ta thấy đồ thị có nét cuối hướng lên nên
Lại có: Đồ thị cắt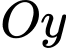 tại điểm có tung độ dương và tọa độ của điểm đó là
tại điểm có tung độ dương và tọa độ của điểm đó là 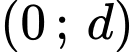
 Đáp án: B
Đáp án: B
Từ đồ thị hình vẽ ta thấy đồ thị có nét cuối hướng lên nên

Lại có: Đồ thị cắt
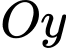 tại điểm có tung độ dương và tọa độ của điểm đó là
tại điểm có tung độ dương và tọa độ của điểm đó là 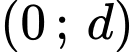
 Đáp án: B
Đáp án: B
Câu 11 [693683]: Chiều cao của các bạn học sinh nữ lớp 12B được ghi lại ở bảng sau:

Khoảng tứ phân vị của mẫu số liệu ghép nhóm trên gần với giá trị nào nhất sau đây?

Khoảng tứ phân vị của mẫu số liệu ghép nhóm trên gần với giá trị nào nhất sau đây?
A, 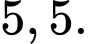
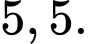
B, 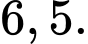
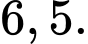
C, 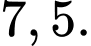
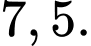
D, 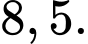
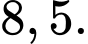
Chọn đáp án C.
Số học sinh nữ của lớp 12B được khảo sát là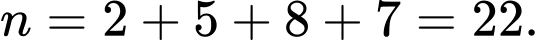
Gọi là chiều cao của 22 người được sắp xếp theo thứ tự không giảm.
là chiều cao của 22 người được sắp xếp theo thứ tự không giảm.
Ta có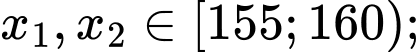
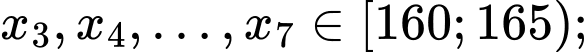
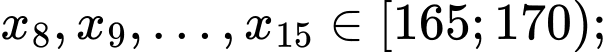
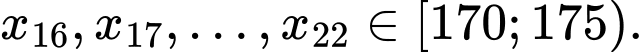 Do đó đối với dãy số liệu
Do đó đối với dãy số liệu  thì
thì
Tứ phân vị thứ nhất của dãy số liệu là
là 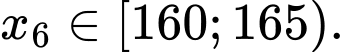 Do đó tứ phân vị thứ nhất của mẫu số liệu ghép nhóm là:
Do đó tứ phân vị thứ nhất của mẫu số liệu ghép nhóm là:
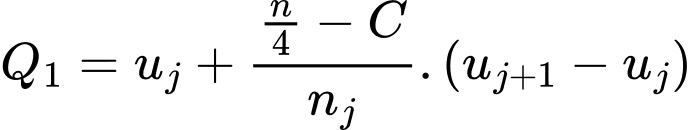
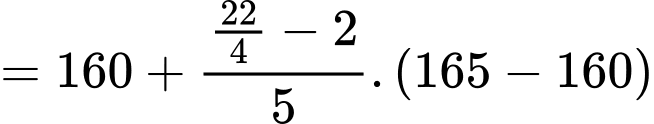
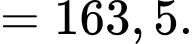
Tứ phân vị thứ ba của dãy số liệu là
là 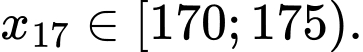 Do đó tứ phân vị thứ ba của mẫu số liệu ghép nhóm là:
Do đó tứ phân vị thứ ba của mẫu số liệu ghép nhóm là:
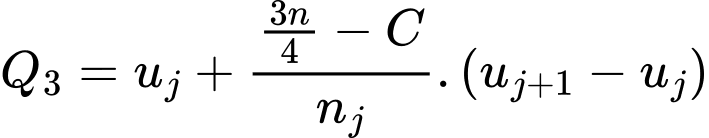
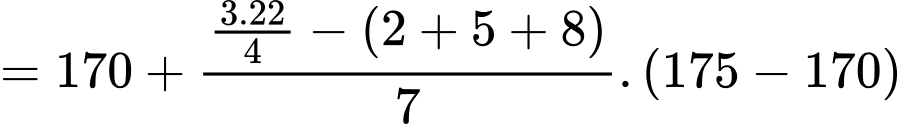
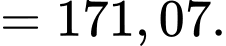
Vậy khoảng tứ phân vị của mẫu số liệu ghép nhóm là:
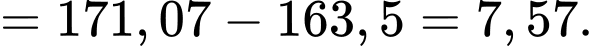 Đáp án: C
Đáp án: C
Số học sinh nữ của lớp 12B được khảo sát là
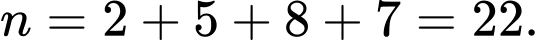
Gọi
 là chiều cao của 22 người được sắp xếp theo thứ tự không giảm.
là chiều cao của 22 người được sắp xếp theo thứ tự không giảm.Ta có
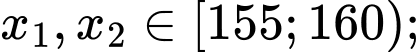
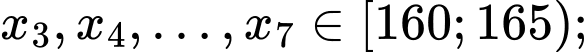
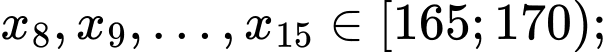
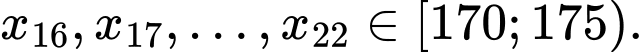 Do đó đối với dãy số liệu
Do đó đối với dãy số liệu  thì
thìTứ phân vị thứ nhất của dãy số liệu
 là
là 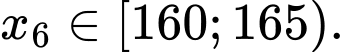 Do đó tứ phân vị thứ nhất của mẫu số liệu ghép nhóm là:
Do đó tứ phân vị thứ nhất của mẫu số liệu ghép nhóm là: 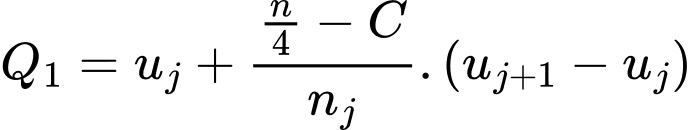
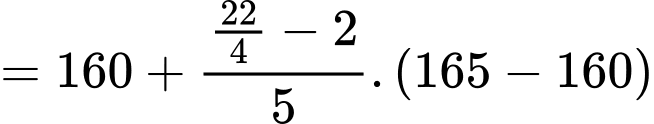
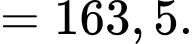
Tứ phân vị thứ ba của dãy số liệu
 là
là 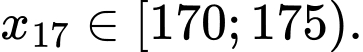 Do đó tứ phân vị thứ ba của mẫu số liệu ghép nhóm là:
Do đó tứ phân vị thứ ba của mẫu số liệu ghép nhóm là: 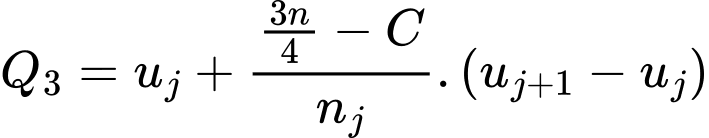
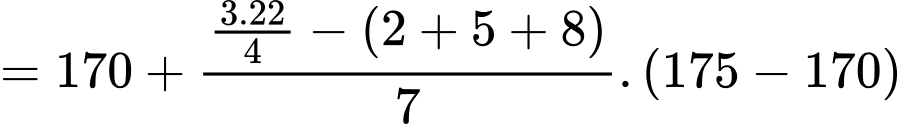
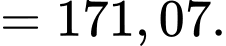
Vậy khoảng tứ phân vị của mẫu số liệu ghép nhóm là:

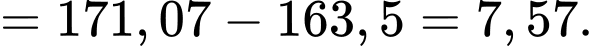 Đáp án: C
Đáp án: C
Câu 12 [693684]: Cho hình lăng trụ tam giác đều  có cạnh
có cạnh 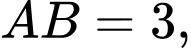
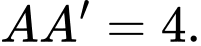 Độ dài của vectơ
Độ dài của vectơ 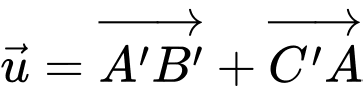 bằng
bằng
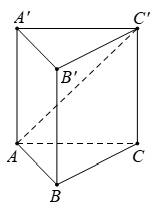
 có cạnh
có cạnh 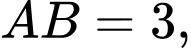
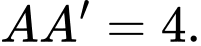 Độ dài của vectơ
Độ dài của vectơ 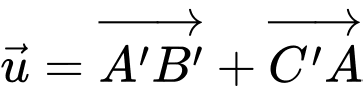 bằng
bằng
A, 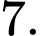
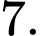
B, 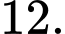
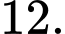
C, 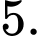
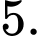
D, 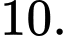
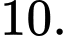
Chọn đáp án C.
Ta có: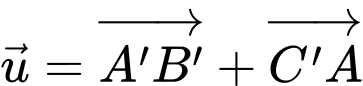
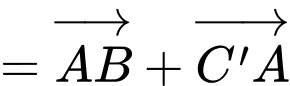
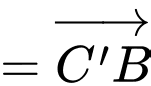
Vậy độ dài của vectơ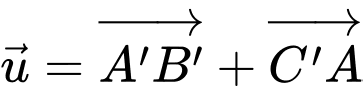 bằng
bằng 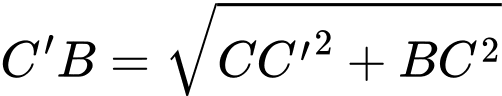
 Đáp án: C
Đáp án: C
Ta có:
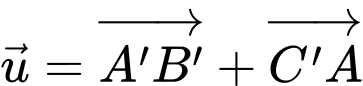
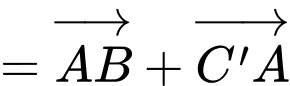
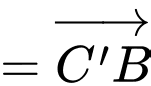
Vậy độ dài của vectơ
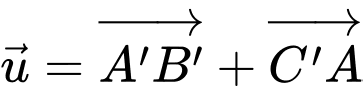 bằng
bằng 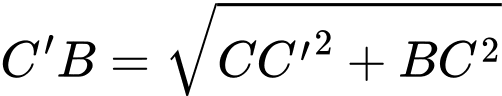
 Đáp án: C
Đáp án: C PHẦN II. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Câu 13 [694446]: Cho hàm số 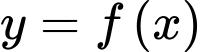 có đạo hàm là
có đạo hàm là 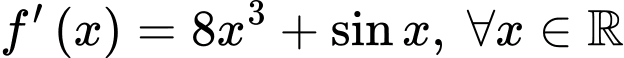 và thoả mãn
và thoả mãn 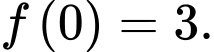
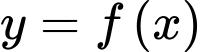 có đạo hàm là
có đạo hàm là 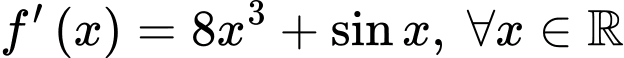 và thoả mãn
và thoả mãn 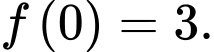
a) Đúng.
Hàm số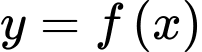 là một nguyên hàm của hàm số
là một nguyên hàm của hàm số 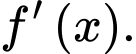
b) Đúng.
Ta có: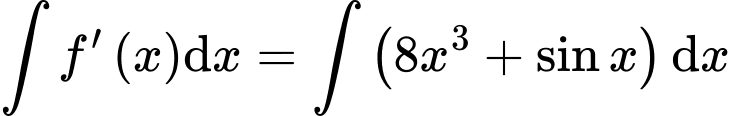
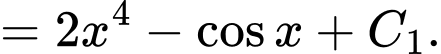
Do đó,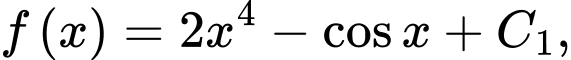 với
với  là hằng số.
là hằng số.
c) Sai.
Ta có:
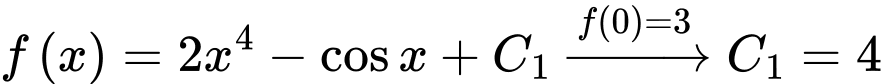
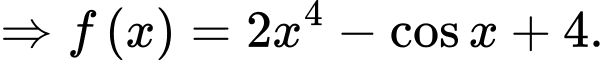
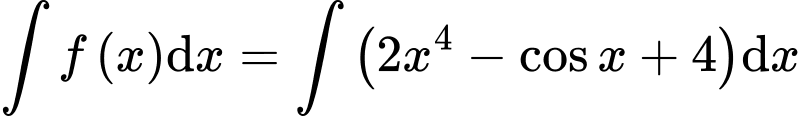
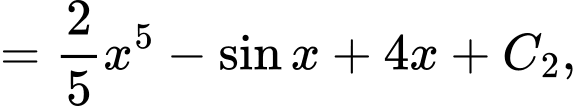 với
với 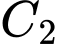 là hằng số.
là hằng số.
d) Đúng.
Ta có: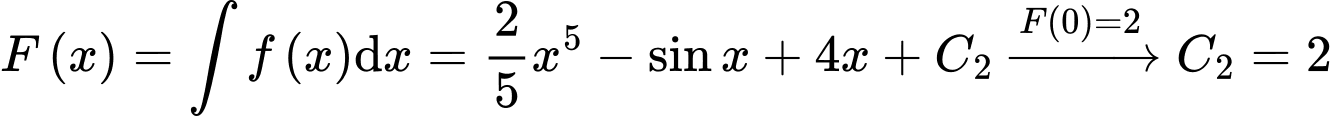
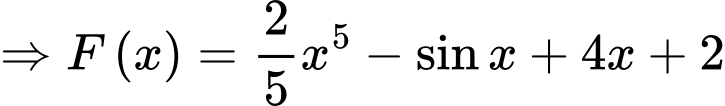
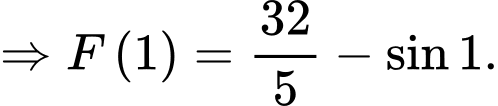
Hàm số
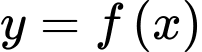 là một nguyên hàm của hàm số
là một nguyên hàm của hàm số 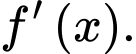
b) Đúng.
Ta có:
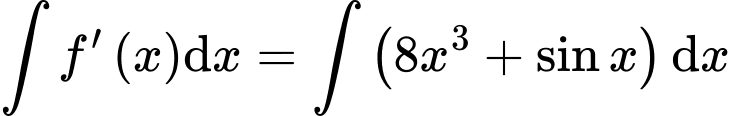
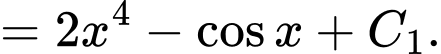
Do đó,
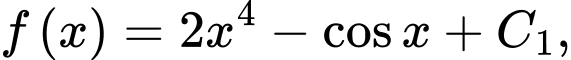 với
với  là hằng số.
là hằng số.c) Sai.
Ta có:
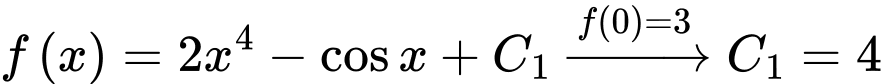
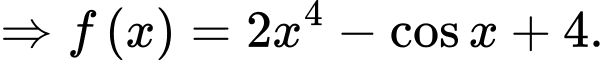
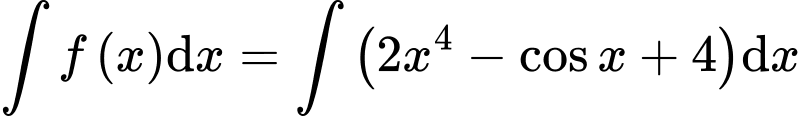
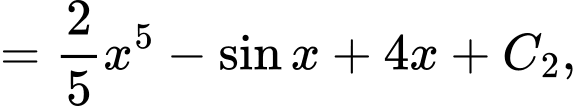 với
với 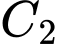 là hằng số.
là hằng số.d) Đúng.
Ta có:
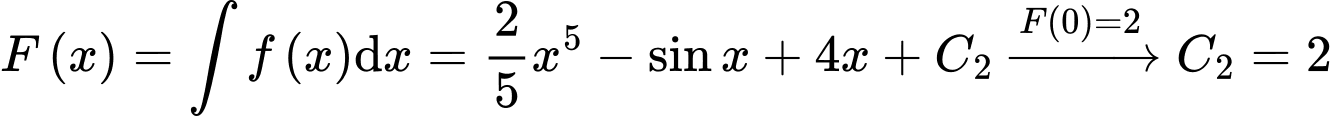
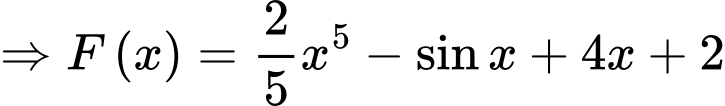
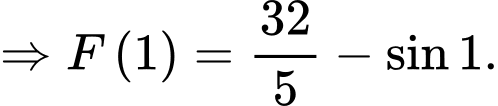
Câu 14 [702784]: Một hòn đá được ném từ một cây cầu với quỹ đạo ban đầu là 25° so với phương nằm ngang. Vào thời điểm nó di chuyển 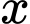 (m) theo phương ngang, chiều cao của hòn đá so với mặt nước dưới cầu được cho bởi
(m) theo phương ngang, chiều cao của hòn đá so với mặt nước dưới cầu được cho bởi 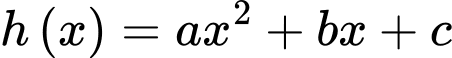 (mét) với
(mét) với 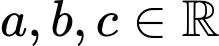 . Hòn đá được ném từ độ cao 3 mét so với mặt nước và đạt độ cao cực đại khi
. Hòn đá được ném từ độ cao 3 mét so với mặt nước và đạt độ cao cực đại khi 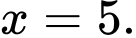
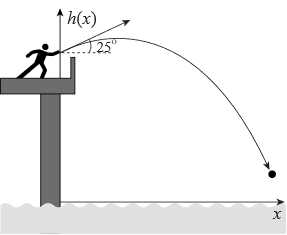
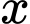 (m) theo phương ngang, chiều cao của hòn đá so với mặt nước dưới cầu được cho bởi
(m) theo phương ngang, chiều cao của hòn đá so với mặt nước dưới cầu được cho bởi 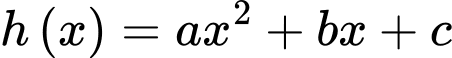 (mét) với
(mét) với 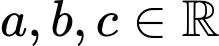 . Hòn đá được ném từ độ cao 3 mét so với mặt nước và đạt độ cao cực đại khi
. Hòn đá được ném từ độ cao 3 mét so với mặt nước và đạt độ cao cực đại khi 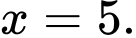

a) Đúng.
Do hòn đá được ném từ độ cao 3 mét so với mặt nước nên ta có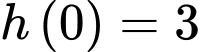
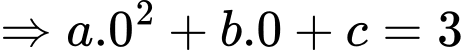
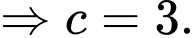
b) Đúng.
Ta có: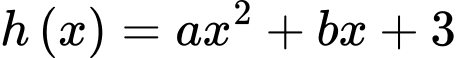
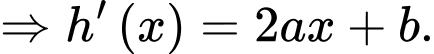
c) Sai.
Hòn đá đạt độ cao cực đại khi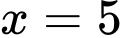 nên
nên  hay
hay 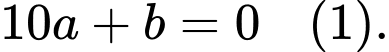
Hòn đá được ném từ một cây cầu với quỹ đạo ban đầu là 25° so với phương nằm ngang nên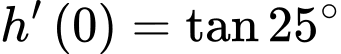
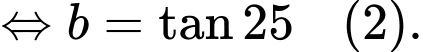
Từ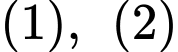 ta có:
ta có: 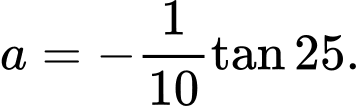
Do đó: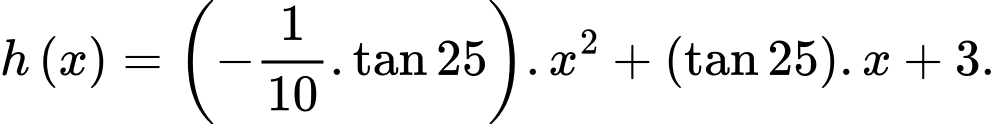
Độ cao lớn nhất của hòn đá so với mặt nước là
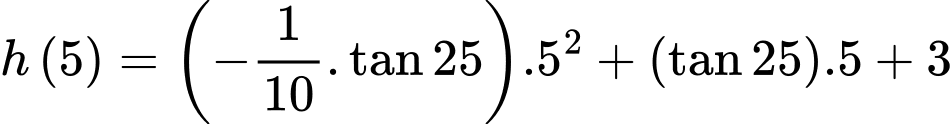
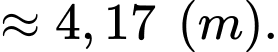
d) Sai.
Ta có: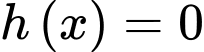
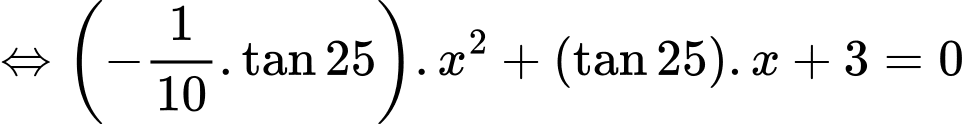
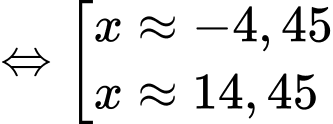
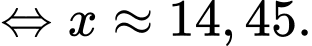
Vậy hòn đá rơi xuống nước tại vị trí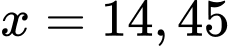 mét.
mét.
Do hòn đá được ném từ độ cao 3 mét so với mặt nước nên ta có
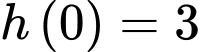
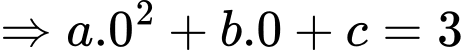
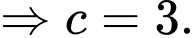
b) Đúng.
Ta có:
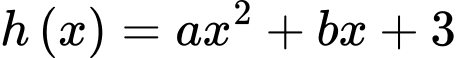
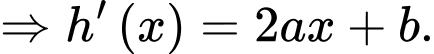
c) Sai.
Hòn đá đạt độ cao cực đại khi
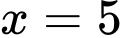 nên
nên  hay
hay 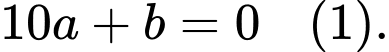
Hòn đá được ném từ một cây cầu với quỹ đạo ban đầu là 25° so với phương nằm ngang nên
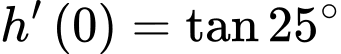
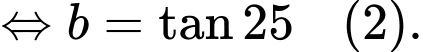
Từ
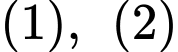 ta có:
ta có: 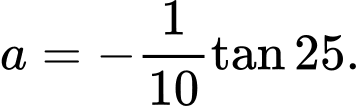
Do đó:
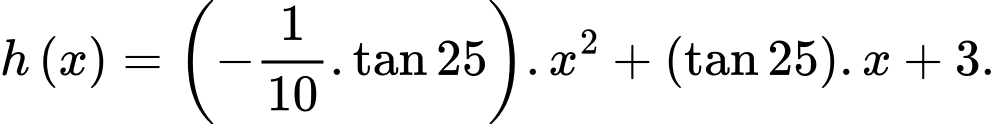
Độ cao lớn nhất của hòn đá so với mặt nước là
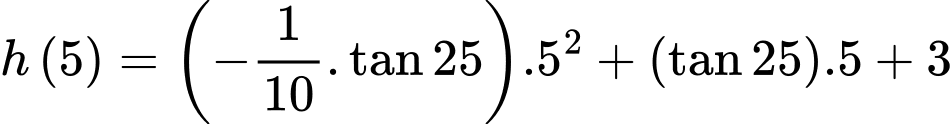
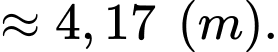
d) Sai.
Ta có:
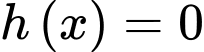
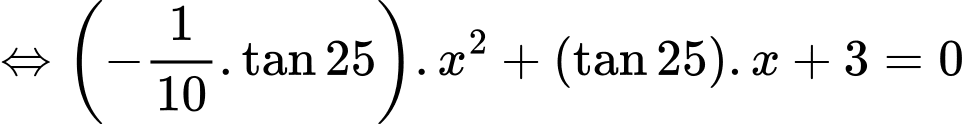
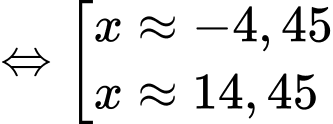
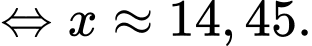
Vậy hòn đá rơi xuống nước tại vị trí
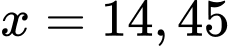 mét.
mét.
Câu 15 [700497]: Tỉ lệ học sinh tiêm vắc xin phòng bệnh Thủy Đậu trong một trường 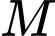 là
là 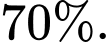 Trong số những học sinh đã tiêm phòng, tỉ lệ mắc bệnh Thủy Đậu là
Trong số những học sinh đã tiêm phòng, tỉ lệ mắc bệnh Thủy Đậu là 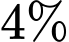 , còn trong số học sinh chưa tiêm, tỉ lệ mắc bệnh là
, còn trong số học sinh chưa tiêm, tỉ lệ mắc bệnh là 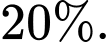 Gặp ngẫu nhiên một học sinh ở trường đó. Biết học sinh đó bị bệnh Thủy Đậu.
Gặp ngẫu nhiên một học sinh ở trường đó. Biết học sinh đó bị bệnh Thủy Đậu.
Gọi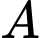 là biến cố: “Gặp học sinh mắc bệnh Thủy Đậu”.
là biến cố: “Gặp học sinh mắc bệnh Thủy Đậu”.
Gọi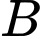 là biến cố: “Gặp học sinh đã tiêm vắc xin phòng bệnh Thủy Đậu”.
là biến cố: “Gặp học sinh đã tiêm vắc xin phòng bệnh Thủy Đậu”.
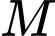 là
là 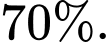 Trong số những học sinh đã tiêm phòng, tỉ lệ mắc bệnh Thủy Đậu là
Trong số những học sinh đã tiêm phòng, tỉ lệ mắc bệnh Thủy Đậu là 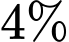 , còn trong số học sinh chưa tiêm, tỉ lệ mắc bệnh là
, còn trong số học sinh chưa tiêm, tỉ lệ mắc bệnh là 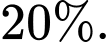 Gặp ngẫu nhiên một học sinh ở trường đó. Biết học sinh đó bị bệnh Thủy Đậu.
Gặp ngẫu nhiên một học sinh ở trường đó. Biết học sinh đó bị bệnh Thủy Đậu. Gọi
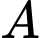 là biến cố: “Gặp học sinh mắc bệnh Thủy Đậu”.
là biến cố: “Gặp học sinh mắc bệnh Thủy Đậu”.Gọi
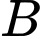 là biến cố: “Gặp học sinh đã tiêm vắc xin phòng bệnh Thủy Đậu”.
là biến cố: “Gặp học sinh đã tiêm vắc xin phòng bệnh Thủy Đậu”.
a) Sai.
Tỉ lệ học sinh tiêm vắc xin phòng bệnh Thủy Đậu trong một trường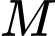 là 70% nên
là 70% nên 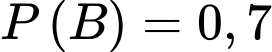
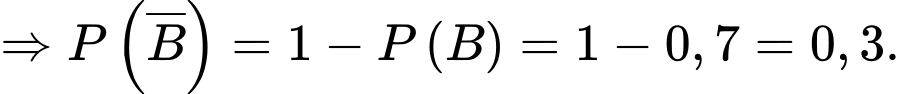
b) Đúng.
Trong số những học sinh đã tiêm phòng, tỉ lệ mắc bệnh Thủy Đậu là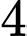 còn trong số học sinh chưa tiêm , tỉ lệ mắc bệnh là
còn trong số học sinh chưa tiêm , tỉ lệ mắc bệnh là 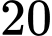 nên
nên 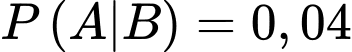 và
và 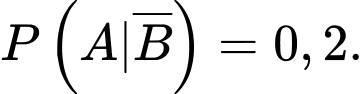
c) Sai.
Ta có sơ đồ cây sau:
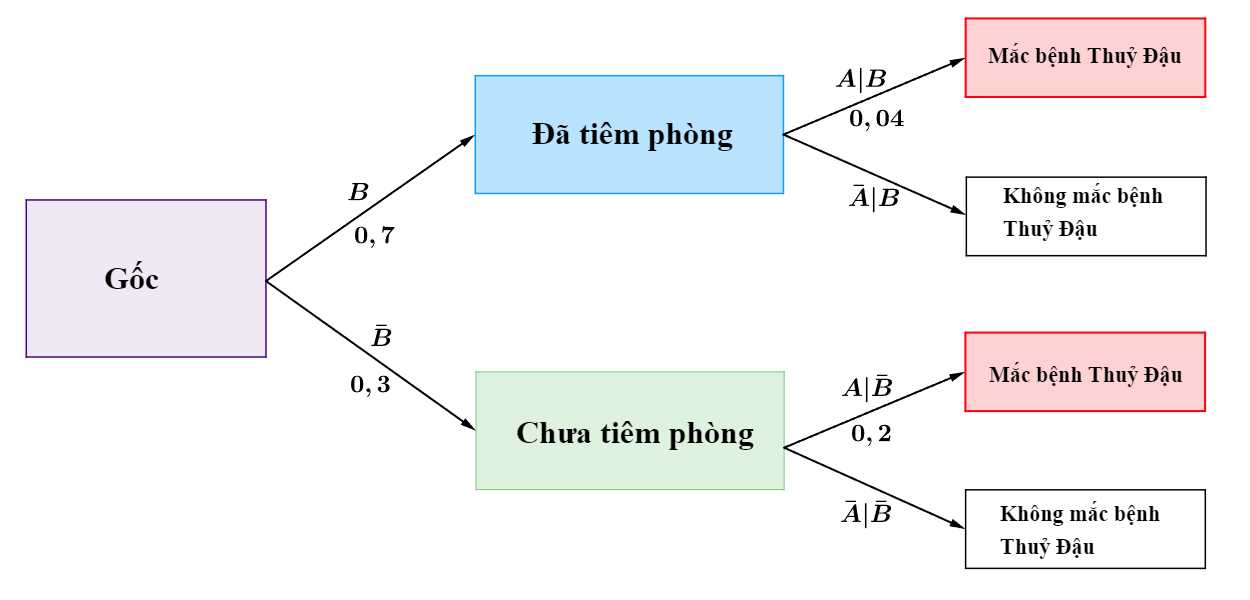
Áp dụng công thức xác suất toàn phần, ta có xác suất gặp học sinh bị bệnh Thủy Đậu là
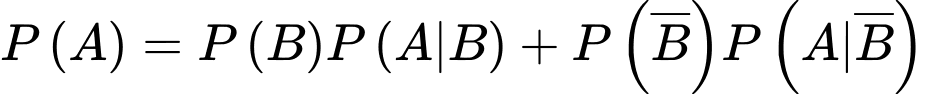
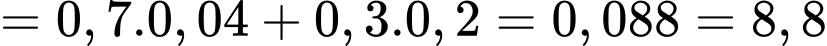
d) Đúng.
Xác suất học sinh đó không tiêm vắc xin phòng bệnh Thủy Đậu là
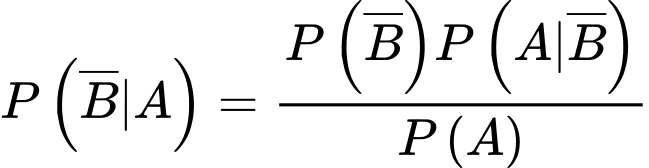
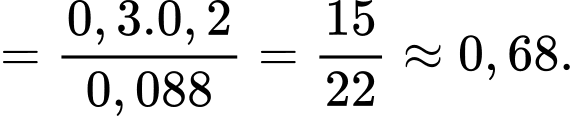
Tỉ lệ học sinh tiêm vắc xin phòng bệnh Thủy Đậu trong một trường
 là 70% nên
là 70% nên 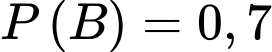
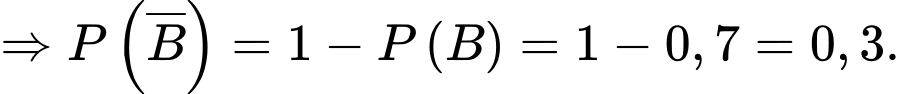
b) Đúng.
Trong số những học sinh đã tiêm phòng, tỉ lệ mắc bệnh Thủy Đậu là
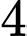 còn trong số học sinh chưa tiêm , tỉ lệ mắc bệnh là
còn trong số học sinh chưa tiêm , tỉ lệ mắc bệnh là 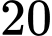 nên
nên 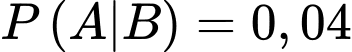 và
và 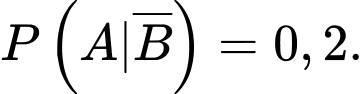
c) Sai.
Ta có sơ đồ cây sau:

Áp dụng công thức xác suất toàn phần, ta có xác suất gặp học sinh bị bệnh Thủy Đậu là
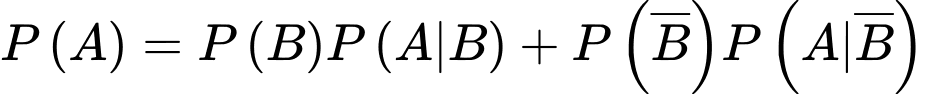
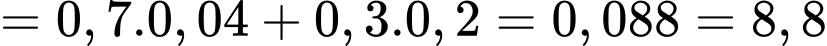
d) Đúng.
Xác suất học sinh đó không tiêm vắc xin phòng bệnh Thủy Đậu là
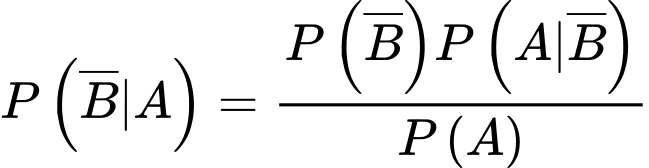
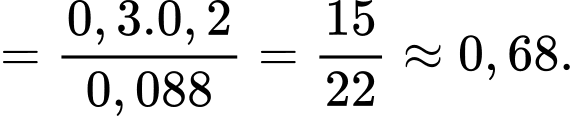
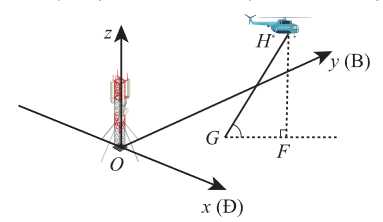
Câu 16 [700498]: Hình vẽ minh hoạ đường bay của một chiếc trực thăng 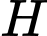 cất cánh từ một sân bay. Xét hệ trục toạ độ
cất cánh từ một sân bay. Xét hệ trục toạ độ 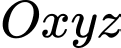 có gốc toạ độ
có gốc toạ độ  là chân tháp điều khiển của sân bay; trục
là chân tháp điều khiển của sân bay; trục 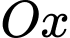 là hướng đông, trục
là hướng đông, trục 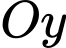 là hướng bắc và trục
là hướng bắc và trục  là trục thẳng đứng, đơn vị trên mỗi trục là kilômét. Trực thăng cất cánh từ điểm
là trục thẳng đứng, đơn vị trên mỗi trục là kilômét. Trực thăng cất cánh từ điểm  Vectơ
Vectơ 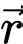 chỉ vị trí của trực thăng tại thời điểm
chỉ vị trí của trực thăng tại thời điểm 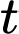 phút sau khi cất cánh
phút sau khi cất cánh 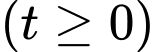 có toạ độ là:
có toạ độ là: 
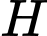 cất cánh từ một sân bay. Xét hệ trục toạ độ
cất cánh từ một sân bay. Xét hệ trục toạ độ 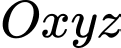 có gốc toạ độ
có gốc toạ độ  là chân tháp điều khiển của sân bay; trục
là chân tháp điều khiển của sân bay; trục 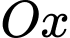 là hướng đông, trục
là hướng đông, trục 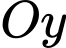 là hướng bắc và trục
là hướng bắc và trục  là trục thẳng đứng, đơn vị trên mỗi trục là kilômét. Trực thăng cất cánh từ điểm
là trục thẳng đứng, đơn vị trên mỗi trục là kilômét. Trực thăng cất cánh từ điểm  Vectơ
Vectơ 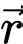 chỉ vị trí của trực thăng tại thời điểm
chỉ vị trí của trực thăng tại thời điểm 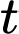 phút sau khi cất cánh
phút sau khi cất cánh 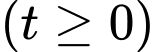 có toạ độ là:
có toạ độ là: 

a) Đúng.
Tại thời điểm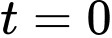 thì
thì 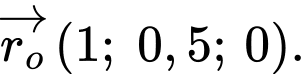
Trực thăng cất cánh tại điểm nên
nên 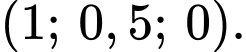
b) Sai.
Tại thời điểm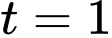 , trực thăng bay tới vị trí
, trực thăng bay tới vị trí 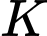 thuộc đường thẳng
thuộc đường thẳng 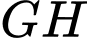 với
với 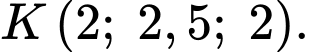
Đường thẳng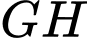 đi qua điểm
đi qua điểm 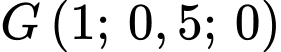 và có vectơ chỉ phương
và có vectơ chỉ phương 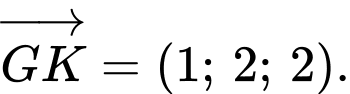
Phương trình đường thẳng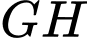 là
là 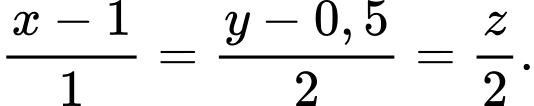
c) Đúng.
Gọi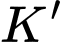 là hình chiếu của
là hình chiếu của 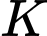 lên mặt phẳng
lên mặt phẳng 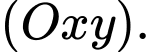 Suy ra
Suy ra 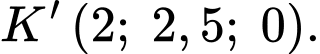
Vì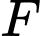 là hình chiếu của
là hình chiếu của 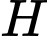 lên mặt phẳng
lên mặt phẳng 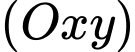 nên
nên 
Suy ra đường thẳng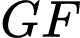 có một vectơ chỉ phương là
có một vectơ chỉ phương là 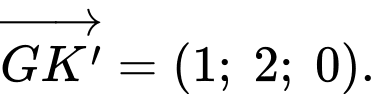
Phương trình tham số của đường thẳng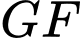 là
là 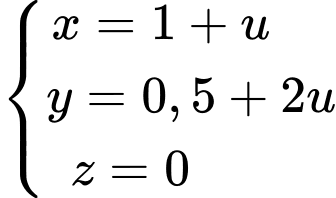 (
(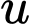 là tham số).
là tham số).
Vậy đường thẳng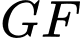 đi qua điểm
đi qua điểm 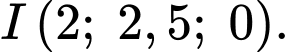
d) Đúng.
Ta có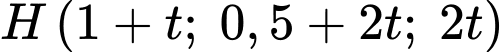 , khi đó
, khi đó 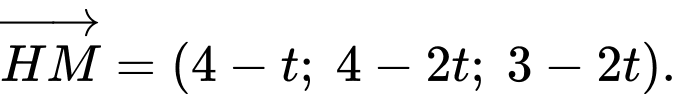
Đường thẳng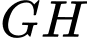 có vectơ chỉ phương
có vectơ chỉ phương 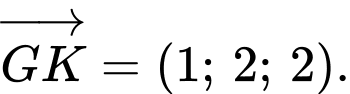
 vuông góc với đường bay
vuông góc với đường bay 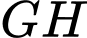 khi
khi 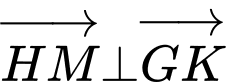
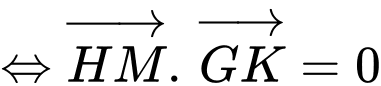
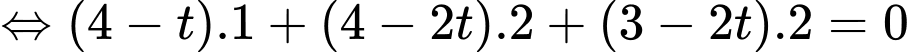
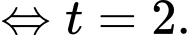
Khi đó khoảng cách từ đỉnh núi đến máy bay trực thăng là
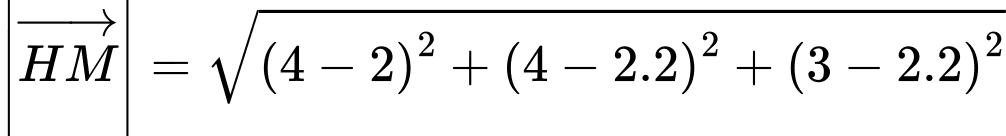
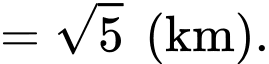
Tại thời điểm
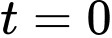 thì
thì 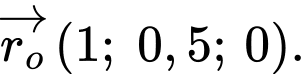
Trực thăng cất cánh tại điểm
 nên
nên 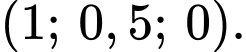
b) Sai.
Tại thời điểm
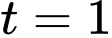 , trực thăng bay tới vị trí
, trực thăng bay tới vị trí 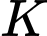 thuộc đường thẳng
thuộc đường thẳng 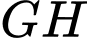 với
với 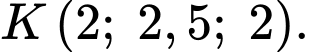
Đường thẳng
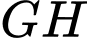 đi qua điểm
đi qua điểm 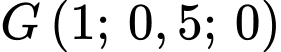 và có vectơ chỉ phương
và có vectơ chỉ phương 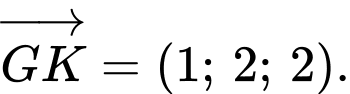
Phương trình đường thẳng
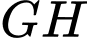 là
là 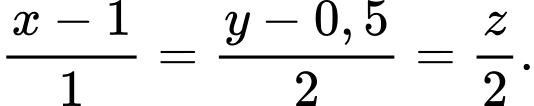
c) Đúng.
Gọi
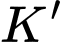 là hình chiếu của
là hình chiếu của 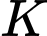 lên mặt phẳng
lên mặt phẳng 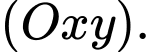 Suy ra
Suy ra 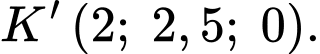
Vì
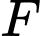 là hình chiếu của
là hình chiếu của 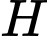 lên mặt phẳng
lên mặt phẳng 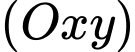 nên
nên 
Suy ra đường thẳng
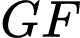 có một vectơ chỉ phương là
có một vectơ chỉ phương là 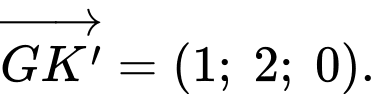
Phương trình tham số của đường thẳng
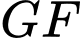 là
là 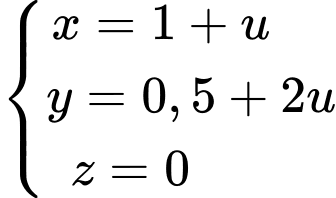 (
(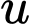 là tham số).
là tham số).Vậy đường thẳng
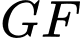 đi qua điểm
đi qua điểm 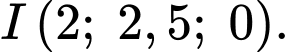
d) Đúng.
Ta có
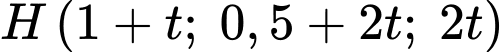 , khi đó
, khi đó 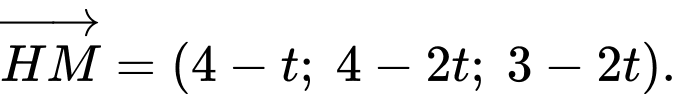
Đường thẳng
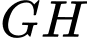 có vectơ chỉ phương
có vectơ chỉ phương 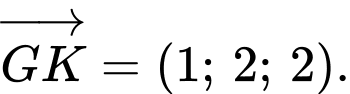
 vuông góc với đường bay
vuông góc với đường bay 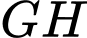 khi
khi 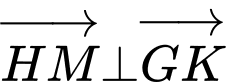
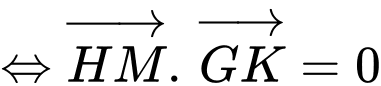
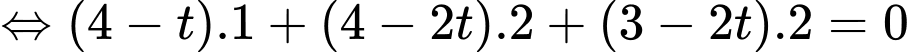
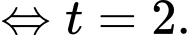
Khi đó khoảng cách từ đỉnh núi đến máy bay trực thăng là
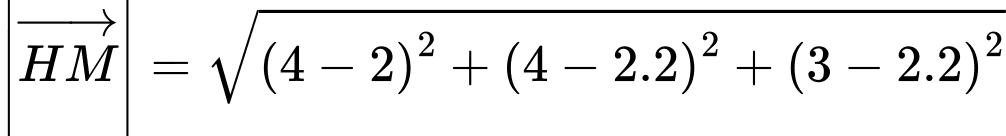
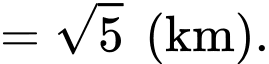
PHẦN III. Thí sinh trả lời từ câu 1 đến câu 6.
Câu 17 [693688]: Cho hình chóp 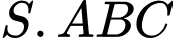 có đáy
có đáy 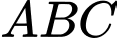 là tam giác vuông tại
là tam giác vuông tại  với
với 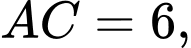
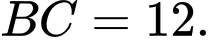 Cạnh bên
Cạnh bên 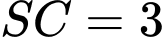 và
và 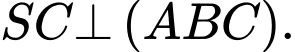 Gọi
Gọi 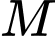 là trung điểm cạnh
là trung điểm cạnh 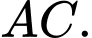 Khoảng cách giữa hai đường thẳng
Khoảng cách giữa hai đường thẳng 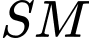 và
và  bằng bao nhiêu?
bằng bao nhiêu?
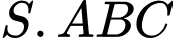 có đáy
có đáy 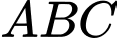 là tam giác vuông tại
là tam giác vuông tại  với
với 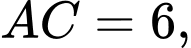
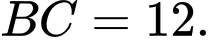 Cạnh bên
Cạnh bên 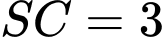 và
và 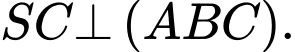 Gọi
Gọi 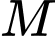 là trung điểm cạnh
là trung điểm cạnh 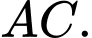 Khoảng cách giữa hai đường thẳng
Khoảng cách giữa hai đường thẳng 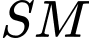 và
và  bằng bao nhiêu?
bằng bao nhiêu?
Điền đáp án: 
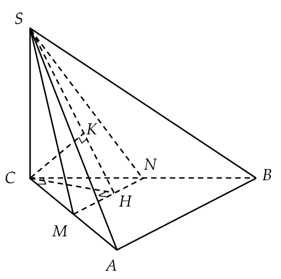
Gọi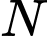 là trung điểm của
là trung điểm của 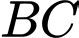
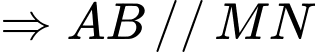 mà
mà 
Ta có: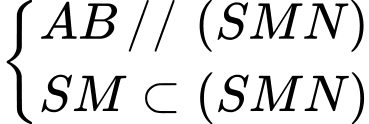
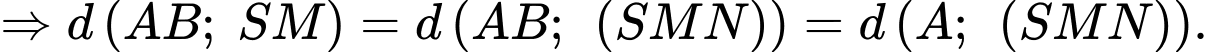
Do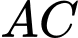 cắt
cắt 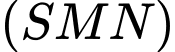 tại
tại 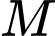 nên:
nên: 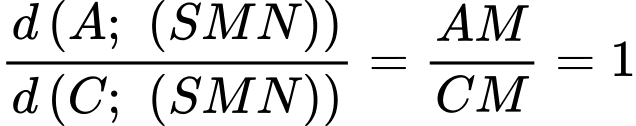
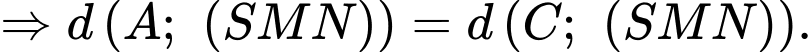
Kẻ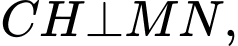
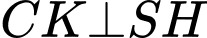 suy ra
suy ra 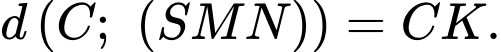
Tam giác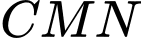 vuông tại
vuông tại  , đường cao
, đường cao 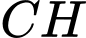 , ta có
, ta có 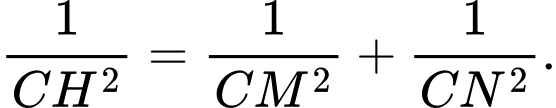
Tam giác vuông tại
vuông tại  , đường cao
, đường cao 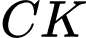 , ta có
, ta có 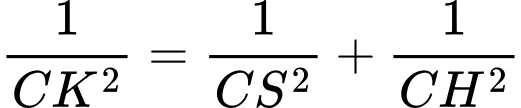
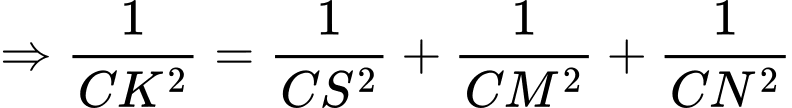
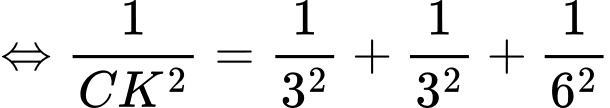
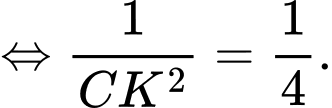
Vậy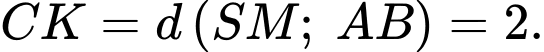
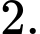

Gọi
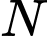 là trung điểm của
là trung điểm của 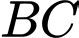
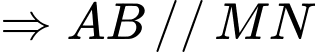 mà
mà 
Ta có:
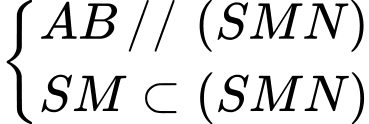
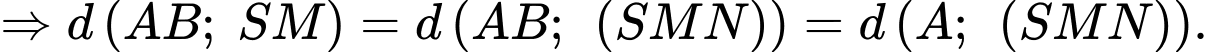
Do
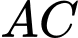 cắt
cắt 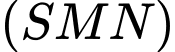 tại
tại 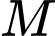 nên:
nên: 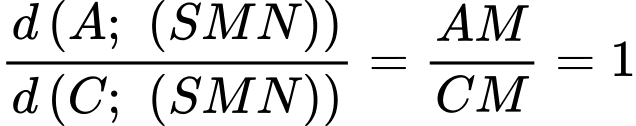
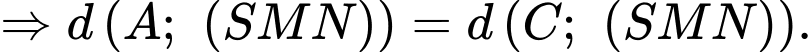
Kẻ
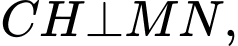
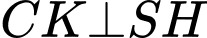 suy ra
suy ra 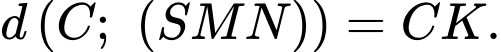
Tam giác
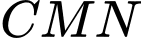 vuông tại
vuông tại  , đường cao
, đường cao 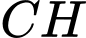 , ta có
, ta có 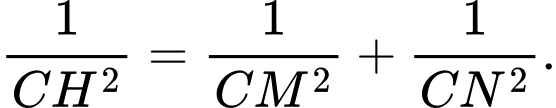
Tam giác
 vuông tại
vuông tại  , đường cao
, đường cao 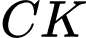 , ta có
, ta có 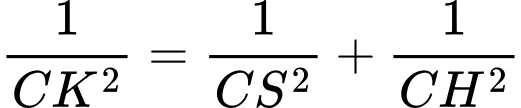
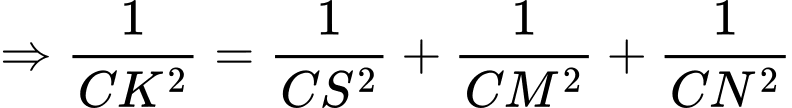
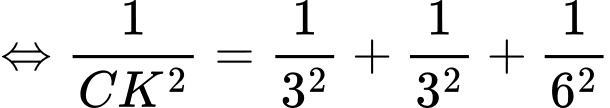
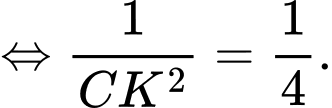
Vậy
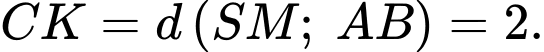
Câu 18 [693689]: Để làm một quả bóng như hình bên, người ta dùng một số mảnh da hình lục giác đều và hình ngũ giác đều có các cạnh bằng nhau, rồi khâu các cạnh chung của từng hai mảnh một sao cho cứ mỗi hình ngũ giác đều có cạnh chung với năm hình lục giác đều (hình vẽ). Hỏi cần dùng bao nhiêu mảnh da để làm mỗi quả bóng?


Điền đáp án: 32.
Gọi số ngũ giác màu sẫm là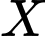 , số lục giác màu sáng là
, số lục giác màu sáng là 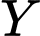 .
.
Mỗi lục giác chỉ có 3 cạnh tiếp xúc với các ngũ giác, mỗi ngũ giác có 5 cạnh tiếp xúc với các lục giác.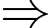 Tổng số cạnh chung của các lục giác và ngũ giác là
Tổng số cạnh chung của các lục giác và ngũ giác là 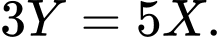 (1)
(1)
Do đó số lượng ngũ giác và lục giác theo tỷ lệ là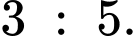
Theo định lý Euler thì ta có:
thì ta có:
Số đỉnh: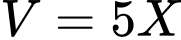
Số cạnh: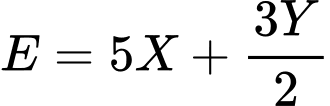
Số mặt: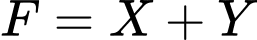
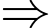
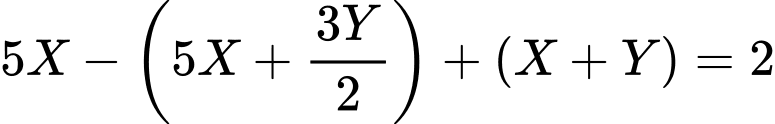
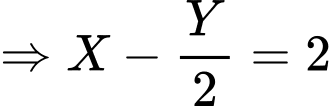 (2)
(2)
Từ (1) và (2)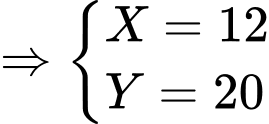
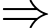 Cần dùng 32 mảnh.
Cần dùng 32 mảnh.
Gọi số ngũ giác màu sẫm là
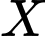 , số lục giác màu sáng là
, số lục giác màu sáng là 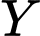 .
. Mỗi lục giác chỉ có 3 cạnh tiếp xúc với các ngũ giác, mỗi ngũ giác có 5 cạnh tiếp xúc với các lục giác.
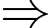 Tổng số cạnh chung của các lục giác và ngũ giác là
Tổng số cạnh chung của các lục giác và ngũ giác là 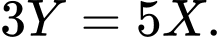 (1)
(1)Do đó số lượng ngũ giác và lục giác theo tỷ lệ là
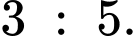
Theo định lý Euler
 thì ta có:
thì ta có: Số đỉnh:
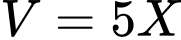
Số cạnh:
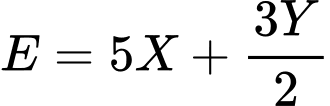
Số mặt:
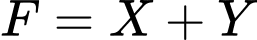
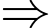
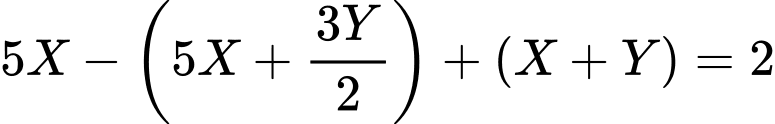
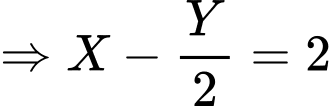 (2)
(2)Từ (1) và (2)
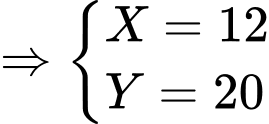
 Cần dùng 32 mảnh.
Cần dùng 32 mảnh.
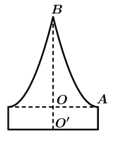
Câu 19 [693690]: Chuẩn bị cho đêm hội diễn văn nghệ chào đón năm mới, bạn An đã làm một chiếc mũ “cách điệu” cho ông già Noel có dáng một khối tròn xoay. Mặt cắt qua trục của chiếc mũ như hình vẽ bên dưới. Biết rằng 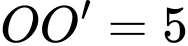

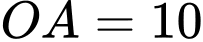

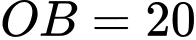
 đường cong
đường cong  là một phần của parabol có đỉnh là điểm
là một phần của parabol có đỉnh là điểm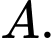 Thể tích của chiếc mũ bằng bao nhiêu centimet khối? (kết quả làm tròn đến hàng đơn vị).
Thể tích của chiếc mũ bằng bao nhiêu centimet khối? (kết quả làm tròn đến hàng đơn vị).
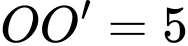

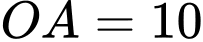

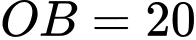
 đường cong
đường cong  là một phần của parabol có đỉnh là điểm
là một phần của parabol có đỉnh là điểm Thể tích của chiếc mũ bằng bao nhiêu centimet khối? (kết quả làm tròn đến hàng đơn vị).
Thể tích của chiếc mũ bằng bao nhiêu centimet khối? (kết quả làm tròn đến hàng đơn vị).
Điền đáp án: 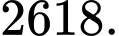
Gọi là thể tích của chiếc mũ,
là thể tích của chiếc mũ, 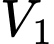 là thể tích của khối trụ có chiều cao là
là thể tích của khối trụ có chiều cao là 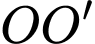 , bán kính đáy là
, bán kính đáy là 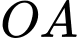 nên
nên 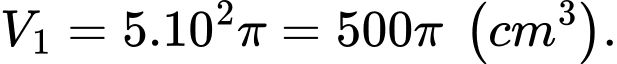
Gọi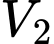 là thể tích phần còn lại của chiếc mũ.
là thể tích phần còn lại của chiếc mũ.
Chọn hệ trục toạ độ có là gốc toạ độ,
là gốc toạ độ, 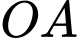 nằm trên
nằm trên 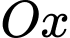 ,
, 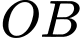 nằm trên
nằm trên 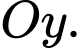
Khi đó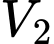 là thể tích khối tròn xoay khi quay hình phẳng giới hạn bởi nhánh parabol
là thể tích khối tròn xoay khi quay hình phẳng giới hạn bởi nhánh parabol  và trục
và trục 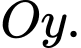
Phương trình parabol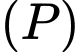 chứa nhánh
chứa nhánh  có dạng
có dạng 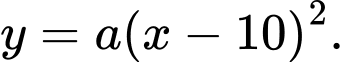
Vì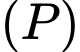 đi qua điểm
đi qua điểm 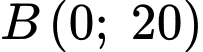 nên
nên 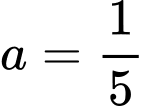 , do đó
, do đó 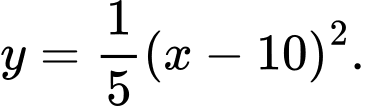
Suy ra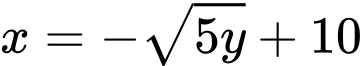 (do
(do  ).
).
Vậy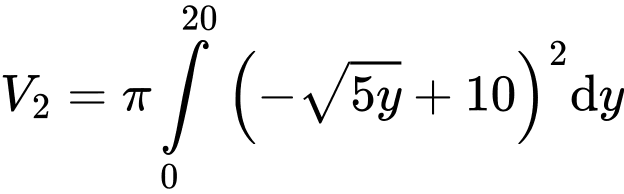
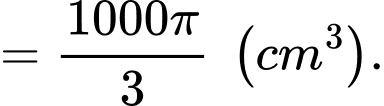
Vậy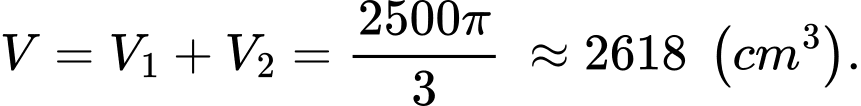
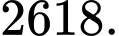
Gọi
 là thể tích của chiếc mũ,
là thể tích của chiếc mũ, 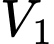 là thể tích của khối trụ có chiều cao là
là thể tích của khối trụ có chiều cao là 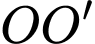 , bán kính đáy là
, bán kính đáy là 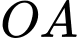 nên
nên 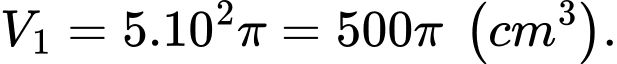
Gọi
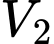 là thể tích phần còn lại của chiếc mũ.
là thể tích phần còn lại của chiếc mũ.Chọn hệ trục toạ độ có
 là gốc toạ độ,
là gốc toạ độ, 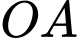 nằm trên
nằm trên 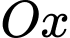 ,
, 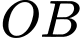 nằm trên
nằm trên 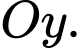
Khi đó
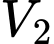 là thể tích khối tròn xoay khi quay hình phẳng giới hạn bởi nhánh parabol
là thể tích khối tròn xoay khi quay hình phẳng giới hạn bởi nhánh parabol  và trục
và trục 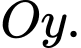
Phương trình parabol
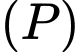 chứa nhánh
chứa nhánh  có dạng
có dạng 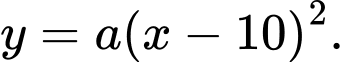
Vì
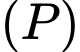 đi qua điểm
đi qua điểm 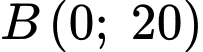 nên
nên 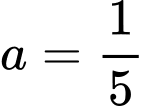 , do đó
, do đó 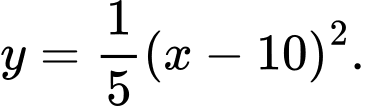
Suy ra
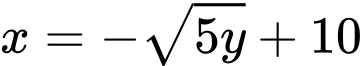 (do
(do  ).
). Vậy
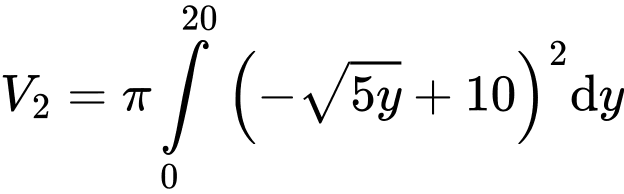
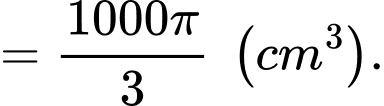
Vậy
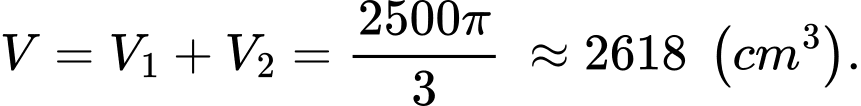
Câu 20 [693692]: Trong không gian 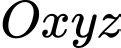 (đơn vị đo là km), bốn chiếc máy bay ở bốn hướng khác nhau khi vừa bay vào vùng phủ sóng của một chiếc ra đa thì trên ra đa cùng một lúc báo tín hiệu phát hiện mục tiêu. Tại thời điểm ra đa phát hiện mục tiêu thì 4 chiếc máy bay ở vị trí có tọa độ lần lượt là
(đơn vị đo là km), bốn chiếc máy bay ở bốn hướng khác nhau khi vừa bay vào vùng phủ sóng của một chiếc ra đa thì trên ra đa cùng một lúc báo tín hiệu phát hiện mục tiêu. Tại thời điểm ra đa phát hiện mục tiêu thì 4 chiếc máy bay ở vị trí có tọa độ lần lượt là 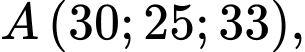
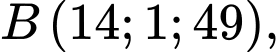
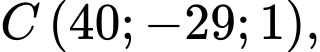
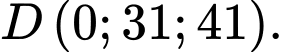 Hỏi bán kính vùng phủ sóng của rada là bao nhiêu km?
Hỏi bán kính vùng phủ sóng của rada là bao nhiêu km?
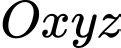 (đơn vị đo là km), bốn chiếc máy bay ở bốn hướng khác nhau khi vừa bay vào vùng phủ sóng của một chiếc ra đa thì trên ra đa cùng một lúc báo tín hiệu phát hiện mục tiêu. Tại thời điểm ra đa phát hiện mục tiêu thì 4 chiếc máy bay ở vị trí có tọa độ lần lượt là
(đơn vị đo là km), bốn chiếc máy bay ở bốn hướng khác nhau khi vừa bay vào vùng phủ sóng của một chiếc ra đa thì trên ra đa cùng một lúc báo tín hiệu phát hiện mục tiêu. Tại thời điểm ra đa phát hiện mục tiêu thì 4 chiếc máy bay ở vị trí có tọa độ lần lượt là 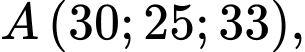
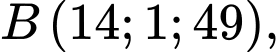
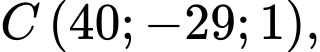
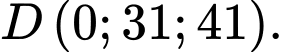 Hỏi bán kính vùng phủ sóng của rada là bao nhiêu km?
Hỏi bán kính vùng phủ sóng của rada là bao nhiêu km?
Điền đáp án: 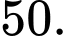
Gọi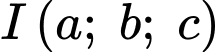 là tâm của mặt cầu đi qua bốn điểm
là tâm của mặt cầu đi qua bốn điểm 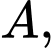
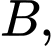
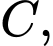
 Khi đó:
Khi đó:  .
.
Ta có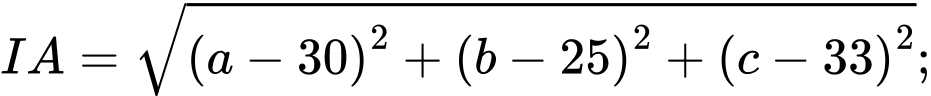
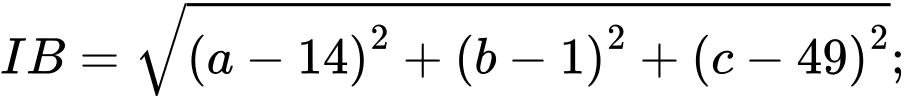
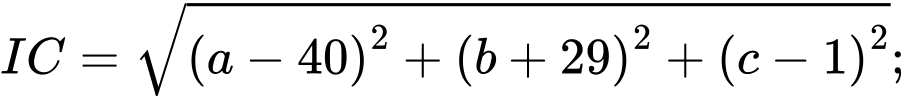
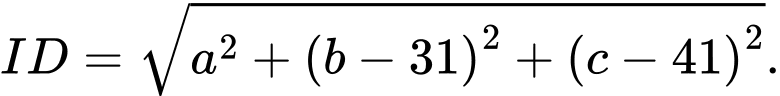
Ta có: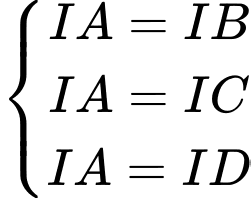
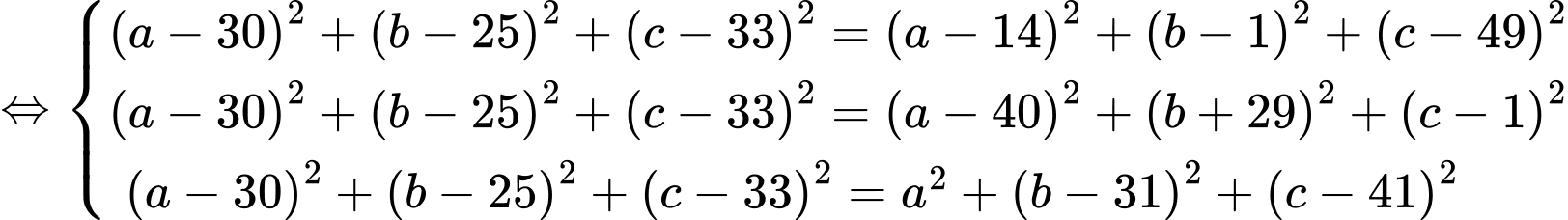
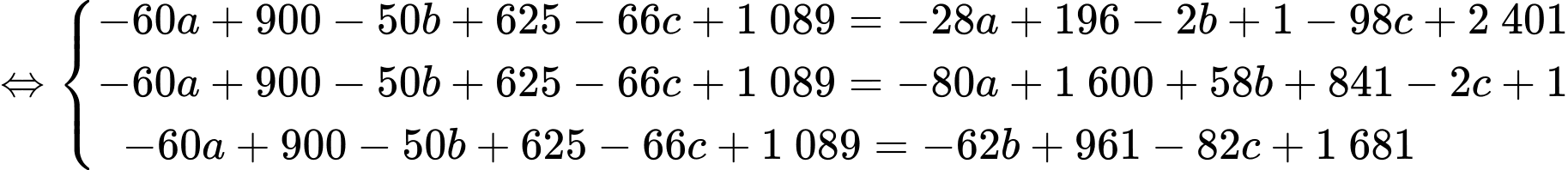
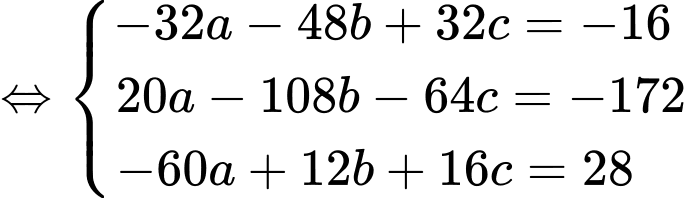
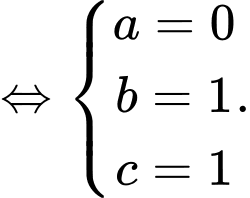
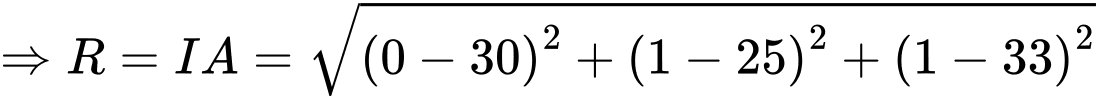
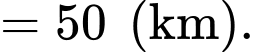
Vậy bán kính vùng phủ sóng của radar là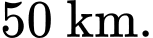
Gọi
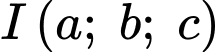 là tâm của mặt cầu đi qua bốn điểm
là tâm của mặt cầu đi qua bốn điểm 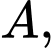
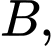
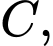
 Khi đó:
Khi đó:  .
.Ta có
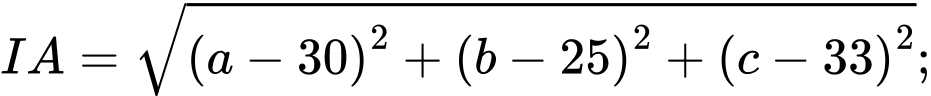
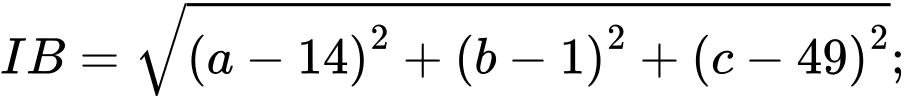
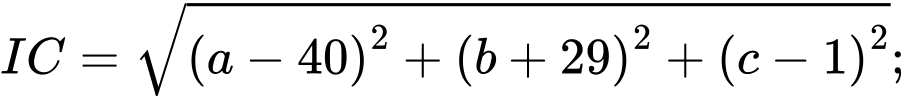
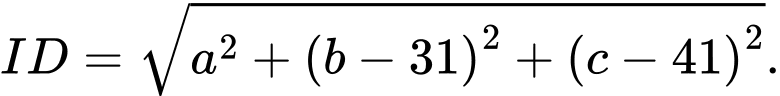
Ta có:
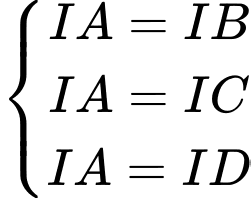
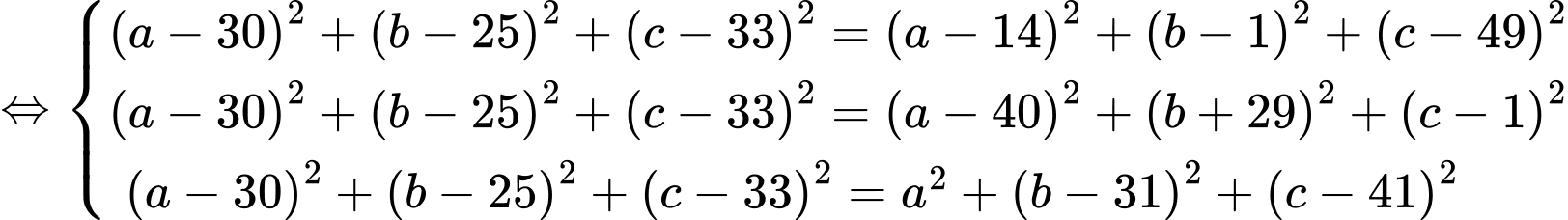
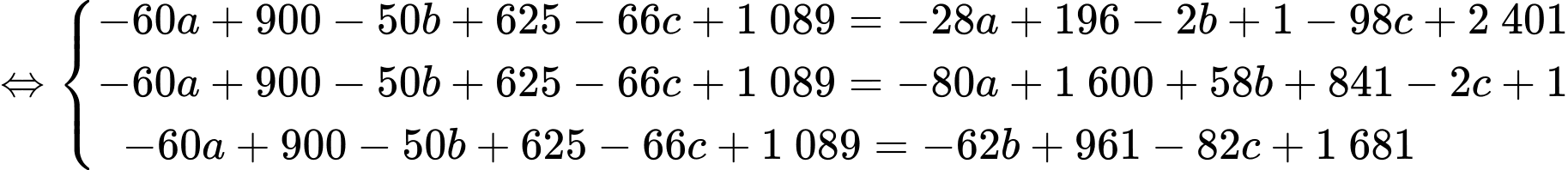
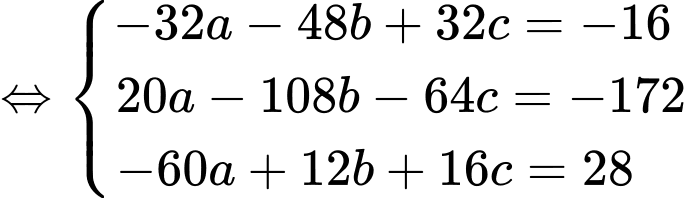
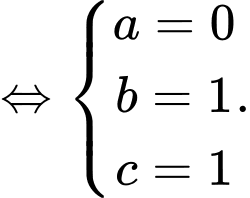
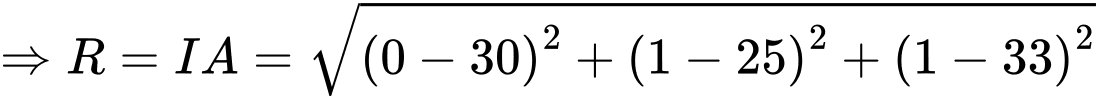
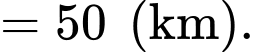
Vậy bán kính vùng phủ sóng của radar là
Câu 21 [700499]: Tại một phòng khám chuyên khoa tỷ lệ người đến khám có bệnh là 0,8. Người ta áp dụng phương pháp chẩn đoán mới thì thấy nếu khẳng định có bệnh thì đúng 9 trên 10 trường hợp; còn nếu khẳng định không bệnh thì đúng 5 trên 10 trường hợp. Hỏi xác suất chẩn đoán đúng là bao nhiêu %. Biết rằng chẩn đoán đúng là khi người bị bệnh được chẩn đoán có bệnh hoặc người không bị bệnh được chẩn đoán không bị bệnh.
Điền đáp án: 80.
Gọi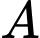 là biến cố “Khẳng định có bệnh”
là biến cố “Khẳng định có bệnh”
 là biến cố “Khẳng định không bệnh”
là biến cố “Khẳng định không bệnh”
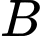 là biến cố “Chẩn đoán đúng”
là biến cố “Chẩn đoán đúng”
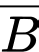 là biến cố “Chẩn đoán sai”
là biến cố “Chẩn đoán sai”
Từ dữ kiện đề bài, ta có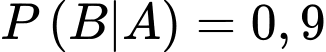
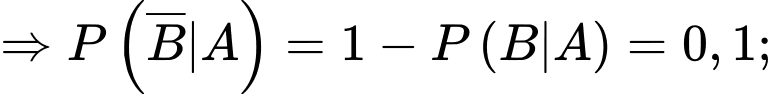
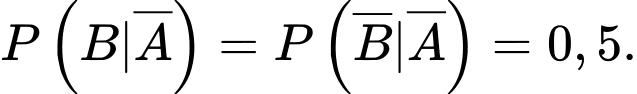
Giả sử
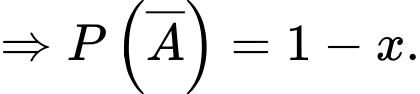
Từ đó, ta có sơ đồ cây sau:
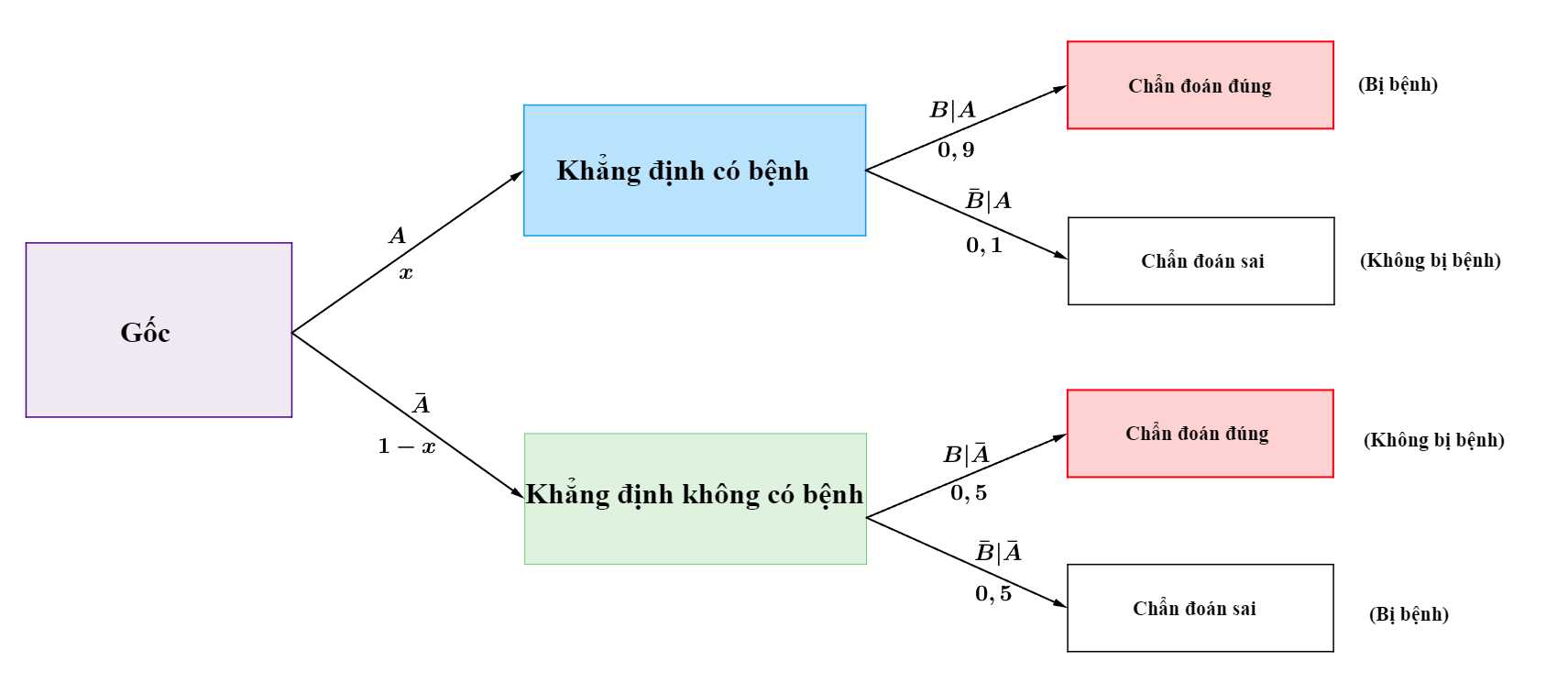
Theo công thức xác suất toàn phần, xác suất người đến khám có bệnh bằng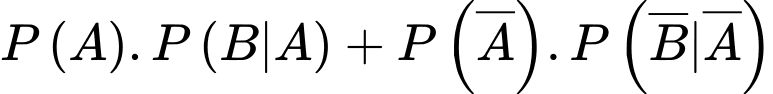
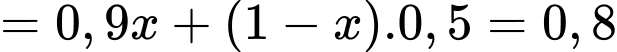
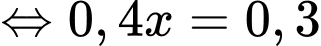
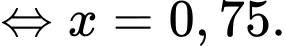
Suy ra xác suất chẩn đoán đúng bằng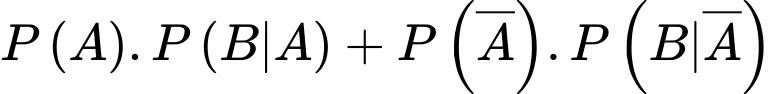
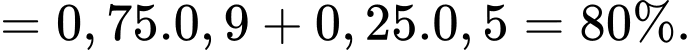
Gọi
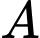 là biến cố “Khẳng định có bệnh”
là biến cố “Khẳng định có bệnh” là biến cố “Khẳng định không bệnh”
là biến cố “Khẳng định không bệnh”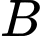 là biến cố “Chẩn đoán đúng”
là biến cố “Chẩn đoán đúng”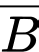 là biến cố “Chẩn đoán sai”
là biến cố “Chẩn đoán sai”Từ dữ kiện đề bài, ta có
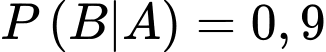
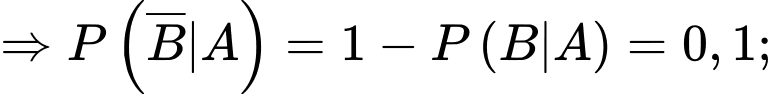
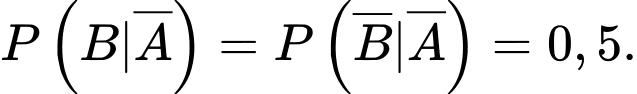
Giả sử

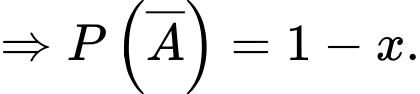
Từ đó, ta có sơ đồ cây sau:

Theo công thức xác suất toàn phần, xác suất người đến khám có bệnh bằng
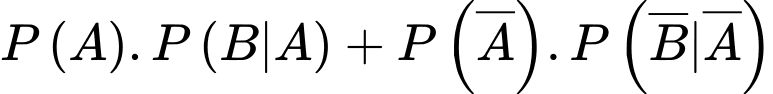
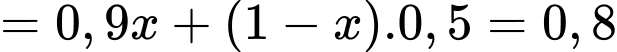
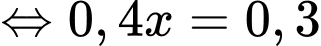
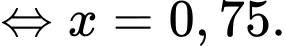
Suy ra xác suất chẩn đoán đúng bằng
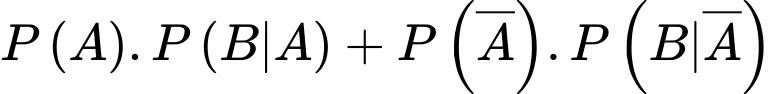
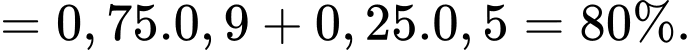
Câu 22 [695182]: Một thành phố nằm trên một con sông chảy qua hẻm núi. Hẻm có chiều ngang 80m, một bên cao  và một bên cao
và một bên cao  Một cây cầu sẽ được xây dựng bắc qua sông và hẻm núi. Sơ đồ thiết kế của cây cầu được gắn hệ trục tọa độ như hình vẽ dưới đây.
Một cây cầu sẽ được xây dựng bắc qua sông và hẻm núi. Sơ đồ thiết kế của cây cầu được gắn hệ trục tọa độ như hình vẽ dưới đây.
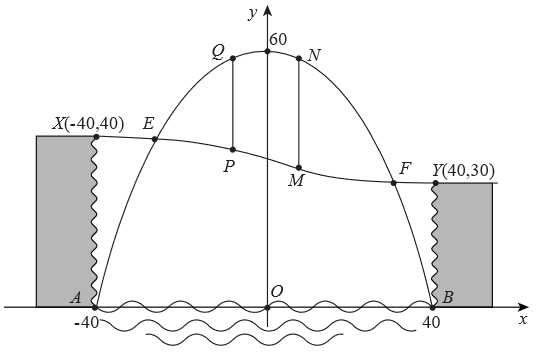
Con đường xuyên qua hẻm núi được mô hình hóa bằng phương trình:
xuyên qua hẻm núi được mô hình hóa bằng phương trình: 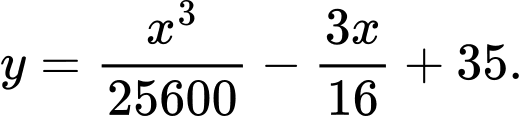 Hai cột đỡ dọc
Hai cột đỡ dọc 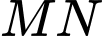 và
và 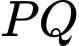 ( song song với trục
( song song với trục 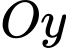 ) là đoạn nối giữa khung của Parabol và đường
) là đoạn nối giữa khung của Parabol và đường  Tính tổng độ dài đoạn
Tính tổng độ dài đoạn 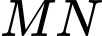 và
và 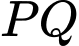 biết rằng
biết rằng 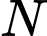 và
và  là hai điểm đối xứng qua
là hai điểm đối xứng qua 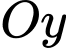 ;
; 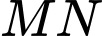 là đoạn có độ dài lớn nhất ( làm tròn kết quả đến hàng phần chục).
là đoạn có độ dài lớn nhất ( làm tròn kết quả đến hàng phần chục).
 và một bên cao
và một bên cao  Một cây cầu sẽ được xây dựng bắc qua sông và hẻm núi. Sơ đồ thiết kế của cây cầu được gắn hệ trục tọa độ như hình vẽ dưới đây.
Một cây cầu sẽ được xây dựng bắc qua sông và hẻm núi. Sơ đồ thiết kế của cây cầu được gắn hệ trục tọa độ như hình vẽ dưới đây.
Con đường
 xuyên qua hẻm núi được mô hình hóa bằng phương trình:
xuyên qua hẻm núi được mô hình hóa bằng phương trình: 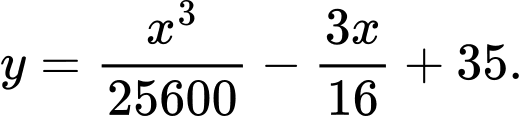 Hai cột đỡ dọc
Hai cột đỡ dọc 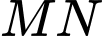 và
và 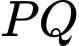 ( song song với trục
( song song với trục 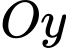 ) là đoạn nối giữa khung của Parabol và đường
) là đoạn nối giữa khung của Parabol và đường  Tính tổng độ dài đoạn
Tính tổng độ dài đoạn 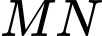 và
và 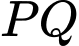 biết rằng
biết rằng 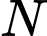 và
và  là hai điểm đối xứng qua
là hai điểm đối xứng qua 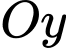 ;
; 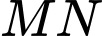 là đoạn có độ dài lớn nhất ( làm tròn kết quả đến hàng phần chục).
là đoạn có độ dài lớn nhất ( làm tròn kết quả đến hàng phần chục).
Điền đáp án: 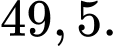
Phương trình Parabol đi qua 4 điểm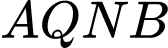 là
là 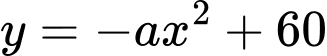 .
.
Parabol đi qua điểm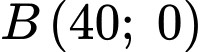 nên
nên 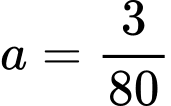
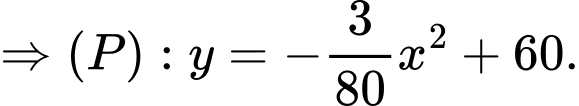
Gọi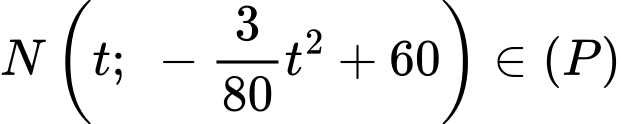
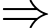 Phương trình
Phương trình 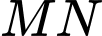 là
là 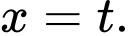
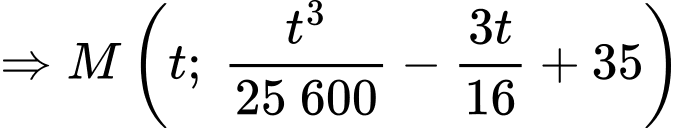
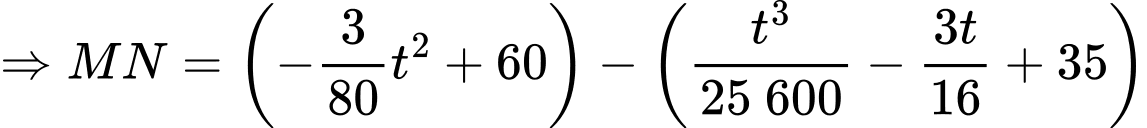
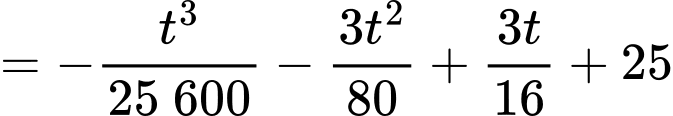
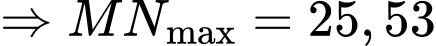 khi
khi 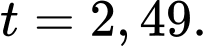
Suy ra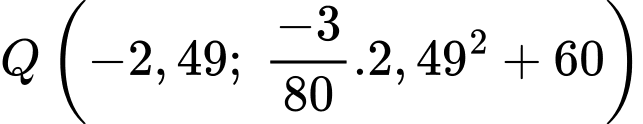
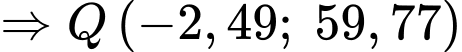
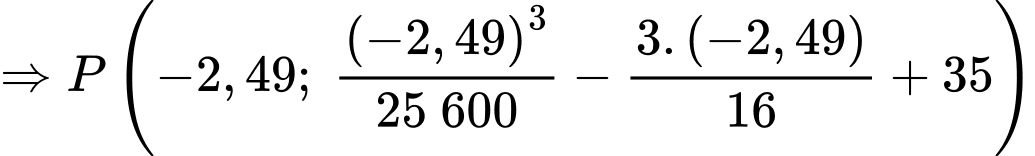
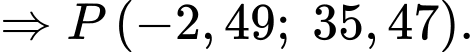
Vậy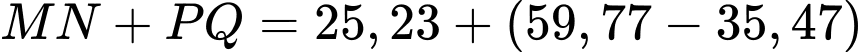
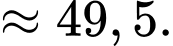
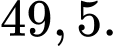
Phương trình Parabol đi qua 4 điểm
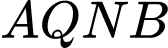 là
là 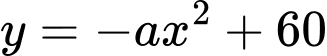 .
.Parabol đi qua điểm
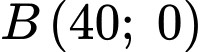 nên
nên 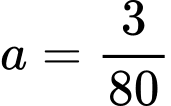
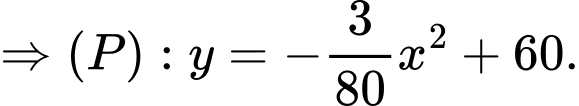
Gọi
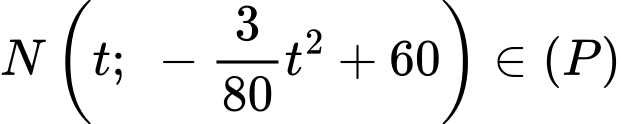
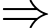 Phương trình
Phương trình 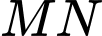 là
là 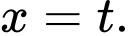
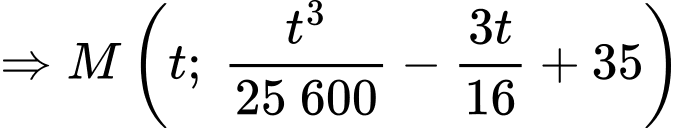
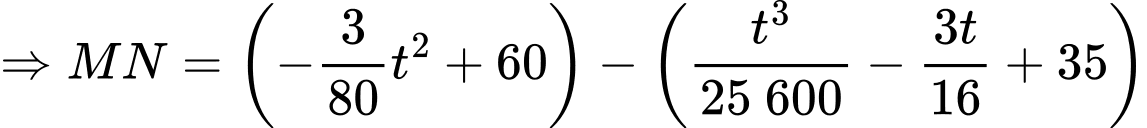
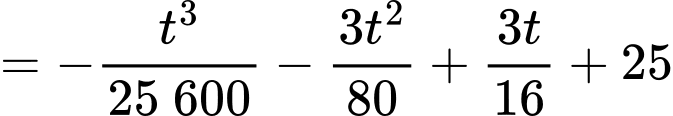
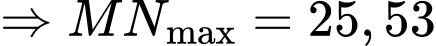 khi
khi 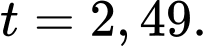
Suy ra
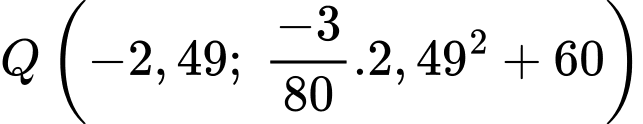
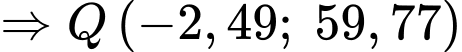
Vậy