PHẦN I. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Câu 1 [677850]: Trong không gian 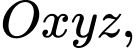 Cho mặt phẳng
Cho mặt phẳng 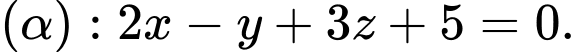 Vectơ nào dưới đây là một vectơ pháp tuyến của
Vectơ nào dưới đây là một vectơ pháp tuyến của  ?
?
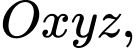 Cho mặt phẳng
Cho mặt phẳng 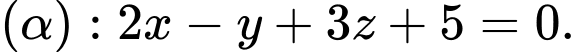 Vectơ nào dưới đây là một vectơ pháp tuyến của
Vectơ nào dưới đây là một vectơ pháp tuyến của  ?
? A, 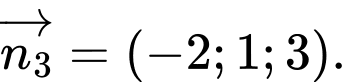
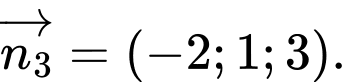
B, 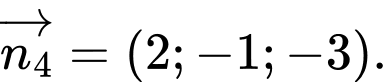
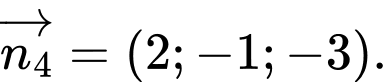
C, 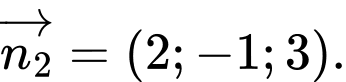
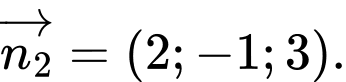
D, 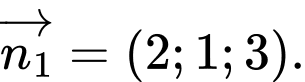
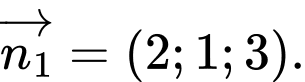
Chọn đáp án C. Đáp án: C
Câu 2 [508151]: Cho hàm số 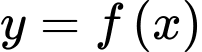 liên tục trên
liên tục trên 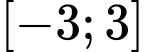 và có bảng xét dấu của đạo hàm như hình bên dưới.
và có bảng xét dấu của đạo hàm như hình bên dưới.
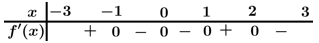
Mệnh đề nào sau đây sai?
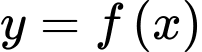 liên tục trên
liên tục trên 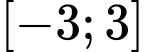 và có bảng xét dấu của đạo hàm như hình bên dưới.
và có bảng xét dấu của đạo hàm như hình bên dưới.Mệnh đề nào sau đây sai?
A, Hàm số đạt cực tiểu tại 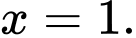
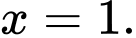
B, Hàm số đạt cực đại tại 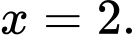
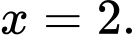
C, Hàm số đạt cực đại tại 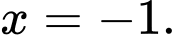
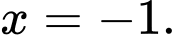
D, Hàm số đạt cực tiểu tại 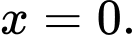
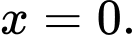
Chọn đáp án D.
Ta có bảng biến thiên:
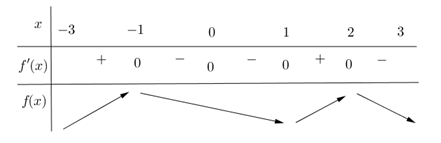
Vậy hàm số đạt cực tiểu tại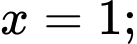 hàm số đạt cực đại tại
hàm số đạt cực đại tại 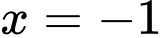 và
và 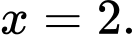 Đáp án: D
Đáp án: D
Ta có bảng biến thiên:

Vậy hàm số đạt cực tiểu tại
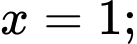 hàm số đạt cực đại tại
hàm số đạt cực đại tại 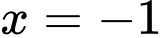 và
và 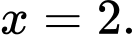 Đáp án: D
Đáp án: D
Câu 3 [677848]: Tập xác định của hàm số 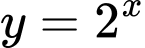 là
là
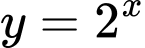 là
là A, 
B, 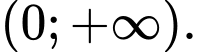
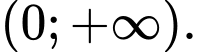
C, 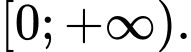
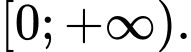
D, 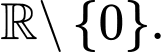
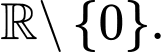
Chọn đáp án A.
Hàm số mũ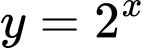 xác định với mọi
xác định với mọi 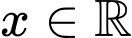 nên tập xác định là
nên tập xác định là 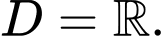 Đáp án: A
Đáp án: A
Hàm số mũ
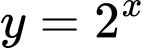 xác định với mọi
xác định với mọi 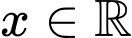 nên tập xác định là
nên tập xác định là 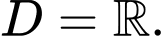 Đáp án: A
Đáp án: A
Câu 4 [898230]: Cho 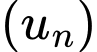 là cấp số cộng có
là cấp số cộng có 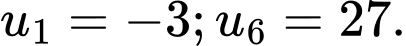 Tìm công sai
Tìm công sai 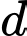 của
của 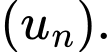
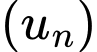 là cấp số cộng có
là cấp số cộng có 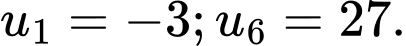 Tìm công sai
Tìm công sai 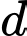 của
của 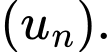
A, 

B, 

C, 

D, 

Chọn đáp án D.
Ta có: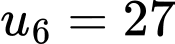
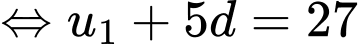
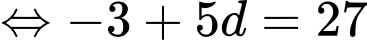
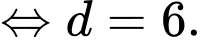 Đáp án: D
Đáp án: D
Ta có:
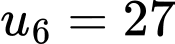
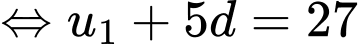
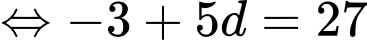
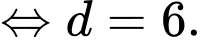 Đáp án: D
Đáp án: D
Câu 5 [527869]: Cho hình chóp tứ giác 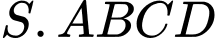 có đáy
có đáy 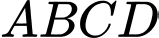 là hình vuông cạnh
là hình vuông cạnh 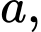
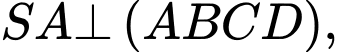
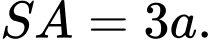 Thể tích
Thể tích  của hình chóp
của hình chóp  là
là
 có đáy
có đáy  là hình vuông cạnh
là hình vuông cạnh 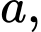
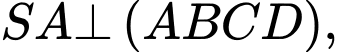
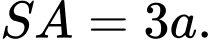 Thể tích
Thể tích  của hình chóp
của hình chóp 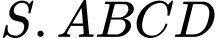 là
là A, 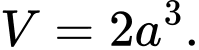
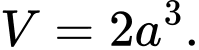
B, 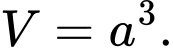
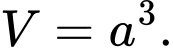
C, 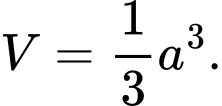
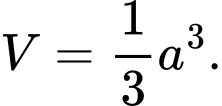
D, 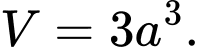
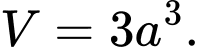
Chọn đáp án B.
Ta có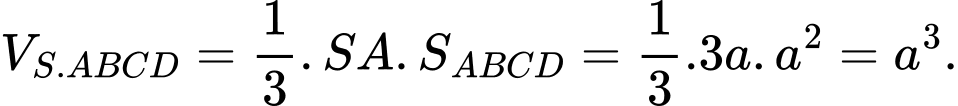 Đáp án: B
Đáp án: B
Ta có
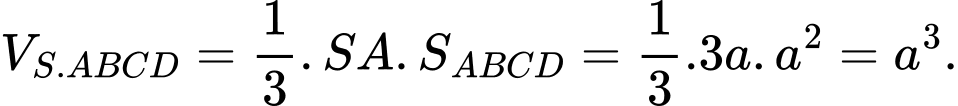 Đáp án: B
Đáp án: B
Câu 6 [890697]: Nguyên hàm  bằng
bằng
 bằng
bằng A, 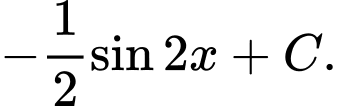
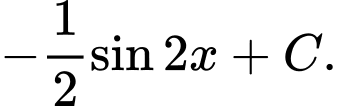
B, 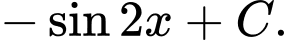
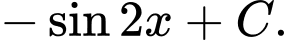
C, 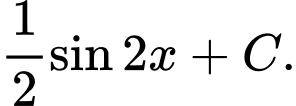
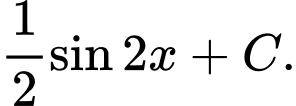
D, 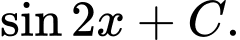
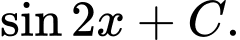
Chọn đáp án C.
Ta có :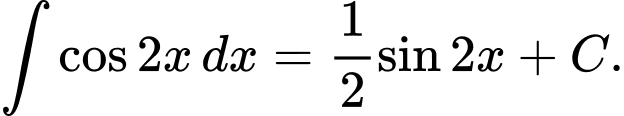 Đáp án: C
Đáp án: C
Ta có :
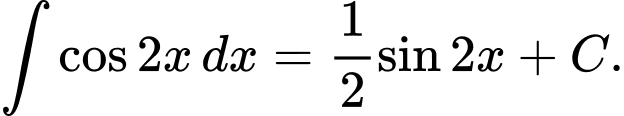 Đáp án: C
Đáp án: C
Câu 7 [601731]: Đồ thị của hàm số nào sau đây có tiệm cận đứng là đường thẳng 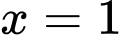 và tiệm cận ngang là đường thẳng
và tiệm cận ngang là đường thẳng 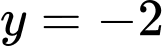 ?
?
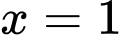 và tiệm cận ngang là đường thẳng
và tiệm cận ngang là đường thẳng 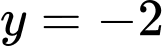 ?
? A, 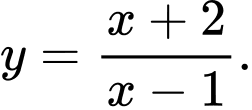
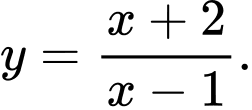
B, 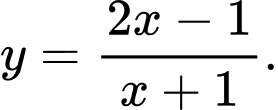
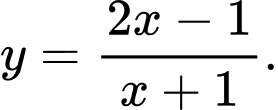
C, 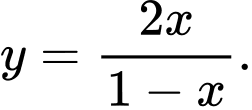
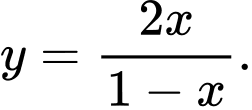
D, 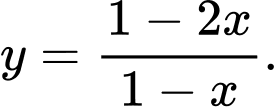
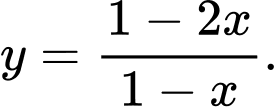
Chọn đáp án C.
Xét hàm số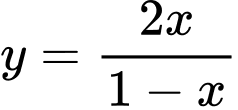 thỏa mãn:
thỏa mãn: 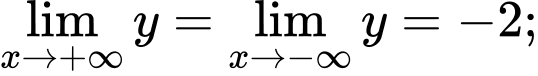
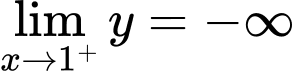 và
và 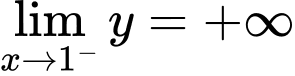 .
.
Vậy đồ thị hàm số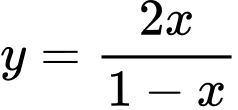 có tiệm cận đứng là đường thẳng
có tiệm cận đứng là đường thẳng 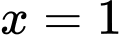 và tiệm cận ngang là đường thẳng
và tiệm cận ngang là đường thẳng 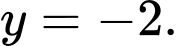 Đáp án: C
Đáp án: C
Xét hàm số
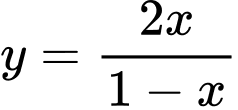 thỏa mãn:
thỏa mãn: 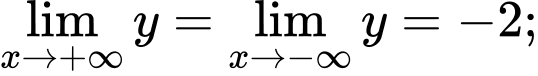
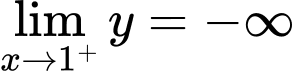 và
và 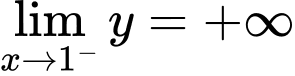 .
. Vậy đồ thị hàm số
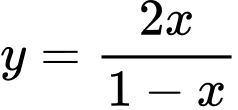 có tiệm cận đứng là đường thẳng
có tiệm cận đứng là đường thẳng 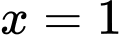 và tiệm cận ngang là đường thẳng
và tiệm cận ngang là đường thẳng 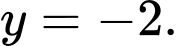 Đáp án: C
Đáp án: C
Câu 8 [693777]: Tập nghiệm của bất phương trình 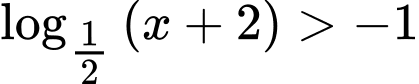 là
là
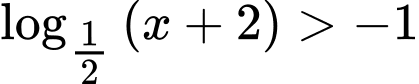 là
là A, 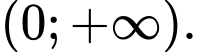
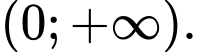
B, 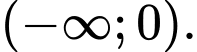
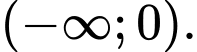
C, 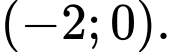
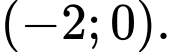
D, 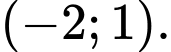
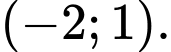
Chọn đáp án C.
ĐKXĐ:
Ta có: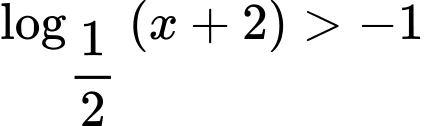
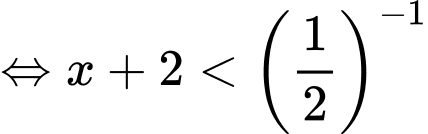

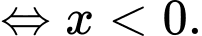
Vậy tập nghiệm của bất phương trình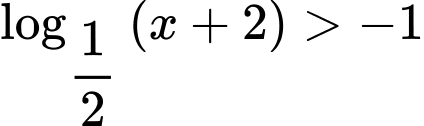 là
là 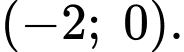 Đáp án: C
Đáp án: C
ĐKXĐ:

Ta có:
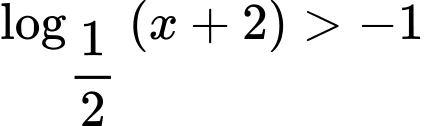
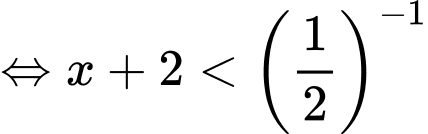

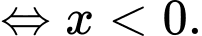
Vậy tập nghiệm của bất phương trình
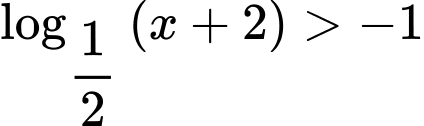 là
là 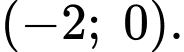 Đáp án: C
Đáp án: C
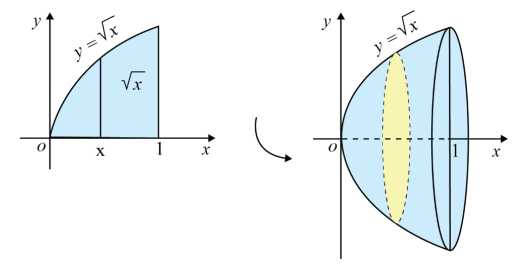
Câu 9 [693778]: Tính thể tích khối tròn xoay sinh ra khi quay quanh trục 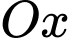 hình phẳng giới hạn bởiđồ thị hàm số
hình phẳng giới hạn bởiđồ thị hàm số 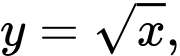 trục hoành và hai đường thẳng
trục hoành và hai đường thẳng 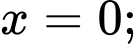
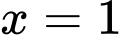 (hình vẽ)
(hình vẽ)
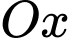 hình phẳng giới hạn bởiđồ thị hàm số
hình phẳng giới hạn bởiđồ thị hàm số 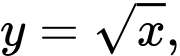 trục hoành và hai đường thẳng
trục hoành và hai đường thẳng 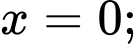
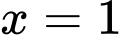 (hình vẽ)
(hình vẽ)
A, 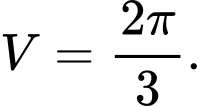
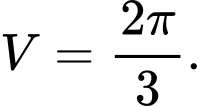
B, 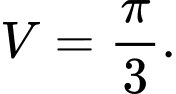
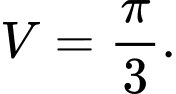
C, 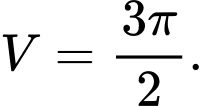
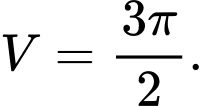
D, 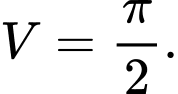
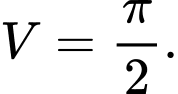
Chọn đáp án D.
Thể tích khối tròn xoay sinh ra khi quay quanh trục hình phẳng giới hạn bởi đồ thị hàm số
hình phẳng giới hạn bởi đồ thị hàm số 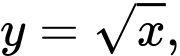 trục hoành và hai đường thẳng
trục hoành và hai đường thẳng 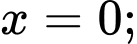
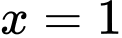 là
là
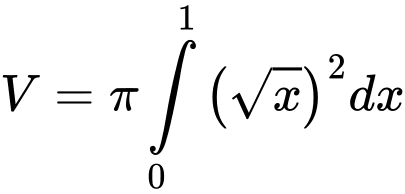
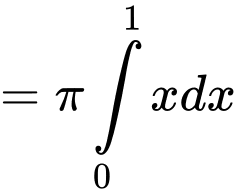
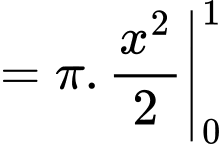
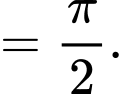 Đáp án: D
Đáp án: D
Thể tích khối tròn xoay sinh ra khi quay quanh trục
 hình phẳng giới hạn bởi đồ thị hàm số
hình phẳng giới hạn bởi đồ thị hàm số 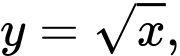 trục hoành và hai đường thẳng
trục hoành và hai đường thẳng 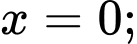
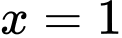 là
là 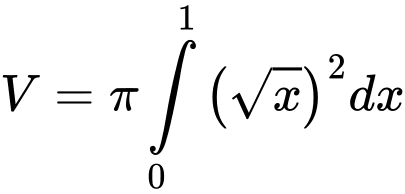
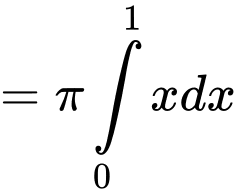
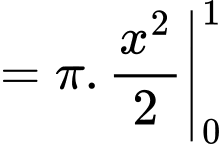
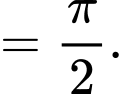 Đáp án: D
Đáp án: D
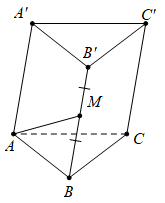
Câu 10 [975604]: Cho hình lăng trụ  Gọi
Gọi 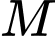 là trung điểm của cạnh
là trung điểm của cạnh 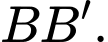 Đặt
Đặt 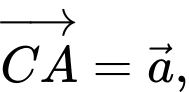
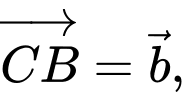
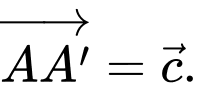 Khẳng định nào dưới đây là đúng?
Khẳng định nào dưới đây là đúng?
 Gọi
Gọi 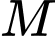 là trung điểm của cạnh
là trung điểm của cạnh 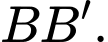 Đặt
Đặt 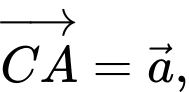
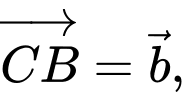
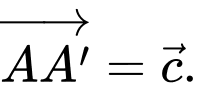 Khẳng định nào dưới đây là đúng?
Khẳng định nào dưới đây là đúng? A, 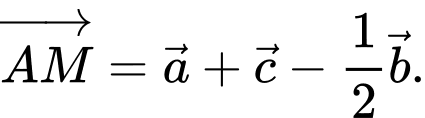
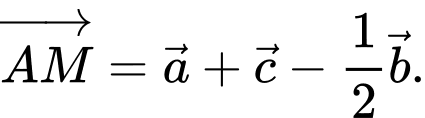
B, 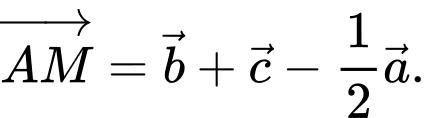
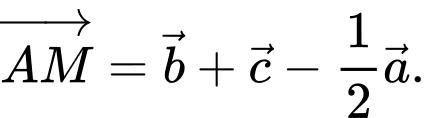
C, 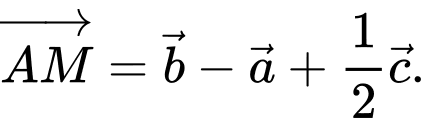
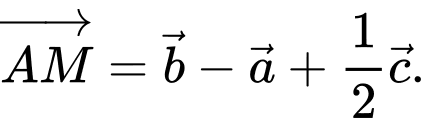
D, 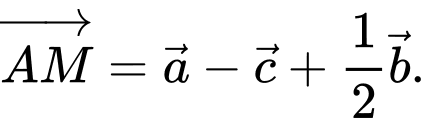
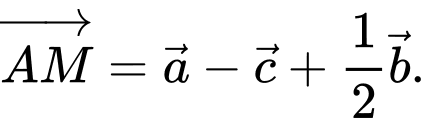
Chọn đáp án C.
Ta có:
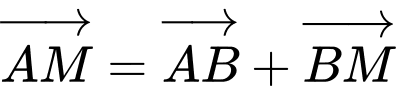
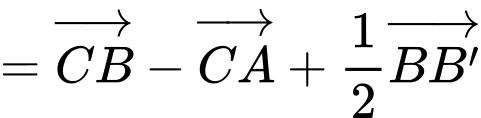
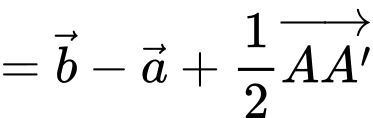
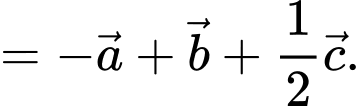 Đáp án: C
Đáp án: C

Ta có:
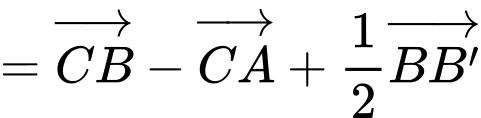
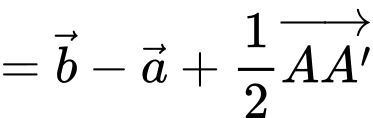
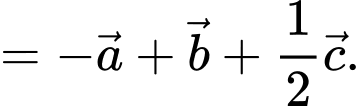 Đáp án: C
Đáp án: C
Câu 11 [898349]: Trong không gian với hệ trục toạ độ 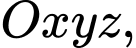 cho hai điểm
cho hai điểm 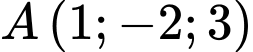 và
và 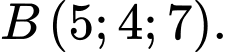 Phương trình mặt cầu nhận
Phương trình mặt cầu nhận  làm đường kính là
làm đường kính là
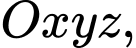 cho hai điểm
cho hai điểm 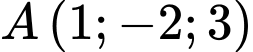 và
và 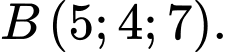 Phương trình mặt cầu nhận
Phương trình mặt cầu nhận  làm đường kính là
làm đường kính là A, 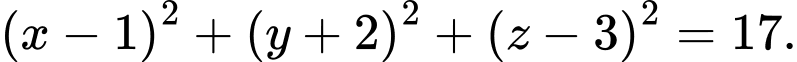
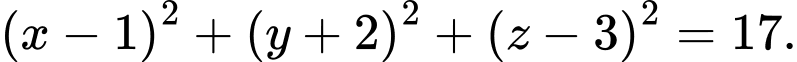
B, 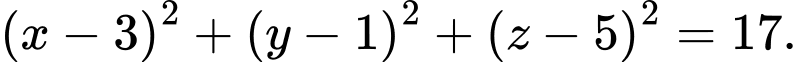
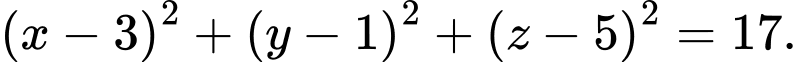
C, 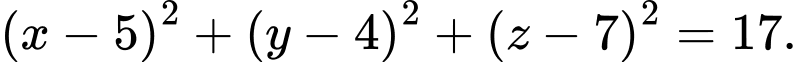
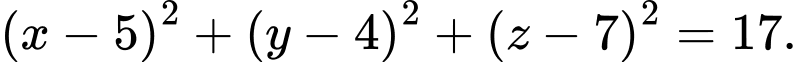
D, 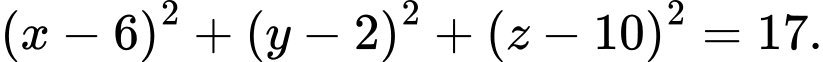
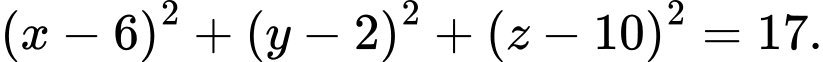
Chọn đáp án B.
Gọi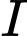 là tâm của mặt cầu suy ra
là tâm của mặt cầu suy ra 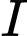 là trung điểm của
là trung điểm của 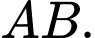 Suy ra
Suy ra 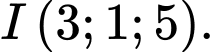
Ta có bán kính của mặt cầu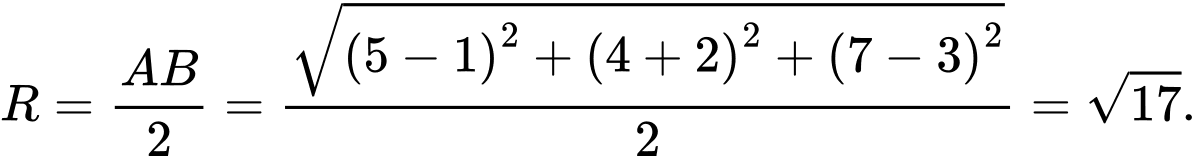
Vậy phương trình mặt cầu nhận làm đường kính là
làm đường kính là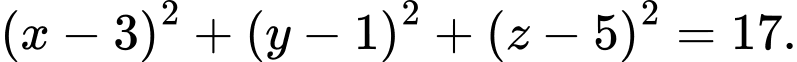 Đáp án: B
Đáp án: B
Gọi
 là tâm của mặt cầu suy ra
là tâm của mặt cầu suy ra  là trung điểm của
là trung điểm của 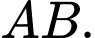 Suy ra
Suy ra 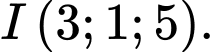
Ta có bán kính của mặt cầu
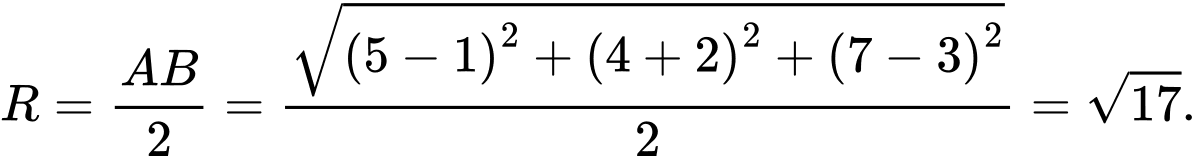
Vậy phương trình mặt cầu nhận
 làm đường kính là
làm đường kính là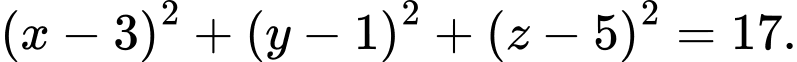 Đáp án: B
Đáp án: B
Câu 12 [693779]: Một bệnh viện thống kê chiều cao của 50 trẻ sơ sinh 12 ngày tuổi một cách ngẫu nhiên. Kết quả thu được như sau:

Bộ giá trị nào sau đây là tứ phân vị của mẫu số liệu ghép nhóm trên?

Bộ giá trị nào sau đây là tứ phân vị của mẫu số liệu ghép nhóm trên?
A, 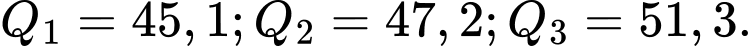
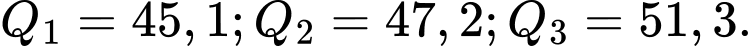
B, 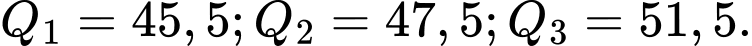
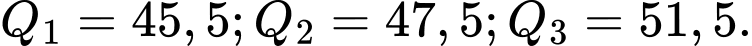
C, 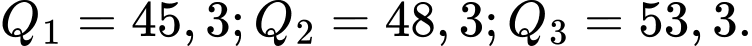
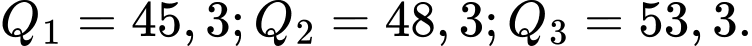
D, 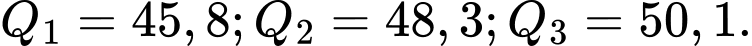
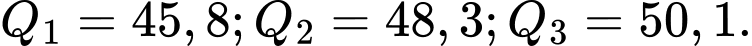
Chọn đáp án D.

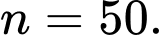
Nhóm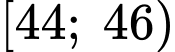 là nhóm đầu tiên có tần số tích luỹ lớn hơn hoặc bằng
là nhóm đầu tiên có tần số tích luỹ lớn hơn hoặc bằng 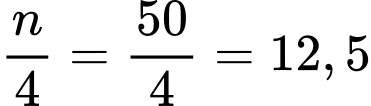 nên chứa tứ phân vị thứ nhất.
nên chứa tứ phân vị thứ nhất.
Ta có: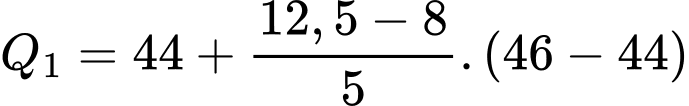
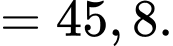
Nhóm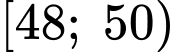 là nhóm đầu tiên có tần số tích luỹ lớn hơn hoặc bằng
là nhóm đầu tiên có tần số tích luỹ lớn hơn hoặc bằng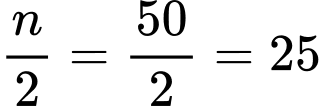 nên chứa tứ phân vị thứ ba.
nên chứa tứ phân vị thứ ba.
Ta có: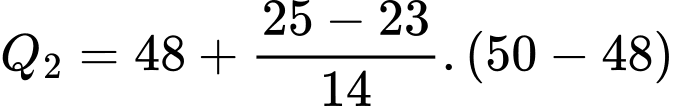
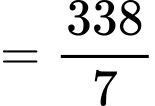
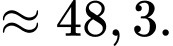
Nhóm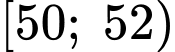 là nhóm đầu tiên có tần số tích luỹ lớn hơn hoặc bằng
là nhóm đầu tiên có tần số tích luỹ lớn hơn hoặc bằng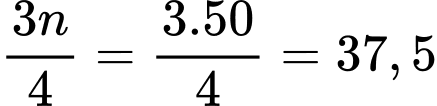 nên chứa tứ phân vị thứ ba.
nên chứa tứ phân vị thứ ba.
Ta có: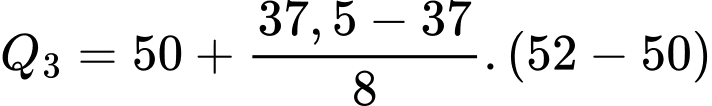
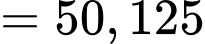
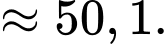 Đáp án: D
Đáp án: D

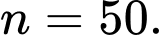
Nhóm
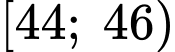 là nhóm đầu tiên có tần số tích luỹ lớn hơn hoặc bằng
là nhóm đầu tiên có tần số tích luỹ lớn hơn hoặc bằng 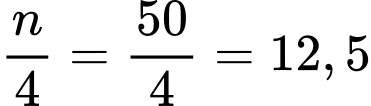 nên chứa tứ phân vị thứ nhất.
nên chứa tứ phân vị thứ nhất. Ta có:
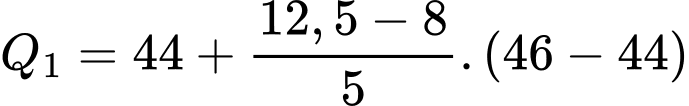
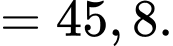
Nhóm
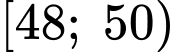 là nhóm đầu tiên có tần số tích luỹ lớn hơn hoặc bằng
là nhóm đầu tiên có tần số tích luỹ lớn hơn hoặc bằng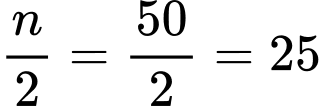 nên chứa tứ phân vị thứ ba.
nên chứa tứ phân vị thứ ba. Ta có:
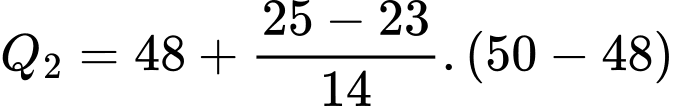
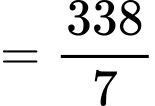
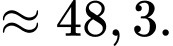
Nhóm
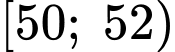 là nhóm đầu tiên có tần số tích luỹ lớn hơn hoặc bằng
là nhóm đầu tiên có tần số tích luỹ lớn hơn hoặc bằng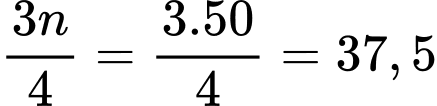 nên chứa tứ phân vị thứ ba.
nên chứa tứ phân vị thứ ba. Ta có:
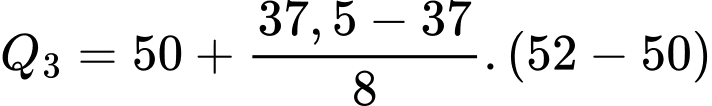
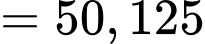
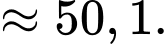 Đáp án: D
Đáp án: D PHẦN II. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Câu 13 [693780]: Khảo sát 100 người trong đó có 49 nam và 51 nữ về việc có nuôi thú cưng không thì được bảng sau
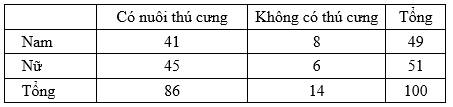
Chọn ngẫu nhiên một người trong số người được khảo sát.

Chọn ngẫu nhiên một người trong số người được khảo sát.
Gọi 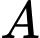 là biến cố “Người đó nuôi thú cưng”
là biến cố “Người đó nuôi thú cưng”
Gọi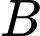 là biến cố “Người đó là nam”.
là biến cố “Người đó là nam”.
a) Sai.
Xác suất người đó là nam là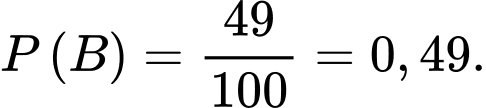
b) Đúng.
Xác suất người đó nuôi thú cưng là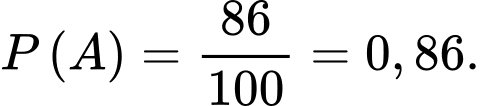
c) Sai.
Xác suất người đó là nam và nuôi thú cưng là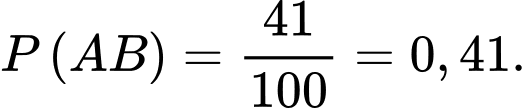
d) Đúng.
Xác suất người đó nuôi thú cưng khi biết người được chọn là nam là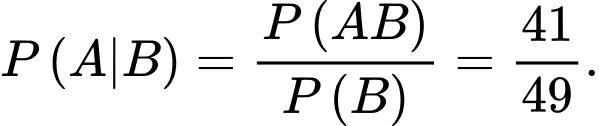
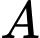 là biến cố “Người đó nuôi thú cưng”
là biến cố “Người đó nuôi thú cưng”
Gọi
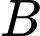 là biến cố “Người đó là nam”.
là biến cố “Người đó là nam”.
a) Sai.
Xác suất người đó là nam là
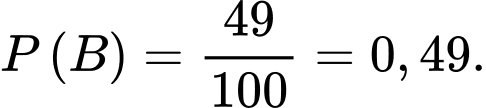
b) Đúng.
Xác suất người đó nuôi thú cưng là
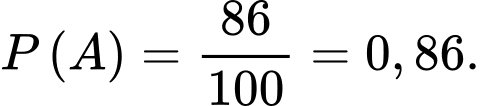
c) Sai.
Xác suất người đó là nam và nuôi thú cưng là
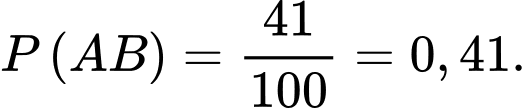
d) Đúng.
Xác suất người đó nuôi thú cưng khi biết người được chọn là nam là
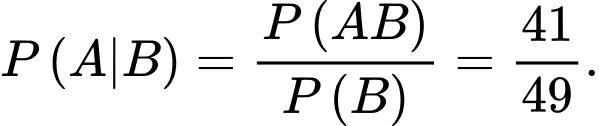
Câu 14 [693781]: Trong không gian với hệ tọa độ  một cabin cáp treo xuất phát từ điểm
một cabin cáp treo xuất phát từ điểm 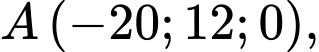 chuyển động thẳng đều theo đường cáp và cùng chiều với vectơ
chuyển động thẳng đều theo đường cáp và cùng chiều với vectơ 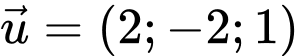 với tốc độ là
với tốc độ là 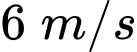 (Đơn vị trên mỗi trục tọa độ là mét); giả sử sau
(Đơn vị trên mỗi trục tọa độ là mét); giả sử sau 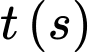 kể từ lúc xuất phát
kể từ lúc xuất phát 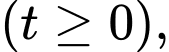 cabin đến điểm
cabin đến điểm 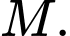

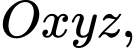 một cabin cáp treo xuất phát từ điểm
một cabin cáp treo xuất phát từ điểm 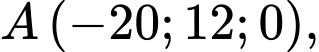 chuyển động thẳng đều theo đường cáp và cùng chiều với vectơ
chuyển động thẳng đều theo đường cáp và cùng chiều với vectơ 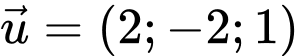 với tốc độ là
với tốc độ là 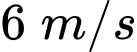 (Đơn vị trên mỗi trục tọa độ là mét); giả sử sau
(Đơn vị trên mỗi trục tọa độ là mét); giả sử sau 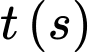 kể từ lúc xuất phát
kể từ lúc xuất phát 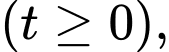 cabin đến điểm
cabin đến điểm 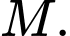

a) Đúng.
Do tốc độ di chuyển của cabin là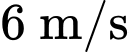 nên sau
nên sau  thì độ dài đoạn
thì độ dài đoạn 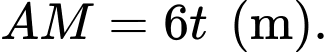
b) Sai.
Vectơ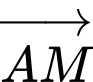 cùng phương với vectơ
cùng phương với vectơ 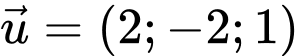 nên
nên 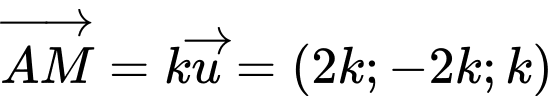
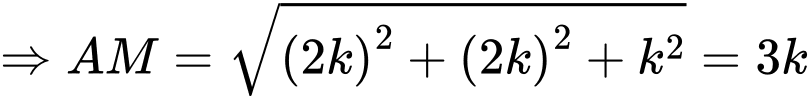
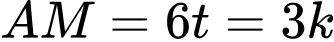
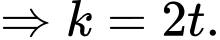
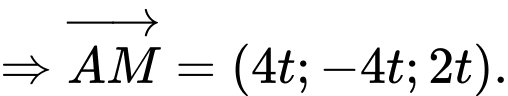
c) Sai.
Phương trình tham số của đường dây cáp là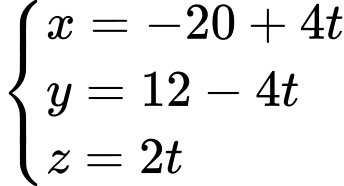 (
(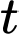 là tham số).
là tham số).
Toạ độ điểm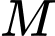 sau
sau  là
là 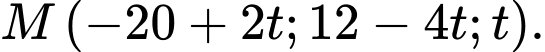
d) Đúng.
Khoảng cách giữa người quan sát và cabin là độ dài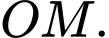
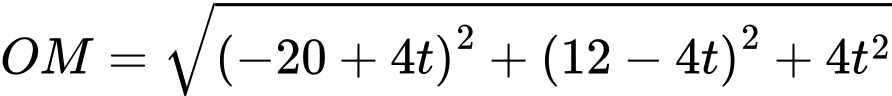
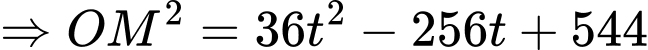
Ta thấy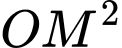 đạt giá trị nhỏ nhất khi
đạt giá trị nhỏ nhất khi 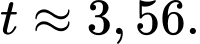
Do tốc độ di chuyển của cabin là
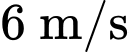 nên sau
nên sau  thì độ dài đoạn
thì độ dài đoạn 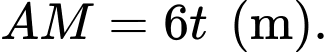
b) Sai.
Vectơ
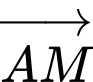 cùng phương với vectơ
cùng phương với vectơ 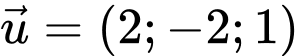 nên
nên 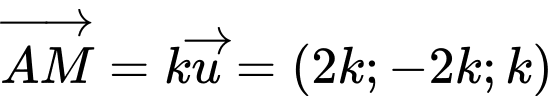
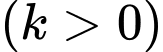
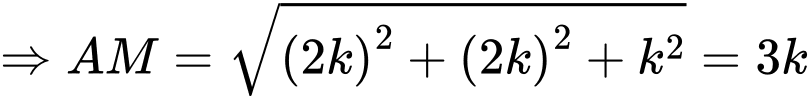
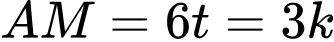
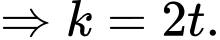
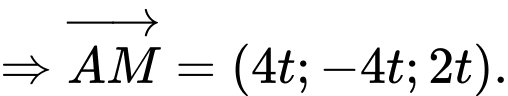
c) Sai.
Phương trình tham số của đường dây cáp là
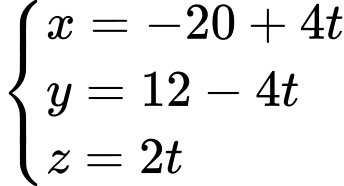 (
( là tham số).
là tham số).Toạ độ điểm
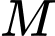 sau
sau  là
là 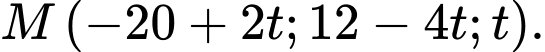
d) Đúng.
Khoảng cách giữa người quan sát và cabin là độ dài
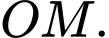
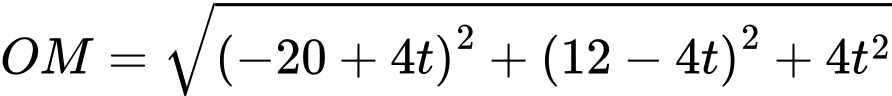
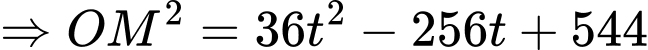
Ta thấy
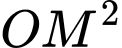 đạt giá trị nhỏ nhất khi
đạt giá trị nhỏ nhất khi 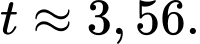
Câu 15 [693782]: Độ cứng 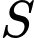 của một thanh gỗ hình chữ nhật tỉ lệ thuận với tích của chiều rộng
của một thanh gỗ hình chữ nhật tỉ lệ thuận với tích của chiều rộng 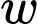 và bình phương chiều dài
và bình phương chiều dài 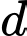 của nó (theo đơn vị cm). Biết rằng nếu thanh gỗ có chiều dài là 6cm, chiều rộng là 3cm thì độ cứng của nó bằng
của nó (theo đơn vị cm). Biết rằng nếu thanh gỗ có chiều dài là 6cm, chiều rộng là 3cm thì độ cứng của nó bằng 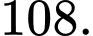 Một khúc gỗ hình tròn có đường kính là
Một khúc gỗ hình tròn có đường kính là 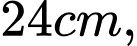 người ta cắt thành một thanh gỗ hình chữ nhật như hình vẽ sau:
người ta cắt thành một thanh gỗ hình chữ nhật như hình vẽ sau:
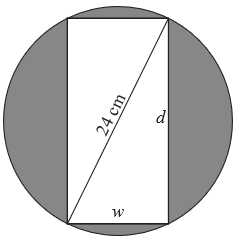
Mệnh đề sau đúng hay sai?
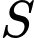 của một thanh gỗ hình chữ nhật tỉ lệ thuận với tích của chiều rộng
của một thanh gỗ hình chữ nhật tỉ lệ thuận với tích của chiều rộng 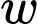 và bình phương chiều dài
và bình phương chiều dài 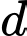 của nó (theo đơn vị cm). Biết rằng nếu thanh gỗ có chiều dài là 6cm, chiều rộng là 3cm thì độ cứng của nó bằng
của nó (theo đơn vị cm). Biết rằng nếu thanh gỗ có chiều dài là 6cm, chiều rộng là 3cm thì độ cứng của nó bằng 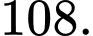 Một khúc gỗ hình tròn có đường kính là
Một khúc gỗ hình tròn có đường kính là 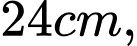 người ta cắt thành một thanh gỗ hình chữ nhật như hình vẽ sau:
người ta cắt thành một thanh gỗ hình chữ nhật như hình vẽ sau:
Mệnh đề sau đúng hay sai?
a) Đúng.
Áp dụng định lý Pythagore: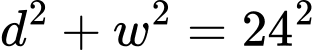
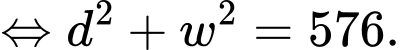
b) Sai.
Độ cứng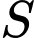 của một thanh gỗ hình chữ nhật tỉ lệ thuận với tích của chiều rộng
của một thanh gỗ hình chữ nhật tỉ lệ thuận với tích của chiều rộng 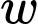 và bình phương chiều dài
và bình phương chiều dài 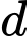 của nó
của nó 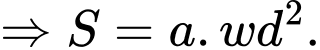
Nếu thanh gỗ có chiều dài là 6 cm, chiều rộng là 3 cm thì độ cứng của nó bằng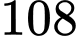
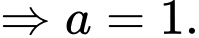
Vậy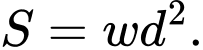
c) Sai.
Từ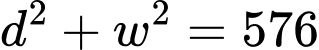 ta có
ta có 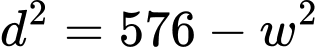
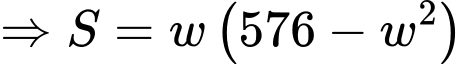
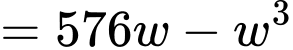
Ta có: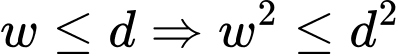
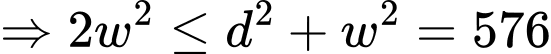
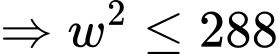
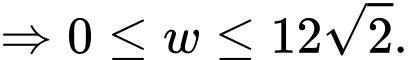
d) Đúng.
Xét hàm số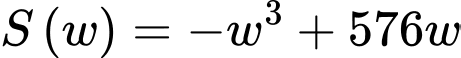 , ta có
, ta có 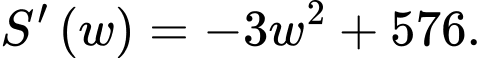
Với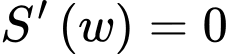 ta có
ta có 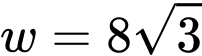 hoặc
hoặc 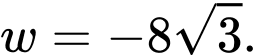
Vậy độ cứng lớn nhất của miếng gỗ cắt ra được là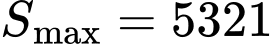 khi
khi 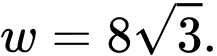
Áp dụng định lý Pythagore:
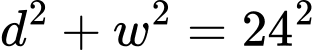
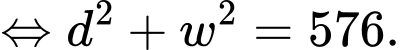
b) Sai.
Độ cứng
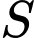 của một thanh gỗ hình chữ nhật tỉ lệ thuận với tích của chiều rộng
của một thanh gỗ hình chữ nhật tỉ lệ thuận với tích của chiều rộng 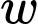 và bình phương chiều dài
và bình phương chiều dài 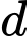 của nó
của nó 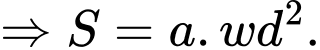
Nếu thanh gỗ có chiều dài là 6 cm, chiều rộng là 3 cm thì độ cứng của nó bằng
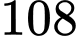
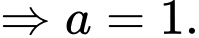
Vậy
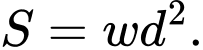
c) Sai.
Từ
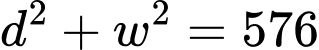 ta có
ta có 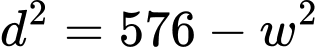
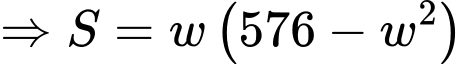
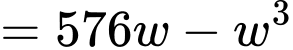
Ta có:
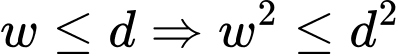
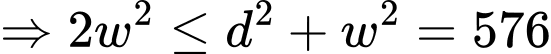
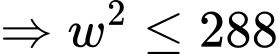
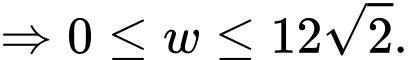
d) Đúng.
Xét hàm số
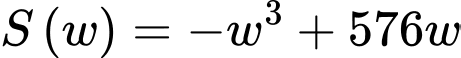 , ta có
, ta có 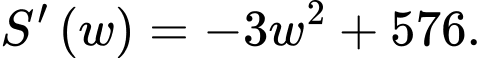
Với
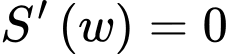 ta có
ta có 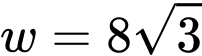 hoặc
hoặc 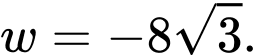
Vậy độ cứng lớn nhất của miếng gỗ cắt ra được là
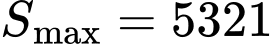 khi
khi 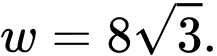
Câu 16 [693783]: Một ly trà sữa dạng hình nón cụt, có đường kính đáy ly là 6 cm, đường kính miệng ly là 9cm, chiều cao 13, 4 cm, ở miệng ly có sử dụng một nắp đậy có hình dạng nửa mặt cầu và ở đỉnh của nửa mặt cầu này có một hình tròn có đường kính 2cm để cắm ống hút, mặt phẳng chứa hình tròn này song song với mặt phẳng chứa miệng ly (tham khảo hình vẽ)
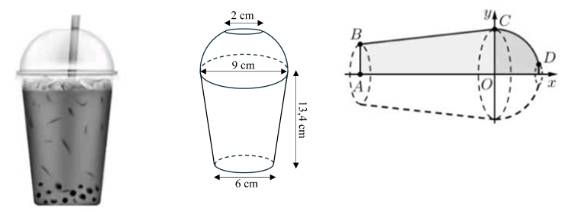
Chọn hệ trục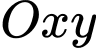 (đơn vị trên trục là centimet) với trục
(đơn vị trên trục là centimet) với trục 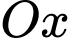 đi qua tâm của 2 đáy hình nón cụt và gốc toạ độ
đi qua tâm của 2 đáy hình nón cụt và gốc toạ độ  trùng với tâm của đáy lớn như hình vẽ.
trùng với tâm của đáy lớn như hình vẽ.

Chọn hệ trục
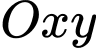 (đơn vị trên trục là centimet) với trục
(đơn vị trên trục là centimet) với trục 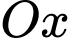 đi qua tâm của 2 đáy hình nón cụt và gốc toạ độ
đi qua tâm của 2 đáy hình nón cụt và gốc toạ độ  trùng với tâm của đáy lớn như hình vẽ.
trùng với tâm của đáy lớn như hình vẽ.
a) Đúng.
Phương trình đường thẳng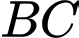 có dạng
có dạng 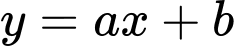 đi qua 2 điểm
đi qua 2 điểm 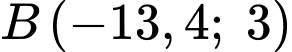 và
và 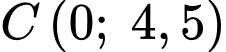 nên
nên
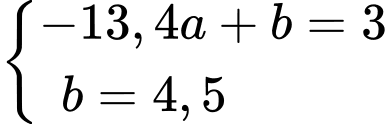
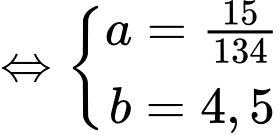
Vậy phương trình đường thẳng là
là 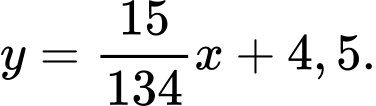
b) Đúng.
Phương trình đường tròn tâm bán kính
bán kính 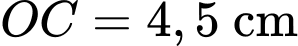 là
là 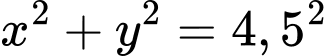 .
.
Do đường tròn đi qua điểm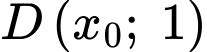 nên
nên 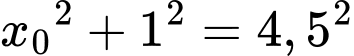
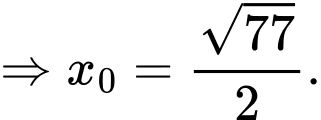
Vậy toạ độ điểm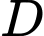 là
là 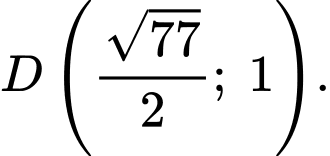
c) Đúng.
Thể tích bên trong ly không bao gồm nắp là
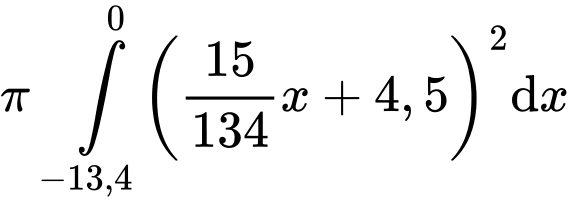
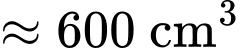
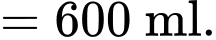
d) Đúng.
Đường tròn nắp ly có phương trình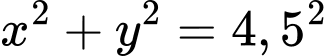
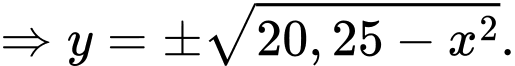
Ta xét phần dương của nắp ly, ta có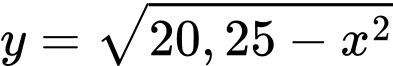 .
.
Thế tích nắp ly là: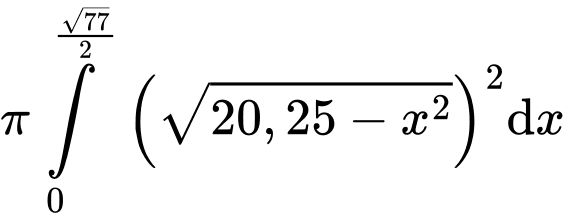
Vậy thể tích bên trong ly bao gồm cả thể tích nắp là:
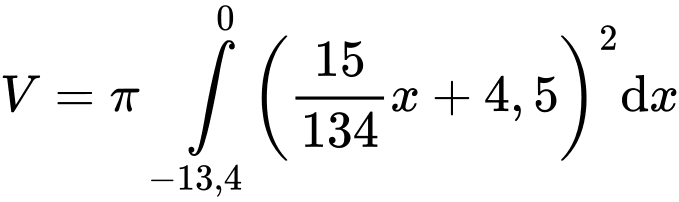
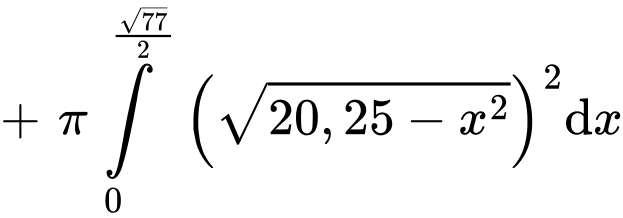
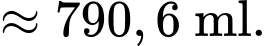
Phương trình đường thẳng
 có dạng
có dạng 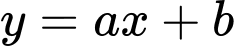 đi qua 2 điểm
đi qua 2 điểm 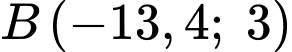 và
và 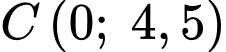 nên
nên
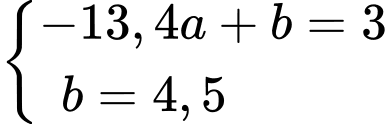
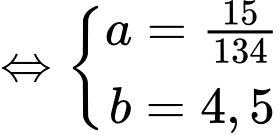
Vậy phương trình đường thẳng
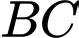 là
là 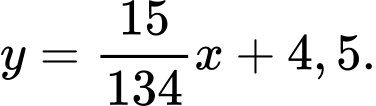
b) Đúng.
Phương trình đường tròn tâm
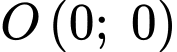 bán kính
bán kính 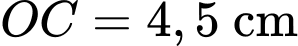 là
là 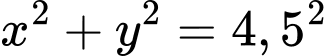 .
.
Do đường tròn đi qua điểm
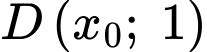 nên
nên 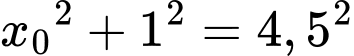
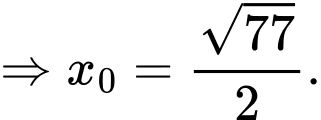
Vậy toạ độ điểm
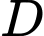 là
là 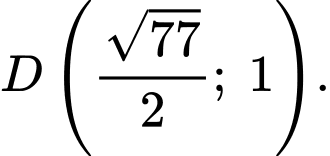
c) Đúng.
Thể tích bên trong ly không bao gồm nắp là
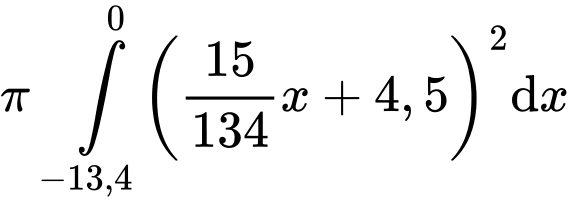
d) Đúng.
Đường tròn nắp ly có phương trình
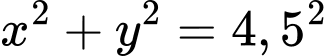
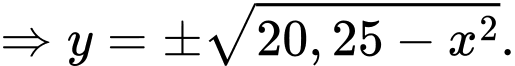
Ta xét phần dương của nắp ly, ta có
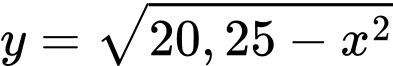 .
.
Thế tích nắp ly là:
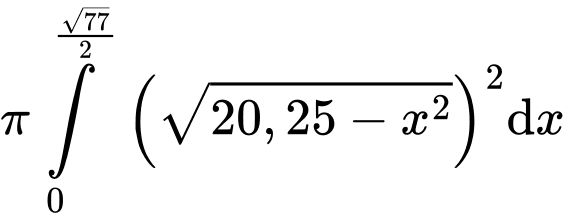
Vậy thể tích bên trong ly bao gồm cả thể tích nắp là:
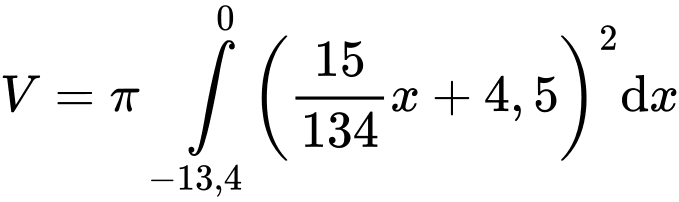
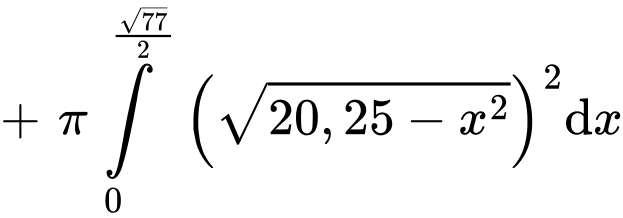
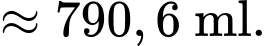
PHẦN III. Thí sinh trả lời từ câu 1 đến câu 6.
Câu 17 [693784]: Cho hình chóp 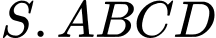 có đáy
có đáy 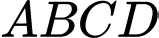 là hình vuông cạnh bằng
là hình vuông cạnh bằng 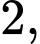
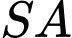 vuông góc với mặt phẳng đáy và
vuông góc với mặt phẳng đáy và 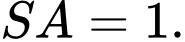 Gọi
Gọi 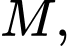
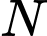 lần lượt là trung điểm của
lần lượt là trung điểm của 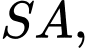
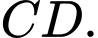 Côsin của góc giữa hai đường thẳng
Côsin của góc giữa hai đường thẳng 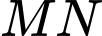 và
và  bằng bao nhiêu? (làm tròn kết quả đến hàng phần trăm).
bằng bao nhiêu? (làm tròn kết quả đến hàng phần trăm).
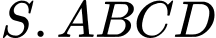 có đáy
có đáy 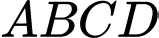 là hình vuông cạnh bằng
là hình vuông cạnh bằng 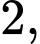
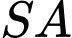 vuông góc với mặt phẳng đáy và
vuông góc với mặt phẳng đáy và 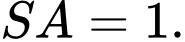 Gọi
Gọi 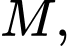
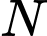 lần lượt là trung điểm của
lần lượt là trung điểm của 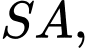
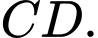 Côsin của góc giữa hai đường thẳng
Côsin của góc giữa hai đường thẳng 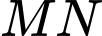 và
và  bằng bao nhiêu? (làm tròn kết quả đến hàng phần trăm).
bằng bao nhiêu? (làm tròn kết quả đến hàng phần trăm).
Điền đáp án: 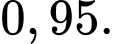
Chọn hệ trục toạ độ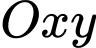 như hình dưới đây:
như hình dưới đây:
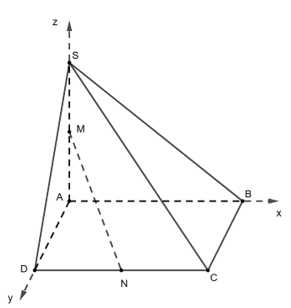
Gọi điểm là gốc toạ độ
là gốc toạ độ 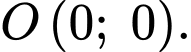
Ta có:
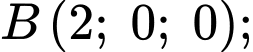
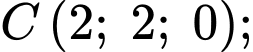
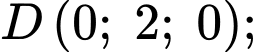
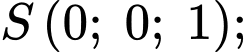
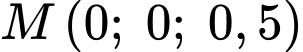 là trung điểm của
là trung điểm của 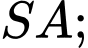
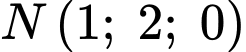 là trung điểm của
là trung điểm của 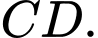
Suy ra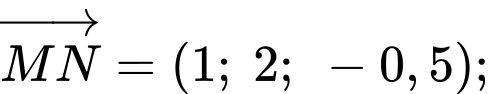
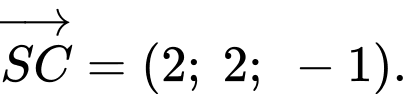
Tích vô hướng: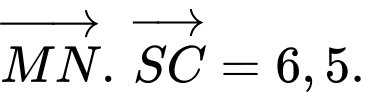
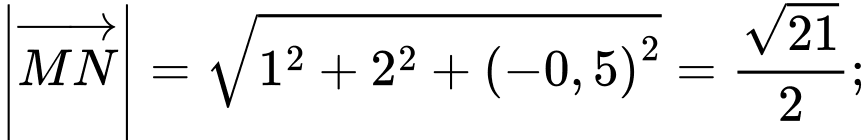
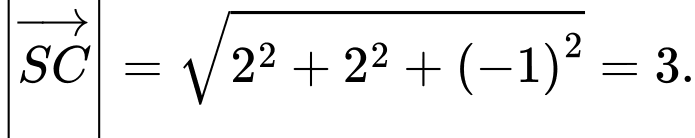
Gọi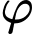 là góc giữa hai đường thẳng
là góc giữa hai đường thẳng 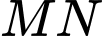 và
và 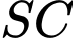 , khi đó:
, khi đó:
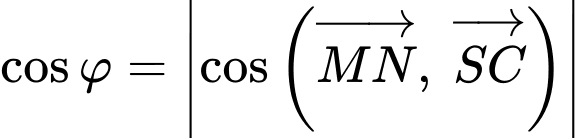
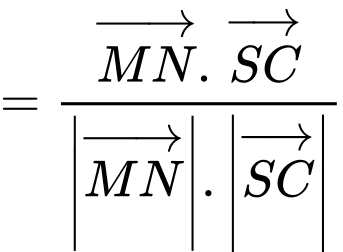
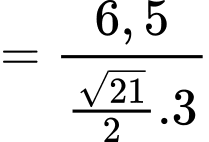
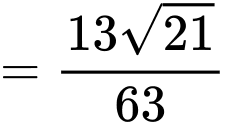
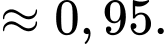
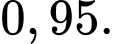
Chọn hệ trục toạ độ
 như hình dưới đây:
như hình dưới đây:
Gọi điểm
 là gốc toạ độ
là gốc toạ độ 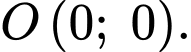
Ta có:
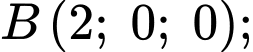
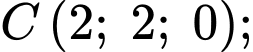
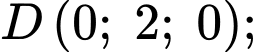
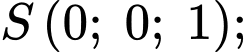
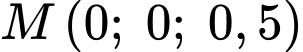 là trung điểm của
là trung điểm của 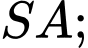
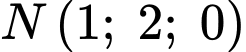 là trung điểm của
là trung điểm của 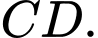
Suy ra
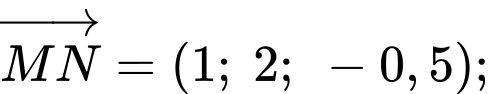
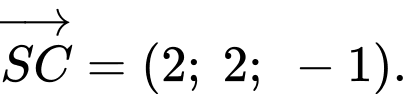
Tích vô hướng:
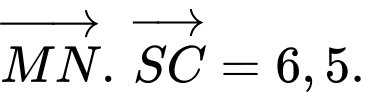
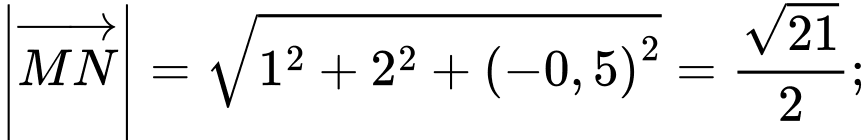
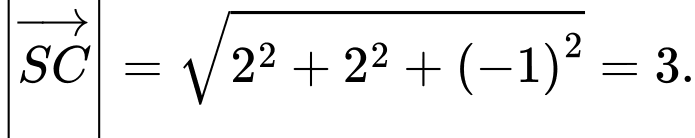
Gọi
 là góc giữa hai đường thẳng
là góc giữa hai đường thẳng  và
và 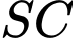 , khi đó:
, khi đó:
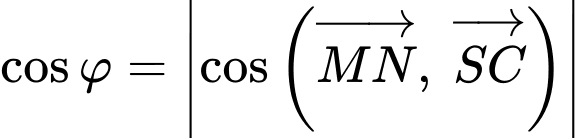
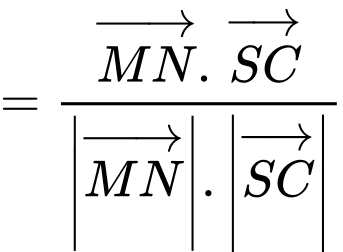
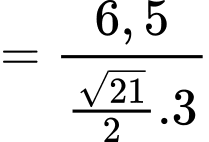
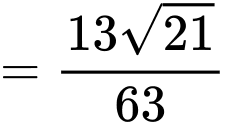
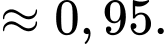
Câu 18 [693786]: Gieo hai con xúc xắc cân đối và đồng chất. Tính xác suất để tổng số chấm xuất hiện trên hai con xúc xắc đó không nhỏ hơn  nếu biết rằng ít nhất một con xúc xắc xuất hiện mặt 5 chấm (kết quả làm tròn đến hàng phần trăm).
nếu biết rằng ít nhất một con xúc xắc xuất hiện mặt 5 chấm (kết quả làm tròn đến hàng phần trăm).
 nếu biết rằng ít nhất một con xúc xắc xuất hiện mặt 5 chấm (kết quả làm tròn đến hàng phần trăm).
nếu biết rằng ít nhất một con xúc xắc xuất hiện mặt 5 chấm (kết quả làm tròn đến hàng phần trăm).
Điền đáp án: 0,27.
Gọi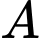 là biến cố: “Tổng số chấm xuất hiện trên hai con xúc xắc đó không nhỏ hơn 10”.
là biến cố: “Tổng số chấm xuất hiện trên hai con xúc xắc đó không nhỏ hơn 10”.
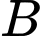 là biến cố: “Ít nhất một con xúc xắc xuất hiện mặt 5 chấm”.
là biến cố: “Ít nhất một con xúc xắc xuất hiện mặt 5 chấm”.
Ta cần tính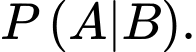
Số phần tử của không gian mẫu là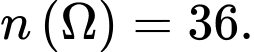
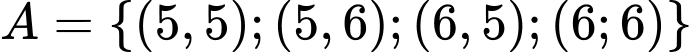 .
.
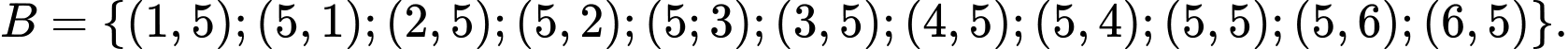
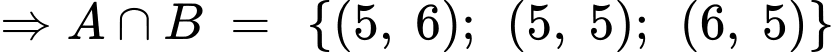
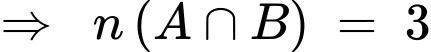
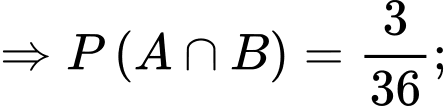
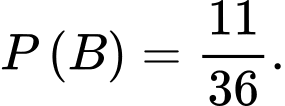
Vậy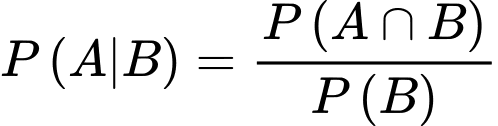
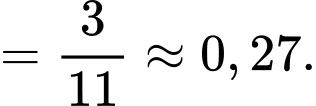
Gọi
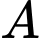 là biến cố: “Tổng số chấm xuất hiện trên hai con xúc xắc đó không nhỏ hơn 10”.
là biến cố: “Tổng số chấm xuất hiện trên hai con xúc xắc đó không nhỏ hơn 10”. 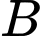 là biến cố: “Ít nhất một con xúc xắc xuất hiện mặt 5 chấm”.
là biến cố: “Ít nhất một con xúc xắc xuất hiện mặt 5 chấm”. Ta cần tính
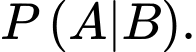
Số phần tử của không gian mẫu là
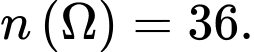
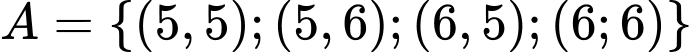 .
. 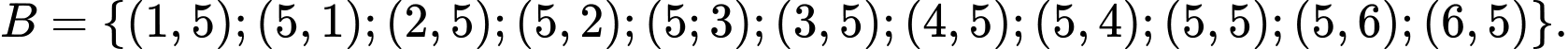
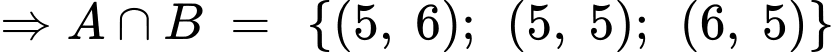
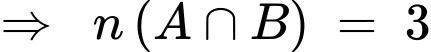
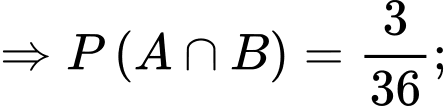
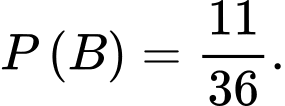
Vậy
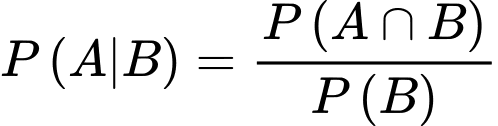
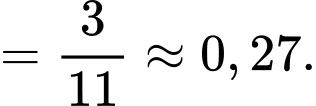
Câu 19 [693838]: Chủ của một nhà hàng muốn làm tường rào bao quanh 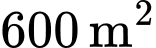 đất để làm bãi đỗ xe. Ba cạnh của khu đất sẽ được rào bằng một loại thép với chi phí 14 000 đồng một mét, riêng mặt thứ tư do tiếp giáp với mặt bên của nhà hàng nên được xây bằng tường gạch xi măng với chi phí là 28 000 đồng mỗi mét. Biết rằng cổng vào của khu đỗ xe là
đất để làm bãi đỗ xe. Ba cạnh của khu đất sẽ được rào bằng một loại thép với chi phí 14 000 đồng một mét, riêng mặt thứ tư do tiếp giáp với mặt bên của nhà hàng nên được xây bằng tường gạch xi măng với chi phí là 28 000 đồng mỗi mét. Biết rằng cổng vào của khu đỗ xe là 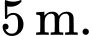 Tìm chu vi của khu đất khi chi phí nguyên liệu bỏ ra là ít nhất, biết rằng khu đất rào được có dạng hình chữ nhật.
Tìm chu vi của khu đất khi chi phí nguyên liệu bỏ ra là ít nhất, biết rằng khu đất rào được có dạng hình chữ nhật.
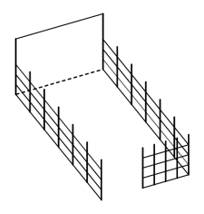
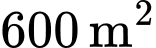 đất để làm bãi đỗ xe. Ba cạnh của khu đất sẽ được rào bằng một loại thép với chi phí 14 000 đồng một mét, riêng mặt thứ tư do tiếp giáp với mặt bên của nhà hàng nên được xây bằng tường gạch xi măng với chi phí là 28 000 đồng mỗi mét. Biết rằng cổng vào của khu đỗ xe là
đất để làm bãi đỗ xe. Ba cạnh của khu đất sẽ được rào bằng một loại thép với chi phí 14 000 đồng một mét, riêng mặt thứ tư do tiếp giáp với mặt bên của nhà hàng nên được xây bằng tường gạch xi măng với chi phí là 28 000 đồng mỗi mét. Biết rằng cổng vào của khu đỗ xe là 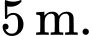 Tìm chu vi của khu đất khi chi phí nguyên liệu bỏ ra là ít nhất, biết rằng khu đất rào được có dạng hình chữ nhật.
Tìm chu vi của khu đất khi chi phí nguyên liệu bỏ ra là ít nhất, biết rằng khu đất rào được có dạng hình chữ nhật.
Điền đáp án: 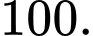
Gọi chiều dài phần rào không chứa cửa là
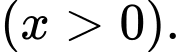
Diện tích miếng đất là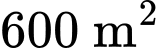 nên chiều dài phần bờ tường là
nên chiều dài phần bờ tường là 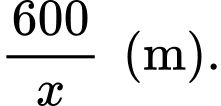
Phần rào chứa cửa của khu đỗ xe dài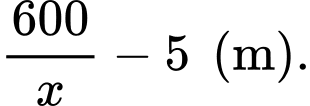
Tổng chi phí là: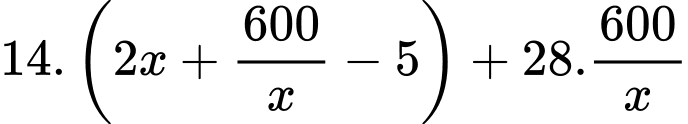 (nghìn đồng)
(nghìn đồng)
Xét hàm số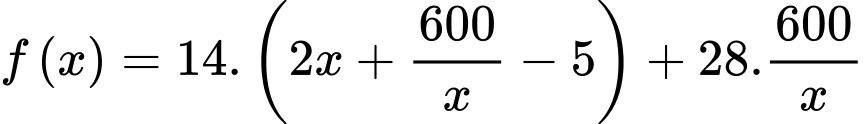
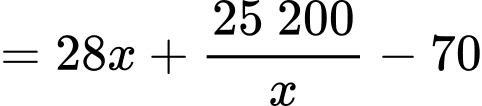
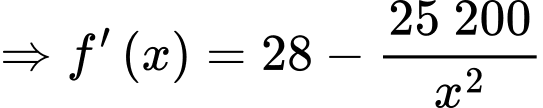 .
.
Ta có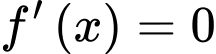
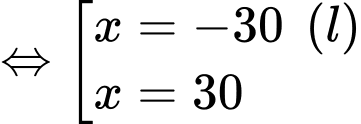
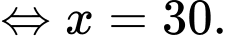
Lập bảng biến thiên, ta tìm được giá trị nhỏ nhất của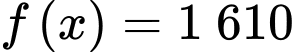 trên
trên 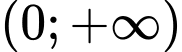 tại
tại 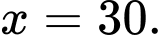
Chu vi của khu đất khi đó là
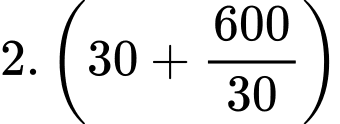
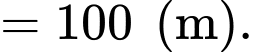
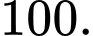
Gọi chiều dài phần rào không chứa cửa là

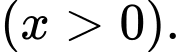
Diện tích miếng đất là
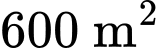 nên chiều dài phần bờ tường là
nên chiều dài phần bờ tường là 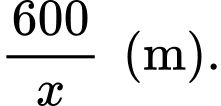
Phần rào chứa cửa của khu đỗ xe dài
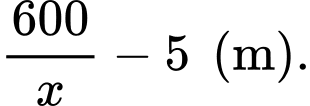
Tổng chi phí là:
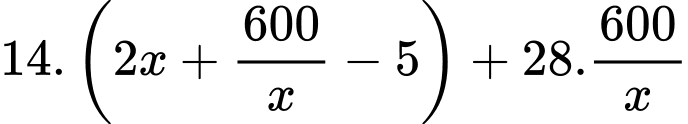 (nghìn đồng)
(nghìn đồng)Xét hàm số
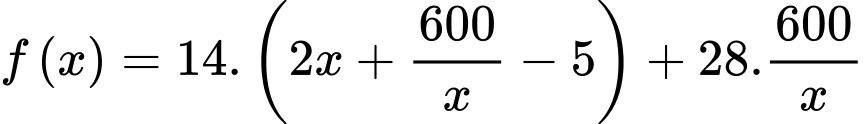
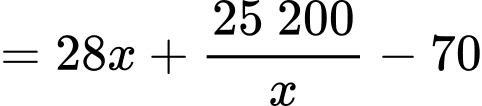
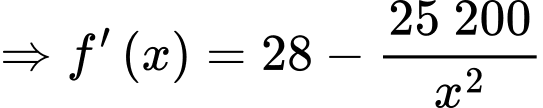 .
.Ta có
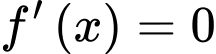
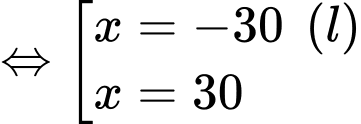
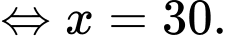
Lập bảng biến thiên, ta tìm được giá trị nhỏ nhất của
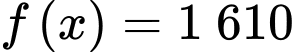 trên
trên 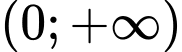 tại
tại 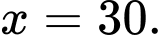
Chu vi của khu đất khi đó là
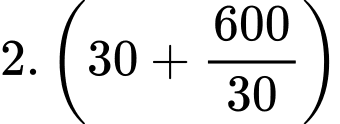
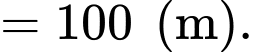
Câu 20 [693785]: Trong lễ tổng kết năm học 2021-2022, lớp 10A1 nhận được 20 cuốn sách gồm 5 cuốn sách Toán, 7 cuốn sách Vật lí, 8 cuốn sách Hóa học, các sách cùng môn là giống nhau. Số sách này được chia đều cho 10 học sinh trong lớp, mỗi học sinh chỉ nhận được hai cuốn sách khác môn học. Bình và Bảo là 2 trong số 10 học sinh đó. Hỏi có bao nhiêu cách chia quà sao cho 2 cuốn sách mà Bình nhận được giống 2 cuốn sách của Bảo.
Điền đáp án: 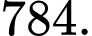
Vì mỗi học sinh chỉ nhận được hai cuốn sách khác môn học nên từ 20 quyển sách ta chia ra làm 10 phần quà. Trong đó mỗi phần quà đó hoặc là gồm 1 cuốn sách Toán và 1 cuốn sách Vật lí (loại 1), hoặc là gồm 1 cuổn sách Toán và 1 cuổn sách Hóa (loại 2), hoặc là gồm 1 cuốn sách Vật lí và 1 cuốn sách Hóa (loại 3).
Gọi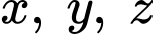 lần lượt là phần quà loại 1, loại 2 và loại 3 .
lần lượt là phần quà loại 1, loại 2 và loại 3 .
Ta có: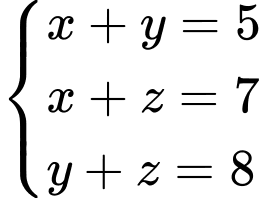
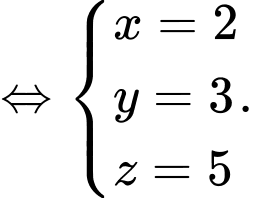
Số cách chia quà sao cho 2 cuốn sách mà Bình và Bảo nhận được đều là quà loại 1 là: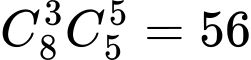 cách.
cách.
Số cách chia quà sao cho 2 cuốn sách mà Bình và Bảo nhận được đều là quà loại 2 là: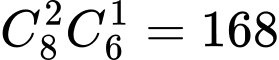 cách.
cách.
Số cách chia quà sao cho 2 cuốn sách mà Bình và Bảo nhận được đều là quà loại 3 là: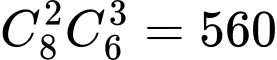 cách.
cách.
Số cách chia phần quà sao cho 2 cuốn sách mà Bình nhận được giống 2 cuốn sách của Bảo là: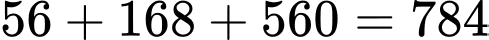 cách.
cách.
Vì mỗi học sinh chỉ nhận được hai cuốn sách khác môn học nên từ 20 quyển sách ta chia ra làm 10 phần quà. Trong đó mỗi phần quà đó hoặc là gồm 1 cuốn sách Toán và 1 cuốn sách Vật lí (loại 1), hoặc là gồm 1 cuổn sách Toán và 1 cuổn sách Hóa (loại 2), hoặc là gồm 1 cuốn sách Vật lí và 1 cuốn sách Hóa (loại 3).
Gọi
 lần lượt là phần quà loại 1, loại 2 và loại 3 .
lần lượt là phần quà loại 1, loại 2 và loại 3 .Ta có:
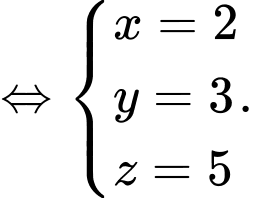
Số cách chia quà sao cho 2 cuốn sách mà Bình và Bảo nhận được đều là quà loại 1 là:
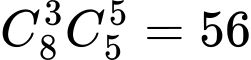 cách.
cách.Số cách chia quà sao cho 2 cuốn sách mà Bình và Bảo nhận được đều là quà loại 2 là:
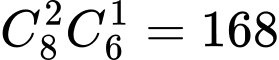 cách.
cách.Số cách chia quà sao cho 2 cuốn sách mà Bình và Bảo nhận được đều là quà loại 3 là:
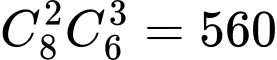 cách.
cách.Số cách chia phần quà sao cho 2 cuốn sách mà Bình nhận được giống 2 cuốn sách của Bảo là:
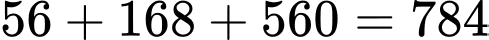 cách.
cách.
Câu 21 [700642]: Trong không gian 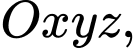 cho ba đường thẳng
cho ba đường thẳng 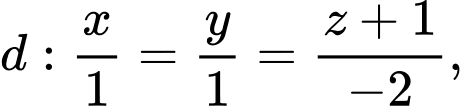
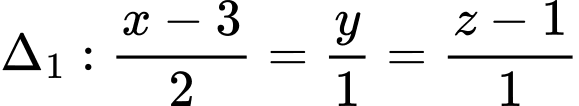 và
và 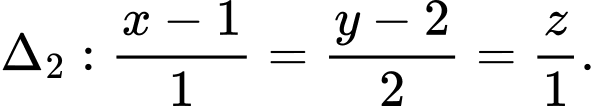 Đường thẳng
Đường thẳng  vuông góc với
vuông góc với 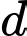 đồng thời cắt
đồng thời cắt 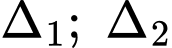 tương ứng tại
tương ứng tại 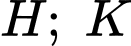 sao cho độ dài
sao cho độ dài 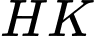 nhỏ nhất. Biết rằng
nhỏ nhất. Biết rằng  có một vectơ chỉ phương là
có một vectơ chỉ phương là 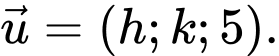 Giá trị của
Giá trị của  bằng bao nhiêu?
bằng bao nhiêu?
 cho ba đường thẳng
cho ba đường thẳng 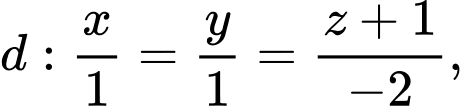
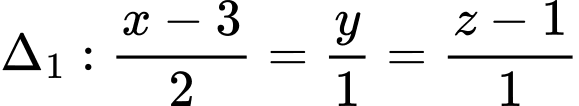 và
và 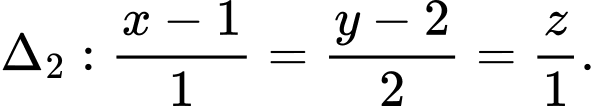 Đường thẳng
Đường thẳng  vuông góc với
vuông góc với 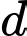 đồng thời cắt
đồng thời cắt 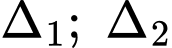 tương ứng tại
tương ứng tại 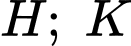 sao cho độ dài
sao cho độ dài 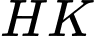 nhỏ nhất. Biết rằng
nhỏ nhất. Biết rằng  có một vectơ chỉ phương là
có một vectơ chỉ phương là 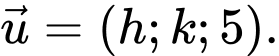 Giá trị của
Giá trị của  bằng bao nhiêu?
bằng bao nhiêu?
Điền đáp án: 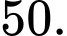
Giả sử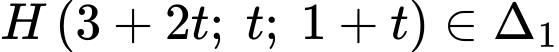 ,
, 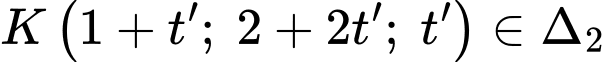 , ta có
, ta có 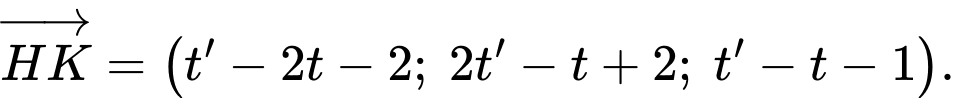
Đường thẳng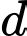 có vectơ chỉ phương là
có vectơ chỉ phương là 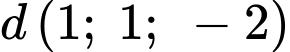 .
.
Vì nên
nên  nên
nên 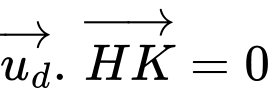
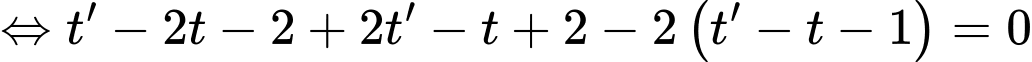
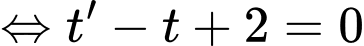
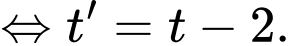
Suy ra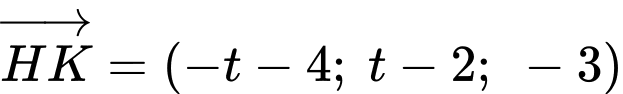
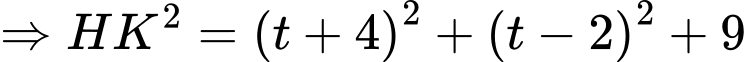
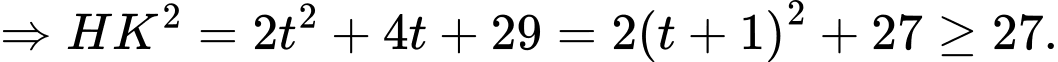
Do đó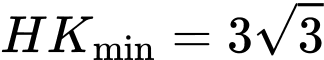 khi
khi 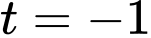 .
.
Khi đó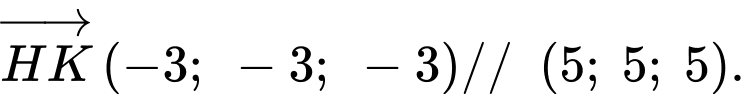
Suy ra đường thẳng nhận
nhận 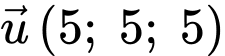 là một VTCP
là một VTCP 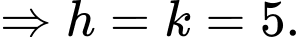
Vậy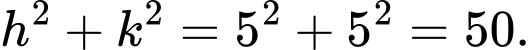
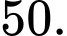
Giả sử
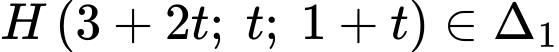 ,
, 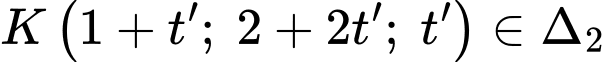 , ta có
, ta có 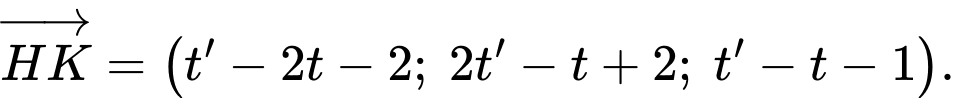
Đường thẳng
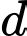 có vectơ chỉ phương là
có vectơ chỉ phương là 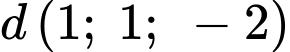 .
.Vì
 nên
nên  nên
nên 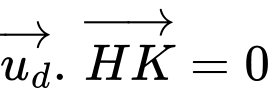
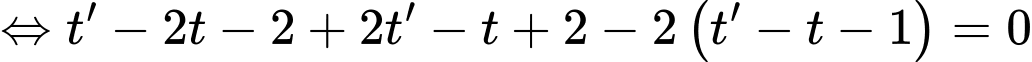
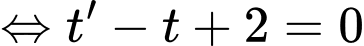
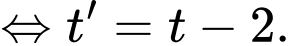
Suy ra
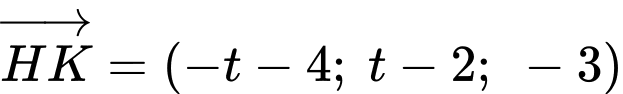
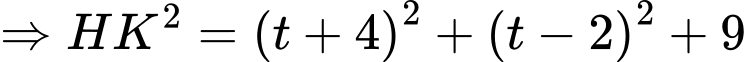
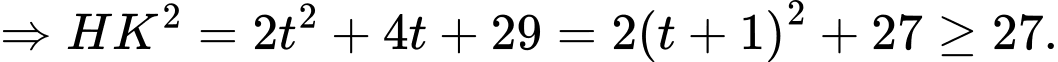
Do đó
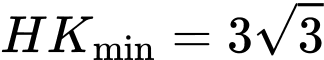 khi
khi 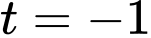 .
. Khi đó
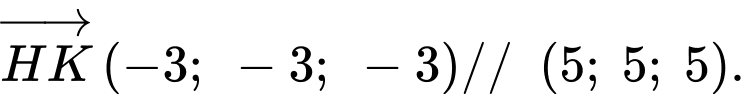
Suy ra đường thẳng
 nhận
nhận 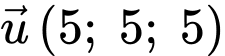 là một VTCP
là một VTCP 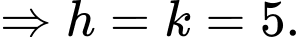
Vậy
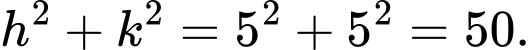
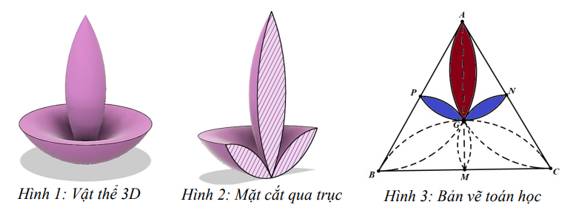
Câu 22 [693787]: Một người thiết kế mô hình một cái đèn ngủ bằng nhựa có hình dạng như hình vẽ 3D ở hình 1. Hình 2 là mặt cắt bởi mặt phẳng cắt đi qua trục của đèn, hình 3 là bản vẽ toán học. Tam giác 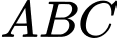 trong hình 3 là tam giác đều cạnh
trong hình 3 là tam giác đều cạnh 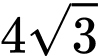 dm và
dm và 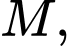
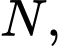
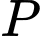 là trung điểm các cạnh,
là trung điểm các cạnh,  là trọng tâm của tam giác. Phần tô đậm trong hình 3 được tạo bởi giao nhau của các cặp cung tròn đi qua 3 điểm là :
là trọng tâm của tam giác. Phần tô đậm trong hình 3 được tạo bởi giao nhau của các cặp cung tròn đi qua 3 điểm là : 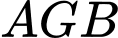 và
và 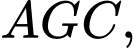
 và
và 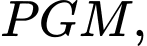
 và
và  (xem hình vẽ). Biết rằng chiếc đèn ngủ được tạo thành khi xoay phần tô đậm trong hình 3 quanh trục là đường thẳng
(xem hình vẽ). Biết rằng chiếc đèn ngủ được tạo thành khi xoay phần tô đậm trong hình 3 quanh trục là đường thẳng 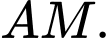 Chi phí trung bình để sản xuất chiếc đèn ngủ là
Chi phí trung bình để sản xuất chiếc đèn ngủ là 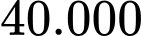 đồng trên mỗi
đồng trên mỗi 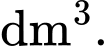 Chi phí để sản xuất đèn ngủ trên bằng bao nhiêu nghìn đồng? Làm tròn đến hàng đơn vị
Chi phí để sản xuất đèn ngủ trên bằng bao nhiêu nghìn đồng? Làm tròn đến hàng đơn vị
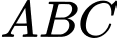 trong hình 3 là tam giác đều cạnh
trong hình 3 là tam giác đều cạnh 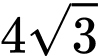 dm và
dm và 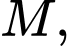
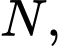
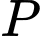 là trung điểm các cạnh,
là trung điểm các cạnh,  là trọng tâm của tam giác. Phần tô đậm trong hình 3 được tạo bởi giao nhau của các cặp cung tròn đi qua 3 điểm là :
là trọng tâm của tam giác. Phần tô đậm trong hình 3 được tạo bởi giao nhau của các cặp cung tròn đi qua 3 điểm là : 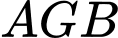 và
và 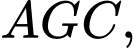
 và
và 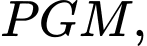
 và
và  (xem hình vẽ). Biết rằng chiếc đèn ngủ được tạo thành khi xoay phần tô đậm trong hình 3 quanh trục là đường thẳng
(xem hình vẽ). Biết rằng chiếc đèn ngủ được tạo thành khi xoay phần tô đậm trong hình 3 quanh trục là đường thẳng 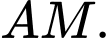 Chi phí trung bình để sản xuất chiếc đèn ngủ là
Chi phí trung bình để sản xuất chiếc đèn ngủ là 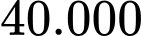 đồng trên mỗi
đồng trên mỗi 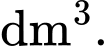 Chi phí để sản xuất đèn ngủ trên bằng bao nhiêu nghìn đồng? Làm tròn đến hàng đơn vị
Chi phí để sản xuất đèn ngủ trên bằng bao nhiêu nghìn đồng? Làm tròn đến hàng đơn vị
Điền đáp án: 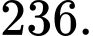
Đường tròn đi qua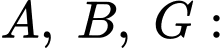
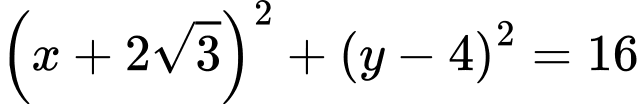
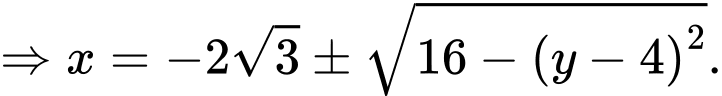
Đường tròn đi qua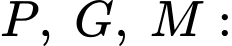
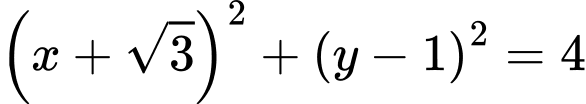
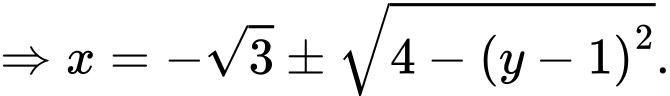
Đường tròn đi qua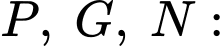
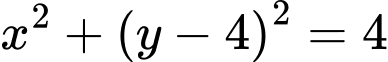
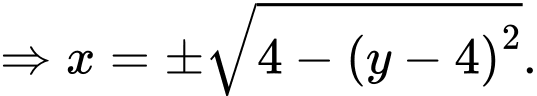
Lấy
Thể tích của đèn ngủ là
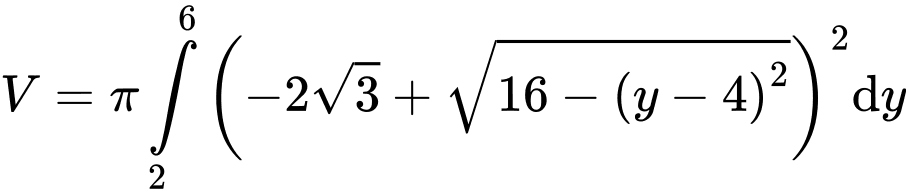
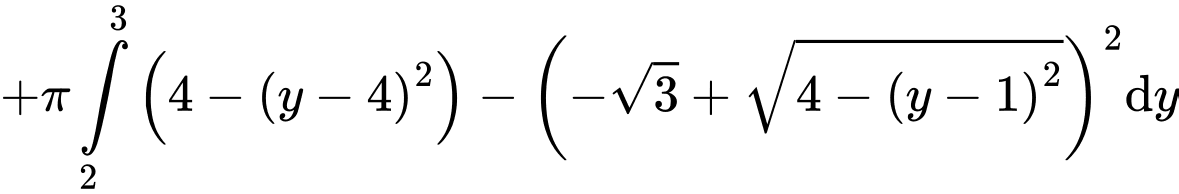
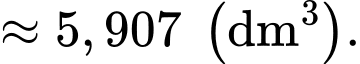
Chi phí để sản xuất đèn ngủ là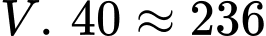 (nghìn đồng).
(nghìn đồng).
Đường tròn đi qua
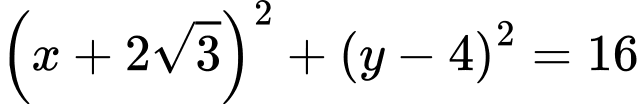
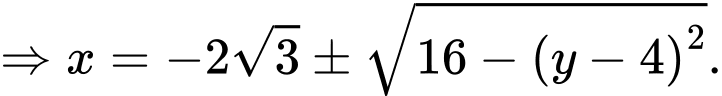
Đường tròn đi qua
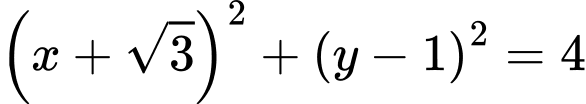
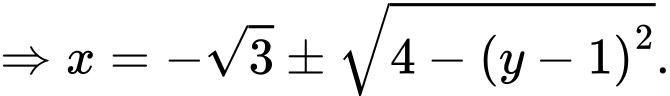
Đường tròn đi qua
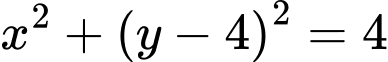
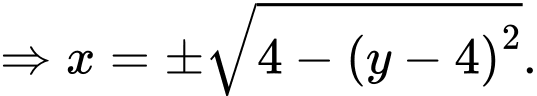
Lấy

Thể tích của đèn ngủ là
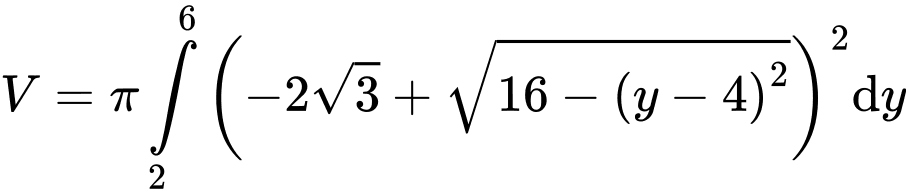
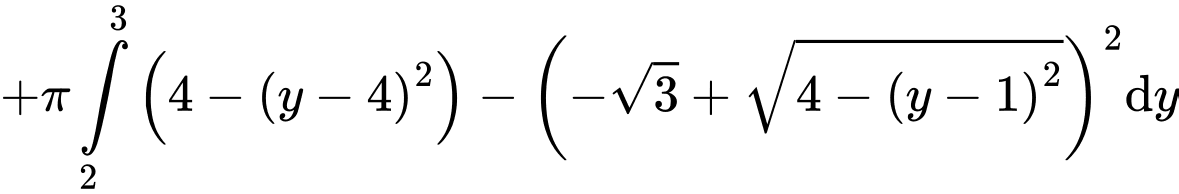
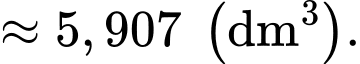
Chi phí để sản xuất đèn ngủ là
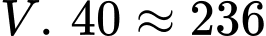 (nghìn đồng).
(nghìn đồng).