PHẦN I. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Câu 1 [693824]: Với 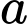 là số thực dương tuỳ ý,
là số thực dương tuỳ ý, 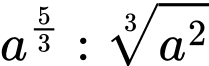 bằng
bằng
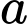 là số thực dương tuỳ ý,
là số thực dương tuỳ ý, 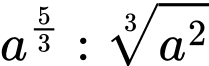 bằng
bằng A, 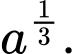
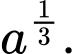
B, 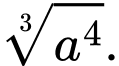
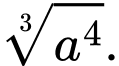
C, 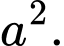
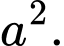
D, 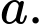
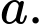
Chọn đáp án D.
Ta có: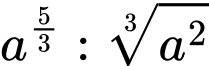
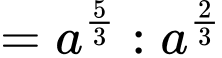
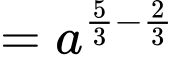
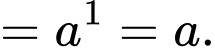 Đáp án: D
Đáp án: D
Ta có:
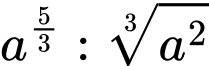
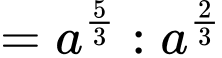
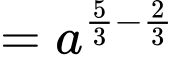
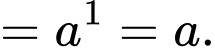 Đáp án: D
Đáp án: D
Câu 2 [257454]: Cho hàm số bậc bốn 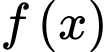 có bảng biến thiên như sau:
có bảng biến thiên như sau:
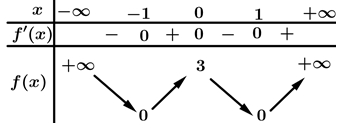
Hàm số đã cho đồng biến trên khoảng nào dưới đây?
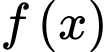 có bảng biến thiên như sau:
có bảng biến thiên như sau:
Hàm số đã cho đồng biến trên khoảng nào dưới đây?
A, 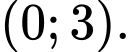
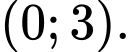
B, 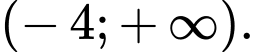
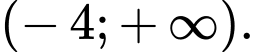
C, 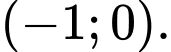
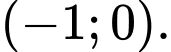
D, 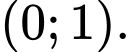
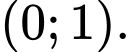
Chọn đáp án C.
Dựa vào bảng biến thiên, ta thấy hàm số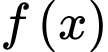 đồng biến trên các khoảng
đồng biến trên các khoảng 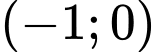 và
và 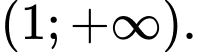 Đáp án: C
Đáp án: C
Dựa vào bảng biến thiên, ta thấy hàm số
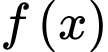 đồng biến trên các khoảng
đồng biến trên các khoảng 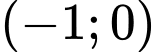 và
và 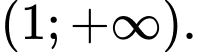 Đáp án: C
Đáp án: C
Câu 3 [257464]: Trong không gian 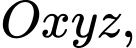 cho hai điểm
cho hai điểm 
 Trọng tâm của tam giác
Trọng tâm của tam giác 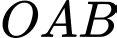 có tọa độ là
có tọa độ là
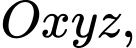 cho hai điểm
cho hai điểm 
 Trọng tâm của tam giác
Trọng tâm của tam giác 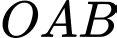 có tọa độ là
có tọa độ là A, 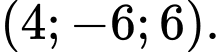
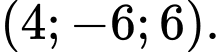
B, 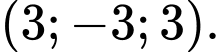
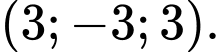
C, 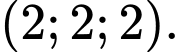
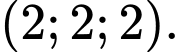
D, 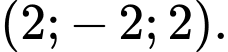
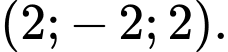
Chọn đáp án D.
Chú ý: Trọng tâm của tam giác
của tam giác 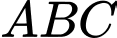 có tọa độ là
có tọa độ là 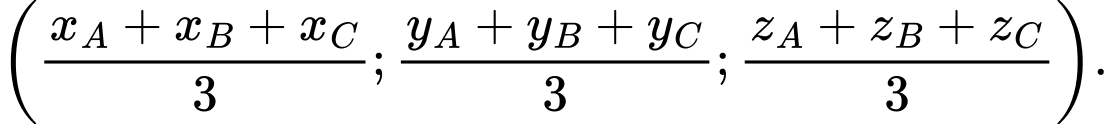
Áp dụng công thức, tọa độ trọng tâm của tam giác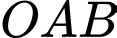 là
là 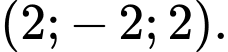 Đáp án: D
Đáp án: D
Chú ý: Trọng tâm
 của tam giác
của tam giác 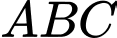 có tọa độ là
có tọa độ là 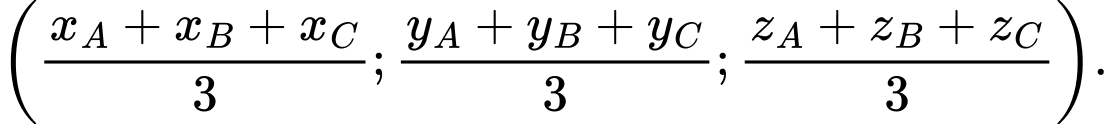
Áp dụng công thức, tọa độ trọng tâm của tam giác
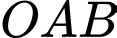 là
là 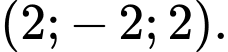 Đáp án: D
Đáp án: D
Câu 4 [693825]: Cho dãy số 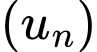 với
với 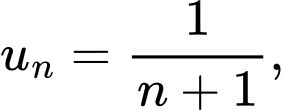
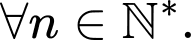 Giá trị của
Giá trị của 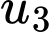 bằng
bằng
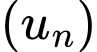 với
với 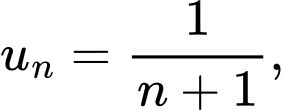
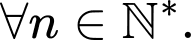 Giá trị của
Giá trị của 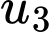 bằng
bằng A, 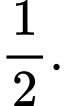
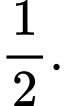
B, 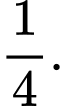
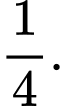
C, 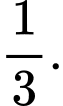
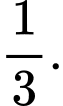
D, 
Chọn đáp án B.
Với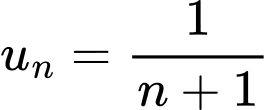 ta có:
ta có: 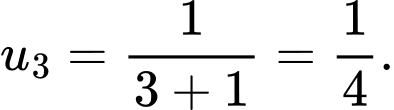 Đáp án: B
Đáp án: B
Với
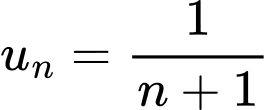 ta có:
ta có: 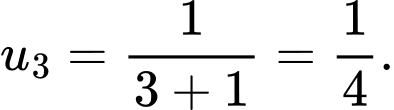 Đáp án: B
Đáp án: B
Câu 5 [693826]: Họ nguyên hàm của hàm số 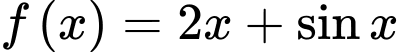 là
là
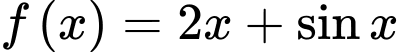 là
là A, 

B, 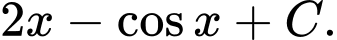
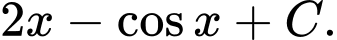
C, 

D, 

Chọn đáp án A.
Ta có: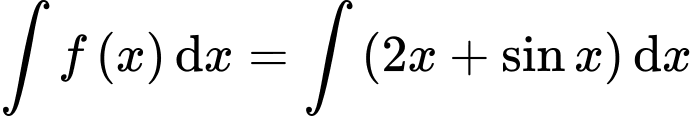
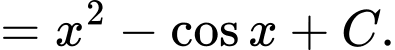 Đáp án: A
Đáp án: A
Ta có:
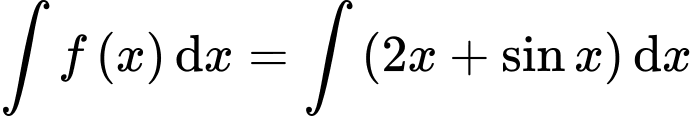
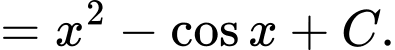 Đáp án: A
Đáp án: A
Câu 6 [693827]: Cho hình hộp 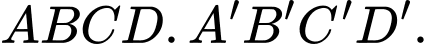 Vectơ nào sau đây cùng phương với
Vectơ nào sau đây cùng phương với 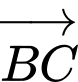 ?
?
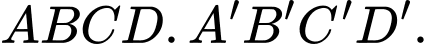 Vectơ nào sau đây cùng phương với
Vectơ nào sau đây cùng phương với 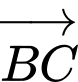 ?
? A, 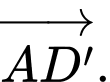
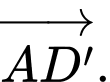
B, 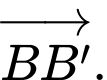
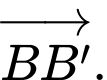
C, 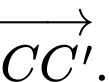
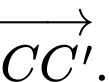
D, 

Chọn đáp án D.
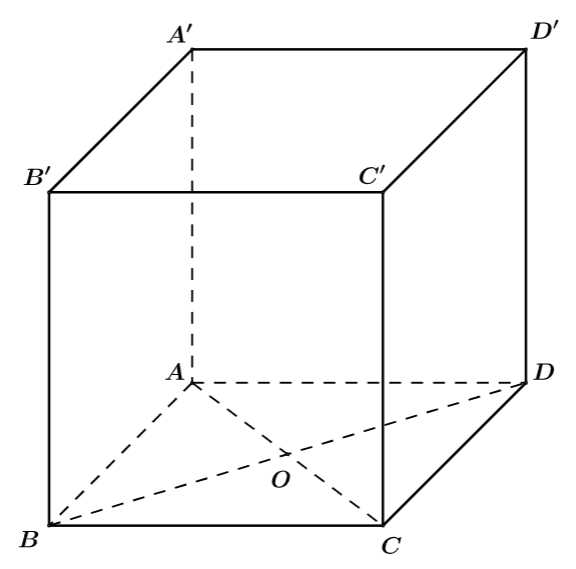
Từ hình vẽ ta có vectơ cùng phương với
cùng phương với 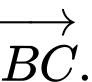 Đáp án: D
Đáp án: D

Từ hình vẽ ta có vectơ
 cùng phương với
cùng phương với 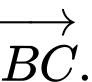 Đáp án: D
Đáp án: D
Câu 7 [257439]: Số nghiệm của phương trình 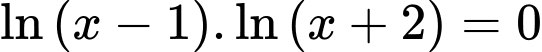 là
là
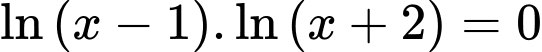 là
là A, 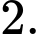
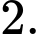
B, 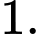
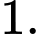
C, 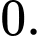
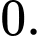
D, 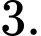
Chọn đáp án B.
Điều kiện xác định: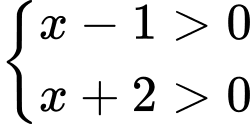
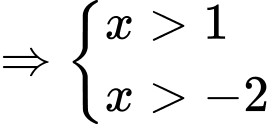
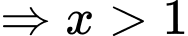 .
.
Ta có phương trình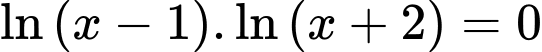
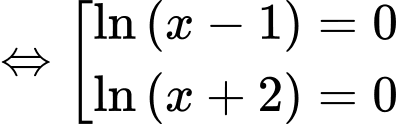
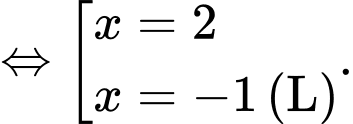
Vậy phương trình có 1 nghiệm thực. Đáp án: B
Điều kiện xác định:
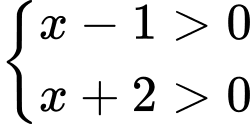
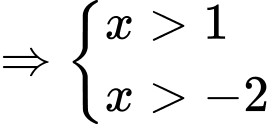
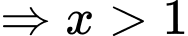 .
.Ta có phương trình
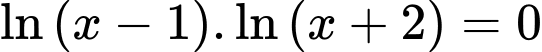
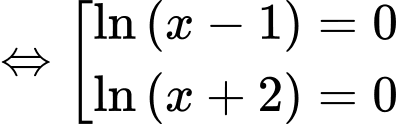
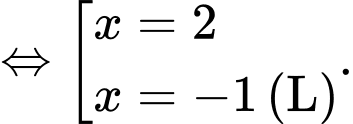
Vậy phương trình có 1 nghiệm thực. Đáp án: B
Câu 8 [693828]: Trong không gian 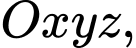 góc giữa hai mặt phẳng
góc giữa hai mặt phẳng 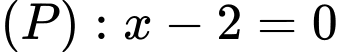 và
và 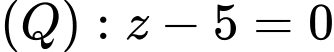 là
là
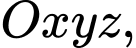 góc giữa hai mặt phẳng
góc giữa hai mặt phẳng 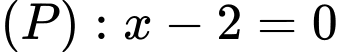 và
và 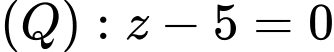 là
là A, 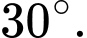
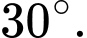
B, 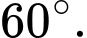
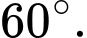
C, 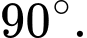
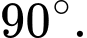
D, 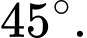
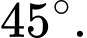
Chọn đáp án C.
Ta có: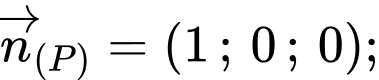
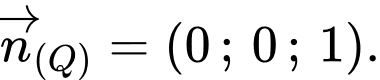
Suy ra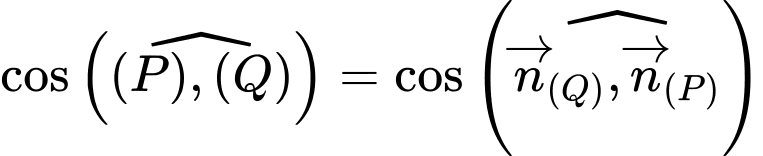
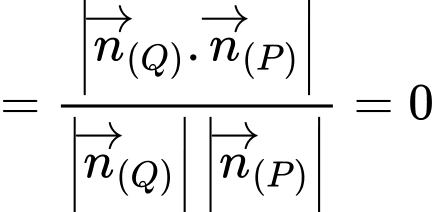
 Đáp án: C
Đáp án: C
Ta có:
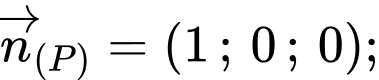
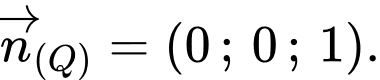
Suy ra
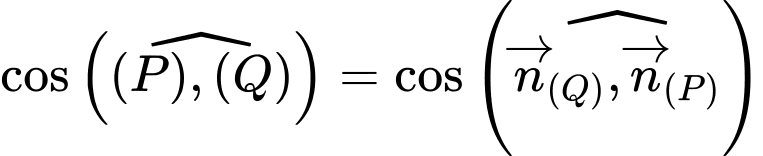
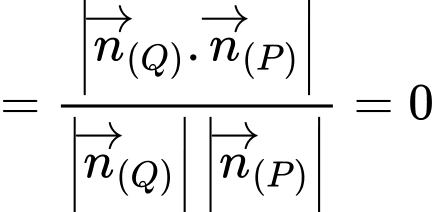
 Đáp án: C
Đáp án: C
Câu 9 [693829]: Cho hàm số 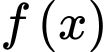 có đạo hàm liên tục trên đoạn
có đạo hàm liên tục trên đoạn 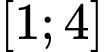 và thoả mãn
và thoả mãn 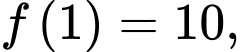
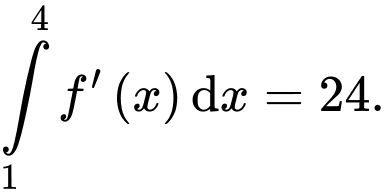 Giá trị của
Giá trị của 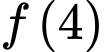 bằng
bằng
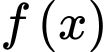 có đạo hàm liên tục trên đoạn
có đạo hàm liên tục trên đoạn 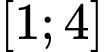 và thoả mãn
và thoả mãn 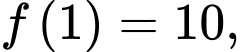
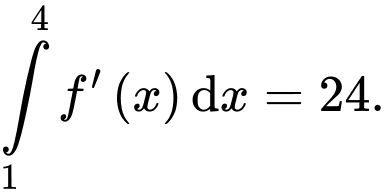 Giá trị của
Giá trị của 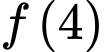 bằng
bằng A, 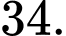
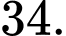
B, 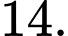
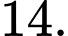
C, 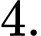
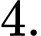
D, 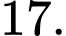
Chọn đáp án A.
Ta có: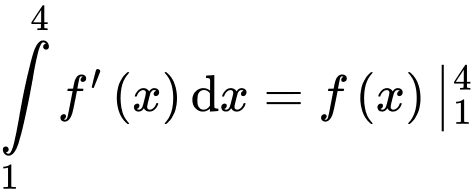
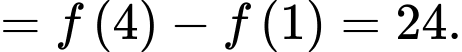
Mà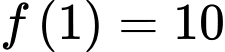
Nên ta được: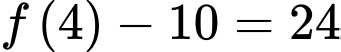
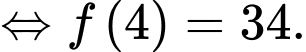 Đáp án: A
Đáp án: A
Ta có:
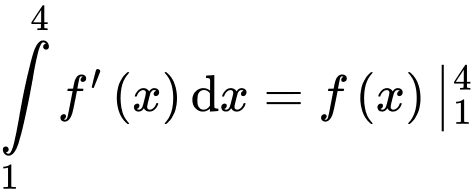
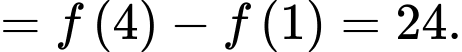
Mà
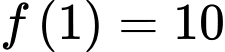
Nên ta được:
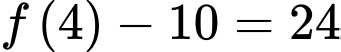
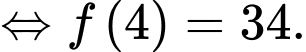 Đáp án: A
Đáp án: A
Câu 10 [693830]: Mức thưởng tết (đơn vị: triệu đồng) cho các nhân viên của một công ty được thống kê trong bảng sau:

Tứ phân vị thứ nhất của mẫu số liệu trên thuộc nhóm nào sau đây?

Tứ phân vị thứ nhất của mẫu số liệu trên thuộc nhóm nào sau đây?
A, 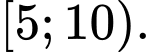
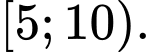
B, 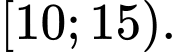
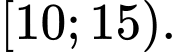
C, 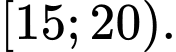
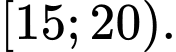
D, 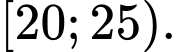
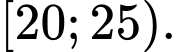
Chọn đáp án B.
Số nhân viên của công ty được khảo sát là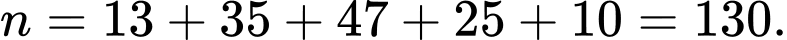
Gọi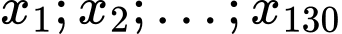 là mức thưởng tết của 130 người được sắp xếp theo thứ tự không giảm.
là mức thưởng tết của 130 người được sắp xếp theo thứ tự không giảm.
Ta có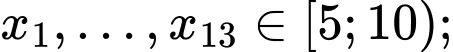
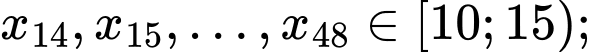
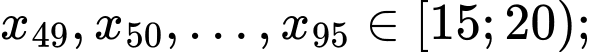
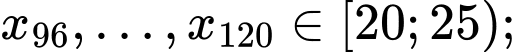
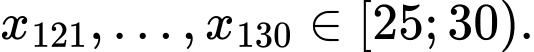 Do đó đối với dãy số liệu
Do đó đối với dãy số liệu 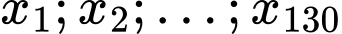 thì
thì
Tứ phân vị thứ nhất của dãy số liệu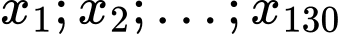 là
là 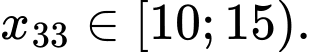
Do đó tứ phân vị thứ nhất của mẫu số liệu thuộc nhóm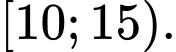 Đáp án: B
Đáp án: B
Số nhân viên của công ty được khảo sát là
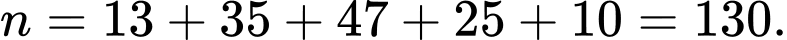
Gọi
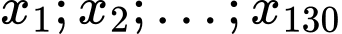 là mức thưởng tết của 130 người được sắp xếp theo thứ tự không giảm.
là mức thưởng tết của 130 người được sắp xếp theo thứ tự không giảm.
Ta có
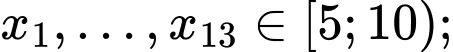
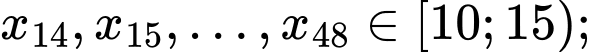
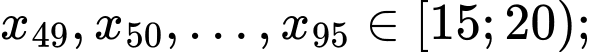
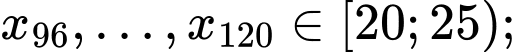
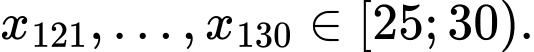 Do đó đối với dãy số liệu
Do đó đối với dãy số liệu 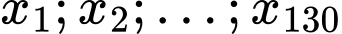 thì
thì
Tứ phân vị thứ nhất của dãy số liệu
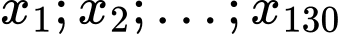 là
là 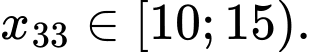
Do đó tứ phân vị thứ nhất của mẫu số liệu thuộc nhóm
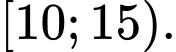 Đáp án: B
Đáp án: B
Câu 11 [693832]: Cho hình lăng trụ đứng  có đáy là tam giác vuông cân tại
có đáy là tam giác vuông cân tại 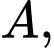
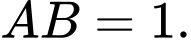 Khoảng cách từ điểm
Khoảng cách từ điểm 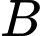 đến mặt phẳng
đến mặt phẳng 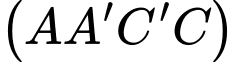 bằng
bằng
 có đáy là tam giác vuông cân tại
có đáy là tam giác vuông cân tại 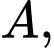
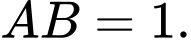 Khoảng cách từ điểm
Khoảng cách từ điểm 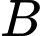 đến mặt phẳng
đến mặt phẳng 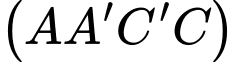 bằng
bằng A, 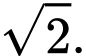
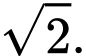
B, 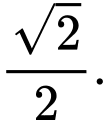
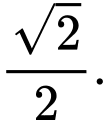
C, 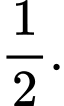
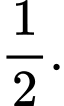
D, 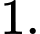
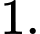
Chọn đáp án D.
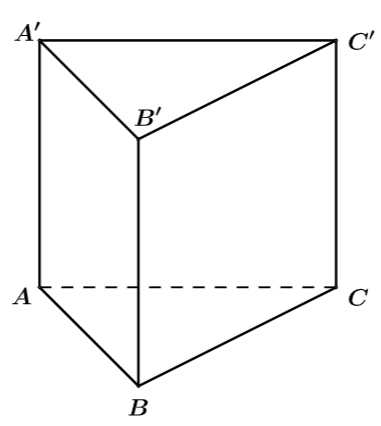
Ta có: là hình lăng trụ đứng
là hình lăng trụ đứng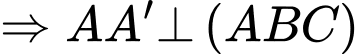
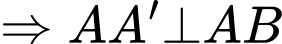
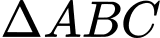 vuông cân tại
vuông cân tại 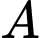

Mà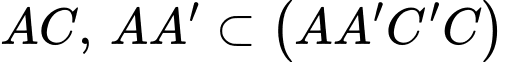

Vậy khoảng cách từ điểm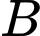 đến mặt phẳng
đến mặt phẳng 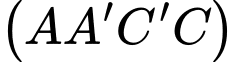 bằng
bằng 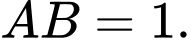 Đáp án: D
Đáp án: D

Ta có:
 là hình lăng trụ đứng
là hình lăng trụ đứng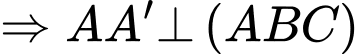
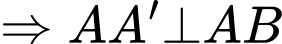
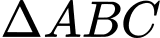 vuông cân tại
vuông cân tại 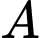

Mà
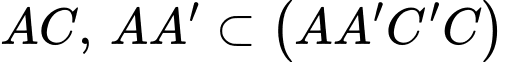

Vậy khoảng cách từ điểm
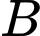 đến mặt phẳng
đến mặt phẳng 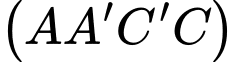 bằng
bằng 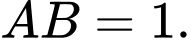 Đáp án: D
Đáp án: D
Câu 12 [693831]: Cho hàm số 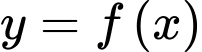 có đạo hàm
có đạo hàm 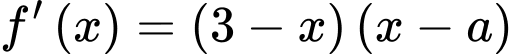 với
với 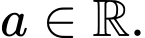 Tất cả giá trị của
Tất cả giá trị của 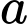 để hàm số đã cho đạt cực đại tại điểm
để hàm số đã cho đạt cực đại tại điểm 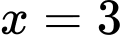 là
là
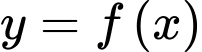 có đạo hàm
có đạo hàm 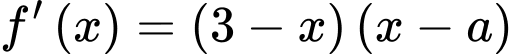 với
với 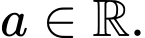 Tất cả giá trị của
Tất cả giá trị của 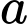 để hàm số đã cho đạt cực đại tại điểm
để hàm số đã cho đạt cực đại tại điểm 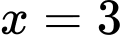 là
là A, 

B, 

C, 

D, 

Chọn đáp án A.
Ta có: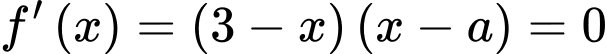
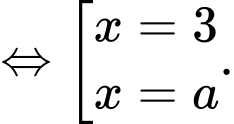
Để hàm số đạt cực đại tại điểm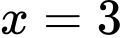 thì phương trình không có nghiệm kép nên nghiệm
thì phương trình không có nghiệm kép nên nghiệm 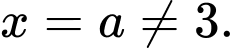 Và qua điểm cực đại
Và qua điểm cực đại 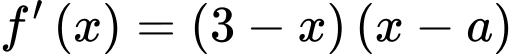 đổi dấu “dương” sang “âm” nên ta xét dấu
đổi dấu “dương” sang “âm” nên ta xét dấu 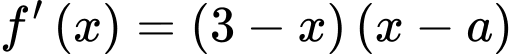 :
:
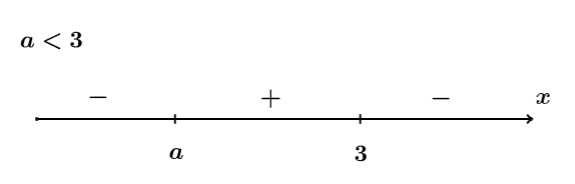
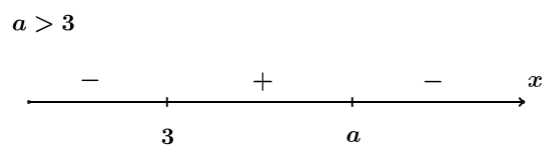
Từ trục xét dấu ta suy ra để hàm số đạt cực đại tại điểm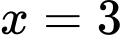 thì
thì  Đáp án: A
Đáp án: A
Ta có:
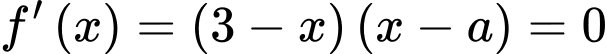
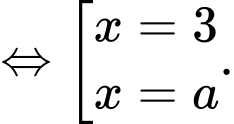
Để hàm số đạt cực đại tại điểm
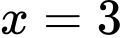 thì phương trình không có nghiệm kép nên nghiệm
thì phương trình không có nghiệm kép nên nghiệm 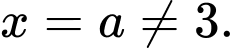 Và qua điểm cực đại
Và qua điểm cực đại 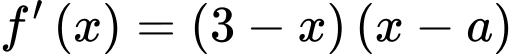 đổi dấu “dương” sang “âm” nên ta xét dấu
đổi dấu “dương” sang “âm” nên ta xét dấu 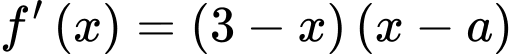 :
:

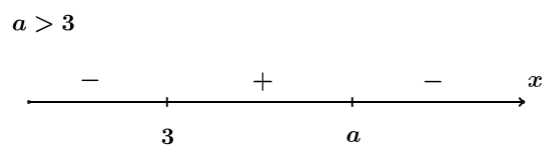
Từ trục xét dấu ta suy ra để hàm số đạt cực đại tại điểm
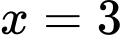 thì
thì  Đáp án: A
Đáp án: A PHẦN II. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Câu 13 [693833]: Trong không gian với tọa độ Oxyz, cho mặt cầu 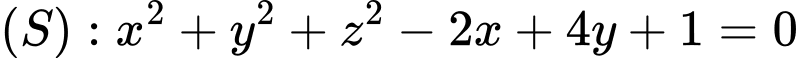 và mặt phẳng
và mặt phẳng 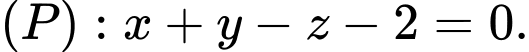
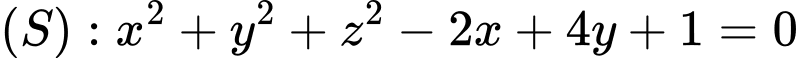 và mặt phẳng
và mặt phẳng 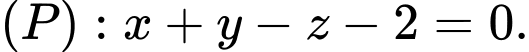
a) Sai.
Mặt cầu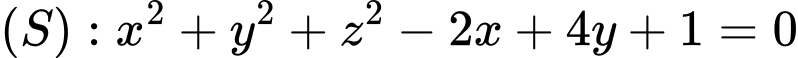 có tâm
có tâm 
b) Sai.
Bán kính mặt cầu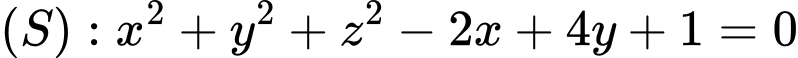 là
là 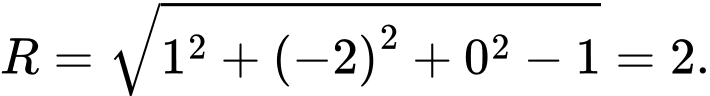
c) Đúng.
Khoảng cách từ tâm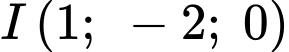 của mặt cầu
của mặt cầu 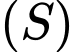 đến mặt phẳng
đến mặt phẳng 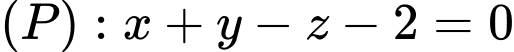 là
là
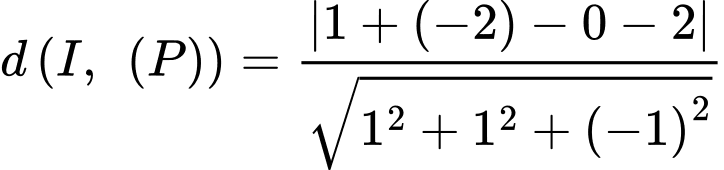

d) Đúng.
Ta thấy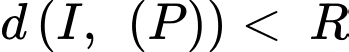 nên
nên 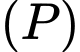 cắt mặt cầu
cắt mặt cầu 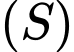 theo giao tuyến là một đường tròn với bán kính
theo giao tuyến là một đường tròn với bán kính 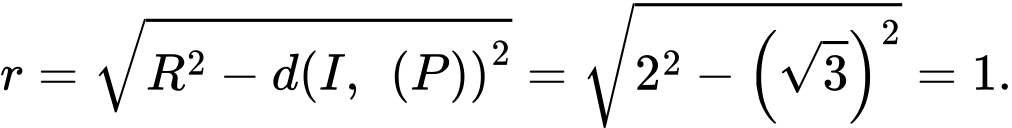
Mặt cầu
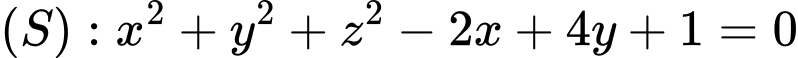 có tâm
có tâm 
b) Sai.
Bán kính mặt cầu
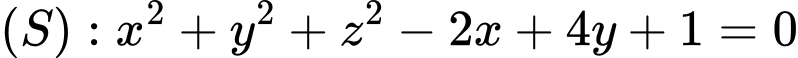 là
là 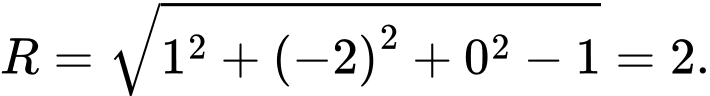
c) Đúng.
Khoảng cách từ tâm
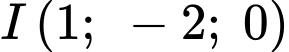 của mặt cầu
của mặt cầu 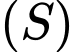 đến mặt phẳng
đến mặt phẳng 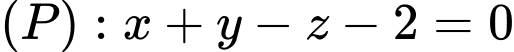 là
là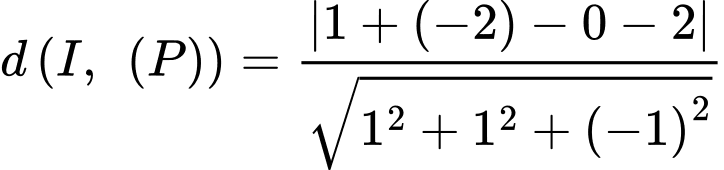

d) Đúng.
Ta thấy
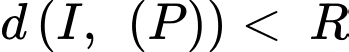 nên
nên 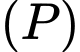 cắt mặt cầu
cắt mặt cầu 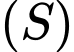 theo giao tuyến là một đường tròn với bán kính
theo giao tuyến là một đường tròn với bán kính 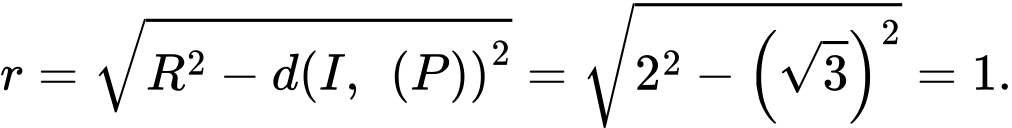
Câu 14 [695593]: Người ta muốn thiết kế một lồng nuôi cá có bề mặt hình chữ nhật bao gồm phần mặt nước có diện tích bằng 54 m² và phần đường đi xung quanh với kích thước (đơn vị: m) như hình vẽ:
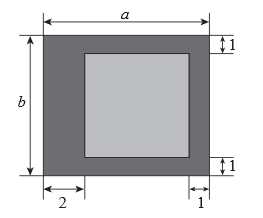

a) Đúng.
Kích thước hình chữ nhật phần mặt nước là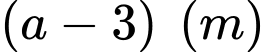 và
và 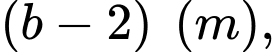 với
với 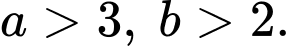
b) Sai.
Diện tích phần mặt nước là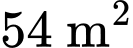 nên
nên 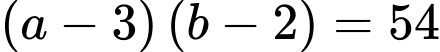
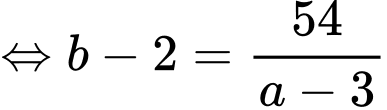
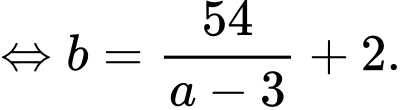
c) Sai.
Diện tích cả lồng nuôi cá là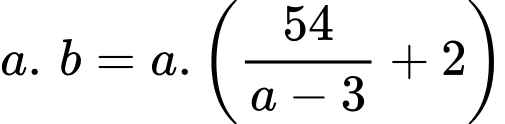
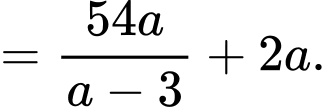
Diện tích phần đường đi là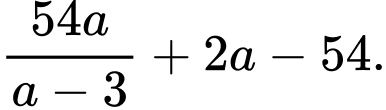
d) Đúng.
Xét hàm số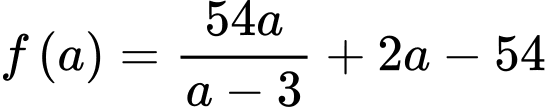
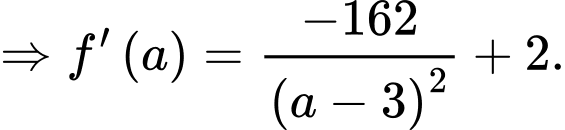
Ta có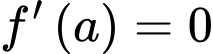
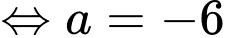 (loại) hoặc
(loại) hoặc 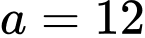 (thoả mãn).
(thoả mãn).
Tính giá trị của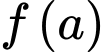 tại điểm cực trị, ta có diện tích phần đường đi nhỏ nhất khi
tại điểm cực trị, ta có diện tích phần đường đi nhỏ nhất khi 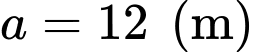 và có diện tích
và có diện tích 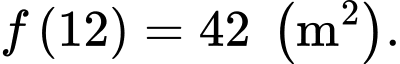
Kích thước hình chữ nhật phần mặt nước là
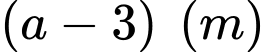 và
và 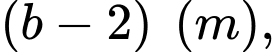 với
với 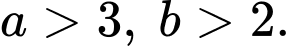
b) Sai.
Diện tích phần mặt nước là
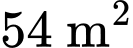 nên
nên 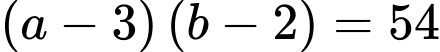
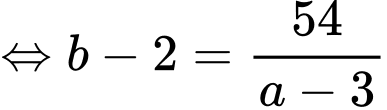
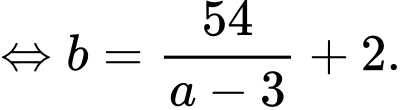
c) Sai.
Diện tích cả lồng nuôi cá là
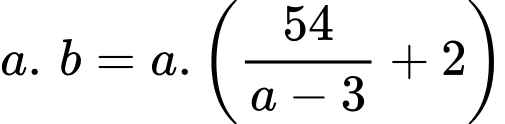
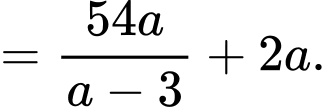
Diện tích phần đường đi là
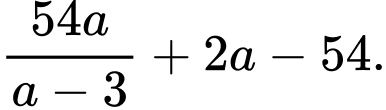
d) Đúng.
Xét hàm số
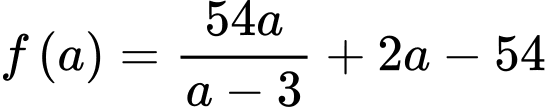
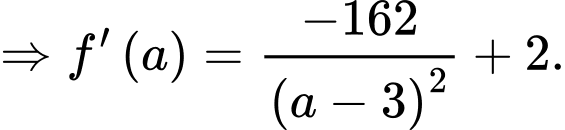
Ta có
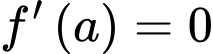
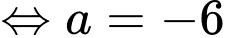 (loại) hoặc
(loại) hoặc 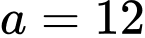 (thoả mãn).
(thoả mãn).
Tính giá trị của
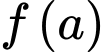 tại điểm cực trị, ta có diện tích phần đường đi nhỏ nhất khi
tại điểm cực trị, ta có diện tích phần đường đi nhỏ nhất khi 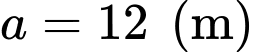 và có diện tích
và có diện tích 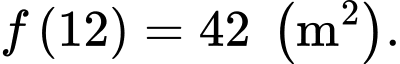
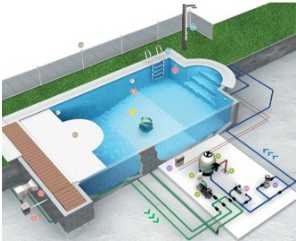
Câu 15 [703158]: Hệ thống lọc nước bể bơi vô cùng quan trọng để nguồn nước được làm sạch thường xuyên và giữ vệ sinh cho người bơi. Trong quá trình vận hành lọc nước thì lượng nước trong bể sẽ thay đổi theo thời gian. Lượng nước trong bể giảm nếu hệ thống đang xả nước bẩn ra khỏi bể và tăng nếu hệ thống đang cấp thêm nước sạch cho bể. Biết rằng 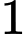 gallon gần bằng
gallon gần bằng 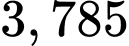 lít, dung tích của bể là
lít, dung tích của bể là 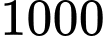 gallon và thời điểm
gallon và thời điểm 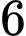 giờ sáng bể chứa
giờ sáng bể chứa 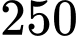 gallon nước. Hàm số
gallon nước. Hàm số 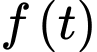 liên tục trên đoạn
liên tục trên đoạn 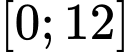 biểu thị cho tốc độ thay đổi lượng nước trong bể theo thời gian
biểu thị cho tốc độ thay đổi lượng nước trong bể theo thời gian 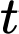 giờ, từ thời điểm
giờ, từ thời điểm 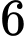 giờ sáng đến
giờ sáng đến 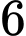 giờ chiều được cho bởi hàm số
giờ chiều được cho bởi hàm số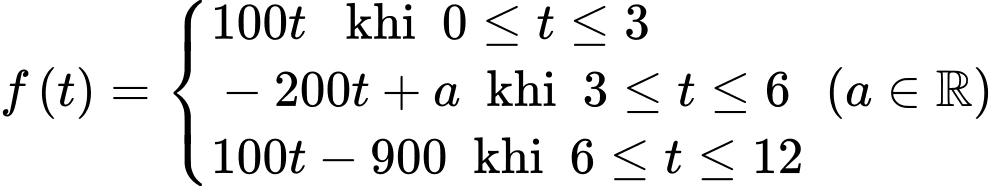 với mốc thời gian
với mốc thời gian 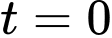 tại thời điểm
tại thời điểm  giờ sáng.
giờ sáng.
 gallon gần bằng
gallon gần bằng 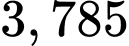 lít, dung tích của bể là
lít, dung tích của bể là 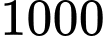 gallon và thời điểm
gallon và thời điểm 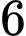 giờ sáng bể chứa
giờ sáng bể chứa 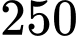 gallon nước. Hàm số
gallon nước. Hàm số 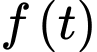 liên tục trên đoạn
liên tục trên đoạn 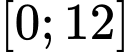 biểu thị cho tốc độ thay đổi lượng nước trong bể theo thời gian
biểu thị cho tốc độ thay đổi lượng nước trong bể theo thời gian 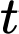 giờ, từ thời điểm
giờ, từ thời điểm 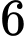 giờ sáng đến
giờ sáng đến 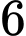 giờ chiều được cho bởi hàm số
giờ chiều được cho bởi hàm số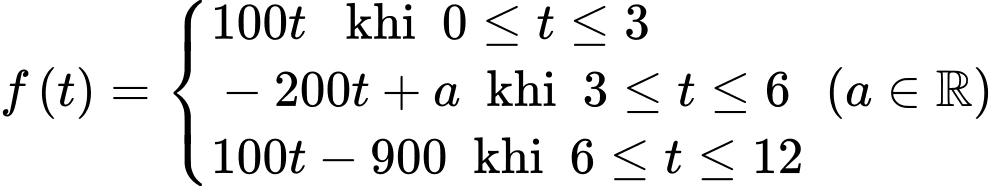 với mốc thời gian
với mốc thời gian 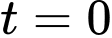 tại thời điểm
tại thời điểm 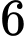 giờ sáng.
giờ sáng.
a) Sai.
Do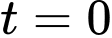 tại thời điểm
tại thời điểm 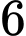 giờ sáng nên tại thời điểm
giờ sáng nên tại thời điểm 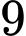 giờ sáng thì
giờ sáng thì 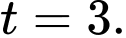
Ta có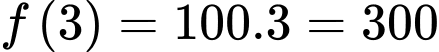 gallon/giờ.
gallon/giờ.
b) Đúng.
Với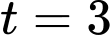 ,
, 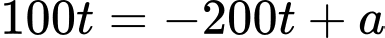

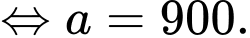
c) Sai.
Tại giờ trưa (tương đương
giờ trưa (tương đương 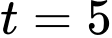 ), tốc độ thay đổi lượng nước trong bể là
), tốc độ thay đổi lượng nước trong bể là
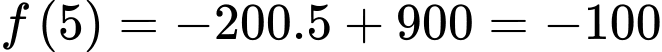 gallon/giờ.
gallon/giờ.
Tại giờ chiều (tương đương
giờ chiều (tương đương 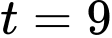 ), tốc độ thay đổi lượng nước trong bể là
), tốc độ thay đổi lượng nước trong bể là
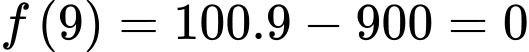 gallon/giờ.
gallon/giờ.
d) Sai.
Từ giờ sáng đến giờ chiều tức là
giờ chiều tức là 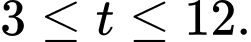
Từ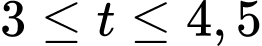 lượng nước đang tăng
lượng nước đang tăng
Lượng nước trong bể bắt đầu giảm từ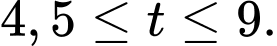
Lượng nước trong bể bắt đầu tăng trở lại từ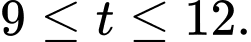
Lượng nước trong bể từ giờ chiều đến
giờ chiều đến  giờ chiều là
giờ chiều là
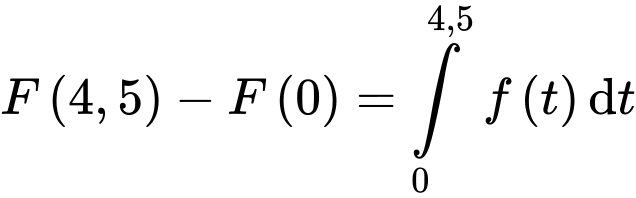
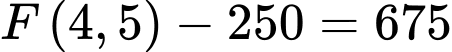
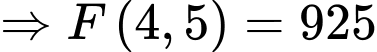 (gallon).
(gallon).
Lại có: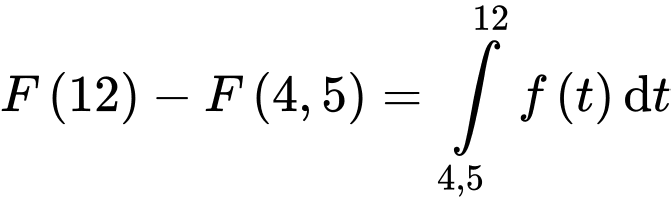
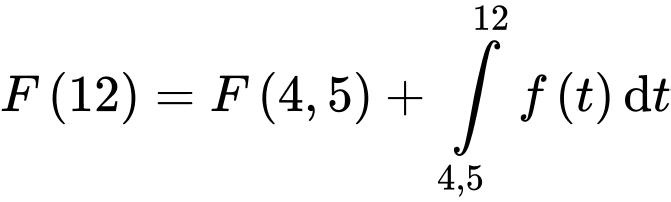
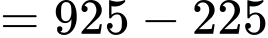
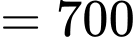 (gallon).
(gallon).
Do
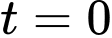 tại thời điểm
tại thời điểm 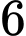 giờ sáng nên tại thời điểm
giờ sáng nên tại thời điểm 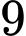 giờ sáng thì
giờ sáng thì 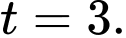
Ta có
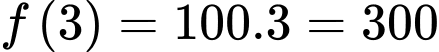 gallon/giờ.
gallon/giờ.b) Đúng.
Với
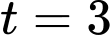 ,
, 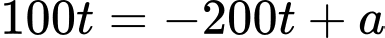

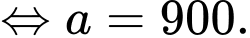
c) Sai.
Tại
 giờ trưa (tương đương
giờ trưa (tương đương 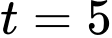 ), tốc độ thay đổi lượng nước trong bể là
), tốc độ thay đổi lượng nước trong bể là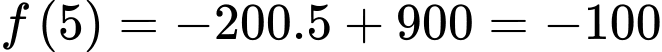 gallon/giờ.
gallon/giờ.Tại
 giờ chiều (tương đương
giờ chiều (tương đương 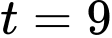 ), tốc độ thay đổi lượng nước trong bể là
), tốc độ thay đổi lượng nước trong bể là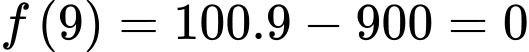 gallon/giờ.
gallon/giờ.d) Sai.
Từ giờ sáng đến
 giờ chiều tức là
giờ chiều tức là 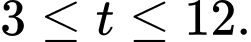
Từ
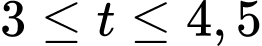 lượng nước đang tăng
lượng nước đang tăng Lượng nước trong bể bắt đầu giảm từ
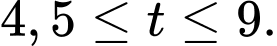
Lượng nước trong bể bắt đầu tăng trở lại từ
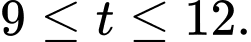
Lượng nước trong bể từ
 giờ chiều đến
giờ chiều đến  giờ chiều là
giờ chiều là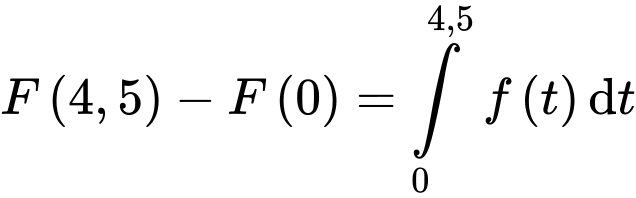
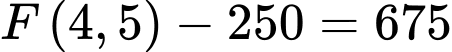
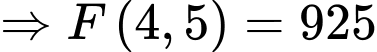 (gallon).
(gallon).Lại có:
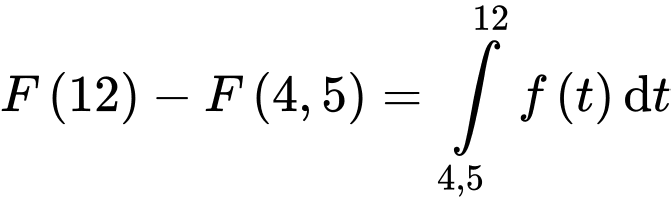
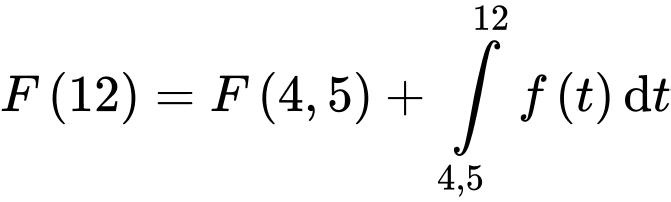
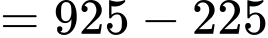
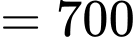 (gallon).
(gallon).
Câu 16 [693836]: Chuồng  có
có 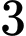 con gà trống và
con gà trống và 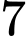 con gà mái, chuồng
con gà mái, chuồng 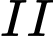 có
có 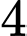 con gà trống và
con gà trống và 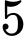 con gà mái. Có
con gà mái. Có 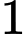 con gà từ chuồng
con gà từ chuồng 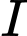 sang chuồng
sang chuồng 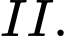 Sau đó, có
Sau đó, có 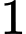 con gà từ chuồng
con gà từ chuồng 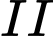 chạy ra ngoài.
chạy ra ngoài.
Gọi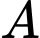 là biến cố có
là biến cố có 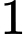 con gà mái từ chuồng
con gà mái từ chuồng 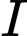 sang chuồng
sang chuồng 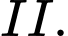
Gọi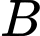 là biến cố một con gà từ chuồng
là biến cố một con gà từ chuồng 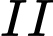 chạy ra ngoài là gà trống.
chạy ra ngoài là gà trống.
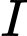 có
có 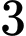 con gà trống và
con gà trống và 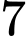 con gà mái, chuồng
con gà mái, chuồng 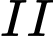 có
có 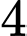 con gà trống và
con gà trống và 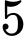 con gà mái. Có
con gà mái. Có 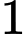 con gà từ chuồng
con gà từ chuồng 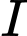 sang chuồng
sang chuồng 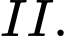 Sau đó, có
Sau đó, có 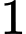 con gà từ chuồng
con gà từ chuồng 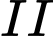 chạy ra ngoài.
chạy ra ngoài. Gọi
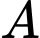 là biến cố có
là biến cố có 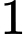 con gà mái từ chuồng
con gà mái từ chuồng 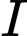 sang chuồng
sang chuồng 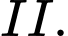
Gọi
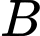 là biến cố một con gà từ chuồng
là biến cố một con gà từ chuồng 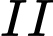 chạy ra ngoài là gà trống.
chạy ra ngoài là gà trống.
a) Đúng.
Ta có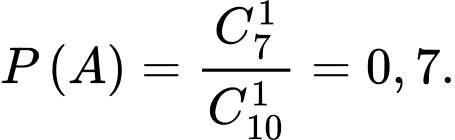
Gọi là biến cố “Có
là biến cố “Có 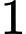 con gà trống từ chuồng
con gà trống từ chuồng 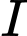 sang chuồng
sang chuồng 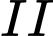 ”.
”.
Suy ra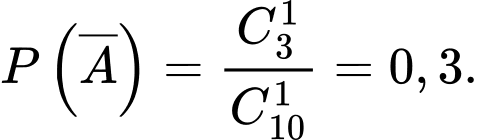
b) Sai.
Ta có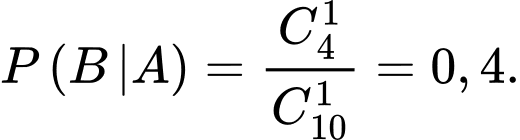
c) Đúng.
Ta có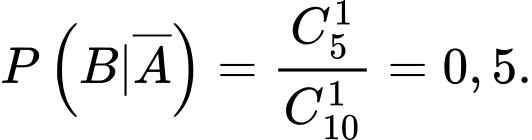
Ta có sơ đồ cây sau:
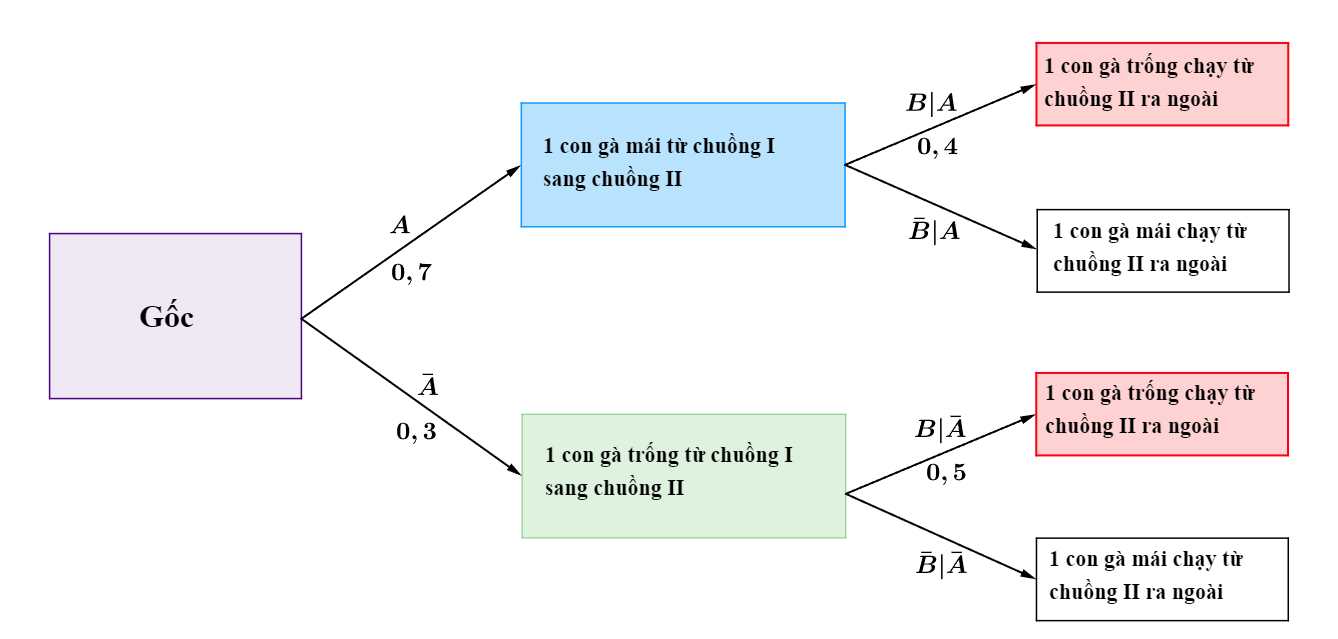
Áp dụng công thức xác suất toàn phần, ta có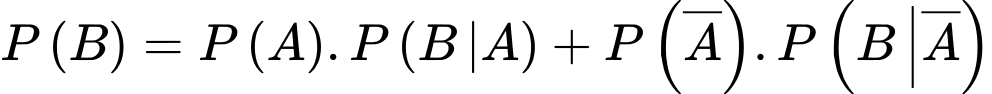
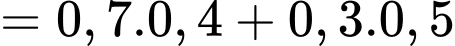
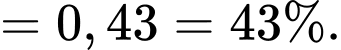
d) Đúng.
Ta có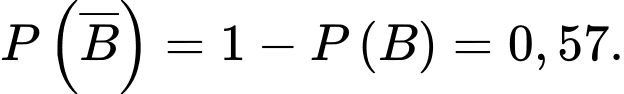
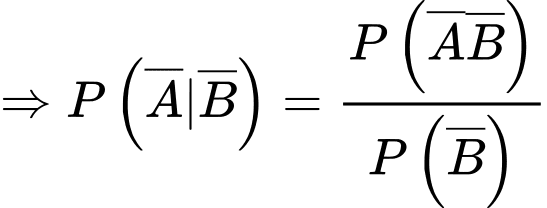
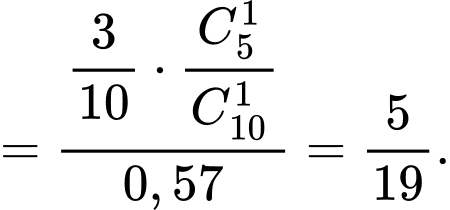
Ta có
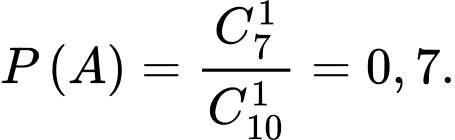
Gọi
 là biến cố “Có
là biến cố “Có 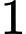 con gà trống từ chuồng
con gà trống từ chuồng 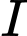 sang chuồng
sang chuồng 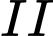 ”.
”. Suy ra
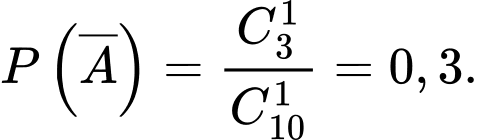
b) Sai.
Ta có
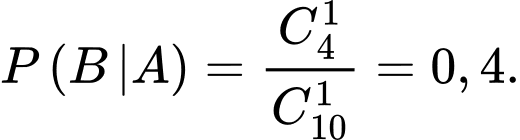
c) Đúng.
Ta có
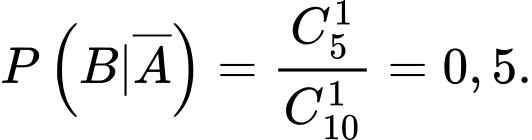
Ta có sơ đồ cây sau:

Áp dụng công thức xác suất toàn phần, ta có
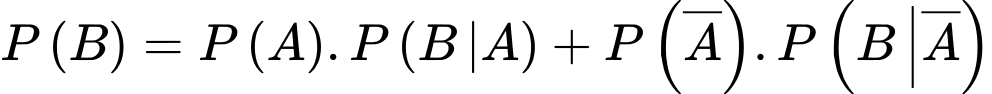
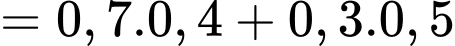
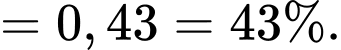
d) Đúng.
Ta có
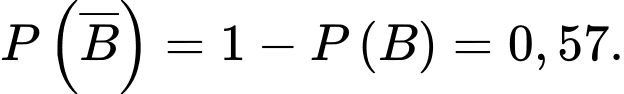
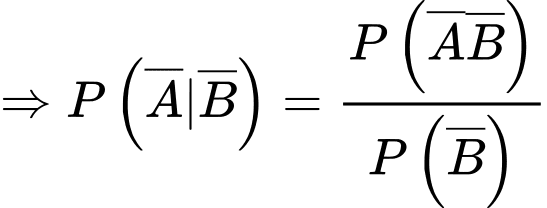
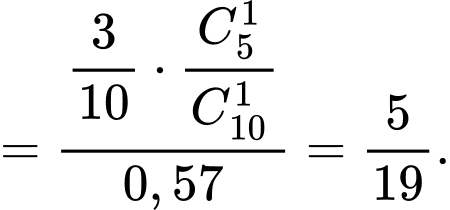
PHẦN III. Thí sinh trả lời từ câu 1 đến câu 6.
Câu 17 [289651]: Cho hình chóp 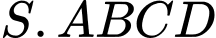 có đáy
có đáy 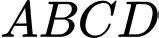 là hình vuông cạnh
là hình vuông cạnh 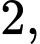 tam giác
tam giác 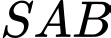 vuông cân tại và nằm trong mặt phẳng vuông góc với đáy. Gọi
vuông cân tại và nằm trong mặt phẳng vuông góc với đáy. Gọi 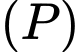 là mặt phẳng chứa
là mặt phẳng chứa 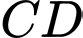 và vuông góc với
và vuông góc với 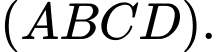 Trên
Trên 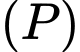 lấy điểm
lấy điểm 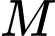 bất kỳ, thể tích khối tứ diện
bất kỳ, thể tích khối tứ diện 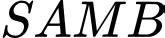 bằng bao nhiêu? (làm tròn kết quả đến hàng phần trăm).
bằng bao nhiêu? (làm tròn kết quả đến hàng phần trăm).
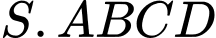 có đáy
có đáy 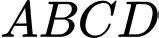 là hình vuông cạnh
là hình vuông cạnh 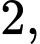 tam giác
tam giác 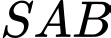 vuông cân tại và nằm trong mặt phẳng vuông góc với đáy. Gọi
vuông cân tại và nằm trong mặt phẳng vuông góc với đáy. Gọi 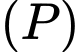 là mặt phẳng chứa
là mặt phẳng chứa 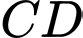 và vuông góc với
và vuông góc với 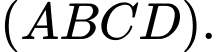 Trên
Trên 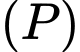 lấy điểm
lấy điểm 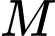 bất kỳ, thể tích khối tứ diện
bất kỳ, thể tích khối tứ diện 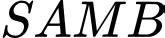 bằng bao nhiêu? (làm tròn kết quả đến hàng phần trăm).
bằng bao nhiêu? (làm tròn kết quả đến hàng phần trăm). 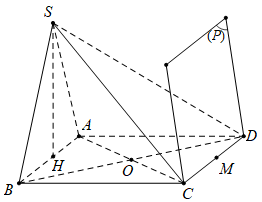
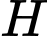 là trung điểm
là trung điểm  , vì tam giác
, vì tam giác 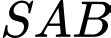 vuông cân tại
vuông cân tại 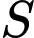 nên
nên  và
và 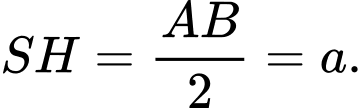
Suy ra diện tích tam giác
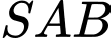 là:
là: 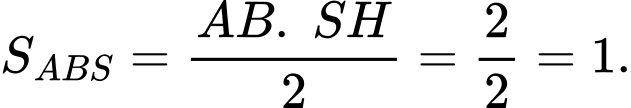
Vì
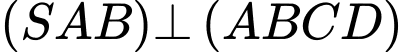 , lại có
, lại có  nên
nên 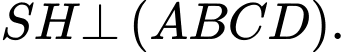
Mặt khác:
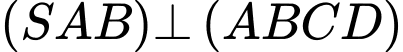 và
và 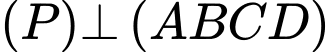 nên
nên 
Lấy điểm
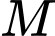 trên
trên 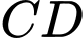 , vì
, vì  nên
nên 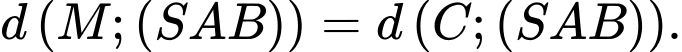
Ta có
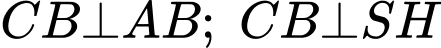 nên
nên 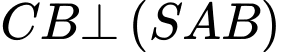 hay
hay 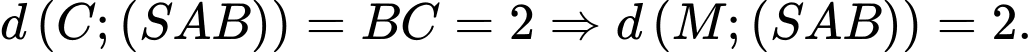
Vậy thể tích khối tứ diện
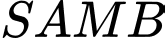 là:
là: 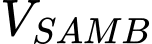
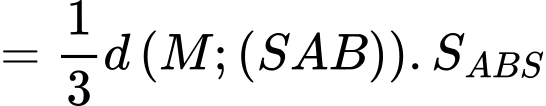
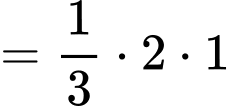
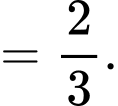
Câu 18 [693837]: Chị Lan vừa mua một chiếc máy tính xách tay mới với giá 25 triệu đồng vào ngày 20/9/2022 bằng thẻ tín dụng của ngân hàng Y. Thẻ tín dụng này được phát hành vào ngày 10/9/2022. Ngân hàng Y có chế độ không tính lãi trong 45 ngày đầu và cộng thêm khuyến mãi 15 ngày tiếp theo không tính lãi. Sau thời gian này, ngân hàng sẽ tính lãi với lãi suất 18%/năm (tính lãi kép theo ngày). Chị Lan dự định sẽ hoàn tiền cho ngân hàng vào ngày 10/12/2022. Chị Lan phải trả thêm bao nhiêu nghìn đồng tiền lãi so với giá gốc cho ngân hàng vào ngày 10/12/2022? (kết quả làm tròn đến hàng đơn vị).
Điền đáp án: 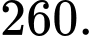
Ngân hàng miễn lãi trong 45 ngày đầu + 15 ngày khuyến mãi = 60 ngày miễn lãi.
Thời gian tính lãi là từ ngày 20/11/2022 đến ngày 10/12/2022 nên số ngày có lãi là 21 ngày.
Lãi suất hàng năm là 18%/năm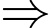 Lãi suất hàng ngày là
Lãi suất hàng ngày là 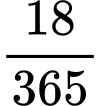
Số tiền chị Lan phải trả cho ngân hàng vào ngày 10/12/2022 là:
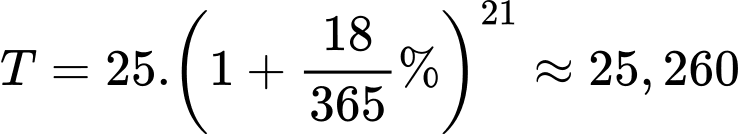 ( triệu đồng ).
( triệu đồng ).
Số tiền lãi chị Lan phải trả cho ngân hàng là :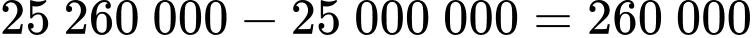 (đồng).
(đồng).
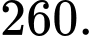
Ngân hàng miễn lãi trong 45 ngày đầu + 15 ngày khuyến mãi = 60 ngày miễn lãi.
Thời gian tính lãi là từ ngày 20/11/2022 đến ngày 10/12/2022 nên số ngày có lãi là 21 ngày.
Lãi suất hàng năm là 18%/năm
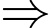 Lãi suất hàng ngày là
Lãi suất hàng ngày là 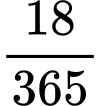
Số tiền chị Lan phải trả cho ngân hàng vào ngày 10/12/2022 là:
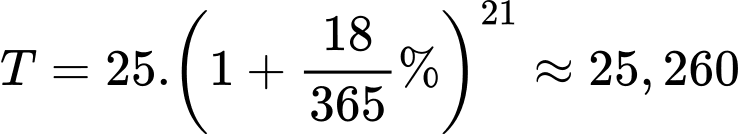 ( triệu đồng ).
( triệu đồng ).Số tiền lãi chị Lan phải trả cho ngân hàng là :
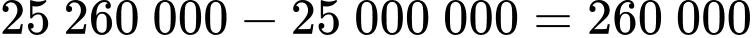 (đồng).
(đồng).
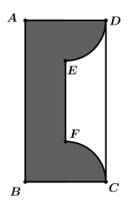
Câu 19 [693839]: Một vật trang trí có dạng khối tròn xoay tạo thành khi quay miền  (phần tô đậm trong hình vẽ) quay xung quanh trục
(phần tô đậm trong hình vẽ) quay xung quanh trục 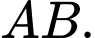 Miền
Miền  được giới hạn bởi các cạnh
được giới hạn bởi các cạnh 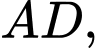

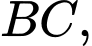
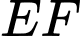 và các cung phần tư của các đường tròn bán kính bằng
và các cung phần tư của các đường tròn bán kính bằng 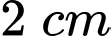 với tâm lần lượt là trung điểm của
với tâm lần lượt là trung điểm của 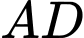 và
và 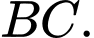 Biết
Biết 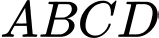 là hình chữ nhật có cạnh
là hình chữ nhật có cạnh 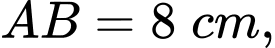
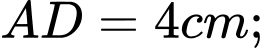 điểm
điểm 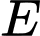 cách
cách 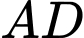 một đoạn bằng
một đoạn bằng 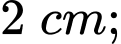 điểm
điểm 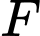 cách
cách 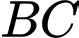 một đoạn bằng
một đoạn bằng 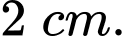 Thể tích của vật thể trang trí trên là bao nhiêu centimetkhối? (quy tròn đến hàng phần mười)
Thể tích của vật thể trang trí trên là bao nhiêu centimetkhối? (quy tròn đến hàng phần mười)
 (phần tô đậm trong hình vẽ) quay xung quanh trục
(phần tô đậm trong hình vẽ) quay xung quanh trục 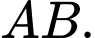 Miền
Miền  được giới hạn bởi các cạnh
được giới hạn bởi các cạnh 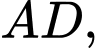

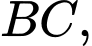
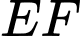 và các cung phần tư của các đường tròn bán kính bằng
và các cung phần tư của các đường tròn bán kính bằng 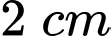 với tâm lần lượt là trung điểm của
với tâm lần lượt là trung điểm của 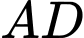 và
và 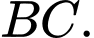 Biết
Biết 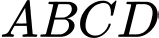 là hình chữ nhật có cạnh
là hình chữ nhật có cạnh 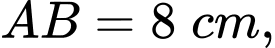
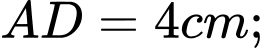 điểm
điểm 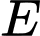 cách
cách 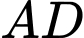 một đoạn bằng
một đoạn bằng 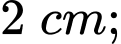 điểm
điểm 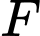 cách
cách 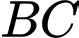 một đoạn bằng
một đoạn bằng 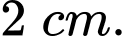 Thể tích của vật thể trang trí trên là bao nhiêu centimetkhối? (quy tròn đến hàng phần mười)
Thể tích của vật thể trang trí trên là bao nhiêu centimetkhối? (quy tròn đến hàng phần mười)
Điền đáp án: 
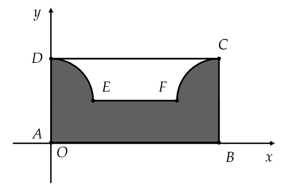
Gắn hệ trục toạ độ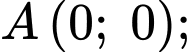
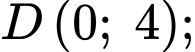
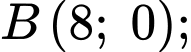
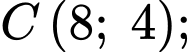
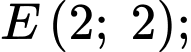
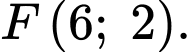
Phương trình đường tròn đi qua hai điểm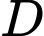 và
và 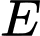 là
là 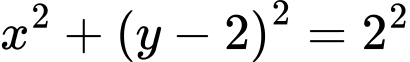
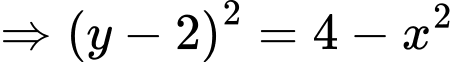
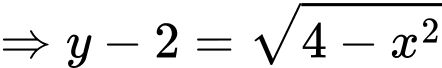 (do lấy nửa trên của đường tròn)
(do lấy nửa trên của đường tròn) 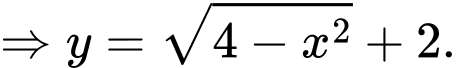
Thể tích của vật thể trang trí là
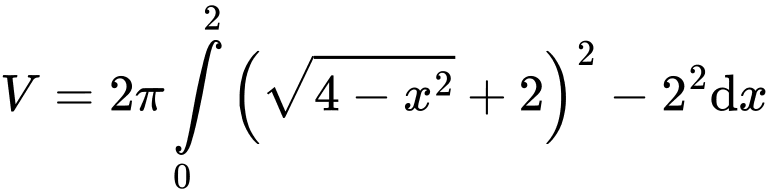
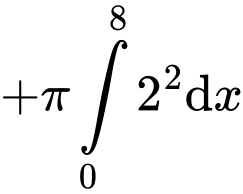
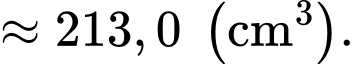

Gắn hệ trục toạ độ
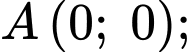
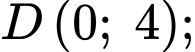
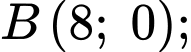
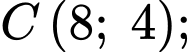
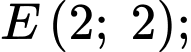
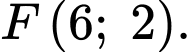
Phương trình đường tròn đi qua hai điểm
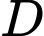 và
và 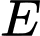 là
là 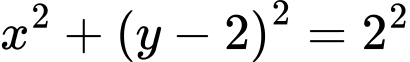
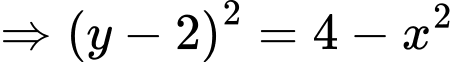
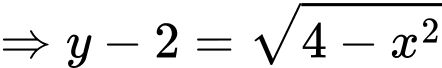 (do lấy nửa trên của đường tròn)
(do lấy nửa trên của đường tròn) 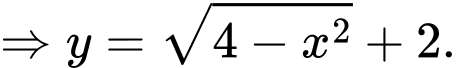
Thể tích của vật thể trang trí là
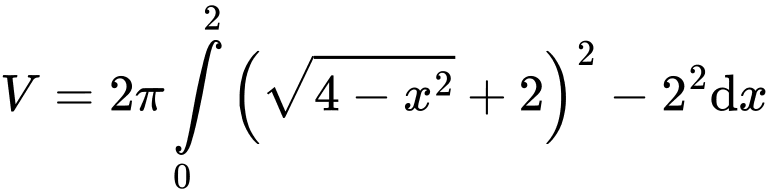
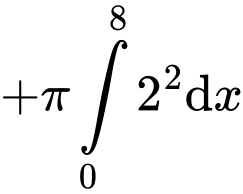
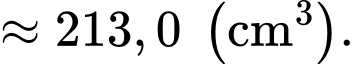
Câu 20 [702632]: Trong quân sự, một máy bay chiến đấu của đối phương có thể xuất hiện ở vị trí X với xác suất 0,55. Nếu máy bay đó không xuất hiện ở vị trí X thì nó xuất hiện ở vị trí Y. Để phòng thủ, các bệ phóng tên lửa được bố trí tại các vị trí X và Y. Khi máy bay đối phương xuất hiện ở vị trí X hoặc Y thì tên lửa sẽ được phóng để hạ máy bay đó. Xét phương án tác chiến sau: Nếu máy bay xuất hiện tại X thì bắn 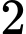 quả tên lửa và nếu máy bay xuất hiện tại Y thì bắn một quả tên lửa. Biết rằng, xác suất bắn trúng máy bay của mỗi quả tên lửa là 0,8 và các bệ phóng tên lửa hoạt động độc lập. Máy bay bị bắn hạ nếu nó trúng ít nhất
quả tên lửa và nếu máy bay xuất hiện tại Y thì bắn một quả tên lửa. Biết rằng, xác suất bắn trúng máy bay của mỗi quả tên lửa là 0,8 và các bệ phóng tên lửa hoạt động độc lập. Máy bay bị bắn hạ nếu nó trúng ít nhất 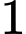 quả tên lửa. Biết máy bay bị bắn hạ trong phương án tác chiến trên. Tính xác suất máy bay bị bắn hạ ở vị trí X. (kết quả làm tròn đến hàng phần trăm).
quả tên lửa. Biết máy bay bị bắn hạ trong phương án tác chiến trên. Tính xác suất máy bay bị bắn hạ ở vị trí X. (kết quả làm tròn đến hàng phần trăm).
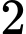 quả tên lửa và nếu máy bay xuất hiện tại Y thì bắn một quả tên lửa. Biết rằng, xác suất bắn trúng máy bay của mỗi quả tên lửa là 0,8 và các bệ phóng tên lửa hoạt động độc lập. Máy bay bị bắn hạ nếu nó trúng ít nhất
quả tên lửa và nếu máy bay xuất hiện tại Y thì bắn một quả tên lửa. Biết rằng, xác suất bắn trúng máy bay của mỗi quả tên lửa là 0,8 và các bệ phóng tên lửa hoạt động độc lập. Máy bay bị bắn hạ nếu nó trúng ít nhất 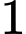 quả tên lửa. Biết máy bay bị bắn hạ trong phương án tác chiến trên. Tính xác suất máy bay bị bắn hạ ở vị trí X. (kết quả làm tròn đến hàng phần trăm).
quả tên lửa. Biết máy bay bị bắn hạ trong phương án tác chiến trên. Tính xác suất máy bay bị bắn hạ ở vị trí X. (kết quả làm tròn đến hàng phần trăm).
Điền đáp án: 0,59.
Gọi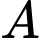 là biến cố “Máy bay xuất hiện tại vị trí X”
là biến cố “Máy bay xuất hiện tại vị trí X”
 là biến cố “Máy bay xuất hiện tại vị trí Y”
là biến cố “Máy bay xuất hiện tại vị trí Y”
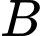 là biến cố “Máy bay bị bắn hạ”
là biến cố “Máy bay bị bắn hạ”
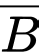 là biến cố “Máy bay không bị bắn hạ”
là biến cố “Máy bay không bị bắn hạ”
Yêu cầu bài toán Tính
Tính 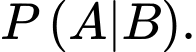
Từ giả thiết, ta có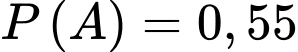
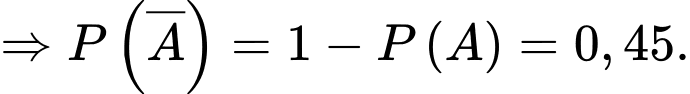
+) Xác suất máy bay bị bắn hạ tại vị trí Y là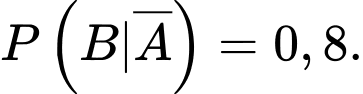
+) Xác suất máy bay không bị bắn hạ tại vị trí X là Vì máy bay bị bắn hạ nếu bị trúng ít nhất 1 quả tên lửa do đó bay không bị bắn hạ khi và chỉ khi cả 2 quả tên lửa đều không bắn trúng (và xác suất không bắn trúng là
Vì máy bay bị bắn hạ nếu bị trúng ít nhất 1 quả tên lửa do đó bay không bị bắn hạ khi và chỉ khi cả 2 quả tên lửa đều không bắn trúng (và xác suất không bắn trúng là 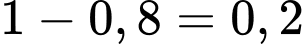 ). Nên
). Nên 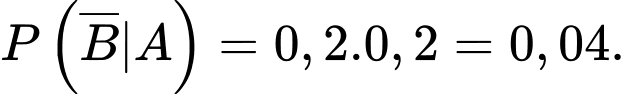
Suy ra xác suất máy bay bị bắn hạ tại vị trí A là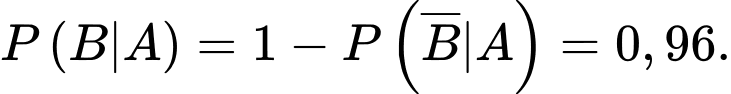
Từ đó, ta có sơ đồ cây sau:
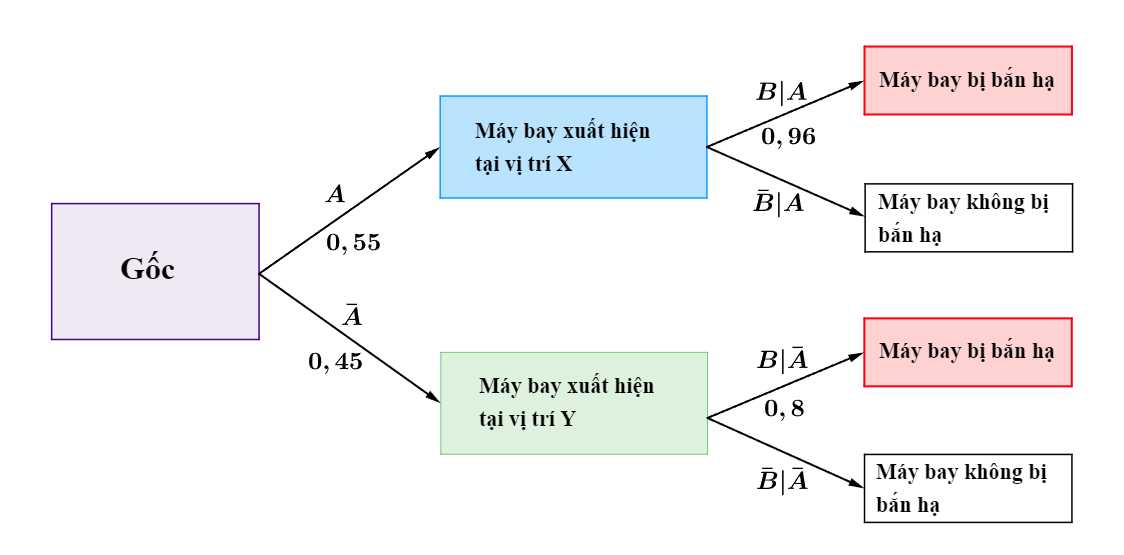
Áp dụng công thức xác suất toàn phần, ta có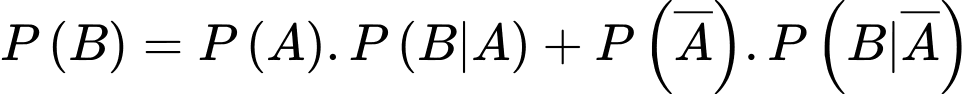
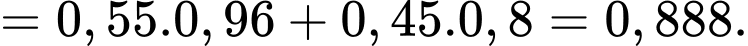
Áp dụng công thức Bayes, ta có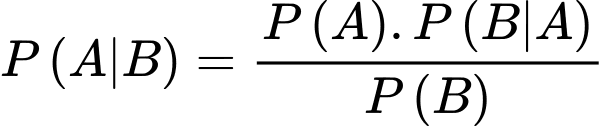
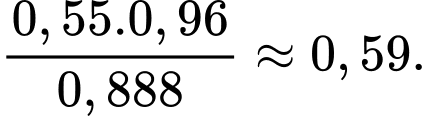
Gọi
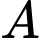 là biến cố “Máy bay xuất hiện tại vị trí X”
là biến cố “Máy bay xuất hiện tại vị trí X”
 là biến cố “Máy bay xuất hiện tại vị trí Y”
là biến cố “Máy bay xuất hiện tại vị trí Y”
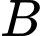 là biến cố “Máy bay bị bắn hạ”
là biến cố “Máy bay bị bắn hạ”
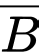 là biến cố “Máy bay không bị bắn hạ”
là biến cố “Máy bay không bị bắn hạ”
Yêu cầu bài toán
 Tính
Tính 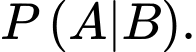
Từ giả thiết, ta có
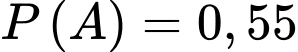
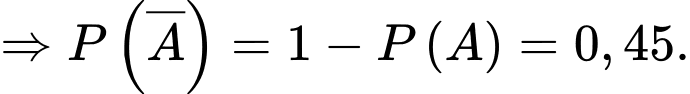
+) Xác suất máy bay bị bắn hạ tại vị trí Y là
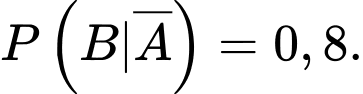
+) Xác suất máy bay không bị bắn hạ tại vị trí X là
 Vì máy bay bị bắn hạ nếu bị trúng ít nhất 1 quả tên lửa do đó bay không bị bắn hạ khi và chỉ khi cả 2 quả tên lửa đều không bắn trúng (và xác suất không bắn trúng là
Vì máy bay bị bắn hạ nếu bị trúng ít nhất 1 quả tên lửa do đó bay không bị bắn hạ khi và chỉ khi cả 2 quả tên lửa đều không bắn trúng (và xác suất không bắn trúng là 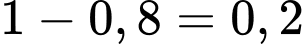 ). Nên
). Nên 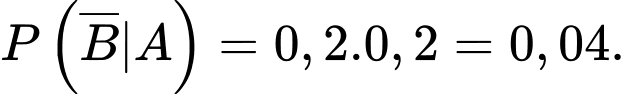
Suy ra xác suất máy bay bị bắn hạ tại vị trí A là
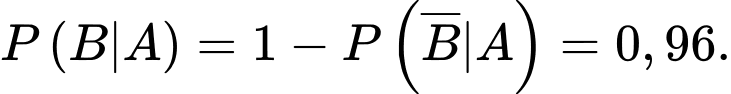
Từ đó, ta có sơ đồ cây sau:

Áp dụng công thức xác suất toàn phần, ta có
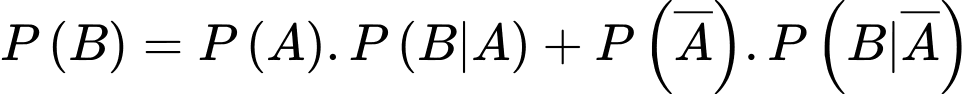
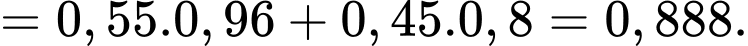
Áp dụng công thức Bayes, ta có
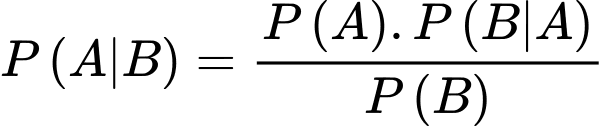
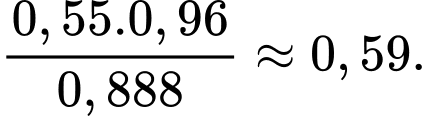
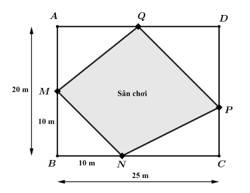
Câu 21 [696409]: Một công viên hình chữ nhật 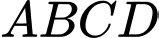 có kích thước
có kích thước  x
x có hai vị trí
có hai vị trí 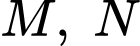 cố định lần lượt thuộc cạnh
cố định lần lượt thuộc cạnh  và
và 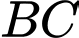 sao cho
sao cho 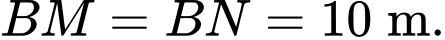 Trên cạnh
Trên cạnh 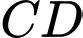 và
và 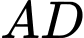 người ta xác định hai điểm
người ta xác định hai điểm 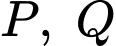 để xây dựng sân chơi
để xây dựng sân chơi 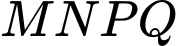 sao cho
sao cho 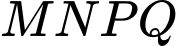 là hình thang có
là hình thang có 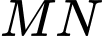 song song với
song song với 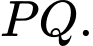 Diện tích lớn nhất của sân chơi là bao nhiêu mét vuông. Làm tròn đến hàng đơn vị.
Diện tích lớn nhất của sân chơi là bao nhiêu mét vuông. Làm tròn đến hàng đơn vị.
 có kích thước
có kích thước  x
x có hai vị trí
có hai vị trí  cố định lần lượt thuộc cạnh
cố định lần lượt thuộc cạnh  và
và  sao cho
sao cho 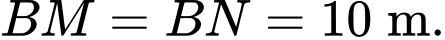 Trên cạnh
Trên cạnh 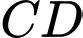 và
và 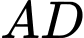 người ta xác định hai điểm
người ta xác định hai điểm 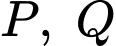 để xây dựng sân chơi
để xây dựng sân chơi 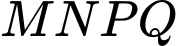 sao cho
sao cho 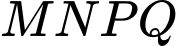 là hình thang có
là hình thang có 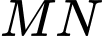 song song với
song song với 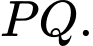 Diện tích lớn nhất của sân chơi là bao nhiêu mét vuông. Làm tròn đến hàng đơn vị.
Diện tích lớn nhất của sân chơi là bao nhiêu mét vuông. Làm tròn đến hàng đơn vị.
Điền đáp án: 
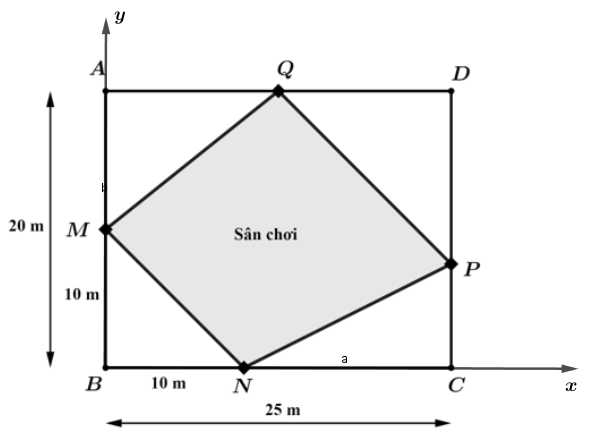
Chọn hệ trục toạ độ như hình vẽ.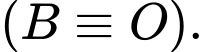
Khi đó: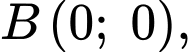
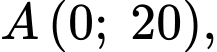
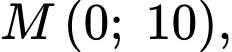
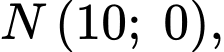
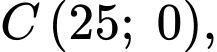
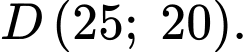
Phương trình đường thẳng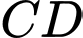 là:
là: 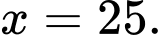
Phương trình đường thẳng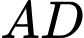 là:
là: 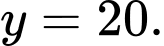
Gọi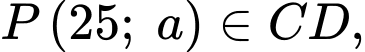
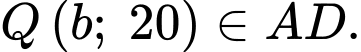
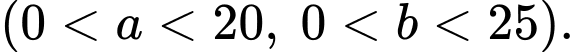
Khi đó: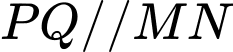
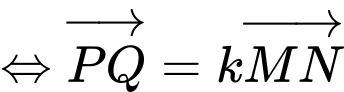
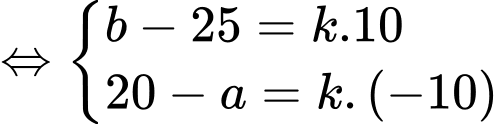
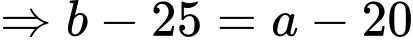
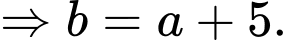
Do đó: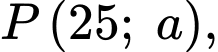
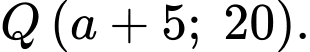
Diện tích sân chơi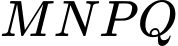 là:
là:
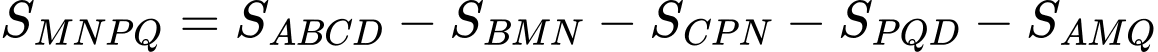
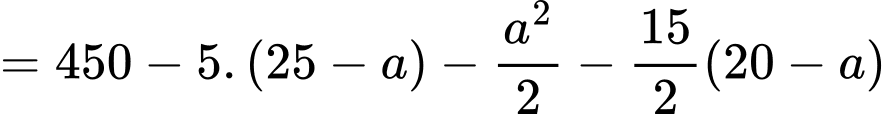
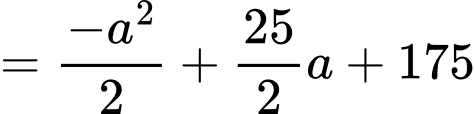
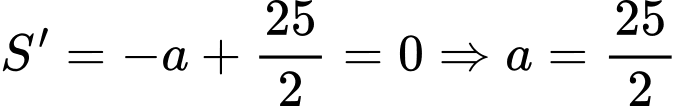
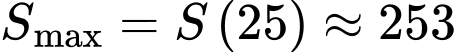
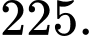

Chọn hệ trục toạ độ như hình vẽ.
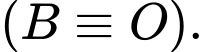
Khi đó:
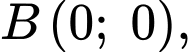
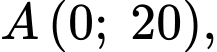
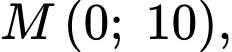
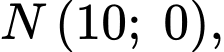
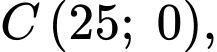
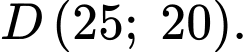
Phương trình đường thẳng
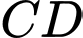 là:
là: 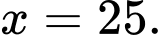
Phương trình đường thẳng
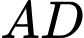 là:
là: 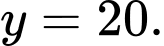
Gọi
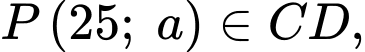
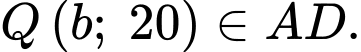
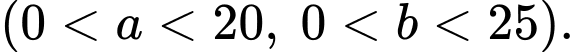
Khi đó:
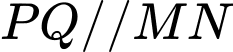
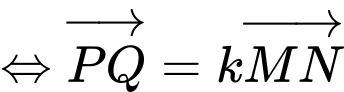
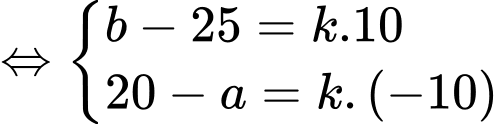
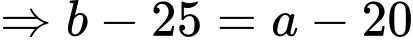
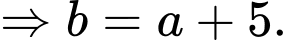
Do đó:
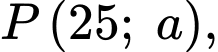
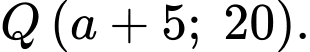
Diện tích sân chơi
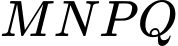 là:
là: 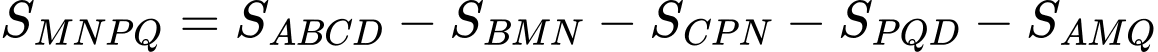
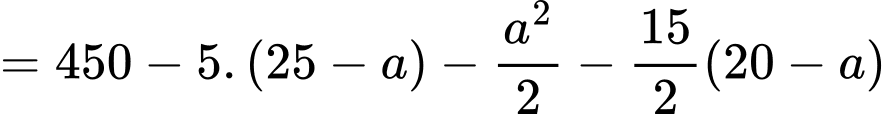
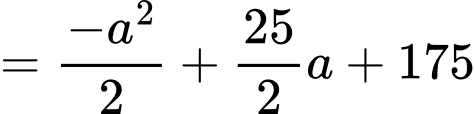
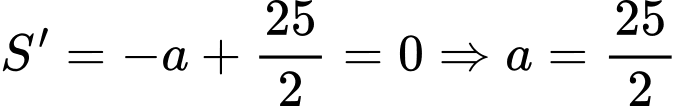
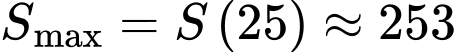
Câu 22 [693841]: Trong không gian 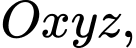 cho tam giác
cho tam giác 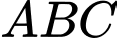 vuông tại
vuông tại 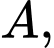
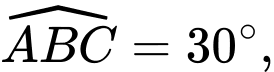
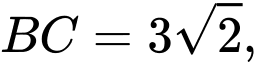 đường thẳng
đường thẳng 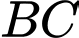 có phương trình
có phương trình 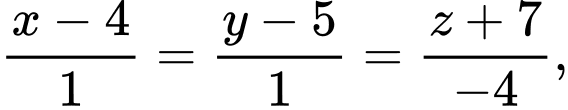 đường thẳng
đường thẳng  nằm trong mặt phẳng
nằm trong mặt phẳng 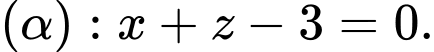 Biết đỉnh
Biết đỉnh  có cao độ âm. Tính hoành độ đỉnh
có cao độ âm. Tính hoành độ đỉnh 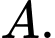
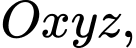 cho tam giác
cho tam giác 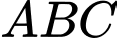 vuông tại
vuông tại 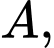
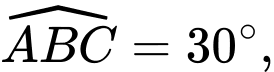
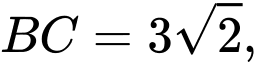 đường thẳng
đường thẳng 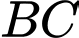 có phương trình
có phương trình 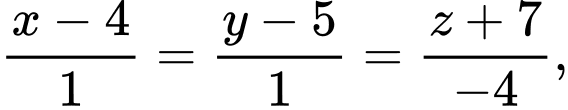 đường thẳng
đường thẳng  nằm trong mặt phẳng
nằm trong mặt phẳng 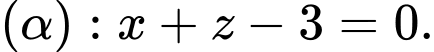 Biết đỉnh
Biết đỉnh  có cao độ âm. Tính hoành độ đỉnh
có cao độ âm. Tính hoành độ đỉnh 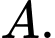
Đáp án: 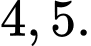
Toạ độ điểm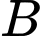 là nghiệm của hệ phương trình
là nghiệm của hệ phương trình 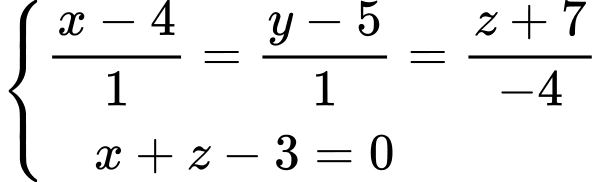
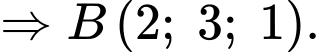
Do nên
nên 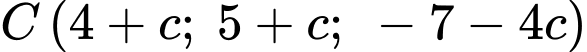
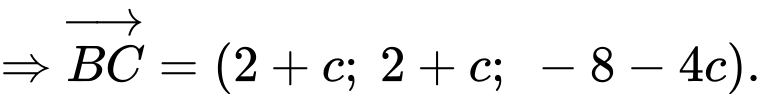
Theo giả thiết, ta có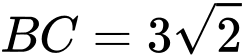
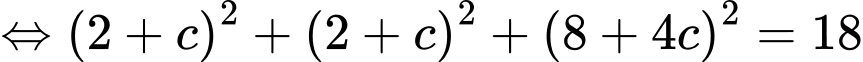
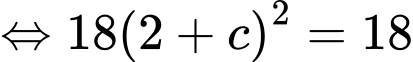
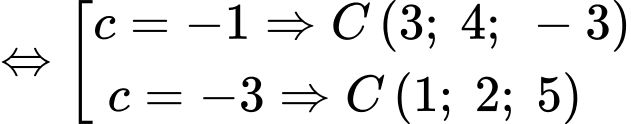
Mà đỉnh có toạ độ âm nên
có toạ độ âm nên 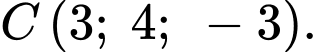
Gọi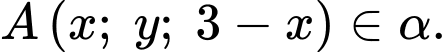
Do nên
nên 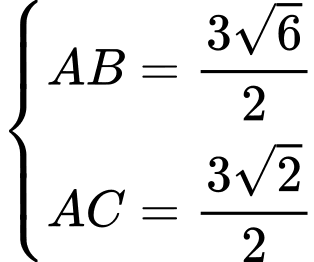
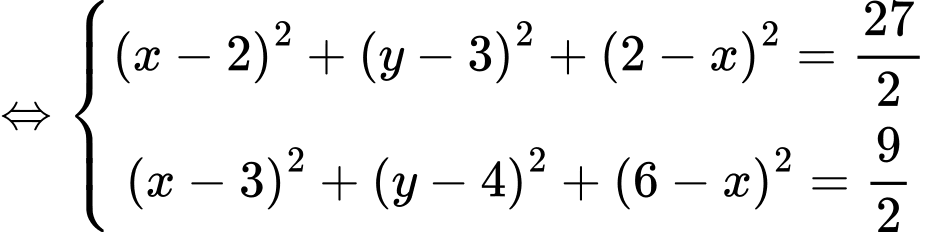
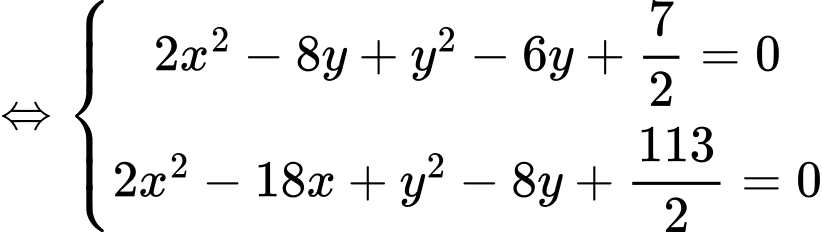
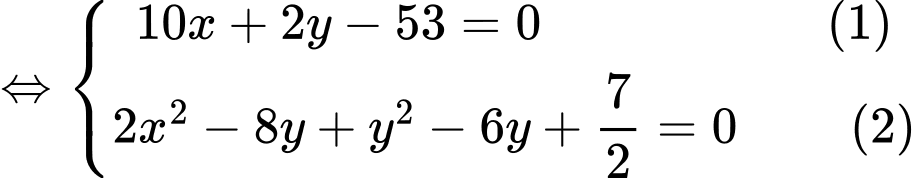
Từ ta có
ta có 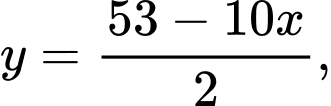 thay vào
thay vào  ta có:
ta có: 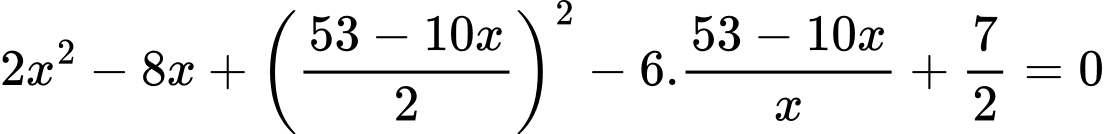
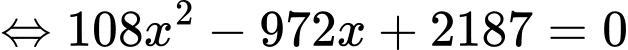
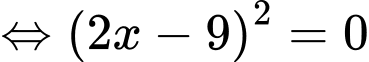
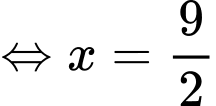
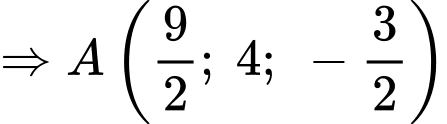 .
.
Vậy hoành độ đỉnh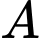 là
là 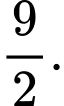
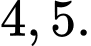
Toạ độ điểm
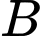 là nghiệm của hệ phương trình
là nghiệm của hệ phương trình 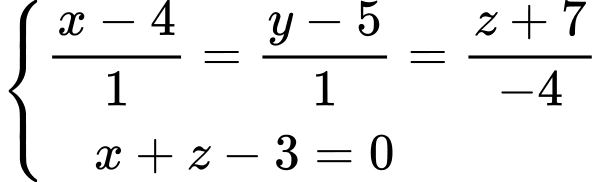
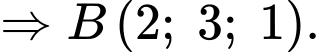
Do
 nên
nên 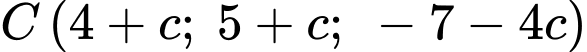
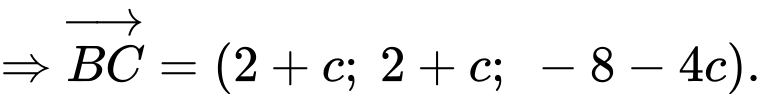
Theo giả thiết, ta có
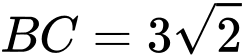
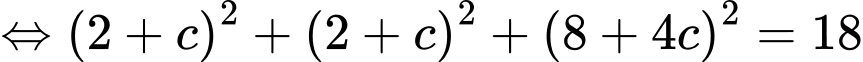
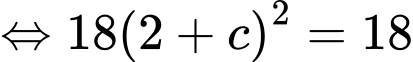
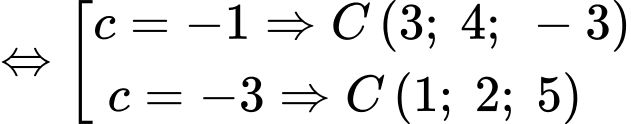
Mà đỉnh
 có toạ độ âm nên
có toạ độ âm nên 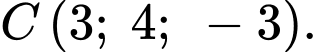
Gọi
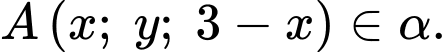
Do
 nên
nên 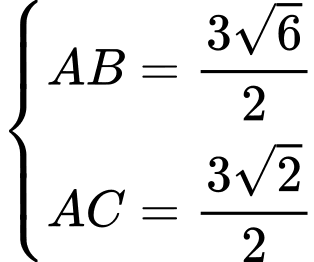
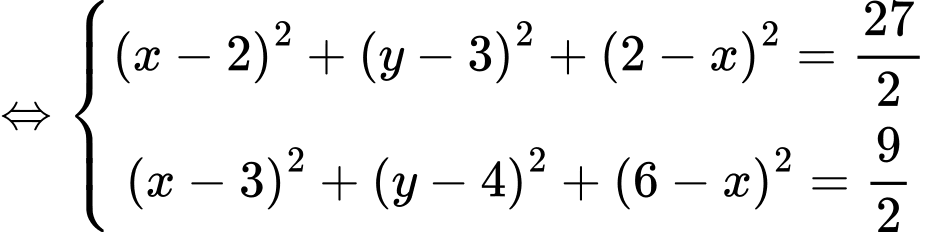
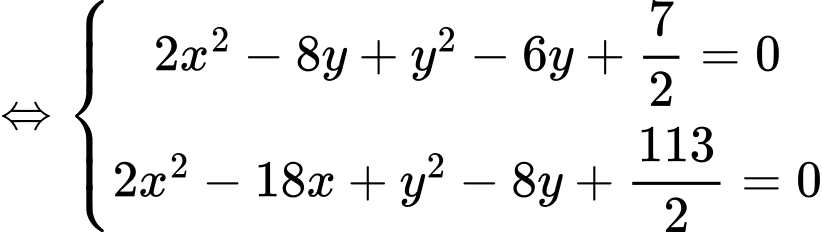
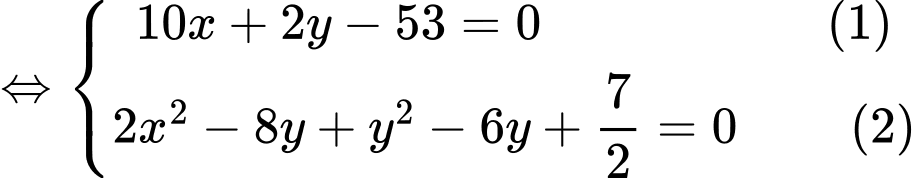
Từ
 ta có
ta có 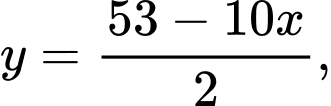 thay vào
thay vào  ta có:
ta có: 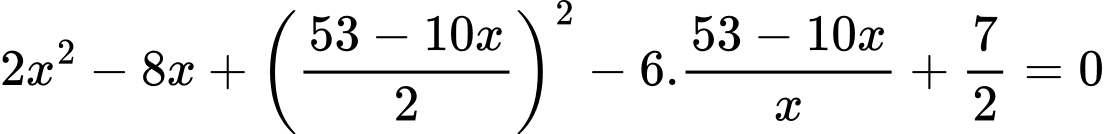
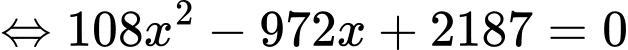
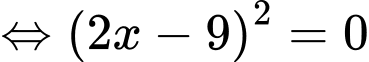
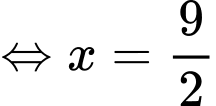
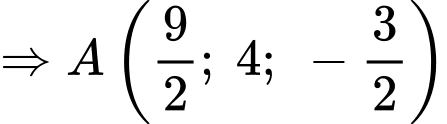 .
.Vậy hoành độ đỉnh
 là
là