PHẦN I. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Câu 1 [322640]: Giá trị nhỏ nhất của hàm số 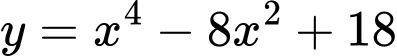 trên
trên 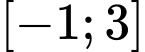 bằng
bằng
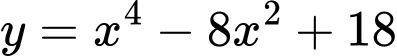 trên
trên 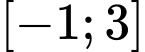 bằng
bằng A, 
B, 
C, 
D, 

Chọn đáp án A.
Đặt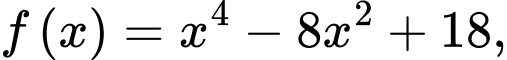 khi đó
khi đó 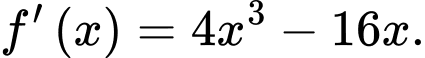
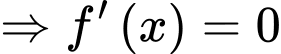
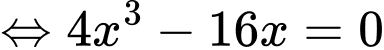
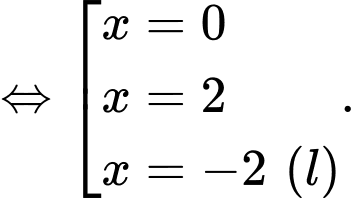
Ta có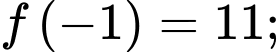
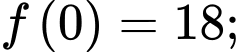
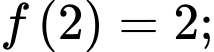
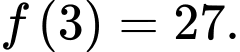
Từ đó suy ra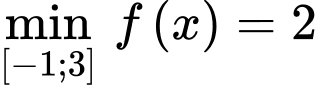 khi
khi 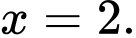 Đáp án: A
Đáp án: A
Đặt
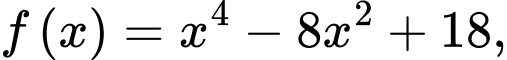 khi đó
khi đó 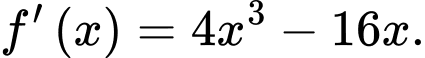
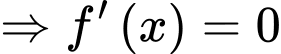
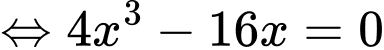
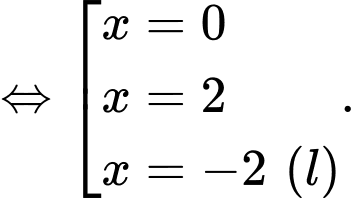
Ta có
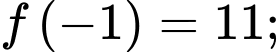
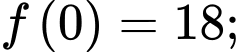
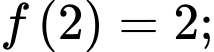
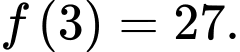
Từ đó suy ra
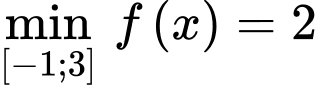 khi
khi 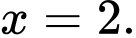 Đáp án: A
Đáp án: A
Câu 2 [322833]: Trong không gian 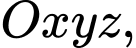 cho mặt cầu
cho mặt cầu 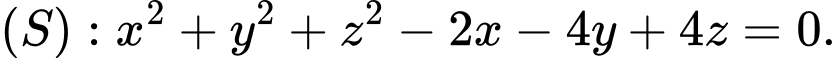 Đường kính mặt cầu
Đường kính mặt cầu  bằng
bằng
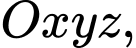 cho mặt cầu
cho mặt cầu 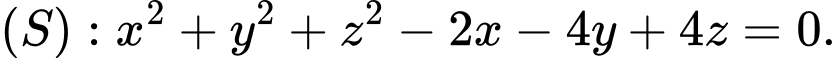 Đường kính mặt cầu
Đường kính mặt cầu 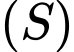 bằng
bằng A, 
B, 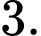
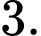
C, 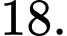
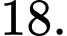
D, 
Chọn đáp án D.
Ta có:
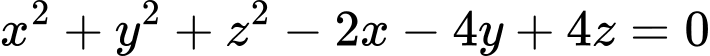
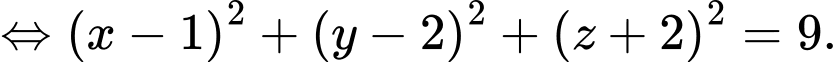
Suy ra bán kính của mặt cầu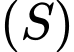 là
là 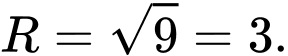
Vậy đường kính mặt cầu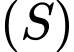 bằng
bằng 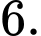 Đáp án: D
Đáp án: D
Ta có:
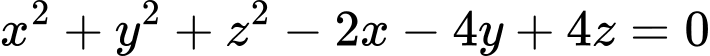
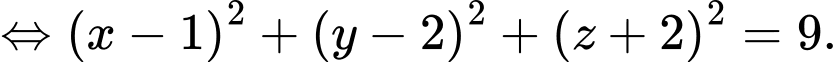
Suy ra bán kính của mặt cầu
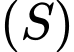 là
là 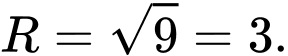
Vậy đường kính mặt cầu
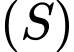 bằng
bằng 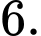 Đáp án: D
Đáp án: D
Câu 3 [326638]: Cho lăng trụ tam giác đều có độ dài cạnh đáy bằng
có độ dài cạnh đáy bằng 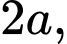 cạnh bên bằng
cạnh bên bằng 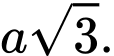 Tính thể tích
Tính thể tích  của lăng trụ.
của lăng trụ.
 có độ dài cạnh đáy bằng
có độ dài cạnh đáy bằng 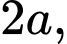 cạnh bên bằng
cạnh bên bằng 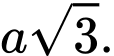 Tính thể tích
Tính thể tích  của lăng trụ.
của lăng trụ. A, 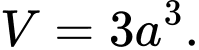
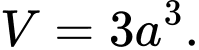
B, 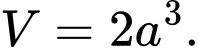
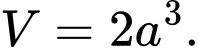
C, 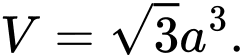
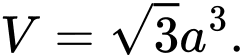
D, 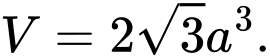
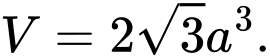
Chọn đáp án A.
Ta có thể tích lăng trụ là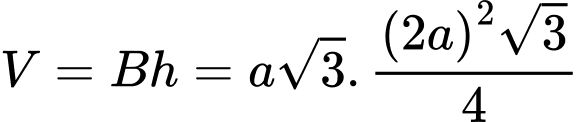
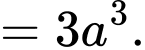 Đáp án: A
Đáp án: A
Ta có thể tích lăng trụ là
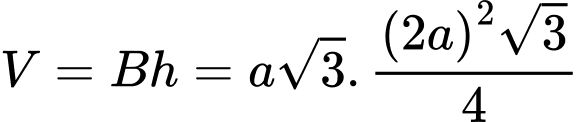
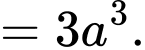 Đáp án: A
Đáp án: A
Câu 4 [511846]: Cho hàm số 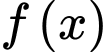 có đồ thị như hình vẽ. Hàm số đã cho nghịch biến trên khoảng nào dưới đây?
có đồ thị như hình vẽ. Hàm số đã cho nghịch biến trên khoảng nào dưới đây?
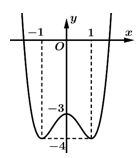
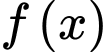 có đồ thị như hình vẽ. Hàm số đã cho nghịch biến trên khoảng nào dưới đây?
có đồ thị như hình vẽ. Hàm số đã cho nghịch biến trên khoảng nào dưới đây?
A, 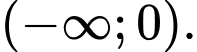
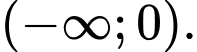
B, 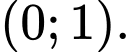
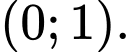
C, 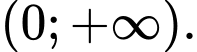
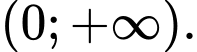
D, 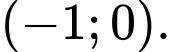
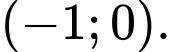
Chọn đáp án B.
Dựa vào hình vẽ, suy ra hàm số đã cho nghịch biến trên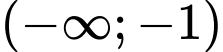 và
và 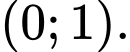 Đáp án: B
Đáp án: B
Dựa vào hình vẽ, suy ra hàm số đã cho nghịch biến trên
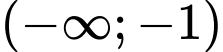 và
và 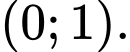 Đáp án: B
Đáp án: B
Câu 5 [512467]: 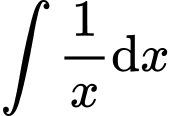 bằng
bằng
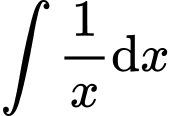 bằng
bằng A, 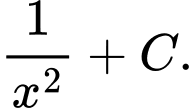
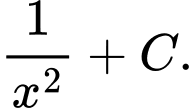
B, 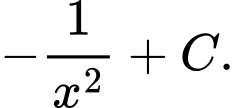
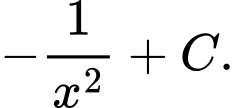
C, 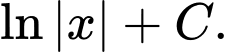
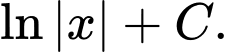
D, 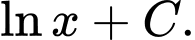
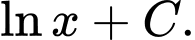
Chọn đáp án C.
Ta có: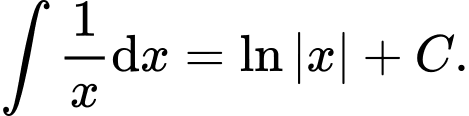 Đáp án: C
Đáp án: C
Ta có:
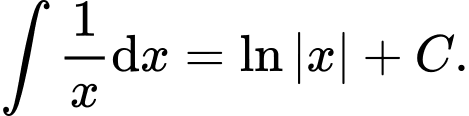 Đáp án: C
Đáp án: C
Câu 6 [529644]: Cho 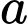 là số thực dương và khác
là số thực dương và khác  Giá trị của biểu thức
Giá trị của biểu thức 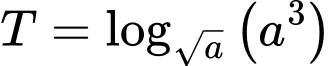 bằng
bằng
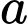 là số thực dương và khác
là số thực dương và khác 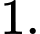 Giá trị của biểu thức
Giá trị của biểu thức 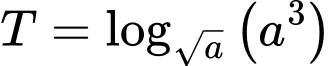 bằng
bằng A, 

B, 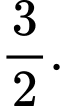
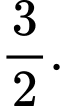
C, 
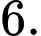
D, 
Chọn đáp án C.
Ta có: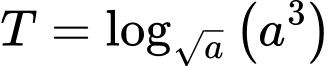
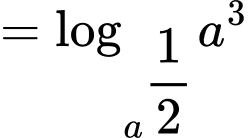
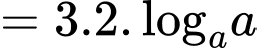
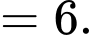 Đáp án: C
Đáp án: C
Ta có:
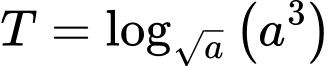
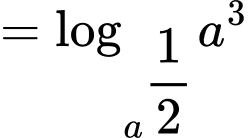
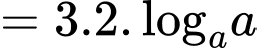
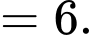 Đáp án: C
Đáp án: C
Câu 7 [529672]: Tập nghiệm 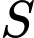 của bất phương trình
của bất phương trình 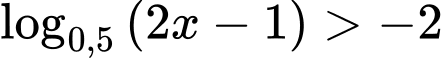 là
là
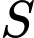 của bất phương trình
của bất phương trình 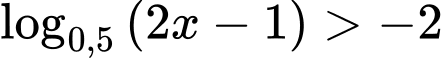 là
là A, 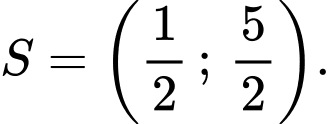
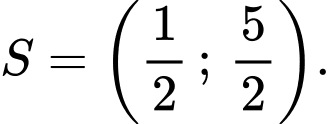
B, 
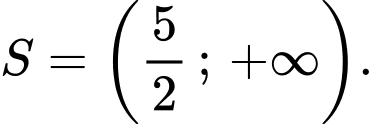
C, 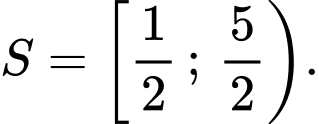
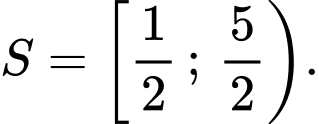
D, 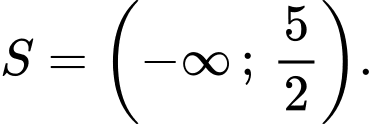
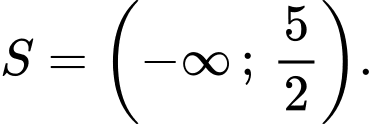
Chọn đáp án A.
Ta có:
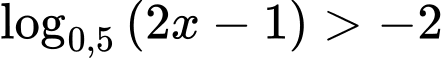
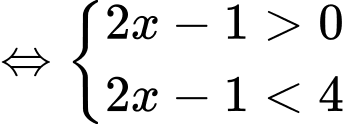
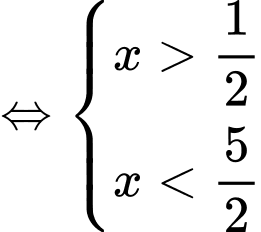
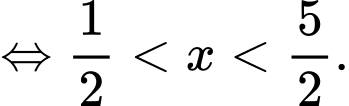
Vậy tập nghiệm của bất phương trình là: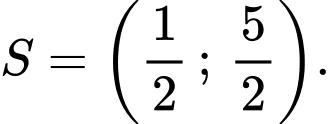 Đáp án: A
Đáp án: A
Ta có:
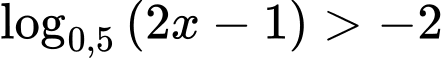
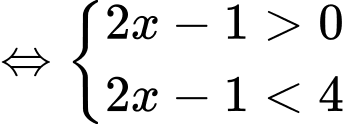
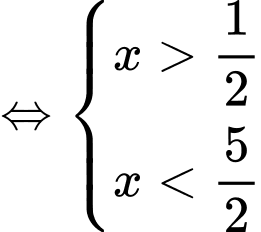
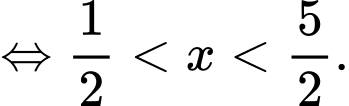
Vậy tập nghiệm của bất phương trình là:
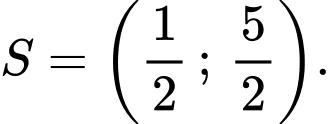 Đáp án: A
Đáp án: A
Câu 8 [810099]: Cho cấp số nhân 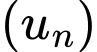 với
với 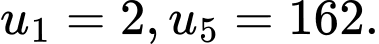 Công bội
Công bội 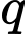 của cấp số nhân bằng
của cấp số nhân bằng
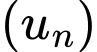 với
với 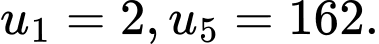 Công bội
Công bội 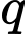 của cấp số nhân bằng
của cấp số nhân bằng A, 

B, 

C, 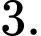
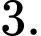
D, 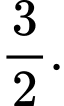
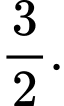
Chọn đáp án C.
Ta có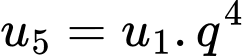
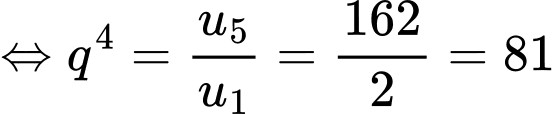
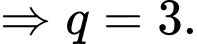 Đáp án: C
Đáp án: C
Ta có
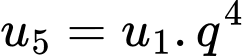
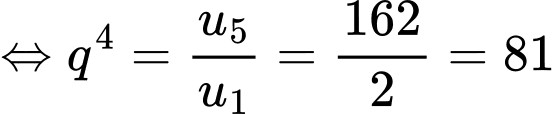
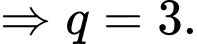 Đáp án: C
Đáp án: C
Câu 9 [810101]: Trong không gian  cho mặt phẳng
cho mặt phẳng 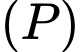 có phương trình là
có phương trình là 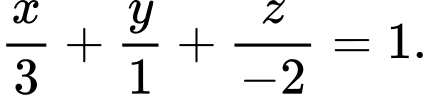 Véc tơ nào sau đây là một véc tơ pháp tuyến của
Véc tơ nào sau đây là một véc tơ pháp tuyến của 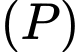 ?
?
 cho mặt phẳng
cho mặt phẳng 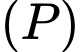 có phương trình là
có phương trình là 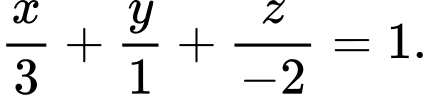 Véc tơ nào sau đây là một véc tơ pháp tuyến của
Véc tơ nào sau đây là một véc tơ pháp tuyến của 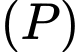 ?
? A, 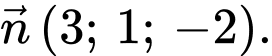
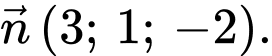
B, 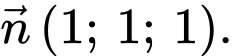
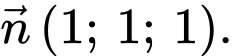
C, 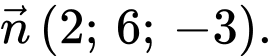
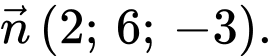
D, 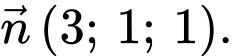
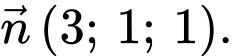
Chọn đáp án C.
Mặt phẳng có phương trình là
có phương trình là 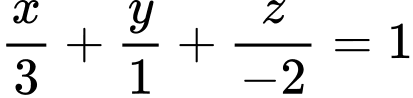
 VTPT
VTPT 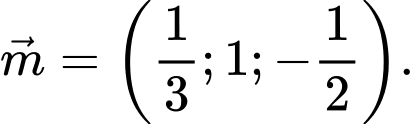
Vậy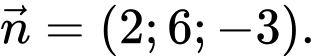 Đáp án: C
Đáp án: C
Mặt phẳng
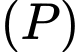 có phương trình là
có phương trình là 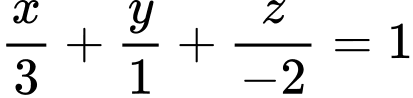
 VTPT
VTPT 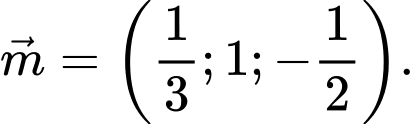
Vậy
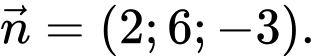 Đáp án: C
Đáp án: C
Câu 10 [810103]: Biết 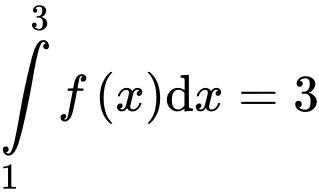 và
và 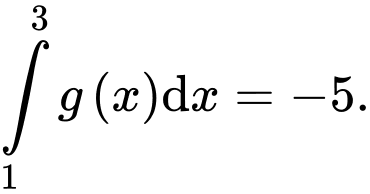 Giá trị của
Giá trị của 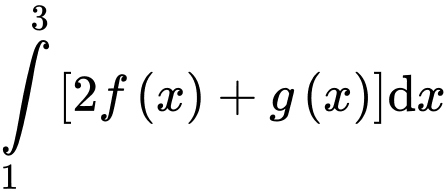 bằng
bằng
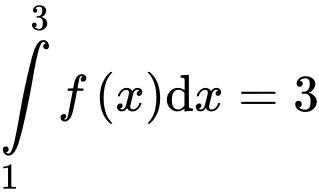 và
và 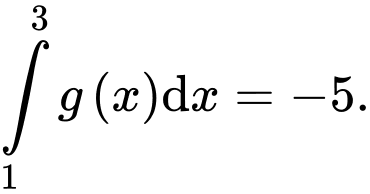 Giá trị của
Giá trị của 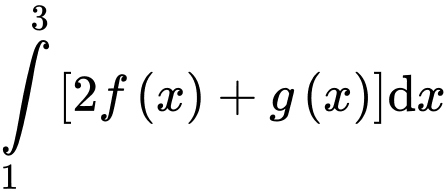 bằng
bằng A, 
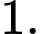
B, 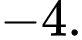
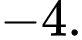
C, 

D, 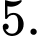
Chọn đáp án A.
Ta có: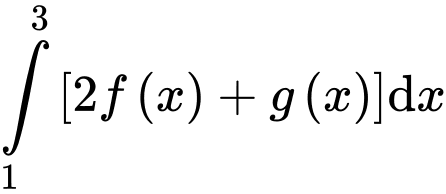
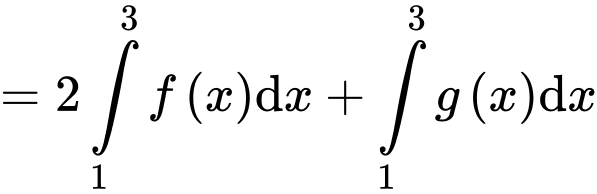
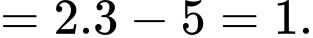 Đáp án: A
Đáp án: A
Ta có:
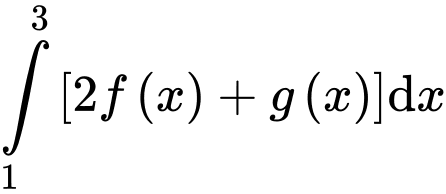
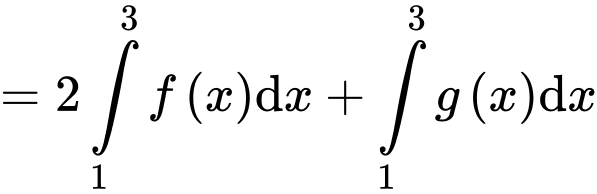
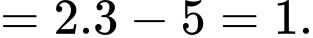 Đáp án: A
Đáp án: A
Câu 11 [694718]: Cho hình lập phương  với
với 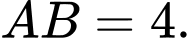 Tính
Tính 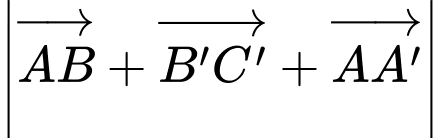 ?
?
 với
với 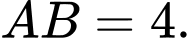 Tính
Tính 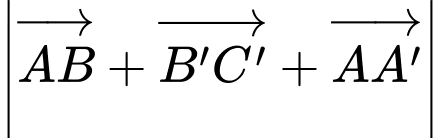 ?
? A, 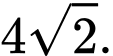
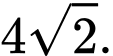
B, 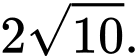
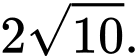
C, 

D, 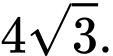
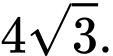
Chọn đáp án D.
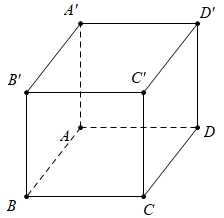
Ta có:
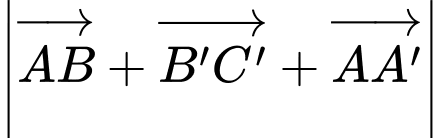
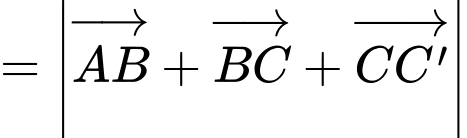
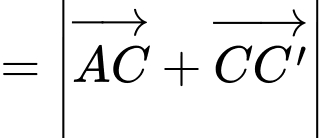
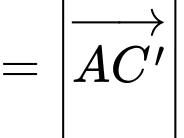
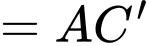
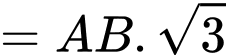
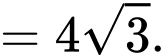 Đáp án: D
Đáp án: D

Ta có:
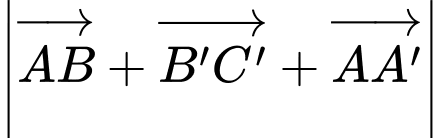
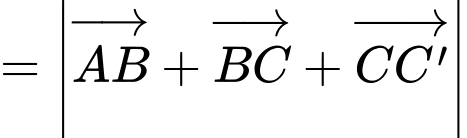
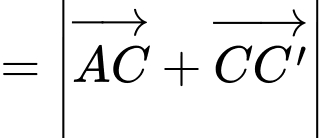
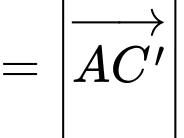
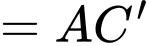
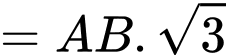
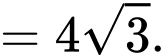 Đáp án: D
Đáp án: D
Câu 12 [694719]: Bảng dưới đây thống kê cự li ném tạ của một vận động viên.

Độ lệch chuẩn của mẫu số liệu ghép nhóm trên gần bằng giá trị nào sau đây nhất?

Độ lệch chuẩn của mẫu số liệu ghép nhóm trên gần bằng giá trị nào sau đây nhất?
A, 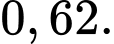
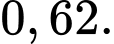
B, 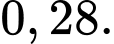
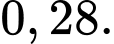
C, 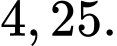
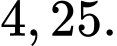
D, 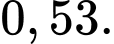
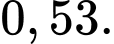
Chọn đáp án D.
Số trung bình của mấu số liệu ghép nhóm là
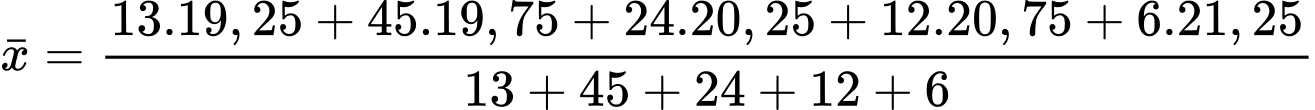
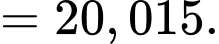
Phương sai của mẫu số liệu ghép nhóm là
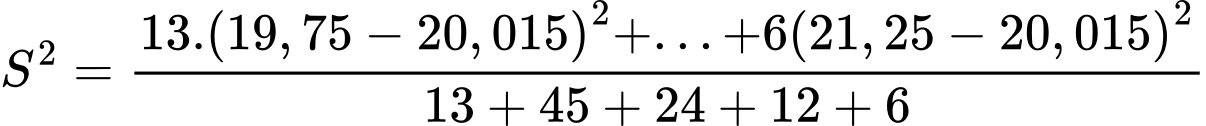

Độ lệch chuẩn của mẫu số liệu ghép nhóm là
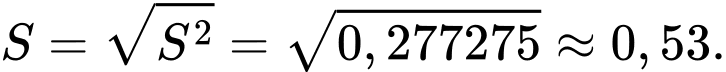 Đáp án: D
Đáp án: D
Số trung bình của mấu số liệu ghép nhóm là
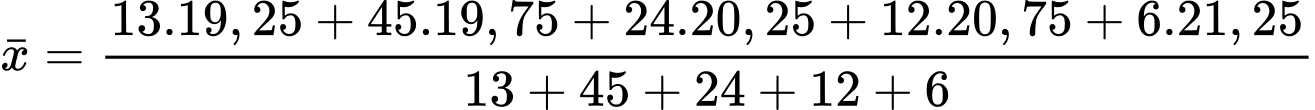
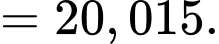
Phương sai của mẫu số liệu ghép nhóm là
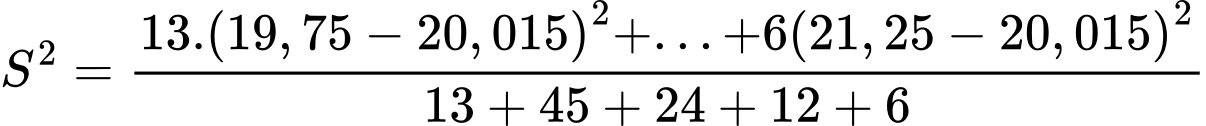

Độ lệch chuẩn của mẫu số liệu ghép nhóm là
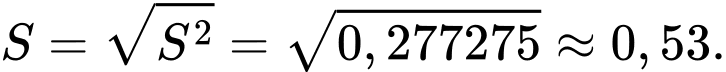 Đáp án: D
Đáp án: D PHẦN II. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Câu 13 [694720]: Trong không gian 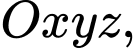 cho điểm
cho điểm 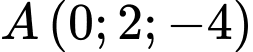 và hai đường thẳng
và hai đường thẳng 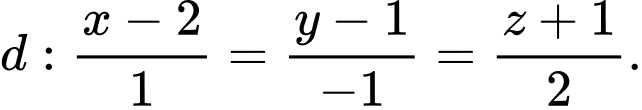 Gọi
Gọi 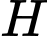 là hình chiếu của
là hình chiếu của 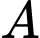 trên đường thẳng
trên đường thẳng 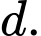
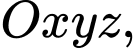 cho điểm
cho điểm 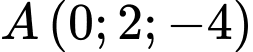 và hai đường thẳng
và hai đường thẳng 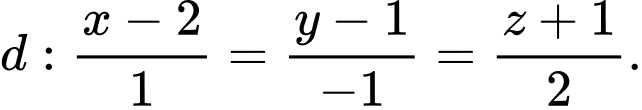 Gọi
Gọi 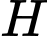 là hình chiếu của
là hình chiếu của 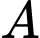 trên đường thẳng
trên đường thẳng 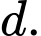
a) Đúng.
Một vectơ chỉ phương của đường thẳng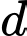 là
là 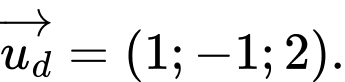
b) Sai.
Toạ độ điểm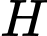 thuộc
thuộc 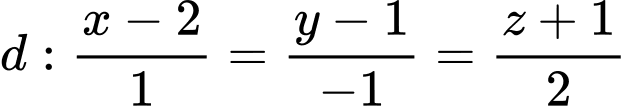 theo tham số
theo tham số 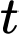 là
là 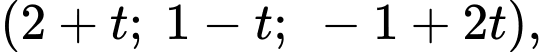
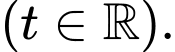
c) Sai.
Ta có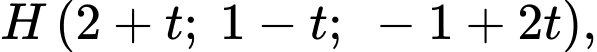
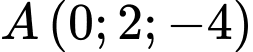
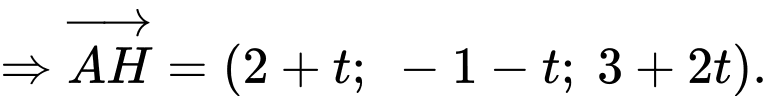
Do là hình chiếu của
là hình chiếu của  lên
lên 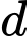 nên
nên 
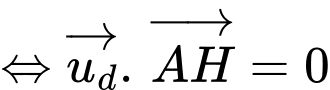
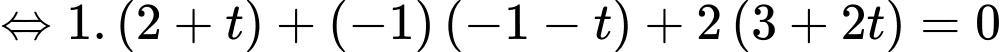
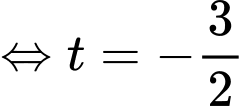
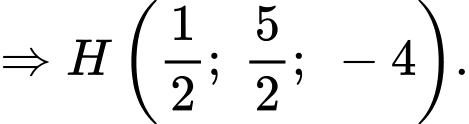
d) Sai.
Ta có: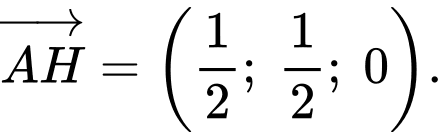
Vì với nên đường thẳng
nên đường thẳng  có vô số vectơ chỉ phương và kết quả thay đổi nên không xác định được tổng đó.
có vô số vectơ chỉ phương và kết quả thay đổi nên không xác định được tổng đó.
Nên kết luận trên sai.
Một vectơ chỉ phương của đường thẳng
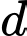 là
là 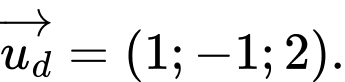
b) Sai.
Toạ độ điểm
 thuộc
thuộc 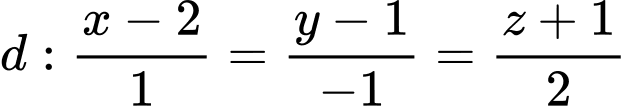 theo tham số
theo tham số 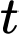 là
là 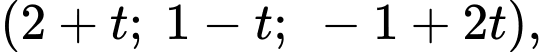
c) Sai.
Ta có
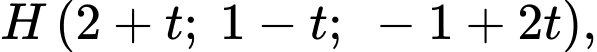
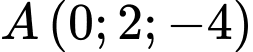
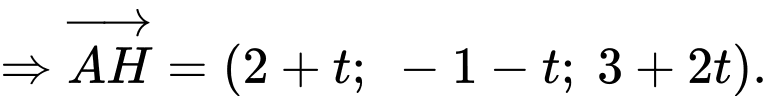
Do
 là hình chiếu của
là hình chiếu của  lên
lên 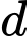 nên
nên 
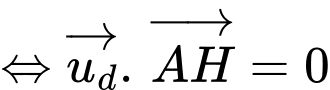
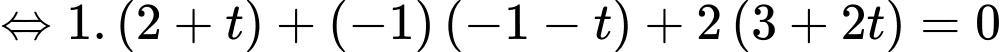
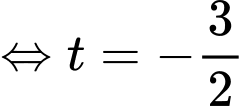
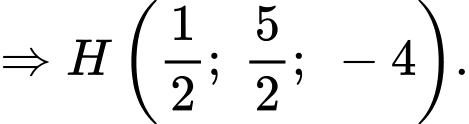
d) Sai.
Ta có:
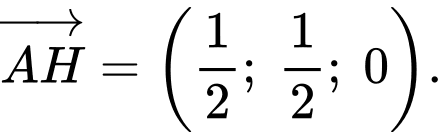
Vì với
 nên đường thẳng
nên đường thẳng  có vô số vectơ chỉ phương và kết quả thay đổi nên không xác định được tổng đó.
có vô số vectơ chỉ phương và kết quả thay đổi nên không xác định được tổng đó.Nên kết luận trên sai.
Câu 14 [694721]: Nhà xe khoán cho hai tài xế An và Bình mỗi người lần lượt nhận 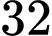 lít và
lít và 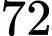 lít xăng trong một tháng. Biết rằng trong một ngày tổng số xăng cả hai người sử dụng là 10 lít. Biết số lít xăng tiêu thụ trong các ngày là như nhau. Gọi
lít xăng trong một tháng. Biết rằng trong một ngày tổng số xăng cả hai người sử dụng là 10 lít. Biết số lít xăng tiêu thụ trong các ngày là như nhau. Gọi 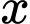 (lít)
(lít) 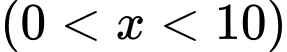 là số xăng An sử dụng trong
là số xăng An sử dụng trong 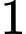 ngày và hàm số
ngày và hàm số 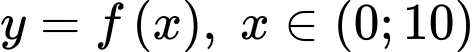 là tổng số ngày An và Bình sử dụng hết số xăng được khoán.
là tổng số ngày An và Bình sử dụng hết số xăng được khoán.
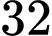 lít và
lít và 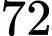 lít xăng trong một tháng. Biết rằng trong một ngày tổng số xăng cả hai người sử dụng là 10 lít. Biết số lít xăng tiêu thụ trong các ngày là như nhau. Gọi
lít xăng trong một tháng. Biết rằng trong một ngày tổng số xăng cả hai người sử dụng là 10 lít. Biết số lít xăng tiêu thụ trong các ngày là như nhau. Gọi 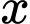 (lít)
(lít) 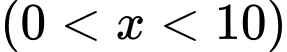 là số xăng An sử dụng trong
là số xăng An sử dụng trong 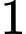 ngày và hàm số
ngày và hàm số 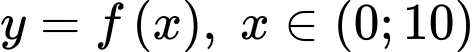 là tổng số ngày An và Bình sử dụng hết số xăng được khoán.
là tổng số ngày An và Bình sử dụng hết số xăng được khoán.
a) Đúng.
Do trong một ngày tổng số xăng cả hai người sử dụng là 10 lít nên số xăng Bình sử dụng trong 1 ngày là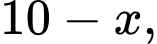
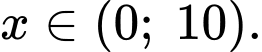
b) Sai.
Tổng số ngày An và Bình sử dụng hết số xăng được khoán là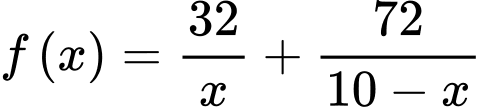 ,
, 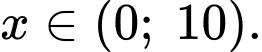
c) Sai.
Ta có:
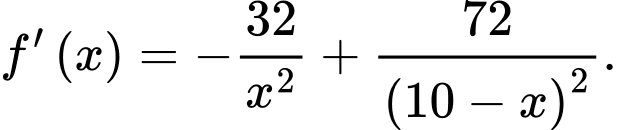
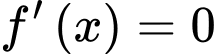
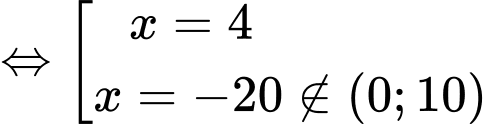 .
.
d) Đúng.
Bảng biến thiên của hàm số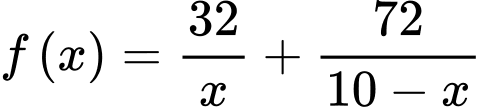 ,
,  là
là
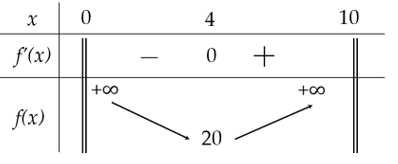
Theo bảng biến thiên, tổng số ngày ít nhất để hai tài xế sử dụng hết số xăng được khoán là 20 ngày.
Do trong một ngày tổng số xăng cả hai người sử dụng là 10 lít nên số xăng Bình sử dụng trong 1 ngày là
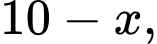
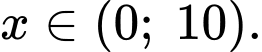
b) Sai.
Tổng số ngày An và Bình sử dụng hết số xăng được khoán là
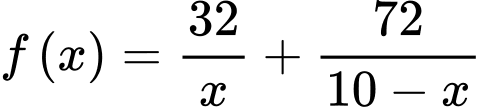 ,
, 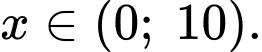
c) Sai.
Ta có:
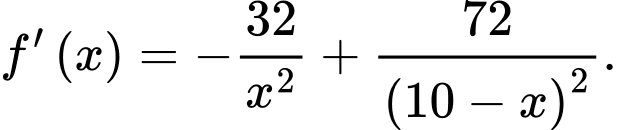
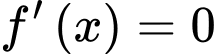
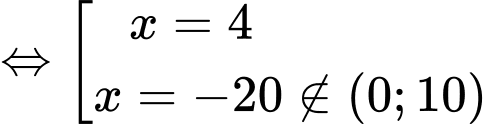 .
.d) Đúng.
Bảng biến thiên của hàm số
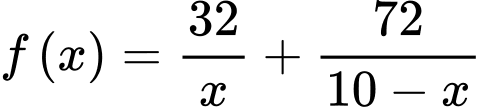 ,
,  là
là 
Theo bảng biến thiên, tổng số ngày ít nhất để hai tài xế sử dụng hết số xăng được khoán là 20 ngày.
Câu 15 [700893]: Một kỹ sư muốn thiết kế một mẫu vật bằng cách mô phỏng bản vẽ dưới dạng hình vẽ. Trước tiên vẽ một hình chữ nhật có kích thước  , sau đó sử dụng hệ trục
, sau đó sử dụng hệ trục 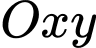 vẽ đường cong
vẽ đường cong 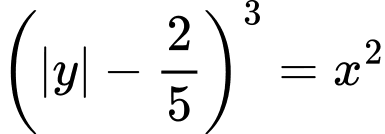 nằm trong hình chữ nhật (tham khảo hình vẽ). Gọi
nằm trong hình chữ nhật (tham khảo hình vẽ). Gọi  là phần hình phẳng được tô màu đậm và đường cong ở góc phần tư thứ nhất có phương trình
là phần hình phẳng được tô màu đậm và đường cong ở góc phần tư thứ nhất có phương trình 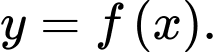
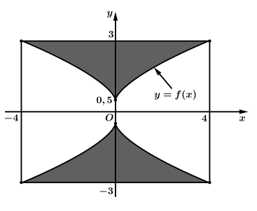
 , sau đó sử dụng hệ trục
, sau đó sử dụng hệ trục 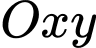 vẽ đường cong
vẽ đường cong 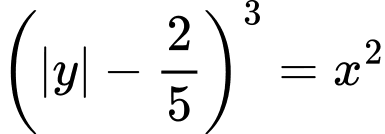 nằm trong hình chữ nhật (tham khảo hình vẽ). Gọi
nằm trong hình chữ nhật (tham khảo hình vẽ). Gọi  là phần hình phẳng được tô màu đậm và đường cong ở góc phần tư thứ nhất có phương trình
là phần hình phẳng được tô màu đậm và đường cong ở góc phần tư thứ nhất có phương trình 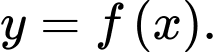

a) Sai.
Ta có: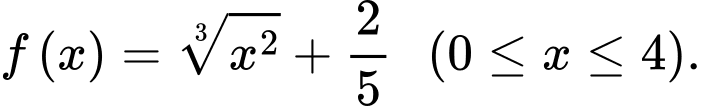
b) Sai.
Diện tích hình phẳng là
là
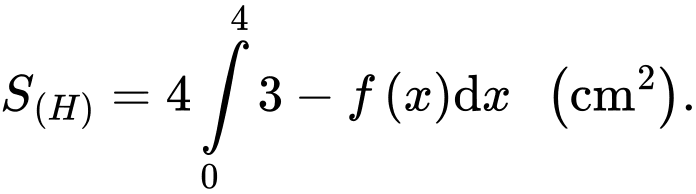
c) Sai.
Diện tích hình chữ nhật là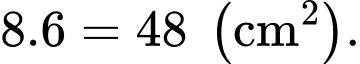
Sau khi cắt bỏ hình phẳng thì diện tích phần còn lại là
thì diện tích phần còn lại là
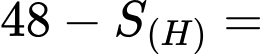
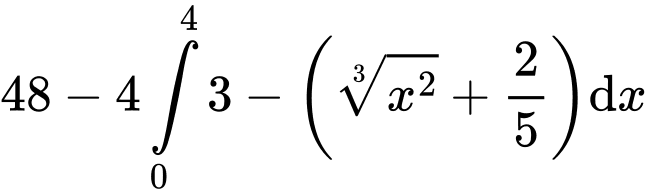
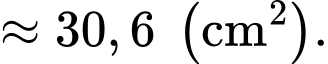
d) Sai.
Thể tích phần đồng hồ cát là
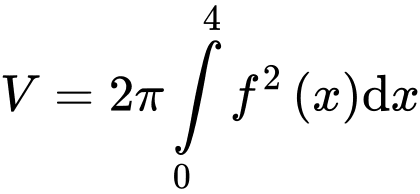
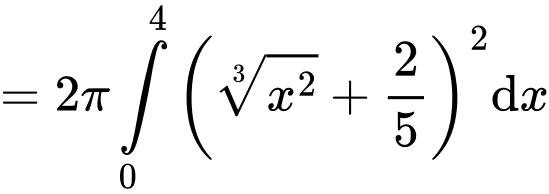
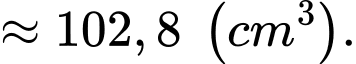
Ta có:
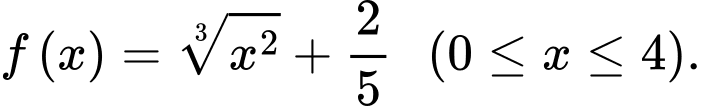
b) Sai.
Diện tích hình phẳng
 là
là 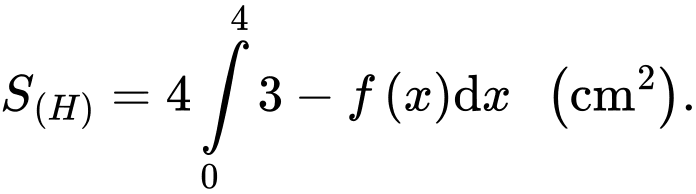
c) Sai.
Diện tích hình chữ nhật là
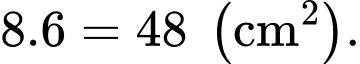
Sau khi cắt bỏ hình phẳng
 thì diện tích phần còn lại là
thì diện tích phần còn lại là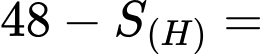
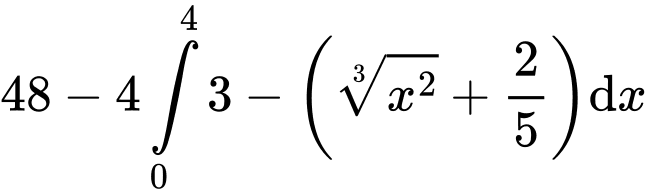
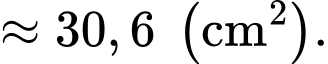
d) Sai.
Thể tích phần đồng hồ cát là
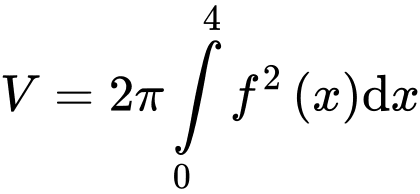
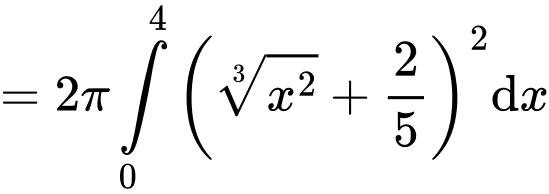
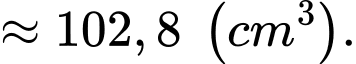
Câu 16 [700894]: Một kho hàng do hai nhà máy sản xuất. Biết tỉ lệ sản phẩm đóng góp của nhà máy một bằng 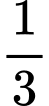 sản phẩm đóng góp của nhà máy hai và tỉ lệ phế phẩm do nhà máy một, nhà máy hai sản xuất lần lượt là
sản phẩm đóng góp của nhà máy hai và tỉ lệ phế phẩm do nhà máy một, nhà máy hai sản xuất lần lượt là 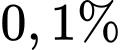 và
và 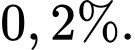
Gọi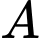 là biến cố: “ Sản phẩm được chọn là phế phẩm”. Chọn ngẫu nhiên một sản phẩm trong kho.
là biến cố: “ Sản phẩm được chọn là phế phẩm”. Chọn ngẫu nhiên một sản phẩm trong kho.
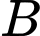 là biến cố: “Sản phẩm được chọn thuộc nhà máy một”.
là biến cố: “Sản phẩm được chọn thuộc nhà máy một”.
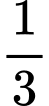 sản phẩm đóng góp của nhà máy hai và tỉ lệ phế phẩm do nhà máy một, nhà máy hai sản xuất lần lượt là
sản phẩm đóng góp của nhà máy hai và tỉ lệ phế phẩm do nhà máy một, nhà máy hai sản xuất lần lượt là 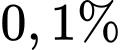 và
và 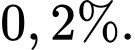
Gọi
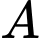 là biến cố: “ Sản phẩm được chọn là phế phẩm”. Chọn ngẫu nhiên một sản phẩm trong kho.
là biến cố: “ Sản phẩm được chọn là phế phẩm”. Chọn ngẫu nhiên một sản phẩm trong kho.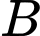 là biến cố: “Sản phẩm được chọn thuộc nhà máy một”.
là biến cố: “Sản phẩm được chọn thuộc nhà máy một”.
a) Đúng.
b) Sai.
 là xác suất sản phẩm được chọn là phế phẩm khi biết sản phẩm được chọn thuộc nhà máy hai và tỉ lệ này bằng 0,2% nên
là xác suất sản phẩm được chọn là phế phẩm khi biết sản phẩm được chọn thuộc nhà máy hai và tỉ lệ này bằng 0,2% nên 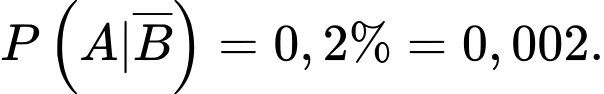
c) Sai.
Vì tỉ lệ đóng góp của nhà máy một bằng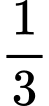 sản phẩm đóng góp của nhà máy hai nên suy ra
sản phẩm đóng góp của nhà máy hai nên suy ra 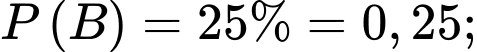
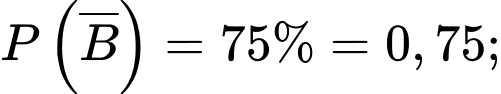
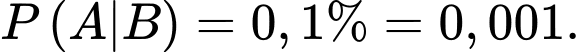
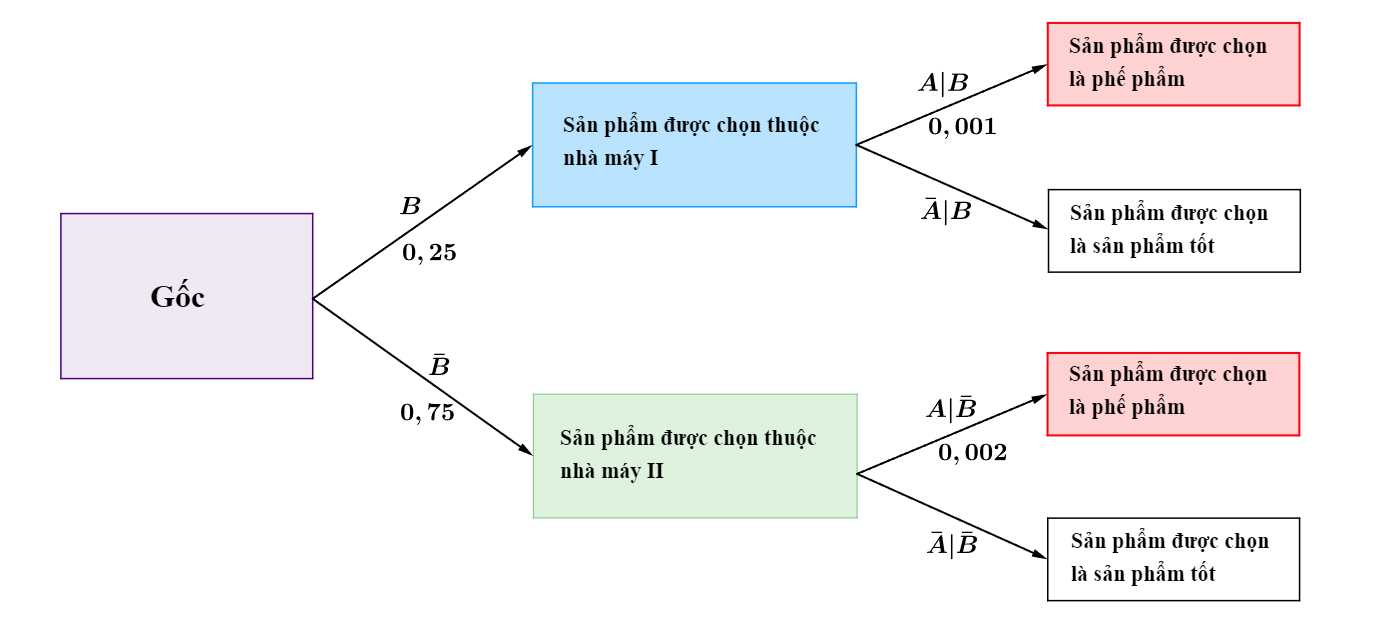
Từ đó, ta có sơ đồ cây sau:
Áp dụng công thức xác suất toàn phần, ta có xác suất chọn được phế phẩm là
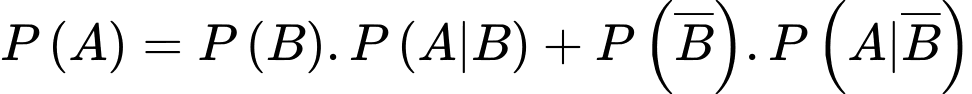
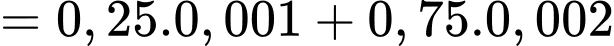
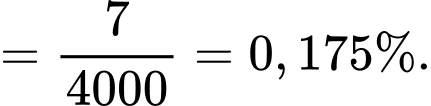
d) Đúng.
Yêu cầu bài toán Tính
Tính 
Áp dụng công thức Bayes, ta có: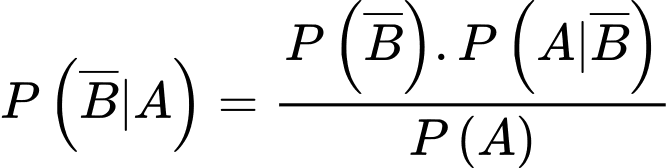
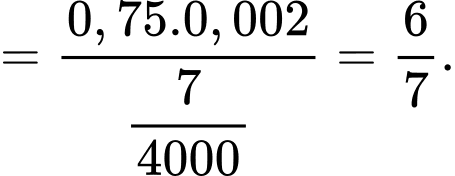
b) Sai.
 là xác suất sản phẩm được chọn là phế phẩm khi biết sản phẩm được chọn thuộc nhà máy hai và tỉ lệ này bằng 0,2% nên
là xác suất sản phẩm được chọn là phế phẩm khi biết sản phẩm được chọn thuộc nhà máy hai và tỉ lệ này bằng 0,2% nên 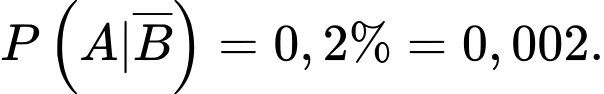
c) Sai.
Vì tỉ lệ đóng góp của nhà máy một bằng
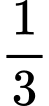 sản phẩm đóng góp của nhà máy hai nên suy ra
sản phẩm đóng góp của nhà máy hai nên suy ra 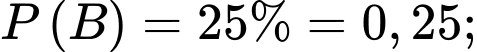
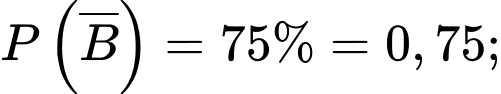
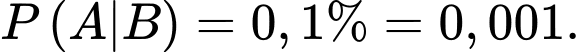
Từ đó, ta có sơ đồ cây sau:

Áp dụng công thức xác suất toàn phần, ta có xác suất chọn được phế phẩm là
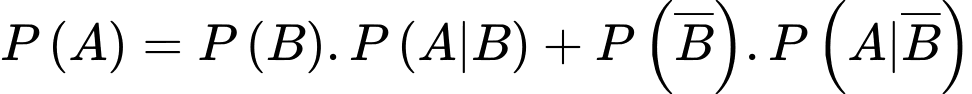
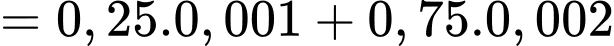
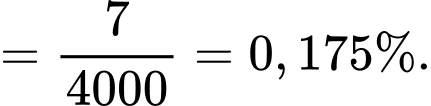
d) Đúng.
Yêu cầu bài toán
 Tính
Tính 
Áp dụng công thức Bayes, ta có:
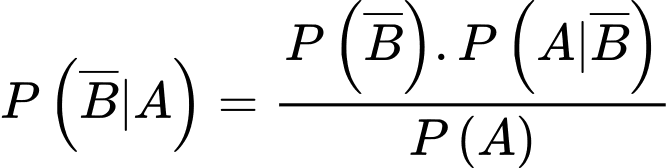
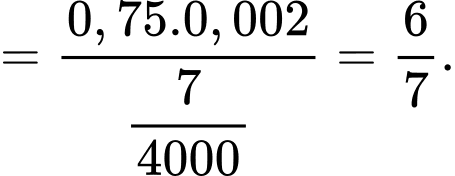
PHẦN III. Thí sinh trả lời từ câu 1 đến câu 6.
Câu 17 [693111]: Trong không gian 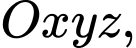 cho mặt cầu
cho mặt cầu 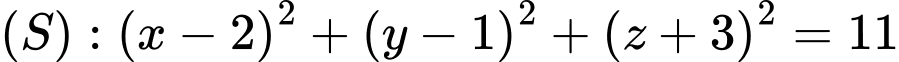 và điểm
và điểm 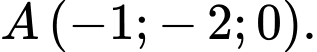 Gọi
Gọi  là đường tròn giao tuyến giữa mặt cầu
là đường tròn giao tuyến giữa mặt cầu 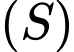 và mặt phẳng
và mặt phẳng 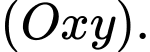 Biết
Biết 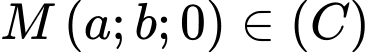 sao cho đoạn thẳng
sao cho đoạn thẳng  dài nhất. Giá trị của biểu thức
dài nhất. Giá trị của biểu thức 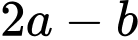 bằng bao nhiêu?
bằng bao nhiêu?
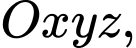 cho mặt cầu
cho mặt cầu 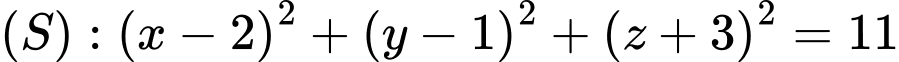 và điểm
và điểm 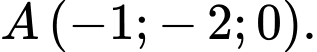 Gọi
Gọi  là đường tròn giao tuyến giữa mặt cầu
là đường tròn giao tuyến giữa mặt cầu 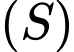 và mặt phẳng
và mặt phẳng 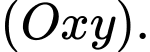 Biết
Biết 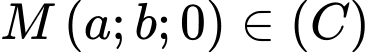 sao cho đoạn thẳng
sao cho đoạn thẳng  dài nhất. Giá trị của biểu thức
dài nhất. Giá trị của biểu thức 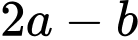 bằng bao nhiêu?
bằng bao nhiêu?
Mặt phẳng 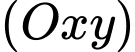 có phương trình là
có phương trình là 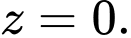
Thay vào mặt cầu
vào mặt cầu 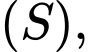 ta được
ta được 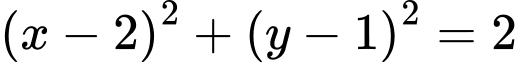
Do đó đường tròn giao tuyến giữa mặt cầu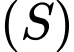 và
và  là
là
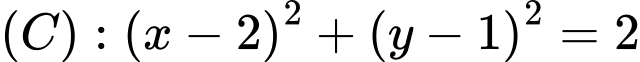 có tâm
có tâm 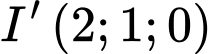 và
và 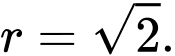
 có độ dài lớn nhất khi
có độ dài lớn nhất khi 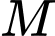 nằm trên đường thẳng
nằm trên đường thẳng 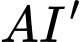 và
và 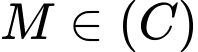
Ta có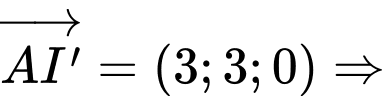 phương trình đường thẳng
phương trình đường thẳng 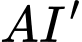 là
là 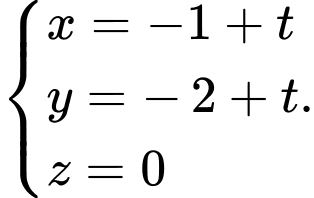
Khi đó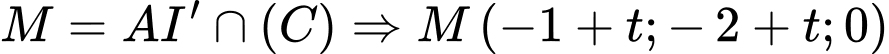
Thay toạ độ điểm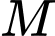 vào
vào  ta được
ta được 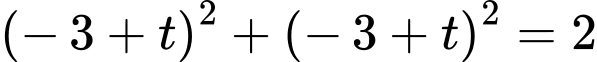
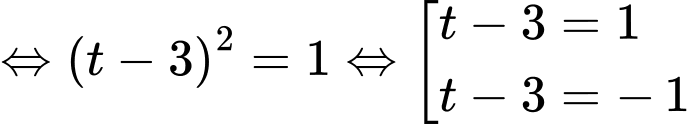
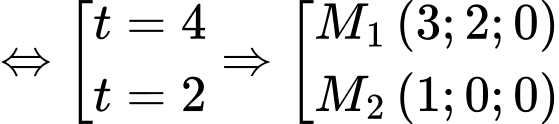
Lại có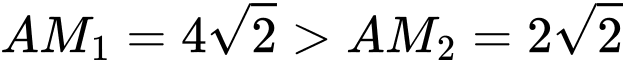 nên
nên  lớn nhất khi
lớn nhất khi 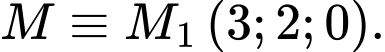
Vậy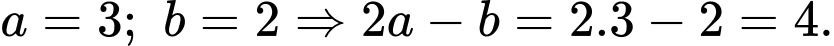
 có phương trình là
có phương trình là 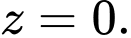
Thay
 vào mặt cầu
vào mặt cầu 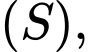 ta được
ta được 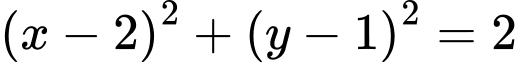
Do đó đường tròn giao tuyến giữa mặt cầu
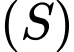 và
và 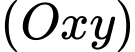 là
là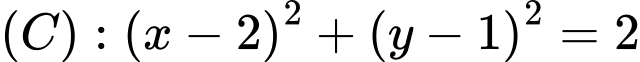 có tâm
có tâm 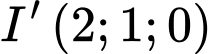 và
và 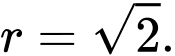
 có độ dài lớn nhất khi
có độ dài lớn nhất khi  nằm trên đường thẳng
nằm trên đường thẳng 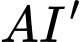 và
và 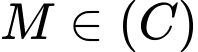
Ta có
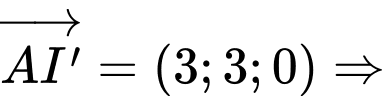 phương trình đường thẳng
phương trình đường thẳng 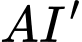 là
là 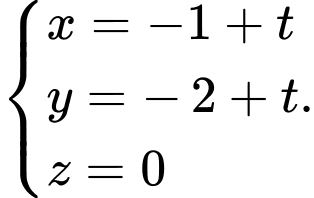
Khi đó
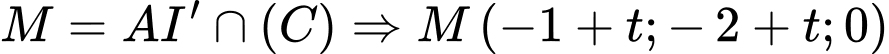
Thay toạ độ điểm
 vào
vào  ta được
ta được 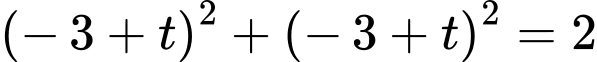
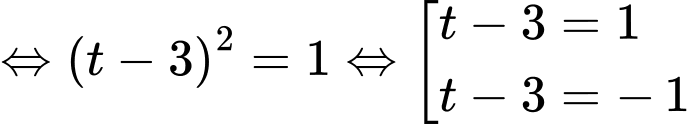
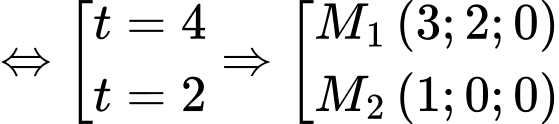
Lại có
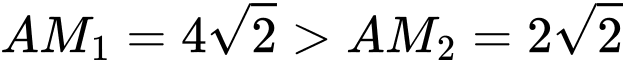 nên
nên  lớn nhất khi
lớn nhất khi 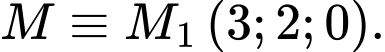
Vậy
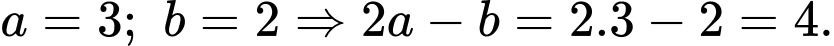
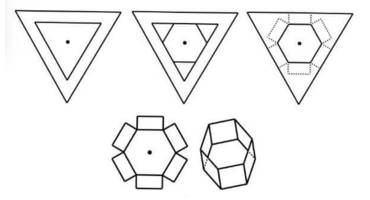
Câu 18 [693788]: Cho một tấm tôn hình một tam giác đều có cạnh bằng  Người ta thiết kế một hình lục giác đều và sáu hình chữ nhật ở phía ngoài lục giác có một cạnh bằng cạnh của lục giác, một cạnh bằng
Người ta thiết kế một hình lục giác đều và sáu hình chữ nhật ở phía ngoài lục giác có một cạnh bằng cạnh của lục giác, một cạnh bằng  với
với 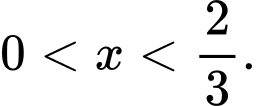 Sau đó người ta cắt theo nét đứt đoạn để thu được hình hợp bởi một lục giác đều và sáu hình chữ nhật. Sau đó gấp các hình chữ nhật để tạo thành khối lăng trụ lục giác đều (tham khảo hình vẽ dưới đây). Thể tích của khối lăng trụ lớn nhất bằng bao nhiêu đề-xi-mét khối
Sau đó người ta cắt theo nét đứt đoạn để thu được hình hợp bởi một lục giác đều và sáu hình chữ nhật. Sau đó gấp các hình chữ nhật để tạo thành khối lăng trụ lục giác đều (tham khảo hình vẽ dưới đây). Thể tích của khối lăng trụ lớn nhất bằng bao nhiêu đề-xi-mét khối  (làm tròn kết quả đến hàng phần mười)?
(làm tròn kết quả đến hàng phần mười)?
 Người ta thiết kế một hình lục giác đều và sáu hình chữ nhật ở phía ngoài lục giác có một cạnh bằng cạnh của lục giác, một cạnh bằng
Người ta thiết kế một hình lục giác đều và sáu hình chữ nhật ở phía ngoài lục giác có một cạnh bằng cạnh của lục giác, một cạnh bằng  với
với 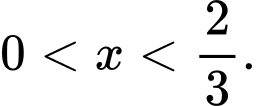 Sau đó người ta cắt theo nét đứt đoạn để thu được hình hợp bởi một lục giác đều và sáu hình chữ nhật. Sau đó gấp các hình chữ nhật để tạo thành khối lăng trụ lục giác đều (tham khảo hình vẽ dưới đây). Thể tích của khối lăng trụ lớn nhất bằng bao nhiêu đề-xi-mét khối
Sau đó người ta cắt theo nét đứt đoạn để thu được hình hợp bởi một lục giác đều và sáu hình chữ nhật. Sau đó gấp các hình chữ nhật để tạo thành khối lăng trụ lục giác đều (tham khảo hình vẽ dưới đây). Thể tích của khối lăng trụ lớn nhất bằng bao nhiêu đề-xi-mét khối 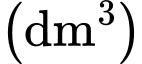 (làm tròn kết quả đến hàng phần mười)?
(làm tròn kết quả đến hàng phần mười)?
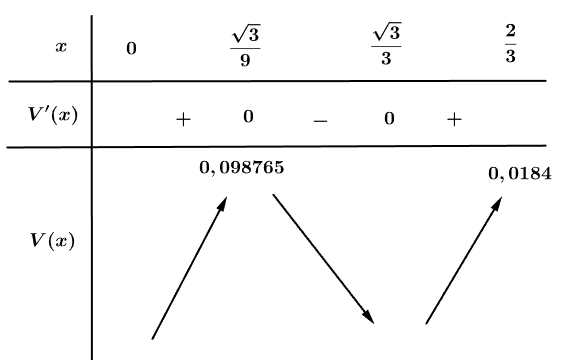
Điền đáp án: 98,8.
Để tính thể tích khối lăng trụ tạo thành, ta cần tìm chiều cao và diện tích đáy (là hình lục giác đều).
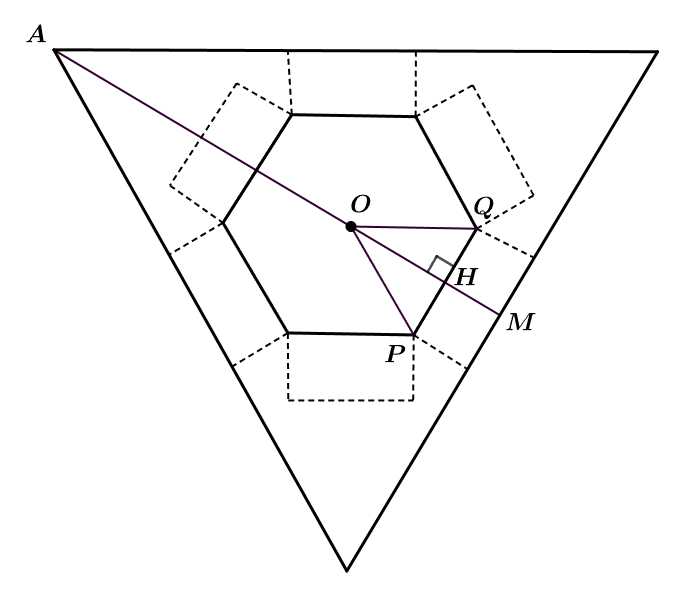
Gọi là trọng tâm của hình tam giác đều (nên
là trọng tâm của hình tam giác đều (nên  là giao điểm của 3 đường trung tuyến). Vẽ
là giao điểm của 3 đường trung tuyến). Vẽ  là trung tuyến của tam giác đều. Ta kí hiệu các điểm
là trung tuyến của tam giác đều. Ta kí hiệu các điểm  như hình vẽ trên.
như hình vẽ trên.
Theo giả thiết, hình chữ nhật có 1 cạnh bằng cạnh của hình lục giác, một cạnh bằng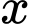 (m). Do đó
(m). Do đó 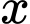 là chiều rộng của hình chữ nhật.
là chiều rộng của hình chữ nhật.
Ta có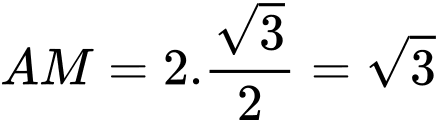 (theo công thức tính nhanh chiều cao của tam giác đều)
(theo công thức tính nhanh chiều cao của tam giác đều)
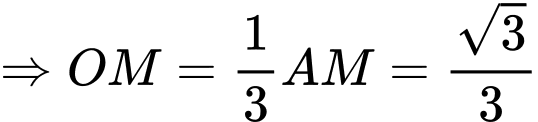 (Tính chất 3 đường trung tuyến của tam giác)
(Tính chất 3 đường trung tuyến của tam giác)
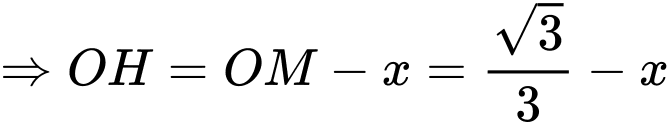
Tam giác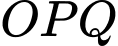 là tam giác đều (theo tính chất của lục giác đều), ta có
là tam giác đều (theo tính chất của lục giác đều), ta có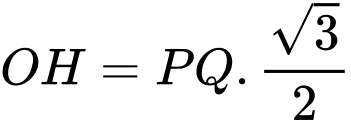
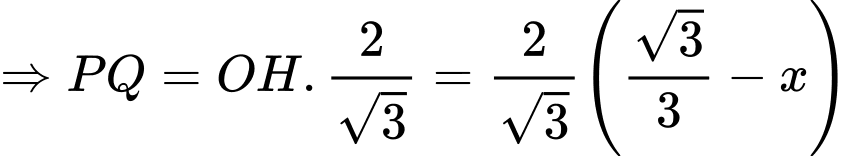 (thay
(thay 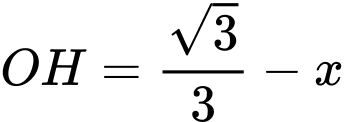 vào)
vào)
Suy ra diện tích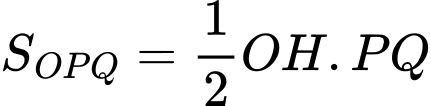
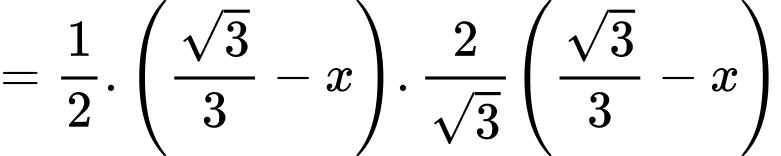
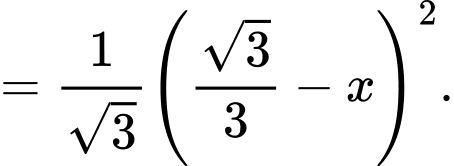
Diện tích lục giác đều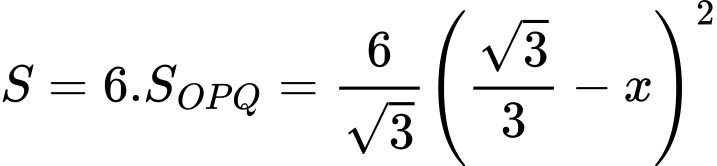
Suy ra thể tích lăng trụ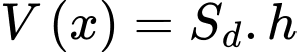
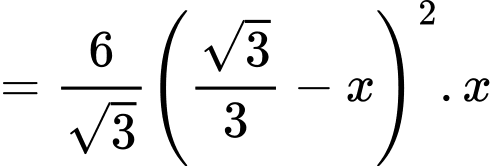
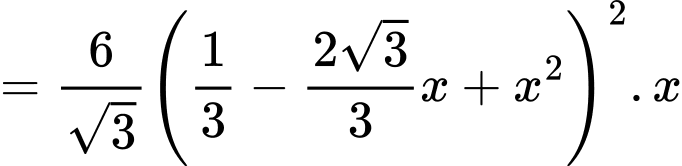
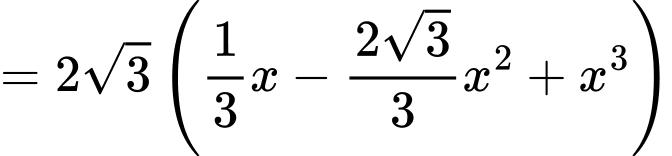
Để tìm thể tích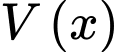 Max, ta khảo sát hàm số
Max, ta khảo sát hàm số 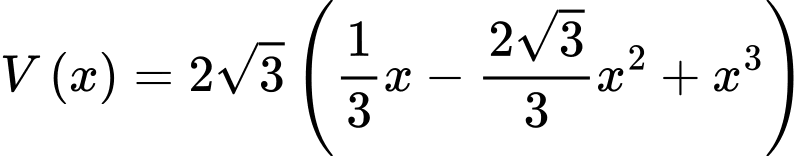 trên khoảng
trên khoảng 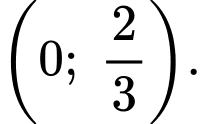
Ta có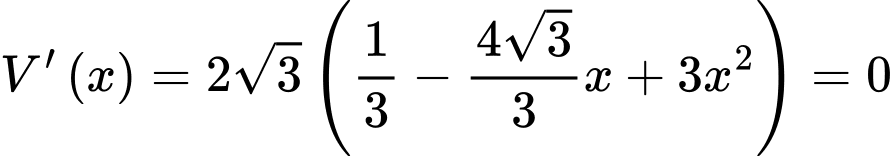
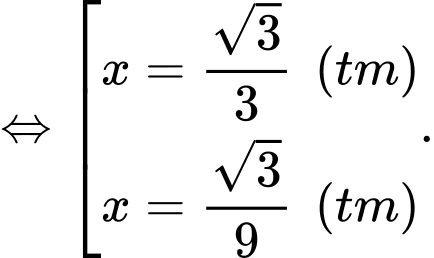
Bảng biến thiên của
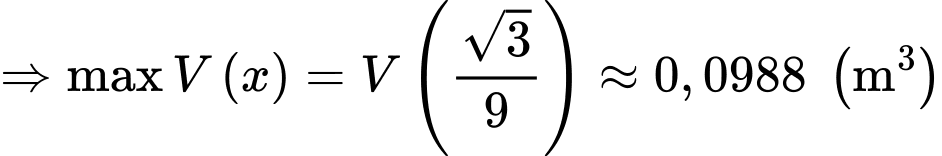
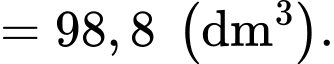
Để tính thể tích khối lăng trụ tạo thành, ta cần tìm chiều cao và diện tích đáy (là hình lục giác đều).

Gọi
 là trọng tâm của hình tam giác đều (nên
là trọng tâm của hình tam giác đều (nên  là giao điểm của 3 đường trung tuyến). Vẽ
là giao điểm của 3 đường trung tuyến). Vẽ  là trung tuyến của tam giác đều. Ta kí hiệu các điểm
là trung tuyến của tam giác đều. Ta kí hiệu các điểm  như hình vẽ trên.
như hình vẽ trên.Theo giả thiết, hình chữ nhật có 1 cạnh bằng cạnh của hình lục giác, một cạnh bằng
 (m). Do đó
(m). Do đó 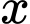 là chiều rộng của hình chữ nhật.
là chiều rộng của hình chữ nhật.Ta có
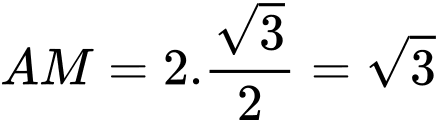 (theo công thức tính nhanh chiều cao của tam giác đều)
(theo công thức tính nhanh chiều cao của tam giác đều) 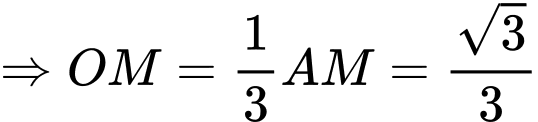 (Tính chất 3 đường trung tuyến của tam giác)
(Tính chất 3 đường trung tuyến của tam giác) 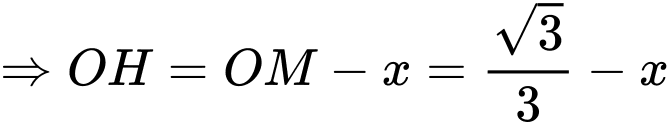
Tam giác
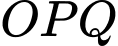 là tam giác đều (theo tính chất của lục giác đều), ta có
là tam giác đều (theo tính chất của lục giác đều), ta có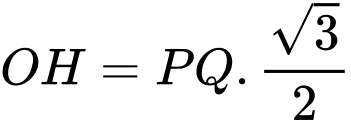
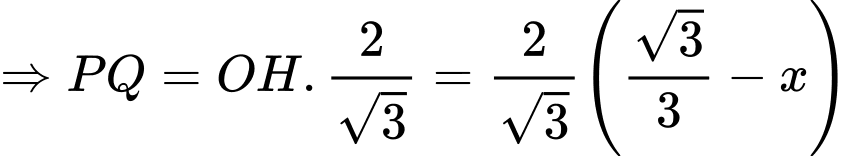 (thay
(thay 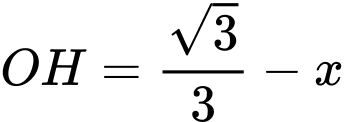 vào)
vào)Suy ra diện tích
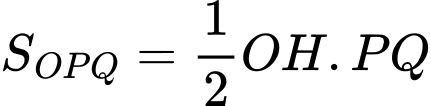
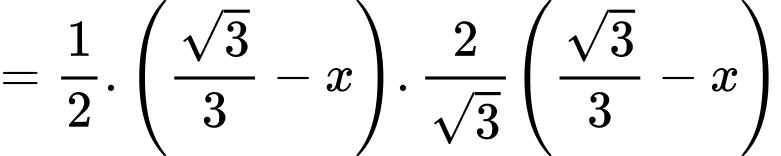
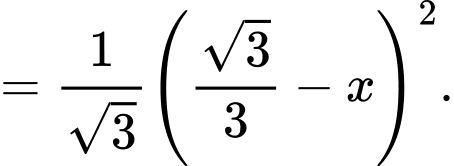
Diện tích lục giác đều
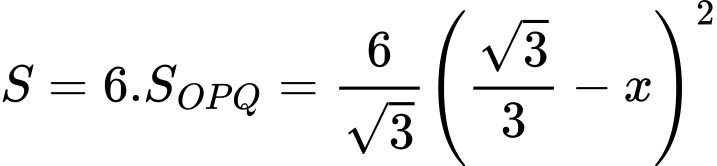
Suy ra thể tích lăng trụ
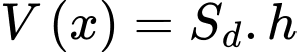
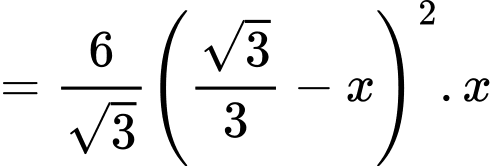
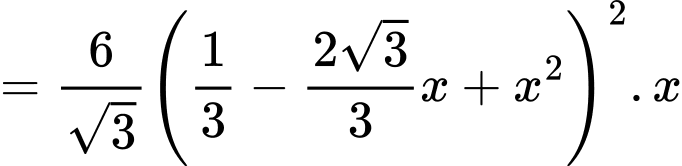
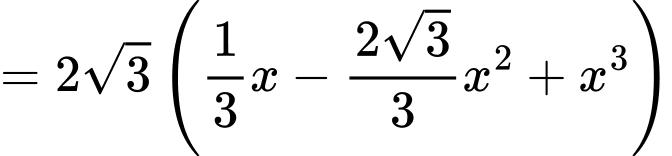
Để tìm thể tích
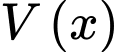 Max, ta khảo sát hàm số
Max, ta khảo sát hàm số 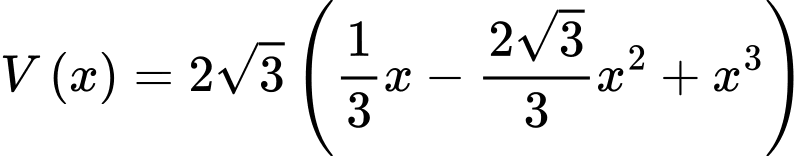 trên khoảng
trên khoảng 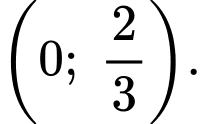
Ta có
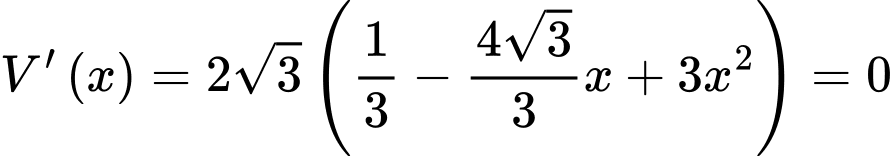
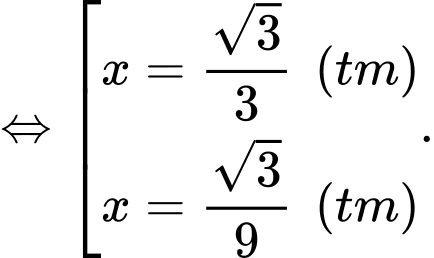
Bảng biến thiên của
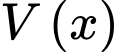

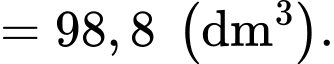
Câu 19 [694724]: Cho hình chóp tứ giác đều 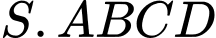 có tất cả các cạnh bằng
có tất cả các cạnh bằng 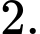 Gọi
Gọi 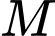 là trung điểm của
là trung điểm của 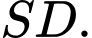 Tang của góc giữa đường thẳng
Tang của góc giữa đường thẳng 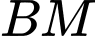 và mặt phẳng
và mặt phẳng 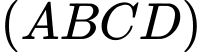 bằng bao nhiêu? (làm tròn kết quả đến hàng phần mười).
bằng bao nhiêu? (làm tròn kết quả đến hàng phần mười).
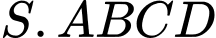 có tất cả các cạnh bằng
có tất cả các cạnh bằng 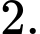 Gọi
Gọi 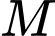 là trung điểm của
là trung điểm của 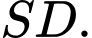 Tang của góc giữa đường thẳng
Tang của góc giữa đường thẳng 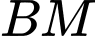 và mặt phẳng
và mặt phẳng 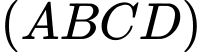 bằng bao nhiêu? (làm tròn kết quả đến hàng phần mười).
bằng bao nhiêu? (làm tròn kết quả đến hàng phần mười). 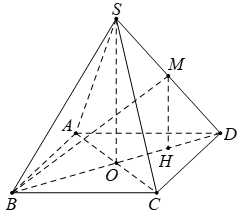
Gọi
 là tâm hình vuông
là tâm hình vuông 
Gọi
 là trung điểm
là trung điểm 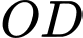
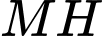 là đường trung bình của
là đường trung bình của 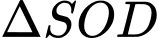
Do đó
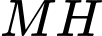 //
// 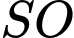

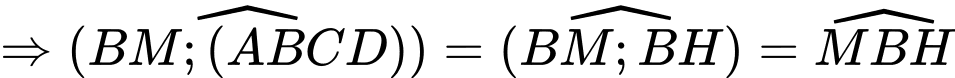
Tam giác
 vuông tại
vuông tại  có
có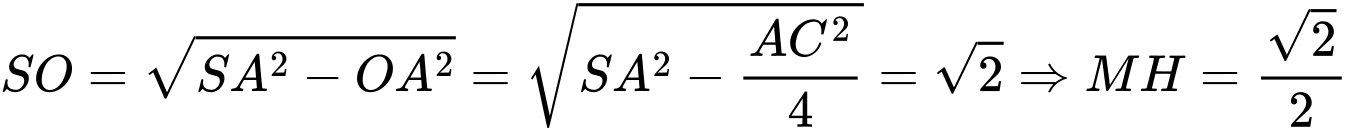
Lại có
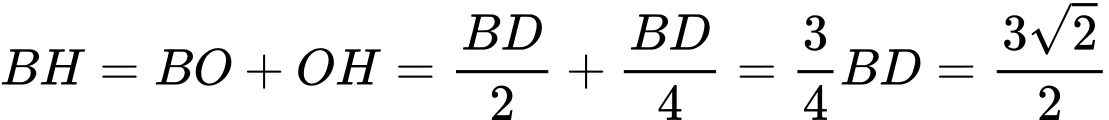
Vậy
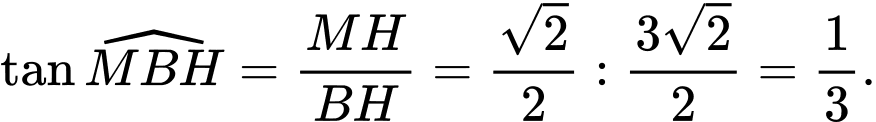
Câu 20 [694725]: Công ty A có kế hoạch tổ chức tour du lịch tâm linh tại tỉnh Bắc Giang đi qua 5 địa điểm: Đền Xương Giang, Chùa Bổ Đà, Chùa Vĩnh Nghiêm, Thiền viện Trúc lâm Phượng Hoàng, Đền Ngọc Lâm. Hành khách sẽ xuất phát từ Đền Xương Giang và đi thăm mỗi địa điểm đúng một lần. Qua khảo sát thực địa, công ty xây dựng được lược đồ như hình (khoảng cách giữa mỗi cặp địa điểm được ghi trên đường nối). Để tiết kiệm chi phí, công ty dự định chọn tuyến đường có tổng độ dài ngắn nhất. Độ dài của tuyến đường này là bao nhiêu km?
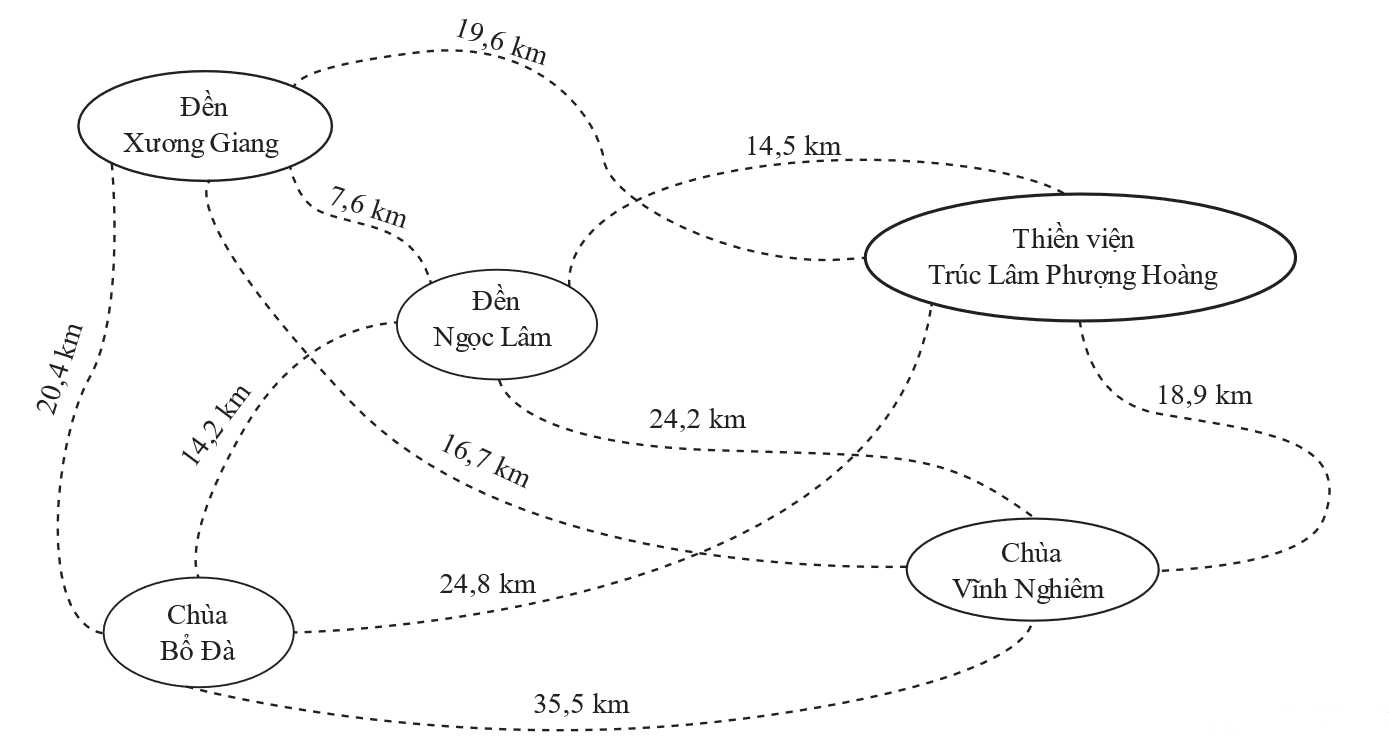

Điền đáp án: 64,3.
Ta sử dụng thuật toán láng giếng gần nhất.
+) Tuyến 1: Đền Xương Giang Đền Ngọc Lâm
Đền Ngọc Lâm  Chùa Bổ Đà
Chùa Bổ Đà  Thiền viện Trúc Lâm Phượng Hoàng
Thiền viện Trúc Lâm Phượng Hoàng  Chùa Vĩnh Nghiêm.
Chùa Vĩnh Nghiêm.
Độ dài quãng đường là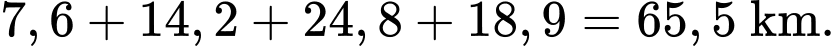
+) Tuyến 2: Đền Xương Giang Chùa Vĩnh Nghiêm
Chùa Vĩnh Nghiêm  Thiền viện Trúc Lâm Phượng Hoàng
Thiền viện Trúc Lâm Phượng Hoàng  Đền Ngọc Lâm
Đền Ngọc Lâm  Chùa Bổ Đà.
Chùa Bổ Đà.
Độ dài quãng đường là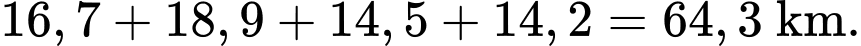
+) Tuyến 3: Đền Xương Giang Chùa Bổ Đà
Chùa Bổ Đà  Đền Ngọc Lâm
Đền Ngọc Lâm  Thiền viện Trúc Lâm Phượng Hoàng
Thiền viện Trúc Lâm Phượng Hoàng  Chùa Vĩnh Nghiêm.
Chùa Vĩnh Nghiêm.
Độ dài quãng đường là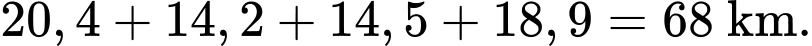
+) Tuyến 4: Đền Xương Giang Thiền viện Trúc Lâm Phượng Hoàng
Thiền viện Trúc Lâm Phượng Hoàng  Chùa Vĩnh Nghiêm
Chùa Vĩnh Nghiêm  Đền Ngọc Lâm
Đền Ngọc Lâm  Chùa Bổ Đà.
Chùa Bổ Đà.
Độ dài quãng đường là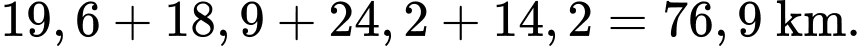
Ta sử dụng thuật toán láng giếng gần nhất.
+) Tuyến 1: Đền Xương Giang
 Đền Ngọc Lâm
Đền Ngọc Lâm  Chùa Bổ Đà
Chùa Bổ Đà  Thiền viện Trúc Lâm Phượng Hoàng
Thiền viện Trúc Lâm Phượng Hoàng  Chùa Vĩnh Nghiêm.
Chùa Vĩnh Nghiêm. Độ dài quãng đường là
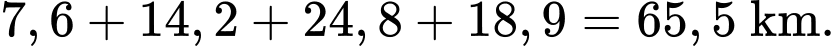
+) Tuyến 2: Đền Xương Giang
 Chùa Vĩnh Nghiêm
Chùa Vĩnh Nghiêm  Thiền viện Trúc Lâm Phượng Hoàng
Thiền viện Trúc Lâm Phượng Hoàng  Đền Ngọc Lâm
Đền Ngọc Lâm  Chùa Bổ Đà.
Chùa Bổ Đà. Độ dài quãng đường là
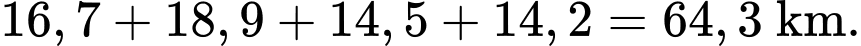
+) Tuyến 3: Đền Xương Giang
 Chùa Bổ Đà
Chùa Bổ Đà  Đền Ngọc Lâm
Đền Ngọc Lâm  Thiền viện Trúc Lâm Phượng Hoàng
Thiền viện Trúc Lâm Phượng Hoàng  Chùa Vĩnh Nghiêm.
Chùa Vĩnh Nghiêm. Độ dài quãng đường là
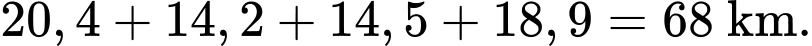
+) Tuyến 4: Đền Xương Giang
 Thiền viện Trúc Lâm Phượng Hoàng
Thiền viện Trúc Lâm Phượng Hoàng  Chùa Vĩnh Nghiêm
Chùa Vĩnh Nghiêm  Đền Ngọc Lâm
Đền Ngọc Lâm  Chùa Bổ Đà.
Chùa Bổ Đà. Độ dài quãng đường là
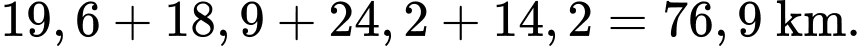
Câu 21 [694728]: Trong một nghiên cứu của V.A.Tucker và K. Schmidt-Koenig, người ta đã xác định rằng năng lượng 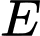 tiêu thụ bởi một con chim trong chuyến bay thay đổi theo tốc độ
tiêu thụ bởi một con chim trong chuyến bay thay đổi theo tốc độ  của con chim. Đối với một loại vẹt đuôi dài, mức tiêu hao năng lượng thay đổi theo tốc độ được cho bởi
của con chim. Đối với một loại vẹt đuôi dài, mức tiêu hao năng lượng thay đổi theo tốc độ được cho bởi 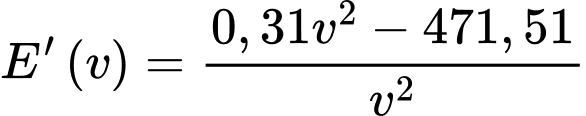 với
với  trong đó
trong đó 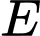 được tính bằng Jun. Quan sát cho thấy vẹt đuôi dài có xu hướng bay với tốc độ
được tính bằng Jun. Quan sát cho thấy vẹt đuôi dài có xu hướng bay với tốc độ  để làm giảm tiêu hao năng lượng xuống còn tối thiểu
để làm giảm tiêu hao năng lượng xuống còn tối thiểu 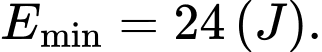 Trong 4 giờ quan sát con vẹt bay với vận tốc tăng đều đặn từ
Trong 4 giờ quan sát con vẹt bay với vận tốc tăng đều đặn từ  đến
đến  Tại thời điểm giờ đầu tiên quan sát, mức năng lượng tiêu hao của con vẹt đó bằng bao nhiêu Jun? (làm tròn đến hàng phần mười).
Tại thời điểm giờ đầu tiên quan sát, mức năng lượng tiêu hao của con vẹt đó bằng bao nhiêu Jun? (làm tròn đến hàng phần mười).
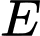 tiêu thụ bởi một con chim trong chuyến bay thay đổi theo tốc độ
tiêu thụ bởi một con chim trong chuyến bay thay đổi theo tốc độ  của con chim. Đối với một loại vẹt đuôi dài, mức tiêu hao năng lượng thay đổi theo tốc độ được cho bởi
của con chim. Đối với một loại vẹt đuôi dài, mức tiêu hao năng lượng thay đổi theo tốc độ được cho bởi 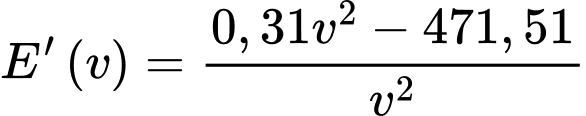 với
với  trong đó
trong đó 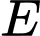 được tính bằng Jun. Quan sát cho thấy vẹt đuôi dài có xu hướng bay với tốc độ
được tính bằng Jun. Quan sát cho thấy vẹt đuôi dài có xu hướng bay với tốc độ  để làm giảm tiêu hao năng lượng xuống còn tối thiểu
để làm giảm tiêu hao năng lượng xuống còn tối thiểu 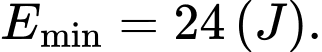 Trong 4 giờ quan sát con vẹt bay với vận tốc tăng đều đặn từ
Trong 4 giờ quan sát con vẹt bay với vận tốc tăng đều đặn từ  đến
đến  Tại thời điểm giờ đầu tiên quan sát, mức năng lượng tiêu hao của con vẹt đó bằng bao nhiêu Jun? (làm tròn đến hàng phần mười).
Tại thời điểm giờ đầu tiên quan sát, mức năng lượng tiêu hao của con vẹt đó bằng bao nhiêu Jun? (làm tròn đến hàng phần mười).
Điền đáp án: 24,2.
Để tính được mức năng lượng tiêu hao của con vẹt tại thời điểm giờ đầu tiên quan sát, ta cần tìm được vận tốc vào thời điểm đó là bao nhiêu.
Ta có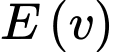 là hàm số thể hiện mức năng lượng tiêu hao của con vẹt khi bay với vận tốc
là hàm số thể hiện mức năng lượng tiêu hao của con vẹt khi bay với vận tốc 
Theo công thức nguyên hàm, ta có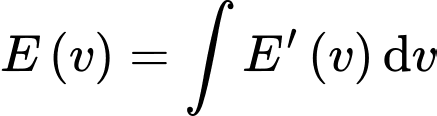
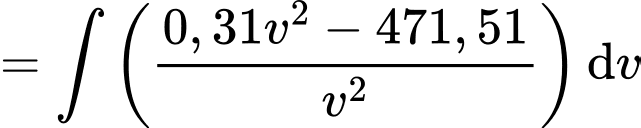 (Áp dụng các công thức nguyên hàm sau:
(Áp dụng các công thức nguyên hàm sau: 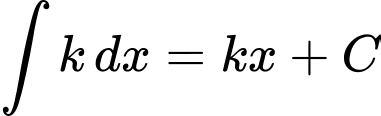 với
với  là hằng số;
là hằng số; 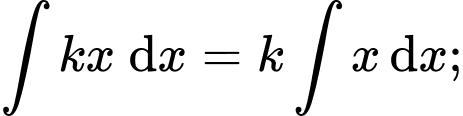
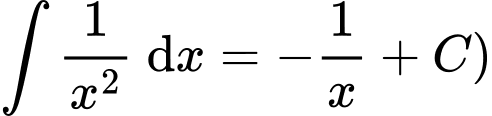
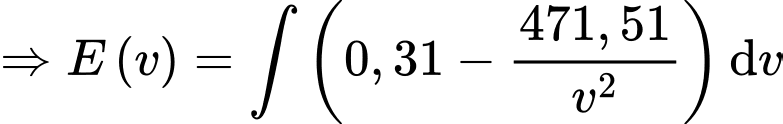
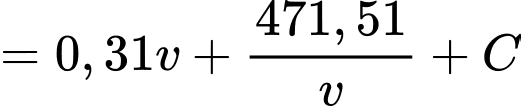
Ta có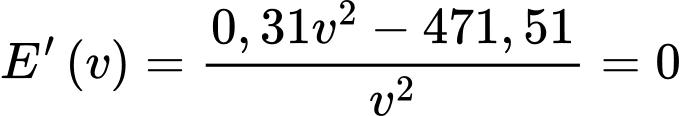
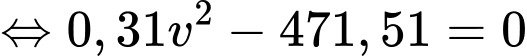
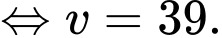 (Loại
(Loại 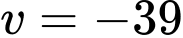 vì
vì

Bảng biến thiên
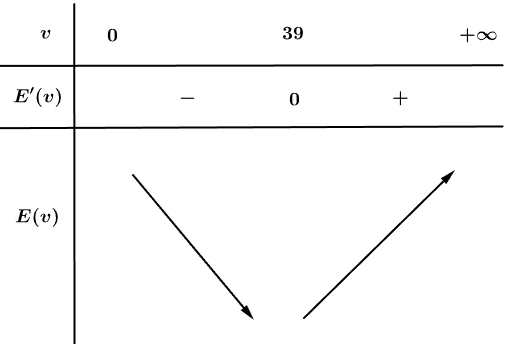
Từ bảng biến thiên, suy ra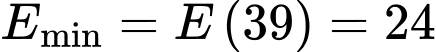
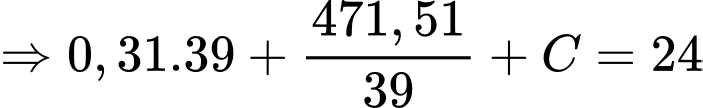 (Thay
(Thay 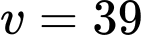 vào phương trình)
vào phương trình)
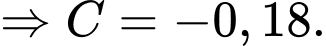
Suy ra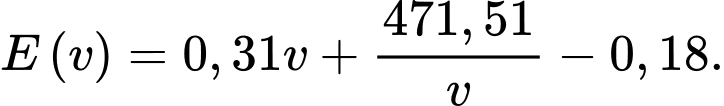
Vì trong 4 giờ (tức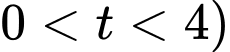 quan sát con vẹt bay với vận tốc tăng đều đặn từ
quan sát con vẹt bay với vận tốc tăng đều đặn từ  đến
đến  nên phương trình vận tốc ở đây là 1 đường thẳng và hàm này đồng biến.
nên phương trình vận tốc ở đây là 1 đường thẳng và hàm này đồng biến.
Giả sử hàm số
Từ giả thiết, ta có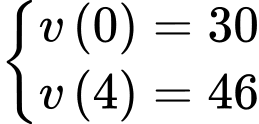
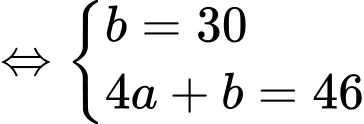
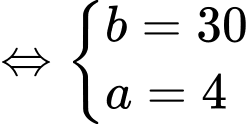
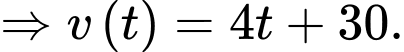
Suy ra vận tốc ban đầu vào lúc quan sát là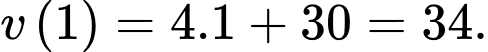 (thay
(thay 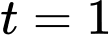 vào phương trình vận tốc)
vào phương trình vận tốc)
Vậy tại thời điểm quan sát, mức năng lượng tiêu hao của con vẹt là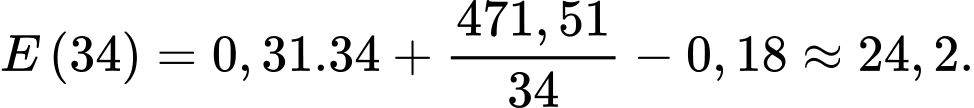
Để tính được mức năng lượng tiêu hao của con vẹt tại thời điểm giờ đầu tiên quan sát, ta cần tìm được vận tốc vào thời điểm đó là bao nhiêu.
Ta có
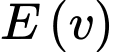 là hàm số thể hiện mức năng lượng tiêu hao của con vẹt khi bay với vận tốc
là hàm số thể hiện mức năng lượng tiêu hao của con vẹt khi bay với vận tốc 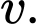
Theo công thức nguyên hàm, ta có
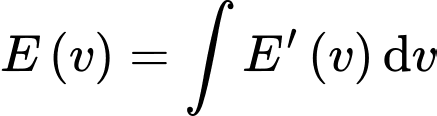
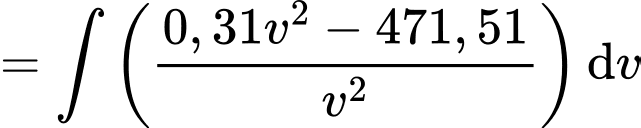 (Áp dụng các công thức nguyên hàm sau:
(Áp dụng các công thức nguyên hàm sau: 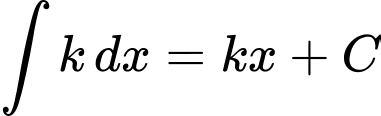 với
với  là hằng số;
là hằng số; 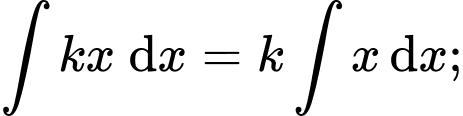
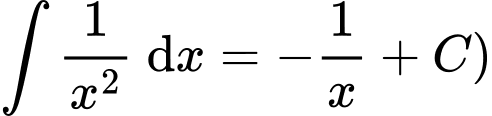
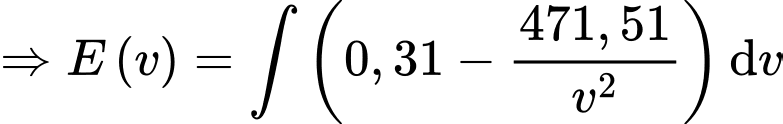
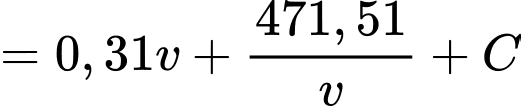
Ta có
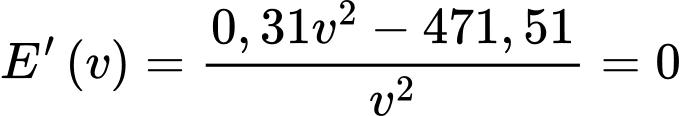
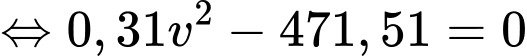
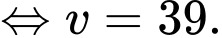 (Loại
(Loại 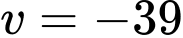 vì
vì

Bảng biến thiên

Từ bảng biến thiên, suy ra
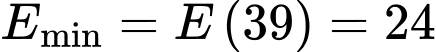
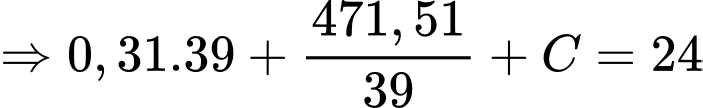 (Thay
(Thay 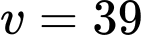 vào phương trình)
vào phương trình)
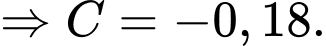
Suy ra
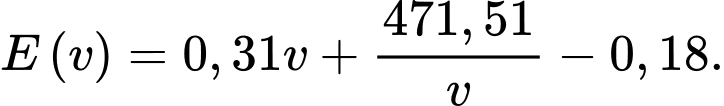
Vì trong 4 giờ (tức
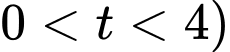 quan sát con vẹt bay với vận tốc tăng đều đặn từ
quan sát con vẹt bay với vận tốc tăng đều đặn từ  đến
đến  nên phương trình vận tốc ở đây là 1 đường thẳng và hàm này đồng biến.
nên phương trình vận tốc ở đây là 1 đường thẳng và hàm này đồng biến.
Giả sử hàm số

Từ giả thiết, ta có
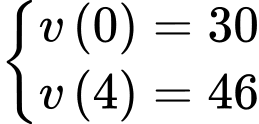
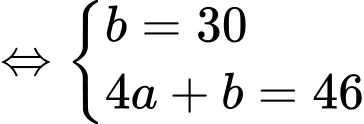
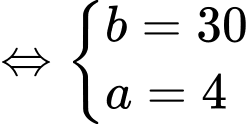
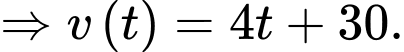
Suy ra vận tốc ban đầu vào lúc quan sát là
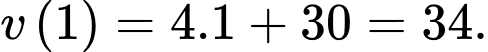 (thay
(thay  vào phương trình vận tốc)
vào phương trình vận tốc)
Vậy tại thời điểm quan sát, mức năng lượng tiêu hao của con vẹt là
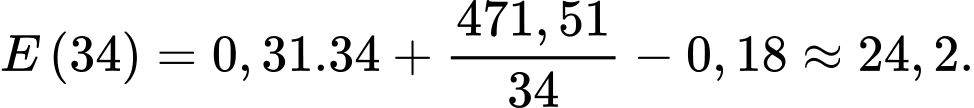
Câu 22 [700895]: Một em bé này mắc một trong 2 bệnh Bạch hầu hoặc Ho gà. Thống kê tình hình mắc bệnh trong nhiều năm thì thấy rằng xác suất mắc bệnh Bạch hầu cao gấp đôi xác suất mắc bệnh Ho gà. Bệnh viện đã tiến hành thực hiện 2 xét nghiệm y học 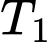 và
và 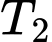 (một cách độc lập). Biết rằng nếu có bệnh Bạch hầu thì xét nghiệm
(một cách độc lập). Biết rằng nếu có bệnh Bạch hầu thì xét nghiệm 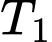 cho kết quả dương tính với xác suất 0,9, xét nghiệm
cho kết quả dương tính với xác suất 0,9, xét nghiệm 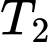 cho kết quả dương tính với xác suất 0,75. Trong trường hợp có bệnh Ho gà xét nghiệm
cho kết quả dương tính với xác suất 0,75. Trong trường hợp có bệnh Ho gà xét nghiệm 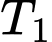 cho kết quả dương tính với xác suất 0,05 và xét nghiệm
cho kết quả dương tính với xác suất 0,05 và xét nghiệm 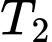 cho kết quả dương tính với xác suất 0,1. Giả sử rằng kết quả của 2 xét nghiệm
cho kết quả dương tính với xác suất 0,1. Giả sử rằng kết quả của 2 xét nghiệm 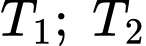 đều dương tính. Xác suất mắc bệnh Bạch hầu của em bé bị bệnh là bao nhiêu % (làm tròn kết quả đến hàng phần mười).
đều dương tính. Xác suất mắc bệnh Bạch hầu của em bé bị bệnh là bao nhiêu % (làm tròn kết quả đến hàng phần mười).
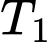 và
và 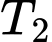 (một cách độc lập). Biết rằng nếu có bệnh Bạch hầu thì xét nghiệm
(một cách độc lập). Biết rằng nếu có bệnh Bạch hầu thì xét nghiệm 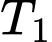 cho kết quả dương tính với xác suất 0,9, xét nghiệm
cho kết quả dương tính với xác suất 0,9, xét nghiệm 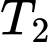 cho kết quả dương tính với xác suất 0,75. Trong trường hợp có bệnh Ho gà xét nghiệm
cho kết quả dương tính với xác suất 0,75. Trong trường hợp có bệnh Ho gà xét nghiệm 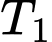 cho kết quả dương tính với xác suất 0,05 và xét nghiệm
cho kết quả dương tính với xác suất 0,05 và xét nghiệm 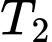 cho kết quả dương tính với xác suất 0,1. Giả sử rằng kết quả của 2 xét nghiệm
cho kết quả dương tính với xác suất 0,1. Giả sử rằng kết quả của 2 xét nghiệm 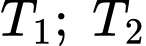 đều dương tính. Xác suất mắc bệnh Bạch hầu của em bé bị bệnh là bao nhiêu % (làm tròn kết quả đến hàng phần mười).
đều dương tính. Xác suất mắc bệnh Bạch hầu của em bé bị bệnh là bao nhiêu % (làm tròn kết quả đến hàng phần mười).
Điền đáp án: 99,6.
Gọi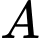 là biến cố “Em bé mắc bệnh Bạch hầu”
là biến cố “Em bé mắc bệnh Bạch hầu”
 là biến cố “Em bé mắc bệnh Ho gà”.
là biến cố “Em bé mắc bệnh Ho gà”.
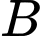 là biến cố “Xét nghiệm
là biến cố “Xét nghiệm 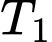 và
và 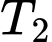 đều có kết quả dương tính”.
đều có kết quả dương tính”.
Theo giả thiết: Xác suất mắc bệnh Bạch hầu cao gấp đôi xác suất mắc bệnh Ho gà nên suy ra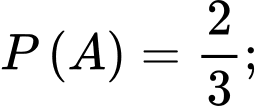
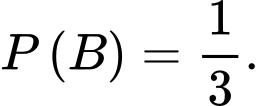
Xác suất xét nghiệm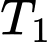 và
và 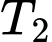 đều có kết quả dương tính khi biết em bé mắc bệnh Bạch hầu là
đều có kết quả dương tính khi biết em bé mắc bệnh Bạch hầu là 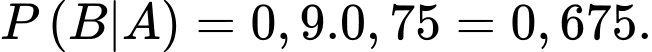
Tương tự, ta có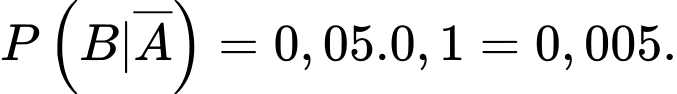
Yêu cầu bài toán Tính
Tính 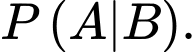
Ta có sơ đồ cây sau:
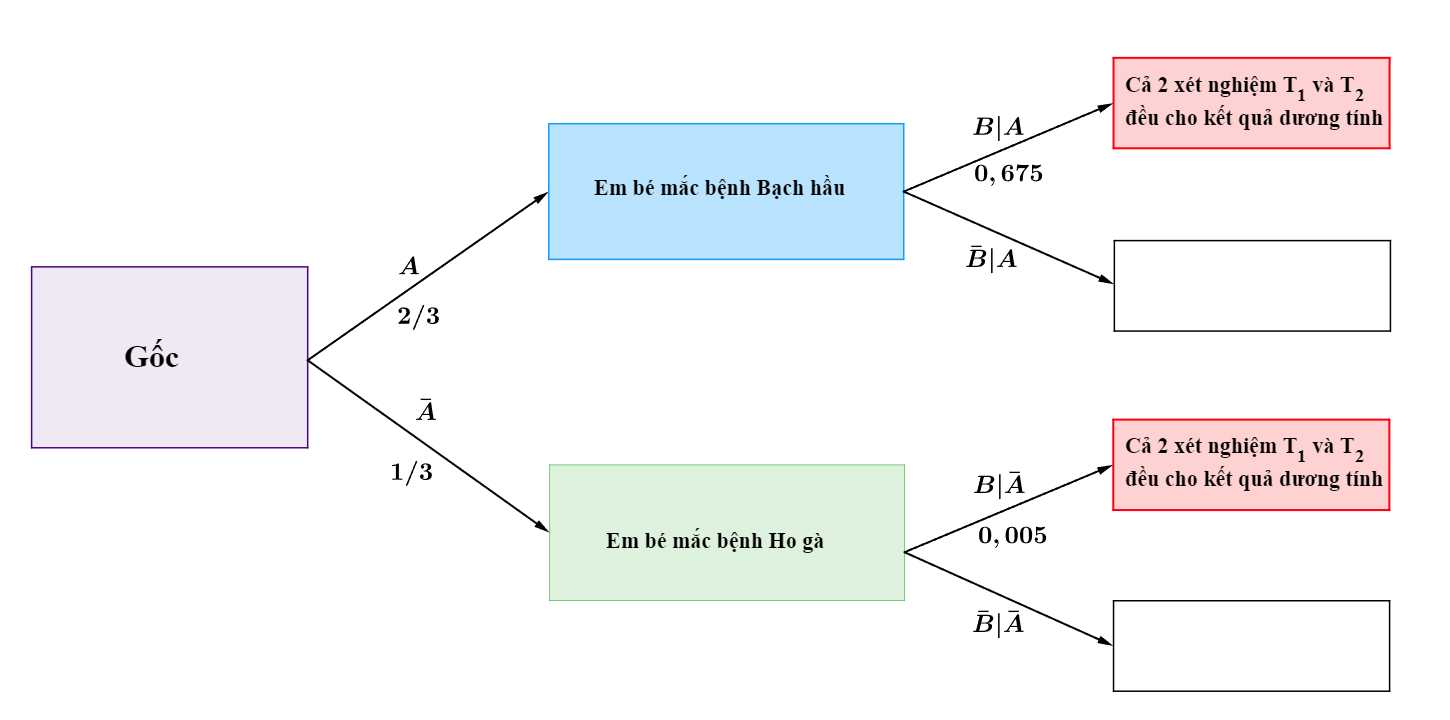
Áp dụng công thức xác suất toàn phần, ta có
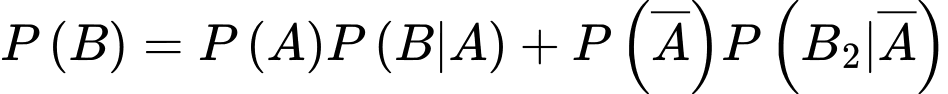
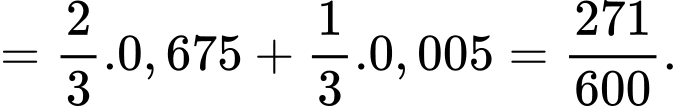
Áp dụng công thức Bayes, ta có
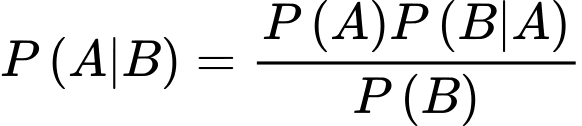
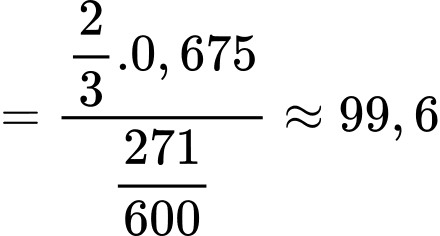
Như vậy trong tập hợp các bệnh nhân có xét nghiệm và
và  đều dương tính thì có 99,6% là mắc bệnh Bạch hầu.
đều dương tính thì có 99,6% là mắc bệnh Bạch hầu.
Gọi
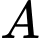 là biến cố “Em bé mắc bệnh Bạch hầu”
là biến cố “Em bé mắc bệnh Bạch hầu” là biến cố “Em bé mắc bệnh Ho gà”.
là biến cố “Em bé mắc bệnh Ho gà”.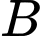 là biến cố “Xét nghiệm
là biến cố “Xét nghiệm 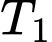 và
và 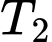 đều có kết quả dương tính”.
đều có kết quả dương tính”.Theo giả thiết: Xác suất mắc bệnh Bạch hầu cao gấp đôi xác suất mắc bệnh Ho gà nên suy ra
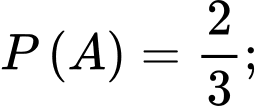
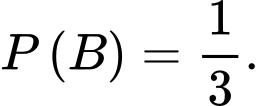
Xác suất xét nghiệm
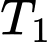 và
và 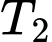 đều có kết quả dương tính khi biết em bé mắc bệnh Bạch hầu là
đều có kết quả dương tính khi biết em bé mắc bệnh Bạch hầu là 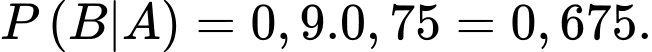
Tương tự, ta có
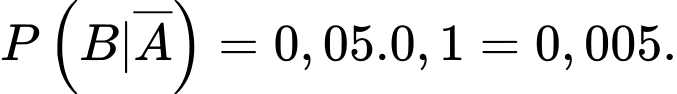
Yêu cầu bài toán
 Tính
Tính 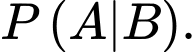
Ta có sơ đồ cây sau:

Áp dụng công thức xác suất toàn phần, ta có
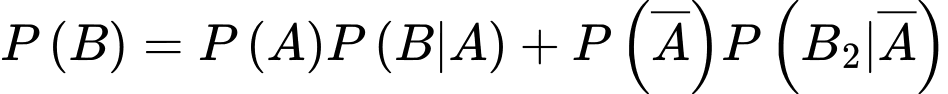
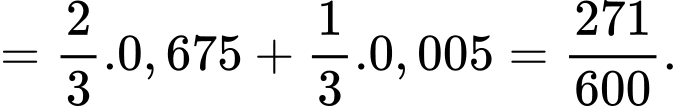
Áp dụng công thức Bayes, ta có
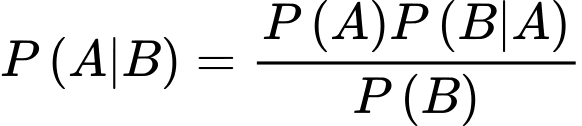
Như vậy trong tập hợp các bệnh nhân có xét nghiệm
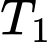 và
và 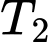 đều dương tính thì có 99,6% là mắc bệnh Bạch hầu.
đều dương tính thì có 99,6% là mắc bệnh Bạch hầu.