PHẦN I. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Câu 1 [694279]: Nếu 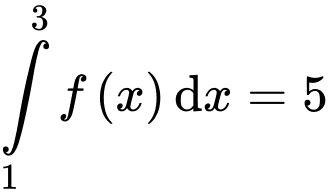 thì
thì 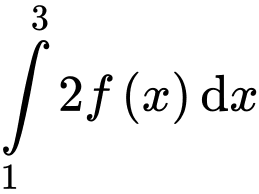 bằng
bằng
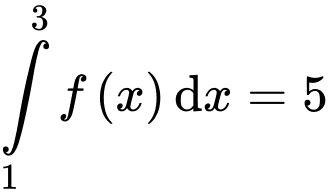 thì
thì 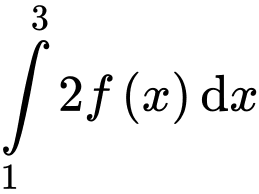 bằng
bằng A, 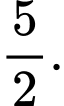
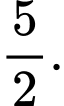
B, 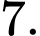
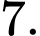
C, 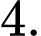
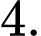
D, 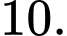
Chọn đáp án D.
Ta có: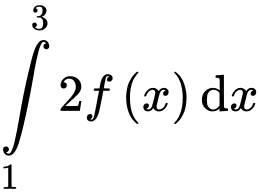
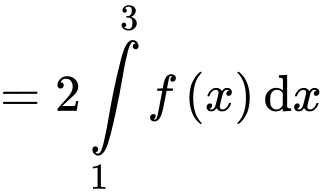
 Đáp án: D
Đáp án: D
Ta có:
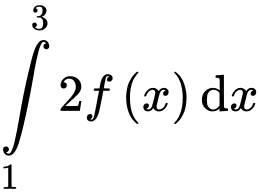
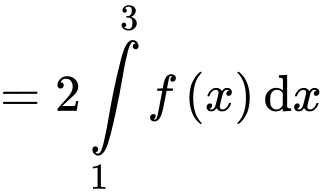
 Đáp án: D
Đáp án: D
Câu 2 [257698]: Cho cấp số nhân 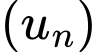 với
với 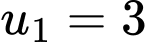 và công bội
và công bội 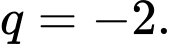 Giá trị của
Giá trị của 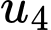 bằng
bằng
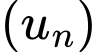 với
với 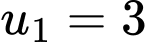 và công bội
và công bội 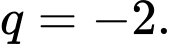 Giá trị của
Giá trị của 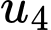 bằng
bằng A, 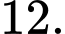
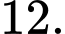
B, 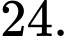
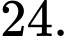
C, 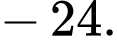
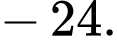
D, 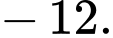
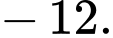
Chọn đáp án C.
Ta có cấp số nhân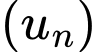 với
với 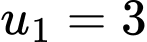 và công bội
và công bội 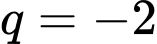
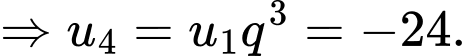
Đáp án: C
Ta có cấp số nhân
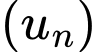 với
với 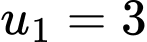 và công bội
và công bội 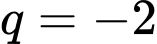
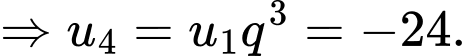
Đáp án: C
Câu 3 [257836]: Cho khối hộp có diện tích đáy là 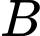 và chiều cao là
và chiều cao là 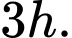 Thể tích
Thể tích  của khối hộp đã cho là
của khối hộp đã cho là
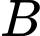 và chiều cao là
và chiều cao là 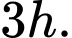 Thể tích
Thể tích  của khối hộp đã cho là
của khối hộp đã cho là A, 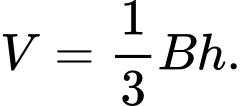
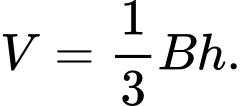
B, 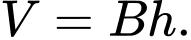
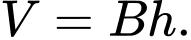
C, 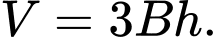
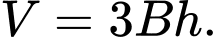
D, 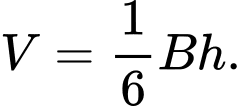
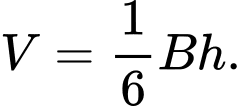
Chọn đáp án C.
Thể tích của khối hộp đã cho là
của khối hộp đã cho là 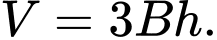 Đáp án: C
Đáp án: C
Thể tích
 của khối hộp đã cho là
của khối hộp đã cho là 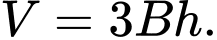 Đáp án: C
Đáp án: C Sử dụng thông tin dưới đây để trả lời câu 4 và câu 5
Cho hàm số y = f(x) liên tục trên đoạn [1;5] và có đồ thị trên như hình vẽ sau
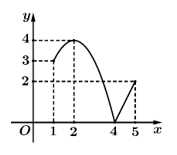

Câu 4 [700896]: Trên đoạn 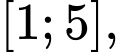 hàm số đã cho đạt giá trị lớn nhất tại điểm
hàm số đã cho đạt giá trị lớn nhất tại điểm
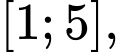 hàm số đã cho đạt giá trị lớn nhất tại điểm
hàm số đã cho đạt giá trị lớn nhất tại điểm A, 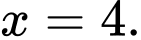
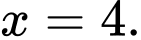
B, 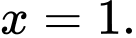
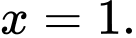
C, 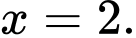
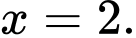
D, 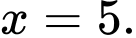
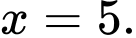
Chọn đáp án C.
Từ đồ thị hình vẽ ta có: Trên đoạn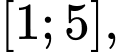 hàm số đã cho đạt giá trị lớn nhất tại điểm
hàm số đã cho đạt giá trị lớn nhất tại điểm 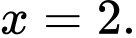 Đáp án: C
Đáp án: C
Từ đồ thị hình vẽ ta có: Trên đoạn
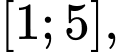 hàm số đã cho đạt giá trị lớn nhất tại điểm
hàm số đã cho đạt giá trị lớn nhất tại điểm 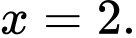 Đáp án: C
Đáp án: C
Câu 5 [700897]: Giá trị cực tiểu của hàm số 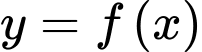 trên đoạn
trên đoạn 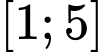 là
là
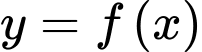 trên đoạn
trên đoạn 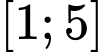 là
là A, 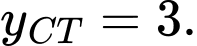
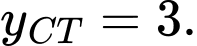
B, 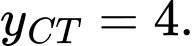
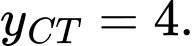
C, 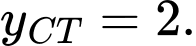
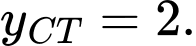
D, 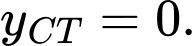
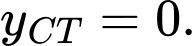
Chọn đáp án D.
Từ đồ thị hình vẽ ta có: Trên đoạn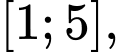 giá trị cực tiểu của hàm số
giá trị cực tiểu của hàm số 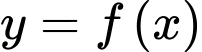 là
là 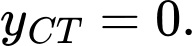 Đáp án: D
Đáp án: D
Từ đồ thị hình vẽ ta có: Trên đoạn
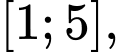 giá trị cực tiểu của hàm số
giá trị cực tiểu của hàm số 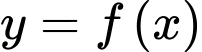 là
là 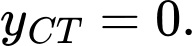 Đáp án: D
Đáp án: D
Câu 6 [694281]: Trong không gian 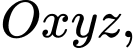 điểm
điểm 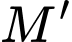 đối xứng với điểm
đối xứng với điểm 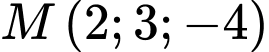 qua gốc toạ độ
qua gốc toạ độ  có toạ độ là
có toạ độ là
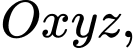 điểm
điểm 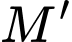 đối xứng với điểm
đối xứng với điểm 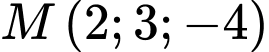 qua gốc toạ độ
qua gốc toạ độ  có toạ độ là
có toạ độ là A, 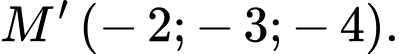
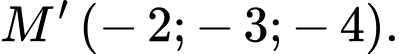
B, 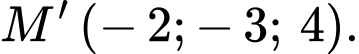
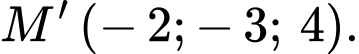
C, 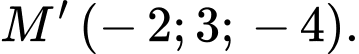
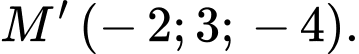
D, 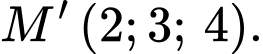
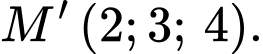
Chọn đáp án B.
Trong không gian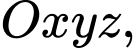 điểm
điểm 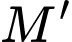 đối xứng với điểm
đối xứng với điểm 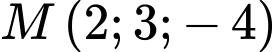 qua gốc toạ độ
qua gốc toạ độ  nên ta có
nên ta có  là trung điểm của
là trung điểm của 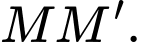
Nên ta có: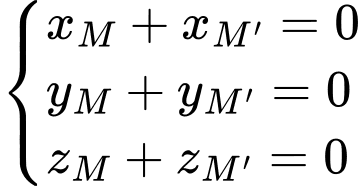
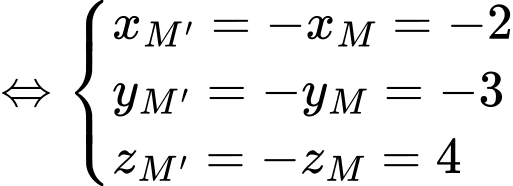
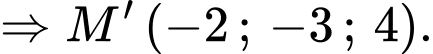 Đáp án: B
Đáp án: B
Trong không gian
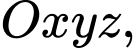 điểm
điểm 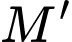 đối xứng với điểm
đối xứng với điểm 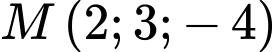 qua gốc toạ độ
qua gốc toạ độ  nên ta có
nên ta có  là trung điểm của
là trung điểm của 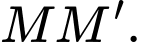
Nên ta có:
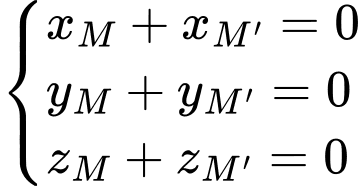
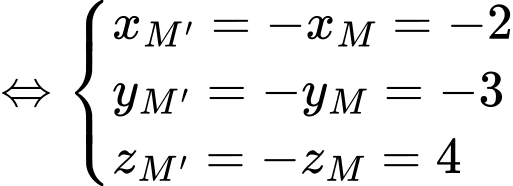
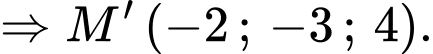 Đáp án: B
Đáp án: B
Câu 7 [257671]: Hàm số nào dưới đây có tập xác định là  ?
?
 ?
? A, 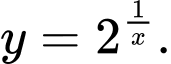
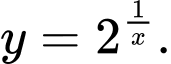
B, 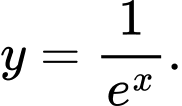
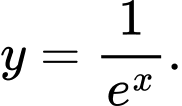
C, 

D, 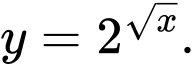
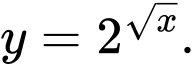
Chọn đáp án B.
Với mọi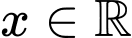 ta có
ta có 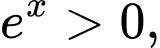 suy ra tập xác định của hàm số
suy ra tập xác định của hàm số 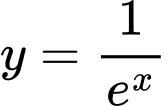 là
là 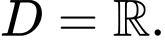 Đáp án: B
Đáp án: B
Với mọi
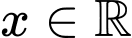 ta có
ta có 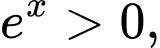 suy ra tập xác định của hàm số
suy ra tập xác định của hàm số 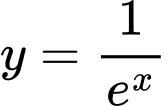 là
là 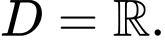 Đáp án: B
Đáp án: B
Câu 8 [694282]: Cho hàm số 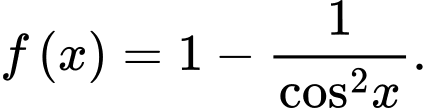 Khẳng định nào sau đây đúng?
Khẳng định nào sau đây đúng?
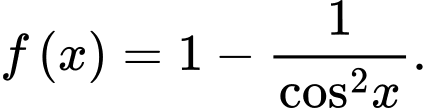 Khẳng định nào sau đây đúng?
Khẳng định nào sau đây đúng? A, 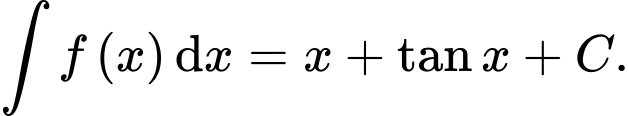
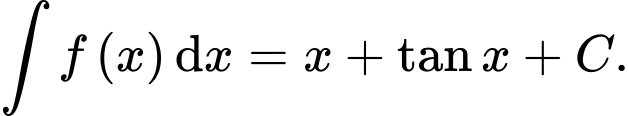
B, 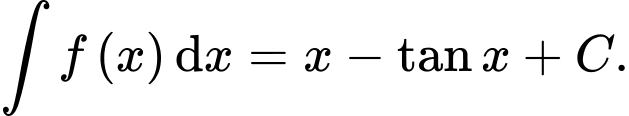
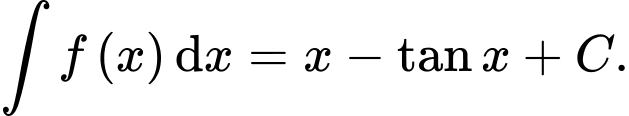
C, 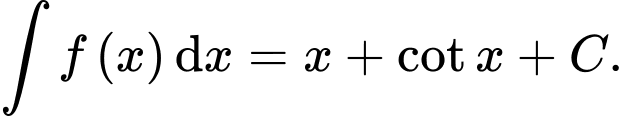
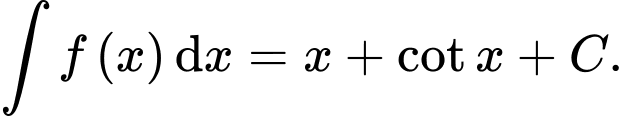
D, 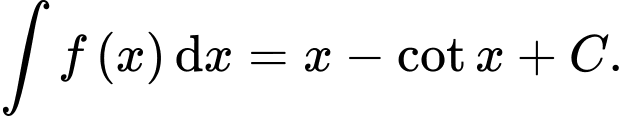
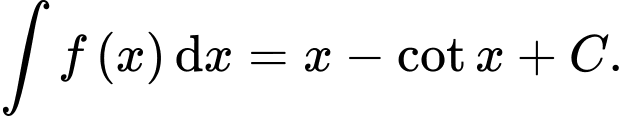
Chọn đáp án B.
Ta có: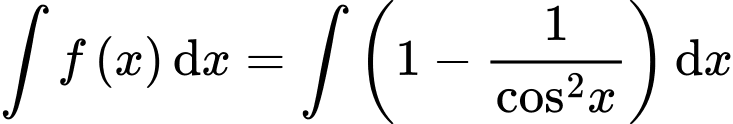
 Đáp án: B
Đáp án: B
Ta có:
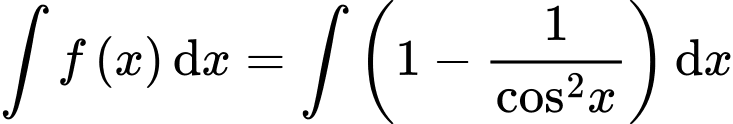
 Đáp án: B
Đáp án: B
Câu 9 [694283]: Thống kê số phút học bài ở nhà buổi tối của 100 học sinh ta có bảng phân bố tần số ghép nhóm như sau:

Số học sinh học bài ở nhà buổi tối ít hơn 120 phút là

Số học sinh học bài ở nhà buổi tối ít hơn 120 phút là
A, 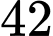 học sinh.
học sinh.
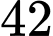 học sinh.
học sinh.B, 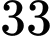 học sinh.
học sinh.
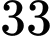 học sinh.
học sinh.C, 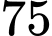 học sinh.
học sinh.
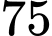 học sinh.
học sinh.D, 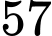 học sinh.
học sinh.
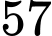 học sinh.
học sinh.
Chọn đáp án C.
Số học sinh học bài ở nhà buổi tối ít hơn 120 phút là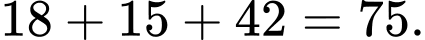 Đáp án: C
Đáp án: C
Số học sinh học bài ở nhà buổi tối ít hơn 120 phút là
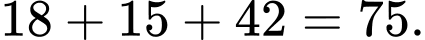 Đáp án: C
Đáp án: C
Câu 10 [694284]: Trong không gian 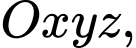 đường thẳng đi qua hai điểm
đường thẳng đi qua hai điểm 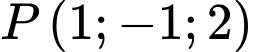 và
và 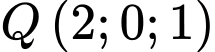 có phương trình tham số là
có phương trình tham số là
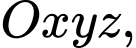 đường thẳng đi qua hai điểm
đường thẳng đi qua hai điểm 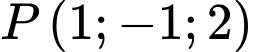 và
và 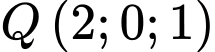 có phương trình tham số là
có phương trình tham số là A, 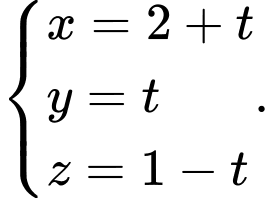
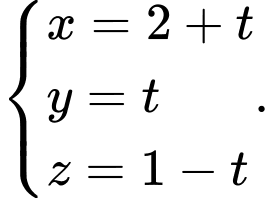
B, 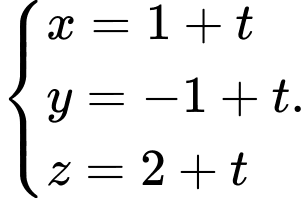
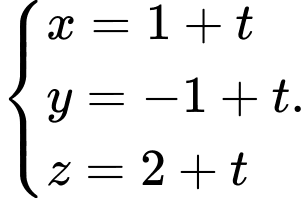
C, 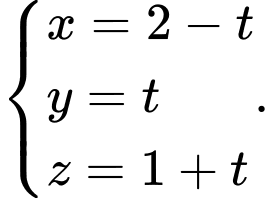
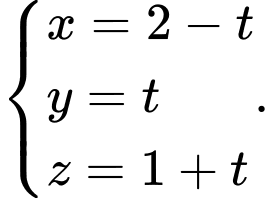
D, 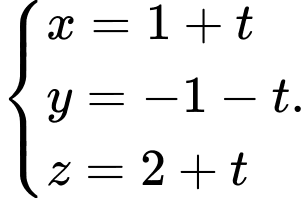
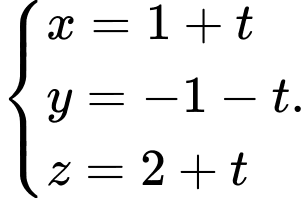
Chọn đáp án A.
Ta có: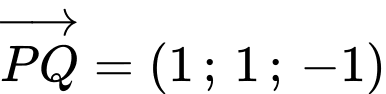
Vậy phương trình đường thẳng đi qua điểm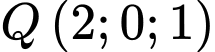 nhận vecto
nhận vecto 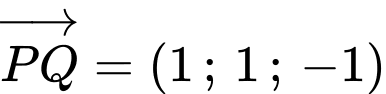 làm vecto chi phương ta có:
làm vecto chi phương ta có:
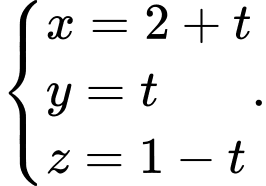 Đáp án: A
Đáp án: A
Ta có:
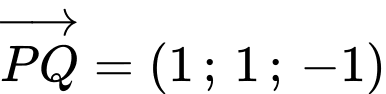
Vậy phương trình đường thẳng đi qua điểm
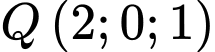 nhận vecto
nhận vecto 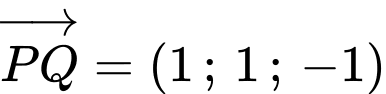 làm vecto chi phương ta có:
làm vecto chi phương ta có:
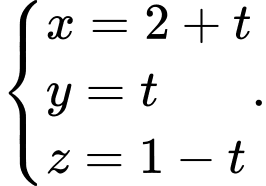 Đáp án: A
Đáp án: A
Câu 11 [257825]: Cho 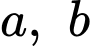 là các số thực dương thỏa mãn
là các số thực dương thỏa mãn 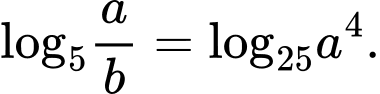 Khẳng định nào sau đây đúng?
Khẳng định nào sau đây đúng?
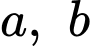 là các số thực dương thỏa mãn
là các số thực dương thỏa mãn 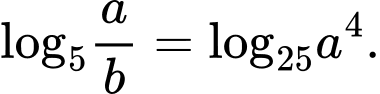 Khẳng định nào sau đây đúng?
Khẳng định nào sau đây đúng? A, 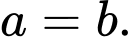
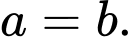
B, 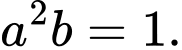
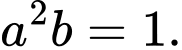
C, 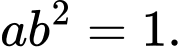
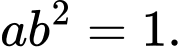
D, 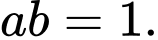
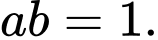
Chọn đáp án D.
Ta có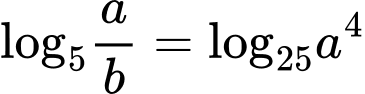
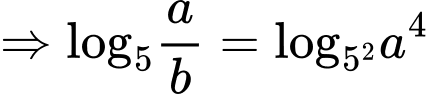
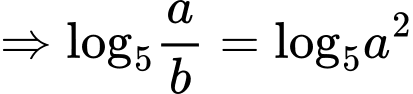
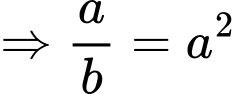
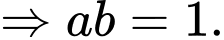 Đáp án: D
Đáp án: D
Ta có
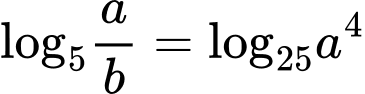
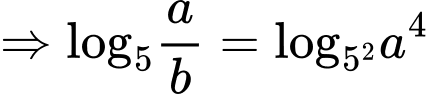
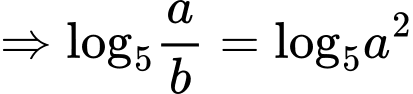
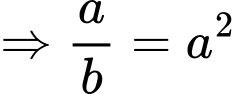
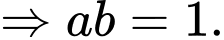 Đáp án: D
Đáp án: D
Câu 12 [694285]: Cho hình chóp tứ giác đều 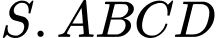 có tất cả các cạnh bằng
có tất cả các cạnh bằng 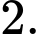 Gọi
Gọi 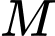 là trung điểm
là trung điểm 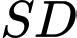 (minh hoạ như hình bên). Giá trị của
(minh hoạ như hình bên). Giá trị của 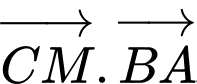 bằng
bằng
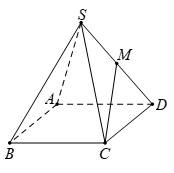
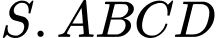 có tất cả các cạnh bằng
có tất cả các cạnh bằng 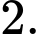 Gọi
Gọi 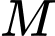 là trung điểm
là trung điểm 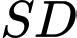 (minh hoạ như hình bên). Giá trị của
(minh hoạ như hình bên). Giá trị của 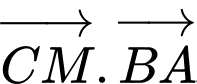 bằng
bằng
A, 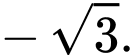
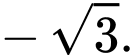
B, 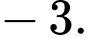
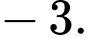
C, 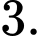
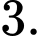
D, 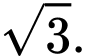
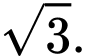
Chọn đáp án C.
Ta có: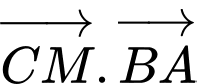
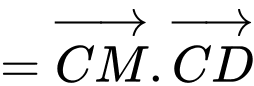
Do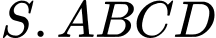 là hình chóp tứ giác đều.
là hình chóp tứ giác đều.
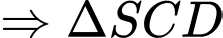 đều.
đều.
Với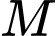 là trung điểm
là trung điểm 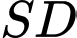
 là đường cao, đường trung tuyến, đường phân giác của
là đường cao, đường trung tuyến, đường phân giác của 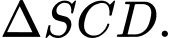
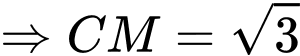
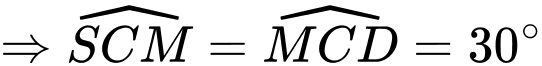
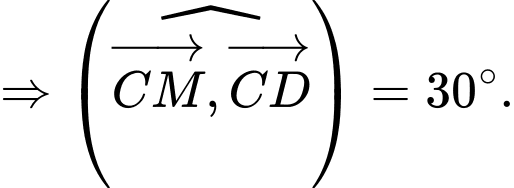
Ta có: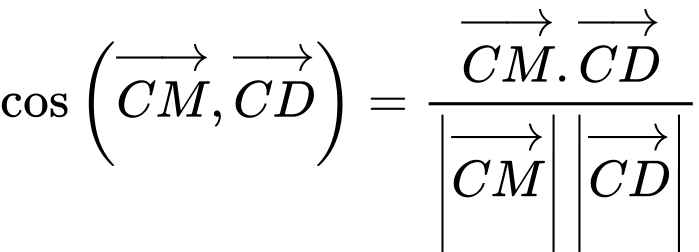
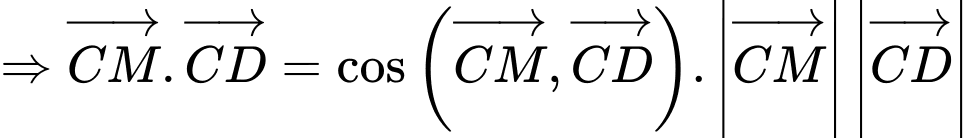
 Đáp án: C
Đáp án: C
Ta có:
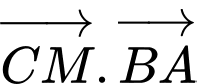
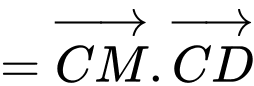
Do
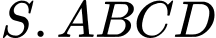 là hình chóp tứ giác đều.
là hình chóp tứ giác đều.
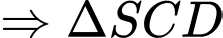 đều.
đều.
Với
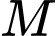 là trung điểm
là trung điểm 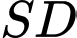
 là đường cao, đường trung tuyến, đường phân giác của
là đường cao, đường trung tuyến, đường phân giác của 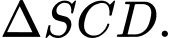
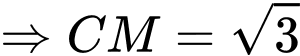
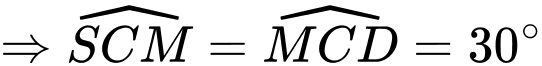
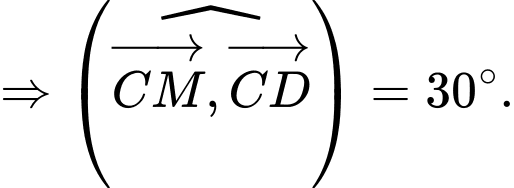
Ta có:
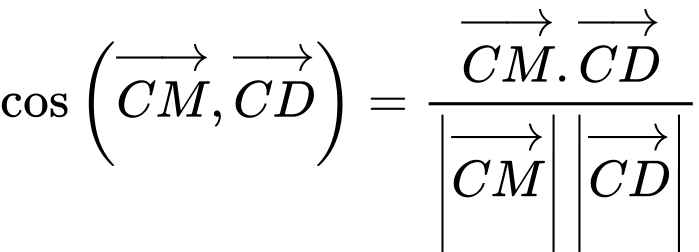
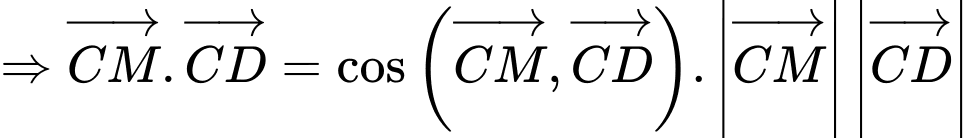
 Đáp án: C
Đáp án: C PHẦN II. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Câu 13 [694286]: Trong không gian với hệ tọa độ 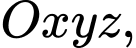 cho ba điểm
cho ba điểm 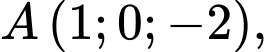
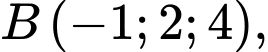
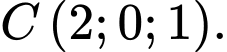 Gọi
Gọi 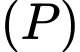 là mặt phẳng đi qua
là mặt phẳng đi qua 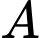 và vuông góc với
và vuông góc với 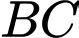
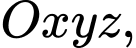 cho ba điểm
cho ba điểm 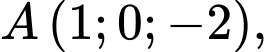
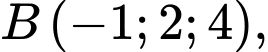
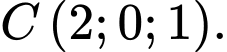 Gọi
Gọi 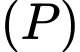 là mặt phẳng đi qua
là mặt phẳng đi qua 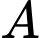 và vuông góc với
và vuông góc với 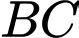
a) Đúng.
Ta có: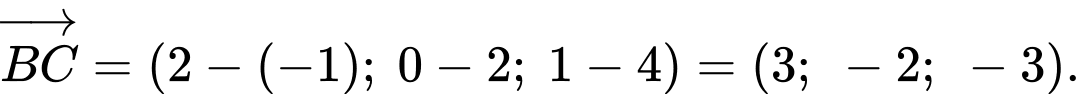
b) Sai.
Đường thẳng BC có vectơ chỉ phương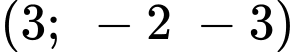 , đi qua điểm
, đi qua điểm 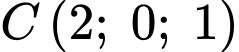 có phương trình
có phương trình
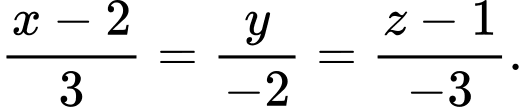
c) Đúng.
Mặt phẳng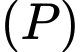 đi qua
đi qua 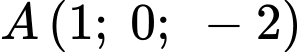 có vectơ pháp tuyến
có vectơ pháp tuyến 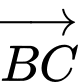 có phương trình
có phương trình
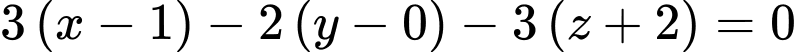

d) Sai.
Do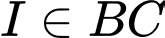 nên
nên 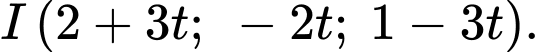
Mặt khác nên
nên 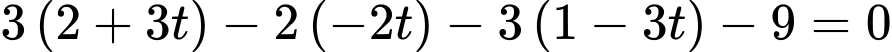
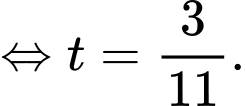
Vậy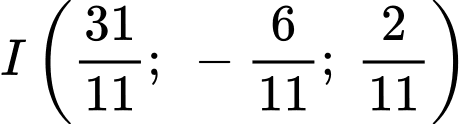
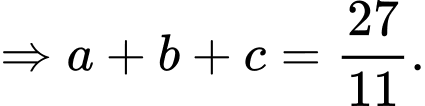
Ta có:
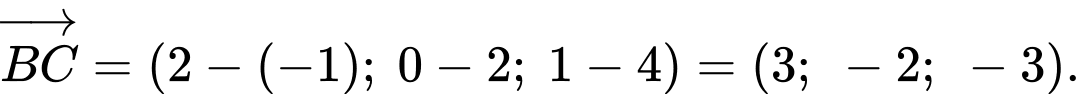
b) Sai.
Đường thẳng BC có vectơ chỉ phương
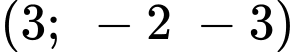 , đi qua điểm
, đi qua điểm 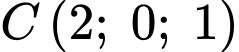 có phương trình
có phương trình
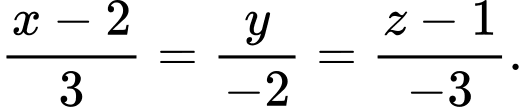
c) Đúng.
Mặt phẳng
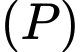 đi qua
đi qua 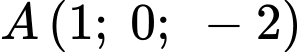 có vectơ pháp tuyến
có vectơ pháp tuyến 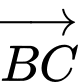 có phương trình
có phương trình
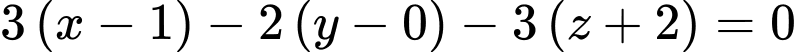

d) Sai.
Do
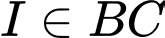 nên
nên 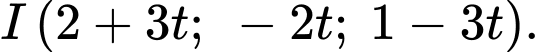
Mặt khác
 nên
nên 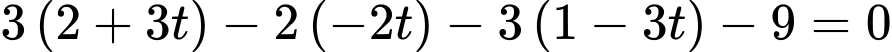
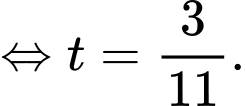
Vậy
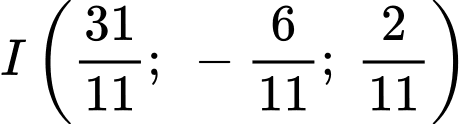
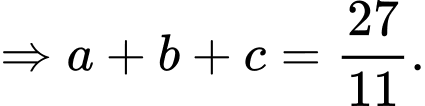
Câu 14 [694287]: Hộp I có 5 bi trắng và 5 bi đen. Hộp II có 6 bi trắng và 4 bi đen. Bỏ hai viên bi từ hộp I sang hộp II. Sau đó lấy ra 1 viên bi. Sau đó lấy ra ngẫu nhiên 1 viên bi từ hộp II.
Gọi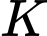 là biến cố: “lấy bi ra từ hộp II của hộp I”.
là biến cố: “lấy bi ra từ hộp II của hộp I”.
Gọi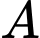 là biến cố: “lấy được bi trắng”.
là biến cố: “lấy được bi trắng”.
Gọi
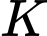 là biến cố: “lấy bi ra từ hộp II của hộp I”.
là biến cố: “lấy bi ra từ hộp II của hộp I”.Gọi
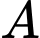 là biến cố: “lấy được bi trắng”.
là biến cố: “lấy được bi trắng”.
a) Đúng.
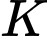 là biến cố “Lấy bi ra từ hộp II là của hộp I”.
là biến cố “Lấy bi ra từ hộp II là của hộp I”.
Suy ra xác suất để bi được lấy ra từ hộp II là của hộp I là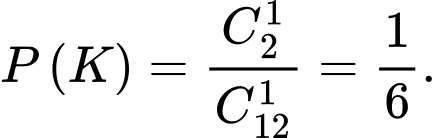
b) Sai.
 là biến cố “Lấy bi ra từ hộp II là của hộp II.
là biến cố “Lấy bi ra từ hộp II là của hộp II.
Suy ra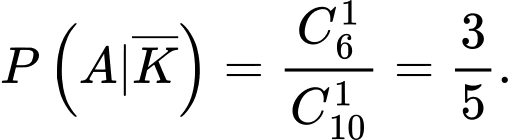
c) Sai.
Ta có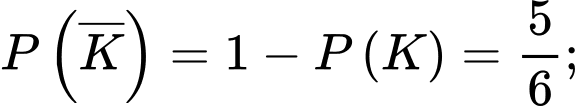
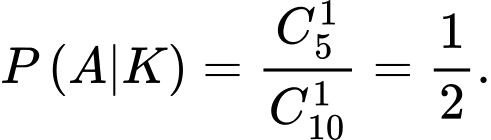
Từ đó, ta có sơ đồ cây sau:
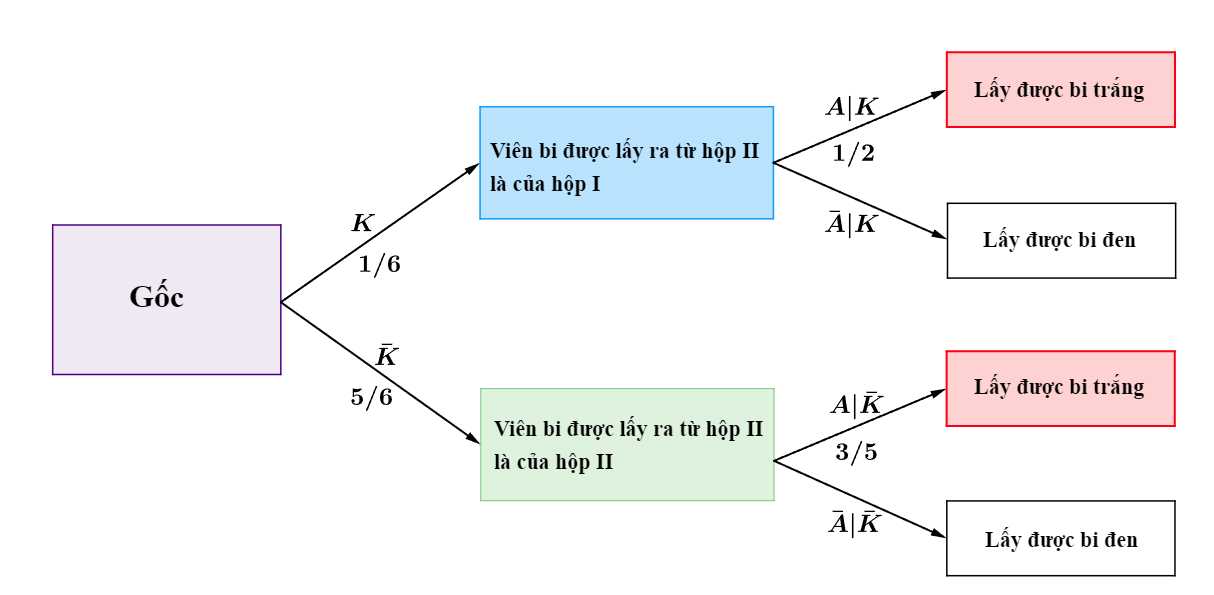
Áp dụng công thức xác suất toàn phần, ta có
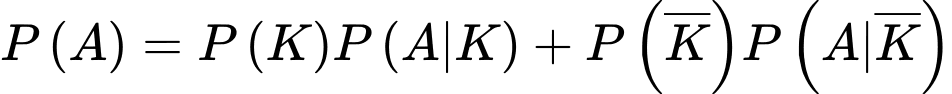
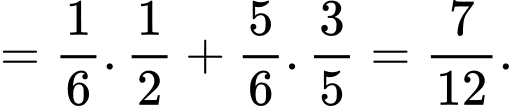
d) Đúng.
Áp dụng công thức Bayes, ta có xác suất để lấy được bi trắng của hộp I là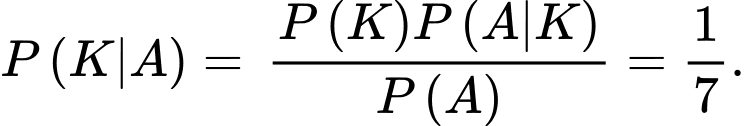
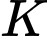 là biến cố “Lấy bi ra từ hộp II là của hộp I”.
là biến cố “Lấy bi ra từ hộp II là của hộp I”.Suy ra xác suất để bi được lấy ra từ hộp II là của hộp I là
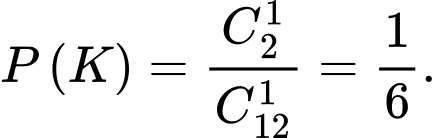
b) Sai.
 là biến cố “Lấy bi ra từ hộp II là của hộp II.
là biến cố “Lấy bi ra từ hộp II là của hộp II.Suy ra
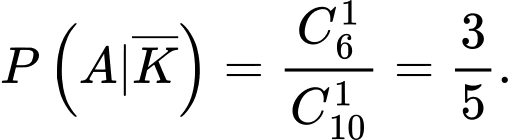
c) Sai.
Ta có
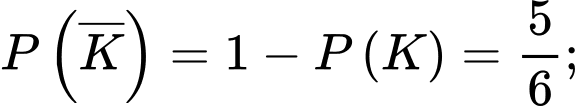
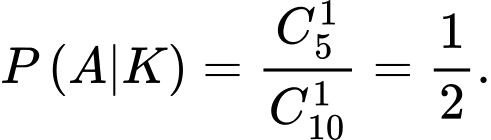
Từ đó, ta có sơ đồ cây sau:

Áp dụng công thức xác suất toàn phần, ta có
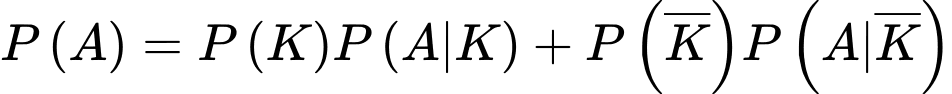
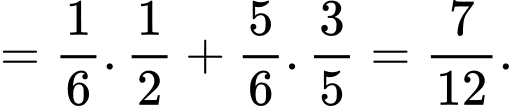
d) Đúng.
Áp dụng công thức Bayes, ta có xác suất để lấy được bi trắng của hộp I là
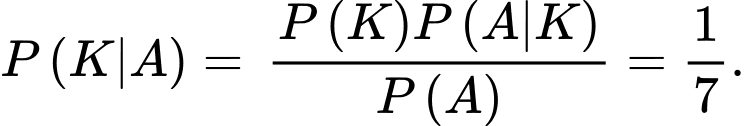
Câu 15 [700898]: Một xe ô tô đang chạy trên một đoạn đường với tốc độ 72 km/h thì người lái xe bất ngờ phát hiện chướng ngại vật trên đường cách đó 80 m. Người lái xe phản ứng một giây sau đó bằng cách đạp phanh khẩn cấp. Kể từ thời điểm này, ô tô chuyển động chậm dần đều với tốc độ 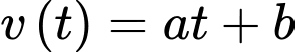 (m/s), trong đó
(m/s), trong đó 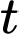 là thời gian tính bằng giây kể từ lúc đạp phanh. Rất may mắn xe đã dừng hẳn cách chướng ngại vật một khoảng 40 mét nên không xảy ra va chạm.
là thời gian tính bằng giây kể từ lúc đạp phanh. Rất may mắn xe đã dừng hẳn cách chướng ngại vật một khoảng 40 mét nên không xảy ra va chạm.
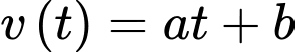 (m/s), trong đó
(m/s), trong đó 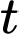 là thời gian tính bằng giây kể từ lúc đạp phanh. Rất may mắn xe đã dừng hẳn cách chướng ngại vật một khoảng 40 mét nên không xảy ra va chạm.
là thời gian tính bằng giây kể từ lúc đạp phanh. Rất may mắn xe đã dừng hẳn cách chướng ngại vật một khoảng 40 mét nên không xảy ra va chạm.
a) Sai.


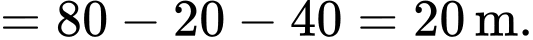
b) Đúng.
Đổi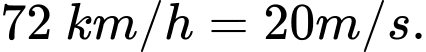
Ta có: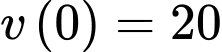
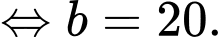
c) Sai.
Xe dừng hẳn khi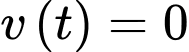 hay
hay 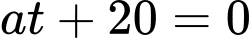
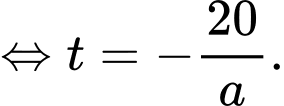
Ta có: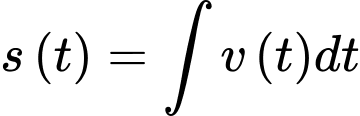
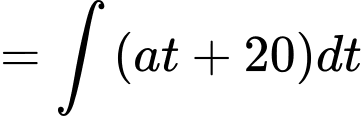
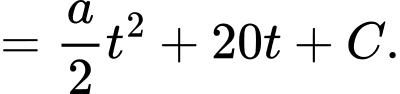
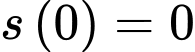 nên
nên 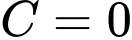
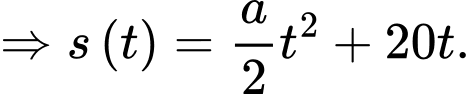
Quãng đường xe đi được kể từ lúc đạp phanh đến khi dừng hẳn là:
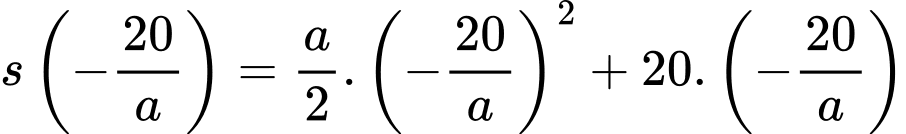
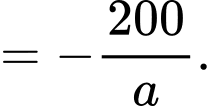
Quãng đường xe ô tô đã di chuyển kể từ khi đạp phanh đến khi dừng hẳn là 40 mét nên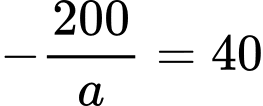 hay
hay 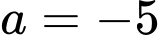
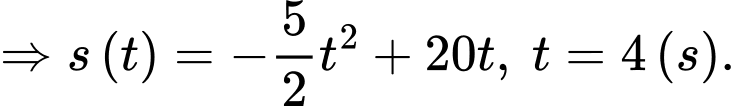
d) Sai.
Vận tốc trung bình của ô tô từ lúc phát hiện chướng ngại vật đến khi dừng hẳn là
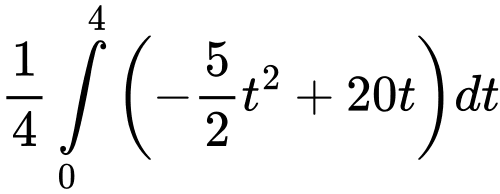
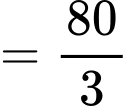
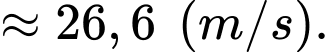


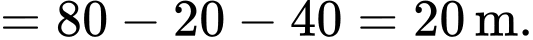
b) Đúng.
Đổi
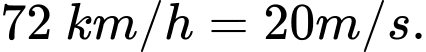
Ta có:
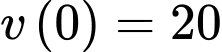
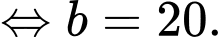
c) Sai.
Xe dừng hẳn khi
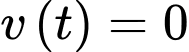 hay
hay 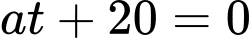
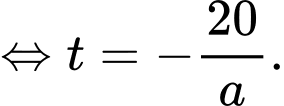
Ta có:
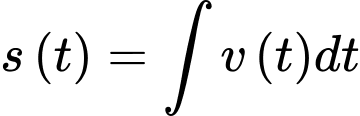
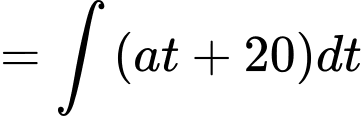
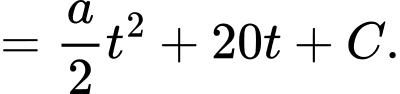
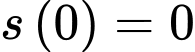 nên
nên 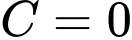
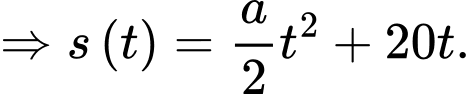
Quãng đường xe đi được kể từ lúc đạp phanh đến khi dừng hẳn là:
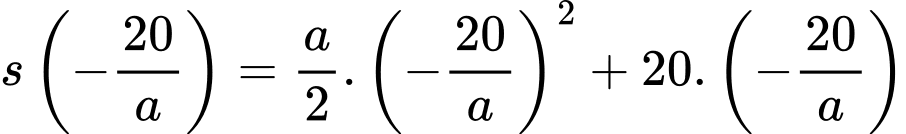
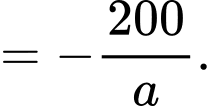
Quãng đường xe ô tô đã di chuyển kể từ khi đạp phanh đến khi dừng hẳn là 40 mét nên
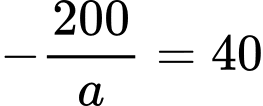 hay
hay 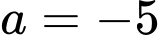
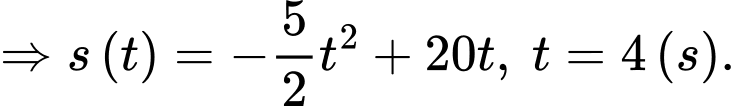
d) Sai.
Vận tốc trung bình của ô tô từ lúc phát hiện chướng ngại vật đến khi dừng hẳn là
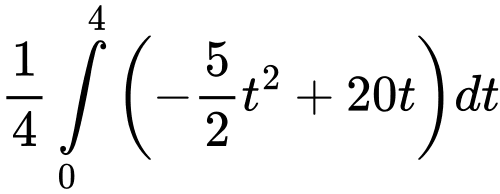
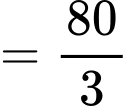
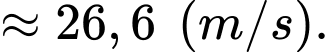
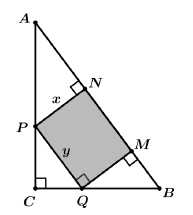
Câu 16 [694289]: Cho hình chữ nhật 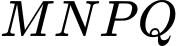 có hai cạnh là
có hai cạnh là 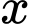 và
và 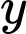 nội tiếp tam giác
nội tiếp tam giác 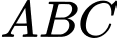 vuông tại
vuông tại  Biết tam giác
Biết tam giác 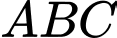 có độ dài các cạnh góc vuông là
có độ dài các cạnh góc vuông là 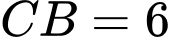 và
và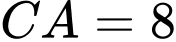 như hình vẽ:
như hình vẽ:
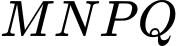 có hai cạnh là
có hai cạnh là 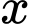 và
và 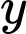 nội tiếp tam giác
nội tiếp tam giác 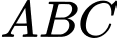 vuông tại
vuông tại  Biết tam giác
Biết tam giác 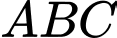 có độ dài các cạnh góc vuông là
có độ dài các cạnh góc vuông là 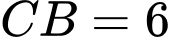 và
và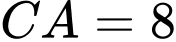 như hình vẽ:
như hình vẽ:
a) Đúng.
Độ dài cạnh huyền của tam giác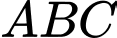 là
là
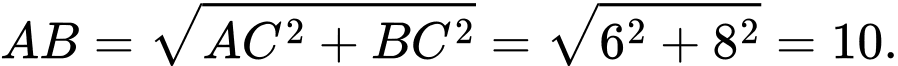
b) Sai.
Xét tam giác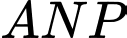 ta có:
ta có: 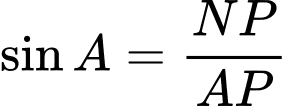
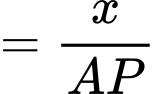
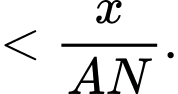
Xét tam giác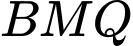 ta có:
ta có: 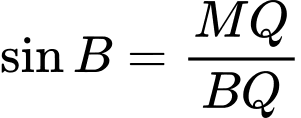
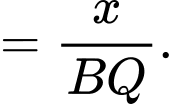
c) Đúng.
Ta có:
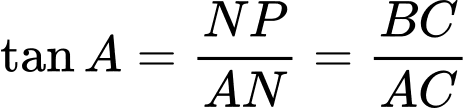
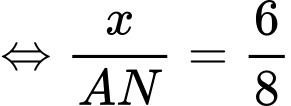
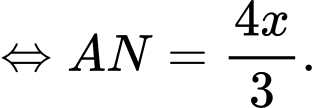
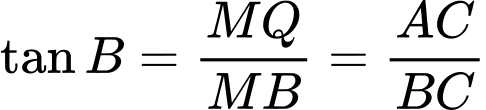
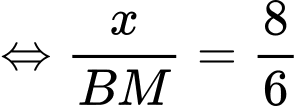
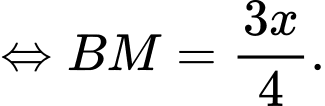
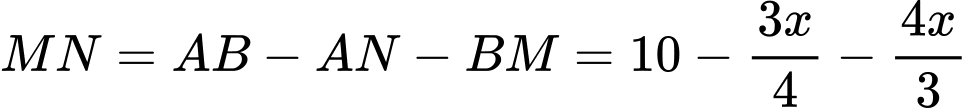
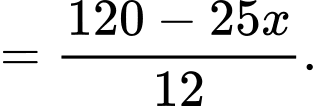
Diện tích hình chữ nhật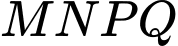 là:
là:

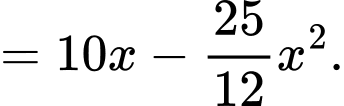
d) Sai.
Ta có: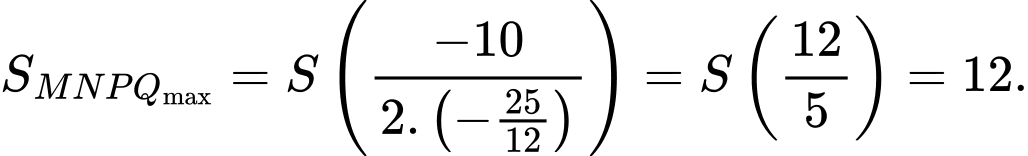
Khi đó, dện tích tam giác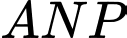 là
là
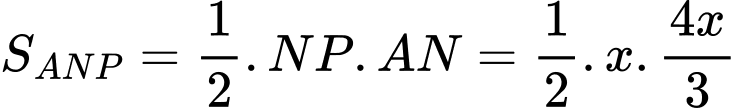
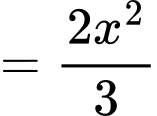
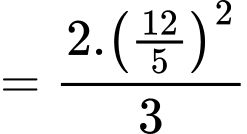
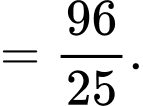
Độ dài cạnh huyền của tam giác
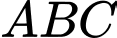 là
là 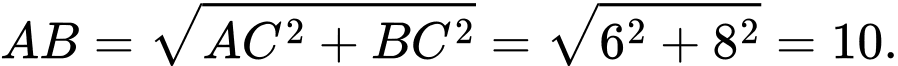
b) Sai.
Xét tam giác
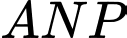 ta có:
ta có: 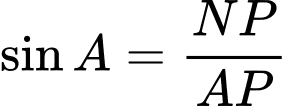
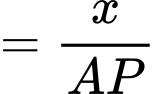
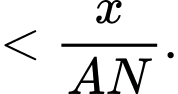
Xét tam giác
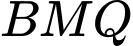 ta có:
ta có: 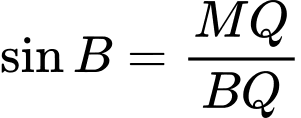
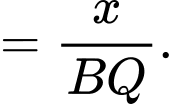
c) Đúng.
Ta có:
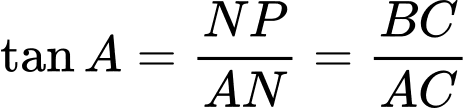
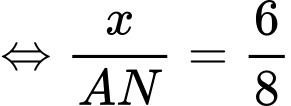
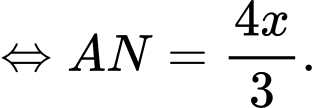
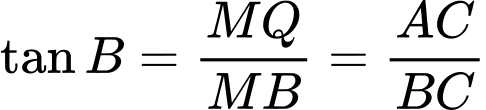
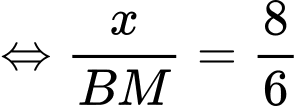
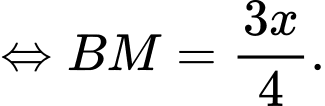
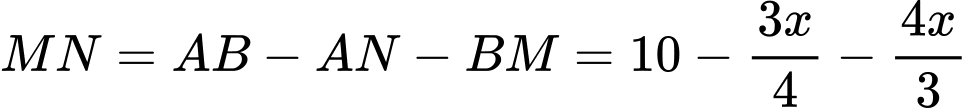
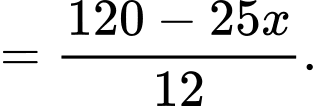
Diện tích hình chữ nhật
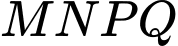 là:
là: 
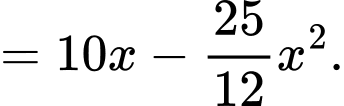
d) Sai.
Ta có:
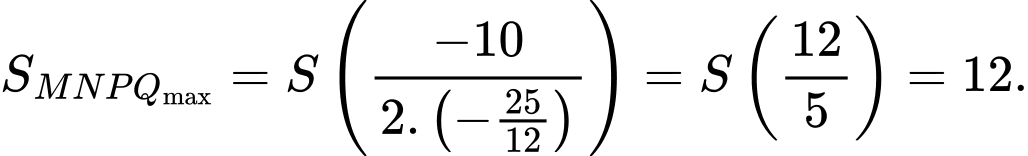
Khi đó, dện tích tam giác
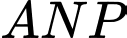 là
là 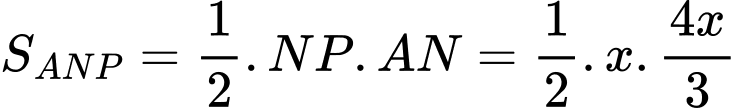
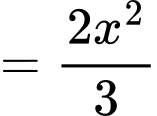
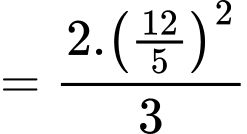
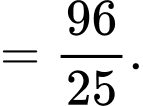
PHẦN III. Thí sinh trả lời từ câu 1 đến câu 6.
Câu 17 [694290]: Cho hình chóp 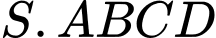 có đáy là hình vuông,
có đáy là hình vuông, 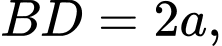 cạnh bên
cạnh bên 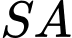 vuông góc với mặt phẳng đáy và
vuông góc với mặt phẳng đáy và 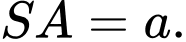 Số đo của góc nhị diện
Số đo của góc nhị diện 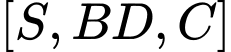 bằng bao nhiêu độ?
bằng bao nhiêu độ?
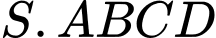 có đáy là hình vuông,
có đáy là hình vuông, 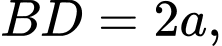 cạnh bên
cạnh bên 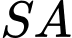 vuông góc với mặt phẳng đáy và
vuông góc với mặt phẳng đáy và 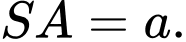 Số đo của góc nhị diện
Số đo của góc nhị diện 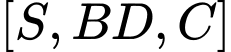 bằng bao nhiêu độ?
bằng bao nhiêu độ?
Điền đáp án: 
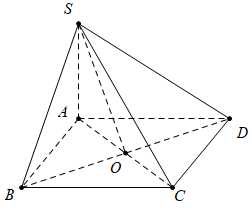
Gọi là giao điểm của 2 đường chéo hình vuông
là giao điểm của 2 đường chéo hình vuông 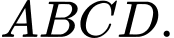 Khi đó:
Khi đó: 
Ta có:
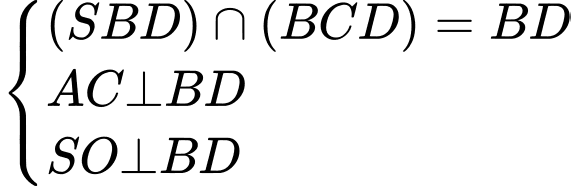
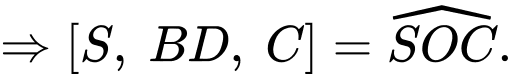
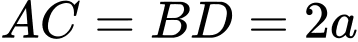
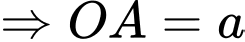
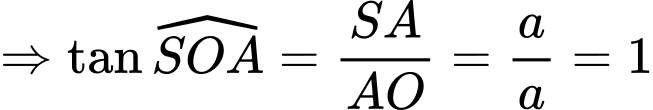
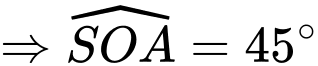
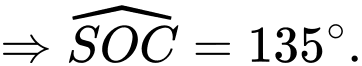
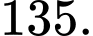

Gọi
 là giao điểm của 2 đường chéo hình vuông
là giao điểm của 2 đường chéo hình vuông 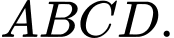 Khi đó:
Khi đó: 
Ta có:
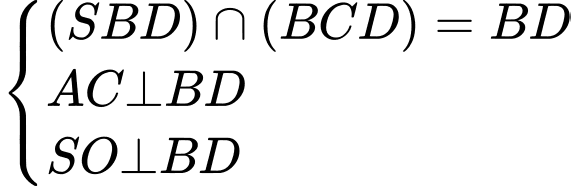
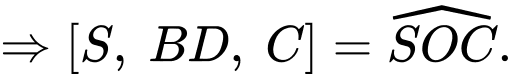
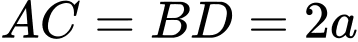
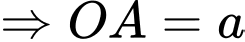
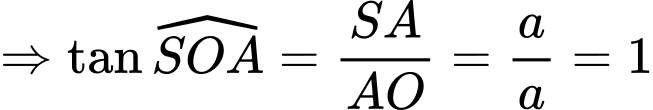
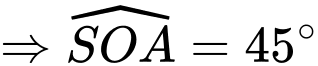
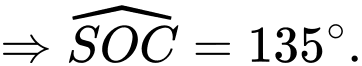
Câu 18 [695244]: Tổng số điểm vòng bảng của 4 đội trong một giải đấu bóng đá bằng 16. Biết rằng, mỗi đội thi đấu vòng tròn 1 lượt, vậy có bao nhiêu trận hòa trong vòng bảng? (Hai đội bất kỳ sẽ phải gặp nhau 1 lần trong vòng bảng và cách tính điểm như sau: đội thắng được 3 điểm, đội thua được 0 điểm, hoà thì mỗi đội được 1 điểm).
Điền đáp án: 2.
Số trận đấu trong vòng bảng là: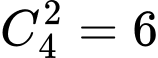 (trận).
(trận).
Nếu cả 6 trận này đều có phân thắng, thua thì tổng số điểm của cả 4 đội sẽ là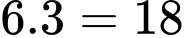 (điểm).
(điểm).
Cứ mỗi trận hòa thì tổng số điểm trên sẽ bị giảm đi là (điểm).
(điểm).
Số điểm bị bớt đi là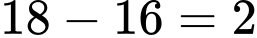 (điểm).
(điểm).
Vậy số trận hòa là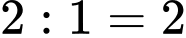 (trận).
(trận).
Số trận đấu trong vòng bảng là:
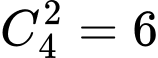 (trận).
(trận).
Nếu cả 6 trận này đều có phân thắng, thua thì tổng số điểm của cả 4 đội sẽ là
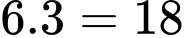 (điểm).
(điểm). Cứ mỗi trận hòa thì tổng số điểm trên sẽ bị giảm đi là
 (điểm).
(điểm).
Số điểm bị bớt đi là
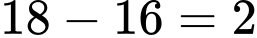 (điểm).
(điểm).
Vậy số trận hòa là
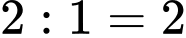 (trận).
(trận).
Câu 19 [693132]: Một người đi săn, xác suất người thợ săn này bắn trúng thú trong mỗi lần bắn tỉ lệ nghịch với khoảng cách bắn. Trong một lần đi săn, anh ta bắn lần đầu ở khoảng cách  với xác suất trúng thú là 50%. Nếu bị trượt, anh ta sẽ bắn viên thứ hai ở khoảng cách
với xác suất trúng thú là 50%. Nếu bị trượt, anh ta sẽ bắn viên thứ hai ở khoảng cách 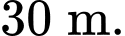 Nếu lại trượt, anh ta sẽ bắn viên thứ ba ở khoảng cách
Nếu lại trượt, anh ta sẽ bắn viên thứ ba ở khoảng cách 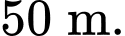 Người thợ săn sẽ dừng bắn nếu bắn trúng thú và chỉ bắn tối đa ba lần. Biết rằng anh ta đã bắn trúng thú, xác suất người thợ săn bắn trúng ở lần bắn thứ ba là bao nhiêu phần trăm (làm tròn kết quả đến hàng phần trăm).
Người thợ săn sẽ dừng bắn nếu bắn trúng thú và chỉ bắn tối đa ba lần. Biết rằng anh ta đã bắn trúng thú, xác suất người thợ săn bắn trúng ở lần bắn thứ ba là bao nhiêu phần trăm (làm tròn kết quả đến hàng phần trăm).
 với xác suất trúng thú là 50%. Nếu bị trượt, anh ta sẽ bắn viên thứ hai ở khoảng cách
với xác suất trúng thú là 50%. Nếu bị trượt, anh ta sẽ bắn viên thứ hai ở khoảng cách 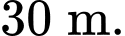 Nếu lại trượt, anh ta sẽ bắn viên thứ ba ở khoảng cách
Nếu lại trượt, anh ta sẽ bắn viên thứ ba ở khoảng cách 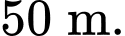 Người thợ săn sẽ dừng bắn nếu bắn trúng thú và chỉ bắn tối đa ba lần. Biết rằng anh ta đã bắn trúng thú, xác suất người thợ săn bắn trúng ở lần bắn thứ ba là bao nhiêu phần trăm (làm tròn kết quả đến hàng phần trăm).
Người thợ săn sẽ dừng bắn nếu bắn trúng thú và chỉ bắn tối đa ba lần. Biết rằng anh ta đã bắn trúng thú, xác suất người thợ săn bắn trúng ở lần bắn thứ ba là bao nhiêu phần trăm (làm tròn kết quả đến hàng phần trăm).
Điền đáp án: 9,09.
Gọi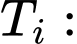 “Thợ săn bắn trúng ở lần thứ
“Thợ săn bắn trúng ở lần thứ 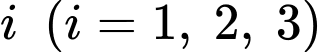 ”.
”.
(Vì khi bắn trúng thợ săn sẽ dừng bắn nên 3 biến cố này không độc lập)
Vì xác suất bắn trúng trong mỗi lần bắn tỉ lệ nghịch với khoảng cách bắn nên ta có tích 2 giá trị tương ứng của chúng luôn không đổi (tính chất của 2 đại lượng tỉ lệ nghịch). Giả sử hằng số đó bằng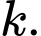
Suy ra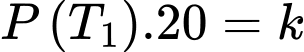
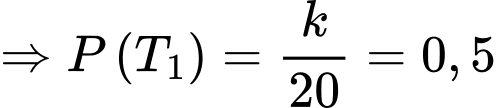
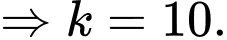
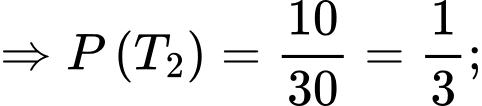
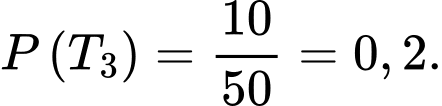
Suy ra xác suất người thợ săn bắn trượt ở lần 1, 2, 3 lần lượt là 0,5;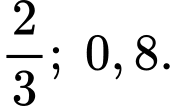
Gọi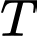 là biến cố “Thợ săn bắn trúng”
là biến cố “Thợ săn bắn trúng”
Ta có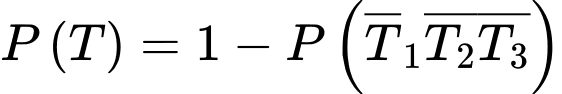
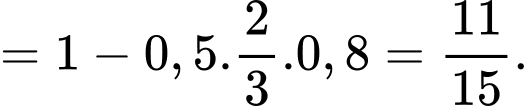
Gọi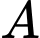 là biến cố: “Cung thủ bắn trúng ở lần thứ ba”
là biến cố: “Cung thủ bắn trúng ở lần thứ ba”
Khi đó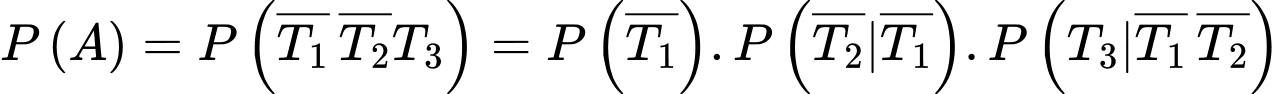
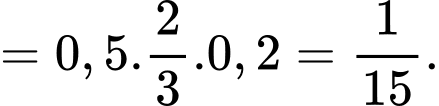
Ta có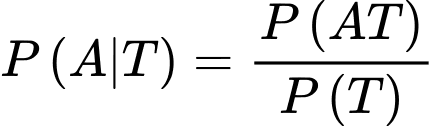
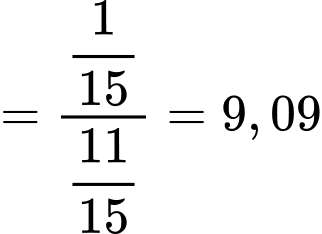 (Vì
(Vì  nên
nên 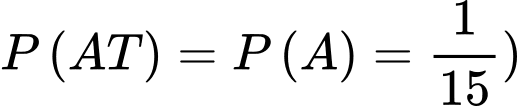
Gọi
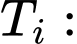 “Thợ săn bắn trúng ở lần thứ
“Thợ săn bắn trúng ở lần thứ 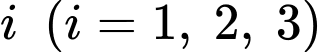 ”.
”.(Vì khi bắn trúng thợ săn sẽ dừng bắn nên 3 biến cố này không độc lập)
Vì xác suất bắn trúng trong mỗi lần bắn tỉ lệ nghịch với khoảng cách bắn nên ta có tích 2 giá trị tương ứng của chúng luôn không đổi (tính chất của 2 đại lượng tỉ lệ nghịch). Giả sử hằng số đó bằng
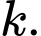
Suy ra
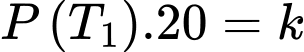
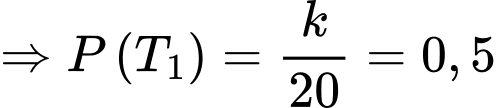
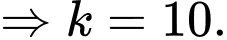
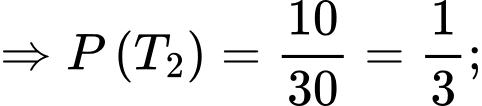
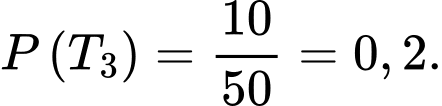
Suy ra xác suất người thợ săn bắn trượt ở lần 1, 2, 3 lần lượt là 0,5;
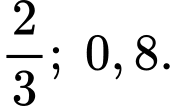
Gọi
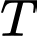 là biến cố “Thợ săn bắn trúng”
là biến cố “Thợ săn bắn trúng”Ta có
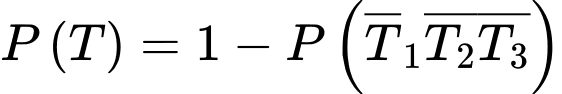
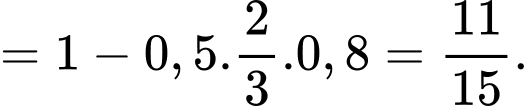
Gọi
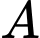 là biến cố: “Cung thủ bắn trúng ở lần thứ ba”
là biến cố: “Cung thủ bắn trúng ở lần thứ ba”Khi đó
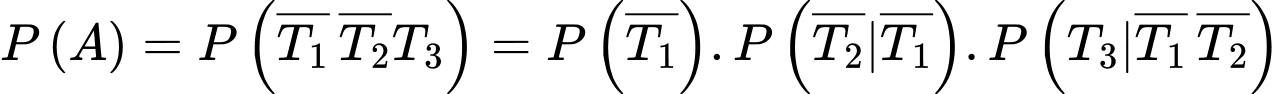
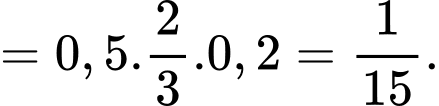
Ta có
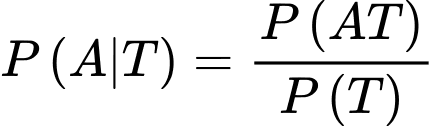
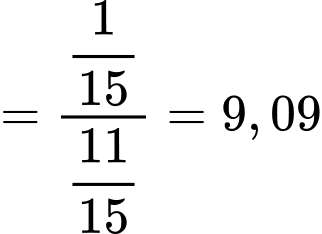 (Vì
(Vì  nên
nên 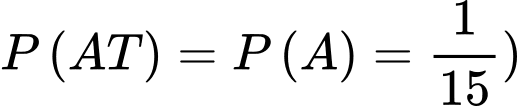
Câu 20 [694293]: Trong không gian cho mặt cầu 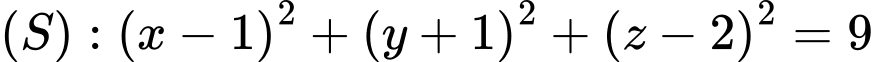 và điểm
và điểm 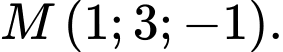 Từ điểm
Từ điểm 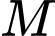 kẻ các tiếp tuyến
kẻ các tiếp tuyến 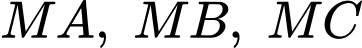 với mặt cầu
với mặt cầu 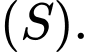 Tâm của đường tròn ngoại tiếp tam giác
Tâm của đường tròn ngoại tiếp tam giác 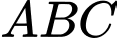 là điểm
là điểm 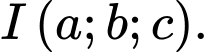 Giá trị của
Giá trị của 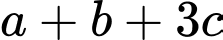 bằng bao nhiêu?
bằng bao nhiêu?
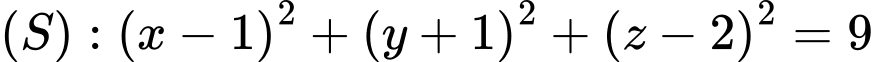 và điểm
và điểm 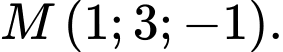 Từ điểm
Từ điểm 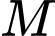 kẻ các tiếp tuyến
kẻ các tiếp tuyến 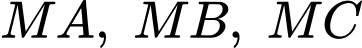 với mặt cầu
với mặt cầu 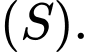 Tâm của đường tròn ngoại tiếp tam giác
Tâm của đường tròn ngoại tiếp tam giác 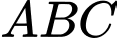 là điểm
là điểm 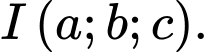 Giá trị của
Giá trị của 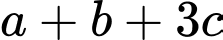 bằng bao nhiêu?
bằng bao nhiêu?
Điền đáp án: 4,2.
Mặt cầu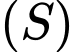 có phương trình:
có phương trình: 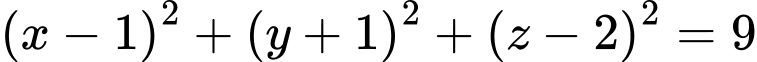 có tâm
có tâm 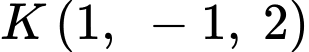 và bán kính mặt cầu là
và bán kính mặt cầu là 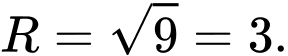
Từ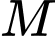 kẻ tiếp tuyến tới
kẻ tiếp tuyến tới 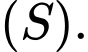
Suy ra tập hợp tiếp điểm là đường tròn tâm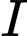 bán kính
bán kính 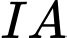
Có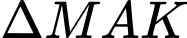 là tam giác vuông tại
là tam giác vuông tại 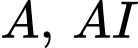 là đường cao
là đường cao
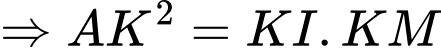
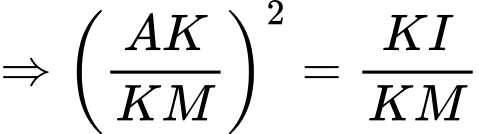
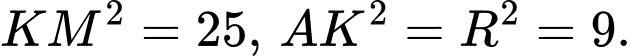
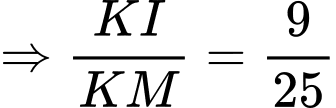
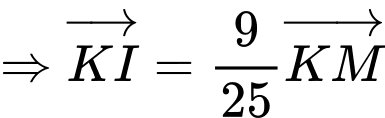
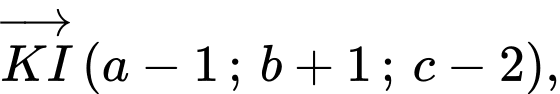
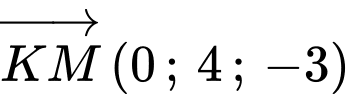
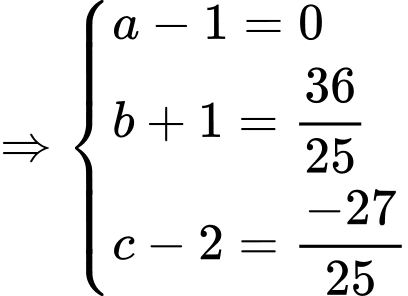
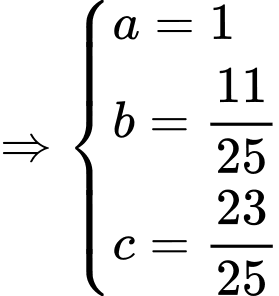
Vậy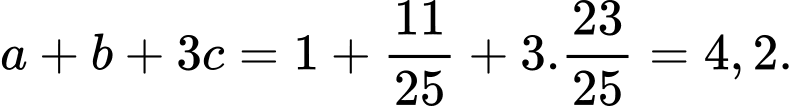
Mặt cầu
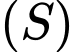 có phương trình:
có phương trình: 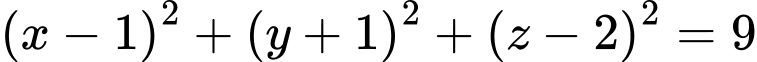 có tâm
có tâm 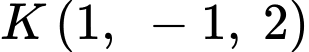 và bán kính mặt cầu là
và bán kính mặt cầu là 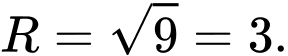
Từ
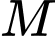 kẻ tiếp tuyến tới
kẻ tiếp tuyến tới 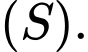
Suy ra tập hợp tiếp điểm là đường tròn tâm
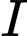 bán kính
bán kính 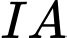
Có
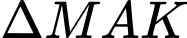 là tam giác vuông tại
là tam giác vuông tại 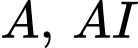 là đường cao
là đường cao
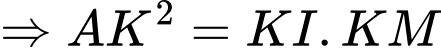
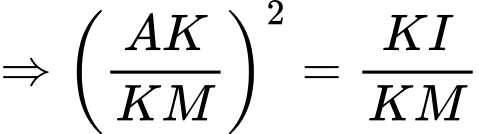
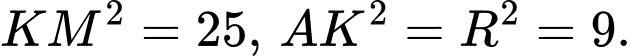
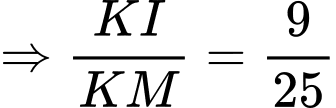
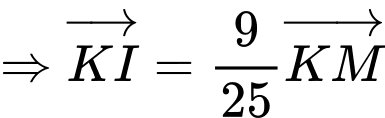
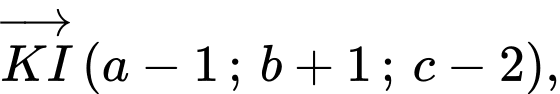
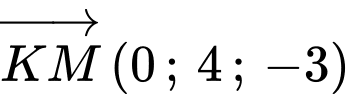
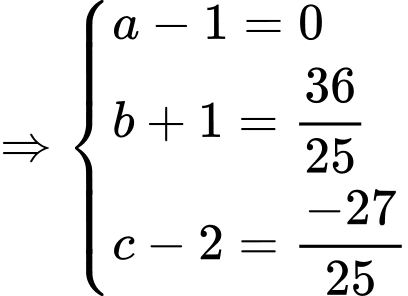
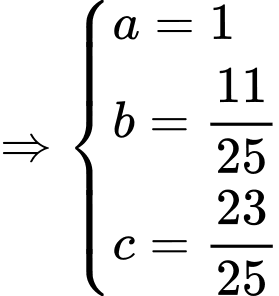
Vậy
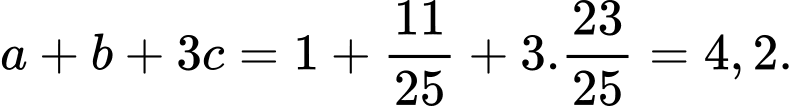
Câu 21 [694294]: Trên hệ tọa độ 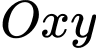 một vườn hoa có dạng parabol
một vườn hoa có dạng parabol 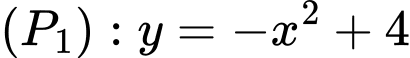 cắt trục hoành tại hai điểm
cắt trục hoành tại hai điểm 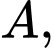
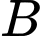 và đường thẳng
và đường thẳng 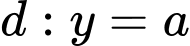
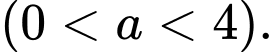 Xét parabol
Xét parabol 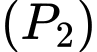 đi qua
đi qua 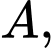
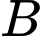 và có đỉnh thuộc đường thẳng
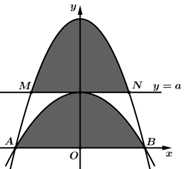
và có đỉnh thuộc đường thẳng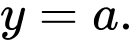 Hai phần tô đậm có diện tích bằng nhau. Biết rằng đơn vị trên các trục tọa độ là 10 mét, phần tô đậm dùng để trồng hoa với chi phí là
Hai phần tô đậm có diện tích bằng nhau. Biết rằng đơn vị trên các trục tọa độ là 10 mét, phần tô đậm dùng để trồng hoa với chi phí là  đồng mỗi mét vuông, phần còn lại dùng để trồng cỏ với chi phí là
đồng mỗi mét vuông, phần còn lại dùng để trồng cỏ với chi phí là  đồng mỗi mét vuông. Số tiền mà người ta bỏ ra để trang trí vườn hoa bằng bao nhiêu triệu đồng? Làm tròn kết quả đến hàng đơn vị.
đồng mỗi mét vuông. Số tiền mà người ta bỏ ra để trang trí vườn hoa bằng bao nhiêu triệu đồng? Làm tròn kết quả đến hàng đơn vị.
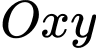 một vườn hoa có dạng parabol
một vườn hoa có dạng parabol 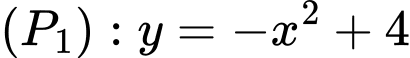 cắt trục hoành tại hai điểm
cắt trục hoành tại hai điểm 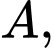
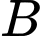 và đường thẳng
và đường thẳng 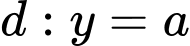
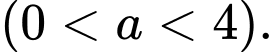 Xét parabol
Xét parabol 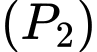 đi qua
đi qua 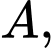
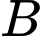 và có đỉnh thuộc đường thẳng
và có đỉnh thuộc đường thẳng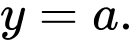 Hai phần tô đậm có diện tích bằng nhau. Biết rằng đơn vị trên các trục tọa độ là 10 mét, phần tô đậm dùng để trồng hoa với chi phí là
Hai phần tô đậm có diện tích bằng nhau. Biết rằng đơn vị trên các trục tọa độ là 10 mét, phần tô đậm dùng để trồng hoa với chi phí là  đồng mỗi mét vuông, phần còn lại dùng để trồng cỏ với chi phí là
đồng mỗi mét vuông, phần còn lại dùng để trồng cỏ với chi phí là  đồng mỗi mét vuông. Số tiền mà người ta bỏ ra để trang trí vườn hoa bằng bao nhiêu triệu đồng? Làm tròn kết quả đến hàng đơn vị.
đồng mỗi mét vuông. Số tiền mà người ta bỏ ra để trang trí vườn hoa bằng bao nhiêu triệu đồng? Làm tròn kết quả đến hàng đơn vị.
Điền đáp án: 
Gọi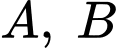 là các giao điểm của
là các giao điểm của 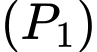 và trục hoành, ta có:
và trục hoành, ta có: 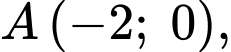
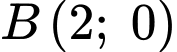
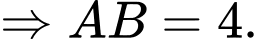
Gọi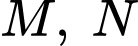 là các giao điểm của
là các giao điểm của 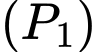 và đường thẳng
và đường thẳng 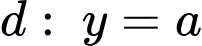
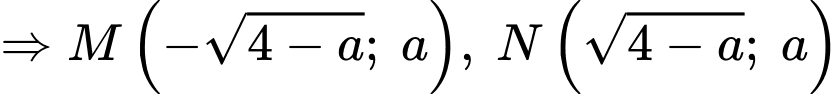
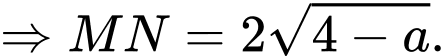
Phương trình parabol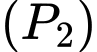 có đỉnh
có đỉnh 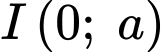 có dạng
có dạng 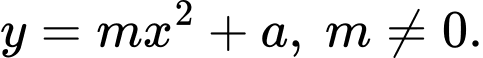
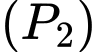 đi qua hai điểm
đi qua hai điểm 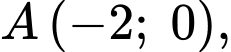
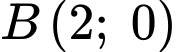 nên
nên 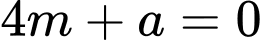
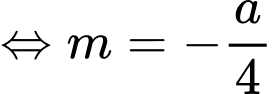
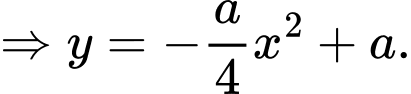
Diện tích phần tô đậm giới hạn bởi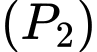 và trục hoành là:
và trục hoành là:
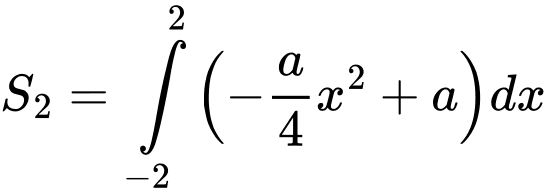
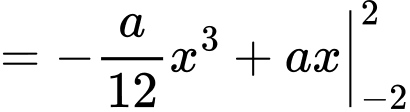
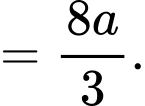
Diện tích phần tô đậm giới hạn bởi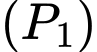 và
và  là:
là:
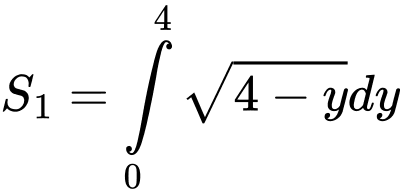
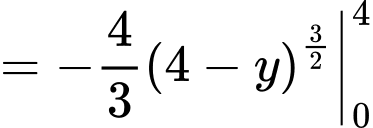
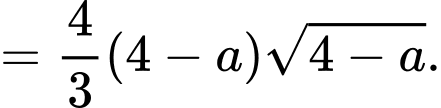
Theo giả thiết ta có: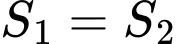
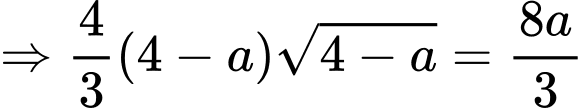
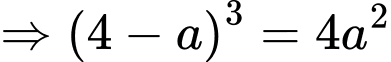
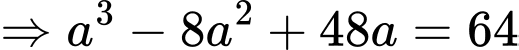
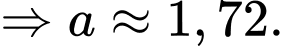
Diện tích phần tô đậm dùng để hoa là: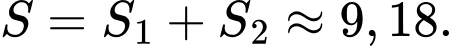
Diện tích phần tô đậm dùng để cỏ là:
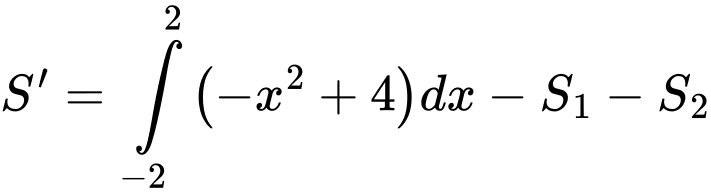
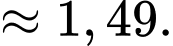
Số tiền mà người ta bỏ ra để trang trí khu vườn bằng

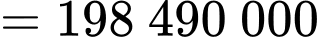 (đồng)
(đồng) 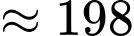 (triệu đồng).
(triệu đồng).
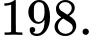
Gọi
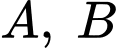 là các giao điểm của
là các giao điểm của 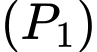 và trục hoành, ta có:
và trục hoành, ta có: 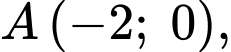
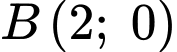
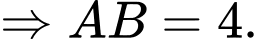
Gọi
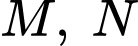 là các giao điểm của
là các giao điểm của 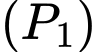 và đường thẳng
và đường thẳng 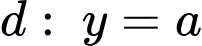
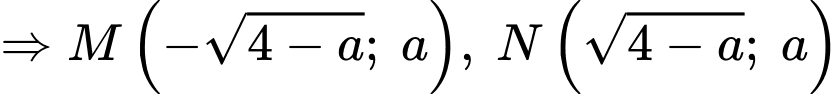
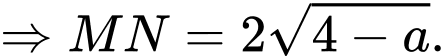
Phương trình parabol
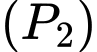 có đỉnh
có đỉnh 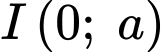 có dạng
có dạng 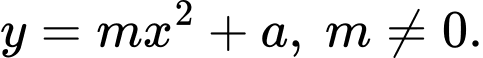
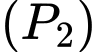 đi qua hai điểm
đi qua hai điểm 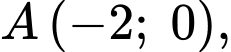
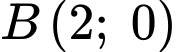 nên
nên 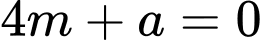
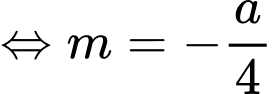
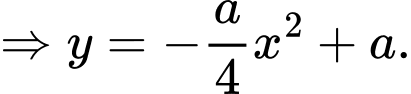
Diện tích phần tô đậm giới hạn bởi
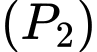 và trục hoành là:
và trục hoành là: 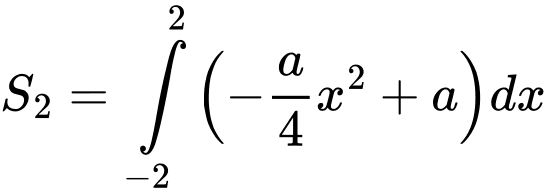
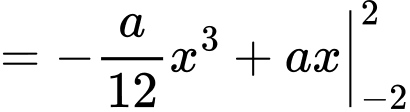
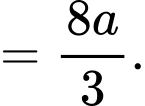
Diện tích phần tô đậm giới hạn bởi
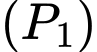 và
và  là:
là: 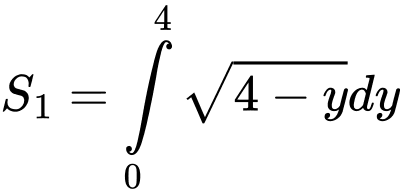
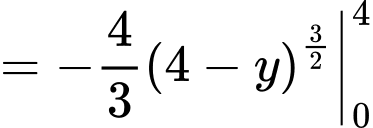
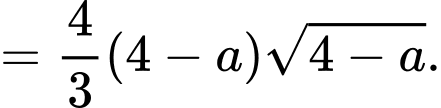
Theo giả thiết ta có:
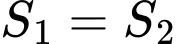
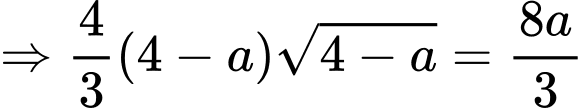
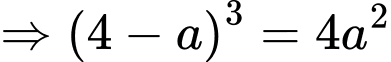
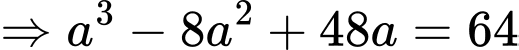
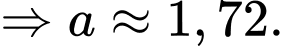
Diện tích phần tô đậm dùng để hoa là:
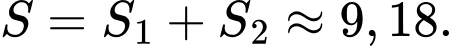
Diện tích phần tô đậm dùng để cỏ là:
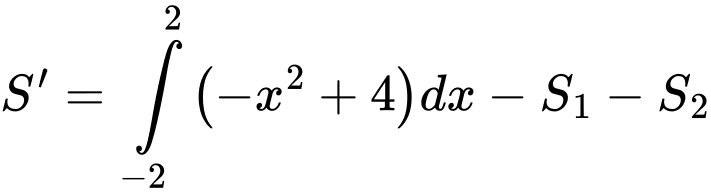
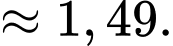
Số tiền mà người ta bỏ ra để trang trí khu vườn bằng

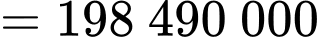 (đồng)
(đồng) 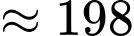 (triệu đồng).
(triệu đồng).
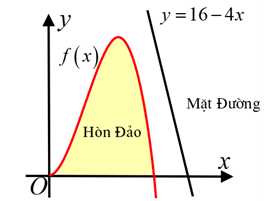
Câu 22 [694295]: Một hòn đảo nằm trong một hồ nước. Biết rằng đường cong tạo nên hòn đảo được mô hình hóa vào hệ trục tọa độ 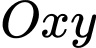 là một phần của đồ thị hàm số bậc ba
là một phần của đồ thị hàm số bậc ba 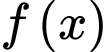 (tham khảo hình vẽ bên). Vị trí điểm cực đại là
(tham khảo hình vẽ bên). Vị trí điểm cực đại là 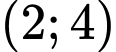 với đơn vị của hệ trục là
với đơn vị của hệ trục là 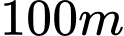 và vị trí điểm cực tiểu là gốc tọa độ
và vị trí điểm cực tiểu là gốc tọa độ  Mặt đường chạy trên một đường thẳng có phương trình
Mặt đường chạy trên một đường thẳng có phương trình 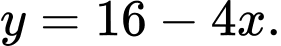 Người ta muốn làm một cây cầu có dạng một đoạn thẳng nối từ hòn đảo ra mặt đường. Độ dài ngắn nhất của cây cầu bằng bao nhiêu mét ? (làm tròn đến một chữ số thập phân sau dấu phẩy)
Người ta muốn làm một cây cầu có dạng một đoạn thẳng nối từ hòn đảo ra mặt đường. Độ dài ngắn nhất của cây cầu bằng bao nhiêu mét ? (làm tròn đến một chữ số thập phân sau dấu phẩy)
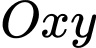 là một phần của đồ thị hàm số bậc ba
là một phần của đồ thị hàm số bậc ba 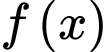 (tham khảo hình vẽ bên). Vị trí điểm cực đại là
(tham khảo hình vẽ bên). Vị trí điểm cực đại là 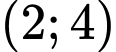 với đơn vị của hệ trục là
với đơn vị của hệ trục là 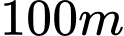 và vị trí điểm cực tiểu là gốc tọa độ
và vị trí điểm cực tiểu là gốc tọa độ  Mặt đường chạy trên một đường thẳng có phương trình
Mặt đường chạy trên một đường thẳng có phương trình 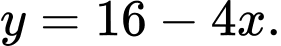 Người ta muốn làm một cây cầu có dạng một đoạn thẳng nối từ hòn đảo ra mặt đường. Độ dài ngắn nhất của cây cầu bằng bao nhiêu mét ? (làm tròn đến một chữ số thập phân sau dấu phẩy)
Người ta muốn làm một cây cầu có dạng một đoạn thẳng nối từ hòn đảo ra mặt đường. Độ dài ngắn nhất của cây cầu bằng bao nhiêu mét ? (làm tròn đến một chữ số thập phân sau dấu phẩy)
Điền đáp án: 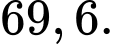
Do hà số đạt cực đại tại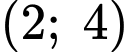 và đạt cực tiểu tại
và đạt cực tiểu tại 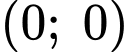 nên
nên 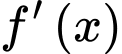 có hai nghiệm
có hai nghiệm 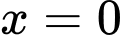 và
và 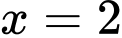
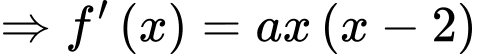
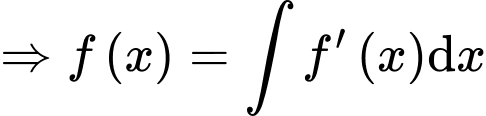
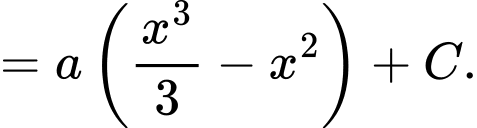
Ta có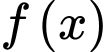 đi qua điểm
đi qua điểm 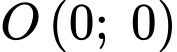 nên
nên 
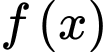 đi qua điểm
đi qua điểm 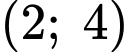 nên
nên 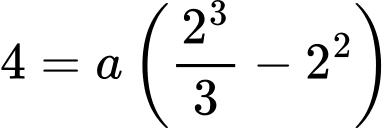
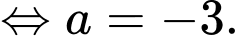
Suy ra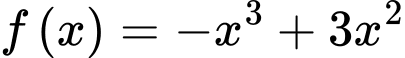
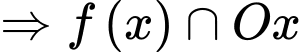 tại
tại 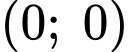 và
và 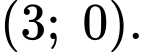
Gọi vị trí đặt cầu là điểm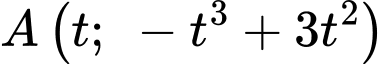 thuộc đồ thị hàm số
thuộc đồ thị hàm số 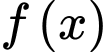 .
.
Ta có phương trình mặt đường là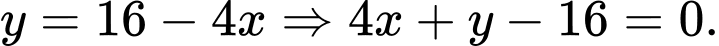
Độ dài cây cầu là:
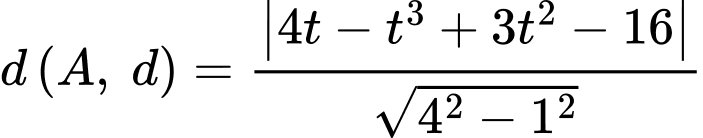
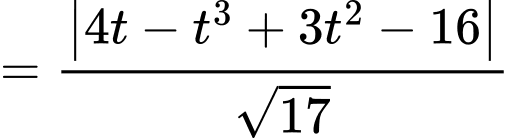
Lập bảng biến thiên tại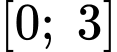 để tìm min của hàm số
để tìm min của hàm số 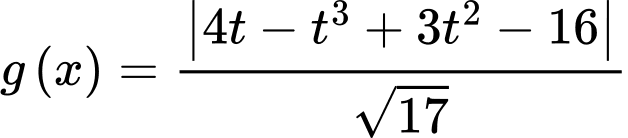
 nhỏ nhất bằng
nhỏ nhất bằng 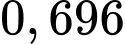 khi
khi 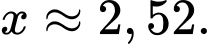
Vậy độ dài cây cầu ngắn nhất là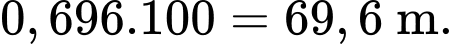
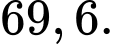
Do hà số đạt cực đại tại
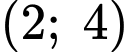 và đạt cực tiểu tại
và đạt cực tiểu tại 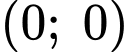 nên
nên 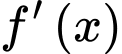 có hai nghiệm
có hai nghiệm 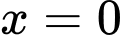 và
và 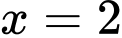
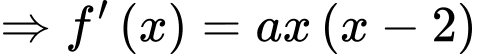
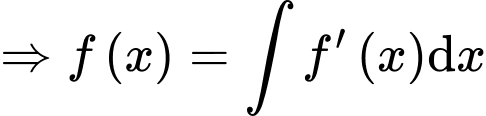
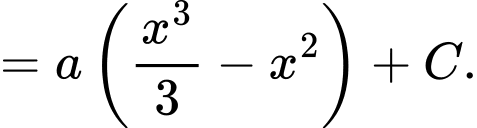
Ta có
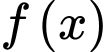 đi qua điểm
đi qua điểm 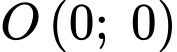 nên
nên 
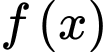 đi qua điểm
đi qua điểm 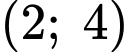 nên
nên 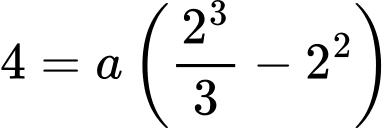
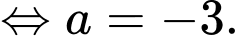
Suy ra
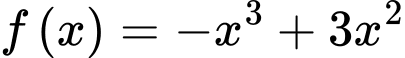
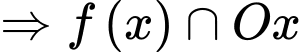 tại
tại 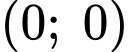 và
và 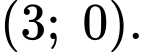
Gọi vị trí đặt cầu là điểm
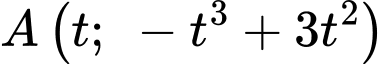 thuộc đồ thị hàm số
thuộc đồ thị hàm số 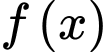 .
.
Ta có phương trình mặt đường là
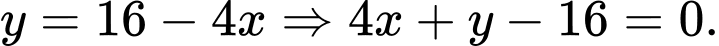
Độ dài cây cầu là:
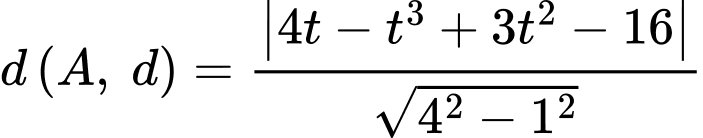
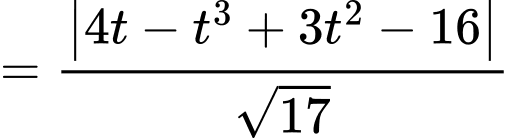
Lập bảng biến thiên tại
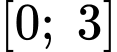 để tìm min của hàm số
để tìm min của hàm số 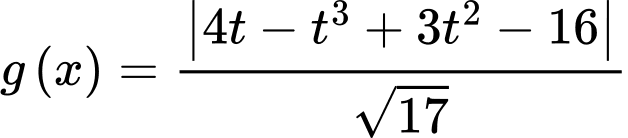
 nhỏ nhất bằng
nhỏ nhất bằng 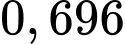 khi
khi 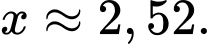
Vậy độ dài cây cầu ngắn nhất là