PHẦN I. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Câu 1 [134803]: Cho 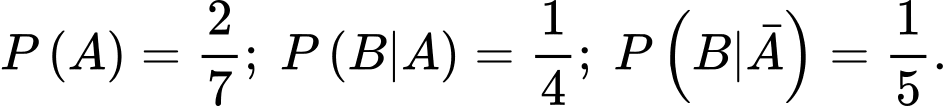 Giá trị
Giá trị  là
là
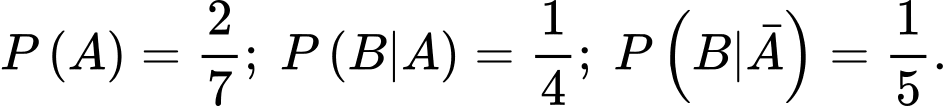 Giá trị
Giá trị  là
là A, 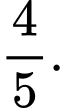
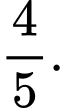
B, 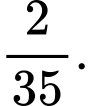
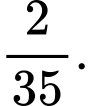
C, 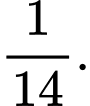
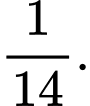
D, 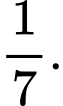
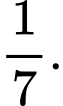
Chọn đáp án D.
Ta có: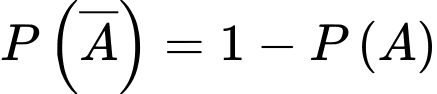
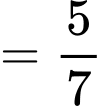
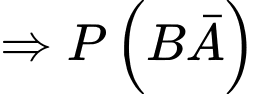
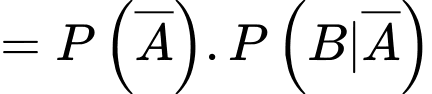
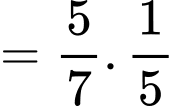
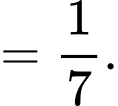 Đáp án: D
Đáp án: D
Ta có:
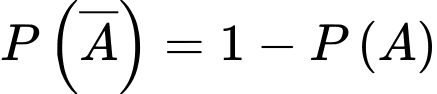
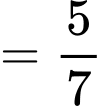
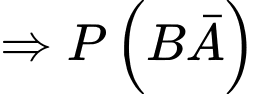
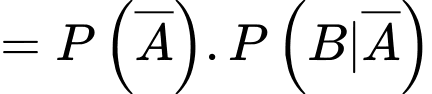
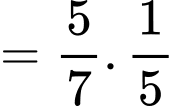
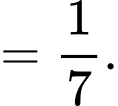 Đáp án: D
Đáp án: D
Câu 2 [695194]: Cho hình lăng trụ tam giác  Đặt
Đặt 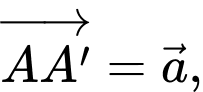
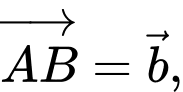
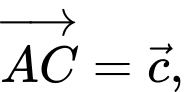
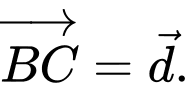 Trong các biểu thức véctơ sau đây, biểu thức nào đúng?
Trong các biểu thức véctơ sau đây, biểu thức nào đúng?
 Đặt
Đặt 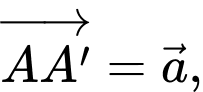
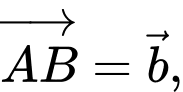
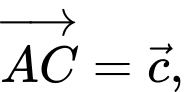
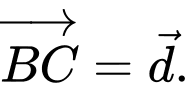 Trong các biểu thức véctơ sau đây, biểu thức nào đúng?
Trong các biểu thức véctơ sau đây, biểu thức nào đúng? A, 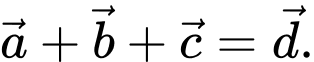
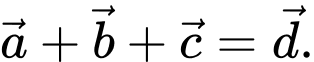
B, 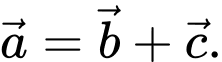
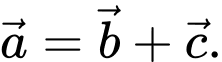
C, 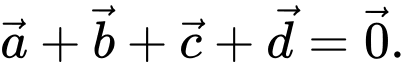
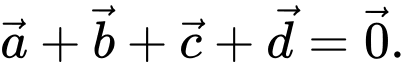
D, 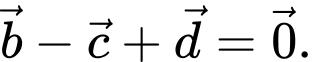
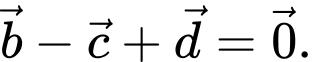
Chọn đáp án D.
Ta có: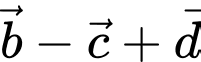
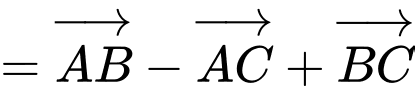
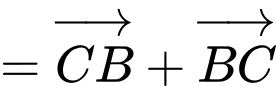
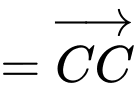
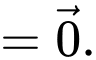 Đáp án: D
Đáp án: D
Ta có:
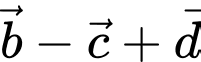
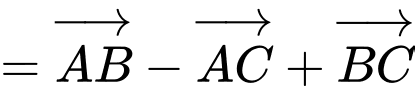
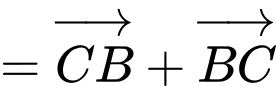
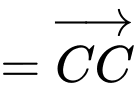
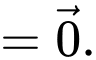 Đáp án: D
Đáp án: D
Câu 3 [328043]: Cho hàm số 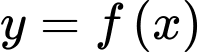 có bảng biến thiên như sau:
có bảng biến thiên như sau:
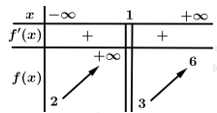
Tổng số tiệm cận ngang và tiệm cận đứng của đồ thị hàm số đã cho là
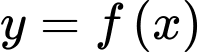 có bảng biến thiên như sau:
có bảng biến thiên như sau:
Tổng số tiệm cận ngang và tiệm cận đứng của đồ thị hàm số đã cho là
A, 4.
B, 3.
C, 1.
D, 2.
Chọn đáp án B.
TXĐ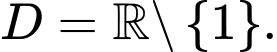
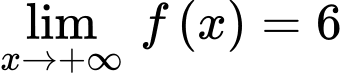 nên đường thẳng
nên đường thẳng 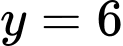 là đường tiệm cận ngang của đồ thị hàm số.
là đường tiệm cận ngang của đồ thị hàm số.
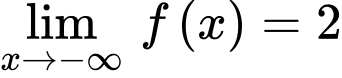 nên đường thẳng
nên đường thẳng 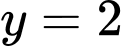 là đường tiệm cận ngang của đồ thị hàm số.
là đường tiệm cận ngang của đồ thị hàm số.
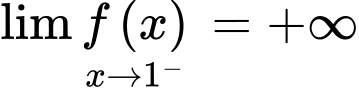 nên đường thẳng
nên đường thẳng 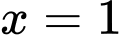 là đường tiệm cận đứng của đồ thị hàm số.
là đường tiệm cận đứng của đồ thị hàm số.
Vậy đồ thị hàm số có tất cả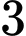 đường tiệm cận đứng và tiệm cận ngang. Đáp án: B
đường tiệm cận đứng và tiệm cận ngang. Đáp án: B
TXĐ
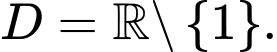
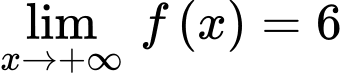 nên đường thẳng
nên đường thẳng 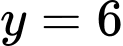 là đường tiệm cận ngang của đồ thị hàm số.
là đường tiệm cận ngang của đồ thị hàm số.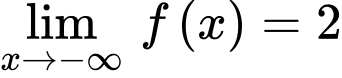 nên đường thẳng
nên đường thẳng 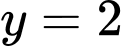 là đường tiệm cận ngang của đồ thị hàm số.
là đường tiệm cận ngang của đồ thị hàm số.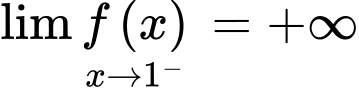 nên đường thẳng
nên đường thẳng 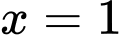 là đường tiệm cận đứng của đồ thị hàm số.
là đường tiệm cận đứng của đồ thị hàm số.Vậy đồ thị hàm số có tất cả
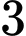 đường tiệm cận đứng và tiệm cận ngang. Đáp án: B
đường tiệm cận đứng và tiệm cận ngang. Đáp án: B
Câu 4 [511859]: Cho hình chóp 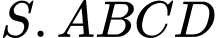 có đáy
có đáy 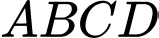 là hình vuông cạnh
là hình vuông cạnh 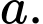 Cạnh
Cạnh 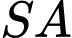 vuông góc với mặt phẳng đáy và có độ dài là
vuông góc với mặt phẳng đáy và có độ dài là 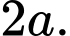 Thể tích khối tứ diện
Thể tích khối tứ diện 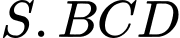 bằng
bằng
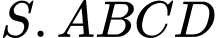 có đáy
có đáy 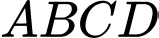 là hình vuông cạnh
là hình vuông cạnh 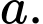 Cạnh
Cạnh 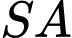 vuông góc với mặt phẳng đáy và có độ dài là
vuông góc với mặt phẳng đáy và có độ dài là 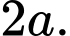 Thể tích khối tứ diện
Thể tích khối tứ diện  bằng
bằng A, 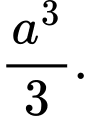
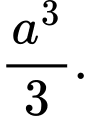
B, 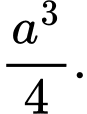
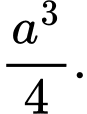
C, 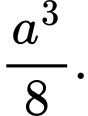
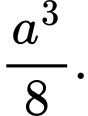
D, 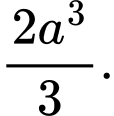
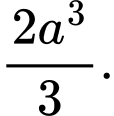
Chọn đáp án A.
Thể tích khối tứ diện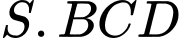 bằng
bằng
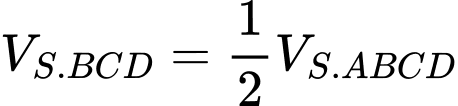
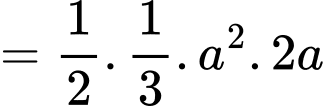
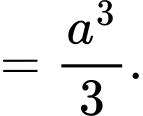 Đáp án: A
Đáp án: A
Thể tích khối tứ diện
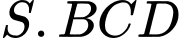 bằng
bằng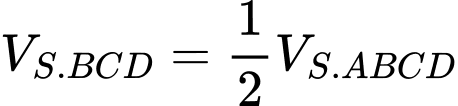
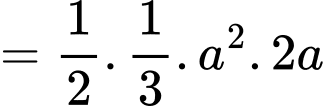
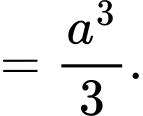 Đáp án: A
Đáp án: A
Câu 5 [677853]: Nghiệm của phương trình 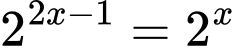 là
là
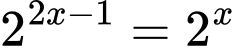 là
là A, 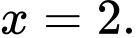
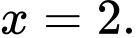
B, 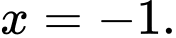
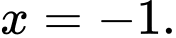
C, 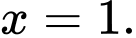
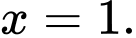
D, 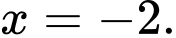
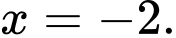
Chọn đáp án C.
Ta có: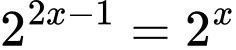
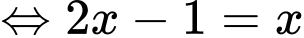
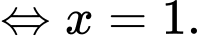 Đáp án: C
Đáp án: C
Ta có:
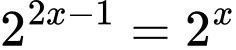
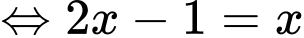
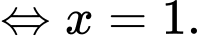 Đáp án: C
Đáp án: C
Câu 6 [522988]: Cho cấp số cộng 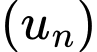 có số hạng đầu
có số hạng đầu 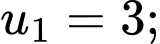 công sai
công sai 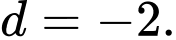 Số hạng
Số hạng 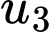 của cấp số cộng đã cho bằng
của cấp số cộng đã cho bằng
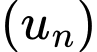 có số hạng đầu
có số hạng đầu 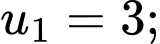 công sai
công sai 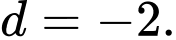 Số hạng
Số hạng 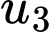 của cấp số cộng đã cho bằng
của cấp số cộng đã cho bằng A, 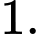
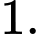
B, 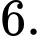
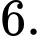
C, 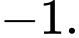
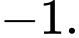
D, 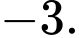
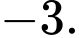
Chọn đáp án C.
Ta có: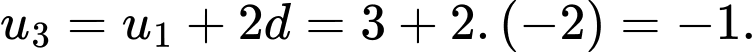 Đáp án: C
Đáp án: C
Ta có:
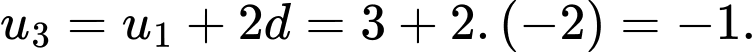 Đáp án: C
Đáp án: C
Câu 7 [328093]: Cho hàm số 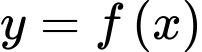 có bảng biến thiên như hình dưới đây. Khẳng định nào sau đây là đúng?
có bảng biến thiên như hình dưới đây. Khẳng định nào sau đây là đúng?
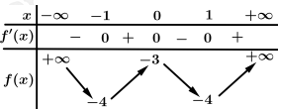
 có bảng biến thiên như hình dưới đây. Khẳng định nào sau đây là đúng?
có bảng biến thiên như hình dưới đây. Khẳng định nào sau đây là đúng?
A, Hàm số đạt cực đại tại 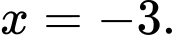
B, Hàm số đạt cực tiểu tại 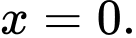
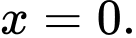
C, Hàm số đạt cực tiểu tại 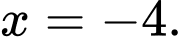
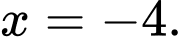
D, Hàm số đạt cực đại tại 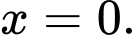
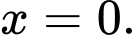
Chọn đáp án D.
Dựa vào bảng biến thiên ta thấy hàm số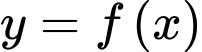 đạt cực đại tại
đạt cực đại tại 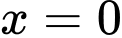 và giá trị cực đại là
và giá trị cực đại là 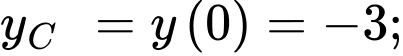 đạt cực tiểu tại
đạt cực tiểu tại 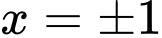 và
và 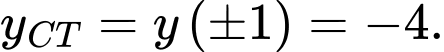 Đáp án: D
Đáp án: D
Dựa vào bảng biến thiên ta thấy hàm số
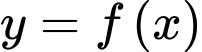 đạt cực đại tại
đạt cực đại tại 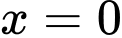 và giá trị cực đại là
và giá trị cực đại là 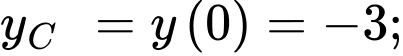 đạt cực tiểu tại
đạt cực tiểu tại 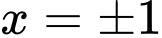 và
và 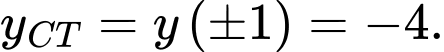 Đáp án: D
Đáp án: D
Câu 8 [677859]: Trong không gian 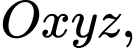 cho đường thẳng
cho đường thẳng 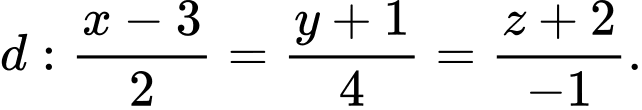 Điểm nào dưới đây thuộc
Điểm nào dưới đây thuộc 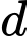 ?
?
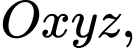 cho đường thẳng
cho đường thẳng 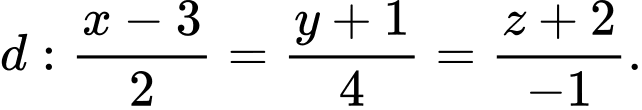 Điểm nào dưới đây thuộc
Điểm nào dưới đây thuộc 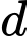 ?
? A, 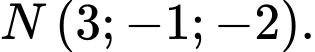
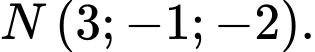
B, 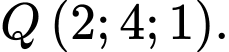
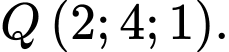
C, 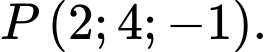
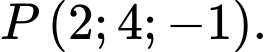
D, 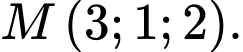
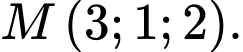
Chọn đáp án A.
Ta có: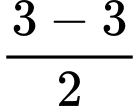
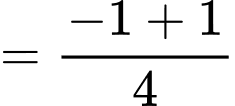
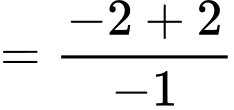
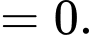
Vậy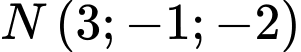 thuộc
thuộc 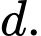 Đáp án: A
Đáp án: A
Ta có:
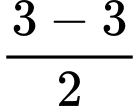
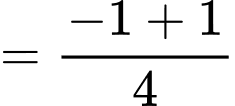
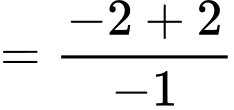
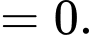
Vậy
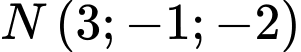 thuộc
thuộc 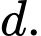 Đáp án: A
Đáp án: A
Câu 9 [677867]: Gọi 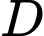 là hình phẳng giới hạn bởi các đường
là hình phẳng giới hạn bởi các đường 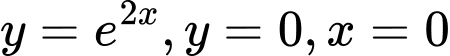 và
và 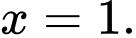 Thể tích khối tròn xoay tạo thành kho quay
Thể tích khối tròn xoay tạo thành kho quay 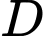 quanh
quanh 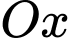 bằng
bằng
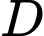 là hình phẳng giới hạn bởi các đường
là hình phẳng giới hạn bởi các đường 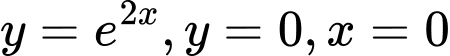 và
và 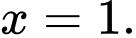 Thể tích khối tròn xoay tạo thành kho quay
Thể tích khối tròn xoay tạo thành kho quay 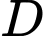 quanh
quanh 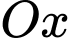 bằng
bằng A, 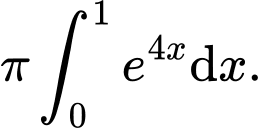
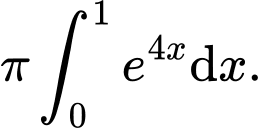
B, 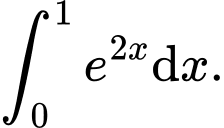
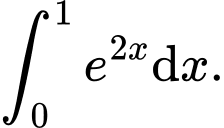
C, 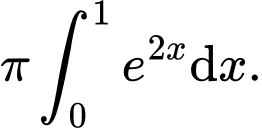
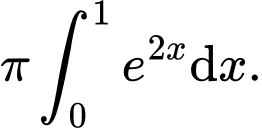
D, 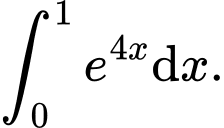
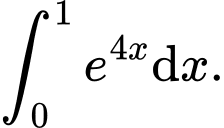
Chọn đáp án A.
Thể tích khối tròn xoay tạo thành kho quay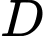 quanh
quanh 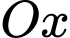 là
là
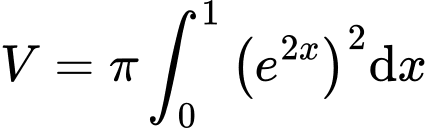
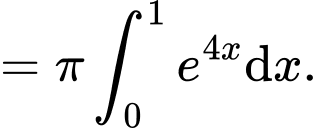 Đáp án: A
Đáp án: A
Thể tích khối tròn xoay tạo thành kho quay
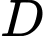 quanh
quanh 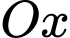 là
là 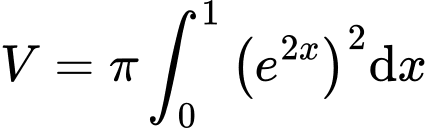
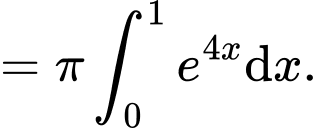 Đáp án: A
Đáp án: A
Câu 10 [677869]: Trong không gian 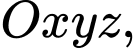 cho điểm
cho điểm 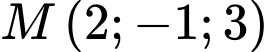 và mặt phẳng
và mặt phẳng 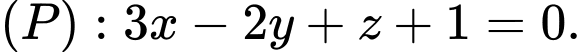 Phương trình mặt phẳng đi qua
Phương trình mặt phẳng đi qua 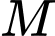 và song song với
và song song với 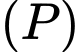 là
là
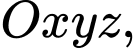 cho điểm
cho điểm 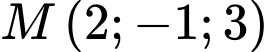 và mặt phẳng
và mặt phẳng 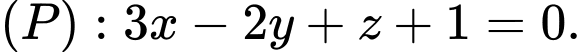 Phương trình mặt phẳng đi qua
Phương trình mặt phẳng đi qua 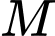 và song song với
và song song với 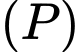 là
là A, 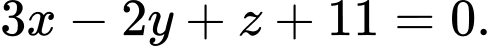
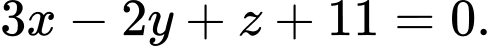
B, 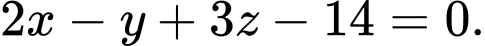
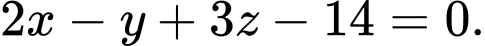
C, 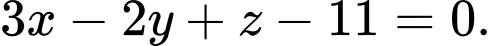
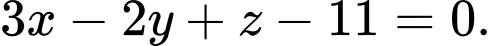
D, 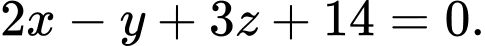
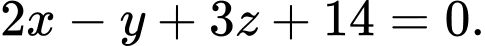
Chọn đáp án C.
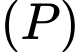 nhận
nhận 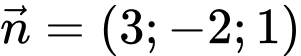 làm vectơ pháp tuyến.
làm vectơ pháp tuyến.
Mặt phẳng đã cho song song với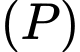 nên cũng nhận nhận
nên cũng nhận nhận 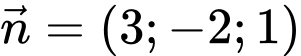 làm vectơ pháp tuyến.
làm vectơ pháp tuyến.
Vậy mặt phẳng đi qua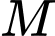 và song song với
và song song với 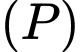 có phương trình là
có phương trình là
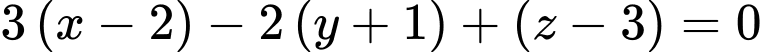
 Đáp án: C
Đáp án: C
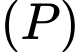 nhận
nhận 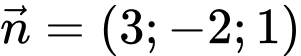 làm vectơ pháp tuyến.
làm vectơ pháp tuyến.Mặt phẳng đã cho song song với
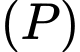 nên cũng nhận nhận
nên cũng nhận nhận 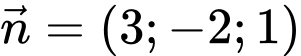 làm vectơ pháp tuyến.
làm vectơ pháp tuyến.Vậy mặt phẳng đi qua
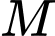 và song song với
và song song với 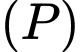 có phương trình là
có phương trình là 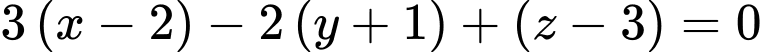
 Đáp án: C
Đáp án: C
Câu 11 [677873]: Với 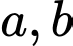 là các số thực dương tùy ý thỏa mãn
là các số thực dương tùy ý thỏa mãn 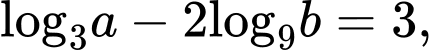 mệnh đề nào dưới đây đúng?
mệnh đề nào dưới đây đúng?
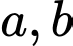 là các số thực dương tùy ý thỏa mãn
là các số thực dương tùy ý thỏa mãn 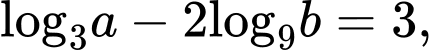 mệnh đề nào dưới đây đúng?
mệnh đề nào dưới đây đúng? A, 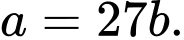
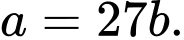
B, 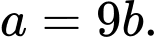
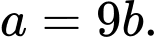
C, 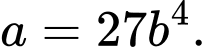
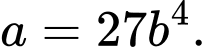
D, 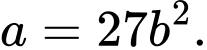
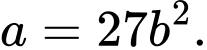
Chọn đáp án A.
Ta có: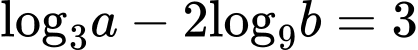
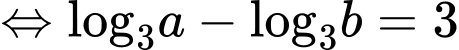
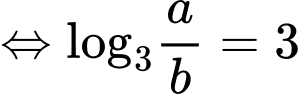
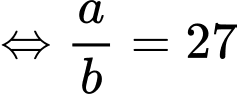
 Đáp án: A
Đáp án: A
Ta có:
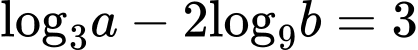
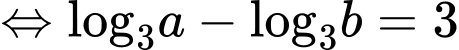
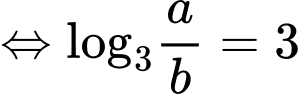
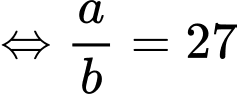
 Đáp án: A
Đáp án: A
Câu 12 [808665]: Họ nguyên hàm của hàm số 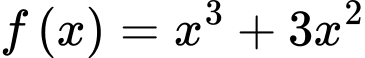 là
là
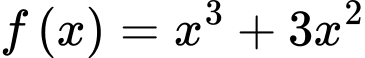 là
là A, 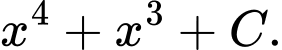
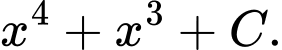
B, 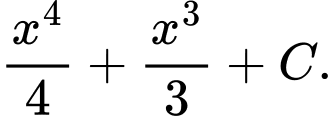
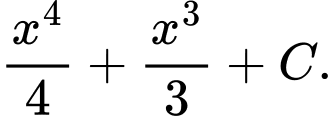
C, 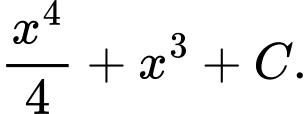
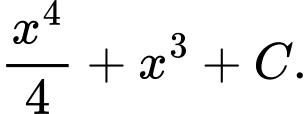
D, 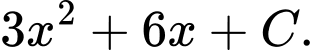
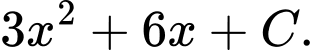
Chọn đáp án C.
Áp dụng công thức nguyên hàm: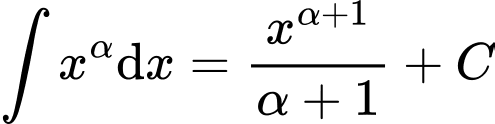 và các tính chất nguyên hàm, ta có:
và các tính chất nguyên hàm, ta có:
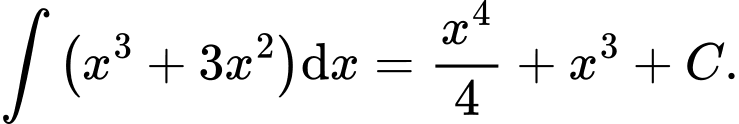 Đáp án: C
Đáp án: C
Áp dụng công thức nguyên hàm:
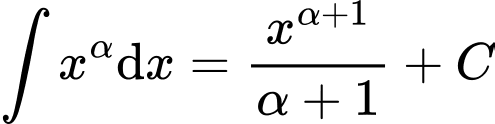 và các tính chất nguyên hàm, ta có:
và các tính chất nguyên hàm, ta có:  Đáp án: C
Đáp án: C PHẦN II. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
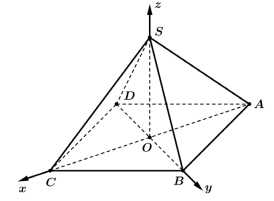
Câu 13 [695195]: Cho hình chóp tứ giác đều 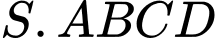 có cạnh đáy bằng
có cạnh đáy bằng 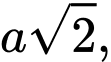 chiều cao bằng
chiều cao bằng 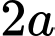 và
và  là tâm của đáy. Bằng cách thiết lập hệ trục tọa độ
là tâm của đáy. Bằng cách thiết lập hệ trục tọa độ 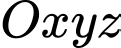 như hình vẽ, với gốc toạ độ
như hình vẽ, với gốc toạ độ  tia
tia 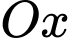 trùng với tia
trùng với tia 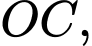 tia
tia 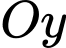 trùng với tia
trùng với tia 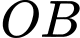 và tia
và tia  trùng với tia
trùng với tia 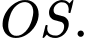
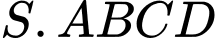 có cạnh đáy bằng
có cạnh đáy bằng 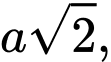 chiều cao bằng
chiều cao bằng 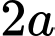 và
và  là tâm của đáy. Bằng cách thiết lập hệ trục tọa độ
là tâm của đáy. Bằng cách thiết lập hệ trục tọa độ 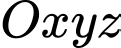 như hình vẽ, với gốc toạ độ
như hình vẽ, với gốc toạ độ  tia
tia 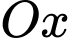 trùng với tia
trùng với tia 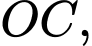 tia
tia 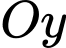 trùng với tia
trùng với tia 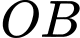 và tia
và tia  trùng với tia
trùng với tia 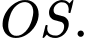

a) Sai.
Vì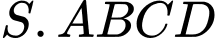 là hình chóp tứ giác đều nên
là hình chóp tứ giác đều nên 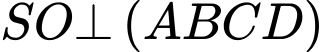 và
và 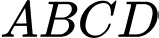 là hình vuông.
là hình vuông.
Suy ra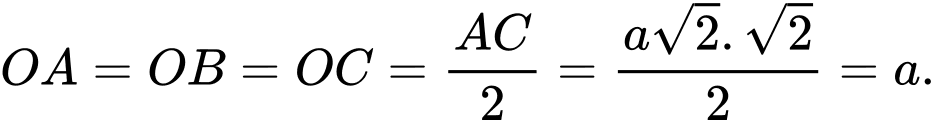
b) Đúng.
Dựa vào hình vẽ, ta có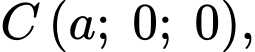
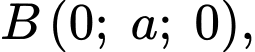
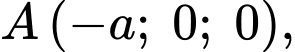
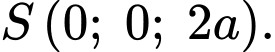
c) Đúng.
Phương trình mặt phẳng đi qua ba điểm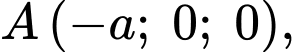
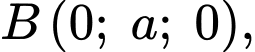
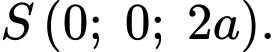 là
là 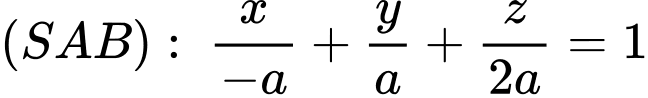

 Một vectơ pháp tuyến của mặt phẳng
Một vectơ pháp tuyến của mặt phẳng 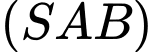 là
là 
d) Sai.
Khoảng cách từ điểm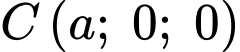 đến
đến 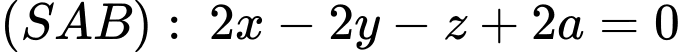 là
là
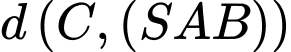
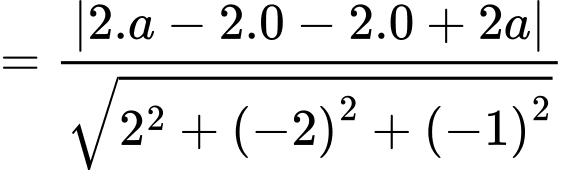
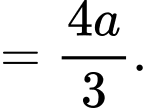
Vì
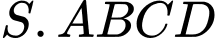 là hình chóp tứ giác đều nên
là hình chóp tứ giác đều nên 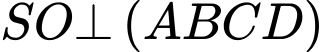 và
và  là hình vuông.
là hình vuông.Suy ra
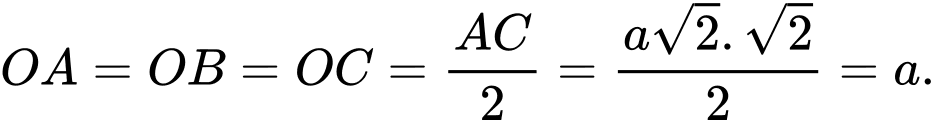
b) Đúng.
Dựa vào hình vẽ, ta có
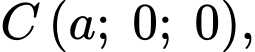
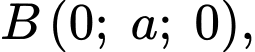
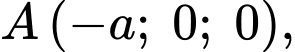
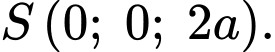
c) Đúng.
Phương trình mặt phẳng đi qua ba điểm
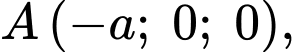
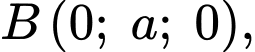
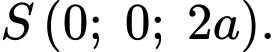 là
là 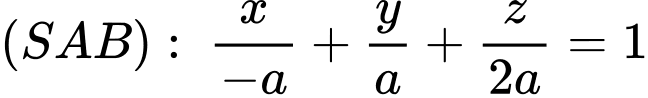

 Một vectơ pháp tuyến của mặt phẳng
Một vectơ pháp tuyến của mặt phẳng 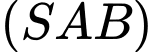 là
là 
d) Sai.
Khoảng cách từ điểm
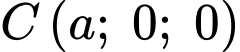 đến
đến 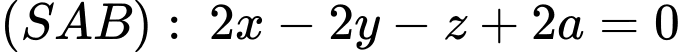 là
là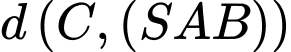
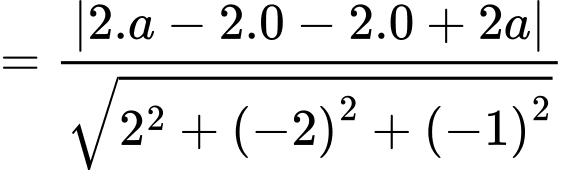
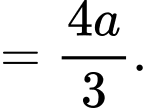
Câu 14 [695196]: Biểu đồ dưới đây mô tả kết quả điều tra về mức lương khởi điểm (đơn vị: triệu đồng) của một số công nhân ở hai khu vực 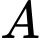 và
và 
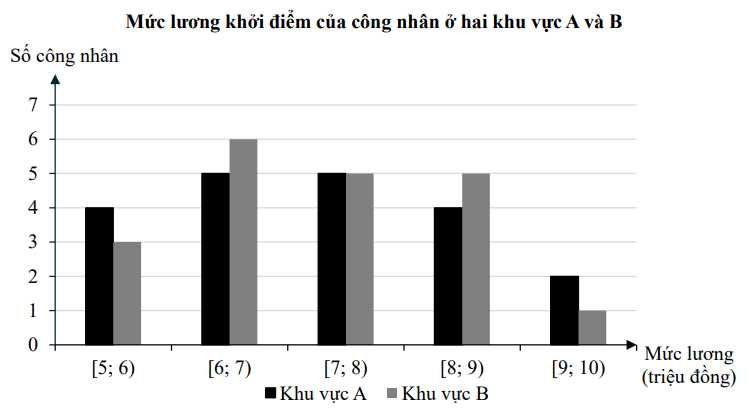
 và
và 

a) Sai.
Khoảng biến thiên của mẫu số liệu ghép nhóm là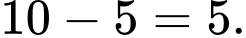
b) Đúng.
Xét mẫu số liệu của khu vực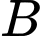 :
:
Cỡ mẫu là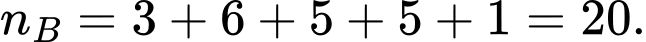
Số trung bình của mẫu số liệu ghép nhóm là
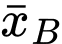
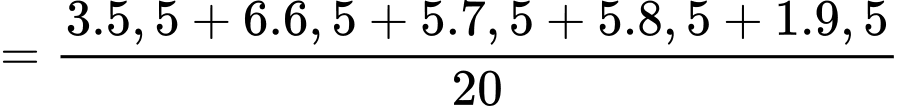
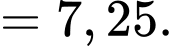
c) Sai.
Phương sai của mẫu số liệu ghép nhóm ứng với khu vực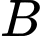 là
là
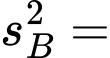
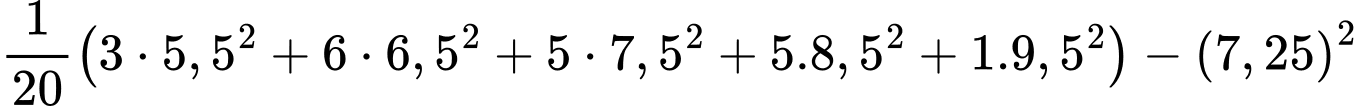
d) Đúng.
+) Xét mẫu số liệu của khu vực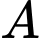 :
:
Cỡ mẫu là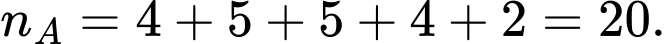
Số trung bình của mẫu số liệu ghép nhóm là
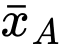
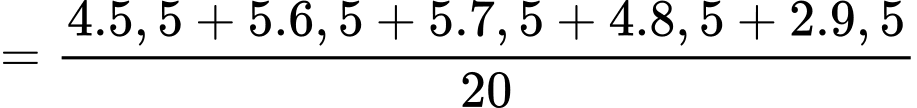
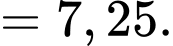
Phương sai của mẫu số liệu ghép nhóm là
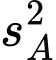
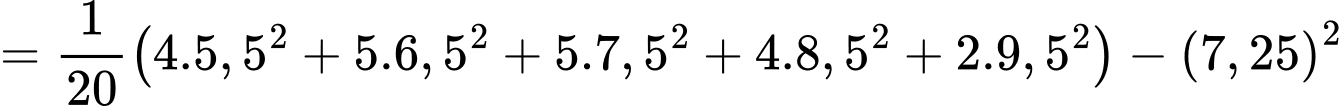
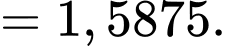
Độ lệch chuẩn của mẫu số liệu ghép nhóm khu vực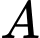 là
là 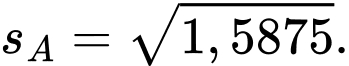
Độ lệch chuẩn của mẫu số liệu ghép nhóm khu vực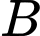 là
là 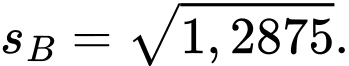
Do nên nếu so sánh theo độ lệch chuẩn của mẫu số liệu ghép nhóm thì mức lương khởi điểm của công nhân khu vực
nên nếu so sánh theo độ lệch chuẩn của mẫu số liệu ghép nhóm thì mức lương khởi điểm của công nhân khu vực 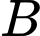 đồng đều hơn của công nhân khu vực
đồng đều hơn của công nhân khu vực 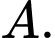
Khoảng biến thiên của mẫu số liệu ghép nhóm là
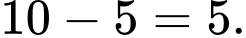
b) Đúng.
Xét mẫu số liệu của khu vực
 :
:
Cỡ mẫu là
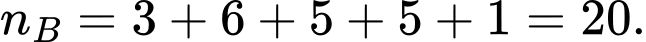
Số trung bình của mẫu số liệu ghép nhóm là
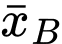
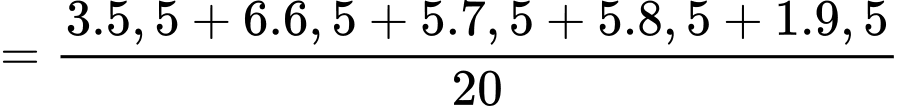
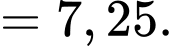
c) Sai.
Phương sai của mẫu số liệu ghép nhóm ứng với khu vực
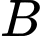 là
là
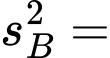
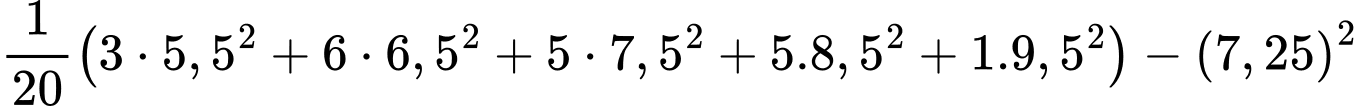
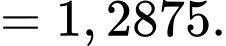
d) Đúng.
+) Xét mẫu số liệu của khu vực
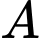 :
:
Cỡ mẫu là
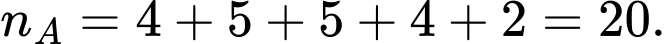
Số trung bình của mẫu số liệu ghép nhóm là
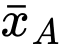
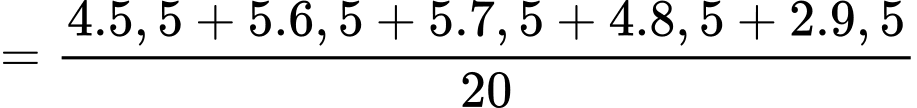
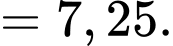
Phương sai của mẫu số liệu ghép nhóm là
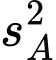
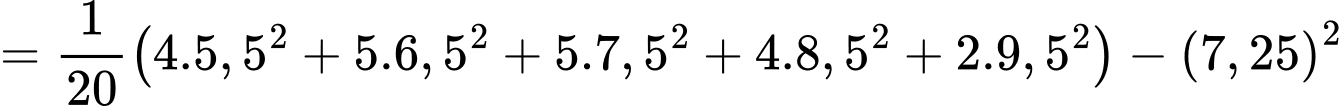
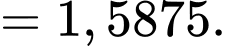
Độ lệch chuẩn của mẫu số liệu ghép nhóm khu vực
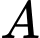 là
là 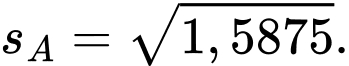
Độ lệch chuẩn của mẫu số liệu ghép nhóm khu vực
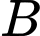 là
là 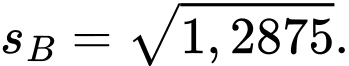
Do
 nên nếu so sánh theo độ lệch chuẩn của mẫu số liệu ghép nhóm thì mức lương khởi điểm của công nhân khu vực
nên nếu so sánh theo độ lệch chuẩn của mẫu số liệu ghép nhóm thì mức lương khởi điểm của công nhân khu vực 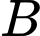 đồng đều hơn của công nhân khu vực
đồng đều hơn của công nhân khu vực 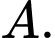
Câu 15 [695197]: Giả sử số lượng của một quần thể nấm men tại môi trường nuôi cấy trong phòng thí nghiệm được mô hình hoá bằng hàm số 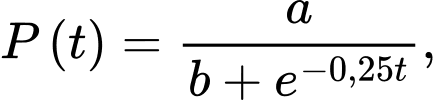
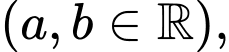 trong đó thời gian
trong đó thời gian 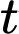 được tính bằng giờ. Tại thời điểm ban đầu
được tính bằng giờ. Tại thời điểm ban đầu 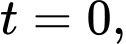 quần thể có 60 tế bào và tăng với tốc độ 10 tế bào/giờ.
quần thể có 60 tế bào và tăng với tốc độ 10 tế bào/giờ.
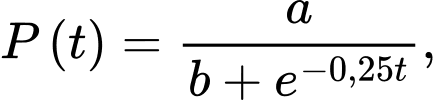
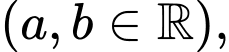 trong đó thời gian
trong đó thời gian 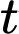 được tính bằng giờ. Tại thời điểm ban đầu
được tính bằng giờ. Tại thời điểm ban đầu 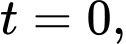 quần thể có 60 tế bào và tăng với tốc độ 10 tế bào/giờ.
quần thể có 60 tế bào và tăng với tốc độ 10 tế bào/giờ. 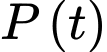 là số lượng vi khuẩn
là số lượng vi khuẩn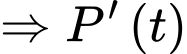 là tốc độ tăng trưởng.
là tốc độ tăng trưởng.a)Đúng.
Tại thời điểm
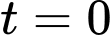 , quần thể có
, quần thể có 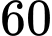 tế bào nên
tế bào nên 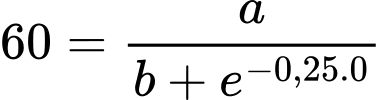
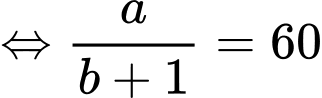
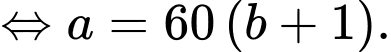
Tốc độ tăng trưởng
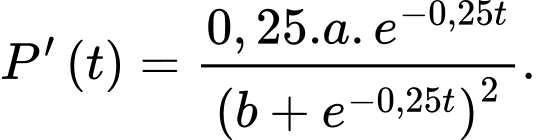
Theo bài ra, ta có
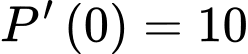
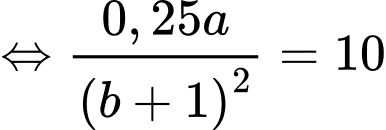
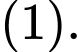
Thay
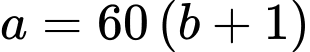 vào
vào  , ta được
, ta được 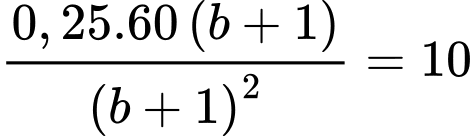
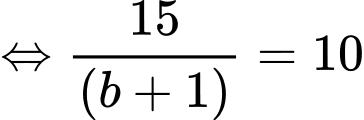
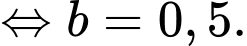
Suy ra
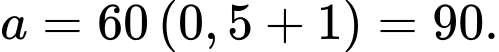
b) Sai.
c) Sai.
Ta có:
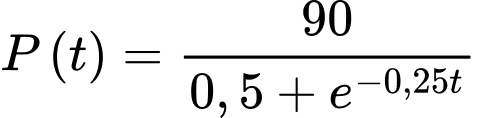
Khi
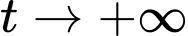 thì
thì 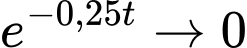 nên
nên 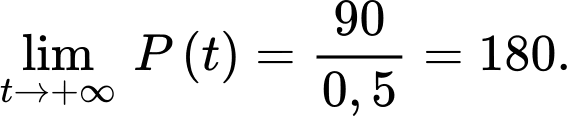
d) Đúng.
Ta có:
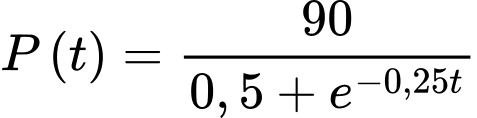
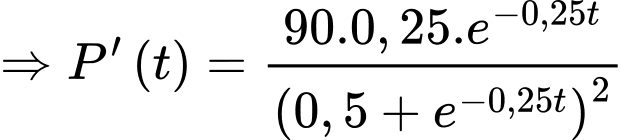
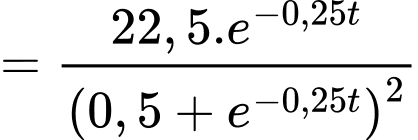
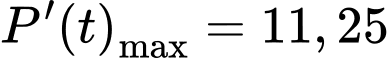 tại
tại 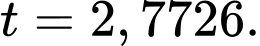
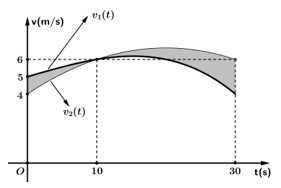
Câu 16 [695198]: Có 2 vận động viên  và
và  chạy trên một đường thẳng với vận tốc lần lượt được biểu diễn bởi đồ thị hàm số
chạy trên một đường thẳng với vận tốc lần lượt được biểu diễn bởi đồ thị hàm số 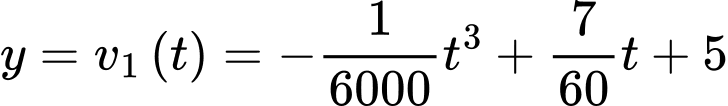 (m/s) và parabol
(m/s) và parabol 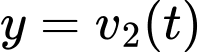 (m/s) như hình vẽ. Biết rằng 2 vận động viên xuất phát cùng một lúc tại cùng một vị trí.
(m/s) như hình vẽ. Biết rằng 2 vận động viên xuất phát cùng một lúc tại cùng một vị trí.
 và
và  chạy trên một đường thẳng với vận tốc lần lượt được biểu diễn bởi đồ thị hàm số
chạy trên một đường thẳng với vận tốc lần lượt được biểu diễn bởi đồ thị hàm số 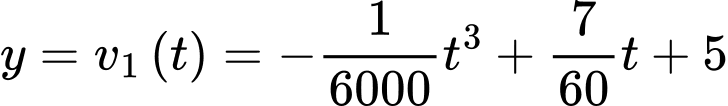 (m/s) và parabol
(m/s) và parabol 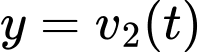 (m/s) như hình vẽ. Biết rằng 2 vận động viên xuất phát cùng một lúc tại cùng một vị trí.
(m/s) như hình vẽ. Biết rằng 2 vận động viên xuất phát cùng một lúc tại cùng một vị trí.
a) Sai.
Quãng đường vận động viên đi được sau
đi được sau  giây là
giây là 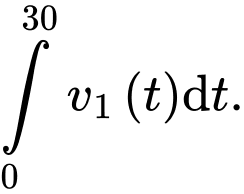
Quãng đường vận động viên đi được sau
đi được sau  giây là
giây là 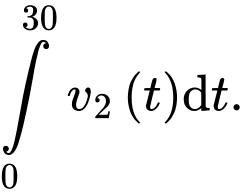
Vậy khoảng cách giữa hai vận động viên sau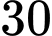 giây kể từ lúc xuất phát bằng diện tích phần tô đậm trong hình vẽ và bằng
giây kể từ lúc xuất phát bằng diện tích phần tô đậm trong hình vẽ và bằng 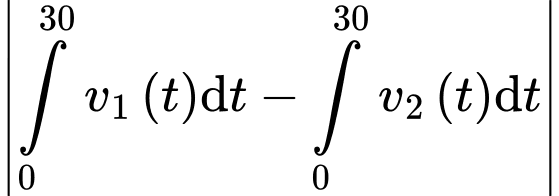
b) Đúng.
Do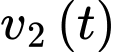 nên hàm số có dạng
nên hàm số có dạng 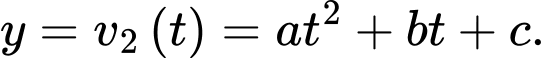
Đồ thị hàm số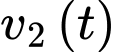 đi qua ba điểm
đi qua ba điểm 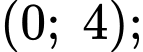
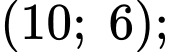
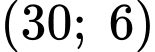 nên ta có:
nên ta có: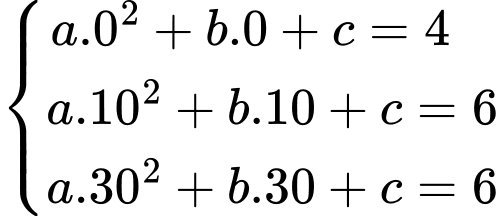
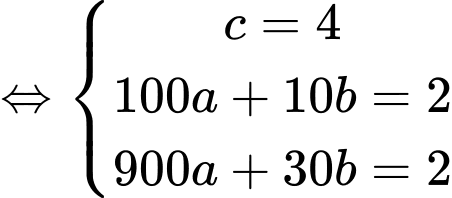
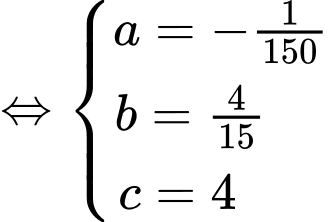
Vậy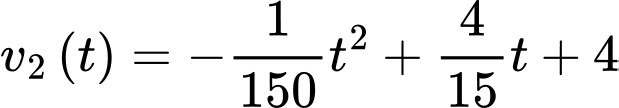
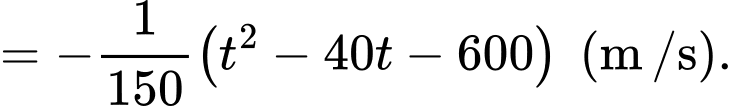
c) Đúng.
Tại thời điểm giây, quãng đường vận động viên
giây, quãng đường vận động viên 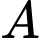 chạy được là
chạy được là
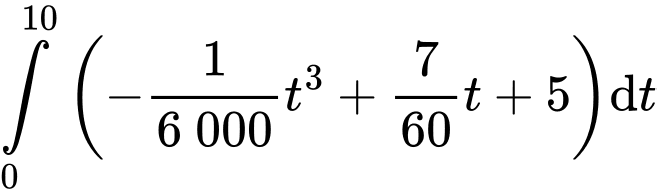
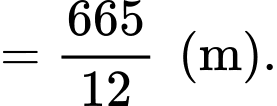
Tại thời điểm 10 giây, quãng đường vận động viên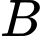 chạy được là
chạy được là
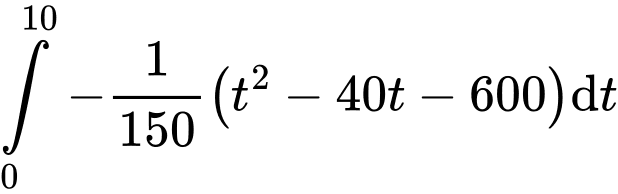
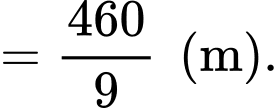
Tại thời điểm 10 giây, vận động viên dẫn trước vận động viên một khoảng bằng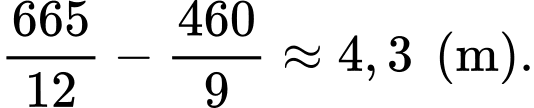
d) Sai.
Sau 30 giây, hai vận đông viên cách nhau một khoảng:
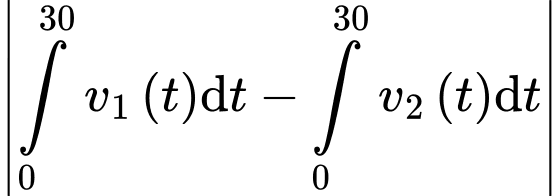
Quãng đường vận động viên
 đi được sau
đi được sau  giây là
giây là 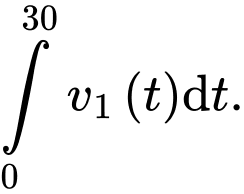
Quãng đường vận động viên
 đi được sau
đi được sau  giây là
giây là 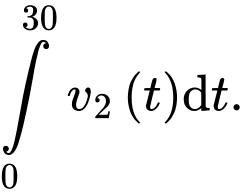
Vậy khoảng cách giữa hai vận động viên sau
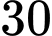 giây kể từ lúc xuất phát bằng diện tích phần tô đậm trong hình vẽ và bằng
giây kể từ lúc xuất phát bằng diện tích phần tô đậm trong hình vẽ và bằng 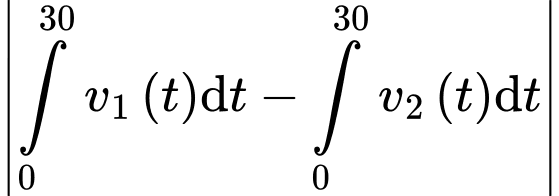
b) Đúng.
Do
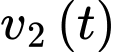 nên hàm số có dạng
nên hàm số có dạng 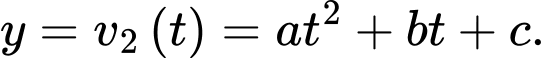
Đồ thị hàm số
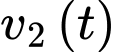 đi qua ba điểm
đi qua ba điểm 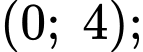
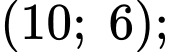
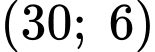 nên ta có:
nên ta có: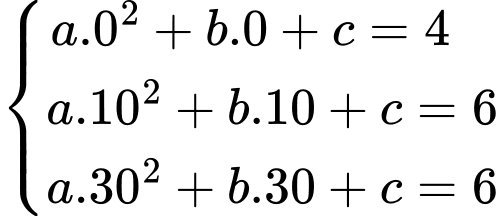
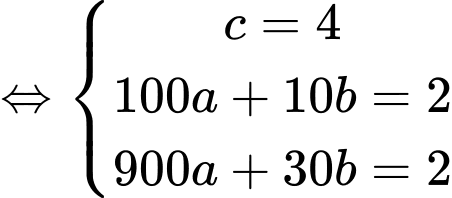
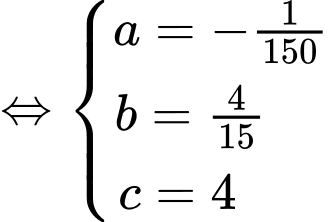
Vậy
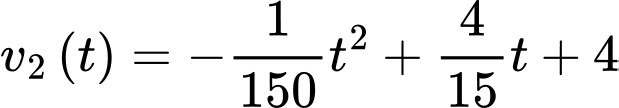
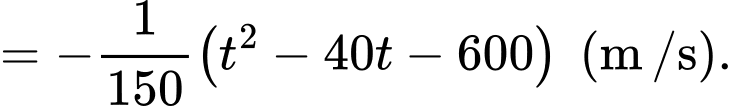
c) Đúng.
Tại thời điểm
 giây, quãng đường vận động viên
giây, quãng đường vận động viên 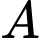 chạy được là
chạy được là
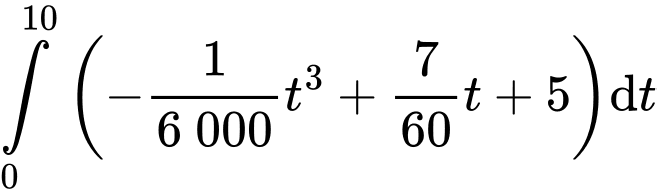
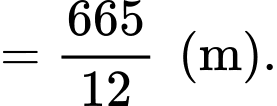
Tại thời điểm 10 giây, quãng đường vận động viên
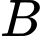 chạy được là
chạy được là
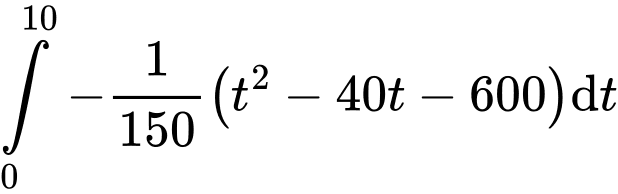
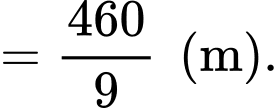
Tại thời điểm 10 giây, vận động viên dẫn trước vận động viên một khoảng bằng
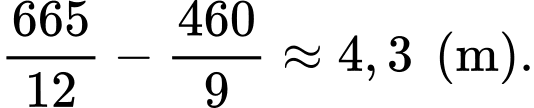
d) Sai.
Sau 30 giây, hai vận đông viên cách nhau một khoảng:
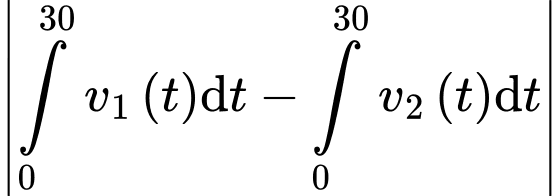
PHẦN III. Thí sinh trả lời từ câu 1 đến câu 6.
Câu 17 [682816]: Trong một phòng thí nghiệm thử nghiệm xe, tốc độ của một chiếc xe là 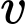 (km/h) tại thời điểm
(km/h) tại thời điểm 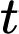 giờ được biểu diễn bởi hàm số
giờ được biểu diễn bởi hàm số 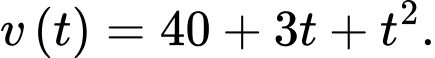 Tỷ lệ tiêu thụ xăng của xe là
Tỷ lệ tiêu thụ xăng của xe là  lít trên mỗi kilômét khi chạy với tốc độ
lít trên mỗi kilômét khi chạy với tốc độ 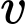 (km/h) được biểu diễn bởi hàm số
(km/h) được biểu diễn bởi hàm số 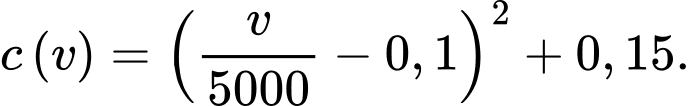 Tìm thời điểm (đơn vị: giờ) mà xe chạy tiết kiệm nhiên liệu nhất trong suốt 24 giờ đầu tiên.
Tìm thời điểm (đơn vị: giờ) mà xe chạy tiết kiệm nhiên liệu nhất trong suốt 24 giờ đầu tiên.
 (km/h) tại thời điểm
(km/h) tại thời điểm 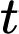 giờ được biểu diễn bởi hàm số
giờ được biểu diễn bởi hàm số 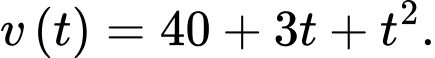 Tỷ lệ tiêu thụ xăng của xe là
Tỷ lệ tiêu thụ xăng của xe là  lít trên mỗi kilômét khi chạy với tốc độ
lít trên mỗi kilômét khi chạy với tốc độ 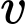 (km/h) được biểu diễn bởi hàm số
(km/h) được biểu diễn bởi hàm số 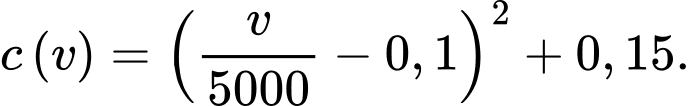 Tìm thời điểm (đơn vị: giờ) mà xe chạy tiết kiệm nhiên liệu nhất trong suốt 24 giờ đầu tiên.
Tìm thời điểm (đơn vị: giờ) mà xe chạy tiết kiệm nhiên liệu nhất trong suốt 24 giờ đầu tiên.
Điền đáp án: 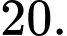
Ta có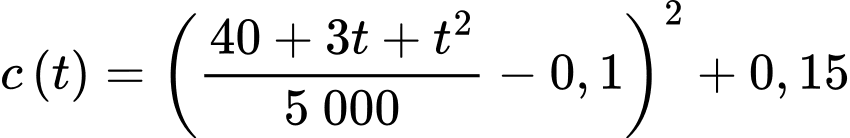
Để tìm thời điểm mà xe chạy tiết kiệm nhiên liệu nhất, ta tìm GTNN của trên
trên 
Ta có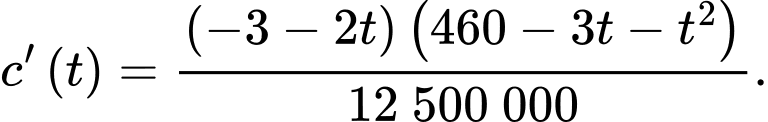
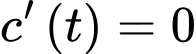
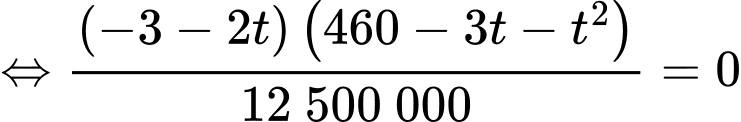
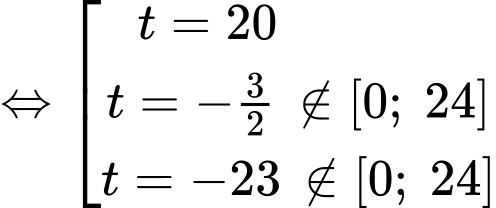
Ta có bảng biến thiên:
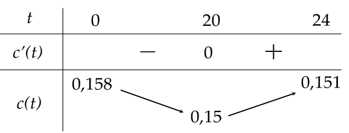
Vậy xe chạy tiết kiệm nhiên liệu nhất là thời điểm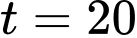 giờ.
giờ.
Ta có
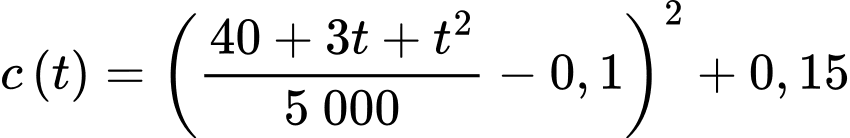
Để tìm thời điểm mà xe chạy tiết kiệm nhiên liệu nhất, ta tìm GTNN của
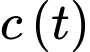 trên
trên 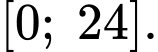
Ta có
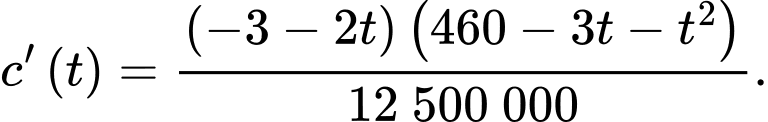
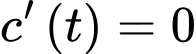
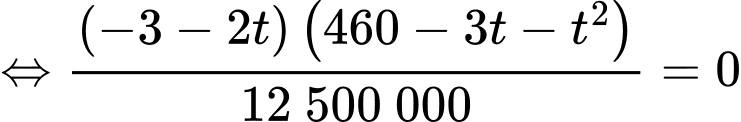
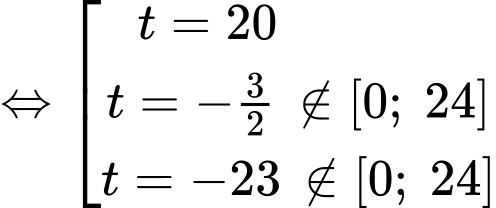
Ta có bảng biến thiên:

Vậy xe chạy tiết kiệm nhiên liệu nhất là thời điểm
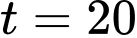 giờ.
giờ.
Câu 18 [695199]: Chín giỏ trứng chứa số trứng lần lượt là: 4, 5, 7, 8, 12, 13, 14, 23 và 24. Bất kỳ ai muốn mua trứng đều phải mua tất cả trứng trong một giỏ. Mai và Đào mỗi người đã mua bốn giỏ. Nếu số quả trứng mà Mai mua gấp ba lần số quả trứng mà Đào mua thì Mai mua nhiều hơn Đào bao nhiêu quả trứng?
Điền đáp án: 
Gọi số trứng trong giỏ còn lại là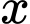 (quả).
(quả).
Ta có tổng số trứng trong 9 giỏ là 110 (quả).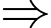 Tổng số trứng mà Mai và Đào mua là
Tổng số trứng mà Mai và Đào mua là 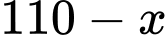 (quả).
(quả).
Gọi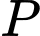 (quả) là số trứng mà Đào mua
(quả) là số trứng mà Đào mua  Số trứng mà Mai mua là
Số trứng mà Mai mua là 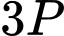 (quả)
(quả)  Số trứng mà Mai mua nhiều hơn Đào mua là
Số trứng mà Mai mua nhiều hơn Đào mua là 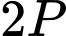 (quả).
(quả).
Ta có: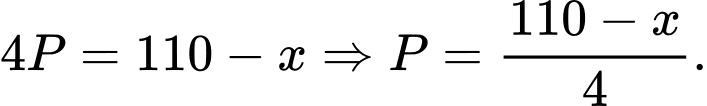
TH1: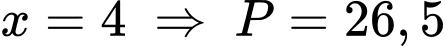 (loại).
(loại).
TH2: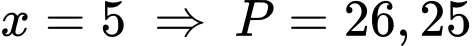 (loại).
(loại).
TH3: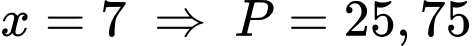 (loại).
(loại).
TH4: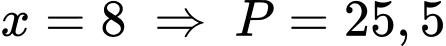 (loại).
(loại).
TH5: (loại).
(loại).
TH6: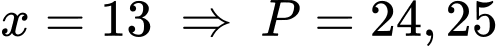 (loại).
(loại).
TH7: (thỏa mãn).
(thỏa mãn).
TH8: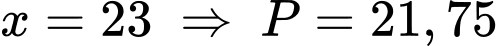 (loại).
(loại).
TH9: (loại).
(loại).
Vậy số trứng mà Mai mua nhiều hơn Đào là 48 quả trứng.
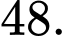
Gọi số trứng trong giỏ còn lại là
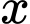 (quả).
(quả).Ta có tổng số trứng trong 9 giỏ là 110 (quả).
 Tổng số trứng mà Mai và Đào mua là
Tổng số trứng mà Mai và Đào mua là 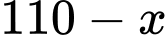 (quả).
(quả).Gọi
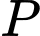 (quả) là số trứng mà Đào mua
(quả) là số trứng mà Đào mua  Số trứng mà Mai mua là
Số trứng mà Mai mua là 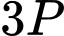 (quả)
(quả)  Số trứng mà Mai mua nhiều hơn Đào mua là
Số trứng mà Mai mua nhiều hơn Đào mua là 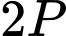 (quả).
(quả).Ta có:
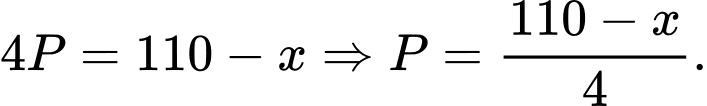
TH1:
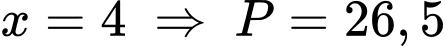 (loại).
(loại).TH2:
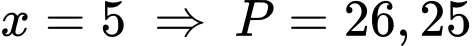 (loại).
(loại).TH3:
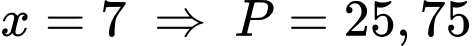 (loại).
(loại).TH4:
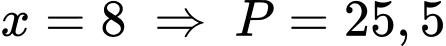 (loại).
(loại).TH5:
 (loại).
(loại).TH6:
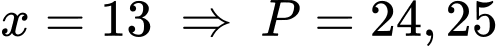 (loại).
(loại).TH7:
 (thỏa mãn).
(thỏa mãn).TH8:
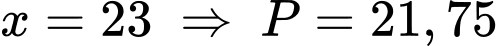 (loại).
(loại).TH9:
 (loại).
(loại).Vậy số trứng mà Mai mua nhiều hơn Đào là 48 quả trứng.
Câu 19 [701398]: Nước bốc hơi khỏi hồ với tốc độ tỷ lệ thuận với thể tích nước còn lại. Giả sử 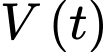 là tổng lượng nước bốc hơi sau
là tổng lượng nước bốc hơi sau 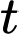 ngày và
ngày và 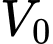 là thể tích nước ban đầu trong hồ thì ta có:
là thể tích nước ban đầu trong hồ thì ta có:  Nếu 50% lượng nước bốc hơi trong 20 ngày, hãy tìm phần trăm lượng nước còn lại sau 50 ngày không mưa (kết quả làm tròn đến hàng phần chục).
Nếu 50% lượng nước bốc hơi trong 20 ngày, hãy tìm phần trăm lượng nước còn lại sau 50 ngày không mưa (kết quả làm tròn đến hàng phần chục).

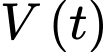 là tổng lượng nước bốc hơi sau
là tổng lượng nước bốc hơi sau 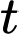 ngày và
ngày và 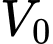 là thể tích nước ban đầu trong hồ thì ta có:
là thể tích nước ban đầu trong hồ thì ta có:  Nếu 50% lượng nước bốc hơi trong 20 ngày, hãy tìm phần trăm lượng nước còn lại sau 50 ngày không mưa (kết quả làm tròn đến hàng phần chục).
Nếu 50% lượng nước bốc hơi trong 20 ngày, hãy tìm phần trăm lượng nước còn lại sau 50 ngày không mưa (kết quả làm tròn đến hàng phần chục).
Điền đáp án: 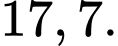
Ta có:
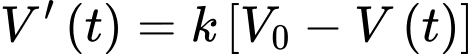
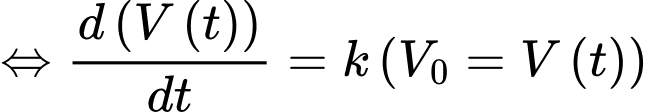
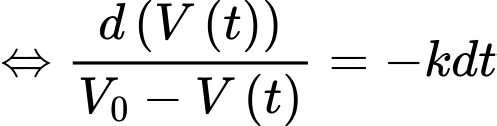
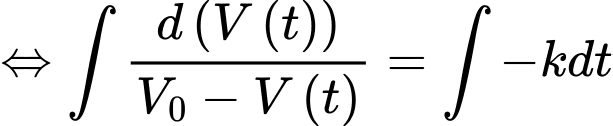

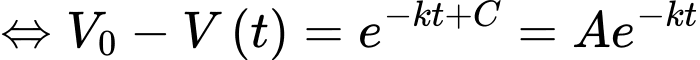
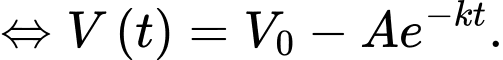
 nên
nên 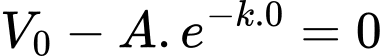
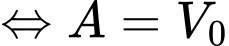

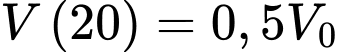
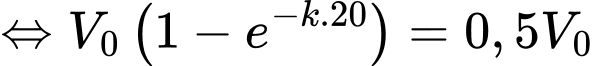
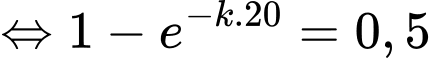
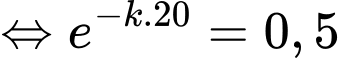
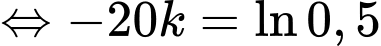
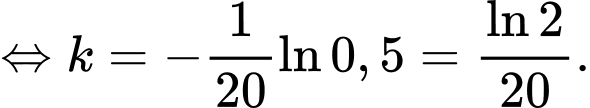
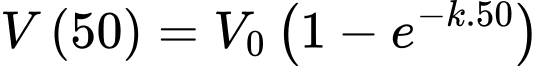
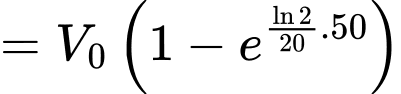
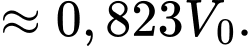
Vậy sau 50 ngày không có mưa, khoảng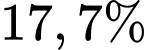 lượng nước ban đầu vẫn còn trong hồ.
lượng nước ban đầu vẫn còn trong hồ.
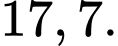
Ta có:
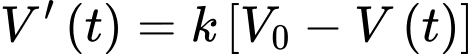
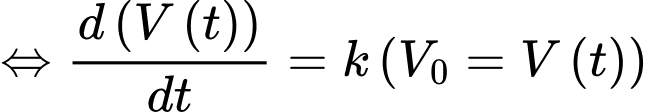
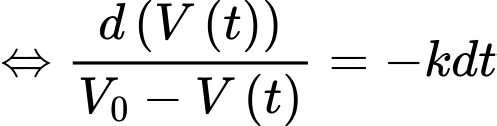
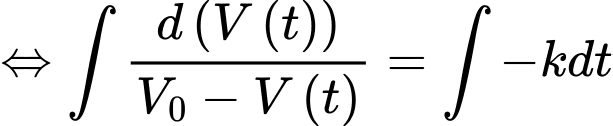

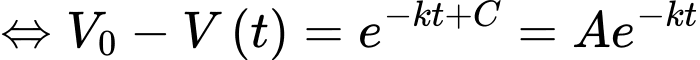
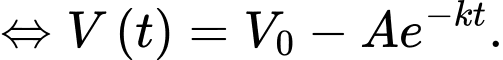
 nên
nên 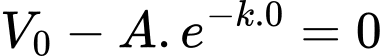
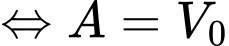

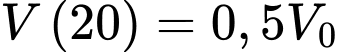
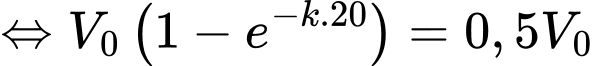
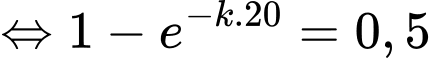
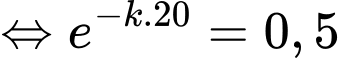
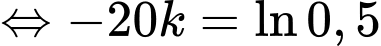
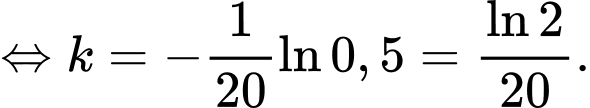
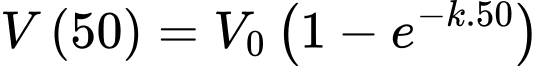
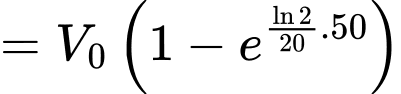
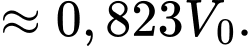
Vậy sau 50 ngày không có mưa, khoảng
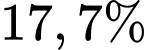 lượng nước ban đầu vẫn còn trong hồ.
lượng nước ban đầu vẫn còn trong hồ.
Câu 20 [695201]: Một chiếc bồn chứa xăng có dạng hình trụ dài 8,5 m và đường kính đáy bằng 2,4 m. Người ta đo được khoảng cách từ mép trên của chiếc bồn đến mặt xăng nằm ngang là 0,6 m. Thể tích xăng chứa trong chiếc bồn đó bằng bao nhiêu mét khối? (bỏ qua độ dày thành bồn, kết quả làm tròn đến hàng phần trăm).


Điền đáp án: 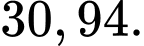
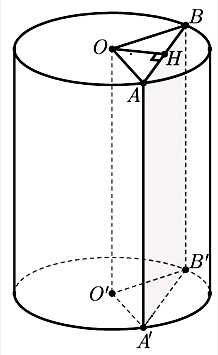
Ký hiệu các điểm như hình vẽ.
Ta có: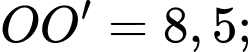
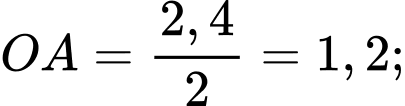
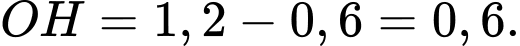
Ta có:

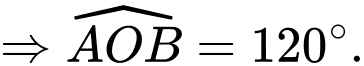
Vì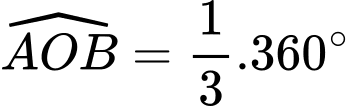 nên thể tích phần hình trụ (phần nhỏ) bị giới hạn bởi mặt phẳng
nên thể tích phần hình trụ (phần nhỏ) bị giới hạn bởi mặt phẳng 
 bằng
bằng 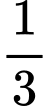 thể tích khối trụ.
thể tích khối trụ.
Suy ra thể tích cần tính bằng
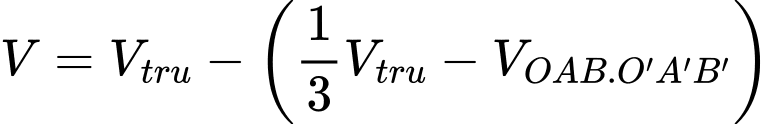
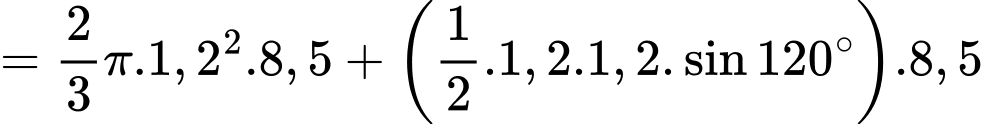
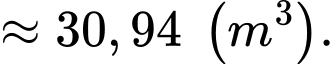
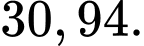

Ký hiệu các điểm như hình vẽ.
Ta có:
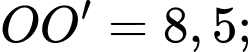
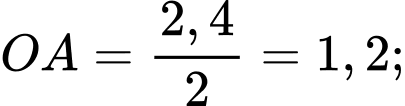
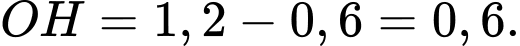
Ta có:


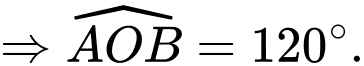
Vì
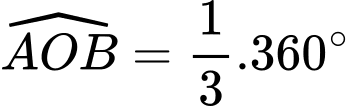 nên thể tích phần hình trụ (phần nhỏ) bị giới hạn bởi mặt phẳng
nên thể tích phần hình trụ (phần nhỏ) bị giới hạn bởi mặt phẳng 
 bằng
bằng 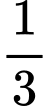 thể tích khối trụ.
thể tích khối trụ.Suy ra thể tích cần tính bằng
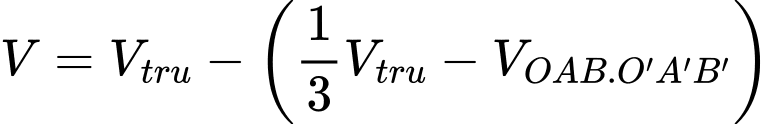
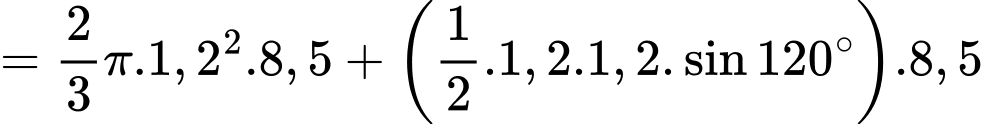
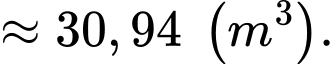
Câu 21 [695204]: Trong không gian 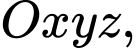 cho điểm
cho điểm 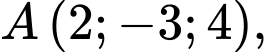 đường thẳng
đường thẳng 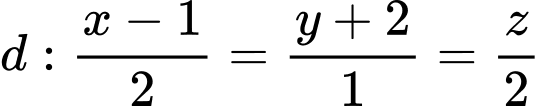 và mặt cầu
và mặt cầu 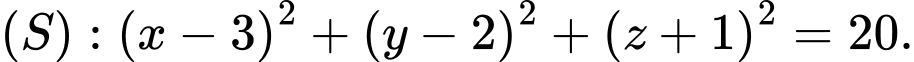 Mặt phẳng
Mặt phẳng 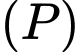 chứa đường thẳng
chứa đường thẳng 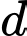 thỏa mãn khoảng cách từ điểm
thỏa mãn khoảng cách từ điểm 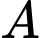 đến
đến 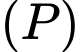 lớn nhất. Mặt cầu
lớn nhất. Mặt cầu 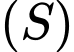 cắt
cắt 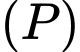 theo đường tròn có bán kính bằng bao nhiêu?
theo đường tròn có bán kính bằng bao nhiêu?
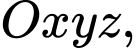 cho điểm
cho điểm 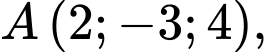 đường thẳng
đường thẳng 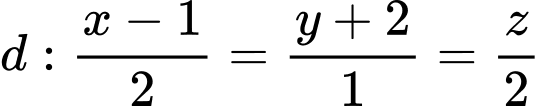 và mặt cầu
và mặt cầu 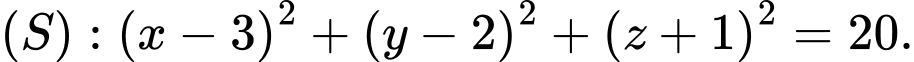 Mặt phẳng
Mặt phẳng 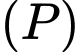 chứa đường thẳng
chứa đường thẳng 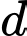 thỏa mãn khoảng cách từ điểm
thỏa mãn khoảng cách từ điểm 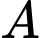 đến
đến 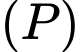 lớn nhất. Mặt cầu
lớn nhất. Mặt cầu 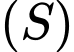 cắt
cắt 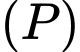 theo đường tròn có bán kính bằng bao nhiêu?
theo đường tròn có bán kính bằng bao nhiêu?
Điền đáp án: 
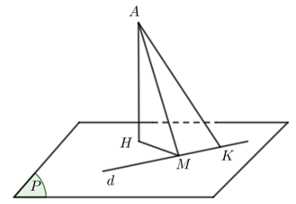
Ta có:
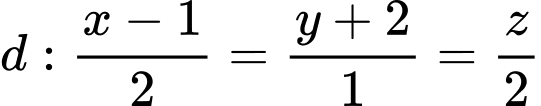 đi qua
đi qua 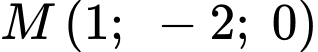 và có VTCP
và có VTCP 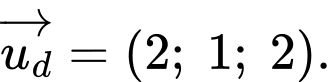
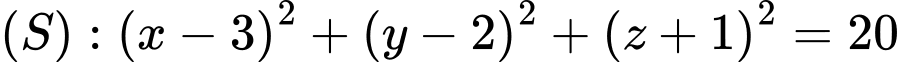 có tâm
có tâm 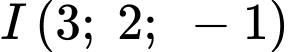 và bán kính
và bán kính 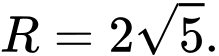
Ta có: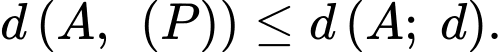
Dấu bằng xảy ra khi: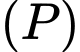 chứa
chứa 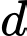 và vuông góc với
và vuông góc với 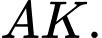
Khi đó: có VTPT
có VTPT 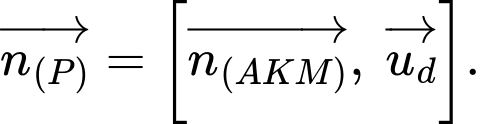
Vì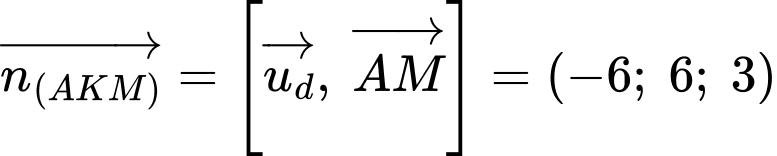
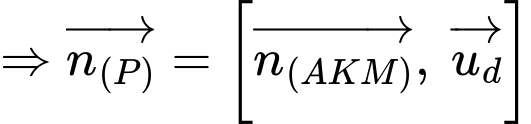
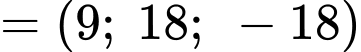
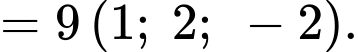
 đi qua
đi qua 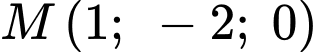 và có VTPT
và có VTPT 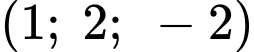 có phương trình là:
có phương trình là: 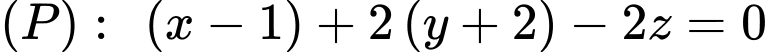
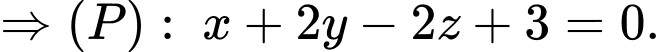
Ta có: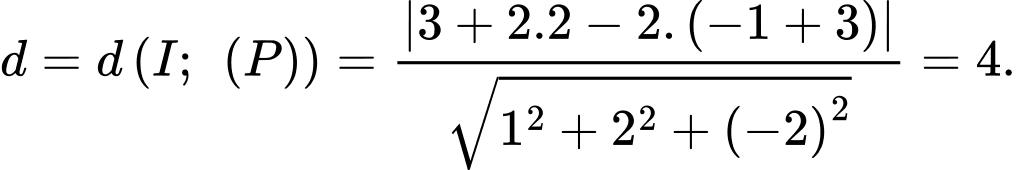
Vậy bán kính đường tròn cần tìm là:
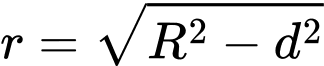
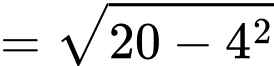
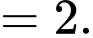
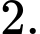

Ta có:
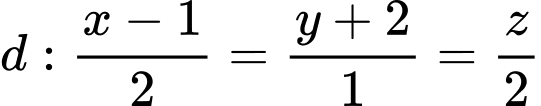 đi qua
đi qua 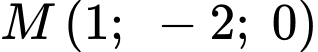 và có VTCP
và có VTCP 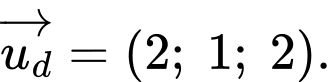
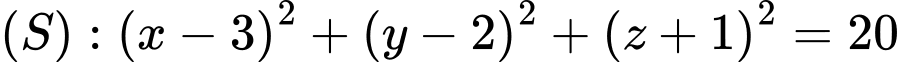 có tâm
có tâm 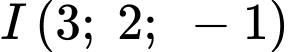 và bán kính
và bán kính 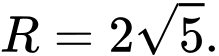
Ta có:
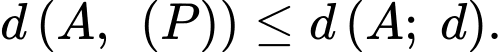
Dấu bằng xảy ra khi:
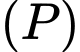 chứa
chứa 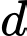 và vuông góc với
và vuông góc với 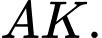
Khi đó:
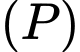 có VTPT
có VTPT 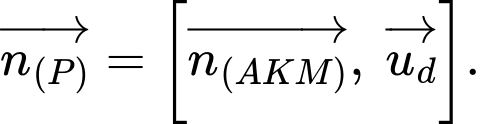
Vì
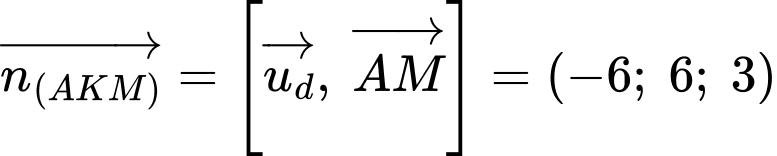
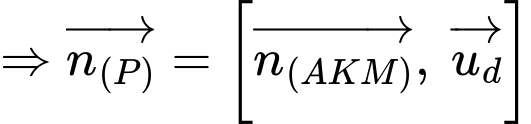
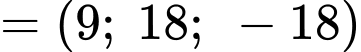
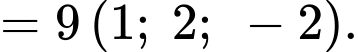
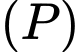 đi qua
đi qua 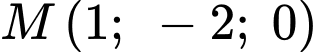 và có VTPT
và có VTPT 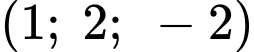 có phương trình là:
có phương trình là: 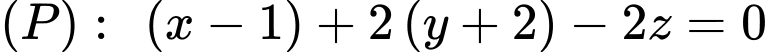
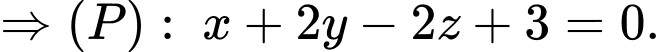
Ta có:
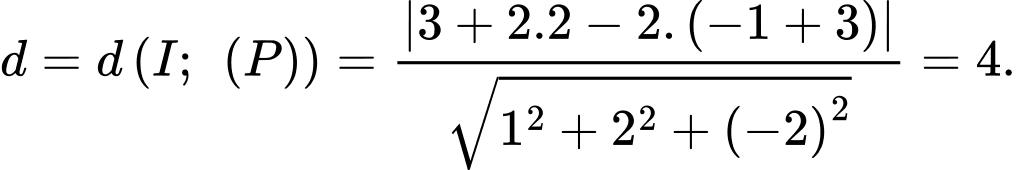
Vậy bán kính đường tròn cần tìm là:
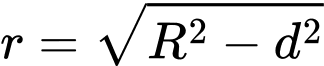
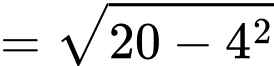
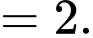
Câu 22 [694841]: Một phiên toà đang nghiên cứu khả năng xảy ra một vụ án T. Theo thống kê người ta thấy xác suất của sự kiện 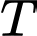 là
là 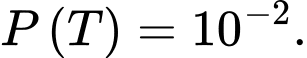 Hai nhân chứng A và B được mời đến dự phiên toà (với độ tin cậy những lời khai của A và B nói đúng với xác suất cùng là 0,9). Giả sử rằng cả A và B độc lập với nhau và đều tuyên bố “T” xảy ra. Khi đó, xác suất xảy ra của T là bao nhiêu %?
Hai nhân chứng A và B được mời đến dự phiên toà (với độ tin cậy những lời khai của A và B nói đúng với xác suất cùng là 0,9). Giả sử rằng cả A và B độc lập với nhau và đều tuyên bố “T” xảy ra. Khi đó, xác suất xảy ra của T là bao nhiêu %?
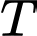 là
là 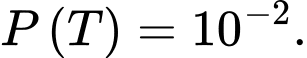 Hai nhân chứng A và B được mời đến dự phiên toà (với độ tin cậy những lời khai của A và B nói đúng với xác suất cùng là 0,9). Giả sử rằng cả A và B độc lập với nhau và đều tuyên bố “T” xảy ra. Khi đó, xác suất xảy ra của T là bao nhiêu %?
Hai nhân chứng A và B được mời đến dự phiên toà (với độ tin cậy những lời khai của A và B nói đúng với xác suất cùng là 0,9). Giả sử rằng cả A và B độc lập với nhau và đều tuyên bố “T” xảy ra. Khi đó, xác suất xảy ra của T là bao nhiêu %?
Điền đáp án: 45.
Gọi là biến cố “Nhân chứng A và B cùng tuyên bố T xảy ra”
là biến cố “Nhân chứng A và B cùng tuyên bố T xảy ra”
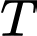 là biến cố “Vụ án “T” xảy ra”
là biến cố “Vụ án “T” xảy ra”
Yêu cầu bài toán Tính
Tính 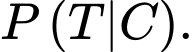
Từ dữ kiện đề bài, ta có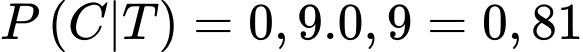 (vì A và B độc lập với nhau);
(vì A và B độc lập với nhau);
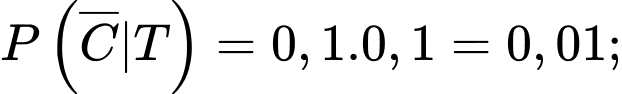
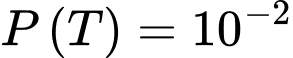
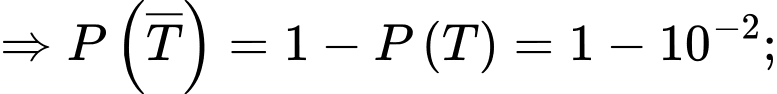
Ta có sơ đồ cây sau:
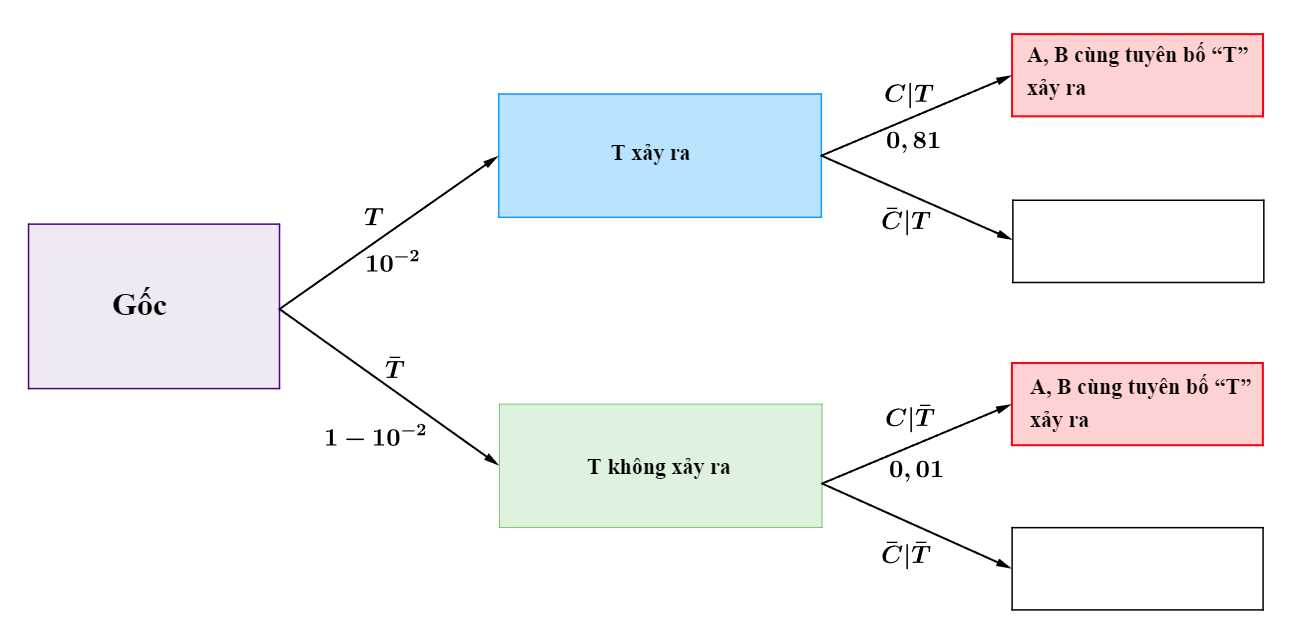
Suy ra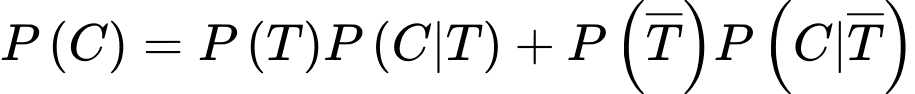
Theo công thức Bayes, ta có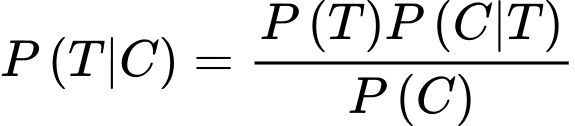
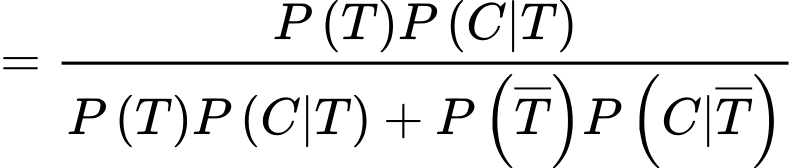
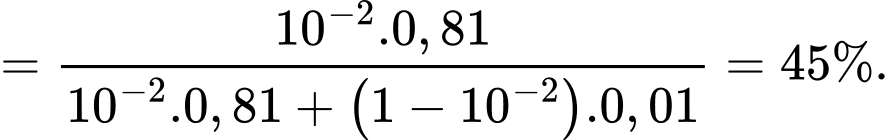
Vậy xác suất xảy ra của T khi biết A và B cùng tuyên bố “T” xảy ra là 45%.
Gọi
 là biến cố “Nhân chứng A và B cùng tuyên bố T xảy ra”
là biến cố “Nhân chứng A và B cùng tuyên bố T xảy ra”
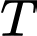 là biến cố “Vụ án “T” xảy ra”
là biến cố “Vụ án “T” xảy ra”
Yêu cầu bài toán
 Tính
Tính 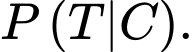
Từ dữ kiện đề bài, ta có
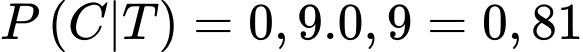 (vì A và B độc lập với nhau);
(vì A và B độc lập với nhau);
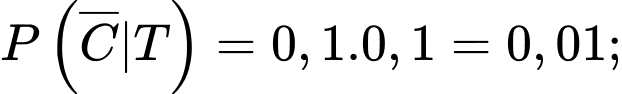
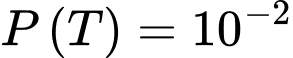
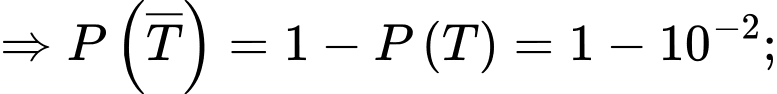
Ta có sơ đồ cây sau:

Suy ra
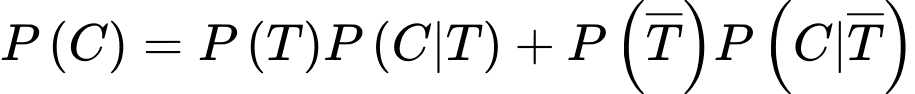
Theo công thức Bayes, ta có
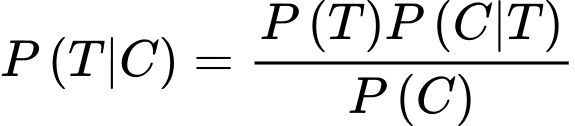
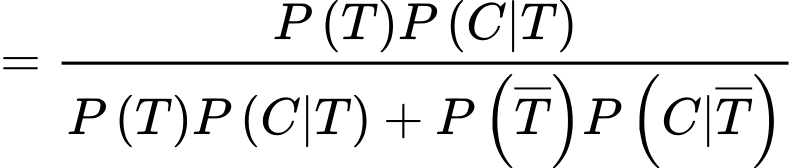
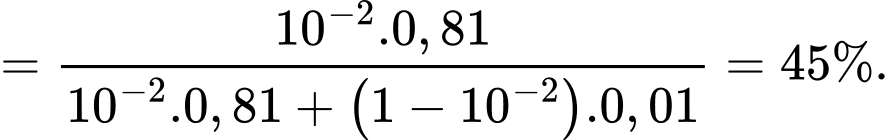
Vậy xác suất xảy ra của T khi biết A và B cùng tuyên bố “T” xảy ra là 45%.