PHẦN I. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Câu 1 [695231]: Trong không gian 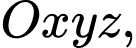 điểm nào dưới đây thuộc mặt phẳng
điểm nào dưới đây thuộc mặt phẳng 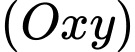 ?
?
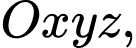 điểm nào dưới đây thuộc mặt phẳng
điểm nào dưới đây thuộc mặt phẳng 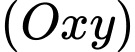 ?
? A, 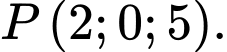
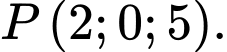
B, 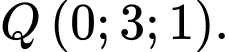
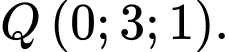
C, 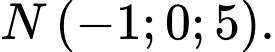
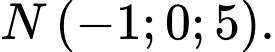
D, 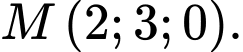
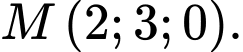
Chọn đáp án D.
Trong không gian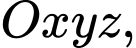 điểm thuộc mặt phẳng
điểm thuộc mặt phẳng 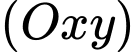 sẽ có cao độ
sẽ có cao độ 
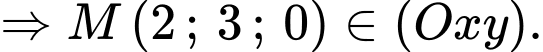 Đáp án: D
Đáp án: D
Trong không gian
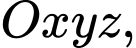 điểm thuộc mặt phẳng
điểm thuộc mặt phẳng 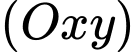 sẽ có cao độ
sẽ có cao độ 
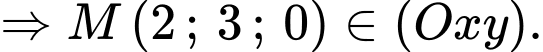 Đáp án: D
Đáp án: D
Câu 2 [695232]: Từ một đội văn nghệ gồm 6 nam và 5 nữ, có bao nhiêu cách chọn một nam và một nữ để hát song ca với nhau?
A, 
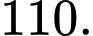
B, 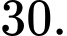
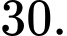
C, 

D, 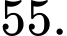
Chọn đáp án B.
Số cách chọn 1 nam, 1 nữ là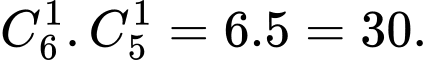 Đáp án: B
Đáp án: B
Số cách chọn 1 nam, 1 nữ là
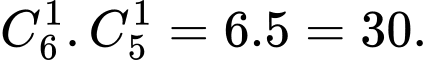 Đáp án: B
Đáp án: B
Câu 3 [333934]: Cho hàm số 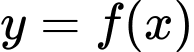 có bảng biến thiên như sau:
có bảng biến thiên như sau:
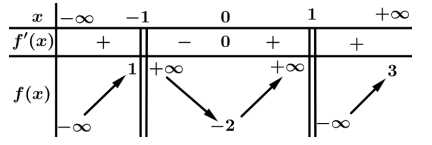
Tổng số tiệm cận đứng và tiệm cận ngang của đồ thị hàm số là
 có bảng biến thiên như sau:
có bảng biến thiên như sau:
Tổng số tiệm cận đứng và tiệm cận ngang của đồ thị hàm số là
Theo bảng biến thiên ta thấy 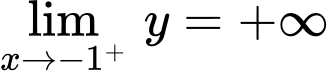
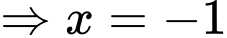 là các tiệm cận đứng bên phải của đồ thị hàm số.
là các tiệm cận đứng bên phải của đồ thị hàm số.
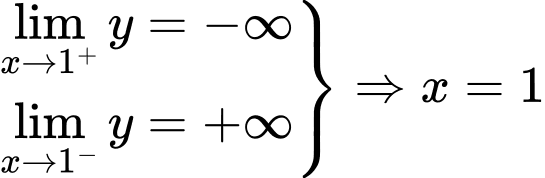 là tiệm cận đứng của đồ thị hàm số.
là tiệm cận đứng của đồ thị hàm số.
Lại có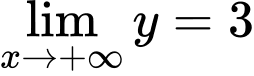
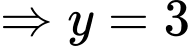 là tiệm cận ngang của đồ thị hàm số.
là tiệm cận ngang của đồ thị hàm số.
Vậy tổng số tiệm cận đứng và tiệm cận ngang của đồ thị hàm số là 3.
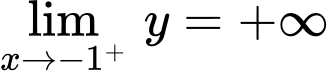
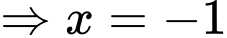 là các tiệm cận đứng bên phải của đồ thị hàm số.
là các tiệm cận đứng bên phải của đồ thị hàm số. 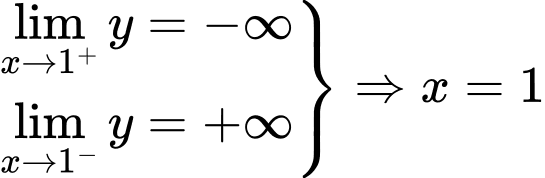 là tiệm cận đứng của đồ thị hàm số.
là tiệm cận đứng của đồ thị hàm số. Lại có
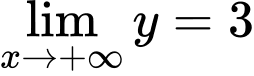
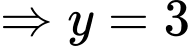 là tiệm cận ngang của đồ thị hàm số.
là tiệm cận ngang của đồ thị hàm số. Vậy tổng số tiệm cận đứng và tiệm cận ngang của đồ thị hàm số là 3.
Câu 4 [695233]: Cho tứ diện đều 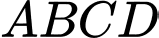 cạnh
cạnh 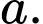 Góc giữa hai vectơ
Góc giữa hai vectơ 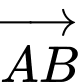 và
và 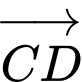 bằng
bằng
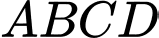 cạnh
cạnh 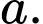 Góc giữa hai vectơ
Góc giữa hai vectơ 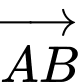 và
và 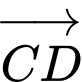 bằng
bằng A, 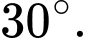
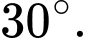
B, 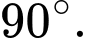
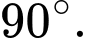
C, 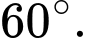
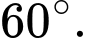
D, 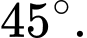
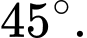
Chọn đáp án B.
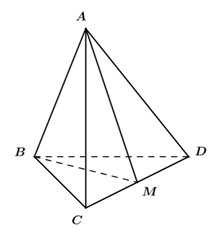
Gọi M là trung điểm của đoạn thẳng CD.
Vì ABCD là tứ diện đều nên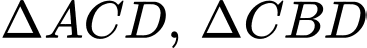 là tam giác đều
là tam giác đều
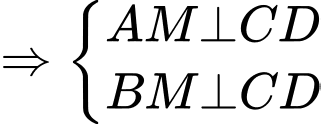
Suy ra mà
mà 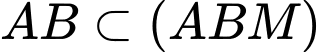 nên
nên  do đó
do đó 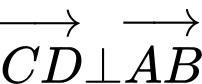
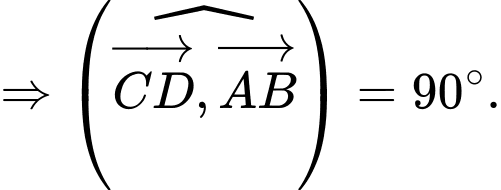 Đáp án: B
Đáp án: B

Gọi M là trung điểm của đoạn thẳng CD.
Vì ABCD là tứ diện đều nên
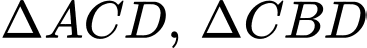 là tam giác đều
là tam giác đều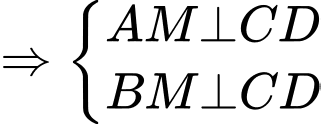
Suy ra
 mà
mà 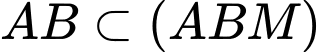 nên
nên  do đó
do đó 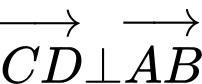
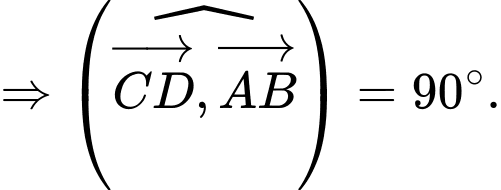 Đáp án: B
Đáp án: B
Câu 5 [695234]: Tập xác định của hàm số 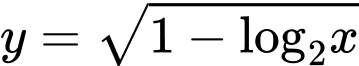 là
là
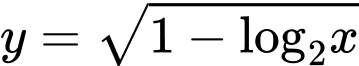 là
là A, 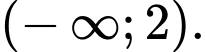
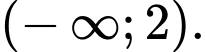
B, 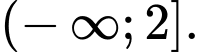
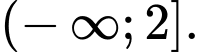
C, 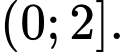
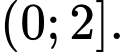
D, 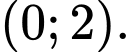
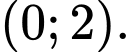
Chọn đáp án C.
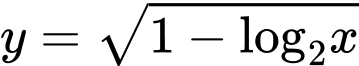
Ta có điều kiện xác định của hàm số là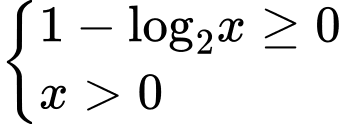
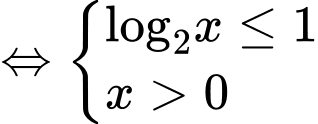
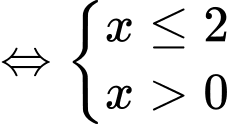
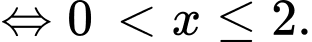 Đáp án: C
Đáp án: C
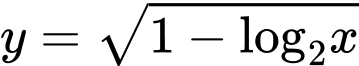
Ta có điều kiện xác định của hàm số là
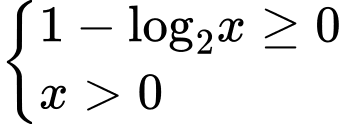
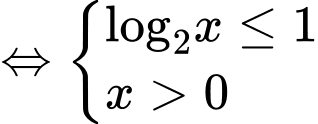
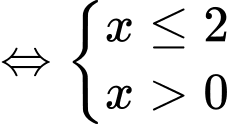
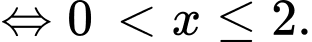 Đáp án: C
Đáp án: C
Câu 6 [258297]: Cho cấp số nhân 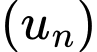 với
với 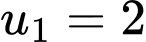 và
và 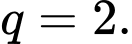 Có bao nhiêu số nguyên dương
Có bao nhiêu số nguyên dương 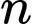 thỏa mãn
thỏa mãn  ?
?
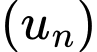 với
với 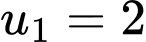 và
và 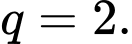 Có bao nhiêu số nguyên dương
Có bao nhiêu số nguyên dương 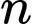 thỏa mãn
thỏa mãn  ?
? A, 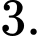
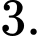
B, 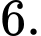
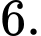
C, 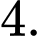
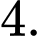
D, 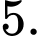
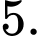
Chọn đáp án D.
Ta có cấp số nhân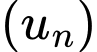 với
với 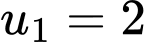 và
và 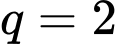
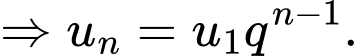
Xét bất phương trình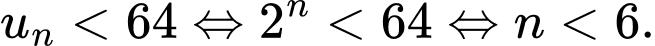 Vậy có 5 giá trị của
Vậy có 5 giá trị của 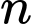 thỏa mãn. Đáp án: D
thỏa mãn. Đáp án: D
Ta có cấp số nhân
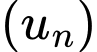 với
với 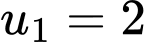 và
và 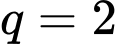
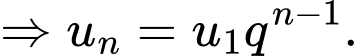
Xét bất phương trình
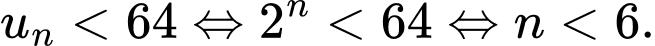 Vậy có 5 giá trị của
Vậy có 5 giá trị của 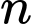 thỏa mãn. Đáp án: D
thỏa mãn. Đáp án: D
Câu 7 [258315]: Cho hàm số 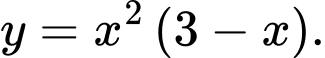 Khẳng định nào sau đây là đúng?
Khẳng định nào sau đây là đúng?
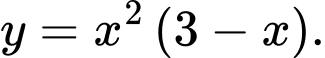 Khẳng định nào sau đây là đúng?
Khẳng định nào sau đây là đúng? A, Hàm số đã cho nghịch biến trên khoảng 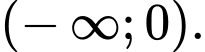
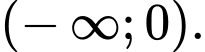
B, Hàm số đã cho nghịch biến trên khoảng 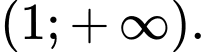
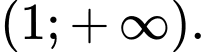
C, Hàm số đã cho nghịch biến trên khoảng 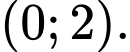
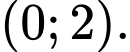
D, Hàm số đã cho nghịch biến trên khoảng 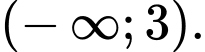
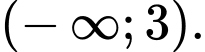
Chọn đáp án A.
Xét hàm số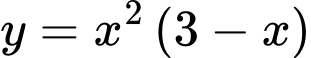 có
có 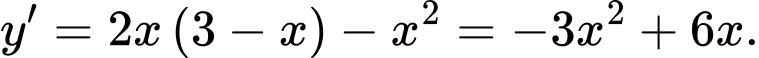
Ta có bất phương trình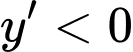
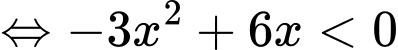
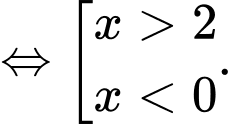
Vậy hàm số nghịch biến trên khoảng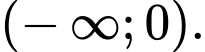 Đáp án: A
Đáp án: A
Xét hàm số
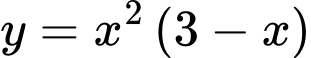 có
có 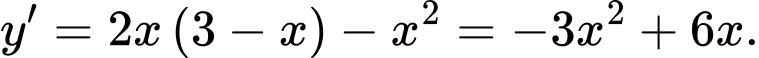
Ta có bất phương trình
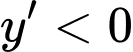
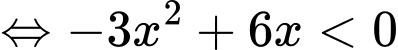
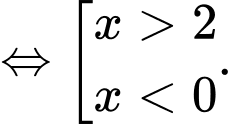
Vậy hàm số nghịch biến trên khoảng
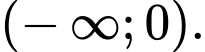 Đáp án: A
Đáp án: A
Câu 8 [695235]: Cho khối lăng trụ tam giác có thể tích 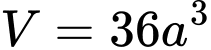 và diện tích đáy
và diện tích đáy 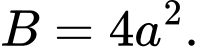 Chiều cao của khối lăng trụ đã cho bằng
Chiều cao của khối lăng trụ đã cho bằng
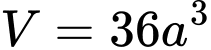 và diện tích đáy
và diện tích đáy 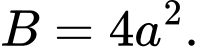 Chiều cao của khối lăng trụ đã cho bằng
Chiều cao của khối lăng trụ đã cho bằng A, 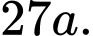
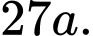
B, 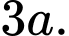
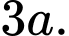
C, 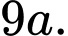
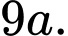
D, 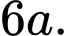
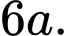
Chọn đáp án C.
Ta có: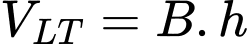
Mà khối lăng trụ tam giác có thể tích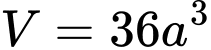 và diện tích đáy
và diện tích đáy 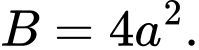
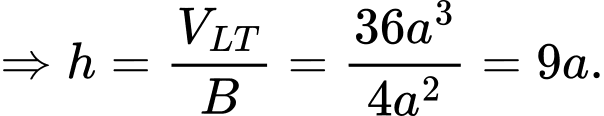 Đáp án: C
Đáp án: C
Ta có:
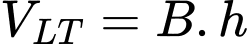
Mà khối lăng trụ tam giác có thể tích
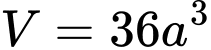 và diện tích đáy
và diện tích đáy 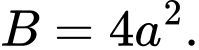
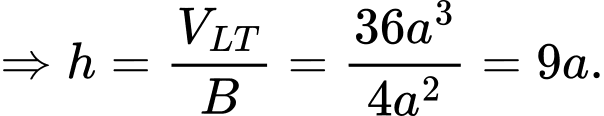 Đáp án: C
Đáp án: C
Câu 9 [695236]: Diện tích hình phẳng giới hạn bởi các đường 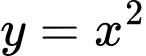 và
và 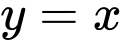 bằng
bằng
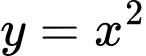 và
và 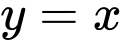 bằng
bằng A, 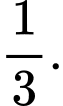
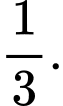
B, 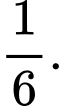
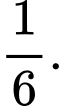
C, 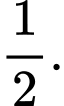
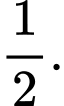
D, 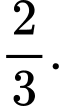
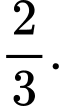
Chọn đáp án B.
Diện tích hình phẳng giới hạn bởi các đường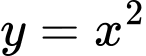 và
và 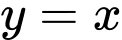 là:
là:
Ta có phương trình hoành độ giao điểm của các đường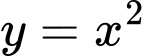 và
và 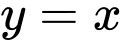 là
là
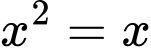
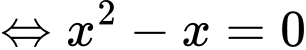
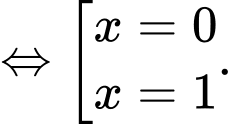
Ta có công thức tính diện tích hình phẳng là:
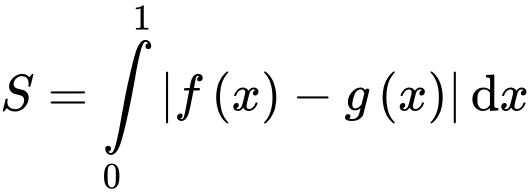
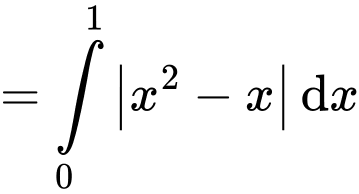
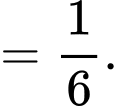 Đáp án: B
Đáp án: B
Diện tích hình phẳng giới hạn bởi các đường
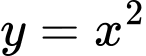 và
và 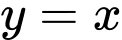 là:
là:
Ta có phương trình hoành độ giao điểm của các đường
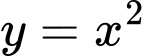 và
và 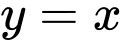 là
là
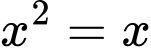
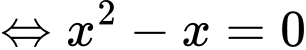
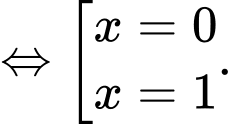
Ta có công thức tính diện tích hình phẳng là:
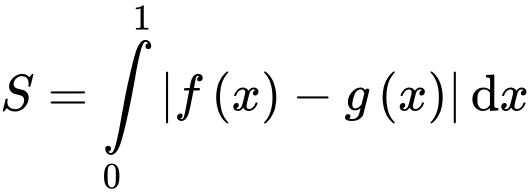
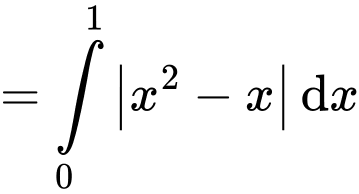
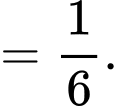 Đáp án: B
Đáp án: B
Câu 10 [695237]: Với 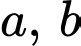 là hai số thực lớn hơn
là hai số thực lớn hơn 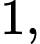
 bằng
bằng
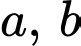 là hai số thực lớn hơn
là hai số thực lớn hơn 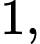
 bằng
bằng A, 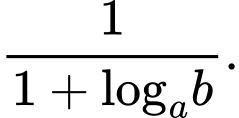
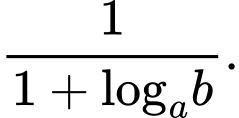
B, 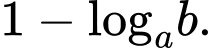
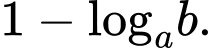
C, 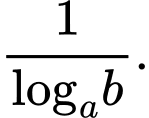
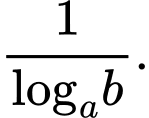
D, 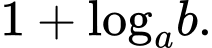
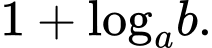
Chọn đáp án A.
Ta có:
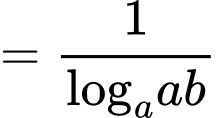
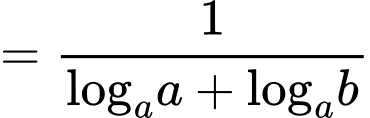
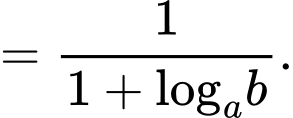 Đáp án: A
Đáp án: A
Ta có:

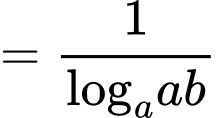
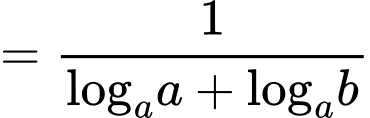
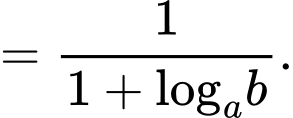 Đáp án: A
Đáp án: A
Câu 11 [695238]: Một vật chuyển động với vận tốc 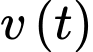 (m/s) có gia tốc
(m/s) có gia tốc 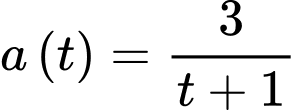 (m/s2). Vận tốc ban đầu của vật là 6 (m/s). Hỏi sau 10 giây vận tốc của vật bằng bao nhiêu? (làm tròn kết quả đến hàng đơn vị).
(m/s2). Vận tốc ban đầu của vật là 6 (m/s). Hỏi sau 10 giây vận tốc của vật bằng bao nhiêu? (làm tròn kết quả đến hàng đơn vị).
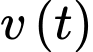 (m/s) có gia tốc
(m/s) có gia tốc 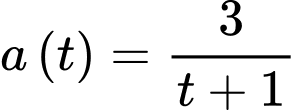 (m/s2). Vận tốc ban đầu của vật là 6 (m/s). Hỏi sau 10 giây vận tốc của vật bằng bao nhiêu? (làm tròn kết quả đến hàng đơn vị).
(m/s2). Vận tốc ban đầu của vật là 6 (m/s). Hỏi sau 10 giây vận tốc của vật bằng bao nhiêu? (làm tròn kết quả đến hàng đơn vị). A,  (m/s).
(m/s).
 (m/s).
(m/s).B,  (m/s).
(m/s).
 (m/s).
(m/s).C, 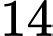 (m/s).
(m/s).
 (m/s).
(m/s).D,  (m/s).
(m/s).
 (m/s).
(m/s).
Chọn đáp án B.
Ta có: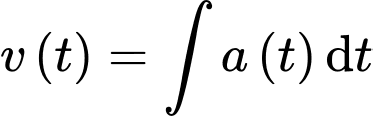
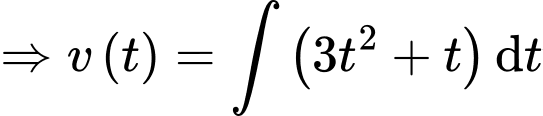
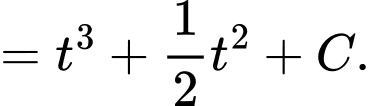
Vận tốc ban đầu của chất điểm là 2 (m/s)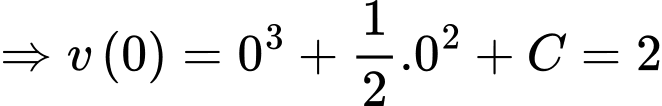
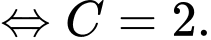
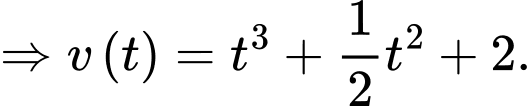
Sau 2 giây vận tốc của chất điểm là: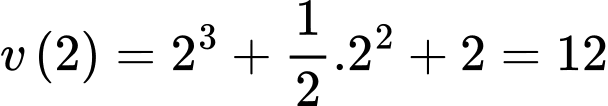 (m/s).
Đáp án: B
(m/s).
Đáp án: B
Ta có:
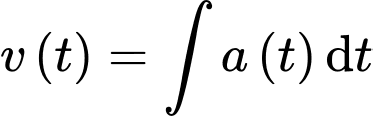
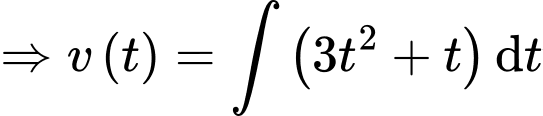
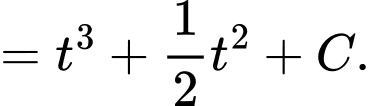
Vận tốc ban đầu của chất điểm là 2 (m/s)
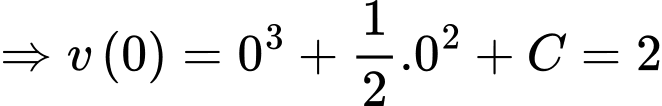
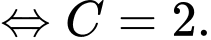
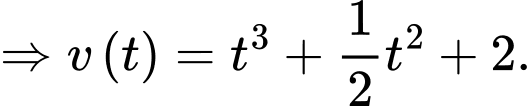
Sau 2 giây vận tốc của chất điểm là:
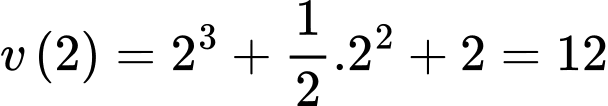 (m/s).
Đáp án: B
(m/s).
Đáp án: B
Câu 12 [258332]: Trong không gian 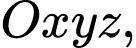 cho hai điểm
cho hai điểm 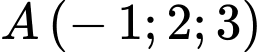 và
và  Phương trình đường trung tuyến
Phương trình đường trung tuyến 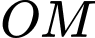 của tam giác
của tam giác 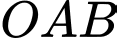 là
là
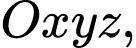 cho hai điểm
cho hai điểm 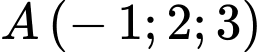 và
và  Phương trình đường trung tuyến
Phương trình đường trung tuyến 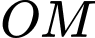 của tam giác
của tam giác 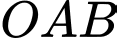 là
là A, 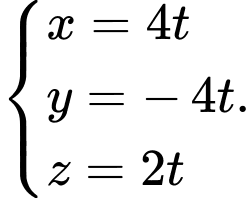
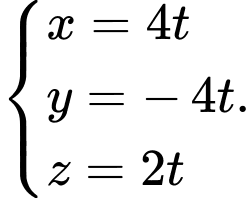
B, 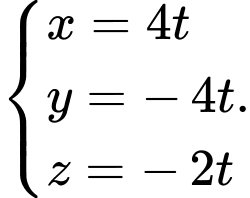
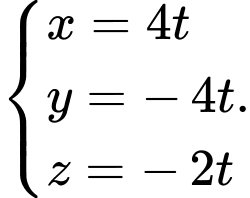
C, 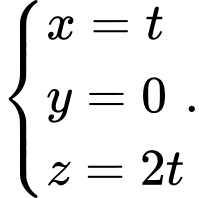
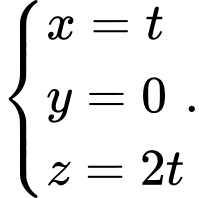
D, 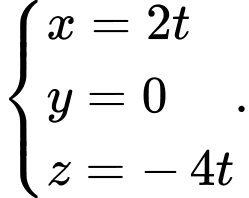
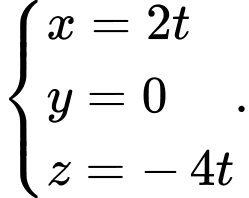
Chọn đáp án C.
Điểm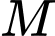 là trung điểm của
là trung điểm của  nên tọa độ của
nên tọa độ của 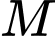 là
là 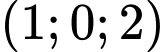 , suy ra
, suy ra 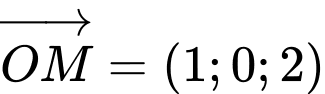 .
.
Phương trình đường thẳng đi qua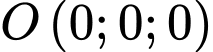 và nhận
và nhận 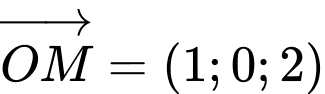 làm một VTCP là:
làm một VTCP là: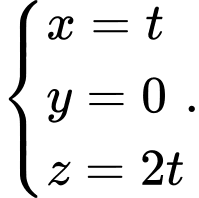 Đáp án: C
Đáp án: C
Điểm
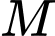 là trung điểm của
là trung điểm của  nên tọa độ của
nên tọa độ của 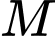 là
là 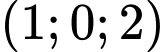 , suy ra
, suy ra 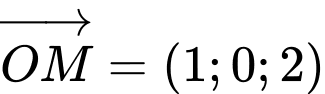 .
.Phương trình đường thẳng đi qua
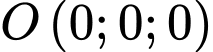 và nhận
và nhận 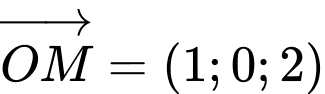 làm một VTCP là:
làm một VTCP là: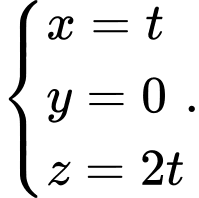 Đáp án: C
Đáp án: C PHẦN II. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Câu 13 [695239]: Cho hàm số 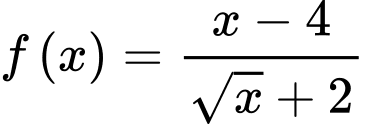 liên tục trên khoảng
liên tục trên khoảng 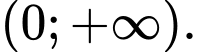 Gọi
Gọi 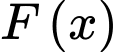 là một nguyên hàm của hàm số
là một nguyên hàm của hàm số 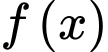 trên khoảng
trên khoảng 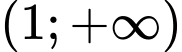 thỏa mãn
thỏa mãn 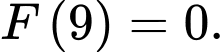
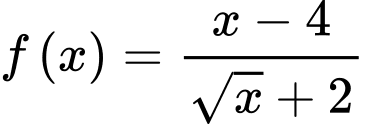 liên tục trên khoảng
liên tục trên khoảng 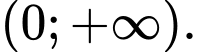 Gọi
Gọi 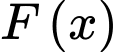 là một nguyên hàm của hàm số
là một nguyên hàm của hàm số 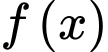 trên khoảng
trên khoảng 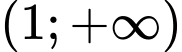 thỏa mãn
thỏa mãn 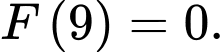
a) Sai.
Với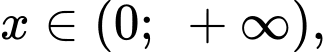 ta có:
ta có: 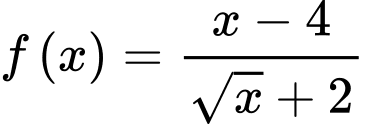
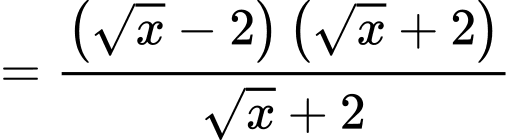
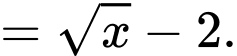
b) Sai.
Ta có: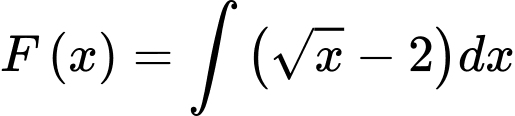
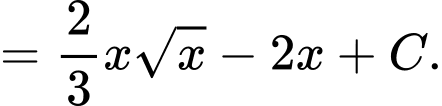
c) Sai.
Ta có:
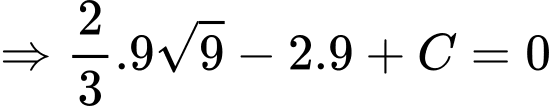
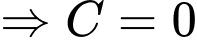
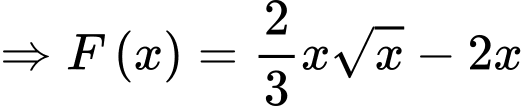
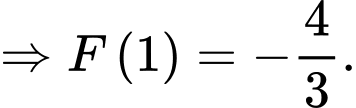
d) Sai.
Ta có: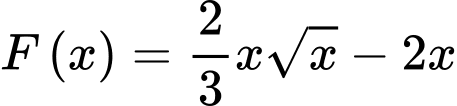
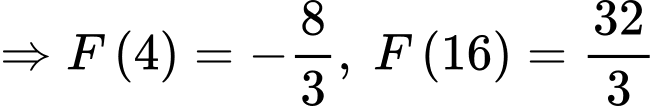
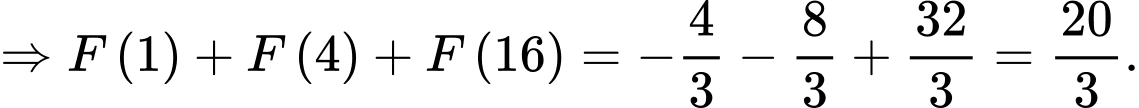
Với
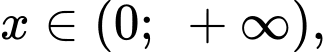 ta có:
ta có: 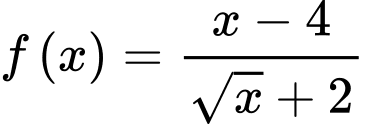
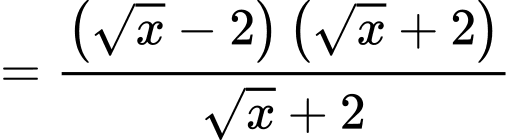
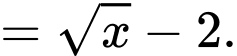
b) Sai.
Ta có:
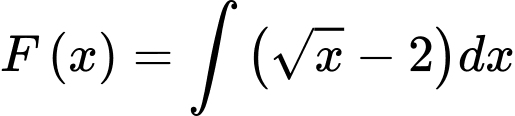
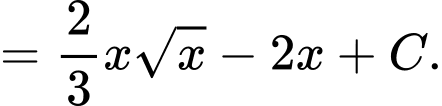
c) Sai.
Ta có:

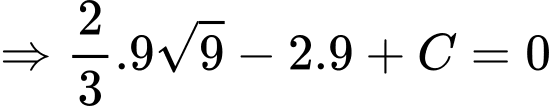
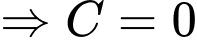
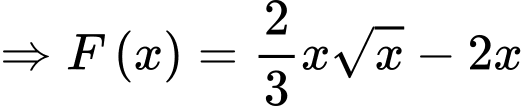
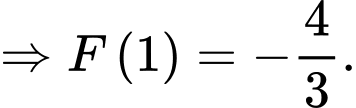
d) Sai.
Ta có:
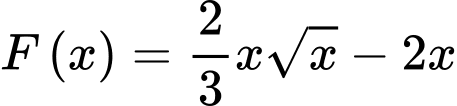
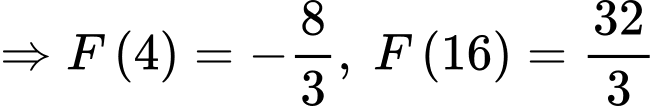
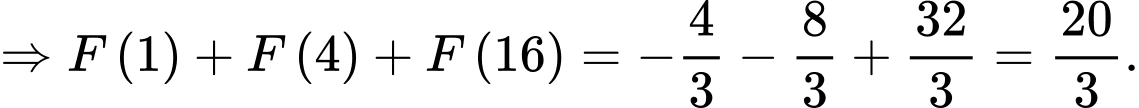
Câu 14 [695240]: Một sân vận động được xây dựng theo mô hình là hình chóp cụt  có hai đáy song song với nhau. Mặt sân
có hai đáy song song với nhau. Mặt sân 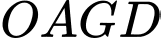 là hình chữ nhật và được gắn hệ trục
là hình chữ nhật và được gắn hệ trục 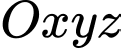 như hình vẽ dưới (đơn vị trên mỗi trục tọa độ là mét). Mặt sân
như hình vẽ dưới (đơn vị trên mỗi trục tọa độ là mét). Mặt sân 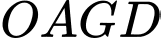 có chiều dài
có chiều dài 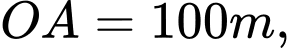 chiều rộng
chiều rộng 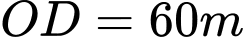 và tọa độ điểm
và tọa độ điểm 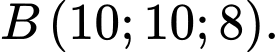
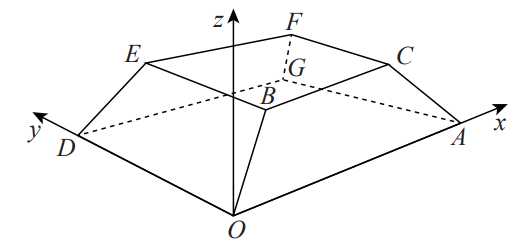
 có hai đáy song song với nhau. Mặt sân
có hai đáy song song với nhau. Mặt sân 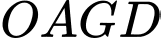 là hình chữ nhật và được gắn hệ trục
là hình chữ nhật và được gắn hệ trục 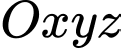 như hình vẽ dưới (đơn vị trên mỗi trục tọa độ là mét). Mặt sân
như hình vẽ dưới (đơn vị trên mỗi trục tọa độ là mét). Mặt sân 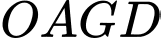 có chiều dài
có chiều dài 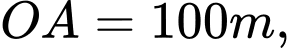 chiều rộng
chiều rộng 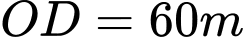 và tọa độ điểm
và tọa độ điểm 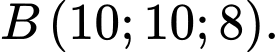

a) Đúng.
Ta có: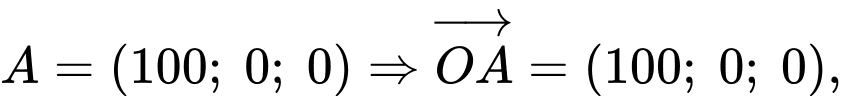
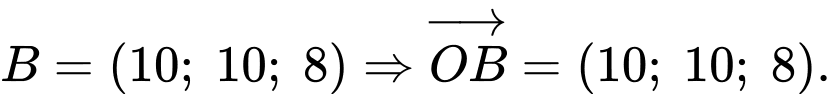
b) Sai.
Vectơ tích có hướng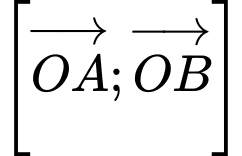 có toạ độ là
có toạ độ là 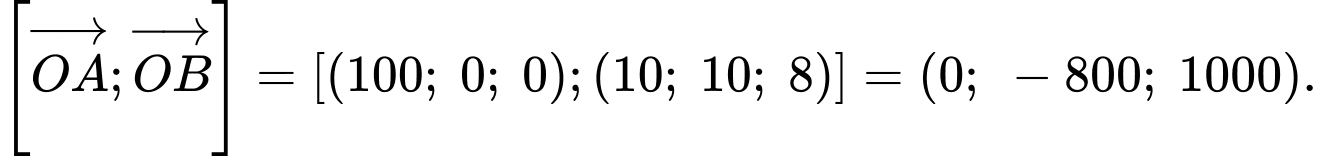
c) Sai.
Phương trình mặt phẳng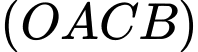 có vectơ pháp tuyến
có vectơ pháp tuyến 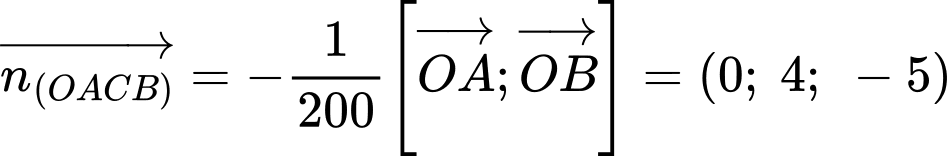 và đi qua
và đi qua 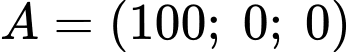 là:
là:  hay
hay 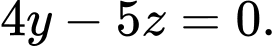
d) Sai.
Mặt phẳng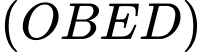 đi qua trục
đi qua trục 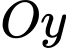 nên phương trình có dạng
nên phương trình có dạng 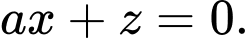
Mặt phẳng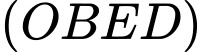 đi qua
đi qua 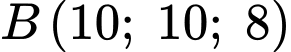 nên
nên 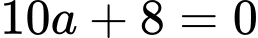
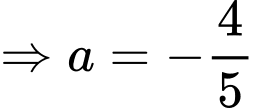
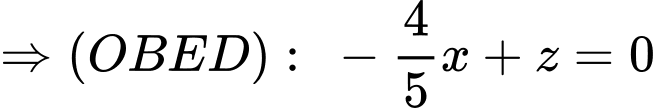 hay
hay 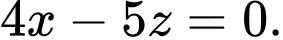
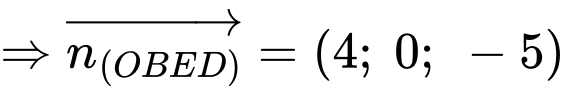
Góc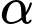 giữa hai mặt phẳng
giữa hai mặt phẳng 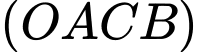 và
và 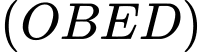 là:
là:
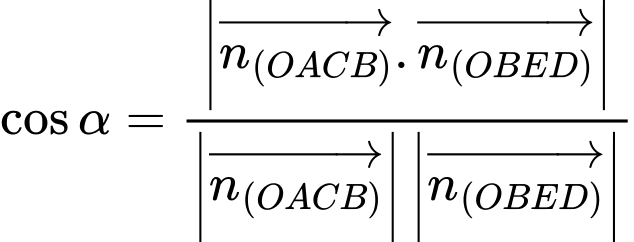
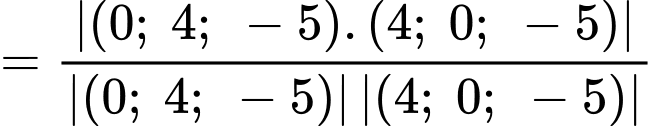
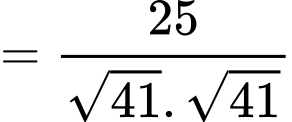
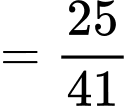
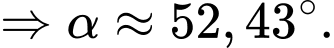
Ta có:
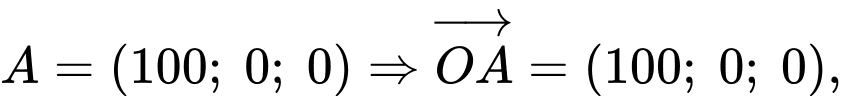
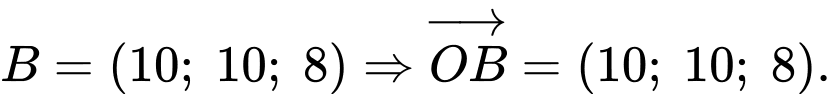
b) Sai.
Vectơ tích có hướng
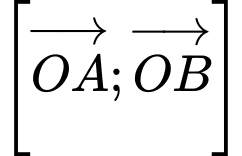 có toạ độ là
có toạ độ là 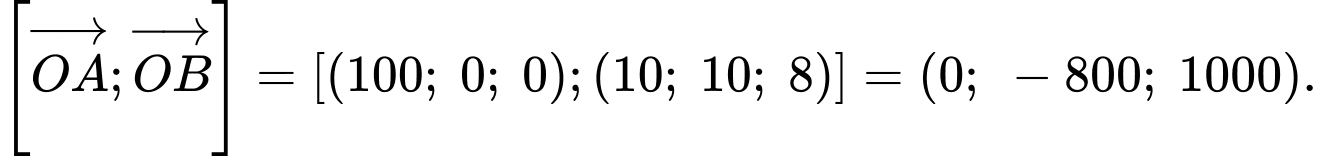
c) Sai.
Phương trình mặt phẳng
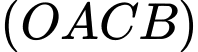 có vectơ pháp tuyến
có vectơ pháp tuyến 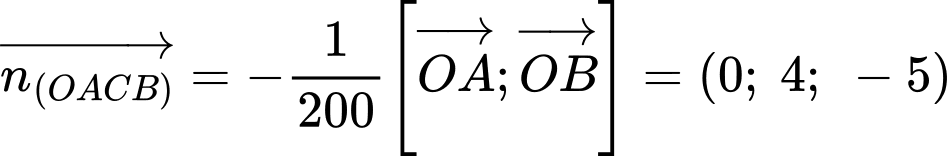 và đi qua
và đi qua 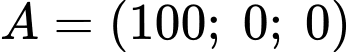 là:
là:  hay
hay 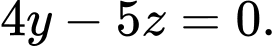
d) Sai.
Mặt phẳng
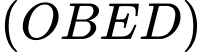 đi qua trục
đi qua trục 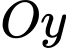 nên phương trình có dạng
nên phương trình có dạng 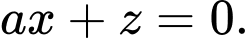
Mặt phẳng
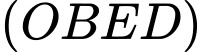 đi qua
đi qua 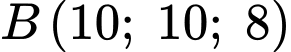 nên
nên 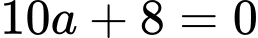
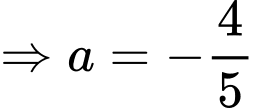
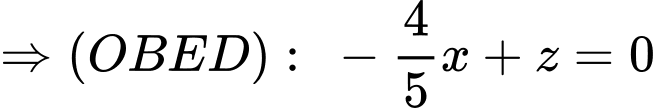 hay
hay 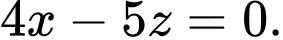
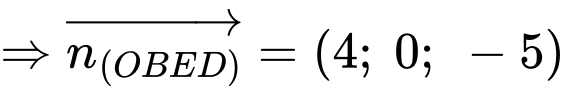
Góc
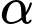 giữa hai mặt phẳng
giữa hai mặt phẳng 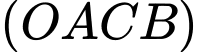 và
và 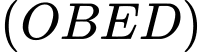 là:
là: 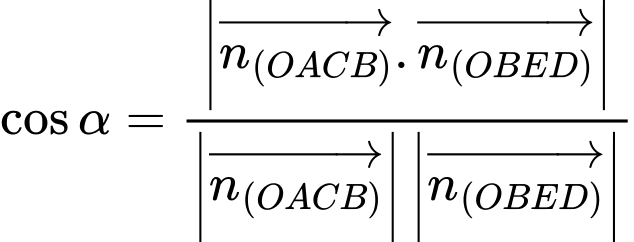
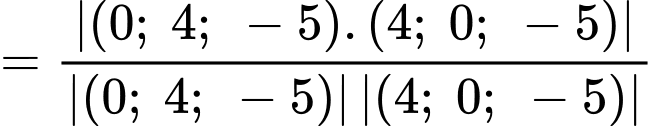
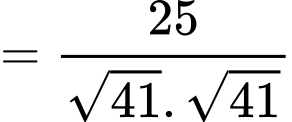
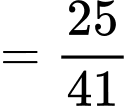
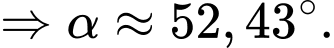
Câu 15 [695241]: Một cơ sở sản xuất khăn mặt đang bán mỗi chiếc khăn với giá 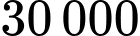 đồng một chiếc và mỗi tháng cơ sở bán được trung bình
đồng một chiếc và mỗi tháng cơ sở bán được trung bình 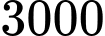 chiếc khăn. Cơ sở sản xuất đang có kế hoạch tăng giá bán để có lợi nhận tốt hơn. Sau khi tham khảo thị trường, người quản lý thấy rằng nếu từ mức giá
chiếc khăn. Cơ sở sản xuất đang có kế hoạch tăng giá bán để có lợi nhận tốt hơn. Sau khi tham khảo thị trường, người quản lý thấy rằng nếu từ mức giá 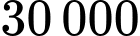 đồng mà cứ tăng giá thêm
đồng mà cứ tăng giá thêm 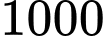 đồng thì mỗi tháng sẽ bán ít hơn
đồng thì mỗi tháng sẽ bán ít hơn 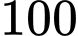 chiếc. Biết vốn sản xuất một chiếc khăn không thay đổi là
chiếc. Biết vốn sản xuất một chiếc khăn không thay đổi là 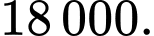 Gọi số tiền cần tăng giá mỗi chiếc khăn là
Gọi số tiền cần tăng giá mỗi chiếc khăn là 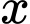 (nghìn đồng và
(nghìn đồng và  ).
).
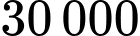 đồng một chiếc và mỗi tháng cơ sở bán được trung bình
đồng một chiếc và mỗi tháng cơ sở bán được trung bình 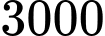 chiếc khăn. Cơ sở sản xuất đang có kế hoạch tăng giá bán để có lợi nhận tốt hơn. Sau khi tham khảo thị trường, người quản lý thấy rằng nếu từ mức giá
chiếc khăn. Cơ sở sản xuất đang có kế hoạch tăng giá bán để có lợi nhận tốt hơn. Sau khi tham khảo thị trường, người quản lý thấy rằng nếu từ mức giá 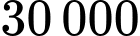 đồng mà cứ tăng giá thêm
đồng mà cứ tăng giá thêm 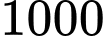 đồng thì mỗi tháng sẽ bán ít hơn
đồng thì mỗi tháng sẽ bán ít hơn 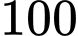 chiếc. Biết vốn sản xuất một chiếc khăn không thay đổi là
chiếc. Biết vốn sản xuất một chiếc khăn không thay đổi là 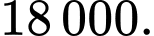 Gọi số tiền cần tăng giá mỗi chiếc khăn là
Gọi số tiền cần tăng giá mỗi chiếc khăn là 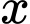 (nghìn đồng và
(nghìn đồng và  ).
).
a) Đúng.
Vì cứ tăng giá thêm một nghìn đồng thì số khăn bán ra giảm 100 chiếc nên tăng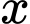 nghìn đồng thì số khăn bán ra giảm
nghìn đồng thì số khăn bán ra giảm 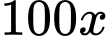 chiếc.
chiếc.
Do đó, tổng số khăn bán ra mỗi tháng là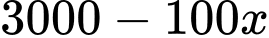 chiếc.
chiếc.
b) Sai.
Sau khi tăng giá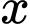 (nghìn đồng) mỗi chiếc thì giá mỗi chiếc khăn là
(nghìn đồng) mỗi chiếc thì giá mỗi chiếc khăn là  (nghìn đồng) và vốn sản xuất một chiếc khăn không thay đổi là 18 nghìn đồng nên mỗi chiếc khăn thu được số lãi là
(nghìn đồng) và vốn sản xuất một chiếc khăn không thay đổi là 18 nghìn đồng nên mỗi chiếc khăn thu được số lãi là 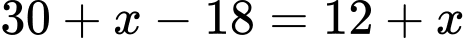 ( nghìn đồng).
( nghìn đồng).
c) Đúng.
Sau khi tăng giá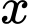 (nghìn đồng) thì mỗi tháng bán được
(nghìn đồng) thì mỗi tháng bán được 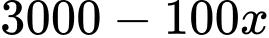 chiếc và mỗi chiếc khăn thu được số lãi là
chiếc và mỗi chiếc khăn thu được số lãi là 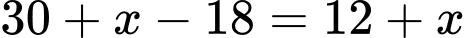 ( nghìn đồng) nên tổng lợi nhuận một tháng là:
( nghìn đồng) nên tổng lợi nhuận một tháng là:
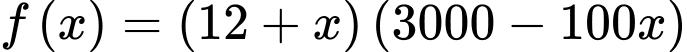
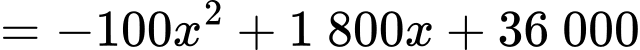 (nghìn đồng).
(nghìn đồng).
d) Đúng.
Xét hàm số trên
trên 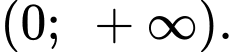
Ta có: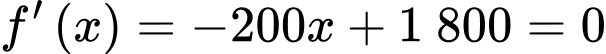
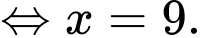
Lập bảng biến thiên của hàm số ta có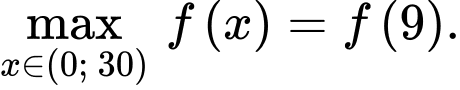
Vậy để lợi nhuận lớn nhất thì mỗi chiếc khăn có giá là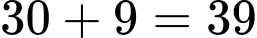 (nghìn đồng).
(nghìn đồng).
Vì cứ tăng giá thêm một nghìn đồng thì số khăn bán ra giảm 100 chiếc nên tăng
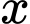 nghìn đồng thì số khăn bán ra giảm
nghìn đồng thì số khăn bán ra giảm 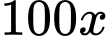 chiếc.
chiếc. Do đó, tổng số khăn bán ra mỗi tháng là
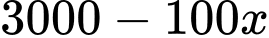 chiếc.
chiếc.
b) Sai.
Sau khi tăng giá
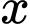 (nghìn đồng) mỗi chiếc thì giá mỗi chiếc khăn là
(nghìn đồng) mỗi chiếc thì giá mỗi chiếc khăn là  (nghìn đồng) và vốn sản xuất một chiếc khăn không thay đổi là 18 nghìn đồng nên mỗi chiếc khăn thu được số lãi là
(nghìn đồng) và vốn sản xuất một chiếc khăn không thay đổi là 18 nghìn đồng nên mỗi chiếc khăn thu được số lãi là 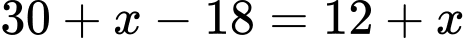 ( nghìn đồng).
( nghìn đồng).
c) Đúng.
Sau khi tăng giá
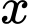 (nghìn đồng) thì mỗi tháng bán được
(nghìn đồng) thì mỗi tháng bán được 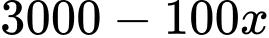 chiếc và mỗi chiếc khăn thu được số lãi là
chiếc và mỗi chiếc khăn thu được số lãi là 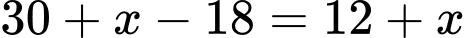 ( nghìn đồng) nên tổng lợi nhuận một tháng là:
( nghìn đồng) nên tổng lợi nhuận một tháng là:
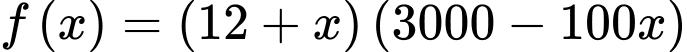
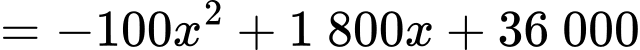 (nghìn đồng).
(nghìn đồng).
d) Đúng.
Xét hàm số
 trên
trên 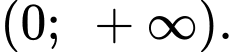
Ta có:
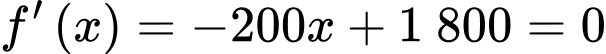
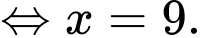
Lập bảng biến thiên của hàm số ta có
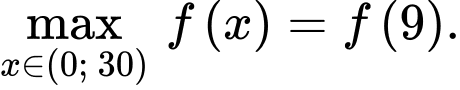
Vậy để lợi nhuận lớn nhất thì mỗi chiếc khăn có giá là
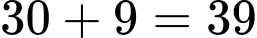 (nghìn đồng).
(nghìn đồng).
Câu 16 [695242]: Giả sử trong một nhóm người có 10 người nhiễm bệnh A, 90 người còn lại không nhiễm bệnh A. Để phát hiện ra người nhiễm bệnh A, người ta tiến hành xét nghiệm tất cả mọi người của nhóm đó. Một loại xét nghiệm cho kết quả như sau: Đối với người nhiễm bệnh A xác suất xét nghiệm có kết quả dương tính là 80%, còn đối với người không nhiễm bệnh A thì xác suất xét nghiệm có phản ứng dương tính là 9%. Gọi là một người trong nhóm được xét nghiệm.
Xét các biến cố
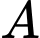 : “X có kết quả xét nghiệm dương tính”
: “X có kết quả xét nghiệm dương tính”
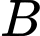 : “X là người nhiễm bệnh”
: “X là người nhiễm bệnh”
Xét các biến cố
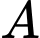 : “X có kết quả xét nghiệm dương tính”
: “X có kết quả xét nghiệm dương tính”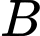 : “X là người nhiễm bệnh”
: “X là người nhiễm bệnh”
Xét các biến cố
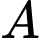 : “X có kết quả xét nghiệm dương tính”.
: “X có kết quả xét nghiệm dương tính”.
 : “X có kết quả xét nghiệm âm tính”.
: “X có kết quả xét nghiệm âm tính”.
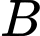 : “X là người nhiễm bệnh”.
: “X là người nhiễm bệnh”.
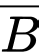 : “X là người không bị nhiễm bệnh”.
: “X là người không bị nhiễm bệnh”.
a) Sai.
Xác suất X là người bị nhiễm bệnh là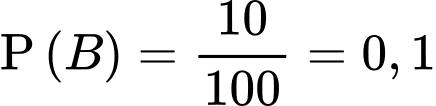 .
.
Xác suất X là người không bị nhiễm bệnh là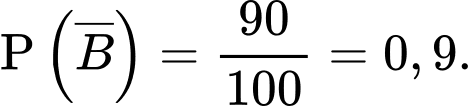
Đối với người nhiễm bệnh thì xác suất xét nghiệm có kết quả dương tính là 80% nên ta có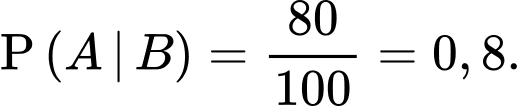
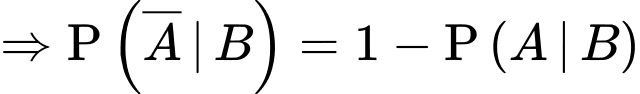
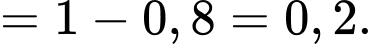
b) Sai.
Đối với người không nhiễm bệnh thì xác suất xét nghiệm có phản ứng dương tính là 9% nên ta có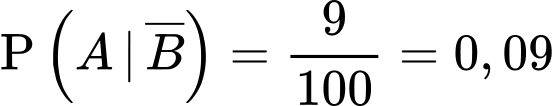 .
.
 .
.
c) Đúng.
Ta có sơ đồ cây sau:

Áp dụng công thức xác suất toàn phần, ta có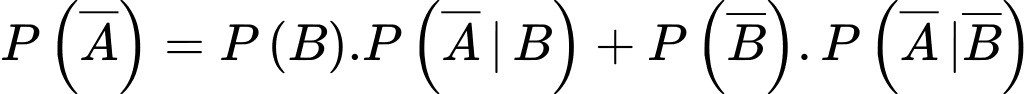
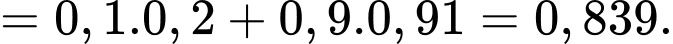
Xác suất để X là người nhiễm bệnh, biết X có kết quả xét nghiệm âm tính là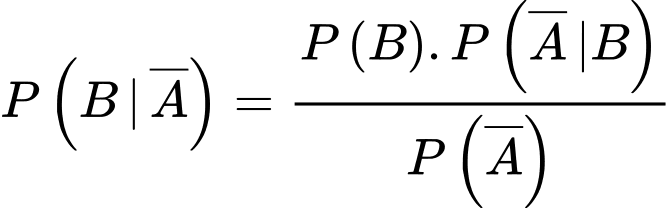
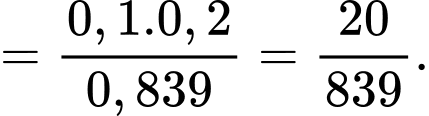
d) Sai.
Xác suất để X là người không bị nhiễm bệnh, biết X có kết quả xét nghiệm âm tính là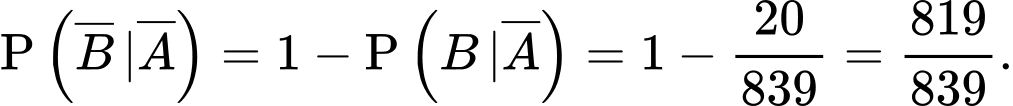
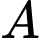 : “X có kết quả xét nghiệm dương tính”.
: “X có kết quả xét nghiệm dương tính”.
 : “X có kết quả xét nghiệm âm tính”.
: “X có kết quả xét nghiệm âm tính”.
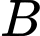 : “X là người nhiễm bệnh”.
: “X là người nhiễm bệnh”.
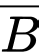 : “X là người không bị nhiễm bệnh”.
: “X là người không bị nhiễm bệnh”.
a) Sai.
Xác suất X là người bị nhiễm bệnh là
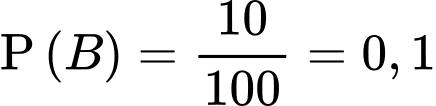 .
.
Xác suất X là người không bị nhiễm bệnh là
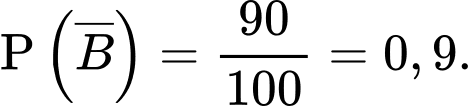
Đối với người nhiễm bệnh thì xác suất xét nghiệm có kết quả dương tính là 80% nên ta có
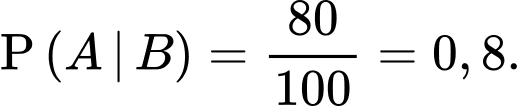
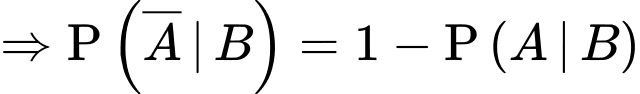
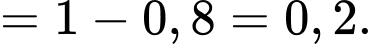
b) Sai.
Đối với người không nhiễm bệnh thì xác suất xét nghiệm có phản ứng dương tính là 9% nên ta có
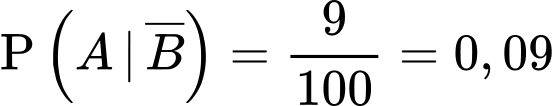 .
.
 .
.
c) Đúng.
Ta có sơ đồ cây sau:

Áp dụng công thức xác suất toàn phần, ta có
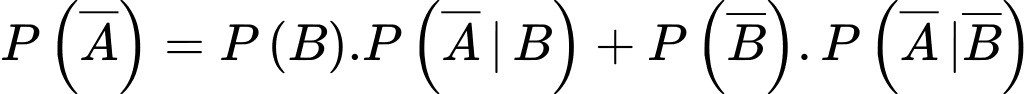
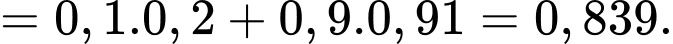
Xác suất để X là người nhiễm bệnh, biết X có kết quả xét nghiệm âm tính là
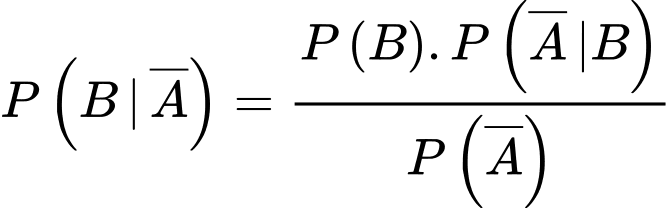
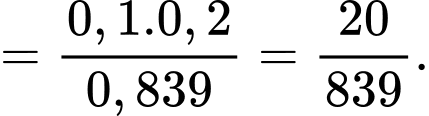
d) Sai.
Xác suất để X là người không bị nhiễm bệnh, biết X có kết quả xét nghiệm âm tính là
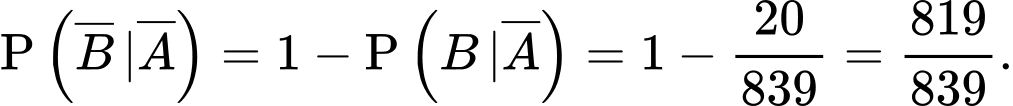
PHẦN III. Thí sinh trả lời từ câu 1 đến câu 6.
Câu 17 [695243]: Cho hình hộp đứng  có đáy
có đáy 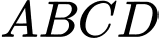 là hình thoi cạnh bằng
là hình thoi cạnh bằng 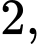 tam giác
tam giác 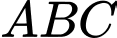 đều,
đều, 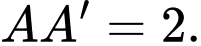 Gọi
Gọi 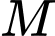 là trung điểm của cạnh
là trung điểm của cạnh 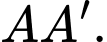 Khoảng cách từ
Khoảng cách từ 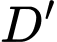 đến mặt phẳng
đến mặt phẳng 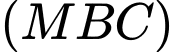 bằng bao nhiêu? (làm tròn kết quả đến hàng phần mười).
bằng bao nhiêu? (làm tròn kết quả đến hàng phần mười).
 có đáy
có đáy 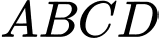 là hình thoi cạnh bằng
là hình thoi cạnh bằng 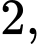 tam giác
tam giác 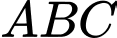 đều,
đều, 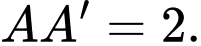 Gọi
Gọi 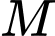 là trung điểm của cạnh
là trung điểm của cạnh 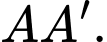 Khoảng cách từ
Khoảng cách từ 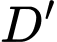 đến mặt phẳng
đến mặt phẳng 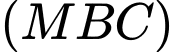 bằng bao nhiêu? (làm tròn kết quả đến hàng phần mười).
bằng bao nhiêu? (làm tròn kết quả đến hàng phần mười).
Điền đáp án: 
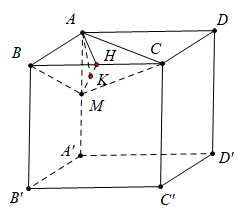
Ta có:

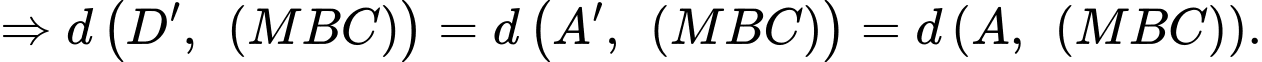
Gọi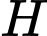 là trung điểm của
là trung điểm của 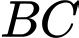
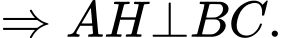
Mặt khác,
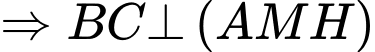
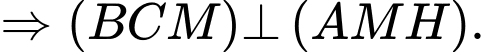
Ta có: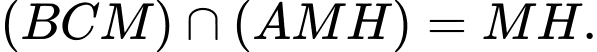
Kẻ
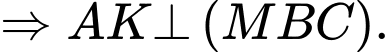
Xét tam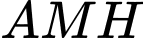 vuông tại
vuông tại 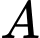 ta có:
ta có:
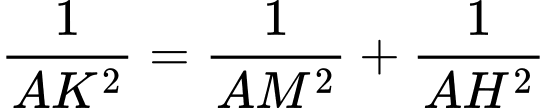
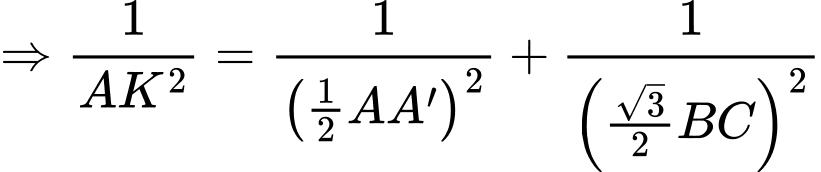
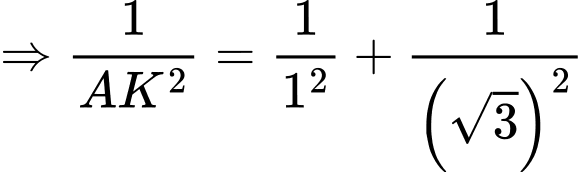
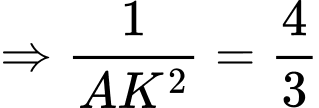
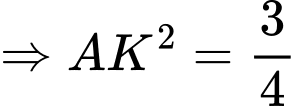
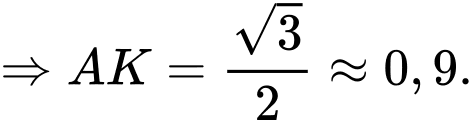
Vậy khoảng cách từ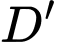 đến mặt phẳng
đến mặt phẳng 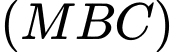 bằng
bằng 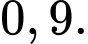
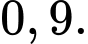

Ta có:


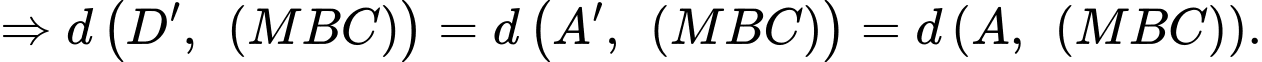
Gọi
 là trung điểm của
là trung điểm của 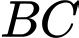
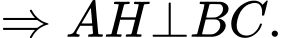
Mặt khác,

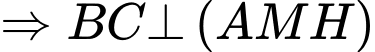
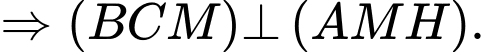
Ta có:
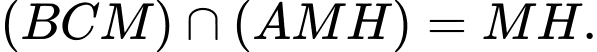
Kẻ

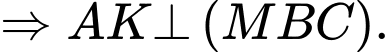
Xét tam
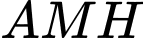 vuông tại
vuông tại 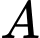 ta có:
ta có: 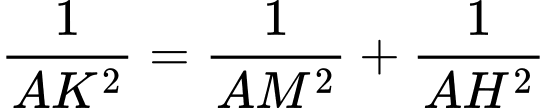
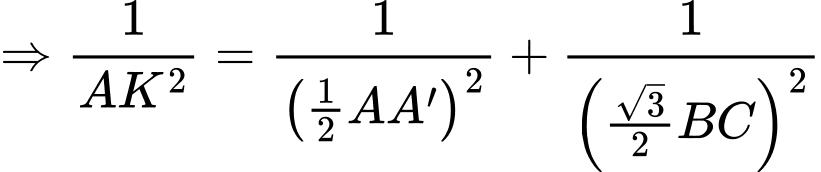
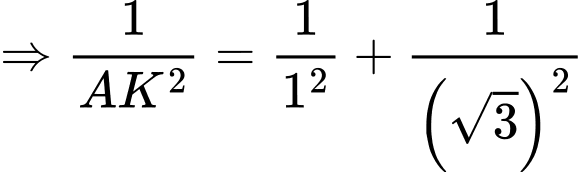
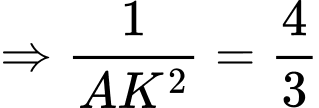
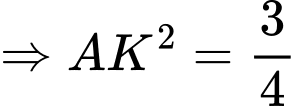
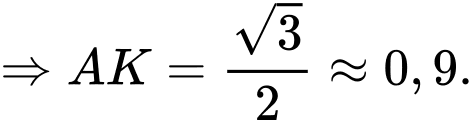
Vậy khoảng cách từ
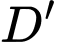 đến mặt phẳng
đến mặt phẳng 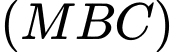 bằng
bằng 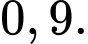
Câu 18 [695245]: Trong không gian 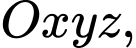 cho hai mặt phẳng
cho hai mặt phẳng 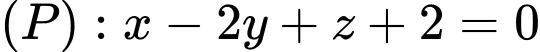 và
và 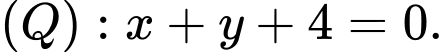 Gọi
Gọi 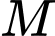 là điểm thuộc mặt phẳng
là điểm thuộc mặt phẳng 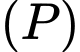 sao cho điểm đối xứng của
sao cho điểm đối xứng của 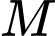 qua mặt phẳng
qua mặt phẳng  nằm trên trục hoành. Tung độ của điểm
nằm trên trục hoành. Tung độ của điểm 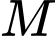 bằng bao nhiêu?
bằng bao nhiêu?
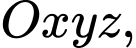 cho hai mặt phẳng
cho hai mặt phẳng 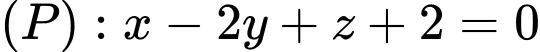 và
và 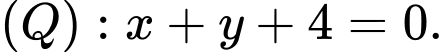 Gọi
Gọi 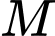 là điểm thuộc mặt phẳng
là điểm thuộc mặt phẳng 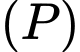 sao cho điểm đối xứng của
sao cho điểm đối xứng của 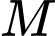 qua mặt phẳng
qua mặt phẳng  nằm trên trục hoành. Tung độ của điểm
nằm trên trục hoành. Tung độ của điểm 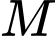 bằng bao nhiêu?
bằng bao nhiêu?
Điền đáp án: 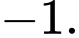
Gọi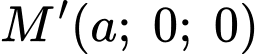 là điểm đối xứng của
là điểm đối xứng của 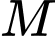 qua mặt phẳng
qua mặt phẳng  nằm trên trục hoành.
nằm trên trục hoành.
Gọi là đường thằng qua
là đường thằng qua 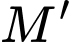 và vuông góc với
và vuông góc với 
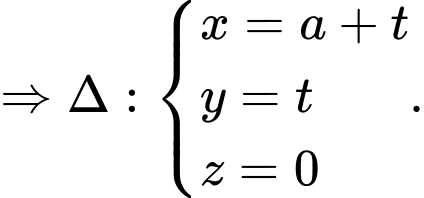
Gọi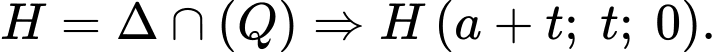

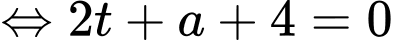
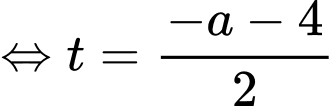
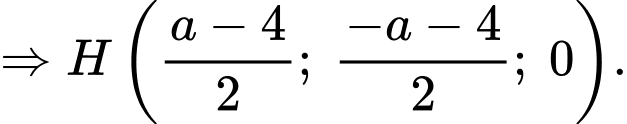
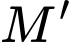 là điểm đối xứng
là điểm đối xứng 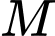 qua
qua 
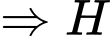 là trung điểm của
là trung điểm của 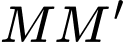
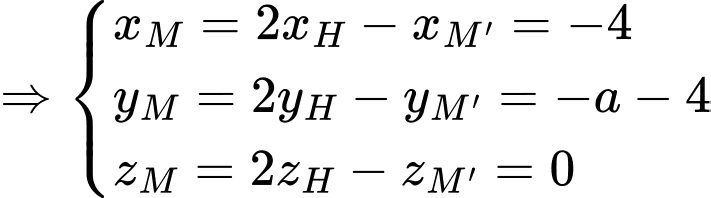
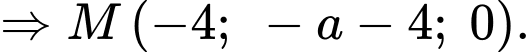
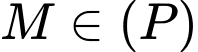

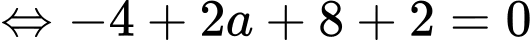

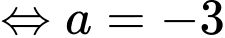
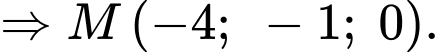
Vậy tung độ của điểm là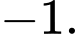
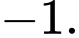
Gọi
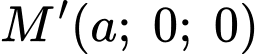 là điểm đối xứng của
là điểm đối xứng của 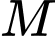 qua mặt phẳng
qua mặt phẳng  nằm trên trục hoành.
nằm trên trục hoành.
Gọi
 là đường thằng qua
là đường thằng qua 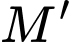 và vuông góc với
và vuông góc với 
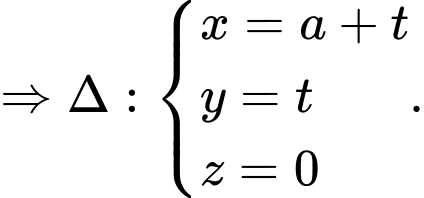
Gọi
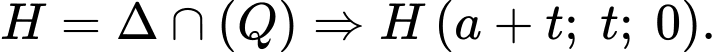

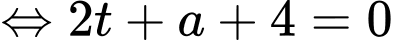
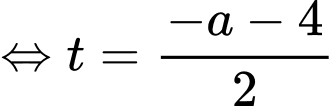
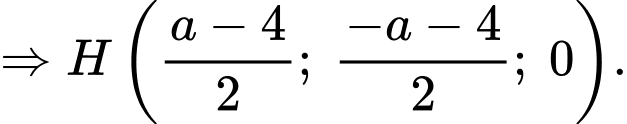
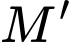 là điểm đối xứng
là điểm đối xứng 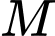 qua
qua 
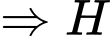 là trung điểm của
là trung điểm của 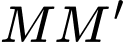
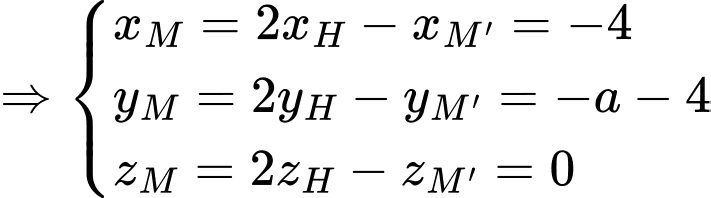
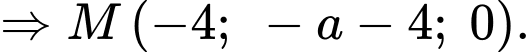
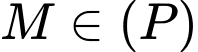

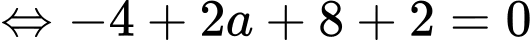

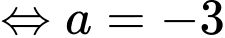
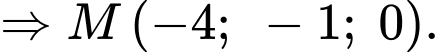
Vậy tung độ của điểm là
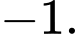
Câu 19 [695246]: Trong kinh tế học, người ta tính toán thu nhập của một khoản đầu tư thông qua công thức 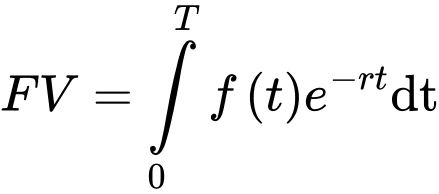 trong đó với khoảng thời gian
trong đó với khoảng thời gian 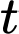 thì
thì 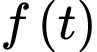 là tốc độ sinh lời,
là tốc độ sinh lời, 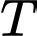 là thời gian đầu tư và
là thời gian đầu tư và 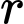 là lãi suất hàng kỳ. Hoàng đang cố gắng để cân nhắc giữa hai khoản đầu tư. Khoản đầu tư thứ nhất có giá 1.000 đô la và dự kiến sẽ tạo ra một dòng thu nhập liên tục với tốc độ
là lãi suất hàng kỳ. Hoàng đang cố gắng để cân nhắc giữa hai khoản đầu tư. Khoản đầu tư thứ nhất có giá 1.000 đô la và dự kiến sẽ tạo ra một dòng thu nhập liên tục với tốc độ 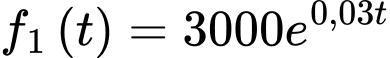 đô la mỗi năm. Khoản đầu tư thứ hai có giá 4.000 đô la và được ước tính sẽ tạo ra thu nhập với tốc độ không đổi là
đô la mỗi năm. Khoản đầu tư thứ hai có giá 4.000 đô la và được ước tính sẽ tạo ra thu nhập với tốc độ không đổi là 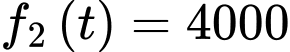 đô la mỗi năm. Giả sử lãi suất hàng năm hiện hành vẫn cố định ở mức 5% mỗi năm và được tính lãi kép liên tục. Em hãy giúp Hoàng chọn khoảng đầu tư lời hơn bằng cách tính số đô la chênh lệch giữa hai khoản đầu tư sau 5 năm (lấy giá trị dương). Làm tròn đến hàng đơn vị.
đô la mỗi năm. Giả sử lãi suất hàng năm hiện hành vẫn cố định ở mức 5% mỗi năm và được tính lãi kép liên tục. Em hãy giúp Hoàng chọn khoảng đầu tư lời hơn bằng cách tính số đô la chênh lệch giữa hai khoản đầu tư sau 5 năm (lấy giá trị dương). Làm tròn đến hàng đơn vị.
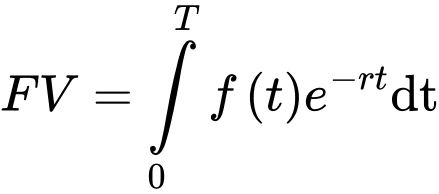 trong đó với khoảng thời gian
trong đó với khoảng thời gian 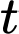 thì
thì 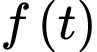 là tốc độ sinh lời,
là tốc độ sinh lời, 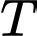 là thời gian đầu tư và
là thời gian đầu tư và 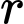 là lãi suất hàng kỳ. Hoàng đang cố gắng để cân nhắc giữa hai khoản đầu tư. Khoản đầu tư thứ nhất có giá 1.000 đô la và dự kiến sẽ tạo ra một dòng thu nhập liên tục với tốc độ
là lãi suất hàng kỳ. Hoàng đang cố gắng để cân nhắc giữa hai khoản đầu tư. Khoản đầu tư thứ nhất có giá 1.000 đô la và dự kiến sẽ tạo ra một dòng thu nhập liên tục với tốc độ 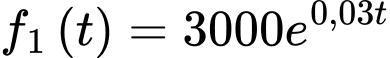 đô la mỗi năm. Khoản đầu tư thứ hai có giá 4.000 đô la và được ước tính sẽ tạo ra thu nhập với tốc độ không đổi là
đô la mỗi năm. Khoản đầu tư thứ hai có giá 4.000 đô la và được ước tính sẽ tạo ra thu nhập với tốc độ không đổi là 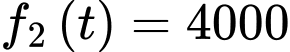 đô la mỗi năm. Giả sử lãi suất hàng năm hiện hành vẫn cố định ở mức 5% mỗi năm và được tính lãi kép liên tục. Em hãy giúp Hoàng chọn khoảng đầu tư lời hơn bằng cách tính số đô la chênh lệch giữa hai khoản đầu tư sau 5 năm (lấy giá trị dương). Làm tròn đến hàng đơn vị.
đô la mỗi năm. Giả sử lãi suất hàng năm hiện hành vẫn cố định ở mức 5% mỗi năm và được tính lãi kép liên tục. Em hãy giúp Hoàng chọn khoảng đầu tư lời hơn bằng cách tính số đô la chênh lệch giữa hai khoản đầu tư sau 5 năm (lấy giá trị dương). Làm tròn đến hàng đơn vị.
Điền đáp án: 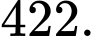
Lợi nhuận của một khoản đầu tư chính là sự chênh lệch giữa thu nhập và chi phi.
Xét lợi nhuận của khoản đầu tư thứ nhất:
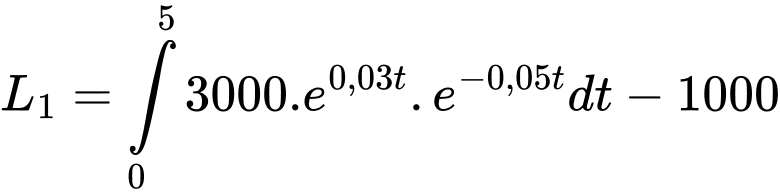
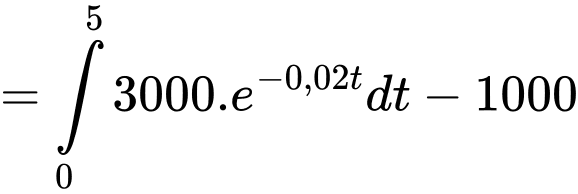
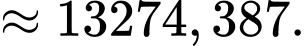
Xét lợi nhuận của khoản đầu tư thứ hai:
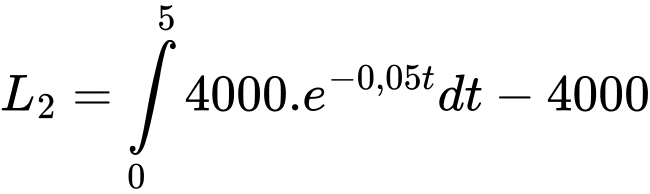

Sự chênh lệch lợi nhuận giữa hai khoản đầu tư là:
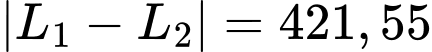
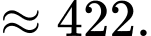
Lợi nhuận của một khoản đầu tư chính là sự chênh lệch giữa thu nhập và chi phi.
Xét lợi nhuận của khoản đầu tư thứ nhất:
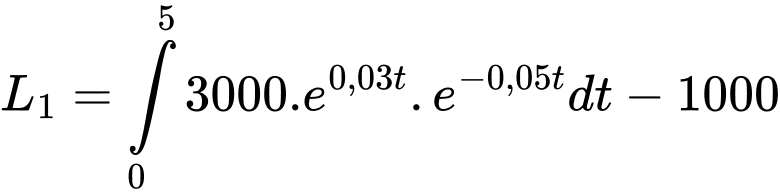
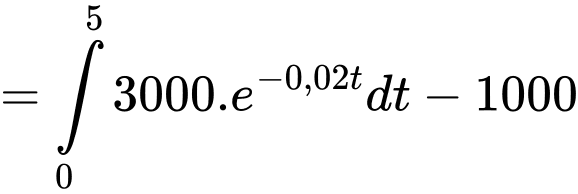
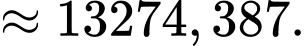
Xét lợi nhuận của khoản đầu tư thứ hai:
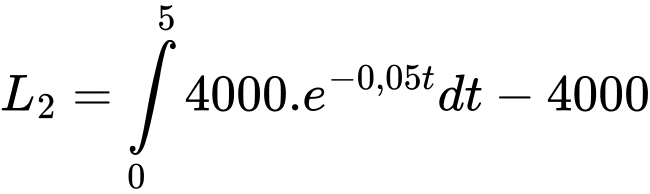

Sự chênh lệch lợi nhuận giữa hai khoản đầu tư là:
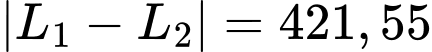
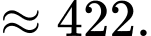
Câu 20 [695280]: Có hai hộp đựng phiếu thi, mỗi phiếu ghi một câu hỏi. Hộp thứ nhất có  phiếu và hộp thứ hai có
phiếu và hộp thứ hai có 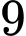 phiếu. Sinh viên A đi thi chỉ thuộc
phiếu. Sinh viên A đi thi chỉ thuộc  câu ở hộp thứ nhất và
câu ở hộp thứ nhất và 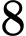 câu ở hộp thứ hai. Thầy giáo rút ngẫu nhiên ra 1 phiếu từ hộp thứ nhất bỏ vào hộp thứ hai, sau đó cho sinh viên A rút ngẫu nhiên ra 2 phiếu từ hộp thứ hai, xác suất để sinh viên đó rút được hai câu thuộc là bao nhiêu (làm tròn kết quả đến hàng phần trăm).
câu ở hộp thứ hai. Thầy giáo rút ngẫu nhiên ra 1 phiếu từ hộp thứ nhất bỏ vào hộp thứ hai, sau đó cho sinh viên A rút ngẫu nhiên ra 2 phiếu từ hộp thứ hai, xác suất để sinh viên đó rút được hai câu thuộc là bao nhiêu (làm tròn kết quả đến hàng phần trăm).
 phiếu và hộp thứ hai có
phiếu và hộp thứ hai có 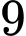 phiếu. Sinh viên A đi thi chỉ thuộc
phiếu. Sinh viên A đi thi chỉ thuộc  câu ở hộp thứ nhất và
câu ở hộp thứ nhất và 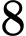 câu ở hộp thứ hai. Thầy giáo rút ngẫu nhiên ra 1 phiếu từ hộp thứ nhất bỏ vào hộp thứ hai, sau đó cho sinh viên A rút ngẫu nhiên ra 2 phiếu từ hộp thứ hai, xác suất để sinh viên đó rút được hai câu thuộc là bao nhiêu (làm tròn kết quả đến hàng phần trăm).
câu ở hộp thứ hai. Thầy giáo rút ngẫu nhiên ra 1 phiếu từ hộp thứ nhất bỏ vào hộp thứ hai, sau đó cho sinh viên A rút ngẫu nhiên ra 2 phiếu từ hộp thứ hai, xác suất để sinh viên đó rút được hai câu thuộc là bao nhiêu (làm tròn kết quả đến hàng phần trăm).
Điền đáp án: 0,74.
Gọi là biến cố “Thầy giáo rút 1 câu thuộc từ hộp 1 bỏ vào hộp 2”. Khi đó hộp 2 có 9 câu thuộc và 1 câu không thuộc.
là biến cố “Thầy giáo rút 1 câu thuộc từ hộp 1 bỏ vào hộp 2”. Khi đó hộp 2 có 9 câu thuộc và 1 câu không thuộc.
Gọi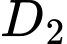 là biến cố “Thầy giáo rút 1 câu không thuộc từ hộp 1 bỏ vào hộp 2”. Khi đó hộp 2 có 8 câu thuộc và 2 câu không thuộc.
là biến cố “Thầy giáo rút 1 câu không thuộc từ hộp 1 bỏ vào hộp 2”. Khi đó hộp 2 có 8 câu thuộc và 2 câu không thuộc.
Gọi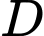 là biến cố “Sinh viên rút ra 2 câu thuộc”
là biến cố “Sinh viên rút ra 2 câu thuộc”
Yêu cầu bài toán Tính
Tính 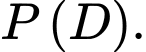
Ta có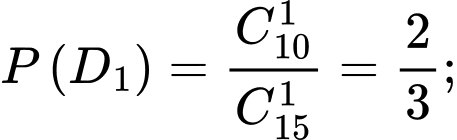
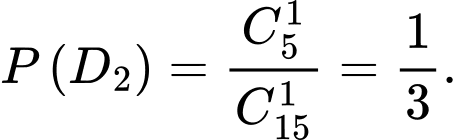
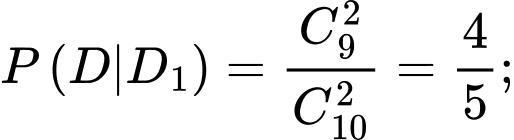
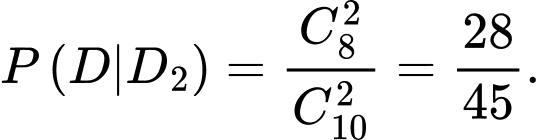
Ta có sơ đồ cây sau:
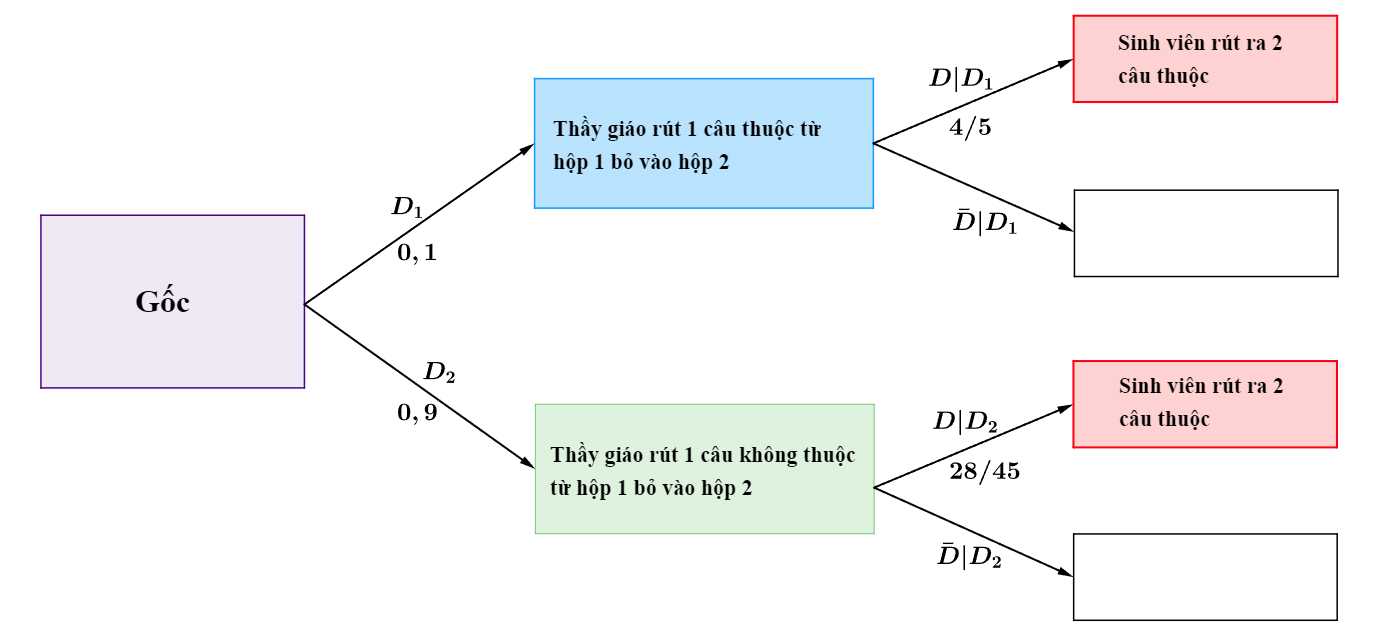
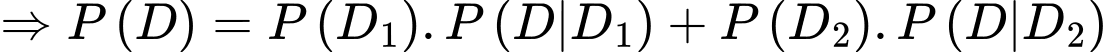
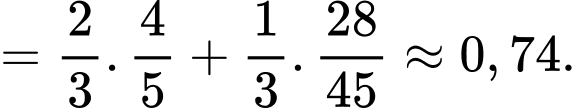
Gọi
 là biến cố “Thầy giáo rút 1 câu thuộc từ hộp 1 bỏ vào hộp 2”. Khi đó hộp 2 có 9 câu thuộc và 1 câu không thuộc.
là biến cố “Thầy giáo rút 1 câu thuộc từ hộp 1 bỏ vào hộp 2”. Khi đó hộp 2 có 9 câu thuộc và 1 câu không thuộc.
Gọi
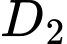 là biến cố “Thầy giáo rút 1 câu không thuộc từ hộp 1 bỏ vào hộp 2”. Khi đó hộp 2 có 8 câu thuộc và 2 câu không thuộc.
là biến cố “Thầy giáo rút 1 câu không thuộc từ hộp 1 bỏ vào hộp 2”. Khi đó hộp 2 có 8 câu thuộc và 2 câu không thuộc.
Gọi
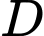 là biến cố “Sinh viên rút ra 2 câu thuộc”
là biến cố “Sinh viên rút ra 2 câu thuộc”
Yêu cầu bài toán
 Tính
Tính 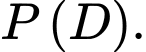
Ta có
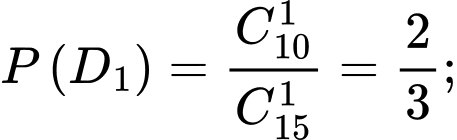
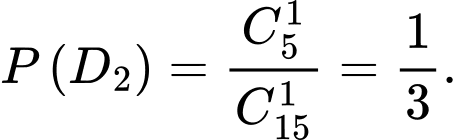
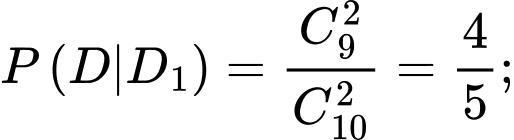
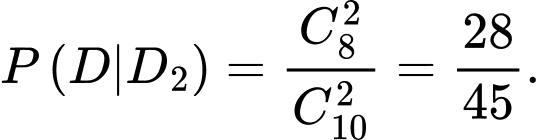
Ta có sơ đồ cây sau:

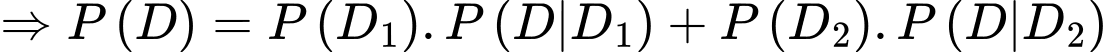
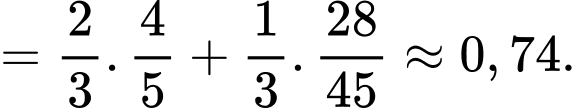
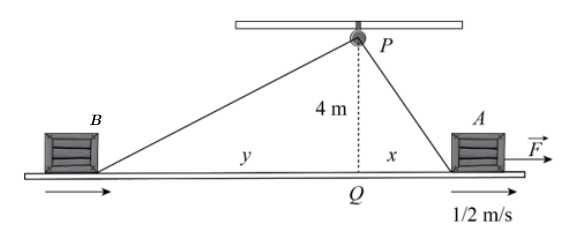
Câu 21 [695248]: Có hai thùng hàng A và B đặt trên sàn kho. Hai thùng được nối với nhau bằng một sợi dây dài 15 m, mỗi thùng được móc vào một đầu dây ở sát mặt sàn. Sợi dây luôn căng và được kéo qua ròng rọc P gắn trên xà nhà, cao hơn điểm Q trên sàn 4 mét (điểm Q là hình chiếu của P xuống sàn ) (tham khảo hình vẽ). Biết rằng trong quá trình di chuyển, hai thùng hàng luôn nằm trên mặt sàn và lực ma sát coi như bằng 0. Nếu thùng A cách Q 3 m và đang được kéo ra xa Q với tốc độ không đổi 0,5 m/s, hỏi thùng B đang di chuyển về phía Q với tốc độ bao nhiêu m/s? Làm tròn đến hàng phần trăm.
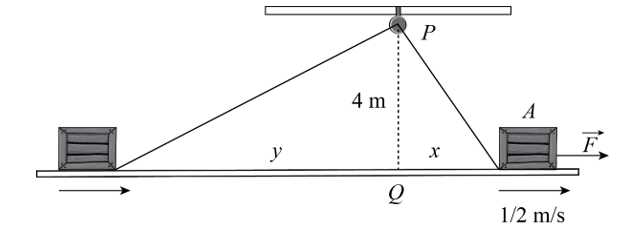

Điền đáp án: 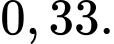
Ta có: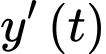 là tốc độ di chuyển của
là tốc độ di chuyển của 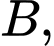
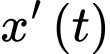 là tốc độ di chuyển của
là tốc độ di chuyển của 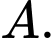
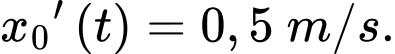
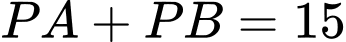
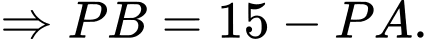
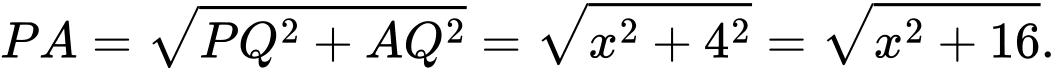
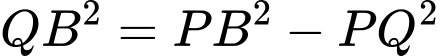 hay
hay 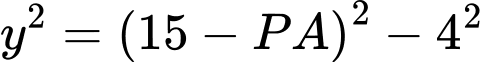 hay
hay 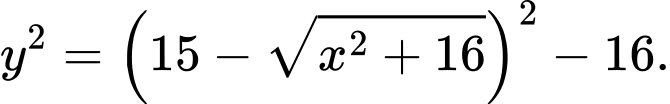
Với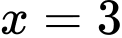 ta có:
ta có: 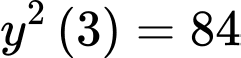 hay
hay 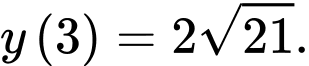
Ta có: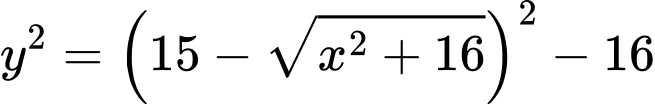
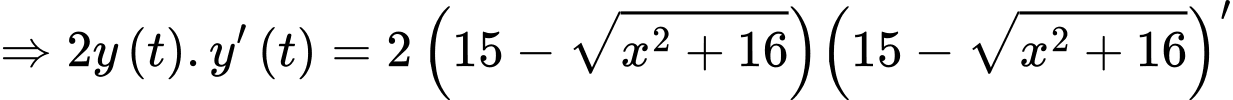
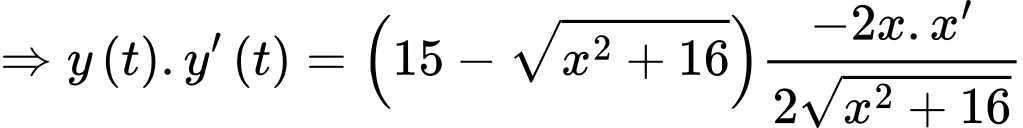
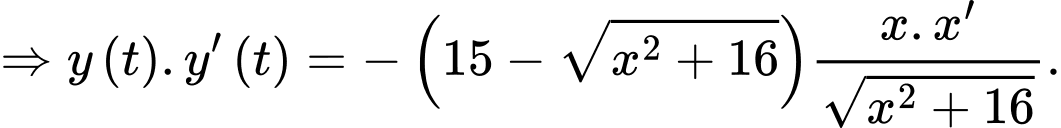
Với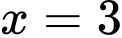 ta có:
ta có: 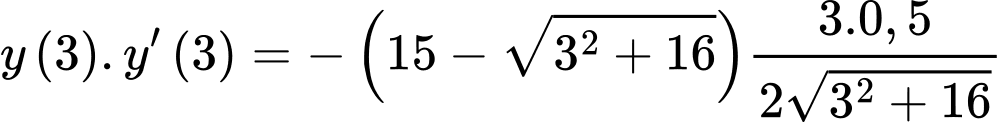
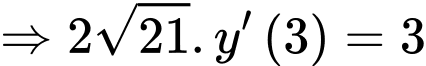
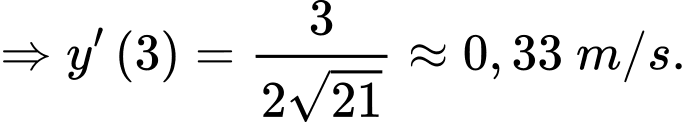
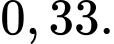

Ta có:
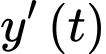 là tốc độ di chuyển của
là tốc độ di chuyển của 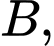
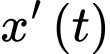 là tốc độ di chuyển của
là tốc độ di chuyển của 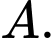
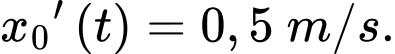
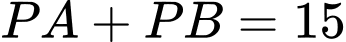
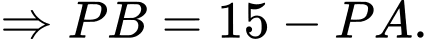
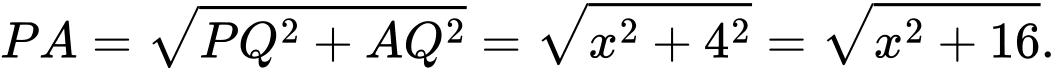
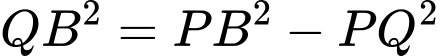 hay
hay 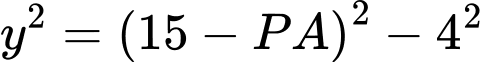 hay
hay 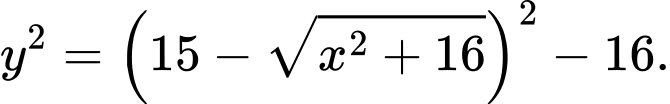
Với
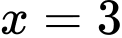 ta có:
ta có: 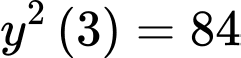 hay
hay 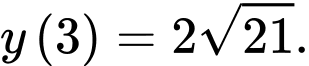
Ta có:
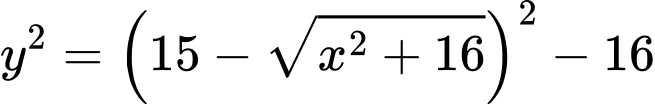
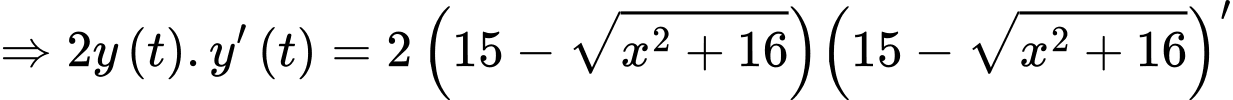
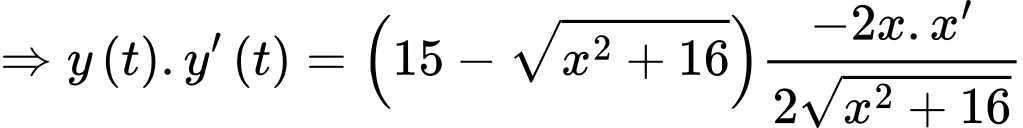
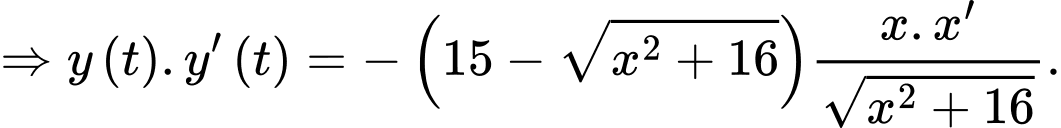
Với
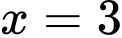 ta có:
ta có: 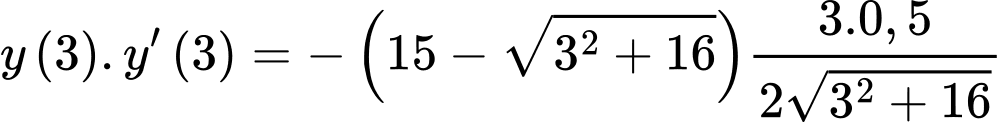
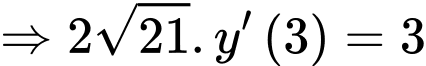
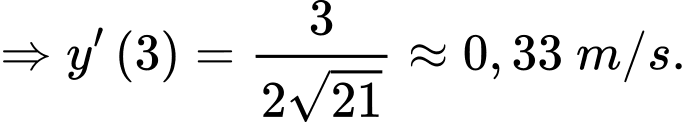
Câu 22 [693108]: Để tiết kiệm chi phí sản xuất ra một dây giày thể thao mà vẫn đảm bảo về chất lượng và tính thẩm mỹ dành cho người tiêu dùng, nhà thiết kế đang muốn tối ưu chiều dài của nó. Trên một chiếc giày có 8 lỗ xỏ dây được chia đều dọc 2 bên, các lỗ cách đều nhau ở mỗi dọc và cùng nằm trên một đường thẳng. Hai lỗ ở dưới mỗi dọc cùng nằm trên một đường thẳng vuông góc với đường thẳng ở mỗi dọc và hai lỗ cách nhau 50 mm, khoảng cách từ lỗ dưới cùng đến lỗ trên cùng ở 1 bên dọc là 80 mm. Dây giày phải đi qua hai lỗ xỏ ở dưới mỗi dọc và sau đó đan chéo qua các lỗ xỏ kế tiếp cho đến khi đến hai lỗ xỏ ở trên cùng mỗi dọc. Sau khi đi qua hai lỗ xỏ cuối cùng, mỗi đầu của dây thừa ít nhất 200 mm để người tiêu dùng có thể buộc thành nút. Vậy chiều dài tối thiểu của dây giày là bao nhiêu milimét? (coi chiều dài sợ dây khi xỏ qua lỗ là không đánh kể).
Điền đáp số: 
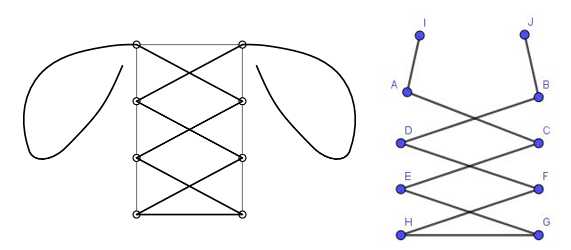
Hình chữ nhật được chia thành 3 hình chữ nhật nhỏ hơn có chiều rộng là và chiều dài là
và chiều dài là 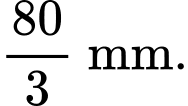
Theo Định lý Pythagore, đường chéo của hình chữ nhật là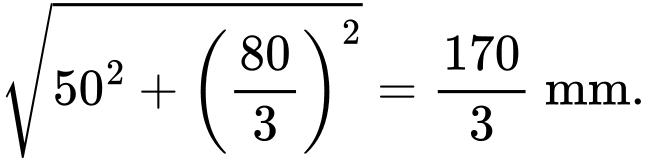
Có tất cả 6 đường chéo và phần mở rộng ít nhất là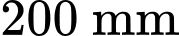 ở mỗi cạnh.
ở mỗi cạnh.
Do đó, chiều dài tối thiểu của dây giày tính bằng milimét là
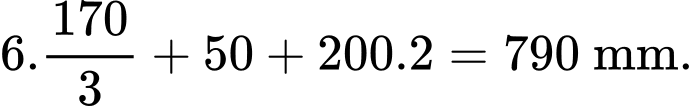
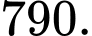

Hình chữ nhật được chia thành 3 hình chữ nhật nhỏ hơn có chiều rộng là
 và chiều dài là
và chiều dài là 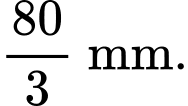
Theo Định lý Pythagore, đường chéo của hình chữ nhật là
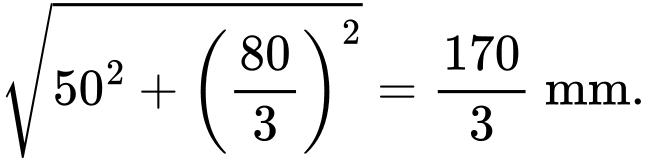
Có tất cả 6 đường chéo và phần mở rộng ít nhất là
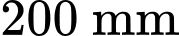 ở mỗi cạnh.
ở mỗi cạnh. Do đó, chiều dài tối thiểu của dây giày tính bằng milimét là