PHẦN I. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Câu 1 [904492]: Phương trình 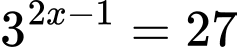 có nghiệm là
có nghiệm là
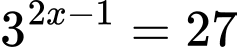 có nghiệm là
có nghiệm là A, 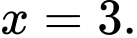
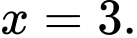
B, 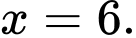
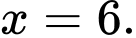
C, 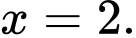
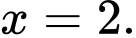
D, 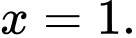
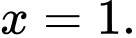
Chọn đáp án C.
Ta có: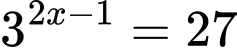
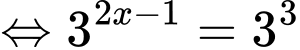
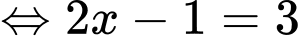
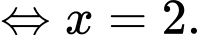 Đáp án: C
Đáp án: C
Ta có:
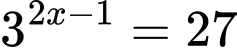
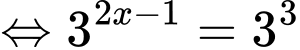
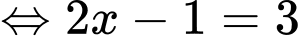
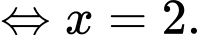 Đáp án: C
Đáp án: C
Câu 2 [801217]: Trong không gian  vectơ nào dưới đây là một vectơ pháp tuyến của mặt phẳng
vectơ nào dưới đây là một vectơ pháp tuyến của mặt phẳng 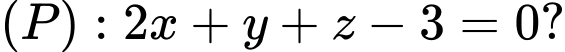
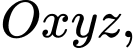 vectơ nào dưới đây là một vectơ pháp tuyến của mặt phẳng
vectơ nào dưới đây là một vectơ pháp tuyến của mặt phẳng 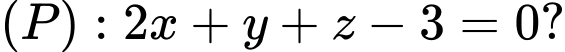
A, 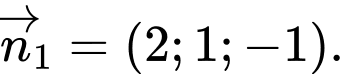
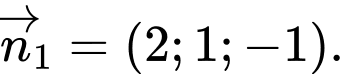
B, 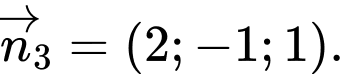
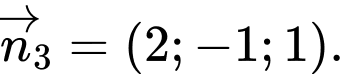
C, 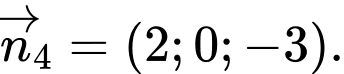
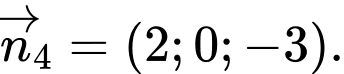
D, 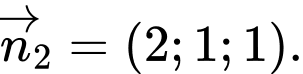
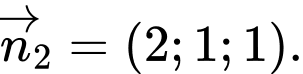
Chọn đáp án D. Đáp án: D
Câu 3 [801228]: Cho cấp số cộng 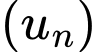 có
có 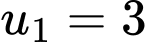 và công sai
và công sai  Số hạng
Số hạng 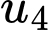 bằng
bằng
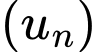 có
có 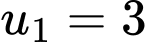 và công sai
và công sai  Số hạng
Số hạng 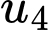 bằng
bằng A, 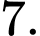
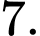
B, 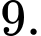
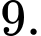
C, 
D, 

Chọn đáp án B.
Ta có: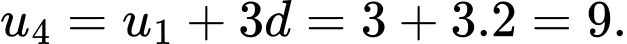 Đáp án: B
Đáp án: B
Ta có:
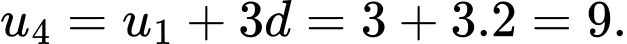 Đáp án: B
Đáp án: B
Câu 4 [904470]: Khẳng định nào sau đây đúng ?
A, 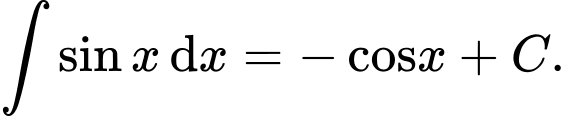
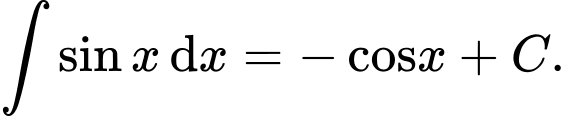
B, 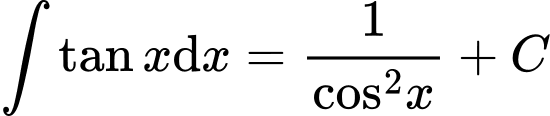
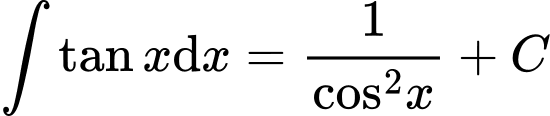
C, 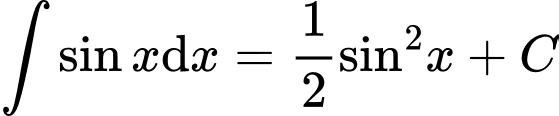
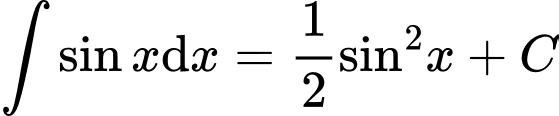
D, 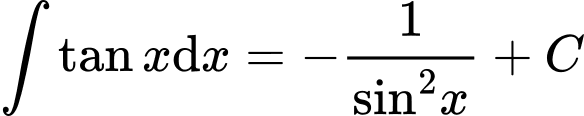
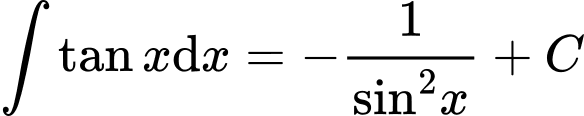
Chọn đáp án A. Đáp án: A
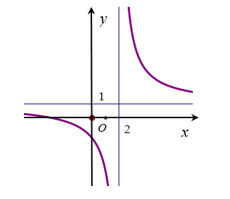
Câu 5 [904476]: Đường cong trong hình vẽ là đồ thị của hàm số nào sau đây ?
 .
.
 .
. A, 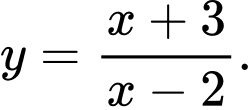
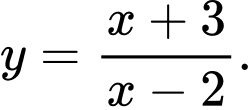
B, 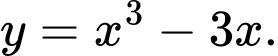
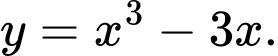
C, 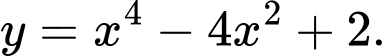
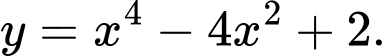
D, 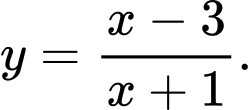
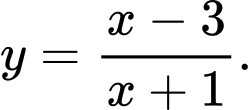
Chọn đáp án A.
Đồ thị trong hình vẽ là của hàm số có dạng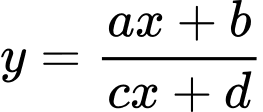
 Loại B, C.
Loại B, C.
Đồ thị trong hàm vẽ nghịch biến trên từng khoảng và
và 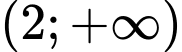
 Loại D. Đáp án: A
Loại D. Đáp án: A
Đồ thị trong hình vẽ là của hàm số có dạng
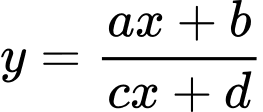
 Loại B, C.
Loại B, C. Đồ thị trong hàm vẽ nghịch biến trên từng khoảng
 và
và 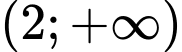
 Loại D. Đáp án: A
Loại D. Đáp án: A
Câu 6 [904495]: Với 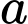 là số thực dương tùy ý khác 1,
là số thực dương tùy ý khác 1, 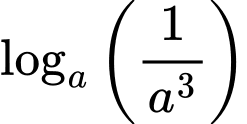 bằng
bằng
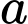 là số thực dương tùy ý khác 1,
là số thực dương tùy ý khác 1, 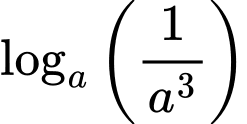 bằng
bằng A, 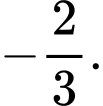
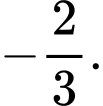
B, 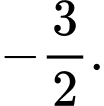
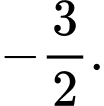
C, 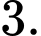
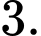
D, 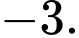
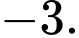
Chọn đáp án D.
Ta có: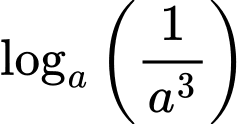
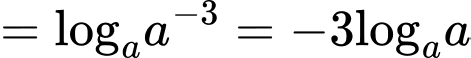
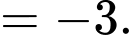 Đáp án: D
Đáp án: D
Ta có:
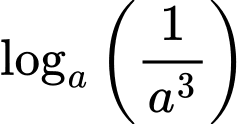
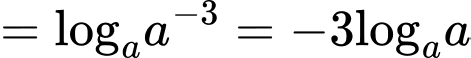
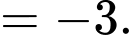 Đáp án: D
Đáp án: D
Câu 7 [695249]: Trong không gian  cho mặt phẳng
cho mặt phẳng 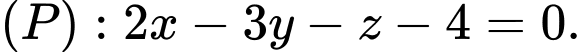 Phương trình nào dưới đây là phương trình tham số của đường thẳng đi qua điểm
Phương trình nào dưới đây là phương trình tham số của đường thẳng đi qua điểm 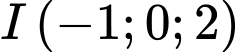 và vuông góc với
và vuông góc với 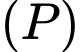 ?
?
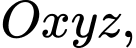 cho mặt phẳng
cho mặt phẳng 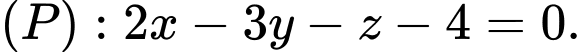 Phương trình nào dưới đây là phương trình tham số của đường thẳng đi qua điểm
Phương trình nào dưới đây là phương trình tham số của đường thẳng đi qua điểm 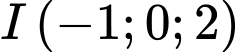 và vuông góc với
và vuông góc với 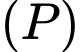 ?
? A, 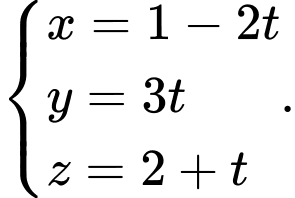
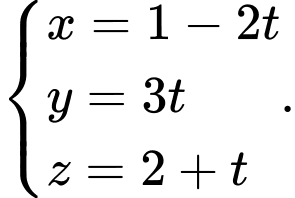
B, 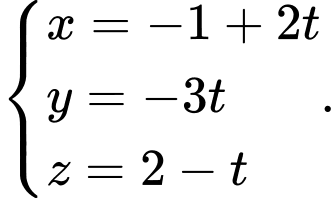
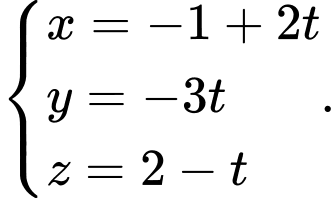
C, 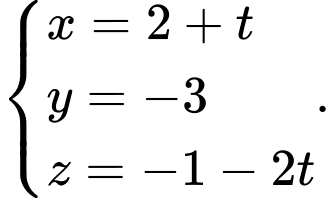
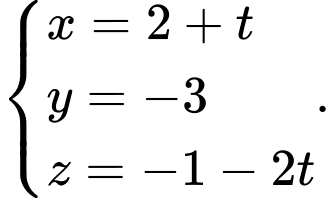
D, 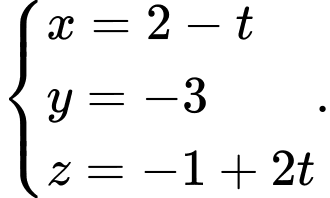
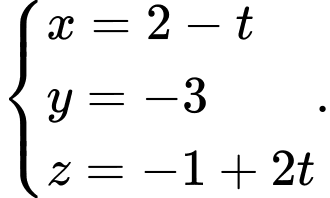
Chọn đáp án B.
Phương trình đường thẳng vuông góc có dạng
có dạng 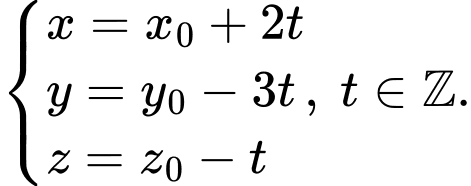
Phương trình đưởng thẳng này đi qua điểm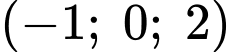 nên
nên 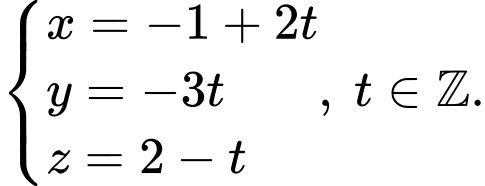 Đáp án: B
Đáp án: B
Phương trình đường thẳng vuông góc
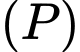 có dạng
có dạng 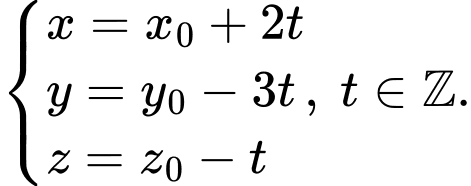
Phương trình đưởng thẳng này đi qua điểm
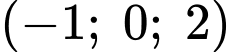 nên
nên 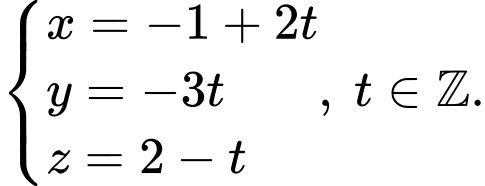 Đáp án: B
Đáp án: B
Câu 8 [681581]: Cho tứ diện đều 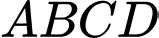 có cạnh bằng
có cạnh bằng 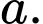 Tích vô hướng
Tích vô hướng 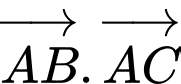 bằng
bằng
 có cạnh bằng
có cạnh bằng  Tích vô hướng
Tích vô hướng 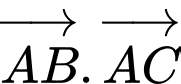 bằng
bằng A, 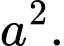
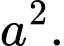
B, 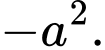
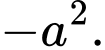
C, 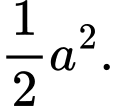
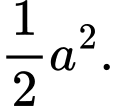
D, 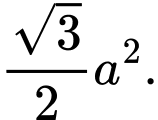
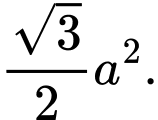
Chọn đáp án C.
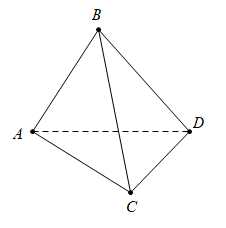
Vì là tứ diện đều cạnh
là tứ diện đều cạnh  nên
nên  là tam giác đều cạnh
là tam giác đều cạnh 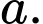
Do đó,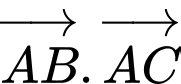
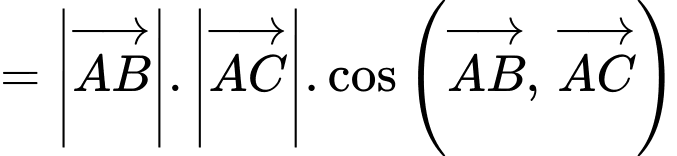
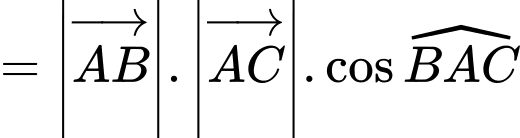
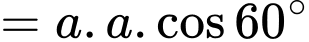
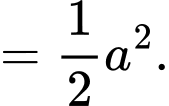 Đáp án: C
Đáp án: C

Vì
 là tứ diện đều cạnh
là tứ diện đều cạnh 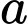 nên
nên 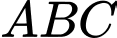 là tam giác đều cạnh
là tam giác đều cạnh 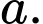
Do đó,
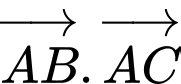
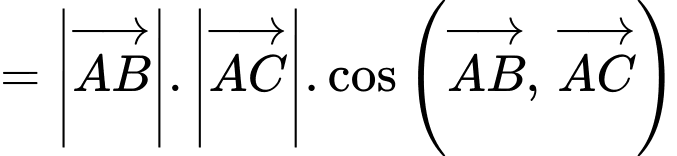
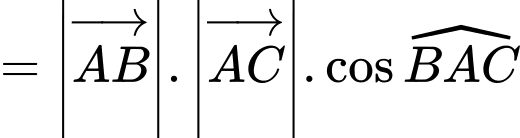
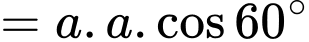
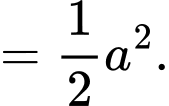 Đáp án: C
Đáp án: C
Câu 9 [695250]: Thành tích môn nhảy cao của các vận động viên tại một giải điền kinh dành cho học sinh trung học phổ thông như sau:
Tính độ lệch chuẩn của mẫu số liệu ghép nhóm trên (làm tròn đến hàng phần trăm).

Tính độ lệch chuẩn của mẫu số liệu ghép nhóm trên (làm tròn đến hàng phần trăm).
A, 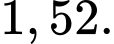
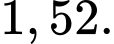
B, 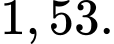
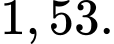
C, 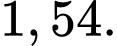
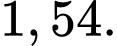
D, 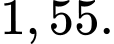
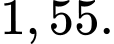
Sách mới với nhiều bài tập nên không tránh khỏi sai sót, các em sửa lại đề giúp thầy như trên Web nhé!
Chọn đáp án B.
Số trung bình của mấu số liệu ghép nhóm là
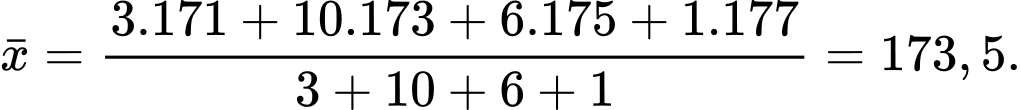
Phương sai của mẫu số liệu ghép nhóm là
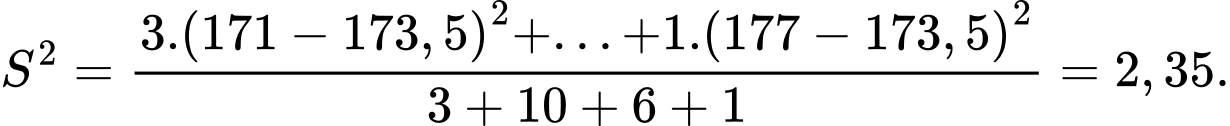
Độ lệch chuẩn của mẫu số liệu ghép nhóm là
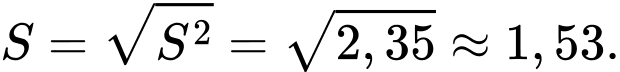 Đáp án: B
Đáp án: B
Chọn đáp án B.
Số trung bình của mấu số liệu ghép nhóm là
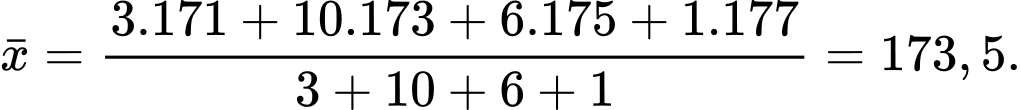
Phương sai của mẫu số liệu ghép nhóm là
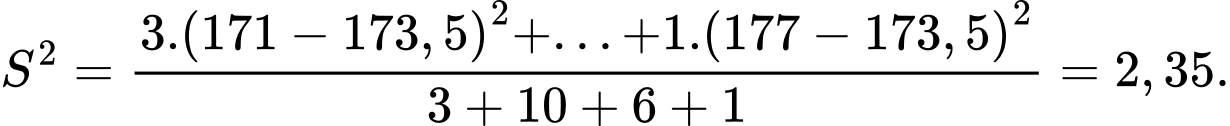
Độ lệch chuẩn của mẫu số liệu ghép nhóm là
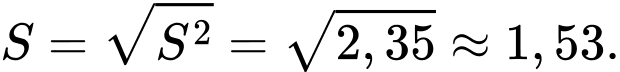 Đáp án: B
Đáp án: B
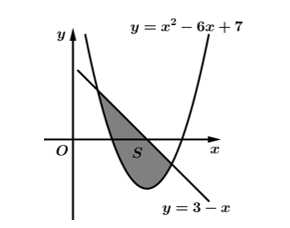
Câu 10 [808412]: Tính diện tích hình phẳng  giới hạn bởi đồ thị hàm số
giới hạn bởi đồ thị hàm số 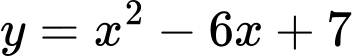 và đường thẳng
và đường thẳng 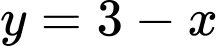
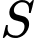 giới hạn bởi đồ thị hàm số
giới hạn bởi đồ thị hàm số 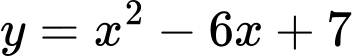 và đường thẳng
và đường thẳng 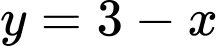

A, 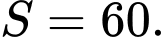
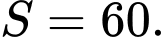
B, 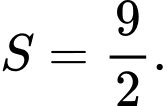
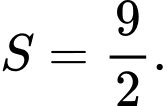
C, 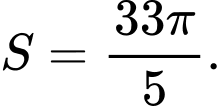
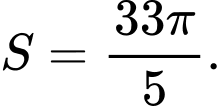
D, 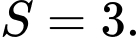
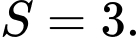
Chọn đáp án B.
Phương trình hoành độ giao điểm của đồ thị hàm số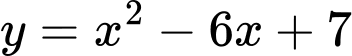 và đường thẳng
và đường thẳng 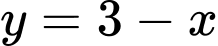 là
là
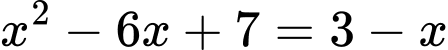
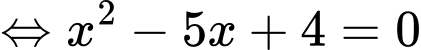

Dễ nhận thấy trên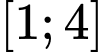 , đường thẳng
, đường thẳng 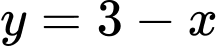 nằm phía trên đồ thị hàm số
nằm phía trên đồ thị hàm số 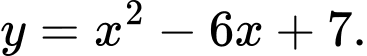
Khi đó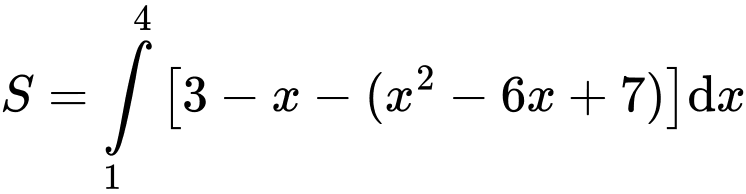
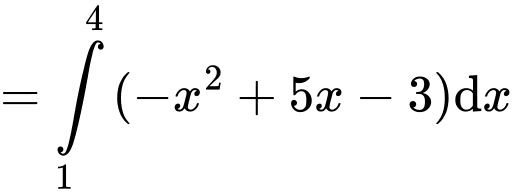
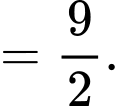 Đáp án: B
Đáp án: B
Phương trình hoành độ giao điểm của đồ thị hàm số
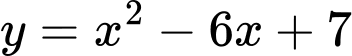 và đường thẳng
và đường thẳng 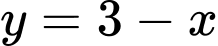 là
là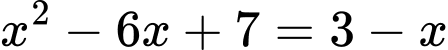
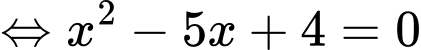

Dễ nhận thấy trên
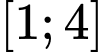 , đường thẳng
, đường thẳng 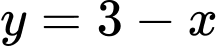 nằm phía trên đồ thị hàm số
nằm phía trên đồ thị hàm số 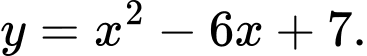
Khi đó
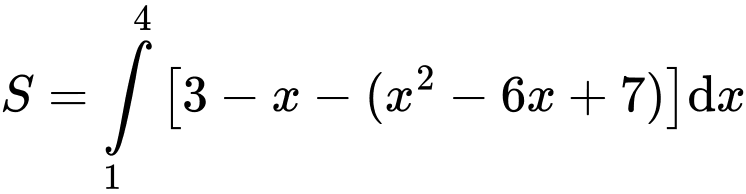
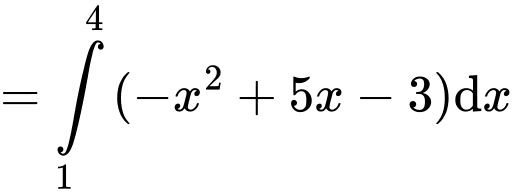
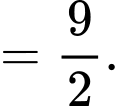 Đáp án: B
Đáp án: B
Câu 11 [513194]: Cho hình chóp đều 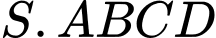 có
có 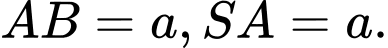 Thể tích khối chóp
Thể tích khối chóp 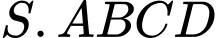 bằng
bằng
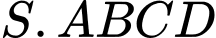 có
có 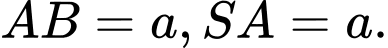 Thể tích khối chóp
Thể tích khối chóp 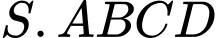 bằng
bằng A, 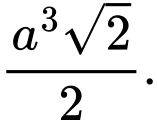
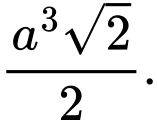
B, 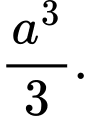
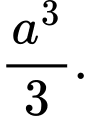
C, 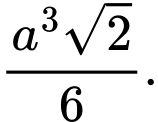
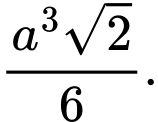
D, 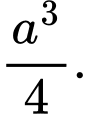
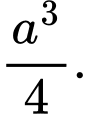
Chọn đáp án C.
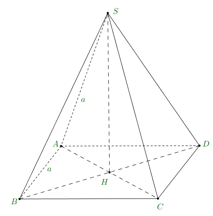
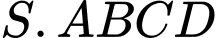 là hình chóp đều nên:
là hình chóp đều nên: 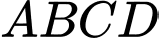 là hình vuông,
là hình vuông, 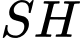 là đường cao của hình chóp.
là đường cao của hình chóp.
Ta có:
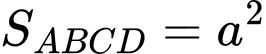

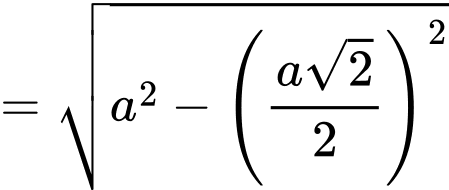
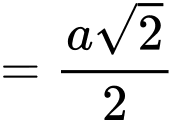
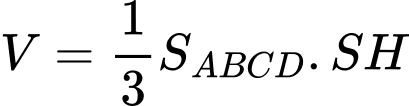
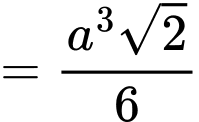 Đáp án: C
Đáp án: C

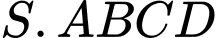 là hình chóp đều nên:
là hình chóp đều nên: 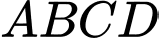 là hình vuông,
là hình vuông, 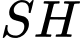 là đường cao của hình chóp.
là đường cao của hình chóp. Ta có:
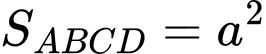

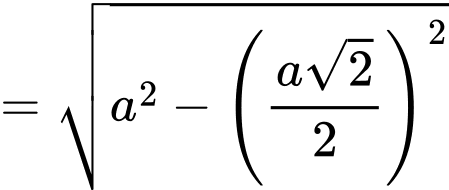
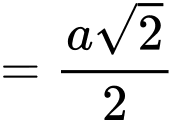
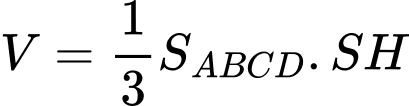
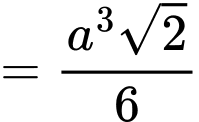 Đáp án: C
Đáp án: C
Câu 12 [904496]: Hàm số 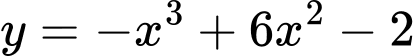 đồng biến trên khoảng
đồng biến trên khoảng
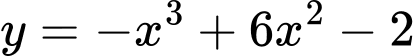 đồng biến trên khoảng
đồng biến trên khoảng A, 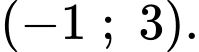
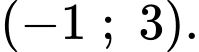
B, 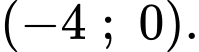
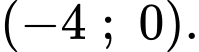
C, 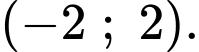
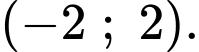
D, 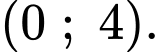
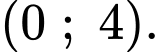
Chọn đáp án D.
Tập xác định: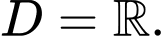
Ta có: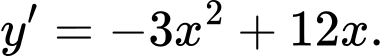
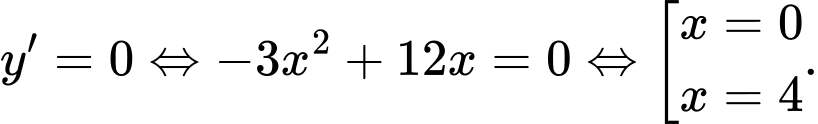
Bảng biến thiên
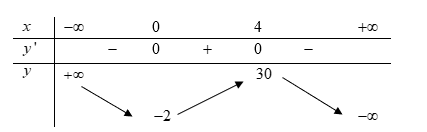
Dựa vào BBT suy ra hàm số đồng biến trên khoảng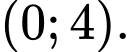 Đáp án: D
Đáp án: D
Tập xác định:
Ta có:
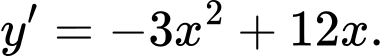
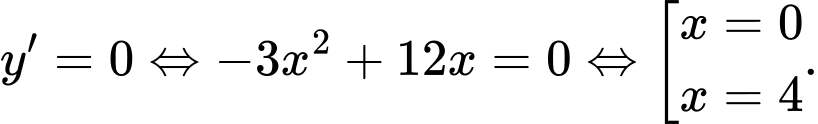
Bảng biến thiên

Dựa vào BBT suy ra hàm số đồng biến trên khoảng
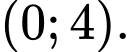 Đáp án: D
Đáp án: D PHẦN II. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
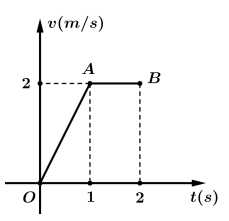
Câu 13 [695251]: Một vật chuyển động với vận tốc 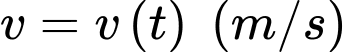
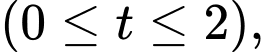
 tính bằng giây, được cho bởi đồ thị trong hình sau:
tính bằng giây, được cho bởi đồ thị trong hình sau:
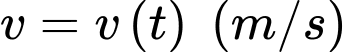
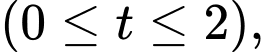
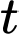 tính bằng giây, được cho bởi đồ thị trong hình sau:
tính bằng giây, được cho bởi đồ thị trong hình sau:
a) Sai.
Vì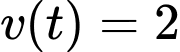 khi
khi 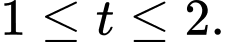
b) Đúng.
Vì nguyên hàm của vận tốc trong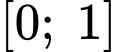 chính là quãng đường trong 1 giây đầu tiên.
chính là quãng đường trong 1 giây đầu tiên.
c) Sai.
Hai cận của tích phân phải từ 1 đến 2.
d) Đúng.
Quãng đường vật đi được trong 2 giây đầu tiên là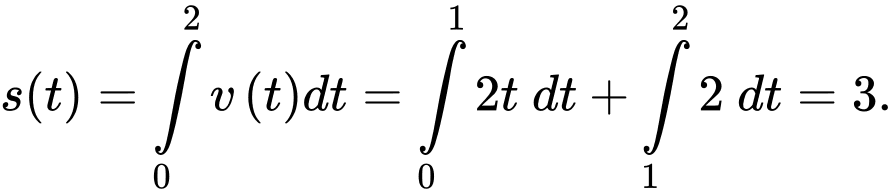
Vì
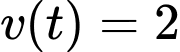 khi
khi 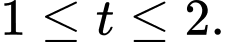
b) Đúng.
Vì nguyên hàm của vận tốc trong
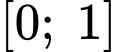 chính là quãng đường trong 1 giây đầu tiên.
chính là quãng đường trong 1 giây đầu tiên.c) Sai.
Hai cận của tích phân phải từ 1 đến 2.
d) Đúng.
Quãng đường vật đi được trong 2 giây đầu tiên là
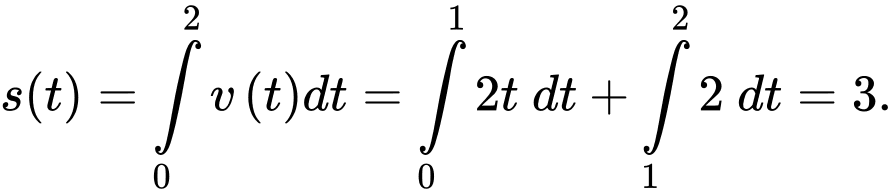
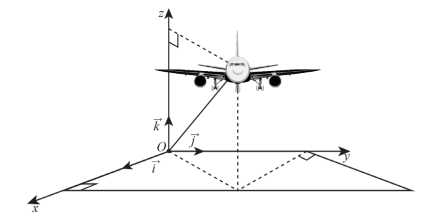
Câu 14 [695252]: Một chiếc máy bay đang bay trên không trung (coi vận tốc gió không đáng kể). Xét hệ trục tọa độ 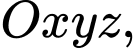 được gắn như hình vẽ, trong đó gốc
được gắn như hình vẽ, trong đó gốc  là vị trí của trạm kiểm soát không lưu, mặt đất trùng với mặt phẳng
là vị trí của trạm kiểm soát không lưu, mặt đất trùng với mặt phẳng  và
và 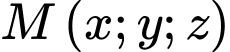 (km) biểu thị vị trí máy bay trên không trung. Tại thời điểm 8h máy bay đang ở vị trí
(km) biểu thị vị trí máy bay trên không trung. Tại thời điểm 8h máy bay đang ở vị trí 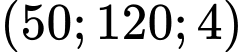 và chuyển động với vận tốc
và chuyển động với vận tốc 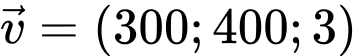 (km/h).
(km/h).
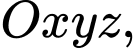 được gắn như hình vẽ, trong đó gốc
được gắn như hình vẽ, trong đó gốc  là vị trí của trạm kiểm soát không lưu, mặt đất trùng với mặt phẳng
là vị trí của trạm kiểm soát không lưu, mặt đất trùng với mặt phẳng 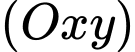 và
và 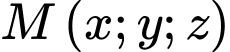 (km) biểu thị vị trí máy bay trên không trung. Tại thời điểm 8h máy bay đang ở vị trí
(km) biểu thị vị trí máy bay trên không trung. Tại thời điểm 8h máy bay đang ở vị trí 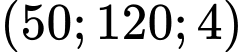 và chuyển động với vận tốc
và chuyển động với vận tốc 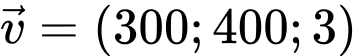 (km/h).
(km/h).
a) Đúng.
Khoảng cách giữa máy bay và trạm kiểm soát không lưu là
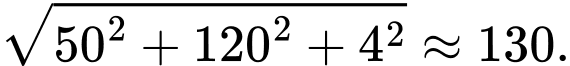
b) Sai.
Ta có phương trình chuyển động của máy bay bắt đầu ở thời điểm 8h là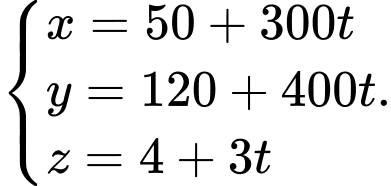
Độ cao của máy bay so vối mặt đất tại thời điểm 9h là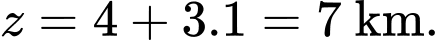
c) Sai.
Tọa độ của máy bay tại thời điểm 10h là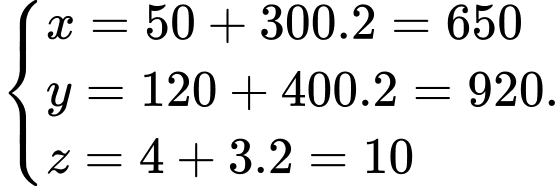
Khoảng cách giữa máy bay và tháp truyền hình là
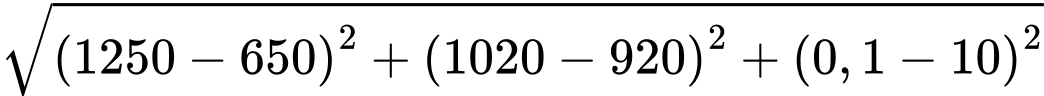
d) Đúng.
Phương trình chuyển động của máy bay ở thời điểm 10h là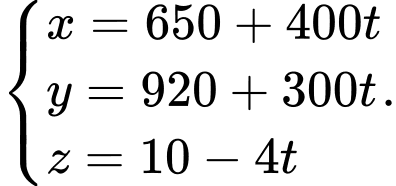
Để máy bay hạ cánh thì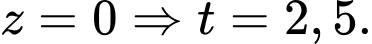
Khoảng cách giữa máy bay và trạm kiểm soát không lưu là
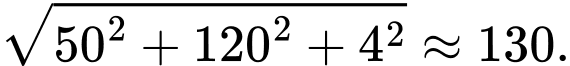
b) Sai.
Ta có phương trình chuyển động của máy bay bắt đầu ở thời điểm 8h là
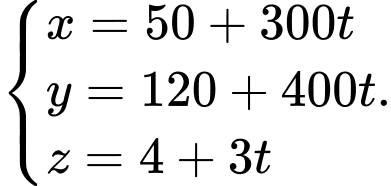
Độ cao của máy bay so vối mặt đất tại thời điểm 9h là
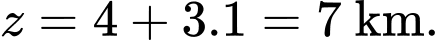
c) Sai.
Tọa độ của máy bay tại thời điểm 10h là
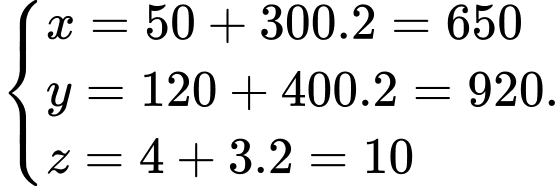
Khoảng cách giữa máy bay và tháp truyền hình là
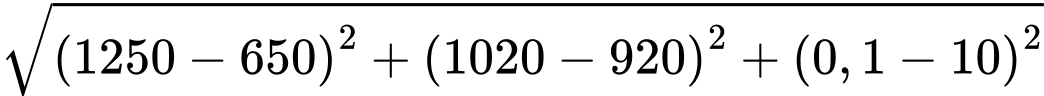
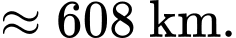
d) Đúng.
Phương trình chuyển động của máy bay ở thời điểm 10h là
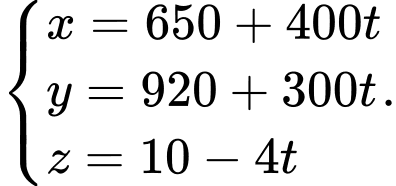
Để máy bay hạ cánh thì
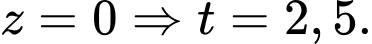
Câu 15 [695253]: Một công ty kim cương thống kê có 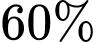 người mua kim cương là nam, có
người mua kim cương là nam, có 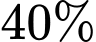 số người mua kim cương là nam trên
số người mua kim cương là nam trên 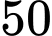 tuổi và
tuổi và 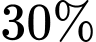 số người mua kim cương là nữ trên
số người mua kim cương là nữ trên 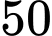 tuổi ( giả sử chỉ có 2 giới tính nam và nữ ).
tuổi ( giả sử chỉ có 2 giới tính nam và nữ ).
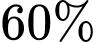 người mua kim cương là nam, có
người mua kim cương là nam, có 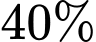 số người mua kim cương là nam trên
số người mua kim cương là nam trên 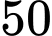 tuổi và
tuổi và 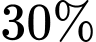 số người mua kim cương là nữ trên
số người mua kim cương là nữ trên 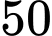 tuổi ( giả sử chỉ có 2 giới tính nam và nữ ).
tuổi ( giả sử chỉ có 2 giới tính nam và nữ ).
a) Đúng.
Gọi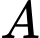 là biến cố “Người mua kim cương là nam”. Ta có
là biến cố “Người mua kim cương là nam”. Ta có 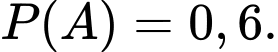
Khi đó là biến cố “Người mua kim cương là nữ ”.
là biến cố “Người mua kim cương là nữ ”.
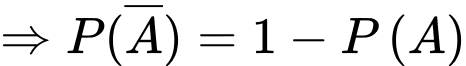
b) Sai.
Gọi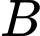 là biến cố “Người mua kim cương trên 50 tuổi”.
là biến cố “Người mua kim cương trên 50 tuổi”.
Theo giả thiết: có 40% số người mua kim cương là nam trên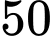 tuổi suy ra
tuổi suy ra 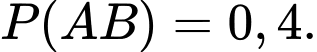
Theo yêu cầu của đề bài ta cần tính: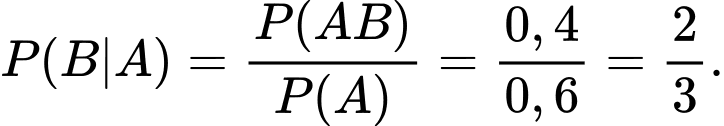
c) Đúng.
Tương tự, phần b). Theo giả thiết: có 30% số người mua kim cương là nữ trên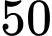 tuổi suy ra
tuổi suy ra 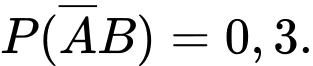
Theo yêu cầu của đề bài ta cần tính :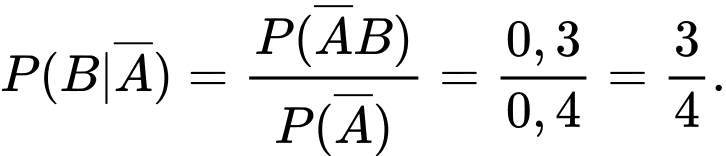
d) Sai.
Dựa vào kết quả ở câu b) và câu c) ta có tỉ lệ đó bằng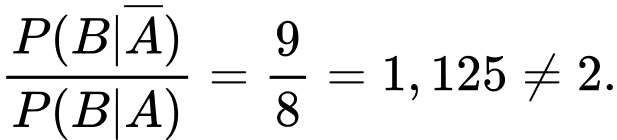
Do đó, tỉ lệ người trên 50 tuổi trong số những người nam cao hơn tỉ lệ người trên tuổi trong số những người nữ là 1,125 lần.
tuổi trong số những người nữ là 1,125 lần.
Gọi
 là biến cố “Người mua kim cương là nam”. Ta có
là biến cố “Người mua kim cương là nam”. Ta có 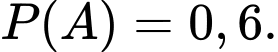
Khi đó
 là biến cố “Người mua kim cương là nữ ”.
là biến cố “Người mua kim cương là nữ ”.
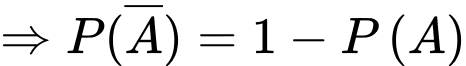
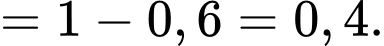
b) Sai.
Gọi
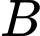 là biến cố “Người mua kim cương trên 50 tuổi”.
là biến cố “Người mua kim cương trên 50 tuổi”.
Theo giả thiết: có 40% số người mua kim cương là nam trên
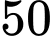 tuổi suy ra
tuổi suy ra 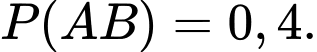
Theo yêu cầu của đề bài ta cần tính:
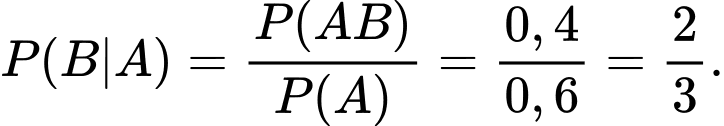
c) Đúng.
Tương tự, phần b). Theo giả thiết: có 30% số người mua kim cương là nữ trên
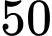 tuổi suy ra
tuổi suy ra 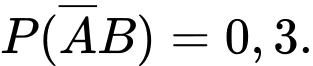
Theo yêu cầu của đề bài ta cần tính :
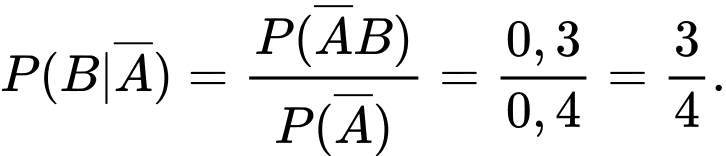
d) Sai.
Dựa vào kết quả ở câu b) và câu c) ta có tỉ lệ đó bằng
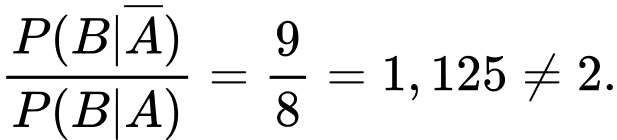
Do đó, tỉ lệ người trên 50 tuổi trong số những người nam cao hơn tỉ lệ người trên
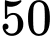 tuổi trong số những người nữ là 1,125 lần.
tuổi trong số những người nữ là 1,125 lần.
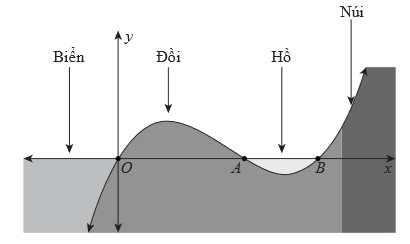
Câu 16 [701558]: Hình vẽ sau mô phỏng một mặt cắt ngang của một phần hòn đảo X, trên hòn đảo X có một lớp đất cạnh một bở biển, phần nhô lên cao là đỉnh của một quả đồi và phần chũng tạo thành một hồ nước tự nhiên. Trên hệ tọa độ 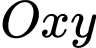 , đường cong
, đường cong 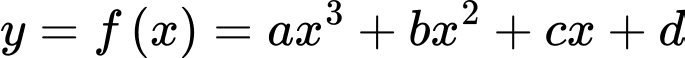 với
với 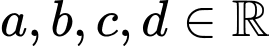 mô phỏng độ cao của lớp đất bên cạnh bờ biển với trục
mô phỏng độ cao của lớp đất bên cạnh bờ biển với trục 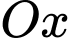 là mực nước biển, đơn vị trên các hệ trục là một kilomet. Biết khoảng cách giữa hai bên chân đôi là
là mực nước biển, đơn vị trên các hệ trục là một kilomet. Biết khoảng cách giữa hai bên chân đôi là 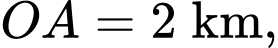 chiều dài của hồ là
chiều dài của hồ là 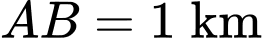 và ngọn đồi cao 528 m.
và ngọn đồi cao 528 m.
 , đường cong
, đường cong 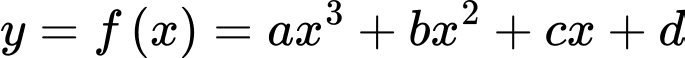 với
với 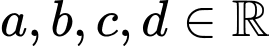 mô phỏng độ cao của lớp đất bên cạnh bờ biển với trục
mô phỏng độ cao của lớp đất bên cạnh bờ biển với trục  là mực nước biển, đơn vị trên các hệ trục là một kilomet. Biết khoảng cách giữa hai bên chân đôi là
là mực nước biển, đơn vị trên các hệ trục là một kilomet. Biết khoảng cách giữa hai bên chân đôi là 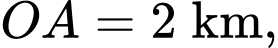 chiều dài của hồ là
chiều dài của hồ là 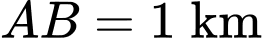 và ngọn đồi cao 528 m.
và ngọn đồi cao 528 m.
a) Sai.
Phương trình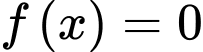 có 3 nghiệm là
có 3 nghiệm là 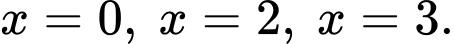
b) Đúng.
Vì hàm số có 3 nghiệm là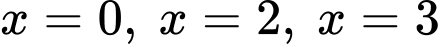 nên có dạng như trên.
nên có dạng như trên.
c) Đúng.
Ta thấy đỉnh ngọn đồi chính là điểm cực đại của đồ thị hàm số đã cho.
Ta có: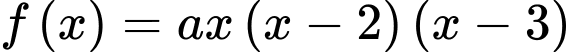
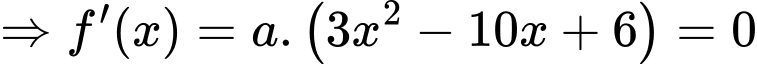
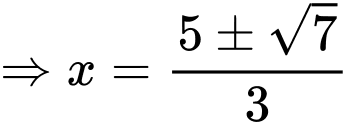 .
.
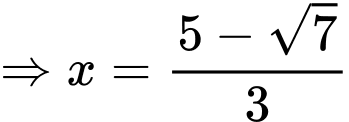 là điểm cực đại của hàm số đã cho.
là điểm cực đại của hàm số đã cho.
Vì ngọn đồi cao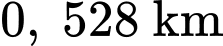 nên ta có:
nên ta có:
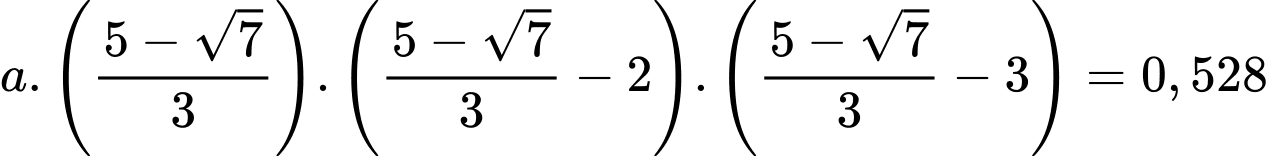
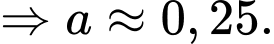
d) Sai.
Dựa vào hình vẽ ta thấy điểm thấp nhất của hồ chính là điểm cực tiểu của đồ thị hàm số đã cho.
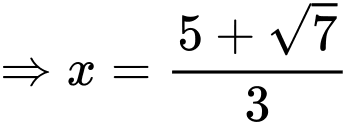 là điểm cực tiểu của hàm số đã cho.
là điểm cực tiểu của hàm số đã cho.
Độ sâu của hồ là
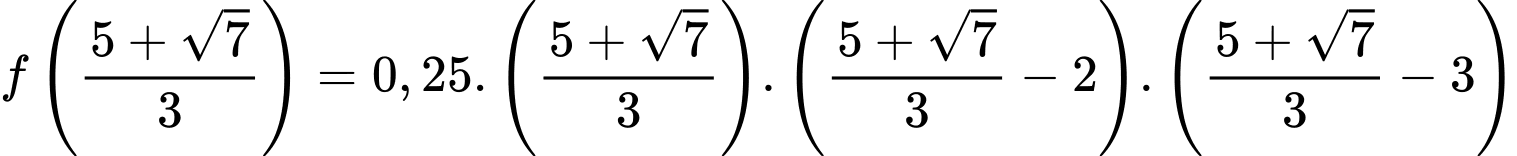
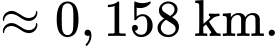
Phương trình
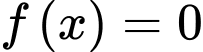 có 3 nghiệm là
có 3 nghiệm là 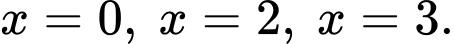
b) Đúng.
Vì hàm số có 3 nghiệm là
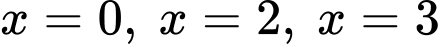 nên có dạng như trên.
nên có dạng như trên.
c) Đúng.
Ta thấy đỉnh ngọn đồi chính là điểm cực đại của đồ thị hàm số đã cho.
Ta có:
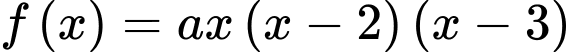
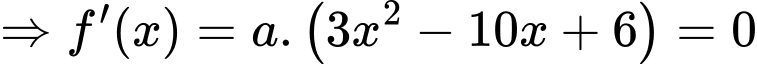
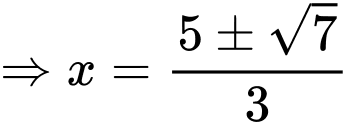 .
.
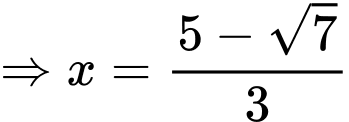 là điểm cực đại của hàm số đã cho.
là điểm cực đại của hàm số đã cho.
Vì ngọn đồi cao
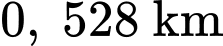 nên ta có:
nên ta có:
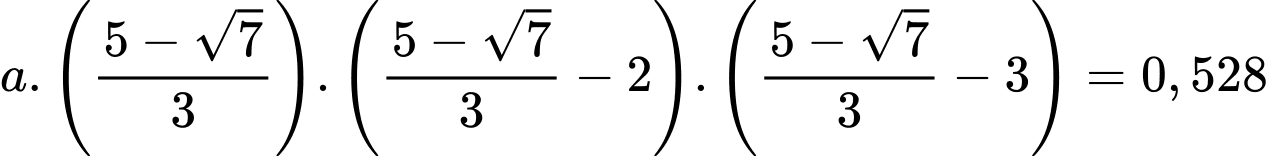
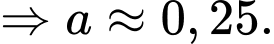
d) Sai.
Dựa vào hình vẽ ta thấy điểm thấp nhất của hồ chính là điểm cực tiểu của đồ thị hàm số đã cho.
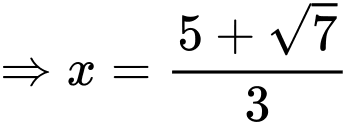 là điểm cực tiểu của hàm số đã cho.
là điểm cực tiểu của hàm số đã cho.
Độ sâu của hồ là
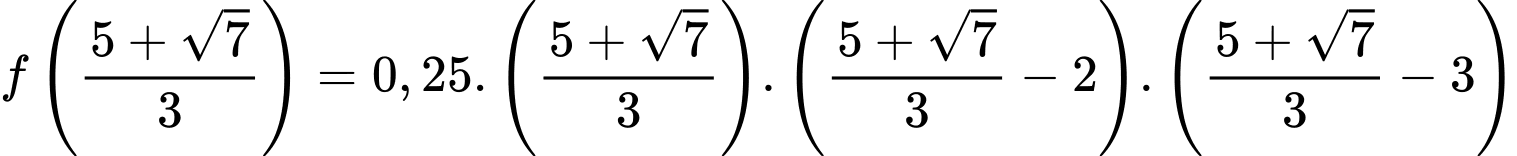
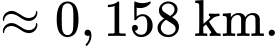
PHẦN III. Thí sinh trả lời từ câu 1 đến câu 6.
Câu 17 [695255]: Cho hình lăng trụ tam giác  có đáy là tam giác đều cạnh bằng
có đáy là tam giác đều cạnh bằng 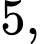 độ dài cạnh bên bằng
độ dài cạnh bên bằng 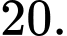 Biết mặt phẳng
Biết mặt phẳng 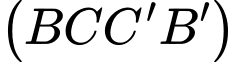 vuông góc với mặt phẳng đáy và
vuông góc với mặt phẳng đáy và 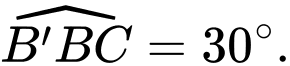 Thể tích của khối chóp
Thể tích của khối chóp 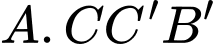 bằng bao nhiêu? (làm tròn kết quả đến hàng phần mười).
bằng bao nhiêu? (làm tròn kết quả đến hàng phần mười).
 có đáy là tam giác đều cạnh bằng
có đáy là tam giác đều cạnh bằng 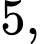 độ dài cạnh bên bằng
độ dài cạnh bên bằng 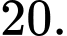 Biết mặt phẳng
Biết mặt phẳng 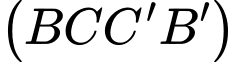 vuông góc với mặt phẳng đáy và
vuông góc với mặt phẳng đáy và 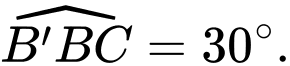 Thể tích của khối chóp
Thể tích của khối chóp  bằng bao nhiêu? (làm tròn kết quả đến hàng phần mười).
bằng bao nhiêu? (làm tròn kết quả đến hàng phần mười).
Điền đáp án: 36,1.
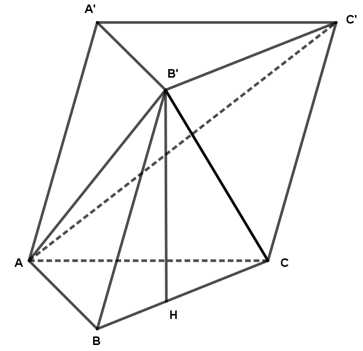
Kẻ .
.
Mà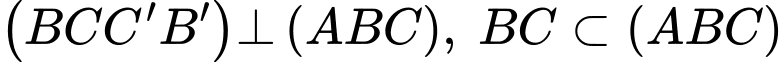
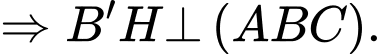
Xét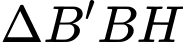 vuông tại
vuông tại 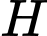 có:
có: 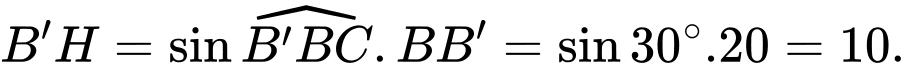
Thể tích hình chóp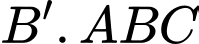 là
là
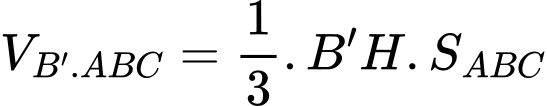
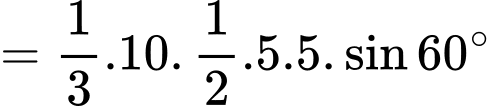
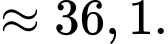
Vì đi qua trung điểm của
đi qua trung điểm của 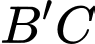 nên
nên 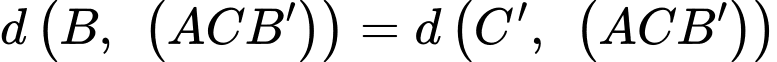
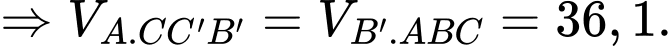

Kẻ
 .
.Mà
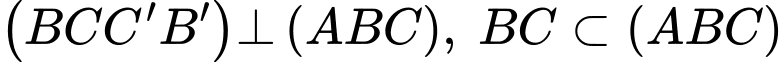
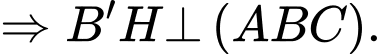
Xét
 vuông tại
vuông tại  có:
có: 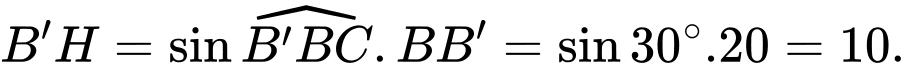
Thể tích hình chóp
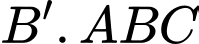 là
là 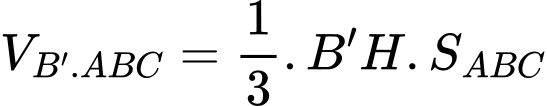
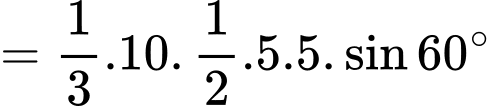
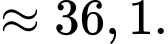
Vì
 đi qua trung điểm của
đi qua trung điểm của 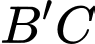 nên
nên 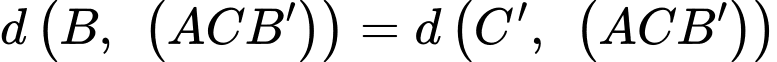
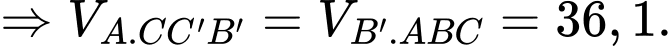
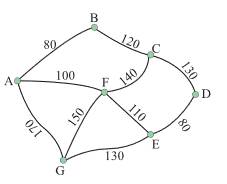
Câu 18 [695256]: Các khu cắm trại tại một công viên được mô phỏng như hình vẽ bên (đơn vị: mét). Bác bảo vệ đang ở khu cắm tại A và phải kiểm tra tất cả các khu cắm trại B, C, D, E, F và G (không nhất thiết phải theo thứ tự đó). Vậy quãng đường ngắn nhất bác bảo vệ có thể đi và điểm kiểm tra cuối cùng ở khu cắm tại D là

Điền đáp án: 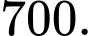
Áp dụng kĩ thuật người láng giềng gần nhất, bác bảo vệ sẽ ưu tiên di chuyển đến những khu cắm trại gần nhất và chưa được đi đến trước đó.
 Quãng đường đi của bác bảo vệ là:
Quãng đường đi của bác bảo vệ là: 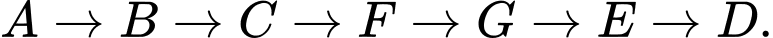
Vậy quãng đường ngắn nhất bác bảo vệ có thể đi là:
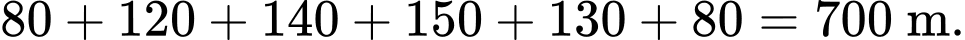
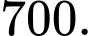
Áp dụng kĩ thuật người láng giềng gần nhất, bác bảo vệ sẽ ưu tiên di chuyển đến những khu cắm trại gần nhất và chưa được đi đến trước đó.
 Quãng đường đi của bác bảo vệ là:
Quãng đường đi của bác bảo vệ là: 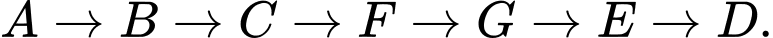
Vậy quãng đường ngắn nhất bác bảo vệ có thể đi là:
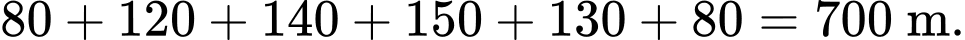
Câu 19 [695257]: Trong không gian với hệ tọa độ 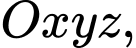 cho hình vuông
cho hình vuông 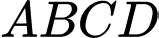 biết
biết 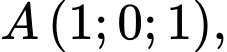
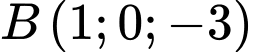 và điểm
và điểm 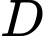 có hoành độ âm. Mặt phẳng
có hoành độ âm. Mặt phẳng 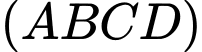 đi qua gốc tọa độ
đi qua gốc tọa độ  Hình vuông
Hình vuông 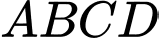 có tâm
có tâm 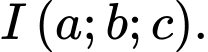 Tính
Tính 
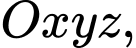 cho hình vuông
cho hình vuông 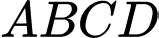 biết
biết 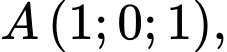
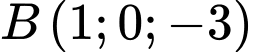 và điểm
và điểm 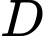 có hoành độ âm. Mặt phẳng
có hoành độ âm. Mặt phẳng 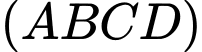 đi qua gốc tọa độ
đi qua gốc tọa độ  Hình vuông
Hình vuông 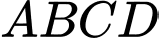 có tâm
có tâm 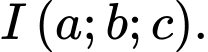 Tính
Tính 
Điền đáp án: -9.
Mặt phẳng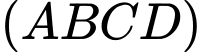 có:
có: 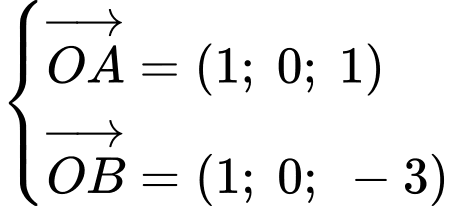
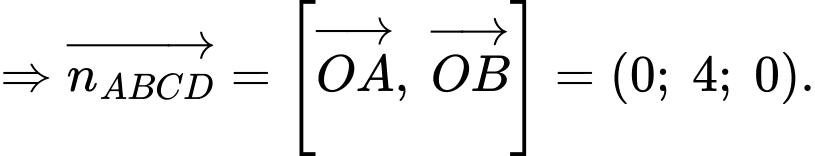
 Phương trình mặt phẳng
Phương trình mặt phẳng 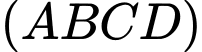 là
là 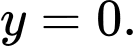
Gọi .
.
Ta có: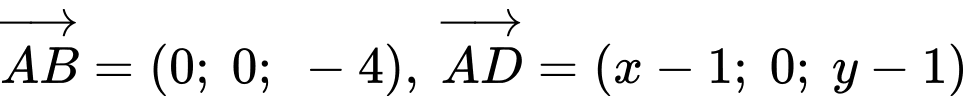

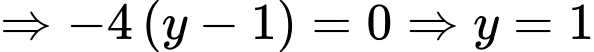
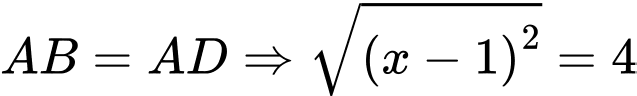
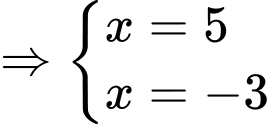
 ( do
( do 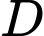 có hoành độ âm)
có hoành độ âm)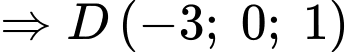 .
.
Do tâm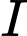 là trung điểm của
là trung điểm của 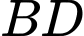
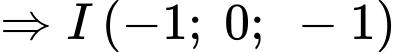
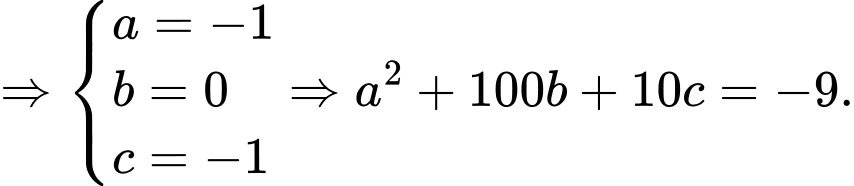
Mặt phẳng
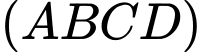 có:
có: 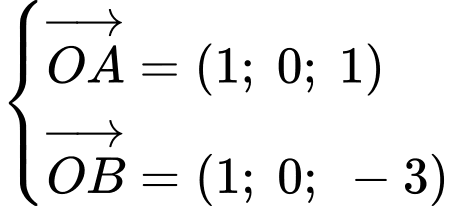
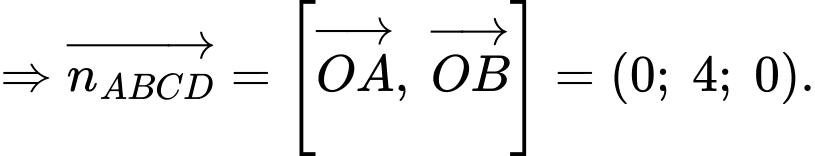
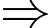 Phương trình mặt phẳng
Phương trình mặt phẳng 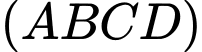 là
là 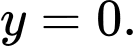
Gọi
 .
.Ta có:
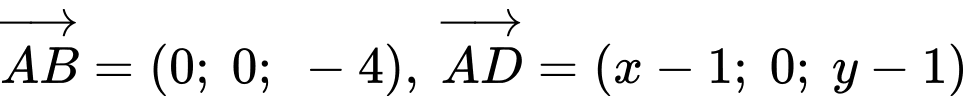

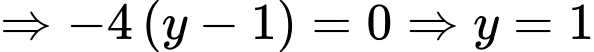
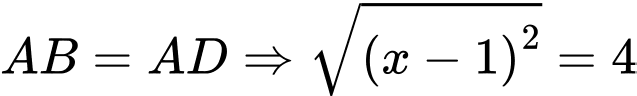
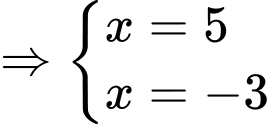
 ( do
( do 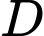 có hoành độ âm)
có hoành độ âm)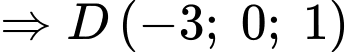 .
.Do tâm
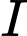 là trung điểm của
là trung điểm của 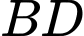
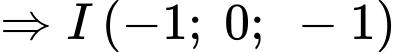
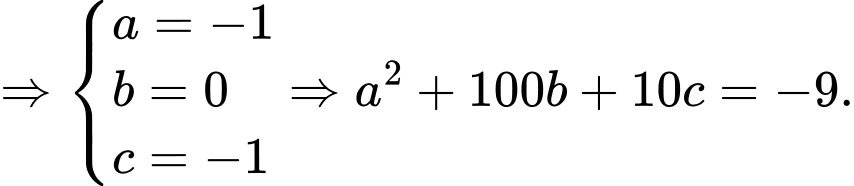
Câu 20 [693540]: Một người lái tàu nhanh đang thử nghiệm một chiếc tàu mới. Từ trạng thái nghỉ, Ông bắt đầu thử nghiệm bằng cách tăng tốc độ của tàu một cách đều đặn cho đến khi đạt được 5 km/h trong vòng 1 phút. Vì đang ở khu vực không được tạo sóng, ông giữ tốc độ này trong 5 phút. Sau khi rời khỏi khu vực không được tạo sóng, ông tăng tốc độ của tàu đều đặn lên đến 45 km/h trong vòng 2 phút. Ông giữ tốc độ này trong 5 phút rồi tăng tốc độ của tàu đều đặn lên 80 km/h trong vòng 1 phút. Sau khi giữ tốc độ này trong 5 phút, ông giảm tốc độ của tàu một cách đều đặn trong vòng 4 phút cho đến khi dừng hẳn. Tính quãng đường mà ông ta đã thử nghiệm chiếc tàu (đơn vị kilomet, làm tròn đến hàng phần mười).


Điền đáp án: 15,4.
Phương trình chuyển động của tàu được biểu thị theo đồ thị vận tốc ( ) và thời gian (h).
) và thời gian (h).
Ta giả sử tàu bắt đầu chuyển động tại vị trí gốc tọa độ O.
+) Trong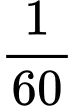 giờ đầu tiên:
giờ đầu tiên:
Phương trình chuyển động của tàu có dạng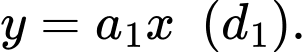
Điểm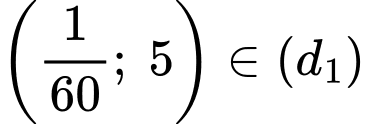
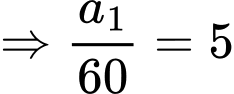
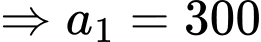
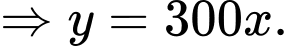
Quãng đường tàu đi được là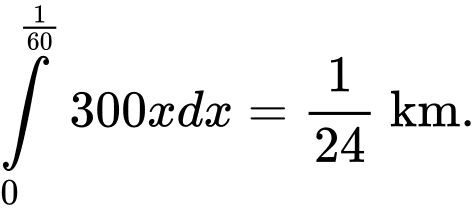
+) Trong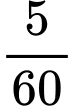 giờ tiếp theo:
giờ tiếp theo:
Quãng đường tàu đi được là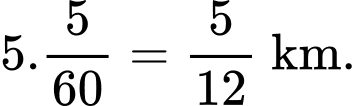
+) Trong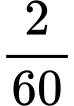 giờ tiếp theo:
giờ tiếp theo:
Phương trình chuyển động của tàu có dạng .
.
Tại thời điểm trước đó, tàu đang ở điểm có tọa độ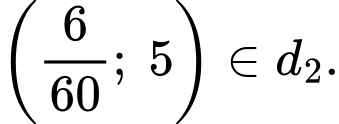
Vì tàu tăng tốc độ trong vòng 2 phút nên ta có điểm
trong vòng 2 phút nên ta có điểm 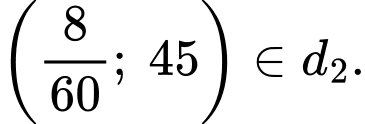
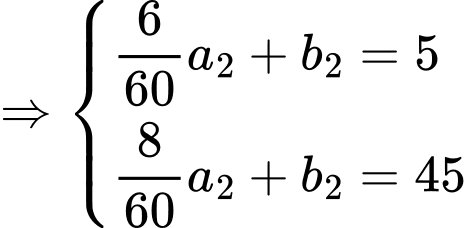
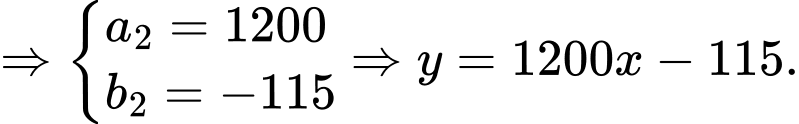
Quãng đường tàu đi được là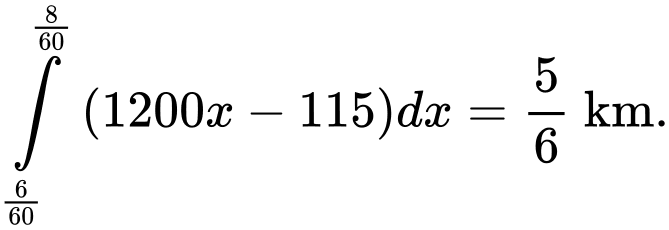
+) Trong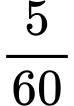 giờ tiếp theo:
giờ tiếp theo:
Quãng đường tàu đi được là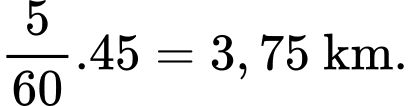
+) Trong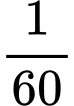 giờ tiếp theo:
giờ tiếp theo:
Phương trình chuyển động của tàu có dạng .
.
Tại thời điểm trước đó, tàu đang ở điểm có tọa độ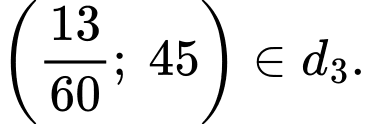
Vì tàu tăng tốc độ trong vòng 1 phút nên ta có điểm
trong vòng 1 phút nên ta có điểm 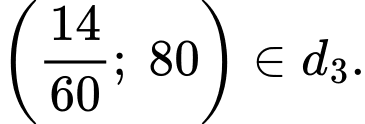
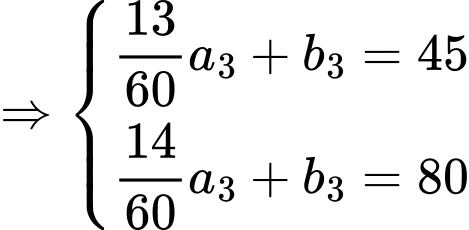
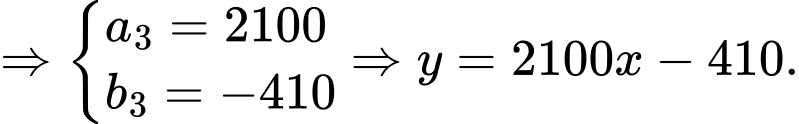
Quãng đường tàu đi được là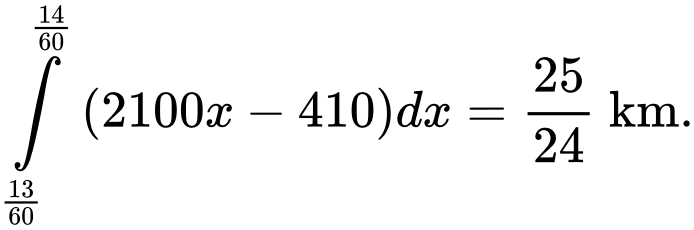
+) Trong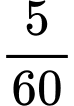 giờ tiếp theo:
giờ tiếp theo:
Quãng đường tàu đi được là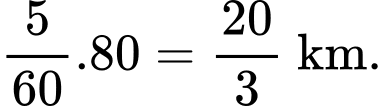
+) Trong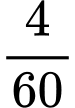 giờ tiếp theo:
giờ tiếp theo:
Phương trình chuyển động của tàu có dạng .
.
Tại thời điểm trước đó, tàu đang ở điểm có tọa độ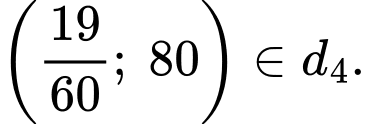
Vì tàu giảm tốc độ một cách đều đặn trong vòng 4 phút cho đến khi dừng hẳn nên ta có điểm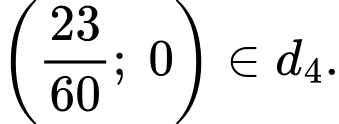
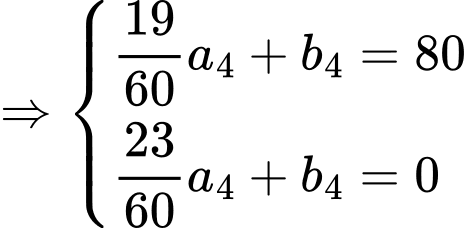
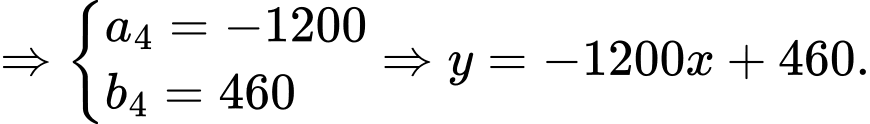
Quãng đường tàu đi được là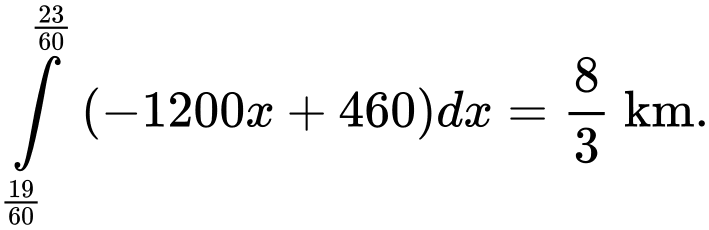
+) Quãng đường mà ông ta đã thử nghiệm chiếc tàu là
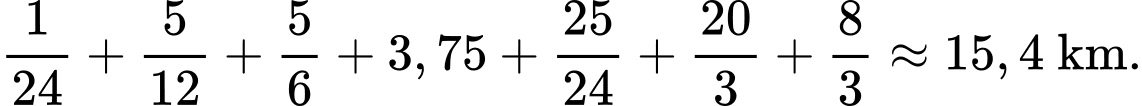
Phương trình chuyển động của tàu được biểu thị theo đồ thị vận tốc (
 ) và thời gian (h).
) và thời gian (h).
Ta giả sử tàu bắt đầu chuyển động tại vị trí gốc tọa độ O.
+) Trong
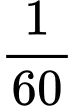 giờ đầu tiên:
giờ đầu tiên: Phương trình chuyển động của tàu có dạng
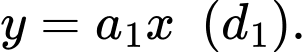
Điểm
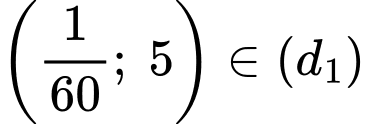
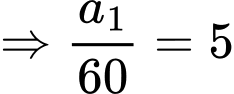
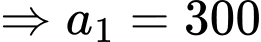
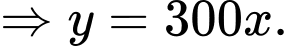
Quãng đường tàu đi được là
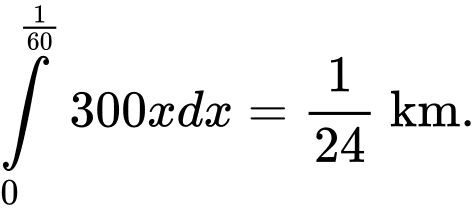
+) Trong
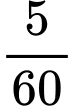 giờ tiếp theo:
giờ tiếp theo: Quãng đường tàu đi được là
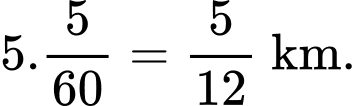
+) Trong
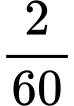 giờ tiếp theo:
giờ tiếp theo: Phương trình chuyển động của tàu có dạng
 .
.
Tại thời điểm trước đó, tàu đang ở điểm có tọa độ
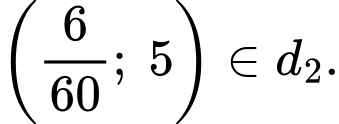
Vì tàu tăng tốc độ
 trong vòng 2 phút nên ta có điểm
trong vòng 2 phút nên ta có điểm 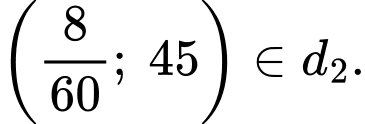
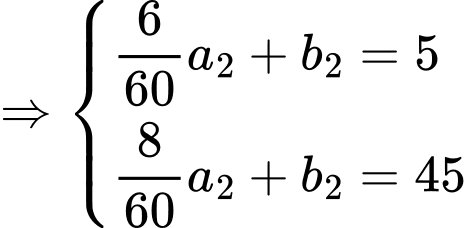
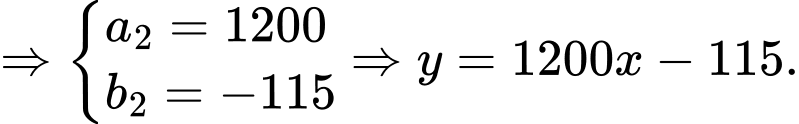
Quãng đường tàu đi được là
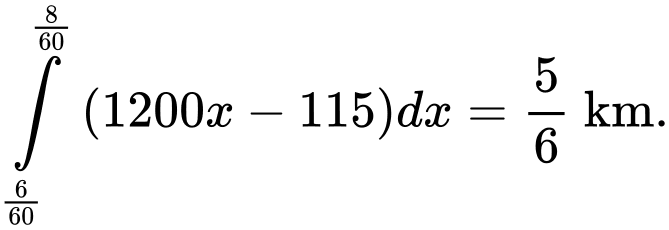
+) Trong
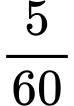 giờ tiếp theo:
giờ tiếp theo: Quãng đường tàu đi được là
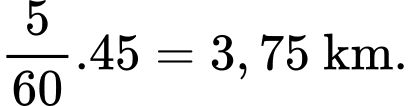
+) Trong
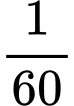 giờ tiếp theo:
giờ tiếp theo: Phương trình chuyển động của tàu có dạng
 .
.
Tại thời điểm trước đó, tàu đang ở điểm có tọa độ
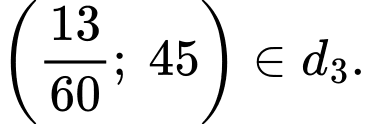
Vì tàu tăng tốc độ
 trong vòng 1 phút nên ta có điểm
trong vòng 1 phút nên ta có điểm 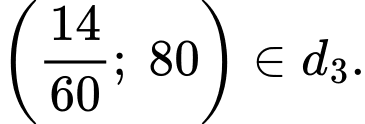
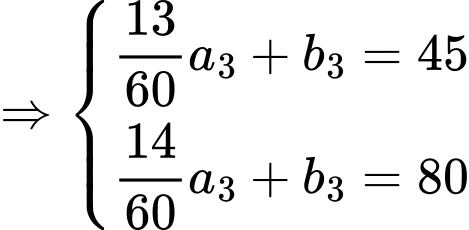
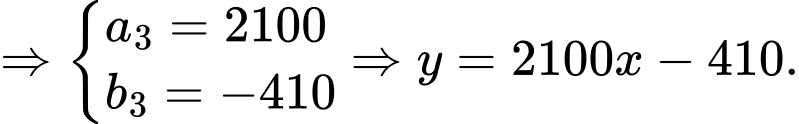
Quãng đường tàu đi được là
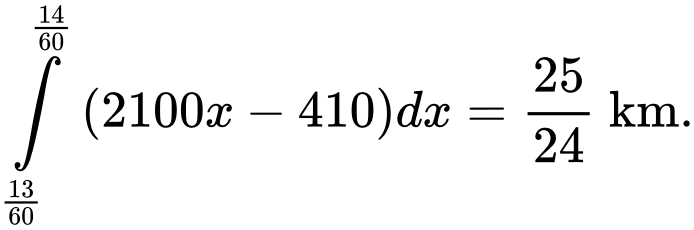
+) Trong
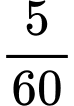 giờ tiếp theo:
giờ tiếp theo: Quãng đường tàu đi được là
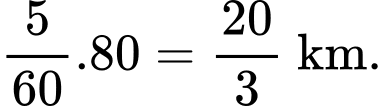
+) Trong
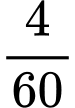 giờ tiếp theo:
giờ tiếp theo: Phương trình chuyển động của tàu có dạng
 .
.
Tại thời điểm trước đó, tàu đang ở điểm có tọa độ
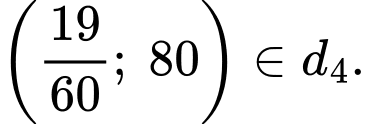
Vì tàu giảm tốc độ một cách đều đặn trong vòng 4 phút cho đến khi dừng hẳn nên ta có điểm
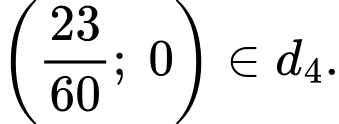
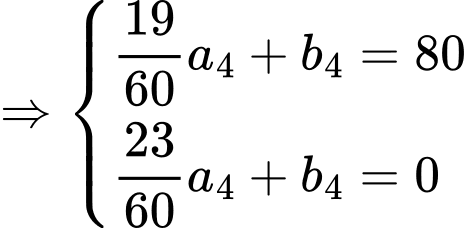
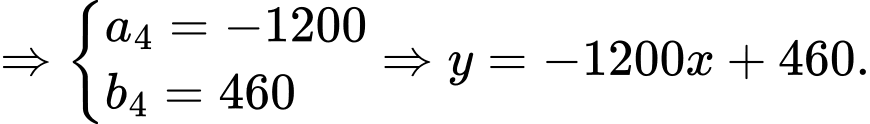
Quãng đường tàu đi được là
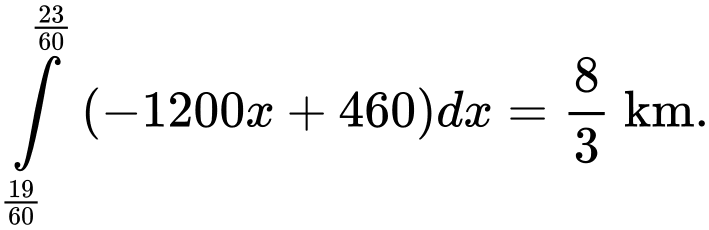
+) Quãng đường mà ông ta đã thử nghiệm chiếc tàu là
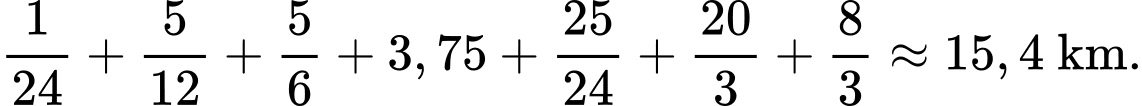
Câu 21 [693094]: Một cái hồ rộng có hình chữ nhật. Tại một góc nhỏ của hồ người ta đóng một cái cọc ở vị trí 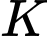 cách bờ
cách bờ  là 1 m và cách bờ
là 1 m và cách bờ 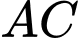 là 8 m, rồi dùng một cây sào ngăn một góc nhỏ của hồ để thả bèo (tham khảo hình vẽ bên). Tính chiều dài ngắn nhất của cây sào để cây sào có thể chạm vào 2 bờ
là 8 m, rồi dùng một cây sào ngăn một góc nhỏ của hồ để thả bèo (tham khảo hình vẽ bên). Tính chiều dài ngắn nhất của cây sào để cây sào có thể chạm vào 2 bờ 
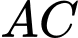 và cây cọc
và cây cọc 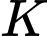 (bỏ qua đường kính của sào, làm tròn kết quả đến hàng phần mười).
(bỏ qua đường kính của sào, làm tròn kết quả đến hàng phần mười).
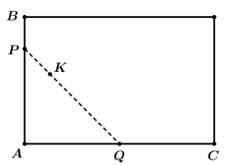
 cách bờ
cách bờ  là 1 m và cách bờ
là 1 m và cách bờ  là 8 m, rồi dùng một cây sào ngăn một góc nhỏ của hồ để thả bèo (tham khảo hình vẽ bên). Tính chiều dài ngắn nhất của cây sào để cây sào có thể chạm vào 2 bờ
là 8 m, rồi dùng một cây sào ngăn một góc nhỏ của hồ để thả bèo (tham khảo hình vẽ bên). Tính chiều dài ngắn nhất của cây sào để cây sào có thể chạm vào 2 bờ 
 và cây cọc
và cây cọc 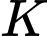 (bỏ qua đường kính của sào, làm tròn kết quả đến hàng phần mười).
(bỏ qua đường kính của sào, làm tròn kết quả đến hàng phần mười).
Điền đáp án: 11,2.
Giả sử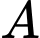 trùng với gốc tọa độ trong mặt phẳng
trùng với gốc tọa độ trong mặt phẳng 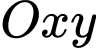 , đoạn
, đoạn 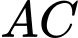 nằm trên trục
nằm trên trục 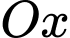 , đoạn
, đoạn  nằm trên trục
nằm trên trục 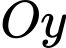
 và
và  cắt 2 trục
cắt 2 trục 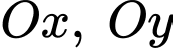 lần lượt tại 2 điểm
lần lượt tại 2 điểm 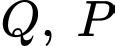 có dạng
có dạng 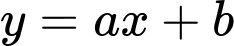
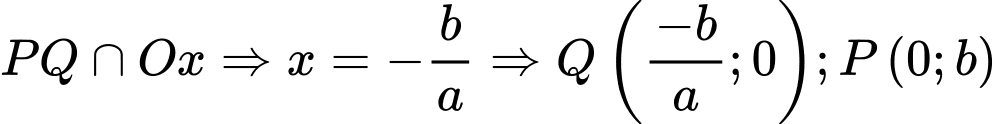
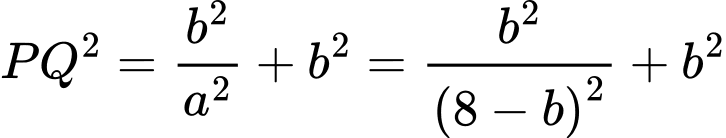
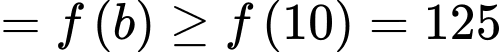
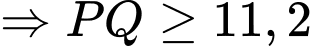
 Chiều dài ngắn nhất của cây sào là
Chiều dài ngắn nhất của cây sào là 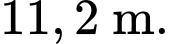
Giả sử
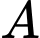 trùng với gốc tọa độ trong mặt phẳng
trùng với gốc tọa độ trong mặt phẳng 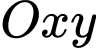 , đoạn
, đoạn 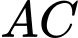 nằm trên trục
nằm trên trục 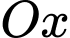 , đoạn
, đoạn  nằm trên trục
nằm trên trục 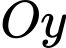
 và
và 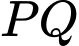 cắt 2 trục
cắt 2 trục 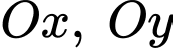 lần lượt tại 2 điểm
lần lượt tại 2 điểm 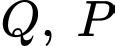 có dạng
có dạng 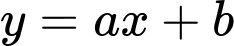
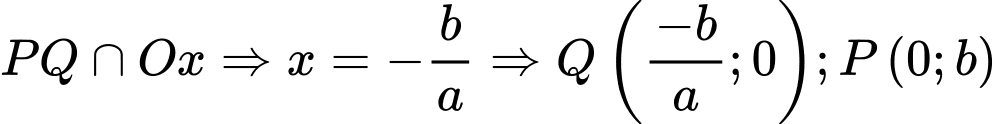
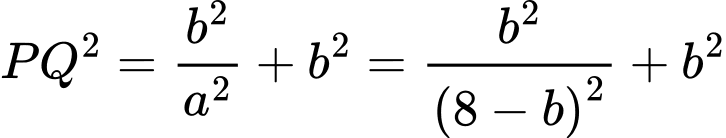
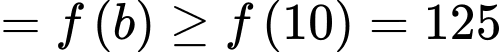
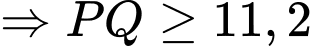
 Chiều dài ngắn nhất của cây sào là
Chiều dài ngắn nhất của cây sào là 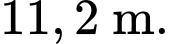
Câu 22 [693693]: Tại một địa phương trong dân số, tỷ lệ bệnh sốt rét là 20%, tỷ lệ lách to là 30%. Trong số người bị sốt rét thì tỷ lệ lách to chiếm 80%. Cần khám ít nhất bao nhiêu người để có ít nhất một người có lách to và không sốt rét với xác suất ít nhất là 90%?
Điền đáp án: 16.
Gọi là biến cố “Người đó bị mắc bệnh sốt rét”.
là biến cố “Người đó bị mắc bệnh sốt rét”.
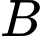 là biến cố “Người đó lách to”.
là biến cố “Người đó lách to”.
Từ giả thiết, ta có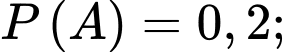
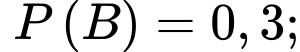
Trong số người bị sốt rét thì tỷ lệ lách to chiếm 80% nên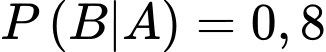
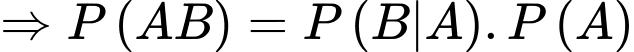
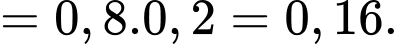
Khi đó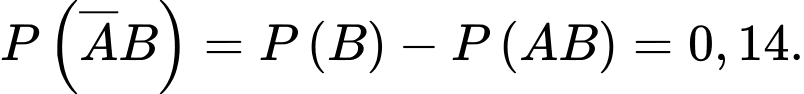
Gọi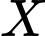 là biến cố: “Khám
là biến cố: “Khám 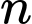 người có ít nhất 1 người có lách to và không sốt rét”
người có ít nhất 1 người có lách to và không sốt rét”
Khi đó là biến cố “Khám
là biến cố “Khám 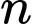 người không có ai có lách to và không sốt rét”
người không có ai có lách to và không sốt rét”
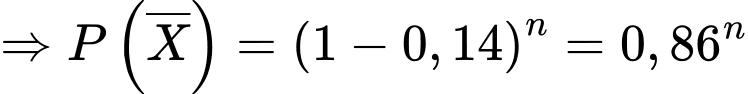
Suy ra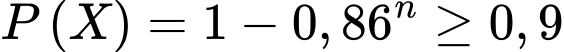
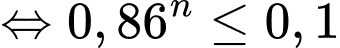
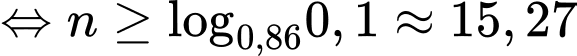
Vậy cần khám ít nhất 16 người.
Gọi
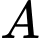 là biến cố “Người đó bị mắc bệnh sốt rét”.
là biến cố “Người đó bị mắc bệnh sốt rét”.
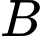 là biến cố “Người đó lách to”.
là biến cố “Người đó lách to”.
Từ giả thiết, ta có
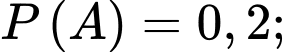
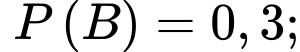
Trong số người bị sốt rét thì tỷ lệ lách to chiếm 80% nên
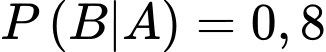
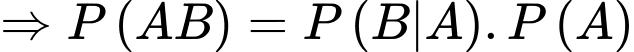
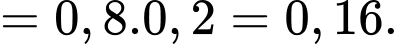
Khi đó
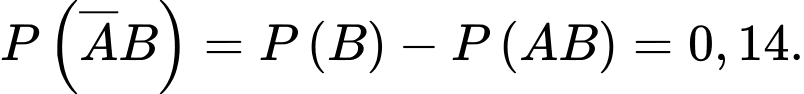
Gọi
 là biến cố: “Khám
là biến cố: “Khám  người có ít nhất 1 người có lách to và không sốt rét”
người có ít nhất 1 người có lách to và không sốt rét”
Khi đó
 là biến cố “Khám
là biến cố “Khám 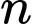 người không có ai có lách to và không sốt rét”
người không có ai có lách to và không sốt rét”
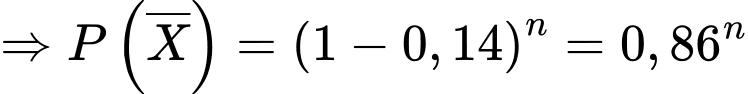
Suy ra
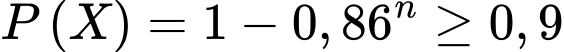
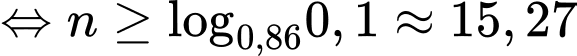
Vậy cần khám ít nhất 16 người.
Câu 23 [870500]: Một chủ mỏ than phải chi 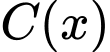 đô la mỗi ngày để duy trì sản xuất
đô la mỗi ngày để duy trì sản xuất 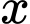 tấn than, trong đó
tấn than, trong đó 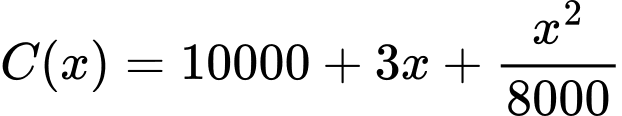 (USD/ ngày), mỗi một tấn than chủ mỏ than thu về được số tiền là
(USD/ ngày), mỗi một tấn than chủ mỏ than thu về được số tiền là 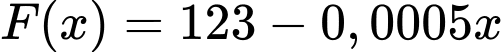 đô la. Khi sản lượng đạt 12000 tấn thì anh ta bắt đầu tăng chi phí sản xuất với tốc độ là 1200 đô la mỗi ngày. Vào thời điểm lợi nhuận thu về đạt lớn nhất thì sản lượng than được sản xuất tăng với tốc độ bao nhiêu tấn mỗi ngày? Làm tròn đến hàng phần mười.
đô la. Khi sản lượng đạt 12000 tấn thì anh ta bắt đầu tăng chi phí sản xuất với tốc độ là 1200 đô la mỗi ngày. Vào thời điểm lợi nhuận thu về đạt lớn nhất thì sản lượng than được sản xuất tăng với tốc độ bao nhiêu tấn mỗi ngày? Làm tròn đến hàng phần mười.
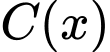 đô la mỗi ngày để duy trì sản xuất
đô la mỗi ngày để duy trì sản xuất 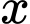 tấn than, trong đó
tấn than, trong đó 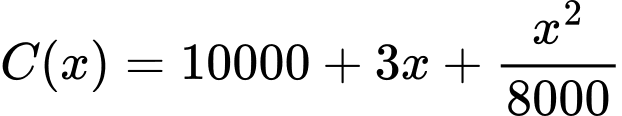 (USD/ ngày), mỗi một tấn than chủ mỏ than thu về được số tiền là
(USD/ ngày), mỗi một tấn than chủ mỏ than thu về được số tiền là 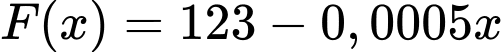 đô la. Khi sản lượng đạt 12000 tấn thì anh ta bắt đầu tăng chi phí sản xuất với tốc độ là 1200 đô la mỗi ngày. Vào thời điểm lợi nhuận thu về đạt lớn nhất thì sản lượng than được sản xuất tăng với tốc độ bao nhiêu tấn mỗi ngày? Làm tròn đến hàng phần mười.
đô la. Khi sản lượng đạt 12000 tấn thì anh ta bắt đầu tăng chi phí sản xuất với tốc độ là 1200 đô la mỗi ngày. Vào thời điểm lợi nhuận thu về đạt lớn nhất thì sản lượng than được sản xuất tăng với tốc độ bao nhiêu tấn mỗi ngày? Làm tròn đến hàng phần mười.
Câu 24 [870505]: Trong không gian 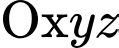 , cho đường thẳng
, cho đường thẳng 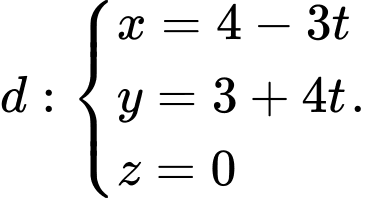 Gọi
Gọi  là hình chiếu vuông góc của
là hình chiếu vuông góc của  trên
trên 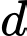 . Điểm
. Điểm 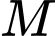 di động trên tia
di động trên tia 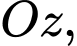 điểm
điểm 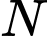 di động trên đường thẳng
di động trên đường thẳng 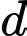 sao cho
sao cho 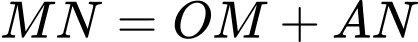 . Gọi
. Gọi 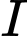 là trung điểm đoạn thẳng OA . Diện tích tam giác
là trung điểm đoạn thẳng OA . Diện tích tam giác 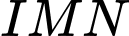 đạt giá trị nhỏ nhất bằng bao nhiêu? Làm tròn đến hàng phần trăm.
đạt giá trị nhỏ nhất bằng bao nhiêu? Làm tròn đến hàng phần trăm.
 , cho đường thẳng
, cho đường thẳng 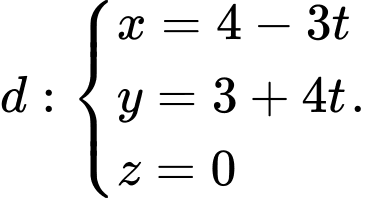 Gọi
Gọi  là hình chiếu vuông góc của
là hình chiếu vuông góc của  trên
trên  . Điểm
. Điểm 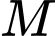 di động trên tia
di động trên tia 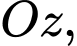 điểm
điểm 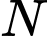 di động trên đường thẳng
di động trên đường thẳng 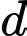 sao cho
sao cho 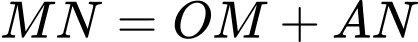 . Gọi
. Gọi 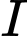 là trung điểm đoạn thẳng OA . Diện tích tam giác
là trung điểm đoạn thẳng OA . Diện tích tam giác 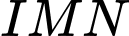 đạt giá trị nhỏ nhất bằng bao nhiêu? Làm tròn đến hàng phần trăm.
đạt giá trị nhỏ nhất bằng bao nhiêu? Làm tròn đến hàng phần trăm.