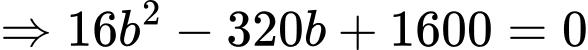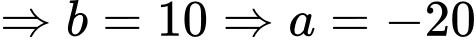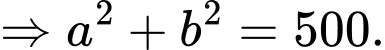PHẦN I. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Câu 1 [695267]: Cho mẫu số liệu ghép nhóm có bảng tần số ghép nhóm như sau:

Giá trị đại diện của nhóm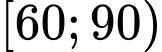 là
là

Giá trị đại diện của nhóm
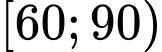 là
là A, 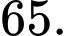
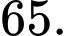
B, 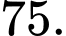
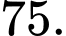
C, 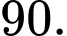
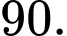
D, 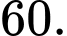
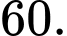
Chọn đáp án B.
Giá trị đại diện của nhóm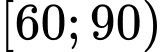 là
là 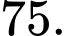 Đáp án: B
Đáp án: B
Giá trị đại diện của nhóm
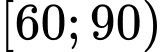 là
là  Đáp án: B
Đáp án: B
Câu 2 [695261]: Hàm số nào dưới đây là hàm số mũ?
A, 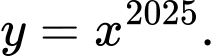
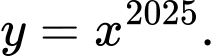
B, 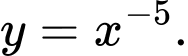
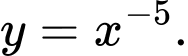
C, 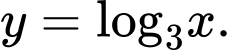
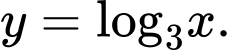
D, 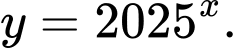
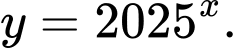
Chọn đáp án D.
Hàm số mũ có dạng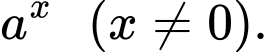 Do dó hàm số
Do dó hàm số 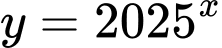 là hàm số mũ. Đáp án: D
là hàm số mũ. Đáp án: D
Hàm số mũ có dạng
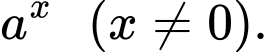 Do dó hàm số
Do dó hàm số 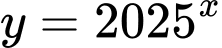 là hàm số mũ. Đáp án: D
là hàm số mũ. Đáp án: D
Câu 3 [695262]: Trong không gian 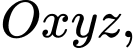 cho điểm
cho điểm 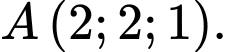 Tính độ dài đoạn thẳng
Tính độ dài đoạn thẳng 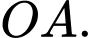
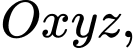 cho điểm
cho điểm 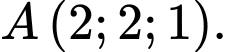 Tính độ dài đoạn thẳng
Tính độ dài đoạn thẳng 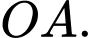
A, 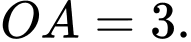
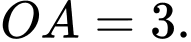
B, 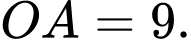
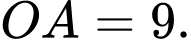
C, 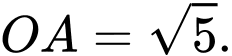
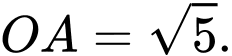
D, 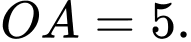
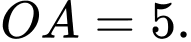
Chọn đáp án A.
Độ dài đoạn thẳng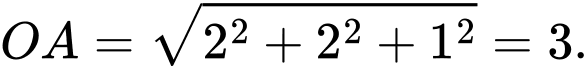 Đáp án: A
Đáp án: A
Độ dài đoạn thẳng
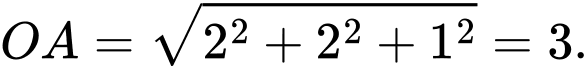 Đáp án: A
Đáp án: A
Câu 4 [149141]: Cho hàm số 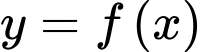 có đạo hàm là hàm liên tục trên
có đạo hàm là hàm liên tục trên 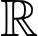 thỏa mãn
thỏa mãn 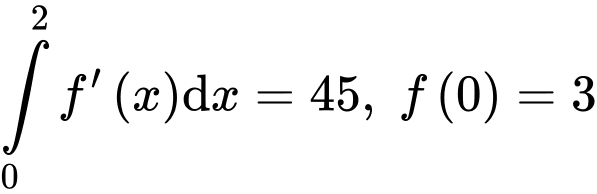 . Giá trị của biểu thức
. Giá trị của biểu thức 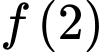 bằng
bằng
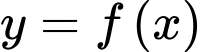 có đạo hàm là hàm liên tục trên
có đạo hàm là hàm liên tục trên 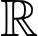 thỏa mãn
thỏa mãn 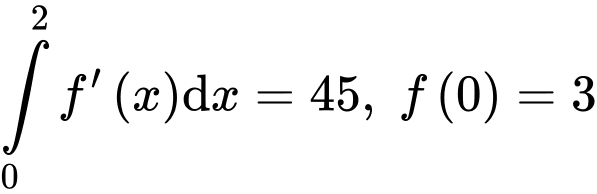 . Giá trị của biểu thức
. Giá trị của biểu thức 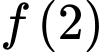 bằng
bằng A, 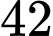 .
.
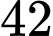 .
.B,  .
.
 .
.C, 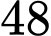 .
.
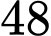 .
.D, 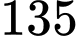 .
.
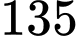 .
.
Chọn đáp án C.
Ta có: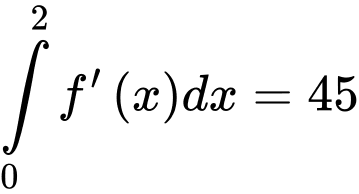 a
a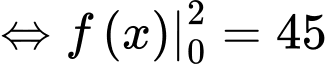
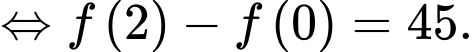
Mà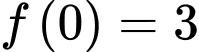 nên
nên 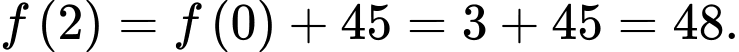 Đáp án: C
Đáp án: C
Ta có:
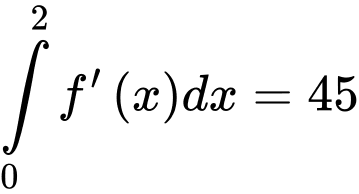 a
a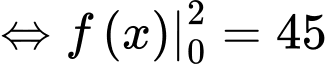
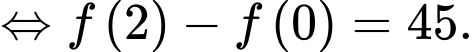
Mà
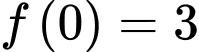 nên
nên 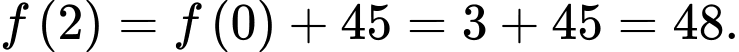 Đáp án: C
Đáp án: C
Câu 5 [695265]: Cho hình chóp 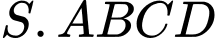 có đáy
có đáy 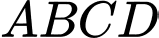 là hình chữ nhật,
là hình chữ nhật, 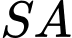 vuông góc với mặt phẳng đáy. Góc giữa đường thẳng
vuông góc với mặt phẳng đáy. Góc giữa đường thẳng 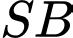 và mặt phẳng
và mặt phẳng 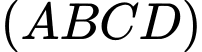 là
là
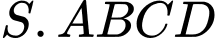 có đáy
có đáy 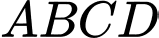 là hình chữ nhật,
là hình chữ nhật, 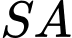 vuông góc với mặt phẳng đáy. Góc giữa đường thẳng
vuông góc với mặt phẳng đáy. Góc giữa đường thẳng 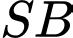 và mặt phẳng
và mặt phẳng 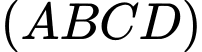 là
là A, 

B, 

C, 

D, 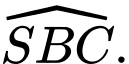
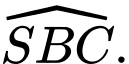
Chọn đáp án C.
Góc giữa đường thẳng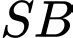 và mặt phẳng
và mặt phẳng 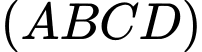 là
là  Đáp án: C
Đáp án: C
Góc giữa đường thẳng
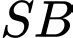 và mặt phẳng
và mặt phẳng 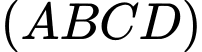 là
là  Đáp án: C
Đáp án: C
Câu 6 [695266]: Với 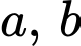 là các số thực dương tuỳ ý và
là các số thực dương tuỳ ý và 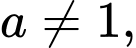
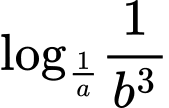 bằng
bằng
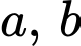 là các số thực dương tuỳ ý và
là các số thực dương tuỳ ý và 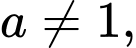
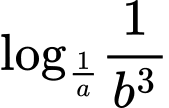 bằng
bằng A, 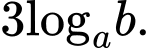
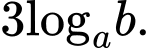
B, 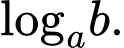
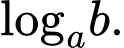
C, 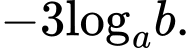
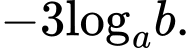
D, 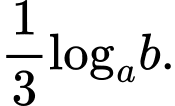
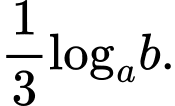
Chọn đáp án A.
Ta có:
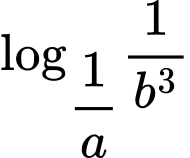
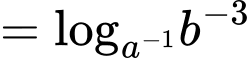
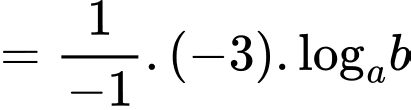
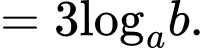 Đáp án: A
Đáp án: A
Ta có:
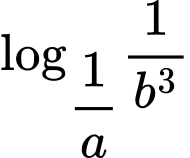
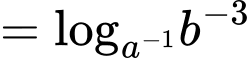
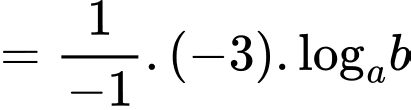
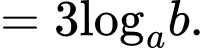 Đáp án: A
Đáp án: A
Câu 7 [801372]: Cho hàm số 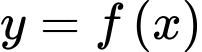 xác định trên
xác định trên 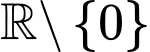 , liên tục trên mỗi khoảng xác định và có bảng biến thiên như sau:
, liên tục trên mỗi khoảng xác định và có bảng biến thiên như sau:
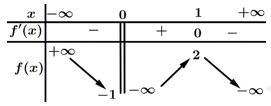
Hàm số đã cho có bao nhiêu điểm cực trị?
 xác định trên
xác định trên 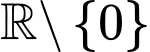 , liên tục trên mỗi khoảng xác định và có bảng biến thiên như sau:
, liên tục trên mỗi khoảng xác định và có bảng biến thiên như sau:
Hàm số đã cho có bao nhiêu điểm cực trị?
A, 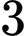 .
.
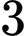 .
.B,  .
.
 .
.C, 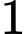 .
.
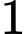 .
.D, 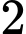 .
.
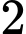 .
.
Chọn đáp án C.
Từ bảng biến thiên ta thấy hàm số đã cho xác định và có đạo hàm đổi dấu qua điểm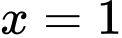 nên hàm số chỉ có 1 điểm cực trị là điểm
nên hàm số chỉ có 1 điểm cực trị là điểm 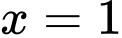 . Đáp án: C
. Đáp án: C
Từ bảng biến thiên ta thấy hàm số đã cho xác định và có đạo hàm đổi dấu qua điểm
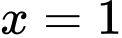 nên hàm số chỉ có 1 điểm cực trị là điểm
nên hàm số chỉ có 1 điểm cực trị là điểm 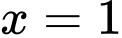 . Đáp án: C
. Đáp án: C
Câu 8 [695268]: Trong không gian 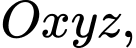 cho hai vectơ
cho hai vectơ 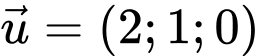 và
và 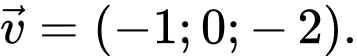 Tính
Tính 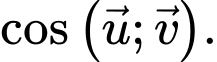
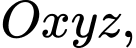 cho hai vectơ
cho hai vectơ 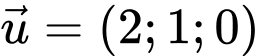 và
và 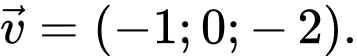 Tính
Tính 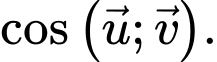
A, 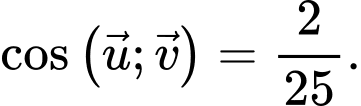
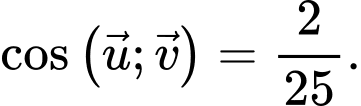
B, 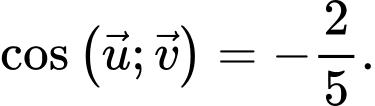
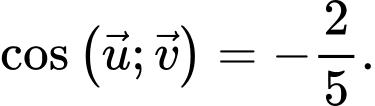
C, 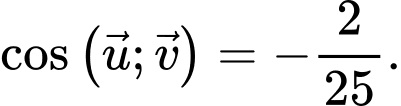
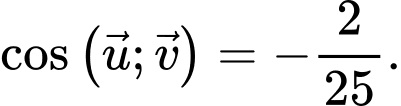
D, 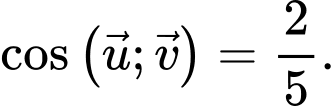
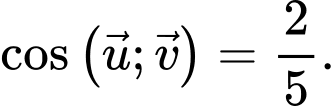
Chọn đáp án B.
Ta có:
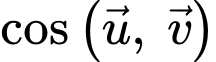
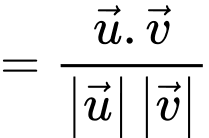
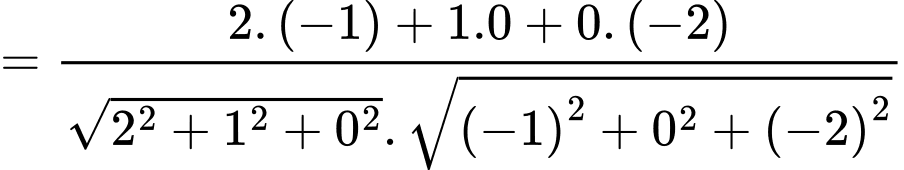
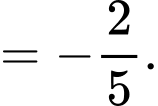 Đáp án: B
Đáp án: B
Ta có:
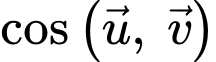
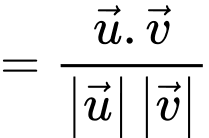
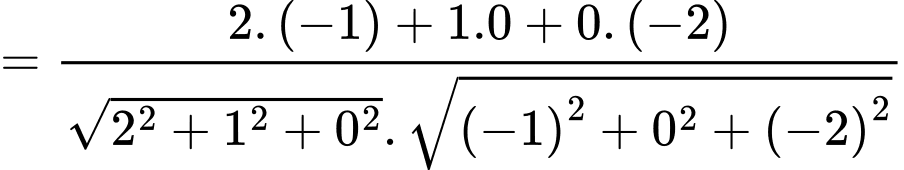
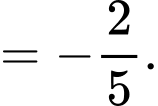 Đáp án: B
Đáp án: B
Câu 9 [604994]: Cho cấp số nhân 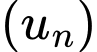 có số hạng đầu
có số hạng đầu 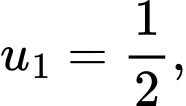 công bội
công bội 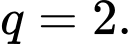 Giá trị của
Giá trị của 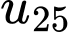 bằng
bằng
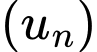 có số hạng đầu
có số hạng đầu 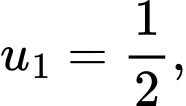 công bội
công bội 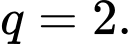 Giá trị của
Giá trị của 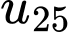 bằng
bằng A, 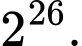
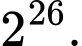
B, 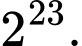
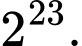
C, 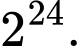
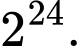
D, 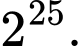
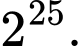
Chọn đáp án B.
Ta có: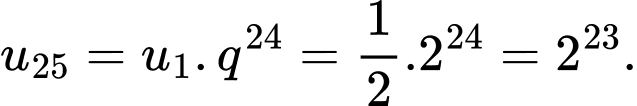 Đáp án: B
Đáp án: B
Ta có:
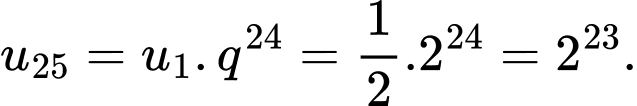 Đáp án: B
Đáp án: B
Câu 10 [695270]: Cho hình lăng trụ  Gọi
Gọi 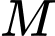 là trung điểm của cạnh
là trung điểm của cạnh 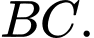 Khẳng định nào sau đây đúng?
Khẳng định nào sau đây đúng?
 Gọi
Gọi 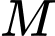 là trung điểm của cạnh
là trung điểm của cạnh 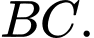 Khẳng định nào sau đây đúng?
Khẳng định nào sau đây đúng? A, 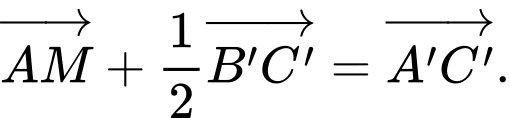
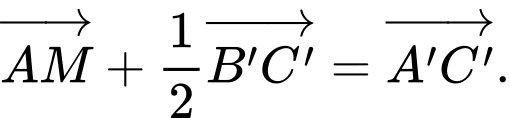
B, 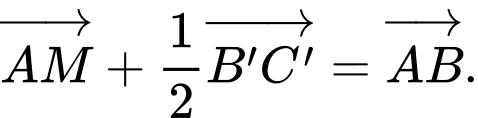
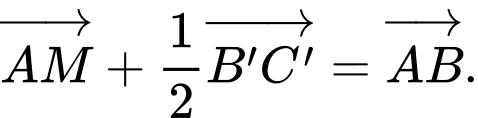
C, 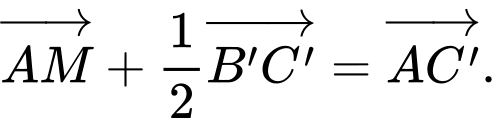
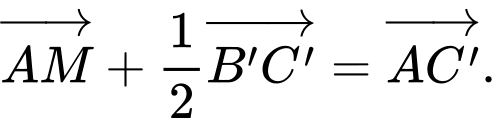
D, 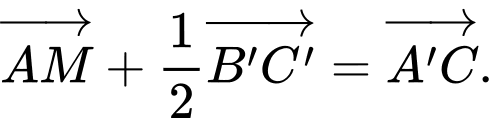
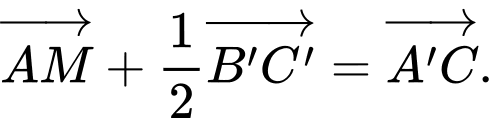
Chọn đáp án A.
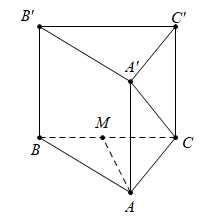
Ta có:
 là trung điểm của
là trung điểm của  nên
nên 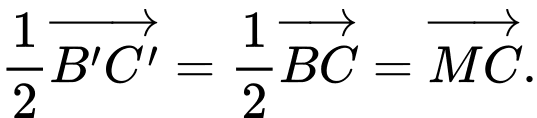
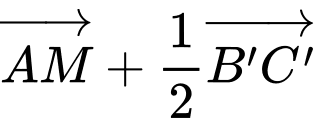
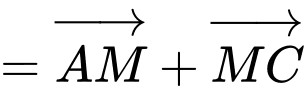
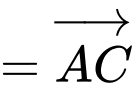
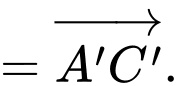 Đáp án: A
Đáp án: A

Ta có:
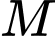 là trung điểm của
là trung điểm của 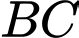 nên
nên 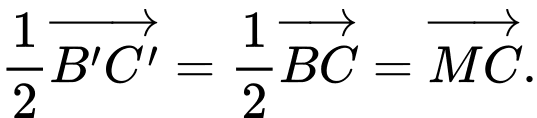
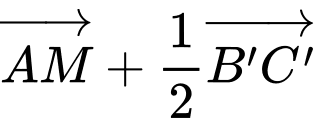
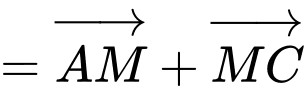
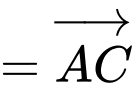
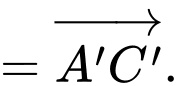 Đáp án: A
Đáp án: A
Câu 11 [695263]: Cho hàm số 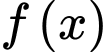 xác định trên
xác định trên 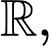 có bảng xét dấu đạo hàm như sau:
có bảng xét dấu đạo hàm như sau:
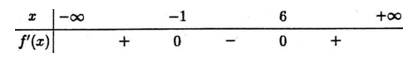
Khẳng định nào sau đây đúng?
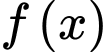 xác định trên
xác định trên 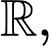 có bảng xét dấu đạo hàm như sau:
có bảng xét dấu đạo hàm như sau: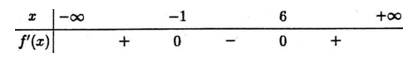
Khẳng định nào sau đây đúng?
A, 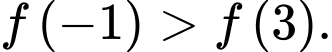
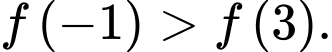
B, 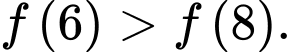
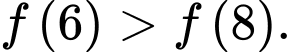
C, 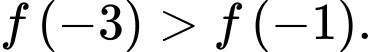
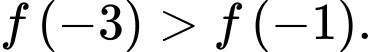
D, 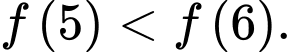
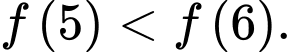
Chọn đáp án A.
Dựa vào bảng xét dấu đạo hàm ta có:
- Hàm số nghịch biến trên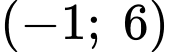 nên
nên 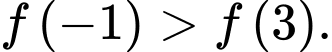
- Hàm số đồng biến trên nên
nên 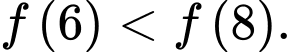
- Hàm số đồng biến trên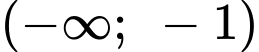 nên
nên 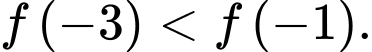
- Hàm số nghịch biến trên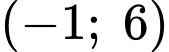 nên
nên 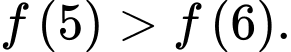 Đáp án: A
Đáp án: A
Dựa vào bảng xét dấu đạo hàm ta có:
- Hàm số nghịch biến trên
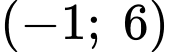 nên
nên 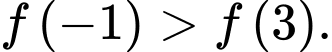
- Hàm số đồng biến trên
 nên
nên 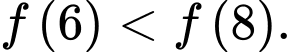
- Hàm số đồng biến trên
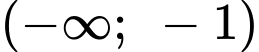 nên
nên 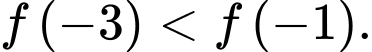
- Hàm số nghịch biến trên
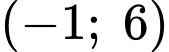 nên
nên 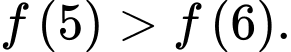 Đáp án: A
Đáp án: A
Câu 12 [695272]: Cho 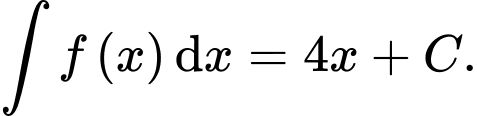 Họ nguyên hàm của hàm số
Họ nguyên hàm của hàm số 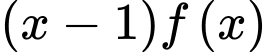 là
là
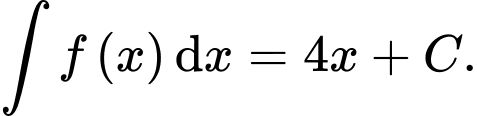 Họ nguyên hàm của hàm số
Họ nguyên hàm của hàm số 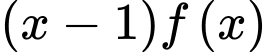 là
là A, 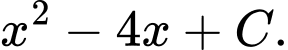
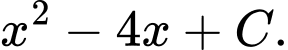
B, 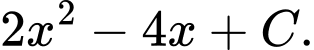
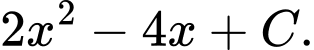
C, 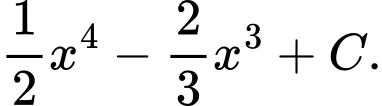
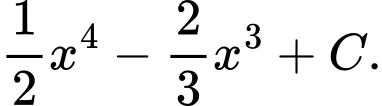
D, 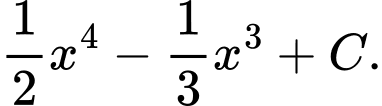
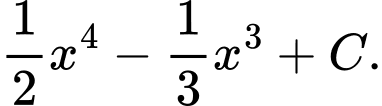
Chọn đáp án B.
Ta có:
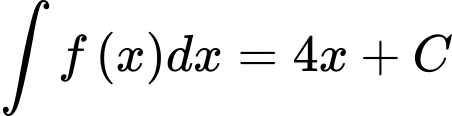

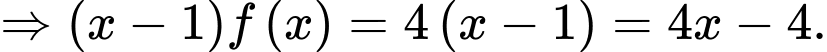
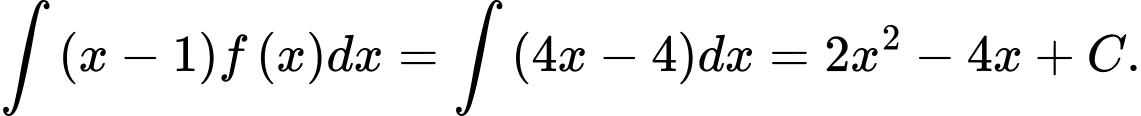 Đáp án: B
Đáp án: B
Ta có:
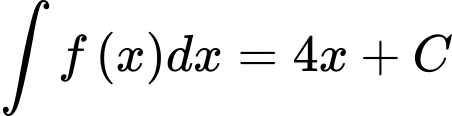

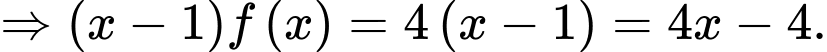
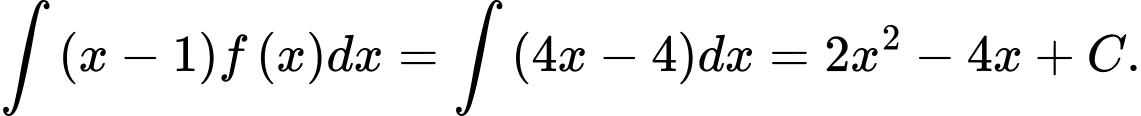 Đáp án: B
Đáp án: B PHẦN II. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Câu 13 [695273]: Cho hàm số 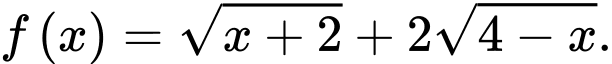
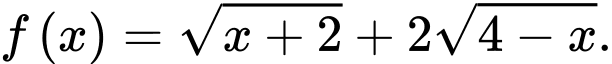
a) Đúng.
Điều kiện xác định là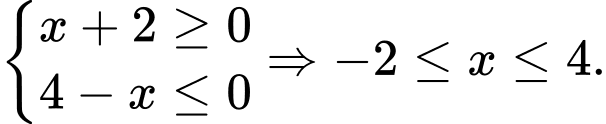
b) Đúng.
Áp dụng công thức đạo hàm :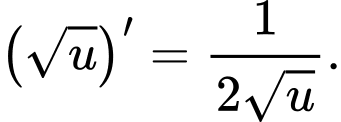
c) Đúng.
Ta có: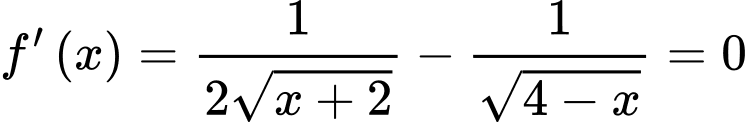

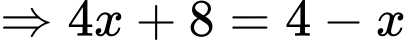
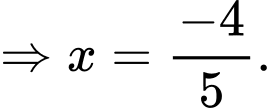
d) Sai.
Ta có:
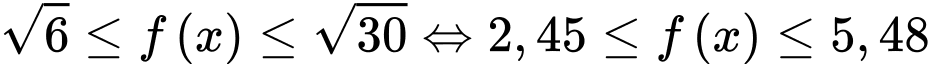
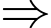 Tập giá trị của
Tập giá trị của 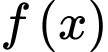 có 3 số nguyên.
có 3 số nguyên.
Điều kiện xác định là
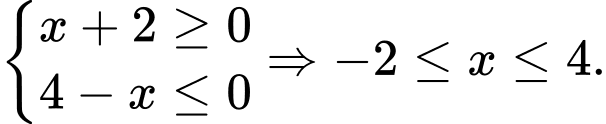
b) Đúng.
Áp dụng công thức đạo hàm :
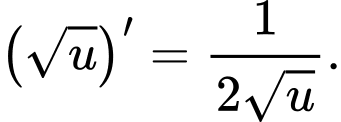
c) Đúng.
Ta có:
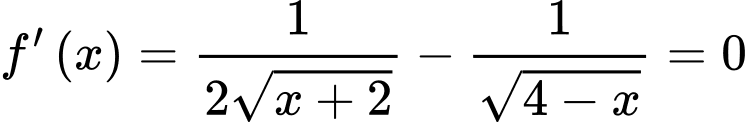

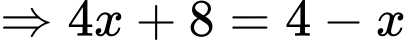
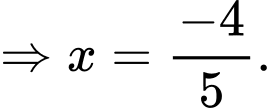
d) Sai.
Ta có:
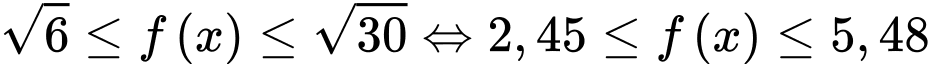
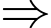 Tập giá trị của
Tập giá trị của 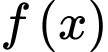 có 3 số nguyên.
có 3 số nguyên.
Câu 14 [695274]: Một công ty kinh doanh 2 mặt hàng là 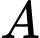 và
và 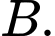 Xác suất có lãi của mặt hàng
Xác suất có lãi của mặt hàng 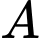 là
là 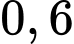 và xác suất có lãi của mặt hàng
và xác suất có lãi của mặt hàng 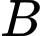 là
là 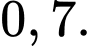 Xác suất chỉ có mặt hàng
Xác suất chỉ có mặt hàng 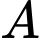 có lãi là
có lãi là 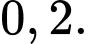
Gọi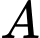 là biến cố: “Mặt hàng
là biến cố: “Mặt hàng 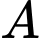 có lãi”
có lãi”
Gọi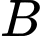 là biến cố: “Mặt hàng
là biến cố: “Mặt hàng 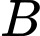 có lãi”.
có lãi”.
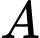 và
và 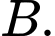 Xác suất có lãi của mặt hàng
Xác suất có lãi của mặt hàng 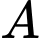 là
là 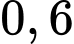 và xác suất có lãi của mặt hàng
và xác suất có lãi của mặt hàng 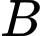 là
là 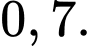 Xác suất chỉ có mặt hàng
Xác suất chỉ có mặt hàng 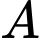 có lãi là
có lãi là 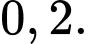
Gọi
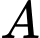 là biến cố: “Mặt hàng
là biến cố: “Mặt hàng 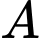 có lãi”
có lãi”Gọi
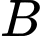 là biến cố: “Mặt hàng
là biến cố: “Mặt hàng 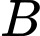 có lãi”.
có lãi”.
a) Đúng.
Có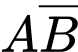 là biến cố “Mặt hàng A có lãi và mặt hàng B không có lãi” hay “Chỉ có mặt hàng A có lãi”
là biến cố “Mặt hàng A có lãi và mặt hàng B không có lãi” hay “Chỉ có mặt hàng A có lãi” 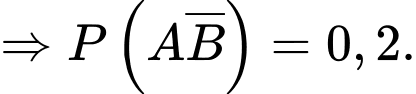
b) Sai.
 là biến cố “Cả 2 mặt hàng có lãi”
là biến cố “Cả 2 mặt hàng có lãi”  Yêu cầu bài toán là tính
Yêu cầu bài toán là tính 
Vì mặt hàng A có lãi khi A có lãi và B có lãi hoặc A có lãi và B không có lãi nên ta có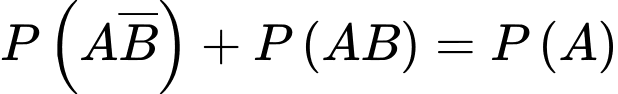
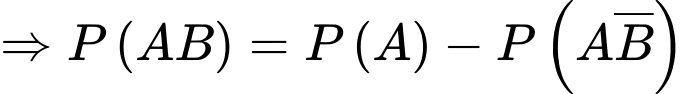
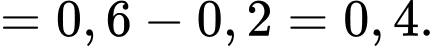
c) Đúng.
Gọi là biến cố “Có đúng một mặt hàng có lãi”
là biến cố “Có đúng một mặt hàng có lãi”
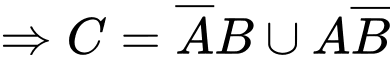 mà
mà  và
và 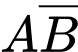 là các biến cố xung khắc
là các biến cố xung khắc

Có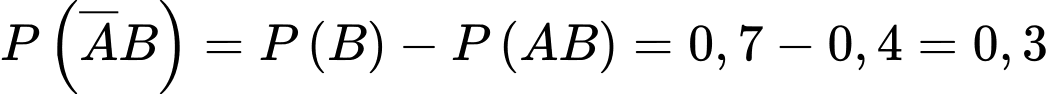 và
và 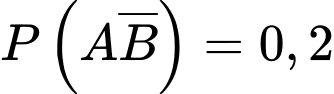
Vậy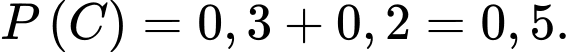
d) Đúng.
Gọi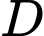 là biến cố: “Mặt hàng
là biến cố: “Mặt hàng 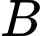 có lãi biết mặt hàng
có lãi biết mặt hàng 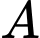 không có lãi”
không có lãi” 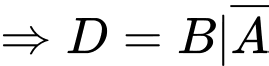
Khi đó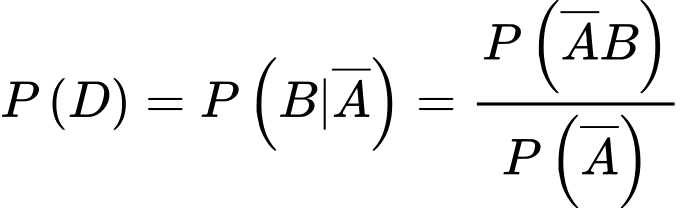
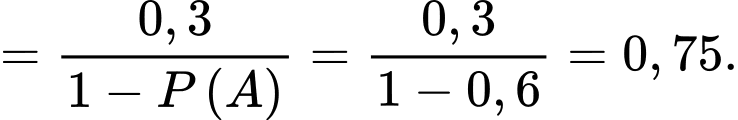
Có
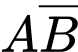 là biến cố “Mặt hàng A có lãi và mặt hàng B không có lãi” hay “Chỉ có mặt hàng A có lãi”
là biến cố “Mặt hàng A có lãi và mặt hàng B không có lãi” hay “Chỉ có mặt hàng A có lãi” 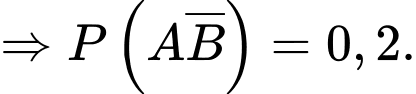
b) Sai.
 là biến cố “Cả 2 mặt hàng có lãi”
là biến cố “Cả 2 mặt hàng có lãi”  Yêu cầu bài toán là tính
Yêu cầu bài toán là tính 
Vì mặt hàng A có lãi khi A có lãi và B có lãi hoặc A có lãi và B không có lãi nên ta có
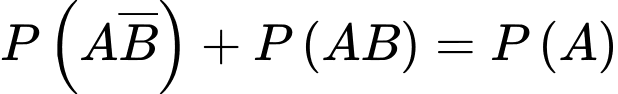
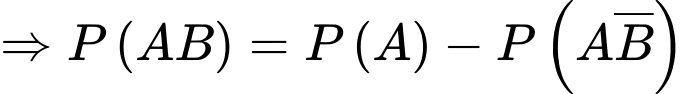
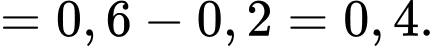
c) Đúng.
Gọi
 là biến cố “Có đúng một mặt hàng có lãi”
là biến cố “Có đúng một mặt hàng có lãi”
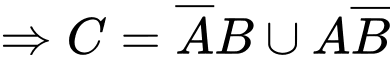 mà
mà  và
và 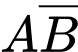 là các biến cố xung khắc
là các biến cố xung khắc

Có
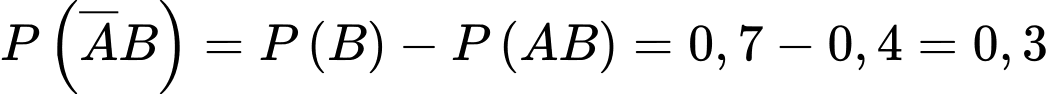 và
và 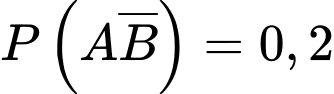
Vậy
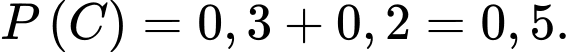
d) Đúng.
Gọi
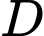 là biến cố: “Mặt hàng
là biến cố: “Mặt hàng 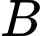 có lãi biết mặt hàng
có lãi biết mặt hàng 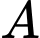 không có lãi”
không có lãi” 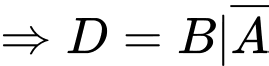
Khi đó
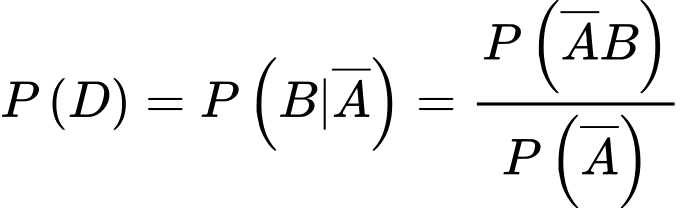
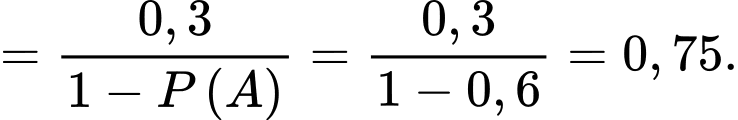
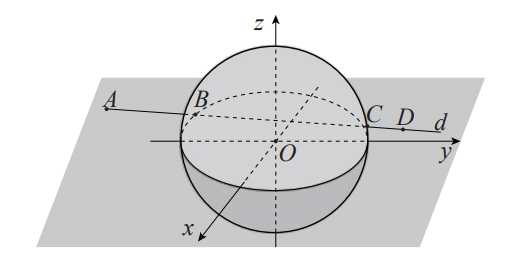
Câu 15 [695275]: Trong không gian hệ trục tọa độ 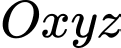 (đơn vị trên mỗi trục là kilômét), đài kiểm soát không lưu của một sân bay ở vị trí
(đơn vị trên mỗi trục là kilômét), đài kiểm soát không lưu của một sân bay ở vị trí 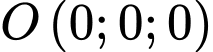 và được thiết kế phát hiện máy bay ở khoảng cách tối đa
và được thiết kế phát hiện máy bay ở khoảng cách tối đa 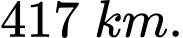 Một máy bay đang chuyển động theo đường thẳng
Một máy bay đang chuyển động theo đường thẳng 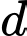 từ điểm
từ điểm 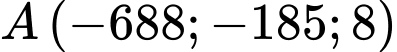 đến điểm
đến điểm 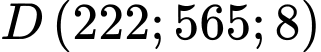 và hướng về đài kiểm soát không lưu (như hình vẽ).
và hướng về đài kiểm soát không lưu (như hình vẽ).
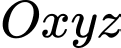 (đơn vị trên mỗi trục là kilômét), đài kiểm soát không lưu của một sân bay ở vị trí
(đơn vị trên mỗi trục là kilômét), đài kiểm soát không lưu của một sân bay ở vị trí 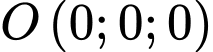 và được thiết kế phát hiện máy bay ở khoảng cách tối đa
và được thiết kế phát hiện máy bay ở khoảng cách tối đa 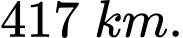 Một máy bay đang chuyển động theo đường thẳng
Một máy bay đang chuyển động theo đường thẳng 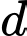 từ điểm
từ điểm 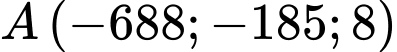 đến điểm
đến điểm 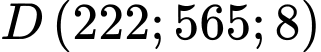 và hướng về đài kiểm soát không lưu (như hình vẽ).
và hướng về đài kiểm soát không lưu (như hình vẽ).
a) Đúng.
Vectơ chỉ phương của đường thẳng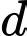 là
là 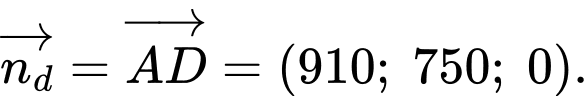
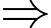 Phương trình đường thẳng
Phương trình đường thẳng  là
là 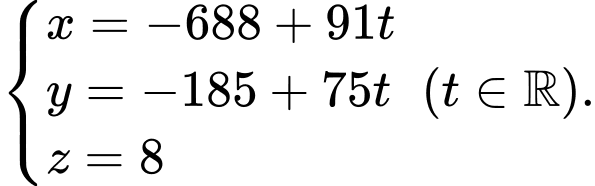
b) Đúng.
Tọa độ của vị trí sớm nhất chính là giao điểm của đường thẳng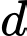 với mặt cầu tâm
với mặt cầu tâm  bán kính
bán kính 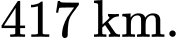
Phương trình mặt cầu tâm là
là 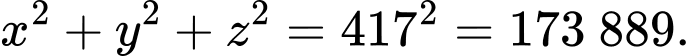
Phương trình đường thẳng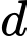 là
là 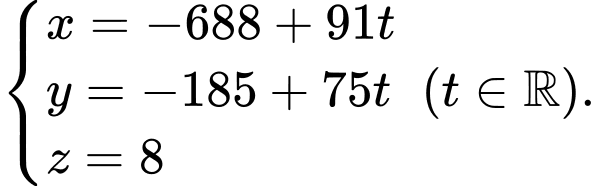
Thay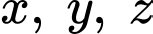 vào phương trình mặt cầu tâm
vào phương trình mặt cầu tâm  ta được:
ta được: 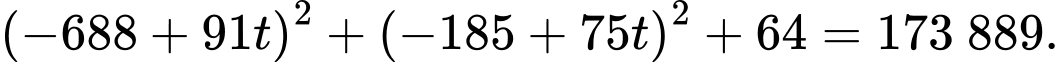
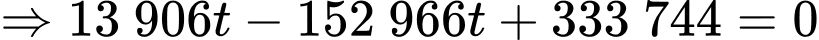
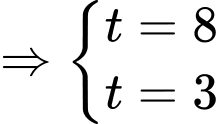
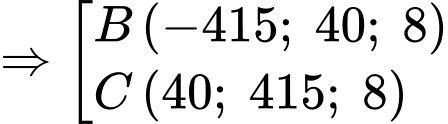 hoặc
hoặc 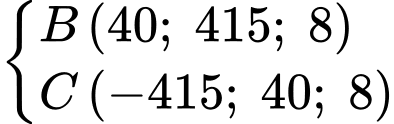
+)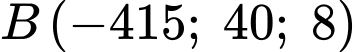 ,
, 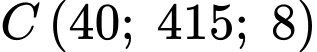 ,
, 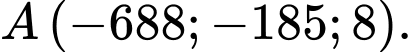
Ta có: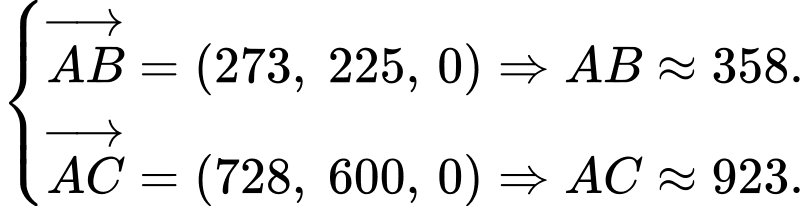
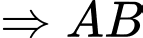
Vectơ chỉ phương của đường thẳng
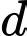 là
là 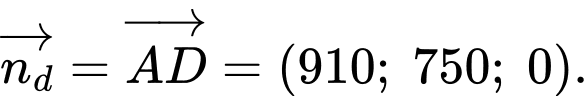
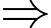 Phương trình đường thẳng
Phương trình đường thẳng 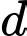 là
là 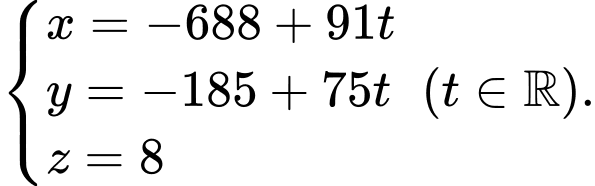
b) Đúng.
Tọa độ của vị trí sớm nhất chính là giao điểm của đường thẳng
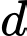 với mặt cầu tâm
với mặt cầu tâm  bán kính
bán kính 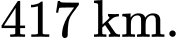
Phương trình mặt cầu tâm
 là
là 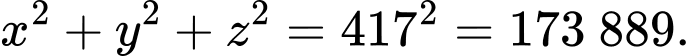
Phương trình đường thẳng
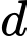 là
là 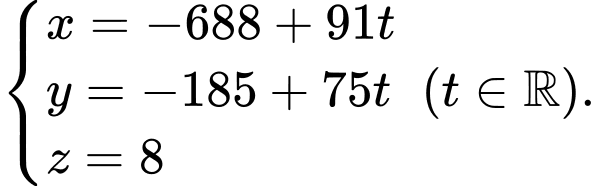
Thay
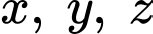 vào phương trình mặt cầu tâm
vào phương trình mặt cầu tâm  ta được:
ta được: 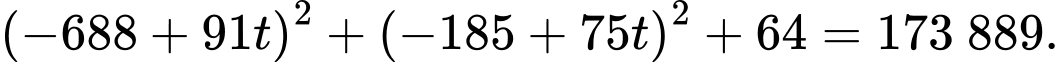
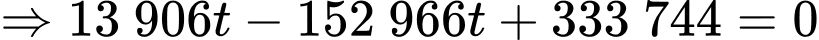
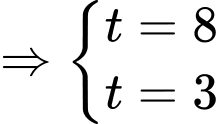
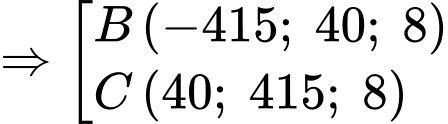 hoặc
hoặc 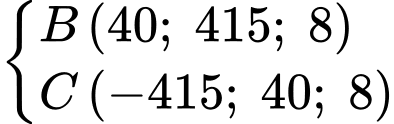
+)
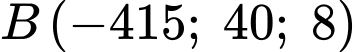 ,
, 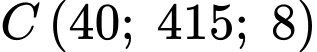 ,
, 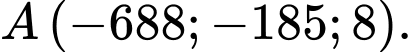
Ta có:
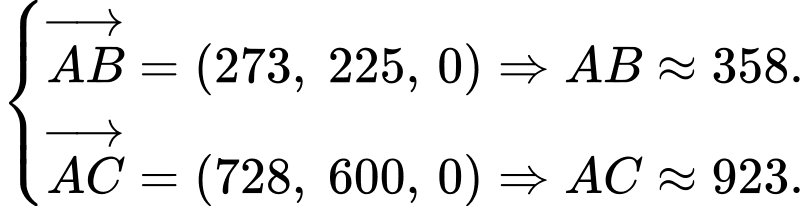
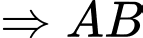
Câu 16 [695276]: Một cuộc khảo sát thị trường cho thấy khi một loại máy lọc không khí mới được giới thiệu ra thị trường, hàm lợi nhuận 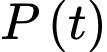 sau
sau 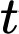 tháng là nguyên hàm của hàm tốc độ sinh lời
tháng là nguyên hàm của hàm tốc độ sinh lời 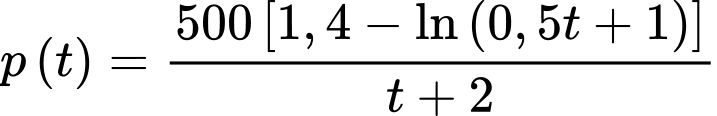 (chục triệu đồng mỗi tháng). Biết rằng công ty phải chi 1 tỷ đồng để sản xuất máy lọc không khí.
(chục triệu đồng mỗi tháng). Biết rằng công ty phải chi 1 tỷ đồng để sản xuất máy lọc không khí.
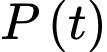 sau
sau 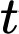 tháng là nguyên hàm của hàm tốc độ sinh lời
tháng là nguyên hàm của hàm tốc độ sinh lời 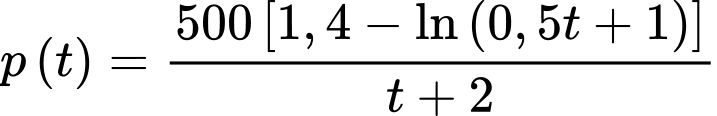 (chục triệu đồng mỗi tháng). Biết rằng công ty phải chi 1 tỷ đồng để sản xuất máy lọc không khí.
(chục triệu đồng mỗi tháng). Biết rằng công ty phải chi 1 tỷ đồng để sản xuất máy lọc không khí.
a) Đúng.
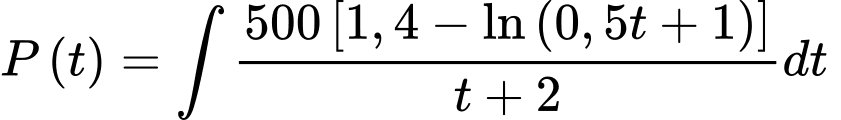
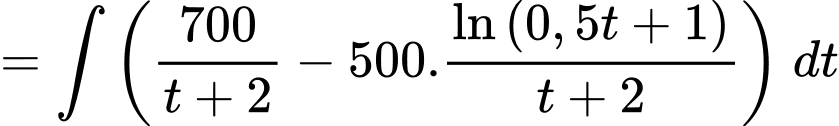
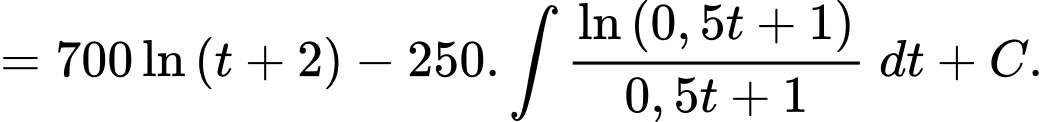
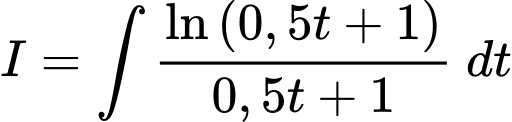
Đặt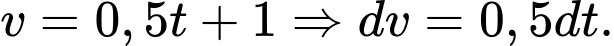
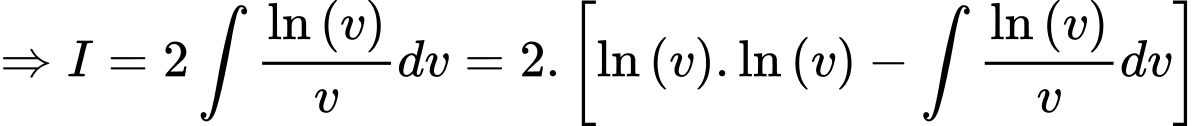
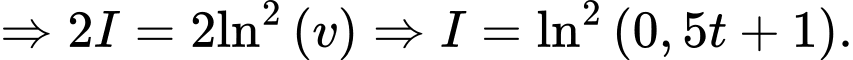
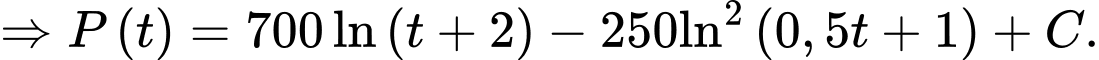
b) Đúng.
Ta có:
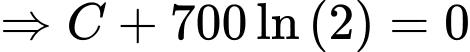
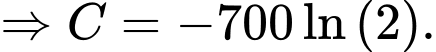
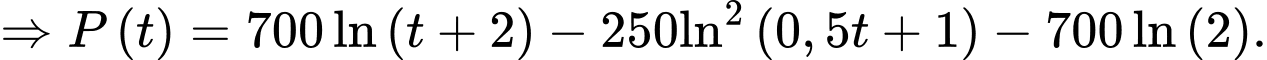
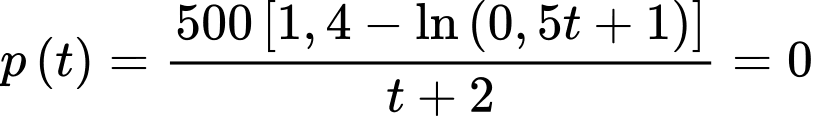
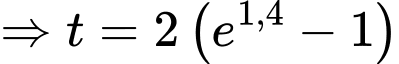 là điểm cực đại của đồ thị hàm
là điểm cực đại của đồ thị hàm 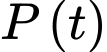 .
.
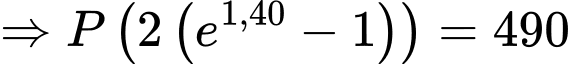 (chục triệu đồng)
(chục triệu đồng) 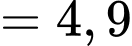 (tỷ đồng).
(tỷ đồng).
Vì công ty ban đầu đã chi 1 tỷ đồng để sản xuất máy lọc không khí nên lợi nhuận cực đại là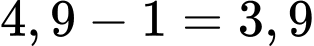 (tỷ đồng).
(tỷ đồng).
c) Sai.
Ta có :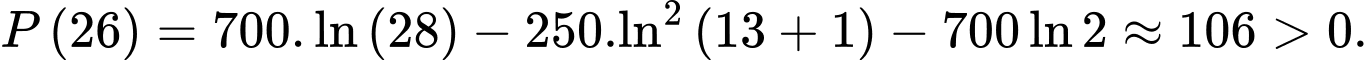
d) Đúng.
Ta có lợi nhuận đạt cực đại tại thời điểm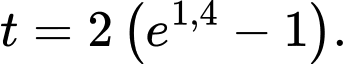
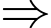 Thời điểm sau khi đạt cực đại 12 tháng là
Thời điểm sau khi đạt cực đại 12 tháng là 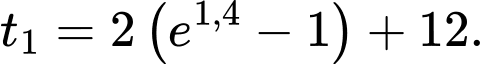
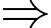
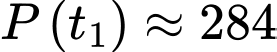 chục triệu đồng
chục triệu đồng 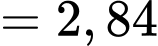 tỷ đồng.
tỷ đồng.
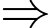 Lợi nhuận tại thời điểm sau khi đạt cực đại 12 tháng là
Lợi nhuận tại thời điểm sau khi đạt cực đại 12 tháng là 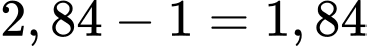 tỷ đồng.
tỷ đồng.
Mà lợi nhuận cực đại là 3,9 tỷ đồng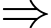 Lợi nhuận cực đại lớn hơn 2 lần lợi nhuận sản phẩm sau khi đạt cực đại 12 tháng.
Lợi nhuận cực đại lớn hơn 2 lần lợi nhuận sản phẩm sau khi đạt cực đại 12 tháng.
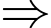 Sản phẩm trên không phải là một trào lưu.
Sản phẩm trên không phải là một trào lưu.
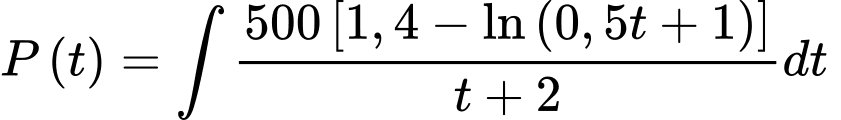
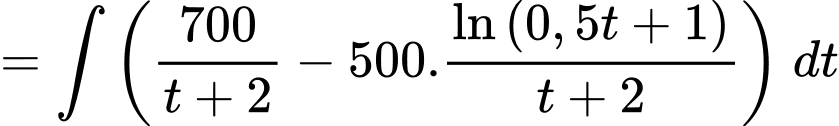
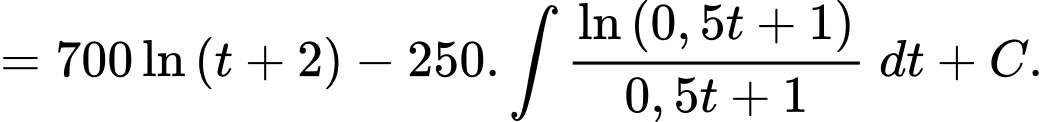
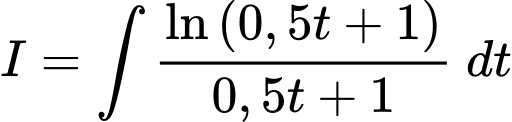
Đặt
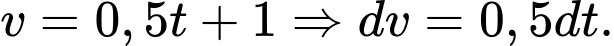
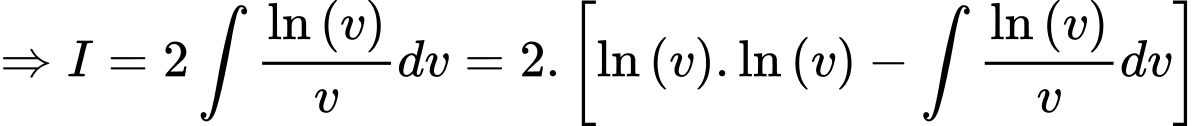
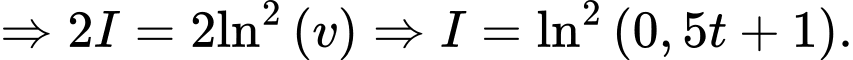
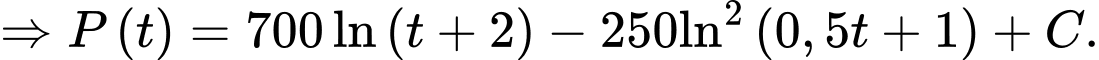
b) Đúng.
Ta có:

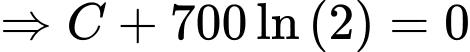
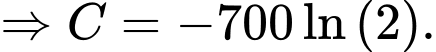
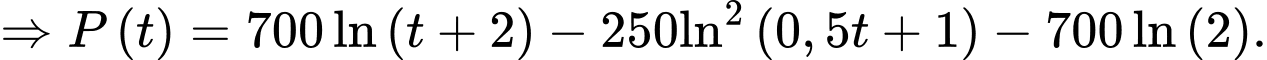
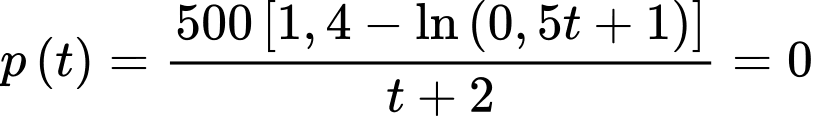
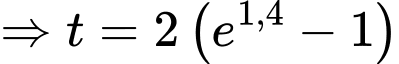 là điểm cực đại của đồ thị hàm
là điểm cực đại của đồ thị hàm 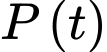 .
.
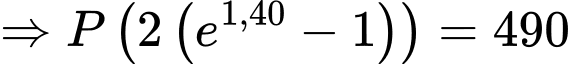 (chục triệu đồng)
(chục triệu đồng) 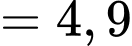 (tỷ đồng).
(tỷ đồng).
Vì công ty ban đầu đã chi 1 tỷ đồng để sản xuất máy lọc không khí nên lợi nhuận cực đại là
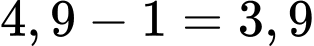 (tỷ đồng).
(tỷ đồng). c) Sai.
Ta có :
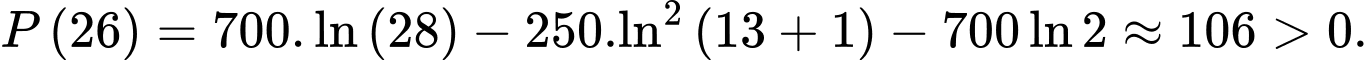
d) Đúng.
Ta có lợi nhuận đạt cực đại tại thời điểm
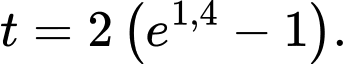
 Thời điểm sau khi đạt cực đại 12 tháng là
Thời điểm sau khi đạt cực đại 12 tháng là 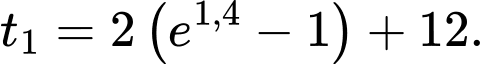
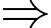
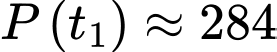 chục triệu đồng
chục triệu đồng 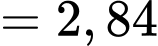 tỷ đồng.
tỷ đồng.
 Lợi nhuận tại thời điểm sau khi đạt cực đại 12 tháng là
Lợi nhuận tại thời điểm sau khi đạt cực đại 12 tháng là 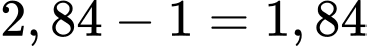 tỷ đồng.
tỷ đồng.
Mà lợi nhuận cực đại là 3,9 tỷ đồng
 Lợi nhuận cực đại lớn hơn 2 lần lợi nhuận sản phẩm sau khi đạt cực đại 12 tháng.
Lợi nhuận cực đại lớn hơn 2 lần lợi nhuận sản phẩm sau khi đạt cực đại 12 tháng.
 Sản phẩm trên không phải là một trào lưu.
Sản phẩm trên không phải là một trào lưu.
PHẦN III. Thí sinh trả lời từ câu 1 đến câu 6.
Câu 17 [695277]: Cho hình chóp 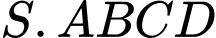 có đáy là hình vuông cạnh
có đáy là hình vuông cạnh 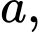
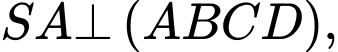 số đo của góc nhị diện
số đo của góc nhị diện 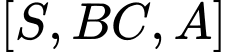 bằng
bằng 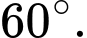 Khoảng cách giữa hai đường thẳng
Khoảng cách giữa hai đường thẳng 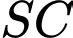 và
và 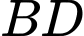 bằng
bằng 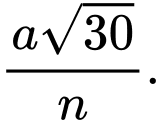 Giá trị của
Giá trị của 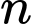 bằng bao nhiêu?
bằng bao nhiêu?
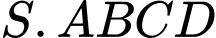 có đáy là hình vuông cạnh
có đáy là hình vuông cạnh 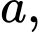
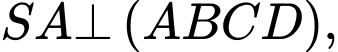 số đo của góc nhị diện
số đo của góc nhị diện 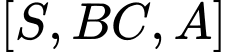 bằng
bằng 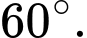 Khoảng cách giữa hai đường thẳng
Khoảng cách giữa hai đường thẳng 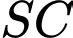 và
và 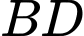 bằng
bằng 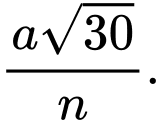 Giá trị của
Giá trị của 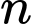 bằng bao nhiêu?
bằng bao nhiêu?
Điền đáp án: 10.
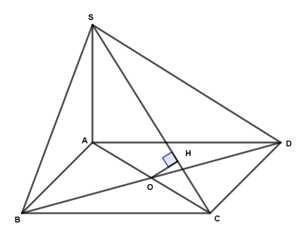

Ta có:
Mà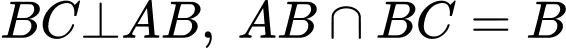
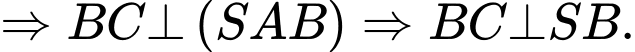
Mà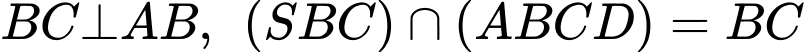
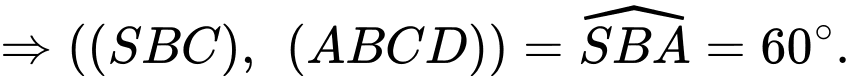
Gọi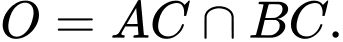 Kẻ
Kẻ 
Ta có: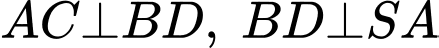

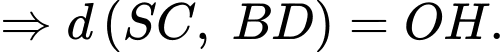
Xét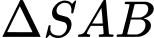 vuông tại
vuông tại 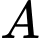 có :
có : 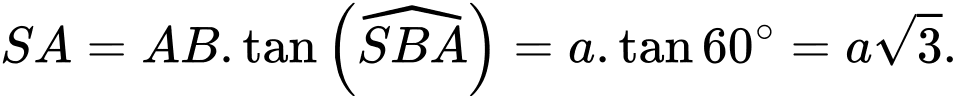
Xét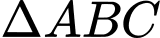 vuông tại
vuông tại 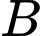 có:
có: 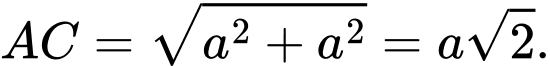
Xét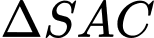 vuông tại
vuông tại 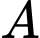 có:
có: 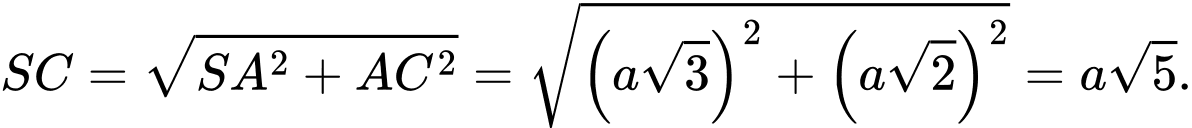
Xét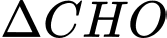 và
và 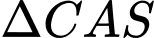 có:
có:  chung,
chung, 

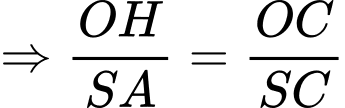
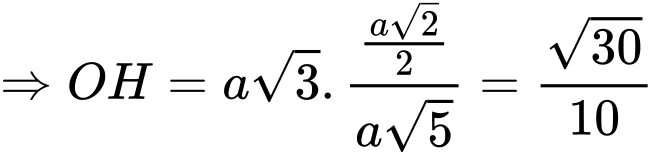
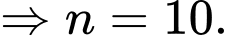


Ta có:

Mà
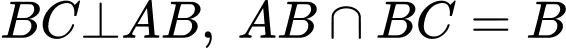
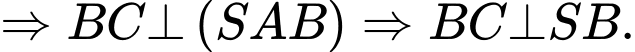
Mà
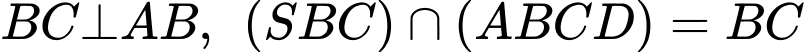
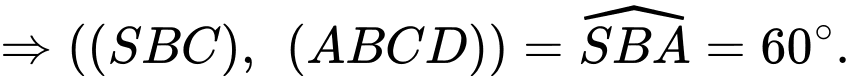
Gọi
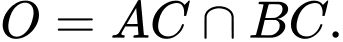 Kẻ
Kẻ 
Ta có:
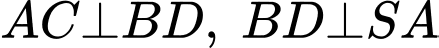

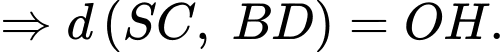
Xét
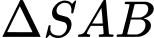 vuông tại
vuông tại 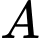 có :
có : 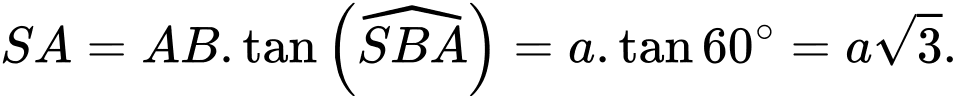
Xét
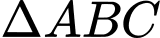 vuông tại
vuông tại 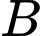 có:
có: 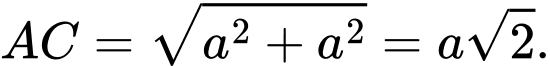
Xét
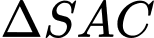 vuông tại
vuông tại 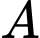 có:
có: 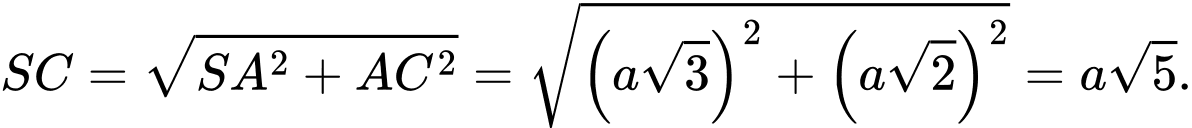
Xét
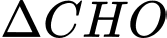 và
và 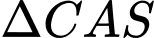 có:
có:  chung,
chung, 

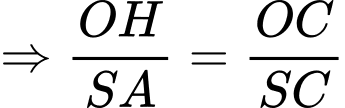
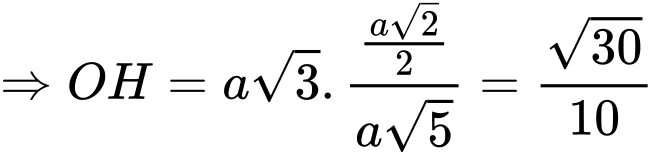
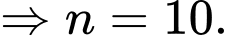
Câu 18 [695278]: Một siêu thị chạy chương trình khuyến mãi cho nước tăng lực có giá niêm yết là 9000 (đồng/lon) như sau:
- Nếu mua 1 lon thì không giảm giá.
- Nếu mua 2 lon thì lon thứ hai được giảm 500 đồng.
- Nếu mua 3 lon thì lon thứ hai được giảm 500 đồng và lon thứ ba được giảm giá 10%.
- Nếu mua trên 3 lon thì lon thứ hai được giảm 500 đồng, lon thứ ba được giảm 10% và những lon thứ tư trở đi đều được giảm thêm 2% trên giá đã giảm của lon thứ ba.
Hòa phải trả 422 500 đồng để thanh toán khi mua những lon nước tăng lực trên. Hòa đã mua bao nhiêu lon nước?
- Nếu mua 1 lon thì không giảm giá.
- Nếu mua 2 lon thì lon thứ hai được giảm 500 đồng.
- Nếu mua 3 lon thì lon thứ hai được giảm 500 đồng và lon thứ ba được giảm giá 10%.
- Nếu mua trên 3 lon thì lon thứ hai được giảm 500 đồng, lon thứ ba được giảm 10% và những lon thứ tư trở đi đều được giảm thêm 2% trên giá đã giảm của lon thứ ba.
Hòa phải trả 422 500 đồng để thanh toán khi mua những lon nước tăng lực trên. Hòa đã mua bao nhiêu lon nước?
Điền đáp án: 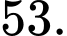
Gọi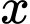 là số lon nước Hoà mua được.
là số lon nước Hoà mua được.
Khi đó, ta có: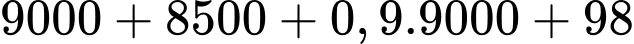
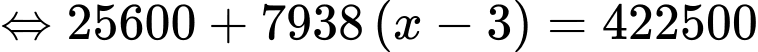
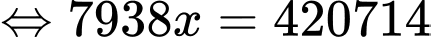
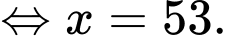
Vậy Hoà mua được 53 lon nước.
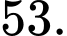
Gọi
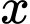 là số lon nước Hoà mua được.
là số lon nước Hoà mua được. Khi đó, ta có:
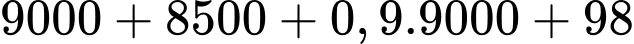
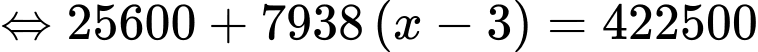
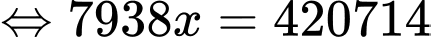
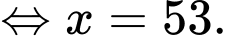
Vậy Hoà mua được 53 lon nước.
Câu 19 [695279]: Chướng ngại vật “tường cong” trong một sân thi đấu X-Game là một khối bê tông có chiều cao từ mặt đất lên là 3 m. Giao của mặt tường cong và mặt đất là đoạn thẳng 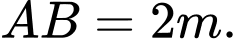 Thiết diện của khối tường cong cắt bởi mặt phẳng vuông góc với
Thiết diện của khối tường cong cắt bởi mặt phẳng vuông góc với  tại
tại 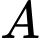 là một hình tam giác vuông cong
là một hình tam giác vuông cong  với
với 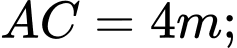
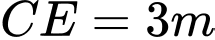 và cạnh cong
và cạnh cong 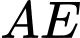 nằm trên một đường Parabol có trục đối xứng vuông góc với mặt đất. Tại vị trí
nằm trên một đường Parabol có trục đối xứng vuông góc với mặt đất. Tại vị trí 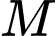 là trung điểm của
là trung điểm của 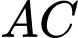 thì tường cong có độ cao
thì tường cong có độ cao 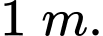
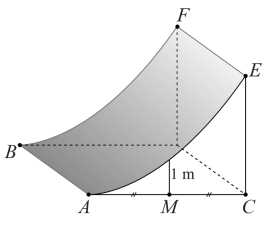
Thể tích bê tông cần sử dụng để tạo nên khối tường cong đó là bao nhiêu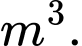 Viết kết quả làm tròn đến hàng phần chục.
Viết kết quả làm tròn đến hàng phần chục.
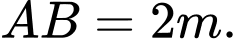 Thiết diện của khối tường cong cắt bởi mặt phẳng vuông góc với
Thiết diện của khối tường cong cắt bởi mặt phẳng vuông góc với  tại
tại 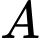 là một hình tam giác vuông cong
là một hình tam giác vuông cong  với
với 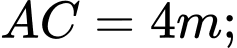
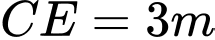 và cạnh cong
và cạnh cong 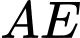 nằm trên một đường Parabol có trục đối xứng vuông góc với mặt đất. Tại vị trí
nằm trên một đường Parabol có trục đối xứng vuông góc với mặt đất. Tại vị trí 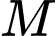 là trung điểm của
là trung điểm của 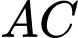 thì tường cong có độ cao
thì tường cong có độ cao 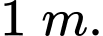

Thể tích bê tông cần sử dụng để tạo nên khối tường cong đó là bao nhiêu
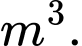 Viết kết quả làm tròn đến hàng phần chục.
Viết kết quả làm tròn đến hàng phần chục.
Điền đáp án: 9,33.
Giả sử điểm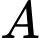 trùng với gốc tọa độ
trùng với gốc tọa độ  trong mặt phẳng
trong mặt phẳng 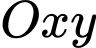 ,
, 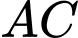 nằm trên trục
nằm trên trục 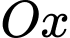 .
.
Phương trình parabol đi qua 2 điểm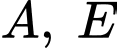 có dạng
có dạng 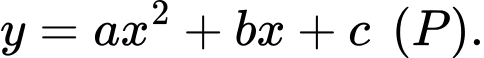
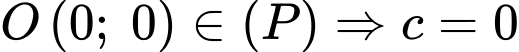
Tại điểm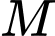 có hoành độ bằng 2 thì tường cao
có hoành độ bằng 2 thì tường cao 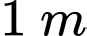 nên ta có điểm
nên ta có điểm 
 .
.
Điểm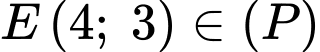

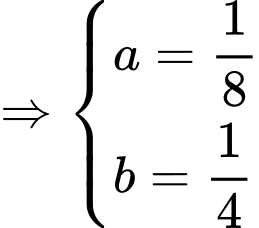
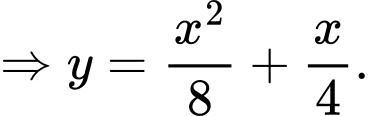
Diện tích hình phẳng giới hạn bởi parabol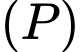 , đường thẳng
, đường thẳng 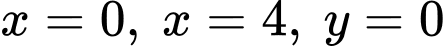 là
là
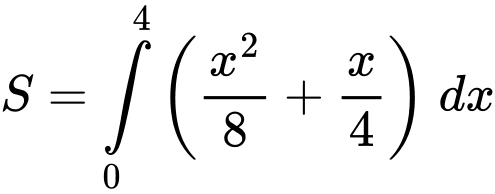
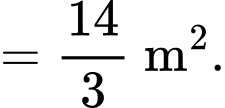
Thể tích bê tông cần sử dụng để tạo nên khối tường cong đó là
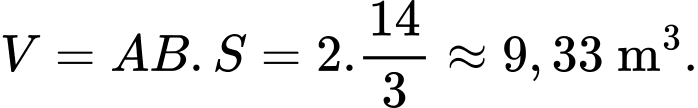
Giả sử điểm
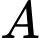 trùng với gốc tọa độ
trùng với gốc tọa độ  trong mặt phẳng
trong mặt phẳng 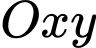 ,
, 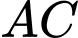 nằm trên trục
nằm trên trục 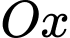 .
.
Phương trình parabol đi qua 2 điểm
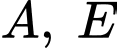 có dạng
có dạng 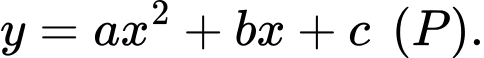
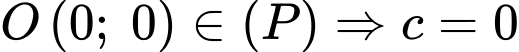
Tại điểm
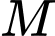 có hoành độ bằng 2 thì tường cao
có hoành độ bằng 2 thì tường cao 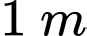 nên ta có điểm
nên ta có điểm 
 .
.
Điểm
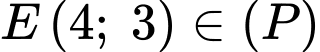

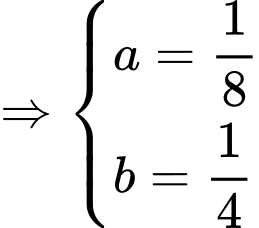
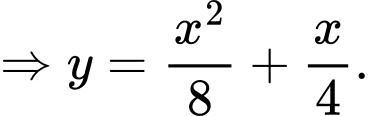
Diện tích hình phẳng giới hạn bởi parabol
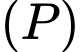 , đường thẳng
, đường thẳng 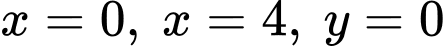 là
là
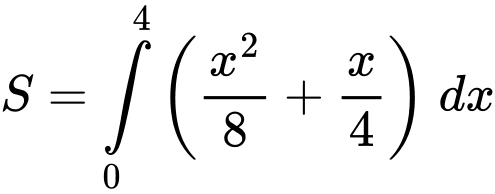
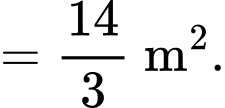
Thể tích bê tông cần sử dụng để tạo nên khối tường cong đó là
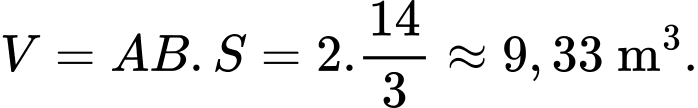
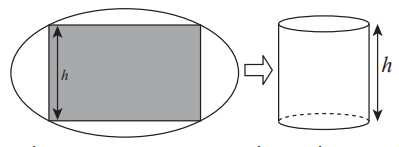
Câu 20 [695281]: Người ta cần cắt một tấm tôn có hình dạng là một elip với độ dài trục lớn bằng 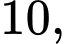 độ dài trục bé bằng
độ dài trục bé bằng 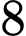 để được một tấm tôn có dạng hình chữ nhật nội tiếp elip. Sau đó gò tấm tôn hình chữ nhật đó để thu được một hình trụ không có đáy như hình vẽ. Thể tích lớn nhất của khối trụ thu được bằng bao nhiêu? (làm tròn kết quả đến hàng phần mười).
để được một tấm tôn có dạng hình chữ nhật nội tiếp elip. Sau đó gò tấm tôn hình chữ nhật đó để thu được một hình trụ không có đáy như hình vẽ. Thể tích lớn nhất của khối trụ thu được bằng bao nhiêu? (làm tròn kết quả đến hàng phần mười).
 độ dài trục bé bằng
độ dài trục bé bằng 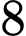 để được một tấm tôn có dạng hình chữ nhật nội tiếp elip. Sau đó gò tấm tôn hình chữ nhật đó để thu được một hình trụ không có đáy như hình vẽ. Thể tích lớn nhất của khối trụ thu được bằng bao nhiêu? (làm tròn kết quả đến hàng phần mười).
để được một tấm tôn có dạng hình chữ nhật nội tiếp elip. Sau đó gò tấm tôn hình chữ nhật đó để thu được một hình trụ không có đáy như hình vẽ. Thể tích lớn nhất của khối trụ thu được bằng bao nhiêu? (làm tròn kết quả đến hàng phần mười).
Điền đáp án: 24,50.
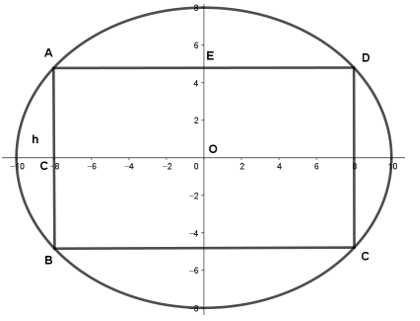
Phương trình elip có dạng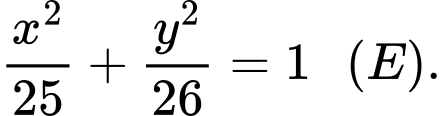
Theo hình vẽ ta có: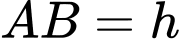 ,
, 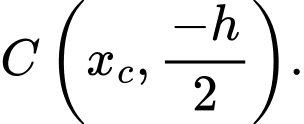
Thay tọa độ điểm vào phương trình elip ta được:
vào phương trình elip ta được: 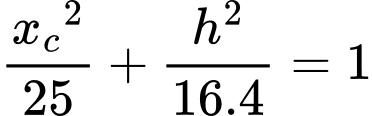
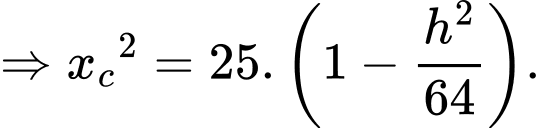
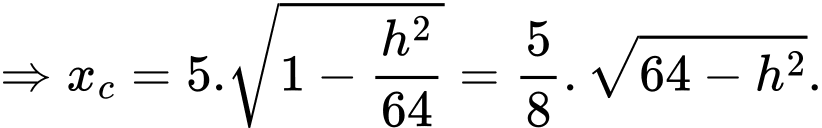
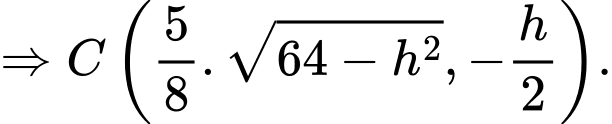
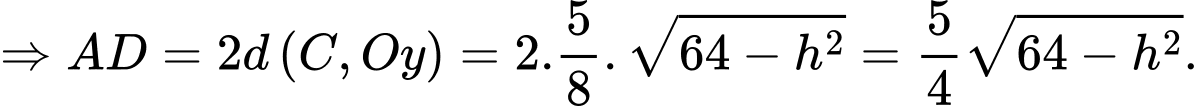
Khi gò tấm tôn lại ta sẽ được đáy của tấm tôn có hình tròn và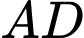 chính là chu vi của hình tròn đó.
chính là chu vi của hình tròn đó.
Gọi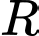 là bán kính của hình tròn đáy thì ta có:
là bán kính của hình tròn đáy thì ta có: 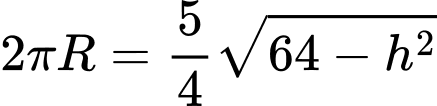
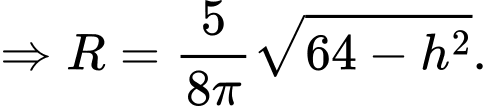
Thể tích của khối trụ là
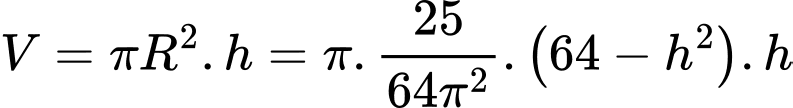
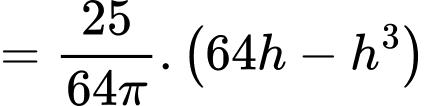
Xét hàm số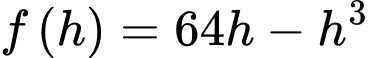
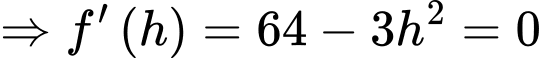
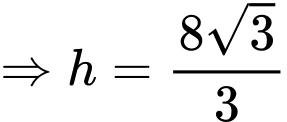 chính là điểm cực đại của đồ thị hàm số đã cho.
chính là điểm cực đại của đồ thị hàm số đã cho.
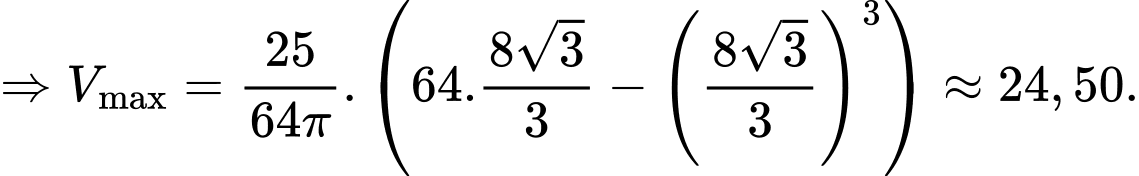

Phương trình elip có dạng
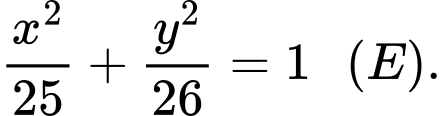
Theo hình vẽ ta có:
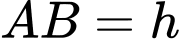 ,
, 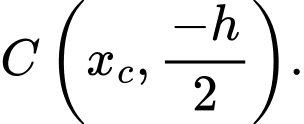
Thay tọa độ điểm
 vào phương trình elip ta được:
vào phương trình elip ta được: 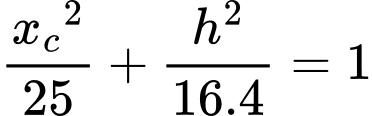
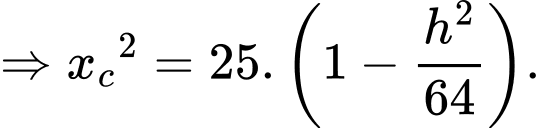
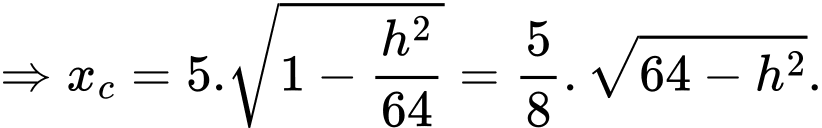
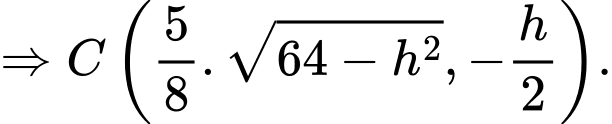
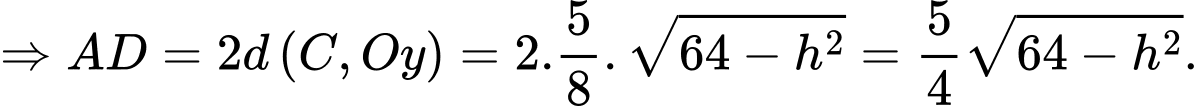
Khi gò tấm tôn lại ta sẽ được đáy của tấm tôn có hình tròn và
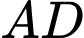 chính là chu vi của hình tròn đó.
chính là chu vi của hình tròn đó.
Gọi
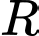 là bán kính của hình tròn đáy thì ta có:
là bán kính của hình tròn đáy thì ta có: 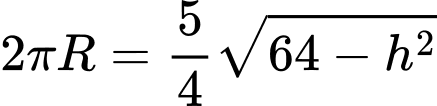
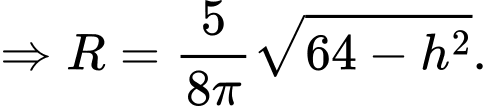
Thể tích của khối trụ là
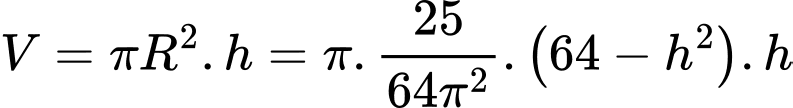
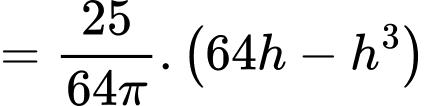
Xét hàm số
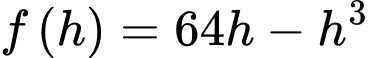
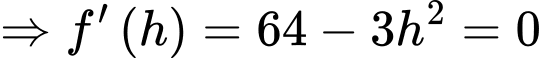
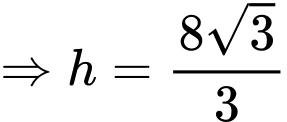 chính là điểm cực đại của đồ thị hàm số đã cho.
chính là điểm cực đại của đồ thị hàm số đã cho.
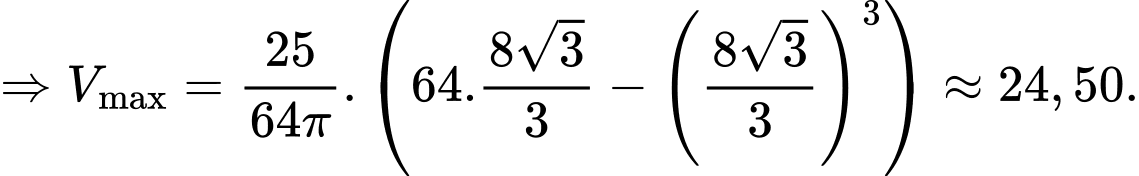
Câu 21 [695247]: Ở thị trấn của tôi, trời mưa một phần ba số ngày. Nếu trời mưa, sẽ có khả năng xảy ra ùn tắc giao thông với xác suất 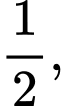 nếu trời không mưa, sẽ có khả năng xảy ra ùn tắc giao thông là
nếu trời không mưa, sẽ có khả năng xảy ra ùn tắc giao thông là 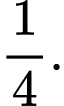 Nếu trời mưa và có ùn tắc giao thông, tôi sẽ đến muộn làm việc với xác suất
Nếu trời mưa và có ùn tắc giao thông, tôi sẽ đến muộn làm việc với xác suất 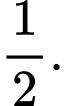 Mặt khác, xác suất đến muộn là
Mặt khác, xác suất đến muộn là 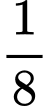 nếu trời không mưa và không có ùn tắc giao thông. Trong các tình huống khác (mưa và không có ùn tắc giao thông, không mưa và có ùn tắc giao thông), xác suất đến muộn của tôi đều là 0,25. Chọn một ngày ngẫu nhiên mà tôi đi làm muộn, vậy xác suất trời mưa vào ngày hôm đó là bao nhiêu %? Kết quả làm tròn đến hàng phần mười.
nếu trời không mưa và không có ùn tắc giao thông. Trong các tình huống khác (mưa và không có ùn tắc giao thông, không mưa và có ùn tắc giao thông), xác suất đến muộn của tôi đều là 0,25. Chọn một ngày ngẫu nhiên mà tôi đi làm muộn, vậy xác suất trời mưa vào ngày hôm đó là bao nhiêu %? Kết quả làm tròn đến hàng phần mười.
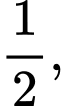 nếu trời không mưa, sẽ có khả năng xảy ra ùn tắc giao thông là
nếu trời không mưa, sẽ có khả năng xảy ra ùn tắc giao thông là 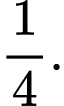 Nếu trời mưa và có ùn tắc giao thông, tôi sẽ đến muộn làm việc với xác suất
Nếu trời mưa và có ùn tắc giao thông, tôi sẽ đến muộn làm việc với xác suất 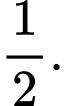 Mặt khác, xác suất đến muộn là
Mặt khác, xác suất đến muộn là 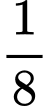 nếu trời không mưa và không có ùn tắc giao thông. Trong các tình huống khác (mưa và không có ùn tắc giao thông, không mưa và có ùn tắc giao thông), xác suất đến muộn của tôi đều là 0,25. Chọn một ngày ngẫu nhiên mà tôi đi làm muộn, vậy xác suất trời mưa vào ngày hôm đó là bao nhiêu %? Kết quả làm tròn đến hàng phần mười.
nếu trời không mưa và không có ùn tắc giao thông. Trong các tình huống khác (mưa và không có ùn tắc giao thông, không mưa và có ùn tắc giao thông), xác suất đến muộn của tôi đều là 0,25. Chọn một ngày ngẫu nhiên mà tôi đi làm muộn, vậy xác suất trời mưa vào ngày hôm đó là bao nhiêu %? Kết quả làm tròn đến hàng phần mười.
Điền đáp án: 54,5.
Từ giả thiết đề bài, ta có sơ đồ cây sau:
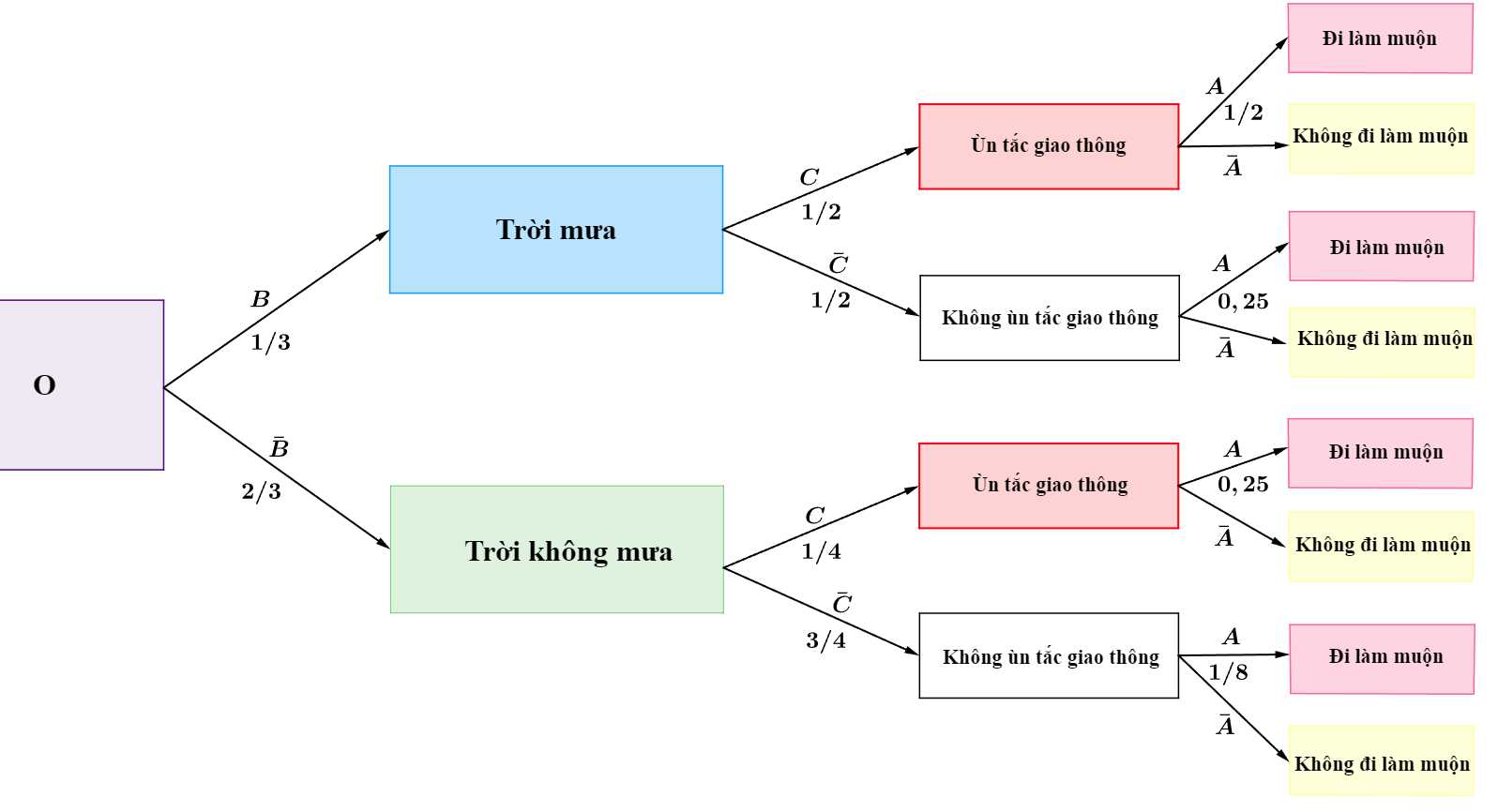
Theo công thức xác suất có điều kiện, ta có
P (trời mưa|đi làm muộn) = P(trời mưa và đi làm muộn)/P(đi làm muộn)
+) P(trời mưa và đi làm muộn)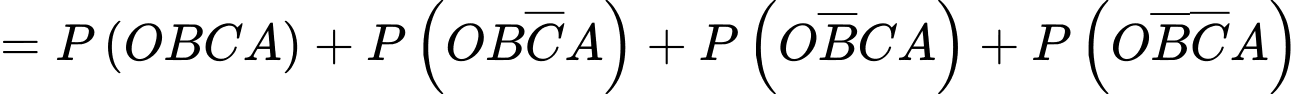
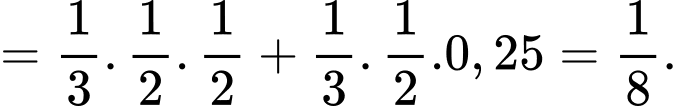
+) P(đi làm muộn)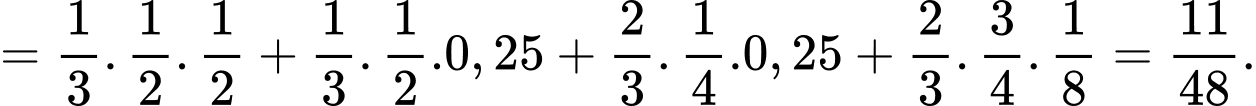
Suy ra P (trời mưa|đi làm muộn)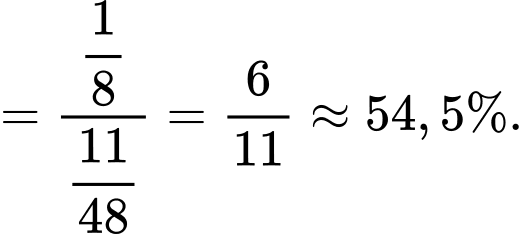
Từ giả thiết đề bài, ta có sơ đồ cây sau:

Theo công thức xác suất có điều kiện, ta có
P (trời mưa|đi làm muộn) = P(trời mưa và đi làm muộn)/P(đi làm muộn)
+) P(trời mưa và đi làm muộn)
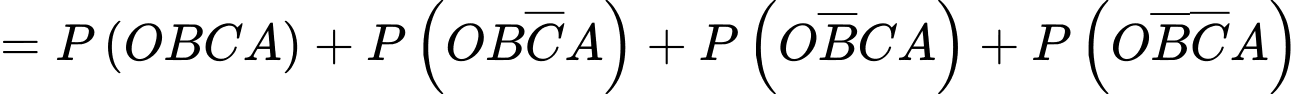
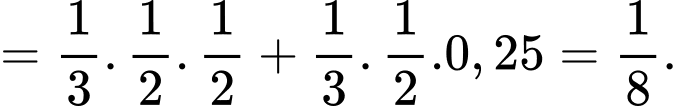
+) P(đi làm muộn)
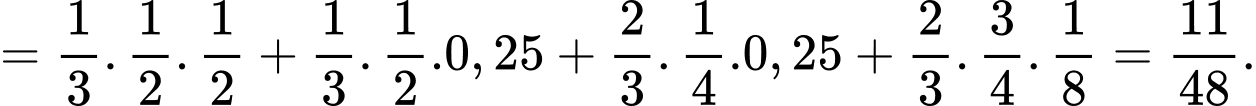
Suy ra P (trời mưa|đi làm muộn)
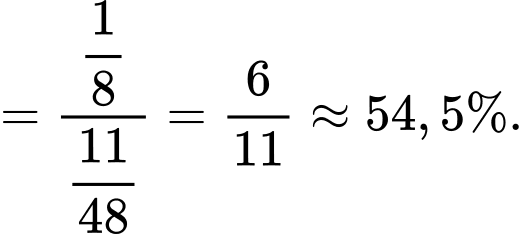
Câu 22 [695282]: Trong không gian với hệ tọa độ 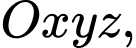 cho điểm
cho điểm 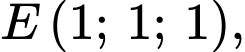 mặt cầu
mặt cầu 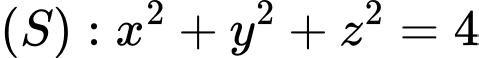 và mặt phẳng
và mặt phẳng 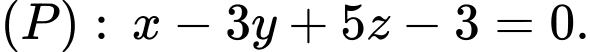 Gọi
Gọi  là đường thẳng đi qua
là đường thẳng đi qua 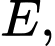 nằm trong
nằm trong 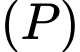 và cắt mặt cầu
và cắt mặt cầu 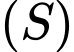 tại hai điểm
tại hai điểm 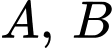 sao cho tam giác
sao cho tam giác 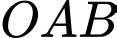 là tam giác đều. Đường thẳng
là tam giác đều. Đường thẳng  có một vecto chỉ phương là
có một vecto chỉ phương là 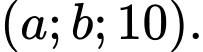 Tính
Tính 
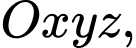 cho điểm
cho điểm 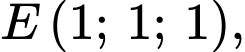 mặt cầu
mặt cầu 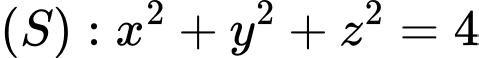 và mặt phẳng
và mặt phẳng 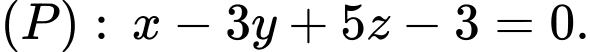 Gọi
Gọi  là đường thẳng đi qua
là đường thẳng đi qua 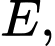 nằm trong
nằm trong 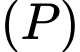 và cắt mặt cầu
và cắt mặt cầu 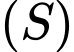 tại hai điểm
tại hai điểm 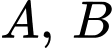 sao cho tam giác
sao cho tam giác 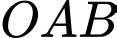 là tam giác đều. Đường thẳng
là tam giác đều. Đường thẳng  có một vecto chỉ phương là
có một vecto chỉ phương là 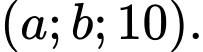 Tính
Tính 
Điền đáp án: 500.
Gọi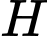 là chân đường vuông góc kẻ từ
là chân đường vuông góc kẻ từ  đến đường thẳng
đến đường thẳng  .
.
Do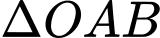 đều có đường cao
đều có đường cao 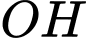 nên
nên 
Ta có: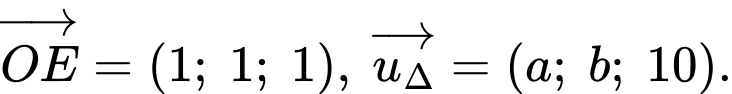
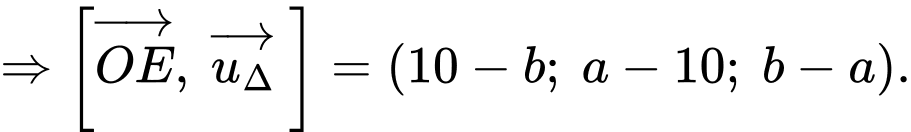
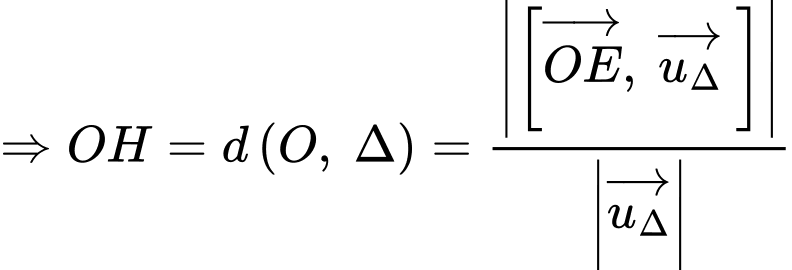
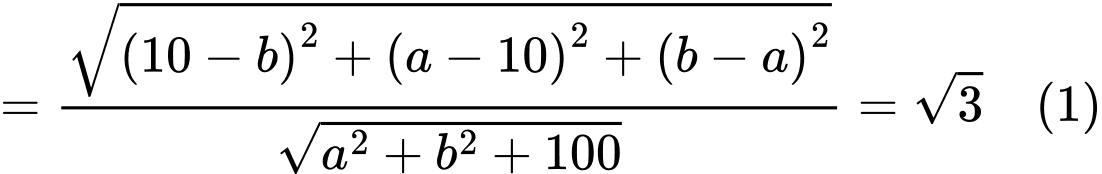 .
.
Ta có: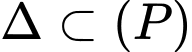
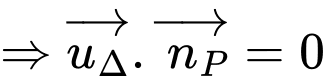
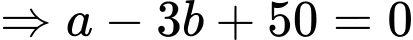
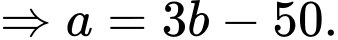
Thay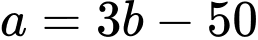 vào (1) ta được:
vào (1) ta được:
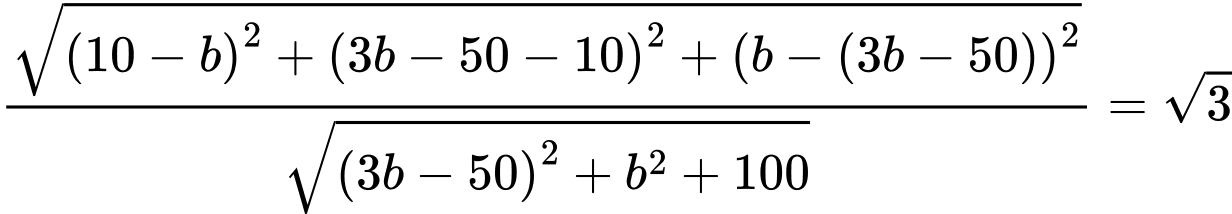
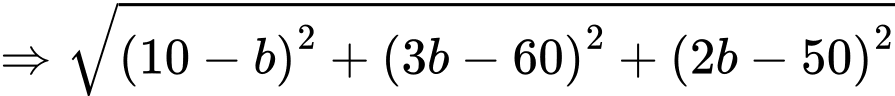
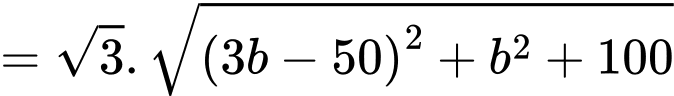
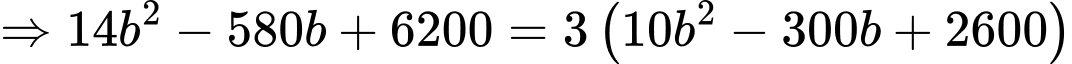
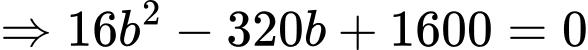
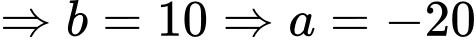
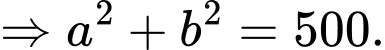
Gọi
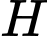 là chân đường vuông góc kẻ từ
là chân đường vuông góc kẻ từ  đến đường thẳng
đến đường thẳng  .
.
Do
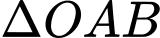 đều có đường cao
đều có đường cao 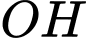 nên
nên 
Ta có:
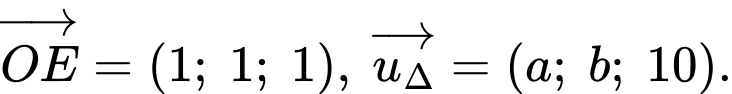
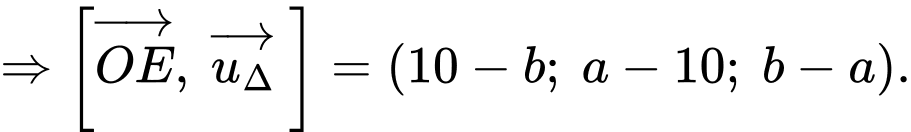
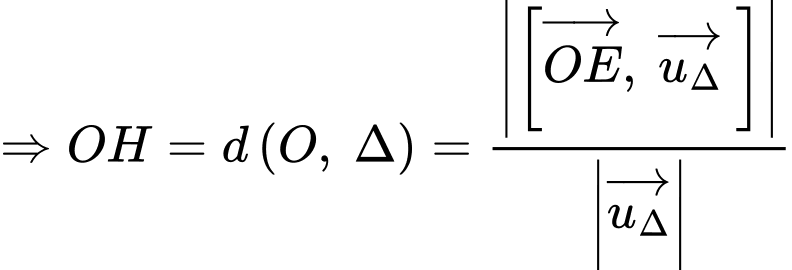
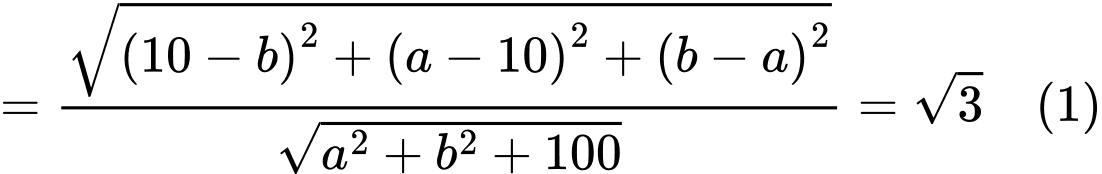 .
.
Ta có:
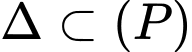
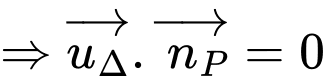
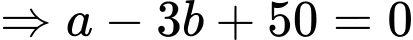
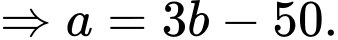
Thay
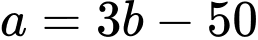 vào (1) ta được:
vào (1) ta được: