PHẦN I. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Câu 1 [693075]: Cho hàm số 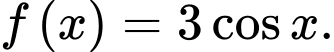 Khẳng định nào dưới đây đúng?
Khẳng định nào dưới đây đúng?
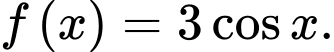 Khẳng định nào dưới đây đúng?
Khẳng định nào dưới đây đúng? A, 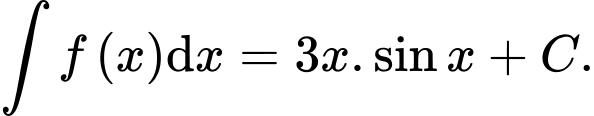
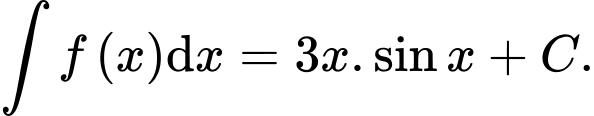
B, 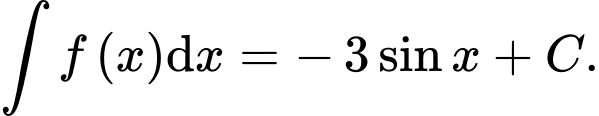
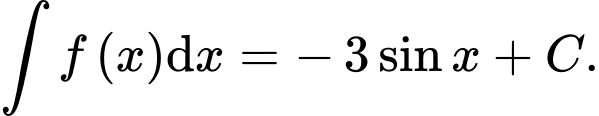
C, 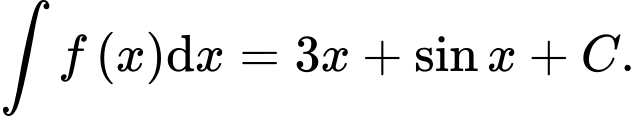
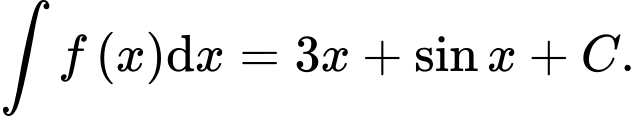
D, 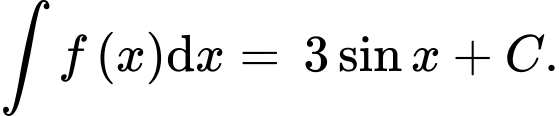
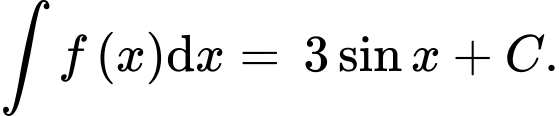
Chọn đáp án D.
Ta có: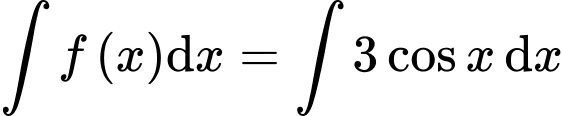

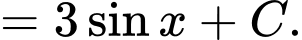 Đáp án: D
Đáp án: D
Ta có:
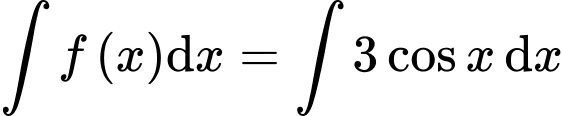

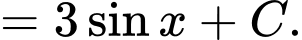 Đáp án: D
Đáp án: D
Câu 2 [255863]: Cho cấp số cộng 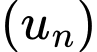 với
với 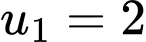 và công sai
và công sai  Giá trị của
Giá trị của 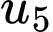 bằng
bằng
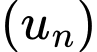 với
với 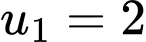 và công sai
và công sai  Giá trị của
Giá trị của 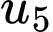 bằng
bằng A, 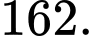
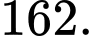
B, 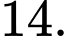
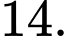
C, 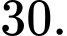
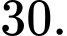
D, 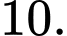
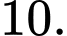
Chọn đáp án B.
Theo giả thiết,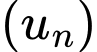 là cấp số cộng có
là cấp số cộng có 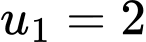 và công sai
và công sai 
Áp dụng công thức CSC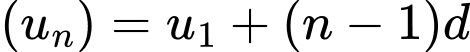 ta có:
ta có:

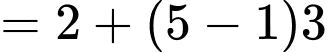
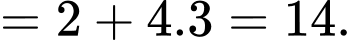 Đáp án: B
Đáp án: B
Theo giả thiết,
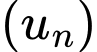 là cấp số cộng có
là cấp số cộng có 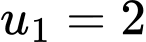 và công sai
và công sai 
Áp dụng công thức CSC
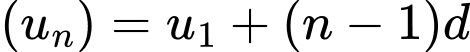 ta có:
ta có:

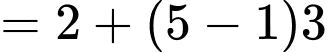
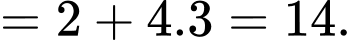 Đáp án: B
Đáp án: B
Câu 3 [693080]: Nghiệm của phương trình 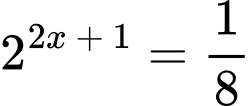 là
là
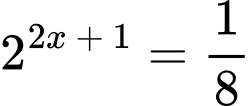 là
là A, 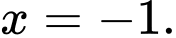
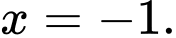
B, 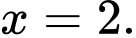
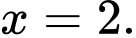
C, 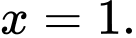
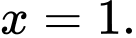
D, 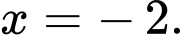
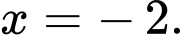
Chọn đáp án D.
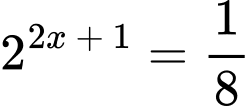
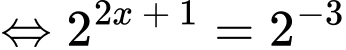
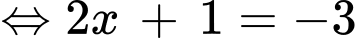
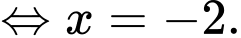 Đáp án: D
Đáp án: D
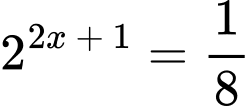
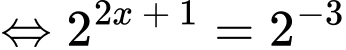
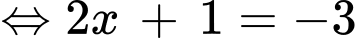
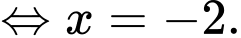 Đáp án: D
Đáp án: D
Câu 4 [255864]: Cho hình phẳng  giới hạn bởi đường cong
giới hạn bởi đường cong 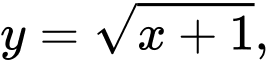 trục hoành và các đường thẳng
trục hoành và các đường thẳng 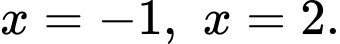 Thể tích
Thể tích  của khối tròn xoay tạo thành khi quay
của khối tròn xoay tạo thành khi quay  quanh trục hoành được tính bởi công thức nào dưới đây?
quanh trục hoành được tính bởi công thức nào dưới đây?
 giới hạn bởi đường cong
giới hạn bởi đường cong 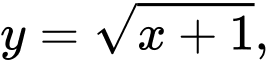 trục hoành và các đường thẳng
trục hoành và các đường thẳng 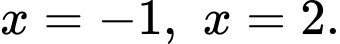 Thể tích
Thể tích  của khối tròn xoay tạo thành khi quay
của khối tròn xoay tạo thành khi quay  quanh trục hoành được tính bởi công thức nào dưới đây?
quanh trục hoành được tính bởi công thức nào dưới đây? A, 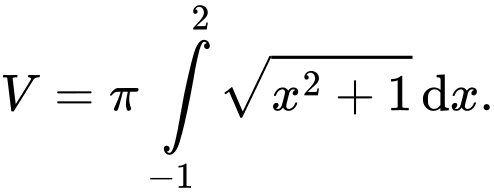
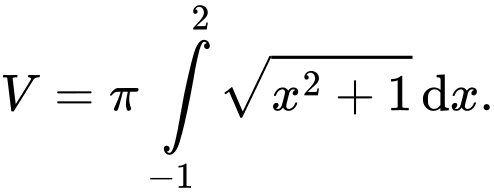
B, 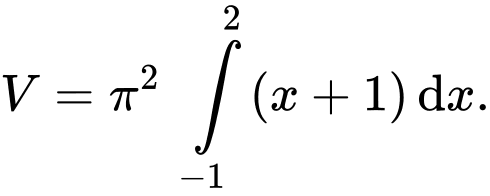
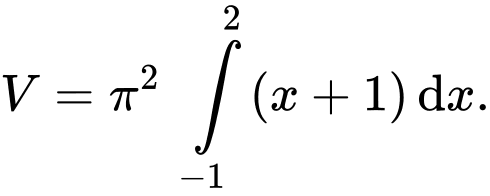
C, 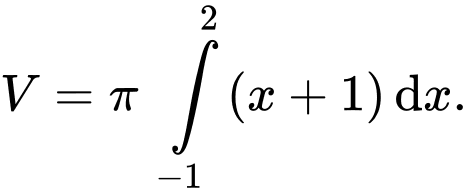
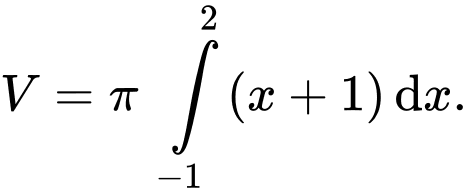
D, 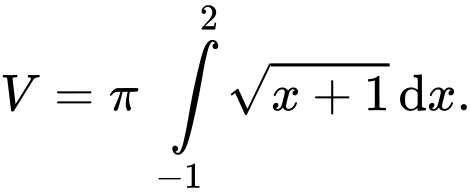
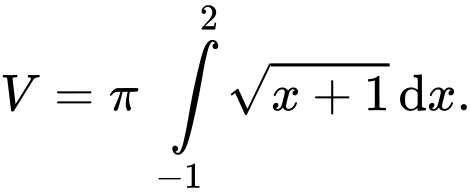
Chọn đáp án C.
Thể tích khối tròn xoay được sinh ra khi quay hình phẳng giới hạn bởi các đường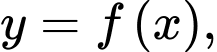 trục hoành và hai đường thẳng
trục hoành và hai đường thẳng 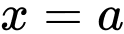 ,
, 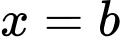 quanh trục
quanh trục 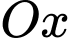 là:
là: 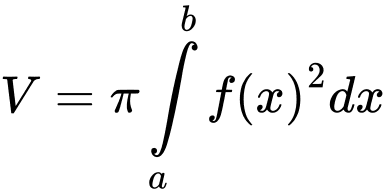
Áp dụng công thức, ta có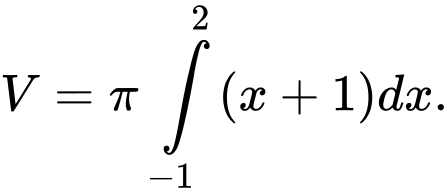 Đáp án: C
Đáp án: C
Thể tích khối tròn xoay được sinh ra khi quay hình phẳng giới hạn bởi các đường
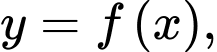 trục hoành và hai đường thẳng
trục hoành và hai đường thẳng 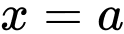 ,
, 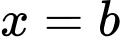 quanh trục
quanh trục 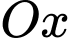 là:
là: 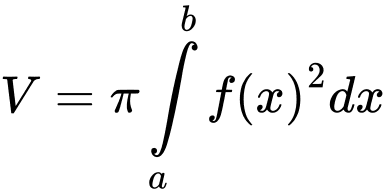
Áp dụng công thức, ta có
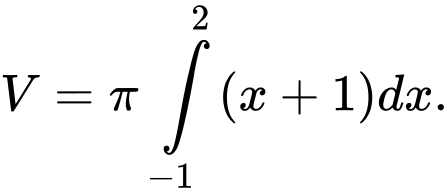 Đáp án: C
Đáp án: C
Câu 5 [693076]: Tập xác định của hàm số 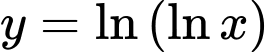 là
là
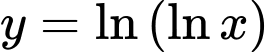 là
là A, 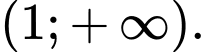
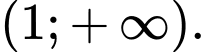
B, 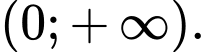
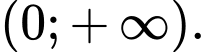
C, 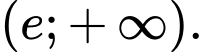
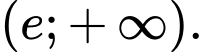
D, 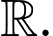
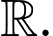
Chọn đáp án A.
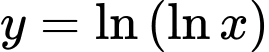
Hàm số có nghĩa khi: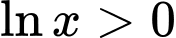
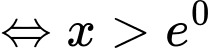
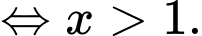
Vậy tập xác định của hàm số là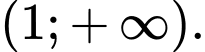 Đáp án: A
Đáp án: A
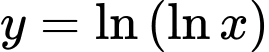
Hàm số có nghĩa khi:
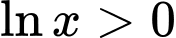
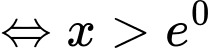
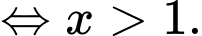
Vậy tập xác định của hàm số là
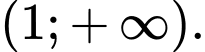 Đáp án: A
Đáp án: A Sử dụng thông tin dưới đây để trả lời câu 6 và câu 7
Trong không gian với hệ toạ độ Oxyz, cho ba điểm A(1; - 2; - 1), B(1;0;2) và C(0;2;1).
Câu 6 [697136]: Độ dài vectơ 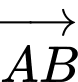 bằng
bằng
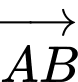 bằng
bằng A, 
B, 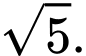
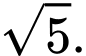
C, 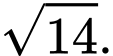
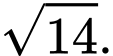
D, 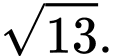
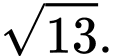
Chọn đáp án D.
Theo bài ta có: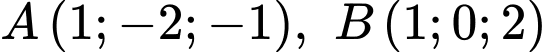
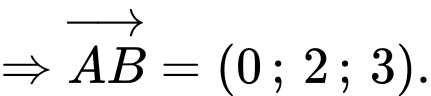
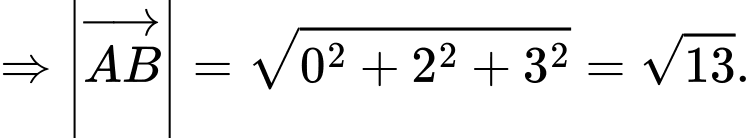 Đáp án: D
Đáp án: D
Theo bài ta có:
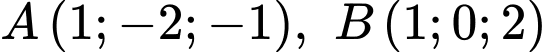
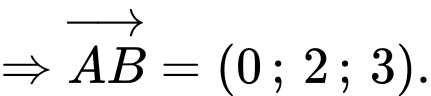
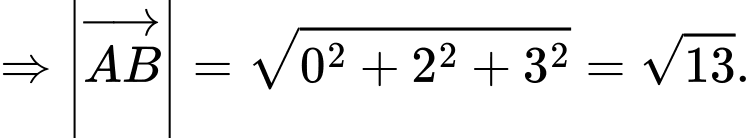 Đáp án: D
Đáp án: D
Câu 7 [697137]: Mặt phẳng đi qua 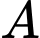 và vuông góc với đường thẳng
và vuông góc với đường thẳng 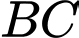 có phương trình là
có phương trình là
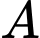 và vuông góc với đường thẳng
và vuông góc với đường thẳng 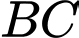 có phương trình là
có phương trình là A, 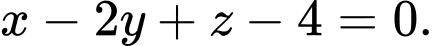
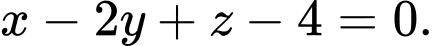
B, 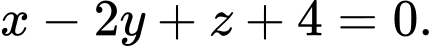
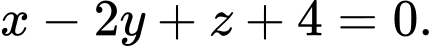
C, 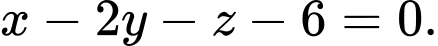
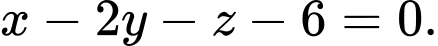
D, 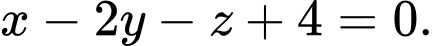
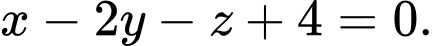
Chọn đáp án A.
Theo giả thiết, mặt phẳng đi qua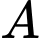 và vuông góc với đường thẳng
và vuông góc với đường thẳng 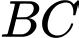 nên ta suy ra: Mặt phẳng đi qua
nên ta suy ra: Mặt phẳng đi qua 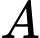 và nhận
và nhận 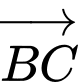 làm vecto pháp tuyến.
làm vecto pháp tuyến.
Ta có: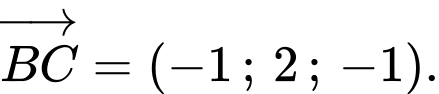
Mặt phẳng đi qua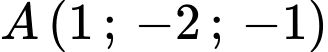 và có vecto pháp tuyến
và có vecto pháp tuyến 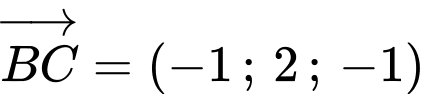 có phương trình là:
có phương trình là:

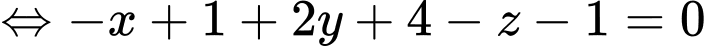
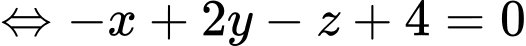
 Đáp án: A
Đáp án: A
Theo giả thiết, mặt phẳng đi qua
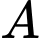 và vuông góc với đường thẳng
và vuông góc với đường thẳng 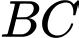 nên ta suy ra: Mặt phẳng đi qua
nên ta suy ra: Mặt phẳng đi qua 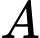 và nhận
và nhận 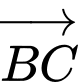 làm vecto pháp tuyến.
làm vecto pháp tuyến.Ta có:
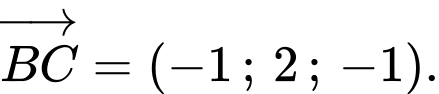
Mặt phẳng đi qua
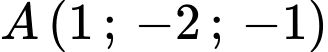 và có vecto pháp tuyến
và có vecto pháp tuyến 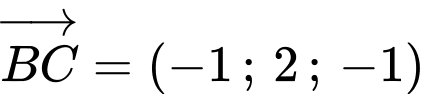 có phương trình là:
có phương trình là:
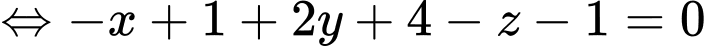
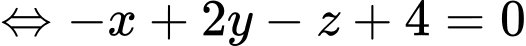
 Đáp án: A
Đáp án: A
Câu 8 [693078]: Thống kê thu nhập theo tháng (đơn vị: triệu đồng) của một nhóm người chạy xe máy “Xanh SM” được cho trong bảng sau:

Tứ phân vị thứ ba của mẫu số liệu ghép nhóm trên là

Tứ phân vị thứ ba của mẫu số liệu ghép nhóm trên là
A, 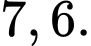
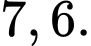
B, 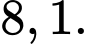
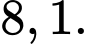
C, 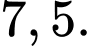
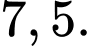
D, 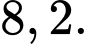
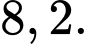
Chọn đáp án A.
Số người chạy xe máy “Xanh SM” được khảo sát là
Gọi là thu nhập của 22 người được sắp xếp theo thứ tự không giảm.
là thu nhập của 22 người được sắp xếp theo thứ tự không giảm.
Ta có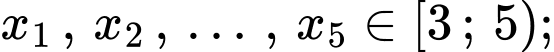
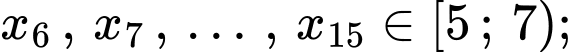
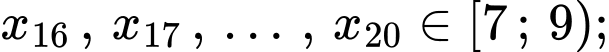
 Do đó đối với dãy số liệu
Do đó đối với dãy số liệu  thì
thì
Tứ phân vị thứ ba của dãy số liệu là
là 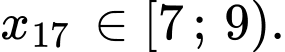 Do đó tứ phân vị thứ ba của mẫu số liệu ghép nhóm là:
Do đó tứ phân vị thứ ba của mẫu số liệu ghép nhóm là:
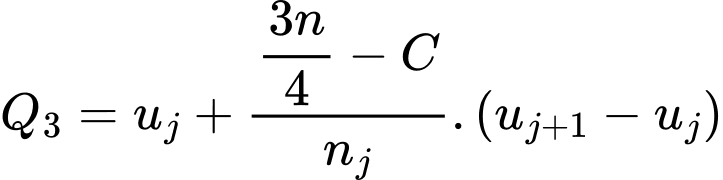
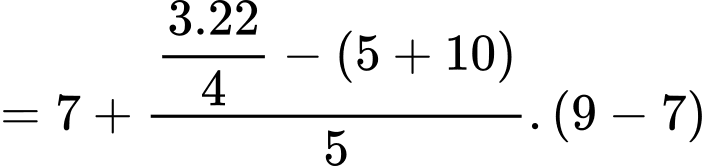
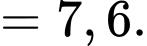 Đáp án: A
Đáp án: A
Số người chạy xe máy “Xanh SM” được khảo sát là

Gọi
 là thu nhập của 22 người được sắp xếp theo thứ tự không giảm.
là thu nhập của 22 người được sắp xếp theo thứ tự không giảm.Ta có
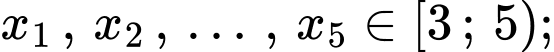
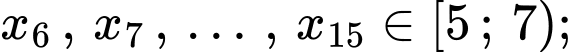
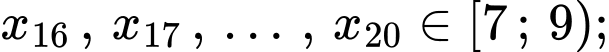
 Do đó đối với dãy số liệu
Do đó đối với dãy số liệu  thì
thìTứ phân vị thứ ba của dãy số liệu
 là
là 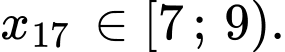 Do đó tứ phân vị thứ ba của mẫu số liệu ghép nhóm là:
Do đó tứ phân vị thứ ba của mẫu số liệu ghép nhóm là: 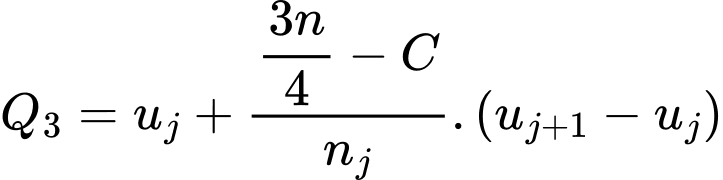
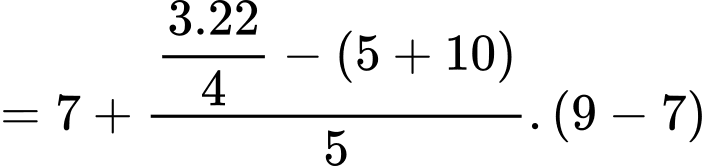
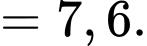 Đáp án: A
Đáp án: A
Câu 9 [566004]: Hàm số 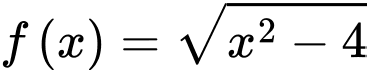 đồng biến trên khoảng nào dưới đây?
đồng biến trên khoảng nào dưới đây?
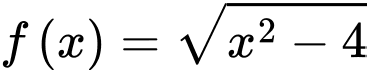 đồng biến trên khoảng nào dưới đây?
đồng biến trên khoảng nào dưới đây? A, 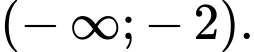
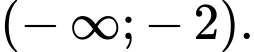
B, 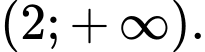
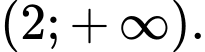
C, 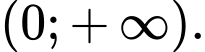
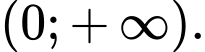
D, 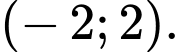
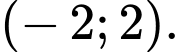
Chọn đáp án B.
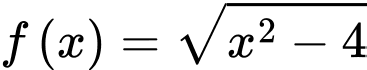
ĐK: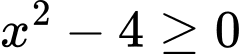
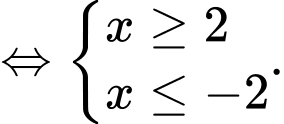
Xét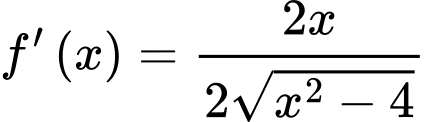
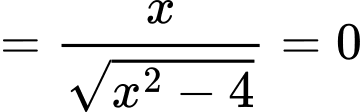 (
( và
và  )
)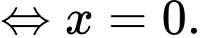
Ta có BBT hàm số:
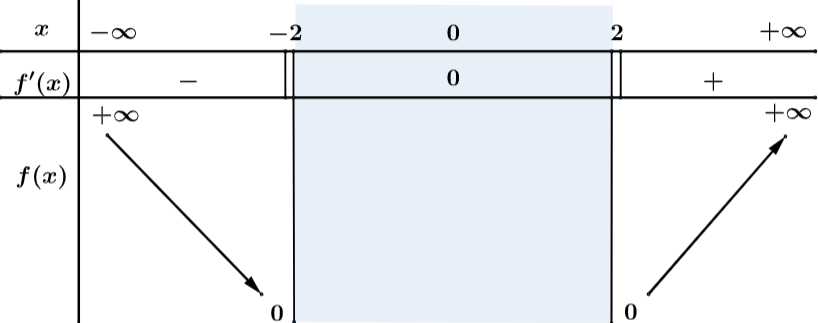
Từ BBT ta suy ra hàm số đồng biến trên khoảng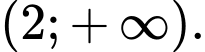 Đáp án: B
Đáp án: B
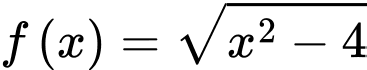
ĐK:
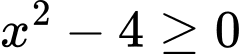
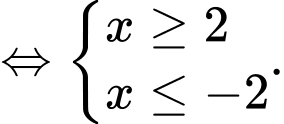
Xét
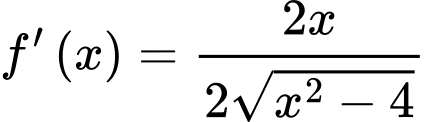
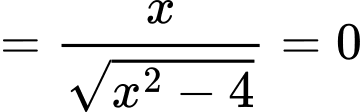 (
( và
và  )
)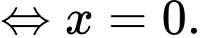
Ta có BBT hàm số:

Từ BBT ta suy ra hàm số đồng biến trên khoảng
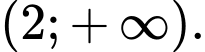 Đáp án: B
Đáp án: B
Câu 10 [693079]: Cho hình chóp tứ giác 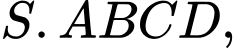 gọi
gọi 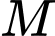 và
và 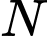 lần lượt là trung điểm của
lần lượt là trung điểm của 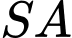 và
và  Mặt phẳng nào sau đây song song với đường thẳng
Mặt phẳng nào sau đây song song với đường thẳng 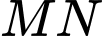 ?
?
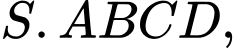 gọi
gọi 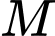 và
và 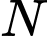 lần lượt là trung điểm của
lần lượt là trung điểm của 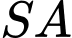 và
và  Mặt phẳng nào sau đây song song với đường thẳng
Mặt phẳng nào sau đây song song với đường thẳng 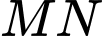 ?
? A, 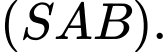
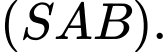
B, 

C, 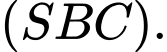
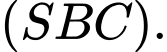
D, 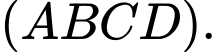
Chọn đáp án D.
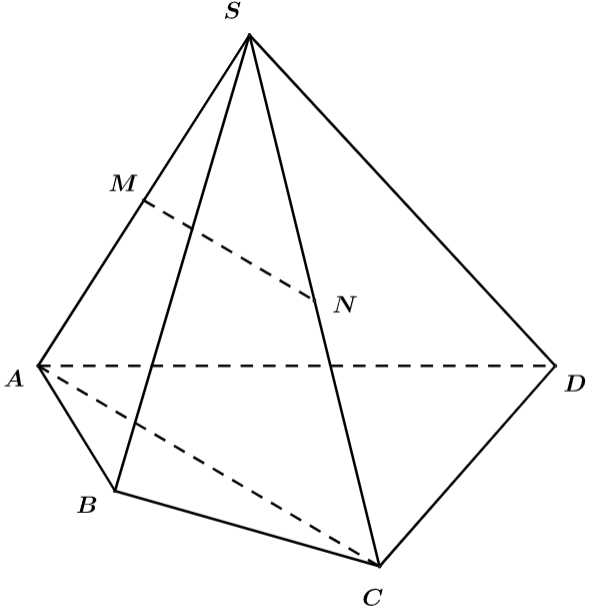
Ta có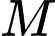 và
và 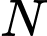 lần lượt là trung điểm của
lần lượt là trung điểm của 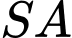 và
và 
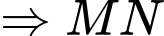 là đường trung bình của
là đường trung bình của 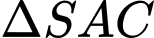
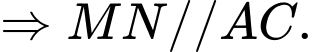
Mặt khác: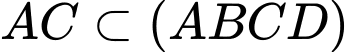
 Đáp án: D
Đáp án: D

Ta có
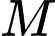 và
và 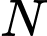 lần lượt là trung điểm của
lần lượt là trung điểm của 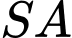 và
và 
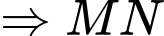 là đường trung bình của
là đường trung bình của 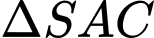
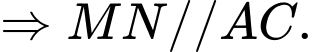
Mặt khác:
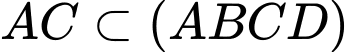
 Đáp án: D
Đáp án: D
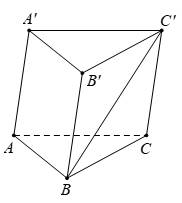
Câu 11 [693081]: Cho hình lăng trụ tam giác  (minh hoạ như hình bên). Đặt
(minh hoạ như hình bên). Đặt 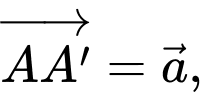
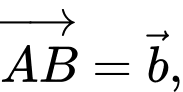
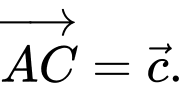 Phát biểu nào sau đây là đúng?
Phát biểu nào sau đây là đúng?
 (minh hoạ như hình bên). Đặt
(minh hoạ như hình bên). Đặt 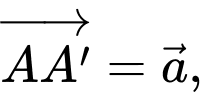
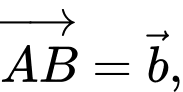
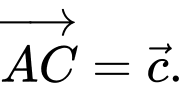 Phát biểu nào sau đây là đúng?
Phát biểu nào sau đây là đúng?
A, 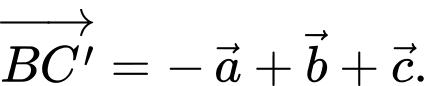
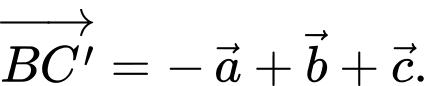
B, 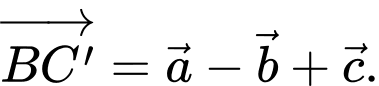
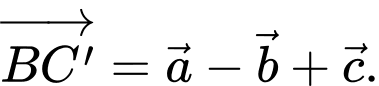
C, 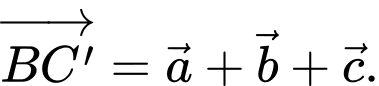
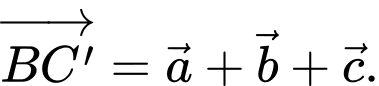
D, 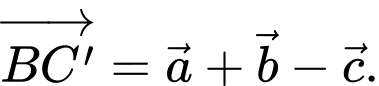
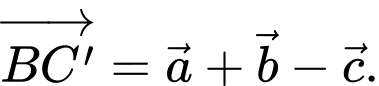
Chọn đáp án B.
Ta có: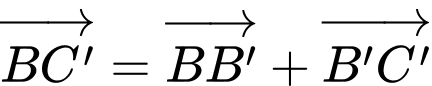
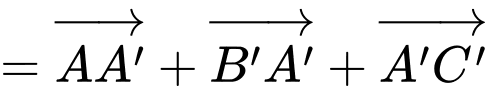
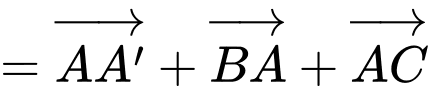
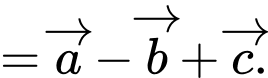 Đáp án: B
Đáp án: B
Ta có:
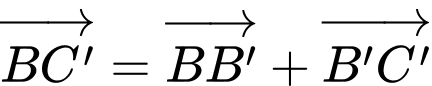
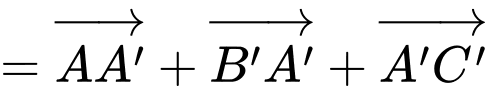
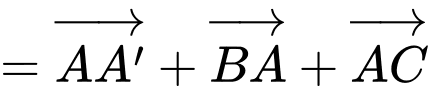
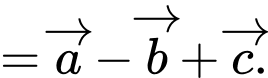 Đáp án: B
Đáp án: B
Câu 12 [693082]: Cho hàm số 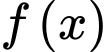 liên tục trên
liên tục trên 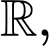 có bảng xét dấu của
có bảng xét dấu của 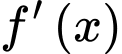 như sau:
như sau:
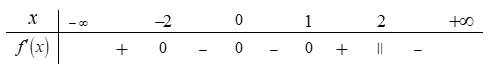
Số điểm cực đại của hàm số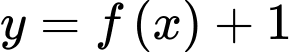 là
là
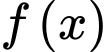 liên tục trên
liên tục trên 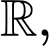 có bảng xét dấu của
có bảng xét dấu của 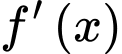 như sau:
như sau: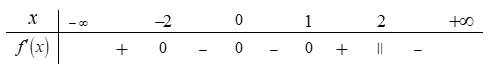
Số điểm cực đại của hàm số
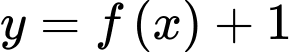 là
là A, 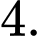
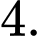
B, 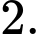
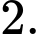
C, 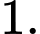
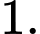
D, 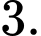
Chọn đáp án B.
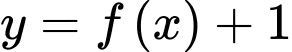
Ta có: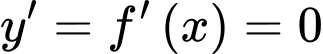
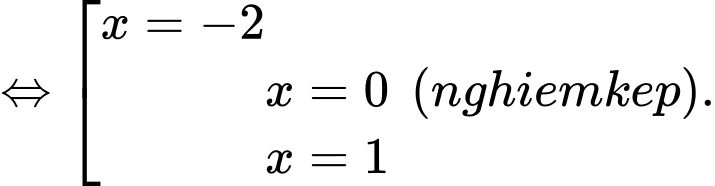
Ta có bảng xét dấu giống với đề bài.
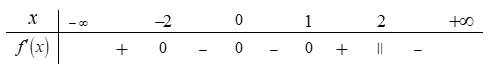
Vậy số điểm cực đại của hàm số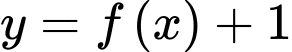 là 2 điểm. Đáp án: B
là 2 điểm. Đáp án: B
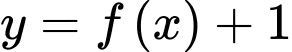
Ta có:
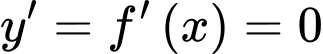
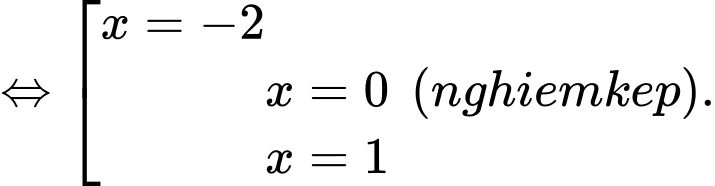
Ta có bảng xét dấu giống với đề bài.
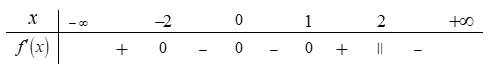
Vậy số điểm cực đại của hàm số
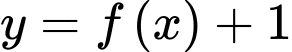 là 2 điểm. Đáp án: B
là 2 điểm. Đáp án: B PHẦN II. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Câu 13 [693085]: Cho hàm số 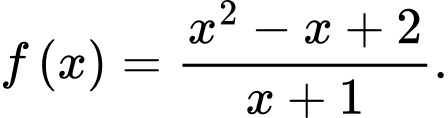
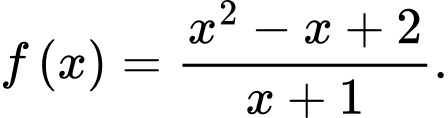
a) Đúng.
Ta có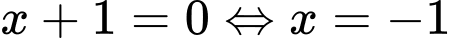 và
và 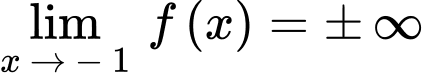
Suy ra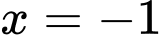 là tiệm cận đứng của đồ thị hàm số.
là tiệm cận đứng của đồ thị hàm số.
b) Đúng.
Ta có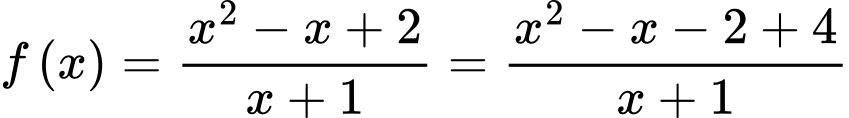
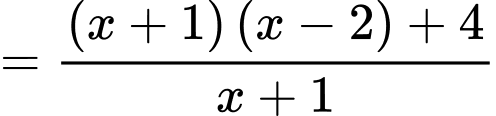
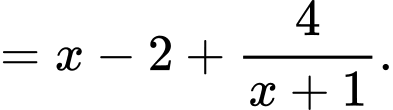
Suy ra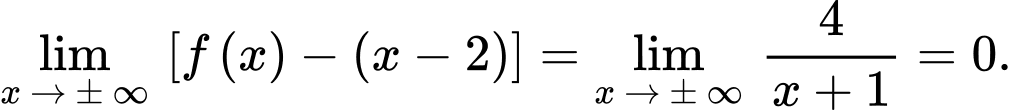
Do đó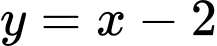 là tiệm cận xiên của đồ thị hàm số.
là tiệm cận xiên của đồ thị hàm số.
c) Đúng.
Với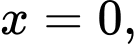 thay vào phương trình tiệm cận xiên, ta được
thay vào phương trình tiệm cận xiên, ta được 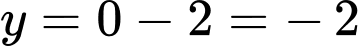
Suy ra tiệm cận xiên của đồ thị hàm số đi qua điểm có toạ độ là
d) Sai.
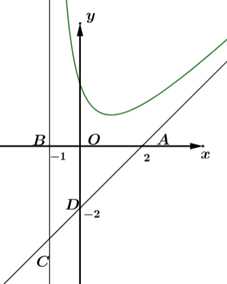
Tiệm cận xiên cắt trục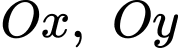 lần lượt tại
lần lượt tại 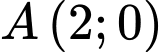 và
và 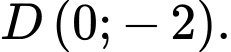
Giao điểm của hai đường TCĐ và TCX là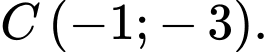
Tiệm cận đứng cắt trục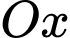 tại điểm
tại điểm 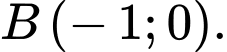
Giao điểm của hai trục toạ độ là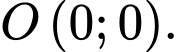
Do đó hai đường tiệm cận cùng với hai trục toạ độ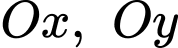 tạo thành tứ giác
tạo thành tứ giác 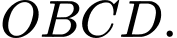
Dễ thấy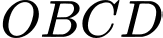 là hình thang vuông tại
là hình thang vuông tại 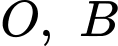
Suy ra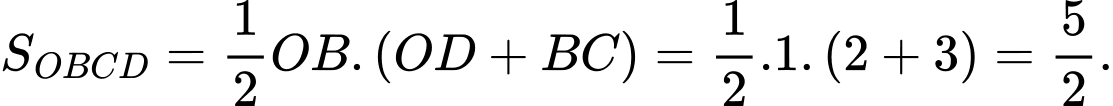
Ta có
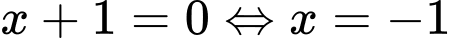 và
và 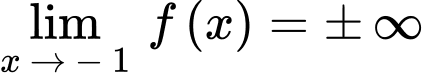
Suy ra
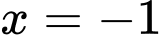 là tiệm cận đứng của đồ thị hàm số.
là tiệm cận đứng của đồ thị hàm số.
b) Đúng.
Ta có
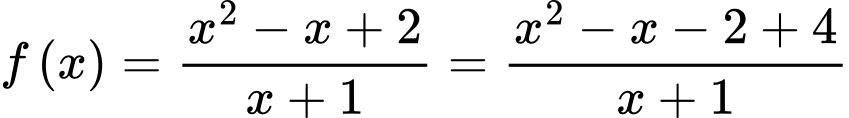
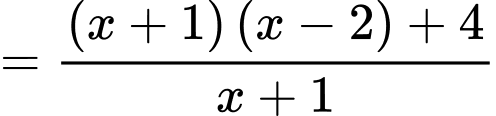
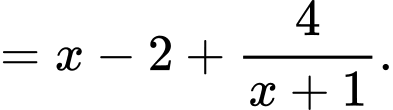
Suy ra
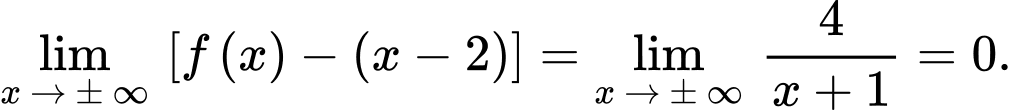
Do đó
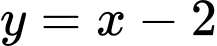 là tiệm cận xiên của đồ thị hàm số.
là tiệm cận xiên của đồ thị hàm số.
c) Đúng.
Với
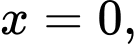 thay vào phương trình tiệm cận xiên, ta được
thay vào phương trình tiệm cận xiên, ta được 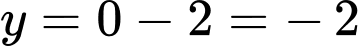
Suy ra tiệm cận xiên của đồ thị hàm số đi qua điểm có toạ độ là

d) Sai.

Tiệm cận xiên cắt trục
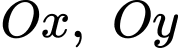 lần lượt tại
lần lượt tại 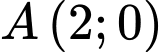 và
và 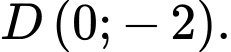
Giao điểm của hai đường TCĐ và TCX là
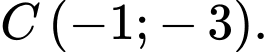
Tiệm cận đứng cắt trục
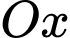 tại điểm
tại điểm 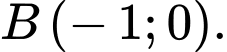
Giao điểm của hai trục toạ độ là
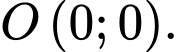
Do đó hai đường tiệm cận cùng với hai trục toạ độ
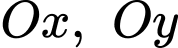 tạo thành tứ giác
tạo thành tứ giác 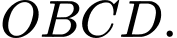
Dễ thấy
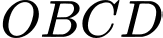 là hình thang vuông tại
là hình thang vuông tại 
Suy ra
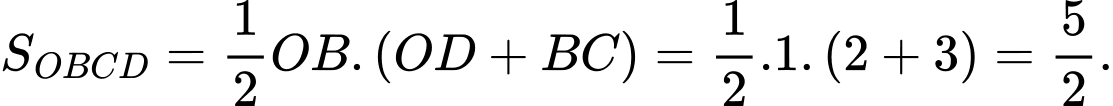
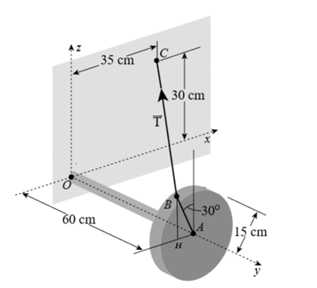
Câu 14 [693087]: Một vật dụng bằng sắt đang nằm trên mặt sàn có tay cầm dài 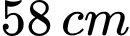 nối với một ống trụ dày
nối với một ống trụ dày 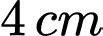 và có đường kính đáy bằng
và có đường kính đáy bằng 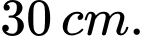 Nếu không giữ thì sẽ luôn có một lực làm vật rung động, để vật đứng yên thì người ta đã nối một đoạn dây từ điểm
Nếu không giữ thì sẽ luôn có một lực làm vật rung động, để vật đứng yên thì người ta đã nối một đoạn dây từ điểm 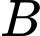 (là một điểm nằm trên đường tròn chính giữa của ống trụ to) đến điểm
(là một điểm nằm trên đường tròn chính giữa của ống trụ to) đến điểm  nằm trên bờ tường. Trên hệ trục
nằm trên bờ tường. Trên hệ trục 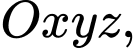 xét gốc tọa độ là điểm gắn ống trụ với bờ tường, bờ tường là mặt phẳng
xét gốc tọa độ là điểm gắn ống trụ với bờ tường, bờ tường là mặt phẳng 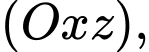 trục
trục 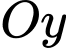 là trục của hình trụ, điểm
là trục của hình trụ, điểm 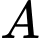 nằm chính giữa ống trụ to, điểm
nằm chính giữa ống trụ to, điểm 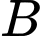 có hoành độ âm, cao độ dương và
có hoành độ âm, cao độ dương và  tạo với trục
tạo với trục  một góc
một góc 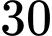 độ, các số liệu được cho như hình vẽ, đơn vị trên các hệ trục tính theo cm. Biết rằng lực căng
độ, các số liệu được cho như hình vẽ, đơn vị trên các hệ trục tính theo cm. Biết rằng lực căng 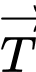 trên đoạn dây
trên đoạn dây 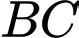 có độ lớn bằng
có độ lớn bằng 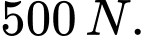
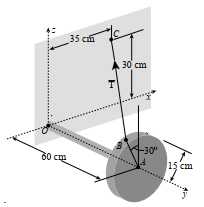
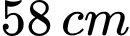 nối với một ống trụ dày
nối với một ống trụ dày 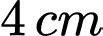 và có đường kính đáy bằng
và có đường kính đáy bằng 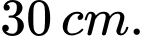 Nếu không giữ thì sẽ luôn có một lực làm vật rung động, để vật đứng yên thì người ta đã nối một đoạn dây từ điểm
Nếu không giữ thì sẽ luôn có một lực làm vật rung động, để vật đứng yên thì người ta đã nối một đoạn dây từ điểm  (là một điểm nằm trên đường tròn chính giữa của ống trụ to) đến điểm
(là một điểm nằm trên đường tròn chính giữa của ống trụ to) đến điểm  nằm trên bờ tường. Trên hệ trục
nằm trên bờ tường. Trên hệ trục 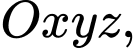 xét gốc tọa độ là điểm gắn ống trụ với bờ tường, bờ tường là mặt phẳng
xét gốc tọa độ là điểm gắn ống trụ với bờ tường, bờ tường là mặt phẳng 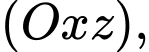 trục
trục 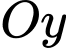 là trục của hình trụ, điểm
là trục của hình trụ, điểm 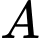 nằm chính giữa ống trụ to, điểm
nằm chính giữa ống trụ to, điểm 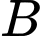 có hoành độ âm, cao độ dương và
có hoành độ âm, cao độ dương và  tạo với trục
tạo với trục  một góc
một góc 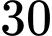 độ, các số liệu được cho như hình vẽ, đơn vị trên các hệ trục tính theo cm. Biết rằng lực căng
độ, các số liệu được cho như hình vẽ, đơn vị trên các hệ trục tính theo cm. Biết rằng lực căng 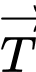 trên đoạn dây
trên đoạn dây 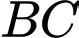 có độ lớn bằng
có độ lớn bằng 

a) Đúng.
Ta có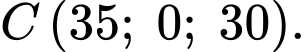
Suy ra hình chiếu của lên mặt phẳng
lên mặt phẳng 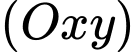 có toạ độ là
có toạ độ là 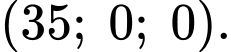
b) Sai.
Theo giả thiết, ta có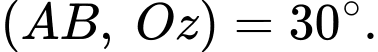
Mà suy ra
suy ra 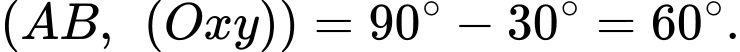
c) Sai.
+) Vì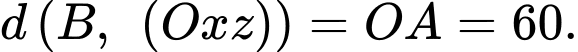 Suy ra tung độ của điểm
Suy ra tung độ của điểm 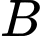 bằng 60.
bằng 60.
+) Gọi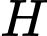 là hình chiếu của
là hình chiếu của 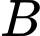 lên mặt phẳng
lên mặt phẳng 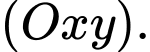
Xét tam giác vuông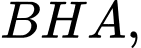 ta có:
ta có: 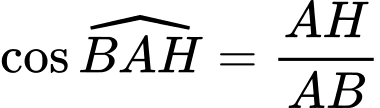
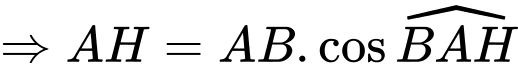

Suy ra hoành độ của điểm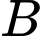 bằng
bằng 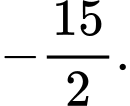
+) Ta có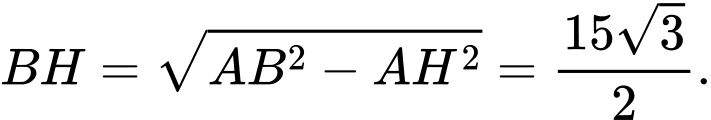 Suy ra cao độ của điểm
Suy ra cao độ của điểm 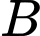 bằng
bằng 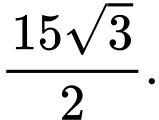
Suy ra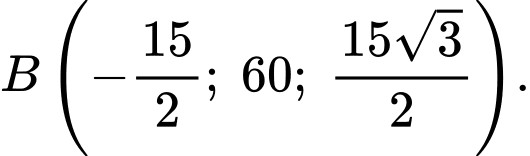
Suy ra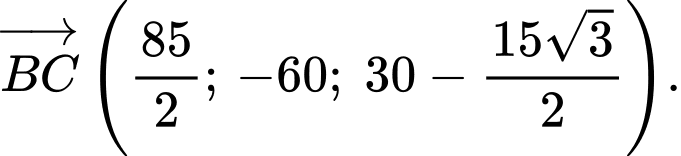
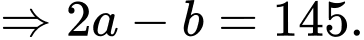
d) Sai.
Kiến thức cần dùng: Nếu 2 vectơ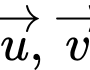 cùng hướng thì suy ra
cùng hướng thì suy ra 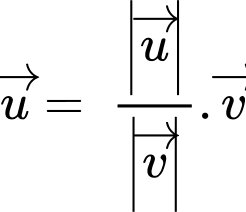
Vì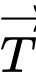 là vectơ lực tác dụng lên đoạn dây
là vectơ lực tác dụng lên đoạn dây 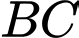 nên
nên 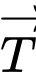 cùng hướng với
cùng hướng với 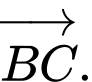
Áp dụng cho 2 vectơ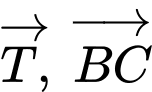 ta có
ta có 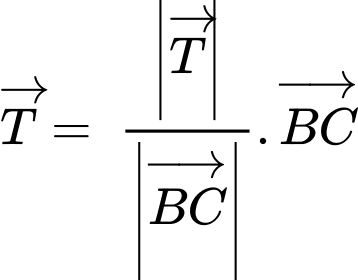
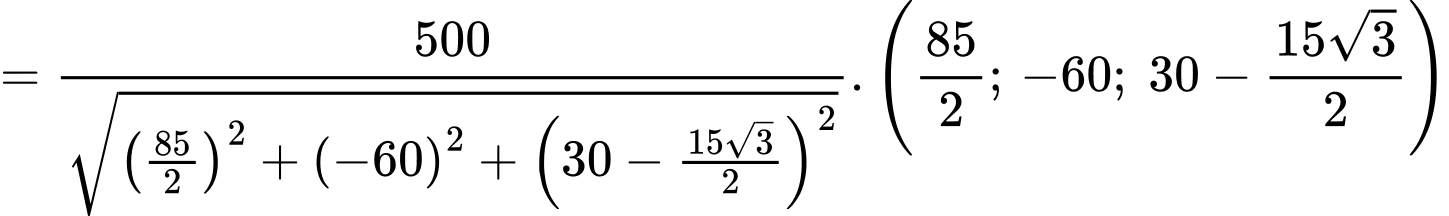
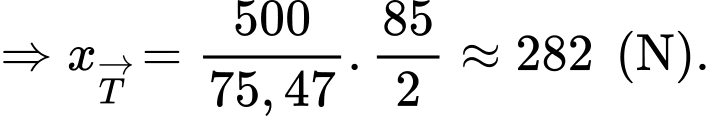
Ta có
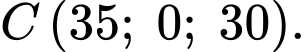
Suy ra hình chiếu của
 lên mặt phẳng
lên mặt phẳng 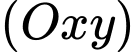 có toạ độ là
có toạ độ là 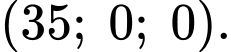
b) Sai.
Theo giả thiết, ta có
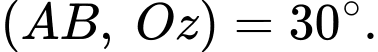
Mà
 suy ra
suy ra 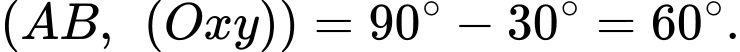
c) Sai.
+) Vì
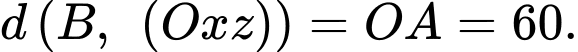 Suy ra tung độ của điểm
Suy ra tung độ của điểm 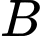 bằng 60.
bằng 60.
+) Gọi
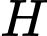 là hình chiếu của
là hình chiếu của 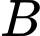 lên mặt phẳng
lên mặt phẳng 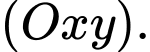

Xét tam giác vuông
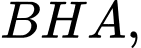 ta có:
ta có: 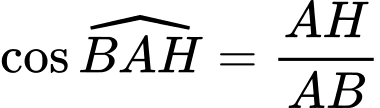
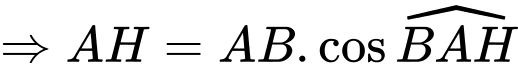

Suy ra hoành độ của điểm
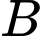 bằng
bằng 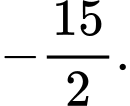
+) Ta có
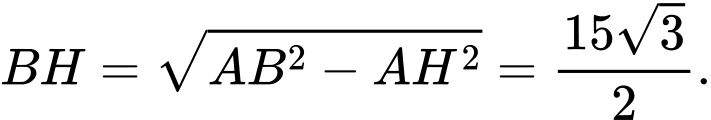 Suy ra cao độ của điểm
Suy ra cao độ của điểm 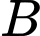 bằng
bằng 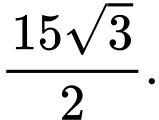
Suy ra
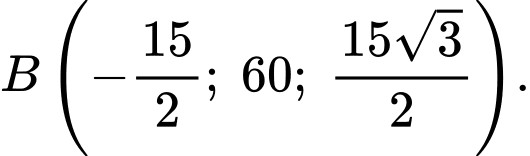
Suy ra
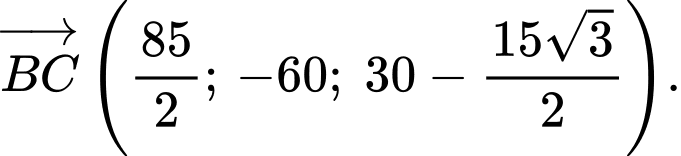
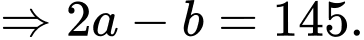
d) Sai.
Kiến thức cần dùng: Nếu 2 vectơ
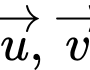 cùng hướng thì suy ra
cùng hướng thì suy ra 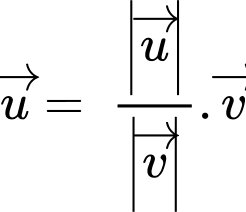
Vì
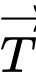 là vectơ lực tác dụng lên đoạn dây
là vectơ lực tác dụng lên đoạn dây 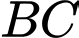 nên
nên 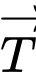 cùng hướng với
cùng hướng với 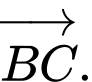
Áp dụng cho 2 vectơ
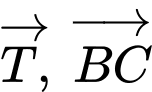 ta có
ta có 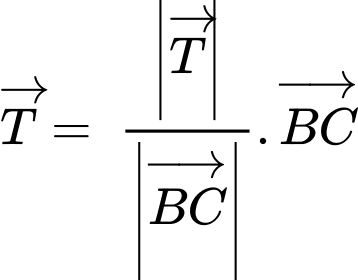
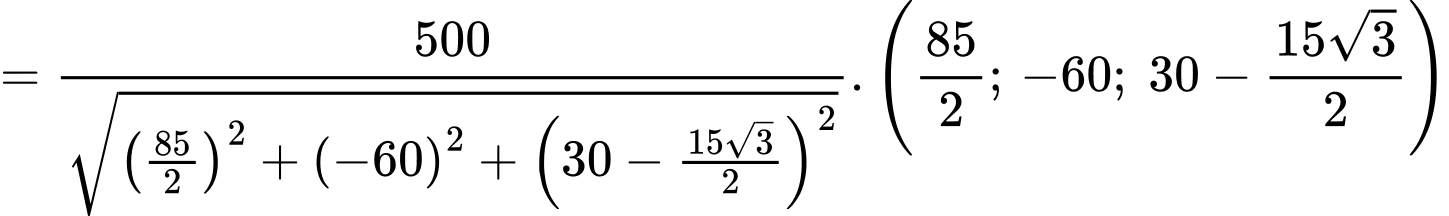
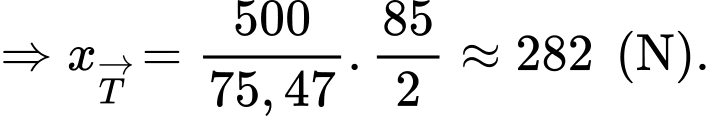
Câu 15 [693088]: Trong một khu dân cư, tỉ lệ người nghiện thuốc lá và chứng ung thư vòm họng là 15%. Có 25% người nghiện thuốc lá, nhưng không bị ung thư vòm họng, 50% người nghiện thuốc lá và cũng không ung thư họng và có 10% số người không nghiện thuốc nhưng mắc ung thư vòm họng.
Gọi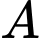 là biến cố “người đó nghiện thuốc lá”
là biến cố “người đó nghiện thuốc lá”
Gọi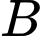 là biến cố “người đó bị ung thư vòm họng”
là biến cố “người đó bị ung thư vòm họng”
Gọi
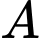 là biến cố “người đó nghiện thuốc lá”
là biến cố “người đó nghiện thuốc lá”Gọi
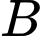 là biến cố “người đó bị ung thư vòm họng”
là biến cố “người đó bị ung thư vòm họng”
a) Sai.
Từ giả thiết, ta suy ra được:
+)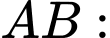 “Người đó nghiện thuốc là và bị ung thư vòm họng”.
“Người đó nghiện thuốc là và bị ung thư vòm họng”.

+) “Người đó không nghiện thuốc lá và bị ung thư vòm họng”.
“Người đó không nghiện thuốc lá và bị ung thư vòm họng”.
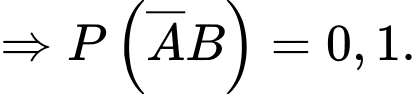
b) Sai.
Ta có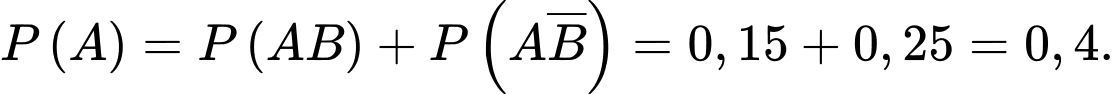
c) Đúng.
Áp dụng công thức, ta có: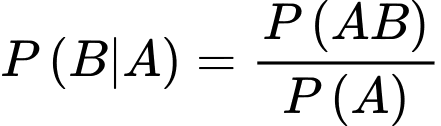
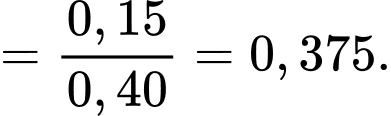
d) Đúng.
Để so sánh nguy cơ mắc ung thư vòm họng của người nghiện thuốc lá trong khu dân cư trên với nguy cơ mắc ung thư vòm họng của người không nghiện thuốc lá. Tức ta cần so sánh với
với 
Ta có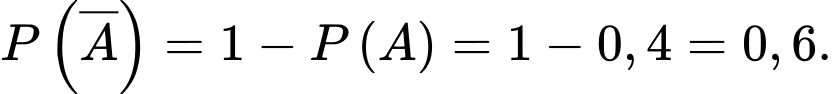
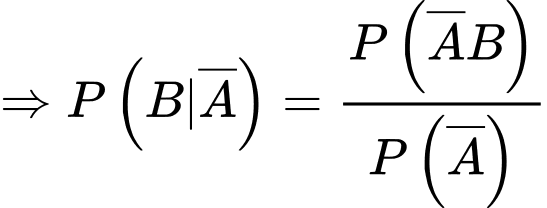
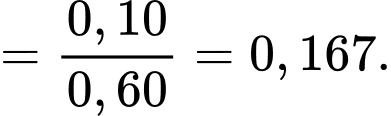
Nhận xét: gấp
gấp 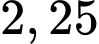 lần
lần  nên có thể thấy nguy cơ của người nghiện thuốc mắc ung thư vòm họng gấp hơn 2 lần người không nghiệm thuốc lá.
nên có thể thấy nguy cơ của người nghiện thuốc mắc ung thư vòm họng gấp hơn 2 lần người không nghiệm thuốc lá.
Từ giả thiết, ta suy ra được:
+)
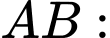 “Người đó nghiện thuốc là và bị ung thư vòm họng”.
“Người đó nghiện thuốc là và bị ung thư vòm họng”.

+)
 “Người đó không nghiện thuốc lá và bị ung thư vòm họng”.
“Người đó không nghiện thuốc lá và bị ung thư vòm họng”.
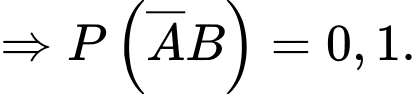
b) Sai.
Ta có
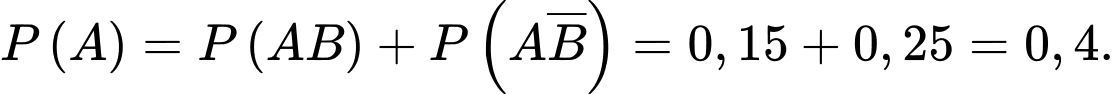
c) Đúng.
Áp dụng công thức, ta có:
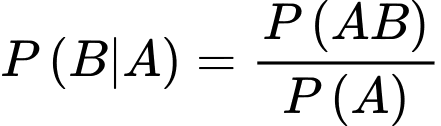
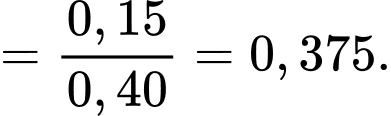
d) Đúng.
Để so sánh nguy cơ mắc ung thư vòm họng của người nghiện thuốc lá trong khu dân cư trên với nguy cơ mắc ung thư vòm họng của người không nghiện thuốc lá. Tức ta cần so sánh
 với
với 
Ta có
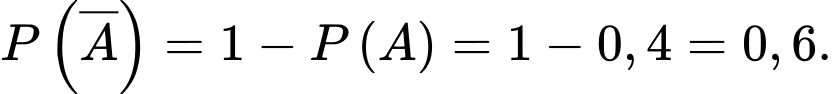
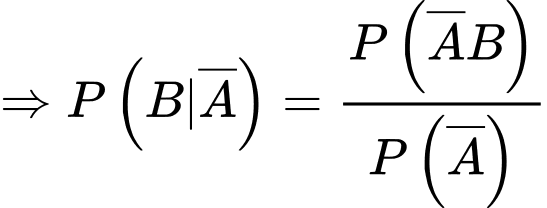
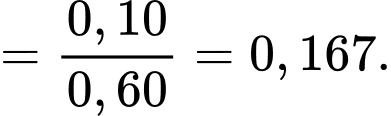
Nhận xét:
 gấp
gấp 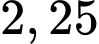 lần
lần  nên có thể thấy nguy cơ của người nghiện thuốc mắc ung thư vòm họng gấp hơn 2 lần người không nghiệm thuốc lá.
nên có thể thấy nguy cơ của người nghiện thuốc mắc ung thư vòm họng gấp hơn 2 lần người không nghiệm thuốc lá.
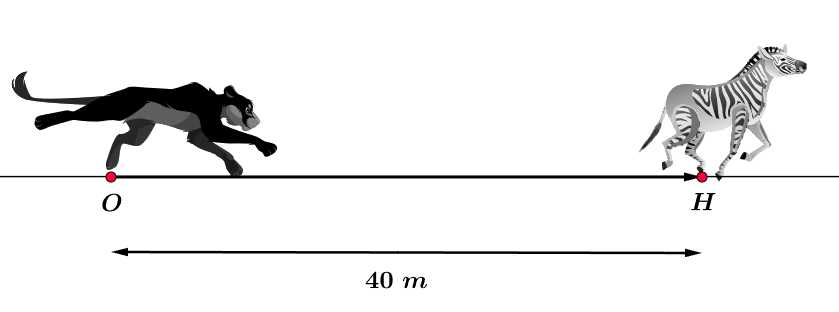
Câu 16 [702909]: Một con sư tử đang đuổi theo một con ngựa vằn. Con ngựa vằn nhận ra con sư tử khi con sư tử cách xa nó 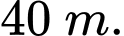 Từ thời điểm này, con sư tử đuổi con ngựa vằn với tốc độ
Từ thời điểm này, con sư tử đuổi con ngựa vằn với tốc độ 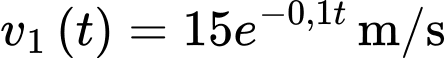 và con ngựa vằn chạy trốn với tốc độ
và con ngựa vằn chạy trốn với tốc độ 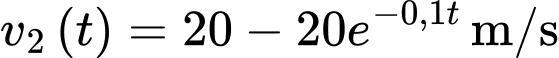 trên cùng một đường thẳng (với
trên cùng một đường thẳng (với 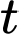 tính theo giây và
tính theo giây và 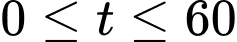 ).
).

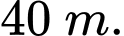 Từ thời điểm này, con sư tử đuổi con ngựa vằn với tốc độ
Từ thời điểm này, con sư tử đuổi con ngựa vằn với tốc độ 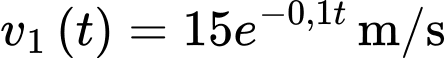 và con ngựa vằn chạy trốn với tốc độ
và con ngựa vằn chạy trốn với tốc độ 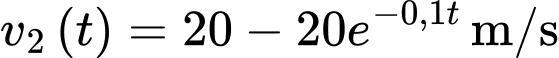 trên cùng một đường thẳng (với
trên cùng một đường thẳng (với 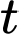 tính theo giây và
tính theo giây và 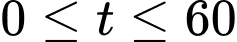 ).
).
a) Sai.
Tại thời điểm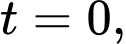 vận tốc của con ngựa vằn là
vận tốc của con ngựa vằn là 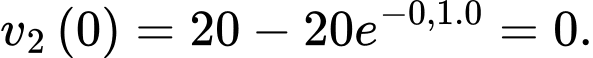
b) Đúng.
+) Ta có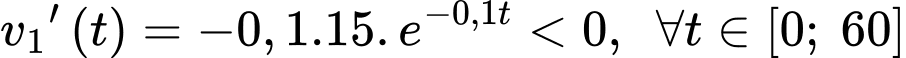
Suy ra tốc độ của sư tử giảm dần theo thời gian.
+) Ta có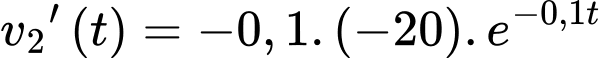
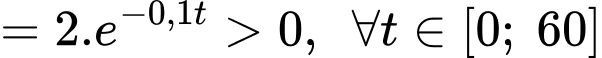
Suy ra tốc độ của ngựa vằn tăng dần theo thời gian.
Vậy tốc độ của sư tử giảm dần theo thời gian, trong khi tốc độ của ngựa vằn tăng dần theo thời gian.
c) Sai.
Vì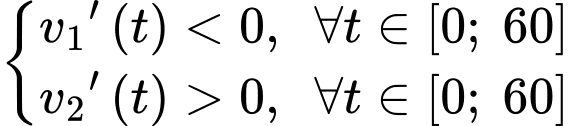
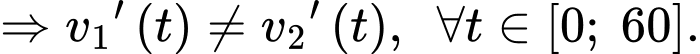
d) Sai.
Gọi quãng đường chạy được của sư tử và ngựa vằn lần lượt là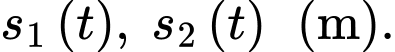
+) Ta có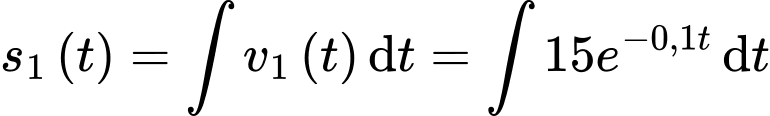
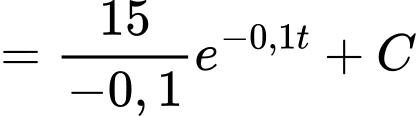
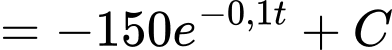
Coi điểm là vị trí xuất phát ban đầu, ta có tại thời điểm xuất phát
là vị trí xuất phát ban đầu, ta có tại thời điểm xuất phát 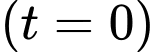 quãng đường mà sư tử chạy được bằng 0
quãng đường mà sư tử chạy được bằng 0
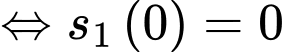
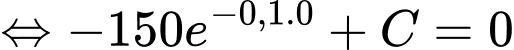
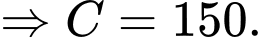
Vậy
+) Ta có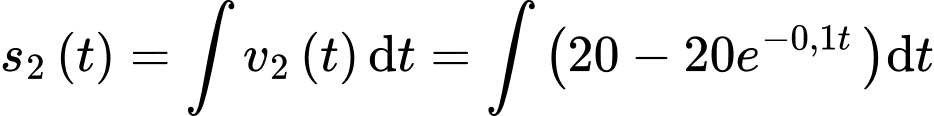
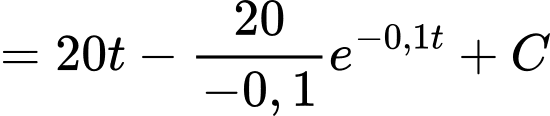
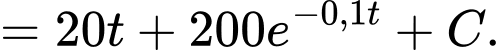
So với vị trí xuất phát ban đầu tại thời điểm
tại thời điểm 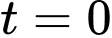 ngựa vằn chạy được quãng đường là
ngựa vằn chạy được quãng đường là 

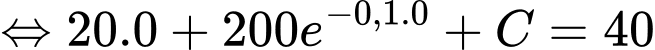
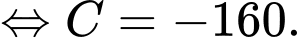
Vậy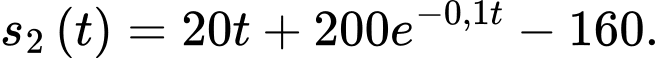
Suy ra khoảng cách giữa sư tử và ngựa vằn là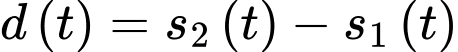
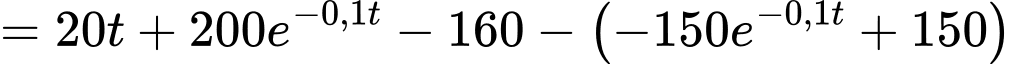
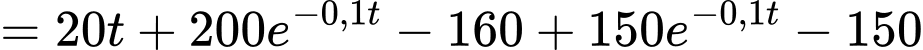

*) Xét hàm số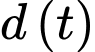 trên đoạn
trên đoạn 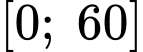
Ta có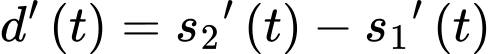
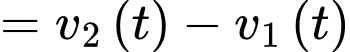
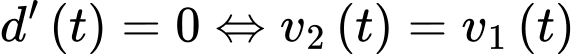
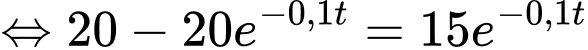
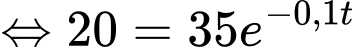
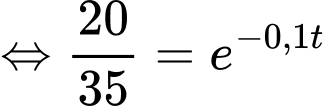
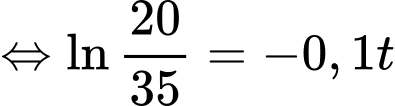
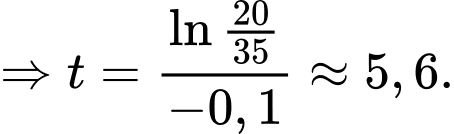
Bảng biến thiên
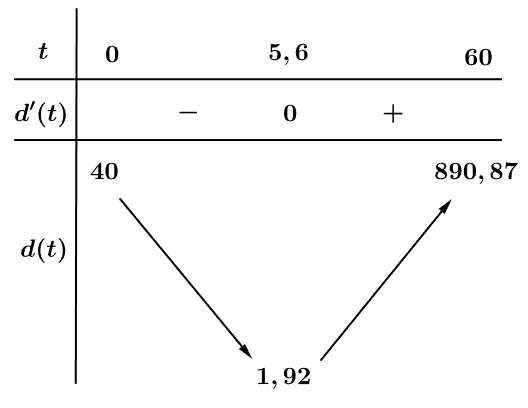
Vậy sư tử ở gần ngữa vằn nhất khi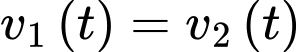 và khoảng cách ngắn nhất giữa chúng là 1,92 mét.
và khoảng cách ngắn nhất giữa chúng là 1,92 mét.
Tại thời điểm
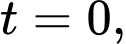 vận tốc của con ngựa vằn là
vận tốc của con ngựa vằn là 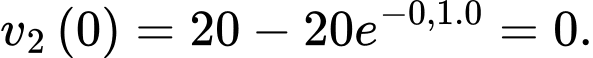
b) Đúng.
+) Ta có
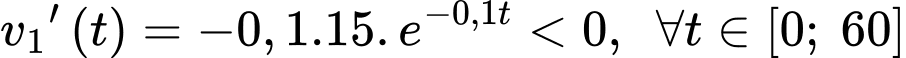
Suy ra tốc độ của sư tử giảm dần theo thời gian.
+) Ta có
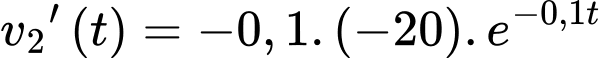
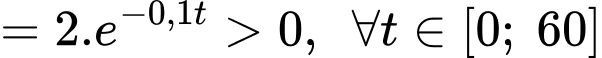
Suy ra tốc độ của ngựa vằn tăng dần theo thời gian.
Vậy tốc độ của sư tử giảm dần theo thời gian, trong khi tốc độ của ngựa vằn tăng dần theo thời gian.
c) Sai.
Vì
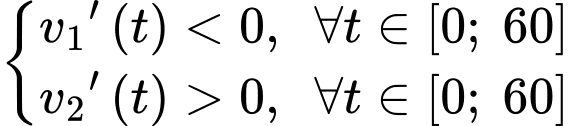
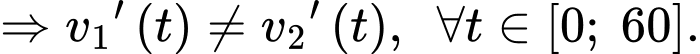
d) Sai.
Gọi quãng đường chạy được của sư tử và ngựa vằn lần lượt là
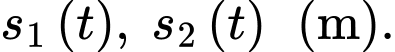

+) Ta có
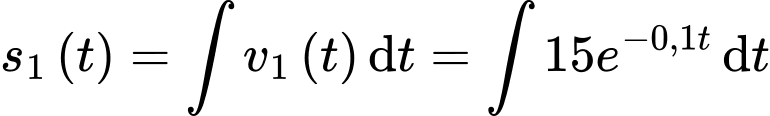
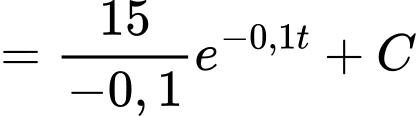
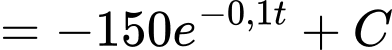
Coi điểm
 là vị trí xuất phát ban đầu, ta có tại thời điểm xuất phát
là vị trí xuất phát ban đầu, ta có tại thời điểm xuất phát 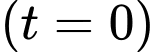 quãng đường mà sư tử chạy được bằng 0
quãng đường mà sư tử chạy được bằng 0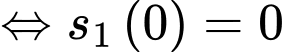
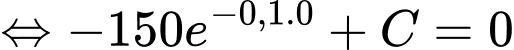
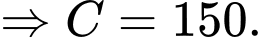
Vậy

+) Ta có
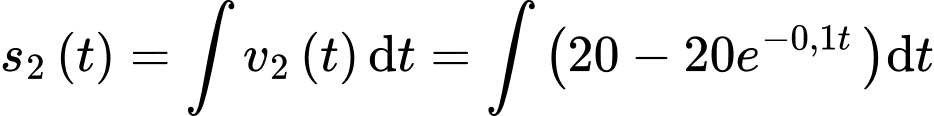
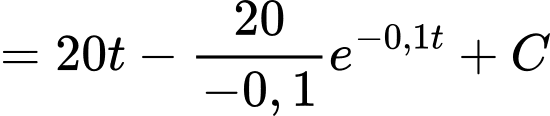
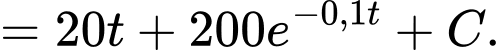
So với vị trí xuất phát ban đầu
 tại thời điểm
tại thời điểm 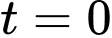 ngựa vằn chạy được quãng đường là
ngựa vằn chạy được quãng đường là 

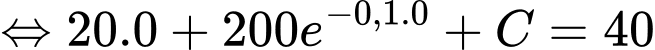
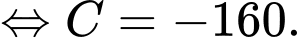
Vậy
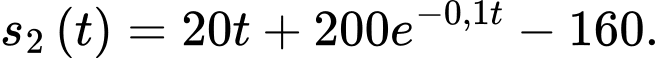
Suy ra khoảng cách giữa sư tử và ngựa vằn là
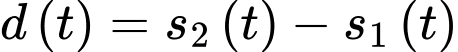
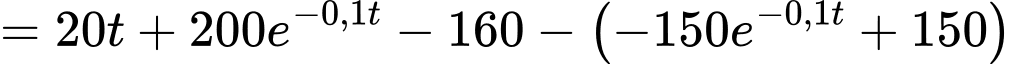
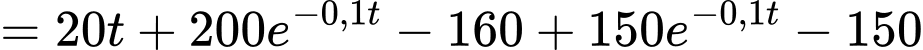

*) Xét hàm số
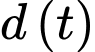 trên đoạn
trên đoạn 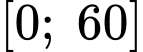
Ta có
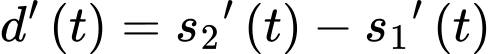
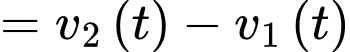
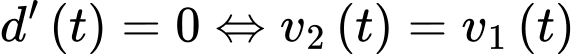
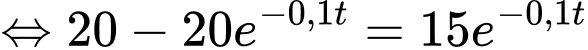
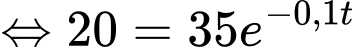
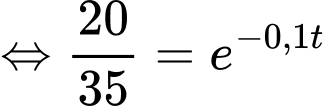
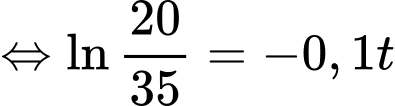
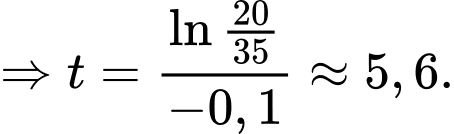
Bảng biến thiên

Vậy sư tử ở gần ngữa vằn nhất khi
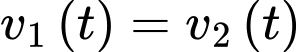 và khoảng cách ngắn nhất giữa chúng là 1,92 mét.
và khoảng cách ngắn nhất giữa chúng là 1,92 mét. PHẦN III. Thí sinh trả lời từ câu 1 đến câu 6.
Câu 17 [693089]: Cho hình chóp 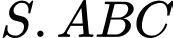 có cạnh bên
có cạnh bên 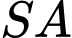 vuông góc với mặt phẳng
vuông góc với mặt phẳng 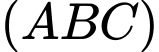 và
và 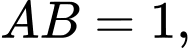
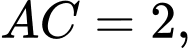
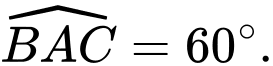 Khoảng cách giữa hai đường thẳng
Khoảng cách giữa hai đường thẳng 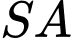 và
và 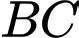 bằng bao nhiêu? (làm tròn kết quả đến hàng phần mười).
bằng bao nhiêu? (làm tròn kết quả đến hàng phần mười).
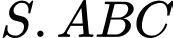 có cạnh bên
có cạnh bên 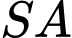 vuông góc với mặt phẳng
vuông góc với mặt phẳng 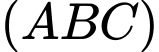 và
và 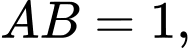
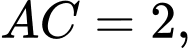
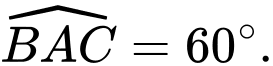 Khoảng cách giữa hai đường thẳng
Khoảng cách giữa hai đường thẳng 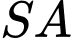 và
và 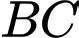 bằng bao nhiêu? (làm tròn kết quả đến hàng phần mười).
bằng bao nhiêu? (làm tròn kết quả đến hàng phần mười).
Điền đáp án: 1,0.
Kẻ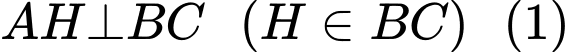
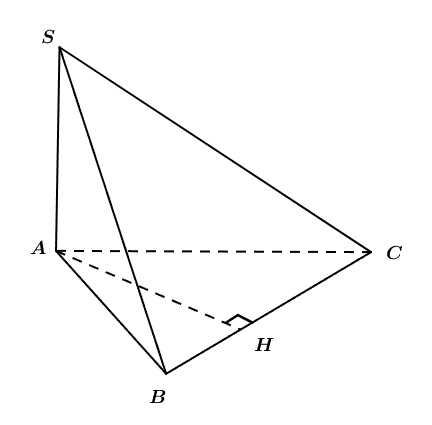
Theo giả thiết, ta có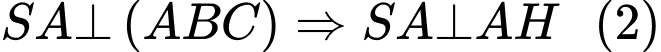
Từ (1) và (2) ta suy ra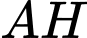 là đường vuông góc chung của 2 đường thẳng
là đường vuông góc chung của 2 đường thẳng 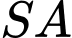 và
và 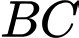
Hay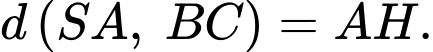
+) Theo định lý Cosin ta có: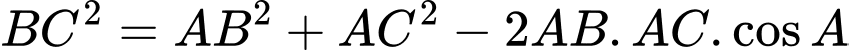
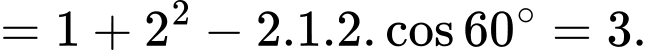
Trong tam giác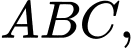 ta có
ta có 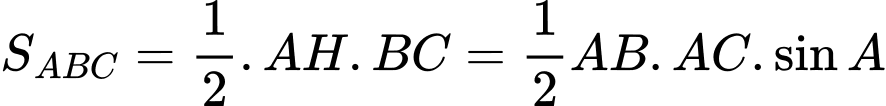
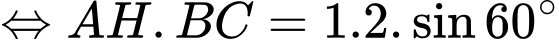
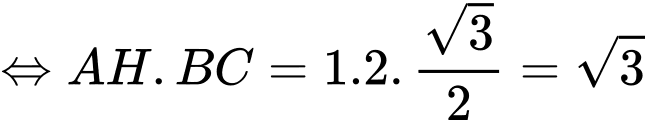
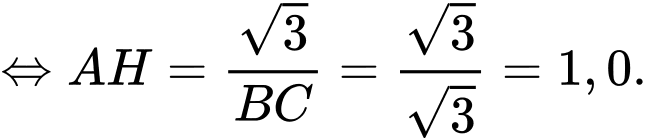
Kẻ
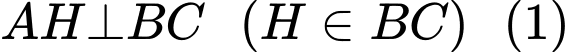

Theo giả thiết, ta có
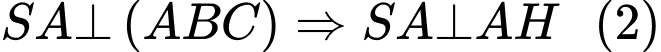
Từ (1) và (2) ta suy ra
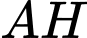 là đường vuông góc chung của 2 đường thẳng
là đường vuông góc chung của 2 đường thẳng 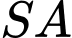 và
và 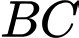
Hay
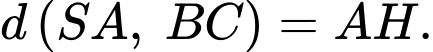
+) Theo định lý Cosin ta có:
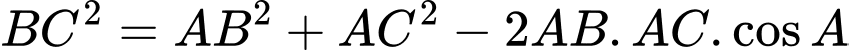
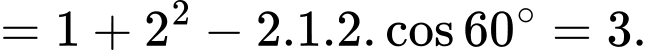
Trong tam giác
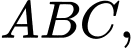 ta có
ta có 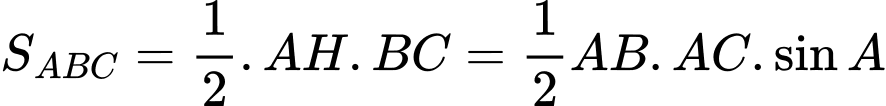
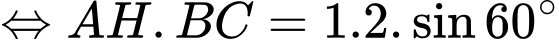
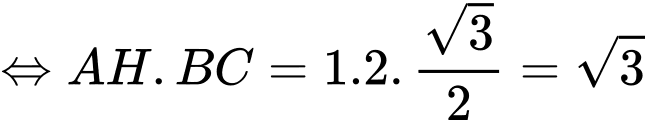
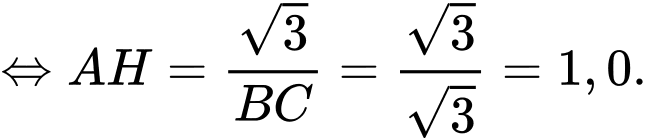
Câu 18 [693090]: Trong một vườn cây ăn trái, có ba loại cây: cây cam, cây chanh và cây bưởi. Sau 3 năm, số cây cam tăng gấp ba lần, số cây chanh tăng gấp hai lần và cây bưởi tăng gấp bốn lần số lượng cây ban đầu. Tổng số cây sau 3 năm là 330 cây. Biết rằng ban đầu số lượng cây bưởi bằng trung bình cộng của số lượng cây cam và cây chanh. Sau 3 năm thu hoạch, tổng số cây cam và cây chanh tăng thêm nhiều hơn 15 cây so với số cây bưởi tăng thêm. Vậy tổng số cây cam và cây bưởi ban đầu là bao nhiêu?
Điền đáp án: 
Gọi số cây cam, cây chanh, cây bưởi lần lượt là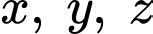 ( cây)
( cây) 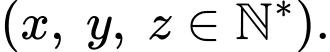
Vì sau 3 năm, số cây cam tăng gấp ba lần, số cây chanh tăng gấp hai lần và cây bưởi tăng gấp bốn lần số lượng ban đầu nên ta có số số cây cam, cây chanh, cây bưởi sau 3 năm lần lượt là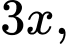
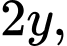
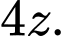
Tổng số cây sau 3 năm là 330 cây nên ta có phương trình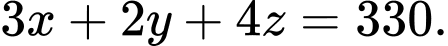
Số lượng cây bưởi ban đầu bằng trung bình cộng của số lượng cây cam và cây chanh nên ta có phương trình: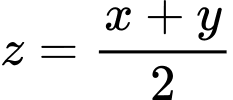
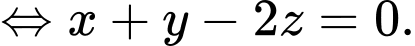
Sau 3 năm thu hoạch, tổng số cây cam và cây chanh tăng thêm nhiều hơn 15 cây so với số cây bưởi tăng thêm nên ta có phương trình: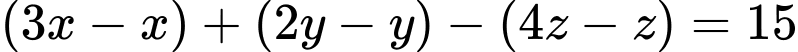
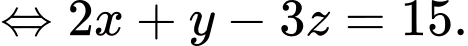
Theo đề bài ta có hệ phương trình: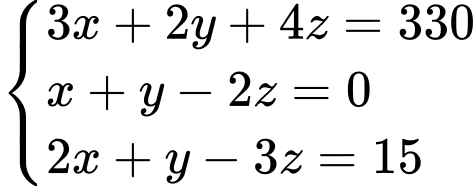
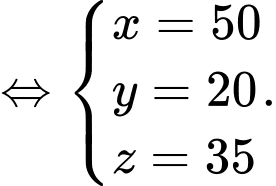
Tổng số cây cam và cây bưởi ban đầu là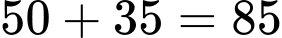 cây.
cây.
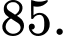
Gọi số cây cam, cây chanh, cây bưởi lần lượt là
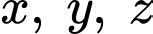 ( cây)
( cây) 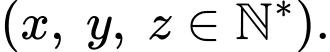
Vì sau 3 năm, số cây cam tăng gấp ba lần, số cây chanh tăng gấp hai lần và cây bưởi tăng gấp bốn lần số lượng ban đầu nên ta có số số cây cam, cây chanh, cây bưởi sau 3 năm lần lượt là
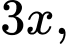
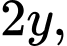
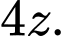
Tổng số cây sau 3 năm là 330 cây nên ta có phương trình
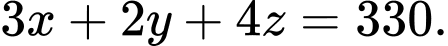
Số lượng cây bưởi ban đầu bằng trung bình cộng của số lượng cây cam và cây chanh nên ta có phương trình:
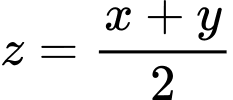
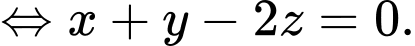
Sau 3 năm thu hoạch, tổng số cây cam và cây chanh tăng thêm nhiều hơn 15 cây so với số cây bưởi tăng thêm nên ta có phương trình:
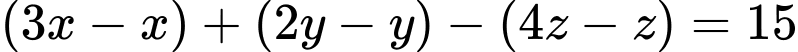
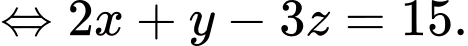
Theo đề bài ta có hệ phương trình:
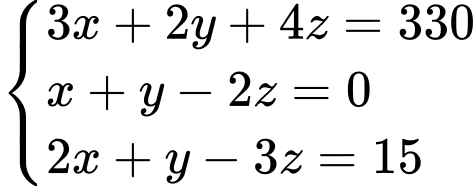
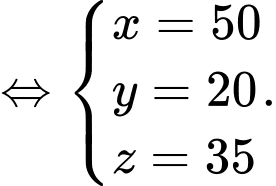
Tổng số cây cam và cây bưởi ban đầu là
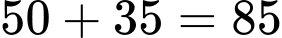 cây.
cây.
Câu 19 [693093]: Có hai bình như sau: Bình A chứa 5 bi đỏ, 3 bi trắng và 8 bi xanh; bình B chứa 3 bi đỏ và 5 bi trắng. Gieo một con xúc xắc ngẫu nhiên: Nếu mặt 3 hoặc mặt 5 xuất hiện thì chọn ngẫu nhiên một bi từ bình B; các trường hợp khác thì chọn ngẫu nhiên một bi từ bình A. Nếu viên bi trắng được chọn ra, hãy tính xác suất để mặt 5 của con xúc xắc xuất hiện.
Điền đáp án: 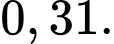
Gọi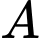 là biến cố: “Gieo được mặt 3 hoặc mặt 5” ta có:
là biến cố: “Gieo được mặt 3 hoặc mặt 5” ta có: 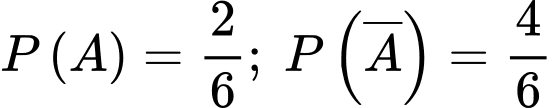
Ta có sơ đồ cây sau:
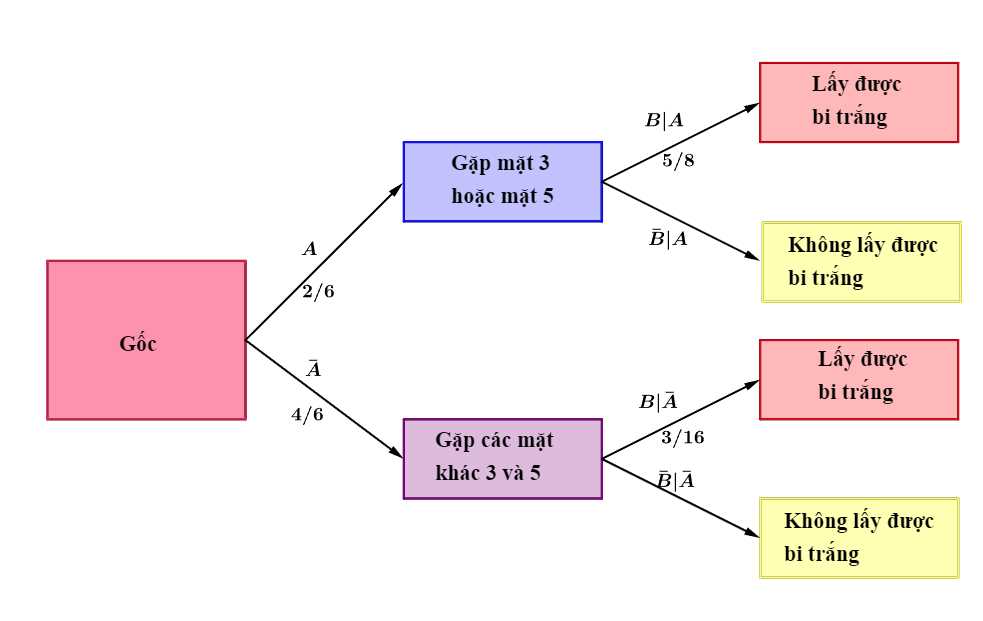
Gọi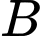 là biến cố: “Bi chọn ra là bi trắng” ta có:
là biến cố: “Bi chọn ra là bi trắng” ta có: 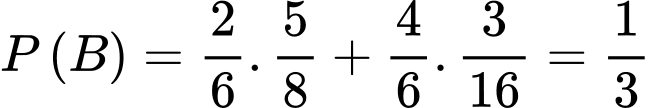
Theo công thức Bayes, ta có:
Xác suất để mặt 3 hoặc mặt 5 xuất hiện khi biết viên bi trắng được trọn ra là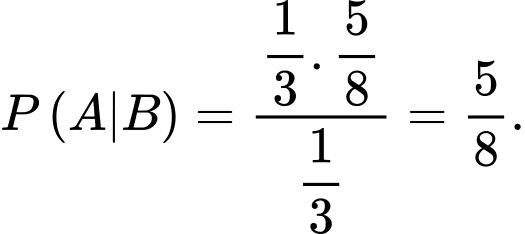
Vì xác suất mặt 3 hoặc mặt 5 xuất hiện là như nhau nên xác suất xuất hiện mặt 5 chấm là: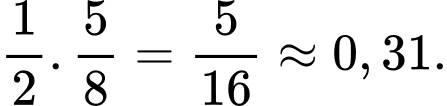
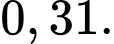
Gọi
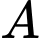 là biến cố: “Gieo được mặt 3 hoặc mặt 5” ta có:
là biến cố: “Gieo được mặt 3 hoặc mặt 5” ta có: 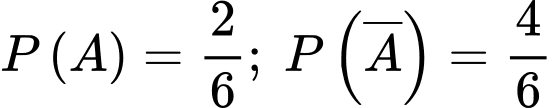
Ta có sơ đồ cây sau:

Gọi
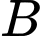 là biến cố: “Bi chọn ra là bi trắng” ta có:
là biến cố: “Bi chọn ra là bi trắng” ta có: 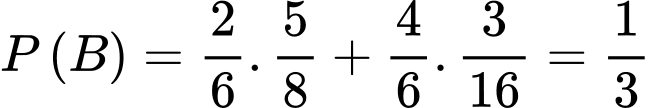
Theo công thức Bayes, ta có:
Xác suất để mặt 3 hoặc mặt 5 xuất hiện khi biết viên bi trắng được trọn ra là
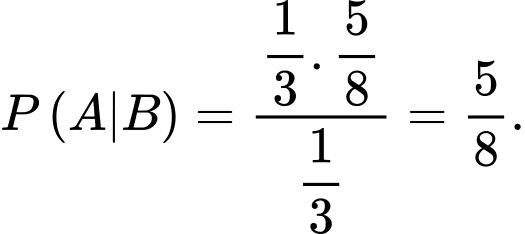
Vì xác suất mặt 3 hoặc mặt 5 xuất hiện là như nhau nên xác suất xuất hiện mặt 5 chấm là:
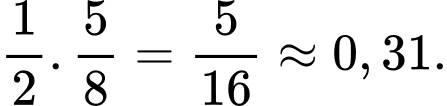
Câu 20 [693314]: Cần trục chân đế là kiểu cột quay được sử dụng để phục vụ công việc xếp dỡ hàng hóa chủ yếu ngoài các cảng bến, bãi (hình ảnh minh họa). Ta chọn hệ trục 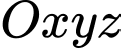 thỏa trục
thỏa trục 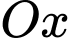 trùng với trục chân đế, trục
trùng với trục chân đế, trục 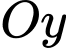 vuông góc với trục
vuông góc với trục 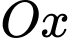 và trục
và trục  trùng với trục cần cẩu (theo đơn vị mét, như hình vẽ). Gọi
trùng với trục cần cẩu (theo đơn vị mét, như hình vẽ). Gọi 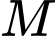 là vị trí tại đỉnh cần cẩu,
là vị trí tại đỉnh cần cẩu, 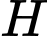 là hình chiếu của
là hình chiếu của 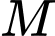 lên
lên 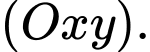

Biết tay cần của cần trục dài
của cần trục dài 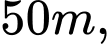 trục cần
trục cần 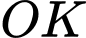 dài
dài 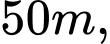
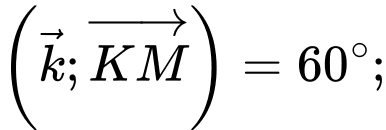
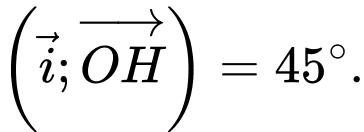 Biết điểm
Biết điểm 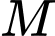 có toạ độ
có toạ độ 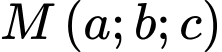 trong hệ toạ độ
trong hệ toạ độ 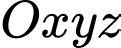 trên, tính
trên, tính 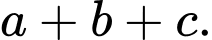 (làm tròn kết quả đến hàng đơn vị).
(làm tròn kết quả đến hàng đơn vị).
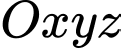 thỏa trục
thỏa trục 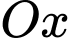 trùng với trục chân đế, trục
trùng với trục chân đế, trục 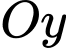 vuông góc với trục
vuông góc với trục 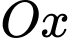 và trục
và trục  trùng với trục cần cẩu (theo đơn vị mét, như hình vẽ). Gọi
trùng với trục cần cẩu (theo đơn vị mét, như hình vẽ). Gọi 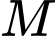 là vị trí tại đỉnh cần cẩu,
là vị trí tại đỉnh cần cẩu, 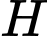 là hình chiếu của
là hình chiếu của 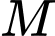 lên
lên 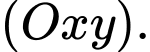

Biết tay cần
 của cần trục dài
của cần trục dài 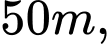 trục cần
trục cần 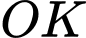 dài
dài 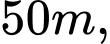
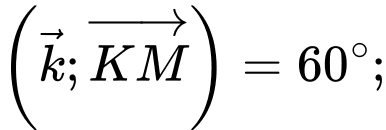
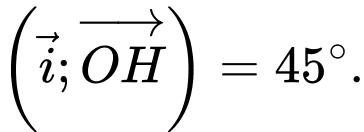 Biết điểm
Biết điểm 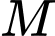 có toạ độ
có toạ độ 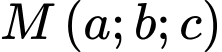 trong hệ toạ độ
trong hệ toạ độ 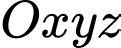 trên, tính
trên, tính 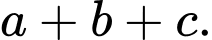 (làm tròn kết quả đến hàng đơn vị).
(làm tròn kết quả đến hàng đơn vị).
Điền đáp án: 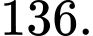
Ta gọi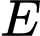 là hình chiếu của
là hình chiếu của 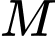 lên
lên 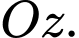

Ta có:
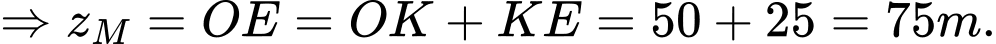
Ta có: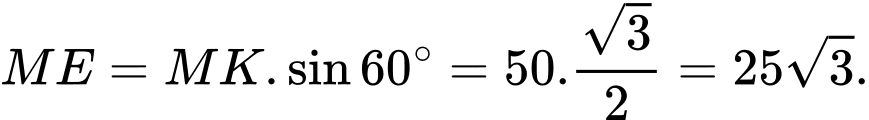
Suy ra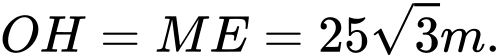
Gọi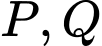 lần lượt là hình chiếu của
lần lượt là hình chiếu của 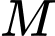 lên
lên 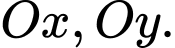
Vì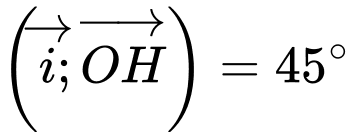
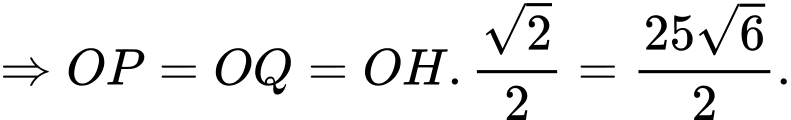
Vậy điểm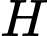 có tọa độ
có tọa độ 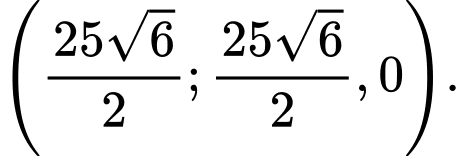
Ta có: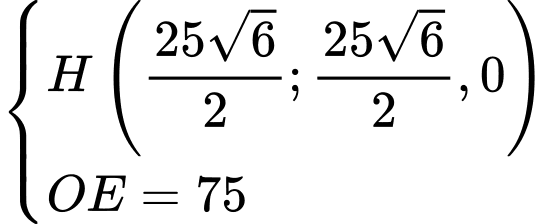
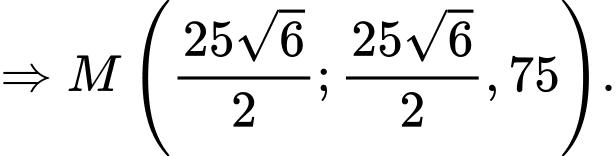
Suy ra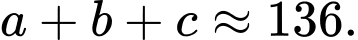
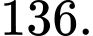
Ta gọi
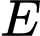 là hình chiếu của
là hình chiếu của 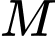 lên
lên 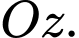

Ta có:

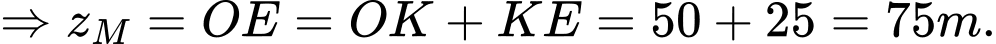
Ta có:
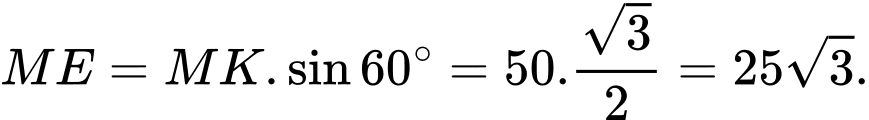
Suy ra
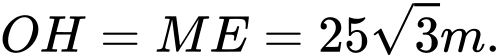
Gọi
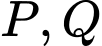 lần lượt là hình chiếu của
lần lượt là hình chiếu của 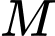 lên
lên 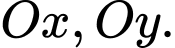
Vì
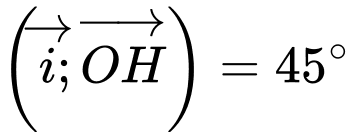
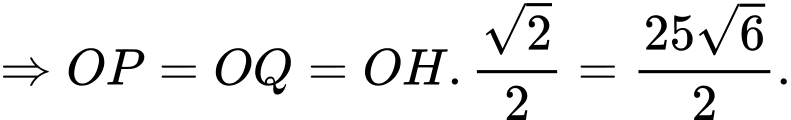
Vậy điểm
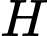 có tọa độ
có tọa độ 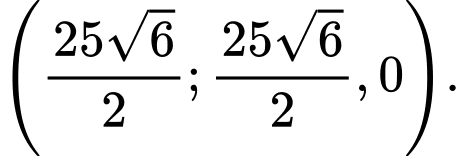
Ta có:
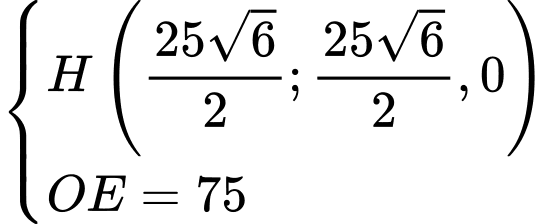
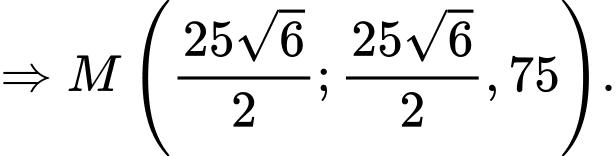
Suy ra
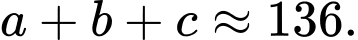
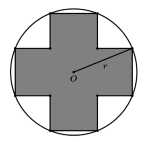
Câu 21 [703025]: Hai hình chữ nhật bằng nhau, nội tiếp trong đường tròn tâm  bán kính
bán kính 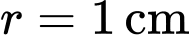 tạo thành một hình chữ thập đối xứng (như hình vẽ bên). Diện tích lớn nhất của hình chữ thập là bao nhiêu
tạo thành một hình chữ thập đối xứng (như hình vẽ bên). Diện tích lớn nhất của hình chữ thập là bao nhiêu 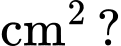 (kết quả làm tròn đến hàng phần trăm).
(kết quả làm tròn đến hàng phần trăm).
 bán kính
bán kính 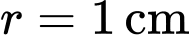 tạo thành một hình chữ thập đối xứng (như hình vẽ bên). Diện tích lớn nhất của hình chữ thập là bao nhiêu
tạo thành một hình chữ thập đối xứng (như hình vẽ bên). Diện tích lớn nhất của hình chữ thập là bao nhiêu 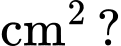 (kết quả làm tròn đến hàng phần trăm).
(kết quả làm tròn đến hàng phần trăm).
Điền đáp án: 2,47.
Ta kí hiệu các điểm trên hình như sau:
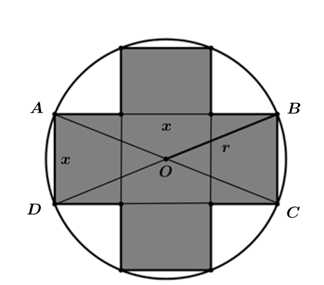
(Nhận xét: các đường chéo của 2 hình chữ nhật sẽ trùng với đường kính của đường tròn tâm .)
.)
Đặt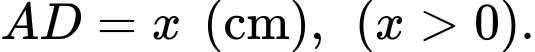
Trong tam giác vuông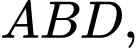 ta có
ta có 
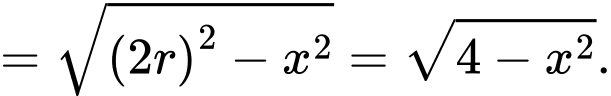
Diện tích của hình chữ thập Diện tích hình vuông (là giao của 2 hình chữ nhật)
Diện tích hình vuông (là giao của 2 hình chữ nhật)
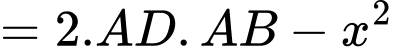
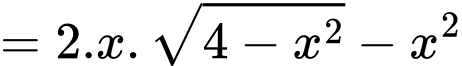
Xét hàm số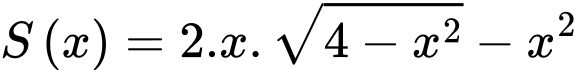 trên khoảng
trên khoảng 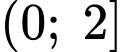
Ta có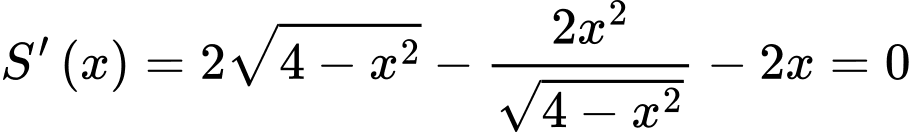
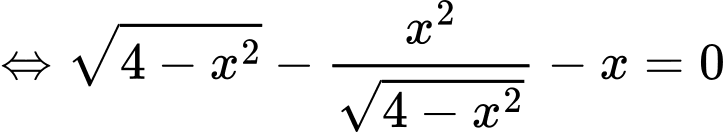
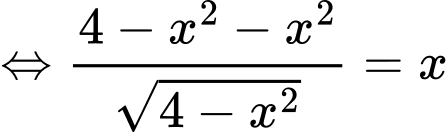
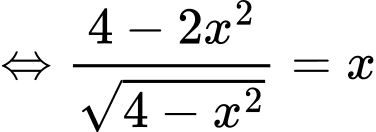

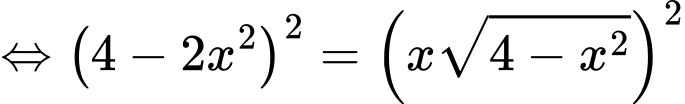
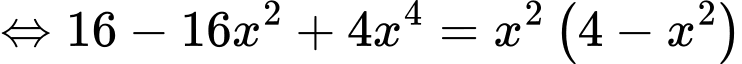
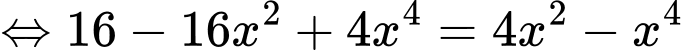

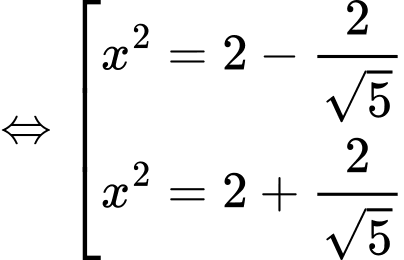
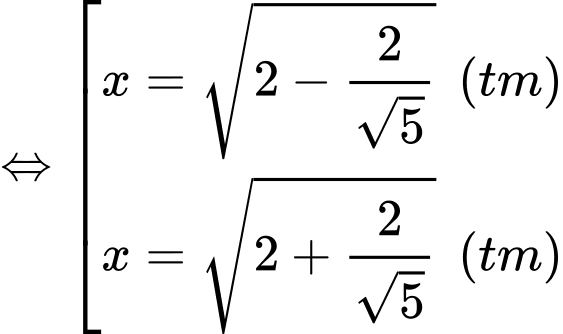
Ta có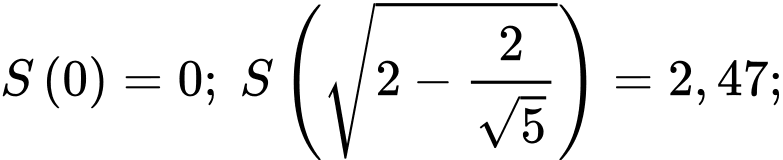
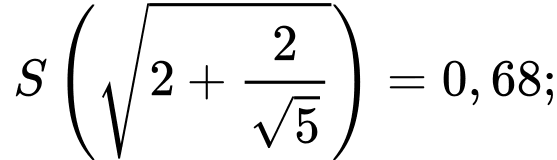
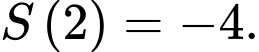
Vậy diện tích lớn nhất của hình chữ thập là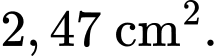
Ta kí hiệu các điểm trên hình như sau:

(Nhận xét: các đường chéo của 2 hình chữ nhật sẽ trùng với đường kính của đường tròn tâm
 .)
.)
Đặt
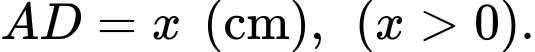
Trong tam giác vuông
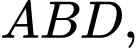 ta có
ta có 
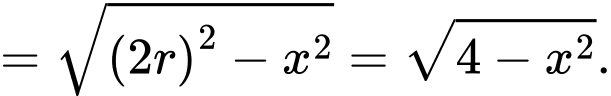
Diện tích của hình chữ thập
 Diện tích hình vuông (là giao của 2 hình chữ nhật)
Diện tích hình vuông (là giao của 2 hình chữ nhật)
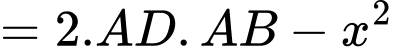
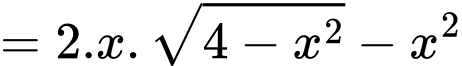
Xét hàm số
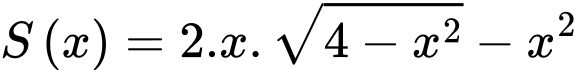 trên khoảng
trên khoảng 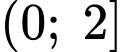
Ta có
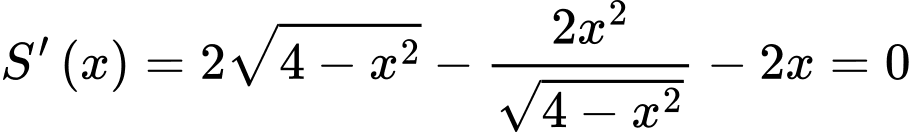
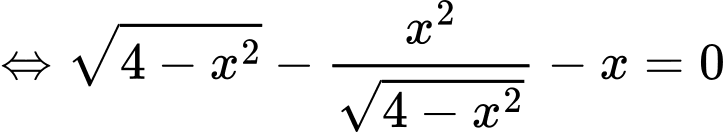
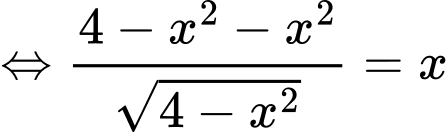
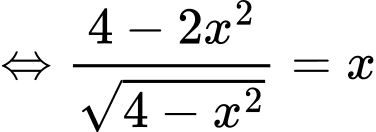

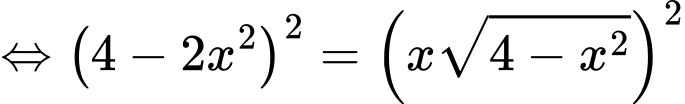
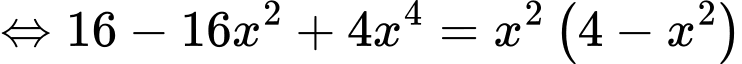
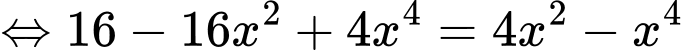

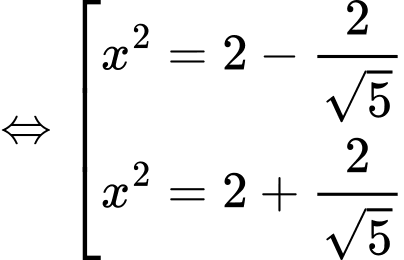
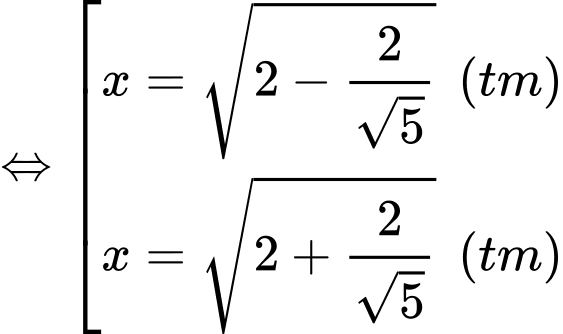
Ta có
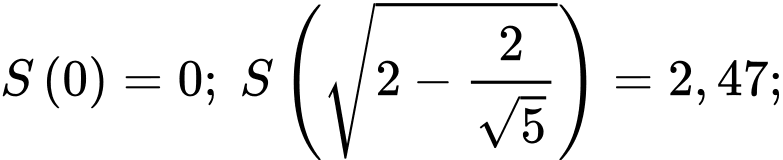
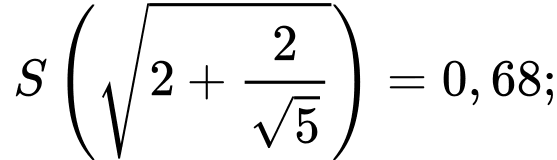
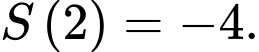
Vậy diện tích lớn nhất của hình chữ thập là
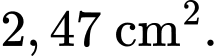
Câu 22 [703002]: Trên một mặt hồ phẳng rộng 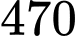 mét vuông, một đợt tảo lam độc hại phát triển với tốc độ tỷ lệ thuận với căn bậc hai kích thước hiện tại của nó. Nếu ta gọi
mét vuông, một đợt tảo lam độc hại phát triển với tốc độ tỷ lệ thuận với căn bậc hai kích thước hiện tại của nó. Nếu ta gọi 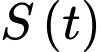 là diện tích của đợt tảo này sau
là diện tích của đợt tảo này sau 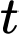 ngày thì
ngày thì 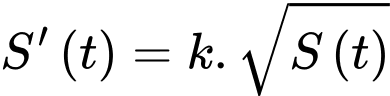 (trong đó
(trong đó 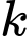 là hằng số thực).
là hằng số thực).

Khi mới phát hiện, đợt tảo này bao phủ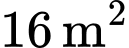 mặt hồ. Diện tích của nó tăng gấp đôi trong
mặt hồ. Diện tích của nó tăng gấp đôi trong 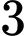 ngày tiếp theo, hỏi sau bao ngày tính từ lúc phát hiện đợt tảo này phủ kín mặt hồ? (kết quả làm tròn đến hàng đơn vị).
ngày tiếp theo, hỏi sau bao ngày tính từ lúc phát hiện đợt tảo này phủ kín mặt hồ? (kết quả làm tròn đến hàng đơn vị).
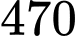 mét vuông, một đợt tảo lam độc hại phát triển với tốc độ tỷ lệ thuận với căn bậc hai kích thước hiện tại của nó. Nếu ta gọi
mét vuông, một đợt tảo lam độc hại phát triển với tốc độ tỷ lệ thuận với căn bậc hai kích thước hiện tại của nó. Nếu ta gọi 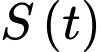 là diện tích của đợt tảo này sau
là diện tích của đợt tảo này sau 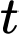 ngày thì
ngày thì 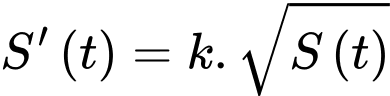 (trong đó
(trong đó 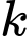 là hằng số thực).
là hằng số thực).
Khi mới phát hiện, đợt tảo này bao phủ
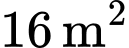 mặt hồ. Diện tích của nó tăng gấp đôi trong
mặt hồ. Diện tích của nó tăng gấp đôi trong 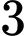 ngày tiếp theo, hỏi sau bao ngày tính từ lúc phát hiện đợt tảo này phủ kín mặt hồ? (kết quả làm tròn đến hàng đơn vị).
ngày tiếp theo, hỏi sau bao ngày tính từ lúc phát hiện đợt tảo này phủ kín mặt hồ? (kết quả làm tròn đến hàng đơn vị).
Điền đáp án: 32.
Ta có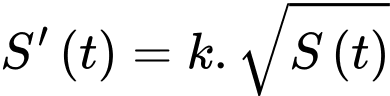
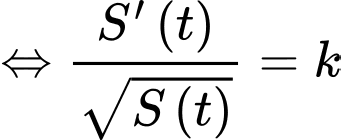
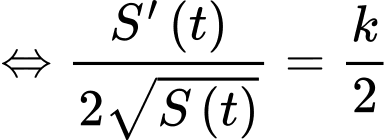
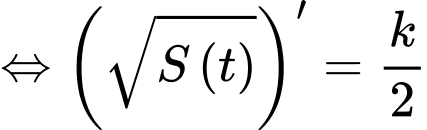
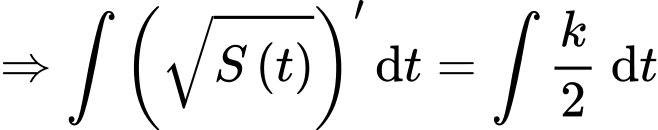
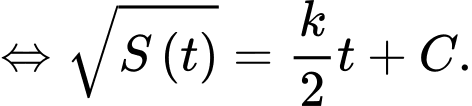
Theo giả thiết, ta có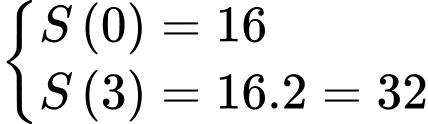
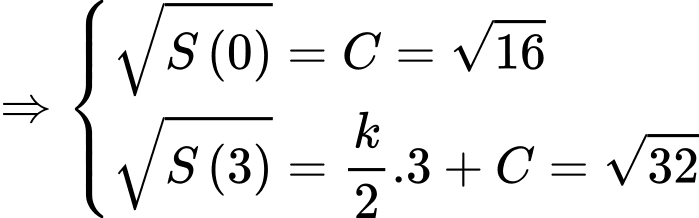
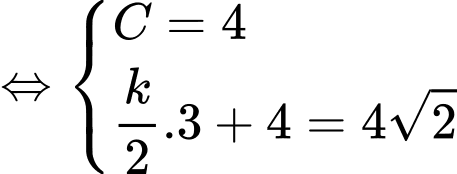
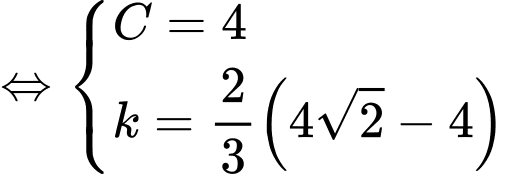
Suy ra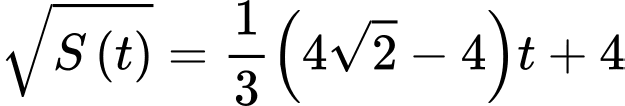
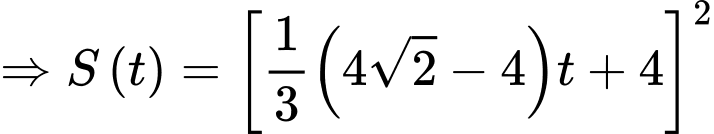
Để tảo phủ kín mặt hồ thì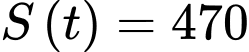
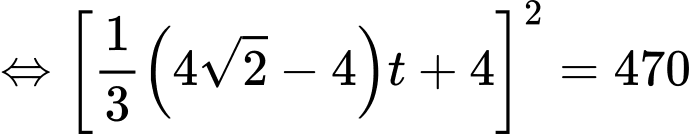
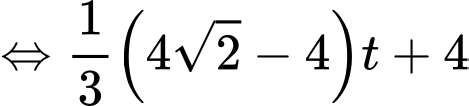

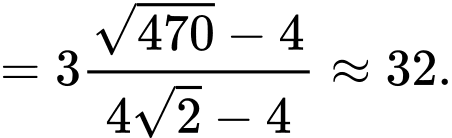
Vậy sau 32 ngày thì tảo sẽ phủ kín mặt hồ.
Ta có
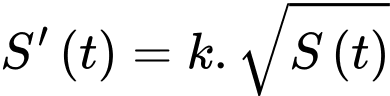
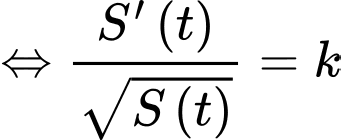
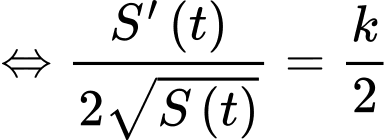
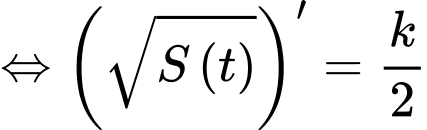
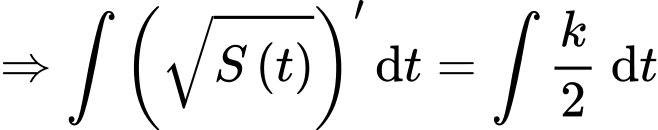
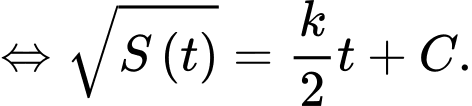
Theo giả thiết, ta có
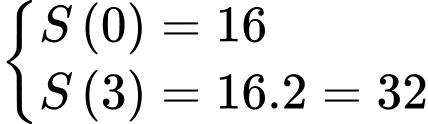
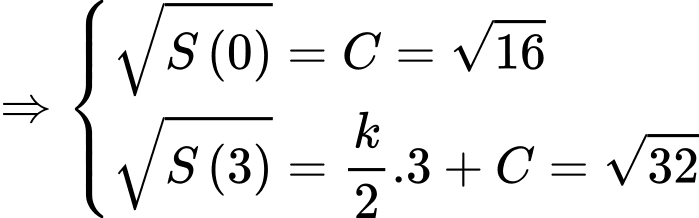
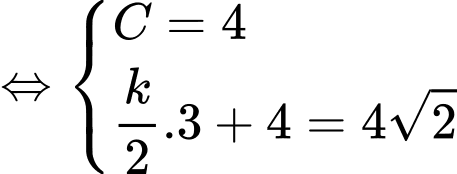
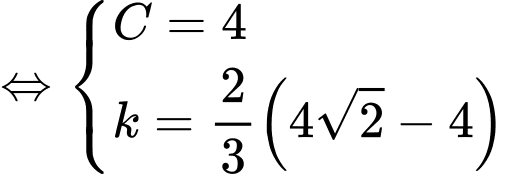
Suy ra
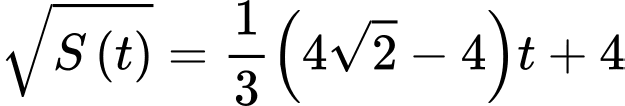
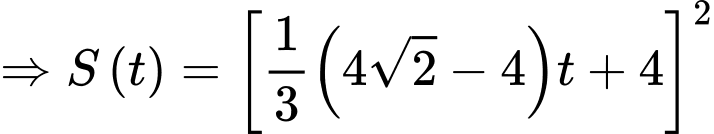
Để tảo phủ kín mặt hồ thì
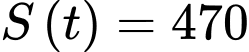
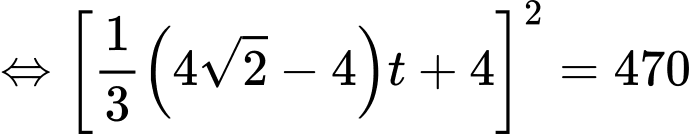
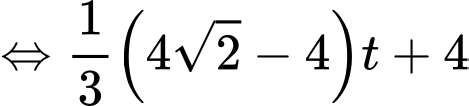

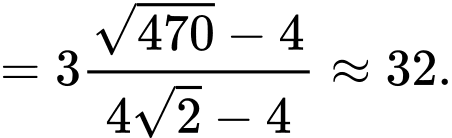
Vậy sau 32 ngày thì tảo sẽ phủ kín mặt hồ.