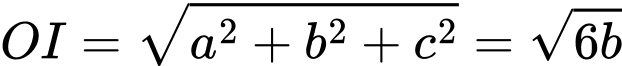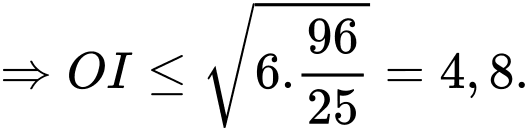PHẦN I. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Câu 1 [801224]: Với số thực dương 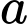 tuỳ ý, biểu thức
tuỳ ý, biểu thức 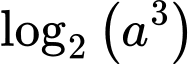 bằng
bằng
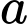 tuỳ ý, biểu thức
tuỳ ý, biểu thức 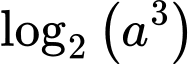 bằng
bằng A, 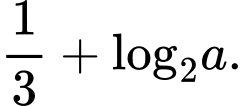
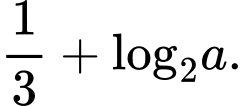
B, 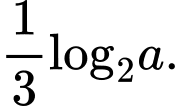
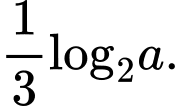
C, 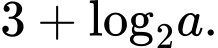
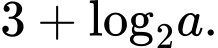
D, 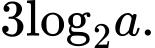
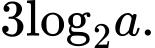
Chọn đáp án D.
Ta có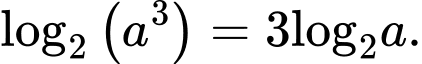 Đáp án: D
Đáp án: D
Ta có
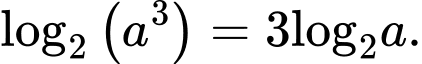 Đáp án: D
Đáp án: D
Câu 2 [511374]: Cho cấp số nhân có 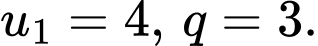 Hãy tính giá trị của
Hãy tính giá trị của 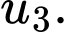
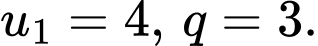 Hãy tính giá trị của
Hãy tính giá trị của 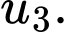
A, 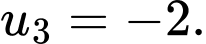
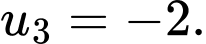
B, 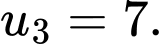
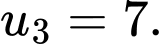
C, 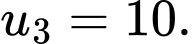
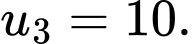
D, 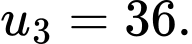
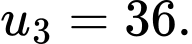
Chọn đáp án D.
Có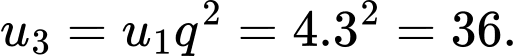 Đáp án: D
Đáp án: D
Có
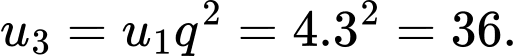 Đáp án: D
Đáp án: D
Câu 3 [380260]: Cho hình lập phương 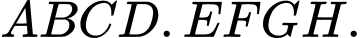 Hãy xác định góc giữa hai vectơ
Hãy xác định góc giữa hai vectơ 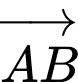 và
và 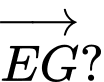
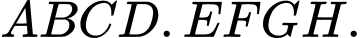 Hãy xác định góc giữa hai vectơ
Hãy xác định góc giữa hai vectơ 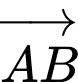 và
và 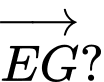
A, 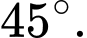
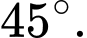
B, 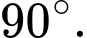
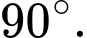
C, 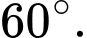
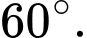
D, 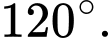
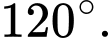
Chọn đáp án A.
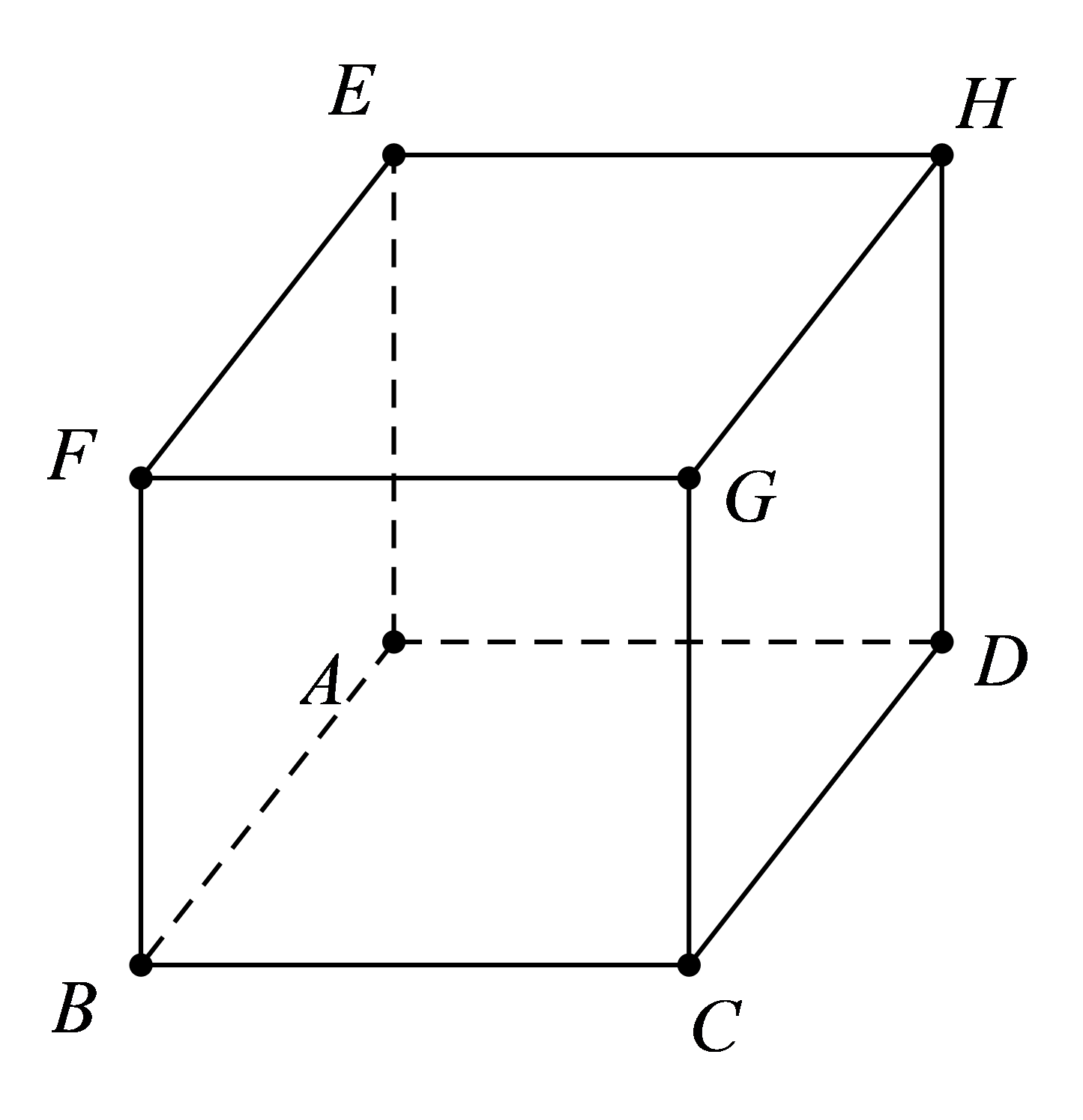
Ta có: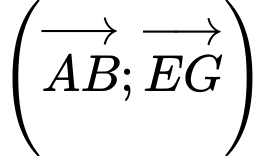
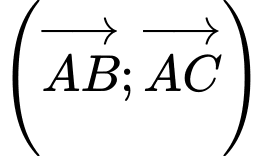
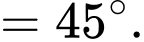 Đáp án: A
Đáp án: A
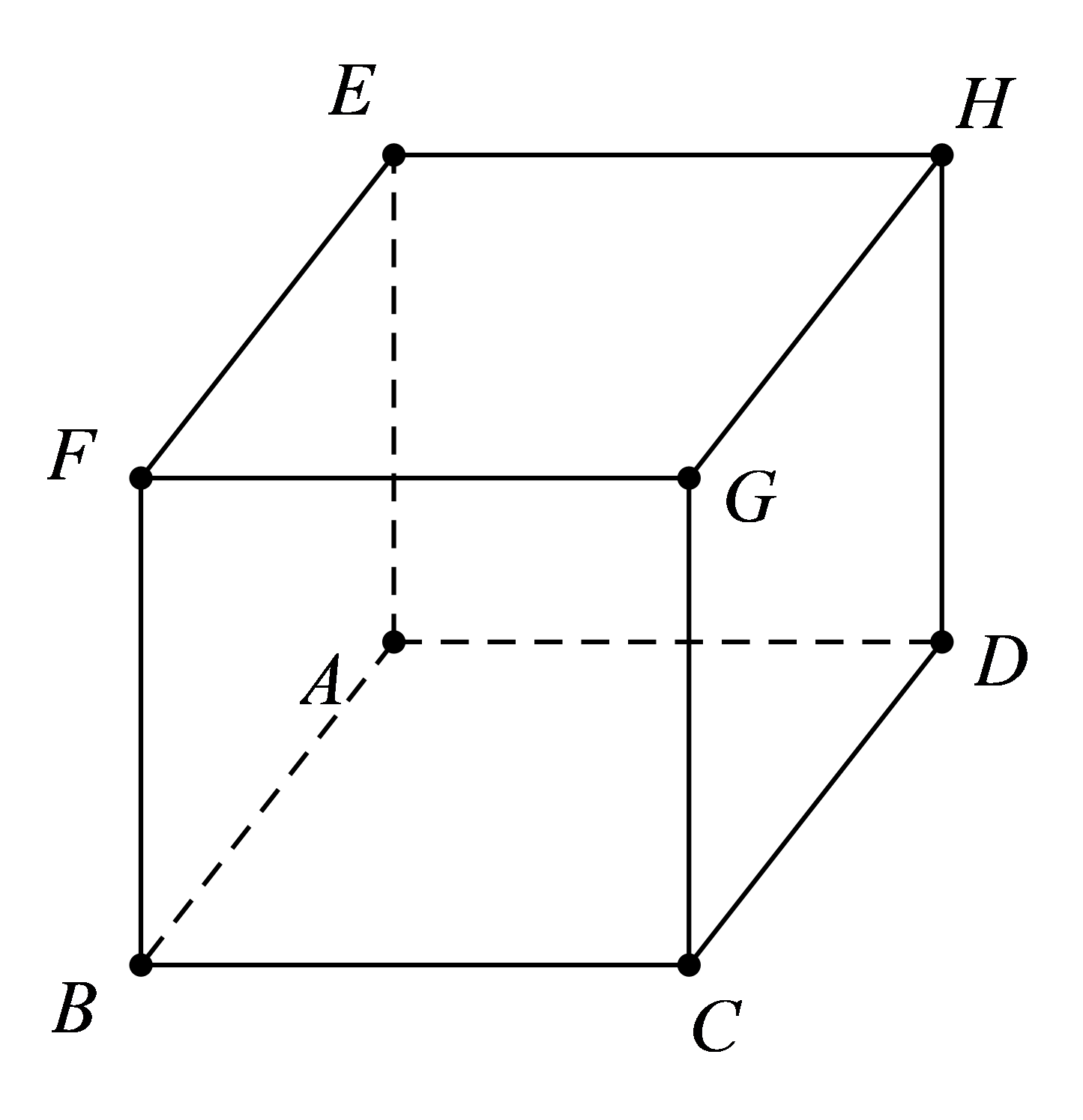
Ta có:
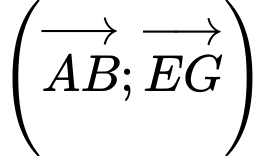
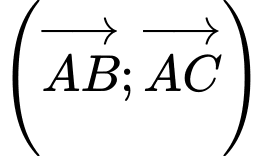
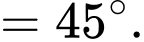 Đáp án: A
Đáp án: A
Câu 4 [808407]: Biết 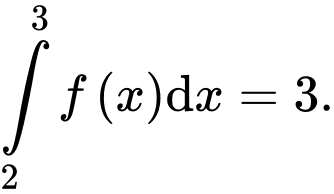 Giá trị của
Giá trị của 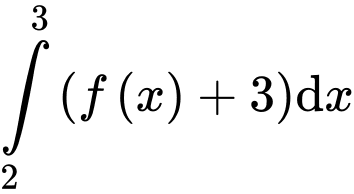 bằng
bằng
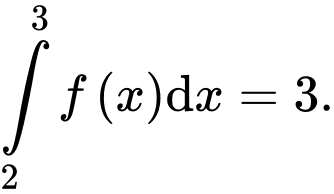 Giá trị của
Giá trị của 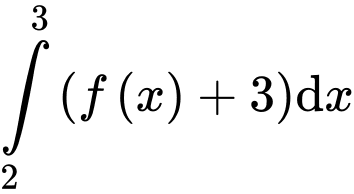 bằng
bằng A, 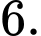
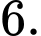
B, 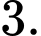
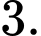
C, 
D, 
Chọn đáp án A.
Ta có: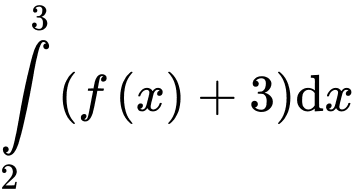
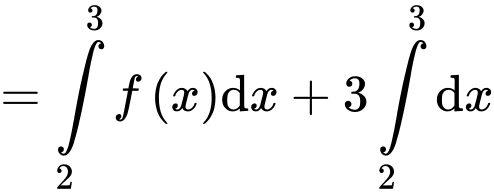
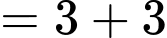
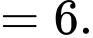 Đáp án: A
Đáp án: A
Ta có:
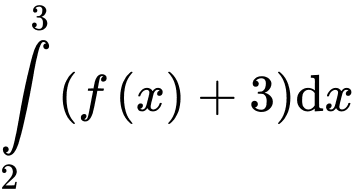
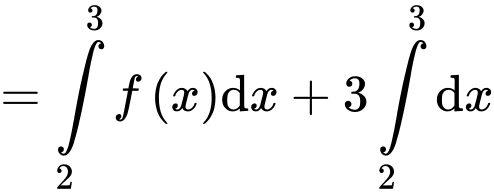
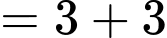
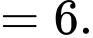 Đáp án: A
Đáp án: A
Câu 5 [528543]: Tập nghiệm của bất phương trình 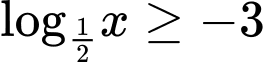 là
là
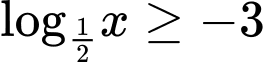 là
là A, 

B, 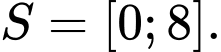
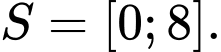
C, 

D, 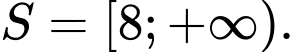
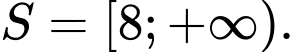
Chọn đáp án A.
Vì cơ số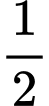 bé hơn
bé hơn 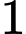 nên ta có:
nên ta có: 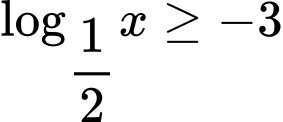
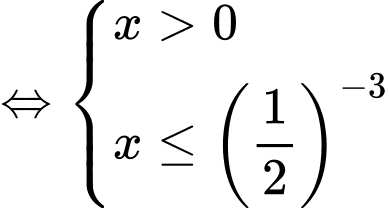
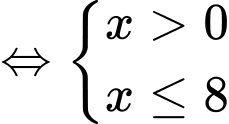
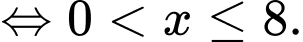
Vậy tập nghiệm của bất phương trình là Đáp án: A
Đáp án: A
Vì cơ số
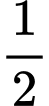 bé hơn
bé hơn 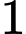 nên ta có:
nên ta có: 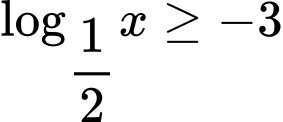
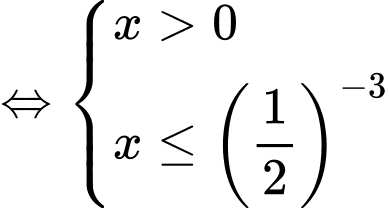
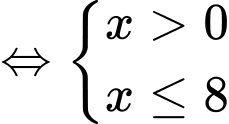
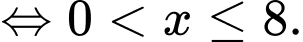
Vậy tập nghiệm của bất phương trình là
 Đáp án: A
Đáp án: A
Câu 6 [808745]: Trong không gian 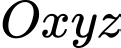 cho mặt cầu
cho mặt cầu 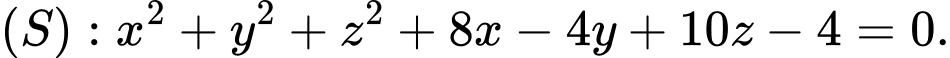 Khi đó
Khi đó 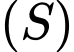 có tâm
có tâm 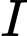 và bán kính
và bán kính 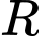 lần lượt là
lần lượt là
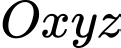 cho mặt cầu
cho mặt cầu 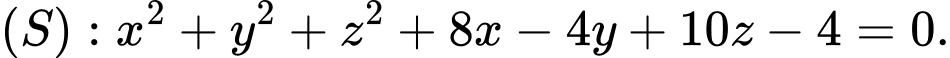 Khi đó
Khi đó 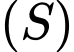 có tâm
có tâm 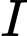 và bán kính
và bán kính 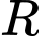 lần lượt là
lần lượt là A, 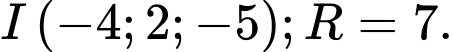
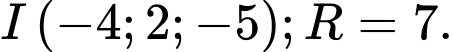
B, 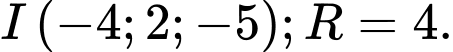
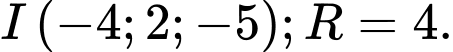
C, 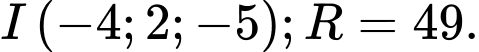
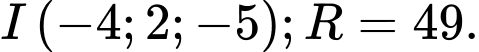
D, 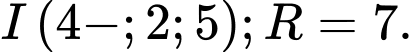
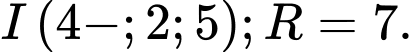
Chọn đáp án A.
Mặt cầu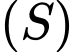 có tâm
có tâm 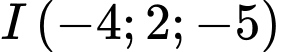 và bán kính
và bán kính 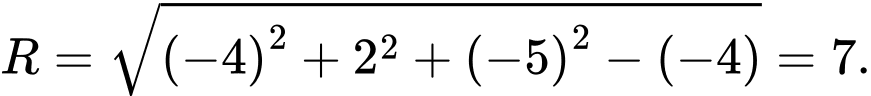 Đáp án: A
Đáp án: A
Mặt cầu
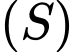 có tâm
có tâm 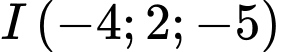 và bán kính
và bán kính 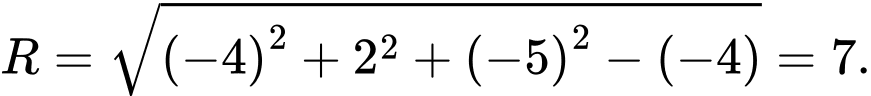 Đáp án: A
Đáp án: A
Câu 7 [329247]: Biết rằng thể tích của một khối lập phương bằng 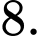 Tính tổng diện tích các mặt của hình lập phương đó.
Tính tổng diện tích các mặt của hình lập phương đó.
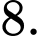 Tính tổng diện tích các mặt của hình lập phương đó.
Tính tổng diện tích các mặt của hình lập phương đó. A, 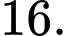
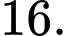
B, 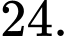
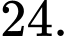
C, 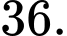
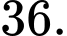
D, 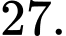
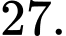
Chọn đáp án B.
Gọi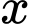 là độ dài cạnh hình lập phương. Theo giả thiết, ta có
là độ dài cạnh hình lập phương. Theo giả thiết, ta có 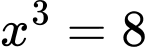
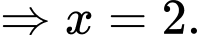
Tính tổng diện tích các mặt của hình lập phương đó là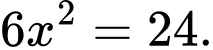 Đáp án: B
Đáp án: B
Gọi
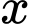 là độ dài cạnh hình lập phương. Theo giả thiết, ta có
là độ dài cạnh hình lập phương. Theo giả thiết, ta có 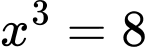
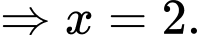
Tính tổng diện tích các mặt của hình lập phương đó là
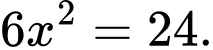 Đáp án: B
Đáp án: B
Câu 8 [512846]: Diện tích 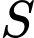 của hình phẳng giới hạn bởi các đường
của hình phẳng giới hạn bởi các đường 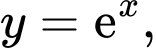
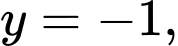
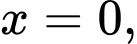
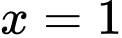 được tính bởi công thức nào dưới đây?
được tính bởi công thức nào dưới đây?
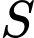 của hình phẳng giới hạn bởi các đường
của hình phẳng giới hạn bởi các đường 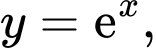
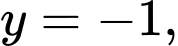
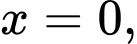
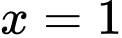 được tính bởi công thức nào dưới đây?
được tính bởi công thức nào dưới đây? A, 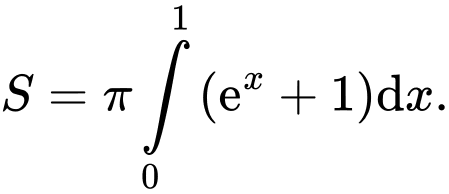
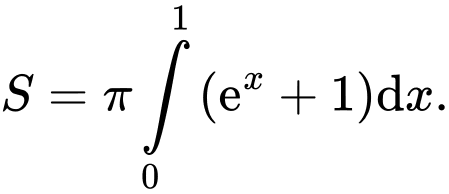
B, 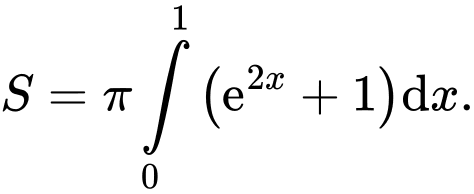
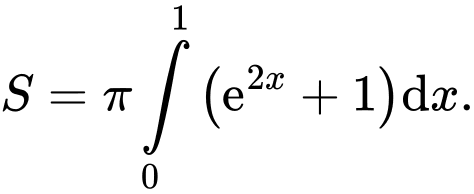
C, 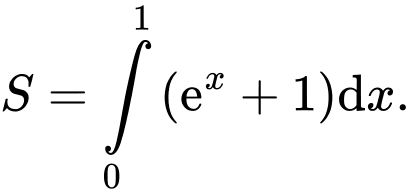
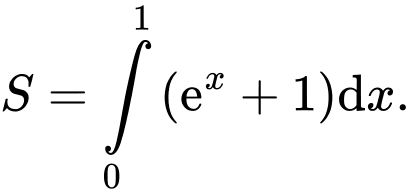
D, 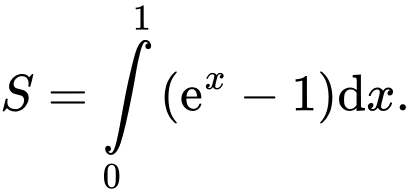
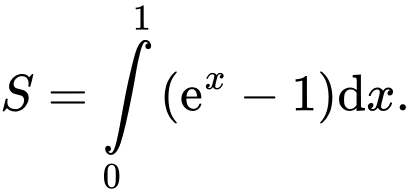
Chọn đáp án C.
ta có: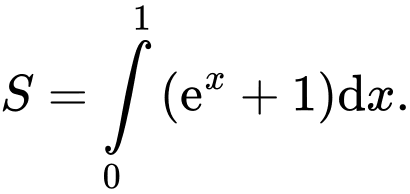 Đáp án: C
Đáp án: C
ta có:
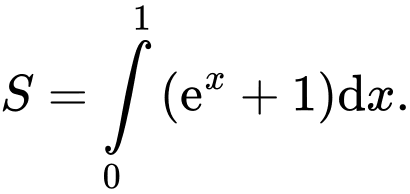 Đáp án: C
Đáp án: C
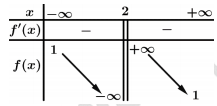
Câu 9 [30671]: Bảng biến thiên ở bên là của hàm số nào?

A, 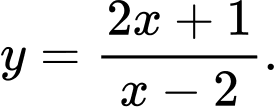
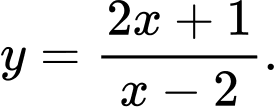
B, 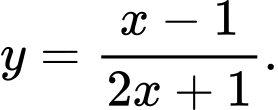
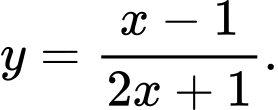
C, 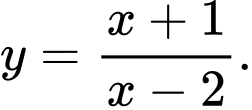
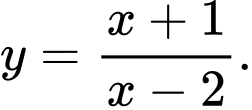
D, 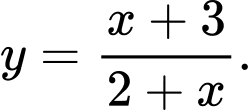
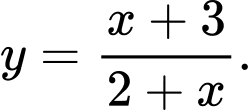
Chọn đáp án C.
Do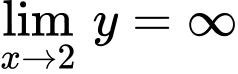
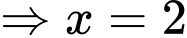 là tiệm cận đứng của hàm số nên loại B, D.
là tiệm cận đứng của hàm số nên loại B, D.
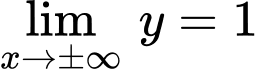
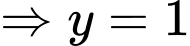 là tiệm cận ngang của hàm số nên loại A. Đáp án: C
là tiệm cận ngang của hàm số nên loại A. Đáp án: C
Do
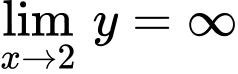
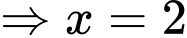 là tiệm cận đứng của hàm số nên loại B, D.
là tiệm cận đứng của hàm số nên loại B, D.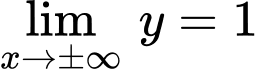
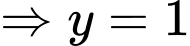 là tiệm cận ngang của hàm số nên loại A. Đáp án: C
là tiệm cận ngang của hàm số nên loại A. Đáp án: C
Câu 10 [808784]: Trong không gian 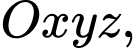 cho điểm
cho điểm 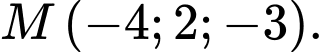 Tìm toạ độ điểm
Tìm toạ độ điểm 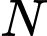 đối xứng với
đối xứng với 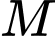 qua trục
qua trục 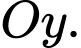
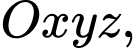 cho điểm
cho điểm 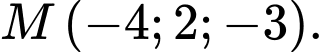 Tìm toạ độ điểm
Tìm toạ độ điểm 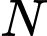 đối xứng với
đối xứng với 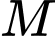 qua trục
qua trục 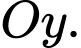
A, 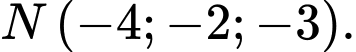
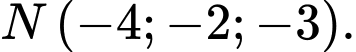
B, 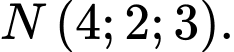
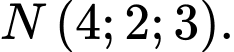
C, 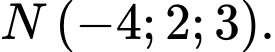
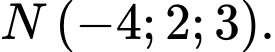
D, 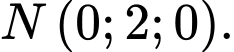
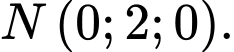
Chọn đáp án B.
Tìm toạ độ điểm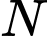 đối xứng với
đối xứng với 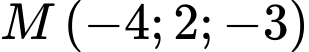 qua trục
qua trục 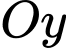
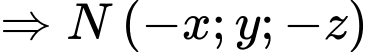
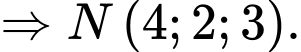 Đáp án: B
Đáp án: B
Tìm toạ độ điểm
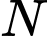 đối xứng với
đối xứng với 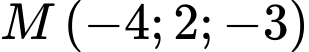 qua trục
qua trục 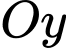
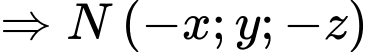
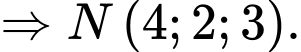 Đáp án: B
Đáp án: B
Câu 11 [390481]: Một trang báo điện tử thống kê thời gian người sử dụng đọc thông tin trên trang trong mỗi lần truy cập ở bảng sau:

Khoảng tứ phân vị của mẫu số liệu ghép nhóm trên (làm tròn đến hàng phần trăm) là:
A, 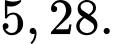
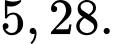
B, 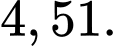
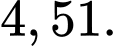
C, 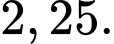
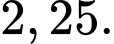
D, 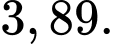
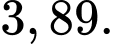
Chọn đáp án D.

Nhóm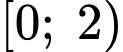 là nhóm đầu tiên có tần số tích luỹ lớn hơn hoặc bằng
là nhóm đầu tiên có tần số tích luỹ lớn hơn hoặc bằng 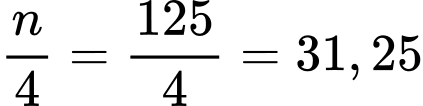 nên chứa tứ phân vị thứ nhất.
nên chứa tứ phân vị thứ nhất.
Ta có: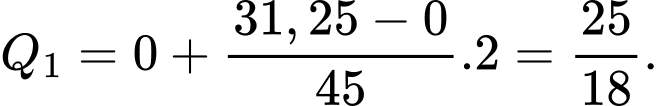
Nhóm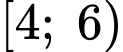 là nhóm đầu tiên có tần số tích luỹ lớn hơn hoặc bằng
là nhóm đầu tiên có tần số tích luỹ lớn hơn hoặc bằng
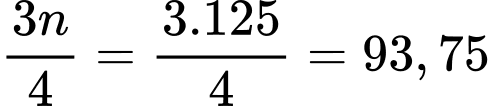 nên chứa tứ phân vị thứ ba.
nên chứa tứ phân vị thứ ba.
Ta có: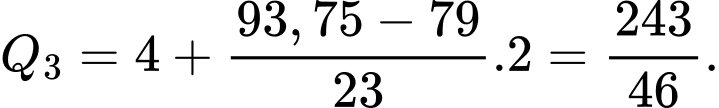
Suy ra khoảng tứ phân vị của MSL ghép nhóm trên là:
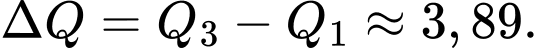 Đáp án: D
Đáp án: D

Nhóm
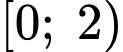 là nhóm đầu tiên có tần số tích luỹ lớn hơn hoặc bằng
là nhóm đầu tiên có tần số tích luỹ lớn hơn hoặc bằng 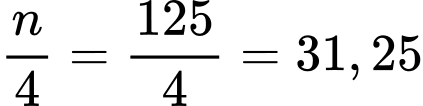 nên chứa tứ phân vị thứ nhất.
nên chứa tứ phân vị thứ nhất. Ta có:
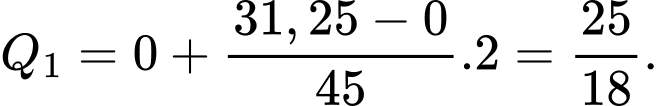
Nhóm
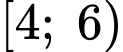 là nhóm đầu tiên có tần số tích luỹ lớn hơn hoặc bằng
là nhóm đầu tiên có tần số tích luỹ lớn hơn hoặc bằng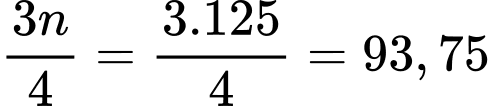 nên chứa tứ phân vị thứ ba.
nên chứa tứ phân vị thứ ba. Ta có:
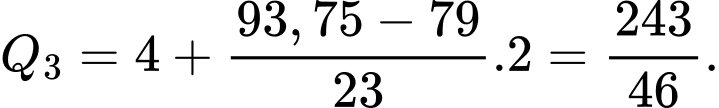
Suy ra khoảng tứ phân vị của MSL ghép nhóm trên là:
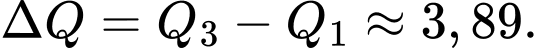 Đáp án: D
Đáp án: D
Câu 12 [681582]: Tiệm cận xiên của đồ thị hàm số 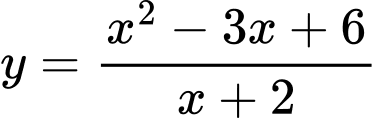 là đường thẳng:
là đường thẳng:
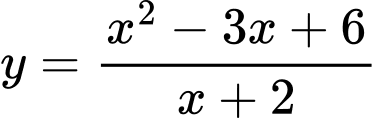 là đường thẳng:
là đường thẳng: A, 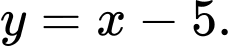
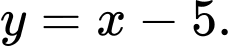
B, 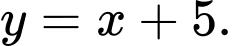
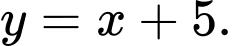
C, 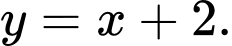
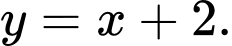
D, 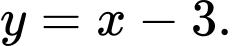
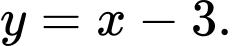
Chọn đáp án A.
Tập xác định của hàm số là
Ta có: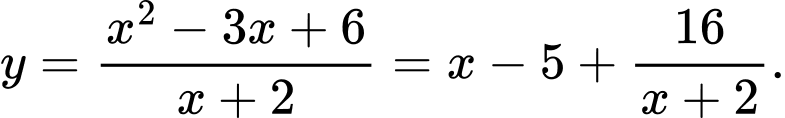
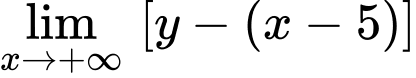
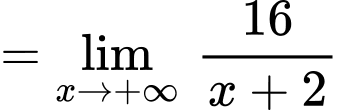
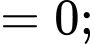
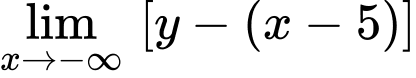
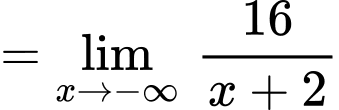
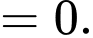
Vậy đường thẳng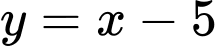 là tiệm cận xiên của đồ thị hàm số đã cho. Đáp án: A
là tiệm cận xiên của đồ thị hàm số đã cho. Đáp án: A
Tập xác định của hàm số là

Ta có:
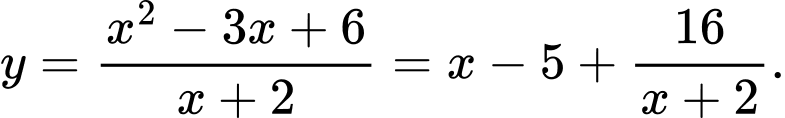
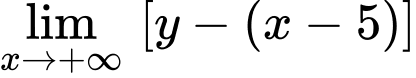
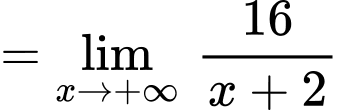
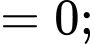
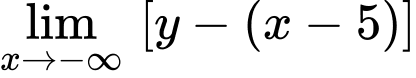
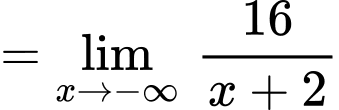
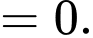
Vậy đường thẳng
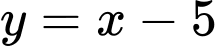 là tiệm cận xiên của đồ thị hàm số đã cho. Đáp án: A
là tiệm cận xiên của đồ thị hàm số đã cho. Đáp án: A PHẦN II. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Câu 13 [695175]: Trong không gian 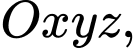 cho mặt phẳng
cho mặt phẳng 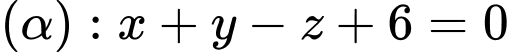 có vectơ pháp tuyến
có vectơ pháp tuyến 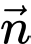 và đường thẳng
và đường thẳng 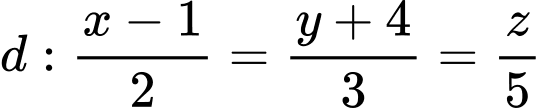 có vectơ chỉ phương
có vectơ chỉ phương 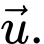
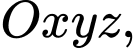 cho mặt phẳng
cho mặt phẳng 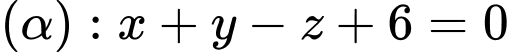 có vectơ pháp tuyến
có vectơ pháp tuyến 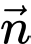 và đường thẳng
và đường thẳng 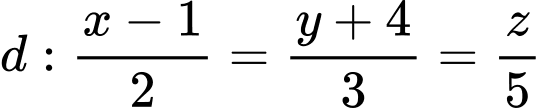 có vectơ chỉ phương
có vectơ chỉ phương 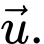
a) Sai.
Vectơ chỉ phương của đường thẳng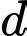 là
là 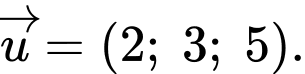
b) Sai.
Thay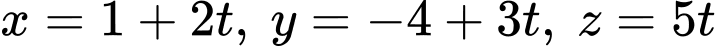 vào phương trình mặt phẳng
vào phương trình mặt phẳng  ta được:
ta được:
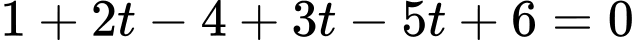
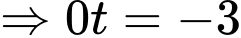 ( vô lý).
( vô lý).
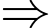 Đường thẳng
Đường thẳng 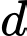 không cắt mặt phẳng
không cắt mặt phẳng 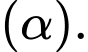
c) Đúng.
Vì là đường thẳng đi qua
là đường thẳng đi qua 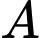 và vuông góc với
và vuông góc với  .
.
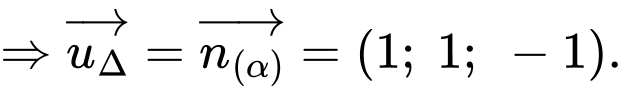
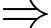 Phương trình đường thẳng
Phương trình đường thẳng  đi qua điểm
đi qua điểm 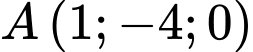 và vuông góc với
và vuông góc với  là
là
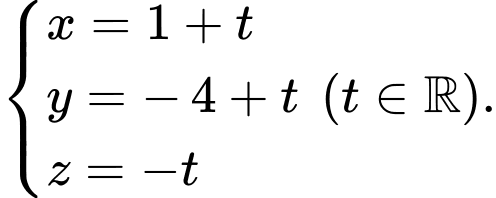
d) Đúng.
Theo câu c) ta có phương trình đường thẳng đi qua điểm
đi qua điểm 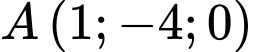 và vuông góc với
và vuông góc với  là
là 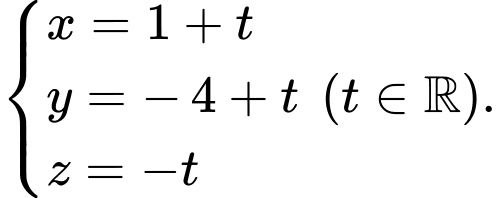
Gọi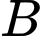 là hình chiếu của điểm
là hình chiếu của điểm 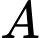 trên mặt phẳng
trên mặt phẳng  .
.
Thay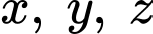 vào phương trình mặt phẳng
vào phương trình mặt phẳng  ta được:
ta được:

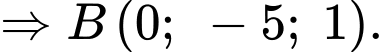
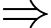 Phương trình hình chiếu vuông góc của
Phương trình hình chiếu vuông góc của 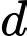 trên
trên  đi qua điểm
đi qua điểm 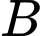 là
là 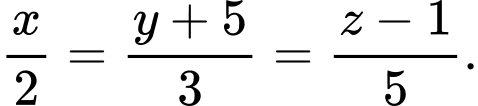
Vectơ chỉ phương của đường thẳng
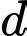 là
là 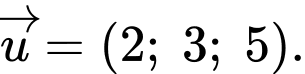
b) Sai.
Thay
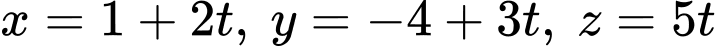 vào phương trình mặt phẳng
vào phương trình mặt phẳng  ta được:
ta được:
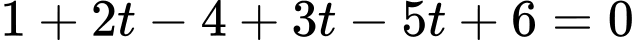
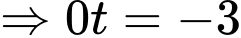 ( vô lý).
( vô lý).
 Đường thẳng
Đường thẳng 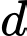 không cắt mặt phẳng
không cắt mặt phẳng 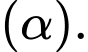
c) Đúng.
Vì
 là đường thẳng đi qua
là đường thẳng đi qua 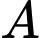 và vuông góc với
và vuông góc với  .
.
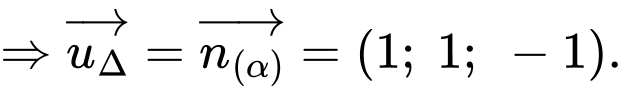
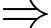 Phương trình đường thẳng
Phương trình đường thẳng  đi qua điểm
đi qua điểm 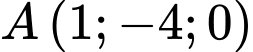 và vuông góc với
và vuông góc với  là
là
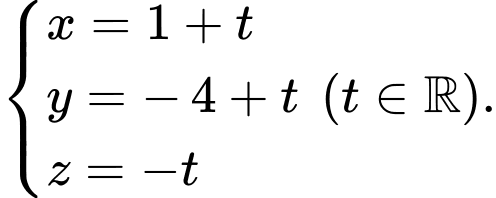
d) Đúng.
Theo câu c) ta có phương trình đường thẳng
 đi qua điểm
đi qua điểm 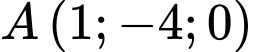 và vuông góc với
và vuông góc với  là
là 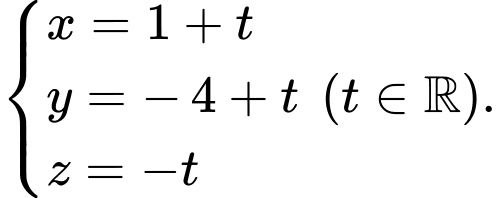
Gọi
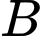 là hình chiếu của điểm
là hình chiếu của điểm 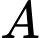 trên mặt phẳng
trên mặt phẳng  .
.
Thay
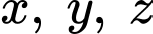 vào phương trình mặt phẳng
vào phương trình mặt phẳng  ta được:
ta được:

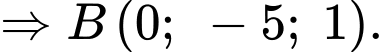
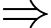 Phương trình hình chiếu vuông góc của
Phương trình hình chiếu vuông góc của 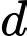 trên
trên  đi qua điểm
đi qua điểm 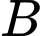 là
là 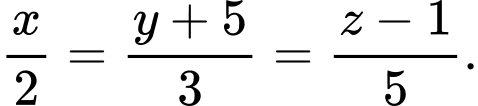
Câu 14 [693686]: Sự phân huỷ của rác thải hữu cơ có trong nước sẽ làm tiêu hao oxygen hoà tan trong nước. Nồng độ oxygen (mg/l) trong một hồ nước sau 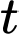 giờ
giờ 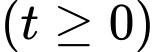 khi một lượng rác thải hữu cơ bị xả vào hồ được mô phỏng bởi hàm số
khi một lượng rác thải hữu cơ bị xả vào hồ được mô phỏng bởi hàm số 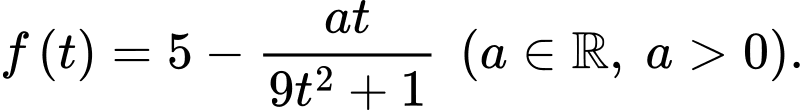 Biết rằng nồng độ oxygen trong hồ nước thấp nhất đo được là
Biết rằng nồng độ oxygen trong hồ nước thấp nhất đo được là 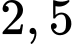 (mg/l).
(mg/l).
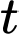 giờ
giờ 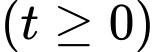 khi một lượng rác thải hữu cơ bị xả vào hồ được mô phỏng bởi hàm số
khi một lượng rác thải hữu cơ bị xả vào hồ được mô phỏng bởi hàm số 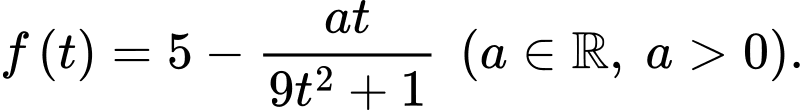 Biết rằng nồng độ oxygen trong hồ nước thấp nhất đo được là
Biết rằng nồng độ oxygen trong hồ nước thấp nhất đo được là 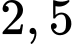 (mg/l).
(mg/l).
a) Đúng.
Thay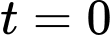 vào hàm
vào hàm 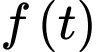 ta được:
ta được: 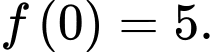
b) Sai.
Xét hàm số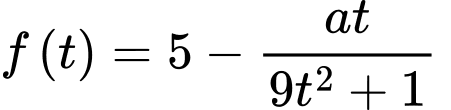
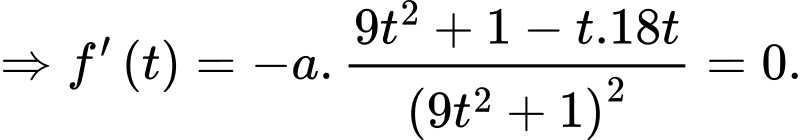
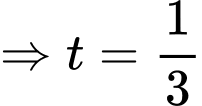 là điểm cực tiểu của đồ thị hàm số đã cho.
là điểm cực tiểu của đồ thị hàm số đã cho.
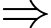 Nồng độ oxygen trong hồ nước thấp nhất sau
Nồng độ oxygen trong hồ nước thấp nhất sau 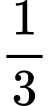 giờ = 20 phút.
giờ = 20 phút.
c) Sai.
Theo câu b) ta có nồng độ oxygen trong hồ nước thấp nhất sau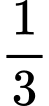 giờ.
giờ.
Vì nồng độ oxygen trong hồ nước thấp nhất đo được là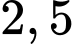 (mg/l) nên ta thay
(mg/l) nên ta thay 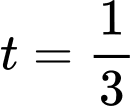 vào hàm
vào hàm 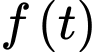 ta được:
ta được: 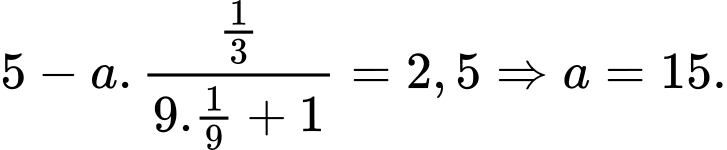
d) Đúng.
Thay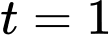 vào hàm
vào hàm 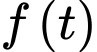 ta được:
ta được: 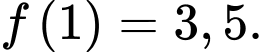
Thay
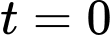 vào hàm
vào hàm 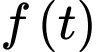 ta được:
ta được: 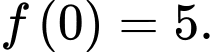
b) Sai.
Xét hàm số
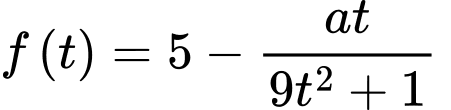
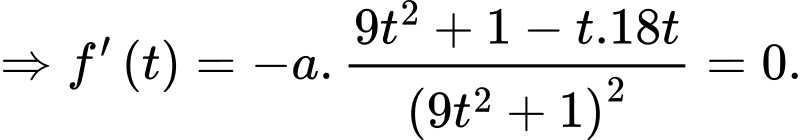
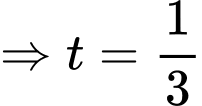 là điểm cực tiểu của đồ thị hàm số đã cho.
là điểm cực tiểu của đồ thị hàm số đã cho.
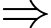 Nồng độ oxygen trong hồ nước thấp nhất sau
Nồng độ oxygen trong hồ nước thấp nhất sau 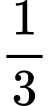 giờ = 20 phút.
giờ = 20 phút.
c) Sai.
Theo câu b) ta có nồng độ oxygen trong hồ nước thấp nhất sau
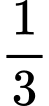 giờ.
giờ.
Vì nồng độ oxygen trong hồ nước thấp nhất đo được là
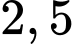 (mg/l) nên ta thay
(mg/l) nên ta thay 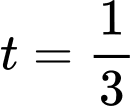 vào hàm
vào hàm 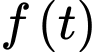 ta được:
ta được: 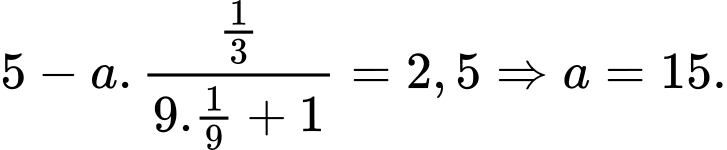
d) Đúng.
Thay
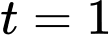 vào hàm
vào hàm 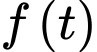 ta được:
ta được: 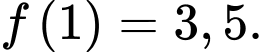
Câu 15 [695177]: Một cái hồ nước ước tính có hình tròn, đường kính 400dm (xem hình). Bắt đầu từ tâm, độ sâu của nước được đo mỗi 25 dm và ghi lại trong bảng với 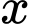 có đơn vị dm.
có đơn vị dm.
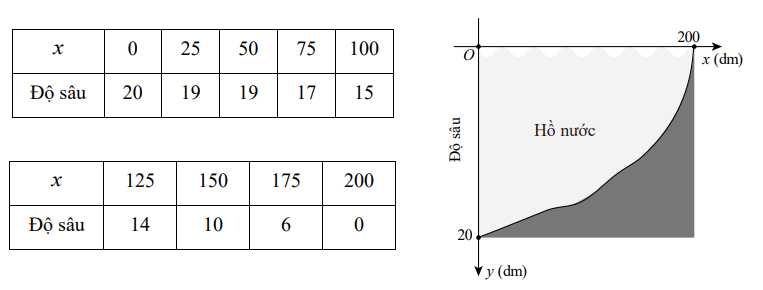
Người ta xây dựng một hàm số bậc hai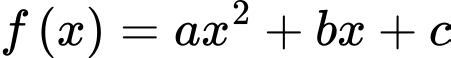
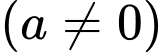 để mô phỏng tương đối độ sâu của cái ao theo số liệu ở bảng 1, tức là trên hệ trục tọa độ
để mô phỏng tương đối độ sâu của cái ao theo số liệu ở bảng 1, tức là trên hệ trục tọa độ 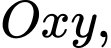 đồ thị của hàm số đó đi qua các điểm
đồ thị của hàm số đó đi qua các điểm 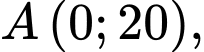
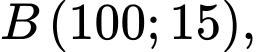
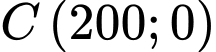 và đơn vị trên các trục tọa độ là dm. Gọi
và đơn vị trên các trục tọa độ là dm. Gọi 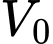 là thể tích của hồ nước. Dựa vào hàm số
là thể tích của hồ nước. Dựa vào hàm số 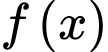 tìm được ta có:
tìm được ta có:
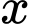 có đơn vị dm.
có đơn vị dm.
Người ta xây dựng một hàm số bậc hai
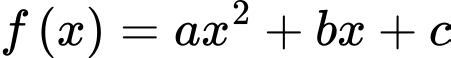
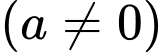 để mô phỏng tương đối độ sâu của cái ao theo số liệu ở bảng 1, tức là trên hệ trục tọa độ
để mô phỏng tương đối độ sâu của cái ao theo số liệu ở bảng 1, tức là trên hệ trục tọa độ 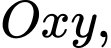 đồ thị của hàm số đó đi qua các điểm
đồ thị của hàm số đó đi qua các điểm 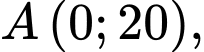
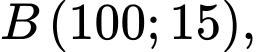
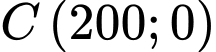 và đơn vị trên các trục tọa độ là dm. Gọi
và đơn vị trên các trục tọa độ là dm. Gọi 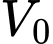 là thể tích của hồ nước. Dựa vào hàm số
là thể tích của hồ nước. Dựa vào hàm số 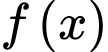 tìm được ta có:
tìm được ta có:
a) Sai.
Dựa theo hình vẽ ta thấy độ sâu lớn nhất của ao là
b) Sai.
Thể tích của hồ nước chính là thể tích giới hạn bởi hàm số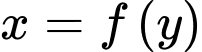 và các đường thẳng
và các đường thẳng 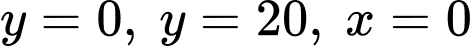 khi quay quanh trục
khi quay quanh trục 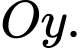
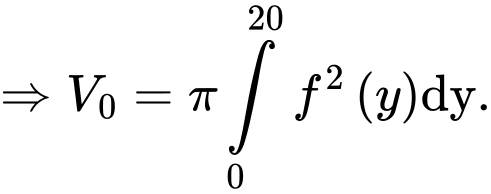
c) Sai.
Thay tọa độ các điểm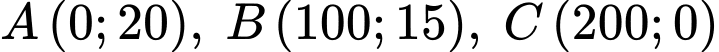 vào phương trình hàm số
vào phương trình hàm số 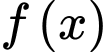 ta được hệ phương trình sau:
ta được hệ phương trình sau: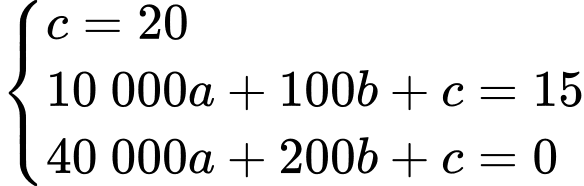
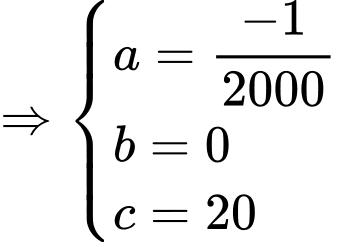
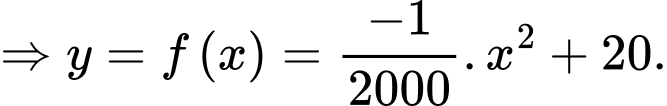
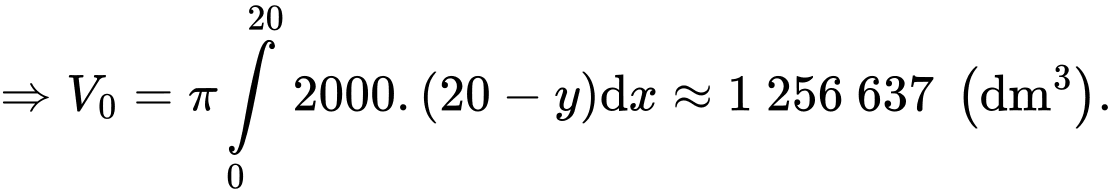
d) Sai.
Thể tích hồ nước bốc hơi trong 10 ngày là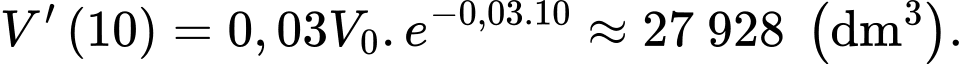
Thể tích nước còn lại trong hồ là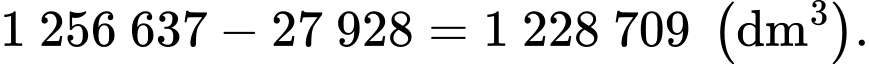
Dựa theo hình vẽ ta thấy độ sâu lớn nhất của ao là

b) Sai.
Thể tích của hồ nước chính là thể tích giới hạn bởi hàm số
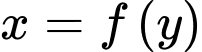 và các đường thẳng
và các đường thẳng 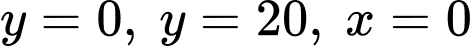 khi quay quanh trục
khi quay quanh trục 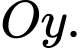
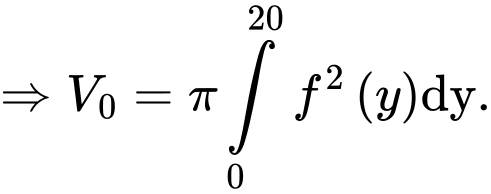
c) Sai.
Thay tọa độ các điểm
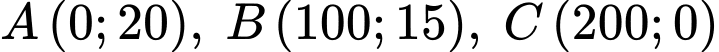 vào phương trình hàm số
vào phương trình hàm số 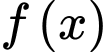 ta được hệ phương trình sau:
ta được hệ phương trình sau: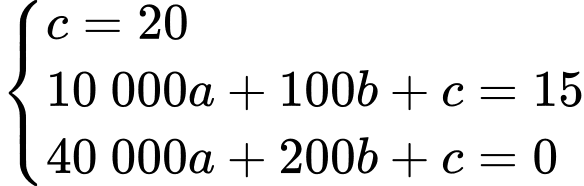
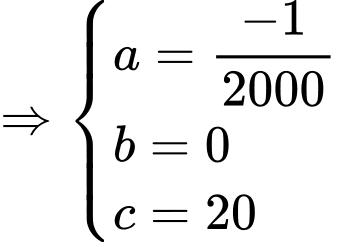
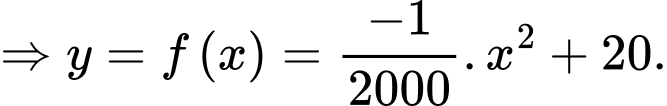
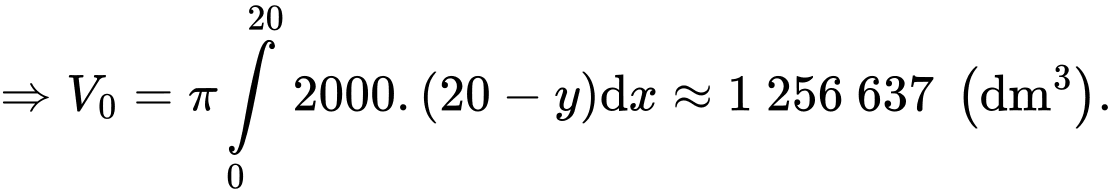
d) Sai.
Thể tích hồ nước bốc hơi trong 10 ngày là
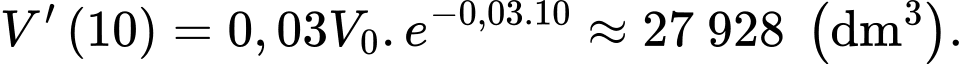
Thể tích nước còn lại trong hồ là
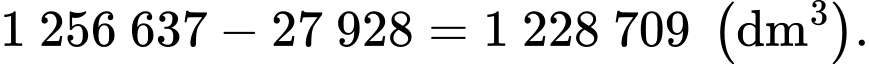
Câu 16 [695178]: Một cặp trẻ sinh đôi có thể do cùng một trứng (sinh đôi thật) hay do hai trứng khác nhau sinh ra (sinh đôi giả). Các cặp sinh đôi thật luôn có cùng giới tính. Cặp sinh đôi giả thì giới tính của mỗi đứa độc lập với nhau và có xác suất 0,5 là con trai. Thống kê cho thấy 34% cặp sinh đôi đều là trai, 30% cặp sinh đôi đều là gái và 36% cặp sinh đôi có giới tính khác nhau.
Gọi A là biến cố “Cặp sinh đôi thật”
Gọi B là biến cố “Cặp sinh đôi có cùng giới tính”
Gọi A là biến cố “Cặp sinh đôi thật”
Gọi B là biến cố “Cặp sinh đôi có cùng giới tính”
a) Đúng.
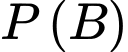 là xác suất cặp sinh đôi có cùng giới tính (tức cặp sinh đôi là trai hoặc cặp sinh đôi là gái) nên
là xác suất cặp sinh đôi có cùng giới tính (tức cặp sinh đôi là trai hoặc cặp sinh đôi là gái) nên 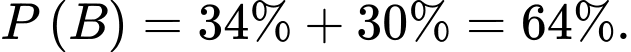
b) Đúng.
 là xác suất cặp sinh đôi có cùng giới tính khi biết đó là cặp sinh đôi thật.
là xác suất cặp sinh đôi có cùng giới tính khi biết đó là cặp sinh đôi thật.
Vì giả thiết cho: “Các cặp sinh đôi thật luôn có cùng giới tính” nên xác suất trên chắc chắn xảy ra hay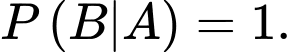
c) Đúng.
Giả sử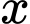 là xác suất cặp sinh đôi cùng trứng.
là xác suất cặp sinh đôi cùng trứng.
Suy ra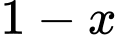 là xác suất cặp sinh đôi khác trứng.
là xác suất cặp sinh đôi khác trứng.
Ta có sơ đồ cây sau:
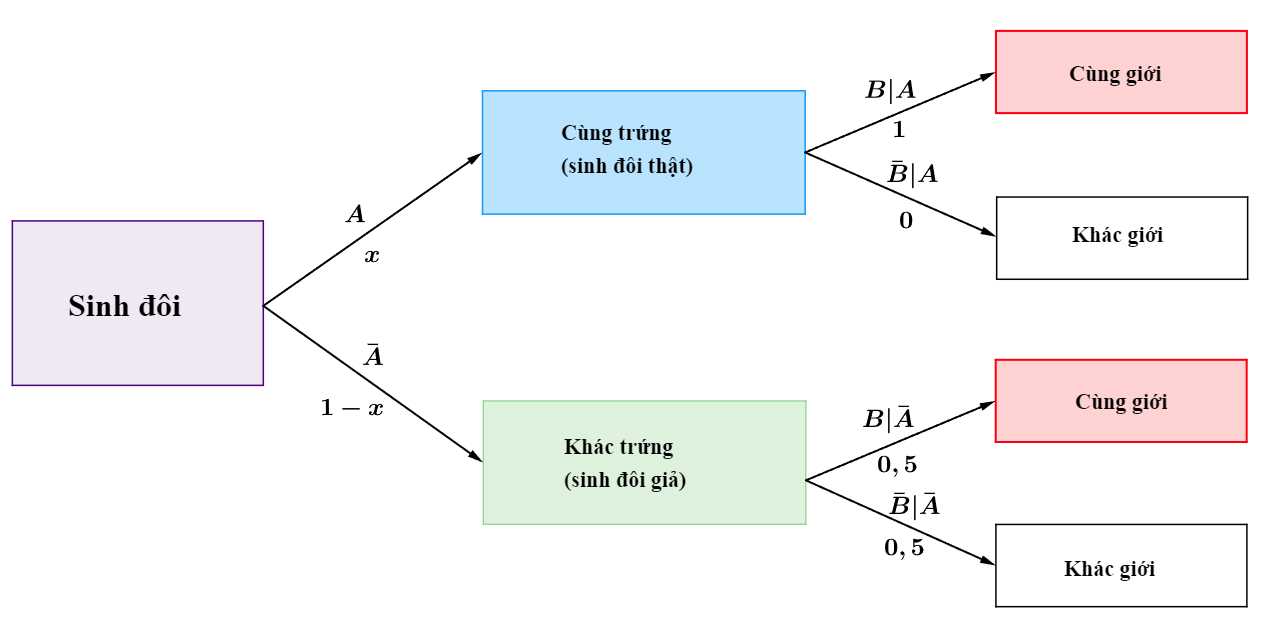
Áp dụng công thức xác suất toàn phần, ta có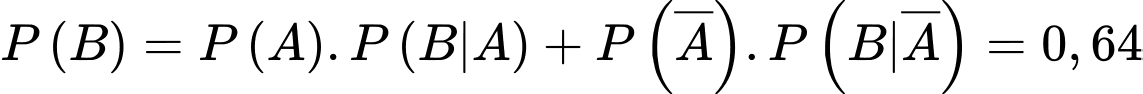
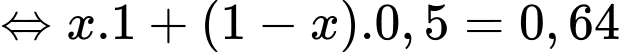
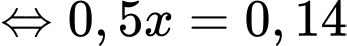
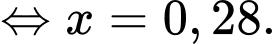
Suy ra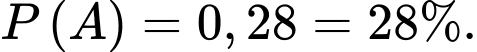
d) Đúng.
YCBT Tính
Tính 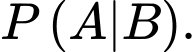
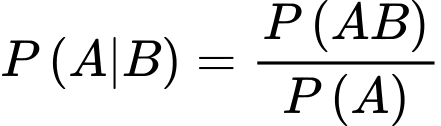
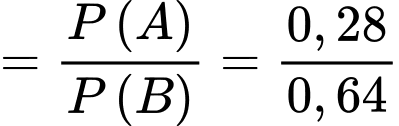
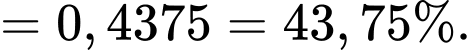
(Vì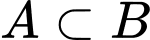 nên
nên 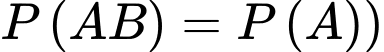
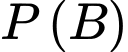 là xác suất cặp sinh đôi có cùng giới tính (tức cặp sinh đôi là trai hoặc cặp sinh đôi là gái) nên
là xác suất cặp sinh đôi có cùng giới tính (tức cặp sinh đôi là trai hoặc cặp sinh đôi là gái) nên 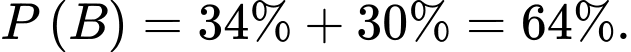
b) Đúng.
 là xác suất cặp sinh đôi có cùng giới tính khi biết đó là cặp sinh đôi thật.
là xác suất cặp sinh đôi có cùng giới tính khi biết đó là cặp sinh đôi thật.Vì giả thiết cho: “Các cặp sinh đôi thật luôn có cùng giới tính” nên xác suất trên chắc chắn xảy ra hay
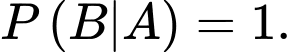
c) Đúng.
Giả sử
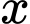 là xác suất cặp sinh đôi cùng trứng.
là xác suất cặp sinh đôi cùng trứng.Suy ra
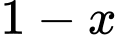 là xác suất cặp sinh đôi khác trứng.
là xác suất cặp sinh đôi khác trứng.Ta có sơ đồ cây sau:

Áp dụng công thức xác suất toàn phần, ta có
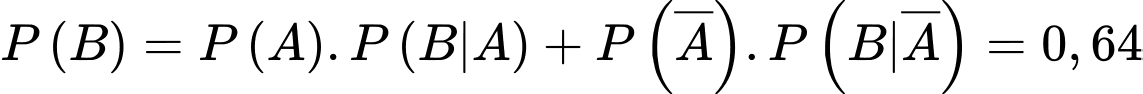
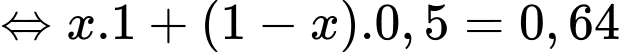
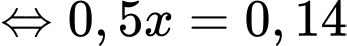
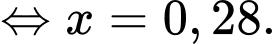
Suy ra
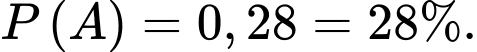
d) Đúng.
YCBT
 Tính
Tính 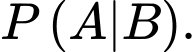
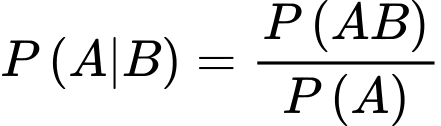
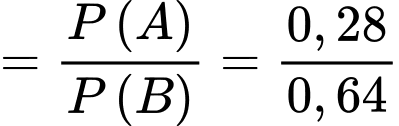
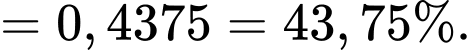
(Vì
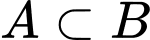 nên
nên 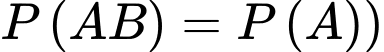
PHẦN III. Thí sinh trả lời từ câu 1 đến câu 6.
Câu 17 [695179]: Giá đỡ ba chân ở Hình vẽ đang được mở sao cho ba góc chân cách đều nhau một khoảng cách bằng 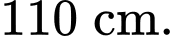 Tính chiều cao của giá đỡ, biết các chân của giá đỡ dài
Tính chiều cao của giá đỡ, biết các chân của giá đỡ dài 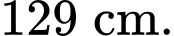 (Kết quả làm tròn đến hàng đơn vị)
(Kết quả làm tròn đến hàng đơn vị)
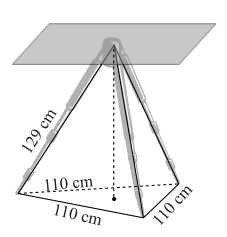
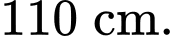 Tính chiều cao của giá đỡ, biết các chân của giá đỡ dài
Tính chiều cao của giá đỡ, biết các chân của giá đỡ dài 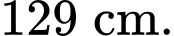 (Kết quả làm tròn đến hàng đơn vị)
(Kết quả làm tròn đến hàng đơn vị)
Điền đáp án: 112.
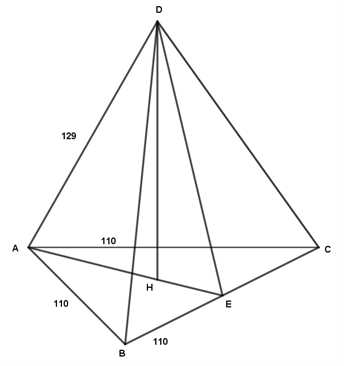
Gọi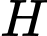 là chân đường cao kẻ từ
là chân đường cao kẻ từ 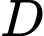 xuống mặt phẳng
xuống mặt phẳng 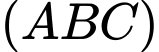 ,
, 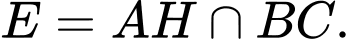
Vì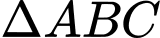 đều các cạnh bên của tứ diện đều bằng nhau nên
đều các cạnh bên của tứ diện đều bằng nhau nên 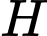 là trọng tâm của tam giác
là trọng tâm của tam giác 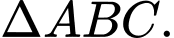
Xét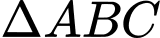 đều có:
đều có: 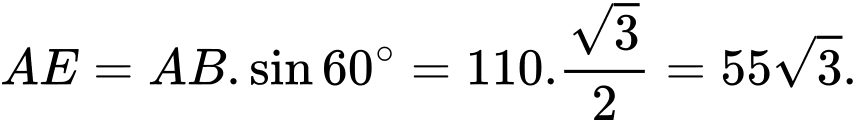
Do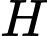 là trọng tâm của tam giác
là trọng tâm của tam giác 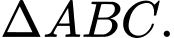
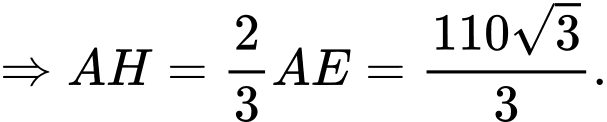
Chiều cao của giá đỡ là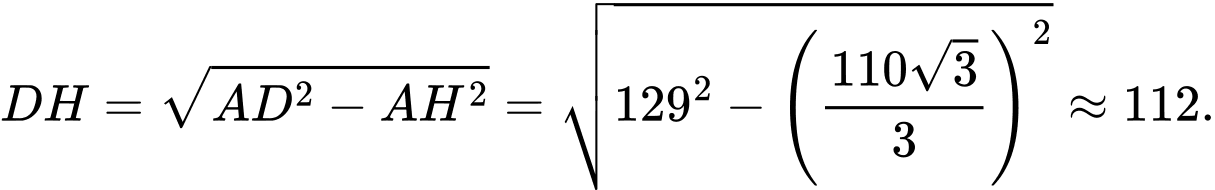

Gọi
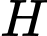 là chân đường cao kẻ từ
là chân đường cao kẻ từ 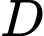 xuống mặt phẳng
xuống mặt phẳng 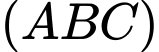 ,
, 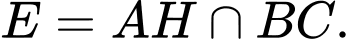
Vì
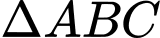 đều các cạnh bên của tứ diện đều bằng nhau nên
đều các cạnh bên của tứ diện đều bằng nhau nên 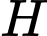 là trọng tâm của tam giác
là trọng tâm của tam giác 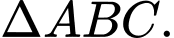
Xét
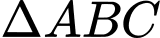 đều có:
đều có: 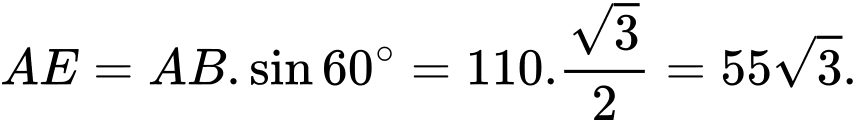
Do
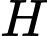 là trọng tâm của tam giác
là trọng tâm của tam giác 
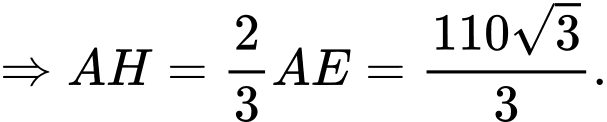
Chiều cao của giá đỡ là
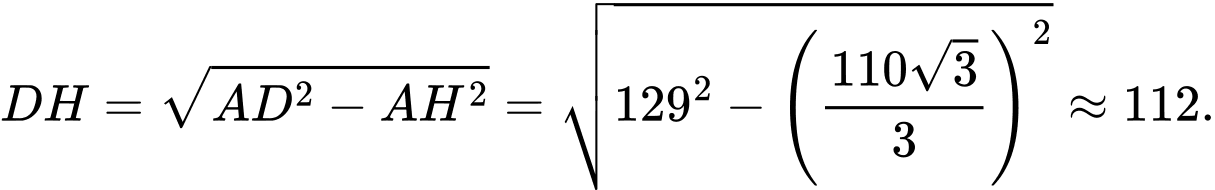
Câu 18 [695180]: Có 4 người và 1 đèn pin muốn qua sông phải đi qua 1 cây cầu. Biết cây cầu chỉ đi 1 lần tối đa được 2 người và phải có đèn pin mới có thể di chuyển trên cầu. A đi qua cầu hết 1 phút, B hết 2 phút, C hết 5 phút, D hết 10 phút. Hai người đi cùng nhau thì phải đi với tốc độ của người đi chậm hơn. Hỏi mất ít nhất bao nhiêu phút để tất cả đều qua được sông?
Điền đáp án: 
Để mất ít thời gian nhất ta sẽ cho 4 người đi theo lộ trình sau:

Tổng thời gian để tất cả đều qua được sông là:
 phút.
phút.
Để mất ít thời gian nhất ta sẽ cho 4 người đi theo lộ trình sau:

Tổng thời gian để tất cả đều qua được sông là:
 phút.
phút.
Câu 19 [699144]: Ba khẩu súng độc lập bắn vào một mục tiêu. Xác suất để khẩu thứ nhất bắn trúng bằng 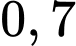 để khẩu thứ hai bắn trúng bằng
để khẩu thứ hai bắn trúng bằng 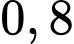 để khẩu thứ ba bắn trúng bằng
để khẩu thứ ba bắn trúng bằng 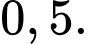 Mỗi khẩu bắn 1 viên. Tính xác suất để khẩu thứ nhất bắn trúng biết rằng chỉ có 2 viên trúng mục tiêu (kết quả làm tròn đến hàng phần trăm).
Mỗi khẩu bắn 1 viên. Tính xác suất để khẩu thứ nhất bắn trúng biết rằng chỉ có 2 viên trúng mục tiêu (kết quả làm tròn đến hàng phần trăm).
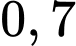 để khẩu thứ hai bắn trúng bằng
để khẩu thứ hai bắn trúng bằng 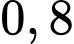 để khẩu thứ ba bắn trúng bằng
để khẩu thứ ba bắn trúng bằng 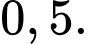 Mỗi khẩu bắn 1 viên. Tính xác suất để khẩu thứ nhất bắn trúng biết rằng chỉ có 2 viên trúng mục tiêu (kết quả làm tròn đến hàng phần trăm).
Mỗi khẩu bắn 1 viên. Tính xác suất để khẩu thứ nhất bắn trúng biết rằng chỉ có 2 viên trúng mục tiêu (kết quả làm tròn đến hàng phần trăm).
Điền đáp án: 0,74.
Gọi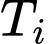 là biến cố “Khẩu thứ
là biến cố “Khẩu thứ 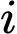 bắn trúng mục tiêu, với
bắn trúng mục tiêu, với 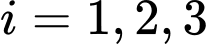 ”
”
Khi đó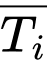 là biến cố “Khẩu thứ
là biến cố “Khẩu thứ 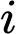 bắn trượtmục tiêu, với
bắn trượtmục tiêu, với 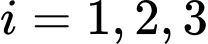 ”
”
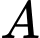 là biến cố “Chỉ có 2 viên trúng mục tiêu”
là biến cố “Chỉ có 2 viên trúng mục tiêu”
YCBT Tính
Tính 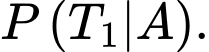
Theo công thức xác suất điều kiện, ta có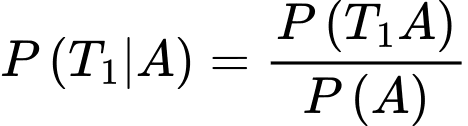
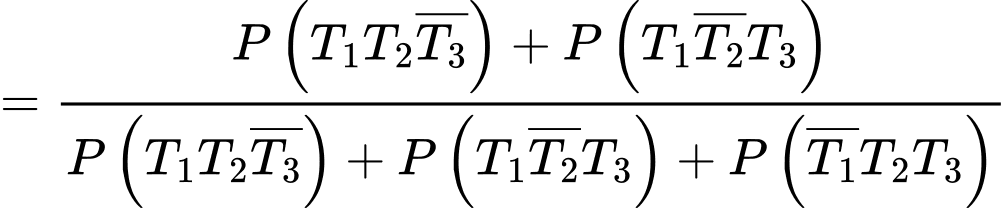
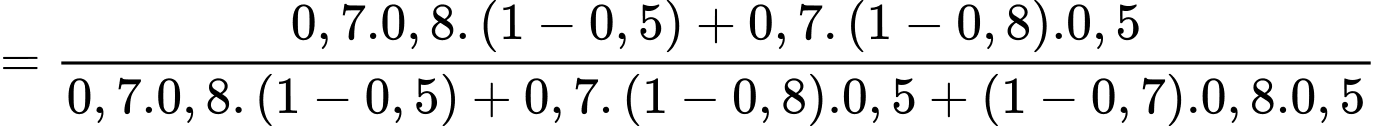
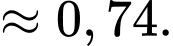
Gọi
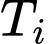 là biến cố “Khẩu thứ
là biến cố “Khẩu thứ 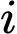 bắn trúng mục tiêu, với
bắn trúng mục tiêu, với 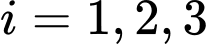 ”
”Khi đó
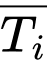 là biến cố “Khẩu thứ
là biến cố “Khẩu thứ 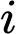 bắn trượtmục tiêu, với
bắn trượtmục tiêu, với 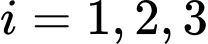 ”
”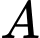 là biến cố “Chỉ có 2 viên trúng mục tiêu”
là biến cố “Chỉ có 2 viên trúng mục tiêu”YCBT
 Tính
Tính 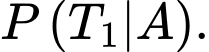
Theo công thức xác suất điều kiện, ta có
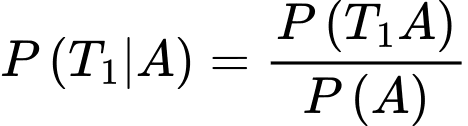
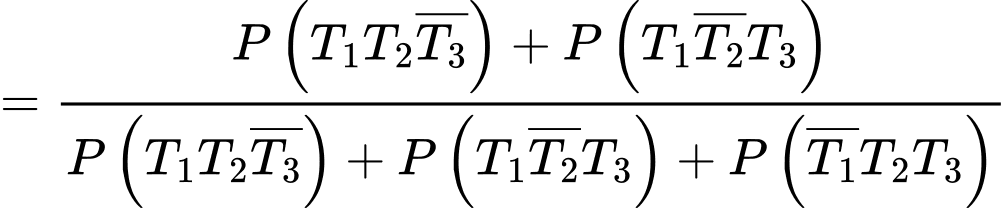
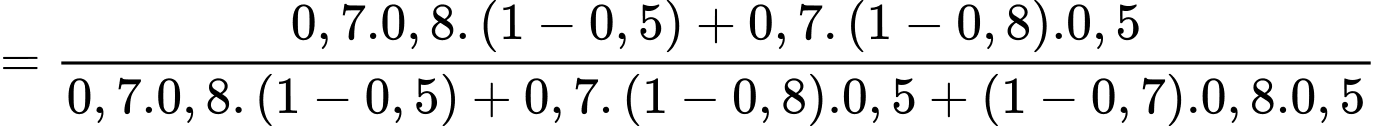
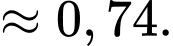
Câu 20 [695258]: Theo thống kê tại một nhà máy X, nếu áp dụng tuần làm việc 40 giờ thì mỗi tuần có 100 công nhân đi làm và mỗi công nhân làm được 120 sản phẩm trong một giờ. Nếu tăng thời gian làm việc thêm 2 giờ mỗi tuần thì sẽ có 1 công nhân nghỉ việc và năng suất lao động giảm 5 sản phẩm/1 công nhân/1 giờ. Ngoài ra, số phế phẩm mỗi tuần ước tính là 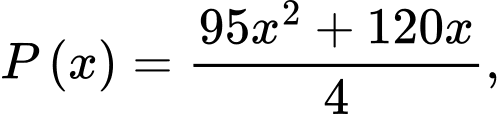 với
với 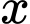 là thời gian làm việc trong một tuần (đơn vị: giờ). Nhà máy cần áp dụng thời gian làm việc mỗi tuần bao nhiêu giờ để số lượng sản phẩm thu được mỗi tuần là lớn nhất?
là thời gian làm việc trong một tuần (đơn vị: giờ). Nhà máy cần áp dụng thời gian làm việc mỗi tuần bao nhiêu giờ để số lượng sản phẩm thu được mỗi tuần là lớn nhất?
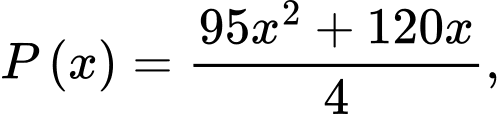 với
với 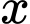 là thời gian làm việc trong một tuần (đơn vị: giờ). Nhà máy cần áp dụng thời gian làm việc mỗi tuần bao nhiêu giờ để số lượng sản phẩm thu được mỗi tuần là lớn nhất?
là thời gian làm việc trong một tuần (đơn vị: giờ). Nhà máy cần áp dụng thời gian làm việc mỗi tuần bao nhiêu giờ để số lượng sản phẩm thu được mỗi tuần là lớn nhất?
Điền đáp án: 36.
Gọi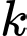 là số lần tăng thời gian làm việc lên 2 giờ một tuần.
là số lần tăng thời gian làm việc lên 2 giờ một tuần.
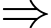 Thời gian làm việc trong 1 tuần của 1 công nhân là
Thời gian làm việc trong 1 tuần của 1 công nhân là 
Số công nhân làm việc trong 1 tuần sau khi tăng thời gian làm việc là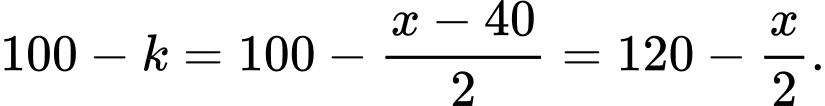
Năng suất lao động trong 1 giờ của 1 công nhân sau khi tăng thời gian làm việc là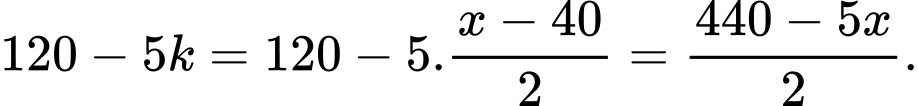
Số sản phẩm thu được mỗi tuần là
Xét hàm số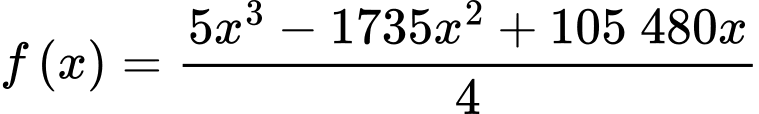
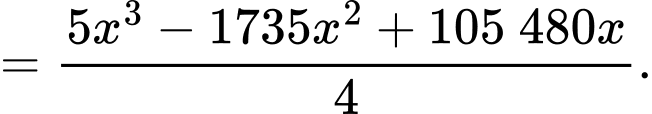
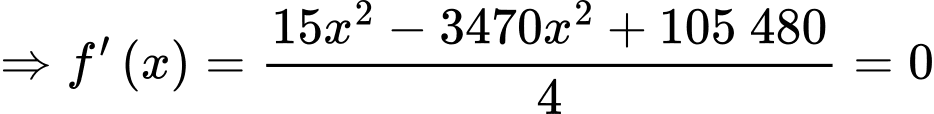
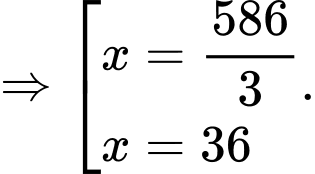
Ta có bảng biến thiên:
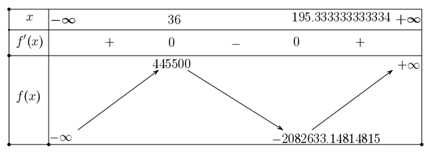
Dựa vào bảng biến thiên ta thấy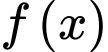 đạt giá trị lớn nhất tại
đạt giá trị lớn nhất tại 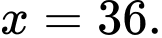
Gọi
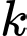 là số lần tăng thời gian làm việc lên 2 giờ một tuần.
là số lần tăng thời gian làm việc lên 2 giờ một tuần.
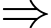 Thời gian làm việc trong 1 tuần của 1 công nhân là
Thời gian làm việc trong 1 tuần của 1 công nhân là 
Số công nhân làm việc trong 1 tuần sau khi tăng thời gian làm việc là
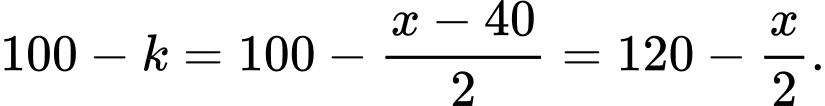
Năng suất lao động trong 1 giờ của 1 công nhân sau khi tăng thời gian làm việc là
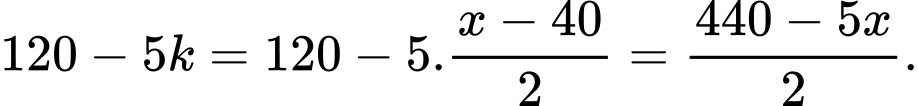
Số sản phẩm thu được mỗi tuần là

Xét hàm số
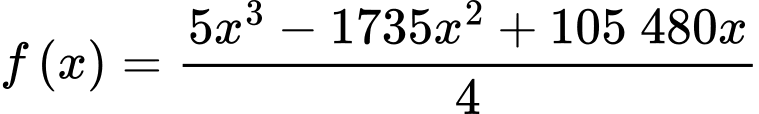
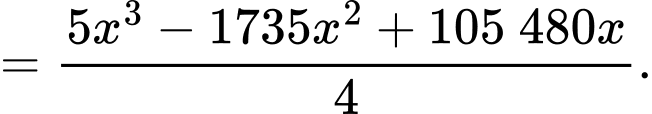
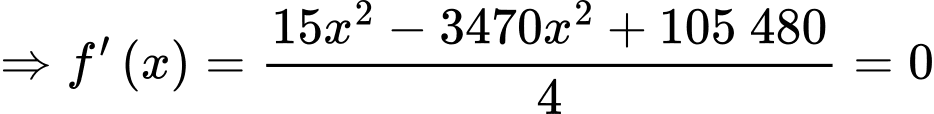
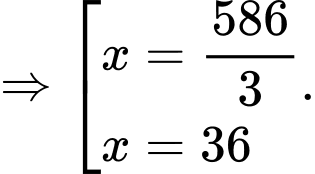
Ta có bảng biến thiên:

Dựa vào bảng biến thiên ta thấy
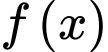 đạt giá trị lớn nhất tại
đạt giá trị lớn nhất tại 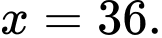
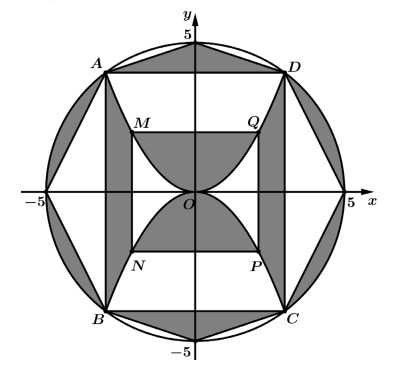
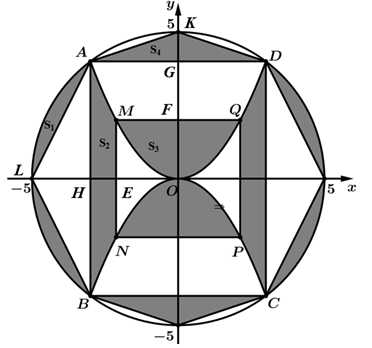
Câu 21 [695183]: Nhà thiết kế muốn trang trí một biển quảng cáo có dạng hình tròn tâm  bán kính
bán kính  phía trong được trang trí bởi hai hình chữ nhật
phía trong được trang trí bởi hai hình chữ nhật 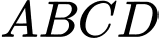 và
và 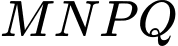 có độ dài cạnh là
có độ dài cạnh là 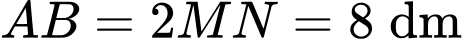 và hai đường parabol đối xứng nhau chung đỉnh
và hai đường parabol đối xứng nhau chung đỉnh  trong đó hình chữ nhật
trong đó hình chữ nhật 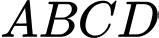 nội tiếp đường tròn tâm
nội tiếp đường tròn tâm  còn Parabol nằm phía trên trục hoành đi qua các điểm
còn Parabol nằm phía trên trục hoành đi qua các điểm 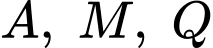 và
và 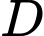 (như hình vẽ). Hỏi diện tích phần tô đậm bằng bao nhiêu deximet vuông (làm tròn kết quả đến hang phần mười).
(như hình vẽ). Hỏi diện tích phần tô đậm bằng bao nhiêu deximet vuông (làm tròn kết quả đến hang phần mười).
 bán kính
bán kính  phía trong được trang trí bởi hai hình chữ nhật
phía trong được trang trí bởi hai hình chữ nhật 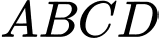 và
và 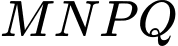 có độ dài cạnh là
có độ dài cạnh là 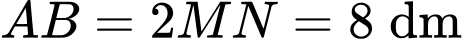 và hai đường parabol đối xứng nhau chung đỉnh
và hai đường parabol đối xứng nhau chung đỉnh  trong đó hình chữ nhật
trong đó hình chữ nhật 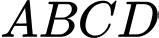 nội tiếp đường tròn tâm
nội tiếp đường tròn tâm  còn Parabol nằm phía trên trục hoành đi qua các điểm
còn Parabol nằm phía trên trục hoành đi qua các điểm 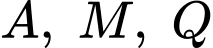 và
và 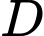 (như hình vẽ). Hỏi diện tích phần tô đậm bằng bao nhiêu deximet vuông (làm tròn kết quả đến hang phần mười).
(như hình vẽ). Hỏi diện tích phần tô đậm bằng bao nhiêu deximet vuông (làm tròn kết quả đến hang phần mười).
Điền đáp án: 34,0.
Gọi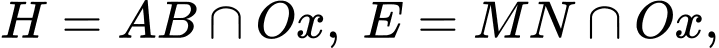
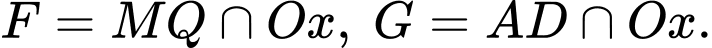
Phương trình hình tròn tâm bán kính
bán kính 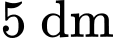 là
là 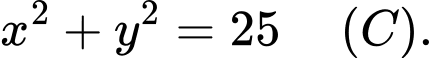
Vì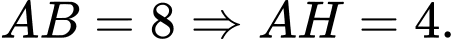
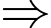 Tung độ của điểm
Tung độ của điểm 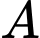 là 4.
là 4.
Thay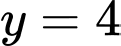 vào phương trình đường tròn
vào phương trình đường tròn  ta được:
ta được:
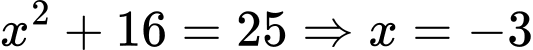
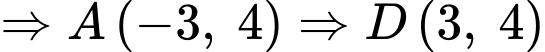 (do
(do 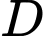 đối xứng với
đối xứng với 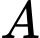 qua
qua 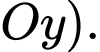
Gọi phương trình parabol đi qua các điểm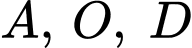 có dạng
có dạng 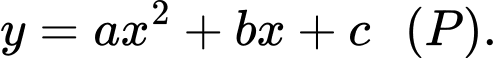
Thay tọa độ của các điểm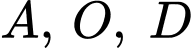 vào phương trình parabol
vào phương trình parabol 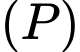 ta được hệ phương trình sau:
ta được hệ phương trình sau: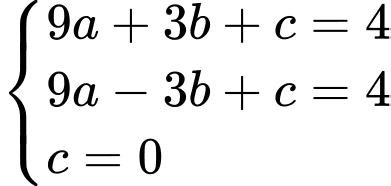
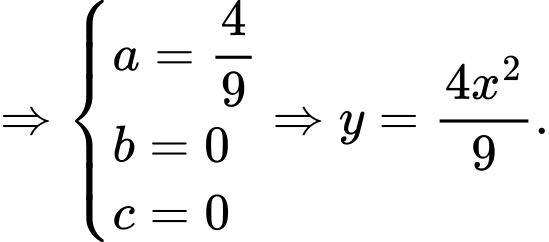
Vì
 Tung độ của điểm
Tung độ của điểm 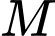 là 2.
là 2.
Thay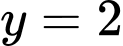 vào phương trình parabol
vào phương trình parabol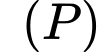 ta được:
ta được: 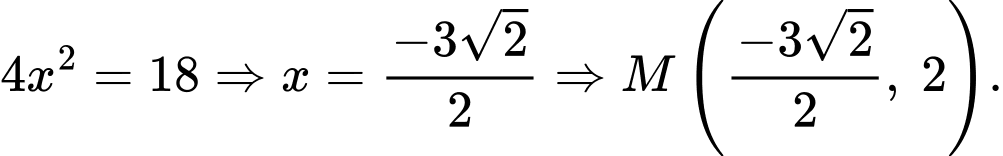
Phương trình của đường tròn tâm bán kính
bán kính 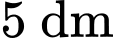 trong góc phần tư thứ II là
trong góc phần tư thứ II là 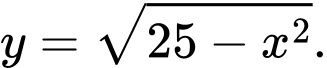 Ta ký hiệu:
Ta ký hiệu:
Diện tích giới hạn bởi đường tròn tâm và đoạn
và đoạn 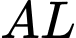 là
là 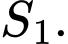
Diện tích giới hạn bởi parabol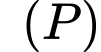 , đường thẳng
, đường thẳng 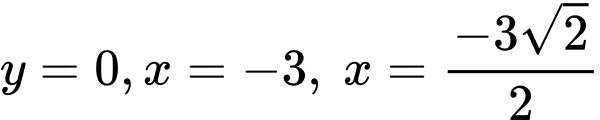 là
là 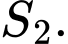
Diện tích giới hạn bởi parabol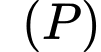 , đoạn
, đoạn 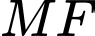 , đường thẳng
, đường thẳng 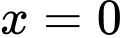 là
là 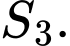
Diện tích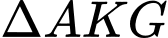 là
là 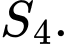
Ta có:
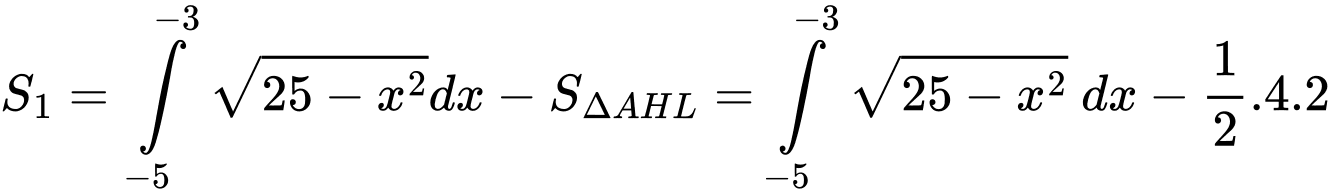
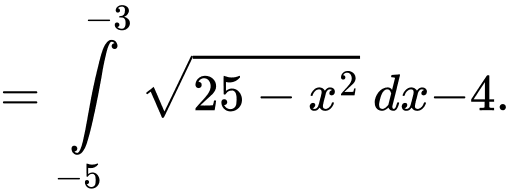
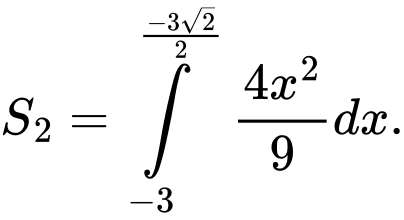
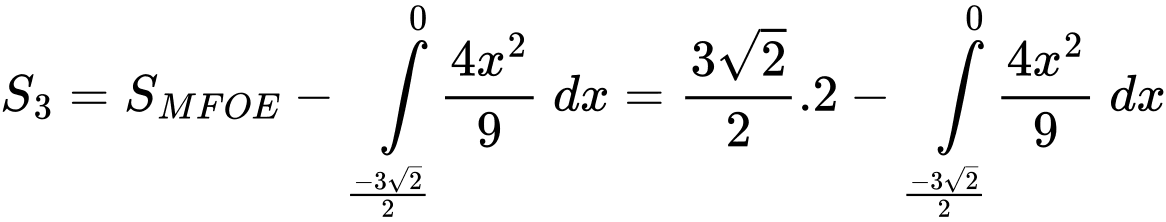
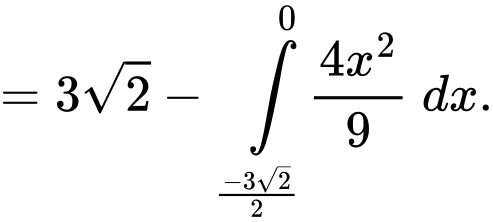
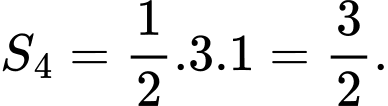
Ta bấm máy tính thì được diện tích phần tô đậm là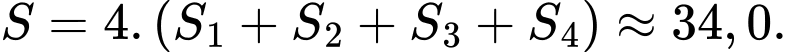

Gọi
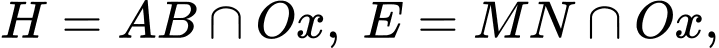
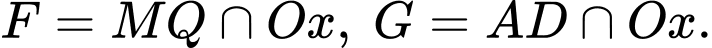
Phương trình hình tròn tâm
 bán kính
bán kính 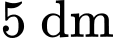 là
là 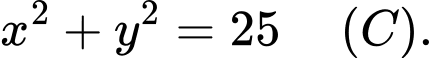
Vì
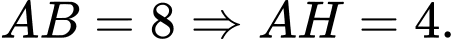
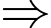 Tung độ của điểm
Tung độ của điểm 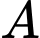 là 4.
là 4.Thay
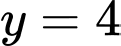 vào phương trình đường tròn
vào phương trình đường tròn  ta được:
ta được: 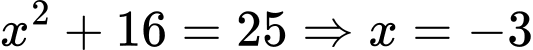
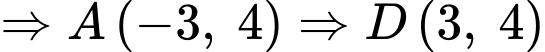 (do
(do 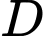 đối xứng với
đối xứng với 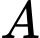 qua
qua 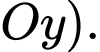
Gọi phương trình parabol đi qua các điểm
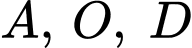 có dạng
có dạng 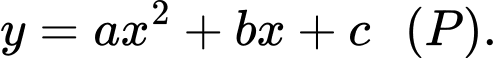
Thay tọa độ của các điểm
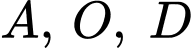 vào phương trình parabol
vào phương trình parabol 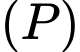 ta được hệ phương trình sau:
ta được hệ phương trình sau: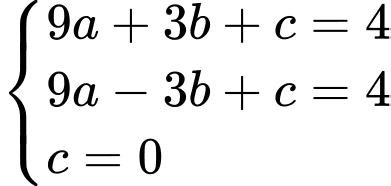
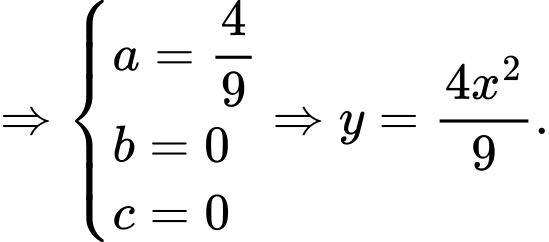
Vì

 Tung độ của điểm
Tung độ của điểm 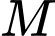 là 2.
là 2.Thay
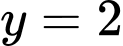 vào phương trình parabol
vào phương trình parabol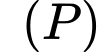 ta được:
ta được: 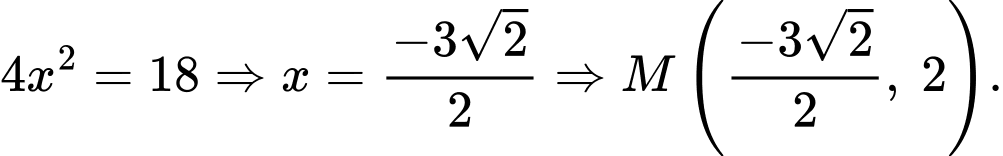
Phương trình của đường tròn tâm
 bán kính
bán kính 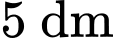 trong góc phần tư thứ II là
trong góc phần tư thứ II là 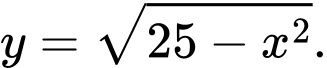 Ta ký hiệu:
Ta ký hiệu: Diện tích giới hạn bởi đường tròn tâm
 và đoạn
và đoạn 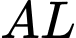 là
là 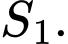
Diện tích giới hạn bởi parabol
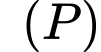 , đường thẳng
, đường thẳng 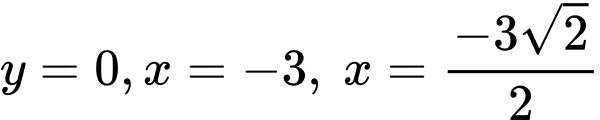 là
là 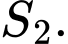
Diện tích giới hạn bởi parabol
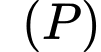 , đoạn
, đoạn 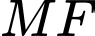 , đường thẳng
, đường thẳng 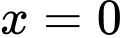 là
là 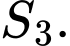
Diện tích
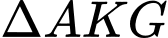 là
là 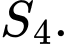
Ta có:
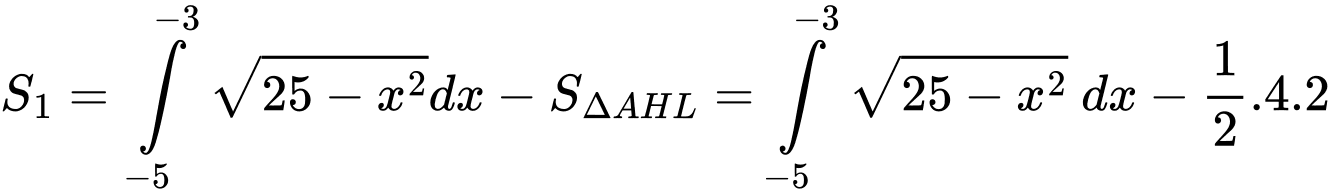
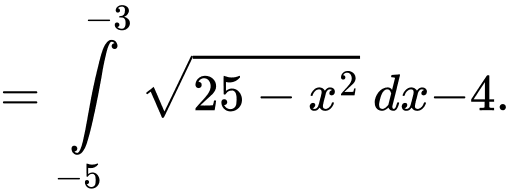
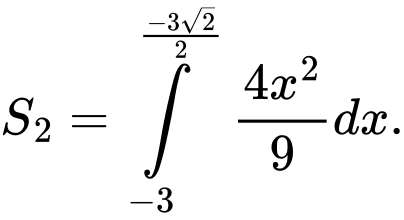
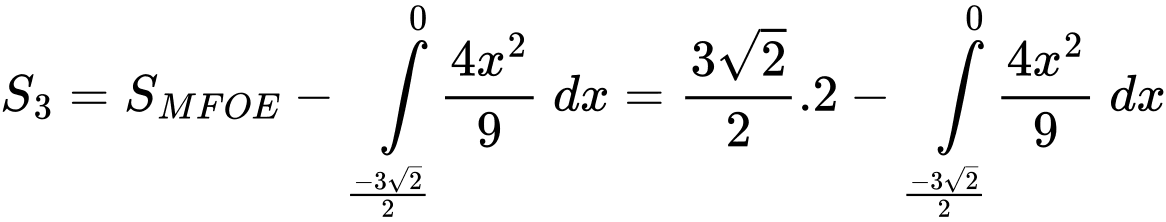
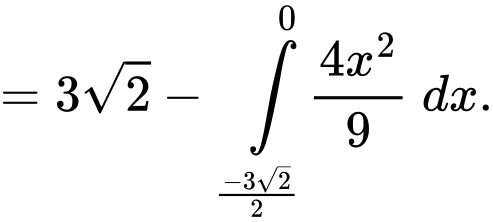
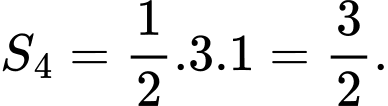
Ta bấm máy tính thì được diện tích phần tô đậm là
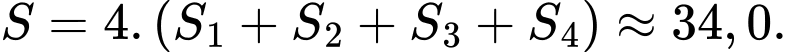
Câu 22 [695184]: Trong không gian với hệ tọa độ 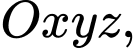 cho hai mặt cầu
cho hai mặt cầu 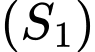 và
và 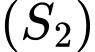 có phương trình lần lượt là
có phương trình lần lượt là 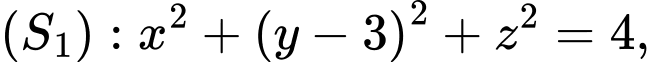
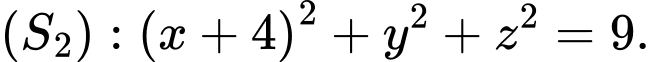 Mặt cầu
Mặt cầu 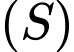 có bán kính bằng 1, tâm I và tiếp xúc ngoài với cả hai mặt cầu
có bán kính bằng 1, tâm I và tiếp xúc ngoài với cả hai mặt cầu 
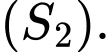 Khoảng cách từ gốc tọa độ O đến điểm I lớn nhất bằng bao nhiêu?
Khoảng cách từ gốc tọa độ O đến điểm I lớn nhất bằng bao nhiêu?
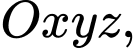 cho hai mặt cầu
cho hai mặt cầu 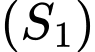 và
và 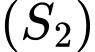 có phương trình lần lượt là
có phương trình lần lượt là 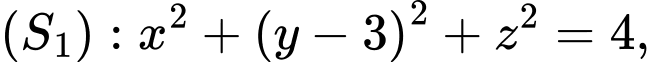
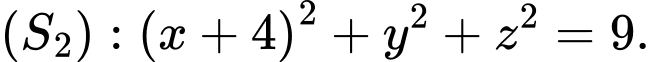 Mặt cầu
Mặt cầu 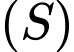 có bán kính bằng 1, tâm I và tiếp xúc ngoài với cả hai mặt cầu
có bán kính bằng 1, tâm I và tiếp xúc ngoài với cả hai mặt cầu 
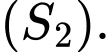 Khoảng cách từ gốc tọa độ O đến điểm I lớn nhất bằng bao nhiêu?
Khoảng cách từ gốc tọa độ O đến điểm I lớn nhất bằng bao nhiêu?
Điền đáp án: 4,8.
Gọi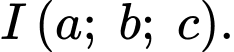
Ta có: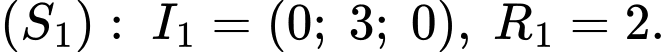
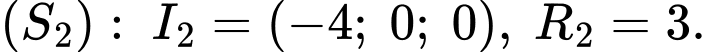
Vì mặt cầu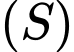 có bán kính bằng 1, tâm
có bán kính bằng 1, tâm 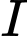 và tiếp xúc ngoài với cả hai mặt cầu
và tiếp xúc ngoài với cả hai mặt cầu 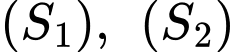 nên ta có:
nên ta có:
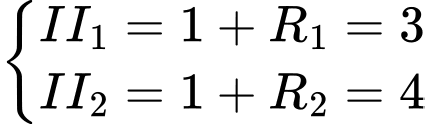
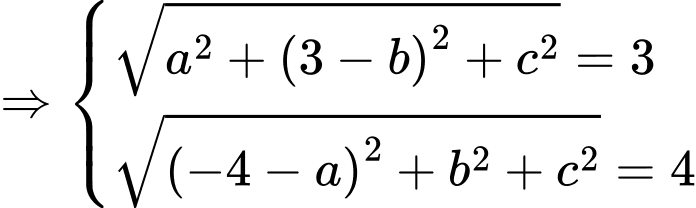
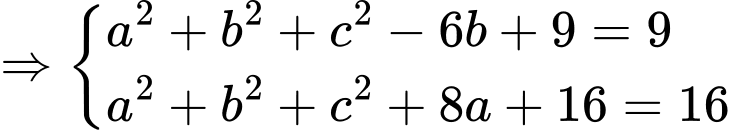
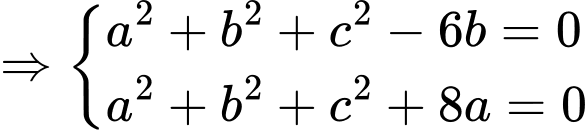
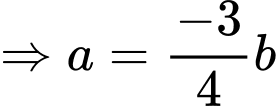
Thay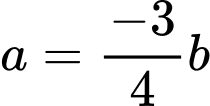 vào
vào 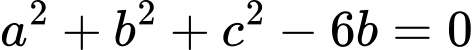 ta được:
ta được:
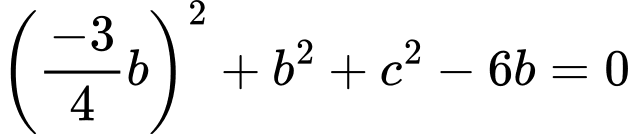
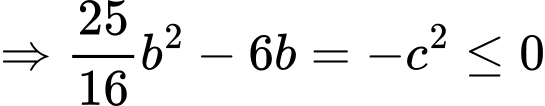
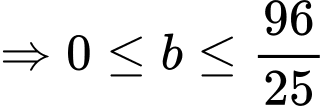
Khoảng cách từ gốc tọa độ đến điểm
đến điểm 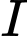 là
là
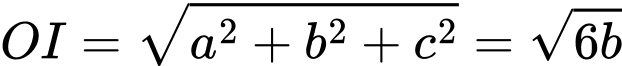
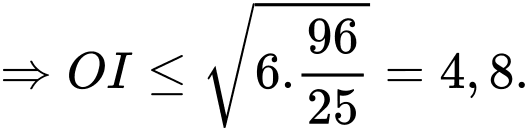
Gọi
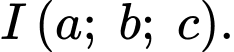
Ta có:
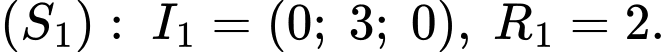
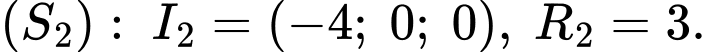
Vì mặt cầu
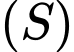 có bán kính bằng 1, tâm
có bán kính bằng 1, tâm 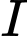 và tiếp xúc ngoài với cả hai mặt cầu
và tiếp xúc ngoài với cả hai mặt cầu 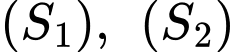 nên ta có:
nên ta có:
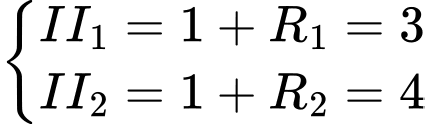
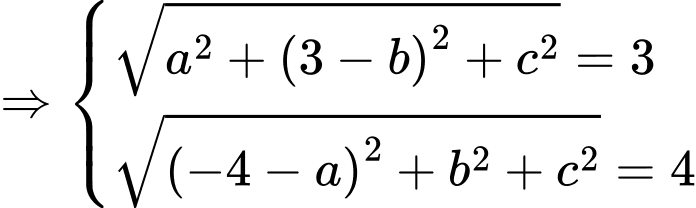
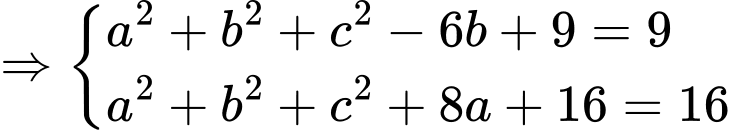
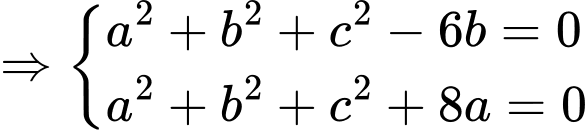
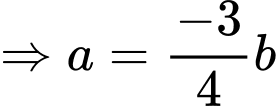
Thay
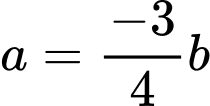 vào
vào 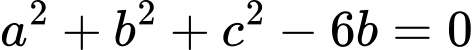 ta được:
ta được:
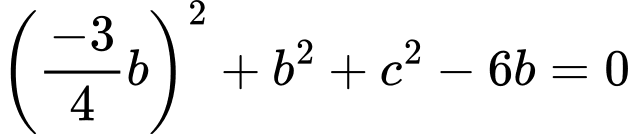
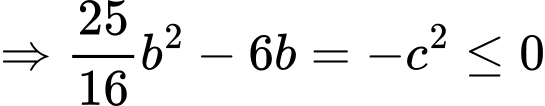
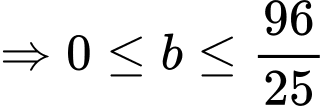
Khoảng cách từ gốc tọa độ
 đến điểm
đến điểm  là
là