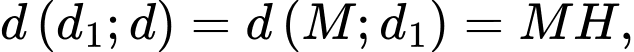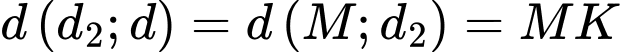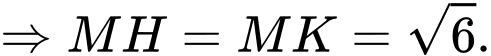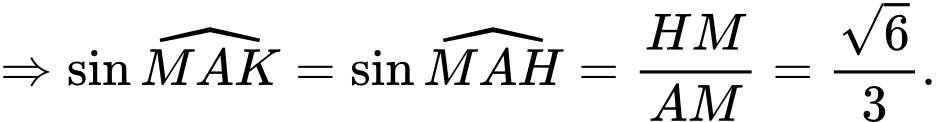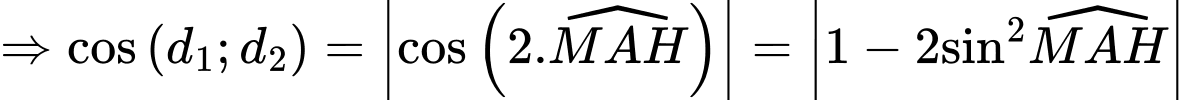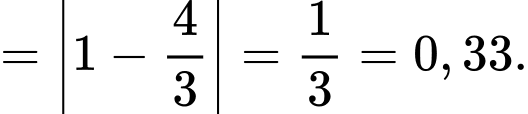PHẦN I. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Câu 1 [255816]: Cho hàm số 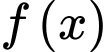 có bảng biến thiên như sau:
có bảng biến thiên như sau:
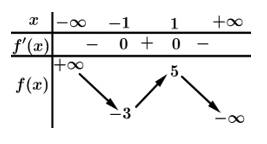
Hàm số đã cho đồng biến trên khoảng nào trong các khoảng dưới đây?
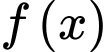 có bảng biến thiên như sau:
có bảng biến thiên như sau:
Hàm số đã cho đồng biến trên khoảng nào trong các khoảng dưới đây?
A, 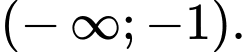
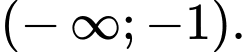
B, 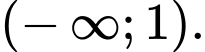
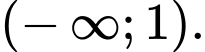
C, 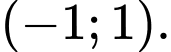
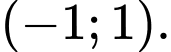
D, 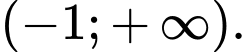
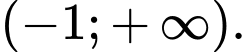
Chọn đáp án C.
Hàm số đồng biến trên khoảng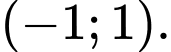 Đáp án: C
Đáp án: C
Hàm số đồng biến trên khoảng
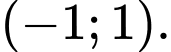 Đáp án: C
Đáp án: C
Câu 2 [695284]: Cho khối chóp và khối lăng trụ có diện tích đáy, chiều cao tương ứng bằng nhau và có thể tích lần lượt là  Tỉ số
Tỉ số 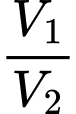 bằng
bằng
 Tỉ số
Tỉ số 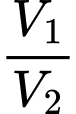 bằng
bằng A, 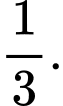
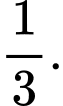
B, 
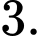
C, 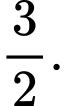
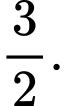
D, 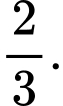
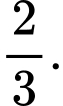
Chọn đáp án A.
Ta có: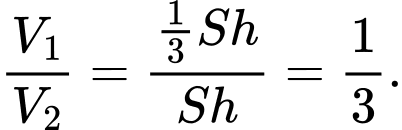 Đáp án: A
Đáp án: A
Ta có:
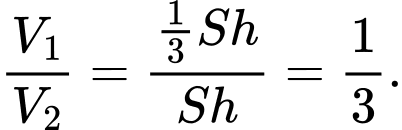 Đáp án: A
Đáp án: A
Câu 3 [695285]: Cho 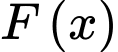 là một nguyên hàm của hàm số
là một nguyên hàm của hàm số 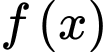 trên
trên 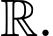 Khẳng định nào sau đây đúng?
Khẳng định nào sau đây đúng?
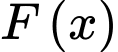 là một nguyên hàm của hàm số
là một nguyên hàm của hàm số 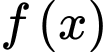 trên
trên  Khẳng định nào sau đây đúng?
Khẳng định nào sau đây đúng? A, 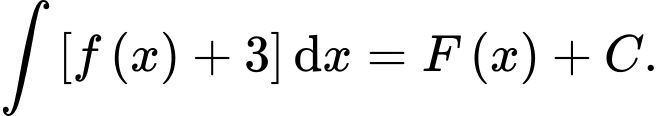
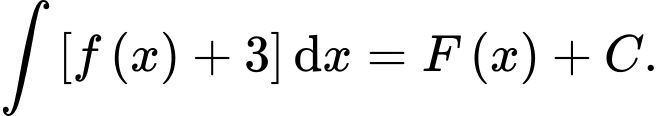
B, 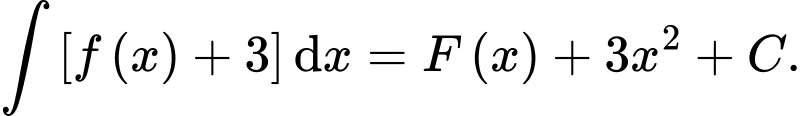
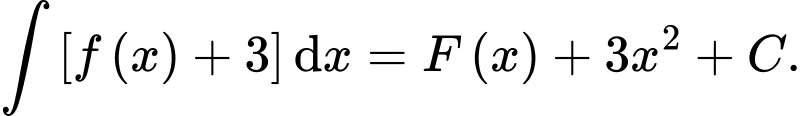
C, 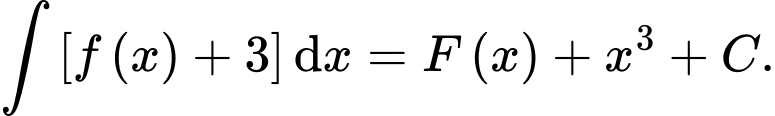
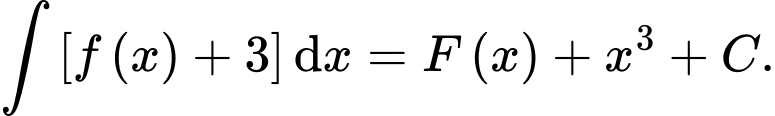
D, 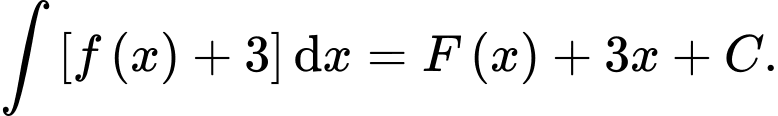
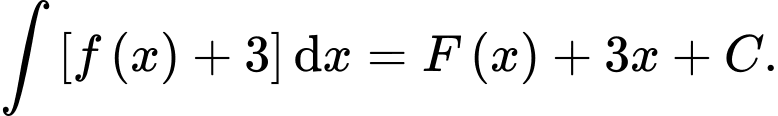
Chọn đáp án D.
Ta có: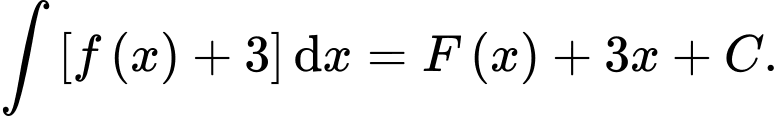 Đáp án: D
Đáp án: D
Ta có:
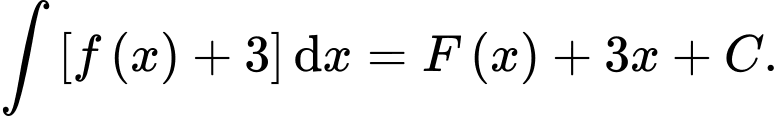 Đáp án: D
Đáp án: D
Câu 4 [695286]: Trong không gian 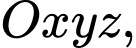 mặt phẳng song song với mặt phẳng
mặt phẳng song song với mặt phẳng 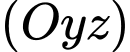 và đi qua điểm
và đi qua điểm 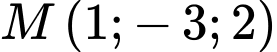 có phương trình là
có phương trình là
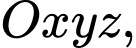 mặt phẳng song song với mặt phẳng
mặt phẳng song song với mặt phẳng 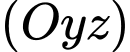 và đi qua điểm
và đi qua điểm 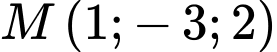 có phương trình là
có phương trình là A, 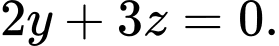
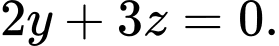
B, 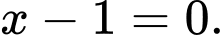
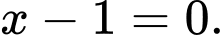
C, 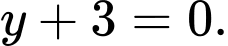
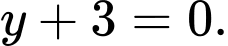
D, 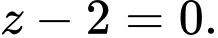
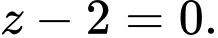
Chọn đáp án B.
Mặt phẳng song song với mặt phẳng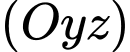 có phương trình dạng
có phương trình dạng 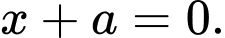
Mặt phẳng này đi qua điểm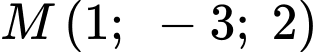 nên
nên 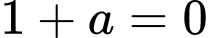
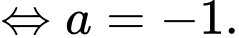
Vậy mặt phẳng song song với mặt phẳng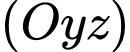 và đi qua điểm
và đi qua điểm 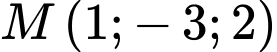 có phương trình là
có phương trình là 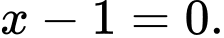 Đáp án: B
Đáp án: B
Mặt phẳng song song với mặt phẳng
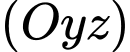 có phương trình dạng
có phương trình dạng 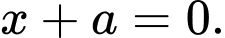
Mặt phẳng này đi qua điểm
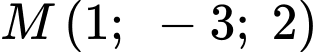 nên
nên 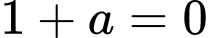
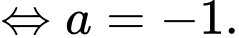
Vậy mặt phẳng song song với mặt phẳng
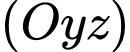 và đi qua điểm
và đi qua điểm 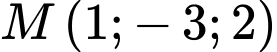 có phương trình là
có phương trình là 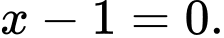 Đáp án: B
Đáp án: B
Câu 5 [695287]: Đạo hàm của hàm số 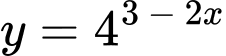 là
là
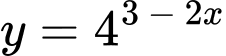 là
là A, 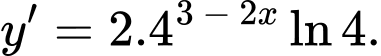
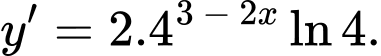
B, 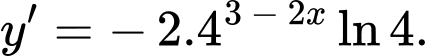
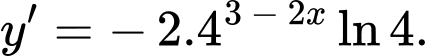
C, 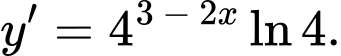
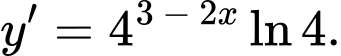
D, 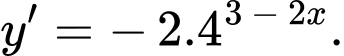
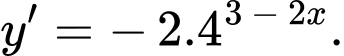
Chọn đáp án B.
Đạo hàm của hàm số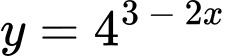 là
là 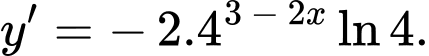 Đáp án: B
Đáp án: B
Đạo hàm của hàm số
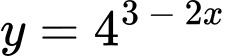 là
là 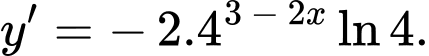 Đáp án: B
Đáp án: B
Câu 6 [695288]: Trong không gian cho hai vectơ 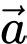 và
và 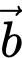 khác
khác 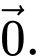 Tích vô hướng của hai vectơ
Tích vô hướng của hai vectơ 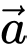 và
và 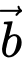 được tính bằng công thức nào sau đây?
được tính bằng công thức nào sau đây?
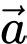 và
và 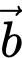 khác
khác 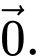 Tích vô hướng của hai vectơ
Tích vô hướng của hai vectơ 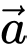 và
và 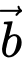 được tính bằng công thức nào sau đây?
được tính bằng công thức nào sau đây? A, 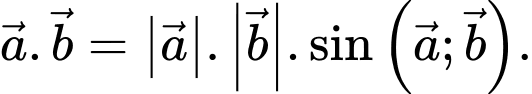
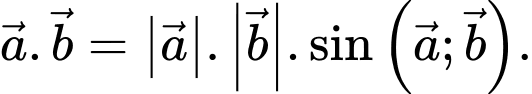
B, 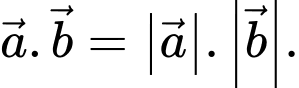
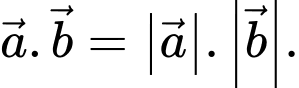
C, 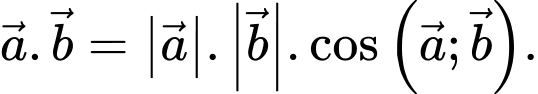
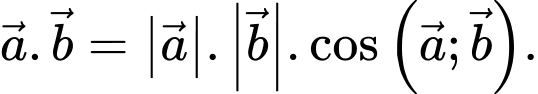
D, 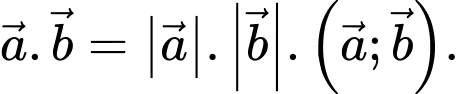
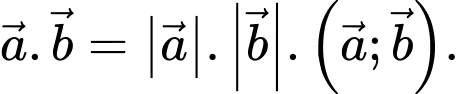
Chọn đáp án C.
Tích vô hướng của hai vectơ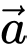 và
và 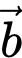 được tính bằng công thức
được tính bằng công thức 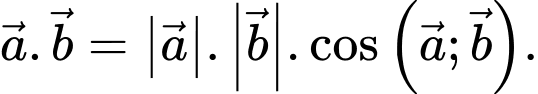 Đáp án: C
Đáp án: C
Tích vô hướng của hai vectơ
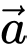 và
và 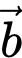 được tính bằng công thức
được tính bằng công thức 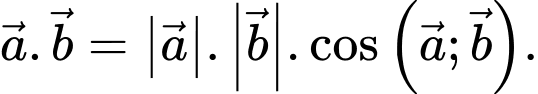 Đáp án: C
Đáp án: C
Câu 7 [348898]: Cho hàm số 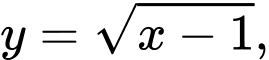 khi đó
khi đó 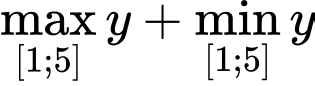 bằng
bằng
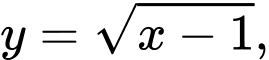 khi đó
khi đó 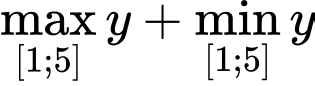 bằng
bằng A, 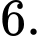
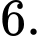
B, 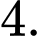
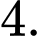
C, 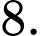
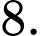
D, 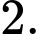
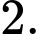
Chọn đáp án D.
Ta có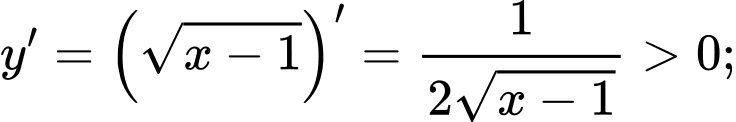
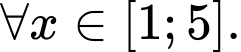
Suy ra hàm số đã cho đồng biến trên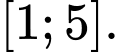
Do đó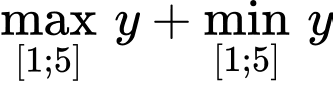
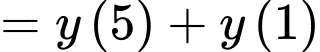
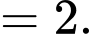 Đáp án: D
Đáp án: D
Ta có
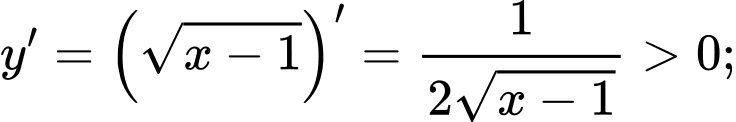
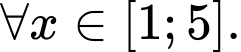
Suy ra hàm số đã cho đồng biến trên
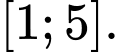
Do đó
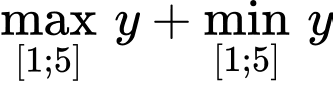
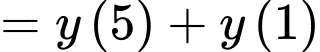
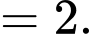 Đáp án: D
Đáp án: D
Câu 8 [695289]: Trong không gian  toạ độ giao điểm của đường thẳng
toạ độ giao điểm của đường thẳng 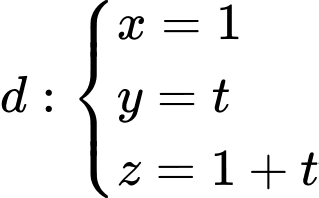 và mặt phẳng
và mặt phẳng 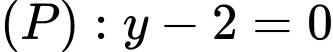 là
là
 toạ độ giao điểm của đường thẳng
toạ độ giao điểm của đường thẳng 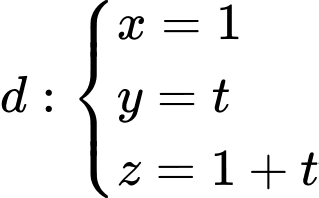 và mặt phẳng
và mặt phẳng 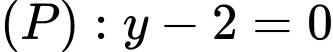 là
là A, điểm 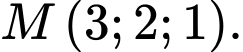
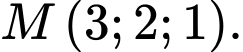
B, điểm 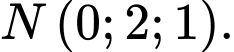
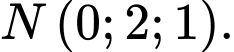
C, điểm 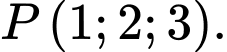
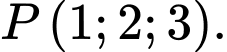
D, điểm 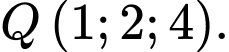
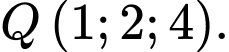
Chọn đáp án C.
Toạ độ giao điểm của đường thẳng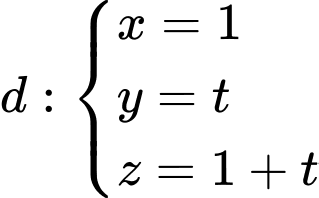 và mặt phẳng
và mặt phẳng 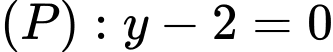 là điểm
là điểm 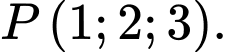 Đáp án: C
Đáp án: C
Toạ độ giao điểm của đường thẳng
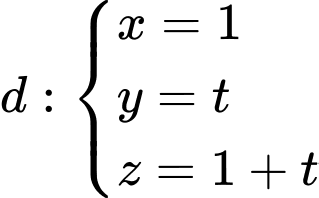 và mặt phẳng
và mặt phẳng 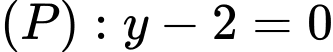 là điểm
là điểm 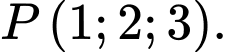 Đáp án: C
Đáp án: C
Câu 9 [695290]: Cho dãy số 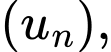 biết
biết 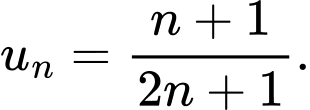 Hỏi
Hỏi 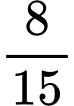 là số hạng thứ mấy của
là số hạng thứ mấy của 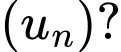
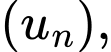 biết
biết 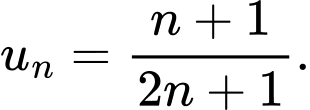 Hỏi
Hỏi 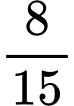 là số hạng thứ mấy của
là số hạng thứ mấy của 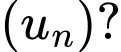
A, 7.
B, 6.
C, 5.
D, 8.
Chọn đáp án A.
Ta có: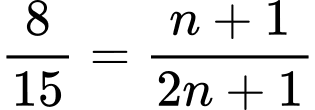
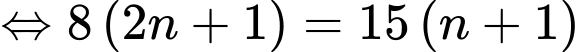
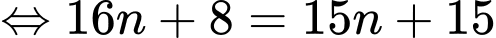
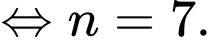
Vậy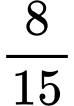 là số hạng thứ 7 của
là số hạng thứ 7 của 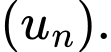 Đáp án: A
Đáp án: A
Ta có:
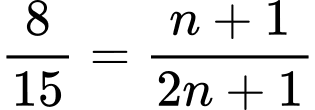
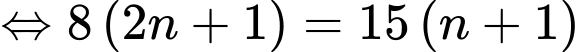
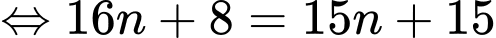
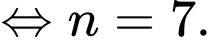
Vậy
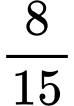 là số hạng thứ 7 của
là số hạng thứ 7 của 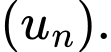 Đáp án: A
Đáp án: A
Câu 10 [695283]: Với 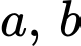 là các số thực tuỳ ý lớn hơn
là các số thực tuỳ ý lớn hơn 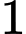 thoả mãn
thoả mãn 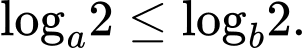 Khẳng định nào sau đây đúng?
Khẳng định nào sau đây đúng?
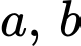 là các số thực tuỳ ý lớn hơn
là các số thực tuỳ ý lớn hơn 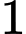 thoả mãn
thoả mãn 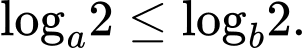 Khẳng định nào sau đây đúng?
Khẳng định nào sau đây đúng? A, 

B, 

C, 

D, 

Chọn đáp án A.
Ta có: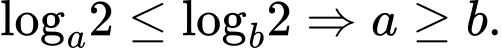 Đáp án: A
Đáp án: A
Ta có:
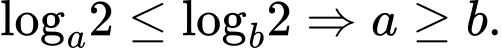 Đáp án: A
Đáp án: A
Câu 11 [695291]: Thời gian trung bình sử dụng ChatGPT trên một ngày của một nhóm học sinh được ghi lại trong bảng dưới đây.
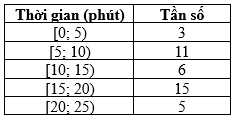
Tính tứ phân vị thứ nhất của mẫu số liệu ghép nhóm trên (làm tròn kết quả đến hàng phần mười; đơn vị phút).

Tính tứ phân vị thứ nhất của mẫu số liệu ghép nhóm trên (làm tròn kết quả đến hàng phần mười; đơn vị phút).
A, 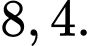
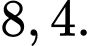
B, 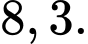
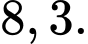
C, 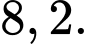
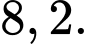
D, 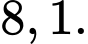
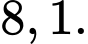
Chọn đáp án C.
Cỡ mẫu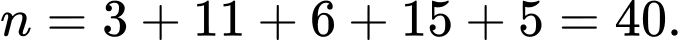
Gọi là mẫu số liệu được sắp xếp theo thứ tự không giảm.
là mẫu số liệu được sắp xếp theo thứ tự không giảm.
Ta có: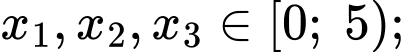
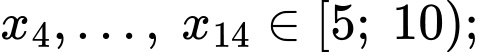
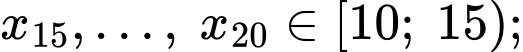
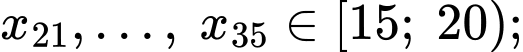
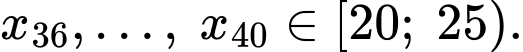
Tứ phân vị thứ nhất của mẫu số liệu gốc là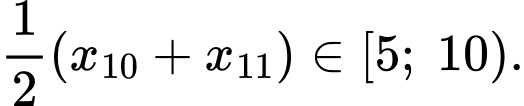 Do đó, tứ phân vị thứ nhất của mẫu số liệu ghép nhóm là:
Do đó, tứ phân vị thứ nhất của mẫu số liệu ghép nhóm là:
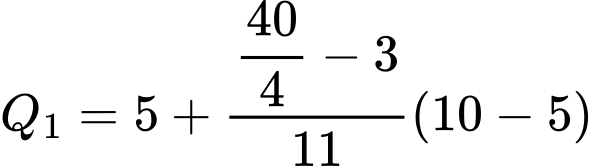
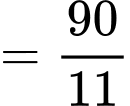
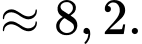 Đáp án: C
Đáp án: C
Cỡ mẫu
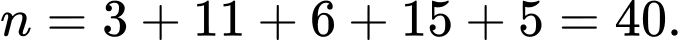
Gọi
 là mẫu số liệu được sắp xếp theo thứ tự không giảm.
là mẫu số liệu được sắp xếp theo thứ tự không giảm.Ta có:
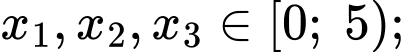
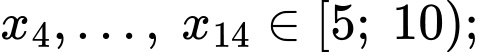
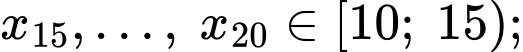
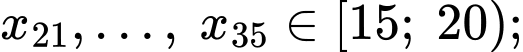
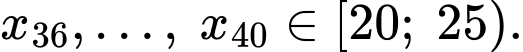
Tứ phân vị thứ nhất của mẫu số liệu gốc là
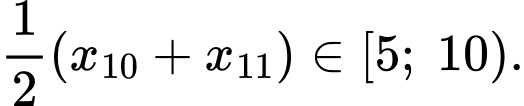 Do đó, tứ phân vị thứ nhất của mẫu số liệu ghép nhóm là:
Do đó, tứ phân vị thứ nhất của mẫu số liệu ghép nhóm là: 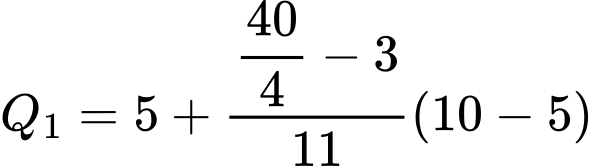
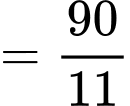
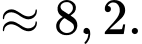 Đáp án: C
Đáp án: C
Câu 12 [348883]: Nếu 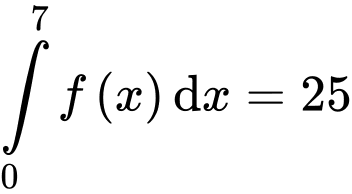 và
và 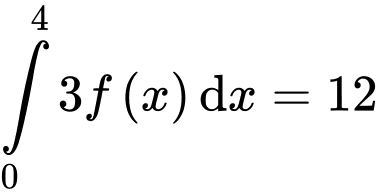 thì
thì 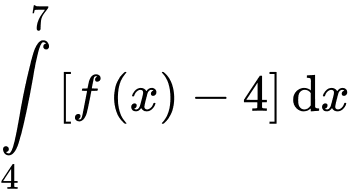 bằng
bằng
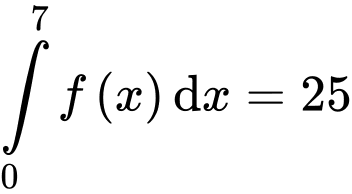 và
và 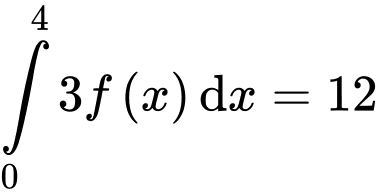 thì
thì 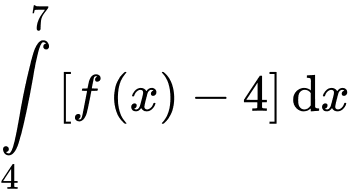 bằng
bằng A, 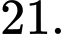
B, 
C, 
D, 
Chọn đáp án D.
Ta có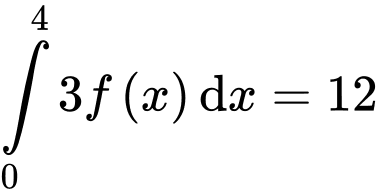
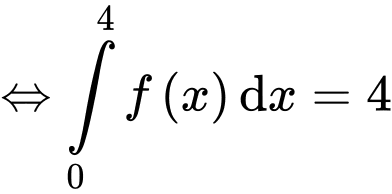
Lại có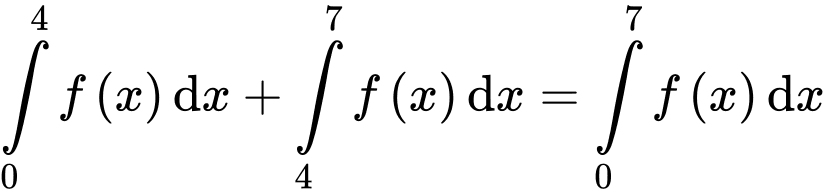
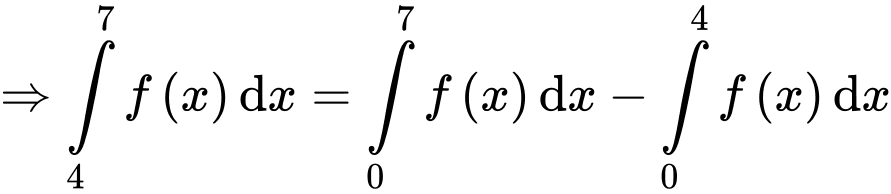
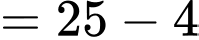
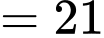
Do đó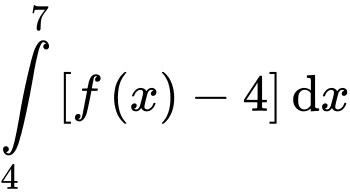
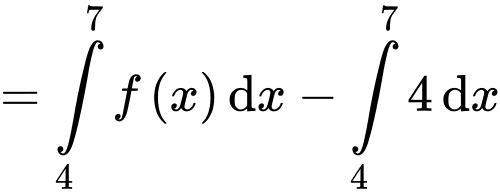

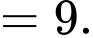 Đáp án: D
Đáp án: D
Ta có
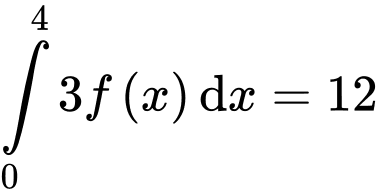
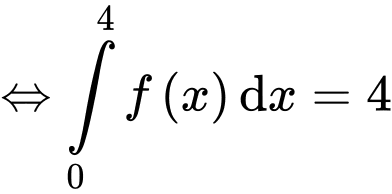
Lại có
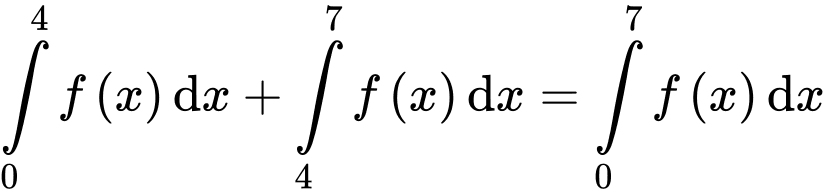
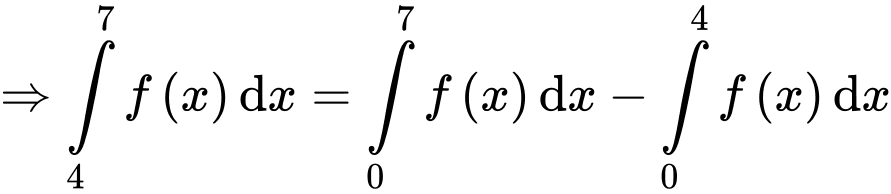
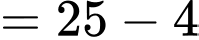
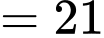
Do đó
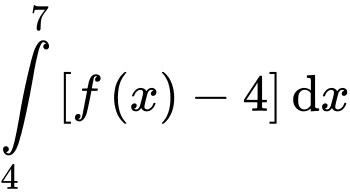
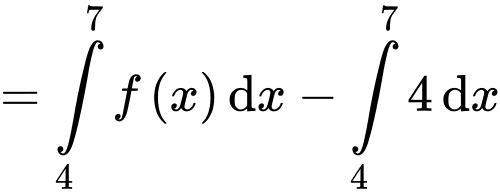

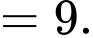 Đáp án: D
Đáp án: D PHẦN II. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Câu 13 [695292]: Cho hình lăng trụ tam giác đều  có
có 
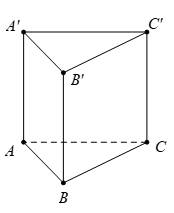
 có
có 

a) Đúng.
Ta có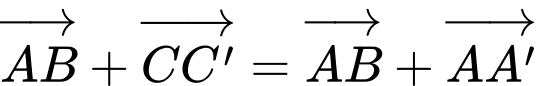
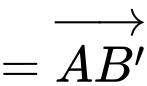 (theo quy tắc hình bình hành)
(theo quy tắc hình bình hành)
Vậy mệnh đề đúng.
b) Sai.
Ta có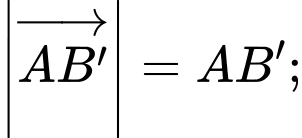
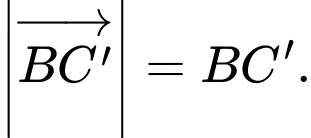
Lại có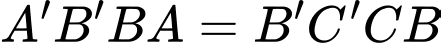 (do lăng trụ đã cho là lăng trụ tam giác đều)
(do lăng trụ đã cho là lăng trụ tam giác đều)
Suy ra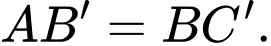
Xét tam giác vuông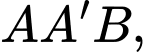 ta có
ta có 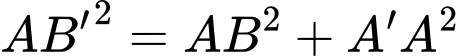 (Áp dụng định lý Pytago)
(Áp dụng định lý Pytago)
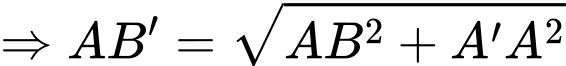
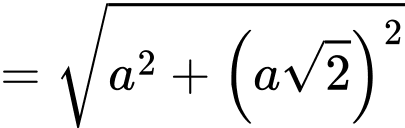
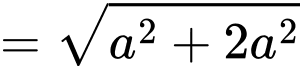
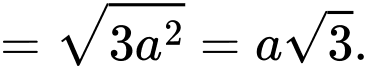
Vậy mệnh đề sai.
c) Sai.
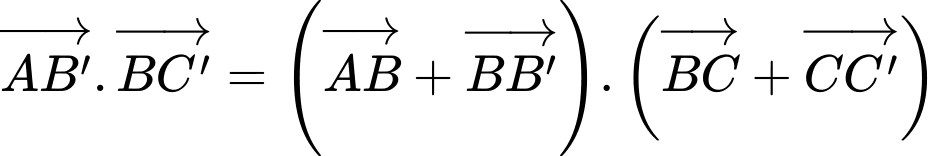
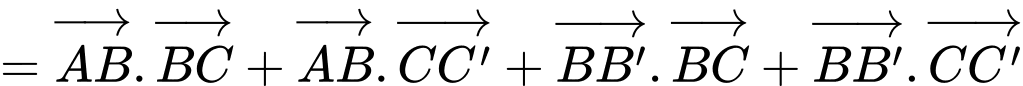
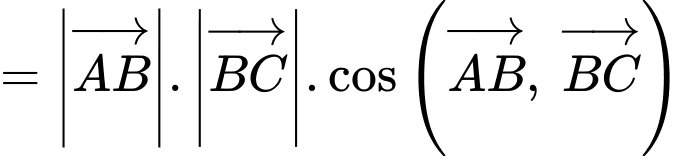
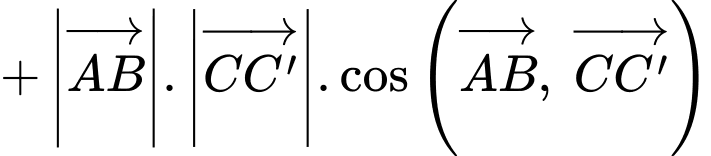
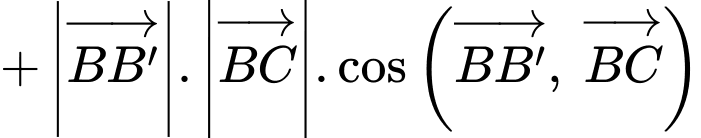
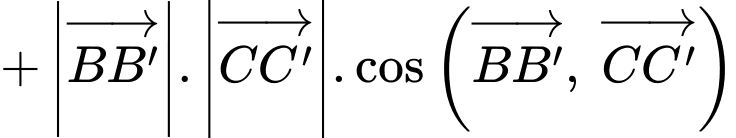
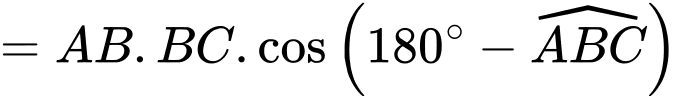
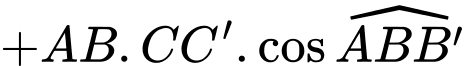
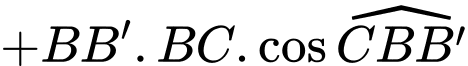
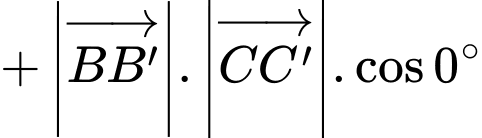

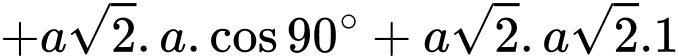
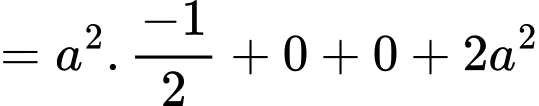
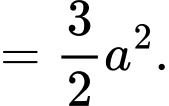
Note: Vì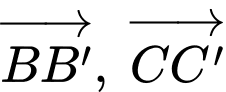 là 2 vectơ cùng phương cùng hướng, mà góc giữa 2 vectơ cùng hướng bằng
là 2 vectơ cùng phương cùng hướng, mà góc giữa 2 vectơ cùng hướng bằng 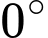 nên
nên 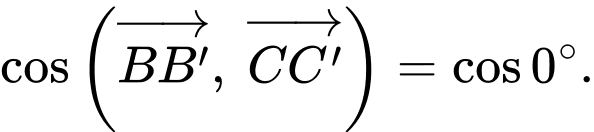
Vậy mệnh đề sai.
d) Đúng.
Áp dụng công thức tích vô hướng của 2 vectơ, ta có
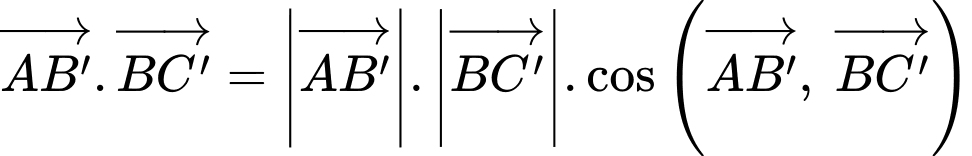
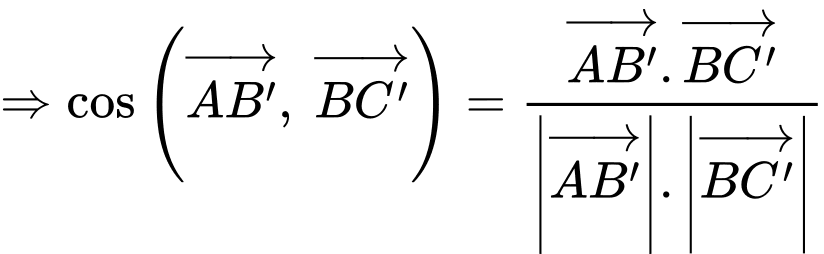
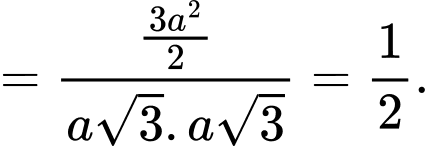
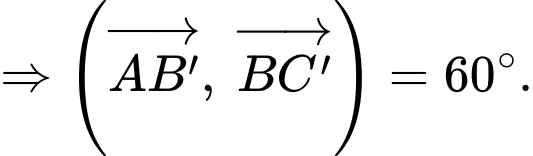
Vậy mệnh đề đúng.
Ta có
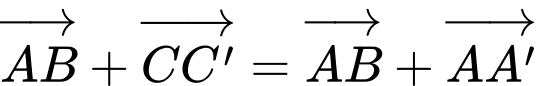
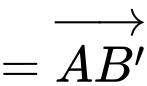 (theo quy tắc hình bình hành)
(theo quy tắc hình bình hành)Vậy mệnh đề đúng.
b) Sai.
Ta có
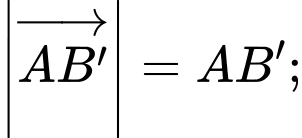
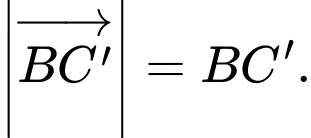
Lại có
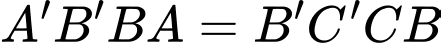 (do lăng trụ đã cho là lăng trụ tam giác đều)
(do lăng trụ đã cho là lăng trụ tam giác đều) Suy ra
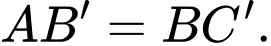
Xét tam giác vuông
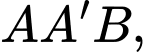 ta có
ta có 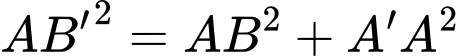 (Áp dụng định lý Pytago)
(Áp dụng định lý Pytago)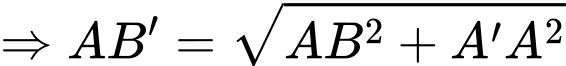
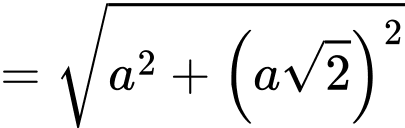
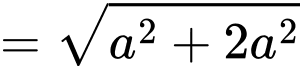
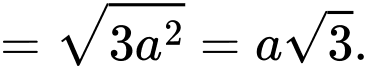
Vậy mệnh đề sai.
c) Sai.
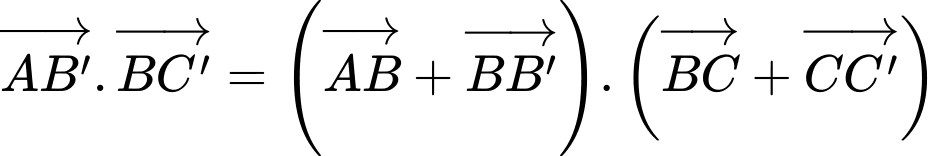
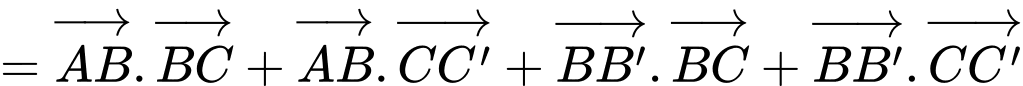
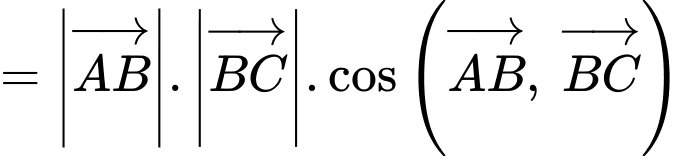
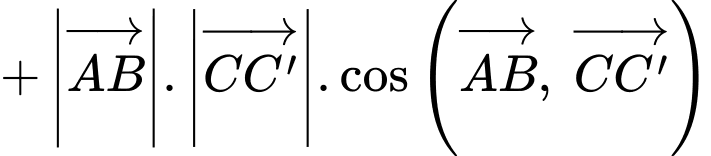
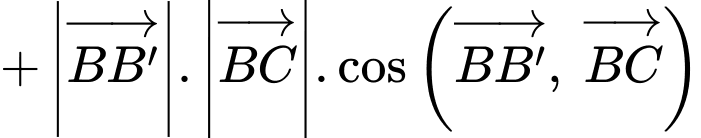
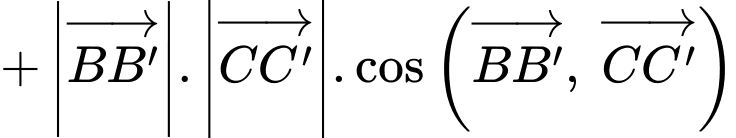
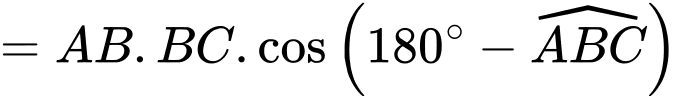
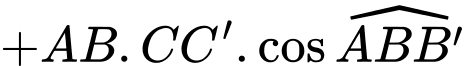
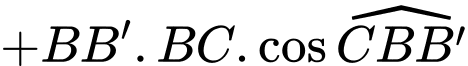
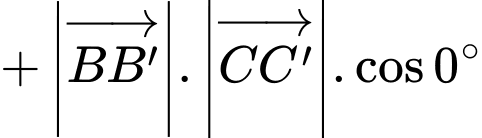

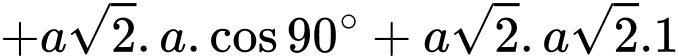
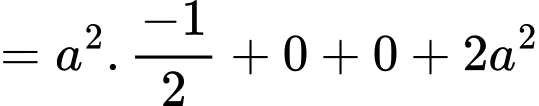
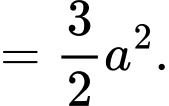
Note: Vì
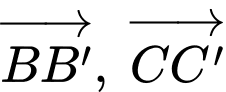 là 2 vectơ cùng phương cùng hướng, mà góc giữa 2 vectơ cùng hướng bằng
là 2 vectơ cùng phương cùng hướng, mà góc giữa 2 vectơ cùng hướng bằng 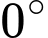 nên
nên 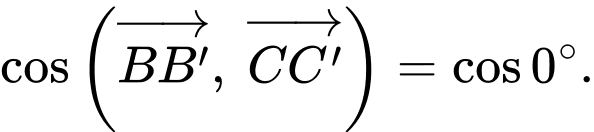
Vậy mệnh đề sai.
d) Đúng.
Áp dụng công thức tích vô hướng của 2 vectơ, ta có
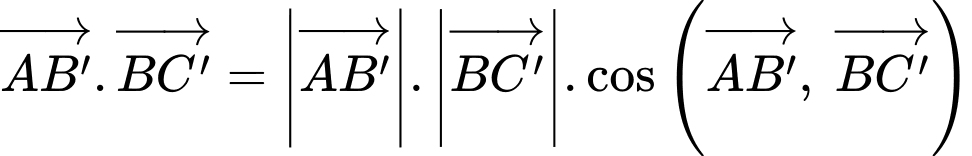
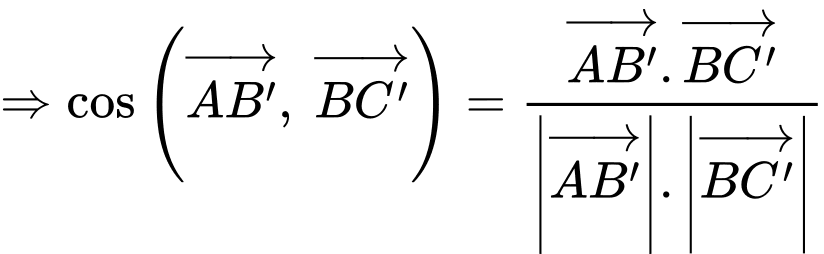
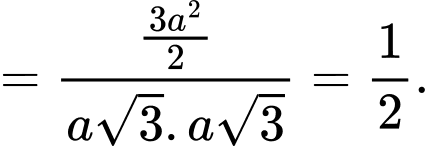
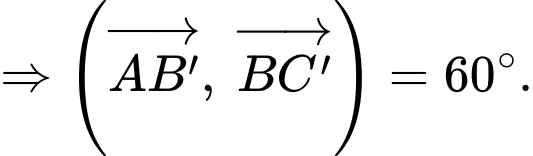
Vậy mệnh đề đúng.
Câu 14 [702324]: Trong 1 lô hàng 10 sản phẩm có 2 sản phẩm xấu còn lại là các sản phẩm tốt, chọn ngẫu nhiên không hoàn lại mỗi lần một sản phẩm để phát hiện ra 2 sản phẩm xấu, khi nào chọn được sản phẩm xấu thứ 2 thì dừng lại.
a) Sai.
Xác suất lần thứ nhất chọn được một sản phẩm xấu là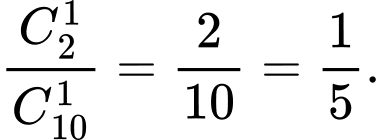
b) Sai.
Xác suất dừng lại ở lần chọn thứ hai (tức lần 1 và lần 2 đều chọn được sản phẩm xấu) là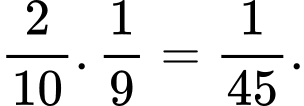
c) Sai.
Gọi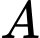 là biến cố “Dừng lại ở lần chọn thứ 3”.
là biến cố “Dừng lại ở lần chọn thứ 3”.
Để dừng lại ở lần thứ 3, có 2 trường hợp xảy ra:
+) Lần 1 lấy được sản phẩm xấu, lần 2 và lần 3 lấy được sản phẩm tốt;
+) Lần 2 lấy được sản phẩm xấu, lần 1 và lần 3 lấy được sản phẩm tốt;
Khi đó, xác suất dừng lại ở lần chọn thứ 3 là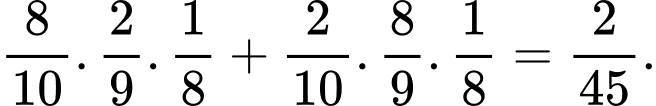
d) Đúng.
Gọi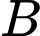 là biến cố “Lần đầu chọn được sản phẩm xấu”
là biến cố “Lần đầu chọn được sản phẩm xấu”
Ta có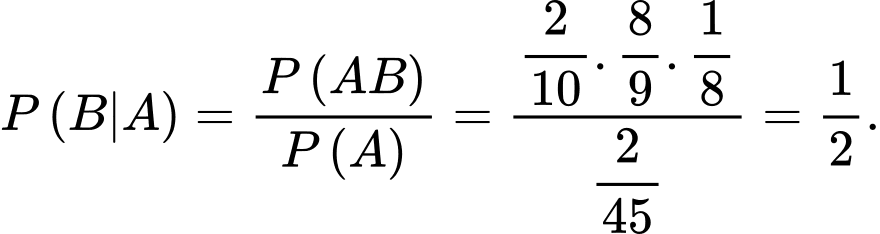
Xác suất lần thứ nhất chọn được một sản phẩm xấu là
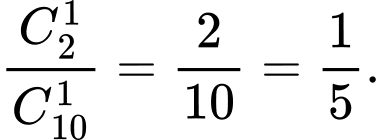
b) Sai.
Xác suất dừng lại ở lần chọn thứ hai (tức lần 1 và lần 2 đều chọn được sản phẩm xấu) là
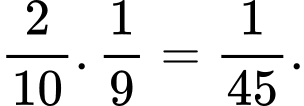
c) Sai.
Gọi
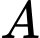 là biến cố “Dừng lại ở lần chọn thứ 3”.
là biến cố “Dừng lại ở lần chọn thứ 3”.Để dừng lại ở lần thứ 3, có 2 trường hợp xảy ra:
+) Lần 1 lấy được sản phẩm xấu, lần 2 và lần 3 lấy được sản phẩm tốt;
+) Lần 2 lấy được sản phẩm xấu, lần 1 và lần 3 lấy được sản phẩm tốt;
Khi đó, xác suất dừng lại ở lần chọn thứ 3 là
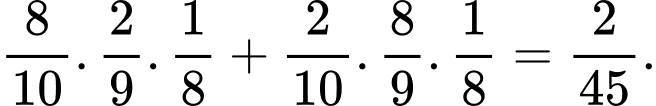
d) Đúng.
Gọi
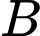 là biến cố “Lần đầu chọn được sản phẩm xấu”
là biến cố “Lần đầu chọn được sản phẩm xấu”Ta có
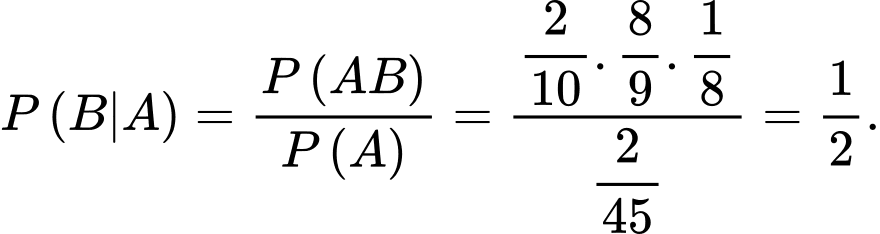
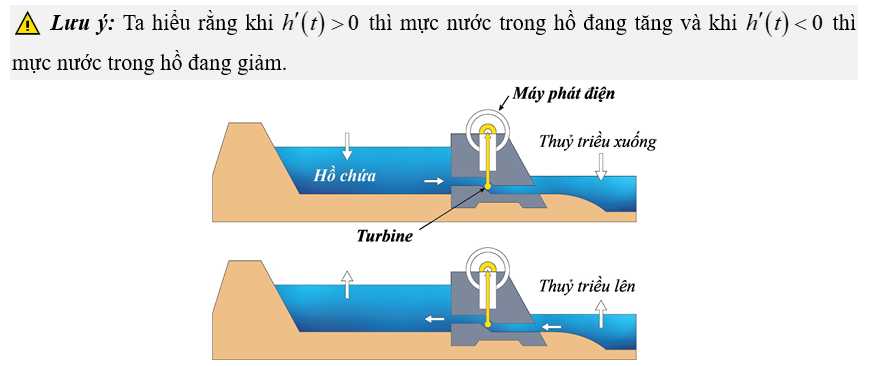
Câu 15 [702879]: Mực nước 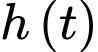 trong hồ chứa của nhà máy điện thuỷ triều thay đổi trong suốt một ngày do nước chảy ra (khi thuỷ triều xuống) và nước chảy vào (khi thuỷ triều lên). Sự thay đổi của mực nước trong hồ chứa được mô phỏng bởi hàm số
trong hồ chứa của nhà máy điện thuỷ triều thay đổi trong suốt một ngày do nước chảy ra (khi thuỷ triều xuống) và nước chảy vào (khi thuỷ triều lên). Sự thay đổi của mực nước trong hồ chứa được mô phỏng bởi hàm số 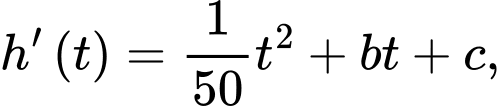 trong đó
trong đó 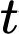 tính bằng giờ
tính bằng giờ 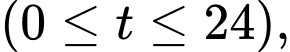
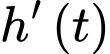 tính bằng mét/ giờ. Tại thời điểm
tính bằng mét/ giờ. Tại thời điểm 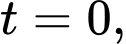 mực nước trong hồ chứa là
mực nước trong hồ chứa là 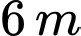 và đang tăng với tốc độ
và đang tăng với tốc độ 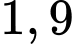 mét/ giờ. Mực nước trong trong hồ chứa lớn nhất lúc
mét/ giờ. Mực nước trong trong hồ chứa lớn nhất lúc 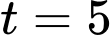 giờ.
giờ.
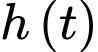 trong hồ chứa của nhà máy điện thuỷ triều thay đổi trong suốt một ngày do nước chảy ra (khi thuỷ triều xuống) và nước chảy vào (khi thuỷ triều lên). Sự thay đổi của mực nước trong hồ chứa được mô phỏng bởi hàm số
trong hồ chứa của nhà máy điện thuỷ triều thay đổi trong suốt một ngày do nước chảy ra (khi thuỷ triều xuống) và nước chảy vào (khi thuỷ triều lên). Sự thay đổi của mực nước trong hồ chứa được mô phỏng bởi hàm số 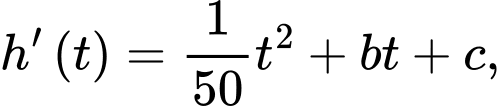 trong đó
trong đó 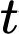 tính bằng giờ
tính bằng giờ 
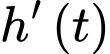 tính bằng mét/ giờ. Tại thời điểm
tính bằng mét/ giờ. Tại thời điểm 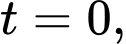 mực nước trong hồ chứa là
mực nước trong hồ chứa là 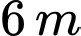 và đang tăng với tốc độ
và đang tăng với tốc độ 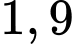 mét/ giờ. Mực nước trong trong hồ chứa lớn nhất lúc
mét/ giờ. Mực nước trong trong hồ chứa lớn nhất lúc 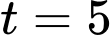 giờ.
giờ.
a) Sai.
Dựa vào giả thiết: tại thời điểm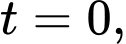 mực nước trong hồ tăng với tốc độ 1,9 mét/giờ. (với
mực nước trong hồ tăng với tốc độ 1,9 mét/giờ. (với 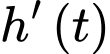 là hàm biểu diễn tốc độ tăng/giảm của mực nước) Ta suy ra
là hàm biểu diễn tốc độ tăng/giảm của mực nước) Ta suy ra 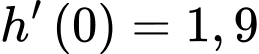
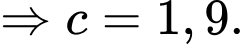
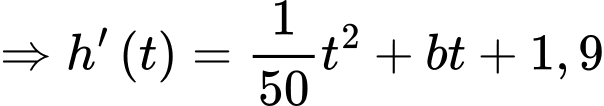
Vậy mệnh đề sai.
b) Đúng.
Dựa vào giả thiết: “Mực nước trong hồ chứa lớn nhất lúc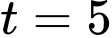 giờ” suy ra
giờ” suy ra 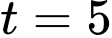 là giá trị cực đại của hàm số (Vì khi xét giá trị lớn nhất của hàm số
là giá trị cực đại của hàm số (Vì khi xét giá trị lớn nhất của hàm số 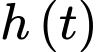 trên đoạn
trên đoạn 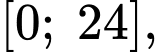 ta cần so sánh giữa các giá trị tại 2 đầu mút và các giá trị cực trị, mà giá trị lớn nhất của hàm số đạt tại
ta cần so sánh giữa các giá trị tại 2 đầu mút và các giá trị cực trị, mà giá trị lớn nhất của hàm số đạt tại 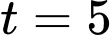 không phải là đầu mút do đó
không phải là đầu mút do đó 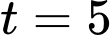 phải là cực trị của hàm số (cụ thể là cực đại)).
phải là cực trị của hàm số (cụ thể là cực đại)).
Suy ra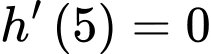
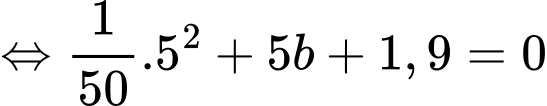
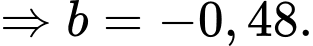
Vậy mệnh đề đúng.
c) Sai.
Để xác định mức nước trong hồ chứa tăng giảm trong các khoảng thời gian nào, ta tìm khoảng đồng biến, nghịch biến của hàm số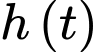 bằng cách khảo sát hàm số
bằng cách khảo sát hàm số 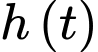 trên đoạn
trên đoạn 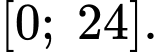
Ta có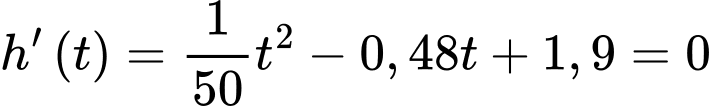
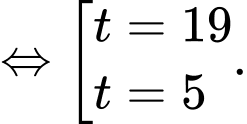
Ta có trục xét dấu sau:

Vậy mực nước trong hồ chứa khoảng thời gian từ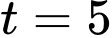 giờ đến
giờ đến 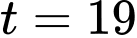 giờ và tăng trong các khoảng thời gian còn lại.
giờ và tăng trong các khoảng thời gian còn lại.
Vậy mệnh đề sai.
d) Đúng.
Ta có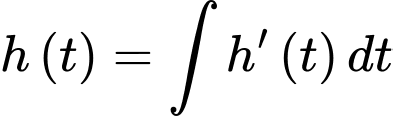
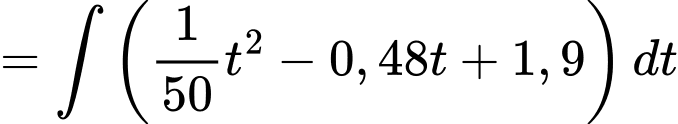
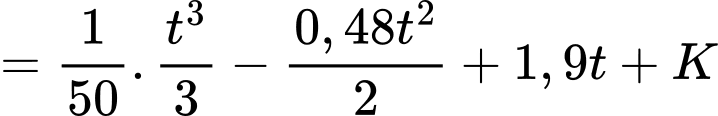
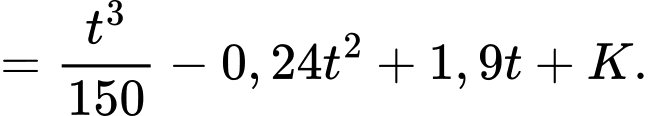
Theo dữ kiện đề bài, tại thời điểm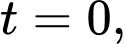 mực nước trong hồ chứa là 6 m suy ra
mực nước trong hồ chứa là 6 m suy ra
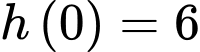
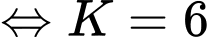
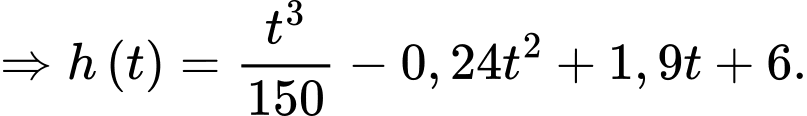
Mực nước trong hồ chứa thấp nhất là tại thời điểm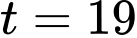 và
và 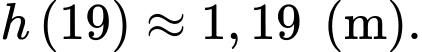
Vậy mệnh đề đúng.
Dựa vào giả thiết: tại thời điểm
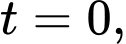 mực nước trong hồ tăng với tốc độ 1,9 mét/giờ. (với
mực nước trong hồ tăng với tốc độ 1,9 mét/giờ. (với 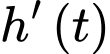 là hàm biểu diễn tốc độ tăng/giảm của mực nước) Ta suy ra
là hàm biểu diễn tốc độ tăng/giảm của mực nước) Ta suy ra 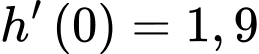
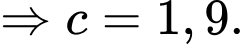
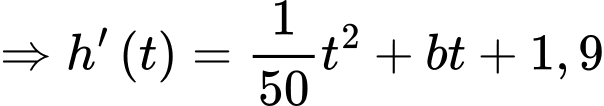
Vậy mệnh đề sai.
b) Đúng.
Dựa vào giả thiết: “Mực nước trong hồ chứa lớn nhất lúc
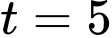 giờ” suy ra
giờ” suy ra 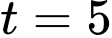 là giá trị cực đại của hàm số (Vì khi xét giá trị lớn nhất của hàm số
là giá trị cực đại của hàm số (Vì khi xét giá trị lớn nhất của hàm số 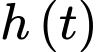 trên đoạn
trên đoạn 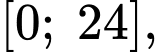 ta cần so sánh giữa các giá trị tại 2 đầu mút và các giá trị cực trị, mà giá trị lớn nhất của hàm số đạt tại
ta cần so sánh giữa các giá trị tại 2 đầu mút và các giá trị cực trị, mà giá trị lớn nhất của hàm số đạt tại 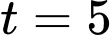 không phải là đầu mút do đó
không phải là đầu mút do đó 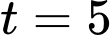 phải là cực trị của hàm số (cụ thể là cực đại)).
phải là cực trị của hàm số (cụ thể là cực đại)).
Suy ra
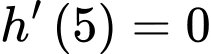
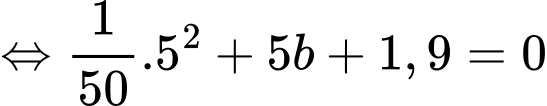
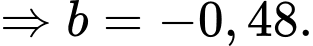
Vậy mệnh đề đúng.
c) Sai.
Để xác định mức nước trong hồ chứa tăng giảm trong các khoảng thời gian nào, ta tìm khoảng đồng biến, nghịch biến của hàm số
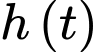 bằng cách khảo sát hàm số
bằng cách khảo sát hàm số 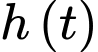 trên đoạn
trên đoạn 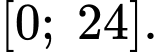
Ta có
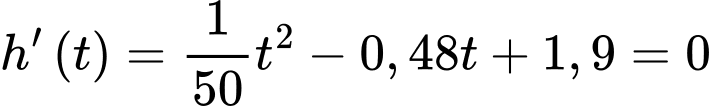
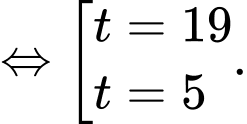
Ta có trục xét dấu sau:

Vậy mực nước trong hồ chứa khoảng thời gian từ
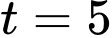 giờ đến
giờ đến 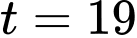 giờ và tăng trong các khoảng thời gian còn lại.
giờ và tăng trong các khoảng thời gian còn lại.
Vậy mệnh đề sai.
d) Đúng.
Ta có
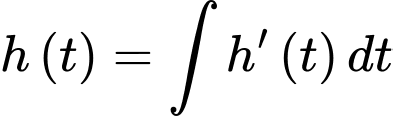
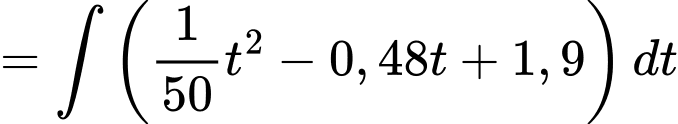
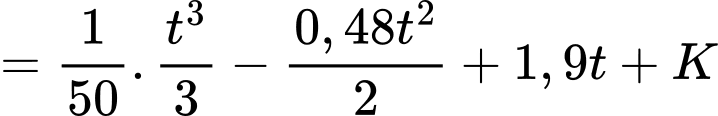
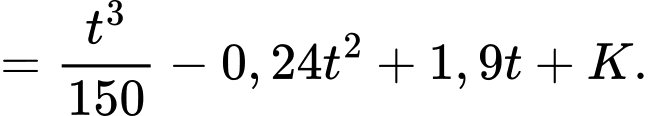
Theo dữ kiện đề bài, tại thời điểm
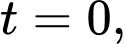 mực nước trong hồ chứa là 6 m suy ra
mực nước trong hồ chứa là 6 m suy ra
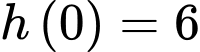
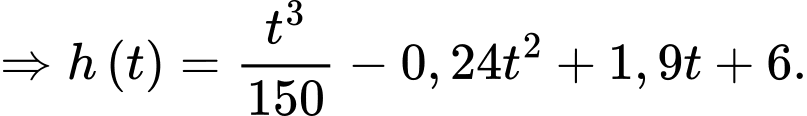
Mực nước trong hồ chứa thấp nhất là tại thời điểm
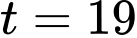 và
và 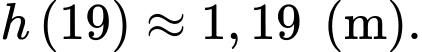
Vậy mệnh đề đúng.
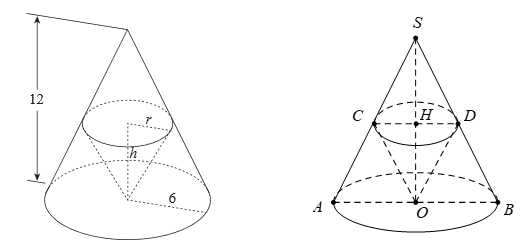
Câu 16 [695295]: Hình vẽ dưới cho thấy hai hình nón tròn xoay, một hình nón  có bán kính
có bán kính 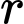 (cm), chiều cao
(cm), chiều cao 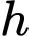 (cm) nằm úp bên trong hình nón
(cm) nằm úp bên trong hình nón  có bán kính bằng 6 cm, chiều cao bằng 12 cm. Hai đáy hình nón song song với nhau và đỉnh của hình nón nhỏ
có bán kính bằng 6 cm, chiều cao bằng 12 cm. Hai đáy hình nón song song với nhau và đỉnh của hình nón nhỏ 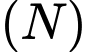 là tâm đáy của hình nón lớn (tham khảo hình vẽ). Kí hiệu thể tích hình nón
là tâm đáy của hình nón lớn (tham khảo hình vẽ). Kí hiệu thể tích hình nón 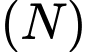 nằm úp bên trong là
nằm úp bên trong là 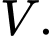
 có bán kính
có bán kính  (cm), chiều cao
(cm), chiều cao  (cm) nằm úp bên trong hình nón
(cm) nằm úp bên trong hình nón  có bán kính bằng 6 cm, chiều cao bằng 12 cm. Hai đáy hình nón song song với nhau và đỉnh của hình nón nhỏ
có bán kính bằng 6 cm, chiều cao bằng 12 cm. Hai đáy hình nón song song với nhau và đỉnh của hình nón nhỏ 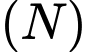 là tâm đáy của hình nón lớn (tham khảo hình vẽ). Kí hiệu thể tích hình nón
là tâm đáy của hình nón lớn (tham khảo hình vẽ). Kí hiệu thể tích hình nón 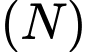 nằm úp bên trong là
nằm úp bên trong là 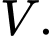

a) Đúng.
b) Đúng.
Từ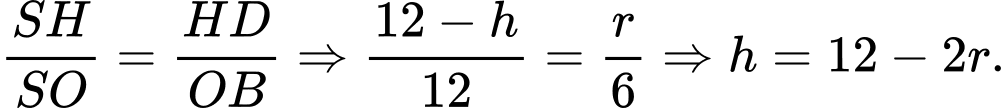
c) Đúng.
Thể tích hình nón là
là 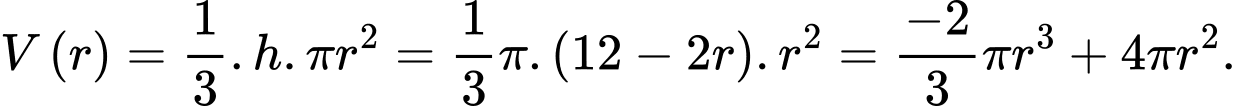
d) Đúng.
Xét hàm số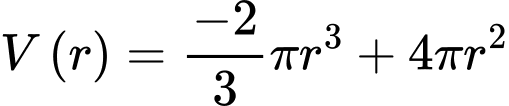
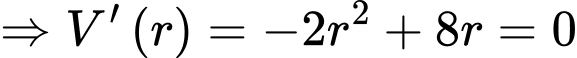
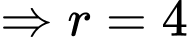 là điểm cực đại của đồ thị hàm số trên.
là điểm cực đại của đồ thị hàm số trên.
 đạt giá trị lớn nhất tại
đạt giá trị lớn nhất tại 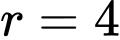 và bằng
và bằng 
b) Đúng.
Từ
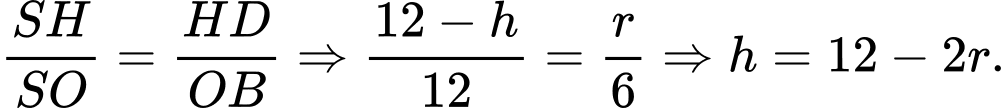
c) Đúng.
Thể tích hình nón
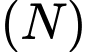 là
là 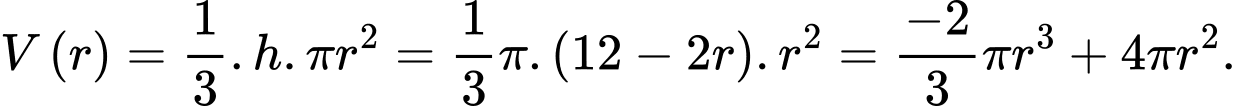
d) Đúng.
Xét hàm số
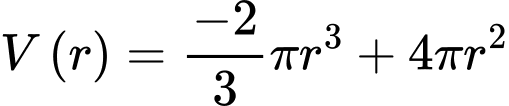
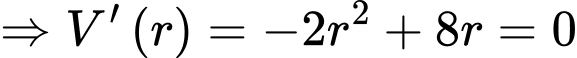
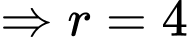 là điểm cực đại của đồ thị hàm số trên.
là điểm cực đại của đồ thị hàm số trên. đạt giá trị lớn nhất tại
đạt giá trị lớn nhất tại 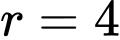 và bằng
và bằng 
PHẦN III. Thí sinh trả lời từ câu 1 đến câu 6.
Câu 17 [695296]: Một ống khói có cấu trúc gồm một khối chóp cụt tứ giác đều có thể tích 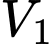 và một khối hộp chữ nhật có thể tích
và một khối hộp chữ nhật có thể tích 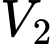 ghép lại với nhau như hình bên dưới. Cho biết bản vẽ hình chiếu của ống khói với phương chiếu trùng với phương của một cạnh đáy khối chóp cụt như hình vẽ, hãy tính tỉ số thể tích
ghép lại với nhau như hình bên dưới. Cho biết bản vẽ hình chiếu của ống khói với phương chiếu trùng với phương của một cạnh đáy khối chóp cụt như hình vẽ, hãy tính tỉ số thể tích 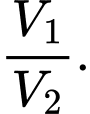 Kết quả làm tròn đến hàng phần trăm.
Kết quả làm tròn đến hàng phần trăm.
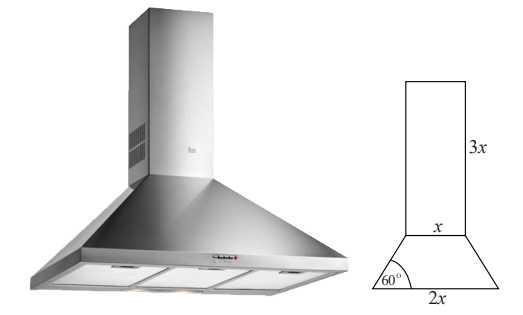
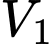 và một khối hộp chữ nhật có thể tích
và một khối hộp chữ nhật có thể tích 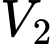 ghép lại với nhau như hình bên dưới. Cho biết bản vẽ hình chiếu của ống khói với phương chiếu trùng với phương của một cạnh đáy khối chóp cụt như hình vẽ, hãy tính tỉ số thể tích
ghép lại với nhau như hình bên dưới. Cho biết bản vẽ hình chiếu của ống khói với phương chiếu trùng với phương của một cạnh đáy khối chóp cụt như hình vẽ, hãy tính tỉ số thể tích 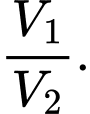 Kết quả làm tròn đến hàng phần trăm.
Kết quả làm tròn đến hàng phần trăm.
Điền đáp án: 0,67.
Vì phần dưới của ống khói là 1 khối chóp cụt đều, do đó 2 đáy của khối chóp cụt này là hình vuông (với độ dài đáy lớn bằng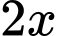 và độ dài đáy nhỏ bằng
và độ dài đáy nhỏ bằng 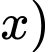 , dẫn đến 2 đáy của khối hộp chữ nhật cũng là hình vuông (có độ dài là
, dẫn đến 2 đáy của khối hộp chữ nhật cũng là hình vuông (có độ dài là 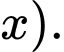
Để tính thể tích của 2 khối trên, ta áp dụng các công thức sau:
+) Tính thể tích của khối hộp chữ nhật: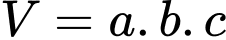 với
với 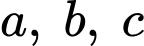 lần lượt là chiều dài, chiều rộng và chiều cao của hình.
lần lượt là chiều dài, chiều rộng và chiều cao của hình.
+) Tính thể tích của khối chóp cụt: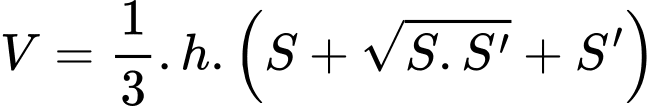 với
với 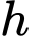 là chiều cao của khối chóp,
là chiều cao của khối chóp, 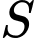 là diện tích đáy lớn và
là diện tích đáy lớn và 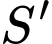 là diện tích đáy nhỏ của khối chóp cụt.
là diện tích đáy nhỏ của khối chóp cụt.
Dựa vào hình chiếu đã cho, ta có:
+) Khối hộp chữ nhật có đáy là hình vuông cạnh bằng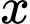 và chiều cao bằng
và chiều cao bằng 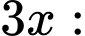
Suy ra thể tích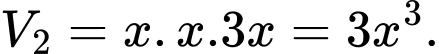
+) Kẻ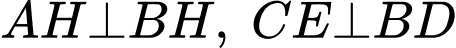 và kí hiệu các điểm như hình vẽ sau:
và kí hiệu các điểm như hình vẽ sau:
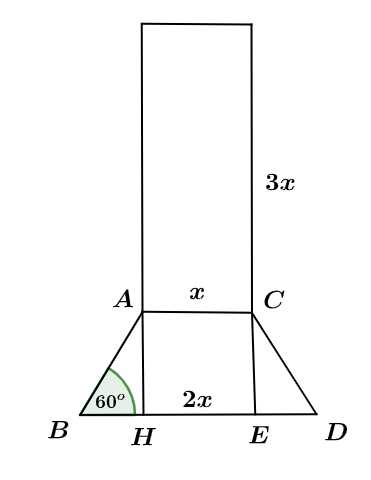
Khi đó, ta có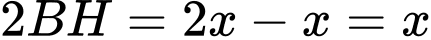
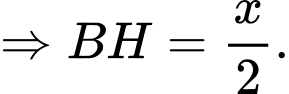
Xét tam giác vuông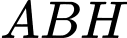 vuông tại
vuông tại 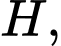 ta có
ta có 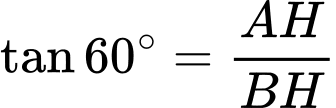
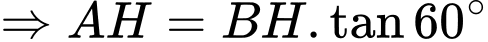
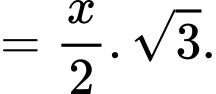
Khối chóp cụt đều có chiều cao là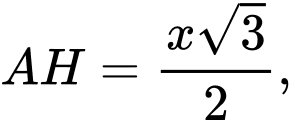 diện tích đáy lớn là
diện tích đáy lớn là 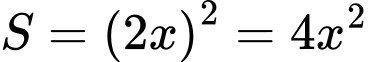 và diện tích đáy nhỏ là
và diện tích đáy nhỏ là 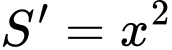 có thể tích bằng
có thể tích bằng
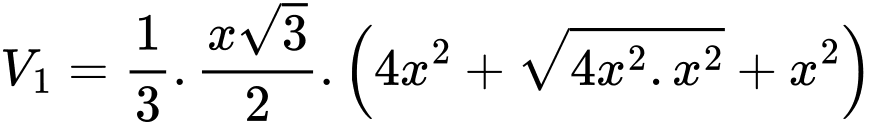
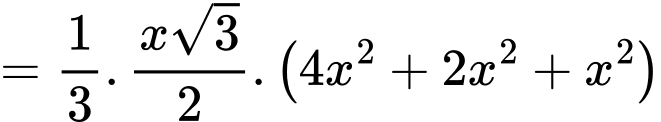
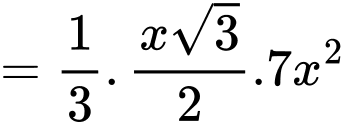
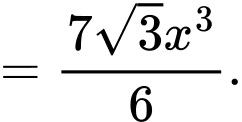
Suy ra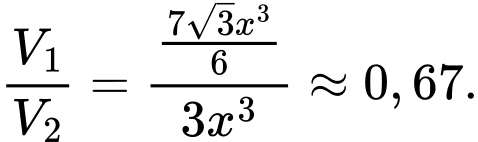
Vì phần dưới của ống khói là 1 khối chóp cụt đều, do đó 2 đáy của khối chóp cụt này là hình vuông (với độ dài đáy lớn bằng
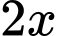 và độ dài đáy nhỏ bằng
và độ dài đáy nhỏ bằng 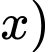 , dẫn đến 2 đáy của khối hộp chữ nhật cũng là hình vuông (có độ dài là
, dẫn đến 2 đáy của khối hộp chữ nhật cũng là hình vuông (có độ dài là 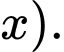
Để tính thể tích của 2 khối trên, ta áp dụng các công thức sau:
+) Tính thể tích của khối hộp chữ nhật:
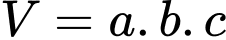 với
với 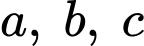 lần lượt là chiều dài, chiều rộng và chiều cao của hình.
lần lượt là chiều dài, chiều rộng và chiều cao của hình.
+) Tính thể tích của khối chóp cụt:
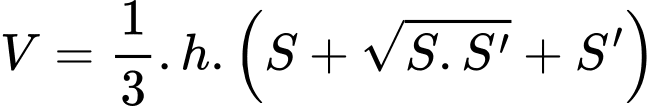 với
với 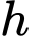 là chiều cao của khối chóp,
là chiều cao của khối chóp, 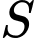 là diện tích đáy lớn và
là diện tích đáy lớn và 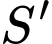 là diện tích đáy nhỏ của khối chóp cụt.
là diện tích đáy nhỏ của khối chóp cụt.
Dựa vào hình chiếu đã cho, ta có:
+) Khối hộp chữ nhật có đáy là hình vuông cạnh bằng
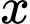 và chiều cao bằng
và chiều cao bằng 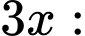
Suy ra thể tích
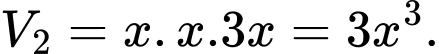
+) Kẻ
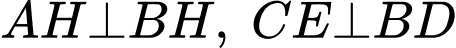 và kí hiệu các điểm như hình vẽ sau:
và kí hiệu các điểm như hình vẽ sau:
Khi đó, ta có
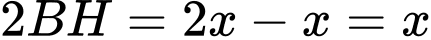
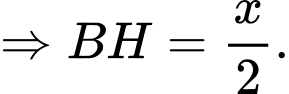
Xét tam giác vuông
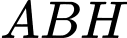 vuông tại
vuông tại 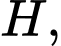 ta có
ta có 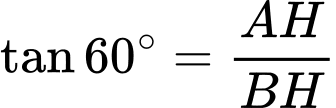
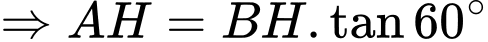
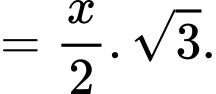
Khối chóp cụt đều có chiều cao là
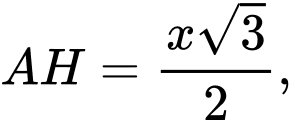 diện tích đáy lớn là
diện tích đáy lớn là 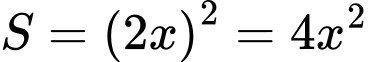 và diện tích đáy nhỏ là
và diện tích đáy nhỏ là 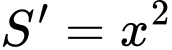 có thể tích bằng
có thể tích bằng
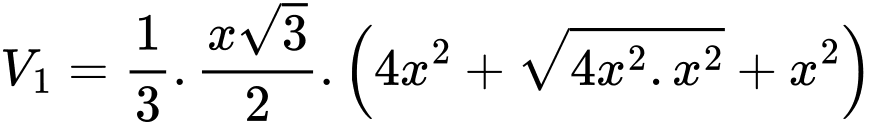
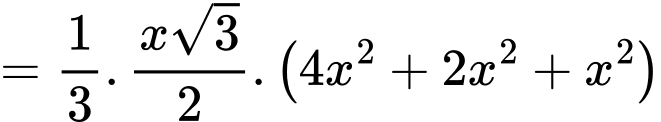
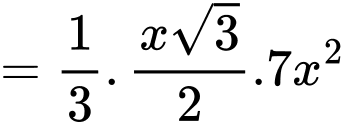
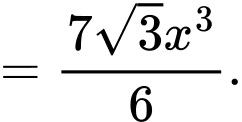
Suy ra
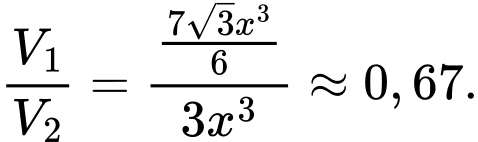
Câu 18 [695297]: Xe xúc tuyết phải dọn tuyết bằng cách lái xe dọc theo tất cả các con đường được hiển thị như hình vẽ (đơn vị: km).
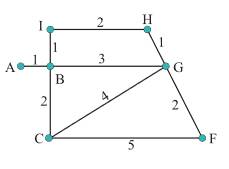
Quãng đường ngắn nhất xe xúc tuyết phải đi bằng bao nhiêu km?

Quãng đường ngắn nhất xe xúc tuyết phải đi bằng bao nhiêu km?
Điền đáp án: 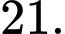
Nhận thấy đây là đồ thị vô hướng có hai đỉnh bậc lẻ Có đường đi Euler.
Có đường đi Euler.
Để xe xúc tuyết đi được quãng đường ngắn nhất thì xe chỉ đi qua các con đường đúng một lần.
Một trong số các cách đi của xe là: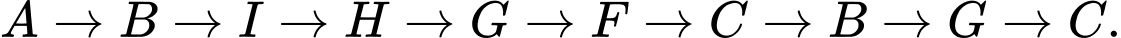
Quãng đường ngắn nhất xe xúc tuyết phải đi là:

Nhận thấy đây là đồ thị vô hướng có hai đỉnh bậc lẻ
 Có đường đi Euler.
Có đường đi Euler.Để xe xúc tuyết đi được quãng đường ngắn nhất thì xe chỉ đi qua các con đường đúng một lần.
Một trong số các cách đi của xe là:
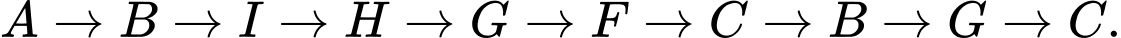
Quãng đường ngắn nhất xe xúc tuyết phải đi là:

Câu 19 [695298]: Một chiếc máy bay có thể xuất hiện ở vị trí A với xác suất 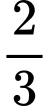 và ở vị trí B với xác suất
và ở vị trí B với xác suất 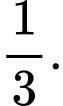 Người ta bố trí 1 khẩu đặt tại A, 3 khẩu đặt tại B. Biết rằng xác suất bắn trúng máy bay của mỗi khẩu pháo là 0,7 và các khẩu pháo hoạt động độc lập với nhau. Giả sử máy bay bị bắn trúng thì xác suất máy bay bị bắn trúng tại vị trí A là bao nhiêu? Kết quả làm tròn đến hàng phần trăm?
Người ta bố trí 1 khẩu đặt tại A, 3 khẩu đặt tại B. Biết rằng xác suất bắn trúng máy bay của mỗi khẩu pháo là 0,7 và các khẩu pháo hoạt động độc lập với nhau. Giả sử máy bay bị bắn trúng thì xác suất máy bay bị bắn trúng tại vị trí A là bao nhiêu? Kết quả làm tròn đến hàng phần trăm?
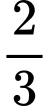 và ở vị trí B với xác suất
và ở vị trí B với xác suất 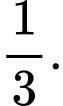 Người ta bố trí 1 khẩu đặt tại A, 3 khẩu đặt tại B. Biết rằng xác suất bắn trúng máy bay của mỗi khẩu pháo là 0,7 và các khẩu pháo hoạt động độc lập với nhau. Giả sử máy bay bị bắn trúng thì xác suất máy bay bị bắn trúng tại vị trí A là bao nhiêu? Kết quả làm tròn đến hàng phần trăm?
Người ta bố trí 1 khẩu đặt tại A, 3 khẩu đặt tại B. Biết rằng xác suất bắn trúng máy bay của mỗi khẩu pháo là 0,7 và các khẩu pháo hoạt động độc lập với nhau. Giả sử máy bay bị bắn trúng thì xác suất máy bay bị bắn trúng tại vị trí A là bao nhiêu? Kết quả làm tròn đến hàng phần trăm?
Điền đáp án: 0,59.
Gọi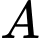 là biến cố “Máy bay xuất hiện ở vị trí A”
là biến cố “Máy bay xuất hiện ở vị trí A”
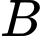 là biến cố “Máy bay bị bắn trúng”
là biến cố “Máy bay bị bắn trúng”
Khi đó là biến cố “Máy bay xuất hiện ở vị trí B” và
là biến cố “Máy bay xuất hiện ở vị trí B” và 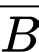 là biến cố “Máy bay không bị bắn trúng”
là biến cố “Máy bay không bị bắn trúng”
Yêu cầu bài toán Tính
Tính 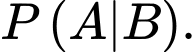
(Theo công thức xác suất có điều kiện, ta có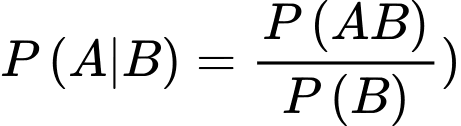
Vì có 3 khẩu đặt tại B nên để máy bay rơi cần ít nhất một khẩu bắn trúng. Xác suất để ít nhất một khẩu tại B bắn trúng máy bay là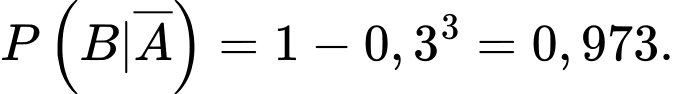
Ta có sơ đồ cây sau:
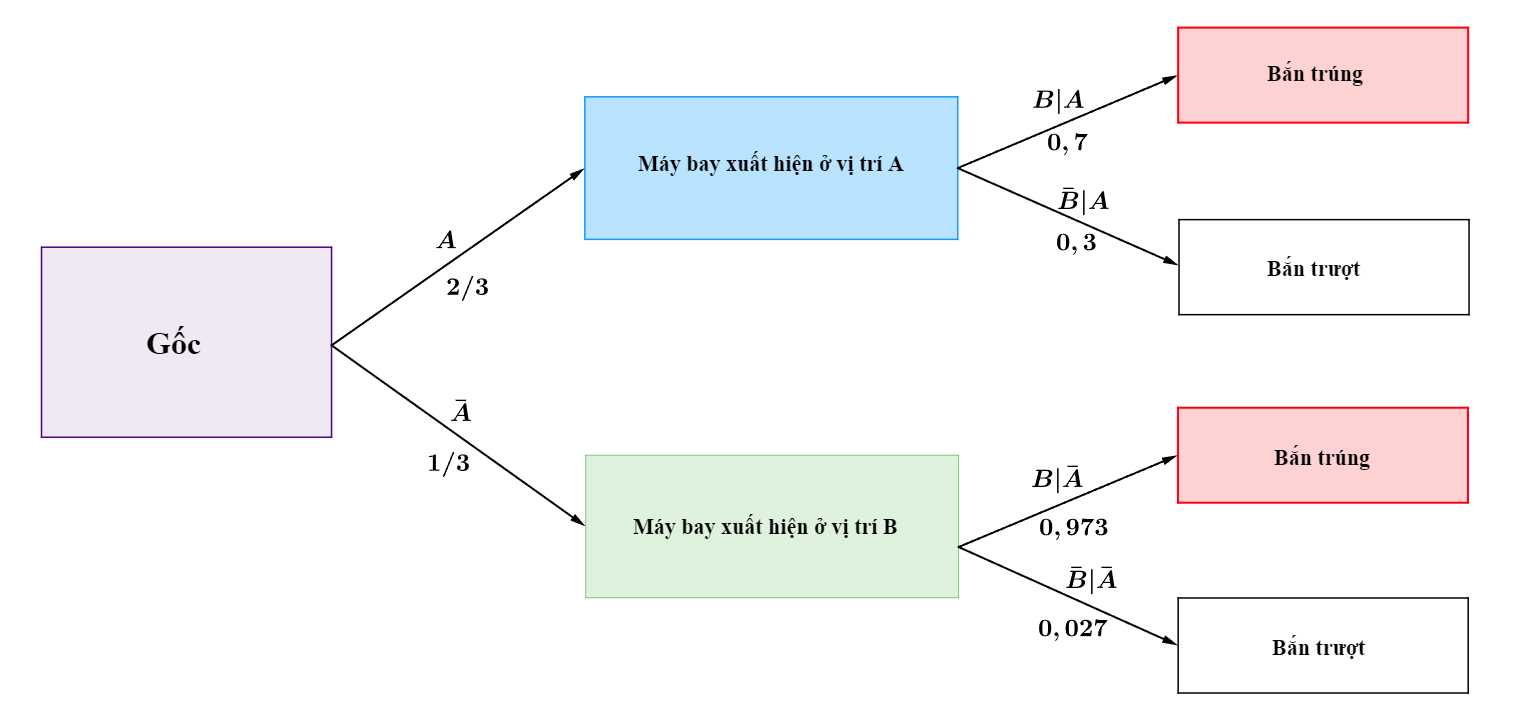
Suy ra xác suất để máy bay rơi (bị bắn trúng) là: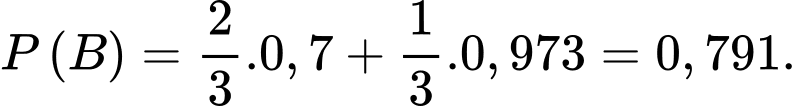
Xác suất cần tìm là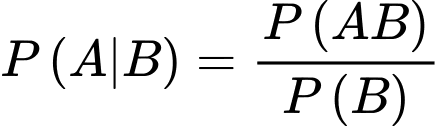
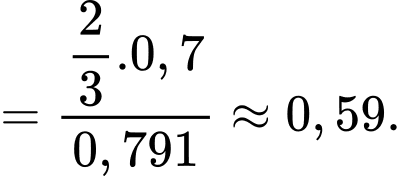
Gọi
 là biến cố “Máy bay xuất hiện ở vị trí A”
là biến cố “Máy bay xuất hiện ở vị trí A” là biến cố “Máy bay bị bắn trúng”
là biến cố “Máy bay bị bắn trúng”Khi đó
 là biến cố “Máy bay xuất hiện ở vị trí B” và
là biến cố “Máy bay xuất hiện ở vị trí B” và 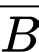 là biến cố “Máy bay không bị bắn trúng”
là biến cố “Máy bay không bị bắn trúng”Yêu cầu bài toán
 Tính
Tính 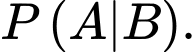
(Theo công thức xác suất có điều kiện, ta có
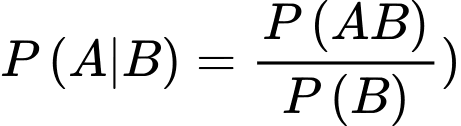
Vì có 3 khẩu đặt tại B nên để máy bay rơi cần ít nhất một khẩu bắn trúng. Xác suất để ít nhất một khẩu tại B bắn trúng máy bay là
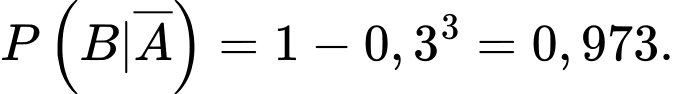
Ta có sơ đồ cây sau:

Suy ra xác suất để máy bay rơi (bị bắn trúng) là:
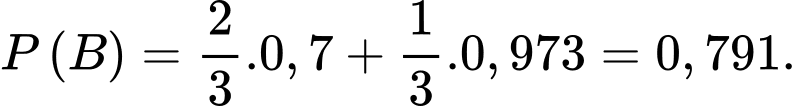
Xác suất cần tìm là
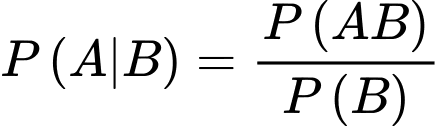
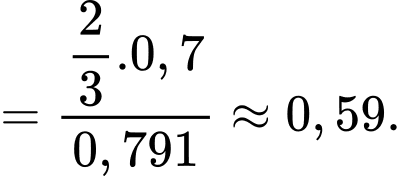
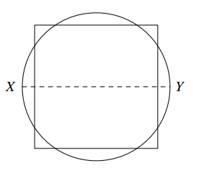
Câu 20 [695300]: Cho hình vuông có độ dài cạnh bằng 8  và một hình tròn có bán kính 5
và một hình tròn có bán kính 5  được xếp chồng lên nhau sao cho tâm của hình tròn trùng với tâm của hình vuông như hình vẽ bên. Thể tích của vật thể tròn xoay tạo thành khi quay mô hình trên quanh trục
được xếp chồng lên nhau sao cho tâm của hình tròn trùng với tâm của hình vuông như hình vẽ bên. Thể tích của vật thể tròn xoay tạo thành khi quay mô hình trên quanh trục  bằng bao nhiêu
bằng bao nhiêu  ? (làm tròn kết quả đến hàng phần trăm).
? (làm tròn kết quả đến hàng phần trăm).
 và một hình tròn có bán kính 5
và một hình tròn có bán kính 5  được xếp chồng lên nhau sao cho tâm của hình tròn trùng với tâm của hình vuông như hình vẽ bên. Thể tích của vật thể tròn xoay tạo thành khi quay mô hình trên quanh trục
được xếp chồng lên nhau sao cho tâm của hình tròn trùng với tâm của hình vuông như hình vẽ bên. Thể tích của vật thể tròn xoay tạo thành khi quay mô hình trên quanh trục  bằng bao nhiêu
bằng bao nhiêu  ? (làm tròn kết quả đến hàng phần trăm).
? (làm tròn kết quả đến hàng phần trăm).
Điền đáp án: 0,54.
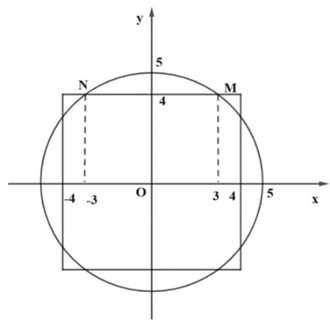
Khi đó phương trình đường tròn có dạng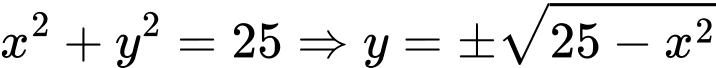 .
.
Một phần tư đường tròn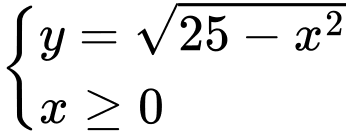 cắt các đường
cắt các đường 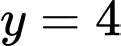 và
và  lần lượt tại
lần lượt tại 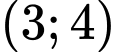 và
và 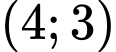 .
.
Do đó thể tích của mô hình khi quay quanh trục là
là 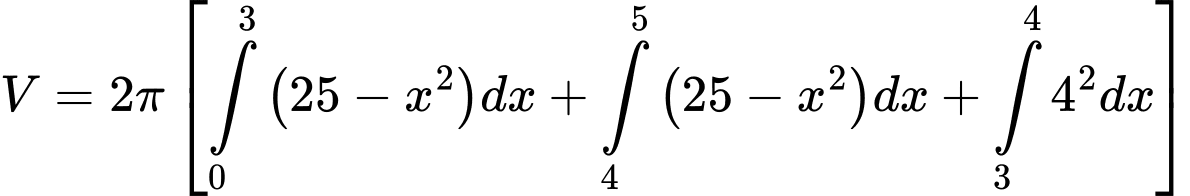
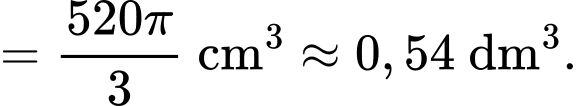

Khi đó phương trình đường tròn có dạng
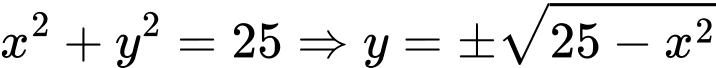 .
.Một phần tư đường tròn
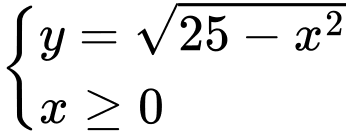 cắt các đường
cắt các đường 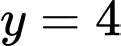 và
và  lần lượt tại
lần lượt tại 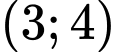 và
và 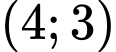 .
.Do đó thể tích của mô hình khi quay quanh trục
 là
là 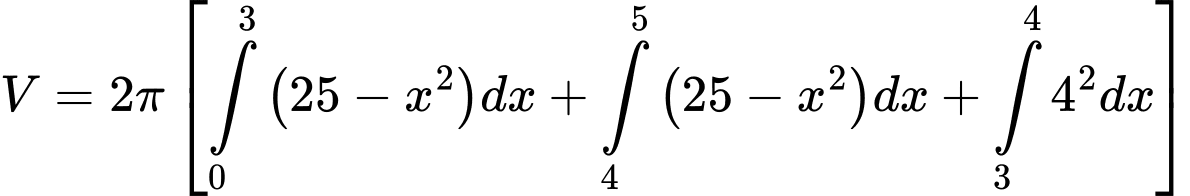
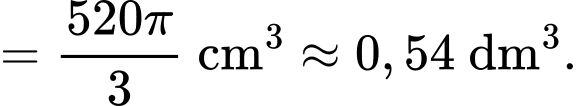
Câu 21 [693131]: Bác Nam dự định làm một máng thoát nước mưa từ một miếng tôn hình chữ nhật có chiều dài 8 m và chiều rộng 45 cm. Bác Nam chia chiều rộng của miếng tôn thành ba phần bằng nhau, mỗi phần dài 15 cm, rồi gập hai bên lên một góc 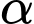 (đơn vị radian) như hình vẽ dưới đây.
(đơn vị radian) như hình vẽ dưới đây.
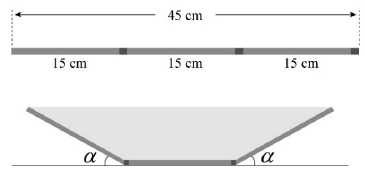
Gọi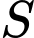
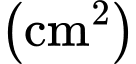 là diện tích của mặt cắt ngang của máng nước. Tìm góc
là diện tích của mặt cắt ngang của máng nước. Tìm góc 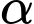 (làm tròn kết quả đến chữ số thứ hai sau dấu phẩy) để diện tích
(làm tròn kết quả đến chữ số thứ hai sau dấu phẩy) để diện tích 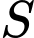 là lớn nhất (sẽ cho phép nước thoát qua máng nhiều nhất).
là lớn nhất (sẽ cho phép nước thoát qua máng nhiều nhất).
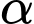 (đơn vị radian) như hình vẽ dưới đây.
(đơn vị radian) như hình vẽ dưới đây.
Gọi
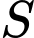
 là diện tích của mặt cắt ngang của máng nước. Tìm góc
là diện tích của mặt cắt ngang của máng nước. Tìm góc 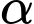 (làm tròn kết quả đến chữ số thứ hai sau dấu phẩy) để diện tích
(làm tròn kết quả đến chữ số thứ hai sau dấu phẩy) để diện tích 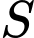 là lớn nhất (sẽ cho phép nước thoát qua máng nhiều nhất).
là lớn nhất (sẽ cho phép nước thoát qua máng nhiều nhất).
Điền đáp án: 1,05.
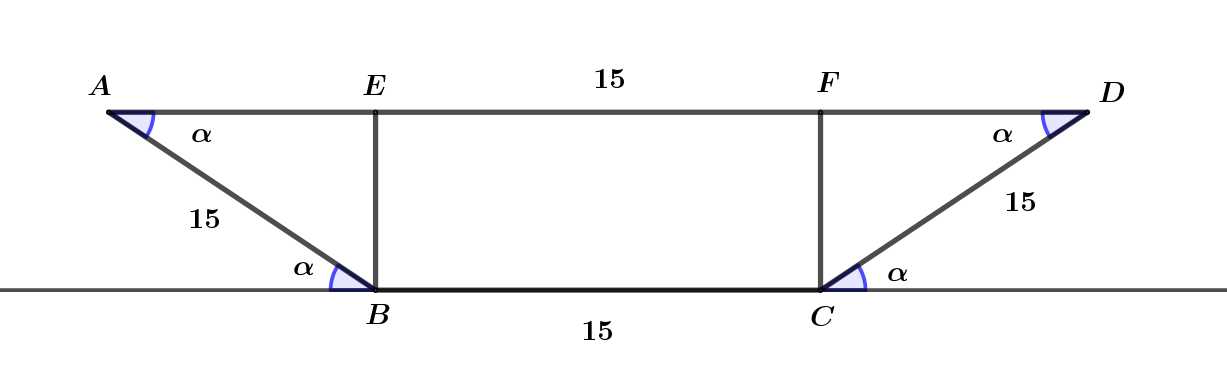
Điều kiện: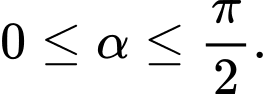
Xét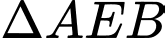 vuông tại
vuông tại  có:
có: 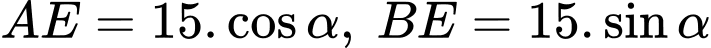
Xét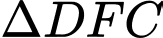 vuông tại
vuông tại 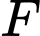 có:
có: 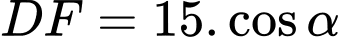
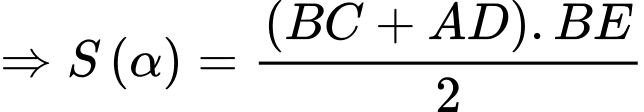
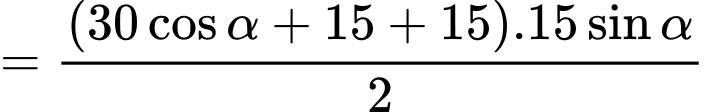
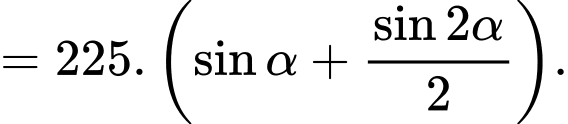
Xét hàm số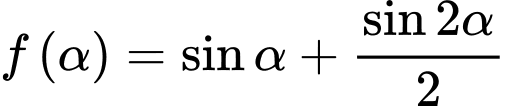
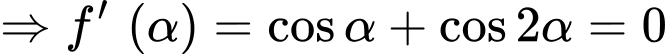
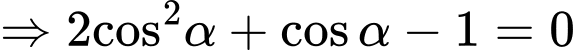
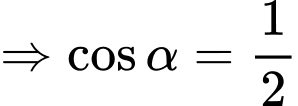
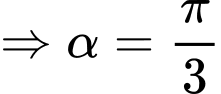 là điểm cực đại của đồ thị hàm số
là điểm cực đại của đồ thị hàm số 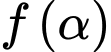 .
.
Ta có :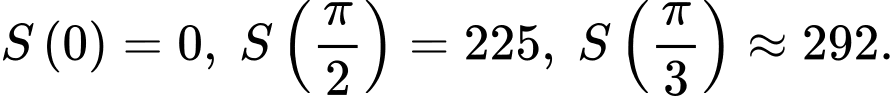
 Diện tích
Diện tích 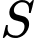 đạt giá trị lớn nhất tại
đạt giá trị lớn nhất tại 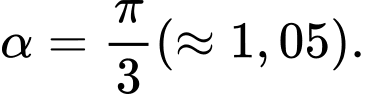

Điều kiện:
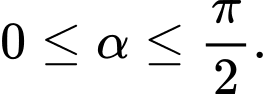
Xét
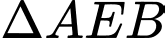 vuông tại
vuông tại 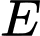 có:
có: 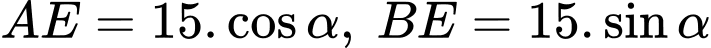
Xét
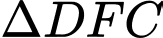 vuông tại
vuông tại  có:
có: 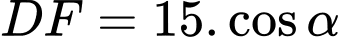
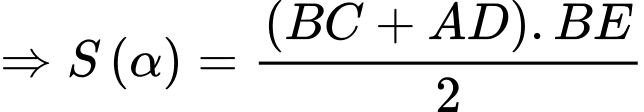
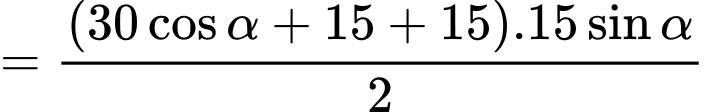
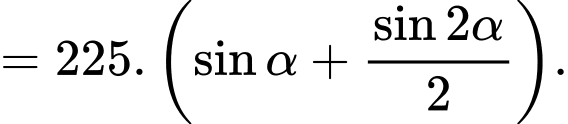
Xét hàm số
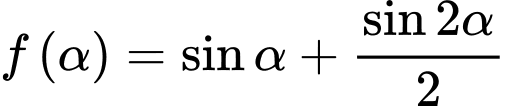
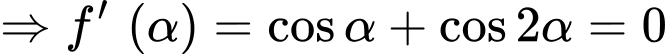
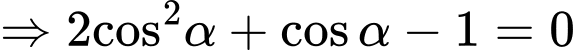
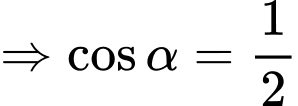
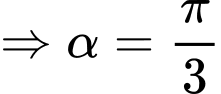 là điểm cực đại của đồ thị hàm số
là điểm cực đại của đồ thị hàm số 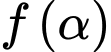 .
.
Ta có :
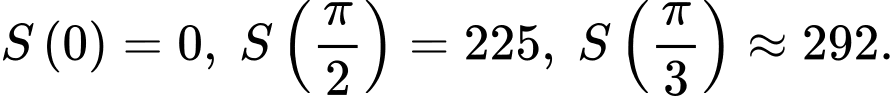
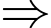 Diện tích
Diện tích 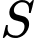 đạt giá trị lớn nhất tại
đạt giá trị lớn nhất tại 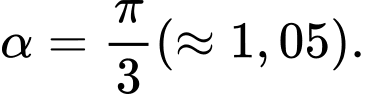
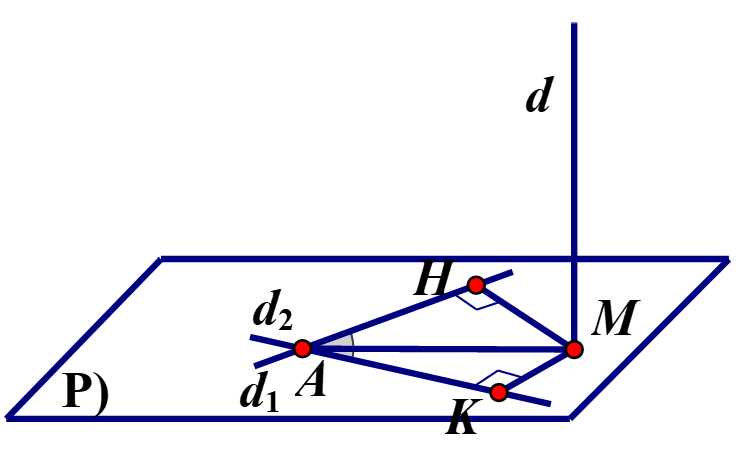
Câu 22 [695301]: Trong không gian 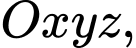 cho điểm
cho điểm 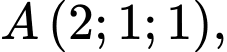 mặt phẳng
mặt phẳng 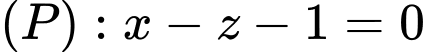 và đường thẳng
và đường thẳng 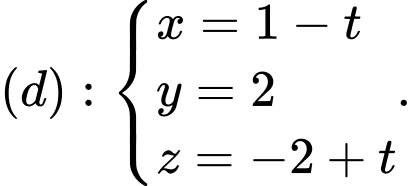 Gọi
Gọi 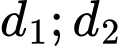 là các đường thẳng đi qua
là các đường thẳng đi qua 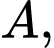 nằm trong
nằm trong 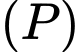 và đều có khoảng cách đến đường thẳng
và đều có khoảng cách đến đường thẳng 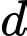 bằng
bằng 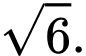 Tính côsin của góc giữa hai đường thẳng
Tính côsin của góc giữa hai đường thẳng 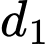 và
và 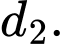 (làm tròn kết quả đến hàng phần trăm).
(làm tròn kết quả đến hàng phần trăm).
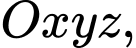 cho điểm
cho điểm 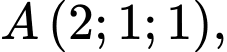 mặt phẳng
mặt phẳng 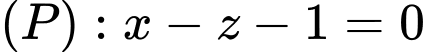 và đường thẳng
và đường thẳng 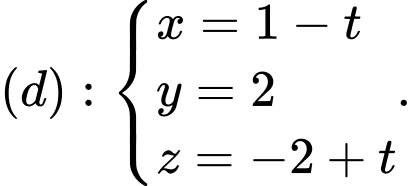 Gọi
Gọi 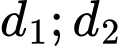 là các đường thẳng đi qua
là các đường thẳng đi qua 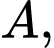 nằm trong
nằm trong 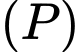 và đều có khoảng cách đến đường thẳng
và đều có khoảng cách đến đường thẳng 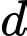 bằng
bằng 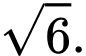 Tính côsin của góc giữa hai đường thẳng
Tính côsin của góc giữa hai đường thẳng 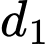 và
và 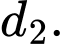 (làm tròn kết quả đến hàng phần trăm).
(làm tròn kết quả đến hàng phần trăm).
Điền đáp án: 0,33.
Ta có: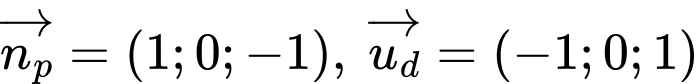
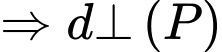 và
và 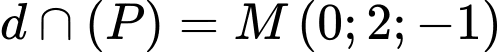
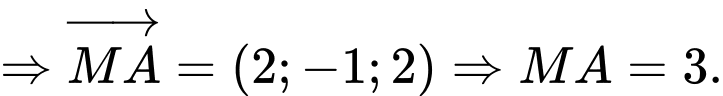
Gọi lần lượt là hình chiếu vuông góc của
lần lượt là hình chiếu vuông góc của 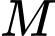 lên
lên 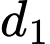 và
và 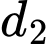 , ta có
, ta có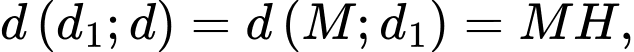
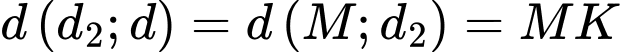
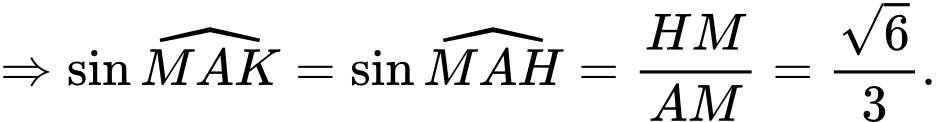
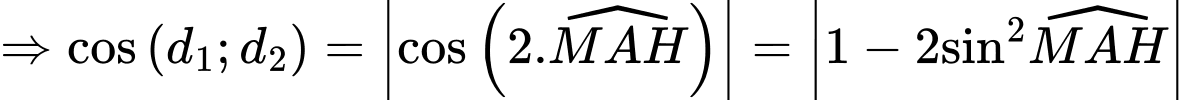
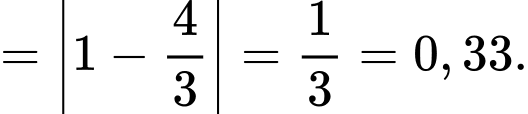

Ta có:
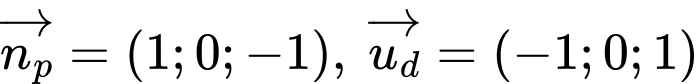
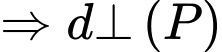 và
và 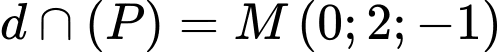
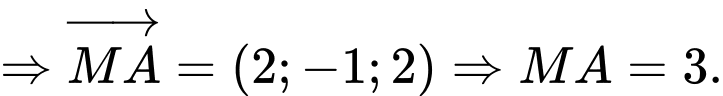
Gọi
 lần lượt là hình chiếu vuông góc của
lần lượt là hình chiếu vuông góc của 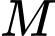 lên
lên 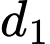 và
và 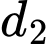 , ta có
, ta có