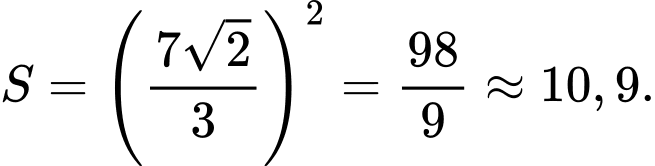PHẦN I. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Câu 1 [326618]: Phương trình 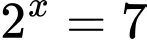 có nghiệm là
có nghiệm là
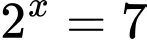 có nghiệm là
có nghiệm là A, 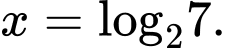
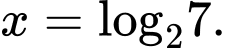
B, 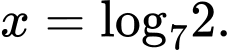
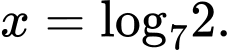
C, 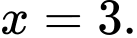
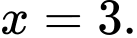
D, 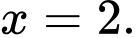
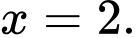
Chọn đáp án A.
Ta có: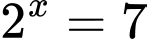
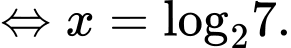 Đáp án: A
Đáp án: A
Ta có:
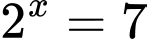
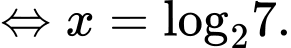 Đáp án: A
Đáp án: A
Câu 2 [807064]: Trong không gian với hệ tọa độ 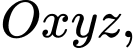 đường thẳng nào sau đây có vectơ chỉ phương là
đường thẳng nào sau đây có vectơ chỉ phương là 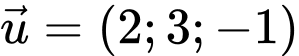
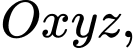 đường thẳng nào sau đây có vectơ chỉ phương là
đường thẳng nào sau đây có vectơ chỉ phương là 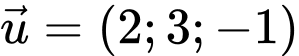
A, 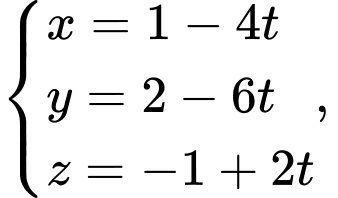
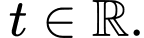
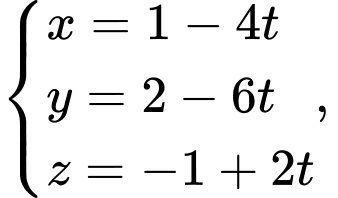
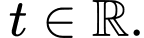
B, 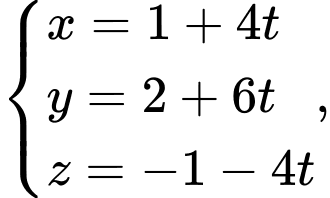

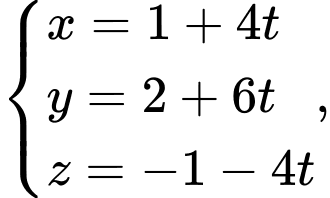

C, 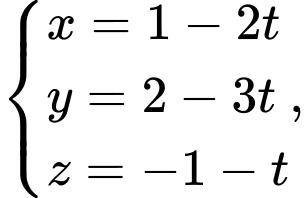

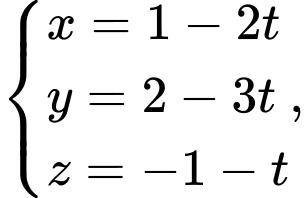

D, 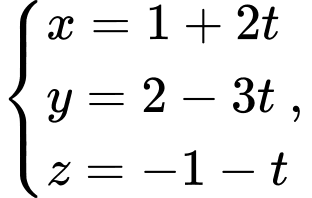
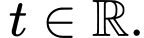
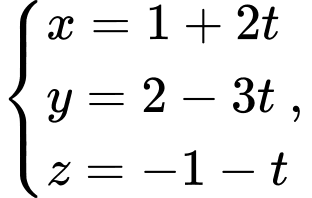
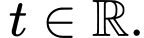
Chọn đáp án A.
Đường thẳng ở đáp án A có vectơ chỉ phương là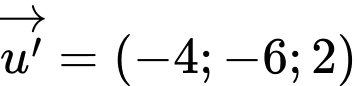
 Đường thằng này có một vectơ chỉ phương là
Đường thằng này có một vectơ chỉ phương là 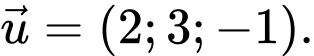 Đáp án: A
Đáp án: A
Đường thẳng ở đáp án A có vectơ chỉ phương là
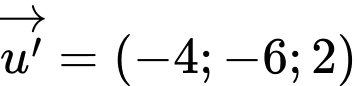
 Đường thằng này có một vectơ chỉ phương là
Đường thằng này có một vectơ chỉ phương là 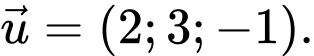 Đáp án: A
Đáp án: A
Câu 3 [521726]: Hàm số nào sau đây không có cực trị?
A, 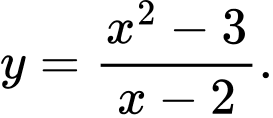
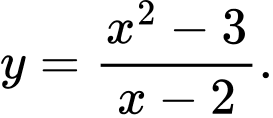
B, 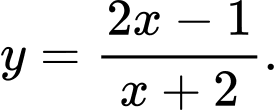
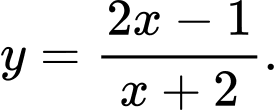
C, 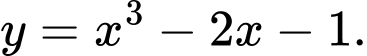
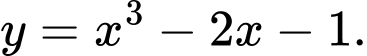
D, 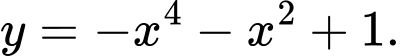
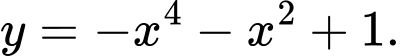
Chọn đáp án B. Đáp án: B
Câu 4 [547579]: Một cuộc khảo sát đã tiến hành xác định tuổi (theo năm) của 120 chiếc ô tô. Kết quả điều tra được cho trong bảng sau.

Có bao nhiêu ô tô có độ tuổi dưới 12 năm?

Có bao nhiêu ô tô có độ tuổi dưới 12 năm?
A, 26.
B, 37.
C, 45.
D, 75.
Chọn đáp án D.
Số ô tô có độ tuổi dưới 12 năm là: Đáp án: D
Đáp án: D
Số ô tô có độ tuổi dưới 12 năm là:
 Đáp án: D
Đáp án: D
Câu 5 [512588]: Cho hàm số 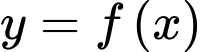 có đồ thị như hình vẽ bên. Hàm số đã cho đồng biến trên khoảng nào dưới đây?
có đồ thị như hình vẽ bên. Hàm số đã cho đồng biến trên khoảng nào dưới đây?
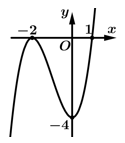
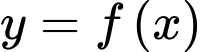 có đồ thị như hình vẽ bên. Hàm số đã cho đồng biến trên khoảng nào dưới đây?
có đồ thị như hình vẽ bên. Hàm số đã cho đồng biến trên khoảng nào dưới đây?
A, 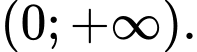
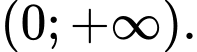
B, 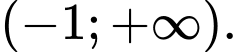
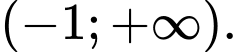
C, 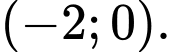
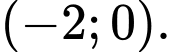
D, 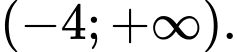
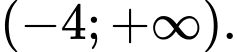
Chọn đáp án A.
Nhìn đồ thị ta thấy hàm số đồng biến trên khoảng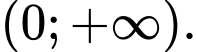 Đáp án: A
Đáp án: A
Nhìn đồ thị ta thấy hàm số đồng biến trên khoảng
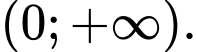 Đáp án: A
Đáp án: A
Câu 6 [677752]: Cho cấp số nhân 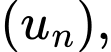 biết
biết 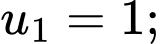
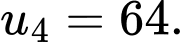 Công bội
Công bội 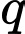 của cấp số nhân bằng
của cấp số nhân bằng
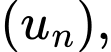 biết
biết 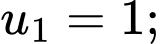
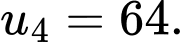 Công bội
Công bội 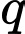 của cấp số nhân bằng
của cấp số nhân bằng A, 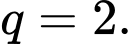
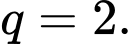
B, 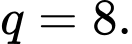
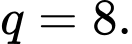
C, 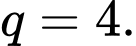
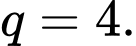
D, 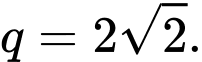
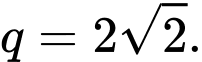
Chọn đáp án C.
Ta có: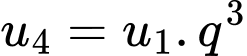
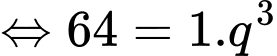
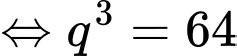
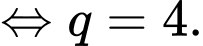 Đáp án: C
Đáp án: C
Ta có:
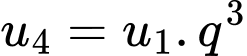
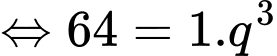
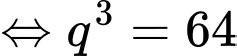
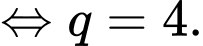 Đáp án: C
Đáp án: C
Câu 7 [808404]: Biết 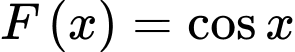 là một nguyên hàm của hàm số
là một nguyên hàm của hàm số 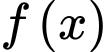 trên
trên 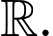 Giá trị của
Giá trị của 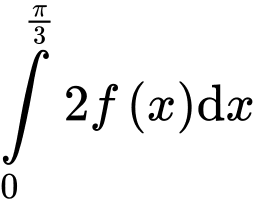 bằng
bằng
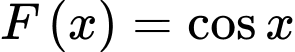 là một nguyên hàm của hàm số
là một nguyên hàm của hàm số 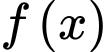 trên
trên 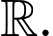 Giá trị của
Giá trị của 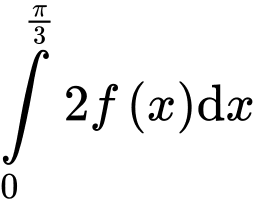 bằng
bằng A, 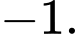
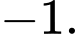
B, 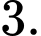
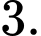
C, 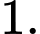
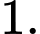
D, 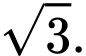
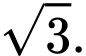
Chọn đáp án A.
Ta có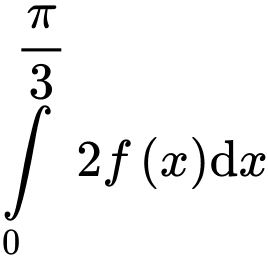

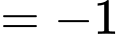 Đáp án: A
Đáp án: A
Ta có
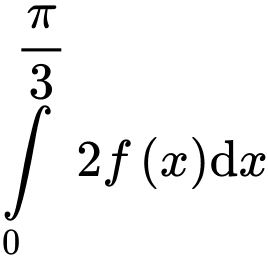

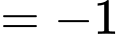 Đáp án: A
Đáp án: A Sử dụng thông tin dưới đây để trả lời câu 8 và câu 9
Cho hình lăng trụ đứng ABC.A'B'C' có tất cả các cạnh bằng nhau và bằng 4 (tham khảo hình bên).
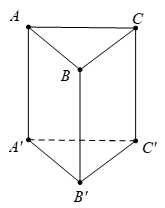

Câu 8 [702518]: Góc giữa đường thẳng 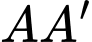 và
và 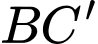 bằng
bằng
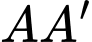 và
và 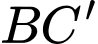 bằng
bằng A, 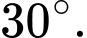
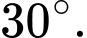
B, 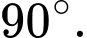
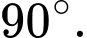
C, 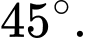
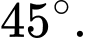
D, 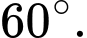
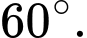
Chọn đáp án C.
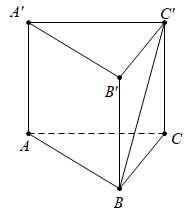
Ta có: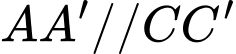
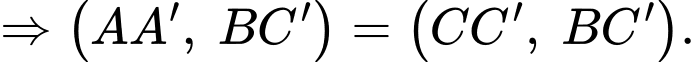
Mặt khác tam giác vuông tại
vuông tại  có
có 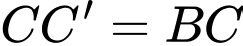 nên là tam giác vuông cân.
nên là tam giác vuông cân.
Vậy góc giữa hai đường thẳng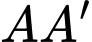 và
và 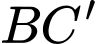 bằng
bằng 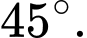 Đáp án: C
Đáp án: C

Ta có:
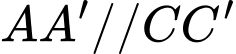
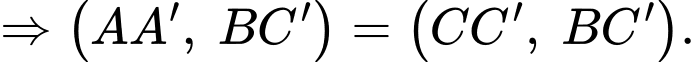
Mặt khác tam giác
 vuông tại
vuông tại  có
có 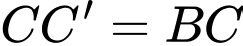 nên là tam giác vuông cân.
nên là tam giác vuông cân. Vậy góc giữa hai đường thẳng
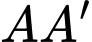 và
và 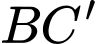 bằng
bằng 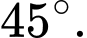 Đáp án: C
Đáp án: C
Câu 9 [702519]: Tính giá trị của 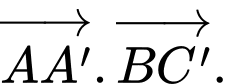
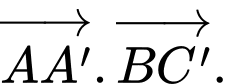
A, 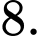
B, 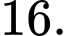
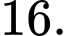
C, 

D, 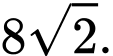
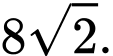
Chọn đáp án B.
Ta có:
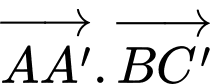
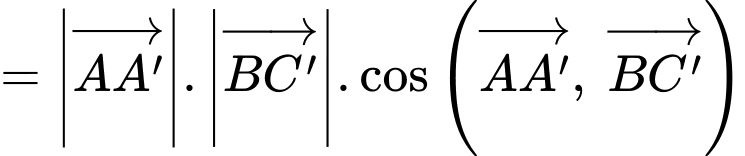
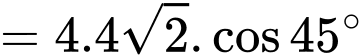
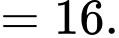 Đáp án: B
Đáp án: B
Ta có:
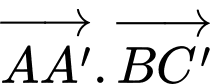
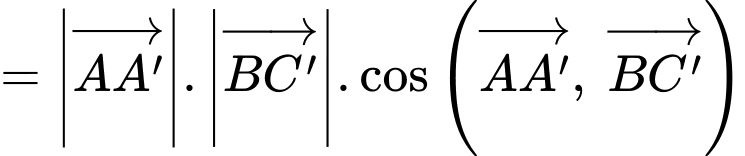
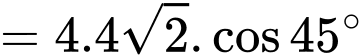
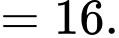 Đáp án: B
Đáp án: B
Câu 10 [508142]: Gọi 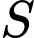 là tập nghiệm của phương trình
là tập nghiệm của phương trình 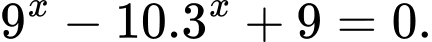 Tổng các phần tử của
Tổng các phần tử của 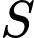 bằng
bằng
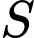 là tập nghiệm của phương trình
là tập nghiệm của phương trình 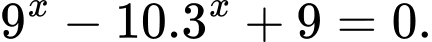 Tổng các phần tử của
Tổng các phần tử của 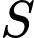 bằng
bằng A, 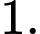
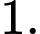
B, 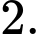
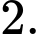
C, 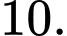
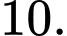
D, 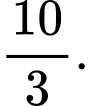
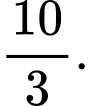
Chọn đáp án B.
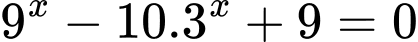

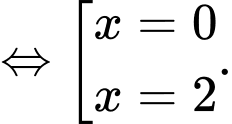
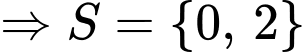
Vậy tổng các phần tử của bằng
bằng 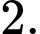 Đáp án: B
Đáp án: B
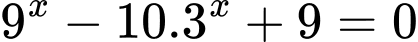

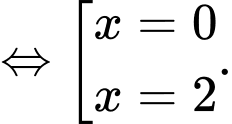
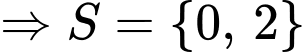
Vậy tổng các phần tử của
 bằng
bằng 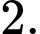 Đáp án: B
Đáp án: B
Câu 11 [317409]: Họ tất cả các nguyên hàm của hàm số 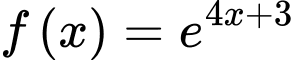 là
là
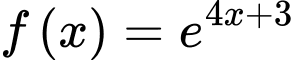 là
là A, 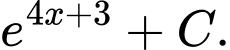
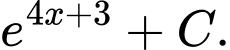
B, 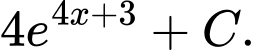
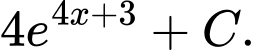
C, 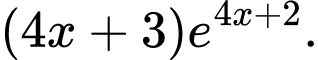
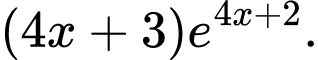
D, 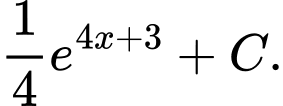
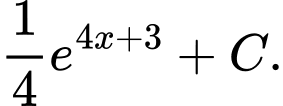
Chọn đáp án D.
Ta có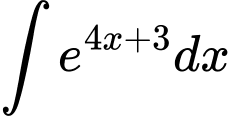
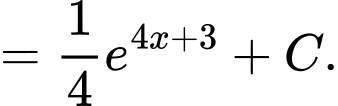 Đáp án: D
Đáp án: D
Ta có
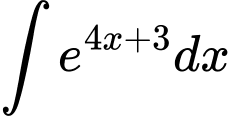
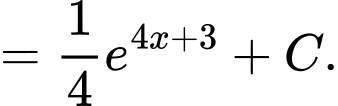 Đáp án: D
Đáp án: D
Câu 12 [808956]: Trong không gian 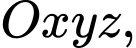 mặt cầu có tâm
mặt cầu có tâm 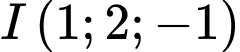 và tiếp xúc với mặt phẳng
và tiếp xúc với mặt phẳng 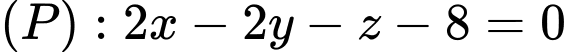 có phương trình là
có phương trình là
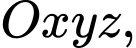 mặt cầu có tâm
mặt cầu có tâm 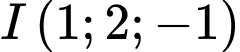 và tiếp xúc với mặt phẳng
và tiếp xúc với mặt phẳng 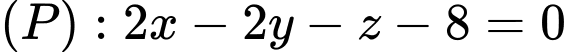 có phương trình là
có phương trình là A, 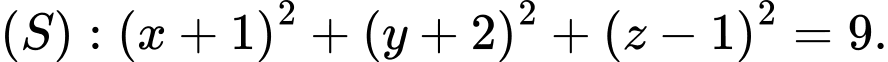
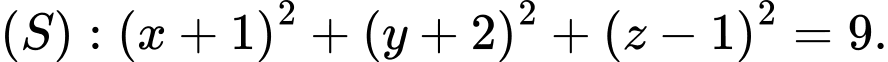
B, 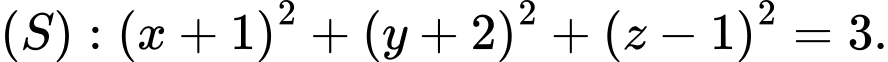
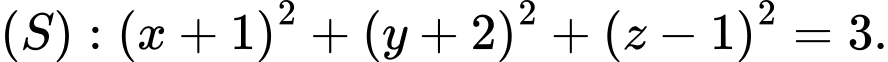
C, 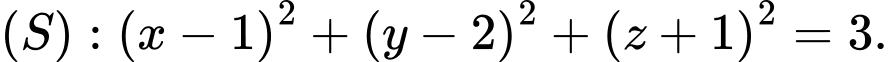
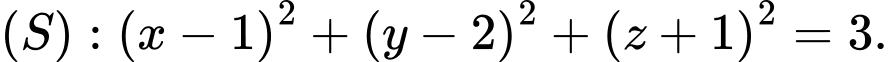
D, 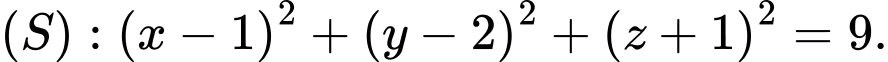
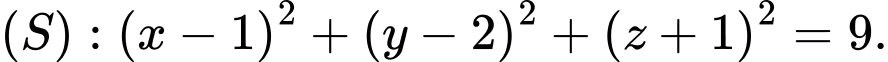
Chọn đáp án D.
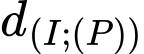
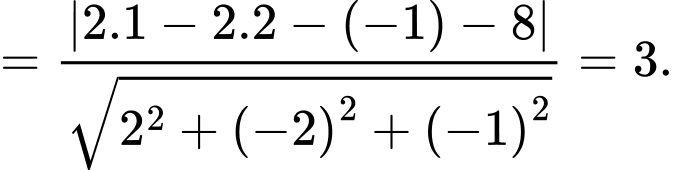
Mặt cầu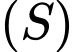 tiếp xúc với mặt phẳng
tiếp xúc với mặt phẳng 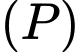 nên
nên 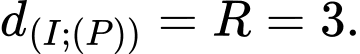
Vậy phương trình mặt cầu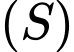 tâm
tâm 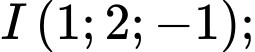 bán kính
bán kính 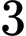 là
là
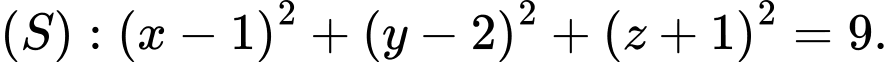 Đáp án: D
Đáp án: D
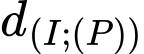
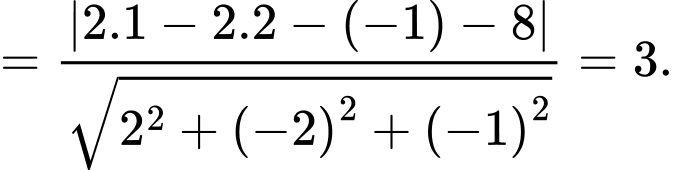
Mặt cầu
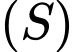 tiếp xúc với mặt phẳng
tiếp xúc với mặt phẳng 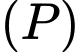 nên
nên 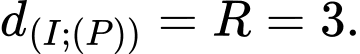
Vậy phương trình mặt cầu
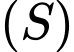 tâm
tâm 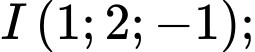 bán kính
bán kính 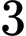 là
là 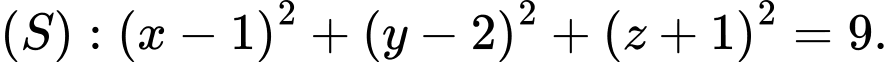 Đáp án: D
Đáp án: D PHẦN II. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Câu 13 [687486]: Cho hàm số 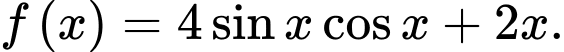
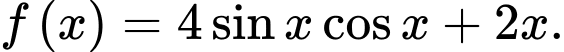
a) Đúng.
Thay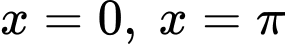 vào hàm số
vào hàm số 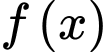 ta được:
ta được: 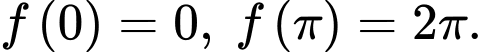
b) Sai.
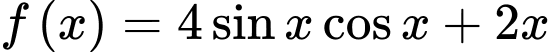
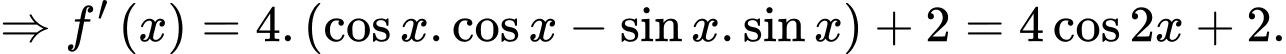
c) Đúng.
Ta có:

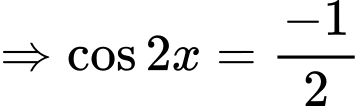
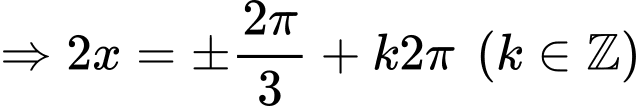
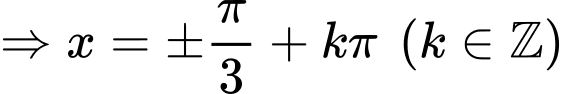
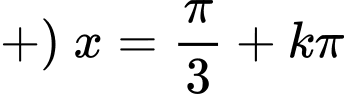 .
.
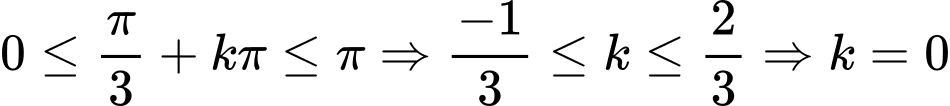 .
.
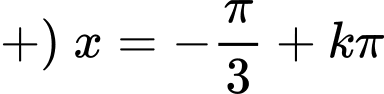 .
.
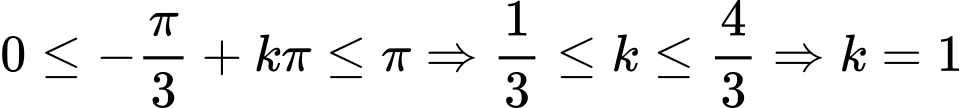 .
.
d) Sai.
Theo câu c) ta có 2 điểm cực trị của hàm số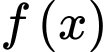 là
là 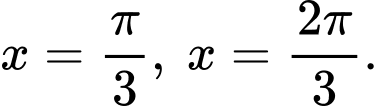
Ta có: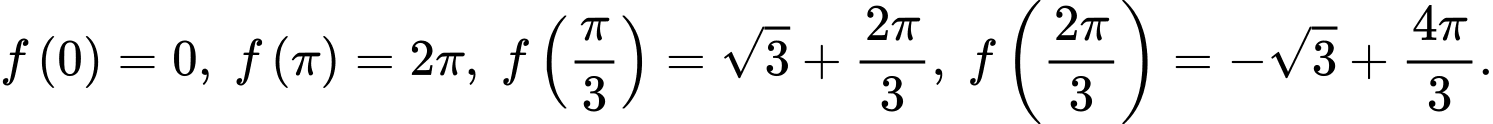
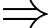 Giá trị lớn nhất của
Giá trị lớn nhất của 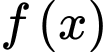 trên đoạn
trên đoạn 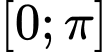 là
là 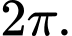
Thay
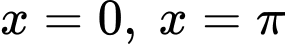 vào hàm số
vào hàm số 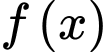 ta được:
ta được: 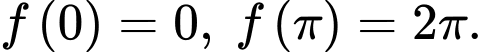
b) Sai.
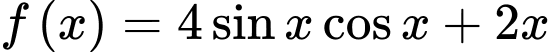
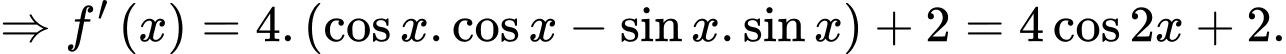
c) Đúng.
Ta có:

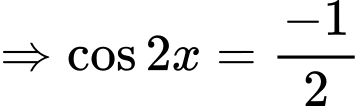
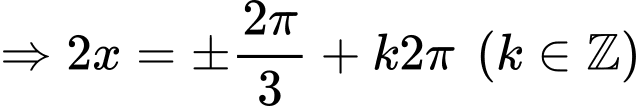
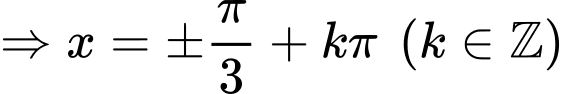
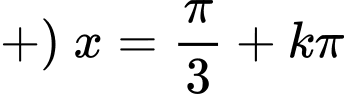 .
.
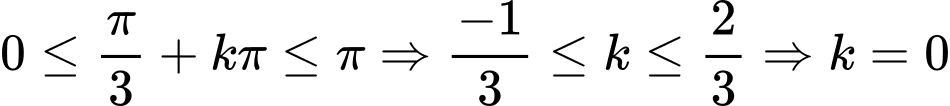 .
.
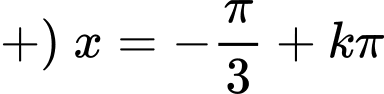 .
.
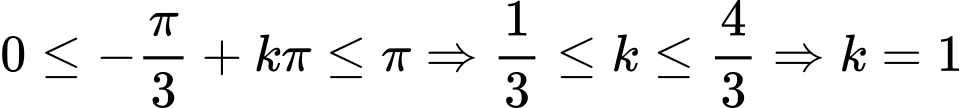 .
.
d) Sai.
Theo câu c) ta có 2 điểm cực trị của hàm số
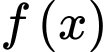 là
là 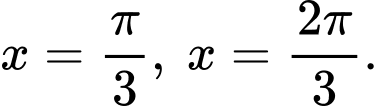
Ta có:
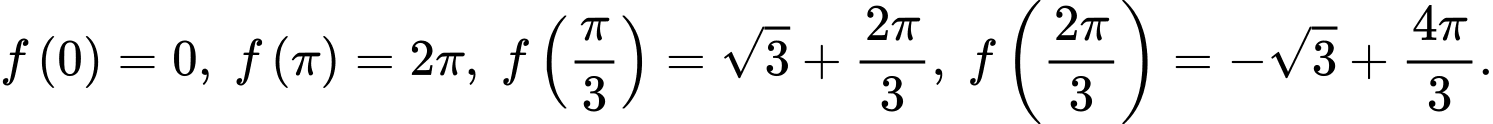
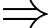 Giá trị lớn nhất của
Giá trị lớn nhất của 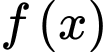 trên đoạn
trên đoạn 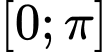 là
là 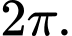
Câu 14 [695514]: Một khinh khí cầu bay với độ cao (so với mặt đất) tại thời điểm 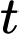 là
là 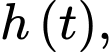 trong đó
trong đó 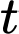 tính bằng phút,
tính bằng phút, 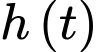 tính bằng mét. Vận tốc bay của khinh khí cầu được cho bởi hàm số
tính bằng mét. Vận tốc bay của khinh khí cầu được cho bởi hàm số 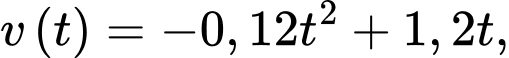 với
với 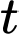 tính bằng phút,
tính bằng phút, 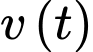 tính bằng mét/phút. Từ thời điểm xuất phát
tính bằng mét/phút. Từ thời điểm xuất phát 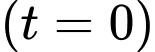 thì
thì 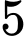 phút sau khi xuất phát, khinh khí cầu đã ở độ cao
phút sau khi xuất phát, khinh khí cầu đã ở độ cao 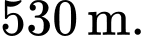
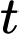 là
là 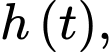 trong đó
trong đó 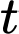 tính bằng phút,
tính bằng phút, 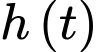 tính bằng mét. Vận tốc bay của khinh khí cầu được cho bởi hàm số
tính bằng mét. Vận tốc bay của khinh khí cầu được cho bởi hàm số 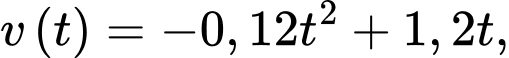 với
với 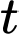 tính bằng phút,
tính bằng phút, 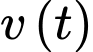 tính bằng mét/phút. Từ thời điểm xuất phát
tính bằng mét/phút. Từ thời điểm xuất phát 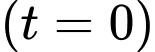 thì
thì 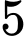 phút sau khi xuất phát, khinh khí cầu đã ở độ cao
phút sau khi xuất phát, khinh khí cầu đã ở độ cao 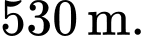
(Nguồn: A. Bigalke et al., Mathematik, Grundkurs ma – 1, Cornelsen 2016).
a) Đúng.
Ta có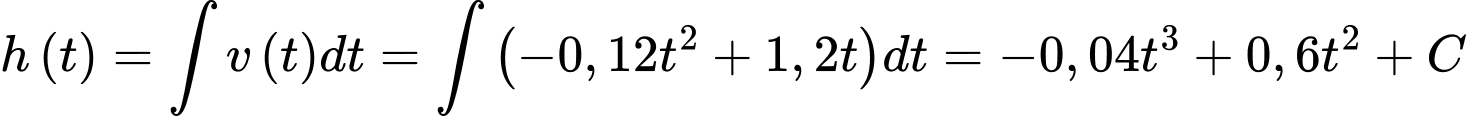 .
.
Khi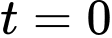 thì
thì 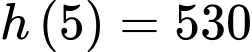 suy ra
suy ra 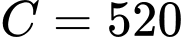 .
.
Vậy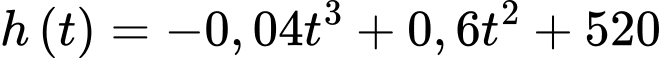
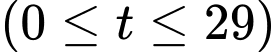
b) Đúng.
Độ cao tối đa của khinh khí cầu khi bay chính là giá trị lớn nhất của hàm số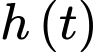 trên đoạn
trên đoạn 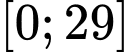 .
.
Ta có: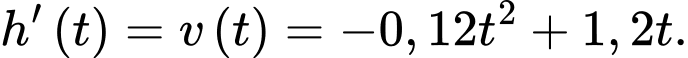
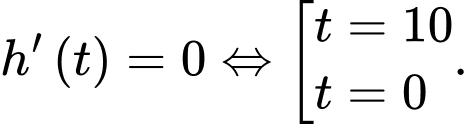
Có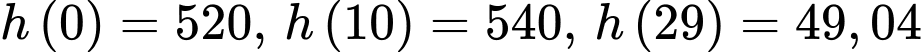 nên
nên 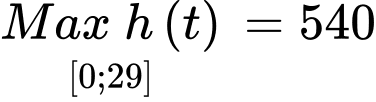 khi
khi 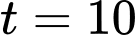 .
.
Độ cao tối đa của khinh khí cầu khi bay là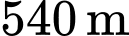 .
.
c) Đúng.
Khinh khí cầu trở lại độ cao khi xuất phát tức có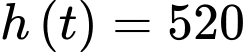 với
với 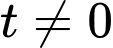 .
.
Ta có phương trình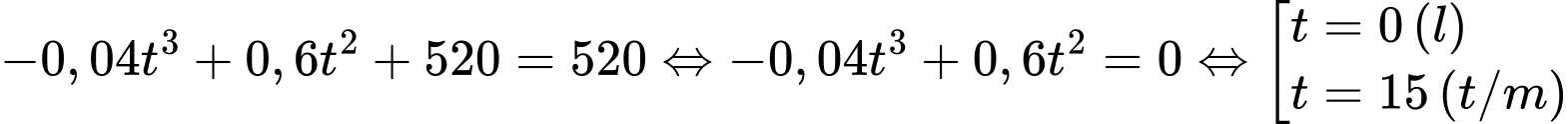
Vậy sau phút từ khi xuất phát thì khinh khí cầu trở lại độ cao khi bắt đầu xuất phát.
phút từ khi xuất phát thì khinh khí cầu trở lại độ cao khi bắt đầu xuất phát.
d) Đúng.
Khinh khí cầu tiếp đất khi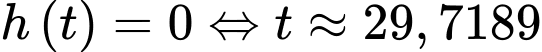
Vận tốc của khinh khí cầu khi đó là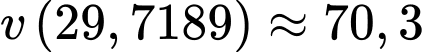 mét/phút.
mét/phút.
Ta có
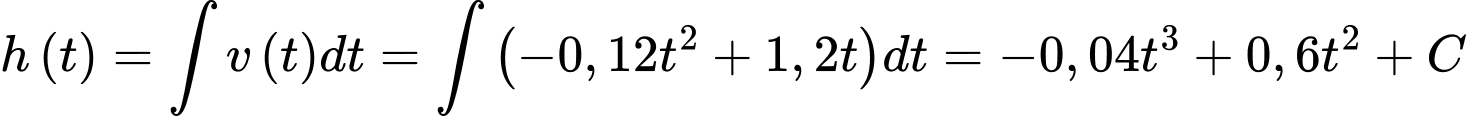 .
.
Khi
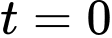 thì
thì 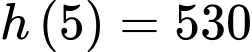 suy ra
suy ra 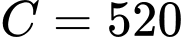 .
.
Vậy
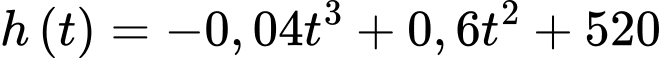
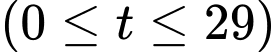
b) Đúng.
Độ cao tối đa của khinh khí cầu khi bay chính là giá trị lớn nhất của hàm số
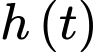 trên đoạn
trên đoạn 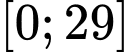 .
.
Ta có:
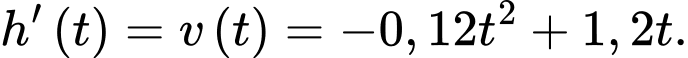
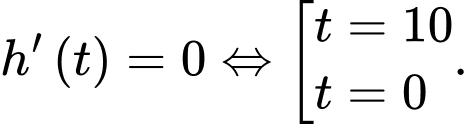
Có
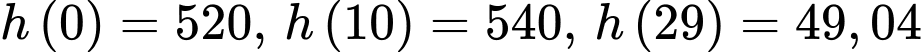 nên
nên 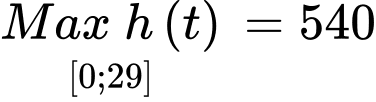 khi
khi 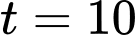 .
.
Độ cao tối đa của khinh khí cầu khi bay là
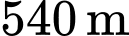 .
.
c) Đúng.
Khinh khí cầu trở lại độ cao khi xuất phát tức có
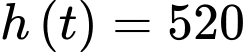 với
với 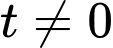 .
.
Ta có phương trình
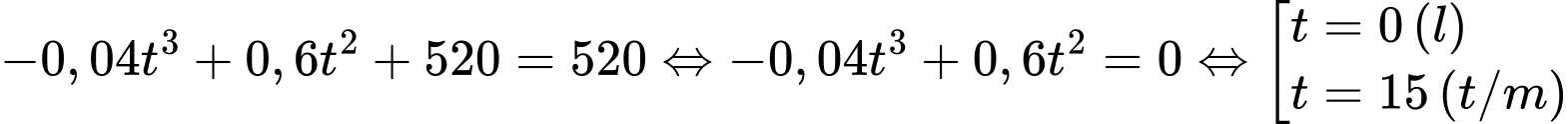
Vậy sau
 phút từ khi xuất phát thì khinh khí cầu trở lại độ cao khi bắt đầu xuất phát.
phút từ khi xuất phát thì khinh khí cầu trở lại độ cao khi bắt đầu xuất phát.
d) Đúng.
Khinh khí cầu tiếp đất khi
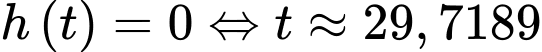
Vận tốc của khinh khí cầu khi đó là
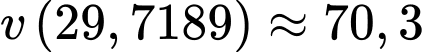 mét/phút.
mét/phút.
Câu 15 [695528]: Hai công nhân cần phải hoàn thành số sản phẩm nhất định. Công nhân thứ nhất phải làm 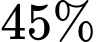 số sản phẩm, công nhân thứ hai phải làm
số sản phẩm, công nhân thứ hai phải làm 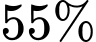 số sản phẩm. Khả năng xảy ra sai sót của công nhân thứ nhất là
số sản phẩm. Khả năng xảy ra sai sót của công nhân thứ nhất là 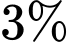 và của công nhân thứ hai là
và của công nhân thứ hai là 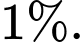 Chọn ngẫu nhiên
Chọn ngẫu nhiên 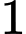 sản phẩm. Gọi
sản phẩm. Gọi 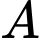 là biến cố “Sản phẩm được chọn là của công nhân thứ nhất”,
là biến cố “Sản phẩm được chọn là của công nhân thứ nhất”,  là biến cố “Sản phẩm được chọn bị lỗi”.
là biến cố “Sản phẩm được chọn bị lỗi”.
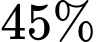 số sản phẩm, công nhân thứ hai phải làm
số sản phẩm, công nhân thứ hai phải làm 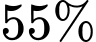 số sản phẩm. Khả năng xảy ra sai sót của công nhân thứ nhất là
số sản phẩm. Khả năng xảy ra sai sót của công nhân thứ nhất là 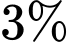 và của công nhân thứ hai là
và của công nhân thứ hai là 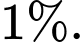 Chọn ngẫu nhiên
Chọn ngẫu nhiên 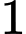 sản phẩm. Gọi
sản phẩm. Gọi 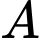 là biến cố “Sản phẩm được chọn là của công nhân thứ nhất”,
là biến cố “Sản phẩm được chọn là của công nhân thứ nhất”, 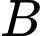 là biến cố “Sản phẩm được chọn bị lỗi”.
là biến cố “Sản phẩm được chọn bị lỗi”.
a) Sai.
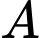 là biến cố “Sản phẩm được chọn là của công nhân thứ nhất”
là biến cố “Sản phẩm được chọn là của công nhân thứ nhất”
Do công nhân thứ nhất phải làm 45% số sản phẩm nên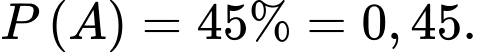
b) Đúng.
Do tỉ lệ sản phẩm lỗi của công nhân thứ nhất là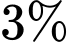 nên
nên 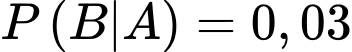 .
.
c) Sai.
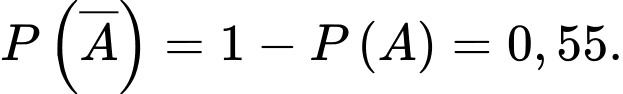
Do tỉ lệ sản phẩm bị lỗi của công nhân số hai là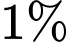 nên
nên 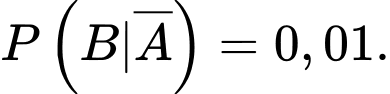
Ta có sơ đồ cây sau:
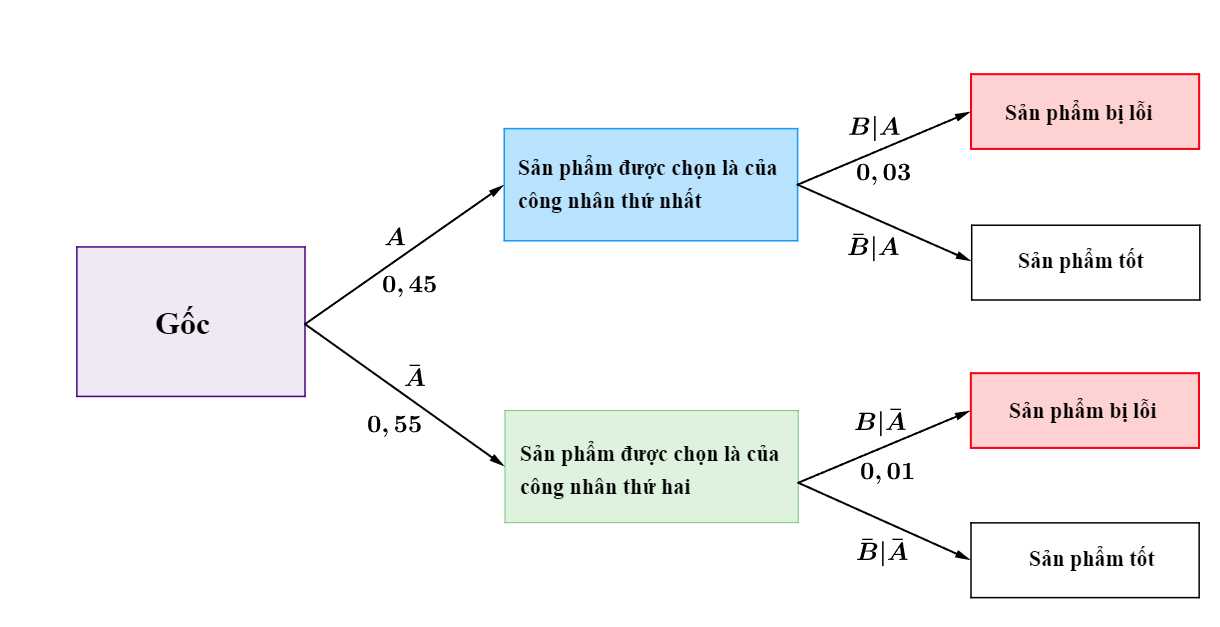
Vậy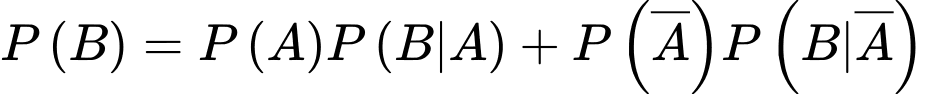
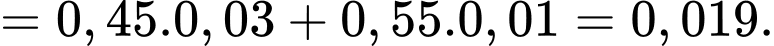
d) Đúng.
Xác suất để sản phẩm được chọn là sản phẩm của công nhân thứ nhất bị lỗi là
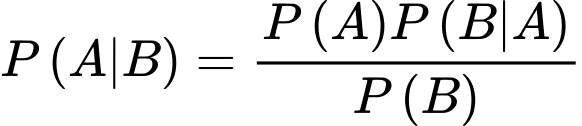
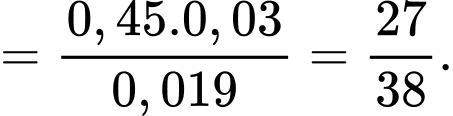
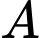 là biến cố “Sản phẩm được chọn là của công nhân thứ nhất”
là biến cố “Sản phẩm được chọn là của công nhân thứ nhất”Do công nhân thứ nhất phải làm 45% số sản phẩm nên
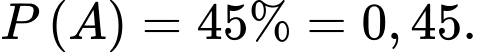
b) Đúng.
Do tỉ lệ sản phẩm lỗi của công nhân thứ nhất là
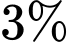 nên
nên 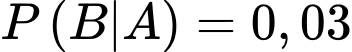 .
.c) Sai.
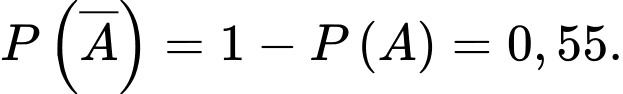
Do tỉ lệ sản phẩm bị lỗi của công nhân số hai là
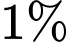 nên
nên 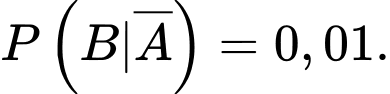
Ta có sơ đồ cây sau:

Vậy
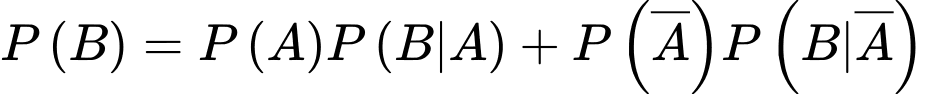
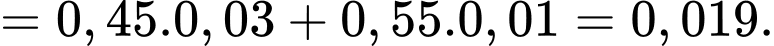
d) Đúng.
Xác suất để sản phẩm được chọn là sản phẩm của công nhân thứ nhất bị lỗi là
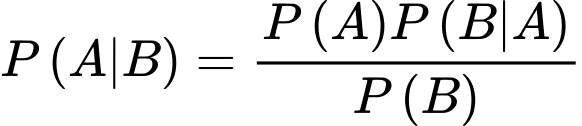
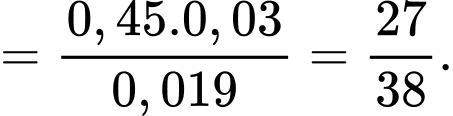
Câu 16 [702520]: Trong không gian với hệ toạ độ 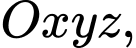 cho tam giác
cho tam giác 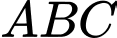 với toạ độ 3 điểm là
với toạ độ 3 điểm là 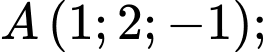
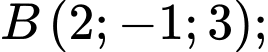
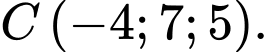
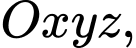 cho tam giác
cho tam giác 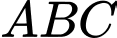 với toạ độ 3 điểm là
với toạ độ 3 điểm là 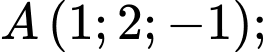
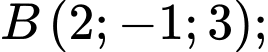
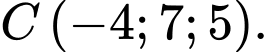
a) Đúng.
Áp dụng công thức tọa độ của vecto khi biến tọa độ 2 điểm.
b) Đúng.
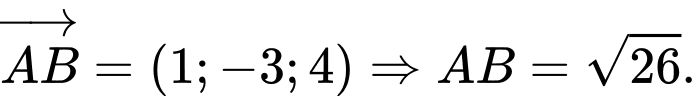
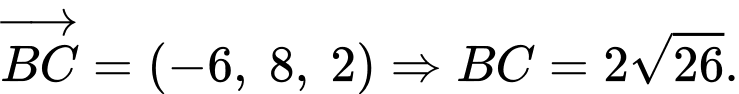
c) Sai.
Ta có: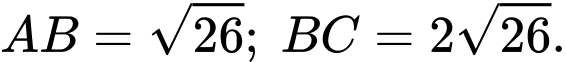
Theo tính chất đường phân giác ta có: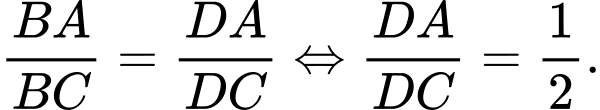
Do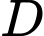 nằm giữa 2 điểm
nằm giữa 2 điểm 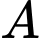 và
và  nên:
nên:
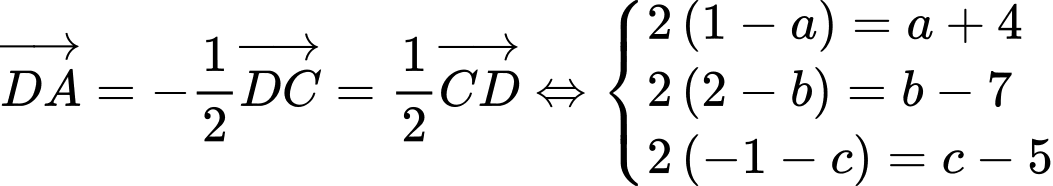
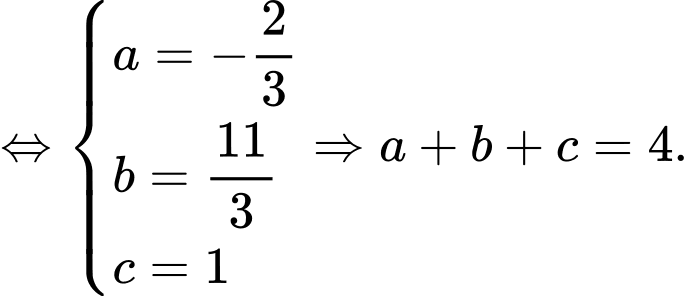
d) Đúng.
Theo câu c) ta có: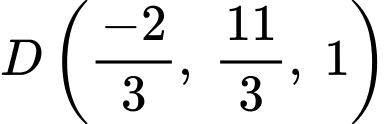
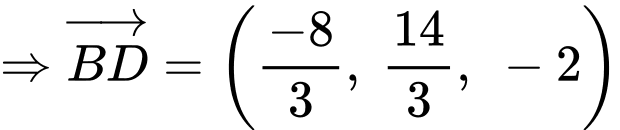
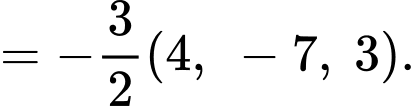
Phương trình tham số đường phân giác của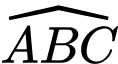 là
là
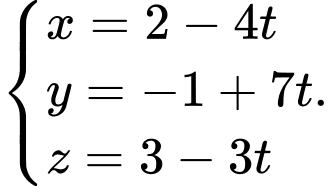
Thay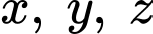 vào phương trình mặt phẳng
vào phương trình mặt phẳng 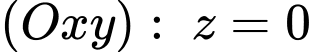 ta được:
ta được: 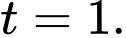
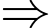 Đường phân giác của góc
Đường phân giác của góc 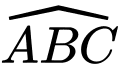 cắt mặt phẳng
cắt mặt phẳng 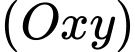 tại điểm có tọa độ
tại điểm có tọa độ 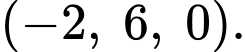
Áp dụng công thức tọa độ của vecto khi biến tọa độ 2 điểm.
b) Đúng.
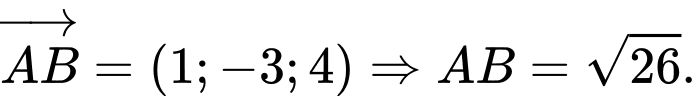
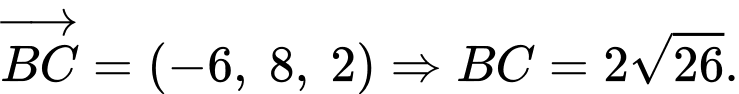
c) Sai.
Ta có:
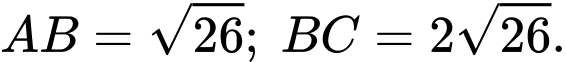
Theo tính chất đường phân giác ta có:
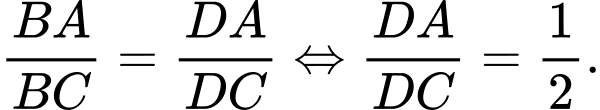
Do
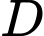 nằm giữa 2 điểm
nằm giữa 2 điểm 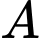 và
và  nên:
nên:
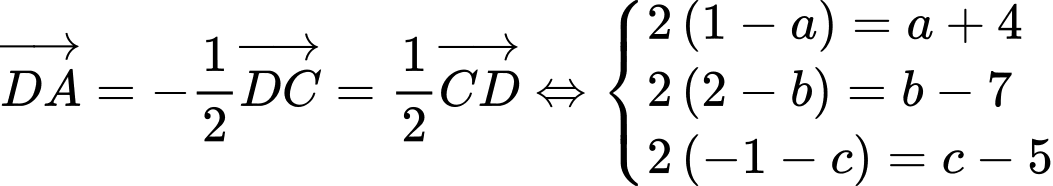
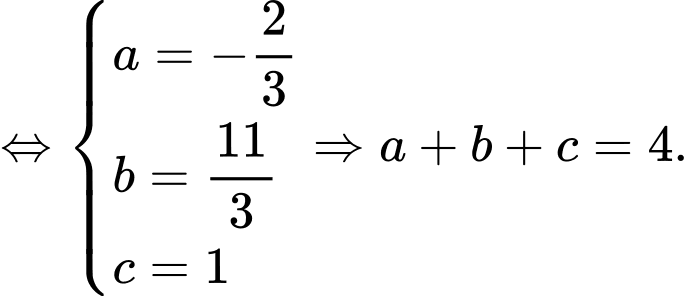
d) Đúng.
Theo câu c) ta có:
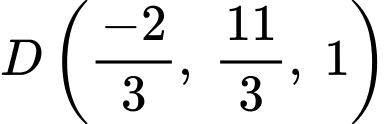
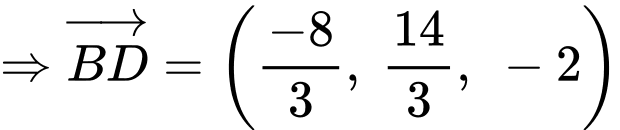
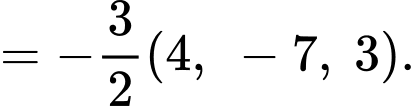
Phương trình tham số đường phân giác của
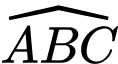 là
là
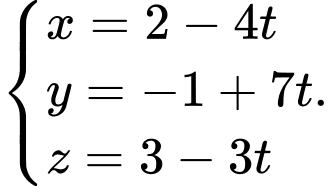
Thay
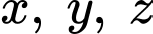 vào phương trình mặt phẳng
vào phương trình mặt phẳng 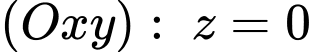 ta được:
ta được: 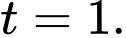
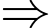 Đường phân giác của góc
Đường phân giác của góc 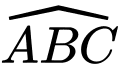 cắt mặt phẳng
cắt mặt phẳng 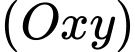 tại điểm có tọa độ
tại điểm có tọa độ 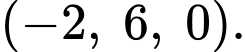
PHẦN III. Thí sinh trả lời từ câu 1 đến câu 6.
Câu 17 [695517]: Cho hình lăng trụ đứng  có đáy
có đáy 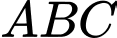 là tam giác đều cạnh
là tam giác đều cạnh 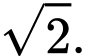
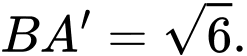 Khoảng cách giữa hai đường thẳng
Khoảng cách giữa hai đường thẳng 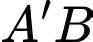 và
và 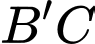 là bao nhiêu? (làm tròn kết quả đến hàng phần trăm)
là bao nhiêu? (làm tròn kết quả đến hàng phần trăm)
 có đáy
có đáy 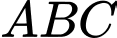 là tam giác đều cạnh
là tam giác đều cạnh 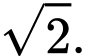
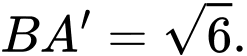 Khoảng cách giữa hai đường thẳng
Khoảng cách giữa hai đường thẳng 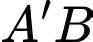 và
và 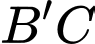 là bao nhiêu? (làm tròn kết quả đến hàng phần trăm)
là bao nhiêu? (làm tròn kết quả đến hàng phần trăm)
Điền đáp án: 0,67.
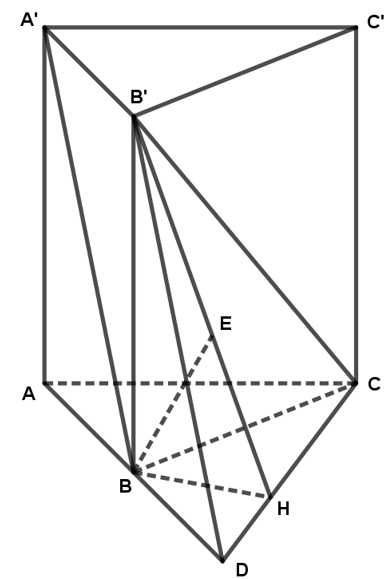
Kẻ 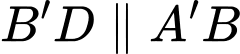
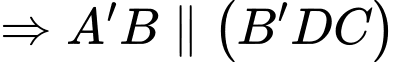
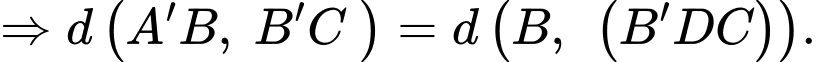
Vì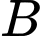 là trung điểm
là trung điểm 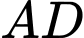
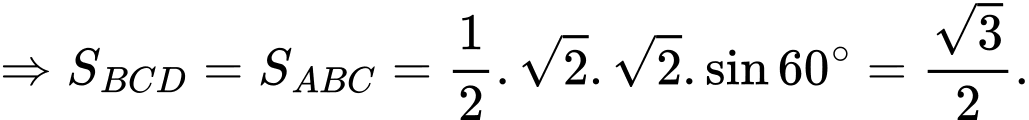
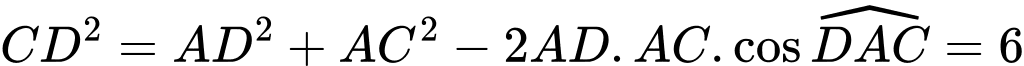
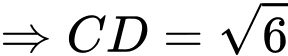
Kẻ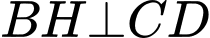
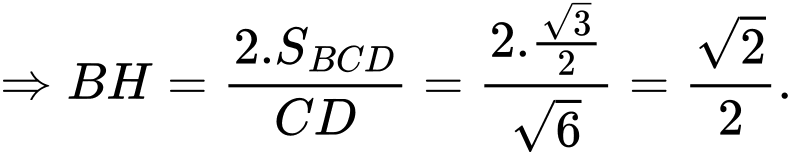
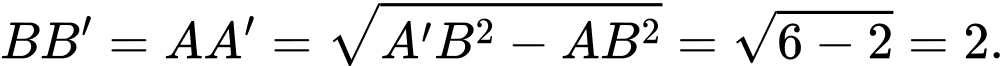
Xét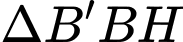 vuông tại có:
vuông tại có: 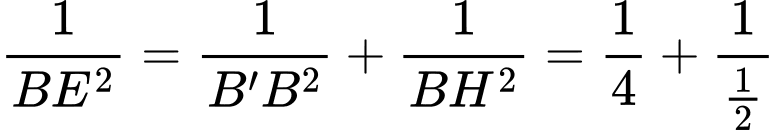
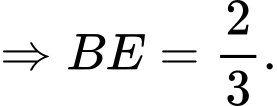
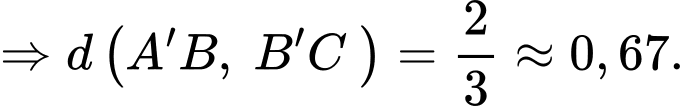

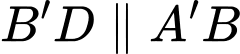
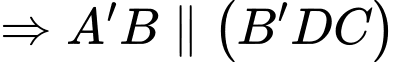
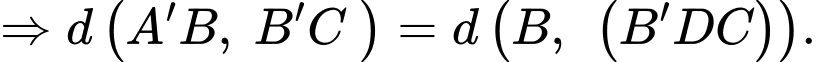
Vì
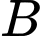 là trung điểm
là trung điểm 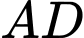
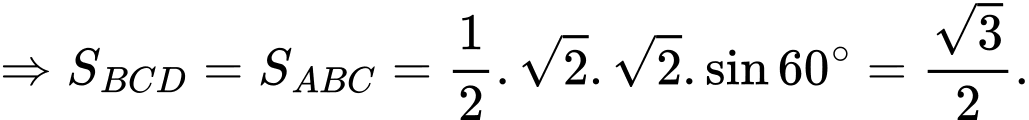
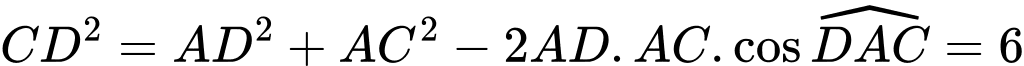
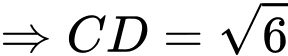
Kẻ
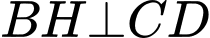
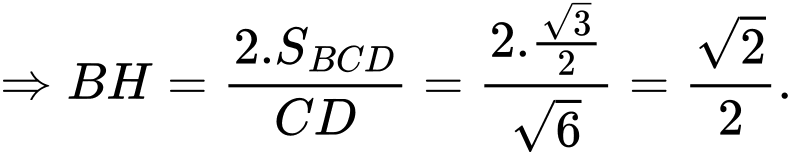
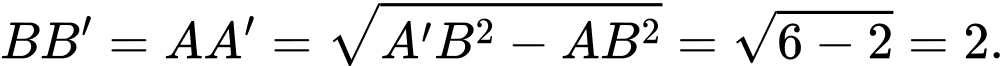
Xét
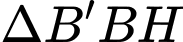 vuông tại có:
vuông tại có: 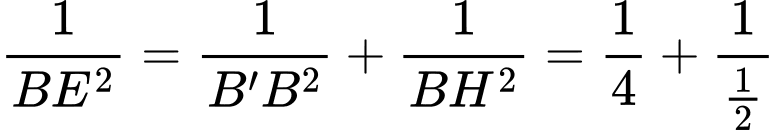
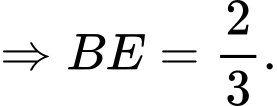
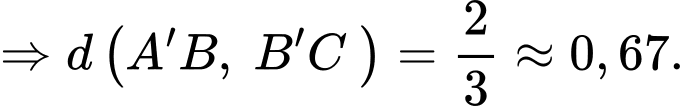
Câu 18 [695518]: Một công ty sản xuất hai loại thiết bị dạy học A và B dành cho môn Toán lớp 12. Mỗi sản phẩm loại A cần 9 giờ lao động để gia công và 1 giờ lao động để hoàn thiện. Mỗi sản phẩm loại B cần 12 giờ lao động để gia công và 3 giờ lao động để hoàn thiện. Số giờ lao động tối đa có sẵn mỗi tuần cho gia công và hoàn thiện lần lượt là 180 giờ và 30 giờ. Công ty thu được lợi nhuận là 80 000 đồng trên mỗi sản phẩm loại A và 120 000 đồng trên mỗi sản phẩm loại B. Cần sản xuất 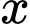 sản phẩm loại A và
sản phẩm loại A và 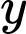 sản phẩm loại B mỗi tuần để có được lợi nhuận tối đa. Lợi nhuận tối đa mỗi tuần là bao nhiêu nghìn đồng?
sản phẩm loại B mỗi tuần để có được lợi nhuận tối đa. Lợi nhuận tối đa mỗi tuần là bao nhiêu nghìn đồng?
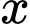 sản phẩm loại A và
sản phẩm loại A và 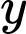 sản phẩm loại B mỗi tuần để có được lợi nhuận tối đa. Lợi nhuận tối đa mỗi tuần là bao nhiêu nghìn đồng?
sản phẩm loại B mỗi tuần để có được lợi nhuận tối đa. Lợi nhuận tối đa mỗi tuần là bao nhiêu nghìn đồng?
Điền đáp án: 1680.
Lợi nhuận của công ty là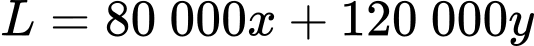 (đồng)
(đồng)
Theo đề bài ta có hệ bất phương trình: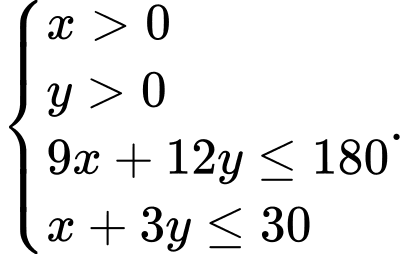
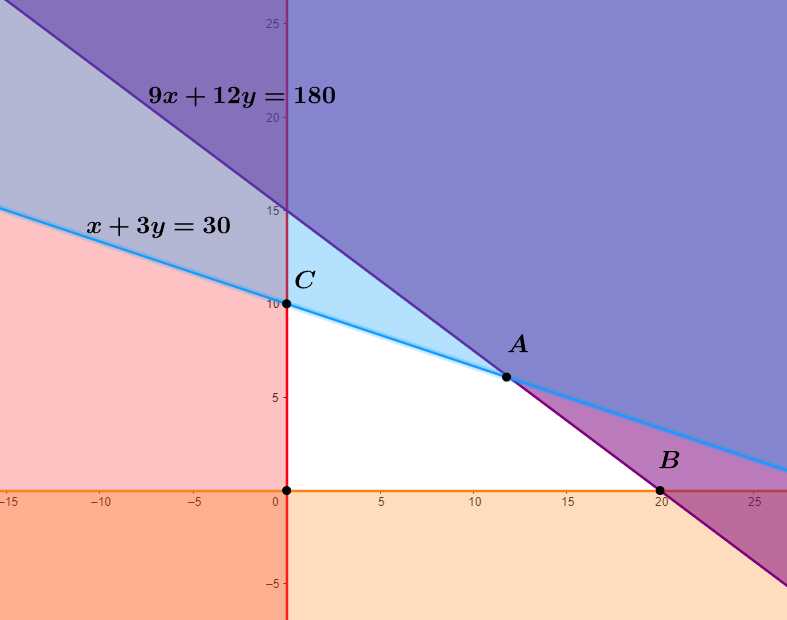
Miền giá trị của hệ bất phương trình trên chính là tứ giác OBAC.
Hàm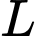 đạt giá trị lớn nhất tại các đỉnh của tứ giác trên.
đạt giá trị lớn nhất tại các đỉnh của tứ giác trên.
Tại điểm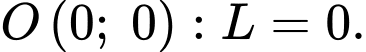
Tại điểm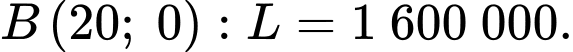
Tại điểm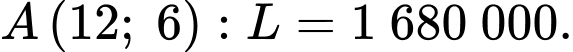
Tại điểm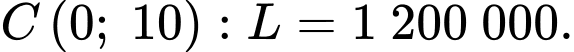
Vậy lợi nhuận cao nhất là 1 680 000 đồng.
Lợi nhuận của công ty là
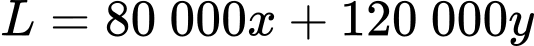 (đồng)
(đồng)Theo đề bài ta có hệ bất phương trình:
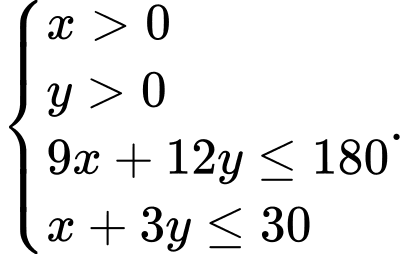

Miền giá trị của hệ bất phương trình trên chính là tứ giác OBAC.
Hàm
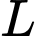 đạt giá trị lớn nhất tại các đỉnh của tứ giác trên.
đạt giá trị lớn nhất tại các đỉnh của tứ giác trên.Tại điểm
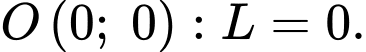
Tại điểm
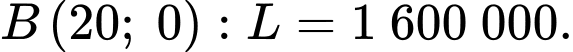
Tại điểm
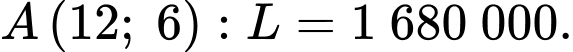
Tại điểm
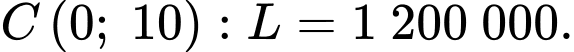
Vậy lợi nhuận cao nhất là 1 680 000 đồng.
Câu 19 [695519]: Hộp thứ nhất có 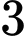 viên bi xanh và
viên bi xanh và 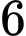 viên vi đỏ. Hộp thứ hai có
viên vi đỏ. Hộp thứ hai có 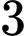 viên vi xanh và
viên vi xanh và 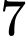 viên bi đỏ. Các viên bi có cùng kích thức và khối lượng. Lấy ngẫu nhiên ra một viên bi từ hộp thứ nhất chuyển sang hộp thứ hai. Sau đó lại lấy ngẫu nhiên đồng thời hai viên từ hộp thứ hai, biết rằng hai bi lấy ra từ hộp thứ hai là bi màu đỏ, xác suất viên bi lấy ra từ hộp thứ nhất cũng là bi màu đỏ là bao nhiêu, viết kết quả làm tròn đến hàng phần trăm.
viên bi đỏ. Các viên bi có cùng kích thức và khối lượng. Lấy ngẫu nhiên ra một viên bi từ hộp thứ nhất chuyển sang hộp thứ hai. Sau đó lại lấy ngẫu nhiên đồng thời hai viên từ hộp thứ hai, biết rằng hai bi lấy ra từ hộp thứ hai là bi màu đỏ, xác suất viên bi lấy ra từ hộp thứ nhất cũng là bi màu đỏ là bao nhiêu, viết kết quả làm tròn đến hàng phần trăm.
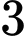 viên bi xanh và
viên bi xanh và 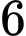 viên vi đỏ. Hộp thứ hai có
viên vi đỏ. Hộp thứ hai có 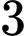 viên vi xanh và
viên vi xanh và 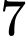 viên bi đỏ. Các viên bi có cùng kích thức và khối lượng. Lấy ngẫu nhiên ra một viên bi từ hộp thứ nhất chuyển sang hộp thứ hai. Sau đó lại lấy ngẫu nhiên đồng thời hai viên từ hộp thứ hai, biết rằng hai bi lấy ra từ hộp thứ hai là bi màu đỏ, xác suất viên bi lấy ra từ hộp thứ nhất cũng là bi màu đỏ là bao nhiêu, viết kết quả làm tròn đến hàng phần trăm.
viên bi đỏ. Các viên bi có cùng kích thức và khối lượng. Lấy ngẫu nhiên ra một viên bi từ hộp thứ nhất chuyển sang hộp thứ hai. Sau đó lại lấy ngẫu nhiên đồng thời hai viên từ hộp thứ hai, biết rằng hai bi lấy ra từ hộp thứ hai là bi màu đỏ, xác suất viên bi lấy ra từ hộp thứ nhất cũng là bi màu đỏ là bao nhiêu, viết kết quả làm tròn đến hàng phần trăm.
Điền đáp án: 0,73.
Gọi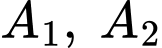 lần lượt là các biến cố lấy ra một bi một màu xanh và một bi màu đỏ ở hộp thứ nhất. Nên
lần lượt là các biến cố lấy ra một bi một màu xanh và một bi màu đỏ ở hộp thứ nhất. Nên 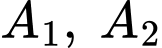 là hệ biến cố đầy đủ.
là hệ biến cố đầy đủ.
Gọi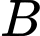 là biến cố “Hai bi lấy ra từ hộp thứ hai là màu đỏ”
là biến cố “Hai bi lấy ra từ hộp thứ hai là màu đỏ”
YCBT Tính
Tính 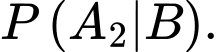
Ta có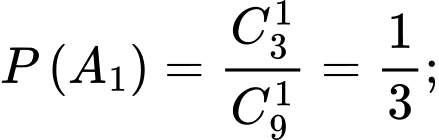
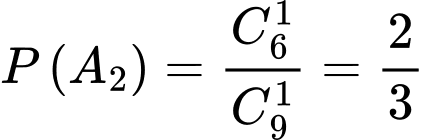
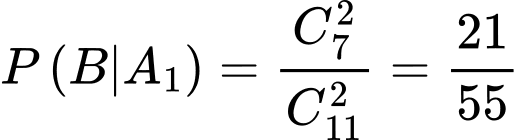 ;
; 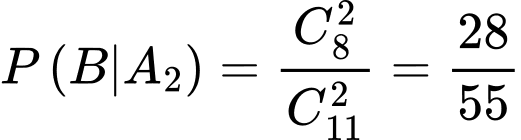
Ta có sơ đồ cây sau:
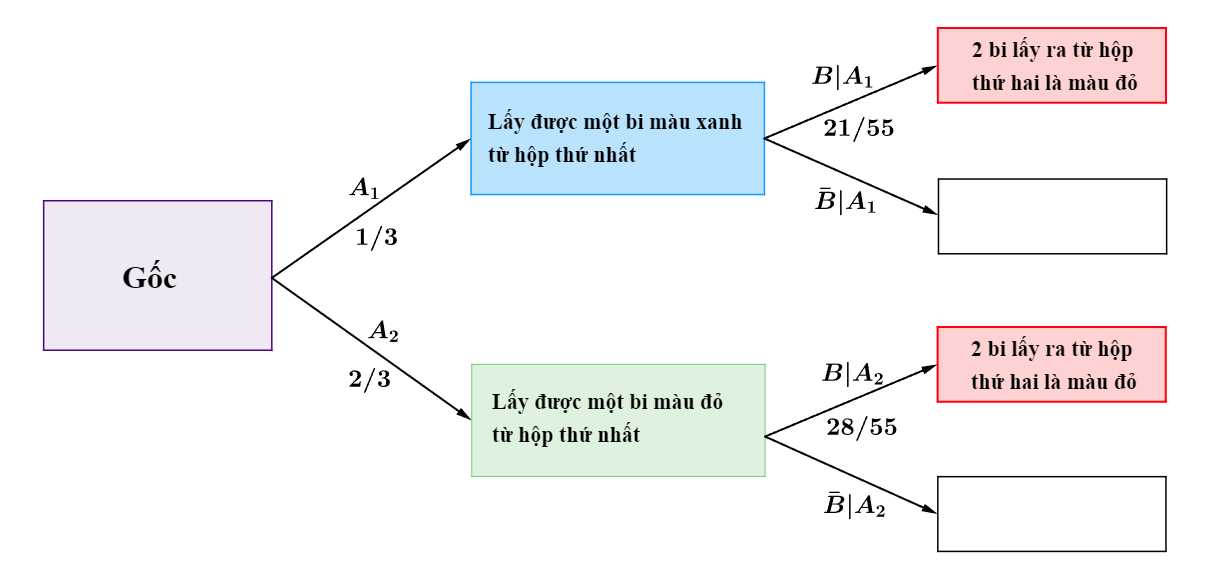
Áp dụng công thức xác suất toàn phần, ta có
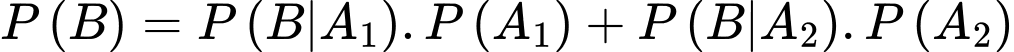
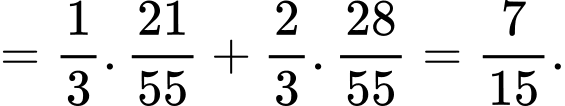
Xác suất viên bi lấy ra từ hộp thứ nhất màu đỏ, biết rằng hai bi lấy ra từ hộp thứ hai màu đỏ, ta áp dụng công thức Bayes, ta được
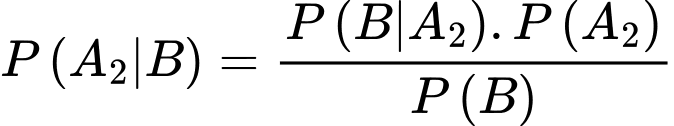
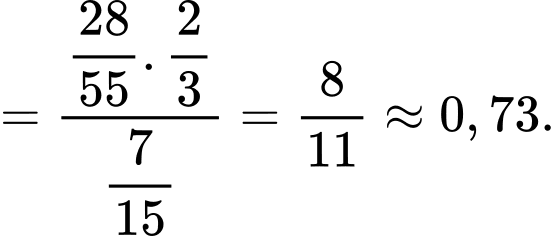
Gọi
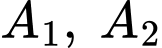 lần lượt là các biến cố lấy ra một bi một màu xanh và một bi màu đỏ ở hộp thứ nhất. Nên
lần lượt là các biến cố lấy ra một bi một màu xanh và một bi màu đỏ ở hộp thứ nhất. Nên 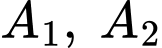 là hệ biến cố đầy đủ.
là hệ biến cố đầy đủ.Gọi
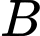 là biến cố “Hai bi lấy ra từ hộp thứ hai là màu đỏ”
là biến cố “Hai bi lấy ra từ hộp thứ hai là màu đỏ”YCBT
 Tính
Tính 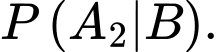
Ta có
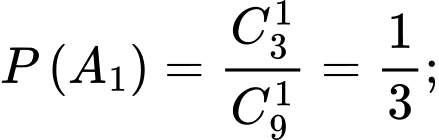
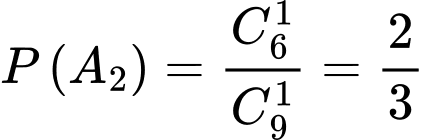
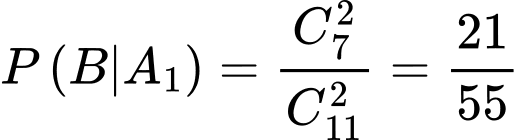 ;
; 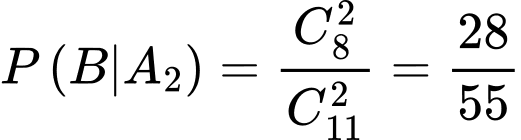
Ta có sơ đồ cây sau:

Áp dụng công thức xác suất toàn phần, ta có
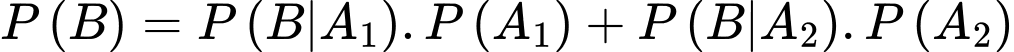
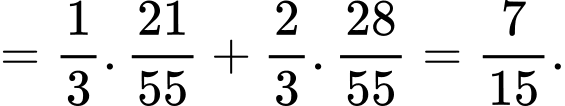
Xác suất viên bi lấy ra từ hộp thứ nhất màu đỏ, biết rằng hai bi lấy ra từ hộp thứ hai màu đỏ, ta áp dụng công thức Bayes, ta được
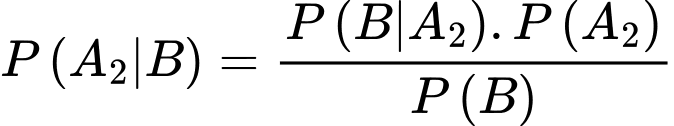
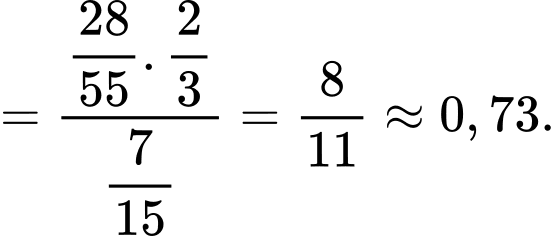
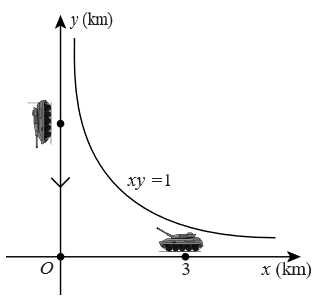
Câu 20 [696346]: Một quân nhân đang ở trong một chiếc xe tăng 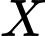 (loại quân sự) di chuyển dọc theo trục
(loại quân sự) di chuyển dọc theo trục 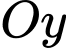 về phía gốc tọa độ. Tại thời điểm xe cách gốc tọa độ 4 km, và 10 phút sau xe cách gốc tọa độ 2 km. Tốc độ của xe (km/h) tỉ lệ nghịch với khoảng cách của xe (km) đến gốc tọa độ. Biết rằng một xe tăng địch đang chờ ở tại điểm
về phía gốc tọa độ. Tại thời điểm xe cách gốc tọa độ 4 km, và 10 phút sau xe cách gốc tọa độ 2 km. Tốc độ của xe (km/h) tỉ lệ nghịch với khoảng cách của xe (km) đến gốc tọa độ. Biết rằng một xe tăng địch đang chờ ở tại điểm 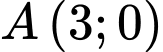 trên trục
trên trục  nhưng có một bức tường cao dọc theo đường cong (tất cả khoảng cách tính bằng km) ngăn cản bạn nhìn thấy vị trí chính xác của nó. Tại thời điểm đầu tiên quân địch phát hiện xe tăng, tốc độ của xe tăng
nhưng có một bức tường cao dọc theo đường cong (tất cả khoảng cách tính bằng km) ngăn cản bạn nhìn thấy vị trí chính xác của nó. Tại thời điểm đầu tiên quân địch phát hiện xe tăng, tốc độ của xe tăng 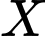 bằng bao nhiêu km/h? (làm tròn kết quả đến hàng phần mười).
bằng bao nhiêu km/h? (làm tròn kết quả đến hàng phần mười).
 (loại quân sự) di chuyển dọc theo trục
(loại quân sự) di chuyển dọc theo trục 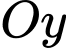 về phía gốc tọa độ. Tại thời điểm xe cách gốc tọa độ 4 km, và 10 phút sau xe cách gốc tọa độ 2 km. Tốc độ của xe (km/h) tỉ lệ nghịch với khoảng cách của xe (km) đến gốc tọa độ. Biết rằng một xe tăng địch đang chờ ở tại điểm
về phía gốc tọa độ. Tại thời điểm xe cách gốc tọa độ 4 km, và 10 phút sau xe cách gốc tọa độ 2 km. Tốc độ của xe (km/h) tỉ lệ nghịch với khoảng cách của xe (km) đến gốc tọa độ. Biết rằng một xe tăng địch đang chờ ở tại điểm 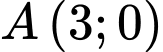 trên trục
trên trục  nhưng có một bức tường cao dọc theo đường cong (tất cả khoảng cách tính bằng km) ngăn cản bạn nhìn thấy vị trí chính xác của nó. Tại thời điểm đầu tiên quân địch phát hiện xe tăng, tốc độ của xe tăng
nhưng có một bức tường cao dọc theo đường cong (tất cả khoảng cách tính bằng km) ngăn cản bạn nhìn thấy vị trí chính xác của nó. Tại thời điểm đầu tiên quân địch phát hiện xe tăng, tốc độ của xe tăng 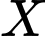 bằng bao nhiêu km/h? (làm tròn kết quả đến hàng phần mười).
bằng bao nhiêu km/h? (làm tròn kết quả đến hàng phần mười).
Điền đáp án: 27.
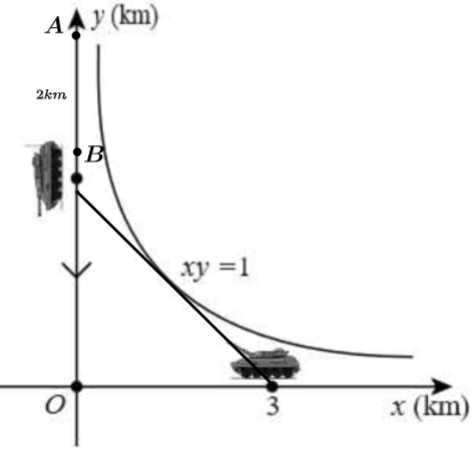
Ta có đường cong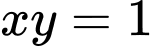
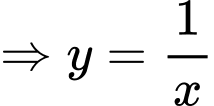
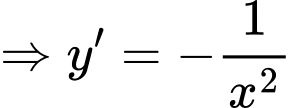
Xét tại thời điểm đầu tiên quân địch phát hiện xe tăng ta có phương trình tiếp tuyến của đường cong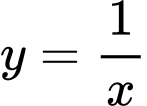 có dạng:
có dạng:
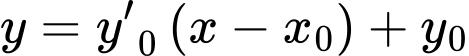
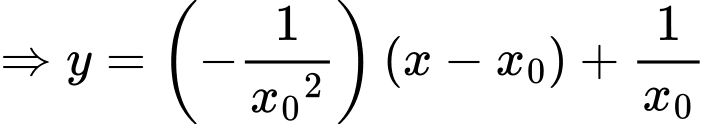
Ta có tiếp tuyến đi qua điểm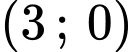 điểm xe địch đứng
điểm xe địch đứng
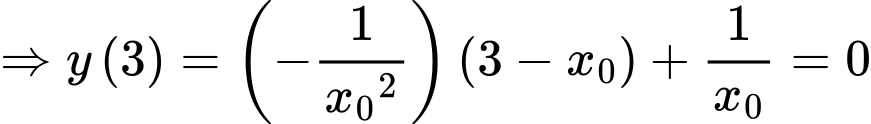
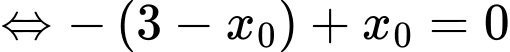
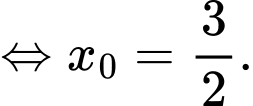
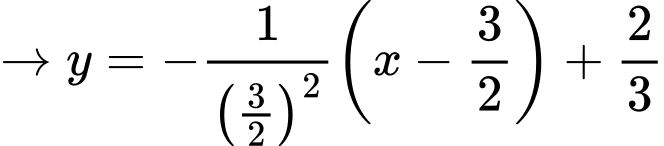
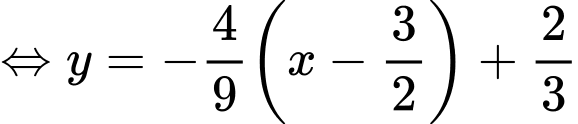
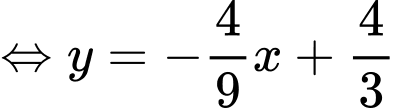
Tọa độ vị trí xe tăng ta lúc địch thấy tại điểm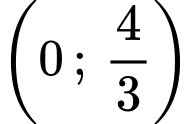
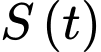 là quãng đường xe đi,
là quãng đường xe đi, 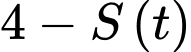 là khoảng cách từ xe đến O.
là khoảng cách từ xe đến O.
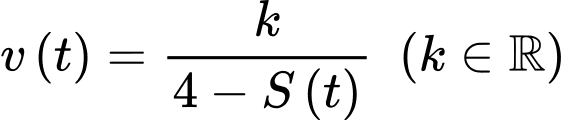
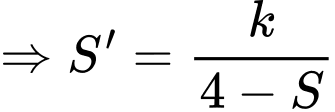
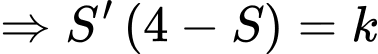
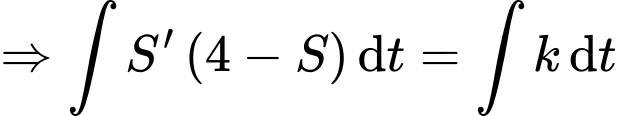
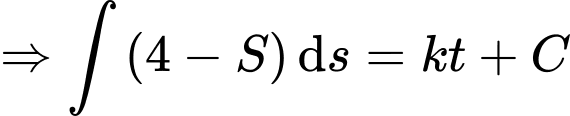
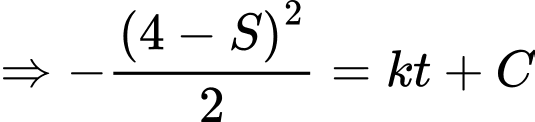
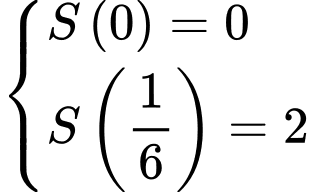
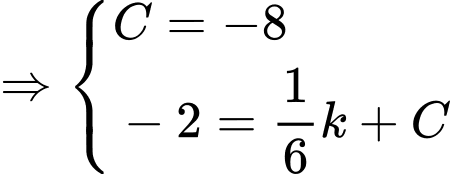
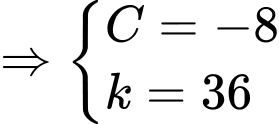
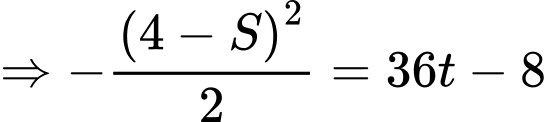
+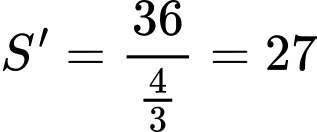
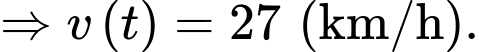

Ta có đường cong
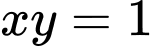
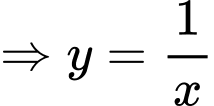
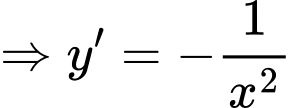
Xét tại thời điểm đầu tiên quân địch phát hiện xe tăng ta có phương trình tiếp tuyến của đường cong
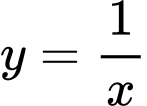 có dạng:
có dạng:
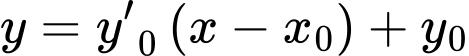
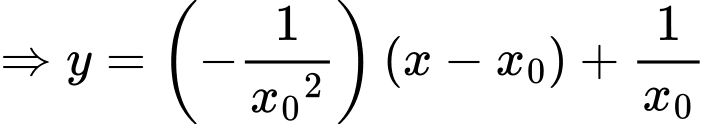
Ta có tiếp tuyến đi qua điểm
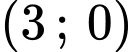 điểm xe địch đứng
điểm xe địch đứng
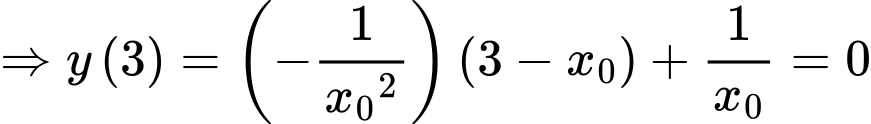
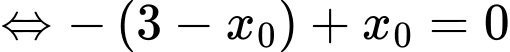
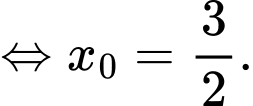
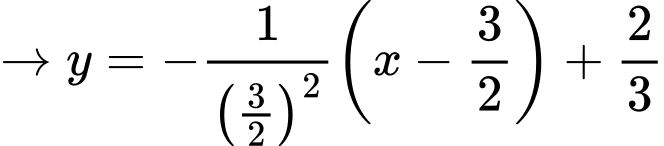
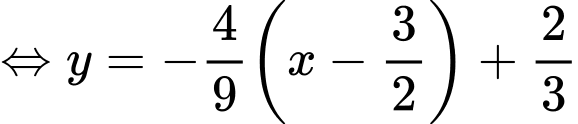
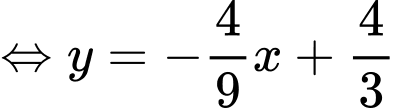
Tọa độ vị trí xe tăng ta lúc địch thấy tại điểm
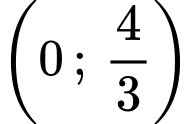
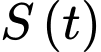 là quãng đường xe đi,
là quãng đường xe đi, 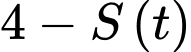 là khoảng cách từ xe đến O.
là khoảng cách từ xe đến O.
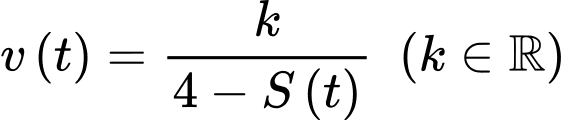
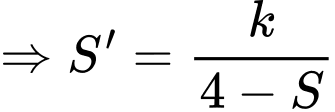
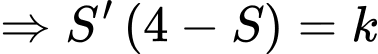
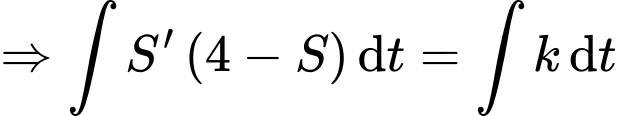
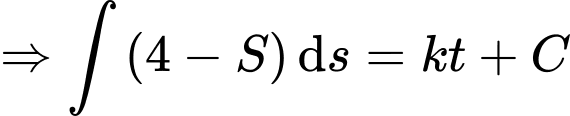
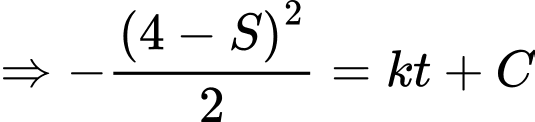
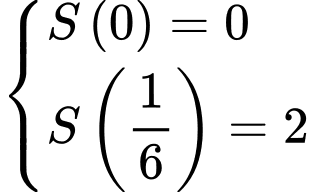
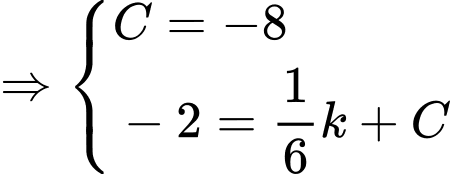
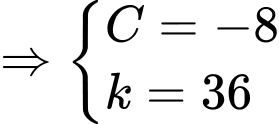
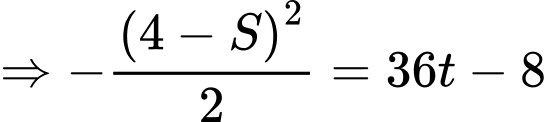
+
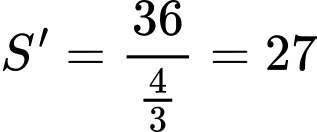
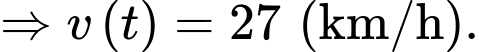
Câu 21 [695521]: Trong không gian với hệ tọa độ 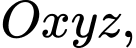 cho hai mặt cầu
cho hai mặt cầu 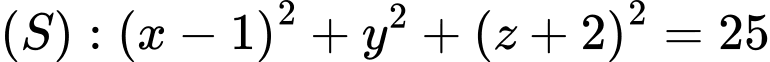 và điểm
và điểm 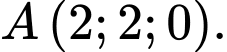 Gọi d là đường thẳng nằm trong mặt phẳng
Gọi d là đường thẳng nằm trong mặt phẳng 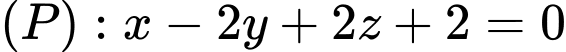 và đi qua điểm A sao cho d cắt (S) theo một dây cung có độ dài nhỏ nhất. Biết d có một véc tơ chỉ phương là
và đi qua điểm A sao cho d cắt (S) theo một dây cung có độ dài nhỏ nhất. Biết d có một véc tơ chỉ phương là 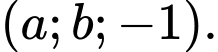 Giá trị của a + b bằng bao nhiêu?
Giá trị của a + b bằng bao nhiêu?
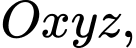 cho hai mặt cầu
cho hai mặt cầu 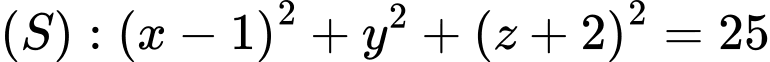 và điểm
và điểm 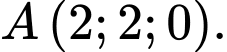 Gọi d là đường thẳng nằm trong mặt phẳng
Gọi d là đường thẳng nằm trong mặt phẳng 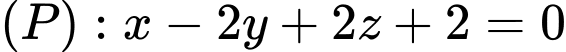 và đi qua điểm A sao cho d cắt (S) theo một dây cung có độ dài nhỏ nhất. Biết d có một véc tơ chỉ phương là
và đi qua điểm A sao cho d cắt (S) theo một dây cung có độ dài nhỏ nhất. Biết d có một véc tơ chỉ phương là 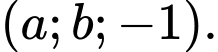 Giá trị của a + b bằng bao nhiêu?
Giá trị của a + b bằng bao nhiêu?
Điền đáp án: 2.
Mặt cầu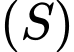 có :
có : 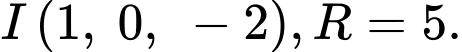
Gọi là hình chiều của
là hình chiều của 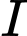 xuống mặt phẳng
xuống mặt phẳng 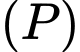 .
.
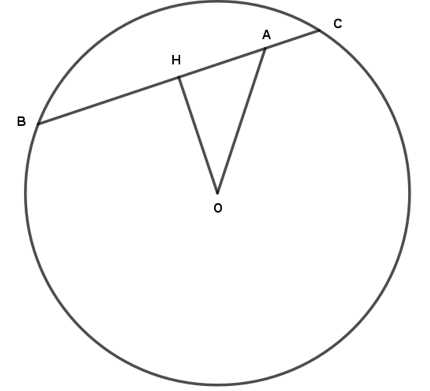
Mặt phẳng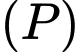 giao với mặt cầu
giao với mặt cầu 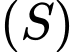 theo đường tròn tâm
theo đường tròn tâm  , đường thẳng
, đường thẳng 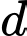 cắt đường trong tâm
cắt đường trong tâm  theo dây cung
theo dây cung 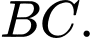
Gọi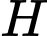 là chân đường cao kẻ từ
là chân đường cao kẻ từ  xuống
xuống 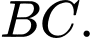
Phương trình đường thẳng vuông góc với mặt phẳng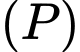 và đi qua điểm
và đi qua điểm 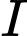 là
là 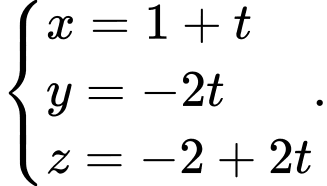
Thay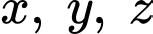 vào phương trình mặt phẳng
vào phương trình mặt phẳng 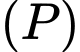 ta được :
ta được :
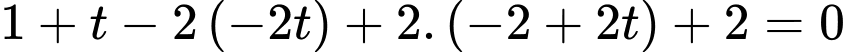
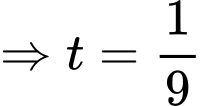
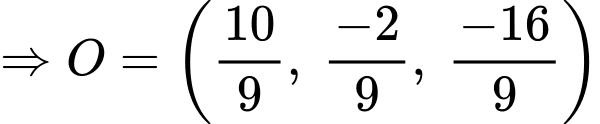
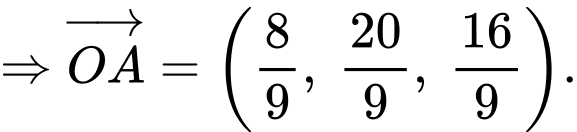
Khoảng cách từ điểm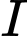 đến mặt phẳng
đến mặt phẳng 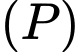 là
là 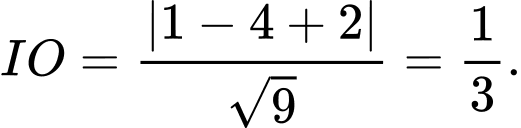

Ta có: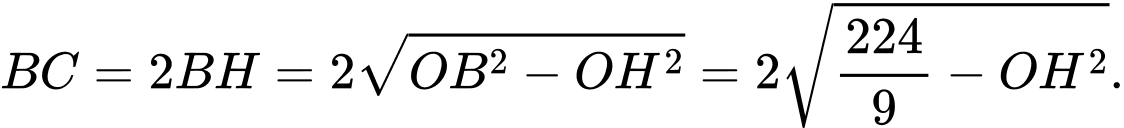
Mà
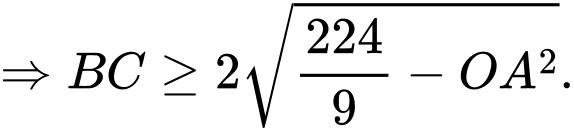
Dấu “=” xảy ra khi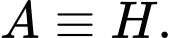
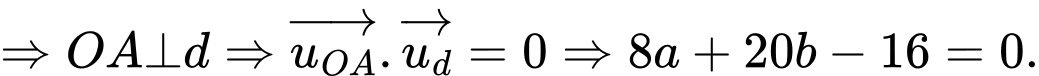 (1)
(1)
Ta có: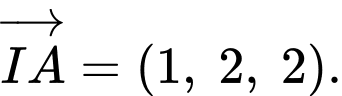
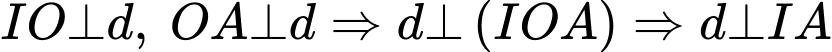
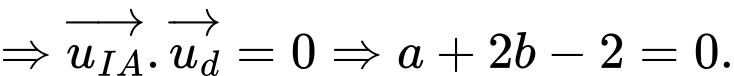 (2)
(2)
Từ (1) và (2)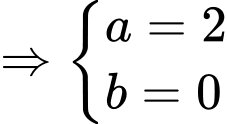
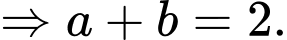
Mặt cầu
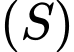 có :
có : 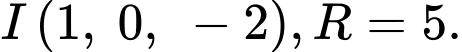
Gọi
 là hình chiều của
là hình chiều của 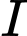 xuống mặt phẳng
xuống mặt phẳng 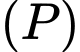 .
.
Mặt phẳng
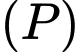 giao với mặt cầu
giao với mặt cầu 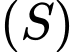 theo đường tròn tâm
theo đường tròn tâm  , đường thẳng
, đường thẳng 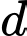 cắt đường trong tâm
cắt đường trong tâm  theo dây cung
theo dây cung 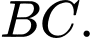
Gọi
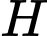 là chân đường cao kẻ từ
là chân đường cao kẻ từ  xuống
xuống 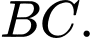

Phương trình đường thẳng vuông góc với mặt phẳng
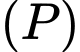 và đi qua điểm
và đi qua điểm 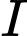 là
là 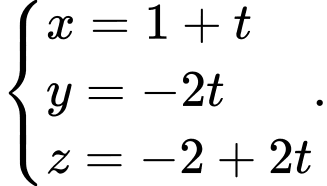
Thay
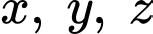 vào phương trình mặt phẳng
vào phương trình mặt phẳng 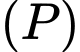 ta được :
ta được :
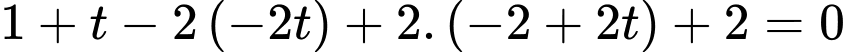
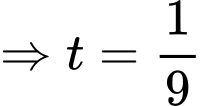
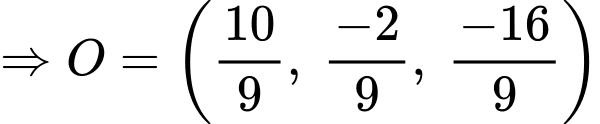
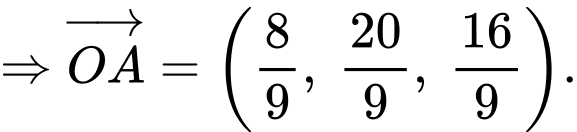
Khoảng cách từ điểm
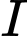 đến mặt phẳng
đến mặt phẳng 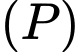 là
là 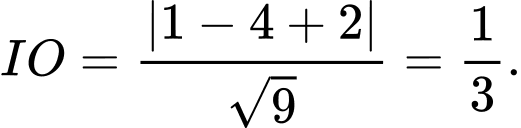

Ta có:
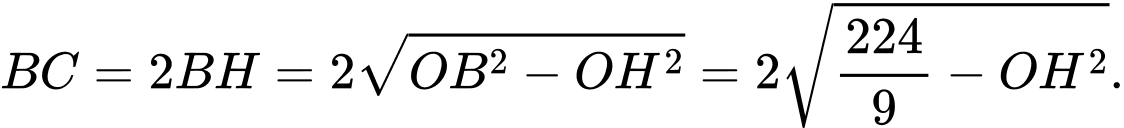
Mà

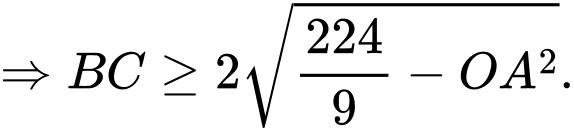
Dấu “=” xảy ra khi
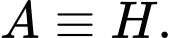
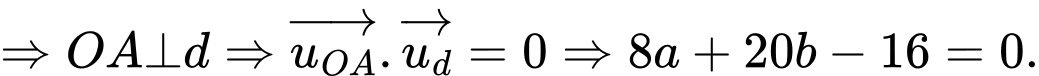 (1)
(1)
Ta có:
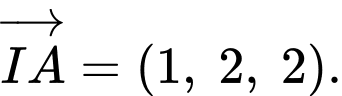
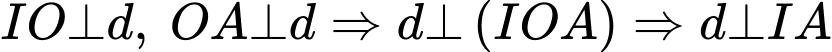
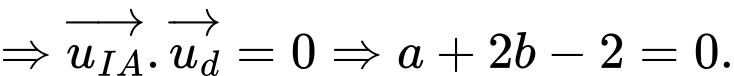 (2)
(2)
Từ (1) và (2)
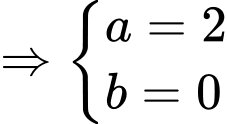
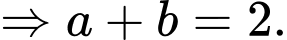
Câu 22 [695522]: Người ta muốn làm một sàn nổi hình vuông nối liền một sân khẩu nổi trên mặt hồ có bở là một nhánh đồ thị của hàm số 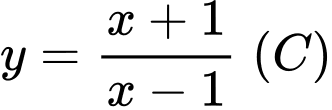 với đất liền là nửa mặt phẳng giới hạn bởi đường thẳng
với đất liền là nửa mặt phẳng giới hạn bởi đường thẳng 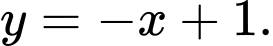 Tính diện tích
Tính diện tích 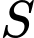 của mặt sản nôi, biết hình vuông có 2 đỉnh năm trên
của mặt sản nôi, biết hình vuông có 2 đỉnh năm trên  hai đỉnh còn lại nằm trên
hai đỉnh còn lại nằm trên 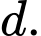
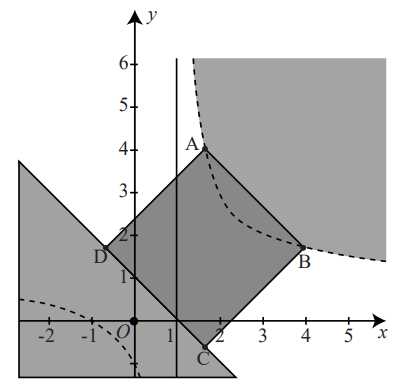
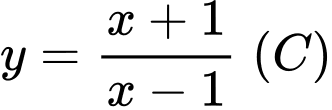 với đất liền là nửa mặt phẳng giới hạn bởi đường thẳng
với đất liền là nửa mặt phẳng giới hạn bởi đường thẳng 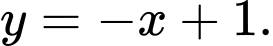 Tính diện tích
Tính diện tích 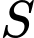 của mặt sản nôi, biết hình vuông có 2 đỉnh năm trên
của mặt sản nôi, biết hình vuông có 2 đỉnh năm trên  hai đỉnh còn lại nằm trên
hai đỉnh còn lại nằm trên 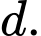

Điền đáp án: 10,9.
Ta có 2 đường tiệm cận của đồ thị hàm số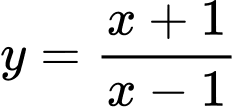 là
là 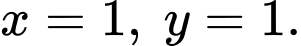
Kẻ đường thẳng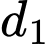 sao cho
sao cho 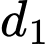 là đường phân giác của góc tạo bởi 2 đường tiệm cận của đồ thị hàm số
là đường phân giác của góc tạo bởi 2 đường tiệm cận của đồ thị hàm số 
Suy ra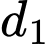 là trục đối xứng của đồ thị và hình vuông.
là trục đối xứng của đồ thị và hình vuông.
Khi đó ta có hình vẽ như sau:
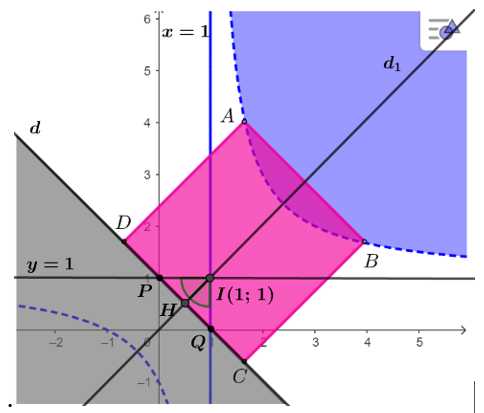
Suy ra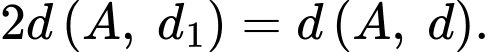
+) Để tìm khoảng cách từ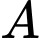 đến
đến 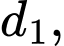 ta cần tìm được phương trình đường thẳng
ta cần tìm được phương trình đường thẳng 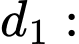
Gọi I là giao điểm của hai đường tiệm cận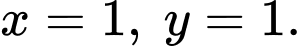
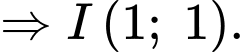
Xét tam giác vuông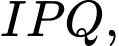 ta có
ta có 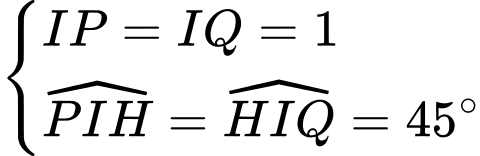 (vì
(vì  là đường phân giác của
là đường phân giác của  )
)
Suy ra hay
hay 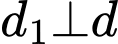
Ta có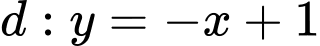 hay
hay 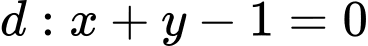 có VTPT là
có VTPT là 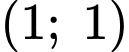
Vì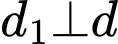 nên tích vô hướng của 2 VTPT của
nên tích vô hướng của 2 VTPT của 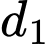 và
và 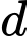 bằng 0 suy ra VTPT của
bằng 0 suy ra VTPT của 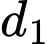 là
là 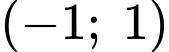
Đường thẳng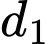 đi qua điểm
đi qua điểm 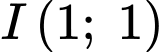 và có VTPT
và có VTPT 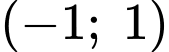 sẽ có phương trình là
sẽ có phương trình là 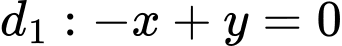
Vì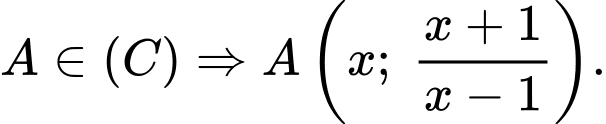
Ta có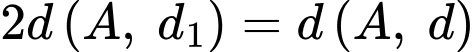
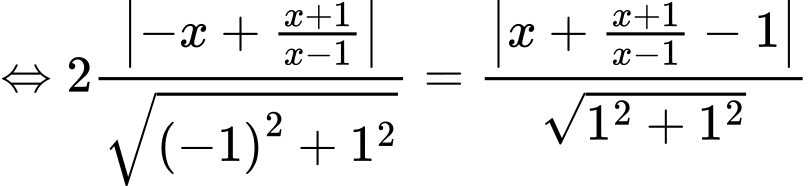
Ấn máy tính, ta tìm được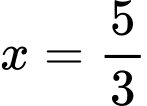
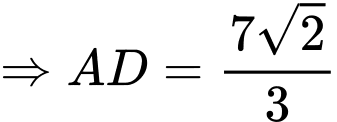
Suy ra diện tích mặt sàn nổi hình vuông là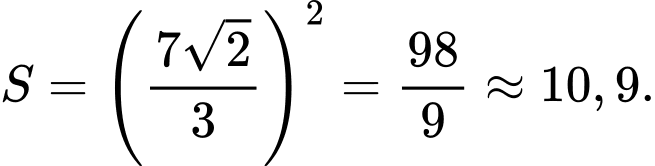
Ta có 2 đường tiệm cận của đồ thị hàm số
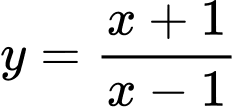 là
là 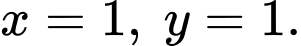
Kẻ đường thẳng
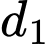 sao cho
sao cho 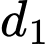 là đường phân giác của góc tạo bởi 2 đường tiệm cận của đồ thị hàm số
là đường phân giác của góc tạo bởi 2 đường tiệm cận của đồ thị hàm số 
Suy ra
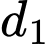 là trục đối xứng của đồ thị và hình vuông.
là trục đối xứng của đồ thị và hình vuông. Khi đó ta có hình vẽ như sau:

Suy ra
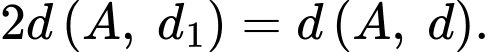
+) Để tìm khoảng cách từ
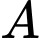 đến
đến 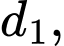 ta cần tìm được phương trình đường thẳng
ta cần tìm được phương trình đường thẳng 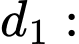
Gọi I là giao điểm của hai đường tiệm cận
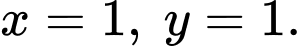
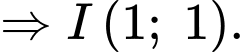
Xét tam giác vuông
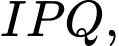 ta có
ta có 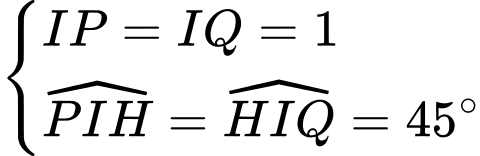 (vì
(vì  là đường phân giác của
là đường phân giác của  )
)Suy ra
 hay
hay 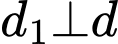
Ta có
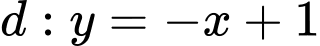 hay
hay 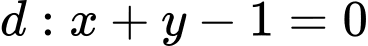 có VTPT là
có VTPT là 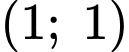
Vì
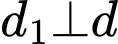 nên tích vô hướng của 2 VTPT của
nên tích vô hướng của 2 VTPT của 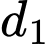 và
và 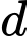 bằng 0 suy ra VTPT của
bằng 0 suy ra VTPT của 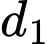 là
là 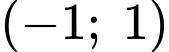
Đường thẳng
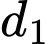 đi qua điểm
đi qua điểm 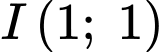 và có VTPT
và có VTPT 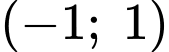 sẽ có phương trình là
sẽ có phương trình là 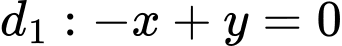
Vì
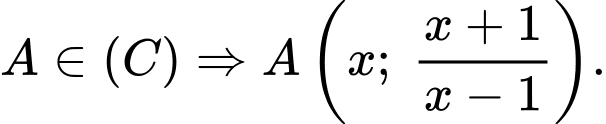
Ta có
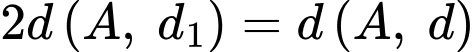
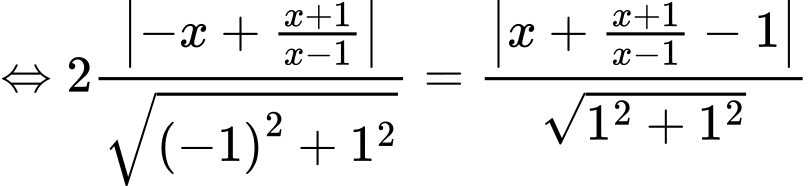
Ấn máy tính, ta tìm được
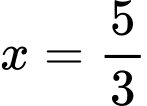
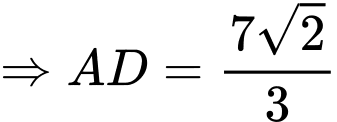
Suy ra diện tích mặt sàn nổi hình vuông là