PHẦN I. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu hỏi thí sinh chỉ chọn một phương án.
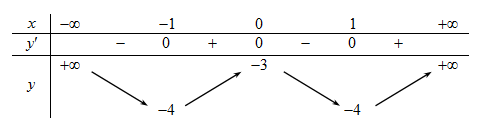
Câu 1 [616642]: Cho hàm số 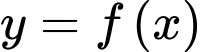 có bảng biến thiên như hình vẽ. Hàm số
có bảng biến thiên như hình vẽ. Hàm số 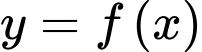 đồng biến trên khoảng nào dưới đây?
đồng biến trên khoảng nào dưới đây?
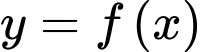 có bảng biến thiên như hình vẽ. Hàm số
có bảng biến thiên như hình vẽ. Hàm số 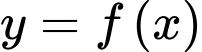 đồng biến trên khoảng nào dưới đây?
đồng biến trên khoảng nào dưới đây?
A, 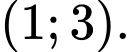
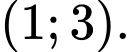
B, 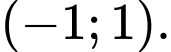
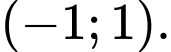
C, 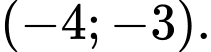
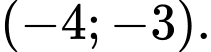
D, 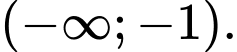
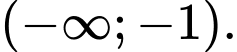
Chọn đáp án A.
Nhìn vào bảng biến thiên ta thấy hàm số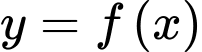 đồng biến trên khoảng
đồng biến trên khoảng 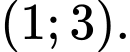 Đáp án: A
Đáp án: A
Nhìn vào bảng biến thiên ta thấy hàm số
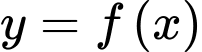 đồng biến trên khoảng
đồng biến trên khoảng 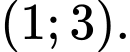 Đáp án: A
Đáp án: A
Câu 2 [620110]: Cho cấp số nhân 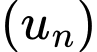 với
với 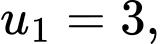
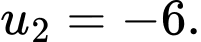 Giá trị
Giá trị 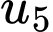 bằng
bằng
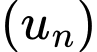 với
với 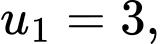
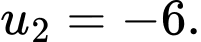 Giá trị
Giá trị 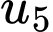 bằng
bằng A, 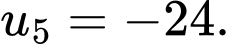
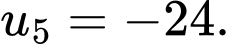
B, 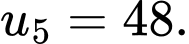
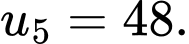
C, 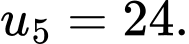
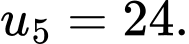
D, 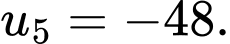
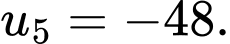
Chọn đáp án B.
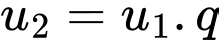
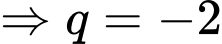
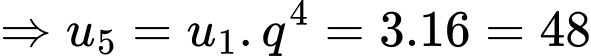 Đáp án: B
Đáp án: B
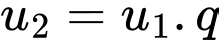
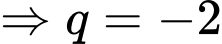
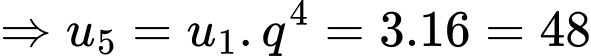 Đáp án: B
Đáp án: B
Câu 3 [695523]: Bảng sau thống kê khối lượng một số quả măng cụt được lựa chọn ngẫu nhiên trong một thùng hàng.

Khoảng biến thiên của mẫu số liệu ghép nhóm trên là:

Khoảng biến thiên của mẫu số liệu ghép nhóm trên là:
A,  gam.
gam.
 gam.
gam.B,  gam.
gam.
 gam.
gam.C, 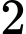 gam.
gam.
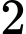 gam.
gam.D, 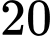 gam.
gam.
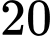 gam.
gam.
Chọn đáp án A.
Khoảng biến thiên của mẫu số liệu ghép nhóm trên là: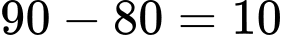 gam. Đáp án: A
gam. Đáp án: A
Khoảng biến thiên của mẫu số liệu ghép nhóm trên là:
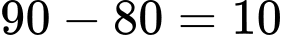 gam. Đáp án: A
gam. Đáp án: A
Câu 4 [977112]: Trong không gian cho hai vectơ 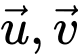 tạo với nhau một góc
tạo với nhau một góc 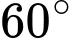 ,
, 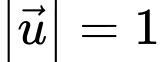 và
và 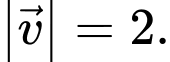 Tích vô hướng
Tích vô hướng 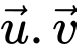 bằng
bằng
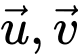 tạo với nhau một góc
tạo với nhau một góc 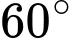 ,
, 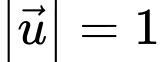 và
và 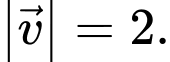 Tích vô hướng
Tích vô hướng 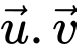 bằng
bằng A, 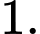
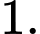
B, 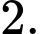
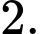
C, 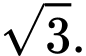
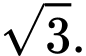
D, 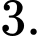
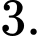
Chọn đáp án A.
Ta có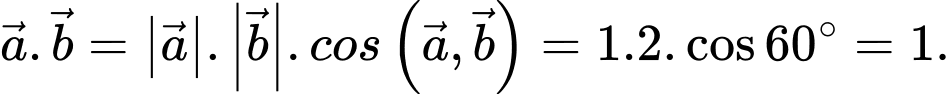 Đáp án: A
Đáp án: A
Ta có
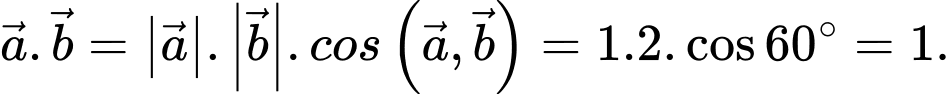 Đáp án: A
Đáp án: A
Câu 5 [618135]: Tìm nguyên hàm của hàm số 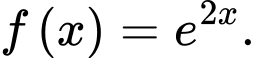
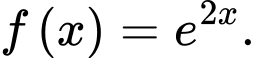
A, 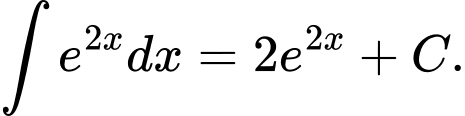
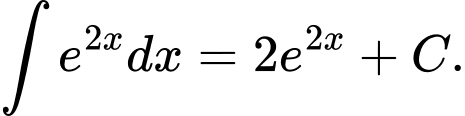
B, 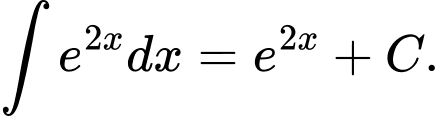
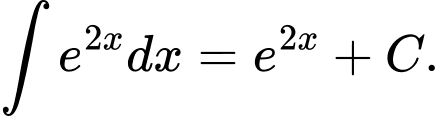
C, 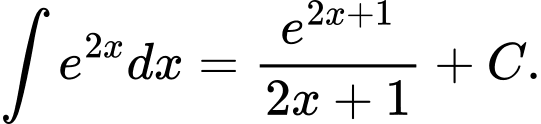
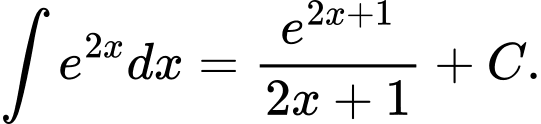
D, 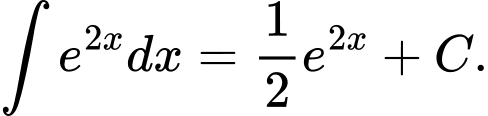
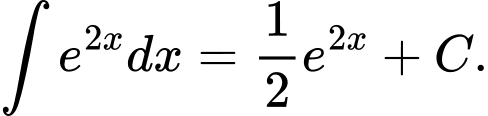
Chọn đáp án D.
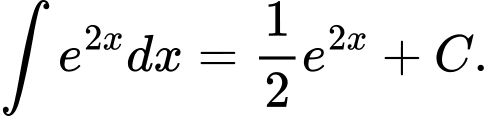 Đáp án: D
Đáp án: D
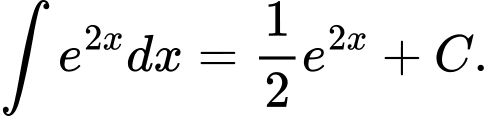 Đáp án: D
Đáp án: D
Câu 6 [50280]: Cho hai số thực dương 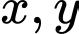 tùy ý. Mệnh đề nào sau đây đúng?
tùy ý. Mệnh đề nào sau đây đúng?
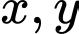 tùy ý. Mệnh đề nào sau đây đúng?
tùy ý. Mệnh đề nào sau đây đúng? A, 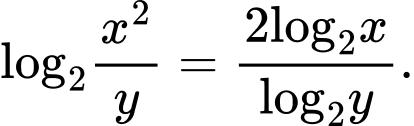
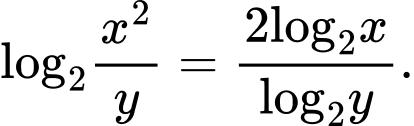
B, 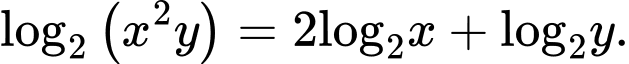
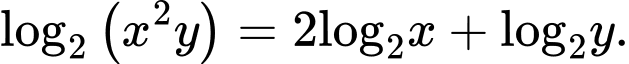
C, 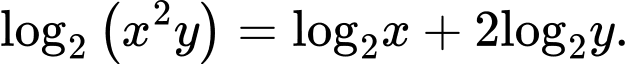
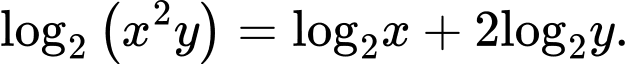
D, 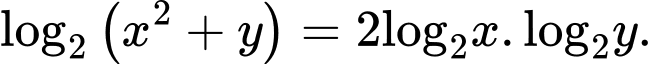
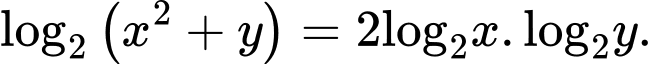
Chọn đáp án B.
Ta có: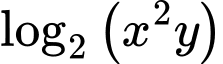
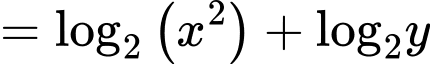
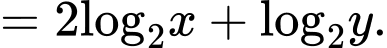 Đáp án: B
Đáp án: B
Ta có:
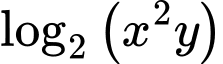
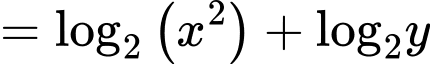
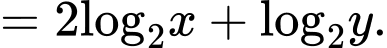 Đáp án: B
Đáp án: B
Câu 7 [149172]: Giả sử 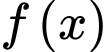 là hàm liên tục trên
là hàm liên tục trên 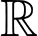 và các số thực
và các số thực 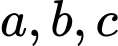 thoả mãn
thoả mãn 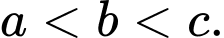 Mệnh đề nào sau đây sai?
Mệnh đề nào sau đây sai?
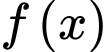 là hàm liên tục trên
là hàm liên tục trên 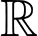 và các số thực
và các số thực 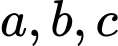 thoả mãn
thoả mãn 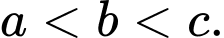 Mệnh đề nào sau đây sai?
Mệnh đề nào sau đây sai? A, 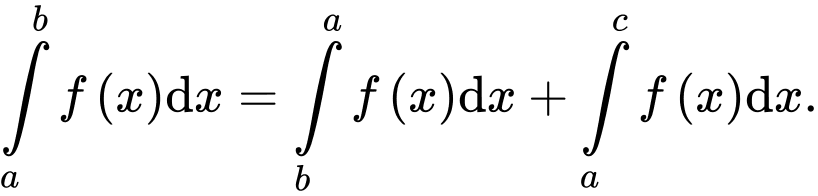
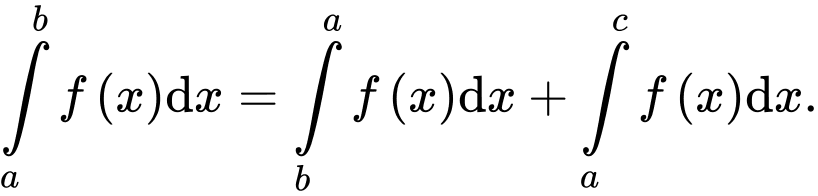
B, 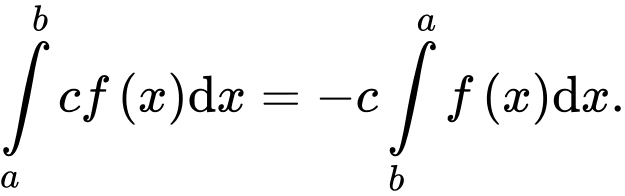
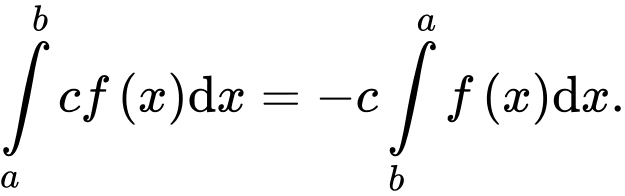
C, 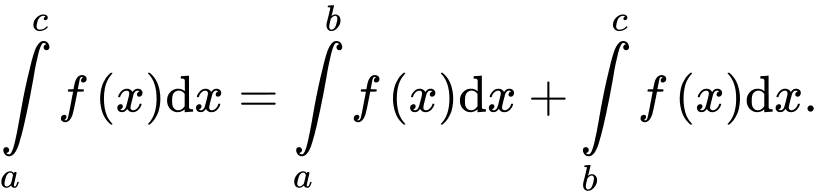
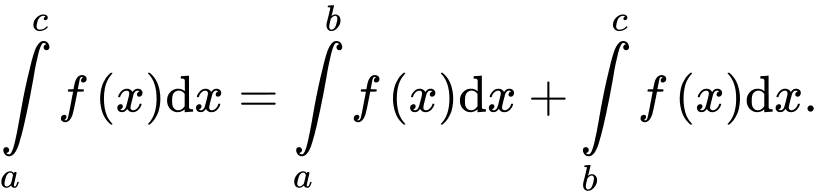
D, 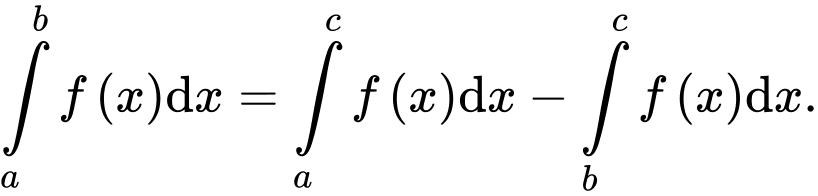
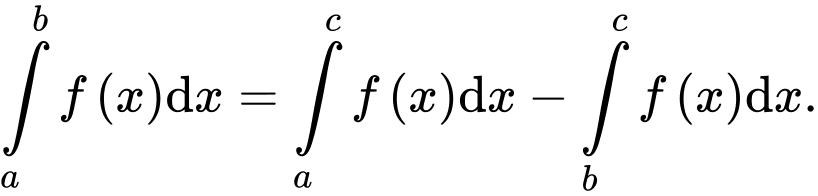
Chọn đáp án A.
Dựa vào tính chất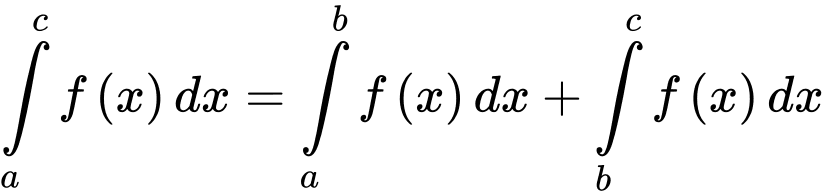 và
và 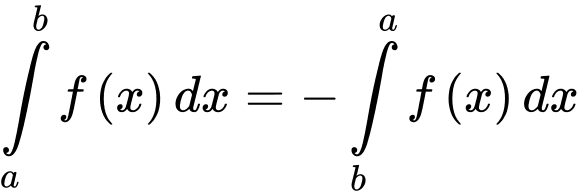
Suy ra đáp án A sai. Đáp án: A
Dựa vào tính chất
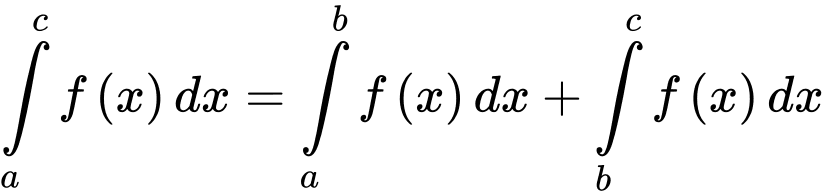 và
và 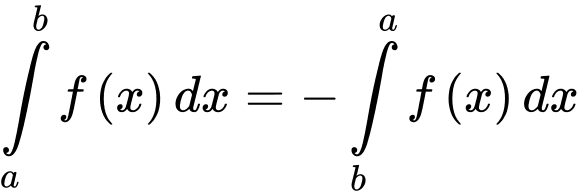
Suy ra đáp án A sai. Đáp án: A
Câu 8 [624473]: Số nghiệm của phương trình 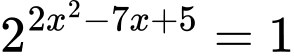 là:
là:
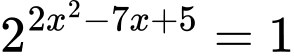 là:
là: A, 
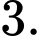
B, 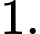
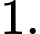
C, 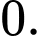
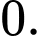
D, 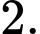
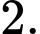
Chọn đáp án D.
Ta có: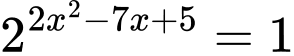
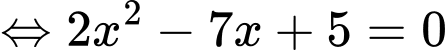
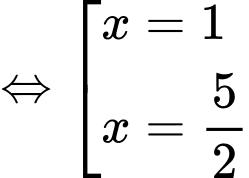
Từ đây ta suy ra phương trình có 2 nghiệm. Đáp án: D
Ta có:
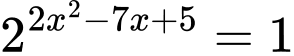
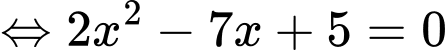
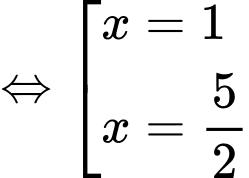
Từ đây ta suy ra phương trình có 2 nghiệm. Đáp án: D
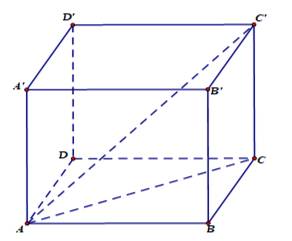
Câu 9 [618094]: Cho khối hộp chữ nhật 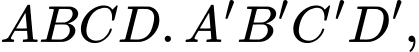 biết
biết 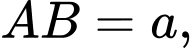
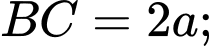
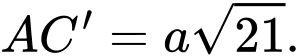 Tính thể tích
Tính thể tích  của khối hộp?
của khối hộp?
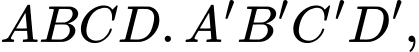 biết
biết 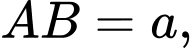
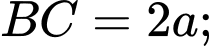
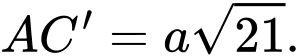 Tính thể tích
Tính thể tích  của khối hộp?
của khối hộp? A, 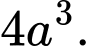
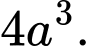
B, 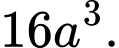
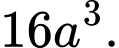
C, 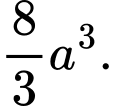
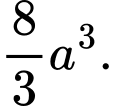
D, 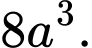
Chọn đáp án D.
Ta có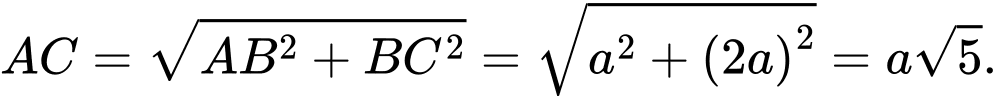
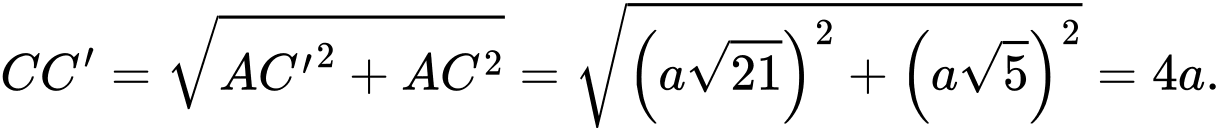
Vậy thể tích V của khối hộp là: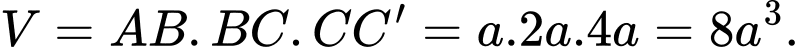 Đáp án: D
Đáp án: D

Ta có
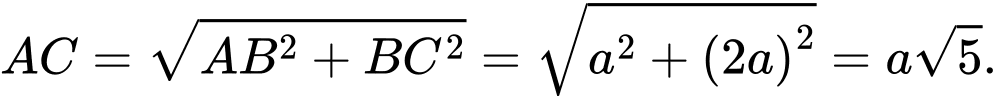
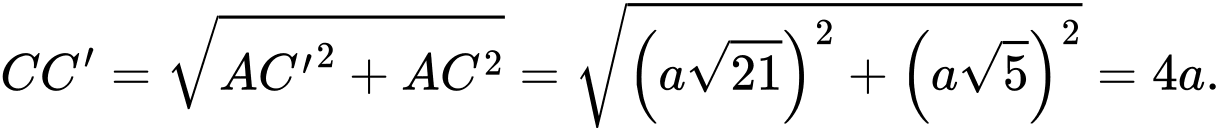
Vậy thể tích V của khối hộp là:
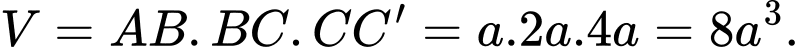 Đáp án: D
Đáp án: D Sử dụng thông tin dưới đây để trả lời câu 10 và câu 11:
Trong không gian tọa độ Oxyz, cho mặt cầu (S): x2+ y2+ z2- 4x + 4y - 4z + 3 = 0 và mặt phẳng (P): x+2y+2z-3=0.
Câu 10 [702521]: Đường kính của mặt cầu 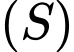 bằng
bằng
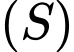 bằng
bằng A, 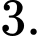
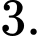
B, 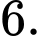
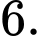
C, 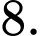
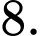
D, 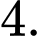
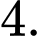
Chọn đáp án B.
Mặt cầu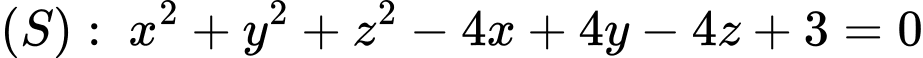 có tâm
có tâm 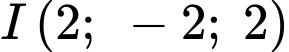 và bán kính
và bán kính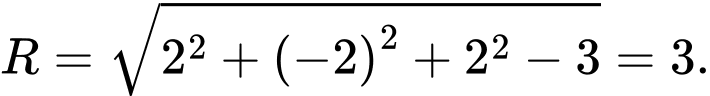
Vậy đường kính của mặt cầu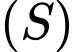 là
là 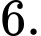 Đáp án: B
Đáp án: B
Mặt cầu
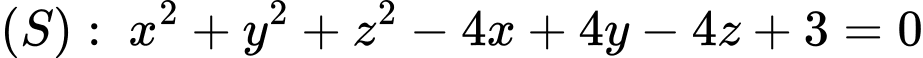 có tâm
có tâm 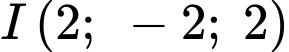 và bán kính
và bán kính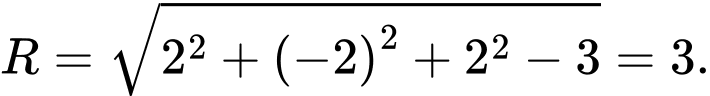
Vậy đường kính của mặt cầu
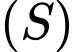 là
là 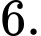 Đáp án: B
Đáp án: B
Câu 11 [702522]: Khoảng cách từ tâm mặt cầu 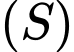 đến mặt phẳng
đến mặt phẳng 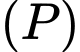 bằng
bằng
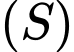 đến mặt phẳng
đến mặt phẳng 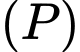 bằng
bằng A, 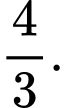
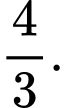
B, 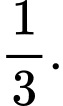
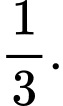
C, 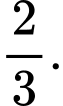
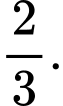
D, 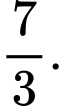
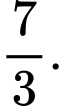
Chọn đáp án B.
Khoảng cách từ tâm mặt cầu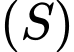 đến
đến 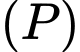 bằng:
bằng:
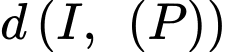
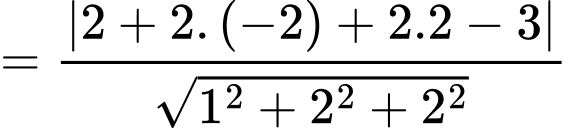
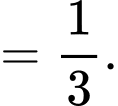 Đáp án: B
Đáp án: B
Khoảng cách từ tâm mặt cầu
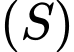 đến
đến 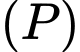 bằng:
bằng: 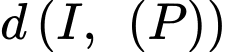
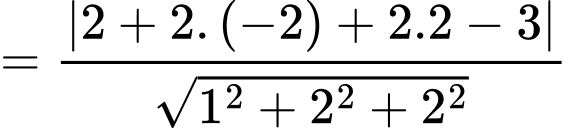
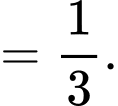 Đáp án: B
Đáp án: B
Câu 12 [360117]: Đường cong ở hình vẽ là đồ thị của hàm số: 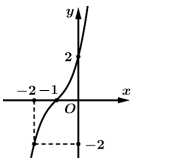

A, 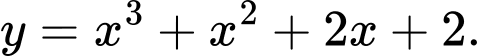
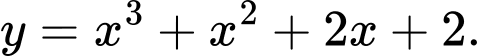
B, 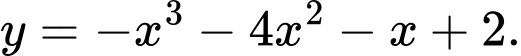
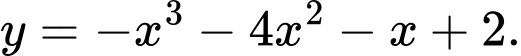
C, 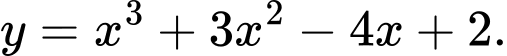
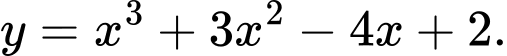
D, 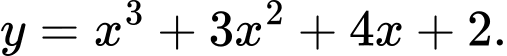
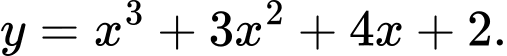
Chọn đáp án D.
Dựa vào đáp án, ta suy ra hàm số là đường: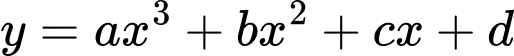
Dựa vào đồ thị ta thấy:
+) Hệ số suy ra loại B.
suy ra loại B.
+) Đồ thị đi qua điểm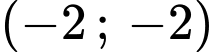 suy ra loại A.
suy ra loại A.
+) Đồ thị đi qua điểm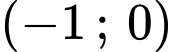 suy ra loại C. Đáp án: D
suy ra loại C. Đáp án: D
Dựa vào đáp án, ta suy ra hàm số là đường:
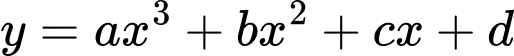
Dựa vào đồ thị ta thấy:
+) Hệ số
 suy ra loại B.
suy ra loại B.+) Đồ thị đi qua điểm
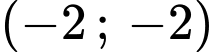 suy ra loại A.
suy ra loại A.+) Đồ thị đi qua điểm
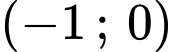 suy ra loại C. Đáp án: D
suy ra loại C. Đáp án: D PHẦN II. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Câu 13 [695525]: Trong không gian với hệ tọa độ 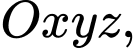 cho đường thẳng
cho đường thẳng 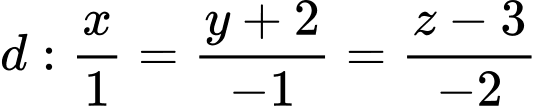 và mặt phẳng
và mặt phẳng 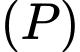 đi qua ba điểm
đi qua ba điểm 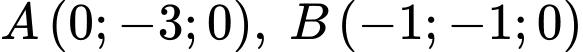 và
và 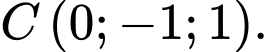
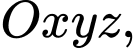 cho đường thẳng
cho đường thẳng 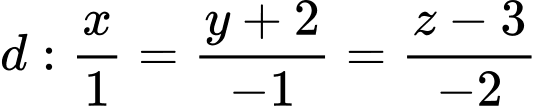 và mặt phẳng
và mặt phẳng 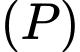 đi qua ba điểm
đi qua ba điểm 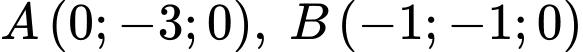 và
và 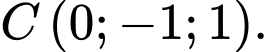
a) Đúng.
b) Đúng.
c) Sai.
Ta có: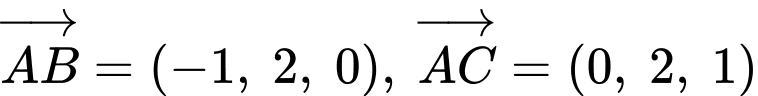
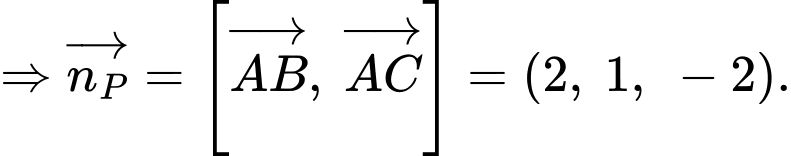
d) Sai.
Phương trình mặt phẳng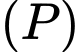 là
là 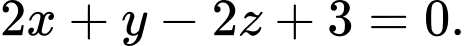
Thay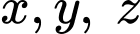 theo
theo 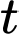 vào phương trình mặt phẳng
vào phương trình mặt phẳng 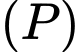 ta được:
ta được:
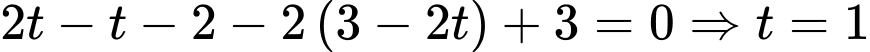

b) Đúng.
c) Sai.
Ta có:
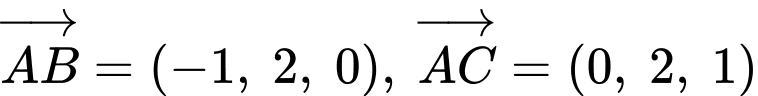
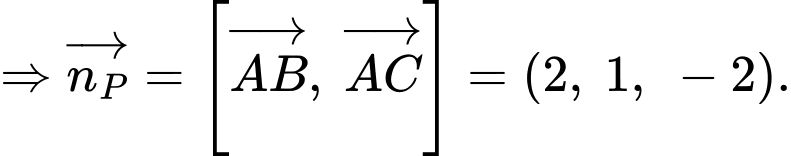
d) Sai.
Phương trình mặt phẳng
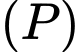 là
là 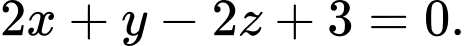
Thay
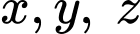 theo
theo 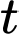 vào phương trình mặt phẳng
vào phương trình mặt phẳng 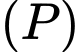 ta được:
ta được: 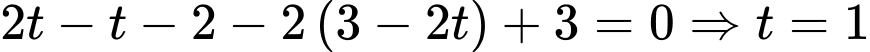

Câu 14 [695526]: Một nhà sản xuất đồ dùng sinh hoạt có chi phí cố định là 150 triệu đồng mỗi tháng và chi phí biến đổi là 15 triệu đồng cho một nghìn đồ dùng (tức là chi phí để sản xuất một nghìn đồ dùng là 15 triệu đồng). Giả sử 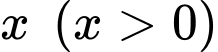 là số lượng đồ dùng, tính bằng nghìn sản phẩm được sản xuất trong mỗi tháng và nhà sản xuất chỉ có thể sản xuất tối đa 300 nghìn sản phẩm trong một tháng.
là số lượng đồ dùng, tính bằng nghìn sản phẩm được sản xuất trong mỗi tháng và nhà sản xuất chỉ có thể sản xuất tối đa 300 nghìn sản phẩm trong một tháng.
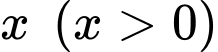 là số lượng đồ dùng, tính bằng nghìn sản phẩm được sản xuất trong mỗi tháng và nhà sản xuất chỉ có thể sản xuất tối đa 300 nghìn sản phẩm trong một tháng.
là số lượng đồ dùng, tính bằng nghìn sản phẩm được sản xuất trong mỗi tháng và nhà sản xuất chỉ có thể sản xuất tối đa 300 nghìn sản phẩm trong một tháng.
a) Đúng.
b) Sai.
Tổng doanh thu của nhà sản suất trong 1 tháng là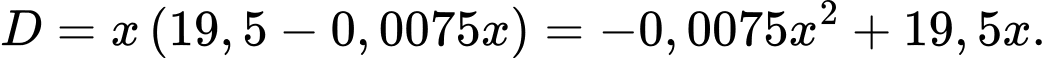
c) Đúng.
Lợi nhuận nhà sản suất kiếm được mỗi 1 tháng là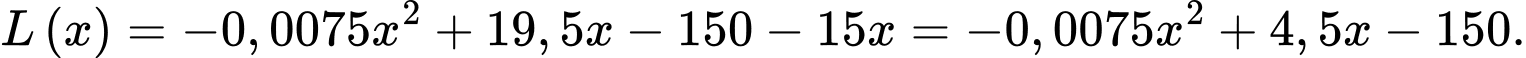
d) Sai.
Xét hàm số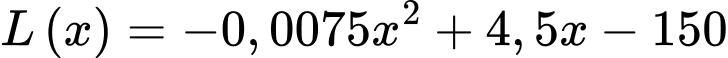
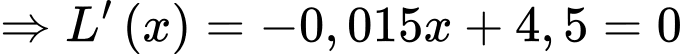
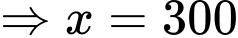 là điểm cực đại của đồ thị hàm số trên.
là điểm cực đại của đồ thị hàm số trên.
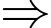 Lợi nhuận tối đa mà nhà sản suất thu được mỗi tháng là
Lợi nhuận tối đa mà nhà sản suất thu được mỗi tháng là 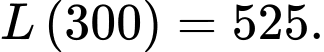
b) Sai.
Tổng doanh thu của nhà sản suất trong 1 tháng là
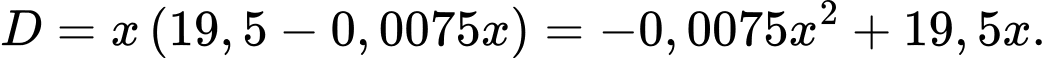
c) Đúng.
Lợi nhuận nhà sản suất kiếm được mỗi 1 tháng là
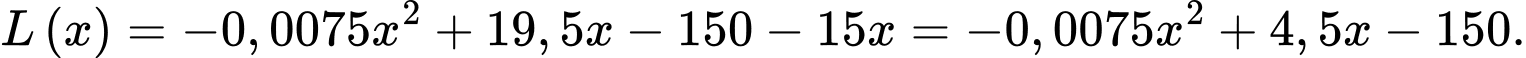
d) Sai.
Xét hàm số
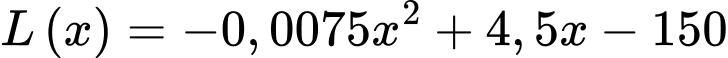
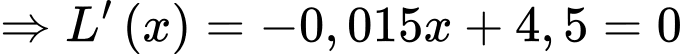
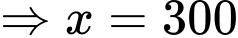 là điểm cực đại của đồ thị hàm số trên.
là điểm cực đại của đồ thị hàm số trên. 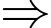 Lợi nhuận tối đa mà nhà sản suất thu được mỗi tháng là
Lợi nhuận tối đa mà nhà sản suất thu được mỗi tháng là 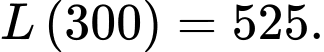
Câu 15 [695515]: Một thùng có các hộp loại I và loại II, trong đó có 2 hộp loại I, mỗi hộp có 13 sản phẩm tốt và 2 phế phẩm và có 3 hộp loại II, mỗi hộp có 6 sản phẩm tốt và 4 phế phẩm. Chọn ngẫu nhiên trong thùng một hộp và từ hộp đó lấy ra hai sản phẩm để kiểm tra.
Gọi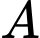 là biến cố: “Chọn được trong thùng một hộp loại I”.
là biến cố: “Chọn được trong thùng một hộp loại I”.
Gọi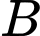 là biến cố: “Chọn được trong thùng một hộp loại II”.
là biến cố: “Chọn được trong thùng một hộp loại II”.
Gọi là biến cố: “Cả 2 sản phẩm lấy ra đều tốt”.
là biến cố: “Cả 2 sản phẩm lấy ra đều tốt”.
Gọi
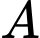 là biến cố: “Chọn được trong thùng một hộp loại I”.
là biến cố: “Chọn được trong thùng một hộp loại I”.Gọi
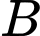 là biến cố: “Chọn được trong thùng một hộp loại II”.
là biến cố: “Chọn được trong thùng một hộp loại II”.Gọi
 là biến cố: “Cả 2 sản phẩm lấy ra đều tốt”.
là biến cố: “Cả 2 sản phẩm lấy ra đều tốt”.
a) Sai.
Xác suất chọn hộp loại I là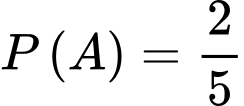 và xác suất chọn hộp loại II là
và xác suất chọn hộp loại II là 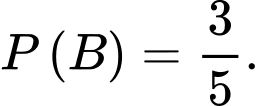
b) Sai.
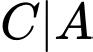 là biến cố “Cả 2 sản phẩm lấy ra đều tốt biết 2 sản phẩm đó lấy ra từ hộp loại I”.
là biến cố “Cả 2 sản phẩm lấy ra đều tốt biết 2 sản phẩm đó lấy ra từ hộp loại I”.
Xác suất lấy được 2 sản phẩm tốt từ hộp loại I là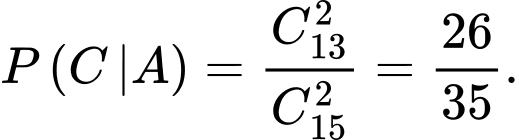
c) Đúng.
Xác suất lấy được 2 sản phẩm tốt từ hộp II là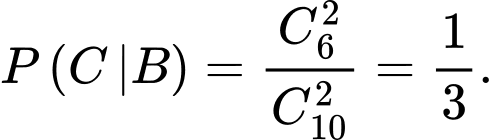
Ta có sơ đồ cây sau:
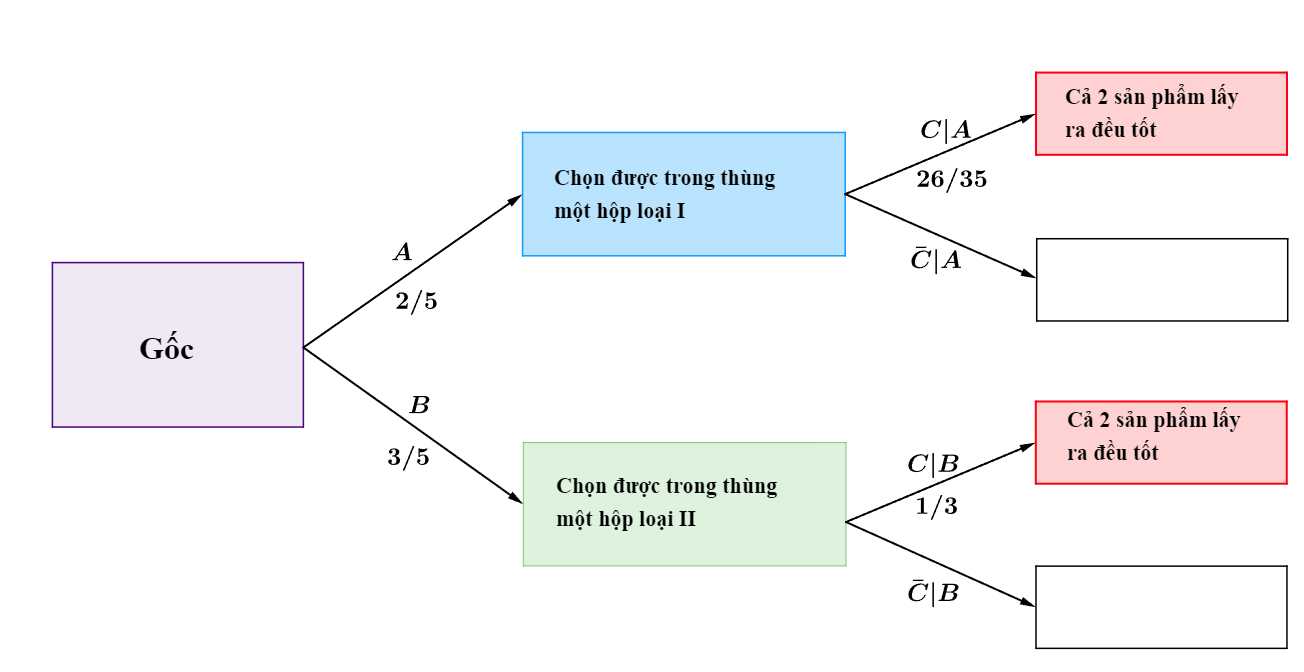
Vậy xác suất hai sản phẩm lấy ra từ một hộp trong thùng đều tốt là
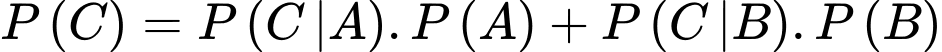
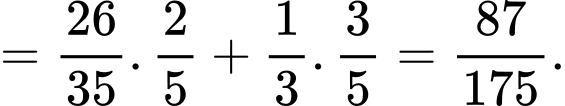
d) Đúng.
Xác suất lấy ra hai sản phẩm đều tốt thuộc hộp loại I là
Công thức Bayes: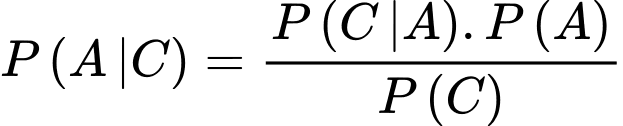
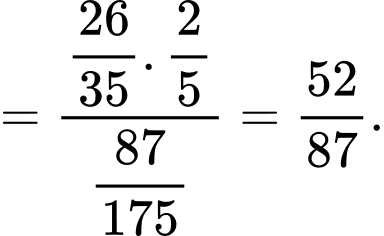
Xác suất chọn hộp loại I là
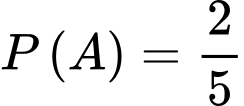 và xác suất chọn hộp loại II là
và xác suất chọn hộp loại II là 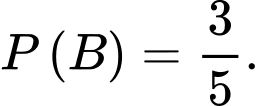
b) Sai.
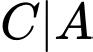 là biến cố “Cả 2 sản phẩm lấy ra đều tốt biết 2 sản phẩm đó lấy ra từ hộp loại I”.
là biến cố “Cả 2 sản phẩm lấy ra đều tốt biết 2 sản phẩm đó lấy ra từ hộp loại I”.Xác suất lấy được 2 sản phẩm tốt từ hộp loại I là
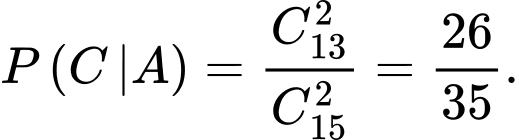
c) Đúng.
Xác suất lấy được 2 sản phẩm tốt từ hộp II là
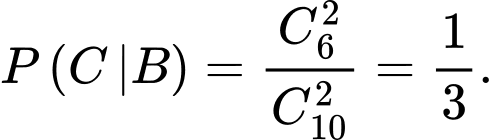
Ta có sơ đồ cây sau:

Vậy xác suất hai sản phẩm lấy ra từ một hộp trong thùng đều tốt là
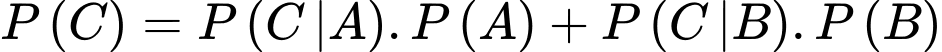
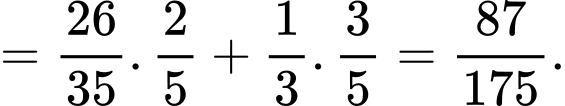
d) Đúng.
Xác suất lấy ra hai sản phẩm đều tốt thuộc hộp loại I là
Công thức Bayes:
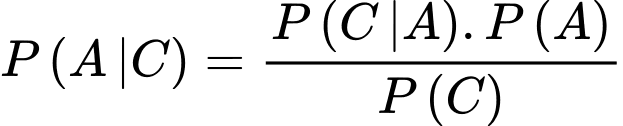
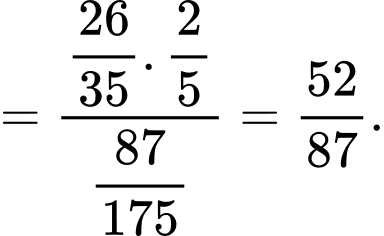
Câu 16 [695527]: Khi đun nước, nhiệt độ ban đầu của nước trong ấm là 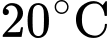 và tăng dần với tốc độ
và tăng dần với tốc độ 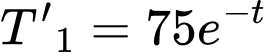 (
( phút)
phút) 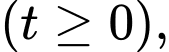 trong đó
trong đó 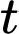 (phút) là thời gian tính từ lúc bếp được bật lên. Khi nước trong ấm đạt
(phút) là thời gian tính từ lúc bếp được bật lên. Khi nước trong ấm đạt 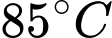 thì bếp được tắt đi và nhiệt độ
thì bếp được tắt đi và nhiệt độ  của nước trong ấm khi này xác định theo công thức
của nước trong ấm khi này xác định theo công thức 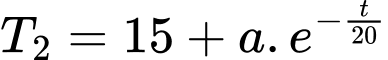
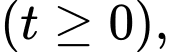 trong đó
trong đó 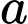 là hằng số và
là hằng số và 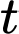 (phút) là thời gian tính từ lúc tắt bếp.
(phút) là thời gian tính từ lúc tắt bếp.
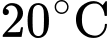 và tăng dần với tốc độ
và tăng dần với tốc độ 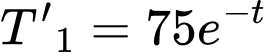 (
( phút)
phút) 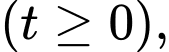 trong đó
trong đó 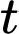 (phút) là thời gian tính từ lúc bếp được bật lên. Khi nước trong ấm đạt
(phút) là thời gian tính từ lúc bếp được bật lên. Khi nước trong ấm đạt 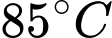 thì bếp được tắt đi và nhiệt độ
thì bếp được tắt đi và nhiệt độ  của nước trong ấm khi này xác định theo công thức
của nước trong ấm khi này xác định theo công thức 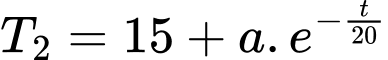
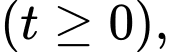 trong đó
trong đó 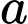 là hằng số và
là hằng số và 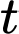 (phút) là thời gian tính từ lúc tắt bếp.
(phút) là thời gian tính từ lúc tắt bếp.
a) Đúng.
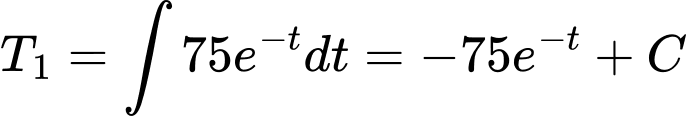 với
với  là hằng số.
là hằng số.
Vì nhiệt độ ban đầu là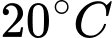 nên
nên 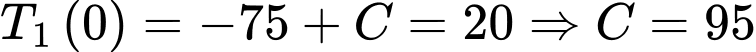
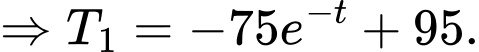
b) Sai.
Vì khi nước trong ấm đạt 85°C thì bếp được tắt đi nên ta có: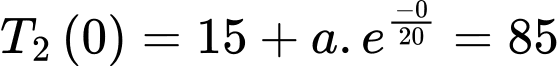
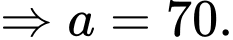
c) Sai.
Ta có: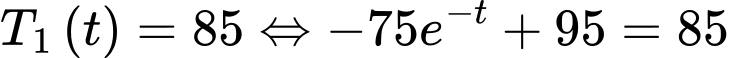
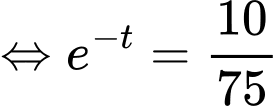
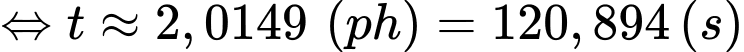
d) Sai.
Theo câu c) ta có sau 2 phút kể từ khi mở bếp thì nước trong ấm đạt nhiệt độ
Sau đó thì nhiệt độ của nước trong ấm sẽ tính theo công thức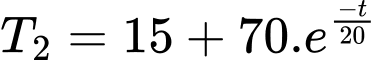
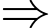 Sau 21 phút kể từ khi bật bếp thì nhiệt độ của ấm là
Sau 21 phút kể từ khi bật bếp thì nhiệt độ của ấm là 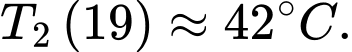
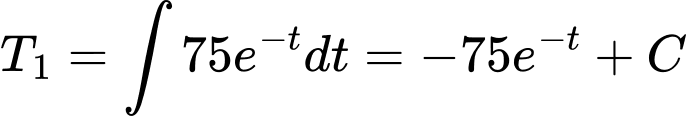 với
với  là hằng số.
là hằng số.Vì nhiệt độ ban đầu là
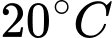 nên
nên 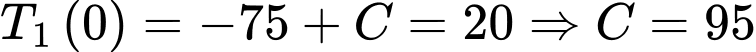
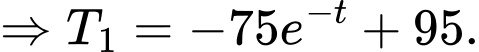
b) Sai.
Vì khi nước trong ấm đạt 85°C thì bếp được tắt đi nên ta có:
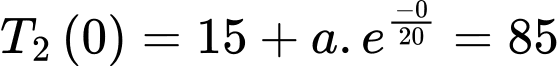
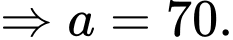
c) Sai.
Ta có:
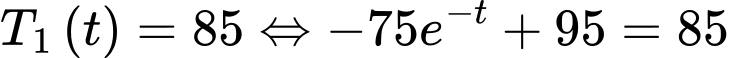
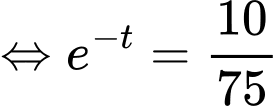
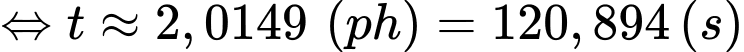
d) Sai.
Theo câu c) ta có sau 2 phút kể từ khi mở bếp thì nước trong ấm đạt nhiệt độ

Sau đó thì nhiệt độ của nước trong ấm sẽ tính theo công thức
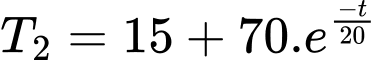
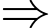 Sau 21 phút kể từ khi bật bếp thì nhiệt độ của ấm là
Sau 21 phút kể từ khi bật bếp thì nhiệt độ của ấm là 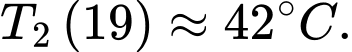
PHẦN III. Thí sinh trả lời từ câu 1 đến câu 6.
Câu 17 [257709]: Cho hình lăng trụ tứ giác đều  có
có 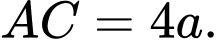 Gọi
Gọi  là tâm của mặt
là tâm của mặt  Biết rằng hai mặt phẳng
Biết rằng hai mặt phẳng 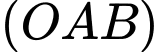 và
và 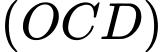 vuông góc với nhau. Thể tích của khối lăng trụ
vuông góc với nhau. Thể tích của khối lăng trụ  bằng
bằng 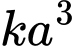 , giá trị của
, giá trị của 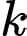 là bao nhiêu? (làm tròn kết quả đến hàng phần mười).
là bao nhiêu? (làm tròn kết quả đến hàng phần mười).
 có
có 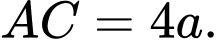 Gọi
Gọi  là tâm của mặt
là tâm của mặt  Biết rằng hai mặt phẳng
Biết rằng hai mặt phẳng 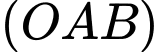 và
và 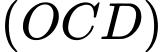 vuông góc với nhau. Thể tích của khối lăng trụ
vuông góc với nhau. Thể tích của khối lăng trụ  bằng
bằng 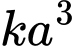 , giá trị của
, giá trị của 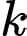 là bao nhiêu? (làm tròn kết quả đến hàng phần mười).
là bao nhiêu? (làm tròn kết quả đến hàng phần mười).
Điền đáp án: 11,3.
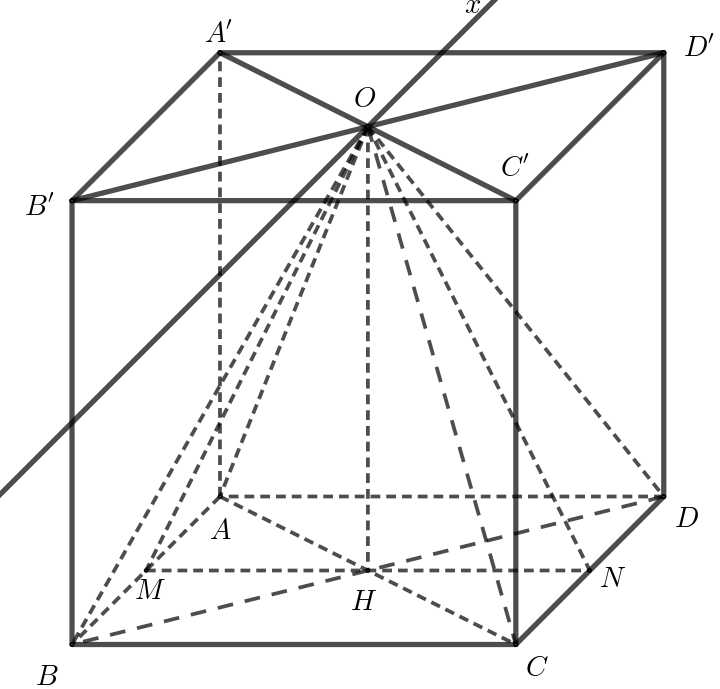 Ta có
Ta có 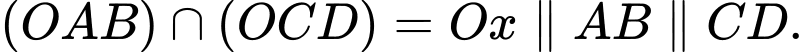
Gọi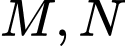 lần lượt là trung điểm của
lần lượt là trung điểm của 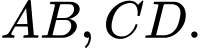
Ta có các tam giác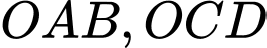 cân tại
cân tại  nên
nên 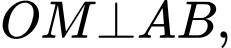

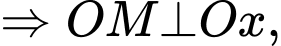

 .
.
Suy ra tam giác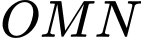 vuông cân tại
vuông cân tại 
Gọi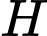 là tâm của hình vuông
là tâm của hình vuông 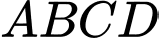
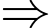
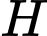 là trung điểm của
là trung điểm của 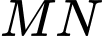
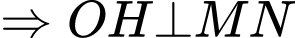 , lại có
, lại có 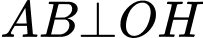 suy ra
suy ra 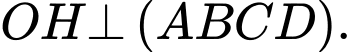
Vậy thể tích của khối lăng trụ bằng:
bằng: 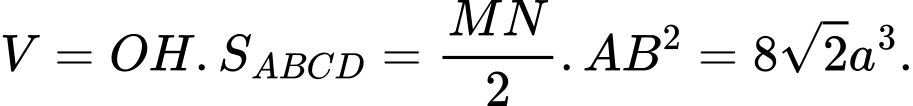
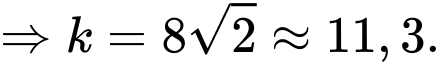

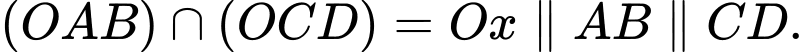
Gọi
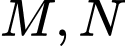 lần lượt là trung điểm của
lần lượt là trung điểm của 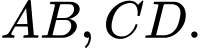
Ta có các tam giác
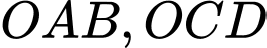 cân tại
cân tại  nên
nên 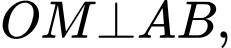

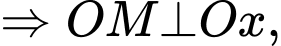

 .
.Suy ra tam giác
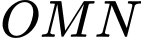 vuông cân tại
vuông cân tại 
Gọi
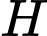 là tâm của hình vuông
là tâm của hình vuông 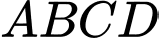
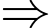
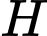 là trung điểm của
là trung điểm của 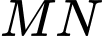
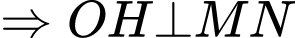 , lại có
, lại có 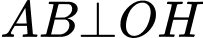 suy ra
suy ra 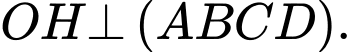
Vậy thể tích của khối lăng trụ
 bằng:
bằng: 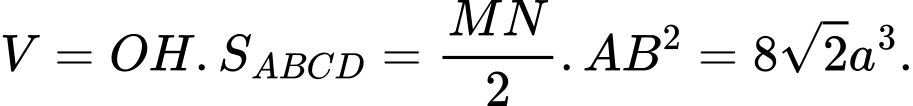
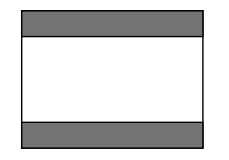
Câu 18 [695529]: Màn hình Tivi có tỷ lệ khung hình là 4:3. Nghĩa là, tỷ lệ giữa chiều dài và chiều rộng là 4:3. Tỷ lệ khung hình của nhiều bộ phim không phải là 4:3, vì vậy đôi khi chúng được chiếu trên màn hình tivi bằng cách “Letterboxing” – có nghĩa là tạo các dải màu tối có chiều rộng bằng nhau ở phía trên và phía dưới của màn hình (như hình minh họa). Giả sử một bộ phim có tỷ lệ khung hình là 2:1 và được chiếu trên màn hình Tivi này với đường chéo 27 inch. Vậy chiều cao của mỗi dải tối là bao nhiêu inch?

Điền đáp án: 2,7.
Giả sử chiều dài và chiều rộng của màn hình lần lượt là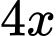 và
và 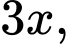 chiều dài và chiều rộng của phim lần lượt là
chiều dài và chiều rộng của phim lần lượt là 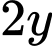 và
và 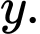
Theo định lý Pythagore, độ dài đường chéo là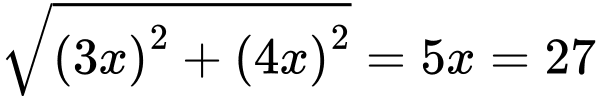
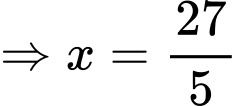 .
.
Vì phim và màn hình có cùng chiều rộng nên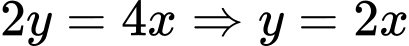 .
.
Do đó, chiều cao của mỗi dải là
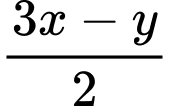
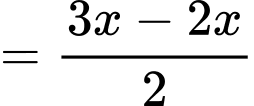
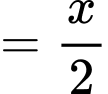
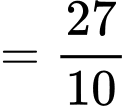
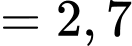 (inch).
(inch).
Giả sử chiều dài và chiều rộng của màn hình lần lượt là
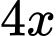 và
và 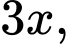 chiều dài và chiều rộng của phim lần lượt là
chiều dài và chiều rộng của phim lần lượt là 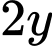 và
và 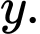
Theo định lý Pythagore, độ dài đường chéo là
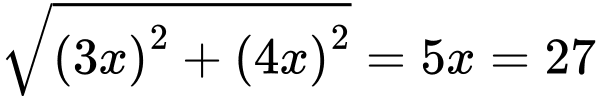
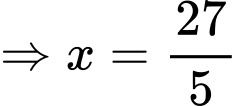 .
.Vì phim và màn hình có cùng chiều rộng nên
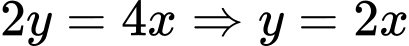 .
.Do đó, chiều cao của mỗi dải là
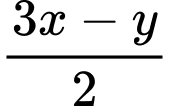
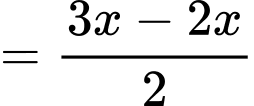
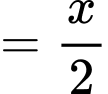
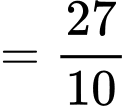
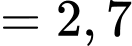 (inch).
(inch).
Câu 19 [695530]: Theo một cuộc khảo sát thống kê, có 40% các vụ tai nạn xe cộ gây chết người là do có người lái xe say rượu. Giả sử tỉ lệ số người say rượu khi lái xe là 4%. Việc say rượu khi lái xe có thể làm tăng khả năng tai nạn chết người lên bao nhiêu lần?
Điền đáp án: 10.
Gọi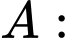 “Lái xe gây tại nạn chết người”
“Lái xe gây tại nạn chết người”
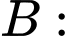 “Người lái xe say rượu”
“Người lái xe say rượu”
YCBT Tính tỉ lệ
Tính tỉ lệ 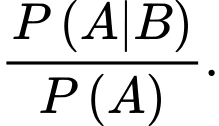
Ta có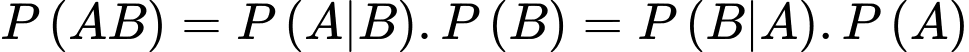
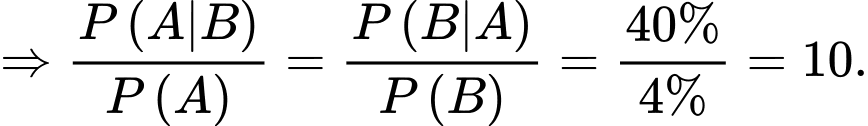
Gọi
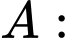 “Lái xe gây tại nạn chết người”
“Lái xe gây tại nạn chết người”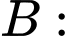 “Người lái xe say rượu”
“Người lái xe say rượu”YCBT
 Tính tỉ lệ
Tính tỉ lệ 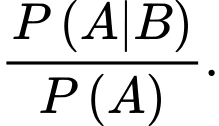
Ta có
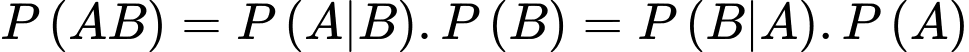
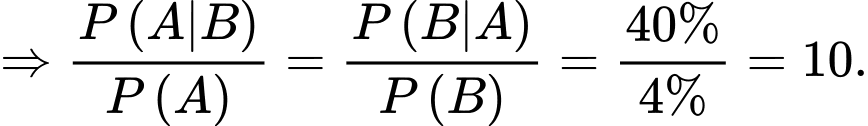
Câu 20 [695531]: Một hàng rào cao 2,4 mét được đặt song song và cách bức tường của ngôi nhà một khoảng bằng 1,5 mét. Chiều dài ngắn nhất của cây thang để nó đúng dưới đất vươn qua hàng rào tựa vào ngôi nhà (tham khảo hình vẽ) là bao nhiêu mét? (làm tròn kết quả đến hàng phần trăm).
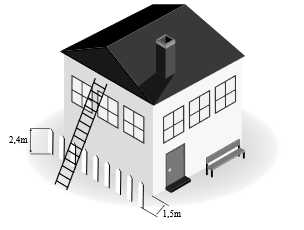

Điền đáp án: 5,47.
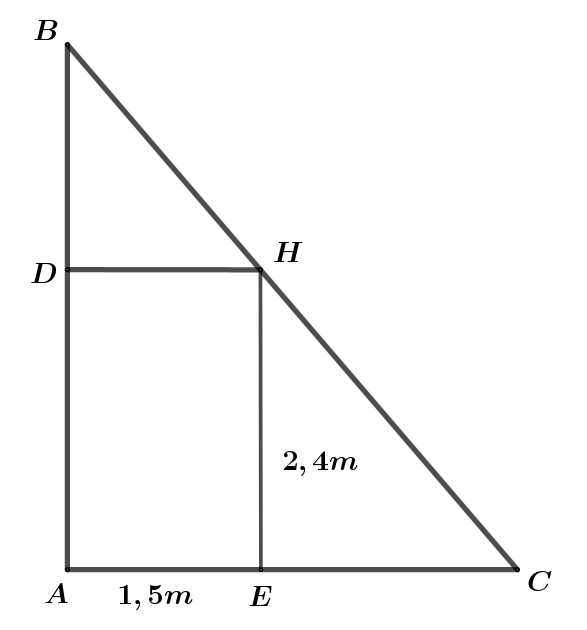
Đặt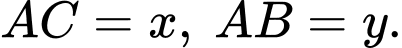
Xét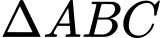 có:
có: 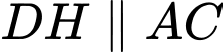
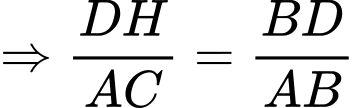
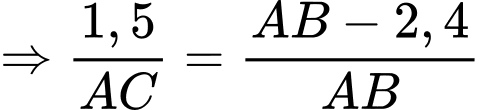
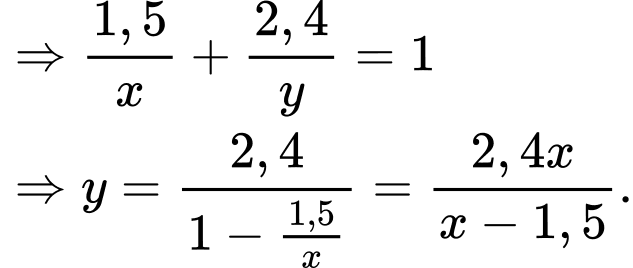
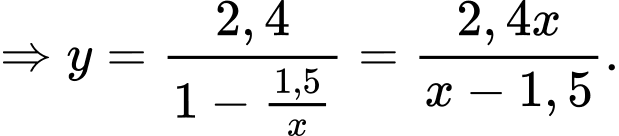
Ta có: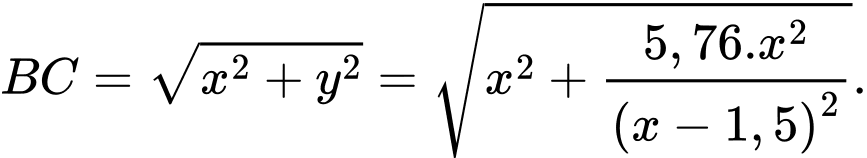
Xét hàm số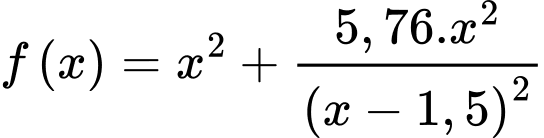
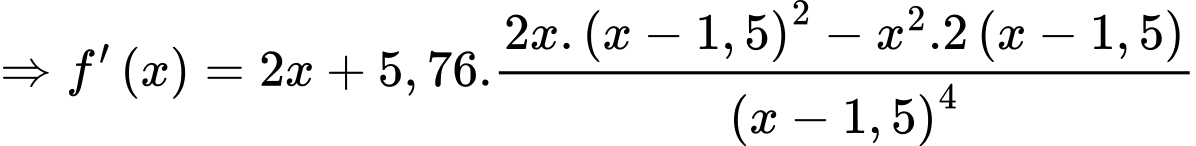
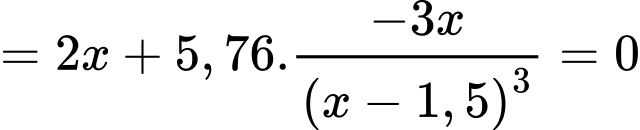
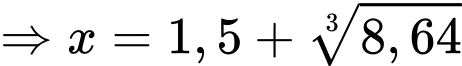 là điểm cực tiểu của đồ thị hàm số đã cho.
là điểm cực tiểu của đồ thị hàm số đã cho.
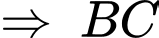 đạt giá trị nhỏ nhất là 5,47 tại
đạt giá trị nhỏ nhất là 5,47 tại 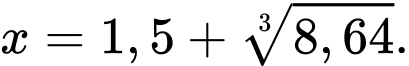

Đặt
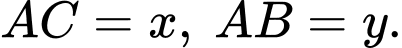
Xét
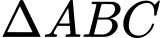 có:
có: 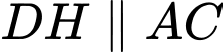
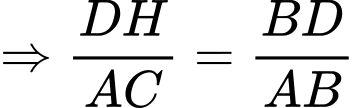
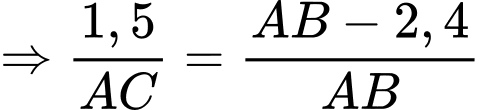
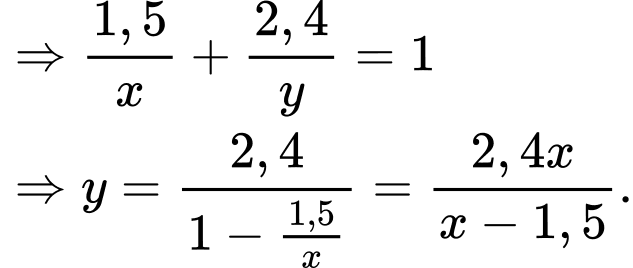
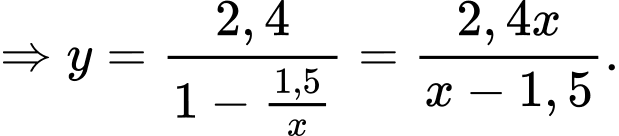
Ta có:
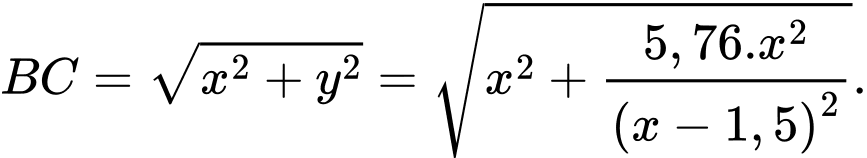
Xét hàm số
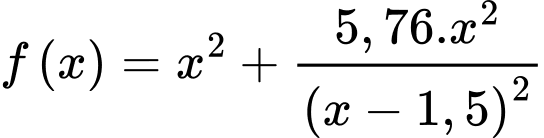
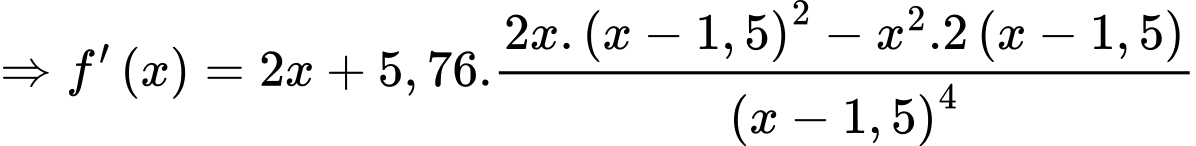
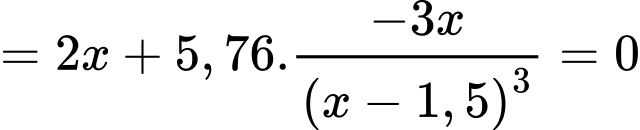
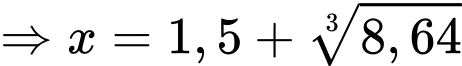 là điểm cực tiểu của đồ thị hàm số đã cho.
là điểm cực tiểu của đồ thị hàm số đã cho. đạt giá trị nhỏ nhất là 5,47 tại
đạt giá trị nhỏ nhất là 5,47 tại 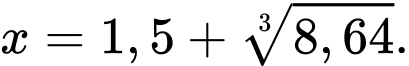
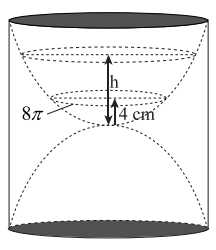
Câu 21 [695532]: Một chiếc đồng hồ cát như hình vẽ, gồm hai phần đối xứng nhau qua mặt phẳng nằm ngang và đặt trong một hình trụ. Thiết diện thẳng đứng qua trục của nó là hai Parabol chung đỉnh và đối xứng nhau qua mặt phẳng nằm ngang. Ban đầu lượng cát dồn hết ở phần trên của đồng hồ thì chiều cao của mực cát bằng 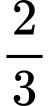 chiều cao của bên đó (xem hình vẽ). Cát chảy từ trên xuống dưới với lưu lượng
chiều cao của bên đó (xem hình vẽ). Cát chảy từ trên xuống dưới với lưu lượng 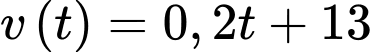 (
(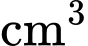 /phút). Khi chiều cao của cát còn thì 4(cm) bề mặt trên cùng của cát tạo thành một đường tròn chu vi bằng
/phút). Khi chiều cao của cát còn thì 4(cm) bề mặt trên cùng của cát tạo thành một đường tròn chu vi bằng 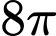 (cm). Biết sau 20 phút thì cát chảy hết xuống phần bên dưới của đồng hồ. Hỏi chiều cao của khối trụ bên ngoài bằng bao nhiêu?( làm trong kết quả đến hàng phần mười)
(cm). Biết sau 20 phút thì cát chảy hết xuống phần bên dưới của đồng hồ. Hỏi chiều cao của khối trụ bên ngoài bằng bao nhiêu?( làm trong kết quả đến hàng phần mười)
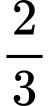 chiều cao của bên đó (xem hình vẽ). Cát chảy từ trên xuống dưới với lưu lượng
chiều cao của bên đó (xem hình vẽ). Cát chảy từ trên xuống dưới với lưu lượng 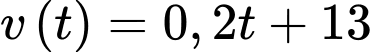 (
(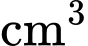 /phút). Khi chiều cao của cát còn thì 4(cm) bề mặt trên cùng của cát tạo thành một đường tròn chu vi bằng
/phút). Khi chiều cao của cát còn thì 4(cm) bề mặt trên cùng của cát tạo thành một đường tròn chu vi bằng 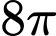 (cm). Biết sau 20 phút thì cát chảy hết xuống phần bên dưới của đồng hồ. Hỏi chiều cao của khối trụ bên ngoài bằng bao nhiêu?( làm trong kết quả đến hàng phần mười)
(cm). Biết sau 20 phút thì cát chảy hết xuống phần bên dưới của đồng hồ. Hỏi chiều cao của khối trụ bên ngoài bằng bao nhiêu?( làm trong kết quả đến hàng phần mười)
Điền đáp án: 36,7.
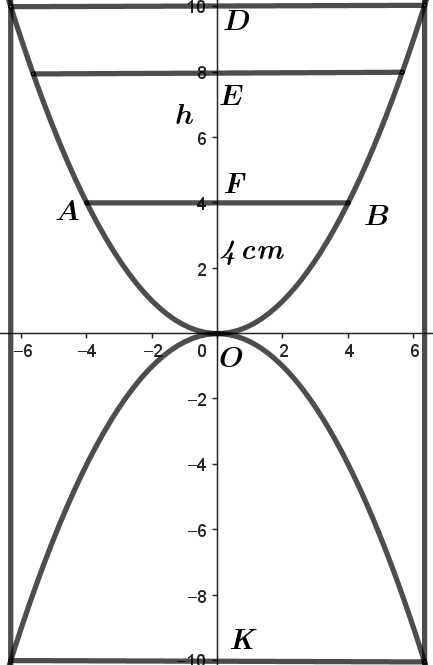
Ta có hình vẽ trên thể hiện mặt cắt của đồng hồ cát qua tâm hình trụ theo phương thẳng đứng của chiều cao.
Ta có: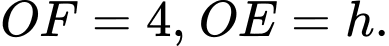
Vì ban đầu lượng cát dồn hết ở phần trên của đồng hồ thì chiều cao của mực cát bằng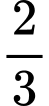 chiều cao của bên đó nên
chiều cao của bên đó nên 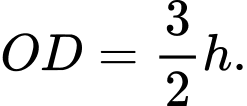
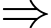 Chiều cao của khối trụ bên ngoài là
Chiều cao của khối trụ bên ngoài là 
Vì khi chiều cao của cát còn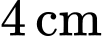 thì bề mặt trên cùng của cát tạo thành một đường tròn có chu vi bằng
thì bề mặt trên cùng của cát tạo thành một đường tròn có chu vi bằng 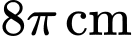
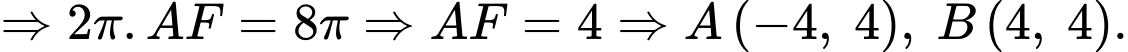
Parabol đi qua gốc tọa độ và 2 điểm
và 2 điểm 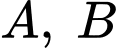 có dạng
có dạng 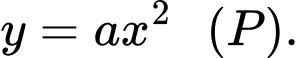
Thay tọa độ điểm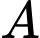 vào phương trình parabol
vào phương trình parabol 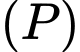 ta được:
ta được: 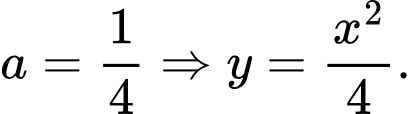
Cát chảy từ trên xuống với tốc độ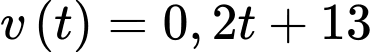 (
(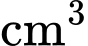 /phút) và sau 20 phút thì các chảy hết xuống phía dưới đồng hồ nên ta có thể tích cát ban đầu dồn hết ở phần trên của đồng hồ là
/phút) và sau 20 phút thì các chảy hết xuống phía dưới đồng hồ nên ta có thể tích cát ban đầu dồn hết ở phần trên của đồng hồ là
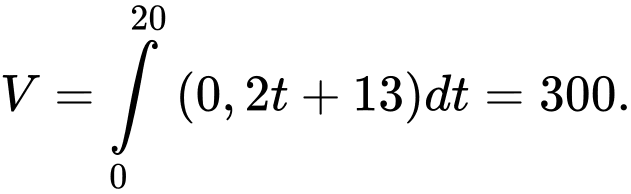
Thể tích giới hạn bởi parabol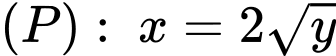 , các đường thẳng
, các đường thẳng 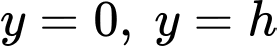 khi quay quanh trục
khi quay quanh trục 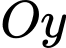 chính là thể tích cát ban đầu dồn hết ở phần trên của đồng hồ nên ta có:
chính là thể tích cát ban đầu dồn hết ở phần trên của đồng hồ nên ta có:
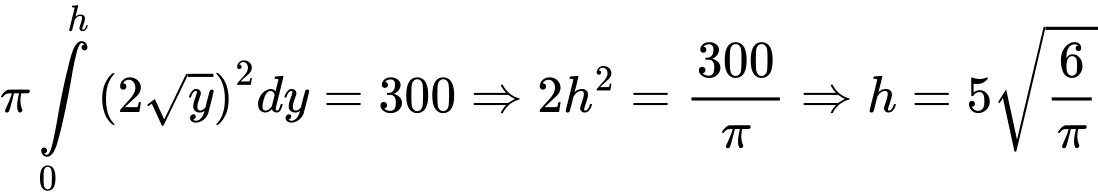
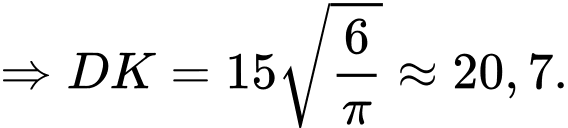

Ta có hình vẽ trên thể hiện mặt cắt của đồng hồ cát qua tâm hình trụ theo phương thẳng đứng của chiều cao.
Ta có:
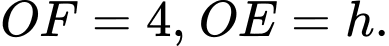
Vì ban đầu lượng cát dồn hết ở phần trên của đồng hồ thì chiều cao của mực cát bằng
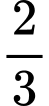 chiều cao của bên đó nên
chiều cao của bên đó nên 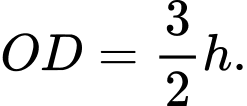
 Chiều cao của khối trụ bên ngoài là
Chiều cao của khối trụ bên ngoài là 
Vì khi chiều cao của cát còn
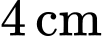 thì bề mặt trên cùng của cát tạo thành một đường tròn có chu vi bằng
thì bề mặt trên cùng của cát tạo thành một đường tròn có chu vi bằng 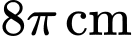
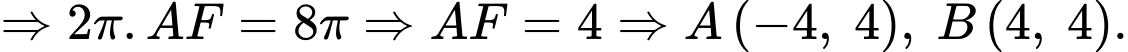
Parabol đi qua gốc tọa độ
 và 2 điểm
và 2 điểm 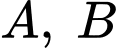 có dạng
có dạng 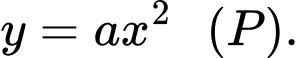
Thay tọa độ điểm
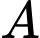 vào phương trình parabol
vào phương trình parabol 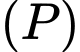 ta được:
ta được: 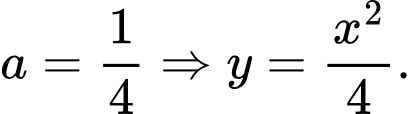
Cát chảy từ trên xuống với tốc độ
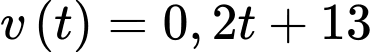 (
(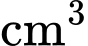 /phút) và sau 20 phút thì các chảy hết xuống phía dưới đồng hồ nên ta có thể tích cát ban đầu dồn hết ở phần trên của đồng hồ là
/phút) và sau 20 phút thì các chảy hết xuống phía dưới đồng hồ nên ta có thể tích cát ban đầu dồn hết ở phần trên của đồng hồ là 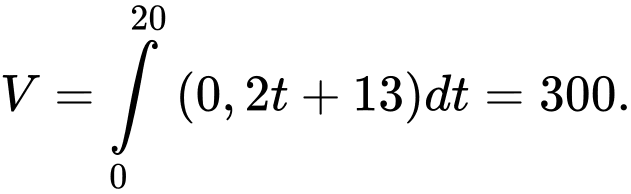
Thể tích giới hạn bởi parabol
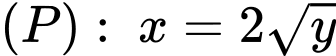 , các đường thẳng
, các đường thẳng 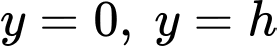 khi quay quanh trục
khi quay quanh trục 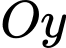 chính là thể tích cát ban đầu dồn hết ở phần trên của đồng hồ nên ta có:
chính là thể tích cát ban đầu dồn hết ở phần trên của đồng hồ nên ta có: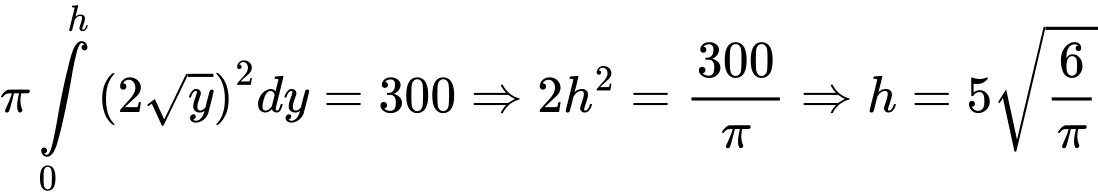
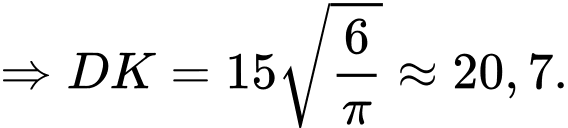
Câu 22 [695533]: Trong không gian 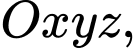 cho điểm
cho điểm 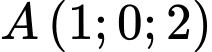 và hai mặt cầu
và hai mặt cầu 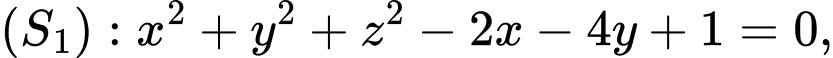
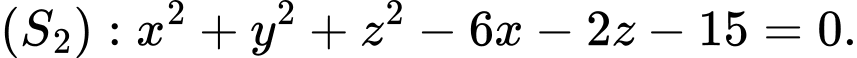 Gọi đường thẳng
Gọi đường thẳng 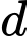 là tiếp tuyến chung của hai mặt cầu
là tiếp tuyến chung của hai mặt cầu 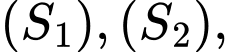
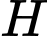 là hình chiếu vuông góc của điểm
là hình chiếu vuông góc của điểm 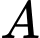 trên đường thẳng
trên đường thẳng 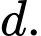 Biết khi
Biết khi 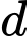 thay đổi thì điểm
thay đổi thì điểm 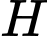 luôn chạy trên một đường tròn
luôn chạy trên một đường tròn  cố định. Bán kính của đường tròn
cố định. Bán kính của đường tròn  bằng bao nhiêu?
bằng bao nhiêu?
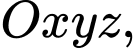 cho điểm
cho điểm 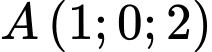 và hai mặt cầu
và hai mặt cầu 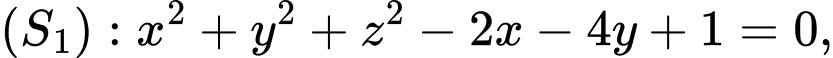
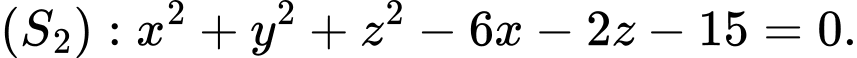 Gọi đường thẳng
Gọi đường thẳng 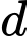 là tiếp tuyến chung của hai mặt cầu
là tiếp tuyến chung của hai mặt cầu 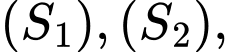
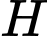 là hình chiếu vuông góc của điểm
là hình chiếu vuông góc của điểm 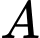 trên đường thẳng
trên đường thẳng 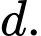 Biết khi
Biết khi 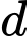 thay đổi thì điểm
thay đổi thì điểm 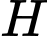 luôn chạy trên một đường tròn
luôn chạy trên một đường tròn  cố định. Bán kính của đường tròn
cố định. Bán kính của đường tròn  bằng bao nhiêu?
bằng bao nhiêu?
Điền đáp án: 1.
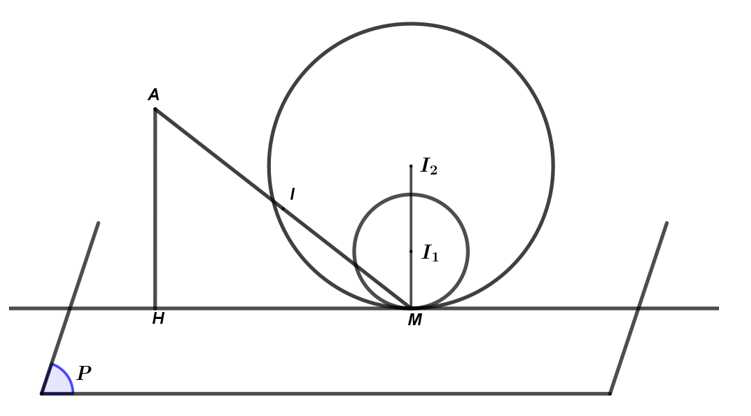
Ta xét: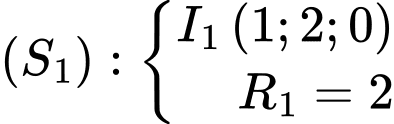 và
và 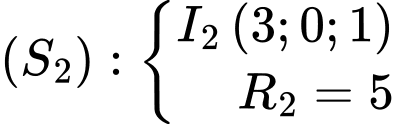 ,
, 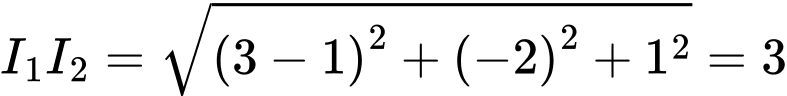
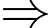
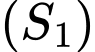 tiếp xúc với
tiếp xúc với 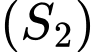 vì tâm
vì tâm 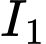 nằm trong mặt cầu
nằm trong mặt cầu 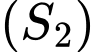
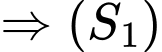 nằm trong
nằm trong 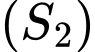 .
.
Gọi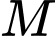 là tiếp điểm của hai mặt cầu.
là tiếp điểm của hai mặt cầu.
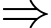 Các tiếp tuyến
Các tiếp tuyến 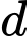 của 2 mặt cầu
của 2 mặt cầu 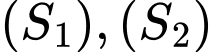 thuộc mặt phẳng
thuộc mặt phẳng 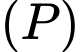 đi qua
đi qua 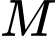 và có vectơ pháp tuyến là
và có vectơ pháp tuyến là 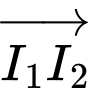 .
.
Ta có: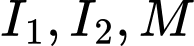 thẳng hàng
thẳng hàng 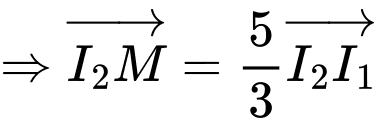
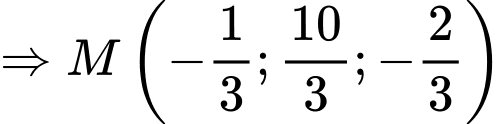 .
.
Phương trình mặt phẳng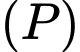 :
: 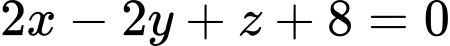 .
.
Ta có: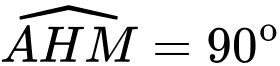 nên
nên 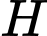 thuộc mặt cầu
thuộc mặt cầu 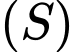 đường kính
đường kính 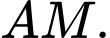
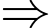
 là giao tuyến của
là giao tuyến của 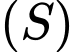 và
và 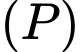 .
.
Gọi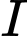 là trung điểm
là trung điểm 
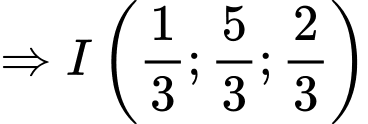 .
.
Ta có: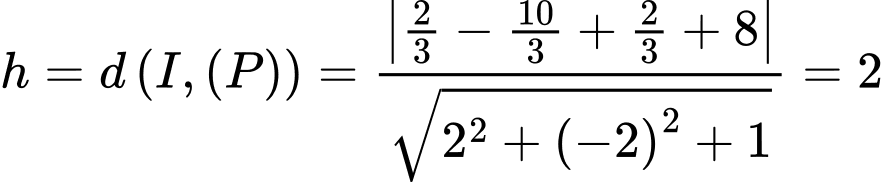 ;
;  .
.
 Bán kính
Bán kính  là
là 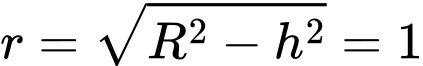 .
.

Ta xét:
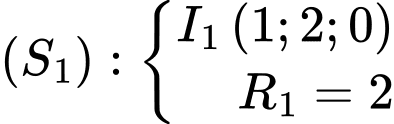 và
và 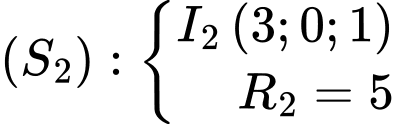 ,
, 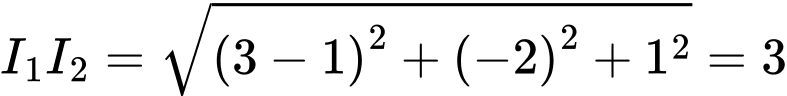
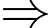
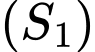 tiếp xúc với
tiếp xúc với 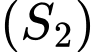 vì tâm
vì tâm 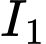 nằm trong mặt cầu
nằm trong mặt cầu 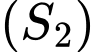
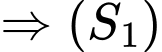 nằm trong
nằm trong 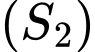 .
.Gọi
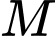 là tiếp điểm của hai mặt cầu.
là tiếp điểm của hai mặt cầu.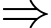 Các tiếp tuyến
Các tiếp tuyến 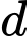 của 2 mặt cầu
của 2 mặt cầu 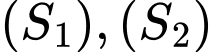 thuộc mặt phẳng
thuộc mặt phẳng 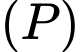 đi qua
đi qua 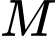 và có vectơ pháp tuyến là
và có vectơ pháp tuyến là 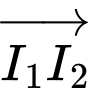 .
.Ta có:
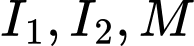 thẳng hàng
thẳng hàng 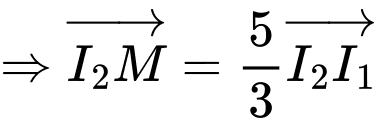
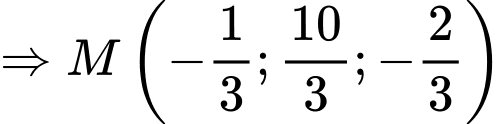 .
.Phương trình mặt phẳng
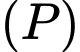 :
: 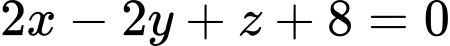 .
.Ta có:
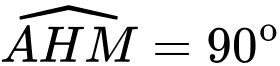 nên
nên 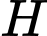 thuộc mặt cầu
thuộc mặt cầu 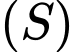 đường kính
đường kính 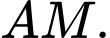
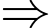
 là giao tuyến của
là giao tuyến của 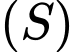 và
và 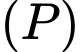 .
.Gọi
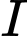 là trung điểm
là trung điểm 
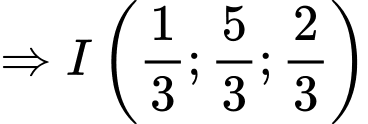 .
.Ta có:
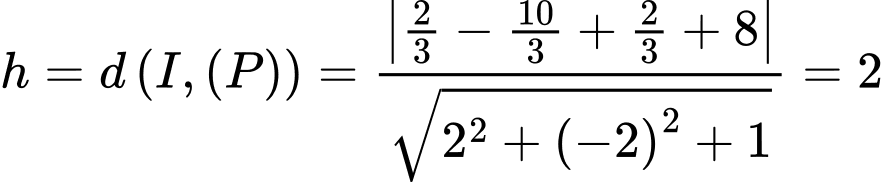 ;
;  .
. Bán kính
Bán kính  là
là 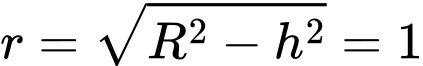 .
.